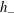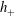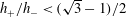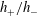1. Introduction
Consider a layer of viscous liquid on a plate inclined at an angle
${\it\alpha}$
. If the layer’s upstream depth
$h_{-}$
exceeds its downstream depth
$h_{+}$
(see figure 1), a smooth hydraulic jump (bore) forms and starts propagating down the slope.
The dynamics of bores have been mostly examined under the assumption that the slope of the free surface, and sometimes its displacement, are small – in which case the governing equations can be simplified using the so-called lubrication theory (Benney Reference Benney1966; Mei Reference Mei1966; Homsy Reference Homsy1974; Lin Reference Lin1974; Nepomnyashchy Reference Nepomnyashchy1974; Bertozzi & Brenner Reference Bertozzi and Brenner1997; Bertozzi et al.
Reference Bertozzi, Münch, Fanton and Cazabat1998; Nepomnyashchy Reference Nepomnyashchy, Shyy and Narayanan1999; Bertozzi & Shearer Reference Bertozzi and Shearer2000; Bertozzi et al.
Reference Bertozzi, Münch, Shearer and Zumbrun2001; Chang & Demekhin Reference Chang and Demekhin2002; Kalliadasis et al.
Reference Kalliadasis, Demekhin, Ruyer-Quil and Velarde2003; Saprykin, Demekhin & Kalliadasis Reference Saprykin, Demekhin and Kalliadasis2005; Mavromoustaki, Matar & Craster Reference Mavromoustaki, Matar and Craster2010). Note that, in all lubrication models, solutions describing steadily propagating bores exist for all values of
${\it\alpha}$
and
$h_{\pm }$
.
Figure 1. The setting: a smooth hydraulic jump (bore) on an inclined plate.
A different situation has been reported for bores with an order-one slope of the free surface by Benilov & Lapin (Reference Benilov and Lapin2011), who examined them numerically in the limit of small Reynolds numbers. It has been shown that, if
${\it\alpha}$
is sufficiently large and/or
${\it\eta}=h_{+}/h_{-}$
is sufficiently small, all bores overturn and no steady solution exists (unlike the above asymptotic models). A similar result has been obtained for flows on the inside of a horizontal rotating cylinder by Benilov, Lapin & O’Brien (Reference Benilov, Lapin and O’Brien2012).
The conclusions of Benilov & Lapin (Reference Benilov and Lapin2011) have been generally confirmed by Benilov (Reference Benilov2014), who used a heuristic depth-averaged model to examine steadily propagating bores with an order-one slope of the free surface. However, even though Benilov (Reference Benilov2014) confirmed the non-existence of steadily propagating bores for large
${\it\alpha}$
and/or small
${\it\eta}$
, the actual region of existence on the
$({\it\eta},{\it\alpha})$
plane was different from that of Benilov & Lapin (Reference Benilov and Lapin2011).
In the present paper, we show that simulations carried out by Benilov & Lapin (Reference Benilov and Lapin2011) lacked accuracy due to an insufficient resolution, resulting in a certain short-scale behaviour being suppressed.
New, more accurate numerical results lead us to an important physical conclusion: even though some bores appear to exist as stable steady solutions under the lubrication theory, they are either unstable or do not exist within the framework of the exact equations. We also show that this behaviour is caused by a stagnation point located at the free surface of the liquid.
This paper has the following structure: in § 2, we introduce the governing equations and, in § 3 and § 4–5, present the numerical and analytical results, respectively.
2. Formulation of the problem
Consider a two-dimensional layer of liquid, of density
${\it\rho}$
and dynamic viscosity
${\it\mu}$
, on a plate inclined at an angle
${\it\alpha}$
. Let the
$x$
and
$z$
axes be directed along, and perpendicular to, the plate (see figure 1). The free surface of the layer is described by the equation
$z=h(x,t)$
, where
$h$
is the layer’s depth and
$t$
is the time.
The spatial coordinates and
$h$
are implied to be non-dimensionalised by the characteristic depth
$H$
. The time
$t$
is non-dimensionalised by
${\it\mu}/H{\it\rho}g\cos {\it\alpha}$
, where
$g$
is the acceleration due to gravity. The
$x$
and
$z$
components of the velocity,
$u$
and
$w$
, and the pressure
$p$
are non-dimensionalised by
$H^{2}{\it\rho}g\cos {\it\alpha}/{\it\mu}$
and
${\it\rho}gH\cos {\it\alpha}$
, respectively. We also introduce the plate’s slope
$$\begin{eqnarray}s=\tan {\it\alpha}.\end{eqnarray}$$
In this work, surface tension is neglected, which implies that the spatial scale
$H$
of the flow is much larger than the capillary scale. Given that, for most liquids, the latter is on the scale of 2–3 mm, this assumption is not very restrictive. Among phenomena within the scope of our model are bores in medium-scale rivulets, as well as landslides and avalanches (for the applicability of liquid models to these, see the monograph by Pudasaini & Hutter (Reference Pudasaini and Hutter2007)).
2.1. The general case
To describe the flow, we shall use the Stokes equations,
$$\begin{eqnarray}\frac{\partial p}{\partial x}=s+\frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial z^{2}},\quad \frac{\partial p}{\partial z}=-1+\frac{\partial ^{2}w}{\partial x^{2}}+\frac{\partial ^{2}w}{\partial z^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0.\end{eqnarray}$$
Let
$U$
be the bore’s non-dimensional speed relative to the plate. Then, it is convenient to have the plate moving in the opposite direction with the matching speed, which implies the following boundary conditions:
$$\begin{eqnarray}u=-U,\quad w=0\quad \text{at }z=0.\end{eqnarray}$$
At the free surface we impose the standard dynamic boundary conditions,
$$\begin{eqnarray}\boldsymbol{Sn}=\mathbf{0}\quad \text{at }z=h,\end{eqnarray}$$
where the stress tensor and the (not necessarily unit) normal are
$$\begin{eqnarray}\boldsymbol{S}=\left[\begin{array}{@{}cc@{}}\displaystyle 2\frac{\partial u}{\partial x}-p & \displaystyle \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\\ \displaystyle \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y} & \displaystyle 2\frac{\partial w}{\partial z}-p\end{array}\right],\quad \boldsymbol{n}=\left[\begin{array}{@{}c@{}}\displaystyle -\frac{\partial h}{\partial x}\\ 1\end{array}\right].\end{eqnarray}$$
Rewriting condition (2.5) in terms of components, we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}-\left(2\frac{\partial u}{\partial x}-p\right)\frac{\partial h}{\partial x}=0\quad \text{at }z=h, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 2\frac{\partial w}{\partial z}-p-\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right)\frac{\partial h}{\partial x}=0\quad \text{at }z=h. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial h}{\partial t}+\frac{\partial }{\partial x}\int _{0}^{h}u\text{d}z=0.\end{eqnarray}$$
Since we are modelling bores, let
$$\begin{eqnarray}h\rightarrow h_{\pm }\quad \text{as }x\rightarrow \pm \infty ,\end{eqnarray}$$
where
$h_{-}$
(
$h_{+}$
) is the liquid’s upstream (downstream) depth.
Assuming the limit
$x\rightarrow \pm \infty$
in (2.2)–(2.4), (2.7)–(2.8) and applying the boundary conditions (2.10), one can obtain
$$\begin{eqnarray}w\rightarrow 0,\quad u\rightarrow s\left(-{\textstyle \frac{1}{2}}z^{2}+zh_{\pm }\right)-U\quad \text{as }x\rightarrow \pm \infty .\end{eqnarray}$$
This work is mostly devoted to steady solutions, for which (2.9) becomes
$$\begin{eqnarray}\int _{0}^{h}u\text{d}z=q,\end{eqnarray}$$
where the constant
$q$
is the non-dimensional flux of the flow along the plate. Assuming the limit
$x\rightarrow \pm \infty$
in (2.12) and applying the boundary conditions (2.10)–(2.11), one can derive the following expressions for the velocity and flux of a steady bore,
$$\begin{eqnarray}U=\frac{s(h_{-}^{2}+h_{-}h_{+}+h_{+}^{2})}{3},\quad q=-\frac{sh_{-}h_{+}(h_{-}+h_{+})}{3}.\end{eqnarray}$$
Note that, without loss of generality, one can set
$h_{-}=1$
(which implies that the scale
$H$
used in the non-dimensionalisation above is the dimensional upstream depth). One can also formulate all results in terms of the downstream-to-upstream depth ratio,
$$\begin{eqnarray}{\it\eta}=\frac{h_{+}}{h_{-}}.\end{eqnarray}$$
2.2. The lubrication theory
The lubrication theory for viscous interfacial flows assumes that the slope of the free surface relative to the plate is small. It can be further shown that, in the problem at hand (where surface tension is not taken into account), this requirement holds only if the hydraulic jump’s amplitude
$(h_{-}-h_{+})/h_{-}$
and/or the inclination angle
${\it\alpha}$
are small. If neither is small, the free surface rapidly develops an order-one slope, even if it was initially small.
We shall consider the limit of small
${\it\alpha}$
,
$$\begin{eqnarray}s\ll 1,\end{eqnarray}$$
and also assume
$$\begin{eqnarray}\frac{\partial h}{\partial x}=O(s),\quad u=O(s),\quad w=O(s^{2}).\end{eqnarray}$$
We shall only need steady lubrication solutions,
$$\begin{eqnarray}u=u_{n}(x,z),\quad w=w_{n}(x,z),\quad p=p_{n}(x,z),\quad h=h_{n}(x),\end{eqnarray}$$
where
$n$
characterises the solution’s accuracy. Note that
$u_{n}$
,
$w_{n}$
,
$p_{n}$
and
$h_{n}$
do not represent the
$n\text{th}$
terms in the expansions of the corresponding fields, but the series themselves truncated at the
$n\text{th}$
term.
For the leading-order approximation,
$n=1$
, the governing equations (2.2)–(2.4), (2.7)–(2.8) and (2.12) yield
$$\begin{eqnarray}\displaystyle & \displaystyle \left.\begin{array}{@{}c@{}}\displaystyle u_{1}=-U+\left(zh_{1}-\frac{z^{2}}{2}\right)\left(s-\frac{\text{d}h_{1}}{\text{d}x}\right),\\ \displaystyle w_{1}=-\frac{z^{3}}{6}\frac{\text{d}^{2}h_{1}}{\text{d}x^{2}}-\frac{z^{2}}{2}\frac{\text{d}}{\text{d}x}\left[h_{1}\left(s-\frac{\text{d}h_{1}}{\text{d}x}\right)\right],\\ p_{1}=h_{1}-z,\end{array}\right\} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -Uh_{1}+\frac{h_{1}^{3}}{3}\left(s-\frac{\text{d}h_{1}}{\text{d}x}\right)=q. & \displaystyle\end{eqnarray}$$
$s$
and
$h_{\pm }$
. We conclude that the lubrication theory does not capture overturning.
The specific form of the
$n\text{th}$
-order equivalents of (2.18)–(2.19) will not be needed, so we just describe briefly how they can be obtained.
The unknowns
$u$
,
$w$
and
$p$
(but not
$h$
) are expanded in powers of
$s^{2}$
, and the Stokes equations are used to relate the first
$n$
terms in these series to
$h$
. To distinguish the series from the exact fields, the subscript
$n$
, representing the accuracy of the expansion, is added. Then, the expression for
$u_{n}$
is substituted in the mass conservation law (2.12), which yields an equation for
$h_{n}$
.
Note that the
$n\text{th}$
-order lubrication solution satisfies the governing equations with the following errors of truncation:
$$\begin{eqnarray}\frac{\partial p_{n}}{\partial x}=s+\frac{\partial ^{2}u_{n}}{\partial x^{2}}+\frac{\partial ^{2}u_{n}}{\partial z^{2}}+O(s^{2n+1}),\quad \frac{\partial p_{n}}{\partial z}=-1+\frac{\partial ^{2}w_{n}}{\partial x^{2}}+\frac{\partial ^{2}w_{n}}{\partial z^{2}}+O(s^{2n}),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial u_{n}}{\partial x}+\frac{\partial w_{n}}{\partial z}=0,\end{eqnarray}$$
$$\begin{eqnarray}u_{n}=-U,\quad w_{n}=0\quad \text{at }z=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u_{n}}{\partial z}+\frac{\partial w_{n}}{\partial x}-\left(2\frac{\partial u_{n}}{\partial x}-p_{n}\right)\frac{\text{d}h_{n}}{\text{d}x}=O(s^{2n+1})\quad \text{at }z=h_{n}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 2\frac{\partial w_{n}}{\partial z}-p_{n}-\left(\frac{\partial u_{n}}{\partial z}+\frac{\partial w_{n}}{\partial x}\right)\frac{\text{d}h_{n}}{\text{d}x}=O(s^{2n})\quad \text{at }z=h_{n}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \int _{0}^{h_{n}}u_{n}\text{d}z=q. & \displaystyle\end{eqnarray}$$
$n=1$
, this can be verified by substituting expressions (2.18) into (2.21) and (2.25).
3. Numerical results
Following Benilov & Lapin (Reference Benilov and Lapin2011) and Benilov et al. (Reference Benilov, Lapin and O’Brien2012), we solved the boundary-value problem (2.2)–(2.4), (2.7)–(2.11) using the COMSOL Multiphysics package. There was, however, an important modification: the present work employed an extra fine mesh near the stagnation point (if the flow involved one). The significance of this modification will be explained later.
In all other respects our numerical approach is the same as that described in Benilov & Lapin (Reference Benilov and Lapin2011) and, in more detail, in § 4.2 of Benilov et al. (Reference Benilov, Lapin and O’Brien2012).
3.1. Three scenarios of the bore evolution
We have carried out numerous simulations, aiming to determine the region in the
$({\it\eta},{\it\alpha})$
plane where stable steady bores exist. The results are shown in figure 2.
Figure 2. Numerical results on the existence of steady bores on the
$({\it\eta},{\it\alpha})$
plane (
${\it\alpha}$
is the plate’s inclination angle,
${\it\eta}=h_{+}/h_{-}$
is the downstream-to-upstream depth ratio). The regions where micro-overturning and overturning proper occur (see figure 3) are labelled ‘MO’ and ‘Overturning’, respectively. The vertical part of the boundary between the existence/MO regions corresponds to condition (4.1). The four ‘black squares’ correspond to the solutions presented in figure 3.
Three scenarios of the bore evolution have been identified:
(i) If
${\it\eta}$
exceeds a certain threshold value (which depends on
${\it\alpha}$
), a stable bore emerges from a wide range of initial conditions. The region in the
$({\it\eta},{\it\alpha})$
plane where this occurs is shown in figure 2 and labelled ‘Steady solutions’. Examples of these are shown in figure 3: observe that, for large
${\it\alpha}$
, the solution has an oscillatory structure, which is rather unusual for a flow without surface tension (for more details, see Benilov & Lapin Reference Benilov and Lapin2011).
Figure 3. Examples of steady bores: the depth
$h$
of the liquid versus
$x$
. The corresponding points in the
$({\it\alpha},{\it\eta})$
plane are shown in figure 2 by ‘black squares’.
Most importantly, none of the existing stable bores involves a stagnation point (SP), which indicates that SPs either destabilise bores or eliminate them as steady solutions. This conclusion can be verified by considering a sequence of bores with parameters approaching the boundary of the existence region: one can observe a rapid decrease of the velocity in a certain part of the flow, near the free surface (see figure 4) – which implies that an SP emerges exactly when the solution ceases to exist.
Figure 4. Examples of steady bores: the surface velocity
$u_{s}$
(normalised by the plate’s slope
$s=\tan {\it\alpha}$
) versus
$x$
. The corresponding graphs of
$h(x)$
are shown in figure 3.
Note that the emergence of the SP at
${\it\alpha}\lesssim 30.7^{\circ }$
occurs differently from that at
${\it\alpha}\gtrsim 30.7^{\circ }$
. In the latter case, the SP appears at the top of the bore’s highest peak (compare figures 3
a,b and 4
a,b), whereas, in the former case, the SP emerges at minus infinity (see figure 4
c,d).
Thus, when a stagnation point appears on the surface of the flow, bores either become unstable or disappear as steady solutions. At this stage, we cannot distinguish between these two possibilities (this question will be discussed in more detail later).
(ii) If
${\it\eta}$
is sufficiently small, all bores overturn, regardless of the initial condition. Two kinds of overturning can be distinguished, differing in the dynamics and scale of the overturning region. The two kinds correspond to two distinct regions in the
$({\it\eta},{\it\alpha})$
plane, labelled in figure 2 as ‘MO’ (micro-overturning) and ‘Overturning’ (overturning proper).
(iia) Overturning proper occurs for smaller values of
${\it\eta}$
and is similar to the usual wave breaking (see an example in figure 5
a).
Figure 5. Two patterns of overturning for
${\it\alpha}=7^{\circ }$
: (a) overturning proper (
${\it\eta}=0.15$
), (b) micro-overturning (
${\it\eta}=0.22$
). The stagnation points are shown by black dots, the insets show blow-ups of the regions near the stagnation points (note that the
$x$
and
$y$
ranges of inset (a) are approximately 16 and 173 times larger than those of inset (b)). The solutions shown as solid and dotted lines are separated in time by (a)
$t=488$
; (b)
$t=326$
, with the dotted line corresponding to the later
$t$
. The corresponding points in the
$({\it\eta},{\it\alpha})$
plane are shown in figure 6 by ‘black squares’.
(iib) The evolution of bores with
${\it\alpha}\lesssim 30.7^{\circ }$
and intermediate
${\it\eta}$
is characterised by a localised burst of short-scale, ‘spiky’ waves (see an example in figure 5
b). These waves contract and grow, eventually developing a singularity (infinite slope of the free surface). Since the spatial scale of the solution in this case is considerably smaller than that in the case of overturning proper, this flow pattern will be referred to as micro-overturning.
The presence/absence of the contracting spatial scale (resulting in spiky waves) allows one to readily distinguish the two kinds of overturning.
Note also that the troughs of spiky waves do not develop into a corner, i.e. the curvature of the free surface there may be large, but is still finite. The breakdown of the solution occurs solely due to overturning (i.e. emergence of a point where the tangent to the free surface is vertical).
Most importantly, both overturning and micro-overturning bores involve an SP, and the point of overturning is located near it – which is why a finer mesh is needed in the near-SP region. This circumstance was not recognised by Benilov & Lapin (Reference Benilov and Lapin2011); as a result, the stagnation region was not properly resolved in their simulations and micro-overturning did not occur.
3.2. Micro-overturning versus overturning proper
Physically, the main difference between micro-overturning and overturning proper is that the latter occurs for bores that do not satisfy the lubrication theory (even if
${\it\alpha}$
is small).
Indeed, using the first-order lubrication equation (2.19), one can deduce that the maximum slope of the free surface in a steady bore is
$$\begin{eqnarray}\max \left|\frac{\text{d}h}{\text{d}x}\right|=\frac{s(2+3{\it\eta}-3{\it\eta}^{2}-2{\it\eta}^{3})^{2}}{27{\it\eta}^{2}(1+{\it\eta})^{2}}.\end{eqnarray}$$
Expression (3.1) indicates that the lubrication theory is applicable when
$$\begin{eqnarray}\frac{s(2+3{\it\eta}-3{\it\eta}^{2}-2{\it\eta}^{3})^{2}}{27{\it\eta}^{2}(1+{\it\eta})^{2}}\ll 1.\end{eqnarray}$$
One can see that, for a sufficiently small
${\it\eta}$
(i.e. for a large hydraulic jump), the lubrication theory does not necessarily hold even if
${\it\alpha}$
– and, hence,
$s$
– are small.
It can now be shown that the boundary between the regions of micro-overturning and overturning proper on the
$({\it\eta},{\it\alpha})$
plane happens to be very close to the curve where the maximum slope of the free surface is equal to 0.6 (see figure 6). This suggests that overturning proper can occur only for bores with order-one slope.
Figure 6. Existence of steady bores on the
$({\it\eta},{\it\alpha})$
plane (as in figure 2) and the applicability of the lubrication theory. The thin solid line corresponds to the maximum slope of the free surface (calculated using expression (3.1)) being 0.6. The two ‘black squares’ correspond to the solutions presented in figure 5.
Thus, the near-SP evolution depends on the slope of the free surface. If it is sufficiently large, one can conjecture that disturbances generated near the SP slide down the slope – which is why overturning proper occurs lower than the SP. It can be further conjectured that, while sliding, short-scale disturbances merge and form a larger-scale overturning flow.
4. An existence condition for stagnation points
As conjectured in the previous section, a steady bore exists and is stable only if it does not involve an SP. Thus, if we prove that, for certain
$({\it\eta},{\it\alpha})$
, the steady bore must involve an SP, our conjecture would imply that such a bore cannot be observed in reality (because it either is unstable or does not exist as a steady state).
4.1. The general case
We shall prove the following statement: if
$$\begin{eqnarray}{\it\eta}<{\textstyle \frac{1}{2}}(\sqrt{3}-1),\end{eqnarray}$$
the steady bore (if it exists) involves an SP.
To prove criterion (4.1), we use asymptotics (2.11) for
$u$
and expression (2.13) for
$U$
to calculate
$$\begin{eqnarray}[(u)_{z=h}]_{x\rightarrow -\infty }=\frac{sh_{-}^{2}}{6}(1-2{\it\eta}-2{\it\eta}^{2}),\quad [(u)_{z=h}]_{x\rightarrow +\infty }=\frac{sh_{+}^{2}}{6}\left(1-\frac{2}{{\it\eta}}-\frac{2}{{\it\eta}^{2}}\right).\end{eqnarray}$$
Given that
${\it\eta}<1$
, one can readily see that
$$\begin{eqnarray}[(u)_{z=h}]_{x\rightarrow +\infty }<0,\end{eqnarray}$$
i.e. the surface flow in front of the bore has the same direction as that of the plate’s motion. The flow behind the bore, in turn, can be directed either way, depending on whether or not
${\it\eta}$
falls into the range (4.1). If it does, then
$$\begin{eqnarray}[(u)_{z=h}]_{x\rightarrow -\infty }>0\quad \text{if }{\it\eta}<{\textstyle \frac{1}{2}}(\sqrt{3}-1).\end{eqnarray}$$
Conditions (4.3)–(4.4) imply that, if (4.1) holds, there exists
$x_{s}$
such that
$$\begin{eqnarray}[(u)_{z=h}]_{x=x_{s}}=0.\end{eqnarray}$$
Recalling that, at the free surface of a steady flow, the normal velocity is zero, and that the surface of a steady non-overturning bore cannot be perpendicular to the plate, equality (4.5) implies that both components of the velocity are zero – hence,
$x_{s}$
is a stagnation point.
Recall that condition (4.1) was conjectured to be a sufficient criterion of non-existence of stable steady bores – hence, the parameter region it describes should not overlap with the existence region in figure 2 (and, evidently, it does not).
Note that, if
${\it\alpha}\lesssim 30.7^{\circ }$
, our numerical results for existing bores indicate that
$(u)_{z=h}$
is a monotonic function of
$x$
(for
${\it\alpha}\ll 1$
, this can also be verified using the lubrication theory). As a result, when
${\it\eta}$
is decreasing while
${\it\alpha}$
is fixed at a value smaller than
$30.7^{\circ }$
, an SP can emerge only at
$x=-\infty$
. Then, using asymptotics (2.11), one can show that criterion (4.1) in this case becomes both sufficient and necessary.
This conclusion agrees with the fact that, for
${\it\alpha}\lesssim 30.7^{\circ }$
, the boundary of the existence region in figure 2 is strictly vertical.
4.2. The lubrication theory
Criterion (4.1) can be illustrated using the first-order lubrication theory (2.18)–(2.19), (2.10).
First we shall use (2.18) to calculate
$(u)_{z=h}$
and then equate it to zero,
$$\begin{eqnarray}h_{1}^{3}\left(\frac{\text{d}h_{1}}{\text{d}x}-s\right)+2Uh_{1}=0\quad \text{at }x=x_{s}.\end{eqnarray}$$
Then, using (2.19) to substitute for
$\text{d}h_{1}/\text{d}x$
, one can deduce that
$$\begin{eqnarray}(h_{1})_{x=x_{s}}=-\frac{3q}{U}.\end{eqnarray}$$
Since, under the lubrication theory, the bore’s profile is monotonic, an SP exists if and only if
$$\begin{eqnarray}h_{+}<(h_{1})_{x=x_{s}}<h_{-}.\end{eqnarray}$$
Substituting expressions (2.13) for
$U$
and
$q$
into (4.7), then inserting the resulting expression for
$(h_{1})_{x=x_{s}}$
into (4.8), one can obtain, as expected, condition (4.1).
Two examples of steady bores, with and without an SP, have been computed using the first-order lubrication theory and are shown in figure 7.
Figure 7. The streamlines for steady bores as described by the lubrication theory (2.18)–(2.19), (2.10). The plate’s inclination angle is
${\it\alpha}=5^{\circ }$
, the non-dimensional upstream depth is
$h_{-}=1$
, the downstream depth is (a)
$h_{+}=0.5$
and (b)
$h_{+}=0.2$
. In (b), observe the recirculation region (its boundary shown as a dotted line) and the SP shown by a black dot. Another SP is located infinitely far to the left, so that the two SPs are connected by the dotted line.
5. The evolution near the stagnation point
Note that the first-order lubrication equation (2.19) is separable. Solving it with the boundary conditions (2.10), one can show that solutions exist for all values of
$s$
and
$h_{\pm }$
. It can be further shown (Bertozzi & Shearer Reference Bertozzi and Shearer2000; Bertozzi et al.
Reference Bertozzi, Münch, Shearer and Zumbrun2001) that all the steady solutions, including those with SPs, are stable under the time-dependent version of the first-order lubrication theory. These two conclusions appear to contradict the conjecture suggested by our numerical results – that stable steady bores with SPs do not exist.
In what follows, the contradiction will be resolved by examining the interaction of a steady lubrication flow and an evolving non-lubrication disturbance localised near the SP.
5.1. Asymptotic equations for small
${\it\alpha}$
Consider a steady bore with an SP, and a small disturbance superposed on the bore. Assuming
${\it\alpha}\ll 1$
and
${\it\eta}\sim 1$
, one can seek a solution in the form
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u=u_{2}(x,z)+\tilde{u} (x,z,t),\\ w=w_{2}(x,z)+\tilde{w}(x,z,t),\\ p=p_{2}(x,z)+\tilde{p}(x,z,t),\\ h=h_{2}(x)+\tilde{h}(x,t),\end{array}\right\}\end{eqnarray}$$
where the variables with tildes describe the disturbance and
$(u_{2},w_{2},p_{2},h_{2})$
represent the steady lubrication solution of the second-order accuracy (the reason why the first-order solution is not used will be explained later). Substituting (5.1) into the exact governing equations (2.2)–(2.4), (2.7)–(2.9) and taking into account the fact that the lubrication solution satisfies (2.20–(2.25), we obtain
$$\begin{eqnarray}\frac{\partial \tilde{p}}{\partial x}=\frac{\partial ^{2}\tilde{u} }{\partial x^{2}}+\frac{\partial ^{2}\tilde{u} }{\partial z^{2}}+O(s^{5}),\quad \frac{\partial \tilde{p}}{\partial z}=\frac{\partial ^{2}\tilde{w}}{\partial x^{2}}+\frac{\partial ^{2}\tilde{w}}{\partial z^{2}}+O(s^{4}),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \tilde{u} }{\partial x}+\frac{\partial \tilde{w}}{\partial z}=0,\end{eqnarray}$$
$$\begin{eqnarray}\tilde{u} =0,\quad \tilde{w}=0\quad \text{at }z=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial u_{2}}{\partial z}+\frac{\partial \tilde{u} }{\partial z}+\frac{\partial w_{2}}{\partial x}+\frac{\partial \tilde{w}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle \quad -\left[2\left(\frac{\partial u_{2}}{\partial x}+\frac{\partial \tilde{u} }{\partial x}\right)-p_{2}-\tilde{p}\right]\left(\frac{\partial h_{2}}{\partial x}+\frac{\partial \tilde{h}}{\partial x}\right)=O(s^{5})\quad \text{at }z=h_{2}+\tilde{h},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 2\left(\frac{\partial w_{2}}{\partial z}+\frac{\partial \tilde{w}}{\partial z}\right)-p_{2}-\tilde{p}\nonumber\\ \displaystyle & & \displaystyle \quad -\left(\frac{\partial u_{2}}{\partial z}+\frac{\partial \tilde{u} }{\partial z}+\frac{\partial w_{2}}{\partial x}+\frac{\partial \tilde{w}}{\partial x}\right)\left(\frac{\partial h_{2}}{\partial x}+\frac{\partial \tilde{h}}{\partial x}\right)=O(s^{4})\quad \text{at }z=h_{2}+\tilde{h},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \tilde{h}}{\partial t}+\frac{\partial }{\partial x}\left[\int _{0}^{h_{2}}\tilde{u} \text{d}z+\int _{h_{2}}^{h_{2}+\tilde{h}}(u_{2}+\tilde{u} )\text{d}z\right]=0.\end{eqnarray}$$
Let the disturbance be localised near the SP in a region of size
${\it\varepsilon}$
, and let
${\it\delta}$
be a characteristic elevation of the free surface due to the disturbance. The time scale
${\it\tau}$
, in turn, should be determined by ‘balancing’ the time derivative in (5.7) with the largest of the remaining terms – which yields
${\it\tau}={\it\varepsilon}^{-1}$
.
The above scales imply the following change of variables:
$$\begin{eqnarray}x_{\mathit{new}}=\frac{x-x_{s}}{{\it\varepsilon}},\quad z_{\mathit{new}}=\frac{z-h_{2}(x_{s})}{{\it\varepsilon}},\quad t_{\mathit{new}}=\frac{t}{{\it\varepsilon}^{-1}},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{u} _{\mathit{new}}=\frac{\tilde{u} }{{\it\delta}{\it\varepsilon}},\quad \tilde{w}_{\mathit{new}}=\frac{\tilde{w}}{{\it\delta}{\it\varepsilon}},\quad \tilde{p}_{\mathit{new}}=\frac{\tilde{p}}{{\it\delta}},\quad \tilde{h}_{\mathit{new}}=\frac{\tilde{h}}{{\it\delta}},\end{eqnarray}$$
where
$x_{s}$
is, again, the coordinate of the SP. We shall further assume that
$$\begin{eqnarray}{\it\delta}\ll {\it\varepsilon}.\end{eqnarray}$$
It turns out that the most general asymptotic model can be derived for the following distinguished limit:
$$\begin{eqnarray}{\it\varepsilon}=s^{2}.\end{eqnarray}$$
Substituting (5.8)–(5.9) into (5.2)–(5.7) and taking into account conditions (5.10)–(5.11), we obtain to leading order (subscripts
$\text{}_{\mathit{new}}$
omitted)
$$\begin{eqnarray}\frac{\partial \tilde{p}}{\partial x}=\frac{\partial ^{2}\tilde{u} }{\partial x^{2}}+\frac{\partial ^{2}\tilde{u} }{\partial z^{2}},\quad \frac{\partial \tilde{p}}{\partial z}=\frac{\partial ^{2}\tilde{w}}{\partial x^{2}}+\frac{\partial ^{2}\tilde{w}}{\partial z^{2}},\quad \frac{\partial \tilde{u} }{\partial x}+\frac{\partial \tilde{w}}{\partial z}=0,\end{eqnarray}$$
$$\begin{eqnarray}\tilde{u} =0,\quad \tilde{w}=0\quad \text{as }z\rightarrow -\infty ,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \tilde{u} }{\partial z}+\frac{\partial \tilde{w}}{\partial x}=0,\quad \tilde{h}+2\frac{\partial \tilde{w}}{\partial z}-\tilde{p}=0\quad \text{at }z=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial \tilde{h}}{\partial t}+\frac{\partial }{\partial x}\left[\int _{-\infty }^{0}\tilde{u} \text{d}z+{\it\beta}x\tilde{h}\right]=0,\end{eqnarray}$$
where
$$\begin{eqnarray}{\it\beta}=-\frac{1}{s^{2}}\left[\frac{\text{d}}{\text{d}x}(u_{2})_{z=h_{2}}\right]_{x=x_{s}}.\end{eqnarray}$$
Equations (5.12)–(5.15) form a closed set describing the dynamics of the disturbance. The coefficient
${\it\beta}$
is to be determined using the steady lubrication solution. Note that, since (5.12)–(5.15) were derived to leading order with respect to all small parameters,
${\it\beta}$
can be calculated using the leading-order lubrication solution as well. Thus, replacing
$u_{2}$
and
$h_{2}$
with
$u_{1}$
and
$h_{1}$
in expression (5.16), and using the first-order expressions (2.18)–(2.19), we obtain
$$\begin{eqnarray}{\it\beta}=\left(\frac{3q}{2s^{2}h_{1}^{2}}\frac{\text{d}h_{1}}{\text{d}x}\right)_{x=x_{s}}.\end{eqnarray}$$
It follows from (2.13) that
$q$
is negative, and so is
$\text{d}h_{1}/\text{d}x$
– hence,
${\it\beta}>0$
(it will be seen later that the sign of
${\it\beta}$
is important physically). Eventually, (2.13) can be used to reduce (5.17) to
$$\begin{eqnarray}{\it\beta}=-\frac{U^{2}}{54q^{3}s^{2}}(2U^{3}-9q^{2}s).\end{eqnarray}$$
Together with (2.13), this expression relates
${\it\beta}$
to the basic parameters
$({\it\eta},{\it\alpha})$
.
Note that, even though the first-order lubrication theory was used for
${\it\beta}$
, the second-order approximation must be used, strictly speaking, in representation (5.1). If the first-order lubrication expansion were used, its error in some of the governing equations would exceed the contribution of the disturbance and, thus, its dynamics would be described incorrectly.
5.2. The solution of (5.12)–(5.15)
We shall first use (5.12)–(5.14) to express
$\tilde{u}$
in terms of
$\tilde{h}$
and then substitute the resulting expression into (5.15).
To do so, we introduce the Fourier transforms
$(\hat{u} ,{\hat{w}},\hat{p},{\hat{h}})$
of the unknowns
$(\tilde{u} ,\tilde{w},\tilde{p},\tilde{h})$
– e.g.
$$\begin{eqnarray}{\hat{h}}(k,t)=\frac{1}{2{\rm\pi}}\int _{-\infty }^{\infty }\tilde{h}(x,t)\text{e}^{-\text{i}kx}\text{d}k.\end{eqnarray}$$
Then, applying the Fourier transformation to (5.12)–(5.15), we obtain
$$\begin{eqnarray}\text{i}k\hat{p}=-k^{2}\hat{u} +\hat{u} _{zz},\quad \hat{p}_{z}=-k^{2}{\hat{w}}+{\hat{w}}_{zz},\quad \text{i}k\hat{u} +w_{z}=0,\end{eqnarray}$$
$$\begin{eqnarray}\hat{u} =0\quad {\hat{w}}=0\quad \text{at }z\rightarrow -\infty ,\end{eqnarray}$$
$$\begin{eqnarray}\hat{u} _{z}+\text{i}k{\hat{w}}=0\quad {\hat{h}}+2{\hat{w}}_{z}-\hat{p}=0\quad \text{at }z=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial {\hat{h}}}{\partial t}+\text{i}k\left(-\frac{{\it\beta}}{2{\rm\pi}}\int _{-\infty }^{\infty }xh\text{e}^{-\text{i}kx}\text{d}x+\int _{-\infty }^{0}\hat{u} \text{d}z\right)=0.\end{eqnarray}$$
(5.20) is a set of linear ordinary differential equations in
$z$
and, thus, can be readily solved. Then, applying the boundary conditions (5.21)–(5.22), one obtains
$$\begin{eqnarray}\hat{u} =\frac{\text{i}\,\text{sgn}\,k}{2}{\hat{h}}z\text{e}^{|k|z},\quad {\hat{w}}=\frac{1}{2}\left(-\frac{1}{|k|}+z\right){\hat{h}}\text{e}^{|k|z},\quad \hat{p}={\hat{h}}\text{e}^{|k|z}.\end{eqnarray}$$
Next, substitution of
$\hat{u}$
into (5.23) yields
$$\begin{eqnarray}\frac{\partial {\hat{h}}}{\partial t}+{\it\beta}k\frac{\partial {\hat{h}}}{\partial k}+\frac{1}{2|k|}{\hat{h}}=0.\end{eqnarray}$$
The general solution of this linear partial differential equation can be readily found by characteristics,
$$\begin{eqnarray}{\hat{h}}={\hat{h}}_{0}(k\text{e}^{-{\it\beta}t})\exp \left(-\frac{\text{e}^{{\it\beta}t}-1}{2{\it\beta}|k|}\right),\end{eqnarray}$$
where
${\hat{h}}_{0}(k)$
is the Fourier transform of the initial condition
$\tilde{h}(x,0)$
. Finally, taking the inverse Fourier transform, we obtain
$$\begin{eqnarray}h(x,t)=\int _{-\infty }^{\infty }{\hat{h}}_{0}(k\text{e}^{-{\it\beta}t})\exp \left(-\frac{\text{e}^{{\it\beta}t}-1}{2{\it\beta}|k|}+\text{i}kx\right)\text{d}k.\end{eqnarray}$$
Two examples of this solution, developing from odd and even initial conditions, are shown in figures 8 a and 8 b, respectively. One can see that, in both cases, the disturbance contracts and grows.
Figure 8. The asymptotic solution (5.25) for
${\it\eta}=0.15$
,
${\it\alpha}=3^{\circ }$
, and two different initial conditions: (a)
$\tilde{h}(x,0)=-x\exp (-x^{2}/2)$
and (b)
$\tilde{h}(x,0)=\exp (-x^{2}/2)$
. The curves labelled 0–2 correspond to
$t=0$
, 0.2, 0.4.
This conclusion can also be extracted from the general solution (5.27). Introducing
$K=k\text{e}^{-{\it\beta}t}$
, one can rewrite it in the form
$$\begin{eqnarray}h(x,t)=\text{e}^{{\it\beta}t}\int _{-\infty }^{\infty }{\hat{h}}_{0}(K)\exp \left(-\frac{1-\text{e}^{-{\it\beta}t}}{2{\it\beta}|K|}+\text{i}K\text{e}^{{\it\beta}t}x\right)\text{d}K.\end{eqnarray}$$
Thus,
$$\begin{eqnarray}h\rightarrow \text{e}^{{\it\beta}t}f(x\text{e}^{{\it\beta}t})\quad \text{as }t\rightarrow \infty ,\end{eqnarray}$$
where
$$\begin{eqnarray}f({\it\xi})=\int _{-\infty }^{\infty }{\hat{h}}_{0}(K)\exp \left[-\frac{1}{2{\it\beta}|K|}+\text{i}K{\it\xi}\right]\text{d}K.\end{eqnarray}$$
One can now see that the long-term behaviour of
$h(x,t)$
is, essentially, self-similar exponential growth and contraction.
5.3. Discussion
(i) To understand the physical meaning of the contraction and growth of solution (5.27), observe that, in the short-wave limit (
$k\gg 1$
), the last term of (5.25) can be omitted and (5.25) becomes
$$\begin{eqnarray}\frac{\partial {\hat{h}}}{\partial t}+{\it\beta}k\frac{\partial {\hat{h}}}{\partial k}\approx 0.\end{eqnarray}$$
Applying the inverse Fourier transformation, one can re-arrange this equation as
$$\begin{eqnarray}\frac{\partial \tilde{h}}{\partial t}-{\it\beta}x\frac{\partial \tilde{h}}{\partial x}\approx {\it\beta}\tilde{h}.\end{eqnarray}$$
This equation describes waves with local speed
$-{\it\beta}x$
(the second term) and growth rate
${\it\beta}$
(the right-hand side). Most importantly, the wave speed is negative for positive
$x$
and vice versa – hence, the waves always converge onto the point
$x=0$
. This effect is purely kinematic, but it is the reason for the contraction of disturbances near the SP.
(ii) Sooner or later the solution’s growth and contraction violate the conditions under which (5.27) was derived. Even though we have no analytical means of describing the further evolution, one can conjecture that the developing nonlinearity causes either overturning or a collapse (closing up) of a wave trough. In either case, the slope of the free surface becomes infinite.
(iii) We have tried to use our numerical solution at a certain time as the initial condition for the asymptotic solution (5.27) and compare the numerical and analytical solutions at larger times. Unfortunately, this did not work out due to the fact that the asymptotic solution is valid only at a very early stage of the evolution, while the disturbance is linear. The numerical solution, on the other hand, is trustworthy only after the initial mesh-scale noise has decayed (for flows with a free surface, such noise is inevitably introduced by the COMSOL package due to its use of triangles to approximate the region occupied by the liquid). As a result, one cannot find a sufficiently wide ‘window’ where both solutions are reliable.
Thus, even though the asymptotic solution exhibits the same qualitative dynamics as the numerical one, we have been unable to achieve quantitative agreement.
(iv) As mentioned above, simulations cannot distinguish unstable steady solutions from non-existent ones. The same is true, albeit less obviously, for our asymptotic results. On the one hand, representation (5.1) describes a perturbation of a steady bore, and (5.25) for the former admits the trivial solution,
${\hat{h}}=0$
, corresponding to the unperturbed bore. On the other hand, the steady-bore part of representation (5.1) is based on the second-order lubrication theory, which does not guarantee the existence of an equivalent solution of the exact equations.
In principle, this issue could be resolved by tracking the steady-bore solution when approaching the boundary of the existence region. If two families of solutions exist before the boundary is reached, merging at the boundary and then disappearing – this would indicate that a saddle-node bifurcation occurs. If, however, a single solution is found, one could explore its stability and see if an eigenmode exists, becoming neutrally stable when approaching the boundary of the existence region (which should rather be called the ‘stability region’ in this case).
Unfortunately, neither of these possibilities can be readily explored.
Firstly, a saddle-node bifurcation typically implies that one of the two merging solutions is unstable – hence, it cannot be found by simulating the evolution equations (which is what we do in this work). Secondly, stability analysis of a free-surface flow is one of the most complicated problems in computational fluid dynamics and, thus, is beyond the scope of the present paper.
This issue, however, was explored by Benilov (Reference Benilov2014) using a relatively simple depth-averaged model (instead of the Stokes equations). It was shown that, in the framework of this model, SPs do eliminate bores as steady solutions. Even though this conclusion cannot be regarded as rigorous, all other results obtained using Benilov’s (Reference Benilov2014) model turned out to be relatively accurate. In particular, it yields an existence region for steady bores which agrees very well with that in our figure 2 – suggesting that the reason why steady bores are not observed in the rest of the parameter space might also be identified correctly.
(v) Note that surface tension can weaken the effect of SPs. This conclusion is suggested by the results of Joseph et al. (Reference Joseph, Nelson, Renardy and Renardy1991), Jeong & Moffatt (Reference Jeong and Moffatt1992), Pozrikidis (Reference Pozrikidis1998) and Peixinho, Mirbod & Morris (Reference Peixinho, Mirbod and Morris2012), who observed stable capillary flows with SPs and/or obtained the solutions describing them. Benilov & Lapin (Reference Benilov and Lapin2011), in turn, observed that increasingly strong surface tension extended the existence region of steady bores to bores with SPs – i.e. it can stop the emergence of singularities in a certain part of the parameter space, but not in all of the parameter space. ‘Spiky waves’, in turn, are affected by capillarity much stronger than overturning, as even weak surface tension can make them significantly smoother.
We also note the results by Pozrikidis (Reference Pozrikidis1998) and Thoroddsen & Tan (Reference Thoroddsen and Tan2004), who observed (numerically and experimentally, respectively) formation of cusps and collapse of troughs of short-scale surface waves similar to our ‘spiky waves’. Interestingly, the latter paper reports the collapse of wave troughs and the resulting entrainment of bubbles only if a surfactant was used – which agrees with our conjecture about the stabilising effect of surface tension.
Finally, the collapse of wave troughs cannot occur without an infinite slope of the interface and, thus, can be interpreted as a kind of micro-overturning.
(vi) Generally, the destabilising effect of SPs on steady flows (when they exist) is well known (Friedlander & Vishik Reference Friedlander and Vishik1991; Lifschitz Reference Lifschitz1991; Lifschitz & Hameiri Reference Lifschitz and Hameiri1991; Lifschitz Reference Lifschitz1995; Lebovitz & Lifschitz Reference Lebovitz and Lifschitz1996; Bayly, Holm & Lifschitz Reference Bayly, Holm and Lifschitz1996; Leblanc Reference Leblanc1997). It has been established, among other things, that steady flows with SPs are unstable, except the cases where the streamlines are circular in the vicinity of the SP (Friedlander & Vishik Reference Friedlander and Vishik1991; Lifschitz Reference Lifschitz1991; Lifschitz & Hameiri Reference Lifschitz and Hameiri1991). Since the streamlines near the SP in the problem at hand are not circular (see figure 7 b), our setting seems to be within the scope of the existing theory.
There are four important differences, however.
Firstly, the unstable disturbances considered in all of the above papers are three dimensional – whereas, in our case, instability occurs in two dimensions.
Secondly, Friedlander & Vishik (Reference Friedlander and Vishik1991), Lifschitz (Reference Lifschitz1991) and Lifschitz & Hameiri (Reference Lifschitz and Hameiri1991) considered ideal fluids, whereas we examine viscous fluids. This difference is important – as, in principle, viscosity could dampen the effect (but it does not).
Thirdly, the SP in our case is located on the free surface – and we claim that, in principle, this circumstance could make it a stabilising influence even though the streamlines are not locally circular. It all depends on whether the flow at the surface is directed towards the SP (as in our case) or away from it. In the latter case, the equivalent of (5.32) is
$$\begin{eqnarray}\frac{\partial \tilde{h}}{\partial t}+{\it\beta}x\frac{\partial \tilde{h}}{\partial x}\approx -{\it\beta}\tilde{h}\end{eqnarray}$$
(where
${\it\beta}$
is still positive). It can be readily verified that all solutions of equation (5.33) spread out and decay – simply because the flow pulls the perturbations away from the SP, while the negative term on the right-hand side of (5.33) causes an exponential decay. A flow with such a geometry of the stagnation point has been computed by Mekias & Vanden-Broeck (Reference Mekias and Vanden-Broeck1991).
Fourthly, an SP with non-circular streamlines inside the liquid’s bulk destabilised the flow, whereas ‘our’ SP is likely to eliminate the steady state altogether (as discussed above).
6. Summary and concluding remarks
Thus, we have examined smooth hydraulic jumps (bores) on an inclined plate. Depending on the inclination angle
${\it\alpha}$
and the downstream-to-upstream depth ratio
${\it\eta}$
, three scenarios have been identified, corresponding to three parameter regions in the
$({\it\eta},{\it\alpha})$
plane (see figure 2):
(i) The flow settles down into a stable steady bore without stagnation points (see examples in figure 3).
(iia) The bore overturns (see an example in figure 5 a).
(iib) A highly localised cluster of short waves is generated in a certain region of the free surface (see figure 5 b). Eventually, one of the waves develops an infinite slope of the interface. This scenario was dubbed ‘micro-overturning’.
Both micro-overturning and overturning proper occur near the flow’s SP, which happens to be located at the free surface. An asymptotic equation (5.25) has been derived for the near-SP dynamics of surface waves, which indicates that they grow and become steeper (because the background flow advects them towards the SP, compressing them in the process).
The results obtained suggest that the effect of free-surface SPs can be different from that of SPs in the bulk of the liquid. Even though some studies do discuss the former (e.g. Scheid et al. Reference Scheid, Delacotte, Dollet, Rio, Restagno, van Nierop, Cantat, Langevin and Stone2010), their effect on the flow’s stability has not been examined and, thus, deserves further investigation.
Note that the lubrication theory yields a stable steady solution for all values of
$({\it\alpha},{\it\eta})$
, including those in regions (iia) and (iib), where the bores should overturn. The problem with region (iia) can be attributed to the inapplicability of the lubrication theory there, as the solutions corresponding to (iia) have an order-one slope of the free surface. The problem with (iib), in turn, is more worrying – as, for a certain part of this region, the lubrication theory yields solutions that appear to be fully consistent with the conditions under which they were derived (small slope of the free surface, etc.).
Finally, note that the present setting is not the first one where the lubrication approximation has been shown to break down. It is also known to do so for falling films (Pumir, Manneville & Pomeau Reference Pumir, Manneville and Pomeau1983; Scheid et al. Reference Scheid, Ruyer-Quil, Thiele, Kabov, Legros and Colinet2005) and rimming flows (Benilov, O’Brien & Sazonov Reference Benilov, O’Brien and Sazonov2003; Benilov Reference Benilov2004). In these cases, however, the lubrication solution blows up in a finite time, which is a different scenario from both (iia) and (iib).
Acknowledgement
The authors acknowledge the support of the Science Foundation Ireland under grants 11/RFP.1/MTH3281 and 12/IA/1683.
