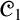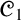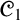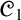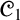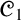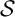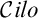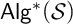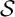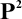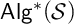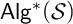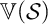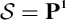1 Introduction
Paraconsistent logics were developed in the last century as a direct challenge to the principle of explosion (valid in both classical and intuitionistic logics) that from a contradiction anything follows. Concretely, ex contradictione sequitur quodlibet is dropped, thus allowing for situations where
![]() $\varphi ,\neg \varphi \not \vdash \psi $
. The study of paraconsistency has emerged in order to cope with inconsistency in a logical way, as motivated for instance by paradoxes of self-reference, or more simply in order to reason soundly in the presence of contradictory information. There are several competing approaches to paraconsistency, most notably, discussive logics, adaptive logics, relevance logics, and logics of formal inconsistency. For a historical account of the development of paraconsistent logics and an overview of some of its applications, ranging from philosophy to artificial intelligence, we refer the reader to [Reference Arruda2, Reference Carnielli, Coniglio and Marcos17, Reference Gabbay and Guenthner34, Reference Marcos42, Reference Priest46–Reference Priest, Tanaka and Weber49, Reference Weber55].
$\varphi ,\neg \varphi \not \vdash \psi $
. The study of paraconsistency has emerged in order to cope with inconsistency in a logical way, as motivated for instance by paradoxes of self-reference, or more simply in order to reason soundly in the presence of contradictory information. There are several competing approaches to paraconsistency, most notably, discussive logics, adaptive logics, relevance logics, and logics of formal inconsistency. For a historical account of the development of paraconsistent logics and an overview of some of its applications, ranging from philosophy to artificial intelligence, we refer the reader to [Reference Arruda2, Reference Carnielli, Coniglio and Marcos17, Reference Gabbay and Guenthner34, Reference Marcos42, Reference Priest46–Reference Priest, Tanaka and Weber49, Reference Weber55].
Da Costa’s paraconsistent logic
![]() ${\mathscr {C}}_1$
, and more generally da Costa’s
${\mathscr {C}}_1$
, and more generally da Costa’s
![]() ${\mathscr {C}}$
-systems
${\mathscr {C}}$
-systems
![]() ${\mathscr {C}}_n$
, originally introduced in [Reference da Costa18], constitute the seminal examples of logics of formal inconsistency. The logics are defined axiomatically, by weakening classical logic (
${\mathscr {C}}_n$
, originally introduced in [Reference da Costa18], constitute the seminal examples of logics of formal inconsistency. The logics are defined axiomatically, by weakening classical logic (
![]() $\mathcal {CL}$
) in such a way that the principle of explosion does not hold in general. However, distinctively, these logics are able to express consistency internally, and enjoy a controlled form of explosion. In
$\mathcal {CL}$
) in such a way that the principle of explosion does not hold in general. However, distinctively, these logics are able to express consistency internally, and enjoy a controlled form of explosion. In
![]() ${\mathscr {C}}_1$
, for instance, the consistency (or classicality) of a formula
${\mathscr {C}}_1$
, for instance, the consistency (or classicality) of a formula
![]() $\varphi $
can be expressed as
$\varphi $
can be expressed as
![]() and
and
![]() $\varphi ^{\circ },\varphi ,\neg \varphi \not \vdash \psi $
.
$\varphi ^{\circ },\varphi ,\neg \varphi \not \vdash \psi $
.
A couple of papers soon followed the seminal work of da Costa in 1963, namely [Reference Arruda and da Costa3, Reference da Costa and Guillaume25], which further developed these recent logical systems. Among the first results about
![]() ${\mathscr {C}}_1$
, one can emphasize the decidability of
${\mathscr {C}}_1$
, one can emphasize the decidability of
![]() ${\mathscr {C}}_1$
, the fact that da Costa’s
${\mathscr {C}}_1$
, the fact that da Costa’s
![]() ${\mathscr {C}}$
-systems form a hierarchy of proper extensions, and the fact that they are not complete w.r.t. finite matrices.Footnote
1
${\mathscr {C}}$
-systems form a hierarchy of proper extensions, and the fact that they are not complete w.r.t. finite matrices.Footnote
1
Semantical investigations of da Costa’s
![]() ${\mathscr {C}}$
-systems were also present since the beginning. Da Costa himself proposed the notion of
${\mathscr {C}}$
-systems were also present since the beginning. Da Costa himself proposed the notion of
![]() ${\mathscr {C}}_n$
-algebras as early as 1966 in [Reference da Costa19], defined the notions of filters and ideals for
${\mathscr {C}}_n$
-algebras as early as 1966 in [Reference da Costa19], defined the notions of filters and ideals for
![]() ${\mathscr {C}}_n$
-algebras in [Reference da Costa20], and later in a collaboration with Sette also defined the notion of
${\mathscr {C}}_n$
-algebras in [Reference da Costa20], and later in a collaboration with Sette also defined the notion of
![]() ${\mathscr {C}}_{\omega }$
-algebras in [Reference da Costa and Sette27]. But perhaps the most successful semantics was the non-truth-functional two-valued semantics developed by Alves and da Costa in [Reference da Costa and Alves22, Reference da Costa and Alves23] and establishing a completeness theorem for
${\mathscr {C}}_{\omega }$
-algebras in [Reference da Costa and Sette27]. But perhaps the most successful semantics was the non-truth-functional two-valued semantics developed by Alves and da Costa in [Reference da Costa and Alves22, Reference da Costa and Alves23] and establishing a completeness theorem for
![]() ${\mathscr {C}}_1$
. The quest for an algebraic counterpart for the logic
${\mathscr {C}}_1$
. The quest for an algebraic counterpart for the logic
![]() ${\mathscr {C}}_1$
was yet to have one further development with the so-called da Costa algebras investigated in [Reference Carnielli and de Alcantara14, Reference Seoane and de Alcantara52] and generalizing the
${\mathscr {C}}_1$
was yet to have one further development with the so-called da Costa algebras investigated in [Reference Carnielli and de Alcantara14, Reference Seoane and de Alcantara52] and generalizing the
![]() ${\mathscr {C}}_1$
-algebras introduced in [Reference da Costa19].
${\mathscr {C}}_1$
-algebras introduced in [Reference da Costa19].
The definite reference on da Costa’s logic would finally arrive in [Reference da Costa21], where the theory of inconsistent formal systems is presented fully developed and where several results from the previous papers mentioned are compiled.
The next big advance on da Costa’s logic would appear in 1980 and tore apart any hope of algebraizing
![]() ${\mathscr {C}}_1$
according to the classical Lindenbaum–Tarski process. Indeed, Mortensen proved in [Reference Mortensen44] that the only congruence on the formula algebra compatible with the theorems of
${\mathscr {C}}_1$
according to the classical Lindenbaum–Tarski process. Indeed, Mortensen proved in [Reference Mortensen44] that the only congruence on the formula algebra compatible with the theorems of
![]() ${\mathscr {C}}_1$
is the identity congruence, and as a consequence the Lindenbaum–Tarski algebra
${\mathscr {C}}_1$
is the identity congruence, and as a consequence the Lindenbaum–Tarski algebra
![]() ${\boldsymbol {Fm}}/{\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}({\mathrm{Thm}}_{{\mathscr {C}}_1})$
is isomorphic to the algebra of formulas
${\boldsymbol {Fm}}/{\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}({\mathrm{Thm}}_{{\mathscr {C}}_1})$
is isomorphic to the algebra of formulas
![]() ${\boldsymbol {Fm}}$
. Still in the 80s, two further contributions to the study of da Costa’s
${\boldsymbol {Fm}}$
. Still in the 80s, two further contributions to the study of da Costa’s
![]() ${\mathscr {C}}$
-systems were published, namely [Reference Mortensen45, Reference Urbas54]. It is worth mentioning that Mortensen’s paper [Reference Mortensen45] already contained material about the logics
${\mathscr {C}}$
-systems were published, namely [Reference Mortensen45, Reference Urbas54]. It is worth mentioning that Mortensen’s paper [Reference Mortensen45] already contained material about the logics
![]() and
and
![]() , under the names
, under the names
![]() $\mathrm {C}_{0.1}$
and
$\mathrm {C}_{0.1}$
and
![]() $\mathrm {C}_{0.2}$
, respectively. As to Urbas’ paper [Reference Urbas54], it provided several counterexamples for very simple properties which fail in
$\mathrm {C}_{0.2}$
, respectively. As to Urbas’ paper [Reference Urbas54], it provided several counterexamples for very simple properties which fail in
![]() ${\mathscr {C}}_1$
. Perhaps the most surprising one is that the consistency formula itself,
${\mathscr {C}}_1$
. Perhaps the most surprising one is that the consistency formula itself,
![]() , turns out not to be interderivable with the formula
, turns out not to be interderivable with the formula
![]() $\neg (\neg \varphi \wedge \varphi )$
. These somehow odd properties made
$\neg (\neg \varphi \wedge \varphi )$
. These somehow odd properties made
![]() ${\mathscr {C}}_1$
a paradigmatic exception among non-classical logics, and in particular among paraconsistent logics.
${\mathscr {C}}_1$
a paradigmatic exception among non-classical logics, and in particular among paraconsistent logics.
One last negative result was put forward in 1991, when Lewin, Mikenberg, and Schwarze proved in [Reference Lewin, Mikenberg and Schwarze39] that
![]() ${\mathscr {C}}_1$
is not algebraizable according to Blok and Pigozzi’s theory. This seemed to leave da Costa’s logic outside of any standard attempt of algebraization. As a result, two alternative algebraizations were proposed, namely behavioral algebraization [Reference Caleiro and Gonçalves12, Reference Caleiro, Gonçalves and Martins13] and possible-translations algebraization [Reference Bueno-Soler and Carnielli9].
${\mathscr {C}}_1$
is not algebraizable according to Blok and Pigozzi’s theory. This seemed to leave da Costa’s logic outside of any standard attempt of algebraization. As a result, two alternative algebraizations were proposed, namely behavioral algebraization [Reference Caleiro and Gonçalves12, Reference Caleiro, Gonçalves and Martins13] and possible-translations algebraization [Reference Bueno-Soler and Carnielli9].
The motivation behind the present work is to study da Costa’s logic from an Abstract Algebraic Logic (AAL) perspective. As we have seen,
![]() ${\mathscr {C}}_1$
had already been subject to extensive research in the literature, but apart from its famous non-algebraizability [Reference Lewin, Mikenberg and Schwarze39] and the side-remark on its non-equivalentiality [Reference Herrmann36, pp. 425–426], a thorough AAL investigation of
${\mathscr {C}}_1$
had already been subject to extensive research in the literature, but apart from its famous non-algebraizability [Reference Lewin, Mikenberg and Schwarze39] and the side-remark on its non-equivalentiality [Reference Herrmann36, pp. 425–426], a thorough AAL investigation of
![]() ${\mathscr {C}}_1$
is still missing.
${\mathscr {C}}_1$
is still missing.
The main new result about da Costa’s logic established in this work is the fact that
![]() ${\mathscr {C}}_1$
does not admit any algebraic semantics in the sense of Blok and Pigozzi (Theorem 5.6), as originally defined in [Reference Blok and Pigozzi6]. Since every algebraizable logic possesses an algebraic semantics (in fact, every truth-equational logic possesses an algebraic semantics), this result generalizes the non-algebraizability of
${\mathscr {C}}_1$
does not admit any algebraic semantics in the sense of Blok and Pigozzi (Theorem 5.6), as originally defined in [Reference Blok and Pigozzi6]. Since every algebraizable logic possesses an algebraic semantics (in fact, every truth-equational logic possesses an algebraic semantics), this result generalizes the non-algebraizability of
![]() ${\mathscr {C}}_1$
established by Lewin, Mikenberg, and Schwarze [Reference Lewin, Mikenberg and Schwarze39]. Although this fact may reinforce the belief that
${\mathscr {C}}_1$
established by Lewin, Mikenberg, and Schwarze [Reference Lewin, Mikenberg and Schwarze39]. Although this fact may reinforce the belief that
![]() ${\mathscr {C}}_1$
is an exception to the standard AAL methods, it satisfies nevertheless a wealth of properties within the theory of protoalgebraic logics. Namely, the class
${\mathscr {C}}_1$
is an exception to the standard AAL methods, it satisfies nevertheless a wealth of properties within the theory of protoalgebraic logics. Namely, the class
![]() ${\mathsf {Mod}}({\mathscr {C}}_1)$
enjoys the Filter Extension Property (FEP), the lattice of
${\mathsf {Mod}}({\mathscr {C}}_1)$
enjoys the Filter Extension Property (FEP), the lattice of
![]() ${\mathscr {C}}_1$
-filters of an arbitrary algebra is distributive, and the join-semilattice of finitely generated
${\mathscr {C}}_1$
-filters of an arbitrary algebra is distributive, and the join-semilattice of finitely generated
![]() ${\mathscr {C}}_1$
-theories is dually Brouwerian (Theorem 3.10).
${\mathscr {C}}_1$
-theories is dually Brouwerian (Theorem 3.10).
The study of
![]() ${\mathscr {C}}_1$
eventually led us to consider the logic
${\mathscr {C}}_1$
eventually led us to consider the logic
![]() ${\mathcal {C}ilo}$
[Reference da Costa, Béziau and Bueno24], a paraconsistent extension of
${\mathcal {C}ilo}$
[Reference da Costa, Béziau and Bueno24], a paraconsistent extension of
![]() ${\mathscr {C}}_1$
introduced by da Costa, Béziau, and Bueno in [Reference da Costa, Béziau and Bueno24], and coined as
${\mathscr {C}}_1$
introduced by da Costa, Béziau, and Bueno in [Reference da Costa, Béziau and Bueno24], and coined as
![]() ${\mathcal {C}ilo}$
in [Reference Carnielli and Marcos16], as well as other paraconsistent axiomatic extensions of
${\mathcal {C}ilo}$
in [Reference Carnielli and Marcos16], as well as other paraconsistent axiomatic extensions of
![]() ${\mathscr {C}}_1$
covered in the literature, including the algebraizable logics
${\mathscr {C}}_1$
covered in the literature, including the algebraizable logics
![]() ,
,
![]() , and
, and
![]() . The choice of which extensions of
. The choice of which extensions of
![]() ${\mathscr {C}}_1$
to consider was mainly guided by [Reference Carnielli and Marcos16, Section 3.10] and is depicted in Figure 1, along with the inclusion relations among them.
${\mathscr {C}}_1$
to consider was mainly guided by [Reference Carnielli and Marcos16, Section 3.10] and is depicted in Figure 1, along with the inclusion relations among them.

Figure 1 Extensions of
![]() ${\mathscr {C}}_1$
under study.
${\mathscr {C}}_1$
under study.
In particular, we will show that every algebra in
![]() ${\mathsf {Alg}}^*({\mathcal {C}ilo})$
contains a Boolean subalgebra (Proposition 9.10). Moreover, for
${\mathsf {Alg}}^*({\mathcal {C}ilo})$
contains a Boolean subalgebra (Proposition 9.10). Moreover, for
![]() , we will prove that every non-trivial subdirectly
, we will prove that every non-trivial subdirectly
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
-irreducible algebra in
${\mathsf {Alg}}^*({\mathcal {S}})$
-irreducible algebra in
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
has cardinality at most
${\mathsf {Alg}}^*({\mathcal {S}})$
has cardinality at most
![]() $3$
(Theorems 11.9, 11.10, and 12.8 of the Leibniz operator). We further classify these logics within the Leibniz hierarchy—the main classification of logics in AAL, which characterizes its member classes in terms of algebraic properties enjoyed by the Leibniz operator—and characterize the quasivariety
$3$
(Theorems 11.9, 11.10, and 12.8 of the Leibniz operator). We further classify these logics within the Leibniz hierarchy—the main classification of logics in AAL, which characterizes its member classes in terms of algebraic properties enjoyed by the Leibniz operator—and characterize the quasivariety
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
and the intrinsic variety
${\mathsf {Alg}}^*({\mathcal {S}})$
and the intrinsic variety
![]() $\mathbb {V}({\mathcal {S}})$
, with
$\mathbb {V}({\mathcal {S}})$
, with
![]() (Propositions 11.11, 11.13, and 12.9 and Corollaries 11.12, 11.14, and 12.10), although the results for Sette’s logic
(Propositions 11.11, 11.13, and 12.9 and Corollaries 11.12, 11.14, and 12.10), although the results for Sette’s logic
![]() were originally established in [Reference Pynko50].
were originally established in [Reference Pynko50].
Finally, we correct a couple of claims found in the literature, namely:
-
• We prove that
 ${\mathcal {C}ilo}$
is not equivalential (Proposition 9.6), and hence not algebraizable either, correcting [Reference Marcos42, p. 183] and [Reference Carnielli and Marcos16, p. 79].
${\mathcal {C}ilo}$
is not equivalential (Proposition 9.6), and hence not algebraizable either, correcting [Reference Marcos42, p. 183] and [Reference Carnielli and Marcos16, p. 79]. -
• We provide new proofs for the algebraizability of
 and
and
 . These logics are among the 8k three-valued logics considered in [Reference Carnielli and Marcos16, Fact 3.82] or [Reference Carnielli, Coniglio and Marcos17, Theorem 135]. However, the proofs of the cited results make use of relations which may not be congruence relations.Footnote
2
. These logics are among the 8k three-valued logics considered in [Reference Carnielli and Marcos16, Fact 3.82] or [Reference Carnielli, Coniglio and Marcos17, Theorem 135]. However, the proofs of the cited results make use of relations which may not be congruence relations.Footnote
2
We decided to organize the paper in three parts.
In Part I of our study, we undertake a thorough investigation of the logic
![]() ${\mathscr {C}}_1$
from an AAL perspective. We start by formally introducing da Costa’s logic
${\mathscr {C}}_1$
from an AAL perspective. We start by formally introducing da Costa’s logic
![]() ${\mathscr {C}}_1$
in Section 3, as well as briefly reviewing the semantics put forward in the literature for
${\mathscr {C}}_1$
in Section 3, as well as briefly reviewing the semantics put forward in the literature for
![]() ${\mathscr {C}}_1$
. In Section 3.1 we fully classify
${\mathscr {C}}_1$
. In Section 3.1 we fully classify
![]() ${\mathscr {C}}_1$
within the Leibniz and Frege hierarchies (both classifications were known in the literature, but we compile these scattered results) and in Section 3.2 we state some consequences of the Deduction-Detachment Theorem for
${\mathscr {C}}_1$
within the Leibniz and Frege hierarchies (both classifications were known in the literature, but we compile these scattered results) and in Section 3.2 we state some consequences of the Deduction-Detachment Theorem for
![]() ${\mathscr {C}}_1$
. In Section 4 we provide two sets of congruence formulas for the logic
${\mathscr {C}}_1$
. In Section 4 we provide two sets of congruence formulas for the logic
![]() ${\mathscr {C}}_1$
. In Section 5.1 we study the class
${\mathscr {C}}_1$
. In Section 5.1 we study the class
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
and the intrinsic variety
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
and the intrinsic variety
![]() $\mathbb {V}({\mathscr {C}}_1)$
, and in Section 5.2 we prove that
$\mathbb {V}({\mathscr {C}}_1)$
, and in Section 5.2 we prove that
![]() ${\mathscr {C}}_1$
admits no algebraic semantics in the sense of Blok and Pigozzi.
${\mathscr {C}}_1$
admits no algebraic semantics in the sense of Blok and Pigozzi.
In Part II we study logics
![]() ${\mathcal {S}}$
such that
${\mathcal {S}}$
such that
![]() ${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
and consider two general conditions upon
${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
and consider two general conditions upon
![]() ${\mathcal {S}}$
under which stronger algebraic results hold, namely:
${\mathcal {S}}$
under which stronger algebraic results hold, namely:
-
1. For every
 ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
 and
and
 $a,b \in A^{\circ }$
,Footnote
3
$a,b \in A^{\circ }$
,Footnote
3
 $$ \begin{align*} \langle a,b \rangle \in {\boldsymbol{\varOmega}}^{\boldsymbol{A}}(F) \quad\Leftrightarrow\quad a \leftrightarrow^{\boldsymbol{A}} b \in F. \end{align*} $$
$$ \begin{align*} \langle a,b \rangle \in {\boldsymbol{\varOmega}}^{\boldsymbol{A}}(F) \quad\Leftrightarrow\quad a \leftrightarrow^{\boldsymbol{A}} b \in F. \end{align*} $$
-
2.
 ${\mathcal {S}}$
is finitary and finitely equivalential with a set of congruence formulas
${\mathcal {S}}$
is finitary and finitely equivalential with a set of congruence formulas
 ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
.
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
.
The abstract investigation of
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
under these assumptions paves the way for the individual study of the envisaged axiomatic extensions of
${\mathsf {Alg}}^*({\mathcal {S}})$
under these assumptions paves the way for the individual study of the envisaged axiomatic extensions of
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
Part III is devoted to the individual detailed analysis of each of the extensions of
![]() ${\mathscr {C}}_1$
. We begin in Section 9 with
${\mathscr {C}}_1$
. We begin in Section 9 with
![]() ${\mathcal {C}ilo}$
. In Section 9.1 we fully classify
${\mathcal {C}ilo}$
. In Section 9.1 we fully classify
![]() ${\mathcal {C}ilo}$
within the Leibniz hierarchy and in Section 9.2 we investigate some algebraic properties of the class
${\mathcal {C}ilo}$
within the Leibniz hierarchy and in Section 9.2 we investigate some algebraic properties of the class
![]() ${\mathsf {Alg}}^*({\mathcal {C}ilo})$
. In Section 10 we consider the extension
${\mathsf {Alg}}^*({\mathcal {C}ilo})$
. In Section 10 we consider the extension
![]() ${\mathcal {C}ilow}$
which allows us to prove that
${\mathcal {C}ilow}$
which allows us to prove that
![]() ${\mathcal {C}ilo}$
is not equivalential. Finally, in Sections 11 and 12 we investigate
${\mathcal {C}ilo}$
is not equivalential. Finally, in Sections 11 and 12 we investigate
![]() ,
,
![]() , and
, and
![]() . It is worth mentioning that Sette’s logic
. It is worth mentioning that Sette’s logic
![]() had already been subject to an AAL investigation in [Reference Pynko50], but we present it here in the unified setting of equivalential extensions of
had already been subject to an AAL investigation in [Reference Pynko50], but we present it here in the unified setting of equivalential extensions of
![]() ${\mathscr {C}}_1$
with set of congruence formulas
${\mathscr {C}}_1$
with set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
.
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
.
2 Preliminaries
We adopt the standard terminology and notation employed in Abstract Algebraic Logic (AAL), and refer the reader to [Reference Font32] for a recent and thorough treatment on the subject. We will here only briefly introduce the AAL notions needed in the sequel. These often rely on ground concepts from Universal Algebra and the theory of sentential logics. Classical references on these subjects are [Reference Burris and Sankappanavar10, Reference Wójcicki56].
We trust the reader is acquainted with the notions of algebra, homomorphism, congruence, variety, and quasivariety. We ought however to fix some notation. Given two algebras
![]() ${\boldsymbol {A}},{\boldsymbol {B}}$
, we denote a homomorphism h from
${\boldsymbol {A}},{\boldsymbol {B}}$
, we denote a homomorphism h from
![]() ${\boldsymbol {A}}$
to
${\boldsymbol {A}}$
to
![]() ${\boldsymbol {B}}$
simply by
${\boldsymbol {B}}$
simply by
![]() $h: {\boldsymbol {A}} \to {\boldsymbol {B}}$
, and the least congruence on
$h: {\boldsymbol {A}} \to {\boldsymbol {B}}$
, and the least congruence on
![]() ${\boldsymbol {A}}$
containing a subset
${\boldsymbol {A}}$
containing a subset
![]() $X \subseteq A \times A$
by
$X \subseteq A \times A$
by
![]() $\Theta ^{\boldsymbol {A}}(X)$
. The set of all congruences on
$\Theta ^{\boldsymbol {A}}(X)$
. The set of all congruences on
![]() ${\boldsymbol {A}}$
will be denoted by
${\boldsymbol {A}}$
will be denoted by
![]() $\mathrm {Co}\, {\boldsymbol {A}}$
; and given a class of algebras
$\mathrm {Co}\, {\boldsymbol {A}}$
; and given a class of algebras
![]() ${\mathsf {K}}$
, the set of all congruences
${\mathsf {K}}$
, the set of all congruences
![]() $\theta \in \mathrm {Co}\, {\boldsymbol {A}}$
such that
$\theta \in \mathrm {Co}\, {\boldsymbol {A}}$
such that
![]() ${\boldsymbol {A}}/\theta \in {\mathsf {K}}$
will be denoted by
${\boldsymbol {A}}/\theta \in {\mathsf {K}}$
will be denoted by
![]() $\mathrm {Co}_{\mathsf {K}}{\boldsymbol {A}}$
, and will be referred to as the set of congruences of
$\mathrm {Co}_{\mathsf {K}}{\boldsymbol {A}}$
, and will be referred to as the set of congruences of
![]() ${\boldsymbol {A}}$
relative to
${\boldsymbol {A}}$
relative to
![]() ${\mathsf {K}}$
, or simply the set
${\mathsf {K}}$
, or simply the set
![]() ${\mathsf {K}}$
-relative congruences of
${\mathsf {K}}$
-relative congruences of
![]() ${\boldsymbol {A}}$
.
${\boldsymbol {A}}$
.
Let
![]() ${\boldsymbol {A}}$
be an algebra. A subset
${\boldsymbol {A}}$
be an algebra. A subset
![]() $B \subseteq A$
is a subuniverse of
$B \subseteq A$
is a subuniverse of
![]() ${\boldsymbol {A}}$
, if it is closed under the operations of
${\boldsymbol {A}}$
, if it is closed under the operations of
![]() ${\boldsymbol {A}}$
. That is, if for every n-ary operation symbol
${\boldsymbol {A}}$
. That is, if for every n-ary operation symbol
![]() $f \in {\mathcal {L}}$
and for every
$f \in {\mathcal {L}}$
and for every
![]() $b_1 , \ldots , b_n \in B$
, it holds that
$b_1 , \ldots , b_n \in B$
, it holds that
![]() $f^{\boldsymbol {A}}(b_1 , \ldots , b_n) \in B$
. An algebra
$f^{\boldsymbol {A}}(b_1 , \ldots , b_n) \in B$
. An algebra
![]() ${\boldsymbol {B}}$
of the same similarity type as
${\boldsymbol {B}}$
of the same similarity type as
![]() ${\boldsymbol {A}}$
is a subalgebra of
${\boldsymbol {A}}$
is a subalgebra of
![]() ${\boldsymbol {A}}$
, fact which we shall denote by
${\boldsymbol {A}}$
, fact which we shall denote by
![]() ${\boldsymbol {B}} \leq {\boldsymbol {A}}$
, if
${\boldsymbol {B}} \leq {\boldsymbol {A}}$
, if
![]() $B \subseteq A$
and for every operation symbol
$B \subseteq A$
and for every operation symbol
![]() $f \in {\mathcal {L}}$
, it holds that
$f \in {\mathcal {L}}$
, it holds that
![]() $f^{\boldsymbol {B}} = f^{\boldsymbol {A}} \!\! \upharpoonright _{B}$
. Clearly, if
$f^{\boldsymbol {B}} = f^{\boldsymbol {A}} \!\! \upharpoonright _{B}$
. Clearly, if
![]() ${\boldsymbol {B}}$
is a subalgebra of
${\boldsymbol {B}}$
is a subalgebra of
![]() ${\boldsymbol {A}}$
, then B is a subuniverse of
${\boldsymbol {A}}$
, then B is a subuniverse of
![]() ${\boldsymbol {A}}$
. Given an algebra
${\boldsymbol {A}}$
. Given an algebra
![]() ${\boldsymbol {A}}$
and a subset
${\boldsymbol {A}}$
and a subset
![]() $X \subseteq A$
, the subuniverse generated by X, which we shall denote by
$X \subseteq A$
, the subuniverse generated by X, which we shall denote by
![]() $\mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(X)$
, is the least subuniverse of
$\mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(X)$
, is the least subuniverse of
![]() ${\boldsymbol {A}}$
containing X.
${\boldsymbol {A}}$
containing X.
Let
![]() ${\boldsymbol {A}}$
be an algebra. A congruence
${\boldsymbol {A}}$
be an algebra. A congruence
![]() $\theta \in \mathrm {Co}\, {\boldsymbol {A}}$
is compatible with a subset
$\theta \in \mathrm {Co}\, {\boldsymbol {A}}$
is compatible with a subset
![]() $F \subseteq A$
, if whenever
$F \subseteq A$
, if whenever
![]() $\langle a,b \rangle \in \theta $
and
$\langle a,b \rangle \in \theta $
and
![]() $a \in F$
, then
$a \in F$
, then
![]() $b \in F$
; in other words,
$b \in F$
; in other words,
![]() $\theta $
does not identify elements inside F with elements outside F. The least congruence on
$\theta $
does not identify elements inside F with elements outside F. The least congruence on
![]() ${\boldsymbol {A}}$
compatible with a given
${\boldsymbol {A}}$
compatible with a given
![]() $F \subseteq A$
is the identity congruence on
$F \subseteq A$
is the identity congruence on
![]() ${\boldsymbol {A}}$
, hereby denoted by
${\boldsymbol {A}}$
, hereby denoted by
![]() $id_{\boldsymbol {A}}$
, while the largest congruence on
$id_{\boldsymbol {A}}$
, while the largest congruence on
![]() ${\boldsymbol {A}}$
compatible with F, which always exists, is known as the Leibniz congruence of F, and is denoted by
${\boldsymbol {A}}$
compatible with F, which always exists, is known as the Leibniz congruence of F, and is denoted by
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. The Leibniz congruence can be lifted to the powerset. Given
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. The Leibniz congruence can be lifted to the powerset. Given
![]() ${\mathscr {C}} \subseteq \mathscr {P}(A)$
, the Tarski congruence of
${\mathscr {C}} \subseteq \mathscr {P}(A)$
, the Tarski congruence of
![]() ${\mathscr {C}}$
is the largest congruence on
${\mathscr {C}}$
is the largest congruence on
![]() ${\boldsymbol {A}}$
compatible with every
${\boldsymbol {A}}$
compatible with every
![]() $F \in {\mathscr {C}}$
; that is,
$F \in {\mathscr {C}}$
; that is,
![]() .
.
Given a class of algebras
![]() ${\mathsf {K}}$
, we denote by
${\mathsf {K}}$
, we denote by
![]() $\mathbb {Q}{\mathsf {K}}$
and
$\mathbb {Q}{\mathsf {K}}$
and
![]() $\mathbb {V}{\mathsf {K}}$
the least quasivariety containing
$\mathbb {V}{\mathsf {K}}$
the least quasivariety containing
![]() ${\mathsf {K}}$
and the least variety containing
${\mathsf {K}}$
and the least variety containing
![]() ${\mathsf {K}}$
, respectively, and we denote by
${\mathsf {K}}$
, respectively, and we denote by
![]() $\mathbb {I}$
,
$\mathbb {I}$
,
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\mathbb {P}_{\scriptscriptstyle \!\mathrm {S}}$
,
$\mathbb {P}_{\scriptscriptstyle \!\mathrm {S}}$
,
![]() $\mathbb {S}$
, and
$\mathbb {S}$
, and
![]() $\mathbb {H}$
the isomorphism, direct product, subdirect product, subalgebra, and homomorphic image operators, respectively. Recall that a trivial algebra is one with a single element universe, and observe that every quasivariety (and hence every variety as well) contains all trivial algebras. We assume the reader is familiar with the notion of subdirectly irreducible algebra, as well as Birkhoff’s famous result characterizing varieties in terms of their subdirectly irreducible elements [Reference Birkhoff5, Theorem 2]. Namely, if
$\mathbb {H}$
the isomorphism, direct product, subdirect product, subalgebra, and homomorphic image operators, respectively. Recall that a trivial algebra is one with a single element universe, and observe that every quasivariety (and hence every variety as well) contains all trivial algebras. We assume the reader is familiar with the notion of subdirectly irreducible algebra, as well as Birkhoff’s famous result characterizing varieties in terms of their subdirectly irreducible elements [Reference Birkhoff5, Theorem 2]. Namely, if
![]() ${\mathsf {K}}$
is a variety, then
${\mathsf {K}}$
is a variety, then
![]() ${\mathsf {K}} = \mathbb {IP}_{\mathrm {S}}({\mathsf {K}}_{\mathrm {s.i.}})$
, where
${\mathsf {K}} = \mathbb {IP}_{\mathrm {S}}({\mathsf {K}}_{\mathrm {s.i.}})$
, where
![]() ${\mathsf {K}}_{\mathrm {s.i.}}$
denotes the set of subdirectly irreducible elements of
${\mathsf {K}}_{\mathrm {s.i.}}$
denotes the set of subdirectly irreducible elements of
![]() ${\mathsf {K}}$
—see for instance [Reference Burris and Sankappanavar10, Corollary 9.7] or [Reference Bergman4, Theorem 3.44].
${\mathsf {K}}$
—see for instance [Reference Burris and Sankappanavar10, Corollary 9.7] or [Reference Bergman4, Theorem 3.44].
A generalization of Birkhoff’s result for quasivarieties will be needed in Section 9.2. Given a class of algebras
![]() ${\mathsf {K}}$
, an algebra
${\mathsf {K}}$
, an algebra
![]() ${\boldsymbol {A}}$
is subdirectly irreducible relative to
${\boldsymbol {A}}$
is subdirectly irreducible relative to
![]() ${\mathsf {K}}$
, or is subdirectly
${\mathsf {K}}$
, or is subdirectly
![]() ${\mathsf {K}}$
-irreducible, if for every subdirect embedding
${\mathsf {K}}$
-irreducible, if for every subdirect embedding
![]() $\alpha : {\boldsymbol {A}} \rightarrow \prod _{i \in I} {\boldsymbol {A}}_i$
, with
$\alpha : {\boldsymbol {A}} \rightarrow \prod _{i \in I} {\boldsymbol {A}}_i$
, with
![]() $\{ {\boldsymbol {A}}_i : i \in I \} \subseteq {\mathsf {K}}$
, there exists
$\{ {\boldsymbol {A}}_i : i \in I \} \subseteq {\mathsf {K}}$
, there exists
![]() $i \in I$
such that
$i \in I$
such that
![]() $\pi _i \circ \alpha : {\boldsymbol {A}} \rightarrow {\boldsymbol {A}}_i$
is an isomorphism. Quasivarieties can also be characterized in terms of their relative subdirectly irreducible elements—this fact is not so well-known as its particular case for varieties, but a proof can be found in [Reference Caicedo11, Corollary 6] or [Reference Gorbunov35, Theorem 3.1.1]; in the latter reference the original result is credited to Mal’cev [Reference Mal’cev41]. Consequently, if
$\pi _i \circ \alpha : {\boldsymbol {A}} \rightarrow {\boldsymbol {A}}_i$
is an isomorphism. Quasivarieties can also be characterized in terms of their relative subdirectly irreducible elements—this fact is not so well-known as its particular case for varieties, but a proof can be found in [Reference Caicedo11, Corollary 6] or [Reference Gorbunov35, Theorem 3.1.1]; in the latter reference the original result is credited to Mal’cev [Reference Mal’cev41]. Consequently, if
![]() ${\mathsf {K}}$
is a quasivariety, then
${\mathsf {K}}$
is a quasivariety, then
![]() ${\mathsf {K}} = \mathbb {IP}_s({\mathsf {K}}_{\mathrm {r.s.i.}})$
, where
${\mathsf {K}} = \mathbb {IP}_s({\mathsf {K}}_{\mathrm {r.s.i.}})$
, where
![]() ${\mathsf {K}}_{\mathrm {r.s.i.}}$
denotes a set of subdirectly
${\mathsf {K}}_{\mathrm {r.s.i.}}$
denotes a set of subdirectly
![]() ${\mathsf {K}}$
-irreducible elements of
${\mathsf {K}}$
-irreducible elements of
![]() ${\mathsf {K}}$
.
${\mathsf {K}}$
.
By a (sentential) logic we understand a structural consequence relation on
![]() $\mathrm {Fm}_{\mathcal {L}}$
, where
$\mathrm {Fm}_{\mathcal {L}}$
, where
![]() $\mathrm {Fm}_{\mathcal {L}}$
denotes the universe of the free algebra of terms
$\mathrm {Fm}_{\mathcal {L}}$
denotes the universe of the free algebra of terms
![]() ${\boldsymbol {Fm}}$
generated by a denumerable set of variables
${\boldsymbol {Fm}}$
generated by a denumerable set of variables
![]() $\mathrm {Var}$
over an algebraic language
$\mathrm {Var}$
over an algebraic language
![]() ${\mathcal {L}}$
. It is common practice to denote by
${\mathcal {L}}$
. It is common practice to denote by
![]() ${\mathcal {S}}$
an arbitrary logic, i.e., the set of all rules of
${\mathcal {S}}$
an arbitrary logic, i.e., the set of all rules of
![]() ${\mathcal {S}}$
, and by
${\mathcal {S}}$
, and by
![]() $\Gamma \vdash _{\mathcal {S}} \varphi $
or
$\Gamma \vdash _{\mathcal {S}} \varphi $
or
![]() $\langle \Gamma ,\varphi \rangle \in \; \vdash _{\mathcal {S}}$
, with
$\langle \Gamma ,\varphi \rangle \in \; \vdash _{\mathcal {S}}$
, with
![]() $\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
, one such particular rule. We abbreviate
$\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
, one such particular rule. We abbreviate
![]() $\varnothing \vdash \varphi $
simply by
$\varnothing \vdash \varphi $
simply by
![]() $\vdash \varphi $
, and the facts
$\vdash \varphi $
, and the facts
![]() $\varphi \vdash _{\mathcal {S}} \psi $
and
$\varphi \vdash _{\mathcal {S}} \psi $
and
![]() $\psi \vdash _{\mathcal {S}} \varphi $
by
$\psi \vdash _{\mathcal {S}} \varphi $
by
![]() $\varphi \dashv \vdash _{\mathcal {S}} \psi $
. The relation identifying such pairs of formulas is called the interderivability relation.
$\varphi \dashv \vdash _{\mathcal {S}} \psi $
. The relation identifying such pairs of formulas is called the interderivability relation.
Let
![]() ${\mathcal {S}}$
be a logic. A logic
${\mathcal {S}}$
be a logic. A logic
![]() ${\mathcal {S}}'$
(in the same language of
${\mathcal {S}}'$
(in the same language of
![]() ${\mathcal {S}}$
) is an extension of
${\mathcal {S}}$
) is an extension of
![]() ${\mathcal {S}}$
, if
${\mathcal {S}}$
, if
![]() $\vdash _{\mathcal {S}} \; \subseteq \; \vdash _{{\mathcal {S}}'}$
, a fact which we will denote simply by
$\vdash _{\mathcal {S}} \; \subseteq \; \vdash _{{\mathcal {S}}'}$
, a fact which we will denote simply by
![]() ${\mathcal {S}} \leq {\mathcal {S}}'$
. Now, let
${\mathcal {S}} \leq {\mathcal {S}}'$
. Now, let
![]() ${\mathcal {L}}'$
be a language such that
${\mathcal {L}}'$
be a language such that
![]() ${\mathcal {L}} \subseteq {\mathcal {L}}'$
. A logic
${\mathcal {L}} \subseteq {\mathcal {L}}'$
. A logic
![]() ${\mathcal {S}}'$
in the language
${\mathcal {S}}'$
in the language
![]() ${\mathcal {L}}'$
is an expansion of
${\mathcal {L}}'$
is an expansion of
![]() ${\mathcal {S}}$
, if for every set of
${\mathcal {S}}$
, if for every set of
![]() ${\mathcal {L}}$
-formulas
${\mathcal {L}}$
-formulas
![]() $\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
,
$\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
,
![]() $\Gamma \vdash _{\mathcal {S}} \varphi \; \Rightarrow \; \Gamma \vdash _{{\mathcal {S}}'} \varphi $
; in case the converse implication also holds, that is for every set of
$\Gamma \vdash _{\mathcal {S}} \varphi \; \Rightarrow \; \Gamma \vdash _{{\mathcal {S}}'} \varphi $
; in case the converse implication also holds, that is for every set of
![]() ${\mathcal {L}}$
-formulas
${\mathcal {L}}$
-formulas
![]() $\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
we have
$\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
we have
![]() $\Gamma \vdash _{\mathcal {S}} \varphi \; \Leftrightarrow \; \Gamma \vdash _{{\mathcal {S}}'} \varphi $
, the logic
$\Gamma \vdash _{\mathcal {S}} \varphi \; \Leftrightarrow \; \Gamma \vdash _{{\mathcal {S}}'} \varphi $
, the logic
![]() ${\mathcal {S}}'$
is called a conservative expansion of
${\mathcal {S}}'$
is called a conservative expansion of
![]() ${\mathcal {S}}$
, and the logic
${\mathcal {S}}$
, and the logic
![]() ${\mathcal {S}}$
is called the
${\mathcal {S}}$
is called the
![]() ${\mathcal {L}}$
-fragment of
${\mathcal {L}}$
-fragment of
![]() ${\mathcal {S}}'$
.
${\mathcal {S}}'$
.
The sets of formulas which are
![]() $\vdash _{\mathcal {S}}$
-closed are called
$\vdash _{\mathcal {S}}$
-closed are called
![]() ${\mathcal {S}}$
-theories. The set of all
${\mathcal {S}}$
-theories. The set of all
![]() ${\mathcal {S}}$
-theories is denoted by
${\mathcal {S}}$
-theories is denoted by
![]() $\mathcal {T}\!h({\mathcal {S}})$
and the least
$\mathcal {T}\!h({\mathcal {S}})$
and the least
![]() ${\mathcal {S}}$
-theory, whose elements are called
${\mathcal {S}}$
-theory, whose elements are called
![]() ${\mathcal {S}}$
-theorems, is denoted by
${\mathcal {S}}$
-theorems, is denoted by
![]() ${\mathrm{Thm}}_{{\mathcal {S}}}$
. A logic
${\mathrm{Thm}}_{{\mathcal {S}}}$
. A logic
![]() ${\mathcal {S}}$
is called inconsistent if
${\mathcal {S}}$
is called inconsistent if
![]() ${\mathrm{Thm}}_{\mathcal {S}} = \mathrm {Fm}_{\mathcal {L}}$
. The notion of
${\mathrm{Thm}}_{\mathcal {S}} = \mathrm {Fm}_{\mathcal {L}}$
. The notion of
![]() ${\mathcal {S}}$
-theory turns out to be an instance of a more general notion, applicable to arbitrary algebras. Given an algebra
${\mathcal {S}}$
-theory turns out to be an instance of a more general notion, applicable to arbitrary algebras. Given an algebra
![]() ${\boldsymbol {A}}$
, an
${\boldsymbol {A}}$
, an
![]() ${\mathcal {S}}$
-filter of
${\mathcal {S}}$
-filter of
![]() ${\boldsymbol {A}}$
is a subset
${\boldsymbol {A}}$
is a subset
![]() $F \subseteq A$
such that, for every homomorphism
$F \subseteq A$
such that, for every homomorphism
![]() $h \colon {\boldsymbol {Fm}} \to {\boldsymbol {A}}$
and every
$h \colon {\boldsymbol {Fm}} \to {\boldsymbol {A}}$
and every
![]() $\Gamma \cup \{ \varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
, if
$\Gamma \cup \{ \varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
, if
![]() $\Gamma \vdash _{\mathcal {S}} \varphi $
and
$\Gamma \vdash _{\mathcal {S}} \varphi $
and
![]() $h(\Gamma ) \subseteq F$
, then
$h(\Gamma ) \subseteq F$
, then
![]() $h(\varphi ) \in F$
. We denote the set of all
$h(\varphi ) \in F$
. We denote the set of all
![]() ${\mathcal {S}}$
-filters of
${\mathcal {S}}$
-filters of
![]() ${\boldsymbol {A}}$
by
${\boldsymbol {A}}$
by
![]() . As claimed,
. As claimed,
![]() . The least
. The least
![]() ${\mathcal {S}}$
-filter of
${\mathcal {S}}$
-filter of
![]() ${\boldsymbol {A}}$
containing
${\boldsymbol {A}}$
containing
![]() $X \subseteq A$
is denoted by
$X \subseteq A$
is denoted by
![]() , and the least
, and the least
![]() ${\mathcal {S}}$
-theory containing
${\mathcal {S}}$
-theory containing
![]() $\Gamma \subseteq \mathrm {Fm}_{\mathcal {L}}$
is denoted by
$\Gamma \subseteq \mathrm {Fm}_{\mathcal {L}}$
is denoted by
![]() .
.
Although the Leibniz and Tarski congruences were defined for arbitrary sets and families of sets, respectively, we shall usually consider them over
![]() ${\mathcal {S}}$
-filters and families of
${\mathcal {S}}$
-filters and families of
![]() ${\mathcal {S}}$
-filters, respectively. The next auxiliary lemma relates the notions of logical filter, Leibniz congruence, and subalgebra.
${\mathcal {S}}$
-filters, respectively. The next auxiliary lemma relates the notions of logical filter, Leibniz congruence, and subalgebra.
Lemma 2.1. Let
![]() ${\mathcal {S}}$
be a logic,
${\mathcal {S}}$
be a logic,
![]() ${\boldsymbol {A}}$
an algebra, and
${\boldsymbol {A}}$
an algebra, and
![]() ${\boldsymbol {B}}$
a subalgebra of
${\boldsymbol {B}}$
a subalgebra of
![]() ${\boldsymbol {A}}$
. For every
${\boldsymbol {A}}$
. For every
![]() ,
,
-
1.

-
2.
 ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\!\downharpoonright _{{\boldsymbol {B}}} \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {B}}(F \cap B)$
.
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\!\downharpoonright _{{\boldsymbol {B}}} \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {B}}(F \cap B)$
.
An
![]() ${\mathcal {L}}$
-equation is a pair of formulas
${\mathcal {L}}$
-equation is a pair of formulas
![]() $\langle \varphi ,\psi \rangle \in \mathrm {Fm}_{\mathcal {L}} \times \mathrm {Fm}_{\mathcal {L}}$
, usually abbreviated as
$\langle \varphi ,\psi \rangle \in \mathrm {Fm}_{\mathcal {L}} \times \mathrm {Fm}_{\mathcal {L}}$
, usually abbreviated as
![]() $\varphi \approx \psi $
. We denote the set of all
$\varphi \approx \psi $
. We denote the set of all
![]() ${\mathcal {L}}$
-equations by
${\mathcal {L}}$
-equations by
![]() $\mathrm {Eq}_{\mathcal {L}}$
. Given a class of algebras
$\mathrm {Eq}_{\mathcal {L}}$
. Given a class of algebras
![]() ${\mathsf {K}}$
, the equational consequence relation relative to
${\mathsf {K}}$
, the equational consequence relation relative to
![]() ${\mathsf {K}}$
is the relation
${\mathsf {K}}$
is the relation
![]() $\vDash _{\mathsf {K}} \; \subseteq \mathscr {P}(\mathrm {Eq}_{\mathcal {L}}) \times \mathrm {Eq}_{\mathcal {L}}$
defined by
$\vDash _{\mathsf {K}} \; \subseteq \mathscr {P}(\mathrm {Eq}_{\mathcal {L}}) \times \mathrm {Eq}_{\mathcal {L}}$
defined by
 $$ \begin{align*} \Pi \vDash_{\mathsf{K}} \varphi \approx \psi\quad \text{iff}\quad & \forall {\boldsymbol{A}} \in {\mathsf{K}} \; \forall h : {\boldsymbol{Fm}} \to {\boldsymbol{A}} \\ & \forall \delta \approx \epsilon \in \Pi \quad h(\delta) = h(\epsilon) \; \Rightarrow \; h(\varphi) = h(\psi). \end{align*} $$
$$ \begin{align*} \Pi \vDash_{\mathsf{K}} \varphi \approx \psi\quad \text{iff}\quad & \forall {\boldsymbol{A}} \in {\mathsf{K}} \; \forall h : {\boldsymbol{Fm}} \to {\boldsymbol{A}} \\ & \forall \delta \approx \epsilon \in \Pi \quad h(\delta) = h(\epsilon) \; \Rightarrow \; h(\varphi) = h(\psi). \end{align*} $$
It is common practice to abbreviate
![]() $\vDash _{\{{\boldsymbol {A}}\}}$
simply by
$\vDash _{\{{\boldsymbol {A}}\}}$
simply by
![]() $\vDash _{\boldsymbol {A}}$
.
$\vDash _{\boldsymbol {A}}$
.
A matrix model of
![]() ${\mathcal {S}}$
is a pair
${\mathcal {S}}$
is a pair
![]() $\langle {\boldsymbol {A}} , F \rangle $
such that
$\langle {\boldsymbol {A}} , F \rangle $
such that
![]() . We denote the class of all matrix models of a logic
. We denote the class of all matrix models of a logic
![]() ${\mathcal {S}}$
by
${\mathcal {S}}$
by
![]() ${\mathsf {Mod}}({\mathcal {S}})$
. A matrix model
${\mathsf {Mod}}({\mathcal {S}})$
. A matrix model
![]() $\langle {\boldsymbol {A}} , F \rangle \in {\mathsf {Mod}}({\mathcal {S}})$
is called reduced if
$\langle {\boldsymbol {A}} , F \rangle \in {\mathsf {Mod}}({\mathcal {S}})$
is called reduced if
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) = id_{\boldsymbol {A}}$
. We denote the class of all reduced matrix models by
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) = id_{\boldsymbol {A}}$
. We denote the class of all reduced matrix models by
![]() ${\mathsf {Mod}}^*({\mathcal {S}})$
.
${\mathsf {Mod}}^*({\mathcal {S}})$
.
Two classes of algebras are usually considered in AAL as naturally, and intrinsically, associated with a logic. These are obtained as follows:

It turns out that
![]() ${\mathsf {Alg}}({\mathcal {S}}) = \mathbb {P}_{\scriptscriptstyle \!\mathrm {S}}\,{\mathsf {Alg}}^*({\mathcal {S}})$
[Reference Font and Jansana33, Theorem 2.23]. When one wishes to associate with a logic
${\mathsf {Alg}}({\mathcal {S}}) = \mathbb {P}_{\scriptscriptstyle \!\mathrm {S}}\,{\mathsf {Alg}}^*({\mathcal {S}})$
[Reference Font and Jansana33, Theorem 2.23]. When one wishes to associate with a logic
![]() ${\mathcal {S}}$
an “algebraic counterpart” which is necessarily a variety, a third class of algebras is often considered, defined by
${\mathcal {S}}$
an “algebraic counterpart” which is necessarily a variety, a third class of algebras is often considered, defined by
It can be proved that
![]() $\mathbb {V}({\mathcal {S}})$
is in fact the least variety containing
$\mathbb {V}({\mathcal {S}})$
is in fact the least variety containing
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, i.e.,
${\mathsf {Alg}}^*({\mathcal {S}})$
, i.e.,
![]() $\mathbb {V}({\mathcal {S}}) = \mathbb {V}\,{\mathsf {Alg}}^*({\mathcal {S}})$
, and it is called the intrinsic variety of
$\mathbb {V}({\mathcal {S}}) = \mathbb {V}\,{\mathsf {Alg}}^*({\mathcal {S}})$
, and it is called the intrinsic variety of
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
2.1 The Leibniz and Frege hierarchies
The main classification of sentential logics in AAL is the so-called Leibniz hierarchy, characterizing logics by means of algebraic properties of the Leibniz operator.Footnote
4
For instance, the Leibniz operator (over the
![]() ${\mathcal {S}}$
-filters of an arbitrary algebra
${\mathcal {S}}$
-filters of an arbitrary algebra
![]() ${\boldsymbol {A}}$
) of an algebraizable logic
${\boldsymbol {A}}$
) of an algebraizable logic
![]() ${\mathcal {S}}$
is an isomorphism between the lattice of
${\mathcal {S}}$
is an isomorphism between the lattice of
![]() ${\mathcal {S}}$
-filters of
${\mathcal {S}}$
-filters of
![]() ${\boldsymbol {A}}$
and the lattice of
${\boldsymbol {A}}$
and the lattice of
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
-relative congruences of
${\mathsf {Alg}}^*({\mathcal {S}})$
-relative congruences of
![]() ${\boldsymbol {A}}$
, which furthermore commutes with inverse images of homomorphisms. In [Reference Lewin, Mikenberg and Schwarze39], the non-algebraizability of
${\boldsymbol {A}}$
, which furthermore commutes with inverse images of homomorphisms. In [Reference Lewin, Mikenberg and Schwarze39], the non-algebraizability of
![]() ${\mathscr {C}}_1$
was established by exhibiting an algebra
${\mathscr {C}}_1$
was established by exhibiting an algebra
![]() ${\boldsymbol {A}}$
where the Leibniz operator over the
${\boldsymbol {A}}$
where the Leibniz operator over the
![]() ${\mathscr {C}}_1$
-filters of
${\mathscr {C}}_1$
-filters of
![]() ${\boldsymbol {A}}$
was not injective.
${\boldsymbol {A}}$
was not injective.
We next introduce the main classes of logics belonging to the Leibniz hierarchy. However, since their characterizations in terms of the algebraic properties of Leibniz operator will not be used in the sequel, we have chosen to define them here in a manner that will suit our purposes better.
Definition 2.2. A logic
![]() ${\mathcal {S}}$
is:
${\mathcal {S}}$
is:
-
(i) protoalgebraic if there exists a set of formulas
 ${\boldsymbol {\rho }}(x,y) \subseteq \mathrm {Fm}_{\mathcal {L}}$
satisfying(R)
${\boldsymbol {\rho }}(x,y) \subseteq \mathrm {Fm}_{\mathcal {L}}$
satisfying(R) $$ \begin{align} \varnothing \vdash_{\mathcal{S}} {\boldsymbol{\rho}}(x,x), \end{align} $$
(MP)
$$ \begin{align} \varnothing \vdash_{\mathcal{S}} {\boldsymbol{\rho}}(x,x), \end{align} $$
(MP) $$ \begin{align} x , {\boldsymbol{\rho}}(x,y) \vdash_{\mathcal{S}} y , \end{align} $$
$$ \begin{align} x , {\boldsymbol{\rho}}(x,y) \vdash_{\mathcal{S}} y , \end{align} $$
-
(ii) equivalential if there exists a set of formulas
 ${\boldsymbol {\rho }}(x,y) \subseteq \mathrm {Fm}_{\mathcal {L}}$
satisfying (R), (MP) and for every n-ary function symbol
${\boldsymbol {\rho }}(x,y) \subseteq \mathrm {Fm}_{\mathcal {L}}$
satisfying (R), (MP) and for every n-ary function symbol
 $f \in \mathcal {L}$
, (RP)
$f \in \mathcal {L}$
, (RP) $$ \begin{align} {\boldsymbol{\rho}}(x_1 ,y_1) \cup \cdots \cup {\boldsymbol{\rho}}(x_n ,y_n) \vdash_{\mathcal{S}} {\boldsymbol{\rho}}\big(f(x_1 \ldots x_n) , f(y_1 \ldots y_n)\big) , \end{align} $$
$$ \begin{align} {\boldsymbol{\rho}}(x_1 ,y_1) \cup \cdots \cup {\boldsymbol{\rho}}(x_n ,y_n) \vdash_{\mathcal{S}} {\boldsymbol{\rho}}\big(f(x_1 \ldots x_n) , f(y_1 \ldots y_n)\big) , \end{align} $$
-
(iii) truth-equational if there exists a set of equations
 ${\boldsymbol {\tau }}(x) \subseteq \mathrm {Eq}_{\mathcal {L}}$
such that
${\boldsymbol {\tau }}(x) \subseteq \mathrm {Eq}_{\mathcal {L}}$
such that  $$ \begin{align*} \forall \langle {\boldsymbol{A}} , F \rangle \in {\mathsf{Mod}}^*({\mathcal{S}}) \; \forall a \in A \quad a \in F \;\Leftrightarrow\; \forall \delta &\approx \epsilon \in {\boldsymbol{\tau}}(x) \; \delta^{\boldsymbol{A}}(a)\\ &= \epsilon^{\boldsymbol{A}}(a), \end{align*} $$
$$ \begin{align*} \forall \langle {\boldsymbol{A}} , F \rangle \in {\mathsf{Mod}}^*({\mathcal{S}}) \; \forall a \in A \quad a \in F \;\Leftrightarrow\; \forall \delta &\approx \epsilon \in {\boldsymbol{\tau}}(x) \; \delta^{\boldsymbol{A}}(a)\\ &= \epsilon^{\boldsymbol{A}}(a), \end{align*} $$
-
(iv) weakly algebraizable if it is protoalgebraic and truth-equational,
-
(v) algebraizable if it is equivalential and truth-equational.
In case the set of congruence formulas in item (ii) is finite, the underlying logic is called finitely equivalential, and if the logic is furthermore truth-equational, it is called finitely algebraizable.
We shall make use of an equivalent formulation of truth-equationality also established by Raftery in [Reference Raftery51, Proposition 22]. A logic
![]() ${\mathcal {S}}$
is truth-equational if and only if there exists a set of equations
${\mathcal {S}}$
is truth-equational if and only if there exists a set of equations
![]() ${\boldsymbol {\tau }}(x) \subseteq \mathrm {Eq}_{\mathcal {L}}$
such that
${\boldsymbol {\tau }}(x) \subseteq \mathrm {Eq}_{\mathcal {L}}$
such that
where
![]() ${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) = \{ \delta ^{\boldsymbol {A}}(a) \approx \epsilon ^{\boldsymbol {A}}(a) : \delta \approx \epsilon \in {\boldsymbol {\tau }}(x) \}$
. Notice that condition (iii) is the particular case of the condition above for reduced
${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) = \{ \delta ^{\boldsymbol {A}}(a) \approx \epsilon ^{\boldsymbol {A}}(a) : \delta \approx \epsilon \in {\boldsymbol {\tau }}(x) \}$
. Notice that condition (iii) is the particular case of the condition above for reduced
![]() ${\mathcal {S}}$
-models.
${\mathcal {S}}$
-models.
Parallel to the Leibniz hierarchy, the Frege hierarchy classifies sentential logics according to some replacement properties, which can also be expressed by the congruentiality of the Frege relation (either over the
![]() ${\mathcal {S}}$
-theories of the underlying logic or over the
${\mathcal {S}}$
-theories of the underlying logic or over the
![]() ${\mathcal {S}}$
-filters of arbitrary algebras). The Frege relation of
${\mathcal {S}}$
-filters of arbitrary algebras). The Frege relation of
![]() $F\subseteq A$
on
$F\subseteq A$
on
![]() ${\boldsymbol {A}}$
(relative to
${\boldsymbol {A}}$
(relative to
![]() ${\mathcal {S}}$
) is defined by
${\mathcal {S}}$
) is defined by
Notice that unlike the Leibniz congruence
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
, the equivalence relation
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
, the equivalence relation
is not necessarily a congruence on
![]() ${\boldsymbol {A}}$
. The relation
${\boldsymbol {A}}$
. The relation
is called the interderivability relation on
![]() ${\boldsymbol {A}}$
, and traditionally
${\boldsymbol {A}}$
, and traditionally
is abbreviated by
![]() $\varphi \dashv \vdash _{\mathcal {S}} \psi $
, as we have seen already on page 482.
$\varphi \dashv \vdash _{\mathcal {S}} \psi $
, as we have seen already on page 482.
The Frege hierarchy comprises four classes of logics, which we next introduce.
Definition 2.3. A logic
![]() ${\mathcal {S}}$
is:
${\mathcal {S}}$
is:
-
(i) self-extensional, if
 ,
, -
(ii) Fregean, if for every
 $T \in \mathcal {T}\!h({\mathcal {S}})$
,
$T \in \mathcal {T}\!h({\mathcal {S}})$
,
 ,
, -
(iii) fully self-extensional, if for every
 ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
 ,
, -
(iv) fully Fregean, if for every
 ${\boldsymbol {A}}$
and every
${\boldsymbol {A}}$
and every
 ,
,
 .
.
2.2 Parameterized sets of congruence formulas
The notion of (parameterized) sets of congruence formulas is a cornerstone of the theory of protoalgebraic logics and will play a prominent role in the present work. In particular, the subtle difference between having parameters or not will be crucial in our study of axiomatic extensions of
![]() ${\mathscr {C}}_1$
. We next compile some auxiliary facts concerning (parameterized) sets of congruence formulas which we will be used in the sequel.
${\mathscr {C}}_1$
. We next compile some auxiliary facts concerning (parameterized) sets of congruence formulas which we will be used in the sequel.
Throughout the rest of the section, let
![]() $x,y \in \mathrm {Var}$
be two fixed distinct variables, and
$x,y \in \mathrm {Var}$
be two fixed distinct variables, and
![]() $\overline {z}$
an arbitrary possibly infinite sequence of variables (distinct from x and y). In particular,
$\overline {z}$
an arbitrary possibly infinite sequence of variables (distinct from x and y). In particular,
![]() $\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
denotes a set of formulas in the variables
$\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
denotes a set of formulas in the variables
![]() $x,y$
and possibly variables
$x,y$
and possibly variables
![]() $\overline {z}$
. For ease of notation, we will use
$\overline {z}$
. For ease of notation, we will use
![]() $c_1,c_2,c_3,\ldots $
to denote the elements of
$c_1,c_2,c_3,\ldots $
to denote the elements of
![]() $\overline {c}$
, and simply write
$\overline {c}$
, and simply write
![]() $\overline {c} \in A$
if all the elements are in A.
$\overline {c} \in A$
if all the elements are in A.
Definition 2.4. Let
![]() ${\mathcal {S}}$
be a logic,
${\mathcal {S}}$
be a logic,
![]() ${\boldsymbol {A}}$
an algebra, and
${\boldsymbol {A}}$
an algebra, and
![]() . A set of formulas
. A set of formulas
![]() $\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
is a set of parameterized congruence formulas for
$\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
is a set of parameterized congruence formulas for
![]() ${\mathcal {S}}$
, if for every
${\mathcal {S}}$
, if for every
![]() ${\boldsymbol {A}}$
, every
${\boldsymbol {A}}$
, every
![]() , and every
, and every
![]() $a,b \in A$
,
$a,b \in A$
,
In case
![]() $\Delta (x,y) \subseteq \mathrm {Fm}_{\mathcal {L}}$
has no parameters, it is called a set of congruence formulas for
$\Delta (x,y) \subseteq \mathrm {Fm}_{\mathcal {L}}$
has no parameters, it is called a set of congruence formulas for
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
The parameters are the variables
![]() $\overline {z}$
, which by no means need be in finite number. But if we pick a formula
$\overline {z}$
, which by no means need be in finite number. But if we pick a formula
![]() $\delta \in \Delta (x,y,\overline {z})$
, then we can write
$\delta \in \Delta (x,y,\overline {z})$
, then we can write
![]() $\delta (x,y,z_1 , \ldots , z_n)$
, with
$\delta (x,y,z_1 , \ldots , z_n)$
, with
![]() $z_1 , \ldots , z_n$
occurring in
$z_1 , \ldots , z_n$
occurring in
![]() $\overline {z}$
. For the sake of notation easiness, when the context is understood we sometimes write simply
$\overline {z}$
. For the sake of notation easiness, when the context is understood we sometimes write simply
![]() $\Delta $
instead of
$\Delta $
instead of
![]() $\Delta (x,y,\overline {z})$
, or
$\Delta (x,y,\overline {z})$
, or
![]() $\Delta (x,y)$
.
$\Delta (x,y)$
.
We shall need yet another important notation. Given a set of formulas
![]() $\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
, let
$\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
, let
The main characterization of a set of parameterized congruence formulas (in fact the original definition for the case without parameters [Reference Czelakowski28, Definition I.10]; for the case with parameters, see [Reference Font32, Exercise 6.28]) is the following:
Theorem 2.5. A set of formulas
![]() $\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
is a set of parameterized congruence formulas for
$\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
is a set of parameterized congruence formulas for
![]() ${\mathcal {S}}$
if and only if the following conditions hold:
${\mathcal {S}}$
if and only if the following conditions hold:
for every n-ary function symbol
![]() $f \in {\mathcal {L}}$
.
$f \in {\mathcal {L}}$
.
Conditions (p-Sym) and (p-Trans) actually follow from the three remaining conditions (see [Reference Font32, Corollary 6.61]), but their presence helps us understand the intuition behind the terminology “congruence formulas.”
As it turns out, Definition 2.4 captures two classes of logics within the Leibniz hierarchy. Indeed, the existence of a set of parameterized congruence formulas characterizes protoalgebraic logics, while the existence of a set of congruence formulas without parameters characterizes equivalential logics (see [Reference Font32, Theorem 6.57 and Definition 6.63]).
The next technical result will be used in Section 10 to prove that the logic
![]() ${\mathcal {C}ilow}$
is not equivalential. The auxiliary lemma is taken from Jansana’s AAL lecture notes [Reference Jansana37, Exercise 4.36, p. 89].
${\mathcal {C}ilow}$
is not equivalential. The auxiliary lemma is taken from Jansana’s AAL lecture notes [Reference Jansana37, Exercise 4.36, p. 89].
Lemma 2.6. If
![]() $\Delta (x,y,\overline {z})$
and
$\Delta (x,y,\overline {z})$
and
![]() $\Delta '(x,y,\overline {z'})$
are two sets of parameterized congruence formulas for
$\Delta '(x,y,\overline {z'})$
are two sets of parameterized congruence formulas for
![]() ${\mathcal {S}}$
, then
${\mathcal {S}}$
, then
![]() $\Delta \langle x,y \rangle \dashv \vdash _{\mathcal {S}} \Delta '\langle x,y \rangle $
.
$\Delta \langle x,y \rangle \dashv \vdash _{\mathcal {S}} \Delta '\langle x,y \rangle $
.
Proposition 2.7. Let
![]() ${\mathcal {S}}$
be an equivalential logic. If
${\mathcal {S}}$
be an equivalential logic. If
![]() $\Delta \subseteq \mathrm {Fm}_{\mathcal {L}}$
is a set of parameterized congruence formulas for
$\Delta \subseteq \mathrm {Fm}_{\mathcal {L}}$
is a set of parameterized congruence formulas for
![]() ${\mathcal {S}}$
, then for every substitution
${\mathcal {S}}$
, then for every substitution
![]() $\sigma : {\boldsymbol {Fm}} \to {\boldsymbol {Fm}}(x,y)$
leaving
$\sigma : {\boldsymbol {Fm}} \to {\boldsymbol {Fm}}(x,y)$
leaving
![]() $x,y$
unchanged and replacing any other variable z with
$x,y$
unchanged and replacing any other variable z with
![]() $\sigma \,z \in \{x,y\}$
,
$\sigma \,z \in \{x,y\}$
,
![]() $\sigma \,\Delta \subseteq \mathrm {Fm}_{\mathcal {L}}(x,y)$
is a set of congruence formulas for
$\sigma \,\Delta \subseteq \mathrm {Fm}_{\mathcal {L}}(x,y)$
is a set of congruence formulas for
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
Proof Let
![]() $\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
be a set of parameterized congruence formulas for
$\Delta (x,y,\overline {z}) \subseteq \mathrm {Fm}_{\mathcal {L}}$
be a set of parameterized congruence formulas for
![]() ${\mathcal {S}}$
and
${\mathcal {S}}$
and
![]() $\Delta '(x,y)$
be a set of congruence formulas (without parameters) for
$\Delta '(x,y)$
be a set of congruence formulas (without parameters) for
![]() ${\mathcal {S}}$
. Notice that
${\mathcal {S}}$
. Notice that
![]() $\Delta '$
must exist by hypothesis. It follows by Lemma 2.6 that
$\Delta '$
must exist by hypothesis. It follows by Lemma 2.6 that
![]() $\Delta \langle x,y \rangle \dashv \vdash _{\mathcal {S}} \Delta '(x,y)$
. It follows by structurality that
$\Delta \langle x,y \rangle \dashv \vdash _{\mathcal {S}} \Delta '(x,y)$
. It follows by structurality that
![]() $\sigma \Delta \langle x,y \rangle \dashv \vdash _{\mathcal {S}} \Delta '(x,y)$
, bearing in mind that
$\sigma \Delta \langle x,y \rangle \dashv \vdash _{\mathcal {S}} \Delta '(x,y)$
, bearing in mind that
![]() $\sigma $
leaves
$\sigma $
leaves
![]() $x,y$
unchanged and replaces any other variable z with
$x,y$
unchanged and replaces any other variable z with
![]() $\sigma \,z \in \{x,y\}$
. Thus
$\sigma \,z \in \{x,y\}$
. Thus
![]() $\sigma \Delta \langle x,y \rangle \subseteq \mathrm {Fm}_{\mathcal {L}}(x,y)$
is also a set of congruence formulas (without parameters) for
$\sigma \Delta \langle x,y \rangle \subseteq \mathrm {Fm}_{\mathcal {L}}(x,y)$
is also a set of congruence formulas (without parameters) for
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
2.3 Algebraic semantics
The notion of algebraic semantics was originally introduced in [Reference Blok and Pigozzi6] (assuming
![]() ${\mathcal {S}}$
is finitary,
${\mathcal {S}}$
is finitary,
![]() ${\mathsf {K}}$
a quasivariety, and
${\mathsf {K}}$
a quasivariety, and
![]() ${\boldsymbol {\tau }}(x)$
finite), and was further investigated per se in [Reference Blok and Rebagliato8]. We choose here to make explicit its dependence on the set of equations
${\boldsymbol {\tau }}(x)$
finite), and was further investigated per se in [Reference Blok and Rebagliato8]. We choose here to make explicit its dependence on the set of equations
![]() ${\boldsymbol {\tau }}$
, following the more works [Reference Blok and Raftery7, Reference Raftery51]. More recent developments on algebraic semantics can be found in [Reference Moraschini43].
${\boldsymbol {\tau }}$
, following the more works [Reference Blok and Raftery7, Reference Raftery51]. More recent developments on algebraic semantics can be found in [Reference Moraschini43].
Definition 2.8. Let
![]() ${\mathcal {S}}$
be a logic and
${\mathcal {S}}$
be a logic and
![]() ${\boldsymbol {\tau }}(x) \subseteq \mathrm {Eq}_{\mathcal {L}}$
. A class of algebras
${\boldsymbol {\tau }}(x) \subseteq \mathrm {Eq}_{\mathcal {L}}$
. A class of algebras
![]() ${\mathsf {K}}$
is a
${\mathsf {K}}$
is a
![]() ${\boldsymbol {\tau }}$
-algebraic semantics for
${\boldsymbol {\tau }}$
-algebraic semantics for
![]() ${\mathcal {S}}$
if for every
${\mathcal {S}}$
if for every
![]() $\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
,
$\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
,
Despite the fact that no characterization of Definition 2.8 in terms of the Leibniz operator is known, there is a close relation between the notion of algebraic semantics and the Leibniz hierarchy. Indeed, algebraizable logics were originally defined (apart from finitariness issues) as those logics
![]() ${\mathcal {S}}$
for which there exist a class of algebras
${\mathcal {S}}$
for which there exist a class of algebras
![]() ${\mathsf {K}}$
, a set of equations in at most one variable
${\mathsf {K}}$
, a set of equations in at most one variable
![]() ${\boldsymbol {\tau }}(x) \subseteq \mathrm {Eq}_{\mathcal {L}}$
, and a set of formulas in at most two variables
${\boldsymbol {\tau }}(x) \subseteq \mathrm {Eq}_{\mathcal {L}}$
, and a set of formulas in at most two variables
![]() ${\boldsymbol {\rho }}(x,y) \subseteq \mathrm {Fm}_{\mathcal {L}}$
, such that
${\boldsymbol {\rho }}(x,y) \subseteq \mathrm {Fm}_{\mathcal {L}}$
, such that
for every
![]() $\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
. It is thus clear by the definitions involved that every algebraizable logic has an algebraic semantics, which in this case is called an equivalent algebraic semantics.
$\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
. It is thus clear by the definitions involved that every algebraizable logic has an algebraic semantics, which in this case is called an equivalent algebraic semantics.
The next result, whose proof can be found in [Reference Raftery51, Corollary 6], will be used for establishing that
![]() ${\mathscr {C}}_1$
admits no algebraic semantics (Theorem 5.6). We state it here for the particular case of protoalgebraic logics.
${\mathscr {C}}_1$
admits no algebraic semantics (Theorem 5.6). We state it here for the particular case of protoalgebraic logics.
Proposition 2.9. If a protoalgebraic logic
![]() ${\mathcal {S}}$
has a
${\mathcal {S}}$
has a
![]() ${\boldsymbol {\tau }}$
-algebraic semantics, then
${\boldsymbol {\tau }}$
-algebraic semantics, then
![]() ${\boldsymbol {\tau }}(T) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}(T)$
for every
${\boldsymbol {\tau }}(T) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}(T)$
for every
![]() $T \in \mathcal {T}\!h({\mathcal {S}})$
.
$T \in \mathcal {T}\!h({\mathcal {S}})$
.
Part I. Da Costa’s logic
![]() $\mathbf {\mathscr {C}}_1$
.
$\mathbf {\mathscr {C}}_1$
.
In the first part of our work we deal exclusively with the logic
![]() ${\mathscr {C}}_1$
and the related family of logics
${\mathscr {C}}_1$
and the related family of logics
![]() ${\mathscr {C}}_n$
, with
${\mathscr {C}}_n$
, with
![]() $n \geq 1$
. Our main goals are to classify
$n \geq 1$
. Our main goals are to classify
![]() ${\mathscr {C}}_1$
within the Leibniz and Frege hierarchies, collect some algebraic consequences of the fact that
${\mathscr {C}}_1$
within the Leibniz and Frege hierarchies, collect some algebraic consequences of the fact that
![]() ${\mathscr {C}}_1$
admits a Deduction-Detachment Theorem (Theorem 3.10), present a set of parameterized congruence formulas for
${\mathscr {C}}_1$
admits a Deduction-Detachment Theorem (Theorem 3.10), present a set of parameterized congruence formulas for
![]() ${\mathscr {C}}_1$
(Theorem 4.3), and prove that
${\mathscr {C}}_1$
(Theorem 4.3), and prove that
![]() ${\mathscr {C}}_1$
does not admit any algebraic semantics whatsoever in the sense of Blok and Pigozzi (Theorem 5.6).
${\mathscr {C}}_1$
does not admit any algebraic semantics whatsoever in the sense of Blok and Pigozzi (Theorem 5.6).
3 The logic
 ${\mathscr {C}}_1$
${\mathscr {C}}_1$
In this section we introduce the logic
![]() ${\mathscr {C}}_1$
alongside with the family of logics
${\mathscr {C}}_1$
alongside with the family of logics
![]() ${\mathscr {C}}_n$
, with
${\mathscr {C}}_n$
, with
![]() $n \geq 1$
. We then proceed to classify
$n \geq 1$
. We then proceed to classify
![]() ${\mathscr {C}}_1$
within the Leibniz and Frege hierarchies and state some algebraic consequences of the Deduction-Detachment Theorem for
${\mathscr {C}}_1$
within the Leibniz and Frege hierarchies and state some algebraic consequences of the Deduction-Detachment Theorem for
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
Throughout the present work we assume fixed the language
where
![]() $\wedge ,\vee ,\to $
are binary operation symbols and
$\wedge ,\vee ,\to $
are binary operation symbols and
![]() $\neg $
is a unary operation symbol. We shall also consider two unary non-primitive connectives
$\neg $
is a unary operation symbol. We shall also consider two unary non-primitive connectives
![]() and
and
![]() , and one binary non-primitive connective
, and one binary non-primitive connective
![]() , with
, with
![]() $\varphi ,\psi \in \mathrm {Fm}_{\mathcal {L}}$
. The traditional Hilbert-style axiomatics for
$\varphi ,\psi \in \mathrm {Fm}_{\mathcal {L}}$
. The traditional Hilbert-style axiomatics for
![]() ${\mathscr {C}}_1$
is presented in the next definition, as given in [Reference da Costa21, pp. 498–499].
${\mathscr {C}}_1$
is presented in the next definition, as given in [Reference da Costa21, pp. 498–499].
Definition 3.1. The logic
![]() ${\mathscr {C}}_1$
is induced by the following Hilbert-style axioms and inference rule:
${\mathscr {C}}_1$
is induced by the following Hilbert-style axioms and inference rule:
By definition,
![]() ${\mathscr {C}}_1$
is obviously a finitary logic, also called a deductive system in the literature. The schemata (Ax1)–(Ax8) axiomatize positive intuitionistic propositional logic (
${\mathscr {C}}_1$
is obviously a finitary logic, also called a deductive system in the literature. The schemata (Ax1)–(Ax8) axiomatize positive intuitionistic propositional logic (
![]() $\mathcal {IL}^+$
), and hence
$\mathcal {IL}^+$
), and hence
![]() ${\mathscr {C}}_1$
is an (axiomatic) extension of
${\mathscr {C}}_1$
is an (axiomatic) extension of
![]() $\mathcal {IL}^+$
. Also, classical propositional logic (
$\mathcal {IL}^+$
. Also, classical propositional logic (
![]() $\mathcal {CL}$
) is an extension of
$\mathcal {CL}$
) is an extension of
![]() ${\mathscr {C}}_1$
, axiomatized relatively to it by the principle of contradiction
${\mathscr {C}}_1$
, axiomatized relatively to it by the principle of contradiction
![]() $\neg (\varphi \wedge \neg \varphi )$
.
$\neg (\varphi \wedge \neg \varphi )$
.
The logic
![]() ${\mathscr {C}}_{\omega }$
is axiomatized by the schemata (Ax1)–(Ax10) and inference rule (MP). It is the weakest among all of da Costa’s
${\mathscr {C}}_{\omega }$
is axiomatized by the schemata (Ax1)–(Ax10) and inference rule (MP). It is the weakest among all of da Costa’s
![]() ${\mathscr {C}}$
-systems. LetFootnote
5
${\mathscr {C}}$
-systems. LetFootnote
5
The logic
![]() ${\mathscr {C}}_n$
, with
${\mathscr {C}}_n$
, with
![]() $n \geq 1$
, is the least extension of
$n \geq 1$
, is the least extension of
![]() ${\mathscr {C}}_{\omega }$
closed under the following additional axiom schemata:
${\mathscr {C}}_{\omega }$
closed under the following additional axiom schemata:
For
![]() $n = 1$
, the logic just defined coincides with the logic
$n = 1$
, the logic just defined coincides with the logic
![]() ${\mathscr {C}}_1$
in Definition 3.1. Da Costa proved in [Reference da Costa18, Théorème 7] (the proof is credited to A. I. Arruda) that his
${\mathscr {C}}_1$
in Definition 3.1. Da Costa proved in [Reference da Costa18, Théorème 7] (the proof is credited to A. I. Arruda) that his
![]() ${\mathscr {C}}$
-systems form a hierarchy of proper extensions, i.e.,
${\mathscr {C}}$
-systems form a hierarchy of proper extensions, i.e.,
The logic
![]() ${\mathscr {C}}_{\omega }$
is not the infimum of the family of logics
${\mathscr {C}}_{\omega }$
is not the infimum of the family of logics
![]() $\{ {\mathscr {C}}_n : n \geq 1 \}$
, although the notation may suggest it. For more details on this issue, see [Reference Carnielli and Marcos15].
$\{ {\mathscr {C}}_n : n \geq 1 \}$
, although the notation may suggest it. For more details on this issue, see [Reference Carnielli and Marcos15].
The following auxiliary facts about
![]() ${\mathscr {C}}_1$
will be used exhaustively in the sequel. See [Reference da Costa, Krause and Bueno26, Theorems 2.1.6, 2.1.8, 2.1.13, and 2.1.14].
${\mathscr {C}}_1$
will be used exhaustively in the sequel. See [Reference da Costa, Krause and Bueno26, Theorems 2.1.6, 2.1.8, 2.1.13, and 2.1.14].
Lemma 3.2.
-
1.
 $\vdash _{{\mathscr {C}}_1} \varphi \leftrightarrow \varphi $
.
$\vdash _{{\mathscr {C}}_1} \varphi \leftrightarrow \varphi $
. -
2.
 $\varphi \leftrightarrow \psi \vdash _{{\mathscr {C}}_1} \psi \leftrightarrow \varphi $
.
$\varphi \leftrightarrow \psi \vdash _{{\mathscr {C}}_1} \psi \leftrightarrow \varphi $
. -
3.
 $\varphi \leftrightarrow \psi , \psi \leftrightarrow \xi \vdash _{{\mathscr {C}}_1} \varphi \leftrightarrow \xi $
.
$\varphi \leftrightarrow \psi , \psi \leftrightarrow \xi \vdash _{{\mathscr {C}}_1} \varphi \leftrightarrow \xi $
. -
4.
 $\varphi \leftrightarrow \psi , \xi \leftrightarrow \zeta \vdash _{{\mathscr {C}}_1} (\varphi \wedge \xi ) \leftrightarrow (\psi \wedge \zeta )$
.
$\varphi \leftrightarrow \psi , \xi \leftrightarrow \zeta \vdash _{{\mathscr {C}}_1} (\varphi \wedge \xi ) \leftrightarrow (\psi \wedge \zeta )$
. -
5.
 $\varphi \leftrightarrow \psi , \xi \leftrightarrow \zeta \vdash _{{\mathscr {C}}_1} (\varphi \vee \xi ) \leftrightarrow (\psi \vee \zeta )$
.
$\varphi \leftrightarrow \psi , \xi \leftrightarrow \zeta \vdash _{{\mathscr {C}}_1} (\varphi \vee \xi ) \leftrightarrow (\psi \vee \zeta )$
. -
6.
 $\varphi \leftrightarrow \psi , \xi \leftrightarrow \zeta \vdash _{{\mathscr {C}}_1} (\varphi \to \xi ) \leftrightarrow (\psi \to \zeta )$
.
$\varphi \leftrightarrow \psi , \xi \leftrightarrow \zeta \vdash _{{\mathscr {C}}_1} (\varphi \to \xi ) \leftrightarrow (\psi \to \zeta )$
. -
7.
 $\psi ^{\circ } , \varphi \to \psi \vdash _{{\mathscr {C}}_1} \neg \psi \to \neg \varphi $
.
$\psi ^{\circ } , \varphi \to \psi \vdash _{{\mathscr {C}}_1} \neg \psi \to \neg \varphi $
. -
8.
 $\varphi ^{\circ } , \psi ^{\circ },\varphi \leftrightarrow \psi \vdash _{{\mathscr {C}}_1} \neg \varphi \leftrightarrow \neg \psi $
.
$\varphi ^{\circ } , \psi ^{\circ },\varphi \leftrightarrow \psi \vdash _{{\mathscr {C}}_1} \neg \varphi \leftrightarrow \neg \psi $
. -
9.
 $\vdash _{{\mathscr {C}}_1} \varphi \to \varphi $
.
$\vdash _{{\mathscr {C}}_1} \varphi \to \varphi $
. -
10.
 $\varphi \to \psi , \psi \to \xi \vdash _{{\mathscr {C}}_1} \varphi \to \xi $
.
$\varphi \to \psi , \psi \to \xi \vdash _{{\mathscr {C}}_1} \varphi \to \xi $
. -
11.
 $\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\varphi \wedge \xi ) \to (\psi \wedge \xi )$
.
$\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\varphi \wedge \xi ) \to (\psi \wedge \xi )$
. -
12.
 $\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\varphi \vee \xi ) \to (\psi \vee \xi )$
.
$\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\varphi \vee \xi ) \to (\psi \vee \xi )$
. -
13.
 $\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\varphi \to \xi ) \to (\psi \to \xi )$
.
$\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\varphi \to \xi ) \to (\psi \to \xi )$
. -
14.
 $\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\xi \wedge \varphi ) \to (\xi \wedge \psi )$
.
$\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\xi \wedge \varphi ) \to (\xi \wedge \psi )$
. -
15.
 $\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\xi \vee \varphi ) \to (\xi \vee \psi )$
.
$\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\xi \vee \varphi ) \to (\xi \vee \psi )$
. -
16.
 $\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\xi \to \varphi ) \to (\xi \to \psi )$
.
$\varphi \to \psi \vdash _{{\mathscr {C}}_1} (\xi \to \varphi ) \to (\xi \to \psi )$
. -
17.
 $\varphi ^{\circ } \vdash _{{\mathscr {C}}_1} (\neg \varphi )^{\circ }$
.
$\varphi ^{\circ } \vdash _{{\mathscr {C}}_1} (\neg \varphi )^{\circ }$
. -
18.
 $ \hphantom{\varphi ^{\circ } }\vdash _{{\mathscr {C}}_1} (\varphi ^{\circ })^{\circ }$
.
$ \hphantom{\varphi ^{\circ } }\vdash _{{\mathscr {C}}_1} (\varphi ^{\circ })^{\circ }$
.
Several semantics have been put forward in the literature for the logic
![]() ${\mathscr {C}}_1$
, namely, behavioral semantics [Reference Caleiro and Gonçalves12, Reference Caleiro, Gonçalves and Martins13], possible-translations semantics [Reference Bueno-Soler and Carnielli9], and the so-called da Costa algebras investigated in [Reference Carnielli and de Alcantara14, Reference Seoane and de Alcantara52] and generalizing the
${\mathscr {C}}_1$
, namely, behavioral semantics [Reference Caleiro and Gonçalves12, Reference Caleiro, Gonçalves and Martins13], possible-translations semantics [Reference Bueno-Soler and Carnielli9], and the so-called da Costa algebras investigated in [Reference Carnielli and de Alcantara14, Reference Seoane and de Alcantara52] and generalizing the
![]() ${\mathscr {C}}_1$
-algebras introduced by da Costa himself in [Reference da Costa19]. Da Costa’s proposal has the drawback (from an AAL point of view) of changing the underlying language of the class of algebras associated with
${\mathscr {C}}_1$
-algebras introduced by da Costa himself in [Reference da Costa19]. Da Costa’s proposal has the drawback (from an AAL point of view) of changing the underlying language of the class of algebras associated with
![]() ${\mathscr {C}}_1$
. One further semantics for
${\mathscr {C}}_1$
. One further semantics for
![]() ${\mathscr {C}}_1$
can be found in the literature, developed by da Costa and Alves in [Reference da Costa and Alves23], and which will be very useful in the sequel. We next introduce da Costa and Alves’s two-valued semantics for the logic
${\mathscr {C}}_1$
can be found in the literature, developed by da Costa and Alves in [Reference da Costa and Alves23], and which will be very useful in the sequel. We next introduce da Costa and Alves’s two-valued semantics for the logic
![]() ${\mathscr {C}}_1$
and state the completeness result w.r.t. this non-truth-functional semantics.
${\mathscr {C}}_1$
and state the completeness result w.r.t. this non-truth-functional semantics.
Definition 3.3. A bivaluation of
![]() ${\mathscr {C}}_1$
is a map
${\mathscr {C}}_1$
is a map
![]() $v : {\boldsymbol {Fm}} \to \{0,1\}$
such that:
$v : {\boldsymbol {Fm}} \to \{0,1\}$
such that:
-
•
 $v(\varphi ) = 0 \;\Rightarrow \; v(\neg \varphi ) = 1$
,
$v(\varphi ) = 0 \;\Rightarrow \; v(\neg \varphi ) = 1$
, -
•
 $v(\neg \neg \varphi ) = 1 \;\Rightarrow \; v(\varphi ) = 1$
,
$v(\neg \neg \varphi ) = 1 \;\Rightarrow \; v(\varphi ) = 1$
, -
•
 $v(\psi ^{\circ }) = v(\varphi \to \psi ) = v(\varphi \to \neg \psi ) = 1 \;\Rightarrow \; v(\varphi ) = 0$
,
$v(\psi ^{\circ }) = v(\varphi \to \psi ) = v(\varphi \to \neg \psi ) = 1 \;\Rightarrow \; v(\varphi ) = 0$
, -
•
 $v(\varphi \to \psi ) = 1 \;\Leftrightarrow \; v(\varphi ) = 0 \text { or } v(\psi ) = 1$
,
$v(\varphi \to \psi ) = 1 \;\Leftrightarrow \; v(\varphi ) = 0 \text { or } v(\psi ) = 1$
, -
•
 $v(\varphi \wedge \psi ) = 1 \;\Leftrightarrow \; v(\varphi ) = 1 \text { and } v(\psi ) = 1$
,
$v(\varphi \wedge \psi ) = 1 \;\Leftrightarrow \; v(\varphi ) = 1 \text { and } v(\psi ) = 1$
, -
•
 $v(\varphi \vee \psi ) = 1 \;\Leftrightarrow \; v(\varphi ) = 1 \text { or } v(\psi ) = 1$
,
$v(\varphi \vee \psi ) = 1 \;\Leftrightarrow \; v(\varphi ) = 1 \text { or } v(\psi ) = 1$
, -
•
 $v(\varphi ^{\circ }) = v(\psi ^{\circ }) = 1 \;\Rightarrow \; v\big ((\varphi \wedge \psi )^{\circ }\big ) = v\big ((\varphi \vee \psi )^{\circ }\big ) = v\big ((\varphi \to \psi )^{\circ }\big ) = 1$
.
$v(\varphi ^{\circ }) = v(\psi ^{\circ }) = 1 \;\Rightarrow \; v\big ((\varphi \wedge \psi )^{\circ }\big ) = v\big ((\varphi \vee \psi )^{\circ }\big ) = v\big ((\varphi \to \psi )^{\circ }\big ) = 1$
.
A bivaluation of
![]() ${\mathscr {C}}_1$
is a model of a formula
${\mathscr {C}}_1$
is a model of a formula
![]() $\varphi \in \mathrm {Fm}_{\mathcal {L}}$
if
$\varphi \in \mathrm {Fm}_{\mathcal {L}}$
if
![]() $v(\varphi ) = 1$
, and it is a model of a set of formulas
$v(\varphi ) = 1$
, and it is a model of a set of formulas
![]() $\Gamma \subseteq \mathrm {Fm}_{\mathcal {L}}$
if
$\Gamma \subseteq \mathrm {Fm}_{\mathcal {L}}$
if
![]() $v(\gamma ) = 1$
, for every
$v(\gamma ) = 1$
, for every
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
Theorem 3.4 da Costa
For every
![]() $\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
,
$\Gamma \cup \{\varphi \} \subseteq \mathrm {Fm}_{\mathcal {L}}$
,
![]() $\Gamma \vdash _{{\mathscr {C}}_1} \varphi $
if and only if every bivaluation v of
$\Gamma \vdash _{{\mathscr {C}}_1} \varphi $
if and only if every bivaluation v of
![]() ${\mathscr {C}}_1$
which is a model of
${\mathscr {C}}_1$
which is a model of
![]() $\Gamma $
is also a model of
$\Gamma $
is also a model of
![]() $\varphi $
.
$\varphi $
.
Given a bivaluation v of
![]() ${\mathscr {C}}_1$
, we have [Reference da Costa and Alves23, Theorem 2]:
${\mathscr {C}}_1$
, we have [Reference da Costa and Alves23, Theorem 2]:
In fact, the connective
![]() $\sim \!$
behaves like classical negation.
$\sim \!$
behaves like classical negation.
3.1 Classification of
 ${\mathscr {C}}_1$
within the Leibniz and Frege hierarchies
${\mathscr {C}}_1$
within the Leibniz and Frege hierarchies
The classification of
![]() ${\mathscr {C}}_1$
(or more generally, of da Costa’s
${\mathscr {C}}_1$
(or more generally, of da Costa’s
![]() ${\mathscr {C}}$
-systems
${\mathscr {C}}$
-systems
![]() ${\mathscr {C}}_n$
) within the Leibniz and Frege hierarchies is scattered along the literature, sometimes appearing as mere observations, and most often without explicit proofs. The notorious exception is the non-algebraizability of
${\mathscr {C}}_n$
) within the Leibniz and Frege hierarchies is scattered along the literature, sometimes appearing as mere observations, and most often without explicit proofs. The notorious exception is the non-algebraizability of
![]() ${\mathscr {C}}_1$
established in [Reference Lewin, Mikenberg and Schwarze39]. We next compile these scattered results and fully classify the logic
${\mathscr {C}}_1$
established in [Reference Lewin, Mikenberg and Schwarze39]. We next compile these scattered results and fully classify the logic
![]() ${\mathscr {C}}_1$
within the Leibniz hierarchy, which since the non-algebraizability result of Lewin, Mikenberg, and Schwarze in 1991, has been enlarged with two further classes of logics (namely, the classes of weakly algebraizable [Reference Czelakowski and Jansana29] and truth-equational logics [Reference Raftery51]).
${\mathscr {C}}_1$
within the Leibniz hierarchy, which since the non-algebraizability result of Lewin, Mikenberg, and Schwarze in 1991, has been enlarged with two further classes of logics (namely, the classes of weakly algebraizable [Reference Czelakowski and Jansana29] and truth-equational logics [Reference Raftery51]).
The protoalgebraicity of
![]() ${\mathscr {C}}_1$
was left as an open question in [Reference Carnielli and Marcos16, p. 81] (perhaps because the condition said to characterize protoalgebraicity in [Reference Carnielli and Marcos16, p. 81] is in fact equivalent to weak algebraizability), but was later observed to hold in [Reference Bueno-Soler and Carnielli9, p. 2]. Indeed, it follows by manipulation of axioms (Ax1), (Ax2), and rule (MP) in Definition 3.1, or at once by Lemma 3.2.11, that
${\mathscr {C}}_1$
was left as an open question in [Reference Carnielli and Marcos16, p. 81] (perhaps because the condition said to characterize protoalgebraicity in [Reference Carnielli and Marcos16, p. 81] is in fact equivalent to weak algebraizability), but was later observed to hold in [Reference Bueno-Soler and Carnielli9, p. 2]. Indeed, it follows by manipulation of axioms (Ax1), (Ax2), and rule (MP) in Definition 3.1, or at once by Lemma 3.2.11, that
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \to y \}$
complies with Definition 2.2 (i).
${\boldsymbol {\rho }}(x,y) = \{ x \to y \}$
complies with Definition 2.2 (i).
Proposition 3.5.
![]() ${\mathscr {C}}_1$
is protoalgebraic.
${\mathscr {C}}_1$
is protoalgebraic.
Proposition 3.5 immediately prompts the question of whether
![]() ${\mathscr {C}}_1$
is furthermore equivalential. The answer this time is negative, as first observed in [Reference Herrmann36, pp. 425–426], and also mentioned in [Reference Font32, Example 6.77]. The proof uses as a counterexample the five-element algebra of [Reference Lewin, Mikenberg and Schwarze39] depicted in Figure 2 (Table 1).
${\mathscr {C}}_1$
is furthermore equivalential. The answer this time is negative, as first observed in [Reference Herrmann36, pp. 425–426], and also mentioned in [Reference Font32, Example 6.77]. The proof uses as a counterexample the five-element algebra of [Reference Lewin, Mikenberg and Schwarze39] depicted in Figure 2 (Table 1).
Proposition 3.6.
![]() ${\mathscr {C}}_1$
is not equivalential.
${\mathscr {C}}_1$
is not equivalential.
Proof Consider the algebra
![]() ${\boldsymbol {A}} = \langle A , \wedge ^{\boldsymbol {A}} , \vee ^{\boldsymbol {A}} , \to ^{\boldsymbol {A}} , \neg ^{\boldsymbol {A}} , 0^{\boldsymbol {A}} ,1^{\boldsymbol {A}} \rangle $
with universe
${\boldsymbol {A}} = \langle A , \wedge ^{\boldsymbol {A}} , \vee ^{\boldsymbol {A}} , \to ^{\boldsymbol {A}} , \neg ^{\boldsymbol {A}} , 0^{\boldsymbol {A}} ,1^{\boldsymbol {A}} \rangle $
with universe
![]() $A = \{ 0,a,b,1,u\}$
, whose lattice operations are given by Figure 2 and with the truth-tables of
$A = \{ 0,a,b,1,u\}$
, whose lattice operations are given by Figure 2 and with the truth-tables of
![]() $\neg ^{\boldsymbol {A}}$
and
$\neg ^{\boldsymbol {A}}$
and
![]() $\to ^{\boldsymbol {A}}$
given by Table 2, respectively. Consider moreover the subalgebra
$\to ^{\boldsymbol {A}}$
given by Table 2, respectively. Consider moreover the subalgebra
![]() ${\boldsymbol {B}}$
with universe
${\boldsymbol {B}}$
with universe
![]() $B = \{ 0,a,b,1\}$
. It is clear that
$B = \{ 0,a,b,1\}$
. It is clear that
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathscr {C}}_1)$
, since for instance
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathscr {C}}_1)$
, since for instance
![]() witnesses
witnesses
![]() $\langle {\boldsymbol {A}} , F \rangle \in {\mathsf {Mod}}^*({\mathscr {C}}_1)$
. Now, fix
$\langle {\boldsymbol {A}} , F \rangle \in {\mathsf {Mod}}^*({\mathscr {C}}_1)$
. Now, fix
![]() . It is not difficult to check that
. It is not difficult to check that
![]() $\langle a,1 \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {B}}(G)$
. Then
$\langle a,1 \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {B}}(G)$
. Then
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {B}}(G) \neq id_{\boldsymbol {B}}$
, and therefore
${\boldsymbol {\varOmega }}^{\boldsymbol {B}}(G) \neq id_{\boldsymbol {B}}$
, and therefore
![]() $\langle {\boldsymbol {B}} , G \rangle \notin {\mathsf {Mod}}^*({\mathscr {C}}_1)$
. We conclude that the class
$\langle {\boldsymbol {B}} , G \rangle \notin {\mathsf {Mod}}^*({\mathscr {C}}_1)$
. We conclude that the class
![]() ${\mathsf {Mod}}^*({\mathscr {C}}_1)$
is not closed under submatrices, and hence
${\mathsf {Mod}}^*({\mathscr {C}}_1)$
is not closed under submatrices, and hence
![]() ${\mathscr {C}}_1$
cannot be equivalential (see for instance [Reference Font32, Theorem 6.73]).
${\mathscr {C}}_1$
cannot be equivalential (see for instance [Reference Font32, Theorem 6.73]).

Figure 2 The algebra
![]() ${\boldsymbol {A}}$
of [Reference Lewin, Mikenberg and Schwarze39] and its
${\boldsymbol {A}}$
of [Reference Lewin, Mikenberg and Schwarze39] and its
![]() ${\mathscr {C}}_1$
-filters.
${\mathscr {C}}_1$
-filters.
Table 1 The algebra
![]() ${\boldsymbol {A}}$
of [Reference Lewin, Mikenberg and Schwarze39] and the Leibniz congruences of its
${\boldsymbol {A}}$
of [Reference Lewin, Mikenberg and Schwarze39] and the Leibniz congruences of its
![]() ${\mathscr {C}}_1$
-filters.
${\mathscr {C}}_1$
-filters.

Table 2 Truth-tables of the connectives
![]() $\neg ^{\boldsymbol {A}}$
and
$\neg ^{\boldsymbol {A}}$
and
![]() $\to ^{\boldsymbol {A}}$
.
$\to ^{\boldsymbol {A}}$
.

We are left to see whether
![]() ${\mathscr {C}}_1$
is truth-equational. But, in fact, this was implicitly established in [Reference Lewin, Mikenberg and Schwarze39]—implicitly, simply because truth-equational logics had not yet been defined in 1991. Indeed, the five-element algebra
${\mathscr {C}}_1$
is truth-equational. But, in fact, this was implicitly established in [Reference Lewin, Mikenberg and Schwarze39]—implicitly, simply because truth-equational logics had not yet been defined in 1991. Indeed, the five-element algebra
![]() ${\boldsymbol {A}}$
exhibited in [Reference Lewin, Mikenberg and Schwarze39] (and reproduced in Figure 2) is such that the Leibniz operator on
${\boldsymbol {A}}$
exhibited in [Reference Lewin, Mikenberg and Schwarze39] (and reproduced in Figure 2) is such that the Leibniz operator on
![]() ${\boldsymbol {A}}$
over the
${\boldsymbol {A}}$
over the
![]() ${\mathscr {C}}_1$
-filters is not injective. Recall that Raftery proved that the Leibniz operator is completely order-reflecting (and hence, injective) on arbitrary algebras for truth-equational logics [Reference Raftery51]. It follows at once that:
${\mathscr {C}}_1$
-filters is not injective. Recall that Raftery proved that the Leibniz operator is completely order-reflecting (and hence, injective) on arbitrary algebras for truth-equational logics [Reference Raftery51]. It follows at once that:
Proposition 3.7.
![]() ${\mathscr {C}}_1$
is not truth-equational.
${\mathscr {C}}_1$
is not truth-equational.
Having in mind Definition 2.2(iv), it follows at once that
![]() ${\mathscr {C}}_1$
is not weakly algebraic. Indeed, Font’s [Reference Font32, Example 6.122.9] generalizes that “neither of the logic
${\mathscr {C}}_1$
is not weakly algebraic. Indeed, Font’s [Reference Font32, Example 6.122.9] generalizes that “neither of the logic
![]() ${\mathscr {C}}_n$
is weakly algebraizable.”
${\mathscr {C}}_n$
is weakly algebraizable.”
As a matter of fact, by direct inspection of Table 2, one sees that truth is not even implicitly definable
Footnote
6
in the class
![]() ${\mathsf {Mod}}^*({\mathscr {C}}_1)$
, which is a weaker condition than equational definability of truth in the class
${\mathsf {Mod}}^*({\mathscr {C}}_1)$
, which is a weaker condition than equational definability of truth in the class
![]() ${\mathsf {Mod}}^*({\mathscr {C}}_1)$
.
${\mathsf {Mod}}^*({\mathscr {C}}_1)$
.
Propositions 3.5–3.7 settle the classification of the logic
![]() ${\mathscr {C}}_1$
within the Leibniz hierarchy. As to the Frege hierarchy, the logic
${\mathscr {C}}_1$
within the Leibniz hierarchy. As to the Frege hierarchy, the logic
![]() ${\mathscr {C}}_1$
falls outside its scope, as first shown by da Costa and Guillaume as early as in [Reference da Costa and Guillaume25].
${\mathscr {C}}_1$
falls outside its scope, as first shown by da Costa and Guillaume as early as in [Reference da Costa and Guillaume25].
Proposition 3.8.
![]() ${\mathscr {C}}_1$
is not self-extensional.
${\mathscr {C}}_1$
is not self-extensional.
Proof For instance,
![]() $\varphi \to \varphi \dashv \vdash _{{\mathscr {C}}_1} \psi \to \psi $
, but the matrix model
$\varphi \to \varphi \dashv \vdash _{{\mathscr {C}}_1} \psi \to \psi $
, but the matrix model
![]() $\langle {\boldsymbol {A}} , \{1,u\} \rangle \in {\mathsf {Mod}}({\mathscr {C}}_1)$
, with
$\langle {\boldsymbol {A}} , \{1,u\} \rangle \in {\mathsf {Mod}}({\mathscr {C}}_1)$
, with
![]() ${\boldsymbol {A}}$
given as in Figure 2, and any homomorphism
${\boldsymbol {A}}$
given as in Figure 2, and any homomorphism
![]() $h : {\boldsymbol {Fm}} \to {\boldsymbol {A}}$
such that
$h : {\boldsymbol {Fm}} \to {\boldsymbol {A}}$
such that
![]() $h(\varphi ) = u$
and
$h(\varphi ) = u$
and
![]() $h(\psi ) = 1$
witness
$h(\psi ) = 1$
witness
![]() $\neg (\varphi \to \varphi ) \not \vdash _{{\mathscr {C}}_1} \neg (\psi \to \psi )$
.
$\neg (\varphi \to \varphi ) \not \vdash _{{\mathscr {C}}_1} \neg (\psi \to \psi )$
.
It is worth mentioning that it was precisely the non-self-extensionality of
![]() ${\mathscr {C}}_1$
that motivated the first algebraic studies about this paraconsistent logic.
${\mathscr {C}}_1$
that motivated the first algebraic studies about this paraconsistent logic.
So far we have only seen one positive result about
![]() ${\mathscr {C}}_1$
, namely that it is protoalgebraic. This fact will be the ground upon which Sections 3.2 and 4 will be built on.
${\mathscr {C}}_1$
, namely that it is protoalgebraic. This fact will be the ground upon which Sections 3.2 and 4 will be built on.
3.2 The Deduction-Detachment Theorem for
 ${\mathscr {C}}_1$
${\mathscr {C}}_1$
Protoalgebraic logics are characterized by possessing a weak form of the Deduction-Detachment Theorem (DDT), the so-called Parameterized Local Deduction-Detachment Theorem (PLDDT). Some famous bridge theorems in AAL establish correspondences between stronger versions of the PLDDT and purely algebraic properties. For instance, for finitary logics, the LDDT (a non-parameterized version of the PLDDT) corresponds to the Filter Extension Property (FEP) of the class of matrix models of the underlying logic, while, again for finitary logics, the DDT (a non-local and non-parameterized version of the PLDDT) corresponds to the property of the lattice of finitely generated filters being dually Brouwerian.
It is easy to check that logic
![]() ${\mathscr {C}}_1$
admits a “classical” DDT witnessed by one single formula with no parameters. In fact, any finitary logic in the language
${\mathscr {C}}_1$
admits a “classical” DDT witnessed by one single formula with no parameters. In fact, any finitary logic in the language
![]() ${\mathcal {L}}$
having (Ax1) and (Ax2) among its axioms and (MP) as its only inference rules satisfies the classical DDT (see [Reference Font32, Theorem 3.72]).
${\mathcal {L}}$
having (Ax1) and (Ax2) among its axioms and (MP) as its only inference rules satisfies the classical DDT (see [Reference Font32, Theorem 3.72]).
Proposition 3.9. For every
![]() $\Gamma \cup \{\varphi ,\psi \} \in \mathrm {Fm}_{\mathcal {L}}$
,
$\Gamma \cup \{\varphi ,\psi \} \in \mathrm {Fm}_{\mathcal {L}}$
,
That is,
![]() $\{ p \to q\}$
is a DD set for the logic
$\{ p \to q\}$
is a DD set for the logic
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
As a consequence of Proposition 3.9, the class
![]() ${\mathsf {Mod}}({\mathscr {C}}_1)$
has the FEP.Footnote
7
We compile this and other algebraic properties of the logic
${\mathsf {Mod}}({\mathscr {C}}_1)$
has the FEP.Footnote
7
We compile this and other algebraic properties of the logic
![]() ${\mathscr {C}}_1$
in the next result, all of which are consequences of more general AAL results for finitary protoalgebraic logics having a DD set—see [Reference Font32, Theorems 6.24 and 6.28 and Corollary 6.30].
${\mathscr {C}}_1$
in the next result, all of which are consequences of more general AAL results for finitary protoalgebraic logics having a DD set—see [Reference Font32, Theorems 6.24 and 6.28 and Corollary 6.30].
Theorem 3.10.
-
1. For every
 ${\boldsymbol {A}}$
, the join-semilattice of the finitely generated
${\boldsymbol {A}}$
, the join-semilattice of the finitely generated
 ${\mathscr {C}}_1$
-filters of
${\mathscr {C}}_1$
-filters of
 ${\boldsymbol {A}}$
is dually Brouwerian.
${\boldsymbol {A}}$
is dually Brouwerian. -
2. The logic
 ${\mathscr {C}}_1$
is filter-distributive.
${\mathscr {C}}_1$
is filter-distributive. -
3. The class
 ${\mathsf {Mod}}({\mathscr {C}}_1)$
has the FEP.
${\mathsf {Mod}}({\mathscr {C}}_1)$
has the FEP.
An observation which will be used in the sequel is that every axiomatic extension of
![]() ${\mathscr {C}}_1$
enjoys the FEP.
${\mathscr {C}}_1$
enjoys the FEP.
The DDT lifts to arbitrary algebras given an underlying protoalgebraic logic—see [Reference Font32, Theorem 3.81]. Once applied to the logic
![]() ${\mathscr {C}}_1$
, we obtain that for every
${\mathscr {C}}_1$
, we obtain that for every
![]() ${\boldsymbol {A}}$
and every
${\boldsymbol {A}}$
and every
![]() $X \cup \{a,b\} \subseteq A$
,
$X \cup \{a,b\} \subseteq A$
,
A consequence of this fact is a characterization of the Frege relation for the logic
![]() ${\mathscr {C}}_1$
. We omit the easy proof.
${\mathscr {C}}_1$
. We omit the easy proof.
Proposition 3.11. For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
, and
![]() $a,b \in A$
,
$a,b \in A$
,
Proposition 3.11 shows us that the classical characterization of the Leibniz congruence of a
![]() $\mathcal {CL}$
-filter defines the Frege relation of a
$\mathcal {CL}$
-filter defines the Frege relation of a
![]() ${\mathscr {C}}_1$
-filter. This relation is not necessarily a congruence, for
${\mathscr {C}}_1$
-filter. This relation is not necessarily a congruence, for
![]() ${\mathscr {C}}_1$
is not (fully) self-extensional.
${\mathscr {C}}_1$
is not (fully) self-extensional.
4 Parameterized congruence formulas for
 ${\mathscr {C}}_1$
${\mathscr {C}}_1$
Our goal in this section is to provide a set of parameterized congruence formulas for the logic
![]() ${\mathscr {C}}_1$
. In fact, we shall provide two such sets, namely in Proposition 4.1 and Theorem 4.3. While the former is a rather trivial one, the latter is fairly complex and will be needed in the sequel.
${\mathscr {C}}_1$
. In fact, we shall provide two such sets, namely in Proposition 4.1 and Theorem 4.3. While the former is a rather trivial one, the latter is fairly complex and will be needed in the sequel.
Since
![]() ${\mathscr {C}}_1$
is protoalgebraic, but not equivalential (recall Propositions 3.5 and 3.6), we know a priori that
${\mathscr {C}}_1$
is protoalgebraic, but not equivalential (recall Propositions 3.5 and 3.6), we know a priori that
![]() ${\mathscr {C}}_1$
admits a set of parameterized congruence formulas, but no set of congruence formulas without parameters. The first set of parameterized congruence formulas we provide for
${\mathscr {C}}_1$
admits a set of parameterized congruence formulas, but no set of congruence formulas without parameters. The first set of parameterized congruence formulas we provide for
![]() ${\mathscr {C}}_1$
is rather trivial, but will be useful in our analysis.
${\mathscr {C}}_1$
is rather trivial, but will be useful in our analysis.
Proposition 4.1. The set
is a set of parameterized congruence formulas for the logic
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
Proof Conditions (p-R), (p-Sym), and (p-Trans) follow by Lemma 3.2.1–3, respectively. Taking
![]() $\xi (w,\overline {z}) = w$
, we have
$\xi (w,\overline {z}) = w$
, we have
![]() $x \leftrightarrow y = \xi (x,\overline {z}) \leftrightarrow \xi (y,\overline {z}) \in \Delta (x,y,\overline {z}) \subseteq \Delta \langle x,y \rangle $
, so clearly
$x \leftrightarrow y = \xi (x,\overline {z}) \leftrightarrow \xi (y,\overline {z}) \in \Delta (x,y,\overline {z}) \subseteq \Delta \langle x,y \rangle $
, so clearly
![]() $x , \Delta \langle x,y \rangle \vdash _{{\mathscr {C}}_1} y$
, that is,
$x , \Delta \langle x,y \rangle \vdash _{{\mathscr {C}}_1} y$
, that is,
![]() $\Delta $
satisfies (p-MP). Finally, notice that
$\Delta $
satisfies (p-MP). Finally, notice that
![]() $\bigcup _{i =1}^n \Delta \langle x_i,y_i \rangle \vdash _{{\mathscr {C}}_1} \Delta \big \langle f(x_1,\ldots ,x_n), f(y_1,\ldots ,y_n) \big \rangle $
holds by extensivity, for every n-ary function symbol
$\bigcup _{i =1}^n \Delta \langle x_i,y_i \rangle \vdash _{{\mathscr {C}}_1} \Delta \big \langle f(x_1,\ldots ,x_n), f(y_1,\ldots ,y_n) \big \rangle $
holds by extensivity, for every n-ary function symbol
![]() $f \in {\mathcal {L}}$
, given our choice of
$f \in {\mathcal {L}}$
, given our choice of
![]() $\Delta $
. Therefore,
$\Delta $
. Therefore,
![]() $\Delta $
satisfies (p-Re). It follows by Theorem 2.5 that
$\Delta $
satisfies (p-Re). It follows by Theorem 2.5 that
![]() $\Delta (x,y,\overline {z})$
is a set of parameterized congruence formulas for the logic
$\Delta (x,y,\overline {z})$
is a set of parameterized congruence formulas for the logic
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
The second set of parameterized congruence formulas for
![]() ${\mathscr {C}}_1$
we consider, on the opposite, is quite complex. In order to establish it we need an auxiliary lemma.
${\mathscr {C}}_1$
we consider, on the opposite, is quite complex. In order to establish it we need an auxiliary lemma.
Lemma 4.2.
-
1.
 $(\neg \psi \wedge \varphi ^{\circ }) \to (\neg \psi \wedge \psi ^{\circ }) , (\neg \varphi \wedge \psi ^{\circ }) \to (\neg \varphi \wedge \varphi ^{\circ }) , \varphi \leftrightarrow \psi \vdash _{{\mathscr {C}}_1} \neg \varphi \leftrightarrow \neg \psi $
.
$(\neg \psi \wedge \varphi ^{\circ }) \to (\neg \psi \wedge \psi ^{\circ }) , (\neg \varphi \wedge \psi ^{\circ }) \to (\neg \varphi \wedge \varphi ^{\circ }) , \varphi \leftrightarrow \psi \vdash _{{\mathscr {C}}_1} \neg \varphi \leftrightarrow \neg \psi $
. -
2.
 $\varphi \leftrightarrow \psi , \varphi ^{\circ } \leftrightarrow \psi ^{\circ } \vdash _{{\mathscr {C}}_1} \neg \varphi \leftrightarrow \neg \psi $
.
$\varphi \leftrightarrow \psi , \varphi ^{\circ } \leftrightarrow \psi ^{\circ } \vdash _{{\mathscr {C}}_1} \neg \varphi \leftrightarrow \neg \psi $
. -
3.
 $\varphi \leftrightarrow \psi , \neg \varphi \leftrightarrow \neg \psi \vdash _{{\mathscr {C}}_1} \varphi ^{\circ } \leftrightarrow \psi ^{\circ }$
.
$\varphi \leftrightarrow \psi , \neg \varphi \leftrightarrow \neg \psi \vdash _{{\mathscr {C}}_1} \varphi ^{\circ } \leftrightarrow \psi ^{\circ }$
. -
4.
 $\varphi \leftrightarrow \psi \vdash _{{\mathscr {C}}_1} (\neg \varphi \leftrightarrow \neg \psi ) \leftrightarrow (\varphi ^{\circ } \leftrightarrow \psi ^{\circ })$
.
$\varphi \leftrightarrow \psi \vdash _{{\mathscr {C}}_1} (\neg \varphi \leftrightarrow \neg \psi ) \leftrightarrow (\varphi ^{\circ } \leftrightarrow \psi ^{\circ })$
.
Proof The proof uses da Costa’s completeness Theorem 3.4.
1. Let
![]() $v : {\boldsymbol {Fm}} \to \{0,1\}$
be a bivaluation such that
$v : {\boldsymbol {Fm}} \to \{0,1\}$
be a bivaluation such that
![]() $v(\neg \varphi \leftrightarrow \neg \psi ) = 0$
and assigning
$v(\neg \varphi \leftrightarrow \neg \psi ) = 0$
and assigning
![]() $1$
to all the premises of our claim. Then,
$1$
to all the premises of our claim. Then,
![]() $v(\neg \varphi ) \neq v(\neg \psi )$
. Assume without loss of generality that
$v(\neg \varphi ) \neq v(\neg \psi )$
. Assume without loss of generality that
![]() $v(\neg \varphi ) = 0$
and
$v(\neg \varphi ) = 0$
and
![]() $v(\neg \psi ) = 1$
. Since
$v(\neg \psi ) = 1$
. Since
![]() $v(\varphi \leftrightarrow \psi ) = 1$
, either
$v(\varphi \leftrightarrow \psi ) = 1$
, either
![]() $v(\varphi ) = v(\psi ) = 0$
or
$v(\varphi ) = v(\psi ) = 0$
or
![]() $v(\varphi ) = v(\psi ) = 1$
. In the first case, it follows that
$v(\varphi ) = v(\psi ) = 1$
. In the first case, it follows that
![]() $v(\neg \varphi ) = v(\neg \psi ) = 1$
, contradicting our assumption. So,
$v(\neg \varphi ) = v(\neg \psi ) = 1$
, contradicting our assumption. So,
![]() $v(\varphi ) = v(\psi ) = 1$
. Next, notice that since
$v(\varphi ) = v(\psi ) = 1$
. Next, notice that since
![]() $v(\neg \varphi ) = 0$
,
$v(\neg \varphi ) = 0$
,
![]() $v(\varphi ^{\circ }) = 1$
. Since moreover
$v(\varphi ^{\circ }) = 1$
. Since moreover
![]() $v(\neg \psi ) = 1$
, it follows
$v(\neg \psi ) = 1$
, it follows
![]() $v(\neg \psi \wedge \varphi ^{\circ }) = 1$
. Finally, notice that
$v(\neg \psi \wedge \varphi ^{\circ }) = 1$
. Finally, notice that
![]() $\neg \psi \wedge \psi ^{\circ } =\, \sim \! \psi $
, and since
$\neg \psi \wedge \psi ^{\circ } =\, \sim \! \psi $
, and since
![]() $v(\psi ) = 1$
, it must be the case
$v(\psi ) = 1$
, it must be the case
![]() $v(\sim \! \psi ) = 0$
. Thus
$v(\sim \! \psi ) = 0$
. Thus
![]() $v\big ((\neg \psi \wedge \varphi ^{\circ }) \to (\neg \psi \wedge \psi ^{\circ })\big ) = 0$
, and we reach a contradiction.
$v\big ((\neg \psi \wedge \varphi ^{\circ }) \to (\neg \psi \wedge \psi ^{\circ })\big ) = 0$
, and we reach a contradiction.
2. Just notice that
![]() $\varphi ^{\circ } \leftrightarrow \psi ^{\circ } \vdash _{{\mathscr {C}}_1} (\neg \psi \wedge \varphi ^{\circ }) \to (\neg \psi \wedge \psi ^{\circ })$
and
$\varphi ^{\circ } \leftrightarrow \psi ^{\circ } \vdash _{{\mathscr {C}}_1} (\neg \psi \wedge \varphi ^{\circ }) \to (\neg \psi \wedge \psi ^{\circ })$
and
![]() $\varphi ^{\circ } \leftrightarrow \psi ^{\circ } \vdash _{{\mathscr {C}}_1} (\neg \varphi \wedge \psi ^{\circ }) \to (\neg \varphi \wedge \varphi ^{\circ })$
, applying Lemma 3.2.16 with
$\varphi ^{\circ } \leftrightarrow \psi ^{\circ } \vdash _{{\mathscr {C}}_1} (\neg \varphi \wedge \psi ^{\circ }) \to (\neg \varphi \wedge \varphi ^{\circ })$
, applying Lemma 3.2.16 with
![]() $\xi = \neg \psi $
and
$\xi = \neg \psi $
and
![]() $\xi = \neg \varphi $
respectively. The result now follows by item 1.
$\xi = \neg \varphi $
respectively. The result now follows by item 1.
3. Let
![]() $v : {\boldsymbol {Fm}} \to \{0,1\}$
be a bivaluation such that
$v : {\boldsymbol {Fm}} \to \{0,1\}$
be a bivaluation such that
![]() $v(\varphi ^{\circ } \leftrightarrow \psi ^{\circ }) = 0$
and
$v(\varphi ^{\circ } \leftrightarrow \psi ^{\circ }) = 0$
and
![]() $v(\varphi \leftrightarrow \psi ) = v(\neg \varphi \leftrightarrow \neg \psi ) = 1$
. Then,
$v(\varphi \leftrightarrow \psi ) = v(\neg \varphi \leftrightarrow \neg \psi ) = 1$
. Then,
![]() $v(\varphi ^{\circ }) \neq v(\psi ^{\circ })$
. Assume without loss of generality that
$v(\varphi ^{\circ }) \neq v(\psi ^{\circ })$
. Assume without loss of generality that
![]() $v(\varphi ^{\circ }) = 0$
and
$v(\varphi ^{\circ }) = 0$
and
![]() $v(\psi ^{\circ }) = 1$
. So it must be the case
$v(\psi ^{\circ }) = 1$
. So it must be the case
![]() $v(\varphi ) = 1$
, otherwise
$v(\varphi ) = 1$
, otherwise
![]() $v(\varphi ^{\circ }) = 1$
. It follows by assumption that
$v(\varphi ^{\circ }) = 1$
. It follows by assumption that
![]() $v(\psi ) = 1$
as well. Similarly, it must be the case
$v(\psi ) = 1$
as well. Similarly, it must be the case
![]() $v(\neg \varphi ) = 1$
, otherwise
$v(\neg \varphi ) = 1$
, otherwise
![]() $v(\varphi ^{\circ }) = 1$
. It follows by assumption that
$v(\varphi ^{\circ }) = 1$
. It follows by assumption that
![]() $v(\neg \psi ) = 1$
as well. So,
$v(\neg \psi ) = 1$
as well. So,
![]() $v(\psi ^{\circ }) = v(\varphi \to \psi ) = v(\varphi \to \neg \psi ) = 1$
. It follows by definition of bivaluation that
$v(\psi ^{\circ }) = v(\varphi \to \psi ) = v(\varphi \to \neg \psi ) = 1$
. It follows by definition of bivaluation that
![]() $v(\varphi ) = 0$
. Thus
$v(\varphi ) = 0$
. Thus
![]() $v(\varphi ^{\circ }) = 1$
, and we reach an absurdity.
$v(\varphi ^{\circ }) = 1$
, and we reach an absurdity.
Compare Lemma 3.2.8 with Lemma 4.2.2. The latter provides a weaker condition in order to establish
![]() $\neg \varphi \leftrightarrow \neg \psi $
, and it will be used exhaustively throughout the rest of the work.
$\neg \varphi \leftrightarrow \neg \psi $
, and it will be used exhaustively throughout the rest of the work.
We still need a couple of auxiliary definitions before stating the main result of this section. For every
![]() $m \in \omega $
and every
$m \in \omega $
and every
![]() $\varphi \in \mathrm {Fm}_{\mathcal {L}}$
, letFootnote
8
$\varphi \in \mathrm {Fm}_{\mathcal {L}}$
, letFootnote
8
In particular,
![]() $\neg ^0 \varphi = \varphi $
and
$\neg ^0 \varphi = \varphi $
and
![]() $\neg ^1 \varphi = \neg \varphi $
. Let us also define
$\neg ^1 \varphi = \neg \varphi $
. Let us also define
 $$ \begin{align*} \Phi_0(x,y) = \big\{ &x \leftrightarrow y \big\} , \\[0.5ex] \Phi_1(x,y,z_1) = \big\{ &\neg^{m_1} (x *_1 z_1) \leftrightarrow \neg^{m_1} (y *_1 z_1) : \\ &*_1 \in \{\wedge,\vee,\to\} , m_1 \in \omega \big\} , \\ \Phi_2(x,y,z_1,z_2) = \big\{ &\neg^{m_2} \big( \neg^{m_1} (x *_1 z_1) *_2 z_2 \big) \leftrightarrow \\ &\neg^{m_2} \big( \neg^{m_1} (y *_1 z_1) *_2 z_2 \big) : \\ &*_1,*_2 \in \{\wedge,\vee,\to\} , m_1,m_2 \in \omega \big\} , \\ \quad\vdots\qquad\qquad&\\ \Phi_n(x,y,z_1,z_2,\ldots,z_n) = \big\{ & \neg^{m_n} \big( \cdots \neg^{m_2} (\neg^{m_1} (x *_1 z_1) *_2 z_2) \cdots *_n z_n \big) \leftrightarrow \\ &\neg^{m_n} \big( \cdots \neg^{m_2} ( \neg^{m_1} (y *_1 z_1) *_2 z_2) \cdots *_n z_n \big) : \\ &*_1,\ldots,*_n \in \{\wedge,\vee,\to\} , m_1,\ldots,m_n \in \omega \big\} , \end{align*} $$
$$ \begin{align*} \Phi_0(x,y) = \big\{ &x \leftrightarrow y \big\} , \\[0.5ex] \Phi_1(x,y,z_1) = \big\{ &\neg^{m_1} (x *_1 z_1) \leftrightarrow \neg^{m_1} (y *_1 z_1) : \\ &*_1 \in \{\wedge,\vee,\to\} , m_1 \in \omega \big\} , \\ \Phi_2(x,y,z_1,z_2) = \big\{ &\neg^{m_2} \big( \neg^{m_1} (x *_1 z_1) *_2 z_2 \big) \leftrightarrow \\ &\neg^{m_2} \big( \neg^{m_1} (y *_1 z_1) *_2 z_2 \big) : \\ &*_1,*_2 \in \{\wedge,\vee,\to\} , m_1,m_2 \in \omega \big\} , \\ \quad\vdots\qquad\qquad&\\ \Phi_n(x,y,z_1,z_2,\ldots,z_n) = \big\{ & \neg^{m_n} \big( \cdots \neg^{m_2} (\neg^{m_1} (x *_1 z_1) *_2 z_2) \cdots *_n z_n \big) \leftrightarrow \\ &\neg^{m_n} \big( \cdots \neg^{m_2} ( \neg^{m_1} (y *_1 z_1) *_2 z_2) \cdots *_n z_n \big) : \\ &*_1,\ldots,*_n \in \{\wedge,\vee,\to\} , m_1,\ldots,m_n \in \omega \big\} , \end{align*} $$
and
 $$ \begin{align*} \Psi_0(x,y) = \big\{ &x \leftrightarrow y \big\} , \\[0.5ex] \Psi_1(x,y,z_1) = \big\{ &\neg^{m_1} (z_1 *_1 x) \leftrightarrow \neg^{m_1} (z_1 *_1 y) : \\ &*_1 \in \{\wedge,\vee,\to\} , m_1 \in \omega \big\} , \\ \Psi_2(x,y,z_1,z_2) = \big\{ &\neg^{m_2} \big( \neg^{m_1} (z_1 * x) *_2 z_2 \big) \leftrightarrow \\ &\neg^{m_2} \big( \neg^{m_1} (z_1 * y) *_2 z_2 \big) : \\ &*_1,*_2 \in \{\wedge,\vee,\to\} , m_1,m_2 \in \omega \big\} , \\ \quad\vdots\qquad\qquad&\\ \Psi_n(x,y,z_1,z_2,\ldots,z_n) = \big\{ &\neg^{m_n} \big(\cdots \neg^{m_2} (\neg^{m_1} (z_1 *_1 x) *_2 z_2) \cdots *_n z_n \big) \leftrightarrow \\ &\neg^{m_n} \big( \cdots \neg^{m_2} (\neg^{m_1} (z_1 *_1 y) *_2 z_2) \cdots *_n z_n \big) : \\ &*_1,\ldots,*_n \in \{\wedge,\vee,\to\} , m_1,\ldots,m_n \in \omega \big\}. \end{align*} $$
$$ \begin{align*} \Psi_0(x,y) = \big\{ &x \leftrightarrow y \big\} , \\[0.5ex] \Psi_1(x,y,z_1) = \big\{ &\neg^{m_1} (z_1 *_1 x) \leftrightarrow \neg^{m_1} (z_1 *_1 y) : \\ &*_1 \in \{\wedge,\vee,\to\} , m_1 \in \omega \big\} , \\ \Psi_2(x,y,z_1,z_2) = \big\{ &\neg^{m_2} \big( \neg^{m_1} (z_1 * x) *_2 z_2 \big) \leftrightarrow \\ &\neg^{m_2} \big( \neg^{m_1} (z_1 * y) *_2 z_2 \big) : \\ &*_1,*_2 \in \{\wedge,\vee,\to\} , m_1,m_2 \in \omega \big\} , \\ \quad\vdots\qquad\qquad&\\ \Psi_n(x,y,z_1,z_2,\ldots,z_n) = \big\{ &\neg^{m_n} \big(\cdots \neg^{m_2} (\neg^{m_1} (z_1 *_1 x) *_2 z_2) \cdots *_n z_n \big) \leftrightarrow \\ &\neg^{m_n} \big( \cdots \neg^{m_2} (\neg^{m_1} (z_1 *_1 y) *_2 z_2) \cdots *_n z_n \big) : \\ &*_1,\ldots,*_n \in \{\wedge,\vee,\to\} , m_1,\ldots,m_n \in \omega \big\}. \end{align*} $$
We are now ready to state the main result of this section.
Theorem 4.3. For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() , and
, and
![]() $a,b \in A$
,
$a,b \in A$
,
 $$ \begin{align*} \langle a,b \rangle \in {\boldsymbol{\varOmega}}^{\boldsymbol{A}}(F) &\Leftrightarrow \forall n \in \omega \; \forall m \in \omega \; \forall c_1,\ldots,c_n \in A, \\ &\quad \Phi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F , \\ &\quad \Psi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F. \end{align*} $$
$$ \begin{align*} \langle a,b \rangle \in {\boldsymbol{\varOmega}}^{\boldsymbol{A}}(F) &\Leftrightarrow \forall n \in \omega \; \forall m \in \omega \; \forall c_1,\ldots,c_n \in A, \\ &\quad \Phi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F , \\ &\quad \Psi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F. \end{align*} $$
Proof For the sake of simplicity, define the relation
![]() $R \subseteq A \times A$
by
$R \subseteq A \times A$
by
 $$ \begin{align*} \langle a,b \rangle \in R &\Leftrightarrow \forall n \in \omega \; \forall m \in \omega \; \forall c_1,\ldots,c_n \in A, \\ &\quad \Phi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F , \\ &\quad \Psi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F. \end{align*} $$
$$ \begin{align*} \langle a,b \rangle \in R &\Leftrightarrow \forall n \in \omega \; \forall m \in \omega \; \forall c_1,\ldots,c_n \in A, \\ &\quad \Phi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F , \\ &\quad \Psi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F. \end{align*} $$
Suppose that
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. It follows by Proposition 4.1 that
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. It follows by Proposition 4.1 that
![]() $a\,Rb$
. Conversely, we claim that R is a congruence relation on
$a\,Rb$
. Conversely, we claim that R is a congruence relation on
![]() ${\boldsymbol {A}}$
compatible with F. It should be clear that R is an equivalence relation on A, given Lemma 3.2.1–3. Notice next that the relation R is compatible with the connective
${\boldsymbol {A}}$
compatible with F. It should be clear that R is an equivalence relation on A, given Lemma 3.2.1–3. Notice next that the relation R is compatible with the connective
![]() $\neg $
, since by construction of R we are ranging
$\neg $
, since by construction of R we are ranging
![]() $\neg ^m a$
and
$\neg ^m a$
and
![]() $\neg ^m b$
over
$\neg ^m b$
over
![]() $m \in \omega $
. We are left to prove that R is also compatible with the binary language operations of
$m \in \omega $
. We are left to prove that R is also compatible with the binary language operations of
![]() ${\mathscr {C}}_1$
. Let
${\mathscr {C}}_1$
. Let
![]() $\langle a_1,b_1 \rangle \in R$
and
$\langle a_1,b_1 \rangle \in R$
and
![]() $\langle a_2,b_2 \rangle \in R$
. We claim that for every
$\langle a_2,b_2 \rangle \in R$
. We claim that for every
![]() $c_1,\ldots ,c_n \in A$
,
$c_1,\ldots ,c_n \in A$
,
with
![]() $* \in \{\wedge ,\vee ,\to \}$
. Let
$* \in \{\wedge ,\vee ,\to \}$
. Let
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $c_1,\ldots ,c_n \in A$
,
$c_1,\ldots ,c_n \in A$
,
![]() $*,*_1,\ldots ,*_n \in \{\wedge ,\vee ,\to \}$
and
$*,*_1,\ldots ,*_n \in \{\wedge ,\vee ,\to \}$
and
![]() $m,m_1,\ldots ,m_n \in \omega $
. Consider
$m,m_1,\ldots ,m_n \in \omega $
. Consider
![]() $\Phi _{n+1}(a_1,b_1,a_2,c_1,\ldots ,c_n)$
with
$\Phi _{n+1}(a_1,b_1,a_2,c_1,\ldots ,c_n)$
with
![]() $m'=0$
,
$m'=0$
,
![]() $m_1'=m,m_2'=m_1,\ldots ,m_{n+1}'=m_n$
. Since
$m_1'=m,m_2'=m_1,\ldots ,m_{n+1}'=m_n$
. Since
![]() $\Phi _{n+1}(a_1,b_1,a_2,c_1,\ldots ,c_n) \subseteq F$
by the assumption
$\Phi _{n+1}(a_1,b_1,a_2,c_1,\ldots ,c_n) \subseteq F$
by the assumption
![]() $\langle a_1,b_1 \rangle \in R$
, we have
$\langle a_1,b_1 \rangle \in R$
, we have
 $$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_1} (\neg^m (a_1 * a_2) *_1 c_1) \cdots *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_1} ( \neg^m (b_1 * a_2) *_1 c_1) \cdots *_n c_n) \in F. \end{align*} $$
$$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_1} (\neg^m (a_1 * a_2) *_1 c_1) \cdots *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_1} ( \neg^m (b_1 * a_2) *_1 c_1) \cdots *_n c_n) \in F. \end{align*} $$
Next, consider
![]() $\Psi _{n+1}(a_2,b_2,b_1,c_1,\ldots ,c_n)$
with
$\Psi _{n+1}(a_2,b_2,b_1,c_1,\ldots ,c_n)$
with
![]() $m'=0$
,
$m'=0$
,
![]() $m_1'=m,m_2'=m_1,\ldots, m_{n+1}'=m_n$
. Since
$m_1'=m,m_2'=m_1,\ldots, m_{n+1}'=m_n$
. Since
![]() $\Psi _{n+1}(a_2,b_2,b_1,c_1,\ldots ,c_n) \subseteq F$
by the assumption
$\Psi _{n+1}(a_2,b_2,b_1,c_1,\ldots ,c_n) \subseteq F$
by the assumption
![]() $\langle a_2,b_2 \rangle \in R$
, we have
$\langle a_2,b_2 \rangle \in R$
, we have
 $$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_1} (\neg^m (b_1 * a_2) *_1 c_1) \cdots *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_1} ( \neg^m (b_1 * b_2) *_1 c_1) \cdots *_n c_n) \in F. \end{align*} $$
$$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_1} (\neg^m (b_1 * a_2) *_1 c_1) \cdots *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_1} ( \neg^m (b_1 * b_2) *_1 c_1) \cdots *_n c_n) \in F. \end{align*} $$
It then follows by transitivity (Lemma 3.2.3) that
 $$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_1} (\neg^m (a_1 * a_2) *_1 c_1) \cdots *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_1} ( \neg^m (b_1 * b_2) *_1 c_1) \cdots *_n c_n) \in F. \end{align*} $$
$$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_1} (\neg^m (a_1 * a_2) *_1 c_1) \cdots *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_1} ( \neg^m (b_1 * b_2) *_1 c_1) \cdots *_n c_n) \in F. \end{align*} $$
Thus,
![]() $\Phi _n\big (\neg ^m (a_1 * a_2), \neg ^m (b_1 * b_2), c_1,\ldots ,c_n\big ) \subseteq F$
.
$\Phi _n\big (\neg ^m (a_1 * a_2), \neg ^m (b_1 * b_2), c_1,\ldots ,c_n\big ) \subseteq F$
.
Similarly, one proves that for every
![]() $c_1,\ldots ,c_n \in A$
,
$c_1,\ldots ,c_n \in A$
,
with
![]() $* \in \{\wedge ,\vee ,\to \}$
. Finally, in order to see that R is compatible with F, let
$* \in \{\wedge ,\vee ,\to \}$
. Finally, in order to see that R is compatible with F, let
![]() $\langle a,b \rangle \in R$
and assume
$\langle a,b \rangle \in R$
and assume
![]() $a \in F$
. Since by assumption
$a \in F$
. Since by assumption
![]() $\Phi _0(a,b) \subseteq F$
, it follows that
$\Phi _0(a,b) \subseteq F$
, it follows that
![]() $a \to b \in F$
, and hence by (MP) that
$a \to b \in F$
, and hence by (MP) that
![]() $b \in F$
. Thus,
$b \in F$
. Thus,
![]() $R \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
$R \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
In other words, Theorem 4.3 tells us that the set
 $$ \begin{align*} \Delta(x,y,\overline{z}) =& \bigcup_{n \in \omega} \bigcup_{m \in \omega} \Phi_n(\neg^m x, \neg^m y, z_1,\ldots,z_n) \; \cup \\ &\bigcup_{n \in \omega} \bigcup_{m \in \omega} \Psi_n(\neg^m x, \neg^m y, z_1,\ldots,z_n) \end{align*} $$
$$ \begin{align*} \Delta(x,y,\overline{z}) =& \bigcup_{n \in \omega} \bigcup_{m \in \omega} \Phi_n(\neg^m x, \neg^m y, z_1,\ldots,z_n) \; \cup \\ &\bigcup_{n \in \omega} \bigcup_{m \in \omega} \Psi_n(\neg^m x, \neg^m y, z_1,\ldots,z_n) \end{align*} $$
is a set of parameterized congruence formulas for the logic
![]() ${\mathscr {C}}_1$
. Although the set
${\mathscr {C}}_1$
. Although the set
![]() $\Delta (x,y,\overline {z})$
above may seem of little more practical usage than the one given in Proposition 4.1, it will be the key to proving Theorem 9.1 later on.
$\Delta (x,y,\overline {z})$
above may seem of little more practical usage than the one given in Proposition 4.1, it will be the key to proving Theorem 9.1 later on.
5 Algebraic semantics for
 ${\mathscr {C}}_1$
${\mathscr {C}}_1$
As we have mentioned in the Introduction, several semantical approaches to the logic
![]() ${\mathscr {C}}_1$
have been put forward in the literature, namely, behavioral semantics [Reference Caleiro and Gonçalves12, Reference Caleiro, Gonçalves and Martins13], possible-translations semantics [Reference Bueno-Soler and Carnielli9], da Costa algebras [Reference Carnielli and de Alcantara14, Reference Seoane and de Alcantara52],
${\mathscr {C}}_1$
have been put forward in the literature, namely, behavioral semantics [Reference Caleiro and Gonçalves12, Reference Caleiro, Gonçalves and Martins13], possible-translations semantics [Reference Bueno-Soler and Carnielli9], da Costa algebras [Reference Carnielli and de Alcantara14, Reference Seoane and de Alcantara52],
![]() ${\mathscr {C}}_1$
-algebras [Reference da Costa19], and a two-valued semantics [Reference da Costa and Alves22, Reference da Costa and Alves23], this latter already introduced in Definition 3.3. From an AAL perspective, however, there are still two natural candidates for a semantical approach left unstudied—the class
${\mathscr {C}}_1$
-algebras [Reference da Costa19], and a two-valued semantics [Reference da Costa and Alves22, Reference da Costa and Alves23], this latter already introduced in Definition 3.3. From an AAL perspective, however, there are still two natural candidates for a semantical approach left unstudied—the class
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
and Blok and Pigozzi’s notion of algebraic semantics. In this section we will investigate both these approaches, and conclude that neither provides a meaningful algebraic counterpart to the logic
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
and Blok and Pigozzi’s notion of algebraic semantics. In this section we will investigate both these approaches, and conclude that neither provides a meaningful algebraic counterpart to the logic
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
5.1 The class
 ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
The first (negative) result on the algebraization of
![]() ${\mathscr {C}}_1$
was established by Mortensen in [Reference Mortensen44], by proving that the only congruence on the formula algebra compatible with the set of
${\mathscr {C}}_1$
was established by Mortensen in [Reference Mortensen44], by proving that the only congruence on the formula algebra compatible with the set of
![]() ${\mathscr {C}}_1$
-theorems is the identity relation. This fact can be re-written as:
${\mathscr {C}}_1$
-theorems is the identity relation. This fact can be re-written as:
Proposition 5.1 Mortensen
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}({\mathrm{Thm}}_{{\mathscr {C}}_1}) = id_{\boldsymbol {Fm}}$
.
${\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}({\mathrm{Thm}}_{{\mathscr {C}}_1}) = id_{\boldsymbol {Fm}}$
.
In light of Proposition 5.1, it follows by Theorem 4.3 that for every
![]() $\varphi ,\psi \in \mathrm {Fm}_{\mathcal {L}}$
,
$\varphi ,\psi \in \mathrm {Fm}_{\mathcal {L}}$
,

Having in mind (1) on page 483, Mortensen’s result can be re-stated as follows:
Proposition 5.2.
![]() ${\boldsymbol {Fm}} \in {\mathsf {Alg}}^*({\mathscr {C}}_1)$
.
${\boldsymbol {Fm}} \in {\mathsf {Alg}}^*({\mathscr {C}}_1)$
.
Proposition 5.2 has a most crucial consequence upon the intrinsic variety of the logic
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
Corollary 5.3. The intrinsic variety of
![]() ${\mathscr {C}}_1$
is the class of all
${\mathscr {C}}_1$
is the class of all
![]() ${\mathcal {L}}$
-algebras. That is,
${\mathcal {L}}$
-algebras. That is,
![]() $\mathbb {V}({\mathscr {C}}_1) = \{ {\boldsymbol {A}} : {\boldsymbol {A}} \text { is an } {\mathcal {L}}\text {-algebra} \}$
.
$\mathbb {V}({\mathscr {C}}_1) = \{ {\boldsymbol {A}} : {\boldsymbol {A}} \text { is an } {\mathcal {L}}\text {-algebra} \}$
.
Proof Since
![]() ${\boldsymbol {Fm}}$
is the absolutely free
${\boldsymbol {Fm}}$
is the absolutely free
![]() ${\mathcal {L}}$
-algebra over the (denumerable) set of variables
${\mathcal {L}}$
-algebra over the (denumerable) set of variables
![]() $\mathrm {Var}$
, it is well-known that
$\mathrm {Var}$
, it is well-known that
![]() $\mathbb {V}({\boldsymbol {Fm}})$
is the class of all
$\mathbb {V}({\boldsymbol {Fm}})$
is the class of all
![]() ${\mathcal {L}}$
-algebras. Moreover
${\mathcal {L}}$
-algebras. Moreover
![]() , bearing in mind that
, bearing in mind that
![]() by protoalgebraicity of
by protoalgebraicity of
![]() ${\mathscr {C}}_1$
and Proposition 5.1, respectively.
${\mathscr {C}}_1$
and Proposition 5.1, respectively.
Corollary 5.3 sets aside the possibility of associating with
![]() ${\mathscr {C}}_1$
its intrinsic variety as the class of algebras one could canonically associate with it.
${\mathscr {C}}_1$
its intrinsic variety as the class of algebras one could canonically associate with it.
Notice that since
![]() ${\mathscr {C}}_1$
is an extension of
${\mathscr {C}}_1$
is an extension of
![]() ${\mathscr {C}}_n$
, we also have
${\mathscr {C}}_n$
, we also have
![]() ${\boldsymbol {Fm}} \in {\mathsf {Alg}}^*({\mathscr {C}}_1) \subseteq {\mathsf {Alg}}^*({\mathscr {C}}_n)$
, for every
${\boldsymbol {Fm}} \in {\mathsf {Alg}}^*({\mathscr {C}}_1) \subseteq {\mathsf {Alg}}^*({\mathscr {C}}_n)$
, for every
![]() $n \geq 1$
. As such, Corollary 5.3 also holds for the logics
$n \geq 1$
. As such, Corollary 5.3 also holds for the logics
![]() ${\mathscr {C}}_n$
, with
${\mathscr {C}}_n$
, with
![]() $n \geq 1$
. Consequently, the intrinsic varieties of all da Costa’s
$n \geq 1$
. Consequently, the intrinsic varieties of all da Costa’s
![]() ${\mathscr {C}}$
-systems coincide. It is an open problem whether the quasivarieties
${\mathscr {C}}$
-systems coincide. It is an open problem whether the quasivarieties
![]() $\mathbb {Q}\,{\mathsf {Alg}}^*({\mathscr {C}}_n)$
, with
$\mathbb {Q}\,{\mathsf {Alg}}^*({\mathscr {C}}_n)$
, with
![]() $n \geq 1$
, also coincide, or even if the classes
$n \geq 1$
, also coincide, or even if the classes
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_n)$
, with
${\mathsf {Alg}}^*({\mathscr {C}}_n)$
, with
![]() $n \geq 1$
, happen to coincide.
$n \geq 1$
, happen to coincide.
Given the fact that the intrinsic variety of a logic is generated by its algebraic counterpart (see page 483), it follows by Corollary 5.3 that
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
generates the variety of all
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
generates the variety of all
![]() ${\mathcal {L}}$
-algebras.
${\mathcal {L}}$
-algebras.
We now proceed to prove that
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not a quasivariety. In order to see that, we borrow the next example from [Reference Urbas54, p. 590], and prove that
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not a quasivariety. In order to see that, we borrow the next example from [Reference Urbas54, p. 590], and prove that
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not closed under subalgebras. Notice that the proof of Theorem 3.6 provides a counterexample for the fact that
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not closed under subalgebras. Notice that the proof of Theorem 3.6 provides a counterexample for the fact that
![]() ${\mathsf {Mod}}^*({\mathscr {C}}_1)$
is not closed under submatrices, but the subalgebra
${\mathsf {Mod}}^*({\mathscr {C}}_1)$
is not closed under submatrices, but the subalgebra
![]() ${\boldsymbol {B}}$
there presented still belongs to
${\boldsymbol {B}}$
there presented still belongs to
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
, because
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
, because
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {B}}(\{1\}) = id_{\boldsymbol {B}}$
and
${\boldsymbol {\varOmega }}^{\boldsymbol {B}}(\{1\}) = id_{\boldsymbol {B}}$
and
![]() .
.
Proposition 5.4.
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not a quasivariety.
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not a quasivariety.
Proof We prove that
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not closed under subalgebras. Consider the algebra
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not closed under subalgebras. Consider the algebra
![]() ${\boldsymbol {A}}$
defined by the truth-tables given in Table 3 and fix
${\boldsymbol {A}}$
defined by the truth-tables given in Table 3 and fix
![]() . First, one must check that
. First, one must check that
![]() and furthermore that
and furthermore that
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) = id_{\boldsymbol {A}}$
(we leave the details to the reader). Thus,
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) = id_{\boldsymbol {A}}$
(we leave the details to the reader). Thus,
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathscr {C}}_1)$
. Now, consider the subalgebra
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathscr {C}}_1)$
. Now, consider the subalgebra
![]() ${\boldsymbol {B}} \leq {\boldsymbol {A}}$
with universe
${\boldsymbol {B}} \leq {\boldsymbol {A}}$
with universe
![]() $B = \{0,4,5\}$
. We have
$B = \{0,4,5\}$
. We have
![]() $\mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(B) = B$
and
$\mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(B) = B$
and
![]() . In fact
. In fact
![]() , because the singletons
, because the singletons
![]() $\{0\}, \{4\}, \{5\}$
are not
$\{0\}, \{4\}, \{5\}$
are not
![]() ${\mathscr {C}}_1$
-filters, and neither are the subsets
${\mathscr {C}}_1$
-filters, and neither are the subsets
![]() $\{0,5\}$
and
$\{0,5\}$
and
![]() $\{4,5\}$
. We now claim that
$\{4,5\}$
. We now claim that
![]() $\langle 0,4 \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {B}}(F \cap B)$
. We shall make use of Theorem 4.3. Notice that
$\langle 0,4 \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {B}}(F \cap B)$
. We shall make use of Theorem 4.3. Notice that
![]() $0 \leftrightarrow 4 = 0 \in F \cap B$
, and since
$0 \leftrightarrow 4 = 0 \in F \cap B$
, and since
![]() $\neg 0 = \neg 4$
, it follows that
$\neg 0 = \neg 4$
, it follows that
![]() $\neg ^m 0 = \neg ^m 4$
, for every
$\neg ^m 0 = \neg ^m 4$
, for every
![]() $m \in \omega $
, and therefore
$m \in \omega $
, and therefore
![]() $\neg ^m 0 \leftrightarrow \neg ^m 4 = 0 \in F \cap B$
. Furthermore, by looking at the truth tables of
$\neg ^m 0 \leftrightarrow \neg ^m 4 = 0 \in F \cap B$
. Furthermore, by looking at the truth tables of
![]() ${\boldsymbol {A}}$
restricted to the subuniverse B, one sees that for every
${\boldsymbol {A}}$
restricted to the subuniverse B, one sees that for every
![]() $*_1,\ldots ,*_n \in \{\wedge ,\vee ,\to \}$
, every
$*_1,\ldots ,*_n \in \{\wedge ,\vee ,\to \}$
, every
![]() $m_1,\ldots ,m_n \in \omega $
, and every
$m_1,\ldots ,m_n \in \omega $
, and every
![]() $c_1,\ldots ,c_n \in A$
,
$c_1,\ldots ,c_n \in A$
,
 $$ \begin{align*} &\neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (0 *_1 c_1) *_2 c_2) \cdots) *_n c_n) = \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (4 *_1 c_1) *_2 c_2) \cdots) *_n c_n), \end{align*} $$
$$ \begin{align*} &\neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (0 *_1 c_1) *_2 c_2) \cdots) *_n c_n) = \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (4 *_1 c_1) *_2 c_2) \cdots) *_n c_n), \end{align*} $$
and
 $$ \begin{align*} &\neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (c_1 *_1 0) *_2 c_2) \cdots) *_n c_n) = \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (c_1 *_1 4) *_2 c_2) \cdots) *_n c_n). \end{align*} $$
$$ \begin{align*} &\neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (c_1 *_1 0) *_2 c_2) \cdots) *_n c_n) = \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (c_1 *_1 4) *_2 c_2) \cdots) *_n c_n). \end{align*} $$
Therefore,
 $$ \begin{align*} &\neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (0 *_1 c_1) *_2 c_2) \cdots) *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (4 *_1 c_1) *_2 c_2) \cdots) *_n c_n) = 0 \in F \cap B, \end{align*} $$
$$ \begin{align*} &\neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (0 *_1 c_1) *_2 c_2) \cdots) *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (4 *_1 c_1) *_2 c_2) \cdots) *_n c_n) = 0 \in F \cap B, \end{align*} $$
and
 $$ \begin{align*} &\neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (c_1 *_1 0) *_2 c_2) \cdots) *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (c_1 *_1 4) *_2 c_2) \cdots) *_n c_n) = 0 \in F \cap B. \end{align*} $$
$$ \begin{align*} &\neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (c_1 *_1 0) *_2 c_2) \cdots) *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (c_1 *_1 4) *_2 c_2) \cdots) *_n c_n) = 0 \in F \cap B. \end{align*} $$
It follows by Theorem 4.3 that
![]() $\langle 0,4 \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {B}}(F \cap B)$
. Thus,
$\langle 0,4 \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {B}}(F \cap B)$
. Thus,
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {B}}(F \cap B) \neq id_{{\boldsymbol {B}}}$
. We conclude that
${\boldsymbol {\varOmega }}^{\boldsymbol {B}}(F \cap B) \neq id_{{\boldsymbol {B}}}$
. We conclude that
![]() ${\boldsymbol {B}} \notin {\mathsf {Alg}}^*({\mathscr {C}}_1)$
and hence
${\boldsymbol {B}} \notin {\mathsf {Alg}}^*({\mathscr {C}}_1)$
and hence
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not closed under subalgebras.
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not closed under subalgebras.
Table 3 Truth-tables of the algebra
![]() ${\boldsymbol {A}}$
of [Reference Urbas54, p. 590].
${\boldsymbol {A}}$
of [Reference Urbas54, p. 590].

Corollary 5.5.
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1) \subsetneq \mathbb {V}({\mathscr {C}}_1)$
.
${\mathsf {Alg}}^*({\mathscr {C}}_1) \subsetneq \mathbb {V}({\mathscr {C}}_1)$
.
Proof Since
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not a quasivariety by Proposition 5.4, it follows at once that
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is not a quasivariety by Proposition 5.4, it follows at once that
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1) \subsetneq \mathbb {Q}{\mathsf {Alg}}^*({\mathscr {C}}_1) \subseteq \mathbb {V}({\mathscr {C}}_1)$
.
${\mathsf {Alg}}^*({\mathscr {C}}_1) \subsetneq \mathbb {Q}{\mathsf {Alg}}^*({\mathscr {C}}_1) \subseteq \mathbb {V}({\mathscr {C}}_1)$
.
In summary, the class
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
seems to be of little interest from an algebraic point of view. Indeed, it is not a quasivariety (Proposition 5.4), the formula algebra
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
seems to be of little interest from an algebraic point of view. Indeed, it is not a quasivariety (Proposition 5.4), the formula algebra
![]() ${\boldsymbol {Fm}}$
belongs to
${\boldsymbol {Fm}}$
belongs to
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
(Proposition 5.2), and the variety generated by
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
(Proposition 5.2), and the variety generated by
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is the class of all
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
is the class of all
![]() ${\mathcal {L}}$
-algebras (Corollary 5.3).
${\mathcal {L}}$
-algebras (Corollary 5.3).
5.2 Algebraic semantics for
 ${\mathscr {C}}_1$
${\mathscr {C}}_1$
Our next goal is to prove that
![]() ${\mathscr {C}}_1$
admits no algebraic semantics in the sense of Blok and Pigozzi, as originally defined in [Reference Blok and Pigozzi6] and introduced in Definition 2.8. We shall appeal to a recent result established in [Reference Moraschini43] characterizing non-trivial protoalgebraic logics with an algebraic semantics and (once again) to Mortensen’s result.
${\mathscr {C}}_1$
admits no algebraic semantics in the sense of Blok and Pigozzi, as originally defined in [Reference Blok and Pigozzi6] and introduced in Definition 2.8. We shall appeal to a recent result established in [Reference Moraschini43] characterizing non-trivial protoalgebraic logics with an algebraic semantics and (once again) to Mortensen’s result.
Theorem 5.6. The logic
![]() ${\mathscr {C}}_1$
has no algebraic semantics.
${\mathscr {C}}_1$
has no algebraic semantics.
Proof Let
![]() $\varphi ,\psi \in \mathrm {Fm}_{\mathcal {L}}$
be two logically equivalent formulas. That is, for every
$\varphi ,\psi \in \mathrm {Fm}_{\mathcal {L}}$
be two logically equivalent formulas. That is, for every
![]() $\xi (x,\overline {z}) \in \mathrm {Fm}_{\mathcal {L}}$
we have
$\xi (x,\overline {z}) \in \mathrm {Fm}_{\mathcal {L}}$
we have
![]() $\xi (\varphi ,\overline {z}) \dashv \vdash _{{\mathscr {C}}_1} \xi (\psi ,\overline {z})$
. It trivially follows that
$\xi (\varphi ,\overline {z}) \dashv \vdash _{{\mathscr {C}}_1} \xi (\psi ,\overline {z})$
. It trivially follows that
![]() $\xi (\varphi ,\overline {z}) \in {\mathrm{Thm}}_{{\mathscr {C}}_1}$
if and only if
$\xi (\varphi ,\overline {z}) \in {\mathrm{Thm}}_{{\mathscr {C}}_1}$
if and only if
![]() $\xi (\psi ,\overline {z}) \in {\mathrm{Thm}}_{{\mathscr {C}}_1}$
. Therefore,
$\xi (\psi ,\overline {z}) \in {\mathrm{Thm}}_{{\mathscr {C}}_1}$
. Therefore,
![]() $\langle \varphi ,\psi \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}({\mathrm{Thm}}_{{\mathscr {C}}_1})$
—see for instance [Reference Font32, Corollary 4.24]. But then
$\langle \varphi ,\psi \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}({\mathrm{Thm}}_{{\mathscr {C}}_1})$
—see for instance [Reference Font32, Corollary 4.24]. But then
![]() $\varphi = \psi $
, in light of Mortensen’s Proposition 5.1. We conclude by [Reference Moraschini43, Theorem 9.3] (which states that a non-trivial protoalgebraic logic admits an algebraic semantics if and only if there are two distinct logically equivalent formulas) that
$\varphi = \psi $
, in light of Mortensen’s Proposition 5.1. We conclude by [Reference Moraschini43, Theorem 9.3] (which states that a non-trivial protoalgebraic logic admits an algebraic semantics if and only if there are two distinct logically equivalent formulas) that
![]() ${\mathscr {C}}_1$
admits no algebraic semantics.
${\mathscr {C}}_1$
admits no algebraic semantics.
The non-algebraizability of da Costa’s logic
![]() ${\mathscr {C}}_1$
established in [Reference Lewin, Mikenberg and Schwarze39] tells us that there exists no triple
${\mathscr {C}}_1$
established in [Reference Lewin, Mikenberg and Schwarze39] tells us that there exists no triple
![]() $\langle {\mathsf {K}} , {\boldsymbol {\tau }} , {\boldsymbol {\rho }} \rangle $
satisfying conditions (ALG1) and (ALG2) for the logic
$\langle {\mathsf {K}} , {\boldsymbol {\tau }} , {\boldsymbol {\rho }} \rangle $
satisfying conditions (ALG1) and (ALG2) for the logic
![]() ${\mathscr {C}}_1$
; in other words,
${\mathscr {C}}_1$
; in other words,
![]() ${\mathscr {C}}_1$
fails to possess an equivalent algebraic semantics. Theorem 5.6 now tells us that there exists no pair
${\mathscr {C}}_1$
fails to possess an equivalent algebraic semantics. Theorem 5.6 now tells us that there exists no pair
![]() $\langle {\mathsf {K}} , {\boldsymbol {\tau }} \rangle $
satisfying condition (ALG1) for the logic
$\langle {\mathsf {K}} , {\boldsymbol {\tau }} \rangle $
satisfying condition (ALG1) for the logic
![]() ${\mathscr {C}}_1$
; in other words,
${\mathscr {C}}_1$
; in other words,
![]() ${\mathscr {C}}_1$
fails to possess an algebraic semantics. Theorem 5.6 definitely leaves out of the picture any attempt to associate with
${\mathscr {C}}_1$
fails to possess an algebraic semantics. Theorem 5.6 definitely leaves out of the picture any attempt to associate with
![]() ${\mathscr {C}}_1$
a canonical class of algebras
${\mathscr {C}}_1$
a canonical class of algebras
![]() ${\mathsf {K}}$
, whose
${\mathsf {K}}$
, whose
![]() ${\mathsf {K}}$
-relative congruences would algebraically translate the logical properties of
${\mathsf {K}}$
-relative congruences would algebraically translate the logical properties of
![]() ${\mathscr {C}}_1$
according to Definition 2.8.
${\mathscr {C}}_1$
according to Definition 2.8.
Having an algebraic semantics is a property preserved by extensions [Reference Blok and Rebagliato8, Theorem 2.15]—the cited result is stated for finitary logics, but for our purposes it suffices. Therefore, an immediate consequence of Theorem 5.6 is the following:
Corollary 5.7. For every
![]() $n \geq 1$
, the logic
$n \geq 1$
, the logic
![]() ${\mathscr {C}}_n$
has no algebraic semantics.
${\mathscr {C}}_n$
has no algebraic semantics.
On the other hand, the property of having an algebraic semantics is not necessarily preserved by expansions, and
![]() ${\mathscr {C}}_1$
provides one such counterexample. Indeed,
${\mathscr {C}}_1$
provides one such counterexample. Indeed,
![]() $\mathcal {IL}^+$
possesses an (equivalent) algebraic semantics—the variety of generalized Heyting algebras, also known as relatively pseudo-complemented lattices—while
$\mathcal {IL}^+$
possesses an (equivalent) algebraic semantics—the variety of generalized Heyting algebras, also known as relatively pseudo-complemented lattices—while
![]() ${\mathscr {C}}_1$
does not.
${\mathscr {C}}_1$
does not.
It is worth mentioning that a (protoalgebraic) logic without any algebraic semantics is not a novel phenomenon in the literature. Indeed, [Reference Blok and Rebagliato8, Section 2.3] investigates a necessary condition for a logic to possess an algebraic semantics, and then builds a very simple logic (with one single axiom schema and the inference rule of Modus Ponens), which fails to satisfy such condition. In fact, this logic has been exhaustively studied from an AAL perspective in [Reference Font31]. Another ad-hoc example of a logic without any algebraic semantics appears in [Reference Raftery51, Example 3]. For the sake of completeness, the negation fragments of
![]() $\mathcal {CL}$
and
$\mathcal {CL}$
and
![]() $\mathcal {IL}$
also fail to admit any algebraic semantics, as observed in [Reference Blok and Rebagliato8, p. 170], as well as the logic
$\mathcal {IL}$
also fail to admit any algebraic semantics, as observed in [Reference Blok and Rebagliato8, p. 170], as well as the logic
![]() $\mathcal {PW}$
having a single binary connective [Reference Raftery51, Example 4]. The novelty of Theorem 5.6 is the fact that such pathological behaviour is here exhibited by a well-established logic, rather than a built-up counterexample, or a mono-connective logic. As a matter of fact, the existence of an interesting logic without an algebraic semantics was posed as an open problem right from the very introduction of this notion by Blok and Pigozzi [Reference Blok and Pigozzi6, p. 18]: “It is an open question if any interesting deductive systems fail to have an algebraic semantics.”
$\mathcal {PW}$
having a single binary connective [Reference Raftery51, Example 4]. The novelty of Theorem 5.6 is the fact that such pathological behaviour is here exhibited by a well-established logic, rather than a built-up counterexample, or a mono-connective logic. As a matter of fact, the existence of an interesting logic without an algebraic semantics was posed as an open problem right from the very introduction of this notion by Blok and Pigozzi [Reference Blok and Pigozzi6, p. 18]: “It is an open question if any interesting deductive systems fail to have an algebraic semantics.”
Part II. From
![]() $\mathbf {\mathscr {C}}_{\mathbf {1}}$
to its extensions.
$\mathbf {\mathscr {C}}_{\mathbf {1}}$
to its extensions.
The second part of our work may be seen as a bridge between the logic
![]() ${\mathscr {C}}_1$
and the extensions of
${\mathscr {C}}_1$
and the extensions of
![]() ${\mathscr {C}}_1$
we intend to study. Indeed, while the results of Section 6 still hold, in particular, for the logic
${\mathscr {C}}_1$
we intend to study. Indeed, while the results of Section 6 still hold, in particular, for the logic
![]() ${\mathscr {C}}_1$
, from Section 7 onwards the results will depend on conditions which
${\mathscr {C}}_1$
, from Section 7 onwards the results will depend on conditions which
![]() ${\mathscr {C}}_1$
fails to satisfy. We were led to such conditions while investigating the same results for several extensions of
${\mathscr {C}}_1$
fails to satisfy. We were led to such conditions while investigating the same results for several extensions of
![]() ${\mathscr {C}}_1$
. The reason for this abstraction is twofold. On the one hand, our new assumptions allow us to establish stronger results than those seen for the logic
${\mathscr {C}}_1$
. The reason for this abstraction is twofold. On the one hand, our new assumptions allow us to establish stronger results than those seen for the logic
![]() ${\mathscr {C}}_1$
. On the other hand, we avoid repeating the same results for each extension of
${\mathscr {C}}_1$
. On the other hand, we avoid repeating the same results for each extension of
![]() ${\mathscr {C}}_1$
under study, while unifying them under a general setting.
${\mathscr {C}}_1$
under study, while unifying them under a general setting.
Ultimately, the goal of this second part is to arrive at Theorems 8.3 and 8.7 concerning the non-trivial algebra subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, where
${\mathsf {Alg}}^*({\mathcal {S}})$
, where
![]() ${\mathcal {S}}$
is an extension of
${\mathcal {S}}$
is an extension of
![]() ${\mathscr {C}}_1$
satisfying the aforementioned conditions. These results will allow us in Part III to characterize the quasivarieties
${\mathscr {C}}_1$
satisfying the aforementioned conditions. These results will allow us in Part III to characterize the quasivarieties
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
and the intrinsic variety
${\mathsf {Alg}}^*({\mathcal {S}})$
and the intrinsic variety
![]() $\mathbb {V}({\mathcal {S}})$
, for some known extensions
$\mathbb {V}({\mathcal {S}})$
, for some known extensions
![]() ${\mathcal {S}}$
of
${\mathcal {S}}$
of
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
6 The subalgebra
 ${\boldsymbol {A}}^{\circ }$
${\boldsymbol {A}}^{\circ }$
In this section we study a special subalgebra whose
![]() ${\mathscr {C}}_1$
-filters satisfy “classical” properties. Most notably, the quotient of such subalgebra over the Leibniz congruence of any of its
${\mathscr {C}}_1$
-filters satisfy “classical” properties. Most notably, the quotient of such subalgebra over the Leibniz congruence of any of its
![]() ${\mathscr {C}}_1$
-filters is a Boolean Algebra (Theorem 6.6). The results of this section lay the groundwork for Sections 7 and 8.
${\mathscr {C}}_1$
-filters is a Boolean Algebra (Theorem 6.6). The results of this section lay the groundwork for Sections 7 and 8.
Throughout the present section let
![]() ${\mathcal {S}}$
be an extension of
${\mathcal {S}}$
be an extension of
![]() ${\mathscr {C}}_1$
, extended itself by
${\mathscr {C}}_1$
, extended itself by
![]() $\mathcal {CL}$
, that is,
$\mathcal {CL}$
, that is,
![]() ${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
. Let also
${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
. Let also
![]() ${\boldsymbol {A}}$
be an arbitrary fixed algebra. Consider the subset
${\boldsymbol {A}}$
be an arbitrary fixed algebra. Consider the subset
![]() and let
and let
![]() ${\boldsymbol {A}}^{\circ }$
be the subalgebra of
${\boldsymbol {A}}^{\circ }$
be the subalgebra of
![]() ${\boldsymbol {A}}$
generated by the subuniverse
${\boldsymbol {A}}$
generated by the subuniverse
![]() $\mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(A^{\circ })$
.
$\mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(A^{\circ })$
.
Let us start by observing that the subset
![]() $A^{\circ }$
is in fact a subuniverse of A.
$A^{\circ }$
is in fact a subuniverse of A.
Lemma 6.1. For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() $A^{\circ } = \mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(A^{\circ })$
.
$A^{\circ } = \mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(A^{\circ })$
.
Proof Let
![]() $a,b \in A^{\circ }$
. That is,
$a,b \in A^{\circ }$
. That is,
![]() . It follows by axioms (Ax12), (Ax13), and (Ax14) and Lemma 3.2.19 that
. It follows by axioms (Ax12), (Ax13), and (Ax14) and Lemma 3.2.19 that
![]() , respectively. That is,
, respectively. That is,
![]() $a \wedge b, a \vee b, a \to b, \neg a \in A^{\circ }$
. Thus,
$a \wedge b, a \vee b, a \to b, \neg a \in A^{\circ }$
. Thus,
![]() $A^{\circ }$
is closed under the language operations.
$A^{\circ }$
is closed under the language operations.
In light of Lemma 6.1, from here on, we shall denote the subuniverse
![]() $\mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(A^{\circ })$
simply by
$\mathrm {Sg}_{\mathcal {L}}^{\boldsymbol {A}}(A^{\circ })$
simply by
![]() $A^{\circ }$
. Another useful observation is that
$A^{\circ }$
. Another useful observation is that
![]() $a^{\circ } \in A^{\circ }$
, for every
$a^{\circ } \in A^{\circ }$
, for every
![]() $a \in A$
. We register this fact for future reference.
$a \in A$
. We register this fact for future reference.
Lemma 6.2. For every
![]() ${\boldsymbol {A}}$
and
${\boldsymbol {A}}$
and
![]() $a \in A$
,
$a \in A$
,
![]() $a^{\circ } \in A^{\circ }$
.
$a^{\circ } \in A^{\circ }$
.
Our first goal is to show that, by restricting ourselves to the subuniverse
![]() $A^{\circ }$
, the Leibniz congruence on
$A^{\circ }$
, the Leibniz congruence on
![]() ${\boldsymbol {A}}^{\circ }$
of
${\boldsymbol {A}}^{\circ }$
of
![]() ${\mathcal {S}}$
-filters of
${\mathcal {S}}$
-filters of
![]() ${\boldsymbol {A}}^{\circ }$
can be “classically” characterized. For ease of notation we shall drop the superscript
${\boldsymbol {A}}^{\circ }$
can be “classically” characterized. For ease of notation we shall drop the superscript
![]() $^{\boldsymbol {A}}$
on
$^{\boldsymbol {A}}$
on
![]() ${a^{\circ }}^{\boldsymbol {A}}$
.
${a^{\circ }}^{\boldsymbol {A}}$
.
Proposition 6.3. For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() and
and
![]() $a,b \in A^{\circ }$
,
$a,b \in A^{\circ }$
,
Proof Let
![]() ${\boldsymbol {A}}$
arbitrary and
${\boldsymbol {A}}$
arbitrary and
![]() . Consider the relation
. Consider the relation
![]() $R \subseteq A^{\circ } \times A^{\circ }$
defined by
$R \subseteq A^{\circ } \times A^{\circ }$
defined by
![]() $x R\, y$
iff
$x R\, y$
iff
![]() $x \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} y \in F$
. Suppose
$x \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} y \in F$
. Suppose
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
. It follows by Proposition 4.1 that
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
. It follows by Proposition 4.1 that
![]() $a \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} b \in F$
. Thus,
$a \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} b \in F$
. Thus,
![]() $a\,Rb$
. Conversely, we claim that R is a congruence relation on
$a\,Rb$
. Conversely, we claim that R is a congruence relation on
![]() ${\boldsymbol {A}}^{\circ }$
compatible with F. First, it should be clear from Lemma 3.2.1–3 that R is an equivalence relation. Next, it follows by Lemma 3.2.4–6 that R is compatible with the language operations
${\boldsymbol {A}}^{\circ }$
compatible with F. First, it should be clear from Lemma 3.2.1–3 that R is an equivalence relation. Next, it follows by Lemma 3.2.4–6 that R is compatible with the language operations
![]() $\wedge , \vee , \to $
, respectively. To see that it is also compatible with the operation
$\wedge , \vee , \to $
, respectively. To see that it is also compatible with the operation
![]() $\neg $
, let
$\neg $
, let
![]() $x,y \in A^{\circ }$
such that
$x,y \in A^{\circ }$
such that
![]() $x R\, y$
. Then,
$x R\, y$
. Then,
![]() . It follows by Lemma 3.2.8 that
. It follows by Lemma 3.2.8 that
![]() $\neg x \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} \neg y \in F$
. Finally, it is clear by (MP) that R is compatible with F. Thus,
$\neg x \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} \neg y \in F$
. Finally, it is clear by (MP) that R is compatible with F. Thus,
![]() $R \subseteq {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
.
$R \subseteq {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
.
Corollary 6.4. For every
![]() ${\boldsymbol {A}}$
and
${\boldsymbol {A}}$
and
,
Corollary 6.4 reinforces the “classical” flavour of the subalgebra
![]() ${\boldsymbol {A}}^{\circ }$
. Recall that the Leibniz congruence and Frege relation coincide on classical filters, for arbitrary algebras.
${\boldsymbol {A}}^{\circ }$
. Recall that the Leibniz congruence and Frege relation coincide on classical filters, for arbitrary algebras.
As it turns out, not only is the Leibniz congruence on
![]() ${\boldsymbol {A}}^{\circ }$
of an
${\boldsymbol {A}}^{\circ }$
of an
![]() ${\mathcal {S}}$
-filter classically defined (Proposition 6.3), but it is actually a congruence relative to
${\mathcal {S}}$
-filter classically defined (Proposition 6.3), but it is actually a congruence relative to
![]() $\mathsf {BA}$
.Footnote
9
(Theorem 6.6) In order to prove it, we compile some auxiliary facts, whose proofs we leave for the reader—item 3 below is proved in [Reference Carnielli and Marcos15, Proposition 4.2].
$\mathsf {BA}$
.Footnote
9
(Theorem 6.6) In order to prove it, we compile some auxiliary facts, whose proofs we leave for the reader—item 3 below is proved in [Reference Carnielli and Marcos15, Proposition 4.2].
Lemma 6.5.
-
1.
 $ \vdash _{{\mathscr {C}}_1} (\varphi \wedge \psi ) \vee \xi \to (\varphi \vee \psi ) \wedge (\psi \vee \xi )$
.
$ \vdash _{{\mathscr {C}}_1} (\varphi \wedge \psi ) \vee \xi \to (\varphi \vee \psi ) \wedge (\psi \vee \xi )$
. -
2.
 $ \vdash _{{\mathscr {C}}_1} (\varphi \vee \psi ) \wedge (\psi \vee \xi ) \to (\varphi \wedge \psi ) \vee \xi $
.
$ \vdash _{{\mathscr {C}}_1} (\varphi \vee \psi ) \wedge (\psi \vee \xi ) \to (\varphi \wedge \psi ) \vee \xi $
. -
3.
 $\varphi \vdash _{{\mathscr {C}}_1} \varphi \leftrightarrow (\psi \vee \neg \psi )$
.
$\varphi \vdash _{{\mathscr {C}}_1} \varphi \leftrightarrow (\psi \vee \neg \psi )$
. -
4.
 $ \vdash _{{\mathscr {C}}_1} (\psi \wedge \neg \psi ) \leftrightarrow \neg \neg (\psi \wedge \neg \psi )$
.
$ \vdash _{{\mathscr {C}}_1} (\psi \wedge \neg \psi ) \leftrightarrow \neg \neg (\psi \wedge \neg \psi )$
. -
5.
 $\varphi ,\varphi ^{\circ },\psi ^{\circ } \vdash _{{\mathscr {C}}_1} (\psi \wedge \neg \psi ) \leftrightarrow \neg \varphi $
.
$\varphi ,\varphi ^{\circ },\psi ^{\circ } \vdash _{{\mathscr {C}}_1} (\psi \wedge \neg \psi ) \leftrightarrow \neg \varphi $
.
Theorem 6.6. For every
![]() ${\boldsymbol {A}}$
and
${\boldsymbol {A}}$
and
![]() ,
,
![]() ${\boldsymbol {A}}^{\circ }/{\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F) \in \mathsf {BA}$
.
${\boldsymbol {A}}^{\circ }/{\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F) \in \mathsf {BA}$
.
Proof Let
![]() ${\boldsymbol {A}}$
arbitrary and
${\boldsymbol {A}}$
arbitrary and
![]() . Fix
. Fix
![]() . We must prove that
. We must prove that
![]() $\langle {\boldsymbol {B}} , \wedge ^{\boldsymbol {B}} , \vee ^{\boldsymbol {B}} , \to ^{\boldsymbol {B}} , \neg ^{\boldsymbol {B}} \rangle $
is a distributive, bounded, and complemented lattice. Let
$\langle {\boldsymbol {B}} , \wedge ^{\boldsymbol {B}} , \vee ^{\boldsymbol {B}} , \to ^{\boldsymbol {B}} , \neg ^{\boldsymbol {B}} \rangle $
is a distributive, bounded, and complemented lattice. Let
![]() $\pi : {\boldsymbol {A}}^{\circ } \to {\boldsymbol {B}}$
be the natural map. For every
$\pi : {\boldsymbol {A}}^{\circ } \to {\boldsymbol {B}}$
be the natural map. For every
![]() $a,b \in A^{\circ }$
, define the relation
$a,b \in A^{\circ }$
, define the relation
![]() $\leq ^{\boldsymbol {B}} \subseteq B \times B$
by
$\leq ^{\boldsymbol {B}} \subseteq B \times B$
by
It is easy to see that
![]() $\leq ^{\boldsymbol {B}}$
is reflexive and transitive, by Lemma 3.2.11 and 12. Furthermore, if
$\leq ^{\boldsymbol {B}}$
is reflexive and transitive, by Lemma 3.2.11 and 12. Furthermore, if
![]() $\pi (a) \leq ^{\boldsymbol {B}} \pi (b)$
and
$\pi (a) \leq ^{\boldsymbol {B}} \pi (b)$
and
![]() $\pi (b) \leq ^{\boldsymbol {B}} \pi (a)$
, that is,
$\pi (b) \leq ^{\boldsymbol {B}} \pi (a)$
, that is,
![]() $a \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} b \in F$
, it follows by Proposition 6.3 that
$a \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} b \in F$
, it follows by Proposition 6.3 that
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
, and hence
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
, and hence
![]() $\pi (a) = \pi (b)$
. So,
$\pi (a) = \pi (b)$
. So,
![]() $\leq ^{\boldsymbol {B}}$
is a partial order on
$\leq ^{\boldsymbol {B}}$
is a partial order on
![]() ${\boldsymbol {B}}$
.
${\boldsymbol {B}}$
.
It follows by (Ax3), (Ax4), and (Ax5) that
![]() $\wedge ^{\boldsymbol {B}}$
is the infimum induced by the order
$\wedge ^{\boldsymbol {B}}$
is the infimum induced by the order
![]() $\leq ^{\boldsymbol {B}}$
, and by (Ax6), (Ax7), and (Ax8) that
$\leq ^{\boldsymbol {B}}$
, and by (Ax6), (Ax7), and (Ax8) that
![]() $\vee ^{\boldsymbol {B}}$
is the supremum induced by the order
$\vee ^{\boldsymbol {B}}$
is the supremum induced by the order
![]() $\leq ^{\boldsymbol {B}}$
. So,
$\leq ^{\boldsymbol {B}}$
. So,
![]() $\langle {\boldsymbol {B}} , \wedge ^{\boldsymbol {B}} , \vee ^{\boldsymbol {B}} \rangle $
is indeed a lattice. Moreover, it follows by Lemma 6.5.1 and 2 that it is a distributive lattice.
$\langle {\boldsymbol {B}} , \wedge ^{\boldsymbol {B}} , \vee ^{\boldsymbol {B}} \rangle $
is indeed a lattice. Moreover, it follows by Lemma 6.5.1 and 2 that it is a distributive lattice.
We next prove that
![]() ${\boldsymbol {B}}$
is limited. Let
${\boldsymbol {B}}$
is limited. Let
![]() $a \in F \subseteq A^{\circ }$
and
$a \in F \subseteq A^{\circ }$
and
![]() $b \in A^{\circ }$
. It follows by (Ax1) and (MP) that
$b \in A^{\circ }$
. It follows by (Ax1) and (MP) that
![]() $b \to ^{{\boldsymbol {A}}^{\circ }} a \in F$
, that is,
$b \to ^{{\boldsymbol {A}}^{\circ }} a \in F$
, that is,
![]() $\pi (b) \leq ^{\boldsymbol {B}} \pi (a)$
. So,
$\pi (b) \leq ^{\boldsymbol {B}} \pi (a)$
. So,
![]() $\pi (a)$
is the top element of B w.r.t. the order
$\pi (a)$
is the top element of B w.r.t. the order
![]() $\leq ^{\boldsymbol {B}}$
. In particular,
$\leq ^{\boldsymbol {B}}$
. In particular,
![]() $\pi (\neg ^{{\boldsymbol {A}}^{\circ }} b) \leq ^{\boldsymbol {B}} \pi (a)$
, i.e.,
$\pi (\neg ^{{\boldsymbol {A}}^{\circ }} b) \leq ^{\boldsymbol {B}} \pi (a)$
, i.e.,
![]() $\neg ^{{\boldsymbol {A}}^{\circ }} b \to ^{{\boldsymbol {A}}^{\circ }} a \in F$
. Since
$\neg ^{{\boldsymbol {A}}^{\circ }} b \to ^{{\boldsymbol {A}}^{\circ }} a \in F$
. Since
![]() $a \in A^{\circ }$
, we have
$a \in A^{\circ }$
, we have
![]() . It follows by Lemma 3.2.7 that
. It follows by Lemma 3.2.7 that
![]() $\neg ^{{\boldsymbol {A}}^{\circ }} a \to ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} b \in F$
. But
$\neg ^{{\boldsymbol {A}}^{\circ }} a \to ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} b \in F$
. But
![]() $\neg ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} b \to ^{{\boldsymbol {A}}^{\circ }} b \in F$
by (Ax10), so by transitivity
$\neg ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} b \to ^{{\boldsymbol {A}}^{\circ }} b \in F$
by (Ax10), so by transitivity
![]() $\neg ^{{\boldsymbol {A}}^{\circ }} a \to ^{{\boldsymbol {A}}^{\circ }} b \in F$
, that is,
$\neg ^{{\boldsymbol {A}}^{\circ }} a \to ^{{\boldsymbol {A}}^{\circ }} b \in F$
, that is,
![]() $\pi (\neg ^{{\boldsymbol {A}}^{\circ }} a) \leq ^{\boldsymbol {B}} \pi (b)$
. Therefore,
$\pi (\neg ^{{\boldsymbol {A}}^{\circ }} a) \leq ^{\boldsymbol {B}} \pi (b)$
. Therefore,
![]() $\neg ^{\boldsymbol {B}} \pi (a)$
is the bottom element of B w.r.t. the order
$\neg ^{\boldsymbol {B}} \pi (a)$
is the bottom element of B w.r.t. the order
![]() $\leq ^{\boldsymbol {B}}$
.
$\leq ^{\boldsymbol {B}}$
.
We are left to prove that
![]() ${\boldsymbol {B}}$
is complemented. Let
${\boldsymbol {B}}$
is complemented. Let
![]() $a \in F \subseteq A^{\circ }$
and
$a \in F \subseteq A^{\circ }$
and
![]() $b \in A^{\circ }$
. It follows by Lemma 6.5.3 that
$b \in A^{\circ }$
. It follows by Lemma 6.5.3 that
![]() $a \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} (b \vee ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} b) \in F$
, and hence
$a \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} (b \vee ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} b) \in F$
, and hence
Moreover, since
![]() and
and
![]() $a \in F$
, it follows by Lemma 6.5.5 that
$a \in F$
, it follows by Lemma 6.5.5 that
![]() $(b \wedge ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} b) \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} a \in F$
, and hence
$(b \wedge ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} b) \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} a \in F$
, and hence
Since we have seen already
![]() $\pi (a)$
and
$\pi (a)$
and
![]() $\neg ^{\boldsymbol {B}} \pi (a)$
to be the top and bottom elements of B, respectively, it follows that
$\neg ^{\boldsymbol {B}} \pi (a)$
to be the top and bottom elements of B, respectively, it follows that
![]() ${\boldsymbol {B}}$
is complemented.
${\boldsymbol {B}}$
is complemented.
7 A sufficient condition for
 ${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
Our goal in this section is to isolate a general condition which will allow us to prove stronger algebraic results than those seen so far for the logic
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
Throughout the present section, let
![]() ${\mathcal {S}}$
be such that
${\mathcal {S}}$
be such that
![]() ${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
and satisfying the following condition: For every
${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
and satisfying the following condition: For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() and
and
![]() $a,b \in A^{\circ }$
,
$a,b \in A^{\circ }$
,
To put it in words, by restricting ourselves to the subuniverse
![]() $A^{\circ }$
, the Leibniz congruence on
$A^{\circ }$
, the Leibniz congruence on
![]() ${\boldsymbol {A}}$
of
${\boldsymbol {A}}$
of
![]() ${\mathcal {S}}$
-filters of
${\mathcal {S}}$
-filters of
![]() ${\boldsymbol {A}}$
can be “classically” characterized. Comparing condition (⋆) with Proposition 6.3, we see that the former is applicable to
${\boldsymbol {A}}$
can be “classically” characterized. Comparing condition (⋆) with Proposition 6.3, we see that the former is applicable to
![]() ${\mathcal {S}}$
-filters of
${\mathcal {S}}$
-filters of
![]() ${\boldsymbol {A}}$
while the latter is applicable to
${\boldsymbol {A}}$
while the latter is applicable to
![]() ${\mathcal {S}}$
-filters of the subalgebra
${\mathcal {S}}$
-filters of the subalgebra
![]() ${\boldsymbol {A}}^{\circ }$
.
${\boldsymbol {A}}^{\circ }$
.
Notice that for every
![]() $a,b \in A^{\circ }$
and every
$a,b \in A^{\circ }$
and every
![]() , we have
, we have
![]() , and hence
, and hence
![]() $a^{\circ } \leftrightarrow b^{\circ } \in F$
. Therefore, condition (⋆) is equivalent to the following condition: For every
$a^{\circ } \leftrightarrow b^{\circ } \in F$
. Therefore, condition (⋆) is equivalent to the following condition: For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() and
and
![]() $a,b \in A^{\circ }$
,
$a,b \in A^{\circ }$
,
and having in mind Lemma 4.2.2, it is also equivalent to the following condition: For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() and
and
![]() $a,b \in A^{\circ }$
,
$a,b \in A^{\circ }$
,
Observe that, as claimed, condition (⋆) does not hold for
![]() ${\mathscr {C}}_1$
. Indeed, consider the algebra
${\mathscr {C}}_1$
. Indeed, consider the algebra
![]() ${\boldsymbol {A}}$
depicted in Figure 2 and fix
${\boldsymbol {A}}$
depicted in Figure 2 and fix
![]() . On the one hand,
. On the one hand,
![]() $a^{\circ } = 1^{\circ } = 1 \in F_0$
and
$a^{\circ } = 1^{\circ } = 1 \in F_0$
and
![]() $a \leftrightarrow 1 \in F_0$
. On the other hand,
$a \leftrightarrow 1 \in F_0$
. On the other hand,
![]() $\langle a,1 \rangle \notin {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F_0) = id_{\boldsymbol {A}}$
.
$\langle a,1 \rangle \notin {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F_0) = id_{\boldsymbol {A}}$
.
In light of Lemma 6.2, a particular case of condition (⋆) arises when dealing with
![]() $a^{\circ },b^{\circ } \in A$
.
$a^{\circ },b^{\circ } \in A$
.
Corollary 7.1. For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() and
and
![]() $a,b \in A$
,
$a,b \in A$
,
The next result is a very important consequence of condition (⋆)—in fact, it is equivalent to it.
Theorem 7.2. For every
![]() ${\boldsymbol {A}}$
and
${\boldsymbol {A}}$
and
![]() ,
,
Proof The inclusion
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\!\downharpoonright _{{\boldsymbol {A}}^{\circ }} \subseteq {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ })$
holds in general by Lemma 2.1.2. As for the converse inclusion, let
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\!\downharpoonright _{{\boldsymbol {A}}^{\circ }} \subseteq {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ })$
holds in general by Lemma 2.1.2. As for the converse inclusion, let
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ })$
. Then
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ })$
. Then
![]() $a \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} b \in F \cap A^{\circ }$
by Proposition 4.1, and therefore
$a \leftrightarrow ^{{\boldsymbol {A}}^{\circ }} b \in F \cap A^{\circ }$
by Proposition 4.1, and therefore
![]() $a \leftrightarrow ^{\boldsymbol {A}} b \in F$
because
$a \leftrightarrow ^{\boldsymbol {A}} b \in F$
because
![]() ${\boldsymbol {A}}^{\circ } \leq {\boldsymbol {A}}$
. Since
${\boldsymbol {A}}^{\circ } \leq {\boldsymbol {A}}$
. Since
![]() $a,b \in A^{\circ }$
, the result now follows by condition (⋆).
$a,b \in A^{\circ }$
, the result now follows by condition (⋆).
Notice that Theorem 7.2 holds for every equivalential extension of
![]() ${\mathscr {C}}_1$
. Indeed, it is known (see [Reference Font32, Lemma 6.72]) that given an equivalential logic
${\mathscr {C}}_1$
. Indeed, it is known (see [Reference Font32, Lemma 6.72]) that given an equivalential logic
![]() ${\mathcal {S}}$
, we have
${\mathcal {S}}$
, we have
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\!\downharpoonright _{{\boldsymbol {B}}} = {\boldsymbol {\varOmega }}^{{\boldsymbol {B}}}(F \cap B)$
, for every algebra
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\!\downharpoonright _{{\boldsymbol {B}}} = {\boldsymbol {\varOmega }}^{{\boldsymbol {B}}}(F \cap B)$
, for every algebra
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() , and every subalgebra
, and every subalgebra
![]() ${\boldsymbol {B}} \leq {\boldsymbol {A}}$
. Theorem 7.2 is simply the particular case for the subalgebra
${\boldsymbol {B}} \leq {\boldsymbol {A}}$
. Theorem 7.2 is simply the particular case for the subalgebra
![]() ${\boldsymbol {A}}^{\circ }$
.
${\boldsymbol {A}}^{\circ }$
.
Theorems 6.6 and 7.2 taken together have one major consequence. As it turns out, the subalgebra
![]() ${\boldsymbol {A}}^{\circ }$
of an algebra
${\boldsymbol {A}}^{\circ }$
of an algebra
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a Boolean algebra.
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a Boolean algebra.
Corollary 7.3. If
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
, then
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
, then
![]() ${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
.
${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
.
Proof Let
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
. Then there exists
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
. Then there exists
![]() such that
such that
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) = id_{\boldsymbol {A}}$
. It follows by Theorem 7.2 that
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) = id_{\boldsymbol {A}}$
. It follows by Theorem 7.2 that
![]() ${\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ }) = {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\!\downharpoonright _{{\boldsymbol {A}}^{\circ }} = id_{\boldsymbol {A}} \downharpoonright _{{\boldsymbol {A}}^{\circ }} = id_{{\boldsymbol {A}}^{\circ }}$
. Since
${\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ }) = {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\!\downharpoonright _{{\boldsymbol {A}}^{\circ }} = id_{\boldsymbol {A}} \downharpoonright _{{\boldsymbol {A}}^{\circ }} = id_{{\boldsymbol {A}}^{\circ }}$
. Since
![]() , it follows by Theorem 6.6 that
, it follows by Theorem 6.6 that
![]() ${\boldsymbol {A}}^{\circ } \cong {\boldsymbol {A}}^{\circ } / {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ }) \in \mathsf {BA}$
.
${\boldsymbol {A}}^{\circ } \cong {\boldsymbol {A}}^{\circ } / {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ }) \in \mathsf {BA}$
.
Corollary 7.3 does not hold for the logic
![]() ${\mathscr {C}}_1$
. Indeed, consider the algebra
${\mathscr {C}}_1$
. Indeed, consider the algebra
![]() ${\boldsymbol {A}}$
whose truth-tables are given as in Table 3. We have
${\boldsymbol {A}}$
whose truth-tables are given as in Table 3. We have
![]() $A^{\circ } = \{ 0,4,5 \}$
. Since
$A^{\circ } = \{ 0,4,5 \}$
. Since
![]() $|A^{\circ }| = 3$
, necessarily
$|A^{\circ }| = 3$
, necessarily
![]() ${\boldsymbol {A}}^{\circ } \notin \mathsf {BA}$
.
${\boldsymbol {A}}^{\circ } \notin \mathsf {BA}$
.
The next two consequences of Corollary 7.3 concern the
![]() ${\mathcal {S}}$
-filters of the subalgebra
${\mathcal {S}}$
-filters of the subalgebra
![]() ${\boldsymbol {A}}^{\circ }$
, and in particular its least element. Given a lattice
${\boldsymbol {A}}^{\circ }$
, and in particular its least element. Given a lattice
![]() $\langle {\boldsymbol {A}} , \wedge , \vee \rangle $
, let
$\langle {\boldsymbol {A}} , \wedge , \vee \rangle $
, let
![]() $\mathrm {Filt}{\boldsymbol {A}}$
denote the set of lattice filters of
$\mathrm {Filt}{\boldsymbol {A}}$
denote the set of lattice filters of
![]() ${\boldsymbol {A}}$
w.r.t. the order
${\boldsymbol {A}}$
w.r.t. the order
![]() $a \leq ^{\boldsymbol {A}} b$
iff
$a \leq ^{\boldsymbol {A}} b$
iff
![]() $a \wedge ^{\boldsymbol {A}} b = a$
iff
$a \wedge ^{\boldsymbol {A}} b = a$
iff
![]() $a \vee ^{\boldsymbol {A}} b = b$
, for every
$a \vee ^{\boldsymbol {A}} b = b$
, for every
![]() $a,b \in A$
. Recall that, given
$a,b \in A$
. Recall that, given
![]() ${\boldsymbol {A}} \in \mathsf {BA}$
, we have
${\boldsymbol {A}} \in \mathsf {BA}$
, we have
![]() .
.
Corollary 7.4. For every
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
,
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
,
![]() .
.
Proof Since
![]() ${\mathcal {S}} \leq \mathcal {CL}$
, the inclusion
${\mathcal {S}} \leq \mathcal {CL}$
, the inclusion
![]() is clear. Conversely, given axioms (Ax4) and (Ax5), we have
is clear. Conversely, given axioms (Ax4) and (Ax5), we have
![]() . Furthermore, since
. Furthermore, since
![]() ${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
by Corollary 7.3, it is well-known that
${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
by Corollary 7.3, it is well-known that
![]() .
.
Corollary 7.5. If
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
, then
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
, then
where
![]() $1$
is the top element of
$1$
is the top element of
![]() ${\boldsymbol {A}}^{\circ }$
.
${\boldsymbol {A}}^{\circ }$
.
Proof It follows by Corollary 7.4 that
![]() , where
, where
![]() $1$
is the top element of
$1$
is the top element of
![]() ${\boldsymbol {A}}^{\circ }$
, having in mind Corollary 7.3. So,
${\boldsymbol {A}}^{\circ }$
, having in mind Corollary 7.3. So,
![]() . Next, since
. Next, since
![]() is an
is an
![]() ${\mathcal {S}}$
-filter of
${\mathcal {S}}$
-filter of
![]() ${\boldsymbol {A}}^{\circ }$
, we have
${\boldsymbol {A}}^{\circ }$
, we have
![]() . So,
. So,
![]() . Finally, let
. Finally, let
![]() . Since both
. Since both
![]() , we have
, we have
![]() . Therefore
. Therefore
![]() , by Proposition 6.3. But
, by Proposition 6.3. But
![]() , using Theorem 7.2 and the fact
, using Theorem 7.2 and the fact
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
. Thus
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
. Thus
![]() $a = 1$
, and therefore
$a = 1$
, and therefore
![]() .
.
8 Subdirectly irreducible algebras relative to
 ${\mathsf {Alg}}^*({\mathcal {S}})$
${\mathsf {Alg}}^*({\mathcal {S}})$
We are now ready to investigate the subdirectly irreducible algebras in
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
relative to
${\mathsf {Alg}}^*({\mathcal {S}})$
relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, and to prove the two main results of Part II (Theorems 8.3 and 8.7), namely:
${\mathsf {Alg}}^*({\mathcal {S}})$
, and to prove the two main results of Part II (Theorems 8.3 and 8.7), namely:
-
1. Let
 ${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
satisfy condition (⋆). If
${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
satisfy condition (⋆). If
 ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a non-trivial algebra subdirectly irreducible relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a non-trivial algebra subdirectly irreducible relative to
 ${\mathsf {Alg}}^*({\mathcal {S}})$
, then
${\mathsf {Alg}}^*({\mathcal {S}})$
, then
 .
. -
2. Let
 ${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
be finitely equivalential with set of congruence formulas
${\mathscr {C}}_1 \leq {\mathcal {S}} \leq \mathcal {CL}$
be finitely equivalential with set of congruence formulas
 ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
. If
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
. If
 ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a non-trivial algebra subdirectly irreducible relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a non-trivial algebra subdirectly irreducible relative to
 ${\mathsf {Alg}}^*({\mathcal {S}})$
, then
${\mathsf {Alg}}^*({\mathcal {S}})$
, then
 $|A| \leq 3$
.
$|A| \leq 3$
.
We start by discarding the case of a trivial (Boolean) algebra in Corollary 7.3. Unless otherwise stated, we continue to assume that the underlying logic
![]() ${\mathcal {S}}$
satisfies condition (⋆).
${\mathcal {S}}$
satisfies condition (⋆).
Lemma 8.1. If
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is non-trivial, then
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is non-trivial, then
![]() ${\boldsymbol {A}}^{\circ }$
is non-trivial.
${\boldsymbol {A}}^{\circ }$
is non-trivial.
Proof If
![]() $A = A^{\circ }$
, then the result follows immediately by assumption. Assume therefore that there exists
$A = A^{\circ }$
, then the result follows immediately by assumption. Assume therefore that there exists
![]() $a \in A - A^{\circ }$
. Suppose for the sake of contradiction that
$a \in A - A^{\circ }$
. Suppose for the sake of contradiction that
![]() $A^{\circ } = \{b\}$
, for some
$A^{\circ } = \{b\}$
, for some
![]() $b \in A$
. Then,
$b \in A$
. Then,
![]() . Fix
. Fix
![]() . We first claim that we can assume, without loss of generality, that
. We first claim that we can assume, without loss of generality, that
![]() $a \in F$
. Indeed notice that
$a \in F$
. Indeed notice that
![]() $b^{\circ } \in A^{\circ }$
, so necessarily
$b^{\circ } \in A^{\circ }$
, so necessarily
![]() . Moreover
. Moreover
![]() $a \to ^{\boldsymbol {A}} b \in F$
, by (Ax1) and (MP). It follows by Lemma 3.2.7 that
$a \to ^{\boldsymbol {A}} b \in F$
, by (Ax1) and (MP). It follows by Lemma 3.2.7 that
![]() $\neg ^{\boldsymbol {A}} b \to ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} a \in F$
. But,
$\neg ^{\boldsymbol {A}} b \to ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} a \in F$
. But,
![]() $\neg ^{\boldsymbol {A}} b = \neg ^{{\boldsymbol {A}}^{\circ }} b = b$
, because
$\neg ^{\boldsymbol {A}} b = \neg ^{{\boldsymbol {A}}^{\circ }} b = b$
, because
![]() ${\boldsymbol {A}}^{\circ } \leq {\boldsymbol {A}}$
and
${\boldsymbol {A}}^{\circ } \leq {\boldsymbol {A}}$
and
![]() $A^{\circ } = \{b\}$
, respectively. It follows by (MP) that
$A^{\circ } = \{b\}$
, respectively. It follows by (MP) that
![]() $\neg ^{\boldsymbol {A}} a \in F$
. Now, if by chance
$\neg ^{\boldsymbol {A}} a \in F$
. Now, if by chance
![]() $\neg ^{\boldsymbol {A}} a = b$
, then
$\neg ^{\boldsymbol {A}} a = b$
, then
![]() $\neg ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} a = \neg ^{\boldsymbol {A}} b = \neg ^{{\boldsymbol {A}}^{\circ }} b = b \in F$
, and therefore by (Ax10) and (MP) we have
$\neg ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} a = \neg ^{\boldsymbol {A}} b = \neg ^{{\boldsymbol {A}}^{\circ }} b = b \in F$
, and therefore by (Ax10) and (MP) we have
![]() $a \in F$
. So, either
$a \in F$
. So, either
![]() $\neg ^{\boldsymbol {A}} a \neq b$
and
$\neg ^{\boldsymbol {A}} a \neq b$
and
![]() $\neg ^{\boldsymbol {A}} a \in F$
, or
$\neg ^{\boldsymbol {A}} a \in F$
, or
![]() $\neg ^{\boldsymbol {A}} a = b$
and
$\neg ^{\boldsymbol {A}} a = b$
and
![]() $a \in F$
. In any case, there exists
$a \in F$
. In any case, there exists
![]() $c \in A - A^{\circ }$
such that
$c \in A - A^{\circ }$
such that
![]() $c \in F$
. Assume therefore that
$c \in F$
. Assume therefore that
![]() $a \in F$
. We next claim that
$a \in F$
. We next claim that
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. On the one hand, since both
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. On the one hand, since both
![]() $a,b \in F$
, we have
$a,b \in F$
, we have
![]() $a \leftrightarrow ^{\boldsymbol {A}} b \in F$
. On the other hand, notice that
$a \leftrightarrow ^{\boldsymbol {A}} b \in F$
. On the other hand, notice that
![]() $a^{\circ } = b^{\circ } = b \in F$
, because
$a^{\circ } = b^{\circ } = b \in F$
, because
![]() $A^{\circ } = \{b\}$
. It follows by condition (⋆) that
$A^{\circ } = \{b\}$
. It follows by condition (⋆) that
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. But
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. But
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) = id_{\boldsymbol {A}}$
, because
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) = id_{\boldsymbol {A}}$
, because
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
. Thus
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
. Thus
![]() $a = b$
, and we reach an absurdity.
$a = b$
, and we reach an absurdity.
Lemma 8.2. For every
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
and every
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
and every
![]() , there exists
, there exists
![]() such that
such that
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(G) \!\!\downharpoonright _{{\boldsymbol {A}}^{\circ }} = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
.
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(G) \!\!\downharpoonright _{{\boldsymbol {A}}^{\circ }} = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
.
Proof Consider the
![]() ${\mathcal {L}}$
-matrix
${\mathcal {L}}$
-matrix
![]() and its
and its
![]() ${\mathcal {L}}$
-submatrix
${\mathcal {L}}$
-submatrix
![]() . Since
. Since
![]() by Corollary 7.5, and the class
by Corollary 7.5, and the class
![]() ${\mathsf {Mod}}({\mathcal {S}})$
has the FEP by the remark following Theorem 3.10.3, we conclude that for every
${\mathsf {Mod}}({\mathcal {S}})$
has the FEP by the remark following Theorem 3.10.3, we conclude that for every
![]() there exists
there exists
![]() such that
such that
![]() $F = G \cap A^{\circ }$
. It now follows by Theorem 7.2 that
$F = G \cap A^{\circ }$
. It now follows by Theorem 7.2 that
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(G) \!\!\downharpoonright _{{\boldsymbol {A}}^{\circ }} = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}\big ( G \cap A^{\circ } \big ) = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
.
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(G) \!\!\downharpoonright _{{\boldsymbol {A}}^{\circ }} = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}\big ( G \cap A^{\circ } \big ) = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F)$
.
We are now able to identify, up to isomorphism, the (Boolean) subalgebra
![]() ${\boldsymbol {A}}^{\circ }$
of any non-trivial algebra
${\boldsymbol {A}}^{\circ }$
of any non-trivial algebra
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
.
${\mathsf {Alg}}^*({\mathcal {S}})$
.
Theorem 8.3. If
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a non-trivial algebra subdirectly irreducible relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a non-trivial algebra subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, then
${\mathsf {Alg}}^*({\mathcal {S}})$
, then
![]() .
.
Proof Let
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
be a non-trivial algebra subdirectly irreducible relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
be a non-trivial algebra subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
. Fix
${\mathsf {Alg}}^*({\mathcal {S}})$
. Fix
![]() and
and
![]() . We claim that
. We claim that
![]() $\vartheta = \min \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
. First, since
$\vartheta = \min \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
. First, since
![]() $\theta \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}$
, there exists
$\theta \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}$
, there exists
![]() such that
such that
![]() $\theta = {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. So,
$\theta = {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. So,
![]() $\vartheta = {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\! \downharpoonright _{{\boldsymbol {A}}^{\circ }} = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ }) \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}^{\circ }$
, using Theorem 7.2. Next, let
$\vartheta = {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \!\! \downharpoonright _{{\boldsymbol {A}}^{\circ }} = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ }) \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}^{\circ }$
, using Theorem 7.2. Next, let
![]() $\alpha \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
. On the one hand, there exists
$\alpha \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
. On the one hand, there exists
![]() such that
such that
![]() $\alpha = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(G)$
. On the other hand, by Lemma 8.2 there exists
$\alpha = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(G)$
. On the other hand, by Lemma 8.2 there exists
![]() such that
such that
![]() $\alpha = {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H) \!\! \downharpoonright _{{\boldsymbol {A}}^{\circ }}$
. Since
$\alpha = {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H) \!\! \downharpoonright _{{\boldsymbol {A}}^{\circ }}$
. Since
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H) \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}$
and
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H) \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}$
and
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H) \neq id_{\boldsymbol {A}}$
(otherwise
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H) \neq id_{\boldsymbol {A}}$
(otherwise
![]() $\alpha = id_{{\boldsymbol {A}}^{\circ }}$
), we must have
$\alpha = id_{{\boldsymbol {A}}^{\circ }}$
), we must have
![]() $\theta \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H)$
. Hence
$\theta \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H)$
. Hence
![]() $\vartheta = \theta \!\! \downharpoonright _{{\boldsymbol {A}}^{\circ }} \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H) \!\! \downharpoonright _{{\boldsymbol {A}}^{\circ }} = \alpha $
. Thus,
$\vartheta = \theta \!\! \downharpoonright _{{\boldsymbol {A}}^{\circ }} \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(H) \!\! \downharpoonright _{{\boldsymbol {A}}^{\circ }} = \alpha $
. Thus,
![]() $\vartheta = \min \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
, as claimed.
$\vartheta = \min \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
, as claimed.
We now claim that
![]() ${\boldsymbol {A}}^{\circ }$
is subdirectly irreducible. We know that
${\boldsymbol {A}}^{\circ }$
is subdirectly irreducible. We know that
![]() , by Corollary 7.4. Therefore,
, by Corollary 7.4. Therefore,
![]() $\vartheta = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ }) \in \mathrm {Co}_{\mathsf {BA}}{\boldsymbol {A}}^{\circ }$
. Moreover, since
$\vartheta = {\boldsymbol {\varOmega }}^{{\boldsymbol {A}}^{\circ }}(F \cap A^{\circ }) \in \mathrm {Co}_{\mathsf {BA}}{\boldsymbol {A}}^{\circ }$
. Moreover, since
![]() $\mathsf {BA} \subseteq {\mathsf {Alg}}^*({\mathcal {S}})$
, it also holds
$\mathsf {BA} \subseteq {\mathsf {Alg}}^*({\mathcal {S}})$
, it also holds
![]() $\vartheta = \min \mathrm {Co}_{\mathsf {BA}}{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
. Finally, since
$\vartheta = \min \mathrm {Co}_{\mathsf {BA}}{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
. Finally, since
![]() $\mathsf {BA}$
is closed under
$\mathsf {BA}$
is closed under
![]() $\mathbb {H}$
,
$\mathbb {H}$
,
![]() $\mathrm {Co}_{\mathsf {BA}}{\boldsymbol {A}}^{\circ } = \mathrm {Co}\,{\boldsymbol {A}}^{\circ }$
, and hence
$\mathrm {Co}_{\mathsf {BA}}{\boldsymbol {A}}^{\circ } = \mathrm {Co}\,{\boldsymbol {A}}^{\circ }$
, and hence
![]() $\vartheta = \min \mathrm {Co}\,{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
. We conclude that
$\vartheta = \min \mathrm {Co}\,{\boldsymbol {A}}^{\circ } - \{id_{{\boldsymbol {A}}^{\circ }}\}$
. We conclude that
![]() ${\boldsymbol {A}}^{\circ }$
is subdirectly irreducible—see [Reference Burris and Sankappanavar10, Theorem 8.4]. Since
${\boldsymbol {A}}^{\circ }$
is subdirectly irreducible—see [Reference Burris and Sankappanavar10, Theorem 8.4]. Since
![]() ${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
is non-trivial by Lemma 8.1, it can only be the case
${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
is non-trivial by Lemma 8.1, it can only be the case
![]() .
.
Having determined the cardinality of the subuniverse
![]() $A^{\circ }$
, given
$A^{\circ }$
, given
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
non-trivial subdirectly irreducible relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
non-trivial subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, we now wish to determine the cardinality of the universe A itself. In fact, we want to prove that
${\mathsf {Alg}}^*({\mathcal {S}})$
, we now wish to determine the cardinality of the universe A itself. In fact, we want to prove that
![]() $|A| \leq 3$
. For this purpose we will need to strengthen our assumption over
$|A| \leq 3$
. For this purpose we will need to strengthen our assumption over
![]() ${\mathcal {S}}$
. The next auxiliary results however still holds under our current assumption, that is,
${\mathcal {S}}$
. The next auxiliary results however still holds under our current assumption, that is,
![]() ${\mathcal {S}}$
satisfying (⋆). In light of Corollary 7.3, let
${\mathcal {S}}$
satisfying (⋆). In light of Corollary 7.3, let
![]() $1$
denote the top element of
$1$
denote the top element of
![]() ${\boldsymbol {A}}^{\circ }$
and let
${\boldsymbol {A}}^{\circ }$
and let
![]() $0 = \neg 1$
.
$0 = \neg 1$
.
Lemma 8.4. Let
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
be a non-trivial subdirectly irreducible algebra relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
be a non-trivial subdirectly irreducible algebra relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
. For every
${\mathsf {Alg}}^*({\mathcal {S}})$
. For every
![]() $a \in A^{\circ }$
,
$a \in A^{\circ }$
,
![]() $a^{\circ } = 1$
; for every
$a^{\circ } = 1$
; for every
![]() $a \in A - A^{\circ }$
,
$a \in A - A^{\circ }$
,
![]() $a^{\circ } = 0$
.
$a^{\circ } = 0$
.
Proof First, it should be clear that for every
![]() $a \in A^{\circ }$
, we have
$a \in A^{\circ }$
, we have
![]() $\neg ^{\boldsymbol {A}} (a \wedge ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} a) = \neg ^{{\boldsymbol {A}}^{\circ }} (a \wedge ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} a) = \neg ^{{\boldsymbol {A}}^{\circ }} 0 = 1$
, because
$\neg ^{\boldsymbol {A}} (a \wedge ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} a) = \neg ^{{\boldsymbol {A}}^{\circ }} (a \wedge ^{{\boldsymbol {A}}^{\circ }} \neg ^{{\boldsymbol {A}}^{\circ }} a) = \neg ^{{\boldsymbol {A}}^{\circ }} 0 = 1$
, because
![]() ${\boldsymbol {A}}^{\circ } \leq {\boldsymbol {A}}$
and
${\boldsymbol {A}}^{\circ } \leq {\boldsymbol {A}}$
and
![]() ${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
. Next, let
${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
. Next, let
![]() $a \in A - A^{\circ }$
. We know by Theorem 8.3 that
$a \in A - A^{\circ }$
. We know by Theorem 8.3 that
![]() . But
. But
![]() $a^{\circ } \in A^{\circ } = \{0,1\}$
, using Lemma 6.2. If
$a^{\circ } \in A^{\circ } = \{0,1\}$
, using Lemma 6.2. If
![]() (recall Corollary 7.5), then
(recall Corollary 7.5), then
![]() $a \in A^{\circ }$
and we reach an absurdity. Necessarily,
$a \in A^{\circ }$
and we reach an absurdity. Necessarily,
![]() $a^{\circ } = 0$
.
$a^{\circ } = 0$
.
Corollary 8.5. Let
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
be a non-trivial subdirectly irreducible algebra relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
be a non-trivial subdirectly irreducible algebra relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
.
${\mathsf {Alg}}^*({\mathcal {S}})$
.
-
1.
 .
. -
2.
 .
. -
3.
 $\mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}} = \{ id_{\boldsymbol {A}} , A \times A \}$
.
$\mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}} = \{ id_{\boldsymbol {A}} , A \times A \}$
.
Proof
1. Let
![]() $a \in A - A^{\circ }$
. Then
$a \in A - A^{\circ }$
. Then
![]() $a^{\circ } = 0$
, by Lemma 8.4. So,
$a^{\circ } = 0$
, by Lemma 8.4. So,
![]() . Since
. Since
![]() $\neg \varphi ^{\circ } = \neg \neg (\varphi \wedge \neg \varphi )$
, it follows by (Ax10) that
$\neg \varphi ^{\circ } = \neg \neg (\varphi \wedge \neg \varphi )$
, it follows by (Ax10) that
![]() , and then by (Ax3) that
, and then by (Ax3) that
![]() . Thus,
. Thus,
![]() . Since
. Since
![]() $A^{\circ } = \{0,1\}$
and
$A^{\circ } = \{0,1\}$
and
![]() , it can only be the case
, it can only be the case
![]() . Indeed, if
. Indeed, if
![]() , then
, then
![]() , so
, so
![]() , using the fact
, using the fact
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
, and it would follow that A is trivial.
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
, and it would follow that A is trivial.
2. It follows immediately by 1.
3. Every
![]() $\theta \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}$
is of the form
$\theta \in \mathrm {Co}_{{\mathsf {Alg}}^*({\mathcal {S}})}{\boldsymbol {A}}$
is of the form
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
with
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
with
![]() , so the result follows by 2, having in mind that
, so the result follows by 2, having in mind that
![]() and
and
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(A) = A \times A$
.
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(A) = A \times A$
.
For the last result of the section let
![]() ${\mathcal {S}}$
be a finitary and finitely equivalential extension of
${\mathcal {S}}$
be a finitary and finitely equivalential extension of
![]() ${\mathscr {C}}_1$
, extended itself by
${\mathscr {C}}_1$
, extended itself by
![]() $\mathcal {CL}$
, with (finite) set of congruence formulas
$\mathcal {CL}$
, with (finite) set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
. Let us first see that our new assumption is stronger than condition (⋆).
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
. Let us first see that our new assumption is stronger than condition (⋆).
Lemma 8.6. If
![]() ${\mathcal {S}}$
is finitely equivalential with a set of congruence formulas
${\mathcal {S}}$
is finitely equivalential with a set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
, then
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
, then
![]() ${\mathcal {S}}$
satisfies (⋆).
${\mathcal {S}}$
satisfies (⋆).
Proof Our hypothesis tells us that for every algebra
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() and
and
![]() $a,b \in A$
,
$a,b \in A$
,
But this clearly implies (⋆⋆)—which is the particular case where
![]() $a,b \in A^{\circ }$
—and we have seen it already to be equivalent to (⋆).
$a,b \in A^{\circ }$
—and we have seen it already to be equivalent to (⋆).
Theorem 8.7. If
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a non-trivial algebra subdirectly irreducible relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a non-trivial algebra subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, then
${\mathsf {Alg}}^*({\mathcal {S}})$
, then
![]() $|A| \leq 3$
.
$|A| \leq 3$
.
Proof Let
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
be a non-trivial algebra subdirectly irreducible relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
be a non-trivial algebra subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
. Then
${\mathsf {Alg}}^*({\mathcal {S}})$
. Then
![]() $|A^{\circ }| = 2$
, by Theorem 8.3. Assume for the sake of contradiction that there exist
$|A^{\circ }| = 2$
, by Theorem 8.3. Assume for the sake of contradiction that there exist
![]() $a,b \in A - A^{\circ }$
, with
$a,b \in A - A^{\circ }$
, with
![]() $a \neq b$
. Then
$a \neq b$
. Then
![]() $a^{\circ }=b^{\circ }=0$
by Lemma 8.4, and therefore
$a^{\circ }=b^{\circ }=0$
by Lemma 8.4, and therefore
![]() . Since
. Since
![]() $\neg \varphi ^{\circ } = \neg \neg (\varphi \wedge \neg \varphi )$
, it follows by (Ax10) that
$\neg \varphi ^{\circ } = \neg \neg (\varphi \wedge \neg \varphi )$
, it follows by (Ax10) that
![]() and
and
![]() , and then by (Ax3) and (Ax4) that
, and then by (Ax3) and (Ax4) that
![]() . Clearly then
. Clearly then
![]() and
and
![]() . Since by hypothesis
. Since by hypothesis
![]() ${\mathcal {S}}$
is finitely equivalential with set of congruence formulas
${\mathcal {S}}$
is finitely equivalential with set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
, it follows that
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
, it follows that
![]() , using the fact
, using the fact
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
. We reach a contradiction. Thus
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
. We reach a contradiction. Thus
![]() $|A - A^{\circ }| \leq 1$
, and hence
$|A - A^{\circ }| \leq 1$
, and hence
![]() $|A| \leq 3$
.
$|A| \leq 3$
.
A careful look at the proof of Theorem 8.7 show us why condition (⋆) does not suffice. We need to extend (⋆) to elements
![]() $a,b \in A - A^{\circ }$
. That is: for every
$a,b \in A - A^{\circ }$
. That is: for every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() and
and
![]() $a,b \in A - A^{\circ }$
,
$a,b \in A - A^{\circ }$
,
An important consequence of our stronger assumption on
![]() ${\mathcal {S}}$
(that is,
${\mathcal {S}}$
(that is,
![]() ${\mathcal {S}}$
is finitary and finitely equivalential) is that the class of algebraic reducts of
${\mathcal {S}}$
is finitary and finitely equivalential) is that the class of algebraic reducts of
![]() ${\mathcal {S}}$
is a quasivariety—see [Reference Font32, Corollary 6.80]. Quasivarieties are fully determined by their relative subdirectly irreducible algebras. In Part III, we will characterize the quasivariety
${\mathcal {S}}$
is a quasivariety—see [Reference Font32, Corollary 6.80]. Quasivarieties are fully determined by their relative subdirectly irreducible algebras. In Part III, we will characterize the quasivariety
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
in terms of the subdirectly irreducible algebras in
${\mathsf {Alg}}^*({\mathcal {S}})$
in terms of the subdirectly irreducible algebras in
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
relative to
${\mathsf {Alg}}^*({\mathcal {S}})$
relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, for the equivalential extensions of
${\mathsf {Alg}}^*({\mathcal {S}})$
, for the equivalential extensions of
![]() ${\mathscr {C}}_1$
considered in the literature
${\mathscr {C}}_1$
considered in the literature
![]() . In light of Theorem 8.7, we will do this by determining the truth-tables of the three-element algebras in
. In light of Theorem 8.7, we will do this by determining the truth-tables of the three-element algebras in
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
${\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
.
${\mathsf {Alg}}^*({\mathcal {S}})$
.
Part III. Axiomatic extensions of
![]() $\mathbf {\mathscr {C}}_{\mathbf {1}}$
.
$\mathbf {\mathscr {C}}_{\mathbf {1}}$
.
In this last part we extend our AAL study of
![]() ${\mathscr {C}}_1$
to some of its paraconsistent extensions considered in the literature. To settle the scope of the logics under study, we shall focus ourselves on the so-called
${\mathscr {C}}_1$
to some of its paraconsistent extensions considered in the literature. To settle the scope of the logics under study, we shall focus ourselves on the so-called
![]() $d{\mathscr {C}}$
-systems, according to the terminology of [Reference Carnielli and Marcos16, Section 3.8] or [Reference Carnielli, Coniglio and Marcos17, Section 5.1]. In particular, we shall be mainly interested in the logics
$d{\mathscr {C}}$
-systems, according to the terminology of [Reference Carnielli and Marcos16, Section 3.8] or [Reference Carnielli, Coniglio and Marcos17, Section 5.1]. In particular, we shall be mainly interested in the logics
![]() ${\mathcal {C}ilo}$
,
${\mathcal {C}ilo}$
,
![]() ${\mathcal {C}ilow}$
,
${\mathcal {C}ilow}$
,
![]() ${\mathcal {C}ibv}$
,
${\mathcal {C}ibv}$
,
![]() ,
,
![]() , and
, and
![]() —recall Figure 1 for the inclusion relations among these logics.
—recall Figure 1 for the inclusion relations among these logics.
In the sequel we will only classify sentential logics within the Leibniz hierarchy, leaving aside the Frege hierarchy. The reason for this omission is that every extension of
![]() ${\mathscr {C}}_1$
(weaker than
${\mathscr {C}}_1$
(weaker than
![]() $\mathcal {CL}$
) is not self-extensional—see [Reference Carnielli and Marcos16, Corollary 3.65]—and therefore falls outside the Frege hierarchy.
$\mathcal {CL}$
) is not self-extensional—see [Reference Carnielli and Marcos16, Corollary 3.65]—and therefore falls outside the Frege hierarchy.
9 The logic
 ${\mathcal {C}ilo}$
${\mathcal {C}ilo}$
The goals of this section are to introduce the logic
![]() ${\mathcal {C}ilo}$
, prove that it satisfies condition (⋆) (Corollary 9.2), and classify it within the Leibniz hierarchy (Propositions 9.6 and 9.9). We finish with a brief discussion about the class
${\mathcal {C}ilo}$
, prove that it satisfies condition (⋆) (Corollary 9.2), and classify it within the Leibniz hierarchy (Propositions 9.6 and 9.9). We finish with a brief discussion about the class
![]() ${\mathsf {Alg}}^*({\mathcal {C}ilo})$
in order to clarify a couple of incorrect claims in the literature.
${\mathsf {Alg}}^*({\mathcal {C}ilo})$
in order to clarify a couple of incorrect claims in the literature.
We first consider an extension of
![]() ${\mathscr {C}}_1$
introduced by da Costa, Béziau, and Bueno in [Reference da Costa, Béziau and Bueno24]. We follow the presentation of [Reference Carnielli and Marcos16], as well as the notation adopted there—the reason for choosing the notation
${\mathscr {C}}_1$
introduced by da Costa, Béziau, and Bueno in [Reference da Costa, Béziau and Bueno24]. We follow the presentation of [Reference Carnielli and Marcos16], as well as the notation adopted there—the reason for choosing the notation
![]() ${\mathcal {C}ilo}$
of [Reference Carnielli and Marcos16] instead of the original notation
${\mathcal {C}ilo}$
of [Reference Carnielli and Marcos16] instead of the original notation
![]() ${\mathscr {C}}_1^+$
of [Reference da Costa, Béziau and Bueno24] is so that it does not collide with the notation of the strong version of
${\mathscr {C}}_1^+$
of [Reference da Costa, Béziau and Bueno24] is so that it does not collide with the notation of the strong version of
![]() ${\mathscr {C}}_1$
[Reference Albuquerque, Font and Jansana1]. Let us define the logic
${\mathscr {C}}_1$
[Reference Albuquerque, Font and Jansana1]. Let us define the logic
![]() ${\mathcal {C}ilo}$
as the logic axiomatized by (Ax1)–(Ax11) plus (MP), together with the following axioms:
${\mathcal {C}ilo}$
as the logic axiomatized by (Ax1)–(Ax11) plus (MP), together with the following axioms:
Clearly the logic
![]() ${\mathcal {C}ilo}$
is an extension of
${\mathcal {C}ilo}$
is an extension of
![]() ${\mathscr {C}}_1$
, that is
${\mathscr {C}}_1$
, that is
![]() ${\mathscr {C}}_1 \leq {\mathcal {C}ilo}$
, and therefore Lemma 3.2 still holds for the consequence relation
${\mathscr {C}}_1 \leq {\mathcal {C}ilo}$
, and therefore Lemma 3.2 still holds for the consequence relation
![]() $\vdash _{{\mathcal {C}ilo}}$
. In particular,
$\vdash _{{\mathcal {C}ilo}}$
. In particular,
Although the axiomatization of
![]() ${\mathcal {C}ilo}$
resembles that of
${\mathcal {C}ilo}$
resembles that of
![]() ${\mathscr {C}}_1$
, the logic
${\mathscr {C}}_1$
, the logic
![]() ${\mathcal {C}ilo}$
is stronger enough to obtain better results than those seen for
${\mathcal {C}ilo}$
is stronger enough to obtain better results than those seen for
![]() ${\mathscr {C}}_1$
, at least from an AAL point of view. By “stronger enough,” we mean
${\mathscr {C}}_1$
, at least from an AAL point of view. By “stronger enough,” we mean
![]() ${\mathcal {C}ilo}$
satisfies (⋆).
${\mathcal {C}ilo}$
satisfies (⋆).
To begin with, let us stress that
![]() , for an arbitrary algebra
, for an arbitrary algebra
![]() ${\boldsymbol {A}}$
, and therefore the results seen so far for
${\boldsymbol {A}}$
, and therefore the results seen so far for
![]() ${\mathscr {C}}_1$
-filters are also applicable to
${\mathscr {C}}_1$
-filters are also applicable to
![]() ${\mathcal {C}ilo}$
-filters. In particular, and having in mind that sets of parameterized congruence formulas are preserved by extensions, for every algebra
${\mathcal {C}ilo}$
-filters. In particular, and having in mind that sets of parameterized congruence formulas are preserved by extensions, for every algebra
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() , and
, and
![]() $a,b \in A$
,
$a,b \in A$
,
 $$ \begin{align*} \langle a,b \rangle \in {\boldsymbol{\varOmega}}^{\boldsymbol{A}}(F) \quad\Leftrightarrow\quad &\forall n \in \omega \; \forall m \in \omega \; \forall c_1,\ldots,c_n \in A, \\ &\Phi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F , \\ &\Psi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F. \end{align*} $$
$$ \begin{align*} \langle a,b \rangle \in {\boldsymbol{\varOmega}}^{\boldsymbol{A}}(F) \quad\Leftrightarrow\quad &\forall n \in \omega \; \forall m \in \omega \; \forall c_1,\ldots,c_n \in A, \\ &\Phi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F , \\ &\Psi_n^{\boldsymbol{A}}(\neg^m a, \neg^m b, c_1,\ldots,c_n) \subseteq F. \end{align*} $$
We now prove that
![]() ${\mathcal {C}ilo}$
satisfies (⋆). The proof makes use of the (rather complex) set of parameterized congruence formulas given in Theorem 4.3. It is interesting to observe where the axioms (Ax12a)–(Ax14a) play its role, and why the axioms (Ax12)–(Ax14) do not suffice for our purposes.
${\mathcal {C}ilo}$
satisfies (⋆). The proof makes use of the (rather complex) set of parameterized congruence formulas given in Theorem 4.3. It is interesting to observe where the axioms (Ax12a)–(Ax14a) play its role, and why the axioms (Ax12)–(Ax14) do not suffice for our purposes.
Theorem 9.1. Let
![]() ${\boldsymbol {A}}$
be arbitrary,
${\boldsymbol {A}}$
be arbitrary,
![]() , and
, and
![]() $a,b \in A$
. If
$a,b \in A$
. If
![]() $a^{\circ },b^{\circ } \in F$
, then
$a^{\circ },b^{\circ } \in F$
, then
Proof If
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
, then
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
, then
![]() $a \leftrightarrow b \in F$
by Proposition 4.1. Conversely, assume
$a \leftrightarrow b \in F$
by Proposition 4.1. Conversely, assume
![]() $a \leftrightarrow b \in F$
. We claim that for every
$a \leftrightarrow b \in F$
. We claim that for every
![]() $c_1,\ldots ,c_n \in A$
,
$c_1,\ldots ,c_n \in A$
,
The proof goes by induction on
![]() $n \in \omega $
.
$n \in \omega $
.
Basis: We must prove that for every
![]() $m \in \omega $
,
$m \in \omega $
,
![]() $\neg ^m a \leftrightarrow \neg ^m b \in F$
. The proof goes by induction on
$\neg ^m a \leftrightarrow \neg ^m b \in F$
. The proof goes by induction on
![]() $m \in \omega $
. Assume first
$m \in \omega $
. Assume first
![]() $m=0$
. It follows by assumption that
$m=0$
. It follows by assumption that
![]() $a \leftrightarrow b \in F$
. Assume now that
$a \leftrightarrow b \in F$
. Assume now that
![]() $m> 0$
. On the one hand, we have
$m> 0$
. On the one hand, we have
![]() $\neg ^m a \leftrightarrow \neg ^m b \in F$
, by inductive hypothesis. On the other hand, since
$\neg ^m a \leftrightarrow \neg ^m b \in F$
, by inductive hypothesis. On the other hand, since
![]() $a^{\circ },b^{\circ } \in F$
, it follows by m applications of Lemma 3.2.19 that
$a^{\circ },b^{\circ } \in F$
, it follows by m applications of Lemma 3.2.19 that
![]() $(\neg ^m a)^{\circ },(\neg ^m b)^{\circ } \in F$
. So it follows by Lemma 3.2.8 that
$(\neg ^m a)^{\circ },(\neg ^m b)^{\circ } \in F$
. So it follows by Lemma 3.2.8 that
![]() $\neg ^{m+1} a \leftrightarrow \neg ^{m+1} b \in F$
. Thus,
$\neg ^{m+1} a \leftrightarrow \neg ^{m+1} b \in F$
. Thus,
![]() $\bigcup _{m \in \omega } \Phi _0(\neg ^m a, \neg ^m b) \subseteq F$
.
$\bigcup _{m \in \omega } \Phi _0(\neg ^m a, \neg ^m b) \subseteq F$
.
Step: Let
![]() $m,m_1,\ldots ,m_{n+1} \in \omega $
,
$m,m_1,\ldots ,m_{n+1} \in \omega $
,
![]() $c_1,\ldots ,c_{n+1} \in A$
, and
$c_1,\ldots ,c_{n+1} \in A$
, and
![]() $*_1,\ldots ,*_{n+1} \in \{ \wedge , \vee , \to \}$
.
$*_1,\ldots ,*_{n+1} \in \{ \wedge , \vee , \to \}$
.
-
•
 $\Phi _{n+1}(\neg ^m a, \neg ^m b, c_1, c_2,\ldots ,c_{n+1})$
with
$\Phi _{n+1}(\neg ^m a, \neg ^m b, c_1, c_2,\ldots ,c_{n+1})$
with
 $m_{n+1} = 0$
: It follows by inductive hypothesis that
$m_{n+1} = 0$
: It follows by inductive hypothesis that
 $\Phi _n(\neg ^m a, \neg ^m b, c_1,\ldots ,c_n) \subseteq F$
. Therefore, Since moreover
$\Phi _n(\neg ^m a, \neg ^m b, c_1,\ldots ,c_n) \subseteq F$
. Therefore, Since moreover $$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2) \cdots *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_2} ( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2) \cdots *_n c_n) \in F. \end{align*} $$
$$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2) \cdots *_n c_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_2} ( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2) \cdots *_n c_n) \in F. \end{align*} $$
 $c_{n+1} \leftrightarrow c_{n+1} \in F$
by Lemma 3.2.1, it follows by Lemma 3.2.4–6 that Thus,
$c_{n+1} \leftrightarrow c_{n+1} \in F$
by Lemma 3.2.1, it follows by Lemma 3.2.4–6 that Thus, $$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2) \cdots *_n c_n) *_{n+1} c_{n+1} \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_2} ( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2) \cdots *_n c_n) *_{n+1} c_{n+1} \in F. \end{align*} $$
$$ \begin{align*} &\neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2) \cdots *_n c_n) *_{n+1} c_{n+1} \leftrightarrow \\ &\neg^{m_n} ( \cdots \neg^{m_2} ( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2) \cdots *_n c_n) *_{n+1} c_{n+1} \in F. \end{align*} $$
 $\Phi _{n+1}(\neg ^m a, \neg ^m b, c_1, c_2,\ldots ,c_{n+1}) \subseteq F$
.
$\Phi _{n+1}(\neg ^m a, \neg ^m b, c_1, c_2,\ldots ,c_{n+1}) \subseteq F$
.
-
•
 $\Phi _{n+1}(\neg ^m a, \neg ^m b, c_1, c_2,\ldots ,c_{n+1})$
with
$\Phi _{n+1}(\neg ^m a, \neg ^m b, c_1, c_2,\ldots ,c_{n+1})$
with
 $m_{n+1}> 0$
: Since
$m_{n+1}> 0$
: Since
 $a^{\circ } \in F$
by hypothesis, it follows by m applications of Lemma 3.2.19 that
$a^{\circ } \in F$
by hypothesis, it follows by m applications of Lemma 3.2.19 that
 $(\neg ^m a)^{\circ } \in F$
. It then follows by (Ax12a)–(Ax14a) that
$(\neg ^m a)^{\circ } \in F$
. It then follows by (Ax12a)–(Ax14a) that
 $(\neg ^m a *_1 c_1)^{\circ } \in F$
; then by
$(\neg ^m a *_1 c_1)^{\circ } \in F$
; then by
 $m_1$
applications of Lemma 3.2.19 that
$m_1$
applications of Lemma 3.2.19 that
 $\big ( \neg ^{m_1} (\neg ^m a *_1 c_1) \big )^{\circ } \in F$
; and again by (Ax12a)–(Ax14a) that
$\big ( \neg ^{m_1} (\neg ^m a *_1 c_1) \big )^{\circ } \in F$
; and again by (Ax12a)–(Ax14a) that
 $\big ( \neg ^{m_1} (\neg ^m a *_1 c_1) *_2 c_2\big )^{\circ } \in F$
; and so on, until we obtain (2)Similarly,
$\big ( \neg ^{m_1} (\neg ^m a *_1 c_1) *_2 c_2\big )^{\circ } \in F$
; and so on, until we obtain (2)Similarly, $$ \begin{align} \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big)^{\circ} \in F. \end{align} $$
(3)Moreover, it follows by inductive hypothesis that
$$ \begin{align} \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big)^{\circ} \in F. \end{align} $$
(3)Moreover, it follows by inductive hypothesis that $$ \begin{align} \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big)^{\circ} \in F. \end{align} $$
So by Lemma 3.2.4–6,
$$ \begin{align} \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big)^{\circ} \in F. \end{align} $$
So by Lemma 3.2.4–6, $$ \begin{align*} &\neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) \leftrightarrow \\ &\neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) \in F. \end{align*} $$
(4)It finally follows by (2), (3), (4) and Lemma 3.2.8 that
$$ \begin{align*} &\neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) \leftrightarrow \\ &\neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) \in F. \end{align*} $$
(4)It finally follows by (2), (3), (4) and Lemma 3.2.8 that $$ \begin{align} &\neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \leftrightarrow \notag \\ &\neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \in F. \end{align} $$
(5)Having arrived here, by (2) and Lemma 3.2.19 we have
$$ \begin{align} &\neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \leftrightarrow \notag \\ &\neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \in F. \end{align} $$
(5)Having arrived here, by (2) and Lemma 3.2.19 we have $$ \begin{align} &\neg \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \leftrightarrow \notag \\ &\neg \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \in F. \end{align} $$
(6)Similarly, by (3) and Lemma 3.2.19 we have
$$ \begin{align} &\neg \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \leftrightarrow \notag \\ &\neg \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \in F. \end{align} $$
(6)Similarly, by (3) and Lemma 3.2.19 we have $$ \begin{align} \Big( \neg \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \Big)^{\circ} \in F. \end{align} $$
(7)This time it follows by (5)–(7) and Lemma 3.2.8 that
$$ \begin{align} \Big( \neg \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \Big)^{\circ} \in F. \end{align} $$
(7)This time it follows by (5)–(7) and Lemma 3.2.8 that $$ \begin{align} \Big( \neg \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \Big)^{\circ} \in F. \end{align} $$
By repeating this process
$$ \begin{align} \Big( \neg \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \Big)^{\circ} \in F. \end{align} $$
By repeating this process $$ \begin{align*} &\neg^2 \big( \neg^{m_n} \big( \cdots \big( \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots \big) *_n c_n \big) *_{n+1} c_{n+1} \big) \leftrightarrow \\ &\neg^2 \big( \neg^{m_n} \big( \cdots \big( \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots \big) *_n c_n \big) *_{n+1} c_{n+1} \big) \in F. \end{align*} $$
$$ \begin{align*} &\neg^2 \big( \neg^{m_n} \big( \cdots \big( \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots \big) *_n c_n \big) *_{n+1} c_{n+1} \big) \leftrightarrow \\ &\neg^2 \big( \neg^{m_n} \big( \cdots \big( \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots \big) *_n c_n \big) *_{n+1} c_{n+1} \big) \in F. \end{align*} $$
 $m_{n+1}$
times, we eventually obtain Thus,
$m_{n+1}$
times, we eventually obtain Thus, $$ \begin{align*} &\neg^{m_{n+1}} \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \leftrightarrow \\ &\neg^{m_{n+1}} \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \in F. \end{align*} $$
$$ \begin{align*} &\neg^{m_{n+1}} \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m a *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \leftrightarrow \\ &\neg^{m_{n+1}} \big( \neg^{m_n} \big( \cdots \neg^{m_2} \big( \neg^{m_1} (\neg^m b *_1 c_1) *_2 c_2\big) \cdots *_n c_n \big) *_{n+1} c_{n+1} \big) \in F. \end{align*} $$
 $\Phi _{n+1}(\neg ^m a, \neg ^m b, c_1, c_2,\ldots ,c_{n+1}) \subseteq F$
.
$\Phi _{n+1}(\neg ^m a, \neg ^m b, c_1, c_2,\ldots ,c_{n+1}) \subseteq F$
.
We conclude that for every
![]() $c_1,\ldots ,c_n \in A$
,
$c_1,\ldots ,c_n \in A$
,
Similarly, one proves that for every
![]() $c_1,\ldots ,c_n \in A$
,
$c_1,\ldots ,c_n \in A$
,
Since
![]() , it follows by Theorem 4.3 that
, it follows by Theorem 4.3 that
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
Corollary 9.2. The logic
![]() ${\mathcal {C}ilo}$
satisfies (⋆).
${\mathcal {C}ilo}$
satisfies (⋆).
Proof Let
![]() ${\boldsymbol {A}}$
be arbitrary,
${\boldsymbol {A}}$
be arbitrary,
![]() , and
, and
![]() $a,b \in A^{\circ }$
. Then
$a,b \in A^{\circ }$
. Then
![]() . It follows by Theorem 9.1 that
. It follows by Theorem 9.1 that
As a consequence of Corollary 9.2, all the results seen in Section 7 hold for the logic
![]() ${\mathcal {C}ilo}.$
${\mathcal {C}ilo}.$
A particular case of Theorem 9.1 arises when dealing with
![]() $\sim \! a , \sim \! b \in A$
. In order to see it, we first prove an auxiliary lemma.
$\sim \! a , \sim \! b \in A$
. In order to see it, we first prove an auxiliary lemma.
Lemma 9.3.
![]() $\vdash _{{\mathcal {C}ilo}} (\sim \! \varphi )^{\circ }$
.
$\vdash _{{\mathcal {C}ilo}} (\sim \! \varphi )^{\circ }$
.
Proof Since
![]() $\sim \! \varphi = \neg \varphi \wedge \varphi ^{\circ }$
and
$\sim \! \varphi = \neg \varphi \wedge \varphi ^{\circ }$
and
![]() $\vdash _{{\mathcal {C}ilo}} (\varphi ^{\circ })^{\circ }$
by Lemma 3.2.20, it follows by (Ax12a) that
$\vdash _{{\mathcal {C}ilo}} (\varphi ^{\circ })^{\circ }$
by Lemma 3.2.20, it follows by (Ax12a) that
![]() $\vdash _{{\mathcal {C}ilo}} (\neg \varphi \wedge \varphi ^{\circ })^{\circ }$
, that is
$\vdash _{{\mathcal {C}ilo}} (\neg \varphi \wedge \varphi ^{\circ })^{\circ }$
, that is
![]() $\vdash _{{\mathcal {C}ilo}} (\sim \! \varphi )^{\circ }$
.
$\vdash _{{\mathcal {C}ilo}} (\sim \! \varphi )^{\circ }$
.
Corollary 9.4. For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() , and
, and
![]() $a,b \in A$
,
$a,b \in A$
,
9.1 Classification of
 ${\mathcal {C}ilo}$
within the Leibniz hierarchy
${\mathcal {C}ilo}$
within the Leibniz hierarchy
We now address the classification of
![]() ${\mathcal {C}ilo}$
within the Leibniz hierarchy and relate
${\mathcal {C}ilo}$
within the Leibniz hierarchy and relate
![]() ${\mathcal {C}ilo}$
with the strong version of
${\mathcal {C}ilo}$
with the strong version of
![]() ${\mathscr {C}}_1$
.
${\mathscr {C}}_1$
.
Since protoalgebraicity is preserved by extensions, the next result should come with no surprise.
Proposition 9.5.
![]() ${\mathcal {C}ilo}$
is protoalgebraic.
${\mathcal {C}ilo}$
is protoalgebraic.
Proposition 9.5 prompts the question of whether
![]() ${\mathcal {C}ilo}$
is equivalential. The problem this time is harder to grasp than it was for the logic
${\mathcal {C}ilo}$
is equivalential. The problem this time is harder to grasp than it was for the logic
![]() ${\mathscr {C}}_1$
, for we lack a counterexample of a reduced
${\mathscr {C}}_1$
, for we lack a counterexample of a reduced
![]() ${\mathcal {C}ilo}$
-model with a non-reduced
${\mathcal {C}ilo}$
-model with a non-reduced
![]() ${\mathcal {C}ilo}$
-submodel. The strategy to prove that
${\mathcal {C}ilo}$
-submodel. The strategy to prove that
![]() ${\mathcal {C}ilo}$
is not equivalential will make use of another extension,
${\mathcal {C}ilo}$
is not equivalential will make use of another extension,
![]() ${\mathcal {C}ilow}$
, yet to appear, and hence we will have to wait until Proposition 10.3 in order to see in full detail the proof. Nevertheless, we state the next result here, where it belongs naturally.
${\mathcal {C}ilow}$
, yet to appear, and hence we will have to wait until Proposition 10.3 in order to see in full detail the proof. Nevertheless, we state the next result here, where it belongs naturally.
Proposition 9.6.
![]() ${\mathcal {C}ilo}$
is not equivalential.
${\mathcal {C}ilo}$
is not equivalential.
Proposition 9.6 corrects a claim on [Reference Marcos42, p. 183] stating: “The logic
![]() ${\mathcal {C}ilo}$
, for instance, is (finitely) equivalential.”
${\mathcal {C}ilo}$
, for instance, is (finitely) equivalential.”
We are left to address the truth-equationality of
![]() ${\mathcal {C}ilo}$
. Unlike
${\mathcal {C}ilo}$
. Unlike
![]() ${\mathscr {C}}_1$
, the logic
${\mathscr {C}}_1$
, the logic
![]() ${\mathcal {C}ilo}$
has its filters equationally definable, hence being the first truth-equational logic we have come across in our study.
${\mathcal {C}ilo}$
has its filters equationally definable, hence being the first truth-equational logic we have come across in our study.
Lemma 9.7.
![]() $\xi , (\xi \wedge \varphi ) \leftrightarrow (\xi \wedge \psi ) \vdash _{{\mathscr {C}}_1} \varphi \leftrightarrow \psi $
.
$\xi , (\xi \wedge \varphi ) \leftrightarrow (\xi \wedge \psi ) \vdash _{{\mathscr {C}}_1} \varphi \leftrightarrow \psi $
.
Proposition 9.8.
![]() ${\mathcal {C}ilo}$
is truth-equational, witnessed by the set of truth equations
${\mathcal {C}ilo}$
is truth-equational, witnessed by the set of truth equations
![]() ${\boldsymbol {\tau }}(x) = \big \{ {(x^{\circ })}^{\circ } \wedge x \approx {(x^{\circ })}^{\circ } \wedge (x \to x) \big \}$
.
${\boldsymbol {\tau }}(x) = \big \{ {(x^{\circ })}^{\circ } \wedge x \approx {(x^{\circ })}^{\circ } \wedge (x \to x) \big \}$
.
Proof Let
![]() $\langle {\boldsymbol {A}} , F \rangle \in {\mathsf {Mod}}({\mathcal {C}ilo})$
. Assume first
$\langle {\boldsymbol {A}} , F \rangle \in {\mathsf {Mod}}({\mathcal {C}ilo})$
. Assume first
![]() $a \in F$
. Since both
$a \in F$
. Since both
![]() $a \in F$
and
$a \in F$
and
![]() $a \to a \in F$
by assumption and Lemma 3.2.11, respectively, it follows by manipulation of (Ax1) and (MP) that
$a \to a \in F$
by assumption and Lemma 3.2.11, respectively, it follows by manipulation of (Ax1) and (MP) that
![]() $a \leftrightarrow (a \to a) \in F$
. It then follows by Lemma 3.2.16 that
$a \leftrightarrow (a \to a) \in F$
. It then follows by Lemma 3.2.16 that
![]() $\big ( {(a^{\circ })}^{\circ } \wedge a \big ) \leftrightarrow \big ( {(a^{\circ })}^{\circ } \wedge (a \to a) \big ) \in F$
. Moreover, since
$\big ( {(a^{\circ })}^{\circ } \wedge a \big ) \leftrightarrow \big ( {(a^{\circ })}^{\circ } \wedge (a \to a) \big ) \in F$
. Moreover, since
![]() $\big ({(a^{\circ })}^{\circ }\big )^{\circ } \in F$
by Lemma 3.2.20 (taking
$\big ({(a^{\circ })}^{\circ }\big )^{\circ } \in F$
by Lemma 3.2.20 (taking
![]() $\varphi ^{\circ }$
instead of
$\varphi ^{\circ }$
instead of
![]() $\varphi $
), it follows by (Ax12a) that
$\varphi $
), it follows by (Ax12a) that
![]() $\big ( {(a^{\circ })}^{\circ } \wedge a \big )^{\circ } \in F$
and
$\big ( {(a^{\circ })}^{\circ } \wedge a \big )^{\circ } \in F$
and
![]() $\big ( {(a^{\circ })}^{\circ } \wedge (a \to a) \big )^{\circ } \in F$
. It finally follows by Theorem 9.1 that
$\big ( {(a^{\circ })}^{\circ } \wedge (a \to a) \big )^{\circ } \in F$
. It finally follows by Theorem 9.1 that
![]() ${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Conversely, assume
${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Conversely, assume
![]() ${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Then,
${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Then,
![]() $\big ( {(a^{\circ })}^{\circ } \wedge a \big ) \leftrightarrow \big ( {(a^{\circ })}^{\circ } \wedge (a \to a) \big ) \in F$
by Proposition 4.1. Since
$\big ( {(a^{\circ })}^{\circ } \wedge a \big ) \leftrightarrow \big ( {(a^{\circ })}^{\circ } \wedge (a \to a) \big ) \in F$
by Proposition 4.1. Since
![]() ${(a^{\circ })}^{\circ } \in F$
by Lemma 3.2.20, it follows by Lemma 9.7 that
${(a^{\circ })}^{\circ } \in F$
by Lemma 3.2.20, it follows by Lemma 9.7 that
![]() $a \leftrightarrow (a \to a) \in F$
. Next, since
$a \leftrightarrow (a \to a) \in F$
. Next, since
![]() $a \to a \in F$
by Lemma 3.2.11, it follows by (MP) that
$a \to a \in F$
by Lemma 3.2.11, it follows by (MP) that
![]() $a \in F$
. We conclude that
$a \in F$
. We conclude that
![]() $F = \{ a \in A : {\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \}$
, which proves the result.
$F = \{ a \in A : {\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \}$
, which proves the result.
Bearing in mind Definition 2.2, and putting together Propositions 9.5 and 9.8, it follows at once that:
Proposition 9.9.
![]() ${\mathcal {C}ilo}$
is weakly algebraizable.
${\mathcal {C}ilo}$
is weakly algebraizable.
In light of Proposition 9.6, the logic
![]() ${\mathcal {C}ilo}$
is not algebraizable. There are few examples of weakly algebraizable, but not algebraizable, logics in the literature. Namely, the logic of ortholattices
${\mathcal {C}ilo}$
is not algebraizable. There are few examples of weakly algebraizable, but not algebraizable, logics in the literature. Namely, the logic of ortholattices
![]() ${\mathcal {S}}_{\mathrm {OL}}$
, the logic of Andréka and Nemeti
${\mathcal {S}}_{\mathrm {OL}}$
, the logic of Andréka and Nemeti
![]() ${\mathcal {S}}_{\mathrm {AN}}$
, and some assertional logics of protoregular classes—the latter being in fact regularly weakly algebraizable. All these examples, as well as the corresponding proofs of their weak algebraizability, can be found in [Reference Czelakowski and Jansana29, Section 6].
${\mathcal {S}}_{\mathrm {AN}}$
, and some assertional logics of protoregular classes—the latter being in fact regularly weakly algebraizable. All these examples, as well as the corresponding proofs of their weak algebraizability, can be found in [Reference Czelakowski and Jansana29, Section 6].
9.2 The class
 ${\mathsf {Alg}}^*({\mathcal {C}ilo})$
${\mathsf {Alg}}^*({\mathcal {C}ilo})$
The class
![]() ${\mathsf {Alg}}^*({\mathcal {C}ilo})$
enjoys much nicer properties than
${\mathsf {Alg}}^*({\mathcal {C}ilo})$
enjoys much nicer properties than
![]() ${\mathsf {Alg}}^*({\mathscr {C}}_1)$
. Perhaps most notably, Mortensen’s result (recall Proposition 5.2) is no longer valid. We next prove this and other results concerning the class
${\mathsf {Alg}}^*({\mathscr {C}}_1)$
. Perhaps most notably, Mortensen’s result (recall Proposition 5.2) is no longer valid. We next prove this and other results concerning the class
![]() ${\mathsf {Alg}}^*({\mathcal {C}ilo})$
.
${\mathsf {Alg}}^*({\mathcal {C}ilo})$
.
A consequence of Proposition 9.8 is that
![]() ${\mathsf {Alg}}^*({\mathcal {C}ilo})$
is an algebraic semantics for the logic
${\mathsf {Alg}}^*({\mathcal {C}ilo})$
is an algebraic semantics for the logic
![]() ${\mathcal {C}ilo}$
. Indeed, every truth-equational logic
${\mathcal {C}ilo}$
. Indeed, every truth-equational logic
![]() ${\mathcal {S}}$
admits
${\mathcal {S}}$
admits
![]() ${\mathsf {Alg}}({\mathcal {S}})$
as an algebraic semantics—see [Reference Raftery51, Corollary 26]. This contrasts with the situation seen for the logic
${\mathsf {Alg}}({\mathcal {S}})$
as an algebraic semantics—see [Reference Raftery51, Corollary 26]. This contrasts with the situation seen for the logic
![]() ${\mathscr {C}}_1$
—recall Theorem 5.6.
${\mathscr {C}}_1$
—recall Theorem 5.6.
Since
![]() ${\mathcal {C}ilo}$
satisfies (⋆) by Theorem 9.1, it follows by Corollary 7.3 that
${\mathcal {C}ilo}$
satisfies (⋆) by Theorem 9.1, it follows by Corollary 7.3 that
![]() ${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
whenever
${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
whenever
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {C}ilo})$
.
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {C}ilo})$
.
Proposition 9.10. If
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {C}ilo})$
then
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {C}ilo})$
then
![]() ${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
.
${\boldsymbol {A}}^{\circ } \in \mathsf {BA}$
.
The converse of Proposition 9.10 is false. Consider once again the algebra
![]() ${\boldsymbol {A}}$
depicted in Figure 2. We have
${\boldsymbol {A}}$
depicted in Figure 2. We have
![]() , but
, but
![]() ${\boldsymbol {A}} \notin {\mathsf {Alg}}^*({\mathcal {C}ilo})$
—this last fact is easily checked by noticing that no non-trivial
${\boldsymbol {A}} \notin {\mathsf {Alg}}^*({\mathcal {C}ilo})$
—this last fact is easily checked by noticing that no non-trivial
![]() ${\mathscr {C}}_1$
-filter in Table 2 is closed under axioms (Ax12a)–(Ax14a).
${\mathscr {C}}_1$
-filter in Table 2 is closed under axioms (Ax12a)–(Ax14a).
As already claimed, unlike the logic
![]() ${\mathscr {C}}_1$
, Mortensen’s result no longer holds for the logic
${\mathscr {C}}_1$
, Mortensen’s result no longer holds for the logic
![]() ${\mathcal {C}ilo}$
.
${\mathcal {C}ilo}$
.
Proposition 9.11.
![]() ${\boldsymbol {Fm}} \notin {\mathsf {Alg}}^*({\mathcal {C}ilo})$
.
${\boldsymbol {Fm}} \notin {\mathsf {Alg}}^*({\mathcal {C}ilo})$
.
Proof Suppose for the sake of contradiction that
![]() ${\boldsymbol {Fm}} \in {\mathsf {Alg}}^*({\mathcal {C}ilo})$
. Since
${\boldsymbol {Fm}} \in {\mathsf {Alg}}^*({\mathcal {C}ilo})$
. Since
![]() ${\mathcal {C}ilo}$
is a non-trivial logic with theorems, it follows by the observation after Theorem 5.6 that
${\mathcal {C}ilo}$
is a non-trivial logic with theorems, it follows by the observation after Theorem 5.6 that
![]() ${\mathcal {C}ilo}$
admits no algebraic semantics, and we reach a contradiction.
${\mathcal {C}ilo}$
admits no algebraic semantics, and we reach a contradiction.
As a consequence of Proposition 9.11, there exists a non-trivial congruence on
![]() ${\boldsymbol {Fm}}$
compatible with the
${\boldsymbol {Fm}}$
compatible with the
![]() ${\mathcal {C}ilo}$
-theorems—just consider
${\mathcal {C}ilo}$
-theorems—just consider
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}({\mathrm{Thm}}_{{\mathcal {C}ilo}}) \neq id_{\boldsymbol {Fm}}$
. The existence of such a congruence has already been stated in the literature—originally in [Reference da Costa, Béziau and Bueno24, Theorem 3.21], but also in [Reference Carnielli and Marcos16, Fact 3.81] and [Reference Bueno-Soler and Carnielli9, p. 3]. However, from the existence of a non-trivial congruence on
${\boldsymbol {\varOmega }}^{\boldsymbol {Fm}}({\mathrm{Thm}}_{{\mathcal {C}ilo}}) \neq id_{\boldsymbol {Fm}}$
. The existence of such a congruence has already been stated in the literature—originally in [Reference da Costa, Béziau and Bueno24, Theorem 3.21], but also in [Reference Carnielli and Marcos16, Fact 3.81] and [Reference Bueno-Soler and Carnielli9, p. 3]. However, from the existence of a non-trivial congruence on
![]() ${\boldsymbol {Fm}}$
(compatible with
${\boldsymbol {Fm}}$
(compatible with
![]() ${\mathrm{Thm}}_{{\mathcal {C}ilo}}$
) it does not follow that
${\mathrm{Thm}}_{{\mathcal {C}ilo}}$
) it does not follow that
![]() ${\mathcal {C}ilo}$
is algebraizable nor even equivalential, as mentioned in [Reference Carnielli and Marcos16, p. 79] and [Reference Marcos42, p. 118].
${\mathcal {C}ilo}$
is algebraizable nor even equivalential, as mentioned in [Reference Carnielli and Marcos16, p. 79] and [Reference Marcos42, p. 118].
10 The logic
 ${\mathcal {C}ilow}$
${\mathcal {C}ilow}$
The goals of this section are to introduce the logic
![]() ${\mathcal {C}ilow}$
, classify it within the Leibniz hierarchy, and use its classification (namely, the fact that it is not equivalential) to establish that
${\mathcal {C}ilow}$
, classify it within the Leibniz hierarchy, and use its classification (namely, the fact that it is not equivalential) to establish that
![]() ${\mathcal {C}ilo}$
is not equivalential (although formally stated in Proposition 9.6, it is an immediate consequence of Proposition 10.3).
${\mathcal {C}ilo}$
is not equivalential (although formally stated in Proposition 9.6, it is an immediate consequence of Proposition 10.3).
Consider the axiom:
Let us call the logic
![]() ${\mathscr {C}}_1 + \mathrm {( {Ax15})}$
by
${\mathscr {C}}_1 + \mathrm {( {Ax15})}$
by
![]() ${\mathcal {C}ilaw}$
Footnote
10
and the logic
${\mathcal {C}ilaw}$
Footnote
10
and the logic
![]() ${\mathcal {C}ilo} + \mathrm {( {Ax15})}$
by
${\mathcal {C}ilo} + \mathrm {( {Ax15})}$
by
![]() ${\mathcal {C}ilow}$
.Footnote
11
Unlike the logic
${\mathcal {C}ilow}$
.Footnote
11
Unlike the logic
![]() ${\mathcal {C}ilo}$
, the extensions
${\mathcal {C}ilo}$
, the extensions
![]() ${\mathcal {C}ilaw}$
and
${\mathcal {C}ilaw}$
and
![]() ${\mathcal {C}ilow}$
have not been considered in the literature. Our main purpose in considering them is to help us establish that
${\mathcal {C}ilow}$
have not been considered in the literature. Our main purpose in considering them is to help us establish that
![]() ${\mathcal {C}ilo}$
is not equivalential.
${\mathcal {C}ilo}$
is not equivalential.
Putting together Lemma 3.2.8 and (Ax15), we obtain:
Lemma 10.1.
![]() $\neg \varphi \leftrightarrow \neg \psi \vdash _{{\mathcal {C}ilaw}} \neg \neg \varphi \leftrightarrow \neg \neg \psi $
.
$\neg \varphi \leftrightarrow \neg \psi \vdash _{{\mathcal {C}ilaw}} \neg \neg \varphi \leftrightarrow \neg \neg \psi $
.
The classification of the logic
![]() ${\mathcal {C}ilaw}$
within the Leibniz hierarchy coincides with that of
${\mathcal {C}ilaw}$
within the Leibniz hierarchy coincides with that of
![]() ${\mathscr {C}}_1$
. In fact, the exact same counterexample used in the proofs of Propositions 3.6 and 3.7 (that is, the algebra
${\mathscr {C}}_1$
. In fact, the exact same counterexample used in the proofs of Propositions 3.6 and 3.7 (that is, the algebra
![]() ${\boldsymbol {A}}$
in Figure 2) can also be used for the logic
${\boldsymbol {A}}$
in Figure 2) can also be used for the logic
![]() ${\mathcal {C}ilaw}$
. We need only to check that the subsets
${\mathcal {C}ilaw}$
. We need only to check that the subsets
![]() $\{1,u\}$
and
$\{1,u\}$
and
![]() $\{a,1,u\}$
are
$\{a,1,u\}$
are
![]() ${\mathcal {C}ilaw}$
-filters of
${\mathcal {C}ilaw}$
-filters of
![]() ${\boldsymbol {A}}$
. But this is easy, because
${\boldsymbol {A}}$
. But this is easy, because
![]() $(\neg 0)^{\circ } = (\neg a)^{\circ } = (\neg b)^{\circ } = (\neg 1)^{\circ } = (\neg u)^{\circ } = 1$
. Therefore both
$(\neg 0)^{\circ } = (\neg a)^{\circ } = (\neg b)^{\circ } = (\neg 1)^{\circ } = (\neg u)^{\circ } = 1$
. Therefore both
![]() $\{1,u\}$
and
$\{1,u\}$
and
![]() $\{a,1,u\}$
satisfy (Ax15). Therefore,
$\{a,1,u\}$
satisfy (Ax15). Therefore,
![]() ${\mathcal {C}ilaw}$
is neither equivalential nor truth-equational.
${\mathcal {C}ilaw}$
is neither equivalential nor truth-equational.
As for the logic
![]() ${\mathcal {C}ilow}$
, since it extends
${\mathcal {C}ilow}$
, since it extends
![]() ${\mathcal {C}ilo}$
it follows at once by Proposition 9.9 that it is weakly algebraizable.
${\mathcal {C}ilo}$
it follows at once by Proposition 9.9 that it is weakly algebraizable.
We now move on to the main result of this section which is the non-equivalentiality of
![]() ${\mathcal {C}ilow}$
. The next auxiliary lemma makes use of Proposition 2.7 seen in the Preliminaries.
${\mathcal {C}ilow}$
. The next auxiliary lemma makes use of Proposition 2.7 seen in the Preliminaries.
Lemma 10.2. If
![]() ${\mathcal {C}ilow}$
were equivalential, then
${\mathcal {C}ilow}$
were equivalential, then
![]() would be a set of congruence formulas for
would be a set of congruence formulas for
![]() ${\mathcal {C}ilow}$
.
${\mathcal {C}ilow}$
.
Proof Suppose that
![]() ${\mathcal {C}ilow}$
is equivalential. Let
${\mathcal {C}ilow}$
is equivalential. Let
![]() $\sigma : {\boldsymbol {Fm}} \to {\boldsymbol {Fm}}(x,y)$
such that
$\sigma : {\boldsymbol {Fm}} \to {\boldsymbol {Fm}}(x,y)$
such that
![]() $\sigma (x) = x$
,
$\sigma (x) = x$
,
![]() $\sigma (y) = y$
, and
$\sigma (y) = y$
, and
![]() $\sigma (z) = \neg x$
, for every
$\sigma (z) = \neg x$
, for every
![]() $z \in \mathrm {Var} \backslash \{x,y\}$
. It follows by Proposition 2.7 and Theorem 4.3 that
$z \in \mathrm {Var} \backslash \{x,y\}$
. It follows by Proposition 2.7 and Theorem 4.3 that
![]() $\sigma \,\Delta $
is a set of congruence formulas for
$\sigma \,\Delta $
is a set of congruence formulas for
![]() ${\mathcal {C}ilow}$
, where
${\mathcal {C}ilow}$
, where
 $$ \begin{align*} \Delta(x,y,\overline{z}) =& \bigcup_{n \in \omega} \bigcup_{m \in \omega} \Phi_n(\neg^m x, \neg^m y, z_1,\ldots,z_n) \; \cup \\ &\bigcup_{n \in \omega} \bigcup_{m \in \omega} \Psi_n(\neg^m x, \neg^m y, z_1,\ldots,z_n). \end{align*} $$
$$ \begin{align*} \Delta(x,y,\overline{z}) =& \bigcup_{n \in \omega} \bigcup_{m \in \omega} \Phi_n(\neg^m x, \neg^m y, z_1,\ldots,z_n) \; \cup \\ &\bigcup_{n \in \omega} \bigcup_{m \in \omega} \Psi_n(\neg^m x, \neg^m y, z_1,\ldots,z_n). \end{align*} $$
Now, let
![]() $m,n \in \omega $
and
$m,n \in \omega $
and
![]() $\varphi \in \Phi _n(\neg ^m x, \neg ^m y, z_1,\ldots ,z_n)$
. That is,
$\varphi \in \Phi _n(\neg ^m x, \neg ^m y, z_1,\ldots ,z_n)$
. That is,
 $$ \begin{align*} \varphi =\; & \neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (\neg^m x *_1 z_1) *_2 z_2) \cdots) *_n z_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (\neg^m y *_1 z_1) *_2 z_2) \cdots) *_n z_n) , \end{align*} $$
$$ \begin{align*} \varphi =\; & \neg^{m_n} (\cdots (\neg^{m_2} (\neg^{m_1} (\neg^m x *_1 z_1) *_2 z_2) \cdots) *_n z_n) \leftrightarrow \\ &\neg^{m_n} ( \cdots ( \neg^{m_2} ( \neg^{m_1} (\neg^m y *_1 z_1) *_2 z_2) \cdots) *_n z_n) , \end{align*} $$
for some
![]() $*_1,\ldots ,*_n \in \{\wedge ,\vee ,\to \}$
and some
$*_1,\ldots ,*_n \in \{\wedge ,\vee ,\to \}$
and some
![]() $m_1,\ldots ,m_n \in \omega $
. We claim that
$m_1,\ldots ,m_n \in \omega $
. We claim that
The proof of our claim goes by induction on
![]() $n \in \omega $
.
$n \in \omega $
.
Basis:
![]() $\mathbf {n=0}$
:
$\mathbf {n=0}$
:
Then
![]() $\sigma \,\varphi = \neg ^m x \leftrightarrow \neg ^m y$
, for some
$\sigma \,\varphi = \neg ^m x \leftrightarrow \neg ^m y$
, for some
![]() $m \in \omega $
. If
$m \in \omega $
. If
![]() $m=0$
or
$m=0$
or
![]() $m=1$
, then clearly
$m=1$
, then clearly
![]() $x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\varphi $
holds by extensivity. Assume
$x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\varphi $
holds by extensivity. Assume
![]() $m> 1$
. It follows by
$m> 1$
. It follows by
![]() $m-1$
applications of Lemma 10.1 that
$m-1$
applications of Lemma 10.1 that
![]() $\neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \neg ^m x \leftrightarrow \neg ^m y$
. Therefore,
$\neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \neg ^m x \leftrightarrow \neg ^m y$
. Therefore,
![]() $x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\varphi $
.
$x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\varphi $
.
Step:
![]() $\mathbf {n>0}$
:
$\mathbf {n>0}$
:
Then
 $$ \begin{align*} \sigma\varphi \;=\; &\neg^{m_{n+1}} \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n +1}\neg x \big) \leftrightarrow \notag \\ &\neg^{m_{n+1}} \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_{n} \neg x) *_{n+1} \neg x \big) , \end{align*} $$
$$ \begin{align*} \sigma\varphi \;=\; &\neg^{m_{n+1}} \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n +1}\neg x \big) \leftrightarrow \notag \\ &\neg^{m_{n+1}} \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_{n} \neg x) *_{n+1} \neg x \big) , \end{align*} $$
for some
![]() $*_1,\ldots ,*_{n+1} \in \{\wedge ,\vee ,\to \}$
and
$*_1,\ldots ,*_{n+1} \in \{\wedge ,\vee ,\to \}$
and
![]() $m_1,\ldots ,m_{n+1} \in \omega $
. It follows by inductive hypothesis that
$m_1,\ldots ,m_{n+1} \in \omega $
. It follows by inductive hypothesis that
 $$ \begin{align*} x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash_{{\mathcal{C}ilow}} &\neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) \leftrightarrow \\ & \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_n \neg x). \end{align*} $$
$$ \begin{align*} x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash_{{\mathcal{C}ilow}} &\neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) \leftrightarrow \\ & \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_n \neg x). \end{align*} $$
Now, it follows by Lemma 3.2.13–15 (depending on
![]() $*_{n+1} \in \{\wedge ,\vee ,\to \}$
, respectively) that
$*_{n+1} \in \{\wedge ,\vee ,\to \}$
, respectively) that
 $$ \begin{align} & x \leftrightarrow y , \neg x \leftrightarrow \neg y \nonumber\\ \vdash_{{\mathcal{C}ilow}} & \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x \leftrightarrow \notag \\ & \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x. \end{align} $$
$$ \begin{align} & x \leftrightarrow y , \neg x \leftrightarrow \neg y \nonumber\\ \vdash_{{\mathcal{C}ilow}} & \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x \leftrightarrow \notag \\ & \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x. \end{align} $$
If
![]() $m_{n+1} = 0$
, then we are done. If
$m_{n+1} = 0$
, then we are done. If
![]() $m_{n+1}> 0$
, then since
$m_{n+1}> 0$
, then since
![]() $\,\vdash _{{\mathcal {C}ilow}} (\neg x)^{\circ }$
by (Ax15), it follows by (Ax12a)–(Ax14a) (depending on
$\,\vdash _{{\mathcal {C}ilow}} (\neg x)^{\circ }$
by (Ax15), it follows by (Ax12a)–(Ax14a) (depending on
![]() $*_{n+1} \in \{\wedge ,\vee ,\to \}$
, respectively) that
$*_{n+1} \in \{\wedge ,\vee ,\to \}$
, respectively) that
and similarly
It follows by (8)–(10) and Lemma 3.2.8 that
 $$ \begin{align*} & x \leftrightarrow y , \neg x \leftrightarrow \neg y \\ \vdash_{{\mathcal{C}ilow}} &\neg \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x \big) \leftrightarrow \notag \\ & \neg \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x \big). \end{align*} $$
$$ \begin{align*} & x \leftrightarrow y , \neg x \leftrightarrow \neg y \\ \vdash_{{\mathcal{C}ilow}} &\neg \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x \big) \leftrightarrow \notag \\ & \neg \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x \big). \end{align*} $$
It then follows by
![]() $m_{n+1}-1$
applications of Lemma 10.1 that
$m_{n+1}-1$
applications of Lemma 10.1 that
 $$ \begin{align*} & x \leftrightarrow y , \neg x \leftrightarrow \neg y \\ \vdash_{{\mathcal{C}ilow}} &\neg^{m_{n+1}} \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n +1}\neg x \big) \leftrightarrow \notag \\ &\neg^{m_{n+1}} \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x \big). \end{align*} $$
$$ \begin{align*} & x \leftrightarrow y , \neg x \leftrightarrow \neg y \\ \vdash_{{\mathcal{C}ilow}} &\neg^{m_{n+1}} \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m x *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n +1}\neg x \big) \leftrightarrow \notag \\ &\neg^{m_{n+1}} \big( \neg^{m_n} (\cdots \neg^{m_2} (\neg^{m_1} (\neg^m y *_1 \neg x) *_2 \neg x) \cdots *_n \neg x) *_{n+1} \neg x \big). \end{align*} $$
That is,
![]() $x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\varphi $
.
$x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\varphi $
.
We conclude that
![]() $x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\varphi $
, as claimed. Similarly, one proves that
$x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\varphi $
, as claimed. Similarly, one proves that
![]() $x \leftrightarrow y \vdash _{{\mathcal {C}ilow}} \sigma \,\psi $
, with
$x \leftrightarrow y \vdash _{{\mathcal {C}ilow}} \sigma \,\psi $
, with
![]() $\psi \in \Psi _n(\neg ^m x, \neg ^m y, z_1,\ldots ,z_n)$
. Thus
$\psi \in \Psi _n(\neg ^m x, \neg ^m y, z_1,\ldots ,z_n)$
. Thus
![]() $x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\Delta $
, which proves the result.
$x \leftrightarrow y , \neg x \leftrightarrow \neg y \vdash _{{\mathcal {C}ilow}} \sigma \,\Delta $
, which proves the result.
Proposition 10.3. The logic
![]() ${\mathcal {C}ilow}$
is not equivalential.
${\mathcal {C}ilow}$
is not equivalential.
Proof Suppose for the sake of contradiction that
![]() ${\mathcal {C}ilow}$
is equivalential. It follows by Lemma 10.2 that
${\mathcal {C}ilow}$
is equivalential. It follows by Lemma 10.2 that
![]() is a set of congruence formulas for
is a set of congruence formulas for
![]() ${\mathcal {C}ilow}$
. Consider the algebra
${\mathcal {C}ilow}$
. Consider the algebra
![]() ${\boldsymbol {A}}$
whose truth-tables are given in Table 4 and fix
${\boldsymbol {A}}$
whose truth-tables are given in Table 4 and fix
![]() . First of all, one must check that
. First of all, one must check that
![]() . Next, on the one hand
. Next, on the one hand
![]() $a \leftrightarrow ^{\boldsymbol {A}} b = 1 \in F$
and
$a \leftrightarrow ^{\boldsymbol {A}} b = 1 \in F$
and
![]() $\neg ^{\boldsymbol {A}} a \leftrightarrow ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} b = 1 \in F$
. On the other hand,
$\neg ^{\boldsymbol {A}} a \leftrightarrow ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} b = 1 \in F$
. On the other hand,
![]() $\neg ^{\boldsymbol {A}} (a \to ^{\boldsymbol {A}} b) \leftrightarrow ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} (b \to ^{\boldsymbol {A}} b) = 0 \leftrightarrow ^{\boldsymbol {A}} 1 = 0 \notin F$
. Thus
$\neg ^{\boldsymbol {A}} (a \to ^{\boldsymbol {A}} b) \leftrightarrow ^{\boldsymbol {A}} \neg ^{\boldsymbol {A}} (b \to ^{\boldsymbol {A}} b) = 0 \leftrightarrow ^{\boldsymbol {A}} 1 = 0 \notin F$
. Thus
![]() ${\boldsymbol {\rho }}^{\boldsymbol {A}}(a,b) \subseteq F$
, but
${\boldsymbol {\rho }}^{\boldsymbol {A}}(a,b) \subseteq F$
, but
![]() $\langle a,b \rangle \notin {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. We reach a contradiction.
$\langle a,b \rangle \notin {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. We reach a contradiction.
Table 4 Truth-tables of the algebra
![]() ${\boldsymbol {A}}$
.
${\boldsymbol {A}}$
.

Consequently,
![]() ${\mathcal {C}ilow}$
is not algebraizable.
${\mathcal {C}ilow}$
is not algebraizable.
Still concerning the logic
![]() ${\mathcal {C}ilow}$
, it is interesting to observe that the Leibniz congruence of a
${\mathcal {C}ilow}$
, it is interesting to observe that the Leibniz congruence of a
![]() ${\mathcal {C}ilow}$
-filter is “classically” defined for negated elements. Indeed, we have seen this to be the case in Theorem 9.1 for all “well-behaved” elements. But given axiom (Ax15), all negated elements are now “well-behaved.”
${\mathcal {C}ilow}$
-filter is “classically” defined for negated elements. Indeed, we have seen this to be the case in Theorem 9.1 for all “well-behaved” elements. But given axiom (Ax15), all negated elements are now “well-behaved.”
Corollary 10.4. For every
![]() ${\boldsymbol {A}}$
,
${\boldsymbol {A}}$
,
![]() , and
, and
![]() $a,b \in A$
,
$a,b \in A$
,
Compare Corollary 10.4 with Corollary 9.4, seen for the logic
![]() ${\mathcal {C}ilo}$
.
${\mathcal {C}ilo}$
.
As a final note, observe that by considering axiom
one can define the logics
![]() ${\mathcal {C}ilae}$
and
${\mathcal {C}ilae}$
and
![]() ${\mathcal {C}iloe}$
Footnote
12
as the extensions of
${\mathcal {C}iloe}$
Footnote
12
as the extensions of
![]() ${\mathscr {C}}_1$
and
${\mathscr {C}}_1$
and
![]() ${\mathcal {C}ilo}$
by (Ax16), respectively. Although we will not study these logics in detail here, we shall nevertheless include them among the extensions of
${\mathcal {C}ilo}$
by (Ax16), respectively. Although we will not study these logics in detail here, we shall nevertheless include them among the extensions of
![]() ${\mathscr {C}}_1$
in Figure 1.
${\mathscr {C}}_1$
in Figure 1.
11 The logics
 ${\mathcal {C}ibv}$
,
${\mathcal {C}ibv}$
,
 , and
, and

The goals of this section are to introduce the logics
![]() ${\mathcal {C}ibv}$
,
${\mathcal {C}ibv}$
,
![]() , and
, and
![]() , classify
, classify
![]() ${\mathcal {C}ibv}$
within the Leibniz hierarchy (Theorem 11.5)—the classifications of
${\mathcal {C}ibv}$
within the Leibniz hierarchy (Theorem 11.5)—the classifications of
![]() and
and
![]() are known—and characterize the non-trivial algebras in
are known—and characterize the non-trivial algebras in
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
${\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, with
${\mathsf {Alg}}^*({\mathcal {S}})$
, with
![]() (Theorems 11.9 and 11.10, respectively). These last characterizations will allow us to determine the quasivarieties
(Theorems 11.9 and 11.10, respectively). These last characterizations will allow us to determine the quasivarieties
![]() and
and
![]() (Propositions 11.11 and 11.13), as well as the varieties
(Propositions 11.11 and 11.13), as well as the varieties
![]() and
and
![]() (Corollaries 11.12 and 11.14).
(Corollaries 11.12 and 11.14).
So far we have only seen non-equivalential axiomatic extensions of
![]() ${\mathscr {C}}_1$
. In this section we shall consider three equivalential extensions of
${\mathscr {C}}_1$
. In this section we shall consider three equivalential extensions of
![]() ${\mathcal {C}ilo}$
. Following the terminology of [Reference Carnielli and Marcos16, p. 68], let us consider the logic
${\mathcal {C}ilo}$
. Following the terminology of [Reference Carnielli and Marcos16, p. 68], let us consider the logic
![]() ${\mathcal {C}ibv}$
as the logic axiomatized by (Ax1)–(Ax11) and (MP), together with the following axioms:
${\mathcal {C}ibv}$
as the logic axiomatized by (Ax1)–(Ax11) and (MP), together with the following axioms:
The logic
![]() (also called
(also called
![]() ${\mathcal {C}ibvw}$
in [Reference Carnielli and Marcos16, p. 68] and
${\mathcal {C}ibvw}$
in [Reference Carnielli and Marcos16, p. 68] and
![]() $\mathrm {C}_{0.1}$
in [Reference Mortensen45, p. 301])Footnote
13
is the extension of
$\mathrm {C}_{0.1}$
in [Reference Mortensen45, p. 301])Footnote
13
is the extension of
![]() ${\mathcal {C}ibv}$
by axiom (Ax15). The logic
${\mathcal {C}ibv}$
by axiom (Ax15). The logic
![]() (also called
(also called
![]() ${\mathcal {C}ibve}$
in [Reference Carnielli and Marcos16, p. 68] and
${\mathcal {C}ibve}$
in [Reference Carnielli and Marcos16, p. 68] and
![]() $\mathrm {C}_{0.2}$
in [Reference Mortensen45, p. 301]) is the extension of
$\mathrm {C}_{0.2}$
in [Reference Mortensen45, p. 301]) is the extension of
![]() ${\mathcal {C}ibv}$
by axiom (Ax16).
${\mathcal {C}ibv}$
by axiom (Ax16).
The logic
![]() ${\mathcal {C}ibv}$
is the first equivalential (in fact, algebraizable) logic we have come across so far.
${\mathcal {C}ibv}$
is the first equivalential (in fact, algebraizable) logic we have come across so far.
Proposition 11.1. The logic
![]() ${\mathcal {C}ibv}$
is equivalential, witnessed by the set of congruence formulas
${\mathcal {C}ibv}$
is equivalential, witnessed by the set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ \neg ^m x \leftrightarrow \neg ^m y : m \in \omega \}$
.
${\boldsymbol {\rho }}(x,y) = \{ \neg ^m x \leftrightarrow \neg ^m y : m \in \omega \}$
.
Proof We prove that for every
![]() ${\boldsymbol {A}}$
and every
${\boldsymbol {A}}$
and every
![]() ,
,
Fix
![]() ${\boldsymbol {A}}$
and
${\boldsymbol {A}}$
and
![]() . Define the relation
. Define the relation
![]() $R \subseteq A \times A$
by
$R \subseteq A \times A$
by
![]() $\langle a,b \rangle \in R \;\Leftrightarrow \; \forall m\!\in \! \omega \quad \neg ^m a \leftrightarrow \neg ^m b \in F$
. Assume that
$\langle a,b \rangle \in R \;\Leftrightarrow \; \forall m\!\in \! \omega \quad \neg ^m a \leftrightarrow \neg ^m b \in F$
. Assume that
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. It follows by Proposition 4.1 that
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. It follows by Proposition 4.1 that
![]() $a\,Rb$
. Thus,
$a\,Rb$
. Thus,
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \subseteq R$
. Conversely, we claim that R is a congruence relation on
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \subseteq R$
. Conversely, we claim that R is a congruence relation on
![]() ${\boldsymbol {A}}$
compatible with F. It should be clear that it is an equivalence relation on A by Lemma 3.2.1–3. It is also clear by definition of R that it is compatible with the connective
${\boldsymbol {A}}$
compatible with F. It should be clear that it is an equivalence relation on A by Lemma 3.2.1–3. It is also clear by definition of R that it is compatible with the connective
![]() $\neg $
. We are left to prove that R is compatible with the binary language operations of
$\neg $
. We are left to prove that R is compatible with the binary language operations of
![]() ${\mathcal {L}}$
. The proof goes by induction on
${\mathcal {L}}$
. The proof goes by induction on
![]() $m \in \omega $
. Basis: Take
$m \in \omega $
. Basis: Take
![]() $m = 0$
. The compatibility with the language operations
$m = 0$
. The compatibility with the language operations
![]() $\wedge , \vee , \to $
follows by Lemma 3.2.4–6, respectively. Step: Let
$\wedge , \vee , \to $
follows by Lemma 3.2.4–6, respectively. Step: Let
![]() $m>0$
. Let
$m>0$
. Let
![]() $a_1\,R\,b_1$
and
$a_1\,R\,b_1$
and
![]() $a_2\,R\,b_2$
. It follows by axioms (Ax12b)–(Ax14b) that
$a_2\,R\,b_2$
. It follows by axioms (Ax12b)–(Ax14b) that
![]() $(a_1 * a_2)^{\circ } \in F$
and
$(a_1 * a_2)^{\circ } \in F$
and
![]() $(b_1 * b_2)^{\circ } \in F$
, with
$(b_1 * b_2)^{\circ } \in F$
, with
![]() $* \in \{\wedge , \vee , \to \}$
. It then follows by Lemma 3.2.19 (applied m times) that
$* \in \{\wedge , \vee , \to \}$
. It then follows by Lemma 3.2.19 (applied m times) that
![]() $\big (\neg ^m (a_1 * a_2)\big )^{\circ } \in F$
and
$\big (\neg ^m (a_1 * a_2)\big )^{\circ } \in F$
and
![]() $\big (\neg ^m (b_1 * b_2)\big )^{\circ } \in F$
, with
$\big (\neg ^m (b_1 * b_2)\big )^{\circ } \in F$
, with
![]() $* \in \{\wedge , \vee , \to \}$
. Moreover, it follows by inductive hypothesis that
$* \in \{\wedge , \vee , \to \}$
. Moreover, it follows by inductive hypothesis that
![]() $\neg ^m (a_1 * a_2) \leftrightarrow \neg ^m (b_1 * b_2)$
, with
$\neg ^m (a_1 * a_2) \leftrightarrow \neg ^m (b_1 * b_2)$
, with
![]() $* \in \{\wedge , \vee , \to \}$
. Hence, it follows by Lemma 3.2.8 that
$* \in \{\wedge , \vee , \to \}$
. Hence, it follows by Lemma 3.2.8 that
![]() $\neg ^{m+1}(a_1 * a_2) \leftrightarrow \neg ^{m+1} (b_1 * b_2) \in F$
, with
$\neg ^{m+1}(a_1 * a_2) \leftrightarrow \neg ^{m+1} (b_1 * b_2) \in F$
, with
![]() $* \in \{\wedge , \vee , \to \}$
. We conclude that R is compatible with the language operations
$* \in \{\wedge , \vee , \to \}$
. We conclude that R is compatible with the language operations
![]() $\wedge , \vee , \to $
. Finally, taking
$\wedge , \vee , \to $
. Finally, taking
![]() $m = 0$
, it follows by (MP) that R is compatible with F. Thus,
$m = 0$
, it follows by (MP) that R is compatible with F. Thus,
![]() $R \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
$R \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
We now proceed to prove that
![]() ${\mathcal {C}ibv}$
is not finitely equivalential.
${\mathcal {C}ibv}$
is not finitely equivalential.
Lemma 11.2. If
![]() ${\mathcal {C}ibv}$
were finitely equivalential, then there would exist
${\mathcal {C}ibv}$
were finitely equivalential, then there would exist
![]() $k \in \omega $
such that
$k \in \omega $
such that
![]() $\{ \neg ^m x \leftrightarrow \neg ^m y : m \leq k \}$
is a set of congruence formulas for
$\{ \neg ^m x \leftrightarrow \neg ^m y : m \leq k \}$
is a set of congruence formulas for
![]() ${\mathcal {C}ibv}$
.
${\mathcal {C}ibv}$
.
Proof Assume
![]() ${\mathcal {C}ibv}$
is finitely equivalential. Since
${\mathcal {C}ibv}$
is finitely equivalential. Since
![]() ${\mathcal {C}ibv}$
is finitary, it follows by Proposition 11.1 and [Reference Font32, Proposition 6.65.6] that there exists a finite subset of
${\mathcal {C}ibv}$
is finitary, it follows by Proposition 11.1 and [Reference Font32, Proposition 6.65.6] that there exists a finite subset of
![]() $\{ \neg ^m x \leftrightarrow \neg ^m y : m \in \omega \}$
, say
$\{ \neg ^m x \leftrightarrow \neg ^m y : m \in \omega \}$
, say
![]() $\{ \neg ^i x \leftrightarrow \neg ^i y : i \in I , I \text { finite} \}$
, which is still a set of congruence formulas for
$\{ \neg ^i x \leftrightarrow \neg ^i y : i \in I , I \text { finite} \}$
, which is still a set of congruence formulas for
![]() ${\mathcal {C}ibv}$
. Let
${\mathcal {C}ibv}$
. Let
![]() $k = \max \,I$
. Notice that
$k = \max \,I$
. Notice that
Thus
![]() $\{ \neg ^m x \leftrightarrow \neg ^m y : m \leq k \}$
is a set of congruence formulas for
$\{ \neg ^m x \leftrightarrow \neg ^m y : m \leq k \}$
is a set of congruence formulas for
![]() ${\mathcal {C}ibv}$
.
${\mathcal {C}ibv}$
.
Proposition 11.3. The logic
![]() ${\mathcal {C}ibv}$
is not finitely equivalential.
${\mathcal {C}ibv}$
is not finitely equivalential.
Proof Suppose for the sake of contradiction that
![]() ${\mathcal {C}ibv}$
is finitely equivalential. Consider the algebra
${\mathcal {C}ibv}$
is finitely equivalential. Consider the algebra
![]() ${\boldsymbol {A}}_n$
with universe
${\boldsymbol {A}}_n$
with universe
![]() $A_n = \{ 0 , \frac {1}{n-1} , \ldots , \frac {n-2}{n-1} , 1 \}$
. Define the operations
$A_n = \{ 0 , \frac {1}{n-1} , \ldots , \frac {n-2}{n-1} , 1 \}$
. Define the operations
![]() $\neg ^{{\boldsymbol {A}}_n},\wedge ^{{\boldsymbol {A}}_n},\vee ^{{\boldsymbol {A}}_n},\to ^{{\boldsymbol {A}}_n}$
as follows:
$\neg ^{{\boldsymbol {A}}_n},\wedge ^{{\boldsymbol {A}}_n},\vee ^{{\boldsymbol {A}}_n},\to ^{{\boldsymbol {A}}_n}$
as follows:
 $$\begin{align*}\neg^{{\boldsymbol{A}}_n} x = \begin{cases} 1, & \text{if } x=0, \\ x+\frac{1}{n-1}, & \text{if } x \in \{\frac{1}{n-1} , \ldots , \frac{n-2}{n-1}\}, \\ 0, & \text{if } x=1, \end{cases} \end{align*}$$
$$\begin{align*}\neg^{{\boldsymbol{A}}_n} x = \begin{cases} 1, & \text{if } x=0, \\ x+\frac{1}{n-1}, & \text{if } x \in \{\frac{1}{n-1} , \ldots , \frac{n-2}{n-1}\}, \\ 0, & \text{if } x=1, \end{cases} \end{align*}$$
 $$\begin{align*}x \wedge^{{\boldsymbol{A}}_n} y = \begin{cases} 0, & \text{if } x=0 \text{ or } y = 0, \\ 1, & \text{otherwise}, \end{cases} \end{align*}$$
$$\begin{align*}x \wedge^{{\boldsymbol{A}}_n} y = \begin{cases} 0, & \text{if } x=0 \text{ or } y = 0, \\ 1, & \text{otherwise}, \end{cases} \end{align*}$$
 $$\begin{align*}x \vee^{{\boldsymbol{A}}_n} y = \begin{cases} 0, & \text{if } x=0 \text{ and } y = 0, \\ 1, & \text{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}x \vee^{{\boldsymbol{A}}_n} y = \begin{cases} 0, & \text{if } x=0 \text{ and } y = 0, \\ 1, & \text{otherwise,} \end{cases} \end{align*}$$
 $$\begin{align*}x \to^{{\boldsymbol{A}}_n} y = \begin{cases} 0, & \text{if } x\neq0 \text{ and } y = 0, \\ 1, & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}x \to^{{\boldsymbol{A}}_n} y = \begin{cases} 0, & \text{if } x\neq0 \text{ and } y = 0, \\ 1, & \text{otherwise.} \end{cases} \end{align*}$$
For the case
![]() $n=4$
, the truth-tables of
$n=4$
, the truth-tables of
![]() ${\boldsymbol {A}}_4$
are given in Table 5. Under our assumption, it follows by Lemma 11.2 that there exists
${\boldsymbol {A}}_4$
are given in Table 5. Under our assumption, it follows by Lemma 11.2 that there exists
![]() $k \in \omega $
such that
$k \in \omega $
such that
![]() is a set of congruence formulas for
is a set of congruence formulas for
![]() ${\mathcal {C}ibv}$
. Let us consider the algebra
${\mathcal {C}ibv}$
. Let us consider the algebra
![]() ${\boldsymbol {A}}_{k+3}$
and fix
${\boldsymbol {A}}_{k+3}$
and fix
![]() . First of all, notice that
. First of all, notice that
![]() . Next, observe that
. Next, observe that
![]() $\neg ^m \frac {1}{k+2} \leftrightarrow \neg ^m \frac {2}{k+2} = 1 \in F$
, for every
$\neg ^m \frac {1}{k+2} \leftrightarrow \neg ^m \frac {2}{k+2} = 1 \in F$
, for every
![]() $m \leq k$
, but
$m \leq k$
, but
![]() $\neg ^{k+1} \frac {1}{k+2} \leftrightarrow \neg ^{k+1} \frac {2}{k+2} = 1 \leftrightarrow 0 = 0 \notin F$
. Thus
$\neg ^{k+1} \frac {1}{k+2} \leftrightarrow \neg ^{k+1} \frac {2}{k+2} = 1 \leftrightarrow 0 = 0 \notin F$
. Thus
![]() ${\boldsymbol {\rho }}^{\boldsymbol {A}}\big ( \frac {1}{k+2} , \frac {2}{k+2} \big ) \subseteq F$
, but
${\boldsymbol {\rho }}^{\boldsymbol {A}}\big ( \frac {1}{k+2} , \frac {2}{k+2} \big ) \subseteq F$
, but
![]() $\langle \frac {1}{k+2} , \frac {2}{k+2} \rangle \notin {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. We reach a contradiction.
$\langle \frac {1}{k+2} , \frac {2}{k+2} \rangle \notin {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. We reach a contradiction.
Table 5 Truth-tables of the algebra
![]() ${\boldsymbol {A}}_4$
.
${\boldsymbol {A}}_4$
.

Regarding the family
![]() ${\boldsymbol {A}}_n$
, with
${\boldsymbol {A}}_n$
, with
![]() $n \in \omega $
, observe that
$n \in \omega $
, observe that
![]() and
and
![]() $A_3 = {\boldsymbol {S}}$
, where
$A_3 = {\boldsymbol {S}}$
, where
![]() ${\boldsymbol {S}}$
is Sette’s algebra.
${\boldsymbol {S}}$
is Sette’s algebra.
The (few) known examples of equivalential logics which are not finitely equivalential are Herrmann’s logic, Dellunde’s logic, and the local logic associated with the least normal modal system. All these examples can be found in [Reference Font32, Examples 3.42, 3.53, and 6.67.3]. The logic
![]() ${\mathcal {C}ibv}$
provides one further example to this list.
${\mathcal {C}ibv}$
provides one further example to this list.
Since truth-equationality is preserved by extensions, it follows at once by Proposition 9.8 that
![]() ${\mathcal {C}ibv}$
has its filters equationally definable by
${\mathcal {C}ibv}$
has its filters equationally definable by
![]() ${\boldsymbol {\tau }}(x) = \big \{ {(x^{\circ })}^{\circ } \wedge x \approx {(x^{\circ })}^{\circ } \wedge (x \to x) \big \}$
. However, in the case of
${\boldsymbol {\tau }}(x) = \big \{ {(x^{\circ })}^{\circ } \wedge x \approx {(x^{\circ })}^{\circ } \wedge (x \to x) \big \}$
. However, in the case of
![]() ${\mathcal {C}ibv}$
one can identify a simpler set of truth-equations.
${\mathcal {C}ibv}$
one can identify a simpler set of truth-equations.
Proposition 11.4. The logic
![]() ${\mathcal {C}ibv}$
is truth-equational, witnessed by the set of truth-equations
${\mathcal {C}ibv}$
is truth-equational, witnessed by the set of truth-equations
![]() ${\boldsymbol {\tau }}(x) = \{ (x \to x) \to x \approx x \to x \}$
.
${\boldsymbol {\tau }}(x) = \{ (x \to x) \to x \approx x \to x \}$
.
Proof Let
![]() $\langle {\boldsymbol {A}} , F \rangle \in {\mathsf {Mod}}({\mathcal {C}ibv})$
. Assume
$\langle {\boldsymbol {A}} , F \rangle \in {\mathsf {Mod}}({\mathcal {C}ibv})$
. Assume
![]() $a \in F$
. Since
$a \in F$
. Since
![]() $a \to a \in F$
by Lemma 3.2.11, it follows by some easy manipulation of (Ax1) and (MP) that
$a \to a \in F$
by Lemma 3.2.11, it follows by some easy manipulation of (Ax1) and (MP) that
![]() $\big ((a \to a) \to a\big ) \leftrightarrow (a \to a) \in F$
. Moreover, since both
$\big ((a \to a) \to a\big ) \leftrightarrow (a \to a) \in F$
. Moreover, since both
![]() $\big ((a \to a) \to a\big )^{\circ } \in F$
and
$\big ((a \to a) \to a\big )^{\circ } \in F$
and
![]() $(a \to a)^{\circ } \in F$
by (Ax14b), it follows by Theorem 9.1 that
$(a \to a)^{\circ } \in F$
by (Ax14b), it follows by Theorem 9.1 that
![]() ${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Conversely, assume
${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Conversely, assume
![]() ${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Then,
${\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Then,
![]() $\big ((a \to a) \to a\big ) \leftrightarrow (a \to a) \in F$
. Since
$\big ((a \to a) \to a\big ) \leftrightarrow (a \to a) \in F$
. Since
![]() $a \to a \in F$
by Lemma 3.2.11, it follows by (MP) that
$a \to a \in F$
by Lemma 3.2.11, it follows by (MP) that
![]() $(a \to a) \to a$
, and again by (MP) that
$(a \to a) \to a$
, and again by (MP) that
![]() $a \in F$
. We conclude that
$a \in F$
. We conclude that
![]() $F = \{ a \in A : {\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \}$
, which proves the result.
$F = \{ a \in A : {\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \}$
, which proves the result.
The algebraizability of
![]() ${\mathcal {C}ibv}$
is a straightforward consequence of Propositions 11.1 and 11.4. However, in light of Proposition 11.3, the logic
${\mathcal {C}ibv}$
is a straightforward consequence of Propositions 11.1 and 11.4. However, in light of Proposition 11.3, the logic
![]() ${\mathcal {C}ibv}$
is not finitely algebraizable.
${\mathcal {C}ibv}$
is not finitely algebraizable.
Theorem 11.5. The logic
![]() ${\mathcal {C}ibv}$
is algebraizable, with set of congruence formulas
${\mathcal {C}ibv}$
is algebraizable, with set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ \neg ^m x \leftrightarrow \neg ^m y : m \in \omega \}$
and set of truth equations
${\boldsymbol {\rho }}(x,y) = \{ \neg ^m x \leftrightarrow \neg ^m y : m \in \omega \}$
and set of truth equations
![]() ${\boldsymbol {\tau }}(x) = \{ (x \to x) \to x \approx x \to x \}$
.
${\boldsymbol {\tau }}(x) = \{ (x \to x) \to x \approx x \to x \}$
.
Since algebraizability is preserved by extensions, it follows by Theorem 11.5 that both
![]() and
and
![]() are algebraizable. However, as we next prove, these logics admit finite sets of congruence formulas.
are algebraizable. However, as we next prove, these logics admit finite sets of congruence formulas.
Proposition 11.6. The logics
![]() and
and
![]() are finitely equivalential, with a set of congruence formulas
are finitely equivalential, with a set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
.
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
.
Proof Let
![]() ${\mathcal {S}}$
be any of
${\mathcal {S}}$
be any of
![]() . We prove that for every
. We prove that for every
![]() ${\boldsymbol {A}}$
and every
${\boldsymbol {A}}$
and every
![]() ,
,
Fix
![]() ${\boldsymbol {A}}$
and
${\boldsymbol {A}}$
and
![]() . Define the relation
. Define the relation
![]() $R \subseteq A \times A$
by
$R \subseteq A \times A$
by
![]() $\langle a,b \rangle \in R \;\text {iff}\; a \leftrightarrow b \in F \text { and } \neg a \leftrightarrow \neg b \in F$
. Assume that
$\langle a,b \rangle \in R \;\text {iff}\; a \leftrightarrow b \in F \text { and } \neg a \leftrightarrow \neg b \in F$
. Assume that
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. It follows by Proposition 4.1 that
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. It follows by Proposition 4.1 that
![]() $a\,R\,b$
. Thus,
$a\,R\,b$
. Thus,
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \subseteq R$
. Conversely, we claim that R is a congruence relation on
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \subseteq R$
. Conversely, we claim that R is a congruence relation on
![]() ${\boldsymbol {A}}$
compatible with F. It should be clear that it is an equivalence relation on A by Lemma 3.2.1–3. Let
${\boldsymbol {A}}$
compatible with F. It should be clear that it is an equivalence relation on A by Lemma 3.2.1–3. Let
![]() $a_1\,R\,b_1$
and
$a_1\,R\,b_1$
and
![]() $a_2\,R\,b_2$
. On the one hand, it follows by Lemma 3.2.4–6 that
$a_2\,R\,b_2$
. On the one hand, it follows by Lemma 3.2.4–6 that
![]() $(a_1 * a_2) \leftrightarrow (b_1 * b_2) \in F$
, with
$(a_1 * a_2) \leftrightarrow (b_1 * b_2) \in F$
, with
![]() $* \in \{ \wedge ,\vee ,\to \}$
. Moreover,
$* \in \{ \wedge ,\vee ,\to \}$
. Moreover,
![]() $\neg a \leftrightarrow \neg b \in F$
by assumption. On the other hand, it follows by (Ax12b)–(Ax14b) that
$\neg a \leftrightarrow \neg b \in F$
by assumption. On the other hand, it follows by (Ax12b)–(Ax14b) that
![]() $(a_1 * a_2)^{\circ } \in F$
and
$(a_1 * a_2)^{\circ } \in F$
and
![]() $(b_1 * b_2)^{\circ } \in F$
, with
$(b_1 * b_2)^{\circ } \in F$
, with
![]() $* \in \{ \wedge ,\vee ,\to \}$
. It then follows by Lemma 3.2.8 that
$* \in \{ \wedge ,\vee ,\to \}$
. It then follows by Lemma 3.2.8 that
![]() $\neg (a_1 * b_1) \leftrightarrow \neg (a_2 * b_2) \in F$
, with
$\neg (a_1 * b_1) \leftrightarrow \neg (a_2 * b_2) \in F$
, with
![]() $* \in \{ \wedge ,\vee ,\to \}$
. Now if
$* \in \{ \wedge ,\vee ,\to \}$
. Now if
![]() , then it follows by (Ax15) that
, then it follows by (Ax15) that
![]() $(\neg a_1)^{\circ } \in F$
and
$(\neg a_1)^{\circ } \in F$
and
![]() $(\neg b_1)^{\circ } \in F$
. Since
$(\neg b_1)^{\circ } \in F$
. Since
![]() $\neg a_1 \leftrightarrow \neg b_1 \in F$
by assumption, it follows once again by Lemma 3.2.8 that
$\neg a_1 \leftrightarrow \neg b_1 \in F$
by assumption, it follows once again by Lemma 3.2.8 that
![]() $\neg \neg a_1 \leftrightarrow \neg \neg b_1 \in F$
. If
$\neg \neg a_1 \leftrightarrow \neg \neg b_1 \in F$
. If
![]() , then it follows by (Ax10) and (Ax16) that
, then it follows by (Ax10) and (Ax16) that
![]() $a_1 \leftrightarrow \neg \neg a_1 \in F$
and
$a_1 \leftrightarrow \neg \neg a_1 \in F$
and
![]() $b_1 \leftrightarrow \neg \neg b_1 \in F$
. Since
$b_1 \leftrightarrow \neg \neg b_1 \in F$
. Since
![]() $a_1 \leftrightarrow b_1 \in F$
by assumption, it follows by transitivity (Lemma 3.2.3) that
$a_1 \leftrightarrow b_1 \in F$
by assumption, it follows by transitivity (Lemma 3.2.3) that
![]() $\neg \neg a_1 \leftrightarrow \neg \neg b_1 \in F$
. We conclude that R is compatible with the language operations. Finally, it follows by (MP) that R is compatible with F. Thus,
$\neg \neg a_1 \leftrightarrow \neg \neg b_1 \in F$
. We conclude that R is compatible with the language operations. Finally, it follows by (MP) that R is compatible with F. Thus,
![]() $R \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
$R \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
Theorem 11.7. The logics
![]() and
and
![]() are finitely algebraizable, with a set of congruence formulas
are finitely algebraizable, with a set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
and a set of truth equations
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
and a set of truth equations
![]() ${\boldsymbol {\tau }}(x) = \{ (x \to x) \to x \approx x \to x \}$
.
${\boldsymbol {\tau }}(x) = \{ (x \to x) \to x \approx x \to x \}$
.
The algebraizability of
![]() was first established in [Reference Lewin, Mikenberg and Schwarze39, Theorem 2.1]. The algebraizability of
was first established in [Reference Lewin, Mikenberg and Schwarze39, Theorem 2.1]. The algebraizability of
![]() is contained in [Reference Carnielli and Marcos16, Fact 3.82] or [Reference Carnielli, Coniglio and Marcos17, Theorem 135], although it is unclear whether the relations there considered are in fact congruence relations—see the remarks on page 479.
is contained in [Reference Carnielli and Marcos16, Fact 3.82] or [Reference Carnielli, Coniglio and Marcos17, Theorem 135], although it is unclear whether the relations there considered are in fact congruence relations—see the remarks on page 479.
For the next result let
![]() ${\mathcal {S}}$
be a finitary and finitely equivalential extension of
${\mathcal {S}}$
be a finitary and finitely equivalential extension of
![]() ${\mathcal {C}ilo}$
, extended itself by
${\mathcal {C}ilo}$
, extended itself by
![]() $\mathcal {CL}$
, with (finite) set of congruence formulas
$\mathcal {CL}$
, with (finite) set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
. This encompasses both
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
. This encompasses both
![]() and
and
![]() .
.
Theorem 11.8. If
![]() ${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a subdirectly irreducible algebra relative to
${\boldsymbol {A}} \in {\mathsf {Alg}}^*({\mathcal {S}})$
is a subdirectly irreducible algebra relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, then the truth tables of the
${\mathsf {Alg}}^*({\mathcal {S}})$
, then the truth tables of the
![]() ${\mathcal {L}}$
-connectives on
${\mathcal {L}}$
-connectives on
![]() ${\boldsymbol {A}}$
agree with those in Table 6.
${\boldsymbol {A}}$
agree with those in Table 6.
Table 6 The truth-tables of Theorem 11.8.

Proof Let
![]() ${\boldsymbol {A}}$
comply with the assumption. It follows by Theorem 8.7 that
${\boldsymbol {A}}$
comply with the assumption. It follows by Theorem 8.7 that
![]() $|A|\leq 3$
, say
$|A|\leq 3$
, say
![]() $A = \{0,1,a\}$
. We proceed to construct the truth table of
$A = \{0,1,a\}$
. We proceed to construct the truth table of
![]() ${\boldsymbol {A}}$
. Fix
${\boldsymbol {A}}$
. Fix
![]() , having in mind Corollary 8.5.1.
, having in mind Corollary 8.5.1.
-
i. The truth table of the subuniverse
 $A^{\circ } = \{0,1\}$
is obvious, given the fact that
$A^{\circ } = \{0,1\}$
is obvious, given the fact that
 by Theorem 8.3.
by Theorem 8.3. -
ii. Let
 $* \in \{\wedge , \vee , \to \}$
. Notice that since
$* \in \{\wedge , \vee , \to \}$
. Notice that since
 $0^{\circ } = 1^{\circ } = 1 \in F$
, it follows by (Ax12a)–(Ax14a) that
$0^{\circ } = 1^{\circ } = 1 \in F$
, it follows by (Ax12a)–(Ax14a) that
 $(a * 0)^{\circ } , (0 * a)^{\circ } , (a * 1)^{\circ } , (1 * a)^{\circ } \in F$
. But clearly all these elements are in
$(a * 0)^{\circ } , (0 * a)^{\circ } , (a * 1)^{\circ } , (1 * a)^{\circ } \in F$
. But clearly all these elements are in
 $A^{\circ }$
. Therefore,
$A^{\circ }$
. Therefore,
 $(a * 0)^{\circ } , (0 * a)^{\circ } , (a * 1)^{\circ } , (1 * a)^{\circ } \in F \cap A^{\circ } = \{1\}$
, using Corollary 7.5. It follows by Lemma 8.4 that
$(a * 0)^{\circ } , (0 * a)^{\circ } , (a * 1)^{\circ } , (1 * a)^{\circ } \in F \cap A^{\circ } = \{1\}$
, using Corollary 7.5. It follows by Lemma 8.4 that
 $a * 0, 0 * a, a * 1, 1 * a \in \{0,1\}$
. We now reason by cases until we obtain the (incomplete) truth-tables of Table 7.
$a * 0, 0 * a, a * 1, 1 * a \in \{0,1\}$
. We now reason by cases until we obtain the (incomplete) truth-tables of Table 7.Table 7 The truth-tables of the algebra
 ${\boldsymbol {T}}$
[Reference Mortensen45, p. 301].
${\boldsymbol {T}}$
[Reference Mortensen45, p. 301].
-
a. If
 $1 \wedge a = 0$
, then since both
$1 \wedge a = 0$
, then since both
 $a,1 \in F$
, it would follow by (Ax5) and (MP) that
$a,1 \in F$
, it would follow by (Ax5) and (MP) that
 $0 \in F$
, reaching a contradiction. Thus,
$0 \in F$
, reaching a contradiction. Thus,
 $1 \wedge a = 1$
. Mutatis mutandis for
$1 \wedge a = 1$
. Mutatis mutandis for
 $a \wedge 1 = 1$
.
$a \wedge 1 = 1$
. -
b. If
 $0 \wedge a = 1$
, then it would follow by (Ax3) and (MP) that
$0 \wedge a = 1$
, then it would follow by (Ax3) and (MP) that
 $0 \in F$
, reaching a contradiction. Thus,
$0 \in F$
, reaching a contradiction. Thus,
 $0 \wedge a = 0$
. Mutatis mutandis for
$0 \wedge a = 0$
. Mutatis mutandis for
 $a \wedge 0 = 0$
, using (Ax4).
$a \wedge 0 = 0$
, using (Ax4). -
c. Let
 $x \in \{0,1\}$
. If
$x \in \{0,1\}$
. If
 $x \vee a = 0$
, then since
$x \vee a = 0$
, then since
 $a \in F$
, it would follow by (Ax7) that
$a \in F$
, it would follow by (Ax7) that
 $0 \in F$
, reaching a contradiction. Thus,
$0 \in F$
, reaching a contradiction. Thus,
 $x \vee a = 1$
. Mutatis mutandis for
$x \vee a = 1$
. Mutatis mutandis for
 $a \vee x = 1$
, using (Ax6).
$a \vee x = 1$
, using (Ax6). -
d. If
 $a \to 1 = 0$
, then since
$a \to 1 = 0$
, then since
 $1 \in F$
, it would follow by (Ax1) and (MP) that
$1 \in F$
, it would follow by (Ax1) and (MP) that
 $0 \in F$
, reaching a contradiction. Thus,
$0 \in F$
, reaching a contradiction. Thus,
 $a \to 1 = 1$
.
$a \to 1 = 1$
. -
e. If
 $a \to 0 = 1$
, then since
$a \to 0 = 1$
, then since
 $a \in F$
, it would follow by (MP) that
$a \in F$
, it would follow by (MP) that
 $0 \in F$
, reaching a contradiction. Thus,
$0 \in F$
, reaching a contradiction. Thus,
 $a \to 0 = 0$
.
$a \to 0 = 0$
. -
f. If
 $1 \to a = 0$
, then since
$1 \to a = 0$
, then since
 $a \in F$
, it would follow by (Ax1) and (MP) that
$a \in F$
, it would follow by (Ax1) and (MP) that
 $0 \in F$
, reaching a contradiction. Thus,
$0 \in F$
, reaching a contradiction. Thus,
 $1 \to a = 1$
. Mutatis mutandis for
$1 \to a = 1$
. Mutatis mutandis for
 $0 \to a = 1$
.
$0 \to a = 1$
.
-
-
iii. Let
 $* \in \{\wedge , \vee , \to \}$
. We are left to prove that
$* \in \{\wedge , \vee , \to \}$
. We are left to prove that
 $\neg a \neq 0$
and
$\neg a \neq 0$
and
 $a * a \neq 0$
. If
$a * a \neq 0$
. If
 $\neg a = 0$
, then
$\neg a = 0$
, then
 $a^{\circ } = 1$
, contradicting Lemma 8.4. Finally, since
$a^{\circ } = 1$
, contradicting Lemma 8.4. Finally, since
 $a \in F$
, notice that we also have
$a \in F$
, notice that we also have
 $a * a \in F$
. Thus,
$a * a \in F$
. Thus,
 $a * a \neq 0$
.
$a * a \neq 0$
.
This does not necessarily mean that there exist
![]() $2^4$
non-trivial algebras in
$2^4$
non-trivial algebras in
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
${\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
. For instance, any truth-table agreeing with Table 6 and such that
${\mathsf {Alg}}^*({\mathcal {S}})$
. For instance, any truth-table agreeing with Table 6 and such that
![]() $a \wedge a = a$
and
$a \wedge a = a$
and
![]() $\neg a = a$
will not correspond to a non-trivial algebra in
$\neg a = a$
will not correspond to a non-trivial algebra in
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
${\mathsf {Alg}}^*({\mathcal {S}})$
subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
, otherwise
${\mathsf {Alg}}^*({\mathcal {S}})$
, otherwise
![]() $a^{\circ } = \neg (a \wedge \neg a) = \neg (a \wedge a) = \neg a = a$
, contradicting Lemma 8.4. It does mean however that there exist at most
$a^{\circ } = \neg (a \wedge \neg a) = \neg (a \wedge a) = \neg a = a$
, contradicting Lemma 8.4. It does mean however that there exist at most
![]() $12$
non-trivial algebras in
$12$
non-trivial algebras in
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
with three elements subdirectly irreducible relative to
${\mathsf {Alg}}^*({\mathcal {S}})$
with three elements subdirectly irreducible relative to
![]() ${\mathsf {Alg}}^*({\mathcal {S}})$
. We shall see three of them in greater detail—namely, the algebras
${\mathsf {Alg}}^*({\mathcal {S}})$
. We shall see three of them in greater detail—namely, the algebras
![]() ${\boldsymbol {S}}$
,
${\boldsymbol {S}}$
,
![]() ${\boldsymbol {T}}$
, and
${\boldsymbol {T}}$
, and
![]() ${\boldsymbol {R}}$
.
${\boldsymbol {R}}$
.
Given Proposition 11.6, we can apply the general results of Section 8 together with Theorem 11.8 to the logics
![]() and
and
![]() .
.
Theorem 11.9. The only non-trivial algebras in
![]() subdirectly irreducible relative to
subdirectly irreducible relative to
![]() are
are
![]() ,
,
![]() ${\boldsymbol {S}}$
.
${\boldsymbol {S}}$
.
Proof Let
![]() ${\boldsymbol {A}}$
comply with the assumption. The proof goes exactly as in Theorem 11.8, with two further items:
${\boldsymbol {A}}$
comply with the assumption. The proof goes exactly as in Theorem 11.8, with two further items:
-
iv. Let
 $* \in \{\wedge , \vee , \to \}$
. On the one hand, notice that
$* \in \{\wedge , \vee , \to \}$
. On the one hand, notice that
 $(a * a)^{\circ } \in F \cap A^{\circ } = \{1\}$
, using (Ax12b)–(Ax14b). It follows by Lemma 8.4 that
$(a * a)^{\circ } \in F \cap A^{\circ } = \{1\}$
, using (Ax12b)–(Ax14b). It follows by Lemma 8.4 that
 $a * a \in \{0,1\}$
. On the other hand, since
$a * a \in \{0,1\}$
. On the other hand, since
 $a \in F$
, we have
$a \in F$
, we have
 $a * a \in F = \{a,1\}$
. It can only be the case then that
$a * a \in F = \{a,1\}$
. It can only be the case then that
 $a * a = 1$
.
$a * a = 1$
. -
v. Notice that
 $(\neg a)^{\circ } \in F \cap A^{\circ } = \{1\}$
, using (Ax15). It follows by Lemma 8.4 that
$(\neg a)^{\circ } \in F \cap A^{\circ } = \{1\}$
, using (Ax15). It follows by Lemma 8.4 that
 $\neg a \in \{0,1\}$
. But we had seen already in item iii (see the proof of Theorem 11.8) that
$\neg a \in \{0,1\}$
. But we had seen already in item iii (see the proof of Theorem 11.8) that
 $\neg a \neq 0$
. Thus,
$\neg a \neq 0$
. Thus,
 $\neg a = 1$
.
$\neg a = 1$
.
We conclude that
![]() ${\boldsymbol {A}} \cong {\boldsymbol {S}}$
, whose truth-tables are depicted in Table 8.
${\boldsymbol {A}} \cong {\boldsymbol {S}}$
, whose truth-tables are depicted in Table 8.
Table 8 The truth-tables of the algebra
![]() ${\boldsymbol {S}}$
[Reference Sette53, pp. 176 and 179] and [Reference Pynko50, p. 101].
${\boldsymbol {S}}$
[Reference Sette53, pp. 176 and 179] and [Reference Pynko50, p. 101].

Theorem 11.9 generalizes [Reference Lewin, Mikenberg and Schwarze40, Theorem 9], which states that the only subdirectly irreducible algebras in
![]() are
are
![]() and
and
![]() ${\boldsymbol {S}}$
.
${\boldsymbol {S}}$
.
Theorem 11.10. The only non-trivial algebras in
![]() subdirectly irreducible relative to
subdirectly irreducible relative to
![]() are
are
![]() ,
,
![]() ${\boldsymbol {T}}$
.
${\boldsymbol {T}}$
.
Proof Let
![]() ${\boldsymbol {A}}$
comply with the assumption. The proof goes exactly as in Theorem 11.8, with two further items:
${\boldsymbol {A}}$
comply with the assumption. The proof goes exactly as in Theorem 11.8, with two further items:
-
iv. Let
 $* \in \{\wedge , \vee , \to \}$
. On the one hand, notice that
$* \in \{\wedge , \vee , \to \}$
. On the one hand, notice that
 $(a * a)^{\circ } \in F \cap A^{\circ } = \{1\}$
, using (Ax12b)–(Ax14b). It follows by Lemma 8.4 that
$(a * a)^{\circ } \in F \cap A^{\circ } = \{1\}$
, using (Ax12b)–(Ax14b). It follows by Lemma 8.4 that
 $a * a \in \{0,1\}$
. On the other hand, since
$a * a \in \{0,1\}$
. On the other hand, since
 $a \in F$
, we have
$a \in F$
, we have
 $a * a \in F = \{a,1\}$
. It can only be the case then that
$a * a \in F = \{a,1\}$
. It can only be the case then that
 $a * a = 1$
.
$a * a = 1$
. -
v. We know by item iii (see the proof of Theorem 11.8) that
 $\neg a \neq 0$
. Suppose for the sake of contradiction that
$\neg a \neq 0$
. Suppose for the sake of contradiction that
 $\neg a = 1$
. Since
$\neg a = 1$
. Since
 $1 \to a = 1 \in F$
and
$1 \to a = 1 \in F$
and
 $a \to \neg \neg a$
by (Ax16), it follows by transitivity (Lemma 3.2.3) that
$a \to \neg \neg a$
by (Ax16), it follows by transitivity (Lemma 3.2.3) that
 $1 \to \neg \neg a \in F$
, that is
$1 \to \neg \neg a \in F$
, that is
 $1 \to \neg 1 = 1 \to 0 = 0 \in F$
. We reach a contradiction. Thus,
$1 \to \neg 1 = 1 \to 0 = 0 \in F$
. We reach a contradiction. Thus,
 $\neg a = a$
.
$\neg a = a$
.
We conclude that
![]() ${\boldsymbol {A}} \cong {\boldsymbol {T}}$
, whose truth-tables are depicted in Table 8.
${\boldsymbol {A}} \cong {\boldsymbol {T}}$
, whose truth-tables are depicted in Table 8.
Theorems 11.9 and 11.10 allow us to characterize the classes of algebraic reducts of
![]() and
and
![]() , as well as their intrinsic varieties. In the case of
, as well as their intrinsic varieties. In the case of
![]() , the result is already known and even has a lattice characterization, corresponding to the so-called Sette’s algebras.
, the result is already known and even has a lattice characterization, corresponding to the so-called Sette’s algebras.
Proposition 11.11.
![]() .
.
Proof It is easy to check that
![]() . Therefore
. Therefore
![]() , because
, because
![]() is closed under
is closed under
![]() $\mathbb {IP}_{\mathrm {S}}$
. Conversely, let
$\mathbb {IP}_{\mathrm {S}}$
. Conversely, let
![]() . Since
. Since
![]() is a quasivariety, because
is a quasivariety, because
![]() is finitary and finitely equivalential [Reference Font32, Corollary 6.80], it follows by Theorem 11.9 that
is finitary and finitely equivalential [Reference Font32, Corollary 6.80], it follows by Theorem 11.9 that
![]() . Thus,
. Thus,
![]() . The inclusion
. The inclusion
![]() follows once again from the fact that
follows once again from the fact that
![]() is a quasivariety. To prove the converse inclusion notice that since
is a quasivariety. To prove the converse inclusion notice that since
![]() ${\boldsymbol {S}}$
is subdirectly irreducible relative to
${\boldsymbol {S}}$
is subdirectly irreducible relative to
![]() , it follows by Theorem 8.3 that
, it follows by Theorem 8.3 that
![]() , and hence
, and hence
![]() . Finally,
. Finally,
![]() $\mathbb {Q}({\boldsymbol {S}}) = \mathsf {SA}$
by definition of Sette algebra given in [Reference Pynko50, p. 106].
$\mathbb {Q}({\boldsymbol {S}}) = \mathsf {SA}$
by definition of Sette algebra given in [Reference Pynko50, p. 106].
The identity
![]() was first established in [Reference Lewin, Mikenberg and Schwarze38, Corollary 2.2], while the identity
was first established in [Reference Lewin, Mikenberg and Schwarze38, Corollary 2.2], while the identity
![]() $\mathbb {Q}({\boldsymbol {S}}) = \mathsf {SA}$
was established in [Reference Pynko50, Theorem 4.3], together with an axiomatization of Sette’s algebras.
$\mathbb {Q}({\boldsymbol {S}}) = \mathsf {SA}$
was established in [Reference Pynko50, Theorem 4.3], together with an axiomatization of Sette’s algebras.
Interestingly enough, Proposition 11.11 and Pynko’s [Reference Pynko50, Corollary 5.8] provide us with a lattice characterization of the intrinsic variety of
![]() . Quasi-Sette algebras are introduced in [Reference Pynko50, Section 5], and following [Reference Pynko50, Definition 5.1] we shall denote the variety of all quasi-Sette algebras by
. Quasi-Sette algebras are introduced in [Reference Pynko50, Section 5], and following [Reference Pynko50, Definition 5.1] we shall denote the variety of all quasi-Sette algebras by
![]() $\mathsf {QSA}$
.
$\mathsf {QSA}$
.
Corollary 11.12.
![]() .
.
Proof Since
![]() , the identity
, the identity
![]() follows immediately by Proposition 11.11. The identity
follows immediately by Proposition 11.11. The identity
![]() $\mathbb {V}({\boldsymbol {S}}) = \mathsf {QSA}$
was proved in [Reference Pynko50, Corollary 5.8].
$\mathbb {V}({\boldsymbol {S}}) = \mathsf {QSA}$
was proved in [Reference Pynko50, Corollary 5.8].
Proposition 11.13.
![]() .
.
Proof It is easy to check that
![]() . Therefore
. Therefore
![]() , because
, because
![]() is closed under
is closed under
![]() $\mathbb {IP}_{\mathrm {S}}$
. Conversely, let
$\mathbb {IP}_{\mathrm {S}}$
. Conversely, let
![]() . Since
. Since
![]() is a quasivariety, because
is a quasivariety, because
![]() is finitary and finitely equivalential [Reference Font32, Corollary 6.80], it follows by Theorem 11.9 that
is finitary and finitely equivalential [Reference Font32, Corollary 6.80], it follows by Theorem 11.9 that
![]() . Thus,
. Thus,
![]() . The inclusion
. The inclusion
![]() follows once again from the fact that
follows once again from the fact that
![]() is a quasivariety. To prove the converse inclusion notice that since
is a quasivariety. To prove the converse inclusion notice that since
![]() ${\boldsymbol {T}}$
is subdirectly irreducible relative to
${\boldsymbol {T}}$
is subdirectly irreducible relative to
![]() , it follows by Theorem 8.3 that
, it follows by Theorem 8.3 that
![]() , and hence
, and hence
![]() .
.
Corollary 11.14.
![]() .
.
12 The logic

In this last section we introduce the logic
![]() , prove that it coincides with the logic
, prove that it coincides with the logic
![]() ${\mathcal {C}ilor}$
also covered in the literature (Proposition 12.2), and classify it within the Leibniz hierarchy (Theorem 12.7). Similarly to the previous section, we then characterize the non-trivial algebras in
${\mathcal {C}ilor}$
also covered in the literature (Proposition 12.2), and classify it within the Leibniz hierarchy (Theorem 12.7). Similarly to the previous section, we then characterize the non-trivial algebras in
![]() subdirectly irreducible relative to
subdirectly irreducible relative to
![]() (Theorem 12.8) in order to determine the quasivariety
(Theorem 12.8) in order to determine the quasivariety
![]() (Proposition 12.9) and the variety
(Proposition 12.9) and the variety
![]() (Corollary 12.10).
(Corollary 12.10).
Let us define the logic
![]() ${\mathcal {C}ilor}$
Footnote
14
as the (axiomatic) extension of
${\mathcal {C}ilor}$
Footnote
14
as the (axiomatic) extension of
![]() ${\mathcal {C}ilo}$
by the following axioms:
${\mathcal {C}ilo}$
by the following axioms:
The logic
![]() is the extension of
is the extension of
![]() ${\mathcal {C}ilor}$
by the axiom (Ax15).
${\mathcal {C}ilor}$
by the axiom (Ax15).
Before proceeding with the classification of
![]() ${\mathcal {C}ilor}$
and
${\mathcal {C}ilor}$
and
![]() within the Leibniz hierarchy, let us see that these two logics in fact coincide.
within the Leibniz hierarchy, let us see that these two logics in fact coincide.
Lemma 12.1.
-
1.
 $ \vdash _{{\mathscr {C}}_1} (\varphi \wedge \psi ) \wedge \xi \leftrightarrow \varphi \wedge (\psi \wedge \xi )$
.
$ \vdash _{{\mathscr {C}}_1} (\varphi \wedge \psi ) \wedge \xi \leftrightarrow \varphi \wedge (\psi \wedge \xi )$
. -
2.
 $ \vdash _{{\mathcal {C}ilor}} \big ((\varphi \wedge \psi ) \wedge \xi \big )^{\circ } \leftrightarrow \big (\varphi \wedge (\psi \wedge \xi )\big )^{\circ }$
.
$ \vdash _{{\mathcal {C}ilor}} \big ((\varphi \wedge \psi ) \wedge \xi \big )^{\circ } \leftrightarrow \big (\varphi \wedge (\psi \wedge \xi )\big )^{\circ }$
. -
3.
 $ \vdash _{{\mathcal {C}ilor}} \neg \big ((\varphi \wedge \psi ) \wedge \xi \big ) \leftrightarrow \neg \big (\varphi \wedge (\psi \wedge \xi )\big )$
.
$ \vdash _{{\mathcal {C}ilor}} \neg \big ((\varphi \wedge \psi ) \wedge \xi \big ) \leftrightarrow \neg \big (\varphi \wedge (\psi \wedge \xi )\big )$
. -
4.
 $ \vdash _{{\mathcal {C}ilor}} (\varphi \wedge \neg \varphi )^{\circ }$
.
$ \vdash _{{\mathcal {C}ilor}} (\varphi \wedge \neg \varphi )^{\circ }$
. -
5.
 $ \vdash _{{\mathcal {C}ilor}} (\neg \varphi )^{\circ }$
.
$ \vdash _{{\mathcal {C}ilor}} (\neg \varphi )^{\circ }$
.
Proof 1. It follows easily by Definition 3.3 and Theorem 3.4.
2. Notice that
![]() $ \vdash _{{\mathcal {C}ilor}} \big ((\varphi \wedge \psi ) \wedge \xi \big )^{\circ } \leftrightarrow \big ((\varphi ^{\circ } \vee \psi ^{\circ }) \vee \xi ^{\circ }\big )$
by (Ax12) and (Ax12c). Notice also that
$ \vdash _{{\mathcal {C}ilor}} \big ((\varphi \wedge \psi ) \wedge \xi \big )^{\circ } \leftrightarrow \big ((\varphi ^{\circ } \vee \psi ^{\circ }) \vee \xi ^{\circ }\big )$
by (Ax12) and (Ax12c). Notice also that
![]() $ \vdash _{{\mathscr {C}}_1} \big ((\varphi ^{\circ } \vee \psi ^{\circ }) \vee \xi ^{\circ }\big ) \leftrightarrow \big (\varphi ^{\circ } \vee (\psi ^{\circ } \vee \xi ^{\circ })\big )$
by 1. Finally, notice that
$ \vdash _{{\mathscr {C}}_1} \big ((\varphi ^{\circ } \vee \psi ^{\circ }) \vee \xi ^{\circ }\big ) \leftrightarrow \big (\varphi ^{\circ } \vee (\psi ^{\circ } \vee \xi ^{\circ })\big )$
by 1. Finally, notice that
![]() $ \vdash _{{\mathcal {C}ilor}} \big (\varphi ^{\circ } \vee (\psi ^{\circ } \vee \xi ^{\circ })\big ) \leftrightarrow \big (\varphi \wedge (\psi \wedge \xi )\big )^{\circ }$
, again by (Ax12) and (Ax12c). The result now follows by transitivity (Lemma 3.2.3).
$ \vdash _{{\mathcal {C}ilor}} \big (\varphi ^{\circ } \vee (\psi ^{\circ } \vee \xi ^{\circ })\big ) \leftrightarrow \big (\varphi \wedge (\psi \wedge \xi )\big )^{\circ }$
, again by (Ax12) and (Ax12c). The result now follows by transitivity (Lemma 3.2.3).
3. It follows by 1 and 2, together with Lemma 4.2.2.
4. Fix
![]() $\xi = \varphi \wedge \neg \varphi $
. Notice that
$\xi = \varphi \wedge \neg \varphi $
. Notice that
![]() $\xi ^{\circ } = \neg ((\varphi \wedge \neg \varphi ) \wedge \varphi ^{\circ })$
. Having in mind 3, we have
$\xi ^{\circ } = \neg ((\varphi \wedge \neg \varphi ) \wedge \varphi ^{\circ })$
. Having in mind 3, we have
![]() $ \vdash _{{\mathcal {C}ilor}} \neg ((\varphi \wedge \neg \varphi ) \wedge \varphi ^{\circ }) \leftrightarrow \neg (\varphi \wedge \sim \! \varphi )$
. But
$ \vdash _{{\mathcal {C}ilor}} \neg ((\varphi \wedge \neg \varphi ) \wedge \varphi ^{\circ }) \leftrightarrow \neg (\varphi \wedge \sim \! \varphi )$
. But
![]() $ \vdash _{{\mathscr {C}}_1} \neg (\varphi \wedge \sim \! \varphi )$
, fact which can be easily checked using Definition 3.3 da Costa’s completeness Theorem 3.4. Therefore,
$ \vdash _{{\mathscr {C}}_1} \neg (\varphi \wedge \sim \! \varphi )$
, fact which can be easily checked using Definition 3.3 da Costa’s completeness Theorem 3.4. Therefore,
![]() $ \vdash _{{\mathcal {C}ilor}} \neg ((\varphi \wedge \neg \varphi ) \wedge \varphi ^{\circ })$
. That is,
$ \vdash _{{\mathcal {C}ilor}} \neg ((\varphi \wedge \neg \varphi ) \wedge \varphi ^{\circ })$
. That is,
![]() $ \vdash _{{\mathcal {C}ilor}} \xi ^{\circ }$
.
$ \vdash _{{\mathcal {C}ilor}} \xi ^{\circ }$
.
5. It follows by (Ax12c) that
![]() $ \vdash _{{\mathcal {C}ilor}} (\varphi \wedge \neg \varphi )^{\circ } \to \varphi ^{\circ } \vee (\neg \varphi )^{\circ }$
. Therefore by 4 and (MP),
$ \vdash _{{\mathcal {C}ilor}} (\varphi \wedge \neg \varphi )^{\circ } \to \varphi ^{\circ } \vee (\neg \varphi )^{\circ }$
. Therefore by 4 and (MP),
![]() $ \vdash _{{\mathcal {C}ilor}} \varphi ^{\circ } \vee (\neg \varphi )^{\circ }$
. Finally, since
$ \vdash _{{\mathcal {C}ilor}} \varphi ^{\circ } \vee (\neg \varphi )^{\circ }$
. Finally, since
![]() $ \vdash _{{\mathcal {C}ilor}} \varphi ^{\circ } \to (\neg \varphi )^{\circ }$
by Lemma 3.2.19 and
$ \vdash _{{\mathcal {C}ilor}} \varphi ^{\circ } \to (\neg \varphi )^{\circ }$
by Lemma 3.2.19 and
![]() $ \vdash _{{\mathcal {C}ilor}} (\neg \varphi )^{\circ } \to (\neg \varphi )^{\circ }$
by Lemma 3.2.11, it follows by (Ax8) and (MP) that
$ \vdash _{{\mathcal {C}ilor}} (\neg \varphi )^{\circ } \to (\neg \varphi )^{\circ }$
by Lemma 3.2.11, it follows by (Ax8) and (MP) that
![]() $ \vdash _{{\mathcal {C}ilor}} (\neg \varphi )^{\circ }$
.
$ \vdash _{{\mathcal {C}ilor}} (\neg \varphi )^{\circ }$
.
Since
![]() by definition, and
by definition, and
![]() ${\mathcal {C}ilor}$
satisfies axiom (Ax15) by Lemma 12.1.5, both logics coincide.
${\mathcal {C}ilor}$
satisfies axiom (Ax15) by Lemma 12.1.5, both logics coincide.
Proposition 12.2.
![]() .
.
Having considered the logic
![]() ${\mathcal {C}ilor} + \mathrm {( {Ax15})}$
, it is also natural to consider the logic
${\mathcal {C}ilor} + \mathrm {( {Ax15})}$
, it is also natural to consider the logic
![]() ${\mathcal {C}ilor} + \mathrm {( {Ax16})}$
. However, in this case we are in the presence of classical logic.
${\mathcal {C}ilor} + \mathrm {( {Ax16})}$
. However, in this case we are in the presence of classical logic.
Proposition 12.3.
![]() ${\mathcal {C}ilor} + \mathrm {( {Ax16})} = \mathcal {CL}$
.
${\mathcal {C}ilor} + \mathrm {( {Ax16})} = \mathcal {CL}$
.
Proof Let
![]() ${\mathcal {S}} = {\mathcal {C}ilor} + \mathrm {( {Ax16})}$
. We claim that
${\mathcal {S}} = {\mathcal {C}ilor} + \mathrm {( {Ax16})}$
. We claim that
![]() $\vdash _{{\mathcal {S}}} \varphi ^{\circ }$
, for every
$\vdash _{{\mathcal {S}}} \varphi ^{\circ }$
, for every
![]() $\varphi \in \mathrm {Fm}_{\mathcal {L}}$
. On the one hand, since
$\varphi \in \mathrm {Fm}_{\mathcal {L}}$
. On the one hand, since
![]() ${\mathcal {C}ilor}$
satisfies axiom (Ax15) by Lemma 12.1.5, we have
${\mathcal {C}ilor}$
satisfies axiom (Ax15) by Lemma 12.1.5, we have
![]() $\vdash _{\mathcal {S}} (\neg \varphi )^{\circ }$
. Therefore,
$\vdash _{\mathcal {S}} (\neg \varphi )^{\circ }$
. Therefore,
![]() $\vdash _{\mathcal {S}} (\varphi \wedge \neg \varphi ) \to (\neg \varphi )^{\circ }$
. On the other hand, it follows by Lemma 3.2.13, axiom (Ax16) and the fact
$\vdash _{\mathcal {S}} (\varphi \wedge \neg \varphi ) \to (\neg \varphi )^{\circ }$
. On the other hand, it follows by Lemma 3.2.13, axiom (Ax16) and the fact
![]() $\vdash _{{\mathscr {C}}_1} \psi \wedge \delta \leftrightarrow \delta \wedge \psi $
, that
$\vdash _{{\mathscr {C}}_1} \psi \wedge \delta \leftrightarrow \delta \wedge \psi $
, that
![]() $\vdash _{\mathcal {S}} (\varphi \wedge \neg \varphi ) \to (\neg \varphi \wedge \neg \neg \varphi )$
. Moreover, since
$\vdash _{\mathcal {S}} (\varphi \wedge \neg \varphi ) \to (\neg \varphi \wedge \neg \neg \varphi )$
. Moreover, since
![]() $(\neg \varphi )^{\circ } = \neg (\neg \varphi \wedge \neg \neg \varphi )$
, it follows again by (Ax16) that
$(\neg \varphi )^{\circ } = \neg (\neg \varphi \wedge \neg \neg \varphi )$
, it follows again by (Ax16) that
![]() $\vdash _{\mathcal {S}} (\neg \varphi \wedge \neg \neg \varphi ) \to \neg (\neg \varphi )^{\circ }$
. Therefore, it follows by transitivity (Lemma 3.2.3) that
$\vdash _{\mathcal {S}} (\neg \varphi \wedge \neg \neg \varphi ) \to \neg (\neg \varphi )^{\circ }$
. Therefore, it follows by transitivity (Lemma 3.2.3) that
![]() $\vdash _{\mathcal {S}} (\varphi \wedge \neg \varphi ) \to \neg (\neg \varphi )^{\circ }$
. Finally, we have
$\vdash _{\mathcal {S}} (\varphi \wedge \neg \varphi ) \to \neg (\neg \varphi )^{\circ }$
. Finally, we have
![]() $\vdash _{\mathcal {S}} \big ((\neg \varphi )^{\circ }\big )^{\circ }$
by Lemma 3.2.20. Now, fix
$\vdash _{\mathcal {S}} \big ((\neg \varphi )^{\circ }\big )^{\circ }$
by Lemma 3.2.20. Now, fix
![]() . We have by (Ax11),
. We have by (Ax11),
It follows by successive applications of (MP) that
![]() $\vdash _{{\mathcal {S}}} \neg \xi $
. That is
$\vdash _{{\mathcal {S}}} \neg \xi $
. That is
![]() $\vdash _{{\mathcal {S}}} \varphi ^{\circ }$
, as claimed. We conclude that
$\vdash _{{\mathcal {S}}} \varphi ^{\circ }$
, as claimed. We conclude that
![]() ${\mathcal {S}} = \mathcal {CL}$
—see [Reference da Costa, Krause and Bueno26, Theorem 2.1.5].
${\mathcal {S}} = \mathcal {CL}$
—see [Reference da Costa, Krause and Bueno26, Theorem 2.1.5].
Other than
![]() ${\mathscr {C}}_1$
’s axioms, the above proof makes use only of axioms (Ax15) and (Ax16).
${\mathscr {C}}_1$
’s axioms, the above proof makes use only of axioms (Ax15) and (Ax16).
Corollary 12.4.
![]() ${\mathscr {C}}_1 + \mathrm {( {Ax15})} + \mathrm {( {Ax16})} = \mathcal {CL}$
.
${\mathscr {C}}_1 + \mathrm {( {Ax15})} + \mathrm {( {Ax16})} = \mathcal {CL}$
.
Similarly to the logics
![]() and
and
![]() , the logic
, the logic
![]() is also finitely equivalential.
is also finitely equivalential.
Proposition 12.5. The logic
![]() is finitely equivalential, witnessed by the set of congruence formulas
is finitely equivalential, witnessed by the set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , x^{\circ } \leftrightarrow y^{\circ } \}$
.
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , x^{\circ } \leftrightarrow y^{\circ } \}$
.
Proof We prove that for every
![]() ${\boldsymbol {A}}$
and every
${\boldsymbol {A}}$
and every
![]() ,
,
Let
![]() ${\boldsymbol {A}}$
arbitrary and
${\boldsymbol {A}}$
arbitrary and
![]() . Define the relation
. Define the relation
![]() $R \subseteq A \times A$
by
$R \subseteq A \times A$
by
![]() $\langle a,b \rangle \in R \;\text {iff}\; a \leftrightarrow b \in F \text { and } a^{\circ } \leftrightarrow b^{\circ } \in F$
. Assume that
$\langle a,b \rangle \in R \;\text {iff}\; a \leftrightarrow b \in F \text { and } a^{\circ } \leftrightarrow b^{\circ } \in F$
. Assume that
![]() $\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. It follows by Proposition 4.1 that
$\langle a,b \rangle \in {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. It follows by Proposition 4.1 that
![]() $a\,R\,b$
. Thus,
$a\,R\,b$
. Thus,
![]() ${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \subseteq R$
. Conversely, we claim that R is a congruence relation on
${\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \subseteq R$
. Conversely, we claim that R is a congruence relation on
![]() ${\boldsymbol {A}}$
compatible with F. It should be clear that it is an equivalence relation on A by Lemma 3.2.1–3. Let
${\boldsymbol {A}}$
compatible with F. It should be clear that it is an equivalence relation on A by Lemma 3.2.1–3. Let
![]() $a_1\,R\,b_1$
and
$a_1\,R\,b_1$
and
![]() $a_2\,R\,b_2$
. On the one hand, it follows by Lemma 3.2.4–6 that
$a_2\,R\,b_2$
. On the one hand, it follows by Lemma 3.2.4–6 that
![]() $(a_1 * b_1) \leftrightarrow (a_2 * b_2) \in F$
, with
$(a_1 * b_1) \leftrightarrow (a_2 * b_2) \in F$
, with
![]() $* \in \{ \wedge ,\vee ,\to \}$
. Moreover, since both
$* \in \{ \wedge ,\vee ,\to \}$
. Moreover, since both
![]() $a_1 \leftrightarrow b_1 , a_1^{\circ } \leftrightarrow b_1^{\circ } \in F$
by assumption, it follows by Lemma 4.2.2 that
$a_1 \leftrightarrow b_1 , a_1^{\circ } \leftrightarrow b_1^{\circ } \in F$
by assumption, it follows by Lemma 4.2.2 that
![]() $\neg a_1 \leftrightarrow \neg b_1 \in F$
. On the other hand, we have by axioms (Ax12c)–(Ax14c) that
$\neg a_1 \leftrightarrow \neg b_1 \in F$
. On the other hand, we have by axioms (Ax12c)–(Ax14c) that
![]() $(a_1 * a_2)^{\circ } \to a_1^{\circ } \vee a_2^{\circ } \in F$
, with
$(a_1 * a_2)^{\circ } \to a_1^{\circ } \vee a_2^{\circ } \in F$
, with
![]() $* \in \{\wedge , \vee , \to \}$
. Since by assumption
$* \in \{\wedge , \vee , \to \}$
. Since by assumption
![]() $a_1^{\circ } \leftrightarrow b_1^{\circ } \in F$
and
$a_1^{\circ } \leftrightarrow b_1^{\circ } \in F$
and
![]() $a_2^{\circ } \leftrightarrow b_2^{\circ } \in F$
, it follows by Lemma 3.2.5 that
$a_2^{\circ } \leftrightarrow b_2^{\circ } \in F$
, it follows by Lemma 3.2.5 that
![]() $(a_1^{\circ } \vee a_2^{\circ }) \to (b_1^{\circ } \vee b_2^{\circ }) \in F$
,
$(a_1^{\circ } \vee a_2^{\circ }) \to (b_1^{\circ } \vee b_2^{\circ }) \in F$
,
![]() $* \in \{\wedge , \vee , \to \}$
. Moreover, it follows by axioms (Ax12)–(Ax14) that
$* \in \{\wedge , \vee , \to \}$
. Moreover, it follows by axioms (Ax12)–(Ax14) that
![]() $(b_1^{\circ } \vee b_2^{\circ }) \to (b_1 * b_2)^{\circ } \in F$
, with
$(b_1^{\circ } \vee b_2^{\circ }) \to (b_1 * b_2)^{\circ } \in F$
, with
![]() $* \in \{\wedge , \vee , \to \}$
. Thus by transitivity
$* \in \{\wedge , \vee , \to \}$
. Thus by transitivity
![]() $(a_1 * a_2)^{\circ } \to (b_1 * b_2)^{\circ } \in F$
. Similarly, one proves that
$(a_1 * a_2)^{\circ } \to (b_1 * b_2)^{\circ } \in F$
. Similarly, one proves that
![]() $(b_1 * b_2)^{\circ } \to (a_1 * a_2)^{\circ } \in F$
. Thus,
$(b_1 * b_2)^{\circ } \to (a_1 * a_2)^{\circ } \in F$
. Thus,
![]() $(a_1 * a_2)^{\circ } \leftrightarrow (b_1 * b_2)^{\circ } \in F$
. Finally, since
$(a_1 * a_2)^{\circ } \leftrightarrow (b_1 * b_2)^{\circ } \in F$
. Finally, since
![]() $(\neg a_1)^{\circ },(\neg b_1)^{\circ }$
by Lemma 12.1.5, it is clear that
$(\neg a_1)^{\circ },(\neg b_1)^{\circ }$
by Lemma 12.1.5, it is clear that
![]() $(\neg a_1)^{\circ } \leftrightarrow (\neg b_1)^{\circ } \in F$
. We conclude that R is compatible with the language operations. Furthermore, it follows by (MP) that R is compatible with F. Thus,
$(\neg a_1)^{\circ } \leftrightarrow (\neg b_1)^{\circ } \in F$
. We conclude that R is compatible with the language operations. Furthermore, it follows by (MP) that R is compatible with F. Thus,
![]() $R \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
$R \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
.
In light of Lemma 4.2.2, it follows that
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
is also a set of congruence formulas for
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
is also a set of congruence formulas for
![]() .
.
Truth-equationality follows by the fact that
![]() . But similarly to
. But similarly to
![]() ${\mathcal {C}ibv}$
, we can point out another set of truth-equations for
${\mathcal {C}ibv}$
, we can point out another set of truth-equations for
![]() simpler than the one presented for the logic
simpler than the one presented for the logic
![]() ${\mathcal {C}ilo}$
in Proposition 9.8. Indeed,
${\mathcal {C}ilo}$
in Proposition 9.8. Indeed,
![]() admits the same set of truth-equations than classical logic
admits the same set of truth-equations than classical logic
![]() $\mathcal {CL}$
.
$\mathcal {CL}$
.
Proposition 12.6. The logic
![]() is truth-equational, witnessed by the set of truth equations
is truth-equational, witnessed by the set of truth equations
![]() ${\boldsymbol {\tau }}(x) = \{ x \approx x \to x \}$
.
${\boldsymbol {\tau }}(x) = \{ x \approx x \to x \}$
.
Proof Let
![]() . Assume
. Assume
![]() $a \in F$
. Since moreover
$a \in F$
. Since moreover
![]() $a \to a \in F$
by Lemma 3.2.11, we have
$a \to a \in F$
by Lemma 3.2.11, we have
![]() $a \leftrightarrow (a \to a) \in F$
. On the other hand, we have
$a \leftrightarrow (a \to a) \in F$
. On the other hand, we have
![]() $(a \to a)^{\circ } \to a^{\circ } \in F$
by (Ax14c) and
$(a \to a)^{\circ } \to a^{\circ } \in F$
by (Ax14c) and
![]() $a^{\circ } \to (a \to a)^{\circ } \in F$
by (Ax14a). Therefore,
$a^{\circ } \to (a \to a)^{\circ } \in F$
by (Ax14a). Therefore,
![]() $a^{\circ } \leftrightarrow (a \to a)^{\circ } \in F$
. Thus,
$a^{\circ } \leftrightarrow (a \to a)^{\circ } \in F$
. Thus,
![]() ${\boldsymbol {\tau }}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
by Proposition 12.5. Conversely, assume
${\boldsymbol {\tau }}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
by Proposition 12.5. Conversely, assume
![]() ${\boldsymbol {\tau }}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Then,
${\boldsymbol {\tau }}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F)$
. Then,
![]() $a \leftrightarrow (a \to a) \in F$
. Since
$a \leftrightarrow (a \to a) \in F$
. Since
![]() $a \to a \in F$
, it follows by (MP) that
$a \to a \in F$
, it follows by (MP) that
![]() $a \in F$
. We conclude that
$a \in F$
. We conclude that
![]() $F = \{ a \in A : {\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \}$
, which proves the result.
$F = \{ a \in A : {\boldsymbol {\tau }}^{\boldsymbol {A}}(a) \subseteq {\boldsymbol {\varOmega }}^{\boldsymbol {A}}(F) \}$
, which proves the result.
We are now able to classify
![]() within the Leibniz hierarchy.
within the Leibniz hierarchy.
Theorem 12.7. The logic
![]() is finitely algebraizable, with a set of congruence formulas
is finitely algebraizable, with a set of congruence formulas
![]() ${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
and aaa set of truth equations
${\boldsymbol {\rho }}(x,y) = \{ x \leftrightarrow y , \neg x \leftrightarrow \neg y \}$
and aaa set of truth equations
![]() ${\boldsymbol {\tau }}(x) = \{ x \approx x \to x \}$
.
${\boldsymbol {\tau }}(x) = \{ x \approx x \to x \}$
.
The algebraizability of
![]() is contained in [Reference Carnielli and Marcos16, Fact 3.82] or [Reference Carnielli, Coniglio and Marcos17, Theorem 135], again assuming that the relations there considered are in fact congruence relations—see the remarks on page 479. However, the truth-set of Theorem 12.7 is new—the one presented in the cited results is
is contained in [Reference Carnielli and Marcos16, Fact 3.82] or [Reference Carnielli, Coniglio and Marcos17, Theorem 135], again assuming that the relations there considered are in fact congruence relations—see the remarks on page 479. However, the truth-set of Theorem 12.7 is new—the one presented in the cited results is
![]() ${\boldsymbol {\tau }}(x) = \{ (x \to x) \to x \approx x \to x \}$
.
${\boldsymbol {\tau }}(x) = \{ (x \to x) \to x \approx x \to x \}$
.
Proposition 12.5 makes it possible to apply once again the general results of Section 8 together with Theorem 11.8 to the logic
![]() .
.
Theorem 12.8. The only non-trivial algebras in
![]() subdirectly irreducible relative to
subdirectly irreducible relative to
![]() are
are
![]() and
and
![]() ${\boldsymbol {R}}$
.
${\boldsymbol {R}}$
.
Proof Let
![]() ${\boldsymbol {A}}$
comply with the assumption. The proof goes exactly as in Theorem 11.8, with two further items which go as follows:
${\boldsymbol {A}}$
comply with the assumption. The proof goes exactly as in Theorem 11.8, with two further items which go as follows:
-
iv. Let
 $* \in \{\wedge , \vee , \to \}$
. On the one hand, notice that
$* \in \{\wedge , \vee , \to \}$
. On the one hand, notice that
 $(a * a)^{\circ } \in A^{\circ } = \{0,1\}$
. But if
$(a * a)^{\circ } \in A^{\circ } = \{0,1\}$
. But if
 $(a * a)^{\circ } = 1$
, then
$(a * a)^{\circ } = 1$
, then
 $a^{\circ } = 1$
by (Ax12c)–(Ax14c), contradicting Lemma 8.4. So,
$a^{\circ } = 1$
by (Ax12c)–(Ax14c), contradicting Lemma 8.4. So,
 $(a * a)^{\circ } = 0$
. It can only be the case then that
$(a * a)^{\circ } = 0$
. It can only be the case then that
 $a * a = a$
, again by Lemma 8.4.
$a * a = a$
, again by Lemma 8.4. -
v. We have two cases:
-
a. If
 $\neg a = 1$
, then
$\neg a = 1$
, then
 ${\boldsymbol {A}} \cong {\boldsymbol {R}}$
, whose truth-tables are depicted in Table 9.
${\boldsymbol {A}} \cong {\boldsymbol {R}}$
, whose truth-tables are depicted in Table 9.Table 9 The truth-tables of the algebra
 ${\boldsymbol {R}}$
[Reference Carnielli and Marcos16, p. 68].
${\boldsymbol {R}}$
[Reference Carnielli and Marcos16, p. 68].
-
b. If
 $\neg a = a$
, then
$\neg a = a$
, then
 $a^{\circ } = \neg (a \wedge \neg a) = \neg (a \wedge a) = \neg a = a$
, contradicting Lemma 8.4.
$a^{\circ } = \neg (a \wedge \neg a) = \neg (a \wedge a) = \neg a = a$
, contradicting Lemma 8.4.
-
Proposition 12.9.
![]() .
.
Proof It is easy to check that
![]() . Therefore
. Therefore
![]() , because
, because
![]() is closed under
is closed under
![]() $\mathbb {IP}_{\mathrm {S}}$
. Conversely, let
$\mathbb {IP}_{\mathrm {S}}$
. Conversely, let
![]() . Since
. Since
![]() is a quasivariety, because
is a quasivariety, because
![]() is finitary and finitely equivalential [Reference Font32, Corollary 6.80], it follows by Theorem 12.8 that
is finitary and finitely equivalential [Reference Font32, Corollary 6.80], it follows by Theorem 12.8 that
![]() . Thus,
. Thus,
![]() . The inclusion
. The inclusion
![]() follows once again from the fact that
follows once again from the fact that
![]() is a quasivariety. To prove the converse inclusion notice that since
is a quasivariety. To prove the converse inclusion notice that since
![]() ${\boldsymbol {R}}$
is subdirectly irreducible relative to
${\boldsymbol {R}}$
is subdirectly irreducible relative to
![]() , it follows by Theorem 8.3 that
, it follows by Theorem 8.3 that
![]() , and hence
, and hence
![]() .
.
Corollary 12.10.
![]() .
.
The relations between the quasivarieties studied in the second part of this work are depicted in Figure 3. Since
![]() ${\mathcal {C}ibv}$
is not finitely algebraizable (recall Proposition 11.3), we must consider the class
${\mathcal {C}ibv}$
is not finitely algebraizable (recall Proposition 11.3), we must consider the class
![]() $\mathbb {Q}{\mathsf {Alg}}^*({\mathcal {C}ibv})$
, unlike the classes of algebraic reducts of the remaining algebraizable logics studied.
$\mathbb {Q}{\mathsf {Alg}}^*({\mathcal {C}ibv})$
, unlike the classes of algebraic reducts of the remaining algebraizable logics studied.

Figure 3 Quasivarieties under study.
Our last result sums up the completeness results for the logics
![]() ,
,
![]() , and
, and
![]() . These are all known—see [Reference Sette53, Proposition 9] for 1, [Reference Mortensen45, Theorem 5.3]Footnote
15
for 2, and [Reference Carnielli and Marcos16, Theorem 3.69]Footnote
16
for 3. We state it for the sake of completeness and also to provide a unified AAL proof for the three logics.Footnote
17
. These are all known—see [Reference Sette53, Proposition 9] for 1, [Reference Mortensen45, Theorem 5.3]Footnote
15
for 2, and [Reference Carnielli and Marcos16, Theorem 3.69]Footnote
16
for 3. We state it for the sake of completeness and also to provide a unified AAL proof for the three logics.Footnote
17
Proof Fix
![]() , with
, with
![]() ${\boldsymbol {A}} = {\boldsymbol {S}},{\boldsymbol {R}},{\boldsymbol {T}}$
, and let
${\boldsymbol {A}} = {\boldsymbol {S}},{\boldsymbol {R}},{\boldsymbol {T}}$
, and let
![]() , respectively. Notice that
, respectively. Notice that
![]() $\{{\boldsymbol {A}}\}$
is a
$\{{\boldsymbol {A}}\}$
is a
![]() ${\boldsymbol {\tau }}$
-algebraic semantics for
${\boldsymbol {\tau }}$
-algebraic semantics for
![]() ${\mathcal {S}}$
, with
${\mathcal {S}}$
, with
![]() , because
, because
![]() $\{a,1\}$
is precisely the subset of elements of A satisfying the equation
$\{a,1\}$
is precisely the subset of elements of A satisfying the equation
![]() $(x \to x) \to x \approx x \to x$
on
$(x \to x) \to x \approx x \to x$
on
![]() ${\boldsymbol {A}}$
. Bearing in mind that
${\boldsymbol {A}}$
. Bearing in mind that
![]() ${\mathcal {S}}$
is finitary (for it is defined by a finite matrix), it follows by [Reference Blok and Rebagliato8, Proposition 2.2] that
${\mathcal {S}}$
is finitary (for it is defined by a finite matrix), it follows by [Reference Blok and Rebagliato8, Proposition 2.2] that
![]() $\mathbb {Q}({\boldsymbol {A}})$
is also a
$\mathbb {Q}({\boldsymbol {A}})$
is also a
![]() ${\boldsymbol {\tau }}$
-algebraic semantics for
${\boldsymbol {\tau }}$
-algebraic semantics for
![]() ${\mathcal {S}}$
. But
${\mathcal {S}}$
. But
![]() $\mathbb {Q}({\boldsymbol {A}}) = {\mathsf {Alg}}^*({\mathcal {S}}')$
, by Propositions 11.11, 11.13, and 12.9 (depending on
$\mathbb {Q}({\boldsymbol {A}}) = {\mathsf {Alg}}^*({\mathcal {S}}')$
, by Propositions 11.11, 11.13, and 12.9 (depending on
![]() ${\boldsymbol {A}} = {\boldsymbol {S}},{\boldsymbol {R}},{\boldsymbol {T}}$
). Therefore both
${\boldsymbol {A}} = {\boldsymbol {S}},{\boldsymbol {R}},{\boldsymbol {T}}$
). Therefore both
![]() ${\mathcal {S}}$
and
${\mathcal {S}}$
and
![]() ${\mathcal {S}}'$
are the
${\mathcal {S}}'$
are the
![]() ${\boldsymbol {\tau }}$
-assertional logic w.r.t.
${\boldsymbol {\tau }}$
-assertional logic w.r.t.
![]() $\mathbb {Q}({\boldsymbol {A}})$
, and hence must coincide.
$\mathbb {Q}({\boldsymbol {A}})$
, and hence must coincide.
As future lines of research, one can point out finding lattice characterizations of
![]() -algebras and
-algebras and
![]() -algebras, analogous to that of Sette’s algebras
-algebras, analogous to that of Sette’s algebras
![]() $\mathsf {SA}$
for
$\mathsf {SA}$
for
![]() -algebras; and lattice characterizations of the intrinsic varieties
-algebras; and lattice characterizations of the intrinsic varieties
![]() and
and
![]() , analogous to that of quasi-Sette’s algebras
, analogous to that of quasi-Sette’s algebras
![]() $\mathsf {QSA}$
for
$\mathsf {QSA}$
for
![]() .
.
Acknowledgements
The authors wish to thank Ramon Jansana for his comments on a preliminary version of the paper. The first author also thanks Josep Maria Font for sharing his own articles of da Costa’s early works, and Carlos Caleiro for introducing him in the first place to paraconsistent logics. The authors are indebted to the anonymous referee for many valuable comments and suggestions which helped improve a previous version of the paper, and in particular for bringing our attention to the paper [Reference Moraschini43] and for the simpler arguments used in the proofs of Proposition 2.7 and Theorem 5.6. This research was funded by FCT/MCTES through national funds and when applicable co-funded EU funds under the project UIDB/EEA/50008/2020.