Published online by Cambridge University Press: 03 March 2004
Directed energy and turbulence structure are shown to be crucial in understanding the growth of self-similar Rayleigh–Taylor and incompressible Richtmyer–Meshkov turbulent mixing zones. Averaging over the mixing zone is used to analyze the response of a modified k–ε model and a turbulent two-fluid model. Three different transport regimes are then identified by considering self-similar variable acceleration RT flows (SSVARTs), which appear as promising reference flows for model testing.
Mixing instabilities between two stratified fluids of different densities induced by acceleration or gravitation are found in many flows of basic and applied physics (astrophysics, inertial confinement fusion, etc.). The Rayleigh–Taylor (RT) and Richtmyer–Meshkov (IRM) instabilities, where acceleration is respectively constant and impulsive, are two important idealized plane cases commonly used to understand and predict the main features of such flows (Sharp, 1984; Kull, 1991; Inogamov, 1999). In the final stage of such instabilities, a fully developed turbulent regime appears in the mixing layer, whose growth follows a more or less steep power law, depending on the influence of dissipation and molecular mixing. This late time behavior, of practical importance in many applications, can be studied through experiments and modeling, although it is analytically untractable from first principles (Sharp, 1984; Kull, 1991; Inogamov, 1999). Qualitative analysis of other turbulent layers (wakes, jets, etc.) have been available for many decades (see, for instance, Tennekes & Lumley, 1972), but do not seem to have been given for RT and IRM situations. The aim of the present work is to provide a similar insight on the ensemble-averaged flow fields of gravitationally induced mixing layers, in order to eventually suggest a new basis of elementary modeling. The extensively investigated case of the Kelvin–Helmoltz (KH) turbulent mixing zones (TMZ) will also be considered here as a reference.
The instabilities considered here will all be for initially plane ideal interfaces, in the incompressible and fully developed turbulent limits, and between two fluids of vanishingly small density difference (
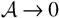
, zero Atwood number limit). Furthermore, since only broad qualitative features will be discussed, all the relevant quantities will be averaged over the width of the TMZ, L(t). This is the bulk averaging approximation, already used for the analysis of Atwood number dependency (Dimonte, 2000). Throughout the following discussion, all bulk averages will be given without their explicit calculations, which are mostly straightforward and can also be found in a previous work (Llor, 2001a).
In the
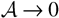
limit, experiments and numerical simulations show that the average volume fraction profiles of the fluids in the TMZs are practically linear functions of the longitudinal coordinate, x (Read & Youngs, 1983; Burrows et al. 1984; Read, 1984; and the numerous collected references in Dimonte & Schneider, 1997; Llor, 2001a). Using the mass conservation equations, the average longitudinal fluid velocities in the TMZ are also found to be linear in x, and their difference is constant throughout the TMZ, given by δUx(t) = (d/dt)L(t)/2 (Llor, 2001a).
These volume fraction and velocity profiles, together with a TMZ growth law, directly provide three important terms of the overall energy balance: KI(t), the total input energy (converted from gravitational energy (RT) or mean transverse kinetic energy (KH)), KM(t), the mean kinetic energy, and KD(t), here called “directed” kinetic energy. KM is calculated from the one-fluid (Favre) mean longitudinal velocity, and KD is the excess of mean kinetic energy introduced when going from a one-fluid to a two-fluid average field description:
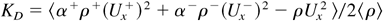
(+ and −: fluid indices, α±, ρ±, Ux±: volume fractions, densities and longitudinal velocities of fluids, ρ: Reynolds average density, Ux: Favre average velocity, and 〈.〉: bulk average). For

, KD is simply related to the TMZ growth law by KD ≈ (δUx)2/12 = (dL/dt)2/48 whereas KM is vanishingly small as
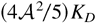
(Llor, 2001a) and will be ignored here. The growth laws and the resulting KI and KD /KI are given in Table 1 (Llor, 2001a).
Basic self-similar TMZ growth laws

The available data (Read & Youngs, 1983; Burrows et al. 1984; Read, 1984, and references in Dimonte & Schneider, 1997; Llor, 2001a) from experiments and numerical simulations can be summarized by two basic bulk parameters, as collected in Table 2: the coefficient in L(t),
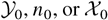
for RT, IRM, or KH, respectively, and the turbulent kinetic energy, K. Using the results of Table 1, KD is found to be negligible compared to K in the IRM and KH cases, whereas it is of similar order in the RT case. This reflects a striking difference of the energy distribution that motivates the need, already pointed out by various authors (Dimonte, 2000; Read, 1984; Youngs, 1989), of two-fluid modeling in the RT case instead of one fluid for IRM and KH. In the RT case, it also justifies distinguishing the (single-fluid) turbulent kinetic energy, as measured in experiments, from the two-fluid turbulent kinetic energy, defined as KT = K − KD. Furthermore, since KD is associated to purely longitudinal velocity components, it has a major contribution to the overall Reynolds tensor anisotropy.
Bulk-averaged parameters of self-similar RT, IRM, and KH TMZs, as obtained from experiments and numerical simulations (estimated to ±20% from various sources), the modified k–ε model, and Youngs' two-fluid model

From the self-similar evolution of KI − KD − KT, one can determine the bulk-averaged turbulent energy transfer to intermediate scales in the TMZs, E (also called spectral flux), or the closely related nondimensional parameter:
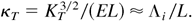
Λi is an average integral length scale (the typical size of the largest eddies) and κT thus stands as an effective Knudsen number of the turbulent transport (Tennekes & Lumley, 1972), previously called Von Kármán number in Llor, 2001b. E is characteristic of large scales and, for unsteady flows as considered here, it is close but not equal to the (small scale) energy dissipation rate. However, expression (2) assumes the existence of an inertial range to relate Λi and E, as is indeed observed even for the RT case (Dalziel et al., 1999). The effective Knudsen numbers found for the three TMZs, reported in Table 2, differ by a factor of up to 7 that reflects striking structural differences: if, as commonly accepted, the KH TMZ accommodates typically one large eddy in its width, the IRM TMZ accommodates two and the RT seven.
The energy balance is of utmost importance in testing the physical relevance and accuracy of models. As examples, two elementary Reynolds-Averaged Navier–Stokes (RANS)-based statistical turbulent mixing models have been examined: a modified k–ε model (Andronov et al., 1979; Gauthier & Bonnet, 1990; Bonnet et al., 1992), and a two-fluid turbulent model introduced by Youngs (1989). Here again, bulk averaging has been applied to simplify the model PDEs into ODEs (Llor, 2001a), as listed in Table 3, to reveal the basic phenomena that are captured. Self-similar solutions to the ODEs are then given by algebraic equations, in analytical form for the two models considered here (Llor, 2001a). With the recommended values of the coefficients, the modeled bulk-averaged quantities were obtained as listed in Table 2 (Llor, 2001a). The corresponding initial conditions, which must be compatible with the self-similarity constraint, are thus given by the listed solutions taken at a given finite time.
Bulk-averaged equations of the modified k–ε and Youngs' two-fluid models for RT type mixing in the incompressible, limits (ζ ≈ 3/2: bulk correction factor). In the KH case, not explicitly given here, Π becomes the Reynolds stress production, Cε0 is replaced by Cε1, and an equation in Λ must also be added to Youngs' model (Llor, 2001a)

Most deviations between modeled and measured results fall in a ±30% range and can be attributed to experimental and numerical errors (for instance, K in the IRM case is estimated from a single numerical study), bulk-averaging bias (these are not expected to exceed ±10%; Llor, 2001a), and limited “universality” of the models (k–ε is typically optimized to capture boundary layers). Within this margin, reasonable estimates of all the basic quantities in the IRM and KH cases are obtained from both models, but significant discrepancies are observed in the RT case:
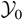
is twice too low in the modified k–ε, and κT is overestimated by 15- and 7-fold factors, respectively, with the k–ε and two-fluid models. Particularly striking is the κT value for the k–ε that would indicate typical eddies' sizes over twice larger that the TMZ width!
For the modified k–ε, these inconsistencies result from the purely diffusive modeling of the TMZ growth as visible on the L(t) equation in Table 3. The IRM and KH cases are therefore properly captured, but for the RT case, the directed transport is replaced by an unphysically enhanced turbulent diffusion, obtained by increasing Λi (or κT): After substitution with the measured RT quantities in Table 2, the L(t) equation is incompatible with any reasonable values of the standard k–ε model constants Cμ and σc. The analytical results also show that no combination of σρ and Cε0 values can make the model to capture at once
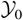
, κT, and K/KI (Llor, 2001a).
As in any two-fluid approach, the TMZ growth in Youngs' model is simply driven by directed transport as shown by the L(t) equation in Table 3. The model specificity stands in the two evolution equations for quantities kT and λ (besides the usual four equations for mass and momentum, with (δU)2 drag force, turbulent diffusion, and added-mass effects). λ is used to provide a closure of the characteristic length scales for both turbulence and drag between the fluids: λi = Ci λ/Cμ and λd = λ/Cd, respectively (notations kT, λ, Cd, and Ci, respectively, stand here for k, L, c1, and c2 in Youngs publications). The production term in the λ equation dominates the other terms and is proportional to δUx in the RT and IRM cases. This means that λ, as δUx, is almost uniform across the TMZ and its bulk average, Λ = 〈λ〉, behaves as L. Simple calculations (Llor, 2001a) show that, in any gravitationally induced instability such as RT and IRM, Λ = L/2, hence, κT = Ci /(2Cμ) ≈ 0.58, and in the KH case, this value is corrected by a factor close to 1 which depends only on Cd. Here again, the sevenfold span of experimental κT values observed between the RT and KH cases cannot be captured.
The strong overestimation of κT can generate major modeling errors whenever changes in turbulent structure or viscosity become essential, as in the case of combined RT and KH. However, in the RT case, the κT distortions of the k–ε and two-fluid models play different roles in connection with the modeled TMZ growth processes: In the former, transport proceeds by enhanced turbulent diffusion, thus forcing large κT values, whereas in the latter, directed transport dominates, and the κT value is incidental.
Regardless of turbulence structure, that is, of κT, the competition between the two transport processes becomes more visible in self-similar variable acceleration RT (SSVARTs) flows, although experimental or numerical data are not yet available. They are defined by
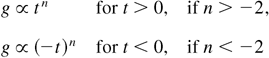
(n = 0 is standard RT). Such flows were previously considered for n > −1 only by Neuvazhaev (1983) who gave their TMZ growth rates as captured by his specific model. The extension for n values below −2 is dictated by the unsuitable decreasing behavior of L(t) as tn+2 for n < −2 if g ∝ tn. The TMZ would then experience an unphysical complete demixing down to L = 0 under a positive, instability-inducing gravity field. Although experimentally very demanding or even out of reach, SSVARTs at nonnegligible values of n can be investigated through numerical simulations. It will only be assumed here that SSVARTs do exist a priori as Reynolds (ensemble) averages, yielding
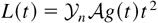
in the incompressible,
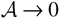
limits, where
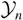
is positive.
For a SSVART to be stable, it must eventually “forget,” for late t, any added perturbation on its initial state at time t0 taken as origin. A necessary condition is provided by KI(t), which behaves as a(± t)2n+2 + b(± t)−(n+2): The first term is the expected self-similar law produced by the time integration of gδU, whereas the second is due to the dilution as 1/L of any initial deviation of KI(t0). a and b being positive, the contribution of KI(t0) is thus forgotten when t → ∞ or −t → 0 unless −2 < n < −4/3. This result does not take into account the spectral transfer and dissipation of KI(t0). Therefore, a critical value nc exists between −2 and −4/3 such that, for −2 < n < nc, the behavior of SSVARTs is dominated by KI(t0), and L(t) grows necessarily as tnc+2 at late times. This is exactly the situation of IRM mixing; hence the result nc = n0 − 2.
The bulk-averaged k–ε and two-fluid models in Table 3 estimate
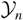
as listed in Table 4 (Llor, 2001a). Also given are the results from scaled free fall and Read's formula (Read & Youngs, 1983; Burrows et al. 1984; Read, 1984), which are the simplest approximations of any two-fluid description such as Youngs' in Table 3: the former by assuming Π = 0 and scaling g into
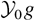
(thus

), and the latter (explicitly solved as
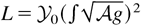
) by assuming that the directed transport dominates diffusion, the production and destruction of KD are balanced, and the ratio ΛD /L is independent of g(t) (Llor, 2001a). Unscaled free fall (if
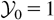
) provides an upper bound to TMZ growth, and Read's formula has been found to retrieve the TMZ growth to within 2% on the presently available variable acceleration experiments (Burrows et al., 1984; Dimonte, 2000).
Analytical expressions of , as obtained from the bulk-averaged models (Table 3) and their approximations

The k–ε modeled
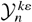
displays two poles at n1 = n0kε − 2 = −(4Cε2 − 3)/(3Cε2 − 3) ≈ −1.7 and n2 = −(4Cε0 − 3)/(3Cε0 − 3) ≈ 0.89.
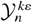
is thus negative outside the −1.7 to 0.89 interval, but the range of physically acceptable n values is certainly much wider. Again, the model is unable to capture the directed transport effects that are enhanced when increasing n.
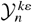
can be made positive for all n < −2 and n > n1 by setting Cε0 = 3/2, a value reassuringly close to Cε1 that causes turbulence to be produced at the integral length scale. However, it is then found that
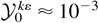
for the recommended value of σρ = 2, or that
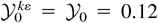
for σρ ≈ 0.017, both extremes being physically unacceptable.
The two-fluid modeled
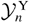
also displays two simple poles, at n1Y = n0Y − 2 and n2Y = −2, being positive outside the poles, over the widest range of physically acceptable n values. Scaled free fall and Read's approximation again display two simple poles: n2 is always preserved at −2, but n1 is respectively increased to −4/3 and decreased to −2.
The plot of
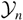
in Figure 1, as scaled by (1 − n/n1Y)−1(1 − n/n2Y)−1, shows the existence of three continuously connected growth regimes, loosely defined by:

Scaled representation of (Table 4), as obtained from Youngs' two-fluid model (solid line), scaled free fall (dot dashed line), and Read's approximation (dashed line). SSVARTs are not stable in the shaded interval of n.
Single-fluid models, such as the modified k–ε, appear unnatural to describe directed transport and are limited to the first regime. In the second regime, the widest, both scaled free fall and Read's approximations provide surprisingly good accuracies of about ±30% compared to a full two-fluid model, but fail in the first and third, where they either diverge or vanish. They limit the range of acceptable responses because their RM poles take the extreme values −2 and −4/3. Only a full two-fluid model, such as Youngs', is able to capture all three regimes at once in a physically acceptable manner, even though it misses some important features such as dissipation of density fluctuations (Linden & Redondo, 1991; Youngs, 1995; Dalziel et al. 1999), effective Knudsen number (present work).
SSVARTs are currently being investigated by numerical means (Youngs & Llor, 2002). Values of bulk parameters such as
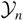
, κT, and KD /KI should then significantly strengthen constraints for model testing. Yet, with the limited present knowledge on two special cases (n = −2 + n0 and n = 0) and on free fall, SSVARTs clearly show the importance of directed transport and turbulence structure for elementary modeling. This is most naturally performed within a two-fluid approach. A two-fluid model consistent with the experimental results in Table 2 (and most noticeably κT) was recently proposed (Bailly & Llor, 2002; Llor & Bailly, this issue).
I am greatly indebted toward D.L. Youngs, J. Magnaudet, O. Simonin, P. Mignon and B. Desjardins for helpful discussions.

Basic self-similar TMZ growth laws

Bulk-averaged parameters of self-similar RT, IRM, and KH TMZs, as obtained from experiments and numerical simulations (estimated to ±20% from various sources), the modified k–ε model, and Youngs' two-fluid model

Bulk-averaged equations of the modified k–ε and Youngs' two-fluid models for RT type mixing in the incompressible, limits (ζ ≈ 3/2: bulk correction factor). In the KH case, not explicitly given here, Π becomes the Reynolds stress production, Cε0 is replaced by Cε1, and an equation in Λ must also be added to Youngs' model (Llor, 2001a)

Analytical expressions of , as obtained from the bulk-averaged models (Table 3) and their approximations

Scaled representation of (Table 4), as obtained from Youngs' two-fluid model (solid line), scaled free fall (dot dashed line), and Read's approximation (dashed line). SSVARTs are not stable in the shaded interval of n.