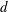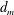1 Introduction
Viscoplastic fluids constitute a special class of non-Newtonian fluids. They are uniquely characterized by exhibition of a threshold shear stress (known as yield stress), below which they do not undergo deformation and show ideal rigid-solid behaviour. When the shear stress is more than the yield stress, the fluid behaves as viscous (Bird, Dai & Yarusso Reference Bird, Dai and Yarusso1983). Such fluids find applications in varied fields such as food and dairy processing, oil exploration, biological fluids, etc. (Chhabra & Richardson Reference Chhabra and Richardson1999; Balmforth, Frigaard & Ovarlez Reference Balmforth, Frigaard and Ovarlez2014; Tripathi et al. Reference Tripathi, Yadav, Beg and Kumar2018). Viscoplastic behaviour is exhibited by colloidal gels, emulsions, slurries, suspensions, nanocomposites, drilling muds, cement, etc. Stability analysis of fluid flow is essential to determine the physical scenario under which there is departure from laminar behaviour, so that it can be either avoided or exploited for potential enhancement in heat and mass transfer. One of the earliest attempts at stability analysis of Poiseuille flow of viscoplastic fluids was made by Pavlov, Romanov & Simkhovich (Reference Pavlov, Romanov and Simkhovich1974). By means of changing the scale of the characteristic length and velocity parameters, the problem was reduced to Couette–Poiseuille flow of a Newtonian fluid, and thus inferred to be stable for infinitesimal disturbances. Pavlov, Romanov & Simkhovich (Reference Pavlov, Romanov and Simkhovich1975) further extended the work to consider the scenario of finite-amplitude disturbances to explain the experimental findings on transition to turbulence of viscoplastic fluids. One of the major limitations of Pavlov et al. was that they considered the analogous Newtonian stability problem, without commenting on three-dimensional perturbations. In the case of Newtonian fluids, Squire’s theorem asserts that a two-dimensional perturbation is able to make a flow unstable at lower Reynolds number, compared to three-dimensional perturbations (Squire Reference Squire1933; Drazin & Reiid Reference Drazin and Reiid2004). However, Squire’s theorem is not applicable for Bingham (viscoplastic) fluids, as rightly pointed out by subsequent researchers (Frigaard, Howison & Sobey Reference Frigaard, Howison and Sobey1994; Nouar & Frigaard Reference Nouar and Frigaard2001; Nouar et al. Reference Nouar, Kabouya, Dusek and Mamou2007; Métivier & Nouar Reference Métivier and Nouar2011). A comprehensive modal linear stability analysis (incorporating perturbation in the yield surface) of Poiseuille flow of a Bingham fluid was undertaken by Frigaard et al. (Reference Frigaard, Howison and Sobey1994). The study revealed that the system is unconditionally linearly stable for a one-dimensional perturbation.
Linear stability analysis of two-layer channel flow involving viscoplastic fluids was also undertaken, and it was shown that multilayer flow comprising two Bingham fluids is more stable than the equivalent flow of either fluid alone (Pinarbasi & Liakopoulos Reference Pinarbasi and Liakopoulos1995; Frigaard Reference Frigaard2001). Pinarbasi & Liakopoulos (Reference Pinarbasi and Liakopoulos1995) performed the analysis systematically by first starting with a two-layer Newtonian fluid flow, and showed that replacing the Newtonian fluid with a Bingham fluid at the bottom layer stabilizes the interface between the two fluids. Having two Bingham fluids stabilized the flow even further, with an increase in yield stress favouring stability. They concluded the study by analysing the behaviour of two shear-thinning fluids, and demonstrated that an increase in shear thinning leads to flow destabilization. Linear stability analysis of two-layer channel flow consisting of a viscoplastic fluid and a Newtonian fluid subject to two- and three-dimensional perturbations was undertaken by Sahu et al. (Reference Sahu, Valluri, Spelt and Matar2007) and Sahu & Matar (Reference Sahu and Matar2010). However, there is a major difference in the assumptions of the analyses performed by Frigaard (Reference Frigaard2001) and Sahu et al. (Reference Sahu, Valluri, Spelt and Matar2007). In the case of viscoplastic fluids, yield stress is known to influence the growth of waves at the interface, consequently affecting the rate of removal of the highly viscous layer. The study by Frigaard (Reference Frigaard2001) considered the presence of a plug zone in between the Newtonian fluid and the unyielded zone of the Bingham fluid. As a result, the interfacial modes were suppressed in their study, resulting in super-stable two-layer flows similar to pressure-driven single-fluid flow. Sahu et al. (Reference Sahu, Valluri, Spelt and Matar2007) removed this interfacial plug zone in their analysis. Owing to this, the interfacial modes no longer remained suppressed. This resulted in an interesting observation: enhancement of dimensionless yield stress (quantified by Bingham number) prior to the development of a plug zone had a destabilizing effect. Nouar & Frigaard (Reference Nouar and Frigaard2001) carried out a nonlinear energy stability analysis of the Poiseuille flow of a Bingham fluid, and observed that the critical energy Reynolds number increases as
![]() $Bn^{0.5}$
for large values of
$Bn^{0.5}$
for large values of
![]() $Bn$
,
$Bn$
,
![]() $Bn$
being the Bingham number (the ratio of the yield stress to the viscous stress of the fluid). In their analysis, the yield stress of the fluid did not directly contribute to the viscous dissipation. Instead, the effect of yield stress was implicitly present in the Reynolds number through the modification of the yielded zone width, and also through the gradient of the base velocity profile. Frigaard & Nouar (Reference Frigaard and Nouar2003) analysed the linear stability of the Poiseuille flow of a Bingham fluid to three-dimensional disturbances, and determined the eigenvalue bounds. For large
$Bn$
being the Bingham number (the ratio of the yield stress to the viscous stress of the fluid). In their analysis, the yield stress of the fluid did not directly contribute to the viscous dissipation. Instead, the effect of yield stress was implicitly present in the Reynolds number through the modification of the yielded zone width, and also through the gradient of the base velocity profile. Frigaard & Nouar (Reference Frigaard and Nouar2003) analysed the linear stability of the Poiseuille flow of a Bingham fluid to three-dimensional disturbances, and determined the eigenvalue bounds. For large
![]() $Bn$
, they observed the variation of critical Reynolds number as
$Bn$
, they observed the variation of critical Reynolds number as
![]() $Bn^{0.75}$
. However, they did not consider the limiting case of
$Bn^{0.75}$
. However, they did not consider the limiting case of
![]() $Bn$
close to zero. Nevertheless, the limiting problem was attempted by Métivier, Nouar & Brancher (Reference Métivier, Nouar and Brancher2005). In comparison with a Newtonian fluid, they observed a discontinuity of the critical conditions. Thus, the critical conditions for
$Bn$
close to zero. Nevertheless, the limiting problem was attempted by Métivier, Nouar & Brancher (Reference Métivier, Nouar and Brancher2005). In comparison with a Newtonian fluid, they observed a discontinuity of the critical conditions. Thus, the critical conditions for
![]() $Bn\rightarrow 0$
are different compared to a Newtonian fluid
$Bn\rightarrow 0$
are different compared to a Newtonian fluid
![]() $(Bn=0)$
. This discontinuity arises because of the assumption of a plug zone. They opined that the replacement of the plug zone by assuming a suitable biviscous model could possibly eradicate the discontinuity.
$(Bn=0)$
. This discontinuity arises because of the assumption of a plug zone. They opined that the replacement of the plug zone by assuming a suitable biviscous model could possibly eradicate the discontinuity.
Non-modal stability analyses for plane Poiseuille as well as Hagen–Poiseuille flow of viscoplastic fluids (Bingham and Herschel–Bulkley) have also been performed (Nouar et al.
Reference Nouar, Kabouya, Dusek and Mamou2007; Liu & Liu Reference Liu and Liu2014; Bentrad et al.
Reference Bentrad, Esmael, Nouar, Lefevre and Messaoudene2017; Liu, Ding & Hu Reference Liu, Ding and Hu2018). The study by Nouar et al. (Reference Nouar, Kabouya, Dusek and Mamou2007) involved demonstration of the shape of optimal perturbation, and its variation with dimensionless yield stress. The reduction in the transient energy growth observed in their study, compared to plane Poiseuille flow of a Newtonian fluid, may be attributed to increase in the viscous dissipation caused by the viscoplastic behaviour of the fluid. The stability of Rayleigh–Bénard–Poiseuille (RBP) flow for viscoplastic fluids was studied, both with and without the assumption of thermal dependence, as well as by considering the effect of wall slip (Métivier & Nouar Reference Métivier and Nouar2008, Reference Métivier and Nouar2009, Reference Métivier and Nouar2011; Métivier, Frigaard & Nouar Reference Métivier, Frigaard and Nouar2009; Métivier, Nouar & Brancher Reference Métivier, Nouar and Brancher2010; Métivier & Magnin Reference Métivier and Magnin2011). The stabilizing effect of
![]() $Bn$
in these studies is possibly because of the vanishing of velocity perturbations at the yield surface for smaller values of
$Bn$
in these studies is possibly because of the vanishing of velocity perturbations at the yield surface for smaller values of
![]() $Bn$
, and augmentation in effective viscous dissipation at higher values of
$Bn$
, and augmentation in effective viscous dissipation at higher values of
![]() $Bn$
. Nouar & Bottaro (Reference Nouar and Bottaro2010) studied the stability of a Bingham fluid in a channel with emphasis on eigenvalue sensitivity analysis. They observed that very weak defects can successfully excite exponentially amplified streamwise travelling waves. However, they neglected a fundamental fact that the stability operator encountered in shear planar flow of the fluid is non-normal in nature. Thus, ignoring the interplay between transient amplifications and exponential growth was a major limitation in their analysis. Moyers-Gonzalez, Burghelea & Mak (Reference Moyers-Gonzalez, Burghelea and Mak2011) performed linear stability analysis for plane Poiseuille flow of an elastoviscoplastic fluid, a marked departure from the traditional consideration of a viscoplastic fluid. Instead of assuming a direct solid–fluid transition regime, they considered a solid–fluid coexistence regime where the behaviour of the material is viscoelastic. The findings of their study resemble those of a normal viscoplastic fluid, possibly because the viscoelastic core is limited to a region away from the wall boundary. In addition to flow in parallel channels, the stability of viscoplastic fluids has also been analysed for an annular geometry (Kabouya & Nouar Reference Kabouya and Nouar2003; Moyers-Gonzalez, Frigaard & Nouar Reference Moyers-Gonzalez, Frigaard and Nouar2004; Peng & Zhu Reference Peng and Zhu2004; Caton Reference Caton2006; Landry, Frigaard & Martinez Reference Landry, Frigaard and Martinez2006; Soleimani & Sadeghy Reference Soleimani and Sadeghy2010, Reference Soleimani and Sadeghy2011; Madani et al.
Reference Madani, Martinez, Olson and Frigaard2013).
$Bn$
. Nouar & Bottaro (Reference Nouar and Bottaro2010) studied the stability of a Bingham fluid in a channel with emphasis on eigenvalue sensitivity analysis. They observed that very weak defects can successfully excite exponentially amplified streamwise travelling waves. However, they neglected a fundamental fact that the stability operator encountered in shear planar flow of the fluid is non-normal in nature. Thus, ignoring the interplay between transient amplifications and exponential growth was a major limitation in their analysis. Moyers-Gonzalez, Burghelea & Mak (Reference Moyers-Gonzalez, Burghelea and Mak2011) performed linear stability analysis for plane Poiseuille flow of an elastoviscoplastic fluid, a marked departure from the traditional consideration of a viscoplastic fluid. Instead of assuming a direct solid–fluid transition regime, they considered a solid–fluid coexistence regime where the behaviour of the material is viscoelastic. The findings of their study resemble those of a normal viscoplastic fluid, possibly because the viscoelastic core is limited to a region away from the wall boundary. In addition to flow in parallel channels, the stability of viscoplastic fluids has also been analysed for an annular geometry (Kabouya & Nouar Reference Kabouya and Nouar2003; Moyers-Gonzalez, Frigaard & Nouar Reference Moyers-Gonzalez, Frigaard and Nouar2004; Peng & Zhu Reference Peng and Zhu2004; Caton Reference Caton2006; Landry, Frigaard & Martinez Reference Landry, Frigaard and Martinez2006; Soleimani & Sadeghy Reference Soleimani and Sadeghy2010, Reference Soleimani and Sadeghy2011; Madani et al.
Reference Madani, Martinez, Olson and Frigaard2013).
As stated in the beginning, viscoplastic fluids assume importance due to their widespread presence in various physically relevant systems (e.g. blood flow, drilling mud, toothpaste). An understanding of the conditions under which flow transition occurs in viscoplastic fluids may possibly lead to better design of flow equipment involving the flow of such fluids. Stability studies on a Bingham fluid in a non-porous channel show that the critical Reynolds number increases with the Bingham number of the fluid (Frigaard et al. Reference Frigaard, Howison and Sobey1994; Balmforth et al. Reference Balmforth, Frigaard and Ovarlez2014). Thus, yield stress adds to the stability of the flow in general for non-porous channels. Actually, the plug region of the Bingham flow helps in resisting transition even when finite perturbations are introduced in the channel. But stability analysis of the flow of viscoplastic fluids over a porous layer has remained unexplored till now. However, several real-life applications, like oil recovery, biological transport, deep filtration, etc., involve the flow of viscoplastic fluids over porous media (Herzig, Leclerc & Goff Reference Herzig, Leclerc and Goff1970; Dash, Mehta & Jayaraman Reference Dash, Mehta and Jayaraman1996; Mandal & Bera Reference Mandal and Bera2015). Hence, stability analysis of viscoplastic fluid flow over a porous media is of considerable interest. Although studies exploring the analytical solutions for the flow of Bingham fluids involving a porous interface exist (Chen & Zhu Reference Chen and Zhu2008; Sengupta & De Reference Sengupta and De2019), there has been no stability analysis on the same. This lack of literature on the stability analysis of viscoplastic fluids involving porous media has necessitated the current study. Linear stability analysis is important, as it provides an upper limit on the critical Reynolds number necessary for flow to become unstable, leading to undesirable flow manifestations, like unwanted mixing. In addition, it provides useful insight into the role played by yield stress in viscoplastic fluids. The Bingham model, while providing a simplistic representation of viscoplastic fluids, also incorporates the essential element of viscoplastic behaviour, i.e. yield stress, thereby making the analysis intriguing.
To the best of the authors’ knowledge, there are no reported studies on the stability analysis of Bingham fluids over a porous layer for any kind of flow configuration. In addition, non-modal stability analysis for flow over porous media is rare. For analysing fluid flow over a porous layer, earlier studies have adopted modal analysis (Chang, Chen & Straughan Reference Chang, Chen and Straughan2006; Hill & Straughan Reference Hill and Straughan2008, Reference Hill and Straughan2009; Deepu, Anand & Basu Reference Deepu, Anand and Basu2015; Chang, Chen & Chang Reference Chang, Chen and Chang2017). A literature review suggests that variation in porous layer parameters, like permeability, depth ratio, slip parameter, etc., can induce instability via the fluid–porous interface in the case of Newtonian fluids (Chang et al.
Reference Chang, Chen and Straughan2006; Hill & Straughan Reference Hill and Straughan2008; Chang et al.
Reference Chang, Chen and Chang2017). Linear stability analysis shows that the critical Reynolds number for porous configuration (
![]() $Re_{cr}$
) can be as low as approximately 2500, which is significantly lower than that of non-porous configuration
$Re_{cr}$
) can be as low as approximately 2500, which is significantly lower than that of non-porous configuration
![]() $(Re_{cr}=5772)$
(Chang et al.
Reference Chang, Chen and Straughan2006). In fact, in the case of a fluid–porous system, there is a rapid change in velocity at the interface, which is difficult to avoid. This velocity gradient at the interface is known to influence the flow transition characteristics significantly. Thus, the authors are interested in exploring how the presence of a porous layer affects the flow transition in the case of Bingham fluids. This was the major motivation behind attempting the current study.
$(Re_{cr}=5772)$
(Chang et al.
Reference Chang, Chen and Straughan2006). In fact, in the case of a fluid–porous system, there is a rapid change in velocity at the interface, which is difficult to avoid. This velocity gradient at the interface is known to influence the flow transition characteristics significantly. Thus, the authors are interested in exploring how the presence of a porous layer affects the flow transition in the case of Bingham fluids. This was the major motivation behind attempting the current study.
Bingham flows are obviously known to be more stable. Thus, the current study aims to investigate whether the presence of the porous layer is able to impact this stable flow. Since the modal analysis underpredicts the experimentally observed critical point in many cases, a non-modal analysis is attempted (because, for example, modal analysis predicts
![]() $Re_{cr}=5772$
for plane Poiseuille flow of Newtonian fluids, while it is around 2000 in real experimental observations). Moreover, a literature review reveals that non-modal studies on Bingham fluids in non-porous channels have shown the presence of a transient growth that decays at large time (Nouar et al.
Reference Nouar, Kabouya, Dusek and Mamou2007). Thus, there is substantial evidence that non-modal studies give insight into the transient amplifications for Newtonian as well as non-Newtonian fluids. However, to the best of our knowledge, non-modal analysis in a fluid–porous system is rare in the open literature. Moreover, in a practical scenario, a porous layer has a high possibility to exhibit directional variations in the permeability (Straughan & Walker Reference Straughan and Walker1996; Malashetty & Mahantesh Reference Malashetty and Mahantesh2010). Thus, it is imperative to consider anisotropy and inhomogeneity of the porous layer, and analyse its effects on the flow stability for an exhaustive understanding of practical applications involving fluid–porous systems.
$Re_{cr}=5772$
for plane Poiseuille flow of Newtonian fluids, while it is around 2000 in real experimental observations). Moreover, a literature review reveals that non-modal studies on Bingham fluids in non-porous channels have shown the presence of a transient growth that decays at large time (Nouar et al.
Reference Nouar, Kabouya, Dusek and Mamou2007). Thus, there is substantial evidence that non-modal studies give insight into the transient amplifications for Newtonian as well as non-Newtonian fluids. However, to the best of our knowledge, non-modal analysis in a fluid–porous system is rare in the open literature. Moreover, in a practical scenario, a porous layer has a high possibility to exhibit directional variations in the permeability (Straughan & Walker Reference Straughan and Walker1996; Malashetty & Mahantesh Reference Malashetty and Mahantesh2010). Thus, it is imperative to consider anisotropy and inhomogeneity of the porous layer, and analyse its effects on the flow stability for an exhaustive understanding of practical applications involving fluid–porous systems.
In the modal analysis, asymptotic long-time stability behaviour is analysed. However, the response to infinitesimal perturbations at short times has not been explored for a porous configuration. This necessitates the analysis of the response to external excitations and initial conditions, in order to gain a more holistic understanding of the fluid flow transition. In terms of non-modal analysis, the resolvent and the growth functions give an indication about the amplification of the external excitations and the initial conditions. The importance of non-modal analysis can be stressed by the fact that there is always a possibility for occurrence of subcritical transition if a non-normal linear stability operator is present, as in shear flows (Schmid & Henningson Reference Schmid and Henningson1992; Henningson, Lundbladh & Johansson Reference Henningson, Lundbladh and Johansson1993; Reddy & Henningson Reference Reddy and Henningson1993). Mathematically, it implies that there is a possibility for energy extraction from the basic flow by a perturbation subspace. This may lead to a transient growth, even though there is no long-time instability.
In the current work, an attempt has been made to carry out temporal linear stability analysis of Poiseuille flow of a Bingham fluid overlying an anisotropic and inhomogeneous porous layer. The constitutive equation for a Bingham fluid has been considered together with the governing conservation equations, and the base velocity profile is derived for the chosen flow configuration. Thereafter, an Orr–Sommerfeld equation-like framework is obtained. Since traditional eigenvalue analysis did not yield any unstable eigenvalue, non-modal analysis has also been attempted. The effect of the porous layer parameters on the stability behaviour has been identified in terms of transient growth curves. Critical energy Reynolds-number curves are also obtained in order to comprehend the kinetic energy of the perturbations. To gain insight regarding the short-time behaviour, the initial growth rate and pseudospectra curves are also constructed. The authors believe that the present study provides a much-needed framework for a basic understanding of the stability of viscoplastic fluids over a porous layer. The current study is envisaged to be of critical help in the better design of equipment dealing with Bingham-type flow, as observed in the case of drilling mud, nanocomposites, etc. As already emphasized, studies involving non-modal stability analysis for flow over porous media are rare for non-Newtonian fluids. The current work aims to bridge this gap.
2 Problem formulation
The geometry of the flow configuration is elucidated in figure 1. A Bingham fluid of density
![]() $\unicode[STIX]{x1D70C}$
flows in a channel overlying a porous medium having thickness
$\unicode[STIX]{x1D70C}$
flows in a channel overlying a porous medium having thickness
![]() $d_{m}$
. There are two distinct flow regions: an unobstructed layer of fluid where no porous medium is present, and a porous layer beneath it, where the fluid flows through the porous medium in the axial direction, i.e. in the same direction as that of the unobstructed zone. The thickness of the unobstructed zone (also referred to hereafter as the fluid layer, being the zone where no porous medium is present) is
$d_{m}$
. There are two distinct flow regions: an unobstructed layer of fluid where no porous medium is present, and a porous layer beneath it, where the fluid flows through the porous medium in the axial direction, i.e. in the same direction as that of the unobstructed zone. The thickness of the unobstructed zone (also referred to hereafter as the fluid layer, being the zone where no porous medium is present) is
![]() $d$
(extending from
$d$
(extending from
![]() $z=0$
to
$z=0$
to
![]() $d$
). The porous medium is of thickness
$d$
). The porous medium is of thickness
![]() $d_{m}$
. The porous layer is saturated with the same fluid. The bottom of the porous layer is impermeable, i.e. at
$d_{m}$
. The porous layer is saturated with the same fluid. The bottom of the porous layer is impermeable, i.e. at
![]() $z=-d_{m}$
,
$z=-d_{m}$
,
![]() $w_{m}=0$
, where
$w_{m}=0$
, where
![]() $w_{m}$
refers to the normal velocity component in the porous layer. The flow occurs under the action of an applied constant pressure gradient
$w_{m}$
refers to the normal velocity component in the porous layer. The flow occurs under the action of an applied constant pressure gradient
![]() $(-\text{d}p/\text{d}x)$
in the
$(-\text{d}p/\text{d}x)$
in the
![]() $x$
direction. The yield surfaces are located at
$x$
direction. The yield surfaces are located at
![]() $z=z_{01}$
and
$z=z_{01}$
and
![]() $z_{02}$
. It may be noted that the velocity profile is expected to be asymmetric with respect to the centreline of the channel
$z_{02}$
. It may be noted that the velocity profile is expected to be asymmetric with respect to the centreline of the channel
![]() $(z=d/2)$
, due to the presence of the porous layer. This is evident from the schematic given in figure 1.
$(z=d/2)$
, due to the presence of the porous layer. This is evident from the schematic given in figure 1.

Figure 1. Flow configuration for plane Poiseuille flow of a Bingham fluid overlying a porous layer.
2.1 Governing equations
Now, the mass conservation equation and Cauchy’s momentum equation in the fluid layer are given as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\\ \displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}\boldsymbol{u}}{\text{D}t}=-\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\\ \displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}\boldsymbol{u}}{\text{D}t}=-\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D749}.\end{array}\right\}\end{eqnarray}$$
Equation (2.1) is simplified to obtain the
![]() $x$
-momentum equation as
$x$
-momentum equation as
In the above equation,
![]() $\unicode[STIX]{x1D70F}$
is the shear stress of the fluid.
$\unicode[STIX]{x1D70F}$
is the shear stress of the fluid.
The constitutive relation for a Bingham fluid is expressed as
 $$\begin{eqnarray}\left.\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}\frac{\text{d}u}{\text{d}z}+\unicode[STIX]{x1D70F}_{0}\,\text{sgn}\left(\frac{\text{d}u}{\text{d}z}\right), & |\unicode[STIX]{x1D70F}|\geqslant \unicode[STIX]{x1D70F}_{0},\\ \displaystyle \frac{\text{d}u}{\text{d}z}=0, & |\unicode[STIX]{x1D70F}|<\unicode[STIX]{x1D70F}_{0},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D70F}=\unicode[STIX]{x1D707}\frac{\text{d}u}{\text{d}z}+\unicode[STIX]{x1D70F}_{0}\,\text{sgn}\left(\frac{\text{d}u}{\text{d}z}\right), & |\unicode[STIX]{x1D70F}|\geqslant \unicode[STIX]{x1D70F}_{0},\\ \displaystyle \frac{\text{d}u}{\text{d}z}=0, & |\unicode[STIX]{x1D70F}|<\unicode[STIX]{x1D70F}_{0},\end{array}\right\}\end{eqnarray}$$
where
![]() $u=u(z)$
is the streamwise velocity component,
$u=u(z)$
is the streamwise velocity component,
![]() $\unicode[STIX]{x1D70F}_{0}$
and
$\unicode[STIX]{x1D70F}_{0}$
and
![]() $\unicode[STIX]{x1D707}$
represent the yield stress and the plastic viscosity of the Bingham fluid, and
$\unicode[STIX]{x1D707}$
represent the yield stress and the plastic viscosity of the Bingham fluid, and
![]() $\text{sgn}$
denotes the signum function.
$\text{sgn}$
denotes the signum function.
For characterizing flow in the anisotropic porous medium, the governing equations are
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{m}=0,\\ \displaystyle \left(\frac{\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D712}}\right)\frac{\unicode[STIX]{x2202}\boldsymbol{u}_{m}}{\unicode[STIX]{x2202}t}=-\unicode[STIX]{x1D735}p_{m}-\frac{\unicode[STIX]{x1D707}}{\unicode[STIX]{x1D646}}\boldsymbol{u}_{m}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{m}=0,\\ \displaystyle \left(\frac{\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D712}}\right)\frac{\unicode[STIX]{x2202}\boldsymbol{u}_{m}}{\unicode[STIX]{x2202}t}=-\unicode[STIX]{x1D735}p_{m}-\frac{\unicode[STIX]{x1D707}}{\unicode[STIX]{x1D646}}\boldsymbol{u}_{m}.\end{array}\right\}\end{eqnarray}$$
In the above equation,
![]() $\boldsymbol{u}_{m}$
is the velocity vector in the porous layer, and
$\boldsymbol{u}_{m}$
is the velocity vector in the porous layer, and
![]() $p_{m}$
is the interstitial pressure. Also,
$p_{m}$
is the interstitial pressure. Also,
![]() $\unicode[STIX]{x1D712}$
is the porosity, and
$\unicode[STIX]{x1D712}$
is the porosity, and
![]() $\unicode[STIX]{x1D646}$
is a diagonal tensor used to represent the anisotropic and inhomogeneous permeability of the porous medium. This tensor is expressed as
$\unicode[STIX]{x1D646}$
is a diagonal tensor used to represent the anisotropic and inhomogeneous permeability of the porous medium. This tensor is expressed as
![]() $\unicode[STIX]{x1D646}=K_{x}\unicode[STIX]{x1D702}_{x}(z/d_{m})\boldsymbol{i}\boldsymbol{i}+K_{y}\unicode[STIX]{x1D702}_{y}(z/d_{m})\boldsymbol{j}\boldsymbol{j}+K_{z}\unicode[STIX]{x1D702}_{z}(z/d_{m})\boldsymbol{k}\boldsymbol{k}$
, where
$\unicode[STIX]{x1D646}=K_{x}\unicode[STIX]{x1D702}_{x}(z/d_{m})\boldsymbol{i}\boldsymbol{i}+K_{y}\unicode[STIX]{x1D702}_{y}(z/d_{m})\boldsymbol{j}\boldsymbol{j}+K_{z}\unicode[STIX]{x1D702}_{z}(z/d_{m})\boldsymbol{k}\boldsymbol{k}$
, where
![]() $\boldsymbol{i}$
,
$\boldsymbol{i}$
,
![]() $\boldsymbol{j}$
and
$\boldsymbol{j}$
and
![]() $\boldsymbol{k}$
are the unit vectors in the
$\boldsymbol{k}$
are the unit vectors in the
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
directions, respectively. In this expression,
$z$
directions, respectively. In this expression,
![]() $K_{x}$
,
$K_{x}$
,
![]() $K_{y}$
and
$K_{y}$
and
![]() $K_{z}$
represent the permeabilities in the
$K_{z}$
represent the permeabilities in the
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
directions; and
$z$
directions; and
![]() $\unicode[STIX]{x1D702}_{x}$
,
$\unicode[STIX]{x1D702}_{x}$
,
![]() $\unicode[STIX]{x1D702}_{y}$
and
$\unicode[STIX]{x1D702}_{y}$
and
![]() $\unicode[STIX]{x1D702}_{z}$
denote the respective inhomogeneity functions. A generalized formulation would allow each of these inhomogeneity functions to be multivariate. However, in the present study,
$\unicode[STIX]{x1D702}_{z}$
denote the respective inhomogeneity functions. A generalized formulation would allow each of these inhomogeneity functions to be multivariate. However, in the present study,
![]() $\unicode[STIX]{x1D702}_{x}$
,
$\unicode[STIX]{x1D702}_{x}$
,
![]() $\unicode[STIX]{x1D702}_{y}$
and
$\unicode[STIX]{x1D702}_{y}$
and
![]() $\unicode[STIX]{x1D702}_{z}$
have been assumed to be functions of
$\unicode[STIX]{x1D702}_{z}$
have been assumed to be functions of
![]() $z$
only. This is done in order to ensure that the base solution is not multidimensional in nature. In this study, an exponential variation of the inhomogeneity function is assumed,
$z$
only. This is done in order to ensure that the base solution is not multidimensional in nature. In this study, an exponential variation of the inhomogeneity function is assumed,
![]() $\unicode[STIX]{x1D702}_{x}=\unicode[STIX]{x1D702}_{y}=\unicode[STIX]{x1D702}_{z}=\exp (A_{inh}(1+\bar{z}_{m}))$
, where
$\unicode[STIX]{x1D702}_{x}=\unicode[STIX]{x1D702}_{y}=\unicode[STIX]{x1D702}_{z}=\exp (A_{inh}(1+\bar{z}_{m}))$
, where
![]() $A_{inh}$
is the inhomogeneity factor (Chen & Hsu Reference Chen and Hsu1991), and
$A_{inh}$
is the inhomogeneity factor (Chen & Hsu Reference Chen and Hsu1991), and
![]() $\bar{z}_{m}$
is the dimensionless distance in the porous layer (as defined later in (2.10)). Continuity of pressure is assumed at the fluid–porous interface, i.e.
$\bar{z}_{m}$
is the dimensionless distance in the porous layer (as defined later in (2.10)). Continuity of pressure is assumed at the fluid–porous interface, i.e.
![]() $p=p_{m}$
(Beavers & Joseph Reference Beavers and Joseph1967).
$p=p_{m}$
(Beavers & Joseph Reference Beavers and Joseph1967).
The velocity profile in the porous layer is given by the plane Buckingham–Reiner model (Rees Reference Rees and Vafai2015). In the present notation of variables, it is expressed as
 $$\begin{eqnarray}u_{m}=-\frac{K_{x}\unicode[STIX]{x1D702}_{x}}{\unicode[STIX]{x1D707}}\left[1-\frac{3}{2}\left(\frac{\unicode[STIX]{x1D6FC}_{0}}{\displaystyle \left|\frac{\text{d}p}{\text{d}x}\right|}\right)+\frac{1}{2}\left(\frac{\unicode[STIX]{x1D6FC}_{0}}{\displaystyle \left|\frac{\text{d}p}{\text{d}x}\right|}\right)^{\!3}\right]\left(\frac{\text{d}p}{\text{d}x}\right),\quad \text{for }\left|\frac{\text{d}p}{\text{d}x}\right|>\unicode[STIX]{x1D6FC}_{0},\end{eqnarray}$$
$$\begin{eqnarray}u_{m}=-\frac{K_{x}\unicode[STIX]{x1D702}_{x}}{\unicode[STIX]{x1D707}}\left[1-\frac{3}{2}\left(\frac{\unicode[STIX]{x1D6FC}_{0}}{\displaystyle \left|\frac{\text{d}p}{\text{d}x}\right|}\right)+\frac{1}{2}\left(\frac{\unicode[STIX]{x1D6FC}_{0}}{\displaystyle \left|\frac{\text{d}p}{\text{d}x}\right|}\right)^{\!3}\right]\left(\frac{\text{d}p}{\text{d}x}\right),\quad \text{for }\left|\frac{\text{d}p}{\text{d}x}\right|>\unicode[STIX]{x1D6FC}_{0},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}_{0}=(\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D70F}_{0})/\sqrt{K_{x}}$
is essentially the threshold gradient, i.e. the limiting pressure gradient for flow to occur, and
$\unicode[STIX]{x1D6FC}_{0}=(\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D70F}_{0})/\sqrt{K_{x}}$
is essentially the threshold gradient, i.e. the limiting pressure gradient for flow to occur, and
![]() $\unicode[STIX]{x1D6FD}_{0}$
is a dimensionless parameter. When the applied pressure gradient is unable to exceed the threshold gradient, there is no flow in the porous layer. It may be observed that the velocity in the porous layer continuously approaches zero, as the limiting pressure gradient is attained. This is a characteristic feature of Bingham flow in porous media, as also confirmed by pore-scale studies (Balhoff & Thompson Reference Balhoff and Thompson2004; Nash & Rees Reference Nash and Rees2017).
$\unicode[STIX]{x1D6FD}_{0}$
is a dimensionless parameter. When the applied pressure gradient is unable to exceed the threshold gradient, there is no flow in the porous layer. It may be observed that the velocity in the porous layer continuously approaches zero, as the limiting pressure gradient is attained. This is a characteristic feature of Bingham flow in porous media, as also confirmed by pore-scale studies (Balhoff & Thompson Reference Balhoff and Thompson2004; Nash & Rees Reference Nash and Rees2017).
The authors recognize the prevalence of the Darcy–Brinkman model for describing porous layer flow. Brinkman (Reference Brinkman1949) suggested the incorporation of a viscous stress component in the Darcy equation. The study describes an ‘effective viscosity’ to be used in the viscous stress term. However, it seems that there is a lack of consensus in the literature regarding the definition of this effective viscosity (Liu & Liu Reference Liu and Liu2009). In addition, it appears that most researchers have agreed upon the fact that the Brinkman model is applicable for high-porosity configurations (Nield & Bejan Reference Nield and Bejan2006; Auriault Reference Auriault2009). A detailed Stokesian dynamics study for flow in porous media was carried out by Durlofsky & Brady (Reference Durlofsky and Brady1987), and they concluded that Brinkman’s equation should be used for porosity greater than 0.95. On the contrary, in our analysis, we considered a porosity of only 0.1, for which the validity of the Brinkman model is undoubtedly debatable. Typical application of a viscoplastic fluid flow over a porous layer is in oil recovery, where drilling fluid flows over porous soil. The porosity of major varieties of soil lies in the range of 0.1–0.4 (Association of Swiss Road and Traffic Engineers 1999; Das Reference Das2013). Other researchers who have considered the porosity in a similar range (0.1–0.4) have also neglected the Brinkman model for the similar reason of a low-porosity configuration (Chang et al. Reference Chang, Chen and Straughan2006; Deepu et al. Reference Deepu, Anand and Basu2015, Reference Deepu, Kallurkar, Anand and Basu2016; Chang et al. Reference Chang, Chen and Chang2017). Only researchers who have carried out the analysis for a ‘highly porous material’ have adopted the Brinkman model (Hill & Straughan Reference Hill and Straughan2008, Reference Hill and Straughan2009). These are the major factors why the Brinkman model is not considered to describe the flow in porous medium in this study. Incorporation of the Brinkman model can be suitably done in a future study, exploring the stability of a flow configuration consisting of a highly porous medium.
2.2 Boundary conditions
At the upper wall, the no-slip boundary condition is assumed, i.e.
The fluid–porous interface
![]() $(z=0)$
is described by the Beavers–Joseph boundary condition (Beavers & Joseph Reference Beavers and Joseph1967), i.e.
$(z=0)$
is described by the Beavers–Joseph boundary condition (Beavers & Joseph Reference Beavers and Joseph1967), i.e.
where
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
is the Beavers–Joseph constant. For a Bingham fluid, the velocity remains invariant within the plug zone. In addition, both the velocity and its gradient are assumed to be continuous at both yield surfaces. Therefore,
$\unicode[STIX]{x1D6FC}_{BJ}$
is the Beavers–Joseph constant. For a Bingham fluid, the velocity remains invariant within the plug zone. In addition, both the velocity and its gradient are assumed to be continuous at both yield surfaces. Therefore,
and
2.3 Non-dimensionalization
The variables are made non-dimensional as follows:
where
![]() $U_{p}=(d^{2}/\unicode[STIX]{x1D707})(-\text{d}p/\text{d}x)$
.
$U_{p}=(d^{2}/\unicode[STIX]{x1D707})(-\text{d}p/\text{d}x)$
.
2.3.1 Non-dimensional governing equations
Equation (2.2) may be represented in terms of non-dimensional variables as
i.e.
where
![]() $l_{1}$
is the integration constant.
$l_{1}$
is the integration constant.
The constitutive relation for a Bingham fluid (2.3) may be represented in dimensionless form as
 $$\begin{eqnarray}\left.\begin{array}{@{}ll@{}}\displaystyle \bar{\unicode[STIX]{x1D70F}}=\frac{\text{d}\bar{u}}{\text{d}\bar{z}}+Bn\,\text{sgn}\left(\frac{\text{d}\bar{u}}{\text{d}\bar{z}}\right), & |\bar{\unicode[STIX]{x1D70F}}|\geqslant Bn,\\ \displaystyle \frac{\text{d}\bar{u}}{\text{d}\bar{z}}=0, & |\bar{\unicode[STIX]{x1D70F}}|<Bn.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}ll@{}}\displaystyle \bar{\unicode[STIX]{x1D70F}}=\frac{\text{d}\bar{u}}{\text{d}\bar{z}}+Bn\,\text{sgn}\left(\frac{\text{d}\bar{u}}{\text{d}\bar{z}}\right), & |\bar{\unicode[STIX]{x1D70F}}|\geqslant Bn,\\ \displaystyle \frac{\text{d}\bar{u}}{\text{d}\bar{z}}=0, & |\bar{\unicode[STIX]{x1D70F}}|<Bn.\end{array}\right\}\end{eqnarray}$$
In the above equation,
![]() $Bn=(\unicode[STIX]{x1D70F}_{0}d)/(\unicode[STIX]{x1D707}U_{p})$
is the Bingham number of the fluid.
$Bn=(\unicode[STIX]{x1D70F}_{0}d)/(\unicode[STIX]{x1D707}U_{p})$
is the Bingham number of the fluid.
2.3.2 Non-dimensional boundary conditions
The boundary conditions (2.6)–(2.9) may be recast in terms of dimensionless variables:
where
![]() $\unicode[STIX]{x1D6FF}=\sqrt{K_{x}}/d_{m}$
represents the Darcy number, and
$\unicode[STIX]{x1D6FF}=\sqrt{K_{x}}/d_{m}$
represents the Darcy number, and
![]() $\hat{d}=d/d_{m}$
is the ratio of the thicknesses of the fluid and the porous layers;
$\hat{d}=d/d_{m}$
is the ratio of the thicknesses of the fluid and the porous layers;
![]() $\hat{d}$
is referred to as the depth ratio of the channel.
$\hat{d}$
is referred to as the depth ratio of the channel.
2.4 Base flow – analytical solution
The velocity profile may be derived by solving (2.11) subject to boundary conditions (2.13)–(2.16). For the region
![]() $0\leqslant \bar{z}\leqslant \bar{z}_{01}$
(i.e. the lower shear zone),
$0\leqslant \bar{z}\leqslant \bar{z}_{01}$
(i.e. the lower shear zone),
![]() $\text{d}\bar{u}/\text{d}\bar{z}>0$
, i.e. the velocity gradient is positive. The velocity may be given as
$\text{d}\bar{u}/\text{d}\bar{z}>0$
, i.e. the velocity gradient is positive. The velocity may be given as
In the upper shear zone (i.e.
![]() $\bar{z}_{02}\leqslant \bar{z}\leqslant 1$
),
$\bar{z}_{02}\leqslant \bar{z}\leqslant 1$
),
![]() $\text{d}\bar{u}/\text{d}\bar{z}<0$
. The velocity is expressed as
$\text{d}\bar{u}/\text{d}\bar{z}<0$
. The velocity is expressed as
where
![]() $l_{2}$
and
$l_{2}$
and
![]() $l_{3}$
are the integration constants.
$l_{3}$
are the integration constants.
For the intermediate unyielded zone
![]() $(\bar{z}_{01}\leqslant \bar{z}\leqslant \bar{z}_{02})$
, the velocity is constant, given by
$(\bar{z}_{01}\leqslant \bar{z}\leqslant \bar{z}_{02})$
, the velocity is constant, given by
![]() $\bar{u}|_{\bar{z}=\bar{z}_{01}}=\bar{u}|_{\bar{z}=\bar{z}_{02}}$
.
$\bar{u}|_{\bar{z}=\bar{z}_{01}}=\bar{u}|_{\bar{z}=\bar{z}_{02}}$
.
2.4.1 Velocity profile in the fluid layer
The dimensionless base velocity in the fluid layer may be given as (
![]() $\bar{v}$
and
$\bar{v}$
and
![]() $\bar{w}$
represent the dimensionless spanwise and normal velocity components)
$\bar{w}$
represent the dimensionless spanwise and normal velocity components)
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \begin{array}{@{}rcl@{}}\displaystyle \bar{u}(\bar{z})\, & = & \displaystyle \left(l_{1}\bar{z}-\frac{\bar{z}^{2}}{2}-Bn\,\bar{z}\right)+l_{2},\quad 0\leqslant \bar{z}\leqslant \bar{z}_{01},\\ \displaystyle \, & = & \displaystyle \frac{\bar{z}_{01}^{2}}{2}+l_{2},\quad \bar{z}_{01}\leqslant \bar{z}\leqslant \bar{z}_{02},\\ \, & = & \displaystyle \left(l_{1}\bar{z}-\frac{\bar{z}^{2}}{2}+Bn\,\bar{z}\right)+l_{3},\quad \bar{z}_{02}\leqslant \bar{z}\leqslant 1,\end{array}\\ \bar{v}=0,\quad \bar{w}=0,\quad 0\leqslant \bar{z}\leqslant 1,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \begin{array}{@{}rcl@{}}\displaystyle \bar{u}(\bar{z})\, & = & \displaystyle \left(l_{1}\bar{z}-\frac{\bar{z}^{2}}{2}-Bn\,\bar{z}\right)+l_{2},\quad 0\leqslant \bar{z}\leqslant \bar{z}_{01},\\ \displaystyle \, & = & \displaystyle \frac{\bar{z}_{01}^{2}}{2}+l_{2},\quad \bar{z}_{01}\leqslant \bar{z}\leqslant \bar{z}_{02},\\ \, & = & \displaystyle \left(l_{1}\bar{z}-\frac{\bar{z}^{2}}{2}+Bn\,\bar{z}\right)+l_{3},\quad \bar{z}_{02}\leqslant \bar{z}\leqslant 1,\end{array}\\ \bar{v}=0,\quad \bar{w}=0,\quad 0\leqslant \bar{z}\leqslant 1,\end{array}\right\}\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle & \displaystyle l_{2}=\left[\frac{\displaystyle 1-4Bn(1-Bn)+\frac{2\bar{u}_{m}(0)\unicode[STIX]{x1D6FC}_{BJ}\hat{d}(1-2Bn)}{\unicode[STIX]{x1D6FF}\sqrt{\unicode[STIX]{x1D702}_{x}(0)}}}{\displaystyle 2\left(1+\frac{\unicode[STIX]{x1D6FC}_{BJ}\hat{d}(1-2Bn)}{\unicode[STIX]{x1D6FF}\sqrt{\unicode[STIX]{x1D702}_{x}(0)}}\right)}\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle l_{2}=\left[\frac{\displaystyle 1-4Bn(1-Bn)+\frac{2\bar{u}_{m}(0)\unicode[STIX]{x1D6FC}_{BJ}\hat{d}(1-2Bn)}{\unicode[STIX]{x1D6FF}\sqrt{\unicode[STIX]{x1D702}_{x}(0)}}}{\displaystyle 2\left(1+\frac{\unicode[STIX]{x1D6FC}_{BJ}\hat{d}(1-2Bn)}{\unicode[STIX]{x1D6FF}\sqrt{\unicode[STIX]{x1D702}_{x}(0)}}\right)}\right], & \displaystyle\end{eqnarray}$$
The locations of the yield surfaces at
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
are expressed as
$\bar{z}_{02}$
are expressed as
Using (2.22) and (2.23), it is observed that
It is evident that the plug region should be within the fluid volume. Therefore, the following constraint is imposed on
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
:
$\bar{z}_{02}$
:
In addition, it may be inferred from (2.24) and (2.25) that
2.4.2 Velocity profile in the porous layer
The non-dimensional velocity profile in the porous layer is obtained as
where
 $$\begin{eqnarray}l_{4}=\frac{\unicode[STIX]{x1D6FF}^{2}}{\hat{d}^{2}}\left[1-\frac{3}{2}\left(\frac{\unicode[STIX]{x1D6FD}_{0}Bn\,\hat{d}}{\unicode[STIX]{x1D6FF}}\right)+\frac{1}{2}\left(\frac{\unicode[STIX]{x1D6FD}_{0}Bn\,\hat{d}}{\unicode[STIX]{x1D6FF}}\right)^{\!3}\right].\end{eqnarray}$$
$$\begin{eqnarray}l_{4}=\frac{\unicode[STIX]{x1D6FF}^{2}}{\hat{d}^{2}}\left[1-\frac{3}{2}\left(\frac{\unicode[STIX]{x1D6FD}_{0}Bn\,\hat{d}}{\unicode[STIX]{x1D6FF}}\right)+\frac{1}{2}\left(\frac{\unicode[STIX]{x1D6FD}_{0}Bn\,\hat{d}}{\unicode[STIX]{x1D6FF}}\right)^{\!3}\right].\end{eqnarray}$$
When the threshold gradient is not reached (i.e. when
![]() $\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FD}_{0}\hat{d}<Bn$
), the velocity is zero in the porous layer.
$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FD}_{0}\hat{d}<Bn$
), the velocity is zero in the porous layer.
2.5 Stability analysis
In earlier studies on stability analysis of viscoplastic fluids, there was no existence of the porous layer. As a result, the flow profile was symmetric about the middle of the plug zone. This eliminated the need to consider both the shear zones in the analysis. Stability analysis for the decoupled problem was carried out only for the upper shear zone. Here, it may be noted that the flow configuration consists of an upper shear zone, a plug zone, a lower shear zone and a porous layer. The complexity of the current study is enhanced by the fact that the velocity profile is asymmetric about the middle of the plug zone. There are two flow domains, separated by a plug zone discontinuity. One is the domain I comprising the porous layer and the lower shear zone, extending from
![]() $z=-d_{m}$
to
$z=-d_{m}$
to
![]() $z_{01}$
. The other is the domain II, consisting of the upper shear zone, extending from
$z_{01}$
. The other is the domain II, consisting of the upper shear zone, extending from
![]() $z=z_{02}$
to
$z=z_{02}$
to
![]() $d$
. Fortunately, it may be noted that the maximum velocity is the same for both domains, and is realized at the interface of the shear and plug zones. It is evident that the governing perturbation equations will be the same for both the shear zones. Since the maximum realizable velocity is the same in either of the two shear zones, for the current study, we carry out the stability analysis for the domain I. In other words, we study the zone extending from
$d$
. Fortunately, it may be noted that the maximum velocity is the same for both domains, and is realized at the interface of the shear and plug zones. It is evident that the governing perturbation equations will be the same for both the shear zones. Since the maximum realizable velocity is the same in either of the two shear zones, for the current study, we carry out the stability analysis for the domain I. In other words, we study the zone extending from
![]() $z=-d_{m}$
to
$z=-d_{m}$
to
![]() $z_{01}$
(comprising the porous layer and the lower shear zone). Henceforth,
$z_{01}$
(comprising the porous layer and the lower shear zone). Henceforth,
![]() $z_{01}$
is represented as
$z_{01}$
is represented as
![]() $z_{0}$
for the sake of simplicity.
$z_{0}$
for the sake of simplicity.
2.5.1 Perturbation equations
Now, we allow a perturbation to the system in the form
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u=\overline{u}+u^{\prime },\quad v=\overline{v}+v^{\prime },\quad w=\overline{w}+w^{\prime },\\ u_{m}=\overline{u_{m}}+u_{m}^{\prime },\quad v_{m}=\overline{v_{m}}+v_{m}^{\prime },\quad w_{m}=\overline{w_{m}}+w_{m}^{\prime },\\ p=\overline{p}+p^{\prime },\quad z_{0}=\overline{z_{0}}+h^{\prime },\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u=\overline{u}+u^{\prime },\quad v=\overline{v}+v^{\prime },\quad w=\overline{w}+w^{\prime },\\ u_{m}=\overline{u_{m}}+u_{m}^{\prime },\quad v_{m}=\overline{v_{m}}+v_{m}^{\prime },\quad w_{m}=\overline{w_{m}}+w_{m}^{\prime },\\ p=\overline{p}+p^{\prime },\quad z_{0}=\overline{z_{0}}+h^{\prime },\end{array}\right\}\end{eqnarray}$$
where
![]() $\bar{u}$
and
$\bar{u}$
and
![]() $u^{\prime }$
respectively denote
$u^{\prime }$
respectively denote
![]() $x$
-direction steady-state velocity, and the velocity perturbation. The rest of the variables also have analogous meanings.
$x$
-direction steady-state velocity, and the velocity perturbation. The rest of the variables also have analogous meanings.
The perturbation equations for the fluid layer are given as (
![]() $\text{D}=\text{d}/\text{d}z$
; in addition, we write
$\text{D}=\text{d}/\text{d}z$
; in addition, we write
![]() $\bar{u}=U$
for convenience in the following equations)
$\bar{u}=U$
for convenience in the following equations)
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}u^{\prime }}{\unicode[STIX]{x2202}t}+U\frac{\unicode[STIX]{x2202}u^{\prime }}{\unicode[STIX]{x2202}x}+w^{\prime }\text{D}U & = & \displaystyle -\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}x}+\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}u^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\frac{1}{|\text{D}U|}\left(\unicode[STIX]{x1D6FB}^{2}u^{\prime }-\frac{\unicode[STIX]{x2202}^{2}w^{\prime }}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}z}-\frac{\unicode[STIX]{x2202}^{2}u^{\prime }}{\unicode[STIX]{x2202}z^{2}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}u^{\prime }}{\unicode[STIX]{x2202}t}+U\frac{\unicode[STIX]{x2202}u^{\prime }}{\unicode[STIX]{x2202}x}+w^{\prime }\text{D}U & = & \displaystyle -\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}x}+\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}u^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\frac{1}{|\text{D}U|}\left(\unicode[STIX]{x1D6FB}^{2}u^{\prime }-\frac{\unicode[STIX]{x2202}^{2}w^{\prime }}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}z}-\frac{\unicode[STIX]{x2202}^{2}u^{\prime }}{\unicode[STIX]{x2202}z^{2}}\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}t}+U\frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}x} & = & \displaystyle -\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}y}+\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}v^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[\frac{\unicode[STIX]{x1D6FB}^{2}v^{\prime }}{|\text{D}U|}+\left(\frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}z}+\frac{\unicode[STIX]{x2202}w^{\prime }}{\unicode[STIX]{x2202}y}\right)\left\{\frac{\text{d}}{\text{d}z}\left(\frac{1}{|\text{D}U|}\right)\right\}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}t}+U\frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}x} & = & \displaystyle -\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}y}+\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}v^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[\frac{\unicode[STIX]{x1D6FB}^{2}v^{\prime }}{|\text{D}U|}+\left(\frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}z}+\frac{\unicode[STIX]{x2202}w^{\prime }}{\unicode[STIX]{x2202}y}\right)\left\{\frac{\text{d}}{\text{d}z}\left(\frac{1}{|\text{D}U|}\right)\right\}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}w^{\prime }}{\unicode[STIX]{x2202}t}+U\frac{\unicode[STIX]{x2202}w^{\prime }}{\unicode[STIX]{x2202}x} & = & \displaystyle -\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}z}+\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}w^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[2\left(\frac{\unicode[STIX]{x2202}w^{\prime }}{\unicode[STIX]{x2202}z}\right)\left\{\frac{\text{d}}{\text{d}z}\left(\frac{1}{|\text{D}U|}\right)\right\}+\frac{\displaystyle \unicode[STIX]{x1D6FB}^{2}w^{\prime }-\frac{\unicode[STIX]{x2202}^{2}w^{\prime }}{\unicode[STIX]{x2202}x^{2}}-\frac{\unicode[STIX]{x2202}^{2}u^{\prime }}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}z}}{|\text{D}U|}\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}w^{\prime }}{\unicode[STIX]{x2202}t}+U\frac{\unicode[STIX]{x2202}w^{\prime }}{\unicode[STIX]{x2202}x} & = & \displaystyle -\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}z}+\frac{1}{Re}\unicode[STIX]{x1D6FB}^{2}w^{\prime }\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[2\left(\frac{\unicode[STIX]{x2202}w^{\prime }}{\unicode[STIX]{x2202}z}\right)\left\{\frac{\text{d}}{\text{d}z}\left(\frac{1}{|\text{D}U|}\right)\right\}+\frac{\displaystyle \unicode[STIX]{x1D6FB}^{2}w^{\prime }-\frac{\unicode[STIX]{x2202}^{2}w^{\prime }}{\unicode[STIX]{x2202}x^{2}}-\frac{\unicode[STIX]{x2202}^{2}u^{\prime }}{\unicode[STIX]{x2202}x\unicode[STIX]{x2202}z}}{|\text{D}U|}\right].\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The perturbation equations for the porous layer are expressed as
It is known that Squire’s transformation is not valid for Bingham fluids (Frigaard et al. Reference Frigaard, Howison and Sobey1994; Métivier & Nouar Reference Métivier and Nouar2011). Thus, to perform stability analysis, we assume three-dimensional disturbances of the form
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u^{\prime }=\hat{u} (z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\quad v^{\prime }=\hat{v}(z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\quad w^{\prime }={\hat{w}}(z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\\ u_{m}^{\prime }=\hat{u} _{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m})},\quad v_{m}^{\prime }=\hat{v}_{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m})},\\ w_{m}^{\prime }={\hat{w}}_{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m})},\\ p^{\prime }=\hat{p}(z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\quad p_{m}^{\prime }=\hat{p}_{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\quad h^{\prime }={\hat{h}}(t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u^{\prime }=\hat{u} (z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\quad v^{\prime }=\hat{v}(z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\quad w^{\prime }={\hat{w}}(z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\\ u_{m}^{\prime }=\hat{u} _{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m})},\quad v_{m}^{\prime }=\hat{v}_{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m})},\\ w_{m}^{\prime }={\hat{w}}_{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m})},\\ p^{\prime }=\hat{p}(z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\quad p_{m}^{\prime }=\hat{p}_{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\quad h^{\prime }={\hat{h}}(t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)},\end{array}\right\}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are the real streamwise and spanwise wavenumbers, respectively. It is to be noted that yield stress fluids are unique in the sense that the yield surface also undergoes perturbation. Hence, perturbation in the yield surface is also being considered. Incorporation of the above disturbance expressions (2.38) in the governing perturbation equations (2.30)–(2.37) results in an initial value problem (the hats are dropped from
$\unicode[STIX]{x1D6FD}$
are the real streamwise and spanwise wavenumbers, respectively. It is to be noted that yield stress fluids are unique in the sense that the yield surface also undergoes perturbation. Hence, perturbation in the yield surface is also being considered. Incorporation of the above disturbance expressions (2.38) in the governing perturbation equations (2.30)–(2.37) results in an initial value problem (the hats are dropped from
![]() $u$
,
$u$
,
![]() $v$
, etc., for convenience). Thus, in the following equations,
$v$
, etc., for convenience). Thus, in the following equations,
![]() $u$
is essentially
$u$
is essentially
![]() $\hat{u}$
. Also,
$\hat{u}$
. Also,
![]() $\mathbb{Q}=\text{D}^{2}-(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})$
. In addition, we write
$\mathbb{Q}=\text{D}^{2}-(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})$
. In addition, we write
![]() $\bar{u}=U$
for convenience in the following equations, wherever applicable.
$\bar{u}=U$
for convenience in the following equations, wherever applicable.
For the fluid layer, the following set of equations is obtained:
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}t} & = & \displaystyle -\text{i}\unicode[STIX]{x1D6FC}Uv-\text{i}\unicode[STIX]{x1D6FD}p+\frac{1}{Re}\mathbb{Q}v\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[\frac{1}{|\text{D}U|}\mathbb{Q}v+(\text{D}v+\text{i}\unicode[STIX]{x1D6FD}w)\left\{\text{D}\left(\frac{1}{|\text{D}U|}\right)\right\}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}t} & = & \displaystyle -\text{i}\unicode[STIX]{x1D6FC}Uv-\text{i}\unicode[STIX]{x1D6FD}p+\frac{1}{Re}\mathbb{Q}v\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[\frac{1}{|\text{D}U|}\mathbb{Q}v+(\text{D}v+\text{i}\unicode[STIX]{x1D6FD}w)\left\{\text{D}\left(\frac{1}{|\text{D}U|}\right)\right\}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t} & = & \displaystyle -\text{i}\unicode[STIX]{x1D6FC}Uw-\text{D}p+\frac{1}{Re}\mathbb{Q}w\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[(2\text{D}w)\left\{\text{D}\left(\frac{1}{|\text{D}U|}\right)\right\}+\frac{(\text{D}^{2}-\unicode[STIX]{x1D6FD}^{2})w-\text{i}\unicode[STIX]{x1D6FC}\text{D}u}{|\text{D}U|}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t} & = & \displaystyle -\text{i}\unicode[STIX]{x1D6FC}Uw-\text{D}p+\frac{1}{Re}\mathbb{Q}w\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[(2\text{D}w)\left\{\text{D}\left(\frac{1}{|\text{D}U|}\right)\right\}+\frac{(\text{D}^{2}-\unicode[STIX]{x1D6FD}^{2})w-\text{i}\unicode[STIX]{x1D6FC}\text{D}u}{|\text{D}U|}\right].\end{eqnarray}$$
For the porous layer, the following initial value problem is obtained:
where
![]() $\unicode[STIX]{x1D709}_{1}=K_{x}/K_{y}$
and
$\unicode[STIX]{x1D709}_{1}=K_{x}/K_{y}$
and
![]() $\unicode[STIX]{x1D709}_{2}=K_{x}/K_{z}$
respectively denote the spanwise and normal anisotropy parameters. Also,
$\unicode[STIX]{x1D709}_{2}=K_{x}/K_{z}$
respectively denote the spanwise and normal anisotropy parameters. Also,
![]() $\text{D}_{p}=\text{d}/\text{d}z_{m}$
. The Reynolds numbers in the two layers are related as
$\text{D}_{p}=\text{d}/\text{d}z_{m}$
. The Reynolds numbers in the two layers are related as
 $$\begin{eqnarray}Re=\hat{d}Re_{m}\left(\frac{\displaystyle l_{2}+\frac{\bar{z}_{01}^{2}}{2}}{l_{4}\unicode[STIX]{x1D702}_{x}(0)}\right).\end{eqnarray}$$
$$\begin{eqnarray}Re=\hat{d}Re_{m}\left(\frac{\displaystyle l_{2}+\frac{\bar{z}_{01}^{2}}{2}}{l_{4}\unicode[STIX]{x1D702}_{x}(0)}\right).\end{eqnarray}$$
For modal analysis, the disturbance expressions in the governing perturbation equations (2.30)–(2.37) are replaced, using the following relations:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u^{\prime }=\hat{u} (z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\quad v^{\prime }=\hat{v}(z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\quad w^{\prime }={\hat{w}}(z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\\ u_{m}^{\prime }=\hat{u} _{m}(z_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})},\quad v_{m}^{\prime }=\hat{v}_{m}(z_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})},\\ w_{m}^{\prime }={\hat{w}}_{m}(z_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})},\\ p^{\prime }=\hat{p}(z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\quad z_{0}^{\prime }=\hat{z}_{0}(z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\\ p_{m}^{\prime }=\hat{p}_{m}(z_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})},\quad h^{\prime }={\hat{h}}(t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u^{\prime }=\hat{u} (z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\quad v^{\prime }=\hat{v}(z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\quad w^{\prime }={\hat{w}}(z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\\ u_{m}^{\prime }=\hat{u} _{m}(z_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})},\quad v_{m}^{\prime }=\hat{v}_{m}(z_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})},\\ w_{m}^{\prime }={\hat{w}}_{m}(z_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})},\\ p^{\prime }=\hat{p}(z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\quad z_{0}^{\prime }=\hat{z}_{0}(z)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)},\\ p_{m}^{\prime }=\hat{p}_{m}(z_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})},\quad h^{\prime }={\hat{h}}(t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)}.\end{array}\right\}\end{eqnarray}$$
Thus, the following eigenvalue problem is obtained in the fluid and the porous layers:
 $$\begin{eqnarray}\displaystyle -\text{i}cv & = & \displaystyle -\text{i}\unicode[STIX]{x1D6FC}Uv-\text{i}\unicode[STIX]{x1D6FD}p+\frac{1}{Re}\mathbb{Q}v\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[\frac{1}{|\text{D}U|}\mathbb{Q}v+(\text{D}v+\text{i}\unicode[STIX]{x1D6FD}w)\left\{\text{D}\left(\frac{1}{|\text{D}U|}\right)\right\}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\text{i}cv & = & \displaystyle -\text{i}\unicode[STIX]{x1D6FC}Uv-\text{i}\unicode[STIX]{x1D6FD}p+\frac{1}{Re}\mathbb{Q}v\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[\frac{1}{|\text{D}U|}\mathbb{Q}v+(\text{D}v+\text{i}\unicode[STIX]{x1D6FD}w)\left\{\text{D}\left(\frac{1}{|\text{D}U|}\right)\right\}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle -\text{i}cw & = & \displaystyle -\text{i}\unicode[STIX]{x1D6FC}Uw-\text{D}p+\frac{1}{Re}\mathbb{Q}w\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[(2\text{D}w)\left\{\text{D}\left(\frac{1}{|\text{D}U|}\right)\right\}+\frac{(\text{D}^{2}-\unicode[STIX]{x1D6FD}^{2})w-\text{i}\unicode[STIX]{x1D6FC}\text{D}u}{|\text{D}U|}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\text{i}cw & = & \displaystyle -\text{i}\unicode[STIX]{x1D6FC}Uw-\text{D}p+\frac{1}{Re}\mathbb{Q}w\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Bn}{Re}\left[(2\text{D}w)\left\{\text{D}\left(\frac{1}{|\text{D}U|}\right)\right\}+\frac{(\text{D}^{2}-\unicode[STIX]{x1D6FD}^{2})w-\text{i}\unicode[STIX]{x1D6FC}\text{D}u}{|\text{D}U|}\right],\end{eqnarray}$$
At the yield surface (interface of yielded and unyielded zone), the following boundary conditions prevail:
Other boundary conditions are obtained from the Beavers–Joseph condition at the fluid–porous interface, along with the continuity of normal and spanwise velocity, and pressure.
Thus, at the fluid–porous interface
![]() $(\bar{z}=\bar{z}_{m}=0)$
, we have
$(\bar{z}=\bar{z}_{m}=0)$
, we have
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{D}u(0)=\frac{\unicode[STIX]{x1D6FC}_{BJ}\hat{d}}{\unicode[STIX]{x1D6FF}\sqrt{\unicode[STIX]{x1D702}_{x}(0)}}\left[u(0)-\frac{\hat{d}Re_{m}}{Re}u_{m}(0)\right],\\ \displaystyle Re\,v(0)=\hat{d}Re_{m}v_{m}(0),\\ Re\,w(0)=\hat{d}Re_{m}w_{m}(0),\\ \displaystyle p(0)=\frac{\hat{d}^{2}}{Re}Re_{m}p_{m}(0).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{D}u(0)=\frac{\unicode[STIX]{x1D6FC}_{BJ}\hat{d}}{\unicode[STIX]{x1D6FF}\sqrt{\unicode[STIX]{x1D702}_{x}(0)}}\left[u(0)-\frac{\hat{d}Re_{m}}{Re}u_{m}(0)\right],\\ \displaystyle Re\,v(0)=\hat{d}Re_{m}v_{m}(0),\\ Re\,w(0)=\hat{d}Re_{m}w_{m}(0),\\ \displaystyle p(0)=\frac{\hat{d}^{2}}{Re}Re_{m}p_{m}(0).\end{array}\right\}\end{eqnarray}$$
At the bottom surface of the porous layer (
![]() $z=-d_{m}$
, or
$z=-d_{m}$
, or
![]() $\bar{z}_{m}=-1$
), we have
$\bar{z}_{m}=-1$
), we have
The following relation exists among the wavenumbers
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}_{m},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}_{m})$
in the fluid and porous layers:
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}_{m},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}_{m})$
in the fluid and porous layers:
Equations (2.49)–(2.56) are second order in
![]() $u$
,
$u$
,
![]() $v$
,
$v$
,
![]() $w$
, and first order in
$w$
, and first order in
![]() $w_{m}$
,
$w_{m}$
,
![]() $p$
,
$p$
,
![]() $p_{m}$
. For solving the same, we are seemingly using 12 boundary conditions (2.57)–(2.59). In other words, the system is apparently over-specified. However, a careful observation will reveal the reality that is typical of yield stress fluids. In (2.57), the relation for
$p_{m}$
. For solving the same, we are seemingly using 12 boundary conditions (2.57)–(2.59). In other words, the system is apparently over-specified. However, a careful observation will reveal the reality that is typical of yield stress fluids. In (2.57), the relation for
![]() $\text{D}u$
essentially specifies the condition for the amplitude of the perturbation of the yield surface. Thus, the relation basically defines
$\text{D}u$
essentially specifies the condition for the amplitude of the perturbation of the yield surface. Thus, the relation basically defines
![]() $h$
, and not
$h$
, and not
![]() $u$
. The relations for
$u$
. The relations for
![]() $\text{D}v$
and
$\text{D}v$
and
![]() $\text{D}w$
are also required, as they take care of the singularity of
$\text{D}w$
are also required, as they take care of the singularity of
![]() $|\text{D}U|^{-1}$
as the yield surface is approached. The same has been elucidated by other researchers as well (Frigaard & Nouar Reference Frigaard and Nouar2003; Nouar et al.
Reference Nouar, Kabouya, Dusek and Mamou2007).
$|\text{D}U|^{-1}$
as the yield surface is approached. The same has been elucidated by other researchers as well (Frigaard & Nouar Reference Frigaard and Nouar2003; Nouar et al.
Reference Nouar, Kabouya, Dusek and Mamou2007).
It may be highlighted here that the disturbance waves arising in the fluid and porous layers are the same, i.e. they have the same wavelength. As a result, the dimensional wavenumbers, being the reciprocal of wavelength, are also the same in the two layers. However, in our analysis, we are considering non-dimensional wavenumbers, namely
![]() $\unicode[STIX]{x1D6FC}$
in the fluid layer and
$\unicode[STIX]{x1D6FC}$
in the fluid layer and
![]() $\unicode[STIX]{x1D6FC}_{m}$
in the porous layer:
$\unicode[STIX]{x1D6FC}_{m}$
in the porous layer:
![]() $\unicode[STIX]{x1D6FC}$
is non-dimensionalized with respect to
$\unicode[STIX]{x1D6FC}$
is non-dimensionalized with respect to
![]() $d$
(thickness of the fluid layer), while
$d$
(thickness of the fluid layer), while
![]() $\unicode[STIX]{x1D6FC}_{m}$
is made non-dimensional with respect to
$\unicode[STIX]{x1D6FC}_{m}$
is made non-dimensional with respect to
![]() $d_{m}$
(thickness of the porous layer). Thus,
$d_{m}$
(thickness of the porous layer). Thus,
![]() $\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FC}_{m}$
(in fact,
$\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FC}_{m}$
(in fact,
![]() $\unicode[STIX]{x1D6FC}=\hat{d}\unicode[STIX]{x1D6FC}_{m}$
, as already stated; in fact,
$\unicode[STIX]{x1D6FC}=\hat{d}\unicode[STIX]{x1D6FC}_{m}$
, as already stated; in fact,
![]() $\unicode[STIX]{x1D6FD}=\hat{d}\unicode[STIX]{x1D6FD}_{m}$
as well). In a similar way, the non-dimensional distances in the two layers are related as
$\unicode[STIX]{x1D6FD}=\hat{d}\unicode[STIX]{x1D6FD}_{m}$
as well). In a similar way, the non-dimensional distances in the two layers are related as
![]() $\hat{d}x=x_{m}$
and
$\hat{d}x=x_{m}$
and
![]() $\hat{d}y=y_{m}$
. Thus, the Fourier expressions are identical in the two layers, i.e.
$\hat{d}y=y_{m}$
. Thus, the Fourier expressions are identical in the two layers, i.e.
![]() $\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)}=\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})}$
. The modal expressions
$\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y-ct)}=\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m}-c_{m}t_{m})}$
. The modal expressions
![]() $u$
and
$u$
and
![]() $u^{\prime }$
differ in the
$u^{\prime }$
differ in the
![]() $z$
direction, which is logical, as the base profiles are also different in the two layers. These assumptions are in conformity with earlier studies (Chang et al.
Reference Chang, Chen and Straughan2006; Hill & Straughan Reference Hill and Straughan2008; Deepu et al.
Reference Deepu, Anand and Basu2015; Chang et al.
Reference Chang, Chen and Chang2017).
$z$
direction, which is logical, as the base profiles are also different in the two layers. These assumptions are in conformity with earlier studies (Chang et al.
Reference Chang, Chen and Straughan2006; Hill & Straughan Reference Hill and Straughan2008; Deepu et al.
Reference Deepu, Anand and Basu2015; Chang et al.
Reference Chang, Chen and Chang2017).
2.6 Numerical solution
We have assumed porosity
![]() $\unicode[STIX]{x1D712}=0.1$
throughout. Unless otherwise explicitly specified, the parameters assume the following values:
$\unicode[STIX]{x1D712}=0.1$
throughout. Unless otherwise explicitly specified, the parameters assume the following values:
![]() $Bn=0.2$
,
$Bn=0.2$
,
![]() $\unicode[STIX]{x1D6FD}_{0}=0.016$
,
$\unicode[STIX]{x1D6FD}_{0}=0.016$
,
![]() $\hat{d}=0.3$
,
$\hat{d}=0.3$
,
![]() $\unicode[STIX]{x1D6FC}_{BJ}=0.2$
,
$\unicode[STIX]{x1D6FC}_{BJ}=0.2$
,
![]() $\unicode[STIX]{x1D6FF}=0.001$
,
$\unicode[STIX]{x1D6FF}=0.001$
,
![]() $\unicode[STIX]{x1D709}_{1}=2$
,
$\unicode[STIX]{x1D709}_{1}=2$
,
![]() $\unicode[STIX]{x1D709}_{2}=2$
and
$\unicode[STIX]{x1D709}_{2}=2$
and
![]() $A_{inh}=2$
. For modal analysis, the resultant generalized eigenvalue problem of the form
$A_{inh}=2$
. For modal analysis, the resultant generalized eigenvalue problem of the form
![]() $\unicode[STIX]{x1D63C}\unicode[STIX]{x1D653}=c\unicode[STIX]{x1D63D}\unicode[STIX]{x1D653}$
is solved via the Chebyshev spectral collocation method using QZ decomposition. Here,
$\unicode[STIX]{x1D63C}\unicode[STIX]{x1D653}=c\unicode[STIX]{x1D63D}\unicode[STIX]{x1D653}$
is solved via the Chebyshev spectral collocation method using QZ decomposition. Here,
![]() $\unicode[STIX]{x1D653}=(u,v,w,p)$
, and
$\unicode[STIX]{x1D653}=(u,v,w,p)$
, and
![]() $\unicode[STIX]{x1D63C}$
and
$\unicode[STIX]{x1D63C}$
and
![]() $\unicode[STIX]{x1D63D}$
are the matrices comprising Chebyshev derivatives. The discretization of the equations is carried out on the Gauss–Lobatto grid, consisting of
$\unicode[STIX]{x1D63D}$
are the matrices comprising Chebyshev derivatives. The discretization of the equations is carried out on the Gauss–Lobatto grid, consisting of
![]() $(N+1)$
collocation points. The details of the spectral collocation method using Chebyshev polynomials have been discussed by Schmid & Henningson (Reference Schmid and Henningson2001). MATLAB 2014b software was used for the computation. The calculations were checked with increasing number of Chebyshev polynomials (
$(N+1)$
collocation points. The details of the spectral collocation method using Chebyshev polynomials have been discussed by Schmid & Henningson (Reference Schmid and Henningson2001). MATLAB 2014b software was used for the computation. The calculations were checked with increasing number of Chebyshev polynomials (
![]() $N=32$
, 64, 96, 128, 192, 256, 384, 512). It was observed that for
$N=32$
, 64, 96, 128, 192, 256, 384, 512). It was observed that for
![]() $N=192$
, the first 50 eigenvalues (sorted in terms of increasing imaginary part) gave accuracy up to five digits. In other words, the first five digits remained invariant with further increase in
$N=192$
, the first 50 eigenvalues (sorted in terms of increasing imaginary part) gave accuracy up to five digits. In other words, the first five digits remained invariant with further increase in
![]() $N$
. Hence, all the computations reported in this paper were carried out with
$N$
. Hence, all the computations reported in this paper were carried out with
![]() $N=192$
.
$N=192$
.
2.7 Non-modal analysis and energy growth
For non-modal analysis, the following linear initial value problem needs to be solved:
where
![]() $\boldsymbol{q}$
is expressed as
$\boldsymbol{q}$
is expressed as
![]() $\boldsymbol{q}=(\hat{u} ,\hat{v},{\hat{w}},\hat{p})^{\text{T}}$
, and
$\boldsymbol{q}=(\hat{u} ,\hat{v},{\hat{w}},\hat{p})^{\text{T}}$
, and
![]() $\unicode[STIX]{x1D647}$
is defined as
$\unicode[STIX]{x1D647}$
is defined as
![]() $\unicode[STIX]{x1D647}=-\text{i}\unicode[STIX]{x1D63D}^{-1}\unicode[STIX]{x1D63C}$
. The solution is expressed as
$\unicode[STIX]{x1D647}=-\text{i}\unicode[STIX]{x1D63D}^{-1}\unicode[STIX]{x1D63C}$
. The solution is expressed as
![]() $\boldsymbol{q}(t)=\boldsymbol{q}(0)\exp (-\text{i}\unicode[STIX]{x1D647}t)$
, where
$\boldsymbol{q}(t)=\boldsymbol{q}(0)\exp (-\text{i}\unicode[STIX]{x1D647}t)$
, where
![]() $\boldsymbol{q}(0)$
is the initial value of the perturbation variables.
$\boldsymbol{q}(0)$
is the initial value of the perturbation variables.
2.7.1 Response to initial conditions: growth function
In the above context, the growth function defines the maximum possible amplification of the initial condition, and is mathematically expressed as
where
![]() $\Vert \cdot \Vert$
is the norm.
$\Vert \cdot \Vert$
is the norm.
In general, for a flow stability problem, if the Reynolds number
![]() $Re$
is less than the critical energy Reynolds number
$Re$
is less than the critical energy Reynolds number
![]() $Re_{1}$
, then the growth function
$Re_{1}$
, then the growth function
![]() $G(t)$
is never greater than unity, i.e.
$G(t)$
is never greater than unity, i.e.
![]() $G_{max}=1$
. In such a case, optimal time
$G_{max}=1$
. In such a case, optimal time
![]() $t_{opt}$
is zero. On the other hand, if the Reynolds number is greater than the critical Reynolds number
$t_{opt}$
is zero. On the other hand, if the Reynolds number is greater than the critical Reynolds number
![]() $Re_{2}$
, then one of the eigenvalues of the linear Orr–Sommerfeld operator has a positive imaginary part, and the flow becomes unstable. Mathematically, the growth function becomes unbounded at infinite time. In the case of
$Re_{2}$
, then one of the eigenvalues of the linear Orr–Sommerfeld operator has a positive imaginary part, and the flow becomes unstable. Mathematically, the growth function becomes unbounded at infinite time. In the case of
![]() $Re_{1}<Re<Re_{2}$
, modal analysis yields no unstable eigenvalue and thus the flow is linearly stable. However, a transient growth is observed which decays with time. For the current work, stability analysis is performed for a vast range of Reynolds numbers, but no unstable eigenvalues are obtained. Thus, for analysing non-modal behaviour, a Reynolds number higher than the critical energy Reynolds number
$Re_{1}<Re<Re_{2}$
, modal analysis yields no unstable eigenvalue and thus the flow is linearly stable. However, a transient growth is observed which decays with time. For the current work, stability analysis is performed for a vast range of Reynolds numbers, but no unstable eigenvalues are obtained. Thus, for analysing non-modal behaviour, a Reynolds number higher than the critical energy Reynolds number
![]() $Re_{1}$
is taken into consideration.
$Re_{1}$
is taken into consideration.
2.7.2 Response to external excitations: resolvent
Let us assume that a flow configuration is subjected to an input signal
![]() $V$
, represented as
$V$
, represented as
where
![]() $\unicode[STIX]{x1D714}$
is the frequency of
$\unicode[STIX]{x1D714}$
is the frequency of
![]() $V$
, and
$V$
, and
![]() $\unicode[STIX]{x1D714}$
is assumed to be complex. Then, the relationship among the input signal
$\unicode[STIX]{x1D714}$
is assumed to be complex. Then, the relationship among the input signal
![]() $V$
and the response
$V$
and the response
![]() $U$
is given by the following differential equation:
$U$
is given by the following differential equation:
Solution of the above equation leads to the following expression for
![]() $U$
:
$U$
:
In the above relation,
![]() $\unicode[STIX]{x1D644}$
is the identity matrix, and
$\unicode[STIX]{x1D644}$
is the identity matrix, and
![]() $(\unicode[STIX]{x1D714}\unicode[STIX]{x1D644}-\unicode[STIX]{x1D647})^{-1}$
is referred to as the resolvent;
$(\unicode[STIX]{x1D714}\unicode[STIX]{x1D644}-\unicode[STIX]{x1D647})^{-1}$
is referred to as the resolvent;
![]() $\unicode[STIX]{x1D647}$
has already been defined earlier. For an input signal of frequency
$\unicode[STIX]{x1D647}$
has already been defined earlier. For an input signal of frequency
![]() $\unicode[STIX]{x1D714}$
, the maximum amplification of the external excitation,
$\unicode[STIX]{x1D714}$
, the maximum amplification of the external excitation,
![]() $R(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})$
, is given by the norm of the resolvent operator. Thus,
$R(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})$
, is given by the norm of the resolvent operator. Thus,
where
![]() $\unicode[STIX]{x1D644}$
is the identity matrix, and
$\unicode[STIX]{x1D644}$
is the identity matrix, and
![]() $\unicode[STIX]{x1D714}$
is the eigenvalue of
$\unicode[STIX]{x1D714}$
is the eigenvalue of
![]() $\unicode[STIX]{x1D647}$
, such that
$\unicode[STIX]{x1D647}$
, such that
![]() $\Vert (\unicode[STIX]{x1D714}\unicode[STIX]{x1D644}-\unicode[STIX]{x1D647})^{-1}\Vert \rightarrow \infty$
. In mathematical terms, the resolvent norm is equivalent to amplification of the response under external forcing. In this context, it is essential to discuss the definition of the ‘
$\Vert (\unicode[STIX]{x1D714}\unicode[STIX]{x1D644}-\unicode[STIX]{x1D647})^{-1}\Vert \rightarrow \infty$
. In mathematical terms, the resolvent norm is equivalent to amplification of the response under external forcing. In this context, it is essential to discuss the definition of the ‘
![]() $\unicode[STIX]{x1D700}$
-pseudospectrum’. A basic understanding of the pseudospectrum is critical to non-modal stability analysis. For any
$\unicode[STIX]{x1D700}$
-pseudospectrum’. A basic understanding of the pseudospectrum is critical to non-modal stability analysis. For any
![]() $\unicode[STIX]{x1D700}\geqslant 0$
, the pseudospectrum of
$\unicode[STIX]{x1D700}\geqslant 0$
, the pseudospectrum of
![]() $\unicode[STIX]{x1D647}$
is defined as (Trefethen & Embree Reference Trefethen and Embree2005)
$\unicode[STIX]{x1D647}$
is defined as (Trefethen & Embree Reference Trefethen and Embree2005)
With a variation in
![]() $\unicode[STIX]{x1D700}$
, contours of pseudospectra are obtained. When
$\unicode[STIX]{x1D700}$
, contours of pseudospectra are obtained. When
![]() $\unicode[STIX]{x1D700}=0$
, the pseudospectrum reduces to the spectrum, i.e. the set of eigenvalues obtained from normal mode analysis. Thus, with increasing
$\unicode[STIX]{x1D700}=0$
, the pseudospectrum reduces to the spectrum, i.e. the set of eigenvalues obtained from normal mode analysis. Thus, with increasing
![]() $\unicode[STIX]{x1D700}$
, there is deviation from the traditional eigenvalue analysis. In a non-modal stability analysis problem, there are two major components that need to be explored. One is the response of the system to external excitations, the other being the transient growth of the initial conditions. The resolvent norm describes the maximum possible amplification in response to external excitations. On the other hand, transient growth of the initial conditions is expressed by the growth function
$\unicode[STIX]{x1D700}$
, there is deviation from the traditional eigenvalue analysis. In a non-modal stability analysis problem, there are two major components that need to be explored. One is the response of the system to external excitations, the other being the transient growth of the initial conditions. The resolvent norm describes the maximum possible amplification in response to external excitations. On the other hand, transient growth of the initial conditions is expressed by the growth function
![]() $G(t)$
. In the current study, we have considered only the response to initial conditions, i.e.
$G(t)$
. In the current study, we have considered only the response to initial conditions, i.e.
![]() $G(t)$
. The pseudospectrum has been studied only in the limiting case of Newtonian fluids, in order to validate our simulation methodology with that of the existing literature.
$G(t)$
. The pseudospectrum has been studied only in the limiting case of Newtonian fluids, in order to validate our simulation methodology with that of the existing literature.
2.8 Energy stability
For carrying out energy stability analysis, the perturbation kinetic energy is quantified as
 $$\begin{eqnarray}\displaystyle E & = & \displaystyle \frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{8\unicode[STIX]{x03C0}^{2}}\left[\frac{1}{z_{0}}\int _{0}^{z_{0}}\int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FD}}(u_{r}^{\prime 2}+v_{r}^{\prime 2}+w_{r}^{\prime 2})\,\text{d}y\,\text{d}x\,\text{d}z\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D6FD}_{m}}{8\unicode[STIX]{x03C0}^{2}}\left[\int _{-1}^{0}\int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{m}}\int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FD}_{m}}(u_{mr}^{\prime 2}+v_{mr}^{\prime 2}+w_{mr}^{\prime 2})\,\text{d}y_{m}\,\text{d}x_{m}\,\text{d}z_{m}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E & = & \displaystyle \frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{8\unicode[STIX]{x03C0}^{2}}\left[\frac{1}{z_{0}}\int _{0}^{z_{0}}\int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FD}}(u_{r}^{\prime 2}+v_{r}^{\prime 2}+w_{r}^{\prime 2})\,\text{d}y\,\text{d}x\,\text{d}z\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FC}_{m}\unicode[STIX]{x1D6FD}_{m}}{8\unicode[STIX]{x03C0}^{2}}\left[\int _{-1}^{0}\int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{m}}\int _{0}^{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FD}_{m}}(u_{mr}^{\prime 2}+v_{mr}^{\prime 2}+w_{mr}^{\prime 2})\,\text{d}y_{m}\,\text{d}x_{m}\,\text{d}z_{m}\right],\end{eqnarray}$$
where
![]() $u_{r}^{\prime }=\text{Real}(\hat{u} (z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)})$
,
$u_{r}^{\prime }=\text{Real}(\hat{u} (z,t)\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}x+\unicode[STIX]{x1D6FD}y)})$
,
![]() $u_{mr}^{\prime }=\text{Real}(\hat{u} _{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m})})$
, and so on. No energy growth is possible if
$u_{mr}^{\prime }=\text{Real}(\hat{u} _{m}(z_{m},t_{m})\text{e}^{\text{i}(\unicode[STIX]{x1D6FC}_{m}x_{m}+\unicode[STIX]{x1D6FD}_{m}y_{m})})$
, and so on. No energy growth is possible if
![]() $\text{d}E/\text{d}t<0$
as
$\text{d}E/\text{d}t<0$
as
![]() $t\rightarrow \infty$
(Butler & Farrell Reference Butler and Farrell1992). Thus, the condition for no energy growth may be expressed as
$t\rightarrow \infty$
(Butler & Farrell Reference Butler and Farrell1992). Thus, the condition for no energy growth may be expressed as
with
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D644}_{3}(\boldsymbol{u}) & = & \displaystyle Bn\left[\left\langle \frac{3|\text{D}w|^{2}+(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})|u|^{2}}{|\text{D}U|}\right\rangle \right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left\langle \frac{(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})|\unicode[STIX]{x1D6FC}u-\text{i}\text{D}w|^{2}+|\unicode[STIX]{x1D6FC}\text{D}u-\text{i}(\text{D}^{2}w+\unicode[STIX]{x1D6FD}w)|^{2}}{\unicode[STIX]{x1D6FD}^{2}|\text{D}U|}\right\rangle \right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D644}_{3}(\boldsymbol{u}) & = & \displaystyle Bn\left[\left\langle \frac{3|\text{D}w|^{2}+(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})|u|^{2}}{|\text{D}U|}\right\rangle \right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left\langle \frac{(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})|\unicode[STIX]{x1D6FC}u-\text{i}\text{D}w|^{2}+|\unicode[STIX]{x1D6FC}\text{D}u-\text{i}(\text{D}^{2}w+\unicode[STIX]{x1D6FD}w)|^{2}}{\unicode[STIX]{x1D6FD}^{2}|\text{D}U|}\right\rangle \right].\end{eqnarray}$$
In the above expressions, the following terminology is applicable:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle |u|^{2}=u_{r}^{2}+u_{i}^{2},\quad |\boldsymbol{u}|^{2}=|u|^{2}+\left|\frac{-\unicode[STIX]{x1D6FC}u+\text{i}\text{D}w}{\unicode[STIX]{x1D6FD}}\right|^{2}+|w|^{2},\\ \displaystyle \langle \cdot \rangle =\int _{0}^{z_{0}}(\cdot )\,\text{d}z,\quad \unicode[STIX]{x27E6}\cdot \unicode[STIX]{x27E7}=\int _{-1}^{0}(\cdot )\,\text{d}z_{m},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle |u|^{2}=u_{r}^{2}+u_{i}^{2},\quad |\boldsymbol{u}|^{2}=|u|^{2}+\left|\frac{-\unicode[STIX]{x1D6FC}u+\text{i}\text{D}w}{\unicode[STIX]{x1D6FD}}\right|^{2}+|w|^{2},\\ \displaystyle \langle \cdot \rangle =\int _{0}^{z_{0}}(\cdot )\,\text{d}z,\quad \unicode[STIX]{x27E6}\cdot \unicode[STIX]{x27E7}=\int _{-1}^{0}(\cdot )\,\text{d}z_{m},\end{array}\right\}\end{eqnarray}$$
and
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{i}$
are the real and imaginary components of the perturbation. The corresponding variational problem needs to be solved. The Euler equations for the same may be given as
$u_{i}$
are the real and imaginary components of the perturbation. The corresponding variational problem needs to be solved. The Euler equations for the same may be given as
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\text{D}^{2}-\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2})^{2}w\nonumber\\ \displaystyle & & \displaystyle \qquad +\,Bn\left[-4(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})\text{D}\left(\frac{\text{D}w}{|\text{D}U|}\right)-\text{i}(\text{D}^{2}+\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})\left\{\frac{\text{D}(-\unicode[STIX]{x1D6FC}u+\text{i}\text{D}w)+\text{i}\unicode[STIX]{x1D6FD}^{2}w}{|\text{D}U|}\right\}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{\unicode[STIX]{x1D706}}{2}[(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})u\text{D}U+\text{i}\unicode[STIX]{x1D6FC}\text{D}(w\text{D}U)],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\text{D}^{2}-\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2})^{2}w\nonumber\\ \displaystyle & & \displaystyle \qquad +\,Bn\left[-4(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})\text{D}\left(\frac{\text{D}w}{|\text{D}U|}\right)-\text{i}(\text{D}^{2}+\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})\left\{\frac{\text{D}(-\unicode[STIX]{x1D6FC}u+\text{i}\text{D}w)+\text{i}\unicode[STIX]{x1D6FD}^{2}w}{|\text{D}U|}\right\}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{\unicode[STIX]{x1D706}}{2}[(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})u\text{D}U+\text{i}\unicode[STIX]{x1D6FC}\text{D}(w\text{D}U)],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})(\text{D}^{2}-\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2})u-\text{i}\unicode[STIX]{x1D6FC}\text{D}(\text{D}^{2}-\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2})w-Bn\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left[\frac{(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})^{2}u-\text{i}\unicode[STIX]{x1D6FC}^{3}\text{D}w}{|\text{D}U|}+\unicode[STIX]{x1D6FC}\text{D}\left(\frac{\text{D}(\text{i}\text{D}w-\unicode[STIX]{x1D6FC}u)}{|\text{D}U|}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}^{2}}{2}w\text{D}U,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})(\text{D}^{2}-\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2})u-\text{i}\unicode[STIX]{x1D6FC}\text{D}(\text{D}^{2}-\unicode[STIX]{x1D6FC}^{2}-\unicode[STIX]{x1D6FD}^{2})w-Bn\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\left[\frac{(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FD}^{2})^{2}u-\text{i}\unicode[STIX]{x1D6FC}^{3}\text{D}w}{|\text{D}U|}+\unicode[STIX]{x1D6FC}\text{D}\left(\frac{\text{D}(\text{i}\text{D}w-\unicode[STIX]{x1D6FC}u)}{|\text{D}U|}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D706}\unicode[STIX]{x1D6FD}^{2}}{2}w\text{D}U,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{\unicode[STIX]{x1D6FF}^{2}}\left[\frac{\text{D}_{p}^{2}u_{m}}{\unicode[STIX]{x1D702}_{x}}-\left(\frac{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D6FC}_{m}^{2}}{\unicode[STIX]{x1D702}_{y}}+\frac{\unicode[STIX]{x1D709}_{2}\unicode[STIX]{x1D6FD}_{m}^{2}}{\unicode[STIX]{x1D702}_{z}}\right)(u_{m}+\text{i}\text{D}_{p}w_{m})-\frac{\text{D}_{p}\unicode[STIX]{x1D702}_{x}\text{D}_{p}(u_{m}+\text{i}\text{D}_{p}w_{m})}{\unicode[STIX]{x1D702}_{x}^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\text{i}\unicode[STIX]{x1D706}}{\hat{d}\unicode[STIX]{x1D712}}\left(\frac{l_{4}\unicode[STIX]{x1D702}_{x}(0)}{\displaystyle l_{2}+\frac{\bar{z}_{01}^{2}}{2}}\right)(\text{D}_{p}^{2}-\unicode[STIX]{x1D6FC}_{m}^{2}-\unicode[STIX]{x1D6FD}_{m}^{2})(u_{m}+\text{i}\text{D}_{p}w_{m}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{\unicode[STIX]{x1D6FF}^{2}}\left[\frac{\text{D}_{p}^{2}u_{m}}{\unicode[STIX]{x1D702}_{x}}-\left(\frac{\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D6FC}_{m}^{2}}{\unicode[STIX]{x1D702}_{y}}+\frac{\unicode[STIX]{x1D709}_{2}\unicode[STIX]{x1D6FD}_{m}^{2}}{\unicode[STIX]{x1D702}_{z}}\right)(u_{m}+\text{i}\text{D}_{p}w_{m})-\frac{\text{D}_{p}\unicode[STIX]{x1D702}_{x}\text{D}_{p}(u_{m}+\text{i}\text{D}_{p}w_{m})}{\unicode[STIX]{x1D702}_{x}^{2}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\text{i}\unicode[STIX]{x1D706}}{\hat{d}\unicode[STIX]{x1D712}}\left(\frac{l_{4}\unicode[STIX]{x1D702}_{x}(0)}{\displaystyle l_{2}+\frac{\bar{z}_{01}^{2}}{2}}\right)(\text{D}_{p}^{2}-\unicode[STIX]{x1D6FC}_{m}^{2}-\unicode[STIX]{x1D6FD}_{m}^{2})(u_{m}+\text{i}\text{D}_{p}w_{m}).\end{eqnarray}$$
The above eigenvalue problem in
![]() $\unicode[STIX]{x1D706}$
is solved subject to the following boundary conditions:
$\unicode[STIX]{x1D706}$
is solved subject to the following boundary conditions:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u(z_{0})=0,\quad w(z_{0})=0,\quad \text{D}w(z_{0})=0,\\ \displaystyle \text{D}u(0)=\frac{\unicode[STIX]{x1D6FC}_{BJ}\hat{d}}{\unicode[STIX]{x1D6FF}\sqrt{\unicode[STIX]{x1D702}_{x}(0)}}\left[u(0)-\frac{\hat{d}Re_{m}}{Re}u_{m}(0)\right],\quad Re\,w(0)=\hat{d}Re_{m}w_{m}(0),\quad \text{D}w_{m}(0)=0,\\ u_{m}(-1)=0,\quad w_{m}(-1)=0,\quad \text{D}w_{m}(-1)=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u(z_{0})=0,\quad w(z_{0})=0,\quad \text{D}w(z_{0})=0,\\ \displaystyle \text{D}u(0)=\frac{\unicode[STIX]{x1D6FC}_{BJ}\hat{d}}{\unicode[STIX]{x1D6FF}\sqrt{\unicode[STIX]{x1D702}_{x}(0)}}\left[u(0)-\frac{\hat{d}Re_{m}}{Re}u_{m}(0)\right],\quad Re\,w(0)=\hat{d}Re_{m}w_{m}(0),\quad \text{D}w_{m}(0)=0,\\ u_{m}(-1)=0,\quad w_{m}(-1)=0,\quad \text{D}w_{m}(-1)=0.\end{array}\right\}\end{eqnarray}$$
As already emphasized earlier, the solution gives the conditions for no energy growth. The solution methodology for this eigenvalue problem set is also Chebyshev spectral collocation (presented in § 2.6). The results are discussed subsequently in § 3.4.
3 Results and discussion
3.1 Validation
For the purpose of validation, we compare our findings with two different studies (both modal and non-modal) reported in the literature, in the limiting cases. First, we compare our non-modal results with that obtained for Poiseuille flow of a Newtonian fluid. As discussed in the preceding section, the pseudospectrum for Poiseuille flow of a Newtonian fluid
![]() $(Bn=0)$
is constructed in order to validate our findings with the literature. The same is depicted in figure 2(a,b). Both streamwise
$(Bn=0)$
is constructed in order to validate our findings with the literature. The same is depicted in figure 2(a,b). Both streamwise
![]() $(\unicode[STIX]{x1D6FC}\neq 0,~\unicode[STIX]{x1D6FD}=0)$
as well as spanwise
$(\unicode[STIX]{x1D6FC}\neq 0,~\unicode[STIX]{x1D6FD}=0)$
as well as spanwise
![]() $(\unicode[STIX]{x1D6FC}=0,~\unicode[STIX]{x1D6FD}\neq 0)$
perturbations are considered at
$(\unicode[STIX]{x1D6FC}=0,~\unicode[STIX]{x1D6FD}\neq 0)$
perturbations are considered at
![]() $Re=3000$
. It is found that the response to streamwise perturbation is a spectrum consisting of the A, P and S branches. On the other hand, the spectrum for the spanwise perturbation is a single vertical branch. Our results coincide with those of Reddy & Henningson (Reference Reddy and Henningson1993), thereby validating the current numerical approach. In addition, we have also validated our modal stability results with Poiseuille flow of a Newtonian fluid overlying a porous layer, as reported by Chang et al. (Reference Chang, Chen and Straughan2006). Figure 2(c) shows the neutral stability curve in the case of streamwise perturbation for the set (
$Re=3000$
. It is found that the response to streamwise perturbation is a spectrum consisting of the A, P and S branches. On the other hand, the spectrum for the spanwise perturbation is a single vertical branch. Our results coincide with those of Reddy & Henningson (Reference Reddy and Henningson1993), thereby validating the current numerical approach. In addition, we have also validated our modal stability results with Poiseuille flow of a Newtonian fluid overlying a porous layer, as reported by Chang et al. (Reference Chang, Chen and Straughan2006). Figure 2(c) shows the neutral stability curve in the case of streamwise perturbation for the set (
![]() $Bn=0$
,
$Bn=0$
,
![]() $A_{inh}=0$
,
$A_{inh}=0$
,
![]() $K_{y}=1$
,
$K_{y}=1$
,
![]() $K_{z}=1$
). The neutral stability results reported in the literature by Chang et al. (Reference Chang, Chen and Straughan2006) are also displayed on the same plot (figure 2a in Chang et al.
Reference Chang, Chen and Straughan2006). As evident from the figure, they show a satisfactory match.
$K_{z}=1$
). The neutral stability results reported in the literature by Chang et al. (Reference Chang, Chen and Straughan2006) are also displayed on the same plot (figure 2a in Chang et al.
Reference Chang, Chen and Straughan2006). As evident from the figure, they show a satisfactory match.

Figure 2. Validation with literature. (a,b) Comparison with Reddy & Henningson (Reference Reddy and Henningson1993) for (a) streamwise (
![]() $\unicode[STIX]{x1D6FC}=1,~\unicode[STIX]{x1D6FD}=0$
) and (b) spanwise
$\unicode[STIX]{x1D6FC}=1,~\unicode[STIX]{x1D6FD}=0$
) and (b) spanwise
![]() $(\unicode[STIX]{x1D6FC}=0,~\unicode[STIX]{x1D6FD}=2)$
perturbations. (c) Comparison with Chang et al. (Reference Chang, Chen and Straughan2006) for
$(\unicode[STIX]{x1D6FC}=0,~\unicode[STIX]{x1D6FD}=2)$
perturbations. (c) Comparison with Chang et al. (Reference Chang, Chen and Straughan2006) for
![]() $Bn=0$
. For (a), the boundaries of the
$Bn=0$
. For (a), the boundaries of the
![]() $\unicode[STIX]{x1D700}$
-pseudospectra from outer to inner are
$\unicode[STIX]{x1D700}$
-pseudospectra from outer to inner are
![]() $\unicode[STIX]{x1D700}=10^{-1},~10^{-2},~10^{-3},~10^{-4}$
. For (b), they are
$\unicode[STIX]{x1D700}=10^{-1},~10^{-2},~10^{-3},~10^{-4}$
. For (b), they are
![]() $\unicode[STIX]{x1D700}=10^{-1},~10^{-2}$
. In (a,b), the legend denotes the following: RH-EV, eigenvalues reported by Reddy & Henningson (Reference Reddy and Henningson1993); CS-EV, eigenvalues obtained in the current study; RH-PS, pseudospectra reported by Reddy & Henningson (Reference Reddy and Henningson1993); CS-PS, pseudospectra obtained in the current study.
$\unicode[STIX]{x1D700}=10^{-1},~10^{-2}$
. In (a,b), the legend denotes the following: RH-EV, eigenvalues reported by Reddy & Henningson (Reference Reddy and Henningson1993); CS-EV, eigenvalues obtained in the current study; RH-PS, pseudospectra reported by Reddy & Henningson (Reference Reddy and Henningson1993); CS-PS, pseudospectra obtained in the current study.
3.2 Variation of
 $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
 $\bar{z}_{02}$
$\bar{z}_{02}$
As already discussed in the beginning, the existence of a plug zone is a characteristic feature of yield stress fluids. The thickness of the plug zone can be determined from the location of yield surfaces,
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
. Thus, studying the variations of
$\bar{z}_{02}$
. Thus, studying the variations of
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
with various parameters can provide useful insight into flow characteristics. Figure 3 demonstrates the effect of Bingham number, as well as various porous layer parameters, on
$\bar{z}_{02}$
with various parameters can provide useful insight into flow characteristics. Figure 3 demonstrates the effect of Bingham number, as well as various porous layer parameters, on
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
. Figure 3(a) shows that, although the variations of both
$\bar{z}_{02}$
. Figure 3(a) shows that, although the variations of both
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
are monotonic with
$\bar{z}_{02}$
are monotonic with
![]() $Bn$
, the trends are opposite to each other. The lower yield surface
$Bn$
, the trends are opposite to each other. The lower yield surface
![]() $\bar{z}_{01}$
reduces with
$\bar{z}_{01}$
reduces with
![]() $Bn$
, unlike
$Bn$
, unlike
![]() $\bar{z}_{02}$
, which increases monotonically. Physically, this represents widening of the plug zone with
$\bar{z}_{02}$
, which increases monotonically. Physically, this represents widening of the plug zone with
![]() $Bn$
. The values of
$Bn$
. The values of
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
coincide at
$\bar{z}_{02}$
coincide at
![]() $Bn=0$
, indicating no plug zone (Newtonian fluid). Essentially, as yield stress increases, there is a gradual transition from single shear (Newtonian) to double shear flow with a plug zone in the middle. Figure 3(b,c) reveals that both
$Bn=0$
, indicating no plug zone (Newtonian fluid). Essentially, as yield stress increases, there is a gradual transition from single shear (Newtonian) to double shear flow with a plug zone in the middle. Figure 3(b,c) reveals that both
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
increase with depth ratio
$\bar{z}_{02}$
increase with depth ratio
![]() $\hat{d}$
and slip parameter
$\hat{d}$
and slip parameter
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
. However, there is saturation at higher values of
$\unicode[STIX]{x1D6FC}_{BJ}$
. However, there is saturation at higher values of
![]() $\hat{d}$
and
$\hat{d}$
and
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
. Increase in
$\unicode[STIX]{x1D6FC}_{BJ}$
. Increase in
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
translates to rise in velocity gradient at the fluid–porous interface. This results in higher momentum transfer in the transverse direction, leading to plug behaviour in the upper shear zone and a more pronounced lower shear zone, represented by an upward shift of both the yield surfaces (Sengupta & De Reference Sengupta and De2019). Of course, there cannot be prolonged monotonic rise of the interface velocity gradient, leading to saturation at higher values of
$\unicode[STIX]{x1D6FC}_{BJ}$
translates to rise in velocity gradient at the fluid–porous interface. This results in higher momentum transfer in the transverse direction, leading to plug behaviour in the upper shear zone and a more pronounced lower shear zone, represented by an upward shift of both the yield surfaces (Sengupta & De Reference Sengupta and De2019). Of course, there cannot be prolonged monotonic rise of the interface velocity gradient, leading to saturation at higher values of
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
. As per the Beavers–Joseph condition, depth ratio is also proportional to the interface velocity gradient, thereby exhibiting similar trend as that of
$\unicode[STIX]{x1D6FC}_{BJ}$
. As per the Beavers–Joseph condition, depth ratio is also proportional to the interface velocity gradient, thereby exhibiting similar trend as that of
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
. As shown in figure 3(d), the trend is reverse for
$\unicode[STIX]{x1D6FC}_{BJ}$
. As shown in figure 3(d), the trend is reverse for
![]() $\unicode[STIX]{x1D6FF}$
. Darcy number represents the permeability of the porous layer. As the porous layer becomes more permeable, the porous layer velocity increases. Thus, there is a reduction in the velocity gradient at the fluid–porous interface, resulting in a downward shift of the yield surfaces with
$\unicode[STIX]{x1D6FF}$
. Darcy number represents the permeability of the porous layer. As the porous layer becomes more permeable, the porous layer velocity increases. Thus, there is a reduction in the velocity gradient at the fluid–porous interface, resulting in a downward shift of the yield surfaces with
![]() $\unicode[STIX]{x1D6FF}$
. In figure 3(e), the yield surfaces exhibit an asymmetric variation with inhomogeneity factor
$\unicode[STIX]{x1D6FF}$
. In figure 3(e), the yield surfaces exhibit an asymmetric variation with inhomogeneity factor
![]() $A_{inh}$
with respect to
$A_{inh}$
with respect to
![]() $A_{inh}=0$
, in addition to being non-monotonic. For
$A_{inh}=0$
, in addition to being non-monotonic. For
![]() $A_{inh}>0$
, there is a reduction in the values of
$A_{inh}>0$
, there is a reduction in the values of
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
. Increase in inhomogeneity amounts to increase in overall permeability of the porous medium. Owing to this, the trend of a downward shift in the yield surfaces with
$\bar{z}_{02}$
. Increase in inhomogeneity amounts to increase in overall permeability of the porous medium. Owing to this, the trend of a downward shift in the yield surfaces with
![]() $A_{inh}$
somewhat resembles the behaviour of
$A_{inh}$
somewhat resembles the behaviour of
![]() $\unicode[STIX]{x1D6FF}$
. High negative values of
$\unicode[STIX]{x1D6FF}$
. High negative values of
![]() $A_{inh}$
indicate drastic (exponential) reduction in the permeability, due to which the fluid–porous interface almost behaves as an impermeable wall. Thus, the porous layer no longer affects the location of the yield surfaces, due to which both
$A_{inh}$
indicate drastic (exponential) reduction in the permeability, due to which the fluid–porous interface almost behaves as an impermeable wall. Thus, the porous layer no longer affects the location of the yield surfaces, due to which both
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
become almost invariant at large negative
$\bar{z}_{02}$
become almost invariant at large negative
![]() $A_{inh}$
.
$A_{inh}$
.

Figure 3. Variation of
![]() $\bar{z}_{01}$
and
$\bar{z}_{01}$
and
![]() $\bar{z}_{02}$
with various parameters: (a) Bingham number; (b) depth ratio; (c) slip coefficient; (d) Darcy number; and (e) inhomogeneity factor.
$\bar{z}_{02}$
with various parameters: (a) Bingham number; (b) depth ratio; (c) slip coefficient; (d) Darcy number; and (e) inhomogeneity factor.
3.3 Eigenvalue spectra
The dependence of the normal modes on
![]() $Bn$
is shown in figures 4–6, in addition to the effect of the various parameters of the porous layer. It is observed that increase in
$Bn$
is shown in figures 4–6, in addition to the effect of the various parameters of the porous layer. It is observed that increase in
![]() $Bn$
from 0.01 to 0.1 leads to reduction in
$Bn$
from 0.01 to 0.1 leads to reduction in
![]() $c_{i}$
. However, there is no value of
$c_{i}$
. However, there is no value of
![]() $c_{i}>0$
in each of the cases. Unlike non-porous channel shear flow, there is no vertical S branch here. Instead, there is an oblique branch at approximately
$c_{i}>0$
in each of the cases. Unlike non-porous channel shear flow, there is no vertical S branch here. Instead, there is an oblique branch at approximately
![]() $c_{r}=0.48$
(the oblique line is represented by dotted line in figure 4
a). The complex interplay of the fluid and porous modes makes the branches oblique. Also, two distinct branches can be located on either side of this oblique line, similar to A and P branches of non-porous Newtonian flow. Reduction in the value of
$c_{r}=0.48$
(the oblique line is represented by dotted line in figure 4
a). The complex interplay of the fluid and porous modes makes the branches oblique. Also, two distinct branches can be located on either side of this oblique line, similar to A and P branches of non-porous Newtonian flow. Reduction in the value of
![]() $c_{i}$
is due to the increase in the viscoplasticity of the fluid with
$c_{i}$
is due to the increase in the viscoplasticity of the fluid with
![]() $Bn$
. Thus, the flow becomes increasingly stable with increased
$Bn$
. Thus, the flow becomes increasingly stable with increased
![]() $Bn$
(even though it is never linearly unstable).
$Bn$
(even though it is never linearly unstable).
Figures 4–6 explore the effects of the porous layer parameters on the spectra. The P and S branches are not very sharp, unlike the case of non-porous flow configuration. Although these A and P branches are diffused, there is an interesting observation regarding the imaginary part of the eigenvalues. To explain the same, let us observe the two modes marked 1 and 2 in figure 4(a). Their coordinates in figure 4(a) are as follows: mode 1
![]() $(0.53624,-0.06912)$
and mode 2
$(0.53624,-0.06912)$
and mode 2
![]() $(0.72222,-0.06976)$
. Thus, for
$(0.72222,-0.06976)$
. Thus, for
![]() $\hat{d}=0.1$
, mode 1 would dominate the transition behaviour. But as
$\hat{d}=0.1$
, mode 1 would dominate the transition behaviour. But as
![]() $\hat{d}$
is increased to 1 in figure 4(b), the coordinates for the two modes are: mode 1
$\hat{d}$
is increased to 1 in figure 4(b), the coordinates for the two modes are: mode 1
![]() $(0.53624,-0.11480)$
and mode 2
$(0.53624,-0.11480)$
and mode 2
![]() $(0.72222,-0.11411)$
. So, mode 2 becomes dominant in this case. Thus, with increase in depth ratio from 0.1 to 1, there is a ‘switching’ of the modes carrying the maximum value of
$(0.72222,-0.11411)$
. So, mode 2 becomes dominant in this case. Thus, with increase in depth ratio from 0.1 to 1, there is a ‘switching’ of the modes carrying the maximum value of
![]() $c_{i}$
, from mode 1 to mode 2. Similar behaviour of mode switching is also observed in the case of slip parameter and permeability, depicted in figures 5 and 6. Thus, slip parameter and permeability also induce mode switching in the eigenvalue spectra. However, the mode switching is not explicitly demonstrated in figures 5 and 6, to avoid repetition. The mode switching phenomenon leads to the development of unique behaviour in the neutral curves, as discussed later in § 3.4.
$c_{i}$
, from mode 1 to mode 2. Similar behaviour of mode switching is also observed in the case of slip parameter and permeability, depicted in figures 5 and 6. Thus, slip parameter and permeability also induce mode switching in the eigenvalue spectra. However, the mode switching is not explicitly demonstrated in figures 5 and 6, to avoid repetition. The mode switching phenomenon leads to the development of unique behaviour in the neutral curves, as discussed later in § 3.4.

Figure 4. Eigenvalue spectra studying the effect of depth ratio
![]() $\hat{d}$
: (a)
$\hat{d}$
: (a)
![]() $\hat{d}=0.1$
and (b)
$\hat{d}=0.1$
and (b)
![]() $\hat{d}=1$
. Dotted lines represent the oblique branches.
$\hat{d}=1$
. Dotted lines represent the oblique branches.

Figure 5. Eigenvalue spectra studying the effect of slip parameter
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
: (a)
$\unicode[STIX]{x1D6FC}_{BJ}$
: (a)
![]() $\unicode[STIX]{x1D6FC}_{BJ}=0.1$
and (b)
$\unicode[STIX]{x1D6FC}_{BJ}=0.1$
and (b)
![]() $\unicode[STIX]{x1D6FC}_{BJ}=0.4$
. Dotted lines represent the oblique branches.
$\unicode[STIX]{x1D6FC}_{BJ}=0.4$
. Dotted lines represent the oblique branches.

Figure 6. Eigenvalue spectra studying the effect of Darcy number
![]() $\unicode[STIX]{x1D6FF}$
: (a)
$\unicode[STIX]{x1D6FF}$
: (a)
![]() $\unicode[STIX]{x1D6FF}=0.0001$
and (b)
$\unicode[STIX]{x1D6FF}=0.0001$
and (b)
![]() $\unicode[STIX]{x1D6FF}=0.001$
. Dotted lines represent the oblique branches.
$\unicode[STIX]{x1D6FF}=0.001$
. Dotted lines represent the oblique branches.
3.3.1 Effect of the porous modes
In order to have a better understanding of the effect of viscoplasticity on porous modes, the effect of
![]() $Bn$
on the eigenfunction is studied. As demonstrated in figure 7, for low
$Bn$
on the eigenfunction is studied. As demonstrated in figure 7, for low
![]() $Bn$
(
$Bn$
(
![]() $Bn=0.01$
), there is a flow reversal near the interface. Also, there is significant protrusion of the momentum into the porous layer. With gradual increase in
$Bn=0.01$
), there is a flow reversal near the interface. Also, there is significant protrusion of the momentum into the porous layer. With gradual increase in
![]() $Bn$
to
$Bn$
to
![]() $Bn=0.05$
, the degree of protrusion reduces. The extent of flow reversal is also less. But both these effects of flow reversal and protrusion are exhibited at this stage. However, with further increase in
$Bn=0.05$
, the degree of protrusion reduces. The extent of flow reversal is also less. But both these effects of flow reversal and protrusion are exhibited at this stage. However, with further increase in
![]() $Bn$
to 0.1, there is no more protrusion. Only flow reversal near the interface is observed. For higher
$Bn$
to 0.1, there is no more protrusion. Only flow reversal near the interface is observed. For higher
![]() $Bn$
(
$Bn$
(
![]() $Bn=0.2$
), even the flow reversal ceases to exist. All these effects reveal the effect of the porous layer in deciding the mode of stability. At lower
$Bn=0.2$
), even the flow reversal ceases to exist. All these effects reveal the effect of the porous layer in deciding the mode of stability. At lower
![]() $Bn$
, Newtonian flow characteristics are more dominant. Thus, there is significant perturbation in the porous layer as well, in addition to the fluid layer. This is the cause of the flow reversal and protrusion in figure 7(a,b). At this stage, the effects of the fluid layer and the porous layer on flow transition are comparable. As
$Bn$
, Newtonian flow characteristics are more dominant. Thus, there is significant perturbation in the porous layer as well, in addition to the fluid layer. This is the cause of the flow reversal and protrusion in figure 7(a,b). At this stage, the effects of the fluid layer and the porous layer on flow transition are comparable. As
![]() $Bn$
further increases to 0.1, the protrusion of the perturbation becomes negligible, owing to the onset of yield stress effects. At even higher
$Bn$
further increases to 0.1, the protrusion of the perturbation becomes negligible, owing to the onset of yield stress effects. At even higher
![]() $Bn$
, the viscoplastic effects dominate the porous layer completely. As a result, the porous layer is unable to influence the transition behaviour. The dominant role is now played by the fluid layer alone.
$Bn$
, the viscoplastic effects dominate the porous layer completely. As a result, the porous layer is unable to influence the transition behaviour. The dominant role is now played by the fluid layer alone.

Figure 7. Variation of the eigenfunctions with
![]() $Bn$
: (a)
$Bn$
: (a)
![]() $Bn=0.01$
; (b)
$Bn=0.01$
; (b)
![]() $Bn=0.05$
; (c)
$Bn=0.05$
; (c)
![]() $Bn=0.1$
; and (d)
$Bn=0.1$
; and (d)
![]() $Bn=0.2$
. Here
$Bn=0.2$
. Here
![]() $u_{m}$
is the eigenfunction corresponding to the domain
$u_{m}$
is the eigenfunction corresponding to the domain
![]() $-1\leqslant z_{m}\leqslant 0,$
whereas
$-1\leqslant z_{m}\leqslant 0,$
whereas
![]() $u$
is the eigenfunction corresponding to the domain
$u$
is the eigenfunction corresponding to the domain
![]() $0\leqslant z\leqslant 1.$
Solid lines refer to the real components, while the dashed lines refer to the imaginary components.
$0\leqslant z\leqslant 1.$
Solid lines refer to the real components, while the dashed lines refer to the imaginary components.

Figure 8. Plots of energy Reynolds number versus spanwise wavenumber (
![]() $\unicode[STIX]{x1D6FC}=0$
) to depict the effects of: (a) depth ratio
$\unicode[STIX]{x1D6FC}=0$
) to depict the effects of: (a) depth ratio
![]() $\hat{d}$
; (b) slip parameter
$\hat{d}$
; (b) slip parameter
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
; (c) Darcy number
$\unicode[STIX]{x1D6FC}_{BJ}$
; (c) Darcy number
![]() $\unicode[STIX]{x1D6FF}$
; (d) inhomogeneity factor
$\unicode[STIX]{x1D6FF}$
; (d) inhomogeneity factor
![]() $A_{inh}$
; (e) spanwise anisotropy parameter
$A_{inh}$
; (e) spanwise anisotropy parameter
![]() $\unicode[STIX]{x1D709}_{1}$
; and (f) normal anisotropy parameter
$\unicode[STIX]{x1D709}_{1}$
; and (f) normal anisotropy parameter
![]() $\unicode[STIX]{x1D709}_{2}$
. The numbers in the panels denote the respective values of the parameters. Here
$\unicode[STIX]{x1D709}_{2}$
. The numbers in the panels denote the respective values of the parameters. Here
![]() $Bn=0.2$
in all cases.
$Bn=0.2$
in all cases.
3.4 Non-modal analysis
3.4.1 Neutral stability
As already discussed, in the current study, modal analysis did not yield any unstable eigenvalue for
![]() $Bn>0$
. Thus, non-modal study is attempted in order to investigate the possible sources of perturbation amplifications. First, the conditions for no energy growth are explored, i.e. when
$Bn>0$
. Thus, non-modal study is attempted in order to investigate the possible sources of perturbation amplifications. First, the conditions for no energy growth are explored, i.e. when
![]() $G(t)$
is never greater than unity. Therefore, in figure 8(a–f), the neutral stability curves are constructed for critical energy Reynolds number
$G(t)$
is never greater than unity. Therefore, in figure 8(a–f), the neutral stability curves are constructed for critical energy Reynolds number
![]() $Re_{1}$
versus the spanwise disturbances
$Re_{1}$
versus the spanwise disturbances
![]() $\unicode[STIX]{x1D6FD}$
. Spanwise disturbances are selected, as they have been found to be the source of greater amplification of perturbations (Reddy & Henningson Reference Reddy and Henningson1993; Liu & Liu Reference Liu and Liu2014; Liu et al.
Reference Liu, Ding and Hu2018). It is observed that the curves are multimodal, as opposed to the unimodal curves obtained for flow of viscoplastic fluids in a non-porous environment (Liu et al.
Reference Liu, Ding and Hu2018). The additional modes are imparted by the existence of the porous layer. Figure 8(a) delineates the effect of depth ratio
$\unicode[STIX]{x1D6FD}$
. Spanwise disturbances are selected, as they have been found to be the source of greater amplification of perturbations (Reddy & Henningson Reference Reddy and Henningson1993; Liu & Liu Reference Liu and Liu2014; Liu et al.
Reference Liu, Ding and Hu2018). It is observed that the curves are multimodal, as opposed to the unimodal curves obtained for flow of viscoplastic fluids in a non-porous environment (Liu et al.
Reference Liu, Ding and Hu2018). The additional modes are imparted by the existence of the porous layer. Figure 8(a) delineates the effect of depth ratio
![]() $\hat{d}$
on critical energy Reynolds number. It is found that, with increase in the depth ratio from 0.1 to 3, there is a shift in the dominant mode of critical
$\hat{d}$
on critical energy Reynolds number. It is found that, with increase in the depth ratio from 0.1 to 3, there is a shift in the dominant mode of critical
![]() $Re_{1}$
towards long-wave (i.e. small-
$Re_{1}$
towards long-wave (i.e. small-
![]() $\unicode[STIX]{x1D6FD}$
) perturbations. This exhibition of multimodal behaviour can be traced back to the phenomenon of mode switching, as discussed in § 3.3. Mode switching leads to multiple critical points in the neutral curve, dictated by the relative influence of the fluid layer and porous layer modes. The complex interaction between the porous and fluid modes decides the dominant mode of instability, depending on the value of the porous layer parameters. Figure 8(b) demonstrates the effect of the Beavers–Joseph coefficient
$\unicode[STIX]{x1D6FD}$
) perturbations. This exhibition of multimodal behaviour can be traced back to the phenomenon of mode switching, as discussed in § 3.3. Mode switching leads to multiple critical points in the neutral curve, dictated by the relative influence of the fluid layer and porous layer modes. The complex interaction between the porous and fluid modes decides the dominant mode of instability, depending on the value of the porous layer parameters. Figure 8(b) demonstrates the effect of the Beavers–Joseph coefficient
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
, which is essentially a slip parameter. As slip parameter increases from 0.2 to 0.4, the fluid layer mode dominates the criticality. The only difference is that, at higher values of slip parameter
$\unicode[STIX]{x1D6FC}_{BJ}$
, which is essentially a slip parameter. As slip parameter increases from 0.2 to 0.4, the fluid layer mode dominates the criticality. The only difference is that, at higher values of slip parameter
![]() $(\unicode[STIX]{x1D6FC}_{BJ}>0.2)$
, the shifting of dominant modes is less significant. As far as the effect of the permeability (in terms of Darcy number) is concerned, it depicts an opposite trend. Thus, the long-wave perturbation is dominant with increasing permeability. With higher Darcy number, the critical energy Reynolds number is lowered. This is because with lower permeability there is a greater flow resistance in the porous layer. As a result, more fluid is pushed into the fluid layer, establishing the dominance of the fluid layer mode in deciding the stability of the system. The effect of the inhomogeneity factor
$(\unicode[STIX]{x1D6FC}_{BJ}>0.2)$
, the shifting of dominant modes is less significant. As far as the effect of the permeability (in terms of Darcy number) is concerned, it depicts an opposite trend. Thus, the long-wave perturbation is dominant with increasing permeability. With higher Darcy number, the critical energy Reynolds number is lowered. This is because with lower permeability there is a greater flow resistance in the porous layer. As a result, more fluid is pushed into the fluid layer, establishing the dominance of the fluid layer mode in deciding the stability of the system. The effect of the inhomogeneity factor
![]() $A_{inh}$
is depicted in figure 8(d). Porous layer modes are found to be dominant with
$A_{inh}$
is depicted in figure 8(d). Porous layer modes are found to be dominant with
![]() $A_{inh}$
. This is possibly because an increase in
$A_{inh}$
. This is possibly because an increase in
![]() $A_{inh}$
is found to lower the value of
$A_{inh}$
is found to lower the value of
![]() $\bar{z}_{01}$
significantly for
$\bar{z}_{01}$
significantly for
![]() $A_{inh}>0$
(figure 3), leading to the porous modes becoming more prominent. Also, there is a monotonic lowering of criticality with
$A_{inh}>0$
(figure 3), leading to the porous modes becoming more prominent. Also, there is a monotonic lowering of criticality with
![]() $A_{inh}$
due to the prominence of porous modes. Thus, inhomogeneity acts as a destabilizing agent. The effects of anisotropy factors
$A_{inh}$
due to the prominence of porous modes. Thus, inhomogeneity acts as a destabilizing agent. The effects of anisotropy factors
![]() $\unicode[STIX]{x1D709}_{1}$
and
$\unicode[STIX]{x1D709}_{1}$
and
![]() $\unicode[STIX]{x1D709}_{2}$
on the transition behaviour are depicted in figure 8(e,f). The criticality is found to lower with decrease in the anisotropic parameters. Decrease in anisotropic parameters implies relative increase in the values of
$\unicode[STIX]{x1D709}_{2}$
on the transition behaviour are depicted in figure 8(e,f). The criticality is found to lower with decrease in the anisotropic parameters. Decrease in anisotropic parameters implies relative increase in the values of
![]() $K_{y}$
and
$K_{y}$
and
![]() $K_{z}$
. Thus, the permeabilities enhance in the spanwise and normal directions. This increases the total volume of fluid flowing through the porous layer, for a fixed
$K_{z}$
. Thus, the permeabilities enhance in the spanwise and normal directions. This increases the total volume of fluid flowing through the porous layer, for a fixed
![]() $K_{x}$
. This increased volume of fluid contributes to the momentum enhancement in the porous layer, and thus, is responsible for the lowering of criticality. Thus, the anisotropy parameters generally aid stabilization of flow.
$K_{x}$
. This increased volume of fluid contributes to the momentum enhancement in the porous layer, and thus, is responsible for the lowering of criticality. Thus, the anisotropy parameters generally aid stabilization of flow.
3.4.2 Growth rate
Figure 9 shows the effects of the porous layer parameters on the growth rate curves for a spanwise perturbation. It is observed that, with increase in depth ratio in figure 9(a), the maximum possible growth as well as the time corresponding to maximum growth is reduced. However, beyond
![]() $\hat{d}=$
1, the reduction is not substantial. The slip parameter also depicts a similar tendency in figure 9(b), but the reduction in
$\hat{d}=$
1, the reduction is not substantial. The slip parameter also depicts a similar tendency in figure 9(b), but the reduction in
![]() $G(t)$
is significant even at high slip coefficient, i.e. at high velocity gradient at the fluid–porous interface. As far as permeability is concerned in figure 9(c), increase in Darcy number leads to monotonic increase in the maximum growth, as well as the time of maximum growth. These effects illustrate the relative roles played by each of the porous layer parameters in deciding the non-modal growth. With increase in depth ratio, the fluid layer gradually grows in thickness. Thus, both the porous and the fluid layers simultaneously contribute to intermediate growth. This explains the growth characteristics with
$G(t)$
is significant even at high slip coefficient, i.e. at high velocity gradient at the fluid–porous interface. As far as permeability is concerned in figure 9(c), increase in Darcy number leads to monotonic increase in the maximum growth, as well as the time of maximum growth. These effects illustrate the relative roles played by each of the porous layer parameters in deciding the non-modal growth. With increase in depth ratio, the fluid layer gradually grows in thickness. Thus, both the porous and the fluid layers simultaneously contribute to intermediate growth. This explains the growth characteristics with
![]() $\hat{d}$
. For the slip parameter, increase signifies increased momentum transfer across the interface, thus establishing the dominance of the fluid layer in influencing the criticality. Increase in permeability (characterized by the Darcy number) assists relatively greater flow in the porous layer. Thus, with increase in permeability, the porous layer is able to influence the transient amplifications. Thus, the complex interactions among these parameters decide the short-time growth.
$\hat{d}$
. For the slip parameter, increase signifies increased momentum transfer across the interface, thus establishing the dominance of the fluid layer in influencing the criticality. Increase in permeability (characterized by the Darcy number) assists relatively greater flow in the porous layer. Thus, with increase in permeability, the porous layer is able to influence the transient amplifications. Thus, the complex interactions among these parameters decide the short-time growth.

Figure 9. Growth rate curves depicting the effects of: (a) depth ratio
![]() $\hat{d}$
; (b) slip parameter
$\hat{d}$
; (b) slip parameter
![]() $\unicode[STIX]{x1D6FC}_{BJ}$
; and (c) Darcy number
$\unicode[STIX]{x1D6FC}_{BJ}$
; and (c) Darcy number
![]() $\unicode[STIX]{x1D6FF}$
. The numbers in the panels denote the respective values of the parameters. Here
$\unicode[STIX]{x1D6FF}$
. The numbers in the panels denote the respective values of the parameters. Here
![]() $Re=600$
and
$Re=600$
and
![]() $\unicode[STIX]{x1D6FD}=4$
in all cases.
$\unicode[STIX]{x1D6FD}=4$
in all cases.
In further discussions, we consider oblique perturbations (
![]() $\unicode[STIX]{x1D6FC}\neq 0,~\unicode[STIX]{x1D6FD}\neq 0$
), and the effect of the parameters of the porous layer on the same. Figure 10 describes the effect of viscoplasticity, in terms of contours of maximum growth in the plane of streamwise and spanwise perturbations. At
$\unicode[STIX]{x1D6FC}\neq 0,~\unicode[STIX]{x1D6FD}\neq 0$
), and the effect of the parameters of the porous layer on the same. Figure 10 describes the effect of viscoplasticity, in terms of contours of maximum growth in the plane of streamwise and spanwise perturbations. At
![]() $Bn=0.01$
, the maximum growth is achieved by a spanwise perturbation. As the perturbations become oblique, the maximum growth is reduced. It is observed from figure 10(a) that the disturbance is streamwise at lower values of optimal, whereas it turns into a spanwise disturbance at the highest value of
$Bn=0.01$
, the maximum growth is achieved by a spanwise perturbation. As the perturbations become oblique, the maximum growth is reduced. It is observed from figure 10(a) that the disturbance is streamwise at lower values of optimal, whereas it turns into a spanwise disturbance at the highest value of
![]() $G_{max}$
. This is in conformity with earlier studies highlighting the role of spanwise disturbances in amplifying growth (Liu & Liu Reference Liu and Liu2014; Liu et al.
Reference Liu, Ding and Hu2018). Nouar et al. (Reference Nouar, Kabouya, Dusek and Mamou2007) also constructed contours of
$G_{max}$
. This is in conformity with earlier studies highlighting the role of spanwise disturbances in amplifying growth (Liu & Liu Reference Liu and Liu2014; Liu et al.
Reference Liu, Ding and Hu2018). Nouar et al. (Reference Nouar, Kabouya, Dusek and Mamou2007) also constructed contours of
![]() $G_{max}$
for plane Bingham–Poiseuille flow. Their results are also presented in figure 10(a), for the sake of comparison. It is observed from figure 10(a) that, for a particular combination of
$G_{max}$
for plane Bingham–Poiseuille flow. Their results are also presented in figure 10(a), for the sake of comparison. It is observed from figure 10(a) that, for a particular combination of
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
, the
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
, the
![]() $G_{max}$
values obtained in the current study are higher than those of Nouar et al. (Reference Nouar, Kabouya, Dusek and Mamou2007). This is because of the dominant role played by the porous layer in the present study for low
$G_{max}$
values obtained in the current study are higher than those of Nouar et al. (Reference Nouar, Kabouya, Dusek and Mamou2007). This is because of the dominant role played by the porous layer in the present study for low
![]() $Bn$
, as demonstrated in figure 7. Figure 10(b) depicts the contours of
$Bn$
, as demonstrated in figure 7. Figure 10(b) depicts the contours of
![]() $G_{max}$
for
$G_{max}$
for
![]() $Bn=0.1$
. A decrease in
$Bn=0.1$
. A decrease in
![]() $G_{max}$
with
$G_{max}$
with
![]() $Bn$
is observed, for the same combination of
$Bn$
is observed, for the same combination of
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
. The decrease in maximum growth with increased viscoplasticity is due to the enhanced viscous dissipation. From figure 10(a,b), it is found that the magnitude of optimal growth reduces with
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
. The decrease in maximum growth with increased viscoplasticity is due to the enhanced viscous dissipation. From figure 10(a,b), it is found that the magnitude of optimal growth reduces with
![]() $Bn$
. Thus, although there is asymptotic long-time decay, viscoplasticity plays a stabilizing role in amplifying the short-time growth.
$Bn$
. Thus, although there is asymptotic long-time decay, viscoplasticity plays a stabilizing role in amplifying the short-time growth.

Figure 10. Effect of Bingham number: contours of
![]() $G_{max}$
at (a)
$G_{max}$
at (a)
![]() $Bn=0.02$
and (b)
$Bn=0.02$
and (b)
![]() $Bn=0.1$
. In (a), dashed lines refer to the studies of Nouar et al. (Reference Nouar, Kabouya, Dusek and Mamou2007).
$Bn=0.1$
. In (a), dashed lines refer to the studies of Nouar et al. (Reference Nouar, Kabouya, Dusek and Mamou2007).

Figure 11. Effect of Darcy number: contours of
![]() $G_{max}$
at (a)
$G_{max}$
at (a)
![]() $\unicode[STIX]{x1D6FF}=5\times 10^{-4}$
and (b)
$\unicode[STIX]{x1D6FF}=5\times 10^{-4}$
and (b)
![]() $\unicode[STIX]{x1D6FF}=5\times 10^{-3}$
.
$\unicode[STIX]{x1D6FF}=5\times 10^{-3}$
.
Figures 11–13 depict the effects of Darcy number, depth ratio and slip parameter with regards to the oblique perturbations. In figure 11, with increase in permeability, the optimal perturbation is increased. It increases from 150 to 290 as the permeability increases from
![]() $\unicode[STIX]{x1D6FF}=5\times 10^{-4}$
to
$\unicode[STIX]{x1D6FF}=5\times 10^{-4}$
to
![]() $5\times 10^{-3}$
. This again demonstrates the destabilizing role played by permeability in creating short-time amplifications. The reason for this is the increased momentum in the porous layer with permeability. Also, as the perturbations turn from spanwise to oblique to streamwise, the maximum growth is lowered. However, at higher permeability, the perturbation producing maximum growth is oblique, although the streamwise component is negligible compared to the spanwise component.
$5\times 10^{-3}$
. This again demonstrates the destabilizing role played by permeability in creating short-time amplifications. The reason for this is the increased momentum in the porous layer with permeability. Also, as the perturbations turn from spanwise to oblique to streamwise, the maximum growth is lowered. However, at higher permeability, the perturbation producing maximum growth is oblique, although the streamwise component is negligible compared to the spanwise component.
Figure 12 expresses the effect of depth ratio. It is observed that the maximum growth is reduced with the increase in fluid layer thickness. Thus, as the relative influence of the fluid layer compared to the porous layer is increased in the flow system, there is a reduction in transient amplifications. The fluid modes restrict the growth of amplifications, leading to the reduction in the magnitudes of
![]() $G_{max}$
. At very low depth ratio, the fluid layer has a small thickness, and a large part of the momentum is influenced by the porous layer. This explains the trend of the maximum growth with depth ratio. A similar behaviour is depicted by slip parameter in figure 13. At lower slip coefficient, the maximum growth perturbation is spanwise in nature. However, as the slip coefficient is increased, the perturbation becomes oblique.
$G_{max}$
. At very low depth ratio, the fluid layer has a small thickness, and a large part of the momentum is influenced by the porous layer. This explains the trend of the maximum growth with depth ratio. A similar behaviour is depicted by slip parameter in figure 13. At lower slip coefficient, the maximum growth perturbation is spanwise in nature. However, as the slip coefficient is increased, the perturbation becomes oblique.

Figure 12. Effect of depth ratio: contours of
![]() $G_{max}$
at (a)
$G_{max}$
at (a)
![]() $\hat{d}=0.3$
and (b)
$\hat{d}=0.3$
and (b)
![]() $\hat{d}=3$
.
$\hat{d}=3$
.

Figure 13. Effect of slip parameter: contours of
![]() $G_{max}$
at (a)
$G_{max}$
at (a)
![]() $\unicode[STIX]{x1D6FC}_{BJ}=0.05$
and (b)
$\unicode[STIX]{x1D6FC}_{BJ}=0.05$
and (b)
![]() $\unicode[STIX]{x1D6FC}_{BJ}=0.2$
.
$\unicode[STIX]{x1D6FC}_{BJ}=0.2$
.
3.5 Mechanism of transient growth
The shape of the optimal perturbation is explored in detail in figure 14. Figure 14(a) shows the shape of the optimal perturbation for
![]() $Bn=0.02$
and
$Bn=0.02$
and
![]() $\hat{d}=0.3$
. It is observed that the perturbation is spanwise. Moreover, the optimal perturbations also protrude into the porous layer. This explains the significance of the porous layer in deciding the flow transition characteristics, as also revealed in figure 7. Figure 14(b,c) displays the optimal perturbations for a high value of depth ratio (
$\hat{d}=0.3$
. It is observed that the perturbation is spanwise. Moreover, the optimal perturbations also protrude into the porous layer. This explains the significance of the porous layer in deciding the flow transition characteristics, as also revealed in figure 7. Figure 14(b,c) displays the optimal perturbations for a high value of depth ratio (
![]() $\hat{d}=3$
) for two different Bingham numbers,
$\hat{d}=3$
) for two different Bingham numbers,
![]() $Bn=0.02$
and 0.3. From the plots, it is observed that, at lower
$Bn=0.02$
and 0.3. From the plots, it is observed that, at lower
![]() $Bn$
, the optimal perturbation consists of spanwise streaks. However, it becomes oblique with larger
$Bn$
, the optimal perturbation consists of spanwise streaks. However, it becomes oblique with larger
![]() $Bn$
. This obliqueness of the optimal perturbation is possibly because of the fact that the effective viscosity of the Bingham fluid varies in a nonlinear fashion across the width of the channel. Moreover, at higher depth ratio, there is no protrusion of the optimal perturbation into the porous layer. The perturbations are confined to the fluid layer alone. This explains the relative significance of the fluid and the porous layers at high depth ratio.
$Bn$
. This obliqueness of the optimal perturbation is possibly because of the fact that the effective viscosity of the Bingham fluid varies in a nonlinear fashion across the width of the channel. Moreover, at higher depth ratio, there is no protrusion of the optimal perturbation into the porous layer. The perturbations are confined to the fluid layer alone. This explains the relative significance of the fluid and the porous layers at high depth ratio.
It is worth while to discuss the mechanism of transient growth occurring here. In the case of inviscid shear flow, the streamwise component of the velocity perturbation has been found to grow linearly with time (Ellingsen & Palm Reference Ellingsen and Palm1975). This mechanism is commonly referred to as ‘lift-up’ (Reddy & Henningson Reference Reddy and Henningson1993; Trefethen et al.
Reference Trefethen, Trefethen, Reddy and Driscoll1993). However, for viscous shear flows, viscous dissipation plays an important role. In this case, there is initial linear growth of the streamwise velocity with time due to lift-up, and consequent damping due to viscosity (Butler & Farrell Reference Butler and Farrell1992; Farrell & Ioannou Reference Farrell and Ioannou1993; Trefethen et al.
Reference Trefethen, Trefethen, Reddy and Driscoll1993). The interplay of lift-up and Orr mechanisms contributes to transient growth of the oblique disturbances (Farrell & Ioannou Reference Farrell and Ioannou1993). They both act simultaneously, and the interaction between the two leads to the development of the transient growth. In our analysis, in the case of lower
![]() $Bn$
, the shape of the optimal disturbance is found to be similar to that reported by Reddy & Henningson (Reference Reddy and Henningson1993) in the case of plane Newtonian–Poiseuille flow. It is known that the lift-up mechanism dominates transient growth in the case of such perturbations. However, at higher
$Bn$
, the shape of the optimal disturbance is found to be similar to that reported by Reddy & Henningson (Reference Reddy and Henningson1993) in the case of plane Newtonian–Poiseuille flow. It is known that the lift-up mechanism dominates transient growth in the case of such perturbations. However, at higher
![]() $Bn$
, the perturbation becomes oblique in shape. As discussed, when the perturbation is oblique, both lift-up and Orr mechanisms become comparable. Thus, it may be said that transient growth is dominated by lift-up at lower
$Bn$
, the perturbation becomes oblique in shape. As discussed, when the perturbation is oblique, both lift-up and Orr mechanisms become comparable. Thus, it may be said that transient growth is dominated by lift-up at lower
![]() $Bn$
, while both lift-up and Orr mechanisms contribute to transient response at higher
$Bn$
, while both lift-up and Orr mechanisms contribute to transient response at higher
![]() $Bn$
.
$Bn$
.

Figure 14. Optimal perturbation at
![]() $x=0$
,
$x=0$
,
![]() $Re=600$
for: (a)
$Re=600$
for: (a)
![]() $\hat{d}=0.3$
,
$\hat{d}=0.3$
,
![]() $Bn=0.02$
; (b)
$Bn=0.02$
; (b)
![]() $\hat{d}=3$
,
$\hat{d}=3$
,
![]() $Bn=0.02$
; and (c)
$Bn=0.02$
; and (c)
![]() $\hat{d}=3$
,
$\hat{d}=3$
,
![]() $Bn=0.3$
. Contour levels from outer to inner denote the values of
$Bn=0.3$
. Contour levels from outer to inner denote the values of
![]() $u$
in the following order
$u$
in the following order
![]() $[0.1,0.3,0.5,0.7,0.9]$
.
$[0.1,0.3,0.5,0.7,0.9]$
.
3.6 Description of the fluid–porous interface and the porous layer
As may be observed from the expressions of the velocity profiles, there is a discontinuity in the axial velocity profile at the interface between the fluid and the porous layers. This discontinuity arises because of the Beavers–Joseph boundary condition, which is generally obtained from experimental study, and thus backed by experimental verification. The authors acknowledge the existence of more refined interface conditions that have been proposed in recent times, for example, the ones by Ochoa-Tapia & Whitaker (Reference Ochoa-Tapia and Whitaker1995a ,Reference Ochoa-Tapia and Whitaker b ) and Bars & Worster (Reference Bars and Worster2006). However, each of these interface conditions also carries its own set of limitations. For example, the validity of the Bars–Worster boundary condition is questionable in the case of a sharp fluid–porous interface (Bars & Worster Reference Bars and Worster2006). In addition, some of these conditions, like the boundary condition by Ochoa-Tapia & Whitaker, are generally used together with the Brinkman model. The limitations of the Brinkman model with regard to the current study have already been discussed in § 2.1. Taking all these factors into consideration, the current study uses the Beavers–Joseph condition to model the fluid–porous interface. The same has been adopted by other researchers as well (Chang et al. Reference Chang, Chen and Straughan2006; Deepu et al. Reference Deepu, Anand and Basu2015, Reference Deepu, Kallurkar, Anand and Basu2016; Chang et al. Reference Chang, Chen and Chang2017).
It may be mentioned that the Forchheimer model is not considered in the current analysis. Incorporation of the Forchheimer model ensures that the inertial effects are taken care of (Lyubimova et al.
Reference Lyubimova, Lyubimov, Baydina, Kolchanova and Tsiberkin2016). The Forchheimer model is generally considered when the Reynolds number in the porous layer
![]() $(Re_{m})$
is high. However, in the present study,
$(Re_{m})$
is high. However, in the present study,
![]() $Re_{m}$
in the porous layer is less than
$Re_{m}$
in the porous layer is less than
![]() $Re$
by approximately four orders of magnitude. This can be easily checked from the relation (2.47) between
$Re$
by approximately four orders of magnitude. This can be easily checked from the relation (2.47) between
![]() $Re$
and
$Re$
and
![]() $Re_{m}$
. By taking representative values of the parameters (
$Re_{m}$
. By taking representative values of the parameters (
![]() $Bn=0.2$
,
$Bn=0.2$
,
![]() $\unicode[STIX]{x1D6FD}_{0}=0.016$
,
$\unicode[STIX]{x1D6FD}_{0}=0.016$
,
![]() $\hat{d}=0.3$
,
$\hat{d}=0.3$
,
![]() $\unicode[STIX]{x1D6FC}_{BJ}=0.2$
,
$\unicode[STIX]{x1D6FC}_{BJ}=0.2$
,
![]() $\unicode[STIX]{x1D6FF}=0.001$
,
$\unicode[STIX]{x1D6FF}=0.001$
,
![]() $A_{inh}=2$
),
$A_{inh}=2$
),
![]() $Re/Re_{m}=1.29\times 10^{4}$
. Therefore,
$Re/Re_{m}=1.29\times 10^{4}$
. Therefore,
![]() $Re_{m}$
is significantly small even for a seemingly high
$Re_{m}$
is significantly small even for a seemingly high
![]() $Re$
. Thus, there is negligible inertial effect in the porous layer. This is the primary reason behind neglecting inertial effects by a majority of researchers (Chang et al.
Reference Chang, Chen and Straughan2006; Hill & Straughan Reference Hill and Straughan2008, Reference Hill and Straughan2009; Deepu et al.
Reference Deepu, Anand and Basu2015, Reference Deepu, Kallurkar, Anand and Basu2016; Chang et al.
Reference Chang, Chen and Chang2017).
$Re$
. Thus, there is negligible inertial effect in the porous layer. This is the primary reason behind neglecting inertial effects by a majority of researchers (Chang et al.
Reference Chang, Chen and Straughan2006; Hill & Straughan Reference Hill and Straughan2008, Reference Hill and Straughan2009; Deepu et al.
Reference Deepu, Anand and Basu2015, Reference Deepu, Kallurkar, Anand and Basu2016; Chang et al.
Reference Chang, Chen and Chang2017).
4 Conclusion
The current study provides interesting insights into flow transition for Bingham fluids overlying an anisotropic and inhomogeneous porous layer. A linear stability analysis subject to infinitesimal perturbations shows the existence of fluid layer and porous layer modes, and the interplay between them in deciding the dominant mode of instability. Plots of critical energy Reynolds number versus the wavenumber are constructed to comprehend the conditions for no energy growth. The effects of permeability of the porous medium (in terms of Darcy number), the depth ratio (relative thicknesses of the fluid and porous layers), the slip coefficient and the yield stress (in terms of Bingham number) on criticality are assessed. The effect of anisotropy in the porous medium is found to be stabilizing. On the other hand, the inhomogeneity of the medium lowers the critical point, and is thus destabilizing in nature. The optimal perturbations are found to be spanwise at lower
![]() $Bn$
, while they become oblique at higher
$Bn$
, while they become oblique at higher
![]() $Bn$
. It is observed that the lift-up mechanism dominates the transient growth at lower
$Bn$
. It is observed that the lift-up mechanism dominates the transient growth at lower
![]() $Bn$
, while at higher
$Bn$
, while at higher
![]() $Bn$
, both lift-up and Orr mechanisms contribute to transient amplifications. It is envisaged that the present analysis would help in having a fundamental understanding of flow stability involving viscoplastic fluids in a porous channel configuration. In addition, it would also consequently lead to better designing of flow equipment involving viscoplastic fluid flow.
$Bn$
, both lift-up and Orr mechanisms contribute to transient amplifications. It is envisaged that the present analysis would help in having a fundamental understanding of flow stability involving viscoplastic fluids in a porous channel configuration. In addition, it would also consequently lead to better designing of flow equipment involving viscoplastic fluid flow.