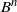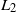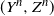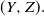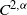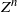1. Introduction
Let ![]() $(\Omega, {\mathcal{F}}, {\mathbb{P}})$ be a complete probability space carrying the standard Brownian motion
$(\Omega, {\mathcal{F}}, {\mathbb{P}})$ be a complete probability space carrying the standard Brownian motion ![]() $B= (B_t)_{t \ge 0}$ and assume that
$B= (B_t)_{t \ge 0}$ and assume that ![]() $({\mathcal{F}}_t)_{t\ge 0}$ is the augmented natural filtration. Let (Y, Z) be the solution of the forward-backward stochastic differential equation (FBSDE)
$({\mathcal{F}}_t)_{t\ge 0}$ is the augmented natural filtration. Let (Y, Z) be the solution of the forward-backward stochastic differential equation (FBSDE)
 \begin{align}X_s&= x + \int_0^s b(r,X_r) dr + \int_0^s \sigma(r,X_r) dB_r,\notag \\[3pt] Y_s&= g( X_T) + \int_s^T f(r,X_r,Y_r,Z_r)dr - \int_s^T Z_r dB_r, \quad \quad 0 \leq s \leq T.\end{align}
\begin{align}X_s&= x + \int_0^s b(r,X_r) dr + \int_0^s \sigma(r,X_r) dB_r,\notag \\[3pt] Y_s&= g( X_T) + \int_s^T f(r,X_r,Y_r,Z_r)dr - \int_s^T Z_r dB_r, \quad \quad 0 \leq s \leq T.\end{align}Let ![]() $(Y^n,Z^n)$ be the solution of the FBSDE if the Brownian motion B is replaced by a scaled random walk
$(Y^n,Z^n)$ be the solution of the FBSDE if the Brownian motion B is replaced by a scaled random walk ![]() $B^n$ given by
$B^n$ given by
 \begin{eqnarray} B^n_{t} =\sqrt{h} \sum_{i=1}^{[t/h] }\varepsilon_i, \quad \quad 0 \leq t \leq T, \end{eqnarray}
\begin{eqnarray} B^n_{t} =\sqrt{h} \sum_{i=1}^{[t/h] }\varepsilon_i, \quad \quad 0 \leq t \leq T, \end{eqnarray}where ![]() $h= \tfrac{T}{n}$ and
$h= \tfrac{T}{n}$ and ![]() $(\varepsilon_i)_{i=1,2, \dots}$ is a sequence of independent and identically distributed (i.i.d.) Rademacher random variables. Then
$(\varepsilon_i)_{i=1,2, \dots}$ is a sequence of independent and identically distributed (i.i.d.) Rademacher random variables. Then ![]() $(Y^n,Z^n)$ solves the discretized FBSDE
$(Y^n,Z^n)$ solves the discretized FBSDE
 \begin{align}X^n_s &= x + \int_{(0,s]} b(r,X^n_{r-}) d[B^n]_r + \int_{(0,s]} \sigma(r,X^n_{r-}) dB^n_r, \notag \\[3pt] Y^n_s &= g(X^n_T) + \int_{(s,T]} f(r,X^n_{r-}Y^n_{r-},Z^n_{r-})d[B^n]_r - \int_{(s,T]} Z^n _{r-} dB^n_r, \quad 0 \le s \leq T.\end{align}
\begin{align}X^n_s &= x + \int_{(0,s]} b(r,X^n_{r-}) d[B^n]_r + \int_{(0,s]} \sigma(r,X^n_{r-}) dB^n_r, \notag \\[3pt] Y^n_s &= g(X^n_T) + \int_{(s,T]} f(r,X^n_{r-}Y^n_{r-},Z^n_{r-})d[B^n]_r - \int_{(s,T]} Z^n _{r-} dB^n_r, \quad 0 \le s \leq T.\end{align} Many authors have investigated the approximation of backward stochastic differential equations (BSDEs) using random walks, analytically as well as numerically (see, for example, [Reference Briand, Delyon and Mémin7], [Reference Jańczak-Borkowska26, [Reference Ma, Protter, San Martín and Torres29], [Reference Martínez, San Martín and Torres31], [Reference Mémin, Peng and Xu32], [Reference Peng and Xu33], [Reference Cheridito and Stadje16]). In 2001, Briand et al. [Reference Briand, Delyon and Mémin7] showed weak convergence of ![]() $(Y^n,Z^n)$ to (Y, Z) for a Lipschitz continuous generator f and a terminal condition in
$(Y^n,Z^n)$ to (Y, Z) for a Lipschitz continuous generator f and a terminal condition in ![]() $L_2.$ The rate of convergence of this method remained an open problem. Bouchard and Touzi in [Reference Bouchard and Touzi6] and Zhang in [Reference Zhang42] proposed instead of random walks an approach based on the dynamic programming equation, for which they established a rate of convergence. But this approach involves conditional expectations. Various methods to approximate these conditional expectations have been developed ([Reference Gobet, Lemor and Warin23], [Reference Crisan, Manolarakis and Touzi17], [Reference Chassagneux and Garcia Trillos12]). Also, forward methods have been introduced to approximate (1): a branching diffusion method ([Reference Henry-Labordère, Tan and Touzi24]), a multilevel Picard approximation ([Reference Weinan, Hutzenthaler, Jentzen and Kruse39]), and Wiener chaos expansion ([Reference Briand and Labart8]). Many extensions of (1) have been considered, among them schemes for reflected BSDEs ([Reference Bally and Pagès3], [Reference Chassagneux and Richou14]), high order schemes ([Reference Chassagneux9], [Reference Chassagneux and Crisan10]), fully-coupled BSDEs ([Reference Delarue and Menozzi18], [Reference Bender and Zhang5]), quadratic BSDEs ([Reference Chassagneux and Richou13]), BSDEs with jumps ([Reference Geiss and Labart21]), and McKean–Vlasov BSDEs ([Reference Alanko1], [Reference Chaudru de Raynal and Garcia Trillos15], [Reference Chassagneux, Crisan and Delarue11]).
$L_2.$ The rate of convergence of this method remained an open problem. Bouchard and Touzi in [Reference Bouchard and Touzi6] and Zhang in [Reference Zhang42] proposed instead of random walks an approach based on the dynamic programming equation, for which they established a rate of convergence. But this approach involves conditional expectations. Various methods to approximate these conditional expectations have been developed ([Reference Gobet, Lemor and Warin23], [Reference Crisan, Manolarakis and Touzi17], [Reference Chassagneux and Garcia Trillos12]). Also, forward methods have been introduced to approximate (1): a branching diffusion method ([Reference Henry-Labordère, Tan and Touzi24]), a multilevel Picard approximation ([Reference Weinan, Hutzenthaler, Jentzen and Kruse39]), and Wiener chaos expansion ([Reference Briand and Labart8]). Many extensions of (1) have been considered, among them schemes for reflected BSDEs ([Reference Bally and Pagès3], [Reference Chassagneux and Richou14]), high order schemes ([Reference Chassagneux9], [Reference Chassagneux and Crisan10]), fully-coupled BSDEs ([Reference Delarue and Menozzi18], [Reference Bender and Zhang5]), quadratic BSDEs ([Reference Chassagneux and Richou13]), BSDEs with jumps ([Reference Geiss and Labart21]), and McKean–Vlasov BSDEs ([Reference Alanko1], [Reference Chaudru de Raynal and Garcia Trillos15], [Reference Chassagneux, Crisan and Delarue11]).
The aim of this paper is to study the rate of the ![]() $L_2$-approximation of
$L_2$-approximation of ![]() $(Y^n_t,Z^n_t)$ to
$(Y^n_t,Z^n_t)$ to ![]() $(Y_t,Z_t)$ when X satisfies (1). For this, we generate the random walk
$(Y_t,Z_t)$ when X satisfies (1). For this, we generate the random walk ![]() $B^n$ by Skorokhod embedding from the Brownian motion B. In this case the
$B^n$ by Skorokhod embedding from the Brownian motion B. In this case the ![]() $L_p$-convergence of
$L_p$-convergence of ![]() $B^n$ to B is of order
$B^n$ to B is of order ![]() $h^{\frac{1}{4}}$ for any
$h^{\frac{1}{4}}$ for any ![]() $p>0.$ The special case
$p>0.$ The special case ![]() $X=B$ has already been studied in [Reference Geiss, Labart and Luoto22], assuming a locally
$X=B$ has already been studied in [Reference Geiss, Labart and Luoto22], assuming a locally ![]() $\alpha$-Hölder continuous terminal function g and a Lipschitz continuous generator. An estimate for the rate of convergence was obtained which is of order
$\alpha$-Hölder continuous terminal function g and a Lipschitz continuous generator. An estimate for the rate of convergence was obtained which is of order ![]() $h^{\frac{\alpha}{4}}$ for the
$h^{\frac{\alpha}{4}}$ for the ![]() $L_2$-norm of
$L_2$-norm of ![]() $Y^n_t-Y_t,$ and of order
$Y^n_t-Y_t,$ and of order ![]() $\tfrac{h^{\frac{\alpha}{4}}}{\sqrt{T-t}}$ for the
$\tfrac{h^{\frac{\alpha}{4}}}{\sqrt{T-t}}$ for the ![]() $L_2$-norm of
$L_2$-norm of ![]() $Z^n_t-Z_t.$
$Z^n_t-Z_t.$
In the present paper, where we assume that X is a solution of the stochastic differential equation (SDE) in (1), rather strong conditions on the smoothness and boundedness of f and g and also of b and ![]() $\sigma$ are needed. In Theorem 3.1, the main result of the paper, we show that the convergence rate for
$\sigma$ are needed. In Theorem 3.1, the main result of the paper, we show that the convergence rate for ![]() $(Y^n_t,Z^n_t)$ to
$(Y^n_t,Z^n_t)$ to ![]() $(Y_t,Z_t)$ in
$(Y_t,Z_t)$ in ![]() $L_2$ is of order
$L_2$ is of order ![]() $h^{\frac{1}{4}\wedge \frac{\alpha}{2}}$ provided that gʹʹ is locally
$h^{\frac{1}{4}\wedge \frac{\alpha}{2}}$ provided that gʹʹ is locally ![]() $\alpha$-Hölder continuous. To the best of our knowledge, these are the first cases in which a convergence rate for the approximation of FBSDEs using random walks has been obtained.
$\alpha$-Hölder continuous. To the best of our knowledge, these are the first cases in which a convergence rate for the approximation of FBSDEs using random walks has been obtained.
Remark 1.1. For the diffusion setting—in contrast to the case ![]() $X=B$—we can derive the convergence rate for
$X=B$—we can derive the convergence rate for ![]() $(Y^n_t,Z^n_t)$ to
$(Y^n_t,Z^n_t)$ to ![]() $(Y_t,Z_t)$ in
$(Y_t,Z_t)$ in ![]() $L_2$ only under strong smoothness conditions on the coefficients, which include also that gʹʹ is locally
$L_2$ only under strong smoothness conditions on the coefficients, which include also that gʹʹ is locally ![]() $\alpha$-Hölder continuous (see Assumption 2.3 below). These requirements appear to be necessary. This becomes visible in Subsection 2.2.2 where we introduce a discretized Malliavin weight to obtain a representation
$\alpha$-Hölder continuous (see Assumption 2.3 below). These requirements appear to be necessary. This becomes visible in Subsection 2.2.2 where we introduce a discretized Malliavin weight to obtain a representation ![]() $\hat Z^n$ for
$\hat Z^n$ for ![]() $Z^n.$ While it holds that
$Z^n.$ While it holds that ![]() $\hat Z^n =Z^n$ when
$\hat Z^n =Z^n$ when ![]() $X=B,$ in our case
$X=B,$ in our case ![]() $\hat Z^n$ does not coincide with
$\hat Z^n$ does not coincide with ![]() $Z^n.$ However, one can show that the difference
$Z^n.$ However, one can show that the difference ![]() $\hat Z^n_t -Z^n_t$ converges to 0 in
$\hat Z^n_t -Z^n_t$ converges to 0 in ![]() $L_2$ as
$L_2$ as ![]() $n \to \infty$ using a Hölder continuity property (see (63) in Remark 4.1) for the space derivative of the generator in (3). For this Hölder continuity property to hold one needs enough smoothness in space from the solution
$n \to \infty$ using a Hölder continuity property (see (63) in Remark 4.1) for the space derivative of the generator in (3). For this Hölder continuity property to hold one needs enough smoothness in space from the solution ![]() $u^n$ to the finite difference equation associated to the discretized FBSDE (3). Provided that Assumption 2.3 holds, we show the smoothness properties for
$u^n$ to the finite difference equation associated to the discretized FBSDE (3). Provided that Assumption 2.3 holds, we show the smoothness properties for ![]() $u^n$ in Proposition 4.2, applying methods known for Lévy driven BSDEs.
$u^n$ in Proposition 4.2, applying methods known for Lévy driven BSDEs.
The paper is organized as follows. Section 2 contains the setting, the main assumptions, and the approximative representation ![]() $\hat{Z}^n$ of
$\hat{Z}^n$ of ![]() $Z^n.$ Our main results about the approximation rate for the case of no generator (i.e.
$Z^n.$ Our main results about the approximation rate for the case of no generator (i.e. ![]() $f=0$) and for the general case are in Section 3. One can see that in contrast to what is known for time discretization schemes, for random walk schemes the Lipschitz generator seems to cause more difficulties than the terminal condition: while in the case
$f=0$) and for the general case are in Section 3. One can see that in contrast to what is known for time discretization schemes, for random walk schemes the Lipschitz generator seems to cause more difficulties than the terminal condition: while in the case ![]() $f=0$ we need that gʹ is locally
$f=0$ we need that gʹ is locally ![]() $\alpha$-Hölder continuous, in the case
$\alpha$-Hölder continuous, in the case ![]() $f\neq0$ this property is required for
$f\neq0$ this property is required for ![]() $g^{\prime\prime}.$ In Section 4 we recall some needed facts about Malliavin weights, the regularity of solutions to BSDEs, and properties of the associated partial differential equations (PDEs). Finally, we sketch how to prove growth and smoothness properties of solutions to the finite difference equation associated to the discretized FBSDE. Section 5 contains technical results which mainly arise from the fact that the construction of the random walk by Skorokhod embedding forces us to compare our processes on different ‘timelines’, one coming from the stopping times of the Skorokhod embedding, the other from the equidistant deterministic times due to the quadratic variation process
$g^{\prime\prime}.$ In Section 4 we recall some needed facts about Malliavin weights, the regularity of solutions to BSDEs, and properties of the associated partial differential equations (PDEs). Finally, we sketch how to prove growth and smoothness properties of solutions to the finite difference equation associated to the discretized FBSDE. Section 5 contains technical results which mainly arise from the fact that the construction of the random walk by Skorokhod embedding forces us to compare our processes on different ‘timelines’, one coming from the stopping times of the Skorokhod embedding, the other from the equidistant deterministic times due to the quadratic variation process ![]() $[B^n].$
$[B^n].$
2. Preliminaries
2.1. The SDE and its approximation scheme
We introduce
and its discretized counterpart
 \begin{align} X^n_{t_k} = x + h\sum_{j=1}^k b(t_j,X^n_{t_{j-1}}) + \sqrt{h} \sum_{j=1}^k \sigma(t_j,X^n_{t_{j-1}}) {\varepsilon}_j, \quad \quad t_j\coloneqq j\tfrac{T}{n}, \,\, j=0,\ldots,n,\end{align}
\begin{align} X^n_{t_k} = x + h\sum_{j=1}^k b(t_j,X^n_{t_{j-1}}) + \sqrt{h} \sum_{j=1}^k \sigma(t_j,X^n_{t_{j-1}}) {\varepsilon}_j, \quad \quad t_j\coloneqq j\tfrac{T}{n}, \,\, j=0,\ldots,n,\end{align}where ![]() $(\varepsilon_i)_{i=1,2, \dots}$ is a sequence of i.i.d. Rademacher random variables. Letting
$(\varepsilon_i)_{i=1,2, \dots}$ is a sequence of i.i.d. Rademacher random variables. Letting
it follows that the associated discrete-time random walk ![]() $(B^n_{t_k})_{k=0}^n$ is
$(B^n_{t_k})_{k=0}^n$ is ![]() $(\mathcal{G}_k)_{k=0}^n$-adapted. Recall (2) and
$(\mathcal{G}_k)_{k=0}^n$-adapted. Recall (2) and ![]() $h= \tfrac{T}{n}.$ If we extend the sequence
$h= \tfrac{T}{n}.$ If we extend the sequence ![]() $(X^n_{t_k})_{k\ge0}$ to a process in continuous time by defining
$(X^n_{t_k})_{k\ge0}$ to a process in continuous time by defining ![]() $X^n_t \coloneqq X^n_{t_k} $ for
$X^n_t \coloneqq X^n_{t_k} $ for ![]() $t \in [t_k, t_{k+1}),$ it is the solution of the forward SDE (3).
$t \in [t_k, t_{k+1}),$ it is the solution of the forward SDE (3).
We formulate our first assumptions. Assumption 2.1(ii) will not be used explicitly for our estimates, but it is required for Theorem 4.1 below.
(i)
 $b, \sigma \in C_b^{0,2}([0,T]\times {\mathbb{R}}),$ in the sense that the derivatives of order
$b, \sigma \in C_b^{0,2}([0,T]\times {\mathbb{R}}),$ in the sense that the derivatives of order  $k=0,1,2$ with respect to the space variable are continuous and bounded on
$k=0,1,2$ with respect to the space variable are continuous and bounded on  $[0,T]\times {\mathbb{R}}$.
$[0,T]\times {\mathbb{R}}$.(ii) The first and second derivatives of b and
 $\sigma$ with respect to the space variable are assumed to be
$\sigma$ with respect to the space variable are assumed to be  $\gamma$-Hölder continuous (for some
$\gamma$-Hölder continuous (for some  $\gamma \in (0,1],$ with respect to the parabolic metric
$\gamma \in (0,1],$ with respect to the parabolic metric  $d((t,x),(\bar t, \bar x))=(|t- \bar t| + |x- \bar x|^2)^{\frac{1}{2}})$ on all compact subsets of
$d((t,x),(\bar t, \bar x))=(|t- \bar t| + |x- \bar x|^2)^{\frac{1}{2}})$ on all compact subsets of  $[0, T ] \times {\mathbb{R}}$.
$[0, T ] \times {\mathbb{R}}$.(iii)
 $b, \sigma$ are
$b, \sigma$ are  ${\frac{1}{2}}$-Hölder continuous in time, uniformly in space.
${\frac{1}{2}}$-Hölder continuous in time, uniformly in space.(iv)
 $\sigma(t,x) \ge \delta >0$ for all (t, x).
$\sigma(t,x) \ge \delta >0$ for all (t, x).
(i) g is locally Hölder continuous with order
 $\alpha \in (0,1]$ and polynomially bounded in the following sense: there exist
$\alpha \in (0,1]$ and polynomially bounded in the following sense: there exist  $p_0 \ge 0, C_g>0$ such that
(6)
$p_0 \ge 0, C_g>0$ such that
(6) \begin{align} \forall (x, \bar x) \in {\mathbb{R}}^2, \quad |g(x)-g( \bar x)|\le C_g(1+|x|^{p_0}+ | \bar x|^{p_0})|x- \bar x|^{\alpha}.\end{align}
\begin{align} \forall (x, \bar x) \in {\mathbb{R}}^2, \quad |g(x)-g( \bar x)|\le C_g(1+|x|^{p_0}+ | \bar x|^{p_0})|x- \bar x|^{\alpha}.\end{align}(ii) The function
 $(t,x,y,z) \mapsto f (t,x,y,z)$ on
$(t,x,y,z) \mapsto f (t,x,y,z)$ on  $[0,T] \times {\mathbb{R}}^3$ satisfies
(7)
$[0,T] \times {\mathbb{R}}^3$ satisfies
(7) \begin{eqnarray} |f(t,x,y,z) - f(\bar t, \bar x, \bar y, \bar z)| \le L_f\Big(\sqrt{t- \bar t} + |x- \bar x| + |y- \bar y|+|z- \bar z|\Big). \end{eqnarray}
\begin{eqnarray} |f(t,x,y,z) - f(\bar t, \bar x, \bar y, \bar z)| \le L_f\Big(\sqrt{t- \bar t} + |x- \bar x| + |y- \bar y|+|z- \bar z|\Big). \end{eqnarray}
Notice that (6) implies
for some ![]() $K>0.$ From the continuity of f we conclude that
$K>0.$ From the continuity of f we conclude that
Notation:
•
 $\|\cdot\|_p\coloneqq \|\cdot\|_{L_p({\mathbb{P}})}$ for
$\|\cdot\|_p\coloneqq \|\cdot\|_{L_p({\mathbb{P}})}$ for  $p\ge 1$. For
$p\ge 1$. For  $p=2$ we write simply
$p=2$ we write simply  $\|\cdot\|$.
$\|\cdot\|$.• If a is a function, C(a) represents a generic constant which depends on a and possibly also on its derivatives.
•
 ${\mathbb{E}}_{0,x}\coloneqq {\mathbb{E}}(\cdot|X_0=x)$.
${\mathbb{E}}_{0,x}\coloneqq {\mathbb{E}}(\cdot|X_0=x)$.• Let
 $\phi$ be a
$\phi$ be a  $C^{0,1}([0,T]\times {\mathbb{R}})$ function. Then
$C^{0,1}([0,T]\times {\mathbb{R}})$ function. Then  $\phi_x$ denotes
$\phi_x$ denotes  $\partial_x \phi$, the partial derivative of
$\partial_x \phi$, the partial derivative of  $\phi$ with respect to x.
$\phi$ with respect to x.
2.2. The FBSDE and its approximation scheme
Recall the FBSDE (1) and its approximation (3). The backward equation in (3) can equivalently be written in the form
 \begin{align}Y^n_{t_k} &= g(X^n_T) + h\sum_{m=k}^{n-1} f(t_{m+1},X^n_{t_m},Y^n_{t_m},Z^n_{t_m}) - \sqrt{h}\sum_{m=k}^{n-1}Z^n_{t_m} {\varepsilon}_{m+1}, \quad 0 \leq k \leq n,\end{align}
\begin{align}Y^n_{t_k} &= g(X^n_T) + h\sum_{m=k}^{n-1} f(t_{m+1},X^n_{t_m},Y^n_{t_m},Z^n_{t_m}) - \sqrt{h}\sum_{m=k}^{n-1}Z^n_{t_m} {\varepsilon}_{m+1}, \quad 0 \leq k \leq n,\end{align}if one puts ![]() $X^n_r\coloneqq X^n_{t_m}$,
$X^n_r\coloneqq X^n_{t_m}$, ![]() $Y^n_r\coloneqq Y^n_{t_m}$, and
$Y^n_r\coloneqq Y^n_{t_m}$, and ![]() $Z_r^n \coloneqq {Z}_{t_m}^n$ for
$Z_r^n \coloneqq {Z}_{t_m}^n$ for ![]() $r \in [t_m, t_{m+1})$.
$r \in [t_m, t_{m+1})$.
Remark 2.1. Equations (3) and (9) do not contain any martingale orthogonal to the random walk ![]() $B^n$, since we are in a special case where the orthogonal martingale is zero (see [Reference Briand, Delyon and Mémin7, p. 3] or [Reference Privault34, Proposition 1.7.5]). Indeed, for the symmetric simple random walk
$B^n$, since we are in a special case where the orthogonal martingale is zero (see [Reference Briand, Delyon and Mémin7, p. 3] or [Reference Privault34, Proposition 1.7.5]). Indeed, for the symmetric simple random walk ![]() $B^n$ the predictable representation property holds; i.e. for any
$B^n$ the predictable representation property holds; i.e. for any ![]() $\mathcal{G}_n$-measurable (see (5)) random variable
$\mathcal{G}_n$-measurable (see (5)) random variable ![]() $\xi= F(\varepsilon_1, \dots, \varepsilon_n)$ there exists a representation
$\xi= F(\varepsilon_1, \dots, \varepsilon_n)$ there exists a representation
where ![]() $c \in {\mathbb{R}}$ and
$c \in {\mathbb{R}}$ and ![]() $h_m$ is
$h_m$ is ![]() $\mathcal{G}_{m-1}$-measurable for
$\mathcal{G}_{m-1}$-measurable for ![]() $m=1,\ldots,n$. To see this, consider
$m=1,\ldots,n$. To see this, consider
Put ![]() $c= {\mathbb{E}} [F(\varepsilon_1, \ldots, \varepsilon_n)].$ Our aim is to determine a
$c= {\mathbb{E}} [F(\varepsilon_1, \ldots, \varepsilon_n)].$ Our aim is to determine a ![]() $\mathcal{G}_{m-1}$-measurable
$\mathcal{G}_{m-1}$-measurable ![]() $h_m$ such that
$h_m$ such that
We define
By the tower property it holds that
 \begin{align*}&F_m(\varepsilon_1, \ldots, \varepsilon_m) - F_{m-1}(\varepsilon_1, \ldots, \varepsilon_{m-1}) \\[2pt] &\quad= F_m(\varepsilon_1,\ldots, \varepsilon_m) - {\mathbb{E}}[F_m(\varepsilon_1, \ldots, \varepsilon_m)| \mathcal{G}_{m-1}] \\[2pt] &\quad= F_m(\varepsilon_1,\ldots, \varepsilon_m) -\frac{F_m(\varepsilon_1,\ldots, \varepsilon_{m-1},1) +F_m(\varepsilon_1,\ldots, \varepsilon_{m-1},-1) }{2} \\[2pt] &\quad=\frac{F_m(\varepsilon_1,\ldots, \varepsilon_{m-1},1) -F_m(\varepsilon_1,\ldots, \varepsilon_{m-1},-1) }{2} \varepsilon_m;\end{align*}
\begin{align*}&F_m(\varepsilon_1, \ldots, \varepsilon_m) - F_{m-1}(\varepsilon_1, \ldots, \varepsilon_{m-1}) \\[2pt] &\quad= F_m(\varepsilon_1,\ldots, \varepsilon_m) - {\mathbb{E}}[F_m(\varepsilon_1, \ldots, \varepsilon_m)| \mathcal{G}_{m-1}] \\[2pt] &\quad= F_m(\varepsilon_1,\ldots, \varepsilon_m) -\frac{F_m(\varepsilon_1,\ldots, \varepsilon_{m-1},1) +F_m(\varepsilon_1,\ldots, \varepsilon_{m-1},-1) }{2} \\[2pt] &\quad=\frac{F_m(\varepsilon_1,\ldots, \varepsilon_{m-1},1) -F_m(\varepsilon_1,\ldots, \varepsilon_{m-1},-1) }{2} \varepsilon_m;\end{align*}hence
One can derive an equation for ![]() $Z^n = (Z^n_{t_k})_{k=0}^{n-1}$ if one multiplies (9) by
$Z^n = (Z^n_{t_k})_{k=0}^{n-1}$ if one multiplies (9) by ![]() ${\varepsilon}_{k+1}$ and takes the conditional expectation with respect to
${\varepsilon}_{k+1}$ and takes the conditional expectation with respect to ![]() ${\mathcal{G}}_k$, so that
${\mathcal{G}}_k$, so that
 \begin{eqnarray} Z^n_{t_k} &=& \frac{{\mathbb{E}}^{{\mathcal{G}}}_{k}\big(g(X^n_T) {\varepsilon}_{k+1}\big)}{\sqrt{h}} +{\mathbb{E}}^{{\mathcal{G}}}_{k}\Bigg( \sqrt{ h}\sum_{m=k+1}^{n-1}f( t_{m+1},X^n_{t_m}, Y^n_{t_m} , Z^n_{t_m}) {\varepsilon}_{k+1}\Bigg ), \, 0\le k \le n-1, \end{eqnarray}
\begin{eqnarray} Z^n_{t_k} &=& \frac{{\mathbb{E}}^{{\mathcal{G}}}_{k}\big(g(X^n_T) {\varepsilon}_{k+1}\big)}{\sqrt{h}} +{\mathbb{E}}^{{\mathcal{G}}}_{k}\Bigg( \sqrt{ h}\sum_{m=k+1}^{n-1}f( t_{m+1},X^n_{t_m}, Y^n_{t_m} , Z^n_{t_m}) {\varepsilon}_{k+1}\Bigg ), \, 0\le k \le n-1, \end{eqnarray}where ![]() ${\mathbb{E}}^{{\mathcal{G}}}_k\coloneqq {\mathbb{E}}(\cdot|{\mathcal{G}}_k)$.
${\mathbb{E}}^{{\mathcal{G}}}_k\coloneqq {\mathbb{E}}(\cdot|{\mathcal{G}}_k)$.
Remark 2.2. For n large enough, the BSDE (3) has a unique solution ![]() $({Y}^n,{Z}^n)$ (see [Reference Toldo36, Proposition 1.2]), and
$({Y}^n,{Z}^n)$ (see [Reference Toldo36, Proposition 1.2]), and ![]() $({Y}^n_{t_k}, {Z}^n_{t_k})_{k=0}^{n-1}$ is adapted to the filtration
$({Y}^n_{t_k}, {Z}^n_{t_k})_{k=0}^{n-1}$ is adapted to the filtration ![]() $({\mathcal{G}}_k)_{k=0}^{n-1}.$
$({\mathcal{G}}_k)_{k=0}^{n-1}.$
2.2.1. Representation for Z
We will use the following representation for Z, due to Ma and Zhang (see [Reference Ma and Zhang30, Theorem 4.2]):
where ![]() ${\mathbb{E}}_t \coloneqq {\mathbb{E}}(\cdot|{\mathcal{F}}_t),$ and for all
${\mathbb{E}}_t \coloneqq {\mathbb{E}}(\cdot|{\mathcal{F}}_t),$ and for all ![]() $s \in (t,T]$, we have (cf. Lemma 4.1)
$s \in (t,T]$, we have (cf. Lemma 4.1)
where ![]() $\nabla X = (\nabla X_s)_{s \in [0,T]}$ is the variational process; i.e., it solves
$\nabla X = (\nabla X_s)_{s \in [0,T]}$ is the variational process; i.e., it solves
with ![]() $(X_s)_{s \in [0,T]}$ given in (1).
$(X_s)_{s \in [0,T]}$ given in (1).
Remark 2.3. In the following we will assume that gʹʹ exists. In such a case we have the following representation for Z:
2.2.2. Approximation for  $Z^n$
$Z^n$
In this section we state the discrete counterpart to (11), which, in the general case of a forward process X, does not coincide with ![]() $Z^n$ (given by (10)). In contrast to the continuous-time case, where the variational process and the Malliavin derivative are connected by
$Z^n$ (given by (10)). In contrast to the continuous-time case, where the variational process and the Malliavin derivative are connected by ![]() $\tfrac{\nabla X_t}{\nabla X_s} = \tfrac{D_sX_t }{\sigma(s,X_s)}$ (
$\tfrac{\nabla X_t}{\nabla X_s} = \tfrac{D_sX_t }{\sigma(s,X_s)}$ (![]() $s \le t$), we cannot expect equality for the corresponding expressions if we use the discretized versions of the processes
$s \le t$), we cannot expect equality for the corresponding expressions if we use the discretized versions of the processes ![]() $(\nabla X_t)_t$ and
$(\nabla X_t)_t$ and ![]() $(D_s X_t)_{s\le t}$ introduced in (16). This counterpart
$(D_s X_t)_{s\le t}$ introduced in (16). This counterpart ![]() $\hat{Z}^n$ to Z is a key tool in the proof of the convergence of
$\hat{Z}^n$ to Z is a key tool in the proof of the convergence of ![]() $Z^n$ to Z. As we will see in the proof of Theorem 3.1, the study of
$Z^n$ to Z. As we will see in the proof of Theorem 3.1, the study of ![]() $\|Z^n_{t_k}-Z_{t_k}\|$ goes through the study of
$\|Z^n_{t_k}-Z_{t_k}\|$ goes through the study of ![]() $\|Z^n_{t_k}-\hat{Z}^n_{t_k}\|$ and
$\|Z^n_{t_k}-\hat{Z}^n_{t_k}\|$ and ![]() $\|\hat{Z}^n_{t_k}-Z_{t_k}\|$.
$\|\hat{Z}^n_{t_k}-Z_{t_k}\|$.
Before defining the discretized versions of ![]() $(\nabla X_t)_t$ and
$(\nabla X_t)_t$ and ![]() $(D_s X_t)_{s \le t}$, we briefly introduce the discretized Malliavin derivative. We refer the reader to [Reference Bender and Parczewski4] for more information on this topic.
$(D_s X_t)_{s \le t}$, we briefly introduce the discretized Malliavin derivative. We refer the reader to [Reference Bender and Parczewski4] for more information on this topic.
Definition 2.1. (Definition of ![]() $T_{_{m,+}}$,
$T_{_{m,+}}$, ![]() $T_{_{m,-}}$ and
$T_{_{m,-}}$ and ![]() $\mathcal{D}^n_m$) For any function
$\mathcal{D}^n_m$) For any function ![]() $F\,:\,\{-1,1 \}^n \to {\mathbb{R}}$, the mappings
$F\,:\,\{-1,1 \}^n \to {\mathbb{R}}$, the mappings ![]() $T_{_{m,+}}$ and
$T_{_{m,+}}$ and ![]() $T_{_{m,-}}$ are defined by
$T_{_{m,-}}$ are defined by
For any ![]() $\xi= F(\varepsilon_1, \dots, \varepsilon_n)$, the discretized Malliavin derivative is defined by
$\xi= F(\varepsilon_1, \dots, \varepsilon_n)$, the discretized Malliavin derivative is defined by
Definition 2.2. (Definition of ![]() $\phi_x^{(k,l)}$) Let
$\phi_x^{(k,l)}$) Let ![]() $\phi$ be a
$\phi$ be a ![]() $C^{0,1}([0,T]\times {\mathbb{R}})$ function. We define
$C^{0,1}([0,T]\times {\mathbb{R}})$ function. We define
If ![]() $\mathcal{D}^n_{k} X^n_{t_{\ell-1}}\neq 0$, the second ‘
$\mathcal{D}^n_{k} X^n_{t_{\ell-1}}\neq 0$, the second ‘![]() $\coloneqq $’ holds as an identity.
$\coloneqq $’ holds as an identity.
We are now able to define the discretized versions of ![]() $(\nabla X_t)_t$ and
$(\nabla X_t)_t$ and ![]() $(D_s X_t)_{s \le t}$.
$(D_s X_t)_{s \le t}$.
Definition 2.3. (Discretized processes ![]() $(\nabla X^{n,t_k,x}_{t_m})_{m \in \{k,\dots,n\}}$ and
$(\nabla X^{n,t_k,x}_{t_m})_{m \in \{k,\dots,n\}}$ and ![]() $(\mathcal{D}^n_k X^{n}_{t_m})_{m \in \{k,\dots,n\}}$) For all m in
$(\mathcal{D}^n_k X^{n}_{t_m})_{m \in \{k,\dots,n\}}$) For all m in ![]() $\{k,\dots,n\}$ we define
$\{k,\dots,n\}$ we define
 \begin{align} \nabla X^{n,t_k,x}_{t_m} &= 1 + h\sum_{l=k+1}^m b_x(t_l,X^{n,t_k,x}_{t_{l-1}})\nabla X^{n,t_k,x}_{t_{l-1}} \notag \\[2pt] &\quad + \sqrt{h}\!\! \sum_{l=k+1}^m \sigma_x(t_l,X^{n,t_k,x}_{t_{l-1}})\nabla X^{n,t_k,x}_{t_{l-1}} {\varepsilon}_l, \,\, \quad 0\le k \le n, \notag \\[2pt] \mathcal{D}^n_k X^n_{t_m} & = \sigma(t_{k},X^n_{t_{k-1}}) + h\sum_{l=k+1}^m b_x^{(k,l)} \mathcal{D}^n_k X^n_{t_{l-1}} \notag \\[2pt] & \quad+ \sqrt{h} \sum_{l=k+1}^m \sigma_x^{(k,l)} (\mathcal{D}^n_k X^n_{t_{l-1}}) {\varepsilon}_l, \quad 0<k \le n. \end{align}
\begin{align} \nabla X^{n,t_k,x}_{t_m} &= 1 + h\sum_{l=k+1}^m b_x(t_l,X^{n,t_k,x}_{t_{l-1}})\nabla X^{n,t_k,x}_{t_{l-1}} \notag \\[2pt] &\quad + \sqrt{h}\!\! \sum_{l=k+1}^m \sigma_x(t_l,X^{n,t_k,x}_{t_{l-1}})\nabla X^{n,t_k,x}_{t_{l-1}} {\varepsilon}_l, \,\, \quad 0\le k \le n, \notag \\[2pt] \mathcal{D}^n_k X^n_{t_m} & = \sigma(t_{k},X^n_{t_{k-1}}) + h\sum_{l=k+1}^m b_x^{(k,l)} \mathcal{D}^n_k X^n_{t_{l-1}} \notag \\[2pt] & \quad+ \sqrt{h} \sum_{l=k+1}^m \sigma_x^{(k,l)} (\mathcal{D}^n_k X^n_{t_{l-1}}) {\varepsilon}_l, \quad 0<k \le n. \end{align}(i) Although
 $\nabla X^{n,t_k,X^n_{t_k}}_{t_m}$ is not equal to
we can show that the difference of these terms converges in
$\nabla X^{n,t_k,X^n_{t_k}}_{t_m}$ is not equal to
we can show that the difference of these terms converges in \begin{equation*}\frac{\mathcal{D}^n_{k+1}X^n_{t_m} }{\sigma(t_{k+1},X^n_{t_k})},\end{equation*}
\begin{equation*}\frac{\mathcal{D}^n_{k+1}X^n_{t_m} }{\sigma(t_{k+1},X^n_{t_k})},\end{equation*} $L_p$ (see Lemma 5.4).
$L_p$ (see Lemma 5.4).(ii) With the notation introduced above, (10) can be rewritten as
(17) \begin{eqnarray} Z^n_{t_k} &=& {\mathbb{E}}^{{\mathcal{G}}}_{k} \big ( \mathcal{D}^n_{k+1} g(X^n_T) \big) +{\mathbb{E}}^{{\mathcal{G}}}_{k}\Bigg(h\sum_{m=k+1}^{n-1} \mathcal{D}^n_{k+1} f( t_{m+1},X^n_{t_m}, Y^n_{t_m} , Z^n_{t_m}) \Bigg). \end{eqnarray}
\begin{eqnarray} Z^n_{t_k} &=& {\mathbb{E}}^{{\mathcal{G}}}_{k} \big ( \mathcal{D}^n_{k+1} g(X^n_T) \big) +{\mathbb{E}}^{{\mathcal{G}}}_{k}\Bigg(h\sum_{m=k+1}^{n-1} \mathcal{D}^n_{k+1} f( t_{m+1},X^n_{t_m}, Y^n_{t_m} , Z^n_{t_m}) \Bigg). \end{eqnarray}
In order to define the discrete counterpart to (11), we first define the discrete counterpart to ![]() $(N^t_s)_{s \in [t,T]}$ given in (12):
$(N^t_s)_{s \in [t,T]}$ given in (12):
 \begin{eqnarray} N^{n,t_k}_{t_{\ell}}\coloneqq \sqrt{h} \sum_{m=k+1}^\ell \frac{\nabla X^{n,t_k,X^n_{t_k}}_{t_{m-1}}}{\sigma(t_m, X^n_{t_{m-1}})} \frac{{\varepsilon}_m}{t_\ell - t_k}, \quad k
< \ell \leq n.\end{eqnarray}
\begin{eqnarray} N^{n,t_k}_{t_{\ell}}\coloneqq \sqrt{h} \sum_{m=k+1}^\ell \frac{\nabla X^{n,t_k,X^n_{t_k}}_{t_{m-1}}}{\sigma(t_m, X^n_{t_{m-1}})} \frac{{\varepsilon}_m}{t_\ell - t_k}, \quad k
< \ell \leq n.\end{eqnarray}Notice that there is some constant ![]() $\widehat \kappa_2>0$ depending on
$\widehat \kappa_2>0$ depending on ![]() $b,\sigma,T,\delta$ such that
$b,\sigma,T,\delta$ such that
Definition 2.4. (Discrete counterpart to (14).) Let the process ![]() $\hat{Z}^n = (\hat{Z}^n_{t_k})_{k=0}^{n-1}$ be defined by
$\hat{Z}^n = (\hat{Z}^n_{t_k})_{k=0}^{n-1}$ be defined by
 \begin{align} \hat{Z}^n_{t_k} \coloneqq {\mathbb{E}}^{{\mathcal{G}}}_{k} \big( \mathcal{D}^n_{k+1} g(X^n_T) \big) + {\mathbb{E}}^{{\mathcal{G}}}_{k} \Bigg( h\sum_{m= k+1}^{n-1}f( t_{m+1}, X^n_{t_m}, Y^n_{t_m}, Z^n_{t_m}) N^{n,t_k}_{t_m}\Bigg) \sigma(t_{k+1},X^n_{t_k}).\end{align}
\begin{align} \hat{Z}^n_{t_k} \coloneqq {\mathbb{E}}^{{\mathcal{G}}}_{k} \big( \mathcal{D}^n_{k+1} g(X^n_T) \big) + {\mathbb{E}}^{{\mathcal{G}}}_{k} \Bigg( h\sum_{m= k+1}^{n-1}f( t_{m+1}, X^n_{t_m}, Y^n_{t_m}, Z^n_{t_m}) N^{n,t_k}_{t_m}\Bigg) \sigma(t_{k+1},X^n_{t_k}).\end{align}Remark 2.5. In (20) the approximate expression ![]() ${\mathbb{E}}^{{\mathcal{G}}}_{k} ({ g(X^n_T) N^{n,t_k}_{t_n} \sigma(t_{k+1},X^n_{t_k}) })$ also could have been used, but since we will assume that gʹʹ exists, we work with the correct term.
${\mathbb{E}}^{{\mathcal{G}}}_{k} ({ g(X^n_T) N^{n,t_k}_{t_n} \sigma(t_{k+1},X^n_{t_k}) })$ also could have been used, but since we will assume that gʹʹ exists, we work with the correct term.
The study of the convergence ![]() ${\mathbb{E}}^{{\mathcal{G}}}_{0,x} | Z^n_{t_k} - \hat{Z}^n_{t_k}|^2$ requires stronger assumptions on the coefficients b,
${\mathbb{E}}^{{\mathcal{G}}}_{0,x} | Z^n_{t_k} - \hat{Z}^n_{t_k}|^2$ requires stronger assumptions on the coefficients b, ![]() $\sigma$, f, and g.
$\sigma$, f, and g.
Assumption 2.3. Assumptions 2.1 and 2.2 hold. Additionally, we assume that all first and second derivatives with respect to the variables x, y, z of b(t, x), ![]() $\sigma(t,x)$, and f(t, x, y, z) exist and are bounded Lipschitz functions with respect to these variables, uniformly in time. Moreover, gʹʹ satisfies (6).
$\sigma(t,x)$, and f(t, x, y, z) exist and are bounded Lipschitz functions with respect to these variables, uniformly in time. Moreover, gʹʹ satisfies (6).
Proposition 2.1. If Assumption 2.3 holds, then
where ![]() ${\mathbb{E}}^{{\mathcal{G}}}_{0,x}\coloneqq {\mathbb{E}}^{{\mathcal{G}}}(\cdot|X_0=x)$, the function
${\mathbb{E}}^{{\mathcal{G}}}_{0,x}\coloneqq {\mathbb{E}}^{{\mathcal{G}}}(\cdot|X_0=x)$, the function ![]() $\hat \Psi$ is defined in (62) below, and
$\hat \Psi$ is defined in (62) below, and ![]() $C_{\hyperref[Pro2.1]{\scriptstyle\textcolor{blue}{2.1}}}$ depends on b,
$C_{\hyperref[Pro2.1]{\scriptstyle\textcolor{blue}{2.1}}}$ depends on b, ![]() $\sigma$, f, g, T,
$\sigma$, f, g, T, ![]() $p_0$, and
$p_0$, and ![]() $\delta$.
$\delta$.
Proof. According to [Reference Briand, Delyon and Mémin7, Proposition 5.1] one has the representations
where ![]() $u^n$ is the solution of the finite difference equation (44) with terminal condition
$u^n$ is the solution of the finite difference equation (44) with terminal condition ![]() $u^n(t_n,x)= g(x).$ Notice that by the definition of
$u^n(t_n,x)= g(x).$ Notice that by the definition of ![]() $\mathcal{D}^n_{m+1}$ in (15) the expression
$\mathcal{D}^n_{m+1}$ in (15) the expression ![]() $\mathcal{D}^n_{m+1} u^n(t_{m+1},X^{n}_{t_{m+1}})$ depends in fact on
$\mathcal{D}^n_{m+1} u^n(t_{m+1},X^{n}_{t_{m+1}})$ depends in fact on ![]() $X^{n}_{t_m}.$ Hence we can put
$X^{n}_{t_m}.$ Hence we can put
 \begin{align*} f(t_{m+1}, X^n_{t_m}, Y^n_{t_m}, Z^n_{t_m})&= f(t_{m+1}, X^n_{t_m}, u^n(t_m, X^n_{t_m}), \mathcal{D}^n_{m+1} u^n(t_{m+1},X^{n}_{t_{m+1}}))\\[2pt] &\eqqcolon F^n(t_{m+1}, X^n_{t_{m}}).\end{align*}
\begin{align*} f(t_{m+1}, X^n_{t_m}, Y^n_{t_m}, Z^n_{t_m})&= f(t_{m+1}, X^n_{t_m}, u^n(t_m, X^n_{t_m}), \mathcal{D}^n_{m+1} u^n(t_{m+1},X^{n}_{t_{m+1}}))\\[2pt] &\eqqcolon F^n(t_{m+1}, X^n_{t_{m}}).\end{align*}From (20) and (17) we conclude the following (we use ![]() ${\mathbb{E}}\coloneqq {\mathbb{E}}^{{\mathcal{G}}}_{0,x}$ for
${\mathbb{E}}\coloneqq {\mathbb{E}}^{{\mathcal{G}}}_{0,x}$ for ![]() $\|\cdot \|$):
$\|\cdot \|$):
 \begin{align*} & \| Z^n_{t_k} - \hat{Z}^n_{t_k} \| \\[2pt] &\quad =\Bigg \| {\mathbb{E}}^{{\mathcal{G}}}_k \Bigg ( h\sum_{m=k+1}^{n-1} \mathcal{D}^n_{k+1} f(t_{m+1},X^n_{t_m}, Y^n_{t_m}, Z^n_{t_m}) \Bigg) \\[2pt] &
\quad \quad - {\mathbb{E}}^{{\mathcal{G}}}_k \Bigg(h\sum_{m=k+1}^{n-1}f( t_{m+1}, X^n_{t_m}, Y^n_{t_m}, Z^n_{t_m}) N^{n,t_k}_{t_m} \sigma(t_{k+1},X^n_{t_k}) \Bigg) \notag\Bigg \| \\[2pt]
&\quad\le\sum_{m=k+1}^{n-1}\!\! \frac{h}{m - k} \! \sum_{\ell=k+1}^m \!\left\| {\mathbb{E}}^{{\mathcal{G}}}_k \! \left[\! \mathcal{D}^n_{k+1} F^n(t_{m+1}, X^n_{t_m})- \mathcal{D}^n_{ \ell } F^n(t_{m+1}, X^n_{t_m}) \frac{\sigma(t_{k+1},X^n_{t_k})\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell -1 }}}{\sigma(t_\ell, X^n_{t_{\ell - 1}})} \right] \right \|\!.\end{align*}
\begin{align*} & \| Z^n_{t_k} - \hat{Z}^n_{t_k} \| \\[2pt] &\quad =\Bigg \| {\mathbb{E}}^{{\mathcal{G}}}_k \Bigg ( h\sum_{m=k+1}^{n-1} \mathcal{D}^n_{k+1} f(t_{m+1},X^n_{t_m}, Y^n_{t_m}, Z^n_{t_m}) \Bigg) \\[2pt] &
\quad \quad - {\mathbb{E}}^{{\mathcal{G}}}_k \Bigg(h\sum_{m=k+1}^{n-1}f( t_{m+1}, X^n_{t_m}, Y^n_{t_m}, Z^n_{t_m}) N^{n,t_k}_{t_m} \sigma(t_{k+1},X^n_{t_k}) \Bigg) \notag\Bigg \| \\[2pt]
&\quad\le\sum_{m=k+1}^{n-1}\!\! \frac{h}{m - k} \! \sum_{\ell=k+1}^m \!\left\| {\mathbb{E}}^{{\mathcal{G}}}_k \! \left[\! \mathcal{D}^n_{k+1} F^n(t_{m+1}, X^n_{t_m})- \mathcal{D}^n_{ \ell } F^n(t_{m+1}, X^n_{t_m}) \frac{\sigma(t_{k+1},X^n_{t_k})\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell -1 }}}{\sigma(t_\ell, X^n_{t_{\ell - 1}})} \right] \right \|\!.\end{align*}With the notation introduced in Definition 2.2 applied to ![]() $F^n$,
$F^n$,
 \begin{align*}& \left \| \mathcal{D}^n_{k+1}F^n(t_{m+1}, X^n_{t_m})-\mathcal{D}^n_\ell F^n(t_{m+1}, X^n_{t_m}) \frac{\sigma(t_{k+1},X^n_{t_k})\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell-1}}}{\sigma(t_\ell,X^n_{t_{\ell-1}})} \right \| \\[2pt]
& \quad \le \| (\mathcal{D}^n_{k+1}X^n_{t_m} )( F^{n,(k+1,m+1)}_x -F^{n,(\ell,m+1)}_x) \| \\[2pt]
&\qquad+ \,\left \| F^{n,(\ell,m+1)}_x \left( (\mathcal{D}^n_{k+1} X^n_{t_m}) -(\mathcal{D}^n_\ell X^n_{t_m}) \frac{\sigma(t_{k+1},X^n_{t_k})\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell-1}}}{\sigma(t_\ell,X^n_{t_{\ell-1}})} \right)\right \| \\[2pt] &\quad\eqqcolon A_1 +A_2.\end{align*}
\begin{align*}& \left \| \mathcal{D}^n_{k+1}F^n(t_{m+1}, X^n_{t_m})-\mathcal{D}^n_\ell F^n(t_{m+1}, X^n_{t_m}) \frac{\sigma(t_{k+1},X^n_{t_k})\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell-1}}}{\sigma(t_\ell,X^n_{t_{\ell-1}})} \right \| \\[2pt]
& \quad \le \| (\mathcal{D}^n_{k+1}X^n_{t_m} )( F^{n,(k+1,m+1)}_x -F^{n,(\ell,m+1)}_x) \| \\[2pt]
&\qquad+ \,\left \| F^{n,(\ell,m+1)}_x \left( (\mathcal{D}^n_{k+1} X^n_{t_m}) -(\mathcal{D}^n_\ell X^n_{t_m}) \frac{\sigma(t_{k+1},X^n_{t_k})\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell-1}}}{\sigma(t_\ell,X^n_{t_{\ell-1}})} \right)\right \| \\[2pt] &\quad\eqqcolon A_1 +A_2.\end{align*}For ![]() $A_1$ we use Definition 2.2 again and exploit the fact that
$A_1$ we use Definition 2.2 again and exploit the fact that
is locally ![]() $\alpha$-Hölder continuous according to (63). By Hölder’s inequality and Lemma 5.4 Parts (i) and (iii),
$\alpha$-Hölder continuous according to (63). By Hölder’s inequality and Lemma 5.4 Parts (i) and (iii),
 \begin{align*}A_1 & \leq \| {\mathcal{D}}^n_{k+1} X^n_{t_m}\|_4\int_{0}^1 \| F^n_x(t_{m+1}, \vartheta T_{_{k+1,+}} X^n_{t_m} + (1-\vartheta) T_{_{k+1,-}}X^n_{t_m}) \\[2pt] &\quad \quad \quad \quad\quad \quad- F^n_x(t_{m+1}, \vartheta T_{_{\ell,+}} X^n_{t_m} + (1-\vartheta) T_{_{\ell,-}} X^n_{t_m})\|_4 d\vartheta \\[2pt] & \leq C(b,\sigma,f,g,T,p_0) \hat \Psi(x) h^{\frac{\alpha}{2}}.\end{align*}
\begin{align*}A_1 & \leq \| {\mathcal{D}}^n_{k+1} X^n_{t_m}\|_4\int_{0}^1 \| F^n_x(t_{m+1}, \vartheta T_{_{k+1,+}} X^n_{t_m} + (1-\vartheta) T_{_{k+1,-}}X^n_{t_m}) \\[2pt] &\quad \quad \quad \quad\quad \quad- F^n_x(t_{m+1}, \vartheta T_{_{\ell,+}} X^n_{t_m} + (1-\vartheta) T_{_{\ell,-}} X^n_{t_m})\|_4 d\vartheta \\[2pt] & \leq C(b,\sigma,f,g,T,p_0) \hat \Psi(x) h^{\frac{\alpha}{2}}.\end{align*}For the estimate of ![]() $A_2$ we notice that by our assumptions the
$A_2$ we notice that by our assumptions the ![]() $L_4$-norm of
$L_4$-norm of ![]() $F^{n,(\ell,m+1)}_x $ is bounded by
$F^{n,(\ell,m+1)}_x $ is bounded by ![]() $C \Psi^2(x),$ so that it suffices to estimate
$C \Psi^2(x),$ so that it suffices to estimate
 \begin{eqnarray} && \left \| (\mathcal{D}^n_{k+1} X^n_{t_m}) - (\mathcal{D}^n_\ell X^n_{t_m}) \frac{\sigma(t_{k+1},X^n_{t_k})\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell-1}}}{\sigma(t_\ell, X^n_{t_{\ell-1}})}\right \|_4\notag\\[2pt]
&& \quad\le \left\| (\mathcal{D}^n_{k+1} X^n_{t_m}) - \frac{\sigma( t_{k+1},X^n_{t_k}) \, \mathcal{D}^n_\ell X^n_{t_m}}{ \sigma(t_\ell ,X^n_{t_{\ell-1}}) } \frac{ \mathcal{D}^n_{k+1}X^n_{t_{\ell -1}}}{ \sigma( t_{k+1},X^n_{t_k})}\right\|_4 \notag\\[2pt] && \quad \quad + \left\| \frac{\sigma( t_{k+1},X^n_{t_k}) \, \mathcal{D}^n_\ell X^n_{t_m}}{ \sigma(t_\ell,X^n_{t_{\ell-1}} )}\Bigg (\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell-1}} - \frac{ \mathcal{D}^n_{k+1} X^n_{t_{\ell-1}}}{\sigma( t_{k+1},X^n_{t_k})} \Bigg )\right\|_4. \end{eqnarray}
\begin{eqnarray} && \left \| (\mathcal{D}^n_{k+1} X^n_{t_m}) - (\mathcal{D}^n_\ell X^n_{t_m}) \frac{\sigma(t_{k+1},X^n_{t_k})\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell-1}}}{\sigma(t_\ell, X^n_{t_{\ell-1}})}\right \|_4\notag\\[2pt]
&& \quad\le \left\| (\mathcal{D}^n_{k+1} X^n_{t_m}) - \frac{\sigma( t_{k+1},X^n_{t_k}) \, \mathcal{D}^n_\ell X^n_{t_m}}{ \sigma(t_\ell ,X^n_{t_{\ell-1}}) } \frac{ \mathcal{D}^n_{k+1}X^n_{t_{\ell -1}}}{ \sigma( t_{k+1},X^n_{t_k})}\right\|_4 \notag\\[2pt] && \quad \quad + \left\| \frac{\sigma( t_{k+1},X^n_{t_k}) \, \mathcal{D}^n_\ell X^n_{t_m}}{ \sigma(t_\ell,X^n_{t_{\ell-1}} )}\Bigg (\nabla X^{n,t_k,X^n_{t_k}}_{t_{\ell-1}} - \frac{ \mathcal{D}^n_{k+1} X^n_{t_{\ell-1}}}{\sigma( t_{k+1},X^n_{t_k})} \Bigg )\right\|_4. \end{eqnarray}The second expression on the right-hand side of (22) is bounded by ![]() $C(b,\sigma,T,\delta)h^{\frac{1}{2}}$ as a consequence of Lemma 5.4 Parts (ii) and (iii). To show that the first expression is also bounded by
$C(b,\sigma,T,\delta)h^{\frac{1}{2}}$ as a consequence of Lemma 5.4 Parts (ii) and (iii). To show that the first expression is also bounded by ![]() $C(b,\sigma,T,\delta)h^{\frac{1}{2}}$, we rewrite it using (16) and get
$C(b,\sigma,T,\delta)h^{\frac{1}{2}}$, we rewrite it using (16) and get
 \begin{align}& \left |\frac{ \mathcal{D}^n_{\ell} X^n_{t_m}}{ \sigma(t_\ell,X^n_{t_{\ell-1}})} \mathcal{D}^n_{k+1} X^n_{t_{\ell-1}} - \mathcal{D}^n_{k+1} X^n_{t_m}\right | \nonumber\\[2pt]
& = \Bigg | \Bigg (1+ \sum_{l=\ell+1}^{m} \frac{ \mathcal{D}^n_{\ell} X^n_{t_{l-1}}}{ \sigma(t_\ell,X^n_{t_{\ell-1}}) } ( b_x^{(\ell,l)} h + \sigma_x^{(\ell,l)} \sqrt{h} \varepsilon_l) \Bigg ) \nonumber \\[2pt]
& \quad \quad \times \Bigg (\sigma(t_{k+1},X^n_{t_k})+ \sum_{l=k+2}^{\ell-1}\mathcal{D}^n_{k+1} X^n_{t_{l-1}}( b^{(k+1,l)}_x h + \sigma^{(k+1,l)}_x \sqrt{h} \varepsilon_l) \Bigg ) \nonumber\\[2pt]
& \quad \quad - \Bigg (\sigma(t_{k+1},X^n_{t_k})+ \Bigg (\sum_{l=k+2}^{\ell-1} + \sum_{l=\ell}^{m} \Bigg )\mathcal{D}^n_{k+1} X^n_{t_{l-1}}( b^{(k+1,l)}_x h + \sigma^{(k+1,l)}_x \sqrt{h} \varepsilon_l) \Bigg ) \Bigg | \nonumber\\[2pt]
&\le \big| \mathcal{D}^n_{k+1} X^n_{t_{\ell-1}}( b^{(k+1,\ell)}_x h + \sigma^{(k+1,\ell)}_x \sqrt{h} \varepsilon_\ell)\big| \nonumber\\& \quad + \Bigg | \sum_{l=\ell+1}^{m} \bigg [\frac{ \mathcal{D}^n_{\ell} X^n_{t_{l-1}}}{ \sigma(t_\ell,X^n_{t_{\ell-1}}) }\mathcal{D}^n_{k+1} X^n_{t_{\ell-1}} - \mathcal{D}^n_{k+1} X^n_{t_{l-1}} \bigg] \Big( b^{(\ell,l)}_x h + \sigma^{(\ell,l)}_x \sqrt{h} \varepsilon_l\Big) \Bigg | \nonumber\\
& \quad + \! \Bigg | \sum_{l=\ell+1}^{m} \mathcal{D}^n_{k+1} X^n_{t_{l-1}} \bigg[ b^{(\ell,l)}_x h + \sigma^{(\ell,l)}_x \sqrt{h} \varepsilon_l - \Big(b^{(k+1,l)}_x h + \sigma^{(k+1,l)}_x\sqrt{h} \varepsilon_l\Big) \bigg] \Bigg |.\end{align}
\begin{align}& \left |\frac{ \mathcal{D}^n_{\ell} X^n_{t_m}}{ \sigma(t_\ell,X^n_{t_{\ell-1}})} \mathcal{D}^n_{k+1} X^n_{t_{\ell-1}} - \mathcal{D}^n_{k+1} X^n_{t_m}\right | \nonumber\\[2pt]
& = \Bigg | \Bigg (1+ \sum_{l=\ell+1}^{m} \frac{ \mathcal{D}^n_{\ell} X^n_{t_{l-1}}}{ \sigma(t_\ell,X^n_{t_{\ell-1}}) } ( b_x^{(\ell,l)} h + \sigma_x^{(\ell,l)} \sqrt{h} \varepsilon_l) \Bigg ) \nonumber \\[2pt]
& \quad \quad \times \Bigg (\sigma(t_{k+1},X^n_{t_k})+ \sum_{l=k+2}^{\ell-1}\mathcal{D}^n_{k+1} X^n_{t_{l-1}}( b^{(k+1,l)}_x h + \sigma^{(k+1,l)}_x \sqrt{h} \varepsilon_l) \Bigg ) \nonumber\\[2pt]
& \quad \quad - \Bigg (\sigma(t_{k+1},X^n_{t_k})+ \Bigg (\sum_{l=k+2}^{\ell-1} + \sum_{l=\ell}^{m} \Bigg )\mathcal{D}^n_{k+1} X^n_{t_{l-1}}( b^{(k+1,l)}_x h + \sigma^{(k+1,l)}_x \sqrt{h} \varepsilon_l) \Bigg ) \Bigg | \nonumber\\[2pt]
&\le \big| \mathcal{D}^n_{k+1} X^n_{t_{\ell-1}}( b^{(k+1,\ell)}_x h + \sigma^{(k+1,\ell)}_x \sqrt{h} \varepsilon_\ell)\big| \nonumber\\& \quad + \Bigg | \sum_{l=\ell+1}^{m} \bigg [\frac{ \mathcal{D}^n_{\ell} X^n_{t_{l-1}}}{ \sigma(t_\ell,X^n_{t_{\ell-1}}) }\mathcal{D}^n_{k+1} X^n_{t_{\ell-1}} - \mathcal{D}^n_{k+1} X^n_{t_{l-1}} \bigg] \Big( b^{(\ell,l)}_x h + \sigma^{(\ell,l)}_x \sqrt{h} \varepsilon_l\Big) \Bigg | \nonumber\\
& \quad + \! \Bigg | \sum_{l=\ell+1}^{m} \mathcal{D}^n_{k+1} X^n_{t_{l-1}} \bigg[ b^{(\ell,l)}_x h + \sigma^{(\ell,l)}_x \sqrt{h} \varepsilon_l - \Big(b^{(k+1,l)}_x h + \sigma^{(k+1,l)}_x\sqrt{h} \varepsilon_l\Big) \bigg] \Bigg |.\end{align}We take the ![]() $L_4$-norm of (23) and apply the Burkholder–Davis–Gundy (BDG) inequality and Hölder’s inequality. The second term on the right-hand side of (23) will be used for Gronwall’s lemma, while the first and last terms can be bounded by
$L_4$-norm of (23) and apply the Burkholder–Davis–Gundy (BDG) inequality and Hölder’s inequality. The second term on the right-hand side of (23) will be used for Gronwall’s lemma, while the first and last terms can be bounded by ![]() $ C(b,\sigma,T)h^{\frac{1}{2}},$ using Lemma 5.4(iii). For the last term we also use the Lipschitz continuity of
$ C(b,\sigma,T)h^{\frac{1}{2}},$ using Lemma 5.4(iii). For the last term we also use the Lipschitz continuity of ![]() $b_x$ and
$b_x$ and ![]() $\sigma_x$ in space and Lemma 5.4(i).
$\sigma_x$ in space and Lemma 5.4(i).
3. Main results
In order to compute the mean square distance between the solution to (1) and the solution to (3), we construct the random walk ![]() $B^n$ from the Brownian motion B by Skorokhod embedding. Let
$B^n$ from the Brownian motion B by Skorokhod embedding. Let
Then ![]() $(B_{\tau_{k}} -B_{\tau_{k-1}})_{k=1}^\infty$ is a sequence of i.i.d. random variables with
$(B_{\tau_{k}} -B_{\tau_{k-1}})_{k=1}^\infty$ is a sequence of i.i.d. random variables with
which means that ![]() $\sqrt{h} {\varepsilon}_k \stackrel{d}{=} B_{\tau_{k}}-B_{\tau_{k-1}}\!.$ We will denote by
$\sqrt{h} {\varepsilon}_k \stackrel{d}{=} B_{\tau_{k}}-B_{\tau_{k-1}}\!.$ We will denote by ![]() ${\mathbb{E}}_{\tau_k}\!$ the conditional expectation with respect to
${\mathbb{E}}_{\tau_k}\!$ the conditional expectation with respect to ![]() ${\mathcal{F}}_{\tau_k} \coloneqq {\mathcal{G}}_k.$ In this case we also use the notation
${\mathcal{F}}_{\tau_k} \coloneqq {\mathcal{G}}_k.$ In this case we also use the notation ![]() ${\mathcal{X}}_{\tau_k}\coloneqq X^n_{t_k}$ for all
${\mathcal{X}}_{\tau_k}\coloneqq X^n_{t_k}$ for all ![]() $k =0, \dots,n,$ so that (4) turns into
$k =0, \dots,n,$ so that (4) turns into
 \begin{align*}{\mathcal{X}}_{\tau_k} = x + \sum_{j=1}^k b(t_j,{\mathcal{X}}_{\tau_{j-1}})h + \sum_{j=1}^k \sigma(t_j,{\mathcal{X}}_{\tau_{j-1}})(B_{\tau_j} - B_{\tau_{j-1}}), \quad 0 \leq k \leq n.\end{align*}
\begin{align*}{\mathcal{X}}_{\tau_k} = x + \sum_{j=1}^k b(t_j,{\mathcal{X}}_{\tau_{j-1}})h + \sum_{j=1}^k \sigma(t_j,{\mathcal{X}}_{\tau_{j-1}})(B_{\tau_j} - B_{\tau_{j-1}}), \quad 0 \leq k \leq n.\end{align*}Assumption 3.1. We assume that the random walk ![]() $B^n$ in (3) is given by
$B^n$ in (3) is given by
 \begin{eqnarray*}B^n_{t} = \sum_{k=1}^{[t/h] }(B_{\tau_{k}} -B_{\tau_{k-1}}), \quad \quad 0 \leq t\leq T,\end{eqnarray*}
\begin{eqnarray*}B^n_{t} = \sum_{k=1}^{[t/h] }(B_{\tau_{k}} -B_{\tau_{k-1}}), \quad \quad 0 \leq t\leq T,\end{eqnarray*}where the ![]() $\tau_k$,
$\tau_k$, ![]() $k =1,\ldots,n$, are taken from (24).
$k =1,\ldots,n$, are taken from (24).
Remark 3.1. Note that for ![]() $p>0$ there exists a
$p>0$ there exists a ![]() $C(p) >0$ such that for all
$C(p) >0$ such that for all ![]() $k =1, \dots,n$ it holds that
$k =1, \dots,n$ it holds that
The upper estimate is given in Lemma 5.1. For ![]() $p\in [4,\infty)$ the lower estimate follows from [Reference Ankirchner, Kruse and Urusov2, Proposition 5.3]. We get the lower estimate for
$p\in [4,\infty)$ the lower estimate follows from [Reference Ankirchner, Kruse and Urusov2, Proposition 5.3]. We get the lower estimate for ![]() $p\in (0,4)$ by choosing
$p\in (0,4)$ by choosing ![]() $0<\theta <1$ and
$0<\theta <1$ and ![]() $0<p<p_1$ such that
$0<p<p_1$ such that ![]() $ \frac{1}{4} = \frac{1-\theta}{p} + \frac{\theta}{ p_1}.$ Then it holds by the log-convexity of
$ \frac{1}{4} = \frac{1-\theta}{p} + \frac{\theta}{ p_1}.$ Then it holds by the log-convexity of ![]() $L_p$ norms (see for example [Reference Tao35, Lemma 1.11.5]) that
$L_p$ norms (see for example [Reference Tao35, Lemma 1.11.5]) that
 \begin{equation*}\| B_{\tau_{k}} -B_{t_k}\|^{1-\theta}_p \ge \frac{ \| B_{\tau_{k}} -B_{t_k}\|_4}{ \| B_{\tau_{k}} -B_{t_k}\|^{\theta}_{p_1}} \ge \frac{C(4)^{-1} (t_k h)^{\frac{1}{4}} }{ \big(C(p_1) (t_k h)^{\frac{1}{4}} \big)^{\theta} } \ge \big (C(p) (t_k h)^{\frac{1}{4}} \big )^{1-\theta}. \end{equation*}
\begin{equation*}\| B_{\tau_{k}} -B_{t_k}\|^{1-\theta}_p \ge \frac{ \| B_{\tau_{k}} -B_{t_k}\|_4}{ \| B_{\tau_{k}} -B_{t_k}\|^{\theta}_{p_1}} \ge \frac{C(4)^{-1} (t_k h)^{\frac{1}{4}} }{ \big(C(p_1) (t_k h)^{\frac{1}{4}} \big)^{\theta} } \ge \big (C(p) (t_k h)^{\frac{1}{4}} \big )^{1-\theta}. \end{equation*}Since for ![]() $t\in [t_k,t_{k+1})$ it holds that
$t\in [t_k,t_{k+1})$ it holds that ![]() $B^n_t= B_{\tau_k}$ and
$B^n_t= B_{\tau_k}$ and ![]() $\|B_t -B_{t_k} \|_p \le C(p) h^\frac{1}{2},$ we have for any
$\|B_t -B_{t_k} \|_p \le C(p) h^\frac{1}{2},$ we have for any ![]() $p>0$ that
$p>0$ that
Proposition 3.1 states the convergence rate of ![]() $(Y^n_v,Z^n_v)$ to
$(Y^n_v,Z^n_v)$ to ![]() $(Y_v,Z_v)$ in
$(Y_v,Z_v)$ in ![]() $L_2$ when
$L_2$ when ![]() $f=0$, and Theorem 3.1 generalizes this result to any f which satisfies Assumption 2.3.
$f=0$, and Theorem 3.1 generalizes this result to any f which satisfies Assumption 2.3.
Proposition 3.1. Let Assumptions 2.1 and 3.1 hold. If ![]() $f =0$ and
$f =0$ and ![]() $g \in C^1$ is such that gʹ is a locally
$g \in C^1$ is such that gʹ is a locally ![]() $\alpha$-Hölder continuous function in the sense of (6), then for all
$\alpha$-Hölder continuous function in the sense of (6), then for all ![]() $0 \le v < T$, we have (for sufficiently large n) that
$0 \le v < T$, we have (for sufficiently large n) that
where ![]() $C^y_{\hyperref[Pro3.1]{\scriptstyle\textcolor{blue}{3.1}}}= C(C_g, b, \sigma, T, p_0, \delta)$ and
$C^y_{\hyperref[Pro3.1]{\scriptstyle\textcolor{blue}{3.1}}}= C(C_g, b, \sigma, T, p_0, \delta)$ and ![]() $C^z_{\hyperref[Pro3.1]{\scriptstyle\textcolor{blue}{3.1}}}= C(C_{g'}, b, \sigma, T, p_0, \delta).$
$C^z_{\hyperref[Pro3.1]{\scriptstyle\textcolor{blue}{3.1}}}= C(C_{g'}, b, \sigma, T, p_0, \delta).$
Theorem 3.1. Let Assumptions 2.3 and 3.1 be satisfied. Then for all ![]() $v \in [0,T)$ and large enough n, we have
$v \in [0,T)$ and large enough n, we have
where ![]() $C_{\hyperref[The3.1]{\scriptstyle\textcolor{blue}{3.1}}}= C(b,\sigma,f,g,T,p_0,\delta)$ and
$C_{\hyperref[The3.1]{\scriptstyle\textcolor{blue}{3.1}}}= C(b,\sigma,f,g,T,p_0,\delta)$ and ![]() $\hat{\Psi}$ is given in (62).
$\hat{\Psi}$ is given in (62).
Remark 3.2. As observed above, the filtration ![]() $\mathcal{G}_k$ coincides with
$\mathcal{G}_k$ coincides with ![]() $\mathcal{F}_{\tau_k}$, for all
$\mathcal{F}_{\tau_k}$, for all ![]() $k = 0,\dots,n$. The expectation
$k = 0,\dots,n$. The expectation ![]() ${\mathbb{E}}_{0,x}$ appearing in Proposition 3.1 and in Theorem 3.1 is defined on the probability space
${\mathbb{E}}_{0,x}$ appearing in Proposition 3.1 and in Theorem 3.1 is defined on the probability space ![]() $(\Omega,\mathcal{F},\mathbb{P})$.
$(\Omega,\mathcal{F},\mathbb{P})$.
Remark 3.3. In order to avoid too much notation for the dependencies of the constants, if for example only g is mentioned and not ![]() $C_g,$ this means that the estimate might depend also on the bounds of the derivatives of g.
$C_g,$ this means that the estimate might depend also on the bounds of the derivatives of g.
From (25) one can see that the convergence rates stated in Proposition 3.1 and Theorem 3.1 are the natural ones for this approach. The results are proved in the next two sections. In both proofs, we will use the following remark.
Remark 3.4. Since the process ![]() $(X_t)_{t \ge 0}$ is strong Markov, we can express conditional expectations with the help of an independent copy of B denoted by
$(X_t)_{t \ge 0}$ is strong Markov, we can express conditional expectations with the help of an independent copy of B denoted by ![]() $\tilde B$. For example,
$\tilde B$. For example, ![]() ${\mathbb{E}}_{\tau_k} g(X^n_T) = \tilde {\mathbb{E}} g( \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n})$ for
${\mathbb{E}}_{\tau_k} g(X^n_T) = \tilde {\mathbb{E}} g( \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n})$ for ![]() $0 \leq k \leq n$, where
$0 \leq k \leq n$, where
 \begin{eqnarray} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} = {\mathcal{X}}_{\tau_k}+ \sum_{j=k+1}^n b(t_j, \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_{j-1}})h + \sum_{j=k+1}^n\sigma(t_j, \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_{j-1}})(\tilde B_{\tilde \tau_{j-k}} - \tilde B_{\tilde \tau_{j-k-1}})\end{eqnarray}
\begin{eqnarray} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} = {\mathcal{X}}_{\tau_k}+ \sum_{j=k+1}^n b(t_j, \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_{j-1}})h + \sum_{j=k+1}^n\sigma(t_j, \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_{j-1}})(\tilde B_{\tilde \tau_{j-k}} - \tilde B_{\tilde \tau_{j-k-1}})\end{eqnarray}(we define ![]() $\tilde \tau_k\coloneqq 0$,
$\tilde \tau_k\coloneqq 0$, ![]() $\tilde \tau_j\coloneqq \inf\{ t> \tilde \tau_{j-1}\,:\, |\tilde B_t- \tilde B_{\tilde \tau_{j-1}}| = \sqrt{h} \}$ for
$\tilde \tau_j\coloneqq \inf\{ t> \tilde \tau_{j-1}\,:\, |\tilde B_t- \tilde B_{\tilde \tau_{j-1}}| = \sqrt{h} \}$ for ![]() $j \ge 1$, and
$j \ge 1$, and ![]() $\tau_n \coloneqq \tau_k +\tilde \tau_{n-k}$ for
$\tau_n \coloneqq \tau_k +\tilde \tau_{n-k}$ for ![]() ${n\ge k}$). In fact, to represent the conditional expectations
${n\ge k}$). In fact, to represent the conditional expectations ![]() ${\mathbb{E}}_{t_k}$ and
${\mathbb{E}}_{t_k}$ and ![]() ${\mathbb{E}}_{\tau_k}$, we work here with
${\mathbb{E}}_{\tau_k}$, we work here with ![]() $\tilde {\mathbb{E}}$ and the Brownian motions Bʹ and Bʹʹ, respectively, given by
$\tilde {\mathbb{E}}$ and the Brownian motions Bʹ and Bʹʹ, respectively, given by
3.1. Proof of Proposition 3.1: the approximation rates for the zero generator case
To shorten the notation, we use ![]() ${\mathbb{E}} \coloneqq {\mathbb{E}}_{0,x}.$ Let us first deal with the error of Y. If v belongs to
${\mathbb{E}} \coloneqq {\mathbb{E}}_{0,x}.$ Let us first deal with the error of Y. If v belongs to ![]() $[t_k,t_{k+1})$ we have
$[t_k,t_{k+1})$ we have ![]() $Y^n_v= Y^n_{t_k}$. Then
$Y^n_v= Y^n_{t_k}$. Then
Using Theorem 4.1 we bound ![]() $\|Y_v - Y_{t_k}\|$ by
$\|Y_v - Y_{t_k}\|$ by
(since ![]() $\alpha=1$ can be chosen when g is locally Lipschitz continuous). It remains to bound
$\alpha=1$ can be chosen when g is locally Lipschitz continuous). It remains to bound
By (6) and the Cauchy–Schwarz inequality (with ![]() $\Psi_1\coloneqq C_g(1+|\tilde X^{t_k,X_{t_k}}_{t_n}|^{p_0}+| \tilde {\mathcal{X}}^{\tau_k,{{\mathcal{X}}}_{\tau_k}}_{\tau_n}|^{p_0})$),
$\Psi_1\coloneqq C_g(1+|\tilde X^{t_k,X_{t_k}}_{t_n}|^{p_0}+| \tilde {\mathcal{X}}^{\tau_k,{{\mathcal{X}}}_{\tau_k}}_{\tau_n}|^{p_0})$),
 \begin{align*} | \tilde {\mathbb{E}} g(\tilde X^{t_k,X_{t_k}}_{t_n})-\tilde {\mathbb{E}} g(\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{ \tau_n})|^2 &\le (\tilde {\mathbb{E}} (\Psi_1 |\tilde X^{t_k,X_{t_k}}_{t_n}-\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\ \tau_n}| ))^2 \\[3pt] &\le \tilde {\mathbb{E}} (\Psi_1^2) \tilde {\mathbb{E}} |\tilde X^{t_k,X_{t_k}}_{t_n}-\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{ \tau_n}|^{2}. \end{align*}
\begin{align*} | \tilde {\mathbb{E}} g(\tilde X^{t_k,X_{t_k}}_{t_n})-\tilde {\mathbb{E}} g(\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{ \tau_n})|^2 &\le (\tilde {\mathbb{E}} (\Psi_1 |\tilde X^{t_k,X_{t_k}}_{t_n}-\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\ \tau_n}| ))^2 \\[3pt] &\le \tilde {\mathbb{E}} (\Psi_1^2) \tilde {\mathbb{E}} |\tilde X^{t_k,X_{t_k}}_{t_n}-\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{ \tau_n}|^{2}. \end{align*}Finally, we get by Lemma 5.2(v) that
Let us now deal with the error of Z. We use ![]() $ \|Z_v - Z^n_v \| \le \|Z_v - Z_{t_k}\| + \|Z_{t_k} - Z^n_{t_k}\|$ and the representation
$ \|Z_v - Z^n_v \| \le \|Z_v - Z_{t_k}\| + \|Z_{t_k} - Z^n_{t_k}\|$ and the representation
(see Theorem 4.2), where
 \begin{align} \tilde X^{t,x}_s &= x+\int_t^s b(r, \tilde X^{t,x}_r) dr + \int_t^s \sigma(r,\tilde X^{t,x}_r) d\tilde B_{r-t}, \\[3pt] \nabla \tilde X^{t,x}_s &= 1+\int_t^s b_x(r, \tilde X^{t,x}_r) \nabla \tilde X^{t,x}_r dr + \int_t^s \sigma_x(r,\tilde X^{t,x}_r) \nabla \tilde X^{t,x}_r d\tilde B_{r-t}, \quad 0\le t\le s\le T. \notag \end{align}
\begin{align} \tilde X^{t,x}_s &= x+\int_t^s b(r, \tilde X^{t,x}_r) dr + \int_t^s \sigma(r,\tilde X^{t,x}_r) d\tilde B_{r-t}, \\[3pt] \nabla \tilde X^{t,x}_s &= 1+\int_t^s b_x(r, \tilde X^{t,x}_r) \nabla \tilde X^{t,x}_r dr + \int_t^s \sigma_x(r,\tilde X^{t,x}_r) \nabla \tilde X^{t,x}_r d\tilde B_{r-t}, \quad 0\le t\le s\le T. \notag \end{align}For the first term we get by the assumption on g and Lemma 5.2 Parts (i) and (iii) that
 \begin{eqnarray*} \|Z_v - Z_{t_k}\| &\,=\,& \| \sigma(v,X_v) \tilde {\mathbb{E}} (g'(\tilde X^{v,X_v}_{T}) \nabla \tilde X^{v,X_v}_{T}) - \sigma(t_k,X_{t_k}) \tilde {\mathbb{E}}( g'(\tilde X^{t_k,X_{t_k}}_{T}) \nabla \tilde X^{t_k,X_{t_k}}_{T}) \|\\[4pt] &\,\le\,& \| \sigma(v,X_v) - \sigma(t_k,X_{t_k}) \|_4 \| \tilde {\mathbb{E}} (g'(\tilde X^{v,X_v}_{T}) \nabla \tilde X^{v,X_v}_{T}) \|_4 \\[4pt] && +\, \|\sigma\|_\infty \| \tilde {\mathbb{E}} (g'(\tilde X^{v,X_v}_{T}) \nabla \tilde X^{v,X_v}_{T}) - \tilde {\mathbb{E}}( g'(\tilde X^{t_k,X_{t_k}}_{T}) \nabla \tilde X^{v,X_v}_{T}) \| \\[4pt] && +\, \|\sigma\|_\infty \| \tilde {\mathbb{E}}( g'(\tilde X^{t_k,X_{t_k}}_{T}) \nabla \tilde X^{v,X_v}_{T}) - \tilde {\mathbb{E}}( g'(\tilde X^{t_k,X_{t_k}}_{T}) \nabla \tilde X^{t_k,X_{t_k}}_{T}) \| \\[4pt] &\,\le\, & C( C_{g'},b,\sigma,T,p_0)\Psi(x) \Big [h^{\frac{1}{2}} + \|X_v -X_{t_k} \|_4+ \left ( {\mathbb{E}}\tilde {\mathbb{E}} |\tilde X^{v,X_v}_{T}-\tilde X^{t_k,X_{t_k}}_{T}|^{4\alpha} \right)^\frac{1}{4}\\[4pt] &&+\left ({\mathbb{E}}\tilde {\mathbb{E}} | \nabla \tilde X^{v,X_v}_{T} -\nabla \tilde X^{t_k,X_{t_k}}_{T}|^4 \right)^\frac{1}{4} \Big] \\[4pt] &\,\le\,& C( C_{g'},b,\sigma,T,p_0) \Psi(x) h^\frac{\alpha}{2}.\end{eqnarray*}
\begin{eqnarray*} \|Z_v - Z_{t_k}\| &\,=\,& \| \sigma(v,X_v) \tilde {\mathbb{E}} (g'(\tilde X^{v,X_v}_{T}) \nabla \tilde X^{v,X_v}_{T}) - \sigma(t_k,X_{t_k}) \tilde {\mathbb{E}}( g'(\tilde X^{t_k,X_{t_k}}_{T}) \nabla \tilde X^{t_k,X_{t_k}}_{T}) \|\\[4pt] &\,\le\,& \| \sigma(v,X_v) - \sigma(t_k,X_{t_k}) \|_4 \| \tilde {\mathbb{E}} (g'(\tilde X^{v,X_v}_{T}) \nabla \tilde X^{v,X_v}_{T}) \|_4 \\[4pt] && +\, \|\sigma\|_\infty \| \tilde {\mathbb{E}} (g'(\tilde X^{v,X_v}_{T}) \nabla \tilde X^{v,X_v}_{T}) - \tilde {\mathbb{E}}( g'(\tilde X^{t_k,X_{t_k}}_{T}) \nabla \tilde X^{v,X_v}_{T}) \| \\[4pt] && +\, \|\sigma\|_\infty \| \tilde {\mathbb{E}}( g'(\tilde X^{t_k,X_{t_k}}_{T}) \nabla \tilde X^{v,X_v}_{T}) - \tilde {\mathbb{E}}( g'(\tilde X^{t_k,X_{t_k}}_{T}) \nabla \tilde X^{t_k,X_{t_k}}_{T}) \| \\[4pt] &\,\le\, & C( C_{g'},b,\sigma,T,p_0)\Psi(x) \Big [h^{\frac{1}{2}} + \|X_v -X_{t_k} \|_4+ \left ( {\mathbb{E}}\tilde {\mathbb{E}} |\tilde X^{v,X_v}_{T}-\tilde X^{t_k,X_{t_k}}_{T}|^{4\alpha} \right)^\frac{1}{4}\\[4pt] &&+\left ({\mathbb{E}}\tilde {\mathbb{E}} | \nabla \tilde X^{v,X_v}_{T} -\nabla \tilde X^{t_k,X_{t_k}}_{T}|^4 \right)^\frac{1}{4} \Big] \\[4pt] &\,\le\,& C( C_{g'},b,\sigma,T,p_0) \Psi(x) h^\frac{\alpha}{2}.\end{eqnarray*}We compute the second term using ![]() $Z^n_{t_k} $ as given in (17). Hence, with the notation from Definition 2.2,
$Z^n_{t_k} $ as given in (17). Hence, with the notation from Definition 2.2,
 \begin{eqnarray*} \|Z_{t_k} - Z^n_{t_k}\|^2&\,=\,& {\mathbb{E}} \big | \sigma(t_k,X_{t_k}) \tilde {\mathbb{E}} g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n} - \tilde {\mathbb{E}} \mathcal{D}^n_{k+1} g(\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}) \big |^2 \\[4pt] &\,\le\, & \| \sigma\|_\infty ^2 \, {\mathbb{E}} \left | \tilde {\mathbb{E}} ( g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n} ) - \frac{ \tilde {\mathbb{E}} \mathcal{D}^n_{k+1} g(\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n})}{ \sigma(t_k,X_{t_k}) } \right |^2 \\[4pt] &\,=\,& \| \sigma\|_\infty ^2 \, {\mathbb{E}} \Bigg | \tilde {\mathbb{E}} (g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n} ) - \tilde {\mathbb{E}} \Bigg ( g_x^{(k+1,n+1)} \frac{ \mathcal{D}^n_{k+1} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}}{ \sigma(t_k,X_{t_k}) }\Bigg ) \Bigg |^2. \\[4pt] \end{eqnarray*}
\begin{eqnarray*} \|Z_{t_k} - Z^n_{t_k}\|^2&\,=\,& {\mathbb{E}} \big | \sigma(t_k,X_{t_k}) \tilde {\mathbb{E}} g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n} - \tilde {\mathbb{E}} \mathcal{D}^n_{k+1} g(\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}) \big |^2 \\[4pt] &\,\le\, & \| \sigma\|_\infty ^2 \, {\mathbb{E}} \left | \tilde {\mathbb{E}} ( g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n} ) - \frac{ \tilde {\mathbb{E}} \mathcal{D}^n_{k+1} g(\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n})}{ \sigma(t_k,X_{t_k}) } \right |^2 \\[4pt] &\,=\,& \| \sigma\|_\infty ^2 \, {\mathbb{E}} \Bigg | \tilde {\mathbb{E}} (g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n} ) - \tilde {\mathbb{E}} \Bigg ( g_x^{(k+1,n+1)} \frac{ \mathcal{D}^n_{k+1} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}}{ \sigma(t_k,X_{t_k}) }\Bigg ) \Bigg |^2. \\[4pt] \end{eqnarray*}We insert ![]() $\pm \tilde {\mathbb{E}} ( g_x^{(k+1,n+1)} \nabla \tilde X^{t_k,X_{t_k}}_{t_n})$ and get by the Cauchy–Schwarz inequality that
$\pm \tilde {\mathbb{E}} ( g_x^{(k+1,n+1)} \nabla \tilde X^{t_k,X_{t_k}}_{t_n})$ and get by the Cauchy–Schwarz inequality that
 \begin{eqnarray} && {} \Bigg | \tilde {\mathbb{E}} (g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n}) - \tilde {\mathbb{E}} \Bigg ( g_x^{(k+1,n+1)} \frac{ \mathcal{D}^n_{k+1} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}}{ \sigma(t_k,X_{t_k}) } \Bigg ) \Bigg |^2 \notag\\[4pt]
&&\quad \le\, 2 \tilde {\mathbb{E}} | g'(\tilde X^{t_k,X_{t_k}}_{t_n})- g_x^{(k+1,n+1)}|^2 \tilde {\mathbb{E}} | \nabla \tilde X^{t_k,X_{t_k}}_{t_n} |^2 + 2\tilde {\mathbb{E}} | g_x^{(k+1,n+1)}|^2 \tilde {\mathbb{E}} \Bigg | \nabla \tilde X^{t_k,X_{t_k}}_{t_n} \!- \!\frac{ \mathcal{D}^n_{k+1} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}}{ \sigma(t_k,X_{t_k}) } \Bigg|^2.\nonumber\\ \end{eqnarray}
\begin{eqnarray} && {} \Bigg | \tilde {\mathbb{E}} (g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n}) - \tilde {\mathbb{E}} \Bigg ( g_x^{(k+1,n+1)} \frac{ \mathcal{D}^n_{k+1} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}}{ \sigma(t_k,X_{t_k}) } \Bigg ) \Bigg |^2 \notag\\[4pt]
&&\quad \le\, 2 \tilde {\mathbb{E}} | g'(\tilde X^{t_k,X_{t_k}}_{t_n})- g_x^{(k+1,n+1)}|^2 \tilde {\mathbb{E}} | \nabla \tilde X^{t_k,X_{t_k}}_{t_n} |^2 + 2\tilde {\mathbb{E}} | g_x^{(k+1,n+1)}|^2 \tilde {\mathbb{E}} \Bigg | \nabla \tilde X^{t_k,X_{t_k}}_{t_n} \!- \!\frac{ \mathcal{D}^n_{k+1} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}}{ \sigma(t_k,X_{t_k}) } \Bigg|^2.\nonumber\\ \end{eqnarray}For the estimate of ![]() $ \tilde {\mathbb{E}} | \nabla \tilde X^{t_k,X_{t_k}}_{t_n} |^2$ we use Lemma 5.2. Since gʹ satisfies (6) we proceed with
$ \tilde {\mathbb{E}} | \nabla \tilde X^{t_k,X_{t_k}}_{t_n} |^2$ we use Lemma 5.2. Since gʹ satisfies (6) we proceed with
 \begin{eqnarray*}&& {} \tilde {\mathbb{E}} | g'(\tilde X^{t_k,X_{t_k}}_{t_n})- g_x^{(k+1,n+1)}|^2 \\[2pt] &&\quad\le \int_0^1 \tilde {\mathbb{E}} \Big | g'(\tilde X^{t_k,X_{t_k}}_{t_n})- g'(\vartheta T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}+ (1-\vartheta) T_{_{k+1,-}}\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}) \Big |^2 d \vartheta \\[2pt] &&\quad\le \int_0^1 (\tilde {\mathbb{E}} \Psi_1^4)^{\frac{1}{2}} \Big [ \tilde {\mathbb{E}} \left |\tilde X^{t_k,X_{t_k}}_{t_n}- \vartheta T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} - (1-\vartheta) T_{_{k+1,-}}\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} \right|^{4\alpha} \Big ]^{\frac{1}{2}} d \vartheta,\end{eqnarray*}
\begin{eqnarray*}&& {} \tilde {\mathbb{E}} | g'(\tilde X^{t_k,X_{t_k}}_{t_n})- g_x^{(k+1,n+1)}|^2 \\[2pt] &&\quad\le \int_0^1 \tilde {\mathbb{E}} \Big | g'(\tilde X^{t_k,X_{t_k}}_{t_n})- g'(\vartheta T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}+ (1-\vartheta) T_{_{k+1,-}}\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}) \Big |^2 d \vartheta \\[2pt] &&\quad\le \int_0^1 (\tilde {\mathbb{E}} \Psi_1^4)^{\frac{1}{2}} \Big [ \tilde {\mathbb{E}} \left |\tilde X^{t_k,X_{t_k}}_{t_n}- \vartheta T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} - (1-\vartheta) T_{_{k+1,-}}\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} \right|^{4\alpha} \Big ]^{\frac{1}{2}} d \vartheta,\end{eqnarray*}where ![]() $\Psi_1\coloneqq C_{g'}(1+|\tilde X^{t_k,X_{t_k}}_{t_n}|^{p_0}+|\vartheta T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}+ (1-\vartheta) T_{_{k+1,-}}\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}|^{p_0}). $ For
$\Psi_1\coloneqq C_{g'}(1+|\tilde X^{t_k,X_{t_k}}_{t_n}|^{p_0}+|\vartheta T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}+ (1-\vartheta) T_{_{k+1,-}}\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}|^{p_0}). $ For ![]() $\tilde {\mathbb{E}} \Psi_1^4$ and
$\tilde {\mathbb{E}} \Psi_1^4$ and
 \begin{eqnarray*}&& \tilde {\mathbb{E}} \left |\tilde X^{t_k,X_{t_k}}_{t_n}- (\vartheta T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}+ (1-\vartheta) T_{_{k+1,-}}\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} ) \right|^{ 4\alpha} \\[2pt] &&\quad\le\, 8 \left ( \vartheta^{2\alpha} \tilde {\mathbb{E}} \left |\tilde X^{t_k,X_{t_k}}_{t_n}- T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} \right|^{4\alpha} + (1-\vartheta)^{2\alpha} \tilde {\mathbb{E}} \left |\tilde X^{t_k,X_{t_k}}_{t_n} - T_{_{k+1,-}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} \right|^{4\alpha} \right ) \\[2pt] &&\quad\le\, C(b,\sigma,T) h^{2 \alpha} + C(b,\sigma,T)( |X_{t_k} - {\mathcal{X}}_{\tau_k}|^{4 \alpha}+ h^{\alpha}),\end{eqnarray*}
\begin{eqnarray*}&& \tilde {\mathbb{E}} \left |\tilde X^{t_k,X_{t_k}}_{t_n}- (\vartheta T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}+ (1-\vartheta) T_{_{k+1,-}}\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} ) \right|^{ 4\alpha} \\[2pt] &&\quad\le\, 8 \left ( \vartheta^{2\alpha} \tilde {\mathbb{E}} \left |\tilde X^{t_k,X_{t_k}}_{t_n}- T_{_{k+1,+}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} \right|^{4\alpha} + (1-\vartheta)^{2\alpha} \tilde {\mathbb{E}} \left |\tilde X^{t_k,X_{t_k}}_{t_n} - T_{_{k+1,-}} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n} \right|^{4\alpha} \right ) \\[2pt] &&\quad\le\, C(b,\sigma,T) h^{2 \alpha} + C(b,\sigma,T)( |X_{t_k} - {\mathcal{X}}_{\tau_k}|^{4 \alpha}+ h^{\alpha}),\end{eqnarray*}we use Lemma 5.4 and Lemma 5.2(v). For the last term in (29) we notice that
By Lemma 5.2 we have ![]() ${\mathbb{E}}\tilde {\mathbb{E}} | \nabla \tilde X^{t_k,X_{t_k}}_{t_n}- \nabla \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}|^p \le C(b,\sigma,T,p) h^{\frac{p}{4}},$ and by Lemma 5.4,
${\mathbb{E}}\tilde {\mathbb{E}} | \nabla \tilde X^{t_k,X_{t_k}}_{t_n}- \nabla \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}|^p \le C(b,\sigma,T,p) h^{\frac{p}{4}},$ and by Lemma 5.4,
 \begin{eqnarray*}&& {\mathbb{E}}\tilde {\mathbb{E}} \left | \nabla \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}-\frac{\mathcal{D}^n_{k+1} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}}{ \sigma(t_{k}, X_{t_k})}\right |^p \\[2pt] &&\quad\le\, C(p) {\mathbb{E}}\left | \nabla X^{n,t_k, X^n_{t_k}}_{t_n} - \dfrac{\mathcal{D}^n_{k+1}X^n_{t_n} }{\sigma(t_{k+1},X^n_{t_k})} \right |^p + C(p) {\mathbb{E}}\left | \dfrac{\mathcal{D}^n_{k+1}X^n_{t_n} }{\sigma(t_{k+1},X^n_{t_k})} - \dfrac{\mathcal{D}^n_{k+1}X^n_{t_n} }{\sigma(t_k, X_{t_k})} \right |^p \\[2pt] &&\quad\le\, C(b,\sigma,T,p, \delta) h^{\frac{p}{4}}.\end{eqnarray*}
\begin{eqnarray*}&& {\mathbb{E}}\tilde {\mathbb{E}} \left | \nabla \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}-\frac{\mathcal{D}^n_{k+1} \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_n}}{ \sigma(t_{k}, X_{t_k})}\right |^p \\[2pt] &&\quad\le\, C(p) {\mathbb{E}}\left | \nabla X^{n,t_k, X^n_{t_k}}_{t_n} - \dfrac{\mathcal{D}^n_{k+1}X^n_{t_n} }{\sigma(t_{k+1},X^n_{t_k})} \right |^p + C(p) {\mathbb{E}}\left | \dfrac{\mathcal{D}^n_{k+1}X^n_{t_n} }{\sigma(t_{k+1},X^n_{t_k})} - \dfrac{\mathcal{D}^n_{k+1}X^n_{t_n} }{\sigma(t_k, X_{t_k})} \right |^p \\[2pt] &&\quad\le\, C(b,\sigma,T,p, \delta) h^{\frac{p}{4}}.\end{eqnarray*}Consequently, ![]() $ \|Z_{t_k} - Z^n_{t_k}\|^2 \le C(C_{g'}, b,\sigma,T,p_0,\delta) \Psi^2(x) h^\frac{\alpha}{2}.$
$ \|Z_{t_k} - Z^n_{t_k}\|^2 \le C(C_{g'}, b,\sigma,T,p_0,\delta) \Psi^2(x) h^\frac{\alpha}{2}.$
3.2. Proof of Theorem 3.1: the approximation rates for the general case
Let ![]() $u \,:\, [0,T)\times {\mathbb{R}} \to {\mathbb{R}}$ be the solution of the PDE (38) associated to (1). We use the representations
$u \,:\, [0,T)\times {\mathbb{R}} \to {\mathbb{R}}$ be the solution of the PDE (38) associated to (1). We use the representations ![]() $ Y_s = u(s, X_s)$ and
$ Y_s = u(s, X_s)$ and ![]() $Z_s = \sigma(s, X_s)u_x(s, X_s)$ stated in Theorem 4.2 and define
$Z_s = \sigma(s, X_s)u_x(s, X_s)$ stated in Theorem 4.2 and define
 \begin{align*} \|Y_{t_k}- Y^n_{t_k} \| &\le \| {\mathbb{E}}_{t_k} g(X_T) - {\mathbb{E}}_{\tau_k} g(X^n_T) \| \notag \\[3pt] & \quad + \left \| {\mathbb{E}}_{t_k}\int_{t_k}^T f(s,X_s,Y_s,Z_s)ds - h {\mathbb{E}}_{\tau_k}\sum_{m=k}^{n-1} f(t_{m+1},X^n_{t_m}, Y^n_{t_m},Z^n_{t_m}) \right \|, \end{align*}
\begin{align*} \|Y_{t_k}- Y^n_{t_k} \| &\le \| {\mathbb{E}}_{t_k} g(X_T) - {\mathbb{E}}_{\tau_k} g(X^n_T) \| \notag \\[3pt] & \quad + \left \| {\mathbb{E}}_{t_k}\int_{t_k}^T f(s,X_s,Y_s,Z_s)ds - h {\mathbb{E}}_{\tau_k}\sum_{m=k}^{n-1} f(t_{m+1},X^n_{t_m}, Y^n_{t_m},Z^n_{t_m}) \right \|, \end{align*}where Proposition 3.1 provides the estimate for the terminal condition. We decompose the generator term as follows:
 \begin{align*}& {\mathbb{E}}_{t_k} f(s,X_s,Y_s,Z_s)-{\mathbb{E}}_{\tau_k}f(t_{m+1}, X^n_{t_m},Y^n_{t_m},Z^n_{t_m})\\[2pt] &\quad=[{\mathbb{E}}_{t_k} f(s,X_s,Y_s,Z_s)- {\mathbb{E}}_{t_k}f(t_m,X_{t_m},Y_{t_m},Z_{t_m})] + [{\mathbb{E}}_{t_k}F(t_m,X_{t_m}) -{\mathbb{E}}_{\tau_k}F(t_m, X^n_{t_m})]\\[2pt] & \qquad+ [{\mathbb{E}}_{\tau_k}F(t_m,X^n_{t_m}) \!-\!{\mathbb{E}}_{\tau_k} F(t_m,X_{t_m})] \!+[{\mathbb{E}}_{\tau_k} f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) \!-\! {\mathbb{E}}_{\tau_k}f(t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m})] \\[2pt] &\quad\eqqcolon d_1(s,m) +d_2(m)+ d_3(m)+ d_4(m).\end{align*}
\begin{align*}& {\mathbb{E}}_{t_k} f(s,X_s,Y_s,Z_s)-{\mathbb{E}}_{\tau_k}f(t_{m+1}, X^n_{t_m},Y^n_{t_m},Z^n_{t_m})\\[2pt] &\quad=[{\mathbb{E}}_{t_k} f(s,X_s,Y_s,Z_s)- {\mathbb{E}}_{t_k}f(t_m,X_{t_m},Y_{t_m},Z_{t_m})] + [{\mathbb{E}}_{t_k}F(t_m,X_{t_m}) -{\mathbb{E}}_{\tau_k}F(t_m, X^n_{t_m})]\\[2pt] & \qquad+ [{\mathbb{E}}_{\tau_k}F(t_m,X^n_{t_m}) \!-\!{\mathbb{E}}_{\tau_k} F(t_m,X_{t_m})] \!+[{\mathbb{E}}_{\tau_k} f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) \!-\! {\mathbb{E}}_{\tau_k}f(t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m})] \\[2pt] &\quad\eqqcolon d_1(s,m) +d_2(m)+ d_3(m)+ d_4(m).\end{align*}We use
 \begin{eqnarray*}&& {} \left \| {\mathbb{E}}_{t_k}\int_{t_k}^T f(s,X_s,Y_s,Z_s)ds - h {\mathbb{E}}_{\tau_k}\sum_{m=k}^{n-1} f(t_{m+1}, X^n_{t_m},Y^n_{t_m},Z^n_{t_m}) \right \| \notag\\[2pt] &&\quad \le \sum_{m=k}^{n-1} \left( \left \| \int_{t_m}^{t_{m+1}} d_1(s,m) ds\right \| + h \sum_{i=2}^4 \|d_i(m) \| \right)\end{eqnarray*}
\begin{eqnarray*}&& {} \left \| {\mathbb{E}}_{t_k}\int_{t_k}^T f(s,X_s,Y_s,Z_s)ds - h {\mathbb{E}}_{\tau_k}\sum_{m=k}^{n-1} f(t_{m+1}, X^n_{t_m},Y^n_{t_m},Z^n_{t_m}) \right \| \notag\\[2pt] &&\quad \le \sum_{m=k}^{n-1} \left( \left \| \int_{t_m}^{t_{m+1}} d_1(s,m) ds\right \| + h \sum_{i=2}^4 \|d_i(m) \| \right)\end{eqnarray*}and estimate the expressions on the right-hand side. For the function F defined in (30) we use Assumption 2.3 (which implies that (6) holds for ![]() $\alpha=1$) to derive by Theorem 4.2 and the mean value theorem that for
$\alpha=1$) to derive by Theorem 4.2 and the mean value theorem that for ![]() $x_1, x_2 \in {\mathbb{R}}$ there exists
$x_1, x_2 \in {\mathbb{R}}$ there exists ![]() $\xi \in [\min\{x_1,x_2\},\max\{x_1,x_2\}] $ such that
$\xi \in [\min\{x_1,x_2\},\max\{x_1,x_2\}] $ such that
 \begin{eqnarray} |F(t,x_1) -F(t,x_2)| &\,=\,& |f(t, x_1, u(t, x_1), \sigma(t,x_1)u_x(t, x_1)) - f(t, x_2, u(t, x_2), \sigma(t,x_2)u_x(t, x_2))| \notag \\[3pt] & \,\le\, & C(L_f, \sigma) \left ( 1 + c^2_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi( \xi ) + \frac{c^3_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi(\xi)}{(T-t)^{\frac{1}{2}}} \right )|x_1-x_2| \notag\\[3pt]&\, \le\, & C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \sigma, T) (1+|x_1|^{p_0+1}+|x_2|^{p_0+1}) \frac{|x_1-x_2|}{(T-t)^{\frac{1}{2}}}.\end{eqnarray}
\begin{eqnarray} |F(t,x_1) -F(t,x_2)| &\,=\,& |f(t, x_1, u(t, x_1), \sigma(t,x_1)u_x(t, x_1)) - f(t, x_2, u(t, x_2), \sigma(t,x_2)u_x(t, x_2))| \notag \\[3pt] & \,\le\, & C(L_f, \sigma) \left ( 1 + c^2_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi( \xi ) + \frac{c^3_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi(\xi)}{(T-t)^{\frac{1}{2}}} \right )|x_1-x_2| \notag\\[3pt]&\, \le\, & C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \sigma, T) (1+|x_1|^{p_0+1}+|x_2|^{p_0+1}) \frac{|x_1-x_2|}{(T-t)^{\frac{1}{2}}}.\end{eqnarray}By (7), standard estimates on ![]() $(X_s),$ Theorem 4.1(i), and Proposition 4.1 for
$(X_s),$ Theorem 4.1(i), and Proposition 4.1 for ![]() $p=2$, we immediately get
$p=2$, we immediately get
 \begin{eqnarray*} \| d_1(s,m) \|&\,\le\,& C(L_f, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}, b,\sigma,T) \Psi(x) \,h^{\frac{1}{2}} \\&\,=\,& C(b,\sigma, f,g, T,p_0,\delta) \Psi(x) \,h^{\frac{1}{2}}.\end{eqnarray*}
\begin{eqnarray*} \| d_1(s,m) \|&\,\le\,& C(L_f, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}, b,\sigma,T) \Psi(x) \,h^{\frac{1}{2}} \\&\,=\,& C(b,\sigma, f,g, T,p_0,\delta) \Psi(x) \,h^{\frac{1}{2}}.\end{eqnarray*}For the estimate of ![]() $d_2$ one exploits
$d_2$ one exploits
and then uses (31) and Lemma 5.2(v). This gives
For ![]() $d_3$ we start with Jensen’s inequality and then continue similarly as above to get
$d_3$ we start with Jensen’s inequality and then continue similarly as above to get
and for the last term we get
This implies
 \begin{eqnarray} \| Y_{t_k} - Y^n_{t_k}\| \le C \Psi(x) h^{\frac{1}{4}}+ h L_f \sum_{m=k}^{n-1}( \| Y_{t_m} - Y^n_{t_m}\| + \| Z_{t_m} -Z^n_{t_m}\|),\end{eqnarray}
\begin{eqnarray} \| Y_{t_k} - Y^n_{t_k}\| \le C \Psi(x) h^{\frac{1}{4}}+ h L_f \sum_{m=k}^{n-1}( \| Y_{t_m} - Y^n_{t_m}\| + \| Z_{t_m} -Z^n_{t_m}\|),\end{eqnarray}where ![]() $C= C(L_f, C^y_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}}, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}, C_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}},b,\sigma, T,p_0) = C(b,\sigma, f,g, T,p_0,\delta).$
$C= C(L_f, C^y_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}}, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}, C_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}},b,\sigma, T,p_0) = C(b,\sigma, f,g, T,p_0,\delta).$
For ![]() $\| Z_{t_k} -Z^n_{t_k}\|$ we use the representations (14) and (17), the approximation (20), and Proposition 2.1. Instead of
$\| Z_{t_k} -Z^n_{t_k}\|$ we use the representations (14) and (17), the approximation (20), and Proposition 2.1. Instead of ![]() $N^{n,t_k}_{t_n}$ we will use here the notation
$N^{n,t_k}_{t_n}$ we will use here the notation ![]() $N^{n,\tau_k}_{\tau_n}$ to indicate its measurability with respect to the filtration
$N^{n,\tau_k}_{\tau_n}$ to indicate its measurability with respect to the filtration ![]() $({\mathcal{F}}_t)$. It holds that
$({\mathcal{F}}_t)$. It holds that
 \begin{eqnarray} \|Z^n_{t_k} - Z_{t_k}\| &\le & \| Z^n_{t_k} - \hat Z^n_{t_k}\| + \|Z_{t_k}- \hat Z^n_{t_k}\| \notag\\[3pt] &\le & C_{\hyperref[discreteZand-wrongZdifference]{\scriptstyle\textcolor{blue}{2.1}}} \hat \Psi(x) h^{\frac{\alpha}{2}} + \| \sigma(t_k,X_{t_k}) \tilde {\mathbb{E}} g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n} - \tilde {\mathbb{E}} \mathcal{D}^n_{k+1} g(\tilde X^{n,t_k,X^n_{t_k}}_{t_n}) \| \notag\\[3pt] &&+ \Bigg \|{\mathbb{E}}_{t_{k}}\int_{t_{k+1}}^T f(s,X_s,Y_s,Z_s) N^{t_k}_s ds \, \sigma(t_k,X_{t_k}) \notag \\[3pt] && \quad \quad -{\mathbb{E}}_{\tau_k} h\sum_{m=k+1}^{n-1}f( t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m}) N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \Bigg \| \notag \\&& + \bigg \|{\mathbb{E}}_{t_k}\int_{t_k}^{t_{k+1}} f(s,X_s,Y_s,Z_s) N^{t_k}_s ds \, \sigma(t_k,X_{t_k}) \bigg \| .\end{eqnarray}
\begin{eqnarray} \|Z^n_{t_k} - Z_{t_k}\| &\le & \| Z^n_{t_k} - \hat Z^n_{t_k}\| + \|Z_{t_k}- \hat Z^n_{t_k}\| \notag\\[3pt] &\le & C_{\hyperref[discreteZand-wrongZdifference]{\scriptstyle\textcolor{blue}{2.1}}} \hat \Psi(x) h^{\frac{\alpha}{2}} + \| \sigma(t_k,X_{t_k}) \tilde {\mathbb{E}} g'(\tilde X^{t_k,X_{t_k}}_{t_n}) \nabla \tilde X^{t_k,X_{t_k}}_{t_n} - \tilde {\mathbb{E}} \mathcal{D}^n_{k+1} g(\tilde X^{n,t_k,X^n_{t_k}}_{t_n}) \| \notag\\[3pt] &&+ \Bigg \|{\mathbb{E}}_{t_{k}}\int_{t_{k+1}}^T f(s,X_s,Y_s,Z_s) N^{t_k}_s ds \, \sigma(t_k,X_{t_k}) \notag \\[3pt] && \quad \quad -{\mathbb{E}}_{\tau_k} h\sum_{m=k+1}^{n-1}f( t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m}) N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \Bigg \| \notag \\&& + \bigg \|{\mathbb{E}}_{t_k}\int_{t_k}^{t_{k+1}} f(s,X_s,Y_s,Z_s) N^{t_k}_s ds \, \sigma(t_k,X_{t_k}) \bigg \| .\end{eqnarray}For the terminal condition, Proposition 3.1 provides
We continue with the generator terms and use F defined in (30) to decompose the difference
 \begin{align*}& {\mathbb{E}}_{t_k}f(s,X_s,Y_s,Z_s) N^{t_k}_s \sigma(t_k,X_{t_k})-{\mathbb{E}}_{\tau_k}f( t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m}) N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \\[3pt]&\quad = {\mathbb{E}}_{t_k}f(s,X_s,Y_s,Z_s) N^{t_k}_s \sigma(t_k,X_{t_k}) - {\mathbb{E}}_{t_k}f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) N^{t_k}_{t_m}\sigma(t_k,X_{t_k}) \\[3pt]&\qquad + {\mathbb{E}}_{t_k}F(t_m,X_{t_m}) N^{t_k}_{t_m} \sigma(t_k,X_{t_k}) - {\mathbb{E}}_{\tau_k} F(t_m,X^n_{t_m}) N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \\[3pt]&\qquad + {\mathbb{E}}_{\tau_k}\left [ [ F(t_m,X^n_{t_m}) - F(t_m,X_{t_m})] N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \right ] \\[3pt]&\qquad + {\mathbb{E}}_{\tau_k} \left [ [f(t_m, X_{t_m},Y_{t_m},Z_{t_m})- f(t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m})]N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \right ] \\[3pt]&\quad \eqqcolon {\tt t}_1(s,m)+{\tt t}_2(m)+ {\tt t}_3(m) + {\tt t}_4(m),\end{align*}
\begin{align*}& {\mathbb{E}}_{t_k}f(s,X_s,Y_s,Z_s) N^{t_k}_s \sigma(t_k,X_{t_k})-{\mathbb{E}}_{\tau_k}f( t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m}) N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \\[3pt]&\quad = {\mathbb{E}}_{t_k}f(s,X_s,Y_s,Z_s) N^{t_k}_s \sigma(t_k,X_{t_k}) - {\mathbb{E}}_{t_k}f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) N^{t_k}_{t_m}\sigma(t_k,X_{t_k}) \\[3pt]&\qquad + {\mathbb{E}}_{t_k}F(t_m,X_{t_m}) N^{t_k}_{t_m} \sigma(t_k,X_{t_k}) - {\mathbb{E}}_{\tau_k} F(t_m,X^n_{t_m}) N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \\[3pt]&\qquad + {\mathbb{E}}_{\tau_k}\left [ [ F(t_m,X^n_{t_m}) - F(t_m,X_{t_m})] N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \right ] \\[3pt]&\qquad + {\mathbb{E}}_{\tau_k} \left [ [f(t_m, X_{t_m},Y_{t_m},Z_{t_m})- f(t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m})]N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},X^n_{t_k}) \right ] \\[3pt]&\quad \eqqcolon {\tt t}_1(s,m)+{\tt t}_2(m)+ {\tt t}_3(m) + {\tt t}_4(m),\end{align*}where ![]() $s \in [t_m, t_{m+1})$. For
$s \in [t_m, t_{m+1})$. For ![]() ${\tt t}_1$ we use that
${\tt t}_1$ we use that ![]() ${\mathbb{E}}_{t_k}f(t_m, X_{t_k},Y_{t_k},Z_{t_k}) (N^{t_k}_s -N^{t_k}_{t_m}) =0,$ so that
${\mathbb{E}}_{t_k}f(t_m, X_{t_k},Y_{t_k},Z_{t_k}) (N^{t_k}_s -N^{t_k}_{t_m}) =0,$ so that
 \begin{align*} \|{\tt t}_1(s,m)\| &\le \| {\mathbb{E}}_{t_k}f(s,X_s,Y_s,Z_s) N^{t_k}_s \sigma(t_k,X_{t_k}) - {\mathbb{E}}_{t_k}f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) N^{t_k}_s\sigma(t_k,X_{t_k}) \| \\[3pt] &\quad + \| {\mathbb{E}}_{t_k}(f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) - f(t_m, X_{t_k},Y_{t_k},Z_{t_k}) ) (N^{t_k}_s -N^{t_k}_{t_m})\sigma(t_k,X_{t_k}) \|.\end{align*}
\begin{align*} \|{\tt t}_1(s,m)\| &\le \| {\mathbb{E}}_{t_k}f(s,X_s,Y_s,Z_s) N^{t_k}_s \sigma(t_k,X_{t_k}) - {\mathbb{E}}_{t_k}f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) N^{t_k}_s\sigma(t_k,X_{t_k}) \| \\[3pt] &\quad + \| {\mathbb{E}}_{t_k}(f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) - f(t_m, X_{t_k},Y_{t_k},Z_{t_k}) ) (N^{t_k}_s -N^{t_k}_{t_m})\sigma(t_k,X_{t_k}) \|.\end{align*}As before, we rewrite the conditional expectations with the help of the independent copy ![]() $\tilde B.$ Then
$\tilde B.$ Then
 \begin{align*}& {\mathbb{E}}_{t_k}f(s,X_s,Y_s,Z_s) N^{t_k}_s - {\mathbb{E}}_{t_k}f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) N^{t_k}_s \\[3pt] &\quad = \tilde {\mathbb{E}} [(f(s, \tilde X^{t_k,X_{t_k}}_s, \tilde Y^{t_k,X_{t_k}}_s, \tilde Z^{t_k,X_{t_k}}_s) - f(t_m, \tilde X^{t_k,X_{t_k}}_{t_m}, \tilde Y^{t_k,X_{t_k}}_{t_m},\tilde Z^{t_k,X_{t_k}}_{t_m})) \tilde N^{t_k}_s]\end{align*}
\begin{align*}& {\mathbb{E}}_{t_k}f(s,X_s,Y_s,Z_s) N^{t_k}_s - {\mathbb{E}}_{t_k}f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) N^{t_k}_s \\[3pt] &\quad = \tilde {\mathbb{E}} [(f(s, \tilde X^{t_k,X_{t_k}}_s, \tilde Y^{t_k,X_{t_k}}_s, \tilde Z^{t_k,X_{t_k}}_s) - f(t_m, \tilde X^{t_k,X_{t_k}}_{t_m}, \tilde Y^{t_k,X_{t_k}}_{t_m},\tilde Z^{t_k,X_{t_k}}_{t_m})) \tilde N^{t_k}_s]\end{align*}and
 \begin{align*}& {\mathbb{E}}_{t_k}(f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) - f(t_m, X_{t_k},Y_{t_k},Z_{t_k}) ) (N^{t_k}_s -N^{t_k}_{t_m}) \\[3pt] &\quad = \tilde {\mathbb{E}} [(f(t_m, \tilde X^{t_k,X_{t_k}}_{t_m}, \tilde Y^{t_k,X_{t_k}}_{t_m},\tilde Z^{t_k,X_{t_k}}_{t_m}) - f(t_m, X_{t_k},Y_{t_k},Z_{t_k}) ) (\tilde N^{t_k}_s - \tilde N^{t_k}_{t_m})].\end{align*}
\begin{align*}& {\mathbb{E}}_{t_k}(f(t_m, X_{t_m},Y_{t_m},Z_{t_m}) - f(t_m, X_{t_k},Y_{t_k},Z_{t_k}) ) (N^{t_k}_s -N^{t_k}_{t_m}) \\[3pt] &\quad = \tilde {\mathbb{E}} [(f(t_m, \tilde X^{t_k,X_{t_k}}_{t_m}, \tilde Y^{t_k,X_{t_k}}_{t_m},\tilde Z^{t_k,X_{t_k}}_{t_m}) - f(t_m, X_{t_k},Y_{t_k},Z_{t_k}) ) (\tilde N^{t_k}_s - \tilde N^{t_k}_{t_m})].\end{align*}We apply the conditional Hölder inequality, and from the estimates (37) and
we get
 \begin{eqnarray*} \|{\tt t}_1(s,m)\| &\le & \frac{\kappa_2 \| \sigma \|_{\infty}}{(s-t_k)^{\frac{1}{2}}} \| f(s, X_s, Y_s,Z_s)- f(t_m, X_{t_m},Y_{t_m},Z_{t_m})\| \\ && + C(b,\sigma,T,\delta) \frac{ h^{{\frac{1}{2}}}}{s-t_k}\ \| f(t_m, X_{t_m},Y_{t_m},Z_{t_m})- f(t_k, X_{t_k},Y_{t_k},Z_{t_k}) \| \\& \le & C(L_f, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}},\kappa_2, b,\sigma,T,p_0, \delta) \Psi(x) \frac{h^{\frac{1}{2}} }{(s-t_k)^\frac{1}{2}},\end{eqnarray*}
\begin{eqnarray*} \|{\tt t}_1(s,m)\| &\le & \frac{\kappa_2 \| \sigma \|_{\infty}}{(s-t_k)^{\frac{1}{2}}} \| f(s, X_s, Y_s,Z_s)- f(t_m, X_{t_m},Y_{t_m},Z_{t_m})\| \\ && + C(b,\sigma,T,\delta) \frac{ h^{{\frac{1}{2}}}}{s-t_k}\ \| f(t_m, X_{t_m},Y_{t_m},Z_{t_m})- f(t_k, X_{t_k},Y_{t_k},Z_{t_k}) \| \\& \le & C(L_f, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}},\kappa_2, b,\sigma,T,p_0, \delta) \Psi(x) \frac{h^{\frac{1}{2}} }{(s-t_k)^\frac{1}{2}},\end{eqnarray*}since for ![]() $0\le t <s \le T$ we have by Theorem 4.1 and Proposition 4.1 that
$0\le t <s \le T$ we have by Theorem 4.1 and Proposition 4.1 that
For the estimate of ![]() ${\tt t}_2$, Lemma 5.2, Lemma 5.3, (31), and (37) yield
${\tt t}_2$, Lemma 5.2, Lemma 5.3, (31), and (37) yield
 \begin{align*} \|{\tt t}_2(m)\|&= \| \tilde {\mathbb{E}} F(t_m,\tilde X^{t_k,X_{t_k}}_{t_m}) \tilde N^{t_k}_{t_m} \sigma(t_k,X_{t_k}) - \tilde {\mathbb{E}} F(t_m, \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_m}) \tilde N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k}) \| \\[3pt] &\le \frac{ C(\kappa_2, \sigma)}{(t_m - t_k)^{\frac{1}{2}}} {{\left( {\mathbb{E}} \tilde {\mathbb{E}} (F(t_m,\tilde X^{t_k,X_{t_k}}_{t_m}) - F(t_m, \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_m}))^2 \right)}}^{{\frac{1}{2}}}\\[2pt] &\quad + ( {\mathbb{E}} \tilde {\mathbb{E}} |F(t_m,\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_m})-F(t_m,{\mathcal{X}}_{\tau_k})|^2 \tilde {\mathbb{E}} | \tilde N^{t_k}_{t_m} \sigma(t_k,X_{t_k}) - \tilde N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k}) |^2 )^{\frac{1}{2}} \\[3pt] &\le C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \kappa_2,b,\sigma,T,p_0,\delta) \frac{\Psi(x)}{(T-t_m)^{\frac{1}{2}} } \frac{h^\frac{1}{4}}{ (t_m -t_k)^\frac{1}{2}}.\end{align*}
\begin{align*} \|{\tt t}_2(m)\|&= \| \tilde {\mathbb{E}} F(t_m,\tilde X^{t_k,X_{t_k}}_{t_m}) \tilde N^{t_k}_{t_m} \sigma(t_k,X_{t_k}) - \tilde {\mathbb{E}} F(t_m, \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_m}) \tilde N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k}) \| \\[3pt] &\le \frac{ C(\kappa_2, \sigma)}{(t_m - t_k)^{\frac{1}{2}}} {{\left( {\mathbb{E}} \tilde {\mathbb{E}} (F(t_m,\tilde X^{t_k,X_{t_k}}_{t_m}) - F(t_m, \tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_m}))^2 \right)}}^{{\frac{1}{2}}}\\[2pt] &\quad + ( {\mathbb{E}} \tilde {\mathbb{E}} |F(t_m,\tilde {\mathcal{X}}^{\tau_k,{\mathcal{X}}_{\tau_k}}_{\tau_m})-F(t_m,{\mathcal{X}}_{\tau_k})|^2 \tilde {\mathbb{E}} | \tilde N^{t_k}_{t_m} \sigma(t_k,X_{t_k}) - \tilde N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k}) |^2 )^{\frac{1}{2}} \\[3pt] &\le C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \kappa_2,b,\sigma,T,p_0,\delta) \frac{\Psi(x)}{(T-t_m)^{\frac{1}{2}} } \frac{h^\frac{1}{4}}{ (t_m -t_k)^\frac{1}{2}}.\end{align*}For ![]() ${\tt t}_3$ we use the conditional Hölder inequality, (31), (19), and Lemma 5.2:
${\tt t}_3$ we use the conditional Hölder inequality, (31), (19), and Lemma 5.2:
 \begin{align*} \|{\tt t}_3(m)\|&= \left\|{\mathbb{E}}_{\tau_k}\left [ [F(t_m,X^n_{t_m} ) - F(t_m,X_{t_m})] N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k}) \right ] \right\| \\[2pt] &\le \frac{ C(\widehat\kappa_2, \sigma)}{(t_m - t_k)^{\frac{1}{2}}} \left\| F(t_m, X^n_{t_m} ) - F(t_m,X_{t_m}) \right\| \\ &\le C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}},b,\sigma,T,p_0,\delta) \frac{\Psi(x)}{(T-t_m)^{\frac{1}{2}} } \frac{h^\frac{1}{4}}{ (t_m -t_k)^\frac{1}{2}}.\end{align*}
\begin{align*} \|{\tt t}_3(m)\|&= \left\|{\mathbb{E}}_{\tau_k}\left [ [F(t_m,X^n_{t_m} ) - F(t_m,X_{t_m})] N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k}) \right ] \right\| \\[2pt] &\le \frac{ C(\widehat\kappa_2, \sigma)}{(t_m - t_k)^{\frac{1}{2}}} \left\| F(t_m, X^n_{t_m} ) - F(t_m,X_{t_m}) \right\| \\ &\le C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}},b,\sigma,T,p_0,\delta) \frac{\Psi(x)}{(T-t_m)^{\frac{1}{2}} } \frac{h^\frac{1}{4}}{ (t_m -t_k)^\frac{1}{2}}.\end{align*}The term ![]() ${\tt t}_4$ can be estimated as follows:
${\tt t}_4$ can be estimated as follows:
 \begin{align*} \|{\tt t}_4(m)\|&= \left\| {\mathbb{E}}_{\tau_k} \big [ [f(t_m, X_{t_m},Y_{t_m},Z_{t_m})- f(t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m})]N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k}) \big] \right\| \\[3pt] &\le \frac{C(L_f, b,\sigma,T, \delta)}{ (t_m -t_k)^{\frac{1}{2}}} (h^{\frac{1}{2}} + \| X_{t_m} -X^n_{t_m} \| + \| Y_{t_m} -Y^n_{t_m} \| + \| Z_{t_m} - Z^n_{t_m} \|). \end{align*}
\begin{align*} \|{\tt t}_4(m)\|&= \left\| {\mathbb{E}}_{\tau_k} \big [ [f(t_m, X_{t_m},Y_{t_m},Z_{t_m})- f(t_{m+1}, X^n_{t_m}, Y^n_{t_m},Z^n_{t_m})]N^{n,\tau_k}_{\tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k}) \big] \right\| \\[3pt] &\le \frac{C(L_f, b,\sigma,T, \delta)}{ (t_m -t_k)^{\frac{1}{2}}} (h^{\frac{1}{2}} + \| X_{t_m} -X^n_{t_m} \| + \| Y_{t_m} -Y^n_{t_m} \| + \| Z_{t_m} - Z^n_{t_m} \|). \end{align*}Finally, for the remaining term of the estimate of ![]() $\| Z_{t_k} -Z^n_{t_k}\|, $ we use (35) and (37) to get
$\| Z_{t_k} -Z^n_{t_k}\|, $ we use (35) and (37) to get
Consequently, from (33), (34), and the estimates for the remaining term and for ![]() ${\tt t}_1,\ldots,{\tt t}_4$, it follows that
${\tt t}_1,\ldots,{\tt t}_4$, it follows that
 \begin{align*} \| Z_{t_k} -Z^n_{t_k}\| &\le C_{\hyperref[discreteZand-wrongZdifference]{\scriptstyle\textcolor{blue}{2.1}}} \hat \Psi (x) h^{\frac{\alpha}{2}} + (C^z_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}})^{\frac{1}{2}} \Psi(x) h^\frac{1}{4} + C(L_f, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}},b,\sigma,T, p_0,\kappa_2) \Psi(x) h\\[2pt] &\quad + C(L_f, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}},\kappa_2,b,\sigma,T,p_0,\delta) \Psi(x) h^{\frac{1}{2}} \int_{t_k}^{T} \frac{ds }{ (s-t_k)^\frac{1}{2}}\\[2pt] &\quad + C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \kappa_2, b,\sigma,T,p_0,\delta) h \sum_{m=k+1}^{n-1} \frac{\Psi(x)}{(T-t_m)^{\frac{1}{2}} } \frac{h^\frac{1}{4}}{ (t_m -t_k)^\frac{1}{2}} \\[2pt] &\quad + C(L_f, b,\sigma,T, \delta )h \sum_{m=k+1}^{n-1} (\| Y_{t_m} -Y^n_{t_m} \| + \| Z_{t_m} - Z^n_{t_m} \|)\frac{1}{ (t_m -t_k)^{\frac{1}{2}}} \\[2pt] &\le C(C_{\hyperref[discreteZand-wrongZdifference]{\scriptstyle\textcolor{blue}{2.1}}},C^z_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}}) \hat \Psi (x) h^{\frac{\alpha}{2}\wedge\frac{1}{4}} + C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}},\kappa_2,b,\sigma,T,p_0,\delta) \Psi(x) h^\frac{1}{4} \\[2pt] &\quad + C(L_f, b,\sigma,T, \delta ) \sum_{m=k+1}^{n-1} (\| Y_{t_m} -Y^n_{t_m} \| + \| Z_{t_m} - Z^n_{t_m} \|)\frac{1}{(t_m -t_k)^{\frac{1}{2}}} h.\end{align*}
\begin{align*} \| Z_{t_k} -Z^n_{t_k}\| &\le C_{\hyperref[discreteZand-wrongZdifference]{\scriptstyle\textcolor{blue}{2.1}}} \hat \Psi (x) h^{\frac{\alpha}{2}} + (C^z_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}})^{\frac{1}{2}} \Psi(x) h^\frac{1}{4} + C(L_f, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}},b,\sigma,T, p_0,\kappa_2) \Psi(x) h\\[2pt] &\quad + C(L_f, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}},\kappa_2,b,\sigma,T,p_0,\delta) \Psi(x) h^{\frac{1}{2}} \int_{t_k}^{T} \frac{ds }{ (s-t_k)^\frac{1}{2}}\\[2pt] &\quad + C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \kappa_2, b,\sigma,T,p_0,\delta) h \sum_{m=k+1}^{n-1} \frac{\Psi(x)}{(T-t_m)^{\frac{1}{2}} } \frac{h^\frac{1}{4}}{ (t_m -t_k)^\frac{1}{2}} \\[2pt] &\quad + C(L_f, b,\sigma,T, \delta )h \sum_{m=k+1}^{n-1} (\| Y_{t_m} -Y^n_{t_m} \| + \| Z_{t_m} - Z^n_{t_m} \|)\frac{1}{ (t_m -t_k)^{\frac{1}{2}}} \\[2pt] &\le C(C_{\hyperref[discreteZand-wrongZdifference]{\scriptstyle\textcolor{blue}{2.1}}},C^z_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}}) \hat \Psi (x) h^{\frac{\alpha}{2}\wedge\frac{1}{4}} + C(L_f, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}},C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}},\kappa_2,b,\sigma,T,p_0,\delta) \Psi(x) h^\frac{1}{4} \\[2pt] &\quad + C(L_f, b,\sigma,T, \delta ) \sum_{m=k+1}^{n-1} (\| Y_{t_m} -Y^n_{t_m} \| + \| Z_{t_m} - Z^n_{t_m} \|)\frac{1}{(t_m -t_k)^{\frac{1}{2}}} h.\end{align*}Then we use (32) and the above estimate to get
 \begin{align*}& \| Y_{t_k} - Y^n_{t_k}\| + \| Z_{t_k} -Z^n_{t_k}\| \\[2pt] &\le C(C_{\hyperref[discreteZand-wrongZdifference]{\scriptstyle\textcolor{blue}{2.1}}},C^z_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}})\hat \Psi (x) h^{\frac{\alpha}{2}\wedge\frac{1}{4}} + C(L_f,C^y_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}},C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}, C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \kappa_2, b, \sigma, T,p_0, \delta) \Psi(x) h^\frac{1}{4} \\[3pt] &\quad + C(L_f,b,\sigma,T, \delta) \sum_{m=k+1}^{n-1} (\| Y_{t_m} -Y^n_{t_m} \| + \| Z_{t_m} - Z^n_{t_m} \|)\frac{1}{ (t_m -t_k)^{\frac{1}{2}}} h.\end{align*}
\begin{align*}& \| Y_{t_k} - Y^n_{t_k}\| + \| Z_{t_k} -Z^n_{t_k}\| \\[2pt] &\le C(C_{\hyperref[discreteZand-wrongZdifference]{\scriptstyle\textcolor{blue}{2.1}}},C^z_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}})\hat \Psi (x) h^{\frac{\alpha}{2}\wedge\frac{1}{4}} + C(L_f,C^y_{\hyperref[no f]{\scriptstyle\textcolor{blue}{3.1}}},C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}, C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}, c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \kappa_2, b, \sigma, T,p_0, \delta) \Psi(x) h^\frac{1}{4} \\[3pt] &\quad + C(L_f,b,\sigma,T, \delta) \sum_{m=k+1}^{n-1} (\| Y_{t_m} -Y^n_{t_m} \| + \| Z_{t_m} - Z^n_{t_m} \|)\frac{1}{ (t_m -t_k)^{\frac{1}{2}}} h.\end{align*}Consequently, summarizing the dependencies, there is a ![]() $ C=C(b,\sigma,f,g,T,p_0,\delta)$ such that
$ C=C(b,\sigma,f,g,T,p_0,\delta)$ such that
By Theorem 4.1 (note that by Assumption 2.3 on g we have ![]() $\alpha=1$) it follows that
$\alpha=1$) it follows that
while Proposition 4.1 implies that
and hence we have
with ![]() $C_{\hyperref[the-result]{\scriptstyle\textcolor{blue}{3.1}}} = C_{\hyperref[the-result]{\scriptstyle\textcolor{blue}{3.1}}}(b,\sigma,f,g,T,p_0,\delta).$
$C_{\hyperref[the-result]{\scriptstyle\textcolor{blue}{3.1}}} = C_{\hyperref[the-result]{\scriptstyle\textcolor{blue}{3.1}}}(b,\sigma,f,g,T,p_0,\delta).$
4. Some properties of solutions to BSDEs and their associated PDEs
4.1. Malliavin weights
We use the SDE from (1) started in (t, x),
and recall the Malliavin weight and its properties from [Reference Geiss, Geiss and Gobet20, Subsection 1.1 and Remark 3].
Lemma 4.1. Let ![]() $H\,:\, {\mathbb{R}} \to {\mathbb{R}}$ be a polynomially bounded Borel function. If Assumption 2.1 holds and
$H\,:\, {\mathbb{R}} \to {\mathbb{R}}$ be a polynomially bounded Borel function. If Assumption 2.1 holds and ![]() $X^{t,x}$ is given by (36), then setting
$X^{t,x}$ is given by (36), then setting
implies that ![]() $G \in C^{1,2}([0,T)\times {\mathbb{R}} ).$ Specifically, it holds for
$G \in C^{1,2}([0,T)\times {\mathbb{R}} ).$ Specifically, it holds for ![]() $0 \le t \le r < T$ that
$0 \le t \le r < T$ that
where ![]() $({\mathcal{F}}^t_r)_{r\in [t,T]}$ is the augmented natural filtration of
$({\mathcal{F}}^t_r)_{r\in [t,T]}$ is the augmented natural filtration of ![]() $(B^{t,0}_r)_{r \in [t,T]},$
$(B^{t,0}_r)_{r \in [t,T]},$
and ![]() $\nabla X^{t,x}_s$ is given in (13). Moreover, for
$\nabla X^{t,x}_s$ is given in (13). Moreover, for ![]() $ q \in (0, \infty)$ there exists a
$ q \in (0, \infty)$ there exists a ![]() $\kappa_q>0$ such that
$\kappa_q>0$ such that
and we have
for ![]() $1<q,p < \infty$ with
$1<q,p < \infty$ with ![]() $\frac{1}{p} + \frac{1}{q} =1.$
$\frac{1}{p} + \frac{1}{q} =1.$
4.2. Regularity of solutions to BSDEs
The following result originates from [Reference Geiss, Geiss and Gobet20, Theorem 1], where path-dependent cases were also included. We formulate it only for our Markovian setting but use ![]() ${\mathbb{P}}_{t,x}$ since we are interested in an estimate for all
${\mathbb{P}}_{t,x}$ since we are interested in an estimate for all ![]() $(t,x) \in [0,T) \times {\mathbb{R}}.$ A sketch of a proof of this formulation can be found in [Reference Geiss, Labart and Luoto22].
$(t,x) \in [0,T) \times {\mathbb{R}}.$ A sketch of a proof of this formulation can be found in [Reference Geiss, Labart and Luoto22].
Theorem 4.1. Let Assumptions 2.1 and 2.2 hold. Then for any ![]() $p\in [2,\infty)$ the following assertions are true.
$p\in [2,\infty)$ the following assertions are true.
(i) There exists a constant
 $C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}} >0$ such that for
$C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}} >0$ such that for  $0\le t < s \le T$ and
$0\le t < s \le T$ and  $x\in {\mathbb{R}}$,
$x\in {\mathbb{R}}$,
 \begin{eqnarray*} \| Y_s - Y_t\|_{L_p({\mathbb{P}}_{t,x})} \le C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}} \Psi(x) \left ( \int_t^s (T-r)^{\alpha -1}dr \right )^{\frac{1}{2}}.\end{eqnarray*}
\begin{eqnarray*} \| Y_s - Y_t\|_{L_p({\mathbb{P}}_{t,x})} \le C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}} \Psi(x) \left ( \int_t^s (T-r)^{\alpha -1}dr \right )^{\frac{1}{2}}.\end{eqnarray*}(ii) There exists a constant
 $C^z_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}} >0$ such that for
$C^z_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}} >0$ such that for  $0\le t < s<T$ and
$0\le t < s<T$ and  $x\in {\mathbb{R}},$
$x\in {\mathbb{R}},$ \begin{eqnarray*} \| Z_s - Z_t\|_{L_p({\mathbb{P}}_{t,x})} \le C^z_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}} \Psi(x) \left ( \int_t^s (T-r)^{\alpha -2}dr \right )^{\frac{1}{2}}.\end{eqnarray*}
\begin{eqnarray*} \| Z_s - Z_t\|_{L_p({\mathbb{P}}_{t,x})} \le C^z_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}} \Psi(x) \left ( \int_t^s (T-r)^{\alpha -2}dr \right )^{\frac{1}{2}}.\end{eqnarray*}
The constants ![]() $ C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}$ and
$ C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}$ and ![]() $C^z_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}$ depend on
$C^z_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}$ depend on ![]() $ (L_f, K_f, C_g,c^{1,2}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \kappa_q, b,\sigma, T, p_0,p)$, and
$ (L_f, K_f, C_g,c^{1,2}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \kappa_q, b,\sigma, T, p_0,p)$, and ![]() $\Psi(x)$ is defined in (8).
$\Psi(x)$ is defined in (8).
4.3. Properties of the associated PDE
The theorem below collects properties of the solution to the PDE associated to the FBSDE (1). For a proof see [Reference Zhang43, Theorem 3.2], [Reference Zhang41], and [Reference Geiss, Labart and Luoto22, Theorem 5.4].
Theorem 4.2. Consider the FBSDE (1) and let Assumptions 2.1 and 2.2 hold. Then for the solution u of the associated PDE
 \begin{eqnarray} \left\{ \begin{array}{l} u_t(t,x) + \tfrac{\sigma^2(t,x)}{2} u_{xx}(t,x) + b(t,x) u_x(t,x) + f(t,x,u(t,x), \sigma(t,x) u_x(t,x)) =0,\\[3pt] t\in [0,T), \quad x\in {\mathbb{R}}, \\[3pt] u(T,x)=g(x) , \quad x \in {\mathbb{R}}, \end{array}\right . \end{eqnarray}
\begin{eqnarray} \left\{ \begin{array}{l} u_t(t,x) + \tfrac{\sigma^2(t,x)}{2} u_{xx}(t,x) + b(t,x) u_x(t,x) + f(t,x,u(t,x), \sigma(t,x) u_x(t,x)) =0,\\[3pt] t\in [0,T), \quad x\in {\mathbb{R}}, \\[3pt] u(T,x)=g(x) , \quad x \in {\mathbb{R}}, \end{array}\right . \end{eqnarray}we have the following:
(i)
 $Y_t=u(t,X_t)$ almost surely, where
$Y_t=u(t,X_t)$ almost surely, where  $u(t,x)={\mathbb{E}}_{t,x} \!\left (g(X_T)+\int_t^T\! f(r,X_r,Y_r,Z_r)dr \right )$, and
$u(t,x)={\mathbb{E}}_{t,x} \!\left (g(X_T)+\int_t^T\! f(r,X_r,Y_r,Z_r)dr \right )$, and  $|u(t,x)|\le c^1_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi(x)$ for
$|u(t,x)|\le c^1_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi(x)$ for  $\Psi$ given in (8), where
$\Psi$ given in (8), where  $c^{1}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}$ depends on
$c^{1}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}$ depends on  $L_f$,
$L_f$,  $K_f$,
$K_f$,  $C_g$, T, and
$C_g$, T, and  $p_0$, as well as on the bounds and Lipschitz constants of b and
$p_0$, as well as on the bounds and Lipschitz constants of b and  $\sigma$.
$\sigma$.(ii) (a)
 $\partial_x u$ exists and is continuous in
$\partial_x u$ exists and is continuous in  $[0,T)\times {\mathbb{R}}$.
$[0,T)\times {\mathbb{R}}$.(b)
 $Z^{t,x}_s= u_x(s,X_s^{t,x})\sigma(s,X_s^{t,x})$ almost surely.
$Z^{t,x}_s= u_x(s,X_s^{t,x})\sigma(s,X_s^{t,x})$ almost surely.(c)
where \begin{equation*}|u_x(t,x)|\le \frac{ c^2_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi(x)}{(T-t)^{\frac{1-\alpha}{2}}},\end{equation*}
\begin{equation*}|u_x(t,x)|\le \frac{ c^2_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi(x)}{(T-t)^{\frac{1-\alpha}{2}}},\end{equation*} $c^{2}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}$ depends on
$c^{2}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}$ depends on  $L_f$,
$L_f$,  $K_f$,
$K_f$,  $C_g$, T,
$C_g$, T,  $p_0$, and
$p_0$, and  $\kappa_2= \kappa_2(b,\sigma,T,\delta)$, as well as on the bounds and Lipschitz constants of b and
$\kappa_2= \kappa_2(b,\sigma,T,\delta)$, as well as on the bounds and Lipschitz constants of b and  $\sigma$, and hence
$\sigma$, and hence  $c^{2}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} = c^{2}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}(L_f, K_f, C_g,b,\sigma, T,p_0,\delta).$
$c^{2}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} = c^{2}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}(L_f, K_f, C_g,b,\sigma, T,p_0,\delta).$(iii) (a)
 $\partial^2_x u$ exists and is continuous in
$\partial^2_x u$ exists and is continuous in  $[0,T)\times {\mathbb{R}}$.
$[0,T)\times {\mathbb{R}}$.(b)
where \begin{equation*}|\partial^2_x u(t,x)|\le \frac{ c^3_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi(x)}{(T-t)^{1-\frac{\alpha}{2}}},\end{equation*}
\begin{equation*}|\partial^2_x u(t,x)|\le \frac{ c^3_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} \Psi(x)}{(T-t)^{1-\frac{\alpha}{2}}},\end{equation*} $c^{3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}$ depends on
$c^{3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}$ depends on  $L_f$,
$L_f$,  $C_g$, T,
$C_g$, T,  $p_0$,
$p_0$,  $\kappa_2= \kappa_2(b,\sigma,T,\delta)$,
$\kappa_2= \kappa_2(b,\sigma,T,\delta)$,  $C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}$, and
$C^y_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}$, and  $C^z_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}$, as well as on the bounds and Lipschitz constants of b and
$C^z_{\hyperref[The4.1]{\scriptstyle\textcolor{blue}{4.1}}}$, as well as on the bounds and Lipschitz constants of b and  $\sigma$, and hence
$\sigma$, and hence  $c^{3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} = c^{3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}(L_f, K_f, C_g,b,\sigma, T,p_0,\delta). $
$c^{3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}} = c^{3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}(L_f, K_f, C_g,b,\sigma, T,p_0,\delta). $
Using Assumption 2.3, we are now in a position to improve the bound on ![]() $\| Z_s - Z_t\|_{L_p({\mathbb{P}}_{t,x})}$ given in Theorem 4.1.
$\| Z_s - Z_t\|_{L_p({\mathbb{P}}_{t,x})}$ given in Theorem 4.1.
Proposition 4.1. If Assumption 2.3 holds, then there exists a constant ![]() $C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}} >0$ such that for
$C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}} >0$ such that for ![]() $0\le t < s \le T$ and
$0\le t < s \le T$ and ![]() $x\in {\mathbb{R}},$
$x\in {\mathbb{R}},$
where ![]() $C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}$ depends on
$C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}$ depends on ![]() $c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}$, b,
$c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}$, b, ![]() $\sigma$, f, g, T,
$\sigma$, f, g, T, ![]() $p_0$, and p, and hence
$p_0$, and p, and hence ![]() $C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}= C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}(b,\sigma, f,g,T,p_0,p,\delta).$
$C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}= C_{\hyperref[Pro4.1]{\scriptstyle\textcolor{blue}{4.1}}}(b,\sigma, f,g,T,p_0,p,\delta).$
Proof. From ![]() $Z^{t,x}_s= u_x(s,X_s^{t,x})\sigma(s,X_s^{t,x})$ and
$Z^{t,x}_s= u_x(s,X_s^{t,x})\sigma(s,X_s^{t,x})$ and
we conclude that
It is well-known (see e.g. [Reference El Karoui, Peng and Quenez19]) that the solution ![]() $\nabla Y$ of the linear BSDE
$\nabla Y$ of the linear BSDE
 \begin{align}\nabla Y_s = & g'(X_T) \nabla X_T + \int_{s}^T (f_x(\Theta_r) \nabla X_r + f_y(\Theta_r) \nabla Y_r + f_z(\Theta_r) \nabla Z_r) dr \notag\\[2pt] & - \int_{s}^T \nabla Z_r dB_r, \quad 0 \leq s \leq T,\end{align}
\begin{align}\nabla Y_s = & g'(X_T) \nabla X_T + \int_{s}^T (f_x(\Theta_r) \nabla X_r + f_y(\Theta_r) \nabla Y_r + f_z(\Theta_r) \nabla Z_r) dr \notag\\[2pt] & - \int_{s}^T \nabla Z_r dB_r, \quad 0 \leq s \leq T,\end{align}can be represented as
 \begin{align} \frac{\nabla Y_s}{\nabla X_s} & = {\mathbb{E}}_s \bigg[g'(X_T) \nabla X_T \Gamma^s_T + \int_{s}^T f_x(\Theta_r) \nabla X_r \Gamma^s_rdr \bigg] \frac{1}{\nabla X_s} \notag\\[2pt]
& = \tilde {\mathbb{E}}\bigg[g'(\tilde X^{s, X_s}_T) \nabla \tilde X^{s,X_s}_T \tilde \Gamma^{s,X_s}_T + \int_{s}^T f_x(\tilde \Theta^{s,X_s}_r) \nabla \tilde X^{s,X_s}_r \tilde \Gamma^{s,X_s}_rdr \bigg], \quad 0 \leq t \le s \leq T,\end{align}
\begin{align} \frac{\nabla Y_s}{\nabla X_s} & = {\mathbb{E}}_s \bigg[g'(X_T) \nabla X_T \Gamma^s_T + \int_{s}^T f_x(\Theta_r) \nabla X_r \Gamma^s_rdr \bigg] \frac{1}{\nabla X_s} \notag\\[2pt]
& = \tilde {\mathbb{E}}\bigg[g'(\tilde X^{s, X_s}_T) \nabla \tilde X^{s,X_s}_T \tilde \Gamma^{s,X_s}_T + \int_{s}^T f_x(\tilde \Theta^{s,X_s}_r) \nabla \tilde X^{s,X_s}_r \tilde \Gamma^{s,X_s}_rdr \bigg], \quad 0 \leq t \le s \leq T,\end{align}where ![]() $\Theta_r \coloneqq (r,X_r,Y_r,Z_r)$,
$\Theta_r \coloneqq (r,X_r,Y_r,Z_r)$, ![]() $\Gamma^s$ denotes the adjoint process given by
$\Gamma^s$ denotes the adjoint process given by
and
where ![]() $\tilde B$ denotes an independent copy of B. Notice that
$\tilde B$ denotes an independent copy of B. Notice that ![]() $\nabla X^{t,x}_t=1,$ so that
$\nabla X^{t,x}_t=1,$ so that
Then, by (39),
 \begin{eqnarray*}\| Z_s - Z_t\|_{L_p({\mathbb{P}}_{t,x})} &\le&C(\sigma) \bigg [ \bigg\|\frac{\nabla Y_s}{\nabla X_s} - \frac{\nabla Y_t}{\nabla X_t} \bigg\|_{L_{p}({\mathbb{P}}_{t,x})} \\[3pt] &&+ \|\nabla Y_t\|_{L_{2p}({\mathbb{P}}_{t,x})} [(s-t)^{\frac{1}{2}} \!+ \| X^{t,x}_s -x\|_{L_{2p}({\mathbb{P}}_{t,x})}] \bigg ].\end{eqnarray*}
\begin{eqnarray*}\| Z_s - Z_t\|_{L_p({\mathbb{P}}_{t,x})} &\le&C(\sigma) \bigg [ \bigg\|\frac{\nabla Y_s}{\nabla X_s} - \frac{\nabla Y_t}{\nabla X_t} \bigg\|_{L_{p}({\mathbb{P}}_{t,x})} \\[3pt] &&+ \|\nabla Y_t\|_{L_{2p}({\mathbb{P}}_{t,x})} [(s-t)^{\frac{1}{2}} \!+ \| X^{t,x}_s -x\|_{L_{2p}({\mathbb{P}}_{t,x})}] \bigg ].\end{eqnarray*}Since ![]() $(\nabla Y_s, \nabla Z_s)$ is the solution to the linear BSDE (40) with bounded
$(\nabla Y_s, \nabla Z_s)$ is the solution to the linear BSDE (40) with bounded ![]() $f_x, f_y, f_z,$ we have that
$f_x, f_y, f_z,$ we have that ![]() $\|\nabla Y_t\|_{L_{2p}({\mathbb{P}}_{t,x})} \le C(b,\sigma,f,g,T,p).$ Obviously,
$\|\nabla Y_t\|_{L_{2p}({\mathbb{P}}_{t,x})} \le C(b,\sigma,f,g,T,p).$ Obviously, ![]() $ \| X^{t,x}_s -x\|_{L_{2p}({\mathbb{P}}_{t,x})} \le C(b,\sigma,T,p) (s-t)^{\frac{1}{2}}.$ So it remains to show that
$ \| X^{t,x}_s -x\|_{L_{2p}({\mathbb{P}}_{t,x})} \le C(b,\sigma,T,p) (s-t)^{\frac{1}{2}}.$ So it remains to show that
We intend to use (41) in the following. There is a certain degree of freedom in how to connect B and ![]() $\tilde B$ in order to compute conditional expectations. Here, unlike in (27), we define the processes
$\tilde B$ in order to compute conditional expectations. Here, unlike in (27), we define the processes
as driving Brownian motions for ![]() $\tfrac{\nabla Y_s}{\nabla X_s}$ and
$\tfrac{\nabla Y_s}{\nabla X_s}$ and ![]() $\tfrac{\nabla Y_t}{\nabla X_t},$ respectively. This will especially simplify the estimate for
$\tfrac{\nabla Y_t}{\nabla X_t},$ respectively. This will especially simplify the estimate for ![]() $ \tilde {\mathbb{E}} |\tilde \Gamma^{s,X_s}_T -\tilde \Gamma^{t,x}_T|^ q $ below. From the above relations we get the following (with
$ \tilde {\mathbb{E}} |\tilde \Gamma^{s,X_s}_T -\tilde \Gamma^{t,x}_T|^ q $ below. From the above relations we get the following (with ![]() $X_s\coloneqq X^{t,x}_s $):
$X_s\coloneqq X^{t,x}_s $):
 \begin{align*}\bigg\|\frac{\nabla Y_s}{\nabla X_s} - \frac{\nabla Y_t}{\nabla X_t} \bigg\|_{L_{p}({\mathbb{P}}_{t,x})} & \leq \left \| \tilde {\mathbb{E}} \Big[g'(\tilde X^{s, X_s}_T) \nabla \tilde X^{s,X_s}_T \tilde \Gamma^{s,X_s}_T - g'(\tilde X^{t,x}_T) \nabla \tilde X^{t,x}_T \tilde \Gamma^{t,x}_T \Big] \right \|_p\\[2pt] & \quad + \int_t^s \left\| \tilde {\mathbb{E}} \Big[ f_x(\tilde \Theta^{t,x}_r) \nabla \tilde X^{t,x}_r \tilde \Gamma^{t,x}_r\Big]\right\|_p dr \\[2pt] & \quad +\left\| \int_s^T \tilde {\mathbb{E}} \Big[ f_x(\tilde \Theta^{s,X_s}_r) \nabla \tilde X^{s,X_s}_r\tilde \Gamma^{s,X_s}_r- f_x(\tilde \Theta^{t,x}_r) \nabla \tilde X^{t,x}_r \tilde \Gamma^{t,x}_r \Big] dr \right\|_p\\[2pt] & \eqqcolon J_1 + J_2 + J_3.\end{align*}
\begin{align*}\bigg\|\frac{\nabla Y_s}{\nabla X_s} - \frac{\nabla Y_t}{\nabla X_t} \bigg\|_{L_{p}({\mathbb{P}}_{t,x})} & \leq \left \| \tilde {\mathbb{E}} \Big[g'(\tilde X^{s, X_s}_T) \nabla \tilde X^{s,X_s}_T \tilde \Gamma^{s,X_s}_T - g'(\tilde X^{t,x}_T) \nabla \tilde X^{t,x}_T \tilde \Gamma^{t,x}_T \Big] \right \|_p\\[2pt] & \quad + \int_t^s \left\| \tilde {\mathbb{E}} \Big[ f_x(\tilde \Theta^{t,x}_r) \nabla \tilde X^{t,x}_r \tilde \Gamma^{t,x}_r\Big]\right\|_p dr \\[2pt] & \quad +\left\| \int_s^T \tilde {\mathbb{E}} \Big[ f_x(\tilde \Theta^{s,X_s}_r) \nabla \tilde X^{s,X_s}_r\tilde \Gamma^{s,X_s}_r- f_x(\tilde \Theta^{t,x}_r) \nabla \tilde X^{t,x}_r \tilde \Gamma^{t,x}_r \Big] dr \right\|_p\\[2pt] & \eqqcolon J_1 + J_2 + J_3.\end{align*}Since gʹ is Lipschitz continuous and of polynomial growth, we have
by Hölder’s inequality and the ![]() $L_q$-boundedness for any
$L_q$-boundedness for any ![]() $q >0$ of all the factors, as well as from the estimates for
$q >0$ of all the factors, as well as from the estimates for ![]() $ \tilde X^{s, X_s}_T - \tilde X^{t,x}_T$ and
$ \tilde X^{s, X_s}_T - \tilde X^{t,x}_T$ and ![]() $\nabla \tilde X^{s,X_s}_T - \nabla \tilde X^{t,x}_T $ as in Lemma 5.2. For the
$\nabla \tilde X^{s,X_s}_T - \nabla \tilde X^{t,x}_T $ as in Lemma 5.2. For the ![]() $\Gamma$ differences we first apply the inequalities of Hölder and BDG:
$\Gamma$ differences we first apply the inequalities of Hölder and BDG:
 \begin{align*} \tilde {\mathbb{E}} |\tilde \Gamma^{s,X_s}_T -\tilde \Gamma^{t,x}_T|^ q \le C(T,q)& \bigg [ (s-t)^{q-1} \tilde {\mathbb{E}} \int_t^s |f_y(\tilde \Theta^{s,X_s}_r) \tilde \Gamma^{s,X_s}_r|^q dr + \tilde {\mathbb{E}} \bigg(\int_t^s |f_z (\tilde \Theta^{s,X_s}_r) \tilde \Gamma^{s,X_s}_r |^2 dr \bigg)^\frac{q}{2} \\[3pt] &\quad + \tilde {\mathbb{E}} \int_s^T |f_y(\tilde \Theta^{s,X_s}_r) \tilde \Gamma^{s,X_s}_r - f_y(\tilde \Theta^{t,x}_r) \tilde \Gamma^{t,x}_r|^q dr \\[3pt] &\quad + \tilde {\mathbb{E}} \bigg( \int_s^T |f_z(\tilde \Theta^{s,X_s}_r) \tilde \Gamma^{s,X_s}_r- f_z(\tilde \Theta^{t,x}_r) \tilde \Gamma^{t,x}_r|^2 dr \bigg)^\frac{q}{2} \bigg ]. \end{align*}
\begin{align*} \tilde {\mathbb{E}} |\tilde \Gamma^{s,X_s}_T -\tilde \Gamma^{t,x}_T|^ q \le C(T,q)& \bigg [ (s-t)^{q-1} \tilde {\mathbb{E}} \int_t^s |f_y(\tilde \Theta^{s,X_s}_r) \tilde \Gamma^{s,X_s}_r|^q dr + \tilde {\mathbb{E}} \bigg(\int_t^s |f_z (\tilde \Theta^{s,X_s}_r) \tilde \Gamma^{s,X_s}_r |^2 dr \bigg)^\frac{q}{2} \\[3pt] &\quad + \tilde {\mathbb{E}} \int_s^T |f_y(\tilde \Theta^{s,X_s}_r) \tilde \Gamma^{s,X_s}_r - f_y(\tilde \Theta^{t,x}_r) \tilde \Gamma^{t,x}_r|^q dr \\[3pt] &\quad + \tilde {\mathbb{E}} \bigg( \int_s^T |f_z(\tilde \Theta^{s,X_s}_r) \tilde \Gamma^{s,X_s}_r- f_z(\tilde \Theta^{t,x}_r) \tilde \Gamma^{t,x}_r|^2 dr \bigg)^\frac{q}{2} \bigg ]. \end{align*}Since ![]() $f_y$ and
$f_y$ and ![]() $f_z$ are bounded we have
$f_z$ are bounded we have ![]() $\tilde {\mathbb{E}} | \tilde \Gamma^{s,X_s}_r|^q + \tilde {\mathbb{E}} |\tilde \Gamma^{t,x}_r |^q \le C(f,T,q). $ Similarly to (31), since
$\tilde {\mathbb{E}} | \tilde \Gamma^{s,X_s}_r|^q + \tilde {\mathbb{E}} |\tilde \Gamma^{t,x}_r |^q \le C(f,T,q). $ Similarly to (31), since ![]() $f_x, f_y,f_z$ are Lipschitz continuous with respect to the space variables,
$f_x, f_y,f_z$ are Lipschitz continuous with respect to the space variables,
 \begin{align*} |f_x(\tilde \Theta^{s,X_s}_r) - f_x(\tilde \Theta^{t,x}_r) |&= |f_x(r, \tilde X_r^{s,X_s}, u(r, \tilde X_r^{s,X_s}), \sigma(r, \tilde X_r^{s,X_s}) u_x(r, \tilde X_r^{s,X_s}) ) \\[3pt] & \quad - f_x(r, \tilde X_r^{t,x}, u(r, \tilde X_r^{t,x}), \sigma(r, \tilde X_r^{t,x}) u_x(r, \tilde X_r^{t,x}) )| \\[3pt] &\le C(c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \sigma, f, T) (1+|\tilde X_r^{s,X_s}|^{p_0+1}+|\tilde X_r^{t,x}|^{p_0+1}) \frac{|\tilde X_r^{s,X_s}-\tilde X_r^{t,x}|}{(T-r)^{\frac{1}{2}}}, \end{align*}
\begin{align*} |f_x(\tilde \Theta^{s,X_s}_r) - f_x(\tilde \Theta^{t,x}_r) |&= |f_x(r, \tilde X_r^{s,X_s}, u(r, \tilde X_r^{s,X_s}), \sigma(r, \tilde X_r^{s,X_s}) u_x(r, \tilde X_r^{s,X_s}) ) \\[3pt] & \quad - f_x(r, \tilde X_r^{t,x}, u(r, \tilde X_r^{t,x}), \sigma(r, \tilde X_r^{t,x}) u_x(r, \tilde X_r^{t,x}) )| \\[3pt] &\le C(c^{2,3}_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}, \sigma, f, T) (1+|\tilde X_r^{s,X_s}|^{p_0+1}+|\tilde X_r^{t,x}|^{p_0+1}) \frac{|\tilde X_r^{s,X_s}-\tilde X_r^{t,x}|}{(T-r)^{\frac{1}{2}}}, \end{align*}so that Lemma 5.2 yields
 \begin{equation*}\tilde {\mathbb{E}} |f_x(\tilde \Theta^{s,X_s}_r) -f_x(\tilde \Theta^{t,x}_r) |^q \le C(c_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}^{2,3}, b,\sigma, f, T,p_0,q) (1+|X_s|^{p_0+1}+|x|^{p_0+1})^q \frac{ |X_s-x|^q + |s-t|^\frac{q}{2}}{ (T-r)^{\frac{1}{2}}}.\end{equation*}
\begin{equation*}\tilde {\mathbb{E}} |f_x(\tilde \Theta^{s,X_s}_r) -f_x(\tilde \Theta^{t,x}_r) |^q \le C(c_{\hyperref[betterZ]{\scriptstyle\textcolor{blue}{4.2}}}^{2,3}, b,\sigma, f, T,p_0,q) (1+|X_s|^{p_0+1}+|x|^{p_0+1})^q \frac{ |X_s-x|^q + |s-t|^\frac{q}{2}}{ (T-r)^{\frac{1}{2}}}.\end{equation*}The same holds for ![]() $|f_y(\tilde \Theta^{s,X_s}_r) - f_y(\tilde \Theta^{t,x}_r) |$ and
$|f_y(\tilde \Theta^{s,X_s}_r) - f_y(\tilde \Theta^{t,x}_r) |$ and ![]() $|f_z(\tilde \Theta^{s,X_s}_r) - f_z(\tilde \Theta^{t,x}_r) |.$ Applying these inequalities and Gronwall’s lemma, we arrive at
$|f_z(\tilde \Theta^{s,X_s}_r) - f_z(\tilde \Theta^{t,x}_r) |.$ Applying these inequalities and Gronwall’s lemma, we arrive at
for ![]() $p> 0.$
$p> 0.$
For ![]() $J_2\le C (t-s)$ it is enough to realise that the integrand is bounded. The estimate for
$J_2\le C (t-s)$ it is enough to realise that the integrand is bounded. The estimate for ![]() $J_3$ follows similarly to that of
$J_3$ follows similarly to that of ![]() $J_1.$
$J_1.$
4.4. Properties of the solution to the finite difference equation
Recall the definition of ![]() $ \mathcal{D}^n_m$ given in (15). By (4),
$ \mathcal{D}^n_m$ given in (15). By (4),
so that
While for the solution to the PDE (38) one can observe in Theorem 4.2 the well-known smoothing property which implies that u is differentiable on ![]() $[0,T)\times {\mathbb{R}}$ even though g is only Hölder continuous, in the following proposition, for the solution
$[0,T)\times {\mathbb{R}}$ even though g is only Hölder continuous, in the following proposition, for the solution ![]() $u^n$ to the finite difference equation we have to require from g the same regularity as we want for
$u^n$ to the finite difference equation we have to require from g the same regularity as we want for ![]() $u^n.$
$u^n.$
Proposition 4.2. Let Assumption 2.3 hold and assume that ![]() $u^n$ is a solution of
$u^n$ is a solution of
 \begin{align} & u^n(t_m,x) -h f(t_{m+1}, x,u^n(t_m,x), \mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x})) \notag \\[2pt] &\quad= {\frac{1}{2}} [T_{_{m+1,+}} u^n(t_{m+1}, X_{t_{m+1}}^{n,t_m,x }) + T_{_{m+1,-}} u^n(t_{m+1}, X_{t_{m+1}}^{n,t_m,x })], \quad m = 0, \dots, n-1, \end{align}
\begin{align} & u^n(t_m,x) -h f(t_{m+1}, x,u^n(t_m,x), \mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x})) \notag \\[2pt] &\quad= {\frac{1}{2}} [T_{_{m+1,+}} u^n(t_{m+1}, X_{t_{m+1}}^{n,t_m,x }) + T_{_{m+1,-}} u^n(t_{m+1}, X_{t_{m+1}}^{n,t_m,x })], \quad m = 0, \dots, n-1, \end{align}with terminal condition ![]() $u^n(t_n,x)= g(x).$ Then, for sufficiently small h, the map
$u^n(t_n,x)= g(x).$ Then, for sufficiently small h, the map ![]() $x \mapsto u^n(t_m,x)$ is
$x \mapsto u^n(t_m,x)$ is ![]() $C^2,$ and it holds that
$C^2,$ and it holds that
and
uniformly in ![]() $ m=0,\dots,n-1$. The constants
$ m=0,\dots,n-1$. The constants ![]() $C_{u^n\!,1}$,
$C_{u^n\!,1}$, ![]() $C_{u^n\!,2}$, and
$C_{u^n\!,2}$, and ![]() $C_{u^n\!,3}$ depend on the bounds of f, g, b,
$C_{u^n\!,3}$ depend on the bounds of f, g, b, ![]() $\sigma$, and their derivatives, and on T and
$\sigma$, and their derivatives, and on T and ![]() $p_0$.
$p_0$.
Proof. Step 1. From (44), since g is ![]() $C^2$ and
$C^2$ and ![]() $f_y$ is bounded, for sufficiently small h we conclude by induction (backwards in time) that
$f_y$ is bounded, for sufficiently small h we conclude by induction (backwards in time) that ![]() $u^n_x(t_m,x)$ exists for
$u^n_x(t_m,x)$ exists for ![]() $m=0,\ldots,n-1,$ and that
$m=0,\ldots,n-1,$ and that
 \begin{align*}u_x^n(t_m,x)&=h f_x(t_{m+1}, x,u^n(t_m,x), \mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x})) \\[3pt] &\quad +h f_y(t_{m+1}, x,u^n(t_m,x), \mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x})) \, u_x^n(t_m,x) \\[3pt] &\quad +h f_z(t_{m+1}, x,u^n(t_m,x), \mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x})) \, \partial_x\mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x}) \\[3pt] &\quad +\tfrac{1}{2}\Big ( \partial_xT_{_{m+1,+}} u^n(t_{m+1}, X_{t_{m+1}}^{n,t_m,x }) + \partial_xT_{_{m+1,-}} u^n(t_{m+1}, X_{t_{m+1}}^{n,t_m,x} )\Big). \end{align*}
\begin{align*}u_x^n(t_m,x)&=h f_x(t_{m+1}, x,u^n(t_m,x), \mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x})) \\[3pt] &\quad +h f_y(t_{m+1}, x,u^n(t_m,x), \mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x})) \, u_x^n(t_m,x) \\[3pt] &\quad +h f_z(t_{m+1}, x,u^n(t_m,x), \mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x})) \, \partial_x\mathcal{D}^n_{m+1} u^n(t_{m+1},X_{t_{m+1}}^{n,t_m,x}) \\[3pt] &\quad +\tfrac{1}{2}\Big ( \partial_xT_{_{m+1,+}} u^n(t_{m+1}, X_{t_{m+1}}^{n,t_m,x }) + \partial_xT_{_{m+1,-}} u^n(t_{m+1}, X_{t_{m+1}}^{n,t_m,x} )\Big). \end{align*}Similarly one can show that ![]() $u^n_{xx}(t_m,x)$ exists and solves the derivative of the previous equation.
$u^n_{xx}(t_m,x)$ exists and solves the derivative of the previous equation.
Step 2. As stated in the proof of Proposition 2.1, the finite difference equation (44) is the associated equation to (9) in the sense that we have the representations (21). We will use that ![]() $u^n(t_m,x) =Y_{t_m}^{n,t_m,x}$ and exploit the BSDE
$u^n(t_m,x) =Y_{t_m}^{n,t_m,x}$ and exploit the BSDE
 \begin{align} Y_{t_m}^{n,t_m,x}&= g(X_T^{n,t_m,x}) +\int_{(t_m,T]} f(s,X^{n,t_m,x}_{s-},Y^{n,t_m,x}_{s-},Z^{n,t_m,x}_{s-})d[B^n]_s \notag \\[3pt] &\quad - \int_{(t_m,T]} Z^{n,t_m,x} _{s-} dB^n_s, \end{align}
\begin{align} Y_{t_m}^{n,t_m,x}&= g(X_T^{n,t_m,x}) +\int_{(t_m,T]} f(s,X^{n,t_m,x}_{s-},Y^{n,t_m,x}_{s-},Z^{n,t_m,x}_{s-})d[B^n]_s \notag \\[3pt] &\quad - \int_{(t_m,T]} Z^{n,t_m,x} _{s-} dB^n_s, \end{align}in which we will drop the superscript ![]() $t_m,x$ from now on. For
$t_m,x$ from now on. For ![]() $u^n_x(t_m,x)$ we will consider
$u^n_x(t_m,x)$ we will consider
 \begin{align} \nabla Y^n_{t_m}\coloneqq \partial_x Y_{t_m}^{n} &= g'(X_T^{n}) \partial_x X_T^{n} +\int_{(t_m,T]} f_x \partial_x X_{s-}^{n} + f_y \partial_x Y_{s-}^{n} + f_z \partial_x Z_{s-}^{n}d[B^n]_s \notag \\[3pt] & \quad -\int_{(t_m,T]} \partial_x Z_{s-}^{n} dB^n_s.\end{align}
\begin{align} \nabla Y^n_{t_m}\coloneqq \partial_x Y_{t_m}^{n} &= g'(X_T^{n}) \partial_x X_T^{n} +\int_{(t_m,T]} f_x \partial_x X_{s-}^{n} + f_y \partial_x Y_{s-}^{n} + f_z \partial_x Z_{s-}^{n}d[B^n]_s \notag \\[3pt] & \quad -\int_{(t_m,T]} \partial_x Z_{s-}^{n} dB^n_s.\end{align}Similarly as in the proof of [Reference Ma and Zhang30, Theorem 3.1], the BSDE (47) can be derived from (46) as a limit of difference quotients with respect to x. Notice that the generator of (47) is random but has the same Lipschitz constant and linear growth bound as f. Assumption 2.3 allows us to find a ![]() $p_0\ge 0$ and a
$p_0\ge 0$ and a ![]() $K>0$ such that
$K>0$ such that
In order to get estimates simultaneously for (46) and (47) we prove the following lemma.
Lemma 4.2. We fix n and assume a BSDE
with ![]() $\xi^n = g(X_T^{n,t_m,x}) $ or
$\xi^n = g(X_T^{n,t_m,x}) $ or ![]() $\xi^n = g'(X_T^{n,t_m,x}) \partial_x X_T^{n,t_m,x} $, and
$\xi^n = g'(X_T^{n,t_m,x}) \partial_x X_T^{n,t_m,x} $, and ![]() $\textsf{X}_s\coloneqq X_s^{n,t_m,x}$ or
$\textsf{X}_s\coloneqq X_s^{n,t_m,x}$ or ![]() $\textsf{X}_s\coloneqq \partial_x X_s^{n,t_m,x}$, such that
$\textsf{X}_s\coloneqq \partial_x X_s^{n,t_m,x}$, such that ![]() $\textsf{f}:\Omega \times [0,T] \times {\mathbb{R}}^3 \to {\mathbb{R}} $ is measurable and satisfies
$\textsf{f}:\Omega \times [0,T] \times {\mathbb{R}}^3 \to {\mathbb{R}} $ is measurable and satisfies
Then for any ![]() $p \ge 2,$
$p \ge 2,$
(i)
for \begin{equation*} {\mathbb{E}} |\textsf{Y}_{t_k}|^p + \frac{\gamma_p}{4} {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-}|^2 d[B^n]_s \le C\Psi^p(x)\end{equation*}
\begin{equation*} {\mathbb{E}} |\textsf{Y}_{t_k}|^p + \frac{\gamma_p}{4} {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-}|^2 d[B^n]_s \le C\Psi^p(x)\end{equation*} $k=m,\ldots,n$ and some
$k=m,\ldots,n$ and some  $\gamma_p>0,$
$\gamma_p>0,$(ii)
 $ {\mathbb{E}} \sup_{t_m < s \le T}|\textsf{Y}_{s-}|^p \le C \Psi^p(x), $ and
$ {\mathbb{E}} \sup_{t_m < s \le T}|\textsf{Y}_{s-}|^p \le C \Psi^p(x), $ and(iii)
 $ {\mathbb{E}} \Big ( \int_{(t_m,T]} |\textsf{Z}_{s-}|^2 d[B^n]_s \Big)^{\frac{p}{2}} \le C\Psi^p(x),$
$ {\mathbb{E}} \Big ( \int_{(t_m,T]} |\textsf{Z}_{s-}|^2 d[B^n]_s \Big)^{\frac{p}{2}} \le C\Psi^p(x),$
for some constant ![]() $ C=C(b,\sigma, f,g,T,p,p_0)$.
$ C=C(b,\sigma, f,g,T,p,p_0)$.
Proof.
(i) By Itô’s formula (see [Reference Jacod and Shiryaev25, Theorem 4.57]) we get for
 $p\ge 2$ that
(50)Following the proof of [Reference Kruse and Popier27, Proposition 2] (which is carried out there in the Lévy process setting but can be done also for martingales with jumps, like
$p\ge 2$ that
(50)Following the proof of [Reference Kruse and Popier27, Proposition 2] (which is carried out there in the Lévy process setting but can be done also for martingales with jumps, like \begin{align} |\textsf{Y}_{t_k}|^p& = | \xi^n|^p - p \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \textsf{Z}_{s-} dB^n_s \notag \\[3pt] &\quad + \ p \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-})d[B^n]_s \notag\\[3pt] &\quad - \sum_{s \in (t_k,T]} [|\textsf{Y}_s|^p - |\textsf{Y}_{s-}|^p - p \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} (\textsf{Y}_s-\textsf{Y}_{s-})].\end{align}
\begin{align} |\textsf{Y}_{t_k}|^p& = | \xi^n|^p - p \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \textsf{Z}_{s-} dB^n_s \notag \\[3pt] &\quad + \ p \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-})d[B^n]_s \notag\\[3pt] &\quad - \sum_{s \in (t_k,T]} [|\textsf{Y}_s|^p - |\textsf{Y}_{s-}|^p - p \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} (\textsf{Y}_s-\textsf{Y}_{s-})].\end{align} $B^n$) we can use the estimate
where
$B^n$) we can use the estimate
where \begin{eqnarray*} - \!\sum_{s \in (t_k,T]} [ |\textsf{Y}_s|^p \,{-}\, |\textsf{Y}_{s-}|^p \,{-}\, p \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} (\textsf{Y}_s\,{-}\,\textsf{Y}_{s-})]\le {-} \gamma_p \!\sum_{s \in (t_k,T]} |\textsf{Y}_{s-}|^{p-2} (\textsf{Y}_s{-}\textsf{Y}_{s-})^2,\end{eqnarray*}
\begin{eqnarray*} - \!\sum_{s \in (t_k,T]} [ |\textsf{Y}_s|^p \,{-}\, |\textsf{Y}_{s-}|^p \,{-}\, p \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} (\textsf{Y}_s\,{-}\,\textsf{Y}_{s-})]\le {-} \gamma_p \!\sum_{s \in (t_k,T]} |\textsf{Y}_{s-}|^{p-2} (\textsf{Y}_s{-}\textsf{Y}_{s-})^2,\end{eqnarray*} $\gamma_p >0$ is computed in [Reference Yao40, Lemma A4]. Since
we have
$\gamma_p >0$ is computed in [Reference Yao40, Lemma A4]. Since
we have \begin{equation*} \textsf{Y}_{t_{\ell+1}} - \textsf{Y}_{{t_{\ell+1}}-}=\textsf{f}(t_{\ell+1},\textsf{X}_{t_\ell},\textsf{Y}_{t_\ell}, \textsf{Z}_{t_\ell})h- \textsf{Z}_{t_\ell} \sqrt{h} {\varepsilon}_{\ell+1}\end{equation*}Hence we get from (50) that
\begin{equation*} \textsf{Y}_{t_{\ell+1}} - \textsf{Y}_{{t_{\ell+1}}-}=\textsf{f}(t_{\ell+1},\textsf{X}_{t_\ell},\textsf{Y}_{t_\ell}, \textsf{Z}_{t_\ell})h- \textsf{Z}_{t_\ell} \sqrt{h} {\varepsilon}_{\ell+1}\end{equation*}Hence we get from (50) that \begin{align*}& - \sum_{s \in (t_k,T]} [ |\textsf{Y}_s|^p - |\textsf{Y}_{s-}|^p - p \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} (\textsf{Y}_s-\textsf{Y}_{s-})] \\[3pt] &\quad\le - \gamma_p \,\sum_{\ell=k}^{n-1} |\textsf{Y}_{t_\ell} |^{p-2} \, \Big (\textsf{f}(t_{\ell+1},\textsf{X}_{t_\ell},\textsf{Y}_{t_\ell}, \textsf{Z}_{t_\ell})h - \textsf{Z}_{t_\ell} \sqrt{h} {\varepsilon}_{\ell+1} \Big)^2 \\[3pt] &\quad= - \gamma_p \, h \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, \textsf{f}^2(s,\textsf{X}_{s-},\textsf{Y}_{s-},\textsf{Z}_{s-})d[B^n]_s - \gamma_p \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-}|^2 d[B^n]_s \\[3pt] &\qquad + 2 \gamma_p \, \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-}) \textsf{Z}_{s-}(B^n_s-B^n_{s-}) d[B^n]_s.\end{align*}From Young’s inequality and (49) we conclude that there is a
\begin{align*}& - \sum_{s \in (t_k,T]} [ |\textsf{Y}_s|^p - |\textsf{Y}_{s-}|^p - p \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} (\textsf{Y}_s-\textsf{Y}_{s-})] \\[3pt] &\quad\le - \gamma_p \,\sum_{\ell=k}^{n-1} |\textsf{Y}_{t_\ell} |^{p-2} \, \Big (\textsf{f}(t_{\ell+1},\textsf{X}_{t_\ell},\textsf{Y}_{t_\ell}, \textsf{Z}_{t_\ell})h - \textsf{Z}_{t_\ell} \sqrt{h} {\varepsilon}_{\ell+1} \Big)^2 \\[3pt] &\quad= - \gamma_p \, h \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, \textsf{f}^2(s,\textsf{X}_{s-},\textsf{Y}_{s-},\textsf{Z}_{s-})d[B^n]_s - \gamma_p \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-}|^2 d[B^n]_s \\[3pt] &\qquad + 2 \gamma_p \, \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-}) \textsf{Z}_{s-}(B^n_s-B^n_{s-}) d[B^n]_s.\end{align*}From Young’s inequality and (49) we conclude that there is a \begin{align*} |\textsf{Y}_{t_k}|^p&\le | \xi^n|^p- p \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \textsf{Z}_{s-} dB^n_s \\[3pt] &\quad + p\int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \, \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-})d[B^n]_s \notag\\[3pt] &\quad - \gamma_p \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, |\textsf{Z}_{s-}|^2 d[B^n]_s \\[3pt] &\quad + 2 \gamma_p \, \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-}) \textsf{Z}_{s-}(B^n_s-B^n_{s-}) d[B^n]_s.\end{align*}
\begin{align*} |\textsf{Y}_{t_k}|^p&\le | \xi^n|^p- p \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \textsf{Z}_{s-} dB^n_s \\[3pt] &\quad + p\int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \, \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-})d[B^n]_s \notag\\[3pt] &\quad - \gamma_p \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, |\textsf{Z}_{s-}|^2 d[B^n]_s \\[3pt] &\quad + 2 \gamma_p \, \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-}) \textsf{Z}_{s-}(B^n_s-B^n_{s-}) d[B^n]_s.\end{align*} $ c'= c'(p,K_f,L_f, \gamma_p)>0$ such that
and for
$ c'= c'(p,K_f,L_f, \gamma_p)>0$ such that
and for \begin{eqnarray*} p|\textsf{Y}_{s-} |^{p-1}\, |\textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-},\textsf{Z}_{s-})|\le \tfrac{\gamma_p}{4} |\textsf{Y}_{s-} |^{p-2} \, |\textsf{Z}_{s-}|^2 + c'(1+| \textsf{X}_{s-}|^p + |\textsf{Y}_{s-} |^p),\end{eqnarray*}
\begin{eqnarray*} p|\textsf{Y}_{s-} |^{p-1}\, |\textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-},\textsf{Z}_{s-})|\le \tfrac{\gamma_p}{4} |\textsf{Y}_{s-} |^{p-2} \, |\textsf{Z}_{s-}|^2 + c'(1+| \textsf{X}_{s-}|^p + |\textsf{Y}_{s-} |^p),\end{eqnarray*} $ \sqrt{h} < \tfrac{1}{8 (L_f + K_f)}$ we find a
$ \sqrt{h} < \tfrac{1}{8 (L_f + K_f)}$ we find a  $c^{\prime\prime} =c^{\prime\prime}(p, L_f, K_f, \gamma_p )>0$ such that
Then for
$c^{\prime\prime} =c^{\prime\prime}(p, L_f, K_f, \gamma_p )>0$ such that
Then for \begin{align*} & 2 \gamma_p \, \sqrt{h} |\textsf{Y}_{s-} |^{p-2} \, |\textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-},\textsf{Z}_{s-})| | \textsf{Z}_{s-}| \le \tfrac{ \gamma_p}{4} |\textsf{Y}_{s-} |^{p-2} \, | \textsf{Z}_{s-}|^2\\[3pt] &\quad + c^{\prime\prime} \,(1+|\textsf{X}_{s-}|^p +|\textsf{Y}_{s-}|^p).\end{align*}
\begin{align*} & 2 \gamma_p \, \sqrt{h} |\textsf{Y}_{s-} |^{p-2} \, |\textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-},\textsf{Z}_{s-})| | \textsf{Z}_{s-}| \le \tfrac{ \gamma_p}{4} |\textsf{Y}_{s-} |^{p-2} \, | \textsf{Z}_{s-}|^2\\[3pt] &\quad + c^{\prime\prime} \,(1+|\textsf{X}_{s-}|^p +|\textsf{Y}_{s-}|^p).\end{align*} $c=c'+c^{\prime\prime}$ we have
(51)By standard methods, approximating the terminal condition and the generator by bounded functions, it follows that for any
$c=c'+c^{\prime\prime}$ we have
(51)By standard methods, approximating the terminal condition and the generator by bounded functions, it follows that for any \begin{align} |\textsf{Y}_{t_k}|^p&\le | \xi^n|^p - p \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2}\, \textsf{Z}_{s-} dB^n_s + c\int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p + |\textsf{Y}_{s-} |^p d[B^n]_s \notag\\[3pt] &\quad - \tfrac{\gamma_p}{2} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, |\textsf{Z}_{s-}|^2 d[B^n]_s.\end{align}
\begin{align} |\textsf{Y}_{t_k}|^p&\le | \xi^n|^p - p \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2}\, \textsf{Z}_{s-} dB^n_s + c\int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p + |\textsf{Y}_{s-} |^p d[B^n]_s \notag\\[3pt] &\quad - \tfrac{\gamma_p}{2} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} \, |\textsf{Z}_{s-}|^2 d[B^n]_s.\end{align} $a>0$,
Hence
$a>0$,
Hence \begin{equation*}{\mathbb{E}} \sup_{t_k \le s\le T} |\textsf{Y}_s|^a < \infty \quad \text{ and } \quad {\mathbb{E}} \bigg (\int_{(t_k,T]} |\textsf{Z}_{s-}|^2 d[B^n]_s \bigg)^{\frac{a}{2}}
< \infty.\end{equation*}
\begin{equation*}{\mathbb{E}} \sup_{t_k \le s\le T} |\textsf{Y}_s|^a < \infty \quad \text{ and } \quad {\mathbb{E}} \bigg (\int_{(t_k,T]} |\textsf{Z}_{s-}|^2 d[B^n]_s \bigg)^{\frac{a}{2}}
< \infty.\end{equation*} $ \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \textsf{Z}_{s-} dB^n_s$ has expectation zero. Taking the expectation in (51) yields
(52)Since
$ \int_{(t_k,T]} \textsf{Y}_{s-} |\textsf{Y}_{s-} |^{p-2} \textsf{Z}_{s-} dB^n_s$ has expectation zero. Taking the expectation in (51) yields
(52)Since \begin{align} &{\mathbb{E}} |\textsf{Y}_{t_k}|^p + \tfrac{\gamma_p}{2} {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-}|^{p-2} |\textsf{Z}_{s-}|^2 d[B^n]_s\le {\mathbb{E}}| \xi^n|^p \nonumber\\[3pt] &\quad + c {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p + |\textsf{Y}_{s-} |^p d[B^n]_s.\end{align}
\begin{align} &{\mathbb{E}} |\textsf{Y}_{t_k}|^p + \tfrac{\gamma_p}{2} {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-}|^{p-2} |\textsf{Z}_{s-}|^2 d[B^n]_s\le {\mathbb{E}}| \xi^n|^p \nonumber\\[3pt] &\quad + c {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p + |\textsf{Y}_{s-} |^p d[B^n]_s.\end{align} ${\mathbb{E}}| \xi^n|^p$ and
${\mathbb{E}}| \xi^n|^p$ and  $ {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p d[B^n]_s$ are polynomially bounded in x, Gronwall’s lemma gives
and inserting this into (52) yields
$ {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p d[B^n]_s$ are polynomially bounded in x, Gronwall’s lemma gives
and inserting this into (52) yields \begin{eqnarray*}&& {} \| \textsf{Y}_{t_k}\|_p \le C(b,\sigma, f,g, T,p,p_0) (1 + |x|^{ p_0+1}), \quad k=m,\ldots,n,\end{eqnarray*}
\begin{eqnarray*}&& {} \| \textsf{Y}_{t_k}\|_p \le C(b,\sigma, f,g, T,p,p_0) (1 + |x|^{ p_0+1}), \quad k=m,\ldots,n,\end{eqnarray*} \begin{align*} & \bigg ({\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-}|^2 d[B^n]_s \bigg )^\frac{1}{p} \le C(b,\sigma,f,g,T,p,p_0) (1 + |x|^{ p_0+1}),\\[3pt] &\quad k=m,\ldots,n-1.\end{align*}
\begin{align*} & \bigg ({\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-}|^2 d[B^n]_s \bigg )^\frac{1}{p} \le C(b,\sigma,f,g,T,p,p_0) (1 + |x|^{ p_0+1}),\\[3pt] &\quad k=m,\ldots,n-1.\end{align*}(ii) From (51) we derive by the inequality of BDG and Young’s inequality that for
 ${t_m \le t_k\,{\le}\,T}$,
We assume that h is sufficiently small so that we find a
${t_m \le t_k\,{\le}\,T}$,
We assume that h is sufficiently small so that we find a \begin{align*}& {\mathbb{E}} \sup_{t_k < s \le T}|\textsf{Y}_{s-}|^p \\[3pt]
&\quad \le {\mathbb{E}}| \xi^n|^p + C(p) {\mathbb{E}} \bigg ( \int_{(t_k,T]} |\textsf{Y}_{s-} |^{2p-2} |\textsf{Z}_{s-} |^2 d[B^n]_s\bigg)^{\frac{1}{2}}\\[3pt]
&\qquad +c{\mathbb{E}} \int_{(t_k,T]}1+| \textsf{X}_{s-}|^p + |\textsf{Y}_{s-} |^p d[B^n]_s \notag\\
&\quad \le {\mathbb{E}}| \xi^n|^p + c {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p d[B^n]_s \notag\\[2pt]
&\qquad + C(p) {\mathbb{E}} \left [ \sup_{t_k < s \le T} |\textsf{Y}_{s-} |^{\frac{p}{2}} \left ( \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-} |^2 d[B^n]_s\right )^{\frac{1}{2}} \right ]\\[3pt]
&\qquad + c {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^pd[B^n]_s \\[3pt] &\quad \le {\mathbb{E}}| \xi^n|^p + c {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p d[B^n]_s + C(p) {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-} |^2 d[B^n]_s \\[3pt] &\qquad + {\mathbb{E}} \sup_{t_k
< s \le T} |\textsf{Y}_{s-} |^p( \tfrac{1}{4} + c (T-t_k)).\end{align*}
\begin{align*}& {\mathbb{E}} \sup_{t_k < s \le T}|\textsf{Y}_{s-}|^p \\[3pt]
&\quad \le {\mathbb{E}}| \xi^n|^p + C(p) {\mathbb{E}} \bigg ( \int_{(t_k,T]} |\textsf{Y}_{s-} |^{2p-2} |\textsf{Z}_{s-} |^2 d[B^n]_s\bigg)^{\frac{1}{2}}\\[3pt]
&\qquad +c{\mathbb{E}} \int_{(t_k,T]}1+| \textsf{X}_{s-}|^p + |\textsf{Y}_{s-} |^p d[B^n]_s \notag\\
&\quad \le {\mathbb{E}}| \xi^n|^p + c {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p d[B^n]_s \notag\\[2pt]
&\qquad + C(p) {\mathbb{E}} \left [ \sup_{t_k < s \le T} |\textsf{Y}_{s-} |^{\frac{p}{2}} \left ( \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-} |^2 d[B^n]_s\right )^{\frac{1}{2}} \right ]\\[3pt]
&\qquad + c {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^pd[B^n]_s \\[3pt] &\quad \le {\mathbb{E}}| \xi^n|^p + c {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p d[B^n]_s + C(p) {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-} |^2 d[B^n]_s \\[3pt] &\qquad + {\mathbb{E}} \sup_{t_k
< s \le T} |\textsf{Y}_{s-} |^p( \tfrac{1}{4} + c (T-t_k)).\end{align*} $t_k$ with
$t_k$ with  $c (T-t_k) < \tfrac{1}{4}.$ We rearrange the inequality to have
$c (T-t_k) < \tfrac{1}{4}.$ We rearrange the inequality to have  $ {\mathbb{E}} \sup_{t_k < s \le T} |\textsf{Y}_{s-} |^p$ on the left-hand side, and from (i) we conclude that
Now we may repeat the above step for
$ {\mathbb{E}} \sup_{t_k < s \le T} |\textsf{Y}_{s-} |^p$ on the left-hand side, and from (i) we conclude that
Now we may repeat the above step for \begin{align*} {\mathbb{E}} \sup_{t_k
< s \le T}|\textsf{Y}_{s-}|^p &\le 2 {\mathbb{E}} | \xi^n|^p + 2c {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p d[B^n]_s \\[3pt] &\quad + 2C(p) {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-} |^2 d[B^n]_s \\[3pt] &\le C(b,\sigma, f,g, T,p,p_0) (1+|x|^{(p_0+1)p}). \end{align*}
\begin{align*} {\mathbb{E}} \sup_{t_k
< s \le T}|\textsf{Y}_{s-}|^p &\le 2 {\mathbb{E}} | \xi^n|^p + 2c {\mathbb{E}} \int_{(t_k,T]} 1+| \textsf{X}_{s-}|^p d[B^n]_s \\[3pt] &\quad + 2C(p) {\mathbb{E}} \int_{(t_k,T]} |\textsf{Y}_{s-} |^{p-2} |\textsf{Z}_{s-} |^2 d[B^n]_s \\[3pt] &\le C(b,\sigma, f,g, T,p,p_0) (1+|x|^{(p_0+1)p}). \end{align*} ${\mathbb{E}} \sup_{t_\ell < s \le t_k}|\textsf{Y}_{s-}|^p$ with
${\mathbb{E}} \sup_{t_\ell < s \le t_k}|\textsf{Y}_{s-}|^p$ with  $c (t_k-t_\ell) < \tfrac{1}{4}$ and
$c (t_k-t_\ell) < \tfrac{1}{4}$ and  $\xi^n=\textsf{Y}_T$ replaced by
$\xi^n=\textsf{Y}_T$ replaced by  $\textsf{Y}_{t_k},$ and continue doing so until we eventually get the assertion (ii).
$\textsf{Y}_{t_k},$ and continue doing so until we eventually get the assertion (ii).(iii) We proceed from (48):
so that by (49) and the inequalities of BDG and Hölder we have that \begin{align*} &\sup_{k\le \ell\le n} \Big | \int_{(t_\ell,T]} \textsf{Z}_{s-} dB^n_s \Big|^p\\[3pt] &\quad \le C(p) \bigg ( | \xi^n|^p + \sup_{k\le \ell \le n} |\textsf{Y}_{t_\ell}|^p + \Big |\int_{(t_k,T]} | \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-}) | \,d[B^n]_s\Big |^p \bigg),\end{align*}Hence for
\begin{align*} &\sup_{k\le \ell\le n} \Big | \int_{(t_\ell,T]} \textsf{Z}_{s-} dB^n_s \Big|^p\\[3pt] &\quad \le C(p) \bigg ( | \xi^n|^p + \sup_{k\le \ell \le n} |\textsf{Y}_{t_\ell}|^p + \Big |\int_{(t_k,T]} | \textsf{f}(s,\textsf{X}_{s-},\textsf{Y}_{s-}, \textsf{Z}_{s-}) | \,d[B^n]_s\Big |^p \bigg),\end{align*}Hence for \begin{align*}& {\mathbb{E}} \bigg ( \int_{(t_k,T]} |\textsf{Z}_{s-}|^2 d[B^n]_s \bigg)^{\frac{p}{2}} \\[2pt]
&\quad\le C(p) \bigg ( {\mathbb{E}} | \xi^n|^p + {\mathbb{E}} \sup_{k\le \ell\le n} | \textsf{Y}_{t_\ell}|^p \bigg) +C(p,L_f,K_f) {\mathbb{E}} \bigg(\int_{(t_k,T]} 1+|\textsf{X}_{s-}|+| \textsf{Y}_{s-}|d[B^n]_s\bigg)^p \\[2pt]
&\qquad +C(p,L_f,K_f) (T-t_k)^{\frac{p}{2}} {\mathbb{E}} \left (\int_{(t_k,T]} |\textsf{Z}_{s-}|^2d[B^n]_s\right )^{\frac{p}{2}}. \end{align*}
\begin{align*}& {\mathbb{E}} \bigg ( \int_{(t_k,T]} |\textsf{Z}_{s-}|^2 d[B^n]_s \bigg)^{\frac{p}{2}} \\[2pt]
&\quad\le C(p) \bigg ( {\mathbb{E}} | \xi^n|^p + {\mathbb{E}} \sup_{k\le \ell\le n} | \textsf{Y}_{t_\ell}|^p \bigg) +C(p,L_f,K_f) {\mathbb{E}} \bigg(\int_{(t_k,T]} 1+|\textsf{X}_{s-}|+| \textsf{Y}_{s-}|d[B^n]_s\bigg)^p \\[2pt]
&\qquad +C(p,L_f,K_f) (T-t_k)^{\frac{p}{2}} {\mathbb{E}} \left (\int_{(t_k,T]} |\textsf{Z}_{s-}|^2d[B^n]_s\right )^{\frac{p}{2}}. \end{align*} $C(p,L_f,K_f) (T-t_k)^{\frac{p}{2}} <{\frac{1}{2}}$ we derive from the assertion (ii) and from the growth properties of the other terms that
(53)Repeating this procedure eventually yields (iii).
$C(p,L_f,K_f) (T-t_k)^{\frac{p}{2}} <{\frac{1}{2}}$ we derive from the assertion (ii) and from the growth properties of the other terms that
(53)Repeating this procedure eventually yields (iii). \begin{align} {\mathbb{E}} \bigg ( \int_{(t_k,T]} |{\textsf{Z}_{s-}}|^2 d[B^n]_s \bigg)^{\frac{p}{2}} \le C(b,\sigma, f,g,T,p,p_0) (1+|x|^{(p_0+1)p}).\end{align}
\begin{align} {\mathbb{E}} \bigg ( \int_{(t_k,T]} |{\textsf{Z}_{s-}}|^2 d[B^n]_s \bigg)^{\frac{p}{2}} \le C(b,\sigma, f,g,T,p,p_0) (1+|x|^{(p_0+1)p}).\end{align}
Step 3. Applying Lemma 4.2 to (46) and (47) we see that for all ![]() $m =0,\ldots,n$ we have
$m =0,\ldots,n$ we have
and
Our next aim is to show that ![]() $u^n_{xx}(t_m,x)$ is locally Lipschitz in x. We first show that
$u^n_{xx}(t_m,x)$ is locally Lipschitz in x. We first show that ![]() $u^n_{xx}(t_m,x)$ has polynomial growth. We introduce the BSDE which describes
$u^n_{xx}(t_m,x)$ has polynomial growth. We introduce the BSDE which describes ![]() $u^n_{xx}(t_m,x)$, for simplicity writing
$u^n_{xx}(t_m,x)$, for simplicity writing
and consider
 \begin{align} \partial_x^2 Y_{t_m}^{n}&=g^{\prime\prime}(X_T^{n}) ( \partial_x X_T^{n})^2 + g'(X_T^{n}) \partial_x^2 X_T^{n} \notag\\[3pt] & \quad+\int_{(t_m,T]} \sum_{\substack{a \in \{0,1,2\}^3 \\ i_1+i_2+i_3=2}} (D^a f)(s,X_{s-}^{n},Y^{n}_{s-},Z^{n}_{s-}) (\partial_x X_{s-}^{n})^{i_1} (\partial_x Y^{n}_{s-})^{i_2} (\partial_x Z^{n}_{s-})^{i_3} d[B^n]_s \notag \\[3pt] &\quad + \int_{(t_m,T]} \sum_{\substack{a \in \{0, 1\}^3\\ i_1+i_2+i_3=1}} (D^a f)(s,X_{s-}^{n},Y^{n}_{s-},Z^{n}_{s-}) (\partial_x^2 X_{s-}^{n})^{i_1} (\partial_x^2 Y^{n}_{s-})^{i_2} (\partial_x^2 Z^{n}_{s-})^{i_3} d[B^n]_s \notag \\[3pt] &\quad -\int_{(t_m,T]} \partial_x^2 Z^n_{s-} dB^n_s.\end{align}
\begin{align} \partial_x^2 Y_{t_m}^{n}&=g^{\prime\prime}(X_T^{n}) ( \partial_x X_T^{n})^2 + g'(X_T^{n}) \partial_x^2 X_T^{n} \notag\\[3pt] & \quad+\int_{(t_m,T]} \sum_{\substack{a \in \{0,1,2\}^3 \\ i_1+i_2+i_3=2}} (D^a f)(s,X_{s-}^{n},Y^{n}_{s-},Z^{n}_{s-}) (\partial_x X_{s-}^{n})^{i_1} (\partial_x Y^{n}_{s-})^{i_2} (\partial_x Z^{n}_{s-})^{i_3} d[B^n]_s \notag \\[3pt] &\quad + \int_{(t_m,T]} \sum_{\substack{a \in \{0, 1\}^3\\ i_1+i_2+i_3=1}} (D^a f)(s,X_{s-}^{n},Y^{n}_{s-},Z^{n}_{s-}) (\partial_x^2 X_{s-}^{n})^{i_1} (\partial_x^2 Y^{n}_{s-})^{i_2} (\partial_x^2 Z^{n}_{s-})^{i_3} d[B^n]_s \notag \\[3pt] &\quad -\int_{(t_m,T]} \partial_x^2 Z^n_{s-} dB^n_s.\end{align}We denote the generator of this BSDE by ![]() $\hat f$ and notice that it is of the structure
$\hat f$ and notice that it is of the structure
Here ![]() $f_0(\omega, t)$ denotes the integrand of the first integral on the right-hand side of (55), and from the previous results one concludes that
$f_0(\omega, t)$ denotes the integrand of the first integral on the right-hand side of (55), and from the previous results one concludes that ![]() ${\mathbb{E}} (\!\int_{(t_m,T]} |f_0(s-\!)| d[B^n]_s)^p < \infty.$ The functions
${\mathbb{E}} (\!\int_{(t_m,T]} |f_0(s-\!)| d[B^n]_s)^p < \infty.$ The functions ![]() $f_1(t) = (D^{(1,0,0)} f)(t, \cdot) = (\partial_x f)(t, \cdot)$,
$f_1(t) = (D^{(1,0,0)} f)(t, \cdot) = (\partial_x f)(t, \cdot)$, ![]() $f_2(t) = (\partial_y f)(t, \cdot)$, and
$f_2(t) = (\partial_y f)(t, \cdot)$, and ![]() $f_3(t) = (\partial_z f)(t, \cdot)$ are bounded by our assumptions. We put
$f_3(t) = (\partial_z f)(t, \cdot)$ are bounded by our assumptions. We put
Denoting the solution by ![]() $(\hat{\textsf{Y}}, \hat{\textsf{Z}})$, we get for
$(\hat{\textsf{Y}}, \hat{\textsf{Z}})$, we get for ![]() $C(f_3 ) (T-t_m) \le \tfrac{1}{2}$ that
$C(f_3 ) (T-t_m) \le \tfrac{1}{2}$ that
 \begin{eqnarray} && {} {\mathbb{E}} |\hat{\textsf{Y}}_{t_m}|^2 + {\frac{1}{2}} {\mathbb{E}} \int_{(t_m,T]} |\hat{\textsf{Z}}_{s-}|^2 d[B^n]_s \notag\\&
\le\,& C \bigg [ {\mathbb{E}} |\hat \xi^n|^2 + {\mathbb{E}} \bigg (\int_{(t_m,T]} |f_0( s-) | d[B^n]_s \bigg )^2 + {\mathbb{E}} \int_{(t_m,T]} |\hat{\textsf{X}}_{s-}|^2 + |\hat{\textsf{Y}}_{s-} |^2 d[B^n]_s \bigg].\end{eqnarray}
\begin{eqnarray} && {} {\mathbb{E}} |\hat{\textsf{Y}}_{t_m}|^2 + {\frac{1}{2}} {\mathbb{E}} \int_{(t_m,T]} |\hat{\textsf{Z}}_{s-}|^2 d[B^n]_s \notag\\&
\le\,& C \bigg [ {\mathbb{E}} |\hat \xi^n|^2 + {\mathbb{E}} \bigg (\int_{(t_m,T]} |f_0( s-) | d[B^n]_s \bigg )^2 + {\mathbb{E}} \int_{(t_m,T]} |\hat{\textsf{X}}_{s-}|^2 + |\hat{\textsf{Y}}_{s-} |^2 d[B^n]_s \bigg].\end{eqnarray}Now we derive the polynomial growth ![]() ${\mathbb{E}} | \hat \xi^n|^2 \le C \Psi^2(x) $ from the properties of gʹ and gʹʹ and from the fact that
${\mathbb{E}} | \hat \xi^n|^2 \le C \Psi^2(x) $ from the properties of gʹ and gʹʹ and from the fact that ![]() ${\mathbb{E}} \sup_{t_m< s \le T} |\partial^j_x X_{s}^{n}|^p$ is bounded for
${\mathbb{E}} \sup_{t_m< s \le T} |\partial^j_x X_{s}^{n}|^p$ is bounded for ![]() $j=1,2$ under our assumptions. Then the estimate
$j=1,2$ under our assumptions. Then the estimate
can be derived from Lemma 4.2 Parts (ii) and (iii), so that Gronwall’s lemma implies
Finally, to show (45), one uses (55) and derives an inequality as in (56), but now for the difference ![]() $\partial_x^2 Y_{t_m}^{n,t_m,x}-\partial_x^2 Y_{t_m}^{n,t_m,\bar x}.$
$\partial_x^2 Y_{t_m}^{n,t_m,x}-\partial_x^2 Y_{t_m}^{n,t_m,\bar x}.$
Before proving (45), let us state the following lemma.
Lemma 4.3 Let Assumption 2.3 hold. We have
for some constant ![]() $C=C(b,\sigma,f,g,T,p,p_0)$.
$C=C(b,\sigma,f,g,T,p,p_0)$.
Proof of Lemma 4.3. Proof of (58): Introduce ![]() $G(t_{k+1}, x) \coloneqq \mathcal{D}^n_{k+1} u^n(t_{k+1}, X^{n,t_k,x}_{t_{k+1}})$. Using the relations (42)–(43) and the bounds (54) and (57) for
$G(t_{k+1}, x) \coloneqq \mathcal{D}^n_{k+1} u^n(t_{k+1}, X^{n,t_k,x}_{t_{k+1}})$. Using the relations (42)–(43) and the bounds (54) and (57) for ![]() $u^n_x$ and
$u^n_x$ and ![]() $u^n_{xx}$, respectively, one obtains
$u^n_{xx}$, respectively, one obtains
uniformly in ![]() $t_{k+1}$. Since
$t_{k+1}$. Since ![]() $Z^{n,t_m,x}_{t_k} = \mathcal{D}^n_{k+1} u^n(t_{k+1}, X^{n,t_k, \eta}_{t_{k+1}}) = G(t_{k+1}, \eta)$, where
$Z^{n,t_m,x}_{t_k} = \mathcal{D}^n_{k+1} u^n(t_{k+1}, X^{n,t_k, \eta}_{t_{k+1}}) = G(t_{k+1}, \eta)$, where ![]() $\eta = X^{n,t_m,x}_{t_k}$, the previous bound yields
$\eta = X^{n,t_m,x}_{t_k}$, the previous bound yields
uniformly for each ![]() $t_m \leq t_k < T$. The inequality (58) then follows by applying the Cauchy–Schwarz inequality and standard
$t_m \leq t_k < T$. The inequality (58) then follows by applying the Cauchy–Schwarz inequality and standard ![]() $L_p$-estimates for the process
$L_p$-estimates for the process ![]() $X^n$.
$X^n$.
Proof of (59): This can be shown similarly to Lemma 4.2(iii), by considering the BSDE for the difference ![]() $\partial_x Y_{t_m}^{n,t_m,x}-\partial_x Y_{t_m}^{n,t_m,\bar x}$ instead of (47) itself.
$\partial_x Y_{t_m}^{n,t_m,x}-\partial_x Y_{t_m}^{n,t_m,\bar x}$ instead of (47) itself.
Proof of (60): This can again be shown by repeating the proof of Lemma 4.2(iii), but now for the BSDE (55).
We return to the main proof. By our assumptions we have
where we use ![]() $|x-\bar x|^2 \le C(1+|x|^2+|\bar x|^2) |x-\bar x|^{2\alpha}.$ (The term
$|x-\bar x|^2 \le C(1+|x|^2+|\bar x|^2) |x-\bar x|^{2\alpha}.$ (The term ![]() $|x-\bar x|^2$ appears, for example, in the estimate of
$|x-\bar x|^2$ appears, for example, in the estimate of ![]() $(\partial_x X_T^{n,t_m,x })^2 - ( \partial_x X_T^{n,t_m, \bar x })^2$.) To see that
$(\partial_x X_T^{n,t_m,x })^2 - ( \partial_x X_T^{n,t_m, \bar x })^2$.) To see that
we check the terms with the highest polynomial growth. We have to deal with terms like
and
for example. We bound the first term by using (53) and (58):
 \begin{eqnarray*} && {} {\mathbb{E}} \bigg (\int_{(t_m,T]} | Z^{n,t_m,x}_{s-}- Z^{n,t_m,\bar x}_{s-} | \,|\partial_xZ^{n,t_m,x}_{s-}|^{2} d[B^n]_s \bigg )^2 \\[3pt]
&&\quad\le\, \bigg( {\mathbb{E}} \sup_s | Z^{n,t_m,x}_{s-}- Z^{n,t_m,\bar x}_{s-} |^4 \bigg)^{\frac{1}{2}} \bigg ({\mathbb{E}} \bigg (\int_{(t_m,T]} |\partial_x Z^{n,t_m,x}_{s-}|^{2} d[B^n]_s \bigg )^4 \bigg )^{\frac{1}{2}}\\[3pt] &&\quad\le\, C( \Psi^4(x) + \Psi^4(\bar x) )|x-\bar x|^2 \Psi^4(x). \end{eqnarray*}
\begin{eqnarray*} && {} {\mathbb{E}} \bigg (\int_{(t_m,T]} | Z^{n,t_m,x}_{s-}- Z^{n,t_m,\bar x}_{s-} | \,|\partial_xZ^{n,t_m,x}_{s-}|^{2} d[B^n]_s \bigg )^2 \\[3pt]
&&\quad\le\, \bigg( {\mathbb{E}} \sup_s | Z^{n,t_m,x}_{s-}- Z^{n,t_m,\bar x}_{s-} |^4 \bigg)^{\frac{1}{2}} \bigg ({\mathbb{E}} \bigg (\int_{(t_m,T]} |\partial_x Z^{n,t_m,x}_{s-}|^{2} d[B^n]_s \bigg )^4 \bigg )^{\frac{1}{2}}\\[3pt] &&\quad\le\, C( \Psi^4(x) + \Psi^4(\bar x) )|x-\bar x|^2 \Psi^4(x). \end{eqnarray*}We bound the second term by using (53) and (59):
 \begin{align*} & {\mathbb{E}} \bigg (\int_{(t_m,T]} |\partial_x Z^{n,t_m,x}_{s-}|^2- |\partial_x Z^{n,t_m, \bar x}_{s-}|^{2} d[B^n]_s \bigg )^2 \\[3pt] &\quad\le C {\mathbb{E}} \int_{(t_m,T]} |\partial_x Z^{n,t_m,x}_{s-}|^2+ |\partial_x Z^{n,t_m, \bar x}_{s-}|^{2} d[B^n]_s \int_{(t_m,T]} |\partial_x Z^{n,t_m,x}_{s-}- \partial_x Z^{n,t_m, \bar x}_{s-}|^{2} d[B^n]_s \\[3pt] &\quad\le C( \Psi^2(x) + \Psi^2(\bar x) ) ( \Psi^8(x) + \Psi^8(\bar x) )|x-\bar x|^2 \\ &\quad\le C( \Psi^{10}(x) + \Psi^{10}(\bar x) ) (|x|^{2-2\alpha} +|\bar x|^{2-2\alpha}) |x-\bar x|^{2\alpha} \\[3pt] &\quad\le C( \Psi^{10}(x) + \Psi^{10}(\bar x) ) (1+|x|^{2} +|\bar x|^{2}) |x-\bar x|^{2\alpha}. \end{align*}
\begin{align*} & {\mathbb{E}} \bigg (\int_{(t_m,T]} |\partial_x Z^{n,t_m,x}_{s-}|^2- |\partial_x Z^{n,t_m, \bar x}_{s-}|^{2} d[B^n]_s \bigg )^2 \\[3pt] &\quad\le C {\mathbb{E}} \int_{(t_m,T]} |\partial_x Z^{n,t_m,x}_{s-}|^2+ |\partial_x Z^{n,t_m, \bar x}_{s-}|^{2} d[B^n]_s \int_{(t_m,T]} |\partial_x Z^{n,t_m,x}_{s-}- \partial_x Z^{n,t_m, \bar x}_{s-}|^{2} d[B^n]_s \\[3pt] &\quad\le C( \Psi^2(x) + \Psi^2(\bar x) ) ( \Psi^8(x) + \Psi^8(\bar x) )|x-\bar x|^2 \\ &\quad\le C( \Psi^{10}(x) + \Psi^{10}(\bar x) ) (|x|^{2-2\alpha} +|\bar x|^{2-2\alpha}) |x-\bar x|^{2\alpha} \\[3pt] &\quad\le C( \Psi^{10}(x) + \Psi^{10}(\bar x) ) (1+|x|^{2} +|\bar x|^{2}) |x-\bar x|^{2\alpha}. \end{align*}While all the other terms can be easily estimated using the results we have obtained already, for
 \begin{align*}{\mathbb{E}} \bigg ( &\int_{(t_m,T]} |(f_3^{t_m,x} (s-\!) -f_3^{t_m,\bar x}(s-\!))\partial^2_x Z^{n,t_m,x}_{s-} |d[B^n]_s \bigg)^2 \\[3pt] &\le\, C( \Psi^{12}(x) + \Psi^{12}(\bar x) ) (1+|x|^{2} +|\bar x|^{2}) |x-\bar x|^{2\alpha}\end{align*}
\begin{align*}{\mathbb{E}} \bigg ( &\int_{(t_m,T]} |(f_3^{t_m,x} (s-\!) -f_3^{t_m,\bar x}(s-\!))\partial^2_x Z^{n,t_m,x}_{s-} |d[B^n]_s \bigg)^2 \\[3pt] &\le\, C( \Psi^{12}(x) + \Psi^{12}(\bar x) ) (1+|x|^{2} +|\bar x|^{2}) |x-\bar x|^{2\alpha}\end{align*}we need the bound (60).
The result then follows from Gronwall’s lemma.
Remark 4.1. Under Assumption 2.3 we conclude that by Proposition 4.2 there exists a constant ![]() $C = C(b,\sigma, f,g, T,p,p_0) > 0$ such that
$C = C(b,\sigma, f,g, T,p,p_0) > 0$ such that
 \begin{align} |u^n(t_m,x) - u^n(t_m,\bar x) | &\le C( 1+ \Psi(x) + \Psi(\bar x))|x-\bar{x}|, \notag \\[3pt] |\mathcal{D}^n_{m+1} u^n(t_{m+1},X^{n,t_m,x}_{t_{m+1}})-\mathcal{D}^n_{m+1} u^n(t_{m+1},X^{n,t_m,x}_{t_{m+1}})| &\le C( 1+ \Psi^2(x) + \Psi^2(\bar x))|x-\bar{x}|, \notag \\[3pt] |u_x^n(t_m,x) - u_x^n(t_m,\bar x) | &\le C( 1+ \Psi^2(x) + \Psi^2(\bar x))|x-\bar{x}|, \notag \\[3pt] |\partial_x \mathcal{D}^n_{m+1} u^n(t_{m+1}, X^{n,t_m,x}_{t_{m+1}}) - \partial_x \mathcal{D}^n_{m+1} u^n(t_{m+1}, X^{n,t_m,{\bar x}}_{t_{m+1}})| &\leq C(1+ \hat{\Psi}(x) + \hat{\Psi}(\bar x))|x-\bar{x}|^{\alpha}, \notag \\[3pt] |\partial_x \mathcal{D}^n_{m+1} u^n(t_{m+1}, X^{n,t_m,x}_{t_{m+1}})| &\le C(1+ \Psi^2(x)), \end{align}
\begin{align} |u^n(t_m,x) - u^n(t_m,\bar x) | &\le C( 1+ \Psi(x) + \Psi(\bar x))|x-\bar{x}|, \notag \\[3pt] |\mathcal{D}^n_{m+1} u^n(t_{m+1},X^{n,t_m,x}_{t_{m+1}})-\mathcal{D}^n_{m+1} u^n(t_{m+1},X^{n,t_m,x}_{t_{m+1}})| &\le C( 1+ \Psi^2(x) + \Psi^2(\bar x))|x-\bar{x}|, \notag \\[3pt] |u_x^n(t_m,x) - u_x^n(t_m,\bar x) | &\le C( 1+ \Psi^2(x) + \Psi^2(\bar x))|x-\bar{x}|, \notag \\[3pt] |\partial_x \mathcal{D}^n_{m+1} u^n(t_{m+1}, X^{n,t_m,x}_{t_{m+1}}) - \partial_x \mathcal{D}^n_{m+1} u^n(t_{m+1}, X^{n,t_m,{\bar x}}_{t_{m+1}})| &\leq C(1+ \hat{\Psi}(x) + \hat{\Psi}(\bar x))|x-\bar{x}|^{\alpha}, \notag \\[3pt] |\partial_x \mathcal{D}^n_{m+1} u^n(t_{m+1}, X^{n,t_m,x}_{t_{m+1}})| &\le C(1+ \Psi^2(x)), \end{align}uniformly in ![]() $m = 0,1, \dots, n-1$, where
$m = 0,1, \dots, n-1$, where
In addition, for
we have
uniformly in ![]() $m = 0,1, \dots, n-1$. The latter inequality follows from the assumption that the partial derivatives of f are bounded and Lipschitz continuous with respect to the spatial variables, from estimates proved in Proposition 4.2, and from those stated in (61) above.
$m = 0,1, \dots, n-1$. The latter inequality follows from the assumption that the partial derivatives of f are bounded and Lipschitz continuous with respect to the spatial variables, from estimates proved in Proposition 4.2, and from those stated in (61) above.
From the calculations it can be seen that in general Assumption 2.3 cannot be weakened if one needs ![]() $ \partial_x F^n(t_{m+1}, x)$ to be locally
$ \partial_x F^n(t_{m+1}, x)$ to be locally ![]() $\alpha$-Hölder continuous.
$\alpha$-Hölder continuous.
5. Technical results and estimates
In this section we collect some facts which are needed for the proofs of our results. We start with properties of the stopping times used to construct a random walk.
Lemma 5.1 (Proposition 11.1 in [Reference Walsh38], Lemma A.1 in [Reference Geiss, Labart and Luoto22]) For all ![]() $0 \leq k \leq m \leq n$ and
$0 \leq k \leq m \leq n$ and ![]() $p > 0$, it holds for
$p > 0$, it holds for ![]() $h = \tfrac{T}{n}$ and
$h = \tfrac{T}{n}$ and ![]() $\tau_k$ as defined in (24) that
$\tau_k$ as defined in (24) that
(i)
 ${\mathbb{E}} \tau_k = kh$;
${\mathbb{E}} \tau_k = kh$;(ii)
 ${\mathbb{E}} |\tau_1 |^p \leq C(p) h^p$;
${\mathbb{E}} |\tau_1 |^p \leq C(p) h^p$;(iii)
 ${\mathbb{E}} | B_{\tau_k} - B_{t_k}|^{2p} \leq C(p) {\mathbb{E}} |\tau_k - t_k|^p \leq C(p) (t_k h)^{\frac{p}{2}}. $
${\mathbb{E}} | B_{\tau_k} - B_{t_k}|^{2p} \leq C(p) {\mathbb{E}} |\tau_k - t_k|^p \leq C(p) (t_k h)^{\frac{p}{2}}. $
The next lemma lists some estimates concerning the diffusion X defined by (28) and its discretization (26), where we assume that B and ![]() $\tilde B$ are connected as in (27).
$\tilde B$ are connected as in (27).
Lemma 5.2 Under Assumption 2.1 on b and ![]() $\sigma$, for
$\sigma$, for ![]() $p \geq 2$ there exists a constant
$p \geq 2$ there exists a constant ![]() $C=C(b,\sigma,T,p) >0$ such that the following hold:
$C=C(b,\sigma,T,p) >0$ such that the following hold:
(i)
 $ {\mathbb{E}}\big|X^{s,y}_{T} - X^{t,x}_T\big|^p \leq C ( |y-x|^p + |s-t|^{\frac{p}{2}}), \quad x,y \in {\mathbb{R}}, \, s,t \in [0,T]. $
$ {\mathbb{E}}\big|X^{s,y}_{T} - X^{t,x}_T\big|^p \leq C ( |y-x|^p + |s-t|^{\frac{p}{2}}), \quad x,y \in {\mathbb{R}}, \, s,t \in [0,T]. $(ii)
 $ \tilde {\mathbb{E}} \sup_{\tilde \tau_l \wedge t_{m} \le r \le \tilde \tau_{l+1} \wedge t_{m}} |\tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}|^{p} \le C h^{\frac{p}{4}}, \quad 0\le k\le n, \, 0 \le l \le n-k-1, \, 0 \leq m \le n-k.$
$ \tilde {\mathbb{E}} \sup_{\tilde \tau_l \wedge t_{m} \le r \le \tilde \tau_{l+1} \wedge t_{m}} |\tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}|^{p} \le C h^{\frac{p}{4}}, \quad 0\le k\le n, \, 0 \le l \le n-k-1, \, 0 \leq m \le n-k.$(iii)
 $ {\mathbb{E}}|\nabla X^{s,y}_T - \nabla X^{t,x}_T |^p \le C( |y-x|^p + |s-t|^{\frac{p}{2}}), \quad x,y \in {\mathbb{R}}, \, s,t \in [0,T]. $
$ {\mathbb{E}}|\nabla X^{s,y}_T - \nabla X^{t,x}_T |^p \le C( |y-x|^p + |s-t|^{\frac{p}{2}}), \quad x,y \in {\mathbb{R}}, \, s,t \in [0,T]. $(iv)
 $ {\mathbb{E}} \sup_{0 \leq l \leq m} \big|\nabla X^{n,t_k,x}_{t_k+t_l}\big|^{p} \leq C, \quad 0 \leq k \leq n, \, 0 \le m \le n-k. $
$ {\mathbb{E}} \sup_{0 \leq l \leq m} \big|\nabla X^{n,t_k,x}_{t_k+t_l}\big|^{p} \leq C, \quad 0 \leq k \leq n, \, 0 \le m \le n-k. $(v)
 $\tilde {\mathbb{E}}\big|\tilde X^{t_k,x}_{t_k+ t_m}-\tilde {\mathcal{X}}^{\tau_k,y}_{\tau_k +\tilde \tau_m}\big|^p \le C ( |x - y|^p+ h^{\frac{p}{4}}), \quad 0 \leq k \leq n,\, 0 \leq m \le n-k.$
$\tilde {\mathbb{E}}\big|\tilde X^{t_k,x}_{t_k+ t_m}-\tilde {\mathcal{X}}^{\tau_k,y}_{\tau_k +\tilde \tau_m}\big|^p \le C ( |x - y|^p+ h^{\frac{p}{4}}), \quad 0 \leq k \leq n,\, 0 \leq m \le n-k.$(vi)
 $\tilde {\mathbb{E}} | \nabla \tilde X_{t_k+ t_m }^{t_k, x} - \nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_m}^{\tau_k,y}|^p \le C( |x - y |^p+ h^{\frac{p}{4}}), \quad 0 \leq k \leq n, \, 0 \leq m \le n-k.$
$\tilde {\mathbb{E}} | \nabla \tilde X_{t_k+ t_m }^{t_k, x} - \nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_m}^{\tau_k,y}|^p \le C( |x - y |^p+ h^{\frac{p}{4}}), \quad 0 \leq k \leq n, \, 0 \leq m \le n-k.$
Proof.
(i) This estimate is well-known.
(ii) For the stochastic integral we use the inequality of BDG and then, since b and
 $\sigma $ are bounded, we get by Lemma 5.1(ii) that
$\sigma $ are bounded, we get by Lemma 5.1(ii) that
 \begin{eqnarray*}&& {} \tilde {\mathbb{E}} \sup_{\tilde \tau_l \wedge t_{m} \le r \le \tilde \tau_{l+1} \wedge t_{m}} |\tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}|^{p} \\[3pt] && \quad\le\, C(p)(\|{b}\|^p_{\infty} \tilde{\mathbb{E}} | \tilde \tau_{l+1}- \tilde \tau_l |^p + \|{\sigma}\|^p_{\infty} {\mathbb{E}} | \tilde \tau_{l+1}- \tilde \tau_l|^{\frac{p}{2}}) \le C(b,\sigma, T,p) \, h^{\frac{p}{2}}.\end{eqnarray*}
\begin{eqnarray*}&& {} \tilde {\mathbb{E}} \sup_{\tilde \tau_l \wedge t_{m} \le r \le \tilde \tau_{l+1} \wedge t_{m}} |\tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}|^{p} \\[3pt] && \quad\le\, C(p)(\|{b}\|^p_{\infty} \tilde{\mathbb{E}} | \tilde \tau_{l+1}- \tilde \tau_l |^p + \|{\sigma}\|^p_{\infty} {\mathbb{E}} | \tilde \tau_{l+1}- \tilde \tau_l|^{\frac{p}{2}}) \le C(b,\sigma, T,p) \, h^{\frac{p}{2}}.\end{eqnarray*}(iii) This can be easily seen because the process
 $(\nabla X^{s,y}_r)_{r \in [s,T]} $ solves the linear SDE (13) with bounded coefficients.
$(\nabla X^{s,y}_r)_{r \in [s,T]} $ solves the linear SDE (13) with bounded coefficients.(iv) The process solves (65). The estimate follows from the inequality of BDG and Gronwall’s lemma.
(v) Recall that from (4) and (26) we have
and \begin{equation*}\tilde {\mathcal{X}}^{\tau_k,y}_{\tau_k+\tilde \tau_m} = \tilde X^{n,t_k,y}_{t_k+t_m} = y + \int_{(0, t_m]} b(t_k+ r, \tilde X^{n,t_k,y}_{t_k+r-}) d[\tilde B^n, \tilde B^n]_r + \int_{(0, t_m]} \sigma(t_k+r,\tilde X^{n,t_k,y}_{t_k+r-}) d \tilde B^n_{r},\end{equation*}
\begin{equation*}\tilde {\mathcal{X}}^{\tau_k,y}_{\tau_k+\tilde \tau_m} = \tilde X^{n,t_k,y}_{t_k+t_m} = y + \int_{(0, t_m]} b(t_k+ r, \tilde X^{n,t_k,y}_{t_k+r-}) d[\tilde B^n, \tilde B^n]_r + \int_{(0, t_m]} \sigma(t_k+r,\tilde X^{n,t_k,y}_{t_k+r-}) d \tilde B^n_{r},\end{equation*} $\tilde X^{t_k,x}_{t_k+t_m} $ is given by
To compare the stochastic integrals of the previous two equations we use the relation
$\tilde X^{t_k,x}_{t_k+t_m} $ is given by
To compare the stochastic integrals of the previous two equations we use the relation \begin{equation*}\tilde X^{t_k,x}_{t_k+t_m} = x + \int_0^{t_m} b(t_k+r, \tilde X^{t_k,x}_{t_k+r}) dr + \int_0^{t_m} \sigma(t_k+r,\tilde X^{t_k,y}_{t_k+r}) d \tilde B_r.\end{equation*}We define an ‘increasing’ map,
\begin{equation*}\tilde X^{t_k,x}_{t_k+t_m} = x + \int_0^{t_m} b(t_k+r, \tilde X^{t_k,x}_{t_k+r}) dr + \int_0^{t_m} \sigma(t_k+r,\tilde X^{t_k,y}_{t_k+r}) d \tilde B_r.\end{equation*}We define an ‘increasing’ map, \begin{equation*} \int_{(0, t_m]} \sigma(t_k+r,\tilde X^{n,t_k,y}_{t_k+r-}) d \tilde B^n_r = \int_0^\infty \sum_{l=0}^{m-1} \sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}) {\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r.\end{equation*}
\begin{equation*} \int_{(0, t_m]} \sigma(t_k+r,\tilde X^{n,t_k,y}_{t_k+r-}) d \tilde B^n_r = \int_0^\infty \sum_{l=0}^{m-1} \sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}) {\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r.\end{equation*} $i(r) \coloneqq t_{l+1} $ for
$i(r) \coloneqq t_{l+1} $ for  $r \in (t_l,t_{l+1}]$, and a ‘decreasing’ map,
$r \in (t_l,t_{l+1}]$, and a ‘decreasing’ map,  $d(r) \coloneqq t_{l} $ for
$d(r) \coloneqq t_{l} $ for  $r \in (t_l,t_{l+1}]$, and split the differences as follows (using Assumption 2.1(iii) for the coefficient b):
(64)We estimate the terms on the right-hand side as follows: by standard estimates for SDEs with bounded coefficients one has that
$r \in (t_l,t_{l+1}]$, and split the differences as follows (using Assumption 2.1(iii) for the coefficient b):
(64)We estimate the terms on the right-hand side as follows: by standard estimates for SDEs with bounded coefficients one has that \begin{align} & \tilde {\mathbb{E}}\big|\tilde X^{t_k,x}_{t_k+t_m}- \tilde X^{n,t_k,y}_{t_k+t_m}\big|^p \notag \\[3pt] &\,\, \le C(b,p) \left (\! |x - y|^p + \tilde {\mathbb{E}} \!\int_0^{t_m} |r- i(r)|^{\frac{p}{2}} +| \tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+d(r)} |^p + | \tilde X^{t_k,x}_{t_k+d(r)}- \tilde X^{n,t_k,y}_{t_k+d(r)} |^p dr \!\right)\notag\\[3pt] &\qquad +C(p) \tilde {\mathbb{E}} | \int_{t_{m} \wedge \tilde \tau_{m}}^{t_{m}} \sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r}) d \tilde B_r|^p \notag \\[3pt] &\qquad + C(p) \tilde {\mathbb{E}} | \int_{t_{m} \wedge \tilde \tau_{m}}^{\tilde \tau_{m}} \sum_{l=0}^{ m-1} \sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}){\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r|^p\notag \\[3pt] &\qquad + C(p) \tilde {\mathbb{E}} | \int_0^{t_{m} \wedge \tilde \tau_{m}} \!\!\!\! \sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r}) - \sum_{l=0}^{m-1} \sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}){\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r|^p.\end{align}By the BDG inequality, the fact that
\begin{align} & \tilde {\mathbb{E}}\big|\tilde X^{t_k,x}_{t_k+t_m}- \tilde X^{n,t_k,y}_{t_k+t_m}\big|^p \notag \\[3pt] &\,\, \le C(b,p) \left (\! |x - y|^p + \tilde {\mathbb{E}} \!\int_0^{t_m} |r- i(r)|^{\frac{p}{2}} +| \tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+d(r)} |^p + | \tilde X^{t_k,x}_{t_k+d(r)}- \tilde X^{n,t_k,y}_{t_k+d(r)} |^p dr \!\right)\notag\\[3pt] &\qquad +C(p) \tilde {\mathbb{E}} | \int_{t_{m} \wedge \tilde \tau_{m}}^{t_{m}} \sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r}) d \tilde B_r|^p \notag \\[3pt] &\qquad + C(p) \tilde {\mathbb{E}} | \int_{t_{m} \wedge \tilde \tau_{m}}^{\tilde \tau_{m}} \sum_{l=0}^{ m-1} \sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}){\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r|^p\notag \\[3pt] &\qquad + C(p) \tilde {\mathbb{E}} | \int_0^{t_{m} \wedge \tilde \tau_{m}} \!\!\!\! \sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r}) - \sum_{l=0}^{m-1} \sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}){\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r|^p.\end{align}By the BDG inequality, the fact that \begin{eqnarray*} \tilde {\mathbb{E}} \int_0^{t_m} |r- i(r)|^{\frac{p}{2}} +| \tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+d(r)} |^p dr \le C(b,\sigma,T,p) h^\frac{p}{2}.\end{eqnarray*}
\begin{eqnarray*} \tilde {\mathbb{E}} \int_0^{t_m} |r- i(r)|^{\frac{p}{2}} +| \tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+d(r)} |^p dr \le C(b,\sigma,T,p) h^\frac{p}{2}.\end{eqnarray*} $\sigma$ is bounded, and Lemma 5.1, we conclude that
Finally, by the BDG inequality,
$\sigma$ is bounded, and Lemma 5.1, we conclude that
Finally, by the BDG inequality, \begin{eqnarray*}&& {} \tilde {\mathbb{E}} \bigg | \int_{t_{m} \wedge \tilde \tau_{m}}^{t_{m}} \sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r}) d \tilde B_r\bigg |^p + \tilde {\mathbb{E}} \bigg | \int_{t_{m} \wedge \tilde \tau_{m}}^{\tilde \tau_{m}} \sum_{l=0}^{m-1} \sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}){\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r \bigg|^p \\&& \quad\le C(\sigma,p) \|\sigma\|^p_\infty \tilde {\mathbb{E}} |\tilde\tau_{m}-t_{m}|^\frac{p}{2} \le C(\sigma,p) ( t_{m} h)^\frac{p}{4}.\end{eqnarray*}Moreover, since
\begin{eqnarray*}&& {} \tilde {\mathbb{E}} \bigg | \int_{t_{m} \wedge \tilde \tau_{m}}^{t_{m}} \sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r}) d \tilde B_r\bigg |^p + \tilde {\mathbb{E}} \bigg | \int_{t_{m} \wedge \tilde \tau_{m}}^{\tilde \tau_{m}} \sum_{l=0}^{m-1} \sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}){\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r \bigg|^p \\&& \quad\le C(\sigma,p) \|\sigma\|^p_\infty \tilde {\mathbb{E}} |\tilde\tau_{m}-t_{m}|^\frac{p}{2} \le C(\sigma,p) ( t_{m} h)^\frac{p}{4}.\end{eqnarray*}Moreover, since \begin{eqnarray*} && {} \tilde {\mathbb{E}} \Bigg | \int_0^{t_{m} \wedge \tilde \tau_{m}} \!\!\!\! \sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r}) - \sum_{l=0}^{m-1}\sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}){\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r \Bigg|^p \\[-2pt]
&&\quad\le\, C(p) \tilde {\mathbb{E}} \Bigg ( \int_0^{t_{m}} \sum_{l=0}^{m-1}|\sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r})-\sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}})|^2 {\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) dr\Bigg )^\frac{p}{2} \\[-2pt]
&&\quad\le\, C(\sigma,p)\tilde {\mathbb{E}} \Bigg ( \sum_{l=0}^{m-1}\int_{\tilde \tau_l \wedge t_{m}}^{\tilde \tau_{l+1} \wedge t_{m}}\!\!\!\!|\tilde \tau_{l+1}-t_{l+1}|^\frac{p}{2} + |\tilde \tau_l -t_{l+1} |^\frac{p}{2} + |\tilde X^{t_k,x}_{t_k +r}- \tilde X^{t_k,x}_{t_k+\tilde \tau_l \wedge t_{m}}|^p \\&& \qquad +\, |\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}-\tilde X^{n,t_k,y}_{t_{k+l}} |^p dr\Bigg ) \\[-2pt]
&&\quad\le\, C(\sigma,T,p) \Bigg ( h^\frac{p}{2} + \max_{1\le l<m} ( \tilde {\mathbb{E}} |\tilde \tau_l -t_l|^p)^{\frac{1}{2}}\\[-2pt]
&& \qquad +\, \max_{0\le l<m} \Bigg( \tilde {\mathbb{E}} \sup_{\tilde \tau_l \wedge t_{m} \le r \le \tilde \tau_{l+1} \wedge t_{m}} |\tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}|^{2p} \Bigg)^{\frac{1}{2}} \\
&& \qquad +\, \tilde {\mathbb{E}} \sum_{l=0}^{m-1} |\tilde X^{t_k,x}_{t_k+\tilde \tau_l \wedge t_{m}} -\tilde X^{n,t_k,y}_{t_{k+l}} |^p (\tilde \tau_{l+1} - \tilde \tau_l ) \Bigg ). \end{eqnarray*}
\begin{eqnarray*} && {} \tilde {\mathbb{E}} \Bigg | \int_0^{t_{m} \wedge \tilde \tau_{m}} \!\!\!\! \sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r}) - \sum_{l=0}^{m-1}\sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}}){\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) d \tilde B_r \Bigg|^p \\[-2pt]
&&\quad\le\, C(p) \tilde {\mathbb{E}} \Bigg ( \int_0^{t_{m}} \sum_{l=0}^{m-1}|\sigma(t_k+r,\tilde X^{t_k,x}_{t_k+r})-\sigma(t_{k+l+1},\tilde X^{n,t_k,y}_{t_{k+l}})|^2 {\textbf{1}}_{(\tilde \tau_l, \tilde \tau_{l+1}]}(r) dr\Bigg )^\frac{p}{2} \\[-2pt]
&&\quad\le\, C(\sigma,p)\tilde {\mathbb{E}} \Bigg ( \sum_{l=0}^{m-1}\int_{\tilde \tau_l \wedge t_{m}}^{\tilde \tau_{l+1} \wedge t_{m}}\!\!\!\!|\tilde \tau_{l+1}-t_{l+1}|^\frac{p}{2} + |\tilde \tau_l -t_{l+1} |^\frac{p}{2} + |\tilde X^{t_k,x}_{t_k +r}- \tilde X^{t_k,x}_{t_k+\tilde \tau_l \wedge t_{m}}|^p \\&& \qquad +\, |\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}-\tilde X^{n,t_k,y}_{t_{k+l}} |^p dr\Bigg ) \\[-2pt]
&&\quad\le\, C(\sigma,T,p) \Bigg ( h^\frac{p}{2} + \max_{1\le l<m} ( \tilde {\mathbb{E}} |\tilde \tau_l -t_l|^p)^{\frac{1}{2}}\\[-2pt]
&& \qquad +\, \max_{0\le l<m} \Bigg( \tilde {\mathbb{E}} \sup_{\tilde \tau_l \wedge t_{m} \le r \le \tilde \tau_{l+1} \wedge t_{m}} |\tilde X^{t_k,x}_{t_k+r}- \tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}|^{2p} \Bigg)^{\frac{1}{2}} \\
&& \qquad +\, \tilde {\mathbb{E}} \sum_{l=0}^{m-1} |\tilde X^{t_k,x}_{t_k+\tilde \tau_l \wedge t_{m}} -\tilde X^{n,t_k,y}_{t_{k+l}} |^p (\tilde \tau_{l+1} - \tilde \tau_l ) \Bigg ). \end{eqnarray*} $\tilde \tau_{l+1} - \tilde \tau_l$ is independent of
$\tilde \tau_{l+1} - \tilde \tau_l$ is independent of  $|\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}} -\tilde X^{n,t_k,y}_{t_k+t_l} |^p$, by Lemma 5.1(i) we getUsing Lemma 5.1(iii), one concludes similarly as in the proof of (ii) that
$|\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}} -\tilde X^{n,t_k,y}_{t_k+t_l} |^p$, by Lemma 5.1(i) we getUsing Lemma 5.1(iii), one concludes similarly as in the proof of (ii) that \begin{eqnarray*}&& {} \tilde {\mathbb{E}} \sum_{l=0}^{m-1} |\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}} -\tilde X^{n,t_k,y}_{t_{k+l}} |^p (\tilde \tau_{l+1} - \tilde \tau_l ) \\
&&\quad=\, \tilde {\mathbb{E}} \sum_{l=0}^{m-1} |\tilde X^{t_k,x}_{t_k+\tilde \tau_l \wedge t_{m}} -\tilde X^{n,t_k,y}_{t_{k+l}} |^p (t_{l+1} - t_l )\\
&&\quad\le\, C(T,p) \bigg ( \tilde {\mathbb{E}} \int_0^{t_m} |\tilde X^{t_k,x}_{t_k+d(r)} -\tilde X^{n,t_k,y}_{t_k+d(r)} |^p dr + \max_{0\le l<m} \tilde {\mathbb{E}} |\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}- \tilde X^{t_k,x}_{t_k+t_l}|^p \bigg ). \end{eqnarray*}Then (64) combined with the above estimates implies that
\begin{eqnarray*}&& {} \tilde {\mathbb{E}} \sum_{l=0}^{m-1} |\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}} -\tilde X^{n,t_k,y}_{t_{k+l}} |^p (\tilde \tau_{l+1} - \tilde \tau_l ) \\
&&\quad=\, \tilde {\mathbb{E}} \sum_{l=0}^{m-1} |\tilde X^{t_k,x}_{t_k+\tilde \tau_l \wedge t_{m}} -\tilde X^{n,t_k,y}_{t_{k+l}} |^p (t_{l+1} - t_l )\\
&&\quad\le\, C(T,p) \bigg ( \tilde {\mathbb{E}} \int_0^{t_m} |\tilde X^{t_k,x}_{t_k+d(r)} -\tilde X^{n,t_k,y}_{t_k+d(r)} |^p dr + \max_{0\le l<m} \tilde {\mathbb{E}} |\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}- \tilde X^{t_k,x}_{t_k+t_l}|^p \bigg ). \end{eqnarray*}Then (64) combined with the above estimates implies that \begin{equation*} \tilde {\mathbb{E}} |\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}- \tilde X^{t_k,x}_{t_k+t_l}|^p\le C(b,\sigma,T,p) h^\frac{p}{4} .\end{equation*}Gronwall’s lemma yields
\begin{equation*} \tilde {\mathbb{E}} |\tilde X^{t_k,x}_{t_k+ \tilde \tau_l \wedge t_{m}}- \tilde X^{t_k,x}_{t_k+t_l}|^p\le C(b,\sigma,T,p) h^\frac{p}{4} .\end{equation*}Gronwall’s lemma yields \begin{eqnarray*}\tilde {\mathbb{E}}\big|\tilde X^{t_k,x}_{t_k+t_m}- \tilde X^{n,t_k,y}_{t_k+t_m}\big|^p\le C(b,\sigma,T,p) \bigg ( |x - y|^p + h^\frac{p}{4} + \tilde {\mathbb{E}} \int_0^{t_m} |\tilde X^{t_k,x}_{t_k+ d(r)} -\tilde X^{n,t_k,y}_{t_k+d(r)} |^p dr \bigg ). \end{eqnarray*}
\begin{eqnarray*}\tilde {\mathbb{E}}\big|\tilde X^{t_k,x}_{t_k+t_m}- \tilde X^{n,t_k,y}_{t_k+t_m}\big|^p\le C(b,\sigma,T,p) \bigg ( |x - y|^p + h^\frac{p}{4} + \tilde {\mathbb{E}} \int_0^{t_m} |\tilde X^{t_k,x}_{t_k+ d(r)} -\tilde X^{n,t_k,y}_{t_k+d(r)} |^p dr \bigg ). \end{eqnarray*} \begin{equation*}\tilde {\mathbb{E}}\big|\tilde X^{t_k,x}_{t_k+t_m}- \tilde X^{n,t_k,y}_{t_k+t_m}\big|^p\le C(b,\sigma,T,p) ( |x - y|^p + h^\frac{p}{4}). \end{equation*}
\begin{equation*}\tilde {\mathbb{E}}\big|\tilde X^{t_k,x}_{t_k+t_m}- \tilde X^{n,t_k,y}_{t_k+t_m}\big|^p\le C(b,\sigma,T,p) ( |x - y|^p + h^\frac{p}{4}). \end{equation*}(vi) We have
(65)and \begin{align} \nabla \tilde X^{n,t_k, y}_{t_k+ t_m}= 1 &+ \int_{(0,t_m]} b_x (t_k+ r,X^{n, t_k, y}_{t_k+r-}) \nabla \tilde X^{n,t_k, y}_{t_k+r-} d[\tilde B^n,\tilde B^n]_r \! \notag\\&+ \int_{(0,t_m]} \sigma_x(t_k+ r, \tilde X^{n,t_k,y}_{t_k+r-}) \nabla \tilde X^{n,t_k, y}_{t_k+r-} d \tilde B^n_r\end{align}(66)
\begin{align} \nabla \tilde X^{n,t_k, y}_{t_k+ t_m}= 1 &+ \int_{(0,t_m]} b_x (t_k+ r,X^{n, t_k, y}_{t_k+r-}) \nabla \tilde X^{n,t_k, y}_{t_k+r-} d[\tilde B^n,\tilde B^n]_r \! \notag\\&+ \int_{(0,t_m]} \sigma_x(t_k+ r, \tilde X^{n,t_k,y}_{t_k+r-}) \nabla \tilde X^{n,t_k, y}_{t_k+r-} d \tilde B^n_r\end{align}(66) \begin{eqnarray} \nabla \tilde X^{t_k,x}_{t_k+t_m} = 1 + \int_0^{t_m} b_x(t_k+ r, \tilde X^{t_k,x}_{t_k+r}) \nabla \tilde X^{t_k,x}_{t_k+r}dr + \int_0^{t_m} \sigma_x(t_k+ r,\tilde X^{t_k,x}_{t_k+r}) \nabla \tilde X^{t_k,x}_{t_k+r}d \tilde B_{r}.\qquad \end{eqnarray}
\begin{eqnarray} \nabla \tilde X^{t_k,x}_{t_k+t_m} = 1 + \int_0^{t_m} b_x(t_k+ r, \tilde X^{t_k,x}_{t_k+r}) \nabla \tilde X^{t_k,x}_{t_k+r}dr + \int_0^{t_m} \sigma_x(t_k+ r,\tilde X^{t_k,x}_{t_k+r}) \nabla \tilde X^{t_k,x}_{t_k+r}d \tilde B_{r}.\qquad \end{eqnarray}
We may proceed similarly as in (v), except that this time the coefficients are not bounded but have linear growth. Here one uses that the integrands are bounded in any ![]() $L_p({\mathbb{P}}).$
$L_p({\mathbb{P}}).$
Finally, we estimate the difference between the continuous-time Malliavin weight and its discrete-time counterpart.
Lemma 5.3 Let B and ![]() $\tilde B$ be connected via (27). Under Assumption 2.1 it holds that
$\tilde B$ be connected via (27). Under Assumption 2.1 it holds that
 \begin{equation*} \tilde {\mathbb{E}}|\tilde N^{t_k}_{t_m}\sigma(t_k,X_{t_k})-\tilde N^{n,\tau_k}_{\tilde \tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k})|^2 \leq C(b,\sigma,T,\delta) \frac{ |X_{t_k} - {\mathcal{X}}_{\tau_k}|^2+ h^\frac{1}{2}}{(t_m-t_k)^{\frac{3}{2}}}, \quad m=k+1,\ldots,n. \end{equation*}
\begin{equation*} \tilde {\mathbb{E}}|\tilde N^{t_k}_{t_m}\sigma(t_k,X_{t_k})-\tilde N^{n,\tau_k}_{\tilde \tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k})|^2 \leq C(b,\sigma,T,\delta) \frac{ |X_{t_k} - {\mathcal{X}}_{\tau_k}|^2+ h^\frac{1}{2}}{(t_m-t_k)^{\frac{3}{2}}}, \quad m=k+1,\ldots,n. \end{equation*} Proof. For ![]() $N^{n,\tau_k}_{\tilde \tau_m}$ and
$N^{n,\tau_k}_{\tilde \tau_m}$ and ![]() $N^{t_k}_{t_{m}}$ given by (12) and (18), respectively, we introduce the notation
$N^{t_k}_{t_{m}}$ given by (12) and (18), respectively, we introduce the notation
with
 \begin{eqnarray*} a_{t_k+s}\!\coloneqq \! \!\nabla \tilde X_{t_k+s}^{t_k, X_{t_k}}\frac{\sigma(t_k,X_{t_k})}{\sigma(t_k\!+\!s,\tilde X_{t_k+s}^{t_k,X_{t_k}})},\qquad a_{\tau_k+s}^n \!\coloneqq \! \sum_{\ell=1}^{m-k}\! \nabla \tilde {\mathcal{X}}_{\tau_k + \tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}}\! \frac{\sigma(t_{k+1},{\mathcal{X}}_{\tau_k})}{\sigma(t_{k+\ell},\tilde {\mathcal{X}}_{\tau_k+ \tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}})} {\textbf{1}}_{s \in (\tilde \tau_{\ell-1}, \tilde \tau_\ell]}. \end{eqnarray*}
\begin{eqnarray*} a_{t_k+s}\!\coloneqq \! \!\nabla \tilde X_{t_k+s}^{t_k, X_{t_k}}\frac{\sigma(t_k,X_{t_k})}{\sigma(t_k\!+\!s,\tilde X_{t_k+s}^{t_k,X_{t_k}})},\qquad a_{\tau_k+s}^n \!\coloneqq \! \sum_{\ell=1}^{m-k}\! \nabla \tilde {\mathcal{X}}_{\tau_k + \tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}}\! \frac{\sigma(t_{k+1},{\mathcal{X}}_{\tau_k})}{\sigma(t_{k+\ell},\tilde {\mathcal{X}}_{\tau_k+ \tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}})} {\textbf{1}}_{s \in (\tilde \tau_{\ell-1}, \tilde \tau_\ell]}. \end{eqnarray*}By the inequality of BDG,
 \begin{align*}& (t_m-t_k)^2 \tilde {\mathbb{E}}|\tilde N^{t_k}_{t_m} \sigma(t_k,X_{t_k})-\tilde N^{n,\tau_k}_{\tilde \tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k})|^2 \\ &\quad = \tilde {\mathbb{E}} \Big|\int_{0}^{t_{m-k}} a_{t_k+s} d\tilde B_s -\int_{0}^{\tilde \tau_{m-k}} a^n_{\tau_k+s} d\tilde B_{s}\Big|^2\\[3pt] &\quad = \tilde {\mathbb{E}} \int_{0}^{t_{m-k}\wedge \tilde \tau_{m-k}} (a_{t_k+s} - a^n_{\tau_k+s})^2 ds + \tilde {\mathbb{E}} \int_{0}^{\infty} a_{t_k+s}^2 {\textbf{1}}_{(\tilde \tau_{m-k},t_{m-k}]}(s) ds\\[3pt] &\qquad + \tilde {\mathbb{E}} \int_{0}^{\infty} (a^n_{\tau_k+s})^2 {\textbf{1}}_{(t_{m-k},\tilde \tau_{m-k}]}(s) ds\\[3pt] &\quad \leq \sum_{\ell=1}^{m-k} {{\left( \tilde {\mathbb{E}} \sup_{s \in [0, t_{m-k}] \cap (\tilde \tau_{\ell-1}, \tilde \tau_{\ell}]}\big|a_{t_k+s} - a^n_{ \tau_k +\tilde \tau_{\ell}}\big|^4\right)}}^{\frac{1}{2}} (\tilde {\mathbb{E}} |\tilde \tau_{\ell} -\tilde \tau_{\ell-1}|^2)^{\frac{1}{2}} \\[3pt] &\qquad + {{\left(\tilde {\mathbb{E}} \sup_{s \in [0, t_{m-k}]} |a_{t_k+s}|^4 + \tilde {\mathbb{E}} \max_{1 \leq \ell \leq m-k} |a^n_{\tau_k +\tilde \tau_{\ell}}|^4\right)}}^{\frac{1}{2}} (\tilde {\mathbb{E}} |t_{m-k} -\tilde \tau_{m-k}|^2 )^{\frac{1}{2}}.\end{align*}
\begin{align*}& (t_m-t_k)^2 \tilde {\mathbb{E}}|\tilde N^{t_k}_{t_m} \sigma(t_k,X_{t_k})-\tilde N^{n,\tau_k}_{\tilde \tau_m} \sigma(t_{k+1},{\mathcal{X}}_{\tau_k})|^2 \\ &\quad = \tilde {\mathbb{E}} \Big|\int_{0}^{t_{m-k}} a_{t_k+s} d\tilde B_s -\int_{0}^{\tilde \tau_{m-k}} a^n_{\tau_k+s} d\tilde B_{s}\Big|^2\\[3pt] &\quad = \tilde {\mathbb{E}} \int_{0}^{t_{m-k}\wedge \tilde \tau_{m-k}} (a_{t_k+s} - a^n_{\tau_k+s})^2 ds + \tilde {\mathbb{E}} \int_{0}^{\infty} a_{t_k+s}^2 {\textbf{1}}_{(\tilde \tau_{m-k},t_{m-k}]}(s) ds\\[3pt] &\qquad + \tilde {\mathbb{E}} \int_{0}^{\infty} (a^n_{\tau_k+s})^2 {\textbf{1}}_{(t_{m-k},\tilde \tau_{m-k}]}(s) ds\\[3pt] &\quad \leq \sum_{\ell=1}^{m-k} {{\left( \tilde {\mathbb{E}} \sup_{s \in [0, t_{m-k}] \cap (\tilde \tau_{\ell-1}, \tilde \tau_{\ell}]}\big|a_{t_k+s} - a^n_{ \tau_k +\tilde \tau_{\ell}}\big|^4\right)}}^{\frac{1}{2}} (\tilde {\mathbb{E}} |\tilde \tau_{\ell} -\tilde \tau_{\ell-1}|^2)^{\frac{1}{2}} \\[3pt] &\qquad + {{\left(\tilde {\mathbb{E}} \sup_{s \in [0, t_{m-k}]} |a_{t_k+s}|^4 + \tilde {\mathbb{E}} \max_{1 \leq \ell \leq m-k} |a^n_{\tau_k +\tilde \tau_{\ell}}|^4\right)}}^{\frac{1}{2}} (\tilde {\mathbb{E}} |t_{m-k} -\tilde \tau_{m-k}|^2 )^{\frac{1}{2}}.\end{align*}The assertion then follows from Lemma 5.1 and from the estimates
So it remains to prove these inequalities. We put
 \begin{equation*} \tilde K^{t_k}_{t_k+s} \coloneqq \frac{\sigma(t_k,X_{t_k})}{\sigma(t_k+s,\tilde X_{t_k+s}^{t_k,X_{t_k}})} \quad \text{ and } \quad \tilde K^{n,\tau_k}_{\tau_k+\tilde \tau_{\ell-1}}\coloneqq \frac{\sigma(t_{k+1}, {\mathcal{X}}_{\tau_k})}{\sigma(t_{k+\ell}, \tilde {\mathcal{X}}^{\tau_k, {\mathcal{X}}_{\tau_k}}_{\tau_k +\tilde \tau_{\ell-1}})}\end{equation*}
\begin{equation*} \tilde K^{t_k}_{t_k+s} \coloneqq \frac{\sigma(t_k,X_{t_k})}{\sigma(t_k+s,\tilde X_{t_k+s}^{t_k,X_{t_k}})} \quad \text{ and } \quad \tilde K^{n,\tau_k}_{\tau_k+\tilde \tau_{\ell-1}}\coloneqq \frac{\sigma(t_{k+1}, {\mathcal{X}}_{\tau_k})}{\sigma(t_{k+\ell}, \tilde {\mathcal{X}}^{\tau_k, {\mathcal{X}}_{\tau_k}}_{\tau_k +\tilde \tau_{\ell-1}})}\end{equation*}and notice that by Assumption 2.1 both expressions are bounded by ![]() $ \|{\sigma}\|_{\infty}\delta^{-1}.$ To show (67) let us split
$ \|{\sigma}\|_{\infty}\delta^{-1}.$ To show (67) let us split ![]() $a_{t_k+s}- a^n_{\tau_k+ \tilde \tau_\ell}$ in the following way:
$a_{t_k+s}- a^n_{\tau_k+ \tilde \tau_\ell}$ in the following way:
 \begin{align*} a_{t_k+s}- a^n_{\tau_k+ \tilde \tau_\ell} &= \tilde K^{t_k}_{t_k+s} (\nabla \tilde X_{t_k+s}^{t_k, X_{t_k}} -\nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}}) + \nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}} ( \tilde K^{t_k}_{t_k+s} - \tilde K^{t_k}_{t_k +t_{\ell-1}}) \\[3pt] &\quad + \tilde K^{t_k}_{t_k +t_{\ell-1}} ( \nabla \tilde X_{t_k+ t_{\ell-1} }^{t_k, X_{t_k}} - \nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}} ) + \nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}} ( \tilde K^{t_k}_{t_k+ t_{\ell-1}} - \tilde K^{n,\tau_k}_{\tau_k +\tilde \tau_{\ell-1}}). \end{align*}
\begin{align*} a_{t_k+s}- a^n_{\tau_k+ \tilde \tau_\ell} &= \tilde K^{t_k}_{t_k+s} (\nabla \tilde X_{t_k+s}^{t_k, X_{t_k}} -\nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}}) + \nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}} ( \tilde K^{t_k}_{t_k+s} - \tilde K^{t_k}_{t_k +t_{\ell-1}}) \\[3pt] &\quad + \tilde K^{t_k}_{t_k +t_{\ell-1}} ( \nabla \tilde X_{t_k+ t_{\ell-1} }^{t_k, X_{t_k}} - \nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}} ) + \nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}} ( \tilde K^{t_k}_{t_k+ t_{\ell-1}} - \tilde K^{n,\tau_k}_{\tau_k +\tilde \tau_{\ell-1}}). \end{align*}Then
 \begin{eqnarray*}&& {} \tilde {\mathbb{E}} \sup_{s \in [\tilde \tau_{\ell-1} \wedge t_{m-k}, \tilde \tau_{\ell} \wedge t_{m-k}]} | \tilde K^{t_k}_{t_k+s} (\nabla \tilde X_{t_k+s}^{t_k, X_{t_k}} -\nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}})|^4 \\[3pt] &\le\,& \|{\sigma}\|^4_{\infty}\delta^{-4} \tilde {\mathbb{E}} \sup_{s \in [\tilde \tau_{\ell-1} \wedge t_{m-k}, \tilde \tau_{\ell} \wedge t_{m-k}]} | \nabla \tilde X_{t_k+s}^{t_k, X_{t_k}} -\nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}}|^4\le C(b,\sigma,T,\delta) h,\end{eqnarray*}
\begin{eqnarray*}&& {} \tilde {\mathbb{E}} \sup_{s \in [\tilde \tau_{\ell-1} \wedge t_{m-k}, \tilde \tau_{\ell} \wedge t_{m-k}]} | \tilde K^{t_k}_{t_k+s} (\nabla \tilde X_{t_k+s}^{t_k, X_{t_k}} -\nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}})|^4 \\[3pt] &\le\,& \|{\sigma}\|^4_{\infty}\delta^{-4} \tilde {\mathbb{E}} \sup_{s \in [\tilde \tau_{\ell-1} \wedge t_{m-k}, \tilde \tau_{\ell} \wedge t_{m-k}]} | \nabla \tilde X_{t_k+s}^{t_k, X_{t_k}} -\nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}}|^4\le C(b,\sigma,T,\delta) h,\end{eqnarray*}since one can show similarly to Lemma 5.2(ii) that
Notice that ![]() $\nabla \tilde X_t^{t_k, X_{t_k}}$ and
$\nabla \tilde X_t^{t_k, X_{t_k}}$ and ![]() $\nabla \tilde {\mathcal{X}}_{\tau_m}^{\tau_k,{\mathcal{X}}_{\tau_k}} $ solve the linear SDEs (66) and (65), respectively. Therefore,
$\nabla \tilde {\mathcal{X}}_{\tau_m}^{\tau_k,{\mathcal{X}}_{\tau_k}} $ solve the linear SDEs (66) and (65), respectively. Therefore,
For the second term we get
 \begin{eqnarray*}&& {} \tilde {\mathbb{E}} \sup_{s \in [\tilde \tau_{\ell-1} \wedge t_{m-k}, \tilde \tau_{\ell} \wedge t_{m-k}]} | \nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}} ( \tilde K^{t_k}_{t_k+s} - \tilde K^{t_k}_{t_k +t_{\ell-1}}) |^4 \\&&\quad\le C(\sigma, \delta) (\tilde {\mathbb{E}} | \nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}}|^8 )^{\frac{1}{2}} (\tilde {\mathbb{E}} \sup_{s \in [\tilde \tau_{\ell-1} \wedge t_{m-k}, \tilde \tau_{\ell} \wedge t_{m-k}]} (| t_\ell-s|^4 + | \tilde X_{t_k+s}^{t_k,X_{t_k}}-\tilde X_{t_k+t_\ell}^{t_k,X_{t_k}}|^8)^{\frac{1}{2}} \\ &&\quad\le C(b,\sigma,T,\delta) h.\end{eqnarray*}
\begin{eqnarray*}&& {} \tilde {\mathbb{E}} \sup_{s \in [\tilde \tau_{\ell-1} \wedge t_{m-k}, \tilde \tau_{\ell} \wedge t_{m-k}]} | \nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}} ( \tilde K^{t_k}_{t_k+s} - \tilde K^{t_k}_{t_k +t_{\ell-1}}) |^4 \\&&\quad\le C(\sigma, \delta) (\tilde {\mathbb{E}} | \nabla \tilde X_{t_k + t_{\ell-1}}^{t_k, X_{t_k}}|^8 )^{\frac{1}{2}} (\tilde {\mathbb{E}} \sup_{s \in [\tilde \tau_{\ell-1} \wedge t_{m-k}, \tilde \tau_{\ell} \wedge t_{m-k}]} (| t_\ell-s|^4 + | \tilde X_{t_k+s}^{t_k,X_{t_k}}-\tilde X_{t_k+t_\ell}^{t_k,X_{t_k}}|^8)^{\frac{1}{2}} \\ &&\quad\le C(b,\sigma,T,\delta) h.\end{eqnarray*}For the third term, Lemma 5.2(vi) implies that
The last term we estimate similarly to the second one:
 \begin{align*}& \tilde {\mathbb{E}} |\nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}} ( \tilde K^{t_k}_{t_k+ t_{\ell-1}} - \tilde K^{n,\tau_k}_{\tau_k +\tilde \tau_{\ell-1}})|^4\\[3pt] &\quad \leq C(\sigma, \delta)(\tilde {\mathbb{E}} | \nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}} |^8 )^{\frac{1}{2}} ( |X_{t_k} - {\mathcal{X}}_{\tau_k}|^{8} + \tilde {\mathbb{E}} | {\mathcal{X}}^{\tau_k, {\mathcal{X}}_{\tau_k}}_{\tau_k +\tilde \tau_{\ell-1}}-\tilde X_{t_k+t_{\ell-1}}^{t_k,X_{t_k}}|^8)^{\frac{1}{2}} \\[3pt] & \quad \leq C(b,\sigma,T, \delta) (|X_{t_k} - {\mathcal{X}}_{\tau_k}|^4 + h).\end{align*}
\begin{align*}& \tilde {\mathbb{E}} |\nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}} ( \tilde K^{t_k}_{t_k+ t_{\ell-1}} - \tilde K^{n,\tau_k}_{\tau_k +\tilde \tau_{\ell-1}})|^4\\[3pt] &\quad \leq C(\sigma, \delta)(\tilde {\mathbb{E}} | \nabla \tilde {\mathcal{X}}_{\tau_k +\tilde \tau_{\ell-1}}^{\tau_k,{\mathcal{X}}_{\tau_k}} |^8 )^{\frac{1}{2}} ( |X_{t_k} - {\mathcal{X}}_{\tau_k}|^{8} + \tilde {\mathbb{E}} | {\mathcal{X}}^{\tau_k, {\mathcal{X}}_{\tau_k}}_{\tau_k +\tilde \tau_{\ell-1}}-\tilde X_{t_k+t_{\ell-1}}^{t_k,X_{t_k}}|^8)^{\frac{1}{2}} \\[3pt] & \quad \leq C(b,\sigma,T, \delta) (|X_{t_k} - {\mathcal{X}}_{\tau_k}|^4 + h).\end{align*}To see (68), use the estimates (69).
We close this section with estimates concerning the effect of ![]() $T_{_{m,{\pm}}}$ and the discretized Malliavin derivative
$T_{_{m,{\pm}}}$ and the discretized Malliavin derivative ![]() $\mathcal{D}^n_k$ (see Definition 2.1) on
$\mathcal{D}^n_k$ (see Definition 2.1) on ![]() $X^n.$
$X^n.$
Lemma 5.4 Under Assumption 2.1, and for ![]() $p\ge 2,$ we have the following:
$p\ge 2,$ we have the following:
(i)
 ${\mathbb{E}} |X^n_{t_l}- T_{_{m,{\pm}}}X^n_{t_l}|^p \leq C(b,\sigma,T,p) h^{\frac{p}{2}}, \quad 1 \leq l, m \leq n$.
${\mathbb{E}} |X^n_{t_l}- T_{_{m,{\pm}}}X^n_{t_l}|^p \leq C(b,\sigma,T,p) h^{\frac{p}{2}}, \quad 1 \leq l, m \leq n$.(ii)
 ${\mathbb{E}}\bigg | \nabla X^{n,t_k,X^n_{t_k}}_{t_m} - \dfrac{\mathcal{D}^n_{k+1}X^n_{t_m} }{\sigma(t_{k+1},X^n_{t_k})} \bigg|^p \le C(b,\sigma,T,p) h^{\frac{p}{2}}, \quad 0 \le k < m \le n$.
${\mathbb{E}}\bigg | \nabla X^{n,t_k,X^n_{t_k}}_{t_m} - \dfrac{\mathcal{D}^n_{k+1}X^n_{t_m} }{\sigma(t_{k+1},X^n_{t_k})} \bigg|^p \le C(b,\sigma,T,p) h^{\frac{p}{2}}, \quad 0 \le k < m \le n$.(iii)
 ${\mathbb{E}} |\mathcal{D}^n_k X^n_{t_m} |^p \le C(b,\sigma,T,p), \quad0 \le k \leq m \leq n$.
${\mathbb{E}} |\mathcal{D}^n_k X^n_{t_m} |^p \le C(b,\sigma,T,p), \quad0 \le k \leq m \leq n$.
Proof.
(i) By definition,
 $T_{_{m, \pm}}X^n_{t_l} = X^n_{t_l}$ for
$T_{_{m, \pm}}X^n_{t_l} = X^n_{t_l}$ for  $l \leq m -1, $ and for
$l \leq m -1, $ and for  $l\ge m$ we have
By the properties of b and
$l\ge m$ we have
By the properties of b and \begin{align*}T_{_{m, \pm}}X^n_{t_l} &= X^n_{t_{m-1}} + b(t_m,X^n_{t_{m-1}})h \pm \sigma(t_m,X^n_{t_{m-1}}) \sqrt{h} \\[3pt] &\quad + \ h \sum_{j=m+1}^{ {l}} b(t_j, T_{_{m,\pm}}X^n_{t_{j-1}})+ \sqrt{h} \sum_{j=m+1}^{ {l}} \sigma(t_{ j}, T_{_{m,\pm}}X^n_{t_{j-1}}){\varepsilon}_j.\end{align*}
\begin{align*}T_{_{m, \pm}}X^n_{t_l} &= X^n_{t_{m-1}} + b(t_m,X^n_{t_{m-1}})h \pm \sigma(t_m,X^n_{t_{m-1}}) \sqrt{h} \\[3pt] &\quad + \ h \sum_{j=m+1}^{ {l}} b(t_j, T_{_{m,\pm}}X^n_{t_{j-1}})+ \sqrt{h} \sum_{j=m+1}^{ {l}} \sigma(t_{ j}, T_{_{m,\pm}}X^n_{t_{j-1}}){\varepsilon}_j.\end{align*} $\sigma$, and thanks to the inequality of BDG and Hölder’s inequality, we see that
It remains to apply Gronwall’s lemma.
$\sigma$, and thanks to the inequality of BDG and Hölder’s inequality, we see that
It remains to apply Gronwall’s lemma. \begin{align*}& {\mathbb{E}}|X^n_{t_l}- T_{_{m, \pm}}X^n_{t_l}|^p\\
& \quad\leq C(p) \Bigg( {\mathbb{E}}\big|\sigma(t_m,X^n_{t_{m-1}}) \sqrt{h}(1 \pm\varepsilon_m)\big|^p+ h^{p} {\mathbb{E}} \Bigg| \sum_{j = m+1 }^l \big(b(t_j, X^n_{t_{j-1}}) - b(t_j, T_{_{m,\pm}}X^n_{t_{j-1}})\big)\Bigg|^p\\
& \quad \quad + h^{\frac{p}{2}} {\mathbb{E}} \Bigg |\sum_{j=m+1}^l \big(\sigma(t_j, X^n_{t_{j-1}}) - \sigma(t_j, T_{_{m,\pm}} X^n_{t_{j-1}})\big)^2 \Bigg |^{\frac{p}{2}} \Bigg )\\
& \quad\leq C(p) \Bigg ( \|{\sigma}\|_{\infty}^p h^{\frac{p}{2}} + h (\|{b_x}\|_{\infty}^p t_{l-m}^{p-1} + \|{\sigma_x}\|_{\infty}^pt_{l-m}^{{\frac{p}{2}}-1}) \sum_{j=m+1}^l {\mathbb{E}}|X^n_{t_{j-1}}- T_{_{m,\pm}}X^n_{t_{j-1}}|^p \Bigg ).\end{align*}
\begin{align*}& {\mathbb{E}}|X^n_{t_l}- T_{_{m, \pm}}X^n_{t_l}|^p\\
& \quad\leq C(p) \Bigg( {\mathbb{E}}\big|\sigma(t_m,X^n_{t_{m-1}}) \sqrt{h}(1 \pm\varepsilon_m)\big|^p+ h^{p} {\mathbb{E}} \Bigg| \sum_{j = m+1 }^l \big(b(t_j, X^n_{t_{j-1}}) - b(t_j, T_{_{m,\pm}}X^n_{t_{j-1}})\big)\Bigg|^p\\
& \quad \quad + h^{\frac{p}{2}} {\mathbb{E}} \Bigg |\sum_{j=m+1}^l \big(\sigma(t_j, X^n_{t_{j-1}}) - \sigma(t_j, T_{_{m,\pm}} X^n_{t_{j-1}})\big)^2 \Bigg |^{\frac{p}{2}} \Bigg )\\
& \quad\leq C(p) \Bigg ( \|{\sigma}\|_{\infty}^p h^{\frac{p}{2}} + h (\|{b_x}\|_{\infty}^p t_{l-m}^{p-1} + \|{\sigma_x}\|_{\infty}^pt_{l-m}^{{\frac{p}{2}}-1}) \sum_{j=m+1}^l {\mathbb{E}}|X^n_{t_{j-1}}- T_{_{m,\pm}}X^n_{t_{j-1}}|^p \Bigg ).\end{align*}(ii) By the inequality of BDG and Hölder’s inequality,
Since by Lemma 5.4(i) we conclude that \begin{align*}&{\mathbb{E}}\!\left | \nabla X^{n,t_k,X^n_{t_k}}_{t_m} - \frac{ \mathcal{D}^n_{k+1} X^n_{t_{m}}}{\sigma( t_{k+1},X^n_{t_k})} \right |^p\\[3pt] &\quad \le C(p,T) \bigg ( | b_x(t_{k+1}, X^n_{t_k})h + \sigma_x(t_{k+1},X^n_{t_k}) \sqrt{h} {\varepsilon}_{k+1}|^p \notag \\[3pt]
& \qquad + h^p \sum_{l=k+2}^{m} {\mathbb{E}} \bigg| b_x(t_l, X^n_{t_{l-1}}) \nabla X^{n,t_k,X^n_{t_k}}_{t_{l-1}} - b_x^{(k+1,l)} \frac{\mathcal{D}^n_{k+1} X^n_{t_{l-1}}}{\sigma( t_{k+1},X^n_{t_k})} \bigg|^p \nonumber\\[3pt]& \qquad + h^{\frac{p}{2}} \!\!\! \sum_{l=k+2}^{m} {\mathbb{E}} \bigg|\sigma_x(t_l, X^n_{t_{l-1}}) \nabla X^{n,t_k,X^n_{t_k}}_{t_{l-1}} -\sigma_x^{(k+1,l)} \frac{\mathcal{D}^n_{k+1} X^n_{t_{l-1}}}{\sigma(t_{k+1},X^n_{t_k})} \bigg|^{p} \bigg ).\end{align*}and Lemma 5.2 implies that
\begin{align*}&{\mathbb{E}}\!\left | \nabla X^{n,t_k,X^n_{t_k}}_{t_m} - \frac{ \mathcal{D}^n_{k+1} X^n_{t_{m}}}{\sigma( t_{k+1},X^n_{t_k})} \right |^p\\[3pt] &\quad \le C(p,T) \bigg ( | b_x(t_{k+1}, X^n_{t_k})h + \sigma_x(t_{k+1},X^n_{t_k}) \sqrt{h} {\varepsilon}_{k+1}|^p \notag \\[3pt]
& \qquad + h^p \sum_{l=k+2}^{m} {\mathbb{E}} \bigg| b_x(t_l, X^n_{t_{l-1}}) \nabla X^{n,t_k,X^n_{t_k}}_{t_{l-1}} - b_x^{(k+1,l)} \frac{\mathcal{D}^n_{k+1} X^n_{t_{l-1}}}{\sigma( t_{k+1},X^n_{t_k})} \bigg|^p \nonumber\\[3pt]& \qquad + h^{\frac{p}{2}} \!\!\! \sum_{l=k+2}^{m} {\mathbb{E}} \bigg|\sigma_x(t_l, X^n_{t_{l-1}}) \nabla X^{n,t_k,X^n_{t_k}}_{t_{l-1}} -\sigma_x^{(k+1,l)} \frac{\mathcal{D}^n_{k+1} X^n_{t_{l-1}}}{\sigma(t_{k+1},X^n_{t_k})} \bigg|^{p} \bigg ).\end{align*}and Lemma 5.2 implies that \begin{align*}{\mathbb{E}} |b_x^{(k+1,l)} - b_x(t_l, X^n_{t_{l-1}})|^{2p} + {\mathbb{E}} |\sigma_x^{(k+1,l)} - \sigma_x(t_l, X^n_{t_{l-1}})|^{2p} \leq C(b,\sigma,T,p) h^{p},\end{align*}the assertion follows by Gronwall’s lemma.
\begin{align*}{\mathbb{E}} |b_x^{(k+1,l)} - b_x(t_l, X^n_{t_{l-1}})|^{2p} + {\mathbb{E}} |\sigma_x^{(k+1,l)} - \sigma_x(t_l, X^n_{t_{l-1}})|^{2p} \leq C(b,\sigma,T,p) h^{p},\end{align*}the assertion follows by Gronwall’s lemma. \begin{equation*} {\mathbb{E}} \sup_{k+1 \leq l \leq m} \Big |\nabla X^{n,t_k,X^n_{t_k}}_{t_{l-1}}\Big|^{2p} \leq C(b,\sigma,T,p),\end{equation*}
\begin{equation*} {\mathbb{E}} \sup_{k+1 \leq l \leq m} \Big |\nabla X^{n,t_k,X^n_{t_k}}_{t_{l-1}}\Big|^{2p} \leq C(b,\sigma,T,p),\end{equation*}(iii) This is an immediate consequence of (i).
Acknowledgement
Christel Geiss would like to thank the Erwin Schrödinger Institute, Vienna, where a part of this work was written, for its hospitality and support.