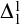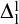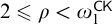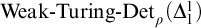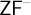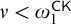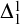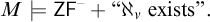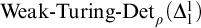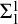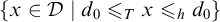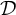Introduction
A most important result in the study of infinite games is Harvey Friedman’s [Reference Friedman3], where it is shown that a proof of determinacy, for Borel games, would require
$\aleph _{1}$
iterations of the power set operation—and this is precisely what Tony Martin used in his landmark proof [Reference Martin7].
Our focus here is on the Turing determinacy results of [Reference Friedman3], concentrating instead on the theory
${\mathsf {ZF}^{-\!}}$
, rather than Zermelo’s
${\mathsf {Z}}$
. In the
${\Delta ^{1}_{1}}$
realm, Friedman essentially shows that the determinacy of Turing closed
$\Delta ^{1}_{1}$
games—henceforth,
${\textrm{Turing-Det}(\Delta ^{1}_{1})}$
—implies the consistency of the theories
${\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{\nu }\textrm{ exists''}$
, for all
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
. He does produce a level-by-level analysis entailing, e.g., that the determinacy of Turing closed
${\Sigma ^{0}_{n+6}}$
games implies the consistency of
${\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{n}\textrm{ exists''}$
.Footnote
1
,
Footnote
2
Importantly, it was further observed by Friedman (unpublished) that these results extend to produce transitive models, rather than just consistency statements. See Martin’s forthcoming book [Reference Martin9] for details, see also Van Wesep’s [Reference Van Wesep13].
We forgo in this paper the level-by-level analysis to provide, in §3, a simple proof of the existence of transitive models of
${\mathsf {ZF}^{-\!}}$
with uncountable cardinals, from
${\textrm{Turing-Det}(\Delta ^{1}_{1})}$
. In so doing, we show that the full force of Turing determinacy isn’t needed. The main result is Theorem 3.1, with a simply stated corollary. For context, by Martin’s Lemma (see 1.2),
${\textrm{Turing-Det}(\Delta ^{1}_{1})}$
is equivalent to:
-
• Every cofinal
$\Delta ^{1}_{1}$
set of Turing degrees contains a cone of degrees—i.e., a set
$\{ x \in {\mathcal {D}} \mid d_{0} \mathbin {\leqslant _{T}} x \}$
.
Theorem (3.1)
Let
$2 \leqslant \rho < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, and assume every
$\Delta ^{1}_{1}$
set of reals, cofinal in the Turing degrees, contains two Turing distinct,
${\Delta ^{0}_{\rho }}$
-equivalent reals. For every
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, there is a transitive model:
$M \models {\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{\nu }\textrm{ exists''}$
.
Corollary (3.2)
If every cofinal
$\Delta ^{1}_{1}$
set of Turing degrees contains both a degree and its jump, then for every
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, there is a transitive model:
${M \models {\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{\nu }\textrm{ exists''}}$
.
In §4 several results are derived, showing that
${\textrm{Turing-Det}(\Delta ^{1}_{1})}$
imparts weak determinacy properties to the class
$\Sigma ^{1}_{1}$
, such as [4.4]:
-
• Every cofinal
$\Sigma ^{1}_{1}$
set of degrees includes a set
$\{\mkern 1mu {x \in {\mathcal {D}}} \mid d_{0} \mathbin {\leqslant _{T}} x \; \&\; x \mathbin {\leqslant _{h}} d_{0} \}$
, for some
$d_{0} \in {\mathcal {D}}$
.
Or, from Borel Turing determinacy, [4.3]:
-
• If
$(A_k)_{k < \omega}$
is a sequence of cofinal analytic subsets of
${\mathcal {D}}$
, then
is cofinal in
${\mathcal {D}}$
.
I wish to thank Tony Martin for inspiring exchanges on the present results. He provided the argument for Remark 2.3, below, and observed that my first proof of Theorem 4.6 was needlessly complex. Parts of §4 go back to the author’s dissertation [Reference Sami12], it is a pleasure to acknowledge Robert Solovay’s direction. Lastly, thanks are due to the referee for thoughtful suggestions.
1 Preliminaries and notation
The effective descriptive set theory we shall need, as well as basic hyperarithmetic theory, is from Moschovakis’ [Reference Moschovakis11], whose terminology and notation we follow. For the theory of admissible sets, we refer to Barwise’s [Reference Barwise1]. Standard facts about the
${\mathbb {L}}$
-hierarchy are used without explicit mention: see Devlin’s [Reference Devlin2], or Van Wesep’s [Reference Van Wesep13].
${\mathcal {N}} = \omega ^{\omega } = {\mathbb {N}}^{\mathbb {N}}$
denotes Baire’s space (the set of reals), and
${\mathcal {D}}$
the set of Turing degrees. Subsets of
${\mathcal {D}}$
shall be identified with the corresponding (Turing closed) sets of reals.
$\mathbin {\leqslant _{T}}$
,
$\mathbin {\leqslant _{h}}$
, and
$\mathrel {\equiv _{T}}$
,
$\mathrel {\equiv _{h}}$
denote, respectively, Turing and hyperarithmetic (i.e.,
$\Delta ^{1}_{1}$
) reducibility, and equivalence.
1.1 The ambient theories
Our base theory is
${\mathsf {ZF}^{-\!}}$
, Zermelo–Fraenkel set theory stripped of the Power Set axiom.Footnote
3
${\mathcal {N}}$
or
${\mathcal {D}}$
may be proper classes in this context, yet speaking of their ‘subsets’ (
$\Delta ^{1}_{1}$
,
$\Sigma ^{1}_{1}$
, Borel or analytic) can be handled as usual, as these sets are codable by integers, or reals. Amenities such as
$\aleph _{1}$
or
${\mathbb {L}_{\omega _{1}}}$
aren’t available but, since our results here are global (i.e.,
$\Delta ^{1}_{1}$
) rather than local, the reader may use instead the more comfortable
${\mathsf {ZF}^{-\!}} + \textrm{``}{\mathcal {P}}^{2}(\omega ) \textrm{ exists''}$
.
${\mathsf {KP}_{\infty }}$
is the theory Kripke–Platek
$+$
Infinity. Much of the argumentation below involves
$\omega $
-models of
${\mathsf {KP}_{\infty }}\!--$
familiarity with their properties is assumed.
1.2 Turing determinacy
A set of reals
$A \subseteq {\mathcal {N}}$
is said to be Turing-cofinal if, for every
$x \in {\mathcal {N}}$
, there is
$y \in A$
, such that
$x \mathbin {\leqslant _{T}} y$
. A Turing cone is a set
$ \operatorname {\mathrm {\operatorname {Cone}}}(c) = {\{{x \in {\mathcal {N}}} \mid {c \mathbin {\leqslant _{T}} x} \}}$
, where
$c \in {\mathcal {N}}$
. For a class of sets of reals
$\Gamma $
,
${\textrm{Det}(\Gamma )}$
is the statement that infinite games
${\textrm{G}_{\omega }(A)}$
where
$A \in \Gamma $
are determined, whereas
${\textrm{Turing-Det}(\Gamma )}$
stands for the determinacy of games
${\textrm{G}_{\omega }(A)}$
restricted to Turing closed sets
$A \in \Gamma $
. Recall the following easy, yet central:
Martin’s Lemma [Reference Martin6]
For a Turing closed set
$A \subseteq {\mathcal {N}}$
, the infinite game
${\textrm{G}_{\omega }(A)}$
is determined iff A or its complement contains a Turing cone.⊣
1.3 Constructibility and condensation
For an ordinal
$\lambda> 0$
, and
$X \subseteq {\mathbb {L}_{\lambda }}$
,
${\mathsf {H}^{\mathbb {L}_{\lambda }}\mkern -2mu}(X)$
denotes the set of elements of
${\mathbb {L}_{\lambda }}$
definable from parameters in X, and
its transitive collapse. For
$X = \varnothing $
, one simply writes
${\mathsf {H}^{\mathbb {L}_{\lambda }}\mkern -2mu}$
and
. Gödel’s Condensation Lemma is the relevant tool here. Note that, since
, all elements of
${\mathbb {L}_{\lambda }}$
are definable in
${\mathbb {L}_{\lambda }}$
from ordinal parameters.
1.4 Reflection
The following reflection principle will be used a few times, to make for shorter proofs.Footnote
4
A property
$\Phi (X)$
of subsets
$X \subseteq {\mathcal {N}}$
is said to be “
${\Pi ^{1}_{1}}$
on
$\Sigma ^{1}_{1}$
” if, for any
$\Sigma ^{1}_{1}$
relation
$U \subseteq {\mathcal {N}} \times {\mathcal {N}}$
, the set
${\{\mkern 1mu {x \in {\mathcal {N}}} \mid \Phi (U_{x}) \}}$
is
${\Pi ^{1}_{1}}$
.
A simple example of such a property: let
$A \subseteq {\mathcal {N}}$
be
$\Sigma ^{1}_{1}$
, and set:
$\Theta (X) \Leftrightarrow X \cap A = \varnothing $
.
$\Theta (X)$
is a
${\Pi ^{1}_{1}}$
on
$\Sigma ^{1}_{1}$
property.
Theorem. Let
$\Phi (X)$
be a
${\Pi ^{1}_{1}}$
on
$\Sigma ^{1}_{1}$
property. For any
$\Sigma ^{1}_{1}$
set
$S \subseteq {\mathcal {N}}$
such that
$\Phi (S)$
there is a
$\Delta ^{1}_{1}$
set
$D \supseteq S$
such that
$\Phi (D)$
.
Proof See Kechris’ [Reference Kechris5, §35] for a boldface version, easily transcribed to lightface.
2 Weak-Turing-Determinacy
Examining what’s needed to derive the existence of transitive models from Turing determinacy hypotheses, it is possible to isolate a seemingly weaker statement. For
$1 \leqslant \rho < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, let
$x \mathrel {\equiv _{\rho }} y$
denote
${\Delta ^{0}_{\rho }}$
-equivalence on
${\mathcal {N}}$
, that is:
$x \in {\Delta ^{0}_{\rho }}(y) \mathrel {\&} y \in {\Delta ^{0}_{\rho }}(x)$
.
$\mathrel {\equiv _{1}}$
is just Turing equivalence.
Definition 2.1. For a class
$\Gamma $
, and
$2 \leqslant \rho < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, define
${\textrm{Weak-Turing-Det}_{\rho }(\Gamma )}$
:
Every Turing-cofinal set of reals
$A \in \Gamma $
has two Turing distinct elements
$x, y \in A$
such that
$x \mathrel {\equiv _{\rho }} y$
.
For any recursive
$\rho \geqslant 2$
,
${\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})}$
will suffice to derive the existence of transitive models of
${\mathsf {ZF}^{-\!}}$
with uncountable cardinals. The property lifts from
$\Delta ^{1}_{1}$
to
$\Sigma ^{1}_{1}-\kern-5pt-\kern-2pt-$
note that it is, a priori, asymmetric.
Theorem 2.2. Let
$2 \leqslant \rho < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
,
$$ \begin{align*} {{\rm Weak}\textrm{-}{\rm Turing}\textrm{-}{\rm Det}_{\rho}(\Delta^{1}_{1})} \mathrel{\;{=}\mkern-10mu{\Rightarrow}\;} {{\rm Weak}\textrm{-}{\rm Turing}\textrm{-}{\rm Det}_{\rho}(\Sigma^{1}_{1})}. \end{align*} $$
Proof Assume
${\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})}$
. Let
$S \in \Sigma ^{1}_{1}$
and suppose there are no Turing distinct
$x, y \in S$
such that
$x \mathrel {\equiv _{\rho }} y$
, that is
$$ \begin{align*} \forall x,y \mkern1mu (x, y \in S \;\&\; x \mathrel{\equiv_{\rho}} y \mathrel{\;{=}\mkern-10mu{\Rightarrow}\;} x \mathrel{\equiv_{T}} y). \end{align*} $$
This is a statement
$\Phi (S)$
, where
$\Phi (X)$
is easily checked to be a
${\Pi ^{1}_{1}}$
on
$\Sigma ^{1}_{1}$
property. Reflection yields a
$\Delta ^{1}_{1}$
set
$D \supseteq S$
such that
$\Phi (D)$
. By
${\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})}$
, D is not Turing-cofinal; a fortiori, S isn’t either.
Remark 2.3. One may be tempted to substitute for
${\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})}$
a simpler hypothesis:
Every Turing-cofinal
$\Delta ^{1}_{1}$
set of reals has Turing distinct elements
$x, y$
, such that
$x \mathrel {\equiv _{h}} y$
.
It turns out to be too weak and, indeed, provable in Analysis. (Tony Martin, private communication: building on his paper [Reference Martin8], he shows that every uncountable
$\Delta ^{1}_{1}$
set of reals contains two Turing distinct reals, in every hyperdegree
$\geqslant $
Kleene’s
${\mathcal {O}}$
.)
The simpler, weaker, condition does suffice however when asserted about the class
$\Sigma ^{1}_{1}$
, see Theorem 3.13, below.
3 Transitive models from Weak-Turing-Determinacy
We state the main result, and a simple special case. The proof is postponed towards the end of the present section.
Theorem 3.1. Let
$2 \leqslant \rho < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, and assume
${{\rm Weak}\textrm{-}{\rm Turing}\textrm{-}{\rm Det}_{\rho }(\Delta ^{1}_{1})}$
. For every
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, there is a transitive model:
$M \models {\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{\nu }\textrm{ exists''}$
.
Corollary 3.2. If every cofinal
$\Delta ^{1}_{1}$
set of Turing degrees contains both a degree and its jump, then for every
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, there is a transitive model:
${M \models {\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{\nu } \textrm{ exists''}}$
.
$\bullet $
Term models.
Given a completeFootnote
5
theory
$U \supseteq {\mathsf {KP}_{\infty } + (\mathbb {V}=\mathbb {L})}$
, one constructs its term model. To be specific: owing to the presence of the axiom
${\mathbb {V}} = {\mathbb {L}}$
, to every formula
$\psi (v)$
is associated
such that
, just take for
the formula
$\psi (v) \land (\forall w <_{\mathbb {L}} v \mkern 1mu) \neg \psi (w)$
.
Let now
${(\varphi _{n}(v))_{n < \omega }}$
be a recursive in U enumeration of the formulas
$\varphi (v)$
, in the single free variable
$v$
, having
. Using, as metalinguistic device,
$(\boldsymbol {\iota }\mkern .8mu v) \varphi (v)$
for “the unique
$v$
such that
$\varphi (v)$
” set:
and define on
$M_{U}$
the relation
$\in _{U}$
:
$(M_{U}, \in _{U})$
is a prime model of U and, U being complete,
$(M_{U}, {\in _{U}}) \mathbin {\leqslant _{T}} U$
. Using the canonical
$1{\textrm{-}}1$
enumeration
$\omega \to M_{U}$
, substitute
$\omega $
for
$M_{U}$
and remap
$\in _{U}$
accordingly. The resulting model
${\mathcal {M}_{U}} = (\omega , \in ^{\mathcal {M}_{U}})$
shall be called the term model of U. The function
$U \mapsto {\mathcal {M}_{U}}$
is recursive, and
${\mathcal {M}_{U}} \mathrel {\equiv _{h}} U$
, uniformly.
Whenever
${\mathcal {M}_{U}}$
is an
$\omega $
-model, we say that
$a \subseteq \omega $
is realized in
${\mathcal {M}_{U}}$
if there is
$\mathring {a} \in \omega $
such that
$a = {\{\mkern 1mu {k \in \omega } \mid k^{\mathcal {M}_{U}} \!\in ^{\mathcal {M}_{U}}\! \mathring {a} \}}$
. We state, for later reference, a couple of standard facts.
Proposition 3.3. Let U be as above. If
${\mathcal {M}_{U}}$
is an
$\omega $
-model, and
$a \subseteq \omega $
is realized in
${\mathcal {M}_{U}}$
, then:
-
(1) For all
$x \mathbin {\leqslant _{h}} a$
, x is realized in
${\mathcal {M}_{U}}$
. -
(2)
$a \mathbin {\leqslant _{T}} U$
. Hence U is not realized in
${\mathcal {M}_{U}}$
, lest the Turing jump
$U^{\prime }$
be realized in
${\mathcal {M}_{U}}$
, causing
$U^{\prime } \mathbin {\leqslant _{T}} U$
.⊣
Note that if
$U = { \operatorname {\mathrm {\operatorname {Th}}}(\mathbb {L}_{\alpha }})$
, where
$\alpha $
is admissible, then
${\mathcal {M}_{U}}$
is a copy of
${\mathsf {H}^{\mathbb {L}_{\alpha }}\mkern -2mu}$
. Hence
${\mathcal {M}_{U}} \cong {\mathbb {L}_{\beta }}$
, for some
$\beta \leqslant \alpha $
. The following easy proposition is quite familiar.
Proposition 3.4. Assume
${\mathbb {V}} = {\mathbb {L}}$
. For cofinally many countable admissible
$\alpha $
’s,
${\mathbb {L}_{\alpha }} = {\mathsf {H}^{\mathbb {L}_{\alpha }}\mkern -2mu}$
, equivalently:
$\mathcal {M}_{{ \operatorname {\mathrm {\operatorname {Th}}}(\mathbb {L}_{\alpha }})}\cong {\mathbb {L}_{\alpha }}$
.
Proof Suppose not. Let
$\lambda $
be the sup of the admissible
$\alpha $
’s having
${\mathbb {L}_{\alpha }} = {\mathsf {H}^{\mathbb {L}_{\alpha }}\mkern -2mu}$
, and let
$\kappa> \lambda $
be the first admissible such that
$\lambda $
is countable in
${\mathbb {L}_{\kappa }}$
. Since
$\lambda $
is definable and countable in
${\mathbb {L}_{\kappa }}$
,
$\lambda \cup \{\lambda \} \subseteq {\mathsf {H}^{\mathbb {L}_{\kappa }}\mkern -2mu}$
. It follows readily that
, a contradiction.
$\bullet $
Cardinality in the constructible levels.
Set theory within the confines of
${\mathbb {L}_{\lambda }}$
,
$\lambda $
an arbitrary limit ordinal, imposes some contortions. For technical convenience, the notion of cardinal needs to be slightly twisted—for a time only.
Definition 3.5.
-
(1) For an ordinal
$\alpha $
,
$ \operatorname {\mathrm {\operatorname {Card}}}(\alpha ) = \min _{\xi \leqslant \alpha }(\textit {there is a surjection}\ \xi \to \alpha )$
. -
(2)
$\alpha $
is a cardinal if
$\alpha = \operatorname {\mathrm {\operatorname {Card}}}(\alpha )$
. -
(3)
$ \operatorname {\mathrm {\operatorname {Card}}}_{\lambda } \subseteq {\mathbb {L}_{\lambda }}$
is the class of infinite cardinals as computed in
${\mathbb {L}_{\lambda }}$
.
3.6. Note that, for
$\lambda $
limit, from a surjection
$g \colon \gamma \to \alpha $
in
${\mathbb {L}_{\lambda }}$
, one can extract
$a \subseteq \gamma $
and
${\vartriangleleft } \subseteq a \times a$
such that
,Footnote
6
and both
$(a, \vartriangleleft )$
,
$g \mathord {\upharpoonright } a$
are in
${\mathbb {L}_{\lambda }}$
. Further, if
$\lambda $
is admissible, in
${\mathbb {L}_{\lambda }}$
the altered notion of cardinality and the standard one coincide.
Convention 3.7. For simplicity’s sake, the assertion
$\textrm{``}\aleph _{\nu } \textrm{ exists in } {\mathbb {L}_{\lambda }}\textrm{''}$
should be understood as:
There is an isomorphism
, where J is an initial segment of
$ \operatorname {\mathrm {\operatorname {Card}}}_{\lambda }$
.
Note that its negation is equivalent in
${\mathsf {KP}_{\infty }}$
to: There is
$\kappa \leqslant \nu $
such that
$ \operatorname {\mathrm {\operatorname {Card}}}_{\lambda } \cong \kappa $
. The notation
$\aleph _{\nu }^{\mathbb {L}_{\lambda }}$
carries the obvious meaning.
We need the following result, readily proved using the Jensen techniques of [Reference Jensen4]. A direct proof is provided in the Appendix.
Proposition 3.8. For
$\lambda $
a limit ordinal, if
${\mathbb {L}_{\lambda }} \models \textrm{``}\boldsymbol {\mu }> \omega \textrm{ is a successor cardinal''}$
then
${\mathbb {L}_{\mu }} \models {\mathsf {ZF}^{-\!}}$
.
$\bullet $
The theories
${\mathsf {T}_{\nu }}$
.
Let
${\mathcal {M}}$
be an
$\omega $
-model of
${\mathsf {KP}_{\infty }}$
. The wellfounded part of
$\mathbb {O}\textrm{n}^{\mathcal {M}}$
‘includes’
$\omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
. For
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, pick
$e_{\nu }$
a recursive index for a wellordering
$<_{e_{\nu }}$
of a subset of
$\omega $
, of length
$\nu $
. Using
$e_{\nu }$
, statements about
$\nu $
can tentatively be expressed in
${\mathsf {KP}_{\infty }}$
. In
${\mathcal {M}}$
, the truth of such statements is independent of the choice of
$e_{\nu }$
. Indeed,
$<_{e_{\nu }}$
is realized in
${\mathcal {M}}$
, and its realization is isomorphic in
${\mathcal {M}}$
to the
${\mathcal {M}}$
-ordinal of order-type
$\nu $
, to be denoted
$\nu ^{\mathcal {M}}$
. For a formula
$\varphi (x, \ldots )$
, we write
${\mathcal {M}} \models \varphi (\underline {\nu }, \ldots )$
, instead of a ‘translated’
${\mathcal {M}} \models \varphi ^{\ast }(e_{\nu }, \ldots )$
.
Definition 3.9. For
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
,
${\mathsf {T}_{\nu }}$
is the theory
$$ \begin{align*} {\mathsf{KP}_{\infty} + (\mathbb{V}=\mathbb{L})} + \textrm{ ``for all limit } \lambda, \aleph_{\nu+1} \textrm{ doesn't exist in } {\mathbb{L}_{\lambda}}\textrm{''}. \end{align*} $$
This definition is clearly lacking: a recursive index
$e_{\nu }$
coding the ordinal
$\nu $
is not made explicit. This is immaterial, as we shall be interested only in
$\omega $
-models of
${\mathsf {T}_{\nu }}$
. They possess the following rigidity property.
Lemma 3.10. Let
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, and
${\mathcal {M}_{1}}$
,
${\mathcal {M}_{2}}$
be
$\omega $
-models of
${\mathsf {T}_{\nu }}$
. Let
$u \in \mathbb {O}\textrm{n}^{\mathcal {M}_{1}}$
, and
$w, w_{\ast } \in \mathbb {O}\textrm{n}^{\mathcal {M}_{2}}$
, for any two isomorphisms
and
,
$f = f_{\ast }$
.
Proof By an easy reduction, it suffices to prove this for u, a limit
${\mathcal {M}_{1}}$
-ordinal.
Let
$<_{1}$
denote the ordering of
$\mathbb {O}\textrm{n}^{\mathcal {M}_{1}}$
in
${\mathcal {M}_{1}}$
, and set
${\mathcal {C}}_{u} = {\{\mkern 1mu {c <_{1} u} \mid {\mathcal {M}_{1}} \models \boldsymbol {c} \in \operatorname {\mathrm {\operatorname {Card}}}_{\boldsymbol {u}} \}}$
.
The relevant claim here is that
$({\mathcal {C}}_{u}, <_{1})$
is wellordered. Indeed, since
${\mathcal {M}_{1}} \models {\mathsf {T}_{\underline {\nu }}}$
,
$$ \begin{align*} {\mathcal{M}_{1}} \models \textrm{``}{\aleph_{\underline{\nu} +1}} \textrm{ doesn't exist in } {\mathbb{L}_{\boldsymbol{u}}}\textrm{''}. \end{align*} $$
Hence, as observed in 3.7, there is
$k \in \mathbb {O}\textrm{n}^{\mathcal {M}_{1}}$
with
$$ \begin{align*} {\mathcal{M}_{1}} \models \boldsymbol{k} \leqslant \underline{\nu}+1 \; \&\; \operatorname{\mathrm{\operatorname{Card}}}_{\boldsymbol{u}} \cong \boldsymbol{k}. \end{align*} $$
The isomorphism in
${\mathcal {M}_{1}}$
induces an actual isomorphism
$({\mathcal {C}}_{u}, <_{1}) \cong ({\{\mkern 1mu {x} \mid x <_{1} k \}}, <_{1})$
. Since
${\mathcal {M}_{1}}$
is an
$\omega $
-model,
$\nu ^{\mathcal {M}_{1}}$
(and hence, k) is in its wellfounded part, thus the claim.
First, we check that f and
$f_{\ast }$
agree on the
${\mathcal {M}_{1}}$
-ordinals
$o <_{1} u$
, using induction on
${\mathcal {C}}_{u}$
. Clearly, for
$o \leqslant _{1} \omega ^{\mathcal {M}_{1}}$
,
$f(o)=f_{\ast }(o)$
. Set
$\kappa _{u}(o) = \operatorname {\mathrm {\operatorname {Card}}}(o)$
, as evaluated in
${\mathbb {L}_{u}^{\!{\mathcal {M}_{1}}}}$
, and show by induction on
$c \in {\mathcal {C}}_{u}$
:
The inductive hypothesis, for
$c^{\prime } <_{1} c$
, yields, for all
$o <_{1} c$
,
$f(o) = f_{\ast }(o)$
, hence
$f(c) = f_{\ast }(c)$
. Let now
$o <_{1} u$
have
$\kappa _{u}(o) = c$
. Inside
${\mathbb {L}_{u}^{\!{\mathcal {M}_{1}}}}$
,
$(o, \in )$
is isomorphic to an ordering
$s = (a, \vartriangleleft )$
, where
$a \subseteq c$
and
${\vartriangleleft } \subseteq c \times c$
, (see 3.6). Since f and
$f_{\ast }$
agree on the
${\mathcal {M}_{1}}$
-ordinals up to c, one readily gets
$f(s) = f_{\ast }(s)$
. In
${\mathcal {M}_{2}}$
now, the common value
$f(s)$
is isomorphic to both the ordinals
$f(o)$
and
$f_{\ast }(o)$
, hence
$f(o) = f_{\ast }(o)$
.
This entails
$w = w_{\ast }$
and
${\mathbb {L}_{w}^{\!{\mathcal {M}_{2}}}} = {\mathbb {L}_{w_{\ast }}^{\!{\mathcal {M}_{2}}}}$
. Now, any
$x \in {\mathbb {L}_{u}^{\!{\mathcal {M}_{1}}}}$
is definable in
${\mathbb {L}_{u}^{\!{\mathcal {M}_{1}}}}$
from
${\mathcal {M}_{1}}$
-ordinals (see 1.3), thus
$f(x)$
and
$f_{\ast }(x)$
satisfy in
${\mathbb {L}_{w}^{\!{\mathcal {M}_{2}}}}$
the same definition from equal parameters, hence
$f(x) = f_{\ast }(x)$
.
$\bullet $
Pseudo-wellfounded models.
A relation
${\vartriangleleft } \subseteq \omega \times \omega $
is said to be pseudo-wellfounded if every nonempty
$\Delta ^{1}_{1}(\vartriangleleft )$
subset of
$\omega $
has a
$\vartriangleleft $
-minimal element. By the standard computation, this is a
$\Sigma ^{1}_{1}$
property.Footnote
7
Indeed, we may define it, for
$\boldsymbol {E} \subseteq \omega \times \omega $
, as:
$$ \begin{align*} {\textrm{pseudo-WF}(\boldsymbol{E})} \;\Leftrightarrow^{\textrm{def}}\, (\forall X \mathbin{\leqslant_{h}} \boldsymbol{E} \mkern1mu)\bigl(X \neq \varnothing \mathrel{\;{=}\mkern-10mu{\Rightarrow}\;} (\exists k \,{\in}\, X \mkern1mu)(\forall m \,{\in}\, X \mkern1mu)\neg(m \,{\boldsymbol{E}}\, k)\bigr). \end{align*} $$
Definition 3.11. For
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
,
$\mathcal {S}_{\nu }$
is the set of theories:
$$ \begin{align*} {\mathcal{S}_{\nu}} = {\{\mkern1mu {U} \mid U \textrm{ is a complete extension of } {\mathsf{T}_{\nu}}, \textrm{ and } {\mathcal{M}_{U}} \textrm{ is pseudo-wellfounded} \}}. \end{align*} $$
Easily,
${\mathcal {S}_{\nu }}$
is
$\Sigma ^{1}_{1}$
. Indeed, the first clause in its definition is arithmetical, while the second reads “
${\textrm{pseudo-WF}(\in ^{\mathcal {M}_{U}})}$
,” where the function
$U \mapsto {\in ^{\mathcal {M}_{U}}}$
is recursive.
Note further: for
$U \in {\mathcal {S}_{\nu }}$
,
${\mathcal {M}_{U}}$
is an
$\omega $
-model. The sets
${\mathcal {S}_{\nu }}$
play a central role in the proof. They are sparse, in the following sense.
Proposition 3.12. For
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, no two distinct members of
${\mathcal {S}_{\nu }}$
have the same hyperdegree.
Proof Let
$U_{1}, U_{2} \in {\mathcal {S}_{\nu }}$
have
$U_{1} \mathrel {\equiv _{h}} U_{2}$
, and let
${\mathcal {M}_{1}}$
,
${\mathcal {M}_{2}}$
stand for
${\mathcal {M}_{U_{1}}}$
,
${\mathcal {M}_{U_{2}}}$
. We’ll obtain
$U_{1} = U_{2}$
by showing
${\mathcal {M}_{1}} \cong {\mathcal {M}_{2}}$
. Define a relation between ‘ordinals’
$u \in {\mathcal {M}_{1}}$
and
$w \in {\mathcal {M}_{2}}$
:
Set
$I_{1} = \operatorname {\mathrm {\operatorname {Dom}}}(\simeq )$
, and
$I_{2} = \operatorname {\mathrm {\operatorname {Im}}}(\simeq )$
.
$I_{1}$
and
$I_{2}$
are initial segments of
$\mathbb {O}\textrm{n}^{\mathcal {M}_{1}}$
and
$\mathbb {O}\textrm{n}^{\mathcal {M}_{2}}$
, respectively. Using Lemma 3.10, the relation “
$u \simeq w$
” defines a bijection
$I_{1} \to I_{2}$
which is, indeed, the restriction of an isomorphism
Note that, by the same lemma,
The RHS here reads:
$\exists !f \mkern 1mu {\mathcal {I}}(\hspace{2pt}f, U_{1}, u, U_{2}, w)$
, where
${\mathcal {I}}$
is a
$\Delta ^{1}_{1}$
predicate, hence:
By the standard computation, the relation “
$u \simeq w$
” is
$\Delta ^{1}_{1}(U_{1} \oplus U_{2})\ [\, = \Delta ^{1}_{1}(U_{1}) = \Delta ^{1}_{1}(U_{2})]$
. Consequently,
$I_{1}$
and
$I_{2}$
are also
$\Delta ^{1}_{1}(U_{1})\ [\, = \Delta ^{1}_{1}(U_{2})]$
.
${\mathcal {M}_{1}}$
,
${\mathcal {M}_{2}}$
being pseudo-wellfounded,
$\mathbb {O}\textrm{n}^{\mathcal {M}_{1}} - I_{1}$
and
$\mathbb {O}\textrm{n}^{\mathcal {M}_{2}} - I_{2}$
each, if nonempty, has a minimum. Denote
$m_{1}, m_{2}$
the respective potential minima, and consider the cases:
-
–
$\mathbb {O}\textrm{n}^{\mathcal {M}_{1}} - I_{1}$
and
$\mathbb {O}\textrm{n}^{\mathcal {M}_{2}} - I_{2}$
are both nonempty. This isn’t possible, as
$\boldsymbol {F}$
would be the isomorphism
, entailing
$m_{1} \in I_{1}$
and
$m_{2} \in I_{2}$
. -
–
$I_{1} = \mathbb {O}\textrm{n}^{\mathcal {M}_{1}}$
and
$\mathbb {O}\textrm{n}^{\mathcal {M}_{2}} - I_{2} \ne \varnothing $
. Here
, and
.
$U_{1}$
is now the theory of
${\mathbb {L}_{m_{2}}^{\!{\mathcal {M}_{2}}}}$
, hence is realized in
${\mathcal {M}_{2}}$
. Since
$U_{2} \mathrel {\equiv _{h}} U_{1}$
, by Prop. 3.3(1),
$U_{2}$
is also realized in
${\mathcal {M}_{2}}$
(that’s
${\mathcal {M}_{U_{2}}}$
). This contradicts (2) of the same proposition. -
– The third case, symmetric of the previous one, is equally impossible.
-
– The remaining case:
$I_{1} = \mathbb {O}\textrm{n}^{\mathcal {M}_{1}}$
and
$I_{2} = \mathbb {O}\textrm{n}^{\mathcal {M}_{2}}$
. Here
and
, thus
is the desired isomorphism.
Proof of Theorem 3.1 Our hypothesis is
${\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})}$
, and we may work entirely in
${\mathbb {L}}$
.
Fix any
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, towards a transitive model of
${\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{\nu }\textrm{ exists''}$
.
Claim. There is a limit ordinal
$\lambda $
, such that:
${\aleph _{\nu +1}}$
exists in
${\mathbb {L}_{\lambda }}$
.
Suppose no such
$\lambda $
exists. It follows that for all admissible
$\alpha> \omega $
,
$\mathbb {L}_{\alpha } \models {\mathsf {T}_{\nu }}$
. This entails that
${\mathcal {S}_{\nu }}$
is Turing-cofinal: indeed, since
${\mathbb {V}} = {\mathbb {L}}$
, using Proposition 3.4, given
$x \subseteq \omega $
there is an
$\alpha> \omega $
, admissible, such that
$x \in {\mathbb {L}_{\alpha }}$
and
${\mathcal {M}_{{ \operatorname {\mathrm {\operatorname {Th}}}(\mathbb {L}_{\alpha }})}} \cong {\mathbb {L}_{\alpha }}$
. Thus
$x \mathbin {\leqslant _{T}} { \operatorname {\mathrm {\operatorname {Th}}}(\mathbb {L}_{\alpha }})$
and,
${\mathcal {M}_{ \operatorname {\mathrm {\operatorname {Th}}}({\mathbb {L}_{\alpha }})}}$
being wellfounded,
${ \operatorname {\mathrm {\operatorname {Th}}}(\mathbb {L}_{\alpha }}) \in {\mathcal {S}_{\nu }}$
.
Invoking now
${\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})}$
and Theorem 2.2,
${\textrm{Weak-Turing-Det}_{\rho }(\Sigma ^{1}_{1})}$
holds. Hence, there are distinct
$U_{1}, U_{2} \in {\mathcal {S}_{\nu }}$
such that
$U_{1} \mathrel {\equiv _{\rho }} U_{2}$
, contradicting the previous proposition. ⊣Claim
Let now
$\lambda $
be as claimed, and set
$\mu = {\aleph _{\nu +1}^{\mathbb {L}_{\lambda }}}$
. In
${\mathbb {L}_{\lambda }}$
,
$\mu $
is a successor cardinal hence, by Prop. 3.8,
${\mathbb {L}_{\mu }} \models {\mathsf {ZF}^{-\!}}$
. Further, for
$\xi \leqslant \nu $
,
${\aleph _{\xi }^{\mathbb {L}_{\lambda }}} < \mu $
and
${\aleph _{\xi }^{\mathbb {L}_{\lambda }}}$
is an
$\mathbb {L}_{\mu }$
-cardinal (now in the usual sense), hence
${\mathbb {L}_{\mu }} \models {\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{\nu }\textrm{ exists''}$
.
Note the following byproduct of the previous proposition, and the proof just given (substituting
$U_{1} \mathrel {\equiv _{h}} U_{2}$
for
$U_{1} \mathrel {\equiv _{\rho }} U_{2}$
, in the proof)—in contradistinction to Remark 2.3.
Theorem 3.13. Assume every Turing-cofinal
$\Sigma ^{1}_{1}$
set of reals has two Turing distinct elements
$x, y$
, such that
$x \mathrel {\equiv _{h}} y$
. For every
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
, there is a transitive model:
$M \models {\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{\nu }\textrm{ exists''}$
.⊣
An easy consequence of the main result:
${\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})}$
implies full
$\Delta ^{1}_{1}$
determinacy. The proof proceeds via Martin’s Borel determinacy theorem: no direct argument is known for this sort of implication—apparently first observed by Friedman for
${\textrm{Turing-Det}(\Delta ^{1}_{1})}$
.
Theorem 3.14. For
$2 \leqslant \rho < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
,
$\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})$
implies
$\textrm{Det}(\Delta ^{1}_{1})$
.
Proof Assume
${\textrm{Weak-Turing-Det}_{\rho }(\Delta ^{1}_{1})}$
. Let
$A \subseteq {\mathcal {N}}$
be
$\Delta ^{1}_{1}$
, say
$A \in {\Sigma ^{0}_{\nu }}$
where
$\nu < \omega _{1}^{\scriptscriptstyle \mathsf {CK}}$
. Applying Theorem 3.1, there is a transitive
$M \models {\mathsf {ZF}^{-\!}} + \textrm{``}\aleph _{\nu }\textrm{ exists''}$
. Invoking (non-optimally) Martin’s main result from [Reference Martin8] inside M,
${\Sigma ^{0}_{\nu }}$
games are determined. The statement “the game
${\textrm{G}_{\omega }(A)}$
is determined” is
${\Sigma ^{1}_{2}}$
. By Mostowki’s absoluteness theorem, being true in M, it holds in the universe:
${\textrm{G}_{\omega }(A)}$
is indeed determined.
4
$\Delta ^{1}_{1}$
determinacy and properties of
$\Sigma ^{1}_{1}$
sets
We proceed now to show that
$\Delta ^{1}_{1}$
determinacy imparts weak determinacy properties to the class
$\Sigma ^{1}_{1}$
. In view of Theorem 3.14, there is no point, here, in working from weaker hypotheses.
Definition 4.1. The hyp-Turing cone with vertex
$d \in {\mathcal {D}}$
is the set of degrees
$$ \begin{align*} \operatorname{\mathrm{\operatorname{Cone}}}_{h}(d) = \operatorname{\mathrm{\operatorname{Cone}}}(d) \cap \Delta^{1}_{1}(d) = \{\mkern1mu x \in {\mathcal{D}} \mid d \mathbin{\leqslant_{T}} x\; \&\; x \mathbin{\leqslant_{h}} d \}. \end{align*} $$
${\textrm{Hyp-Turing-Det}(\Gamma )}$
is the statement: Every cofinal set of degrees
$A \in \Gamma $
contains a hyp-Turing cone.
Theorem 4.2. Assume
${{\rm Turing}\textrm{-}{\rm Det}(\Delta ^{1}_{1})}$
. If
$ (S_k)_{k < \omega}$
is a
$\Sigma ^{1}_{1}$
sequence of Turing-cofinal sets of degrees, then
—and, indeed,
contains a hyp-Turing cone.
Proof Let the
$S_{k}$
’s be given as the sections of a
$\Sigma ^{1}_{1}$
relation
$S \subseteq \omega \times {\mathcal {N}}$
, and assume
contains no hyp-Turing cone:
, i.e.,
This is a statement
$\Phi (S)$
, where
$\Phi (X)$
is a
${\Pi ^{1}_{1}}$
on
$\Sigma ^{1}_{1}$
property of subsets
$X \subseteq \omega \times {\mathcal {N}}$
. Reflection yields a
$\Delta ^{1}_{1}$
relation
$D \supseteq S$
such that
$\Phi (D)$
. Shrink D, if need be, to ensure that its sections
$D_{k}$
are Turing closed, preserving
$\Phi (D)$
and
$D \supseteq S$
. Now,
$D_{k} \supseteq S_{k}$
and
contains no hyp-Turing cone. A contradiction ensues using
${\textrm{Turing-Det}(\Delta ^{1}_{1})}\, +$
Martin’s Lemma: each
$D_{k}$
, being cofinal in
${\mathcal {D}}$
, contains a Turing cone hence, easily, so does
.
The converse is immediate. Indeed, if
${\textrm{Turing-Det}(\Delta ^{1}_{1})}$
fails, by Martin’s Lemma there is a
$\Delta ^{1}_{1}$
set
$A \subseteq {\mathcal {D}}$
, such that both A and
${\sim }A$
are cofinal in
${\mathcal {D}}$
, and the
$\Delta ^{1}_{1}$
sequence
$\langle A, {\sim }A \rangle $
has empty intersection. Relativizing 4.2, one readily gets:
Corollary 4.3. Assume Borel Turing determinacy. If
$(A_k)_{k < \omega}$
is a sequence of cofinal analytic sets of Turing degrees, then
is cofinal in
${\mathcal {D}}$
.⊣
An interesting special case of 4.2, where the ‘sequence’
$(S_{k})_{k<1}$
is a single
$\Sigma ^{1}_{1}$
term.
Theorem 4.4.
${{\rm Turing}\textrm{-}{\rm Det}(\Delta ^{1}_{1})}$
implies
${{\rm Hyp}\textrm{-}{\rm Turing}\textrm{-}{\rm Det}(\Sigma ^{1}_{1})}$
.⊣
In view of Theorem 3.14, the implication is an equivalence. A similar result obtains for full determinacy.
Definition 4.5. For a game
${\textrm{G}_{\omega }(A)}$
, a strategy
$\sigma $
for Player I is called a hyp-winning strategy if
$\forall \tau \mathbin {\leqslant _{h}} \sigma \mkern 1mu(\sigma {*}\tau \in A)$
, i.e., applying
$\sigma $
, Player I wins against any
$\Delta ^{1}_{1}(\sigma )$
sequence of moves by Player II.
Theorem 4.6. Assume
${{\rm Det}(\Delta ^{1}_{1})}$
. For
$S \in \Sigma ^{1}_{1}$
, one of the following holds for
${{\rm G}_{\omega }(S)}$
,
-
(1) Player I has a hyp-winning strategy.
-
(2) Player II has a winning strategy.
Proof Let S be
$\Sigma ^{1}_{1}$
, and assume Player I has no hyp-winning strategy for
${\textrm{G}_{\omega }(S)}$
, that is:
$\forall \sigma \mkern 1mu \exists \tau \mathbin {\leqslant _{h}} \sigma \mkern 1mu(\sigma {*}\tau \notin S)$
. Much as in the proof of 4.2, Reflection yields a
$\Delta ^{1}_{1}$
set
$D \supseteq S$
such that Player I has no hyp-winning strategy for
${\textrm{G}_{\omega }(D)}$
, hence no winning strategy. Invoking
${\textrm{Det}(\Delta ^{1}_{1})}$
, Player II has a winning strategy for
${\textrm{G}_{\omega }(D)}$
which is, a fortiori, winning for
${\textrm{G}_{\omega }(S)}$
.
5 Appendix
The point of the present section is to sketch a proof of Proposition 3.8, without dissecting the
${\mathbb {L}}$
construction—albeit with a recourse to admissible sets. Finer results most certainly hold.
${\mathcal {F}}$
is the set of formulas,
${\mathcal {F}} \in \mathbb {L}_{\omega +1}$
, and
$\models _{\mathbb {L}_{\alpha }}$
is the satisfaction relation for
${\mathbb {L}_{\alpha }}$
,
$$ \begin{align*} {\models_{{\mathbb{L}_{\alpha}}}} (\varphi,\vec{s}) \mathrel{\;{\mathrel{{\Leftarrow}\mkern-16mu{\Rightarrow}}}\;} \varphi \in {\mathcal{F}} \; \& \; \vec{s}\ \in {\mathbb{L}_{\alpha}^{\!<\omega}} \; \& \; {\mathbb{L}_{\alpha}} \models \varphi[\vec{s}]. \end{align*} $$
Apart from the classic Condensation Lemma (see 1.3), we shall need the following familiar result: For any limit
$\lambda> \omega $
, and
$\beta < \lambda $
,
$\models _{{\mathbb {L}_{\beta }}} \in {\mathbb {L}_{\lambda }}$
. See [Reference Van Wesep13, §7.1].
Notation. Let
$X \mathrel {\gg ^{\mkern -4mu{\lambda }}} Y$
abbreviate
$\exists f \,{\in }\, {\mathbb {L}_{\lambda }} \mkern 1mu(\hspace{2pt}f \colon X \twoheadrightarrow Y)$
, where ‘
$\twoheadrightarrow $
’ stands for surjective map.
Reminder. Here, “
$\mu $
is an
$\mathbb {L}_{\lambda }$
-cardinal” means: “for no
$\xi < \mu $
, does
$\xi \mathrel {\gg ^{\mkern -4mu{\lambda }}} \mu $
” (see 3.5).
Lemma 5.1. Let
$\lambda> \omega $
be limit. For
$0 < \alpha \leqslant \gamma < \lambda $
, and
,
${\alpha }^{< \omega } \mathrel {\gg ^{\mkern -4mu{\lambda }}} \beta $
.
Proof Observe that
${\mathbb {L}_{\beta }} = {\mathsf {H}^{\mathbb {L}_{\beta }}\mkern -2mu}(\alpha )$
, and
$\beta < \lambda $
. In
${\mathbb {L}_{\beta }}$
, every
$\xi < \beta $
is the unique solution of some formula
$\varphi (v, \vec {\boldsymbol {\eta }})$
, where
$\vec {\eta } \in {\alpha }^{< \omega }$
. Thus, using
$\models _{{\mathbb {L}_{\beta }}} \in {\mathbb {L}_{\lambda }}$
, one readily derives
${\mathcal {F}}\times {\alpha }^{< \omega } \mathrel {\gg ^{\mkern -4mu{\lambda }}} \beta $
. Using an injection
${\mathcal {F}}\times {\alpha }^{< \omega } \to {\alpha }^{< \omega }$
in
${\mathbb {L}_{\lambda }}$
, one gets
${\alpha }^{< \omega } \mathrel {\gg ^{\mkern -4mu{\lambda }}} \beta $
.
Proposition 5.2. Let
$\lambda> \omega $
be a limit ordinal, and
$\omega < \mu < \lambda $
, an
$\mathbb {L}_{\lambda }$
-cardinal.
-
(1) For
$0 < \alpha < \mu \leqslant \gamma < \lambda $
, and
. (A downward Löwenheim–Skolem property). -
(2)
$\mu $
is admissible.
Proof We check (1) and (2) simultaneously, by induction on
$\mu $
.
(1) Set
. Note that, for
,
, it follows that
is an
$\mathbb {L}_{\lambda }$
-cardinal, and clearly
.
We claim that
. If
$\mu = {\aleph _{1}^{\mathbb {L}_{\lambda }}}$
, then
. Else, if
then, by induction,
is admissible, yielding an
-definable map
. Whence
, and thus
, contradicting “
$\mu $
is an
$\mathbb {L}_{\lambda }$
-cardinal.”
Now, given
$0 < \alpha < \mu \leqslant \gamma < \lambda $
, and
, the previous lemma yields
${\alpha }^{< \omega } \mathrel {\gg ^{\mkern -4mu{\lambda }}} \beta $
. Hence, since
,
$\beta < \mu $
.
(2) To show that
$\mu $
is admissible, only
$\Delta _{0}$
Collection needs checking.
Say
${\mathbb {L}_{\mu }} \models \forall x \,{\in }\, \boldsymbol {a} \mkern 1mu \exists y \mkern 1mu \varphi (x, y, \vec {\boldsymbol {p}})$
, where
$\varphi $
is
$\Delta _{0}$
, and
$a, \vec {p} \in {\mathbb {L}_{\mu }}$
. Pick
$\alpha < \mu $
with
$a,\vec {p} \in {\mathbb {L}_{\alpha }}$
and set
:
${\mathbb {L}_{\beta }} \models \forall x \,{\in }\, \boldsymbol {a} \mkern 1mu \exists y \mkern 1mu \varphi (x, y, \vec {\boldsymbol {p}})$
. Applying (1),
$\beta < \mu $
, thus
$b =^{\textrm{def}} {\mathbb {L}_{\beta }} \in {\mathbb {L}_{\mu }}$
. By
$\Delta _{0}$
absoluteness,
${\mathbb {L}_{\mu }} \models \forall x \,{\in }\, \boldsymbol {a} \mkern 1mu \exists y \,{\in }\, \boldsymbol {b} \mkern 1mu \varphi (x,y,\vec {\boldsymbol {p}})$
.
Proposition 3.8. For
$\lambda $
limit,
${\mathbb {L}_{\lambda }} \models \textrm{``}\boldsymbol {\mu }> \omega \textrm{ is a successor cardinal}\textrm{''} \mathrel {\;{=}\mkern -10mu{\Rightarrow }\;} {{\mathbb {L}_{\mu }} \models {\mathsf {ZF}^{-\!}}}$
.
Proof Set
$\pi =$
the cardinal preceding
$\mu $
in
${\mathbb {L}}_{\lambda }$
. We argue that
$\pi $
is the largest cardinal in
${\mathbb {L}_{\mu }}$
. Indeed, for
$\pi \leqslant \eta < \mu $
, pick
$\gamma < \lambda $
such that
$\exists f \in {\mathbb {L}_{\gamma }} \mkern 1mu(\hspace{2pt}f \colon \pi \twoheadrightarrow \eta )$
, and set
. We get
$\exists f \in {\mathbb {L}_{\beta }} \mkern 1mu(\hspace{2pt}f \colon \pi \twoheadrightarrow \eta )$
and, invoking 5.2(1),
$\beta < \mu $
. Hence
${\mathbb {L}_{\mu }} \models \exists f \mkern 1mu(\hspace{2pt}f \colon \boldsymbol {\pi } \twoheadrightarrow \boldsymbol {\eta })$
.
Next:
$\mu $
is regular in
${\mathbb {L}_{\lambda }}$
. The usual
${\mathsf {ZFC}}$
proof for the regularity of infinite successors goes through here: for each nonzero
$\eta < \mu $
, using
$<_{{\mathbb {L}_{\mu }}}$
, select
$f_{\eta } \in {\mathbb {L}_{\mu }}$
,
$f_{\eta } \colon \pi \twoheadrightarrow \eta $
, and note that the sequence
$(\hspace{2pt}f_{\eta })_{0 < \eta < \mu }$
is in
${\mathbb {L}_{\mu +1}} \subseteq {\mathbb {L}_{\lambda }}$
, etc.
Finally, to show
${\mathbb {L}_{\mu }} \models {\mathsf {ZF}^{-\!}}$
: since by 5.2(2)
$\mu $
is admissible, using the standard definable bijection
$\mu \to {\mathbb {L}_{\mu }}$
, it suffices to verify Replacement for
${\mathbb {L}_{\mu }}$
class-functions
$\mu \to \mu $
.
Let therefore
$F \colon \mu \to \mu $
be
${\mathbb {L}_{\mu }}$
-definable, from parameters
$\vec {p}$
. Given a set of ordinals
$s \in {\mathbb {L}_{\mu }}$
, s is bounded in
$\mu $
. By regularity of
$\mu $
in
${\mathbb {L}_{\lambda }}$
,
$F[s]$
is bounded as well. Pick
$\alpha < \mu $
, with
$F[s] \subseteq \alpha $
and
$s, \vec {p} \in {\mathbb {L}_{\alpha }}$
:
$F[s]$
is definable over
${\mathbb {L}_{\mu }}$
from
$s, \vec {p} \in {\mathbb {L}_{\alpha }}$
, and
${\mathbb {L}_{\alpha }} \subseteq {\mathsf {H}^{\mathbb {L}_{\mu }}\mkern -2mu}(\alpha ) \prec {\mathbb {L}_{\mu }}$
. Set
, applying 5.2(1),
$\beta < \mu $
, and thus
${F[s] \in {\mathbb {L}_{\beta +1}} \subseteq {\mathbb {L}_{\mu }}}$
.
