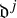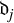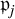1 Introduction
In recent years, complex structures on nilpotent Lie algebras have been shown to be very useful for understanding some geometric and algebraic properties of nilmanifolds. In [Reference Cordero, Fernández, Gray and Ugarte3, Reference Cordero, Fernández, Gray and Ugarte4], Cordero et al. introduced
![]() $\textit {nilpotent complex structures} $
, studied
$\textit {nilpotent complex structures} $
, studied
![]() $6$
-dimensional nilpotent Lie algebras with nilpotent complex structures and provided a classification. Since the ascending central series is not necessarily J-invariant, they introduced a J-invariant ascending central series to characterise nilpotent complex structures. More recently, Latorre, Ugarte and Villacampa defined the space of nilpotent complex structures on nilpotent Lie algebras and studied complex structures on nilpotent Lie algebras with one-dimensional centre [Reference Latorre, Ugarte and Villacampa10, Reference Latorre, Ugarte and Villacampa11]. They also provided a theorem describing the ascending central series of
$6$
-dimensional nilpotent Lie algebras with nilpotent complex structures and provided a classification. Since the ascending central series is not necessarily J-invariant, they introduced a J-invariant ascending central series to characterise nilpotent complex structures. More recently, Latorre, Ugarte and Villacampa defined the space of nilpotent complex structures on nilpotent Lie algebras and studied complex structures on nilpotent Lie algebras with one-dimensional centre [Reference Latorre, Ugarte and Villacampa10, Reference Latorre, Ugarte and Villacampa11]. They also provided a theorem describing the ascending central series of
![]() $8$
-dimensional nilpotent Lie algebras with complex structures. In [Reference Gao, Zhao and Zheng7], Gao et al. studied the relation between the step of a nilpotent Lie algebra and the smallest integer
$8$
-dimensional nilpotent Lie algebras with complex structures. In [Reference Gao, Zhao and Zheng7], Gao et al. studied the relation between the step of a nilpotent Lie algebra and the smallest integer
![]() $j_0$
such that the J-invariant ascending central series stops. Furthermore, they introduced a J-invariant descending central series, which is another tool to characterise nilpotent complex structures. These papers use the language of differential forms to characterise nilpotent complex structures. Our proofs are purely Lie algebraic.
$j_0$
such that the J-invariant ascending central series stops. Furthermore, they introduced a J-invariant descending central series, which is another tool to characterise nilpotent complex structures. These papers use the language of differential forms to characterise nilpotent complex structures. Our proofs are purely Lie algebraic.
Let G be a Lie group and
![]() $\mathfrak {g} \cong T_eG$
be its Lie algebra, which we always assume to be real, unless otherwise stated. A linear isomorphism
$\mathfrak {g} \cong T_eG$
be its Lie algebra, which we always assume to be real, unless otherwise stated. A linear isomorphism
![]() $J:TG \rightarrow TG$
is an
$J:TG \rightarrow TG$
is an
![]() $\textit {almost complex structure}$
if
$\textit {almost complex structure}$
if
![]() $J^2 = -I.$
By the Newlander–Nirenberg theorem [Reference Newlander and Nirenberg13], an almost complex structure J corresponds to a left invariant complex structure on G if and only if
$J^2 = -I.$
By the Newlander–Nirenberg theorem [Reference Newlander and Nirenberg13], an almost complex structure J corresponds to a left invariant complex structure on G if and only if
for all
![]() $X,Y \in \mathfrak {g}.$
Since we are interested only in Lie algebras in this paper, from now on, we will write J for
$X,Y \in \mathfrak {g}.$
Since we are interested only in Lie algebras in this paper, from now on, we will write J for
![]() $J_e.$
We will refer to (1.1) as the
$J_e.$
We will refer to (1.1) as the
![]() $\textit {Newlander--Nirenberg condition}.$
$\textit {Newlander--Nirenberg condition}.$
2 Complex structures on nilpotent Lie algebras
In this section, we consider some properties of the central series of a nilpotent Lie algebra with complex structure J and define a J-invariant central series. We define nilpotent complex structures, and relate their properties to the dimension of the centre
![]() $\mathfrak {z}$
of a nilpotent Lie algebra.
$\mathfrak {z}$
of a nilpotent Lie algebra.
Definition 2.1 (see, for example, [Reference Knapp9]).
Let
![]() $\mathfrak {g}$
be a Lie algebra. The
$\mathfrak {g}$
be a Lie algebra. The
![]() $\textit {descending} \textit{central series}$
and
$\textit {descending} \textit{central series}$
and
![]() $\textit {ascending central series}$
of
$\textit {ascending central series}$
of
![]() $\mathfrak {g} $
are denoted by
$\mathfrak {g} $
are denoted by
![]() $\mathfrak {c}_j(\mathfrak {g})$
and
$\mathfrak {c}_j(\mathfrak {g})$
and
![]() $\mathfrak {c}^j(\mathfrak {g})$
, respectively, for all
$\mathfrak {c}^j(\mathfrak {g})$
, respectively, for all
![]() $j \geq 0 ,$
and defined inductively by
$j \geq 0 ,$
and defined inductively by
Remark 2.2.
-
(i) Notice that
 $\mathfrak {c}^1(\mathfrak {g})=\mathfrak {Z}(\mathfrak {g}) $
,
$\mathfrak {c}^1(\mathfrak {g})=\mathfrak {Z}(\mathfrak {g}) $
,
 $\mathfrak {c}_1(\mathfrak {g}) = [\mathfrak {g},\mathfrak {g}]$
and
$\mathfrak {c}_1(\mathfrak {g}) = [\mathfrak {g},\mathfrak {g}]$
and
 $ \mathfrak {c}^{j}(\mathfrak {g})/\mathfrak {c}^{j-1}(\mathfrak {g}) = \mathfrak {Z}(\mathfrak {g}/ \mathfrak {c}^{j-1}(\mathfrak {g}))$
for all
$ \mathfrak {c}^{j}(\mathfrak {g})/\mathfrak {c}^{j-1}(\mathfrak {g}) = \mathfrak {Z}(\mathfrak {g}/ \mathfrak {c}^{j-1}(\mathfrak {g}))$
for all
 $j \geq 1$
, where
$j \geq 1$
, where
 $\mathfrak {Z}(\cdot )$
means the centre of a Lie algebra. Furthermore,
$\mathfrak {Z}(\cdot )$
means the centre of a Lie algebra. Furthermore,
 $\mathfrak {c}_j(\mathfrak {g})/\mathfrak {c}_{j+1}(\mathfrak {g}) \subseteq \mathfrak {Z} (\mathfrak {n}/\mathfrak {c}_{j+1}(\mathfrak {g}))$
for all
$\mathfrak {c}_j(\mathfrak {g})/\mathfrak {c}_{j+1}(\mathfrak {g}) \subseteq \mathfrak {Z} (\mathfrak {n}/\mathfrak {c}_{j+1}(\mathfrak {g}))$
for all
 $j \geq 0.$
It is clear that
$j \geq 0.$
It is clear that
 $\mathfrak {c}^j(\mathfrak {g})$
and
$\mathfrak {c}^j(\mathfrak {g})$
and
 $\mathfrak {c}_j(\mathfrak {g})$
are ideals of
$\mathfrak {c}_j(\mathfrak {g})$
are ideals of
 $\mathfrak {g}$
for all
$\mathfrak {g}$
for all
 $j \geq 0$
.
$j \geq 0$
. -
(ii) A Lie algebra
 $\mathfrak {g}$
is called
$\mathfrak {g}$
is called
 $\textit {nilpotent of step }k $
, for some
$\textit {nilpotent of step }k $
, for some
 $k \in \mathbb {N},$
if
$k \in \mathbb {N},$
if
 $\mathfrak {c}_k(\mathfrak {g}) = \{0\}$
and
$\mathfrak {c}_k(\mathfrak {g}) = \{0\}$
and
 $\mathfrak {c}_{k-1}(\mathfrak {g}) \neq \{0\}.$
We will denote nilpotent Lie algebras by
$\mathfrak {c}_{k-1}(\mathfrak {g}) \neq \{0\}.$
We will denote nilpotent Lie algebras by
 $\mathfrak {n}$
in this paper. (See, for example, [Reference Hilgert and Neeb8, Section 5.2] or [Reference Knapp9].)
$\mathfrak {n}$
in this paper. (See, for example, [Reference Hilgert and Neeb8, Section 5.2] or [Reference Knapp9].)
2.1 J-invariant central series and nilpotent complex structures
Following [Reference Cordero, Fernández, Gray and Ugarte3, Definition 1], we define the
![]() $\textit {J-invariant ascending central series}\ \mathfrak {d}^{\,j}$
for nilpotent Lie algebras and introduce
$\textit {J-invariant ascending central series}\ \mathfrak {d}^{\,j}$
for nilpotent Lie algebras and introduce
![]() $\textit {nilpotent complex structures}$
on nilpotent Lie algebras. Furthermore, we recall the definition of the
$\textit {nilpotent complex structures}$
on nilpotent Lie algebras. Furthermore, we recall the definition of the
![]() $\textit {J-invariant descending central series}\ \mathfrak {d}_j$
[Reference Gao, Zhao and Zheng7, Definition 2.7].
$\textit {J-invariant descending central series}\ \mathfrak {d}_j$
[Reference Gao, Zhao and Zheng7, Definition 2.7].
Definition 2.3. Let
![]() $ \mathfrak {n} $
be a Lie algebra with a complex structure
$ \mathfrak {n} $
be a Lie algebra with a complex structure
![]() $J.$
Define a sequence of J-invariant ideals of
$J.$
Define a sequence of J-invariant ideals of
![]() $\mathfrak {n}$
by
$\mathfrak {n}$
by
![]() $\mathfrak {d}^0 = \{0\}$
and
$\mathfrak {d}^0 = \{0\}$
and
for all
![]() $ j \geq 1.$
We call the sequence
$ j \geq 1.$
We call the sequence
![]() $\mathfrak {d}^{\,j}$
the J-
$\mathfrak {d}^{\,j}$
the J-
![]() $\textit {invariant ascending central series}$
. The complex structure J is called
$\textit {invariant ascending central series}$
. The complex structure J is called
![]() $\textit {nilpotent of step }j_0$
if there exists
$\textit {nilpotent of step }j_0$
if there exists
![]() $j_0 \in \mathbb {N}$
such that
$j_0 \in \mathbb {N}$
such that
![]() $\mathfrak {d}^{\,j_0} = \mathfrak {n}$
and
$\mathfrak {d}^{\,j_0} = \mathfrak {n}$
and
![]() $\mathfrak {d}^{\,j_0-1} \subset \mathfrak {n}$
.
$\mathfrak {d}^{\,j_0-1} \subset \mathfrak {n}$
.
We define inductively the J-
![]() $\textit {invariant descending central series}$
by
$\textit {invariant descending central series}$
by
Remark 2.4.
-
(i) For the ascending J-invariant central series
 $\mathfrak {d}^{\,j}$
, In particular,
$\mathfrak {d}^{\,j}$
, In particular, $$ \begin{align*} \mathfrak{d}^{\,j} / \mathfrak{d}^{\,j-1} = \mathfrak{Z}(\mathfrak{n}/\mathfrak{d}^{\,j-1}) \cap J\mathfrak{Z}(\mathfrak{n}/\mathfrak{d}^{\,j-1}) \quad \text{for all } j \geq 1. \end{align*} $$
$$ \begin{align*} \mathfrak{d}^{\,j} / \mathfrak{d}^{\,j-1} = \mathfrak{Z}(\mathfrak{n}/\mathfrak{d}^{\,j-1}) \cap J\mathfrak{Z}(\mathfrak{n}/\mathfrak{d}^{\,j-1}) \quad \text{for all } j \geq 1. \end{align*} $$
 $\mathfrak {d}^1 = \mathfrak {z} \cap J\mathfrak {z},$
which is the largest J-invariant subspace of
$\mathfrak {d}^1 = \mathfrak {z} \cap J\mathfrak {z},$
which is the largest J-invariant subspace of
 $\mathfrak {z} $
and, if J is nilpotent, then
$\mathfrak {z} $
and, if J is nilpotent, then
 $\mathfrak {d}^1 \neq \{0\}$
. The nilpotency of J implies that the ascending J-invariant central series
$\mathfrak {d}^1 \neq \{0\}$
. The nilpotency of J implies that the ascending J-invariant central series
 $\mathfrak {d}^{\,j}$
of
$\mathfrak {d}^{\,j}$
of
 $\mathfrak {n}$
is strictly increasing until
$\mathfrak {n}$
is strictly increasing until
 $\mathfrak {d}^{\,j_0} = \mathfrak {n}$
. Furthermore, if
$\mathfrak {d}^{\,j_0} = \mathfrak {n}$
. Furthermore, if
 $\mathfrak {n}$
is a step k nilpotent Lie algebra with a nilpotent complex structure J of step
$\mathfrak {n}$
is a step k nilpotent Lie algebra with a nilpotent complex structure J of step
 $j_0$
, then
$j_0$
, then
 $k \leq j_0 \leq \tfrac 12\dim \mathfrak {n}$
(see, for example, [Reference Cordero, Fernández, Gray and Ugarte3, Reference Gao, Zhao and Zheng7]).
$k \leq j_0 \leq \tfrac 12\dim \mathfrak {n}$
(see, for example, [Reference Cordero, Fernández, Gray and Ugarte3, Reference Gao, Zhao and Zheng7]).
-
(ii) By definition, if
 $\mathfrak {n}$
admits a nilpotent complex structure, then
$\mathfrak {n}$
admits a nilpotent complex structure, then
 $\mathfrak {n}$
is nilpotent.
$\mathfrak {n}$
is nilpotent. -
(iii) For all
 $j \geq 0,$
it is clear that
$j \geq 0,$
it is clear that
 $ \mathfrak {c}_j(\mathfrak {n}) + J \mathfrak {c}_j(\mathfrak {n}) \subseteq \mathfrak {d}_j$
; furthermore,
$ \mathfrak {c}_j(\mathfrak {n}) + J \mathfrak {c}_j(\mathfrak {n}) \subseteq \mathfrak {d}_j$
; furthermore,
 $\mathfrak {d}_j \unlhd \mathfrak {n}$
and
$\mathfrak {d}_j \unlhd \mathfrak {n}$
and
 $\mathfrak {d}^{\,j} \unlhd \mathfrak {n}$
where
$\mathfrak {d}^{\,j} \unlhd \mathfrak {n}$
where
 $\unlhd $
is the notation for an ideal.
$\unlhd $
is the notation for an ideal. -
(iv) Let
 $ \mathfrak {n} $
be a Lie algebra with a complex structure
$ \mathfrak {n} $
be a Lie algebra with a complex structure
 $J.$
Then J preserves all terms of
$J.$
Then J preserves all terms of
 $ \mathfrak {c}^j(\mathfrak {n})$
if and only if
$ \mathfrak {c}^j(\mathfrak {n})$
if and only if
 $\mathfrak {d}^{\,j} = \mathfrak {c}^j(\mathfrak {n})$
for all
$\mathfrak {d}^{\,j} = \mathfrak {c}^j(\mathfrak {n})$
for all
 $j \geq 0$
[Reference Cordero, Fernández, Gray and Ugarte3, Corollary 5]. Similarly, J preserves all terms of
$j \geq 0$
[Reference Cordero, Fernández, Gray and Ugarte3, Corollary 5]. Similarly, J preserves all terms of
 $\mathfrak {c}_j(\mathfrak {n})$
if and only if
$\mathfrak {c}_j(\mathfrak {n})$
if and only if
 $\mathfrak {d}_j = \mathfrak {c}_j(\mathfrak {n})$
for all
$\mathfrak {d}_j = \mathfrak {c}_j(\mathfrak {n})$
for all
 $j.$
$j.$
The following lemma provides a connection between J-invariant ascending and descending central series.
Lemma 2.5. Let
![]() $\mathfrak {n}$
be a Lie algebra with a complex structure J.
$\mathfrak {n}$
be a Lie algebra with a complex structure J.
-
(i) If J is nilpotent of step
 $j_0$
, then
$j_0$
, then
 $\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian. Conversely, if there exists
$\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian. Conversely, if there exists
 $j_0\in \mathbb {N}$
such that
$j_0\in \mathbb {N}$
such that
 $\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian, then J is nilpotent of step at most
$\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian, then J is nilpotent of step at most
 $j_0.$
$j_0.$
-
(ii) If J is nilpotent of step
 $j_0$
, then
$j_0$
, then
 $\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j} $
for all
$\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j} $
for all
 $j \geq 0 $
. Conversely, if there exists
$j \geq 0 $
. Conversely, if there exists
 $j_0 \in \mathbb {N}$
such that
$j_0 \in \mathbb {N}$
such that
 $\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j} $
for all
$\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j} $
for all
 $j \geq 0,$
then J is nilpotent of step at most
$j \geq 0,$
then J is nilpotent of step at most
 $j_0.$
$j_0.$
Proof. For part (i), suppose that J is nilpotent of step
![]() $j_0$
. By definition,
$j_0$
. By definition,
![]() $\mathfrak {d}^{\,j_0} = \mathfrak {n}$
and
$\mathfrak {d}^{\,j_0} = \mathfrak {n}$
and
![]() $\mathfrak {d}^{\,j_0-1} \subset \mathfrak {n}$
. Then
$\mathfrak {d}^{\,j_0-1} \subset \mathfrak {n}$
. Then
![]() $\mathfrak {Z}(\mathfrak {n}/\mathfrak {d}^{\,j_0-1}) \cap J\mathfrak {Z}(\mathfrak {n}/ \mathfrak {d}^{\,j_0-1}) = \mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
. It is obvious that
$\mathfrak {Z}(\mathfrak {n}/\mathfrak {d}^{\,j_0-1}) \cap J\mathfrak {Z}(\mathfrak {n}/ \mathfrak {d}^{\,j_0-1}) = \mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
. It is obvious that
![]() $ \mathfrak {Z}(\mathfrak {n}/\mathfrak {d}^{\,j_0-1}) = \mathfrak {n}/\mathfrak {d}^{\,j_0-1}.$
Hence,
$ \mathfrak {Z}(\mathfrak {n}/\mathfrak {d}^{\,j_0-1}) = \mathfrak {n}/\mathfrak {d}^{\,j_0-1}.$
Hence,
![]() $\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian.
$\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian.
Conversely, suppose that there exists
![]() $j_0 \in \mathbb {N}$
such that
$j_0 \in \mathbb {N}$
such that
![]() $ \mathfrak {n}/ \mathfrak {d}^{\,j_0-1}$
is Abelian. Then
$ \mathfrak {n}/ \mathfrak {d}^{\,j_0-1}$
is Abelian. Then
![]() $ \{0\} \neq \mathfrak {c}_1(\mathfrak {n}) \subseteq \mathfrak {d}^{\,j_0-1}$
. For all
$ \{0\} \neq \mathfrak {c}_1(\mathfrak {n}) \subseteq \mathfrak {d}^{\,j_0-1}$
. For all
![]() $X \in \mathfrak {n},$
we have
$X \in \mathfrak {n},$
we have
![]() $[X,\mathfrak {n}] \subseteq \mathfrak {d}^{\,j_0 - 1} \text { and } [JX,\mathfrak {n}] \subseteq \mathfrak {d}^{\,j_0 -1}$
. We deduce that
$[X,\mathfrak {n}] \subseteq \mathfrak {d}^{\,j_0 - 1} \text { and } [JX,\mathfrak {n}] \subseteq \mathfrak {d}^{\,j_0 -1}$
. We deduce that
![]() $ \mathfrak {n} = \mathfrak {d}^{\,j_0}$
and therefore J is nilpotent of step at most
$ \mathfrak {n} = \mathfrak {d}^{\,j_0}$
and therefore J is nilpotent of step at most
![]() $j_0$
.
$j_0$
.
For part (ii), assume that J is nilpotent of step
![]() $j_0.$
By definition,
$j_0.$
By definition,
![]() $\mathfrak {d}_0 = \mathfrak {n} = \mathfrak {d}^{\,j_0}.$
Next, assume that
$\mathfrak {d}_0 = \mathfrak {n} = \mathfrak {d}^{\,j_0}.$
Next, assume that
![]() $\mathfrak {d}_{s-1} \subseteq \mathfrak {d}^{\,j_0-s+1}$
for some
$\mathfrak {d}_{s-1} \subseteq \mathfrak {d}^{\,j_0-s+1}$
for some
![]() $s \in \mathbb {N}.$
Then
$s \in \mathbb {N}.$
Then
Hence, by induction,
![]() $\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j} $
for all
$\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j} $
for all
![]() $j \geq 0.$
$j \geq 0.$
Conversely, suppose that there exists
![]() $j_0 \in \mathbb {N}$
such that
$j_0 \in \mathbb {N}$
such that
![]() $\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j} $
for all
$\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j} $
for all
![]() $j \geq 0$
. In particular,
$j \geq 0$
. In particular,
![]() $ \mathfrak {d}_1 \subseteq \mathfrak {d}^{\,j_0 -1}.$
By definition,
$ \mathfrak {d}_1 \subseteq \mathfrak {d}^{\,j_0 -1}.$
By definition,
![]() $\mathfrak {c}_1(\mathfrak {n}) \subseteq \mathfrak {d}_1.$
It follows that
$\mathfrak {c}_1(\mathfrak {n}) \subseteq \mathfrak {d}_1.$
It follows that
and thus
![]() $\mathfrak {n}/\mathfrak {d}^{\,j_0 -1}$
is Abelian. From Lemma 2.5, J is nilpotent of step at most
$\mathfrak {n}/\mathfrak {d}^{\,j_0 -1}$
is Abelian. From Lemma 2.5, J is nilpotent of step at most
![]() $j_0.$
$j_0.$
Remark 2.6. Under the condition of Lemma 2.5, if J is nilpotent of step
![]() $j_0,$
then
$j_0,$
then
![]() $\mathfrak {d}_{j_0-1} \subseteq \mathfrak {d}^1 \subseteq \mathfrak {z}$
and
$\mathfrak {d}_{j_0-1} \subseteq \mathfrak {d}^1 \subseteq \mathfrak {z}$
and
![]() $\mathfrak {d}_{j_0-1}$
is Abelian. Furthermore, there exists
$\mathfrak {d}_{j_0-1}$
is Abelian. Furthermore, there exists
![]() $j_0 \in \mathbb {N}$
such that
$j_0 \in \mathbb {N}$
such that
![]() $\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian if and only if
$\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian if and only if
![]() $\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0-j}$
for all
$\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0-j}$
for all
![]() $j \geq 0.$
This is proved by induction as in the proof of Lemma 2.5.
$j \geq 0.$
This is proved by induction as in the proof of Lemma 2.5.
Corollary 2.7. Let
![]() $\mathfrak {n}$
be a step k nilpotent Lie algebra with a complex structure
$\mathfrak {n}$
be a step k nilpotent Lie algebra with a complex structure
![]() $J.$
Then J is nilpotent of step k if and only if
$J.$
Then J is nilpotent of step k if and only if
![]() $\mathfrak {d}_j \subseteq \mathfrak {d}^{k-j}$
for all
$\mathfrak {d}_j \subseteq \mathfrak {d}^{k-j}$
for all
![]() $j \geq 0$
.
$j \geq 0$
.
Proof. Suppose that J is nilpotent of step
![]() $k.$
By Lemma 2.5,
$k.$
By Lemma 2.5,
![]() $\mathfrak {d}_j \subseteq \mathfrak {d}^{k-j}$
for all
$\mathfrak {d}_j \subseteq \mathfrak {d}^{k-j}$
for all
![]() $j \geq 0.$
Conversely, assume that
$j \geq 0.$
Conversely, assume that
![]() $\mathfrak {d}_j \subseteq \mathfrak {d}^{k-j}$
for all
$\mathfrak {d}_j \subseteq \mathfrak {d}^{k-j}$
for all
![]() $j.$
Again by Lemma 2.5, J is nilpotent of step at most
$j.$
Again by Lemma 2.5, J is nilpotent of step at most
![]() $k.$
Furthermore, it follows that
$k.$
Furthermore, it follows that
![]() $ \{0\} \neq \mathfrak {c}_{k-1}(\mathfrak {n}) \subseteq \mathfrak {d}_{k-1}.$
Therefore,
$ \{0\} \neq \mathfrak {c}_{k-1}(\mathfrak {n}) \subseteq \mathfrak {d}_{k-1}.$
Therefore,
![]() $\mathfrak {d}_{k-1} \neq \{0\} $
and J is nilpotent of step
$\mathfrak {d}_{k-1} \neq \{0\} $
and J is nilpotent of step
![]() $k.$
$k.$
Remark 2.8. From Remark 2.6, J is nilpotent of step k if and only if
![]() $\mathfrak {n}/\mathfrak {d}^{k-1}$
is Abelian.
$\mathfrak {n}/\mathfrak {d}^{k-1}$
is Abelian.
We introduce a new descending central series whose descending ‘rate’ is slower than that of
![]() $\mathfrak {c}_j(\mathfrak {n})$
but faster than that of
$\mathfrak {c}_j(\mathfrak {n})$
but faster than that of
![]() $\mathfrak {d}_j.$
$\mathfrak {d}_j.$
Definition 2.9. Let J be a complex structure on a Lie algebra
![]() $\mathfrak {n}.$
We define the sequence
$\mathfrak {n}.$
We define the sequence
![]() $\mathfrak {p}_j$
inductively by
$\mathfrak {p}_j$
inductively by
Remark 2.10. It is clear that
![]() $\mathfrak {p}_{j+1} \subseteq \mathfrak {p}_j$
for all
$\mathfrak {p}_{j+1} \subseteq \mathfrak {p}_j$
for all
![]() $j \geq 0.$
Furthermore,
$j \geq 0.$
Furthermore,
![]() $\mathfrak {p}_j \unlhd \mathfrak {n}$
since
$\mathfrak {p}_j \unlhd \mathfrak {n}$
since
![]() $[\mathfrak {p}_j,\mathfrak {n}] \subseteq \mathfrak {p}_{j+1} \subseteq \mathfrak {p}_j$
for all
$[\mathfrak {p}_j,\mathfrak {n}] \subseteq \mathfrak {p}_{j+1} \subseteq \mathfrak {p}_j$
for all
![]() $j \geq 0$
.
$j \geq 0$
.
Lemma 2.11. Let
![]() $\mathfrak {n}$
be a Lie algebra with a complex structure
$\mathfrak {n}$
be a Lie algebra with a complex structure
![]() $J $
. Then
$J $
. Then
![]() $ \mathfrak {c}_j(\mathfrak {n}) \subseteq \mathfrak {p}_j$
for all
$ \mathfrak {c}_j(\mathfrak {n}) \subseteq \mathfrak {p}_j$
for all
![]() $j \geq 0$
. Furthermore,
$j \geq 0$
. Furthermore,
![]() $\mathfrak {p}_j \subseteq \mathfrak {d}_j $
and
$\mathfrak {p}_j \subseteq \mathfrak {d}_j $
and
![]() $ J \mathfrak {p}_j \subseteq \mathfrak {d}_j $
for all
$ J \mathfrak {p}_j \subseteq \mathfrak {d}_j $
for all
![]() $j \geq 0$
.
$j \geq 0$
.
Proof. By definition,
![]() $\mathfrak {c}_0(\mathfrak {n}) = \mathfrak {n} = \mathfrak {p}_0.$
It follows, by induction, that
$\mathfrak {c}_0(\mathfrak {n}) = \mathfrak {n} = \mathfrak {p}_0.$
It follows, by induction, that
![]() $ \mathfrak {c}_j(\mathfrak {n}) \subseteq \mathfrak {p}_j$
for all
$ \mathfrak {c}_j(\mathfrak {n}) \subseteq \mathfrak {p}_j$
for all
![]() ${j \geq 0}$
. Using (2.2),
${j \geq 0}$
. Using (2.2),
![]() $[\mathfrak {d}_{j-1},\mathfrak {n}] \subseteq \mathfrak {d}_j $
. By definition,
$[\mathfrak {d}_{j-1},\mathfrak {n}] \subseteq \mathfrak {d}_j $
. By definition,
![]() $ \mathfrak {p}_0 = \mathfrak {n} = \mathfrak {d}_0 \mbox { and } J\mathfrak {p}_0 = J\mathfrak {n} = \mathfrak {n} = \mathfrak {d}_0$
. Next, suppose that
$ \mathfrak {p}_0 = \mathfrak {n} = \mathfrak {d}_0 \mbox { and } J\mathfrak {p}_0 = J\mathfrak {n} = \mathfrak {n} = \mathfrak {d}_0$
. Next, suppose that
![]() $\mathfrak {p}_s \subseteq \mathfrak {d}_s \mbox { and } J\mathfrak {p}_s \subseteq \mathfrak {d}_s$
for some
$\mathfrak {p}_s \subseteq \mathfrak {d}_s \mbox { and } J\mathfrak {p}_s \subseteq \mathfrak {d}_s$
for some
![]() $s \in \mathbb {N}.$
Then by (2.3),
$s \in \mathbb {N}.$
Then by (2.3),
By induction,
![]() $ \mathfrak {p}_j \subseteq \mathfrak {d}_j $
and
$ \mathfrak {p}_j \subseteq \mathfrak {d}_j $
and
![]() $J\mathfrak {p}_j \subseteq \mathfrak {d}_j $
for all
$J\mathfrak {p}_j \subseteq \mathfrak {d}_j $
for all
![]() $j \geq 0.$
$j \geq 0.$
Remark 2.12.
-
(i) Notice that
 $\mathfrak {p}_j/\mathfrak {p}_{j+1} \subseteq \mathfrak {Z}(\mathfrak {n}/\mathfrak {p}_{j+1})$
for all
$\mathfrak {p}_j/\mathfrak {p}_{j+1} \subseteq \mathfrak {Z}(\mathfrak {n}/\mathfrak {p}_{j+1})$
for all
 $j \geq 0.$
Indeed, for all
$j \geq 0.$
Indeed, for all
 $P \in \mathfrak {p}_j$
and
$P \in \mathfrak {p}_j$
and
 $Y \in \mathfrak {n},$
since
$Y \in \mathfrak {n},$
since
 $[P,Y] \subseteq \mathfrak {p}_{j+1},$
it is enough to deduce Hence,
$[P,Y] \subseteq \mathfrak {p}_{j+1},$
it is enough to deduce Hence, $$ \begin{align*}[P+ \mathfrak{p}_{j+1},Y + \mathfrak{p}_{j+1}] =[P,Y] + \mathfrak{p}_{j+1} \subseteq \mathfrak{p}_{j+1}. \end{align*} $$
$$ \begin{align*}[P+ \mathfrak{p}_{j+1},Y + \mathfrak{p}_{j+1}] =[P,Y] + \mathfrak{p}_{j+1} \subseteq \mathfrak{p}_{j+1}. \end{align*} $$
 $\mathfrak {p}_j/\mathfrak {p}_{j+1} \subseteq \mathfrak {Z}(\mathfrak {n}/\mathfrak {p}_{j+1})$
.
$\mathfrak {p}_j/\mathfrak {p}_{j+1} \subseteq \mathfrak {Z}(\mathfrak {n}/\mathfrak {p}_{j+1})$
.
-
(ii) By Lemma 2.11,
 $ \mathfrak {p}_j + J \mathfrak {p}_j \subseteq \mathfrak {d}_j$
for all
$ \mathfrak {p}_j + J \mathfrak {p}_j \subseteq \mathfrak {d}_j$
for all
 $j \geq 0$
. We show that
$j \geq 0$
. We show that
 $\mathfrak {p}_j + J \mathfrak {p}_j \unlhd \mathfrak {n}$
for all
$\mathfrak {p}_j + J \mathfrak {p}_j \unlhd \mathfrak {n}$
for all
 $j \geq 0.$
Indeed, for all
$j \geq 0.$
Indeed, for all
 $P,P' \in \mathfrak {p}_j,$
$P,P' \in \mathfrak {p}_j,$
 $$ \begin{align*}\underbrace{[P+JP',\mathfrak{n}]}_{\subseteq [\mathfrak{p}_j + J \mathfrak{p}_j,\mathfrak{n}]} \subseteq \underbrace{[P,\mathfrak{n}]}_{\subseteq \mathfrak{p}_{j+1}} + \underbrace{[JP',\mathfrak{n}]}_{\subseteq \mathfrak{p}_{j+1}} \subseteq \mathfrak{p}_{j+1} \subseteq \mathfrak{p}_{j+1} + J\mathfrak{p}_{j+1}\subseteq \mathfrak{p}_j + J\mathfrak{p}_j.\end{align*} $$
$$ \begin{align*}\underbrace{[P+JP',\mathfrak{n}]}_{\subseteq [\mathfrak{p}_j + J \mathfrak{p}_j,\mathfrak{n}]} \subseteq \underbrace{[P,\mathfrak{n}]}_{\subseteq \mathfrak{p}_{j+1}} + \underbrace{[JP',\mathfrak{n}]}_{\subseteq \mathfrak{p}_{j+1}} \subseteq \mathfrak{p}_{j+1} \subseteq \mathfrak{p}_{j+1} + J\mathfrak{p}_{j+1}\subseteq \mathfrak{p}_j + J\mathfrak{p}_j.\end{align*} $$
Hence,
![]() $\mathfrak {p}_j + J \mathfrak {p}_j \unlhd \mathfrak {n}$
. From part (ii), we can show that
$\mathfrak {p}_j + J \mathfrak {p}_j \unlhd \mathfrak {n}$
. From part (ii), we can show that
![]() $\mathfrak {p}_j + J\mathfrak {p}_j$
is a J-invariant descending central series. Indeed, for all
$\mathfrak {p}_j + J\mathfrak {p}_j$
is a J-invariant descending central series. Indeed, for all
![]() $T = P + JP' \in \mathfrak {p}_j + J \mathfrak {p}_j$
and
$T = P + JP' \in \mathfrak {p}_j + J \mathfrak {p}_j$
and
![]() $Y \in \mathfrak {n},$
$Y \in \mathfrak {n},$
Theorem 2.13. Let
![]() $\mathfrak {n}$
be a Lie algebra with a complex structure
$\mathfrak {n}$
be a Lie algebra with a complex structure
![]() $J.$
The following are equivalent:
$J.$
The following are equivalent:
-
(i) J is nilpotent of step
 $j_0;$
$j_0;$
-
(ii)
 $ \mathfrak {p}_{j_0} = \{0\}$
and
$ \mathfrak {p}_{j_0} = \{0\}$
and
 $ \mathfrak {p}_{j_0-1} \neq \{0\};$
$ \mathfrak {p}_{j_0-1} \neq \{0\};$
-
(iii)
 $ \mathfrak {d}_{j_0} = \{0\}$
and
$ \mathfrak {d}_{j_0} = \{0\}$
and
 $\mathfrak {d}_{j_0 - 1} \neq \{0\}$
.
$\mathfrak {d}_{j_0 - 1} \neq \{0\}$
.
Proof. We first show that (i) and (ii) are equivalent. Assume that J is nilpotent of step
![]() $j_0.$
From Lemma 2.5(ii),
$j_0.$
From Lemma 2.5(ii),
![]() $\mathfrak {d}_{j_0-1} \subseteq \mathfrak {d}^1.$
Hence, by Lemma 2.11,
$\mathfrak {d}_{j_0-1} \subseteq \mathfrak {d}^1.$
Hence, by Lemma 2.11,
Thus,
![]() $ \mathfrak {p}_{j_0}= \{0\} $
. Assume, by contradiction, that
$ \mathfrak {p}_{j_0}= \{0\} $
. Assume, by contradiction, that
![]() $ \mathfrak {p}_{j_0-1} = \{0\}.$
We show by induction that
$ \mathfrak {p}_{j_0-1} = \{0\}.$
We show by induction that
![]() $\mathfrak {p}_{j_0-j-1} + J\mathfrak {p}_{j_0-j-1} \subseteq \mathfrak {d}^{\,j} $
for all
$\mathfrak {p}_{j_0-j-1} + J\mathfrak {p}_{j_0-j-1} \subseteq \mathfrak {d}^{\,j} $
for all
![]() $j \geq 0 $
. By definition,
$j \geq 0 $
. By definition,
![]() $ \mathfrak {p}_{j_0-1} + J \mathfrak {p}_{j_0-1} = \{0\} = \mathfrak {d}^0.$
Next, suppose that
$ \mathfrak {p}_{j_0-1} + J \mathfrak {p}_{j_0-1} = \{0\} = \mathfrak {d}^0.$
Next, suppose that
![]() $ \mathfrak {p}_{j_0-s-1} + J \mathfrak {p}_{j_0-s-1}\subseteq \mathfrak {d}^s $
for some
$ \mathfrak {p}_{j_0-s-1} + J \mathfrak {p}_{j_0-s-1}\subseteq \mathfrak {d}^s $
for some
![]() $s \in \mathbb {N}.$
Then from Remark 2.12(ii),
$s \in \mathbb {N}.$
Then from Remark 2.12(ii),
This implies, using (2.1),
![]() $\mathfrak {p}_{j_0-s-2} +J \mathfrak {p}_{j_0-s-2} \subseteq \mathfrak {d}^{s+1}.$
By induction,
$\mathfrak {p}_{j_0-s-2} +J \mathfrak {p}_{j_0-s-2} \subseteq \mathfrak {d}^{s+1}.$
By induction,
![]() $\mathfrak {p}_{j_0-j-1} + J\mathfrak {p}_{j_0-j-1} \subseteq \mathfrak {d}^{\,j} $
for all
$\mathfrak {p}_{j_0-j-1} + J\mathfrak {p}_{j_0-j-1} \subseteq \mathfrak {d}^{\,j} $
for all
![]() $j \geq 0.$
In particular, let
$j \geq 0.$
In particular, let
![]() $j = j_0-1.$
Then
$j = j_0-1.$
Then
![]() $\mathfrak {n} \subseteq \mathfrak {d}^{\,j_0-1}$
, which implies that J is nilpotent of step
$\mathfrak {n} \subseteq \mathfrak {d}^{\,j_0-1}$
, which implies that J is nilpotent of step
![]() $j_0-1$
by definition. This is a contradiction. Therefore,
$j_0-1$
by definition. This is a contradiction. Therefore,
![]() $ \mathfrak {p}_{j_0-1} \neq \{0\}.$
$ \mathfrak {p}_{j_0-1} \neq \{0\}.$
Conversely, suppose that
![]() $ \mathfrak {p}_{j_0} = \{0\}$
and
$ \mathfrak {p}_{j_0} = \{0\}$
and
![]() $ \mathfrak {p}_{j_0-1} \neq \{0\}$
. We show that J is nilpotent of step
$ \mathfrak {p}_{j_0-1} \neq \{0\}$
. We show that J is nilpotent of step
![]() $j_0.$
By definition,
$j_0.$
By definition,
![]() $ \mathfrak {p}_{j_0} + J \mathfrak {p}_{j_0} = \{0\} = \mathfrak {d}^0 $
. It follows, by induction, that
$ \mathfrak {p}_{j_0} + J \mathfrak {p}_{j_0} = \{0\} = \mathfrak {d}^0 $
. It follows, by induction, that
![]() $\mathfrak {p}_{j_0-j} + J\mathfrak {p}_{j_0-j} \subseteq \mathfrak {d}^{\,j} $
for all
$\mathfrak {p}_{j_0-j} + J\mathfrak {p}_{j_0-j} \subseteq \mathfrak {d}^{\,j} $
for all
![]() $j \geq 0.$
Hence,
$j \geq 0.$
Hence,
![]() $\mathfrak {p}_{j_0-j} \subseteq \mathfrak {d}^{\,j}$
. In particular, let
$\mathfrak {p}_{j_0-j} \subseteq \mathfrak {d}^{\,j}$
. In particular, let
![]() $j =j_0-1.$
Then
$j =j_0-1.$
Then
![]() $\mathfrak {p}_1 = [\mathfrak {n},\mathfrak {n}] \subseteq \mathfrak {d}^{\,j_0-1}$
, which implies that
$\mathfrak {p}_1 = [\mathfrak {n},\mathfrak {n}] \subseteq \mathfrak {d}^{\,j_0-1}$
, which implies that
![]() $\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian. By Lemma 2.5, J is nilpotent of step at most
$\mathfrak {n}/\mathfrak {d}^{\,j_0-1}$
is Abelian. By Lemma 2.5, J is nilpotent of step at most
![]() $j_0.$
$j_0.$
We next show that
![]() $\mathfrak {d}^{\,j_0-1} \neq \mathfrak {n}$
. Assume, by contradiction, that
$\mathfrak {d}^{\,j_0-1} \neq \mathfrak {n}$
. Assume, by contradiction, that
![]() $ \mathfrak {n}= \mathfrak {d}^{\,j_0-1}.$
We show by induction that
$ \mathfrak {n}= \mathfrak {d}^{\,j_0-1}.$
We show by induction that
![]() $\mathfrak {p}_{j-1} \subseteq \mathfrak {d}^{\,j_0-j}$
for all
$\mathfrak {p}_{j-1} \subseteq \mathfrak {d}^{\,j_0-j}$
for all
![]() $j \geq 1$
. By definition,
$j \geq 1$
. By definition,
![]() $\mathfrak {p}_0 = \mathfrak {n}= \mathfrak {d}^{\,j_0-1}.$
Next, suppose that
$\mathfrak {p}_0 = \mathfrak {n}= \mathfrak {d}^{\,j_0-1}.$
Next, suppose that
![]() $\mathfrak {p}_{s-1} \subseteq \mathfrak {d}^{\,j_0-s}$
for some
$\mathfrak {p}_{s-1} \subseteq \mathfrak {d}^{\,j_0-s}$
for some
![]() $s \in \mathbb {N}.$
Then
$s \in \mathbb {N}.$
Then
By induction,
![]() $\mathfrak {p}_{j-1} \subseteq \mathfrak {d}^{\,j_0-j}$
for all
$\mathfrak {p}_{j-1} \subseteq \mathfrak {d}^{\,j_0-j}$
for all
![]() $j \geq 1.$
In particular, let
$j \geq 1.$
In particular, let
![]() $j = j_0.$
We deduce that
$j = j_0.$
We deduce that
![]() $ \mathfrak {p}_{j_0-1} \subseteq \mathfrak {d}^0 = \{0\}.$
This implies that
$ \mathfrak {p}_{j_0-1} \subseteq \mathfrak {d}^0 = \{0\}.$
This implies that
![]() $ \mathfrak {p}_{j_0-1} = \{0\}$
which is a contradiction. Hence,
$ \mathfrak {p}_{j_0-1} = \{0\}$
which is a contradiction. Hence,
![]() $\mathfrak {d}^{\,j_0-1} \neq \mathfrak {n}.$
By definition, J is nilpotent of step
$\mathfrak {d}^{\,j_0-1} \neq \mathfrak {n}.$
By definition, J is nilpotent of step
![]() $j_0.$
$j_0.$
We now show (i) and (iii) are equivalent. Since J is nilpotent of step
![]() $j_0,$
it follows from Lemma 2.5(ii) that
$j_0,$
it follows from Lemma 2.5(ii) that
![]() $\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j}$
for all
$\mathfrak {d}_j \subseteq \mathfrak {d}^{\,j_0 - j}$
for all
![]() $j \geq 0.$
In particular, let
$j \geq 0.$
In particular, let
![]() $j = j_0.$
By definition,
$j = j_0.$
By definition,
![]() $\mathfrak {d}_{j_0} = \mathfrak {d}^0 = \{0\}.$
We show that
$\mathfrak {d}_{j_0} = \mathfrak {d}^0 = \{0\}.$
We show that
![]() $\mathfrak {d}_{j_0-1} \neq \{0\}.$
By Lemma 2.11,
$\mathfrak {d}_{j_0-1} \neq \{0\}.$
By Lemma 2.11,
![]() $\{0\} \neq \mathfrak {p}_{j_0-1} + J \mathfrak {p}_{j_0-1} \subseteq \mathfrak {d}_{j_0-1}.$
Hence,
$\{0\} \neq \mathfrak {p}_{j_0-1} + J \mathfrak {p}_{j_0-1} \subseteq \mathfrak {d}_{j_0-1}.$
Hence,
![]() $\mathfrak {d}_{j_0-1} \neq \{0\}.$
$\mathfrak {d}_{j_0-1} \neq \{0\}.$
Conversely, assume that
![]() $\mathfrak {d}_{j_0} = \{0\}$
and
$\mathfrak {d}_{j_0} = \{0\}$
and
![]() $\mathfrak {d}_{j_0-1} \neq \{0\}$
. From the definition,
$\mathfrak {d}_{j_0-1} \neq \{0\}$
. From the definition,
![]() $[\mathfrak {d}_{j_0-1},\mathfrak {n}] \subseteq \mathfrak {d}_{j_0} = \{0\}.$
Hence,
$[\mathfrak {d}_{j_0-1},\mathfrak {n}] \subseteq \mathfrak {d}_{j_0} = \{0\}.$
Hence,
![]() $\{0\} \neq \mathfrak {d}_{j_0-1} \subseteq \mathfrak {d}^1.$
Next, assume that
$\{0\} \neq \mathfrak {d}_{j_0-1} \subseteq \mathfrak {d}^1.$
Next, assume that
![]() $\mathfrak {d}_{j_0-s} \subseteq \mathfrak {d}^s$
for some
$\mathfrak {d}_{j_0-s} \subseteq \mathfrak {d}^s$
for some
![]() $s \in \mathbb {N}.$
Then by definition,
$s \in \mathbb {N}.$
Then by definition,
By (2.1),
![]() $\mathfrak {d}_{j_0-s-1} \subseteq \mathfrak {d}^{s+1}.$
By induction,
$\mathfrak {d}_{j_0-s-1} \subseteq \mathfrak {d}^{s+1}.$
By induction,
![]() $\mathfrak {d}_{j_0-j} \subseteq \mathfrak {d}^{\,j}$
for all
$\mathfrak {d}_{j_0-j} \subseteq \mathfrak {d}^{\,j}$
for all
![]() $j \geq 0.$
Let
$j \geq 0.$
Let
![]() $j= j_0.$
We find that
$j= j_0.$
We find that
![]() $\mathfrak {d}_0 = \mathfrak {n} \subseteq \mathfrak {d}^{\,j_0}.$
Therefore,
$\mathfrak {d}_0 = \mathfrak {n} \subseteq \mathfrak {d}^{\,j_0}.$
Therefore,
![]() $\mathfrak {d}^{\,j_0} = \mathfrak {n}$
and J is nilpotent of step at most
$\mathfrak {d}^{\,j_0} = \mathfrak {n}$
and J is nilpotent of step at most
![]() $j_0.$
$j_0.$
We next show that
![]() $\mathfrak {d}^{\,j_0-1} \neq \mathfrak {n}.$
Suppose not, that is,
$\mathfrak {d}^{\,j_0-1} \neq \mathfrak {n}.$
Suppose not, that is,
![]() $ \mathfrak {n} =\mathfrak {d}^{\,j_0-1}.$
By definition,
$ \mathfrak {n} =\mathfrak {d}^{\,j_0-1}.$
By definition,
![]() $\mathfrak {d}_0 = \mathfrak {n} = \mathfrak {d}^{\,j_0-1}.$
It follows, by induction, that
$\mathfrak {d}_0 = \mathfrak {n} = \mathfrak {d}^{\,j_0-1}.$
It follows, by induction, that
![]() $\mathfrak {d}_{j-1} \subseteq \mathfrak {d}^{\,j_0-j}$
for all
$\mathfrak {d}_{j-1} \subseteq \mathfrak {d}^{\,j_0-j}$
for all
![]() $j \geq 1$
. Let
$j \geq 1$
. Let
![]() $j = j_0.$
We find that
$j = j_0.$
We find that
![]() $ \mathfrak {d}_{j_0-1} \subseteq \{0\}$
, a contradiction. Hence,
$ \mathfrak {d}_{j_0-1} \subseteq \{0\}$
, a contradiction. Hence,
![]() $\mathfrak {d}^{\,j_0-1} \neq \mathfrak {n} $
and J is nilpotent of step
$\mathfrak {d}^{\,j_0-1} \neq \mathfrak {n} $
and J is nilpotent of step
![]() $j_0.$
$j_0.$
Finally, since (i) is equivalent to both (ii) and (iii), we conclude that (ii) and (iii) are equivalent.
Remark 2.14. Suppose that a Lie algebra
![]() $\mathfrak {n}$
admits a nilpotent complex structure J of step
$\mathfrak {n}$
admits a nilpotent complex structure J of step
![]() $j_0.$
Then
$j_0.$
Then
for all
![]() $ j \geq 0$
.
$ j \geq 0$
.
It is shown, in [Reference Cordero, Fernández, Gray and Ugarte3, Corollary 7], that if
![]() $\mathfrak {c}_j(\mathfrak {n})$
is J-invariant for all
$\mathfrak {c}_j(\mathfrak {n})$
is J-invariant for all
![]() $j \geq 0,$
then J is nilpotent. We will provide a different approach to this.
$j \geq 0,$
then J is nilpotent. We will provide a different approach to this.
Corollary 2.15. Let
![]() $\mathfrak {n}$
be a step k nilpotent Lie algebra with a complex structure
$\mathfrak {n}$
be a step k nilpotent Lie algebra with a complex structure
![]() $J.$
Suppose that all
$J.$
Suppose that all
![]() $\mathfrak {c}_j(\mathfrak {n})$
are J-invariant. Then
$\mathfrak {c}_j(\mathfrak {n})$
are J-invariant. Then
![]() $\mathfrak {p}_j = \mathfrak {c}_j(\mathfrak {n})$
for all
$\mathfrak {p}_j = \mathfrak {c}_j(\mathfrak {n})$
for all
![]() $j \geq 0.$
Furthermore, J is nilpotent of step k.
$j \geq 0.$
Furthermore, J is nilpotent of step k.
Proof. Since all
![]() $\mathfrak {c}_j(\mathfrak {n})$
are J-invariant, by definition,
$\mathfrak {c}_j(\mathfrak {n})$
are J-invariant, by definition,
![]() $\mathfrak {p}_0 = \mathfrak {n} = \mathfrak {c}_0(\mathfrak {n}).$
By induction,
$\mathfrak {p}_0 = \mathfrak {n} = \mathfrak {c}_0(\mathfrak {n}).$
By induction,
![]() $ \mathfrak {p}_j = \mathfrak {c}_j(\mathfrak {n}) $
for all
$ \mathfrak {p}_j = \mathfrak {c}_j(\mathfrak {n}) $
for all
![]() $j \geq 0.$
Therefore,
$j \geq 0.$
Therefore,
![]() $\mathfrak {p}_k = \mathfrak {c}_k(\mathfrak {n}) = \{0\}$
and
$\mathfrak {p}_k = \mathfrak {c}_k(\mathfrak {n}) = \{0\}$
and
![]() $\mathfrak {p}_{k-1} = \mathfrak {c}_{k-1}(\mathfrak {n}) \neq \{0\}$
. By Theorem 2.13, J is nilpotent of step
$\mathfrak {p}_{k-1} = \mathfrak {c}_{k-1}(\mathfrak {n}) \neq \{0\}$
. By Theorem 2.13, J is nilpotent of step
![]() $k.$
$k.$
Corollary 2.16. Let
![]() $\mathfrak {n}$
be a step k nilpotent Lie algebra with a nilpotent complex structure J of step k. Suppose that
$\mathfrak {n}$
be a step k nilpotent Lie algebra with a nilpotent complex structure J of step k. Suppose that
![]() $\mathfrak {c}_{k-1}(\mathfrak {n}) = \mathfrak {z}$
. Then
$\mathfrak {c}_{k-1}(\mathfrak {n}) = \mathfrak {z}$
. Then
![]() $\mathfrak {z}$
is J-invariant.
$\mathfrak {z}$
is J-invariant.
Proof. Since J is nilpotent of step
![]() $k,$
by (2.4),
$k,$
by (2.4),
Hence,
![]() $J\mathfrak {z} = \mathfrak {z}.$
$J\mathfrak {z} = \mathfrak {z}.$
Corollary 2.17. Let
![]() $\mathfrak {n}$
be a Lie algebra with a nilpotent complex structure J of step
$\mathfrak {n}$
be a Lie algebra with a nilpotent complex structure J of step
![]() $j_0$
. Then for all
$j_0$
. Then for all
![]() $j \geq 1, \mathfrak {d}_{j_0-j}$
is not contained in
$j \geq 1, \mathfrak {d}_{j_0-j}$
is not contained in
![]() $\mathfrak {d}^{\,j-1}$
.
$\mathfrak {d}^{\,j-1}$
.
Proof. Since J is nilpotent of step
![]() $j_0,$
by Theorem 2.13,
$j_0,$
by Theorem 2.13,
![]() $\mathfrak {d}_{j_0-1} \neq \{0\} = \mathfrak {d}^0$
. Hence,
$\mathfrak {d}_{j_0-1} \neq \{0\} = \mathfrak {d}^0$
. Hence,
![]() $\mathfrak {d}_{j_0-1}$
is not contained in
$\mathfrak {d}_{j_0-1}$
is not contained in
![]() $\mathfrak {d}^0.$
Next, suppose that
$\mathfrak {d}^0.$
Next, suppose that
![]() $\mathfrak {d}_{j_0-s+1}$
is not contained in
$\mathfrak {d}_{j_0-s+1}$
is not contained in
![]() $\mathfrak {d}^{s-2}$
for some integer
$\mathfrak {d}^{s-2}$
for some integer
![]() $s \geq 2.$
We show that
$s \geq 2.$
We show that
![]() $\mathfrak {d}_{j_0-s}$
is not contained in
$\mathfrak {d}_{j_0-s}$
is not contained in
![]() $\mathfrak {d}^{s-1}.$
Suppose not, that is,
$\mathfrak {d}^{s-1}.$
Suppose not, that is,
![]() $\mathfrak {d}_{j_0-s} \subseteq \mathfrak {d}^{s-1}.$
Then
$\mathfrak {d}_{j_0-s} \subseteq \mathfrak {d}^{s-1}.$
Then
It follows that
![]() $\mathfrak {d}_{j_0-s+1} \subseteq \mathfrak {d}^{s-2}.$
This is a contradiction. Hence,
$\mathfrak {d}_{j_0-s+1} \subseteq \mathfrak {d}^{s-2}.$
This is a contradiction. Hence,
![]() $\mathfrak {d}_{j_0-s}$
is not contained in
$\mathfrak {d}_{j_0-s}$
is not contained in
![]() $ \mathfrak {d}^{s-1}.$
By induction, for all
$ \mathfrak {d}^{s-1}.$
By induction, for all
![]() $j \geq 1, \mathfrak {d}_{j_0-j}$
is not contained in
$j \geq 1, \mathfrak {d}_{j_0-j}$
is not contained in
![]() $\mathfrak {d}^{\,j-1}$
.
$\mathfrak {d}^{\,j-1}$
.
We investigate the possible range of
![]() $\dim \mathfrak {z}$
for a Lie algebra
$\dim \mathfrak {z}$
for a Lie algebra
![]() $\mathfrak {n}$
with a nilpotent complex structure
$\mathfrak {n}$
with a nilpotent complex structure
![]() $J.$
$J.$
Proposition 2.18. Let
![]() $\mathfrak {n}$
be a non-Abelian Lie algebra of dimension
$\mathfrak {n}$
be a non-Abelian Lie algebra of dimension
![]() $2n$
with a nilpotent complex structure
$2n$
with a nilpotent complex structure
![]() $J.$
Then
$J.$
Then
![]() $ 2 \leq \dim \mathfrak {z} \leq 2n-2.$
$ 2 \leq \dim \mathfrak {z} \leq 2n-2.$
Proof. Recall that
![]() $ \mathfrak {d}^1 = \mathfrak {z} \cap J \mathfrak {z}$
, which is the largest J-invariant subspace of
$ \mathfrak {d}^1 = \mathfrak {z} \cap J \mathfrak {z}$
, which is the largest J-invariant subspace of
![]() $\mathfrak {z}$
. Since J is nilpotent, it is clear that
$\mathfrak {z}$
. Since J is nilpotent, it is clear that
![]() $ \mathfrak {d}^1 \neq \{0\}.$
Furthermore, since
$ \mathfrak {d}^1 \neq \{0\}.$
Furthermore, since
![]() $ \mathfrak {d}^1$
is J-invariant, it follows that
$ \mathfrak {d}^1$
is J-invariant, it follows that
![]() $ 2 \leq \dim \mathfrak {d}^1 \leq \dim \mathfrak {z}.$
Then the lower bound of
$ 2 \leq \dim \mathfrak {d}^1 \leq \dim \mathfrak {z}.$
Then the lower bound of
![]() $\dim \mathfrak {z}$
is
$\dim \mathfrak {z}$
is
![]() $2.$
$2.$
Next, we show that the upper bound of
![]() $\dim \mathfrak {z}$
is
$\dim \mathfrak {z}$
is
![]() $2n-2.$
Since
$2n-2.$
Since
![]() $\mathfrak {n}$
is non-Abelian, it is possible to find
$\mathfrak {n}$
is non-Abelian, it is possible to find
![]() $X,Y \in \mathfrak {n}$
such that
$X,Y \in \mathfrak {n}$
such that
![]() $0 \neq [X,Y] \in \mathfrak {c}_1(\mathfrak {n}).$
Then
$0 \neq [X,Y] \in \mathfrak {c}_1(\mathfrak {n}).$
Then
![]() $ \mathrm {span} \{X,Y\}$
is
$ \mathrm {span} \{X,Y\}$
is
![]() $2$
-dimensional and
$2$
-dimensional and
![]() $ \mathrm {span} \{X,Y\} \cap \mathfrak {z} = \{0\}.$
Hence,
$ \mathrm {span} \{X,Y\} \cap \mathfrak {z} = \{0\}.$
Hence,
![]() $\dim \mathfrak {z} \leq 2n -2.$
$\dim \mathfrak {z} \leq 2n -2.$
In conclusion,
![]() $2 \leq \dim \mathfrak {z} \leq 2n - 2.$
$2 \leq \dim \mathfrak {z} \leq 2n - 2.$
Remark 2.19. From Proposition 2.18, we can further conclude that if
![]() $\dim \mathfrak {z} = 1,$
then the complex structure J on
$\dim \mathfrak {z} = 1,$
then the complex structure J on
![]() $\mathfrak {n}$
is nonnilpotent. In particular, the Lie algebra of
$\mathfrak {n}$
is nonnilpotent. In particular, the Lie algebra of
![]() $n \times n$
upper triangular matrices does not admit a nilpotent complex structure.
$n \times n$
upper triangular matrices does not admit a nilpotent complex structure.
3 Stratified Lie algebras with complex structures
In this section, we consider a special type of nilpotent Lie algebras:
![]() $\textit {stratified Lie} \textit{algebras}$
. Recent results on nilpotent Lie algebras with a stratification can be found in [Reference Cowling, Li, Ottazzi and Wu5, Reference Cowling and Ottazzi6, Reference Le Donne12]. We start with the definition of stratified Lie algebras.
$\textit {stratified Lie} \textit{algebras}$
. Recent results on nilpotent Lie algebras with a stratification can be found in [Reference Cowling, Li, Ottazzi and Wu5, Reference Cowling and Ottazzi6, Reference Le Donne12]. We start with the definition of stratified Lie algebras.
Definition 3.1. A nilpotent Lie algebra
![]() $\mathfrak {n}$
is said to admit a
$\mathfrak {n}$
is said to admit a
![]() $\textit {step k stratification}$
if it has a vector space decomposition of the form
$\textit {step k stratification}$
if it has a vector space decomposition of the form
![]() $\mathfrak {n}_1 \oplus \mathfrak {n}_2 \oplus \cdots \oplus \mathfrak {n}_k,$
where
$\mathfrak {n}_1 \oplus \mathfrak {n}_2 \oplus \cdots \oplus \mathfrak {n}_k,$
where
![]() $\mathfrak {n}_k \neq \{0\},$
satisfying the bracket generating property
$\mathfrak {n}_k \neq \{0\},$
satisfying the bracket generating property
![]() $[\mathfrak {n}_1,\mathfrak {n}_k] = \{0\}$
and
$[\mathfrak {n}_1,\mathfrak {n}_k] = \{0\}$
and
A Lie algebra
![]() $\mathfrak {n}$
that admits a stratification is called a
$\mathfrak {n}$
that admits a stratification is called a
![]() $\textit {stratified Lie algebra}.$
A complex structure J on a stratified Lie algebra
$\textit {stratified Lie algebra}.$
A complex structure J on a stratified Lie algebra
![]() $\mathfrak {n}$
is said to be
$\mathfrak {n}$
is said to be
![]() $\textit {strata-preserving}$
if it preserves each layer of the stratification.
$\textit {strata-preserving}$
if it preserves each layer of the stratification.
Remark 3.2. Let
![]() $\mathfrak {n}$
be a step k stratified Lie algebra. By induction,
$\mathfrak {n}$
be a step k stratified Lie algebra. By induction,
 $$ \begin{align} \mathfrak{c}_j(\mathfrak{n}) =\bigoplus_{ j+1\leq l \leq k} \mathfrak{n}_l \quad \text{for all } j \geq 0. \end{align} $$
$$ \begin{align} \mathfrak{c}_j(\mathfrak{n}) =\bigoplus_{ j+1\leq l \leq k} \mathfrak{n}_l \quad \text{for all } j \geq 0. \end{align} $$
Proposition 3.3. Let
![]() $\mathfrak {n}$
be a
$\mathfrak {n}$
be a
![]() $2n$
-dimensional step n nilpotent Lie algebra for some
$2n$
-dimensional step n nilpotent Lie algebra for some
![]() $n \in \mathbb {N}$
. Suppose that
$n \in \mathbb {N}$
. Suppose that
![]() $\dim \mathfrak {c}_j(\mathfrak {n}) = 2n-2j$
for
$\dim \mathfrak {c}_j(\mathfrak {n}) = 2n-2j$
for
![]() $1 \leq j \leq n.$
Then
$1 \leq j \leq n.$
Then
![]() $\mathfrak {n}$
does not admit a stratification.
$\mathfrak {n}$
does not admit a stratification.
Proof. Assume, by contradiction, that
![]() $\mathfrak {n}$
admits a stratification. By (3.1),
$\mathfrak {n}$
admits a stratification. By (3.1),
![]() $ \mathfrak {c}_j(\mathfrak {n})=\bigoplus _{j+1 \leq l \leq n} \mathfrak {n}_l$
and
$ \mathfrak {c}_j(\mathfrak {n})=\bigoplus _{j+1 \leq l \leq n} \mathfrak {n}_l$
and
![]() $\dim \mathfrak {c}_1(\mathfrak {n}) = 2n-2$
, so
$\dim \mathfrak {c}_1(\mathfrak {n}) = 2n-2$
, so
![]() $\dim \mathfrak {n}_1 =2.$
Since
$\dim \mathfrak {n}_1 =2.$
Since
![]() $\mathfrak {n}$
is a stratified Lie algebra,
$\mathfrak {n}$
is a stratified Lie algebra,
![]() $\mathfrak {n}_2 = [\mathfrak {n}_1,\mathfrak {n}_1].$
Thus,
$\mathfrak {n}_2 = [\mathfrak {n}_1,\mathfrak {n}_1].$
Thus,
![]() $\dim \mathfrak {n}_2 = 1$
and
$\dim \mathfrak {n}_2 = 1$
and
![]() $\dim \mathfrak {c}_2(\mathfrak {n}) = 2n-3> 2n-4.$
This is a contradiction.
$\dim \mathfrak {c}_2(\mathfrak {n}) = 2n-3> 2n-4.$
This is a contradiction.
Proposition 3.4. Let
![]() $\mathfrak {n}$
be a step k stratified Lie algebra with a complex structure J and
$\mathfrak {n}$
be a step k stratified Lie algebra with a complex structure J and
![]() $k \geq 2$
. Suppose that
$k \geq 2$
. Suppose that
![]() $\dim \mathfrak {n}_1 =2.$
Then J is not strata-preserving.
$\dim \mathfrak {n}_1 =2.$
Then J is not strata-preserving.
Proof. Suppose, by contradiction, that there exists a strata-preserving complex structure
![]() $J.$
Then
$J.$
Then
![]() $\dim \mathfrak {n}_j \in 2\mathbb {N}$
for all
$\dim \mathfrak {n}_j \in 2\mathbb {N}$
for all
![]() $j \geq 1.$
However,
$j \geq 1.$
However,
![]() $\dim \mathfrak {n}_1= 2 $
implies that
$\dim \mathfrak {n}_1= 2 $
implies that
![]() ${\dim \mathfrak {n}_2 =1,}$
which contradicts the assumption that
${\dim \mathfrak {n}_2 =1,}$
which contradicts the assumption that
![]() $\dim \mathfrak {n}_2 \in 2 \mathbb {N}.$
Hence,
$\dim \mathfrak {n}_2 \in 2 \mathbb {N}.$
Hence,
![]() $\mathfrak {n}$
does not have a strata-preserving complex structure.
$\mathfrak {n}$
does not have a strata-preserving complex structure.
Remark 3.5. Let
![]() $\mathfrak {n}$
be a step
$\mathfrak {n}$
be a step
![]() $3$
stratified Lie algebra with a strata-preserving complex structure. Arguing in a similar way as in Proposition 3.4, we conclude that
$3$
stratified Lie algebra with a strata-preserving complex structure. Arguing in a similar way as in Proposition 3.4, we conclude that
![]() $\dim \mathfrak {n} \neq 4$
or
$\dim \mathfrak {n} \neq 4$
or
![]() $6.$
$6.$
We show that there always exists a stratification on a step
![]() $2$
nilpotent Lie algebra with a strata-preserving complex structure J.
$2$
nilpotent Lie algebra with a strata-preserving complex structure J.
Theorem 3.6. Let
![]() $\mathfrak {n}$
be a step
$\mathfrak {n}$
be a step
![]() $2$
nilpotent Lie algebra with a complex structure
$2$
nilpotent Lie algebra with a complex structure
![]() $J.$
Suppose that
$J.$
Suppose that
![]() $\mathfrak {c}_1(\mathfrak {n})$
is J-invariant. Then
$\mathfrak {c}_1(\mathfrak {n})$
is J-invariant. Then
![]() $\mathfrak {n}$
admits a J-invariant stratification.
$\mathfrak {n}$
admits a J-invariant stratification.
Proof. Define a J-invariant inner product
![]() $\psi $
by
$\psi $
by
where
![]() $\phi $
is an inner product on
$\phi $
is an inner product on
![]() $\mathfrak {n}.$
We show that there exists a stratification on
$\mathfrak {n}.$
We show that there exists a stratification on
![]() $\mathfrak {n}$
such that
$\mathfrak {n}$
such that
![]() $\mathfrak {n}_1$
and
$\mathfrak {n}_1$
and
![]() $\mathfrak {n}_2$
are J-invariant. Define
$\mathfrak {n}_2$
are J-invariant. Define
![]() $\mathfrak {n}_2 = [\mathfrak {n},\mathfrak {n}]$
and
$\mathfrak {n}_2 = [\mathfrak {n},\mathfrak {n}]$
and
![]() $ \mathfrak {n}_1 = \mathfrak {n}_2^\perp $
, the orthogonal complement of
$ \mathfrak {n}_1 = \mathfrak {n}_2^\perp $
, the orthogonal complement of
![]() $ \mathfrak {n}_2$
with respect to
$ \mathfrak {n}_2$
with respect to
![]() $\psi $
. Then
$\psi $
. Then
![]() $\mathfrak {n}_2 = \mathfrak {c}_1(\mathfrak {n})$
is J-invariant and by definition,
$\mathfrak {n}_2 = \mathfrak {c}_1(\mathfrak {n})$
is J-invariant and by definition,
![]() $\mathfrak {n}= \mathfrak {n}_1 \oplus \mathfrak {n}_2$
. Also note that
$\mathfrak {n}= \mathfrak {n}_1 \oplus \mathfrak {n}_2$
. Also note that
This implies that
![]() $\mathfrak {n}_1$
generates
$\mathfrak {n}_1$
generates
![]() $\mathfrak {n}.$
Thus, J is a complex structure that preserves both
$\mathfrak {n}.$
Thus, J is a complex structure that preserves both
![]() $\mathfrak {n}_1$
and
$\mathfrak {n}_1$
and
![]() $\mathfrak {n}_2$
.
$\mathfrak {n}_2$
.
Remark 3.7.
-
(i) Let
 $\mathfrak {g}$
be an arbitrary Lie algebra. A complex structure J on
$\mathfrak {g}$
be an arbitrary Lie algebra. A complex structure J on
 $\mathfrak {g}$
is called
$\mathfrak {g}$
is called
 $\textit {bi-invariant}$
if
$\textit {bi-invariant}$
if
 $J[X,Y] = [JX,Y]$
for all
$J[X,Y] = [JX,Y]$
for all
 $X,Y \in \mathfrak {g}.$
That is,
$X,Y \in \mathfrak {g}.$
That is,
 $J \circ \operatorname {ad} = \operatorname {ad} \circ J.$
A complex structure J is called
$J \circ \operatorname {ad} = \operatorname {ad} \circ J.$
A complex structure J is called
 $\textit {Abelian}$
if
$\textit {Abelian}$
if
 $[X,Y] = [JX,JY]$
for all
$[X,Y] = [JX,JY]$
for all
 $X,Y \in \mathfrak {g}.$
See, for example, [Reference Barberis and Dotti2, Reference Remm14]. Notice that J preserves all terms of
$X,Y \in \mathfrak {g}.$
See, for example, [Reference Barberis and Dotti2, Reference Remm14]. Notice that J preserves all terms of
 $\mathfrak {c}_j(\mathfrak {n})$
and
$\mathfrak {c}_j(\mathfrak {n})$
and
 $\mathfrak {c}^j(\mathfrak {n})$
if J is bi-invariant, while if J is Abelian, J only preserves all terms of
$\mathfrak {c}^j(\mathfrak {n})$
if J is bi-invariant, while if J is Abelian, J only preserves all terms of
 $\mathfrak {c}^j(\mathfrak {n}).$
$\mathfrak {c}^j(\mathfrak {n}).$
-
(ii) Suppose that
 $\mathfrak {n}$
is a step k stratified Lie algebra with a bi-invariant complex structure
$\mathfrak {n}$
is a step k stratified Lie algebra with a bi-invariant complex structure
 $J.$
From (3.1),
$J.$
From (3.1),
 $ \mathfrak {c}_j(\mathfrak {n}) = \bigoplus _{j+1 \leq l \leq k} \mathfrak {n}_l$
and it is clear that
$ \mathfrak {c}_j(\mathfrak {n}) = \bigoplus _{j+1 \leq l \leq k} \mathfrak {n}_l$
and it is clear that
 $\dim \mathfrak {n}_j \in 2 \mathbb {N}$
for all
$\dim \mathfrak {n}_j \in 2 \mathbb {N}$
for all
 $ j \in \{1,\ldots ,k\}.$
$ j \in \{1,\ldots ,k\}.$
Proposition 3.8. Let
![]() $\mathfrak {n}$
be a step k stratified Lie algebra with a strata-preserving complex structure
$\mathfrak {n}$
be a step k stratified Lie algebra with a strata-preserving complex structure
![]() $J.$
Then
$J.$
Then
![]() $J\mathfrak {c}_j(\mathfrak {n}) = \mathfrak {c}_j(\mathfrak {n})$
for all
$J\mathfrak {c}_j(\mathfrak {n}) = \mathfrak {c}_j(\mathfrak {n})$
for all
![]() $j \geq 0 $
and J is nilpotent of step k.
$j \geq 0 $
and J is nilpotent of step k.
Proof. We first show that
![]() $J\mathfrak {c}_j(\mathfrak {n}) = \mathfrak {c}_j(\mathfrak {n})$
for all
$J\mathfrak {c}_j(\mathfrak {n}) = \mathfrak {c}_j(\mathfrak {n})$
for all
![]() $j \geq 0.$
Recall, from (2.1), that
$j \geq 0.$
Recall, from (2.1), that
![]() $\mathfrak {c}_j(\mathfrak {n}) = \bigoplus _{j+1 \leq l \leq k} \mathfrak {n}_l$
and hence
$\mathfrak {c}_j(\mathfrak {n}) = \bigoplus _{j+1 \leq l \leq k} \mathfrak {n}_l$
and hence
![]() $ J\mathfrak {c}_j(\mathfrak {n}) =\mathfrak {c}_j(\mathfrak {n}) $
for all
$ J\mathfrak {c}_j(\mathfrak {n}) =\mathfrak {c}_j(\mathfrak {n}) $
for all
![]() $j \geq 0.$
By Corollary 2.15, J is nilpotent of step
$j \geq 0.$
By Corollary 2.15, J is nilpotent of step
![]() $k.$
$k.$
It is known that every step
![]() $2$
nilpotent Lie algebra may be stratified (see, for example, [Reference Le Donne12]). We will provide another proof in Theorem 3.9, that every complex structure on a step
$2$
nilpotent Lie algebra may be stratified (see, for example, [Reference Le Donne12]). We will provide another proof in Theorem 3.9, that every complex structure on a step
![]() $2$
nilpotent Lie algebra is nilpotent of step
$2$
nilpotent Lie algebra is nilpotent of step
![]() $2$
or
$2$
or
![]() $3$
(compare [Reference Gao, Zhao and Zheng7, Theorem 1.3] and [Reference Rollenske15, Proposition 3.3]). In what follows, we denote by
$3$
(compare [Reference Gao, Zhao and Zheng7, Theorem 1.3] and [Reference Rollenske15, Proposition 3.3]). In what follows, we denote by
![]() $\mathfrak {k} = \mathfrak {n}_2 \cap J\mathfrak {n}_2$
the largest J-invariant subspace contained in
$\mathfrak {k} = \mathfrak {n}_2 \cap J\mathfrak {n}_2$
the largest J-invariant subspace contained in
![]() $\mathfrak {n}_2$
and we also remind the reader that
$\mathfrak {n}_2$
and we also remind the reader that
![]() $\mathfrak {d}^1 = \mathfrak {z} \cap J\mathfrak {z} $
is the largest J-invariant subspace contained in
$\mathfrak {d}^1 = \mathfrak {z} \cap J\mathfrak {z} $
is the largest J-invariant subspace contained in
![]() $\mathfrak {z}.$
$\mathfrak {z}.$
Theorem 3.9. Let
![]() $ \mathfrak {n} = \mathfrak {n}_1 \oplus \mathfrak {n}_2$
be a step
$ \mathfrak {n} = \mathfrak {n}_1 \oplus \mathfrak {n}_2$
be a step
![]() $2$
nilpotent Lie algebra with a complex structure J and a J-invariant inner product
$2$
nilpotent Lie algebra with a complex structure J and a J-invariant inner product
![]() $\psi $
.
$\psi $
.
-
(i) If
 $\mathfrak {k} = \{0\}$
, then
$\mathfrak {k} = \{0\}$
, then
 $ \mathfrak {d}_1$
is Abelian and J is nilpotent of step
$ \mathfrak {d}_1$
is Abelian and J is nilpotent of step
 $2.$
$2.$
-
(ii) If
 $\{0\} \neq \mathfrak {k} \subset \mathfrak {n}_2$
, then J is nilpotent of step
$\{0\} \neq \mathfrak {k} \subset \mathfrak {n}_2$
, then J is nilpotent of step
 $3.$
$3.$
-
(iii) If
 $\mathfrak {n}_2 = \mathfrak {k}$
, then J is strata-preserving and nilpotent of step
$\mathfrak {n}_2 = \mathfrak {k}$
, then J is strata-preserving and nilpotent of step
 $2.$
$2.$
In conclusion, J is nilpotent of either step
![]() $2$
or
$2$
or
![]() $3$
.
$3$
.
Proof. We start with parts (i) and (ii) together. Suppose that
![]() $J\mathfrak {n}_2 \neq \mathfrak {n}_2.$
Then,
$J\mathfrak {n}_2 \neq \mathfrak {n}_2.$
Then,
![]() $\mathfrak {p}_2 = [J\mathfrak {n}_2,\mathfrak {n}] \subseteq \mathfrak {n}_2.$
For all
$\mathfrak {p}_2 = [J\mathfrak {n}_2,\mathfrak {n}] \subseteq \mathfrak {n}_2.$
For all
![]() $Z_2 \in \mathfrak {n}_2$
and
$Z_2 \in \mathfrak {n}_2$
and
![]() $X,JX \in \mathfrak {n},$
by the Newlander–Nirenberg condition,
$X,JX \in \mathfrak {n},$
by the Newlander–Nirenberg condition,
This implies that
![]() $\mathfrak {p}_2$
is J-invariant in
$\mathfrak {p}_2$
is J-invariant in
![]() $\mathfrak {n}_2$
. We now consider the following two possibilities.
$\mathfrak {n}_2$
. We now consider the following two possibilities.
-
(i) If
 $\mathfrak {k} = \{0\},$
then from (3.2),
$\mathfrak {k} = \{0\},$
then from (3.2),
 $\mathfrak {p}_2 = \{0\}.$
By Theorem 2.13, J is nilpotent of step
$\mathfrak {p}_2 = \{0\}.$
By Theorem 2.13, J is nilpotent of step
 $2.$
$2.$
-
(ii) If
 $\{0\} \neq \mathfrak {k} \subset \mathfrak {n}_2,$
since
$\{0\} \neq \mathfrak {k} \subset \mathfrak {n}_2,$
since
 $\{0\} \neq \mathfrak {p}_2 \subseteq \mathfrak {k}$
and
$\{0\} \neq \mathfrak {p}_2 \subseteq \mathfrak {k}$
and
 $J\mathfrak {p}_2 \subset \mathfrak {n}_2$
, then by definition,
$J\mathfrak {p}_2 \subset \mathfrak {n}_2$
, then by definition,
 $\mathfrak {p}_3 = \{0\}.$
By Theorem 2.13, J is nilpotent of step
$\mathfrak {p}_3 = \{0\}.$
By Theorem 2.13, J is nilpotent of step
 $3$
.
$3$
.
Finally, for part (iii), suppose that
![]() $\mathfrak {n}_2 = \mathfrak {k}.$
We find that J preserves
$\mathfrak {n}_2 = \mathfrak {k}.$
We find that J preserves
![]() $\mathfrak {n}_2.$
By Theorem 3.6, J is strata-preserving. From Corollary 3.8, J is nilpotent of step
$\mathfrak {n}_2.$
By Theorem 3.6, J is strata-preserving. From Corollary 3.8, J is nilpotent of step
![]() $2.$
$2.$
In conclusion, J is either nilpotent of step
![]() $2$
or
$2$
or
![]() $3.$
$3.$
Remark 3.10.
-
(i) If J is nilpotent of step
 $3,$
then there does not necessarily exist a J-invariant stratification.
$3,$
then there does not necessarily exist a J-invariant stratification. -
(ii) We recall, from [Reference Gao, Zhao and Zheng7, Theorem 1.3], if
 $\mathfrak {z}$
is not J-invariant, then J is nilpotent of step
$\mathfrak {z}$
is not J-invariant, then J is nilpotent of step
 $3.$
From Theorem 3.9, we derive Table 1.
$3.$
From Theorem 3.9, we derive Table 1.Table 1 Nilpotency of J.

From Table 1, if J is nilpotent of step
![]() $2$
, then J is either strata-preserving or centre-preserving. More precisely, we conclude that either
$2$
, then J is either strata-preserving or centre-preserving. More precisely, we conclude that either
![]() $\mathfrak {k} =\mathfrak {n}_2 \cap J\mathfrak {n}_2 =\{0\}$
or
$\mathfrak {k} =\mathfrak {n}_2 \cap J\mathfrak {n}_2 =\{0\}$
or
![]() $J\mathfrak {n}_2 = \mathfrak {n}_2.$
Indeed, if
$J\mathfrak {n}_2 = \mathfrak {n}_2.$
Indeed, if
![]() $\mathfrak {n}$
is step
$\mathfrak {n}$
is step
![]() $2$
nilpotent Lie algebra with a nilpotent complex structure J of step
$2$
nilpotent Lie algebra with a nilpotent complex structure J of step
![]() $2, J$
may not be strata-preserving.
$2, J$
may not be strata-preserving.
An even dimensional nilpotent Lie algebra with
![]() $\dim \mathfrak {c}_1(\mathfrak {n}) = 1$
has step
$\dim \mathfrak {c}_1(\mathfrak {n}) = 1$
has step
![]() $2$
. There does not exist a J-invariant stratification for dimensional reasons. We give the following result for
$2$
. There does not exist a J-invariant stratification for dimensional reasons. We give the following result for
![]() $\dim \mathfrak {c}_1(\mathfrak {n}) \geq 2.$
$\dim \mathfrak {c}_1(\mathfrak {n}) \geq 2.$
Theorem 3.11. Let
![]() $\mathfrak {n}$
be a step
$\mathfrak {n}$
be a step
![]() $2$
stratified Lie algebra with a complex structure J.
$2$
stratified Lie algebra with a complex structure J.
-
(i) Suppose that
 $\dim \mathfrak {n}_2 =2$
. Then
$\dim \mathfrak {n}_2 =2$
. Then-
(a) J is nilpotent of step
 $2;$
$2;$
-
(b) if
 $\dim \mathfrak {d}^1 = 2,$
then
$\dim \mathfrak {d}^1 = 2,$
then
 $J\mathfrak {n}_2 = \mathfrak {n}_2$
.
$J\mathfrak {n}_2 = \mathfrak {n}_2$
.
-
-
(ii) Suppose that
 $\dim \mathfrak {n}_2 = 2l$
for some
$\dim \mathfrak {n}_2 = 2l$
for some
 $l \geq 2 \in \mathbb {N}$
. Furthermore, assume that
$l \geq 2 \in \mathbb {N}$
. Furthermore, assume that
 $\dim \mathfrak {d}^1 \leq 4l-2$
and
$\dim \mathfrak {d}^1 \leq 4l-2$
and
 $J\mathfrak {n}_2 \neq \mathfrak {n}_2$
. Then J is nilpotent of step
$J\mathfrak {n}_2 \neq \mathfrak {n}_2$
. Then J is nilpotent of step
 $3.$
$3.$
Proof. By Theorem 3.9, J is nilpotent of either step
![]() $2$
or
$2$
or
![]() $3.$
$3.$
Start with part (i). Assume that
![]() $\dim \mathfrak {n}_2 =2.$
For part (a), notice that J could be either strata-preserving or not. If J is strata-preserving, by Theorem 3.9(iii), J is nilpotent of step
$\dim \mathfrak {n}_2 =2.$
For part (a), notice that J could be either strata-preserving or not. If J is strata-preserving, by Theorem 3.9(iii), J is nilpotent of step
![]() $2$
. Otherwise, J is not strata-preserving. Since
$2$
. Otherwise, J is not strata-preserving. Since
![]() $\dim \mathfrak {n}_2 =2 $
, it follows that
$\dim \mathfrak {n}_2 =2 $
, it follows that
![]() $\mathfrak {k} = \{0\}.$
Then by Theorem 3.9(i), J is Abelian and hence nilpotent of step
$\mathfrak {k} = \{0\}.$
Then by Theorem 3.9(i), J is Abelian and hence nilpotent of step
![]() $2.$
$2.$
Next, for part (b), recall that
![]() $\mathfrak {d}^1 = \mathfrak {z} \cap J\mathfrak {z}$
is the largest J-invariant subspace of
$\mathfrak {d}^1 = \mathfrak {z} \cap J\mathfrak {z}$
is the largest J-invariant subspace of
![]() $\mathfrak {z} $
. Suppose that
$\mathfrak {z} $
. Suppose that
![]() $\mathfrak {n}_2$
is not J-invariant. Then
$\mathfrak {n}_2$
is not J-invariant. Then
![]() $\mathfrak {k} = \{0\}.$
From part (i), J is nilpotent of step
$\mathfrak {k} = \{0\}.$
From part (i), J is nilpotent of step
![]() $2.$
It follows, from Theorem 2.13, that
$2.$
It follows, from Theorem 2.13, that
![]() $\mathfrak {d}_2 = \{0\}$
and
$\mathfrak {d}_2 = \{0\}$
and
![]() $\mathfrak {d}_1 \subseteq \mathfrak {d}^1.$
But
$\mathfrak {d}_1 \subseteq \mathfrak {d}^1.$
But
![]() $\dim \mathfrak {d}_1 = \dim \mathfrak {n}_2 \oplus J\mathfrak {n}_2 = 4> \dim \mathfrak {d}^1.$
This is a contradiction. Hence,
$\dim \mathfrak {d}_1 = \dim \mathfrak {n}_2 \oplus J\mathfrak {n}_2 = 4> \dim \mathfrak {d}^1.$
This is a contradiction. Hence,
![]() $J\mathfrak {n}_2 = \mathfrak {n}_2$
.
$J\mathfrak {n}_2 = \mathfrak {n}_2$
.
We now show part (ii). Notice that
![]() $l \neq 1.$
Otherwise
$l \neq 1.$
Otherwise
![]() $\dim \mathfrak {n}_2 = \dim \mathfrak {d}^1 = 2.$
This implies that
$\dim \mathfrak {n}_2 = \dim \mathfrak {d}^1 = 2.$
This implies that
![]() $J\mathfrak {n}_2 = \mathfrak {n}_2.$
Suppose, by contradiction, that J is not nilpotent of step
$J\mathfrak {n}_2 = \mathfrak {n}_2.$
Suppose, by contradiction, that J is not nilpotent of step
![]() $3.$
Hence, J is nilpotent of step
$3.$
Hence, J is nilpotent of step
![]() $2.$
Then from Remark 3.10(ii),
$2.$
Then from Remark 3.10(ii),
![]() $\mathfrak {k} = \{0\} $
and by definition,
$\mathfrak {k} = \{0\} $
and by definition,
![]() $\mathfrak {d}_1 = \mathfrak {n}_2 \oplus J\mathfrak {n}_2\subseteq \mathfrak {d}^1.$
However,
$\mathfrak {d}_1 = \mathfrak {n}_2 \oplus J\mathfrak {n}_2\subseteq \mathfrak {d}^1.$
However,
![]() $\dim \mathfrak {d}_1 = 4l> \dim \mathfrak {d}^1.$
This is a contradiction. Hence,
$\dim \mathfrak {d}_1 = 4l> \dim \mathfrak {d}^1.$
This is a contradiction. Hence,
![]() $\mathfrak {k} \neq \{0\}.$
By Theorem 3.9(ii), J is nilpotent of step
$\mathfrak {k} \neq \{0\}.$
By Theorem 3.9(ii), J is nilpotent of step
![]() $3.$
$3.$
Remark 3.12. We can extend the statement of part (i) into a higher step stratification as follows. Let
![]() $\mathfrak {n}$
be a step k stratified Lie algebra with a nilpotent complex structure J of step k. Suppose that
$\mathfrak {n}$
be a step k stratified Lie algebra with a nilpotent complex structure J of step k. Suppose that
![]() $\dim \mathfrak {n}_k = 2$
and
$\dim \mathfrak {n}_k = 2$
and
![]() $\dim \mathfrak {d}^1 =2 $
. Then
$\dim \mathfrak {d}^1 =2 $
. Then
![]() $J\mathfrak {n}_k = \mathfrak {n}_k.$
$J\mathfrak {n}_k = \mathfrak {n}_k.$
Corollary 3.13. Let
![]() $\mathfrak {n} = \mathfrak {n}_1 \oplus \mathfrak {n}_2$
be a step
$\mathfrak {n} = \mathfrak {n}_1 \oplus \mathfrak {n}_2$
be a step
![]() $2$
stratified Lie algebra with a complex structure J such that
$2$
stratified Lie algebra with a complex structure J such that
![]() $\dim \mathfrak {n}_2 = 2.$
Then J is centre-preserving or strata-preserving or both. Furthermore, suppose that
$\dim \mathfrak {n}_2 = 2.$
Then J is centre-preserving or strata-preserving or both. Furthermore, suppose that
![]() $2 \leq \dim \mathfrak {z} \leq 3$
or
$2 \leq \dim \mathfrak {z} \leq 3$
or
![]() $\dim \mathfrak {z} = 4$
and
$\dim \mathfrak {z} = 4$
and
![]() $J\mathfrak {z} \neq \mathfrak {z}.$
Then there exists a J-invariant stratification.
$J\mathfrak {z} \neq \mathfrak {z}.$
Then there exists a J-invariant stratification.
Proof. By Theorem 3.11, J is nilpotent of step
![]() $2$
. Then by Table 1,
$2$
. Then by Table 1,
![]() $J\mathfrak {n}_2 = \mathfrak {n}_2$
or
$J\mathfrak {n}_2 = \mathfrak {n}_2$
or
![]() $J\mathfrak {z} = \mathfrak {z}$
or both if
$J\mathfrak {z} = \mathfrak {z}$
or both if
![]() $\mathfrak {n}_2 = \mathfrak {z}$
.
$\mathfrak {n}_2 = \mathfrak {z}$
.
Furthermore,
![]() $\dim \mathfrak {d}^1 = 2$
since
$\dim \mathfrak {d}^1 = 2$
since
![]() $2 \leq \dim \mathfrak {z} \leq 3$
or
$2 \leq \dim \mathfrak {z} \leq 3$
or
![]() $\dim \mathfrak {z} = 4$
and
$\dim \mathfrak {z} = 4$
and
![]() $J\mathfrak {z} \neq \mathfrak {z}.$
By Theorem 3.11(ii),
$J\mathfrak {z} \neq \mathfrak {z}.$
By Theorem 3.11(ii),
![]() $J\mathfrak {n}_2 = \mathfrak {n}_2$
. Furthermore, by Theorem 3.6, there exists a J-invariant stratification.
$J\mathfrak {n}_2 = \mathfrak {n}_2$
. Furthermore, by Theorem 3.6, there exists a J-invariant stratification.
Suppose that
![]() $\mathfrak {n}$
is a
$\mathfrak {n}$
is a
![]() $6$
-dimensional step
$6$
-dimensional step
![]() $2$
nilpotent Lie algebra with a complex structure. In [Reference Cordero, Fernández, Gray and Ugarte4, Table 1], there is a complete classification of complex structures on these algebras. However, no information is provided on whether or not J preserves the strata.
$2$
nilpotent Lie algebra with a complex structure. In [Reference Cordero, Fernández, Gray and Ugarte4, Table 1], there is a complete classification of complex structures on these algebras. However, no information is provided on whether or not J preserves the strata.
Corollary 3.14 [Reference Andrada, Barberis and Dotti1, Reference Cordero, Fernández, Gray and Ugarte4].
Let
![]() $\mathfrak {n}$
be a
$\mathfrak {n}$
be a
![]() $6$
-dimensional step
$6$
-dimensional step
![]() $2$
nilpotent Lie algebra with a complex structure
$2$
nilpotent Lie algebra with a complex structure
![]() $J $
such that
$J $
such that
![]() $\dim \mathfrak {c}_1(\mathfrak {n}) =2.$
Then
$\dim \mathfrak {c}_1(\mathfrak {n}) =2.$
Then
![]() $\mathfrak {n}$
admits a J-invariant stratification.
$\mathfrak {n}$
admits a J-invariant stratification.
Proof. By Theorem 3.9 and Proposition 2.18, J is nilpotent and
![]() $2 \leq \dim \mathfrak {z} \leq 4$
. If
$2 \leq \dim \mathfrak {z} \leq 4$
. If
![]() $\dim \mathfrak {z} = 4, \dim \mathfrak {c}_1(\mathfrak {n}) = 1$
and J is not strata-preserving due to dimensional reasons. We omit this case. Next, assume that
$\dim \mathfrak {z} = 4, \dim \mathfrak {c}_1(\mathfrak {n}) = 1$
and J is not strata-preserving due to dimensional reasons. We omit this case. Next, assume that
![]() $\dim \mathfrak {z} \leq 3.$
The result is a direct consequence of Corollary 3.13.
$\dim \mathfrak {z} \leq 3.$
The result is a direct consequence of Corollary 3.13.
In what follows, we focus on higher step stratified Lie algebras with complex structures.
Proposition 3.15. Let
![]() $\mathfrak {n}$
be a step
$\mathfrak {n}$
be a step
![]() $3$
stratified Lie algebra with a complex structure J. Suppose that
$3$
stratified Lie algebra with a complex structure J. Suppose that
![]() $J\mathfrak {n}_3 = \mathfrak {n}_3$
. Then J is nilpotent of step
$J\mathfrak {n}_3 = \mathfrak {n}_3$
. Then J is nilpotent of step
![]() $3.$
$3.$
Proof. By the definition of the descending central series
![]() $\mathfrak {p}_j$
in (2.3), it follows that
$\mathfrak {p}_j$
in (2.3), it follows that
![]() $\{0\} \neq \mathfrak {p}_2 = \mathfrak {n}_3 + [J\mathfrak {c}_1(\mathfrak {n}),\mathfrak {n}].$
On the one hand, suppose that
$\{0\} \neq \mathfrak {p}_2 = \mathfrak {n}_3 + [J\mathfrak {c}_1(\mathfrak {n}),\mathfrak {n}].$
On the one hand, suppose that
![]() $[J\mathfrak {c}_1(\mathfrak {n}),\mathfrak {n}] = \{0\}.$
We deduce that
$[J\mathfrak {c}_1(\mathfrak {n}),\mathfrak {n}] = \{0\}.$
We deduce that
![]() $\mathfrak {p}_2 = \mathfrak {n}_3$
and hence
$\mathfrak {p}_2 = \mathfrak {n}_3$
and hence
![]() $\mathfrak {p}_3 = \{0\}$
by definition. Using Theorem 2.13, J is nilpotent of step
$\mathfrak {p}_3 = \{0\}$
by definition. Using Theorem 2.13, J is nilpotent of step
![]() $3.$
On the other hand, suppose that
$3.$
On the other hand, suppose that
![]() $ [J\mathfrak {c}_1(\mathfrak {n}),\mathfrak {n}] \neq \{0\}.$
Then by the Newlander–Nirenberg condition, for all
$ [J\mathfrak {c}_1(\mathfrak {n}),\mathfrak {n}] \neq \{0\}.$
Then by the Newlander–Nirenberg condition, for all
![]() $U \in \mathfrak {c}_1(\mathfrak {n})$
and
$U \in \mathfrak {c}_1(\mathfrak {n})$
and
![]() $X,JX \in \mathfrak {n}$
,
$X,JX \in \mathfrak {n}$
,
Hence,
![]() $[J\mathfrak {c}_1(\mathfrak {n}),\mathfrak {n}] \subseteq \mathfrak {n}_3.$
This implies that
$[J\mathfrak {c}_1(\mathfrak {n}),\mathfrak {n}] \subseteq \mathfrak {n}_3.$
This implies that
![]() $\mathfrak {p}_2 \subseteq \mathfrak {n}_3$
and therefore
$\mathfrak {p}_2 \subseteq \mathfrak {n}_3$
and therefore
![]() $J\mathfrak {p}_2 \subseteq \mathfrak {n}_3.$
Then
$J\mathfrak {p}_2 \subseteq \mathfrak {n}_3.$
Then
![]() $\mathfrak {p}_3 = [\mathfrak {p}_2,\mathfrak {n}] + [J\mathfrak {p}_2,\mathfrak {n}] = \{0\}.$
Again by Theorem 2.13, J is nilpotent of step
$\mathfrak {p}_3 = [\mathfrak {p}_2,\mathfrak {n}] + [J\mathfrak {p}_2,\mathfrak {n}] = \{0\}.$
Again by Theorem 2.13, J is nilpotent of step
![]() $3.$
$3.$
Proposition 3.16. Let
![]() $\mathfrak {n}$
be an
$\mathfrak {n}$
be an
![]() $8$
-dimensional step
$8$
-dimensional step
![]() $3$
stratified Lie algebra with a complex structure J such that
$3$
stratified Lie algebra with a complex structure J such that
![]() $2\dim \mathfrak {n}_3 = \dim \mathfrak {c}_1(\mathfrak {n}) = 4$
. Suppose that
$2\dim \mathfrak {n}_3 = \dim \mathfrak {c}_1(\mathfrak {n}) = 4$
. Suppose that
![]() $J\mathfrak {n}_3 \neq \mathfrak {n}_3$
and
$J\mathfrak {n}_3 \neq \mathfrak {n}_3$
and
![]() $\dim \mathfrak {z} \leq 3.$
Then J is nilpotent of step
$\dim \mathfrak {z} \leq 3.$
Then J is nilpotent of step
![]() $4.$
Furthermore,
$4.$
Furthermore,
![]() $\mathfrak {d}_2 = \mathfrak {n}_3 \oplus J\mathfrak {n}_3$
.
$\mathfrak {d}_2 = \mathfrak {n}_3 \oplus J\mathfrak {n}_3$
.
Proof. Since
![]() $\mathfrak {n}_3 \subseteq \mathfrak {z}, \dim \mathfrak {z} \geq 2.$
By [Reference Latorre, Ugarte and Villacampa10, Corollary 3.12], J is nilpotent. Then using Remark 2.4(i),
$\mathfrak {n}_3 \subseteq \mathfrak {z}, \dim \mathfrak {z} \geq 2.$
By [Reference Latorre, Ugarte and Villacampa10, Corollary 3.12], J is nilpotent. Then using Remark 2.4(i),
![]() $3 \leq j_0 \leq 4$
, where
$3 \leq j_0 \leq 4$
, where
![]() $j_0$
is the nilpotent step of
$j_0$
is the nilpotent step of
![]() $J.$
Suppose, by contradiction, that J is nilpotent of step
$J.$
Suppose, by contradiction, that J is nilpotent of step
![]() $3.$
It follows, from equation (2.4), that
$3.$
It follows, from equation (2.4), that
![]() $\mathfrak {n}_3 + J\mathfrak {n}_3 \subseteq \mathfrak {d}_2 \subseteq \mathfrak {d}^1 \subseteq \mathfrak {z}.$
On the one hand, since
$\mathfrak {n}_3 + J\mathfrak {n}_3 \subseteq \mathfrak {d}_2 \subseteq \mathfrak {d}^1 \subseteq \mathfrak {z}.$
On the one hand, since
![]() $\dim \mathfrak {z} \leq 3, \dim \mathfrak {d}^1 =2.$
On the other hand, since
$\dim \mathfrak {z} \leq 3, \dim \mathfrak {d}^1 =2.$
On the other hand, since
![]() $J\mathfrak {n}_3 \neq \mathfrak {n}_3$
and
$J\mathfrak {n}_3 \neq \mathfrak {n}_3$
and
![]() $\dim \mathfrak {n}_3 = 2, \mathfrak {n}_3 \cap J\mathfrak {n}_3 = \{0\}$
and therefore
$\dim \mathfrak {n}_3 = 2, \mathfrak {n}_3 \cap J\mathfrak {n}_3 = \{0\}$
and therefore
![]() $ \dim \mathfrak {n}_3 \oplus J\mathfrak {n}_3 = 4> \dim \mathfrak {d}^1.$
This is a contradiction. So J is nilpotent of step
$ \dim \mathfrak {n}_3 \oplus J\mathfrak {n}_3 = 4> \dim \mathfrak {d}^1.$
This is a contradiction. So J is nilpotent of step
![]() $4.$
$4.$
We now show that
![]() $\mathfrak {d}_2 = \mathfrak {n}_3 \oplus J\mathfrak {n}_3$
. It is sufficient to show that
$\mathfrak {d}_2 = \mathfrak {n}_3 \oplus J\mathfrak {n}_3$
. It is sufficient to show that
![]() $\mathfrak {d}_2 \subseteq \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
By definition,
$\mathfrak {d}_2 \subseteq \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
By definition,
For all
![]() $ T,T' \in \mathfrak {d}_1,$
we may write
$ T,T' \in \mathfrak {d}_1,$
we may write
![]() $T = U + JV$
and
$T = U + JV$
and
![]() $T' = U' + JV'$
where
$T' = U' + JV'$
where
![]() $U,V,U',V' \in \mathfrak {c}_1(\mathfrak {n}).$
Then
$U,V,U',V' \in \mathfrak {c}_1(\mathfrak {n}).$
Then
 $$ \begin{align} 0 \neq [T,X] + J[T',X']= \underbrace{[U,X]+J[U',X']}_{\in \mathfrak{n}_3 \oplus J\mathfrak{n}_3 } +[JV,X] + J[JV',X']. \end{align} $$
$$ \begin{align} 0 \neq [T,X] + J[T',X']= \underbrace{[U,X]+J[U',X']}_{\in \mathfrak{n}_3 \oplus J\mathfrak{n}_3 } +[JV,X] + J[JV',X']. \end{align} $$
By the Newlander–Nirenberg condition,
Hence,
![]() $ [JV,X] + J[JV', X'] \in \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
From (3.3),
$ [JV,X] + J[JV', X'] \in \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
From (3.3),
![]() $[T,X] + J[T',X'] \in \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
Hence
$[T,X] + J[T',X'] \in \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
Hence
![]() $\mathfrak {d}_2 \subseteq \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
In conclusion,
$\mathfrak {d}_2 \subseteq \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
In conclusion,
![]() $\mathfrak {d}_2 = \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
$\mathfrak {d}_2 = \mathfrak {n}_3 \oplus J\mathfrak {n}_3.$
Acknowledgements
The results of this paper are contained in the author’s Master of Science thesis at the University of New South Wales, prepared under the supervision of Michael Cowling and Alessandro Ottazzi. I would like to give deep thanks to both of them, for guiding and sharing their views on mathematics. They also provided very useful comments and suggestions on the project.