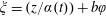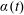1 Introduction
Helical vortices appear in various technological devices with swirl, e.g. in the wake of windmills (Vermeer, Sorensen & Crespo Reference Vermeer, Sorensen and Crespo2003), or as wing tip vortices, in particular, on delta wings (Mitchell, Morton & Forsythe Reference Mitchell, Morton and Forsythe1997). Furthermore, helical vortex structures were observed by Sarpkaya (Reference Sarpkaya1971) who performed experiments with swirling flows in a cylindrical tube and observed three different types of vortex breakdown, where one of them is of helical type.
Helically symmetric flows are further observed as natural phenomena, e.g. in laboratory plasma applications (kink instabilities in the ‘straight tokamak’ approximations, e.g. Johnson et al. (Reference Johnson, Oberman, Kulsrud and Frieman1958), Schnack, Caramana & Nebel (Reference Schnack, Caramana and Nebel1985)), and astrophysical phenomena such as astrophysical jets (Bogoyavlenskij Reference Bogoyavlenskij2000).
In a more theoretical context, flows with a helical symmetry in general have been considered in various contributions in the past. For example, Delbende, Rossi & Daube (Reference Delbende, Rossi and Daube2012) developed a direct numerical simulation code for the helical invariant Navier–Stokes equations in a generalized vorticity–streamfunction formulation. Dritschel (Reference Dritschel1991) reduced the three-dimensional Euler equations to a linear equation, assuming that the flow has helical symmetry and consists of a rigidly rotating basic part and a Beltrami disturbance part. Further, he derived exact solutions for flows in a straight pipe of circular cross-section. Helical flows for a Maxwell fluid between two infinite coaxial circular cylinders were considered by Jamil & Fetecau (Reference Jamil and Fetecau2010). Using the finite Hankel transform, they obtained exact solutions which satisfy all imposed initial and boundary conditions. A detailed overview on helical flows may be taken from Kelbin, Cheviakov & Oberlack (Reference Kelbin, Cheviakov and Oberlack2013).
In mathematical physics, symmetries and conservation laws (CLs) are considered to be one of the most fundamental objects. For example, in fluid mechanics, CLs describe physical quantities such as the conservation of mass, energy, momentum or angular momentum. In practice, local CLs are of fundamental importance for several reasons. They are essential for numerical simulations with modern numerical methods, where the equations are assumed to be in divergence form, e.g. for discontinuous Galerkin methods (see Zienkiewicz et al. Reference Zienkiewicz, Taylor, Sherwin and Peiro2003). Additionally, they give the possibility to easily find potential variables (see Bluman, Cheviakov & Anco Reference Bluman, Cheviakov and Anco2010), which in turn leads to a reduction of the dependent variables and new analytical solutions. Further, CLs are used to establish the existence and uniqueness of solutions as well as in the analysis of stability and global behaviour of solutions (Bluman et al. Reference Bluman, Cheviakov and Anco2010).
For three-dimensional time-dependent fluid flows, CLs were studied in very much detail in Cheviakov & Oberlack (Reference Cheviakov and Oberlack2014). Therein, they considered higher-order CL multipliers and obtained an infinite family of vorticity CLs. Further, Rosenhaus & Shankar (Reference Rosenhaus and Shankar2015) considered the correspondence between symmetries and CLs. They introduced subsymmetries to find further infinite sets of CLs of the Euler equations, involving arbitrary functions of the dependent variables.
Most importantly, additional CLs appear to exist in reduced dimensions such as in plane or axisymmetric flows. Recently new CLs for Euler and Navier–Stokes equations were found for helically invariant flows (see Kelbin et al.
Reference Kelbin, Cheviakov and Oberlack2013). Therein they considered a helical coordinate system, given by the radius
![]() $r$
and a helical variable
$r$
and a helical variable
![]() $\unicode[STIX]{x1D709}=az+b\unicode[STIX]{x1D711}$
, arising from a linear combination of the cylindrical coordinates
$\unicode[STIX]{x1D709}=az+b\unicode[STIX]{x1D711}$
, arising from a linear combination of the cylindrical coordinates
![]() $z$
and
$z$
and
![]() $\unicode[STIX]{x1D711}$
. The parameters
$\unicode[STIX]{x1D711}$
. The parameters
![]() $a$
and
$a$
and
![]() $b$
, involved in this coordinate, were assumed to be constant. Further, the authors expressed the three-dimensional, incompressible Euler and Navier–Stokes equations in a helical symmetric setting and finally obtained new CLs for primitive variables as well as for the vorticity formulation. Interestingly enough, they also derived new CLs for plane and axisymmetric flows. Due to many citations the publication of Kelbin, Cheviakov & Oberlack (Reference Kelbin, Cheviakov and Oberlack2013) is subsequently denoted as KCO.
$b$
, involved in this coordinate, were assumed to be constant. Further, the authors expressed the three-dimensional, incompressible Euler and Navier–Stokes equations in a helical symmetric setting and finally obtained new CLs for primitive variables as well as for the vorticity formulation. Interestingly enough, they also derived new CLs for plane and axisymmetric flows. Due to many citations the publication of Kelbin, Cheviakov & Oberlack (Reference Kelbin, Cheviakov and Oberlack2013) is subsequently denoted as KCO.
In a fluid dynamical context, divergence-type local CLs usually have the form
where
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D731}=\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6F7}^{i}=\unicode[STIX]{x2202}_{1}\unicode[STIX]{x1D6F7}^{1}+\unicode[STIX]{x2202}_{2}\unicode[STIX]{x1D6F7}^{2}+\cdots +\unicode[STIX]{x2202}_{n-1}\unicode[STIX]{x1D6F7}^{n-1}$
denotes the spatial divergence. The quantity
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D731}=\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6F7}^{i}=\unicode[STIX]{x2202}_{1}\unicode[STIX]{x1D6F7}^{1}+\unicode[STIX]{x2202}_{2}\unicode[STIX]{x1D6F7}^{2}+\cdots +\unicode[STIX]{x2202}_{n-1}\unicode[STIX]{x1D6F7}^{n-1}$
denotes the spatial divergence. The quantity
![]() $\unicode[STIX]{x1D6E9}$
is called density, whereas
$\unicode[STIX]{x1D6E9}$
is called density, whereas
![]() $\unicode[STIX]{x1D6F7}^{i}$
are the spatial fluxes of the CL.
$\unicode[STIX]{x1D6F7}^{i}$
are the spatial fluxes of the CL.
In order to compute a globally conserved quantity one may integrate (1.1) over a fluid domain
![]() $\unicode[STIX]{x1D6FA}$
and apply Gauss’s theorem
$\unicode[STIX]{x1D6FA}$
and apply Gauss’s theorem
where
![]() $\text{d}^{n}x$
defines the volume element while
$\text{d}^{n}x$
defines the volume element while
![]() $\text{d}a$
corresponds to a surface element on
$\text{d}a$
corresponds to a surface element on
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. Assuming that the fluxes
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
. Assuming that the fluxes
![]() $\unicode[STIX]{x1D6F7}^{i}$
vanish on the boundary
$\unicode[STIX]{x1D6F7}^{i}$
vanish on the boundary
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
or if periodicity is assumed and the domain
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
or if periodicity is assumed and the domain
![]() $\unicode[STIX]{x1D6FA}$
is time-independent
$\unicode[STIX]{x1D6FA}$
is time-independent
![]() $(\unicode[STIX]{x1D6FA}\neq \unicode[STIX]{x1D6FA}(t))$
, one obtains the global conserved quantity given by
$(\unicode[STIX]{x1D6FA}\neq \unicode[STIX]{x1D6FA}(t))$
, one obtains the global conserved quantity given by
In practice, one is interested in finding non-trivial CLs (1.1) since trivial CLs usually do not carry a physical or mathematical meaning. To distinguish between trivial and non-trivial CLs, we first explicate the meaning of trivial CLs.
Following Bluman et al. (Reference Bluman, Cheviakov and Anco2010), a trivial CL of the first type arises when each of its fluxes
![]() $\unicode[STIX]{x1D6F7}$
vanish identically on the solutions of a given system of partial differential equations. A trivial CL of the second type is a CL that vanishes identically as a differential identity, e.g.
$\unicode[STIX]{x1D6F7}$
vanish identically on the solutions of a given system of partial differential equations. A trivial CL of the second type is a CL that vanishes identically as a differential identity, e.g.
![]() $(\text{div}(\text{curl}(\cdot ))\equiv 0)$
.
$(\text{div}(\text{curl}(\cdot ))\equiv 0)$
.
The definition of trivial CLs leads to the definition of equivalence and linear dependence of CLs: two CLs
![]() $\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6F7}^{i}=0$
and
$\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6F7}^{i}=0$
and
![]() $\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6F9}^{i}=0$
are equivalent if
$\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6F9}^{i}=0$
are equivalent if
![]() $\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D6F7}^{i}-\unicode[STIX]{x1D6F9}^{i})=0$
is a trivial CL. An equivalence class of CLs consists of all CLs that can be reduced to a class of non-trivial CLs.
$\unicode[STIX]{x2202}_{i}(\unicode[STIX]{x1D6F7}^{i}-\unicode[STIX]{x1D6F9}^{i})=0$
is a trivial CL. An equivalence class of CLs consists of all CLs that can be reduced to a class of non-trivial CLs.
A set of
![]() $l$
CLs
$l$
CLs
![]() $\{\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6F7}_{j}^{i}=0\}_{j=1}^{l}$
is linearly dependent if there exists a set of constants
$\{\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D6F7}_{j}^{i}=0\}_{j=1}^{l}$
is linearly dependent if there exists a set of constants
![]() $\{a^{(j)}\}_{j=1}^{l}$
which are not all zero such that the linear combination
$\{a^{(j)}\}_{j=1}^{l}$
which are not all zero such that the linear combination
is a trivial CL (Bluman et al. Reference Bluman, Cheviakov and Anco2010). The direct method (see e.g. Anco & Bluman Reference Anco and Bluman2002a ), described and employed in the following, seeks non-trivial sets of local CLs of a given PDE system in non-conservative form.
The direct method is based on two key ideas. The first idea can be explained as follows: consider an arbitrary and non-conservative PDE system given by
It is proven in Anco & Bluman (Reference Anco and Bluman2002b
) that a PDE system only admits non-trivial CLs arising from linear combinations of these equations with multipliers of
![]() $k$
th order given by
$k$
th order given by
If the multipliers (1.6) are known, they yield divergence expressions of the form
for arbitrary functions
![]() $\boldsymbol{U}(\boldsymbol{x})$
and
$\boldsymbol{U}(\boldsymbol{x})$
and
![]() $D_{i}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{i}$
. The multipliers
$D_{i}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{i}$
. The multipliers
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
are of the form (1.6) and can be chosen to depend on all dependent and independent variables
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
are of the form (1.6) and can be chosen to depend on all dependent and independent variables
![]() $\boldsymbol{x}$
and
$\boldsymbol{x}$
and
![]() $\boldsymbol{U}$
as well as on derivatives
$\boldsymbol{U}$
as well as on derivatives
![]() $\unicode[STIX]{x2202}_{k}\boldsymbol{U}$
up to a certain order
$\unicode[STIX]{x2202}_{k}\boldsymbol{U}$
up to a certain order
![]() $k$
. A priori it is not known up to which order one may choose the multipliers. On solutions
$k$
. A priori it is not known up to which order one may choose the multipliers. On solutions
![]() $\boldsymbol{U}(\boldsymbol{x})=\boldsymbol{u}(\boldsymbol{x})$
of the PDE system (1.5) one obtains the CL
$\boldsymbol{U}(\boldsymbol{x})=\boldsymbol{u}(\boldsymbol{x})$
of the PDE system (1.5) one obtains the CL
To calculate the multipliers
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
, the second key idea is to apply the Euler operator
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
, the second key idea is to apply the Euler operator
![]() $\text{E}_{U^{j}}$
with respect to
$\text{E}_{U^{j}}$
with respect to
![]() $U^{j}$
to (1.7). The Euler operator has the property to annihilate an expression if, and only if, it is a divergence expression
$U^{j}$
to (1.7). The Euler operator has the property to annihilate an expression if, and only if, it is a divergence expression
![]() $D_{i}\unicode[STIX]{x1D6E4}^{i}$
, and is given by
$D_{i}\unicode[STIX]{x1D6E4}^{i}$
, and is given by
for each
![]() $j=1\ldots m$
, while
$j=1\ldots m$
, while
![]() $D_{i}$
is defined above.
$D_{i}$
is defined above.
In order to derive the multipliers
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
, we apply the Euler operator (1.9) to (1.7). Based on the above, the right-hand side vanishes identically and one obtains
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
, we apply the Euler operator (1.9) to (1.7). Based on the above, the right-hand side vanishes identically and one obtains
which holds for arbitrary functions
![]() $\boldsymbol{U}(\boldsymbol{x})$
. Expanding all derivatives in (1.10), a set of linear determining equations for all multipliers
$\boldsymbol{U}(\boldsymbol{x})$
. Expanding all derivatives in (1.10), a set of linear determining equations for all multipliers
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
arises, where the quantities
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
arises, where the quantities
![]() $\boldsymbol{x},\boldsymbol{U},\unicode[STIX]{x2202}_{1}\boldsymbol{U},\ldots ,\unicode[STIX]{x2202}_{k}\boldsymbol{U}$
have to be treated as independent variables. Once the CL multipliers are derived, one may compute the density and fluxes using (1.8). For details, see e.g. Bluman et al. (Reference Bluman, Cheviakov and Anco2010).
$\boldsymbol{x},\boldsymbol{U},\unicode[STIX]{x2202}_{1}\boldsymbol{U},\ldots ,\unicode[STIX]{x2202}_{k}\boldsymbol{U}$
have to be treated as independent variables. Once the CL multipliers are derived, one may compute the density and fluxes using (1.8). For details, see e.g. Bluman et al. (Reference Bluman, Cheviakov and Anco2010).
The main goal of the current contribution is twofold. First, we develop a new helical coordinate system with a time-dependent pitch and, thereof, derived a reduced system of helically invariant Euler and Navier–Stokes equations in primitive variables and vorticity formulation. Second, for both formulations, we derive new local CLs applying the direct construction method. The new results will be compared to the classical case with constant pitch considered in KCO, where various new CLs in primitive variables and in vorticity formulation were derived.
2 Helically invariant Navier–Stokes equations in a time-dependent helical coordinate system
In a cylindrical coordinate system the three-dimensional time-dependent Navier–Stokes equations for a viscous and incompressible fluid without external forces are given by
The Navier–Stokes equations (2.1) are invariant under the helical symmetry, which relies on the combination of two common Lie symmetry groups: (i) generalized Galilean invariance, which comprises axial translation and classical Galilean boost, and (ii) a rotation group about the same axis. Without restricting generality we choose the coordinate system as such that the common symmetry axis lies along the
![]() $z$
-axis.
$z$
-axis.
The global form of the two parameter Lie symmetry group is given by
Using the symmetry group (2.2a )–(2.2d ), we derived a set of independent variables (i.e. the time-dependent helical coordinates) and dependent variables (for details see appendix A), which are given by
In the limiting case
![]() $b=0$
, the helical symmetry reduces to an axial symmetry and the similarity variable (2.3b
) becomes
$b=0$
, the helical symmetry reduces to an axial symmetry and the similarity variable (2.3b
) becomes
![]() $\unicode[STIX]{x1D709}=z/\unicode[STIX]{x1D6FC}$
, although it is still time-dependent owing to the scaling of the
$\unicode[STIX]{x1D709}=z/\unicode[STIX]{x1D6FC}$
, although it is still time-dependent owing to the scaling of the
![]() $z$
-coordinate by the parameter function
$z$
-coordinate by the parameter function
![]() $\unicode[STIX]{x1D6FC}(t)$
. In the opposite case
$\unicode[STIX]{x1D6FC}(t)$
. In the opposite case
![]() $1/\unicode[STIX]{x1D6FC}=0$
, in which helical symmetry reduces to a planar symmetry, the time dependence of the coordinate system vanishes and the classical planar case as discussed in KCO is retained.
$1/\unicode[STIX]{x1D6FC}=0$
, in which helical symmetry reduces to a planar symmetry, the time dependence of the coordinate system vanishes and the classical planar case as discussed in KCO is retained.
Inverting the equations (2.3e
)–(2.3h
) and replacing the cylindrical coordinates
![]() $(r,\unicode[STIX]{x1D711},z)$
by the helical coordinates
$(r,\unicode[STIX]{x1D711},z)$
by the helical coordinates
![]() $(r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, one obtains the relations given by
$(r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, one obtains the relations given by

Figure 1. An illustration of the helix
![]() $\unicode[STIX]{x1D709}=\text{const.}$
with parameter function
$\unicode[STIX]{x1D709}=\text{const.}$
with parameter function
![]() $\unicode[STIX]{x1D6FC}(t)$
(cf. KCO).
$\unicode[STIX]{x1D6FC}(t)$
(cf. KCO).
2.1 The Navier–Stokes equations in primitive variables
In order to obtain the reduced system of helically invariant Navier–Stokes equations we introduce the new variables (2.3e
)–(2.3h
) into the system (2.1) and impose helical invariance, i.e.
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}\equiv 0$
, which eliminates
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}\equiv 0$
, which eliminates
![]() $\unicode[STIX]{x1D702}$
from the system. From this, we obtain the helical invariant continuity equation and the three components of the momentum equations in the
$\unicode[STIX]{x1D702}$
from the system. From this, we obtain the helical invariant continuity equation and the three components of the momentum equations in the
![]() $r$
-,
$r$
-,
![]() $\unicode[STIX]{x1D702}$
- and
$\unicode[STIX]{x1D702}$
- and
![]() $\unicode[STIX]{x1D709}$
-direction
$\unicode[STIX]{x1D709}$
-direction
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -{\displaystyle \frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}}u_{\unicode[STIX]{x1D709}}^{r}\unicode[STIX]{x1D709}+u_{\unicode[STIX]{x1D70F}}^{r}+u^{r}u_{r}^{r}+\frac{1}{B}u^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{r}-\frac{B^{2}}{r}\left(\frac{b}{r}u^{\unicode[STIX]{x1D709}}+\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =-\tilde{p}_{r}+\unicode[STIX]{x1D708}\left[\frac{1}{r}\left(ru_{r}^{r}\right)_{r}+\frac{1}{B^{2}}u_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{r}-\frac{1}{r^{2}}u^{r}-\frac{2bB}{r^{2}}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\frac{b}{r}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -{\displaystyle \frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}}u_{\unicode[STIX]{x1D709}}^{r}\unicode[STIX]{x1D709}+u_{\unicode[STIX]{x1D70F}}^{r}+u^{r}u_{r}^{r}+\frac{1}{B}u^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{r}-\frac{B^{2}}{r}\left(\frac{b}{r}u^{\unicode[STIX]{x1D709}}+\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}\right)^{2}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =-\tilde{p}_{r}+\unicode[STIX]{x1D708}\left[\frac{1}{r}\left(ru_{r}^{r}\right)_{r}+\frac{1}{B^{2}}u_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{r}-\frac{1}{r^{2}}u^{r}-\frac{2bB}{r^{2}}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\frac{b}{r}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \dot{\unicode[STIX]{x1D6FC}}\frac{b}{r}u^{\unicode[STIX]{x1D709}}+\dot{\unicode[STIX]{x1D6FC}}\frac{b^{2}B^{2}}{r^{2}\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+u_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D702}}+u^{r}u_{r}^{\unicode[STIX]{x1D702}}+\frac{B^{2}}{r\unicode[STIX]{x1D6FC}^{2}}u^{r}u^{\unicode[STIX]{x1D702}}+\frac{1}{B}u^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =-B\ddot{\unicode[STIX]{x1D6FC}}\frac{b}{r}\unicode[STIX]{x1D709}\!+\unicode[STIX]{x1D708}\!\left[\!\frac{1}{r}\left(ru_{r}^{\unicode[STIX]{x1D702}}\right)_{r}\!+\frac{1}{B^{2}}u_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\!\left(\!{\displaystyle \frac{{\displaystyle \frac{B^{2}}{\unicode[STIX]{x1D6FC}^{2}}}\left({\displaystyle \frac{B^{2}}{\unicode[STIX]{x1D6FC}^{2}}}-2\!\right)}{r^{2}}}\!\right)\!u^{\unicode[STIX]{x1D702}}\!+\frac{2bB}{r^{2}\unicode[STIX]{x1D6FC}}\!\left(u_{\unicode[STIX]{x1D709}}^{r}-\!\left(Bu^{\unicode[STIX]{x1D709}}\right)_{r}\right)\!\right]\!,\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \dot{\unicode[STIX]{x1D6FC}}\frac{b}{r}u^{\unicode[STIX]{x1D709}}+\dot{\unicode[STIX]{x1D6FC}}\frac{b^{2}B^{2}}{r^{2}\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+u_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D702}}+u^{r}u_{r}^{\unicode[STIX]{x1D702}}+\frac{B^{2}}{r\unicode[STIX]{x1D6FC}^{2}}u^{r}u^{\unicode[STIX]{x1D702}}+\frac{1}{B}u^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =-B\ddot{\unicode[STIX]{x1D6FC}}\frac{b}{r}\unicode[STIX]{x1D709}\!+\unicode[STIX]{x1D708}\!\left[\!\frac{1}{r}\left(ru_{r}^{\unicode[STIX]{x1D702}}\right)_{r}\!+\frac{1}{B^{2}}u_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\!\left(\!{\displaystyle \frac{{\displaystyle \frac{B^{2}}{\unicode[STIX]{x1D6FC}^{2}}}\left({\displaystyle \frac{B^{2}}{\unicode[STIX]{x1D6FC}^{2}}}-2\!\right)}{r^{2}}}\!\right)\!u^{\unicode[STIX]{x1D702}}\!+\frac{2bB}{r^{2}\unicode[STIX]{x1D6FC}}\!\left(u_{\unicode[STIX]{x1D709}}^{r}-\!\left(Bu^{\unicode[STIX]{x1D709}}\right)_{r}\right)\!\right]\!,\qquad \quad\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -2\dot{\unicode[STIX]{x1D6FC}}\frac{bB^{2}}{r\unicode[STIX]{x1D6FC}^{2}}u^{\unicode[STIX]{x1D702}}-\dot{\unicode[STIX]{x1D6FC}}\frac{b^{2}B^{2}}{r^{2}\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+u_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D709}}+u^{r}u_{r}^{\unicode[STIX]{x1D709}}+\frac{b^{2}B^{2}}{r^{3}}u^{r}u^{\unicode[STIX]{x1D709}}+\frac{1}{B}u^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+\frac{2bB^{2}}{r^{2}\unicode[STIX]{x1D6FC}}u^{r}u^{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =-\frac{1}{B}\tilde{p}_{\unicode[STIX]{x1D709}}+B\frac{\ddot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D708}\!\left[\!\frac{1}{r}\left(ru_{r}^{\unicode[STIX]{x1D709}}\right)_{r}+{\displaystyle \frac{1}{B^{2}}}u_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+{\displaystyle \frac{{\displaystyle \frac{B^{4}}{\unicode[STIX]{x1D6FC}^{4}}}-1}{r^{2}}}u^{\unicode[STIX]{x1D709}}+\frac{2bB}{r}\!\left(\frac{b}{r^{2}}u_{\unicode[STIX]{x1D709}}^{r}+\left(\frac{B}{\unicode[STIX]{x1D6FC}r}u^{\unicode[STIX]{x1D702}}\right)_{r}\right)\!\right]\!.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -2\dot{\unicode[STIX]{x1D6FC}}\frac{bB^{2}}{r\unicode[STIX]{x1D6FC}^{2}}u^{\unicode[STIX]{x1D702}}-\dot{\unicode[STIX]{x1D6FC}}\frac{b^{2}B^{2}}{r^{2}\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+u_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D709}}+u^{r}u_{r}^{\unicode[STIX]{x1D709}}+\frac{b^{2}B^{2}}{r^{3}}u^{r}u^{\unicode[STIX]{x1D709}}+\frac{1}{B}u^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+\frac{2bB^{2}}{r^{2}\unicode[STIX]{x1D6FC}}u^{r}u^{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =-\frac{1}{B}\tilde{p}_{\unicode[STIX]{x1D709}}+B\frac{\ddot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D708}\!\left[\!\frac{1}{r}\left(ru_{r}^{\unicode[STIX]{x1D709}}\right)_{r}+{\displaystyle \frac{1}{B^{2}}}u_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+{\displaystyle \frac{{\displaystyle \frac{B^{4}}{\unicode[STIX]{x1D6FC}^{4}}}-1}{r^{2}}}u^{\unicode[STIX]{x1D709}}+\frac{2bB}{r}\!\left(\frac{b}{r^{2}}u_{\unicode[STIX]{x1D709}}^{r}+\left(\frac{B}{\unicode[STIX]{x1D6FC}r}u^{\unicode[STIX]{x1D702}}\right)_{r}\right)\!\right]\!.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
2.2 Navier–Stokes equations in vorticity formulation
The generic Navier–Stokes equations in vorticity formulation are given by
Following KCO, we introduce a local orthogonal basis system to compute the helical vorticity components
![]() $\unicode[STIX]{x1D714}^{r},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}$
. The unit vectors are given by
$\unicode[STIX]{x1D714}^{r},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}$
. The unit vectors are given by
The vorticity vector in the helical basis is given by
The helical vorticity components are related to the cylindrical vorticity components given by
The definition of vorticity (2.6b ) in cylindrical coordinates is given by
Replacing the expressions for the velocity components (2.4a
)–(2.4c
) and their derivatives and, further, assuming helical invariance
![]() $(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}\equiv 0)$
one obtains the respective components of
$(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D702}\equiv 0)$
one obtains the respective components of
![]() $\unicode[STIX]{x1D74E}$
given by
$\unicode[STIX]{x1D74E}$
given by
Employing a transformation similarly to the Navier–Stokes equations in primitive variables, one obtains the helically invariant Navier–Stokes equations in vorticity formulation given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}^{r}+u_{r}\unicode[STIX]{x1D714}_{r}^{r}+{\displaystyle \frac{1}{B}}u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\unicode[STIX]{x1D714}^{r}u_{r}^{r}+\frac{1}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{r}+\unicode[STIX]{x1D708}\left[\frac{1}{r}\left(r\unicode[STIX]{x1D714}_{r}^{r}\right)_{r}+\frac{1}{B^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{r}-\frac{1}{r^{2}}\unicode[STIX]{x1D714}^{r}-\frac{2bB}{r^{2}}\left(\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\frac{b}{r}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right)\right],\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}\unicode[STIX]{x1D709}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}^{r}+u_{r}\unicode[STIX]{x1D714}_{r}^{r}+{\displaystyle \frac{1}{B}}u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\unicode[STIX]{x1D714}^{r}u_{r}^{r}+\frac{1}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{r}+\unicode[STIX]{x1D708}\left[\frac{1}{r}\left(r\unicode[STIX]{x1D714}_{r}^{r}\right)_{r}+\frac{1}{B^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{r}-\frac{1}{r^{2}}\unicode[STIX]{x1D714}^{r}-\frac{2bB}{r^{2}}\left(\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\frac{b}{r}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right)\right],\qquad \quad\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{b}{r}\dot{\unicode[STIX]{x1D6FC}}\left(-\frac{b^{2}}{r^{2}}+\frac{1}{\unicode[STIX]{x1D6FC}^{2}}\right)B^{2}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D709}-\frac{b^{2}\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}r^{2}}B^{2}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D702}}+u^{r}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}+\frac{1}{B}u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad -{\displaystyle \frac{B^{2}}{r\unicode[STIX]{x1D6FC}^{2}}}(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r})+{\displaystyle \frac{2bB^{2}}{\unicode[STIX]{x1D6FC}r^{2}}}(u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}-u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\unicode[STIX]{x1D714}^{r}u_{r}^{\unicode[STIX]{x1D702}}+\frac{1}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\unicode[STIX]{x1D708}\!\left[\!\frac{1}{r}\left(r\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}\right)_{r}+\frac{1}{B^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\frac{B^{2}\left(\!{\displaystyle \frac{1}{\unicode[STIX]{x1D6FC}^{2}}}B^{2}-2\!\right)}{\unicode[STIX]{x1D6FC}^{2}r^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{2bB}{\unicode[STIX]{x1D6FC}r^{2}}\left(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}-(B\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}})_{r}\right)\!\right]\!,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{b}{r}\dot{\unicode[STIX]{x1D6FC}}\left(-\frac{b^{2}}{r^{2}}+\frac{1}{\unicode[STIX]{x1D6FC}^{2}}\right)B^{2}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D709}-\frac{b^{2}\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}r^{2}}B^{2}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D702}}+u^{r}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}+\frac{1}{B}u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad -{\displaystyle \frac{B^{2}}{r\unicode[STIX]{x1D6FC}^{2}}}(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r})+{\displaystyle \frac{2bB^{2}}{\unicode[STIX]{x1D6FC}r^{2}}}(u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}-u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\unicode[STIX]{x1D714}^{r}u_{r}^{\unicode[STIX]{x1D702}}+\frac{1}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\unicode[STIX]{x1D708}\!\left[\!\frac{1}{r}\left(r\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}\right)_{r}+\frac{1}{B^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\frac{B^{2}\left(\!{\displaystyle \frac{1}{\unicode[STIX]{x1D6FC}^{2}}}B^{2}-2\!\right)}{\unicode[STIX]{x1D6FC}^{2}r^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{2bB}{\unicode[STIX]{x1D6FC}r^{2}}\left(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}-(B\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}})_{r}\right)\!\right]\!,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D709}+\frac{b^{2}\dot{\unicode[STIX]{x1D6FC}}}{r^{2}\unicode[STIX]{x1D6FC}}B^{2}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D709}}+u^{r}(\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}})_{r}+{\displaystyle \frac{1}{B}}u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+{\displaystyle \frac{1-{\displaystyle \frac{B^{2}}{\unicode[STIX]{x1D6FC}^{2}}}}{r}}(u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}-u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\unicode[STIX]{x1D714}^{r}u_{r}^{\unicode[STIX]{x1D709}}+\frac{1}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D708}\left[\frac{1}{r}\left(r\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D709}}\right)_{r}+\frac{1}{B^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+\frac{{\displaystyle \frac{1}{\unicode[STIX]{x1D6FC}^{4}}}B^{4}-1}{r^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad +\frac{2bB}{r}\left(\frac{b}{r^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}+\left(\frac{B}{\unicode[STIX]{x1D6FC}r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)_{r}\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D709}+\frac{b^{2}\dot{\unicode[STIX]{x1D6FC}}}{r^{2}\unicode[STIX]{x1D6FC}}B^{2}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D709}}+u^{r}(\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}})_{r}+{\displaystyle \frac{1}{B}}u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+{\displaystyle \frac{1-{\displaystyle \frac{B^{2}}{\unicode[STIX]{x1D6FC}^{2}}}}{r}}(u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}-u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\unicode[STIX]{x1D714}^{r}u_{r}^{\unicode[STIX]{x1D709}}+\frac{1}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D708}\left[\frac{1}{r}\left(r\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D709}}\right)_{r}+\frac{1}{B^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}+\frac{{\displaystyle \frac{1}{\unicode[STIX]{x1D6FC}^{4}}}B^{4}-1}{r^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad +\frac{2bB}{r}\left(\frac{b}{r^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}+\left(\frac{B}{\unicode[STIX]{x1D6FC}r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)_{r}\right)\right].\end{eqnarray}$$
3 Conservation laws of the helically invariant Euler system in time-dependent helical coordinates
In order to seek local CLs, we subsequently apply the direct construction method (Bluman et al.
Reference Bluman, Cheviakov and Anco2010) to the Euler system (2.5a
)–(2.5d
) with
![]() $\unicode[STIX]{x1D708}=0$
in primitive variables as well as in vorticity formulation (2.12a
)–(2.12d
) with
$\unicode[STIX]{x1D708}=0$
in primitive variables as well as in vorticity formulation (2.12a
)–(2.12d
) with
![]() $\unicode[STIX]{x1D708}=0$
. In both cases, the CL multipliers
$\unicode[STIX]{x1D708}=0$
. In both cases, the CL multipliers
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
are chosen to be of zeroth order and, thus, only depend on the dependent and independent variables
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
are chosen to be of zeroth order and, thus, only depend on the dependent and independent variables
Computations with CL multipliers of first order, i.e.
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
in (3.1) containing first derivatives of
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D70E}}$
in (3.1) containing first derivatives of
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\tilde{p}$
, have also been done. However, no additional multipliers exist and, hence, also no extended set of CLs.
$\tilde{p}$
, have also been done. However, no additional multipliers exist and, hence, also no extended set of CLs.
All computations to derive local CLs were conducted with the aid of the symbolic software package GEM for Maple (Cheviakov Reference Cheviakov2007) and the Maple rifsimp tool. Further, with these tools we also obtained the corresponding fluxes of the general form
![]() $\unicode[STIX]{x1D6E4}^{i}$
in equation (1.8). The relation between the fluxes
$\unicode[STIX]{x1D6E4}^{i}$
in equation (1.8). The relation between the fluxes
![]() $\unicode[STIX]{x1D6E4}^{i}$
and the density
$\unicode[STIX]{x1D6E4}^{i}$
and the density
![]() $\unicode[STIX]{x1D6E9}$
and the spatial fluxes
$\unicode[STIX]{x1D6E9}$
and the spatial fluxes
![]() $\unicode[STIX]{x1D6F7}^{i}$
in equation (1.1) can be derived as follows.
$\unicode[STIX]{x1D6F7}^{i}$
in equation (1.1) can be derived as follows.
In the helical setting, any divergence form reads
while a divergence expression of an evolution process in helically symmetric form reads
which is apparently not identical to (3.2a
) due to metric terms. However, multiplying (3.2b
) by
![]() $r$
and using (3.2a
) leads to
$r$
and using (3.2a
) leads to
Comparing the left- and right-hand side of (3.3) one obtains
Subsequently, we always list the density
![]() $\unicode[STIX]{x1D6E9}$
and the spatial fluxes
$\unicode[STIX]{x1D6E9}$
and the spatial fluxes
![]() $\unicode[STIX]{x1D731}$
for each CL. The obvious CLs, such as the continuity equations
$\unicode[STIX]{x1D731}$
for each CL. The obvious CLs, such as the continuity equations
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
,
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0$
,
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}=0$
and the scaling of these equations with a time-dependent function leading to
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}=0$
and the scaling of these equations with a time-dependent function leading to
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(G(t)\boldsymbol{u})=0$
,
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(G(t)\boldsymbol{u})=0$
,
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }(G(t)\unicode[STIX]{x1D74E})=0$
, will not be listed explicitly.
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }(G(t)\unicode[STIX]{x1D74E})=0$
, will not be listed explicitly.
In the next section we seek local CLs that arise from the helically invariant Euler equations in primitive variables, given by (2.5) with
![]() $\unicode[STIX]{x1D708}=0$
. These CLs will be denoted by the prefix ‘EP’. The CLs obtained from the helically invariant Euler system in vorticity formulation will be denoted by the prefix ‘EV’.
$\unicode[STIX]{x1D708}=0$
. These CLs will be denoted by the prefix ‘EP’. The CLs obtained from the helically invariant Euler system in vorticity formulation will be denoted by the prefix ‘EV’.
3.1 Primitive variables
EP1. Extension of the conservation of the
 $z$
-projection of momentum
$z$
-projection of momentum
The first CL is given by
EP2. Extension of the conservation of the
 $z$
-projection of angular momentum
$z$
-projection of angular momentum
The second CL is given by
EP3. Extension of the conservation of the generalized momenta/angular momenta
Here we obtain an infinite family of CLs
The density and the spatial fluxes contain the first and second time derivative of
![]() $\unicode[STIX]{x1D6FC}$
. Referring to KCO, the quantity
$\unicode[STIX]{x1D6FC}$
. Referring to KCO, the quantity
can be physically interpreted as a ‘blend’ of momentum and angular momentum density in the
![]() $\unicode[STIX]{x1D702}$
-direction since with the use of (2.3e
) and
$\unicode[STIX]{x1D702}$
-direction since with the use of (2.3e
) and
![]() $z=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D702})$
the quantity reads
$z=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D702})$
the quantity reads
where the term
![]() $(b/\unicode[STIX]{x1D6FC})\dot{\unicode[STIX]{x1D6FC}}z$
describes the relative movement. For the special cases
$(b/\unicode[STIX]{x1D6FC})\dot{\unicode[STIX]{x1D6FC}}z$
describes the relative movement. For the special cases
![]() $b=0$
the quantity is proportional to the angular momentum density in the
$b=0$
the quantity is proportional to the angular momentum density in the
![]() $z$
-direction
$z$
-direction
![]() $\tilde{\unicode[STIX]{x1D701}}\sim (r/\unicode[STIX]{x1D6FC})u^{\unicode[STIX]{x1D711}}$
in (3.10) while for
$\tilde{\unicode[STIX]{x1D701}}\sim (r/\unicode[STIX]{x1D6FC})u^{\unicode[STIX]{x1D711}}$
in (3.10) while for
![]() $1/\unicode[STIX]{x1D6FC}=0$
it is proportional to the linear momentum density in the
$1/\unicode[STIX]{x1D6FC}=0$
it is proportional to the linear momentum density in the
![]() $z$
-direction
$z$
-direction
![]() $\tilde{\unicode[STIX]{x1D701}}\sim u^{z}$
in (3.10) (
$\tilde{\unicode[STIX]{x1D701}}\sim u^{z}$
in (3.10) (
![]() $\unicode[STIX]{x1D6FC}=\text{const.}$
corresponds to EP4 in KCO).
$\unicode[STIX]{x1D6FC}=\text{const.}$
corresponds to EP4 in KCO).
Comparing the above results to the classical cases one observes that the only quantity which is not conserved is kinetic energy. In the next section we will see that also helicity is not conserved. In order to ensure that this proposition is appropriate in any helical, time-dependent coordinate system, we will prove the non-existence of conservation of energy and helicity in appendices B and C.
3.2 The vorticity formulation
The following CLs are derived from the helically invariant Euler equations in vorticity formulation, consisting of the continuity equation for velocity as well as for vorticity, equations (2.5a
) and (2.12a
), the equations defining the vorticity components (2.11) and the vorticity dynamics equations (2.12b
)–(2.12d
) with
![]() $\unicode[STIX]{x1D708}=0$
. Similar to the multipliers (3.1) for the primitive variables we assume the present multipliers to be of the form
$\unicode[STIX]{x1D708}=0$
. Similar to the multipliers (3.1) for the primitive variables we assume the present multipliers to be of the form
i.e. we limit ourselves again to zeroth-order multipliers.
EV1. Extended family of conservation laws involving
 $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}$
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}$
The family of CLs is given by
EV2. Vorticity conservation law
The CL is given by the density and fluxes
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(-\frac{B}{r^{2}}\left(\frac{r^{3}}{\unicode[STIX]{x1D6FC}^{3}}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r}\right)-b^{3}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)\right)-\frac{2B}{\unicode[STIX]{x1D6FC}^{2}}u^{r}\left(-\frac{b}{r}u^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{B}{r^{2}}\dot{\unicode[STIX]{x1D6FC}}\left(-r^{3}u^{\unicode[STIX]{x1D709}}-2\unicode[STIX]{x1D6FC}^{3}b^{3}u^{\unicode[STIX]{x1D702}}-\unicode[STIX]{x1D6FC}r^{2}bu^{\unicode[STIX]{x1D702}}+\frac{2}{B}\unicode[STIX]{x1D6FC}^{2}r^{2}\unicode[STIX]{x1D709}u^{r}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(-\frac{B}{r^{2}}\left(\frac{r^{3}}{\unicode[STIX]{x1D6FC}^{3}}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r}\right)-b^{3}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)\right)-\frac{2B}{\unicode[STIX]{x1D6FC}^{2}}u^{r}\left(-\frac{b}{r}u^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{B}{r^{2}}\dot{\unicode[STIX]{x1D6FC}}\left(-r^{3}u^{\unicode[STIX]{x1D709}}-2\unicode[STIX]{x1D6FC}^{3}b^{3}u^{\unicode[STIX]{x1D702}}-\unicode[STIX]{x1D6FC}r^{2}bu^{\unicode[STIX]{x1D702}}+\frac{2}{B}\unicode[STIX]{x1D6FC}^{2}r^{2}\unicode[STIX]{x1D709}u^{r}\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(\frac{B}{\unicode[STIX]{x1D6FC}^{3}}\left(\left(u^{r}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+r\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)\right)+\frac{2bB}{\unicode[STIX]{x1D6FC}^{2}r}u^{\unicode[STIX]{x1D702}}u^{\unicode[STIX]{x1D709}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{B^{2}}{r^{2}}\dot{\unicode[STIX]{x1D6FC}}\left(b^{3}\unicode[STIX]{x1D6FC}^{3}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-2b^{2}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-r^{3}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-2r^{2}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-\frac{r^{3}}{B}u^{r}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(\frac{B}{\unicode[STIX]{x1D6FC}^{3}}\left(\left(u^{r}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+r\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)\right)+\frac{2bB}{\unicode[STIX]{x1D6FC}^{2}r}u^{\unicode[STIX]{x1D702}}u^{\unicode[STIX]{x1D709}}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{B^{2}}{r^{2}}\dot{\unicode[STIX]{x1D6FC}}\left(b^{3}\unicode[STIX]{x1D6FC}^{3}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-2b^{2}\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-r^{3}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-2r^{2}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-\frac{r^{3}}{B}u^{r}\right).\end{eqnarray}$$
The assumption
![]() $b=0$
leads to
$b=0$
leads to
![]() $\unicode[STIX]{x1D6E9}=-\unicode[STIX]{x1D6FC}^{2}r\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}$
. Corresponding to KCO problems, where the velocity vanishes on the boundary of the time-independent flow domain
$\unicode[STIX]{x1D6E9}=-\unicode[STIX]{x1D6FC}^{2}r\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}$
. Corresponding to KCO problems, where the velocity vanishes on the boundary of the time-independent flow domain
![]() $\unicode[STIX]{x1D6FA}\neq \unicode[STIX]{x1D6FA}(t)$
, the quantity
$\unicode[STIX]{x1D6FA}\neq \unicode[STIX]{x1D6FA}(t)$
, the quantity
![]() $\unicode[STIX]{x1D6FC}^{2}r\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}$
corresponds to the conservation of linear momentum in the
$\unicode[STIX]{x1D6FC}^{2}r\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}$
corresponds to the conservation of linear momentum in the
![]() $z$
-direction since
$z$
-direction since
where
![]() $\unicode[STIX]{x1D6FC}(t)$
is the parameter function (
$\unicode[STIX]{x1D6FC}(t)$
is the parameter function (
![]() $\unicode[STIX]{x1D6FC}=\text{const.}$
corresponds to EV4 in KCO).
$\unicode[STIX]{x1D6FC}=\text{const.}$
corresponds to EV4 in KCO).
EV3. Vorticity conservation law
The CL is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9} & = & \displaystyle -\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\left(\frac{r^{2}b^{2}}{B^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{3}}\left(-\frac{b}{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\right)\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\left(\frac{r^{2}b^{2}}{B^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{3}B}\unicode[STIX]{x1D714}^{z}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9} & = & \displaystyle -\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\left(\frac{r^{2}b^{2}}{B^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{3}}\left(-\frac{b}{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\right)\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\left(\frac{r^{2}b^{2}}{B^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{3}B}\unicode[STIX]{x1D714}^{z}\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\frac{rB}{\unicode[STIX]{x1D6FC}^{3}}\Bigg(2u^{r}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}+\frac{b}{r}u^{\unicode[STIX]{x1D709}}\right)+b\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{r^{4}+r^{2}\unicode[STIX]{x1D6FC}^{2}b^{2}+b^{4}\unicode[STIX]{x1D6FC}^{4}}{r^{3}\unicode[STIX]{x1D6FC}}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)+\dot{\unicode[STIX]{x1D6FC}}\left(\frac{b}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}+2\unicode[STIX]{x1D6FC}^{2}\frac{b^{4}}{r^{3}}u^{\unicode[STIX]{x1D702}}+\frac{b^{2}}{r}u^{\unicode[STIX]{x1D702}}\right)\!\!\Bigg)\!,\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\frac{rB}{\unicode[STIX]{x1D6FC}^{3}}\Bigg(2u^{r}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}+\frac{b}{r}u^{\unicode[STIX]{x1D709}}\right)+b\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{r^{4}+r^{2}\unicode[STIX]{x1D6FC}^{2}b^{2}+b^{4}\unicode[STIX]{x1D6FC}^{4}}{r^{3}\unicode[STIX]{x1D6FC}}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)+\dot{\unicode[STIX]{x1D6FC}}\left(\frac{b}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}+2\unicode[STIX]{x1D6FC}^{2}\frac{b^{4}}{r^{3}}u^{\unicode[STIX]{x1D702}}+\frac{b^{2}}{r}u^{\unicode[STIX]{x1D702}}\right)\!\!\Bigg)\!,\qquad \quad\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(-\frac{1}{\unicode[STIX]{x1D6FC}^{3}}bB\right)\Bigg(\left(u^{r}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+r\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,2\frac{r}{\unicode[STIX]{x1D6FC}b}u^{\unicode[STIX]{x1D702}}u^{\unicode[STIX]{x1D709}}+\dot{\unicode[STIX]{x1D6FC}}\left(B\frac{r}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{r}{\unicode[STIX]{x1D6FC}}u^{r}-\frac{r^{4}+r^{2}\unicode[STIX]{x1D6FC}^{2}b^{2}+b^{4}\unicode[STIX]{x1D6FC}^{4}}{r^{2}\unicode[STIX]{x1D6FC}^{2}b}B\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\Bigg).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(-\frac{1}{\unicode[STIX]{x1D6FC}^{3}}bB\right)\Bigg(\left(u^{r}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+r\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,2\frac{r}{\unicode[STIX]{x1D6FC}b}u^{\unicode[STIX]{x1D702}}u^{\unicode[STIX]{x1D709}}+\dot{\unicode[STIX]{x1D6FC}}\left(B\frac{r}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{r}{\unicode[STIX]{x1D6FC}}u^{r}-\frac{r^{4}+r^{2}\unicode[STIX]{x1D6FC}^{2}b^{2}+b^{4}\unicode[STIX]{x1D6FC}^{4}}{r^{2}\unicode[STIX]{x1D6FC}^{2}b}B\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\Bigg).\end{eqnarray}$$
EV4. Vorticity conservation law
We further obtain a family of CLs given by the density and fluxes
EV5. Vorticity conservation law
In this case the CL multipliers again depend on an arbitrary function
![]() $M=M(\unicode[STIX]{x1D709},r,t)$
and one obtains the following family of CLs, given by the density and fluxes
$M=M(\unicode[STIX]{x1D709},r,t)$
and one obtains the following family of CLs, given by the density and fluxes
4 Conservation laws of the helically invariant Navier–Stokes system in time-dependent coordinates
Presently, the application of the direct method to the reduced Navier–Stokes system (2.5a )–(2.5d ) in primitive variables leads to two new CLs. For the related vorticity formulation (2.12a )–(2.12d ) five new CLs will be derived. For the present calculations all multipliers (3.1) have been chosen to be of zeroth order. Similarly to the classical case, all new present CLs are subsets of those admitted by the helically symmetric Euler equations in the previous section. Whereas the densities are the same, the fluxes are extended by additional viscous terms.
4.1 Primitive variables
NSP1. Extension of the conservation of the
 $z$
-projection of momentum
$z$
-projection of momentum
The CL is respectively defined by the density and fluxes
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{2}\left(u^{\unicode[STIX]{x1D709}}B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)+\frac{B}{\unicode[STIX]{x1D6FC}}p\right)\nonumber\\ \displaystyle & & \displaystyle -\unicode[STIX]{x1D6FC}^{2}\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D6FC}\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}B^{2}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)-\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x1D6FC}^{2}}{B}\left(B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)\right)_{\unicode[STIX]{x1D709}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{2}\left(u^{\unicode[STIX]{x1D709}}B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)+\frac{B}{\unicode[STIX]{x1D6FC}}p\right)\nonumber\\ \displaystyle & & \displaystyle -\unicode[STIX]{x1D6FC}^{2}\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D6FC}\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}B^{2}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)-\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x1D6FC}^{2}}{B}\left(B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)\right)_{\unicode[STIX]{x1D709}}.\end{eqnarray}$$
(
![]() $\unicode[STIX]{x1D6FC}=\text{const.}$
corresponds to NSP1 in KCO).
$\unicode[STIX]{x1D6FC}=\text{const.}$
corresponds to NSP1 in KCO).
NSP2. Extension of the conservation of generalized momentum
For the present viscous case, the family of CLs for the helical Euler system (3.7) reduces to one single CL, given by the density and fluxes
4.2 The vorticity formulation
In the case of CLs in vorticity formulation we obtained five distinct cases all of which are one-to-one extensions of the five cases in KCO.
NSV1. Extension of an infinite family of vorticity conservation laws
The family of CLs (3.12) is extended by the viscous terms and the density and fluxes are given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \frac{1}{r}\left(q(t)\left[u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}-\unicode[STIX]{x1D714}^{r}u^{\unicode[STIX]{x1D711}}\right]+\dot{q}(t)B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)-\dot{\unicode[STIX]{x1D6FC}}q(t)B\left(\frac{1}{\unicode[STIX]{x1D6FC}^{2}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}\right)\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{q(t)}{r}\unicode[STIX]{x1D708}\left[\frac{B}{r\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{b^{2}}{r\left({\displaystyle \frac{r^{2}}{\unicode[STIX]{x1D6FC}^{2}}}+b^{2}\right)}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}+B\left(\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}+\frac{b}{r}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D709}}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \frac{1}{r}\left(q(t)\left[u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}-\unicode[STIX]{x1D714}^{r}u^{\unicode[STIX]{x1D711}}\right]+\dot{q}(t)B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)-\dot{\unicode[STIX]{x1D6FC}}q(t)B\left(\frac{1}{\unicode[STIX]{x1D6FC}^{2}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}\right)\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{q(t)}{r}\unicode[STIX]{x1D708}\left[\frac{B}{r\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{b^{2}}{r\left({\displaystyle \frac{r^{2}}{\unicode[STIX]{x1D6FC}^{2}}}+b^{2}\right)}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}+B\left(\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}+\frac{b}{r}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D709}}\right)\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle -\frac{B}{r\unicode[STIX]{x1D6FC}}\left(q(t)\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)+\dot{q}(t)u^{r}+q(t)\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}-q(t)\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}u^{r}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{q(t)}{r^{4}}B\unicode[STIX]{x1D708}\left[\frac{r^{3}}{B}\left(\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\frac{b}{r}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right)+2br\unicode[STIX]{x1D714}^{r}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle -\frac{B}{r\unicode[STIX]{x1D6FC}}\left(q(t)\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)+\dot{q}(t)u^{r}+q(t)\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}-q(t)\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}u^{r}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{q(t)}{r^{4}}B\unicode[STIX]{x1D708}\left[\frac{r^{3}}{B}\left(\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}+\frac{b}{r}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right)+2br\unicode[STIX]{x1D714}^{r}\right],\end{eqnarray}$$
NSV2. Extension of the vorticity conservation law
This CL is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(-\frac{B}{r^{2}}\left(\frac{r^{3}}{\unicode[STIX]{x1D6FC}^{3}}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r}\right)-b^{3}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)\right)-\frac{2B}{\unicode[STIX]{x1D6FC}^{2}}u^{r}\left(-\frac{b}{r}u^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{B}{r^{2}}\dot{\unicode[STIX]{x1D6FC}}\left(-r^{3}u^{\unicode[STIX]{x1D709}}-2\unicode[STIX]{x1D6FC}^{3}b^{3}u^{\unicode[STIX]{x1D702}}-\unicode[STIX]{x1D6FC}r^{2}bu^{\unicode[STIX]{x1D702}}+\frac{2}{B}\unicode[STIX]{x1D6FC}^{2}r^{2}\unicode[STIX]{x1D709}u^{r}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\unicode[STIX]{x1D708}\left[\frac{r^{2}}{B^{2}}\left(\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{b}{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)-r^{3}\left(\frac{1}{\unicode[STIX]{x1D6FC}^{3}}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}-\frac{b^{3}}{r^{3}}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D709}}\right)+\frac{b}{\unicode[STIX]{x1D6FC}}B^{2}r\left(\frac{b^{3}}{r^{3}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}^{3}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\!\right]\!,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(-\frac{B}{r^{2}}\left(\frac{r^{3}}{\unicode[STIX]{x1D6FC}^{3}}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r}\right)-b^{3}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)\right)-\frac{2B}{\unicode[STIX]{x1D6FC}^{2}}u^{r}\left(-\frac{b}{r}u^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{B}{r^{2}}\dot{\unicode[STIX]{x1D6FC}}\left(-r^{3}u^{\unicode[STIX]{x1D709}}-2\unicode[STIX]{x1D6FC}^{3}b^{3}u^{\unicode[STIX]{x1D702}}-\unicode[STIX]{x1D6FC}r^{2}bu^{\unicode[STIX]{x1D702}}+\frac{2}{B}\unicode[STIX]{x1D6FC}^{2}r^{2}\unicode[STIX]{x1D709}u^{r}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\unicode[STIX]{x1D708}\left[\frac{r^{2}}{B^{2}}\left(\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{b}{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)-r^{3}\left(\frac{1}{\unicode[STIX]{x1D6FC}^{3}}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}-\frac{b^{3}}{r^{3}}\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D709}}\right)+\frac{b}{\unicode[STIX]{x1D6FC}}B^{2}r\left(\frac{b^{3}}{r^{3}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}^{3}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\!\right]\!,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(\frac{B}{\unicode[STIX]{x1D6FC}^{3}}\left(\left(u^{r}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+r\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)\right)+\frac{2bB}{\unicode[STIX]{x1D6FC}^{2}r}u^{\unicode[STIX]{x1D702}}u^{\unicode[STIX]{x1D709}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{B^{2}}{r^{2}}\dot{\unicode[STIX]{x1D6FC}}\left(b^{3}\unicode[STIX]{x1D6FC}^{3}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-2b\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-r^{3}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-2r^{2}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-\frac{r^{3}}{B}u^{r}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}^{4}\frac{2bB}{\unicode[STIX]{x1D6FC}^{2}r}\unicode[STIX]{x1D708}\left[\left(1-\frac{b^{2}\unicode[STIX]{x1D6FC}^{2}}{r^{2}}\right)\unicode[STIX]{x1D714}^{r}+\frac{r^{2}\unicode[STIX]{x1D6FC}^{2}}{2bB}\left(\frac{1}{\unicode[STIX]{x1D6FC}^{3}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}-\frac{b^{3}}{r^{3}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(\frac{B}{\unicode[STIX]{x1D6FC}^{3}}\left(\left(u^{r}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+r\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)\right)+\frac{2bB}{\unicode[STIX]{x1D6FC}^{2}r}u^{\unicode[STIX]{x1D702}}u^{\unicode[STIX]{x1D709}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{B^{2}}{r^{2}}\dot{\unicode[STIX]{x1D6FC}}\left(b^{3}\unicode[STIX]{x1D6FC}^{3}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-2b\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-r^{3}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-2r^{2}\unicode[STIX]{x1D709}u^{\unicode[STIX]{x1D709}}-\frac{r^{3}}{B}u^{r}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}^{4}\frac{2bB}{\unicode[STIX]{x1D6FC}^{2}r}\unicode[STIX]{x1D708}\left[\left(1-\frac{b^{2}\unicode[STIX]{x1D6FC}^{2}}{r^{2}}\right)\unicode[STIX]{x1D714}^{r}+\frac{r^{2}\unicode[STIX]{x1D6FC}^{2}}{2bB}\left(\frac{1}{\unicode[STIX]{x1D6FC}^{3}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}-\frac{b^{3}}{r^{3}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right)\right],\end{eqnarray}$$
NSV3. Extension of the vorticity conservation law
This CL is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9} & = & \displaystyle -\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\left(\frac{r^{2}b^{2}}{B^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{3}}\left(-\frac{b}{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\right)\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\left(\frac{r^{2}b^{2}}{B^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{3}B}\unicode[STIX]{x1D714}^{z}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9} & = & \displaystyle -\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\left(\frac{r^{2}b^{2}}{B^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{3}}\left(-\frac{b}{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{1}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\right)\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FC}^{4}\frac{B}{r^{2}}\left(\frac{r^{2}b^{2}}{B^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{3}B}\unicode[STIX]{x1D714}^{z}\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\frac{rB}{\unicode[STIX]{x1D6FC}^{3}}\Bigg(2u^{r}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}+\frac{b}{r}u^{\unicode[STIX]{x1D709}}\right)+b\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{r^{4}+r^{2}\unicode[STIX]{x1D6FC}^{2}b^{2}+b^{4}\unicode[STIX]{x1D6FC}^{4}}{r^{3}\unicode[STIX]{x1D6FC}}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)+\dot{\unicode[STIX]{x1D6FC}}\left(\frac{b}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}+2\unicode[STIX]{x1D6FC}^{2}\frac{b^{4}}{r^{3}}u^{\unicode[STIX]{x1D702}}+\frac{b^{2}}{r}u^{\unicode[STIX]{x1D702}}\right)\Bigg)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}^{4}\unicode[STIX]{x1D708}~\Bigg[4\frac{B}{\unicode[STIX]{x1D6FC}^{3}}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}+\frac{b}{r}u^{\unicode[STIX]{x1D709}}\right)-\frac{br}{\unicode[STIX]{x1D6FC}^{3}}B\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}+\frac{B}{r^{3}}\left(b^{4}-\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{4}}-\frac{r^{6}}{\unicode[STIX]{x1D6FC}^{4}r^{2}+\unicode[STIX]{x1D6FC}^{6}b^{2}}\right)\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{B}{\unicode[STIX]{x1D6FC}^{4}r^{2}}\left(r^{4}+\unicode[STIX]{x1D6FC}^{2}r^{2}b^{2}+\unicode[STIX]{x1D6FC}^{4}b^{4}\right)\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D709}}+\frac{b}{\unicode[STIX]{x1D6FC}B}\left(2+\frac{r^{4}}{\left(r^{2}+\unicode[STIX]{x1D6FC}^{2}b^{2}\right)^{2}}\right)\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\Bigg],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\frac{rB}{\unicode[STIX]{x1D6FC}^{3}}\Bigg(2u^{r}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}+\frac{b}{r}u^{\unicode[STIX]{x1D709}}\right)+b\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{r}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{r^{4}+r^{2}\unicode[STIX]{x1D6FC}^{2}b^{2}+b^{4}\unicode[STIX]{x1D6FC}^{4}}{r^{3}\unicode[STIX]{x1D6FC}}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)+\dot{\unicode[STIX]{x1D6FC}}\left(\frac{b}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}+2\unicode[STIX]{x1D6FC}^{2}\frac{b^{4}}{r^{3}}u^{\unicode[STIX]{x1D702}}+\frac{b^{2}}{r}u^{\unicode[STIX]{x1D702}}\right)\Bigg)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}^{4}\unicode[STIX]{x1D708}~\Bigg[4\frac{B}{\unicode[STIX]{x1D6FC}^{3}}\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}+\frac{b}{r}u^{\unicode[STIX]{x1D709}}\right)-\frac{br}{\unicode[STIX]{x1D6FC}^{3}}B\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D702}}+\frac{B}{r^{3}}\left(b^{4}-\frac{r^{4}}{\unicode[STIX]{x1D6FC}^{4}}-\frac{r^{6}}{\unicode[STIX]{x1D6FC}^{4}r^{2}+\unicode[STIX]{x1D6FC}^{6}b^{2}}\right)\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{B}{\unicode[STIX]{x1D6FC}^{4}r^{2}}\left(r^{4}+\unicode[STIX]{x1D6FC}^{2}r^{2}b^{2}+\unicode[STIX]{x1D6FC}^{4}b^{4}\right)\unicode[STIX]{x1D714}_{r}^{\unicode[STIX]{x1D709}}+\frac{b}{\unicode[STIX]{x1D6FC}B}\left(2+\frac{r^{4}}{\left(r^{2}+\unicode[STIX]{x1D6FC}^{2}b^{2}\right)^{2}}\right)\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\Bigg],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(-\frac{1}{\unicode[STIX]{x1D6FC}^{3}}bB\right)\Bigg(\left(u^{r}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+r\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,2\frac{r}{\unicode[STIX]{x1D6FC}b}u^{\unicode[STIX]{x1D702}}u^{\unicode[STIX]{x1D709}}+\dot{\unicode[STIX]{x1D6FC}}\left(B\frac{r}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{r}{\unicode[STIX]{x1D6FC}}u^{r}-\frac{r^{4}+r^{2}\unicode[STIX]{x1D6FC}^{2}b^{2}+b^{4}\unicode[STIX]{x1D6FC}^{4}}{r^{2}\unicode[STIX]{x1D6FC}^{2}b}B\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\Bigg)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}^{4}\unicode[STIX]{x1D708}~\Bigg[\frac{1}{\unicode[STIX]{x1D6FC}^{4}r^{2}}\left(r^{4}+\unicode[STIX]{x1D6FC}^{2}r^{2}b^{2}+\unicode[STIX]{x1D6FC}^{4}b^{4}\right)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}-\frac{br}{\unicode[STIX]{x1D6FC}^{3}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}-\frac{4bB}{\unicode[STIX]{x1D6FC}^{3}r}u^{r}+\frac{2B^{4}b}{r^{3}}\unicode[STIX]{x1D714}^{r}\Bigg],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle \unicode[STIX]{x1D6FC}^{4}\left(-\frac{1}{\unicode[STIX]{x1D6FC}^{3}}bB\right)\Bigg(\left(u^{r}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+r\left(u^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,2\frac{r}{\unicode[STIX]{x1D6FC}b}u^{\unicode[STIX]{x1D702}}u^{\unicode[STIX]{x1D709}}+\dot{\unicode[STIX]{x1D6FC}}\left(B\frac{r}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\frac{r}{\unicode[STIX]{x1D6FC}}u^{r}-\frac{r^{4}+r^{2}\unicode[STIX]{x1D6FC}^{2}b^{2}+b^{4}\unicode[STIX]{x1D6FC}^{4}}{r^{2}\unicode[STIX]{x1D6FC}^{2}b}B\unicode[STIX]{x1D709}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\Bigg)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}^{4}\unicode[STIX]{x1D708}~\Bigg[\frac{1}{\unicode[STIX]{x1D6FC}^{4}r^{2}}\left(r^{4}+\unicode[STIX]{x1D6FC}^{2}r^{2}b^{2}+\unicode[STIX]{x1D6FC}^{4}b^{4}\right)\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}-\frac{br}{\unicode[STIX]{x1D6FC}^{3}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D702}}-\frac{4bB}{\unicode[STIX]{x1D6FC}^{3}r}u^{r}+\frac{2B^{4}b}{r^{3}}\unicode[STIX]{x1D714}^{r}\Bigg],\end{eqnarray}$$
NSV4. Extension of an infinite family of vorticity conservation laws
The family of CLs (3.16), which holds for the helically invariant Euler equations, is carried over to the viscous case without change, as the viscosity does not appear explicitly (
![]() $\unicode[STIX]{x1D6FC}=\text{const.}$
corresponds to NSV4 in KCO).
$\unicode[STIX]{x1D6FC}=\text{const.}$
corresponds to NSV4 in KCO).
NSV5. Extension of an infinite family of vorticity conservation laws
The infinite set of CLs (3.17) is extended by a viscous term. Its density and fluxes read
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \frac{M_{\unicode[STIX]{x1D709}}}{B}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)-M_{t}\unicode[STIX]{x1D714}^{r}+\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{r}\left(M+\unicode[STIX]{x1D709}M_{\unicode[STIX]{x1D709}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D708}\left[-\frac{M_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}}{B^{2}}\unicode[STIX]{x1D714}^{r}-\frac{M_{r}}{r}\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}-\frac{2bBM_{\unicode[STIX]{x1D709}}}{\unicode[STIX]{x1D6FC}r^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\left(\frac{BM_{\unicode[STIX]{x1D709}}}{\unicode[STIX]{x1D6FC}^{2}r}+\frac{M_{r\unicode[STIX]{x1D709}}}{B}\right)\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-\frac{M_{\unicode[STIX]{x1D709}}}{rB}\left(r\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)_{r}\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{r} & = & \displaystyle \frac{M_{\unicode[STIX]{x1D709}}}{B}\left(u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right)-M_{t}\unicode[STIX]{x1D714}^{r}+\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{r}\left(M+\unicode[STIX]{x1D709}M_{\unicode[STIX]{x1D709}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D708}\left[-\frac{M_{\unicode[STIX]{x1D709}\unicode[STIX]{x1D709}}}{B^{2}}\unicode[STIX]{x1D714}^{r}-\frac{M_{r}}{r}\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}-\frac{2bBM_{\unicode[STIX]{x1D709}}}{\unicode[STIX]{x1D6FC}r^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}+\left(\frac{BM_{\unicode[STIX]{x1D709}}}{\unicode[STIX]{x1D6FC}^{2}r}+\frac{M_{r\unicode[STIX]{x1D709}}}{B}\right)\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-\frac{M_{\unicode[STIX]{x1D709}}}{rB}\left(r\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)_{r}\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle M_{r}\left(u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}-u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)-M_{t}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\left(M\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-B\unicode[STIX]{x1D709}M_{r}\unicode[STIX]{x1D714}^{r}\right)+\unicode[STIX]{x1D708}\left[\left(\frac{2B}{\unicode[STIX]{x1D6FC}^{2}r}-\frac{2}{rB}\right)M_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\frac{M_{r\unicode[STIX]{x1D709}}}{B}\unicode[STIX]{x1D714}^{r}-\frac{M_{r}}{B}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}+\frac{2bB^{2}M_{r}}{\unicode[STIX]{x1D6FC}r^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-\left(\frac{2B^{2}M_{r}}{\unicode[STIX]{x1D6FC}^{2}r}+r\left(\frac{M_{r}}{r}\right)_{r}\right)\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-\frac{M_{\unicode[STIX]{x1D709}}}{B^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\unicode[STIX]{x1D709}} & = & \displaystyle M_{r}\left(u^{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}-u^{r}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)-M_{t}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}+\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\left(M\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-B\unicode[STIX]{x1D709}M_{r}\unicode[STIX]{x1D714}^{r}\right)+\unicode[STIX]{x1D708}\left[\left(\frac{2B}{\unicode[STIX]{x1D6FC}^{2}r}-\frac{2}{rB}\right)M_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D714}^{r}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\frac{M_{r\unicode[STIX]{x1D709}}}{B}\unicode[STIX]{x1D714}^{r}-\frac{M_{r}}{B}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{r}+\frac{2bB^{2}M_{r}}{\unicode[STIX]{x1D6FC}r^{2}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D702}}-\left(\frac{2B^{2}M_{r}}{\unicode[STIX]{x1D6FC}^{2}r}+r\left(\frac{M_{r}}{r}\right)_{r}\right)\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}-\frac{M_{\unicode[STIX]{x1D709}}}{B^{2}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D709}}\right],\end{eqnarray}$$
5 Summary and conclusions
In the current contribution the classical case of a helical coordinate system is extended to a new time-dependent helical coordinate system by applying the method of group invariant reduction. Based on these new coordinates, a reduced system of time-dependent helically invariant Euler and Navier–Stokes equations was derived, where the spatial dependence of all dependent variables has been reduced by one. For the development of the new helical coordinate system, we considered the helical symmetry of the Euler and Navier–Stokes equations, which relies on the combination of two Lie symmetry groups: (i) generalized Galilean invariance, which comprises classical Galilean group and axial translation and (ii) the rotation about the same axis. Compared to the coordinate system that is used for classical helical flows (see e.g. KCO), where all coordinates are time-independent, the present helical coordinate
![]() $\unicode[STIX]{x1D709}$
is time-dependent. Nevertheless, particularly for the helical coordinate, there is a good analogy between the classical and the extended case. The only difference is that the parameter
$\unicode[STIX]{x1D709}$
is time-dependent. Nevertheless, particularly for the helical coordinate, there is a good analogy between the classical and the extended case. The only difference is that the parameter
![]() $a$
in the classical helical setting is replaced by the time-dependent parameter
$a$
in the classical helical setting is replaced by the time-dependent parameter
![]() $1/\unicode[STIX]{x1D6FC}(t)$
. Moreover, the helically invariant Euler and Navier–Stokes equations are extended by terms involving the time derivative of the parameter function
$1/\unicode[STIX]{x1D6FC}(t)$
. Moreover, the helically invariant Euler and Navier–Stokes equations are extended by terms involving the time derivative of the parameter function
![]() $\unicode[STIX]{x1D6FC}(t)$
.
$\unicode[STIX]{x1D6FC}(t)$
.
Furthermore, new local CLs were sought, which were obtained from the new helically invariant system of equations. However, for every CL in KCO, a corresponding CL has been found for time-dependent coordinates, except for the conservation of energy and helicity. Due to their great importance in a physical context, their absence was proven in appendices B and C.
For the helically invariant Euler equations in primitive variables an extension of the conservation of the
![]() $z$
-projection of momentum and angular momentum was obtained. Further, an infinite family of CLs holds for helical flows in time-dependent coordinates, which may be considered a blend of momentum and angular momentum.
$z$
-projection of momentum and angular momentum was obtained. Further, an infinite family of CLs holds for helical flows in time-dependent coordinates, which may be considered a blend of momentum and angular momentum.
For the helically invariant Euler equations in vorticity formulation, three extended families of CLs were obtained. The family of CLs EV1 (3.12) involves the vorticity component
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}$
and depends on the arbitrary function
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}$
and depends on the arbitrary function
![]() $q(t)$
. The family of CLs EV4 (3.16) is a combination of the continuity equation for vorticity (2.12a
) and the equations defining the vorticity components (2.11). The family of CLs (EV5) is a subset of the infinite family of CLs for helical flows presented in Cheviakov & Oberlack (Reference Cheviakov and Oberlack2014). Further, two new CLs, which are extensions of the classical case, hold (formulae (3.13) and (3.15)).
$q(t)$
. The family of CLs EV4 (3.16) is a combination of the continuity equation for vorticity (2.12a
) and the equations defining the vorticity components (2.11). The family of CLs (EV5) is a subset of the infinite family of CLs for helical flows presented in Cheviakov & Oberlack (Reference Cheviakov and Oberlack2014). Further, two new CLs, which are extensions of the classical case, hold (formulae (3.13) and (3.15)).
For the viscous case in primitive variables, extensions of the conservation of the
![]() $z$
-projection of momentum and generalized momentum were obtained (formulae (4.1), (4.3)).
$z$
-projection of momentum and generalized momentum were obtained (formulae (4.1), (4.3)).
Finally, for the viscous case in vorticity formulation, all the CLs obtained for the inviscid case are carried over and extended by a viscous term. They were listed in the § 4.2.
In summary, with the use of the Lie symmetries, a setting to describe helical flows with a time-dependent moving pitch could be derived in a straightforward way. Moreover, the assumption of helical invariance gives rise to new CLs which exist in addition to the known CL in three dimensions, e.g. conservation of mass, momentum and energy.
One objective for future work is seeking exact solutions of the helical invariant Navier–Stokes equations (2.5). However, it is rather difficult to find an appropriate ansatz for a solution of the equations even for the classical helical case with a constant pitch. The stability of special solutions to the Navier–Stokes equations is a topic of countless publications, although very little is known for helical flows. However, it is known that many swirling flows are unstable to helical disturbances, in fact, very often these are the most unstable modes. In this sense, the present study may be valuable for the understanding of the nonlinear stability of these flows.
Acknowledgements
The authors are grateful to the Germany Research Foundation (DFG) under grant no. OB 96/41-1 for financial support, and to Y. Wang and D. Plümacher for their helpful comments and various inspiring discussions.
Appendix A. Derivation of the time-dependent helical coordinates
Presently, we derived a new time-dependent helical coordinate system for the Euler and Navier–Stokes equations by using the method of group invariant reduction. Here, group invariance is meant in the sense of reduction of the spatial coordinates such as e.g. a reduction to plane flows.
The derivation is based on the helical symmetry which is a combination of the generalized Galilean invariance and the rotation group, given by (2.2). The corresponding infinitesimal generators for rotation and generalized Galilean invariance of the Euler and Navier–Stokes equations are given by (see e.g. Oberlack Reference Oberlack2000)
A new extended helical symmetry of the Euler and Navier–Stokes equations consists of a superposition of a rotation group
![]() $X_{R}$
and the generalized Galilean symmetry
$X_{R}$
and the generalized Galilean symmetry
![]() $X_{G}$
. To maintain the nomenclature to earlier results on helical flows (see e.g. KCO), we choose the following linear combination of symmetries (A 1a
) and (A 1b
) to obtain
$X_{G}$
. To maintain the nomenclature to earlier results on helical flows (see e.g. KCO), we choose the following linear combination of symmetries (A 1a
) and (A 1b
) to obtain
For the final aim of a helically symmetric coordinate system we need to define
![]() $\unicode[STIX]{x1D702}(r,\unicode[STIX]{x1D711},z,t)$
to be the variable, which should be eliminated from the system of equations such that the reduced system only contains two spatial variables.
$\unicode[STIX]{x1D702}(r,\unicode[STIX]{x1D711},z,t)$
to be the variable, which should be eliminated from the system of equations such that the reduced system only contains two spatial variables.
Based on this idea, we derive a new set of variables, i.e. the reduced helical coordinates
![]() $(\tilde{r},\unicode[STIX]{x1D709})$
, the helical velocities
$(\tilde{r},\unicode[STIX]{x1D709})$
, the helical velocities
![]() $(\tilde{u} ^{r},u^{\unicode[STIX]{x1D702}},u^{\unicode[STIX]{x1D709}})$
and the pressure
$(\tilde{u} ^{r},u^{\unicode[STIX]{x1D702}},u^{\unicode[STIX]{x1D709}})$
and the pressure
![]() $\tilde{p}$
summarized in the vector
$\tilde{p}$
summarized in the vector
For their derivation we employ the method of canonical coordinates (see e.g. Bluman et al. Reference Bluman, Cheviakov and Anco2010), which results in two linear partial differential equations of first order, given by
which is a translational symmetry in
![]() $\unicode[STIX]{x1D702}$
.
$\unicode[STIX]{x1D702}$
.
Substituting (A 3) in (A 5a ) leads to
which can be equivalently written in the form of a characteristic system
Solving the system (A 8), we obtain a general solution of equation (A 7) for the helical variable
![]() $\unicode[STIX]{x1D702}$
given by
$\unicode[STIX]{x1D702}$
given by
Similarly, substituting (A 3) in (A 5b ) yields
and, written in the equivalent form of the characteristic system, we obtain
A general solution of (A 11) reads
where
![]() $\boldsymbol{F}=(f^{1},f^{2},f^{3},f^{4},f^{5},f^{6},f^{7})$
is a vector consisting of seven arbitrary functions depending on the arguments given in (A 12).
$\boldsymbol{F}=(f^{1},f^{2},f^{3},f^{4},f^{5},f^{6},f^{7})$
is a vector consisting of seven arbitrary functions depending on the arguments given in (A 12).
The specific new helical coordinates may now be manufactured from (A 9) and (A 12), respectively. In order to keep the complexity for the resulting Euler and Navier–Stokes equations in the helical coordinate system as low as possible, we choose the new independent coordinates as given in (2.3a )–(2.3d ).
Analogous to the classical case the helical velocity components and the pressure are given by (2.3e )–(2.3h ). They are a particular choice of the special solutions of (A 12).
Appendix B. Proof of the absence of conservation of kinetic energy in time-dependent helical coordinates
It is well known that for the three-dimensional time-dependent Euler system, the kinetic energy is conserved in every coordinate system. In the present section we will prove that in our spatially reduced time-dependent helically symmetric coordinate system the conservation of kinetic energy does not hold.
The proof can be done by contradiction: we rewrite the kinetic energy in conserved form in the helical time-dependent coordinates, i.e.
![]() $(r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
defined in (2.3a
)–(2.3d
). However, after imposing helical invariance, i.e. eliminating any
$(r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
defined in (2.3a
)–(2.3d
). However, after imposing helical invariance, i.e. eliminating any
![]() $\unicode[STIX]{x1D702}$
-dependence from the velocity and pressure, we would expect an energy equation, which is independent of
$\unicode[STIX]{x1D702}$
-dependence from the velocity and pressure, we would expect an energy equation, which is independent of
![]() $\unicode[STIX]{x1D702}$
. However, we obtain an equation involving the helical coordinate
$\unicode[STIX]{x1D702}$
. However, we obtain an equation involving the helical coordinate
![]() $\unicode[STIX]{x1D702}$
itself. As a result, it is not possible to write an energy conservation equation in a helically symmetric time-dependent coordinate system. The following steps may clarify the proceeding.
$\unicode[STIX]{x1D702}$
itself. As a result, it is not possible to write an energy conservation equation in a helically symmetric time-dependent coordinate system. The following steps may clarify the proceeding.
The energy equation can be written in a cylindrical coordinate system
where the fluxes read
![]() $K$
denotes the kinetic energy density, given by
$K$
denotes the kinetic energy density, given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\left(rK\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left(ru^{r}\left(K+p\right)\right)-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\left(rK\right)\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle +\,\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\left(\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\left(rK\right)+\left(\frac{r}{\unicode[STIX]{x1D6FC}}u^{z}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\right)\left(K+p\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(bu^{\unicode[STIX]{x1D711}}\left(K+p\right)\right)=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\left(rK\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left(ru^{r}\left(K+p\right)\right)-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\left(rK\right)\nonumber\\ \displaystyle & & \displaystyle \quad \displaystyle +\,\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\left(\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\left(rK\right)+\left(\frac{r}{\unicode[STIX]{x1D6FC}}u^{z}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\right)\left(K+p\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\left(bu^{\unicode[STIX]{x1D711}}\left(K+p\right)\right)=0.\end{eqnarray}$$
Since the helical invariant coordinate
![]() $\unicode[STIX]{x1D702}$
itself only occurs in the velocity component
$\unicode[STIX]{x1D702}$
itself only occurs in the velocity component
![]() $u^{z}$
and in the pressure
$u^{z}$
and in the pressure
![]() $p$
, these variables will be replaced by their corresponding helical expressions. Assuming helical invariance and simplifying, the energy equation reads
$p$
, these variables will be replaced by their corresponding helical expressions. Assuming helical invariance and simplifying, the energy equation reads
 $$\begin{eqnarray}\displaystyle & & \displaystyle R\left(\unicode[STIX]{x1D748},\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D748}\right)+\left[\dot{\unicode[STIX]{x1D6FC}}\left(r\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\hat{u} _{\unicode[STIX]{x1D709}}-r\hat{u} _{\unicode[STIX]{x1D70F}}-bu_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\hat{u} +bu^{\unicode[STIX]{x1D711}}\dot{\unicode[STIX]{x1D6FC}}+bu^{\unicode[STIX]{x1D711}}\hat{u} _{\unicode[STIX]{x1D709}}-\frac{r}{\unicode[STIX]{x1D6FC}}\hat{u} _{\unicode[STIX]{x1D709}}\hat{u} \right.\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\left.+\,\left(u^{r}+ru_{r}^{r}\right)\left(-\hat{u} -ru^{r}\hat{u} _{r}\right)-2\hat{u} \hat{u} _{\unicode[STIX]{x1D709}}-\left(u^{r}u_{\unicode[STIX]{x1D709}}^{r}+u^{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\right)-\tilde{p}_{\unicode[STIX]{x1D709}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.+\,\ddot{\unicode[STIX]{x1D6FC}}\left(-r\hat{u} +r\unicode[STIX]{x1D6FC}bu_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D709}+\left(u^{r}+ru_{r}^{r}\right)\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D709}+r\unicode[STIX]{x1D709}\hat{u} _{\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D6FC}\hat{u} \right)\right]\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[\dot{\unicode[STIX]{x1D6FC}}\left(r\ddot{\unicode[STIX]{x1D6FC}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}r\hat{u} _{\unicode[STIX]{x1D709}}+\frac{1}{2}\left(u^{r}+ru_{r}^{r}\right)\dot{\unicode[STIX]{x1D6FC}}+\frac{1}{2}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\dot{\unicode[STIX]{x1D6FC}}+\frac{1}{2}\frac{r}{\unicode[STIX]{x1D6FC}}\dot{\unicode[STIX]{x1D6FC}}\hat{u} _{\unicode[STIX]{x1D709}}+\dot{\unicode[STIX]{x1D6FC}}\hat{u} _{\unicode[STIX]{x1D709}}-\ddot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.+\,\ddot{\unicode[STIX]{x1D6FC}}\left(-\frac{1}{2}r\unicode[STIX]{x1D6FC}bu_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}-\frac{1}{2}\left(u^{r}+ru_{r}^{r}\right)\unicode[STIX]{x1D6FC}-\frac{1}{2}r\right)\right]\unicode[STIX]{x1D702}^{2}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle R\left(\unicode[STIX]{x1D748},\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D748}\right)+\left[\dot{\unicode[STIX]{x1D6FC}}\left(r\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\hat{u} _{\unicode[STIX]{x1D709}}-r\hat{u} _{\unicode[STIX]{x1D70F}}-bu_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\hat{u} +bu^{\unicode[STIX]{x1D711}}\dot{\unicode[STIX]{x1D6FC}}+bu^{\unicode[STIX]{x1D711}}\hat{u} _{\unicode[STIX]{x1D709}}-\frac{r}{\unicode[STIX]{x1D6FC}}\hat{u} _{\unicode[STIX]{x1D709}}\hat{u} \right.\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\left.+\,\left(u^{r}+ru_{r}^{r}\right)\left(-\hat{u} -ru^{r}\hat{u} _{r}\right)-2\hat{u} \hat{u} _{\unicode[STIX]{x1D709}}-\left(u^{r}u_{\unicode[STIX]{x1D709}}^{r}+u^{\unicode[STIX]{x1D711}}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\right)-\tilde{p}_{\unicode[STIX]{x1D709}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.+\,\ddot{\unicode[STIX]{x1D6FC}}\left(-r\hat{u} +r\unicode[STIX]{x1D6FC}bu_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D709}+\left(u^{r}+ru_{r}^{r}\right)\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D709}+r\unicode[STIX]{x1D709}\hat{u} _{\unicode[STIX]{x1D709}}+\unicode[STIX]{x1D6FC}\hat{u} \right)\right]\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left[\dot{\unicode[STIX]{x1D6FC}}\left(r\ddot{\unicode[STIX]{x1D6FC}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}r\hat{u} _{\unicode[STIX]{x1D709}}+\frac{1}{2}\left(u^{r}+ru_{r}^{r}\right)\dot{\unicode[STIX]{x1D6FC}}+\frac{1}{2}u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\dot{\unicode[STIX]{x1D6FC}}+\frac{1}{2}\frac{r}{\unicode[STIX]{x1D6FC}}\dot{\unicode[STIX]{x1D6FC}}\hat{u} _{\unicode[STIX]{x1D709}}+\dot{\unicode[STIX]{x1D6FC}}\hat{u} _{\unicode[STIX]{x1D709}}-\ddot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.+\,\ddot{\unicode[STIX]{x1D6FC}}\left(-\frac{1}{2}r\unicode[STIX]{x1D6FC}bu_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}-\frac{1}{2}\left(u^{r}+ru_{r}^{r}\right)\unicode[STIX]{x1D6FC}-\frac{1}{2}r\right)\right]\unicode[STIX]{x1D702}^{2}=0,\end{eqnarray}$$
where
![]() $R$
is the collection of all
$R$
is the collection of all
![]() $\unicode[STIX]{x1D702}$
-independent terms and thus is a function of the helical dependent and independent variables
$\unicode[STIX]{x1D702}$
-independent terms and thus is a function of the helical dependent and independent variables
![]() $\unicode[STIX]{x1D748}\in \mathbb{R}^{7}$
defined in (A 4) and their first derivatives
$\unicode[STIX]{x1D748}\in \mathbb{R}^{7}$
defined in (A 4) and their first derivatives
![]() $\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D748}(j\in \{r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}\})$
.
$\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D748}(j\in \{r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}\})$
.
Here, the quantity
![]() $\hat{u}$
is the short form of the
$\hat{u}$
is the short form of the
![]() $\unicode[STIX]{x1D702}$
-independent part of the
$\unicode[STIX]{x1D702}$
-independent part of the
![]() $u^{z}$
-velocity component, given by
$u^{z}$
-velocity component, given by
Apparently, (B 8) displays the above-mentioned contradiction as velocity and pressure are assumed to be independent of
![]() $\unicode[STIX]{x1D702}$
, while the equation still contains
$\unicode[STIX]{x1D702}$
, while the equation still contains
![]() $\unicode[STIX]{x1D702}$
. For
$\unicode[STIX]{x1D702}$
. For
![]() $\unicode[STIX]{x1D6FC}=\text{const.}$
all
$\unicode[STIX]{x1D6FC}=\text{const.}$
all
![]() $\unicode[STIX]{x1D702}$
-dependent terms vanish in equation (B 8) and, hence, the conservation of energy only holds true for the classical helically symmetric case.
$\unicode[STIX]{x1D702}$
-dependent terms vanish in equation (B 8) and, hence, the conservation of energy only holds true for the classical helically symmetric case.
Appendix C. Proof of the absence of conservation of helicity in time-dependent helical coordinates
In this section we prove that for the case of Euler’s equations the conservation of helicity in helically symmetric flows in a spatially reduced time-dependent coordinate system does not hold. The proof is done in the same manner as for the conservation of kinetic energy. In cylindrical coordinates the density and fluxes of helicity conservation are given by
where
![]() $h=\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}=u^{r}\unicode[STIX]{x1D714}^{r}+u^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}+u^{z}\unicode[STIX]{x1D714}^{z}$
is helicity and
$h=\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}=u^{r}\unicode[STIX]{x1D714}^{r}+u^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}+u^{z}\unicode[STIX]{x1D714}^{z}$
is helicity and
 $$\begin{eqnarray}\displaystyle \phantom{E} & = & \displaystyle \frac{1}{2}\left[\left(u^{r}\right)^{2}+B^{2}\left(\frac{b}{r}u^{\unicode[STIX]{x1D709}}+\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}\right)^{2}+\left(B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)-\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\right)^{2}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\tilde{p}-\frac{1}{2}\ddot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\left(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D702}\right)^{2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \phantom{E} & = & \displaystyle \frac{1}{2}\left[\left(u^{r}\right)^{2}+B^{2}\left(\frac{b}{r}u^{\unicode[STIX]{x1D709}}+\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D702}}\right)^{2}+\left(B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)-\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\right)^{2}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\tilde{p}-\frac{1}{2}\ddot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6FC}\left(\unicode[STIX]{x1D709}-\unicode[STIX]{x1D702}\right)^{2}\end{eqnarray}$$
Rewriting the helicity conservation equation in the full three-dimensional helical coordinate system
![]() $(r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
we obtain
$(r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\left(rh\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left(r\unicode[STIX]{x1D714}^{r}\left(K+p-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}-\left(u^{\unicode[STIX]{x1D702}}\right)^{2}+2B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}-\dot{\unicode[STIX]{x1D6FC}}^{2}\unicode[STIX]{x1D702}^{2}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\left(rh\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\Bigg(\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\left(rh\right)+\left(\frac{r}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\left(K+p-\left(u^{r}\right)^{2}\right)+\left(\frac{r}{B}u^{\unicode[STIX]{x1D709}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\right)h\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\frac{r}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\left(\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-2B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}+\dot{\unicode[STIX]{x1D6FC}}^{2}\unicode[STIX]{x1D702}^{2}\right)\Bigg)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\Bigg(b\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}\Big(K+p\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,\left(u^{r}\right)^{2}\Big)-b\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}\left(\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-2B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}+\dot{\unicode[STIX]{x1D6FC}}^{2}\unicode[STIX]{x1D702}^{2}\right)+bu^{\unicode[STIX]{x1D711}}h\Bigg)=0.\qquad \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\left(rh\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left(r\unicode[STIX]{x1D714}^{r}\left(K+p-\left(u^{\unicode[STIX]{x1D709}}\right)^{2}-\left(u^{\unicode[STIX]{x1D702}}\right)^{2}+2B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}-\dot{\unicode[STIX]{x1D6FC}}^{2}\unicode[STIX]{x1D702}^{2}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\left(rh\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\Bigg(\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\left(rh\right)+\left(\frac{r}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\right)\left(K+p-\left(u^{r}\right)^{2}\right)+\left(\frac{r}{B}u^{\unicode[STIX]{x1D709}}-\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}\right)h\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\frac{r}{B}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D709}}\left(\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-2B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}+\dot{\unicode[STIX]{x1D6FC}}^{2}\unicode[STIX]{x1D702}^{2}\right)\Bigg)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}\Bigg(b\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}\Big(K+p\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\,\left(u^{r}\right)^{2}\Big)-b\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}\left(\left(u^{\unicode[STIX]{x1D709}}\right)^{2}+\left(u^{\unicode[STIX]{x1D702}}\right)^{2}-2B\left(\frac{1}{\unicode[STIX]{x1D6FC}}u^{\unicode[STIX]{x1D709}}-\frac{b}{r}u^{\unicode[STIX]{x1D702}}\right)\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}+\dot{\unicode[STIX]{x1D6FC}}^{2}\unicode[STIX]{x1D702}^{2}\right)+bu^{\unicode[STIX]{x1D711}}h\Bigg)=0.\qquad \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
In a second step imposing helical invariance onto equation (C 6), i.e. vorticity, velocity and pressure are
![]() $\unicode[STIX]{x1D702}$
-independent, the helicity equation yields
$\unicode[STIX]{x1D702}$
-independent, the helicity equation yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \tilde{R}\left(\unicode[STIX]{x1D748},\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D748}\right)+\Bigg[\dot{\unicode[STIX]{x1D6FC}}\Bigg(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}\frac{r}{\unicode[STIX]{x1D6FC}}\hat{u} -r\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}^{z}+\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}r\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}+b\left(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\hat{u} -\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}\hat{u} _{\unicode[STIX]{x1D709}}-u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D714}^{z}-u^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}\hat{u} +r\hat{u} _{r}\unicode[STIX]{x1D714}^{r}-\left(ru^{r}\unicode[STIX]{x1D714}^{z}\right)_{r}\Bigg)+\ddot{\unicode[STIX]{x1D6FC}}\Bigg(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}r\unicode[STIX]{x1D709}+b\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}+\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D709}\Bigg)\Bigg]\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\Bigg[\dot{\unicode[STIX]{x1D6FC}}\frac{1}{2}\Bigg(-r\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}+b\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\dot{\unicode[STIX]{x1D6FC}}-\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}\dot{\unicode[STIX]{x1D6FC}}\Bigg)+\ddot{\unicode[STIX]{x1D6FC}}\Bigg(\frac{1}{2}r\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}-b\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D6FC}-\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}\unicode[STIX]{x1D6FC}\Bigg)\Bigg]\unicode[STIX]{x1D702}^{2}=0,\quad \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \tilde{R}\left(\unicode[STIX]{x1D748},\unicode[STIX]{x2202}_{j}\unicode[STIX]{x1D748}\right)+\Bigg[\dot{\unicode[STIX]{x1D6FC}}\Bigg(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}\frac{r}{\unicode[STIX]{x1D6FC}}\hat{u} -r\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}^{z}+\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D709}r\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}+b\left(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\hat{u} -\dot{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D711}}\hat{u} _{\unicode[STIX]{x1D709}}-u_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D714}^{z}-u^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}\hat{u} +r\hat{u} _{r}\unicode[STIX]{x1D714}^{r}-\left(ru^{r}\unicode[STIX]{x1D714}^{z}\right)_{r}\Bigg)+\ddot{\unicode[STIX]{x1D6FC}}\Bigg(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}r\unicode[STIX]{x1D709}+b\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}+\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D709}\Bigg)\Bigg]\unicode[STIX]{x1D702}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad +\,\Bigg[\dot{\unicode[STIX]{x1D6FC}}\frac{1}{2}\Bigg(-r\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}\frac{\dot{\unicode[STIX]{x1D6FC}}}{\unicode[STIX]{x1D6FC}}+b\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\dot{\unicode[STIX]{x1D6FC}}-\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}\dot{\unicode[STIX]{x1D6FC}}\Bigg)+\ddot{\unicode[STIX]{x1D6FC}}\Bigg(\frac{1}{2}r\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{z}-b\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D6FC}-\left(r\unicode[STIX]{x1D714}^{r}\right)_{r}\unicode[STIX]{x1D6FC}\Bigg)\Bigg]\unicode[STIX]{x1D702}^{2}=0,\quad \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
![]() $\tilde{R}$
is a collection of all
$\tilde{R}$
is a collection of all
![]() $\unicode[STIX]{x1D702}$
-independent terms and thus is a function of the reduced helical independent and dependent variables
$\unicode[STIX]{x1D702}$
-independent terms and thus is a function of the reduced helical independent and dependent variables
![]() $\tilde{\unicode[STIX]{x1D748}}\in \mathbb{R}^{10}$
, which consist of the two helical coordinates
$\tilde{\unicode[STIX]{x1D748}}\in \mathbb{R}^{10}$
, which consist of the two helical coordinates
![]() $(r,\unicode[STIX]{x1D709})$
, the time
$(r,\unicode[STIX]{x1D709})$
, the time
![]() $(t)$
, the three velocity components, pressure and the three vorticity components and their first derivatives
$(t)$
, the three velocity components, pressure and the three vorticity components and their first derivatives
![]() $\unicode[STIX]{x2202}_{j}\tilde{\unicode[STIX]{x1D748}}$
, for
$\unicode[STIX]{x2202}_{j}\tilde{\unicode[STIX]{x1D748}}$
, for
![]() $j\in \{r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}\}$
. As for the energy equation, the contradiction becomes apparent, as in (C 7)
$j\in \{r,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70F}\}$
. As for the energy equation, the contradiction becomes apparent, as in (C 7)
![]() $\unicode[STIX]{x1D702}$
-independence of all dependent variables was employed, still the equation contains
$\unicode[STIX]{x1D702}$
-independence of all dependent variables was employed, still the equation contains
![]() $\unicode[STIX]{x1D702}$
explicitly.
$\unicode[STIX]{x1D702}$
explicitly.
Likewise for the kinetic energy, for
![]() $\unicode[STIX]{x1D6FC}=\text{const.}$
all
$\unicode[STIX]{x1D6FC}=\text{const.}$
all
![]() $\unicode[STIX]{x1D702}$
-dependent terms vanish in (C 7) and the conservation of helicity holds for the classical helically symmetric case.
$\unicode[STIX]{x1D702}$
-dependent terms vanish in (C 7) and the conservation of helicity holds for the classical helically symmetric case.