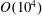1 Introduction
Solid particles dispersed in natural or technical flows are in general non-spherical. Their shape ranges from approximately spherical as sand grains via approximately ellipsoidal as cellulose wood fibres to complex ice crystals in atmospheric clouds. The relevance of the particle shape regarding the overall multiphase dynamics has been emphasized in various studies (Voth & Soldati Reference Voth and Soldati2017). However, unlike the idealized case of spherical particles, the response of turbulent flows to the presence of dispersed non-spherical particles of finite size still is barely understood – despite the numerous fields of application.
Numerical studies based on Euler–Lagrange point-particle models have shown that small inertial spheroids dampen the turbulence production and dissipation rates in turbulent channel flow by clustering in the near wall region and aligning their orientation with respect to the mean flow direction (Zhao, George & van Wachem Reference Zhao, George and van Wachem2016). In one of the few studies considering the two-way coupling of angular momentum between the phases, Andersson, Zhao & Barri (Reference Andersson, Zhao and Barri2012) demonstrated that the torque of very small particles tends to mitigate turbulence attenuation. State-of-the-art point-particle models for general ellipsoidal particle shapes are, strictly speaking, restricted to particle major diameters below the Kolmogorov length (
![]() $d_{p}^{maj}<\unicode[STIX]{x1D702}$
) which experience creeping flow conditions, i.e. particle Reynolds numbers
$d_{p}^{maj}<\unicode[STIX]{x1D702}$
) which experience creeping flow conditions, i.e. particle Reynolds numbers
![]() $Re_{p}\ll 1$
. Analytical expressions for the hydrodynamic drag and torque are available for this case (Voth & Soldati Reference Voth and Soldati2017). The systematic exploration of a larger parameter space is exacerbated by the lack of generalized models, which led to relaxing these conditions in some contributions, i.e. cases involving
$Re_{p}\ll 1$
. Analytical expressions for the hydrodynamic drag and torque are available for this case (Voth & Soldati Reference Voth and Soldati2017). The systematic exploration of a larger parameter space is exacerbated by the lack of generalized models, which led to relaxing these conditions in some contributions, i.e. cases involving
![]() $Re_{p}>1$
(Marchioli, Zhao & Andersson Reference Marchioli, Zhao and Andersson2016) or
$Re_{p}>1$
(Marchioli, Zhao & Andersson Reference Marchioli, Zhao and Andersson2016) or
![]() $d_{p}^{maj}>\unicode[STIX]{x1D702}$
(Marchioli & Soldati Reference Marchioli and Soldati2013). In fact, while recent studies indicate that point-particle models have the potential to perform adequately at
$d_{p}^{maj}>\unicode[STIX]{x1D702}$
(Marchioli & Soldati Reference Marchioli and Soldati2013). In fact, while recent studies indicate that point-particle models have the potential to perform adequately at
![]() $d_{p}\sim \unicode[STIX]{x1D702}$
for spherical particles (Fröhlich et al.
Reference Fröhlich, Schneiders, Meinke and Schröder2018), significantly more research is needed to manifest their validity in this regime, in particular for non-spherical particles.
$d_{p}\sim \unicode[STIX]{x1D702}$
for spherical particles (Fröhlich et al.
Reference Fröhlich, Schneiders, Meinke and Schröder2018), significantly more research is needed to manifest their validity in this regime, in particular for non-spherical particles.
In principle, the modelling issue can be avoided using particle-resolved simulations. However, these are limited by computational resources and the efficiency of numerical codes and become increasingly expensive with decreasing particle diameters. Therefore, the majority of particle-resolved studies focused on
![]() $d_{p}^{vol}\gg \unicode[STIX]{x1D702}$
, where
$d_{p}^{vol}\gg \unicode[STIX]{x1D702}$
, where
![]() $d_{p}^{vol}$
describes the diameter of a volume-equivalent spherical particle. Although meaningful computations can only be performed for a relatively small number of particles and academic flow problems, they are essential to derive new particle and turbulence models. The available studies on non-spherical particles mostly considered neutrally buoyant ellipsoids with
$d_{p}^{vol}$
describes the diameter of a volume-equivalent spherical particle. Although meaningful computations can only be performed for a relatively small number of particles and academic flow problems, they are essential to derive new particle and turbulence models. The available studies on non-spherical particles mostly considered neutrally buoyant ellipsoids with
![]() $d_{p}^{vol}\gg \unicode[STIX]{x1D702}$
dispersed in turbulent channel flow (Do-Quang et al.
Reference Do-Quang, Amberg, Brethouwer and Johansson2014; Ardekani et al.
Reference Ardekani, Costa, Breugem, Picano and Brandt2017; Eshghinejadfard, Hosseini & Thévenin Reference Eshghinejadfard, Hosseini and Thévenin2017; Ardekani & Brandt Reference Ardekani and Brandt2019). These studies demonstrated prolate and oblate spheroids to accumulate in streak structures near the wall, to preferentially align their rotational motion, and dampen the wall-normal velocity fluctuations. For prolate particles, this effect was less pronounced since their larger angular velocities create additional counteracting stresses (Ardekani & Brandt Reference Ardekani and Brandt2019). Measurements of the turbulence response to non-spherical particles are intricate as well due to the overlap of fluid and particle scales and the rotational degrees of freedom. Experimental studies of large (
$d_{p}^{vol}\gg \unicode[STIX]{x1D702}$
dispersed in turbulent channel flow (Do-Quang et al.
Reference Do-Quang, Amberg, Brethouwer and Johansson2014; Ardekani et al.
Reference Ardekani, Costa, Breugem, Picano and Brandt2017; Eshghinejadfard, Hosseini & Thévenin Reference Eshghinejadfard, Hosseini and Thévenin2017; Ardekani & Brandt Reference Ardekani and Brandt2019). These studies demonstrated prolate and oblate spheroids to accumulate in streak structures near the wall, to preferentially align their rotational motion, and dampen the wall-normal velocity fluctuations. For prolate particles, this effect was less pronounced since their larger angular velocities create additional counteracting stresses (Ardekani & Brandt Reference Ardekani and Brandt2019). Measurements of the turbulence response to non-spherical particles are intricate as well due to the overlap of fluid and particle scales and the rotational degrees of freedom. Experimental studies of large (
![]() $d_{p}^{vol}\gg \unicode[STIX]{x1D702}$
) neutrally buoyant particles have detailed the rotational dynamics of elongated particles and their interaction with homogeneous isotropic turbulence. Bellani et al. (Reference Bellani, Byron, Collignon, Meyer and Variano2012) found that prolate ellipsoids with an aspect ratio of two release more energy at small fluid scales than spheres. Bordoloi & Variano (Reference Bordoloi and Variano2017) reported that large cylindrical particles do not exhibit a preferential rotation about the symmetry axis which is in contrast to results for much smaller particles. Additionally, they demonstrated the volume-equivalent diameter
$d_{p}^{vol}\gg \unicode[STIX]{x1D702}$
) neutrally buoyant particles have detailed the rotational dynamics of elongated particles and their interaction with homogeneous isotropic turbulence. Bellani et al. (Reference Bellani, Byron, Collignon, Meyer and Variano2012) found that prolate ellipsoids with an aspect ratio of two release more energy at small fluid scales than spheres. Bordoloi & Variano (Reference Bordoloi and Variano2017) reported that large cylindrical particles do not exhibit a preferential rotation about the symmetry axis which is in contrast to results for much smaller particles. Additionally, they demonstrated the volume-equivalent diameter
![]() $d_{p}^{vol}$
to be the relevant parameter classifying the rotational particle motion of non-spherical particles. For much smaller (
$d_{p}^{vol}$
to be the relevant parameter classifying the rotational particle motion of non-spherical particles. For much smaller (
![]() $d_{p}^{vol}/\unicode[STIX]{x1D702}\approx 0.3$
) and heavy fibres, Sabban, Cohen & van Hout (Reference Sabban, Cohen and van Hout2017) reported the particles to preferentially align with the flow, exhibiting reduced rotation rates compared to neutrally buoyant fibres. However, to determine the velocity disturbances due to the particles for the case
$d_{p}^{vol}/\unicode[STIX]{x1D702}\approx 0.3$
) and heavy fibres, Sabban, Cohen & van Hout (Reference Sabban, Cohen and van Hout2017) reported the particles to preferentially align with the flow, exhibiting reduced rotation rates compared to neutrally buoyant fibres. However, to determine the velocity disturbances due to the particles for the case
![]() $d_{p}^{vol}\sim \unicode[STIX]{x1D702}$
, a sub-Kolmogorov spatial resolution is required in experiments which has been achieved only in few studies on spherical particles (Tanaka & Eaton Reference Tanaka and Eaton2010).
$d_{p}^{vol}\sim \unicode[STIX]{x1D702}$
, a sub-Kolmogorov spatial resolution is required in experiments which has been achieved only in few studies on spherical particles (Tanaka & Eaton Reference Tanaka and Eaton2010).
One of the open questions regarding finite-size, non-spherical particles in turbulence is how the particles affect the turbulent kinetic energy budget and what is the contribution of the rotational particle motion. In Schneiders, Meinke & Schröder (Reference Schneiders, Meinke and Schröder2017a
) an analytical expression for the particle-induced dissipation rate of arbitrarily shaped particles was derived from first principles, however, the subsequent validation was only performed for spherical particles. In the present study, we evidence this mechanistic model to accurately describe the dissipation rate generated by larger particles of ellipsoidal shape. We then quantify the proportion of the dissipation rate directly and indirectly resulting from the rotational particle motion. To this end, we investigate the modulation of decaying homogeneous isotropic turbulence by solid spheres and ellipsoids. This extends our previous analysis on
![]() $45\,000$
spherical particles at
$45\,000$
spherical particles at
![]() $d_{p}\approx \unicode[STIX]{x1D702}$
(Schneiders et al.
Reference Schneiders, Meinke and Schröder2017a
) to non-spherical particle shapes and slightly increased volume-equivalent particle diameters. By conducting direct particle–fluid simulations, the stresses on the fluid–particle interfaces, which determine the multiphase interaction, are precisely captured while strictly conserving mass, momentum and energy. These computationally intensive simulations are enabled by the use of dynamic mesh refinement and a numerical scheme with high accuracy at the particle surfaces.
$d_{p}\approx \unicode[STIX]{x1D702}$
(Schneiders et al.
Reference Schneiders, Meinke and Schröder2017a
) to non-spherical particle shapes and slightly increased volume-equivalent particle diameters. By conducting direct particle–fluid simulations, the stresses on the fluid–particle interfaces, which determine the multiphase interaction, are precisely captured while strictly conserving mass, momentum and energy. These computationally intensive simulations are enabled by the use of dynamic mesh refinement and a numerical scheme with high accuracy at the particle surfaces.
2 Computational set-up and scope of the analysis
2.1 Flow configuration
Solid spheres and ellipsoids dispersed in decaying homogeneous isotropic turbulence are considered. The initial single-phase turbulent field, adopted from Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
), obeys the model energy spectrum
![]() $E(\unicode[STIX]{x1D705})=(3u_{0}^{2}/2)(\unicode[STIX]{x1D705}/\unicode[STIX]{x1D705}_{p}^{2})\exp (-\unicode[STIX]{x1D705}/\unicode[STIX]{x1D705}_{p})$
, with the root-mean-square (r.m.s.) velocity
$E(\unicode[STIX]{x1D705})=(3u_{0}^{2}/2)(\unicode[STIX]{x1D705}/\unicode[STIX]{x1D705}_{p}^{2})\exp (-\unicode[STIX]{x1D705}/\unicode[STIX]{x1D705}_{p})$
, with the root-mean-square (r.m.s.) velocity
![]() $u_{0}$
and the peak wavenumber
$u_{0}$
and the peak wavenumber
![]() $\unicode[STIX]{x1D705}_{p}=8\unicode[STIX]{x03C0}/L$
. It is computed in a cubic domain of edge length
$\unicode[STIX]{x1D705}_{p}=8\unicode[STIX]{x03C0}/L$
. It is computed in a cubic domain of edge length
![]() $L$
, discretized by a uniform background mesh of
$L$
, discretized by a uniform background mesh of
![]() $512^{3}$
Cartesian cells. The initial Taylor-scale Reynolds number is
$512^{3}$
Cartesian cells. The initial Taylor-scale Reynolds number is
![]() $Re_{\unicode[STIX]{x1D706},0}=79.1$
and the turbulent Mach number
$Re_{\unicode[STIX]{x1D706},0}=79.1$
and the turbulent Mach number
![]() $Ma_{t}=0.1$
such that compressibility effects can be considered negligible (Lele Reference Lele1994).
$Ma_{t}=0.1$
such that compressibility effects can be considered negligible (Lele Reference Lele1994).
One of the challenges in particle-resolved simulations of statistically unsteady turbulence is the definition of the initial position and velocity of the particles. In most cases, the initial particle state is unknown. Its determination would require precise experimental measurements, which are in general not available, or an additional simulation. However, since the initial conditions in such a companion simulation again are unknown, this leads to a catch-22 situation. In principle, the consideration of forced, statistically steady turbulence would alleviate this problem. However, as elucidated by Lucci, Ferrante & Elghobashi (Reference Lucci, Ferrante and Elghobashi2010), the application of forced isotropic turbulence to study two-way coupling effects is inappropriate due to the interference of the forcing scheme with the particle momentum coupling. It prevents to distinguish the responsible mechanisms of fluid–particle interaction, especially at small wavenumbers. Therefore, we adopt the initialization procedure used in Lucci et al. (Reference Lucci, Ferrante and Elghobashi2010), Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a ) (among other studies), as discussed in the following.
When the turbulent flow is fully developed, indicated by the convergence of the velocity-derivative skewness to approximately
![]() $-0.5$
, the particles are released at random locations with random orientations. Their linear and angular velocities are determined by the local state of the flow field. Although this procedure significantly increases the level of total kinetic energy due to the high particle mass loading, it minimizes the initial slip velocities and therefore the initial strength of the shear layer between the particles and the continuous phase. The particle-induced viscous dissipation is kept at a relatively small level as well. For instance, one may relate this situation to a turbulent jet issuing from a pipe carrying heavy inertial particles. In such cases, the fluid kinetic energy decays more rapidly over the jet distance than the particle kinetic energy due to their high inertia (Lau & Nathan Reference Lau and Nathan2014). Even higher relative particle kinetic energies have been created in experimental measurements of particle-induced grid turbulence (Geiss et al.
Reference Geiss, Dreizler, Stojanovic, Chrigui, Sadiki and Janicka2004).
$-0.5$
, the particles are released at random locations with random orientations. Their linear and angular velocities are determined by the local state of the flow field. Although this procedure significantly increases the level of total kinetic energy due to the high particle mass loading, it minimizes the initial slip velocities and therefore the initial strength of the shear layer between the particles and the continuous phase. The particle-induced viscous dissipation is kept at a relatively small level as well. For instance, one may relate this situation to a turbulent jet issuing from a pipe carrying heavy inertial particles. In such cases, the fluid kinetic energy decays more rapidly over the jet distance than the particle kinetic energy due to their high inertia (Lau & Nathan Reference Lau and Nathan2014). Even higher relative particle kinetic energies have been created in experimental measurements of particle-induced grid turbulence (Geiss et al.
Reference Geiss, Dreizler, Stojanovic, Chrigui, Sadiki and Janicka2004).
The injection time is at the non-dimensional time
![]() $t_{i}^{\ast }=t_{i}\unicode[STIX]{x1D716}_{0}/u_{0}^{2}=0.28$
, where
$t_{i}^{\ast }=t_{i}\unicode[STIX]{x1D716}_{0}/u_{0}^{2}=0.28$
, where
![]() $\unicode[STIX]{x1D716}_{0}$
is the initial dissipation rate. The Kolmogorov length at
$\unicode[STIX]{x1D716}_{0}$
is the initial dissipation rate. The Kolmogorov length at
![]() $t_{i}$
is
$t_{i}$
is
![]() $\unicode[STIX]{x1D702}_{i}=0.0019L$
and the Taylor length
$\unicode[STIX]{x1D702}_{i}=0.0019L$
and the Taylor length
![]() $\unicode[STIX]{x1D706}_{i}=0.028L$
. The three principal axes of the spheroids are denoted
$\unicode[STIX]{x1D706}_{i}=0.028L$
. The three principal axes of the spheroids are denoted
![]() $d_{\widehat{x}}$
,
$d_{\widehat{x}}$
,
![]() $d_{\widehat{y}}$
and
$d_{\widehat{y}}$
and
![]() $d_{\widehat{z}}$
. They correspond to the particle-frame coordinates
$d_{\widehat{z}}$
. They correspond to the particle-frame coordinates
![]() $(\widehat{\boldsymbol{x}},\widehat{\boldsymbol{y}},\widehat{\boldsymbol{z}})$
, where
$(\widehat{\boldsymbol{x}},\widehat{\boldsymbol{y}},\widehat{\boldsymbol{z}})$
, where
![]() $\widehat{\boldsymbol{z}}$
is the direction of the symmetry axis of the spheroids. The aspect ratio
$\widehat{\boldsymbol{z}}$
is the direction of the symmetry axis of the spheroids. The aspect ratio
![]() $\unicode[STIX]{x1D6FD}=d_{\widehat{z}}/d_{\widehat{x}}$
defines oblates (
$\unicode[STIX]{x1D6FD}=d_{\widehat{z}}/d_{\widehat{x}}$
defines oblates (
![]() $\unicode[STIX]{x1D6FD}<1$
), prolates (
$\unicode[STIX]{x1D6FD}<1$
), prolates (
![]() $\unicode[STIX]{x1D6FD}>1$
) and spherical particles (
$\unicode[STIX]{x1D6FD}>1$
) and spherical particles (
![]() $\unicode[STIX]{x1D6FD}=1$
).
$\unicode[STIX]{x1D6FD}=1$
).
Table 1 lists several non-dimensional parameters of the considered cases at release time. The particle-free turbulent field (case 0) is the reference case for the particle-laden cases. The four particle-laden problems include spherical particles (case S), oblates with
![]() $\unicode[STIX]{x1D6FD}=1/4$
(case O4) and prolates with
$\unicode[STIX]{x1D6FD}=1/4$
(case O4) and prolates with
![]() $\unicode[STIX]{x1D6FD}=4$
and
$\unicode[STIX]{x1D6FD}=4$
and
![]() $\unicode[STIX]{x1D6FD}=8$
(cases P4 and P8). While
$\unicode[STIX]{x1D6FD}=8$
(cases P4 and P8). While
![]() $\unicode[STIX]{x1D6FD}$
is varied, the number of particles (
$\unicode[STIX]{x1D6FD}$
is varied, the number of particles (
![]() $N_{p}=12\,000$
), the volumetric particle diameter
$N_{p}=12\,000$
), the volumetric particle diameter
![]() $d_{p}^{vol}=(d_{\widehat{x}}\,d_{\widehat{y}}\,d_{\widehat{z}})^{1/3}$
, the density ratio of particles and fluid (
$d_{p}^{vol}=(d_{\widehat{x}}\,d_{\widehat{y}}\,d_{\widehat{z}})^{1/3}$
, the density ratio of particles and fluid (
![]() $\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}=1000$
), the volume fraction (
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}=1000$
), the volume fraction (
![]() $\unicode[STIX]{x1D719}_{v}=6.5\times 10^{-4}$
) and the particle mass loading (
$\unicode[STIX]{x1D719}_{v}=6.5\times 10^{-4}$
) and the particle mass loading (
![]() $\unicode[STIX]{x1D719}_{m}=0.65$
) are constant. Note that compared to our previous study (Schneiders et al.
Reference Schneiders, Meinke and Schröder2017a
) we have increased the volumetric particle diameter by approximately a factor of two to provoke more significant finite-size effects. The particle volume fraction is kept approximately constant to remain in the dilute flow regime (Balachandar & Eaton Reference Balachandar and Eaton2010) such that the number of particles becomes smaller. The particle Stokes numbers have been estimated using particle relaxation times
$\unicode[STIX]{x1D719}_{m}=0.65$
) are constant. Note that compared to our previous study (Schneiders et al.
Reference Schneiders, Meinke and Schröder2017a
) we have increased the volumetric particle diameter by approximately a factor of two to provoke more significant finite-size effects. The particle volume fraction is kept approximately constant to remain in the dilute flow regime (Balachandar & Eaton Reference Balachandar and Eaton2010) such that the number of particles becomes smaller. The particle Stokes numbers have been estimated using particle relaxation times
![]() $\unicode[STIX]{x1D70F}_{p}$
approximated for uniformly distributed particle orientations (Voth & Soldati Reference Voth and Soldati2017). That is, the differences in the Stokes numbers among the cases are solely due to shape effects. Note that the particle relaxation times have not been corrected with respect to the finite particle Reynolds numbers of
$\unicode[STIX]{x1D70F}_{p}$
approximated for uniformly distributed particle orientations (Voth & Soldati Reference Voth and Soldati2017). That is, the differences in the Stokes numbers among the cases are solely due to shape effects. Note that the particle relaxation times have not been corrected with respect to the finite particle Reynolds numbers of
![]() $Re_{p}=O(10)$
encountered in this study. Therefore, the Stokes numbers given in table 1 are too high by roughly a factor two, but it facilitates the comparison with different studies since the a priori unknown statistical distribution of particle Reynolds numbers is absent.
$Re_{p}=O(10)$
encountered in this study. Therefore, the Stokes numbers given in table 1 are too high by roughly a factor two, but it facilitates the comparison with different studies since the a priori unknown statistical distribution of particle Reynolds numbers is absent.
Table 1. Parameters of the five simulations at injection time
![]() $t_{i}^{\ast }=0.28$
: particle aspect ratio
$t_{i}^{\ast }=0.28$
: particle aspect ratio
![]() $\unicode[STIX]{x1D6FD}$
; particle-to-fluid density ratio
$\unicode[STIX]{x1D6FD}$
; particle-to-fluid density ratio
![]() $\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}$
; ratio of volumetric, minor and major particle diameter
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}$
; ratio of volumetric, minor and major particle diameter
![]() $d_{p}^{vol/min/maj}$
to the Kolmogorov length
$d_{p}^{vol/min/maj}$
to the Kolmogorov length
![]() $\unicode[STIX]{x1D702}$
, Taylor scale
$\unicode[STIX]{x1D702}$
, Taylor scale
![]() $\unicode[STIX]{x1D706}$
and integral length
$\unicode[STIX]{x1D706}$
and integral length
![]() $\ell$
; the corresponding Stokes numbers
$\ell$
; the corresponding Stokes numbers
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}/\unicode[STIX]{x1D706}/\ell }$
; and particle mass loading
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}/\unicode[STIX]{x1D706}/\ell }$
; and particle mass loading
![]() $\unicode[STIX]{x1D719}_{m}$
.
$\unicode[STIX]{x1D719}_{m}$
.

2.2 Relevance of the considered parameter space
The particles in the present study behave ballistically with respect to the smallest flow scales. This is the inevitable consequence of realizing a significant particle mass loading for
![]() $d_{p}^{vol}\approx 2.5\unicode[STIX]{x1D702}$
, yet staying in the dilute flow regime. The ratios of
$d_{p}^{vol}\approx 2.5\unicode[STIX]{x1D702}$
, yet staying in the dilute flow regime. The ratios of
![]() $d_{p}^{vol}/\unicode[STIX]{x1D702}$
and
$d_{p}^{vol}/\unicode[STIX]{x1D702}$
and
![]() $\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}$
can be considered representative for many gas–solid environments, e.g. turbulent jets carrying pulverized fuel particles (Lau & Nathan Reference Lau and Nathan2014; Qi, Nathan & Lau Reference Qi, Nathan and Lau2015). However, due to computational limitations, the Reynolds number
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}$
can be considered representative for many gas–solid environments, e.g. turbulent jets carrying pulverized fuel particles (Lau & Nathan Reference Lau and Nathan2014; Qi, Nathan & Lau Reference Qi, Nathan and Lau2015). However, due to computational limitations, the Reynolds number
![]() $Re_{\unicode[STIX]{x1D706}}$
still is small compared to such environments, such that the integral turbulent length scale
$Re_{\unicode[STIX]{x1D706}}$
still is small compared to such environments, such that the integral turbulent length scale
![]() $\ell$
is not large enough compared to
$\ell$
is not large enough compared to
![]() $d_{p}$
to create a pronounced preferential concentration or orientation behaviour. In other words, the ratio of the particle and integral turbulent time scale
$d_{p}$
to create a pronounced preferential concentration or orientation behaviour. In other words, the ratio of the particle and integral turbulent time scale
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\ell }$
is not small enough for the particles to completely relax from their initial state before the carrier phase turbulence has dissipated most of its energy. The ratios of
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\ell }$
is not small enough for the particles to completely relax from their initial state before the carrier phase turbulence has dissipated most of its energy. The ratios of
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
and
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
and
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\ell }$
are of the same order of magnitude as cases F (
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\ell }$
are of the same order of magnitude as cases F (
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}=149$
) and G (
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}=149$
) and G (
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}=178$
) in Lucci et al. (Reference Lucci, Ferrante and Elghobashi2010) for significantly larger (
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}=178$
) in Lucci et al. (Reference Lucci, Ferrante and Elghobashi2010) for significantly larger (
![]() $d_{p}\sim \unicode[STIX]{x1D706}$
) spherical particles. We have stopped the simulations at
$d_{p}\sim \unicode[STIX]{x1D706}$
) spherical particles. We have stopped the simulations at
![]() $T^{\ast }=3$
, which still covers only a fraction of the particle relaxation time, i.e. ranging between
$T^{\ast }=3$
, which still covers only a fraction of the particle relaxation time, i.e. ranging between
![]() $(T^{\ast }/\unicode[STIX]{x1D70F}_{p}^{\ast })\approx 0.2$
for case S and
$(T^{\ast }/\unicode[STIX]{x1D70F}_{p}^{\ast })\approx 0.2$
for case S and
![]() $(T^{\ast }/\unicode[STIX]{x1D70F}_{p}^{\ast })\approx 0.3$
for case P8 due to the ballistic nature of the particles. This is demonstrated in figure 1, illustrating the alignment of the particle motion with the fluid motion for case P8 at
$(T^{\ast }/\unicode[STIX]{x1D70F}_{p}^{\ast })\approx 0.3$
for case P8 due to the ballistic nature of the particles. This is demonstrated in figure 1, illustrating the alignment of the particle motion with the fluid motion for case P8 at
![]() $t^{\ast }=2$
. The orientation distribution function (o.d.f.) between the particle velocity
$t^{\ast }=2$
. The orientation distribution function (o.d.f.) between the particle velocity
![]() $\boldsymbol{v}_{p}$
and the ambient fluid velocity
$\boldsymbol{v}_{p}$
and the ambient fluid velocity
![]() $\boldsymbol{U}_{p}$
(figure 1
a) only shows a low alignment between the particle and the fluid motion. To demonstrate that this is the consequence of particle inertia, we compare this distribution to the results of a separate simulation with the exact same set-up, despite the density ratio being set to
$\boldsymbol{U}_{p}$
(figure 1
a) only shows a low alignment between the particle and the fluid motion. To demonstrate that this is the consequence of particle inertia, we compare this distribution to the results of a separate simulation with the exact same set-up, despite the density ratio being set to
![]() $\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}=100$
. In the latter case, a pronounced alignment of the particle motion with the local fluid motion is observed since the particle relaxation time is one order of magnitude smaller. A similar trend is observed for the alignment between the particle symmetry axis and the fluid rotation (figure 1
b), where only a poor tendency for the inertial particles to preferentially orient with respect to the fluid vorticity is observed. The same behaviour is found for the orientation of the symmetry axis with respect to the relative velocity direction (not shown). That is, the position and orientation of the particles remain mostly stochastic in the cases considered in this study.
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}=100$
. In the latter case, a pronounced alignment of the particle motion with the local fluid motion is observed since the particle relaxation time is one order of magnitude smaller. A similar trend is observed for the alignment between the particle symmetry axis and the fluid rotation (figure 1
b), where only a poor tendency for the inertial particles to preferentially orient with respect to the fluid vorticity is observed. The same behaviour is found for the orientation of the symmetry axis with respect to the relative velocity direction (not shown). That is, the position and orientation of the particles remain mostly stochastic in the cases considered in this study.

Figure 1. Alignment of the particle motion with the local fluid motion at
![]() $t^{\ast }=2$
for case P8 and two ratios of
$t^{\ast }=2$
for case P8 and two ratios of
![]() $\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}$
: Orientation distribution function (o.d.f.) of the angle between the particle velocity and the ambient fluid velocity,
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}$
: Orientation distribution function (o.d.f.) of the angle between the particle velocity and the ambient fluid velocity,
![]() $\angle (\boldsymbol{v}_{p},\boldsymbol{U}_{p})$
(a), and between the particle symmetry axis and the ambient fluid rotation,
$\angle (\boldsymbol{v}_{p},\boldsymbol{U}_{p})$
(a), and between the particle symmetry axis and the ambient fluid rotation,
![]() $\angle (\widehat{\unicode[STIX]{x1D734}}_{p},\widehat{\boldsymbol{z}})$
(b).
$\angle (\widehat{\unicode[STIX]{x1D734}}_{p},\widehat{\boldsymbol{z}})$
(b).
The weak particle response has certain consequences for the applicability of the following analysis and necessitates defining of the focus of the present study. We emphasize that the disparity between the dissipative time scale and the particle relaxation time in combination with the limited Reynolds number and thus the lack of very large-scale turbulent structures precludes the current set-up from an analysis of particle transport and associated effects such as particle dispersion, clustering or preferential orientation. The strict focus of the present study is to investigate the direct energy transfer between the carrier phase and finite-size particles and the additional dissipation rate induced by the particles at higher wavenumbers. The shape effects of these processes are identified. This is achieved by resolving all relevant scales of the fluid and the particle phase in a direct sense, i.e. without turbulence models and without applying models to indirectly represent the particle surface or the hydrodynamic interactions. The influence of gravity is neglected. This facilitates the fundamental understanding of the particle–turbulence interaction and can be justified for several fields of applications. Consider a turbulent round air jet at standard atmospheric conditions with a bulk velocity of
![]() $U=100~\text{m}~\text{s}^{-1}$
, a nozzle diameter of
$U=100~\text{m}~\text{s}^{-1}$
, a nozzle diameter of
![]() $D=0.5~\text{m}$
and carrying spherical particles with
$D=0.5~\text{m}$
and carrying spherical particles with
![]() $d_{p}=100~\unicode[STIX]{x03BC}\text{m}$
and
$d_{p}=100~\unicode[STIX]{x03BC}\text{m}$
and
![]() $\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}=1000$
as encountered in various technical environments (Lau & Nathan Reference Lau and Nathan2014). The Kolmogorov length scale
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}=1000$
as encountered in various technical environments (Lau & Nathan Reference Lau and Nathan2014). The Kolmogorov length scale
![]() $\unicode[STIX]{x1D702}$
over the jet distance
$\unicode[STIX]{x1D702}$
over the jet distance
![]() $x$
can be estimated by
$x$
can be estimated by
![]() $(\unicode[STIX]{x1D702}/D)=0.38Re_{D}^{-3/4}(x/D)$
(Antonia, Satyaprakash & Hussain Reference Antonia, Satyaprakash and Hussain1980), where
$(\unicode[STIX]{x1D702}/D)=0.38Re_{D}^{-3/4}(x/D)$
(Antonia, Satyaprakash & Hussain Reference Antonia, Satyaprakash and Hussain1980), where
![]() $Re_{D}\approx 3\times 10^{6}$
, e.g. yielding
$Re_{D}\approx 3\times 10^{6}$
, e.g. yielding
![]() $d_{p}/\unicode[STIX]{x1D702}\approx 4$
at
$d_{p}/\unicode[STIX]{x1D702}\approx 4$
at
![]() $x=10D$
. If the jet issues from a pipe with the same value of
$x=10D$
. If the jet issues from a pipe with the same value of
![]() $Re_{D}$
, one observes
$Re_{D}$
, one observes
![]() $d_{p}\approx \unicode[STIX]{x1D702}$
at the pipe centre line (Morrison, Vallikivi & Smits Reference Morrison, Vallikivi and Smits2016) where the turbulence is approximately isotropic. The particle terminal velocity due to gravity is
$d_{p}\approx \unicode[STIX]{x1D702}$
at the pipe centre line (Morrison, Vallikivi & Smits Reference Morrison, Vallikivi and Smits2016) where the turbulence is approximately isotropic. The particle terminal velocity due to gravity is
![]() $v_{t}=g\unicode[STIX]{x1D70F}_{p}=0.36~\text{m}~\text{s}^{-1}$
, assuming Stokes flow conditions for an order-of-magnitude evaluation. Considering a moderate turbulence intensity of 10 %, the ratio of the settling velocity to the velocity fluctuations is small, i.e.
$v_{t}=g\unicode[STIX]{x1D70F}_{p}=0.36~\text{m}~\text{s}^{-1}$
, assuming Stokes flow conditions for an order-of-magnitude evaluation. Considering a moderate turbulence intensity of 10 %, the ratio of the settling velocity to the velocity fluctuations is small, i.e.
![]() $v_{t}/u^{\prime }=0.036$
. That is, the ratio of the total particle kinetic energy due to gravitational settling to the turbulent kinetic energy of the flow is small,
$v_{t}/u^{\prime }=0.036$
. That is, the ratio of the total particle kinetic energy due to gravitational settling to the turbulent kinetic energy of the flow is small,
![]() $\unicode[STIX]{x1D719}_{m}(v_{t}/u^{\prime })^{2}\ll 1$
, at the pipe centre line and in the near to intermediate field of the jet, despite
$\unicode[STIX]{x1D719}_{m}(v_{t}/u^{\prime })^{2}\ll 1$
, at the pipe centre line and in the near to intermediate field of the jet, despite
![]() $d_{p}\gtrsim \unicode[STIX]{x1D702}$
.
$d_{p}\gtrsim \unicode[STIX]{x1D702}$
.
It goes without saying that turbulent two-phase jets in technical processes exhibit significantly higher
![]() $Re_{\unicode[STIX]{x1D706}}$
than in the present study. Due to computational limitations, the simultaneous resolution of the particle scale and turbulent length scales found in most real-world problems is currently impossible. Although single-phase turbulent jets are self-similar at sufficiently high Reynolds numbers (Antonia et al.
Reference Antonia, Satyaprakash and Hussain1980), this property is generally lost for multiphase jets. Since the real Reynolds numbers cannot be resolved, one has to choose whether to match the particle Stokes number with respect to the dissipative scales or the integral length scales or any scale in between. For studies on particles in anisotropic turbulence, an integral-scale Stokes number is often stipulated to study the particle phase statistics (Lau & Nathan Reference Lau and Nathan2014). Since the focus of the present study is on the energy transport between the phases, we choose to match the Stokes number with respect to the Kolmogorov scale. That is, the response of the particles to very large flow scales is neither covered nor is the turbulence decay time long enough to create a significant energy record due to gravitational settling. In other words, the time span covered is small compared to the typical turnover time of integral-scale vortices found, e.g. in technical free jets or atmospheric flows. The lack of particle response to the turbulent fluctuations leaves the particles approximately randomly distributed and oriented throughout the simulations. That is, all relative velocity directions and incidence angles of the particles are covered at various particle Reynolds numbers. In some sense, this stochastic distribution of the particle phase renders the presented results generic with respect to effects due to preferential motion of the particles. To strengthen this generality, many of the subsequent analyses are performed for individual particles and not just in a statistical sense. For instance, the inferences about the local kinetic energy balances will be demonstrated to apply per particle and thus can be considered applicable also to systems in which large turbulent length scales induce preferentially concentrated or oriented particles. These mechanisms are not directly impacted by the interaction with very large flow scales, even though an indirect interaction would originate from the spectral transport of kinetic energy. That is, we expect these results to be relevant for a wide range of applications and different flow set-ups. However, we explicitly do not encourage to extend the current set-up to investigate mechanisms associated with particle transport.
$Re_{\unicode[STIX]{x1D706}}$
than in the present study. Due to computational limitations, the simultaneous resolution of the particle scale and turbulent length scales found in most real-world problems is currently impossible. Although single-phase turbulent jets are self-similar at sufficiently high Reynolds numbers (Antonia et al.
Reference Antonia, Satyaprakash and Hussain1980), this property is generally lost for multiphase jets. Since the real Reynolds numbers cannot be resolved, one has to choose whether to match the particle Stokes number with respect to the dissipative scales or the integral length scales or any scale in between. For studies on particles in anisotropic turbulence, an integral-scale Stokes number is often stipulated to study the particle phase statistics (Lau & Nathan Reference Lau and Nathan2014). Since the focus of the present study is on the energy transport between the phases, we choose to match the Stokes number with respect to the Kolmogorov scale. That is, the response of the particles to very large flow scales is neither covered nor is the turbulence decay time long enough to create a significant energy record due to gravitational settling. In other words, the time span covered is small compared to the typical turnover time of integral-scale vortices found, e.g. in technical free jets or atmospheric flows. The lack of particle response to the turbulent fluctuations leaves the particles approximately randomly distributed and oriented throughout the simulations. That is, all relative velocity directions and incidence angles of the particles are covered at various particle Reynolds numbers. In some sense, this stochastic distribution of the particle phase renders the presented results generic with respect to effects due to preferential motion of the particles. To strengthen this generality, many of the subsequent analyses are performed for individual particles and not just in a statistical sense. For instance, the inferences about the local kinetic energy balances will be demonstrated to apply per particle and thus can be considered applicable also to systems in which large turbulent length scales induce preferentially concentrated or oriented particles. These mechanisms are not directly impacted by the interaction with very large flow scales, even though an indirect interaction would originate from the spectral transport of kinetic energy. That is, we expect these results to be relevant for a wide range of applications and different flow set-ups. However, we explicitly do not encourage to extend the current set-up to investigate mechanisms associated with particle transport.
3 Computational method
The numerical method and computational parameters are discussed in detail in Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
) and are briefly summarized in the following. The direct particle–fluid simulations are performed using a cell-centred finite-volume scheme for the compressible Navier–Stokes equations formulated on locally refined Cartesian meshes. The particle surfaces are accurately tracked using level sets. A Cartesian cut-cell scheme is used to couple the fluid stresses to the particle motion. The benefits of the cut-cell approach lie in the strict conservation of fluid mass, momentum and energy at these interfaces, the sharp and accurate resolution of the particle surface stresses and its robustness for fluid–structure interaction. As a consequence, the hydrodynamic force and torque acting on each particle can directly be evaluated by integrating the normal and shear stresses over the discrete particle surfaces
![]() $\unicode[STIX]{x1D6E4}_{p}$
, i.e.
$\unicode[STIX]{x1D6E4}_{p}$
, i.e.
where
![]() $\boldsymbol{r}_{p}$
denotes the particle mass centre. The Newton and Euler equations governing the linear and rotational motion of the particles are solved using a second-order accurate scheme. A dynamic mesh refinement technique is applied to adaptively resolve the flow field in the vicinity of the particles, see Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
). In this study, four grid levels are used starting from the uniform background mesh. Due to the larger curvature and more complex shape of the ellipsoids, the finest mesh resolution is the same as in Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
), although the volumetric particle diameter was increased. The mesh spacing at the fluid–solid interfaces is
$\boldsymbol{r}_{p}$
denotes the particle mass centre. The Newton and Euler equations governing the linear and rotational motion of the particles are solved using a second-order accurate scheme. A dynamic mesh refinement technique is applied to adaptively resolve the flow field in the vicinity of the particles, see Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
). In this study, four grid levels are used starting from the uniform background mesh. Due to the larger curvature and more complex shape of the ellipsoids, the finest mesh resolution is the same as in Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
), although the volumetric particle diameter was increased. The mesh spacing at the fluid–solid interfaces is
![]() $d_{p}^{vol}/\unicode[STIX]{x0394}x\approx 20$
and
$d_{p}^{vol}/\unicode[STIX]{x0394}x\approx 20$
and
![]() $d_{p}^{min}/\unicode[STIX]{x0394}x\gtrsim 8$
in all particle-laden cases. The number of mesh cells varies over time and ranges from approximately
$d_{p}^{min}/\unicode[STIX]{x0394}x\gtrsim 8$
in all particle-laden cases. The number of mesh cells varies over time and ranges from approximately
![]() $10^{9}$
in case S to
$10^{9}$
in case S to
![]() $1.5\times 10^{9}$
for case P8 due to the larger particle surface area therein. The turbulent flow structures, the near particle vortical structures and the local mesh refinement are illustrated in figure 2 for case P8 at time
$1.5\times 10^{9}$
for case P8 due to the larger particle surface area therein. The turbulent flow structures, the near particle vortical structures and the local mesh refinement are illustrated in figure 2 for case P8 at time
![]() $t^{\ast }=1$
. It shows a volume rendering of
$t^{\ast }=1$
. It shows a volume rendering of
![]() $Q/\langle \unicode[STIX]{x1D714}^{2}\rangle _{0}$
, i.e. the second invariant of the velocity gradient tensor normalized by the mean enstrophy obtained in case 0 at the same time level. The strong amplification of enstrophy close to the particles is clearly visible.
$Q/\langle \unicode[STIX]{x1D714}^{2}\rangle _{0}$
, i.e. the second invariant of the velocity gradient tensor normalized by the mean enstrophy obtained in case 0 at the same time level. The strong amplification of enstrophy close to the particles is clearly visible.

Figure 2. Volume rendering of the second invariant of the velocity gradient tensor,
![]() $Q$
, for case P8 normalized by the reference enstrophy
$Q$
, for case P8 normalized by the reference enstrophy
![]() $\langle \unicode[STIX]{x1D714}^{2}\rangle _{0}$
at
$\langle \unicode[STIX]{x1D714}^{2}\rangle _{0}$
at
![]() $t^{\ast }=1$
(top); close-up view with a slice of the computational mesh (bottom). Particles are light grey, high fluid rotation rates are indicated by dark blue regions.
$t^{\ast }=1$
(top); close-up view with a slice of the computational mesh (bottom). Particles are light grey, high fluid rotation rates are indicated by dark blue regions.
The continuous motion of the particles causes the locally refined mesh to rapidly vary over space and time. To enable the distributed-memory computations on current supercomputers, a dynamic load balancing strategy was developed to maintain an equally distributed number of computational cells, i.e. a balanced memory and work load, across the different compute cores. The solver has thoroughly been validated for solid body motion in viscous compressible and approximately incompressible flow including isotropic turbulent flow fields. For details the reader is referred to Schneiders et al. (Reference Schneiders, Günther, Meinke and Schröder2016, and references therein).
4 Impact of particle shape and orientation on kinetic energy budget
4.1 Balance of kinetic energies
Let
![]() $E_{k}=\int _{\unicode[STIX]{x1D6F6}_{f}}e_{k}\,\text{d}V$
denote the total fluid kinetic energy, integrated within the global fluid volume
$E_{k}=\int _{\unicode[STIX]{x1D6F6}_{f}}e_{k}\,\text{d}V$
denote the total fluid kinetic energy, integrated within the global fluid volume
![]() $\unicode[STIX]{x1D6F6}_{f}$
, where
$\unicode[STIX]{x1D6F6}_{f}$
, where
![]() $e_{k}=\unicode[STIX]{x1D70C}\boldsymbol{u}^{2}/2$
is the local kinetic energy. The summed kinetic energy of the particles,
$e_{k}=\unicode[STIX]{x1D70C}\boldsymbol{u}^{2}/2$
is the local kinetic energy. The summed kinetic energy of the particles,
![]() $K=\sum _{p=1}^{N_{p}}(m_{p}\boldsymbol{v}_{p}^{2}+\unicode[STIX]{x1D74E}_{p}^{T}\boldsymbol{{\mathcal{I}}}_{p}\unicode[STIX]{x1D74E}_{p})/2$
, is determined using the linear and angular particle velocities,
$K=\sum _{p=1}^{N_{p}}(m_{p}\boldsymbol{v}_{p}^{2}+\unicode[STIX]{x1D74E}_{p}^{T}\boldsymbol{{\mathcal{I}}}_{p}\unicode[STIX]{x1D74E}_{p})/2$
, is determined using the linear and angular particle velocities,
![]() $\boldsymbol{v}_{p}$
and
$\boldsymbol{v}_{p}$
and
![]() $\unicode[STIX]{x1D74E}_{p}$
, and the moment-of-inertia tensor
$\unicode[STIX]{x1D74E}_{p}$
, and the moment-of-inertia tensor
![]() $\boldsymbol{{\mathcal{I}}}_{p}$
. Note that for fluid points which are infinitesimally small, the rotational fluid motion does not affect the linear kinetic energy. The decay rates of
$\boldsymbol{{\mathcal{I}}}_{p}$
. Note that for fluid points which are infinitesimally small, the rotational fluid motion does not affect the linear kinetic energy. The decay rates of
![]() $E_{k}$
and
$E_{k}$
and
![]() $K$
are determined by
$K$
are determined by
where the term
describes the conservative, direct transfer of kinetic energy via stresses acting at the fluid–particle interfaces (Schneiders et al. Reference Schneiders, Meinke and Schröder2017a ) and
defines the global dissipation rate. The pressure-dilatation term
![]() $(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})p$
contributes approximately
$(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})p$
contributes approximately
![]() $0.2\,\%$
to the total dissipation rate in the single-phase case, since the flow field is approximately divergence free. Hence, the total energy of the system decays as
$0.2\,\%$
to the total dissipation rate in the single-phase case, since the flow field is approximately divergence free. Hence, the total energy of the system decays as
![]() $\text{d}(E_{k}+K)/\text{d}t=-{\mathcal{E}}(t)$
. The temporal distributions of
$\text{d}(E_{k}+K)/\text{d}t=-{\mathcal{E}}(t)$
. The temporal distributions of
![]() $E_{k}$
,
$E_{k}$
,
![]() $K$
,
$K$
,
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() $\unicode[STIX]{x1D6F9}$
are shown in figure 3. The kinetic energy budgets in the present cases show a qualitatively similar behaviour to the slightly smaller spherical particles (
$\unicode[STIX]{x1D6F9}$
are shown in figure 3. The kinetic energy budgets in the present cases show a qualitatively similar behaviour to the slightly smaller spherical particles (
![]() $d_{p}\approx \unicode[STIX]{x1D702}$
) in Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
). Until
$d_{p}\approx \unicode[STIX]{x1D702}$
) in Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
). Until
![]() $t^{\ast }=1$
, the particles reduce the fluid kinetic energy by approximately 5.7 % in case S, 7.1 % in cases O4 and P4 and 8.7 % in case P8, compared to the single-phase flow (figure 3
a). The strong amplification of the dissipation rate (figure 3
b) is due to the velocity gradients generated close to the particle surfaces which amplify the strain rate and enstrophy of the ambient flow field. At
$t^{\ast }=1$
, the particles reduce the fluid kinetic energy by approximately 5.7 % in case S, 7.1 % in cases O4 and P4 and 8.7 % in case P8, compared to the single-phase flow (figure 3
a). The strong amplification of the dissipation rate (figure 3
b) is due to the velocity gradients generated close to the particle surfaces which amplify the strain rate and enstrophy of the ambient flow field. At
![]() $t^{\ast }=1$
the increase of
$t^{\ast }=1$
the increase of
![]() ${\mathcal{E}}$
relative to the single-phase flow is 41 % in case S, 53 % in cases O4 and P4 and 65 % in case P8. This extra dissipation is partially compensated by the continuous release of particle energy via
${\mathcal{E}}$
relative to the single-phase flow is 41 % in case S, 53 % in cases O4 and P4 and 65 % in case P8. This extra dissipation is partially compensated by the continuous release of particle energy via
![]() $\unicode[STIX]{x1D6F9}$
(figure 3
b) owing to the high inertia of the particles. The variation of
$\unicode[STIX]{x1D6F9}$
(figure 3
b) owing to the high inertia of the particles. The variation of
![]() $\unicode[STIX]{x1D6F9}$
follows a similar trend as the additional dissipation rate
$\unicode[STIX]{x1D6F9}$
follows a similar trend as the additional dissipation rate
![]() ${\mathcal{E}}$
, relative to case 0, and both significantly increase with the aspect ratio
${\mathcal{E}}$
, relative to case 0, and both significantly increase with the aspect ratio
![]() $\unicode[STIX]{x1D6FD}$
. These opposed effects lead to the rather moderate damping of fluid kinetic energy
$\unicode[STIX]{x1D6FD}$
. These opposed effects lead to the rather moderate damping of fluid kinetic energy
![]() $E_{k}$
with a relatively small influence by the particle shape. On the contrary, the strong dependence of
$E_{k}$
with a relatively small influence by the particle shape. On the contrary, the strong dependence of
![]() $\unicode[STIX]{x1D6F9}$
on the particle shape leads to significant differences in the decay rates of the particle kinetic energy
$\unicode[STIX]{x1D6F9}$
on the particle shape leads to significant differences in the decay rates of the particle kinetic energy
![]() $K$
(figure 3
a). Clearly, the spherical particles transfer the least amount of energy to the fluid and the decay rate of
$K$
(figure 3
a). Clearly, the spherical particles transfer the least amount of energy to the fluid and the decay rate of
![]() $K$
increases with the aspect ratio
$K$
increases with the aspect ratio
![]() $\unicode[STIX]{x1D6FD}$
. The almost identical decay of
$\unicode[STIX]{x1D6FD}$
. The almost identical decay of
![]() $K$
for cases P4 and O4 is explained by the comparable particle relaxation times (cf. table 1) leading to a similar development of the average particle velocities. As a consequence, the variation of
$K$
for cases P4 and O4 is explained by the comparable particle relaxation times (cf. table 1) leading to a similar development of the average particle velocities. As a consequence, the variation of
![]() ${\mathcal{E}}$
,
${\mathcal{E}}$
,
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $E_{k}$
is almost alike for P4 and O4 as well.
$E_{k}$
is almost alike for P4 and O4 as well.

Figure 3. Temporal variation of (a) the fluid kinetic energy
![]() $E_{k}$
and the particle kinetic energy
$E_{k}$
and the particle kinetic energy
![]() $K$
, both normalized by their initial values; (b) the viscous dissipation rate
$K$
, both normalized by their initial values; (b) the viscous dissipation rate
![]() ${\mathcal{E}}$
and the interphase energy exchange
${\mathcal{E}}$
and the interphase energy exchange
![]() $\unicode[STIX]{x1D6F9}$
, both normalized by
$\unicode[STIX]{x1D6F9}$
, both normalized by
![]() ${\mathcal{E}}_{ref}=\unicode[STIX]{x1D70C}L^{2}u_{0}^{3}$
.
${\mathcal{E}}_{ref}=\unicode[STIX]{x1D70C}L^{2}u_{0}^{3}$
.
To understand the integral behaviour of
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() ${\mathcal{E}}$
, the local balance of fluid kinetic energy in the vicinity of each particle is examined. In Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
) an analytical model for the particle-induced dissipation rate was derived from first principles and independently of the particle shape, while assuming the particle to not be significantly larger than the smallest flow scale. Following this analysis, the instantaneous dissipation rate around each particle reads
${\mathcal{E}}$
, the local balance of fluid kinetic energy in the vicinity of each particle is examined. In Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
) an analytical model for the particle-induced dissipation rate was derived from first principles and independently of the particle shape, while assuming the particle to not be significantly larger than the smallest flow scale. Following this analysis, the instantaneous dissipation rate around each particle reads
where
![]() $\unicode[STIX]{x1D6F4}_{p}$
describes a certain volume of fluid around the particle at time
$\unicode[STIX]{x1D6F4}_{p}$
describes a certain volume of fluid around the particle at time
![]() $t$
,
$t$
,
![]() $\boldsymbol{U}_{p}-\boldsymbol{v}_{p}$
the relative fluid velocity experienced by the particle and
$\boldsymbol{U}_{p}-\boldsymbol{v}_{p}$
the relative fluid velocity experienced by the particle and
![]() $\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p}$
the relative rotational velocity. The quantity
$\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p}$
the relative rotational velocity. The quantity
![]() ${\mathcal{I}}_{f}$
is a fluid inertia term describing the local acceleration of the fluid elements and contributes little to the above equation when particle inertia dominates over fluid inertia (Schneiders et al.
Reference Schneiders, Meinke and Schröder2017a
). In the present study it is approximated as
${\mathcal{I}}_{f}$
is a fluid inertia term describing the local acceleration of the fluid elements and contributes little to the above equation when particle inertia dominates over fluid inertia (Schneiders et al.
Reference Schneiders, Meinke and Schröder2017a
). In the present study it is approximated as
![]() ${\mathcal{I}}_{f}\approx \int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D70C}(\boldsymbol{u}-\boldsymbol{U}_{p})\boldsymbol{\cdot }(\text{d}\boldsymbol{u}/\text{d}t)\,\text{d}V$
. The fluid volume
${\mathcal{I}}_{f}\approx \int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D70C}(\boldsymbol{u}-\boldsymbol{U}_{p})\boldsymbol{\cdot }(\text{d}\boldsymbol{u}/\text{d}t)\,\text{d}V$
. The fluid volume
![]() $\unicode[STIX]{x1D6F4}_{p}$
needs to be chosen, on the one hand, large enough to capture the majority of velocity disturbances induced by the particles and on the other hand small enough to not catch up disturbances by adjacent particles and background turbulence. In the following, we set
$\unicode[STIX]{x1D6F4}_{p}$
needs to be chosen, on the one hand, large enough to capture the majority of velocity disturbances induced by the particles and on the other hand small enough to not catch up disturbances by adjacent particles and background turbulence. In the following, we set
where
![]() $\unicode[STIX]{x1D6FF}_{p}(\boldsymbol{x})=\min |\boldsymbol{x}-\unicode[STIX]{x1D6E4}_{p}|$
denotes the distance of the point
$\unicode[STIX]{x1D6FF}_{p}(\boldsymbol{x})=\min |\boldsymbol{x}-\unicode[STIX]{x1D6E4}_{p}|$
denotes the distance of the point
![]() $\boldsymbol{x}$
to the particle surface
$\boldsymbol{x}$
to the particle surface
![]() $\unicode[STIX]{x1D6E4}_{p}$
and
$\unicode[STIX]{x1D6E4}_{p}$
and
![]() $\unicode[STIX]{x1D6E5}=1.5d_{p}^{vol}$
, as justified further below.
$\unicode[STIX]{x1D6E5}=1.5d_{p}^{vol}$
, as justified further below.
4.2 Reconstruction of the ambient fluid velocity
 $\boldsymbol{U}_{p}$
and rotation rate
$\boldsymbol{U}_{p}$
and rotation rate
 $\unicode[STIX]{x1D734}_{p}$
$\unicode[STIX]{x1D734}_{p}$
In the following we demonstrate that (4.4) is still applicable when non-spherical particles are considered with major axes significantly larger than the Kolmogorov length scale. A generalized definition of the velocity
![]() $\boldsymbol{U}_{p}$
will be applied. This quantity is often interpreted as the ‘undisturbed fluid velocity seen by the particles’, however, this notion is clearly inappropriate for
$\boldsymbol{U}_{p}$
will be applied. This quantity is often interpreted as the ‘undisturbed fluid velocity seen by the particles’, however, this notion is clearly inappropriate for
![]() $d_{p}^{maj}\gtrsim \unicode[STIX]{x1D702}$
or for substantial two-way interactions, i.e. when the particle-induced disturbances overlap with the length scales of the flow. In such cases, a suitable definition of
$d_{p}^{maj}\gtrsim \unicode[STIX]{x1D702}$
or for substantial two-way interactions, i.e. when the particle-induced disturbances overlap with the length scales of the flow. In such cases, a suitable definition of
![]() $\boldsymbol{U}_{p}$
is required to translate results from particle-resolved simulations or experiments (Bellani & Variano Reference Bellani and Variano2012) to the various modelling approaches in non-uniform multiphase flow, for instance, to define the particle Reynolds number
$\boldsymbol{U}_{p}$
is required to translate results from particle-resolved simulations or experiments (Bellani & Variano Reference Bellani and Variano2012) to the various modelling approaches in non-uniform multiphase flow, for instance, to define the particle Reynolds number
![]() $Re_{p}=|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|d_{p}^{vol}/\unicode[STIX]{x1D708}$
. Here, we refer to
$Re_{p}=|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|d_{p}^{vol}/\unicode[STIX]{x1D708}$
. Here, we refer to
![]() $\boldsymbol{U}_{p}$
as the ambient fluid velocity with respect to each particle. In experimental studies, this relative velocity is sometimes determined with respect to the global mean flow velocity, i.e.
$\boldsymbol{U}_{p}$
as the ambient fluid velocity with respect to each particle. In experimental studies, this relative velocity is sometimes determined with respect to the global mean flow velocity, i.e.
![]() $\overline{Re_{p}}=|\overline{\boldsymbol{U}}-\boldsymbol{v}_{p}|d_{p}^{vol}/\unicode[STIX]{x1D708}$
(Geiss et al.
Reference Geiss, Dreizler, Stojanovic, Chrigui, Sadiki and Janicka2004; Lau & Nathan Reference Lau and Nathan2014), which clearly does not reflect the state of the local flow about the particles but rather represents a statistical quantity. For particles larger than the Kolmogorov length scale, estimating the so-called undisturbed fluid velocity at the particle centre was shown to be inappropriate by Bagchi & Balachandar (Reference Bagchi and Balachandar2003). They also investigated how averaging the fluid velocity
$\overline{Re_{p}}=|\overline{\boldsymbol{U}}-\boldsymbol{v}_{p}|d_{p}^{vol}/\unicode[STIX]{x1D708}$
(Geiss et al.
Reference Geiss, Dreizler, Stojanovic, Chrigui, Sadiki and Janicka2004; Lau & Nathan Reference Lau and Nathan2014), which clearly does not reflect the state of the local flow about the particles but rather represents a statistical quantity. For particles larger than the Kolmogorov length scale, estimating the so-called undisturbed fluid velocity at the particle centre was shown to be inappropriate by Bagchi & Balachandar (Reference Bagchi and Balachandar2003). They also investigated how averaging the fluid velocity
![]() $\boldsymbol{u}$
over increasing volumes around the particle affects the accuracy of particle force models in frozen turbulence. In particle-resolved simulations of turbulent channel flow, Kidanemariam et al. (Reference Kidanemariam, Chan-Braun, Doychev and Uhlmann2013) have proposed to average the fluid velocity over a segment of a spherical shell at a distance of
$\boldsymbol{u}$
over increasing volumes around the particle affects the accuracy of particle force models in frozen turbulence. In particle-resolved simulations of turbulent channel flow, Kidanemariam et al. (Reference Kidanemariam, Chan-Braun, Doychev and Uhlmann2013) have proposed to average the fluid velocity over a segment of a spherical shell at a distance of
![]() $1.5d_{p}$
from a spherical particle. However, they truncate a part of the reconstruction region based on the wall-normal direction, which complicates the generalization of their scheme. Burton & Eaton (Reference Burton and Eaton2005) reconstructed the undisturbed fluid velocity in isotropic turbulence using a separate simulation without particles. This approach is not suitable for pronounced two-way coupling effects which significantly alter the development of the background turbulent flow. For large (
$1.5d_{p}$
from a spherical particle. However, they truncate a part of the reconstruction region based on the wall-normal direction, which complicates the generalization of their scheme. Burton & Eaton (Reference Burton and Eaton2005) reconstructed the undisturbed fluid velocity in isotropic turbulence using a separate simulation without particles. This approach is not suitable for pronounced two-way coupling effects which significantly alter the development of the background turbulent flow. For large (
![]() $d_{p}\gg \unicode[STIX]{x1D702}$
) spherical particles in isotropic turbulence with gravity, Fornari, Picano & Brandt (Reference Fornari, Picano and Brandt2016) computed
$d_{p}\gg \unicode[STIX]{x1D702}$
) spherical particles in isotropic turbulence with gravity, Fornari, Picano & Brandt (Reference Fornari, Picano and Brandt2016) computed
![]() $\boldsymbol{U}_{p}$
by averaging
$\boldsymbol{U}_{p}$
by averaging
![]() $\boldsymbol{u}$
over spherical shells around the particle and performed a parameter study to identify a suitable shell radius. However, even for large shells with a distance of
$\boldsymbol{u}$
over spherical shells around the particle and performed a parameter study to identify a suitable shell radius. However, even for large shells with a distance of
![]() $5d_{p}$
to particle surface, the mean values of
$5d_{p}$
to particle surface, the mean values of
![]() $\boldsymbol{U}_{p}$
do not fully converge in their study. They attribute this effect to the disturbances by the pronounced particle wakes emerging from gravitational settling.
$\boldsymbol{U}_{p}$
do not fully converge in their study. They attribute this effect to the disturbances by the pronounced particle wakes emerging from gravitational settling.
To the best of our knowledge, the methods to reconstruct
![]() $\boldsymbol{U}_{p}$
proposed in the literature are restricted to spherical particles and their accuracy has not been discussed in detail. In the following, a new scheme to reconstruct
$\boldsymbol{U}_{p}$
proposed in the literature are restricted to spherical particles and their accuracy has not been discussed in detail. In the following, a new scheme to reconstruct
![]() $\boldsymbol{U}_{p}$
is described which is applicable to spherical and non-spherical particles and also allows us to determine
$\boldsymbol{U}_{p}$
is described which is applicable to spherical and non-spherical particles and also allows us to determine
![]() $\unicode[STIX]{x1D734}_{p}$
. The accuracy and robustness of the scheme are evidenced via a parameter sensitivity study. One may require that a suitable definition of
$\unicode[STIX]{x1D734}_{p}$
. The accuracy and robustness of the scheme are evidenced via a parameter sensitivity study. One may require that a suitable definition of
![]() $\boldsymbol{U}_{p}$
(i) maximizes the correlation of the particle acceleration
$\boldsymbol{U}_{p}$
(i) maximizes the correlation of the particle acceleration
![]() $\text{d}\boldsymbol{v}_{p}/\text{d}t$
with
$\text{d}\boldsymbol{v}_{p}/\text{d}t$
with
![]() $\boldsymbol{U}_{p}$
, while (ii) minimizes the bias of
$\boldsymbol{U}_{p}$
, while (ii) minimizes the bias of
![]() $\boldsymbol{U}_{p}$
by
$\boldsymbol{U}_{p}$
by
![]() $\boldsymbol{v}_{p}$
. For instance, at finite particle Reynolds number the particle wake may bias the reconstruction of
$\boldsymbol{v}_{p}$
. For instance, at finite particle Reynolds number the particle wake may bias the reconstruction of
![]() $\boldsymbol{U}_{p}$
(Fornari et al.
Reference Fornari, Picano and Brandt2016). Therefore, we propose to estimate
$\boldsymbol{U}_{p}$
(Fornari et al.
Reference Fornari, Picano and Brandt2016). Therefore, we propose to estimate
![]() $\boldsymbol{U}_{p}$
from the upwind region of the particle using a Gaussian weighting function, i.e.
$\boldsymbol{U}_{p}$
from the upwind region of the particle using a Gaussian weighting function, i.e.
with the upwind-biased weighting function
where
![]() $\angle (\boldsymbol{n}_{p},\boldsymbol{F}_{p})$
is the angle between the hydrodynamic force vector
$\angle (\boldsymbol{n}_{p},\boldsymbol{F}_{p})$
is the angle between the hydrodynamic force vector
![]() $\boldsymbol{F}_{p}$
and the normal vector
$\boldsymbol{F}_{p}$
and the normal vector
![]() $\boldsymbol{n}_{p}$
towards the closest particle surface point. The limiting angle
$\boldsymbol{n}_{p}$
towards the closest particle surface point. The limiting angle
![]() $\unicode[STIX]{x1D703}^{up}$
separates the upwind and the wake regions as illustrated by figure 4(a). The reconstruction region
$\unicode[STIX]{x1D703}^{up}$
separates the upwind and the wake regions as illustrated by figure 4(a). The reconstruction region
is additionally defined by the minimum distance
![]() $\unicode[STIX]{x1D6FF}^{min}$
and its width
$\unicode[STIX]{x1D6FF}^{min}$
and its width
![]() $\unicode[STIX]{x1D70E}$
. The maximum weight is obtained at
$\unicode[STIX]{x1D70E}$
. The maximum weight is obtained at
![]() $\unicode[STIX]{x1D6FF}_{0}=(\unicode[STIX]{x1D6FF}^{min}+\unicode[STIX]{x1D6FF}^{max})/2=\unicode[STIX]{x1D6FF}^{min}+\unicode[STIX]{x1D70E}/2$
, representing the mid-radius of the reconstruction region
$\unicode[STIX]{x1D6FF}_{0}=(\unicode[STIX]{x1D6FF}^{min}+\unicode[STIX]{x1D6FF}^{max})/2=\unicode[STIX]{x1D6FF}^{min}+\unicode[STIX]{x1D70E}/2$
, representing the mid-radius of the reconstruction region
![]() $\widetilde{\unicode[STIX]{x1D6F4}}_{p}$
(see figure 4
a). The ambient fluid rotation
$\widetilde{\unicode[STIX]{x1D6F4}}_{p}$
(see figure 4
a). The ambient fluid rotation
![]() $\unicode[STIX]{x1D734}_{p}$
is evaluated analogously to (4.6).
$\unicode[STIX]{x1D734}_{p}$
is evaluated analogously to (4.6).

Figure 4. Reconstruction of the ambient fluid velocity
![]() $\boldsymbol{U}_{p}$
: (a) illustration of the reconstruction scheme in the plane spanned by the hydrodynamic force vector
$\boldsymbol{U}_{p}$
: (a) illustration of the reconstruction scheme in the plane spanned by the hydrodynamic force vector
![]() $\widehat{\boldsymbol{F}}_{p}$
and the particle symmetry axis direction
$\widehat{\boldsymbol{F}}_{p}$
and the particle symmetry axis direction
![]() $\widehat{\boldsymbol{z}}$
. A Gaussian weight is applied in the upwind region defined by
$\widehat{\boldsymbol{z}}$
. A Gaussian weight is applied in the upwind region defined by
![]() $\angle (\boldsymbol{F}_{p},\boldsymbol{n}_{p})<\unicode[STIX]{x1D703}^{up}$
, where
$\angle (\boldsymbol{F}_{p},\boldsymbol{n}_{p})<\unicode[STIX]{x1D703}^{up}$
, where
![]() $\boldsymbol{n}_{p}$
is the normal vector to the closest surface point. The illustration shows
$\boldsymbol{n}_{p}$
is the normal vector to the closest surface point. The illustration shows
![]() $\unicode[STIX]{x1D703}^{up}=120^{\circ }$
and
$\unicode[STIX]{x1D703}^{up}=120^{\circ }$
and
![]() $d_{p}^{min}=1.5d_{p}^{vol}$
, while the thickness
$d_{p}^{min}=1.5d_{p}^{vol}$
, while the thickness
![]() $\unicode[STIX]{x1D70E}$
was increased for better visualization. Colouring is shown for
$\unicode[STIX]{x1D70E}$
was increased for better visualization. Colouring is shown for
![]() $\langle |\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{v}_{p}|/|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|\rangle$
and the isocontour (
$\langle |\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{v}_{p}|/|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|\rangle$
and the isocontour (
![]() $\cdots \cdots$
) is at level 1.0. (b) Resulting velocity pattern
$\cdots \cdots$
) is at level 1.0. (b) Resulting velocity pattern
![]() $\langle |\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{U}_{p}|/|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|\rangle$
in the plane spanned by
$\langle |\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{U}_{p}|/|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|\rangle$
in the plane spanned by
![]() $\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
and the particle symmetry axis direction
$\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
and the particle symmetry axis direction
![]() $\widehat{\boldsymbol{z}}$
. Isocontours are shown at levels 0.2 (- - - -) and 0.4 (
$\widehat{\boldsymbol{z}}$
. Isocontours are shown at levels 0.2 (- - - -) and 0.4 (
![]() $\cdots \cdots$
). Ensemble averaging was performed for all particles in the range
$\cdots \cdots$
). Ensemble averaging was performed for all particles in the range
![]() $40^{\circ }\leqslant \unicode[STIX]{x1D6FC}_{p}\leqslant 50^{\circ }$
in case P4.
$40^{\circ }\leqslant \unicode[STIX]{x1D6FC}_{p}\leqslant 50^{\circ }$
in case P4.

Figure 5. Influence of the parameters
![]() $\unicode[STIX]{x1D6FF}^{min}$
(a,b),
$\unicode[STIX]{x1D6FF}^{min}$
(a,b),
![]() $\unicode[STIX]{x1D703}^{up}$
(c,d) and
$\unicode[STIX]{x1D703}^{up}$
(c,d) and
![]() $\unicode[STIX]{x1D70E}$
(e,f) on the magnitude of the reconstructed linear (left) and rotational (right) relative velocity vector at
$\unicode[STIX]{x1D70E}$
(e,f) on the magnitude of the reconstructed linear (left) and rotational (right) relative velocity vector at
![]() $t^{\ast }=1$
. While one parameter is varied in each figure, the other two parameters are constant at the reference values
$t^{\ast }=1$
. While one parameter is varied in each figure, the other two parameters are constant at the reference values
![]() $\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
,
$\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
,
![]() $\unicode[STIX]{x1D703}^{up}=120^{\circ }$
, and
$\unicode[STIX]{x1D703}^{up}=120^{\circ }$
, and
![]() $\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
.
$\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
.
In the following, we discuss the choice of the three parameters
![]() $\unicode[STIX]{x1D703}^{up}$
,
$\unicode[STIX]{x1D703}^{up}$
,
![]() $\unicode[STIX]{x1D6FF}^{min}$
and
$\unicode[STIX]{x1D6FF}^{min}$
and
![]() $\unicode[STIX]{x1D70E}$
. The reconstruction region should exclude the region
$\unicode[STIX]{x1D70E}$
. The reconstruction region should exclude the region
![]() $\unicode[STIX]{x1D6F4}_{p}$
defined in (4.4), since the latter represents the range of the particle-induced velocity disturbances. Figure 5 demonstrates how varying the parameters
$\unicode[STIX]{x1D6F4}_{p}$
defined in (4.4), since the latter represents the range of the particle-induced velocity disturbances. Figure 5 demonstrates how varying the parameters
![]() $\unicode[STIX]{x1D703}^{up}$
,
$\unicode[STIX]{x1D703}^{up}$
,
![]() $\unicode[STIX]{x1D6FF}^{min}$
and
$\unicode[STIX]{x1D6FF}^{min}$
and
![]() $\unicode[STIX]{x1D70E}$
affects the reconstruction of
$\unicode[STIX]{x1D70E}$
affects the reconstruction of
![]() $\boldsymbol{U}_{p}$
and
$\boldsymbol{U}_{p}$
and
![]() $\unicode[STIX]{x1D734}_{p}$
. To this end, the average values of the absolute relative velocities
$\unicode[STIX]{x1D734}_{p}$
. To this end, the average values of the absolute relative velocities
![]() $\langle |\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|/|\boldsymbol{v}_{p}|\rangle$
and relative rotational velocities
$\langle |\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|/|\boldsymbol{v}_{p}|\rangle$
and relative rotational velocities
![]() $\langle |\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p}|/|\unicode[STIX]{x1D74E}_{p}|\rangle$
have been evaluated at
$\langle |\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p}|/|\unicode[STIX]{x1D74E}_{p}|\rangle$
have been evaluated at
![]() $t^{\ast }=1$
. While one parameter is varied in each figure, the other two parameters are constant at the reference values
$t^{\ast }=1$
. While one parameter is varied in each figure, the other two parameters are constant at the reference values
![]() $\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
,
$\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
,
![]() $\unicode[STIX]{x1D703}^{up}=120^{\circ }$
and
$\unicode[STIX]{x1D703}^{up}=120^{\circ }$
and
![]() $\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
. Figures 5(a) and 5(b) show the influence of varying
$\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
. Figures 5(a) and 5(b) show the influence of varying
![]() $\unicode[STIX]{x1D6FF}^{min}$
. It can be seen that at distances below
$\unicode[STIX]{x1D6FF}^{min}$
. It can be seen that at distances below
![]() $\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
, the linear and rotational fluid velocities rapidly reduce towards the particle velocity
$\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
, the linear and rotational fluid velocities rapidly reduce towards the particle velocity
![]() $\boldsymbol{u}_{p}$
and
$\boldsymbol{u}_{p}$
and
![]() $\unicode[STIX]{x1D74E}_{p}$
. This illustrates the particle-induced disturbances which are to be avoided. The absolute relative velocities reach a plateau beyond
$\unicode[STIX]{x1D74E}_{p}$
. This illustrates the particle-induced disturbances which are to be avoided. The absolute relative velocities reach a plateau beyond
![]() $\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
and slowly decay when the reconstruction region is moved further away from the particle. This increasing decorrelation of the reconstructed values of
$\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
and slowly decay when the reconstruction region is moved further away from the particle. This increasing decorrelation of the reconstructed values of
![]() $\boldsymbol{U}_{p}$
and
$\boldsymbol{U}_{p}$
and
![]() $\unicode[STIX]{x1D734}_{p}$
from the local state of the flow near the particle is due to filtering effects when increasing the radius of the reconstruction region.
$\unicode[STIX]{x1D734}_{p}$
from the local state of the flow near the particle is due to filtering effects when increasing the radius of the reconstruction region.
This is further evidenced by the increase of the squared deviation between the local velocities
![]() $\boldsymbol{u}(x)$
and the estimated
$\boldsymbol{u}(x)$
and the estimated
![]() $\boldsymbol{U}_{p}$
within each
$\boldsymbol{U}_{p}$
within each
![]() $\widetilde{\unicode[STIX]{x1D6F4}}_{p}$
, using the same weights as in (4.6). This root-mean-square deviation is computed as
$\widetilde{\unicode[STIX]{x1D6F4}}_{p}$
, using the same weights as in (4.6). This root-mean-square deviation is computed as
 $$\begin{eqnarray}\displaystyle \text{r.m.s. dev.}=\frac{1}{u_{0}}\left\{\left[\int _{\widetilde{\unicode[STIX]{x1D6F4}}_{p}}{\mathcal{C}}_{p}^{up}(\boldsymbol{x})\,\text{d}V\right]^{-1}\int _{\widetilde{\unicode[STIX]{x1D6F4}}_{p}}{\mathcal{C}}_{p}^{up}(\boldsymbol{x})[\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{U}_{p}]^{2}\,\text{d}V\right\}^{1/2}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{r.m.s. dev.}=\frac{1}{u_{0}}\left\{\left[\int _{\widetilde{\unicode[STIX]{x1D6F4}}_{p}}{\mathcal{C}}_{p}^{up}(\boldsymbol{x})\,\text{d}V\right]^{-1}\int _{\widetilde{\unicode[STIX]{x1D6F4}}_{p}}{\mathcal{C}}_{p}^{up}(\boldsymbol{x})[\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{U}_{p}]^{2}\,\text{d}V\right\}^{1/2}, & & \displaystyle\end{eqnarray}$$
and then averaged over all particles. The r.m.s. deviation of
![]() $\unicode[STIX]{x1D734}_{p}$
is analogously computed. Note that the particle velocities
$\unicode[STIX]{x1D734}_{p}$
is analogously computed. Note that the particle velocities
![]() $\boldsymbol{v}_{p}$
and
$\boldsymbol{v}_{p}$
and
![]() $\unicode[STIX]{x1D74E}_{p}$
only indirectly influence (4.9) via the no-slip condition on the particle surface. The r.m.s. deviation of the velocities increases with
$\unicode[STIX]{x1D74E}_{p}$
only indirectly influence (4.9) via the no-slip condition on the particle surface. The r.m.s. deviation of the velocities increases with
![]() $\unicode[STIX]{x1D6FF}^{min}$
due to the growing radius of the reconstruction region
$\unicode[STIX]{x1D6FF}^{min}$
due to the growing radius of the reconstruction region
![]() $\widetilde{\unicode[STIX]{x1D6F4}}_{p}$
, i.e. the increasing filtering effect with respect to the smallest flow scales. At small
$\widetilde{\unicode[STIX]{x1D6F4}}_{p}$
, i.e. the increasing filtering effect with respect to the smallest flow scales. At small
![]() $\unicode[STIX]{x1D6FF}^{min}$
, the r.m.s. deviation of
$\unicode[STIX]{x1D6FF}^{min}$
, the r.m.s. deviation of
![]() $\unicode[STIX]{x1D734}_{p}$
sharply increases due to the counter-rotating vortices attached to the particle surface. The decay of the rotational motion
$\unicode[STIX]{x1D734}_{p}$
sharply increases due to the counter-rotating vortices attached to the particle surface. The decay of the rotational motion
![]() $\unicode[STIX]{x1D734}_{p}$
with
$\unicode[STIX]{x1D734}_{p}$
with
![]() $\unicode[STIX]{x1D6FF}^{min}$
is faster compared to
$\unicode[STIX]{x1D6FF}^{min}$
is faster compared to
![]() $\boldsymbol{U}_{p}$
since the velocity gradient defines smaller length scales.
$\boldsymbol{U}_{p}$
since the velocity gradient defines smaller length scales.
Figures 5(c) and 5(d) show the influence of
![]() $\unicode[STIX]{x1D703}^{up}$
on the velocity reconstruction. It can be seen that beyond
$\unicode[STIX]{x1D703}^{up}$
on the velocity reconstruction. It can be seen that beyond
![]() $\unicode[STIX]{x1D703}^{up}=135^{\circ }$
the magnitude of
$\unicode[STIX]{x1D703}^{up}=135^{\circ }$
the magnitude of
![]() $\boldsymbol{U}_{p}-\boldsymbol{v}_{p}$
decreases due to the reduced velocity in the particle wake. On the contrary, the magnitude of
$\boldsymbol{U}_{p}-\boldsymbol{v}_{p}$
decreases due to the reduced velocity in the particle wake. On the contrary, the magnitude of
![]() $\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p}$
slightly increases due to the increased vorticity in the particle wake. The higher vorticity also causes a steep increase of the r.m.s. deviation of the relative rotational velocity. In the limit
$\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p}$
slightly increases due to the increased vorticity in the particle wake. The higher vorticity also causes a steep increase of the r.m.s. deviation of the relative rotational velocity. In the limit
![]() $\unicode[STIX]{x1D703}^{up}=180^{\circ }$
, no upwind-biased reconstruction is applied and the inclusion of the particle wake deteriorates the estimated values of
$\unicode[STIX]{x1D703}^{up}=180^{\circ }$
, no upwind-biased reconstruction is applied and the inclusion of the particle wake deteriorates the estimated values of
![]() $\boldsymbol{U}_{p}$
and
$\boldsymbol{U}_{p}$
and
![]() $\unicode[STIX]{x1D734}_{p}$
. Varying the width of the reconstruction region
$\unicode[STIX]{x1D734}_{p}$
. Varying the width of the reconstruction region
![]() $\unicode[STIX]{x1D70E}$
has a negligible influence on the velocity reconstruction (figure 5
e,f). The magnitude of
$\unicode[STIX]{x1D70E}$
has a negligible influence on the velocity reconstruction (figure 5
e,f). The magnitude of
![]() $\unicode[STIX]{x1D734}_{p}$
slightly decorrelates with increasing
$\unicode[STIX]{x1D734}_{p}$
slightly decorrelates with increasing
![]() $\unicode[STIX]{x1D70E}$
, i.e. increasing
$\unicode[STIX]{x1D70E}$
, i.e. increasing
![]() $\unicode[STIX]{x1D6FF}^{max}$
, while the r.m.s. deviation slightly increases with
$\unicode[STIX]{x1D6FF}^{max}$
, while the r.m.s. deviation slightly increases with
![]() $\unicode[STIX]{x1D70E}$
due to the growing reconstruction volume. In contrast to
$\unicode[STIX]{x1D70E}$
due to the growing reconstruction volume. In contrast to
![]() $\unicode[STIX]{x1D6FF}^{min}$
, variations in
$\unicode[STIX]{x1D6FF}^{min}$
, variations in
![]() $\unicode[STIX]{x1D70E}$
only produce minor filtering effects since the mid-radius
$\unicode[STIX]{x1D70E}$
only produce minor filtering effects since the mid-radius
![]() $\unicode[STIX]{x1D6FF}_{0}$
of the reconstruction region
$\unicode[STIX]{x1D6FF}_{0}$
of the reconstruction region
![]() $\widetilde{\unicode[STIX]{x1D6F4}}_{p}$
only grows slowly.
$\widetilde{\unicode[STIX]{x1D6F4}}_{p}$
only grows slowly.
The curves show a very similar trend for the different cases which results from the definition of
![]() $\unicode[STIX]{x1D6FF}^{min}$
in terms of the volumetric particle diameter
$\unicode[STIX]{x1D6FF}^{min}$
in terms of the volumetric particle diameter
![]() $d_{p}^{vol}$
. This proves the applicability of the reconstruction scheme to the ellipsoidal particle shapes which are considered in this study. The method is robust for particles with
$d_{p}^{vol}$
. This proves the applicability of the reconstruction scheme to the ellipsoidal particle shapes which are considered in this study. The method is robust for particles with
![]() $d_{p}^{vol}\sim \unicode[STIX]{x1D702}$
and
$d_{p}^{vol}\sim \unicode[STIX]{x1D702}$
and
![]() $d_{p}^{maj}\lesssim \unicode[STIX]{x1D706}$
. For larger particles, pronounced filtering effects are expected and in this case the above and similar reconstruction schemes require careful validation regarding the sensitivity of the measured quantities.
$d_{p}^{maj}\lesssim \unicode[STIX]{x1D706}$
. For larger particles, pronounced filtering effects are expected and in this case the above and similar reconstruction schemes require careful validation regarding the sensitivity of the measured quantities.
In addition to the magnitude of the relative velocities, we verify that the direction of the ambient fluid velocity is suitably reconstructed. For the spherical particles, the relative linear and rotational velocities should align with the hydrodynamic force and torque vectors, i.e.
![]() $\text{cos}(\boldsymbol{F}_{p},\boldsymbol{U}_{p}-\boldsymbol{v}_{p})\approx 1$
and
$\text{cos}(\boldsymbol{F}_{p},\boldsymbol{U}_{p}-\boldsymbol{v}_{p})\approx 1$
and
![]() $\text{cos}(\boldsymbol{T}_{p},\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p})\approx 1$
. Figure 6 shows the development of this alignment while varying
$\text{cos}(\boldsymbol{T}_{p},\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p})\approx 1$
. Figure 6 shows the development of this alignment while varying
![]() $\unicode[STIX]{x1D6FF}^{min}$
and
$\unicode[STIX]{x1D6FF}^{min}$
and
![]() $\unicode[STIX]{x1D703}^{up}$
, whereas
$\unicode[STIX]{x1D703}^{up}$
, whereas
![]() $\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
. It is seen in figure 6(a) that for increasing distances
$\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
. It is seen in figure 6(a) that for increasing distances
![]() $\unicode[STIX]{x1D6FF}^{min}$
, the relative velocities tend to decorrelate from the particle acceleration. Again, this effect is more pronounced for the rotational motion due the smaller length scales. Choosing too narrow an upwind region (
$\unicode[STIX]{x1D6FF}^{min}$
, the relative velocities tend to decorrelate from the particle acceleration. Again, this effect is more pronounced for the rotational motion due the smaller length scales. Choosing too narrow an upwind region (
![]() $\unicode[STIX]{x1D703}^{up}<90^{\circ }$
) deteriorates the reconstruction of the flow direction, see figure 6(b). This effect is explained by the finite particle size, i.e. for decreasing
$\unicode[STIX]{x1D703}^{up}<90^{\circ }$
) deteriorates the reconstruction of the flow direction, see figure 6(b). This effect is explained by the finite particle size, i.e. for decreasing
![]() $\unicode[STIX]{x1D703}^{up}$
the reconstruction volume becomes too small compared to the ambient flow length scale. As opposed to the magnitude of the relative velocities, the flow direction is hardly biased by the particle wake since the latter is axisymmetric for the particle Reynolds numbers encountered in the present study. However, for higher particle Reynolds number the upwind bias may become essential to reproduce the incident flow direction.
$\unicode[STIX]{x1D703}^{up}$
the reconstruction volume becomes too small compared to the ambient flow length scale. As opposed to the magnitude of the relative velocities, the flow direction is hardly biased by the particle wake since the latter is axisymmetric for the particle Reynolds numbers encountered in the present study. However, for higher particle Reynolds number the upwind bias may become essential to reproduce the incident flow direction.

Figure 6. Influence of the parameters
![]() $\unicode[STIX]{x1D6FF}^{min}$
(a) and
$\unicode[STIX]{x1D6FF}^{min}$
(a) and
![]() $\unicode[STIX]{x1D703}^{up}$
(b) on the direction of the reconstructed linear and rotational relative velocity vectors for case S at
$\unicode[STIX]{x1D703}^{up}$
(b) on the direction of the reconstructed linear and rotational relative velocity vectors for case S at
![]() $t^{\ast }=1$
. The relative velocities should align with the hydrodynamic force and torque vectors, i.e.
$t^{\ast }=1$
. The relative velocities should align with the hydrodynamic force and torque vectors, i.e.
![]() $\text{cos}(\boldsymbol{F}_{p},\boldsymbol{U}_{p}-\boldsymbol{v}_{p})\approx 1$
and
$\text{cos}(\boldsymbol{F}_{p},\boldsymbol{U}_{p}-\boldsymbol{v}_{p})\approx 1$
and
![]() $\text{cos}(\boldsymbol{T}_{p},\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p})\approx 1$
. While one parameter is varied in each figure, the other two parameters are constant at the reference values
$\text{cos}(\boldsymbol{T}_{p},\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p})\approx 1$
. While one parameter is varied in each figure, the other two parameters are constant at the reference values
![]() $\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
,
$\unicode[STIX]{x1D6FF}^{min}=d_{p}^{vol}$
,
![]() $\unicode[STIX]{x1D703}^{up}=120^{\circ }$
and
$\unicode[STIX]{x1D703}^{up}=120^{\circ }$
and
![]() $\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
.
$\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
.
In light of the above results, the fluid velocities should be reconstructed with
![]() $d_{p}^{vol}<\unicode[STIX]{x1D6FF}^{min}<1.5d_{p}^{vol}$
and
$d_{p}^{vol}<\unicode[STIX]{x1D6FF}^{min}<1.5d_{p}^{vol}$
and
![]() $90^{\circ }<\unicode[STIX]{x1D703}^{up}<135^{\circ }$
. The parameter
$90^{\circ }<\unicode[STIX]{x1D703}^{up}<135^{\circ }$
. The parameter
![]() $\unicode[STIX]{x1D70E}$
has a minor impact on the reconstructed ambient flow, while small values of
$\unicode[STIX]{x1D70E}$
has a minor impact on the reconstructed ambient flow, while small values of
![]() $\unicode[STIX]{x1D70E}$
tend to decrease filtering effects. In this range, the best correlation of the reconstructed velocities with the particle acceleration and the least bias due to the near-particle shear layer or the particle wake are observed. For the following analyses, we set
$\unicode[STIX]{x1D70E}$
tend to decrease filtering effects. In this range, the best correlation of the reconstructed velocities with the particle acceleration and the least bias due to the near-particle shear layer or the particle wake are observed. For the following analyses, we set
![]() $\unicode[STIX]{x1D6FF}^{min}=1.5d_{p}^{vol}$
,
$\unicode[STIX]{x1D6FF}^{min}=1.5d_{p}^{vol}$
,
![]() $\unicode[STIX]{x1D703}^{up}=120^{\circ }$
and
$\unicode[STIX]{x1D703}^{up}=120^{\circ }$
and
![]() $\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
. The velocity reconstruction is demonstrated in figure 4 for case P4 at
$\unicode[STIX]{x1D70E}=0.1d_{p}^{vol}$
. The velocity reconstruction is demonstrated in figure 4 for case P4 at
![]() $t^{\ast }=1$
. Figure 4(a) illustrates the reconstruction volume with non-zero weight
$t^{\ast }=1$
. Figure 4(a) illustrates the reconstruction volume with non-zero weight
![]() ${\mathcal{C}}_{p}^{up}$
in the upwind region. It shows the average velocity distribution
${\mathcal{C}}_{p}^{up}$
in the upwind region. It shows the average velocity distribution
![]() $\langle |\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{v}_{p}|/|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|\rangle$
in the plane spanned by
$\langle |\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{v}_{p}|/|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|\rangle$
in the plane spanned by
![]() $\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
and the particle symmetry axis direction
$\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
and the particle symmetry axis direction
![]() $\widehat{\boldsymbol{z}}$
. Ensemble averaging was performed for all particles in the range
$\widehat{\boldsymbol{z}}$
. Ensemble averaging was performed for all particles in the range
![]() $40^{\circ }\leqslant \unicode[STIX]{x1D6FC}_{p}\leqslant 50^{\circ }$
, where
$40^{\circ }\leqslant \unicode[STIX]{x1D6FC}_{p}\leqslant 50^{\circ }$
, where
![]() $\unicode[STIX]{x1D6FC}_{p}\equiv \angle (\widehat{\boldsymbol{z}},\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p})$
describes the inclination angle between the symmetry axis and the relative velocity vector. Figure 4(a) demonstrates that a bias of
$\unicode[STIX]{x1D6FC}_{p}\equiv \angle (\widehat{\boldsymbol{z}},\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p})$
describes the inclination angle between the symmetry axis and the relative velocity vector. Figure 4(a) demonstrates that a bias of
![]() $\boldsymbol{U}_{p}$
by the particle wake is avoided using the proposed reconstruction scheme. Figure 4(b) shows the resulting velocity distribution
$\boldsymbol{U}_{p}$
by the particle wake is avoided using the proposed reconstruction scheme. Figure 4(b) shows the resulting velocity distribution
![]() $\langle |\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{U}_{p}|/|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|\rangle$
, i.e. relative to the ambient velocity
$\langle |\boldsymbol{u}(\boldsymbol{x})-\boldsymbol{U}_{p}|/|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|\rangle$
, i.e. relative to the ambient velocity
![]() $\boldsymbol{U}_{p}$
. The small deviation between
$\boldsymbol{U}_{p}$
. The small deviation between
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\boldsymbol{U}_{p}$
in front of the particle confirms the upwind bias in the determination of the ambient velocity. The quick decorrelation of
$\boldsymbol{U}_{p}$
in front of the particle confirms the upwind bias in the determination of the ambient velocity. The quick decorrelation of
![]() $\boldsymbol{u}(\boldsymbol{x})$
and
$\boldsymbol{u}(\boldsymbol{x})$
and
![]() $\boldsymbol{U}_{p}$
with increasing distance from the particle illustrates the overlap of the small flow scales and the particle scale. The Kolmogorov length scale
$\boldsymbol{U}_{p}$
with increasing distance from the particle illustrates the overlap of the small flow scales and the particle scale. The Kolmogorov length scale
![]() $\unicode[STIX]{x1D702}_{i}$
and Taylor length scale
$\unicode[STIX]{x1D702}_{i}$
and Taylor length scale
![]() $\unicode[STIX]{x1D706}_{i}$
at release time are indicated for reference.
$\unicode[STIX]{x1D706}_{i}$
at release time are indicated for reference.
The proposed definitions of
![]() $\boldsymbol{U}_{p}$
and
$\boldsymbol{U}_{p}$
and
![]() $\unicode[STIX]{x1D734}_{p}$
have been further verified by ensuring that their distribution shortly after release of the particles recovers the probability density functions of the global fluid velocity field
$\unicode[STIX]{x1D734}_{p}$
have been further verified by ensuring that their distribution shortly after release of the particles recovers the probability density functions of the global fluid velocity field
![]() $\boldsymbol{u}$
and vorticity field
$\boldsymbol{u}$
and vorticity field
![]() $\unicode[STIX]{x1D74E}$
. Note that these distributions will in general not coincide for particles larger than in the present study, due to the emerging filtering effects of the reconstruction scheme, i.e. due to the inherent filtering effects in the motion of finite-size particles. Additionally, a good agreement of the directly evaluated particle force
$\unicode[STIX]{x1D74E}$
. Note that these distributions will in general not coincide for particles larger than in the present study, due to the emerging filtering effects of the reconstruction scheme, i.e. due to the inherent filtering effects in the motion of finite-size particles. Additionally, a good agreement of the directly evaluated particle force
![]() $\boldsymbol{F}_{p}$
and the estimate
$\boldsymbol{F}_{p}$
and the estimate
![]() $0.5\,C_{D}(Re_{p})\unicode[STIX]{x1D70C}|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|^{2}A_{p}$
, using the empirical drag coefficient
$0.5\,C_{D}(Re_{p})\unicode[STIX]{x1D70C}|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|^{2}A_{p}$
, using the empirical drag coefficient
![]() $C_{D}(Re_{p})=24(1+0.15Re_{p}^{0.687})/Re_{p}$
by Schiller & Naumann (Reference Schiller and Naumann1933), is observed for the majority of the spherical particles at
$C_{D}(Re_{p})=24(1+0.15Re_{p}^{0.687})/Re_{p}$
by Schiller & Naumann (Reference Schiller and Naumann1933), is observed for the majority of the spherical particles at
![]() $t^{\ast }\geqslant 1$
(not shown).
$t^{\ast }\geqslant 1$
(not shown).
As noted earlier, the ambient fluid velocity
![]() $\boldsymbol{U}_{p}$
represents the ‘link’ between the energy balances of particle-resolved simulations, experimental measurements, point-particle schemes and other approaches. However, in contrast to the present simulations in which
$\boldsymbol{U}_{p}$
represents the ‘link’ between the energy balances of particle-resolved simulations, experimental measurements, point-particle schemes and other approaches. However, in contrast to the present simulations in which
![]() $\boldsymbol{U}_{p}$
depicts a quantity derived from the results and does not explicitly enter the simulations, the formulation of
$\boldsymbol{U}_{p}$
depicts a quantity derived from the results and does not explicitly enter the simulations, the formulation of
![]() $\boldsymbol{U}_{p}$
is one of the key components defining the accuracy of any point-particle scheme. Point-particle models for finite-size particles at
$\boldsymbol{U}_{p}$
is one of the key components defining the accuracy of any point-particle scheme. Point-particle models for finite-size particles at
![]() $d_{p}\gtrsim \unicode[STIX]{x1D702}$
are yet in the early stages of development (Balachandar & Eaton Reference Balachandar and Eaton2010; Fröhlich et al.
Reference Fröhlich, Schneiders, Meinke and Schröder2018; Mehrabadi et al.
Reference Mehrabadi, Horwitz, Subramaniam and Mani2018). One of the challenges involves the interpolation of
$d_{p}\gtrsim \unicode[STIX]{x1D702}$
are yet in the early stages of development (Balachandar & Eaton Reference Balachandar and Eaton2010; Fröhlich et al.
Reference Fröhlich, Schneiders, Meinke and Schröder2018; Mehrabadi et al.
Reference Mehrabadi, Horwitz, Subramaniam and Mani2018). One of the challenges involves the interpolation of
![]() $\boldsymbol{U}_{p}$
at the particle location while avoiding self-induced disturbances (Mehrabadi et al.
Reference Mehrabadi, Horwitz, Subramaniam and Mani2018). At the same time, an operator for the reverse projection of the particle force onto the fluid momentum equations is required to retain momentum and energy conservation. For instance, Mehrabadi et al. (Reference Mehrabadi, Horwitz, Subramaniam and Mani2018) have considered a Laplacian term to measure and remove the particle-induced disturbances. This approach was demonstrated to be accurate when
$\boldsymbol{U}_{p}$
at the particle location while avoiding self-induced disturbances (Mehrabadi et al.
Reference Mehrabadi, Horwitz, Subramaniam and Mani2018). At the same time, an operator for the reverse projection of the particle force onto the fluid momentum equations is required to retain momentum and energy conservation. For instance, Mehrabadi et al. (Reference Mehrabadi, Horwitz, Subramaniam and Mani2018) have considered a Laplacian term to measure and remove the particle-induced disturbances. This approach was demonstrated to be accurate when
![]() $(d_{p}/\unicode[STIX]{x1D706})^{2}\ll 1$
which is given in their study of spherical particles at
$(d_{p}/\unicode[STIX]{x1D706})^{2}\ll 1$
which is given in their study of spherical particles at
![]() $d_{p}\approx \unicode[STIX]{x1D702}$
. At increasing particle sizes, the overlap of the turbulent scales and the scale of the particle-induced velocity disturbances exacerbates such an approach. While recent studies demonstrate that the spatial extents of the interpolation and projection operators at
$d_{p}\approx \unicode[STIX]{x1D702}$
. At increasing particle sizes, the overlap of the turbulent scales and the scale of the particle-induced velocity disturbances exacerbates such an approach. While recent studies demonstrate that the spatial extents of the interpolation and projection operators at
![]() $d_{p}\approx \unicode[STIX]{x1D702}$
should be chosen large enough to avoid self-induced disturbances (Fröhlich et al.
Reference Fröhlich, Schneiders, Meinke and Schröder2018; Balachandar, Liu & Lakhote Reference Balachandar, Liu and Lakhote2019), our results above suggest that, if these volumes become too large, the reconstruction may suffer from significant filtering effects (figure 5) and errors in the reconstructed relative velocity direction (figure 6). Moreover, it is obvious that too large a projection region will diffuse hydrodynamic particle–particle interactions. Therefore, the projection and interpolation operators for
$d_{p}\approx \unicode[STIX]{x1D702}$
should be chosen large enough to avoid self-induced disturbances (Fröhlich et al.
Reference Fröhlich, Schneiders, Meinke and Schröder2018; Balachandar, Liu & Lakhote Reference Balachandar, Liu and Lakhote2019), our results above suggest that, if these volumes become too large, the reconstruction may suffer from significant filtering effects (figure 5) and errors in the reconstructed relative velocity direction (figure 6). Moreover, it is obvious that too large a projection region will diffuse hydrodynamic particle–particle interactions. Therefore, the projection and interpolation operators for
![]() $d_{p}>\unicode[STIX]{x1D702}$
necessitate careful construction. Moreover, modelling the rotational motion of the particles requires the reconstruction of the ambient fluid rotation and strain rates, which has hardly been discussed in the literature. The derivation of accurate and robust interpolation and force projection schemes for non-spherical, finite-size particles in point-particle applications is an intricate problem on its own and beyond the scope of the present study.
$d_{p}>\unicode[STIX]{x1D702}$
necessitate careful construction. Moreover, modelling the rotational motion of the particles requires the reconstruction of the ambient fluid rotation and strain rates, which has hardly been discussed in the literature. The derivation of accurate and robust interpolation and force projection schemes for non-spherical, finite-size particles in point-particle applications is an intricate problem on its own and beyond the scope of the present study.
4.3 Particle-induced dissipation rate of non-spherical particles
Using the above definitions, the validity of model (4.4) is verified for the present cases in figure 7. Ensemble averaging was performed using 10 bins in the range
![]() $0\leqslant {\mathcal{E}}_{p}/{\mathcal{E}}_{p,ref}\leqslant 25$
, with
$0\leqslant {\mathcal{E}}_{p}/{\mathcal{E}}_{p,ref}\leqslant 25$
, with
![]() ${\mathcal{E}}_{p,ref}=\unicode[STIX]{x1D70C}u_{0}^{3}d_{p}^{2}$
, for each case. It can be seen that the model closely reproduces the dissipation rate
${\mathcal{E}}_{p,ref}=\unicode[STIX]{x1D70C}u_{0}^{3}d_{p}^{2}$
, for each case. It can be seen that the model closely reproduces the dissipation rate
![]() $\int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D716}\,\text{d}V$
which directly has been integrated for each particle. Since for its derivation no assumptions were made on the particle shape (Schneiders et al.
Reference Schneiders, Meinke and Schröder2017a
), the model exhibits a good agreement with the data irrespective of the aspect ratio
$\int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D716}\,\text{d}V$
which directly has been integrated for each particle. Since for its derivation no assumptions were made on the particle shape (Schneiders et al.
Reference Schneiders, Meinke and Schröder2017a
), the model exhibits a good agreement with the data irrespective of the aspect ratio
![]() $\unicode[STIX]{x1D6FD}$
. Even for case P8, in which the major axis of the ellipsoids is of the order of the Taylor length scale (cf. table 1), no substantial deterioration of the model quality is observed. The standard deviation of the data in figure 7 increases with higher values of
$\unicode[STIX]{x1D6FD}$
. Even for case P8, in which the major axis of the ellipsoids is of the order of the Taylor length scale (cf. table 1), no substantial deterioration of the model quality is observed. The standard deviation of the data in figure 7 increases with higher values of
![]() $\int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D716}\,\text{d}V$
. The statistical sampling at these values becomes less significant, corresponding to the relatively small number of particles at larger relative velocities, i.e. larger
$\int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D716}\,\text{d}V$
. The statistical sampling at these values becomes less significant, corresponding to the relatively small number of particles at larger relative velocities, i.e. larger
![]() $Re_{p}$
. On average,
$Re_{p}$
. On average,
![]() $\langle Re_{p}\rangle \approx 14$
at
$\langle Re_{p}\rangle \approx 14$
at
![]() $t^{\ast }=1$
while values of
$t^{\ast }=1$
while values of
![]() ${\mathcal{E}}_{p}/{\mathcal{E}}_{p,ref}=25$
correspond to
${\mathcal{E}}_{p}/{\mathcal{E}}_{p,ref}=25$
correspond to
![]() $Re_{p}\approx 30$
. Only few particles attain higher values of
$Re_{p}\approx 30$
. Only few particles attain higher values of
![]() $Re_{p}$
. The slight tendency of the model to underpredict
$Re_{p}$
. The slight tendency of the model to underpredict
![]() $\int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D716}\,\text{d}V$
is due to the relatively large volume fraction of the particle phase which leads to a mutual overlap of adjacent
$\int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D716}\,\text{d}V$
is due to the relatively large volume fraction of the particle phase which leads to a mutual overlap of adjacent
![]() $\unicode[STIX]{x1D6F4}_{p}$
. These hydrodynamic interactions increase with the aspect ratio of the particles, causing the average particle-to-particle distance to decrease although the volume fraction remains constant. Note that figures 4–7, which are shown at
$\unicode[STIX]{x1D6F4}_{p}$
. These hydrodynamic interactions increase with the aspect ratio of the particles, causing the average particle-to-particle distance to decrease although the volume fraction remains constant. Note that figures 4–7, which are shown at
![]() $t^{\ast }=1$
, are qualitatively representative for the data at all later time levels.
$t^{\ast }=1$
, are qualitatively representative for the data at all later time levels.

Figure 7. Particle-induced dissipation rate, directly computed by the volume integral
![]() $\int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D716}\,\text{d}V$
, versus the analytical model
$\int _{\unicode[STIX]{x1D6F4}_{p}}\unicode[STIX]{x1D716}\,\text{d}V$
, versus the analytical model
![]() ${\mathcal{E}}_{p}$
in (4.4), both normalized by
${\mathcal{E}}_{p}$
in (4.4), both normalized by
![]() ${\mathcal{E}}_{p,ref}=\unicode[STIX]{x1D70C}u_{0}^{3}d_{p}^{2}$
at time level
${\mathcal{E}}_{p,ref}=\unicode[STIX]{x1D70C}u_{0}^{3}d_{p}^{2}$
at time level
![]() $t^{\ast }=1$
. Error bars indicate the standard deviation.
$t^{\ast }=1$
. Error bars indicate the standard deviation.
It has to be emphasized that the good agreement of the above model is not the outcome of calibrating the definitions of
![]() $\unicode[STIX]{x1D6F4}_{p}$
and
$\unicode[STIX]{x1D6F4}_{p}$
and
![]() $\boldsymbol{U}_{p}$
. This is substantiated by figure 8, which shows the convergence of the evaluated dissipation rate
$\boldsymbol{U}_{p}$
. This is substantiated by figure 8, which shows the convergence of the evaluated dissipation rate
![]() $\int _{\unicode[STIX]{x1D6F4}_{p}}\!\unicode[STIX]{x1D716}\,\text{d}V$
when increasing the integration distance
$\int _{\unicode[STIX]{x1D6F4}_{p}}\!\unicode[STIX]{x1D716}\,\text{d}V$
when increasing the integration distance
![]() $\unicode[STIX]{x1D6E5}$
, i.e. the volume
$\unicode[STIX]{x1D6E5}$
, i.e. the volume
![]() $\unicode[STIX]{x1D6F4}_{p}$
, at time
$\unicode[STIX]{x1D6F4}_{p}$
, at time
![]() $t^{\ast }=2$
for cases S and P8. When enlarging the integration region
$t^{\ast }=2$
for cases S and P8. When enlarging the integration region
![]() $\unicode[STIX]{x1D6F4}_{p}$
, a convergence of the correlation shown in figure 7 is observed although the volume
$\unicode[STIX]{x1D6F4}_{p}$
, a convergence of the correlation shown in figure 7 is observed although the volume
![]() $\unicode[STIX]{x1D6F4}_{p}$
rapidly grows by the cube of the distance
$\unicode[STIX]{x1D6F4}_{p}$
rapidly grows by the cube of the distance
![]() $\unicode[STIX]{x1D6E5}$
. At the same time, the scattering of the data increases due to the aforementioned particle–particle interferences which become more probable to be captured when increasing
$\unicode[STIX]{x1D6E5}$
. At the same time, the scattering of the data increases due to the aforementioned particle–particle interferences which become more probable to be captured when increasing
![]() $\unicode[STIX]{x1D6F4}_{p}$
. At
$\unicode[STIX]{x1D6F4}_{p}$
. At
![]() $\unicode[STIX]{x1D6E5}=1.5d_{p}^{vol}$
, most of the particle-induced dissipation is captured in all cases. Likewise, as previously demonstrated in figure 5, an increase of the reconstruction region for the determination of
$\unicode[STIX]{x1D6E5}=1.5d_{p}^{vol}$
, most of the particle-induced dissipation is captured in all cases. Likewise, as previously demonstrated in figure 5, an increase of the reconstruction region for the determination of
![]() $\boldsymbol{U}_{p}$
mostly introduces filtering effects but only slowly deteriorates the quality of the model (4.4). That is, the presented model is very robust with respect to these definitions if the particle-induced disturbances are captured by
$\boldsymbol{U}_{p}$
mostly introduces filtering effects but only slowly deteriorates the quality of the model (4.4). That is, the presented model is very robust with respect to these definitions if the particle-induced disturbances are captured by
![]() $\unicode[STIX]{x1D6F4}_{p}$
and are avoided by
$\unicode[STIX]{x1D6F4}_{p}$
and are avoided by
![]() $\widetilde{\unicode[STIX]{x1D6F4}_{p}}$
.
$\widetilde{\unicode[STIX]{x1D6F4}_{p}}$
.

Figure 8. Convergence of the particle-induced dissipation rate with increasing radius
![]() $\unicode[STIX]{x1D6E5}$
of the integration volume, shown for cases S (a) and P8 (b) at
$\unicode[STIX]{x1D6E5}$
of the integration volume, shown for cases S (a) and P8 (b) at
![]() $t^{\ast }=2$
: The integrated dissipation rate converges towards the model prediction while
$t^{\ast }=2$
: The integrated dissipation rate converges towards the model prediction while
![]() $|\unicode[STIX]{x1D6F4}_{p}|$
grows by
$|\unicode[STIX]{x1D6F4}_{p}|$
grows by
![]() $\unicode[STIX]{x1D6E5}^{3}$
.
$\unicode[STIX]{x1D6E5}^{3}$
.
Combining the model for
![]() ${\mathcal{E}}_{p}$
and the definition of
${\mathcal{E}}_{p}$
and the definition of
![]() $\unicode[STIX]{x1D6F9}_{p}$
, it follows that the influence of an individual particle on the fluid kinetic energy balance, when fluid inertia can be neglected and the flow is dilute, effectively reduces to
$\unicode[STIX]{x1D6F9}_{p}$
, it follows that the influence of an individual particle on the fluid kinetic energy balance, when fluid inertia can be neglected and the flow is dilute, effectively reduces to
![]() $\unicode[STIX]{x1D6F9}_{p}-{\mathcal{E}}_{p}=-\boldsymbol{F}_{p}\boldsymbol{\cdot }\boldsymbol{U}_{p}-\boldsymbol{T}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{p}$
. The share of the rotational terms in the values of
$\unicode[STIX]{x1D6F9}_{p}-{\mathcal{E}}_{p}=-\boldsymbol{F}_{p}\boldsymbol{\cdot }\boldsymbol{U}_{p}-\boldsymbol{T}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{p}$
. The share of the rotational terms in the values of
![]() ${\mathcal{E}}_{p}$
and
${\mathcal{E}}_{p}$
and
![]() $\unicode[STIX]{x1D6F9}_{p}$
is small in the present cases due to the absence of mean shear. Let
$\unicode[STIX]{x1D6F9}_{p}$
is small in the present cases due to the absence of mean shear. Let
![]() ${\mathcal{E}}_{p}^{rot}=\boldsymbol{T}_{p}\boldsymbol{\cdot }(\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p})$
denote the rotational component of
${\mathcal{E}}_{p}^{rot}=\boldsymbol{T}_{p}\boldsymbol{\cdot }(\unicode[STIX]{x1D734}_{p}-\unicode[STIX]{x1D74E}_{p})$
denote the rotational component of
![]() ${\mathcal{E}}_{p}\approx {\mathcal{E}}_{p}^{lin}+{\mathcal{E}}_{p}^{rot}$
. The overall fraction of
${\mathcal{E}}_{p}\approx {\mathcal{E}}_{p}^{lin}+{\mathcal{E}}_{p}^{rot}$
. The overall fraction of
![]() ${\mathcal{E}}_{p}^{rot}$
at
${\mathcal{E}}_{p}^{rot}$
at
![]() $t^{\ast }=1$
amounts to roughly 2.5 % for case P8, 0.8 % for case P4, 0.4 % for case O4 and 0.2 % for case S. These values slowly decay over time due to the minor interaction of the particles with the small flow scales. Although a substantial number of particles in case P8 attain states with
$t^{\ast }=1$
amounts to roughly 2.5 % for case P8, 0.8 % for case P4, 0.4 % for case O4 and 0.2 % for case S. These values slowly decay over time due to the minor interaction of the particles with the small flow scales. Although a substantial number of particles in case P8 attain states with
![]() ${\mathcal{E}}_{p}^{rot}\sim {\mathcal{E}}_{p}^{lin}$
when
${\mathcal{E}}_{p}^{rot}\sim {\mathcal{E}}_{p}^{lin}$
when
![]() $|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|$
is small, these do not contribute significantly to the global dissipation since
$|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|$
is small, these do not contribute significantly to the global dissipation since
![]() ${\mathcal{E}}_{p}^{lin}\sim |\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|^{2}$
. However, for the prolates
${\mathcal{E}}_{p}^{lin}\sim |\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|^{2}$
. However, for the prolates
![]() ${\mathcal{E}}_{p}^{rot}$
grows by the power of
${\mathcal{E}}_{p}^{rot}$
grows by the power of
![]() $3$
–
$3$
–
![]() $4$
with
$4$
with
![]() $\unicode[STIX]{x1D6FD}$
, such that substantially larger values may be observed for longer fibres.
$\unicode[STIX]{x1D6FD}$
, such that substantially larger values may be observed for longer fibres.

Figure 9. Particle orientation impact on energy budget: average particle-induced dissipation
![]() ${\mathcal{E}}_{p}$
(a) and energy transfer
${\mathcal{E}}_{p}$
(a) and energy transfer
![]() $\unicode[STIX]{x1D6F9}_{p}$
(b) normalized by the expected dissipation of a sphere
$\unicode[STIX]{x1D6F9}_{p}$
(b) normalized by the expected dissipation of a sphere
![]() ${\mathcal{E}}_{p}^{sphere}$
and as a function of the particle alignment
${\mathcal{E}}_{p}^{sphere}$
and as a function of the particle alignment
![]() $\text{cos}(\unicode[STIX]{x1D6FC}_{p})$
at
$\text{cos}(\unicode[STIX]{x1D6FC}_{p})$
at
![]() $t^{\ast }=1$
.
$t^{\ast }=1$
.
The direct contribution of the rotational particle motion to the energy balance via
![]() ${\mathcal{E}}_{p}^{rot}$
and the rotational terms in
${\mathcal{E}}_{p}^{rot}$
and the rotational terms in
![]() $\unicode[STIX]{x1D6F9}_{p}$
may become more significant in anisotropic turbulence. It is emphasized, however, that the rotational motion also indirectly influences
$\unicode[STIX]{x1D6F9}_{p}$
may become more significant in anisotropic turbulence. It is emphasized, however, that the rotational motion also indirectly influences
![]() ${\mathcal{E}}_{p}$
and
${\mathcal{E}}_{p}$
and
![]() $\unicode[STIX]{x1D6F9}_{p}$
via the linear force
$\unicode[STIX]{x1D6F9}_{p}$
via the linear force
![]() $\boldsymbol{F}_{p}$
, leading to the significant differences in
$\boldsymbol{F}_{p}$
, leading to the significant differences in
![]() $\unicode[STIX]{x1D6F9}_{p}$
and
$\unicode[STIX]{x1D6F9}_{p}$
and
![]() ${\mathcal{E}}_{p}$
between cases S and P8 (figure 3). That is, the absolute values of
${\mathcal{E}}_{p}$
between cases S and P8 (figure 3). That is, the absolute values of
![]() ${\mathcal{E}}_{p}$
and
${\mathcal{E}}_{p}$
and
![]() $\unicode[STIX]{x1D6F9}_{p}$
tend to be significantly larger for the non-spherical particles. This is demonstrated in figure 9, which shows the impact of the particle orientation on the average values of
$\unicode[STIX]{x1D6F9}_{p}$
tend to be significantly larger for the non-spherical particles. This is demonstrated in figure 9, which shows the impact of the particle orientation on the average values of
![]() ${\mathcal{E}}_{p}$
and
${\mathcal{E}}_{p}$
and
![]() $\unicode[STIX]{x1D6F9}_{p}$
. To remove the dependence of these terms on the instantaneous particle Reynolds number, they are non-dimensionalized by the expected value for a spherical particle of the same volume and same
$\unicode[STIX]{x1D6F9}_{p}$
. To remove the dependence of these terms on the instantaneous particle Reynolds number, they are non-dimensionalized by the expected value for a spherical particle of the same volume and same
![]() $Re_{p}$
. Using (4.4) and neglecting the in this case subordinate rotational component, it can be estimated as
$Re_{p}$
. Using (4.4) and neglecting the in this case subordinate rotational component, it can be estimated as
![]() ${\mathcal{E}}_{p}^{sphere}=0.5\,C_{D}(Re_{p})\unicode[STIX]{x1D70C}|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|^{3}A_{p}$
, with the drag coefficient
${\mathcal{E}}_{p}^{sphere}=0.5\,C_{D}(Re_{p})\unicode[STIX]{x1D70C}|\boldsymbol{U}_{p}-\boldsymbol{v}_{p}|^{3}A_{p}$
, with the drag coefficient
![]() $C_{D}(Re_{p})$
defined above and
$C_{D}(Re_{p})$
defined above and
![]() $A_{p}=\unicode[STIX]{x03C0}(d_{p}^{vol})^{2}/4$
. Ensemble averaging was performed using 10 bins in the range
$A_{p}=\unicode[STIX]{x03C0}(d_{p}^{vol})^{2}/4$
. Ensemble averaging was performed using 10 bins in the range
![]() $0\leqslant |\text{cos}(\unicode[STIX]{x1D6FC}_{p})|\leqslant 1$
. As expected, the spherical particles in case S show a uniform distribution with respect to their orientation while the average value of
$0\leqslant |\text{cos}(\unicode[STIX]{x1D6FC}_{p})|\leqslant 1$
. As expected, the spherical particles in case S show a uniform distribution with respect to their orientation while the average value of
![]() ${\mathcal{E}}_{p}$
is close to
${\mathcal{E}}_{p}$
is close to
![]() ${\mathcal{E}}_{p}^{sphere}$
. This agreement again confirms the accurate reconstruction of the velocity
${\mathcal{E}}_{p}^{sphere}$
. This agreement again confirms the accurate reconstruction of the velocity
![]() $\boldsymbol{U}_{p}$
. The average value of
$\boldsymbol{U}_{p}$
. The average value of
![]() $|\unicode[STIX]{x1D6F9}_{p}|$
is slightly smaller than
$|\unicode[STIX]{x1D6F9}_{p}|$
is slightly smaller than
![]() ${\mathcal{E}}_{p}$
as anticipated from the net kinetic energy decay (figure 3).
${\mathcal{E}}_{p}$
as anticipated from the net kinetic energy decay (figure 3).
For the non-spherical particles the smallest values of
![]() $|\unicode[STIX]{x1D6F9}_{p}|$
and
$|\unicode[STIX]{x1D6F9}_{p}|$
and
![]() ${\mathcal{E}}_{p}$
are observed when their surface perpendicular to the direction of
${\mathcal{E}}_{p}$
are observed when their surface perpendicular to the direction of
![]() $\boldsymbol{U}_{p}-\boldsymbol{v}_{p}$
is minimal, i.e. when
$\boldsymbol{U}_{p}-\boldsymbol{v}_{p}$
is minimal, i.e. when
![]() $|\text{cos}(\unicode[STIX]{x1D6FC}_{p})|=1$
for prolate particles and
$|\text{cos}(\unicode[STIX]{x1D6FC}_{p})|=1$
for prolate particles and
![]() $|\text{cos}(\unicode[STIX]{x1D6FC}_{p})|=0$
for oblate particles. Even though the projected area in this case is smaller than for the spheres, the increased total surface area leads to similar values of
$|\text{cos}(\unicode[STIX]{x1D6FC}_{p})|=0$
for oblate particles. Even though the projected area in this case is smaller than for the spheres, the increased total surface area leads to similar values of
![]() $|\unicode[STIX]{x1D6F9}_{p}|$
and
$|\unicode[STIX]{x1D6F9}_{p}|$
and
![]() ${\mathcal{E}}_{p}$
. As the particles change their alignment with the relative flow direction,
${\mathcal{E}}_{p}$
. As the particles change their alignment with the relative flow direction,
![]() $|\unicode[STIX]{x1D6F9}_{p}|$
and
$|\unicode[STIX]{x1D6F9}_{p}|$
and
![]() ${\mathcal{E}}_{p}$
substantially increase with the aspect ratio of the particles. For instance, in case P8 the particle-induced dissipation rate is approximately
${\mathcal{E}}_{p}$
substantially increase with the aspect ratio of the particles. For instance, in case P8 the particle-induced dissipation rate is approximately
![]() $2.4$
times higher on average than for the spherical particles when
$2.4$
times higher on average than for the spherical particles when
![]() $\widehat{\boldsymbol{z}}$
and
$\widehat{\boldsymbol{z}}$
and
![]() $\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
are orthogonal. This behaviour explains why the total dissipation and energy transfer rates strongly increase with the aspect ratio (figure 3). In the present cases, the particle orientation is almost uniform. In general, the global energy balance highly depends on the distribution of the particle orientations and also the particle Reynolds numbers.
$\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
are orthogonal. This behaviour explains why the total dissipation and energy transfer rates strongly increase with the aspect ratio (figure 3). In the present cases, the particle orientation is almost uniform. In general, the global energy balance highly depends on the distribution of the particle orientations and also the particle Reynolds numbers.

Figure 10. Average relative fluid kinetic energy
![]() $\langle e_{k}-\overline{e_{k}}\rangle /u_{0}^{2}$
in the plane spanned by
$\langle e_{k}-\overline{e_{k}}\rangle /u_{0}^{2}$
in the plane spanned by
![]() $\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
and
$\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
and
![]() $\widehat{\boldsymbol{z}}_{p}$
: case S (a) and case P8 for three classes of orientations
$\widehat{\boldsymbol{z}}_{p}$
: case S (a) and case P8 for three classes of orientations
![]() $\unicode[STIX]{x1D6FC}_{p}$
(b–d). Isocontours are shown at
$\unicode[STIX]{x1D6FC}_{p}$
(b–d). Isocontours are shown at
![]() $-0.05$
(
$-0.05$
(
![]() $\cdots \cdots$
) and 0.25 (- - - -).
$\cdots \cdots$
) and 0.25 (- - - -).
In figure 10 the impact of the particle orientation in case P8 is illustrated by the average pattern of fluid kinetic energy, subtracted by the global mean value
![]() $\overline{e_{k}}=E_{k}/|\unicode[STIX]{x1D6F6}_{f}|$
. The flow patterns were evaluated in the plane spanned by
$\overline{e_{k}}=E_{k}/|\unicode[STIX]{x1D6F6}_{f}|$
. The flow patterns were evaluated in the plane spanned by
![]() $\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
and the symmetry axis direction
$\widehat{\boldsymbol{U}}_{p}-\widehat{\boldsymbol{v}}_{p}$
and the symmetry axis direction
![]() $\widehat{\boldsymbol{z}}$
. For P8, averaging was performed for subsets of particles with
$\widehat{\boldsymbol{z}}$
. For P8, averaging was performed for subsets of particles with
![]() $0^{\circ }\leqslant |\unicode[STIX]{x1D6FC}_{p}|\leqslant 10^{\circ }$
,
$0^{\circ }\leqslant |\unicode[STIX]{x1D6FC}_{p}|\leqslant 10^{\circ }$
,
![]() $40^{\circ }\leqslant |\unicode[STIX]{x1D6FC}_{p}|\leqslant 50^{\circ }$
and
$40^{\circ }\leqslant |\unicode[STIX]{x1D6FC}_{p}|\leqslant 50^{\circ }$
and
![]() $80^{\circ }\leqslant |\unicode[STIX]{x1D6FC}_{p}|\leqslant 90^{\circ }$
, i.e. with a slight smoothing effect due to the variation of
$80^{\circ }\leqslant |\unicode[STIX]{x1D6FC}_{p}|\leqslant 90^{\circ }$
, i.e. with a slight smoothing effect due to the variation of
![]() $\unicode[STIX]{x1D6FC}_{p}$
by
$\unicode[STIX]{x1D6FC}_{p}$
by
![]() $\pm 5^{\circ }$
. These states are compared to the flow pattern obtained for case S. It can be seen that the fluid kinetic energy sharply increases close to the particle surface where the ambient fluid tends to move at the particle velocity. For small
$\pm 5^{\circ }$
. These states are compared to the flow pattern obtained for case S. It can be seen that the fluid kinetic energy sharply increases close to the particle surface where the ambient fluid tends to move at the particle velocity. For small
![]() $|\unicode[STIX]{x1D6FC}_{p}|$
, the projected area of the P8 particles is smaller than for the spheres and thus the peak increase of
$|\unicode[STIX]{x1D6FC}_{p}|$
, the projected area of the P8 particles is smaller than for the spheres and thus the peak increase of
![]() $e_{k}$
at the particle surfaces is smaller than for S, corresponding to smaller relative velocities. At increasing
$e_{k}$
at the particle surfaces is smaller than for S, corresponding to smaller relative velocities. At increasing
![]() $|\unicode[STIX]{x1D6FC}_{p}|$
, the prolates tend to act as bluff bodies for the local fluid flow and an increasing region of fluid is accelerated or decelerated in the wake region of the particles while
$|\unicode[STIX]{x1D6FC}_{p}|$
, the prolates tend to act as bluff bodies for the local fluid flow and an increasing region of fluid is accelerated or decelerated in the wake region of the particles while
![]() $\boldsymbol{U}_{p}-\boldsymbol{v}_{p}$
increases. The resulting strong velocity gradients lead to the intense strain rate and therefore larger dissipation rate for the ellipsoidal particles.
$\boldsymbol{U}_{p}-\boldsymbol{v}_{p}$
increases. The resulting strong velocity gradients lead to the intense strain rate and therefore larger dissipation rate for the ellipsoidal particles.
5 Final remarks and implications for point-particle modeling
Direct particle–fluid simulations of heavy spheres and ellipsoids interacting with decaying isotropic turbulence were conducted, extending the results on spherical particles of Kolmogorov length scale size (Schneiders et al.
Reference Schneiders, Meinke and Schröder2017a
) to
![]() $O(10^{4})$
non-spherical particles. The particle minor and major axes in the considered cases range between Kolmogorov and Taylor length scale size. By explicitly resolving the stresses acting on the fluid–particle interfaces, the modulation of the turbulent flow was precisely captured.
$O(10^{4})$
non-spherical particles. The particle minor and major axes in the considered cases range between Kolmogorov and Taylor length scale size. By explicitly resolving the stresses acting on the fluid–particle interfaces, the modulation of the turbulent flow was precisely captured.
The development of Euler–Lagrange point-particle models capable of representing non-spherical particles at
![]() $d_{p}^{vol}\gtrsim \unicode[STIX]{x1D702}$
is a major challenge for the prediction of two-phase flows in various applications. One of the open questions concerns the two-way interaction since the particle scale and the smallest flow scales overlap. Using the expression for the particle-induced dissipation rate (4.4), the local kinetic energy balance induced by individual particles can be assessed. Analogously to the discussion for spherical particles in Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
), the conservation of energy by two-way coupled Lagrangian point-particle models is discussed for non-spherical particles in the following. The linear motion leads to a net impact of
$d_{p}^{vol}\gtrsim \unicode[STIX]{x1D702}$
is a major challenge for the prediction of two-phase flows in various applications. One of the open questions concerns the two-way interaction since the particle scale and the smallest flow scales overlap. Using the expression for the particle-induced dissipation rate (4.4), the local kinetic energy balance induced by individual particles can be assessed. Analogously to the discussion for spherical particles in Schneiders et al. (Reference Schneiders, Meinke and Schröder2017a
), the conservation of energy by two-way coupled Lagrangian point-particle models is discussed for non-spherical particles in the following. The linear motion leads to a net impact of
![]() $-\boldsymbol{F}_{p}\boldsymbol{\cdot }\boldsymbol{U}_{p}$
on the fluid kinetic energy balance due to an individual particle. This corresponds to the feedback term which is applied in the majority of two-way coupled point-particle particle schemes, where
$-\boldsymbol{F}_{p}\boldsymbol{\cdot }\boldsymbol{U}_{p}$
on the fluid kinetic energy balance due to an individual particle. This corresponds to the feedback term which is applied in the majority of two-way coupled point-particle particle schemes, where
![]() $\boldsymbol{U}_{p}$
is usually defined as the fluid velocity interpolated at the particle position. Note that sometimes approaches to reduce self-induced disturbances are included, see e.g. Mehrabadi et al. (Reference Mehrabadi, Horwitz, Subramaniam and Mani2018), Balachandar et al. (Reference Balachandar, Liu and Lakhote2019). It follows that these schemes implicitly account for the particle-induced dissipation without explicitly resolving the responsible velocity gradients and disturbance length scales. They can therefore be expected to accurately reproduce the distribution of kinetic energy whenever
$\boldsymbol{U}_{p}$
is usually defined as the fluid velocity interpolated at the particle position. Note that sometimes approaches to reduce self-induced disturbances are included, see e.g. Mehrabadi et al. (Reference Mehrabadi, Horwitz, Subramaniam and Mani2018), Balachandar et al. (Reference Balachandar, Liu and Lakhote2019). It follows that these schemes implicitly account for the particle-induced dissipation without explicitly resolving the responsible velocity gradients and disturbance length scales. They can therefore be expected to accurately reproduce the distribution of kinetic energy whenever
![]() $\boldsymbol{F}_{p}$
and
$\boldsymbol{F}_{p}$
and
![]() $\boldsymbol{U}_{p}$
are accurately determined for all particle orientations. The present results indicate that a bias of
$\boldsymbol{U}_{p}$
are accurately determined for all particle orientations. The present results indicate that a bias of
![]() $\boldsymbol{F}_{p}$
or
$\boldsymbol{F}_{p}$
or
![]() $\boldsymbol{U}_{p}$
by self-induced disturbances or filtering effects can lead to significant errors in the determination of the energy exchange between the phases.
$\boldsymbol{U}_{p}$
by self-induced disturbances or filtering effects can lead to significant errors in the determination of the energy exchange between the phases.
An analogous inspection of the rotational terms leads to an effective impact of
![]() $-\boldsymbol{T}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{p}$
on the fluid kinetic energy balance per particle. In Andersson et al. (Reference Andersson, Zhao and Barri2012) a torque coupling scheme for small non-spherical particles was proposed based on an analogy to micropolar fluids. In their approach, the Stokes shear tensor is altered by an anti-symmetric particle stress tensor
$-\boldsymbol{T}_{p}\boldsymbol{\cdot }\unicode[STIX]{x1D734}_{p}$
on the fluid kinetic energy balance per particle. In Andersson et al. (Reference Andersson, Zhao and Barri2012) a torque coupling scheme for small non-spherical particles was proposed based on an analogy to micropolar fluids. In their approach, the Stokes shear tensor is altered by an anti-symmetric particle stress tensor
![]() $\unicode[STIX]{x1D749}_{p}$
such that
$\unicode[STIX]{x1D749}_{p}$
such that
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D749}_{p}\equiv \unicode[STIX]{x1D735}\times \boldsymbol{T}_{p}$
is subtracted from the fluid momentum equations. The resulting term in the energy balance follows from multiplication with the local fluid velocity, i.e.
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D749}_{p}\equiv \unicode[STIX]{x1D735}\times \boldsymbol{T}_{p}$
is subtracted from the fluid momentum equations. The resulting term in the energy balance follows from multiplication with the local fluid velocity, i.e.
![]() $-\boldsymbol{U}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{T}_{p})=-(\unicode[STIX]{x1D735}\times \boldsymbol{U})\boldsymbol{\cdot }\boldsymbol{T}_{p}=-\unicode[STIX]{x1D734}\boldsymbol{\cdot }\boldsymbol{T}_{p}$
, corresponding to the rotational transfer term above, i.e. implicitly accounting for the rotationally induced dissipation. That is, unless the magnitude of this term is orders of magnitude smaller than its linear counterpart, a torque coupling scheme proves necessary for the conservation of energy in these models. In any case, even if this direct rotational contribution is small, the present results evidence the linear part of the two-way coupling rate,
$-\boldsymbol{U}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\times \boldsymbol{T}_{p})=-(\unicode[STIX]{x1D735}\times \boldsymbol{U})\boldsymbol{\cdot }\boldsymbol{T}_{p}=-\unicode[STIX]{x1D734}\boldsymbol{\cdot }\boldsymbol{T}_{p}$
, corresponding to the rotational transfer term above, i.e. implicitly accounting for the rotationally induced dissipation. That is, unless the magnitude of this term is orders of magnitude smaller than its linear counterpart, a torque coupling scheme proves necessary for the conservation of energy in these models. In any case, even if this direct rotational contribution is small, the present results evidence the linear part of the two-way coupling rate,
![]() $-\boldsymbol{F}_{p}\boldsymbol{\cdot }\boldsymbol{U}_{p}$
, to be highly dependent on the orientation and the shape of the particles, i.e. to be indirectly impacted by the rotational motion. Therefore, an orientation-sensitive model for the particle drag is required to reproduce the balance of fluid kinetic energy.
$-\boldsymbol{F}_{p}\boldsymbol{\cdot }\boldsymbol{U}_{p}$
, to be highly dependent on the orientation and the shape of the particles, i.e. to be indirectly impacted by the rotational motion. Therefore, an orientation-sensitive model for the particle drag is required to reproduce the balance of fluid kinetic energy.
Provided that the hydrodynamic force and torque acting on the particle are known as a function of the particle Reynolds number and the orientation of the particle, the particle-induced dissipation rate can be evaluated by (4.4). The remaining quantities are typically available in point-particle schemes. At increasing particle diameter, the fluid inertia term
![]() ${\mathcal{I}}_{f}$
becomes more significant. However, unlike spherical particles for which a ‘standard drag curve’ is established (Clift, Grace & Weber Reference Clift, Grace and Weber1978), no such expression exists for ellipsoidal or general particle shapes. Generalized correlations have been developed for specific particle shapes (Sanjeevi, Kuipers & Padding Reference Sanjeevi, Kuipers and Padding2018; Andersson & Jiang Reference Andersson and Jiang2019) and attempts have been made to provide curve fits covering a broader parameter space using particle-resolved simulations (Ouchene et al.
Reference Ouchene, Khalij, Arcen and Tanièrea2016). However, as discussed by Andersson & Jiang (Reference Andersson and Jiang2019) such simulations face several numerical challenges, specifically for moderate particle Reynolds numbers, and they conclude that ‘the accuracy of already existing formulas can hardly be assessed’. The importance of such fluid inertia corrections for point-particle simulations of spherical particles has recently been evidenced by conducting direct comparisons with particle-resolved simulations (Schneiders, Meinke & Schröder Reference Schneiders, Meinke and Schröder2017b
; Mehrabadi et al.
Reference Mehrabadi, Horwitz, Subramaniam and Mani2018). In conclusion, improved models for the orientation-dependent hydrodynamic drag and torque are the prerequisite to reproduce the local and global energy balance in the presence of non-spherical particles of finite size. Moreover, whereas two-way coupling projection schemes have been discussed for finite-size spherical particles (Fröhlich et al.
Reference Fröhlich, Schneiders, Meinke and Schröder2018), similar approaches have yet to be investigated for non-spherical particles of finite size.
${\mathcal{I}}_{f}$
becomes more significant. However, unlike spherical particles for which a ‘standard drag curve’ is established (Clift, Grace & Weber Reference Clift, Grace and Weber1978), no such expression exists for ellipsoidal or general particle shapes. Generalized correlations have been developed for specific particle shapes (Sanjeevi, Kuipers & Padding Reference Sanjeevi, Kuipers and Padding2018; Andersson & Jiang Reference Andersson and Jiang2019) and attempts have been made to provide curve fits covering a broader parameter space using particle-resolved simulations (Ouchene et al.
Reference Ouchene, Khalij, Arcen and Tanièrea2016). However, as discussed by Andersson & Jiang (Reference Andersson and Jiang2019) such simulations face several numerical challenges, specifically for moderate particle Reynolds numbers, and they conclude that ‘the accuracy of already existing formulas can hardly be assessed’. The importance of such fluid inertia corrections for point-particle simulations of spherical particles has recently been evidenced by conducting direct comparisons with particle-resolved simulations (Schneiders, Meinke & Schröder Reference Schneiders, Meinke and Schröder2017b
; Mehrabadi et al.
Reference Mehrabadi, Horwitz, Subramaniam and Mani2018). In conclusion, improved models for the orientation-dependent hydrodynamic drag and torque are the prerequisite to reproduce the local and global energy balance in the presence of non-spherical particles of finite size. Moreover, whereas two-way coupling projection schemes have been discussed for finite-size spherical particles (Fröhlich et al.
Reference Fröhlich, Schneiders, Meinke and Schröder2018), similar approaches have yet to be investigated for non-spherical particles of finite size.
Acknowledgements
This work has been funded by the German Research Foundation (DFG) within the framework of the SFB/Transregio 129 ‘Oxyflame’ (subproject B2). The support is gratefully acknowledged. Computing resources were provided by the High Performance Computing Center Stuttgart (HLRS) and by the Jülich Supercomputing Centre (JSC) within a Large-Scale Project of the Gauss Centre for Supercomputing (GCS).