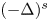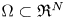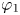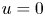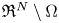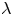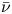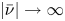1. Introduction
In this paper, we consider the following fractional problem
\begin{equation} \begin{cases} \displaystyle (-\Delta )^{s}u=g(u)-\bar{\nu}\varphi_{1}, & \text{in}\ \Omega,\\ \displaystyle u=0, & \text{in}\ {{\mathfrak R}}^{N}\backslash \Omega, \end{cases}\end{equation}
where 
$\bar {\nu }\in {{\mathfrak R}}$, 
$s\in (0,1)$, 
$\Omega \subset {{\mathfrak R}}^{N}\,(N> 2s)$ is a bounded domain with smooth boundary and 
$\varphi _{1}$ is the first positive eigenfunction of the fractional Laplace under the condition 
$u=0$ in 
${{\mathfrak R}}^{N}\setminus \Omega$. 
$g(t)$ has superlinear growth and satisfies
\[ \underset{t\to+\infty}{\lim}\frac{g(t)}{t}=\alpha>\underset{t\to-\infty}{\lim}\frac{g(t)}{t}=\beta. \]
Here 
$\alpha =+\infty$ and 
$\beta =-\infty$ are allowed. For any 
$\Omega \subset {{\mathfrak R}}^{N}$ and 
$u\in C_{0}^{\infty }(\Omega )$, we have 
$u=0$ in 
${{\mathfrak R}}^{N}\backslash \Omega$. The fractional Laplace operator 
$(-\Delta )^{s}$ is defined as follows:
\[ (-\Delta)^{s} u(y)=C_{N,s}P.V.\int_{{{\mathfrak R}}^{N}}{\frac{u(y)-u(z)}{|y-z|^{N+2s}}}\textrm{d}z, \]
where 
$P.V.$ stands for the principle value and 
$C_{N,s}$ is a normalization constant (see for instance [Reference Nezza, Palatucci and Valdinoci14]).
In particular, if 
$s=1$, equation (1.1) reduces to
\begin{equation} \begin{cases} \displaystyle -\Delta u=g(u)-\bar{\nu}\varphi_{1}, & \text{in}\ \Omega,\\ \displaystyle u=0, & \text{on}\ \partial \Omega. \end{cases}\end{equation}
Equation (1.2) has been studied first by Ambrosetti et al. in [Reference Ambrosetti and Prodi2], and many results were obtained there, the readers can refer to [Reference Dancer and Yan5–Reference Dancer and Yan7, Reference Lazer and McKenna10–Reference Li, Yan and Yang12, Reference Wei and Yan22]. It is well known (e.g. [Reference Ambrosetti and Prodi2]) that the location of 
$\alpha$, 
$\beta$ with respect to the spectrum of 
$(-\Delta , H_{0}^{1}(\Omega ))$ has great influence on the number of solutions to equation (1.2). Let 
$0<\Lambda _{1}<\Lambda _{2}\leq \Lambda _{3} \leq \cdots \leq \Lambda _{i}\leq \cdots$ be the eigenvalues of Laplace 
$-\Delta$ in 
$H_0^{1}(\Omega )$. In [Reference Lazer and McKenna10] Lazer and McKenna made a conjecture that equation (1.2) has an unbounded number of solutions as 
$\bar {\nu }\to +\infty$ if 
$\alpha =+\infty$, 
$\beta <\Lambda _{1}$, and 
$g(t)$ does not grow too rapidly.
There were several works related to the Lazer-McKenna conjecture. Breuer et al. [Reference Breuer, McKenna and Plum3] used numerical method to show that equation (1.2) has at least four solutions if 
$g(t)=t^{2}$ and 
$\Omega$ is a unit square in 
${{\mathfrak R}}^{2}$. Dancer et al. [Reference Dancer and Yan5] proved the Lazer-McKenna conjecture if 
$g(t)=|t|^{p}$, where 
$p\in (1,(N+2)/(N-2))$ and 
$N\geq 3$. Moreover, it is shown in [Reference Dancer and Yan6] that the Lazer-McKenna conjecture is also true if 
$g(t)=t_{+}^{p}+\lambda t$, where 
$u_{+}=\max (u,0)$, 
$N\geq 3$, 
$p\in (1,(N+2)/(N-2))$, 
$\lambda <\Lambda _{1}$ or 
$\lambda \in (\Lambda _{i},\Lambda _{i+1})$ for 
$i\geq 1$. Later on, Li et al. [Reference Li, Yan and Yang11, Reference Li, Yan and Yang12] and Wei et al. [Reference Wei and Yan22] proved the Lazer-McKenna conjecture if 
$g(t)=t_{+}^{2^{*}-1}+\lambda t$, where 
$N\geq 6$, 
$2^{*}=(2N)/(N-2)$ and 
$\lambda \in (0,\Lambda _{1})$ or 
$\lambda \in (\Lambda _{i},\Lambda _{i+1})$ for 
$i\geq 1$. Recently, in [Reference Abdellaoui, Dieb and Mahmoudi1], Abdellaoui et al. extended the results in [Reference Dancer and Yan5] to fractional Laplace and proved the fractional version of conjecture. This inspires us to consider problem (1.1). Our goal in this paper is to prove the fractional version of the Lazer-McKenna conjecture, extending the results in [Reference Li, Yan and Yang12]. More precisely, we consider the following equation
\begin{equation} \begin{cases} \displaystyle (-\Delta )^{s}u=u_{+}^{2^{*}_{s}-1}+\lambda u-\bar{\nu}\varphi_{1}, & \text{in}\ \Omega,\\ \displaystyle u=0, & \text{in}\ {{\mathfrak R}}^{N}\backslash \Omega, \end{cases} \end{equation}
where 
$\lambda \in {{\mathfrak R}}$, 
$2^{*}_{s}=({2N}/{N-2s}),\,N>2s$.
Let 
$\lambda _{1}<\lambda _{2}\leq \lambda _{3}\leq \cdots \leq \lambda _{i}\leq \cdots$ be the eigenvalues of fractional Laplace 
$(-\Delta )^{s}$ under the condition 
$u=0$ in 
${{\mathfrak R}}^{N}\setminus \Omega$. Indeed, it follows from [Reference Servadei and Valdinoci20] that
\[ \lambda_{1}=\underset{u\in X_{0}^{s}(\Omega)\backslash\{0\}}{\min}\frac{\int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}({|u(y)-u(z)|^{2}}/{|y-z|^{N+2s}})\textrm{d}y\textrm{d}z}{\int_{\Omega}|u|^{2}}, \]
where 
$X_{0}^{s}(\Omega )$ is given by
\[ X_{0}^{s}(\Omega)=\Big\{u\in H^{s}({{\mathfrak R}}^{N}): u=0\ \text{in}\ {{\mathfrak R}}^{N}\backslash\Omega\Big\}, \]with the norm
\[ \|u\|:=\Bigg(\int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}\frac{|u(y)-u(z)|^{2}}{|y-z|^{N+2s}}\textrm{d}y\textrm{d}z\Bigg)^{{1}/{2}}. \]
Furthermore, by [Reference Servadei and Valdinoci20], 
$\lambda _{1}$ is simple and 
$\varphi _{1}>0$ in 
$\Omega$.
Throughout this paper, we always assume that 
$\lambda$ and 
$\bar {\nu }$ satisfy one of the following conditions:
(
$C_{1}$) 
$\lambda \in (0,\lambda _{1})$ and 
$\bar {\nu }>0$;
(
$C_{2}$) 
$\lambda \in (\lambda _{i},\lambda _{i+1})$ for some 
$i\geq 1$ and 
$\bar {\nu }<0$.
The main result in this paper can be stated as follows:
Theorem 1.1 Suppose that 
$0< s<1$, (
$C_{1}$) or (
$C_{2}$) is satisfied. Then the number of the solutions for equation (1.3) tends to infinity as 
$|\bar {\nu }|\to +\infty$ if 
$N> 6s$.
Obviously, 
$-({\bar {\nu }}/{\lambda _{1}-\lambda })\varphi _{1}$ is a negative solution of equation (1.3). We will construct solutions of equation (1.3) redin the form
\[ u={-}\frac{\bar{\nu}}{\lambda_{1}-\lambda}\varphi_{1}+v. \]
Then 
$v$ solves
\begin{equation} \begin{cases}\displaystyle (-\Delta )^{s}v-\lambda v=(v-\nu\varphi_{1})_{+}^{2^{*}_{s}-1}, & \text{in}\ \Omega,\\ \displaystyle v=0, & \text{in}\ {{\mathfrak R}}^{N}\backslash \Omega, \end{cases} \end{equation}
where 
$\nu =({\bar {\nu }}/{\lambda _{1}-\lambda })$. Thus 
$\nu \to +\infty$ as 
$|\bar {\nu }|\to +\infty$.
In the sequel, we mainly consider equation (1.4). We will use Lyapunov-Schmidt reduction method to construct peak solutions of equation (1.4). This method has been widely used to study elliptic problems, see for examples [Reference Peng and Wang15–Reference Peng, Wang and Yan18, Reference Wei and Yan24] and the references therein. The advantage of this method is that we can not only prove the existence of many solutions but also obtain the profile of these solutions. Without loss of generality, we always assume that 
$\underset {y\in \Omega }{\max }\varphi _{1}(y)=1$ and we denote 
$S=\{ z\in \Omega : \varphi _{1}(z)=1\}$.
It is well known that
\[ U_{x_{j},\mu_{j}}=b_{0}\Bigg(\frac{\mu_{j}}{1+\mu_{j}^{2}|y-x_{j}|^{2}}\Bigg)^{{N-2s}/{2}}, \]with
\[ b_{0}=2^{{N-2s}/{2}}\frac{\Gamma({N+2s}/{2})}{\Gamma({N-2s}/{2})}, \]solves equation
\begin{equation} (-\Delta )^{s}u=u^{2^{*}_{s}-1}, \quad u>0,\quad \text{in}\ {{\mathfrak R}}^{N}, \end{equation}
where 
$x_{j}\in {{\mathfrak R}}^{N}$ and 
$\mu _{j}\in (0,\infty )$. In order to simplify notations, we denote 
$U=U_{0,1}$. Furthermore, in [Reference Dávila, del Pino and Sire8], it is shown that 
$U$ is non-degenerate, in the sense that, if 
$\phi$ solves the linearized equation of equation (1.5)
\[ (-\Delta )^{s}\phi=(2^{*}_{s}-1)U^{2^{*}_{s}-2}\phi,\quad \text{in}\ {{\mathfrak R}}^{N}, \]
then 
$\phi$ is a linear combination of
\[ \frac{N-2s}{2}U+x\cdot \nabla U,\quad \frac{\partial U}{\partial x_{i}},\quad i=1,\ldots,N. \]
Let 
$PU_{x_{j},\mu _{j}}$ be the solution of
\begin{equation} \begin{cases}\displaystyle (-\Delta )^{s}PU_{x_{j},\mu_{j}}=U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}, & \text{in}\ \Omega,\\ \displaystyle PU_{x_{j},\mu_{j}}=0, & \text{in}\ {{\mathfrak R}}^{N}\backslash \Omega. \end{cases} \end{equation}
We will choose 
$PU_{x_{j},\mu _{j}}$ as a building block of approximate solution. Moreover, we have
Theorem 1.2 Let 
$k>0$ be an integer and 
$N> 6s$. Then there exists 
$\nu _{k}>0$ such that for any 
$\nu \geq \nu _{k}$, equation (1.4) has a solution of the form
\[ v_{\nu}=\sum_{j=1}^{k}PU_{x_{\nu,j},\mu_{\nu,j}}+\phi_{\nu,k}, \]
satisfying that as 
$\nu \to \infty$,
(i)
$\phi _{\nu ,k}\in X_{0}^{s}(\Omega )$ and $\|\phi _{\nu ,k}\|\to 0$;(ii)
$\mu _{\nu ,j}\nu ^{-2/(N-6s)}\to t_{0}>0$;(iii)
$\nu ^{2/(N-6s)} |x_{\nu ,i}-x_{\nu ,j}|\to +\infty$ for $i\neq j$;(iv)
$x_{\nu ,j}\to x_{j}^{*}\in \Omega$ with $x_{j}^{*}\in S$;where the constant
$t_{0}$ is defined in (2.1).
In order to expand energy (see appendix B), we have to estimate
\[ \Psi_{x_{j},\mu_{j}}=U_{x_{j},\mu_{j}}-PU_{x_{j},\mu_{j}}. \]
If 
$s=1$, then 
$\Psi _{x_{j},\mu _{j}}$ solves
\[ \begin{cases} \displaystyle -\Delta \Psi_{x_{j},\mu_{j}}=0, & \text{in}\ \Omega,\\ \displaystyle \Psi_{x_{j},\mu_{j}}=U_{x_{j},\mu_{j}}, & \text{on}\ \partial \Omega. \end{cases}\]
Using comparison principle, we can easily obtain the leading term of 
$\Psi _{x_{j},\mu _{j}}$, for much details, the reader can see [Reference Rey19]. In order to overcome these difficulties due to the fractional Laplace, considering that many mathematics applied 
$s$-harmonic extension method (see [Reference Caffarelli and Silvestre4]) and studied a new local problem
\[ \begin{cases}\displaystyle div(y_{N+1}^{1-2s} \nabla\Phi)=0, & \text{in}\ {{\mathfrak R}}_{+}^{N+1},\\ \displaystyle \Phi=U_{x_{j},\mu_{j}}, & \text{on}\ {{\mathfrak R}}^{N}\backslash \Omega\times \{0\},\\ \displaystyle \underset{y_{N+1}\to 0^{+}}{\lim}y_{N+1}^{1-2s}\dfrac{\partial \Phi}{\partial y_{N+1}}=0, & \text{on}\ \Omega\times \{0\}, \end{cases} \]
we turn to obtain the leading term of 
$\Psi _{x_{j},\mu _{j}}$ by convolution formula of Green function with 
$U_{x_{j},\mu _{j}}^{2^{*}_{s}-1}$. This idea is mainly from [Reference Dávila, López Rios and Sire9, Reference Long, Yan and Yang13]. For much details, the readers can see appendix A. On the other hand, in order to solve critical points of 
$K(x,\mu )$ (see § 3), we will use a type of gradient flow method (see [Reference Wei and Yan22, Reference Wei and Yan23]). Indeed, we cannot prove the existence of critical points of 
$K(x,\mu )$ by using maximization procedure as in [Reference Dancer and Yan5, Reference Dancer and Yan6]. Furthermore, in [Reference Li, Yan and Yang12], Li et al. proved that 
$K(x,\mu )$ has a saddle point such that 
$K(x,\mu )$ attained the minimum at 
$\mu _{i}$ direction and attained maximum at 
$x_{i}$ direction. Compared with [Reference Li, Yan and Yang12], the gradient flow method we used in this paper will simply be the procedure very much to obtain critical points.
To end this section, we introduce some notations. We define 
$H^{s}({{\mathfrak R}}^{N})$ the classical Sobolev space
\[ H^{s}({{\mathfrak R}}^{N})=\Bigg\{u\in L^{2}({{\mathfrak R}}^{N}): \int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}\frac{|u(y)-u(z)|^{2}}{|y-z|^{N+2s}}\textrm{d}y\textrm{d}z<\infty\Bigg\}, \]with the norm
\[ \|u\|_{H^{s}({{\mathfrak R}}^{N})}=\Bigg(\int_{{{\mathfrak R}}^{N}}u^{2}+\int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}\frac{|u(y)-u(z)|^{2}}{|y-z|^{N+2s}}\textrm{d}y\textrm{d}z\Bigg)^{{1}/{2}}. \]
We also define 
$D^{s,2}({{\mathfrak R}}^{N})$ as follows
\[ D^{s,2}({{\mathfrak R}}^{N})=\Bigg\{u\in L^{2_{s}^{*}}({{\mathfrak R}}^{N}): \int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}\frac{|u(y)-u(z)|^{2}}{|y-z|^{N+2s}}\textrm{d}y\textrm{d}z<\infty\Bigg\}, \]with the norm
\[ \|u\|:=\Bigg(\int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}\frac{|u(y)-u(z)|^{2}}{|y-z|^{N+2s}}\textrm{d}y\textrm{d}z\Bigg)^{{1}/{2}}. \]
We recall that 
$X_{0}^{s}(\Omega )$ is a Hilbert space with the product
\[ \langle u, v\rangle=\int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}\frac{(u(y)-u(z))(v(y)-v(z))}{|y-z|^{N+2s}}\textrm{d}y\textrm{d}z. \]By [Reference Nezza, Palatucci and Valdinoci14], we can see that
\[ \int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}\frac{|u(y)-u(z)|^{2}}{|y-z|^{N+2s}}\textrm{d}y\textrm{d}z=2C_{N,s}^{{-}1}\int_{{{\mathfrak R}}^{N}}|(-\Delta)^{({s}/{2})}u|^{2}, \]
where the constant 
$C_{N,s}$ is given by
\[ C_{N,s}=\Bigg(\int_{{{\mathfrak R}}^{N}}\frac{1-\cos(\xi_{1})}{|\xi|^{N+2s}}\Bigg)^{{-}1}. \]
We can also refer to [Reference Servadei and Valdinoci20, Reference Servadei and Valdinoci21] for more properties of 
$X_{0}^{s}(\Omega )$.
Our paper is organized as follows. In § 2, we will carry out the reduction procedure. Then, we will study the reduced finite dimensional problem and prove theorem 1.2 in § 3. Our notations are standard. We will use 
$C$ to denote different positive constant from line to line.
2. Finite dimensional reduction
Define
\begin{eqnarray*} &D_{k,\nu}=\Big\{(x,\mu): \mu_{j} \in\big[(t_{0}-L\nu^{{-}s\tau})\nu^{2/(N-6s)},(t_{0}+L\nu^{{-}s\tau})\nu^{2/(N-6s)}\big], \\ & \quad\quad\quad\quad |\varphi_{1}(x_{j})-1|\leq \nu^{{-}s\tau},|x_{i}-x_{j}|^{N-2s}\geq \nu^{-(2N-8s)/(N-6s)+s\tau}, i\neq j\Big\}, \end{eqnarray*}
where 
$x_{j}\in \Omega$, 
$j=1,\ldots , k$, 
$x=(x_{1},\ldots ,x_{k})$, 
$\mu =(\mu _{1},\ldots ,\mu _{k})$, 
$\tau$ is a small constant, 
$L$ is a fixed large positive constant and 
$t_{0}$ is given by
\begin{equation} t_{0}=\Bigg(\frac{A_{3}(N-2s)}{4s\lambda A_{2}}\Bigg)^{2/(N-6s)}. \end{equation}
Here the positive constants 
$A_{2}$ and 
$A_{3}$ are defined in lemma B.1. Let
\[ \varepsilon_{ij}=\frac{1}{\mu_{i}^{(N-2s)/2}\mu_{j}^{(N-2s)/2}|x_{i}-x_{j}|^{N-2s}},\quad i\neq j. \]
Then, for 
$(x,\mu )\in D_{k,\nu }$, we have
\[ \varepsilon_{ij}\leq C\nu^{{-}4s/(N-6s)-s\tau}. \]We set
\[ E_{x,\mu,k}=\Bigg\{\phi\in X_{0}^{s}(\Omega): \Bigg\langle \phi,\frac{\partial PU_{x_{j},\mu_{j}}}{\partial x_{jl}}\Bigg\rangle=\Bigg\langle \phi,\frac{\partial PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\Bigg\rangle=0 \Bigg\}, \]
where 
$x_{j}=(x_{j1},\ldots ,x_{jN})\in {{\mathfrak R}}^{N}$, 
$j=1,\ldots ,k$, 
$l=1,\ldots ,N$.
Define the energy functional corresponding to equation (1.4) as follows
\[ I_{\nu}(v)=\frac{1}{2}\int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}\frac{|v(y)-v(z)|^{2}}{|y-z|^{N+2s}}\textrm{d}y\textrm{d}z-\frac{1}{2}\int_{\Omega}\lambda v^{2}-\frac{1}{2^{*}_{s}}\int_{\Omega}(v-\nu\varphi_{1})_{+}^{2^{*}_{s}}. \]Let
\[ J_{\nu}(x,\mu,\phi)=I_{\nu}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}+\phi\Bigg),\ (x,\mu)\in D_{k,\nu},\ \phi\in E_{x,\mu,k}. \]
Then we expand 
$J_{\nu }(x,\mu ,\phi )$ at 
$\phi =0$ as follows
\[ J_{\nu}(x,\mu,\phi)=J_{\nu}(x,0)+l_{\nu}(\phi)+\frac{1}{2}Q_{\nu}(\phi,\phi)-R_{\nu}(\phi), \]where
\begin{align} l_{\nu}(\phi)&=\sum_{j=1}^{k}\langle PU_{x_{j},\mu_{j}},\phi\rangle-\sum_{j=1}^{k}\int_{\Omega}\lambda PU_{x_{j},\mu_{j}}\phi-\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-1}\phi, \end{align}
\begin{align} Q_{\nu}(\phi,\psi)&=\langle \phi,\psi\rangle-\int_{\Omega}\lambda \phi\psi-(2^{*}_{s}-1)\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-2}\phi\psi, \end{align}and
\begin{align} R_{\nu}(\phi)&=\frac{1}{2^{*}_{s}}\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}+\phi-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}}-\frac{1}{2^{*}_{s}}\int_{\Omega} \Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}} \nonumber\\ &\quad -\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-1}\phi\notag\\ &\quad -\frac{2^{*}_{s}-1}{2}\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-2}\phi^{2}. \end{align} Now we estimate 
$l_{\nu }(\phi )$, 
$Q_{\nu }(\phi ,\psi )$ and 
$R_{\nu }(\phi )$ respectively.
Lemma 2.1 For any 
$\phi \in X_{0}^{s}(\Omega )$, we have
\[ l_{\nu}(\phi)=O\Bigg(\sum_{j=1}^{k}\frac{\lambda}{\mu_{j}^{2s}}+\sum_{j=1}^{k}\frac{\nu^{({1}/{2})+\sigma}}{\mu_{j}^{({N-2s}/{2})(({1}/{2})+\sigma)}}+\sum_{i\neq j}\varepsilon_{ij}^{({1}/{2})+\sigma}\Bigg)\|\phi\|. \]Proof. Rewrite 
$l_{\nu }(\phi )$ as follows:
\begin{align*} l_{\nu}(\phi)&=\Bigg\{\sum_{j=1}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\phi-\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-1}\phi\Bigg\}-\sum_{j=1}^{k}\int_{\Omega}\lambda PU_{x_{j},\mu_{j}}\phi \\ &=: l_{1}-l_{2}. \end{align*}Note that
\[ (a-b)_+^{2^{*}_{s}-1}=a^{2^{*}_{s}-1}+O(a^{2^{*}_{s}-1-(({1}/{2})+\sigma)}b^{({1}/{2})+\sigma}), \quad \forall a,b>0, \]
where 
$\sigma >0$ is a small constant. Then we have
\begin{align} l_{1}&=\sum_{j=1}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\phi-\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-1}\phi\nonumber\\ &=\sum_{j=1}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\phi-\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}\Bigg)^{2^{*}_{s}-1}\phi\nonumber\\ &\quad+O\Bigg(\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}\Bigg)^{2^{*}_{s}-1-(({1}/{2})+\sigma)}(\nu\varphi_{1})^{({1}/{2})+\sigma}\phi\Bigg) \nonumber\\ &=\sum_{j=1}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\phi-\int_{\Omega}\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\phi+O\Bigg(\sum_{i\neq j}\int_{\Omega}PU_{x_{j},\mu_{j}}^{({2^{*}_{s}-1}/{2})}PU_{x_{i},\mu_{i}}^{({2^{*}_{s}-1}/{2})}\phi\Bigg)\nonumber\\ &\quad+O\Bigg(\int_{\Omega}\Bigg(\sum_{j=1}^{k}U_{x_{j},\mu_{j}}\Bigg)^{2^{*}_{s}-1-(({1}/{2})+\sigma)}\phi\Bigg)\nu^{\frac{1}{2}+\sigma} \nonumber\\ &=\sum_{j=1}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\phi-\sum_{j=1}^{k}\int_{\Omega}PU_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\phi+O\Bigg(\sum_{i\neq j}\int_{\Omega}U_{x_{j},\mu_{j}}^{({2^{*}_{s}-1}/{2})}U_{x_{i},\mu_{i}}^{({2^{*}_{s}-1}/{2})}\phi\Bigg)\nonumber\\ &\quad+O\Bigg(\sum_{j=1}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1-(({1}/{2})+\sigma)}\phi\Bigg)\nu^{({1}/{2})+\sigma} \nonumber\\ &=\sum_{j=1}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\phi-\sum_{j=1}^{k}\int_{\Omega}(U_{x_{j},\mu_{j}}-\Psi_{x_{j},\mu_{j}})^{2^{*}_{s}-1}\phi\nonumber\\ &\quad+O\Bigg(\sum_{i\neq j}\int_{\Omega}U_{x_{j},\mu_{j}}^{({2^{*}_{s}-1}/{2})}U_{x_{i},\mu_{i}}^{({2^{*}_{s}-1}/{2})}\phi\Bigg)+O\Bigg(\sum_{j=1}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1-(({1}/{2})+\sigma)}\phi\Bigg)\nu^{({1}/{2})+\sigma} \nonumber\\ &=\sum_{j=1}^{k}\int_{\Omega}(2^{*}_{s}-1)U_{x_{j},\mu_{j}}^{2^{*}_{s}-2}\Psi_{x_{j},\mu_{j}}\phi+O\Bigg(\sum_{j=1}^{k}\int_{\Omega}\Psi_{x_{j}}^{2^{*}_{s}-1}\phi\Bigg)\nonumber\\ &\quad+O\Bigg(\sum_{i\neq j}\int_{\Omega}U_{x_{j},\mu_{j}}^{({2^{*}_{s}-1}/{2})}U_{x_{i},\mu_{i}}^{({2^{*}_{s}-1}/{2})}\phi\Bigg)+O\Bigg(\sum_{j=1}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1-(({1}/{2})+\sigma)}\phi\Bigg)\nu^{({1}/{2})+\sigma}. \end{align}
Define 
$\Omega _{j}=\{ z: \mu _{j}^{-1}z+x_{j}\in \Omega \}$, we choose 
$\sigma >0$ small enough such that
\[ (N-2s)(2^{*}_{s}-1- \Bigg(\frac{1}{2}+\sigma)\Bigg)\frac{2N}{N+2s}=N\Bigg(2-\frac{N-2s}{N+2s}\Bigg)-\sigma\frac{2N(N-2s)}{N+2s}>N. \]Then
\begin{align}
&\int_{\Omega}|U_{x_{j},\mu_{j}}^{2^{*}_{s}-1-(\frac{1}{2}+\sigma)}\phi|\notag\\
&\quad \leq
C\mu_{j}^{-\frac{N-2s}{2}(\frac{1}{2}+\sigma)}\Bigg(\int_{\Omega_{j}}\Bigg(\frac{1}{(1+|z|^{2})^{({N-2s}/{2})(2^{*}_{s}-1-(\frac{1}{2}+\sigma))}}\Bigg)^{\frac{2N}{N+2s}}\Bigg)^{\frac{N+2s}{2N}}\|\phi\|\nonumber\\
&\quad\leq
C\mu_{j}^{-\frac{N-2s}{2}(\frac{1}{2}+\sigma)}\|\phi\|.
\end{align}By lemma A.2, we have
\begin{align}
\int_{\Omega}|U_{x_{j},\mu_{j}}^{2^{*}_{s}-2}\Psi_{x_{j},\mu_{j}}\phi|&\leq
C\mu_{j}^{{-}N+2s}\Bigg(\int_{\Omega_{j}}\frac{1}{(1+|z|^{2})^{({4sN}/{N+2s})}}\Bigg)^{({N+2s}/{2N})}\|\phi\|\notag\\
&\leq
\frac{C}{\mu_{j}^{({N+2s}/{2})}}\|\phi\|,
\end{align}the second inequality is because of
\[ \Bigg(\int_{\Omega_{j}}\frac{1}{(1+|z|^{2})^{({4sN}/{N+2s})}}\Bigg)^{({N+2s}/{2N})}=O\Bigg(\mu_{j}^{({N-6s}/{2})}\Bigg). \]
In fact, let 
$R>0$ be such that 
$\Omega \subset B_{R}(x_j)$, we have 
$\Omega _j\subset B_{\mu _jR}(0)$. Thus,
\begin{align*} \int_{\Omega_{j}}\frac{1}{(1+|z|^{2})^{({4sN}/{N+2s})}}&\leq \int_{B_{\mu_jR}(0)}\frac{1}{(1+|z|^{2})^{({4sN}/{N+2s})}}\\ & \leq \int_{B_{1}(0)}+\int_{B_{\mu_jR}(0)\backslash B_{1}(0)}\frac{1}{(1+|z|^{2})^{({4sN}/{N+2s})}}\\ &\leq C+C\int_{1}^{\mu_jR}r^{N-1-({8sN}/{N+2s})}\textrm{d}r\\ &\leq C\mu_{j}^{N-({8sN}/{N+2s})}. \end{align*}By Hölder inequality, we have
\begin{align} &\int_{\Omega}U_{x_{j},\mu_{j}}^{({2^{*}_{s}-1}/{2})}U_{x_{i},\mu_{i}}^{({2^{*}_{s}-1}/{2})}\phi\leq \Bigg(\int_{\Omega}U_{x_{j},\mu_{j}}^{({2^{*}_{s}}/{2})}U_{x_{i},\mu_{i}}^{({2^{*}_{s}}/{2})}\Bigg)^{({N+2s}/{2N})}\|\phi\|\nonumber\\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\leq \frac{C[\log(\mu_{i}\mu_{j})]^{({N+2s}/{2N})}}{\mu_{i}^{({N+2s}/{4})}\mu_{j}^{({N+2s}/{4})}|x_{i}-x_{j}|^{({N+2s}/{2})}}\|\phi\|, \end{align}the second inequality is because of
\[ \int_{\Omega}U_{x_{j},\mu_{j}}^{({2^{*}_{s}}/{2})}U_{x_{i},\mu_{i}}^{({2^{*}_{s}}/{2})}\leq C|x_i-x_j|^{{-}N}\mu_{j}^{-({N}/{2})}\mu_{i}^{-({N}/{2})}\log(\mu_i\mu_j). \]In fact, define
\[ \tilde{\Omega}_1=\{y\in \Omega~:~|y-x_i|\geq |y-x_j|\},\quad \tilde{\Omega}_2=\{y\in \Omega~:~|y-x_i|<|y-x_j|\}. \]
For all 
$y\in \tilde {\Omega }_1$, we have
\[ |x_i-x_j|\leq |x_{i}-y|+|y-x_{j}|\leq 2|y-x_{i}|. \]Hence, we have
\begin{align*} \int_{\tilde{\Omega}_1}U_{x_{j},\mu_{j}}^{({2^{*}_{s}}/{2})}U_{x_{i},\mu_{i}}^{({2^{*}_{s}}/{2})}&=b_{0}^{2^{*}_s}\int_{\tilde{\Omega}_1}\frac{\mu_j^{({N}/{2})}}{(1+\mu_{j}^{2}|y-x_{j}|^{2})^{({N}/{2})}}\cdot \frac{\mu_i^{({N}/{2})}}{(1+\mu_{i}^{2}|y-x_{i}|^{2})^{({N}/{2})}}\\ &\leq 2^{N}b_{0}^{2^{*}_s}\mu_{i}^{-({N}/{2})}|x_i-x_j|^{{-}N}\int_{\tilde{\Omega}_1}\frac{\mu_j^{({N}/{2})}}{(1+\mu_{j}^{2}|y-x_{j}|^{2})^{({N}/{2})}}\\ & \leq 2^{N}b_{0}^{2^{*}_s}\mu_{i}^{-({N}/{2})}|x_i-x_j|^{{-}N}\int_{\Omega}\frac{\mu_j^{({N}/{2})}}{(1+\mu_{j}^{2}|y-x_{j}|^{2})^{({N}/{2})}}\\ &\leq 2^{N}b_{0}^{2^{*}_s}\mu_{i}^{-({N}/{2})}|x_i-x_j|^{{-}N}\int_{B_{R}(x_j)}\frac{\mu_j^{({N}/{2})}}{(1+\mu_{j}^{2}|y-x_{j}|^{2})^{({N}/{2})}}\\ &=2^{N}b_{0}^{2^{*}_s}|x_i-x_j|^{{-}N}\mu_{j}^{-({N}/{2})}\mu_{i}^{({N}/{2})}\int_{B_{\mu_jR}(0)}\frac{1}{(1+|z|^{2})^{({N}/{2})}}\\ &\leq C|x_i-x_j|^{{-}N}\mu_{j}^{-({N}/{2}}\mu_{i}^{-({N}/{2})}\log\mu_j. \end{align*}Similarly, we have
\[ \int_{\tilde{\Omega}_2}U_{x_{j},\mu_{j}}^{({2^{*}_{s}}/{2})}U_{x_{i},\mu_{i}}^{({2^{*}_{s}}/{2})}\leq C|x_i-x_j|^{{-}N}\mu_{j}^{-({N}/{2})}\mu_{i}^{-({N}/{2})}\log\mu_i. \]Combining (2.5)–(2.8) with lemma A.2, we can obtain that
\begin{equation} l_{1}=O\Bigg(\sum_{j=1}^{k}\frac{1}{\mu_{j}^{({N+2s}/{2})}}+\sum_{j=1}^{k}\frac{\nu^{({1}/{2})+\sigma}}{\mu_{j}^{({N-2s}/{2}(({1}/{2})+\sigma)}}+\sum_{i\neq j}\varepsilon_{ij}^{({1}/{2})+\sigma}\Bigg)\|\phi\|. \end{equation}On the other hand,
\begin{align}
|l_{2}|&=\Bigg|\sum_{j=1}^{k}\int_{\Omega}\lambda
PU_{x_{j},\mu_{j}}\phi\Bigg|\leq
\sum_{j=1}^{k}\int_{\Omega}\lambda
U_{x_{j},\mu_{j}}|\phi|\notag\\
&\leq
\sum_{j=1}^{k}\lambda\Bigg(\int_{\Omega}
U_{x_{j},\mu_{j}}^{({2N}/{N+2s})}\Bigg)^{({N+2s}/{2N})}\|\phi\|\nonumber\\
&\leq
\sum_{j=1}^{k}\frac{\lambda}{\mu_{j}^{2s}}\Bigg(\int_{\Omega_{j}}
\frac{1}{(1+|z|^{2})^{({N(N-2s)}/{N+2s})}}\Bigg)^{({N+2s}/{2N})}\|\phi\|\notag\\
&\leq
\sum_{j=1}^{k}\frac{C\lambda}{\mu_{j}^{2s}}\|\phi\|,
\end{align}
the last inequality follows from 
$({2N(N-2s)}/{N+2s})>N$ since 
$N>6s$.
Lemma 2.2 For any 
$\phi ,\psi \in X_{0}^{s}(\Omega )$, there exists constant 
$C>0$ such that
\[ |Q_{\nu}(\phi,\psi)|\leq C\|\phi\|\|\psi\|, \]
where 
$C$ is independent of 
$\nu$.
Proof. Using Hölder inequality, we can easily check this conclusion.
It follows from lemma 2.2 that 
$Q_{\nu }(\phi ,\psi )$ is a bounded bi-linear functional in 
$X_{0}^{s}(\Omega )$. Then there exists a bounded linear operator 
$Q_{\nu }$ from 
$E_{x,\mu ,k}$ to 
$E_{x,\mu ,k}$ such that
\begin{equation} Q_{\nu}(\phi,\psi)=\langle Q_{\nu}\phi,\psi\rangle,\quad \forall \phi,\psi\in E_{x,\mu,k}. \end{equation}
Now, we intend to prove that operator 
$Q_{\nu }$ is invertible in 
$E_{x,\mu ,k}$.
Proposition 2.3 There exists constant 
$\rho >0$, independent of 
$\nu$ and 
$(x,\mu )\in D_{k,\nu }$, such that
\[ \|Q_{\nu}\phi\|\geq \rho\|\phi\|,\quad \phi\in E_{x,\mu,k}. \]Proof. We argue by contradiction. Assume that there exist 
$\nu _{n}\to \infty$, 
$(x_{n},\mu _{n})\in D_{\nu _{n},k}$, 
$x_{j,n}\to x_{j}^{*}\in S$ and 
$\phi _{n}\in E_{x_{n},\mu _{n},k}$ such that
\[ \|Q_{\nu}\phi_{n}\|=o(1)\|\phi_{n}\|. \]
Without loss of generality, we may assume that 
$\|\phi _{n}\|=1$. Let 
$\tilde {\phi }_{i,n}(y)=\mu _{i,n}^{-(N-2s)/2}\phi _{n}(\mu _{i,n}^{-1}y+x_{i,n})$, 
$\Omega _{i,n}\,{=}\,\{y: \mu _{i,n}^{-1}y+x_{i,n}\in \Omega \}$. Then 
$\|\tilde {\phi }_{i,n}\|\,{=}\,\|\phi _{n}\|\,{=}\,1$. Thus, we may assume that there exists 
$\tilde {\phi }_{i}\in D^{s,2}({{\mathfrak R}}^{N})$ such that
\[ \begin{split} & \tilde{\phi}_{i,n} \rightharpoonup \tilde{\phi}_{i}\ \ \ \text{in}\ {{D}^{s,2}}\left( {{{{\mathfrak R}}}^{N}} \right),\\ & \tilde{\phi}_{i,n} \to \tilde{\phi}_{i}\ \ \ \text{in}\ L_{loc}^{2}\left( {{{{\mathfrak R}}}^{N}} \right),\\ & \tilde{\phi}_{i,n} \to \tilde{\phi}_{i}\ \ \ a.e. ~\text{on}\ {{{{\mathfrak R}}}^{N}}. \end{split} \]
We claim that 
$\tilde {\phi }_{i}$ solves
\begin{equation} (-\Delta)^{s}\tilde{\phi}_i-(2^{*}_{s}-1)U^{2^{*}_{s}-2}\tilde{\phi}_{i}=0. \end{equation}In fact, it is sufficient to show that
\begin{equation} \int_{{{\mathfrak R}}^{N}}(-\Delta)^{s}\tilde{\phi}_{i}\eta-\int_{{{\mathfrak R}}^{N}}(2^{*}_{s}-1)U^{2^{*}_{s}-2}\tilde{\phi}_{i}\eta=0,\quad \text{for all}\ \eta\in C_{0}^{\infty}({{\mathfrak R}}^{N}). \end{equation}Since
\begin{align} &\langle
\phi_{n},\eta\rangle-\int_{\Omega}\lambda
\phi_{n}\eta-(2^{*}_{s}-1)\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-2}\phi_{n}\eta\nonumber\\
&\quad =Q_{\nu}(\phi_{n},\eta)=\langle
Q_{\nu}\phi_{n},\eta\rangle=o(1)\|\eta\|,\quad \forall
\eta\in E_{x_{n},\mu_{n},k},
\end{align}we have
\begin{align}
&\int_{{{\mathfrak
R}}^{N}}(-\Delta)^{s}\tilde{\phi}_{i,n}\tilde{\eta}-\frac{\lambda}{\mu_{i,n}^{2s}}\int_{\Omega_{i,n}}
\tilde{\phi}_{i,n}\tilde{\eta}\nonumber\\
&\qquad-(2^{*}_{s}-1)\int_{\Omega_{i,n}}\Bigg(\sum_{j=1}^{k}\tilde{U}_{j,n}-\nu_{n}\mu_{i,n}^{-({N-2s}/{2})}\varphi_{1}(\mu_{i,n}^{{-}1}+x_{i,n})\Bigg)_{+}^{2^{*}_{s}-2}\tilde{\phi}_{i,n}\tilde{\eta}\nonumber\\
&\quad =o(1)\|\tilde{\eta}\|,\quad \forall \tilde{\eta}\in
\tilde{E}_{x_{n},\mu_{n},k},
\end{align}
where 
$\tilde {\eta }(y)=\eta (\mu _{i,n}^{-1}y+x_{i,n})$, 
$\tilde {U}_{j,n}=\mu _{i,n}^{-(N-2s)/2}PU_{x_{j,n},\mu _{j,n}}(\mu _{i,n}^{-1}y+x_{i,n})$,
\begin{align*}
\tilde{E}_{x_{n},\mu_{n},k}&=\Bigg\{\tilde{\eta}\in
X_{0}^{s}(\Omega_{i,n}): \int_{{{\mathfrak
R}}^{N}}(-\Delta)^{\frac{s}{2}}\tilde{V}_{j,l,n}(-\Delta)^{\frac{s}{2}}\tilde{\eta}\\
&\qquad =\int_{{{\mathfrak
R}}^{N}}(-\Delta)^{\frac{s}{2}}\tilde{V}_{j,n}(-\Delta)^{\frac{s}{2}}\tilde{\eta}=0\Bigg\},
\end{align*}
where 
$l=1,\ldots ,N$, 
$j=1,\ldots ,k$ and 
$\tilde {V}_{j,l,n}$, 
$\tilde {V}_{j,n}$ are given by
\[ \tilde{V}_{j,l,n}(y)=\mu_{i,n}^{-(N-2s)/2}\mu_{i,n}^{{-}1}\frac{\partial PU_{x_{j,n},\mu_{j,n}}(z)}{\partial x_{jl}}\Big|_{z=\mu_{i,n}^{{-}1}y+x_{i,n}}, \]
\[ \tilde{V}_{j,n}(y)=\mu_{i,n}^{-(N-2s)/2}\mu_{i,n}\frac{\partial PU_{\varepsilon_{n},x_{j,n}}(z)}{\partial \mu_{j}}\Big|_{z=\mu_{i,n}^{{-}1}y+x_{i,n}}. \]
For any 
$\eta \in C_{0}^{\infty }({{\mathfrak R}}^{N})$, we can choose 
$a_{j,l,n}$ and 
$b_{j,n}$ such that
\[ \tilde{\eta}=\eta-\sum_{j=1}^{k}\sum_{l=1}^{N}a_{j,l,n}\tilde{V}_{j,l,n}+\sum_{j=1}^{k}b_{j,n}\tilde{V}_{j,n}\in \tilde{E}_{x_{n},\mu_{n},k}. \]
Noting that 
$\eta$ has compact support and the support of 
$\tilde {V}_{j,l,n}$ and 
$\tilde {V}_{j,n}$ moves to infinity as 
$n\to \infty$ if 
$i\neq j$. Thus, we can see that 
$a_{j,l,n}\to 0$ and 
$b_{j,n}\to 0$ if 
$i\neq j$. Furthermore, we can check that 
$a_{i,l,n}$ and 
$b_{i,n}$ are bounded. Since 
$(x_{n},\mu _{n})\in D_{\nu _{n},k}$, then 
$\nu _{n}\mu _{i,n}^{-(N-2s)/2}\to 0$. Substituting 
$\tilde {\eta }$ in (2.15) and letting 
$n\to \infty$, we derive that
\begin{align}
&\int_{{{\mathfrak
R}}^{N}}(-\Delta)^{s}\tilde{\phi}_{i}\eta-(2^{*}_{s}-1)\int_{{{\mathfrak
R}}^{N}}U^{2^{*}_{s}-2}\tilde{\phi}_{i}\eta\nonumber\\
&\quad =\sum_{l=1}^{k}a_{il}\Bigg(\int_{{{\mathfrak
R}}^{N}}(-\Delta)^{\frac{s}{2}}\tilde{\phi}_{i}(-\Delta)^{\frac{s}{2}}\frac{\partial
U}{\partial
x_{l}}-(2^{*}_{s}-1)U^{2^{*}_{s}-2}\tilde{\phi}_{i}\frac{\partial
U}{\partial x_{l}}\Bigg)\nonumber\\
&\qquad+b_{i}\Bigg(\int_{{{\mathfrak
R}}^{N}}(-\Delta)^{\frac{s}{2}}\tilde{\phi}_{i}(-\Delta)^{\frac{s}{2}}\frac{\partial
U}{\partial
\mu}-(2^{*}_{s}-1)U^{2^{*}_{s}-2}\tilde{\phi}_{i}\frac{\partial
U}{\partial \mu}\Bigg),
\end{align}
where 
$a_{i,l}=\underset {n\to \infty }{\lim }a_{i,l,n}$ and 
$b_{i}=\underset {n\to \infty }{\lim }b_{i,n}$. On the other hand,
\begin{equation} \int_{{{\mathfrak R}}^{N}}(-\Delta)^{\frac{s}{2}}\tilde{\phi}_{i}(-\Delta)^{\frac{s}{2}}\frac{\partial U}{\partial x_{l}}-(2^{*}_{s}-1)U^{2^{*}_{s}-2}\tilde{\phi}_{i}\frac{\partial U}{\partial x_{l}}=0. \end{equation}and
\begin{equation} \int_{{{\mathfrak R}}^{N}}(-\Delta)^{\frac{s}{2}}\tilde{\phi}_{i}(-\Delta)^{\frac{s}{2}}\frac{\partial U}{\partial \mu}-(2^{*}_{s}-1)U^{2^{*}_{s}-2}\tilde{\phi}_{i}\frac{\partial U}{\partial \mu}=0. \end{equation}Thus, (2.13) follows from (2.16)–(2.18). Therefore, we have proved this claim.
We recall that 
$U$ is non-degenerate, that is, if 
$\tilde {\phi }_{i}$ solves (2.12), then there exists some constants 
$\bar {c}_{l}$ and 
$\bar {c}$ such that
\[ \tilde{\phi}_{i}=\sum_{l=1}^{N}\bar{c}_{l}\frac{\partial U}{\partial x_{l}}+\bar{c}\frac{\partial U}{\partial \mu}. \]
Note that 
$\phi _{n}\in E_{x_{n},\mu _{n},k}$, then 
$\tilde {\phi }_{i,n}\in \tilde {E}_{x_{n},\mu _{n},k}$. So we can obtain that
\[ \int_{{{\mathfrak R}}^{N}}(-\Delta)^{\frac{s}{2}}\tilde{\phi}_{i}(-\Delta)^{\frac{s}{2}}\frac{\partial U}{\partial \mu}=0, \]and
\[ \int_{{{\mathfrak R}}^{N}}(-\Delta)^{\frac{s}{2}}\tilde{\phi}_{i}(-\Delta)^{\frac{s}{2}}\frac{\partial U}{\partial x_{l}}=0,\quad l=1,\ldots,N, \]
which imply that 
$\tilde {\phi }_{i}=0$. Then for any 
$R>0$,
\[ \int_{B_{\mu_{i,n}^{{-}1}R}(x_{i,n})}\phi_{n}^{2}=\mu_{i,n}^{2s}\int_{B_{R}(0)}\tilde{\phi}_{i,n}^{2}=o(\mu_{i,n}^{2s}). \]Moreover, we have
\begin{align} \int_{B_{\mu_{i,n}^{{-}1}R}(x_{i,n})}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-2}\phi_{n}^{2}\leq C\int_{B_{\mu_{i,n}^{{-}1}R}(x_{i,n})} U_{x_{i,n},\mu_{i,n}}^{2^{*}_{s}-2}\phi_{n}^{2}=o(1). \end{align}Thus,
\begin{align} &\int_{\Omega}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-2}\phi_{n}^{2}\nonumber\\ & \quad= \sum_{i=1}^{k}\int_{\Omega\backslash B_{\mu_{i,n}^{{-}1}R}(x_{i,n})}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-2}\phi_{n}^{2}+o(1)\nonumber\\ & \quad\leq C\sum_{i=1}^{k}\int_{\Omega\backslash B_{\mu_{i,n}^{{-}1}R}(x_{i,n})}(PU_{x_{i},\mu_{i}}-\nu\varphi_{1})_{+}^{2^{*}_{s}-2}\phi_{n}^{2}+o(1)\nonumber\\ & \quad\leq C\sum_{i=1}^{k}\int_{\Omega\backslash B_{\mu_{i,n}^{{-}1}R}(x_{i,n})}U_{x_{i},\mu_{i}}^{2^{*}_{s}-2}\phi_{n}^{2}+o(1)\nonumber\\ & \quad\leq C\sum_{i=1}^{k}\Bigg(\int_{\Omega_{i,n}\backslash B_{R(0)}}U^{2^{*}_{s}}\Bigg)^{({s}/{N})}\|\phi_{n}\|^{2}+o(1)=o_{R}(1)+o(1), \end{align}
where 
$o_{R}(1)\to 0$ as 
$R\to \infty$. Combining (2.14) with (2.20), we deduce that
\begin{equation} \int_{{{\mathfrak R}}^{N}}(-\Delta)^{\frac{s}{2}}\phi_{n}(-\Delta)^{\frac{s}{2}}\eta-\int_{\Omega}\lambda \phi_{n}\eta=o(1)\|\eta\|,\quad \forall \eta\in E_{x_{n},\mu_{n},k}. \end{equation}
Note that 
$\phi _{n}\in X_{0}^{s}(\Omega )$ and 
$\|\phi _{n}\|=1$. We may assume that there exits 
$\phi \in X_{0}^{s}(\Omega )$ such that
\[ \begin{split} & \phi_{n} \rightharpoonup \phi\ \ \ \text{weakly in}\ X_{0}^{s}(\Omega),\\ & \phi_{n} \to \phi\ \ \ \text{strongly in}\ L^{2}(\Omega).\\ \end{split} \]
We claim that 
$\phi =0$. Indeed, for any 
$\eta \in C_{0}^{\infty }(\Omega )$, we choose 
$c_{j,l,n}$ such that
\[ \bar{\eta}=\eta-\sum_{j=1}^{k}\sum_{l=1}^{N}c_{j,l,n}\frac{\partial PU_{x_{j,n},\mu_{j,n}}}{\partial x_{jl}}-d_{j,n}\frac{\partial PU_{x_{j,n},\mu_{j,n}}}{\partial \mu_{j}}\in E_{x_{n},\mu_{n},k}. \]
In order to estimate 
$c_{j,l,n}$ and 
$d_{j,n}$, multiplying (2.21) by 
$\frac {\partial PU_{x_{i,n},\mu _{i,n}}}{\partial x_{ih}}$ and 
$\frac {\partial PU_{x_{i,n},\mu _{i,n}}}{\partial \mu _{i}}$ respectively, we have
\begin{equation} \Bigg\langle\eta,\frac{\partial PU_{x_{i,n},\mu_{i,n}}}{\partial x_{ih}}\Bigg\rangle-\sum_{j=1}^{k}\sum_{l=1}^{N}c_{j,l,n}\Bigg\langle\frac{\partial PU_{x_{j,n},\mu_{j,n}}}{\partial x_{jl}},\frac{\partial PU_{x_{i,n},\mu_{i,n}}}{\partial x_{ih}}\Bigg\rangle=0, \end{equation}and
\begin{equation} \Bigg\langle\eta,\frac{\partial PU_{x_{i,n},\mu_{i,n}}}{\partial \mu_{i}}\Bigg\rangle-\sum_{j=1}^{k}d_{j,n}\Bigg\langle\frac{\partial PU_{x_{j,n},\mu_{j,n}}}{\partial \mu_{j}},\frac{\partial PU_{x_{i,n},\mu_{i,n}}}{\partial \mu_{i}}\Bigg\rangle=0. \end{equation}Note that
\begin{equation} \Bigg\langle\eta,\frac{\partial PU_{x_{j,n},\mu_{j,n}}}{\partial x_{jh}}\Bigg\rangle=(2^{*}_{s}-1)\int_{\Omega}U_{x_{j,n},\mu_{j,n}}^{2^{*}_{s}-2}\frac{\partial U_{x_{j,n},\mu_{j,n}}}{\partial x_{jh}}\eta=O\Bigg(\frac{\mu_{j}}{\mu_{j}^{({N-2s}/{2})}}\Bigg), \end{equation}and
\begin{equation} \Bigg\langle\eta,\frac{\partial PU_{x_{j,n},\mu_{j,n}}}{\partial \mu_{j}}\Bigg\rangle=(2^{*}_{s}-1)\int_{\Omega}U_{x_{j,n},\mu_{j,n}}^{2^{*}_{s}-2}\frac{\partial U_{x_{j,n},\mu_{j,n}}}{\partial \mu_{j}}\eta=O\Bigg(\frac{\mu_{j}^{{-}1}}{\mu_{j}^{({N-2s}/{2})}}\Bigg). \end{equation}
Combining (2.22) with (2.24), we see that 
$c_{j,l,n}=O(\mu _{j}^{-1}\mu _{j}^{-(N-2s)/2})$. By (2.23) and (2.25), we obtain that 
$d_{j,n}=O(\mu _{j}\mu _{j}^{-(N-2s)/2})$. Thus,
\begin{align}
&\Bigg|c_{j,l,n}\Bigg(\Bigg\langle\frac{\partial
PU_{x_{j,n},\mu_{j,n}}}{\partial
x_{jl}},\phi_{n}\Bigg\rangle-\lambda\int_{\Omega}\frac{\partial
PU_{x_{j,n},\mu_{j,n}}}{\partial
x_{jl}}\phi_{n}\Bigg)\Bigg|\nonumber\\ &\quad \leq
C\frac{1}{\mu_{j}^{({N-2s}/{2})}}\Bigg(\int_{\Omega}U_{x_{j,n},\mu_{j,n}}^{2^{*}_{s}-1}|\phi_{n}|+\int_{\Omega}U_{x_{j,n},\mu_{j,n}}|\phi_{n}|\Bigg)\nonumber\\
&\quad \leq
C\frac{1}{\mu_{j}^{({N-2s}/{2})}}\Bigg[\Bigg(\int_{\Omega}U_{x_{j,n},\mu_{j,n}}^{2^{*}_{s}}\Bigg)^{({N+2s}/{2N})}+\Bigg(\int_{\Omega}U_{x_{j,n},\mu_{j,n}}^{({2N}/{N+2s})}\Bigg)^{({N+2s}/{2N})}\Bigg]\|\phi_{n}\|\nonumber\\
&\quad \leq
C\Bigg[\frac{1}{\mu_{j}^{({N-2s}/{2})}}+\frac{1}{\mu_{j}^{({N+2s}/{2})}}\Bigg(\int_{\Omega_{j,n}}\frac{1}{(1+|y|^{2})^{({N(N-2s)}/{N+2s})}}\Bigg)^{({N+2s}/{2N})}\Bigg]\|\phi_{n}\|\nonumber\\
&\quad \leq
C\frac{1}{\mu_{j}^{({N-2s}/{2})}}+\frac{1}{\mu_{j}^{({N+2s}/{2})}},
\end{align}
the last inequality follows from 
$({2N(N-2s)}/{N+2s})>N$ since 
$N>6s$. Using the similar computation, we also have
\begin{equation} \Bigg|d_{j,n}\Bigg(\Bigg\langle\frac{\partial PU_{x_{j,n},\mu_{j,n}}}{\partial \mu_{j}},\phi_{n}\Bigg\rangle-\lambda\int_{\Omega}\frac{\partial PU_{x_{j,n},\mu_{j,n}}}{\partial \mu_{j}}\phi_{n}\Bigg)\Bigg|=O\Bigg(\frac{1}{\mu_{j}^{({N-2s}/{2})}}\Bigg). \end{equation}
Inserting 
$\bar {\eta }$ into (2.21), combining (2.26) with (2.27) and letting 
$n\to \infty$, we can deduce that
\begin{equation} \int_{{{\mathfrak R}}^{N}}(-\Delta)^{\frac{s}{2}}\phi(-\Delta)^{\frac{s}{2}}\eta-\int_{\Omega}\lambda \phi\eta=0. \end{equation}
Since 
$\lambda \neq \lambda _{i}$, 
$\phi =0$. Hence, the claim is completed.
Taking 
$\eta =\phi _{n}$ in (2.21), we derive that
\[ \int_{{{\mathfrak R}}^{N}}|(-\Delta)^{\frac{s}{2}}\phi_{n}|^{2}=\int_{\Omega}\lambda \phi_{n}^{2}+o(1)\|\phi_{n}\|=o(1)+o(1)\|\phi_{n}\| \]
which contradicts with 
$\|\phi _{n}\|=1$.
Lemma 2.4 For any 
$\phi \in X_{0}^{s}(\Omega )$, it holds
\[ D^{i}R_{\nu}(\phi)=O(\|\phi\|^{2^{*}_{s}-i}),\quad i=0,1,2. \]Proof. Using the fact that for 
$a,b>0$,
\[ (a+b)^{p}=a^{p}+pa^{p-1}b+\frac{p(p-1)}{2}a^{p-2}b^{2}+O(b^{p}),\quad p>2, \]we can easily check this conclusion. Here, we omit it.
Proposition 2.5 There exists 
$\nu _{k}>0$ such that for 
$\nu \geq \nu _{k}$, there exists a 
$C^{1}$-map 
$\phi _{\nu ,x,\mu }: D_{k,\nu }\to X_{0}^{s}(\Omega )$, such that 
$\phi _{\nu ,x,\mu }\in E_{x,\mu ,k}$ satisfies
\begin{equation} \Bigg\langle I^{\prime}_{\nu}\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}+\phi_{\nu,x,\mu}\Bigg),\eta\Bigg\rangle=0,\quad \forall \eta\in E_{x,\mu,k}. \end{equation}Furthermore,
\[ \|\phi_{\nu,x,\mu}\|=O\Bigg(\sum_{j=1}^{k}\frac{\lambda}{\mu_{j}^{2s}}+\sum_{j=1}^{k}\frac{\nu^{({1}/{2})+\sigma}}{\mu_{j}^{({N-2s}/{2})(({1}/{2})+\sigma)}}+\sum_{i\neq j}\varepsilon_{ij}^{({1}/{2})+\sigma}\Bigg), \]
where 
$\sigma$ is a small positive constant.
Proof. Set
\[ \mathcal{N}_{x,\mu,k}\,{=}\,\Bigg\{\phi: \phi\in E_{x,\mu,k}, \|\phi\|\leq \sum_{j=1}^{k}\frac{\lambda}{\mu_{j}^{2s-\sigma}}+\sum_{j=1}^{k}\frac{\nu^{({1+\sigma}/{2})}}{\mu_{j}^{({N-2s}/{2})({1+\sigma}/{2})}}+\sum_{i\neq j}\varepsilon_{ij}^{({1+\sigma}/{2})}\Bigg\}. \]
First, by lemma 2.1, we see that 
$l_{\nu }(\phi )$ is a bounded linear functional in 
$E_{x,\mu ,k}$. Then, there exists 
$l_{\nu }$ such that
\[ l_{\nu}(\phi)=\langle l_{\nu},\phi\rangle,\quad \forall \phi\in E_{x,\mu,k}. \]Combining this with (2.11), we can obtain that (2.29) is equivalent to
\begin{equation} l_{\nu}+Q_{\nu}\phi+R_{\nu}^{\prime}(\phi)=0. \end{equation}
It follows from proposition 2.3 that 
$Q_{\nu }$ is invertible in 
$E_{x,\mu ,k}$ and
\[ \|Q_{\nu}^{{-}1}\|\leq \rho^{{-}1}. \]Thus, (2.30) can be written as
\begin{equation} \phi=\mathcal{A}\phi:={-}Q_{\nu}^{{-}1}l_{\nu}-Q_{\nu}^{{-}1}R_{\nu}^{\prime}(\phi). \end{equation}
Now, we prove that 
$\mathcal {A}$ is a contraction map from 
$\mathcal {N}_{x,\mu ,k}$ to 
$\mathcal {N}_{x,\mu ,k}$.
On one hand, for any 
$\phi _{1}$, 
$\phi _{2}\in \mathcal {N}_{x,\mu ,k}$, using lemma 2.4, we have
\begin{align*}
\|\mathcal{A}(\phi_{1})-\mathcal{A}(\phi_{2})\|&=\|Q_{\nu}^{{-}1}R_{\nu}^{\prime}(\phi_{1})-Q_{\nu}^{{-}1}R_{\nu}^{\prime}(\phi_{2})\|\\
&\leq
\rho^{{-}1}\|R_{\nu}^{\prime}(\phi_{1})-R_{\nu}^{\prime}(\phi_{2})\|\\
&\leq
C(\|\phi_{1}\|^{2^{*}_{s}-2}+\|\phi_{2}\|^{2^{*}_{s}-2})\|\phi_{1}-\phi_{2}\|\\
&\leq
\frac{1}{2}\|\phi_{1}-\phi_{2}\|,
\end{align*}
if 
$\nu$ is large enough. Hence, 
$\mathcal {A}$ is a contraction map.
On the other hand, for any 
$\phi \in \mathcal {N}_{x,\mu ,k}$, applying lemma 2.1 and lemma 2.4 again, we have
\begin{align*}
\|\mathcal{A}\phi\|
&\leq\rho^{{-}1}\|l_{\nu}\|+\rho^{{-}1}\|R_{\nu}^{\prime}(\phi)\|\leq
C(\|l_{\nu}\|+\|\phi\|^{2^{*}_{s}-1})\\ & \leq
C\Bigg(\sum_{j=1}^{k}\frac{\lambda}{\mu_{j}^{2s}}+\sum_{j=1}^{k}\frac{\nu^{({1}/{2})+\sigma}}{\mu_{j}^{({N-2s}/{2})({1}/{2}+\sigma)}}+\sum_{i\neq
j}\varepsilon_{ij}^{({1}/{2})+\sigma}\Bigg)\\ &\leq
\sum_{j=1}^{k}\frac{\lambda}{\mu_{j}^{2s-\sigma}}+\sum_{j=1}^{k}\frac{\nu^{({1+\sigma}/{2})}}{\mu_{j}^{({N-2s}/{2})({1+\sigma}/{2})}}+\sum_{i\neq
j}\varepsilon_{ij}^{({1+\sigma}/{2})},
\end{align*}
if 
$\nu$ is large enough. Therefore, 
$\mathcal {A}$ is a contraction map from 
$\mathcal {N}_{x,\mu ,k}$ to 
$\mathcal {N}_{x,\mu ,k}$. By contraction mapping theorem, there exists a unique 
$\phi _{\nu ,x,\mu }\in \mathcal {N}_{x,\mu ,k}$ such that (2.31) holds. Moreover,
\[ \|\phi_{\nu,x,\mu}\|\leq C\Bigg(\sum_{j=1}^{k}\frac{\lambda}{\mu_{j}^{2s}}+\sum_{j=1}^{k}\frac{\nu^{({1}/{2})+\sigma}}{\mu_{j}^{({N-2s}/{2})({1}/{2}+\sigma)}}+\sum_{i\neq j}\varepsilon_{ij}^{({1}/{2})+\sigma}\Bigg). \]3. Proof of main result
In this section, we will choose suitable 
$(x,\mu )\in D_{k,\nu }$ such that
\[ v_{\nu}=\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}+\phi_{\nu,x,\mu} \]is a solution of equation (1.4). We define
\[ K(x,\mu)=J_{\nu}(x,\mu,\phi_{\nu,x,\mu}),\quad (x,\mu)\in D_{k,\nu}, \]
where 
$\phi _{\nu ,x,\mu }$ is obtained in proposition 2.5. Using proposition 2.5 and lemma B.2, we deduce that
\begin{align}
K(x,\mu)&=J_{\nu}(x,\mu,0)+O(\|\phi_{\nu,x,\mu}\|^{2})\nonumber\\
& =
kA_{1}-\sum_{j=1}^{k}\Bigg(\frac{\lambda
A_{2}}{\mu_{j}^{2s}}-\frac{\varphi_{1}(x_{j})A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}\Bigg)-\sum_{i\neq
j}^{k}\frac{1}{2}b_{0}(A_{3}+b_{0}\lambda
A(x_{i},x_{j}))\varepsilon_{ij} \nonumber\\
&\quad +
O\Bigg(\sum_{j=1}^{k}\Bigg(\frac{1}{\mu_{j}^{2s+2\sigma}}+\frac{\nu}{\mu_{j}^{\frac{N}{2}}}+\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)+\sum_{i\neq
j}\varepsilon_{ij}^{1+\sigma}\Bigg)\nonumber\\
&= kA_{1}-\sum_{j=1}^{k}\Bigg(\frac{\lambda
A_{2}}{\mu_{j}^{2s}}-\frac{\varphi_{1}(x_{j})A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}\Bigg)-\sum_{i\neq
j}^{k}\frac{1}{2}b_{0}(A_{3}+b_{0}\lambda
A(x_{i},x_{j}))\varepsilon_{ij} \nonumber\\
&\quad +
O\Bigg(\frac{1}{\nu^{({4s(1+\sigma)}/{N-6s})}}\Bigg),
\end{align}
where the positive constants 
$A_{1}$, 
$A_{2}$, 
$A_{3}$ 
$A(x_{i},x_{j})$ are defined in lemma B.2 and 
$\sigma >0$ is a small constant.
Now, we intend to estimate the derivative of 
$K(x,\mu )$. It follows from proposition 2.5 that there exist constants 
$c_{ih}$, 
$d_{i}$, 
$i=1,\ldots ,k$, 
$h=1,\ldots ,N$ such that
\begin{equation} \frac{\partial J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial\phi_{\nu,x,\mu}}=\sum_{i=1}^{k}\sum_{h=1}^{N}c_{ih}\frac{\partial PU_{x_{i},\mu_{i}}}{\partial x_{ih}}+\sum_{i=1}^{k}d_{i}\frac{\partial PU_{x_{i},\mu_{i}}}{\partial \mu_{i}}. \end{equation}Thus
\begin{align*}
\frac{\partial K(x,\mu)}{\partial \mu_{j}}&=\frac{\partial
J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial
\mu_{j}}+\Bigg\langle \frac{\partial
J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\phi_{\nu,x,\mu}},\frac{\partial\phi_{\nu,x,\mu}}{\partial
\mu_{j}}\Bigg\rangle\\
& =
\frac{\partial J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial
\mu_{j}}+\sum_{i=1}^{k}\sum_{h=1}^{N}c_{ih}\Bigg\langle\frac{\partial
PU_{x_{i},\mu_{i}}}{\partial
x_{ih}},\frac{\partial\phi_{\nu,x,\mu}}{\partial
\mu_{j}}\Bigg\rangle\\
&\quad+\sum_{i=1}^{k}d_{i}\Bigg\langle\frac{\partial
PU_{x_{i},\mu_{i}}}{\partial
\mu_{i}},\frac{\partial\phi_{\nu,x,\mu}}{\partial
\mu_{j}}\Bigg\rangle. \end{align*}
Hence, we have to estimate 
$({\partial J_{\nu }(x,\mu ,\phi _{\nu ,x,\mu })}/{\partial \mu _{j})}$, 
$c_{ih}$ and 
$d_{i}$.
Lemma 3.1 Let 
$\phi _{\nu ,x,\mu }$ be obtained in proposition 2.5. Then
\begin{align}
\frac{\partial J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial
\mu_{j}}=\frac{2s\lambda
A_{2}}{\mu_{j}^{2s+1}}-\frac{N-2s}{2}\frac{\varphi_{1}(x_{j})A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})+1}}+\frac{1}{\mu_{j}}O\Bigg(\frac{1}{\nu^{({4s(1+\sigma)}/{N-6s})}}\Bigg),
\end{align}and
\begin{equation} \frac{\partial J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial x_{ji}}= \mu_{j}O\Bigg(\frac{1}{\mu_{j}^{N-2s}}+\frac{\nu}{\mu_{j}^{({N}/{2})}}+\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}+\sum_{i\neq j}\varepsilon_{ij}\Bigg), \end{equation}
where 
$\sigma >0$ is a small constant, constants 
$A_{2}$, 
$A_{3}$ are defined in lemma B.1.
Proof. By a direct computation, we have
\begin{align}
\frac{\partial J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial
\mu_{j}}&=\Bigg\langle
I_\nu^{\prime}\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}+\phi_{\nu,x,\mu}\Bigg),
\frac{\partial PU_{x_{j},\mu_{j}}}{\partial
\mu_{j}}\Bigg\rangle\nonumber\\
&=\Bigg\langle
I_\nu^{\prime}\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}\Bigg),
\frac{\partial PU_{x_{j},\mu_{j}}}{\partial
\mu_{j}}\Bigg\rangle-\lambda\int_{\Omega}\phi_{\nu,x,\mu}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\nonumber\\
&\quad-\int_{\Omega}\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}+\phi_{\nu,x,\mu}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\nonumber\\
&\quad +\int_{\Omega}\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}
\end{align}It follows from proposition 2.5 and (2.10) that
\begin{align}
\Bigg|\int_{\Omega}\phi_{\nu,x,\mu}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\Bigg|&\leq
\frac{C}{\mu_{j}}\Bigg(\int_{\Omega}|\phi_{\nu,x,\mu}|
U_{x_{j},\mu_{j}}\Bigg)\notag\\
&\leq
\frac{C}{\mu_{j}}\frac{\|\phi_{\nu,x,\mu}\|}{\mu_{j}^{2s}}\leq\frac{C}{\mu_{j}}\Bigg(\frac{1}{\nu^{({4s(1+\sigma)}/{N-6s})}}\Bigg).
\end{align}Note that
\begin{align}
&\int_{\Omega}\Bigg[\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}+\phi_{\nu,x,\mu}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-1}-\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-1}\Bigg]\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\nonumber\\
&\quad =(2^{*}_{s}-1)\int_{\Omega}\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-2}\phi_{\nu,x,\mu}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\notag\\
&\qquad
+O\Bigg(\int_{\Omega}\phi_{\nu,x,\mu}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\Bigg).
\end{align}Then, using lemma A.2, proposition 2.5 and Hölder inequality, we obtain that
\begin{align}
\Bigg|\int_{\Omega}\phi_{\nu,x,\mu}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial
\mu_{j}}\Bigg|&\leq\frac{C}{\mu_{j}}\int_{\Omega}|\phi_{\nu,x,\mu}^{2^{*}_{s}-1}U_{x_{j},\mu_{j}}|
\leq
\frac{C}{\mu_{j}}\|\phi_{\nu,x,\mu}\|^{2^{*}_{s}-1}\notag\\
&\leq\frac{C}{\mu_{j}}\Bigg(\frac{1}{\nu^{({4s(1+\sigma)}/{N-6s})}}\Bigg).
\end{align}On the other hand, by a similar computation in (B.7), we can obtain
\begin{align}
&\int_{\Omega}\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-2}\phi_{\nu,x,\mu}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\nonumber\\
&\quad =\int_{\Omega}\Bigg(\sum_{i=1}^{k}U_{x_{i},\mu_{i}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-2}\phi_{\nu,x,\mu}\frac{\partial
U_{x_{j},\mu_{j}}}{\partial
\mu_{j}}+\frac{1}{\mu_{j}}O\Bigg(\frac{\|\phi_{\nu,x,\mu}\|}{\mu_{j}^{({N-2s}/{2})}}\Bigg)\nonumber\\
&\quad =\int_{\Omega}\Bigg(\sum_{i=1}^{k}U_{x_{i},\mu_{i}}\Bigg)^{2^{*}_{s}-2}\phi_{\nu,x,\mu}\frac{\partial
U_{x_{j},\mu_{j}}}{\partial
\mu_{j}}+\frac{1}{\mu_{j}}O\Bigg(\frac{\|\phi_{\nu,x,\mu}\|}{\mu_{j}^{({N-2s}/{2})}}\Bigg)\nonumber\\
&\quad \quad+O\Bigg(\frac{1}{\mu_{j}}\int_{\Omega}\Bigg(\sum_{i=1}^{k}U_{x_{i},\mu_{i}}\Bigg)^{2^{*}_{s}-2-(({1}/{2})+\sigma)}|\nu\varphi_{1}|^{({1}/{2})+\sigma}|\phi_{\nu,x,\mu}|
U_{x_{j},\mu_{j}}\Bigg)\nonumber\\
&\quad =\int_{\Omega}\Bigg[\Bigg(\sum_{i=1}^{k}U_{x_{i},\mu_{i}}\Bigg)^{2^{*}_{s}-2}-U_{x_{j},\mu_{j}}^{2^{*}_{s}-2}\Bigg]\phi_{\nu,x,\mu}\frac{\partial
U_{x_{j},\mu_{j}}}{\partial
\mu_{j}}+\frac{1}{\mu_{j}}O\Bigg(\frac{\|\phi_{\nu,x,\mu}\|}{\mu_{j}^{({N-2s}/{2})}}\Bigg)\nonumber\\
&\quad \quad+\frac{1}{\mu_{j}}O\Bigg(\sum_{i=1}^{k}\frac{\nu^{({1}/{2})+\sigma}\|\phi_{\nu,x,\mu}\|}{\mu_{i}^{({(N-2s)}/{2})({1}/{2}+\sigma)}}\Bigg)\nonumber\\
&\quad =\frac{1}{\mu_{j}}\int_{\Omega}\sum_{i\neq
j}U_{x_{i},\mu_{i}}^{({2^{*}_{s}-1}/{2})}U_{x_{j},\mu_{j}}^{({2^{*}_{s}-1}/{2})}|\phi_{\nu,x,\mu}|\notag\\
&\qquad +\frac{1}{\mu_{j}}O\Bigg(\frac{\|\phi_{\nu,x,\mu}\|}{\mu_{j}^{({N-2s}/{2})}}\Bigg)+\frac{1}{\mu_{j}}O\Bigg(\sum_{i=1}^{k}\frac{\nu^{({1}/{2})+\sigma}\|\phi_{\nu,x,\mu}\|}{\mu_{i}^{({(N-2s)}/{2})({1}/{2})+\sigma)}}\Bigg)\nonumber\\
&\quad =\frac{1}{\mu_{j}}\sum_{i\neq
j}\varepsilon_{ij}^{({1}/{2})+\sigma}\|\phi_{\nu,x,\mu}\|+\frac{1}{\mu_{j}}O\Bigg(\frac{\|\phi_{\nu,x,\mu}\|}{\mu_{j}^{({N-2s}/{2})}}\Bigg)\notag\\
&\qquad +\frac{1}{\mu_{j}}O\Bigg(\sum_{i=1}^{k}\frac{\nu^{({1}/{2})+\sigma}\|\phi_{\nu,x,\mu}\|}{\mu_{i}^{({(N-2s)}/{2})({1}/{2}+\sigma)}}\Bigg).
\end{align}Lemma 3.2 Let 
$c_{jl}$ and 
$d_{j}$ be defined in (3.2). Then
\[ c_{jl}=\mu_{j}^{{-}1}O\Bigg(\frac{1}{\mu_{j}^{N-2s}}+\frac{\nu}{\mu_{j}^{{N}/{2}}}+\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}+\sum_{i\neq j}\varepsilon_{ij}\Bigg), \]and
\[ d_{j}=\mu_{j}O\Bigg(\frac{1}{\mu_{j}^{2s}}+\frac{\nu }{\mu_{j}^{({N-2s}/{2})}}+\frac{1}{\nu^{({4s(1+\sigma)}/{N-6s})}}\Bigg). \]Proof. Multiplying 
$({\partial PU_{x_{j},\mu _{j}}}/{\partial \mu _{j})}$ and 
$({\partial PU_{x_{j},\mu _{j}}}/{\partial x_{jl})}$ by (3.2), respectively, we obtain
\begin{align}
&\sum_{i=1}^{k}\sum_{h=1}^{N}c_{ih}\Bigg\langle\frac{\partial
PU_{x_{i},\mu_{i}}}{\partial x_{ih}},\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial
\mu_{j}}\Bigg\rangle+\sum_{i=1}^{k}d_{i}\Bigg\langle\frac{\partial
PU_{x_{i},\mu_{i}}}{\partial \mu_{i}},\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial
\mu_{j}}\Bigg\rangle\nonumber\\
&\quad =\Bigg\langle\frac{\partial
J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial\phi_{\nu,x,\mu}},\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\Bigg\rangle,
\end{align}and
\begin{align}
&\sum_{i=1}^{k}\sum_{h=1}^{N}c_{ih}\Bigg\langle\frac{\partial
PU_{x_{i},\mu_{i}}}{\partial x_{ih}},\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial
x_{jl}}\Bigg\rangle+\sum_{i=1}^{k}d_{i}\Bigg\langle\frac{\partial
PU_{x_{i},\mu_{i}}}{\partial \mu_{i}},\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial x_{jl}}\Bigg\rangle\nonumber\\
&\quad =\Bigg\langle\frac{\partial
J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial\phi_{\nu,x,\mu}},\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial x_{jl}}\Bigg\rangle.
\end{align}On the other hand, by a direct computation, we have
\begin{equation} \Bigg\langle\frac{\partial J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial\phi_{\nu,x,\mu}},\frac{\partial PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\Bigg\rangle=\frac{\partial J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial \mu_{j}} \end{equation}and
\begin{equation} \Bigg\langle\frac{\partial J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial\phi_{\nu,x,\mu}},\frac{\partial PU_{x_{j},\mu_{j}}}{\partial x_{jl}}\Bigg\rangle=\frac{\partial J_{\nu}(x,\mu,\phi_{\nu,x,\mu})}{\partial x_{jl}} \end{equation}Combining (3.10)–(3.13) with lemma 3.1, we can complete the proof.
Based on lemma 3.1 and lemma 3.2, we can conclude the following conclusion.
Proposition 3.3 Let 
$(x,\mu )\in D_{k,\nu }$. Then
\begin{equation} \frac{\partial K(x,\mu)}{\partial \mu_{j}}=\frac{2s\lambda A_{2}}{\mu_{j}^{2s+1}}-\frac{N-2s}{2}\frac{\varphi_{1}(x_{j})A_{3}\nu }{\mu_{j}^{({N-2s}/{2})+1}}+\frac{1}{\mu_{j}}O\Bigg(\frac{1}{\nu^{({4s(1+\sigma)}/{N-6s})}}\Bigg), \end{equation}
where 
$\sigma >0$ is a small constant.
Define
\[ f(t)={-}\frac{\lambda A_{2}}{t^{2s}}+\frac{A_{3} }{t^{({N-2s}/{2})}}. \]
Then it is easy to check that 
$f(t)$ has unique minimum point
\[ t_{0}=\Bigg(\frac{A_{3}(N-2s)}{4s\lambda A_{2}}\Bigg)^{2/(N-6s)} \]
on 
$(0,\infty )$. Let
\[ \alpha_{2}=kA_{1}+\eta,\quad \alpha_{1}=kA_{1}+kf(t_{0})\nu^{-({4s}/{N-6s})}-\nu^{-({4s}/{N-6s})-({3s}/{2})\tau}, \]
where 
$\eta >0$ is a small fixed constant. Denote
\[ K^{\alpha}=\Bigg\{ (x,\mu)\in D_{k,\nu}, K(x,\mu)\leq \alpha\Bigg\}. \]Consider the following flow
\[
\begin{cases} \displaystyle \dfrac{\textrm{d}
x(t)}{\textrm{d}t}={-}D_{x}K(x(t),\mu(t)),& t>0,\\
\displaystyle \dfrac{\textrm{d}
\mu(t)}{\textrm{d}t}={-}D_{\mu}K(x(t),\mu(t)), & t>0,\\
\displaystyle (x(0),\mu(0))=(x_{0},\mu_{0})\in
K^{\alpha_{2}}. \end{cases} \]We have
Proposition 3.4 Let 
$N>6s$. Then the flow does not leave 
$D_{k,\nu }$ before it reaches 
$K^{\alpha _{1}}$.
Proof. Denote
\[ \mu_{j}=t_{j}\nu^{2/(N-6s)},\quad t_{j}\in [t_{0}-L\nu^{{-}s\tau}, t_{0}+L\nu^{{-}s\tau}],\quad j=1,\ldots,k. \]
Suppose that 
$\mu _{j}=(t_{0}+L\nu ^{-s\tau })\nu ^{2/(N-6s)}$ for some 
$j$. Then by (3.14), we have
\begin{align*}
\frac{\partial K(x,\mu)}{\partial
\mu_{j}}&=f^{\prime}(t_{j})\nu^{-({4s+2}/{N-6s})}+O\Bigg((1-\varphi_{1}(x_{j}))\nu^{-({4s+2}/{N-6s})}
\Bigg)\\
&\quad +O\Bigg({\nu^{-({2+4s+4s\sigma}/{N-6s})}}\Bigg)\nonumber\\
&=
f^{\prime}(t_{j})\nu^{-({4s+2}/{N-6s})}+O\Bigg(\nu^{-({4s+2}/{N-6s})-s\tau}
\Bigg)\nonumber\\ & =
f^{\prime\prime}(t_{0})\nu^{-({4s+2}/{N-6s})}L\nu^{{-}s\tau}+O\Bigg(L^{2}\nu^{{-}2s\tau}\nu^{-({4s+2}/{N-6s})}\Bigg)\\
&\quad +O\Bigg(\nu^{-({4s+2}/{N-6s})-s\tau}
\Bigg)>0, \end{align*}
if we choose 
$L>0$ is large.
Similarly, if 
$\mu _{j}=(t_{0}-L\nu ^{-s\tau })\nu ^{2/(N-6s)}$ for some 
$j$. Then by (3.14), we have
\begin{align*} \frac{\partial
K(x,\mu)}{\partial
\mu_{j}}&={-}f^{\prime\prime}(t_{0})\nu^{-({4s+2}/{N-6s})}L\nu^{{-}s\tau}+O\Bigg(L^{2}\nu^{{-}2s\tau}\nu^{-({4s+2}/{N-6s})}\Bigg)\\
&\quad +O\Bigg(\nu^{-({4s+2}/{N-6s})-s\tau}
\Bigg)<0. \end{align*}
So the flow does not leave 
$D_{k,\nu }$.
Now, we suppose that 
$|x_{i}-x_{j}|^{N-2s}= \nu ^{-(2N-8s)/(N-6s)+s\tau }$. Then we have
\[ \varepsilon_{ij}\geq C_{1}\nu^{-({4s}/{N-6s})-s\tau}. \]Thus, applying (3.1), we can derive
\begin{align}
K(x,\mu)&\leq kA_{1}-\sum_{j=1}^{k}\Bigg(\frac{\lambda
A_{2}}{\mu_{j}^{2s}}-\frac{A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}\Bigg)\nonumber\\
&\quad-\sum_{i\neq
j}^{k}\frac{1}{2}b_{0}(A_{3}+b_{0}\lambda
A(x_{i},x_{j}))\varepsilon_{ij}+O\Bigg({\nu^{-({4s+4s\sigma}/{N-6s})}}\Bigg)\nonumber\\
&\leq
kA_{1}+\sum_{j=1}^{k}f(t_{j})\nu^{({4s}/{N-6s})}-C_{1}\nu^{-({4s}/{N-6s})-s\tau}+O\Bigg({\nu^{-({4s}/{N-6s})-2s\tau}}\Bigg)\nonumber\\
&=
kA_{1}+kf(t_{0})\nu^{-({4s}/{N-6s})}+O\Bigg(\nu^{-({4s}/{N-6s})}L^{2}\nu^{{-}2s\tau}\Bigg)\notag\\
&\quad -C_{1}\nu^{-({4s}/{N-6s})-s\tau}
+O\Bigg({\nu^{-({4s}/{N-6s})-2s\tau}}\Bigg)<\alpha_{1},
\end{align}
where the last equality follows from the fact that 
$f(t_{j})=f(t_{0})+O(|t-t_{j}|^{2})$.
On the other hand, if 
$|\varphi _{1}(x_{j})-1|= \nu ^{-s\tau }$, then using (3.1), we can obtain
\begin{align}
K(x,\mu)&=kA_{1}-\sum_{j=1}^{k}\Bigg(\frac{\lambda
A_{2}}{\mu_{j}^{2s}}-\frac{A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}\Bigg)-\sum_{j=1}^{k}\frac{1-\varphi_{1}(x_{j})A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}\nonumber\\ &\quad
- \sum_{i\neq j}^{k}\frac{1}{2}b_{0}(A_{3}+b_{0}\lambda
A(x_{i},x_{j}))\varepsilon_{ij}
+O\Bigg({\nu^{-({4s+4s\sigma}/{N-6s})}}\Bigg)\nonumber\\
&=
kA_{1}+\sum_{j=1}^{k}f(t_{j})\nu^{-({4s}/{N-6s})}-\sum_{j=1}^{k}\frac{A_{3}
}{t_{j}^{({N-2s}/{2})}}\nu^{-({4s}/{N-6s})-s\tau}\nonumber\\
&\quad - \sum_{i\neq
j}^{k}\frac{1}{2}b_{0}(A_{3}+b_{0}\lambda
A(x_{i},x_{j}))\varepsilon_{ij}
+O\Bigg({\nu^{-({4s+4s\sigma}/{N-6s})}}\Bigg)\nonumber\\
&\leq
kA_{1}+\sum_{j=1}^{k}f(t_{j})\nu^{-({4s}/{N-6s})}-\sum_{j=1}^{k}\frac{A_{3}
}{t_{j}^{({N-2s}/{2})}}\nu^{-({4s}/{N-6s})-s\tau}\notag\\
&\quad +O\Bigg({\nu^{-({4s}/{N-6s})-2s\tau}}\Bigg)\nonumber\\
&=
kA_{1}+kf(t_{0})\nu^{-({4s}/{N-6s})}+O\Bigg(\nu^{-({4s}/{N-6s})}L^{2}\nu^{{-}2s\tau}\Bigg)\nonumber\\
&\quad - \sum_{j=1}^{k}\frac{A_{3}
}{t_{j}^{({N-2s}/{2})}}\nu^{-({4s}/{N-6s})-s\tau}+O\Bigg({\nu^{-({4s}/{N-6s})-2s\tau}}\Bigg)<\alpha_{1}.
\end{align}Thus, we complete the proof.
Proof of theorem 1.2 We will prove that 
$K(x,\mu )$ has a critical point in 
$D_{k,\nu }$. Define
\[ \Gamma=\Big\{ h: h(x,\mu)=(h_{1}(x,\mu),h_{2}(x,\mu))\in D_{k,\nu}, (x,\mu)\in D_{k,\nu}\Big\}, \]
where 
$h_1(x,\mu )=x$ if 
$x\in \partial D_{k,\nu }^{1}$. Here we denote 
$D^{1}_{k,\nu }=\{x: (x,\mu )\in D_{k,\nu }\}$ and define the boundary of 
$D^{1}_{k,\nu }$ by 
$\partial D_{\nu ,k}^{1}$. Furthermore, we denote 
$D^{2}_{k,\nu }=\{\mu : (x,\mu )\in D_{k,\nu }\}$.
Let
\[ c_{\nu}=\underset{h\in\Gamma}{\inf}\underset{(x,\mu)\in D_{k,\nu}}{\max} K(h(x,\mu)). \]
We claim that 
$c_{\nu }$ is a critical value of 
$K$. In order to prove this claim, it is sufficient to prove that
(i)
$\alpha _{1}< c_{\nu }<\alpha _{2}$,(ii)
$\underset {(x,\mu )\in \partial D_{\nu ,k}^{1}\times D_{\nu ,k}^{2}}{\sup }K(h(x,\mu ))<\alpha _{1}$, $\forall \, h\in \Gamma$.
Obviously, (ii) directly follows from (3.15) and (3.16).
Now, we prove (i). Using (3.1), we can easily check that 
$c_{\nu }<\alpha _{2}$.
For any 
$h=(h_{1},h_{2})\in \Gamma$, by the definition of 
$h$, we have 
${h}_{1}(x,\mu )=x$ if 
$x \in \partial D_{\nu ,k}^{1}$. Define
\[ \tilde{h}_{1}(x)=h_{1}(x,t_{0}\nu^{{-}2/(N-6s)}). \]
Then 
$\tilde {h}_{1}(x)=x$ for any 
$x \in \partial D_{\nu ,k}^{1}$. Thus, by degree argument, we can obtain
\[ \text{deg}(\tilde{h}_{1}, D_{\nu,k}^{1}, \xi)=1,\quad \forall\, \xi\in D_{\nu,k}^{1}. \]
Hence, for any 
$\xi \in D_{\nu ,k}^{1}$, there exists 
$\tilde {x}\in D_{\nu ,k}^{1}$ such that
\[ \tilde{h}_{1}(\tilde{x})=\xi. \]
Let 
$\tilde {\mu }=h_{2}(\tilde {x},t_{0}\nu ^{-2/(N-6s)})$. Then we have
\[ \underset{(x,\mu)\in D_{\nu,k}}{\max}K(h(x,\mu))\geq K(h(\tilde{x},t_{0}\nu^{{-}2/(N-6s)}))=K(\xi,\tilde{\mu}). \]
Choose 
$\xi _{j}\in \Omega$ such that 
$dist(\xi _{j},S)\leq \nu ^{-s\tau }$ and 
$|\xi _{i}-\xi _{j}|\geq c_{1}\nu ^{-s\tau }$, where 
$c_{1}$ is a small positive constant. By a direct computation, we have
\begin{equation} \tilde{\varepsilon}_{ij}:=\frac{1}{\mu_{i}^{({N-2s}/{2})}\mu_{j}^{({N-2s}/{2})}|\xi_{i}-\xi_{j}|^{N-2s}}=O\Bigg(\nu^{(N-2s)\tau-({2(N-2s)}/{N-6s})}\Bigg). \end{equation}Combining (3.1) with (3.17), we obtain
\begin{align*}
K(\xi,\mu)&=kA_{1}-\sum_{j=1}^{k}\Bigg(\frac{\lambda
A_{2}}{\mu_{j}^{2s}}-\frac{A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}\Bigg)-\sum_{j=1}^{k}\frac{1-\varphi_{1}(x_{j})A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}\nonumber\\
&\quad- \sum_{i\neq j}^{k}\frac{1}{2}b_{0}(A_{3}+b_{0}\lambda
A(x_{i},x_{j}))\tilde{\varepsilon}_{ij}
+O\Bigg({\nu^{-({4s+4s\sigma}/{N-6s})}}\Bigg)\nonumber\\
& = kA_{1}+\sum_{j=1}^{k}f(t_{j})\nu^{-({4s}/{N-6s})}+O(\nu^{-({4s}/{N-6s})-2s\tau})\notag\\
&\quad +O\Bigg(\nu^{(N-2s)\tau-({2(N-2s)}/{N-6s})}\Bigg)\nonumber\\
& = kA_{1}+kf(t_{0})\nu^{-({4s}/{N-6s})}+O\Bigg(\nu^{-({4s}/{N-6s})}L^{2}\nu^{{-}2s\tau}\Bigg)\notag\\
&\quad +O(\nu^{-({4s}/{N-6s})-2s\tau})\nonumber\\
&\geq \alpha_{1}+\frac{1}{2}\nu^{-({4s}/{N-6s})-({3s}/{2})\tau}>\alpha_{1}.
\end{align*}Consequently, we complete the proof.
Appendix A. Basic estimate
In this section, we always suppose that 
$dist(x_{j},\partial \Omega )\geq \delta >0$, where 
$\delta$ is a small constant. Let 
$G(y,z)$ be the Green's function of 
$(-\Delta )^{s}$ in 
$\Omega$. That is, 
$G$ satisfies
\[ \begin{cases}\displaystyle (-\Delta )^{s}G(y,\cdot)=\delta_{y}, \ & \text{in}\ \Omega,\\ \displaystyle G(y,\cdot)=0, & \text{in}\ {{\mathfrak R}}^{N}\backslash\Omega, \end{cases} \]
where 
$\delta _{y}$ denotes the Dirac mass at the point 
$y$. The regular part of 
$G$ is given by
\[ H(y,z)=\Gamma(y,z)-G(y,z), \]
where 
$\Gamma (y,z)$ is given by
\[ \Gamma(y,z)=\frac{C_{N,s}}{|y-z|^{N-2s}}. \]Let
\[ \Psi_{x_{j},\mu_{j}}=U_{x_{j},\mu_{j}}-PU_{x_{j},\mu_{j}}. \]Then we have
Lemma A.1 It holds
\[ 0\leq PU_{x_{j},\mu_{j}}\leq U_{x_{j},\mu_{j}},\quad 0\leq \Psi_{x_{j},\mu_{j}}\leq U_{x_{j},\mu_{j}}. \]Proof. By proposition 2.4 in [Reference Long, Yan and Yang13], we can see that 
$G(y,z)\geq 0$ and 
$H(y,z)\geq 0$. Then
\[ PU_{x_{j},\mu_{j}}=\int_{\Omega}G(y,z)U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}dz\geq 0 \]and
\begin{align*}
\Psi_{x_{j},\mu_{j}}&=\int_{{{\mathfrak
R}}^{N}}\Gamma(y,z)U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\textrm{d}z-\int_{\Omega}G(y,z)U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\textrm{d}z\\
&= \int_{{{\mathfrak
R}}^{N}\backslash\Omega}\Gamma(y,z)U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\textrm{d}z+\int_{\Omega}H(y,z)U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\textrm{d}z\geq
0. \end{align*}Lemma A.2 We have
\begin{align} \Psi_{x_{j},\mu_{j}}&=\frac{c_{0}}{\mu_{j}^{({N-2s}/{2})}}(H(y,x_{j})+o(1)), \end{align}
\begin{align} \frac{\partial\Psi_{x_{j},\mu_{j}}}{\partial\mu_{j}}&={-}\frac{N-2s}{2}\frac{c_{0}}{\mu_{j}\mu_{j}^{({N-2s}/{2})}}(H(y,x_{j})+o(1)), \end{align}
\begin{align} \frac{\partial\Psi_{x_{j},\mu_{j}}}{\partial x_{ji}}&=\frac{c_{0}}{\mu_{j}^{({N-2s}/{2})}}\Bigg(\frac{\partial H(y,x_{j})}{\partial x_{ji}}+o(1)\Bigg), \end{align}
where 
$j=1,\ldots ,k$, 
$i=1,\ldots ,N$ and 
$c_{0}=\int _{{{\mathfrak R}}^{N}}U^{2^{*}_{s}-1}$.
Proof. Note that
\[ U_{x_{j},\mu_{j}}(y)=\int_{{{\mathfrak R}}^{N}}\Gamma(y,z)U_{x_{j},\mu_{j}}^{2_{s}^{*}-1}(z)\textrm{d}z, \]and
\[ PU_{x_{j},\mu_{j}}(y)=\int_{\Omega}G(y,z)U_{x_{j},\mu_{j}}^{2_{s}^{*}-1}(z)\textrm{d}z. \]Then, we have
\begin{align*}
\Psi_{x_{j},\mu_{j}}&=\int_{{{\mathfrak
R}}^{N}}\Gamma(y,z)U_{x_{j},\mu_{j}}^{2_{s}^{*}-1}(z)\textrm{d}z-\int_{\Omega}G(y,z)U_{x_{j},\mu_{j}}^{2_{s}^{*}-1}(z)\textrm{d}z\\
&= \int_{{{\mathfrak
R}}^{N}\backslash\Omega}\Gamma(y,z)U_{x_{j},\mu_{j}}^{2_{s}^{*}-1}(z)\textrm{d}z+\int_{\Omega}H(y,z)U_{x_{j},\mu_{j}}^{2_{s}^{*}-1}(z)\textrm{d}z\\
& =
O\Bigg(\frac{1}{\mu_{j}^{({N+2s}/{2})}}\int_{{{\mathfrak
R}}^{N}\backslash\Omega}\frac{1}{|z-y|^{N-2s}}\frac{1}{|z-x_{j}|^{N+2s}}\textrm{d}z\Bigg)\\
&\quad +
\frac{1}{\mu_{j}^{({N-2s}/{2})}}\int_{\Omega_{j}}H(y,\mu_{j}^{{-}1}z+x_{j})U^{2_{s}^{*}-1}(z)\textrm{d}z\\
&=
O\Bigg(\frac{1}{\mu_{j}^{({N+2s}/{2})}}\Bigg)+\frac{H(y,x_{j})}{\mu_{j}^{({N-2s}/{2})}}\int_{{{\mathfrak
R}}^{N}}U^{2_{s}^{*}-1}\\
&\quad +
O\Bigg(\frac{1}{\mu_{j}^{({N-2s}/{2})}}\int_{\Omega_{j}}\frac{\mu_{j}^{{-}1}|z|}{(1+|z|)^{N+2s}\textrm{d}z}\Bigg)\\
&=
O\Bigg(\frac{1}{\mu_{j}^{({N+2s}/{2})}}\Bigg)+\frac{H(y,x_{j})}{\mu_{j}^{({N-2s}/{2})}}\int_{{{\mathfrak
R}}^{N}}U^{2_{s}^{*}-1}+O\Bigg(\frac{1}{\mu_{j}^{({N}/{2})}}\Bigg),
\end{align*}
the last equality follows from (B.3), where 
$\Omega _{j}=\{z : \mu _{j}^{-1}z+x_{j}\in \Omega \}$. By a similar argument above, we can prove (A.2) and (A.3).
Appendix B. Energy expand
In this section, we will expand 
$J_{\nu }(x,\mu ,0)$ and its derivatives. First, we recall that the energy function corresponding to equation (1.4) is given by
\[ I_\nu(v)=\frac{1}{2}\int_{{{\mathfrak R}}^{N}}\int_{{{\mathfrak R}}^{N}}\frac{|v(y)-v(z)|^{2}}{|y-z|^{N+2s}}\textrm{d}y\textrm{d}z-\frac{1}{2}\int_{\Omega}\lambda v^{2}-\frac{1}{2^{*}_{s}}\int_{\Omega}(v-\nu \varphi_{1})_{+}^{2^{*}_{s}}. \]Lemma B.1 We have
\begin{align*}
I_\nu(PU_{x_{j},\mu_{j}})&=A_{1}-\frac{\lambda
A_{2}}{\mu_{j}^{2s}}+\frac{\varphi_{1}(x_{j})A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}+O\Bigg(\frac{1}{\mu_{j}^{N-2s}}\Bigg)+O\Bigg(\frac{\nu}{\mu_{j}^{({N}/{2})}}\Bigg)\\
&\quad +O\Bigg(\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg),
\end{align*}
where 
$\sigma$ is a small positive constant and 
$A_{1}$, 
$A_{2}$, 
$A_{3}$ are defined by
\[ A_{1}=\Bigg(\frac{1}{2}-\frac{1}{2^{*}_{s}}\Bigg)\int_{{{\mathfrak R}}^{N}}U^{2_{s}^{*}}, \quad A_{2}=\frac{1}{2}\int_{{{\mathfrak R}}^{N}}U^{2},\quad A_{3}=\int_{{{\mathfrak R}}^{N}}U^{2^{*}_{s}-1}. \]Proof. By a direct computation, we have
\begin{align}
I_\nu(PU_{x_{j},\mu_{j}})&=\frac{1}{2}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}PU_{x_{j},\mu_{j}}-\frac{\lambda}{2}\int_{\Omega}(PU_{x_{j},\mu_{j}})^{2}-\frac{1}{2^{*}_{s}}\int_{\Omega}(PU_{x_{j},\mu_{j}}-\nu \varphi_{1})_{+}^{2^{*}_{s}} \nonumber\\
&= \frac{1}{2}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}}-\frac{1}{2}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\Psi_{x_{j},\mu_{j}}-\frac{\lambda}{2}\int_{\Omega}U_{x_{j},\mu_{j}}^{2}\notag\\
&\quad +O\Bigg(\int_{\Omega}U_{x_{j},\mu_{j}}\Psi_{x_{j},\mu_{j}}\Bigg)\nonumber\\
&\quad-\frac{1}{2^{*}_{s}}\int_{\Omega}(U_{x_{j},\mu_{j}}-\nu
\varphi_{1})_{+}^{2^{*}_{s}} +O\Bigg(\int_{\Omega}(U_{x_{j},\mu_{j}}-\nu
\varphi_{1})_{+}^{2^{*}_{s}-1}\Psi_{x_{j},\mu_{j}}\Bigg)\nonumber\\
&= \frac{1}{2}\int_{{{\mathfrak
R}}^{N}}U^{2^{*}_{s}}-\frac{\lambda}{2\mu_{j}^{2s}}\int_{{{\mathfrak
R}}^{N}}U^{2}+O\Bigg(\frac{1}{\mu_{j}^{N-2s}}\Bigg)\notag\\
&\quad +O\Bigg(\frac{1}{\mu_{j}^{N-2s}}\int_{\Omega}\frac{1}{|y-x_{j}|^{N-2s}}\Bigg)\nonumber\\
&\quad-\frac{1}{2^{*}_{s}}\int_{\Omega}(U_{x_{j},\mu_{j}}-\nu
\varphi_{1})_{+}^{2^{*}_{s}}+O\Bigg(\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\Psi_{x_{j},\mu_{j}}\Bigg)\nonumber\\
&= \frac{1}{2}\int_{{{\mathfrak
R}}^{N}}U^{2^{*}_{s}}-\frac{\lambda
A_{2}}{\mu_{j}^{2s}}-\frac{1}{2^{*}_{s}}\int_{\Omega}(U_{x_{j},\mu_{j}}-\nu
\varphi_{1})_{+}^{2^{*}_{s}}+O\Bigg(\frac{1}{\mu_{j}^{N-2s}}\Bigg).
\end{align}
Let 
$R>0$ such that 
$\Omega \subset B_{R}(x_{j})$. Choose 
$\sigma$ small such that 
$N+2s-\sigma (N-2s)>N$. Using the following estimate
\[ (a-b)_{+}^{2^{*}_{s}}=a^{2^{*}_{s}}-2_{s}^{*}a^{2^{*}_{s}-1}b+O(a^{2^{*}_{s}-1-\sigma}b^{1+\sigma}),\quad a,b>0, \]we find
\begin{align}
\int_{\Omega}(U_{x_{j},\mu_{j}}-\nu
\varphi_{1})_{+}^{2^{*}_{s}}&=\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}}-2^{*}_{s}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\nu
\varphi_{1}+O\Bigg(\nu^{1+\sigma}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1-\sigma}\Bigg)\nonumber\\
& =
\int_{{{\mathfrak
R}}^{N}}U^{2^{*}_{s}}-\frac{2^{*}_{s}\varphi_{1}(x_{j})\nu
}{\mu_{j}^{({N-2s}/{2})}}\int_{{{\mathfrak
R}}^{N}}U^{2^{*}_{s}-1}+O\Bigg(\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)\nonumber\\
&\quad+\frac{\nu}{\mu_{j}^{({N-2s}/{2})}}O\Bigg(\int_{B_{\mu_{j}R(0)}}\frac{\mu_{j}^{{-}1}|y|}{1+|y|^{N+2s}}\Bigg)\notag\\
&=
\int_{{{\mathfrak
R}}^{N}}U^{2^{*}_{s}}-\frac{2^{*}_{s}\varphi_{1}(x_{j})A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}\nonumber\\
&\quad+O\Bigg(\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)+O\Bigg(\frac{\nu}{\mu_{j}^{({N}/{2})}}\Bigg),
\end{align}the last equality is due to the following estimate
\begin{equation} \int_{B_{\mu_{j}R(0)}}\frac{\mu_{j}^{{-}1}|y|}{1+|y|^{N+2s}}= \begin{cases} \mu_{j}^{{-}1} & \text{if}\ \frac{1}{2}< s<1,\\ \mu_{j}^{{-}1}\log\mu_{j} & \text{if}\ s=\frac{1}{2},\\ \mu_{j}^{{-}2s} & \text{if}\ 0< s<\frac{1}{2}. \end{cases} \end{equation}Lemma B.2 We have
\begin{align*}
I_\nu\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}\Bigg)&=kA_{1}-\sum_{j=1}^{k}\Bigg(\frac{\lambda
A_{2}}{\mu_{j}^{2s}}-\frac{\varphi_{1}(x_{j})A_{3}\nu
}{\mu_{j}^{({N-2s}/{2})}}\Bigg)\\
&\quad -\sum_{i\neq
j}^{k}\frac{1}{2}b_{0}(A_{3}+b_{0}\lambda
A(x_{i},x_{j}))\varepsilon_{ij}\\
&\quad+O\Bigg(\sum_{j=1}^{k}\Bigg(\frac{1}{\mu_{j}^{N-2s}}+\frac{\nu}{\mu_{j}^{\frac{N}{2}}}+\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)+\sum_{i\neq
j}\varepsilon_{ij}^{1+\sigma}\Bigg),
\end{align*}
where 
$A_{2}$, 
$A_{3}$ are defined in lemma B.1, 
$\sigma$ is a small positive constant and 
$A(x_{i},x_{j})$ is defined by
\[ A(x_{i},x_{j})=\int_{\Omega}\Bigg(\frac{1}{|y-x_{i}|^{N-2s}}+\frac{1}{|y-x_{j}|^{N-2s}}\Bigg)<\infty. \]Proof. By a direct computation, we have
\begin{align}
I_\nu\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}\Bigg)&=\sum_{j=1}^{k}I_\nu(PU_{x_{j},\mu_{j}})+\frac{1}{2}\sum_{i\neq
j}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}PU_{x_{i},\mu_{i}}\notag\\
&\quad -\frac{\lambda}{2}\sum_{i\neq
j}\int_{\Omega}PU_{x_{j},\mu_{j}}PU_{x_{i},\mu_{i}}\nonumber\\
&\quad-\frac{1}{2^{*}_{s}}\int_{\Omega}\Bigg(\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu
\varphi_{1}\Bigg)_{+}^{2^{*}_{s}}-\sum_{j=1}^{k}(PU_{x_{j},\mu_{j}}-\nu
\varphi_{1})_{+}^{2^{*}_{s}}\Bigg).
\end{align}
Noting that for 
$i\neq j$, we have
\begin{align}
\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}PU_{x_{i},\mu_{i}}
&=\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}U_{x_{i},\mu_{i}}-\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\Psi_{x_{i},\mu_{i}}\nonumber\\
& =
\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}U_{x_{i},\mu_{i}}+O\Big(\frac{1}{\mu_{j}^{({N-2s}/{2})}\mu_{i}^{({N-2s}/{2})}}\Bigg)\nonumber\\
&=
\frac{b_{0}}{\mu_{j}^{({N-2s}/{2})}\mu_{i}^{({N-2s}/{2})}|x_{i}-x_{j}|^{N-2s}}\int_{{{\mathfrak
R}}^{N}}U^{2^{*}_{s}-1}\notag\\
&\quad +O\Bigg(\frac{1}{\mu_{j}^{({N-2s}/{2})}\mu_{i}^{({N-2s}/{2})}}\Bigg)\nonumber\\
& =
b_{0}A_{3}\varepsilon_{ij}+O\Bigg(\frac{1}{\mu_{j}^{({N-2s}/{2})}\mu_{i}^{({N-2s}/{2})}}\Bigg),
\end{align}and
\begin{align}
\int_{\Omega}PU_{x_{j},\mu_{j}}PU_{x_{i},\mu_{i}}&=\int_{\Omega}U_{x_{j},\mu_{j}}U_{x_{i},\mu_{i}}+O\Bigg(\frac{1}{\mu_{j}^{({N-2s}/{2})}\mu_{i}^{({N-2s}/{2})}}\Bigg)\nonumber\\
&=b_{0}^{2}\varepsilon_{ij}\int_{\Omega}\Bigg(\frac{1}{|y-x_{i}|^{N-2s}}+\frac{1}{|y-x_{j}|^{N-2s}}\Bigg)\notag\\
&\quad +O\Bigg(\frac{1}{\mu_{j}^{({N-2s}/{2})}\mu_{i}^{({N-2s}/{2})}}\Bigg)\nonumber\\
&=b_{0}^{2}\varepsilon_{ij}A(x_{i},x_{j})+O\Bigg(\frac{1}{\mu_{j}^{({N-2s}/{2})}\mu_{i}^{({N-2s}/{2})}}\Bigg).
\end{align}Now we estimate the last term in (B.4). By a similar computation as (B.2), we obtain that
\begin{align}
&\int_{\Omega}\Bigg(\Bigg(\sum_{j=1}^{k}PU_{x_{j},\mu_{j}}-\nu
\varphi_{1}\Bigg)_{+}^{2^{*}_{s}}-\sum_{j=1}^{k}(PU_{x_{j},\mu_{j}}-\nu
\varphi_{1})_{+}^{2^{*}_{s}}\Bigg)\nonumber\\
&\quad =\int_{\Omega}\Bigg(\Bigg(\sum_{j=1}^{k}U_{x_{j},\mu_{j}}-\nu
\varphi_{1}\Bigg)_{+}^{2^{*}_{s}}-\sum_{j=1}^{k}(U_{x_{j},\mu_{j}}-\nu
\varphi_{1})_{+}^{2^{*}_{s}}\Bigg)+O\Bigg(\sum_{j=1}^{k}\frac{1}{\mu_{j}^{N-2s}}\Bigg)\nonumber\\
&\quad =\int_{\Omega}\Bigg(\sum_{j=1}^{k}U_{x_{j},\mu_{j}}\Bigg)^{\!2^{*}_{s}}-{2^{*}_{s}}\int_{\Omega}\Bigg(\sum_{j=1}^{k}U_{x_{j},\mu_{j}}\Bigg)^{\!2^{*}_{s}-1}\nu
\varphi_{1}+O\Bigg(\sum_{j=1}^{k}\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)\nonumber\\
&\qquad-\sum_{j=1}^{k}\int_{\Omega}\Bigg(U_{x_{j},\mu_{j}}^{2^{*}_{s}}-2^{*}_{s}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\nu
\varphi_{1}\Bigg)+O\Bigg(\sum_{j=1}^{k}\frac{1}{\mu_{j}^{N-2s}}\Bigg)\nonumber\\
&\quad =\int_{\Omega}\Bigg(\Bigg(\sum_{j=1}^{k}U_{x_{j},\mu_{j}}\Bigg)^{2^{*}_{s}}-\sum_{j=1}^{k}\int_{\Omega}\Bigg(\sum_{j=1}^{k}U_{x_{j},\mu_{j}}\Bigg)^{2^{*}_{s}}\Bigg)+O\Bigg(\sum_{j=1}^{k}\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)\nonumber\\
&\qquad-2^{*}_{s}\int_{\Omega}\Bigg(\sum_{j=1}^{k}U_{x_{j},\mu_{j}}\Bigg)^{2^{*}_{s}-1}-\sum_{j=1}^{k}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\Bigg)\nu
\varphi_{1}+O\Bigg(\sum_{j=1}^{k}\frac{1}{\mu_{j}^{N-2s}}\Bigg)\nonumber\\
&\quad =2^{*}_{s}\sum_{i\neq
j}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}U_{x_{i},\mu_{i}}+O\Bigg(\sum_{i\neq
j}^{k}\int_{\Omega}U_{x_{j},\mu_{j}}^{\frac{2^{*}_{s}}{2}}U_{x_{i},\mu_{i}}^{\frac{2^{*}_{s}}{2}}\Bigg)\notag\\
&\qquad +O\Bigg(\sum_{j=1}^{k}\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)
+O\Bigg(\int_{\Omega}\sum_{i\neq
j}^{k}U_{x_{j},\mu_{j}}^{\frac{2^{*}_{s}-1}{2}}U_{x_{i},\mu_{i}}^{\frac{2^{*}_{s}-1}{2}}\nu
\varphi_{1}\Bigg)\notag\\
&\qquad +O\Bigg(\sum_{j=1}^{k}\frac{1}{\mu_{j}^{N-2s}}\Bigg)\nonumber\\
&\quad =\sum_{i\neq
j}^{k}b_{0}2^{*}_{s}A_{3}\varepsilon_{ij}+O\Bigg(\sum_{i\neq
j}^{k}
\frac{\log(\mu_{i}\mu_{j})}{\mu_{j}^{({N}/{2})}\mu_{i}^{({N}/{2})}|x_{i}-x_{j}|^{N}}\Bigg)\notag\\
&\qquad +O\Bigg(\sum_{j=1}^{k}\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)\nonumber\\
&\qquad+O\Bigg(\sum_{i\neq j}^{k}
\frac{\nu}{\mu_{j}^{({N+2}/{4})}\mu_{i}^{({N+2}/{4})}|x_{i}-x_{j}|^{({N+2}/{2})}}\Bigg)+O\Bigg(\sum_{j=1}^{k}\frac{1}{\mu_{j}^{N-2s}}\Bigg).
\end{align}Lemma B.3 We have
\begin{align*} &\frac{\partial J_{\nu}(x,\mu,0)}{\partial \mu_{j}}=\frac{2s\lambda A_{2}}{\mu_{j}^{2s+1}}-\frac{N-2s}{2}\frac{\varphi_{1}(x_{j})A_{3}\nu }{\mu_{j}^{({N-2s}/{2})+1}}\\ &\quad +\frac{1}{\mu_{j}}O\Bigg(\frac{1}{\mu_{j}^{N-2s}}+\frac{\nu}{\mu_{j}^{({N}/{2})}}+\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}+\sum_{i\neq j}\varepsilon_{ij}\Bigg), \end{align*}
where 
$A_{2}$, 
$A_{3}$ are defined in lemma B.1 and 
$\sigma >0$ is a small constant.
Proof. By a direct computation, we have
\begin{align*}
\frac{\partial J_{\nu}(x,\mu,0)}{\partial
\mu_{j}}&=\Bigg\langle
I_\nu^{\prime}\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}\Bigg),\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial
\mu_{j}}\Bigg\rangle\nonumber\\
&=
\int_{\Omega}\sum_{i=1}^{k}U_{x_{i},\mu_{i}}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial
\mu_{j}}-\lambda\sum_{i=1}^{k}\int_{\Omega}PU_{x_{i},\mu_{i}}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\nonumber\\
&\quad-\int_{\Omega}\Bigg(\sum_{i=1}^{k}PU_{x_{i},\mu_{i}}-\nu\varphi_{1}\Bigg)_{+}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\nonumber\\
& =
\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial
\mu_{j}}-\lambda\int_{\Omega}PU_{x_{j},\mu_{j}}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\notag\\
&\quad +O\Bigg(\sum_{i\neq
j}\int_{\Omega}PU_{x_{i},\mu_{i}}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\Bigg)\nonumber\\
&\quad-\int_{\Omega}(PU_{x_{j},\mu_{j}}-\nu\varphi_{1})_{+}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}+O\Bigg(\sum_{i\neq
j}\int_{\Omega}U_{x_{i},\mu_{i}}^{2^{*}_{s}-1}\frac{\partial
P U_{x_{j},\mu_{j}}}{\partial \mu_{j}}\Bigg)\nonumber\\
& =
\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial
\mu_{j}}-\lambda\int_{\Omega}PU_{x_{j},\mu_{j}}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}+O\Bigg(\sum_{i\neq
j}\frac{\varepsilon_{ij}}{\mu_{j}}\Bigg)\nonumber\\
&\quad-\int_{\Omega}(PU_{x_{j},\mu_{j}}-\nu\varphi_{1})_{+}^{2^{*}_{s}-1}\frac{\partial
PU_{x_{j},\mu_{j}}}{\partial \mu_{j}}\nonumber\\
&=
\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-1}\frac{\partial
U_{x_{j},\mu_{j}}}{\partial
\mu_{j}}-\lambda\int_{\Omega}U_{x_{j},\mu_{j}}\frac{\partial
U_{x_{j},\mu_{j}}}{\partial
\mu_{j}}\notag\\
&\quad -\int_{\Omega}(U_{x_{j},\mu_{j}}-\nu\varphi_{1})_{+}^{2^{*}_{s}-1}\frac{\partial
U_{x_{j},\mu_{j}}}{\partial \mu_{j}} \nonumber\\
&\quad+\frac{1}{\mu_{j}}O\Bigg(\frac{1}{\mu_{j}^{N-2s}}\Bigg)+O\Bigg(\sum_{i\neq
j}\frac{\varepsilon_{ij}}{\mu_{j}}\Bigg) \nonumber\\
& = \frac{2s\lambda
A_{2}}{\mu_{j}^{2s+1}}+(2^{*}_{s}-1)\int_{\Omega}U_{x_{j},\mu_{j}}^{2^{*}_{s}-2}\frac{\partial
U_{x_{j},\mu_{j}}}{\partial
\mu_{j}}\nu\varphi_{1}+\frac{1}{\mu_{j}}O\Bigg(\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)\nonumber\\
&\quad+\frac{1}{\mu_{j}}O\Bigg(\frac{1}{\mu_{j}^{N-2s}}\Bigg)+O\Bigg(\sum_{i\neq
j}\frac{\varepsilon_{ij}}{\mu_{j}}\Bigg) \nonumber\\
&= \frac{2s\lambda
A_{2}}{\mu_{j}^{2s+1}}-\frac{N-2s}{2}\frac{A_{3}\varphi_{1}(x_{j})\nu}{\mu_{j}^{({N-2s}/{2})+1}}+O\Bigg(\frac{\nu}{\mu_{j}\mu_{j}^{({N}/{2})}}\Bigg)\notag\\
&\quad +\frac{1}{\mu_{j}}O\Bigg(\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}\Bigg)
+O\Bigg(\sum_{i\neq j}\frac{\varepsilon_{ij}}{\mu_{j}}\Bigg).
\end{align*}Using the similar computation, we can conclude the following result.
Lemma B.4 We have
\[ \frac{\partial J_{\nu}(x,\mu,0)}{\partial x_{ji}}= \mu_{j}O\Bigg(\frac{1}{\mu_{j}^{N-2s}}+\frac{\nu}{\mu_{j}^{({N}/{2})}}+\frac{\nu^{1+\sigma}}{\mu_{j}^{({(N-2s)(1+\sigma)}/{2})}}+\sum_{i\neq j}\varepsilon_{ij}\Bigg). \]Acknowledgments
The authors would like to express their gratitude to the reviewers for careful reading and helpful suggestions which led to an improvement of the original manuscript. This research was supported by the National Natural Science Foundation of China (No.11831009; No.12071169).
