Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T07:43:21.423Z Has data issue: false hasContentIssue false
  • English
  • Français

Spread of parasites in metapopulations: an experimental study of the effects of host migration rate and local host population size

Published online by Cambridge University Press:  21 October 2004

J. E. LOPEZ ,
L. P. GALLINOT  and
M. J. WADE
J. E. LOPEZ
Affiliation:
Biology Department, Indiana University, 1001 East 3rd Street, Bloomington, IN 47405, USA Current address: Biology Department, Grand Valley State University, 1 Campus Drive, Allendale, MI 49401, USA.
L. P. GALLINOT
Affiliation:
Biology Department, Indiana University, 1001 East 3rd Street, Bloomington, IN 47405, USA
M. J. WADE
Affiliation:
Biology Department, Indiana University, 1001 East 3rd Street, Bloomington, IN 47405, USA
Rights & Permissions [Opens in a new window]

Abstract

We established experimental metapopulations of the flour beetle, Tribolium castaneum, and its ectoparasitic mite, Acarophenax tribolii, to investigate the effects of host migration rate and local host population size on the spread of mite infections. Global prevalence across our metapopulations was less than half the observed within-patch prevalence, so that spatial structure alone afforded a great deal of protection to hosts against parasite infection. Our results showed further that migration played a determining role in occupancy, the number of patches infected within a metapopulation, while host population size played a determining role in local prevalence, the fraction of hosts infected within local patches. Local and global prevalence appeared to reach equilibrium levels on 2 different time-scales. Local host prevalence reached equilibrium values within 30 days of receiving an infected host migrant. Global prevalence increased more slowly and was clearly dependent upon occupancy, the number of host patches with at least 1 infected host, which in turn depended on the level of host migration among host patches. The effect of population size was not limited to local prevalence in patches without spatial structure but extended to sets of patches across the metapopulation. Lloyd's index of patchiness differed significantly between metapopulations with small versus large numbers of hosts. Although parasites were aggregated on hosts for both local patch sizes, they tended to aggregate to a much greater degree at the smaller host patch size. We discuss our empirical findings in light of current epidemiological theory.

Keywords

metapopulationprevalencehost-parasite interactionshost population sizeLloyd's indexpatchinessspatial structureparasite distribution
Type
Research Article
Information
Parasitology , Volume 130 , Issue 3 , March 2005 , pp. 323 - 332
Copyright
2004 Cambridge University Press

INTRODUCTION

Spatial structure is a feature of many populations under natural conditions and many other populations are subdivided as a result of anthropogenic habitat fragmentation. In both cases, the spatial structure and migration patterns of hosts can modify host-parasite interactions (Thrall & Burdon, 1997; Ericson, Burdon & Muller, 1999) and lead to changes in parasite prevalence (e.g. Dwyer, 1991; Grosholz, 1993; Burdon, Ericson & Muller, 1995). While the spatial structure of host populations can have significant effects on the dynamics of host and parasite populations, host-parasite interactions are generally modelled assuming a single, randomly mixing host population (Anderson & May, 1978, 1979, 1981, 1991; May & Anderson, 1978, 1979). These models have been applied with some success to human populations, and to other organisms with large, widespread and randomly mixing populations. In such populations, the theory predicts that parasite prevalence is independent of host population size.

In contrast, many natural populations have a conspicuous spatial structure with discrete patches connected by migration and are called metapopulations. The dynamics of metapopulations are different from those of large, well-mixed populations (Hastings, 1990; Gotelli, 1991; Hanski, 1991; Hanski & Gilpin, 1991; Hassell, Comins & May, 1991; Gotelli & Kelley, 1993; Hanski, 1994; Bascompte & Solé, 1995; Murdoch, 1996; Smith, Ericson & Burdon, 2003), but the consequences of such spatial structure on host-parasite interactions are less well understood. Some models of the spread of diseases in structured populations (Post, DeAngelis & Travis, 1983; Bolker & Grenfell, 1993; Grenfell, Bolker & Kleckzkowski, 1995; Sattenspiel & Dietz, 1995; Lloyd & May, 1996; Ferguson, May & Anderson, 1997; Earn, Rohani & Grenfell, 1998) have investigated the effects of spatial heterogeneity. For example, models that divide the host population into patches and allow infected hosts from one patch to migrate to and infect susceptible hosts in other patches show that in order for the disease to persist, at least one host patch must be large enough to sustain an endemic infection (Post et al. 1983). This is similar to the condition required for persistence of parasites in single, homogeneously mixing host populations, namely that the host population be above the threshold density. Cellular automata models reach similar conclusions (Holmes, 1997). Thus, in these models, adding spatial heterogeneity affects only the quantitative behaviour of epidemics.

In metapopulations, patch size and migration rate among host patches can be critical factors determining parasite prevalence. Structured metapopulation models find that patch size is one of the key factors influencing pathogen dynamics (Smith et al. 2003). When the introduction of parasites into uninfected host patches depends on host migration, Hess' (1996) model predicts extinction of both host and parasite populations at low migration rates but increased likelihood of host persistence and greater parasite prevalence at higher rates.

Experimental and field investigations also indicate that the effects of spatial heterogeneity on pathogen-host dynamics can be different from the predictions of models that do not consider spatial structure (Dwyer, 1991; Grosholz, 1993; Burdon et al. 1995; Ericson et al. 1999). For example, in a field study of the prevalence of iridovirus infection in pill bugs (Porcellio scaber), Grosholz (1993) found an inverse relationship between viral prevalence and host population size although models predict no relationship. Viral prevalence was high when host numbers were low because hosts tended to aggregate to a greater degree under summer environmental conditions. Conversely, virus prevalence was low when hosts were more numerous because hosts tended to be less clustered. Similarly, in a study of the transmission of nuclear polyhedrosis virus in the Douglas-fir tussock moth (Orgyia pseudotsugata), Dwyer (1991) found that, although virus transmission within patches was proportional to the local density of hosts, the spatial distribution of the parasite affected the relationship between host density and transmission. Field studies of plant metapopulations identify patch size as a key factor in interactions with pathogenic fungi (Burdon et al. 1995; Ericson et al. 1999; Smith et al. 2003). Collectively, these results indicate that host population size and spatial structure are important variables in the interactions of hosts and parasites but, in studies of natural populations, many factors cannot be controlled.

Taken together, available models and data point to the key roles played by migration and local host population size in the dynamics of host-parasite interactions in metapopulations (Dwyer, 1991; Grosholz, 1993; Hess, 1996), but there are no empirical tests of the effects of these factors on the prevalence of parasites. We have experimentally manipulated these two factors under controlled laboratory conditions and measured their effects on the spread, prevalence and distribution of parasites.

In a metapopulation, the occurrence of parasites can be measured at 3 different levels, (1) the proportion of infected patches, (2) the proportion of infected hosts within a patch, and (3) the proportion of infected hosts across all patches. To distinguish among these measures of parasite occurrence, we use ‘occupancy’ to refer to the proportion of infected patches. Other authors use the term ‘incidence’, but we prefer occupancy to avoid confusion with ‘incidence rate’, a measure of number of new infections per unit time used in epidemiology (Margolis et al. 1982). We use ‘local prevalence’ to refer to the proportion of infected hosts within patches and ‘global prevalence’ to refer to the proportion of infected hosts in the metapopulation as a whole. All these measures are of interest and may be affected differently by host population size and migration. Specifically, we expect that occupancy should be affected most strongly by the rate of host migration among patches because parasite spread from patch to patch depends on host migration. Local prevalence should be influenced by immigration rate and local conditions affecting parasite establishment such as host population size and dynamics, and the time elapsed since the arrival of the parasite in an uninfected patch. Global prevalence should be affected by the interaction of migration rate and local dynamics because migration spreads the parasite among patches (occupancy) but local conditions determine parasite establishment.

In our experiment, we investigated the effect of host population size and host migration rate on the 3 different measures of prevalence: occupancy, local prevalence and global prevalence. We also considered the effects of these factors on the distribution of parasites among hosts.

MATERIALS AND METHODS

We set up 16 laboratory metapopulations of the flour beetle, Tribolium castaneum to study the effects host population size and migration rate on parasite prevalence. Each metapopulation consisted of 25 patches. In order to manipulate host population size, patches in 8 metapopulations were small (SS) while in the other 8 metapopulations, patches were large (LS). Each patch in the SS treatments started with 8 g of medium and 8 adult beetles. In the LS treatments, each patch started with 36 g of medium and 36 adult beetles. The medium consisted of 95% stone ground, unbleached flour and 5% Brewers' yeast by weight that was sifted through a 28 mesh sieve and was ‘sterilized’ in a drying oven at 60 °C for 24 h prior to the start of the experiment. While the size of host populations varied among treatments, the density of hosts was held constant by using different size containers and different amounts of media. The experiment started with 1 host beetle per gram of media in both population size treatments. During the course of the experiment, beetles reproduced and increased in numbers. However, the SS patches had significantly lower numbers of beetles than the LS patches (see Results section). The density of hosts per unit of media also increased but did not differ among treatments. Therefore, host density is not confounded with host population size. For the duration of the experiment, metapopulations were maintained in incubators at 29 °C and 70% RH. Each vial was stoppered with a dispo-plug to prevent uncontrolled migration of beetles or parasites among cultures (see below).

Twenty-four h after establishing the uninfected metapopulations as described above, we introduced mites, Acarophenax tribolii, into one of the 25 patches in each metapopulation. A. tribolii is an ectoparasitic mite that attacks Tribolium eggs, larvae, pupae and adults causing increased mortality, reduced larval development rate, and reduced fecundity in females (unpublished data). Its entire life-cycle, from egg to adult, is only 3 days. Since the mites are too small to handle as single individuals, we selected 3 infected hosts harbouring at least 5 mites on the ventral exoskeleton, killed them, and placed all 3 carcasses in the patch chosen for infection. Mites crawled from the dead hosts and spread through the patch infecting new hosts. Preliminary tests showed that the variation in number of mites on the infected carcasses did not affect prevalence or abundance of mites in the infected patch 7–14 days after infection.

After the parasite introduction, the movement of host beetles among patches caused mites to spread from the patch of initial inoculation to other patches. We moved beetles among patches at weekly intervals, imposing high rates of migration on some metapopulations and low rates on others. In the low migration (LM) treatments, each week we moved 1 randomly chosen beetle from each patch to a randomly chosen destination patch. In the high migration (HM) treatment, each week we randomly moved 4 beetles from each patch to randomly chosen destination patches. The random selection of the migrating beetles means that the rate of migration for infected and uninfected hosts was proportional to their abundance. Thus, migration into and out of patches was random and independent of patch or host infection. In population genetic theory, this pattern of migration is called ‘island model’ migration (cf. Wade, 1982) and it is characteristic of many of the metapopulation models of disease spread. We not only took precautions to prevent the uncontrolled spread of mites among patches other than by our controlled movement of host beetles but also maintained uninfected ‘sentinel’ populations in the same experimental chambers. These were stoppered, mite-free host populations that received no migrants throughout the experiment. Mites never appeared in these uninfected sentinel populations indicating that mites did not spread among patches independent of our manipulations. In total, there were 16 metapopulations consisting of 4 replicates of each combination of host population size and migration rate (4 replicates per treatment×2 population size treatments×2 migration rate treatments×25 patches per metapopulation=400 patches).

Ninety days after the start of the experiment, we sampled 30 randomly chosen beetles from each patch in each metapopulation (30 beetles per patch×25 patches=750 beetles per metapopulation×16 metapopulations=12000 beetles) in order to measure the prevalence and distribution of mites. We dissected each of these sampled hosts and censused all mites on the exoskeleton and under the elytra and wings using a dissecting microscope. From these data, we estimated 3 measures of parasite infection: (1) occupancy, the proportion of patches in which at least one host was infected out of the 25 patches in the metapopulation; (2) local prevalence, the proportion of infected beetles out of the 30 beetles sampled from each patch; and, (3) global prevalence, the proportion of infected beetles out of the 750 sampled from the 25 patches in each metapopulation. Although the probability of detecting infection in samples of 30 beetles varies with the size of the population, such differences are only meaningful when prevalence is low, less than 15%. In our experiment, average mite prevalence was generally much higher (see Results section). As a result, our estimates are not biased by variation in local host population size.

Because of the labour involved in sampling the patches, the experiment was blocked over time with 2 replicates of each treatment per block. Replicates 3 and 4 (block 2) had to be sampled at 60 days instead of 90 days owing to an uncontrolled fungal infection that began to grow in the medium of some patches. The fungal infection appeared to be distributed randomly across patches, treatments, and replicates, with less than 12% of patches showing signs of fungal infection. The fungus was detected before it could interfere with our treatments.

The effects of population size, migration rate, and block were analysed using generalized linear mixed models (GLMM) with binomial errors and logit link (Wilson, Grenfell & Shaw, 1996) using the GLIMMIX macro in SAS (Littell et al. 1996). Population size (small, large), migration rate (low, high) and the population size-by-migration interaction were included as fixed factors. Block, metapopulation replicates, and (where appropriate) patch were introduced as random factors to remove their effect. In the analysis of occupancy, the response variable was the status of each patch in a metapopulation (infected or uninfected) with block and metapopulation as random effects. In the analysis of local prevalence, the response variable was the status of each beetle in the sample (infected or uninfected), with block, metapopulation and patch as random effects. Finally, in the analysis of global prevalence, the response variable was the status of each beetle sampled across the 25 patches in the metapopulation (infected or uninfected), with block and metapopulation included as random effects. We also looked for correlations between local prevalence and the length of time a patch had been infected, and between local prevalence and the number of parasites per host. General linear models with negative binomial or Poisson errors and log or logit links did not fit the data well. Instead, we report results of simple linear regressions that fit the data very well. For the linear regressions, we used standard transformations to meet model assumptions (Zar, 1994): arcsine-square root transformation for prevalence, and natural log of the square root for the number of mites per host.

To quantify the distribution of mites on beetles, we used Lloyd's Patchiness index (Lloyd, 1967). It is common practice to quantify parasite distributions using the negative binomial parameter, k (Wilson & Grenfell, 1997). When the distribution of parasites on hosts is aggregated, k is a good measure of the degree of aggregation. Because parasites are usually aggregated, k is applicable to a wide range of host-parasite systems. However, one of the limitations of k is that it does not quantify over-dispersed distributions. Preliminary data and earlier studies (Lopez, 2004) showed that A. tribolii mites are slightly over-dispersed on T. castaneum hosts. A. tribolii mites were not aggregated in 24·1% of our samples. Therefore, k was not a good measure of mite distribution for nearly ¼ of our samples. Another disadvantage of the negative binomial parameter is that comparisons among samples are unreliable because k is highly dependent on the average number of parasites per host (Scott, 1987); k could not be compared among treatments in our study, or to estimates from other studies. Lloyd's Patchiness index, on the other hand, provides a standardized measure that allows for comparisons among samples. Lloyd's Patchiness index has not been widely used by parasitologists although its properties are very well suited for the analysis of parasite distributions. Lloyd defined Patchiness (P) as:

where m is the mean number of parasites per host, and m* is the ‘mean crowding’ of parasites. Lloyd's mean crowding, m*, measures the average number of other parasites that an individual parasite experiences on a host and is given by

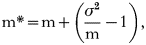
where σ2 is the variance in the number of parasites per host. Put another way, “the amount by which the ratio of variance to mean exceeds unity, added to the mean itself, gives the ‘mean crowding’” (Lloyd, 1967, p4) and can be interpreted as the number of other parasites that the average parasite encounters. Mean crowding exceeds mean parasite density when parasite loads are aggregated on particular hosts and is less than the mean when parasites are over-dispersed. Thus, P>1 indicates that parasites are aggregated, and P<1 indicates that parasites are overdispersed. We used ANOVA to look for differences in P among treatments.

In addition to the final sample after 90 days, we checked replicates 1 and 2 at days 7, 14, 28, 35, and 77 to monitor the spread of the mite. In these checks, we sampled 30 randomly chosen beetles from each patch and examined them for the presence or absence of mites only on the exoskeleton, but not under the elytra, and returned the live hosts to the source patch. This measure underestimates mite presence because some hosts harbour mites only under their wings with no mites visible on the exoskeleton. Although a less thorough sampling method than the 90-day destructive host dissection, these measurements were sufficiently fine-scale for us to detect the spread of infection among patches, and the treatments can still be compared because the same protocol was used to obtain all the samples.

RESULTS

Occupancy

We found that higher migration rates resulted in greater occupancy, i.e. higher numbers of infected patches, and lower migration rates caused low occupancy (Fig. 1). Of 25 patches in each metapopulation, 46·3% (S.E.=0·214) were infected in the HM while only 14·1% (S.E.=0·106) of the patches were infected in the LM treatments (F1,394=39·50, P<0·0001; estimates were calculated in the logit scale during the GLMM analyses but have been converted to proportions for reporting). This represents an average increase in prevalence of 328·4% as migration rate increased 4-fold, from 1 to 4 migrant hosts per patch per week.

Fig. 1. Occupancy. The number of infected patches in experimental metapopulations differed significantly between the high and low migration treatments. Parasites spread to more patches when migration was high. The effect of population size was not significant.

The effect of the size of host populations, on the other hand, was smaller and not statistically significant. In metapopulations consisting of large patches (LS treatment), 32·0% (S.E.=0·189) of the patches were infected patches compared with 23·1% (S.E.=0·154) of infected patches in metapopulations with small patches (SS treatment), a difference that was not statistically significant (F1,394=3·05, P=0·082).

The interaction of migration rate and population size on occupancy after 90 days was significant (F1,394=5·47, P=0·020). Occupancy was higher in the LS treatment than in the SS treatment when the migration was high but not when the migration rate was low (Fig. 1).

Our fine-scale temporal monitoring of exoskeletal mites in block 1 metapopulations showed that the occupancy rate increased with time and that the increase was faster with high migration than with low migration rates (Fig. 2). The regression of occupancy on time explained 78·1% of the variance and was significant (F3,36=47·24, P<10−5). The slope of the regression was low in the LM treatments (β=0·0017 day−1) and high in the HM treatments (β=0·0061 day−1). The difference of 0·0043 in the slopes was significant (F1,36=23·30, P=2·5×10−5).

Fig. 2. Occupancy and time. Occupancy increased faster and reached higher levels when migration rate was high. While not surprising, this may be the first experimental demonstration of the effect of migration on the spread of parasites.

Local prevalence

The prevalence of mites in infected patches was affected by both migration and population size. First, we found that local prevalence was higher in the LS treatments than in the SS treatments (Fig. 3). In small populations, 22·9% (S.E.=0·151) of the hosts were infected while nearly twice as many hosts, 43·1% (S.E.=0·210), were infected in large populations (F1,3682=100·16, P<0·0001). There was also a smaller but significant effect of migration rate. In the LM treatments, prevalence was lower (29·3%) (S.E.=0·178), than in the HM treatments, where 35·1% (S.E.=0·195) of the hosts were infected (F1,3682=7·68, P=0·0056). The interaction between migration and host population size effects was not significant (F1,3682=1·98, P<0·159).

Fig. 3. Local prevalence. Local prevalence, arcsine-square root transformed to meet statistical assumptions, was affected by population size but not by migration rate. Local prevalence was greater in large populations. The effect of population size on prevalence is not predicted by the most commonly used models of host-parasite population dynamics.

Our periodic checks for exoskeletal mites in block 1 revealed that the size of local host populations was not the only factor affecting local prevalence. The proportion of infected hosts in a patch also depended on the time elapsed since the arrival of an infected host immigrant. The fine-scale monitoring permitted us to estimate the date of onset of the mite infection in local patches as the host migration event preceding the date of first mite detection. The scatter plot of the data (Fig. 4) showed that prevalence increased rapidly in the first 20 days following infection. Between days 20 and 60, prevalence plateaued and remained constant, but because our samples contained no populations infected between 20 and 60 days, it was not possible to obtain a reliable estimate of the breakpoint. Regression models using growth and power functions did not fit the data well or the data did not conform to the assumptions. However, piecewise regression (Neter, Wasserman & Kutner, 1990) of local prevalence against the duration of infection with breakpoint=30 days fit very well (F2,90=27·013, P<10−6), and the data conformed to all the assumptions of linear regression. This analysis showed a significant positive correlation before 30 days that accounted for 37·5% of the variance (prevalence=b0+b1X, where the intercept b0=−0·0258 was not significantly different from zero (t90=−0·269, P=0·789) and b1=2·364 represents the increase in prevalence per day (t90=5·229, P<10−6)). For patches infected more than 30 days, the slope of the relationship became b2=0·431 and is not significantly different from zero (t90=0·812, P=0·419). The difference in slopes, b2 − b1=−1·893 is significant (t290=−4·187, P=0·00007). These data indicate that, once established, a mite infection reaches a stable level of prevalence in a local host population within 30 days, which is 6–7 mite generations and, at most, 1 host generation.

Fig. 4. Local prevalence and time. The prevalence of infection is higher in populations that have been infected longer. The data show that prevalence increases in the 30 days following infection. After 30 days, prevalence remains constant.

As might be expected, the number of mites per host had a strong positive correlation with local prevalence (Fig. 5). A regression of arcsine transformed local prevalence on the (natural log of the square root of the) number of mites per host was significant and accounted for 89·5% of the variance (F1,126=1082·72, P<10−63). Without transformations, the relationship between mite abundance and prevalence was not linear. Prevalence increased as mites multiplied, but was eventually limited either because it reached a more or less stable equilibrium value as was the case in most of our host populations, or because it reached the maximal value of 100% as it did in 6·5% of our host patches.

Fig. 5. Prevalence and mite abundance. There is a strong positive relationship between local prevalence and number of mites per host. When data are transformed as indicated on the axes, the regression explains 89·5% of the variance (F1,126=1082·7, P<10−63). This indicates that the average host has more mites when more hosts are infected.

Global prevalence

Global prevalence, i.e. prevalence across the entire metapopulation, was affected by both migration rate and host population size (F1,12E3=488·66, P<0·0001, and F1,12E3=111·52, P<0·0001 respectively). Global prevalence in the HM treatments, 17·3% (S.E.=0·145), was 4 times that in the LM treatments, 4·6% (S.E.=0·045). The SS metapopulations had half the level of global prevalence (6·6%, S.E.=0·063) than the LS metapopulations (12·5%, S.E.=0·110). The interaction between migration rate and population size effects was also significant (F1,12E3=36·30, P<0·0001). Population size affected global prevalence when the migration rate was high but not when it was low (Fig. 6).

Fig. 6. Global prevalence. Both migration rate and population size had effects on global prevalence. Global prevalence was significantly higher in large metapopulations and at high migration rates. The effect of migration rate was greater in block 1 than in block 2.

Parasite distribution

The distribution of mites on beetles, measured using Lloyd's patchiness index, differed significantly between small and large patches (F1,124=11·894, P=0·004; patchiness was square-root transformed for this analysis). Patchiness in small populations (7·578±1·940) was twice that observed in large populations (3·563±1·902). Thus, although parasites were aggregated in both small and large populations, the degree of aggregation in small populations was more than twice that in large populations. The migration rate did not influence the distribution of parasites (F1,124=1·772, P=0·186), nor were there interactions between population size and migration (F1,124=1·300, P=0·256).

DISCUSSION

The spread of a mite infection throughout a metapopulation depends on the arrival of infected hosts through migration and the subsequent establishment of a local infection within patches. Our experiment provides the first empirical evidence of effects of host population size and host migration rate on the prevalence and distribution of parasites in spatially structured host populations. Our results showed that the prevalence of parasites in host populations with spatial structure is more than quantitatively different from expectations based on homogenously mixing populations. The differences observed in our experimental metapopulations are qualitatively different from some of the predictions of theoretical models that assume homogeneously mixing host populations. At different spatial scales, different factors affected parasite prevalence. The migration of hosts among patches was positively related to parasite occupancy, local prevalence and global prevalence. The size of the host population, which is not expected to affect prevalence, was positively related with both local and global prevalence. The effects of host migration rate and host population size sometimes interact.

At the level of parasite occupancy, we found that migration was a key variable in the spread of parasites among patches. The interaction of migration with host population size indicates that local conditions affect the likelihood of parasite establishment. While not surprising, ours may be the first experimental demonstration of the effect of migration on the spread of parasites, and the first empirical confirmation of Hess' (1996) model.

While we did not find an effect of host population size on parasite occupancy, others have. Burdon et al. (1995) found a significant positive correlation between the size of Filipendula ulmaria host populations and the occupancy of the rust pathogen Triphragmium ulmariae. The apparent discrepancy is resolved when we consider that, in the field, the likelihood of successful infection of a host patch may depend on the size of the patch not only because local conditions affect parasite establishment but also because larger patches are more easily encountered by migrants. Due to our manipulations, the likelihood that migrating beetles encountered a host population was held constant at 100%. In our experiment, population size could have affected occupancy only through effects on the likelihood of parasite establishment (but not on the likelihood of encountering the host patch). Therefore, the absence of a population size effect on occupancy is most appropriately interpreted as indicating that population size did not affect parasite establishment.

The effect of host population size on local prevalence, on the other hand, was unexpected and noteworthy. In studies of host–parasite population dynamics, host density, but not host population size, is considered important in the transmission process, and prevalence is predicted to be unrelated to host population size. After controlling for host density, we found that host population size had a significant effect on local prevalence. This result contradicts predictions from models that assume density-dependent transmission (e.g. Anderson & May, 1978, 1981). Whether departures from model predictions are due to the spatial structure of our experimental metapopulations or to features particular to our study system cannot be determined here. However, our results are consistent with field observations in other systems (e.g. Jennersten, Nilsson & Wastljung, 1983; Grosholz, 1993). Effects of host population size like those we observed are predicted by models that assume frequency-dependent parasite transmission among hosts (de Jong, Diekmann & Heesterbeek, 1995), or models in which alternative hosts are available (Holt & Pickering, 1985). Our data do not directly test different transmission models but, using Lloyd's patchiness index, we find that mites tended to aggregate to a much greater degree in the smaller host populations than in larger host populations. This would appear to be a type of positive frequency-dependent transmission. However, we do not know whether this change in the distribution of mite numbers per host is owing to behaviours of the mite, the host, or some interaction between the two species. It does support the criticism that the untested use of density-dependent transmission functions may not be widely appropriate (McCallum, Barlow & Hone, 2001).

Of course, local prevalence is determined by many factors in addition to the size of local host populations. We found that ongoing introduction of parasites as a result of host migration contributes to the prevalence observed in a local patch. Our data also confirmed that local prevalence increases gradually from the time a parasite is introduced to a patch until equilibrium is reached. While not at all surprising, the lag time between the time a parasite arrives in a new population and the time when it reaches equilibrium is seldom so clearly demonstrated. Comparing Figs 2 and 4 we can see that occupancy and local prevalence approach equilibrium at different rates. Occupancy is still increasing after 90 days while local prevalence asymptotes after 30 days. Thus, equilibrium prevalence at different spatial scales is reached in different time-frames.

At the metapopulation level, global prevalence was influenced by migration and population size. We saw that both larger patches and larger metapopulations had a higher proportion of infected individuals than did their smaller counterparts. Thus, the effect of population size was not limited to local prevalence in patches without spatial structure but extended to sets of patches with metapopulation structure. The effect of population size at the metapopulation scale has the same implications as for local prevalence.

But, how does prevalence compare between populations with and without spatial structure? Our data provide an indirect answer to this question. At the global or metapopulation level, spatial structure protected some hosts from infection. Hosts in patches that are isolated or otherwise, lucky to avoid infection, find themselves beyond the reach of parasites, at least temporarily. While in a homogeneously mixing population every individual can be potentially infected, individuals in patches not yet reached by the parasite are not at risk of infection. Note that in our study, global prevalence was always much lower than local prevalence, averaging 25% and 60% infection respectively. The difference is even more dramatic when we remember that large populations have greater prevalence and metapopulations are 25 times bigger than single patches. Clearly, the metapopulation structure prevented (or at least retarded) infection of a large proportion of hosts.

Studies of childhood infectious diseases also support these conclusions. Measles epidemics across cities in England and Wales find dynamics that conform to the island-mainland metapopulation model (reviewed by Grenfell & Harwood, 1997). Measles infections fade out in cities below a ‘critical community size’ but are susceptible to reinfection when the pool of susceptible hosts increases following an outbreak. Fadeouts are not observed in larger communities. The dynamics of measles outbreaks are complicated by the immunity acquired by recovered hosts. Nevertheless, community (or patch) size affects pathogen persistence, and the spatial dispersion of communities keeps some communities temporarily uninfected. Thus, spatial structure reduces global measles prevalence as we found in our results. The spatial structure of host communities also promotes the persistence of measles; persistence is more likely when spatial structure is considered (Bolker & Grenfell, 1993; Grenfell et al. 1995; Ferguson et al. 1997; Earn et al. 1998) and other parasites and pathogens, but our data are insufficient to test this prediction as we observed very few mite extinctions.

Our data support the concept that the risk of host extinction as a result of colonization by virulent pathogens may be reduced in spatially structured populations (Maron, Harrison & Greaves, 2001). The effectiveness of any protection afforded by spatial structure would depend on the rate of migration among patches and whether conditions in local patches permit coexistence of hosts and parasites. Fragmentation of host populations, to the extent that it generates spatial structure and limits host migration, may, in fact, protect some hosts from parasitic infection. However, we would not argue that small populations would be preferred as a conservation strategy when parasites are not a large threat for at least two reasons. First, the effect of population size on prevalence is not linear. The reduction of prevalence in small populations occurs only after the host population size falls below a certain threshold (Lopez, 2004), and that threshold could be too low to maintain a viable population. Second, small populations are at risk of extinction from causes other than parasite infection that may offset the benefit of any protection against parasites.

The effects of population size were not limited to local and global prevalence. We found that the distribution of parasites on hosts, measured with Lloyd's (1967) patchiness index, varied consistently between host populations of different size: mites in small host populations aggregated to twice the levels observed in larger host populations. Differences in parasite aggregation are important to the demography and fitness of both hosts and parasites (Dobson, Hudson & Lyles, 1992), so this effect of host population size has important ecological and evolutionary consequences. Mite effects on infected hosts, and on each other, are more intense in small populations. But because mites are more aggregated in small patches, fewer hosts experience the impact of parasitism. The reduced aggregation of parasites in large host populations exposes more hosts to the effects of the parasite. Assuming that changes in parasite aggregation are independent from changes in parasite numbers, this relationship could allow a parasite to regulate a host population size when host populations are large but avoid causing the extinction of the host by aggregating when hosts become less abundant.

To our knowledge, correlations between host population size and parasite distribution have not been previously reported. The effects of population size on prevalence and parasite distribution that we report here deserve further theoretical and experimental investigation.

We thank Jeff Demuth, Jake Moorad, Eric Osnas and 2 anonymous referees for helpful comments and suggestions. Jennifer Schmitt, Melissa Riegel, April Abbott, Adriene Anderson, Melanie Arzigian, Jenny Bruffey, Erin Flaherty, Josh Griswold, Jennifer Howell, Jay Reynolds, Annie Drake, Shareen Iqbal, Maxim Kostylev, Whitney Jones, Renee Luzadder, Ian Sambur, Morgan Schutte, and Katie Hoyt helped collecting data. Financial support was provided by a HHMI Pre-doctoral Fellowship (J.L.) and Indiana University (J.L. and L.G.).

References

REFERENCES

ANDERSON, R. M. & MAY, R. M. ( 1978). Regulation and stability of host-parasite population interactions I. regulatory processes. Journal of Animal Ecology 47, 219–247.Google Scholar
ANDERSON, R. M. & MAY, R. M. ( 1979). Population biology of infectious diseases: Part I. Nature, London 280, 361–367.CrossRefGoogle Scholar
ANDERSON, R. M. & MAY, R. M. ( 1981). The population dynamics of microparasites and their invertebrate hosts. Philosophical Transactions of the Royal Society of London, Series B 291, 451–524.CrossRefGoogle Scholar
ANDERSON, R. M. & MAY, R. M. ( 1991). Infectious Diseases of Humans: Dynamics and Control. Oxford University Press, Oxford.
BASCOMPTE, J. & SOLÉ, R. ( 1995). Rethinking complexity: modeling spatiotemporal dynamics in ecology. Trends in Ecology and Evolution 10, 361–366.CrossRefGoogle Scholar
BOLKER, B. M. & GRENFELL, B. ( 1993). Chaos and biological complexity in measles dynamics. Proceedings of the Royal Society of London, Series B 251, 75–81.CrossRefGoogle Scholar
BURDON, J. J., ERICSON, L. & MULLER, W. J. ( 1995). Temporal and spatial changes in a metapopulation of the rust pathogen Triphragmium ulmariae and its host, Filipendula ulmaria. Journal of Ecology 83, 979–989.CrossRefGoogle Scholar
DE JONG, M., DIEKMANN, O. & HEESTERBEEK, H. ( 1995). How does transmission of infection depend on population size? In Epidemic Models: Their Structure and Relation to Data (ed. Mollison, D.), pp. 84–94. Cambridge University Press, Cambridge.
DOBSON, A. P., HUDSON, P. J. & LYLES, A. M. ( 1992). Macroparasites: worms and others. In Natural Enemies: The Population Biology of Predators, Parasites and Diseases (ed. Crawley, M. J.), pp. 329–348. Blackwell Scientific Publications, Oxford.CrossRef
DWYER, G. ( 1991). The roles of density, stage, and patchiness in the transmission of an insect virus. Ecology 72, 559–574.CrossRefGoogle Scholar
EARN, D. J. D., ROHANI, P. & GRENFELL, B. ( 1998). Persistence, chaos and synchrony in ecology and epidemiology. Proceedings of the Royal Society of London, Series B 265, 7–10.CrossRefGoogle Scholar
ERICSON, L., BURDON, J. J. & MULLER, W. J. ( 1999). Spatial and temporal dynamics of epidemics of the rust fungus Uromyces valerianae on populations of its host Valeriana salina. Journal of Ecology 87, 649–658.CrossRefGoogle Scholar
FERGUSON, N. M., MAY, R. M. & ANDERSON, R. M. ( 1997). Measles: persistence and synchronicity in disease dynamics. In Spatial Ecology: the Role of Space in Population Dynamics and Interspecific Interactions (ed. Tilman, D. & Kareiva, P.), pp. 137–157. Princeton University Press, Princeton, New Jersey.
GOTELLI, N. J. ( 1991). Metapopulation models: The rescue effect, the propagule rain, and the core-satellite hypothesis. American Naturalist 138, 768–776.CrossRefGoogle Scholar
GOTELLI, N. J. & KELLEY, W. G. ( 1993). A general model of metapopulation dynamics. Oikos 68, 36–44.CrossRefGoogle Scholar
GRENFELL, B., BOLKER, B. M. & KLECZKOWSKI, A. ( 1995). Seasonality and extinction in chaotic metapopulations. Proceedings of the Royal Society of London, Series B 259, 97–103.CrossRefGoogle Scholar
GRENFELL, B. & HARWOOD, J. ( 1997). (Meta)population dynamics of infectious diseases. Trends in Ecology and Evolution 12, 395–399.CrossRefGoogle Scholar
GROSHOLZ, E. D. ( 1993). The influence of habitat heterogeneity on host–pathogen population dynamics. Oecologia 96, 347–353.CrossRefGoogle Scholar
HANSKI, I. ( 1991). Single-species metapopulation dynamics: concepts, models and observations. Biological Journal of the Linnean Society 42, 17–38.CrossRefGoogle Scholar
HANSKI, I. ( 1994). Patch-occupancy dynamics in fragmented landscapes. Trends in Ecology and Evolution 9, 131–135.CrossRefGoogle Scholar
HANSKI, I. & GILPIN, M. ( 1991). Metapopulation dynamics: brief history and conceptual domain. Biological Journal of the Linnean Society 42, 3–16.CrossRefGoogle Scholar
HASSELL, M. P., COMINS, H. N. & MAY, R. M. ( 1991). Spatial structure and chaos in insect population dynamics. Nature, London 353, 255–258.CrossRefGoogle Scholar
HASTINGS, A. ( 1990). Spatial heterogeneity and ecological models. Ecology 71, 426–428.CrossRefGoogle Scholar
HESS, G. ( 1996). Disease in metapopulation models: implications for conservation. Ecology 77, 1617–1632.CrossRefGoogle Scholar
HOLMES, E. E. ( 1997). Basic epidemiological concepts in a spatial context. In Spatial Ecology: the Role of Space in Population Dynamics and Interspecific Interactions (ed. Tilman, D. & Kareiva, P.), pp. 111–136. Princeton University Press, Princeton, New Jersey.
HOLT, R. D. & PICKERING, J. ( 1985). Infectious disease and species coexistence: A model of Lotka-Volterra form. American Naturalist 126, 196–211.CrossRefGoogle Scholar
JENNERSTEN, O., NILSSON, S. G. & WASTLJUNG, U. ( 1983). Local plant populations as ecological islands: the infection of Viscaria vulgaris by the fungus Ustilago violacea. Oikos 41, 391–395.CrossRefGoogle Scholar
LITTELL, R. C., MILLIKEN, G. A., STROUP, W. W. & WOLFINGER, R. D. ( 1996). SAS System for Mixed Models, SAS Institute, Inc., Cary, N.C.
LLOYD, A. L. & MAY, R. M. ( 1996). Spatial heterogeneity in epidemic models. Journal of Theoretical Biology 179, 1–11.CrossRefGoogle Scholar
LLOYD, M. ( 1967). Mean crowding. Journal of Animal Ecology 36, 1–30.CrossRefGoogle Scholar
LOPEZ, J. E. ( 2004). Parasite prevalence and the size of hot populations: an experimental test. Journal of Parasitology (in the Press).Google Scholar
MARGOLIS, L., ESCH, G. W., HOLMES, J. C., KURIS, A. M. & SCHAD, G. A. ( 1982). The use of ecological terms in parasitology (report of an ad hoc committee of the American Society of Parasitologists). Journal of Parasitology 68, 131–133.CrossRefGoogle Scholar
MARON, J. L., HARRISON, S. & GREAVES, M. ( 2001). Origin of an insect outbreak: escape in space or time from natural enemies? Oecologia 126, 595–602.Google Scholar
MAY, R. M. & ANDERSON, R. M. ( 1978). Regulation and stability of host-parasite population interactions. II. Destabilizing processes. Journal of Animal Ecology 47, 249–267.Google Scholar
MAY, R. M. & ANDERSON, R. M. ( 1979). Population biology of infectious diseases: Part II. Nature, London 280, 455–461.CrossRefGoogle Scholar
McCALLUM, H., BARLOW, N. & HONE, J. ( 2001). How should pathogen transmission be modeled? Trends in Ecology and Evolution 16, 295–300.Google Scholar
MURDOCH, W. W. ( 1996). Refuge dynamics and metapopulation dynamics: an experimental test. American Naturalist 147, 424–444.CrossRefGoogle Scholar
NETER, J., WASSERMAN, W. & KUTNER, M. H. ( 1990). Applied Linear Statistical Models, Irwin Inc., Homewood, IL, USA.
POST, W. M., DeANGELIS, D. L. & TRAVIS, C. C. ( 1983). Endemic disease in environments with spatially heterogeneous host populations. Mathematical Biosciences 63, 289–302.CrossRefGoogle Scholar
SATTENSPIEL, L. & DIETZ, K. ( 1995). A structured epidemic model incorporating geographic mobility among regions. Mathematical Biosciences 128, 71–91.CrossRefGoogle Scholar
SCOTT, M. E. ( 1987). Temporal changes in aggregation: a laboratory study. Parasitology 94, 583–595.CrossRefGoogle Scholar
SMITH, D. L., ERICSON, L. & BURDON, J. J. ( 2003). Epidemiological patterns at multiple spatial scales: an 11-year study of a Triphragmium ulmariae-Filipendula ulmaria metapopulation. Journal of Ecology 91, 890–903.CrossRefGoogle Scholar
THRALL, P. H. & BURDON, J. J. ( 1997). Host-pathogen dynamics in a metapopulation context: the ecological and evolutionary consequences of being spatial. Journal of Ecology 85, 743–753.CrossRefGoogle Scholar
WADE, M. J. ( 1982). Group selection: migration and the differentiation of small populations. Evolution 36, 949–961.CrossRefGoogle Scholar
WILSON, K. & GRENFELL, B. ( 1997). Generalized linear modelling for parasitologists. Parasitology Today 13, 33–38.CrossRefGoogle Scholar
WILSON, K., GRENFELL, B. & SHAW, D. J. ( 1996). Analysis of aggregated parasite distributions: a comparison of methods. Functional Ecology 10, 592–601.CrossRefGoogle Scholar
ZAR, J. H. ( 1994). Biostatistical Analysis, Prentice Hall, New Jersey.
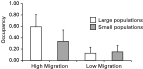
Figure 0

Fig. 1. Occupancy. The number of infected patches in experimental metapopulations differed significantly between the high and low migration treatments. Parasites spread to more patches when migration was high. The effect of population size was not significant.

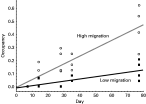
Figure 1

Fig. 2. Occupancy and time. Occupancy increased faster and reached higher levels when migration rate was high. While not surprising, this may be the first experimental demonstration of the effect of migration on the spread of parasites.

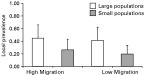
Figure 2

Fig. 3. Local prevalence. Local prevalence, arcsine-square root transformed to meet statistical assumptions, was affected by population size but not by migration rate. Local prevalence was greater in large populations. The effect of population size on prevalence is not predicted by the most commonly used models of host-parasite population dynamics.

Figure 3

Fig. 4. Local prevalence and time. The prevalence of infection is higher in populations that have been infected longer. The data show that prevalence increases in the 30 days following infection. After 30 days, prevalence remains constant.

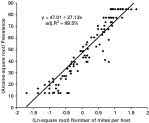
Figure 4

Fig. 5. Prevalence and mite abundance. There is a strong positive relationship between local prevalence and number of mites per host. When data are transformed as indicated on the axes, the regression explains 89·5% of the variance (F1,126=1082·7, P<10−63). This indicates that the average host has more mites when more hosts are infected.

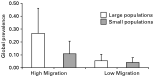
Figure 5

Fig. 6. Global prevalence. Both migration rate and population size had effects on global prevalence. Global prevalence was significantly higher in large metapopulations and at high migration rates. The effect of migration rate was greater in block 1 than in block 2.