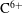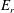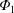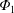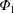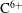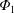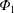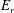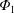1 Introduction
Fusion plasmas contain several ion species other than the fuel ions. Accumulation of such so-called ‘impurity ions’ in the core region could prevent the achievement of steady-state fusion operation by dilution of the fuel ions or energy loss through radiation. Transport of impurity ions is caused by turbulent and neoclassical processes. Although it is thought that the turbulent contribution usually dominates over the neoclassical contribution for bulk plasmas, the contribution of neoclassical transport can also be significant for impurity transport (Burhenn et al. Reference Burhenn, Feng, Ida, Maassberg, McCarthy, Kalinina, Kobayashi, Morita, Nakamura and Nozato2009). The neoclassical flux of species  $a$ is given by
$a$ is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a}\equiv \left\langle \int \,\text{d}^{3}v\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}rf_{a1}\right\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a}\equiv \left\langle \int \,\text{d}^{3}v\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}rf_{a1}\right\rangle ,\end{eqnarray}$$ where  $\boldsymbol{v}_{d}$ denotes the guiding-centre drift velocity,
$\boldsymbol{v}_{d}$ denotes the guiding-centre drift velocity,  $r$ the radial coordinate,
$r$ the radial coordinate,  $f_{a1}$ the non-adiabatic part of the deviation from the local Maxwellian of the species
$f_{a1}$ the non-adiabatic part of the deviation from the local Maxwellian of the species  $a$ and
$a$ and  $\langle \ldots \rangle$ the flux surface average, respectively.
$\langle \ldots \rangle$ the flux surface average, respectively.  $\unicode[STIX]{x1D6E4}_{a}$ can also be expressed by the linear combination of thermodynamic forces:
$\unicode[STIX]{x1D6E4}_{a}$ can also be expressed by the linear combination of thermodynamic forces:
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a}=-n_{a}\mathop{\sum }_{b}\left[D_{11}^{ab}\left(\frac{n_{b}^{\prime }}{n_{b}}+\frac{Z_{b}e\unicode[STIX]{x1D6F7}^{\prime }}{T_{b}}\right)+D_{12}^{ab}\frac{T_{b}^{\prime }}{T_{b}}\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a}=-n_{a}\mathop{\sum }_{b}\left[D_{11}^{ab}\left(\frac{n_{b}^{\prime }}{n_{b}}+\frac{Z_{b}e\unicode[STIX]{x1D6F7}^{\prime }}{T_{b}}\right)+D_{12}^{ab}\frac{T_{b}^{\prime }}{T_{b}}\right],\end{eqnarray}$$ where  $n_{b}$ denotes the density,
$n_{b}$ denotes the density,  $T_{b}$ the temperature and
$T_{b}$ the temperature and  $Z_{b}e$ the charge of species
$Z_{b}e$ the charge of species  $b$, respectively,
$b$, respectively,  $\unicode[STIX]{x1D6F7}$ denotes electrostatic potential and
$\unicode[STIX]{x1D6F7}$ denotes electrostatic potential and  $D_{ij}^{ab}$ the neoclassical transport coefficients and the prime denotes the derivative with respect to the radial coordinate,
$D_{ij}^{ab}$ the neoclassical transport coefficients and the prime denotes the derivative with respect to the radial coordinate,  $r$.
$r$.
For impurity species, the term
 $$\begin{eqnarray}-n_{z}D_{11}^{zz}\frac{Z_{z}e\unicode[STIX]{x1D6F7}^{\prime }}{T_{z}}=n_{z}D_{11}^{zz}\frac{Z_{z}eE_{r}}{T_{z}}\end{eqnarray}$$
$$\begin{eqnarray}-n_{z}D_{11}^{zz}\frac{Z_{z}e\unicode[STIX]{x1D6F7}^{\prime }}{T_{z}}=n_{z}D_{11}^{zz}\frac{Z_{z}eE_{r}}{T_{z}}\end{eqnarray}$$ tends to dominate with increasing charge number  $Z_{z}$, where
$Z_{z}$, where  $E_{r}=-\unicode[STIX]{x1D6F7}^{\prime }$ is the radial electric field and the index
$E_{r}=-\unicode[STIX]{x1D6F7}^{\prime }$ is the radial electric field and the index  $z$ refers to the impurity species. This term drives the impurity inwardly since the coefficient
$z$ refers to the impurity species. This term drives the impurity inwardly since the coefficient  $D_{11}^{zz}$ is positive and the sign of
$D_{11}^{zz}$ is positive and the sign of  $E_{r}$ is expected to be negative in typical fusion-relevant plasmas. In axisymmetric systems, however, the terms involving
$E_{r}$ is expected to be negative in typical fusion-relevant plasmas. In axisymmetric systems, however, the terms involving  $E_{r}=-\unicode[STIX]{x1D6F7}^{\prime }$ in (1.2) are cancelled when the sum over the species is taken and the net contribution of
$E_{r}=-\unicode[STIX]{x1D6F7}^{\prime }$ in (1.2) are cancelled when the sum over the species is taken and the net contribution of  $E_{r}$ to the flux vanishes. The coefficient
$E_{r}$ to the flux vanishes. The coefficient  $D_{12}^{zz}$ is usually positive and it can be larger than the
$D_{12}^{zz}$ is usually positive and it can be larger than the  $D_{11}^{zb}$ terms in absolute value. Then, a sufficiently steep temperature gradient can drive the impurity outwardly. This is called the ‘temperature screening effect’. On the other hand, in non-axisymmetric systems, the cancellation of
$D_{11}^{zb}$ terms in absolute value. Then, a sufficiently steep temperature gradient can drive the impurity outwardly. This is called the ‘temperature screening effect’. On the other hand, in non-axisymmetric systems, the cancellation of  $E_{r}$ terms does not usually occur because neoclassical transport is not intrinsically ambipolar like it is in tokamaks. This is a serious disadvantage of non-axisymmetric devices. Thus, to understand the nature of impurity transport and establish a way to mitigate the impurity accumulation in the core region are crucial tasks for maintaining stable plasma operation.
$E_{r}$ terms does not usually occur because neoclassical transport is not intrinsically ambipolar like it is in tokamaks. This is a serious disadvantage of non-axisymmetric devices. Thus, to understand the nature of impurity transport and establish a way to mitigate the impurity accumulation in the core region are crucial tasks for maintaining stable plasma operation.
With this background, a notable phenomenon has been observed in LHD (Large Helical Device). The phenomenon is called ‘impurity hole’, and it indicates the formation of an extremely hollow density profile of an impurity species in the plasma core region where a negative  $E_{r}$ is expected to exist (Ida et al. Reference Ida, Yoshinuma, Osakabe, Nagaoka, Yokoyama, Funaba, Suzuki, Ido, Shimizu and Murakami2009). The phenomenon had been first observed for carbon
$E_{r}$ is expected to exist (Ida et al. Reference Ida, Yoshinuma, Osakabe, Nagaoka, Yokoyama, Funaba, Suzuki, Ido, Shimizu and Murakami2009). The phenomenon had been first observed for carbon  $\text{C}^{6+}$ and in a later study (Yoshinuma, Ida & Yokoyama Reference Yoshinuma, Ida and Yokoyama2010) it was reported that the same hollow structure can also be formed in the density profile of neon Ne
$\text{C}^{6+}$ and in a later study (Yoshinuma, Ida & Yokoyama Reference Yoshinuma, Ida and Yokoyama2010) it was reported that the same hollow structure can also be formed in the density profile of neon Ne $^{10+}$. The study has also shown that the density in the core becomes hollower for heavier impurities. These observations contradict the prediction of the standard neoclassical transport theory that medium or heavy impurities are expected to be driven inwardly by the negative
$^{10+}$. The study has also shown that the density in the core becomes hollower for heavier impurities. These observations contradict the prediction of the standard neoclassical transport theory that medium or heavy impurities are expected to be driven inwardly by the negative  $E_{r}$. Gyro-kinetic approaches have also been taken, but they indicate that the turbulent
$E_{r}$. Gyro-kinetic approaches have also been taken, but they indicate that the turbulent  $\text{C}^{6+}$ flux also directs inwardly in ion-root plasmas with hollow density profiles. It is also shown that, in such plasmas, the total neoclassical flux can be too large to satisfy the particle balances between turbulent and neoclassical contributions (Nunami et al. Reference Nunami, Sugama, Velasco, Yokoyama, Sato, Nakata and Satake2016, Reference Nunami, Nakata, Sato, Toda, Yamaguchi, Sugama and Yokoyama2017, Reference Nunami, Satake, Fujita, Yamaguchi, Matsuoka, Sato, Toda and Sugama2019, Reference Nunami, Nakata, Toda and Sugama2020). Thus, the validity range of the approximations commonly used for neoclassical simulations has been reconsidered. For example, Helander et al. (Reference Helander, Newton, Mollén and Smith2017) have pointed out that describing collision processes only with the pitch angle scattering operator, as conventionally done, is inadequate for studying impurity transport and, by retaining the friction force part, they have shown the cancellation of the
$\text{C}^{6+}$ flux also directs inwardly in ion-root plasmas with hollow density profiles. It is also shown that, in such plasmas, the total neoclassical flux can be too large to satisfy the particle balances between turbulent and neoclassical contributions (Nunami et al. Reference Nunami, Sugama, Velasco, Yokoyama, Sato, Nakata and Satake2016, Reference Nunami, Nakata, Sato, Toda, Yamaguchi, Sugama and Yokoyama2017, Reference Nunami, Satake, Fujita, Yamaguchi, Matsuoka, Sato, Toda and Sugama2019, Reference Nunami, Nakata, Toda and Sugama2020). Thus, the validity range of the approximations commonly used for neoclassical simulations has been reconsidered. For example, Helander et al. (Reference Helander, Newton, Mollén and Smith2017) have pointed out that describing collision processes only with the pitch angle scattering operator, as conventionally done, is inadequate for studying impurity transport and, by retaining the friction force part, they have shown the cancellation of the  $E_{r}$ terms and hence temperature screening is in fact possible even in non-axisymmetric systems under certain conditions (see also Newton et al. Reference Newton, Helander, Mollén and Smith2017). In order for the cancellation to take place in a helical plasma, the plasma needs to be in a relevant mixed collisionality, where a highly collisional impurity species exists in the low collisional background ion. In addition, the variation of electrostatic potential over the flux surface,
$E_{r}$ terms and hence temperature screening is in fact possible even in non-axisymmetric systems under certain conditions (see also Newton et al. Reference Newton, Helander, Mollén and Smith2017). In order for the cancellation to take place in a helical plasma, the plasma needs to be in a relevant mixed collisionality, where a highly collisional impurity species exists in the low collisional background ion. In addition, the variation of electrostatic potential over the flux surface,  $\unicode[STIX]{x1D6F7}_{1}\equiv \unicode[STIX]{x1D6F7}-\unicode[STIX]{x1D6F7}_{0}$, is required to be sufficiently small (Buller et al. Reference Buller, Smith, Helander, Mollén, Newton and Pusztai2018; Calvo et al. Reference Calvo, Parra, Velasco, Alonso and García-Regaña2018a); here
$\unicode[STIX]{x1D6F7}_{1}\equiv \unicode[STIX]{x1D6F7}-\unicode[STIX]{x1D6F7}_{0}$, is required to be sufficiently small (Buller et al. Reference Buller, Smith, Helander, Mollén, Newton and Pusztai2018; Calvo et al. Reference Calvo, Parra, Velasco, Alonso and García-Regaña2018a); here  $\unicode[STIX]{x1D6F7}_{0}=\unicode[STIX]{x1D6F7}_{0}(r)$ is the flux function part of the electrostatic potential. In Velasco et al. (Reference Velasco, Calvo, Parra, Alonso, Carralero, Estrada, García-Regañ, Huang, Morita and Satake2019), an experimental case in which the temperature screening may be occurring is discussed with numerical analysis.
$\unicode[STIX]{x1D6F7}_{0}=\unicode[STIX]{x1D6F7}_{0}(r)$ is the flux function part of the electrostatic potential. In Velasco et al. (Reference Velasco, Calvo, Parra, Alonso, Carralero, Estrada, García-Regañ, Huang, Morita and Satake2019), an experimental case in which the temperature screening may be occurring is discussed with numerical analysis.
Independently of those works,  $\unicode[STIX]{x1D6F7}_{1}$ itself has been thought to have a non-negligible impact on impurity transport. Although
$\unicode[STIX]{x1D6F7}_{1}$ itself has been thought to have a non-negligible impact on impurity transport. Although  $\unicode[STIX]{x1D6F7}_{1}$ itself is usually smaller by one or two orders of magnitude than the uniform part (Calvo et al. Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018b), the impact of
$\unicode[STIX]{x1D6F7}_{1}$ itself is usually smaller by one or two orders of magnitude than the uniform part (Calvo et al. Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018b), the impact of  $\unicode[STIX]{x1D6F7}_{1}$ in the guiding-centre motions relative to the impact of the magnetic field through the magnetic drift or the mirror force becomes larger proportionally to the charge of the species. Thus, while the effect of
$\unicode[STIX]{x1D6F7}_{1}$ in the guiding-centre motions relative to the impact of the magnetic field through the magnetic drift or the mirror force becomes larger proportionally to the charge of the species. Thus, while the effect of  $\unicode[STIX]{x1D6F7}_{1}$ is usually small for the main ion or electron, it can be essential for highly charged impurities. While measuring such a small variation in electrostatic potential is still challenging in LHD, it is already technically feasible in the smaller device TJ-II and the potential variation has actually been detected in such experiments (Pedrosa et al. Reference Pedrosa, Alonso, García-Regaña, Hidalgo, Velasco, Calvo, Kleiber, Silva and Helander2015; García-Regaña et al. Reference García-Regaña, Estrada, Calvo, Velasco, Alonso, Carralero, Kleiber, Landreman, Mollén and Sánchez2018; Estrada et al. Reference Estrada, Sánchez, García-Regaña, Alonso, Ascasíbar, Calvo, Cappa, Carralero, Hidalgo and Liniers2019). Also, by several simulation studies, it has already been shown that
$\unicode[STIX]{x1D6F7}_{1}$ is usually small for the main ion or electron, it can be essential for highly charged impurities. While measuring such a small variation in electrostatic potential is still challenging in LHD, it is already technically feasible in the smaller device TJ-II and the potential variation has actually been detected in such experiments (Pedrosa et al. Reference Pedrosa, Alonso, García-Regaña, Hidalgo, Velasco, Calvo, Kleiber, Silva and Helander2015; García-Regaña et al. Reference García-Regaña, Estrada, Calvo, Velasco, Alonso, Carralero, Kleiber, Landreman, Mollén and Sánchez2018; Estrada et al. Reference Estrada, Sánchez, García-Regaña, Alonso, Ascasíbar, Calvo, Cappa, Carralero, Hidalgo and Liniers2019). Also, by several simulation studies, it has already been shown that  $\unicode[STIX]{x1D6F7}_{1}$ can have substantial impact on neoclassical impurity transport (see e.g. García-Regaña et al. Reference García-Regaña, Kleiber, Beidler, Turkin, Maassberg and Helander2013, Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017; Calvo et al. Reference Calvo, Parra, Velasco, Alonso and García-Regaña2018a; Mollén et al. Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018; Velasco et al. Reference Velasco, Calvo, García-Regaña, Parra, Satake and Alonso2018). However, all of those calculations have been performed with radially local codes, i.e. the models in which the radial drift in the guiding-centre motion is neglected and dynamics on each flux is separated.
$\unicode[STIX]{x1D6F7}_{1}$ can have substantial impact on neoclassical impurity transport (see e.g. García-Regaña et al. Reference García-Regaña, Kleiber, Beidler, Turkin, Maassberg and Helander2013, Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017; Calvo et al. Reference Calvo, Parra, Velasco, Alonso and García-Regaña2018a; Mollén et al. Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018; Velasco et al. Reference Velasco, Calvo, García-Regaña, Parra, Satake and Alonso2018). However, all of those calculations have been performed with radially local codes, i.e. the models in which the radial drift in the guiding-centre motion is neglected and dynamics on each flux is separated.
In most of the local models, the magnetic drift,  $\boldsymbol{v}_{m}$, is entirely dropped from the equation for the guiding-centre orbit in the configuration space. However, the validity of this approximation for low-collisionality cases is ensured only when the
$\boldsymbol{v}_{m}$, is entirely dropped from the equation for the guiding-centre orbit in the configuration space. However, the validity of this approximation for low-collisionality cases is ensured only when the  $E\times B$ drift,
$E\times B$ drift,  $\boldsymbol{v}_{E}$, is large enough compared with the magnetic drift. When
$\boldsymbol{v}_{E}$, is large enough compared with the magnetic drift. When  $E_{r}$ is close to zero, the helically trapped particles lose their mobility on the flux surface and the contribution of the trapped particles to radial transport significantly increases. Consequently, radial fluxes in the conventional local models show a strong peak around
$E_{r}$ is close to zero, the helically trapped particles lose their mobility on the flux surface and the contribution of the trapped particles to radial transport significantly increases. Consequently, radial fluxes in the conventional local models show a strong peak around  $E_{r}=0$. Such an excessive transport can be largely moderated by the inclusion of the tangential component of the magnetic drift. The tangential
$E_{r}=0$. Such an excessive transport can be largely moderated by the inclusion of the tangential component of the magnetic drift. The tangential  $\boldsymbol{v}_{m}$ moves the trapped particles along the flux surface and can detrap them without collision. Also, the peaking point is shifted from where
$\boldsymbol{v}_{m}$ moves the trapped particles along the flux surface and can detrap them without collision. Also, the peaking point is shifted from where  $E_{r}=0$ to where the particle average of
$E_{r}=0$ to where the particle average of  $\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\equiv \overline{(\boldsymbol{v}_{m}+\boldsymbol{v}_{E})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}$ vanishes on the flux surface, where the overbar denotes the orbit average and
$\overline{\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}\equiv \overline{(\boldsymbol{v}_{m}+\boldsymbol{v}_{E})\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FC}}$ vanishes on the flux surface, where the overbar denotes the orbit average and  $\unicode[STIX]{x1D6FC}$ labels magnetic field lines. As the result, the difference in the radial particle or energy flux of hydrogen ions between calculations with and without the tangential
$\unicode[STIX]{x1D6FC}$ labels magnetic field lines. As the result, the difference in the radial particle or energy flux of hydrogen ions between calculations with and without the tangential  $\boldsymbol{v}_{m}$ can be an order of magnitude (Matsuoka et al. Reference Matsuoka, Satake, Kanno and Sugama2015; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017; Velasco et al. Reference Velasco, Calvo, Parra and García-Regana2020). By evaluating
$\boldsymbol{v}_{m}$ can be an order of magnitude (Matsuoka et al. Reference Matsuoka, Satake, Kanno and Sugama2015; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017; Velasco et al. Reference Velasco, Calvo, Parra and García-Regana2020). By evaluating  $\unicode[STIX]{x1D6F7}_{1}$ and its impact on impurity transport using a local model with the tangential
$\unicode[STIX]{x1D6F7}_{1}$ and its impact on impurity transport using a local model with the tangential  $\boldsymbol{v}_{m}$, Velasco et al. (Reference Velasco, Calvo, García-Regaña, Parra, Satake and Alonso2018) also found that the phase structure of
$\boldsymbol{v}_{m}$, Velasco et al. (Reference Velasco, Calvo, García-Regaña, Parra, Satake and Alonso2018) also found that the phase structure of  $\unicode[STIX]{x1D6F7}_{1}$ can be substantially modified by the tangential
$\unicode[STIX]{x1D6F7}_{1}$ can be substantially modified by the tangential  $\boldsymbol{v}_{m}$. Further, in unoptimised devices such as LHD under the conditions being discussed, the radial component of
$\boldsymbol{v}_{m}$. Further, in unoptimised devices such as LHD under the conditions being discussed, the radial component of  $\boldsymbol{v}_{m}$ can be non-negligible as well (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017). In LHD cases, it has been shown that the hydrogen fluxes obtained by calculation with the full
$\boldsymbol{v}_{m}$ can be non-negligible as well (Calvo et al. Reference Calvo, Parra, Velasco and Alonso2017). In LHD cases, it has been shown that the hydrogen fluxes obtained by calculation with the full  $\boldsymbol{v}_{m}$ can be a few times smaller than those obtained by calculation only with the tangential
$\boldsymbol{v}_{m}$ can be a few times smaller than those obtained by calculation only with the tangential  $\boldsymbol{v}_{m}$ (Matsuoka et al. Reference Matsuoka, Satake, Kanno and Sugama2015; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017). The effect of the radial
$\boldsymbol{v}_{m}$ (Matsuoka et al. Reference Matsuoka, Satake, Kanno and Sugama2015; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017). The effect of the radial  $\boldsymbol{v}_{m}$ appears in the structure of
$\boldsymbol{v}_{m}$ appears in the structure of  $\unicode[STIX]{x1D6F7}_{1}$ as well (Fujita et al. Reference Fujita, Satake, Kanno, Nunami, Nakata and García-Regaña2019). Thus, in order to investigate the structure of
$\unicode[STIX]{x1D6F7}_{1}$ as well (Fujita et al. Reference Fujita, Satake, Kanno, Nunami, Nakata and García-Regaña2019). Thus, in order to investigate the structure of  $\unicode[STIX]{x1D6F7}_{1}$ and its impact on transport in low-collisionality LHD plasmas, global effects should not be neglected.
$\unicode[STIX]{x1D6F7}_{1}$ and its impact on transport in low-collisionality LHD plasmas, global effects should not be neglected.
Recently, we have made two major extensions of a global neoclassical simulation code, FORTEC-3D. The first is to enable it to evaluate  $\unicode[STIX]{x1D6F7}_{1}$ (Fujita et al. Reference Fujita, Satake, Kanno, Nunami, Nakata and García-Regaña2019) and include its effect in a drift-kinetic equation. The second is the implementation of a cross ion-species collision operator to perform multi-ion-species calculation. The collision operator retains both test-particle and field-particle parts and the effects of the momentum and energy exchanges by friction are included (Sugama, Watanabe & Nunami Reference Sugama, Watanabe and Nunami2009; Satake et al. Reference Satake, Nakata, Pianpanit, Sugama, Nunami, Matsuoka, Ishiguro and Kanno2020). Thus, this newly extended code can be used to investigate the effect of
$\unicode[STIX]{x1D6F7}_{1}$ (Fujita et al. Reference Fujita, Satake, Kanno, Nunami, Nakata and García-Regaña2019) and include its effect in a drift-kinetic equation. The second is the implementation of a cross ion-species collision operator to perform multi-ion-species calculation. The collision operator retains both test-particle and field-particle parts and the effects of the momentum and energy exchanges by friction are included (Sugama, Watanabe & Nunami Reference Sugama, Watanabe and Nunami2009; Satake et al. Reference Satake, Nakata, Pianpanit, Sugama, Nunami, Matsuoka, Ishiguro and Kanno2020). Thus, this newly extended code can be used to investigate the effect of  $\unicode[STIX]{x1D6F7}_{1}$ on impurity transport including the global effects. Verification of the numerical schemes in the multi-species version of FORTEC-3D will appear in a separate paper. In this paper, this extended version of the code is applied to impurity transport in LHD plasmas in which hollow carbon density profiles are formed. This paper is organised as follows: the theoretical model used for this study is introduced in § 2. The setup for the calculation is presented in § 3. The result is shown and discussed in § 4. Finally, a conclusion is drawn in § 5.
$\unicode[STIX]{x1D6F7}_{1}$ on impurity transport including the global effects. Verification of the numerical schemes in the multi-species version of FORTEC-3D will appear in a separate paper. In this paper, this extended version of the code is applied to impurity transport in LHD plasmas in which hollow carbon density profiles are formed. This paper is organised as follows: the theoretical model used for this study is introduced in § 2. The setup for the calculation is presented in § 3. The result is shown and discussed in § 4. Finally, a conclusion is drawn in § 5.
2 Theoretical model and numerical method
In this section, the theoretical model used in FORTEC-3D is presented. FORTEC-3D is a Monte Carlo  $\unicode[STIX]{x1D6FF}\,f$ code which solves a drift-kinetic equation with full linearised Landau collision operator without employing the radially local approximation (Satake, Kanno & Sugama Reference Satake, Kanno and Sugama2008; Satake et al. Reference Satake, Idomura, Sugama and Watanabe2010).
$\unicode[STIX]{x1D6FF}\,f$ code which solves a drift-kinetic equation with full linearised Landau collision operator without employing the radially local approximation (Satake, Kanno & Sugama Reference Satake, Kanno and Sugama2008; Satake et al. Reference Satake, Idomura, Sugama and Watanabe2010).
2.1 Drift-kinetic equation
When the guiding-centre coordinates  $\boldsymbol{X}$, the parallel velocity
$\boldsymbol{X}$, the parallel velocity  $v_{\Vert }$ and the magnetic moment
$v_{\Vert }$ and the magnetic moment  $\unicode[STIX]{x1D707}=m_{a}v_{\bot }^{2}/(2B)$ are chosen as the phase-space variables, where
$\unicode[STIX]{x1D707}=m_{a}v_{\bot }^{2}/(2B)$ are chosen as the phase-space variables, where  $B=|\boldsymbol{B}|$ and
$B=|\boldsymbol{B}|$ and  $v_{\bot }$ is the perpendicular velocity, the guiding-centre equations of motion are given by
$v_{\bot }$ is the perpendicular velocity, the guiding-centre equations of motion are given by
 $$\begin{eqnarray}\displaystyle & \displaystyle \dot{\boldsymbol{X}}=v_{\Vert }\boldsymbol{b}+\frac{1}{Z_{a}eB_{\Vert }^{\ast }}\boldsymbol{b}\times (m_{a}v_{\Vert }^{2}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{\boldsymbol{X}}=v_{\Vert }\boldsymbol{b}+\frac{1}{Z_{a}eB_{\Vert }^{\ast }}\boldsymbol{b}\times (m_{a}v_{\Vert }^{2}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \dot{v}_{\Vert }=-\frac{1}{m_{a}v_{\Vert }}\dot{\boldsymbol{X}}\boldsymbol{\cdot }(\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{v}_{\Vert }=-\frac{1}{m_{a}v_{\Vert }}\dot{\boldsymbol{X}}\boldsymbol{\cdot }(\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \dot{\unicode[STIX]{x1D707}}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{\unicode[STIX]{x1D707}}=0, & \displaystyle\end{eqnarray}$$ where  $\boldsymbol{b}=\boldsymbol{B}/B$,
$\boldsymbol{b}=\boldsymbol{B}/B$,  $\boldsymbol{B}^{\ast }=\unicode[STIX]{x1D735}\times \boldsymbol{A}^{\ast }$ is the corrected magnetic field with the guiding-centre vector potential
$\boldsymbol{B}^{\ast }=\unicode[STIX]{x1D735}\times \boldsymbol{A}^{\ast }$ is the corrected magnetic field with the guiding-centre vector potential  $\boldsymbol{A}^{\ast }=\boldsymbol{A}+m_{a}v_{\Vert }\boldsymbol{b}/(Z_{a}e)$,
$\boldsymbol{A}^{\ast }=\boldsymbol{A}+m_{a}v_{\Vert }\boldsymbol{b}/(Z_{a}e)$,  $B_{\Vert }^{\ast }=\boldsymbol{B}^{\ast }\boldsymbol{\cdot }\boldsymbol{b}$ and the overdot denotes the total time derivative
$B_{\Vert }^{\ast }=\boldsymbol{B}^{\ast }\boldsymbol{\cdot }\boldsymbol{b}$ and the overdot denotes the total time derivative  ${\dot{A}}\equiv \,\text{d}A/\text{d}t$ of any function
${\dot{A}}\equiv \,\text{d}A/\text{d}t$ of any function  $A$. It is assumed that
$A$. It is assumed that  $\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t=\unicode[STIX]{x2202}\boldsymbol{A}^{\ast }/\unicode[STIX]{x2202}t=0$ in deriving the equations above.
$\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t=\unicode[STIX]{x2202}\boldsymbol{A}^{\ast }/\unicode[STIX]{x2202}t=0$ in deriving the equations above.
Splitting the distribution function of species  $a$ as
$a$ as  $f_{a}=f_{a0}+f_{a1}$, where
$f_{a}=f_{a0}+f_{a1}$, where  $f_{a1}\ll f_{a0}$, FORTEC-3D solves the equation for
$f_{a1}\ll f_{a0}$, FORTEC-3D solves the equation for  $f_{a1}$. The lowest-order distribution function
$f_{a1}$. The lowest-order distribution function  $f_{a0}$ is given by
$f_{a0}$ is given by
 $$\begin{eqnarray}f_{a0}=f_{aM}\text{e}^{-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}},\end{eqnarray}$$
$$\begin{eqnarray}f_{a0}=f_{aM}\text{e}^{-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}},\end{eqnarray}$$with the local Maxwellian
 $$\begin{eqnarray}f_{aM}=n_{a0}\left(\frac{m_{a}}{2\unicode[STIX]{x03C0}T_{a}}\right)^{3/2}\exp \left[-\frac{m_{a}v_{\Vert }^{2}}{2T_{a}}-\frac{\unicode[STIX]{x1D707}B}{T_{a}}\right].\end{eqnarray}$$
$$\begin{eqnarray}f_{aM}=n_{a0}\left(\frac{m_{a}}{2\unicode[STIX]{x03C0}T_{a}}\right)^{3/2}\exp \left[-\frac{m_{a}v_{\Vert }^{2}}{2T_{a}}-\frac{\unicode[STIX]{x1D707}B}{T_{a}}\right].\end{eqnarray}$$ The first-order drift-kinetic equation for  $f_{a1}$ is then given by
$f_{a1}$ is then given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}f_{a1}}{\unicode[STIX]{x2202}t}+\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{a1}+\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a1}}{\unicode[STIX]{x2202}v_{\Vert }}-C_{TP}(f_{a1})=C_{FP}(f_{a0})+\frac{Z_{a}e}{T_{a}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}_{1}}{\unicode[STIX]{x2202}t}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r\left[\frac{n_{a0}^{\prime }}{n_{a0}}+\frac{Z_{a}e\unicode[STIX]{x1D6F7}_{0}^{\prime }}{T_{a}}+\left(\frac{m_{a}v_{\Vert }^{2}}{2T_{a}}+\frac{\unicode[STIX]{x1D707}B}{T_{a}}-\frac{3}{2}+\frac{Z_{a}e\unicode[STIX]{x1D6F7}_{1}}{T_{a}}\right)\frac{T_{a}^{\prime }}{T_{a}}\right]f_{a0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}f_{a1}}{\unicode[STIX]{x2202}t}+\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{a1}+\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a1}}{\unicode[STIX]{x2202}v_{\Vert }}-C_{TP}(f_{a1})=C_{FP}(f_{a0})+\frac{Z_{a}e}{T_{a}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}_{1}}{\unicode[STIX]{x2202}t}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r\left[\frac{n_{a0}^{\prime }}{n_{a0}}+\frac{Z_{a}e\unicode[STIX]{x1D6F7}_{0}^{\prime }}{T_{a}}+\left(\frac{m_{a}v_{\Vert }^{2}}{2T_{a}}+\frac{\unicode[STIX]{x1D707}B}{T_{a}}-\frac{3}{2}+\frac{Z_{a}e\unicode[STIX]{x1D6F7}_{1}}{T_{a}}\right)\frac{T_{a}^{\prime }}{T_{a}}\right]f_{a0},\end{eqnarray}$$ where  $n_{a0}$ and
$n_{a0}$ and  $T_{a}$ are flux functions,
$T_{a}$ are flux functions,  $m_{a}$ denotes the mass of the species
$m_{a}$ denotes the mass of the species  $a$ and
$a$ and  $C_{TP}(f_{a1})$ and
$C_{TP}(f_{a1})$ and  $C_{FP}(f_{a0})$ are the test-particle part and the field-particle part of the linearised collision operator, respectively,
$C_{FP}(f_{a0})$ are the test-particle part and the field-particle part of the linearised collision operator, respectively,
 $$\begin{eqnarray}\displaystyle & \displaystyle C_{TP}(f_{a1})=\mathop{\sum }_{b}C_{TP}^{ab}(f_{a1},f_{b0}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{TP}(f_{a1})=\mathop{\sum }_{b}C_{TP}^{ab}(f_{a1},f_{b0}), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle C_{FP}(f_{a0})=\mathop{\sum }_{b}C_{FP}^{ab}(f_{a0},f_{b1}). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{FP}(f_{a0})=\mathop{\sum }_{b}C_{FP}^{ab}(f_{a0},f_{b1}). & \displaystyle\end{eqnarray}$$ Strictly speaking, however,  $f_{a0}$ is approximated with
$f_{a0}$ is approximated with  $f_{aM}$ in the linearised collision operator for the present work. Also, the recent attempts to extend the collision operator to include higher-order terms which can be important for impurity transport (Sugama et al. Reference Sugama, Matsuoka, Satake, Nunami and Watanabe2019; Calvo et al. Reference Calvo, Parra, Velasco and García-Regaña2020) are not considered. The equations (2.1)–(2.6) are reduced to the equations for a case without
$f_{aM}$ in the linearised collision operator for the present work. Also, the recent attempts to extend the collision operator to include higher-order terms which can be important for impurity transport (Sugama et al. Reference Sugama, Matsuoka, Satake, Nunami and Watanabe2019; Calvo et al. Reference Calvo, Parra, Velasco and García-Regaña2020) are not considered. The equations (2.1)–(2.6) are reduced to the equations for a case without  $\unicode[STIX]{x1D6F7}_{1}$ by setting
$\unicode[STIX]{x1D6F7}_{1}$ by setting  $\unicode[STIX]{x1D6F7}_{1}=0$. A derivation of the drift-kinetic equation (2.6) is provided in appendix A.
$\unicode[STIX]{x1D6F7}_{1}=0$. A derivation of the drift-kinetic equation (2.6) is provided in appendix A.
Note that in this model, the term corresponding to the so-called  $E\times B$ drift
$E\times B$ drift
 $$\begin{eqnarray}\boldsymbol{v}_{E}\equiv \frac{1}{B_{\Vert }^{\ast }}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{E}\equiv \frac{1}{B_{\Vert }^{\ast }}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}\end{eqnarray}$$is species-dependent due to the denominator
 $$\begin{eqnarray}B_{\Vert }^{\ast }=B+\frac{m_{a}v_{\Vert }}{Z_{a}e}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}\end{eqnarray}$$
$$\begin{eqnarray}B_{\Vert }^{\ast }=B+\frac{m_{a}v_{\Vert }}{Z_{a}e}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}\end{eqnarray}$$and FORTEC-3D does solve (2.1)–(2.3) as written here so that the phase-space volume is conserved (Littlejohn Reference Littlejohn1983). However, the second term in (2.10) is negligible as far as the low-beta approximation
 $$\begin{eqnarray}\unicode[STIX]{x1D735}\times \boldsymbol{b}\simeq \frac{\boldsymbol{B}\times \unicode[STIX]{x1D735}B}{B^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}\times \boldsymbol{b}\simeq \frac{\boldsymbol{B}\times \unicode[STIX]{x1D735}B}{B^{2}}\end{eqnarray}$$ holds. Then,  $\boldsymbol{v}_{E}$ can be approximated as
$\boldsymbol{v}_{E}$ can be approximated as
 $$\begin{eqnarray}\boldsymbol{v}_{E}\simeq \frac{1}{B}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{E}\simeq \frac{1}{B}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}\end{eqnarray}$$ and the value of the  $E\times B$ drift becomes species-independent. Also, it does not affect the basic property that the lowest-order distribution function does not generate radial particle flux:
$E\times B$ drift becomes species-independent. Also, it does not affect the basic property that the lowest-order distribution function does not generate radial particle flux:
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a0}\equiv \left\langle \int \,\text{d}^{3}v(\boldsymbol{v}_{m}+\boldsymbol{v}_{E})\boldsymbol{\cdot }\unicode[STIX]{x1D735}rf_{a0}\right\rangle =0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a0}\equiv \left\langle \int \,\text{d}^{3}v(\boldsymbol{v}_{m}+\boldsymbol{v}_{E})\boldsymbol{\cdot }\unicode[STIX]{x1D735}rf_{a0}\right\rangle =0.\end{eqnarray}$$2.2 Expressions in the Boozer coordinate system
The Boozer coordinate system (Boozer Reference Boozer1981) is used in FORTEC-3D. In this coordinate system, the covariant representation of the magnetic field is given by
 $$\begin{eqnarray}\boldsymbol{B}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D703}+\unicode[STIX]{x1D704}(r)\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}=I(r)\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}+G(r)\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}+\unicode[STIX]{x1D6FD}^{\ast }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D703}+\unicode[STIX]{x1D704}(r)\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D713}=I(r)\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}+G(r)\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}+\unicode[STIX]{x1D6FD}^{\ast }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713},\end{eqnarray}$$ where  $\unicode[STIX]{x1D704}$ is the rotational transform,
$\unicode[STIX]{x1D704}$ is the rotational transform,  $\unicode[STIX]{x1D713}$ is the toroidal magnetic flux divided by
$\unicode[STIX]{x1D713}$ is the toroidal magnetic flux divided by  $2\unicode[STIX]{x03C0}$,
$2\unicode[STIX]{x03C0}$,  $I$ is related to the toroidal current inside the flux surface at
$I$ is related to the toroidal current inside the flux surface at  $r$ and
$r$ and  $G$ is related to the poloidal current outside the surface, respectively. Since
$G$ is related to the poloidal current outside the surface, respectively. Since  $\unicode[STIX]{x1D6FD}^{\ast }$ is related to the Pfirsch–Schlüter current (Boozer Reference Boozer1981) and can be estimated as
$\unicode[STIX]{x1D6FD}^{\ast }$ is related to the Pfirsch–Schlüter current (Boozer Reference Boozer1981) and can be estimated as  $O(\unicode[STIX]{x1D6FD}/a)$, where
$O(\unicode[STIX]{x1D6FD}/a)$, where  $\unicode[STIX]{x1D6FD}$ and
$\unicode[STIX]{x1D6FD}$ and  $a$ are the plasma beta and the minor radius, respectively, we assume low-
$a$ are the plasma beta and the minor radius, respectively, we assume low- $\unicode[STIX]{x1D6FD}$ plasmas and therefore the term
$\unicode[STIX]{x1D6FD}$ plasmas and therefore the term  $\unicode[STIX]{x1D6FD}^{\ast }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$ in (2.14) is ignored in this work. This approximation allows us to put the guiding-centre equations of motion in canonical form. Although we will not write down the equations in canonical form explicitly here, this property has an advantage of ensuring the properties of Hamiltonian systems such as Liouville’s theorem. See § 3.2 of White (Reference White2014) and references therein for a detailed discussion of the construction of the Hamiltonian formulation of the guiding-centre motion. The contravariant representation is given by
$\unicode[STIX]{x1D6FD}^{\ast }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$ in (2.14) is ignored in this work. This approximation allows us to put the guiding-centre equations of motion in canonical form. Although we will not write down the equations in canonical form explicitly here, this property has an advantage of ensuring the properties of Hamiltonian systems such as Liouville’s theorem. See § 3.2 of White (Reference White2014) and references therein for a detailed discussion of the construction of the Hamiltonian formulation of the guiding-centre motion. The contravariant representation is given by
 $$\begin{eqnarray}\boldsymbol{B}=\frac{1}{\sqrt{g}}\frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}r}(\unicode[STIX]{x1D704}\boldsymbol{e}_{\unicode[STIX]{x1D703}}+\boldsymbol{e}_{\unicode[STIX]{x1D701}}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{B}=\frac{1}{\sqrt{g}}\frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}r}(\unicode[STIX]{x1D704}\boldsymbol{e}_{\unicode[STIX]{x1D703}}+\boldsymbol{e}_{\unicode[STIX]{x1D701}}),\end{eqnarray}$$ where  $\boldsymbol{e}_{j}$ is the unit vector in the
$\boldsymbol{e}_{j}$ is the unit vector in the  $j$-direction and the Jacobian
$j$-direction and the Jacobian  $\sqrt{g}$ is given by
$\sqrt{g}$ is given by
 $$\begin{eqnarray}\sqrt{g}=\frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}r}\frac{G+\unicode[STIX]{x1D704}I}{B^{2}}=\frac{(\unicode[STIX]{x1D713}^{\prime }G+\unicode[STIX]{x1D712}^{\prime }I)}{B^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\sqrt{g}=\frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}r}\frac{G+\unicode[STIX]{x1D704}I}{B^{2}}=\frac{(\unicode[STIX]{x1D713}^{\prime }G+\unicode[STIX]{x1D712}^{\prime }I)}{B^{2}},\end{eqnarray}$$ with  $\unicode[STIX]{x1D712}$ the poloidal magnetic flux divided by
$\unicode[STIX]{x1D712}$ the poloidal magnetic flux divided by  $2\unicode[STIX]{x03C0}$.
$2\unicode[STIX]{x03C0}$.
In this coordinate system, the guiding-centre equations of motion are expressed as follows (a derivation is provided in § A.2):
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}r}{\text{d}t}=\frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FE}}\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+\frac{Z_{a}e}{\unicode[STIX]{x1D6FE}}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}r}{\text{d}t}=\frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FE}}\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+\frac{Z_{a}e}{\unicode[STIX]{x1D6FE}}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\unicode[STIX]{x1D703}}{\text{d}t}=\frac{G}{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FF}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })+\frac{v_{\Vert }B}{\unicode[STIX]{x1D6FE}}\left(Z_{a}e\unicode[STIX]{x1D712}^{\prime }-\frac{m_{a}v_{\Vert }}{B}G^{\prime }\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\unicode[STIX]{x1D703}}{\text{d}t}=\frac{G}{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FF}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })+\frac{v_{\Vert }B}{\unicode[STIX]{x1D6FE}}\left(Z_{a}e\unicode[STIX]{x1D712}^{\prime }-\frac{m_{a}v_{\Vert }}{B}G^{\prime }\right), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\unicode[STIX]{x1D701}}{\text{d}t}=-\frac{I}{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FF}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })+\frac{v_{\Vert }B}{\unicode[STIX]{x1D6FE}}\left(Z_{a}e\unicode[STIX]{x1D713}^{\prime }+\frac{m_{a}v_{\Vert }}{B}I^{\prime }\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\unicode[STIX]{x1D701}}{\text{d}t}=-\frac{I}{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FF}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })+\frac{v_{\Vert }B}{\unicode[STIX]{x1D6FE}}\left(Z_{a}e\unicode[STIX]{x1D713}^{\prime }+\frac{m_{a}v_{\Vert }}{B}I^{\prime }\right), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle \frac{\text{d}v_{\Vert }}{\text{d}t} & = & \displaystyle -\frac{v_{\Vert }}{B\unicode[STIX]{x1D6FE}}\left[Z_{a}e\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\unicode[STIX]{x1D6F7}^{\prime }-\unicode[STIX]{x1D707}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)B^{\prime }\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Z_{a}eB}{m_{a}\unicode[STIX]{x1D6FE}}\left[\left(\frac{m_{a}v_{\Vert }}{Z_{a}eB}G^{\prime }-\unicode[STIX]{x1D712}^{\prime }\right)\left(\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}+Z_{a}e\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\left(\frac{m_{a}v_{\Vert }}{Z_{a}eB}I^{\prime }+\unicode[STIX]{x1D713}^{\prime }\right)\left(\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+Z_{a}e\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}v_{\Vert }}{\text{d}t} & = & \displaystyle -\frac{v_{\Vert }}{B\unicode[STIX]{x1D6FE}}\left[Z_{a}e\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\unicode[STIX]{x1D6F7}^{\prime }-\unicode[STIX]{x1D707}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)B^{\prime }\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Z_{a}eB}{m_{a}\unicode[STIX]{x1D6FE}}\left[\left(\frac{m_{a}v_{\Vert }}{Z_{a}eB}G^{\prime }-\unicode[STIX]{x1D712}^{\prime }\right)\left(\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}+Z_{a}e\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\left(\frac{m_{a}v_{\Vert }}{Z_{a}eB}I^{\prime }+\unicode[STIX]{x1D713}^{\prime }\right)\left(\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+Z_{a}e\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)\right],\end{eqnarray}$$where
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}\equiv \unicode[STIX]{x1D707}+\frac{m_{a}v_{\Vert }^{2}}{B}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\equiv \unicode[STIX]{x1D707}+\frac{m_{a}v_{\Vert }^{2}}{B}\end{eqnarray}$$and
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}\equiv Z_{a}eBB_{\Vert }^{\ast }\sqrt{g}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}\equiv Z_{a}eBB_{\Vert }^{\ast }\sqrt{g}\end{eqnarray}$$ are defined.  $\unicode[STIX]{x1D6FF}$ here is not to be confused with the delta function or some ordering parameter. The flux surface average of an arbitrary function
$\unicode[STIX]{x1D6FF}$ here is not to be confused with the delta function or some ordering parameter. The flux surface average of an arbitrary function  $A$ is expressed as
$A$ is expressed as
 $$\begin{eqnarray}\langle A\rangle =\frac{1}{V^{\prime }}\oint \sqrt{g}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}A,\end{eqnarray}$$
$$\begin{eqnarray}\langle A\rangle =\frac{1}{V^{\prime }}\oint \sqrt{g}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}A,\end{eqnarray}$$where
 $$\begin{eqnarray}V^{\prime }=\oint \sqrt{g}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}.\end{eqnarray}$$
$$\begin{eqnarray}V^{\prime }=\oint \sqrt{g}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}.\end{eqnarray}$$The radial particle flux is thus calculated by
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a}=\frac{1}{V^{\prime }}\oint \sqrt{g}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\int \,\text{d}^{3}v{\dot{r}}f_{a1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a}=\frac{1}{V^{\prime }}\oint \sqrt{g}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\int \,\text{d}^{3}v{\dot{r}}f_{a1}.\end{eqnarray}$$2.3 Two-weight  $\unicode[STIX]{x1D6FF}\,f$ method
$\unicode[STIX]{x1D6FF}\,f$ method
The two-weight  $\unicode[STIX]{x1D6FF}\,f$ scheme (Brunner, Valeo & Krommes Reference Brunner, Valeo and Krommes1999; Wang et al. Reference Wang, Nakajima, Okamoto and Murakami1999) is employed in FORTEC-3D. The microscopic dynamics is simulated by marker particles which evolve according to the equations of motion (2.1)–(2.3). In the two-weight
$\unicode[STIX]{x1D6FF}\,f$ scheme (Brunner, Valeo & Krommes Reference Brunner, Valeo and Krommes1999; Wang et al. Reference Wang, Nakajima, Okamoto and Murakami1999) is employed in FORTEC-3D. The microscopic dynamics is simulated by marker particles which evolve according to the equations of motion (2.1)–(2.3). In the two-weight  $\unicode[STIX]{x1D6FF}\,f$ method, the distribution function is split into two parts as
$\unicode[STIX]{x1D6FF}\,f$ method, the distribution function is split into two parts as  $f=f_{0}+f_{1}$, where
$f=f_{0}+f_{1}$, where  $f_{0}$ is an analytically known part and
$f_{0}$ is an analytically known part and  $f_{1}$ is the deviation from that. In this study, the adiabatic response to
$f_{1}$ is the deviation from that. In this study, the adiabatic response to  $\unicode[STIX]{x1D6F7}_{1}$ is included in the
$\unicode[STIX]{x1D6F7}_{1}$ is included in the  $f_{0}$ part (2.4). See García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017) for a discussion of different choices of
$f_{0}$ part (2.4). See García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017) for a discussion of different choices of  $f_{0}$. The species index is omitted for simplicity in this subsection.
$f_{0}$. The species index is omitted for simplicity in this subsection.
The distribution functions are represented by the products of the marker particle distribution  $g(\boldsymbol{Z},t)$ and the weight fields
$g(\boldsymbol{Z},t)$ and the weight fields  $W(\boldsymbol{Z},t)$ and
$W(\boldsymbol{Z},t)$ and  $P(\boldsymbol{Z},t)$, respectively, as
$P(\boldsymbol{Z},t)$, respectively, as
 $$\begin{eqnarray}\displaystyle & f_{0}(\boldsymbol{Z},t)=P(\boldsymbol{Z},t)g(\boldsymbol{Z},t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{0}(\boldsymbol{Z},t)=P(\boldsymbol{Z},t)g(\boldsymbol{Z},t), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & f_{1}(\boldsymbol{Z},t)=W(\boldsymbol{Z},t)g(\boldsymbol{Z},t). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{1}(\boldsymbol{Z},t)=W(\boldsymbol{Z},t)g(\boldsymbol{Z},t). & \displaystyle\end{eqnarray}$$ Each marker particle is assigned two weights  $w_{i}$ and
$w_{i}$ and  $p_{i}$, which are defined as the values of the weight fields
$p_{i}$, which are defined as the values of the weight fields  $W$ and
$W$ and  $P$ at the phase position
$P$ at the phase position  $\boldsymbol{Z}_{i}$, respectively:
$\boldsymbol{Z}_{i}$, respectively:
 $$\begin{eqnarray}\displaystyle & w_{i}(t)=W(\boldsymbol{Z}_{i}(t),t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & w_{i}(t)=W(\boldsymbol{Z}_{i}(t),t), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & p_{i}(t)=P(\boldsymbol{Z}_{i}(t),t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & p_{i}(t)=P(\boldsymbol{Z}_{i}(t),t), & \displaystyle\end{eqnarray}$$ where  $i$ is the particle label. The weights also evolve in time following the equations
$i$ is the particle label. The weights also evolve in time following the equations
 $$\begin{eqnarray}\displaystyle & \displaystyle {\dot{p}}_{i}=\frac{p_{i}}{f_{0}}\dot{\boldsymbol{Z}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{Z}}f_{0}-\frac{Ze}{T}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}_{1}}{\unicode[STIX]{x2202}t}p_{i}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\dot{p}}_{i}=\frac{p_{i}}{f_{0}}\dot{\boldsymbol{Z}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{Z}}f_{0}-\frac{Ze}{T}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}_{1}}{\unicode[STIX]{x2202}t}p_{i}, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle {\dot{w}}_{i}=-\frac{p_{i}}{f_{0}}\left(\dot{\boldsymbol{Z}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{Z}}-C_{\text{FP}}\right)f_{0}+\frac{Ze}{T}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}_{1}}{\unicode[STIX]{x2202}t}p_{i}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\dot{w}}_{i}=-\frac{p_{i}}{f_{0}}\left(\dot{\boldsymbol{Z}}\boldsymbol{\cdot }\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{Z}}-C_{\text{FP}}\right)f_{0}+\frac{Ze}{T}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}_{1}}{\unicode[STIX]{x2202}t}p_{i}, & \displaystyle\end{eqnarray}$$ which are evaluated at  $\boldsymbol{Z}=\boldsymbol{Z}_{i}(t)$. We thus can solve the drift-kinetic equation for
$\boldsymbol{Z}=\boldsymbol{Z}_{i}(t)$. We thus can solve the drift-kinetic equation for  $f_{1}$ by integrating the evolution equations (2.1)–(2.3), (2.30) and (2.31).
$f_{1}$ by integrating the evolution equations (2.1)–(2.3), (2.30) and (2.31).
2.4 Evaluation of electrostatic potential
The electrostatic potential can be decomposed as  $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{0}+\unicode[STIX]{x1D6F7}_{1}$. The first part is a flux function
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{0}+\unicode[STIX]{x1D6F7}_{1}$. The first part is a flux function  $\unicode[STIX]{x1D6F7}_{0}=\unicode[STIX]{x1D6F7}_{0}(r)$ and generates a radial electric field
$\unicode[STIX]{x1D6F7}_{0}=\unicode[STIX]{x1D6F7}_{0}(r)$ and generates a radial electric field  $E_{r}=-\unicode[STIX]{x1D6F7}_{0}^{\prime }$. The radial electric field
$E_{r}=-\unicode[STIX]{x1D6F7}_{0}^{\prime }$. The radial electric field  $E_{r}$ is determined so that it satisfies the ambipolar condition
$E_{r}$ is determined so that it satisfies the ambipolar condition
 $$\begin{eqnarray}\mathop{\sum }_{a}Z_{a}\unicode[STIX]{x1D6E4}_{a}=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a}Z_{a}\unicode[STIX]{x1D6E4}_{a}=0.\end{eqnarray}$$ In FORTEC-3D,  $E_{r}=-\unicode[STIX]{x1D6F7}_{0}^{\prime }$ can be given as a fixed input parameter or it also can be internally solved by the equation (2a) in Satake et al. (Reference Satake, Kanno and Sugama2008).
$E_{r}=-\unicode[STIX]{x1D6F7}_{0}^{\prime }$ can be given as a fixed input parameter or it also can be internally solved by the equation (2a) in Satake et al. (Reference Satake, Kanno and Sugama2008).
The second part  $\unicode[STIX]{x1D6F7}_{1}=\unicode[STIX]{x1D6F7}_{1}(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D701})$ is the non-flux function part. It is assumed that
$\unicode[STIX]{x1D6F7}_{1}=\unicode[STIX]{x1D6F7}_{1}(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D701})$ is the non-flux function part. It is assumed that  $\langle \unicode[STIX]{x1D6F7}_{1}\rangle =0$ in the present study. See appendix B for the justification of this assumption. The non-uniform part
$\langle \unicode[STIX]{x1D6F7}_{1}\rangle =0$ in the present study. See appendix B for the justification of this assumption. The non-uniform part  $\unicode[STIX]{x1D6F7}_{1}$ is determined by the following argument. From (2.4), the density of species
$\unicode[STIX]{x1D6F7}_{1}$ is determined by the following argument. From (2.4), the density of species  $a$ takes the form
$a$ takes the form
 $$\begin{eqnarray}n_{a}=n_{a0}\exp (-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a})+n_{a1}\end{eqnarray}$$
$$\begin{eqnarray}n_{a}=n_{a0}\exp (-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a})+n_{a1}\end{eqnarray}$$and imposing quasi-neutrality up to the first order yields the expression
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{1} & = & \displaystyle \frac{1}{e}\left(\mathop{\sum }_{I}Z_{I}^{2}\frac{n_{I0}}{T_{I}}+\frac{n_{e0}}{T_{e}}\right)^{-1}\mathop{\sum }_{I}Z_{I}n_{I1}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{e}\left(\mathop{\sum }_{I}Z_{I}^{2}\frac{n_{I0}}{T_{I}}+\frac{n_{e0}}{T_{e}}\right)^{-1}\mathop{\sum }_{I}Z_{I}\int \,\text{d}^{3}vf_{I1},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{1} & = & \displaystyle \frac{1}{e}\left(\mathop{\sum }_{I}Z_{I}^{2}\frac{n_{I0}}{T_{I}}+\frac{n_{e0}}{T_{e}}\right)^{-1}\mathop{\sum }_{I}Z_{I}n_{I1}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{e}\left(\mathop{\sum }_{I}Z_{I}^{2}\frac{n_{I0}}{T_{I}}+\frac{n_{e0}}{T_{e}}\right)^{-1}\mathop{\sum }_{I}Z_{I}\int \,\text{d}^{3}vf_{I1},\end{eqnarray}$$ where the subscript  $I$ refers to the ion species. In deriving the above expression,
$I$ refers to the ion species. In deriving the above expression,  $Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}\ll 1$ is assumed for all species. As we shall see below, this assumption is reasonable for the present study. However, the assumption does not hold for high-
$Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}\ll 1$ is assumed for all species. As we shall see below, this assumption is reasonable for the present study. However, the assumption does not hold for high- $Z$ impurities. Also, the adiabatic response of electrons is assumed, i.e.
$Z$ impurities. Also, the adiabatic response of electrons is assumed, i.e.  $n_{e1}=0$. The spatial structure of
$n_{e1}=0$. The spatial structure of  $\unicode[STIX]{x1D6F7}_{1}$ is thus determined by the superposition of the ion density variations
$\unicode[STIX]{x1D6F7}_{1}$ is thus determined by the superposition of the ion density variations  $n_{I1}$, weighted by the charge number
$n_{I1}$, weighted by the charge number  $Z_{I}$. Note here that in some studies,
$Z_{I}$. Note here that in some studies,  $\unicode[STIX]{x1D6F7}_{1}$ is evaluated by considering only the contribution of the main ion. When the contribution of impurities is taken into account as (2.34), the value of
$\unicode[STIX]{x1D6F7}_{1}$ is evaluated by considering only the contribution of the main ion. When the contribution of impurities is taken into account as (2.34), the value of  $\unicode[STIX]{x1D6F7}_{1}$ usually becomes smaller since the impurity contributions are included in the factor
$\unicode[STIX]{x1D6F7}_{1}$ usually becomes smaller since the impurity contributions are included in the factor  $\sum _{I}Z_{I}^{2}n_{I0}/T_{I}$ in the denominator. In this study,
$\sum _{I}Z_{I}^{2}n_{I0}/T_{I}$ in the denominator. In this study,  $\unicode[STIX]{x1D6F7}_{1}$ is evaluated during the self-consistent calculation of the set of equations (2.1)–(2.3), (2.6) and (2.34). It has been pointed out that the contribution of kinetic electrons to
$\unicode[STIX]{x1D6F7}_{1}$ is evaluated during the self-consistent calculation of the set of equations (2.1)–(2.3), (2.6) and (2.34). It has been pointed out that the contribution of kinetic electrons to  $\unicode[STIX]{x1D6F7}_{1}$ can be significant, especially in electron-root plasmas (García-Regaña et al. Reference García-Regaña, Estrada, Calvo, Velasco, Alonso, Carralero, Kleiber, Landreman, Mollén and Sánchez2018). However, it is numerically too costly for the present version of FORTEC-3D to solve kinetic electrons with ion species together.
$\unicode[STIX]{x1D6F7}_{1}$ can be significant, especially in electron-root plasmas (García-Regaña et al. Reference García-Regaña, Estrada, Calvo, Velasco, Alonso, Carralero, Kleiber, Landreman, Mollén and Sánchez2018). However, it is numerically too costly for the present version of FORTEC-3D to solve kinetic electrons with ion species together.
2.5 Evaluation of the flux driven by  $\unicode[STIX]{x1D6F7}_{1}$
$\unicode[STIX]{x1D6F7}_{1}$
In the Boozer coordinate system, the radial particle flux driven by  $\unicode[STIX]{x1D6F7}_{1}$ through the
$\unicode[STIX]{x1D6F7}_{1}$ through the  $E\times B$ drift,
$E\times B$ drift,  $\boldsymbol{v}_{E1}$, is expressed as
$\boldsymbol{v}_{E1}$, is expressed as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{v_{E1}}(r) & = & \displaystyle \frac{1}{V^{\prime }(r)}\oint \sqrt{g}(\boldsymbol{X})\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\int \,\text{d}^{3}v\frac{1}{B(\boldsymbol{X})B_{\Vert }^{\ast }(\boldsymbol{X},\boldsymbol{v})\sqrt{g}(\boldsymbol{X})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(I(r)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}(\boldsymbol{X})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G(r)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}(\boldsymbol{X})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)f_{a1}(\boldsymbol{X},\boldsymbol{v}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{v_{E1}}(r) & = & \displaystyle \frac{1}{V^{\prime }(r)}\oint \sqrt{g}(\boldsymbol{X})\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\int \,\text{d}^{3}v\frac{1}{B(\boldsymbol{X})B_{\Vert }^{\ast }(\boldsymbol{X},\boldsymbol{v})\sqrt{g}(\boldsymbol{X})}\nonumber\\ \displaystyle & & \displaystyle \times \,\left(I(r)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}(\boldsymbol{X})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G(r)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}(\boldsymbol{X})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)f_{a1}(\boldsymbol{X},\boldsymbol{v}),\end{eqnarray}$$ where  $\boldsymbol{X}=(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D701})$ and
$\boldsymbol{X}=(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D701})$ and  $\boldsymbol{v}=(v_{\Vert },\unicode[STIX]{x1D707})$. This quantity can be evaluated in two different ways. One is to simply perform the integral and the other is to use Fourier series expansion. If the low-beta approximation
$\boldsymbol{v}=(v_{\Vert },\unicode[STIX]{x1D707})$. This quantity can be evaluated in two different ways. One is to simply perform the integral and the other is to use Fourier series expansion. If the low-beta approximation
 $$\begin{eqnarray}\frac{1}{B(\boldsymbol{X})B_{\Vert }^{\ast }(\boldsymbol{X},\boldsymbol{v})}\simeq \frac{1}{B^{2}(\boldsymbol{X})}\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{B(\boldsymbol{X})B_{\Vert }^{\ast }(\boldsymbol{X},\boldsymbol{v})}\simeq \frac{1}{B^{2}(\boldsymbol{X})}\end{eqnarray}$$is used, the velocity integral can readily be performed and we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{v_{E1}}(r)=\frac{1}{V^{\prime }(r)}\oint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\bar{v}_{E1}(\boldsymbol{X})n_{a1}(\boldsymbol{X}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{v_{E1}}(r)=\frac{1}{V^{\prime }(r)}\oint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\bar{v}_{E1}(\boldsymbol{X})n_{a1}(\boldsymbol{X}),\end{eqnarray}$$where we have defined
 $$\begin{eqnarray}\bar{v}_{E1}\equiv \frac{1}{B^{2}}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\simeq \sqrt{g}\boldsymbol{v}_{E1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r.\end{eqnarray}$$
$$\begin{eqnarray}\bar{v}_{E1}\equiv \frac{1}{B^{2}}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\simeq \sqrt{g}\boldsymbol{v}_{E1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r.\end{eqnarray}$$ Thus, if we expand  $\bar{v}_{E1}$ and
$\bar{v}_{E1}$ and  $n_{a1}$ in Fourier series, respectively, and put them into (2.37), only the products of the same modes survive and the equation is formally reduced to the following form:
$n_{a1}$ in Fourier series, respectively, and put them into (2.37), only the products of the same modes survive and the equation is formally reduced to the following form:
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{v_{E1}}(r)=\frac{1}{V^{\prime }(r)}\mathop{\sum }_{m,n}C_{m,n}\left[\tilde{v}_{E1}^{m,n(c)}(r){\tilde{n}}_{a1}^{m,n(c)}(r)+\tilde{v}_{E1}^{m,n(s)}(r){\tilde{n}}_{a1}^{m,n(s)}(r)\right],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{v_{E1}}(r)=\frac{1}{V^{\prime }(r)}\mathop{\sum }_{m,n}C_{m,n}\left[\tilde{v}_{E1}^{m,n(c)}(r){\tilde{n}}_{a1}^{m,n(c)}(r)+\tilde{v}_{E1}^{m,n(s)}(r){\tilde{n}}_{a1}^{m,n(s)}(r)\right],\end{eqnarray}$$ where  $C_{m,n}$ are normalisation coefficients and
$C_{m,n}$ are normalisation coefficients and  $\tilde{v}_{E1}^{m,n(c)}$,
$\tilde{v}_{E1}^{m,n(c)}$,  $\tilde{v}_{E1}^{m,n(s)}$,
$\tilde{v}_{E1}^{m,n(s)}$,  ${\tilde{n}}_{a1}^{m,n(c)}$ and
${\tilde{n}}_{a1}^{m,n(c)}$ and  ${\tilde{n}}_{a1}^{m,n(s)}$ are the Fourier coefficients of cosine- and sine-
${\tilde{n}}_{a1}^{m,n(s)}$ are the Fourier coefficients of cosine- and sine- $(m,n)$ modes of
$(m,n)$ modes of  $\bar{v}_{E1}$ and
$\bar{v}_{E1}$ and  $n_{a1}$, respectively. In the present article, Fourier coefficients of a quantity
$n_{a1}$, respectively. In the present article, Fourier coefficients of a quantity  $A(\boldsymbol{X})$ are defined as follows:
$A(\boldsymbol{X})$ are defined as follows:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\tilde{A}^{m,n(c)}(r)={\displaystyle \frac{1}{2\unicode[STIX]{x03C0}^{2}}}\displaystyle \iint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}A(\boldsymbol{X})\cos (m\unicode[STIX]{x1D703}-nN\unicode[STIX]{x1D701}),\\ \tilde{A}^{m,n(s)}(r)={\displaystyle \frac{1}{2\unicode[STIX]{x03C0}^{2}}}\displaystyle \iint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}A(\boldsymbol{X})\sin (m\unicode[STIX]{x1D703}-nN\unicode[STIX]{x1D701}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\tilde{A}^{m,n(c)}(r)={\displaystyle \frac{1}{2\unicode[STIX]{x03C0}^{2}}}\displaystyle \iint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}A(\boldsymbol{X})\cos (m\unicode[STIX]{x1D703}-nN\unicode[STIX]{x1D701}),\\ \tilde{A}^{m,n(s)}(r)={\displaystyle \frac{1}{2\unicode[STIX]{x03C0}^{2}}}\displaystyle \iint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}A(\boldsymbol{X})\sin (m\unicode[STIX]{x1D703}-nN\unicode[STIX]{x1D701}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$ where  $N$ is the toroidal period number (
$N$ is the toroidal period number ( $N=10$ for LHD). Note that the flux driven by the magnetic drift,
$N=10$ for LHD). Note that the flux driven by the magnetic drift,  $\boldsymbol{v}_{m}$, cannot be put in the form of (2.37) and therefore also not in the form of (2.39) since
$\boldsymbol{v}_{m}$, cannot be put in the form of (2.37) and therefore also not in the form of (2.39) since  $\boldsymbol{v}_{m}$ essentially depends on the velocity variables (and the dependence cannot be approximated away).
$\boldsymbol{v}_{m}$ essentially depends on the velocity variables (and the dependence cannot be approximated away).
Although the first method is more simple and straightforward for evaluating  $\unicode[STIX]{x1D6E4}_{v_{E1}}$, this second method has an advantage that it enables us to see how each mode contributes to the additional flux. The
$\unicode[STIX]{x1D6E4}_{v_{E1}}$, this second method has an advantage that it enables us to see how each mode contributes to the additional flux. The  $\text{C}^{6+}$ flux will be evaluated by these two different methods below.
$\text{C}^{6+}$ flux will be evaluated by these two different methods below.
3 Setup for the ion transport calculation
We consider an LHD hydrogen plasma which contains two different impurity species, helium  $\text{He}^{2+}$ and carbon
$\text{He}^{2+}$ and carbon  $\text{C}^{6+}$. Electrons are assumed to be adiabatic in solving the transport of ion species and in the quasineutrality condition. The standard LHD configuration with a major radius
$\text{C}^{6+}$. Electrons are assumed to be adiabatic in solving the transport of ion species and in the quasineutrality condition. The standard LHD configuration with a major radius  $R_{0}=3.7~\text{m}$ and a minor radius
$R_{0}=3.7~\text{m}$ and a minor radius  $a=0.62~\text{m}$ is considered. The magnetic field strength and its Fourier spectrum are represented in figure 1. The density and temperature profiles are shown in figures 2 and 3. One of the features which characterises an impurity hole plasma is the steepness of its ion temperature gradient. This profile has been used for several impurity hole studies (Nunami et al. Reference Nunami, Sugama, Velasco, Yokoyama, Sato, Nakata and Satake2016, Reference Nunami, Nakata, Sato, Toda, Yamaguchi, Sugama and Yokoyama2017, Reference Nunami, Satake, Fujita, Yamaguchi, Matsuoka, Sato, Toda and Sugama2019, Reference Nunami, Nakata, Toda and Sugama2020; Mollén et al. Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018). In this profile, impurity ions comprise a relatively large portion of the total ion density. The effective charge
$a=0.62~\text{m}$ is considered. The magnetic field strength and its Fourier spectrum are represented in figure 1. The density and temperature profiles are shown in figures 2 and 3. One of the features which characterises an impurity hole plasma is the steepness of its ion temperature gradient. This profile has been used for several impurity hole studies (Nunami et al. Reference Nunami, Sugama, Velasco, Yokoyama, Sato, Nakata and Satake2016, Reference Nunami, Nakata, Sato, Toda, Yamaguchi, Sugama and Yokoyama2017, Reference Nunami, Satake, Fujita, Yamaguchi, Matsuoka, Sato, Toda and Sugama2019, Reference Nunami, Nakata, Toda and Sugama2020; Mollén et al. Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018). In this profile, impurity ions comprise a relatively large portion of the total ion density. The effective charge  $Z_{\text{eff}}=\sum _{I}n_{I}Z_{I}^{2}/n_{e}$ varies from 1.85 to 2.14 along the minor radius and its average value over the minor radius is 2.02. Although the trace approximation of the impurities is thus not appropriate, impurity contributions are treated as trace quantities in the evaluation of the ambipolar radial electric field in this study for the reason of computational cost. Since the ambipolar radial electric field is determined by the condition (2.32), the approximation can still be justified if the impurity contribution to the total ion particle flux turns out to be small enough compared with the main ion contribution. However, when the net impurity contribution is comparable with the main ion contribution, the ambipolar-
$Z_{\text{eff}}=\sum _{I}n_{I}Z_{I}^{2}/n_{e}$ varies from 1.85 to 2.14 along the minor radius and its average value over the minor radius is 2.02. Although the trace approximation of the impurities is thus not appropriate, impurity contributions are treated as trace quantities in the evaluation of the ambipolar radial electric field in this study for the reason of computational cost. Since the ambipolar radial electric field is determined by the condition (2.32), the approximation can still be justified if the impurity contribution to the total ion particle flux turns out to be small enough compared with the main ion contribution. However, when the net impurity contribution is comparable with the main ion contribution, the ambipolar- $E_{r}$ is to be modified from the ones obtained by the pure H calculations. Although the detail of how the presence of impurities affects the ambipolar condition depends on the case, positive impurity fluxes usually enhance the ambipolar-
$E_{r}$ is to be modified from the ones obtained by the pure H calculations. Although the detail of how the presence of impurities affects the ambipolar condition depends on the case, positive impurity fluxes usually enhance the ambipolar- $E_{r}$ in the negative direction.
$E_{r}$ in the negative direction.

Figure 1. The magnetic field strength on the flux surface at  $r/a=0.2$ (a), 0.5 (b) and 0.8 (c) and the major Fourier components of the magnetic field (d). The value of the cosine-
$r/a=0.2$ (a), 0.5 (b) and 0.8 (c) and the major Fourier components of the magnetic field (d). The value of the cosine- $(0,0)$ component in (d) is adjusted by subtracting 2.5 for visualisation purpose.
$(0,0)$ component in (d) is adjusted by subtracting 2.5 for visualisation purpose.  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and
$\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and  $N=10$.
$N=10$.

Figure 2. Radial profiles of densities.

Figure 3. Radial profiles of temperatures. All the ion species are assumed to be in thermal equilibrium with each other.

Figure 4. The normalised collisionality,  $\unicode[STIX]{x1D708}_{a}^{\ast }$, of
$\unicode[STIX]{x1D708}_{a}^{\ast }$, of  $\text{H}^{1+}$ (red),
$\text{H}^{1+}$ (red),  $\text{He}^{2+}$ (green),
$\text{He}^{2+}$ (green),  $\text{C}^{6+}$ (blue) and the lower bound of the Pfirsch–Schlülter regime (magenta).
$\text{C}^{6+}$ (blue) and the lower bound of the Pfirsch–Schlülter regime (magenta).

Figure 5. Radial profiles of the ambipolar radial electric fields for the ion-root case obtained by a DKES/PENTA local calculation (solid blue line) and the electron-root case obtained by a FORTEC-3D global calculation (red line), respectively. An electron-root found by the local calculation is also plotted (dashed blue line).
In figure 4, the normalised collisionality,  $\unicode[STIX]{x1D708}_{a}^{\ast }$, of each ion species is plotted. Here the quantity is defined by
$\unicode[STIX]{x1D708}_{a}^{\ast }$, of each ion species is plotted. Here the quantity is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D708}_{a}^{\ast }\equiv \mathop{\sum }_{b}\frac{R\unicode[STIX]{x1D708}_{ab}/\unicode[STIX]{x1D716}^{3/2}}{\unicode[STIX]{x1D704}v_{Ta}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{a}^{\ast }\equiv \mathop{\sum }_{b}\frac{R\unicode[STIX]{x1D708}_{ab}/\unicode[STIX]{x1D716}^{3/2}}{\unicode[STIX]{x1D704}v_{Ta}},\end{eqnarray}$$ with the collision frequency between species  $a$ and
$a$ and  $b$
$b$
 $$\begin{eqnarray}\unicode[STIX]{x1D708}_{ab}=\frac{Z_{a}^{2}Z_{b}^{2}\text{e}^{4}n_{b}\ln \unicode[STIX]{x1D6EC}}{3\unicode[STIX]{x03C0}^{3/2}\unicode[STIX]{x1D700}_{0}^{2}m_{a}^{2}v_{T_{a}}^{3}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{ab}=\frac{Z_{a}^{2}Z_{b}^{2}\text{e}^{4}n_{b}\ln \unicode[STIX]{x1D6EC}}{3\unicode[STIX]{x03C0}^{3/2}\unicode[STIX]{x1D700}_{0}^{2}m_{a}^{2}v_{T_{a}}^{3}},\end{eqnarray}$$ where  $\unicode[STIX]{x1D716}=r/R$ is the inverse aspect ratio,
$\unicode[STIX]{x1D716}=r/R$ is the inverse aspect ratio,  $v_{Ta}=\sqrt{2T_{a}/m_{a}}$ is the thermal velocity of species
$v_{Ta}=\sqrt{2T_{a}/m_{a}}$ is the thermal velocity of species  $a$,
$a$,  $\ln \unicode[STIX]{x1D6EC}$ is the Coulomb logarithm and
$\ln \unicode[STIX]{x1D6EC}$ is the Coulomb logarithm and  $\unicode[STIX]{x1D700}_{0}$ is the vacuum permittivity, respectively. The sum in (3.1) is taken over all the ion species including the species
$\unicode[STIX]{x1D700}_{0}$ is the vacuum permittivity, respectively. The sum in (3.1) is taken over all the ion species including the species  $a$ itself. In the figure, the magenta line represents the lower bound of the Pfirsch–Schlülter regime. The banana regime in the axisymmetric limit corresponds to
$a$ itself. In the figure, the magenta line represents the lower bound of the Pfirsch–Schlülter regime. The banana regime in the axisymmetric limit corresponds to
 $$\begin{eqnarray}\unicode[STIX]{x1D708}_{a}^{\ast }<1\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{a}^{\ast }<1\end{eqnarray}$$ and the intermediate region between  $\unicode[STIX]{x1D708}_{a}^{\ast }=1$ and the magenta line to the plateau regime. In the present case,
$\unicode[STIX]{x1D708}_{a}^{\ast }=1$ and the magenta line to the plateau regime. In the present case,  $\text{H}^{1+}$ and
$\text{H}^{1+}$ and  $\text{He}^{2+}$ are in the
$\text{He}^{2+}$ are in the  $1/\unicode[STIX]{x1D708}$ or
$1/\unicode[STIX]{x1D708}$ or  $\sqrt{\unicode[STIX]{x1D708}}\sim \unicode[STIX]{x1D708}$ regime.
$\sqrt{\unicode[STIX]{x1D708}}\sim \unicode[STIX]{x1D708}$ regime.  $\text{C}^{6+}$ is not so highly collisional to be in the Pfirsch–Schlülter regime and belongs in the plateau regime.
$\text{C}^{6+}$ is not so highly collisional to be in the Pfirsch–Schlülter regime and belongs in the plateau regime.
3.1 Ambipolar radial electric field
The ambipolar condition has been determined by two different (sets of) numerical codes. One is a set of local codes DKES/PENTA and the other is the global code FORTEC-3D. Both FORTEC-3D and DKES/PENTA determined the ambipolar condition by assuming a pure H plasma. Both solutions are represented in figure 5. The red line corresponds to the global solution and the solid blue line to the local solution. As can be seen, those solutions are completely different. The sign of the global solution is positive. In other words, the global calculation indicates that the plasma is in electron-root, not in ion-root. It is not necessarily surprising that the global calculation yields different solutions from local ones. As mentioned in the introduction, it is known that the magnetic drift (even only the tangential component of it) can significantly change the dependence of neoclassical transport on  $E_{r}$ (Matsuoka et al. Reference Matsuoka, Satake, Kanno and Sugama2015; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017; Velasco et al. Reference Velasco, Calvo, Parra and García-Regana2020). In Velasco et al. (Reference Velasco, Calvo, Satake, Alonso, Nunami, Yokoyama, Sato, Estrada, Fontdecaba and Liniers2017), the ambipolar conditions for such impurity hole plasmas are investigated based on the collisionality and it is argued that, even if an impurity hole plasma is in ion-root, the plasma profiles are very close to the condition for
$E_{r}$ (Matsuoka et al. Reference Matsuoka, Satake, Kanno and Sugama2015; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017; Velasco et al. Reference Velasco, Calvo, Parra and García-Regana2020). In Velasco et al. (Reference Velasco, Calvo, Satake, Alonso, Nunami, Yokoyama, Sato, Estrada, Fontdecaba and Liniers2017), the ambipolar conditions for such impurity hole plasmas are investigated based on the collisionality and it is argued that, even if an impurity hole plasma is in ion-root, the plasma profiles are very close to the condition for  $E_{r}$ to become positive. In fact, as represented by the dashed line in figure 5, a positive solution is found by the local codes as well. The solution is stable and physically possible. Its existence suggests that the gap between the local and global solutions is not as large as it appears. Yet, we adopt the ion-root (represented by the solid blue line) as our ‘local solution’ since similar solutions are used in previous local studies. We thus investigate the difference of
$E_{r}$ to become positive. In fact, as represented by the dashed line in figure 5, a positive solution is found by the local codes as well. The solution is stable and physically possible. Its existence suggests that the gap between the local and global solutions is not as large as it appears. Yet, we adopt the ion-root (represented by the solid blue line) as our ‘local solution’ since similar solutions are used in previous local studies. We thus investigate the difference of  $\unicode[STIX]{x1D6F7}_{1}$ structure and its impact on impurity transport between the cases, each with the local and the global solutions, respectively.
$\unicode[STIX]{x1D6F7}_{1}$ structure and its impact on impurity transport between the cases, each with the local and the global solutions, respectively.
However, whether the sign of the ambipolar- $E_{r}$ is positive or negative is the most crucial issue in the impurity hole study. If the sign of ambipolar-
$E_{r}$ is positive or negative is the most crucial issue in the impurity hole study. If the sign of ambipolar- $E_{r}$ turns out to be positive in real impurity hole plasmas, the scenario is completely changed and the impurity hole phenomenon could be explained by standard neoclassical theory arguments. Nunami et al. (Reference Nunami, Satake, Fujita, Yamaguchi, Matsuoka, Sato, Toda and Sugama2019, Reference Nunami, Nakata, Toda and Sugama2020) have intensively investigated the condition for both solutions by considering the contributions of turbulence and external torque. The result of the study also seems to support the possibility of the positive solution.
$E_{r}$ turns out to be positive in real impurity hole plasmas, the scenario is completely changed and the impurity hole phenomenon could be explained by standard neoclassical theory arguments. Nunami et al. (Reference Nunami, Satake, Fujita, Yamaguchi, Matsuoka, Sato, Toda and Sugama2019, Reference Nunami, Nakata, Toda and Sugama2020) have intensively investigated the condition for both solutions by considering the contributions of turbulence and external torque. The result of the study also seems to support the possibility of the positive solution.
There is measurement data on the ambipolar- $E_{r}$ profile in an impurity hole plasma and it indicates that the sign of the ambipolar-
$E_{r}$ profile in an impurity hole plasma and it indicates that the sign of the ambipolar- $E_{r}$ near the magnetic axis is indeed negative (Ido et al. Reference Ido, Shimizu, Nishiura, Nagaoka, Yokoyama, Ida, Yoshinuma, Toi, Itoh and Nakano2010). However, it also shows that the sign of
$E_{r}$ near the magnetic axis is indeed negative (Ido et al. Reference Ido, Shimizu, Nishiura, Nagaoka, Yokoyama, Ida, Yoshinuma, Toi, Itoh and Nakano2010). However, it also shows that the sign of  $E_{r}$ transits to positive at some outer radius. Impurity hole has been observed in plasmas with several different
$E_{r}$ transits to positive at some outer radius. Impurity hole has been observed in plasmas with several different  $n$–
$n$– $T$ profiles (Nakamura et al. Reference Nakamura, Tamura, Yoshinuma, Suzuki, Yoshimura, Kobayashi, Yokoyama, Nunami, Nakata and Nagaoka2017), but the measurement data on ambipolar-
$T$ profiles (Nakamura et al. Reference Nakamura, Tamura, Yoshinuma, Suzuki, Yoshimura, Kobayashi, Yokoyama, Nunami, Nakata and Nagaoka2017), but the measurement data on ambipolar- $E_{r}$ has been reported only for the case mentioned above. The
$E_{r}$ has been reported only for the case mentioned above. The  $n$–
$n$– $T$ profile used in this study is close to but not the same as that in the measured case. Thus, our global solution for the ambipolar condition does not necessarily contradict the existing experimental data.
$T$ profile used in this study is close to but not the same as that in the measured case. Thus, our global solution for the ambipolar condition does not necessarily contradict the existing experimental data.
Since the following concerns remain, however, we cannot simply accept the electron-root as the correct solution yet. First, the positive solution is, as mentioned above, obtained by a single ion-species calculation and the contribution of impurities to the ambipolar condition is not considered. Second, the  $\unicode[STIX]{x1D6F7}_{1}$ effect is not included in the ambipolar condition as well. In contrast, negative solutions similar to our local solution have been obtained by self-consistent calculations for multi-ion-species plasmas including
$\unicode[STIX]{x1D6F7}_{1}$ effect is not included in the ambipolar condition as well. In contrast, negative solutions similar to our local solution have been obtained by self-consistent calculations for multi-ion-species plasmas including  $\unicode[STIX]{x1D6F7}_{1}$ (Mollén et al. Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018). How
$\unicode[STIX]{x1D6F7}_{1}$ (Mollén et al. Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018). How  $\unicode[STIX]{x1D6F7}_{1}$ affects the radial particle fluxes in our electron-root case will be examined below.
$\unicode[STIX]{x1D6F7}_{1}$ affects the radial particle fluxes in our electron-root case will be examined below.
In any case, the primary purpose of this study is not to examine the ambipolar condition, but to apply the newly extended code to impurity transport in a real helical configuration. Thus, we hold both possibilities here and investigate two cases corresponding to each solution, respectively. Both cases have the same background parameters (such as the magnetic field configuration, densities and temperatures) except for the radial electric field.
4 Simulation results
In this section, calculation results of the cases with and without  $\unicode[STIX]{x1D6F7}_{1}$ for each ion-root case and electron-root case are shown and compared to see the impact of
$\unicode[STIX]{x1D6F7}_{1}$ for each ion-root case and electron-root case are shown and compared to see the impact of  $\unicode[STIX]{x1D6F7}_{1}$ on the radial particle transport. The result of the ion-root case, which is mainly focused on, is shown first and the result of the electron-root case follows.
$\unicode[STIX]{x1D6F7}_{1}$ on the radial particle transport. The result of the ion-root case, which is mainly focused on, is shown first and the result of the electron-root case follows.
4.1 Ion-root case
In figure 6, the radial profiles of particle fluxes are compared between the cases with and without  $\unicode[STIX]{x1D6F7}_{1}$. The red lines represent the fluxes for the case without
$\unicode[STIX]{x1D6F7}_{1}$. The red lines represent the fluxes for the case without  $\unicode[STIX]{x1D6F7}_{1}$ and the green lines for the case with
$\unicode[STIX]{x1D6F7}_{1}$ and the green lines for the case with  $\unicode[STIX]{x1D6F7}_{1}$. Before discussing the impact of
$\unicode[STIX]{x1D6F7}_{1}$. Before discussing the impact of  $\unicode[STIX]{x1D6F7}_{1}$, it is worth commenting on the result without
$\unicode[STIX]{x1D6F7}_{1}$, it is worth commenting on the result without  $\unicode[STIX]{x1D6F7}_{1}$. The
$\unicode[STIX]{x1D6F7}_{1}$. The  $\text{H}^{1+}$ flux obtained by our global calculation is smaller by one order than that obtained by local calculations for similar plasmas (Mollén et al. Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018). On the other hand, the values of the
$\text{H}^{1+}$ flux obtained by our global calculation is smaller by one order than that obtained by local calculations for similar plasmas (Mollén et al. Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018). On the other hand, the values of the  $\text{He}^{2+}$ and
$\text{He}^{2+}$ and  $\text{C}^{6+}$ fluxes in our global result are of the same order as those in the local study. In this ion-root case, the plasma profile belongs in a parameter region where the discrepancy in the
$\text{C}^{6+}$ fluxes in our global result are of the same order as those in the local study. In this ion-root case, the plasma profile belongs in a parameter region where the discrepancy in the  $\text{H}^{1+}$ fluxes between global and local (neglecting the entire
$\text{H}^{1+}$ fluxes between global and local (neglecting the entire  $\boldsymbol{v}_{m}$) calculations becomes the largest (Matsuoka et al. Reference Matsuoka, Satake, Kanno and Sugama2015; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017). This significant difference in the main ion flux directly affects the ambipolar condition. Thus, it is natural that the solutions of the ambipolar condition turn out to be qualitatively different between the global and the local simulations and an ion-root is not found by the global simulation.
$\boldsymbol{v}_{m}$) calculations becomes the largest (Matsuoka et al. Reference Matsuoka, Satake, Kanno and Sugama2015; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017). This significant difference in the main ion flux directly affects the ambipolar condition. Thus, it is natural that the solutions of the ambipolar condition turn out to be qualitatively different between the global and the local simulations and an ion-root is not found by the global simulation.

Figure 6. Radial particle fluxes of  $\text{H}^{1+}$ (a),
$\text{H}^{1+}$ (a),  $\text{He}^{2+}$ (b) and
$\text{He}^{2+}$ (b) and  $\text{C}^{6+}$ (c) for the ion-root case without (red) and with (green)
$\text{C}^{6+}$ (c) for the ion-root case without (red) and with (green)  $\unicode[STIX]{x1D6F7}_{1}$, respectively.
$\unicode[STIX]{x1D6F7}_{1}$, respectively.

Figure 7. From left, structures of  $\unicode[STIX]{x1D6F7}_{1}$,
$\unicode[STIX]{x1D6F7}_{1}$,  $n_{H.1}$,
$n_{H.1}$,  $n_{He,1}$ and
$n_{He,1}$ and  $n_{C,1}$ on the flux surface at
$n_{C,1}$ on the flux surface at  $r/a=0.2$ for the ion-root case. Figures (a–d) represent the results without
$r/a=0.2$ for the ion-root case. Figures (a–d) represent the results without  $\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with
$\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with  $\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.
$\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and
$\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and  $N=10$.
$N=10$.
Now, let us examine the  $\unicode[STIX]{x1D6F7}_{1}$ effect on the particle fluxes. In Mollén et al. (Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018), it is shown that the
$\unicode[STIX]{x1D6F7}_{1}$ effect on the particle fluxes. In Mollén et al. (Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018), it is shown that the  $\text{C}^{6+}$ flux in ion-root plasmas is inwardly enhanced by
$\text{C}^{6+}$ flux in ion-root plasmas is inwardly enhanced by  $\unicode[STIX]{x1D6F7}_{1}$ while the
$\unicode[STIX]{x1D6F7}_{1}$ while the  $\text{H}^{1+}$ and the
$\text{H}^{1+}$ and the  $\text{He}^{2+}$ fluxes are outwardly driven. A similar result has also been obtained for the
$\text{He}^{2+}$ fluxes are outwardly driven. A similar result has also been obtained for the  $\text{C}^{6+}$ flux in Velasco et al. (Reference Velasco, Calvo, García-Regaña, Parra, Satake and Alonso2018). Figure 6 shows that our global result for the
$\text{C}^{6+}$ flux in Velasco et al. (Reference Velasco, Calvo, García-Regaña, Parra, Satake and Alonso2018). Figure 6 shows that our global result for the  $\text{C}^{6+}$ flux is qualitatively analogous to those local results. That is, the
$\text{C}^{6+}$ flux is qualitatively analogous to those local results. That is, the  $\text{C}^{6+}$ flux is driven further inwardly, not outwardly. This means that
$\text{C}^{6+}$ flux is driven further inwardly, not outwardly. This means that  $\unicode[STIX]{x1D6F7}_{1}$ contributes to the impurity accumulation, rather than mitigate it. On the other hand, positive enhancement is seen in the
$\unicode[STIX]{x1D6F7}_{1}$ contributes to the impurity accumulation, rather than mitigate it. On the other hand, positive enhancement is seen in the  $\text{H}^{1+}$ and
$\text{H}^{1+}$ and  $\text{He}^{2+}$ fluxes, especially at outer radii
$\text{He}^{2+}$ fluxes, especially at outer radii  $r/a>0.8$.
$r/a>0.8$.
Let us look into the structures of  $\unicode[STIX]{x1D6F7}_{1}$ and density variation of each ion species to see which results in the modification of the particle fluxes in figure 6. In figure 7, the phase structures of the normalised
$\unicode[STIX]{x1D6F7}_{1}$ and density variation of each ion species to see which results in the modification of the particle fluxes in figure 6. In figure 7, the phase structures of the normalised  $\unicode[STIX]{x1D6F7}_{1}$ and the density variation of each ion species on the flux surface at
$\unicode[STIX]{x1D6F7}_{1}$ and the density variation of each ion species on the flux surface at  $r/a=0.2$ are shown. Figure 7(a–d) represent the results without
$r/a=0.2$ are shown. Figure 7(a–d) represent the results without  $\unicode[STIX]{x1D6F7}_{1}$ and figure 7(e–h) the result with
$\unicode[STIX]{x1D6F7}_{1}$ and figure 7(e–h) the result with  $\unicode[STIX]{x1D6F7}_{1}$. Here ‘
$\unicode[STIX]{x1D6F7}_{1}$. Here ‘ $\unicode[STIX]{x1D6F7}_{1}$ for the case without
$\unicode[STIX]{x1D6F7}_{1}$ for the case without  $\unicode[STIX]{x1D6F7}_{1}$’ means
$\unicode[STIX]{x1D6F7}_{1}$’ means  $\unicode[STIX]{x1D6F7}_{1}$ constructed from the solutions of the drift-kinetic equation neglecting
$\unicode[STIX]{x1D6F7}_{1}$ constructed from the solutions of the drift-kinetic equation neglecting  $\unicode[STIX]{x1D6F7}_{1}$ through (2.34). When the difference in
$\unicode[STIX]{x1D6F7}_{1}$ through (2.34). When the difference in  $\unicode[STIX]{x1D6F7}_{1}$ between the cases with and without
$\unicode[STIX]{x1D6F7}_{1}$ between the cases with and without  $\unicode[STIX]{x1D6F7}_{1}$ in this sense becomes significant, the necessity of the self-consistent calculation is indicated. Figures 8 and 9 make the same comparison at
$\unicode[STIX]{x1D6F7}_{1}$ in this sense becomes significant, the necessity of the self-consistent calculation is indicated. Figures 8 and 9 make the same comparison at  $r/a=0.5$ and
$r/a=0.5$ and  $r/a=0.8$, respectively. The amplitude of
$r/a=0.8$, respectively. The amplitude of  $\unicode[STIX]{x1D6F7}_{1}$ is smaller than earlier local results overall and the factor
$\unicode[STIX]{x1D6F7}_{1}$ is smaller than earlier local results overall and the factor  $Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}$ is at most the order of
$Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}$ is at most the order of  $10^{-1}$ even for
$10^{-1}$ even for  $\text{C}^{6+}$ in this case (for example,
$\text{C}^{6+}$ in this case (for example,  $e\unicode[STIX]{x1D6F7}_{1}/T_{i}=1.0\times 10^{-2}$ at
$e\unicode[STIX]{x1D6F7}_{1}/T_{i}=1.0\times 10^{-2}$ at  $r/a=0.5$ roughly amounts to 30 V of
$r/a=0.5$ roughly amounts to 30 V of  $\unicode[STIX]{x1D6F7}_{1}$ in this case). The comparison of the density structures above implies that
$\unicode[STIX]{x1D6F7}_{1}$ in this case). The comparison of the density structures above implies that  $\unicode[STIX]{x1D6F7}_{1}$ is too small to strongly modify the spectrum compositions of the ion species over the flux surface.
$\unicode[STIX]{x1D6F7}_{1}$ is too small to strongly modify the spectrum compositions of the ion species over the flux surface.

Figure 8. From left, structures of  $\unicode[STIX]{x1D6F7}_{1}$,
$\unicode[STIX]{x1D6F7}_{1}$,  $n_{H.1}$,
$n_{H.1}$,  $n_{He,1}$ and
$n_{He,1}$ and  $n_{C,1}$ on the flux surface at
$n_{C,1}$ on the flux surface at  $r/a=0.5$ for the ion-root case. Figures (a–d) represent the results without
$r/a=0.5$ for the ion-root case. Figures (a–d) represent the results without  $\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with
$\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with  $\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.
$\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and
$\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and  $N=10$.
$N=10$.

Figure 9. From left, structures of  $\unicode[STIX]{x1D6F7}_{1}$,
$\unicode[STIX]{x1D6F7}_{1}$,  $n_{H.1}$,
$n_{H.1}$,  $n_{He,1}$ and
$n_{He,1}$ and  $n_{C,1}$ on the flux surface at
$n_{C,1}$ on the flux surface at  $r/a=0.8$ for the ion-root case. Figures (a–d) represent the results without
$r/a=0.8$ for the ion-root case. Figures (a–d) represent the results without  $\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with
$\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with  $\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.
$\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and
$\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and  $N=10$.
$N=10$.
This can also be seen in figure 10, which represents the Fourier spectra of density variations of the ion species for the cases with and without  $\unicode[STIX]{x1D6F7}_{1}$. The density variations are expanded in real trigonometric series. Only leading modes are plotted and reddish colours are assigned to cosine modes and bluish colours to sine modes. Although the Fourier spectra are evaluated on 50 flux surfaces in FORTEC-3D, only the values at
$\unicode[STIX]{x1D6F7}_{1}$. The density variations are expanded in real trigonometric series. Only leading modes are plotted and reddish colours are assigned to cosine modes and bluish colours to sine modes. Although the Fourier spectra are evaluated on 50 flux surfaces in FORTEC-3D, only the values at  $r/a=0.0,0.2,\ldots ,1.0$ are plotted for visualisation purpose. The mode compositions are not largely affected by the inclusion of
$r/a=0.0,0.2,\ldots ,1.0$ are plotted for visualisation purpose. The mode compositions are not largely affected by the inclusion of  $\unicode[STIX]{x1D6F7}_{1}$. One point worth noting is that the phase structure of
$\unicode[STIX]{x1D6F7}_{1}$. One point worth noting is that the phase structure of  $\text{C}^{6+}$ is qualitatively different from those of the other two species.
$\text{C}^{6+}$ is qualitatively different from those of the other two species.  $\text{H}^{1+}$ or
$\text{H}^{1+}$ or  $\text{He}^{2+}$ mainly consists of stellarator symmetric components, which are preserved under the transformation
$\text{He}^{2+}$ mainly consists of stellarator symmetric components, which are preserved under the transformation  $(\unicode[STIX]{x1D703},\unicode[STIX]{x1D701})\rightarrow (-\unicode[STIX]{x1D703},-\unicode[STIX]{x1D701})$, as expected for the ions in the
$(\unicode[STIX]{x1D703},\unicode[STIX]{x1D701})\rightarrow (-\unicode[STIX]{x1D703},-\unicode[STIX]{x1D701})$, as expected for the ions in the  $\sqrt{\unicode[STIX]{x1D708}}$ regime (Calvo et al. Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018b). On the other hand, the main components in the density spectrum of
$\sqrt{\unicode[STIX]{x1D708}}$ regime (Calvo et al. Reference Calvo, Velasco, Parra, Alonso and García-Regaña2018b). On the other hand, the main components in the density spectrum of  $\text{C}^{6+}$, which is in the plateau regime, change their signs under the same transformation.
$\text{C}^{6+}$, which is in the plateau regime, change their signs under the same transformation.

Figure 10. Fourier spectra of  $n_{H,1}$ (a,d),
$n_{H,1}$ (a,d),  $n_{He,1}$ (b,e) and
$n_{He,1}$ (b,e) and  $n_{C,1}$ (c,f) for the ion-root case. Figures (a–c) represent the results without
$n_{C,1}$ (c,f) for the ion-root case. Figures (a–c) represent the results without  $\unicode[STIX]{x1D6F7}_{1}$ and (d–f) the results with
$\unicode[STIX]{x1D6F7}_{1}$ and (d–f) the results with  $\unicode[STIX]{x1D6F7}_{1}$.
$\unicode[STIX]{x1D6F7}_{1}$.

Figure 11. Fourier spectra of  $\bar{v}_{E1}$ (a) and
$\bar{v}_{E1}$ (a) and  $\unicode[STIX]{x1D6F7}_{1}$ (b) for the ion-root case.
$\unicode[STIX]{x1D6F7}_{1}$ (b) for the ion-root case.
The spectrum of  $\bar{v}_{E1}$ is plotted in figure 11 as well as the spectrum of
$\bar{v}_{E1}$ is plotted in figure 11 as well as the spectrum of  $\unicode[STIX]{x1D6F7}_{1}$ itself. For
$\unicode[STIX]{x1D6F7}_{1}$ itself. For  $\text{H}^{1+}$ and
$\text{H}^{1+}$ and  $\text{He}^{2+}$, following (2.39), most of the cosine modes in their density spectra couple with the same modes in the
$\text{He}^{2+}$, following (2.39), most of the cosine modes in their density spectra couple with the same modes in the  $\bar{v}_{E1}$ spectrum having the same signs. These effective couplings result in the outward enhancement of the
$\bar{v}_{E1}$ spectrum having the same signs. These effective couplings result in the outward enhancement of the  $\text{He}^{2+}$ flux and
$\text{He}^{2+}$ flux and  $\text{H}^{1+}$ flux at
$\text{H}^{1+}$ flux at  $r/a>0.8$. On the other hand, the sine-
$r/a>0.8$. On the other hand, the sine- $(1,0)$ mode dominates in the
$(1,0)$ mode dominates in the  $\text{C}^{6+}$ spectrum. The value of this mode peaks around
$\text{C}^{6+}$ spectrum. The value of this mode peaks around  $r/a=0.6$ and the mode couples with
$r/a=0.6$ and the mode couples with  $\bar{v}_{E1}$ having the opposite sign and results in the inward enhancement of the particle flux.
$\bar{v}_{E1}$ having the opposite sign and results in the inward enhancement of the particle flux.
In figure 12(a), the radial  $\text{C}^{6+}$ flux driven by
$\text{C}^{6+}$ flux driven by  $v_{E1}$ is plotted as well as the total
$v_{E1}$ is plotted as well as the total  $\text{C}^{6+}$ flux for the case with
$\text{C}^{6+}$ flux for the case with  $\unicode[STIX]{x1D6F7}_{1}$. The red line represents the total
$\unicode[STIX]{x1D6F7}_{1}$. The red line represents the total  $\text{C}^{6+}$ flux calculated by the integral (1.1). The green line represents the
$\text{C}^{6+}$ flux calculated by the integral (1.1). The green line represents the  $v_{E1}$-driven part of the
$v_{E1}$-driven part of the  $\text{C}^{6+}$ flux calculated by the integral (2.35). The blue line is also the
$\text{C}^{6+}$ flux calculated by the integral (2.35). The blue line is also the  $v_{E1}$-driven part of the
$v_{E1}$-driven part of the  $\text{C}^{6+}$ flux, but it is obtained by the sum of the Fourier coefficient products in the form of (2.39). The impact of
$\text{C}^{6+}$ flux, but it is obtained by the sum of the Fourier coefficient products in the form of (2.39). The impact of  $\unicode[STIX]{x1D6F7}_{1}$ on the
$\unicode[STIX]{x1D6F7}_{1}$ on the  $v_{m}$-driven flux is also shown in figure 12(b). The green line represents the
$v_{m}$-driven flux is also shown in figure 12(b). The green line represents the  $\text{C}^{6+}$ flux driven by the magnetic drift for the case without
$\text{C}^{6+}$ flux driven by the magnetic drift for the case without  $\unicode[STIX]{x1D6F7}_{1}$, i.e. the total
$\unicode[STIX]{x1D6F7}_{1}$, i.e. the total  $\text{C}^{6+}$ for the case without
$\text{C}^{6+}$ for the case without  $\unicode[STIX]{x1D6F7}_{1}$. The blue line represents the
$\unicode[STIX]{x1D6F7}_{1}$. The blue line represents the  $\text{C}^{6+}$ flux driven by
$\text{C}^{6+}$ flux driven by  $v_{m}$ for the case with
$v_{m}$ for the case with  $\unicode[STIX]{x1D6F7}_{1}$. It can been seen that the
$\unicode[STIX]{x1D6F7}_{1}$. It can been seen that the  $v_{m}$-driven flux is also enhanced by the inclusion of
$v_{m}$-driven flux is also enhanced by the inclusion of  $\unicode[STIX]{x1D6F7}_{1}$. This is because, as shown in figure 10,
$\unicode[STIX]{x1D6F7}_{1}$. This is because, as shown in figure 10,  $\unicode[STIX]{x1D6F7}_{1}$ amplifies the sine-
$\unicode[STIX]{x1D6F7}_{1}$ amplifies the sine- $(1,0)$ mode in the
$(1,0)$ mode in the  $\text{C}^{6+}$ spectrum and hence strengthens the opposite-sign couplings between the magnetic drift and the
$\text{C}^{6+}$ spectrum and hence strengthens the opposite-sign couplings between the magnetic drift and the  $\text{C}^{6+}$ distribution function as well. Here the sine-
$\text{C}^{6+}$ distribution function as well. Here the sine- $(1,0)$ component of
$(1,0)$ component of  $\boldsymbol{v}_{m}$ represents the grad-
$\boldsymbol{v}_{m}$ represents the grad- $B$ drift by the toroidicity of the magnetic field. Therefore, at least in this case, the presence of
$B$ drift by the toroidicity of the magnetic field. Therefore, at least in this case, the presence of  $\unicode[STIX]{x1D6F7}_{1}$ is unfavourable for impurity accumulation avoidance.
$\unicode[STIX]{x1D6F7}_{1}$ is unfavourable for impurity accumulation avoidance.

Figure 12. (a) The total radial  $\text{C}^{6+}$ flux,
$\text{C}^{6+}$ flux,  $\unicode[STIX]{x1D6E4}_{C}$, for the case with
$\unicode[STIX]{x1D6E4}_{C}$, for the case with  $\unicode[STIX]{x1D6F7}_{1}$ (red), the
$\unicode[STIX]{x1D6F7}_{1}$ (red), the  $v_{E1}$-driven part of
$v_{E1}$-driven part of  $\unicode[STIX]{x1D6E4}_{C}$ calculated by the integral (green) and the
$\unicode[STIX]{x1D6E4}_{C}$ calculated by the integral (green) and the  $v_{E1}$-driven part calculated by the products of the Fourier coefficients (blue). (b) The total radial
$v_{E1}$-driven part calculated by the products of the Fourier coefficients (blue). (b) The total radial  $\text{C}^{6+}$ flux,
$\text{C}^{6+}$ flux,  $\unicode[STIX]{x1D6E4}_{C}$, for the case with
$\unicode[STIX]{x1D6E4}_{C}$, for the case with  $\unicode[STIX]{x1D6F7}_{1}$ (red), the total
$\unicode[STIX]{x1D6F7}_{1}$ (red), the total  $\text{C}^{6+}$ flux (driven only by
$\text{C}^{6+}$ flux (driven only by  $\boldsymbol{v}_{m}$) for the case without
$\boldsymbol{v}_{m}$) for the case without  $\unicode[STIX]{x1D6F7}_{1}$ (green) and the
$\unicode[STIX]{x1D6F7}_{1}$ (green) and the  $v_{m}$-driven part for the case with
$v_{m}$-driven part for the case with  $\unicode[STIX]{x1D6F7}_{1}$ (blue).
$\unicode[STIX]{x1D6F7}_{1}$ (blue).

Figure 13. Radial particle fluxes of  $\text{H}^{1+}$ (a),
$\text{H}^{1+}$ (a),  $\text{He}^{2+}$ (b) and
$\text{He}^{2+}$ (b) and  $\text{C}^{6+}$ (c) for the electron-root case without (red) and with (green)
$\text{C}^{6+}$ (c) for the electron-root case without (red) and with (green)  $\unicode[STIX]{x1D6F7}_{1}$, respectively.
$\unicode[STIX]{x1D6F7}_{1}$, respectively.

Figure 14. From left, structures of  $\unicode[STIX]{x1D6F7}_{1}$,
$\unicode[STIX]{x1D6F7}_{1}$,  $n_{H,1}$,
$n_{H,1}$,  $n_{He,1}$ and
$n_{He,1}$ and  $n_{C,1}$ on the flux surface at
$n_{C,1}$ on the flux surface at $r/a=0.2$ for the electron-root case. Figures (a–d) represent the results without
$r/a=0.2$ for the electron-root case. Figures (a–d) represent the results without  $\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with
$\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with  $\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.
$\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and
$\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and  $N=10$.
$N=10$.

Figure 15. From left, structures of  $\unicode[STIX]{x1D6F7}_{1}$,
$\unicode[STIX]{x1D6F7}_{1}$,  $n_{H,1}$,
$n_{H,1}$,  $n_{He,1}$ and
$n_{He,1}$ and  $n_{C,1}$ on the flux surface at
$n_{C,1}$ on the flux surface at  $r/a=0.8$ for the electron-root case. Figures (a–d) represent the results without
$r/a=0.8$ for the electron-root case. Figures (a–d) represent the results without  $\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with
$\unicode[STIX]{x1D6F7}_{1}$ and (e–h) the results with  $\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.
$\unicode[STIX]{x1D6F7}_{1}$. Note that the scale of the colour contour is different for each figure.  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and
$\unicode[STIX]{x1D701}$ are poloidal and toroidal angle coordinates in the Boozer coordinate system, respectively, and  $N=10$.
$N=10$.
4.2 Electron-root case
In figure 13, the radial particle fluxes with and without  $\unicode[STIX]{x1D6F7}_{1}$ for the electron-root case are compared. Regardless of the species, the radial particle flux is outwardly enhanced by
$\unicode[STIX]{x1D6F7}_{1}$ for the electron-root case are compared. Regardless of the species, the radial particle flux is outwardly enhanced by  $\unicode[STIX]{x1D6F7}_{1}$. The enhancement is largest for
$\unicode[STIX]{x1D6F7}_{1}$. The enhancement is largest for  $\text{C}^{6+}$ and the existence of an outward convection is indicated. However, the enhancements of the
$\text{C}^{6+}$ and the existence of an outward convection is indicated. However, the enhancements of the  $\text{H}^{1+}$ and
$\text{H}^{1+}$ and  $\text{He}^{2+}$ fluxes are not negligible as well. This result implies that the impact of
$\text{He}^{2+}$ fluxes are not negligible as well. This result implies that the impact of  $\unicode[STIX]{x1D6F7}_{1}$ is too large to be ignored in the calculation of the ambipolar condition. Thus, it is expected that an electron-root slightly different from that used in this work would be found by calculation including
$\unicode[STIX]{x1D6F7}_{1}$ is too large to be ignored in the calculation of the ambipolar condition. Thus, it is expected that an electron-root slightly different from that used in this work would be found by calculation including  $\unicode[STIX]{x1D6F7}_{1}$.
$\unicode[STIX]{x1D6F7}_{1}$.
The reason for the strong outward enhancement can be seen in the phase structures of density variations. The spatial structures of  $\unicode[STIX]{x1D6F7}_{1}$ and
$\unicode[STIX]{x1D6F7}_{1}$ and  $n_{I1}$ at
$n_{I1}$ at  $r/a=0.2$ and
$r/a=0.2$ and  $r/a=0.8$ for this case are illustrated in figures 14 and 15, respectively. The amplitude of
$r/a=0.8$ for this case are illustrated in figures 14 and 15, respectively. The amplitude of  $n_{I1}$ and hence of
$n_{I1}$ and hence of  $\unicode[STIX]{x1D6F7}_{1}$ are at the same level as those in the ion-root case. Also, the phase structures of
$\unicode[STIX]{x1D6F7}_{1}$ are at the same level as those in the ion-root case. Also, the phase structures of  $\unicode[STIX]{x1D6F7}_{1}$,
$\unicode[STIX]{x1D6F7}_{1}$,  $\text{H}^{1+}$ and
$\text{H}^{1+}$ and  $\text{He}^{2+}$ seemingly look similar between the ion-root and the electron-root cases. However, the
$\text{He}^{2+}$ seemingly look similar between the ion-root and the electron-root cases. However, the  $\text{C}^{6+}$ density structure is distinctively different between the two cases. By comparing figures 9(d,h) and 15(d,h), it can be seen that the
$\text{C}^{6+}$ density structure is distinctively different between the two cases. By comparing figures 9(d,h) and 15(d,h), it can be seen that the  $\text{C}^{6+}$ density phase is inverted in the
$\text{C}^{6+}$ density phase is inverted in the  $\unicode[STIX]{x1D703}$-direction.
$\unicode[STIX]{x1D703}$-direction.
This can also be seen in terms of Fourier spectra of the density variations and  $\bar{v}_{E}$ shown in figures 16 and 17, respectively. As shown in figure 16, the signs of the sine-
$\bar{v}_{E}$ shown in figures 16 and 17, respectively. As shown in figure 16, the signs of the sine- $(1,0)$ modes in the density spectra are inverted from those in the ion-root case. This is true not only for
$(1,0)$ modes in the density spectra are inverted from those in the ion-root case. This is true not only for  $\text{C}^{6+}$, but also for
$\text{C}^{6+}$, but also for  $\text{H}^{1+}$ and
$\text{H}^{1+}$ and  $\text{He}^{2+}$. Further, this mode is amplified by the inclusion of
$\text{He}^{2+}$. Further, this mode is amplified by the inclusion of  $\unicode[STIX]{x1D6F7}_{1}$. Figure 17 shows that the sine-
$\unicode[STIX]{x1D6F7}_{1}$. Figure 17 shows that the sine- $(1,0)$ mode in the
$(1,0)$ mode in the  $\hat{v}_{E}$ spectrum, which comes from the cosine-
$\hat{v}_{E}$ spectrum, which comes from the cosine- $(1,0)$ mode in the
$(1,0)$ mode in the  $\unicode[STIX]{x1D6F7}_{1}$ spectrum, is negative and is a major component for this case as well. Thus, the inversion of the sine-
$\unicode[STIX]{x1D6F7}_{1}$ spectrum, is negative and is a major component for this case as well. Thus, the inversion of the sine- $(1,0)$ modes in the density spectra leads to strong same-sign couplings and contributes to the outward radial particle fluxes. This sign inversion is not a consequence of the inclusion of
$(1,0)$ modes in the density spectra leads to strong same-sign couplings and contributes to the outward radial particle fluxes. This sign inversion is not a consequence of the inclusion of  $\unicode[STIX]{x1D6F7}_{1}$ but, rather, it seems to be a consequence of the presence of the positive radial electric field.
$\unicode[STIX]{x1D6F7}_{1}$ but, rather, it seems to be a consequence of the presence of the positive radial electric field.

Figure 16. Fourier spectra of  $n_{H,1}$ (a,d),
$n_{H,1}$ (a,d),  $n_{He,1}$ (b,e) and
$n_{He,1}$ (b,e) and  $n_{C,1}$ (c,f) for the electron-root case. Figures (a–c) represent the results without
$n_{C,1}$ (c,f) for the electron-root case. Figures (a–c) represent the results without  $\unicode[STIX]{x1D6F7}_{1}$ and (d–f) the results with
$\unicode[STIX]{x1D6F7}_{1}$ and (d–f) the results with  $\unicode[STIX]{x1D6F7}_{1}$.
$\unicode[STIX]{x1D6F7}_{1}$.

Figure 17. Fourier spectra of  $\bar{v}_{E1}$ (a) and
$\bar{v}_{E1}$ (a) and  $\unicode[STIX]{x1D6F7}_{1}$ (b) for the electron-root case with
$\unicode[STIX]{x1D6F7}_{1}$ (b) for the electron-root case with  $\unicode[STIX]{x1D6F7}_{1}$.
$\unicode[STIX]{x1D6F7}_{1}$.
In figure 18, the contributions of the  $v_{E1}$-driven part (a) and the
$v_{E1}$-driven part (a) and the  $v_{m}$-driven part (b) to the total radial
$v_{m}$-driven part (b) to the total radial  $\text{C}^{6+}$ flux are separately represented. The red lines in the figures represent the total
$\text{C}^{6+}$ flux are separately represented. The red lines in the figures represent the total  $\text{C}^{6+}$ flux for the case with
$\text{C}^{6+}$ flux for the case with  $\unicode[STIX]{x1D6F7}_{1}$. The green and blue lines in figure 18(a) represent the
$\unicode[STIX]{x1D6F7}_{1}$. The green and blue lines in figure 18(a) represent the  $v_{E1}$-driven part of the
$v_{E1}$-driven part of the  $\text{C}^{6+}$ flux, each calculated by the integral and the sum of Fourier coefficients, respectively. In figure 18(b), the green line represents the total
$\text{C}^{6+}$ flux, each calculated by the integral and the sum of Fourier coefficients, respectively. In figure 18(b), the green line represents the total  $\text{C}^{6+}$ flux for the case without
$\text{C}^{6+}$ flux for the case without  $\unicode[STIX]{x1D6F7}_{1}$, which is driven only by
$\unicode[STIX]{x1D6F7}_{1}$, which is driven only by  $\boldsymbol{v}_{m}$. The blue line is the
$\boldsymbol{v}_{m}$. The blue line is the  $v_{m}$-driven flux for the case with
$v_{m}$-driven flux for the case with  $\unicode[STIX]{x1D6F7}_{1}$. As for the ion-root case, the
$\unicode[STIX]{x1D6F7}_{1}$. As for the ion-root case, the  $v_{m}$-driven flux is reinforced by
$v_{m}$-driven flux is reinforced by  $\unicode[STIX]{x1D6F7}_{1}$ as well. The primary cause of this enhancement is the amplification of the sine-
$\unicode[STIX]{x1D6F7}_{1}$ as well. The primary cause of this enhancement is the amplification of the sine- $(1,0)$ mode in the
$(1,0)$ mode in the  $\text{C}^{6+}$ spectrum by
$\text{C}^{6+}$ spectrum by  $\unicode[STIX]{x1D6F7}_{1}$ (see figure 16c,f). As the result, the
$\unicode[STIX]{x1D6F7}_{1}$ (see figure 16c,f). As the result, the  $v_{m}$-driven part becomes at most an order of magnitude larger than the
$v_{m}$-driven part becomes at most an order of magnitude larger than the  $v_{E1}$-driven part.
$v_{E1}$-driven part.

Figure 18. (a) The total radial  $\text{C}^{6+}$ flux,
$\text{C}^{6+}$ flux,  $\unicode[STIX]{x1D6E4}_{C}$, for the case with
$\unicode[STIX]{x1D6E4}_{C}$, for the case with  $\unicode[STIX]{x1D6F7}_{1}$ (red), the
$\unicode[STIX]{x1D6F7}_{1}$ (red), the  $v_{E1}$-driven part of
$v_{E1}$-driven part of  $\unicode[STIX]{x1D6E4}_{C}$ calculated by the integral (green) and the
$\unicode[STIX]{x1D6E4}_{C}$ calculated by the integral (green) and the  $v_{E1}$-driven part calculated by the products of the Fourier coefficients (blue). (b) The total radial
$v_{E1}$-driven part calculated by the products of the Fourier coefficients (blue). (b) The total radial  $\text{C}^{6+}$ flux,
$\text{C}^{6+}$ flux,  $\unicode[STIX]{x1D6E4}_{C}$, for the case with
$\unicode[STIX]{x1D6E4}_{C}$, for the case with  $\unicode[STIX]{x1D6F7}_{1}$ (red), the total
$\unicode[STIX]{x1D6F7}_{1}$ (red), the total  $\text{C}^{6+}$ flux (driven only by
$\text{C}^{6+}$ flux (driven only by  $v_{m}$) for the case without
$v_{m}$) for the case without  $\unicode[STIX]{x1D6F7}_{1}$ (green) and the
$\unicode[STIX]{x1D6F7}_{1}$ (green) and the  $v_{m}$-driven part for the case with
$v_{m}$-driven part for the case with  $\unicode[STIX]{x1D6F7}_{1}$ (blue).
$\unicode[STIX]{x1D6F7}_{1}$ (blue).
4.3 Discussion of the result
For the ion-root case, a result analogous to previous local results has been obtained: the  $\text{C}^{6+}$ flux is driven further inwardly, not outwardly by
$\text{C}^{6+}$ flux is driven further inwardly, not outwardly by  $\unicode[STIX]{x1D6F7}_{1}$. This enhancement is mainly caused by the couplings of the sine-
$\unicode[STIX]{x1D6F7}_{1}$. This enhancement is mainly caused by the couplings of the sine- $(1,0)$ modes between the
$(1,0)$ modes between the  $\text{C}^{6+}$ density spectrum and the radial drift velocities.
$\text{C}^{6+}$ density spectrum and the radial drift velocities.  $\unicode[STIX]{x1D6F7}_{1}$ amplifies this mode and the opposite-sign couplings of the sine-
$\unicode[STIX]{x1D6F7}_{1}$ amplifies this mode and the opposite-sign couplings of the sine- $(1,0)$ modes result in the further inward flux. For the electron-root case, on the other hand, the radial particle flux is outwardly enhanced regardless of the species mainly due to the same-sign couplings of the sine-
$(1,0)$ modes result in the further inward flux. For the electron-root case, on the other hand, the radial particle flux is outwardly enhanced regardless of the species mainly due to the same-sign couplings of the sine- $(1,0)$ modes.
$(1,0)$ modes.
The phase structure of  $\unicode[STIX]{x1D6F7}_{1}$ is mainly determined by the spatial distribution of main ions. The main components in the
$\unicode[STIX]{x1D6F7}_{1}$ is mainly determined by the spatial distribution of main ions. The main components in the  $\unicode[STIX]{x1D6F7}_{1}$ spectrum are then determined by the magnetic field configuration. The spectra of
$\unicode[STIX]{x1D6F7}_{1}$ spectrum are then determined by the magnetic field configuration. The spectra of  $\text{H}^{1+}$ or light impurities such as
$\text{H}^{1+}$ or light impurities such as  $\text{He}^{2+}$ in low-collisionality regimes mainly consist of stellarator symmetric components. Thus, stellarator anti-symmetric modes become dominant in the spectrum of
$\text{He}^{2+}$ in low-collisionality regimes mainly consist of stellarator symmetric components. Thus, stellarator anti-symmetric modes become dominant in the spectrum of  $\bar{v}_{E1}$. On the other hand, stellarator anti-symmetric components were found to be dominant in the
$\bar{v}_{E1}$. On the other hand, stellarator anti-symmetric components were found to be dominant in the  $\text{C}^{6+}$ density spectrum, and these components tend to couple well with both the magnetic drift and the
$\text{C}^{6+}$ density spectrum, and these components tend to couple well with both the magnetic drift and the  $E\times B$ drift. The important question here is ‘with which sign do the leading modes, in particular the sine
$E\times B$ drift. The important question here is ‘with which sign do the leading modes, in particular the sine  $(1,0)$-modes, of the impurity ions couple with the radial drift velocities?’. An induction from our results implies that the sign of
$(1,0)$-modes, of the impurity ions couple with the radial drift velocities?’. An induction from our results implies that the sign of  $E_{r}$ is a key factor to determine the signs of the sine-
$E_{r}$ is a key factor to determine the signs of the sine- $(1,0)$ modes and, for ion-root plasmas, opposite-sign couplings are realised. To avoid those effective negative couplings or turn them into positive ones, either the phase structure of
$(1,0)$ modes and, for ion-root plasmas, opposite-sign couplings are realised. To avoid those effective negative couplings or turn them into positive ones, either the phase structure of  $\unicode[STIX]{x1D6F7}_{1}$ or the impurity density has to be strongly modified. However, we found that
$\unicode[STIX]{x1D6F7}_{1}$ or the impurity density has to be strongly modified. However, we found that  $\unicode[STIX]{x1D6F7}_{1}$ only increases the absolute value of the sine-
$\unicode[STIX]{x1D6F7}_{1}$ only increases the absolute value of the sine- $(1,0)$ mode in the
$(1,0)$ mode in the  $\text{C}^{6+}$ density spectrum and does not seem to affect its sign. Increasing the amplitude of
$\text{C}^{6+}$ density spectrum and does not seem to affect its sign. Increasing the amplitude of  $\unicode[STIX]{x1D6F7}_{1}$ is unlikely to make a qualitative difference either. Thus, our conclusion is that it is difficult for
$\unicode[STIX]{x1D6F7}_{1}$ is unlikely to make a qualitative difference either. Thus, our conclusion is that it is difficult for  $\unicode[STIX]{x1D6F7}_{1}$ to mitigate the inward neoclassical
$\unicode[STIX]{x1D6F7}_{1}$ to mitigate the inward neoclassical  $\text{C}^{6+}$ flux, let alone drive it in the outward direction in ion-root plasmas unless a strong particle or torque source exists.
$\text{C}^{6+}$ flux, let alone drive it in the outward direction in ion-root plasmas unless a strong particle or torque source exists.
The argument above ignores the contribution of kinetic electrons and it is possible that their contribution modifies the  $\unicode[STIX]{x1D6F7}_{1}$ structure (García-Regaña et al. Reference García-Regaña, Estrada, Calvo, Velasco, Alonso, Carralero, Kleiber, Landreman, Mollén and Sánchez2018). Although it is worth examining, however, it is doubtful that the impact of kinetic electrons can be strong enough to reverse the conclusion. On the other hand, our result does not simply support the electron-root scenario either. In the present study, we have demonstrated that
$\unicode[STIX]{x1D6F7}_{1}$ structure (García-Regaña et al. Reference García-Regaña, Estrada, Calvo, Velasco, Alonso, Carralero, Kleiber, Landreman, Mollén and Sánchez2018). Although it is worth examining, however, it is doubtful that the impact of kinetic electrons can be strong enough to reverse the conclusion. On the other hand, our result does not simply support the electron-root scenario either. In the present study, we have demonstrated that  $\unicode[STIX]{x1D6F7}_{1}$ is indeed a necessary factor to study the role of neoclassical transport in the formation of impurity hole, even in a global simulation model. Although it is an important finding that the global simulation alters the ambipolar-
$\unicode[STIX]{x1D6F7}_{1}$ is indeed a necessary factor to study the role of neoclassical transport in the formation of impurity hole, even in a global simulation model. Although it is an important finding that the global simulation alters the ambipolar- $E_{r}$ profile from the prediction by local codes, more detailed and accurate calculation, in which the ambipolar-
$E_{r}$ profile from the prediction by local codes, more detailed and accurate calculation, in which the ambipolar- $E_{r}$ profile is determined without neglecting the effect of
$E_{r}$ profile is determined without neglecting the effect of  $\unicode[STIX]{x1D6F7}_{1}$ on the radial transport, remains for future research.
$\unicode[STIX]{x1D6F7}_{1}$ on the radial transport, remains for future research.
5 Conclusion
We have extended and enabled a global neoclassical code FORTEC-3D to simulate impurity transport including the effect of  $\unicode[STIX]{x1D6F7}_{1}$. One of the motivations for this extension is to investigate the impurity hole phenomenon. In this study, we found that the impact of
$\unicode[STIX]{x1D6F7}_{1}$. One of the motivations for this extension is to investigate the impurity hole phenomenon. In this study, we found that the impact of  $\unicode[STIX]{x1D6F7}_{1}$ on the radial impurity transport in unoptimised devices such as LHD is mainly determined by the couplings of the sine-
$\unicode[STIX]{x1D6F7}_{1}$ on the radial impurity transport in unoptimised devices such as LHD is mainly determined by the couplings of the sine- $(1,0)$ modes between the radial components of the drift velocities and the impurity distribution. Further, the direction of the enhancement of radial particle fluxes by
$(1,0)$ modes between the radial components of the drift velocities and the impurity distribution. Further, the direction of the enhancement of radial particle fluxes by  $\unicode[STIX]{x1D6F7}_{1}$ depends on the ambipolar-
$\unicode[STIX]{x1D6F7}_{1}$ depends on the ambipolar- $E_{r}$ profile. As the result, while our global result provides another support that
$E_{r}$ profile. As the result, while our global result provides another support that  $\unicode[STIX]{x1D6F7}_{1}$ has non-negligible impact on impurity transport, it was shown that
$\unicode[STIX]{x1D6F7}_{1}$ has non-negligible impact on impurity transport, it was shown that  $\unicode[STIX]{x1D6F7}_{1}$ does not drive impurities outwardly in the ion-root plasma. Instead, a possibility that the ambipolar radial electric field in the impurity hole plasma is positive has emerged.
$\unicode[STIX]{x1D6F7}_{1}$ does not drive impurities outwardly in the ion-root plasma. Instead, a possibility that the ambipolar radial electric field in the impurity hole plasma is positive has emerged.
In this study, it has been assumed that the global effects are crucial, since the plasma profile for our ion-root case belongs in the parameter region where the global effects become most remarkable. However, we cannot distinguish between the contributions of the radial component and the tangential component of  $\boldsymbol{v}_{m}$ only in the present global result. Therefore, although we can at least conclude that considering the effects of
$\boldsymbol{v}_{m}$ only in the present global result. Therefore, although we can at least conclude that considering the effects of  $\boldsymbol{v}_{m}$ in the guiding-centre orbit is essential for studying transport in impurity hole plasmas, we cannot tell to what extent the global effects are necessary. Comparison of calculation results between the global model and the local model with the tangential component of the magnetic drift will be made in a separate study.
$\boldsymbol{v}_{m}$ in the guiding-centre orbit is essential for studying transport in impurity hole plasmas, we cannot tell to what extent the global effects are necessary. Comparison of calculation results between the global model and the local model with the tangential component of the magnetic drift will be made in a separate study.
We also found that there are some points to be improved in our calculation method. In particular, simultaneous calculation of global neoclassical transport and ambipolar radial electric field in multi-ion-species plasmas including  $\unicode[STIX]{x1D6F7}_{1}$ is needed. The impact of kinetic electrons may be non-negligible as well. Performing the computation including the effects mentioned above with reasonable numerical resource remains as a future work. On the other hand, the existing experimental data on the ambipolar radial electric fields in impurity hole plasmas are not sufficient as well. Thus, more efforts to accumulate reliable data in both numerical simulation and experimental measurements are needed to reveal the mechanism behind the impurity hole phenomenon.
$\unicode[STIX]{x1D6F7}_{1}$ is needed. The impact of kinetic electrons may be non-negligible as well. Performing the computation including the effects mentioned above with reasonable numerical resource remains as a future work. On the other hand, the existing experimental data on the ambipolar radial electric fields in impurity hole plasmas are not sufficient as well. Thus, more efforts to accumulate reliable data in both numerical simulation and experimental measurements are needed to reveal the mechanism behind the impurity hole phenomenon.
Acknowledgements
This work is performed under the auspices of the NIFS Collaborative Research Program, nos. NIFS18KNST132 and NIFS16KNXN315. The simulations in this article were carried out on the Plasma Simulator in NIFS, Japan and on the JFRS-1 supercomputer system at the Computational Simulation Centre of the International Fusion Energy Research Centre (IFERC-CSC) in Rokkasho Fusion Institute of QST (Aomori, Japan).
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Appendix A. Equations solved by FORTEC-3D
A.1 Derivation of the 5D drift-kinetic equation
The model used in FORTEC-3D is based on Littlejohn’s guiding-centre Lagrangian (Littlejohn Reference Littlejohn1983)
 $$\begin{eqnarray}L=\frac{1}{\unicode[STIX]{x1D716}}(Z_{a}e\boldsymbol{A}+\unicode[STIX]{x1D716}m_{a}v_{\Vert }\boldsymbol{b})\boldsymbol{\cdot }\dot{\boldsymbol{X}}+\unicode[STIX]{x1D716}\frac{m_{a}}{Z_{a}e}\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D709}}-H,\end{eqnarray}$$
$$\begin{eqnarray}L=\frac{1}{\unicode[STIX]{x1D716}}(Z_{a}e\boldsymbol{A}+\unicode[STIX]{x1D716}m_{a}v_{\Vert }\boldsymbol{b})\boldsymbol{\cdot }\dot{\boldsymbol{X}}+\unicode[STIX]{x1D716}\frac{m_{a}}{Z_{a}e}\unicode[STIX]{x1D707}\dot{\unicode[STIX]{x1D709}}-H,\end{eqnarray}$$ where the small parameter  $\unicode[STIX]{x1D716}$ is temporarily introduced and the guiding-centre coordinates
$\unicode[STIX]{x1D716}$ is temporarily introduced and the guiding-centre coordinates  $\boldsymbol{X}$, the parallel velocity
$\boldsymbol{X}$, the parallel velocity  $v_{\Vert }$, the magnetic moment
$v_{\Vert }$, the magnetic moment  $\unicode[STIX]{x1D707}$ and the gyrophase
$\unicode[STIX]{x1D707}$ and the gyrophase  $\unicode[STIX]{x1D709}$ are chosen as the independent variables. The Hamiltonian
$\unicode[STIX]{x1D709}$ are chosen as the independent variables. The Hamiltonian  $H$ is given by
$H$ is given by
 $$\begin{eqnarray}H={\textstyle \frac{1}{2}}m_{a}v_{\Vert }^{2}+\unicode[STIX]{x1D707}B+Z_{a}e\unicode[STIX]{x1D6F7}\end{eqnarray}$$
$$\begin{eqnarray}H={\textstyle \frac{1}{2}}m_{a}v_{\Vert }^{2}+\unicode[STIX]{x1D707}B+Z_{a}e\unicode[STIX]{x1D6F7}\end{eqnarray}$$and the Jacobian for the guiding-centre velocity variables is
 $$\begin{eqnarray}D\equiv \frac{B_{\Vert }^{\ast }}{m_{a}}=\frac{1}{m_{a}}\left(B+\unicode[STIX]{x1D716}\frac{m_{a}v_{\Vert }}{Z_{a}e}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}\right).\end{eqnarray}$$
$$\begin{eqnarray}D\equiv \frac{B_{\Vert }^{\ast }}{m_{a}}=\frac{1}{m_{a}}\left(B+\unicode[STIX]{x1D716}\frac{m_{a}v_{\Vert }}{Z_{a}e}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}\right).\end{eqnarray}$$ For a case with  $\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t=\unicode[STIX]{x2202}\boldsymbol{A}^{\ast }/\unicode[STIX]{x2202}t=0$, the Lagrangian (A 1) gives the equations of motion
$\unicode[STIX]{x2202}\boldsymbol{A}/\unicode[STIX]{x2202}t=\unicode[STIX]{x2202}\boldsymbol{A}^{\ast }/\unicode[STIX]{x2202}t=0$, the Lagrangian (A 1) gives the equations of motion
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\boldsymbol{X}}{\text{d}t}=\frac{\boldsymbol{B}^{\ast }}{B_{\Vert }^{\ast }}v_{\Vert }+\frac{\unicode[STIX]{x1D716}}{Z_{a}eB_{\Vert }^{\ast }}\boldsymbol{b}\times (\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\boldsymbol{X}}{\text{d}t}=\frac{\boldsymbol{B}^{\ast }}{B_{\Vert }^{\ast }}v_{\Vert }+\frac{\unicode[STIX]{x1D716}}{Z_{a}eB_{\Vert }^{\ast }}\boldsymbol{b}\times (\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}v_{\Vert }}{\text{d}t}=-\frac{\dot{\boldsymbol{X}}}{m_{a}v_{\Vert }}\boldsymbol{\cdot }(\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}v_{\Vert }}{\text{d}t}=-\frac{\dot{\boldsymbol{X}}}{m_{a}v_{\Vert }}\boldsymbol{\cdot }(\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}), & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\unicode[STIX]{x1D707}}{\text{d}t}=0 & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}\unicode[STIX]{x1D707}}{\text{d}t}=0 & \displaystyle\end{eqnarray}$$and (A 4) is equivalent to another expression
 $$\begin{eqnarray}v_{\Vert }\boldsymbol{b}+\frac{\unicode[STIX]{x1D716}}{Z_{a}eB_{\Vert }^{\ast }}\boldsymbol{b}\times (m_{a}v_{\Vert }^{2}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}),\end{eqnarray}$$
$$\begin{eqnarray}v_{\Vert }\boldsymbol{b}+\frac{\unicode[STIX]{x1D716}}{Z_{a}eB_{\Vert }^{\ast }}\boldsymbol{b}\times (m_{a}v_{\Vert }^{2}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}),\end{eqnarray}$$ to the order of  $O(\unicode[STIX]{x1D716}^{2})$, which makes it easier to see the correspondence of each term between different trajectory models (see e.g. Landreman et al. Reference Landreman, Smith, Mollén and Helander2014; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017). The parameter
$O(\unicode[STIX]{x1D716}^{2})$, which makes it easier to see the correspondence of each term between different trajectory models (see e.g. Landreman et al. Reference Landreman, Smith, Mollén and Helander2014; Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017). The parameter  $\unicode[STIX]{x1D716}$ is omitted in the rest of this paper.
$\unicode[STIX]{x1D716}$ is omitted in the rest of this paper.
The drift-kinetic equation with the phase-space variables  $\boldsymbol{Z}=(\boldsymbol{X},v_{\Vert },\unicode[STIX]{x1D707})$ can be written as
$\boldsymbol{Z}=(\boldsymbol{X},v_{\Vert },\unicode[STIX]{x1D707})$ can be written as
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}f_{a1}}{\unicode[STIX]{x2202}t}+\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{a1}+\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a1}}{\unicode[STIX]{x2202}v_{\Vert }}-C(f_{a1})=-\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{a0}-\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a0}}{\unicode[STIX]{x2202}v_{\Vert }},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}f_{a1}}{\unicode[STIX]{x2202}t}+\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{a1}+\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a1}}{\unicode[STIX]{x2202}v_{\Vert }}-C(f_{a1})=-\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{a0}-\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a0}}{\unicode[STIX]{x2202}v_{\Vert }},\end{eqnarray}$$ where  $C(f_{a1})$ is the linearised collision operator. Substituting (A 5) into the last term on the right-hand side,
$C(f_{a1})$ is the linearised collision operator. Substituting (A 5) into the last term on the right-hand side,
 $$\begin{eqnarray}-\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a0}}{\unicode[STIX]{x2202}v_{\Vert }}=\dot{v}_{\Vert }\frac{m_{a}v_{\Vert }}{T_{a}}f_{a0},\end{eqnarray}$$
$$\begin{eqnarray}-\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a0}}{\unicode[STIX]{x2202}v_{\Vert }}=\dot{v}_{\Vert }\frac{m_{a}v_{\Vert }}{T_{a}}f_{a0},\end{eqnarray}$$which yields
 $$\begin{eqnarray}-\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a0}}{\unicode[STIX]{x2202}v_{\Vert }}=-\frac{1}{T_{a}}\dot{\boldsymbol{X}}\boldsymbol{\cdot }(Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{0}+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{1}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B)f_{a0},\end{eqnarray}$$
$$\begin{eqnarray}-\dot{v}_{\Vert }\frac{\unicode[STIX]{x2202}f_{a0}}{\unicode[STIX]{x2202}v_{\Vert }}=-\frac{1}{T_{a}}\dot{\boldsymbol{X}}\boldsymbol{\cdot }(Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{0}+Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{1}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B)f_{a0},\end{eqnarray}$$and the last two terms in the bracket cancel with the last term in
 $$\begin{eqnarray}\displaystyle -\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{a0} & = & \displaystyle -\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r\left[\frac{n_{a0}^{\prime }}{n_{a0}}+\left(\frac{m_{a}v_{\Vert }^{2}}{2T_{a}}+\frac{\unicode[STIX]{x1D707}B}{T_{a}}-\frac{3}{2}+\frac{Z_{a}e\unicode[STIX]{x1D6F7}_{1}}{T_{a}}\right)\frac{T_{a}^{\prime }}{T_{a}}\right]f_{a0}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{T_{a}}\dot{\boldsymbol{X}}\boldsymbol{\cdot }(Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{1}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B)f_{a0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{a0} & = & \displaystyle -\dot{\boldsymbol{X}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r\left[\frac{n_{a0}^{\prime }}{n_{a0}}+\left(\frac{m_{a}v_{\Vert }^{2}}{2T_{a}}+\frac{\unicode[STIX]{x1D707}B}{T_{a}}-\frac{3}{2}+\frac{Z_{a}e\unicode[STIX]{x1D6F7}_{1}}{T_{a}}\right)\frac{T_{a}^{\prime }}{T_{a}}\right]f_{a0}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{T_{a}}\dot{\boldsymbol{X}}\boldsymbol{\cdot }(Z_{a}e\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{1}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D735}B)f_{a0},\end{eqnarray}$$leaving the right-hand side of (2.6) other than the collision term.
A.2 Expressions in the Boozer coordinates
Using the relation
 $$\begin{eqnarray}\displaystyle \boldsymbol{b}\times \boldsymbol{V} & = & \displaystyle \frac{1}{B}(I\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}+G\unicode[STIX]{x1D735}\unicode[STIX]{x1D701})\times (V_{r}\unicode[STIX]{x1D735}r+V_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}+V_{\unicode[STIX]{x1D701}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{B\sqrt{g}}[(IV_{\unicode[STIX]{x1D701}}-GV_{\unicode[STIX]{x1D703}})\boldsymbol{e}_{r}+V_{r}(G\boldsymbol{e}_{\unicode[STIX]{x1D703}}-I\boldsymbol{e}_{\unicode[STIX]{x1D701}})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{b}\times \boldsymbol{V} & = & \displaystyle \frac{1}{B}(I\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}+G\unicode[STIX]{x1D735}\unicode[STIX]{x1D701})\times (V_{r}\unicode[STIX]{x1D735}r+V_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}+V_{\unicode[STIX]{x1D701}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D701})\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{B\sqrt{g}}[(IV_{\unicode[STIX]{x1D701}}-GV_{\unicode[STIX]{x1D703}})\boldsymbol{e}_{r}+V_{r}(G\boldsymbol{e}_{\unicode[STIX]{x1D703}}-I\boldsymbol{e}_{\unicode[STIX]{x1D701}})],\end{eqnarray}$$ for an arbitrary vector in the configuration space  $\boldsymbol{V}$ and
$\boldsymbol{V}$ and
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\times \boldsymbol{b} & = & \displaystyle \unicode[STIX]{x1D735}\times \frac{\boldsymbol{B}}{B}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{B}\unicode[STIX]{x1D735}\times \boldsymbol{B}+\frac{1}{B^{2}}\boldsymbol{B}\times \unicode[STIX]{x1D735}B,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\times \boldsymbol{b} & = & \displaystyle \unicode[STIX]{x1D735}\times \frac{\boldsymbol{B}}{B}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{B}\unicode[STIX]{x1D735}\times \boldsymbol{B}+\frac{1}{B^{2}}\boldsymbol{B}\times \unicode[STIX]{x1D735}B,\end{eqnarray}$$ we can express  $\boldsymbol{B}^{\ast }$ as
$\boldsymbol{B}^{\ast }$ as
 $$\begin{eqnarray}\displaystyle \boldsymbol{B}^{\ast } & = & \displaystyle \boldsymbol{B}+\frac{m_{a}v_{\Vert }}{Z_{a}e}\unicode[STIX]{x1D735}\times \boldsymbol{b}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\sqrt{g}}\frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}r}(\unicode[STIX]{x1D704}\boldsymbol{e}_{\unicode[STIX]{x1D703}}+\boldsymbol{e}_{\unicode[STIX]{x1D701}})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{m_{a}v_{\Vert }}{Z_{a}eB\sqrt{g}}\left[\frac{1}{B}\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\boldsymbol{e}_{r}+\left(\frac{B^{\prime }}{B}G-G^{\prime }\right)\boldsymbol{e}_{\unicode[STIX]{x1D703}}-\left(\frac{B^{\prime }}{B}I-I^{\prime }\right)\boldsymbol{e}_{\unicode[STIX]{x1D701}}\right]\!\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{B}^{\ast } & = & \displaystyle \boldsymbol{B}+\frac{m_{a}v_{\Vert }}{Z_{a}e}\unicode[STIX]{x1D735}\times \boldsymbol{b}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\sqrt{g}}\frac{\text{d}\unicode[STIX]{x1D713}}{\text{d}r}(\unicode[STIX]{x1D704}\boldsymbol{e}_{\unicode[STIX]{x1D703}}+\boldsymbol{e}_{\unicode[STIX]{x1D701}})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{m_{a}v_{\Vert }}{Z_{a}eB\sqrt{g}}\left[\frac{1}{B}\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\boldsymbol{e}_{r}+\left(\frac{B^{\prime }}{B}G-G^{\prime }\right)\boldsymbol{e}_{\unicode[STIX]{x1D703}}-\left(\frac{B^{\prime }}{B}I-I^{\prime }\right)\boldsymbol{e}_{\unicode[STIX]{x1D701}}\right]\!\qquad\end{eqnarray}$$ and  $B_{\Vert }^{\ast }$ as
$B_{\Vert }^{\ast }$ as
 $$\begin{eqnarray}B_{\Vert }^{\ast }=B+\frac{m_{a}v_{\Vert }}{Z_{a}e}\frac{GI^{\prime }-IG^{\prime }}{(\unicode[STIX]{x1D713}^{\prime }G+\unicode[STIX]{x1D712}^{\prime }I)}.\end{eqnarray}$$
$$\begin{eqnarray}B_{\Vert }^{\ast }=B+\frac{m_{a}v_{\Vert }}{Z_{a}e}\frac{GI^{\prime }-IG^{\prime }}{(\unicode[STIX]{x1D713}^{\prime }G+\unicode[STIX]{x1D712}^{\prime }I)}.\end{eqnarray}$$ Then, taking the dot products of (A 4) with  $\unicode[STIX]{x1D735}r$,
$\unicode[STIX]{x1D735}r$,  $\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$ yields
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D701}$ yields
 $$\begin{eqnarray}\displaystyle \frac{\text{d}r}{\text{d}t} & = & \displaystyle \frac{1}{Z_{a}eBB_{\Vert }^{\ast }\sqrt{g}}\left[\left(\unicode[STIX]{x1D707}+\frac{m_{a}v_{\Vert }^{2}}{B}\right)\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+Z_{a}e\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right]\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FE}}\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+\frac{Z_{a}e}{\unicode[STIX]{x1D6FE}}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}r}{\text{d}t} & = & \displaystyle \frac{1}{Z_{a}eBB_{\Vert }^{\ast }\sqrt{g}}\left[\left(\unicode[STIX]{x1D707}+\frac{m_{a}v_{\Vert }^{2}}{B}\right)\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+Z_{a}e\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right]\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FE}}\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+\frac{Z_{a}e}{\unicode[STIX]{x1D6FE}}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right),\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D703}}{\text{d}t} & = & \displaystyle \frac{v_{\Vert }}{\sqrt{g}B_{\Vert }^{\ast }}\left[\unicode[STIX]{x1D713}^{\prime }\unicode[STIX]{x1D704}+\frac{m_{a}v_{\Vert }}{Z_{a}eB}\left(\frac{B^{\prime }}{B}G-G^{\prime }\right)\right]+\frac{G}{Z_{a}eBB_{\Vert }^{\ast }\sqrt{g}}(\unicode[STIX]{x1D707}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \frac{G}{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FF}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })+\frac{v_{\Vert }B}{\unicode[STIX]{x1D6FE}}\left(Z_{a}e\unicode[STIX]{x1D712}^{\prime }-\frac{m_{a}v_{\Vert }}{B}G^{\prime }\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D703}}{\text{d}t} & = & \displaystyle \frac{v_{\Vert }}{\sqrt{g}B_{\Vert }^{\ast }}\left[\unicode[STIX]{x1D713}^{\prime }\unicode[STIX]{x1D704}+\frac{m_{a}v_{\Vert }}{Z_{a}eB}\left(\frac{B^{\prime }}{B}G-G^{\prime }\right)\right]+\frac{G}{Z_{a}eBB_{\Vert }^{\ast }\sqrt{g}}(\unicode[STIX]{x1D707}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \frac{G}{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FF}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })+\frac{v_{\Vert }B}{\unicode[STIX]{x1D6FE}}\left(Z_{a}e\unicode[STIX]{x1D712}^{\prime }-\frac{m_{a}v_{\Vert }}{B}G^{\prime }\right),\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D701}}{\text{d}t} & = & \displaystyle \frac{v_{\Vert }}{\sqrt{g}B_{\Vert }^{\ast }}\left[\unicode[STIX]{x1D713}^{\prime }-\frac{m_{a}v_{\Vert }}{Z_{a}eB}\left(\frac{B^{\prime }}{B}I-I^{\prime }\right)\right]-\frac{I}{Z_{a}eBB_{\Vert }^{\ast }\sqrt{g}}(\unicode[STIX]{x1D707}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle -\frac{I}{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FF}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })+\frac{v_{\Vert }B}{\unicode[STIX]{x1D6FE}}\left(Z_{a}e\unicode[STIX]{x1D713}^{\prime }+\frac{m_{a}v_{\Vert }}{B}I^{\prime }\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D701}}{\text{d}t} & = & \displaystyle \frac{v_{\Vert }}{\sqrt{g}B_{\Vert }^{\ast }}\left[\unicode[STIX]{x1D713}^{\prime }-\frac{m_{a}v_{\Vert }}{Z_{a}eB}\left(\frac{B^{\prime }}{B}I-I^{\prime }\right)\right]-\frac{I}{Z_{a}eBB_{\Vert }^{\ast }\sqrt{g}}(\unicode[STIX]{x1D707}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle -\frac{I}{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FF}B^{\prime }+Z_{a}e\unicode[STIX]{x1D6F7}^{\prime })+\frac{v_{\Vert }B}{\unicode[STIX]{x1D6FE}}\left(Z_{a}e\unicode[STIX]{x1D713}^{\prime }+\frac{m_{a}v_{\Vert }}{B}I^{\prime }\right),\end{eqnarray}$$ respectively, and, using these expressions, we obtain the expression of the derivative of  $v_{\Vert }$ as
$v_{\Vert }$ as
 $$\begin{eqnarray}\displaystyle \frac{\text{d}v_{\Vert }}{\text{d}t} & = & \displaystyle -\frac{v_{\Vert }}{B\unicode[STIX]{x1D6FE}}\left[Z_{a}e\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\unicode[STIX]{x1D6F7}^{\prime }-\unicode[STIX]{x1D707}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)B^{\prime }\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Z_{a}eB}{m_{a}\unicode[STIX]{x1D6FE}}\left[\left(\frac{m_{a}v_{\Vert }}{Z_{a}eB}G^{\prime }-\unicode[STIX]{x1D712}^{\prime }\right)\left(\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}+Z_{a}e\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\left(\frac{m_{a}v_{\Vert }}{Z_{a}eB}I^{\prime }+\unicode[STIX]{x1D713}^{\prime }\right)\left(\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+Z_{a}e\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}v_{\Vert }}{\text{d}t} & = & \displaystyle -\frac{v_{\Vert }}{B\unicode[STIX]{x1D6FE}}\left[Z_{a}e\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\unicode[STIX]{x1D6F7}^{\prime }-\unicode[STIX]{x1D707}\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)B^{\prime }\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{Z_{a}eB}{m_{a}\unicode[STIX]{x1D6FE}}\left[\left(\frac{m_{a}v_{\Vert }}{Z_{a}eB}G^{\prime }-\unicode[STIX]{x1D712}^{\prime }\right)\left(\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}+Z_{a}e\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\left(\frac{m_{a}v_{\Vert }}{Z_{a}eB}I^{\prime }+\unicode[STIX]{x1D713}^{\prime }\right)\left(\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}+Z_{a}e\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\right)\right],\end{eqnarray}$$ where  $\unicode[STIX]{x1D6FF}$ and
$\unicode[STIX]{x1D6FF}$ and  $\unicode[STIX]{x1D6FE}$ are defined by (2.21) and (2.22), respectively.
$\unicode[STIX]{x1D6FE}$ are defined by (2.21) and (2.22), respectively.
A.3 Verification of (2.13)
In appendix B of García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017), it is demonstrated that the relation
 $$\begin{eqnarray}\left\langle \int \,\text{d}^{3}v\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}rf_{a0}\right\rangle =0\end{eqnarray}$$
$$\begin{eqnarray}\left\langle \int \,\text{d}^{3}v\boldsymbol{v}_{d}\boldsymbol{\cdot }\unicode[STIX]{x1D735}rf_{a0}\right\rangle =0\end{eqnarray}$$ still holds when  $f_{a0}$ is chosen as
$f_{a0}$ is chosen as  $f_{a0}=f_{aM}\exp (-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a})$ instead of
$f_{a0}=f_{aM}\exp (-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a})$ instead of  $f_{a0}=f_{aM}$. Although the definitions of the drift velocities in our global model differ from those in the models used in García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017) and other local studies, particularly,
$f_{a0}=f_{aM}$. Although the definitions of the drift velocities in our global model differ from those in the models used in García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017) and other local studies, particularly,  $B_{\Vert }^{\ast }(\boldsymbol{X},\boldsymbol{v})$ appears in the denominators of the drift velocities, it can be shown that the relation (2.13) is unaffected.
$B_{\Vert }^{\ast }(\boldsymbol{X},\boldsymbol{v})$ appears in the denominators of the drift velocities, it can be shown that the relation (2.13) is unaffected.
The demonstration of (A 20) for our model is analogous to that in García-Regaña et al. (Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maassberg, Smith and Turkin2017). In our coordinate system, (A 20) or (2.13) can be expressed as
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a0}=\frac{2\unicode[STIX]{x03C0}}{V^{\prime }}\oint \sqrt{g}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\int D\,\text{d}v_{\Vert }\,\text{d}\unicode[STIX]{x1D707}\frac{\text{d}r}{\text{d}t}f_{a0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{a0}=\frac{2\unicode[STIX]{x03C0}}{V^{\prime }}\oint \sqrt{g}\,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\int D\,\text{d}v_{\Vert }\,\text{d}\unicode[STIX]{x1D707}\frac{\text{d}r}{\text{d}t}f_{a0}.\end{eqnarray}$$ Thus, substituting (A 16) into (A 21) cancels the Jacobian,  $D\sqrt{g}$, and leaves
$D\sqrt{g}$, and leaves
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a0} & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{Z_{a}em_{a}}\frac{1}{V^{\prime }}\oint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\int \,\text{d}v_{\Vert }\,\text{d}\unicode[STIX]{x1D707}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{1}{B}\left[\left(\unicode[STIX]{x1D707}+\frac{m_{a}v_{\Vert }^{2}}{B}\right)\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+Z_{a}e\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right]f_{a0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a0} & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{Z_{a}em_{a}}\frac{1}{V^{\prime }}\oint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\int \,\text{d}v_{\Vert }\,\text{d}\unicode[STIX]{x1D707}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{1}{B}\left[\left(\unicode[STIX]{x1D707}+\frac{m_{a}v_{\Vert }^{2}}{B}\right)\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+Z_{a}e\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right]f_{a0}.\end{eqnarray}$$We can then perform the integrals in the velocity space to have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a0} & = & \displaystyle \frac{n_{a0}}{Z_{a}e}\frac{1}{V^{\prime }}\oint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\frac{1}{B^{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{2T_{a}}{B}\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+Z_{a}e\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right]\text{e}^{-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a0} & = & \displaystyle \frac{n_{a0}}{Z_{a}e}\frac{1}{V^{\prime }}\oint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\frac{1}{B^{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{2T_{a}}{B}\left(I\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}B}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)+Z_{a}e\left(I\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6F7}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\right]\text{e}^{-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}}\end{eqnarray}$$and this expression can be transformed into
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a0}=-\frac{n_{a0}}{Z_{a}e}\frac{T_{a}}{V^{\prime }}\oint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\left(I\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\left(\frac{1}{B^{2}}\text{e}^{-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}}\right). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a0}=-\frac{n_{a0}}{Z_{a}e}\frac{T_{a}}{V^{\prime }}\oint \,\text{d}\unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D701}\left(I\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}-G\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right)\left(\frac{1}{B^{2}}\text{e}^{-Z_{a}e\unicode[STIX]{x1D6F7}_{1}/T_{a}}\right). & & \displaystyle\end{eqnarray}$$ Now, it can be seen that the integrals in  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D701}$ vanish due to the periodic dependence of
$\unicode[STIX]{x1D701}$ vanish due to the periodic dependence of  $B$ and
$B$ and  $\unicode[STIX]{x1D6F7}_{1}$ on those angle variables. In figure 19,
$\unicode[STIX]{x1D6F7}_{1}$ on those angle variables. In figure 19,  $\unicode[STIX]{x1D6E4}_{a0}$ for
$\unicode[STIX]{x1D6E4}_{a0}$ for  $\text{C}^{6+}$ is plotted with the
$\text{C}^{6+}$ is plotted with the  $f_{1}$-part defined by (1.1). The numerical error is within the tolerance compared with the
$f_{1}$-part defined by (1.1). The numerical error is within the tolerance compared with the  $f_{1}$-part.
$f_{1}$-part.

Figure 19. Contributions of  $f_{1}$ (red) and
$f_{1}$ (red) and  $f_{0}$ (green) to the radial carbon flux.
$f_{0}$ (green) to the radial carbon flux.
Appendix B. Method for obtaining continuous distribution functions
In this study, continuous forms of physical quantities such as the distribution function,  $f_{a1}$, the density variation,
$f_{a1}$, the density variation,  $n_{a1}$, and the non-uniform part of electrostatic potential,
$n_{a1}$, and the non-uniform part of electrostatic potential,  $\unicode[STIX]{x1D6F7}_{1}$, are obtained by the following method. First, the Boozer configuration space is partitioned into small cells, where the
$\unicode[STIX]{x1D6F7}_{1}$, are obtained by the following method. First, the Boozer configuration space is partitioned into small cells, where the  $r$-direction is divided into
$r$-direction is divided into  $50$ and both the
$50$ and both the  $\unicode[STIX]{x1D703}$- and
$\unicode[STIX]{x1D703}$- and  $\unicode[STIX]{x1D701}$-directions are divided into
$\unicode[STIX]{x1D701}$-directions are divided into  $40$, respectively. Then, at each calculation step, the quantity, of which the continuous distribution we want, is averaged in each cell to obtain its coarse-grained distribution. After several time steps, the coarse-grained distribution is averaged over that period. Finally, the continuous spectrum on each flux surface is obtained by Fourier transformation along angle coordinates,
$40$, respectively. Then, at each calculation step, the quantity, of which the continuous distribution we want, is averaged in each cell to obtain its coarse-grained distribution. After several time steps, the coarse-grained distribution is averaged over that period. Finally, the continuous spectrum on each flux surface is obtained by Fourier transformation along angle coordinates,  $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and  $\unicode[STIX]{x1D701}$. In the
$\unicode[STIX]{x1D701}$. In the  $r$-direction, each Fourier component is interpolated with a third-order spline function. Using this spectrum, smooth functions can be constructed.
$r$-direction, each Fourier component is interpolated with a third-order spline function. Using this spectrum, smooth functions can be constructed.
Regarding this method, another approximation is used for some quantities. In global calculation, the constraint
 $$\begin{eqnarray}\langle f_{a1}\rangle =0\end{eqnarray}$$
$$\begin{eqnarray}\langle f_{a1}\rangle =0\end{eqnarray}$$ cannot usually be imposed due to the radial drift. Thus, the flux surface average of the density variation is not usually equal to zero, that is, its cosine- $(0,0)$ mode,
$(0,0)$ mode,  ${\tilde{n}}_{a1}^{00(c)}$, does not vanish:
${\tilde{n}}_{a1}^{00(c)}$, does not vanish:
 $$\begin{eqnarray}\langle n_{a1}\rangle ={\tilde{n}}_{a1}^{00(c)}\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}\langle n_{a1}\rangle ={\tilde{n}}_{a1}^{00(c)}\neq 0.\end{eqnarray}$$ However, FORTEC-3D adopts adaptive source and sink terms in the drift-kinetic equation (Huang et al. Reference Huang, Satake, Kanno, Sugama and Matsuoka2017), so that  ${\tilde{n}}_{a1}^{00(c)}\ll n_{a0}$ is kept. We thus can ignore
${\tilde{n}}_{a1}^{00(c)}\ll n_{a0}$ is kept. We thus can ignore  ${\tilde{n}}_{a1}^{00(c)}$ and assume that the cosine-
${\tilde{n}}_{a1}^{00(c)}$ and assume that the cosine- $(0,0)$ mode of
$(0,0)$ mode of  $\unicode[STIX]{x1D6F7}_{1}$ is zero as well:
$\unicode[STIX]{x1D6F7}_{1}$ is zero as well:
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D6F7}_{1}\rangle =\tilde{\unicode[STIX]{x1D6F7}}_{1}^{00(c)}=0.\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D6F7}_{1}\rangle =\tilde{\unicode[STIX]{x1D6F7}}_{1}^{00(c)}=0.\end{eqnarray}$$Appendix C. Pressure anisotropy
One may be concerned that the presence of appreciable density variations may be inconsistent with the assumption that the pressure is a flux-surface function in solving the magnetohydrodynamic (MHD) equilibrium. To address this concern, the ratio between the uniform part and the non-uniform part of the total ion pressure
 $$\begin{eqnarray}\frac{p_{I1}}{p_{I0}}=\frac{\displaystyle \mathop{\sum }_{I}n_{I1}}{\displaystyle \mathop{\sum }_{I}n_{I0}}\end{eqnarray}$$
$$\begin{eqnarray}\frac{p_{I1}}{p_{I0}}=\frac{\displaystyle \mathop{\sum }_{I}n_{I1}}{\displaystyle \mathop{\sum }_{I}n_{I0}}\end{eqnarray}$$ is illustrated in figure 20 (the temperatures are assumed to be the same). It can be seen that the ratio is of the order of  $10^{-2}$ or less than that. Thus, while the pressure anisotropy is large enough to generate numerically appreciable
$10^{-2}$ or less than that. Thus, while the pressure anisotropy is large enough to generate numerically appreciable  $\unicode[STIX]{x1D6F7}_{1}$, it is small enough not to affect the MHD equilibrium condition in the macroscopic scale.
$\unicode[STIX]{x1D6F7}_{1}$, it is small enough not to affect the MHD equilibrium condition in the macroscopic scale.

Figure 20. The ratio  $p_{I1}/p_{I0}$ at
$p_{I1}/p_{I0}$ at  $r/a=0.2$ (a),
$r/a=0.2$ (a),  $r/a=0.5$ (b) and
$r/a=0.5$ (b) and  $r/a=0.8$ (c) for the ion-root case with
$r/a=0.8$ (c) for the ion-root case with  $\unicode[STIX]{x1D6F7}_{1}$, respectively.
$\unicode[STIX]{x1D6F7}_{1}$, respectively.