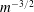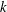1 Introduction
One of the most distinctive properties of a weakly collisional plasma as a physical system is the intricate phase-space dynamics associated with the interaction between electromagnetic fields and charged particles. The signature plasma-physics phenomenon of Landau (Reference Landau1946) damping consists essentially in the removal of free energy from an electromagnetic perturbation and its transfer ‘into phase space’, i.e. into fine-scale structure of the perturbed distribution function in velocity space (‘phase mixing’). It has long been realised that nonlinear effects can lead to Landau damping shutting down, both for broad-spectrum fields and individual monochromatic waves (Vedenov, Velikhov & Sagdeev Reference Vedenov, Velikhov and Sagdeev1962; Mazitov Reference Mazitov1965; O’Neil Reference O’Neil1965; Manheimer & Dupree Reference Manheimer and Dupree1968; Weiland Reference Weiland1992), or even to apparently damped perturbations coming back from phase space, a phenomenon called ‘plasma echo’ (Gould, O’Neil & Malmberg Reference Gould, O’Neil and Malmberg1967; Malmberg et al. Reference Malmberg, Wharton, Gould and O’Neil1968). Fast-forwarding over several decades of plasma-turbulence theory (see Krommes Reference Krommes2015 and Laval, Pesme & Adam Reference Laval, Pesme and Adam2016 for review and references), the notion of ‘phase-space turbulence’, pioneered by Dupree (Reference Dupree1972), has, in the recent years, again become a popular object of study, treated either, Dupree-style, in terms of formation of phase-space structures and their effect on the transport properties of the plasma (Kosuga & Diamond Reference Kosuga and Diamond2011; Lesur, Diamond & Kosuga Reference Lesur, Diamond and Kosuga2014a ,Reference Lesur, Diamond and Kosuga b ; Kosuga et al. Reference Kosuga, Itoh, Diamond, Itoh and Lesur2014, Reference Kosuga, Itoh, Diamond, Itoh and Lesur2017) or in terms of a kinetic cascade carrying free energy to collisional scales in velocity space (Watanabe & Sugama Reference Watanabe and Sugama2004; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Plunk, Quataert and Tatsuno2008, Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Tatsuno et al. Reference Tatsuno, Dorland, Schekochihin, Plunk, Barnes, Cowley and Howes2009; Plunk et al. Reference Plunk, Cowley, Schekochihin and Tatsuno2010; Bañón Navarro et al. Reference Bañón Navarro, Morel, Albrecht-Marc, Carati, Merz, Görler and Jenko2011; Plunk & Tatsuno Reference Plunk and Tatsuno2011; Teaca et al. Reference Teaca, Bañón Navarro, Jenko, Brunner and Villard2012, Reference Teaca, Banón Navarro, Told and Jenko2016; Hatch et al. Reference Hatch, Jenko, Bratanov and Bañón Navarro2014; Kanekar Reference Kanekar2015; Parker et al. Reference Parker, Highcock, Schekochihin and Dellar2016; Schekochihin et al. Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016; Servidio et al. Reference Servidio, Chasapis, Matthaeus, Perrone, Valentini, Parashar, Veltri, Gershman, Russell and Giles2017).
Within the latter strand, a direct precursor to the present study is the paper by Schekochihin et al. (Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016), who proposed, using electrostatic drift-kinetic turbulence as a prototypical example of kinetic turbulence, that a key effect of nonlinearity on phase-space dynamics would be an effective suppression of Landau damping – meaning that the free-energy flux from small to large scales in velocity space associated with stochastic echoes (‘anti-phase-mixing’, or ‘phase unmixing’) largely cancels the phase-mixing flux (‘Landau damping’) from large to small scales. A signature of this effect is a Hermite spectrum of free energy that is steeper for the nonlinear, turbulent perturbations than for the linear, Landau-damped ones (seen in numerical simulations of Watanabe & Sugama Reference Watanabe and Sugama2004, Hatch et al. Reference Hatch, Jenko, Bratanov and Bañón Navarro2014 and Parker et al. Reference Parker, Highcock, Schekochihin and Dellar2016). As a result, the limit of vanishing collisionality ceases to be a singular limit at long wavelengths (as it is in the linear regime; see, e.g. Kanekar et al. Reference Kanekar, Schekochihin, Dorland and Loureiro2015) and most of the entropy production occurs below the Larmor scale (i.e. outside the drift-kinetic approximation).
While some theoretical predictions of Schekochihin et al. (Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016) appear to have found a degree of numerical backing (Parker et al. Reference Parker, Highcock, Schekochihin and Dellar2016), their theory of stochastic echo was a qualitative one, relying on plausible scaling arguments, rather like the theory of hydrodynamic turbulence mostly does to this day (Davidson Reference Davidson2004). In addition to such arguments, understanding of fluid turbulence has benefited greatly from the development of simplified solvable models, the most famous of which is the ‘passive-scalar’ model describing the behaviour of a scalar field chaotically advected by an externally determined random flow (Kraichnan Reference Kraichnan1968, Reference Kraichnan1974, Reference Kraichnan1994; Falkovich, Gawȩdzki & Vergassola Reference Falkovich, Gawȩdzki and Vergassola2001). Under certain assumptions about the nature of this flow, it is possible to solve for the passive-scalar statistics analytically, leading to a number of interesting and non-trivial predictions, some of which appear to carry over qualitatively or even quantitatively to more realistic turbulent systems and all of which have proved stimulating to turbulence theorists. In view of this experience, seeking a maximally simplified but analytically solvable model appears to be worthwhile.
In this paper, we propose such a solvable model, based on the much-studied one-dimensional (1-D) Vlasov–Poisson system. The phase space for this system is two-dimensional (one spatial and one velocity coordinate). The particle distribution function in a turbulent state can be described in terms of its Fourier–Hermite spectrum. We show that, given a stochastic electric field, the only physically sensible solution features zero net free-energy flux from low (‘fluid’) to high (‘kinetic’) Hermite moments, meaning that the Landau damping is suppressed and the low moments are energetically insulated from the rest of the phase space. The underlying mechanism of this suppression is the stochastic-echo effect. The resulting Hermite spectrum is, asymptotically,
![]() $m^{-3/2}$
at large Hermite orders
$m^{-3/2}$
at large Hermite orders
![]() $m$
(compared to
$m$
(compared to
![]() $m^{-1/2}$
for linear Landau damping; see Zocco & Schekochihin Reference Zocco and Schekochihin2011 and Kanekar et al.
Reference Kanekar, Schekochihin, Dorland and Loureiro2015) and so the limit of small collisionality is non-singular (collisional dissipation tends to zero if the collision rate does). The corresponding Fourier spectrum of the low-
$m^{-1/2}$
for linear Landau damping; see Zocco & Schekochihin Reference Zocco and Schekochihin2011 and Kanekar et al.
Reference Kanekar, Schekochihin, Dorland and Loureiro2015) and so the limit of small collisionality is non-singular (collisional dissipation tends to zero if the collision rate does). The corresponding Fourier spectrum of the low-
![]() $m$
Hermite moments is
$m$
Hermite moments is
![]() $m^{-1/2}k^{-2}$
. Surveyed over the entire phase space, the phase-mixing (Landau-damped) and anti-phase-mixing (echoing) components of the distribution function have an interesting and not entirely trivial self-similar structure, which can nevertheless be fully extracted analytically and bears some resemblance to what is seen in various numerical simulations. A finite collision rate imposes a finite wavenumber cutoff on this solution, which is the analogue of the Kolmogorov scale for the Vlasov-kinetic turbulence.
$m^{-1/2}k^{-2}$
. Surveyed over the entire phase space, the phase-mixing (Landau-damped) and anti-phase-mixing (echoing) components of the distribution function have an interesting and not entirely trivial self-similar structure, which can nevertheless be fully extracted analytically and bears some resemblance to what is seen in various numerical simulations. A finite collision rate imposes a finite wavenumber cutoff on this solution, which is the analogue of the Kolmogorov scale for the Vlasov-kinetic turbulence.
The rest of the paper is organised as follows. In § 2, we describe a family of plasma systems that can be reasonably modelled by the equations studied in this paper (electron Langmuir turbulence, ion-acoustic turbulence, Zakharov turbulence). In § 3, we recast these equations in Fourier–Hermite space and introduce the formalism within which the phase mixing and anti-phase-mixing can be studied explicitly (this formalism is similar to one developed by Schekochihin et al. Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016, but with minor adjustments). In § 4, we make the approximations required to render the problem solvable and derive an equation for the Fourier–Hermite spectrum of the distribution function. In § 5, we solve this equation, obtaining the results promised above (a qualitative summary of this solution and an assessment of the effect of finite collisionality on it are given in § 5.4; a quicker, but perhaps less mathematically complete route to it than one pursued in the main text is described in appendix B). Finally, results are summarised and limitations, implications, applications and future directions discussed in § 6.
2 Models: Vlasov–Poisson system and its cousins
The standard Vlasov–Poisson system describes a plasma in the absence of magnetic field. For each species (
![]() $s=e$
electrons or
$s=e$
electrons or
![]() $s=i$
ions), the distribution function obeys the Vlasov–Landau equation
$s=i$
ions), the distribution function obeys the Vlasov–Landau equation
where
![]() $q_{s}$
and
$q_{s}$
and
![]() $m_{s}$
are the charge and mass of the particles, the term in the right-hand side is the collision operator and
$m_{s}$
are the charge and mass of the particles, the term in the right-hand side is the collision operator and
![]() $\unicode[STIX]{x1D719}$
is the electrostatic potential, satisfying Poisson’s equation
$\unicode[STIX]{x1D719}$
is the electrostatic potential, satisfying Poisson’s equation
We are formally splitting the distribution function into mean and perturbed parts,
where
![]() $f_{0s}$
is spatially homogeneous and we assume that there is no mean electric field. Only
$f_{0s}$
is spatially homogeneous and we assume that there is no mean electric field. Only
![]() $\unicode[STIX]{x1D6FF}f_{s}$
enters the Poisson equation (2.2) because the plasma is neutral on average. We do not require that
$\unicode[STIX]{x1D6FF}f_{s}$
enters the Poisson equation (2.2) because the plasma is neutral on average. We do not require that
![]() $\unicode[STIX]{x1D6FF}f_{s}\ll f_{0s}$
everywhere, although we do assume that any temporal evolution of the mean distribution is slow compared to that of the perturbation. We take the mean distribution to be Maxwellian,
$\unicode[STIX]{x1D6FF}f_{s}\ll f_{0s}$
everywhere, although we do assume that any temporal evolution of the mean distribution is slow compared to that of the perturbation. We take the mean distribution to be Maxwellian,
where
![]() $v_{\text{th}s}=\sqrt{2T_{s}/m_{s}}$
is the thermal speed of the particles of species
$v_{\text{th}s}=\sqrt{2T_{s}/m_{s}}$
is the thermal speed of the particles of species
![]() $s$
and
$s$
and
![]() $n_{0s}$
and
$n_{0s}$
and
![]() $T_{s}$
are their number density and temperature, respectively.
$T_{s}$
are their number density and temperature, respectively.
Several simplified models can be constructed, leading to mathematically similar sets of equations.
2.1 Electron Vlasov–Poisson plasma
Assuming cold ions, or, equivalently, restricting our consideration to perturbations with frequencies of the order of the electron plasma frequency,
where
![]() $-e\equiv q_{e}$
, we may set
$-e\equiv q_{e}$
, we may set
![]() $\unicode[STIX]{x1D6FF}f_{i}=0$
. Further restricting our consideration to a single spatial dimension,
$\unicode[STIX]{x1D6FF}f_{i}=0$
. Further restricting our consideration to a single spatial dimension,
![]() $x$
, we have
$x$
, we have
![]() $\unicode[STIX]{x1D6FF}f_{e}=\unicode[STIX]{x1D6FF}f_{e}(x,\boldsymbol{v})$
. We may now introduce the following reduced, non-dimensionalised fields and variables:
$\unicode[STIX]{x1D6FF}f_{e}=\unicode[STIX]{x1D6FF}f_{e}(x,\boldsymbol{v})$
. We may now introduce the following reduced, non-dimensionalised fields and variables:
We may also non-dimensionalise
![]() $t\unicode[STIX]{x1D714}_{\text{p}e}\rightarrow t$
and
$t\unicode[STIX]{x1D714}_{\text{p}e}\rightarrow t$
and
![]() $x/\!\sqrt{2}\,\unicode[STIX]{x1D706}_{\text{D}e}\rightarrow x$
, where
$x/\!\sqrt{2}\,\unicode[STIX]{x1D706}_{\text{D}e}\rightarrow x$
, where
![]() $\unicode[STIX]{x1D706}_{\text{D}e}=v_{\text{th}e}/\sqrt{2}\,\unicode[STIX]{x1D714}_{\text{p}e}$
is the electron Debye length. In this notation, the Vlasov–Poisson system becomes
$\unicode[STIX]{x1D706}_{\text{D}e}=v_{\text{th}e}/\sqrt{2}\,\unicode[STIX]{x1D714}_{\text{p}e}$
is the electron Debye length. In this notation, the Vlasov–Poisson system becomes
where
![]() $-\unicode[STIX]{x1D6FC}$
is twice the inverse Laplacian operator,
$-\unicode[STIX]{x1D6FC}$
is twice the inverse Laplacian operator,
![]() $\unicode[STIX]{x1D6FC}_{k}=2/k^{2}$
in Fourier space. We have added an ‘external’ potential
$\unicode[STIX]{x1D6FC}_{k}=2/k^{2}$
in Fourier space. We have added an ‘external’ potential
![]() $\unicode[STIX]{x1D712}$
to represent energy injection in an analytically convenient fashion (it will also acquire concrete physical meaning in §§ 2.3 and 2.4). Finally, we make a further simplification by using the Lenard & Bernstein (Reference Lenard and Bernstein1958) collision operator
$\unicode[STIX]{x1D712}$
to represent energy injection in an analytically convenient fashion (it will also acquire concrete physical meaning in §§ 2.3 and 2.4). Finally, we make a further simplification by using the Lenard & Bernstein (Reference Lenard and Bernstein1958) collision operator
with the proviso that it must be adjusted to conserve momentum and energy. This will not be a problem as the collision frequency
![]() $\unicode[STIX]{x1D708}$
will always be assumed small and so will only matter for the part of
$\unicode[STIX]{x1D708}$
will always be assumed small and so will only matter for the part of
![]() $g$
that varies quickly with
$g$
that varies quickly with
![]() $v$
.
$v$
.
Besides being interesting in itself, the 1-D Vlasov–Poisson system (2.7)–(2.8) is an appealing minimal model that contains all the ingredients necessary for phase-space turbulence featuring a competition between phase mixing and nonlinearity.
2.2 Ion-acoustic turbulence
Another, mathematically similar, model describes electrostatic perturbations at low frequencies, where it is ion kinetics that matter, namely,
Since
![]() $m_{e}\ll m_{i}$
and assuming
$m_{e}\ll m_{i}$
and assuming
![]() $T_{i}\sim T_{e}$
, the electrons’ velocities are
$T_{i}\sim T_{e}$
, the electrons’ velocities are
![]() $(m_{i}/m_{e})^{1/2}$
larger than the ions’ and so the kinetic equation (2.1) for
$(m_{i}/m_{e})^{1/2}$
larger than the ions’ and so the kinetic equation (2.1) for
![]() $s=e$
becomes, on ion time scales,
$s=e$
becomes, on ion time scales,
This is solved by the Maxwell–Boltzmann distribution
The electrons, therefore, have a Boltzmann response:
assuming
![]() $e\unicode[STIX]{x1D719}/T_{e}\ll 1$
. If
$e\unicode[STIX]{x1D719}/T_{e}\ll 1$
. If
![]() $k\unicode[STIX]{x1D706}_{\text{D}e}\ll 1$
, the Poisson equation (2.2) turns into the quasineutrality constraint:
$k\unicode[STIX]{x1D706}_{\text{D}e}\ll 1$
, the Poisson equation (2.2) turns into the quasineutrality constraint:
where the last equality follows from (2.13) and the ion density perturbation has to be calculated from the perturbed ion distribution function,
![]() $\unicode[STIX]{x1D6FF}n_{i}=\int \text{d}^{3}\boldsymbol{v}\,\unicode[STIX]{x1D6FF}f_{i}$
. Restricting consideration again to 1-D perturbations,
$\unicode[STIX]{x1D6FF}n_{i}=\int \text{d}^{3}\boldsymbol{v}\,\unicode[STIX]{x1D6FF}f_{i}$
. Restricting consideration again to 1-D perturbations,
![]() $\unicode[STIX]{x1D6FF}f_{i}=\unicode[STIX]{x1D6FF}f_{i}(x,\boldsymbol{v})$
, and defining
$\unicode[STIX]{x1D6FF}f_{i}=\unicode[STIX]{x1D6FF}f_{i}(x,\boldsymbol{v})$
, and defining
where
![]() $Ze\equiv q_{i}$
, we find that
$Ze\equiv q_{i}$
, we find that
![]() $g$
again satisfies (2.7). Using (2.14) and again adding an external forcing
$g$
again satisfies (2.7). Using (2.14) and again adding an external forcing
![]() $\unicode[STIX]{x1D712}$
, we have
$\unicode[STIX]{x1D712}$
, we have
This is the same as (2.8), except now
![]() $\unicode[STIX]{x1D6FC}=ZT_{e}/T_{i}$
is a constant rather than a differential operator.
$\unicode[STIX]{x1D6FC}=ZT_{e}/T_{i}$
is a constant rather than a differential operator.
Note that the spatial and temporal coordinates in (2.7) can now be normalised
![]() $x/L\rightarrow x$
and
$x/L\rightarrow x$
and
![]() $tv_{\text{th}i}/L\rightarrow t$
with an entirely arbitrary scale
$tv_{\text{th}i}/L\rightarrow t$
with an entirely arbitrary scale
![]() $L$
because the fundamental dynamics described by the ion equations – (damped) sound waves – does not have a special length scale.
$L$
because the fundamental dynamics described by the ion equations – (damped) sound waves – does not have a special length scale.
2.3 Zakharov turbulence
Models allowing perturbations only on electron or only on ion scales are, in fact, of limited relevance to real plasma turbulence because interactions of Langmuir waves will promote coupling to low-frequency modes at the ion scales while those low-frequency modes will locally alter the plasma frequency, giving rise to a ‘modulational’ nonlinearity in the electron-scale dynamics. Such a ‘two-scale’ system has been extensively studied, mostly using the so-called Zakharov (Reference Zakharov1972) equations, or, to be precise, a version of them in which both the electron and ion densities obey fluid-like equations (see reviews by Rudakov & Tsytovich Reference Rudakov and Tsytovich1978, Thornhill & ter Haar Reference Thornhill and ter Haar1978, Goldman Reference Goldman1984, Zakharov, Musher & Rubenchik Reference Zakharov, Musher and Rubenchik1985, Musher, Rubenchik & Zakharov Reference Musher, Rubenchik and Zakharov1995, Tsytovich Reference Tsytovich1995, Robinson Reference Robinson1997 and Kingsep Reference Kingsep2004, of which the first and the last are the most readable) For electrons, the fluid approximation requires
![]() $k\unicode[STIX]{x1D706}_{\text{D}e}\ll 1$
and for ions,
$k\unicode[STIX]{x1D706}_{\text{D}e}\ll 1$
and for ions,
![]() $T_{i}\ll T_{e}$
, so neither electron nor ion Landau damping are then important (because the phase velocities of the Langmuir and sound waves are much greater than
$T_{i}\ll T_{e}$
, so neither electron nor ion Landau damping are then important (because the phase velocities of the Langmuir and sound waves are much greater than
![]() $v_{\text{th}e}$
and
$v_{\text{th}e}$
and
![]() $v_{\text{th}i}$
, respectively).
$v_{\text{th}i}$
, respectively).
In a traditional approach to plasma turbulence, turbulence is what occurs at the scales (and in parameter regimes) where the dominant interactions are between wave modes (e.g. Langmuir or sound), which conserve fluctuation energy and transfer it, via a ‘cascade’, to scales where waves can interact with particles – usually via Landau damping, linear and/or nonlinear. The latter processes are expected to lead to absorption of the wave energy by particles, i.e. its conversion into heat. Thus, regimes and scale ranges in which kinetic physics matters are viewed as dissipative (analogous to viscous scales in hydrodynamic turbulence).
If one is not committed to such a dismissive attitude to kinetics in the way that a turbulence theorist in search of a fluid model might be, one may wish to explore how Zakharov’s turbulence interfaces with the phase space. While the fluid approximation for electrons at long wavelengths (
![]() $k\unicode[STIX]{x1D706}_{\text{D}e}\ll 1$
) is sensible, the assumption of cold ions and hence unfettered sound propagation is fairly restrictive, so one may wish to remove it. It is then possible to derive a kinetic version of Zakharov’s equations (as Zakharov Reference Zakharov1972 in fact did), in which the ion kinetic equation stays intact [this is (2.1) with
$k\unicode[STIX]{x1D706}_{\text{D}e}\ll 1$
) is sensible, the assumption of cold ions and hence unfettered sound propagation is fairly restrictive, so one may wish to remove it. It is then possible to derive a kinetic version of Zakharov’s equations (as Zakharov Reference Zakharov1972 in fact did), in which the ion kinetic equation stays intact [this is (2.1) with
![]() $s=i$
and
$s=i$
and
![]() $q_{s}=Ze$
], but the potential
$q_{s}=Ze$
], but the potential
![]() $\unicode[STIX]{x1D719}$
in this equation is the ion-time-scale (
$\unicode[STIX]{x1D719}$
in this equation is the ion-time-scale (
![]() ${\sim}1/kv_{\text{th}i}$
) averaged potential – a kind of mean field against the background of electron-time-scale Langmuir oscillations. This mean potential is determined from the Poisson equation, which, since
${\sim}1/kv_{\text{th}i}$
) averaged potential – a kind of mean field against the background of electron-time-scale Langmuir oscillations. This mean potential is determined from the Poisson equation, which, since
![]() $k\unicode[STIX]{x1D706}_{\text{D}e}\ll 1$
, again takes the form of the quasineutrality constraint (2.14), but the ion-time-scale electron-density perturbation now contains both the Boltzmann response and the so-called ponderomotive one – essentially an effective pressure due to the average energy density of the Langmuir oscillations:
$k\unicode[STIX]{x1D706}_{\text{D}e}\ll 1$
, again takes the form of the quasineutrality constraint (2.14), but the ion-time-scale electron-density perturbation now contains both the Boltzmann response and the so-called ponderomotive one – essentially an effective pressure due to the average energy density of the Langmuir oscillations:
where overbars denote averages over the electron time scales and
![]() $\mathfrak{E}$
is the electric field associated with the Langmuir waves. The resulting ion equations are the same as those derived in § 2.2, viz., the kinetic equation (2.7) with the definitions (2.15) (but
$\mathfrak{E}$
is the electric field associated with the Langmuir waves. The resulting ion equations are the same as those derived in § 2.2, viz., the kinetic equation (2.7) with the definitions (2.15) (but
![]() $\unicode[STIX]{x1D719}\rightarrow \bar{\unicode[STIX]{x1D719}}$
) and
$\unicode[STIX]{x1D719}\rightarrow \bar{\unicode[STIX]{x1D719}}$
) and
![]() $\unicode[STIX]{x1D711}$
given by (2.16), or, equivalently, by (2.8), but with the ‘external’ forcing now having a concrete physical meaning:
$\unicode[STIX]{x1D711}$
given by (2.16), or, equivalently, by (2.8), but with the ‘external’ forcing now having a concrete physical meaning:
This forcing is, in fact, not independent of either
![]() $\unicode[STIX]{x1D711}$
or
$\unicode[STIX]{x1D711}$
or
![]() $\unicode[STIX]{x1D6FF}f_{i}$
, as
$\unicode[STIX]{x1D6FF}f_{i}$
, as
![]() $\mathfrak{E}$
satisfies a ‘fluid’ equation for the Langmuir oscillations with the plasma frequency modulated by
$\mathfrak{E}$
satisfies a ‘fluid’ equation for the Langmuir oscillations with the plasma frequency modulated by
![]() $\unicode[STIX]{x1D6FF}\bar{n}_{e}$
(see Zakharov Reference Zakharov1972 or any of the reviews cited above; a systematic derivation of Zakharov’s equations from kinetics, which is surprisingly difficult to locate in the literature, can be found in Schekochihin Reference Schekochihin2017).
$\unicode[STIX]{x1D6FF}\bar{n}_{e}$
(see Zakharov Reference Zakharov1972 or any of the reviews cited above; a systematic derivation of Zakharov’s equations from kinetics, which is surprisingly difficult to locate in the literature, can be found in Schekochihin Reference Schekochihin2017).
Thus, yet again, we have a system of equations that is mathematically similar to the 1-D Vlasov–Poisson system (2.7) and (2.8).
2.4 Stochastic-acceleration problem
A simpler problem than the three preceding ones is to consider a population of ‘test particles’, embedded in an externally imposed, statistically stationary stochastic electric field
![]() $\boldsymbol{E}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
, and seek these particles’ distribution function. It satisfies Vlasov’s equation (2.1), with collision integral now omitted. It can be restricted to one dimension either by fiat or by considering particles in a magnetic field being accelerated by fast electric fluctuations parallel to it. In the limit of the field
$\boldsymbol{E}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
, and seek these particles’ distribution function. It satisfies Vlasov’s equation (2.1), with collision integral now omitted. It can be restricted to one dimension either by fiat or by considering particles in a magnetic field being accelerated by fast electric fluctuations parallel to it. In the limit of the field
![]() $E$
having a short correlation time compared to the characteristic time for particles to become trapped in the potential wells associated with
$E$
having a short correlation time compared to the characteristic time for particles to become trapped in the potential wells associated with
![]() $E$
, the particles’ spatially averaged distribution function is easily shown to satisfy a diffusion equation (Sturrock Reference Sturrock1966):Footnote
1
$E$
, the particles’ spatially averaged distribution function is easily shown to satisfy a diffusion equation (Sturrock Reference Sturrock1966):Footnote
1
where the electric-field correlation function should generally speaking be taken along particles’ trajectories, but, in the limit of short correlation times, it is the same as the Eulerian correlation function.
The solution of (2.19) (assuming an initial
![]() $\unicode[STIX]{x1D6FF}$
-shaped particle distribution) is a 1-D Maxwellian with
$\unicode[STIX]{x1D6FF}$
-shaped particle distribution) is a 1-D Maxwellian with
![]() $v_{\text{th}}^{2}=4Dt$
, expressing gradual secular heating of the test-particle population. At long times, this evolution can be treated as slow compared to the evolution of the perturbation
$v_{\text{th}}^{2}=4Dt$
, expressing gradual secular heating of the test-particle population. At long times, this evolution can be treated as slow compared to the evolution of the perturbation
![]() $\unicode[STIX]{x1D6FF}f$
and so the latter considered to evolve against the background of a quasi-constant Maxwellian equilibrium. With the same normalisations as in § 2.1, the perturbed distribution function again satisfies (2.7), but
$\unicode[STIX]{x1D6FF}f$
and so the latter considered to evolve against the background of a quasi-constant Maxwellian equilibrium. With the same normalisations as in § 2.1, the perturbed distribution function again satisfies (2.7), but
![]() $\unicode[STIX]{x1D711}$
is now an external field with prescribed statistical properties, entirely decoupled from
$\unicode[STIX]{x1D711}$
is now an external field with prescribed statistical properties, entirely decoupled from
![]() $g$
. This, of course, corresponds to setting
$g$
. This, of course, corresponds to setting
![]() $\unicode[STIX]{x1D6FC}=0$
in (2.8).
$\unicode[STIX]{x1D6FC}=0$
in (2.8).
3 Formalism: phase mixing and anti-phase-mixing
The spectral formalism for handling phase-space turbulence that we will use here was developed, for a different problem, by Schekochihin et al. (Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016) (see also Kanekar et al. Reference Kanekar, Schekochihin, Dorland and Loureiro2015, Parker & Dellar Reference Parker and Dellar2015), but there are enough minor differences with this work to justify a detailed recapitulation. However, a reader already familiar with this material might save time by fast forwarding to (3.33) and then working her way backwards whenever anything appears unclear.
3.1 Hermite moments: waves and phase mixing
We will work in the Fourier–Hermite space, decomposing the perturbed distribution as follows
where
![]() $L$
is the system size. The Hermite polynomials
$L$
is the system size. The Hermite polynomials
form a convenient orthogonal basis for handling 1-D perturbations to a Maxwellian. It is in anticipation of the Hermite decomposition that the Lenard–Bernstein collision operator (2.9) was chosen, as the Hermite polynomials are its eigenfunctions:
To enforce momentum and energy conservation, we overrule this with
![]() $C[g_{k,1}]=0$
and
$C[g_{k,1}]=0$
and
![]() $C[g_{k,2}]=0$
.
$C[g_{k,2}]=0$
.
Using the identities
denoting the particle density, flow velocity and temperature by
and noticing that (2.8) then amounts to
we arrive at the following spectral representation of (2.7):
the last equation describing all
![]() $m\geqslant 3$
.
$m\geqslant 3$
.
In the absence of sources, nonlinearities and heat fluxes (
![]() $g_{k,3}=0$
), (3.7)–(3.9) describe 1-D hydrodynamics of plasma waves (Langmuir waves for the electron model and ion-acoustic waves for the ion one). This becomes particularly obvious if we work in terms of the linear eigenfunctions
$g_{k,3}=0$
), (3.7)–(3.9) describe 1-D hydrodynamics of plasma waves (Langmuir waves for the electron model and ion-acoustic waves for the ion one). This becomes particularly obvious if we work in terms of the linear eigenfunctions
denote
![]() $\unicode[STIX]{x1D703}_{k}=T_{k}-2n_{k}$
(the non-adiabatic part of the temperature) and recast (3.7)–(3.9) as follows
$\unicode[STIX]{x1D703}_{k}=T_{k}-2n_{k}$
(the non-adiabatic part of the temperature) and recast (3.7)–(3.9) as follows
At any given
![]() $k$
, the fluctuating fields
$k$
, the fluctuating fields
![]() $n_{k}^{\pm }$
oscillate at frequency
$n_{k}^{\pm }$
oscillate at frequency
![]() $\unicode[STIX]{x1D714}_{k}$
(the Langmuir frequency or the ion sound frequency), with their energy injected by the forcing
$\unicode[STIX]{x1D714}_{k}$
(the Langmuir frequency or the ion sound frequency), with their energy injected by the forcing
![]() $\unicode[STIX]{x1D712}_{k}$
. The nonlinear term, which, since
$\unicode[STIX]{x1D712}_{k}$
. The nonlinear term, which, since
![]() $\unicode[STIX]{x1D711}_{p}=\unicode[STIX]{x1D6FC}_{p}n_{p}+\unicode[STIX]{x1D712}_{p}$
, includes both self-interaction and advection by the external potential
$\unicode[STIX]{x1D711}_{p}=\unicode[STIX]{x1D6FC}_{p}n_{p}+\unicode[STIX]{x1D712}_{p}$
, includes both self-interaction and advection by the external potential
![]() $\unicode[STIX]{x1D712}_{p}$
, can, in general, transfer wave energy to different wavenumbers, drain it or inject it. The term containing
$\unicode[STIX]{x1D712}_{p}$
, can, in general, transfer wave energy to different wavenumbers, drain it or inject it. The term containing
![]() $\unicode[STIX]{x1D703}_{k}$
connects the wave dynamics to the entire hierarchy of higher Hermite moments, which evolve according to (3.10).
$\unicode[STIX]{x1D703}_{k}$
connects the wave dynamics to the entire hierarchy of higher Hermite moments, which evolve according to (3.10).
In a linear system, the latter effect would give rise to Landau damping: the coupling of lower-order Hermite moments to higher-order ones that appears in the second term on the left-hand side of (3.10) ‘phase mixes’ perturbations to ever higher
![]() $m$
’s which represents emergence of ever finer structure in velocity space (at large
$m$
’s which represents emergence of ever finer structure in velocity space (at large
![]() $m$
, the Hermite transform is effectively similar to a Fourier transform in
$m$
, the Hermite transform is effectively similar to a Fourier transform in
![]() $v$
, with ‘frequency’
$v$
, with ‘frequency’
![]() $\sqrt{2m}$
, so moments of order
$\sqrt{2m}$
, so moments of order
![]() $m$
represent velocity-space structures with scale
$m$
represent velocity-space structures with scale
![]() $\unicode[STIX]{x1D6FF}v\sim \unicode[STIX]{x03C0}/\!\sqrt{m}$
). Eventually this activates collisions, however small their frequency
$\unicode[STIX]{x1D6FF}v\sim \unicode[STIX]{x03C0}/\!\sqrt{m}$
). Eventually this activates collisions, however small their frequency
![]() $\unicode[STIX]{x1D708}$
might be, and the dynamics becomes irreversible. In the presence of nonlinearity, the situation is more complicated, with the last term on the left-hand side of (3.10) causing a kind of advection of higher Hermite moments by the wave field
$\unicode[STIX]{x1D708}$
might be, and the dynamics becomes irreversible. In the presence of nonlinearity, the situation is more complicated, with the last term on the left-hand side of (3.10) causing a kind of advection of higher Hermite moments by the wave field
![]() $\unicode[STIX]{x1D711}_{k}$
. This gives rise to filamentation of the distribution function not just in velocity but also in position space (O’Neil Reference O’Neil1965; Manheimer Reference Manheimer1971; Dupree Reference Dupree1972). The resulting coupling between different wavenumbers can trigger plasma echoes (Gould et al.
Reference Gould, O’Neil and Malmberg1967), or anti-phase-mixing, leading to cancellation, on average, of the Landau damping (Parker & Dellar Reference Parker and Dellar2015; Parker et al.
Reference Parker, Highcock, Schekochihin and Dellar2016; Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016). It is with the latter phenomenon that we will be concerned in what follows, as we seek to characterise both spatial and velocity structure of the distribution function in terms of its
$\unicode[STIX]{x1D711}_{k}$
. This gives rise to filamentation of the distribution function not just in velocity but also in position space (O’Neil Reference O’Neil1965; Manheimer Reference Manheimer1971; Dupree Reference Dupree1972). The resulting coupling between different wavenumbers can trigger plasma echoes (Gould et al.
Reference Gould, O’Neil and Malmberg1967), or anti-phase-mixing, leading to cancellation, on average, of the Landau damping (Parker & Dellar Reference Parker and Dellar2015; Parker et al.
Reference Parker, Highcock, Schekochihin and Dellar2016; Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016). It is with the latter phenomenon that we will be concerned in what follows, as we seek to characterise both spatial and velocity structure of the distribution function in terms of its
![]() $k$
and
$k$
and
![]() $m$
spectra.
$m$
spectra.
3.2 Energy fluxes
We can define the energy spectrum of our waves to be
Using (3.12), we find that it evolves according to
The first term on the right-hand side is the energy injection, the last term involves interactions between waves (it does not in general integrate to zero because waves can exchange energy, nonlinearly, with particles), whereas the second term is responsible for energy removal via phase mixing. We can see how this is picked up by higher Hermite moments if we define the Fourier–Hermite spectrum and Hermite fluxFootnote 2
and deduce from (3.10) the evolution equation for the spectrum:
The phase-mixing term in (3.15) is
(the sloshing about of the fluctuation energy associated with the wave motion, represented by the time derivative, averages out in the statistical steady state). The Hermite flux in (3.17) passes energy along to higher
![]() $m$
’s until the collision term is large enough to erase it. Our strategy will be to work out a universal form for
$m$
’s until the collision term is large enough to erase it. Our strategy will be to work out a universal form for
![]() $\unicode[STIX]{x1D6E4}_{k,m}$
in a turbulent plasma at high
$\unicode[STIX]{x1D6E4}_{k,m}$
in a turbulent plasma at high
![]() $m$
. Ideally, one would deduce from that what
$m$
. Ideally, one would deduce from that what
![]() $\unicode[STIX]{x1D6E4}_{k,1}$
is, on average. In practice, we shall be able to predict that if one keeps a certain unspecified order-unity number
$\unicode[STIX]{x1D6E4}_{k,1}$
is, on average. In practice, we shall be able to predict that if one keeps a certain unspecified order-unity number
![]() $m$
of Hermite moments (‘order-unity’ meaning finite and independent of collisionality, however small the latter is), the energy flux
$m$
of Hermite moments (‘order-unity’ meaning finite and independent of collisionality, however small the latter is), the energy flux
![]() $\unicode[STIX]{x1D6E4}_{k,m}$
from/to these moments to/from the rest of phase space is zero in a certain ‘inertial’ range of wave numbers
$\unicode[STIX]{x1D6E4}_{k,m}$
from/to these moments to/from the rest of phase space is zero in a certain ‘inertial’ range of wave numbers
![]() $k$
.
$k$
.
3.3 High-
 $m$
dynamics
$m$
dynamics
Let us focus on the dynamics at
![]() $m\gg 1$
, deep in phase space (one might think of this as the ‘inertial range’ of phase-space turbulence). If
$m\gg 1$
, deep in phase space (one might think of this as the ‘inertial range’ of phase-space turbulence). If
then, to lowest order in
![]() $1/\!\sqrt{m}$
, (3.10) gives us simply
$1/\!\sqrt{m}$
, (3.10) gives us simply
This implies
i.e.
![]() $\text{i}^{m}g_{k,m}$
is either continuous or sign alternating. When
$\text{i}^{m}g_{k,m}$
is either continuous or sign alternating. When
![]() $k>0$
, these two possibilities correspond to phase-mixing and anti-phase-mixing modes, respectively, and vice versa for
$k>0$
, these two possibilities correspond to phase-mixing and anti-phase-mixing modes, respectively, and vice versa for
![]() $k<0$
(Kanekar et al.
Reference Kanekar, Schekochihin, Dorland and Loureiro2015; Parker & Dellar Reference Parker and Dellar2015; Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016). Let us separate these two cases explicitly.
$k<0$
(Kanekar et al.
Reference Kanekar, Schekochihin, Dorland and Loureiro2015; Parker & Dellar Reference Parker and Dellar2015; Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016). Let us separate these two cases explicitly.
In view of (3.20), the function
will be approximately continuous in
![]() $m$
: indeed,
$m$
: indeed,
Therefore, it is legitimate to treat
![]() $m$
as a continuous variable and approximate
$m$
as a continuous variable and approximate
treating the derivative terms as small. Using this approximation, we can cast (3.10) in the following approximate form, valid to lowest order in
![]() $1/\sqrt{m}$
,
$1/\sqrt{m}$
,
Finally, if we define
(3.25) becomes
This is very similar to (3.12) of Schekochihin et al. (Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016) and we have kept their notation for a faithful reader’s convenience.Footnote
3
It is manifest in (3.27) that when
![]() $k>0$
,
$k>0$
,
![]() $\tilde{f}_{k}$
propagates to higher
$\tilde{f}_{k}$
propagates to higher
![]() $s$
(phase mixes) and when
$s$
(phase mixes) and when
![]() $k<0$
, it propagates to lower
$k<0$
, it propagates to lower
![]() $s$
(anti-phase-mixes) and that the coupling between wavenumbers in the nonlinear term can turn phase-mixing perturbations into anti-phase-mixing ones and vice versa.
$s$
(anti-phase-mixes) and that the coupling between wavenumbers in the nonlinear term can turn phase-mixing perturbations into anti-phase-mixing ones and vice versa.
The distribution function itself can be reconstructed from
![]() $\tilde{f}_{k}$
, or, equivalently, from
$\tilde{f}_{k}$
, or, equivalently, from
![]() $G_{k,m}$
, as followsFootnote
4
$G_{k,m}$
, as followsFootnote
4
The fact that, for any given
![]() $k$
, both
$k$
, both
![]() $G_{k,m}$
and
$G_{k,m}$
and
![]() $G_{-k,m}$
are necessary to reconstruct
$G_{-k,m}$
are necessary to reconstruct
![]() $g_{k,m}$
reflects the presence of both phase-mixing and anti-phase-mixing modes in any distribution function. Maintaining a solution of (3.27) with no anti-phase-mixing, viz.,
$g_{k,m}$
reflects the presence of both phase-mixing and anti-phase-mixing modes in any distribution function. Maintaining a solution of (3.27) with no anti-phase-mixing, viz.,
![]() $\tilde{f}_{k}=0$
for all
$\tilde{f}_{k}=0$
for all
![]() $k<0$
, is clearly only possible in the absence of the nonlinearity.
$k<0$
, is clearly only possible in the absence of the nonlinearity.
Finally, if we define
both the Fourier–Hermite spectrum
![]() $C_{k,m}$
and the Hermite flux
$C_{k,m}$
and the Hermite flux
![]() $\unicode[STIX]{x1D6E4}_{k,m}$
, defined in (3.16), can be reconstructed from
$\unicode[STIX]{x1D6E4}_{k,m}$
, defined in (3.16), can be reconstructed from
![]() $F_{k}$
:
$F_{k}$
:
The derivation of these relations relies on (3.28) and on noticing also that
Thus, the Fourier–Hermite spectrum is the average of the spectra of the phase-mixing and anti-phase-mixing modes and the Hermite flux is their difference. It remains to solve for
![]() $F_{k}$
, which, using (3.27), is immediately found to satisfy
$F_{k}$
, which, using (3.27), is immediately found to satisfy
This equation, which is an approximate continuous version of (3.17), is not closed and so we will need a plausible method for handling its right-hand side.
4 Method: Kraichnan–Batchelor limit
4.1 Kraichnan–Kazantsev model
We shall be brutal and obtain a closure for the right-hand side of (3.33) by modelling
![]() $\unicode[STIX]{x1D711}_{p}$
as a random Gaussian white-noise (short-time-correlated) field,Footnote
5
$\unicode[STIX]{x1D711}_{p}$
as a random Gaussian white-noise (short-time-correlated) field,Footnote
5
This assumption, pioneered by Kraichnan (Reference Kraichnan1968) (for the passive-scalar problem) and Kazantsev (Reference Kazantsev1968) (for the turbulent-dynamo problem) is of course quantitatively wrong, but there is a long and encouraging history in fluid dynamics and magneto-hydrodynamics of the resulting closure leading to results that are basically correct (e.g. Kraichnan Reference Kraichnan1974, Reference Kraichnan1994; Zeldovich, Ruzmaikin & Sokoloff Reference Zeldovich, Ruzmaikin and Sokoloff1990; Krommes Reference Krommes1997; Falkovich et al.
Reference Falkovich, Gawȩdzki and Vergassola2001; Boldyrev & Cattaneo Reference Boldyrev and Cattaneo2004; Schekochihin et al.
Reference Schekochihin, Cowley, Taylor, Maron and McWilliams2004a
; Schekochihin, Haynes & Cowley Reference Schekochihin, Haynes and Cowley2004b
; Schekochihin et al.
Reference Schekochihin, Iskakov, Cowley, McWilliams, Proctor and Yousef2007; Bhat & Subramanian Reference Bhat and Subramanian2015). In the present context, what we are doing formally amounts to ignoring the contribution of the density
![]() $n_{k}=g_{k,0}$
to
$n_{k}=g_{k,0}$
to
![]() $\unicode[STIX]{x1D711}_{k}$
in (3.6) and stipulating the statistics (4.1) for the external forcing
$\unicode[STIX]{x1D711}_{k}$
in (3.6) and stipulating the statistics (4.1) for the external forcing
![]() $\unicode[STIX]{x1D712}_{k}$
. Physically, we are assuming that the advecting stochastic electric field can be treated as statistically independent of the phase-space structure of the distribution function. A reader unconvinced that this can ever be a valid approximation for any aspect of the Vlasov problem with a self-consistent electric field, might find comfort in considering the calculations that follow to apply solely to the stochastic-acceleration problem, where
$\unicode[STIX]{x1D712}_{k}$
. Physically, we are assuming that the advecting stochastic electric field can be treated as statistically independent of the phase-space structure of the distribution function. A reader unconvinced that this can ever be a valid approximation for any aspect of the Vlasov problem with a self-consistent electric field, might find comfort in considering the calculations that follow to apply solely to the stochastic-acceleration problem, where
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}$
(§ 2.4).
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D712}$
(§ 2.4).
For a Gaussian field, by the theorem of Furutsu (Reference Furutsu1963) and Novikov (Reference Novikov1965),
Using (3.27) to write an evolution equation for
![]() $\tilde{f}_{k-p}(t)\tilde{f}_{k}^{\ast }(t)$
and then formally integrating it over time, we find
$\tilde{f}_{k-p}(t)\tilde{f}_{k}^{\ast }(t)$
and then formally integrating it over time, we find
 $$\begin{eqnarray}\displaystyle \tilde{f}_{k-p}(t)\tilde{f}_{k}^{\ast }(t) & = & \displaystyle \int ^{t}\text{d}t^{\prime \prime }\left\{-\frac{k}{\sqrt{2}}\tilde{f}_{k-p}\frac{\unicode[STIX]{x2202}\tilde{f}_{k}^{\ast }}{\unicode[STIX]{x2202}s}-\frac{k-p}{\sqrt{2}}\tilde{f}_{k}^{\ast }\frac{\tilde{f}_{k-p}}{\unicode[STIX]{x2202}s}-2\unicode[STIX]{x1D708}s^{2}\tilde{f}_{k-p}\tilde{f}_{k}^{\ast }\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{s}{\sqrt{2}}\mathop{\sum }_{p^{\prime \prime }}p^{\prime \prime }\left[\unicode[STIX]{x1D711}_{p^{\prime \prime }}\tilde{f}_{k-p-p^{\prime \prime }}\tilde{f}_{k}^{\ast }+\unicode[STIX]{x1D711}_{-p^{\prime \prime }}\tilde{f}_{k-p^{\prime \prime }}^{\ast }\tilde{f}_{k-p}\right]\right\}(t^{\prime \prime }).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{f}_{k-p}(t)\tilde{f}_{k}^{\ast }(t) & = & \displaystyle \int ^{t}\text{d}t^{\prime \prime }\left\{-\frac{k}{\sqrt{2}}\tilde{f}_{k-p}\frac{\unicode[STIX]{x2202}\tilde{f}_{k}^{\ast }}{\unicode[STIX]{x2202}s}-\frac{k-p}{\sqrt{2}}\tilde{f}_{k}^{\ast }\frac{\tilde{f}_{k-p}}{\unicode[STIX]{x2202}s}-2\unicode[STIX]{x1D708}s^{2}\tilde{f}_{k-p}\tilde{f}_{k}^{\ast }\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{s}{\sqrt{2}}\mathop{\sum }_{p^{\prime \prime }}p^{\prime \prime }\left[\unicode[STIX]{x1D711}_{p^{\prime \prime }}\tilde{f}_{k-p-p^{\prime \prime }}\tilde{f}_{k}^{\ast }+\unicode[STIX]{x1D711}_{-p^{\prime \prime }}\tilde{f}_{k-p^{\prime \prime }}^{\ast }\tilde{f}_{k-p}\right]\right\}(t^{\prime \prime }).\end{eqnarray}$$
Therefore, its functional derivative is
where
![]() $H(t-t^{\prime })$
is the Heaviside function, expressing the fact that, by causality,
$H(t-t^{\prime })$
is the Heaviside function, expressing the fact that, by causality,
![]() $\tilde{f}(t)$
cannot depend on
$\tilde{f}(t)$
cannot depend on
![]() $\unicode[STIX]{x1D711}(t^{\prime })$
at a future time
$\unicode[STIX]{x1D711}(t^{\prime })$
at a future time
![]() $t^{\prime }>t$
, and ‘
$t^{\prime }>t$
, and ‘
![]() $\cdots \,$
’ stands for terms that vanish when
$\cdots \,$
’ stands for terms that vanish when
![]() $t^{\prime }=t$
. Substituting (4.1) and (4.4) into (4.2) gives
$t^{\prime }=t$
. Substituting (4.1) and (4.4) into (4.2) gives
Finally, using this in (3.33), we get
The
![]() $F_{k}$
term on the right-hand side is an additional, ‘turbulent’ collisionality (turbulent diffusion in velocity space); the
$F_{k}$
term on the right-hand side is an additional, ‘turbulent’ collisionality (turbulent diffusion in velocity space); the
![]() $F_{k-p}$
term is the mode-coupling term responsible for moving energy around and for converting phase-mixing modes into anti-phase-mixing ones or vice versa.
$F_{k-p}$
term is the mode-coupling term responsible for moving energy around and for converting phase-mixing modes into anti-phase-mixing ones or vice versa.
In steady state,
![]() $\unicode[STIX]{x2202}F_{k}/\unicode[STIX]{x2202}t=0$
and (4.6) can be recast in an even simpler form: dividing through by
$\unicode[STIX]{x2202}F_{k}/\unicode[STIX]{x2202}t=0$
and (4.6) can be recast in an even simpler form: dividing through by
![]() $2s^{2}$
, we arrive at
$2s^{2}$
, we arrive at
4.2 Energy budget and collisions
It is an important property of the Kraichnan–Kazantsev model applied to our problem that, in (4.6), the nonlinear interactions disappear under summation over all
![]() $k$
and so the total ‘energy’ of the
$k$
and so the total ‘energy’ of the
![]() $\tilde{f}$
field has a conservation law:
$\tilde{f}$
field has a conservation law:
where
![]() $s_{0}$
is some suitably chosen lower cutoff and the energy balance is between the flux through that cutoff (from or towards the waves at low
$s_{0}$
is some suitably chosen lower cutoff and the energy balance is between the flux through that cutoff (from or towards the waves at low
![]() $m$
) and collisional dissipation. Restating this in the steady state and with the
$m$
) and collisional dissipation. Restating this in the steady state and with the
![]() $\unicode[STIX]{x1D70F}$
variable (4.7),
$\unicode[STIX]{x1D70F}$
variable (4.7),
This energy balance admits two distinct physical scenarios.
One is essentially similar to what happens in the absence of nonlinearity (
![]() $\unicode[STIX]{x1D718}_{p}=0$
): in the limit of small
$\unicode[STIX]{x1D718}_{p}=0$
): in the limit of small
![]() $\unicode[STIX]{x1D708}$
, the spectrum
$\unicode[STIX]{x1D708}$
, the spectrum
![]() $F_{k}$
is independent of
$F_{k}$
is independent of
![]() $\unicode[STIX]{x1D70F}$
(or of
$\unicode[STIX]{x1D70F}$
(or of
![]() $s$
, or of
$s$
, or of
![]() $m$
), giving us the shallow
$m$
), giving us the shallow
![]() $C_{k,m}\propto 1/\sqrt{m}$
slope associated with a Landau-damped solution (Zocco & Schekochihin Reference Zocco and Schekochihin2011; Kanekar et al.
Reference Kanekar, Schekochihin, Dorland and Loureiro2015). Collisions become important at
$C_{k,m}\propto 1/\sqrt{m}$
slope associated with a Landau-damped solution (Zocco & Schekochihin Reference Zocco and Schekochihin2011; Kanekar et al.
Reference Kanekar, Schekochihin, Dorland and Loureiro2015). Collisions become important at
![]() $\unicode[STIX]{x1D70F}\sim \unicode[STIX]{x1D708}^{-1}$
[see (4.7)] and so the dissipation term in the right-hand side of (4.9) is finite and independent of collisionality as
$\unicode[STIX]{x1D70F}\sim \unicode[STIX]{x1D708}^{-1}$
[see (4.7)] and so the dissipation term in the right-hand side of (4.9) is finite and independent of collisionality as
![]() $\unicode[STIX]{x1D708}\rightarrow +0$
. This in turn implies that the integral in left-hand side of (4.9) must be finite and non-zero (in the linear regime,
$\unicode[STIX]{x1D708}\rightarrow +0$
. This in turn implies that the integral in left-hand side of (4.9) must be finite and non-zero (in the linear regime,
![]() $F_{k<0}=0$
, so the integral is always positive and will be finite as long as the wavenumber spectrum decays fast enough).
$F_{k<0}=0$
, so the integral is always positive and will be finite as long as the wavenumber spectrum decays fast enough).
The second scenario arises from any Hermite spectral slope that makes
![]() $F_{k}(\unicode[STIX]{x1D70F})$
decay with
$F_{k}(\unicode[STIX]{x1D70F})$
decay with
![]() $\unicode[STIX]{x1D70F}$
. Then the collisional dissipation vanishes as
$\unicode[STIX]{x1D70F}$
. Then the collisional dissipation vanishes as
![]() $\unicode[STIX]{x1D708}\rightarrow +0$
, i.e. the limit of vanishing collisionality is non-singular in this sense, giving us license simply to set
$\unicode[STIX]{x1D708}\rightarrow +0$
, i.e. the limit of vanishing collisionality is non-singular in this sense, giving us license simply to set
![]() $\unicode[STIX]{x1D708}=0$
in (4.7) and expect to find a legitimate solution. The solution is indeed a legitimate steady-state solution if the integral in the left-hand side of (4.9) vanishes for it, i.e. if the overall energy flux into Hermite space is zero:
$\unicode[STIX]{x1D708}=0$
in (4.7) and expect to find a legitimate solution. The solution is indeed a legitimate steady-state solution if the integral in the left-hand side of (4.9) vanishes for it, i.e. if the overall energy flux into Hermite space is zero:
although there is no a priori requirement that the Hermite flux must vanish at every
![]() $k$
. We shall see that this is exactly the state that emerges in the nonlinear regime.
$k$
. We shall see that this is exactly the state that emerges in the nonlinear regime.
4.3 Batchelor limit
While (4.7) is a closed and compact equation, it is an integral one and not necessarily easily amenable to analytical solution. We are going to make a further simplification by assuming that
![]() $p^{2}\unicode[STIX]{x1D718}_{p}$
decays sufficiently steeply with
$p^{2}\unicode[STIX]{x1D718}_{p}$
decays sufficiently steeply with
![]() $p$
that it is meaningful to consider
$p$
that it is meaningful to consider
![]() $F_{k}$
at
$F_{k}$
at
![]() $|k|\gg p$
, an approach pioneered by Batchelor (Reference Batchelor1959) in the context of passive-scalar mixing (with the more quantitative theory due to Kraichnan Reference Kraichnan1974). We can then expand under the wavenumber sum in (4.7):
$|k|\gg p$
, an approach pioneered by Batchelor (Reference Batchelor1959) in the context of passive-scalar mixing (with the more quantitative theory due to Kraichnan Reference Kraichnan1974). We can then expand under the wavenumber sum in (4.7):
Having noticed that the first term vanishes under summation because it is odd in
![]() $p$
while
$p$
while
![]() $\unicode[STIX]{x1D718}_{p}=\unicode[STIX]{x1D718}_{-p}$
, we obtain a rather simple differential equation:
$\unicode[STIX]{x1D718}_{p}=\unicode[STIX]{x1D718}_{-p}$
, we obtain a rather simple differential equation:
The wavenumber diffusion rate
![]() $\unicode[STIX]{x1D6FE}$
can easily be scaled out.
$\unicode[STIX]{x1D6FE}$
can easily be scaled out.
It turns out (see appendix A) that
![]() $p^{2}\unicode[STIX]{x1D718}_{p}$
must decay more steeply than
$p^{2}\unicode[STIX]{x1D718}_{p}$
must decay more steeply than
![]() $p^{-2}$
at the very least, in order for this approximation to make sense, although it would have to be steeper than
$p^{-2}$
at the very least, in order for this approximation to make sense, although it would have to be steeper than
![]() $p^{-3}$
in order for the
$p^{-3}$
in order for the
![]() $p$
integral that determines
$p$
integral that determines
![]() $\unicode[STIX]{x1D6FE}$
in (4.12) to converge without the need for a high-
$\unicode[STIX]{x1D6FE}$
in (4.12) to converge without the need for a high-
![]() $p$
cutoff. In what follows, we shall effectively assume the advecting electric field to be single scale, with
$p$
cutoff. In what follows, we shall effectively assume the advecting electric field to be single scale, with
![]() $\unicode[STIX]{x1D718}_{p}$
concentrated around some characteristic wavenumber
$\unicode[STIX]{x1D718}_{p}$
concentrated around some characteristic wavenumber
![]() $p$
.
$p$
.
Equation (4.12) makes it clear how the nonlinearity causes anti-phase-mixing. At
![]() $k>0$
, the steady-state equation (4.12) can be thought of as a diffusion equation in
$k>0$
, the steady-state equation (4.12) can be thought of as a diffusion equation in
![]() $k$
(or, to be precise, in
$k$
(or, to be precise, in
![]() $|k|^{3/2}$
; see § 5.1), with
$|k|^{3/2}$
; see § 5.1), with
![]() $\unicode[STIX]{x1D70F}$
playing the role of time. At
$\unicode[STIX]{x1D70F}$
playing the role of time. At
![]() $k<0$
, this ‘time’ reverses, i.e. diffusion turns into anti-diffusion. Whatever energy resides at any given
$k<0$
, this ‘time’ reverses, i.e. diffusion turns into anti-diffusion. Whatever energy resides at any given
![]() $k>0$
and low
$k>0$
and low
![]() $\unicode[STIX]{x1D70F}$
will, as
$\unicode[STIX]{x1D70F}$
will, as
![]() $\unicode[STIX]{x1D70F}$
increases, spread over the
$\unicode[STIX]{x1D70F}$
increases, spread over the
![]() $k$
space. Some of it can spread towards
$k$
space. Some of it can spread towards
![]() $k=0$
, where it crosses into the
$k=0$
, where it crosses into the
![]() $k<0$
territory (the rules of this crossing are established in § 4.4) and diffuses back towards large (negative)
$k<0$
territory (the rules of this crossing are established in § 4.4) and diffuses back towards large (negative)
![]() $k$
and low
$k$
and low
![]() $\unicode[STIX]{x1D70F}$
. This creates an anti-phase-mixing energy flux, which can (and will) cancel the phase-mixing flux. Collisions limit the values of
$\unicode[STIX]{x1D70F}$
. This creates an anti-phase-mixing energy flux, which can (and will) cancel the phase-mixing flux. Collisions limit the values of
![]() $\unicode[STIX]{x1D70F}$
(and of
$\unicode[STIX]{x1D70F}$
(and of
![]() $k$
) available to these phase-space flows. We shall discuss their role more quantitatively in § 5.4, after we have the exact collisionless solution in hand.
$k$
) available to these phase-space flows. We shall discuss their role more quantitatively in § 5.4, after we have the exact collisionless solution in hand.
4.4 Boundary conditions: continuity in
 $k$
space
$k$
space
We would like to be able to treat the solution of (4.7) in the region of low
![]() $|k|\sim p$
, where the Batchelor approximation is not valid, as a continuous extension of the solution of (4.12). In other words, we wish to prove that we can simply solve (4.12) with the boundary conditions
$|k|\sim p$
, where the Batchelor approximation is not valid, as a continuous extension of the solution of (4.12). In other words, we wish to prove that we can simply solve (4.12) with the boundary conditions
where
![]() $k\rightarrow \pm 0$
really means
$k\rightarrow \pm 0$
really means
![]() $k\rightarrow \pm p$
.
$k\rightarrow \pm p$
.
The continuity of
![]() $F_{k}$
across
$F_{k}$
across
![]() $k=0$
and all the way to
$k=0$
and all the way to
![]() $|k|\gg p$
(i.e. to the wavenumbers where the Batchelor approximation holds) can be inferred from (4.7) as follows. Let us ignore collisions and consider sufficiently small
$|k|\gg p$
(i.e. to the wavenumbers where the Batchelor approximation holds) can be inferred from (4.7) as follows. Let us ignore collisions and consider sufficiently small
![]() $k$
(and/or sufficiently large
$k$
(and/or sufficiently large
![]() $\unicode[STIX]{x1D70F}$
) so that the phase-mixing term is small compared to the nonlinear term: from (4.12), this is true for
$\unicode[STIX]{x1D70F}$
) so that the phase-mixing term is small compared to the nonlinear term: from (4.12), this is true for
![]() $|k|\ll (\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{1/3}$
, which can be satisfied already at
$|k|\ll (\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{1/3}$
, which can be satisfied already at
![]() $|k|\gg p$
, at least for
$|k|\gg p$
, at least for
![]() $\unicode[STIX]{x1D70F}\gg p^{3}/\unicode[STIX]{x1D6FE}$
. Then (4.7) reduces to
$\unicode[STIX]{x1D70F}\gg p^{3}/\unicode[STIX]{x1D6FE}$
. Then (4.7) reduces to
If we denote
![]() $p^{2}\unicode[STIX]{x1D718}_{p}=K_{p}$
, assume that the width of this function is smaller than the range of
$p^{2}\unicode[STIX]{x1D718}_{p}=K_{p}$
, assume that the width of this function is smaller than the range of
![]() $k$
in which (4.14) is valid (unlike in appendix A, where the validity of this approach is probed), turn sums in (4.14) into integrals and Fourier transform (4.14), denoting the dual variable by
$k$
in which (4.14) is valid (unlike in appendix A, where the validity of this approach is probed), turn sums in (4.14) into integrals and Fourier transform (4.14), denoting the dual variable by
![]() $x$
, and endowing the transformed functions with hats, we get
$x$
, and endowing the transformed functions with hats, we get
The solution of this equation is
![]() $\hat{F}(x)\propto \unicode[STIX]{x1D6FF}(x)$
. Therefore,
$\hat{F}(x)\propto \unicode[STIX]{x1D6FF}(x)$
. Therefore,
![]() $F_{k}$
is independent of
$F_{k}$
is independent of
![]() $k$
in a range of
$k$
in a range of
![]() $k$
surrounding
$k$
surrounding
![]() $0$
, with characteristic width
$0$
, with characteristic width
![]() ${\sim}p$
, the typical wavenumber of the advecting field
${\sim}p$
, the typical wavenumber of the advecting field
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
The second of the relations (4.13) (the continuity of the derivative) follows from the requirement that there can be no total energy flux in or out of
![]() $k=0$
(because
$k=0$
(because
![]() $C_{k,m}$
must be even in
$C_{k,m}$
must be even in
![]() $k$
by the reality condition). Therefore, from (3.30),
$k$
by the reality condition). Therefore, from (3.30),
5 Solution: universal self-similar phase-space spectrum
Although we are about to entertain ourselves and the reader with an exact solution of (4.12), the morphology of this solution is, in fact, not hard to grasp already by a cursory examination of the equation. We will discuss it post hoc, in § 5.4. A reader with no time for mathematical niceties can start from there and leaf back as necessary.
5.1 Plan of solution
If, as we promised in § 4.2, we are going to discover that phase mixing is substantially or fully suppressed, we must be able find such a solution from (4.12) with
![]() $\unicode[STIX]{x1D708}=0$
. Note that the
$\unicode[STIX]{x1D708}=0$
. Note that the
![]() $\unicode[STIX]{x1D70F}$
variable can now be shifted arbitrarily and so we can choose
$\unicode[STIX]{x1D70F}$
variable can now be shifted arbitrarily and so we can choose
![]() $\unicode[STIX]{x1D70F}=0$
to correspond to any true value of
$\unicode[STIX]{x1D70F}=0$
to correspond to any true value of
![]() $m$
– so let
$m$
– so let
![]() $\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70F}_{0}\rightarrow \unicode[STIX]{x1D70F}$
, where
$\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70F}_{0}\rightarrow \unicode[STIX]{x1D70F}$
, where
![]() $\unicode[STIX]{x1D70F}_{0}$
is the lower cutoff introduced in § 4.2. Physically, the limit
$\unicode[STIX]{x1D70F}_{0}$
is the lower cutoff introduced in § 4.2. Physically, the limit
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
corresponds to going back from the depths of phase space to low
$\unicode[STIX]{x1D70F}\rightarrow 0$
corresponds to going back from the depths of phase space to low
![]() $m$
’s, where the approximations that led to (3.27) break down.
$m$
’s, where the approximations that led to (3.27) break down.
With these further simplifications, equation (4.12) turns into a type of diffusion equation at
![]() $k>0$
and anti-diffusion at
$k>0$
and anti-diffusion at
![]() $k<0$
. Namely, letting
$k<0$
. Namely, letting
we find that
![]() $F^{\pm }$
satisfies
$F^{\pm }$
satisfies
The ‘
![]() $+$
’ version of this equation belongs to a class studied exhaustively by Sutton (Reference Sutton1943), who derived its Green’s functions for all standard initial and boundary-value problems. Armed with these, we are going to construct the full solution in the following way.
$+$
’ version of this equation belongs to a class studied exhaustively by Sutton (Reference Sutton1943), who derived its Green’s functions for all standard initial and boundary-value problems. Armed with these, we are going to construct the full solution in the following way.
(i) First postulate an ‘initial’ condition and a boundary condition for
![]() $F^{+}$
and find the Green’s-function solution for
$F^{+}$
and find the Green’s-function solution for
![]() $F^{+}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709})$
:
$F^{+}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709})$
:
where
![]() $F_{0}^{+}(\unicode[STIX]{x1D709})$
and
$F_{0}^{+}(\unicode[STIX]{x1D709})$
and
![]() $Y(\unicode[STIX]{x1D70F})$
are some unknown functions. Obviously, as we are not interested in spectra that blow up at small scales,
$Y(\unicode[STIX]{x1D70F})$
are some unknown functions. Obviously, as we are not interested in spectra that blow up at small scales,
![]() $F^{+}$
must vanish at
$F^{+}$
must vanish at
![]() $\unicode[STIX]{x1D709}\rightarrow \infty$
and the same will be required of
$\unicode[STIX]{x1D709}\rightarrow \infty$
and the same will be required of
![]() $F^{-}$
.
$F^{-}$
.
(ii) Since we must have continuity,
![]() $F^{+}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709}\rightarrow 0)=F^{-}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709}\rightarrow 0)$
[see (4.13)],
$F^{+}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709}\rightarrow 0)=F^{-}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709}\rightarrow 0)$
[see (4.13)],
![]() $F^{-}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709})$
is found as a Green’s-function solution with an unknown value
$F^{-}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709})$
is found as a Green’s-function solution with an unknown value
![]() $Y(\unicode[STIX]{x1D70F})$
on the boundary. Since the equation for
$Y(\unicode[STIX]{x1D70F})$
on the boundary. Since the equation for
![]() $F^{-}$
is an anti-diffusion equation, the ‘initial’ condition for it must be set at large
$F^{-}$
is an anti-diffusion equation, the ‘initial’ condition for it must be set at large
![]() $\unicode[STIX]{x1D70F}$
and since there can be no energy at
$\unicode[STIX]{x1D70F}$
and since there can be no energy at
![]() $\unicode[STIX]{x1D70F}\rightarrow \infty$
, this ‘initial’ condition is zero. Formally, this can be implemented by choosing some cutoff
$\unicode[STIX]{x1D70F}\rightarrow \infty$
, this ‘initial’ condition is zero. Formally, this can be implemented by choosing some cutoff
![]() $\unicode[STIX]{x1D70F}_{\text{max}}$
, requiring the function to vanish there, solving, and then taking
$\unicode[STIX]{x1D70F}_{\text{max}}$
, requiring the function to vanish there, solving, and then taking
![]() $\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
. The validity of this operation will be confirmed by the finiteness of the result. Thus,
$\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
. The validity of this operation will be confirmed by the finiteness of the result. Thus,
Operationally, the solution can be accomplished by changing variables to
![]() $\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70F}$
, so the anti-diffusion equation turns into a diffusion one. Physically,
$\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70F}$
, so the anti-diffusion equation turns into a diffusion one. Physically,
![]() $\unicode[STIX]{x1D70F}_{\text{max}}\sim 1/\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D70F}_{\text{max}}\sim 1/\unicode[STIX]{x1D708}$
.
(iii) The unknown function
![]() $Y(\unicode[STIX]{x1D70F})$
is now determined by the continuity of the energy flux across
$Y(\unicode[STIX]{x1D70F})$
is now determined by the continuity of the energy flux across
![]() $k=0$
[see (4.13)]. Since
$k=0$
[see (4.13)]. Since
![]() $\unicode[STIX]{x2202}F_{k}/\unicode[STIX]{x2202}k=\pm \unicode[STIX]{x1D709}^{1/3}\unicode[STIX]{x2202}F^{\pm }/\unicode[STIX]{x2202}\unicode[STIX]{x1D709}$
,
$\unicode[STIX]{x2202}F_{k}/\unicode[STIX]{x2202}k=\pm \unicode[STIX]{x1D709}^{1/3}\unicode[STIX]{x2202}F^{\pm }/\unicode[STIX]{x2202}\unicode[STIX]{x1D709}$
,
A key physical constraint is that
![]() $Y(\unicode[STIX]{x1D70F})$
should be a decreasing function, otherwise the assumption that the collisional dissipation is inessential would have to be abandoned.
$Y(\unicode[STIX]{x1D70F})$
should be a decreasing function, otherwise the assumption that the collisional dissipation is inessential would have to be abandoned.
(iv) At this point, we are in possession of the full solution, subject to the unknown function
![]() $F_{0}^{+}(\unicode[STIX]{x1D709})$
. We may now use this solution to determine
$F_{0}^{+}(\unicode[STIX]{x1D709})$
. We may now use this solution to determine
The net Hermite flux (3.31) at
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
, i.e. from low Hermite moments to high ones, is proportional to
$\unicode[STIX]{x1D70F}\rightarrow 0$
, i.e. from low Hermite moments to high ones, is proportional to
![]() $F_{0}^{+}-F_{0}^{-}$
. We will show that there is a solution for which
$F_{0}^{+}-F_{0}^{-}$
. We will show that there is a solution for which
and that this solution is the only physically sound one. Thus, the outcome of this procedure will be a universal structure of the Fourier–Hermite spectrum
![]() $F_{k}(\unicode[STIX]{x1D70F})$
in steady state. An impatient reader can skip what follows to find this spectrum in § 5.3.2 (xe will also find a shorter, more elementary, if perhaps less general, route to this solution in appendix B).
$F_{k}(\unicode[STIX]{x1D70F})$
in steady state. An impatient reader can skip what follows to find this spectrum in § 5.3.2 (xe will also find a shorter, more elementary, if perhaps less general, route to this solution in appendix B).
5.2 Green’s function solution
5.2.1 The ‘
 $+$
’ solution
$+$
’ solution
The solution of the ‘
![]() $+$
’ equation (5.2) satisfying the initial and boundary conditions (5.3) is
$+$
’ equation (5.2) satisfying the initial and boundary conditions (5.3) is
 $$\begin{eqnarray}\displaystyle F^{+}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709}) & = & \displaystyle \frac{\unicode[STIX]{x1D709}^{1/3}\text{e}^{-\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}}{2\unicode[STIX]{x1D70F}}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D702}\,\unicode[STIX]{x1D702}^{2/3}\text{e}^{-\unicode[STIX]{x1D702}^{2}/4\unicode[STIX]{x1D70F}}\text{I}_{1/3}\!\left(\frac{\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}}{2\unicode[STIX]{x1D70F}}\right)F_{0}^{+}(\unicode[STIX]{x1D702})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\left(\frac{1}{2}\unicode[STIX]{x1D709}\right)^{2/3}}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{\unicode[STIX]{x1D70F}}\text{d}\unicode[STIX]{x1D70E}\,\frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}/4(\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70E})}}{(\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70E})^{4/3}}\,Y(\unicode[STIX]{x1D70E}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F^{+}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709}) & = & \displaystyle \frac{\unicode[STIX]{x1D709}^{1/3}\text{e}^{-\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}}{2\unicode[STIX]{x1D70F}}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D702}\,\unicode[STIX]{x1D702}^{2/3}\text{e}^{-\unicode[STIX]{x1D702}^{2}/4\unicode[STIX]{x1D70F}}\text{I}_{1/3}\!\left(\frac{\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}}{2\unicode[STIX]{x1D70F}}\right)F_{0}^{+}(\unicode[STIX]{x1D702})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\left(\frac{1}{2}\unicode[STIX]{x1D709}\right)^{2/3}}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{\unicode[STIX]{x1D70F}}\text{d}\unicode[STIX]{x1D70E}\,\frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}/4(\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70E})}}{(\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70E})^{4/3}}\,Y(\unicode[STIX]{x1D70E}),\end{eqnarray}$$
where
![]() $\text{I}_{1/3}$
is a modified Bessel function of the first kind. The first term in (5.8) is responsible for satisfying the initial condition and is zero at
$\text{I}_{1/3}$
is a modified Bessel function of the first kind. The first term in (5.8) is responsible for satisfying the initial condition and is zero at
![]() $\unicode[STIX]{x1D709}\rightarrow 0$
, the second term is equal to zero at
$\unicode[STIX]{x1D709}\rightarrow 0$
, the second term is equal to zero at
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
and to
$\unicode[STIX]{x1D70F}\rightarrow 0$
and to
![]() $Y(\unicode[STIX]{x1D70F})$
at
$Y(\unicode[STIX]{x1D70F})$
at
![]() $\unicode[STIX]{x1D709}\rightarrow 0$
.
$\unicode[STIX]{x1D709}\rightarrow 0$
.
The associated energy flux at
![]() $\unicode[STIX]{x1D709}\rightarrow 0$
is
$\unicode[STIX]{x1D709}\rightarrow 0$
is
The first term is obtained by expanding
under the integral, mopping up powers of
![]() $\unicode[STIX]{x1D709}$
, then taking
$\unicode[STIX]{x1D709}$
, then taking
![]() $\unicode[STIX]{x1D709}\rightarrow 0$
, and, finally, changing the integration variable to
$\unicode[STIX]{x1D709}\rightarrow 0$
, and, finally, changing the integration variable to
![]() $z=y^{2}/4\unicode[STIX]{x1D70F}$
. The second term in (5.9) takes some work – the derivation can be found in Sutton (Reference Sutton1943) (his equation 7.4).Footnote
6
$z=y^{2}/4\unicode[STIX]{x1D70F}$
. The second term in (5.9) takes some work – the derivation can be found in Sutton (Reference Sutton1943) (his equation 7.4).Footnote
6
5.2.2 The ‘
 $-$
’ solution
$-$
’ solution
To obtain the solution of the ‘
![]() $-$
’ equation (5.2), let
$-$
’ equation (5.2), let
![]() $\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70F}$
and solve
$\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70F}$
and solve
subject to the boundary and initial conditions (5.4), which become, with the new variable,
The solution is the same as (5.8), but with
![]() $F_{0}^{+}$
replaced by
$F_{0}^{+}$
replaced by
![]() $0$
,
$0$
,
![]() $\unicode[STIX]{x1D70F}$
by
$\unicode[STIX]{x1D70F}$
by
![]() $\unicode[STIX]{x1D70F}^{\prime }$
and
$\unicode[STIX]{x1D70F}^{\prime }$
and
![]() $Y(\unicode[STIX]{x1D70E})$
by
$Y(\unicode[STIX]{x1D70E})$
by
![]() $Y(\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70E})$
. Changing the integration variable
$Y(\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70E})$
. Changing the integration variable
![]() $\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70E}\rightarrow \unicode[STIX]{x1D70E}$
and restoring
$\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70E}\rightarrow \unicode[STIX]{x1D70E}$
and restoring
![]() $\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70F}$
, we get
$\unicode[STIX]{x1D70F}^{\prime }=\unicode[STIX]{x1D70F}_{\text{max}}-\unicode[STIX]{x1D70F}$
, we get
Note that taking
![]() $\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
produces no anomalies, assuming
$\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
produces no anomalies, assuming
![]() $Y(\unicode[STIX]{x1D70E})$
does not grow (which would not be physical anyway as even with linear Landau damping,
$Y(\unicode[STIX]{x1D70E})$
does not grow (which would not be physical anyway as even with linear Landau damping,
![]() $Y=\text{const}$
).
$Y=\text{const}$
).
The flux associated with this solution at
![]() $\unicode[STIX]{x1D709}\rightarrow 0$
is found from
$\unicode[STIX]{x1D709}\rightarrow 0$
is found from
![]() $F^{-}(\unicode[STIX]{x1D70F}^{\prime },\unicode[STIX]{x1D709})$
by the same procedure as the second term in (5.9), followed by the same changes of variables as described above. The result is
$F^{-}(\unicode[STIX]{x1D70F}^{\prime },\unicode[STIX]{x1D709})$
by the same procedure as the second term in (5.9), followed by the same changes of variables as described above. The result is
Note that we should not rush into taking
![]() $\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
here before we take the derivative as the integral may well (and indeed will) prove divergent.
$\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
here before we take the derivative as the integral may well (and indeed will) prove divergent.
5.2.3 Continuity of energy flux
Using (5.9) and (5.14), the condition (5.5) becomes
This is an integral equation for
![]() $Y(\unicode[STIX]{x1D70F})$
in terms of the unknown function
$Y(\unicode[STIX]{x1D70F})$
in terms of the unknown function
![]() $F_{0}^{+}$
(or vice versa), but solving it directly is a thankless pursuit. We will cut to the chase and seek a particular solution for which the Hermite flux at
$F_{0}^{+}$
(or vice versa), but solving it directly is a thankless pursuit. We will cut to the chase and seek a particular solution for which the Hermite flux at
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
vanishes.
$\unicode[STIX]{x1D70F}\rightarrow 0$
vanishes.
5.3 Zero-flux solution
From (5.13), we can deduce the spectrum of anti-phase-mixing modes at
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
:
$\unicode[STIX]{x1D70F}\rightarrow 0$
:
Let us explicitly look for such a solution that
![]() $F_{0}^{-}(\unicode[STIX]{x1D709})=F_{0}^{+}(\unicode[STIX]{x1D709})$
. We may then substitute the expression (5.16) for
$F_{0}^{-}(\unicode[STIX]{x1D709})=F_{0}^{+}(\unicode[STIX]{x1D709})$
. We may then substitute the expression (5.16) for
![]() $F_{0}^{+}$
in (5.15) and thus obtain an equation for what
$F_{0}^{+}$
in (5.15) and thus obtain an equation for what
![]() $Y(\unicode[STIX]{x1D70F})$
would have to be in order for the zero-flux solution to be realised. If this
$Y(\unicode[STIX]{x1D70F})$
would have to be in order for the zero-flux solution to be realised. If this
![]() $Y(\unicode[STIX]{x1D70F})$
is physically legitimate (decays with
$Y(\unicode[STIX]{x1D70F})$
is physically legitimate (decays with
![]() $\unicode[STIX]{x1D70F}$
), we can put it back into (5.16) to determine
$\unicode[STIX]{x1D70F}$
), we can put it back into (5.16) to determine
![]() $F_{0}^{\pm }(\unicode[STIX]{x1D709})$
and then use that and
$F_{0}^{\pm }(\unicode[STIX]{x1D709})$
and then use that and
![]() $Y(\unicode[STIX]{x1D70F})$
in (5.8) and (5.13) to determine the Fourier–Hermite spectrum everywhere.
$Y(\unicode[STIX]{x1D70F})$
in (5.8) and (5.13) to determine the Fourier–Hermite spectrum everywhere.
The integral in the right-hand side of (5.15) with (5.16) for
![]() $F_{0}^{+}$
can easily be done after switching the order of
$F_{0}^{+}$
can easily be done after switching the order of
![]() $z$
and
$z$
and
![]() $\unicode[STIX]{x1D70E}$
integrations and changing the integration variable
$\unicode[STIX]{x1D70E}$
integrations and changing the integration variable
![]() $z$
to
$z$
to
![]() $\unicode[STIX]{x1D701}=z(1+\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70E})$
. As a result, (5.15) becomes
$\unicode[STIX]{x1D701}=z(1+\unicode[STIX]{x1D70F}/\unicode[STIX]{x1D70E})$
. As a result, (5.15) becomes
The solution to (5.17) is, up to a multiplicative constant,
which we will presently show by direct substitution. In appendix C, we show that this is indeed the only sensible solution. In appendix B, this scaling with
![]() $\unicode[STIX]{x1D70F}$
emerges via a much simpler (but less rigorous) argument arising from seeking a self-similar solution to our problem.
$\unicode[STIX]{x1D70F}$
emerges via a much simpler (but less rigorous) argument arising from seeking a self-similar solution to our problem.
With (5.18) for
![]() $Y$
, all integrals in (5.17) are standard tabulated ones: the integral in the right-hand side of (5.17) is (after rescaling the integration variable
$Y$
, all integrals in (5.17) are standard tabulated ones: the integral in the right-hand side of (5.17) is (after rescaling the integration variable
![]() $\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70F}\rightarrow \unicode[STIX]{x1D70E}$
)
$\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70F}\rightarrow \unicode[STIX]{x1D70E}$
)
the first integral in the left-hand side is a constant (because
![]() $\unicode[STIX]{x1D70F}$
can scaled out) and the second one is dominated by the upper limit, so it is
$\unicode[STIX]{x1D70F}$
can scaled out) and the second one is dominated by the upper limit, so it is
![]() ${\approx}\ln (\unicode[STIX]{x1D70F}_{\text{max}}/\unicode[STIX]{x1D70F})$
as
${\approx}\ln (\unicode[STIX]{x1D70F}_{\text{max}}/\unicode[STIX]{x1D70F})$
as
![]() $\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
. It then follows immediately that their derivative in the left-hand side of (5.17) is
$\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
. It then follows immediately that their derivative in the left-hand side of (5.17) is
This is equal to (5.19) and so (5.18) is indeed a good solution.
For future reference, these results imply that the energy flux through
![]() $\unicode[STIX]{x1D709}=0$
associated with this solution is
$\unicode[STIX]{x1D709}=0$
associated with this solution is
5.3.1 Reconstruction of the full solution
Now let us describe the full solution for the Fourier–Hermite spectrum that follows from what we have just derived. The spectrum at
![]() $\unicode[STIX]{x1D709}\rightarrow 0$
(
$\unicode[STIX]{x1D709}\rightarrow 0$
(
![]() $k\rightarrow 0$
) is given by (5.18). In our original variables, this means
$k\rightarrow 0$
) is given by (5.18). In our original variables, this means
The spectrum at
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
(low
$\unicode[STIX]{x1D70F}\rightarrow 0$
(low
![]() $m$
) is, via (5.16) and (5.18) (changing integration variable to
$m$
) is, via (5.16) and (5.18) (changing integration variable to
![]() $z=\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70E}$
),
$z=\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70E}$
),
These two scaling laws, the Hermite spectrum (5.22) and the Fourier spectrum (5.23) also hold asymptotically across the entire phase space, at large enough
![]() $m$
and
$m$
and
![]() $k$
, as we shall see shortly.
$k$
, as we shall see shortly.
Using (5.18) in (5.13) and changing the integration variable to
![]() $z=\unicode[STIX]{x1D709}^{2}/4(\unicode[STIX]{x1D70E}-\unicode[STIX]{x1D70F})$
, we find
$z=\unicode[STIX]{x1D709}^{2}/4(\unicode[STIX]{x1D70E}-\unicode[STIX]{x1D70F})$
, we find
 $$\begin{eqnarray}F^{-}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709})=\frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{\infty }\text{d}z\,\frac{\text{e}^{-z}}{\left(\unicode[STIX]{x1D70F}z+\frac{1}{4}\unicode[STIX]{x1D709}^{2}\right)^{2/3}}=\frac{\text{e}^{\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D70F}^{2/3}}\frac{\unicode[STIX]{x1D6E4}\!\left(\displaystyle \frac{1}{3};\frac{\unicode[STIX]{x1D709}^{2}}{4\unicode[STIX]{x1D70F}}\right)}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}.\end{eqnarray}$$
$$\begin{eqnarray}F^{-}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709})=\frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{\infty }\text{d}z\,\frac{\text{e}^{-z}}{\left(\unicode[STIX]{x1D70F}z+\frac{1}{4}\unicode[STIX]{x1D709}^{2}\right)^{2/3}}=\frac{\text{e}^{\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D70F}^{2/3}}\frac{\unicode[STIX]{x1D6E4}\!\left(\displaystyle \frac{1}{3};\frac{\unicode[STIX]{x1D709}^{2}}{4\unicode[STIX]{x1D70F}}\right)}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}.\end{eqnarray}$$
In the first of these expressions, both asymptotics (5.22) and (5.23) are manifest. In the second expression, which is obtained by changing the integration variable
![]() $z+\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}\rightarrow z$
,
$z+\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}\rightarrow z$
,
is an upper incomplete gamma function.
Finally, using (5.23) and (5.18) in (5.8), we find
 $$\begin{eqnarray}\displaystyle F^{+}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709}) & = & \displaystyle \frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D70F}^{2/3}}\left\{1+(-1)^{2/3}\left[\frac{\unicode[STIX]{x1D6E4}\!\left(\displaystyle \frac{1}{3};-\frac{\unicode[STIX]{x1D709}^{2}}{4\unicode[STIX]{x1D70F}}\right)}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}-1\right]\right\}\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D70F}^{2/3}}\left[1+\frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}\text{d}z\,z^{-2/3}\text{e}^{z}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F^{+}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709}) & = & \displaystyle \frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D70F}^{2/3}}\left\{1+(-1)^{2/3}\left[\frac{\unicode[STIX]{x1D6E4}\!\left(\displaystyle \frac{1}{3};-\frac{\unicode[STIX]{x1D709}^{2}}{4\unicode[STIX]{x1D70F}}\right)}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}-1\right]\right\}\nonumber\\ \displaystyle & = & \displaystyle \frac{\text{e}^{-\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D70F}^{2/3}}\left[1+\frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70F}}\text{d}z\,z^{-2/3}\text{e}^{z}\right].\end{eqnarray}$$
The first term inside the bracket comes from the second integral in (5.8) (the boundary-value term) and is obtained by the manipulations analogous to those that led to (5.24). The second term comes from the first integral in (5.8) (the initial-value term), which is turned into a tabulated integral by changing the integration variable to
![]() $z=\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}/2\unicode[STIX]{x1D70F}$
(and then changing
$z=\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}/2\unicode[STIX]{x1D70F}$
(and then changing
![]() $z\rightarrow -z$
to obtain the last integral representation, which is perhaps more transparent than the one in terms of the incomplete gamma function).
$z\rightarrow -z$
to obtain the last integral representation, which is perhaps more transparent than the one in terms of the incomplete gamma function).
5.3.2 Self-similar solution
Assembling (5.24) and (5.26) together and returning them to the original variables, we arrive at the following solution:
 $$\begin{eqnarray}F_{k}(\unicode[STIX]{x1D70F})=\frac{\text{e}^{-k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D70F}^{2/3}}\left\{\begin{array}{@{}l@{}}\displaystyle 1+\frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}\text{d}z\,z^{-2/3}\text{e}^{z},\quad k>0,\\ \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{|k|^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}^{\infty }\text{d}z\,z^{-2/3}\text{e}^{-z},\quad k<0,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}F_{k}(\unicode[STIX]{x1D70F})=\frac{\text{e}^{-k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}}{\unicode[STIX]{x1D70F}^{2/3}}\left\{\begin{array}{@{}l@{}}\displaystyle 1+\frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}\text{d}z\,z^{-2/3}\text{e}^{z},\quad k>0,\\ \displaystyle \frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{|k|^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}^{\infty }\text{d}z\,z^{-2/3}\text{e}^{-z},\quad k<0,\end{array}\right.\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70F}=(2m)^{3/2}/3-\unicode[STIX]{x1D70F}_{0}$
(
$\unicode[STIX]{x1D70F}=(2m)^{3/2}/3-\unicode[STIX]{x1D70F}_{0}$
(
![]() $\unicode[STIX]{x1D70F}_{0}$
is an order-unity offset). Hence the Fourier–Hermite spectrum
$\unicode[STIX]{x1D70F}_{0}$
is an order-unity offset). Hence the Fourier–Hermite spectrum
![]() $C_{k,m}$
and the Hermite flux
$C_{k,m}$
and the Hermite flux
![]() $\unicode[STIX]{x1D6E4}_{k,m}$
can be calculated according to (3.30) and (3.31), respectively.
$\unicode[STIX]{x1D6E4}_{k,m}$
can be calculated according to (3.30) and (3.31), respectively.

Figure 1. The function
![]() $F_{k}(\unicode[STIX]{x1D70F})$
given by (5.27) (with
$F_{k}(\unicode[STIX]{x1D70F})$
given by (5.27) (with
![]() $\unicode[STIX]{x1D6FE}=1$
). The phase-mixing part of the spectrum is on the right (
$\unicode[STIX]{x1D6FE}=1$
). The phase-mixing part of the spectrum is on the right (
![]() $k>0$
), the anti-phase-mixing part on the left (
$k>0$
), the anti-phase-mixing part on the left (
![]() $k<0$
). The total energy is the sum and the Hermite flux the difference of these two. The broader-range scaling behaviour is better represented on a log scale: see figures 2 and 3.
$k<0$
). The total energy is the sum and the Hermite flux the difference of these two. The broader-range scaling behaviour is better represented on a log scale: see figures 2 and 3.

Figure 2. Typical cuts through the solution (5.27) (with
![]() $\unicode[STIX]{x1D6FE}=1$
) at (a) constant
$\unicode[STIX]{x1D6FE}=1$
) at (a) constant
![]() $\unicode[STIX]{x1D70F}$
(
$\unicode[STIX]{x1D70F}$
(
![]() $\unicode[STIX]{x1D70F}=20$
), (b) constant
$\unicode[STIX]{x1D70F}=20$
), (b) constant
![]() $k$
(
$k$
(
![]() $k=7$
). The spectra of phase-mixing modes,
$k=7$
). The spectra of phase-mixing modes,
![]() $F_{k}(\unicode[STIX]{x1D70F})$
, are shown in red and the spectra of anti-phase-mixing modes,
$F_{k}(\unicode[STIX]{x1D70F})$
, are shown in red and the spectra of anti-phase-mixing modes,
![]() $F_{-k}(\unicode[STIX]{x1D70F})$
, in black. The asymptotic scalings (5.23) and (5.22) are shown for reference and convergence to them is manifest in the limits
$F_{-k}(\unicode[STIX]{x1D70F})$
, in black. The asymptotic scalings (5.23) and (5.22) are shown for reference and convergence to them is manifest in the limits
![]() $k\gg (9\unicode[STIX]{x1D70F})^{1/3}$
and
$k\gg (9\unicode[STIX]{x1D70F})^{1/3}$
and
![]() $\unicode[STIX]{x1D70F}\gg k^{3}/9$
, respectively. Two-dimensional plots of
$\unicode[STIX]{x1D70F}\gg k^{3}/9$
, respectively. Two-dimensional plots of
![]() $F_{k}(\unicode[STIX]{x1D70F})$
and of the resulting Hermite flux and total energy spectrum are in figure 3.
$F_{k}(\unicode[STIX]{x1D70F})$
and of the resulting Hermite flux and total energy spectrum are in figure 3.

Figure 3. (a,b) Same as figure 1, but on a log scale and across a broader range of
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D70F}$
. Note the asymptotic features (zero-flux solution, power-law scalings) discussed in §§ 5.3.2 and 5.4. Cf. figure 4. (c) Normalised Hermite flux
$\unicode[STIX]{x1D70F}$
. Note the asymptotic features (zero-flux solution, power-law scalings) discussed in §§ 5.3.2 and 5.4. Cf. figure 4. (c) Normalised Hermite flux
![]() $\bar{\unicode[STIX]{x1D6E4}}$
defined by (5.28). Its contours are straight in the logarithmic coordinates because
$\bar{\unicode[STIX]{x1D6E4}}$
defined by (5.28). Its contours are straight in the logarithmic coordinates because
![]() $\bar{\unicode[STIX]{x1D6E4}}=\bar{\unicode[STIX]{x1D6E4}}(k^{3}/9\unicode[STIX]{x1D70F})$
. (d) Total energy spectrum
$\bar{\unicode[STIX]{x1D6E4}}=\bar{\unicode[STIX]{x1D6E4}}(k^{3}/9\unicode[STIX]{x1D70F})$
. (d) Total energy spectrum
![]() $[F_{k}(\unicode[STIX]{x1D70F})+F_{-k}(\unicode[STIX]{x1D70F})]/2$
[see (3.30)].
$[F_{k}(\unicode[STIX]{x1D70F})+F_{-k}(\unicode[STIX]{x1D70F})]/2$
[see (3.30)].
The solution (5.27) is plotted in figure 1, which shows a pleasingly non-trivial shape. The essential result is, however, extremely simple. The solution is self-similar and could, in fact, have been obtained as such, by a shorter, if marginally less general, route (see appendix B). The similarity variable
![]() $k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}$
determines the demarcation of the phase space into two asymptotic regions: the asymptotic of the spectrum when
$k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}$
determines the demarcation of the phase space into two asymptotic regions: the asymptotic of the spectrum when
![]() $|k|\gg (9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{1/3}$
is (5.23) and the asymptotic when
$|k|\gg (9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{1/3}$
is (5.23) and the asymptotic when
![]() $\unicode[STIX]{x1D70F}\gg |k|^{3}/9\unicode[STIX]{x1D6FE}$
is (5.22) (this is particularly obvious in the second expression in (5.13)). The former describes fluctuations in the ‘wavenumber inertial range’ with a vanishing Hermite flux, the latter fluctuations in the ‘Hermite inertial range’, which also have zero Hermite flux. These scalings are illustrated in figure 2 and the normalised Hermite flux
$\unicode[STIX]{x1D70F}\gg |k|^{3}/9\unicode[STIX]{x1D6FE}$
is (5.22) (this is particularly obvious in the second expression in (5.13)). The former describes fluctuations in the ‘wavenumber inertial range’ with a vanishing Hermite flux, the latter fluctuations in the ‘Hermite inertial range’, which also have zero Hermite flux. These scalings are illustrated in figure 2 and the normalised Hermite flux
is plotted in figure 3(c).
![]() $\bar{\unicode[STIX]{x1D6E4}}$
is a good measure of how different the nonlinear state is from the linear one: for linear Landau-damped perturbations, we would have had
$\bar{\unicode[STIX]{x1D6E4}}$
is a good measure of how different the nonlinear state is from the linear one: for linear Landau-damped perturbations, we would have had
![]() $\bar{\unicode[STIX]{x1D6E4}}=1$
everywhere (Kanekar et al.
Reference Kanekar, Schekochihin, Dorland and Loureiro2015). Note that, as follows immediately from (5.27),
$\bar{\unicode[STIX]{x1D6E4}}=1$
everywhere (Kanekar et al.
Reference Kanekar, Schekochihin, Dorland and Loureiro2015). Note that, as follows immediately from (5.27),
![]() $\bar{\unicode[STIX]{x1D6E4}}=\bar{\unicode[STIX]{x1D6E4}}(k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})$
is a function of the similarity variable only.
$\bar{\unicode[STIX]{x1D6E4}}=\bar{\unicode[STIX]{x1D6E4}}(k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})$
is a function of the similarity variable only.
Another useful result is the overall Hermite spectrum integrated over all wavenumbers. While this, of course, misses the relationship between structure in position and velocity space that we have focused on so closely, it is a good crude measure of how ‘phase mixed’ the distribution is (cf. Hatch et al.
Reference Hatch, Jenko, Bratanov and Bañón Navarro2014; Servidio et al.
Reference Servidio, Chasapis, Matthaeus, Perrone, Valentini, Parashar, Veltri, Gershman, Russell and Giles2017). So, from (3.30) and (5.27), after integrating out the self-similar functional dependence of
![]() $F_{k}(\unicode[STIX]{x1D70F})$
on
$F_{k}(\unicode[STIX]{x1D70F})$
on
![]() $k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}$
, we deduce
$k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}$
, we deduce
This scaling – or, equivalently, the
![]() $k$
-by-
$k$
-by-
![]() $k$
$k$
![]() $C_{k,m}\propto m^{-3/2}$
scaling at large
$C_{k,m}\propto m^{-3/2}$
scaling at large
![]() $m$
(see (5.22)), – being steeper than
$m$
(see (5.22)), – being steeper than
![]() $m^{-1/2}$
, implies that our solution does indeed decay fast enough in
$m^{-1/2}$
, implies that our solution does indeed decay fast enough in
![]() $m$
in order for the collisional dissipation to vanish at vanishing collisionality and so treating the collisionless limit as non-singular was justified (see discussion in § 4.2).Footnote
7
Still, restoring finite
$m$
in order for the collisional dissipation to vanish at vanishing collisionality and so treating the collisionless limit as non-singular was justified (see discussion in § 4.2).Footnote
7
Still, restoring finite
![]() $\unicode[STIX]{x1D708}$
leads to a kind of ‘Kolmogorov scale’ for our kinetic turbulence and to a quantitative measure of the applicability, or otherwise, of the linear approximation, so we are going to do this in § 5.4.
$\unicode[STIX]{x1D708}$
leads to a kind of ‘Kolmogorov scale’ for our kinetic turbulence and to a quantitative measure of the applicability, or otherwise, of the linear approximation, so we are going to do this in § 5.4.
Finally, we may also calculate the overall wavenumber spectrum of the free energy: again integrating out the self-similar functional dependence of
![]() $F_{k}(\unicode[STIX]{x1D70F})$
, we get
$F_{k}(\unicode[STIX]{x1D70F})$
, we get
Since the total variance of the perturbed distribution function is conserved in the Kraichnan–Kazantsev model (see § 4.2), the above result can be made sense of as the classical Batchelor (Reference Batchelor1959) scaling of a passive scalar advected by a single-scale stochastic field.
5.4 Phase-space energy flows and role of collisions
The structure of our self-similar solution of (4.12) is, in fact, easily understood already by means of a qualitative examination of the equation, which is also a useful approach in evaluating the role of collisions. Figure 4 is a cartoon of phase-space energy flows in aid of the discussion that follows (cf. figure 3 a,b).
5.4.1 Phase-mixing region
The phase-mixing term dominates over the nonlinearity when
so the solution is independent of
![]() $\unicode[STIX]{x1D70F}$
in this region (see figure 3
b). This is the linear phase-mixing solution,
$\unicode[STIX]{x1D70F}$
in this region (see figure 3
b). This is the linear phase-mixing solution,
![]() $C_{k,m}\propto 1/\sqrt{m}$
, obtained earlier by Zocco & Schekochihin (Reference Zocco and Schekochihin2011) and Kanekar et al. (Reference Kanekar, Schekochihin, Dorland and Loureiro2015). Its wavenumber scaling,
$C_{k,m}\propto 1/\sqrt{m}$
, obtained earlier by Zocco & Schekochihin (Reference Zocco and Schekochihin2011) and Kanekar et al. (Reference Kanekar, Schekochihin, Dorland and Loureiro2015). Its wavenumber scaling,
![]() $F_{k}\propto 1/k^{2}$
, is, however, a new feature, extracting which required matching with other regions.
$F_{k}\propto 1/k^{2}$
, is, however, a new feature, extracting which required matching with other regions.
A way of making sense of this solution is to go back to the time-dependent (3.27) [or (4.6)] and notice that, for
![]() $k>0$
, whatever solution
$k>0$
, whatever solution
![]() $\tilde{f}_{k}$
(and, therefore,
$\tilde{f}_{k}$
(and, therefore,
![]() $F_{k}$
) exists at low
$F_{k}$
) exists at low
![]() $s$
, it will propagate ‘upwards’ (to higher
$s$
, it will propagate ‘upwards’ (to higher
![]() $s$
) along the characteristic
$s$
) along the characteristic
and it will do so unimpeded by the nonlinearity as long as the time
![]() $t$
is shorter than the nonlinear time
$t$
is shorter than the nonlinear time
![]() $t_{\text{nl}}$
associated with the mode-coupling term in the right-hand side of those equations. In the Kraichnan–Batchelor model,
$t_{\text{nl}}$
associated with the mode-coupling term in the right-hand side of those equations. In the Kraichnan–Batchelor model,
where
![]() $t_{\text{c}}$
is the correlation time of the wave field
$t_{\text{c}}$
is the correlation time of the wave field
![]() $\unicode[STIX]{x1D711}_{p}$
(effectively assumed to be single scale). Requiring
$\unicode[STIX]{x1D711}_{p}$
(effectively assumed to be single scale). Requiring
![]() $t\ll t_{\text{nl}}$
in (5.32), we see that the phase-mixing region of the phase space extends to
$t\ll t_{\text{nl}}$
in (5.32), we see that the phase-mixing region of the phase space extends to
![]() $s^{3}\ll k^{3}/\unicode[STIX]{x1D6FE}$
, which is the same as the condition in (5.31).
$s^{3}\ll k^{3}/\unicode[STIX]{x1D6FE}$
, which is the same as the condition in (5.31).
This gives us a way to estimate how small the wave amplitude must be in order for the nonlinearity and associated effects never to matter: indeed, if the collision time is short compared to the nonlinear time,
the phase-mixed distribution function will thermalise before the echo can bring any energy back from phase space. Putting
![]() $t_{\unicode[STIX]{x1D708}}$
into (5.32) tells us how far into phase space energy will travel:
$t_{\unicode[STIX]{x1D708}}$
into (5.32) tells us how far into phase space energy will travel:
Perhaps the most practically important conclusion from this is that, given the strength of the electric field and, therefore, via (5.33), the value of
![]() $\unicode[STIX]{x1D6FE}$
, we can predict the collisional cutoff wavenumber
$\unicode[STIX]{x1D6FE}$
, we can predict the collisional cutoff wavenumber
![]() $k_{\unicode[STIX]{x1D708}}$
, given by (5.34), at which phase mixing (Landau damping) curtails the universal spectrum that we have derived above: we shall see in a moment that for
$k_{\unicode[STIX]{x1D708}}$
, given by (5.34), at which phase mixing (Landau damping) curtails the universal spectrum that we have derived above: we shall see in a moment that for
![]() $k\gg k_{\unicode[STIX]{x1D708}}$
,
$k\gg k_{\unicode[STIX]{x1D708}}$
,
![]() $\bar{\unicode[STIX]{x1D6E4}}=1$
, i.e. there is no echo flux from high to low Hermite moments.
$\bar{\unicode[STIX]{x1D6E4}}=1$
, i.e. there is no echo flux from high to low Hermite moments.
5.4.2 Diffusion and echo regions
Considering the limit opposite to (5.31), i.e. the region of phase space where
![]() $s\gg kt_{\text{nl}}$
, we get
$s\gg kt_{\text{nl}}$
, we get
i.e.
![]() $k$
-space diffusion dominates. Our self-similar solution (§ 5.3.2) tells us that the appropriate solution in this region is one independent of
$k$
-space diffusion dominates. Our self-similar solution (§ 5.3.2) tells us that the appropriate solution in this region is one independent of
![]() $k$
(see figure 3
a,b) and
$k$
(see figure 3
a,b) and
![]() $F_{k}(\unicode[STIX]{x1D70F})\propto 1/\unicode[STIX]{x1D70F}^{2/3}$
. This solution takes whatever values
$F_{k}(\unicode[STIX]{x1D70F})\propto 1/\unicode[STIX]{x1D70F}^{2/3}$
. This solution takes whatever values
![]() $F_{k}(\unicode[STIX]{x1D70F})$
has at
$F_{k}(\unicode[STIX]{x1D70F})$
has at
![]() $k\sim (\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{1/3}$
(figure 3
b) and transfers them across to
$k\sim (\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{1/3}$
(figure 3
b) and transfers them across to
![]() $k\sim -(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{1/3}$
(figure 3
a), where anti-phase-mixing picks them up and transfers them ‘downwards’ to low Hermite moments (
$k\sim -(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F})^{1/3}$
(figure 3
a), where anti-phase-mixing picks them up and transfers them ‘downwards’ to low Hermite moments (
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
), over times that are again shorter than
$\unicode[STIX]{x1D70F}\rightarrow 0$
), over times that are again shorter than
![]() $t_{\text{nl}}$
(because
$t_{\text{nl}}$
(because
![]() $\unicode[STIX]{x1D70F}\ll |k^{3}|/\unicode[STIX]{x1D6FE}$
again), along the characteristic
$\unicode[STIX]{x1D70F}\ll |k^{3}|/\unicode[STIX]{x1D6FE}$
again), along the characteristic
where
![]() $s_{0}\sim \unicode[STIX]{x1D70F}_{0}^{1/3}\sim |k|/\unicode[STIX]{x1D6FE}^{1/3}$
.
$s_{0}\sim \unicode[STIX]{x1D70F}_{0}^{1/3}\sim |k|/\unicode[STIX]{x1D6FE}^{1/3}$
.
This last piece of the solution is the echo flux. It cancels the phase-mixing flux exactly, provided the energy (
![]() $F_{k}$
) from
$F_{k}$
) from
![]() $k>0$
has been successfully transferred by phase mixing from
$k>0$
has been successfully transferred by phase mixing from
![]() $\unicode[STIX]{x1D70F}=0$
to
$\unicode[STIX]{x1D70F}=0$
to
![]() $\unicode[STIX]{x1D70F}\sim k^{3}/\unicode[STIX]{x1D6FE}$
to be picked up by diffusion and carried over to the anti-phase-mixing region
$\unicode[STIX]{x1D70F}\sim k^{3}/\unicode[STIX]{x1D6FE}$
to be picked up by diffusion and carried over to the anti-phase-mixing region
![]() $k<0$
. For
$k<0$
. For
![]() $k\gg k_{\unicode[STIX]{x1D708}}$
, the energy gets intercepted at
$k\gg k_{\unicode[STIX]{x1D708}}$
, the energy gets intercepted at
![]() $\unicode[STIX]{x1D70F}\sim k/\unicode[STIX]{x1D708}$
[see (5.35)] and thermalised by collisions, so at
$\unicode[STIX]{x1D70F}\sim k/\unicode[STIX]{x1D708}$
[see (5.35)] and thermalised by collisions, so at
![]() $\unicode[STIX]{x1D70F}\sim k^{3}/\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D70F}\sim k^{3}/\unicode[STIX]{x1D6FE}$
,
![]() $F_{k}(\unicode[STIX]{x1D70F})=0$
. This then gives
$F_{k}(\unicode[STIX]{x1D70F})=0$
. This then gives
![]() $F_{-k}(0)=0$
, i.e. no echo flux. Thus,
$F_{-k}(0)=0$
, i.e. no echo flux. Thus,
![]() $k_{\unicode[STIX]{x1D708}}$
is indeed the wavenumber cutoff – a kind of ‘Kolmogorov scale’ for Vlasov-kinetic turbulence – beyond which Landau damping can act as an efficient route to (eventually collisional) dissipation.
$k_{\unicode[STIX]{x1D708}}$
is indeed the wavenumber cutoff – a kind of ‘Kolmogorov scale’ for Vlasov-kinetic turbulence – beyond which Landau damping can act as an efficient route to (eventually collisional) dissipation.
6 Discussion
6.1 Summary
We have considered what is arguably the simplest kinetic turbulence problem available: a 1-D Vlasov–Poisson (§ 2.1; or Vlasov–Boltzmann: see § 2.2) plasma with an energy source. When collisions are vanishingly weak, this gives rise to interesting dynamics across the 2-D (position and velocity) phase space. In a simple approximation where the stochastic electric field mixing the particle distribution can be assumed to have statistics independent of the high-order moments of this distribution, a solvable model can be constructed in the same vein as the Kraichnan–Batchelor model used in the passive-scalar problem. The resulting analytical solution displays the same key features as have been surmised heuristically (Schekochihin et al. Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016) and found numerically (Parker et al. Reference Parker, Highcock, Schekochihin and Dellar2016) for plasma systems with higher-dimensional phase spaces (see § 6.2.5).
Namely, the free-energy flux from low to high Hermite moments is suppressed – i.e. the dissipation channel associated with Landau damping is shut down – for all wavenumbers below a certain cutoff
![]() $k_{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D708})^{1/2}$
(see § 5.4). This cutoff is a kinetic analogue of the Kolmogorov scale: it scales inversely with the collision rate
$k_{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D708})^{1/2}$
(see § 5.4). This cutoff is a kinetic analogue of the Kolmogorov scale: it scales inversely with the collision rate
![]() $\unicode[STIX]{x1D708}$
and increases with the amplitude of the electric perturbations – the latter determines
$\unicode[STIX]{x1D708}$
and increases with the amplitude of the electric perturbations – the latter determines
![]() $\unicode[STIX]{x1D6FE}$
, which is the rate of diffusion of the free energy in
$\unicode[STIX]{x1D6FE}$
, which is the rate of diffusion of the free energy in
![]() $k$
space due to the stochastic electric field. Thus, one might expect a kind of statistical ‘fluidisation’ of the turbulence in the ‘inertial range’ (
$k$
space due to the stochastic electric field. Thus, one might expect a kind of statistical ‘fluidisation’ of the turbulence in the ‘inertial range’ (
![]() $k\ll k_{\unicode[STIX]{x1D708}}$
) – perhaps a welcome development from the point of view of the long history of attempts to reduce kinetics to fluid (or ‘Landau-fluid’) dynamics (see references and further discussion in § 6.2.4).
$k\ll k_{\unicode[STIX]{x1D708}}$
) – perhaps a welcome development from the point of view of the long history of attempts to reduce kinetics to fluid (or ‘Landau-fluid’) dynamics (see references and further discussion in § 6.2.4).
Expanding our interest beyond the effect of phase-space turbulence on the low (‘fluid’) moments of the distribution function and to the structure of this turbulence across the (Fourier–Hermite) phase space, we find the latter cleanly partitioned into two regions: (i) the phase-mixing region
![]() $k\gtrsim \unicode[STIX]{x1D6FE}^{1/3}\sqrt{m}$
, where phase mixing and anti-phase-mixing transfer free energy between lower and higher Hermite moments (cancelling on average), and (ii) the mode-coupling (or diffusion) region
$k\gtrsim \unicode[STIX]{x1D6FE}^{1/3}\sqrt{m}$
, where phase mixing and anti-phase-mixing transfer free energy between lower and higher Hermite moments (cancelling on average), and (ii) the mode-coupling (or diffusion) region
![]() $k\lesssim \unicode[STIX]{x1D6FE}^{1/3}\sqrt{m}$
, where the free energy is transferred between spatial scales (wave numbers) by the advecting action of the stochastic electric field. An overview of how this happens is provided in § 5.4 and figure 4, while the Fourier–Hermite spectrum is derived more formally in § 5 (summarised in § 5.3.2). The resulting scalings are
$k\lesssim \unicode[STIX]{x1D6FE}^{1/3}\sqrt{m}$
, where the free energy is transferred between spatial scales (wave numbers) by the advecting action of the stochastic electric field. An overview of how this happens is provided in § 5.4 and figure 4, while the Fourier–Hermite spectrum is derived more formally in § 5 (summarised in § 5.3.2). The resulting scalings are
 $$\begin{eqnarray}C_{m,k}\sim \left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}^{2/3}m^{3/2}}, & \displaystyle k\lesssim \unicode[STIX]{x1D6FE}^{1/3}\sqrt{m},\quad m\ll \frac{\unicode[STIX]{x1D6FE}^{1/3}}{\unicode[STIX]{x1D708}},\\ \displaystyle \frac{1}{k^{2}\sqrt{m}}, & \displaystyle \unicode[STIX]{x1D6FE}^{1/3}\sqrt{m}\lesssim k\ll k_{\unicode[STIX]{x1D708}}=\left(\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D708}}\right)^{1/2}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}C_{m,k}\sim \left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}^{2/3}m^{3/2}}, & \displaystyle k\lesssim \unicode[STIX]{x1D6FE}^{1/3}\sqrt{m},\quad m\ll \frac{\unicode[STIX]{x1D6FE}^{1/3}}{\unicode[STIX]{x1D708}},\\ \displaystyle \frac{1}{k^{2}\sqrt{m}}, & \displaystyle \unicode[STIX]{x1D6FE}^{1/3}\sqrt{m}\lesssim k\ll k_{\unicode[STIX]{x1D708}}=\left(\frac{\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D708}}\right)^{1/2}.\end{array}\right.\end{eqnarray}$$
6.2 Open issues
There are a number of questions and lines of investigation that all this leaves open. The more immediate and obvious of them are, naturally, to do with how universal these results are, given the radical nature of the approximations that were made in order to obtain them, and how they can be made more general and more applicable to concrete physical problems. Let us itemise these questions briefly.
6.2.1 Multiscale electric fields
What happens outside Batchelor’s approximation (§ 4.3), i.e. when the stochastic electric field cannot be treated as effectively single scale and, therefore, as providing a diffusively accumulating series of small kicks in
![]() $k$
space to the perturbed distribution function? Formally, dealing with this issue is a matter of solving the integral equation (4.7), rather than the differential equation (4.12). A certain (limited) amount of progress on this is made in appendix A, suggesting somewhat steeper wavenumber spectra in the mode-coupling region. While we do not have the full solution, it appears plausible that, even though scalings might change, the overall partitioning of the phase space into (anti-)phase-mixing-dominated and mode-coupling-dominated regions should persist and the Landau damping would still be suppressed. In fact, the conversion between phase-mixing and anti-phase-mixing modes may be quicker in this case than in Batchelor’s limit because the steps in
$k$
space to the perturbed distribution function? Formally, dealing with this issue is a matter of solving the integral equation (4.7), rather than the differential equation (4.12). A certain (limited) amount of progress on this is made in appendix A, suggesting somewhat steeper wavenumber spectra in the mode-coupling region. While we do not have the full solution, it appears plausible that, even though scalings might change, the overall partitioning of the phase space into (anti-)phase-mixing-dominated and mode-coupling-dominated regions should persist and the Landau damping would still be suppressed. In fact, the conversion between phase-mixing and anti-phase-mixing modes may be quicker in this case than in Batchelor’s limit because the steps in
![]() $k$
space need not be as small as in the diffusive regime (cf. Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016).
$k$
space need not be as small as in the diffusive regime (cf. Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016).
6.2.2 Finite-time-correlated electric fields
What happens outside Krachnan’s approximation (§ 4.1), i.e. if the assumption of a short correlation time of the electric field is relaxed? The experience of passive-advection problems in fluid dynamics (see, e.g. Antonsen et al. Reference Antonsen, Fan, Ott and Garcia-Lopez1996; Bhat & Subramanian Reference Bhat and Subramanian2015) suggests that generalising from white to finite-time-correlated advecting field rarely leads to dramatic qualitative changes. In the context of plasma kinetics, however, the limit, opposite to ours, of a long correlation time of the electric field clearly requires special care to capture the phase-space structure that will arise due to particle-trapping effects (Bernstein, Greene & Kruskal Reference Bernstein, Greene and Kruskal1957; O’Neil Reference O’Neil1965; Manheimer Reference Manheimer1971; O’Neil, Winfrey & Malmberg Reference O’Neil, Winfrey and Malmberg1971).
6.2.3 Self-consistent electric fields
How does one construct a fully nonlinear theory of kinetic turbulence, i.e. one in which the stochastic electric field is not prescribed but is determined self-consistently? This requires coupling the high-
![]() $m$
dynamics to the low-
$m$
dynamics to the low-
![]() $m$
‘fluid’ equations derived in § 3.1, i.e. one would have to progress from the vague understanding that the flux to/from high Hermite moments is suppressed to a more quantitative model of how this suppression can be incorporated into a dynamical (‘Landau fluid’; § 6.2.4) or, more likely, statistical model of the low-
$m$
‘fluid’ equations derived in § 3.1, i.e. one would have to progress from the vague understanding that the flux to/from high Hermite moments is suppressed to a more quantitative model of how this suppression can be incorporated into a dynamical (‘Landau fluid’; § 6.2.4) or, more likely, statistical model of the low-
![]() $m$
moments (and how many of them must be kept). Once this is done, it becomes possible to assess to what extent a self-consistent electric field can be compatible with the modelling choices made above: the Batchelor (single scale) and Kraichnan (short correlation time) approximations.
$m$
moments (and how many of them must be kept). Once this is done, it becomes possible to assess to what extent a self-consistent electric field can be compatible with the modelling choices made above: the Batchelor (single scale) and Kraichnan (short correlation time) approximations.
Without claiming to have such a theory, let us offer a few naïve but plausible estimates. Taking the limit of our solution at low
![]() $m$
[the second asymptotic in (6.1)], we find a
$m$
[the second asymptotic in (6.1)], we find a
![]() $k^{-2}$
spectrum. Let us conjecture that this spectrum is established in phase space and imposes itself, via the linear Hermite coupling term in (3.10), on the lower Hermite moments.Footnote
8
So, starting with (3.10) for
$k^{-2}$
spectrum. Let us conjecture that this spectrum is established in phase space and imposes itself, via the linear Hermite coupling term in (3.10), on the lower Hermite moments.Footnote
8
So, starting with (3.10) for
![]() $m=3$
, we may predictFootnote
9
$m=3$
, we may predictFootnote
9
From the wave equation (3.12) and in view of (3.11), we may estimate
Note that, regardless of the size of
![]() $\unicode[STIX]{x1D6FC}_{k}$
,
$\unicode[STIX]{x1D6FC}_{k}$
,
![]() $n_{k}$
is always either much smaller than or comparable to
$n_{k}$
is always either much smaller than or comparable to
![]() $\unicode[STIX]{x1D703}_{k}$
. Therefore,
$\unicode[STIX]{x1D703}_{k}$
. Therefore,
![]() $T_{k}=\unicode[STIX]{x1D703}_{k}+2n_{k}$
in (6.2) can be replaced by
$T_{k}=\unicode[STIX]{x1D703}_{k}+2n_{k}$
in (6.2) can be replaced by
![]() $\unicode[STIX]{x1D703}_{k}$
for the purposes of these crude estimates. This gives us a prediction for the spectra of the ‘wave quantities’:
$\unicode[STIX]{x1D703}_{k}$
for the purposes of these crude estimates. This gives us a prediction for the spectra of the ‘wave quantities’:
At wavenumbers where, in (3.6), the self-consistent term (
![]() $\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D711}_{k}$
) dominates over the ‘external’ one (
$\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D711}_{k}$
) dominates over the ‘external’ one (
![]() $\unicode[STIX]{x1D712}_{k}$
), the electric-field spectrum is
$\unicode[STIX]{x1D712}_{k}$
), the electric-field spectrum is
This tells us that, for example, for Vlasov–Poisson perturbations with
![]() $k\unicode[STIX]{x1D706}_{\text{D}e}\gg 1$
and
$k\unicode[STIX]{x1D706}_{\text{D}e}\gg 1$
and
![]() $\unicode[STIX]{x1D6FC}_{k}=2/k^{2}$
(see § 2.1), we should have
$\unicode[STIX]{x1D6FC}_{k}=2/k^{2}$
(see § 2.1), we should have
![]() $\langle |E_{k}|^{2}\rangle \sim k^{-4}$
, which is a steep enough scaling to justify Batchelor’s approximation.Footnote
10
In contrast, if
$\langle |E_{k}|^{2}\rangle \sim k^{-4}$
, which is a steep enough scaling to justify Batchelor’s approximation.Footnote
10
In contrast, if
![]() $\unicode[STIX]{x1D6FC}_{k}$
is a constant (ion-acoustic perturbations; see §§ 2.2 and 2.3), the self-consistent
$\unicode[STIX]{x1D6FC}_{k}$
is a constant (ion-acoustic perturbations; see §§ 2.2 and 2.3), the self-consistent
![]() $\langle |E_{k}|^{2}\rangle$
is flat (cutoff at
$\langle |E_{k}|^{2}\rangle$
is flat (cutoff at
![]() $k\sim k_{\unicode[STIX]{x1D708}}$
) and our model can only work if the external potential
$k\sim k_{\unicode[STIX]{x1D708}}$
) and our model can only work if the external potential
![]() $\unicode[STIX]{x1D712}_{k}$
plays the dominant part in the nonlinear mode coupling (in the case of ion-scale Zakharov turbulence, § 2.3, this might be a credible possibility as
$\unicode[STIX]{x1D712}_{k}$
plays the dominant part in the nonlinear mode coupling (in the case of ion-scale Zakharov turbulence, § 2.3, this might be a credible possibility as
![]() $\unicode[STIX]{x1D712}_{k}$
is fed by the fast-oscillating electric fields that satisfy an electron-time-scale fluid-like equation and have a tendency to form a large-scale condensate; see Zakharov Reference Zakharov1972 and the reviews cited in § 2.3).
$\unicode[STIX]{x1D712}_{k}$
is fed by the fast-oscillating electric fields that satisfy an electron-time-scale fluid-like equation and have a tendency to form a large-scale condensate; see Zakharov Reference Zakharov1972 and the reviews cited in § 2.3).
Finally, if one is interested in the stochastic-acceleration problem (
![]() $\unicode[STIX]{x1D6FC}_{k}=0$
; § 2.4), the electric field need not be self-consistent and the conclusion from the above considerations is that particles stochastically accelerated by a short-time-correlated electric field cutoff above wavenumber
$\unicode[STIX]{x1D6FC}_{k}=0$
; § 2.4), the electric field need not be self-consistent and the conclusion from the above considerations is that particles stochastically accelerated by a short-time-correlated electric field cutoff above wavenumber
![]() $p$
will develop
$p$
will develop
![]() $k^{-2}$
density, velocity, temperature, etc. spectra at
$k^{-2}$
density, velocity, temperature, etc. spectra at
![]() $k\gg p$
. This appears to be a new result.
$k\gg p$
. This appears to be a new result.
The above discussion should probably not satisfy a discerning reader: clearly, there is much to be done before the link between the ‘kinetic’ and ‘fluid’ moments is established in an analytically solid and quantitative way.
6.2.4 Implications for Landau-fluid closures
The question of what constitutes a quantitatively accurate closure scheme for the first few fluid moments of a kinetic plasma system has been studied in some detail, both analytically and numerically, in the framework of ‘Landau-fluid’ closures (Hammett & Perkins Reference Hammett and Perkins1990; Hammett, Dorland & Perkins Reference Hammett, Dorland and Perkins1992; Dorland & Hammett Reference Dorland and Hammett1993; Hammett et al.
Reference Hammett, Beer, Dorland, Cowley and Smith1993; Beer & Hammett Reference Beer and Hammett1996; Smith Reference Smith1997; Snyder, Hammett & Dorland Reference Snyder, Hammett and Dorland1997; Passot & Sulem Reference Passot and Sulem2004; Goswami, Passot & Sulem Reference Goswami, Passot and Sulem2005; Tassi, Sulem & Passot Reference Tassi, Sulem and Passot2016; Passot, Sulem & Tassi Reference Passot, Sulem and Tassi2017) and, indeed, by their detractors (e.g. Mattor Reference Mattor1992; Weiland Reference Weiland1992). A crude view of the philosophy behind this approach is that linear Landau-damping rates are incorporated explicitly into low-
![]() $m$
fluid equations to model the energy removal process into higher-order moments. This might appear to be inconsistent with the notion, advocated by us, that phase mixing is cancelled by anti-phase-mixing and thus Landau damping is effectively suppressed as a route to thermalisation of the low-
$m$
fluid equations to model the energy removal process into higher-order moments. This might appear to be inconsistent with the notion, advocated by us, that phase mixing is cancelled by anti-phase-mixing and thus Landau damping is effectively suppressed as a route to thermalisation of the low-
![]() $m$
energy. However, the situation is, in fact, more nuanced.
$m$
energy. However, the situation is, in fact, more nuanced.
It was understood already in the course of development of early Landau-fluid models that their performance improves if more fluid moments are included. It was also understood that the cause of this improvement is that nonlinearities in those fluid equations act to reduce the phase-mixing rate to higher-order ‘unresolved’ moments (Beer & Hammett Reference Beer and Hammett1996; Smith Reference Smith1997). It seems plausible that keeping the ‘right’ number of moments is tantamount to keeping enough
![]() $m$
’s to enable the system to have enough anti-phase-mixing to capture the cancellation effect reasonably well – and that if the truncation is done at some
$m$
’s to enable the system to have enough anti-phase-mixing to capture the cancellation effect reasonably well – and that if the truncation is done at some
![]() $m$
that is still smaller than the
$m$
that is still smaller than the
![]() $m$
at which the flux into higher-order moments is fully cancelled (which will depend on
$m$
at which the flux into higher-order moments is fully cancelled (which will depend on
![]() $k$
), some form of Landau-fluid closure may be adequate to mop up the residual flux.
$k$
), some form of Landau-fluid closure may be adequate to mop up the residual flux.
Furthermore, if the cutoff scale
![]() $k_{\unicode[STIX]{x1D708}}$
is finite, i.e. if the collision rate is sufficiently large (equivalently, the velocity-space resolution of a code is limited) and/or the fluctuation amplitude is sufficiently small, the dissipation at
$k_{\unicode[STIX]{x1D708}}$
is finite, i.e. if the collision rate is sufficiently large (equivalently, the velocity-space resolution of a code is limited) and/or the fluctuation amplitude is sufficiently small, the dissipation at
![]() $k\gtrsim k_{\unicode[STIX]{x1D708}}$
should be perfectly well described by the Landau rate corresponding to those
$k\gtrsim k_{\unicode[STIX]{x1D708}}$
should be perfectly well described by the Landau rate corresponding to those
![]() $k$
(see § 5.4). We also saw (figure 3
c) that, at least in our model, cancellation of the Hermite flux required
$k$
(see § 5.4). We also saw (figure 3
c) that, at least in our model, cancellation of the Hermite flux required
![]() $k\gg p$
, i.e. worked in the ‘inertial range’ (
$k\gg p$
, i.e. worked in the ‘inertial range’ (
![]() $p\ll k\ll k_{\unicode[STIX]{x1D708}}$
), rather than at the ‘energy-containing scale’ of the turbulence. It is easy to imagine situations (e.g. in near-marginal tokamak turbulence) in which the scale separation between
$p\ll k\ll k_{\unicode[STIX]{x1D708}}$
), rather than at the ‘energy-containing scale’ of the turbulence. It is easy to imagine situations (e.g. in near-marginal tokamak turbulence) in which the scale separation between
![]() $p$
and
$p$
and
![]() $k_{\unicode[STIX]{x1D708}}$
might not be large.
$k_{\unicode[STIX]{x1D708}}$
might not be large.
Thus, the usefulness of Landau-fluid closures, judiciously applied, is not obviated by the stochastic-echo effect – but it is clearly an interesting topic for exploration how the type of results reported above might help one hone these closures with this effect explicitly in one’s sights.
6.2.5 Three dimensions
What happens when the system is allowed to be three-dimensional in both velocity and position space?
In magnetised, drift-kinetic plasmas, this, in fact, brings in only one extra phase-space variable (
![]() $k_{\bot }$
in addition to
$k_{\bot }$
in addition to
![]() $k_{\Vert }$
, all statistics being isotropic in the plane perpendicular to the magnetic field); phase mixing in drift kinetics is only in
$k_{\Vert }$
, all statistics being isotropic in the plane perpendicular to the magnetic field); phase mixing in drift kinetics is only in
![]() $v_{\Vert }$
, so there is only one velocity-space dimension – provided the equilibrium is isotropic (if it is not, there is also phase-mixing in
$v_{\Vert }$
, so there is only one velocity-space dimension – provided the equilibrium is isotropic (if it is not, there is also phase-mixing in
![]() $v_{\bot }$
; see Dorland & Hammett Reference Dorland and Hammett1993, Mandell, Dorland & Landreman Reference Mandell, Dorland and Landreman2017). The nonlinearity in a magnetised plasma is of a more traditional ‘fluid’ type, viz., it is the advection of
$v_{\bot }$
; see Dorland & Hammett Reference Dorland and Hammett1993, Mandell, Dorland & Landreman Reference Mandell, Dorland and Landreman2017). The nonlinearity in a magnetised plasma is of a more traditional ‘fluid’ type, viz., it is the advection of
![]() $\unicode[STIX]{x1D6FF}f$
by turbulent
$\unicode[STIX]{x1D6FF}f$
by turbulent
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flows. A certain amount of progress has been made (Hatch et al.
Reference Hatch, Jenko, Bratanov and Bañón Navarro2014; Kanekar Reference Kanekar2015; Parker et al.
Reference Parker, Highcock, Schekochihin and Dellar2016; Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016) and is being made with this problem in application both to laboratory-inspired turbulence models and to the solar wind.
$\boldsymbol{E}\times \boldsymbol{B}$
flows. A certain amount of progress has been made (Hatch et al.
Reference Hatch, Jenko, Bratanov and Bañón Navarro2014; Kanekar Reference Kanekar2015; Parker et al.
Reference Parker, Highcock, Schekochihin and Dellar2016; Schekochihin et al.
Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016) and is being made with this problem in application both to laboratory-inspired turbulence models and to the solar wind.
At scales where the finite size of particles’ Larmor orbits is felt, this triggers vigorous nonlinear phase mixing in
![]() $v_{\bot }$
: the ‘entropy cascade’ introduced by Schekochihin et al. (Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Plunk, Quataert and Tatsuno2008, Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009) (but anticipated already by Dorland & Hammett Reference Dorland and Hammett1993) and first numerically diagnosed by Tatsuno et al. (Reference Tatsuno, Dorland, Schekochihin, Plunk, Barnes, Cowley and Howes2009) and Bañón Navarro et al. (Reference Bañón Navarro, Morel, Albrecht-Marc, Carati, Merz, Görler and Jenko2011) (see also Kawamori Reference Kawamori2013, who claims experimental confirmation). Thus, gyrokinetic turbulence has a 5-D phase space. Outside the gyrokinetic approximation, at high frequencies (comparable and exceeding the Larmor frequencies of the particles), the phase space finally becomes six-dimensional, as the distribution function can develop structure also in the gyroangle.
$v_{\bot }$
: the ‘entropy cascade’ introduced by Schekochihin et al. (Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Plunk, Quataert and Tatsuno2008, Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009) (but anticipated already by Dorland & Hammett Reference Dorland and Hammett1993) and first numerically diagnosed by Tatsuno et al. (Reference Tatsuno, Dorland, Schekochihin, Plunk, Barnes, Cowley and Howes2009) and Bañón Navarro et al. (Reference Bañón Navarro, Morel, Albrecht-Marc, Carati, Merz, Görler and Jenko2011) (see also Kawamori Reference Kawamori2013, who claims experimental confirmation). Thus, gyrokinetic turbulence has a 5-D phase space. Outside the gyrokinetic approximation, at high frequencies (comparable and exceeding the Larmor frequencies of the particles), the phase space finally becomes six-dimensional, as the distribution function can develop structure also in the gyroangle.
In a recent promising development, the first harbinger has appeared (Servidio et al. Reference Servidio, Chasapis, Matthaeus, Perrone, Valentini, Parashar, Veltri, Gershman, Russell and Giles2017) of a stage in spacecraft exploration of plasma turbulence in the Earth’s magnetosphere and the solar wind when 3-D Hermite spectra (and, perhaps, 6-D Hermite–Fourier ones) become measurable and thus so much more attractive as a subject for theoretical prediction, now falsifiable (and not necessarily just Hermite spectra; see Howes, Klein & Li Reference Howes, Klein and Li2017 and Klein, Howes & Tenbarge Reference Klein, Howes and Tenbarge2017).
This is a good note to finish on: phase-space turbulence as a new frontier for observation and measurement, as well as theory – for we must hope that the phenomena that are revealed by simple solvable models of kinetic turbulence are not just interesting or aesthetically pleasing but also real.
Acknowledgements
We are grateful to T. Antonsen, F. Califano, P. Dellar, R. Meyrand, J. Parker, D. Ryutov, J. Squire and L. Stipani for discussions of this and related problems, and especially to W. Dorland and G. Hammett, who offered detailed comments on the manuscript. T.A.’s work was supported by the R. Peierls Centre’s and Merton College’s undergraduate summer research bursary schemes. A.A.S.’s work was supported in part by grants from UK STFC and EPSRC. Both authors gratefully acknowledge the hospitality of the Wolfgang Pauli Institute, University of Vienna, where a significant part of this research was performed.
Appendix A. Solutions of (4.7) and the Batchelor approximation
Here we explore how the solutions of (4.7) might change if the electric-field correlation function
![]() $K_{p}=p^{2}\unicode[STIX]{x1D718}_{p}$
does not decay quickly enough in order for the Batchelor approximation [i.e. the expansion (4.11)] to be legitimate – and also under what condition on
$K_{p}=p^{2}\unicode[STIX]{x1D718}_{p}$
does not decay quickly enough in order for the Batchelor approximation [i.e. the expansion (4.11)] to be legitimate – and also under what condition on
![]() $K_{p}$
it is legitimate. Even if it cannot be turned into a differential operator, the mode-coupling integral in the right-hand side of (4.7) will, qualitatively, still provide a kind of smoothing effect in
$K_{p}$
it is legitimate. Even if it cannot be turned into a differential operator, the mode-coupling integral in the right-hand side of (4.7) will, qualitatively, still provide a kind of smoothing effect in
![]() $k$
space (in the Batchelor limit, this was diffusion) and transfer
$k$
space (in the Batchelor limit, this was diffusion) and transfer
![]() $F_{k}$
from positive to negative wavenumbers, causing anti-phase-mixing. One might again expect that this mode-coupling term will dominate over the phase-mixing term,
$F_{k}$
from positive to negative wavenumbers, causing anti-phase-mixing. One might again expect that this mode-coupling term will dominate over the phase-mixing term,
![]() $k\unicode[STIX]{x2202}F_{k}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}$
, at sufficiently small
$k\unicode[STIX]{x2202}F_{k}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}$
, at sufficiently small
![]() $k$
and sufficiently large
$k$
and sufficiently large
![]() $\unicode[STIX]{x1D70F}$
, whereas in the opposite limit, the phase mixing (or anti-phase-mixing) will simply transfer energy ‘vertically’ in the
$\unicode[STIX]{x1D70F}$
, whereas in the opposite limit, the phase mixing (or anti-phase-mixing) will simply transfer energy ‘vertically’ in the
![]() $(k,\unicode[STIX]{x1D70F})$
plane (analogously to figure 4). The solutions of (4.7) in the mode-coupling-dominated region will then be such functions
$(k,\unicode[STIX]{x1D70F})$
plane (analogously to figure 4). The solutions of (4.7) in the mode-coupling-dominated region will then be such functions
![]() $F_{k}$
that the right-hand side of (4.7) vanishes.
$F_{k}$
that the right-hand side of (4.7) vanishes.
It is convenient to write this as follows, converting the wavenumber sum into an integral
Let us assume that
![]() $K_{p}\propto |p|^{\unicode[STIX]{x1D6FC}}$
and
$K_{p}\propto |p|^{\unicode[STIX]{x1D6FC}}$
and
![]() $F_{k}\propto |k|^{\unicode[STIX]{x1D6FD}}$
. Scaling out
$F_{k}\propto |k|^{\unicode[STIX]{x1D6FD}}$
. Scaling out
![]() $|k|^{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}+1}$
and changing the integration variable to
$|k|^{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}+1}$
and changing the integration variable to
![]() $\unicode[STIX]{x1D709}=q/|k|$
, we find that the above integral is proportional to
$\unicode[STIX]{x1D709}=q/|k|$
, we find that the above integral is proportional to
The change of variables
![]() $\unicode[STIX]{x1D702}=1/\unicode[STIX]{x1D709}$
(a 1-D Zakharov transformation; see Zakharov, L’vov & Falkovich Reference Zakharov, L’vov and Falkovich1992) turns this integral into
$\unicode[STIX]{x1D702}=1/\unicode[STIX]{x1D709}$
(a 1-D Zakharov transformation; see Zakharov, L’vov & Falkovich Reference Zakharov, L’vov and Falkovich1992) turns this integral into
This is just
![]() $-I$
and so
$-I$
and so
![]() $I=-I=0$
, as required, if
$I=-I=0$
, as required, if
This is the desired solution satisfying (A 1). It is only valid provided the integral
![]() $I$
converges, the conditions for which are
$I$
converges, the conditions for which are
Otherwise, the integral (A 1) is dominated by what happens at the low- or high-wavenumber cutoffs or at
![]() $|p|=|k-q|\ll |k|$
(i.e.
$|p|=|k-q|\ll |k|$
(i.e.
![]() $\unicode[STIX]{x1D709}\approx 1$
).
$\unicode[STIX]{x1D709}\approx 1$
).
The latter wavenumber range (
![]() $|p|\ll |k|$
) takes over the integral (A 1) for
$|p|\ll |k|$
) takes over the integral (A 1) for
![]() $\unicode[STIX]{x1D6FC}\leqslant -2$
. This corresponds to the flat solution (
$\unicode[STIX]{x1D6FC}\leqslant -2$
. This corresponds to the flat solution (
![]() $\unicode[STIX]{x1D6FD}=0$
) at
$\unicode[STIX]{x1D6FD}=0$
) at
![]() $|k|\lesssim |p|$
that was derived in § 4.4 and that at
$|k|\lesssim |p|$
that was derived in § 4.4 and that at
![]() $|k|\gg |p|$
transitions seamlessly into the Batchelor-limit solution worked out in § 5 (or appendix B). Thus, the condition of validity of the Batchelor approximation is that
$|k|\gg |p|$
transitions seamlessly into the Batchelor-limit solution worked out in § 5 (or appendix B). Thus, the condition of validity of the Batchelor approximation is that
![]() $K_{p}$
must certainly decay more steeply than
$K_{p}$
must certainly decay more steeply than
![]() $|p|^{-2}$
.
$|p|^{-2}$
.
Whether the shallow power-law solutions (A 4) have any interesting physical applications remains to be seen. Presumably, they indicate that when the Batchelor approximation is broken, the
![]() $k$
spectrum in the mode-coupling-dominated region becomes a little steeper than the flat Batchelor-limit solution – with some attendant change in the
$k$
spectrum in the mode-coupling-dominated region becomes a little steeper than the flat Batchelor-limit solution – with some attendant change in the
![]() $\unicode[STIX]{x1D70F}$
spectrum (and also in the
$\unicode[STIX]{x1D70F}$
spectrum (and also in the
![]() $k$
spectrum in the phase-mixing-dominated region), to find which we would need to calculate the solution of (4.7) more precisely, taking into account the fact the power law (A 4) does not, in fact, extend to arbitrarily large
$k$
spectrum in the phase-mixing-dominated region), to find which we would need to calculate the solution of (4.7) more precisely, taking into account the fact the power law (A 4) does not, in fact, extend to arbitrarily large
![]() $k$
.
$k$
.
It is perhaps worth noting that these solutions must be rather particular to the 1-D world, as wavenumber integrals expressing nonlinear mode coupling become quite different in more dimensions (see, e.g. Zakharov et al. Reference Zakharov, L’vov and Falkovich1992).
Appendix B. Self-similar solution of (4.12)
Consider (4.12) with
![]() $\unicode[STIX]{x1D708}=0$
:
$\unicode[STIX]{x1D708}=0$
:
This equation has a self-similar solution of the form
where
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D705})$
satisfies an ordinary differential equation readily obtained by substituting (B 2) into (B 1):
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D705})$
satisfies an ordinary differential equation readily obtained by substituting (B 2) into (B 1):
A standard method for fixing the exponent
![]() $\unicode[STIX]{x1D706}$
for self-similar solutions such as (B 2) is to use some conservation law that the solution must satisfy. In this case, there is indeed a conservation law: (B 1) implies
$\unicode[STIX]{x1D706}$
for self-similar solutions such as (B 2) is to use some conservation law that the solution must satisfy. In this case, there is indeed a conservation law: (B 1) implies
Using (B 2), we find
which would appear to require
to make the integral (B 5) independent of
![]() $\unicode[STIX]{x1D70F}$
. In fact, we know from the argument in § 4.2 that this integral must be zero at
$\unicode[STIX]{x1D70F}$
. In fact, we know from the argument in § 4.2 that this integral must be zero at
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
. In view of (B 4), it must then also be zero at all
$\unicode[STIX]{x1D70F}\rightarrow 0$
. In view of (B 4), it must then also be zero at all
![]() $\unicode[STIX]{x1D70F}$
. Thus, the choice of
$\unicode[STIX]{x1D70F}$
. Thus, the choice of
![]() $\unicode[STIX]{x1D706}=2/3$
cannot really be justified a priori, but it is intriguing because with this value, (B 3) is rendered easily solvable, so we will examine its consequences before discussing its legitimacy.
$\unicode[STIX]{x1D706}=2/3$
cannot really be justified a priori, but it is intriguing because with this value, (B 3) is rendered easily solvable, so we will examine its consequences before discussing its legitimacy.
With
![]() $\unicode[STIX]{x1D706}=2/3$
, (B 3) is solved by the following substitution:
$\unicode[STIX]{x1D706}=2/3$
, (B 3) is solved by the following substitution:
where
![]() $C_{1}$
is an integration constant. Integrating again, we find
$C_{1}$
is an integration constant. Integrating again, we find
where
![]() $C_{2}$
is another integration constant. It is clear that
$C_{2}$
is another integration constant. It is clear that
![]() $C_{2}=0$
, lest
$C_{2}=0$
, lest
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D705})$
blow up at
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D705})$
blow up at
![]() $\unicode[STIX]{x1D705}\rightarrow -\infty$
. Cleaning up the remaining solution by changing the integration variable to
$\unicode[STIX]{x1D705}\rightarrow -\infty$
. Cleaning up the remaining solution by changing the integration variable to
![]() $z=\unicode[STIX]{x1D705}^{\prime }/9$
, setting
$z=\unicode[STIX]{x1D705}^{\prime }/9$
, setting
![]() $C_{1}=\left[9^{1/3}\unicode[STIX]{x1D6E4}(1/3)\right]^{-1}$
(this is arbitrary and done for aesthetic reasons) and using the resulting
$C_{1}=\left[9^{1/3}\unicode[STIX]{x1D6E4}(1/3)\right]^{-1}$
(this is arbitrary and done for aesthetic reasons) and using the resulting
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D705})$
in (B 2), we arrive at the following solution
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D705})$
in (B 2), we arrive at the following solution
If we split the
![]() $k>0$
and
$k>0$
and
![]() $k<0$
cases explicitly, we recover the solution (5.27). It is a simple matter to ascertain that (B 9) has the asymptotics (5.22) and (5.23) when the similarity variable
$k<0$
cases explicitly, we recover the solution (5.27). It is a simple matter to ascertain that (B 9) has the asymptotics (5.22) and (5.23) when the similarity variable
![]() $k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}$
is small or large, respectively. Indeed, changing the integration variable
$k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}$
is small or large, respectively. Indeed, changing the integration variable
![]() $z-k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}\rightarrow -z$
in (B 9), we get
$z-k^{3}/9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}\rightarrow -z$
in (B 9), we get
 $$\begin{eqnarray}F_{k}(\unicode[STIX]{x1D70F})=\frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{\infty }\text{d}z\,\frac{\text{e}^{-z}}{\left|\displaystyle \frac{1}{9\unicode[STIX]{x1D6FE}}k^{3}-\unicode[STIX]{x1D70F}z\right|^{2/3}}\rightarrow \left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{\unicode[STIX]{x1D70F}^{2/3}}, & \displaystyle \frac{|k|^{3}}{9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}\ll 1,\\ \displaystyle \frac{3^{4/3}}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\frac{1}{k^{2}}, & \displaystyle \frac{|k|^{3}}{9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}\gg 1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}F_{k}(\unicode[STIX]{x1D70F})=\frac{1}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\int _{0}^{\infty }\text{d}z\,\frac{\text{e}^{-z}}{\left|\displaystyle \frac{1}{9\unicode[STIX]{x1D6FE}}k^{3}-\unicode[STIX]{x1D70F}z\right|^{2/3}}\rightarrow \left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{\unicode[STIX]{x1D70F}^{2/3}}, & \displaystyle \frac{|k|^{3}}{9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}\ll 1,\\ \displaystyle \frac{3^{4/3}}{\unicode[STIX]{x1D6E4}\!\left(\frac{1}{3}\right)}\frac{1}{k^{2}}, & \displaystyle \frac{|k|^{3}}{9\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70F}}\gg 1.\end{array}\right.\end{eqnarray}$$
This solution manifestly has vanishing Hermite flux (
![]() $F_{k}=F_{-k}$
) at
$F_{k}=F_{-k}$
) at
![]() $\unicode[STIX]{x1D70F}\ll |k^{3}|/9\unicode[STIX]{x1D6FE}$
(as well as in the opposite limit, but this is just a trivial requirement of continuity of
$\unicode[STIX]{x1D70F}\ll |k^{3}|/9\unicode[STIX]{x1D6FE}$
(as well as in the opposite limit, but this is just a trivial requirement of continuity of
![]() $F_{k}$
at
$F_{k}$
at
![]() $k=0$
).
$k=0$
).
Obviously, the above derivation is much more elementary and may, to some readers, be more convincing than that offered in § 5. Methodologically, however, it was not necessarily obvious either that the self-similar solution would prove to be the only one that would have matching (
![]() $k$
by
$k$
by
![]() $k$
) phase-mixing and anti-phase-mixing fluxes at
$k$
) phase-mixing and anti-phase-mixing fluxes at
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
or that this solution would be the only physically acceptable one. As we already indicated above, the choice of
$\unicode[STIX]{x1D70F}\rightarrow 0$
or that this solution would be the only physically acceptable one. As we already indicated above, the choice of
![]() $\unicode[STIX]{x1D706}=2/3$
was merely a convenient conjecture. In order to ascertain that it is the only possible choice, we would have to solve (B 3) for arbitrary
$\unicode[STIX]{x1D706}=2/3$
was merely a convenient conjecture. In order to ascertain that it is the only possible choice, we would have to solve (B 3) for arbitrary
![]() $\unicode[STIX]{x1D706}$
(which can be done in special functions) and then demand that the solutions are positive (i.e. represent physically realisable spectra) and satisfy (4.10). This can be done, but the argument for
$\unicode[STIX]{x1D706}$
(which can be done in special functions) and then demand that the solutions are positive (i.e. represent physically realisable spectra) and satisfy (4.10). This can be done, but the argument for
![]() $\unicode[STIX]{x1D706}=2/3$
given in appendix C is perhaps more mathematically compelling and at any rate no less cumbersome.
$\unicode[STIX]{x1D706}=2/3$
given in appendix C is perhaps more mathematically compelling and at any rate no less cumbersome.
Admittedly, the formal shortcomings of the self-similar route to the answer are probably overcome by its appealing simplicity.
Appendix C. Inevitability of the zero-flux solution (5.18)
Here we exercise due diligence by showing that the solution found in § 5, which we found using an initial guess (5.18), is indeed the only physically and mathematically sensible one.
Let us no longer make an explicit demand for a zero-flux solution, which led us from (5.15) to (5.17), the solution of which was (5.18). Instead of (5.18), let us posit some general power law for the Hermite spectrum at
![]() $\unicode[STIX]{x1D709}\rightarrow 0$
:
$\unicode[STIX]{x1D709}\rightarrow 0$
:
With this ansatz, the left-hand side of (5.15) becomes
 $$\begin{eqnarray}\displaystyle \text{left-hand side of (5.17)} & = & \displaystyle \unicode[STIX]{x1D70F}^{-\unicode[STIX]{x1D706}-(1/3)}\unicode[STIX]{x1D6E4}\!\left({\textstyle \frac{2}{3}}\right)\left[\frac{\unicode[STIX]{x1D6E4}\!\left(\unicode[STIX]{x1D706}+\frac{1}{3}\right)}{\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D706})}-\frac{\left(\unicode[STIX]{x1D706}-\frac{2}{3}\right)\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D706})}{\unicode[STIX]{x1D6E4}\!\left(\frac{5}{3}-\unicode[STIX]{x1D706}\right)}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\underbrace{\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\,\unicode[STIX]{x1D70F}^{(2/3)-\unicode[STIX]{x1D706}}B\!\left(\frac{\unicode[STIX]{x1D70F}}{\unicode[STIX]{x1D70F}_{\text{max}}};\unicode[STIX]{x1D706}-\frac{2}{3},\frac{2}{3}\right)}_{\rightarrow 0\text{ as }\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{left-hand side of (5.17)} & = & \displaystyle \unicode[STIX]{x1D70F}^{-\unicode[STIX]{x1D706}-(1/3)}\unicode[STIX]{x1D6E4}\!\left({\textstyle \frac{2}{3}}\right)\left[\frac{\unicode[STIX]{x1D6E4}\!\left(\unicode[STIX]{x1D706}+\frac{1}{3}\right)}{\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D706})}-\frac{\left(\unicode[STIX]{x1D706}-\frac{2}{3}\right)\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D706})}{\unicode[STIX]{x1D6E4}\!\left(\frac{5}{3}-\unicode[STIX]{x1D706}\right)}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\underbrace{\frac{\text{d}}{\text{d}\unicode[STIX]{x1D70F}}\,\unicode[STIX]{x1D70F}^{(2/3)-\unicode[STIX]{x1D706}}B\!\left(\frac{\unicode[STIX]{x1D70F}}{\unicode[STIX]{x1D70F}_{\text{max}}};\unicode[STIX]{x1D706}-\frac{2}{3},\frac{2}{3}\right)}_{\rightarrow 0\text{ as }\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty },\end{eqnarray}$$
where
![]() $B$
is the incomplete beta function. While the second integral in (5.15), equalling the expression under the derivative in (C 2), is divergent when
$B$
is the incomplete beta function. While the second integral in (5.15), equalling the expression under the derivative in (C 2), is divergent when
![]() $\unicode[STIX]{x1D706}<2/3$
and
$\unicode[STIX]{x1D706}<2/3$
and
![]() $\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
, its
$\unicode[STIX]{x1D70F}_{\text{max}}\rightarrow \infty$
, its
![]() $\unicode[STIX]{x1D70F}$
derivative vanishes in this limit and so the values
$\unicode[STIX]{x1D70F}$
derivative vanishes in this limit and so the values
![]() $\unicode[STIX]{x1D706}<2/3$
are formally allowed. The case
$\unicode[STIX]{x1D706}<2/3$
are formally allowed. The case
![]() $\unicode[STIX]{x1D706}=2/3$
has to be treated differently, but has already been considered in § 5.3. Finally, we must have
$\unicode[STIX]{x1D706}=2/3$
has to be treated differently, but has already been considered in § 5.3. Finally, we must have
![]() $\unicode[STIX]{x1D706}<1$
in order to keep the first integral in (5.15) convergent.
$\unicode[STIX]{x1D706}<1$
in order to keep the first integral in (5.15) convergent.
To calculate the right-hand side of (5.15), we assume a general power law for the phase-mixing part of the Fourier spectrum at
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
,
$\unicode[STIX]{x1D70F}\rightarrow 0$
,
where
![]() $A$
is a constant, and find
$A$
is a constant, and find
In order for (5.15) to be satisfied, we must have
and
 $$\begin{eqnarray}\displaystyle A & = & \displaystyle \displaystyle 2^{2\unicode[STIX]{x1D706}}\unicode[STIX]{x1D6E4}\!\left({\textstyle \frac{2}{3}}\right)\left[\frac{\unicode[STIX]{x1D6E4}\!\left(\unicode[STIX]{x1D706}+\frac{1}{3}\right)}{\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D706})}-\frac{\unicode[STIX]{x1D706}-\frac{2}{3}}{\unicode[STIX]{x1D6E4}\!\left(\frac{5}{3}-\unicode[STIX]{x1D706}\right)}\right]\nonumber\\ \displaystyle & = & \displaystyle \displaystyle 2^{2\unicode[STIX]{x1D706}}\unicode[STIX]{x1D6E4}\!\left({\textstyle \frac{2}{3}}\right)\frac{\unicode[STIX]{x1D706}-\frac{2}{3}}{\unicode[STIX]{x1D6E4}\!\left(\frac{5}{3}-\unicode[STIX]{x1D706}\right)}\left\{\frac{\sin \unicode[STIX]{x03C0}\unicode[STIX]{x1D706}}{\sin \!\left[\unicode[STIX]{x03C0}\left(\unicode[STIX]{x1D706}-\frac{2}{3}\right)\right]}-1\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A & = & \displaystyle \displaystyle 2^{2\unicode[STIX]{x1D706}}\unicode[STIX]{x1D6E4}\!\left({\textstyle \frac{2}{3}}\right)\left[\frac{\unicode[STIX]{x1D6E4}\!\left(\unicode[STIX]{x1D706}+\frac{1}{3}\right)}{\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D706})}-\frac{\unicode[STIX]{x1D706}-\frac{2}{3}}{\unicode[STIX]{x1D6E4}\!\left(\frac{5}{3}-\unicode[STIX]{x1D706}\right)}\right]\nonumber\\ \displaystyle & = & \displaystyle \displaystyle 2^{2\unicode[STIX]{x1D706}}\unicode[STIX]{x1D6E4}\!\left({\textstyle \frac{2}{3}}\right)\frac{\unicode[STIX]{x1D706}-\frac{2}{3}}{\unicode[STIX]{x1D6E4}\!\left(\frac{5}{3}-\unicode[STIX]{x1D706}\right)}\left\{\frac{\sin \unicode[STIX]{x03C0}\unicode[STIX]{x1D706}}{\sin \!\left[\unicode[STIX]{x03C0}\left(\unicode[STIX]{x1D706}-\frac{2}{3}\right)\right]}-1\right\}.\end{eqnarray}$$
The spectrum (C 3) must be positive: within our allowed interval
![]() $\unicode[STIX]{x1D706}<1$
, we can have
$\unicode[STIX]{x1D706}<1$
, we can have
![]() $A>0$
only if
$A>0$
only if
![]() $\unicode[STIX]{x1D706}<5/6$
.
$\unicode[STIX]{x1D706}<5/6$
.
Finally, via (5.16), the ansatz (C 1) implies that the anti-phase-mixing Fourier spectrum at
![]() $\unicode[STIX]{x1D70F}\rightarrow 0$
is
$\unicode[STIX]{x1D70F}\rightarrow 0$
is
(the integral is done by changing the integration variable to
![]() $z=\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70E}$
). In view of (C 5), this is the same scaling as for the phase-mixing spectrum (C 3)! But this means that the condition (4.10) can only be satisfied if the coefficients in (C 7) and (C 3) match. With
$z=\unicode[STIX]{x1D709}^{2}/4\unicode[STIX]{x1D70E}$
). In view of (C 5), this is the same scaling as for the phase-mixing spectrum (C 3)! But this means that the condition (4.10) can only be satisfied if the coefficients in (C 7) and (C 3) match. With
![]() $A$
given by (C 6), this leads us, therefore, to demand
$A$
given by (C 6), this leads us, therefore, to demand
This is satisfied for
![]() $\unicode[STIX]{x1D706}=2/3$
, which hands us back our zero-flux solution (5.18) and everything that it implies.
$\unicode[STIX]{x1D706}=2/3$
, which hands us back our zero-flux solution (5.18) and everything that it implies.
The reason that this has proved to be the only physically acceptable possibility is that for any
![]() $0<\unicode[STIX]{x1D706}<2/3$
, we would have
$0<\unicode[STIX]{x1D706}<2/3$
, we would have
![]() $F_{0}^{+}>F_{0}^{-}$
and their wavenumber scaling would be shallower than
$F_{0}^{+}>F_{0}^{-}$
and their wavenumber scaling would be shallower than
![]() $1/k^{2}$
, causing the integral in (4.10) to blow up. For
$1/k^{2}$
, causing the integral in (4.10) to blow up. For
![]() $2/3<\unicode[STIX]{x1D706}<5/6$
, the integral is finite but negative, meaning that there is no steady state and there is an unphysical net inflow of energy from high
$2/3<\unicode[STIX]{x1D706}<5/6$
, the integral is finite but negative, meaning that there is no steady state and there is an unphysical net inflow of energy from high
![]() $m$
. For even larger values of
$m$
. For even larger values of
![]() $\unicode[STIX]{x1D706}$
, either there is no positive spectrum at all or the energy flux through
$\unicode[STIX]{x1D706}$
, either there is no positive spectrum at all or the energy flux through
![]() $k=0$
blows up. Finally,
$k=0$
blows up. Finally,
![]() $\unicode[STIX]{x1D706}=0$
is not allowed because, even though (C 8) and so (4.10) are satisfied, the right-hand side of (4.9) no longer vanishes at
$\unicode[STIX]{x1D706}=0$
is not allowed because, even though (C 8) and so (4.10) are satisfied, the right-hand side of (4.9) no longer vanishes at
![]() $\unicode[STIX]{x1D708}\rightarrow +0$
and so the steady-state energy budget breaks down, i.e. no such steady-state solution can exist – this is a demonstration that the linear Hermite solution does not work in a nonlinear steady state.
$\unicode[STIX]{x1D708}\rightarrow +0$
and so the steady-state energy budget breaks down, i.e. no such steady-state solution can exist – this is a demonstration that the linear Hermite solution does not work in a nonlinear steady state.