Common ragweed is a native, herbaceous, annual broadleaf weed found throughout temperate North America (Bazzaz Reference Bazzaz1970; Coble et al. Reference Coble, Williams and Ritter1981). The seeds of this species can remain viable in the soil for 39 years or longer (Bassett and Crompton Reference Bassett and Crompton1975) until their dormancy is broken by cold stratification (Bazzaz Reference Bazzaz1970; Willemsen and Rice Reference Willemsen and Rice1972). Common ragweed typically emerges early in the season, from mid-April through May in the Midwest (Werle et al. 2014a). Under favorable conditions, common ragweed plants can reach heights over 2 m (Bassett and Crompton Reference Bassett and Crompton1975; Clewis et al. Reference Clewis, Askew and Wilcut2001). Common ragweed is one of the most prominent hay fever allergens, with the ability to produce more than one billion pollen grains per plant in late summer and early fall (Jordan et al. 2007).
Common ragweed’s early-season emergence gives it a significant competitive advantage if it is not controlled before crop planting in many cropping systems, especially soybean [Glycine max (L.) Merr.] (Coble et al. Reference Coble, Williams and Ritter1981) and peanut (Arachis hypogaea L.) (Clewis et al. Reference Clewis, Askew and Wilcut2001). Common ragweed at a density of four plants per ten meters of row reduced soybean yield by 8% (Jordan et al. 2015). Similarly, Clewis et al. (Reference Clewis, Askew and Wilcut2001) reported that a single common ragweed plant per meter of row reduced peanut yield by 40%. Dickerson and Sweet (Reference Dickerson and Sweet1971) reported that in the absence of competition, a small common ragweed plant (95 g fresh weight) produced 3,135 seeds per plant, and a large plant (2,400 g fresh weight) produced 62,000 seeds.
The overreliance on glyphosate following commercialization of glyphosate-resistant corn (Zea mays L.) and soybean throughout the midwestern United States has led to the evolution of glyphosate-resistant weeds, including common ragweed (Powles Reference Powles2008; Shaner Reference Shaner2014). In the United States, glyphosate-resistant common ragweed was first documented in Missouri in 2004 (Heap Reference Heap2016; Pollard Reference Pollard2007) and has been recently documented in Nebraska (Ganie and Jhala Reference Ganie and Jhala2017). The failure of glyphosate to control glyphosate-resistant common ragweed has forced producers to adopt diversified weed management strategies including mechanical and cultural approaches as well as the use of herbicides with alternate modes of action, both PRE and POST (Beckie Reference Beckie2011; Van Wely et al. Reference Van Wely, Soltani, Robinson, Hooker, Lawton and Sikkema2014, Reference Van Wely, Soltani, Robinson, Hooker, Lawton and Sikkema2015).
Before the extensive use of herbicides, tillage was an important tool for preplant weed control (Burnside Reference Burnside1996; Givens et al. Reference Givens, Shaw, Kruger, Johnson, Weller, Young, Wilson, Owen and Jordan2009). Reduced or no-tillage production systems greatly increased in popularity after glyphosate-resistant crops were introduced in 1996, and the use of glyphosate for weed control widely replaced preplant tillage due to the affordability and effectiveness of glyphosate (Givens et al. Reference Givens, Shaw, Kruger, Johnson, Weller, Young, Wilson, Owen and Jordan2009). The emergence patterns of common lambsquarters (Chenopodium album L.), field pennycress (Thlaspi arevense L.), green foxtail [Setaria viridis (L.) Beauv.], wild buckwheat (Polygonum convolvulus L.), and wild oat (Avena fatua L.) were delayed in conventional tillage systems compared with conservation tillage systems. However, the redroot pigweed (Amaranthus retroflexus L.) and wild mustard (Sinapis arvensis L.) emergence period was not affected by different tillage systems (Bullied et al. Reference Bullied, Marginet and Van Acker2003). Common waterhemp [Amaranthus tuberculatus (Moq.) Sauer] emergence was greater, occurred over a longer period of time, and peaked later in no-till systems compared with chisel plow and moldboard plow systems (Leon and Owen Reference Leon and Owen2006). In a two-year study on a long-term no-till field in Wisconsin, Mulugeta and Stoltenberg (Reference Mulugeta and Stoltenberg1997) observed greater common lambsquarters emergence in one year and greater giant foxtail and redroot pigweed emergence in both years following secondary soil disturbance. Time to 25%, 50%, and 75% total emergence of pitted morningglory (Ipomoea lacunosa L.), and time to 25% sicklepod [Senna obtusifolia (L.) H.S. Irwin & Barneby] emergence was shortened by spring tillage (Norsworthy and Oliveira Reference Norsworthy and Oliveira2007). Control of glyphosate-resistant giant ragweed (Ambrosia trifida L.), a species closely related to common ragweed, with spring tillage before soybean planting is being considered (Ganie et al. Reference Ganie, Sandell, Jugulam, Kruger, Marx and Jhala2016). A study by Kaur et al. (Reference Kaur, Werle, Sandell and Jhala2016) revealed that tillage had no effect on the emergence pattern of glyphosate-resistant giant ragweed, indicating that preplant tillage can be exploited for giant ragweed management. However, the effect of tillage on the emergence pattern of common ragweed is unknown. Understanding the emergence pattern of common ragweed, and its response to spring tillage, would be valuable information for management decisions. If spring tillage does not change common ragweed’s emergence pattern, the weed’s early-season emergence can be employed beneficially to control emerged seedlings with preplant tillage after most seedlings have emerged. To maximize the control of common ragweed using preplant tillage, a model of emergence would be of great value to optimize timing of tillage.
The two main environmental triggers of seedling emergence include soil temperature and soil water content (Grundy Reference Grundy2003). Soil temperature can be used as a predictor of seedling emergence and can be expressed as thermal time (TT) with a growing degree day calculation in which TT is only accumulated above a threshold base temperature (Tbase) (Forcella et al. Reference Forcella, Benech-Arnold, Sanchez and Ghersa2000). Soil temperature and water content can be combined as a predictor and expressed as hydrothermal time (HTT), in which TT accumulates only when the soil temperature is greater than Tbase and the water matric potential is greater than a base matric potential (Ψbase) (Gummerson Reference Gummerson1986). This indicates that time until germination is inversely proportional to the degree which Tbase is exceeded while Ψbase is achieved (Bradford Reference Bradford2002). Seedling emergence can also be modeled using day of year (DOY), in which case the emergence pattern of a species is described by DOY and the environment has no effect on the seedling emergence pattern. The objectives of this study were to evaluate whether spring tillage during emergence would influence the emergence pattern or stimulate additional emergence of common ragweed, and to characterize naturally occurring common ragweed emergence in southeast Nebraska.
Materials and Methods
Field Experiments
Field experiments were conducted in Gage County, Nebraska (40.4465°N, 96.6204°W) in 2014, 2015, and 2016 in a producer’s field with a confirmed glyphosate-resistant common ragweed biotype (Ganie and Jhala Reference Ganie and Jhala2017). The level of glyphosate resistance of this biotype was 7-fold as determined by control estimates, and 19-fold as determined by biomass reduction, compared with a known glyphosate-susceptible common ragweed biotype (Ganie and Jhala Reference Ganie and Jhala2017). The soil was a fine, smectitic, mesic Aquertic Argiudoll (Wymore series silty clay loam; 37.6% silt, 37.6% clay, 24.8% sand) with 2.5% organic matter and a pH of 6.0. The experiment was moved to a new area within the field each year.
The experiment was arranged in a randomized complete block design with four treatments and four replications. Tillage treatments included three tillage timings and an untreated control (no tillage). The plot size was 1.5 m wide by 4.5 m long. Three 0.25-m2 quadrats were evenly spaced within each plot for common ragweed emergence counts. Within each experimental year, the first tillage treatment was implemented one week after the first common ragweed seedlings were observed in the field, with the remaining tillage treatments implemented at two and five weeks after the first tillage treatment. Tillage was simulated using a 50-cm-wide rototiller (Honda FRC800, American Honda, Alpharetta, GA) operated at a depth of 10 cm. Tillage treatments were implemented on May 7, May 21, and June 12 in 2014; April 16, April 30, and May 21 in 2015; and March 31, April 14, and May 5 in 2016. The yearly variation in the timing of tillage treatments was due to variation in timing of common ragweed emergence as influenced by weather conditions (Figure 1).
Figure 1 Daily soil temperature (C) and moisture potential (kPa) at the 2-cm depth, estimated using STM2 (soil temperature and moisture model software) during the common ragweed emergence period in a field experiment conducted in Gage County, Nebraska in 2014, 2015, and 2016.
Data Collection
Newly emerged common ragweed seedlings were counted and removed from each quadrat on a weekly basis from the first week of emergence through the end of June, when common ragweed emergence had ceased. Total emergence in the three quadrats for each plot was summed to obtain total emergence per plot. Weekly emergence data were converted to a percentage of the total number of emerged seedlings in each plot for each year (total emergence per plot). Total emergence per plot was converted to plants m−2. The Soil Temperature and Moisture Model software (STM2) (Spokas and Forcella Reference Spokas and Forcella2009) was used to predict daily soil temperature (C) and moisture (kPa) at the 2-cm depth (Figure 1). Daily precipitation and minimum and maximum air temperature were acquired from the nearest High Plains Regional Climate Center station, which was located near Virginia, Nebraska. The soil texture properties and organic matter (%), along with the latitude, longitude, and elevation (436 m) of the research site, were also used in the software prediction of daily soil temperature (C) and moisture content (matric potential, kPa).
Tillage Effects
The percent total emergence of each plot was modeled with the Weibull function using DOY as the explanatory variable:
$$y{\,\equals\,}asym{\times}\left\{ {1{\minus}{\rm exp}\left[ {{\minus}{\rm exp}\left( {lrc} \right){\times}\left( {x^{{pwr}} } \right)} \right]} \right\},$$
where y is the percent total emergence, x is the independent variable (DOY), and asym is the asymptote (normalized to 100%). Model parameters lrc and pwr are the natural logarithm for the rate of increase and the power to which x is raised, respectively (Crawley Reference Crawley2007). The nls function in the STATS package in R version 3.3.1 (R Core Team 2014) was used to estimate the parameters of the Weibull function. The Weibull function has been shown to appropriately describe crop and weed cumulative emergence (Bridges et al. Reference Bridges, Wu, Sharpe and Chandler1989; Werle et al. Reference Werle, Sandell, Buhler, Hartzler and Lindquist2014a). Time to 10%, 25%, 50%, 75%, and 90% total emergence (T10, T25, T50, T75, and T90) were predicted from each model. Total emergence and T10, T25, T50, T75, and T90 for each plot were subjected to ANOVA and MANOVA, respectively in R version 3.3.1 (R Core Team 2014) with treatments as fixed factors and replications nested within years as random factors in the model. The ANOVA and MANOVA assumptions of normality and homogeneity were tested prior to analysis. Pillai’s Trace test was used to determine significant effects in MANOVA.
Model Configuration
Accumulated HTT was calculated starting from January 1 for each year using the following equation (Gummerson Reference Gummerson1986):
$${\rm HTT}{\,\equals\,}\mathop{\sum}\nolimits_{i{\,\equals\,}1}^n {\left[ {\left( {{\rm T }{\times}{\rm \Psi }} \right){\times}\left( {{\rm T}_{{{\rm mean}}} {\minus}{\rm T}_{{{\rm base}}} } \right)} \right]} ,$$
where T and Ψ represent the temperature and moisture portions of the equation, respectively. If Tmean ≥ Tbase then T=1, otherwise T=0; when Ψmean ≥ Ψbase then Ψ=1, otherwise Ψ=0. Tmean and Ψmean are the average daily soil temperature (C) and the average daily matric potential (kPa) at the 2-cm depth, respectively. Tbase and Ψbase are the minimum threshold temperature (C) and matric potential (kPa) required for seedling emergence, respectively. The starting date of the HTT calculation (January 1) is represented by i, and n represents the number of days after i. T and Ψ can only be 1 or 0; therefore, Tmean − Tbase thermal units are accrued each day when both T and Ψ are sufficient for emergence (T=1 and Ψ=1). Because of inconsistent Tbase values reported for common ragweed in the literature (3.6 C, Shrestha et al. Reference Shrestha, Roman, Thomas and Swanton1999; 4.0 C, Willemsen Reference Willemsen1975b; 13.0 C, Werle et al. 2014a), 16 candidate threshold values ranging from 0 to 15 C were selected. Ψbase values of −33 (wilting point), −750, −1500 (permanent wilting point), and −∞ (analogous to TT) kPa were evaluated, which are similar to those investigated by Werle et al. (2014b).
Fitting the Model
Percent total emergence data for treatments that had similar T10, T25, T50, T75, and T90 values (P > 0.05) were pooled over years. The Weibull function (Eq. 1) was fit to the pooled data. The independent variables tested were 48 combinations of HTT, 16 combinations of TT, and DOY. To ensure an appropriate model fit, data from plots for a specific year were only used if at least 10 seedlings emerged during the season. Using data from plots with a minimum of 10 seedlings prevented plots with minimal emergence from having substantial influence on the model fit. In 2016, 5 out of 16 plots had less than 10 total emerged seedlings; therefore, data from those plots were not included in the model. The nls function in the STATS package in R version 3.3.1 (R Core Team 2014) was used to estimate the Weibull model parameters (lrc and pwr). Model selection was based on the information-theoretic model comparison approach (AIC) (Anderson Reference Anderson2008). The corrected AIC (AICc) and model probability (AICw) were obtained for the 65 models using the aictabCustom function in the AICcmodavg package in R version 3.3.1 (R Core Team 2014). AICc was calculated as
$$AICc{\,\equals\,}{\minus}2LL{\plus}2K\left( {n\,/\left[ {n{\minus}K{\minus}1} \right]} \right){\rm }$$
(Anderson Reference Anderson2008), where LL is the log likelihood of the model parameters (calculated with logLik function in R version 3.3.1 [R Core Team 2014]), K is the number of model parameters, and n is the sample size. Models derived from HTT require an additional input (soil moisture) compared with TT (soil temperature) and DOY; therefore, an additional parameter (K + 1) was added to the HTT model’s AICc computations (Werle et al. 2014a). AICw was calculated as
$$AICw_{i} {\equals}\left[ {{\rm exp}^{{\left( {{\minus}{1 \over {2{\rm \Delta }i}}} \right)}} {\rm \,/\,}\mathop{\sum}\nolimits_{r{\equals}1}^R {{\rm exp}^{{\left( {{\minus}{1 \over {2{\rm \Delta }r}}} \right)}} } } \right]$$
(Anderson Reference Anderson2008), where
${\rm \Delta }i$
is the difference between the model with the lowest AICc and the i
th model, and R represents the total number of models (65). The AICw for each model represents the proportion of the total AICw for all models being compared. The model with the lowest AICc and the highest AICw is considered the “top model” and the best explanation of the results within the group of models being compared (Anderson Reference Anderson2008). The independent variable of the top model indicates the optimum emergence predictor (Tbase and Ψbase or DOY) for this population of common ragweed.
Model Goodness of Fit
To assess goodness of fit, root mean square error (RMSE) and modeling efficiency coefficient (ME) were calculated for the top model. The RMSE was calculated as
$$RMSE{\,\equals\,}\left[ {1/n\mathop{\sum}\nolimits_{i{\,\equals\,}1}^n {\left( {Pi{\minus}Oi} \right)^{2} } } \right]^{{1/2}} $$
(Roman et al. Reference Roman, Murphy and Swanton2000), where Pi and Oi are the predicted and observed values, respectively, and n is the total number of comparisons. The closer the predicted values are to the observed values, the lower the RMSE. The ME was calculated as
$$ME{\equals}1{\minus}\left[ {\mathop{\sum}\nolimits_{i{\equals}1}^n {\left( {Oi{\minus}Pi} \right)^{2} } \,/\,\mathop{\sum}\nolimits_{i{\equals}1}^n {\left( {Oi{\minus}\overline{O} i} \right)^{2} } } \right]$$
(Mayer and Butler Reference Mayer and Butler1993), where
$\bar{O}i$
is the mean observed value. The closer the value of ME is to 1, the more precise the prediction.
Results and Discussion
Spring Tillage
Treatment by year interactions for total common ragweed seedling emergence (plants m−2) and T10, T25, T50, T75, and T90 were not significant (P=0.363 and P=0.311, respectively; Table 1); therefore, only main effects were evaluated. Tillage treatment had no effect on the total emergence in each plot (P=0.875; Table 1). The effect of the tillage treatments on common ragweed emergence was not different between the three years of the study (P=0.349; Table 1). T10, T25, T50, T75, and T90 varied between years (P < 0.001; Table 1), reaching T50 and T90 on DOY 125 and 132 in 2014 (May 5 and May 14), on DOY 110 and 128 in 2015 (April 20 and May 9), and on DOY 93 and 121 in 2016 (April 3 and May 1), respectively (Figure 2). However, tillage treatments had no effect on T10, T25, T50, T75, and T90 within year (P=0.472; Table 1). Willemsen (Reference Willemsen1975a) reported that soil temperature differences (due to seeding depth) affected common ragweed emergence timing, but not the total emergence. In Nebraska, the usual soybean-planting season begins May 5 and ends June 8 (USDA 2010); thus, spring tillage could be used to control emerged common ragweed without altering the species emergence pattern. Because T10, T25, T50, T75, and T90 varied between years, explanatory variables that rely on environmental factors such as temperature and soil moisture could better predict T10, T25, T50, T75, and T90. Predicted soil temperature and water potential at 2 cm varied during the early emergence period (Figure 1), potentially explaining the differences in emergence pattern among years.
Figure 2 Emergence pattern of common ragweed in Gage County, Nebraska, in a field experiment conducted in 2014, 2015, and 2016. As no differences were detected between tillage treatments, data within experimental years were combined. Lines represent the fit of the Weibull function for each year.
Table 1 Influence of spring tillage timing on total common ragweed seedling emergence (total emergence) and time to 10%, 25%, 50%, 75%, and 90% emergence (T10, T25, T50, T75, and T90) in a field experiment conducted in 2014, 2015, and 2016 in Gage County, Nebraska.
a P values were determined with MANOVA based on Pillai’s trace test.
Model Selection and Fit
For model selection, tillage treatments were pooled across years and timings because T10, T25, T50, T75, and T90 did not vary between tillage treatments (P>0.05). When the models were evaluated based on the AIC criterion, TT models had the lowest AICc at base temperatures between 0 and 11 C (Figure 3). This indicated that a TT model was the most appropriate option for predicting common ragweed emergence. Werle et al. (Reference Werle, Sandell, Buhler, Hartzler and Lindquist2014a) reported that the emergence patterns of 13 out of 23 summer annual weed species evaluated in their study were better predicted with TT models than with HTT or DOY models. According to the results from this study, a Tbase of 3 C best predicts the emergence pattern of common ragweed (AICw=0.40; Table 2, Figure 4). The selection of 3 C as the base temperature is not a true base temperature for common ragweed seed germination and seedling emergence, but it is a numerical parameter that best described the emergence pattern. Werle et al. (Reference Werle, Sandell, Buhler, Hartzler and Lindquist2014a) reported a much higher Tbase (13 C) for predicting the emergence pattern of common ragweed in Iowa. The RMSE and ME for the top model were 16.09 and 0.73, respectively, which are within the range reported in the literature. For instance, Werle et al. (Reference Werle, Bernards, Arkebauer and Lindquist2014b) reported the RMSE and ME range for the emergence pattern of several winter annual weeds to be 13.4 to 23.1 and 0.63 to 0.85, respectively.
Figure 3 Corrected information-theoretic model comparison criterion (AICc) of models for common ragweed emergence with threshold soil temperatures (Tbase) ranging from 0 to 15 C based on threshold matric potential (Ψbase) values of −33 (wilting point), −750, −1500 (permanent wilting point), and −∞ (analogous to thermal time, TT). Lower AICc values indicate a better fit of the model to the data. HTT, hydrothermal time.
Figure 4 Weibull function fit to percent total emergence of common ragweed in 2014, 2015, and 2016, with cumulative thermal time calculated with a threshold soil temperature of 3 C. Model parameter asym (horizontal asymptote) was normalized to 100%, while the model parameters lrc (natural logarithm for the rate of increase) and pwr (power to which thermal time is raised) were −18.1718 and 2.8671, respectively. The root mean squared error (RMSE) and modeling efficiency coefficient (ME) for this model were 16.09 and 0.73, respectively.
Table 2 Comparison of K Footnote , AICc, AICw, and LL for the best 6 out of 65 possible models for common ragweed emergence in Nebraska.a Models are ordered from lowest to highest AICc, with the lowest being the best fit (top model). The 6 best models were based on thermal time, and the top model had a Tbase of 3 C.
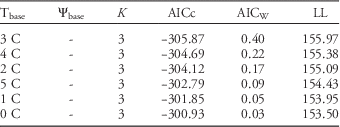
a Abbreviations: AICc, corrected information-theoretic model comparison criterion; AICw, model probability; K, number of model parameters; LL, log likelihood; Tbase, threshold soil temperature; Ψbase, threshold soil matric potential.
Practical Implications
This is the first study that describes the effect of tillage and environmental conditions on the emergence pattern of naturally occurring common ragweed in Nebraska. Soil temperature can be recorded or extrapolated by analyzing data from local weather stations with STM2 software (Spokas and Forcella Reference Spokas and Forcella2009). These data can be converted into TT and used to estimate common ragweed emergence time. The top model from this study predicts 10%, 50%, 75%, and 90% total emergence at 259, 498, 635, and 757 accumulated TT, respectively. Once a preferred threshold is reached, tillage can be implemented to eliminate emerged seedlings before crop planting. Leblanc and Cloutier (Reference Leblanc and Cloutier2002) reported that models of weed emergence could be used for cultivation scheduling. Control of giant ragweed increased with spring tillage prior to soybean planting compared with a no-tillage approach, due to the weed’s early-season, monophasic emergence pattern in Nebraska (Ganie et al. Reference Ganie, Sandell, Jugulam, Kruger, Marx and Jhala2016). In an area adjacent to the study in 2016, tillage was performed on the day of soybean planting (May 26, 2016), and established seedlings were counted before and after tillage. There was 100% control of emerged common ragweed seedlings with the tillage operation, suggesting that spring tillage effectively controls established common ragweed (Barnes, unpublished data). More research is needed to evaluate the efficacy of different types of tillage equipment and tillage depths for the control of common ragweed before crop planting. Common ragweed had a short emergence window in this study, with a TT accumulation of 598 between 10% and 90% predicted emergence. The early, monophasic emergence pattern of common ragweed in Nebraska is a biological characteristic that can be exploited for management prior to crop planting.
Selection pressure resulting from intensive management has led to an extended emergence pattern of giant ragweed in Ohio (Schutte et al. Reference Schutte, Regnier and Harrison2012), Illinois, Indiana, and Wisconsin (Regnier et al. Reference Regnier, Harrison, Loux, Hollowman, Ventatesh, Diekmann, Taylor, Ford, Stoltenberg, Hartzler, Davis, Schutte, Cardina, Mahoney and Johnson2016). This differs from the short, monophasic emergence pattern reported in Nebraska (Kaur et al. Reference Kaur, Werle, Sandell and Jhala2016) and Iowa (Werle et al. Reference Werle, Sandell, Buhler, Hartzler and Lindquist2014a). Wortman et al. (Reference Wortman, Davis, Schutte, Lindquist, Cardina, Felix, Sprague, Dille, Ramirez, Reicks and Clay2012) reported that giant ragweed demographic variation among a common seed lot was attributed to local temperature, rainfall, and elevation differences rather than regional gradients; however, it is important to note that these results should be used as a guide rather than an absolute predictor of common ragweed emergence due to possible biotype differences. Selection pressure can lead to herbicide resistance or shifts in emergence patterns, and therefore integrated weed management programs should be implemented to ensure long-term success. Sbatella and Wilson (Reference Sbatella and Wilson2010) described a kochia [Kochia scoparia (L.) Schrad.] biotype in areas where isoxaflutole had been applied PRE that had elevated seed dormancy and required higher temperatures for germination compared to populations never exposed to isoxaflutole. Ganie et al. (Reference Ganie, Sandell, Jugulam, Kruger, Marx and Jhala2016, Reference Ganie, Lindquist, Jugulam, Kruger, Marx and Jhala2017) also reported the advantages of implementing preplant tillage into integrated glyphosate-resistant giant ragweed management programs in corn and soybean. The ability to predict the emergence pattern of common ragweed allows growers to properly time spring tillage and preplant herbicides in their weed management programs. According to our model, 50% and 90% total emergence can be estimated using a thermal time calculation with a base temperature of 3 C when thermal time accumulates to 498 and 757, respectively. Additionally, thermal time calculations with a Tbase of 3 C can be used to estimate percent emergence. This knowledge can be used to schedule tillage before crops are planted and after most common ragweed seedlings have emerged.
