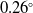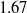1. Introduction
With the development of advanced vision technology and robotics [Reference Huang, Zhou, Chen and Song1], the application fields of robotics are becoming more and more extensive [Reference Ding and Yang2, Reference Peng, Ding, Yang and Xu3]. Vision-based robotic technology is widely used in many fields [Reference Wu, Sun, Wang and Liu4]; typical examples include robotic-assisted minimally invasive surgery [Reference Pachtrachai, Vasconcelos, Dwyer, Hailes and Stoyanov5, Reference Özgüner, Shkurti, Huang, Hao, Jackson, Newman and Çavuşoğlu6], robotic object catching [Reference Kansal and Mukherjee7], and on-orbit services [Reference Ma, Jiang, Li, Gao, Yu, Chen, Liu and Huang8]. Robot vision systems involve eye-in-hand, eye-to-hand, and hybrid forms [Reference Ren, Yang, Song, Qiao, Wu, Xu and Chen9, Reference Su13], in which the robot uses image information as feedback to perform related tasks. Such a system including a robot and a sensor (one or more cameras) equipped at the end of the robot is a typical hand-eye system.
The determination of the robot-world transformation and the hand-eye transformation involved in the hand-eye system is commonly known as hand-eye calibration problems. The mathematical models for the hand-eye calibration problems can all be grouped into the hand-eye equation (
![]() $\boldsymbol{{AX}}=\boldsymbol{{XB}}$
) [Reference Shiu and Ahmad14] and the robot-world and hand-eye equation (
$\boldsymbol{{AX}}=\boldsymbol{{XB}}$
) [Reference Shiu and Ahmad14] and the robot-world and hand-eye equation (
![]() $\boldsymbol{{AX}}=\boldsymbol{{YB}}$
) [Reference Zhuang, Roth and Sudhakar15]. Despite the hand-eye equation can only determine the hand-eye transformation, the dual equation of hand-eye equation can determine the robot-world transformation [Reference Wang, Huang and Song16]. The observation data involved in the robot-world and hand-eye equation consist of absolute poses, while the observation data involved in the dual equations consist of relative motions. Therefore, it is mandatory to compute the robot and camera relative motions before solving hand-eye equation. In other words, simultaneous robot-world and hand-eye calibration based on the robot-world and hand-eye equation (
$\boldsymbol{{AX}}=\boldsymbol{{YB}}$
) [Reference Zhuang, Roth and Sudhakar15]. Despite the hand-eye equation can only determine the hand-eye transformation, the dual equation of hand-eye equation can determine the robot-world transformation [Reference Wang, Huang and Song16]. The observation data involved in the robot-world and hand-eye equation consist of absolute poses, while the observation data involved in the dual equations consist of relative motions. Therefore, it is mandatory to compute the robot and camera relative motions before solving hand-eye equation. In other words, simultaneous robot-world and hand-eye calibration based on the robot-world and hand-eye equation (
![]() $\boldsymbol{{AX}}=\boldsymbol{{YB}}$
) can reduce data generation errors.
$\boldsymbol{{AX}}=\boldsymbol{{YB}}$
) can reduce data generation errors.
Hand-eye calibration was proposed by Shiu et al. [Reference Shiu and Ahmad14] and Tsai et al. [Reference Tsai and Lenz17] and was pointed out that solving the hand-eye equation needs at least two motions with non-parallel rotation axes. Early research mainly focused on linear algorithms. The hand-eye equation can be decoupled into the rotation and translation parts. Estimating the rotation and translation parts sequentially is commonly referred to as the separable solutions. The rotation part of the separable solutions was parameterized based on quaternion [Reference Chou and Kamel18, Reference Malti and Barreto20], Euclidean group [Reference Park and Martin21], and Kronecker product [Reference Andreff, Horaud and Espiau22], and then, the estimated value of rotation was required as a priori information to calculate the translation. However, the separable solutions caused a problem that the error of the rotation is inevitably transferred to the translation part. Obviously, calculating rotation and translation simultaneously can effectively avoid propagation errors. A screw motion can represent rigid body motion based on Chasles theorem, and it is a geometric interpretation that regards rotation and translation as an interdependent entirety [Reference Chen23]. Zhao and Liu [Reference Zhao and Liu24] employed the screw motion theory to establish a hand-eye equation based on quaternion and yielded a simultaneous result for rotation and translation by solving linear equations. Dual quaternions as the algebraic counterpart of screws facilitated a simultaneous solution for the hand-eye rotation and translation using singular value decomposition (SVD) and were proposed in refs. [Reference Daniilidis and Bayro-Corrochano25, Reference Daniilidis26]. Furthermore, a probabilistic method for hand-eye calibration [Reference Ma, Li and Chirikjian27] was feasible even without prior knowledge of the correspondence between the data streams obtained via different systems. Since the linear algorithms are sensitive to possible random noise, a lot of research has been carried out on iterative optimization as an effective method to improve accuracy and robustness. Zhuang and Shiu [Reference Zhuang and Shiu28] solved hand-eye problem based on Gauss–Newton method, which the rotation parameters formulated in Euler angles. The nonlinear least square method was proposed in ref. [Reference Horaud and Dornaika19], where the rotation part was represented by quaternions. Furthermore, Strobl and Hirzinger [Reference Strobl and Hirzinger29] proposed a novel physically based metric on SE(3) that can select the weighting of the rotation part and the translation part automatically. The global optimal method proposed in ref. [Reference Heller, Havlena, Pajdla and Anal30] did not require initial estimates. The cost function constructed by minimizing the reprojection error was proposed in ref. [Reference Malti31], which was lately developed by considering the hand pose errors [Reference Koide and Menegatti32]. There is an exponential mapping between Lie algebra so(3) and the rotation matrix as it belongs to the special orthogonal group SO(3), which makes it easy to obtain the derivative of the rotation matrix. The Jacobian matrix in the Gauss–Newton algorithm can be constructed with the partial derivative of Lie algebra so(3). Yang and Zhao [Reference Yang and Zhao33] applied Gauss–Newton algorithm to optimize the estimation, but the estimation of translation was not accurate enough to be used in practice. Hand-eye calibration has been conducted using extensive methods, but it can only determine the hand-eye transformation.
The robot-world and hand-eye calibration was proposed by Zhuang et al. [Reference Zhuang, Roth and Sudhakar15], and a separable solution based on quaternion was implemented. A new robot-world and hand-eye calibration algorithm based on Kronecker product, which could separably determine the rotation and translation by applying the SVD approach, was presented in ref. [Reference Shah34]. Typically, separate solution based on Kronecker product has good rotation accuracy; however, the position accuracy is often compromised [Reference Ali, Olli, Gotchev and Morales35], while the Kronecker product and the dual quaternions can also be applied to solve rotation and translation simultaneously [Reference Li, Wang and Wu36]. The probabilistic method was also applied on robot-world and hand-eye calibration [Reference Li, Ma, Wang and Chirikjian37]. A nonlinear least square method was presented in robot-world and hand-eye calibration [Reference Dornaika and Horaud38], where the rotation part was represented by a matrix without parameterization. Different parameterization methods of rotation matrices based on Euler angle, axial angle, or quaternion were compared in ref. [Reference Tabb and Ahmad Yousef39]. Zhao and Weng proposed a joint method that gives the solutions of the cameras’ parameters and the hand-eye parameters simultaneously using nonlinear optimization [Reference Zhao and Weng40]. The global optimal methods [Reference Heller, Henrion and Pajdla41, Reference Zhao42] were also found to be instrumental in determining robot-world and hand-eye calibration. Gauss–Newton algorithm in which the Jacobian matrix is constructed by Lie algebra was applied for dual robots [Reference Wu, Wang, Qi, Wu, Ren and Meng10], hybrid system [Reference Ren, Yang, Song, Qiao, Wu, Xu and Chen9], and other conditions [Reference Wu and Ren43]. However, these methods only optimized the rotation part and did not consider rotation and translation simultaneously. In addition, Gauss–Newton algorithm in which the Jacobian matrix is constructed by Lie algebra has not been applied to the classic robot-world and hand-eye calibration. Hence, this study gave a detailed process of optimizing classic robot-world and hand-eye calibration based on the Gauss–Newton algorithm and realized simultaneous estimation of the rotation and the translation.
In this paper, a simultaneous solution for the robot-world and hand-eye equation was proposed. The simultaneous solution includes a closed-form solution that serves as an initial value and an iterative solution. The overdetermined linear equation system corresponding to the closed-form solution was constructed based on the Kronecker product, and such problem was converted into linear null space calculations. Applying SVD on the linear equation system led to the closed-form solution. The Gauss–Newton algorithm is based on Lie algebra to calculate the Jacobian matrix to implement the iterative solution. The contributions of this paper can be listed as:
-
(1) A Jacobian matrix based on Lie algebra that can optimize rotation and translation simultaneously was derived and refined a closed-form solution, thus forming a more complete method.
-
(2) An improved method to solve the singularity problem caused by the parameterization of the rotation matrix was proposed, which can be widely used in the robot-world and hand-eye calibration.
-
(3) The feasibility of the Jacobian matrix has been verified that it can also converge to a better accuracy when other linear method is used as the initial value.
The rest of this article is organized as follows. In Section 2, we derived the left perturbation model of the rotation matrix and constructed the Jacobian matrix based on this model, forming a complete solution including the initial value and the iterative solution. Experiments with simulated data and real data are performed and the results of which are discussed in Section 3. Conclusions are given in Section 4.
2. Proposed method
2.1. Problem formulation
The classic robot-world and hand-eye calibration has the setup similar to the one described in Fig. 1(a), and the corresponding kinematic loop illustrated in Fig. 1(b) can be mapped to the robot-world and hand-eye equation:
where
![]() $\boldsymbol{{A}}$
represents the absolute pose of the robot;
$\boldsymbol{{A}}$
represents the absolute pose of the robot;
![]() $\boldsymbol{{B}}$
represents the absolute pose of the camera;
$\boldsymbol{{B}}$
represents the absolute pose of the camera;
![]() $\boldsymbol{{X}}$
represents the hand-eye transformation; and
$\boldsymbol{{X}}$
represents the hand-eye transformation; and
![]() $\boldsymbol{{Y}}$
represents the robot-world transformation. The camera moves around the calibration checkerboard and collects n images of the checkerboard with the corresponding robot poses, thus leading to the calibration equation system.
$\boldsymbol{{Y}}$
represents the robot-world transformation. The camera moves around the calibration checkerboard and collects n images of the checkerboard with the corresponding robot poses, thus leading to the calibration equation system.

Figure 1. The robot-world and hand-eye kinematics loop
2.2. Closed-form solution
The Kronecker product [Reference Brewer44], usually denoted by
![]() $\otimes$
, can construct a linear equation system for the nonlinear robot-world and hand-eye equation (Eq. (1)). Using an
$\otimes$
, can construct a linear equation system for the nonlinear robot-world and hand-eye equation (Eq. (1)). Using an
![]() $m \times n$
matrix
$m \times n$
matrix
![]() $\boldsymbol{{A}}$
and a
$\boldsymbol{{A}}$
and a
![]() $p \times q$
matrix
$p \times q$
matrix
![]() $\boldsymbol{{B}}$
, a larger matrix with the dimension of
$\boldsymbol{{B}}$
, a larger matrix with the dimension of
![]() $mp\times nq$
can be defined as:
$mp\times nq$
can be defined as:
 \begin{equation} \boldsymbol{{A}} \otimes \boldsymbol{{B}}=\left[\begin{array}{ll} a_{i j} \boldsymbol{{B}} \end{array}\right]=\left[\begin{array}{c@{\quad}c@{\quad}c} a_{11} \boldsymbol{{B}} & \cdots & a_{1n} \boldsymbol{{B}} \\[5pt] \vdots & \ddots & \vdots \\[5pt] a_{m1} \boldsymbol{{B}} & \cdots & a_{mn} \boldsymbol{{B}} \end{array}\right].\end{equation}
\begin{equation} \boldsymbol{{A}} \otimes \boldsymbol{{B}}=\left[\begin{array}{ll} a_{i j} \boldsymbol{{B}} \end{array}\right]=\left[\begin{array}{c@{\quad}c@{\quad}c} a_{11} \boldsymbol{{B}} & \cdots & a_{1n} \boldsymbol{{B}} \\[5pt] \vdots & \ddots & \vdots \\[5pt] a_{m1} \boldsymbol{{B}} & \cdots & a_{mn} \boldsymbol{{B}} \end{array}\right].\end{equation}
In the linear equation system, another linear operator, denoted by
![]() $vec$
, can vectorize a matrix by reordering the coefficients into a single column vector as:
$vec$
, can vectorize a matrix by reordering the coefficients into a single column vector as:
According to the fundamental principle of the Kronecker product [Reference Brewer44]:
Eq. (1) can be represented as the following linear equation system:
 \begin{align} \left[\boldsymbol{{A}} \otimes \boldsymbol{{I}}_{4} \quad-\boldsymbol{{I}}_{4}\otimes \boldsymbol{{B}}^{T} \right]_{16 \times 32} \left\{\begin{array}{c} vec(\boldsymbol{{X}}) \\[5pt] vec(\boldsymbol{{Y}}) \end{array}\right\}_{32 \times 1} = \textbf{0}_{16 \times 1}. \end{align}
\begin{align} \left[\boldsymbol{{A}} \otimes \boldsymbol{{I}}_{4} \quad-\boldsymbol{{I}}_{4}\otimes \boldsymbol{{B}}^{T} \right]_{16 \times 32} \left\{\begin{array}{c} vec(\boldsymbol{{X}}) \\[5pt] vec(\boldsymbol{{Y}}) \end{array}\right\}_{32 \times 1} = \textbf{0}_{16 \times 1}. \end{align}
Each set of data constructs a linear equation of the form
![]() $\boldsymbol{{K}}\boldsymbol{{x}}=\textbf{0}$
, and stacking n linear equations can obtain an overdetermined equation system as follows:
$\boldsymbol{{K}}\boldsymbol{{x}}=\textbf{0}$
, and stacking n linear equations can obtain an overdetermined equation system as follows:
in which
The robot-world and hand-eye calibration problem is transformed into a linear null space calculation, which generates a unique solution based on the constraints of the orthogonal matrix. Applying SVD on the matrix
![]() $\tilde{\boldsymbol{{K}}}$
leads to the right singular vector
$\tilde{\boldsymbol{{K}}}$
leads to the right singular vector
![]() $\boldsymbol{{v}}_{K}$
, which is corresponding to the minimum singular value. Consequently, the matrices
$\boldsymbol{{v}}_{K}$
, which is corresponding to the minimum singular value. Consequently, the matrices
![]() $\boldsymbol{{V}}_{X}$
and
$\boldsymbol{{V}}_{X}$
and
![]() $\boldsymbol{{V}}_{Y}$
extracted from the null space of
$\boldsymbol{{V}}_{Y}$
extracted from the null space of
![]() $\tilde{\boldsymbol{{K}}}$
are proportional to the matrices
$\tilde{\boldsymbol{{K}}}$
are proportional to the matrices
![]() $\boldsymbol{{X}}$
and
$\boldsymbol{{X}}$
and
![]() $\boldsymbol{{Y}}$
, which can be obtained as
$\boldsymbol{{Y}}$
, which can be obtained as
 \begin{equation} \begin{array}{c} \tilde{\boldsymbol{{X}}}=\varphi\boldsymbol{{V}}_{X}; \\[5pt] \tilde{\boldsymbol{{Y}}}=\varphi\boldsymbol{{V}}_{Y}. \end{array}\end{equation}
\begin{equation} \begin{array}{c} \tilde{\boldsymbol{{X}}}=\varphi\boldsymbol{{V}}_{X}; \\[5pt] \tilde{\boldsymbol{{Y}}}=\varphi\boldsymbol{{V}}_{Y}. \end{array}\end{equation}
where
![]() $\boldsymbol{{V}}_{X}=vec^{-1} ( \boldsymbol{{v}}_{K}(1:16) )$
and
$\boldsymbol{{V}}_{X}=vec^{-1} ( \boldsymbol{{v}}_{K}(1:16) )$
and
![]() $\boldsymbol{{V}}_{Y}=vec^{-1} ( \boldsymbol{{v}}_{K}(17:32) )$
. The proportionality factor
$\boldsymbol{{V}}_{Y}=vec^{-1} ( \boldsymbol{{v}}_{K}(17:32) )$
. The proportionality factor
![]() $\varphi$
of the solution
$\varphi$
of the solution
![]() $\boldsymbol{{x}}$
is
$\boldsymbol{{x}}$
is
since
![]() $\varphi$
is determined by the orthogonal constraint:
$\varphi$
is determined by the orthogonal constraint:
![]() $det(\boldsymbol{{R}}_{X})=1$
.
$det(\boldsymbol{{R}}_{X})=1$
.
Meanwhile, it is necessary to go through a re-orthogonalization procedure to guarantee the orthogonality of solutions
![]() $\boldsymbol{{R}}_{X}$
and
$\boldsymbol{{R}}_{X}$
and
![]() $\boldsymbol{{R}}_{Y}$
as the presence of noise. The best re-orthogonalization can be obtained by applying SVD on the approximate matrix as:
$\boldsymbol{{R}}_{Y}$
as the presence of noise. The best re-orthogonalization can be obtained by applying SVD on the approximate matrix as:
and i stands for the unknown
![]() $\boldsymbol{{X}}$
,
$\boldsymbol{{X}}$
,
![]() $\boldsymbol{{Y}}$
.
$\boldsymbol{{Y}}$
.
2.3. Iterative solution
The closed-form solution obtained above can be used as the initial value of the Gauss–Newton algorithm iteration. In turn, the Gauss–Newton algorithm can improve the accuracy and robustness of the closed-form solution. The Gauss–Newton algorithm proposed in this study aims to optimize the rotation and translation parts simultaneously.
Since a rotation matrix belongs to the special orthogonal group SO(3) [Reference Murray, Li and Sastry45], there is an exponential mapping from the ‘axis-angle’ representation of the rotation vector to the rotation matrix as:
where
![]() $\boldsymbol{{I}}_{3}$
is a three order identify matrix;
$\boldsymbol{{I}}_{3}$
is a three order identify matrix;
![]() $[\boldsymbol{\omega}]^{\wedge}$
is the skew-symmetric matrix corresponding to the vector
$[\boldsymbol{\omega}]^{\wedge}$
is the skew-symmetric matrix corresponding to the vector
![]() $\boldsymbol{\omega}$
and is given by:
$\boldsymbol{\omega}$
and is given by:
 \begin{equation} [\boldsymbol{\omega}]^{\wedge}=\left[\begin{array}{c@{\quad}c@{\quad}c} 0 & -\omega_{z} & \omega_{y} \\[5pt] \omega_{z} & 0 & -\omega_{x} \\[5pt] -\omega_{y} & \omega_{x} & 0 \end{array}\right].\end{equation}
\begin{equation} [\boldsymbol{\omega}]^{\wedge}=\left[\begin{array}{c@{\quad}c@{\quad}c} 0 & -\omega_{z} & \omega_{y} \\[5pt] \omega_{z} & 0 & -\omega_{x} \\[5pt] -\omega_{y} & \omega_{x} & 0 \end{array}\right].\end{equation}
![]() $\boldsymbol{\omega}$
is the three independent variables of the rotation matrix based on the ‘axis-angle’ representation and
$\boldsymbol{\omega}$
is the three independent variables of the rotation matrix based on the ‘axis-angle’ representation and
![]() $\boldsymbol{\omega}=\boldsymbol{{k}}\theta$
, where
$\boldsymbol{\omega}=\boldsymbol{{k}}\theta$
, where
![]() $\boldsymbol{{k}}$
is the normalized unit axis of the rotation matrix and
$\boldsymbol{{k}}$
is the normalized unit axis of the rotation matrix and
![]() $\theta$
is the angle of the rotation matrix.
$\theta$
is the angle of the rotation matrix.
The frame transformations and absolute poses involved in the equations (Eq. (1)) have the same mathematical representation, that is, a homogeneous matrix including a rotation matrix and a translation vector. Therefore, Eq. (1) can decouple the rotation part and the translation part, and each can be expressed as a function as follows:
 \begin{equation} \begin{aligned} \boldsymbol{{F}}_{1}(\boldsymbol{\omega}_{X},\boldsymbol{\omega}_{Y})&=\boldsymbol{{R}}_{A} exp \left([ \boldsymbol{\omega}_{X}]^{\wedge}\right) - exp \left([\boldsymbol{\omega}_{Y}]^{\wedge}\right) \boldsymbol{{R}}_{B}; \\[5pt] \boldsymbol{{F}}_{2}(\boldsymbol{\omega}_{Y},\boldsymbol{{t}}_{X},\boldsymbol{{t}}_{Y})&=exp \left([ \boldsymbol{\omega}_{Y}]^{\wedge}\right) \boldsymbol{{t}}_{B} + \boldsymbol{{t}}_{Y} -\boldsymbol{{R}}_{A}\boldsymbol{{t}}_{X} - \boldsymbol{{t}}_{A}. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \boldsymbol{{F}}_{1}(\boldsymbol{\omega}_{X},\boldsymbol{\omega}_{Y})&=\boldsymbol{{R}}_{A} exp \left([ \boldsymbol{\omega}_{X}]^{\wedge}\right) - exp \left([\boldsymbol{\omega}_{Y}]^{\wedge}\right) \boldsymbol{{R}}_{B}; \\[5pt] \boldsymbol{{F}}_{2}(\boldsymbol{\omega}_{Y},\boldsymbol{{t}}_{X},\boldsymbol{{t}}_{Y})&=exp \left([ \boldsymbol{\omega}_{Y}]^{\wedge}\right) \boldsymbol{{t}}_{B} + \boldsymbol{{t}}_{Y} -\boldsymbol{{R}}_{A}\boldsymbol{{t}}_{X} - \boldsymbol{{t}}_{A}. \end{aligned}\end{equation}
The basic method of the theory of Lie groups, which makes it possible to obtain deep results with striking simplicity, consists in reducing questions concerning Lie groups to certain problems of linear algebra [Reference Gorbatsevich, Onishchik and Vinberg46]. It is not convenient to take the derivative of a rotation matrix because the perturbation of a rotation matrix is a multiplication operation. Therefore, taking the derivative of the vector corresponding to the rotation matrix can simplify the problem. The Jacobian matrix of the Gauss–Newton algorithm can be easily calculated by the addition operation of Lie algebra. We use the symbol
![]() $\boldsymbol{{J}}$
to represent the Jacobian matrix, and the iterative formula is
$\boldsymbol{{J}}$
to represent the Jacobian matrix, and the iterative formula is
![]() $\boldsymbol{{J}} \Delta \boldsymbol{{x}}=\boldsymbol{{f}}$
. Let
$\boldsymbol{{J}} \Delta \boldsymbol{{x}}=\boldsymbol{{f}}$
. Let
![]() $(\,)_{i}$
represents the
$(\,)_{i}$
represents the
![]() $i^{th}$
column vector in the bracket, and the Jacobian matrix can be determined by the equation as follows:
$i^{th}$
column vector in the bracket, and the Jacobian matrix can be determined by the equation as follows:
 \begin{align} \boldsymbol{{J}}= \begin{bmatrix} \left[\begin{array}{l} \dfrac{\partial(\boldsymbol{{F}}_{1})_{1}}{\partial \boldsymbol{\omega}_{X}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{2}}{\partial \boldsymbol{\omega}_{X}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{3}}{\partial \boldsymbol{\omega}_{X}} \end{array}\right] &\left[\begin{array}{l} \dfrac{\partial(\boldsymbol{{F}}_{1})_{1}}{\partial\boldsymbol{\omega}_{Y}}\\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{2}}{\partial\boldsymbol{\omega}_{Y}}\\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{3}}{\partial\boldsymbol{\omega}_{Y}} \end{array}\right] &\textbf{0} &\textbf{0}\\[-5pt] \\ \textbf{0} &\dfrac{\partial\boldsymbol{{F}}_{2}}{\partial \boldsymbol{\omega}_{Y}} &\dfrac{\partial\boldsymbol{{F}}_{2}}{\partial \boldsymbol{{t}}_{X}} &\dfrac{\partial\boldsymbol{{F}}_{2}}{\partial \boldsymbol{{t}}_{Y}} \end{bmatrix}.\end{align}
\begin{align} \boldsymbol{{J}}= \begin{bmatrix} \left[\begin{array}{l} \dfrac{\partial(\boldsymbol{{F}}_{1})_{1}}{\partial \boldsymbol{\omega}_{X}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{2}}{\partial \boldsymbol{\omega}_{X}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{3}}{\partial \boldsymbol{\omega}_{X}} \end{array}\right] &\left[\begin{array}{l} \dfrac{\partial(\boldsymbol{{F}}_{1})_{1}}{\partial\boldsymbol{\omega}_{Y}}\\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{2}}{\partial\boldsymbol{\omega}_{Y}}\\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{3}}{\partial\boldsymbol{\omega}_{Y}} \end{array}\right] &\textbf{0} &\textbf{0}\\[-5pt] \\ \textbf{0} &\dfrac{\partial\boldsymbol{{F}}_{2}}{\partial \boldsymbol{\omega}_{Y}} &\dfrac{\partial\boldsymbol{{F}}_{2}}{\partial \boldsymbol{{t}}_{X}} &\dfrac{\partial\boldsymbol{{F}}_{2}}{\partial \boldsymbol{{t}}_{Y}} \end{bmatrix}.\end{align}
The key task of obtaining the Jacobian matrix is to calculate the left perturbation model of the rotation matrix. Taking the first-order approximation of the exponential function, we have
And the principle of cross product:
![]() $[\boldsymbol{{a}}]^{\wedge} \boldsymbol{{b}}=\boldsymbol{{a}} \times \boldsymbol{{b}}=-\boldsymbol{{b}} \times \boldsymbol{{a}}=-[\boldsymbol{{b}}]^{\wedge} \boldsymbol{{a}}$
, which is also instrumental in the calculation of the left perturbation model of the rotation matrix.
$[\boldsymbol{{a}}]^{\wedge} \boldsymbol{{b}}=\boldsymbol{{a}} \times \boldsymbol{{b}}=-\boldsymbol{{b}} \times \boldsymbol{{a}}=-[\boldsymbol{{b}}]^{\wedge} \boldsymbol{{a}}$
, which is also instrumental in the calculation of the left perturbation model of the rotation matrix.
The left perturbation model of the rotation matrix in the help of the operation of Lie algebra is constructed by the following processes:
 \begin{equation} \begin{aligned} \frac{\partial(\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X})}{\partial \boldsymbol{\omega}_{X}} &=\lim_{\partial\boldsymbol{\omega}_{X} \to 0} \frac{\boldsymbol{{R}}_{A}\partial\boldsymbol{{R}}_{X}\boldsymbol{{R}}_{X}-\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X} }{ \partial\boldsymbol{\omega}_{X}}\\[5pt] &=\lim_{\partial \boldsymbol{\omega}_{X} \to 0} \frac{\boldsymbol{{R}}_{A}[\partial\boldsymbol{\omega}_{X}]^{\wedge}\boldsymbol{{R}}_{X}}{\partial\boldsymbol{\omega}_{X}}\\[5pt] &=\lim_{\partial \boldsymbol{\omega}_{X} \to 0} \frac{\boldsymbol{{R}}_{A}[\partial\boldsymbol{\omega}_{X}]^{\wedge}[(\boldsymbol{{R}}_{X})_{1}, (\boldsymbol{{R}}_{X})_{2}, (\boldsymbol{{R}}_{X})_{3} ]}{ \partial\boldsymbol{\omega}_{X}}\\[5pt] &=\lim_{\partial \boldsymbol{\omega}_{X} \to 0} \frac{-\boldsymbol{{R}}_{A}[[(\boldsymbol{{R}}_{X})_{1}]^{\wedge}\partial\boldsymbol{\omega}_{X},[(\boldsymbol{{R}}_{X})_{2}]^{\wedge}\partial\boldsymbol{\omega}_{X},[(\boldsymbol{{R}}_{X})_{3}]^{\wedge}\partial\boldsymbol{\omega}_{X}]}{ \partial\boldsymbol{\omega}_{X}}. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \frac{\partial(\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X})}{\partial \boldsymbol{\omega}_{X}} &=\lim_{\partial\boldsymbol{\omega}_{X} \to 0} \frac{\boldsymbol{{R}}_{A}\partial\boldsymbol{{R}}_{X}\boldsymbol{{R}}_{X}-\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X} }{ \partial\boldsymbol{\omega}_{X}}\\[5pt] &=\lim_{\partial \boldsymbol{\omega}_{X} \to 0} \frac{\boldsymbol{{R}}_{A}[\partial\boldsymbol{\omega}_{X}]^{\wedge}\boldsymbol{{R}}_{X}}{\partial\boldsymbol{\omega}_{X}}\\[5pt] &=\lim_{\partial \boldsymbol{\omega}_{X} \to 0} \frac{\boldsymbol{{R}}_{A}[\partial\boldsymbol{\omega}_{X}]^{\wedge}[(\boldsymbol{{R}}_{X})_{1}, (\boldsymbol{{R}}_{X})_{2}, (\boldsymbol{{R}}_{X})_{3} ]}{ \partial\boldsymbol{\omega}_{X}}\\[5pt] &=\lim_{\partial \boldsymbol{\omega}_{X} \to 0} \frac{-\boldsymbol{{R}}_{A}[[(\boldsymbol{{R}}_{X})_{1}]^{\wedge}\partial\boldsymbol{\omega}_{X},[(\boldsymbol{{R}}_{X})_{2}]^{\wedge}\partial\boldsymbol{\omega}_{X},[(\boldsymbol{{R}}_{X})_{3}]^{\wedge}\partial\boldsymbol{\omega}_{X}]}{ \partial\boldsymbol{\omega}_{X}}. \end{aligned}\end{equation}
According to the left perturbation model of the rotation matrix, a complete and concrete expression of the Jacobian iteration formula
![]() $\boldsymbol{{J}} \Delta \boldsymbol{{x}}=\boldsymbol{{f}}$
can be obtained as:
$\boldsymbol{{J}} \Delta \boldsymbol{{x}}=\boldsymbol{{f}}$
can be obtained as:
 \begin{equation} \begin{bmatrix} \left[\begin{array}{l} -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{1}]^{\wedge}\\[5pt] -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{2}]^{\wedge}\\[5pt] -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{3}]^{\wedge} \end{array}\right] &\left[\begin{array}{l} [(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{1}]^{\wedge}\\[5pt] [(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{2}]^{\wedge}\\[5pt] [(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{3}]^{\wedge} \end{array}\right] &\textbf{0}_{9\times3} &\textbf{0}_{9\times3}\\[5pt] \textbf{0}_{3\times3} &-[\boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}]^{\wedge} &-\boldsymbol{{R}}_{A} &\boldsymbol{{I}}_{3} \end{bmatrix} \begin{Bmatrix} \partial \boldsymbol{\omega}_{X}\\[5pt] \partial \boldsymbol{\omega}_{Y}\\[5pt] \partial \boldsymbol{{t}}_{X}\\[5pt] \partial \boldsymbol{{t}}_{Y} \end{Bmatrix} = - \begin{Bmatrix} (\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X}-\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{1}\\[5pt] (\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X}-\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{2}\\[5pt] (\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X}-\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{3}\\[5pt] \boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}+\boldsymbol{{t}}_{Y}-\boldsymbol{{R}}_{A}\boldsymbol{{t}}_{X}-\boldsymbol{{t}}_{A} \end{Bmatrix} .\end{equation}
\begin{equation} \begin{bmatrix} \left[\begin{array}{l} -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{1}]^{\wedge}\\[5pt] -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{2}]^{\wedge}\\[5pt] -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{3}]^{\wedge} \end{array}\right] &\left[\begin{array}{l} [(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{1}]^{\wedge}\\[5pt] [(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{2}]^{\wedge}\\[5pt] [(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{3}]^{\wedge} \end{array}\right] &\textbf{0}_{9\times3} &\textbf{0}_{9\times3}\\[5pt] \textbf{0}_{3\times3} &-[\boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}]^{\wedge} &-\boldsymbol{{R}}_{A} &\boldsymbol{{I}}_{3} \end{bmatrix} \begin{Bmatrix} \partial \boldsymbol{\omega}_{X}\\[5pt] \partial \boldsymbol{\omega}_{Y}\\[5pt] \partial \boldsymbol{{t}}_{X}\\[5pt] \partial \boldsymbol{{t}}_{Y} \end{Bmatrix} = - \begin{Bmatrix} (\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X}-\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{1}\\[5pt] (\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X}-\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{2}\\[5pt] (\boldsymbol{{R}}_{A}\boldsymbol{{R}}_{X}-\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{3}\\[5pt] \boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}+\boldsymbol{{t}}_{Y}-\boldsymbol{{R}}_{A}\boldsymbol{{t}}_{X}-\boldsymbol{{t}}_{A} \end{Bmatrix} .\end{equation}
Stacking n sets of Eq. (17) leads to
in which
Then, the solution can be obtained as:
![]() $\Delta\boldsymbol{{x}}$
is subsequently used to update
$\Delta\boldsymbol{{x}}$
is subsequently used to update
![]() $\tilde{\boldsymbol{{J}}}$
and
$\tilde{\boldsymbol{{J}}}$
and
![]() $\tilde{\boldsymbol{{f}}}$
, and the process should be repeated until the limit of
$\tilde{\boldsymbol{{f}}}$
, and the process should be repeated until the limit of
![]() $\Delta\boldsymbol{{x}}$
is reached.
$\Delta\boldsymbol{{x}}$
is reached.
2.4. Singular value processing
For an arbitrary rotation matrix
![]() $\boldsymbol{{R}}$
, rotation axis
$\boldsymbol{{R}}$
, rotation axis
![]() $\boldsymbol{{k}}$
is not unique. The results in this study were normalized based on the fact that rotation about an axis
$\boldsymbol{{k}}$
is not unique. The results in this study were normalized based on the fact that rotation about an axis
![]() $\boldsymbol{{k}}$
by an angle of
$\boldsymbol{{k}}$
by an angle of
![]() $\theta(0 \le \theta \le \pi)$
is equivalent to rotation about the axis
$\theta(0 \le \theta \le \pi)$
is equivalent to rotation about the axis
![]() $-\boldsymbol{{k}}$
by the rotation angle of
$-\boldsymbol{{k}}$
by the rotation angle of
![]() $(2\pi - \theta)$
. Therefore, if the rotation angle satisfies
$(2\pi - \theta)$
. Therefore, if the rotation angle satisfies
![]() $0\le \theta \le \pi$
, then
$0\le \theta \le \pi$
, then
![]() $\boldsymbol{\omega}=\boldsymbol{{k}} \theta$
, and if
$\boldsymbol{\omega}=\boldsymbol{{k}} \theta$
, and if
![]() $\pi\le \theta \le 2\pi$
, then
$\pi\le \theta \le 2\pi$
, then
![]() $\boldsymbol{\omega}=-\boldsymbol{{k}} (2\pi-\theta)$
. A more detailed method for extracting the rotation axis
$\boldsymbol{\omega}=-\boldsymbol{{k}} (2\pi-\theta)$
. A more detailed method for extracting the rotation axis
![]() $\boldsymbol{{k}}$
from rotation matrix
$\boldsymbol{{k}}$
from rotation matrix
![]() $\boldsymbol{{R}}$
is presented in refs. [Reference Murray, Li and Sastry45, Reference Fu, Dai, Kun, Chen and Lopez-Custodio47]. But the problem is that the rotation axis
$\boldsymbol{{R}}$
is presented in refs. [Reference Murray, Li and Sastry45, Reference Fu, Dai, Kun, Chen and Lopez-Custodio47]. But the problem is that the rotation axis
![]() $\boldsymbol{{k}}$
cannot be extracted when
$\boldsymbol{{k}}$
cannot be extracted when
![]() $\theta$
is equal to 0 or
$\theta$
is equal to 0 or
![]() $\pi$
. In another words, when the unknown rotation angle of
$\pi$
. In another words, when the unknown rotation angle of
![]() $\boldsymbol{{R}}_{X}$
or
$\boldsymbol{{R}}_{X}$
or
![]() $\boldsymbol{{R}}_{Y}$
is close to 0 or
$\boldsymbol{{R}}_{Y}$
is close to 0 or
![]() $\pi$
, singular phenomenon occurs.
$\pi$
, singular phenomenon occurs.
Song et al. [Reference Song, Du, Wang and Sun48] proposed a method to solve the singularity for the closed-form solutions of the hand-eye calibration, which expressed the unknown hand-eye rotation matrix by two non-singular rotation matrices. However, the singularity of robot-world and hand-eye calibration has not been discussed yet.
The singularity in robot-world and hand-eye calibration is more complicated because both unknown matrices have possible singular values. This study improves a method to solve the singularity problem, which can be widely used for simultaneous robot-world and hand-eye calibration. The specific process is as follows:
-
(1) Firstly, determine whether the angle of the linear estimated rotation matrices
 $\boldsymbol{{R}}_{X}$
and
$\boldsymbol{{R}}_{X}$
and
 $\boldsymbol{{R}}_{Y}$
is close to the singular value or not. Singularity can be divided into three types of results: only
$\boldsymbol{{R}}_{Y}$
is close to the singular value or not. Singularity can be divided into three types of results: only
 $\boldsymbol{{R}}_{X}$
is singular value; only
$\boldsymbol{{R}}_{X}$
is singular value; only
 $\boldsymbol{{R}}_{Y}$
is singular value; both
$\boldsymbol{{R}}_{Y}$
is singular value; both
 $\boldsymbol{{R}}_{X}$
and
$\boldsymbol{{R}}_{X}$
and
 $\boldsymbol{{R}}_{Y}$
are singular values.
$\boldsymbol{{R}}_{Y}$
are singular values. -
(2) According to the result of the first step, select the corresponding processing method.
Only
![]() $\boldsymbol{{R}}_{X}$
is singular value, and the singular value processing process is shown in Fig. 2.
$\boldsymbol{{R}}_{X}$
is singular value, and the singular value processing process is shown in Fig. 2.

Figure 2. Singular value processing flowchart: only
![]() $\boldsymbol{{R}}_{X}$
is singular value.
$\boldsymbol{{R}}_{X}$
is singular value.
Only
![]() $\boldsymbol{{R}}_{Y}$
is singular value, the singular value processing is shown in Fig. 3.
$\boldsymbol{{R}}_{Y}$
is singular value, the singular value processing is shown in Fig. 3.

Figure 3. Singular value processing flowchart: only
![]() $\boldsymbol{{R}}_{Y}$
is singular value.
$\boldsymbol{{R}}_{Y}$
is singular value.
Both
![]() $\boldsymbol{{R}}_{X}$
and
$\boldsymbol{{R}}_{X}$
and
![]() $\boldsymbol{{R}}_{Y}$
are singular values, and the singular value processing is shown in Fig. 4.
$\boldsymbol{{R}}_{Y}$
are singular values, and the singular value processing is shown in Fig. 4.

Figure 4. Singular value processing flowchart: both
![]() $\boldsymbol{{R}}_{X}$
and
$\boldsymbol{{R}}_{X}$
and
![]() $\boldsymbol{{R}}_{Y}$
are singular values.
$\boldsymbol{{R}}_{Y}$
are singular values.
Note that the angle of the rotation of
![]() $\boldsymbol{{X}}_{\text{user}}$
or
$\boldsymbol{{X}}_{\text{user}}$
or
![]() $\boldsymbol{{Y}}_{\text{user}}$
is between 0 and
$\boldsymbol{{Y}}_{\text{user}}$
is between 0 and
![]() $2\pi/3$
according to ref. [Reference Song, Du, Wang and Sun48].
$2\pi/3$
according to ref. [Reference Song, Du, Wang and Sun48].
2.5. Error metrics
For the calculated values
![]() $\hat{\boldsymbol{{R}}}_{X}$
and
$\hat{\boldsymbol{{R}}}_{X}$
and
![]() $\hat{\boldsymbol{{R}}}_{Y}$
, the error metric is defined as:
$\hat{\boldsymbol{{R}}}_{Y}$
, the error metric is defined as:
where
![]() $\boldsymbol{{R}}_{i}$
is the ground truth.
$\boldsymbol{{R}}_{i}$
is the ground truth.
![]() $Rodrigues(\!\bullet\!)$
means to extract the ‘axis-angle’ from the homogeneous matrix, more detailed method in ref. [Reference Murray, Li and Sastry45].
$Rodrigues(\!\bullet\!)$
means to extract the ‘axis-angle’ from the homogeneous matrix, more detailed method in ref. [Reference Murray, Li and Sastry45].
For the calculated values
![]() $\hat{\boldsymbol{{t}}}_{X}$
and
$\hat{\boldsymbol{{t}}}_{X}$
and
![]() $\hat{\boldsymbol{{t}}}_{Y}$
, the error metrics are defined as:
$\hat{\boldsymbol{{t}}}_{Y}$
, the error metrics are defined as:
In order to compare the accuracy of all methods, root mean square was suggested to use,
 \begin{equation} \begin{aligned} \text { Error of}\; \boldsymbol{{R}}&=RMS(\boldsymbol{\theta}^{1}_{\text{error}},\boldsymbol{\theta}^{1}_{\text{error}},\dots,\boldsymbol{\theta}^{N}_{\text{error}}) ;\\[5pt] \text { Error of}\; \boldsymbol{{t}}&=RMS(\boldsymbol{{t}}^{1}_{\text{error}},\boldsymbol{{t}}^{1}_{\text{error}},\dots,\boldsymbol{{t}}^{N}_{\text{error}}). \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \text { Error of}\; \boldsymbol{{R}}&=RMS(\boldsymbol{\theta}^{1}_{\text{error}},\boldsymbol{\theta}^{1}_{\text{error}},\dots,\boldsymbol{\theta}^{N}_{\text{error}}) ;\\[5pt] \text { Error of}\; \boldsymbol{{t}}&=RMS(\boldsymbol{{t}}^{1}_{\text{error}},\boldsymbol{{t}}^{1}_{\text{error}},\dots,\boldsymbol{{t}}^{N}_{\text{error}}). \end{aligned}\end{equation}
where N refers to the number of simulations in the simulation test and the number of verification datasets in the real experimental test.
3. Verification and discussions
In this section, comprehensive tests have been conducted to verify the feasibility and effectiveness of the closed-form solution and the iterative solution. Li et al. [Reference Li, Wang and Wu36] constructed a linear equation system for robot-world and hand-eye calibration based on Kronecker product, which converted such problem into least square calculations. Same as the closed-form solution proposed in this study, Li’s method can solve the rotations and translations problem simultaneously and serve as an initial value for the iterative solution. On the one hand, the Li’s method can verify the feasibility of the closed-form solution as proposed in this study. On the other hand, the iterative solution requires an initial value as a nonlinear method, and the Li’s method can be used to test the convergence efficiency of the iterative solution. The mnemonics ‘Li’ and ‘I-Li’, respectively, indicate the Li’s method and the iterative method with the Li’s method as the initial value. The closed-form solution and the iterative solution proposed in this study, respectively, denote as ‘closed-form’ and ‘iterative’. In order to further improve the credibility of the method proposed in this study, two methods based on dual quaternion are added as reference in the real experiment. One method [Reference Daniilidis26] (denotes as ‘DQ’) solves the rotation and translation problems simultaneously, and the other method [Reference Malti and Barreto20] (denotes as ‘IDQ’) is to solve the rotation and translation problems separately.
An industrial robot (GSK RB03) with 6-degree-of-freedom (6-DOF) and a CMOS camera (Photonfocus
![]() $ MV1-D2048\ast1088-240-CL$
) with an 8 mm lens installed at the end of the robot have been employed for experimentation. The same settings were simulated in the synthesis experiment to closely integrate the simulated and real test results.
$ MV1-D2048\ast1088-240-CL$
) with an 8 mm lens installed at the end of the robot have been employed for experimentation. The same settings were simulated in the synthesis experiment to closely integrate the simulated and real test results.
3.1. Experiments with simulated data
This section presents a detailed account of the number of datasets and the noise effect on the calibration accuracy. The accuracy of the robot-world and hand-eye calibration is affected by the robot configurations distribution [Reference Wu and Ren43], and some data selection methods were elaborated in refs. [Reference Schmidt and Niemann49, Reference Zhang, Shi and Liu50]. Therefore, the robot configurations are selected within the field of view of the monocular camera to maintain consistency with the real experiment.
![]() $\boldsymbol{{A}}_{i}$
(
$\boldsymbol{{A}}_{i}$
(
![]() $i=1,2, \dots ,50$
) came from 50 different robot configurations, which were obtained from the robot control system. Figure 5 shows the distribution of
$i=1,2, \dots ,50$
) came from 50 different robot configurations, which were obtained from the robot control system. Figure 5 shows the distribution of
![]() $\boldsymbol{{A}}_{i}$
. Figure 5(a) is the distribution of the normalized rotation axis. The histograms of the rotation angle and translation norm are shown in Fig. 5(b) and (c), respectively, where the red line refers to the median. Assume that the ground truth of the robot-world and hand-eye transformations are shown in Table I.
$\boldsymbol{{A}}_{i}$
. Figure 5(a) is the distribution of the normalized rotation axis. The histograms of the rotation angle and translation norm are shown in Fig. 5(b) and (c), respectively, where the red line refers to the median. Assume that the ground truth of the robot-world and hand-eye transformations are shown in Table I.
![]() $\boldsymbol{{B}}_{i}$
(
$\boldsymbol{{B}}_{i}$
(
![]() $i=1,2, \dots ,50$
) were obtained through equation:
$i=1,2, \dots ,50$
) were obtained through equation:
![]() $\boldsymbol{{B}}_{i}=\boldsymbol{{Y}}^{-1} \boldsymbol{{A}}_{i} \boldsymbol{{X}}$
. All methods were implemented based on MATLAB2019a. One hundred simulations were performed for each method.
$\boldsymbol{{B}}_{i}=\boldsymbol{{Y}}^{-1} \boldsymbol{{A}}_{i} \boldsymbol{{X}}$
. All methods were implemented based on MATLAB2019a. One hundred simulations were performed for each method.

Figure 5. Distribution of robot configurations.
Table I. The ground truth for the robot-world and hand-eye transformations

Gaussian noise was added to all simulation data as the following equations:
 \begin{equation} \begin{aligned} \boldsymbol{{R}}_{m}^{noise}&=Rot\left(\boldsymbol{{k}},\left(\theta_{m}+\theta_{noise}\right)\right); \\[5pt] \boldsymbol{{t}}_{m}^{noise}&=\boldsymbol{{t}}_{m}+\boldsymbol{{t}}_{noise}, \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \boldsymbol{{R}}_{m}^{noise}&=Rot\left(\boldsymbol{{k}},\left(\theta_{m}+\theta_{noise}\right)\right); \\[5pt] \boldsymbol{{t}}_{m}^{noise}&=\boldsymbol{{t}}_{m}+\boldsymbol{{t}}_{noise}, \end{aligned}\end{equation}
where
![]() $\theta_{noise}$
and
$\theta_{noise}$
and
![]() $\boldsymbol{{t}}_{noise}$
were the amplitude of the rotational noise and the translational noise, both were zero-mean-value.
$\boldsymbol{{t}}_{noise}$
were the amplitude of the rotational noise and the translational noise, both were zero-mean-value.
![]() $\boldsymbol{{t}}_{noise}$
was created by adding noises with the same standard deviation on three directions, respectively. The subscript m denoted
$\boldsymbol{{t}}_{noise}$
was created by adding noises with the same standard deviation on three directions, respectively. The subscript m denoted
![]() $\boldsymbol{{A}}_{i}$
and
$\boldsymbol{{A}}_{i}$
and
![]() $\boldsymbol{{B}}_{j}$
. The synthetic experiment verifies the superiority of the method proposed in this study in terms of accuracy convergence and noise sensitivity. In the accuracy convergence test part, the standard deviation of the rotation noise was
$\boldsymbol{{B}}_{j}$
. The synthetic experiment verifies the superiority of the method proposed in this study in terms of accuracy convergence and noise sensitivity. In the accuracy convergence test part, the standard deviation of the rotation noise was
![]() $\sigma_{\theta_{noise}}=0.1(^{\circ})$
and the noise standard deviation of the translation noise was
$\sigma_{\theta_{noise}}=0.1(^{\circ})$
and the noise standard deviation of the translation noise was
![]() $\sigma_{\boldsymbol{{t}}_{noise}}=[0.1,0.1,0.1]^{T} ({\rm mm})$
. In the noise sensitivity test part, the noise standard deviation
$\sigma_{\boldsymbol{{t}}_{noise}}=[0.1,0.1,0.1]^{T} ({\rm mm})$
. In the noise sensitivity test part, the noise standard deviation
![]() $\sigma_{\theta_{noise}}$
and
$\sigma_{\theta_{noise}}$
and
![]() $\sigma_{\boldsymbol{{t}}_{noise}}$
were set with a maximum amplitude of
$\sigma_{\boldsymbol{{t}}_{noise}}$
were set with a maximum amplitude of
![]() $2(^{\circ})$
in rotation and
$2(^{\circ})$
in rotation and
![]() $[2,2,2]^{T} ({\rm mm})$
in translation and were evenly divided into 10 levels.
$[2,2,2]^{T} ({\rm mm})$
in translation and were evenly divided into 10 levels.
It is noted that the dataset number for the accuracy convergence test ranges from 4 to 50, since the overdetermined system is formed when the dataset number is greater than 3. Figure 6 shows the error curves corresponding to the four methods with different number of datasets, where the errors of
![]() $\boldsymbol{{R}}_{X}$
,
$\boldsymbol{{R}}_{X}$
,
![]() $\boldsymbol{{t}}_{X}$
,
$\boldsymbol{{t}}_{X}$
,
![]() $\boldsymbol{{R}}_{Y,}$
and
$\boldsymbol{{R}}_{Y,}$
and
![]() $\boldsymbol{{t}}_{Y}$
are illustrated in Fig. 6(a), (b), (c), and (d), respectively. Note that the error curves have similar trends, and the accuracy of four methods grows with the number of datasets. However, the numerical value of accuracy and the speed of accuracy convergence are different. The results from ‘closed-form’ and ‘Li’ methods have similar trends, while the results from ‘I-Li’ and ‘iterative’ methods have almost the same trends. This means that the iterative method proposed in this study is suitable for the case where two linear solutions are used as initial values. Figure 6(a) shows that the accuracy of the
$\boldsymbol{{t}}_{Y}$
are illustrated in Fig. 6(a), (b), (c), and (d), respectively. Note that the error curves have similar trends, and the accuracy of four methods grows with the number of datasets. However, the numerical value of accuracy and the speed of accuracy convergence are different. The results from ‘closed-form’ and ‘Li’ methods have similar trends, while the results from ‘I-Li’ and ‘iterative’ methods have almost the same trends. This means that the iterative method proposed in this study is suitable for the case where two linear solutions are used as initial values. Figure 6(a) shows that the accuracy of the
![]() $\boldsymbol{{R}}_{X}$
estimated by four methods converges to a stable value when the number of datasets exceeds 30. When the number of datasets is less than 10, the accuracy of two iterative methods converges faster. In other words, the iterative process can obtain a high-precision solution with data from limited number of robot configurations. Moreover, the accuracy of the iterative methods is better than that of the linear methods. Figure 6(c) shows the error curves of
$\boldsymbol{{R}}_{X}$
estimated by four methods converges to a stable value when the number of datasets exceeds 30. When the number of datasets is less than 10, the accuracy of two iterative methods converges faster. In other words, the iterative process can obtain a high-precision solution with data from limited number of robot configurations. Moreover, the accuracy of the iterative methods is better than that of the linear methods. Figure 6(c) shows the error curves of
![]() $\boldsymbol{{R}}_{Y}$
estimated by four methods, and the results are mostly the same as
$\boldsymbol{{R}}_{Y}$
estimated by four methods, and the results are mostly the same as
![]() $\boldsymbol{{R}}_{X}$
. Figure 6(b) shows the error curves of
$\boldsymbol{{R}}_{X}$
. Figure 6(b) shows the error curves of
![]() $\boldsymbol{{t}}_{X}$
estimated by four methods. The accuracy of the four methods converges a stable value as the number of datasets increases. When the number of datasets is less than 10, the accuracy of two iterative methods is superior to that of two linear methods. Moreover, the accuracy superiority of the iterative methods has not disappeared as the number of datasets increases. Figure 6(d) shows the error curves of
$\boldsymbol{{t}}_{X}$
estimated by four methods. The accuracy of the four methods converges a stable value as the number of datasets increases. When the number of datasets is less than 10, the accuracy of two iterative methods is superior to that of two linear methods. Moreover, the accuracy superiority of the iterative methods has not disappeared as the number of datasets increases. Figure 6(d) shows the error curves of
![]() $\boldsymbol{{t}}_{Y}$
estimated by the four methods, and the downward trends of error curves are similar to that of
$\boldsymbol{{t}}_{Y}$
estimated by the four methods, and the downward trends of error curves are similar to that of
![]() $\boldsymbol{{t}}_{X}$
, but the numerical values are different, which is related to the different amplitudes of
$\boldsymbol{{t}}_{X}$
, but the numerical values are different, which is related to the different amplitudes of
![]() $\boldsymbol{{t}}_{X}$
and
$\boldsymbol{{t}}_{X}$
and
![]() $\boldsymbol{{t}}_{Y}$
[Reference Wu and Ren43]. It can be seen that the iterative methods had faster convergence rate and higher accuracy compared with the linear methods.
$\boldsymbol{{t}}_{Y}$
[Reference Wu and Ren43]. It can be seen that the iterative methods had faster convergence rate and higher accuracy compared with the linear methods.

Figure 6. Accuracy comparison based on different number of datasets.
All 50 sets of data were used in the noise sensitivity test part. Figure 7 shows the error curves corresponding to the four methods with different noise level, where the errors of
![]() $\boldsymbol{{R}}_{X}$
,
$\boldsymbol{{R}}_{X}$
,
![]() $\boldsymbol{{t}}_{X}$
,
$\boldsymbol{{t}}_{X}$
,
![]() $\boldsymbol{{R}}_{Y,}$
and
$\boldsymbol{{R}}_{Y,}$
and
![]() $\boldsymbol{{t}}_{Y}$
are illustrated in Fig. 7(a), (b), (c), and (d), respectively. Generally, the solution errors of the four methods are roughly linearly correlated with the noise level. Figure 7(a) shows the error curves of
$\boldsymbol{{t}}_{Y}$
are illustrated in Fig. 7(a), (b), (c), and (d), respectively. Generally, the solution errors of the four methods are roughly linearly correlated with the noise level. Figure 7(a) shows the error curves of
![]() $\boldsymbol{{R}}_{X}$
, and the iterative methods yield a better performance in robustness. The result of
$\boldsymbol{{R}}_{X}$
, and the iterative methods yield a better performance in robustness. The result of
![]() $\boldsymbol{{R}}_{Y}$
illustrated in Fig. 7(c) has similar trends and amplitudes with the result of
$\boldsymbol{{R}}_{Y}$
illustrated in Fig. 7(c) has similar trends and amplitudes with the result of
![]() $\boldsymbol{{R}}_{X}$
. The results of
$\boldsymbol{{R}}_{X}$
. The results of
![]() $\boldsymbol{{t}}_{X}$
illustrated in Fig. 7(b) are slightly different from the result of
$\boldsymbol{{t}}_{X}$
illustrated in Fig. 7(b) are slightly different from the result of
![]() $\boldsymbol{{t}}_{X}$
illustrated in Fig. 7(d) in amplitude of errors, which is still related to the different amplitudes of
$\boldsymbol{{t}}_{X}$
illustrated in Fig. 7(d) in amplitude of errors, which is still related to the different amplitudes of
![]() $\boldsymbol{{t}}_{X}$
and
$\boldsymbol{{t}}_{X}$
and
![]() $\boldsymbol{{t}}_{Y}$
[Reference Wu and Ren43]. In addition, the slight perturbation of the rotation matrices will cause a larger error in the translation part according to the translation part of Eq. (2.3). Therefore, robot calibration may be an effective method to improve the accuracy of translation estimation. The above results show that iterative optimization can effectively reduce the influence of random noise.
$\boldsymbol{{t}}_{Y}$
[Reference Wu and Ren43]. In addition, the slight perturbation of the rotation matrices will cause a larger error in the translation part according to the translation part of Eq. (2.3). Therefore, robot calibration may be an effective method to improve the accuracy of translation estimation. The above results show that iterative optimization can effectively reduce the influence of random noise.

Figure 7. Accuracy comparison based on different noise level.
3.2. Experiments with real data
The experimental setup corresponding to the robot-world and hand-eye calibration, as shown in Fig. 8, including an industrial robot (GSK RB03) with 6-DOF and a CMOS camera with a 8 mm lens installed at the end of the robot. The intrinsic parameters of the camera were obtained by the Camera Calibration Toolbox for MATLAB [Reference Bouguet51] and Zhang’s method [Reference Zhang and Anal52], which was achieved by a checkerboard with
![]() $7\times10$
calibration grid (each calibration grid is a
$7\times10$
calibration grid (each calibration grid is a
![]() $25\,{\rm mm}\times25\,{\rm mm}$
square).
$25\,{\rm mm}\times25\,{\rm mm}$
square).

Figure 8. Experimental setup.
The experiment process is carried out through the following steps:
-
(1) Camera calibration. Keep the robot fixed and move the checkerboard, and select the poses of the checkerboard in the field of view of the camera based on Zhang’s method [Reference Zhang and Anal52]. Enter the images into Camera Calibration Toolbox for MATLAB, and the intrinsic parameters of camera are listed in Table II.
Table II. Intrinsic parameters of the camera

-
(2) Measurement and calibration. Keep the checkerboard fixed and move the robot to obtain the n configurations for calibration, and the N (
 $N=100$
) configurations for verification.
$N=100$
) configurations for verification.
 $\boldsymbol{{A}}_{i}$
(
$\boldsymbol{{A}}_{i}$
(
 $i=1,2, \dots ,n$
) were obtained from the robot control system.
$i=1,2, \dots ,n$
) were obtained from the robot control system.
 $\boldsymbol{{B}}_{i}$
(
$\boldsymbol{{B}}_{i}$
(
 $i=1,2, \dots ,n$
) were calculated by Zhang’s method [Reference Zhang and Anal52]. The verification data
$i=1,2, \dots ,n$
) were calculated by Zhang’s method [Reference Zhang and Anal52]. The verification data
 $\boldsymbol{{A}}_{i}$
(
$\boldsymbol{{A}}_{i}$
(
 $i=1,2, \dots ,N$
) and
$i=1,2, \dots ,N$
) and
 $\boldsymbol{{B}}_{i}$
(
$\boldsymbol{{B}}_{i}$
(
 $i=1,2, \dots ,N$
) were obtained in the same way.
$i=1,2, \dots ,N$
) were obtained in the same way.In order to solve the robot-world and hand-eye calibration, at least three different poses are required [Reference Shah34]. Consistent with the simulated experiment, take n (
 $n=4,5, \dots ,10$
) datasets to form an overdetermined system for calibration. Run the algorithms and get the calibration results based on all methods.
$n=4,5, \dots ,10$
) datasets to form an overdetermined system for calibration. Run the algorithms and get the calibration results based on all methods. -
(3) Verify the results. Since there is no ground truth in the real experiment, the calibration accuracy can be verified in an indirect way. Calibration accuracy was quantitatively assessed by comparing
 $\boldsymbol{{A}}_{i}$
(
$\boldsymbol{{A}}_{i}$
(
 $i=1,2, \dots ,N$
), using the following equation: (26)The
$i=1,2, \dots ,N$
), using the following equation: (26)The \begin{equation} \hat{\boldsymbol{{A}}}_{i} = \boldsymbol{{Y}}\boldsymbol{{B}}_{i}\boldsymbol{{X}}^{-1}. \end{equation}
\begin{equation} \hat{\boldsymbol{{A}}}_{i} = \boldsymbol{{Y}}\boldsymbol{{B}}_{i}\boldsymbol{{X}}^{-1}. \end{equation}
 $\hat{\boldsymbol{{A}}}_{i}$
and
$\hat{\boldsymbol{{A}}}_{i}$
and
 $\boldsymbol{{A}}_{i}$
(
$\boldsymbol{{A}}_{i}$
(
 $i=1,2, \dots ,N$
) were compared and the errors of all poses (from 4 to 10) in rotation and translation were computed.
$i=1,2, \dots ,N$
) were compared and the errors of all poses (from 4 to 10) in rotation and translation were computed.
The results are shown in Fig. 9. It can be seen that the solutions of Li and closed-form as the initial value of the iterative solution have a faster convergence rate after optimization, which is consistent with the simulation results. In other words, the proposed method can effectively reduce the negative influence of random noise, especially when the measurement information is limited. IDQ method obtains an optimal rotation estimate. This may be due to avoiding the negative effect of translation noise, but the propagation error caused by rotation cannot be ignored. Especially, Fig. 9(b) shows that the translational accuracy estimated by iterative methods outperforms that of the linear methods, and this advantage may be due to the fact that optimizing robot-world and hand-eye calibration with rotation and translation coupling can effectively reduce the propagation error. The proposed method combines the best performance and minimal errors in both rotation and translation using 10 poses. The error is
![]() $0.2632^{\circ}$
in rotation and
$0.2632^{\circ}$
in rotation and
![]() $1.6887$
mm in translation. The calibration error still exists because of the error in robot and vision measuring system.
$1.6887$
mm in translation. The calibration error still exists because of the error in robot and vision measuring system.

Figure 9. Real experiment results: (a) rotation error; (b) translation error.
The calibration accuracy can also be estimated by a global perspective. According to Chasles’s theorem [Reference Chen23], a rigid transformation can be modeled as a rotation with the same angle about an axis not through the origin and a translation along this axis. A screw represented by a vector specified by six independent parameters is exactly equal to the number of degrees of freedom of a rigid body in 3D Euclidean space, which is the most compact representation of a rigid body motion. Therefore, the screw is a better global error evaluation index. The error is denoted as
where
![]() $i=1,2, \dots ,100$
;
$i=1,2, \dots ,100$
;
![]() $Screw(\!\bullet\!)$
means conversion from homogeneous matrix to screw, more detailed method in ref. [Reference Chen23]. The box plots (Fig. 10) show the error distributions. The iterative methods outperform the linear methods in terms of the median error. Meanwhile, the iterative method based on the Li method as the initial value is better, which may be due to the fact that a better initial value can converge to a better iteration result.
$Screw(\!\bullet\!)$
means conversion from homogeneous matrix to screw, more detailed method in ref. [Reference Chen23]. The box plots (Fig. 10) show the error distributions. The iterative methods outperform the linear methods in terms of the median error. Meanwhile, the iterative method based on the Li method as the initial value is better, which may be due to the fact that a better initial value can converge to a better iteration result.

Figure 10. Real experiment results: Error distributions.
In this study, MATLAB R2019a was used to the program implementation of the above four methods, while the hardware used featured Intel(R) Core(TM) i5-10210U CPU @1.60GHz, 8G RAM. Ten poses were used in this test. Table III lists the running time values of the four methods and the number of iterations of the two iterative methods. The runtime data presented in Table III indicate that the iterative solution with the closed-form solution as the initial value is faster than the iterative solution with the reference solution as the initial value.
Table III. Comparison of calculational efficiency

4. Conclusion
This paper proposes a method to solve rotation and translation simultaneously for robot-world and hand-eye calibration. A closed-form initial estimation is originally derived based on Kronecker product for the simultaneous method. Then, the Gauss–Newton algorithm in which the Jacobian matrix is constructed by Lie algebra is applied to the closed-form solution. Additionally, a method to the problem of singularity that can be widely applied to robot-world and hand-eye calibration is elaborated. A comparative analysis with the reference method shows that the proposed method outperforms the later ones in terms of accuracy and robustness, and the proposed method can significantly reduce the propagation error and obtain a higher-precision translation estimation.
CRediT authorship contribution statement
Xiao Wang: conceptualization, formal analysis, investigation, methodology, software, validation, roles/writing – original draft, writing – review and & editing. Hanwen Song: funding acquisition, project administration, resources, and supervision.
Conflicts of interests
The authors declare none.
Acknowledgements
This research was supported by National Natural Science Foundation of China (Grant No. 11872047).
A. Appendix
According to the left perturbation model of the rotation matrix (Eq. (16)), the Jacobian matrix represented by Eq. (14) is derived to Eq. (17). The partial derivative of
![]() $\boldsymbol{{F}}_{1}$
with respect to
$\boldsymbol{{F}}_{1}$
with respect to
![]() $\boldsymbol{\omega}_{X}$
can be represented as
$\boldsymbol{\omega}_{X}$
can be represented as
 \begin{align} \left[\begin{array}{l} \dfrac{\partial(\boldsymbol{{F}}_{1})_{1}}{\partial \boldsymbol{\omega}_{X}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{2}}{\partial \boldsymbol{\omega}_{X}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{3}}{\partial \boldsymbol{\omega}_{X}} \end{array}\right] = \left[\begin{array}{l} -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{1}]^{\wedge^{^{^{^{}}}}}\\[4pt] -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{2}]^{\wedge}\\[4pt] -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{3}]^{\wedge} \end{array}\right].\end{align}
\begin{align} \left[\begin{array}{l} \dfrac{\partial(\boldsymbol{{F}}_{1})_{1}}{\partial \boldsymbol{\omega}_{X}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{2}}{\partial \boldsymbol{\omega}_{X}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{3}}{\partial \boldsymbol{\omega}_{X}} \end{array}\right] = \left[\begin{array}{l} -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{1}]^{\wedge^{^{^{^{}}}}}\\[4pt] -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{2}]^{\wedge}\\[4pt] -\boldsymbol{{R}}_{A}[(\boldsymbol{{R}}_{X})_{3}]^{\wedge} \end{array}\right].\end{align}
Similarly, the partial derivative of
![]() $\boldsymbol{{F}}_{1}$
with respect to
$\boldsymbol{{F}}_{1}$
with respect to
![]() $\boldsymbol{\omega}_{Y}$
can be obtained as
$\boldsymbol{\omega}_{Y}$
can be obtained as
 \begin{equation} \left[\begin{array}{l} \dfrac{\partial(\boldsymbol{{F}}_{1})_{1}}{\partial \boldsymbol{\omega}_{Y}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{2}}{\partial \boldsymbol{\omega}_{Y}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{3}}{\partial \boldsymbol{\omega}_{Y}} \end{array}\right] = \left[\begin{array}{l} {}[(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{1}]^{\wedge^{^{^{^{}}}}}\\[5pt] {}[(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{2}]^{\wedge}\\[4pt] {}[(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{3}]^{\wedge_{_{_{}}}} \end{array}\right].\end{equation}
\begin{equation} \left[\begin{array}{l} \dfrac{\partial(\boldsymbol{{F}}_{1})_{1}}{\partial \boldsymbol{\omega}_{Y}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{2}}{\partial \boldsymbol{\omega}_{Y}} \\[10pt] \dfrac{\partial(\boldsymbol{{F}}_{1})_{3}}{\partial \boldsymbol{\omega}_{Y}} \end{array}\right] = \left[\begin{array}{l} {}[(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{1}]^{\wedge^{^{^{^{}}}}}\\[5pt] {}[(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{2}]^{\wedge}\\[4pt] {}[(\boldsymbol{{R}}_{Y}\boldsymbol{{R}}_{B})_{3}]^{\wedge_{_{_{}}}} \end{array}\right].\end{equation}
![]() $\partial\boldsymbol{{F}}_{2}/\partial \boldsymbol{\omega}_{Y}$
can be calculated easily based on the left perturbation model as
$\partial\boldsymbol{{F}}_{2}/\partial \boldsymbol{\omega}_{Y}$
can be calculated easily based on the left perturbation model as
 \begin{equation} \begin{aligned} \dfrac{\partial\boldsymbol{{F}}_{2}} {\partial \boldsymbol{\omega}_{Y}} & = \dfrac{\partial(\boldsymbol{{R}}_{Y} \boldsymbol{{t}}_{B})}{\partial \boldsymbol{\omega}_{Y}} \\[5pt] & = \lim_{\partial \boldsymbol{\omega}_{Y} \to 0} \dfrac{\partial\boldsymbol{{R}}_{Y} \boldsymbol{{R}}_{Y} \boldsymbol{{t}}_{B}-\boldsymbol{{R}}_{Y} \boldsymbol{{t}}_{B}}{\boldsymbol{\omega}_{Y}}\\[5pt] & = \lim_{\partial \boldsymbol{\omega}_{Y} \to 0} \dfrac{[\partial\boldsymbol{\omega}_{Y}]^{\wedge}\boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}}{\boldsymbol{\omega}_{Y}}\\[5pt] & = \lim_{\partial \boldsymbol{\omega}_{Y} \to 0} \dfrac{-[\partial\boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}]^{\wedge}\boldsymbol{\omega}_{Y}}{\boldsymbol{\omega}_{Y}}\\[5pt] & = \lim_{\partial \boldsymbol{\omega}_{Y} \to 0} -[\partial\boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}]^{\wedge}. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \dfrac{\partial\boldsymbol{{F}}_{2}} {\partial \boldsymbol{\omega}_{Y}} & = \dfrac{\partial(\boldsymbol{{R}}_{Y} \boldsymbol{{t}}_{B})}{\partial \boldsymbol{\omega}_{Y}} \\[5pt] & = \lim_{\partial \boldsymbol{\omega}_{Y} \to 0} \dfrac{\partial\boldsymbol{{R}}_{Y} \boldsymbol{{R}}_{Y} \boldsymbol{{t}}_{B}-\boldsymbol{{R}}_{Y} \boldsymbol{{t}}_{B}}{\boldsymbol{\omega}_{Y}}\\[5pt] & = \lim_{\partial \boldsymbol{\omega}_{Y} \to 0} \dfrac{[\partial\boldsymbol{\omega}_{Y}]^{\wedge}\boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}}{\boldsymbol{\omega}_{Y}}\\[5pt] & = \lim_{\partial \boldsymbol{\omega}_{Y} \to 0} \dfrac{-[\partial\boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}]^{\wedge}\boldsymbol{\omega}_{Y}}{\boldsymbol{\omega}_{Y}}\\[5pt] & = \lim_{\partial \boldsymbol{\omega}_{Y} \to 0} -[\partial\boldsymbol{{R}}_{Y}\boldsymbol{{t}}_{B}]^{\wedge}. \end{aligned}\end{equation}
Meanwhile,
![]() $\partial\boldsymbol{{F}}_{2}/\partial \boldsymbol{{t}}_{X}$
and
$\partial\boldsymbol{{F}}_{2}/\partial \boldsymbol{{t}}_{X}$
and
![]() $\partial\boldsymbol{{F}}_{2}/\partial \boldsymbol{{t}}_{Y}$
can be calculated as
$\partial\boldsymbol{{F}}_{2}/\partial \boldsymbol{{t}}_{Y}$
can be calculated as
 \begin{equation} \begin{aligned} \dfrac{\partial\boldsymbol{{F}}_{2}} {\partial \boldsymbol{{t}}_{X}} &= -\boldsymbol{{R}}_{A};\\[5pt] \dfrac{\partial\boldsymbol{{F}}_{2}} {\partial \boldsymbol{{t}}_{\boldsymbol{{Y}}}} &= \boldsymbol{{I}}_{3}. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \dfrac{\partial\boldsymbol{{F}}_{2}} {\partial \boldsymbol{{t}}_{X}} &= -\boldsymbol{{R}}_{A};\\[5pt] \dfrac{\partial\boldsymbol{{F}}_{2}} {\partial \boldsymbol{{t}}_{\boldsymbol{{Y}}}} &= \boldsymbol{{I}}_{3}. \end{aligned}\end{equation}