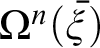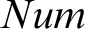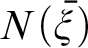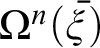2 The ‘ancestral’ problem

Frege’s Begriffsschrift (1879) was the first to maintain that logic is a genuine science assuring impredicative comprehension. It thereby captured inductive proofs within pure logic—proofs that had hitherto been thought to require distinctly arithmetic intuitions of consecutive series. Frege made this point explicitly, and it is important that it came well before he had a working theory of numbers as objects. Frege designed his logic to be the study of functions (understood in a mathematical sense and not as many-one relations). He embraced impredicative comprehension of a hierarchy of levels of functions from entities (each of a given level) to objects. Frege’s functions are “unsaturated” and thus are not themselves objects. It was not until Frege’s Grundlagen (1884) and finally his Grundgesetze (1893) that he was able to put forth a mature theory of numbers as purely logical objects $\overset {,}{z}\, f\, z$ correlated one-to-one to functions $f\, \xi $ by a heterogeneous second-level function $\overset {,}{z}\, \Phi\, z$ . Russell revealed that any such function violates a heterogeneous formulation of Cantor’s power theorem. Russell advocated for Cantor’s work. Frege was never a strong advocate of Cantor and though alarmed by Russell’s discovery, he continued to resist Cantor’s analyses of cardinals and ordinals and the far-reaching implications of his work in mathematics that Whitehead and Russell so lauded.

The formal syntax of Principia has been a subject of continued controversy for more than 100 years. Part of the reason is that the work attempted to set out its formal grammar through a convenience of typical ambiguity. The simple type indices were suppressed throughout the work and as a result it was left to interpreters to add them in ways they thought intended by the semantic statements Russell made in the informal introductory commentaries. As I see it, Principia grammar is that of simple type theory. In the Preface of Principia, both the introduction and summaries are explicitly stated not to be part of the work. Whitehead, who later explicitly disavowed Russell’s introduction to both the first and second edition, never agreed nor was required to agree with Russell’s semantic experiments set out in his introductions.Footnote ¹ Whitehead’s Prefatory Statement of volume 2 reveals that that while he accepted Principia’s no-classes and no-relation-e (no relations-in-extension) theories, he imagined a Realist (objectual) semantics for the formal system of bindable simple type-regimented individual variables. This is in stark contrast to Russell’s appeal in the introduction to the first edition to a nominalistic (modern substitutional) semantics for the simple (impredicative) type-regimented individual variables above the lowest simple type (i.e., variables $\varphi !$ , $\psi !$ , $f!$ , $g!$ , etc., with the exclamation). (The letters $\varphi $ . $\psi $ , f and g are schematic letters for wffs and are not bindable.) Russell’s nominalist semantic interpretation was based on a recursive definition of “truth” (and “falsehood”) whose base case was to be handled by a multiple-relation theory of judgment. The semantics was a disaster. It could not validate *12.n (see below). Ultimately, in 1919 Russell admitted it, and it was Ramsey (not Wittgenstein) who convinced him. Unfortunately, in the absence of an explicit syntax set out, Russell’s nominalistic (modern substitutional) semantic experiment became conflated with the formal theory by interpreters (e.g., Carnap, Church) who endeavored to “fix” the work by offering a syntax guided by the semantics (but ignoring it’s nominalistic orientation). Thus was born ramified types (e.g., Church’s r-types).

Principia embraces simple type regimentation and impredicative comprehension. Had the work given its formal syntax, individual variables of lowest type look like this $x^{o}$ and the individual variables that serve as predicate variables look like this $x^{(t_{1},\ldots,t_{n})}$ . An atomic wffs looks like this:

$$\begin{align*}y^{(t_{1},\ldots ,t_{n})}(x_{1}^{t_{1}},\ldots ,x_{n}^{t_{n}}).\end{align*}$$

Suppressing the simple type indices one needs first to put

$$\begin{align*}\varphi ^{(t_{1},\ldots ,t_{n})}(x_{1}^{t_{1}},\ldots ,x_{n}^{t_{n}})\end{align*}$$

and then to mark the bindable predicate variable one uses an exclamation thus:

$$\begin{align*}\varphi !(x_{1},\ldots ,x_{n}).\end{align*}$$

The definition of a simple type symbol is this:

1. (i) o is a simple type symbol;

2. (ii) if $t_{1},\ldots ,t_{n}$ are simple type symbols then so is ( $t_{1},\ldots ,t_{n});$

3. (iii) there are no other simple type symbols.

For example, there are $x^{o},x^{(o)},x^{((o))}$ etc., and $x^{(o,o)},x^{(o)},x^{((o),o)}$ and so forth. Any individual variable whose simple type index is not o is a predicate variable. In Principia, impredicative comprehension of relations (and properties) in intension is introduced by the following axiom schema:

$$\begin{align*}*12.n\;(\exists\; f)(\varphi (x_{1},\ldots ,x_{n})\;\equiv _{x_{1},\ldots x_{n}}\;f!(x_{1},\ldots ,x_{n})),\end{align*}$$

where the predicate variable $f!$ is not free in $\varphi $ . This impredicative axiom schema is sometimes called the “axiom of reducibility.” The monadic case *12.1 is called the “axiom of classes” and the dyadic case *12.11 is called the “axiom of relations.” It should be noted that impredicativity is not a matter of semantic interpretation. It is a matter of the syntactically unbridled rules of quantification theory governing bindable predicate variables together with syntactic fact that the above axiom schema allows the schematic $\varphi $ to stand in for any wff of the formal language not containing the predicate variable $f!$ free. The syntax is impredicative because it has no order indices on variables.Footnote ²

Principia regards logic as a genuine synthetic a priori science that studies relations-in-intension independently of the contingencies of their exemplification.Footnote ³ The informativity of logic (whether that of Frege or that of Whitehead-Russell) comes directly from its embracing impredicative comprehension. It assures existence and thus is synthetic. Frege’s (and Russell’s) approach to the ‘ancestral’ relation (and its accompanying informative theorem of induction) requires that one admit impredicative comprehension in logic. Principia advances a theory of inductive cardinals that parallels the Fregean impredicative analysis of the ‘ancestral’ relation, while adhering to the Cantorian analysis of cardinality in terms of one-to-one correspondence. Wittgenstein rejected both. Logic is shown, not said and thus it must consist in generalized tautologies. He often put this point, as did Ramsey, as a rejection of *12.n because its instances are not generalized tautologies.

Russell thought impredicative comprehension is the key to the ‘ancestral’ and for that reason it is the key to capturing within logic the “and so on” notion. In fact, this is explicitly stated in Principia in the introduction to section *90 on the ancestral relation (vol. 1, p. 543):

Frege introduces the strong ancestral (where nothing is its own ancestor) using impredicative comprehension. Then the weak ancestral is easily defined in terms of it. Principia introduces the notion of the weak ancestral of $a$ using the following instance of comprehension *12.n:

$$\begin{align*}(\exists\; f)(f!z\;\equiv _{z}\;(\varphi )(\varphi !a\;\wedge\;(x)(\varphi !x\;.\supset .\;\varphi !(x+1))\;.\supset .\;\varphi !z)).\end{align*}$$

For convenience put:

$$\begin{align*}Anc^{a}(z)=df\;(\varphi )(\varphi !a\;\wedge\;(x)(\varphi !x\;.\supset .\;\varphi !(x+1))\;.\supset .\;\varphi !z)).\end{align*}$$

One can then easily arrive at the inductive theorem:

$$\begin{align*}(\varphi )(\varphi !a\;\wedge\;(x)(\varphi !x\;.\supset .\;\varphi !(x+1))\;.\supset .\;(x)(Anc^{a}(x)\;\supset \;\varphi !x)).\end{align*}$$

From that theorem, together with impredicative instance of *12.n, one proves:

Induction:

$$\begin{align*}\displaystyle (\varphi )(\varphi !a\;\wedge\;(x)(Anc^{a}(x)\;\wedge\;\varphi !x\;.\supset .\;\varphi !(x+1))\;.\supset .\end{align*}$$

$$\begin{align*}(x)(Anc^{a}(x)\;\supset \;\varphi !x)).\end{align*}$$

Once 0 is introduced and replaced for a, and with $Anc^{a}(x)$ replaced with $Anc^{0}(x)$ abbreviated as $Num(x)$ , we have mathematical induction. One gets:

Mathematical Induction:

$$\begin{align*}(\varphi )(\varphi !0\;\wedge\;(x)(Num(x)\;\wedge\;\varphi !x\;.\supset .\;\varphi !(x+1))\;.\supset .\end{align*}$$

$$\begin{align*}(x)(Num(x)\;\supset \;\varphi !x)).\end{align*}$$

It is the theorem of induction that provides the analysis of the notion “and so on.”

This history lies importantly behind Wittgenstein’s 1919 letter to Russell which heralded the existence of an Abhandlung on logic and arithmetic that he had compiled sporadically from 1913 through 1917 even while caught up in the first world war. It is one of the most interesting and yet perplexing of the many letters of correspondence between Wittgenstein and Russell. He wrote:

The book, of course, came to be the Tractatus. What did Wittgenstein mean in speaking to Russell of upsetting “our” theory of truth, of classes, and of numbers? The work, at least as Russell interpreted it, was offering an alternative to the approach to these notions that are found in Principia. Thus, rather than saying “upsetting,” a better description would be to say “replacing.” The Tractatus envisioned achieving important results of Principia and certainly a recovery of the uses of the ‘ancestral’ notion. This plan is to do without emulating impredicative comprehension, without emulating classes, numbers and all the rest. Finding a better understanding of Wittgenstein’s endeavor to find a replacement forms the core task of the Tractarian logicist interpretation.

Wittgenstein saw that the “and so on” concept and ‘ancestral’ notion are connected at the chest. But unlike Principia Wittgenstein adopts the “and so on” concept as an indefinable primitive built into his notion of an “operation.” I hold that Wittgenstein’s operations are functions (in Frege’s sense), but comprehension is allowed only when the function is introduced by a “rule” (or recipe for “and so on”) indicated by $\overline {\xi }$ that establishes the general term of the series generated by its applications. Some of these operations, as we shall see, are explicitly characterized recursively. (It is not known whether he required that all operations be recursively defined.) It is my thesis is that Wittgenstein hoped to emulate the use of the ‘ancestral’ relation in arithmetic by appeal to operations. We find:

$TLP$ 4.1273

If we want to express in conceptual notation the general proposition ‘b is a successor of a’, when we require:

$$\begin{align*}aRb\end{align*}$$

$$\begin{align*}(x)(aRx\:\wedge\:xRb)\end{align*}$$

$$\begin{align*}(x,y)(aRx\;\wedge\;xRy\;\wedge\;yRb),\ldots\end{align*}$$

In order to express the general term of a series of forms, we must use a variable, because the concept ‘series of forms’ is a formal concept. (This is what Frege and Russell overlooked; consequently the way in which they want to express general propositions like the ones above is incorrect; it involves a vicious circle.) We can determine the general term of a series of forms by giving its first term, and the general form of the operation that produces the next term out of the proposition that precedes it.

Wittgenstein’s plan is to remake the ‘ancestral’ relation in terms of his formal concept ‘general term of a series’—i.e., the notion of ‘and so on’ which renders the repetition of an operation. Tractatus 6.03 endeavors to do this when it offers [0, $\xi $ , $\xi $ +1] as the general form of an integer (i.e., the use of operations replacing the notion of a natural number). The concept of the general term of a series is thereby given by a structured variable expressing a formal concept which shows (and does not say as Frege and Russell thought) how to go on. Instead of appeals to a proved theorem of mathematical induction of a would-be science of arithmetic, Wittgenstein imagined that one can reveal the correctness of an equation by appeal to the “and so on” of his recursive recipes for arithmetic operations. Instead of using impredicative comprehension, Wittgenstein hoped to capture the ‘ancestral’ relation by appeal to series of iterations of an operation, defined by an “and so on” clause that shows how to generate a consecutive series. The recursive characterization provides the “and so on” pattern for the operation’s continued application.

When Wittgenstein wrote his Tractatus, there had already had been a long history of criticisms of so-called impredicative “definition” and most famously Poincaré regarded it as a “viciously circular” definition. Russell lampooned Poincaré’s proposal to add antecedent clauses on quantifiers that assure vicious circles are avoided. It was Russell’s nominalistic (modern substitutional) semantics for Principia’s bindable predicate variables that forced him to be concerned about vicious circles. His substitutional semantics must put: $(^{i}\varphi )A^{i}\varphi !$ is true iff every wff $B\xi $ of language $L_{i}$ is such that $A[B\xi /\varphi !]$ is true. The wffs of $L_{i}$ must not include the bound variable $^{i}\varphi !$ else the truth-conditions would be viciously circular. There is little doubt that Wittgenstein agreed that it is viciously circular, since he expresses just this criticism at $TLP$ 4.1273. An objection to the impredicativity of *12.n on grounds that it allows viciously circular “definition,” however, is completely vapid and should be ignored. When carefully put, the issue of impredicativity does not concern definition at all. Indeed, all the definitions in Principia are stipulative conveniences of notation. More importantly still, the proper source of Wittgenstein’s objection derives, not from an concern over an alleged “vicious circularity,” but from his rejection of the thesis that mathematical logic is a genuine science (a body of truths). It must be shown, not said. Wittgenstein’s $ab$ -Notation, extended to quantifiers, was designed to to show that logic consists of tautologies and generalized tautologies. And it is clear from a November 1913 letter to RussellFootnote ⁴ that Wittgenstein endeavored to use his $ab$ -Notation to argue that comprehension does not belong to logic.

Russell was keenly interested in Wittgenstein’s ideas. In the letter to Russell of 1919, he speaks of “our” theory of “truth, “classes” and “number.” This is not only suggestive of the many discussions between the two, but also of Russell’s having at some point admitted that his semantic endeavors did not succeed. But once he understood it, Russell never accepted showing. Neither did Ramsey! In his paper “The Foundations of Mathematics,” Ramsey spoke of “propositional functions in extension” which is a phrase he used to characterize a new nominalistic (i.e., substitutional) semantics for Principia’s object language bindable variables. It allows infinite conjunctions and disjunctions in the semantics, but leaves intact the simple type grammar. He wrote (Ramsey, 1925, p. 56):

The comment is ironic because, as Ramsey himself intimates, *12.n and the grammar of Principia’s impredicative simple types remains unchanged.Footnote ⁵ It is Russell’s failed nominalist semantics that Ramsey changed. Relative to Ramsey’s nominalistic semantics, as opposed to Russell’s nominalistic semantics, the axiom schema *12.n of impredicative comprehension is acceptable because valid in the semantics. Russell remarks in his My Philosophical Development that he was pleased but he remained unconvinced (Russell, 1959, p. 26). Wittgenstein was certainly not pleased. Ramsey’s work in “The Foundations of Mathematics” did not adopt showing or the reorientation to functions recursively defined.

Neither was Wittgenstein pleased by Russell’s new experiments in the introduction to the 1925 second edition of Principia which changed the grammar to open the way for the Tractarian ideas of radical extensionality and ramified orders coded into syntax. (Whitehead was unhappy that this new introduction emphasizing Wittgenstein's ideas was included. See Lowe & Schneewind (Reference Lowe and Schneewind1990).) We get important insight into Wittgenstein’s disappointment by noticing the comments Ramsey made in a letter to his mother. The letter reports on the meeting he had with Wittgenstein in 1924 at which he had discussed Russell’s plans for the second edition. Ramsey had seen Russell’s work notes for the new edition and likely he recounted to Wittgenstein that in Russell’ s assessment the Tractarian ideas he worked with do recover mathematical induction but fail to recover Cantor’s work and Analysis. Ramsey indicates to his mother that Wittgenstein was annoyed by Russell’s efforts. At first, his reaction seems quite unwarranted. Why should he be annoyed? Ramsey wrote (Wittgenstein Reference Wittgenstein1973), p. 78):

I think the reason he was annoyed has become clear. Wittgenstein did not see his central Tractarian ideas represented in Russell’s Tractarian-inspired experiments for the new edition’s Introduction. The Tractarian rejection of identity and reorientation to operations was completely ignored. This orientation to operations recursively defined, Wittgenstein thought, was the proper direction of further research. This new orientation is what Wittgenstein meant in saying that Principia must be done “afresh.”

When we understand the history in this way, we can find many passages that offer abductive evidence in favor of it. That is, this historical account offers the better explanation of the existence of passages written later and their content. For example, remembering Wittgenstein’s objection to identity in his My Philosophical Development, Russell wrote (Russell, 1959, p. 115):

The elimination of identity forced Wittgenstein into a combinatorial logic and arithmetic of operations defined by rendering general terms of series. A purely combinatorial logic and arithmetic does indeed jeopardize mathematical logic. Russell’s dalliance with the criticism of identity was short. All the same, he was concerned to understand and assess the viability of Wittgenstein’s technique for recovering arithmetic in a way that, unlike Principia, avoids the need to capture the ‘ancestral’ relation by impredicative comprehension and the need to emulate a theory of classes and relations-in-extension. In a August 13, 1919 letter, we find (Russell, Reference Russell1990, p. 108):

This expresses to Wittgenstein a serious concern over how the ‘ancestral’ relation is supposed have been recovered. Russell did not take the notion of “and so on” to be something that can be adopted as a primitive idea. As noted earlier, he would naturally object that it is the concept of the ancestral relation that captures the “and so on” concept, and it depends upon impredicative comprehension.

In letters as early as August 13, 1919, Russell had written several questions about Wittgenstein’s Abhandlung and its approach to number. At one point he focused on its complete neglect of Cantor’s work. The following is quite revealing Russell (Reference Russell1990):

There is no known evidence of Wittgenstein’s reply. It is conspicuously absent from the replies he did send to Russell on 19 August. This is a casualty of his abandonment of the relation of identity and impredicative comprehension. It commits him to the rejection of Principia’s Cantorian analysis of cardinal numbers in terms of ‘similarity’ (onto relations of one-to-one correspondences). Wittgenstein viewed relations of ‘similarity’ as outside of arithmetic since, without ‘identity’ as a genuine logical relation, they would rely upon contingently exemplified relations of one-one-correspondence (such as physical spatial relations). Such relations are what the Tractatus calls material. They do not belong to the formal relations (all and only of which) are shown. Wittgenstein held that the Cantorian theory thus belongs, not to mathematics, but to physics. Principia, in stark contrast, accepted Cantor’s work as of revolutionary importance. When, some years later, Russell would later write his 1931 review of Frank Ramsey’s Foundations of Mathematics, we find him with the following remark ( $CP$ , vol., 10., p. 113).:

Likely he had Cantor’s work in mind.

Ramsey himself had conducted his own evaluation of Wittgenstein on number and arithmetic. He reported that he studied the Tractarian operations intensely and found them to be unworkable. He wrote (Cuter, Reference Cuter2005):

The Tractarian approach, he thought, must find a way to emulate the commonplace applications of ordinary arithmetic. Ramsey gave the following example:

Now at first blush, one might imagine Ramsey’s concern to have a ready solution. Using numeric quantifiers, such as “ $(\exists x^{n})\varphi x$ ” which says “exactly n-many entities are $\varphi $ ,” one can offer this:

$$\begin{align*}(\exists x^{n})F x\; \wedge\; (\exists x^{m})G x\; .\wedge.\; (P)((\exists x^{n^{2}})Px \equiv (\exists x^{m^{3+2}}x)Px).\end{align*}$$

The general problem Ramsey raised, however, has no such easy remedy. One needs to emulate quantification over numbers. Tractarian accounts, appear to make this impossible. I shall call this “Ramsey’s problem.” It is very hard to believe that Wittgenstein didn’t have something in mind as a reply.

If we start with the Tractarian logicist interpretation, we can then look for abductive arguments that supports it in some of Wittgenstein’s later writing. Their existence and content are best explained as reflections on what had transpired earlier, or further investigations of the viability of techniques formerly advanced. Of course, the later writings of Wittgenstein (from his so called “middle period”) might reflect an entirely new approach departing from any earlier stand he may have taken. But this does not at all indict the perfectly legitimate methodology of advancing abductive arguments in favor of the Tractarian logicist interpretation. There is no methodological flaw in using abductive reasoning, and it would be a significant methodological flaw to presume that any viable interpretation of later writings requires them to belong to a new perspective.

When Wittgenstein returned Cambridge and 1929 and wrote his Philosophische Bemerkungen ( $PB$ ), he included many remarks that corroborate the Tractarian logicist interpretation. They corroborate it, because their existence and contents are expected—i.e., best explained given the Tractarian logicist interpretation is correct. Consider, for example, the following ( $PB$ , p. 25):

The focus of the above seems clearly to be Ramsey’s problem of emulating quantification over numbers. (Indeed, as we shall see, Ramsey’s problem is rather explicitly noted later in the remarks.) The above remarks fit very well with the Tractarian logicism focus on operations. At 125 we have the general term mentioned—i.e., the recipe for the “and so on” of the consecutive series for the natural numbers. The best adbductive explanation of remarks 126 and 129 is that Wittgenstein was returning to the exploration of the Tractarian logicist approach.

Our ultimate goal will be to better understand what Wittgenstein might have had in mind when he hoped to build syntactically structured arithmetic forms that show the proper results of using mathematical induction. As we shall see, Tractarian logicism enables the N-operator account of existential and universal quantification to come to the rescue since all operations are on a par. The N-operator emulates bounded quantification. It is straightforward to extend the technique to emulate bounded quantification over operations generally, and thereby to emulate quantification over the operations of arithmetic in particular. (Interestingly, bounded existential and universal quantifiers are all that one hopes or expects to capture with sum and product in the general theory of recursive functions.) This will solve Ramsey’s problem of emulating quantification over numbers. The new understanding provided will help us to unravel one of the most perplexing features of the Tractatus—its treatment of number and proof by mathematical induction.

3 Operations and rules

Following Frascolla (Reference Frascolla1994, Reference Frascolla1997), the Tractatus was advocating a research program of a combinatorial logic and arithmetic based on functions, some at least recursively defined. Admittedly, what Wittgenstein meant by an “operation” remains a source of difficulty of interpretation. Must it be regarded as a new Tractarian idea tied to showing that has no historical precedent? The Tractarian Logicist interpretation avoids the worry by maintaining that what Wittgenstein meant by an operation is just the notion of a function, but requiring that it be introduced by an explicit rule (or an “and so on” clause). This demystifies his view of an operation. Wittgenstein’s operations (functions) for arithmetic are given by recursive definitions involving numeral exponents. This is consistent with holding that other “and so on” recipes may exist. Nowadays we understand the notion of a function (and a recursively defined function) rather well. (See Mendelson (Reference Mendelson2010).) The study of recursive characterizations of functions by Church in the 1930’s obviously came well after the Tractatus, and later still came the wide acceptance of Church’s Thesis according to which every careful definition of “computable” (e.g., Turing machine, Markov algorithm, abacus, etc.) coincides with the notion of recursiveness. Wittgenstein left such matters open. But it would not be unfair to say that Wittgenstein’s work anticipated subsequent research.

There are many pieces of evidence that enable us to feel confident that an operation, in Wittgenstein’s view, is a function characterized by an “and so on” clause which renders the “general term.” We find:

This requirement of a recipe for how to go on—a recipe given by the structured variable “ ”—is particularly clear as well in Wittgenstein’s Notebooks 1914-1916. Consider the following passages (Wittgenstein Reference Wittgenstein, von Wright and Anscombe1979):

Given all these passages (and many more) one can feel confident that Wittgenstein has in mind the notion of a recipe for generating series, and in the case of arithmetic we know from his explicit definitions in the Tractatus of arithmetic operations ( $TLP$ 6.02; $TLP$ 6.421) that such cases he has in mind are given by recursive recipes. By using the word “recipe” I intend to be charitable in interpreting Wittgenstein’s use of $\overline {\xi }$ as a means of characterizing the “and so on.” The notion might be simply mean “recursive definition,” and as we know all recursive characterizations of functions are built up from what are called the primitive recursive function (together with the $mu$ -recursive function). There is a strong intuition that there can only be denumerably many recursive functions precisely because each has a recipe that has a finite expression.

Anscombe (Reference Anscombe1959) seems first to have noticed the Tractarian logicist idea that all Tractarian operations are the same in kind. She took the Tractarian N-operator to be same in kind as arithmetic operators $\Omega ^{n}\xi$ that are characterized with numeral exponents. Indeed, she goes so far as to say that the N-operator can itself be given numeral exponents. She holds that every N-operation is introduced by by a general term that generates a consecutive series of truth-functions. She writes (Anscombe (Reference Anscombe1959), p. 132):

Consider, for example, the consecutive series 1, 2, 4, 16, $2^{16}$ , … The dots are important because they indicate that a recipe (the general term of the consecutive series) exists which shows how to go on. There are various ways to render such a recipe. One way is through a recursive characterization. For example, one can offer the piece-wise recursive definition:

$$ \begin{align*} f(0)&=1 \\ f(n+1)&=2^{fn} \end{align*}$$

Wittgenstein’ notion of a “general term of a consecutive series” must, of course, be regarded as independent of the mathematical notion of the “general term of a consecutive series” since the latter essentially depends on the consecutive natural ordering of the natural numbers. Consider for example the general term $x^{2}$ generating (as it were) the consecutive series: 0, 1, 4, 9, 16, … As Cantor sees it, the very notion of there being a “general term” relies on the function term $\xi ^{2}$ providing a one-to-one correlation from natural numbers 0, 1, 2, 3, 4, … to the above, respectively. The correlation relies on the consecutive ordering of the natural numbers. So the notion of a general term that Wittgenstein has in mind must not depend on the existence of relations (or functions) on natural numbers that establish such correlations. Anscombe saw that point quite well enough. But she seems to have gone too far toward likening Wittgenstein’s notion of a general term of a series to the mathematical notion of a general term of a consecutive series. Successive order (linear order) is not the same as a consecutive order. To achieve a consecutive ordering of truth-functions, Anscombe has to supply her own recipe. She thereby chooses bases for the N-operator. She assumes that Wittgenstein himself intended this and expected readers to work out what it is. She seems mistaken in thinking that any “general form” of a series must, according to Wittgenstein, assume that the series is consecutively ordered. Nothing discernible in the $\overline {\xi }$ that Wittgenstein used to characterize the general term of truth-functions requires that its intended recipe secures consecutiveness in thexs ordering.

Of course, Whitehead and Russell rejected an ontology of functions and proceeded instead with the ontology of relations in intention, some among which are many-one. Russellian notion of a dyadic relation $\varphi !$ being many-one is this:

$$\begin{align*}(x,y,z)(\varphi !(x,y)\:\wedge\:\varphi !(x,z)\:.\supset .\:y=z).\end{align*}$$

The no relations-e theory uses the the letter $R$ and writes $xRy$ . So there is no chance to conflate a variable $\varphi !$ for a relation in intension with contextually defined variable R for a relation-e (relation in extension). Frege’s function term “ $fx$ ” is quite different. It is a term referring to the y such that $fx=y$ . Russell’s replaces this with “

” which is not a term but is rather an incomplete expression contextually defined. Thus, for example,

Russell’s approach emulates the notion of the composition $f(g\xi )$ of two functions $f\rho $ and $g\xi $ by appeal to the relative product of two many-one relations-e R and S. That is, *12.11 together with the no-relations-e theory, we get:

$$\begin{align*}(\exists T)(xTy\:\equiv _{x,y}\:(\exists z)(xRz\:\wedge\:zSy)).\end{align*}$$

Many interpreters have observed that in the Tractatus, Wittgenstein wrote:

Wittgenstein was certainly in earnest to assure that readers not confuse his notion of an operation with Russell’s notion of a “propositional function.” But his point seems to be that he rejected Principia’s approach and adopted an ontology of functions. Wittgenstein’s notion of an operation departs from Frege’s notion of a function only insofar as he makes the demand that it be given, not by impredicative comprehension, but by an “and so on” recipe (rule, recursive characterization).

The notion of an “operation” in the Tractatus is rather obscure. Arithmetic operators and the N-operator are only very thinly presented in the work. To understand them, one has to uncover that there are rules of calculation embedded in Tractarian notion of an operation. One has to be devoted to uncovering them. Not surprisingly, Wittgenstein was loathe to explicitly state his rules of operation, asking readers of his oracular Tractatus to work them out for themselves. There are many dangers along the way. It should be clear, for example, that one ought not to enter into the confusion that $f(g)$ indicates that a function $g$ is to be put into the argument position of the function sign $f$ . Wittgenstein naturally follows Frege’s in this matter. Function signs must stay in function positions. The notion of a function, of course, rules out “ $f(f)$ ” as meaningless, but obviously one can write “ $f(fx)$ .” Wittgenstein accepts that an operation can take one of its own results as its base and this is just what we expect of functions. Moreover, one does not expect to find a recursive rule of commutation that applies to operations generally. Marking the argument positions of the functions with $\rho $ and $\xi $ , consider:

Such a rule would yield incorrect results in certain cases. Consider the following:

$$\begin{align*}(a\times \rho )((b+\xi ))\quad \qquad i.e.,\;a\times (b+\xi ).\end{align*}$$

This is clearly not the same function as

$$\begin{align*}(b+\rho )((a\times \xi ))\quad \qquad i.e.,\:b+(a\times \xi ).\end{align*}$$

In uncovering the rules of operation, there is a grave risk that the alleged rules “found” in working through examples are merely the invention of the interpreter. The argument for Wittgenstein’s intending a given rule can only be abductive. The rules are uncovered by their being required for working through cases. Oracular and elucidative as it is, the Tractatus offers just enough clues as to what rules of operation Wittgenstein had in mind.

In the case of the N-operator, two of the five discernible rules are rather explicitly stated in the Tractatus. The existence of the others is abductively supported because they are required for the N-operator notation to make good on its promise to render a notation in which all and only logical equivalents have their truth-conditions shown in one and the same way. That is, the N-operator, by design, was intended to extend to quantification theory with identity (where admissible) the result achieved by the $tf$ -notation (formerly the $ab$ -Notation), and truth-tabular notations—that all logically equivalent quantifier-free wffs have the same notation.

The same abductive approach is useful in finding rules of the operations of arithmetic. The existence of general rules of operation are required by the examples of calculation with operations that the Tractatus gives. For instance, we shall see that there is the following:

$$\begin{align*}\text{Rule I:}\ \frac {f(g(h\xi ))}{[f(g\rho )][h(\xi )]}\end{align*}$$

This rule provides for Association. I have written it in this way to indicate (without using an identity sign) that one can replace (substitute) the one operation with the other wherever it occurs. Working through examples, we do find that these rules are implicitly used and required. There is another bit of abductive reasoning we can use. That Wittgenstein intended such rules offers the best explanation of some of the entries in Philosophische Bemerkungen. For example, he writes (PB, p. 198):

This is just what one should expect to find if the Tractatus adopted Rule I.

It is worth pausing to briefly to note that Potter (Reference Potter2000) thinks it likely that Wittgenstein thought all operations are (ultimately) defined (and reduced) to the N-operation. Now we find:

Nothing suggests that the operation O indicated here is built from (reduced to) the N-operator. It is hard to imagine such a reduction, and Wittgenstein explicitly offers recursive characterizations of operations $\Omega ^{n}$ for arithmetic in his Tractatus which seem independent and indefinable by appeal to the N-operator. There are, however, entries in the Tractatus and Notebooks 1914–1916 that suggest that all variables are construed as propositional. Moreover, in the Tractatus, we find:

These do suggest a “reduction” of operations—even arithmetic ones—to the N-operator. But it is hard to feel very confident in the reductive thesis. In fact, $TLP$ 6.01 might be a typo which should have been:

If so, the intent is not to say that all operations are N-operations. Happily, Tractarian Logicism does not need to take a stand on this matter. Tractarian Logicism is an interpretation that is not committed to a reduction of all operations to the N-operation. It simply holds that the N-operator and any other operations are not different in kind.

Why the N-operator? In Landini (Reference Landini2007), I argued that the N-operator was needed because of the limitations of a truth-functional tabular notation, and the limits of the tf-Notation. All such notations were designed to show the truth-conditions of all logical equivalents in one and the same way. For example, fixing the rule of presentation of the rows of the truth-table, one can capture both

$$\begin{align*} & p\:.\vee .\:q \wedge r \\ & p\vee q\:.\wedge .\:p\vee r \end{align*}$$

in one notation, namely:

$$\begin{align*}(t,t,t,f,t,f,t,f)(p,q,r).\end{align*}$$

Wittgenstein knew that this approach (as with the $ab$ -Notation, and $tf$ -Notations) of representation cannot be extended to quantification with relations. It won’t do to use a schematic truth-tabular notation

$$\begin{align*}(\ldots \ldots ._{2^{n}})(p_{1},\ldots ,p_{n}).\end{align*}$$

A change in the size of the domain may well create changes in the positions of the t’s and f’s in a truth-tabular expression (except when only monadic predicates are involved). The N-notation is adopted instead of a schematic truth-tabular notation.

The use of this expression “instead” is important. The “instead” of $TLP$ 5.5-2 expresses the idea that the N-notation is to replace the truth-tabular notation and that it, nonetheless, recovers in a new way the distinctive feature of the truth-tabular notation—namely, that all and only logical equivalents have the same N-notation. Wittgenstein moved on from the Tractarian truth-tabular notion to the N-notation precisely to extend his fundamental idea of showing to the logic of quantification theory with identity. The approach distinguishes the treatment of generality from truth-functions. His treatment of quantification and identity (where admissible) is built into his use of free variables and the “and so on” clause introduced with N-notation.

On the interpretation I am giving, expressions in N-notation are quite literally pictures of truth-conditions, not wffs. For example, the N-notation, “ $N(p,q)$ ,” is a term that pictures/shows something, and it is not a wff that says something. In this respect, the Tractarian N-operator is quite distinct from Sheffer’s “ $p\downarrow q$ ,” which is a wff that says something and is obviously not a term that pictures. Wittgenstein was aware of Sheffer’s result that if Principia’s primitive logical particles $\sim $ and $\vee $ are together adequate to express all truth-functions then so is the dagger by itself (and its dual the stroke). Sheffer has the following:

$$\begin{align*} & p\lor q=df~\sim (p\downarrow q) \\ &p = df\;p\downarrow p. \end{align*}$$

Translation from Sheffer notation into N-notation is made quite easy by employing a very simple technique. Do not define $\sim $ in terms of dagger, but otherwise express the wff in Sheffer’s notation of dagger and $\sim $ . Then express $p\downarrow q$ in the form $\downarrow (p,q)$ . Lastly, replace every occurrence of $\downarrow $ and every occurrence of $\sim $ by an occurrence of N. This technique, however, requires that the N-notation not be dyadic.Footnote ⁶ Thus, e.g., $Np$ , $N(p,q)$ as well as $N(p,q,r)$ , etc., are all allowed without ado. As we shall see, there are rules governing the calculation of sameness which are implicitly embedded in Wittgenstein’s use of $\overline {\xi }$ . For instance, the order of the bases is indifferent so that $N(p,q$ ) is the same as $N(q,p)$ . This rule, which I call $N_{1}$ , was explicitly given by Wittgenstein at $TLP$ 5.501 (quoted below). But there is also the implicit rule $N_{2}$ that repetitions of the same base can vanish, so that e.g., $N(p,p)$ is the same as $Np$ . Moreover, the rule $N_{3}$ assures that embedded occurrence of $NN$ can vanish. In his Notebooks 1914–1916, Wittgenstein wrote:

In the Tractatus we find:

Such passages help to corroborate the interpretation that operations are functions. For example, $NN$ , in $N(NNp,q)$ can vanish to arrive at $N(p,q)$ .

The earliest origins of the N-operator remain unknown. But having tied the notion of an operation to the requirement of an “and so on” recipe giving the general term of a series, we can make some progress concerning finding its beginnings. That is, to trace the origins of the N-operator, we can look again to Wittgenstein’s Notebooks where his notion of an operation as a recipe is unfolding and see how it gets related to quantification. We find the following:

These passages, and many others, suggest that Wittgenstein was trying to find a recipe for the “and so on” operation that captures quantification. The breakthrough passage, indicating Wittgenstein’s idea of the N-operator, is this:

By using a schematic n, Wittgenstein hopes to capture the idea that the infinity of the domain of interpretation (if you will) is shown to be (at least potentially) infinite. Thus quantification that gets emulated in this way is finitely bounded, but the bound is arbitrary. To find N-notations, one finds the Boolean expansions over an n-element domain, where each free variable $x_{i}$ , where $1\leq i\leq n$ , is exclusive (referring to a distinct entity). This idea is rather straightforward and the aim is to represent all and only logical equivalents of quantification theory with identity in one and the same way. The key to Wittgenstein’s approach is that in N-notations, free variables $x_{1},\ldots x_{n}$ are exclusive, where n is schematic. To illustrate,

$$\begin{align*}(x)\sim Fx\end{align*}$$

$$\begin{align*}N(Fx_{1},\ldots ,Fx_{n})\end{align*}$$

All exclusive free variables $x_{1},\ldots ,x_{n}$ have the same widest scope. Compare the following which, because it is logically equivalent, is regarded as having “the same” notation:

$$\begin{align*}\sim (\exists x)Fx\end{align*}$$

$$\begin{align*}N(NN(Fx_{1},\ldots ,Fx_{n}))\end{align*}$$

$$\begin{align*}i.e.\ N(Fx_{1},\ldots ,Fx_{n})\quad rule\:N_{3}\end{align*}$$

Again, there is no confinement of scope needed at all.

The N-notation is designed to realize Wittgenstein’s quest for a logical notation in which logical equivalents have the “same” N-notation. Let’s take another example:

$$\begin{align*}(x)(Fx\:\wedge\;Gx)\end{align*}$$

$$\begin{align*}(Fx_{1}{\wedge}Gx_{1})\;.\wedge.\;,\ldots ,.\wedge.\;(Fx_{n}\;\wedge\;Gx_{n})\end{align*}$$

$$\begin{align*}N(NN(NFx_{1},NGx_{1}),\ldots ,NN(NFx_{n},NGx_{n}))\end{align*}$$

$$\begin{align*}i.e.N(NFx_{1},NGx_{1},\ldots ,NFx_{n},NGx_{n})\quad rule\:N_{3}\end{align*}$$

Compare the N-notation for the following logical equivalent:

$$\begin{align*}(x)(Fx)\;\wedge\;(x)(Gx)\end{align*}$$

$$\begin{align*}(Fx_{1}\;\wedge,\ldots ,\wedge\;Fx_{n})\;.\wedge.\;,\ldots ,.\wedge.\;(Gx_{1}\;\wedge,\ldots ,\wedge\;Gx_{n})\end{align*}$$

$$\begin{align*}N(NN(NFx_{1},\ldots ,NFx_{n}),\ldots ,NN(NGx_{1},\ldots ,NGx_{n}))\quad rule\:N_{3}\end{align*}$$

$$\begin{align*}N(NFx_{1},\ldots ,NFx_{n},\ldots ,NGx_{1},\ldots ,NGx_{n})\quad rule\:N_{1}\end{align*}$$

The rule $N_{1}$ , as we saw, assures the sameness (if you will), since the order of appearance of each of the $p,q$ , etc., in $N(\ldots .p\ldots ..q\ldots .)$ is indifferent. The other step is conducted by rule $N_{3}$ , according to which internal double $NN$ can vanish.

Wittgenstein’s elimination of identity poses no problem for translation into N-notation. The free variables are all independent of one another. To facilitate the translation, Landini (Reference Landini2007) set out a useful notation that followed Wittgenstein in excluding pseudo-statements such as $(x)(x=x)$ . The idea is to banish the identity sign and write $(\forall x^{y})(\varphi x)$ to say that every x other than y is such that $\varphi x$ . Similarly, $(\exists x^{y})(\varphi x)$ says that some x other than y is such that $\varphi x$ . This facilitates the needed expansions for translations into N-notation. Thus, for example, consider the following

$$\begin{align*}(\forall x)(\exists y^{x})(Rxy)\end{align*}$$

$$\begin{align*}(Rx_{1}x_{2}\:\wedge\ldots \wedge\:Rx_{1}x_{n})\:.\vee .\:(Rx_{2}x_{1}\:Rx_{2}x_{3}\:\wedge\ldots \wedge\:Rx_{2}x_{n})\:\end{align*}$$

$$\begin{align*} \vee \ldots \vee \:(Rx_{n}x_{1}\:\wedge\ldots \wedge\:Rx_{n}x_{n-1})\end{align*}$$

$$\begin{align*}i.e.\quad NN(N(N(Rx_{1}x_{2})\:\ldots \:N(Rx_{1}x_{n}))\:,\end{align*}$$

$$\begin{align*}N(N(Rx_{2}x_{1})\:,N(Rx_{2}x_{3}),\ldots ,N(Rx_{2}x_{n}))\:\lor \ldots \lor \end{align*}$$

$$\begin{align*}N(N(Rx_{n}x_{1})\:\ldots \:N(Rx_{n}x_{n-1})).\end{align*}$$

N-notation for relations and identity thereby preserves the feature that the very statement that there are n-many’s entails that there are entities that are not.Footnote ⁷

Interestingly, Geach (Reference Geach1981, Reference Geach1982), Soames (Reference Soames1983, Reference Soames2017) and Fogelin (Reference Fogelin1982, Reference Fogelin1987), each of whom have given their own accounts of the N-operator, have entirely missed the feature that Wittgenstein has no indication whatsoever of scope confining brackets for his N-notation. Landini (Reference Landini2007, Reference Landini2018). argues that this feature is central to Wittgenstein’s expressed goal of having all and only logical equivalents have one and the “same” N-notation. Fogelin and the others each fabricate scope brackets to confine variables in their hope of understanding the N-operator notion. Using scope-confining hard brackets “[, ],” even Fogelin takes it that $(x)Fx$ is represented as $N(Fx$ ), while $\sim (\exists x)Fx$ is represented as the quite different $N[NN(Fx)]$ Fogelin, however, recognized that Wittgenstein’s Tractarian demanded that all variables be confined together. But oddly he tries to derive this from the requirement of “successive operation,” which he reads as consecutive operation and makes part of his scope-confining brackets. In contrast, Geach and Soames invented (variable binding) notions so that one variable may be confined independently of the others. Geach went so far as to alter the Tractarian notation by introducing a minimal class theory so that he can confine variables one at a time using class notations. He fully acknowledged that in doing so he abandons the Tractarian program which maintains at $TLP$ 6.031 that classes are superfluous. In truth, all scope brackets are entirely absent from the Tractatus!

Fogelin, Geach, and Soames never considered Wittgenstein’s concern that the N-notation replaces truth-tabular notation and recovers the centrally important feature of that notation—namely, that all and only logical equivalents one and the same expression. None made this a desideratum for their efforts, though Fogelin noticed that Wittgenstein held that there is a decision recipe for the determination of whether or not a wff is a generalized tautology. In truth, their very efforts to “fix” what they thought was an inadequacy of the Tractatus is the very thing that obliterated the raison d’être of the N-notation—namely, to find a notation in which all and only logical equivalents of quantification theory with identity have the same notation. In N-notations no variables are confined at all. Generality is given wholly by exclusive free variables. They all, as it were, have the same widest scope in N-notation because they all have the same domain of size n, for schematic n. In this way, the Tractarian N-notation is obviously expressively adequate- over any finite domain of n elements, however large n may be. In N-notation, logical equivalents have (in Wittgenstein’s conception of sameness) the same N-notation.

Calculation by operations involves expressing the sameness in a series of substitutions. This applies to calculation by N-operation rules as well as calculation by recursive operation rules generally. The same notation can be profitably adopted for calculating in all cases. According to Tractarian logicist interpretation there is, after all, no difference in kind between such calculations of sameness. For example, consider the following:

$$\begin{align*}\frac {NN(p,NN(Nq,Nr))}{NN(p,Nq,Nr)\;Rule\:N_{3}}\end{align*}$$

Wittgenstein allows this as indicative of showing sameness, not saying it. All steps of calculation are produced by substitution of “identical” (as it were) operations. The method of inference with N-equations and the equations of arithmetic is that of substitution. (Speaking of arithmetic equations, $TLP$ 6.24 says this explicitly.) Now according to the Doctrine of Showing, logical and arithmetic properties are formal and thus shown by structured variables (not said in pseudo-predicates such as identity, number, class, etc). Wittgenstein was well aware that if ‘identity’ were a genuine relation, then arithmetic equations would, after all, say—they would assert truths, and arithmetic would thereby be a science (i.e., a body of truths). Wittgenstein’s objection to identity as a relation entails that he also rejects the functional expressions involving it such as $fx=gx$ . Recalling again that the Tractatus eliminated the identity sign, note that it does not reject what would ordinarily be called the substitution of identical operations. We can write the rule of substitution in a way that avoids the identity sign as follows:

$$\begin{align*}\text{Identity: From }\frac {f\xi }{g\xi } \text{ infer } \frac {k(f\xi )}{k(g\xi )} \end{align*}$$

If f and g are the same operation, then one may substitute them with the context of operation sign k. Here the $\xi $ reminds us that we are dealing with operations, and the notation is meant to indicate that the operations are the same. According to the Tractarian logicist interpretation, Wittgenstein’s view is that tautologies and arithmetic equations are both equational and both are shown as practices of calculation of sameness—just as Waismann noted.

4 Implicit Tractarian N-operator rules

Having set out the N-operator notions for quantification and given some examples, it is time to collect together all the rules for the recursive calculation of whether or not we have a tautology (or a generalized tautology). Here are full set of rules;

$$\begin{align*}N_{1}:\frac {N(p_{1}\ldots p_{i}\ldots p_{j}\ldots p_{n})}{N(p_{1}\ldots p_{j}\ldots p_{i}\ldots p_{n})}\end{align*}$$

$$\begin{align*}N_{2}:\frac {N(p_{1}\ldots p_{i},q_{1}\ldots q_{m},p_{i},p_{j}\ldots p_{n})}{N(p_{1}\ldots p_{j},q_{1}\ldots q_{m},p_{i},\ldots p_{n})}\end{align*}$$

$$\begin{align*}N_{3}:\frac {N(p_{1}\ldots p_{i},NN(q_{1}\ldots q_{m}),p_{j}\ldots p_{n})}{N(p_{1}\ldots p_{i},q_{1}\ldots q_{m},p_{j}\ldots p_{n})}\end{align*}$$

$$\begin{align*}N_{4}:\frac {N(p_{1},\ldots ,p_{i},N(\ldots q_{k}\ldots N(q_{k})\ldots ),p_{j}\ldots p_{n})}{N(p_{1}\ldots p_{i},p_{j}\ldots p_{n})}\end{align*}$$

$$\begin{align*}N_{5}:\frac {N(\ldots NN(p,N(q,r))\ldots )}{N(\ldots N(N(p,Nq),N(p,Nr))\ldots )}\end{align*}$$

As we noted, setting out the rules of N-operation explicitly is something that Wittgenstein was unwilling to do. We have to find them abductively—reasoning that their existence offers the best explanation of what he says about his N-operation and his desire to find a notation in which all and only logical equivalents have the “same” notation. In the Tractatus he does rather explicitly indicate $N_{1}$ and $N_{2}$ and $N_{3}$ fairly clearly. To find the other rules, one must work through examples—working, that is, under the interpretation that Wittgenstein’s goal is a notation where logical equivalents in N-notation are to be “the same.” Interpreters have often missed this, not recognizing this as Wittgenstein goal (though it is clearly expressed as such for his $ab$ -Notation in the 1913 Notes on Logic and letters and the 1914 Notes Dictated to Moore and worknotes). It is by such abductive considerations that the rules emerge. The rules are each legitimated, according to Wittgenstein, by the fact that various “and so on” recipe(s) are given with $\overline {\xi }$ . Consider the following:

Notice that rule $N_{1}$ is explicit in this passage which says that the order is indifferent. That the N-operator sign allows for what looks like multiple-places, is assured by the idea that this can be regarded as a “list” in accordance with $TLP$ 5.50. Thus, we find:

Accordingly, we can write “ $N(Np,Nq)$ ” to picture the truth-conditions of “ $p\wedge q$ ”. And we can write “ $Np$ ” equally well as “ $N(p,p)$ ” to picture the truth conditions of “ $\sim p$ .” Thus, Rule $N_{2}$ is somewhat explicitly revealed in the above passage, for as we have seen Sheffer’s dagger $\sim p$ is captured by $p\downarrow p$ , i.e., $\downarrow (p,p)$ . The other rules have to be extrapolated from examples, but they are all implicit in Wittgenstein’s statement of the above ways in which the may be used with the N-operator. (See Landini (Reference Landini2007) for details.) In N-notation, logical equivalents are “the same” (modulo the N-operator rules of sameness). All and only tautologies of the same bases have the same N-notation—namely $NN(\ldots Np\ldots p\ldots )$ . The following example illustrates the use of these rules so as to determine whether or not a wff is a tautology. We have Peirce’s Law:

$$\begin{align*}p\supset q\:.\supset .\:p\::\supset :\:p\end{align*}$$

$$\begin{align*}\sim (\sim p\downarrow q\;.\downarrow .\;p\;:\downarrow :p)\end{align*}$$

$$\begin{align*}\sim \downarrow (\downarrow (\downarrow (\sim p,q),p),p)\end{align*}$$

$$\begin{align*}NN(N(N(Np,q),p),p)\end{align*}$$

$$\begin{align*}N(N(p,NN(Np,q)),N(p,Np))\quad N_{5}\end{align*}$$

$$\begin{align*}N(N(p,NN(Np,q)))\quad N_{4}\end{align*}$$

$$\begin{align*}NN(p,Np,q)\quad N_{2}\end{align*}$$

The last line of the calculation has the form $NN(\ldots Np\ldots p\ldots )$ of a tautology.

Unfortunately for Wittgenstein, (polyadic) predicate logic is not decidable. The rules of N-notation cannot apply when schematic n is used. We can, of course, apply the N-operator rules to finite subgroups within $N(\ldots ..)$ , but there is no schematic way to proceed globally, even though the bases are always finite in number. If there were a way to apply the rules globally, quantification theory would be decidable by the recipe of $N-$ operator calculation. Since the viability of the rules of N-operator sameness is precisely what Wittgenstein hoped to use to establish the result that quantification theory is not a science, Wittgenstein’s plan fails.

5 Implicit operator rules

Let us next investigate the rules (implicit and explicit) for calculation with arithmetic operations recursively defined. Again, Wittgenstein expected readers to work out the rules for themselves from his examples. The rules are implicit, but clearly a natural feature of the Tractarian account where we find:

Using $\xi ,\rho $ and $\sigma $ as letters indicating the argument paces of a function, the following three rules are natural and quite clearly implicit in the Tractatus:

$$\begin{align*}&\text{Rule I:}\ \frac {f(g(h\xi ))}{[f(g\rho )][h(\xi )]} \\ & \text{Rule II:}\ \frac {[f(g\xi )]^{a}}{f^{a}(g_{\xi }^{a})} \\ &\text{Rule III: }\frac {(f_{\xi }^{a})^{c}}{(f_{\xi }^{a})_{\xi }^{c}}\end{align*}$$

Wittgenstein introduced recursive characterizations of functions by appeal to function (operation) expressions with numeral exponents (i.e., superscripts). The Tractatus offers only the barest sketch of what arithmetic is to become. It should be emphasized as well that the use of identity signs in the statement in the Tractatus of recursive operations does not represent genuine identity (which is a pseudo-relation for Wittgenstein) but rather, as with the Tractarian N-operation, they represent the outcomes of the operation. Thus, what follows could all be rewritten using our line notation:

$$\begin{align*}6.02\ \varOmega _{\xi }^{0}=\xi \end{align*}$$

$$\begin{align*}\varOmega _{\xi }^{m+1}=\varOmega (\varOmega ^{m}\xi )\end{align*}$$

$$\begin{align*}\textrm{(Vienna)}\ \varOmega _{\xi }^{m+n}=\varOmega ^{n}(\varOmega ^{m})\end{align*}$$

$$\begin{align*}6.241\;\Omega ^{mn}_{\xi }=(\varOmega ^{m})_{\xi }^{n}\end{align*}$$

Perhaps Wittgenstein hoped that his 6.02 could do double duty, introducing addition at the same time. I have introduced (Vienna) form the typescript found originally by von Wight in Vienna which is different from other typescripts of the Tractatus. (See von Wright (Reference Wittgenstein and von Wright1971).) Observe that “0”, “m” and “n,” here are not bindable variables for numbers. They are numerals or counters that check off in use the recursive steps down to the base case. Wittgenstein has:

$$\begin{align*}1=df\;0+1\end{align*}$$

$$\begin{align*}2=df\;1+1,\end{align*}$$

$$\begin{align*}3=df\;1+1+1,\text{ and so on.}\end{align*}$$

There are minor difficulties here, however. No provision has been made to assure that, “2 + 3” and “2 × 3” etc., are numerals. We can rectify the situation by a simple amendment of a formation rule: Where “m” and “n” are numerals” $m+n$ ” and “ $m\times n$ ” are numerals. We shall use distinct letters “m”, “n”, “a”, “b”, “c”, etc for distinct numerals. The next thing to ponder in Wittgenstein’s 6.02 is that “1” has been used in the definition of “1.” Likely, Wittgenstein meant to use a slash writing $1=df\;0+/$ .

Observe that there is no expectation that operations (functions) always emulate arithmetic “truths” such as that $0\hspace{2pt} {\neq }\hspace{2pt} 1$ . Indeed, depending on the function in question it may very well be that

$$\begin{align*}\frac {f_{\xi }^{0}}{f_{\xi }^{1}}\end{align*}$$

Our expectations must be tailored to the operation in question that we are dealing with. There is another point to be concerned about as well. A string such as 1+1+1… is not well-formed. We have to know where the brackets go. Let us demand:

$$\begin{align*}3=df\:1+2\end{align*}$$

$$\begin{align*}i.e.,\ 1+(1+1)\end{align*}$$

$$\begin{align*}4=df\:1+3\end{align*}$$

$$\begin{align*}i.e.,\ 1+((1+(1+1))\end{align*}$$

This leads to the question as to why Wittgenstein left out the brackets. Observe that we do find:

This has an important connection with 6.02 that must be deciphered. On the face of it, Wittgenstein’s intent seems to be that the ordering doesn’t matter—that we can order it any way we please. But it does matter to syntax and ignoring this would undermine any hope of the Tractarian system being formally proper. It is here, therefore, that the example reveals that Wittgenstein’s $TLP$ 6.231 tacitly appealed to the general recursion Rule I. The rule is precisely what allows regroupings of the same function. Accordingly, we have the following case:

$$\begin{align*}\frac {f(f(f(f\xi )))}{[f(f\rho )][f(f\xi )]}\end{align*}$$

$$\begin{align*}i.e..,\ \frac {f_{\xi }^{4}}{f_{\rho }^{2}(f_{\xi }^{2})}\end{align*}$$

In short, $TLP$ 6.231 is justified by Rule I transitions. Von Wright said that he remembered seeing a proof of 2+2 = 4 in a Vienna type-script entry at 6.241. Now that the Vienna typescript has been rediscovered, we find:

So laudet der Beweis des Satzes

$$\begin{align*}2+2=4\end{align*}$$

$$\begin{align*}1+1+1+1=4\end{align*}$$

$$\begin{align*}Def.\;1+1=2\end{align*}$$

$$\begin{align*}Def.\;2+2=4\end{align*}$$

This example of a proof of 2+2 = 4 is clearly based on $TLP$ 6.231. Thus it is illicit since the ordering of brackets is a syntactic matter that cannot be slighted and a rule of association + is needed. Happily, the situation is rectified by implicit recursion Rule I. This permits rearranging the brackets. Interestingly, in the Engelmann typescript the entire example at 6.2141 is removed and replaced with a demonstration of 2×2 = 4 together with the recursive definition of multiplication. The change suggests that Wittgenstein felt that readers would understand Rule I and readily work out the case of addition for themselves.

Now we can see that recursive definition (Vienna) of addition together with our general recursive Rule I, generates the following derived rule of association (which we state below with the argument place of the function omitted for convenience):

$$\begin{align*}\text{Association +: }\ \frac{f^{a+(b+c)}}{f^{(a+b)+c}} \qquad \text{Proof: }\qquad \frac {f^{a+(b+c)}}{\frac {f^{b+c}(f^{a})}{\frac {[f^{c}(f^{b})](f^{a})}{\frac {f^{c}(f^{b}(f^{a}))\:Rule\:I}{\frac {f^{c}(f^{a+b})}{f^{(a+b)+c}}}}}}\end{align*}$$

Note that the modern recursive definition of addition follows from Vienna.

$$\begin{align*}m+0=m\qquad \qquad \frac {f^{a+0}}{\frac {f^{0}(f^{a})}{f^{a}}}\end{align*}$$

$$\begin{align*}m+n^{\prime }=(m+n)^{\prime } \qquad \qquad \frac {f^{a+(b+1)}}{\frac {f^{b+1}(f^{a})}{\frac {[f^{1}(f^{b})](f^{a})}{\frac {f^{1}(f^{b}(f^{a}))\ \textit{Rule}\ I}{\frac {f^{1}(f^{a+b})}{f^{(a+b)+1}}}}}}\end{align*}$$

Wittgenstein’s Vienna definition yields the needed equational proof by substitution. In the proof, we again used implicit Rule I from which we obtained Association +. The law of Association + is, therefore, built directly into the definition of the recursive operation + when coupled with recursive Rule I. With this success, let us go on to investigate the case of the Tractarian characterization of multiplication.

As we noted, the Tractatus does offer a definition of multiplication. Now $\varOmega _{\xi }^{ab}$ is to mean $(\varOmega _{\rho }^{a})_{\xi }^{b}$ . This is a relationship of two operations (functions), namely $\varOmega _{\xi }^{a}$ and the higher-level function $\varTheta _{\xi }^{b}$ . Contrast the situation of $\varOmega ^{ba}\xi $ whose meaning is $(\varOmega _{\rho }^{b})_{\xi }^{a}$ . This is a relationship of two operations (functions), namely $\varOmega _{\xi }^{b}$ and the higher-level function $\varTheta _{\xi }^{a}$ . There is an important difference therefore that must be accommodated by recognition of implicit rules governing the interface of such functions of different levels. We have:

$$\begin{align*} & \text{Rule IV: }\ \frac {(\varOmega )_{\xi }^{a}(f_{\rho }^{b})}{(f_{\rho }^{b})_{\xi }^{a}} \\ &\text{Rule V:}\ \frac {[\varOmega {{\hspace {-0.0001pt}}}_{\xi }^{a}(\Theta _{\rho }^{b})](f)}{f_{\rho }^{a}(f{{\hspace {-0.0001pt}}}_{\xi }^{b})}\end{align*}$$

In Rule IV we have a case multiplication. In Rule V we have a case like addition but not permitting regrouping and thus it is quite different from Rule I which permits regrouping. Note that $[\varTheta _{\rho }^{b}]_{\xi }^{a}(f)$ is a case of $\varOmega _{\xi }^{a}[\varTheta _{\xi }^{b}(f)]$ , but it is not a case of $[\varOmega _{\xi }^{a}(\varTheta _{\xi }^{b})](f)$ .

With multiplication recursively characterized, it is easy to see that we can arrive at Association × without appeal to proof by induction. We have:

$$\begin{align*}\text{Association}\times{:}\ \frac {f^{(ca)b}}{f^{c(ab)}}\quad\text{Proof}\quad \frac {f^{(ca)b}}{\frac {(f^{ca})^{b}}{\frac {((f^{c})^{a})^{b}}{\frac {(f^{c})^{ab}}{f^{c(ab)}}}}}\end{align*}$$

Let us next consider the more interesting case of Distribution.

$$\begin{align*}\text{Distribution 1:}\quad \frac {f^{a(b+c)}}{f^{(ab)+(ac)}}\quad\text{Proof}\quad \frac {f^{a(b+c)}}{\frac {(f^{a})^{b+c}}{\frac {(f^{a})^{c}((f^{a})^{b})}{\frac {f^{ac}(f^{ab})}{f^{(ab)+(ac)}}}}}\end{align*}$$

With rule Rule II in place, we arrive at the following:

$$\begin{align*}\text{Distribution 2:}\quad\frac {f^{(b+c)a}}{f^{(ba)+(ca)}}\quad\text{Proof}\quad \frac {f^{(b+c)a}}{\frac {(f^{b+c})^{a}}{\frac {((f^{c}(f^{b})^{a}}{\frac {(f^{c})^{a}((f^{b})^{a})\:Rule\:II}{\frac {f^{ca}(f^{ba})}{f^{(ba)+(ca)}}}}}}\end{align*}$$

Implicit Rule III enables the parallel of the usual recursive definition of multiplication:

$$\begin{align*}a0=0\qquad \qquad \frac {f^{a0}}{\frac {(f^{a})^{0}}{\frac {(f_{\gamma }^{a})_{\xi }^{0}}{\frac {\xi }{f_{\xi }^{0}}}}}\end{align*}$$

$$\begin{align*}ab^{\prime }=(ab)+a\qquad \qquad \frac {f^{a(b+1)}}{\frac {(f^{a})^{b+1}}{\frac {(f^{a})^{1}((f^{a})^{b}}{\frac {f^{a1}(f^{ab})}{\frac {\frac {(f^{a})^{0+/}(f^{ab})}{[f^{a}(f^{a})^{0}](f^{ab})}}{\frac {[f^{a}(\xi )](f^{ab})}{{{\hspace {-0.0001pt}}}^{\frac {f^{a}(f^{ab})\:Rule\:I}{f^{(ab)+a}}}}}}})}}\end{align*}$$

These results were carried out without recourse to any emulation of proof by mathematical induction.

When it comes to a proof of Commutation + and Commutation $\times $ , however, an emulation of mathematical induction seems inescapable. I shall take that up in the next section. For the present we have enough to see that Wittgenstein has, after all, a means for solving Ramsey’s problem of how to emulate quantification over numbers. It is done by simply invoking the N-operator treatment of quantification. Ramsey’s problem boils down to the question of whether the Tractatus can emulate the following

$$\begin{align*}(\exists k)(Num(k)\;\wedge\;k+2=m)\end{align*}$$

$$\begin{align*}(\exists k)(Num(k)\;\wedge\;k\times 2=m).\end{align*}$$

The only way forward is by means of Tractarian Logicism. That is, one can use the N-operator to emulate quantification over the operations used in arithmetic. The application of the N-operator notation readily yields the following:

$$\begin{align*} \begin{array}{l@{\qquad}l} (\exists\; f)\varphi f & (f)\varphi f \\[3pt] \varphi f_{1}\:\lor \ldots \lor \:\varphi f_{n} & \varphi f_{1}\:\wedge\ldots \wedge\:\varphi f_{n} \\[3pt] NN(\varphi f_{1},\ldots ,\varphi f_{n}) & N(N(\varphi f_{1}),\ldots ,N(\varphi f_{n}))\end{array}\end{align*}$$

As we see, this emulates finitely bounded quantification over operations generally, and this includes those operations for arithmetic characterized recursively by expressions with numeral exponents. It is bounded quantification—though the finite bound (given by using schematic n) can be of any finite size.

An important feature emerges. Obviously, there are no numbers at all in the “domain” (as it were) of Wittgenstein’s emulation of quantification over natural numbers. The domain contains operations alone. At first, one may worry that some among the operations are not arithmetic operations. (Let us call those Fregean functions that behave arithmetically, “uniform.’) To illustrate, notice that there are operations f such that, where “ $m$ ” and “ $n$ ” are distinct numerals, we get the following:

$$\begin{align*}\frac {f^{m}\xi }{f^{n}\xi }\end{align*}$$

In arithmetic, of course we get uniformity, so that $0\hspace{2pt} {\neq }\hspace{2pt} 1, 0 \hspace{2pt} {\neq }\hspace{2pt} 2, 1 \hspace{2pt} {\neq }\hspace{2pt} 2$ , and so forth. But this is not to be expected in general for any operation whatsoever. For a given operation, it may well be that m-many applications of it to a base take us to the same outcome as n-many applications of it to that same base. All we have a right to expect is that we get the following rule of inference:

$$\begin{align*}\text{From }\frac {f^{m}(f_{\xi }^{c})}{f^{n}(f_{\xi }^{c})}\text{ infer }\frac {f^{m}\xi }{f^{n}\xi }.\end{align*}$$

(It will be convenient, as before, to sometimes drop the argument place of the function sign.) From this rule it is easy to arrive at the result:

$$\begin{align*}\text{From }\frac {f^{1}}{f^{2}}\text{ infer }\frac {f^{m}}{f^{n}}.\end{align*}$$

That is, from two repetitions yielding the same outcome as one repetition, infer that m repetitions yield the same outcome as n repetitions. Consider the following inference:

$$\begin{align*}\text{From }\frac {k(f^{2})}{f^{6}}\quad and\quad \frac {f^{6}}{f^{4}(f^{2})}\text{ infer }\frac {k}{f^{4}}.\end{align*}$$

Applying k to $f^{2}$ we get $f^{6}$ , which of course is $f^{4}(f{{\hspace {-0.0001pt}}}^{2})$ but we cannot infer that k is the same as $f^{4}$ unless uniformity is involved. If k and f are uniform, the reasoning would be acceptable, since

$$\begin{align*}\frac {k(f^{1})}{f^{5}}, \frac {k(f^{2})}{f^{6}},\frac {k(f^{3})}{f^{7}},\ldots \text{ etc.}\end{align*}$$

What then assures the uniformity? The answer lies the N-operator emulation of quantification. It readily solves the problem that not all operations k will behave the way arithmetic operations behave. That is because, in any given application of N-operation, one requires a recipe determining its use, and thereby Wittgenstein can simply rely on some such recipe to exclude problematic cases. According to the Tractatus, one cannot introduce a predicate “ $Num(k)$ ” to assure that the quantification concerns arithmetic operations k. This is a pseudo-predicate. The uniformity of the operations intended has to be shown. It is shown by the $\overline {\xi }$ clause of N-operator used for the emulation. It allows a recipe for selection, and it seems that one can thereby select as bases, in any given case, just the uniform operations. Thus, we can proceed without introducing any special new signs. The uniformity of the operations selected is shown and not said by any pseudo-predicate “ $Num(k)$ .”

With uniformity understood, we can emulate quantification over numbers, solving Ramsey’s problem. Consider the following cases:

$$\begin{align*}(\exists k)(Num(k)\:\wedge\:2+k=m)\end{align*}$$

$$\begin{align*}(\exists k)\left(\frac {k(f^{2})}{f^{m}}\right)\end{align*}$$

$$\begin{align*}NN\left(\frac {k_{1}(f^{2})}{f^{m}},\ldots,\frac {k_{n}(f^{2})}{f^{m}}\right)\end{align*}$$

The commuted form offers nothing new:

$$\begin{align*}(\exists k)(Num(k)\:\wedge\:k+2=m)\end{align*}$$

$$\begin{align*}(\exists k)\left(\frac {f^{2}(k)}{f^{m}}\right)\end{align*}$$

$$\begin{align*}NN\left(\frac {f^{2}(k_{1})}{f^{m}},\ldots,\frac {f^{2}(k_{n})}{f^{m}}\right).\end{align*}$$

The quantifier has an arbitrary large finite bound. In this cases, recall that the hidden selection recipe $\overline {\xi }$ of application of N-operation is suppose to handle showing, without further premise, that the operations k and f are uniform. In the case of multiplication we have the following:

$$\begin{align*}(\exists k)(Num(k)\:\wedge\:k\times 2=m)\end{align*}$$

$$\begin{align*}(\exists k)\left(\frac {\Omega _{\xi }^{2}(k)}{f_{\xi }^{m}}\right)\end{align*}$$

$$\begin{align*}NN\left(\frac {\Omega _{\xi }^{2}(k_{1})}{f_{\xi }^{m}},\ldots ,\frac {\Omega _{\xi }^{2}(k_{n})}{f_{\xi }^{m}}\right).\end{align*}$$

Alternatively:

$$\begin{align*}(\exists k)\left(\frac {k_{\xi }^{2}}{f_{\xi }^{m}}\right)\end{align*}$$

$$\begin{align*}NN\left(\frac {(k_{1})_{\xi }^{2}}{f_{\xi }^{m}},\ldots ,\frac {(k_{n})_{\xi }^{2}}{f_{\xi }^{m}}\right).\end{align*}$$

Recall that $(\Omega _{\xi }^{2})(k)$ tells us that k is to go into the argument position to form $k_{\xi }^{2}$ . Here we are emulating with the N-operator quantifying over a first-level uniform function $k$ in $k\times 2$ . A special issue arises, however. In expressing the “commuted” form $2\times k$ care must be taken since we shall be quantifying over a higher-level function. But all is well. We have:

$$\begin{align*}(\exists k)(Num(k)\:\wedge\:2\times k=m)\end{align*}$$

$$\begin{align*}(\exists \Omega )\left(\frac {(\Omega )_{\xi }(f_{\sigma }^{2})}{f_{\xi }^{m}}\right)\end{align*}$$

$$\begin{align*}NN\left(\frac {(\Omega _{1})_{\xi }(f_{\sigma }^{2})}{f_{\xi }^{m}},\ldots ,\frac {(\Omega _{n})(f_{\xi }^{2})}{f_{\xi }^{m}}\right).\end{align*}$$

Here the N-operator is emulate quantifying over a higher-level function. (Note that “2” is not itself a function sign and we can’t make the function sign “ $k$ ” into sign that can occupy the position of a numeral.) We can go on to emulate the following as well:

$$\begin{align*}(\exists k,p)(Num(k)\:\wedge\:Num(p)\:.\wedge.\;k\times p=m)\end{align*}$$

$$\begin{align*}(\exists \Omega )(\exists\; f)(\frac {(\Omega )_{\xi }(f_{\sigma })}{f_{\xi }^{m}}).\end{align*}$$

This works because the “higher-level” functions $(\Omega )_{\xi }$ are, e.g., $((k)^{n})_{\xi }$ . This finally addresses Ramsey’s concern that the Tractatus is not viable unless it can emulate quantification over numbers. It can—as long as we can accept the Tractarian logicist interface of the arithmetic operations with the N-operation.

6 Tract-Induct and showing

The Tractarian logicist interpretation says that the N-operator emulates only bounded quantification. This is abductively corroborated from the writings of Wittgenstein’s Philosophische Bemerkungen. Consider the following:

The best explanation of some important features of these passages is that they reflect Tractarian logicist positions. On the emulation of quantification by the N-operator, the quantifiers involved in the definition of the ancestral would, according to the Tractarin logicist interpretation, be finitely bounded—though any bound is allowed. The argument I’m offering is abductive. Admittedly, Wittgenstein does not explicitly mention his N-operator. Nevertheless, that feature is precisely what we find Wittgenstein observing when he rejects the intelligibility of “ $(n)((\exists ^{n}x)\varphi x)$ ” and observes that a proper emulation of quantification would be bounded. We see the trajectory Wittgenstein was exploring. (It should be noted that more abductive evidence may be found in Moore (Reference Moore, Stern, Rogers and Citron2016).)

The problem of finding a Tractarian emulation of proof by Mathematical Induction remains. To this end, note well that it is of no help toward achieving showing to adopt the following as a primitive inference rule:

$$\begin{align*}From\;\vdash \varphi 0\;\wedge\;(m)(\varphi m\;\supset \;\varphi (m+1))\quad \textit{infer}\;\vdash (n)\varphi n.\end{align*}$$

Of course, in a first order elementary arithmetic, one typically adopts a schema of mathematical induction. Its viability relies on the assumption that the intended model of the first-order arithmetic is the domain of natural numbers as abstract particulars. Wittgenstein does not accept an ontology of natural numbers. He cannot, therefore, rely upon such a model theoretic approach.Wittgenstein knew that showing requires more then a technique of evading “ $Num(x)$ ” by simply adopting a convention of using special “numeric” variables, “m” and “ $n.$ ” Tractarian showing respects the requirements of “honest toil,” to borrow a colorful phrase from Russell.We have seen, however, that the N-operator emulation of quantification can emulate the quantification over operations that emulate numbers. This offers a way of using “m” and “n” so that they show the structural features of a system of natural numbers. So the central problem before us concerns the inductive clause

$$\begin{align*}(m)(\varphi m\;\supset\;\varphi (m+1))\end{align*}$$

Unfortunately, Wittgenstein N-operator emulation of quantification has to live with finitely bounded quantifiers. That gets in the way of successfully emulating proof by Mathematical Induction.

It is useful to rehearse the usual inductive proof of Commutation + to show its dependence on universal quantification over numbers in its Inductive Step. The usual proof runs as follows:

$$\begin{align*}\vdash \:(n)(m)(m+n=n+m)\end{align*}$$

$$\begin{align*}Base:\;(m)(m+0=0+m)\end{align*}$$

We prove this base case by a subordinate induction:

$$\begin{align*}Base_{1}:\ 0+0=0+0\end{align*}$$

$$\begin{align*}\textit{Induct}_{1}:\ \textit{Assume}\quad m+0=0+m\quad \textit{Show}\quad m^{\prime}+0=0+m^{\prime}\end{align*}$$

$$\begin{align*}m^{\prime }+0=(m+0){{\hspace {-0.0001pt}}}^{\prime }=(0+m){{\hspace {-0.0001pt}}}^{\prime }=0+m^{\prime }.\end{align*}$$

Next we go on with the main induction:

$$\begin{align*}\textit{Induct}:\textit{Assume}\ (m)(m+n=n+m)\quad \textit{Show}\ (m)(m+n^{\prime }=n^{\prime }+m)\end{align*}$$

We prove this by a subordinate induction:

$$\begin{align*}\textit{Base}_{2}:0+n^{\prime }=n^{\prime }+0\end{align*}$$

$$\begin{align*}\textit{Induct}_{2}:\textit{Assume}\quad m+n^{\prime }=n^{\prime }+m\quad \textit{Show}\quad m^{\prime }+n^{\prime }=n^{\prime }+m^{\prime }\end{align*}$$

By assumption for $Induct$ , instantiating $(m)(m+n=n+m)$ we get

$$\begin{align*}m^{\prime }+n=n+m^{\prime }.\end{align*}$$

This can only happen if the quantifier ranges over all the numbers. Wittgenstein’s bounded schema emulating quantification will not suffice. But with this in place, we get:

$$\begin{align*}m^{\prime }+n^{\prime }=(m^{\prime }+n){{\hspace {-0.0001pt}}}^{\prime }=(n+m^{\prime }){{\hspace {-0.0001pt}}}^{\prime }=(n+m)^{\prime \prime }\end{align*}$$

By assumption for $Induct_{2}$ and our assumption for $Induct$ , we get:

$$\begin{align*}(n+m)^{\prime \prime }=(m+n)^{\prime \prime }=(m+n^{\prime }){{\hspace {-0.0001pt}}}^{\prime }=(n^{\prime }+m)^{\prime }=n^{\prime }+m^{\prime }\end{align*}$$

As we can see, the proof depends essentially on the universal quantifier having within its scope all the natural numbers.

All the same, there are cases where the unboundness is avoided, and this I surmise is why Wittgenstein failed to realize that his arbitrarily bounded quantification is not enough. To see this, consider the following proof of Commutation + using what I call “Tract-Induct.” The approach only works when one can employ stable schematic letters—i.e., when we can fix all the values of the schematic use of n together. We have:

$$\begin{align*}\text{+1 Lemma: }\ \frac {f^{a+1}}{f^{1+a}}\end{align*}$$

$$\begin{align*}\text{(Base) }\ \frac {f^{0+1}}{f^{1+0}}\quad \text{Proof}\quad \frac {f^{0+1}}{\frac {f^{1}(f^{0})}{\frac {f^{0+/}(f^{0})}{\frac {f(f^{0})}{\frac {f}{\frac {\frac {f(f^{0})}{f^{0+/}}}{\frac {f^{1}}{\frac {f^{0}(f^{1})}{f^{1+0}}}}}}}}}\end{align*}$$

$$\begin{align*}\text{(Induction) Assume:}\quad \frac {f^{a+1}}{f^{1+a}}\qquad \text{Show:}\quad \frac {f^{(a+1)+1}}{f^{1+(a+1)}}\end{align*}$$

$$\begin{align*}\text{Proof:}\quad \frac {f^{(a+1)+1}}{\frac {f^{1}(f^{a+1})}{\frac {f^{1}(f^{1+a})\:assumption}{\frac {f^{1}(f^{a}(f^{1}))}{\frac {[f^{1}(f^{a})](f^{1})\:Rule\:I}{\frac {f^{a+1}(f^{1})}{f^{1+(a+1)}}}}}}}\end{align*}$$

With this Lemma in place we can offer a Tract-Induct proof of the following:

$$\begin{align*}\text{Commutation}+\;\frac {f^{a+b}}{f^{b+a}}\end{align*}$$

$$\begin{align*}\text{(Base) }\ \frac {f^{0+1}}{f^{1+0}}\end{align*}$$

$$\begin{align*}\text{(Induction) Assume: }\ \frac {f^{a+b}}{f^{b+a}}\text{ Show }\frac {f^{(a+1)+b}}{f^{b+(a+1)}}\end{align*}$$

$$\begin{align*}\text{Proof: }\ \frac {f^{(a+1)+b}}{\frac {f^{b}(f^{a+1})}{\frac {f^{b}(f^{1}(f^{a}))}{\frac {[f^{b}(f^{1})](f^{a})\:Rule\:I}{\frac {[f^{1}(f^{b})](f^{a})\:Lemma}{\frac {f^{1}(f^{b}(f^{a}))\:Rule\:I}{\frac {f^{1}(f^{a}(f^{b}))\:assumption}{\frac {[f^{1}(f^{a})](f^{b})\:Rule\:I}{\frac {f^{a+1}(f^{b})}{f^{b+(a+1)}}}}}}}}}}\end{align*}$$

This Tract-Induct proof does not depend on having to emulate an unbounded universal quantifier over numbers. (Compare the discussion of Goodstein's interpretation in Marion & Mitsuhiro (Reference Marion, Mitsuhiro and Stern2018).)

Similarly, a proof by Tract-Induct of the commutation of multiplication is also forthcoming. But to facilitate ease of the proofs, let us first prove two lemmas that will make the main proof easy.

$$\begin{align*}\text{Lemma 1: }\ \frac {f^{a1}}{f^{1a}} \text{ Proof }\ \frac {f^{a1}}{\frac {(f^{a})^{1}}{\frac {(f^{a})^{0+/}}{\frac {f^{a}(f^{0})}{\frac {f^{a}}{\frac {(f\xi )^{a}}{\frac {[f(f^{0})]^{a}}{\frac {(f^{0+/})^{a}}{\frac {(f^{1})^{a}}{f^{1a}}}}}}}}}}\end{align*}$$

$$\begin{align*}\text{Lemma 2: }\ \frac {f^{a0}}{f^{0a}}\text{ Proof: }\frac {f^{(a+1)0}}{\frac {(f^{a+1})^{0}}{\frac{\xi}{(f^{0})^{a+1}}}}\end{align*}$$

With this in place we can proceed to a proof of commutation of multiplication:

In this way, proof by Tract-Induct is made possible by Wittgenstein’ s approach to arithmetic in terms of functions (operations) recursively defined with the help of numeral exponents. The lesson is that when proof by mathematical induction takes the form of Tract-Induct, where the numerals are stable throughout the proof then it is allowable.

There is abductive evidence for this in Philosophische Bemerkungen. Wittgenstein wrote ( $PB$ , p. 197):

The letters used in Tract-Induct are stable for any particular numeral assignment and thus the entire Tract-Induct proof acts like a proof-schema which can be repeated for any assignment. The situation is quite unlike the traditional mathematical inductive proof illustrated above which requires the an unbounded quantifier over all numbers. The lesson to be distilled from these examples, therefore, is that in these simple cases the inductive clause

$$\begin{align*}(x)(Num(x)\:.\supset .\:\varphi x\:\supset \:\varphi (x+1))\end{align*}$$

of the usual mathematical induction schema can be successfully reinterpreted as schema expressing “sameness” of outcomes of two recursive functions (operations). That is viable only when there is a stability of form involved with all the schematic letters. What the inductive clause endeavors to establish is not that given functions in question are recursive (since we are given that) but that the two recursive functions are “the same” (i.e., they wherever they operate, they walk down to the same base. In his Philosophische Bemerkungen Wittgenstein’s writings suggest that he knew this. It thereby provides abductive evidence that the Tractarian logicist interpretation is correct. The context of his writing is his criticism of Skolem’s proof of association + by appeal to the traditional principle of Mathematical Induction. Wittgenstein offers the following remarks about what he takes to be the nature of a proper proof of the result ( $PB$ , p. 197):

… But how can it prove this proposition? It obviously points along the series of proofs

That is a stretch of the spiral taken out of the middle. is a stop-gap for what only emerges in the course of the development. If I look at this series, it may strike me that it is akin to the definition A(1); that if I substitute ‘1’ for ‘c’ and ‘1’ for ‘d’, the two systems are the same.

In the proof, at any rate, what is to be proved is not the end of the chain of equations.

The proof shows the spiral form of the law. But not in such a way that it comes out as the conclusion of the chain of inferences.

Though the passage is difficult,Footnote ⁸ it seems clear enough that Wittgenstein is suggesting that, instead of appeal to the traditional proof by mathematical induction (as found in Skolem), we can appeal to our “seeing the spiral pattern.” Wittgenstein’s reference to “definition A(1)” is just to indicate that the definition is that of a recursive function of arithmetic association. Notice again that Wittgenstein writes:

The point he is after is that any finite segment of the recursive walk down in such an inductive proof is itself tantamount to a repetition of the very definition of the recursive function involved. It is by this, he suggests, that one sees the spiral. He writes (p. 199):

To know that you can prove something is to have proved it.

7 + (8+9) = (7+8) + 9. How do I know that this is so, without having to give a particular proof of it? And do I know just as well as if I had given a complete derivation of it? Yes—Then that means it really is proved. What’s more, in that case it cannot have a still better proof; say, by my carrying out the derivation as far as this proposition itself. So it must be possible for me to say after running through one turn of the spiral ‘Stop! I don’t need any more, I can already see how it goes on’. And then every higher step must be purely superfluous and doesn’t make the matter clearer. If I draw all the whorls of the spiral as far as my point, I cannot see that the spiral leads to it any better than if I draw one. It is only that each shows the same thing in a different form.

That seems precisely the idea behind our Tract-Induct. Having been given operations (functions) that we know to be recursive, we may be able see a spiral form emerge from the calculation of these recursive functions in an equation involving them. This, in Wittgenstein’s view, evades the unbounded quantifiers used in the inductive clause of the traditional proof by mathematical induction.

All is well, but for the fact that Tract-Induct (seeing the spiral, understanding the “and so on”) requires that we can reason from a stable and fixed (albeit schematic and arbitrary) use of numerals $a$ , $b,$ etc. This has serious limitations on inductive proofs since it is far from clear that such a stable and fixed use of numerals would suffice. Thus, in spite of Wittgenstein’s having an approach that addresses Ramsey problem of quantification, and in spite of its capturing Tract-Induct, the use of unbounded quantification is still essential. Mathematical Induction in its traditional form is lost, and Wittgenstein seems quite willing to live without it.

It will not suffice to replace the inductive clause with the weaker notion that from any numerical position (arbitrarily bounded) we can recursively get down to the base. To see the spiral at some finite segment of the inductive walk down to the base cannot itself assure that the recursive functions involved do not depart from the spiral elsewhere in the walk down. The problem, in a nutshell, lies in that one cannot transition from any to every even though the walk down of a recursive function to its base is always finite. Recursive combinatorial logic and arithmetic rests with the concept of any, i.e., bounded quantification. Although the bound can be of any finite height, and though one can invent recursive functions to readjust the height, this can never capture the notion of all needed for proof by mathematical induction.