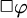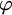1 Introduction
Mereology, as an umbrella term for the general study of parts and wholes, dates back to the early days of philosophy and constitutes an important active sub-field of metaphysics (cf., e.g., the survey by Varzi [Reference Varzi and Zalta47]). In a narrower sense, mereology refers to the formal theory of the part-whole relation initiated by Stanisław Leśniewski (cf., [Reference Simons and Zalta31, Reference Varzi and Zalta47]), aiming at an alternative to set theory as a foundation for mathematics. Despite the fact that it did not quite achieve its initial goal, mereology has become a well-established field on its own. It can also provide tools for formal ontology focusing on the general structure of what there is, regardless of the actual ontological stance, which can be traced back to Husserl’s writings [Reference Gruszczyński and Varzi12, Reference Simons30].
Formulations of mereological theories change over time. The original theory proposed by Leśniewski was formulated in a special logical language based on his system Ontology, which was then recast as a second-order theory by Tarski [Reference Tarski34] and Leonard & Goodman [Reference Leonard and Goodman19]. However, what most logicians nowadays are familiar with might be the first-order approximations of the classical theory, which were started by Goodman [Reference Goodman7] and developed further by Eberle [Reference Eberle5] and Casati & Varzi [Reference Casati and Varzi2], among others. Moreover, there is a series of fruitful research aiming to characterize precisely the classical theory of mereology with finitely many first-order principles, such as [Reference Pietruszczak26, chap. 7], [Reference Niebergall, Alexander and Hannes24, Reference Niebergall, Pettigrew and Horsten25] and the recent work of Tsai [Reference Tsai40]. Also, there are other important traditions of formulations of theories for the parthood relation, including those involving plural quantification that began with [Reference Lewis20]. For an excellent introduction to the basics of mereology, we refer to [Reference Varzi and Zalta47].
In this article, we restrict ourselves to the first-order theories of mereology using a language with equality symbolFootnote
1
![]() $\equiv $
and a special binary predicate symbol P meant to represent ‘part of’ or ‘a part of’ relation.Footnote
2
Various theories have been proposed and studied in the literature featuring different first-order properties of P. For example, it is widely held that the part-whole relation is at least reflexive, transitive and anti-symmetric (see [Reference Varzi and Zalta47] for exceptions), i.e., it is a partial order. The theory with the corresponding axioms for P is called the ground mereology (GM) in the literature of mereology. On top of this, various axioms can be added to capture the composition and decomposition of the parts, resulting in minimal mereology (MM), extensional mereology (EM), extensional closure mereology (CEM), general extensional mereology (GEM), and so on (see, e.g., [Reference Tsai38, sec. 1], [Reference Varzi and Zalta47]).
$\equiv $
and a special binary predicate symbol P meant to represent ‘part of’ or ‘a part of’ relation.Footnote
2
Various theories have been proposed and studied in the literature featuring different first-order properties of P. For example, it is widely held that the part-whole relation is at least reflexive, transitive and anti-symmetric (see [Reference Varzi and Zalta47] for exceptions), i.e., it is a partial order. The theory with the corresponding axioms for P is called the ground mereology (GM) in the literature of mereology. On top of this, various axioms can be added to capture the composition and decomposition of the parts, resulting in minimal mereology (MM), extensional mereology (EM), extensional closure mereology (CEM), general extensional mereology (GEM), and so on (see, e.g., [Reference Tsai38, sec. 1], [Reference Varzi and Zalta47]).
Since mereological theories are about properties of the binary relation of part-whole, it is very natural, at least for a modal logician, to ask whether it is possible to use a modal language, instead of the first-order language, to capture those first-order mereological properties of the part-whole relation and obtain the corresponding modal theories. This is the basic motivation behind the mereological modal theories proposed by this paper. In fact, if we reverse the part-whole relation to whole-part relation and use the standard Kripke semantics for the modality with a set of objects as the domain, then
![]() $\Box \varphi $
has a very natural reading: all parts of the current object are
$\Box \varphi $
has a very natural reading: all parts of the current object are
![]() $\varphi $
. Note that all the modal formulas are evaluated with respect to an object in the domain, and this object exactly is what ‘current’ refers to. Similarly, a modal formula
$\varphi $
. Note that all the modal formulas are evaluated with respect to an object in the domain, and this object exactly is what ‘current’ refers to. Similarly, a modal formula
![]() $\varphi $
captures a property of an object.Footnote
3
$\varphi $
captures a property of an object.Footnote
3
![]() $\Box \varphi \to \varphi $
and
$\Box \varphi \to \varphi $
and
![]() $\Box \varphi \to \Box \Box \varphi $
not only capture the corresponding first-order properties of Reflexivity and Transitivity, but also provide some intuitive readings in the context of mereology, e.g.,
$\Box \varphi \to \Box \Box \varphi $
not only capture the corresponding first-order properties of Reflexivity and Transitivity, but also provide some intuitive readings in the context of mereology, e.g.,
![]() $\Box \varphi \to \Box \Box \varphi $
says that if all parts are
$\Box \varphi \to \Box \Box \varphi $
says that if all parts are
![]() $\varphi $
, then all the parts of the parts are also
$\varphi $
, then all the parts of the parts are also
![]() $\varphi $
.
$\varphi $
.
However, one may complain that the usual modal language seems to be inadequate to capture even the ground mereology, since Anti-symmetry, as a frame property, is not modally definable [Reference Blackburn, de Rijke and Venema1, sec. 3.3]. This motivates us to find a more expressive language for mereological modal theories.
A natural candidate to be added into the modal language is the so-called window modality
![]() studied by van Benthem [Reference van Benthem42], [Reference van Benthem45, p. 412], Humberstone [Reference Humberstone17, Reference Humberstone18], and Gargov et al. [Reference Gargov, Passy, Tinchev and Skordev6].Footnote
4
In our setting,
studied by van Benthem [Reference van Benthem42], [Reference van Benthem45, p. 412], Humberstone [Reference Humberstone17, Reference Humberstone18], and Gargov et al. [Reference Gargov, Passy, Tinchev and Skordev6].Footnote
4
In our setting,
![]() also has a natural reading: all
also has a natural reading: all
![]() $\varphi $
-things are parts of the current object. With the help of
$\varphi $
-things are parts of the current object. With the help of
![]() , many modally undefinable properties become definable in the extended language, such as Irreflexivity, Trichotomy, and Anti-symmetry [Reference Goranko9, sec. 5]. Actually, as also shown by Goranko [Reference Goranko9], every universal first-order formula with the equality
, many modally undefinable properties become definable in the extended language, such as Irreflexivity, Trichotomy, and Anti-symmetry [Reference Goranko9, sec. 5]. Actually, as also shown by Goranko [Reference Goranko9], every universal first-order formula with the equality
![]() $\equiv $
and a binary predicate R can be defined by a modal language with both
$\equiv $
and a binary predicate R can be defined by a modal language with both
![]() $\Box $
and
$\Box $
and
![]() (see also [Reference Goranko and Petkov8, Reference Goranko and Passy10], [Reference van Benthem44, p. 155] for further results).
(see also [Reference Goranko and Petkov8, Reference Goranko and Passy10], [Reference van Benthem44, p. 155] for further results).
Note that the existing results about
![]() do not make the modal rendering of the mereological theories easier. First of all, all the non-trivial mereological properties that we will discuss are not expressible in universal formulas due to the non-trivial quantifier alternations. Technically speaking, as we will see later, most of the first-order properties of mereology are not closed under taking substructures, thus by the Łoś–Tarski Theorem (see, e.g., [Reference Hodges14, p. 143]), the general correspondence method proposed by Goranko [Reference Goranko9] for the universal fragment of first-order logic is not applicable. In contrast, it is highly non-trivial to find the corresponding modal formulas for the first-order mereological properties (or the combinations of several such properties), even if they are indeed definable by the language with
do not make the modal rendering of the mereological theories easier. First of all, all the non-trivial mereological properties that we will discuss are not expressible in universal formulas due to the non-trivial quantifier alternations. Technically speaking, as we will see later, most of the first-order properties of mereology are not closed under taking substructures, thus by the Łoś–Tarski Theorem (see, e.g., [Reference Hodges14, p. 143]), the general correspondence method proposed by Goranko [Reference Goranko9] for the universal fragment of first-order logic is not applicable. In contrast, it is highly non-trivial to find the corresponding modal formulas for the first-order mereological properties (or the combinations of several such properties), even if they are indeed definable by the language with
![]() $\Box $
and
$\Box $
and
![]() . Moreover, having the corresponding modal formulas for the desired first-order properties does not mean the resulting logical system is complete. Actually, showing the completeness for systems using both
. Moreover, having the corresponding modal formulas for the desired first-order properties does not mean the resulting logical system is complete. Actually, showing the completeness for systems using both
![]() $\Box $
and
$\Box $
and
![]() is also highly non-trivial and error-prone (see discussions in Section 4.2).
is also highly non-trivial and error-prone (see discussions in Section 4.2).
Despite the difficulties of using an (extended) modal language to specify mereological theories, there are also some potential technical advantages of using the modal language. First of all, as it is well-known, some modal formulas can express properties that are not first-order definable, such as the McKinsey formula
![]() $\Box \Diamond p\to \Diamond \Box p$
. Over transitive frames, the McKinsey formula boils down to the first-order definable property of Atomicity in mereology. However, over arbitrary frames, the modal formula does not have a first-order correspondence. Another interesting example is that the Grzegorczyk formula
$\Box \Diamond p\to \Diamond \Box p$
. Over transitive frames, the McKinsey formula boils down to the first-order definable property of Atomicity in mereology. However, over arbitrary frames, the modal formula does not have a first-order correspondence. Another interesting example is that the Grzegorczyk formula
![]() $\Box (\Box (p\to \Box p)\to p)\to p$
defines the class of frames that are reflexive, transitive, and anti-symmetric without any infinite ascending chain of distinct elements, which is also not definable but relevant to mereology.Footnote
5
As another example, the mereological property Fusion is essentially second-order, and we will define it by our modal language based on extensional mereology. Another potential advantage is that by using a modest modal language, we may obtain the decidability of the resulting modal logic over the relevant mereology-inspired frames, which we leave for further studies.Footnote
6
$\Box (\Box (p\to \Box p)\to p)\to p$
defines the class of frames that are reflexive, transitive, and anti-symmetric without any infinite ascending chain of distinct elements, which is also not definable but relevant to mereology.Footnote
5
As another example, the mereological property Fusion is essentially second-order, and we will define it by our modal language based on extensional mereology. Another potential advantage is that by using a modest modal language, we may obtain the decidability of the resulting modal logic over the relevant mereology-inspired frames, which we leave for further studies.Footnote
6
In this paper, we mainly focus on the modal definability of existing first-order mereological theories. There can be various taxonomies of mereological properties, e.g., Hovda [Reference Hovda16] discussed different but equivalent formulations of the classical mereology using various versions of fusion. In this paper, we follow the classification by [Reference Tsai38, sec. 1] and [Reference Tsai37, sec. 1]. Note that, we take the whole-part relation R, the converse of the part-whole relation P often used in the mereological theories, as the primitive relation, to have a more natural reading of the
![]() $\Box $
modality. Table 1 is a summary of the first-order theories of mereology (based on R instead of P) that will be studied in this article.Footnote
7
$\Box $
modality. Table 1 is a summary of the first-order theories of mereology (based on R instead of P) that will be studied in this article.Footnote
7
Table 1 First-order theories of mereology

The main contributions of the paper are:
-
• Modal correspondences of the mereological properties Anti-symmetry, Supplementation, Strong Supplementation, Finite Product, and Atomlessness.
-
• Relative modal correspondencesFootnote 8 of the mereological properties Atomicity, Finite Sum, and (the second-order version of) Fusion.
-
• Based on the above correspondences, we modally define all the usual mereological theories according to the classification by Tsai [Reference Tsai37, Reference Tsai38].
-
• We also show that all the aforementioned mereological properties are not definable in the modal logic with
 $\Box $
only. In particular, Atomicity cannot even be (absolutely) defined by the language with both
$\Box $
only. In particular, Atomicity cannot even be (absolutely) defined by the language with both
 $\Box $
and
$\Box $
and
 .
. -
• Incompleteness of the corresponding modal system MGM over frames of the ground mereology and the completeness proof of its extension MGM
 $^{+}$
, where we correct an error in the literature.
$^{+}$
, where we correct an error in the literature.
Related work
Modality and mereology can interact in various ways. As a sub-field of metaphysics, in the philosophical study of mereology, the so-called (weak) modal mereology refers to the view that a possible whole exists in virtue of its parts and the internal relations among its parts, but an actual whole does not [Reference Walsh48]. One can also ask where mereological fusions have their parts necessarily [Reference Uzquiano and Kleinschmidt41]. The formal discussions in this line often involve a language extending the first-order language of mereology with modalities for necessity or tense (e.g., [Reference Simons29, Reference Uzquiano and Kleinschmidt41]). In contrast with such work, the point of our work is to capture the standard first-order mereological theories by using a modal language.
Instead of reasoning about mereological objects, there is a line of research on the modal reasoning about space or spatial regions reflecting some mereological features. Originating from [Reference Tarski33, Reference Tang32], modal logics have been very successful in spatial reasoning (cf., e.g., [Reference van Benthem, Bezhanishvili, Aiello, Pratt-Hartmann and van Benthem46] and the references therein). Compared with the necessity-/tense-readings of modalities in the above philosophical discussions, modal operators in this line of research are often interpreted as spatial concepts, such as the topological interior.
Combining the ideas of topology, geometry and mereology, the research fields of mereotopology and mereogeometry study extensions of the basic ground mereology with various relations of geometrical and topological nature, where modalities also play a role. For instance, to reason about spatial regions, both Lutz & Wolter [Reference Lutz and Wolter21] and Nenov & Vakarelov [Reference Nenov and Vakarelov23] developed modal logics with the corresponding modalities to the eight well-known RCC8 (or Egenhofer-Franzosa) relations about how regions are connected, and study in-depth their meta-properties involving expressiveness and computational complexity. Also, Torrini et al. [Reference Torrini, Stell and Bennett36] proposed a powerful framework extending intuitionistic propositional logics with propositional quantification and a strong modality denoting global truth, which can express a number of mereotopological relations.
In contrast to the above work, where many new modalities capturing various mereotopological relations are used, we stick to the theories of mereology themselves that have the part-whole relation as the only primitive relation, and resort to a simple modal language to describe its properties.
Technically, the closest work to ours in the literature is [Reference Holliday15], where the class of Medvedev frames
Footnote
9
is defined by a formula of the modal language extended with a converse modalityFootnote
10
and any one of the following: nominals in hybrid logic, a difference modality
![]() $[\not =]$
, or a complement modality
$[\not =]$
, or a complement modality
![]() $\boxminus $
. The interpretation of
$\boxminus $
. The interpretation of
![]() $\Box \varphi $
in [Reference Holliday15] is similar to ours: all the non-empty subsets of the current set are
$\Box \varphi $
in [Reference Holliday15] is similar to ours: all the non-empty subsets of the current set are
![]() $\varphi $
. The complement modality
$\varphi $
. The complement modality
![]() $\boxminus $
is inter-definable with the window modality, i.e.,
$\boxminus $
is inter-definable with the window modality, i.e.,
![]() is valid. According to [Reference Holliday15], a Medvedev frame can be characterized as a finite poset with some properties about separativity, reversed convergence, and union. In Section 3.8, we will show that our language can also define all these properties except the finiteness. In [Reference Holliday15], the finiteness is captured by the Grzegorczyk axiom for
is valid. According to [Reference Holliday15], a Medvedev frame can be characterized as a finite poset with some properties about separativity, reversed convergence, and union. In Section 3.8, we will show that our language can also define all these properties except the finiteness. In [Reference Holliday15], the finiteness is captured by the Grzegorczyk axiom for
![]() $\Box $
and its converse variant, in presence of other axioms.
$\Box $
and its converse variant, in presence of other axioms.
As for the (in)completeness results, we follow the general strategy elaborated in the in-depth study by Goranko [Reference Goranko and Petkov8] on the modal logics with both
![]() $\Box $
and
$\Box $
and
![]() over various frame classes.
over various frame classes.
2 Language and semantics
Our language
![]() extends the standard modal language
extends the standard modal language
![]() $\mathcal {L}_{\Box }$
with the window modality
$\mathcal {L}_{\Box }$
with the window modality
![]() .
.
Definition 2.1 (Language)
Let P be a countable set of propositional atoms. Formulas of
are defined as follows:
where
![]() $p\in \mathbf {P}$
. The abbreviations
$p\in \mathbf {P}$
. The abbreviations
![]() $\top $
,
$\top $
,
![]() $\bot $
,
$\bot $
,
![]() $\lor $
,
$\lor $
,
![]() $\to $
and
$\to $
and
![]() $\leftrightarrow $
are defined as usual. Also, we define
$\leftrightarrow $
are defined as usual. Also, we define
and
. In particular, modalities
![]() $\Diamond $
and
$\Diamond $
and
![]() $\Diamond _{u}$
are the dual operators of
$\Diamond _{u}$
are the dual operators of
![]() $\Box $
and
$\Box $
and
![]() $\Box _{u}$
, respectively.
$\Box _{u}$
, respectively.
Intuitively,
![]() $\Box \varphi $
says that all the parts of the current object are
$\Box \varphi $
says that all the parts of the current object are
![]() $\varphi $
;Footnote
11
$\varphi $
;Footnote
11
![]() means that all the objects that are
means that all the objects that are
![]() $\varphi $
are parts of the current object;
$\varphi $
are parts of the current object;
![]() $\Box _{u}\varphi $
reads all objects are
$\Box _{u}\varphi $
reads all objects are
![]() $\varphi $
;
$\varphi $
;
![]() $\blacksquare \varphi $
states that the parts of the current object are exactly the objects that are
$\blacksquare \varphi $
states that the parts of the current object are exactly the objects that are
![]() $\varphi $
, i.e., an object is part of the current object iff it is
$\varphi $
, i.e., an object is part of the current object iff it is
![]() $\varphi $
;
$\varphi $
;
![]() $\Diamond \varphi $
says that at least one part of the current object is
$\Diamond \varphi $
says that at least one part of the current object is
![]() $\varphi $
; and
$\varphi $
; and
![]() $\Diamond _{u}\varphi $
means at least one object is
$\Diamond _{u}\varphi $
means at least one object is
![]() $\varphi $
.
$\varphi $
.
Formulas of
![]() are evaluated in standard relational models
are evaluated in standard relational models
![]() $\mathcal {M}=\langle W,R,V \rangle $
, where W is a non-empty set of objects,
$\mathcal {M}=\langle W,R,V \rangle $
, where W is a non-empty set of objects,
![]() $R\subseteq W\times W$
is a binary relation, and
$R\subseteq W\times W$
is a binary relation, and
![]() $V:\mathbf {P}\to 2^{W}$
is a valuation function. Intuitively, the relation R is intended to be the whole-part relation, i.e.,
$V:\mathbf {P}\to 2^{W}$
is a valuation function. Intuitively, the relation R is intended to be the whole-part relation, i.e.,
![]() $Rxy$
means that y is part of x. As for the valuation function,
$Rxy$
means that y is part of x. As for the valuation function,
![]() $w\in V(p)$
means that the object w has the property p. For any
$w\in V(p)$
means that the object w has the property p. For any
![]() $w\in W$
,
$w\in W$
,
![]() $\langle \mathcal {M},w \rangle $
is called a pointed model. For brevity, we usually write
$\langle \mathcal {M},w \rangle $
is called a pointed model. For brevity, we usually write
![]() $\mathcal {M},w$
instead of
$\mathcal {M},w$
instead of
![]() $\langle \mathcal {M},w \rangle $
. A frame
$\langle \mathcal {M},w \rangle $
. A frame
![]() $\mathcal {F}=\langle W, R \rangle $
is a model without the valuation function. Thus a model can be written as
$\mathcal {F}=\langle W, R \rangle $
is a model without the valuation function. Thus a model can be written as
![]() $\langle \mathcal {F}, V \rangle $
where
$\langle \mathcal {F}, V \rangle $
where
![]() $\mathcal {F}$
is a frame.
$\mathcal {F}$
is a frame.
Remark 2.2. Note that to have an intuitive reading for
![]() $\Box \varphi $
, we take R as the converse of the usual part-whole relation P in the standard mereological theories.
$\Box \varphi $
, we take R as the converse of the usual part-whole relation P in the standard mereological theories.
Definition 2.3 (Semantics.)
Given a pointed model
![]() $\langle \mathcal {M},w \rangle $
and a formula
$\langle \mathcal {M},w \rangle $
and a formula
![]() $\varphi $
of
$\varphi $
of
![]() , we say that
, we say that
![]() $\varphi $
is true in
$\varphi $
is true in
![]() $\mathcal {M}$
at w, written as
$\mathcal {M}$
at w, written as
![]() , when
, when

Based on the above semantics we have the following derived semantics for
![]() $\Box _{u}$
(the universal modality) and
$\Box _{u}$
(the universal modality) and
![]() $\blacksquare $
in accordance with their intuitive readings:
$\blacksquare $
in accordance with their intuitive readings:

Notions of satisfiability, validity and logical consequence are defined as usual. In particular, for any formula
![]() $\varphi $
of
$\varphi $
of
![]() , we write
, we write
![]() , i.e.,
, i.e.,
![]() $\varphi $
is valid on frame
$\varphi $
is valid on frame
![]() $\mathcal {F}$
, if
$\mathcal {F}$
, if
![]() for all
for all
![]() $w\in W$
and all the valuations V on W.
$w\in W$
and all the valuations V on W.
We now introduce some useful notions. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be a frame and
$\mathcal {F}=\langle W,R \rangle $
be a frame and
![]() $w\in W$
, and
$w\in W$
, and
![]() $R(w):=\{v\in W\mid Rwv\}$
is the set of successors of w. Moreover, for all
$R(w):=\{v\in W\mid Rwv\}$
is the set of successors of w. Moreover, for all
![]() ,
,
![]() iff
iff
![]() for all formulas
for all formulas
![]() $\varphi \in \Phi $
. In addition, we say that
$\varphi \in \Phi $
. In addition, we say that
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $\Phi $
-frame if
$\Phi $
-frame if
![]() . For any two classes
. For any two classes
![]() $\mathcal {A},\mathcal {B}$
of frames and formula
$\mathcal {A},\mathcal {B}$
of frames and formula
![]() ,
,
![]() $\varphi ($
absolutely) defines
$\varphi ($
absolutely) defines
![]() $\mathcal {A}$
iff for each frame
$\mathcal {A}$
iff for each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\mathcal {F}\in \mathcal {A}$
iff
$\mathcal {F}\in \mathcal {A}$
iff
![]() $\varphi $
is valid on
$\varphi $
is valid on
![]() $\mathcal {F}$
;
$\mathcal {F}$
;
![]() $\varphi $
defines
$\varphi $
defines
![]() $\mathcal {A}$
relative to
$\mathcal {A}$
relative to
![]() $\mathcal {B}$
iff for any frame
$\mathcal {B}$
iff for any frame
![]() $\mathcal {F}\in \mathcal {B}$
,
$\mathcal {F}\in \mathcal {B}$
,
![]() $\mathcal {F}\in \mathcal {A}$
iff
$\mathcal {F}\in \mathcal {A}$
iff
![]() $\varphi $
is valid on
$\varphi $
is valid on
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
3 Correspondences
In this section, we define the standard theories of mereology listed in Table 1 with
![]() . Recall that
. Recall that
![]() $Rxy$
means
$Rxy$
means
![]() $Pyx$
in the standard mereology, i.e., y is part of x.
$Pyx$
in the standard mereology, i.e., y is part of x.
3.1 Correspondences of ground mereology
Ground mereology (GM) is the ground of all standard first-order theories of mereology. It consists of the following three first-order principles:

Namely, the relation R is a partial order: it is reflexive, transitive and anti-symmetric. The modal correspondences of these properties are familiar to us: Reflexivity and Transitivity correspond to
![]() $\Box p\to p$
(T) and
$\Box p\to p$
(T) and
![]() $\Box p\to \Box \Box p$
(4), respectively, but it is well-known that Anti-symmetry cannot be defined by
$\Box p\to \Box \Box p$
(4), respectively, but it is well-known that Anti-symmetry cannot be defined by
![]() $\Box $
(cf., e.g., [Reference Blackburn, de Rijke and Venema1, sec. 3.3]). With
$\Box $
(cf., e.g., [Reference Blackburn, de Rijke and Venema1, sec. 3.3]). With
![]() , we can also define Anti-symmetry by
, we can also define Anti-symmetry by
![]() as noted by Goranko [Reference Goranko9, p. 97]. However, to ease the completeness proof in Section 4.2, we will use another apparently stronger formula
as noted by Goranko [Reference Goranko9, p. 97]. However, to ease the completeness proof in Section 4.2, we will use another apparently stronger formula
![]() to define this property.Footnote
12
to define this property.Footnote
12
In what follows, we denote by
![]() the satisfaction relation for first-order logic, i.e., taking a frame
the satisfaction relation for first-order logic, i.e., taking a frame
![]() $\langle W, R \rangle $
as a first-order structure where W is the domain and R is the interpretation for the corresponding binary predicate (cf., e.g., [Reference Blackburn, de Rijke and Venema1, sec. 3]).
$\langle W, R \rangle $
as a first-order structure where W is the domain and R is the interpretation for the corresponding binary predicate (cf., e.g., [Reference Blackburn, de Rijke and Venema1, sec. 3]).
Theorem 3.4. For each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() if and only if
if and only if
![]() .
.
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be a frame. For the direction from left to right, suppose that
$\mathcal {F}=\langle W,R \rangle $
be a frame. For the direction from left to right, suppose that
![]() . Then there are
. Then there are
![]() $w,w^{\prime }\in W$
and a valuation V such that
$w,w^{\prime }\in W$
and a valuation V such that
![]() ,
,
![]() and
and
![]() $Rww^{\prime }$
. By the semantics, it holds that
$Rww^{\prime }$
. By the semantics, it holds that
![]() $Rw^{\prime }w$
. Now we have
$Rw^{\prime }w$
. Now we have
![]() $Rww^{\prime }$
and
$Rww^{\prime }$
and
![]() $Rw^{\prime }w$
. However, by
$Rw^{\prime }w$
. However, by
![]() $w\not \in V(q)$
and
$w\not \in V(q)$
and
![]() $w^{\prime }\in V(q)$
, it follows that
$w^{\prime }\in V(q)$
, it follows that
![]() $w\not =w^{\prime }$
. Therefore,
$w\not =w^{\prime }$
. Therefore,
![]() .
.
For the converse direction, assume that
![]() . Then there are
. Then there are
![]() $w,w^{\prime }\in W$
such that
$w,w^{\prime }\in W$
such that
![]() $w\not =w^{\prime }$
,
$w\not =w^{\prime }$
,
![]() $Rww^{\prime }$
and
$Rww^{\prime }$
and
![]() $Rw^{\prime }w$
. Define a valuation V such that
$Rw^{\prime }w$
. Define a valuation V such that
![]() $V(p)=\{w\}$
and
$V(p)=\{w\}$
and
![]() $V(q)=\{w^{\prime }\}$
. Consequently, we obtain
$V(q)=\{w^{\prime }\}$
. Consequently, we obtain
![]() and
and
![]() . Thus,
. Thus,
![]() . The proof is completed.
. The proof is completed.
On top of GM, there are further plausible mereological properties, which are the subjects of other subsections. As mentioned earlier, the original goal of mereology was to replace set theory, and many of the properties in mereology have similar functions to those in set theory: say, in what follows you may find that mereological theories include operations on objects which look similar to the set-theoretic ‘complementation’, ‘union’, ‘intersection’, and so on. However, this by no means indicates mereological concepts can be viewed precisely as set-theoretic ones. Technically, the mereological properties are closer to the properties studied in the theory of partial orders.Footnote 13
3.2 Correspondences of minimal mereology
Minimal mereology (MM) is the minimal standard theory of mereology. It extends GM with the following axiom:
where
![]() $PPxy:= Ryx\land \neg Rxy$
means x is a proper part of y, and
$PPxy:= Ryx\land \neg Rxy$
means x is a proper part of y, and
![]() $Oxy:=\exists z(Rxz\land Ryz)$
states x overlaps y, i.e., they have common parts.
$Oxy:=\exists z(Rxz\land Ryz)$
states x overlaps y, i.e., they have common parts.
Supplementation states that if x is a proper part of y, then y has a part that is disjoint from x. Supplementation is essentially the formula
![]() $\forall x\forall y(Ryx\land \neg Rxy\to \exists z (Ryz\land \neg \exists w(Rxw\land Rzw)))$
. The following result shows that it corresponds to the
$\forall x\forall y(Ryx\land \neg Rxy\to \exists z (Ryz\land \neg \exists w(Rxw\land Rzw)))$
. The following result shows that it corresponds to the
![]() -formula
-formula
![]() $\neg p\land \Diamond \blacksquare p\to \Diamond \Box \neg p$
, which says if the current object s does not have property p and there is a part w of s which has exactly the p-objects as the parts, then there is some part t of s such that all its parts do not have p thus t and w are disjoint.
$\neg p\land \Diamond \blacksquare p\to \Diamond \Box \neg p$
, which says if the current object s does not have property p and there is a part w of s which has exactly the p-objects as the parts, then there is some part t of s such that all its parts do not have p thus t and w are disjoint.
Theorem 3.5. For each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() if and only if
if and only if
![]() .
.
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be a frame. For the direction from left to right, suppose that
$\mathcal {F}=\langle W,R \rangle $
be a frame. For the direction from left to right, suppose that
![]() $\mathcal {F}\nvDash \neg p\land \Diamond \blacksquare p\to \Diamond \Box \neg p$
. Then there exist
$\mathcal {F}\nvDash \neg p\land \Diamond \blacksquare p\to \Diamond \Box \neg p$
. Then there exist
![]() $w\in W$
and a valuation V such that
$w\in W$
and a valuation V such that
![]() . Consequently, there exists
. Consequently, there exists
![]() $w_{1}\in R(w)$
such that
$w_{1}\in R(w)$
such that
![]() . Thus it holds that
. Thus it holds that
![]() $\neg Rw_{1}w$
. Furthermore, from
$\neg Rw_{1}w$
. Furthermore, from
![]() , we know that each
, we know that each
![]() $v\in R(w)$
overlaps
$v\in R(w)$
overlaps
![]() $w_{1}$
. Thus, we do not have
$w_{1}$
. Thus, we do not have
![]() .
.
For the direction from right to left, assume that
![]() and
and
![]() . Then there are
. Then there are
![]() $w,w_{1}\in W$
such that
$w,w_{1}\in W$
such that
![]() $Rww_{1}$
,
$Rww_{1}$
,
![]() $\neg Rw_{1}w$
, and for all
$\neg Rw_{1}w$
, and for all
![]() $o\in R(w)$
, there exists
$o\in R(w)$
, there exists
![]() $o^{\prime }\in W$
with
$o^{\prime }\in W$
with
![]() $Rw_{1}o^{\prime }\land Roo^{\prime }$
. Define a valuation V such that
$Rw_{1}o^{\prime }\land Roo^{\prime }$
. Define a valuation V such that
![]() $V(p)=R(w_{1})$
. Then we obtain
$V(p)=R(w_{1})$
. Then we obtain
![]() . By
. By
![]() , it holds that
, it holds that
![]() . Namely, there exists
. Namely, there exists
![]() $v\in R(w)$
such that
$v\in R(w)$
such that
![]() , so v is disjoint from
, so v is disjoint from
![]() $w_{1}$
. This completes the proof.
$w_{1}$
. This completes the proof.
Remark 3.6. If one prefers to define the proper parthood
![]() $PPxy$
as
$PPxy$
as
![]() $Ryx\land x\not \equiv y$
(see, e.g., [Reference Varzi and Zalta47]), Supplementation then becomes
$Ryx\land x\not \equiv y$
(see, e.g., [Reference Varzi and Zalta47]), Supplementation then becomes
![]() $\forall x\forall y(Ryx\land x\not \equiv y\to \exists z(Ryz\land \neg Ozx))$
. These two versions are not equivalent if we do not assume Anti-symmetry (the reader may find it interesting to see which one is stronger). For the alternative formulation, the reader can check that it corresponds to the modal principle
$\forall x\forall y(Ryx\land x\not \equiv y\to \exists z(Ryz\land \neg Ozx))$
. These two versions are not equivalent if we do not assume Anti-symmetry (the reader may find it interesting to see which one is stronger). For the alternative formulation, the reader can check that it corresponds to the modal principle
![]() $\neg p\land \Diamond (p\land \blacksquare q)\to \Diamond \Box \neg q$
.Footnote
14
$\neg p\land \Diamond (p\land \blacksquare q)\to \Diamond \Box \neg q$
.Footnote
14
In the result above, the modality
![]() is used to define Supplementation. But, is this first-order property also definable with the standard modal language? The following result is a negative answer.
is used to define Supplementation. But, is this first-order property also definable with the standard modal language? The following result is a negative answer.
Proposition 3.7. Supplementation cannot be defined by
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.
Proof. Consider two frames
![]() $\mathcal {F}_{1}=\langle W_{1},R_{1} \rangle $
and
$\mathcal {F}_{1}=\langle W_{1},R_{1} \rangle $
and
![]() $\mathcal {F}_{2}=\langle W_{2},R_{2} \rangle $
depicted in Figure 1. Define a function
$\mathcal {F}_{2}=\langle W_{2},R_{2} \rangle $
depicted in Figure 1. Define a function
![]() $f:W_{1}\to W_{2}$
such that
$f:W_{1}\to W_{2}$
such that
![]() $f(w_{1})=v_{1}$
and
$f(w_{1})=v_{1}$
and
![]() $f(w_{2})=f(w_{3})=v_{2}$
. Then, for any
$f(w_{2})=f(w_{3})=v_{2}$
. Then, for any
![]() $s,t\in W_{1}$
and
$s,t\in W_{1}$
and
![]() $v\in W_{2}$
, if
$v\in W_{2}$
, if
![]() $R_{1}st$
, then
$R_{1}st$
, then
![]() $R_{2}f(s)f(t)$
; if
$R_{2}f(s)f(t)$
; if
![]() $R_{2}f(s)v$
, then there exists
$R_{2}f(s)v$
, then there exists
![]() $u\in W_{1}$
such that
$u\in W_{1}$
such that
![]() $f(u)=v$
and
$f(u)=v$
and
![]() $R_{1}sv$
. Hence, f is a bounded morphism from
$R_{1}sv$
. Hence, f is a bounded morphism from
![]() $\mathcal {F}_{1}$
to
$\mathcal {F}_{1}$
to
![]() $\mathcal {F}_{2}$
(cf. [Reference Blackburn, de Rijke and Venema1, sec. 3.3]). So, for any
$\mathcal {F}_{2}$
(cf. [Reference Blackburn, de Rijke and Venema1, sec. 3.3]). So, for any
![]() $\varphi \in \mathcal {L}_{\Box }$
, if
$\varphi \in \mathcal {L}_{\Box }$
, if
![]() then
then
![]() . If Supplementation can be defined by some formula
. If Supplementation can be defined by some formula
![]() $\varphi ^{\prime }$
of
$\varphi ^{\prime }$
of
![]() $\mathcal {L}_{\Box }$
, then for each frame
$\mathcal {L}_{\Box }$
, then for each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() iff
iff
![]() . However, since
. However, since
![]() and
and
![]() , we know
, we know
![]() and
and
![]() $\mathcal {F}_{2}\nvDash \varphi ^{\prime }$
. By the Goldblatt-Thomason Theorem, Supplementation cannot be defined by
$\mathcal {F}_{2}\nvDash \varphi ^{\prime }$
. By the Goldblatt-Thomason Theorem, Supplementation cannot be defined by
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.

Fig. 1 A bounded morphism (for Supplementation).
3.3 Correspondences of extensional mereology
Extensional mereology (EM) is stronger than MM, which results from replacing Supplementation in MM with Strong Supplementation.
Strong Supplementation states that if object x is not a part of y, then x has a part disjoint from y. This principle is stronger than Supplementation, and it can be easily checked that Strong Supplementation entails Supplementation. Furthermore, formula
![]() $\forall x\forall y(\exists zPPzx\lor \exists zPPzy)\to (x\equiv y\leftrightarrow \forall z(PPzx\leftrightarrow PPzy)))$
is provable in EM, which intuitively states that no composite objects (i.e., objects including proper parts) with the same proper parts can be distinguished (see [Reference Varzi and Zalta47]). By the definition of O, it is not hard to see that Strong Supplementation is essentially the formula
$\forall x\forall y(\exists zPPzx\lor \exists zPPzy)\to (x\equiv y\leftrightarrow \forall z(PPzx\leftrightarrow PPzy)))$
is provable in EM, which intuitively states that no composite objects (i.e., objects including proper parts) with the same proper parts can be distinguished (see [Reference Varzi and Zalta47]). By the definition of O, it is not hard to see that Strong Supplementation is essentially the formula
![]() $\forall x\forall y(\neg Ryx\to \exists z(Rxz\land \neg \exists v(Rzv\land Ryv))$
.
$\forall x\forall y(\neg Ryx\to \exists z(Rxz\land \neg \exists v(Rzv\land Ryv))$
.
Theorem 3.8. For each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() if and only if
if and only if
![]() .
.
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be a frame. From left to right, suppose that
$\mathcal {F}=\langle W,R \rangle $
be a frame. From left to right, suppose that
![]() $\mathcal {F}\nvDash \blacksquare p\to \Box _{u}(\neg p\to \Diamond \Box \neg p)$
. Then there exist
$\mathcal {F}\nvDash \blacksquare p\to \Box _{u}(\neg p\to \Diamond \Box \neg p)$
. Then there exist
![]() $w\in W$
and a valuation V such that
$w\in W$
and a valuation V such that
![]() and
and
![]() $\langle \mathcal {F},V \rangle ,w\nvDash \Box _{u}(\neg p\to \Diamond \Box \neg p)$
. Thus, there exists
$\langle \mathcal {F},V \rangle ,w\nvDash \Box _{u}(\neg p\to \Diamond \Box \neg p)$
. Thus, there exists
![]() $w_{1}\in W$
with
$w_{1}\in W$
with
![]() . Since
. Since
![]() , we have
, we have
![]() $\neg Rww_{1}$
. Moreover, for any
$\neg Rww_{1}$
. Moreover, for any
![]() $v_{1}\in R(w_{1})$
, there exists
$v_{1}\in R(w_{1})$
, there exists
![]() $v_{2}\in R(v_{1})$
such that
$v_{2}\in R(v_{1})$
such that
![]() $Rwv_{2}$
.
$Rwv_{2}$
.
Now, we have
![]() $\neg Rww_{1}$
, and for all
$\neg Rww_{1}$
, and for all
![]() $v_{1}\in W$
, if
$v_{1}\in W$
, if
![]() $Rw_{1}v_{1}$
, then there exists
$Rw_{1}v_{1}$
, then there exists
![]() $v_{2}\in W$
such that
$v_{2}\in W$
such that
![]() $Rv_{1}v_{2}$
and
$Rv_{1}v_{2}$
and
![]() $Rwv_{2}$
. Consequently,
$Rwv_{2}$
. Consequently,
![]() .
.
For the converse direction, assume that
![]() . Therefore, there are
. Therefore, there are
![]() $w,w_{1}\in W$
with
$w,w_{1}\in W$
with
![]() $\neg Rww_{1}\land \forall z(Rw_{1}z\to \exists v(Rzv\land Rwv)))$
.
$\neg Rww_{1}\land \forall z(Rw_{1}z\to \exists v(Rzv\land Rwv)))$
.
Define a valuation V such that
![]() $V(p)=R(w)$
; hence
$V(p)=R(w)$
; hence
![]() . By
. By
![]() $\neg Rww_{1}$
, it holds that
$\neg Rww_{1}$
, it holds that
![]() . Furthermore, for all
. Furthermore, for all
![]() $v_{1}\in R(w_{1})$
, there exists
$v_{1}\in R(w_{1})$
, there exists
![]() $v_{2}\in R(v_{1})$
such that
$v_{2}\in R(v_{1})$
such that
![]() $Rwv_{2}$
. By
$Rwv_{2}$
. By
![]() $V(p)$
, it follows that
$V(p)$
, it follows that
![]() . Consequently,
. Consequently,
![]() $\langle \mathcal {F},V \rangle ,w\nvDash \Box _{u}(\neg p\to \Diamond \Box \neg p)$
. Thus,
$\langle \mathcal {F},V \rangle ,w\nvDash \Box _{u}(\neg p\to \Diamond \Box \neg p)$
. Thus,
![]() $\langle \mathcal {F},V \rangle ,w\nvDash \blacksquare p\to \Box _{u}(\neg p\to \Diamond \Box \neg p)$
.
$\langle \mathcal {F},V \rangle ,w\nvDash \blacksquare p\to \Box _{u}(\neg p\to \Diamond \Box \neg p)$
.
In addition, by the same reasoning as in the proof of Proposition 3.7, we know that Strong Supplementation is not definable in
![]() $\mathcal {L}_{\Box }$
, either.
$\mathcal {L}_{\Box }$
, either.
Proposition 3.9. Strong Supplementation cannot be defined by
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.
3.4 Correspondences of extensional closure mereology
Extensional closure mereology (CEM) is an extension of EM, with the following two axioms which allow us to compose objects:

where
![]() $Uxy:=\exists z(Rzx\land Rzy)$
means x underlaps y, i.e., there exists an object including both x and y as parts.
$Uxy:=\exists z(Rzx\land Rzy)$
means x underlaps y, i.e., there exists an object including both x and y as parts.
Before introducing the correspondence results, let us briefly comment on this theory. By Finite Product, if x overlaps y, then there exists an object whose parts are exactly the common parts of x and y. On the other hand, Finite Sum shows that if x underlaps y, then there exists an object such that the objects overlapping it are exactly those overlapping x or y. Since CEM is an extension of EM, it is extensional, too. Thus the sum and product of two objects are unique.Footnote 15
Unravelling the abbreviations, Finite Product is
![]() $\forall x\forall y(\exists z(Rxz\land Ryz)\to \exists z\forall w(Rzw\leftrightarrow (Rxw\land Ryw)))$
. We can define it by the intuitive formula
$\forall x\forall y(\exists z(Rxz\land Ryz)\to \exists z\forall w(Rzw\leftrightarrow (Rxw\land Ryw)))$
. We can define it by the intuitive formula
![]() $\blacksquare p\land \Diamond _{u} \blacksquare q\land \Diamond (p\land q)\to \Diamond _{u}\blacksquare (p\land q)$
, which says if the current object has exactly the p-objects as parts and there is one object with exactly the q-objects as parts and they indeed overlap then there is one object with exactly those objects in both as parts.
$\blacksquare p\land \Diamond _{u} \blacksquare q\land \Diamond (p\land q)\to \Diamond _{u}\blacksquare (p\land q)$
, which says if the current object has exactly the p-objects as parts and there is one object with exactly the q-objects as parts and they indeed overlap then there is one object with exactly those objects in both as parts.
Theorem 3.10. For each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() iff
iff
![]() .
.
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be a frame. From left to right, suppose that
$\mathcal {F}=\langle W,R \rangle $
be a frame. From left to right, suppose that
![]() and
and
![]() $\mathcal {F}\nvDash \blacksquare p\land \Diamond _{u} \blacksquare q\land \Diamond (p\land q)\to \Diamond _{u}\blacksquare (p\land q)$
. Then there exist
$\mathcal {F}\nvDash \blacksquare p\land \Diamond _{u} \blacksquare q\land \Diamond (p\land q)\to \Diamond _{u}\blacksquare (p\land q)$
. Then there exist
![]() $w\in W$
and a valuation V such that
$w\in W$
and a valuation V such that
![]() . Therefore, there exists
. Therefore, there exists
![]() $v\in W$
with
$v\in W$
with
![]() . Additionally, for any
. Additionally, for any
![]() $o\in W$
, it holds that
$o\in W$
, it holds that
![]() $\langle \mathcal {F},V \rangle ,o\nvDash \blacksquare (p\land q)$
, i.e.,
$\langle \mathcal {F},V \rangle ,o\nvDash \blacksquare (p\land q)$
, i.e.,
![]() .
.
From
![]() , we know that w overlaps v. By
, we know that w overlaps v. By
![]() , there exists
, there exists
![]() $s\in W$
such that for any
$s\in W$
such that for any
![]() $t\in W$
,
$t\in W$
,
![]() $Rst\leftrightarrow (Rwt\land Rvt)$
. Now let us consider the two cases of s. First, when
$Rst\leftrightarrow (Rwt\land Rvt)$
. Now let us consider the two cases of s. First, when
![]() , there exists
, there exists
![]() $s^{\prime }\in R(s)$
such that
$s^{\prime }\in R(s)$
such that
![]() . We now conclude that
. We now conclude that
![]() $\neg Rws^{\prime }\lor \neg Rvs^{\prime }$
, which entails a contradiction. Next, if
$\neg Rws^{\prime }\lor \neg Rvs^{\prime }$
, which entails a contradiction. Next, if
![]() , then there exists
, then there exists
![]() $s^{\prime }\in W$
such that
$s^{\prime }\in W$
such that
![]() and
and
![]() $\neg Rss^{\prime }$
. However, by
$\neg Rss^{\prime }$
. However, by
![]() , we obtain
, we obtain
![]() $Rws^{\prime }\land Rvs^{\prime }$
which also contradicts
$Rws^{\prime }\land Rvs^{\prime }$
which also contradicts
![]() .
.
For the converse direction, assume for reductio that
![]() and
and
![]() . Then there are
. Then there are
![]() $w_{1},w_{2},w_{3}\in W$
with
$w_{1},w_{2},w_{3}\in W$
with
![]() $Rw_{1}w_{3}$
and
$Rw_{1}w_{3}$
and
![]() $Rw_{2}w_{3}$
, and for each
$Rw_{2}w_{3}$
, and for each
![]() $u\in W$
there exists
$u\in W$
there exists
![]() $t\in W$
such that
$t\in W$
such that
![]() $\neg (Rut\leftrightarrow (Rw_{1}t\land Rw_{2}t))$
.
$\neg (Rut\leftrightarrow (Rw_{1}t\land Rw_{2}t))$
.
Define a valuation V such that
![]() $V(p)=R(w_{1})$
and
$V(p)=R(w_{1})$
and
![]() $V(q)=R(w_{2})$
, thus
$V(q)=R(w_{2})$
, thus
![]() . By
. By
![]() $Rw_{1}w_{3}$
and
$Rw_{1}w_{3}$
and
![]() $Rw_{2}w_{3}$
, it holds that
$Rw_{2}w_{3}$
, it holds that
![]() . By assumption, there exists
. By assumption, there exists
![]() $w\in W$
such that
$w\in W$
such that
![]() . Moreover, there exists
. Moreover, there exists
![]() $w^{\prime }\in W$
such that
$w^{\prime }\in W$
such that
![]() $\neg (Rww^{\prime }\leftrightarrow (Rw_{1}w^{\prime }\land Rw_{2}w^{\prime }))$
.
$\neg (Rww^{\prime }\leftrightarrow (Rw_{1}w^{\prime }\land Rw_{2}w^{\prime }))$
.
When
![]() $\neg Rww^{\prime }\land Rw_{1}w^{\prime }\land Rw_{2}w^{\prime }$
, it holds that
$\neg Rww^{\prime }\land Rw_{1}w^{\prime }\land Rw_{2}w^{\prime }$
, it holds that
![]() . Also, we can obtain
. Also, we can obtain
![]() $\langle \mathcal {F},V \rangle ,w\nvDash \Box (p\land q)$
if
$\langle \mathcal {F},V \rangle ,w\nvDash \Box (p\land q)$
if
![]() $Rww^{\prime }\land \neg (Rw_{1}w^{\prime }\land Rw_{2}w^{\prime })$
. Each of them implies a contradiction. Now the proof is completed.
$Rww^{\prime }\land \neg (Rw_{1}w^{\prime }\land Rw_{2}w^{\prime })$
. Each of them implies a contradiction. Now the proof is completed.
Furthermore, this property cannot be defined by the standard modal language:
Proposition 3.11. Finite Product cannot be defined by
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.
Proof. Consider the two frames
![]() $\mathcal {F}=\langle W,R \rangle $
and
$\mathcal {F}=\langle W,R \rangle $
and
![]() $\mathcal {F}^{\prime }=\langle W^{\prime },R^{\prime } \rangle $
depicted in Figure 2. Observe that
$\mathcal {F}^{\prime }=\langle W^{\prime },R^{\prime } \rangle $
depicted in Figure 2. Observe that
![]() $\mathcal {F}^{\prime }=\langle W^{\prime },R^{\prime } \rangle $
is a subframe of
$\mathcal {F}^{\prime }=\langle W^{\prime },R^{\prime } \rangle $
is a subframe of
![]() $\mathcal {F}$
. Moreover, for any
$\mathcal {F}$
. Moreover, for any
![]() $s\in W^{\prime }$
, if
$s\in W^{\prime }$
, if
![]() $Rst$
, then
$Rst$
, then
![]() $t\in W^{\prime }$
. Therefore,
$t\in W^{\prime }$
. Therefore,
![]() $\mathcal {F}^{\prime }$
is a generated subframe of
$\mathcal {F}^{\prime }$
is a generated subframe of
![]() $\mathcal {F}$
. By the well-known Goldblatt–Thomason Theorem, for any
$\mathcal {F}$
. By the well-known Goldblatt–Thomason Theorem, for any
![]() $\varphi \in \mathcal {L}_{\Box }$
,
$\varphi \in \mathcal {L}_{\Box }$
,
![]() follows from
follows from
![]() (see, e.g., [Reference Blackburn, de Rijke and Venema1, sec. 3.3]). However, we have
(see, e.g., [Reference Blackburn, de Rijke and Venema1, sec. 3.3]). However, we have
![]() and
and
![]() . Specifically, in frame
. Specifically, in frame
![]() $\mathcal {F}^{\prime }$
,
$\mathcal {F}^{\prime }$
,
![]() $w_{2}$
and
$w_{2}$
and
![]() $w_{3}$
overlap, but they have no product. Hence the property cannot be defined by
$w_{3}$
overlap, but they have no product. Hence the property cannot be defined by
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.

Fig. 2 A generated subframe (for Finite Product).
Compared with Finite Product, Finite Sum is much more complicated. If Finite Product can be viewed as an analog of intersection in set theory then Finite Sum is an analog of union. Based on this intuition, it seems natural to define it as: if x underlaps y, then there exists an object z whose parts are exactly the parts of x or y, i.e.,
![]() $\forall x\forall y(Uxy\to \exists z\forall w(Rzw\leftrightarrow (Rxw\lor Ryw)))$
. This property can be intuitively captured by
$\forall x\forall y(Uxy\to \exists z\forall w(Rzw\leftrightarrow (Rxw\lor Ryw)))$
. This property can be intuitively captured by
![]() $\Diamond \blacksquare p\land \Diamond \blacksquare q\to \Diamond _{u}\blacksquare (p\lor q)$
.
$\Diamond \blacksquare p\land \Diamond \blacksquare q\to \Diamond _{u}\blacksquare (p\lor q)$
.
Proposition 3.12. For each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() iff
iff
![]() .
.
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be a frame. From left to right, suppose that
$\mathcal {F}=\langle W,R \rangle $
be a frame. From left to right, suppose that
![]() . Then there are
. Then there are
![]() $w_{1},w_{2},w_{3}\in W$
such that
$w_{1},w_{2},w_{3}\in W$
such that
![]() $Rw_{3}w_{1}$
,
$Rw_{3}w_{1}$
,
![]() $Rw_{3}w_{2}$
, and for each
$Rw_{3}w_{2}$
, and for each
![]() $o\in W$
, there is a
$o\in W$
, there is a
![]() $w\in W$
with
$w\in W$
with
![]() $\neg (Row\leftrightarrow (Rw_{1}w\lor Rw_{2}w))$
.
$\neg (Row\leftrightarrow (Rw_{1}w\lor Rw_{2}w))$
.
Define a valuation V such that
![]() $V(p)=R(w_{1})$
and
$V(p)=R(w_{1})$
and
![]() $V(q)=R(w_{2})$
. Now it holds that
$V(q)=R(w_{2})$
. Now it holds that
![]() ,
,
![]() and
and
![]() . Furthermore, for all
. Furthermore, for all
![]() $o\in W$
, if there exists
$o\in W$
, if there exists
![]() $w\in W$
such that
$w\in W$
such that
![]() $Row$
and
$Row$
and
![]() $\neg Rw_{1}w\land \neg Rw_{2}w$
, then
$\neg Rw_{1}w\land \neg Rw_{2}w$
, then
![]() , and if there exists
, and if there exists
![]() $w\in W$
with
$w\in W$
with
![]() $\neg Row$
and
$\neg Row$
and
![]() $Rw_{1}w\lor Rw_{2}w$
, then
$Rw_{1}w\lor Rw_{2}w$
, then
![]() . Each of them shows that for all
. Each of them shows that for all
![]() $o\in W$
,
$o\in W$
,
![]() . Thus we conclude that
. Thus we conclude that
![]() .
.
For the converse direction, assume that
![]() . Then there exist
. Then there exist
![]() $w,w_{1},w_{2}\in W$
and a valuation V such that
$w,w_{1},w_{2}\in W$
and a valuation V such that
![]() $Rww_{1}$
,
$Rww_{1}$
,
![]() $Rww_{2}$
,
$Rww_{2}$
,
![]() $V(p)=R(w_{1})$
and
$V(p)=R(w_{1})$
and
![]() $V(q)=R(w_{2})$
. For all
$V(q)=R(w_{2})$
. For all
![]() $o\in W$
, it holds that
$o\in W$
, it holds that
![]() .
.
If
![]() , then there exists
, then there exists
![]() $o^{\prime }\in W$
such that
$o^{\prime }\in W$
such that
![]() $Roo^{\prime }$
,
$Roo^{\prime }$
,
![]() $\neg Rw_{1}o^{\prime }$
and
$\neg Rw_{1}o^{\prime }$
and
![]() $\neg Rw_{2}o^{\prime }$
. Thus,
$\neg Rw_{2}o^{\prime }$
. Thus,
![]() $\neg (Roo^{\prime }\to (Rw_{1}o^{\prime }\lor Rw_{2}o^{\prime }))$
. If
$\neg (Roo^{\prime }\to (Rw_{1}o^{\prime }\lor Rw_{2}o^{\prime }))$
. If
![]() , then there exists
, then there exists
![]() $o^{\prime }\in W$
with
$o^{\prime }\in W$
with
![]() $\neg Roo^{\prime }$
and
$\neg Roo^{\prime }$
and
![]() $(Rw_{1}o^{\prime }\lor Rw_{2}o^{\prime })$
; consequently,
$(Rw_{1}o^{\prime }\lor Rw_{2}o^{\prime })$
; consequently,
![]() $\neg ((Rw_{1}o^{\prime }\lor Rw_{2}o^{\prime })\to Roo^{\prime })$
. So we have
$\neg ((Rw_{1}o^{\prime }\lor Rw_{2}o^{\prime })\to Roo^{\prime })$
. So we have
![]() $\forall o\exists o^{\prime }\neg (Roo^{\prime }\leftrightarrow (Rw_{1}o^{\prime }\lor Rw_{2}o^{\prime }))$
. This completes the proof.
$\forall o\exists o^{\prime }\neg (Roo^{\prime }\leftrightarrow (Rw_{1}o^{\prime }\lor Rw_{2}o^{\prime }))$
. This completes the proof.
Unfortunately, property
![]() $\forall x\forall y(Uxy\to \exists z\forall w (Rzw\leftrightarrow (Rxw\lor Ryw)))$
is not an ideal alternative to Finite Sum. By this formula, when x underlaps y, there exists z such that
$\forall x\forall y(Uxy\to \exists z\forall w (Rzw\leftrightarrow (Rxw\lor Ryw)))$
is not an ideal alternative to Finite Sum. By this formula, when x underlaps y, there exists z such that
![]() $\forall w(Rzw\leftrightarrow (Rxw\lor Ryw))$
. With Reflexivity, we have
$\forall w(Rzw\leftrightarrow (Rxw\lor Ryw))$
. With Reflexivity, we have
![]() $Rzz$
; consequently,
$Rzz$
; consequently,
![]() $(Rxz\lor Ryz)$
. However, this is not our initial intention: when z is the sum of two different objects x and y, z should not be a part of x or y. Instead, what we expect is that if z is the sum of x and y, then every part of z overlaps x or y, i.e.,
$(Rxz\lor Ryz)$
. However, this is not our initial intention: when z is the sum of two different objects x and y, z should not be a part of x or y. Instead, what we expect is that if z is the sum of x and y, then every part of z overlaps x or y, i.e.,
![]() $\forall x\forall y(Uxy\to \exists z\forall w(Owz\leftrightarrow (Owx\lor Owy)))$
.Footnote
16
Here we obtain a relative definability result based on EM-frames.
$\forall x\forall y(Uxy\to \exists z\forall w(Owz\leftrightarrow (Owx\lor Owy)))$
.Footnote
16
Here we obtain a relative definability result based on EM-frames.
Theorem 3.13. For each EM-frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() iff
iff
![]()
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be an EM-frame. For the direction from left to right, suppose that
$\mathcal {F}=\langle W,R \rangle $
be an EM-frame. For the direction from left to right, suppose that
![]() . Then there exist
. Then there exist
![]() $w\in W$
and a valuation V such that
$w\in W$
and a valuation V such that
![]() .
.
By
![]() , there are
, there are
![]() $w_{1},w_{2}\in R(w)$
such that
$w_{1},w_{2}\in R(w)$
such that
![]() and
and
![]() . By
. By
![]() , for all
, for all
![]() $o\in W$
, either
$o\in W$
, either
![]() or
or
![]() . Now given an arbitrary
. Now given an arbitrary
![]() $w^{\prime }\in W$
, we consider these two cases.
$w^{\prime }\in W$
, we consider these two cases.
If
![]() , then there exists
, then there exists
![]() $w^{\prime \prime }\in R(w^{\prime })$
such that
$w^{\prime \prime }\in R(w^{\prime })$
such that
![]() . Thus
. Thus
![]() $w^{\prime \prime }$
is disjoint from both
$w^{\prime \prime }$
is disjoint from both
![]() $w_{1}$
and
$w_{1}$
and
![]() $w_{2}$
. Furthermore, by Reflexivity,
$w_{2}$
. Furthermore, by Reflexivity,
![]() $Rw^{\prime }w^{\prime \prime }$
entails that objects
$Rw^{\prime }w^{\prime \prime }$
entails that objects
![]() $w^{\prime }$
and
$w^{\prime }$
and
![]() $w^{\prime \prime }$
overlap.
$w^{\prime \prime }$
overlap.
If
![]() , then there exists
, then there exists
![]() $w^{\prime \prime }\in V(p)\cup V(q)$
such that
$w^{\prime \prime }\in V(p)\cup V(q)$
such that
![]() $\neg Rw^{\prime }w^{\prime \prime }$
. W.l.o.g., suppose
$\neg Rw^{\prime }w^{\prime \prime }$
. W.l.o.g., suppose
![]() $w^{\prime \prime }\in V(p)$
. It follows that
$w^{\prime \prime }\in V(p)$
. It follows that
![]() $Rw_{1}w^{\prime \prime }$
since
$Rw_{1}w^{\prime \prime }$
since
![]() . By Strong Supplementation,
. By Strong Supplementation,
![]() $w^{\prime \prime }$
has a successor
$w^{\prime \prime }$
has a successor
![]() $w^{\prime \prime }_{1}$
that is disjoint from
$w^{\prime \prime }_{1}$
that is disjoint from
![]() $w^{\prime }$
. By Transitivity,
$w^{\prime }$
. By Transitivity,
![]() $Rw_{1}w^{\prime \prime }_{1}$
. Thus,
$Rw_{1}w^{\prime \prime }_{1}$
. Thus,
![]() $w^{\prime \prime }_{1}$
overlaps
$w^{\prime \prime }_{1}$
overlaps
![]() $w_{1}$
but
$w_{1}$
but
![]() $w^{\prime \prime }_{1}$
is disjoint from
$w^{\prime \prime }_{1}$
is disjoint from
![]() $w^{\prime }$
. The case for supposing
$w^{\prime }$
. The case for supposing
![]() $w^{\prime \prime }\in V(q)$
is similar.
$w^{\prime \prime }\in V(q)$
is similar.
By these two cases, we can conclude that for all
![]() $o\in W$
, there exists
$o\in W$
, there exists
![]() $o^{\prime }\in W$
such that either o overlaps
$o^{\prime }\in W$
such that either o overlaps
![]() $o^{\prime }$
that is disjoint from both
$o^{\prime }$
that is disjoint from both
![]() $w_{1}$
and
$w_{1}$
and
![]() $w_{2}$
, or that
$w_{2}$
, or that
![]() $o^{\prime }$
is disjoint from o and overlaps
$o^{\prime }$
is disjoint from o and overlaps
![]() $w_{1}$
or
$w_{1}$
or
![]() $w_{2}$
. Each of them indicates that
$w_{2}$
. Each of them indicates that
![]() .
.
For the other direction, assume that
![]() and
and
![]() . Then there are
. Then there are
![]() $w,w_{1},w_{2}\in W$
with
$w,w_{1},w_{2}\in W$
with
![]() $Rww_{1}$
and
$Rww_{1}$
and
![]() $Rww_{2}$
. Moreover, for all
$Rww_{2}$
. Moreover, for all
![]() $o\in W$
, there exists
$o\in W$
, there exists
![]() $o^{\prime }\in W$
such that o overlaps
$o^{\prime }\in W$
such that o overlaps
![]() $o^{\prime }$
, and
$o^{\prime }$
, and
![]() $o^{\prime }$
is disjoint from both
$o^{\prime }$
is disjoint from both
![]() $w_{1}$
and
$w_{1}$
and
![]() $w_{2}$
; or that
$w_{2}$
; or that
![]() $o^{\prime }$
overlaps
$o^{\prime }$
overlaps
![]() $w_{1}$
or
$w_{1}$
or
![]() $w_{2}$
, and o is disjoint from
$w_{2}$
, and o is disjoint from
![]() $o^{\prime }$
(
$o^{\prime }$
(
![]() $\star $
).
$\star $
).
Define a valuation V such that
![]() $V(p)=R(w_{1})$
and
$V(p)=R(w_{1})$
and
![]() $V(q)=R(w_{2})$
. Then,
$V(q)=R(w_{2})$
. Then,
![]() . By the assumption, there exists
. By the assumption, there exists
![]() $o_{1}\in W$
such that
$o_{1}\in W$
such that
![]() . By (
. By (
![]() $\star $
), there is an
$\star $
), there is an
![]() $o^{\prime }$
for this
$o^{\prime }$
for this
![]() $o_{1}$
. Now we consider the two cases stated in (
$o_{1}$
. Now we consider the two cases stated in (
![]() $\star $
).
$\star $
).
First,
![]() $o_{1}$
overlaps
$o_{1}$
overlaps
![]() $o^{\prime }$
, and
$o^{\prime }$
, and
![]() $o^{\prime }$
is disjoint from both
$o^{\prime }$
is disjoint from both
![]() $w_{1}$
and
$w_{1}$
and
![]() $w_{2}$
. It holds directly that
$w_{2}$
. It holds directly that
![]() . Additionally, since
. Additionally, since
![]() $o_{1}$
overlaps
$o_{1}$
overlaps
![]() $o^{\prime }$
, by Transitivity, we have
$o^{\prime }$
, by Transitivity, we have
![]() .
.
Next,
![]() $o^{\prime }$
overlaps
$o^{\prime }$
overlaps
![]() $w_{1}$
or
$w_{1}$
or
![]() $w_{2}$
, and
$w_{2}$
, and
![]() $o^{\prime }$
is disjoint from
$o^{\prime }$
is disjoint from
![]() $o_{1}$
. So,
$o_{1}$
. So,
![]() . Furthermore, since
. Furthermore, since
![]() $o^{\prime }$
is disjoint from
$o^{\prime }$
is disjoint from
![]() $o_{1}$
, we can obtain
$o_{1}$
, we can obtain
![]() .
.
Each of these two cases entails a contradiction. Thus we conclude that if
![]() , then
, then
![]() .
.
Proposition 3.14. Finite Sum cannot be defined by
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.
Proof. Consider the two frames
![]() $\mathcal {F}=\langle W,R \rangle $
and
$\mathcal {F}=\langle W,R \rangle $
and
![]() $\mathcal {F}^{\prime }=\langle W^{\prime },R^{\prime } \rangle $
depicted in Figure 3. As an observation, notice
$\mathcal {F}^{\prime }=\langle W^{\prime },R^{\prime } \rangle $
depicted in Figure 3. As an observation, notice
![]() $\mathcal {F}^{\prime }=\langle W^{\prime },R^{\prime } \rangle $
is a generated subframe of
$\mathcal {F}^{\prime }=\langle W^{\prime },R^{\prime } \rangle $
is a generated subframe of
![]() $\mathcal {F}$
. However, we have
$\mathcal {F}$
. However, we have
![]() and
and
![]() . For instance, in the frame
. For instance, in the frame
![]() $\mathcal {F}^{\prime }$
,
$\mathcal {F}^{\prime }$
,
![]() $s_{3}$
underlaps
$s_{3}$
underlaps
![]() $s_{4}$
, and both of them are parts of
$s_{4}$
, and both of them are parts of
![]() $s_{6}$
. However,
$s_{6}$
. However,
![]() $s_{6}$
also overlaps
$s_{6}$
also overlaps
![]() $s_{5}$
which is disjoint from both
$s_{5}$
which is disjoint from both
![]() $s_{3}$
and
$s_{3}$
and
![]() $s_{4}$
. Hence it cannot be defined by
$s_{4}$
. Hence it cannot be defined by
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.

Fig. 3 A generated subframe (for Finite Sum).
Theorem 3.13 shows that we can define Finite Sum relative to the class of EM-frames. Also, Proposition 3.14 illustrates that the principle cannot be defined by
![]() $\mathcal {L}_{\Box }$
. But, a natural question is:
$\mathcal {L}_{\Box }$
. But, a natural question is:
Open Problem. Can we define Finite Sum absolutely with
![]() ?
?
3.5 Correspondences of general extensional mereology
General extensional mereology (GEM) is a generalization of CEM: when the latter theory allows us to operate finite objects, GEM enables us to operate infinite ones. It is the strongest standard theory of mereology. In particular, GEM is also called classical mereology, since it corresponds to the initial theory of mereology proposed by Leśniewski. Specifically, it extends theory EM with the following principle:
where
![]() $\alpha $
is an arbitrary first-order formula, and variables
$\alpha $
is an arbitrary first-order formula, and variables
![]() $y,z$
do not occur free in
$y,z$
do not occur free in
![]() $\alpha $
.
$\alpha $
.
Fusion is also called Unrestricted Sum, since there is almost no restriction on the property
![]() $\alpha $
. Intuitively, the axiom states that for any non-empty (first-order) property
$\alpha $
. Intuitively, the axiom states that for any non-empty (first-order) property
![]() $\alpha $
, there exists an object such that the objects overlapping it are exactly those overlapping the
$\alpha $
, there exists an object such that the objects overlapping it are exactly those overlapping the
![]() $\alpha $
-objects. This axiom might be the most debatable principle among those we have introduced so far. There are many (equivalent) alternatives to the formulation of GEM employed in the literature, which usually resort to different principles for the notion of fusion, e.g., [Reference Hovda16, sec. 5] and [Reference Tsai40, sec. 2]. All those formulations for fusion are interesting, but as a first attempt, in what follows we just work with the above formula Fusion and leave all others for future inquiry.
$\alpha $
-objects. This axiom might be the most debatable principle among those we have introduced so far. There are many (equivalent) alternatives to the formulation of GEM employed in the literature, which usually resort to different principles for the notion of fusion, e.g., [Reference Hovda16, sec. 5] and [Reference Tsai40, sec. 2]. All those formulations for fusion are interesting, but as a first attempt, in what follows we just work with the above formula Fusion and leave all others for future inquiry.
Replacing the abbreviations, Fusion is
![]() $\exists x\alpha \to \exists z\forall y(\exists v(Ryv\land Rzv)\leftrightarrow \exists x(\alpha \land \exists v(Ryv\land Rxv)))$
. Unlike the previous axioms, it is not a single first-order formula but an axiom schema w.r.t. an arbitrary first-order formula
$\exists x\alpha \to \exists z\forall y(\exists v(Ryv\land Rzv)\leftrightarrow \exists x(\alpha \land \exists v(Ryv\land Rxv)))$
. Unlike the previous axioms, it is not a single first-order formula but an axiom schema w.r.t. an arbitrary first-order formula
![]() $\alpha $
.Footnote
17
This makes it impossible to have a modal correspondence precisely, since we cannot really capture all the first-order formulas using the modal language. However, we can reformulate Fusion a little bit, while keeping its essential idea, with a monadic second-order formula
$\alpha $
.Footnote
17
This makes it impossible to have a modal correspondence precisely, since we cannot really capture all the first-order formulas using the modal language. However, we can reformulate Fusion a little bit, while keeping its essential idea, with a monadic second-order formula
where S denotes a second-order set variable. We call it SO-Fusion. Compared with Fusion, SO-Fusion is a stronger principle since the set S does not need to be first-order definable, which actually brings us closer to the original idea of Leśniewski that every non-empty subset should have a fusion (cf., e.g., [Reference Tsai40, p. 811]). On the technical side, the validity of a modal formula is essentially second-order as discussed in the Correspondence Theory (cf., e.g., [Reference van Benthem, Gabbay and Guenthner43]); thus it is still possible to have a corresponding modal formula.
In the following we will abuse the satisfaction relation
![]() to accommodate monadic second-order formulas in the most natural manner. We have the following result:
to accommodate monadic second-order formulas in the most natural manner. We have the following result:
Theorem 3.15. For each EM-frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() if and only if
if and only if
![]() .
.
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be an EM-frame. From left to right, assume towards a contradiction that
$\mathcal {F}=\langle W,R \rangle $
be an EM-frame. From left to right, assume towards a contradiction that
![]() and
and
![]() . Then there exist
. Then there exist
![]() $w\in W$
and a valuation V such that
$w\in W$
and a valuation V such that
![]() and
and
![]() . Consequently, for every
. Consequently, for every
![]() $o\in W$
, either (1) or (2) holds: (1)
$o\in W$
, either (1) or (2) holds: (1)
![]() ; and (2) o has a successor
; and (2) o has a successor
![]() $o^{\prime }\in W$
such that
$o^{\prime }\in W$
such that
![]() and every
and every
![]() $v\in V(p)$
has no q-successors. Now, consider
$v\in V(p)$
has no q-successors. Now, consider
![]() $V(p)$
as the extension for the predicate S in
$V(p)$
as the extension for the predicate S in
![]() $\mathcal {F}$
, clearly the antecedent
$\mathcal {F}$
, clearly the antecedent
![]() $\exists x Sx$
of SO-Fusion holds; thus we have
$\exists x Sx$
of SO-Fusion holds; thus we have
![]() $\exists z \forall y(Oyz\leftrightarrow \exists x(Sx\land Oyx)) (\star )$
, too. Given an arbitrary
$\exists z \forall y(Oyz\leftrightarrow \exists x(Sx\land Oyx)) (\star )$
, too. Given an arbitrary
![]() $o\in W$
, let us consider the above two cases to see whether o can be the witness for z in
$o\in W$
, let us consider the above two cases to see whether o can be the witness for z in
![]() $(\star )$
.
$(\star )$
.
For (1), if
![]() , then there exists
, then there exists
![]() $o_{1}\in V(p)$
such that
$o_{1}\in V(p)$
such that
![]() $\neg Roo_{1}$
. By Strong Supplementation,
$\neg Roo_{1}$
. By Strong Supplementation,
![]() $o_{1}$
has a successor
$o_{1}$
has a successor
![]() $o_{1}^{\prime }$
that is disjoint from o. Therefore, we have
$o_{1}^{\prime }$
that is disjoint from o. Therefore, we have
![]() $\neg O o_{1}^{\prime }o$
, but
$\neg O o_{1}^{\prime }o$
, but
![]() $(So_{1}\land Oo_{1}^{\prime }o_{1})$
. Thus, o cannot be the witness for z in
$(So_{1}\land Oo_{1}^{\prime }o_{1})$
. Thus, o cannot be the witness for z in
![]() $(\star )$
.
$(\star )$
.
For (2), consider the case that
![]() $Roo^{\prime }$
,
$Roo^{\prime }$
,
![]() , and for each
, and for each
![]() $v\in W$
,
$v\in W$
,
![]() . Since
. Since
![]() $o^{\prime }\in R(o)$
, the two objects overlap trivially. Moreover, for any
$o^{\prime }\in R(o)$
, the two objects overlap trivially. Moreover, for any
![]() $v\in V(p)$
, it is not hard to see that
$v\in V(p)$
, it is not hard to see that
![]() $o^{\prime }$
is disjoint from v. Therefore we have
$o^{\prime }$
is disjoint from v. Therefore we have
![]() $Oo^{\prime }o$
but
$Oo^{\prime }o$
but
![]() $\neg \exists x (Sx\land Oo^{\prime }x)$
. Thus o cannot be the witness for z in
$\neg \exists x (Sx\land Oo^{\prime }x)$
. Thus o cannot be the witness for z in
![]() $(\star )$
either.
$(\star )$
either.
In sum, no
![]() $o\in W$
can be the witness of z in
$o\in W$
can be the witness of z in
![]() $(\star )$
, contradiction.
$(\star )$
, contradiction.
From right to left, suppose that
![]() and
and
![]() . From the latter there is a non-empty set
. From the latter there is a non-empty set
![]() $X\subseteq W$
such that
$X\subseteq W$
such that
![]() $\forall z\exists y\neg (Oyz\leftrightarrow \exists x(Sx \land Oyx)) (\dagger )$
holds when assigning S to X. Now, pick one
$\forall z\exists y\neg (Oyz\leftrightarrow \exists x(Sx \land Oyx)) (\dagger )$
holds when assigning S to X. Now, pick one
![]() $w\in X$
, let
$w\in X$
, let
![]() $V(p)=X$
,
$V(p)=X$
,
![]() $V(q)=\{o\in W\mid \neg \exists x(Xx\land Oxo)\}$
, and we have
$V(q)=\{o\in W\mid \neg \exists x(Xx\land Oxo)\}$
, and we have
![]() . Thus there is a
. Thus there is a
![]() $v\in W$
, such that
$v\in W$
, such that
![]() . Now by
. Now by
![]() $(\dagger )$
, there is
$(\dagger )$
, there is
![]() $v^{\prime }$
such that either (1)
$v^{\prime }$
such that either (1)
![]() $(\neg Ovv^{\prime }\land \exists x(Sx \land Ov^{\prime }x))$
or (2)
$(\neg Ovv^{\prime }\land \exists x(Sx \land Ov^{\prime }x))$
or (2)
![]() $Ovv^{\prime }\land \forall x(Sx \to \neg Ov^{\prime }x)$
.
$Ovv^{\prime }\land \forall x(Sx \to \neg Ov^{\prime }x)$
.
Now consider case (1). Formula
![]() $\exists x(Sx \land Ov^{\prime }x)$
states that there exists
$\exists x(Sx \land Ov^{\prime }x)$
states that there exists
![]() $o\in X$
such that
$o\in X$
such that
![]() $Oov^{\prime }$
, i.e., there is some
$Oov^{\prime }$
, i.e., there is some
![]() $o^{\prime }$
such that
$o^{\prime }$
such that
![]() $Rv^{\prime }o^{\prime }$
and
$Rv^{\prime }o^{\prime }$
and
![]() $Roo^{\prime }$
. Furthermore, since
$Roo^{\prime }$
. Furthermore, since
![]() , we have
, we have
![]() $Rvo$
. Now by Transitivity of EM,
$Rvo$
. Now by Transitivity of EM,
![]() $Rvo^{\prime }$
. However then we obtain
$Rvo^{\prime }$
. However then we obtain
![]() $Ovv^{\prime }$
, contradicting the first conjunct of (1).
$Ovv^{\prime }$
, contradicting the first conjunct of (1).
For case (2), by the second conjunct, we have
![]() $v^{\prime }\in V(q)$
. Moreover, from the definition of the valuation V, it follows that
$v^{\prime }\in V(q)$
. Moreover, from the definition of the valuation V, it follows that
![]() . Now due to the first conjunct of (2), there is an o such that
. Now due to the first conjunct of (2), there is an o such that
![]() $Rvo$
and
$Rvo$
and
![]() $Rv^{\prime }o$
. Then, by Transitivity, we have
$Rv^{\prime }o$
. Then, by Transitivity, we have
![]() . Thus,
. Thus,
![]() . Now by
. Now by
![]() $(\circ )$
,
$(\circ )$
,
![]() , which indicates that there exists an
, which indicates that there exists an
![]() $o^{\prime }\in X$
that has a successor disjoint from any X-point. However, this is impossible since due to Reflexivity,
$o^{\prime }\in X$
that has a successor disjoint from any X-point. However, this is impossible since due to Reflexivity,
![]() $o^{\prime }$
overlaps with any successor. Now we have arrived at a contradiction. This completes the proof.
$o^{\prime }$
overlaps with any successor. Now we have arrived at a contradiction. This completes the proof.
Here a question arises:
Open Problem. Is there a formula of
![]() that corresponds to SO-Fusion?
that corresponds to SO-Fusion?
Instead of answering this question, we now show that the standard modal language is not expressive enough to define Fusion.
Proposition 3.16. Fusion is not definable in
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.
Proof. To prove this result, we consider a special case where
![]() $\alpha $
is
$\alpha $
is
![]() $Rxx$
. Define three frames as follows:
$Rxx$
. Define three frames as follows:
![]() $\mathcal {F}_{1}=\langle \{w_{1}\},\{\langle w_{1},w_{1} \rangle \} \rangle $
,
$\mathcal {F}_{1}=\langle \{w_{1}\},\{\langle w_{1},w_{1} \rangle \} \rangle $
,
![]() $\mathcal {F}_{2}=\langle \{w_{2}\},\{\langle w_{2},w_{2} \rangle \} \rangle $
and
$\mathcal {F}_{2}=\langle \{w_{2}\},\{\langle w_{2},w_{2} \rangle \} \rangle $
and
![]() $\mathcal {F}_{3}=\langle \{w_{1},w_{2}\},\{\langle w_{1},w_{1} \rangle ,\langle w_{2},w_{2} \rangle \} \rangle $
. Each of
$\mathcal {F}_{3}=\langle \{w_{1},w_{2}\},\{\langle w_{1},w_{1} \rangle ,\langle w_{2},w_{2} \rangle \} \rangle $
. Each of
![]() $\mathcal {F}_{1}$
and
$\mathcal {F}_{1}$
and
![]() $\mathcal {F}_{2}$
consists of a reflexive point, and frame
$\mathcal {F}_{2}$
consists of a reflexive point, and frame
![]() $\mathcal {F}_{3}$
is the disjoint union of
$\mathcal {F}_{3}$
is the disjoint union of
![]() $\mathcal {F}_{1}$
and
$\mathcal {F}_{1}$
and
![]() $\mathcal {F}_{2}$
. Now it is not hard to see that when
$\mathcal {F}_{2}$
. Now it is not hard to see that when
![]() $i\in \{1,2\}$
, we have
$i\in \{1,2\}$
, we have
![]() . However, in frame
. However, in frame
![]() $\mathcal {F}_{3}$
both
$\mathcal {F}_{3}$
both
![]() $w_{1}$
and
$w_{1}$
and
![]() $w_{2}$
satisfy the property
$w_{2}$
satisfy the property
![]() $Rxx$
but they are disjoint from each other. So,
$Rxx$
but they are disjoint from each other. So,
![]() . Again, by the Goldblatt–Thomason Theorem, the property cannot be defined by
. Again, by the Goldblatt–Thomason Theorem, the property cannot be defined by
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.
3.6 Correspondences of atomicity and atomlessness
For each standard theory mentioned above, we can also extend it with other properties. For instance, we can stipulate that every object has a part that has no proper part, or that every object has some proper part. The former property is called Atomicity, and the latter one is named as Atomlessness. When an object x has no proper part, we call it an atom (notation,
![]() $Ax$
), which is formally defined as
$Ax$
), which is formally defined as
![]() $Ax:=\neg \exists yPPyx$
. The definitions of the above two principles are as follows:
$Ax:=\neg \exists yPPyx$
. The definitions of the above two principles are as follows:

An atom is also called simple. By its definition, any two different atoms have no common parts. It is important to recognize that Atomicity does not state that everything is ultimately composed of atoms, and it just says that every object contains some atomic part. Furthermore, Atomicity is not compatible with Atomlessness, since an atom has no proper parts. For any
![]() $\text {X}\in \{\text {GM, MM, EM, CEM, GEM}\}$
, we denote by AX and
$\text {X}\in \{\text {GM, MM, EM, CEM, GEM}\}$
, we denote by AX and
![]() $\widetilde {\text {A}}$
X the theories enriching X with Atomicity and Atomlessness respectively.
$\widetilde {\text {A}}$
X the theories enriching X with Atomicity and Atomlessness respectively.
With the definition of Proper Part, we know that
![]() $Ax$
is equivalent to
$Ax$
is equivalent to
![]() $ \forall y(Rxy\to Ryx)$
(Symmetry), which corresponds to formula
$ \forall y(Rxy\to Ryx)$
(Symmetry), which corresponds to formula
![]() $p\to \Box \Diamond p$
(B). In addition, Atomicity is equivalent to
$p\to \Box \Diamond p$
(B). In addition, Atomicity is equivalent to
![]() $\forall x\exists y(Rxy\land \forall z(Ryz\to Rzy))$
, and Atomlessness is equivalent to
$\forall x\exists y(Rxy\land \forall z(Ryz\to Rzy))$
, and Atomlessness is equivalent to
![]() $\forall x\exists y(Rxy\land \neg Ryx)$
. As noted by Blackburn et al. [Reference Blackburn, de Rijke and Venema1, example 3.57], we have the following result:
$\forall x\exists y(Rxy\land \neg Ryx)$
. As noted by Blackburn et al. [Reference Blackburn, de Rijke and Venema1, example 3.57], we have the following result:
Proposition 3.17. For any transitive frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() if and only if
if and only if
![]() .
.
Recall that a GM-frame is transitive and anti-symmetric; thus we have:
Theorem 3.18. For each GM-frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() iff
iff
![]() .
.
Namely, relative to GM-frames, we can define Atomicity with the McKinsey formula, which is an
![]() $\mathcal {L}_{\Box }$
-formula. But, is this principle absolutely definable with the standard modal language? Unfortunately, although this property is closed under taking bounded morphic images, disjoint unions, and generated subframes, the following result still provides us with a negative answer to this question:
$\mathcal {L}_{\Box }$
-formula. But, is this principle absolutely definable with the standard modal language? Unfortunately, although this property is closed under taking bounded morphic images, disjoint unions, and generated subframes, the following result still provides us with a negative answer to this question:
Proposition 3.19. Atomicity cannot be defined by
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.
Proof. To prove this, by the Goldblatt–Thomason Theorem, it suffices to give an example showing that the class of Atomicity-frames does not reflect
Footnote
18
ultrafilter extensions. Consider the frame
![]() $\mathcal {F}=\langle \mathbb {N},< \rangle $
(the natural numbers with the usual
$\mathcal {F}=\langle \mathbb {N},< \rangle $
(the natural numbers with the usual
![]() $<$
relation) and its ultrafilter extension
$<$
relation) and its ultrafilter extension
![]() $ue(\mathcal {F})$
(cf. [Reference Blackburn, de Rijke and Venema1, sec. 3.3]). It is a matter of direct checking that
$ue(\mathcal {F})$
(cf. [Reference Blackburn, de Rijke and Venema1, sec. 3.3]). It is a matter of direct checking that
![]() and
and
![]() . Now the proof is completed.
. Now the proof is completed.
Furthermore, as the following result shows, Atomicity essentially cannot even be defined by our language
![]() .
.
Proposition 3.20. Atomicity is undefinable in
![]() .
.
The result can be proved with the same reasoning as that for Example 4.15 in [Reference Goranko9], which indicated that the first-order property
![]() $\exists xRxx$
is undefinable in
$\exists xRxx$
is undefinable in
![]() . However, the details of the proof involve some results on the expressivity of the language, and it is beyond the scope of this article to explain them. For the reader interested in the details of the proof and the expressivity of
. However, the details of the proof involve some results on the expressivity of the language, and it is beyond the scope of this article to explain them. For the reader interested in the details of the proof and the expressivity of
![]() , we refer to [Reference Goranko9].
, we refer to [Reference Goranko9].
As for Atomlessness, the correspondence result is as follows:
Theorem 3.21. For each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() iff
iff
![]() .
.
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be a frame. For the direction from left to right, suppose for reductio that
$\mathcal {F}=\langle W,R \rangle $
be a frame. For the direction from left to right, suppose for reductio that
![]() and
and
![]() . Then there exist
. Then there exist
![]() $w\in W$
and a valuation V such that
$w\in W$
and a valuation V such that
![]() . Since
. Since
![]() , there exists
, there exists
![]() $v\in W$
with
$v\in W$
with
![]() $Rwv\land \neg Rvw$
. By
$Rwv\land \neg Rvw$
. By
![]() $Rwv$
, it holds that
$Rwv$
, it holds that
![]() . However, from
. However, from
![]() $\neg Rvw$
and
$\neg Rvw$
and
![]() $w\in V(p)$
, we know
$w\in V(p)$
, we know
![]() , which entails a contradiction.
, which entails a contradiction.
For the other direction, suppose that
![]() and
and
![]() . Then there exists
. Then there exists
![]() $w\in W$
such that for all
$w\in W$
such that for all
![]() $w^{\prime }\in W$
,
$w^{\prime }\in W$
,
![]() $Rww^{\prime }$
entails
$Rww^{\prime }$
entails
![]() $Rw^{\prime }w$
. Now define a valuation V such that
$Rw^{\prime }w$
. Now define a valuation V such that
![]() $V(p)=\{w\}$
. Since formula
$V(p)=\{w\}$
. Since formula
![]() is valid, there exists
is valid, there exists
![]() $v\in R(w)$
such that v is not
$v\in R(w)$
such that v is not
![]() . Then we conclude that
. Then we conclude that
![]() $\neg Rvw$
, which entails a contradiction, too. This completes the proof.
$\neg Rvw$
, which entails a contradiction, too. This completes the proof.
Additionally, the following result shows that this property cannot be defined by the standard modal language:
Proposition 3.22. Atomlessness is not definable in
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.
Proof. Consider frames
![]() $\mathcal {F}_{1}=\langle W_{1},R_{1} \rangle $
and
$\mathcal {F}_{1}=\langle W_{1},R_{1} \rangle $
and
![]() $\mathcal {F}_{2}=\langle W_{2},R_{2} \rangle $
depicted in Figure 4. Define a function
$\mathcal {F}_{2}=\langle W_{2},R_{2} \rangle $
depicted in Figure 4. Define a function
![]() $f:W_{1}\to W_{2}$
such that
$f:W_{1}\to W_{2}$
such that
![]() $f(w)=v$
for all
$f(w)=v$
for all
![]() $w\in W_{1}$
. Then f is a bounded morphism from
$w\in W_{1}$
. Then f is a bounded morphism from
![]() $\mathcal {F}_{1}$
to
$\mathcal {F}_{1}$
to
![]() $\mathcal {F}_{2}$
. However, we have
$\mathcal {F}_{2}$
. However, we have
![]() and
and
![]() ; therefore by the Goldblatt–Thomason Theorem, Atomlessness is not definable in
; therefore by the Goldblatt–Thomason Theorem, Atomlessness is not definable in
![]() $\mathcal {L}_{\Box }$
.
$\mathcal {L}_{\Box }$
.

Fig. 4 A bounded morphism (for Atomlessness).
3.7 Summary
So far, we have shown that all the following properties cannot be defined by the standard modal language: Supplementation (Proposition 3.7), Strong Supplementation (Proposition 3.9), Finite Product (Proposition 3.11), Finite Sum (Proposition 3.14), Fusion (Proposition 3.16), Atomicity (Proposition 3.19) and Atomlessness (Proposition 3.22). Also, we have shown that the principle Atomicity cannot be defined by
![]() (Proposition 3.20). But, all these properties are definable (absolutely or relative to some particular class of frames) in
(Proposition 3.20). But, all these properties are definable (absolutely or relative to some particular class of frames) in
![]() . Now we summarize the correspondence results on these properties.
. Now we summarize the correspondence results on these properties.
For each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,

For each GM-frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
For each EM-frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,

Finally, it is worth noting that our results can also be generalized to define some other theories of mereology, say, minimal extensional mereology, which extends theory MM with Finite Product [Reference Tsai38, p. 990].
3.8 A digression: Medvedev frames
To conclude this section, we show that we can define Medvedev frames by
![]() relative to the class of finite frames. According to [Reference Holliday15], a frame
relative to the class of finite frames. According to [Reference Holliday15], a frame
![]() $\langle W,R \rangle $
is a Medvedev frame if it is a finite poset satisfying the following properties:
$\langle W,R \rangle $
is a Medvedev frame if it is a finite poset satisfying the following properties:
-
•
 $\forall x\forall y\exists z(Rzx\land Rzy)$
(Reversed Convergence);
$\forall x\forall y\exists z(Rzx\land Rzy)$
(Reversed Convergence); -
•
 $\forall x\forall y(\forall y^{\prime }(Ryy^{\prime }\to \exists y^{\prime \prime }(Ry^{\prime }y^{\prime \prime }\land Rxy^{\prime \prime }))\to Rxy)$
(Separativity); and
$\forall x\forall y(\forall y^{\prime }(Ryy^{\prime }\to \exists y^{\prime \prime }(Ry^{\prime }y^{\prime \prime }\land Rxy^{\prime \prime }))\to Rxy)$
(Separativity); and -
•
 $\forall x\forall y_{1}\forall y_{2}((Rxy_{1}\land Rxy_{2})\to \exists u(Rxu\land Ruy_{1}\land Ruy_{2}\land \forall v(Ruv\to \exists w(Rvw\land (Ry_{1}w\lor Ry_{2}w)))))$
(Union).
$\forall x\forall y_{1}\forall y_{2}((Rxy_{1}\land Rxy_{2})\to \exists u(Rxu\land Ruy_{1}\land Ruy_{2}\land \forall v(Ruv\to \exists w(Rvw\land (Ry_{1}w\lor Ry_{2}w)))))$
(Union).
We only need to define the first-order property for Reversed Convergence, and the other formulas are already defined by
![]() $\Box $
and
$\Box $
and
![]() $\boxminus $
by Holliday [Reference Holliday15], which can be turned into formulas in our language since
$\boxminus $
by Holliday [Reference Holliday15], which can be turned into formulas in our language since
![]() $\boxminus $
and
$\boxminus $
and
![]() are inter-definable.Footnote
19
are inter-definable.Footnote
19
Proposition 3.23. For each frame
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() iff
iff
![]() .
.
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be a frame. From left to right, suppose that
$\mathcal {F}=\langle W,R \rangle $
be a frame. From left to right, suppose that
![]() $\mathcal {F}\nvDash p\land \Diamond _{u} q\to \Diamond _{u}(\Diamond p\land \Diamond q )$
. Then there exist
$\mathcal {F}\nvDash p\land \Diamond _{u} q\to \Diamond _{u}(\Diamond p\land \Diamond q )$
. Then there exist
![]() $w,v\in W$
and a valuation V such that
$w,v\in W$
and a valuation V such that
![]() ,
,
![]() , and for all
, and for all
![]() $o\in W$
,
$o\in W$
,
![]() $\langle \mathcal {F},V \rangle ,o \nvDash \Diamond p\land \Diamond q$
. We conclude that w and v have no common predecessor, i.e.,
$\langle \mathcal {F},V \rangle ,o \nvDash \Diamond p\land \Diamond q$
. We conclude that w and v have no common predecessor, i.e.,
![]() .
.
From right to left, assume that
![]() and
and
![]() . Then there are
. Then there are
![]() $w,v\in W$
that have not common predecessor. Define the valuation V such that
$w,v\in W$
that have not common predecessor. Define the valuation V such that
![]() $V(p)=\{w\}$
and
$V(p)=\{w\}$
and
![]() $V(q)=\{v\}$
. Consequently,
$V(q)=\{v\}$
. Consequently,
![]() . Since
. Since
![]() , there exists
, there exists
![]() $o\in W$
with
$o\in W$
with
![]() , i.e., o is a common predecessor of w and v, which entails a contradiction.
, i.e., o is a common predecessor of w and v, which entails a contradiction.
Given that our language is able to define those properties of mereology, it is not a surprise that we can also define Medvedev frames relative to finite frames. Essentially, when taking ‘part of’ P as the primitive relation, theory GEM is isomorphic to the inclusion relation restricted to the set of all non-empty subsets of a given set, which is to say a complete Boolean algebra with the zero element removed [Reference Grzegorczyk13, Reference Tarski35]. Although we have this general result, the findings in [Reference Holliday15] are not enough to achieve our goals. At the end of this part, we briefly comment on the modal correspondences of Separativity and Union in [Reference Holliday15].
The principle Separativity is equivalent to Strong Supplementation. Its modal correspondence in [Reference Holliday15] is
![]() (reformulated with window modality), which does correspond to Strong Supplementation. However, formula
(reformulated with window modality), which does correspond to Strong Supplementation. However, formula
![]() $\blacksquare p\to \Box _{u}(\neg p\to \Diamond \Box \neg p)$
, corresponding to Strong Supplementation, has a more natural reading in the context of mereology. In addition, our modal formula contains only one propositional atom, which looks much simpler.
$\blacksquare p\to \Box _{u}(\neg p\to \Diamond \Box \neg p)$
, corresponding to Strong Supplementation, has a more natural reading in the context of mereology. In addition, our modal formula contains only one propositional atom, which looks much simpler.
The modal correspondence of Union in [Reference Holliday15] is
![]() $\Diamond (p_{1}\land \Box q)\land \Diamond (p_{2}\land \Box q)\to \Diamond (\Diamond p_{1}\land \Diamond p_{2}\land \Box \Diamond q)$
. Although the function of mereological ‘sum’ is similar to that of set-theoretic ‘union’ in some sense, this standard modal formula does not correspond to Finite Sum, which follows from Proposition 3.14 directly.
$\Diamond (p_{1}\land \Box q)\land \Diamond (p_{2}\land \Box q)\to \Diamond (\Diamond p_{1}\land \Diamond p_{2}\land \Box \Diamond q)$
. Although the function of mereological ‘sum’ is similar to that of set-theoretic ‘union’ in some sense, this standard modal formula does not correspond to Finite Sum, which follows from Proposition 3.14 directly.
4 Mereological modal logics
In this section, we introduce the mereological modal logics, and show that they are sound. Corresponding to the first-order theories, the modal systems are called modal ground mereology (MGM), modal minimal mereology (MMM), modal extensional mereology (MEM), modal extensional closure mereology (MCEM), and modal general extensional mereology (MGEM), respectively. Also, we prove the incompleteness of MGM over frames and the completeness of an extension of this modal system.
4.1 Logical systems
To get the mereological modal systems, we first introduce two logical systems
![]() $K^{*}$
and
$K^{*}$
and
![]() $K^{\sim }$
: the former one is the minimal system of
$K^{\sim }$
: the former one is the minimal system of
![]() , which has only the operator
, which has only the operator
![]() (besides Boolean connectives
(besides Boolean connectives
![]() $\neg $
and
$\neg $
and
![]() $\land $
), and the latter one is the minimal normal system of
$\land $
), and the latter one is the minimal normal system of
![]() . These two systems are well introduced in [Reference Gargov, Passy, Tinchev and Skordev6, secs. 1 and 2], and we reformulate them with two equivalent systems. Let us begin with
. These two systems are well introduced in [Reference Gargov, Passy, Tinchev and Skordev6, secs. 1 and 2], and we reformulate them with two equivalent systems. Let us begin with
![]() $K^{*}$
, which is defined formally as follows:
$K^{*}$
, which is defined formally as follows:

Let K be the basic normal modal system, we have the following results:
Theorem 4.24 [Reference Gargov, Passy, Tinchev and Skordev6]
For any
![]() $\mathcal {M}=\langle W,R,V \rangle $
,
$\mathcal {M}=\langle W,R,V \rangle $
,
![]() $w\in W$
and
$w\in W$
and
![]() $\varphi \in \mathcal {L}_{\Box }$
, let
$\varphi \in \mathcal {L}_{\Box }$
, let
![]() $\varphi ^{*}$
be the formula obtained by substituting every
$\varphi ^{*}$
be the formula obtained by substituting every
![]() $\Box $
occurring in
$\Box $
occurring in
![]() $\varphi $
with
$\varphi $
with
![]() , and
, and
![]() $\mathcal {M}^{*}:=\langle W,W^{2}\backslash R,V \rangle $
. Then,
$\mathcal {M}^{*}:=\langle W,W^{2}\backslash R,V \rangle $
. Then,
![]() iff
iff
![]() ,
,
![]() iff
iff
![]() , and
, and
![]() iff
iff
![]() .
.
Theorem 4.25 [Reference Gargov, Passy, Tinchev and Skordev6]
Logic
![]() $K^{*}$
is sound, complete, decidable and compact.
$K^{*}$
is sound, complete, decidable and compact.
Compared with
![]() $K^{*}$
, system
$K^{*}$
, system
![]() $K^{\sim }$
is much more complicated: its axioms include not only principles involving
$K^{\sim }$
is much more complicated: its axioms include not only principles involving
![]() $\Box $
and
$\Box $
and
![]() , but also those involving the universal modality
, but also those involving the universal modality
![]() $\Box _{u}$
that can be defined by
$\Box _{u}$
that can be defined by
![]() $\Box $
and
$\Box $
and
![]() . Here is the definition:
. Here is the definition:

Observe that
![]() $\Box _{u}$
is an S5-modality. Moreover, the rules are below derivable in
$\Box _{u}$
is an S5-modality. Moreover, the rules are below derivable in
![]() $K^{\sim }$
:
$K^{\sim }$
:
-
• If
 and
and
 , then
, then
 . (RS)
. (RS) -
• If
 and
and
 , then
, then
 . (RCC)
. (RCC) -
• If
 and
and
 , then
, then
 , where
, where
 $\varphi (\psi /\chi )$
is the formula obtained by substituting each
$\varphi (\psi /\chi )$
is the formula obtained by substituting each
 $\psi $
occurring in
$\psi $
occurring in
 $\varphi $
with
$\varphi $
with
 $\chi $
. (RES)
$\chi $
. (RES)
We omit the proof here, which is by a simple adaption of standard arguments (cf. [Reference Blackburn, de Rijke and Venema1]). Furthermore, as to the relation between
![]() $K^ \sim $
and
$K^ \sim $
and
![]() $K^{*}$
, we have the following result:
$K^{*}$
, we have the following result:
Theorem 4.26.
![]() $K^{\sim }$
is a proper extension of
$K^{\sim }$
is a proper extension of
![]() $K^{*}$
.
$K^{*}$
.
Proof. First, we prove that all inference rules of
![]() $K^{*}$
are derivable in
$K^{*}$
are derivable in
![]() $K^{\sim }$
. To do so, we only need to show that
$K^{\sim }$
. To do so, we only need to show that
![]() $R^{*}2$
is derivable in
$R^{*}2$
is derivable in
![]() $K^{\sim }$
. Suppose that
$K^{\sim }$
. Suppose that
![]() $\neg \varphi $
, i.e.,
$\neg \varphi $
, i.e.,
![]() $\varphi \to \bot $
. From
$\varphi \to \bot $
. From
![]() $R3$
, it follows that
$R3$
, it follows that
![]() . As
. As
![]() is
is
![]() $A7$
, we conclude
$A7$
, we conclude
![]() by
by
![]() $R1$
.
$R1$
.
Next, we show that
![]() :
:

Moreover,
![]() $K^{*}$
has no formula containing modality
$K^{*}$
has no formula containing modality
![]() $\Box $
, but
$\Box $
, but
![]() $K^{\sim }$
has
$K^{\sim }$
has
![]() $R2$
as an inference rule. Thus the proof is completed.
$R2$
as an inference rule. Thus the proof is completed.
By Theorems 4.24 and 4.26, it holds immediately that:
Theorem 4.27. For any
![]() $\mathcal {L}_{\Box }$
-formula
$\mathcal {L}_{\Box }$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() , then
, then
![]() , where
, where
![]() $\varphi ^{*}$
is the formula obtained by substituting every
$\varphi ^{*}$
is the formula obtained by substituting every
![]() $\Box $
occurring in
$\Box $
occurring in
![]() $\varphi $
with
$\varphi $
with
![]() .
.
Consequently, the following result holds:
Proposition 4.28.
![]() .
.
Also, we can prove that:
Proposition 4.29.
![]() .
.
Proof.

Note that formula (8) in the proof above is provable in K, so Theorem 4.27 is applicable. Furthermore, as noted by Gargov et al. [Reference Gargov, Passy, Tinchev and Skordev6, sec. 2], we have the following result:
Theorem 4.30 [Reference Gargov, Passy, Tinchev and Skordev6]
![]() $K^{\sim }$
is sound, complete and decidable.
$K^{\sim }$
is sound, complete and decidable.
Now it is time to introduce the definition of our modal systems. Each of the modal systems is an extension of
![]() $K^{\sim }$
.
$K^{\sim }$
.
Definition 4.31 (Mereological modal systems)
For any
![]() $\text {X}\in \{{GM},{MM},{EM},{CEM},{GEM}\}$
, we denote by MX the logical system extending
$\text {X}\in \{{GM},{MM},{EM},{CEM},{GEM}\}$
, we denote by MX the logical system extending
![]() $K^{\sim }$
with the schemata of the modal correspondences of X. Formally, they are defined as follows:
$K^{\sim }$
with the schemata of the modal correspondences of X. Formally, they are defined as follows:

Also, define
![]() $\text {AMX}:=\text {MX}+\Box \Diamond \varphi \to \Diamond \Box \varphi $
and
$\text {AMX}:=\text {MX}+\Box \Diamond \varphi \to \Diamond \Box \varphi $
and
![]() .
.
Recall that the formula used in MGM to capture Anti-symmetry is slightly different from the one used by Goranko [Reference Goranko9].
With our findings in Section 3, it is easy to see that all the resulting modal systems are sound:
Proposition 4.32 (Soundness)
For any theory
![]() $\text {X}\in \{\text {GM},\text {MM},\text {EM},\text {CEM},\text {GEM}\}$
, systems MX, AMX and
$\text {X}\in \{\text {GM},\text {MM},\text {EM},\text {CEM},\text {GEM}\}$
, systems MX, AMX and
![]() $\tilde {\text {A}}$
MX are sound with respect to X-frames, AX-frames and
$\tilde {\text {A}}$
MX are sound with respect to X-frames, AX-frames and
![]() $\tilde {\text {A}}$
X-frames, respectively.
$\tilde {\text {A}}$
X-frames, respectively.
4.2 Incompleteness of MGM
Now we proceed to study the completeness of MGM. Actually, it is not frame-complete. To prove this result, we need to find a formula
![]() $\varphi $
that is valid on GM-frames but not provable in MGM.
$\varphi $
that is valid on GM-frames but not provable in MGM.
Consider the formula
![]() that is proposed by Goranko [Reference Goranko and Petkov8, p. 321], which in fact also corresponds to Transitivity.Footnote
20
In the context of mereology, it intuitively states that if an object has a part having all
that is proposed by Goranko [Reference Goranko and Petkov8, p. 321], which in fact also corresponds to Transitivity.Footnote
20
In the context of mereology, it intuitively states that if an object has a part having all
![]() $\varphi $
-objects as its parts, then all those objects are also the parts of this object. First, we show that it is valid on GM-frames.
$\varphi $
-objects as its parts, then all those objects are also the parts of this object. First, we show that it is valid on GM-frames.
Proposition 4.33. Formula
![]() is valid on GM-frames.
is valid on GM-frames.
Proof. Let
![]() $\mathcal {F}=\langle W,R \rangle $
be a GM-frame, V a valuation and
$\mathcal {F}=\langle W,R \rangle $
be a GM-frame, V a valuation and
![]() $w\in W$
. Suppose that
$w\in W$
. Suppose that
![]() . Then there exists
. Then there exists
![]() $v\in R(w)$
such that for any
$v\in R(w)$
such that for any
![]() $u\in W$
, if u is
$u\in W$
, if u is
![]() $\varphi $
, then
$\varphi $
, then
![]() $Rvu$
. By Transitivity, all
$Rvu$
. By Transitivity, all
![]() $\varphi $
-points are successors of w. Therefore,
$\varphi $
-points are successors of w. Therefore,
![]() . This completes the proof.
. This completes the proof.
Next, we show that
![]() is not provable in MGM. To do so, we introduce an auxiliary notion of ‘generalized model’ proposed by Gargov et al. [Reference Gargov, Passy, Tinchev and Skordev6]:
is not provable in MGM. To do so, we introduce an auxiliary notion of ‘generalized model’ proposed by Gargov et al. [Reference Gargov, Passy, Tinchev and Skordev6]:
Definition 4.34 (Generalized model and generalized frame)
A generalized model
![]() $\mathcal {M}_{g}=\langle W,R_{1},R_{2},V \rangle $
is a tuple, where W is a non-empty set of objects,
$\mathcal {M}_{g}=\langle W,R_{1},R_{2},V \rangle $
is a tuple, where W is a non-empty set of objects,
![]() $R_{1}$
and
$R_{1}$
and
![]() $R_{2}$
are two binary relations such that
$R_{2}$
are two binary relations such that
![]() $R_{1}\cup R_{2}= W\times W$
, and V is a valuation function defined as usual. Moreover, we call
$R_{1}\cup R_{2}= W\times W$
, and V is a valuation function defined as usual. Moreover, we call
![]() $\mathcal {F}_{g}=\langle W,R_{1},R_{2} \rangle $
a generalized frame.
$\mathcal {F}_{g}=\langle W,R_{1},R_{2} \rangle $
a generalized frame.
It is important to notice that generalized models and frames have two distinguishing features. On the one hand, it always holds that
![]() $R_{1}\cup R_{2}= W\times W$
. On the other hand, generally
$R_{1}\cup R_{2}= W\times W$
. On the other hand, generally
![]() $R_{1}\cap R_{2}\not =\emptyset $
. From now on, we will use the notation ‘
$R_{1}\cap R_{2}\not =\emptyset $
. From now on, we will use the notation ‘
![]() ’ to denote the satisfaction relation w.r.t. generalized models. The truth conditions for Boolean cases are as usual. The semantics for
’ to denote the satisfaction relation w.r.t. generalized models. The truth conditions for Boolean cases are as usual. The semantics for
![]() $\Box $
and
$\Box $
and
![]() are as follows:
are as follows:

Now we are able to show the following result:
Proposition 4.35.
![]() is not provable in MGM.
is not provable in MGM.
Proof. Consider the generalized frame
![]() $\mathcal {F}_{g}$
depicted in Figure 5. It holds that
$\mathcal {F}_{g}$
depicted in Figure 5. It holds that
![]() $R_{1}\cup R_{2}=W\times W$
. Let
$R_{1}\cup R_{2}=W\times W$
. Let
![]() $\varphi :=p$
. We now show that
$\varphi :=p$
. We now show that
![]() . Define a valuation V such that
. Define a valuation V such that
![]() $V(p)=\{v\}$
. Then it follows that
$V(p)=\{v\}$
. Then it follows that
![]() and
and
![]() . Also, we have
. Also, we have
![]() . Consequently,
. Consequently,
![]() .
.

Fig. 5 A generalized frame (
![]() $R_{1}$
is labelled with ‘
$R_{1}$
is labelled with ‘
![]() $1$
’, and
$1$
’, and
![]() $R_{2}$
with ‘
$R_{2}$
with ‘
![]() $2$
’).
$2$
’).
Next, we show that MGM is valid on
![]() $\mathcal {F}_{g}$
. Here we only prove that formulas
$\mathcal {F}_{g}$
. Here we only prove that formulas
![]() $A3$
,
$A3$
,
![]() $A6$
and
$A6$
and
![]() ) are valid on
) are valid on
![]() $\mathcal {F}_{g}$
, and that the validity of
$\mathcal {F}_{g}$
, and that the validity of
![]() -formulas is invariant under
-formulas is invariant under
![]() $R3$
in
$R3$
in
![]() $\mathcal {F}_{g}$
.
$\mathcal {F}_{g}$
.
(1) For each
![]() $x\in \{u,v\}$
, suppose that x is
$x\in \{u,v\}$
, suppose that x is
![]() $\Box _{u}\varphi $
. Thus, x is
$\Box _{u}\varphi $
. Thus, x is
![]() $\Box \varphi $
. Since
$\Box \varphi $
. Since
![]() $R_{1}$
in the frame
$R_{1}$
in the frame
![]() $\mathcal {F}_{g}$
is reflexive, x is
$\mathcal {F}_{g}$
is reflexive, x is
![]() $\varphi $
. Consequently, x is
$\varphi $
. Consequently, x is
![]() $\Box _{u}\varphi \to \varphi $
. Thus,
$\Box _{u}\varphi \to \varphi $
. Thus,
![]() $A3$
is valid on
$A3$
is valid on
![]() $\mathcal {F}_{g}$
.
$\mathcal {F}_{g}$
.
(2) If u is
![]() , then v is
, then v is
![]() $\neg \varphi \land \neg \psi $
, i.e.,
$\neg \varphi \land \neg \psi $
, i.e.,
![]() $\neg (\varphi \lor \psi )$
. So u is
$\neg (\varphi \lor \psi )$
. So u is
![]() . Similarly, when v is
. Similarly, when v is
![]() , we can also prove that v is
, we can also prove that v is
![]() . Thus,
. Thus,
![]() $A6$
is valid on
$A6$
is valid on
![]() $\mathcal {F}_{g}$
.
$\mathcal {F}_{g}$
.
(3) Suppose that u is
![]() . Then, at least one of u and v is
. Then, at least one of u and v is
![]() . If u is
. If u is
![]() , u is
, u is
![]() $\psi $
. Thus,
$\psi $
. Thus,
![]() is true at u. If v is
is true at u. If v is
![]() , then u is
, then u is
![]() $\neg \varphi $
. So formula
$\neg \varphi $
. So formula
![]() is always true at u. Similarly, we can prove that
is always true at u. Similarly, we can prove that
![]() is also true at v.
is also true at v.
(4). Assume that
![]() $\varphi \to \psi $
is valid on
$\varphi \to \psi $
is valid on
![]() $\mathcal {F}_{g}$
. If u is
$\mathcal {F}_{g}$
. If u is
![]() , then v is
, then v is
![]() $\neg \psi \land \varphi $
, i.e.,
$\neg \psi \land \varphi $
, i.e.,
![]() $\neg (\varphi \to \psi )$
, which contradicts our assumption. Similarly, we can prove that v is also
$\neg (\varphi \to \psi )$
, which contradicts our assumption. Similarly, we can prove that v is also
![]() . Therefore the validity of
. Therefore the validity of
![]() -formulas is invariant under
-formulas is invariant under
![]() $R3$
in
$R3$
in
![]() $\mathcal {F}_{g}$
.
$\mathcal {F}_{g}$
.
Hence we conclude that all formulas provable in MGM are valid on
![]() $\mathcal {F}_{g}$
, but
$\mathcal {F}_{g}$
, but
![]() is not. Now the proof is completed.
is not. Now the proof is completed.
By Propositions 4.33 and 4.35, we can obtain the following result:
Theorem 4.36 (Incompleteness of MGM)
MGM is not complete over GM-frames.
At the end of this part, with respect to generalized frames, we show the frame-conditions characterized by formulas
![]() and
and
![]() .
.
Proposition 4.37 [Reference Goranko and Petkov8]
For any generalized frame
![]() $\mathcal {F}_{g}=\langle W,R_{1},R_{2} \rangle $
,
$\mathcal {F}_{g}=\langle W,R_{1},R_{2} \rangle $
,
![]() if and only if
if and only if
![]() .
.
Proof. From left to right, suppose for reductio that
![]() and
and
![]() . Then there are
. Then there are
![]() $w_{1},w_{2},w_{3}\in W$
such that
$w_{1},w_{2},w_{3}\in W$
such that
![]() $R_{1}w_{1}w_{2}$
,
$R_{1}w_{1}w_{2}$
,
![]() $R_{2}w_{1}w_{3}$
and
$R_{2}w_{1}w_{3}$
and
![]() $\neg R_{2}w_{2}w_{3}$
. Define a valuation V such that
$\neg R_{2}w_{2}w_{3}$
. Define a valuation V such that
![]() $V(p)=\{w\in W\mid \neg R_{2}w_{2}w\}$
. Consequently,
$V(p)=\{w\in W\mid \neg R_{2}w_{2}w\}$
. Consequently,
![]() $w_{2}$
is
$w_{2}$
is
![]() . Since
. Since
![]() $R_{1}w_{1}w_{2}$
,
$R_{1}w_{1}w_{2}$
,
![]() $w_{1}$
is
$w_{1}$
is
![]() . Consequently,
. Consequently,
![]() $w_{1}$
is
$w_{1}$
is
![]() . Then, from
. Then, from
![]() $R_{2}w_{1}w_{3}$
we know that
$R_{2}w_{1}w_{3}$
we know that
![]() $w_{3}$
is
$w_{3}$
is
![]() $\neg p$
. Therefore, it holds that
$\neg p$
. Therefore, it holds that
![]() $R_{2}w_{2}w_{3}$
, contradiction.
$R_{2}w_{2}w_{3}$
, contradiction.
From right to left, assume that
![]() . There exist a valuation V and
. There exist a valuation V and
![]() $w_{1}\in W$
such that
$w_{1}\in W$
such that
![]() . So there exists
. So there exists
![]() $w_{2}\in W$
such that
$w_{2}\in W$
such that
![]() $R_{1}w_{1}w_{2}$
and
$R_{1}w_{1}w_{2}$
and
![]() $w_{2}$
is
$w_{2}$
is
![]() . Moreover, as
. Moreover, as
![]() $w_{1}$
is
$w_{1}$
is
![]() , there exists
, there exists
![]() $w_{3}\in W$
with
$w_{3}\in W$
with
![]() $R_{2}w_{1}w_{3}$
and
$R_{2}w_{1}w_{3}$
and
![]() $w_{3}\in V(p)$
. However, since
$w_{3}\in V(p)$
. However, since
![]() $w_{2}$
and
$w_{2}$
and
![]() $w_{3}$
are, respectively,
$w_{3}$
are, respectively,
![]() and p, it holds that
and p, it holds that
![]() $\neg R_{2}w_{2}w_{3}$
. Thus,
$\neg R_{2}w_{2}w_{3}$
. Thus,
![]() . Now the proof is completed.
. Now the proof is completed.
Proposition 4.38. For each generalized frame
![]() $\mathcal {F}_{g}$
,
$\mathcal {F}_{g}$
,
![]() if and only if
if and only if
![]() .
.
Proof. Let
![]() $\mathcal {F}_{g}=\langle W,R_{1},R_{2} \rangle $
be a generalized frame. From left to right, suppose that
$\mathcal {F}_{g}=\langle W,R_{1},R_{2} \rangle $
be a generalized frame. From left to right, suppose that
![]() and
and
![]() . Then there are
. Then there are
![]() $w_{1},w_{2}\in W$
such that
$w_{1},w_{2}\in W$
such that
![]() $R_{1}w_{1}w_{2}$
,
$R_{1}w_{1}w_{2}$
,
![]() $R_{1}w_{2}w_{1}$
,
$R_{1}w_{2}w_{1}$
,
![]() $w_{1}\not =w_{2}$
and
$w_{1}\not =w_{2}$
and
![]() $\neg R_{2}w_{2}w_{1}$
. Define a valuation V such that
$\neg R_{2}w_{2}w_{1}$
. Define a valuation V such that
![]() $V(p)=\{w_{1}\}$
and
$V(p)=\{w_{1}\}$
and
![]() $V(q)=\{w_{2}\}$
. Then,
$V(q)=\{w_{2}\}$
. Then,
![]() $w_{1}$
is
$w_{1}$
is
![]() $p\land \neg q$
, and
$p\land \neg q$
, and
![]() $w_{2}$
is
$w_{2}$
is
![]() . Therefore,
. Therefore,
![]() . Consequently,
. Consequently,
![]() , which entails a contradiction.
, which entails a contradiction.
From right to left, suppose that
![]() . Then there exist a valuation V and
. Then there exist a valuation V and
![]() $w_{1}\in W$
such that
$w_{1}\in W$
such that
![]() . Therefore, there exists
. Therefore, there exists
![]() $w_{2}\in W$
such that
$w_{2}\in W$
such that
![]() $R_{1}w_{1}w_{2}$
and
$R_{1}w_{1}w_{2}$
and
![]() $w_{2}$
is
$w_{2}$
is
![]() . Also, we have
. Also, we have
![]() $w_{1}\not =w_{2}$
. Furthermore, since
$w_{1}\not =w_{2}$
. Furthermore, since
![]() $w_{2}$
is
$w_{2}$
is
![]() , we know
, we know
![]() $\neg R_{2}w_{2}w_{1}$
from
$\neg R_{2}w_{2}w_{1}$
from
![]() $w_{1}\in V(p)$
. With Definition 4.34,
$w_{1}\in V(p)$
. With Definition 4.34,
![]() $R_{1}\cup R_{2}=W\times W$
. Thus we obtain
$R_{1}\cup R_{2}=W\times W$
. Thus we obtain
![]() $R_{1}w_{2}w_{1}$
. Immediately, we conclude that
$R_{1}w_{2}w_{1}$
. Immediately, we conclude that
![]() . The proof is completed.
. The proof is completed.
4.3 Completeness of MGM
 $^{+}$
$^{+}$
We will show that MGM
![]() $^{+}$
, the extension of MGM with
$^{+}$
, the extension of MGM with
![]() , is strongly complete with respect to GM-frames. A version of this result was first given by Goranko [Reference Goranko and Petkov8, theorem 8], but, as we will show later, the proof was flawed.Footnote
21
, is strongly complete with respect to GM-frames. A version of this result was first given by Goranko [Reference Goranko and Petkov8, theorem 8], but, as we will show later, the proof was flawed.Footnote
21
In this section, we fix the proof by giving a different construction of the canonical model. First, we introduce some preliminary notions.
Definition 4.39 (Generalized canonical model)
The generalized canonical model is a tuple
![]() $\mathcal {M}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c},V^{c} \rangle$
:
$\mathcal {M}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c},V^{c} \rangle$
:
-
•
 $W^{c}$
is the class of all maximal consistent sets of
$W^{c}$
is the class of all maximal consistent sets of
 -formulas,
-formulas, -
•
 $R_{1}^{c}wv$
iff
$R_{1}^{c}wv$
iff
 $\Box w\subseteq v$
,
$\Box w\subseteq v$
, -
•
 $R_{2}^{c}wv$
iff
$R_{2}^{c}wv$
iff
 ,
, -
•
 $w\in V^{c}(p)$
iff
$w\in V^{c}(p)$
iff
 $p\in w$
,
$p\in w$
,
where
![]() $\Box w:=\{\varphi \mid \Box \varphi \in w\}$
and
$\Box w:=\{\varphi \mid \Box \varphi \in w\}$
and
![]() . In addition, since
. In addition, since
![]() , we define that
, we define that
![]() $T^{c}wv$
iff
$T^{c}wv$
iff
![]() $\Box _{u}w\subseteq v$
, where
$\Box _{u}w\subseteq v$
, where
![]() $\Box _{u}w:=\{\varphi \mid \Box _{u}\varphi \in w\}$
.
$\Box _{u}w:=\{\varphi \mid \Box _{u}\varphi \in w\}$
.
For any
![]() $w,v\in W^{c}$
, if
$w,v\in W^{c}$
, if
![]() $R_{1}^{c}wv$
, then we call v an
$R_{1}^{c}wv$
, then we call v an
![]() $R_{1}$
-subordinate set of w; if
$R_{1}$
-subordinate set of w; if
![]() $R_{2}^{c}wv$
, then v is an
$R_{2}^{c}wv$
, then v is an
![]() $R_{2}$
-subordinate set of w; and if
$R_{2}$
-subordinate set of w; and if
![]() $T^{c}wv$
, then v is a T-subordinate set of w. Also,
$T^{c}wv$
, then v is a T-subordinate set of w. Also,
![]() $\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
is the generalized canonical frame. As a routine step, we now prove the following ‘existence lemma’ for this new device:
$\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
is the generalized canonical frame. As a routine step, we now prove the following ‘existence lemma’ for this new device:
Lemma 4.40 (Existence lemma for generalized canonical frame)
For the generalized canonical frame
![]() $\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
and
$\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
and
![]() $w\in W^{c}$
, we have:
$w\in W^{c}$
, we have:
-
• If
 $\Diamond \varphi \in w$
, then there exists an
$\Diamond \varphi \in w$
, then there exists an
 $R_{1}^{c}$
-subordinate set v of w such that
$R_{1}^{c}$
-subordinate set v of w such that
 $\varphi \in v$
and
$\varphi \in v$
and -
• If
 , then there exists an
, then there exists an
 $R_{2}^{c}$
-subordinate set v of w such that
$R_{2}^{c}$
-subordinate set v of w such that
 $\neg \varphi \in v$
.
$\neg \varphi \in v$
.
Proof. 1. Assume that
![]() $\Diamond \varphi \in w$
, i.e.,
$\Diamond \varphi \in w$
, i.e.,
![]() $\neg \Box \neg \varphi \in w$
. If
$\neg \Box \neg \varphi \in w$
. If
![]() $\Box w\cup \{\varphi \}$
is inconsistent, then there exists a finite subset
$\Box w\cup \{\varphi \}$
is inconsistent, then there exists a finite subset
![]() $\{\varphi _{1},\cdots ,\varphi _{n}\} ( n\in \mathbb {N})$
of
$\{\varphi _{1},\cdots ,\varphi _{n}\} ( n\in \mathbb {N})$
of
![]() $\Box w$
such that
$\Box w$
such that
![]() . If
. If
![]() $n=0$
, then by
$n=0$
, then by
![]() $R2$
, it holds that
$R2$
, it holds that
![]() , which contradicts
, which contradicts
![]() $\neg \Box \neg \varphi \in w$
. If
$\neg \Box \neg \varphi \in w$
. If
![]() $n>0$
, then it holds that
$n>0$
, then it holds that
![]() . However, from
. However, from
![]() $\Box \varphi _{1},\ldots ,\Box \varphi _{n}\in w$
, we can obtain
$\Box \varphi _{1},\ldots ,\Box \varphi _{n}\in w$
, we can obtain
![]() $\Box \neg \varphi \in w$
, which contradicts
$\Box \neg \varphi \in w$
, which contradicts
![]() $\neg \Box \neg \varphi \in w$
. Thus,
$\neg \Box \neg \varphi \in w$
. Thus,
![]() $\Box w\cup \{\varphi \}$
is consistent. Consequently, there exists a maximal consistent set v with
$\Box w\cup \{\varphi \}$
is consistent. Consequently, there exists a maximal consistent set v with
![]() $\Box w\cup \{\varphi \}\subseteq v$
. Therefore, we conclude that w has an
$\Box w\cup \{\varphi \}\subseteq v$
. Therefore, we conclude that w has an
![]() $R_{1}^{c}$
-subordinate set v with
$R_{1}^{c}$
-subordinate set v with
![]() $\varphi \in v$
.
$\varphi \in v$
.
2. Suppose that
![]() . If
. If
![]() is inconsistent, then there exists a finite subset
is inconsistent, then there exists a finite subset
![]() $\{\varphi _{1},\ldots ,\varphi _{n}\} (n\in \mathbb {N})$
of
$\{\varphi _{1},\ldots ,\varphi _{n}\} (n\in \mathbb {N})$
of
![]() such that
such that
![]() . If
. If
![]() $n=0$
, then
$n=0$
, then
![]() , i.e.,
, i.e.,
![]() . By
. By
![]() $R3$
, it holds that
$R3$
, it holds that
![]() . From
. From
![]() $A7$
and
$A7$
and
![]() $R1$
, we know
$R1$
, we know
![]() , which contradicts
, which contradicts
![]() . If
. If
![]() $n>0$
, then by Theorem 4.26 and the rule
$n>0$
, then by Theorem 4.26 and the rule
![]() $R^{*}2$
, it holds that
$R^{*}2$
, it holds that
![]() . By Proposition 4.28, it follows that
. By Proposition 4.28, it follows that
![]() . Moreover, given Theorem 4.27, it is not hard to see that
. Moreover, given Theorem 4.27, it is not hard to see that
![]() . Therefore, we have
. Therefore, we have
![]() . However, since
. However, since
![]() , it holds that
, it holds that
![]() , which contradicts
, which contradicts
![]() . So
. So
![]() is consistent, and there exists a maximal consistent set v with
is consistent, and there exists a maximal consistent set v with
![]() . Thus, w has an
. Thus, w has an
![]() $R_{2}^{c}$
-subordinate set v such that
$R_{2}^{c}$
-subordinate set v such that
![]() $\neg \varphi \in v$
.
$\neg \varphi \in v$
.
With the result above, by a simple induction on the structure of
![]() $\varphi $
, we can show the following ‘truth lemma’ for the generalized canonical model:
$\varphi $
, we can show the following ‘truth lemma’ for the generalized canonical model:
Lemma 4.41 (Truth lemma for generalized canonical model)
For the generalized canonical model
![]() $\mathcal {M}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c},V^{c} \rangle $
,
$\mathcal {M}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c},V^{c} \rangle $
,
![]() $w\in W^{c}$
and
$w\in W^{c}$
and
![]() , it holds that
, it holds that
![]() iff
iff
![]() $\varphi \in w$
.
$\varphi \in w$
.
Now we are going to show that all axioms of MGM
![]() $^{+}$
are canonical w.r.t. its generalized canonical frame, which will be useful below. In particular, the canonicity of axioms 4 and T is obvious, and we only show the canonicity of the principles
$^{+}$
are canonical w.r.t. its generalized canonical frame, which will be useful below. In particular, the canonicity of axioms 4 and T is obvious, and we only show the canonicity of the principles
![]() and
and
![]() . With Proposition 4.37 and Proposition 4.38, we only need to show Propositions 4.42 and 4.43 below.
. With Proposition 4.37 and Proposition 4.38, we only need to show Propositions 4.42 and 4.43 below.
Proposition 4.42. Let
![]() $\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
be the generalized canonical frame such that for all
$\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
be the generalized canonical frame such that for all
![]() $w\in W^{c}$
,
$w\in W^{c}$
,
![]() . Then for any
. Then for any
![]() $w_{1},w_{2},w_{3}\in W^{c}$
, it holds that
$w_{1},w_{2},w_{3}\in W^{c}$
, it holds that
![]() $R_{1}^{c}w_{1}w_{2}\land R_{2}^{c}w_{1}w_{3}\to R_{2}^{c}w_{2}w_{3}$
.
$R_{1}^{c}w_{1}w_{2}\land R_{2}^{c}w_{1}w_{3}\to R_{2}^{c}w_{2}w_{3}$
.
Proof. Assume towards a contradiction that there are
![]() $w_{1},w_{2},w_{3}\in W^{c}$
such that
$w_{1},w_{2},w_{3}\in W^{c}$
such that
![]() $R_{1}^{c}w_{1}w_{2}\land R_{2}^{c}w_{1}w_{3}\land \neg R_{2}^{c}w_{2}w_{3}$
. Consequently, there exist formulas
$R_{1}^{c}w_{1}w_{2}\land R_{2}^{c}w_{1}w_{3}\land \neg R_{2}^{c}w_{2}w_{3}$
. Consequently, there exist formulas
![]() and
and
![]() $\varphi $
such that
$\varphi $
such that
![]() and
and
![]() $\varphi \in w_{3}$
. Also, from
$\varphi \in w_{3}$
. Also, from
![]() $R_{1}^{c}w_{1}w_{2}$
we know
$R_{1}^{c}w_{1}w_{2}$
we know
![]() . Since
. Since
![]() , it holds that
, it holds that
![]() . In addition, by
. In addition, by
![]() $R_{2}^{c}w_{1}w_{3}$
, it follows that
$R_{2}^{c}w_{1}w_{3}$
, it follows that
![]() $\neg \varphi \in w_{3}$
. Now we have arrived at a contradiction.
$\neg \varphi \in w_{3}$
. Now we have arrived at a contradiction.
Proposition 4.43. Let
![]() $\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
be the generalized canonical frame such that for all
$\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
be the generalized canonical frame such that for all
![]() $w\in W^{c}$
,
$w\in W^{c}$
,
![]() . Then for any
. Then for any
![]() $w,v\in W^{c}$
, it holds that
$w,v\in W^{c}$
, it holds that
![]() $R_{1}^{c}wv\land R_{1}^{c}vw\to R_{2}^{c}vw\lor w\equiv v$
.
$R_{1}^{c}wv\land R_{1}^{c}vw\to R_{2}^{c}vw\lor w\equiv v$
.
Proof. If not, then there are
![]() $w,v\in W^{c}$
such that
$w,v\in W^{c}$
such that
![]() $R_{1}^{c}wv\land R_{1}^{c}vw\land \neg R_{2}^{c}vw\land \neg w\equiv v$
. Since
$R_{1}^{c}wv\land R_{1}^{c}vw\land \neg R_{2}^{c}vw\land \neg w\equiv v$
. Since
![]() $\neg w\equiv v$
, there exists a formula
$\neg w\equiv v$
, there exists a formula
![]() $\psi $
such that
$\psi $
such that
![]() $\neg \psi \in w$
and
$\neg \psi \in w$
and
![]() $\psi \in v$
. By
$\psi \in v$
. By
![]() $\neg R_{2}^{c}vw$
, there exist formulas
$\neg R_{2}^{c}vw$
, there exist formulas
![]() and
and
![]() $\varphi $
such that
$\varphi $
such that
![]() and
and
![]() $\varphi \in w$
. So,
$\varphi \in w$
. So,
![]() , which contradicts the assumption.
, which contradicts the assumption.
Therefore, we now can conclude that:
Proposition 4.44. All axioms of MGM
![]() $^{+}$
are canonical w.r.t. its generalized canonical frame.
$^{+}$
are canonical w.r.t. its generalized canonical frame.
So far so good. However, when considering the relation
![]() $T^{c}$
introduced in Definition 4.39, we will face another crucial challenge, which indicates that we need further ingredients to enrich our framework. Now, to really understand the features of that relation, we introduce the following result:
$T^{c}$
introduced in Definition 4.39, we will face another crucial challenge, which indicates that we need further ingredients to enrich our framework. Now, to really understand the features of that relation, we introduce the following result:
Proposition 4.45. Let
![]() $\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
be the generalized canonical frame. Then:
$\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
be the generalized canonical frame. Then:
-
•
 $T^{c}=R_{1}^{c}\cup R_{2}^{c}$
and
$T^{c}=R_{1}^{c}\cup R_{2}^{c}$
and -
•
 $T^{c}$
is an equivalence relation.
$T^{c}$
is an equivalence relation.
Proof. 1. We now prove that
![]() $T^{c}=R_{1}^{c}\cup R_{2}^{c}$
. From left to right, suppose that there exist
$T^{c}=R_{1}^{c}\cup R_{2}^{c}$
. From left to right, suppose that there exist
![]() $w,v\in W^{c}$
such that
$w,v\in W^{c}$
such that
![]() $T^{c}wv$
,
$T^{c}wv$
,
![]() $\neg R_{1}^{c}wv$
and
$\neg R_{1}^{c}wv$
and
![]() $\neg R_{2}^{c}wv$
. Then it holds that
$\neg R_{2}^{c}wv$
. Then it holds that
![]() $\Box _{u} w\subseteq v$
,
$\Box _{u} w\subseteq v$
,
![]() $\Box w\not \subseteq v$
and
$\Box w\not \subseteq v$
and
![]() . So there exist
. So there exist
![]() such that
such that
![]() $\varphi ,\psi \not \in v$
. Since both w and v are maximal consistent sets, we have
$\varphi ,\psi \not \in v$
. Since both w and v are maximal consistent sets, we have
![]() and
and
![]() $\neg \varphi \land \neg \psi \in v$
. Furthermore, by Proposition 4.29, it holds that
$\neg \varphi \land \neg \psi \in v$
. Furthermore, by Proposition 4.29, it holds that
![]() $\Box _{u}(\neg \psi \to \varphi )\in w$
. However, from
$\Box _{u}(\neg \psi \to \varphi )\in w$
. However, from
![]() $\Box _{u} w\subseteq v$
, we know
$\Box _{u} w\subseteq v$
, we know
![]() $\neg \psi \to \varphi \in v$
, which contradicts
$\neg \psi \to \varphi \in v$
, which contradicts
![]() $\neg \varphi \land \neg \psi \in v$
.
$\neg \varphi \land \neg \psi \in v$
.
From right to left, we first consider the case that there exist
![]() $w,v\in W^{c}$
with
$w,v\in W^{c}$
with
![]() $R_{1}^{c}wv$
and
$R_{1}^{c}wv$
and
![]() $\neg T^{c}wv$
. Then we have
$\neg T^{c}wv$
. Then we have
![]() $\Box w\subseteq v$
and
$\Box w\subseteq v$
and
![]() $\Box _{u} w\not \subseteq v$
. So there exist
$\Box _{u} w\not \subseteq v$
. So there exist
![]() $\Box _{u}\varphi \in w$
and
$\Box _{u}\varphi \in w$
and
![]() $\neg \varphi \in v$
. However, from
$\neg \varphi \in v$
. However, from
![]() ,
,
![]() $\Box \varphi \in w$
and
$\Box \varphi \in w$
and
![]() $\neg \varphi \in v$
, we obtain
$\neg \varphi \in v$
, we obtain
![]() $\neg R_{1}^{c}wv$
, which entails a contradiction. Similarly, when
$\neg R_{1}^{c}wv$
, which entails a contradiction. Similarly, when
![]() $R_{2}^{c}wv$
, we can also obtain
$R_{2}^{c}wv$
, we can also obtain
![]() $T^{c}wv$
.
$T^{c}wv$
.
2. Next we show that
![]() $T^{c}$
is an equivalence relation. For each
$T^{c}$
is an equivalence relation. For each
![]() $w\in W^{c}$
, if
$w\in W^{c}$
, if
![]() $\Box _{u}\varphi \in w$
, then by
$\Box _{u}\varphi \in w$
, then by
![]() $A3$
, we have
$A3$
, we have
![]() $\varphi \in w$
. Thus
$\varphi \in w$
. Thus
![]() $T^{c}$
is reflexive. For any
$T^{c}$
is reflexive. For any
![]() $w_{1},w_{2},w_{3}\in W^{c}$
, if
$w_{1},w_{2},w_{3}\in W^{c}$
, if
![]() $T^{c}w_{1}w_{2}$
and
$T^{c}w_{1}w_{2}$
and
![]() $T^{c}w_{2}w_{3}$
, then
$T^{c}w_{2}w_{3}$
, then
![]() $\Box _{u} w_{1}\subseteq w_{2}$
and
$\Box _{u} w_{1}\subseteq w_{2}$
and
![]() $\Box _{u} w_{2}\subseteq w_{3}$
. For each
$\Box _{u} w_{2}\subseteq w_{3}$
. For each
![]() $\Box _{u}\varphi \in w_{1}$
, by
$\Box _{u}\varphi \in w_{1}$
, by
![]() $A4$
it follows
$A4$
it follows
![]() $\Box _{u}\Box _{u}\varphi \in w_{1}$
. Consequently,
$\Box _{u}\Box _{u}\varphi \in w_{1}$
. Consequently,
![]() $\Box _{u}\varphi \in w_{2}$
. Then we have
$\Box _{u}\varphi \in w_{2}$
. Then we have
![]() $\varphi \in w_{3}$
, i.e.,
$\varphi \in w_{3}$
, i.e.,
![]() $T^{c}w_{1}w_{3}$
. So,
$T^{c}w_{1}w_{3}$
. So,
![]() $T^{c}$
is transitive. For any
$T^{c}$
is transitive. For any
![]() $w,v\in W^{c}$
, if
$w,v\in W^{c}$
, if
![]() $T^{c}wv$
and
$T^{c}wv$
and
![]() $\neg T^{c}vw$
, then
$\neg T^{c}vw$
, then
![]() $\Box _{u}w\subseteq v$
and
$\Box _{u}w\subseteq v$
and
![]() $\Box _{u}v\not \subseteq w$
. By
$\Box _{u}v\not \subseteq w$
. By
![]() $\Box _{u}v\not \subseteq w$
, there exists
$\Box _{u}v\not \subseteq w$
, there exists
![]() $\varphi $
such that
$\varphi $
such that
![]() $\Box _{u}\varphi \in v$
and
$\Box _{u}\varphi \in v$
and
![]() $\varphi \not \in w$
. Since both w and v are maximal consistent sets, we have
$\varphi \not \in w$
. Since both w and v are maximal consistent sets, we have
![]() $\Diamond _{u}\neg \varphi \not \in v$
and
$\Diamond _{u}\neg \varphi \not \in v$
and
![]() $\neg \varphi \in w$
. Moreover, from
$\neg \varphi \in w$
. Moreover, from
![]() $\neg \varphi \in w$
and
$\neg \varphi \in w$
and
![]() $A5$
, it follows that
$A5$
, it follows that
![]() $\Box _{u}\Diamond _{u}\neg \varphi \in w$
. Furthermore,
$\Box _{u}\Diamond _{u}\neg \varphi \in w$
. Furthermore,
![]() $\Diamond _{u}\neg \varphi \in v$
follows from
$\Diamond _{u}\neg \varphi \in v$
follows from
![]() $T^{c}wv$
, which entails contradiction. Therefore, the relation
$T^{c}wv$
, which entails contradiction. Therefore, the relation
![]() $T^{c}$
is symmetric. Now the proof is completed.
$T^{c}$
is symmetric. Now the proof is completed.
Intuitively, the results in Proposition 4.45 are in line with the definition of
![]() $T^{c}$
and our axioms for the universal modality
$T^{c}$
and our axioms for the universal modality
![]() $\Box _{u}$
. However, although
$\Box _{u}$
. However, although
![]() $T^{c}$
forms a partition of the domain
$T^{c}$
forms a partition of the domain
![]() $W^{c}$
, it does not necessarily ‘cover’ the whole model, in the sense that the relation
$W^{c}$
, it does not necessarily ‘cover’ the whole model, in the sense that the relation
![]() $T^{c}$
may be not a total relation, i.e.,
$T^{c}$
may be not a total relation, i.e.,
![]() $T^{c}\not =W^{c}\times W^{c}$
. In other words, generally the occurrence of a formula
$T^{c}\not =W^{c}\times W^{c}$
. In other words, generally the occurrence of a formula
![]() $\Box _{u}\varphi $
in one maximal consistent set cannot guarantee that
$\Box _{u}\varphi $
in one maximal consistent set cannot guarantee that
![]() $\varphi $
occurs in all maximal consistent sets. This definitely has a different spirit with the universal modality that is intended to quantify all objects in a given model. So, the generalized canonical model looks too large. But, how to make it ‘smaller’? To deal with this, following [Reference Gargov, Passy, Tinchev and Skordev6], we introduce a notion of ‘generated generalized canonical model’ as follows:Footnote
22
$\varphi $
occurs in all maximal consistent sets. This definitely has a different spirit with the universal modality that is intended to quantify all objects in a given model. So, the generalized canonical model looks too large. But, how to make it ‘smaller’? To deal with this, following [Reference Gargov, Passy, Tinchev and Skordev6], we introduce a notion of ‘generated generalized canonical model’ as follows:Footnote
22
Definition 4.46 (Generated generalized canonical model)
For the generalized canonical model
![]() $\mathcal {M}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c},V^{c} \rangle $
and
$\mathcal {M}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c},V^{c} \rangle $
and
![]() $w\in W^{c}$
, we say
$w\in W^{c}$
, we say
![]() $\mathcal {M}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c},V^{c}_{w} \rangle $
is its generated generalized canonical model, when
$\mathcal {M}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c},V^{c}_{w} \rangle $
is its generated generalized canonical model, when
-
•
 $W^{c}_{w}=\{v\in W^{c}\mid T^{c}wv\}$
,
$W^{c}_{w}=\{v\in W^{c}\mid T^{c}wv\}$
, -
•
 $R_{1w}^{c}= R_{1}^{c}\cap (W{^{c}_{w}}\times W{^{c}_{w}})$
,
$R_{1w}^{c}= R_{1}^{c}\cap (W{^{c}_{w}}\times W{^{c}_{w}})$
, -
•
 $R_{2w}^{c}= R_{2}^{c}\cap (W{^{c}_{w}}\times W{^{c}_{w}})$
, and
$R_{2w}^{c}= R_{2}^{c}\cap (W{^{c}_{w}}\times W{^{c}_{w}})$
, and -
•
 $V^{c}_{w}(p)=V^{c}(p)\cap W^{c}_{w}$
.
$V^{c}_{w}(p)=V^{c}(p)\cap W^{c}_{w}$
.
We call
![]() $\mathcal {F}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c} \rangle $
a generated generalized canonical frame. Also, define
$\mathcal {F}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c} \rangle $
a generated generalized canonical frame. Also, define
![]() $T^{c}_{w}:=\{v\in W^{c}\mid T^{c}wv\}$
. Then, in the generated generalized canonical frame, it holds that
$T^{c}_{w}:=\{v\in W^{c}\mid T^{c}wv\}$
. Then, in the generated generalized canonical frame, it holds that
![]() $R_{1w}^{c}\cup R_{2w}^{c}= T^{c}_{w}=W{^{c}_{w}}\times W{^{c}_{w}}$
(recall Proposition 4.45). Furthermore, it is not hard to see the following desirable observation: for any
$R_{1w}^{c}\cup R_{2w}^{c}= T^{c}_{w}=W{^{c}_{w}}\times W{^{c}_{w}}$
(recall Proposition 4.45). Furthermore, it is not hard to see the following desirable observation: for any
![]() $v\in W^{c}_{w}$
and
$v\in W^{c}_{w}$
and
![]() $\Box _{u}\varphi $
, when
$\Box _{u}\varphi $
, when
![]() $\Box _{u}\varphi \in v$
, we have
$\Box _{u}\varphi \in v$
, we have
![]() $\varphi \in o$
for any
$\varphi \in o$
for any
![]() $o\in W^{c}_{w}$
. Here it is important to recognize that both the existence lemma (Lemma 4.40) and the truth lemma (Lemma 4.41) for the generalized canonical model also apply to the generated generalized canonical model.
$o\in W^{c}_{w}$
. Here it is important to recognize that both the existence lemma (Lemma 4.40) and the truth lemma (Lemma 4.41) for the generalized canonical model also apply to the generated generalized canonical model.
Lemma 4.47 (Existence lemma for generated generalized canonical frame)
For the generated generalized canonical frame
![]() $\mathcal {F}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c} \rangle $
and
$\mathcal {F}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c} \rangle $
and
![]() $s\in W^{c}_{w}$
, we have:
$s\in W^{c}_{w}$
, we have:
-
• If
 $\Diamond \varphi \in s$
, then there exists some
$\Diamond \varphi \in s$
, then there exists some
 $t\in W^{c}_{w}$
such that
$t\in W^{c}_{w}$
such that
 $R_{1w}^{c}st$
and
$R_{1w}^{c}st$
and
 $\varphi \in t$
and
$\varphi \in t$
and -
• If
 , then there exists some
, then there exists some
 $t\in W^{c}_{w}$
such that
$t\in W^{c}_{w}$
such that
 $R_{2w}^{c}st$
and
$R_{2w}^{c}st$
and
 $\neg \varphi \in v$
.
$\neg \varphi \in v$
.
Proof. Instead of a precise proof for the result, we merely give a few hints why we still have the results for the generated generalized canonical frame. Let
![]() $\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
be the generalized canonical frame,
$\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
be the generalized canonical frame,
![]() $w\in W^{c}$
, and
$w\in W^{c}$
, and
![]() $\mathcal {F}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c} \rangle $
the generated generalized canonical frame. Let
$\mathcal {F}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c} \rangle $
the generated generalized canonical frame. Let
![]() $s\in W^{c}_{w}$
and
$s\in W^{c}_{w}$
and
![]() .
.
Let
![]() $\Diamond \varphi \in s$
. With Lemma 4.40, there exists some
$\Diamond \varphi \in s$
. With Lemma 4.40, there exists some
![]() $t\in W^{c}$
such that
$t\in W^{c}$
such that
![]() $R_{1}^{c}st$
and
$R_{1}^{c}st$
and
![]() $\varphi \in t$
. Therefore, by Proposition 4.45, it follows that
$\varphi \in t$
. Therefore, by Proposition 4.45, it follows that
![]() $T^{c}ws$
and
$T^{c}ws$
and
![]() $T^{c}wt$
. So,
$T^{c}wt$
. So,
![]() $t\in W^{c}_{w}$
. Now, it is easy to see
$t\in W^{c}_{w}$
. Now, it is easy to see
![]() $R_{1w}^{c}st$
. Similarly, we can show the case for
$R_{1w}^{c}st$
. Similarly, we can show the case for
![]() .
.
Lemma 4.48 (Truth lemma for generated generalized canonical model)
For the generated generalized canonical model
![]() $\mathcal {M}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c},V^{c}_{w} \rangle $
,
$\mathcal {M}_{gw}^{c}=\langle W^{c}_{w},R_{1w}^{c},R_{2w}^{c},V^{c}_{w} \rangle $
,
![]() $s\in W^{c}_{w}$
and
$s\in W^{c}_{w}$
and
![]() , it holds that
, it holds that
![]() iff
iff
![]() $\varphi \in s$
.
$\varphi \in s$
.
Similar to that for the generalized canonical model, this can be proved with the help of Lemma 4.47, and we omit the details here. Moreover, for any formula
![]() $\varphi $
and
$\varphi $
and
![]() $u\in W^{c}_{w}$
, it holds that
$u\in W^{c}_{w}$
, it holds that
![]() if and only if
if and only if
![]() . We leave its proof to the reader.
. We leave its proof to the reader.
Note that we have already shown the canonicity of the axioms in MGM
![]() $^{+}$
(Proposition 4.44). As noted by Goranko [Reference Goranko and Petkov8], if the axioms of a logical system X in
$^{+}$
(Proposition 4.44). As noted by Goranko [Reference Goranko and Petkov8], if the axioms of a logical system X in
![]() are canonical, we can prove its completeness by making an extension
are canonical, we can prove its completeness by making an extension
![]() $\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
Footnote
23
of its generated generalized canonical frame
$\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
Footnote
23
of its generated generalized canonical frame
![]() $\mathcal {F}^{c}_{gw}=\langle W_{w}^{c},R^{c}_{1w},R^{c}_{2w} \rangle $
, where
$\mathcal {F}^{c}_{gw}=\langle W_{w}^{c},R^{c}_{1w},R^{c}_{2w} \rangle $
, where
![]() $\mathcal {F}$
satisfies the frame-conditions of
$\mathcal {F}$
satisfies the frame-conditions of
![]() $\mathcal {F}^{c}_{gw}$
, and
$\mathcal {F}^{c}_{gw}$
, and
-
•
 $\mathcal {W}=\bigcup \limits _{v\in W_{w}^{c}}\{v\}\times I_{v}$
, where
$\mathcal {W}=\bigcup \limits _{v\in W_{w}^{c}}\{v\}\times I_{v}$
, where
 $I_{v}$
is an index set for each
$I_{v}$
is an index set for each
 $v\in W_{w}^{c}$
, and
$v\in W_{w}^{c}$
, and -
•
 $\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
iff for any
$\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
iff for any
 $s,t\in W_{w}^{c}$
,
$s,t\in W_{w}^{c}$
,
 $R_{1w}^{c}st\land (R_{2w}^{c}st\Rightarrow S\langle s,i \rangle \langle t,j \rangle )$
, where S is a binary relation s.t.
$R_{1w}^{c}st\land (R_{2w}^{c}st\Rightarrow S\langle s,i \rangle \langle t,j \rangle )$
, where S is a binary relation s.t.
 $R_{1w}^{c}st\land R_{2w}^{c}st\Rightarrow \forall i\in I_{s}(\exists j\in I_{t}\;S\langle s,i \rangle \langle t,j \rangle \land \exists j\in I_{t}\;\neg S\langle s,i \rangle \langle t,j \rangle )$
.
$R_{1w}^{c}st\land R_{2w}^{c}st\Rightarrow \forall i\in I_{s}(\exists j\in I_{t}\;S\langle s,i \rangle \langle t,j \rangle \land \exists j\in I_{t}\;\neg S\langle s,i \rangle \langle t,j \rangle )$
.
The index set
![]() $I_{v}$
in the definition of
$I_{v}$
in the definition of
![]() $\mathcal {W}$
makes copies of objects in
$\mathcal {W}$
makes copies of objects in
![]() $W_{w}^{c}$
, in order to separate pairs of objects which are connected by both
$W_{w}^{c}$
, in order to separate pairs of objects which are connected by both
![]() $R_{1w}^{c}$
and
$R_{1w}^{c}$
and
![]() $R_{2w}^{c}$
. Essentially, the second condition above is to ensure that, if
$R_{2w}^{c}$
. Essentially, the second condition above is to ensure that, if
![]() $R_{1w}^{c}st$
and
$R_{1w}^{c}st$
and
![]() $R_{2w}^{c}st$
, then for all
$R_{2w}^{c}st$
, then for all
![]() $i\in I_{s}$
, there exist
$i\in I_{s}$
, there exist
![]() $j,j^{\prime }\in I_{t}$
with
$j,j^{\prime }\in I_{t}$
with
![]() $\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
and
$\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
and
![]() $\neg \mathcal {R}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. With the definition of
$\neg \mathcal {R}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. With the definition of
![]() $\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
, when
$\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
, when
![]() $\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
, we have
$\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
, we have
![]() $R_{1w}^{c}st$
. On the other hand, since
$R_{1w}^{c}st$
. On the other hand, since
![]() $R_{1w}^{c}\cup R_{2w}^{c}$
is a total relation, i.e.,
$R_{1w}^{c}\cup R_{2w}^{c}$
is a total relation, i.e.,
![]() $R_{1w}^{c}\cup R_{2w}^{c}=W{^{c}_{w}}\times W{^{c}_{w}}$
, it is easy to see that
$R_{1w}^{c}\cup R_{2w}^{c}=W{^{c}_{w}}\times W{^{c}_{w}}$
, it is easy to see that
![]() $\neg \mathcal {R}\langle s,i \rangle \langle t,j \rangle $
is equivalent to
$\neg \mathcal {R}\langle s,i \rangle \langle t,j \rangle $
is equivalent to
![]() $R_{2w}^{c}st\land (R_{1w}^{c}st\Rightarrow \neg S\langle s,i \rangle \langle t,j \rangle )$
.
$R_{2w}^{c}st\land (R_{1w}^{c}st\Rightarrow \neg S\langle s,i \rangle \langle t,j \rangle )$
.
Let
![]() $\mathcal {F}_{g}=\langle W,R_{1},R_{2} \rangle $
be a generalized frame and
$\mathcal {F}_{g}=\langle W,R_{1},R_{2} \rangle $
be a generalized frame and
![]() $w\in W$
. Following [Reference Goranko and Petkov8, p. 317], we say that w has an entry defect (
$w\in W$
. Following [Reference Goranko and Petkov8, p. 317], we say that w has an entry defect (
![]() $d_{i}(w)$
), if there exists
$d_{i}(w)$
), if there exists
![]() $v\in W$
such that
$v\in W$
such that
![]() $R_{1}vw$
and
$R_{1}vw$
and
![]() $R_{2}vw$
. Furthermore, define
$R_{2}vw$
. Furthermore, define
![]() $D_{i}(W):=\{w\in W\mid d_{i}(w)\}$
.
$D_{i}(W):=\{w\in W\mid d_{i}(w)\}$
.
If
![]() $\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
is the generalized canonical frame such that for each
$\mathcal {F}_{g}^{c}=\langle W^{c},R_{1}^{c},R_{2}^{c} \rangle $
is the generalized canonical frame such that for each
![]() $w\in W^{c}$
,
$w\in W^{c}$
,
![]() , then by Proposition 4.42, for all
, then by Proposition 4.42, for all
![]() $v\in D_{i}(W_{w}^{c})$
, it holds that
$v\in D_{i}(W_{w}^{c})$
, it holds that
![]() $R_{2w}^{c}vv$
.
$R_{2w}^{c}vv$
.
As mentioned above, [Reference Goranko and Petkov8, theorem 13(ii)] showed the completeness of a version of MGM
![]() $^{+}$
, but the proof is flawed as shown below. Let
$^{+}$
, but the proof is flawed as shown below. Let
![]() $\mathcal {F}^{c}_{gw}=\langle W_{w}^{c},R^{c}_{1w},R^{c}_{2w} \rangle $
be a generated generalized canonical frame of MGM
$\mathcal {F}^{c}_{gw}=\langle W_{w}^{c},R^{c}_{1w},R^{c}_{2w} \rangle $
be a generated generalized canonical frame of MGM
![]() $^{+}$
. By [Reference Goranko and Petkov8],
$^{+}$
. By [Reference Goranko and Petkov8],
![]() $\mathcal {F}^{c}_{gw}$
is extended to
$\mathcal {F}^{c}_{gw}$
is extended to
![]() $\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
where:
$\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
where:
-
•
 $\mathcal {W}=W_{w}^{c}\times \{0\}\cup D_{i}(W_{w}^{c})\times \mathbb {Z}$
and
$\mathcal {W}=W_{w}^{c}\times \{0\}\cup D_{i}(W_{w}^{c})\times \mathbb {Z}$
and -
•
 $S\langle s,i \rangle \langle t,j \rangle $
iff
$S\langle s,i \rangle \langle t,j \rangle $
iff
 $(Est\land (i<j\lor (i=j\land s\le ^{\prime } t)))\lor (\neg Est\land j\ge 0)$
, where
$(Est\land (i<j\lor (i=j\land s\le ^{\prime } t)))\lor (\neg Est\land j\ge 0)$
, where
 $\le ^{\prime }$
is some linear order in
$\le ^{\prime }$
is some linear order in
 $W_{w}^{c}$
, and
$W_{w}^{c}$
, and
 $Est:=R^{c}_{1w}st\land R^{c}_{1w}ts$
.
$Est:=R^{c}_{1w}st\land R^{c}_{1w}ts$
.
However, the following example shows that the frame
![]() $\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
defined above is not a partial order. More specifically, it is not transitive.
$\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
defined above is not a partial order. More specifically, it is not transitive.
Example 4.49. Let
![]() $w_{1}, w_{2}, w_{3}\in D_{i}(W_{w}^{c})$
. Then for any
$w_{1}, w_{2}, w_{3}\in D_{i}(W_{w}^{c})$
. Then for any
![]() $j\in \{1,2,3\}$
, we have
$j\in \{1,2,3\}$
, we have
![]() $R_{2w}^{c}w_{j}w_{j}$
. Also, since
$R_{2w}^{c}w_{j}w_{j}$
. Also, since
![]() $\mathcal {F}^{c}_{gw}$
is the generated generalized canonical frame of MGM
$\mathcal {F}^{c}_{gw}$
is the generated generalized canonical frame of MGM
![]() $^{+}$
, the relation
$^{+}$
, the relation
![]() $R_{1w}^{c}$
is reflexive. Moreover, consider the following situation
$R_{1w}^{c}$
is reflexive. Moreover, consider the following situation
![]() $s$
:
$s$
:
-
•
 $R_{1w}^{c}w_{1}w_{2}$
,
$R_{1w}^{c}w_{1}w_{2}$
,
 $\neg R_{2w}^{c}w_{1}w_{2}$
,
$\neg R_{2w}^{c}w_{1}w_{2}$
,
 $R_{1w}^{c}w_{1}w_{3}$
,
$R_{1w}^{c}w_{1}w_{3}$
,
 $R_{2w}^{c}w_{1}w_{3} ;$
$R_{2w}^{c}w_{1}w_{3} ;$
-
•
 $R_{1w}^{c}w_{2}w_{3}$
,
$R_{1w}^{c}w_{2}w_{3}$
,
 $R_{2w}^{c}w_{2}w_{3}$
,
$R_{2w}^{c}w_{2}w_{3}$
,
 $\neg R_{1w}^{c}w_{2}w_{1}$
,
$\neg R_{1w}^{c}w_{2}w_{1}$
,
 $R_{2w}^{c}w_{2}w_{1} ;$
and
$R_{2w}^{c}w_{2}w_{1} ;$
and -
•
 $R_{1w}^{c}w_{3}w_{2}$
,
$R_{1w}^{c}w_{3}w_{2}$
,
 $R_{2w}^{c}w_{3}w_{2}$
,
$R_{2w}^{c}w_{3}w_{2}$
,
 $\neg R_{1w}^{c}w_{3}w_{1}$
,
$\neg R_{1w}^{c}w_{3}w_{1}$
,
 $R_{2w}^{c}w_{3}w_{1}$
.
$R_{2w}^{c}w_{3}w_{1}$
.
The relations
![]() $R_{1w}^{c}$
and
$R_{1w}^{c}$
and
![]() $R_{2w}^{c}$
are depicted in Figure 6. For any
$R_{2w}^{c}$
are depicted in Figure 6. For any
![]() $i,j\in \{1,2,3\}$
, we have
$i,j\in \{1,2,3\}$
, we have
![]() $R_{1w}^{c}w_{i}w_{j}$
or
$R_{1w}^{c}w_{i}w_{j}$
or
![]() $R_{2w}^{c}w_{i}w_{j}$
. However, with the definition of
$R_{2w}^{c}w_{i}w_{j}$
. However, with the definition of
![]() $\mathcal {R}$
defined in [Reference Goranko and Petkov8], it holds that
$\mathcal {R}$
defined in [Reference Goranko and Petkov8], it holds that
![]() $\mathcal {R}\langle w_{1},1 \rangle \langle w_{2},-2 \rangle $
,
$\mathcal {R}\langle w_{1},1 \rangle \langle w_{2},-2 \rangle $
,
![]() $\mathcal {R}\langle w_{2},-2 \rangle \langle w_{3},-1 \rangle $
and
$\mathcal {R}\langle w_{2},-2 \rangle \langle w_{3},-1 \rangle $
and
![]() $\neg \mathcal {R}\langle w_{1},1 \rangle \langle w_{3},-1 \rangle $
. Thus the frame is not transitive.
$\neg \mathcal {R}\langle w_{1},1 \rangle \langle w_{3},-1 \rangle $
. Thus the frame is not transitive.

Fig. 6 A counterexample (
![]() $R_{1w}^{c}$
and
$R_{1w}^{c}$
and
![]() $R_{2w}^{c}$
are labelled with ‘
$R_{2w}^{c}$
are labelled with ‘
![]() $1$
’ and ‘
$1$
’ and ‘
![]() $2$
’, respectively).
$2$
’, respectively).
To fix the problem, we extend the generated generalized canonical frame of MGM
![]() $^{+}$
by giving a different S. Although this S still cannot establish the transitivity of the relation in the canonical frame directly, it is close enough to ease our later construction by taking the transitive closure.
$^{+}$
by giving a different S. Although this S still cannot establish the transitivity of the relation in the canonical frame directly, it is close enough to ease our later construction by taking the transitive closure.
Definition 4.50. Given the generated generalized canonical frame of MGM
![]() $^{+} \mathcal {F}^{c}_{gw}=\langle W_{w}^{c},R^{c}_{1w},R^{c}_{2w} \rangle $
, we define the frame
$^{+} \mathcal {F}^{c}_{gw}=\langle W_{w}^{c},R^{c}_{1w},R^{c}_{2w} \rangle $
, we define the frame
![]() $\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
where:
$\mathcal {F}=\langle \mathcal {W},\mathcal {R} \rangle $
where:
-
•
 $\mathcal {W}=W_{w}^{c}\times \{0\}\cup D_{i}(W_{w}^{c})\times \mathbb {Z}$
and
$\mathcal {W}=W_{w}^{c}\times \{0\}\cup D_{i}(W_{w}^{c})\times \mathbb {Z}$
and -
•
 $\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
iff for any
$\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
iff for any
 $s,t\in W_{w}^{c}$
,
$s,t\in W_{w}^{c}$
,
 $R_{1w}^{c}st\land (R_{2w}^{c}st\Rightarrow S\langle s,i \rangle \langle t,j \rangle )$
where:
$R_{1w}^{c}st\land (R_{2w}^{c}st\Rightarrow S\langle s,i \rangle \langle t,j \rangle )$
where: $$ \begin{align*}S\langle s,i \rangle\langle t,j \rangle \text{ iff } (i<j\land j/2\in \mathbb{Z})\lor(s=t\land i=j).\end{align*} $$
$$ \begin{align*}S\langle s,i \rangle\langle t,j \rangle \text{ iff } (i<j\land j/2\in \mathbb{Z})\lor(s=t\land i=j).\end{align*} $$
S tells us how we should connect
![]() $\langle s,i \rangle $
and
$\langle s,i \rangle $
and
![]() $\langle t,j \rangle $
when
$\langle t,j \rangle $
when
![]() $R_{1w}^{c}st$
and
$R_{1w}^{c}st$
and
![]() $R_{2w}^{c}st$
. S defined above is reflexive, and it connects
$R_{2w}^{c}st$
. S defined above is reflexive, and it connects
![]() $\langle s,i \rangle $
and
$\langle s,i \rangle $
and
![]() $\langle t,j \rangle $
if j is even and i is smaller than j.
$\langle t,j \rangle $
if j is even and i is smaller than j.
Let
![]() $\mathcal {F}^{+}=\langle \mathcal {W},\mathcal {R}^{+} \rangle $
be the transitive closure of the frame
$\mathcal {F}^{+}=\langle \mathcal {W},\mathcal {R}^{+} \rangle $
be the transitive closure of the frame
![]() $\mathcal {F}$
defined in Definition 4.50. We will use
$\mathcal {F}$
defined in Definition 4.50. We will use
![]() $\mathcal {F}^{+}$
instead of
$\mathcal {F}^{+}$
instead of
![]() $\mathcal {F}$
to show the completeness. Before the completeness proof we need the following crucial lemma about when we really need to add edges according to the transitive closure.
$\mathcal {F}$
to show the completeness. Before the completeness proof we need the following crucial lemma about when we really need to add edges according to the transitive closure.
Lemma 4.51. If there is an
![]() $\mathcal {R}$
-path
$\mathcal {R}$
-path
![]() $\langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle \dots \langle s_{k}, i_{k} \rangle $
in
$\langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle \dots \langle s_{k}, i_{k} \rangle $
in
![]() $\mathcal {F} ($
i.e., for all
$\mathcal {F} ($
i.e., for all
![]() $1\leq j<k$
,
$1\leq j<k$
,
![]() $\mathcal {R} \langle s_{j}, i_{j} \rangle \langle s_{j+1}, i_{j+1} \rangle )$
where
$\mathcal {R} \langle s_{j}, i_{j} \rangle \langle s_{j+1}, i_{j+1} \rangle )$
where
![]() $3\leq k$
such that it is not the case that
$3\leq k$
such that it is not the case that
![]() $\mathcal {R}\langle s_{1}, i_{1} \rangle \langle s_{k}, i_{k} \rangle $
, then there exists
$\mathcal {R}\langle s_{1}, i_{1} \rangle \langle s_{k}, i_{k} \rangle $
, then there exists
![]() $\langle s_{m}, i_{m} \rangle $
for some
$\langle s_{m}, i_{m} \rangle $
for some
![]() $m<k$
such that:
$m<k$
such that:
-
•
 $\mathcal {R}\langle s_{1}, i_{1} \rangle \langle s_{m}, i_{m} \rangle $
and
$\mathcal {R}\langle s_{1}, i_{1} \rangle \langle s_{m}, i_{m} \rangle $
and
 $\mathcal {R}\langle s_{m}, i_{m} \rangle \langle s_{k}, i_{k} \rangle $
in
$\mathcal {R}\langle s_{m}, i_{m} \rangle \langle s_{k}, i_{k} \rangle $
in
 $\mathcal {F}$
, and
$\mathcal {F}$
, and -
•
 $R_{1w}^{c}s_{1}s_{m}$
,
$R_{1w}^{c}s_{1}s_{m}$
,
 $R_{1w}^{c}s_{m}s_{k}$
,
$R_{1w}^{c}s_{m}s_{k}$
,
 $R_{2w}^{c}s_{1}s_{k}$
,
$R_{2w}^{c}s_{1}s_{k}$
,
 $R_{2w}^{c}s_{m}s_{k}$
but not
$R_{2w}^{c}s_{m}s_{k}$
but not
 $R_{2w}^{c}s_{1}s_{m}$
in
$R_{2w}^{c}s_{1}s_{m}$
in
 $\mathcal {F}^{c}_{gw}$
.
$\mathcal {F}^{c}_{gw}$
.
Proof. We first prove the result given
![]() $k=3$
and then show the general case can be reduced to this basic case.
$k=3$
and then show the general case can be reduced to this basic case.
Suppose
![]() $\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle $
,
$\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle $
,
![]() $\mathcal {R} \langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
, but not
$\mathcal {R} \langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
, but not
![]() $\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
. Then by the definition of
$\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
. Then by the definition of
![]() $\mathcal {R}$
,
$\mathcal {R}$
,
![]() $R_{1w}^{c}s_{1}s_{2}$
and
$R_{1w}^{c}s_{1}s_{2}$
and
![]() $R_{1w}^{c}s_{2}s_{3}$
. By the canonicity of Axiom 4 w.r.t. the generalized canonical
$R_{1w}^{c}s_{2}s_{3}$
. By the canonicity of Axiom 4 w.r.t. the generalized canonical
![]() $\mathcal {F}^{c}_{gw}$
, we have
$\mathcal {F}^{c}_{gw}$
, we have
![]() $R_{1w}^{c}s_{1}s_{3}$
. In the following, we show that
$R_{1w}^{c}s_{1}s_{3}$
. In the following, we show that
![]() $R_{2w}^{c}s_{1}s_{3}$
,
$R_{2w}^{c}s_{1}s_{3}$
,
![]() $R_{2w}^{c}s_{2}s_{3}$
but not
$R_{2w}^{c}s_{2}s_{3}$
but not
![]() $R_{2w}^{c}s_{1}s_{2}$
, namely, the edges between
$R_{2w}^{c}s_{1}s_{2}$
, namely, the edges between
![]() $s_{1}, s_{2}, s_{3}$
are illustrated as below:
$s_{1}, s_{2}, s_{3}$
are illustrated as below:

where we label
![]() $R_{1w}^{c}$
and
$R_{1w}^{c}$
and
![]() $R_{2w}^{c}$
with ‘
$R_{2w}^{c}$
with ‘
![]() $1$
’ and ‘
$1$
’ and ‘
![]() $2$
’, respectively, in the graph, and omit the reflexive links.
$2$
’, respectively, in the graph, and omit the reflexive links.
Since it is not the case that
![]() $\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
but
$\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
but
![]() $R_{1w}^{c}s_{1}s_{3}$
, by the definition of
$R_{1w}^{c}s_{1}s_{3}$
, by the definition of
![]() $\mathcal {R}$
we have
$\mathcal {R}$
we have
![]() $R_{2w}^{c}s_{1}s_{3}$
. Now since
$R_{2w}^{c}s_{1}s_{3}$
. Now since
![]() $R_{1w}^{c}s_{1}s_{2}$
, by Proposition 4.37 we have
$R_{1w}^{c}s_{1}s_{2}$
, by Proposition 4.37 we have
![]() $R_{2w}^{c}s_{2}s_{3}$
.
$R_{2w}^{c}s_{2}s_{3}$
.
Finally, towards contradiction let us assume that
![]() $R_{2w}^{c}s_{1}s_{2}$
. Since
$R_{2w}^{c}s_{1}s_{2}$
. Since
![]() $\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle $
, we have either
$\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle $
, we have either
![]() $\langle s_{1}, i_{1} \rangle =\langle s_{2}, i_{2} \rangle $
or
$\langle s_{1}, i_{1} \rangle =\langle s_{2}, i_{2} \rangle $
or
![]() $i_{1}< i_{2}$
and
$i_{1}< i_{2}$
and
![]() $i_{2}$
is even, according to the definition of
$i_{2}$
is even, according to the definition of
![]() $\mathcal {R}$
. The first case is not possible since
$\mathcal {R}$
. The first case is not possible since
![]() $\mathcal {R} \langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
but it is not the case that
$\mathcal {R} \langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
but it is not the case that
![]() $\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
. Therefore
$\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
. Therefore
![]() $i_{1}< i_{2}$
and
$i_{1}< i_{2}$
and
![]() $i_{2}$
is even. Similarly, since
$i_{2}$
is even. Similarly, since
![]() $\mathcal {R} \langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
,
$\mathcal {R} \langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
,
![]() $R_{1w}^{c}s_{2}s_{3}$
and
$R_{1w}^{c}s_{2}s_{3}$
and
![]() $R_{2w}^{c}s_{2}s_{3}$
we can show that
$R_{2w}^{c}s_{2}s_{3}$
we can show that
![]() $i_{2}< i_{3}$
and
$i_{2}< i_{3}$
and
![]() $i_{3}$
is even. Therefore,
$i_{3}$
is even. Therefore,
![]() $i_{1}<i_{3}$
and
$i_{1}<i_{3}$
and
![]() $i_{3}$
is even. However, this then means that
$i_{3}$
is even. However, this then means that
![]() $\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
according to the definition of
$\mathcal {R} \langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
according to the definition of
![]() $\mathcal {R}$
, which contradicts the assumption. In sum, it cannot be the case that
$\mathcal {R}$
, which contradicts the assumption. In sum, it cannot be the case that
![]() $R_{2w}^{c}s_{1}s_{2}$
.
$R_{2w}^{c}s_{1}s_{2}$
.
For the general case, suppose there is an
![]() $\mathcal {R}$
-path from
$\mathcal {R}$
-path from
![]() $\langle s, i \rangle $
to
$\langle s, i \rangle $
to
![]() $\langle s^{\prime }, i^{\prime } \rangle $
in
$\langle s^{\prime }, i^{\prime } \rangle $
in
![]() $\mathcal {F}$
such that it is not the case that
$\mathcal {F}$
such that it is not the case that
![]() $\mathcal {R}\langle s, i \rangle \langle s^{\prime }, i^{\prime } \rangle $
. Clearly we can shorten the path while keeping the starting and ending points the same, if two non-adjacent points in the path are also connected by
$\mathcal {R}\langle s, i \rangle \langle s^{\prime }, i^{\prime } \rangle $
. Clearly we can shorten the path while keeping the starting and ending points the same, if two non-adjacent points in the path are also connected by
![]() $\mathcal {R}$
. Now let us take one of the shortest subpathsFootnote
24
$\mathcal {R}$
. Now let us take one of the shortest subpathsFootnote
24
![]() $\langle s_{1}, i_{1} \rangle \dots \langle s_{k}, i_{k} \rangle $
for some k, such that
$\langle s_{1}, i_{1} \rangle \dots \langle s_{k}, i_{k} \rangle $
for some k, such that
![]() $\langle s_{1}, i_{1} \rangle =\langle s, i \rangle $
,
$\langle s_{1}, i_{1} \rangle =\langle s, i \rangle $
,
![]() $\langle s_{k}, i_{k} \rangle =\langle s^{\prime }, i^{\prime } \rangle $
, and for all
$\langle s_{k}, i_{k} \rangle =\langle s^{\prime }, i^{\prime } \rangle $
, and for all
![]() $j<k$
,
$j<k$
,
![]() $\mathcal {R} \langle s_{j}, i_{j} \rangle \langle s_{j+1}, i_{j+1} \rangle $
. Note that since it is the shortest in length, it is not the case that
$\mathcal {R} \langle s_{j}, i_{j} \rangle \langle s_{j+1}, i_{j+1} \rangle $
. Note that since it is the shortest in length, it is not the case that
![]() $\mathcal {R} \langle s_{j}, i_{j} \rangle \langle s_{j^{\prime }}, i_{j^{\prime }} \rangle $
for any
$\mathcal {R} \langle s_{j}, i_{j} \rangle \langle s_{j^{\prime }}, i_{j^{\prime }} \rangle $
for any
![]() $j<j^{\prime }\leq k$
.
$j<j^{\prime }\leq k$
.
Note that
![]() $k>2$
, since it is not the case that
$k>2$
, since it is not the case that
![]() $\mathcal {R}\langle s, i \rangle \langle s^{\prime }, i^{\prime } \rangle $
. In the following, we show that k must be
$\mathcal {R}\langle s, i \rangle \langle s^{\prime }, i^{\prime } \rangle $
. In the following, we show that k must be
![]() $3$
, which will reduce the general case to the previous basic case. Suppose
$3$
, which will reduce the general case to the previous basic case. Suppose
![]() $k>3$
and the shortest subpath starts with
$k>3$
and the shortest subpath starts with
![]() $\langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle \langle s_{4}, i_{4} \rangle \dots $
Footnote
25
. Since it is not the case that
$\langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle \langle s_{4}, i_{4} \rangle \dots $
Footnote
25
. Since it is not the case that
![]() $\mathcal {R}\langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
but
$\mathcal {R}\langle s_{1}, i_{1} \rangle \langle s_{3}, i_{3} \rangle $
but
![]() $\mathcal {R}\langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle $
, and
$\mathcal {R}\langle s_{1}, i_{1} \rangle \langle s_{2}, i_{2} \rangle $
, and
![]() $\mathcal {R}\langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
, we can follow the discussion for the basic 3-point case and show
$\mathcal {R}\langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
, we can follow the discussion for the basic 3-point case and show
![]() $R_{2w}^{c}s_{2}s_{3}$
. However, since it is also not the case that
$R_{2w}^{c}s_{2}s_{3}$
. However, since it is also not the case that
![]() $\mathcal {R}\langle s_{2}, i_{2} \rangle \langle s_{4}, i_{4} \rangle $
but
$\mathcal {R}\langle s_{2}, i_{2} \rangle \langle s_{4}, i_{4} \rangle $
but
![]() $\mathcal {R}\langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
, and
$\mathcal {R}\langle s_{2}, i_{2} \rangle \langle s_{3}, i_{3} \rangle $
, and
![]() $\mathcal {R}\langle s_{3}, i_{3} \rangle \langle s_{4}, i_{4} \rangle $
, by the conclusion of the basic 3-point case we have
$\mathcal {R}\langle s_{3}, i_{3} \rangle \langle s_{4}, i_{4} \rangle $
, by the conclusion of the basic 3-point case we have
![]() $\neg R_{2w}^{c}s_{2}s_{3}$
. Now we have a contradiction, thus k can only be 3 if the shortest subpaths are taken.
$\neg R_{2w}^{c}s_{2}s_{3}$
. Now we have a contradiction, thus k can only be 3 if the shortest subpaths are taken.
The above lemma shows that if there is a path such that the starting point and the ending point are not connected by
![]() $\mathcal {R}$
then it is a 3-point path. This means when we build the transitive closure, we just need to add edges in such simple cases, and this is the key to our next lemma.
$\mathcal {R}$
then it is a 3-point path. This means when we build the transitive closure, we just need to add edges in such simple cases, and this is the key to our next lemma.
Lemma 4.52.
![]() $\mathcal {F}^{+}$
is a GM-frame.
$\mathcal {F}^{+}$
is a GM-frame.
Proof. Since
![]() $\mathcal {{R}^{+}}$
is the transitive closure of
$\mathcal {{R}^{+}}$
is the transitive closure of
![]() $\mathcal {R}$
, we just need to show that
$\mathcal {R}$
, we just need to show that
![]() $\mathcal {{R}^{+}}$
is reflexive and anti-symmetric.
$\mathcal {{R}^{+}}$
is reflexive and anti-symmetric.
We first show that
![]() $\mathcal {R}^{+}$
is reflexive. For any
$\mathcal {R}^{+}$
is reflexive. For any
![]() $v\in W_{w}^{c}$
and
$v\in W_{w}^{c}$
and
![]() $i\in I_{v}$
, from
$i\in I_{v}$
, from
![]() $v=v$
and
$v=v$
and
![]() $i=i$
, we know
$i=i$
, we know
![]() $S\langle v,i \rangle \langle v,i \rangle $
. By the canonicity of Axiom T, we have
$S\langle v,i \rangle \langle v,i \rangle $
. By the canonicity of Axiom T, we have
![]() $R_{1w}^{c}vv$
. Consequently,
$R_{1w}^{c}vv$
. Consequently,
![]() $\mathcal {R}\langle v,i \rangle \langle v,i \rangle $
. Therefore,
$\mathcal {R}\langle v,i \rangle \langle v,i \rangle $
. Therefore,
![]() $\mathcal {R}$
is reflexive, so is
$\mathcal {R}$
is reflexive, so is
![]() $\mathcal {R}^{+}$
.
$\mathcal {R}^{+}$
.
We then prove that
![]() $\mathcal {F}^{+}$
is anti-symmetric. If not, then there are
$\mathcal {F}^{+}$
is anti-symmetric. If not, then there are
![]() $\langle w_{1},i \rangle ,\langle w_{2},j \rangle \in \mathcal {W}$
such that
$\langle w_{1},i \rangle ,\langle w_{2},j \rangle \in \mathcal {W}$
such that
![]() $\langle w_{1},i \rangle \not =\langle w_{2},j \rangle $
,
$\langle w_{1},i \rangle \not =\langle w_{2},j \rangle $
,
![]() $\mathcal {R}^{+}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
$\mathcal {R}^{+}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
![]() $\mathcal {R}^{+}\langle w_{2},j \rangle \langle w_{1},i \rangle $
. By the definition of
$\mathcal {R}^{+}\langle w_{2},j \rangle \langle w_{1},i \rangle $
. By the definition of
![]() $\mathcal {R}$
and the discussion above, we know that
$\mathcal {R}$
and the discussion above, we know that
![]() $R_{1w}^{c}w_{1}w_{2}$
and
$R_{1w}^{c}w_{1}w_{2}$
and
![]() $R_{1w}^{c}w_{2}w_{1}$
. Consider the following situations.
$R_{1w}^{c}w_{2}w_{1}$
. Consider the following situations.
First, consider the case that
![]() $\mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
$\mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
![]() $\mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
, i.e., both the edges
$\mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
, i.e., both the edges
![]() $\mathcal {R}^{+}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
$\mathcal {R}^{+}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
![]() $\mathcal {R}^{+}\langle w_{2},j \rangle \langle w_{1},i \rangle $
are not new edges added to the frame when taking the transitive closure. Since
$\mathcal {R}^{+}\langle w_{2},j \rangle \langle w_{1},i \rangle $
are not new edges added to the frame when taking the transitive closure. Since
![]() $R_{1w}^{c}w_{1}w_{2}$
and
$R_{1w}^{c}w_{1}w_{2}$
and
![]() $R_{1w}^{c}w_{2}w_{1}$
, from Proposition 4.43 it follows that
$R_{1w}^{c}w_{2}w_{1}$
, from Proposition 4.43 it follows that
![]() $R_{2w}^{c}w_{2}w_{1}$
or
$R_{2w}^{c}w_{2}w_{1}$
or
![]() $w_{1}\equiv w_{2}$
. If
$w_{1}\equiv w_{2}$
. If
![]() $w_{1}\equiv w_{2}$
, then from
$w_{1}\equiv w_{2}$
, then from
![]() $\langle w_{1},i \rangle \not =\langle w_{2},j \rangle $
it follows that
$\langle w_{1},i \rangle \not =\langle w_{2},j \rangle $
it follows that
![]() $i\not = j$
, which suggests that
$i\not = j$
, which suggests that
![]() $w_{1}\in D_{i}(W_{w}^{c})$
for otherwise
$w_{1}\in D_{i}(W_{w}^{c})$
for otherwise
![]() $i=j=0$
. It then means that there exists
$i=j=0$
. It then means that there exists
![]() $v\in W_{w}^{c}$
such that
$v\in W_{w}^{c}$
such that
![]() $R_{1w}^{c}vw_{1}$
and
$R_{1w}^{c}vw_{1}$
and
![]() $R_{2w}^{c}vw_{1}$
. By Proposition 4.42,
$R_{2w}^{c}vw_{1}$
. By Proposition 4.42,
![]() $R_{2w}^{c}w_{1}w_{1}$
. W.l.o.g., assume
$R_{2w}^{c}w_{1}w_{1}$
. W.l.o.g., assume
![]() $i<j$
. From
$i<j$
. From
![]() $\mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
and
$\mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
and
![]() $R_{2w}^{c}w_{1}w_{1}$
, we can also obtain
$R_{2w}^{c}w_{1}w_{1}$
, we can also obtain
![]() $j<i$
, which entails a contradiction. So it can only be the case that
$j<i$
, which entails a contradiction. So it can only be the case that
![]() $R_{2w}^{c}w_{2}w_{1}$
. Similarly, we have
$R_{2w}^{c}w_{2}w_{1}$
. Similarly, we have
![]() $R_{2w}^{c}w_{1}w_{2}$
. However from the definition of
$R_{2w}^{c}w_{1}w_{2}$
. However from the definition of
![]() $\mathcal {R}$
and
$\mathcal {R}$
and
![]() $\langle w_{1},i \rangle \not =\langle w_{2},j \rangle $
, it follows that
$\langle w_{1},i \rangle \not =\langle w_{2},j \rangle $
, it follows that
![]() $(i<j\land j/2\in \mathbb {Z})$
and
$(i<j\land j/2\in \mathbb {Z})$
and
![]() $(j<i\land i/2\in \mathbb {Z})$
, which is a contradiction, too.
$(j<i\land i/2\in \mathbb {Z})$
, which is a contradiction, too.
Next, consider the case that only one of the two edges is a new edge added when taking transitive closure. W.l.o.g., assume that
![]() $\neg \mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
$\neg \mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
![]() $\mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
. Then the edge from
$\mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
. Then the edge from
![]() $\langle w_{1},i \rangle $
to
$\langle w_{1},i \rangle $
to
![]() $\langle w_{2},j \rangle $
is added in the transitive closure, i.e., there is an
$\langle w_{2},j \rangle $
is added in the transitive closure, i.e., there is an
![]() $\mathcal {R}$
-path (of a length greater than 2) from
$\mathcal {R}$
-path (of a length greater than 2) from
![]() $\langle w_{1},i \rangle $
to
$\langle w_{1},i \rangle $
to
![]() $\langle w_{2},j \rangle $
in
$\langle w_{2},j \rangle $
in
![]() $\mathcal {F}$
. Now by Proposition 4.51, there must be some
$\mathcal {F}$
. Now by Proposition 4.51, there must be some
![]() $\langle w_{3}, k \rangle $
such that
$\langle w_{3}, k \rangle $
such that
![]() $\mathcal {R}\langle w_{1},i \rangle \langle w_{3},k \rangle $
,
$\mathcal {R}\langle w_{1},i \rangle \langle w_{3},k \rangle $
,
![]() $\mathcal {R}\langle w_{3},k \rangle \langle w_{2},j \rangle $
, and moreover
$\mathcal {R}\langle w_{3},k \rangle \langle w_{2},j \rangle $
, and moreover
![]() $R_{1w}^{c}w_{1}w_{3}$
,
$R_{1w}^{c}w_{1}w_{3}$
,
![]() $\neg R_{2w}^{c}w_{1}w_{3}$
,
$\neg R_{2w}^{c}w_{1}w_{3}$
,
![]() $R_{1w}^{c}w_{3}w_{2}$
,
$R_{1w}^{c}w_{3}w_{2}$
,
![]() $R_{2w}^{c}w_{3}w_{2}$
and
$R_{2w}^{c}w_{3}w_{2}$
and
![]() $R_{2w}^{c}w_{1}w_{2}$
. Since
$R_{2w}^{c}w_{1}w_{2}$
. Since
![]() $\mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
, we have
$\mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
, we have
![]() $R_{1w}^{c}w_{2}w_{1}$
. Now by
$R_{1w}^{c}w_{2}w_{1}$
. Now by
![]() $R_{1w}^{c}w_{3}w_{2}$
and
$R_{1w}^{c}w_{3}w_{2}$
and
![]() $R_{1w}^{c}w_{2}w_{1}$
, we have
$R_{1w}^{c}w_{2}w_{1}$
, we have
![]() $R_{1w}^{c}w_{3}w_{1}$
. From Proposition 4.43 and
$R_{1w}^{c}w_{3}w_{1}$
. From Proposition 4.43 and
![]() $R_{1w}^{c}w_{1}w_{3}$
, it holds that
$R_{1w}^{c}w_{1}w_{3}$
, it holds that
![]() $R_{2w}^{c}w_{1}w_{3}\lor w_{1}\equiv w_{3}$
. Note that we already have
$R_{2w}^{c}w_{1}w_{3}\lor w_{1}\equiv w_{3}$
. Note that we already have
![]() $\neg R_{2w}^{c}w_{1}w_{3}$
, so
$\neg R_{2w}^{c}w_{1}w_{3}$
, so
![]() $w_{1}\equiv w_{3}$
. Thus
$w_{1}\equiv w_{3}$
. Thus
![]() $\mathcal {R}\langle w_{1},i \rangle \langle w_{1},k \rangle $
and
$\mathcal {R}\langle w_{1},i \rangle \langle w_{1},k \rangle $
and
![]() $\mathcal {R}\langle w_{1},k \rangle \langle w_{2},j \rangle $
. From
$\mathcal {R}\langle w_{1},k \rangle \langle w_{2},j \rangle $
. From
![]() $\neg \mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
$\neg \mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
![]() $\mathcal {R}\langle w_{1},k \rangle \langle w_{2},j \rangle $
, we know
$\mathcal {R}\langle w_{1},k \rangle \langle w_{2},j \rangle $
, we know
![]() $i\not =k$
. Consequently, we have
$i\not =k$
. Consequently, we have
![]() $w_{1}\in D_{i}(W^{c}_{w})$
, i.e., there exists
$w_{1}\in D_{i}(W^{c}_{w})$
, i.e., there exists
![]() $v\in W^{c}_{w}$
such that
$v\in W^{c}_{w}$
such that
![]() $R_{1w}^{c}vw_{1}$
and
$R_{1w}^{c}vw_{1}$
and
![]() $R_{2w}^{c}vw_{1}$
. However, as
$R_{2w}^{c}vw_{1}$
. However, as
![]() $R_{1w}^{c}vw_{1}$
and
$R_{1w}^{c}vw_{1}$
and
![]() $R_{2w}^{c}vw_{1}$
, by Proposition 4.42 it holds that
$R_{2w}^{c}vw_{1}$
, by Proposition 4.42 it holds that
![]() $R_{2w}^{c}w_{1}w_{1}$
, which contradicts
$R_{2w}^{c}w_{1}w_{1}$
, which contradicts
![]() $\neg R_{2w}^{c}w_{1}w_{3}$
(i.e.,
$\neg R_{2w}^{c}w_{1}w_{3}$
(i.e.,
![]() $\neg R_{2w}^{c}w_{1}w_{1}$
).
$\neg R_{2w}^{c}w_{1}w_{1}$
).
Finally, let us consider the case that
![]() $\neg \mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
$\neg \mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
![]() $\neg \mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
. Since the edges are added in the transitive closure, by Proposition 4.51 there are
$\neg \mathcal {R}\langle w_{2},j \rangle \langle w_{1},i \rangle $
. Since the edges are added in the transitive closure, by Proposition 4.51 there are
![]() $w_{3},w_{4}\in W_{w}^{c}$
in the initial frame
$w_{3},w_{4}\in W_{w}^{c}$
in the initial frame
![]() $\mathcal {F}_{gw}^{c}$
, and
$\mathcal {F}_{gw}^{c}$
, and
![]() $k, h\in \mathbb {Z}$
, such that
$k, h\in \mathbb {Z}$
, such that
-
(1)
 $\mathcal {R}\langle w_{1},i \rangle \langle w_{3},k \rangle $
,
$\mathcal {R}\langle w_{1},i \rangle \langle w_{3},k \rangle $
,
 $\mathcal {R}\langle w_{3},k \rangle \langle w_{2},j \rangle $
,
$\mathcal {R}\langle w_{3},k \rangle \langle w_{2},j \rangle $
,
 $R_{1w}^{c}w_{1}w_{3}$
,
$R_{1w}^{c}w_{1}w_{3}$
,
 $\neg R_{2w}^{c}w_{1}w_{3}$
,
$\neg R_{2w}^{c}w_{1}w_{3}$
,
 $R_{1w}^{c}w_{3}w_{2}$
,
$R_{1w}^{c}w_{3}w_{2}$
,
 $R_{2w}^{c}w_{3}w_{2}$
,
$R_{2w}^{c}w_{3}w_{2}$
,
 $R_{2w}^{c}w_{1}w_{2}$
; and
$R_{2w}^{c}w_{1}w_{2}$
; and -
(2)
 $\mathcal {R}\langle w_{2},i \rangle \langle w_{4},h \rangle $
,
$\mathcal {R}\langle w_{2},i \rangle \langle w_{4},h \rangle $
,
 $\mathcal {R}\langle w_{4},h \rangle \langle w_{1},j \rangle $
,
$\mathcal {R}\langle w_{4},h \rangle \langle w_{1},j \rangle $
,
 $R_{1w}^{c}w_{2}w_{4}$
,
$R_{1w}^{c}w_{2}w_{4}$
,
 $\neg R_{2w}^{c}w_{2}w_{4}$
,
$\neg R_{2w}^{c}w_{2}w_{4}$
,
 $R_{1w}^{c}w_{4}w_{1}$
,
$R_{1w}^{c}w_{4}w_{1}$
,
 $R_{2w}^{c}w_{4}w_{1}$
,
$R_{2w}^{c}w_{4}w_{1}$
,
 $R_{2w}^{c}w_{2}w_{1}$
.
$R_{2w}^{c}w_{2}w_{1}$
.
From
![]() $R_{1w}^{c}w_{3}w_{2}$
in (1) and
$R_{1w}^{c}w_{3}w_{2}$
in (1) and
![]() $R_{1w}^{c}w_{2}w_{1}$
in (2), we have
$R_{1w}^{c}w_{2}w_{1}$
in (2), we have
![]() $R_{1w}^{c}w_{3}w_{1}$
. By Proposition 4.43 and
$R_{1w}^{c}w_{3}w_{1}$
. By Proposition 4.43 and
![]() $R_{1w}^{c}w_{1}w_{3}$
, it follows that
$R_{1w}^{c}w_{1}w_{3}$
, it follows that
![]() $R_{2w}^{c}w_{1}w_{3}\lor w_{1}\equiv w_{3}$
. From
$R_{2w}^{c}w_{1}w_{3}\lor w_{1}\equiv w_{3}$
. From
![]() $\neg R_{2w}^{c}w_{1}w_{3}$
in (1), we obtain
$\neg R_{2w}^{c}w_{1}w_{3}$
in (1), we obtain
![]() $w_{1}\equiv w_{3}$
. Again from (1) we have
$w_{1}\equiv w_{3}$
. Again from (1) we have
![]() $\mathcal {R}\langle w_{1},i \rangle \langle w_{1},k \rangle $
and
$\mathcal {R}\langle w_{1},i \rangle \langle w_{1},k \rangle $
and
![]() $\mathcal {R}\langle w_{1},k \rangle \langle w_{2},j \rangle $
. From
$\mathcal {R}\langle w_{1},k \rangle \langle w_{2},j \rangle $
. From
![]() $\neg \mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
$\neg \mathcal {R}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
![]() $\mathcal {R}\langle w_{1},k \rangle \langle w_{2},j \rangle $
, it holds that
$\mathcal {R}\langle w_{1},k \rangle \langle w_{2},j \rangle $
, it holds that
![]() $i\not =k$
. Consequently, we know
$i\not =k$
. Consequently, we know
![]() $w_{1}\in D_{i}(W^{c}_{w})$
, i.e., there exists
$w_{1}\in D_{i}(W^{c}_{w})$
, i.e., there exists
![]() $v\in W^{c}_{w}$
such that
$v\in W^{c}_{w}$
such that
![]() $R_{1w}^{c}vw_{1}$
and
$R_{1w}^{c}vw_{1}$
and
![]() $R_{2w}^{c}vw_{1}$
. However, as
$R_{2w}^{c}vw_{1}$
. However, as
![]() $R_{1w}^{c}vw_{1}$
and
$R_{1w}^{c}vw_{1}$
and
![]() $R_{2w}^{c}vw_{1}$
, we know
$R_{2w}^{c}vw_{1}$
, we know
![]() $R_{2w}^{c}w_{1}w_{1}$
from Proposition 4.42, which contradicts
$R_{2w}^{c}w_{1}w_{1}$
from Proposition 4.42, which contradicts
![]() $\neg R_{2w}^{c}w_{1}w_{3}$
, i.e.,
$\neg R_{2w}^{c}w_{1}w_{3}$
, i.e.,
![]() $\neg R_{2w}^{c}w_{1}w_{1}$
in (1). Similarly, (2) entails a contradiction, too.
$\neg R_{2w}^{c}w_{1}w_{1}$
in (1). Similarly, (2) entails a contradiction, too.
Therefore, for any
![]() $\langle w_{1},i \rangle ,\langle w_{2},j \rangle \in \mathcal {W}$
, if
$\langle w_{1},i \rangle ,\langle w_{2},j \rangle \in \mathcal {W}$
, if
![]() $\mathcal {R}^{+}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
$\mathcal {R}^{+}\langle w_{1},i \rangle \langle w_{2},j \rangle $
and
![]() $\mathcal {R}^{+}\langle w_{2},j \rangle \langle w_{1},i \rangle $
, then
$\mathcal {R}^{+}\langle w_{2},j \rangle \langle w_{1},i \rangle $
, then
![]() $\langle w_{1},i \rangle =\langle w_{2},j \rangle $
. Thus,
$\langle w_{1},i \rangle =\langle w_{2},j \rangle $
. Thus,
![]() $\mathcal {F}^{+}$
is anti-symmetric.
$\mathcal {F}^{+}$
is anti-symmetric.
All in all,
![]() $\mathcal {F}^{+}$
is reflexive and anti-symmetric. Additionally, it is a transitive closure, so it is a GM-frame.
$\mathcal {F}^{+}$
is reflexive and anti-symmetric. Additionally, it is a transitive closure, so it is a GM-frame.
Now we move to the next step. With the construction of
![]() $\mathcal {F}$
introduced in Definition 4.50, it is an easy exercise to verify that for any
$\mathcal {F}$
introduced in Definition 4.50, it is an easy exercise to verify that for any
![]() $s,t\in W^{c}_{w}$
, if
$s,t\in W^{c}_{w}$
, if
![]() $R_{1w}^{c}st$
and
$R_{1w}^{c}st$
and
![]() $R_{2w}^{c}st$
, then for each
$R_{2w}^{c}st$
, then for each
![]() $i\in I_{s}$
, there exist
$i\in I_{s}$
, there exist
![]() $j,j^{\prime }\in I_{t}$
such that
$j,j^{\prime }\in I_{t}$
such that
![]() $\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
and
$\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
and
![]() $\neg \mathcal {R}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Furthermore, as the relation
$\neg \mathcal {R}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Furthermore, as the relation
![]() $\mathcal {R}^{+}$
is an extension of
$\mathcal {R}^{+}$
is an extension of
![]() $\mathcal {R}$
, we know
$\mathcal {R}$
, we know
![]() $\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
from
$\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
from
![]() $\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
. However, when
$\mathcal {R}\langle s,i \rangle \langle t,j \rangle $
. However, when
![]() $\mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
, is there always another
$\mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
, is there always another
![]() $j^{\prime \prime }\in I_{t}$
such that
$j^{\prime \prime }\in I_{t}$
such that
![]() $\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime \prime } \rangle $
? The following result gives us a positive answer to this:
$\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime \prime } \rangle $
? The following result gives us a positive answer to this:
Lemma 4.53. For all
![]() $s,t\in W^{c}_{w}$
, if
$s,t\in W^{c}_{w}$
, if
![]() $R_{1w}^{c}st$
and
$R_{1w}^{c}st$
and
![]() $R_{2w}^{c}st$
, then for each
$R_{2w}^{c}st$
, then for each
![]() $i\in I_{s}$
, there exist
$i\in I_{s}$
, there exist
![]() $j,j^{\prime }\in I_{t}$
such that
$j,j^{\prime }\in I_{t}$
such that
![]() $\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
and
$\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
and
![]() $\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
.
$\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
.
Proof. As stated above, we only need to show that when
![]() $\neg \mathcal {R}\langle s,i \rangle \langle t,j \rangle $
and
$\neg \mathcal {R}\langle s,i \rangle \langle t,j \rangle $
and
![]() $\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
, there exists
$\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
, there exists
![]() $j^{\prime }\in I_{t}$
such that
$j^{\prime }\in I_{t}$
such that
![]() $\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Let us begin.
$\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Let us begin.
Since the edge from
![]() $\langle s,i \rangle $
to
$\langle s,i \rangle $
to
![]() $\langle t,j \rangle $
is one of those added when building the transitive closure, there must be some
$\langle t,j \rangle $
is one of those added when building the transitive closure, there must be some
![]() $v\in W_{w}^{c}$
such that
$v\in W_{w}^{c}$
such that
![]() $R_{1w}^{c}sv$
,
$R_{1w}^{c}sv$
,
![]() $\neg R_{2w}^{c}sv$
,
$\neg R_{2w}^{c}sv$
,
![]() $R_{1w}^{c}vt$
,
$R_{1w}^{c}vt$
,
![]() $R_{2w}^{c}vt$
and
$R_{2w}^{c}vt$
and
![]() $R_{2w}^{c}st$
. If
$R_{2w}^{c}st$
. If
![]() $s=t$
, then by Proposition 4.43, we know
$s=t$
, then by Proposition 4.43, we know
![]() $R_{2w}^{c}sv\lor s\equiv v$
from
$R_{2w}^{c}sv\lor s\equiv v$
from
![]() $R_{1w}^{c}sv$
and
$R_{1w}^{c}sv$
and
![]() $R_{1w}^{c}vt$
. We already have
$R_{1w}^{c}vt$
. We already have
![]() $\neg R_{2w}^{c}sv$
, so
$\neg R_{2w}^{c}sv$
, so
![]() $s= v$
. However, now
$s= v$
. However, now
![]() $\neg R_{2w}^{c}sv$
contradicts
$\neg R_{2w}^{c}sv$
contradicts
![]() $R_{2w}^{c}st$
.
$R_{2w}^{c}st$
.
Moreover, as
![]() $R_{1w}^{c}st$
and
$R_{1w}^{c}st$
and
![]() $R_{2w}^{c}st$
, it holds that
$R_{2w}^{c}st$
, it holds that
![]() $I_{t}=\mathbb {Z}$
. Consider the case that
$I_{t}=\mathbb {Z}$
. Consider the case that
![]() $j^{\prime }=1$
. Obviously,
$j^{\prime }=1$
. Obviously,
![]() $j^{\prime }/2\not \in \mathbb {Z}$
. Also, since
$j^{\prime }/2\not \in \mathbb {Z}$
. Also, since
![]() $s\not =t$
, we have
$s\not =t$
, we have
![]() $\neg \mathcal {R}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. If
$\neg \mathcal {R}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. If
![]() $\mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
, then there exists
$\mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
, then there exists
![]() $k\in I_{v}$
with
$k\in I_{v}$
with
![]() $\mathcal {R}\langle s,i \rangle \langle v,k \rangle $
and
$\mathcal {R}\langle s,i \rangle \langle v,k \rangle $
and
![]() $\mathcal {R}\langle v,k \rangle \langle t,1 \rangle $
. In addition, since
$\mathcal {R}\langle v,k \rangle \langle t,1 \rangle $
. In addition, since
![]() $R_{2w}^{c}st$
and
$R_{2w}^{c}st$
and
![]() $\neg R_{2w}^{c}sv$
,
$\neg R_{2w}^{c}sv$
,
![]() $t\not =v$
. Therefore, from
$t\not =v$
. Therefore, from
![]() $\mathcal {R}\langle v,k \rangle \langle t,1 \rangle $
, we know
$\mathcal {R}\langle v,k \rangle \langle t,1 \rangle $
, we know
![]() $k<1\land 1/2\in \mathbb {Z}$
which entails a contradiction. Hence,
$k<1\land 1/2\in \mathbb {Z}$
which entails a contradiction. Hence,
![]() $\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Now the proof is completed.
$\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Now the proof is completed.
As mentioned, with the valuable findings in [Reference Goranko and Petkov8], Lemma 4.53 itself has already illustrated the completeness of MGM
![]() $^{+}$
. However, the reader may still have no feeling for how this result can help us to establish the completeness. Therefore, to understand how the lemma above works, we go one step further and show the result more directly in what follows.
$^{+}$
. However, the reader may still have no feeling for how this result can help us to establish the completeness. Therefore, to understand how the lemma above works, we go one step further and show the result more directly in what follows.
Theorem 4.54. MGM
![]() $^{+}$
is strongly complete with respect to GM-frames.
$^{+}$
is strongly complete with respect to GM-frames.
Proof. Let
![]() $\mathcal {M}=\langle \mathcal {F}^{+}, V \rangle $
where
$\mathcal {M}=\langle \mathcal {F}^{+}, V \rangle $
where
![]() $V(\langle s,i \rangle )=V^{c}_{w}(s)$
. By Lemma 4.52,
$V(\langle s,i \rangle )=V^{c}_{w}(s)$
. By Lemma 4.52,
![]() $\mathcal {F}^{+}$
is indeed a GM-frame. In the following we show that
$\mathcal {F}^{+}$
is indeed a GM-frame. In the following we show that
Note that the strong completeness follows if the above claim is true: for each set of MGM
![]() $^{+}$
-consistent formulas, we can extend it to a maximal MGM
$^{+}$
-consistent formulas, we can extend it to a maximal MGM
![]() $^{+}$
-consistent set s by a Lindenbaum-like argument. Then by the truth lemma for the generalized generated canonical model (Lemma 4.48), we have
$^{+}$
-consistent set s by a Lindenbaum-like argument. Then by the truth lemma for the generalized generated canonical model (Lemma 4.48), we have
iff
![]() $\varphi \in s$
. Finally we have
$\varphi \in s$
. Finally we have
for all
![]() $\varphi \in s$
by (
$\varphi \in s$
by (
![]() $\star $
).
$\star $
).
Now we prove the claim
![]() $(\star )$
. The proof goes by induction on
$(\star )$
. The proof goes by induction on
![]() . The Boolean cases are routine, and we only show the cases for
. The Boolean cases are routine, and we only show the cases for
![]() $\Box $
and
$\Box $
and
![]() .
.
Let us begin with that for
![]() $\Box \varphi $
. From left to right, assume towards a contradiction that
$\Box \varphi $
. From left to right, assume towards a contradiction that
![]() and
and
![]() $\mathcal {M}^{c}_{w},s{\nVDash} \Box \varphi $
. By the latter assumption, there exists
$\mathcal {M}^{c}_{w},s{\nVDash} \Box \varphi $
. By the latter assumption, there exists
![]() $t\in W^{c}_{gw}$
such that
$t\in W^{c}_{gw}$
such that
![]() $R_{1w}^{c}st$
and
$R_{1w}^{c}st$
and
![]() . If
. If
![]() $\neg R_{2w}^{c}st$
, then by the construction of
$\neg R_{2w}^{c}st$
, then by the construction of
![]() $\mathcal {R}^{+}$
, for all
$\mathcal {R}^{+}$
, for all
![]() $j\in I_{t}$
,
$j\in I_{t}$
,
![]() $\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
follows directly from
$\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
follows directly from
![]() $R_{1w}^{c}st$
. By the inductive hypothesis, for any
$R_{1w}^{c}st$
. By the inductive hypothesis, for any
![]() $j\in I_{t}$
, we have
$j\in I_{t}$
, we have
![]() iff
iff
![]() . Therefore, we have
. Therefore, we have
![]() contradicting to our assumption. On the other hand, when
contradicting to our assumption. On the other hand, when
![]() $R_{2w}^{c}st$
, it holds that
$R_{2w}^{c}st$
, it holds that
![]() $t\in D_{i}(W_{w}^{c})$
, so
$t\in D_{i}(W_{w}^{c})$
, so
![]() $I_{t}=\mathbb {Z}$
. By Lemma 4.53, there exists
$I_{t}=\mathbb {Z}$
. By Lemma 4.53, there exists
![]() $j^{\prime }\in I_{t}$
such that
$j^{\prime }\in I_{t}$
such that
![]() $\mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Consequently, by the inductive hypothesis, we know
$\mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Consequently, by the inductive hypothesis, we know
![]() that again entails a contradiction.
that again entails a contradiction.
From right to left, suppose that
![]() and
and
![]() . Hence there exists
. Hence there exists
![]() $\langle t,j \rangle \in \mathcal {W}$
with
$\langle t,j \rangle \in \mathcal {W}$
with
![]() $\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
and
$\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
and
![]() . Note that
. Note that
![]() $R_{1w}^{c}st$
follows from
$R_{1w}^{c}st$
follows from
![]() $\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
. Therefore, by the inductive hypothesis, it is not hard to see that
$\mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
. Therefore, by the inductive hypothesis, it is not hard to see that
![]() $\mathcal {M}^{c}_{gw},s\nVDash \Box \varphi $
, which contradicts the assumption.
$\mathcal {M}^{c}_{gw},s\nVDash \Box \varphi $
, which contradicts the assumption.
Now we move to the case for
![]() . For the direction from left to right, suppose for reductio that
. For the direction from left to right, suppose for reductio that
![]() and
and
![]() . Then, there exists
. Then, there exists
![]() $t\in W_{w}^{c}$
such that
$t\in W_{w}^{c}$
such that
![]() $R_{2w}^{c}st$
and
$R_{2w}^{c}st$
and
![]() . When
. When
![]() $\neg R_{1w}^{c}st$
, we have
$\neg R_{1w}^{c}st$
, we have
![]() $\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
for any
$\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
for any
![]() $j\in I_{t}$
. By the inductive hypothesis, for each
$j\in I_{t}$
. By the inductive hypothesis, for each
![]() $j\in I_{t}$
, it holds that
$j\in I_{t}$
, it holds that
![]() iff
iff
![]() . Thus, we have
. Thus, we have
![]() that contradicts the assumption. On the other hand, if
that contradicts the assumption. On the other hand, if
![]() $R_{1w}^{c}st$
, then by Lemma 4.53, that there exists
$R_{1w}^{c}st$
, then by Lemma 4.53, that there exists
![]() $j^{\prime }\in I_{t}$
such that
$j^{\prime }\in I_{t}$
such that
![]() $\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Again by the inductive hypothesis, we have
$\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j^{\prime } \rangle $
. Again by the inductive hypothesis, we have
![]() .
.
For the converse direction, assume that
![]() and
and
![]() . Then there exists
. Then there exists
![]() $\langle t,j \rangle \in \mathcal {W}$
such that
$\langle t,j \rangle \in \mathcal {W}$
such that
![]() $\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
and
$\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
and
![]() . By the inductive hypothesis, we have
. By the inductive hypothesis, we have
![]() . However,
. However,
![]() $R_{2w}^{c}st$
follows from
$R_{2w}^{c}st$
follows from
![]() $\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
, which contradicts
$\neg \mathcal {R}^{+}\langle s,i \rangle \langle t,j \rangle $
, which contradicts
![]() . Now the proof is completed.
. Now the proof is completed.
5 Future work
In this paper, we propose a modal approach to mereological theories. By a modal language extended with the window modality, we modally capture the first-order properties of various mereological theories via frame correspondence. We also correct a mistake in the existing completeness proof for a basic system of mereology by providing a new construction of the canonical model.
We have left several questions open, e.g., the absolute modal correspondences (if any) of Atomicity, Finite Sum and Fusion. Our discussion of the modal axiomatization over the GM-frames (i.e., Ground Mereology) demonstrates that complete mereological modal systems are very hard to obtain. In particular, the incompleteness of the intuitive MGM shows that the extra expressive power brought in by the window modality may help the modal language to define the same frame property in different ways, which may lead to the incompleteness. This suggests that the other modal systems proposed in Definition 4.31 may well be incomplete, even when the extra axiom of MGM
![]() $^{+}$
is added. Another significant difficulty behind the completeness proof for a system using both
$^{+}$
is added. Another significant difficulty behind the completeness proof for a system using both
![]() $\Box $
and
$\Box $
and
![]() is that we need to make the two relations in the generalized canonical frame complement each other, while keeping the important frame properties intact. This is already very hard in the case of GM frames, let alone EM and other much more complicated frames. We probably need new general techniques. Besides completeness, the decidability of our modal systems is also one important issue which we left open for further investigations. We conjecture that using a modal language rather than the first-order language may lead to more decidable (modal) logics.
is that we need to make the two relations in the generalized canonical frame complement each other, while keeping the important frame properties intact. This is already very hard in the case of GM frames, let alone EM and other much more complicated frames. We probably need new general techniques. Besides completeness, the decidability of our modal systems is also one important issue which we left open for further investigations. We conjecture that using a modal language rather than the first-order language may lead to more decidable (modal) logics.
Moreover, if we go back to the basics of our modal approach, there are also some options to be explored. For example, in order to have a more intuitive reading of the
![]() $\Box $
modality, we use the whole-part relation as the primitive relation in our models, in contrast to the part-whole relation used in the literature. It seems to be a non-essential design choice, but it could well affect the modal definability of various mereological properties. Similarly, if we take the proper whole-part relation as primitive, the correspondences of various properties may also change. Finally, instead of modally characterizing the existing first-order theories of mereology, we may also propose new modal theories for its own sake.
$\Box $
modality, we use the whole-part relation as the primitive relation in our models, in contrast to the part-whole relation used in the literature. It seems to be a non-essential design choice, but it could well affect the modal definability of various mereological properties. Similarly, if we take the proper whole-part relation as primitive, the correspondences of various properties may also change. Finally, instead of modally characterizing the existing first-order theories of mereology, we may also propose new modal theories for its own sake.
Acknowledgements
The authors wish to thank Valentin Goranko and Hsing-chien Tsai for their inspiring suggestions and discussions, Malvin Gattinger for pointing out the literature of window modality, David Storrs-Fox and Casper Storm Hansen for their useful feedback at the seminar of CASIP in Beijing, and the four anonymous reviewers whose extensive comments improved the paper. Dazhu Li is supported by the National Social Science Foundation of China [17ZDA026].