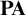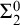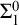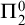1 Summary of mathematical results
This paper consists of mathematical results and a foundational discussion. The former are summarized in the present section; the latter can be found in Section 2. In the remaining sections we provide detailed proofs of all mathematical claims.
First and foremost, our paper is based on a result by Dick de Jongh (unpublished; cf. the introduction to Reference Schmidt[35]) and Diana Schmidt Reference Schmidt[36]: The embeddability relation on finite binary trees yields a well partial order with maximal order type
![]() $\varepsilon _0$
(see below for an explanation). Harvey Friedman Reference Simpson, Harrington, Morley, Sčědrov and Simpson[38] has shown that this type of result yields statements of finite combinatorics that are independent of important mathematical axiom systems. Against this background, many arguments in the present paper may be considered folklore. Nevertheless we find it worthwhile to give an explicit presentation, not least because the arguments are rather sensitive with respect to quantifier complexity and the presence of parameters. At some places we provide more details than the expert may find necessary. The aim is to make the paper as accessible and self-contained as possible.
$\varepsilon _0$
(see below for an explanation). Harvey Friedman Reference Simpson, Harrington, Morley, Sčědrov and Simpson[38] has shown that this type of result yields statements of finite combinatorics that are independent of important mathematical axiom systems. Against this background, many arguments in the present paper may be considered folklore. Nevertheless we find it worthwhile to give an explicit presentation, not least because the arguments are rather sensitive with respect to quantifier complexity and the presence of parameters. At some places we provide more details than the expert may find necessary. The aim is to make the paper as accessible and self-contained as possible.
We write
![]() $\mathcal B$
for the set of finite binary trees. More precisely, we assume that each tree has a distinguished root node, that nodes have either zero or two children, and that left child and right child can be distinguished. Furthermore, we identify isomorphic trees. Formally, we view
$\mathcal B$
for the set of finite binary trees. More precisely, we assume that each tree has a distinguished root node, that nodes have either zero or two children, and that left child and right child can be distinguished. Furthermore, we identify isomorphic trees. Formally, we view
![]() $\mathcal B$
as the least fixed point of the following inductive clauses:
$\mathcal B$
as the least fixed point of the following inductive clauses:
-
(i) There is an element
 $\circ \in \mathcal B$
(the tree that consists of a single root node).
$\circ \in \mathcal B$
(the tree that consists of a single root node). -
(ii) Given s and t in
 $\mathcal B$
, we obtain an element
$\mathcal B$
, we obtain an element
 $\circ (s,t)\in \mathcal B$
(the tree in which the root has left subtree s and right subtree t).
$\circ (s,t)\in \mathcal B$
(the tree in which the root has left subtree s and right subtree t).
For
![]() $s,t\in \mathcal B$
we write
$s,t\in \mathcal B$
we write
![]() $s\leq _{\mathcal B}t$
if there is a tree embedding of s into t. Such an embedding can either map the root to the root and the immediate subtrees of s into the corresponding subtrees of t; or it maps all of s into one subtree of t. Hence we have
$s\leq _{\mathcal B}t$
if there is a tree embedding of s into t. Such an embedding can either map the root to the root and the immediate subtrees of s into the corresponding subtrees of t; or it maps all of s into one subtree of t. Hence we have
![]() $\circ \leq _{\mathcal B}t$
for any
$\circ \leq _{\mathcal B}t$
for any
![]() $t\in \mathcal B$
; we have
$t\in \mathcal B$
; we have
![]() $s\leq _{\mathcal B}\circ $
precisely for
$s\leq _{\mathcal B}\circ $
precisely for
![]() $s=\circ $
; and we have
$s=\circ $
; and we have
 $$ \begin{align*} \circ(s_0,s_1)\leq_{\mathcal B}\circ(t_0,t_1)\quad\Leftrightarrow\quad\begin{cases} s_0\leq_{\mathcal B}t_0\text{ and }s_1\leq_{\mathcal B}t_1,\\ \text{or }\circ(s_0,s_1)\leq_{\mathcal B}t_i\text{ for some }i\in\{0,1\}. \end{cases} \end{align*} $$
$$ \begin{align*} \circ(s_0,s_1)\leq_{\mathcal B}\circ(t_0,t_1)\quad\Leftrightarrow\quad\begin{cases} s_0\leq_{\mathcal B}t_0\text{ and }s_1\leq_{\mathcal B}t_1,\\ \text{or }\circ(s_0,s_1)\leq_{\mathcal B}t_i\text{ for some }i\in\{0,1\}. \end{cases} \end{align*} $$
These clauses provide a recursive definition of
![]() $\leq _{\mathcal B}$
.
$\leq _{\mathcal B}$
.
Recall that a partial order consists of a set X and a binary relation
![]() $\leq _X$
on X that is reflexive, antisymmetric and transitive. A finite or infinite sequence
$\leq _X$
on X that is reflexive, antisymmetric and transitive. A finite or infinite sequence
![]() $x_0,x_1,\ldots $
in X is called good if there are indices
$x_0,x_1,\ldots $
in X is called good if there are indices
![]() $i<j$
such that we have
$i<j$
such that we have
![]() $x_i\leq _X x_j$
; otherwise, the sequence is called bad. If there is no infinite bad sequence, then
$x_i\leq _X x_j$
; otherwise, the sequence is called bad. If there is no infinite bad sequence, then
![]() $(X,\leq _X)$
is called a well partial order (wpo). Equivalently, a partial order
$(X,\leq _X)$
is called a well partial order (wpo). Equivalently, a partial order
![]() $(X,\leq _X)$
is a wpo if, and only if, every subset
$(X,\leq _X)$
is a wpo if, and only if, every subset
![]() $Y\subseteq X$
has a finite “basis”
$Y\subseteq X$
has a finite “basis”
![]() $a\subseteq Y$
with the following property: for any
$a\subseteq Y$
with the following property: for any
![]() $y\in Y$
there is an
$y\in Y$
there is an
![]() $x\in a$
with
$x\in a$
with
![]() $x\leq _X y$
(cf. the argument in Remark 3.1 below).
$x\leq _X y$
(cf. the argument in Remark 3.1 below).
If X is a wpo, then all its linearizations are well orders (since a strictly decreasing sequence in a linearization would be a bad sequence in X). Hence the order type of each linearization is an ordinal number. The supremum of these ordinals is called the maximal order type of X. As shown by D. de Jongh and R. Parikh [Reference Ewald and Sieg8], the maximal order type of any wpo is realized by one of its linearizations (i.e., the supremum is a maximum).
Kruskal’s theorem Reference Kruskal[28] implies that
![]() $(\mathcal B,\leq _{\mathcal B})$
is a well partial order. We point out that the theorem applies to arbitrary (i.e., not necessarily binary) finite trees; the “most general” version of Kruskal’s theorem is investigated in [Reference Friedman14]. Concerning the binary case, de Jongh and Schmidt have proved the finer result that
$(\mathcal B,\leq _{\mathcal B})$
is a well partial order. We point out that the theorem applies to arbitrary (i.e., not necessarily binary) finite trees; the “most general” version of Kruskal’s theorem is investigated in [Reference Friedman14]. Concerning the binary case, de Jongh and Schmidt have proved the finer result that
![]() $\mathcal B$
has maximal order type
$\mathcal B$
has maximal order type
![]() $\varepsilon _0$
, which is the least fixed point of ordinal exponentiation with base
$\varepsilon _0$
, which is the least fixed point of ordinal exponentiation with base
![]() $\omega $
(read [Reference Schmidt36, theorem II.2] in combination with the example after [Reference Schmidt36, definition I.15]). A classical result of G. Gentzen [Reference Gentzen18, Reference Hájek and Pudlák19] establishes
$\omega $
(read [Reference Schmidt36, theorem II.2] in combination with the example after [Reference Schmidt36, definition I.15]). A classical result of G. Gentzen [Reference Gentzen18, Reference Hájek and Pudlák19] establishes
![]() $\varepsilon _0$
as the proof theoretic ordinal of Peano arithmetic (
$\varepsilon _0$
as the proof theoretic ordinal of Peano arithmetic (
![]() $\mathbf {PA}$
). This explains the connection with independence results.
$\mathbf {PA}$
). This explains the connection with independence results.
In the present paper we consider the binary Kruskal theorem (i.e., the result that
![]() $\mathcal B$
is a wpo) in the context of first order arithmetic; an introduction to this setting can be found in [Reference Hasegawa, Jones, Hagiya and Sato20]. We will be particularly interested in questions of quantifier complexity: Recall that a formula lies in the class
$\mathcal B$
is a wpo) in the context of first order arithmetic; an introduction to this setting can be found in [Reference Hasegawa, Jones, Hagiya and Sato20]. We will be particularly interested in questions of quantifier complexity: Recall that a formula lies in the class
![]() $\Delta ^0_0=\Sigma ^0_0=\Pi ^0_0$
if it only contains bounded quantifiers. Since the latter range over a finite domain, the truth of closed
$\Delta ^0_0=\Sigma ^0_0=\Pi ^0_0$
if it only contains bounded quantifiers. Since the latter range over a finite domain, the truth of closed
![]() $\Delta ^0_0$
-formulas is decidable. A
$\Delta ^0_0$
-formulas is decidable. A
![]() $\Sigma ^0_{n+1}$
-formula (
$\Sigma ^0_{n+1}$
-formula (
![]() $\Pi ^0_{n+1}$
-formula) has the form
$\Pi ^0_{n+1}$
-formula) has the form
![]() $\exists _x\varphi $
(the form
$\exists _x\varphi $
(the form
![]() $\forall _x\varphi $
), where
$\forall _x\varphi $
), where
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Pi ^0_n$
-formula (
$\Pi ^0_n$
-formula (
![]() $\Sigma ^0_n$
-formula). Recall that the
$\Sigma ^0_n$
-formula). Recall that the
![]() $\Sigma ^0_1$
-formulas correspond to the computably enumerable relations. A relation is
$\Sigma ^0_1$
-formulas correspond to the computably enumerable relations. A relation is
![]() $\Delta ^0_1$
-definable (in
$\Delta ^0_1$
-definable (in
![]() $\mathbf {PA}$
) if it has a
$\mathbf {PA}$
) if it has a
![]() $\Sigma ^0_1$
-definition and a
$\Sigma ^0_1$
-definition and a
![]() $\Pi ^0_1$
-definition (which
$\Pi ^0_1$
-definition (which
![]() $\mathbf {PA}$
proves to be equivalent). The
$\mathbf {PA}$
proves to be equivalent). The
![]() $\Delta ^0_1$
-relations coincide with the decidable ones.
$\Delta ^0_1$
-relations coincide with the decidable ones.
Working in
![]() $\mathbf {PA}$
, the elements of
$\mathbf {PA}$
, the elements of
![]() $\mathcal B$
can be represented by numerical codes for finite sets of sequences with entries from
$\mathcal B$
can be represented by numerical codes for finite sets of sequences with entries from
![]() $\{0,1\}$
. Note that the relations
$\{0,1\}$
. Note that the relations
![]() $s\in \mathcal B$
and
$s\in \mathcal B$
and
![]() $s\leq _{\mathcal B}t$
are
$s\leq _{\mathcal B}t$
are
![]() $\Delta ^0_1$
-definable in
$\Delta ^0_1$
-definable in
![]() $\mathbf {PA}$
. As mentioned above, the fact that
$\mathbf {PA}$
. As mentioned above, the fact that
![]() $\mathcal B$
is a wpo can be expressed in terms of a finite basis property. To state the latter we abbreviate
$\mathcal B$
is a wpo can be expressed in terms of a finite basis property. To state the latter we abbreviate
In the context of
![]() $\mathbf {PA}$
it is natural to focus on definable sets. Given a formula
$\mathbf {PA}$
it is natural to focus on definable sets. Given a formula
![]() $\varphi (s)$
with a distinguished free variable, the finite basis property for
$\varphi (s)$
with a distinguished free variable, the finite basis property for
![]() $\{s\in \mathcal B\,|\,\varphi (s)\}\subseteq \mathcal B$
can be formalized as
$\{s\in \mathcal B\,|\,\varphi (s)\}\subseteq \mathcal B$
can be formalized as
Note that the quantifiers with subscript
![]() $s\in a$
are bounded, since a is a code for a finite set (cf. [Reference Hasegawa, Jones, Hagiya and Sato20, lemma I.1.32]); in contrast, the quantifiers with subscripts
$s\in a$
are bounded, since a is a code for a finite set (cf. [Reference Hasegawa, Jones, Hagiya and Sato20, lemma I.1.32]); in contrast, the quantifiers with subscripts
![]() $a\subseteq \mathcal B$
and
$a\subseteq \mathcal B$
and
![]() $t\in \mathcal B$
are unbounded. The symbol
$t\in \mathcal B$
are unbounded. The symbol
![]() $\mathcal K$
alludes to Kruskal’s theorem, which implies that all instances
$\mathcal K$
alludes to Kruskal’s theorem, which implies that all instances
![]() $\mathcal K\varphi $
are true (see Remark 3.1 for details). We will be most interested in the axiom scheme
$\mathcal K\varphi $
are true (see Remark 3.1 for details). We will be most interested in the axiom scheme
The superscript of
![]() $\Sigma ^-_1$
emphasizes the fact that no further free variables are allowed. This ensures that each instance of
$\Sigma ^-_1$
emphasizes the fact that no further free variables are allowed. This ensures that each instance of
![]() $\mathcal K\Sigma ^-_1$
is a closed
$\mathcal K\Sigma ^-_1$
is a closed
![]() $\Sigma ^0_2$
-formula.
$\Sigma ^0_2$
-formula.
To motivate the restrictions on the quantifier complexity and the parameters, we recall the notion of computational strength: A computable function
![]() $f:\mathbb N\to \mathbb N$
is provably total in a suitable theory
$f:\mathbb N\to \mathbb N$
is provably total in a suitable theory
![]() $\mathbf T$
if the latter proves
$\mathbf T$
if the latter proves
![]() $\forall _x\exists !_y\varphi (x,y)$
for some
$\forall _x\exists !_y\varphi (x,y)$
for some
![]() $\Sigma ^0_1$
-definition
$\Sigma ^0_1$
-definition
![]() $\varphi $
of the graph of f (where
$\varphi $
of the graph of f (where
![]() $\exists !$
abbreviates the existence of a unique witness). The computational strength of a theory is commonly identified with the collection of its provably total computable functions.
$\exists !$
abbreviates the existence of a unique witness). The computational strength of a theory is commonly identified with the collection of its provably total computable functions.
It is known that the computational strength of a theory does not increase when we add a true
![]() $\Pi ^0_1$
-sentence
$\Pi ^0_1$
-sentence
![]() $\psi $
as an axiom. Essentially, this is due to the fact that the
$\psi $
as an axiom. Essentially, this is due to the fact that the
![]() $\Sigma ^0_1$
-formula
$\Sigma ^0_1$
-formula
![]() $\psi \to \varphi (x,y)$
defines the same graph as
$\psi \to \varphi (x,y)$
defines the same graph as
![]() $\varphi (x,y)$
(note that the definition of provably total function is extensional). A simple but fundamental observation shows that the same is true for closed
$\varphi (x,y)$
(note that the definition of provably total function is extensional). A simple but fundamental observation shows that the same is true for closed
![]() $\Sigma ^0_2$
-axioms: It suffices to note that any true
$\Sigma ^0_2$
-axioms: It suffices to note that any true
![]() $\Sigma ^0_2$
-sentence
$\Sigma ^0_2$
-sentence
![]() $\exists _x\psi (x)$
follows from some true
$\exists _x\psi (x)$
follows from some true
![]() $\Pi ^0_1$
-instance
$\Pi ^0_1$
-instance
![]() $\psi (\overline n)$
(see Proposition 3.2 for details). Note that we may not be able to compute the correct witness
$\psi (\overline n)$
(see Proposition 3.2 for details). Note that we may not be able to compute the correct witness
![]() $n\in \mathbb N$
; this issue will resurface at the end of the present section.
$n\in \mathbb N$
; this issue will resurface at the end of the present section.
The general facts from the previous paragraph imply that
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
has the same computational strength as
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
has the same computational strength as
![]() $\mathbf {PA}$
. At this point it is crucial that we exclude parameters: If the
$\mathbf {PA}$
. At this point it is crucial that we exclude parameters: If the
![]() $\Sigma ^0_1$
-formula
$\Sigma ^0_1$
-formula
![]() $\varphi $
contains further free variables, then the universal closure of
$\varphi $
contains further free variables, then the universal closure of
![]() $\mathcal K\varphi $
is a
$\mathcal K\varphi $
is a
![]() $\Pi ^0_3$
-formula, so that our argument does not longer apply. Note that the version with parameters can be expressed by a single
$\Pi ^0_3$
-formula, so that our argument does not longer apply. Note that the version with parameters can be expressed by a single
![]() $\Pi ^0_3$
-sentence (rather than a scheme), due to the existence of a universal computably enumerable set.
$\Pi ^0_3$
-sentence (rather than a scheme), due to the existence of a universal computably enumerable set.
Next, we explain why
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
is a proper extension of
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
is a proper extension of
![]() $\mathbf {PA}$
. Based on a notation system for the ordinal
$\mathbf {PA}$
. Based on a notation system for the ordinal
![]() $\varepsilon _0$
(see Section 4 for details), transfinite induction can be expressed in first order arithmetic: Given a formula
$\varepsilon _0$
(see Section 4 for details), transfinite induction can be expressed in first order arithmetic: Given a formula
![]() $\psi (\alpha )$
with a distinguished free variable, we set
$\psi (\alpha )$
with a distinguished free variable, we set
 $$ \begin{align*} \operatorname{Prog}_{\varepsilon_0}(\psi)&:\equiv\forall_{\gamma\prec\varepsilon_0}(\forall_{\beta\prec\gamma}\psi(\beta)\rightarrow\psi(\gamma)),\\ \mathcal{TI}(\varepsilon_0,\psi)&:\equiv\operatorname{Prog}_{\varepsilon_0}(\psi)\rightarrow\forall_{\alpha\prec\varepsilon_0}\psi(\alpha). \end{align*} $$
$$ \begin{align*} \operatorname{Prog}_{\varepsilon_0}(\psi)&:\equiv\forall_{\gamma\prec\varepsilon_0}(\forall_{\beta\prec\gamma}\psi(\beta)\rightarrow\psi(\gamma)),\\ \mathcal{TI}(\varepsilon_0,\psi)&:\equiv\operatorname{Prog}_{\varepsilon_0}(\psi)\rightarrow\forall_{\alpha\prec\varepsilon_0}\psi(\alpha). \end{align*} $$
The scheme of parameter-free
![]() $\Pi ^0_1$
-induction up to
$\Pi ^0_1$
-induction up to
![]() $\varepsilon _0$
is the collection
$\varepsilon _0$
is the collection
In Section 4 we show that each instance of
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
can be proved in
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
can be proved in
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
. This is a straightforward consequence of the fact that
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
. This is a straightforward consequence of the fact that
![]() $\varepsilon _0$
is bounded by (and in fact equal to) the maximal order type of
$\varepsilon _0$
is bounded by (and in fact equal to) the maximal order type of
![]() $\mathcal B$
. Nevertheless we find it worthwhile to give a detailed proof, which pays attention to the quantifier complexities and the role of parameters. Gentzen [Reference Gentzen18] has used
$\mathcal B$
. Nevertheless we find it worthwhile to give a detailed proof, which pays attention to the quantifier complexities and the role of parameters. Gentzen [Reference Gentzen18] has used
![]() $\Pi ^0_1$
-induction up to
$\Pi ^0_1$
-induction up to
![]() $\varepsilon _0$
to establish the consistency of
$\varepsilon _0$
to establish the consistency of
![]() $\mathbf {PA}$
. This induction does not require parameters, as we will check in Section 5. Hence the consistency of
$\mathbf {PA}$
. This induction does not require parameters, as we will check in Section 5. Hence the consistency of
![]() $\mathbf {PA}$
can be proved in
$\mathbf {PA}$
can be proved in
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
. The latter must thus be a proper extension, due to Gödel’s second incompleteness theorem.
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
. The latter must thus be a proper extension, due to Gödel’s second incompleteness theorem.
In Section 6 we review the proof that
![]() $\mathcal B$
has maximal order type
$\mathcal B$
has maximal order type
![]() $\varepsilon _0$
. This will allow us to show that, conversely,
$\varepsilon _0$
. This will allow us to show that, conversely,
![]() $\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
proves each instance of
$\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
proves each instance of
![]() $\mathcal K\Sigma ^-_1$
. To complete the picture, we relate transfinite induction and reflection. Let
$\mathcal K\Sigma ^-_1$
. To complete the picture, we relate transfinite induction and reflection. Let
![]() $\operatorname {Pr}_{\mathbf {PA}}(\varphi )$
be a standard formalization of the statement that the formula
$\operatorname {Pr}_{\mathbf {PA}}(\varphi )$
be a standard formalization of the statement that the formula
![]() $\varphi $
is provable in
$\varphi $
is provable in
![]() $\mathbf {PA}$
(see [Reference Hasegawa, Jones, Hagiya and Sato20, sec. I.4(a)]; we will also write
$\mathbf {PA}$
(see [Reference Hasegawa, Jones, Hagiya and Sato20, sec. I.4(a)]; we will also write
![]() $\varphi $
for
$\varphi $
for
![]() $\overline {\ulcorner \varphi \urcorner }$
). Given a sentence
$\overline {\ulcorner \varphi \urcorner }$
). Given a sentence
![]() $\varphi $
of first order arithmetic, we put
$\varphi $
of first order arithmetic, we put
The local (i.e., parameter-free)
![]() $\Sigma ^0_2$
-reflection principle over
$\Sigma ^0_2$
-reflection principle over
![]() $\mathbf {PA}$
is the collection
$\mathbf {PA}$
is the collection
Due to G. Kreisel and A. Lévy Reference Kreisel and Lévy[27], uniform reflection over
![]() $\mathbf {PA}$
is equivalent to
$\mathbf {PA}$
is equivalent to
![]() $\varepsilon _0$
-induction for formulas with parameters. We will show that the proof can be adapted to the parameter free case (which can also be inferred from work of L. Beklemishev [Reference Beklemishev2, Reference Beklemishev3], cf. Remark 5.2 below). This results in Theorem 7.3, which asserts
$\varepsilon _0$
-induction for formulas with parameters. We will show that the proof can be adapted to the parameter free case (which can also be inferred from work of L. Beklemishev [Reference Beklemishev2, Reference Beklemishev3], cf. Remark 5.2 below). This results in Theorem 7.3, which asserts
In view of Goryachev’s theorem (see, e.g., [Reference Lindström30, theorem IV.5]), we can conclude the following (cf. Corollary 7.4 below): Over Peano arithmetic, the
![]() $\Pi ^0_1$
-consequences of
$\Pi ^0_1$
-consequences of
![]() $\mathcal K\Sigma ^-_1$
are precisely those of the finitely iterated consistency statements for
$\mathcal K\Sigma ^-_1$
are precisely those of the finitely iterated consistency statements for
![]() $\mathbf {PA}$
. Due to another result of Kreisel and Lévy Reference Kreisel and Lévy[27], we can also deduce that
$\mathbf {PA}$
. Due to another result of Kreisel and Lévy Reference Kreisel and Lévy[27], we can also deduce that
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
is not contained in any consistent extension of
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
is not contained in any consistent extension of
![]() $\mathbf {PA}$
by a computably enumerable set of
$\mathbf {PA}$
by a computably enumerable set of
![]() $\Pi ^0_2$
-sentences (see Corollary 5.4).
$\Pi ^0_2$
-sentences (see Corollary 5.4).
Concerning the structure of our paper, we point out that the inclusions
![]() $\supseteq $
from (*) are proved in Sections 4 and 5, while the inclusions
$\supseteq $
from (*) are proved in Sections 4 and 5, while the inclusions
![]() $\subseteq $
are proved in Sections 6 and 7. As we will see in the next section, the inclusions
$\subseteq $
are proved in Sections 6 and 7. As we will see in the next section, the inclusions
![]() $\supseteq $
suffice to ensure many (but not all) of the properties that make
$\supseteq $
suffice to ensure many (but not all) of the properties that make
![]() $\mathcal K\Sigma ^-_1$
foundationally significant. Some readers may thus prefer to skip Sections 6 and 7. For others, these sections may constitute the most interesting part of our paper.
$\mathcal K\Sigma ^-_1$
foundationally significant. Some readers may thus prefer to skip Sections 6 and 7. For others, these sections may constitute the most interesting part of our paper.
2 Foundational considerations
In the previous section we have presented an extension of Peano arithmetic by an axiom scheme
![]() $\mathcal K\Sigma ^-_1$
that is related to Kruskal’s theorem. The present section is concerned with the foundational significance of this extension.
$\mathcal K\Sigma ^-_1$
that is related to Kruskal’s theorem. The present section is concerned with the foundational significance of this extension.
Let us first recall some aspects of Hilbert’s program; for a more thorough discussion and further references we refer to the introduction by R. Zach Reference Zach and Zalta[49]. To secure the abstract methods that are central to modern mathematics, Hilbert wanted to justify them by finitist reasoning about natural numbers, which he views as “extralogical concrete objects that are intuitively present as immediate experience prior to all thought” [Reference Hilbert22, p. 171]. (All quotations from [Reference Hilbert22, Reference de Jongh and Parikh23] are translated as in Reference van Heijenoort[48].) The status of the natural numbers entails that certain statements about them are finitistically meaningful. This includes, first of all, statements which assert that a given tuple of numbers satisfies some primitive recursive relation. Such a statement can be verified explicitly, which explains its privileged role, but also entails—as Hilbert [Reference Hilbert22, p. 165] puts it—that it is “of no essential interest when considered by itself.” In addition, one admits universal statements with verifiable instances. According to Hilbert [Reference Hilbert22, p. 173], such a statement can be accepted as “a hypothetical judgement that comes to assert something when a numeral is given.” In contrast, unbounded existential statements are not seen as finitistically meaningful, as “one cannot […] try out all numbers” [Reference de Jongh and Parikh23, p. 73]. At the same time, Hilbert [Reference de Jongh and Parikh23, p. 77f] emphasizes the fact that existential statements play an extremely fruitful role in abstract mathematics. One could even be tempted to say that abstract notions acquire meaning through their role in the mathematical development, a position that seems to resonate with the following statement by Hilbert [Reference de Jongh and Parikh23, p. 79]:
“To make it a universal requirement that each individual formula […] be interpretable by itself is by no means reasonable; on the contrary, a theory by its very nature is such that we do not need to fall back upon intuition or meaning in the midst of some argument.”
However, such a conception of meaning is very different from the finitist one.
The extent of finitist reasoning is commonly identified with primitive recursive arithmetic (
![]() $\mathbf {PRA}$
). This identification has been justified by W. Tait Reference Tait[44]; in Reference Tait, Sieg, Sommer and Talcott[45] he lists and refutes some objections. A quantifier-free formulation seems to be most appropriate: In a such a setting, one can only express statements that are finitistically meaningful; universal statements correspond to open formulas. We will, nevertheless, work in the usual framework of first order arithmetic with quantifiers, since the latter are needed to express our existential statements
$\mathbf {PRA}$
). This identification has been justified by W. Tait Reference Tait[44]; in Reference Tait, Sieg, Sommer and Talcott[45] he lists and refutes some objections. A quantifier-free formulation seems to be most appropriate: In a such a setting, one can only express statements that are finitistically meaningful; universal statements correspond to open formulas. We will, nevertheless, work in the usual framework of first order arithmetic with quantifiers, since the latter are needed to express our existential statements
![]() $\mathcal K\varphi $
. Following C. Smoryński Reference Smoryński and Barwise[42], we agree to identify the finitistically meaningful statements with the
$\mathcal K\varphi $
. Following C. Smoryński Reference Smoryński and Barwise[42], we agree to identify the finitistically meaningful statements with the
![]() $\Pi ^0_1$
-sentences.
$\Pi ^0_1$
-sentences.
More specifically, then, Hilbert’s program suggested to formalize all of abstract mathematics as an axiom system
![]() $\mathbf T$
. In order to obtain a finitist justification, one was supposed to prove the consistency of
$\mathbf T$
. In order to obtain a finitist justification, one was supposed to prove the consistency of
![]() $\mathbf T$
in the theory
$\mathbf T$
in the theory
![]() $\mathbf {PRA}$
. At this point it is important to note that consistency is not merely a minimal requirement: If the consistency of a theory
$\mathbf {PRA}$
. At this point it is important to note that consistency is not merely a minimal requirement: If the consistency of a theory
![]() $\mathbf T$
is provable in
$\mathbf T$
is provable in
![]() $\mathbf {PRA}$
, then the latter proves all
$\mathbf {PRA}$
, then the latter proves all
![]() $\Pi ^0_1$
-theorems of
$\Pi ^0_1$
-theorems of
![]() $\mathbf T$
, i.e., all results that are finitistically meaningful (see [Reference de Jongh and Parikh23, p. 78f]). Gödel’s incompleteness theorems show that Hilbert’s program cannot be carried out: It is impossible for
$\mathbf T$
, i.e., all results that are finitistically meaningful (see [Reference de Jongh and Parikh23, p. 78f]). Gödel’s incompleteness theorems show that Hilbert’s program cannot be carried out: It is impossible for
![]() $\mathbf T$
to prove its own consistency; a fortiori, the consistency of
$\mathbf T$
to prove its own consistency; a fortiori, the consistency of
![]() $\mathbf T$
cannot be established in the weaker theory
$\mathbf T$
cannot be established in the weaker theory
![]() $\mathbf {PRA}$
.
$\mathbf {PRA}$
.
Despite Gödel’s theorems, the aims of Hilbert’s program have been achieved to an astonishing extent: A substantial part of contemporary mathematics can indeed be formalized in rather weak axiom systems (see, e.g., the work of S. Feferman [Reference Fellows and Langston10], as well as U. Kohlenbach’s proof mining program Reference Kohlenbach[24]). In view of these positive results, it is all the more intriguing to ask: Are there natural mathematical theorems that can be expressed but not proved in
![]() $\mathbf {PRA}$
, or in some stronger theory? To count as a natural theorem, the unprovable statement should arise from mathematical practice; it should not involve the logical notions of proof or model. In particular, consistency statements (which are unprovable by Gödel’s theorem) are not seen as examples of this type.
$\mathbf {PRA}$
, or in some stronger theory? To count as a natural theorem, the unprovable statement should arise from mathematical practice; it should not involve the logical notions of proof or model. In particular, consistency statements (which are unprovable by Gödel’s theorem) are not seen as examples of this type.
We do have good examples of true
![]() $\Pi ^0_2$
-statements that are unprovable in relevant axiom systems: The Paris–Harrington principle cannot be proved in Peano arithmetic Reference Paris, Harrington and Barwise[31]; Friedman’s miniaturization of Kruskal’s theorem is independent of an even stronger system Reference Simpson, Harrington, Morley, Sčědrov and Simpson[38], which is associated with predicative mathematics. The situation is less satisfactory when it comes to
$\Pi ^0_2$
-statements that are unprovable in relevant axiom systems: The Paris–Harrington principle cannot be proved in Peano arithmetic Reference Paris, Harrington and Barwise[31]; Friedman’s miniaturization of Kruskal’s theorem is independent of an even stronger system Reference Simpson, Harrington, Morley, Sčědrov and Simpson[38], which is associated with predicative mathematics. The situation is less satisfactory when it comes to
![]() $\Pi ^0_1$
-sentences, which are most important from the finitist viewpoint: The independent statement due to S. Shelah Reference Shelah, Lolli, Longo and Marcja[37] involves notions from model theory, so that its status as a natural mathematical theorem can be questioned. Friedman has presented work on
$\Pi ^0_1$
-sentences, which are most important from the finitist viewpoint: The independent statement due to S. Shelah Reference Shelah, Lolli, Longo and Marcja[37] involves notions from model theory, so that its status as a natural mathematical theorem can be questioned. Friedman has presented work on
![]() $\Pi ^0_1$
-independence from Zermelo–Fraenkel set theory (see, e.g., [Reference Friedman, Robertson, Seymour and Simpson15]), but his results are not yet published in final form. In the present author’s opinion, the search for mathematical
$\Pi ^0_1$
-independence from Zermelo–Fraenkel set theory (see, e.g., [Reference Friedman, Robertson, Seymour and Simpson15]), but his results are not yet published in final form. In the present author’s opinion, the search for mathematical
![]() $\Pi ^0_1$
-sentences that are independent of relevant axiom systems remains one of the most interesting challenges in mathematical logic.
$\Pi ^0_1$
-sentences that are independent of relevant axiom systems remains one of the most interesting challenges in mathematical logic.
The axiom scheme
![]() $\mathcal K\Sigma ^-_1$
from the previous section does not settle the challenge of natural
$\mathcal K\Sigma ^-_1$
from the previous section does not settle the challenge of natural
![]() $\Pi ^0_1$
-independence. The latter can, nevertheless, serve as a benchmark that helps us to assess the foundational significance of
$\Pi ^0_1$
-independence. The latter can, nevertheless, serve as a benchmark that helps us to assess the foundational significance of
![]() $\mathcal K\Sigma ^-_1$
. In the rest of this section we carry out such an assessment.
$\mathcal K\Sigma ^-_1$
. In the rest of this section we carry out such an assessment.
First, we will argue that
![]() $\mathcal K\Sigma ^-_1$
is a natural mathematical commitment. In the previous section we have seen that
$\mathcal K\Sigma ^-_1$
is a natural mathematical commitment. In the previous section we have seen that
![]() $\mathcal K\Sigma ^-_1$
is a restricted version of Kruskal’s theorem. The latter is firmly established as a natural result of mathematical practice. Hence it remains to argue that the restrictions that lead to
$\mathcal K\Sigma ^-_1$
is a restricted version of Kruskal’s theorem. The latter is firmly established as a natural result of mathematical practice. Hence it remains to argue that the restrictions that lead to
![]() $\mathcal K\Sigma ^-_1$
are natural as well.
$\mathcal K\Sigma ^-_1$
are natural as well.
In formulating
![]() $\mathcal K\Sigma ^-_1$
, we have restricted Kruskal’s theorem in two ways: Firstly, we have decided to work with binary rather than arbitrary finite trees. This restriction makes it easier to determine the precise strength of
$\mathcal K\Sigma ^-_1$
, we have restricted Kruskal’s theorem in two ways: Firstly, we have decided to work with binary rather than arbitrary finite trees. This restriction makes it easier to determine the precise strength of
![]() $\mathcal K\Sigma ^-_1$
(i.e., to prove the equivalence with transfinite induction and local reflection), but it is not essential: If we extend our axiom scheme to arbitrary finite trees, then it will imply the consistency of stronger axiom systems; at the same time, it will still not increase the computational strength, since it also consists of
$\mathcal K\Sigma ^-_1$
(i.e., to prove the equivalence with transfinite induction and local reflection), but it is not essential: If we extend our axiom scheme to arbitrary finite trees, then it will imply the consistency of stronger axiom systems; at the same time, it will still not increase the computational strength, since it also consists of
![]() $\Sigma ^0_2$
-statements. The graph minor theorem of N. Robertson and P. Seymour Reference Robertson and Seymour[34] suggests a very intriguing axiom scheme that is even stronger (cf. [Reference Friedman and Sheard16]) but does not have computational strength either (for the same general reason). In summary, the restriction to binary trees is purely pragmatic and does not change the general foundational behavior. Secondly, the scheme
$\Sigma ^0_2$
-statements. The graph minor theorem of N. Robertson and P. Seymour Reference Robertson and Seymour[34] suggests a very intriguing axiom scheme that is even stronger (cf. [Reference Friedman and Sheard16]) but does not have computational strength either (for the same general reason). In summary, the restriction to binary trees is purely pragmatic and does not change the general foundational behavior. Secondly, the scheme
![]() $\mathcal K\Sigma ^-_1$
is a restriction of Kruskal’s theorem insofar as it demands a finite basis for computably enumerable—rather than arbitrary—sets of trees. In the following we give two justifications for the restriction to computably enumerable sets.
$\mathcal K\Sigma ^-_1$
is a restriction of Kruskal’s theorem insofar as it demands a finite basis for computably enumerable—rather than arbitrary—sets of trees. In the following we give two justifications for the restriction to computably enumerable sets.
The first justification is that
![]() $\mathcal K\Sigma ^-_1$
suffices for certain applications in computer science: Assume that P is an upward closed property of finite binary trees, which means that
$\mathcal K\Sigma ^-_1$
suffices for certain applications in computer science: Assume that P is an upward closed property of finite binary trees, which means that
![]() $P(s)$
and
$P(s)$
and
![]() $s\leq _{\mathcal B}t$
imply
$s\leq _{\mathcal B}t$
imply
![]() $P(t)$
. Often (but not always, cf. [Reference Fellows and Langston11, theorem 3]) one will already know that P is decidable. Then P can be defined by a
$P(t)$
. Often (but not always, cf. [Reference Fellows and Langston11, theorem 3]) one will already know that P is decidable. Then P can be defined by a
![]() $\Sigma ^0_1$
-formula, and
$\Sigma ^0_1$
-formula, and
![]() $\mathcal K\Sigma ^-_1$
yields a finite
$\mathcal K\Sigma ^-_1$
yields a finite
![]() $a\subseteq \mathcal B$
such that
$a\subseteq \mathcal B$
such that
![]() $P(t)$
is equivalent to
$P(t)$
is equivalent to
![]() $\exists _{s\in a}s\leq _{\mathcal B}t$
. The latter can be decided in polynomial time (in the size of t). The author knows of no concrete applications in the context of trees, but the analogous argument for the graph minor relation has many applications (see, e.g., [Reference Freund and Pakhomov12]).
$\exists _{s\in a}s\leq _{\mathcal B}t$
. The latter can be decided in polynomial time (in the size of t). The author knows of no concrete applications in the context of trees, but the analogous argument for the graph minor relation has many applications (see, e.g., [Reference Freund and Pakhomov12]).
The second justification for the restriction to computably enumerable sets is based on the idea that one can have reasons to accept
![]() $\mathcal K\Sigma ^-_1$
but not the full Kruskal theorem for binary trees. To make this plausible we recall that
$\mathcal K\Sigma ^-_1$
but not the full Kruskal theorem for binary trees. To make this plausible we recall that
![]() $\mathcal K\Sigma ^-_1$
is equivalent to the principle
$\mathcal K\Sigma ^-_1$
is equivalent to the principle
![]() $\mathcal {TI}(\varepsilon _0,\Pi _1^-)$
of parameter-free
$\mathcal {TI}(\varepsilon _0,\Pi _1^-)$
of parameter-free
![]() $\Pi ^0_1$
-induction up to
$\Pi ^0_1$
-induction up to
![]() $\varepsilon _0$
. The latter is no stronger than induction for decidable (i.e., finitistically meaningful) properties, still up to
$\varepsilon _0$
. The latter is no stronger than induction for decidable (i.e., finitistically meaningful) properties, still up to
![]() $\varepsilon _0$
(see, e.g., [Reference Sommer43, lemma 4.5]). On the other hand, the full Kruskal theorem for binary trees is naturally formulated in second order arithmetic. Over the theory
$\varepsilon _0$
(see, e.g., [Reference Sommer43, lemma 4.5]). On the other hand, the full Kruskal theorem for binary trees is naturally formulated in second order arithmetic. Over the theory
![]() $\mathbf {ACA}_0$
from reverse mathematics (see Reference Simpson[40] for an introduction), it is equivalent both to our statement
$\mathbf {ACA}_0$
from reverse mathematics (see Reference Simpson[40] for an introduction), it is equivalent both to our statement
![]() $\forall _{X\subseteq \mathbb N}\,\mathcal K\varphi $
with
$\forall _{X\subseteq \mathbb N}\,\mathcal K\varphi $
with
![]() $\varphi (s)\equiv s\in X$
and to the well-foundedness of
$\varphi (s)\equiv s\in X$
and to the well-foundedness of
![]() $\varepsilon _0$
(see Reference Rathjen and Weiermann[33] for the crucial direction from well-foundedness to Kruskal’s theorem). Now from a finitist standpoint it makes sense to accept
$\varepsilon _0$
(see Reference Rathjen and Weiermann[33] for the crucial direction from well-foundedness to Kruskal’s theorem). Now from a finitist standpoint it makes sense to accept
![]() $\mathcal {TI}(\varepsilon _0,\Pi _1^-)$
but not the second order statement that
$\mathcal {TI}(\varepsilon _0,\Pi _1^-)$
but not the second order statement that
![]() $\varepsilon _0$
is well-founded. Indeed, Tait [Reference Tait, Sieg, Sommer and Talcott45, p. 411] states that Kreisel Reference Kreisel and Todd[25] accepts quantifier-free induction up to each ordinal below
$\varepsilon _0$
is well-founded. Indeed, Tait [Reference Tait, Sieg, Sommer and Talcott45, p. 411] states that Kreisel Reference Kreisel and Todd[25] accepts quantifier-free induction up to each ordinal below
![]() $\varepsilon _0$
as finitist. Also, G. Takeuti’s justification of transfinite induction is supposed to “involve ‘Gedankenexperimente’ [thought experiments] only on clearly defined operations applied to some concretely given figures” [Reference Takeuti46, p. 97].
$\varepsilon _0$
as finitist. Also, G. Takeuti’s justification of transfinite induction is supposed to “involve ‘Gedankenexperimente’ [thought experiments] only on clearly defined operations applied to some concretely given figures” [Reference Takeuti46, p. 97].
Next, we discuss the fact that
![]() $\mathcal K\Sigma ^-_1$
is a scheme rather than a single statement. In the previous section we have explained that
$\mathcal K\Sigma ^-_1$
is a scheme rather than a single statement. In the previous section we have explained that
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
proves the consistency of
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
proves the consistency of
![]() $\mathbf {PA}$
. Of course, this proof involves only finitely many instances
$\mathbf {PA}$
. Of course, this proof involves only finitely many instances
![]() $\mathcal K\varphi _1,\dots ,\mathcal K\varphi _n$
. However, we see no basis for the claim that these particular instances constitute a natural mathematical commitment—in contrast to the axiom scheme as a whole. In this sense our reference to an axiom scheme is essential. What does this entail? We think that the answer depends on our attitude toward independence phenomena.
$\mathcal K\varphi _1,\dots ,\mathcal K\varphi _n$
. However, we see no basis for the claim that these particular instances constitute a natural mathematical commitment—in contrast to the axiom scheme as a whole. In this sense our reference to an axiom scheme is essential. What does this entail? We think that the answer depends on our attitude toward independence phenomena.
One possibility is to think of independent statements as “unsolvable conjectures.” More explicitly, one might imagine a mathematician immersed in Peano arithmetic, who is challenged to prove or refute the Paris–Harrington principle. The independence result tells us that this mathematician can never succeed. This conception of independence is clearly concerned with single statements rather than schemes. However, one can also think of independence in terms of “potential axioms.” For example, one may view the principle of induction for arbitrary first order formulas as a mathematical commitment beyond the finitist standpoint. This example shows that schemes play a natural role within such a conception of independence.
A broad conception of independence may even incorporate rules, in addition to axiom schemes. In the present context it is interesting to consider the rule

of
![]() $\Pi ^0_1$
-induction along
$\Pi ^0_1$
-induction along
![]() $\varepsilon _0$
, which allows us to infer
$\varepsilon _0$
, which allows us to infer
![]() $\forall _{\alpha \prec \varepsilon _0}\psi (\alpha )$
once we have given a proof of
$\forall _{\alpha \prec \varepsilon _0}\psi (\alpha )$
once we have given a proof of
![]() $\forall _{\gamma \prec \varepsilon _0}(\forall _{\beta \prec \gamma }\psi (\beta )\rightarrow \psi (\gamma ))$
, where
$\forall _{\gamma \prec \varepsilon _0}(\forall _{\beta \prec \gamma }\psi (\beta )\rightarrow \psi (\gamma ))$
, where
![]() $\psi (\alpha )$
can be any
$\psi (\alpha )$
can be any
![]() $\Pi ^0_1$
-formula without further free variables. Note that the rule does not commit us to the contrapositive of the corresponding axiom, i.e., to the least element principle. Hence the rule avoids certain existential commitments, which is well motivated in a finitist context. As shown by Beklemishev [Reference Beklemishev2, theorem 3], the closure of
$\Pi ^0_1$
-formula without further free variables. Note that the rule does not commit us to the contrapositive of the corresponding axiom, i.e., to the least element principle. Hence the rule avoids certain existential commitments, which is well motivated in a finitist context. As shown by Beklemishev [Reference Beklemishev2, theorem 3], the closure of
![]() $\mathbf {PA}$
under the rule of
$\mathbf {PA}$
under the rule of
![]() $\Pi ^0_1$
-induction along
$\Pi ^0_1$
-induction along
![]() $\varepsilon _0$
proves the same theorems as the extension of
$\varepsilon _0$
proves the same theorems as the extension of
![]() $\mathbf {PA}$
by finitely iterated consistency statements. Note that the rule does not refer to logical notions such as proof or model. Insofar as induction up to
$\mathbf {PA}$
by finitely iterated consistency statements. Note that the rule does not refer to logical notions such as proof or model. Insofar as induction up to
![]() $\varepsilon _0$
is a result of mathematical practice, we have a mathematical commitment on the level of
$\varepsilon _0$
is a result of mathematical practice, we have a mathematical commitment on the level of
![]() $\Pi ^0_1$
-statements.
$\Pi ^0_1$
-statements.
Let us now discuss the fact that
![]() $\mathcal K\Sigma ^-_1$
consists of
$\mathcal K\Sigma ^-_1$
consists of
![]() $\Sigma ^0_2$
-statements rather than
$\Sigma ^0_2$
-statements rather than
![]() $\Pi ^0_1$
-statements. At the end of the previous section we have mentioned that there is no computably enumerable set
$\Pi ^0_1$
-statements. At the end of the previous section we have mentioned that there is no computably enumerable set
![]() $\Psi $
of
$\Psi $
of
![]() $\Pi ^0_1$
-sentences (or even
$\Pi ^0_1$
-sentences (or even
![]() $\Pi ^0_2$
-sentences) such that
$\Pi ^0_2$
-sentences) such that
![]() $\mathbf {PA}+\Psi $
is consistent and contains
$\mathbf {PA}+\Psi $
is consistent and contains
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
. This shows that our use of
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
. This shows that our use of
![]() $\Sigma ^0_2$
-sentences is essential in a rather strong sense. How, then, do
$\Sigma ^0_2$
-sentences is essential in a rather strong sense. How, then, do
![]() $\Sigma ^0_2$
- and
$\Sigma ^0_2$
- and
![]() $\Pi ^0_2$
-independence compare from a foundational perspective? To set the stage for this question, we first situate
$\Pi ^0_2$
-independence compare from a foundational perspective? To set the stage for this question, we first situate
![]() $\mathcal K\Sigma ^-_1$
within the context of Gentzen’s ordinal analysis.
$\mathcal K\Sigma ^-_1$
within the context of Gentzen’s ordinal analysis.
Gentzen showed that each purported proof of a contradiction can be reduced to a proof with smaller ordinal label. To establish consistency, one can use this reduction in two different ways: First, it follows that a purported proof p of a contradiction leads to an infinite sequence of such proofs, labeled by a strictly decreasing sequence of ordinals. These sequences are primitive recursive with parameter p. To derive consistency, one can then invoke the primitive recursive well-foundedness of
![]() $\varepsilon _0$
. The latter is, in fact, equivalent to uniform
$\varepsilon _0$
. The latter is, in fact, equivalent to uniform
![]() $\Sigma ^0_1$
-reflection (see [Reference Gentzen17, theorem 4.5]), which can be expressed by a single
$\Sigma ^0_1$
-reflection (see [Reference Gentzen17, theorem 4.5]), which can be expressed by a single
![]() $\Pi ^0_2$
-statement. Secondly, one can use induction on
$\Pi ^0_2$
-statement. Secondly, one can use induction on
![]() $\alpha \prec \varepsilon _0$
to show that no proof with label
$\alpha \prec \varepsilon _0$
to show that no proof with label
![]() $\alpha $
can produce a contradiction. This avoids parameters but involves a universal quantification over ordinals. As we will show, it leads to an equivalence between
$\alpha $
can produce a contradiction. This avoids parameters but involves a universal quantification over ordinals. As we will show, it leads to an equivalence between
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
and
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
and
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
, which are axiom schemes with instances of complexity
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
, which are axiom schemes with instances of complexity
![]() $\Sigma ^0_2$
.
$\Sigma ^0_2$
.
It seems that the route via primitive recursive well-foundedness is preferred in the finitist literature. For example, Takeuti writes that the consistency proof is based on the following [Reference Takeuti46, p. 92]:
“Whenever a concrete method of constructing decreasing sequences of ordinals is given, any such decreasing sequence must be finite.”
This preference may help to explain the pre-eminence of
![]() $\Pi ^0_2$
-independence. As an exception, we mention that L. Beklemishev and A. Visser Reference Beklemishev and Visser[4] have characterized the
$\Pi ^0_2$
-independence. As an exception, we mention that L. Beklemishev and A. Visser Reference Beklemishev and Visser[4] have characterized the
![]() $\Sigma ^0_n$
-consequences of
$\Sigma ^0_n$
-consequences of
![]() $\mathbf {PA}$
(and of its fragments) in terms of iterated reflection. Kreisel Reference Kreisel and Stern[26] has initiated work on finiteness theorems of complexity
$\mathbf {PA}$
(and of its fragments) in terms of iterated reflection. Kreisel Reference Kreisel and Stern[26] has initiated work on finiteness theorems of complexity
![]() $\Sigma ^0_2$
, but here the focus is on proof-mining rather than independence.
$\Sigma ^0_2$
, but here the focus is on proof-mining rather than independence.
We have seen that Gentzen’s consistency proof can be concluded in two subtly different ways. These correspond to different mathematical principles that are independent of Peano arithmetic: It is well known that the strengthened finite Ramsey theorem of J. Paris and L. Harrington is equivalent to uniform
![]() $\Sigma ^0_1$
-reflection (see [Reference Paris, Harrington and Barwise31, theorem 3.1]) and hence to the primitive recursive well-foundedness of
$\Sigma ^0_1$
-reflection (see [Reference Paris, Harrington and Barwise31, theorem 3.1]) and hence to the primitive recursive well-foundedness of
![]() $\varepsilon _0$
. The present paper complements this classical result by the equivalence between the Kruskal scheme
$\varepsilon _0$
. The present paper complements this classical result by the equivalence between the Kruskal scheme
![]() $\mathcal K\Sigma ^-_1$
, the scheme
$\mathcal K\Sigma ^-_1$
, the scheme
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
of local
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
of local
![]() $\Sigma ^0_2$
-reflection, and the transfinite induction principle
$\Sigma ^0_2$
-reflection, and the transfinite induction principle
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
.
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
.
Finally, let us take up the comparison of
![]() $\Sigma ^0_2$
- and
$\Sigma ^0_2$
- and
![]() $\Pi ^0_2$
-independence. Extending Hilbert’s view on
$\Pi ^0_2$
-independence. Extending Hilbert’s view on
![]() $\Pi ^0_1$
-sentences, one could see
$\Pi ^0_1$
-sentences, one could see
![]() $\Pi ^0_2$
-sentences as “hypothetical judgement[s]” [Reference Hilbert22, p. 173] of complexity
$\Pi ^0_2$
-sentences as “hypothetical judgement[s]” [Reference Hilbert22, p. 173] of complexity
![]() $\Sigma ^0_1$
. This might suggest that
$\Sigma ^0_1$
. This might suggest that
![]() $\Pi ^0_2$
-sentences are less abstract—in the finitist sense—than
$\Pi ^0_2$
-sentences are less abstract—in the finitist sense—than
![]() $\Sigma ^0_2$
-statements. From this viewpoint, the independence of
$\Sigma ^0_2$
-statements. From this viewpoint, the independence of
![]() $\mathcal K\Sigma ^-_1$
would be less significant than classical independence results, such as the one by Paris and Harrington.
$\mathcal K\Sigma ^-_1$
would be less significant than classical independence results, such as the one by Paris and Harrington.
On the other hand,
![]() $\Sigma ^0_2$
-independence has particularly interesting properties with respect to provably total functions and computational strength (see the previous section for a definition). An independent
$\Sigma ^0_2$
-independence has particularly interesting properties with respect to provably total functions and computational strength (see the previous section for a definition). An independent
![]() $\Pi ^0_2$
-statement will typically add a provably total function: For the Paris–Harrington principle this is the case by [Reference Paris, Harrington and Barwise31, theorem 3.2]; the general claim is plausible in view of [Reference Gentzen17, theorems 2.24 and 4.5] and [Reference Smith, Harrington, Morley, Sčědrov and Simpson41, theorem 5]. In contrast, we have seen that
$\Pi ^0_2$
-statement will typically add a provably total function: For the Paris–Harrington principle this is the case by [Reference Paris, Harrington and Barwise31, theorem 3.2]; the general claim is plausible in view of [Reference Gentzen17, theorems 2.24 and 4.5] and [Reference Smith, Harrington, Morley, Sčědrov and Simpson41, theorem 5]. In contrast, we have seen that
![]() $\mathcal K\Sigma ^-_1$
does not increase the computational strength of
$\mathcal K\Sigma ^-_1$
does not increase the computational strength of
![]() $\mathbf {PA}$
.
$\mathbf {PA}$
.
The fact that
![]() $\mathcal K\Sigma ^-_1$
does not add provably total functions is interesting in its own right, but it becomes even more relevant in view of the following: The notion of computational strength is a relatively robust extensional invariant. Bounds on provably total functions can be established without the use of Gödel’s theorem, e.g., by induction over cut-free infinite proofs (see Reference Buchholz, Wainer and Simpson[6]). This means that Gödel’s theorem is not needed to prove that the Paris–Harrington principle is independent of
$\mathcal K\Sigma ^-_1$
does not add provably total functions is interesting in its own right, but it becomes even more relevant in view of the following: The notion of computational strength is a relatively robust extensional invariant. Bounds on provably total functions can be established without the use of Gödel’s theorem, e.g., by induction over cut-free infinite proofs (see Reference Buchholz, Wainer and Simpson[6]). This means that Gödel’s theorem is not needed to prove that the Paris–Harrington principle is independent of
![]() $\mathbf {PA}$
(see Reference Cichon[7] for an analogous argument with respect to Goodstein’s theorem). It appears that no similar invariants are available on the level of
$\mathbf {PA}$
(see Reference Cichon[7] for an analogous argument with respect to Goodstein’s theorem). It appears that no similar invariants are available on the level of
![]() $\Sigma ^0_2$
-statements. The only known proof of the fact that
$\Sigma ^0_2$
-statements. The only known proof of the fact that
![]() $\mathbf {PA}$
does not prove all instances of
$\mathbf {PA}$
does not prove all instances of
![]() $\mathcal K\Sigma ^-_1$
appeals to Gödel’s theorem. In our opinion, this means that
$\mathcal K\Sigma ^-_1$
appeals to Gödel’s theorem. In our opinion, this means that
![]() $\mathcal K\Sigma ^-_1$
is a conceptually different and foundationally significant manifestation of mathematical independence.
$\mathcal K\Sigma ^-_1$
is a conceptually different and foundationally significant manifestation of mathematical independence.
3 Analyzing the computational strength
In this section we give a detailed proof of the claim that
![]() $\mathcal K\Sigma ^-_1$
does not increase the computational strength of
$\mathcal K\Sigma ^-_1$
does not increase the computational strength of
![]() $\mathbf {PA}$
. As preparation, we need to show that all instances of
$\mathbf {PA}$
. As preparation, we need to show that all instances of
![]() $\mathcal K\Sigma ^-_1$
are true. In the following remark we argue in a strong meta theory; this will later be superseded by a proof in
$\mathcal K\Sigma ^-_1$
are true. In the following remark we argue in a strong meta theory; this will later be superseded by a proof in
![]() $\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
(see Proposition 7.2).
$\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
(see Proposition 7.2).
Remark 3.1. As a consequence of Kruskal’s theorem Reference Kruskal[28], the partial order
![]() $(\mathcal B,\leq _{\mathcal B})$
does not contain any infinite bad sequence. We will use this fact to justify an arbitrary instance
$(\mathcal B,\leq _{\mathcal B})$
does not contain any infinite bad sequence. We will use this fact to justify an arbitrary instance
of the axiom scheme
![]() $\mathcal K\Sigma ^-_1$
. Aiming at a contradiction, assume that
$\mathcal K\Sigma ^-_1$
. Aiming at a contradiction, assume that
![]() $\mathcal K\varphi $
is false. By a bad
$\mathcal K\varphi $
is false. By a bad
![]() $\varphi $
-sequence we mean a bad sequence
$\varphi $
-sequence we mean a bad sequence
![]() $t_0,t_1,\ldots \subseteq \mathcal B$
such that
$t_0,t_1,\ldots \subseteq \mathcal B$
such that
![]() $\varphi (t_i)$
holds for each i. Note that the empty sequence is a bad
$\varphi (t_i)$
holds for each i. Note that the empty sequence is a bad
![]() $\varphi $
-sequence. Furthermore, each bad
$\varphi $
-sequence. Furthermore, each bad
![]() $\varphi $
-sequence
$\varphi $
-sequence
![]() $t_0,\dots ,t_{n-1}$
can be extended into a bad
$t_0,\dots ,t_{n-1}$
can be extended into a bad
![]() $\varphi $
-sequence
$\varphi $
-sequence
![]() $t_0,\dots ,t_{n-1},t_n$
. To see that this is the case, consider
$t_0,\dots ,t_{n-1},t_n$
. To see that this is the case, consider
![]() $a:=\{t_0,\dots ,t_{n-1}\}$
. As
$a:=\{t_0,\dots ,t_{n-1}\}$
. As
![]() $\forall _{s\in a}\varphi (s)$
holds, the assumption that
$\forall _{s\in a}\varphi (s)$
holds, the assumption that
![]() $\mathcal K\varphi $
is false yields an element
$\mathcal K\varphi $
is false yields an element
![]() $t_n\in \mathcal B$
with
$t_n\in \mathcal B$
with
![]() $\varphi (t_n)$
and
$\varphi (t_n)$
and
![]() $\forall _{s\in a}s\not \leq _{\mathcal B}t_n$
. The latter ensures that
$\forall _{s\in a}s\not \leq _{\mathcal B}t_n$
. The latter ensures that
![]() $t_0,\dots ,t_{n-1},t_n$
is still bad. By dependent choice we now get an infinite bad
$t_0,\dots ,t_{n-1},t_n$
is still bad. By dependent choice we now get an infinite bad
![]() $\varphi $
-sequence, which contradicts Kruskal’s theorem.
$\varphi $
-sequence, which contradicts Kruskal’s theorem.
The following result is folklore, but we provide details in order to make the paper as accessible as possible.
Proposition 3.2. If
![]() $\Psi $
is a set of true
$\Psi $
is a set of true
![]() $\Sigma ^0_2$
-sentences, then the provably total functions of
$\Sigma ^0_2$
-sentences, then the provably total functions of
![]() $\mathbf {PA}+\Psi $
and of
$\mathbf {PA}+\Psi $
and of
![]() $\mathbf {PA}$
coincide. In particular, this applies to
$\mathbf {PA}$
coincide. In particular, this applies to
![]() $\Psi =\mathcal K\Sigma ^-_1$
.
$\Psi =\mathcal K\Sigma ^-_1$
.
Proof. Consider a provably total function
![]() $f:\mathbb N\to \mathbb N$
of the theory
$f:\mathbb N\to \mathbb N$
of the theory
![]() $\mathbf {PA}+\Psi $
. For some
$\mathbf {PA}+\Psi $
. For some
![]() $\Sigma ^0_1$
-definition
$\Sigma ^0_1$
-definition
![]() $\theta (x,y)$
of the graph of f, there are sentences
$\theta (x,y)$
of the graph of f, there are sentences
![]() $\psi _0,\dots ,\psi _{n-1}\in \Psi $
such that we have
$\psi _0,\dots ,\psi _{n-1}\in \Psi $
such that we have
To show that f is a provably total function of
![]() $\mathbf {PA}$
, we will define the graph of f by a modified
$\mathbf {PA}$
, we will define the graph of f by a modified
![]() $\Sigma ^0_1$
-formula
$\Sigma ^0_1$
-formula
![]() $\theta '(x,y)$
such that
$\theta '(x,y)$
such that
![]() $\mathbf {PA}$
alone proves
$\mathbf {PA}$
alone proves
![]() $\forall _x\exists !_y\theta '(x,y)$
. For this purpose we observe that the conjunction
$\forall _x\exists !_y\theta '(x,y)$
. For this purpose we observe that the conjunction
![]() $\psi _0\land \cdots \land \psi _{n-1}$
is equivalent to a true
$\psi _0\land \cdots \land \psi _{n-1}$
is equivalent to a true
![]() $\Sigma ^0_2$
-sentence
$\Sigma ^0_2$
-sentence
![]() $\exists _m\psi (m)$
. Pick a number
$\exists _m\psi (m)$
. Pick a number
![]() $n\in \mathbb N$
such that the
$n\in \mathbb N$
such that the
![]() $\Pi ^0_1$
-sentence
$\Pi ^0_1$
-sentence
![]() $\psi (\overline n)$
is true. Then write
$\psi (\overline n)$
is true. Then write
for a
![]() $\Delta ^0_0$
-formula
$\Delta ^0_0$
-formula
![]() $\theta _0$
. Since
$\theta _0$
. Since
![]() $\psi (\overline n)$
is true and implies each sentence
$\psi (\overline n)$
is true and implies each sentence
![]() $\psi _i$
, we do have
$\psi _i$
, we do have
 $$ \begin{gather*} f(k)=m\quad\Leftrightarrow\quad\mathbb N\vDash\exists_z\theta_0(\overline k,\overline m,z),\\ \mathbf{PA}\vdash\forall_x\exists_y\exists_z\theta_0(x,y,z). \end{gather*} $$
$$ \begin{gather*} f(k)=m\quad\Leftrightarrow\quad\mathbb N\vDash\exists_z\theta_0(\overline k,\overline m,z),\\ \mathbf{PA}\vdash\forall_x\exists_y\exists_z\theta_0(x,y,z). \end{gather*} $$
However, if
![]() $\mathbf {PA}$
does not prove
$\mathbf {PA}$
does not prove
![]() $\psi (\overline n)$
, then it will not prove that the value y is unique. It is well known that one can restore uniqueness by minimizing over the code of the pair
$\psi (\overline n)$
, then it will not prove that the value y is unique. It is well known that one can restore uniqueness by minimizing over the code of the pair
![]() $\langle y,z\rangle $
. Note that minimizing over y alone would lead out of the
$\langle y,z\rangle $
. Note that minimizing over y alone would lead out of the
![]() $\Sigma ^0_1$
-formulas: the minimal y that satisfies
$\Sigma ^0_1$
-formulas: the minimal y that satisfies
![]() $\exists _z\theta _0(x,y,z)$
is specified by a
$\exists _z\theta _0(x,y,z)$
is specified by a
![]() $\Delta ^0_2$
-formula. To provide details we write
$\Delta ^0_2$
-formula. To provide details we write
![]() $w=\langle y,z\rangle $
for a
$w=\langle y,z\rangle $
for a
![]() $\Delta ^0_1$
-definition of Cantor’s pairing function; recall that
$\Delta ^0_1$
-definition of Cantor’s pairing function; recall that
![]() $w=\langle y,z\rangle $
implies
$w=\langle y,z\rangle $
implies
![]() $y,z\leq w$
. Let
$y,z\leq w$
. Let
![]() $\theta '(x,y)$
be the
$\theta '(x,y)$
be the
![]() $\Sigma ^0_1$
-formula
$\Sigma ^0_1$
-formula
It is straightforward to see that
![]() $\theta '$
defines f and that
$\theta '$
defines f and that
![]() $\mathbf {PA}$
proves
$\mathbf {PA}$
proves
![]() $\forall _x\exists !y\theta '(x,y)$
.□
$\forall _x\exists !y\theta '(x,y)$
.□
4 From the finite basis property to transfinite induction
In this section we show that
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
proves each instance of
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
proves each instance of
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
. As we will see, it follows that
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
. As we will see, it follows that
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
is a proper extension of
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
is a proper extension of
![]() $\mathbf {PA}$
. The result of this section is a relatively straightforward consequence of the existing literature. We provide details in order to demonstrate that the argument works out with respect to formula complexity and the role of parameters.
$\mathbf {PA}$
. The result of this section is a relatively straightforward consequence of the existing literature. We provide details in order to demonstrate that the argument works out with respect to formula complexity and the role of parameters.
Let us first recall the usual notation system for ordinals below
![]() $\varepsilon _0$
. According to Cantor’s normal form theorem, any ordinal
$\varepsilon _0$
. According to Cantor’s normal form theorem, any ordinal
![]() $\alpha $
can be uniquely written as
$\alpha $
can be uniquely written as
with
![]() $\alpha =0$
for
$\alpha =0$
for
![]() $n=0$
. For
$n=0$
. For
![]() $\alpha \prec \varepsilon _0=\min \{\gamma \,|\,\omega ^\gamma =\gamma \}$
we have
$\alpha \prec \varepsilon _0=\min \{\gamma \,|\,\omega ^\gamma =\gamma \}$
we have
![]() $\alpha _0\prec \alpha $
. Recursively, this yields finite terms that represent all ordinals below
$\alpha _0\prec \alpha $
. Recursively, this yields finite terms that represent all ordinals below
![]() $\varepsilon _0$
and, simultaneously, a definition of the order on the level of terms. Working in
$\varepsilon _0$
and, simultaneously, a definition of the order on the level of terms. Working in
![]() $\mathbf {PA}$
, one can develop basic ordinal arithmetic in our term system (see, e.g., [Reference Pohlers32, Reference Sommer43]). In the following we always refer to term representations rather than actual ordinals. The set of and the order between terms will also be denoted by
$\mathbf {PA}$
, one can develop basic ordinal arithmetic in our term system (see, e.g., [Reference Pohlers32, Reference Sommer43]). In the following we always refer to term representations rather than actual ordinals. The set of and the order between terms will also be denoted by
![]() $\varepsilon _0$
and
$\varepsilon _0$
and
![]() $\prec $
, respectively (in addition we write
$\prec $
, respectively (in addition we write
![]() $\alpha \prec \varepsilon _0$
to express that
$\alpha \prec \varepsilon _0$
to express that
![]() $\alpha $
is one of our terms).
$\alpha $
is one of our terms).
In the introduction we have defined a set
![]() $\mathcal B$
of binary trees and an embeddability relation
$\mathcal B$
of binary trees and an embeddability relation
![]() $\leq _{\mathcal B}$
. To establish a connection with the ordinals below
$\leq _{\mathcal B}$
. To establish a connection with the ordinals below
![]() $\varepsilon _0$
, it is convenient to have a binary normal form: If
$\varepsilon _0$
, it is convenient to have a binary normal form: If
![]() $\alpha \succ 0$
has Cantor normal form as above, we write
$\alpha \succ 0$
has Cantor normal form as above, we write
Note that
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
can be seen as proper subterms of
$\gamma $
can be seen as proper subterms of
![]() $\alpha $
. The following construction is well-known (cf. [Reference Takeuti46, sec. 12]).
$\alpha $
. The following construction is well-known (cf. [Reference Takeuti46, sec. 12]).
Definition 4.1 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
We construct a function
![]() $f:\varepsilon _0\to \mathcal B$
by setting
$f:\varepsilon _0\to \mathcal B$
by setting
 $$ \begin{align*} f(\alpha)=\begin{cases} \circ & \text{if}\ \alpha=0,\\ \circ(f(\beta),f(\gamma)) & \text{if}\ \alpha=_{\operatorname{NF}}\omega^\beta+\gamma, \end{cases} \end{align*} $$
$$ \begin{align*} f(\alpha)=\begin{cases} \circ & \text{if}\ \alpha=0,\\ \circ(f(\beta),f(\gamma)) & \text{if}\ \alpha=_{\operatorname{NF}}\omega^\beta+\gamma, \end{cases} \end{align*} $$
which amounts to a recursion over term representations of ordinals.
Concerning the formalization in
![]() $\mathbf {PA}$
, we note that f is primitive recursive. Hence f is
$\mathbf {PA}$
, we note that f is primitive recursive. Hence f is
![]() $\mathbf {PA}$
-provably total. In particular, the graph of f is
$\mathbf {PA}$
-provably total. In particular, the graph of f is
![]() $\Delta ^0_1$
-definable in
$\Delta ^0_1$
-definable in
![]() $\mathbf {PA}$
. The following folklore result shows that f satisfies the definition of a quasi embedding.
$\mathbf {PA}$
. The following folklore result shows that f satisfies the definition of a quasi embedding.
Lemma 4.2 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
For
![]() $\alpha ,\beta \prec \varepsilon _0$
, the inequality
$\alpha ,\beta \prec \varepsilon _0$
, the inequality
![]() $f(\alpha )\leq _{\mathcal B}f(\beta )$
implies
$f(\alpha )\leq _{\mathcal B}f(\beta )$
implies
![]() $\alpha \preceq \beta $
.
$\alpha \preceq \beta $
.
Proof. Define a height function
![]() $h:\varepsilon _0\to \mathbb N$
by recursion over terms, setting
$h:\varepsilon _0\to \mathbb N$
by recursion over terms, setting
 $$ \begin{align*} h(\alpha)=\begin{cases} 0 & \text{if}\ \alpha=0,\\ \max\{h(\gamma),h(\delta)\}+1 & \text{if}\ \alpha=_{\operatorname{NF}}\omega^\gamma+\delta. \end{cases} \end{align*} $$
$$ \begin{align*} h(\alpha)=\begin{cases} 0 & \text{if}\ \alpha=0,\\ \max\{h(\gamma),h(\delta)\}+1 & \text{if}\ \alpha=_{\operatorname{NF}}\omega^\gamma+\delta. \end{cases} \end{align*} $$
The claim from the lemma can now be verified by induction over
![]() $h(\beta )$
. For
$h(\beta )$
. For
![]() $\alpha =0$
the implication holds because
$\alpha =0$
the implication holds because
![]() $\alpha \preceq \beta $
is true. In the remaining case we may write
$\alpha \preceq \beta $
is true. In the remaining case we may write
![]() $\alpha =_{\operatorname {NF}}\omega ^\gamma +\delta $
. By the definition of
$\alpha =_{\operatorname {NF}}\omega ^\gamma +\delta $
. By the definition of
![]() $\leq _{\mathcal B}$
, the inequality
$\leq _{\mathcal B}$
, the inequality
![]() $f(\alpha )=\circ (f(\gamma ),f(\delta ))\leq _{\mathcal B}f(\beta )$
fails for
$f(\alpha )=\circ (f(\gamma ),f(\delta ))\leq _{\mathcal B}f(\beta )$
fails for
![]() $f(\beta )=\circ $
. Hence we may also assume
$f(\beta )=\circ $
. Hence we may also assume
![]() $\beta \succ 0$
, say
$\beta \succ 0$
, say
![]() $\beta =_{\operatorname {NF}}\omega ^{\gamma '}+\delta '$
. Again by the definition of
$\beta =_{\operatorname {NF}}\omega ^{\gamma '}+\delta '$
. Again by the definition of
![]() $\leq _{\mathcal B}$
, the inequality
$\leq _{\mathcal B}$
, the inequality
can hold for two reasons: First assume we have
![]() $f(\gamma )\leq _{\mathcal B} f(\gamma ')$
and
$f(\gamma )\leq _{\mathcal B} f(\gamma ')$
and
![]() $f(\delta )\leq _{\mathcal B} f(\delta ')$
. In view of
$f(\delta )\leq _{\mathcal B} f(\delta ')$
. In view of
![]() $h(\gamma '),h(\delta ')<h(\beta )$
, the induction hypothesis yields
$h(\gamma '),h(\delta ')<h(\beta )$
, the induction hypothesis yields
![]() $\gamma \preceq \gamma '$
and
$\gamma \preceq \gamma '$
and
![]() $\delta \preceq \delta '$
. By basic ordinal arithmetic we get
$\delta \preceq \delta '$
. By basic ordinal arithmetic we get
Now assume
![]() $f(\alpha )\leq _{\mathcal B}f(\beta )$
holds because we have
$f(\alpha )\leq _{\mathcal B}f(\beta )$
holds because we have
![]() $f(\alpha )\leq _{\mathcal B}f(\gamma ')$
or
$f(\alpha )\leq _{\mathcal B}f(\gamma ')$
or
![]() $f(\alpha )\leq _{\mathcal B}f(\delta ')$
. Inductively we get
$f(\alpha )\leq _{\mathcal B}f(\delta ')$
. Inductively we get
![]() $\alpha \preceq \gamma '\preceq \omega ^{\gamma '}$
or
$\alpha \preceq \gamma '\preceq \omega ^{\gamma '}$
or
![]() $\alpha \preceq \delta '$
. Either way we have
$\alpha \preceq \delta '$
. Either way we have
![]() $\alpha \preceq \omega ^{\gamma '}+\delta '=\beta $
.□
$\alpha \preceq \omega ^{\gamma '}+\delta '=\beta $
.□
In addition to the lemma itself, we will need the following standard consequence:
Corollary 4.3 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
The function
![]() $f:\varepsilon _0\to \mathcal B$
is injective.
$f:\varepsilon _0\to \mathcal B$
is injective.
Proof. Consider
![]() $\alpha ,\beta \prec \varepsilon _0$
with
$\alpha ,\beta \prec \varepsilon _0$
with
![]() $f(\alpha )=f(\beta )$
. A straightforward induction over
$f(\alpha )=f(\beta )$
. A straightforward induction over
![]() $\mathcal B$
shows that
$\mathcal B$
shows that
![]() $\leq _{\mathcal B}$
is reflexive. Hence we have
$\leq _{\mathcal B}$
is reflexive. Hence we have
![]() $f(\alpha )\leq _{\mathcal B}f(\beta )$
and
$f(\alpha )\leq _{\mathcal B}f(\beta )$
and
![]() $f(\beta )\leq _{\mathcal B}f(\alpha )$
. By the previous lemma this implies
$f(\beta )\leq _{\mathcal B}f(\alpha )$
. By the previous lemma this implies
![]() $\alpha \preceq \beta $
and
$\alpha \preceq \beta $
and
![]() $\beta \preceq \alpha $
. Since the order relation on the ordinals is antisymmetric, we obtain
$\beta \preceq \alpha $
. Since the order relation on the ordinals is antisymmetric, we obtain
![]() $\alpha =\beta $
.□
$\alpha =\beta $
.□
We can now show that the finite basis property implies transfinite induction. The converse implication will be established in Section 7.
Proposition 4.4. Each instance of
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
can be proved in
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
can be proved in
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
.
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
.
Proof. Working in
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
, we establish
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
, we establish
![]() $\mathcal {TI}(\varepsilon _0,\psi )$
for a given
$\mathcal {TI}(\varepsilon _0,\psi )$
for a given
![]() $\Pi ^0_1$
-formula
$\Pi ^0_1$
-formula
![]() $\psi $
with a single free variable. For this purpose we consider the formula
$\psi $
with a single free variable. For this purpose we consider the formula
where
![]() $f:\varepsilon _0\to \mathcal B$
is the function from Definition 4.1. Since the graph of f is
$f:\varepsilon _0\to \mathcal B$
is the function from Definition 4.1. Since the graph of f is
![]() $\Delta ^0_1$
-definable in
$\Delta ^0_1$
-definable in
![]() $\mathbf {PA}$
, we see that
$\mathbf {PA}$
, we see that
![]() $\varphi (t)$
is (provably equivalent to) a
$\varphi (t)$
is (provably equivalent to) a
![]() $\Sigma ^0_1$
-formula with the single free variable t. Hence we may use
$\Sigma ^0_1$
-formula with the single free variable t. Hence we may use
![]() $\mathcal K\varphi $
to get (a code for) a finite set
$\mathcal K\varphi $
to get (a code for) a finite set
![]() $a\subseteq \mathcal B$
that satisfies
$a\subseteq \mathcal B$
that satisfies
First assume that a is empty. Then
![]() $\exists _{s\in a}s\leq _{\mathcal B}t$
fails for all
$\exists _{s\in a}s\leq _{\mathcal B}t$
fails for all
![]() $t\in \mathcal B$
, so that the second conjunct enforces
$t\in \mathcal B$
, so that the second conjunct enforces
![]() $\forall _{t\in \mathcal B}\neg \varphi (t)$
. Given
$\forall _{t\in \mathcal B}\neg \varphi (t)$
. Given
![]() $\alpha \prec \varepsilon _0$
, it is straightforward to see that
$\alpha \prec \varepsilon _0$
, it is straightforward to see that
![]() $\neg \varphi (t)$
for
$\neg \varphi (t)$
for
![]() $t:=f(\alpha )\in \mathcal B$
implies
$t:=f(\alpha )\in \mathcal B$
implies
![]() $\psi (\alpha )$
. We thus have
$\psi (\alpha )$
. We thus have
![]() $\forall _{\alpha \prec \varepsilon _0}\psi (\alpha )$
, which is the conclusion of
$\forall _{\alpha \prec \varepsilon _0}\psi (\alpha )$
, which is the conclusion of
![]() $\mathcal {TI}(\varepsilon _0,\psi )$
. Now assume that the finite set
$\mathcal {TI}(\varepsilon _0,\psi )$
. Now assume that the finite set
![]() $a\subseteq \mathcal B$
is non-empty. Due to
$a\subseteq \mathcal B$
is non-empty. Due to
![]() $\forall _{s\in a}\varphi (s)$
, we see that a is contained in the range of f. Also recall that f is injective. By induction on the cardinality of a, one can infer that there is an ordinal
$\forall _{s\in a}\varphi (s)$
, we see that a is contained in the range of f. Also recall that f is injective. By induction on the cardinality of a, one can infer that there is an ordinal
![]() $\gamma \prec \varepsilon _0$
with
$\gamma \prec \varepsilon _0$
with
Given an ordinal
![]() $\gamma $
with this property, we now establish
$\gamma $
with this property, we now establish
which implies that
![]() $\mathcal {TI}(\varepsilon _0,\psi )$
holds because its antecedent
$\mathcal {TI}(\varepsilon _0,\psi )$
holds because its antecedent
![]() $\operatorname {Prog}_{\varepsilon _0}(\psi )$
fails. Aiming at the first conjunct, we consider an ordinal
$\operatorname {Prog}_{\varepsilon _0}(\psi )$
fails. Aiming at the first conjunct, we consider an ordinal
![]() $\beta \prec \gamma $
. If
$\beta \prec \gamma $
. If
![]() $\psi (\beta )$
was false, then
$\psi (\beta )$
was false, then
![]() $\varphi (t)$
would hold for
$\varphi (t)$
would hold for
![]() $t:=f(\beta )\in \mathcal B$
. Since
$t:=f(\beta )\in \mathcal B$
. Since
![]() $a\subseteq \mathcal B$
witnesses the conclusion of
$a\subseteq \mathcal B$
witnesses the conclusion of
![]() $\mathcal K\varphi $
, we would get an element
$\mathcal K\varphi $
, we would get an element
![]() $s\in a$
with
$s\in a$
with
![]() $s\leq _{\mathcal B}t$
. Writing
$s\leq _{\mathcal B}t$
. Writing
![]() $s=f(\delta )$
with
$s=f(\delta )$
with
![]() $\delta \prec \varepsilon _0$
, we could invoke Lemma 4.2 to conclude
$\delta \prec \varepsilon _0$
, we could invoke Lemma 4.2 to conclude
![]() $\delta \preceq \beta \prec \gamma $
. By the above this would imply
$\delta \preceq \beta \prec \gamma $
. By the above this would imply
![]() $s=f(\delta )\notin a$
, which yields the desired contradiction. To establish the second conjunct we observe that
$s=f(\delta )\notin a$
, which yields the desired contradiction. To establish the second conjunct we observe that
![]() $f(\gamma )\in a$
implies
$f(\gamma )\in a$
implies
![]() $\varphi (f(\gamma ))$
. According to the definition of
$\varphi (f(\gamma ))$
. According to the definition of
![]() $\varphi $
, this means that there is an ordinal
$\varphi $
, this means that there is an ordinal
![]() $\alpha \prec \varepsilon _0$
with
$\alpha \prec \varepsilon _0$
with
![]() $f(\alpha )=f(\gamma )$
and
$f(\alpha )=f(\gamma )$
and
![]() $\neg \psi (\alpha )$
. Since f is injective we get
$\neg \psi (\alpha )$
. Since f is injective we get
![]() $\alpha =\gamma $
and thus
$\alpha =\gamma $
and thus
![]() $\neg \psi (\gamma )$
, as required.□
$\neg \psi (\gamma )$
, as required.□
According to Gentzen’s ordinal analysis [Reference Gentzen18], the consistency of Peano arithmetic is provable in
![]() $\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
. A detailed proof of a stronger result can be found in the next section. Together with Proposition 4.4 and Gödel’s theorem, it follows that
$\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
. A detailed proof of a stronger result can be found in the next section. Together with Proposition 4.4 and Gödel’s theorem, it follows that
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
is a proper extension of
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
is a proper extension of
![]() $\mathbf {PA}$
.
$\mathbf {PA}$
.
5 From transfinite induction to reflection
Working over
![]() $\mathbf {PA}$
, we show that the parameter-free induction scheme
$\mathbf {PA}$
, we show that the parameter-free induction scheme
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
implies the local reflection principle
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
implies the local reflection principle
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
. The converse direction will be established in Section 7. The result is rather similar to one by Kreisel and Lévy Reference Kreisel and Lévy[27], who show that induction with parameters corresponds to uniform reflection. As we will see, the connection with reflection implies that
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
. The converse direction will be established in Section 7. The result is rather similar to one by Kreisel and Lévy Reference Kreisel and Lévy[27], who show that induction with parameters corresponds to uniform reflection. As we will see, the connection with reflection implies that
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
is not contained in any consistent extension of
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
is not contained in any consistent extension of
![]() $\mathbf {PA}$
by a computably enumerable set of
$\mathbf {PA}$
by a computably enumerable set of
![]() $\Pi ^0_2$
-sentences.
$\Pi ^0_2$
-sentences.
As preparation, we review the ordinal analysis of Peano arithmetic and its formalization in
![]() $\mathbf {PA}$
itself. First note that we cannot formalize the usual soundness argument by induction over formal proofs, since there is no arithmetical truth definition that would cover all relevant formulas (due to Tarski Reference Tarski[47]). Even when we restrict attention to theorems of restricted complexity, their proofs may involve detours through more complex lemmata. The method of cut elimination aims to remove such detours in order to permit a soundness argument that is based on partial truth definitions (cf. [Reference Hasegawa, Jones, Hagiya and Sato20, sec. I.1(d)]). However, it is not immediately possible to eliminate complex lemmata from proofs in Peano arithmetic, which may use complex instances of induction in an essential way. To resolve this problem, ordinal analysis transforms the usual finite proofs into infinite proof trees: In the realm of infinite proofs, induction can be deduced from axioms of low complexity, so that cut elimination becomes possible. Soundness can then be proved by transfinite induction over the rank of infinite proof trees.
$\mathbf {PA}$
itself. First note that we cannot formalize the usual soundness argument by induction over formal proofs, since there is no arithmetical truth definition that would cover all relevant formulas (due to Tarski Reference Tarski[47]). Even when we restrict attention to theorems of restricted complexity, their proofs may involve detours through more complex lemmata. The method of cut elimination aims to remove such detours in order to permit a soundness argument that is based on partial truth definitions (cf. [Reference Hasegawa, Jones, Hagiya and Sato20, sec. I.1(d)]). However, it is not immediately possible to eliminate complex lemmata from proofs in Peano arithmetic, which may use complex instances of induction in an essential way. To resolve this problem, ordinal analysis transforms the usual finite proofs into infinite proof trees: In the realm of infinite proofs, induction can be deduced from axioms of low complexity, so that cut elimination becomes possible. Soundness can then be proved by transfinite induction over the rank of infinite proof trees.
Our ordinal analysis works with proofs in a Tait-style sequence calculus. In particular, this means that all formulas are in negation normal form, and that negation is a defined operation based on De Morgan’s laws. Each node in a proof tree deduces a sequent, i.e., a finite set
![]() $\Gamma =\{\varphi _0,\dots ,\varphi _{n-1}\}$
of formulas. The latter is to be interpreted as the disjunction
$\Gamma =\{\varphi _0,\dots ,\varphi _{n-1}\}$
of formulas. The latter is to be interpreted as the disjunction
![]() $\bigvee \Gamma =\varphi _0\lor \dots \lor \varphi _{n-1}$
. In the context of sequents we write
$\bigvee \Gamma =\varphi _0\lor \dots \lor \varphi _{n-1}$
. In the context of sequents we write
![]() $\Gamma ,\varphi $
for
$\Gamma ,\varphi $
for
![]() $\Gamma \cup \{\varphi \}$
. Detours in proofs are implemented via the cut rule
$\Gamma \cup \{\varphi \}$
. Detours in proofs are implemented via the cut rule
which has the following intuitive significance: In order to show
![]() $\bigvee \Gamma $
, it suffices to
$\bigvee \Gamma $
, it suffices to
-
• prove a lemma
 $\varphi $
(more precisely, the left premise proves
$\varphi $
(more precisely, the left premise proves
 $\bigvee \Gamma \lor \varphi $
) and to
$\bigvee \Gamma \lor \varphi $
) and to -
• prove that
 $\varphi $
implies
$\varphi $
implies
 $\bigvee \Gamma $
(i.e., to prove
$\bigvee \Gamma $
(i.e., to prove
 $\bigvee \Gamma \lor \neg \varphi $
, as in the right premise).
$\bigvee \Gamma \lor \neg \varphi $
, as in the right premise).
The crucial feature of the infinite proof system is the
![]() $\omega $
-rule
$\omega $
-rule

which allows to infer
![]() $\forall _n\varphi (n)$
if there is a proof of
$\forall _n\varphi (n)$
if there is a proof of
![]() $\varphi (n)$
for each numeral n. Induction can be derived from the
$\varphi (n)$
for each numeral n. Induction can be derived from the
![]() $\omega $
-rule, since
$\omega $
-rule, since
has a straightforward proof for each number n. It follows that any finite proof in Peano arithmetic can be translated (or “embedded”) into the infinite system.
It is not immediately clear how infinite proof trees can be formalized in Peano arithmetic. In the following we recall a very elegant approach due to Buchholz Reference Buchholz[5] (see his paper for all missing details): The idea is to work with a set
![]() $\mathbf Z^*$
of finite terms. Each term names an infinite proof by specifying its role in the cut elimination process. Specifically, each finite proof d in Peano arithmetic gives rise to a constant symbol
$\mathbf Z^*$
of finite terms. Each term names an infinite proof by specifying its role in the cut elimination process. Specifically, each finite proof d in Peano arithmetic gives rise to a constant symbol
![]() $[d]\in \mathbf Z^*$
, which denotes the translation of d into the infinite system. For each term
$[d]\in \mathbf Z^*$
, which denotes the translation of d into the infinite system. For each term
![]() $h\in \mathbf Z^*$
there is a term
$h\in \mathbf Z^*$
there is a term
![]() $Eh\in \mathbf Z^*$
that names the proof that results from h by a single application of cut elimination. The intermediate steps of cut elimination give rise to auxiliary function symbols. By primitive recursion over terms one can define an ordinal
$Eh\in \mathbf Z^*$
that names the proof that results from h by a single application of cut elimination. The intermediate steps of cut elimination give rise to auxiliary function symbols. By primitive recursion over terms one can define an ordinal
![]() $\mathfrak o(h)\prec \varepsilon _0$
that bounds the rank of the proof tree represented by h; for example, the well-known fact that cut elimination leads to an exponential increase of the ordinal rank suggests the recursive clause
$\mathfrak o(h)\prec \varepsilon _0$
that bounds the rank of the proof tree represented by h; for example, the well-known fact that cut elimination leads to an exponential increase of the ordinal rank suggests the recursive clause
![]() $\mathfrak o(E h)=\omega ^{\mathfrak o(h)}$
. Also by recursion over terms, one can determine the end sequent
$\mathfrak o(E h)=\omega ^{\mathfrak o(h)}$
. Also by recursion over terms, one can determine the end sequent
![]() $\mathfrak e(h)$
, the last rule
$\mathfrak e(h)$
, the last rule
![]() $\mathfrak r(h)$
, the cut rank
$\mathfrak r(h)$
, the cut rank
![]() $\mathfrak d(h)$
, and terms
$\mathfrak d(h)$
, and terms
![]() $\mathfrak s(h,n)\in \mathbf Z^*$
that denote the immediate subtrees of the proof tree that is represented by h. Working in
$\mathfrak s(h,n)\in \mathbf Z^*$
that denote the immediate subtrees of the proof tree that is represented by h. Working in
![]() $\mathbf {PA}$
(or even in
$\mathbf {PA}$
(or even in
![]() $\mathbf {PRA}$
), one can show that the term system
$\mathbf {PRA}$
), one can show that the term system
![]() $\mathbf Z^*$
is “locally correct” (see [Reference Buchholz5, theorem 3.8]); in particular this means that we have
$\mathbf Z^*$
is “locally correct” (see [Reference Buchholz5, theorem 3.8]); in particular this means that we have
![]() $\mathfrak o(\mathfrak s(h,n))\prec \mathfrak o(h)$
, except when
$\mathfrak o(\mathfrak s(h,n))\prec \mathfrak o(h)$
, except when
![]() $\mathfrak r(h)$
signifies an axiom. To ensure “global correctness,” one needs transfinite induction up to
$\mathfrak r(h)$
signifies an axiom. To ensure “global correctness,” one needs transfinite induction up to
![]() $\varepsilon _0$
, which is not available in
$\varepsilon _0$
, which is not available in
![]() $\mathbf {PA}$
. In the sequel we abbreviate
$\mathbf {PA}$
. In the sequel we abbreviate
Intuitively, this asserts that h is a cut-free infinite proof tree with rank
![]() $\alpha $
and end sequent
$\alpha $
and end sequent
![]() $\Gamma $
(note that
$\Gamma $
(note that
![]() $\bigvee \mathfrak e(h)$
implies
$\bigvee \mathfrak e(h)$
implies
![]() $\bigvee \Gamma $
). Crucially, the relation
$\bigvee \Gamma $
). Crucially, the relation
![]() $h\vdash ^\alpha _0\Gamma $
is primitive recursive and hence
$h\vdash ^\alpha _0\Gamma $
is primitive recursive and hence
![]() $\Delta ^0_1$
-definable in
$\Delta ^0_1$
-definable in
![]() $\mathbf {PA}$
. This implies that
$\mathbf {PA}$
. This implies that
is a
![]() $\Sigma ^0_1$
-formula with parameters
$\Sigma ^0_1$
-formula with parameters
![]() $\alpha $
and
$\alpha $
and
![]() $\Gamma $
. We can now show the promised result:
$\Gamma $
. We can now show the promised result:
Proposition 5.1. Each instance of
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
can be proved in
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
can be proved in
![]() $\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
.
$\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
.
Proof. Consider a closed
![]() $\Sigma ^0_2$
-formula
$\Sigma ^0_2$
-formula
![]() $\varphi $
. Working in
$\varphi $
. Working in
![]() $\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
, we assume that we have
$\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
, we assume that we have
![]() $\operatorname {Pr}_{\mathbf {PA}}(\varphi )$
. In order to establish
$\operatorname {Pr}_{\mathbf {PA}}(\varphi )$
. In order to establish
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\varphi )$
, we need to derive
$\operatorname {Rfn}_{\mathbf {PA}}(\varphi )$
, we need to derive
![]() $\varphi $
. We use Buchholz’ formalization of ordinal analysis, as discussed above. By embedding and cut elimination (cf. [Reference Buchholz5, definitions 3.4 and 3.7]), the assumption
$\varphi $
. We use Buchholz’ formalization of ordinal analysis, as discussed above. By embedding and cut elimination (cf. [Reference Buchholz5, definitions 3.4 and 3.7]), the assumption
![]() $\operatorname {Pr}_{\mathbf {PA}}(\varphi )$
implies
$\operatorname {Pr}_{\mathbf {PA}}(\varphi )$
implies
Write
![]() $\Gamma \subseteq \{\varphi \}\cup \Pi ^-_1$
to express that
$\Gamma \subseteq \{\varphi \}\cup \Pi ^-_1$
to express that
![]() $\Gamma $
is a sequent that consists of
$\Gamma $
is a sequent that consists of
![]() $\Pi ^0_1$
-sentences and (possibly) the formula
$\Pi ^0_1$
-sentences and (possibly) the formula
![]() $\varphi $
. The statement that
$\varphi $
. The statement that
![]() $\Gamma $
contains a true
$\Gamma $
contains a true
![]() $\Pi ^0_1$
-sentence can be expressed by a
$\Pi ^0_1$
-sentence can be expressed by a
![]() $\Pi ^0_1$
-formula
$\Pi ^0_1$
-formula
![]() $\operatorname {Tr}_{\Pi ^-_1}(\Gamma )$
(cf. [Reference Hasegawa, Jones, Hagiya and Sato20, theorem I.1.75]). Aiming at a contradiction, we assume that
$\operatorname {Tr}_{\Pi ^-_1}(\Gamma )$
(cf. [Reference Hasegawa, Jones, Hagiya and Sato20, theorem I.1.75]). Aiming at a contradiction, we assume that
![]() $\varphi $
is false. Under this assumption we will derive
$\varphi $
is false. Under this assumption we will derive
arguing by transfinite induction on
![]() $\alpha \prec \varepsilon _0$
. Note that the sentence
$\alpha \prec \varepsilon _0$
. Note that the sentence
![]() $\varphi $
is represented by a fixed numeral. Hence
$\varphi $
is represented by a fixed numeral. Hence
![]() $\alpha $
is the only free variable of the induction formula, and the induction is covered by the scheme
$\alpha $
is the only free variable of the induction formula, and the induction is covered by the scheme
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
. Once the induction is carried out, it is straightforward to derive the desired contradiction: By the above we have
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
. Once the induction is carried out, it is straightforward to derive the desired contradiction: By the above we have
![]() $\mathbf Z^*\vdash ^\alpha _0\{\varphi \}$
for some
$\mathbf Z^*\vdash ^\alpha _0\{\varphi \}$
for some
![]() $\alpha \prec \varepsilon _0$
. However, we cannot have
$\alpha \prec \varepsilon _0$
. However, we cannot have
![]() $\operatorname {Tr}_{\Pi ^-_1}(\{\varphi \})$
, since
$\operatorname {Tr}_{\Pi ^-_1}(\{\varphi \})$
, since
![]() $\varphi $
was assumed to be false (note that this covers both
$\varphi $
was assumed to be false (note that this covers both
![]() $\varphi \in \Pi ^0_1\subseteq \Sigma ^0_2$
and
$\varphi \in \Pi ^0_1\subseteq \Sigma ^0_2$
and
![]() $\varphi \in \Sigma ^0_2\backslash \Pi ^0_1$
). It remains to carry out the induction. In the step we consider a sequent
$\varphi \in \Sigma ^0_2\backslash \Pi ^0_1$
). It remains to carry out the induction. In the step we consider a sequent
![]() $\Gamma \subseteq \{\varphi \}\cup \Pi ^-_1$
and assume
$\Gamma \subseteq \{\varphi \}\cup \Pi ^-_1$
and assume
![]() $h\vdash ^\alpha _0\Gamma $
for some
$h\vdash ^\alpha _0\Gamma $
for some
![]() $h\in \mathbf Z^*$
. We distinguish cases according to the last rule
$h\in \mathbf Z^*$
. We distinguish cases according to the last rule
![]() $\mathfrak r(h)$
. Note that this cannot be a cut, since
$\mathfrak r(h)$
. Note that this cannot be a cut, since
![]() $h\vdash ^\alpha _0\Gamma $
entails
$h\vdash ^\alpha _0\Gamma $
entails
![]() $\mathfrak d(h)=0$
. If
$\mathfrak d(h)=0$
. If
![]() $\mathfrak r(h)$
is an axiom, then
$\mathfrak r(h)$
is an axiom, then
![]() $\mathfrak e(h)\subseteq \Gamma $
contains a true literal (cf. [Reference Buchholz5, definition 2.2]). To complete the proof, we consider the introduction of a quantifier; the introduction of a propositional connective is similar and simpler. First assume that h ends with an
$\mathfrak e(h)\subseteq \Gamma $
contains a true literal (cf. [Reference Buchholz5, definition 2.2]). To complete the proof, we consider the introduction of a quantifier; the introduction of a propositional connective is similar and simpler. First assume that h ends with an
![]() $\omega $
-rule, which introduces a formula
$\omega $
-rule, which introduces a formula
![]() $\forall _n\theta (n)\in \Gamma $
. Due to
$\forall _n\theta (n)\in \Gamma $
. Due to
![]() $\Gamma \subseteq \{\varphi \}\cup \Pi ^-_1$
we see that
$\Gamma \subseteq \{\varphi \}\cup \Pi ^-_1$
we see that
![]() $\forall _n\theta (n)$
must be a
$\forall _n\theta (n)$
must be a
![]() $\Pi ^0_1$
-sentence. Local correctness (see [Reference Buchholz5, theorem 3.8]) yields
$\Pi ^0_1$
-sentence. Local correctness (see [Reference Buchholz5, theorem 3.8]) yields
for all
![]() $n\in \mathbb N$
. The induction hypothesis implies that each sequent
$n\in \mathbb N$
. The induction hypothesis implies that each sequent
![]() $\Gamma ,\theta (n)$
contains a true
$\Gamma ,\theta (n)$
contains a true
![]() $\Pi ^0_1$
-sentence. Hence we get such a sentence in
$\Pi ^0_1$
-sentence. Hence we get such a sentence in
![]() $\Gamma $
, or all instances
$\Gamma $
, or all instances
![]() $\theta (n)$
are true. In the latter case, it follows that
$\theta (n)$
are true. In the latter case, it follows that
![]() $\Gamma $
contains the true
$\Gamma $
contains the true
![]() $\Pi ^0_1$
-sentence
$\Pi ^0_1$
-sentence
![]() $\forall _n\theta (n)$
. Finally, assume that
$\forall _n\theta (n)$
. Finally, assume that
![]() $\mathfrak r(h)$
introduces an existential formula
$\mathfrak r(h)$
introduces an existential formula
![]() $\exists _n\psi (n)$
. In view of
$\exists _n\psi (n)$
. In view of
![]() $\Gamma \subseteq \{\varphi \}\cup \Pi ^-_1$
we must have
$\Gamma \subseteq \{\varphi \}\cup \Pi ^-_1$
we must have
![]() $\exists _n\psi (n)\equiv \varphi $
(note that Reference Buchholz[5] does not work with bounded quantifiers but treats primitive recursive relations as atomic). By local correctness there is some existential witness
$\exists _n\psi (n)\equiv \varphi $
(note that Reference Buchholz[5] does not work with bounded quantifiers but treats primitive recursive relations as atomic). By local correctness there is some existential witness
![]() $k\in \mathbb N$
such that we have
$k\in \mathbb N$
such that we have
The induction hypothesis yields a true
![]() $\Pi ^0_1$
-sentence in
$\Pi ^0_1$
-sentence in
![]() $\Gamma ,\psi (k)$
. To establish
$\Gamma ,\psi (k)$
. To establish
![]() $\operatorname {Tr}_{\Pi ^-_1}(\Gamma )$
it suffices to show that
$\operatorname {Tr}_{\Pi ^-_1}(\Gamma )$
it suffices to show that
![]() $\psi (k)$
cannot be true: if it was, then
$\psi (k)$
cannot be true: if it was, then
![]() $\varphi \equiv \exists _n\psi (n)$
would be true as well, which contradicts our assumption.□
$\varphi \equiv \exists _n\psi (n)$
would be true as well, which contradicts our assumption.□
As mentioned in the introduction, the previous proposition can also be derived from work of Beklemishev:
Remark 5.2. By the paragraph before Proposition 5.18 in Reference Beklemishev[3], the consistency of
![]() $\mathbf {PA}+\operatorname {Con}(\mathbf {PA})$
can be derived by a single application of the (parameter-free) induction rule up to
$\mathbf {PA}+\operatorname {Con}(\mathbf {PA})$
can be derived by a single application of the (parameter-free) induction rule up to
![]() $\varepsilon _0$
over
$\varepsilon _0$
over
![]() $\mathbf {EA}^++\operatorname {Con}(\mathbf {PA})$
, where
$\mathbf {EA}^++\operatorname {Con}(\mathbf {PA})$
, where
![]() $\mathbf {EA}^+$
denotes the extension of elementary arithmetic by superexponentiation. As pointed out by one of the referees, the argument remains valid when the statement
$\mathbf {EA}^+$
denotes the extension of elementary arithmetic by superexponentiation. As pointed out by one of the referees, the argument remains valid when the statement
![]() $\operatorname {Con}(\mathbf {PA})$
is replaced by an arbitrary
$\operatorname {Con}(\mathbf {PA})$
is replaced by an arbitrary
![]() $\Pi ^0_2$
-sentence
$\Pi ^0_2$
-sentence
![]() $\psi $
. In particular, this yields
$\psi $
. In particular, this yields
If we take
![]() $\psi =\neg \varphi $
, then the right side is the contrapositive of local reflection for
$\psi =\neg \varphi $
, then the right side is the contrapositive of local reflection for
![]() $\varphi $
.
$\varphi $
.
The following is folklore (cf. the related result by Kreisel and Lévy [Reference Kreisel and Lévy27, sec. 8]; see also [Reference Beklemishev1, lemma 2] for an argument that takes the formula complexity into account).
Proposition 5.3. There is no computably enumerable set
![]() $\Psi $
of
$\Psi $
of
![]() $\Pi ^0_2$
-sentences such that
$\Pi ^0_2$
-sentences such that
![]() $\mathbf {PA}+\Psi $
is consistent and contains
$\mathbf {PA}+\Psi $
is consistent and contains
![]() $\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
.
$\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
.
Proof. Consider a computably enumerable set
![]() $\Psi $
of
$\Psi $
of
![]() $\Pi ^0_2$
-sentences such that
$\Pi ^0_2$
-sentences such that
![]() $\mathbf {PA}+\Psi $
proves each instance of
$\mathbf {PA}+\Psi $
proves each instance of
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
. We need to show that
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
. We need to show that
![]() $\mathbf {PA}+\Psi $
is inconsistent. According to [Reference Lindström29, theorem 4], there is a single
$\mathbf {PA}+\Psi $
is inconsistent. According to [Reference Lindström29, theorem 4], there is a single
![]() $\Pi ^0_2$
-sentence
$\Pi ^0_2$
-sentence
![]() $\psi $
such that
$\psi $
such that
![]() $\mathbf {PA}+\psi $
is a
$\mathbf {PA}+\psi $
is a
![]() $\Sigma ^0_2$
-conservative extension of
$\Sigma ^0_2$
-conservative extension of
![]() $\mathbf {PA}+\Psi $
. In view of conservativity, it suffices to establish the inconsistency of
$\mathbf {PA}+\Psi $
. In view of conservativity, it suffices to establish the inconsistency of
![]() $\mathbf {PA}+\psi $
. We have
$\mathbf {PA}+\psi $
. We have
since the right side is an instance of
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
. Considering the contrapositive, we learn that
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
. Considering the contrapositive, we learn that
![]() $\mathbf {PA}+\psi $
proves its own consistency statement
$\mathbf {PA}+\psi $
proves its own consistency statement
![]() $\neg \operatorname {Pr}_{\mathbf {PA}}(\neg \psi )$
, so that it is inconsistent by Gödel’s theorem.□
$\neg \operatorname {Pr}_{\mathbf {PA}}(\neg \psi )$
, so that it is inconsistent by Gödel’s theorem.□
By Propositions 4.4 and 5.1 we have
Hence the previous proposition has the following consequence:
Corollary 5.4. There is no computably enumerable set
![]() $\Psi $
of
$\Psi $
of
![]() $\Pi ^0_2$
-sentences such that
$\Pi ^0_2$
-sentences such that
![]() $\mathbf {PA}+\Psi $
is consistent and contains
$\mathbf {PA}+\Psi $
is consistent and contains
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
. In particular, the latter is a proper extension of
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
. In particular, the latter is a proper extension of
![]() $\mathbf {PA}$
.
$\mathbf {PA}$
.
Since any true
![]() $\Sigma ^0_2$
-sentence follows from a true
$\Sigma ^0_2$
-sentence follows from a true
![]() $\Pi ^0_1$
-sentence, there is a set
$\Pi ^0_1$
-sentence, there is a set
![]() $\Xi $
of
$\Xi $
of
![]() $\Pi ^0_1$
-sentences such that
$\Pi ^0_1$
-sentences such that
![]() $\mathbf {PA}+\Xi $
is consistent and contains
$\mathbf {PA}+\Xi $
is consistent and contains
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
. The corollary tells us that
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
. The corollary tells us that
![]() $\Xi $
cannot be computably enumerable.
$\Xi $
cannot be computably enumerable.
6 A primitive recursive reification
In the rest of this paper we complete the proof that
![]() $\mathcal K\Sigma ^-_1$
,
$\mathcal K\Sigma ^-_1$
,
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
and
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
and
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
are equivalent over
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
are equivalent over
![]() $\mathbf {PA}$
. The present section is concerned with a technical result that will be crucial for this purpose.
$\mathbf {PA}$
. The present section is concerned with a technical result that will be crucial for this purpose.
Write
![]() $\operatorname {Bad}^-(\mathcal B)$
for the set of non-empty finite bad sequences in
$\operatorname {Bad}^-(\mathcal B)$
for the set of non-empty finite bad sequences in
![]() $\mathcal B$
. We want to construct a primitive recursive function
$\mathcal B$
. We want to construct a primitive recursive function
![]() $r:\operatorname {Bad}^-(\mathcal B)\rightarrow \varepsilon _0$
such that we have
$r:\operatorname {Bad}^-(\mathcal B)\rightarrow \varepsilon _0$
such that we have
whenever
![]() $\langle t_0,\dots ,t_{n+1}\rangle $
is an element of
$\langle t_0,\dots ,t_{n+1}\rangle $
is an element of
![]() $\operatorname {Bad}^-(\mathcal B)$
, provably in
$\operatorname {Bad}^-(\mathcal B)$
, provably in
![]() $\mathbf {PA}$
(in fact in primitive recursive arithmetic). Such a function is called a reification. It ensures that
$\mathbf {PA}$
(in fact in primitive recursive arithmetic). Such a function is called a reification. It ensures that
![]() $\mathcal B$
is a well partial order with maximal order type at most (and in fact equal to)
$\mathcal B$
is a well partial order with maximal order type at most (and in fact equal to)
![]() $\varepsilon _0$
.
$\varepsilon _0$
.
As mentioned in the introduction, the result that
![]() $\mathcal B$
has maximal order type
$\mathcal B$
has maximal order type
![]() $\varepsilon _0$
is due to de Jongh and Schmidt. Experience shows that maximal order types can be witnessed by effective reifications. For the case of finite (and in particular binary) trees this has been established by M. Rathjen and A. Weiermann [Reference Rathjen and Weiermann33, sec. 2]. Unfortunately, we cannot simply cite their result: In Reference Rathjen and Weiermann[33] it is shown that
$\varepsilon _0$
is due to de Jongh and Schmidt. Experience shows that maximal order types can be witnessed by effective reifications. For the case of finite (and in particular binary) trees this has been established by M. Rathjen and A. Weiermann [Reference Rathjen and Weiermann33, sec. 2]. Unfortunately, we cannot simply cite their result: In Reference Rathjen and Weiermann[33] it is shown that
![]() $\mathbf {ACA_0}$
proves the existence of a reification; however, it is not entirely trivial to see that the constructed reification is (primitive) recursive. In the rest of this section we verify this fact in detail. Some readers may prefer to skip this verification and to continue with the applications in the next section. We point out that the following presentation is influenced by the more general construction in [Reference Hilbert21].
$\mathbf {ACA_0}$
proves the existence of a reification; however, it is not entirely trivial to see that the constructed reification is (primitive) recursive. In the rest of this section we verify this fact in detail. Some readers may prefer to skip this verification and to continue with the applications in the next section. We point out that the following presentation is influenced by the more general construction in [Reference Hilbert21].
The reification of
![]() $\mathcal B$
will depend on reifications of various other orders. In the context of first order arithmetic it helps to think of these orders as types, which are represented by finite expressions.
$\mathcal B$
will depend on reifications of various other orders. In the context of first order arithmetic it helps to think of these orders as types, which are represented by finite expressions.
Definition 6.1 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
The following recursive clauses generate a collection of types and a subcollection of indecomposable types:
-
(i) The symbols
 $\mathfrak B$
and
$\mathfrak B$
and
 $\mathfrak E$
are indecomposable types.
$\mathfrak E$
are indecomposable types. -
(ii) If
 $A,B$
are types, then
$A,B$
are types, then
 $A+B$
is a type.
$A+B$
is a type. -
(iii) If
 $A,B$
are indecomposable types, then
$A,B$
are indecomposable types, then
 $A\times B$
is an indecomposable type.
$A\times B$
is an indecomposable type. -
(iv) If A is any type, then
 $A^*$
is an indecomposable type.
$A^*$
is an indecomposable type.
On an intuitive level, one should think of
![]() $\mathfrak B$
as the collection
$\mathfrak B$
as the collection
![]() $\mathcal B$
of binary trees and of
$\mathcal B$
of binary trees and of
![]() $\mathfrak E$
as the empty order. The expressions
$\mathfrak E$
as the empty order. The expressions
![]() $A+B$
and
$A+B$
and
![]() $A\times B$
refer to the usual notions of sum (disjoint union) and product, while
$A\times B$
refer to the usual notions of sum (disjoint union) and product, while
![]() $A^*$
stands for the set of finite sequences with entries from A (with the order from Higman’s lemma). Officially, the elements of these orders are represented by the terms from Definition 6.2 below, while the order relations are recovered via Definition 6.3.
$A^*$
stands for the set of finite sequences with entries from A (with the order from Higman’s lemma). Officially, the elements of these orders are represented by the terms from Definition 6.2 below, while the order relations are recovered via Definition 6.3.
Note that it is not allowed to form types such as
![]() $(A+B)\times C$
, since
$(A+B)\times C$
, since
![]() $A+B$
is not indecomposable. This restriction corresponds to the notion of normal form from [Reference Hilbert21, definition 4.15]. We will eventually assign an (additively indecomposable) ordinal to each (indecomposable) type that does not contain
$A+B$
is not indecomposable. This restriction corresponds to the notion of normal form from [Reference Hilbert21, definition 4.15]. We will eventually assign an (additively indecomposable) ordinal to each (indecomposable) type that does not contain
![]() $\mathfrak B$
. In particular, the ordinals assigned to product types will be additively indecomposable. This ensures that the ordinal assignment satisfies the monotonicity property from Proposition 6.12 below (cf. the role of indecomposable ordinals in the proof of this proposition, as well as the counterexample in the paragraph after Proposition 5.10 in [Reference Hilbert21]).
$\mathfrak B$
. In particular, the ordinals assigned to product types will be additively indecomposable. This ensures that the ordinal assignment satisfies the monotonicity property from Proposition 6.12 below (cf. the role of indecomposable ordinals in the proof of this proposition, as well as the counterexample in the paragraph after Proposition 5.10 in [Reference Hilbert21]).
As mentioned above, the elements of our orders are represented by terms of the corresponding types. To obtain primitive recursive constructions, it is crucial to work with terms of all types simultaneously. For example, it is neither possible nor necessary to construct all terms of type A before one constructs a term of type
![]() $A^*$
. Let us point out that each term has a unique type, which can be read off by a primitive recursive function. Also recall that
$A^*$
. Let us point out that each term has a unique type, which can be read off by a primitive recursive function. Also recall that
![]() $\mathfrak E$
represents the empty order, so that no terms of this type are specified.
$\mathfrak E$
represents the empty order, so that no terms of this type are specified.
Definition 6.2 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
The following recursive clauses generate a collection of terms. We simultaneously specify the types of these terms:
-
(i) Each binary tree
 $t\in \mathcal B$
is a term of type
$t\in \mathcal B$
is a term of type
 $\mathfrak B$
.
$\mathfrak B$
. -
(ii) If a is a term of type A and B is a type, then
 $\iota _0^Ba$
is a term of type
$\iota _0^Ba$
is a term of type
 $A+B$
. If b is a term of type B and A is a type, then
$A+B$
. If b is a term of type B and A is a type, then
 $\iota _1^Ab$
is a term of type
$\iota _1^Ab$
is a term of type
 $A+B$
.
$A+B$
. -
(iii) If a and b are terms of types A and B, then
 $\langle a,b\rangle $
is a term of type
$\langle a,b\rangle $
is a term of type
 $A\times B$
.
$A\times B$
. -
(iv) If
 $a_0,\dots ,a_{n-1}$
have type A, then
$a_0,\dots ,a_{n-1}$
have type A, then
 $\langle a_0,\dots ,a_{n-1}\rangle _A$
is a term of type
$\langle a_0,\dots ,a_{n-1}\rangle _A$
is a term of type
 $A^*$
.
$A^*$
.
Note that (iii) does only apply when A and B are indecomposable.
One readily constructs a Gödel numbering
![]() $\#$
with the monotonicity properties
$\#$
with the monotonicity properties
 $$ \begin{gather*} \#s,\#t<\#{\circ(s,t)}\text{ for}\ s,t\in\mathfrak B,\qquad\#a<\#\iota_0^Ba,\qquad\#b<\#\iota_1^Ab,\\ \#a,\#b<\#\langle a,b\rangle,\qquad\#a_0,\#\langle a_1,\dots,a_n\rangle_A<\#\langle a_0,\dots,a_n\rangle_A. \end{gather*} $$
$$ \begin{gather*} \#s,\#t<\#{\circ(s,t)}\text{ for}\ s,t\in\mathfrak B,\qquad\#a<\#\iota_0^Ba,\qquad\#b<\#\iota_1^Ab,\\ \#a,\#b<\#\langle a,b\rangle,\qquad\#a_0,\#\langle a_1,\dots,a_n\rangle_A<\#\langle a_0,\dots,a_n\rangle_A. \end{gather*} $$
We will use this Gödel numbering to construct primitive recursive functions by course-of-values recursion. Binary functions can be constructed with the help of the Cantor pairing function, which is monotone in both components. For example, the following definition decides
![]() $a\leq _A a'$
by recursion over the code of
$a\leq _A a'$
by recursion over the code of
![]() $\langle \#a,\#a'\rangle $
.
$\langle \#a,\#a'\rangle $
.
Definition 6.3 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
The relation
![]() $a\leq _A a'$
between terms a and
$a\leq _A a'$
between terms a and
![]() $a'$
of the same type A is generated by the following recursive clauses (i.e., it is the smallest relation that satisfies them):
$a'$
of the same type A is generated by the following recursive clauses (i.e., it is the smallest relation that satisfies them):
-
(i) If
 $s\leq _{\mathcal B} t$
, then
$s\leq _{\mathcal B} t$
, then
 $s\leq _{\mathfrak B} t$
.
$s\leq _{\mathfrak B} t$
. -
(ii) If
 $a\leq _A a'$
, then
$a\leq _A a'$
, then
 $\iota _0^Ba\leq _{A+B}\iota _0^Ba'$
. If
$\iota _0^Ba\leq _{A+B}\iota _0^Ba'$
. If
 $b\leq _B b'$
, then
$b\leq _B b'$
, then
 $\iota _1^Ab\leq _{A+B}\iota _1^Ab'$
.
$\iota _1^Ab\leq _{A+B}\iota _1^Ab'$
. -
(iii) If
 $a\leq _A a'$
and
$a\leq _A a'$
and
 $b\leq _B b'$
, then
$b\leq _B b'$
, then
 $\langle a,b\rangle \leq _{A\times B}\langle a',b'\rangle $
.
$\langle a,b\rangle \leq _{A\times B}\langle a',b'\rangle $
. -
(iv) If there is a strictly increasing
 $f:\{0,\dots ,m-1\}\rightarrow \{0,\dots ,n-1\}$
such that
$f:\{0,\dots ,m-1\}\rightarrow \{0,\dots ,n-1\}$
such that
 $a_i\leq _A a^{\prime }_{f(i)}$
holds for all
$a_i\leq _A a^{\prime }_{f(i)}$
holds for all
 $i<m$
, then
$i<m$
, then
 $\langle a_0,\dots ,a_{m-1}\rangle _A\leq _{A^*}\langle a^{\prime }_0,\dots ,a^{\prime }_{n-1}\rangle _A$
.
$\langle a_0,\dots ,a_{m-1}\rangle _A\leq _{A^*}\langle a^{\prime }_0,\dots ,a^{\prime }_{n-1}\rangle _A$
.
Let us record the expected property:
Lemma 6.4 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
Each relation
![]() $\leq _A$
is a partial order on the terms of type A.
$\leq _A$
is a partial order on the terms of type A.
Proof. First check
![]() $a\leq _A a$
by induction over
$a\leq _A a$
by induction over
![]() $\#a$
, simultaneously for all types A. Then use induction over
$\#a$
, simultaneously for all types A. Then use induction over
![]() $\#a+\#a'$
to verify that
$\#a+\#a'$
to verify that
![]() $a\leq _A a'$
and
$a\leq _A a'$
and
![]() $a'\leq _A a$
imply
$a'\leq _A a$
imply
![]() $a=a'$
. Finally, show
$a=a'$
. Finally, show
![]() $a\leq _A a'\,\&\, a'\leq _A a“\Rightarrow a\leq _Aa”$
by induction over
$a\leq _A a'\,\&\, a'\leq _A a“\Rightarrow a\leq _Aa”$
by induction over
![]() $\#a+\#a'+\#a''$
.□
$\#a+\#a'+\#a''$
.□
From now on we write
![]() $a\in A$
to express that a is a term of type A. Despite this notation, one should keep in mind that A is a finite expression rather than an infinite set. The following provides a substitute for the “missing” types
$a\in A$
to express that a is a term of type A. Despite this notation, one should keep in mind that A is a finite expression rather than an infinite set. The following provides a substitute for the “missing” types
![]() $A\times B$
.
$A\times B$
.
Definition 6.5 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
For arbitrary types A and B we recursively define a type
![]() $A\otimes B$
and terms
$A\otimes B$
and terms
![]() $[a,b]\in A\otimes B$
for all
$[a,b]\in A\otimes B$
for all
![]() $a\in A$
and
$a\in A$
and
![]() $b\in B$
: First put
$b\in B$
: First put
Now consider
![]() $A=C+D$
and an arbitrary B. To save parentheses, we assume that
$A=C+D$
and an arbitrary B. To save parentheses, we assume that
![]() $\otimes $
binds stronger than
$\otimes $
binds stronger than
![]() $+$
. We then define
$+$
. We then define
For indecomposable A and
![]() $B=C+D$
we set
$B=C+D$
we set
The following is readily checked by induction on
![]() $\#a+\#a'+\#b+\#b'$
.
$\#a+\#a'+\#b+\#b'$
.
Lemma 6.6 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
We have
for arbitrary terms
![]() $a,a'\in A$
and
$a,a'\in A$
and
![]() $b,b'\in B$
.
$b,b'\in B$
.
For
![]() $a\in A$
we will abbreviate
$a\in A$
we will abbreviate
Recall that, officially, A is not an infinite set but a finite expression that denotes a type. Similarly,
![]() $a'\in A_a$
does officially refer to a primitive recursive relation between the finite expressions
$a'\in A_a$
does officially refer to a primitive recursive relation between the finite expressions
![]() $a,a'$
and A. Informally,
$a,a'$
and A. Informally,
![]() $A_a$
stands for the set of all
$A_a$
stands for the set of all
![]() $a'\in A$
that can follow a in a bad sequence. It is known that these sets play an important role in the analysis of maximal order types. While
$a'\in A$
that can follow a in a bad sequence. It is known that these sets play an important role in the analysis of maximal order types. While
![]() $A_a$
itself is not a type, it admits a quasi embedding into a type
$A_a$
itself is not a type, it admits a quasi embedding into a type
![]() $A(a)$
, as we show next. To save parentheses we agree on
$A(a)$
, as we show next. To save parentheses we agree on
![]() $A\otimes B\otimes C=(A\otimes B)\otimes C$
and
$A\otimes B\otimes C=(A\otimes B)\otimes C$
and
![]() $[a,b,c]=[[a,b],c]$
. The following construction is similar to the one in [Reference Hilbert21, definition 5.3 and example 5.4].
$[a,b,c]=[[a,b],c]$
. The following construction is similar to the one in [Reference Hilbert21, definition 5.3 and example 5.4].
Definition 6.7 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
By recursion over
![]() $\#a$
we define a type
$\#a$
we define a type
![]() $A(a)$
for each
$A(a)$
for each
![]() $a\in A$
:
$a\in A$
:
-
(i) We have
 $\mathfrak B(\circ )=\mathfrak E$
and
$\mathfrak B(\circ )=\mathfrak E$
and
 $\mathfrak B(\circ (s,t))=(\mathfrak B(s)+\mathfrak B(t))^*$
.
$\mathfrak B(\circ (s,t))=(\mathfrak B(s)+\mathfrak B(t))^*$
. -
(ii) We have
 $(A+B)(\iota _0^Ba)=A(a)+B$
and
$(A+B)(\iota _0^Ba)=A(a)+B$
and
 $(A+B)(\iota _1^Ab)=A+B(b)$
.
$(A+B)(\iota _1^Ab)=A+B(b)$
. -
(iii) We have
 $(A\times B)(\langle a,b\rangle )=A(a)\otimes B+A\otimes B(b)$
.
$(A\times B)(\langle a,b\rangle )=A(a)\otimes B+A\otimes B(b)$
. -
(iv) We have
 $A^*(\langle \rangle _A)=\mathfrak E$
and
$A^*(\langle \rangle _A)=\mathfrak E$
and  $$ \begin{align*} A^*(\langle a_0,\dots,a_n\rangle_A)=A(a_0)^*+A(a_0)^*\otimes A\otimes A^*(\langle a_1,\dots,a_n\rangle_A). \end{align*} $$
$$ \begin{align*} A^*(\langle a_0,\dots,a_n\rangle_A)=A(a_0)^*+A(a_0)^*\otimes A\otimes A^*(\langle a_1,\dots,a_n\rangle_A). \end{align*} $$
As promised, we get the following quasi embeddings:
Proposition 6.8. There is a primitive recursive function e such that
![]() $\mathbf {PA}$
proves the following: For any type A and terms
$\mathbf {PA}$
proves the following: For any type A and terms
![]() $a\in A, b\in A_a$
we have
$a\in A, b\in A_a$
we have
![]() $e_A(a,b)=e(a,b)\in A(a)$
(note that A can be inferred from a). Furthermore we have
$e_A(a,b)=e(a,b)\in A(a)$
(note that A can be inferred from a). Furthermore we have
for any terms
![]() $b,b'\in A_a$
.
$b,b'\in A_a$
.
Proof. The value
![]() $e_A(a,b)$
is defined by recursion over the code of the pair
$e_A(a,b)$
is defined by recursion over the code of the pair
![]() $\langle \#a,\#b\rangle $
, simultaneously for all types A. Once the construction of e is complete, the second part of the proposition can be verified by induction on
$\langle \#a,\#b\rangle $
, simultaneously for all types A. Once the construction of e is complete, the second part of the proposition can be verified by induction on
![]() $\#a+\#b+\#b'$
. In the following we distinguish cases according to the form of a.
$\#a+\#b+\#b'$
. In the following we distinguish cases according to the form of a.
First consider
![]() $a=\circ \in \mathfrak B=A$
. Since
$a=\circ \in \mathfrak B=A$
. Since
![]() $\circ \leq _{\mathfrak B}t$
is true for any
$\circ \leq _{\mathfrak B}t$
is true for any
![]() $t\in \mathfrak B$
, the set
$t\in \mathfrak B$
, the set
![]() $A_a$
is empty and there are no values to define. Now assume
$A_a$
is empty and there are no values to define. Now assume
![]() $a=\circ (s_0,s_1)\in \mathfrak B=A$
. For the term
$a=\circ (s_0,s_1)\in \mathfrak B=A$
. For the term
![]() $b=\circ \in \mathfrak B$
we put
$b=\circ \in \mathfrak B$
we put
Now assume that we have
![]() $b=\circ (t_0,t_1)\in \mathfrak B$
. The condition
$b=\circ (t_0,t_1)\in \mathfrak B$
. The condition
![]() $b\in A_a$
amounts to
$b\in A_a$
amounts to
![]() $\circ (s_0,s_1)\not \leq _{\mathfrak B}\circ (t_0,t_1)$
, which yields
$\circ (s_0,s_1)\not \leq _{\mathfrak B}\circ (t_0,t_1)$
, which yields
![]() $s_0\not \leq _{\mathfrak B}t_0$
or
$s_0\not \leq _{\mathfrak B}t_0$
or
![]() $s_1\not \leq _{\mathfrak B}t_1$
. Let us assume that we have
$s_1\not \leq _{\mathfrak B}t_1$
. Let us assume that we have
![]() $s_0\not \leq _{\mathfrak B}t_0$
, which amounts to
$s_0\not \leq _{\mathfrak B}t_0$
, which amounts to
![]() $t_0\in \mathfrak B_{s_0}$
. We may then refer to the recursively defined value
$t_0\in \mathfrak B_{s_0}$
. We may then refer to the recursively defined value
More formally, the recursive definition of
![]() $e_A(a,b)$
and the inductive verification of
$e_A(a,b)$
and the inductive verification of
![]() $e_A(a,b)\in A(a)$
should be separated. In order to do so, we can agree on a default value for the hypothetical case that the decidable property
$e_A(a,b)\in A(a)$
should be separated. In order to do so, we can agree on a default value for the hypothetical case that the decidable property
![]() $e_{\mathfrak B}(s_0,t_0)\in \mathfrak B(s_0)$
fails; the induction shows that the default value is never called. By
$e_{\mathfrak B}(s_0,t_0)\in \mathfrak B(s_0)$
fails; the induction shows that the default value is never called. By
![]() $\circ (s_0,s_1)\not \leq _{\mathfrak B}\circ (t_0,t_1)$
we also have
$\circ (s_0,s_1)\not \leq _{\mathfrak B}\circ (t_0,t_1)$
we also have
![]() $\circ (s_0,s_1)\not \leq _{\mathfrak B}t_1$
, which amounts to
$\circ (s_0,s_1)\not \leq _{\mathfrak B}t_1$
, which amounts to
![]() $t_1\in \mathfrak B_{\circ (s_0,s_1)}$
and provides
$t_1\in \mathfrak B_{\circ (s_0,s_1)}$
and provides
Let us agree to write
![]() $c_0\star \langle c_1,\dots ,c_n\rangle _C:=\langle c_0,c_1,\dots ,c_n\rangle _C\in C^*$
for terms
$c_0\star \langle c_1,\dots ,c_n\rangle _C:=\langle c_0,c_1,\dots ,c_n\rangle _C\in C^*$
for terms
![]() $c_0,\dots ,c_n$
of a type C. We can now state our recursive clause as
$c_0,\dots ,c_n$
of a type C. We can now state our recursive clause as
 $$ \begin{align*} e_{\mathfrak B}(\circ(s_0,s_1),\circ(t_0,t_1))=\begin{cases} \iota_0^{\mathfrak B(s_1)}e_{\mathfrak B}(s_0,t_0)\star e_{\mathfrak B}(\circ(s_0,s_1),t_1) & \text{if}\ s_0\not\leq_{\mathfrak B}t_0,\\[1ex] \iota_1^{\mathfrak B(s_0)}e_{\mathfrak B}(s_1,t_1)\star e_{\mathfrak B}(\circ(s_0,s_1),t_0) & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} e_{\mathfrak B}(\circ(s_0,s_1),\circ(t_0,t_1))=\begin{cases} \iota_0^{\mathfrak B(s_1)}e_{\mathfrak B}(s_0,t_0)\star e_{\mathfrak B}(\circ(s_0,s_1),t_1) & \text{if}\ s_0\not\leq_{\mathfrak B}t_0,\\[1ex] \iota_1^{\mathfrak B(s_0)}e_{\mathfrak B}(s_1,t_1)\star e_{\mathfrak B}(\circ(s_0,s_1),t_0) & \text{otherwise}. \end{cases} \end{align*} $$
To explain the second case we recall that
![]() $s_1\not \leq _{\mathfrak B}t_1$
must hold if
$s_1\not \leq _{\mathfrak B}t_1$
must hold if
![]() $s_0\not \leq _{\mathfrak B}t_0$
fails.
$s_0\not \leq _{\mathfrak B}t_0$
fails.
Before we state the other recursive clauses, let us verify that the second part of the proposition holds for
![]() $A=\mathfrak B$
. As above we write
$A=\mathfrak B$
. As above we write
![]() $a=\circ (s_0,s_1)$
. In the case of the term
$a=\circ (s_0,s_1)$
. In the case of the term
![]() $b^{\prime }=\circ $
we observe
$b^{\prime }=\circ $
we observe
The consequent of this implication can only hold for
![]() $b=\circ $
. In this case
$b=\circ $
. In this case
![]() $b\leq _{\mathfrak B}b^{\prime }$
is satisfied for any
$b\leq _{\mathfrak B}b^{\prime }$
is satisfied for any
![]() $b^{\prime }\in \mathfrak B$
. Hence it remains to consider terms of the form
$b^{\prime }\in \mathfrak B$
. Hence it remains to consider terms of the form
![]() $b=\circ (t_0,t_1)$
and
$b=\circ (t_0,t_1)$
and
![]() $b^{\prime }=\circ (t_0^{\prime },t_1^{\prime })$
. In general we have
$b^{\prime }=\circ (t_0^{\prime },t_1^{\prime })$
. In general we have
First assume that
![]() $e_{\mathfrak B}(s,b)\leq _{\mathfrak B(s)}e_{\mathfrak B}(s,b^{\prime })$
holds because of
$e_{\mathfrak B}(s,b)\leq _{\mathfrak B(s)}e_{\mathfrak B}(s,b^{\prime })$
holds because of
![]() $e_{\mathfrak B}(s,b)\leq _{\mathfrak B(s)}e_{\mathfrak B}(s,t_i^{\prime })$
. Then the induction hypothesis yields
$e_{\mathfrak B}(s,b)\leq _{\mathfrak B(s)}e_{\mathfrak B}(s,t_i^{\prime })$
. Then the induction hypothesis yields
![]() $b\leq _{\mathfrak B}t_i^{\prime }$
, which implies
$b\leq _{\mathfrak B}t_i^{\prime }$
, which implies
![]() $b\leq _{\mathfrak B}\circ (t_0^{\prime },t_1^{\prime })=b^{\prime }$
. Now assume we have
$b\leq _{\mathfrak B}\circ (t_0^{\prime },t_1^{\prime })=b^{\prime }$
. Now assume we have
![]() $e_{\mathfrak B}(s,b)\leq _{\mathfrak B(s)}e_{\mathfrak B}(s,b^{\prime })$
because there are
$e_{\mathfrak B}(s,b)\leq _{\mathfrak B(s)}e_{\mathfrak B}(s,b^{\prime })$
because there are
![]() $i,j\in \{0,1\}$
with
$i,j\in \{0,1\}$
with
 $$ \begin{align*} \iota_i^{\mathfrak B(s_{1-i})}e_{\mathfrak B}(s_i,t_i)&\leq_{\mathfrak B(s_0)+\mathfrak B(s_1)}\iota_j^{\mathfrak B(s_{1-j})}e_{\mathfrak B}(s_j,t_j^{\prime}),\\[1ex] e_{\mathfrak B}(s,t_{1-i})&\leq_{\mathfrak B(s)}e_{\mathfrak B}(s,t_{1-j}^{\prime}). \end{align*} $$
$$ \begin{align*} \iota_i^{\mathfrak B(s_{1-i})}e_{\mathfrak B}(s_i,t_i)&\leq_{\mathfrak B(s_0)+\mathfrak B(s_1)}\iota_j^{\mathfrak B(s_{1-j})}e_{\mathfrak B}(s_j,t_j^{\prime}),\\[1ex] e_{\mathfrak B}(s,t_{1-i})&\leq_{\mathfrak B(s)}e_{\mathfrak B}(s,t_{1-j}^{\prime}). \end{align*} $$
The first inequality can only hold for
![]() $i=j$
. It yields
$i=j$
. It yields
![]() $e_{\mathfrak B}(s_i,t_i)\leq _{\mathfrak B(s_i)}e_{\mathfrak B}(s_i,t_i^{\prime })$
, which implies
$e_{\mathfrak B}(s_i,t_i)\leq _{\mathfrak B(s_i)}e_{\mathfrak B}(s_i,t_i^{\prime })$
, which implies
![]() $t_i\leq _{\mathfrak B}t_i^{\prime }$
by induction hypothesis. From the second inequality we can infer
$t_i\leq _{\mathfrak B}t_i^{\prime }$
by induction hypothesis. From the second inequality we can infer
![]() $t_{1-i}\leq _{\mathfrak B}t_{1-i}^{\prime }$
. Together we get
$t_{1-i}\leq _{\mathfrak B}t_{1-i}^{\prime }$
. Together we get
![]() $b=\circ (t_0,t_1)\leq _{\mathfrak B}\circ (t_0^{\prime },t_1^{\prime })=b^{\prime }$
, as desired.
$b=\circ (t_0,t_1)\leq _{\mathfrak B}\circ (t_0^{\prime },t_1^{\prime })=b^{\prime }$
, as desired.
Sum and product types are considerably easier to handle. We only state the recursive clauses and leave all verifications to the reader:
 $$ \begin{gather*} \begin{aligned} e_{A+B}(\iota_0^Ba,\iota_0^Ba')&=\iota_0^B e_A(a,a'),\quad & e_{A+B}(\iota_0^Ba,\iota_1^Ab')&=\iota_1^{A(a)}b',\\[1ex] e_{A+B}(\iota_1^Ab,\iota_0^Ba')&=\iota_0^{B(b)}a', & e_{A+B}(\iota_1^Ab,\iota_1^Ab')&=\iota_1^A e_B(b,b'). \end{aligned}\\[1ex] e_{A\times B}(\langle a,b\rangle,\langle a',b'\rangle)=\begin{cases} \iota_0^{A\otimes B(b)}[e_A(a,a'),b'] & \text{if}\ a\not\leq_A a',\\[1ex] \iota_1^{A(a)\otimes B}[a',e_B(b,b')] & \text{otherwise}. \end{cases} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} e_{A+B}(\iota_0^Ba,\iota_0^Ba')&=\iota_0^B e_A(a,a'),\quad & e_{A+B}(\iota_0^Ba,\iota_1^Ab')&=\iota_1^{A(a)}b',\\[1ex] e_{A+B}(\iota_1^Ab,\iota_0^Ba')&=\iota_0^{B(b)}a', & e_{A+B}(\iota_1^Ab,\iota_1^Ab')&=\iota_1^A e_B(b,b'). \end{aligned}\\[1ex] e_{A\times B}(\langle a,b\rangle,\langle a',b'\rangle)=\begin{cases} \iota_0^{A\otimes B(b)}[e_A(a,a'),b'] & \text{if}\ a\not\leq_A a',\\[1ex] \iota_1^{A(a)\otimes B}[a',e_B(b,b')] & \text{otherwise}. \end{cases} \end{gather*} $$
Finally, we consider the case of a type
![]() $A^*$
. For
$A^*$
. For
![]() $a=\langle \rangle _A\in A^*$
it suffices to observe that
$a=\langle \rangle _A\in A^*$
it suffices to observe that
![]() $(A^*)_a$
is empty, since
$(A^*)_a$
is empty, since
![]() $\langle \rangle _A\leq _{A^*}\tau $
holds for any
$\langle \rangle _A\leq _{A^*}\tau $
holds for any
![]() $\tau \in A^*$
. Now consider a term of the form
$\tau \in A^*$
. Now consider a term of the form
![]() $a=a_0\star \sigma \in A^*$
. We write
$a=a_0\star \sigma \in A^*$
. We write
![]() $b=\langle b_0,\dots ,b_{n-1}\rangle _A\in (A^*)_a$
and distinguish two cases. If we have
$b=\langle b_0,\dots ,b_{n-1}\rangle _A\in (A^*)_a$
and distinguish two cases. If we have
![]() $a_0\not \leq _A b_i$
for all
$a_0\not \leq _A b_i$
for all
![]() $i<n$
, then we set
$i<n$
, then we set
Note that this is an element of
![]() $A(a_0)^*+A(a_0)^*\otimes A\otimes A^*(\sigma )=A^*(a)$
, as required. Otherwise we fix the smallest number
$A(a_0)^*+A(a_0)^*\otimes A\otimes A^*(\sigma )=A^*(a)$
, as required. Otherwise we fix the smallest number
![]() $i<n$
with
$i<n$
with
![]() $a_0\leq _A b_i$
. In view of
$a_0\leq _A b_i$
. In view of
![]() $b\in (A^*)_a$
we must have
$b\in (A^*)_a$
we must have
![]() $\sigma \not \leq _{A^*}\langle b_{i+1},\dots ,b_{n-1}\rangle _A$
. We can thus define
$\sigma \not \leq _{A^*}\langle b_{i+1},\dots ,b_{n-1}\rangle _A$
. We can thus define
![]() $e_{A^*}(a,b)$
as
$e_{A^*}(a,b)$
as
Using the induction hypothesis, one readily checks that
![]() $e_{A^*}(a,b)\leq _{A^*(a)}e_{A^*}(a,b')$
implies
$e_{A^*}(a,b)\leq _{A^*(a)}e_{A^*}(a,b')$
implies
![]() $b\leq _{A^*}b'$
.□
$b\leq _{A^*}b'$
.□
Our next aim is to iterate the previous construction along bad sequences. Given a type A, we write
![]() $\sigma \in \operatorname {Bad}(A)$
to express that
$\sigma \in \operatorname {Bad}(A)$
to express that
![]() $\sigma $
is a finite bad sequence in A. This means that we have
$\sigma $
is a finite bad sequence in A. This means that we have
![]() $\sigma =\langle a_0,\dots ,a_{n-1}\rangle $
for terms
$\sigma =\langle a_0,\dots ,a_{n-1}\rangle $
for terms
![]() $a_0,\dots ,a_{n-1}\in A$
that satisfy
$a_0,\dots ,a_{n-1}\in A$
that satisfy
![]() $a_i\not \leq _A a_j$
for all
$a_i\not \leq _A a_j$
for all
![]() $i<j<n$
. If we have
$i<j<n$
. If we have
![]() $\sigma \in \operatorname {Bad}(A)$
and
$\sigma \in \operatorname {Bad}(A)$
and
![]() $\sigma $
is different from the empty sequence
$\sigma $
is different from the empty sequence
![]() $\langle \rangle $
, then we write
$\langle \rangle $
, then we write
![]() $\sigma \in \operatorname {Bad}^-(A)$
. For
$\sigma \in \operatorname {Bad}^-(A)$
. For
![]() $\sigma =\langle a_0,\dots ,a_{n-1}\rangle \in \operatorname {Bad}(A)$
we abbreviate
$\sigma =\langle a_0,\dots ,a_{n-1}\rangle \in \operatorname {Bad}(A)$
we abbreviate
![]() $\sigma ^\frown a=\langle a_0,\dots ,a_{n-1},a\rangle $
and put
$\sigma ^\frown a=\langle a_0,\dots ,a_{n-1},a\rangle $
and put
Once again, note that we officially define a primitive recursive relation
![]() $a\in A_\sigma $
between finite objects, rather than an infinite set
$a\in A_\sigma $
between finite objects, rather than an infinite set
![]() $A_\sigma $
. The expressions
$A_\sigma $
. The expressions
![]() $A(a)$
and
$A(a)$
and
![]() $e_A(a,b)$
have only been explained for
$e_A(a,b)$
have only been explained for
![]() $a\in A$
and
$a\in A$
and
![]() $b\in A_a$
. We will see that the following definition does conform with these restrictions. Before this is established, we may simply assume that some default value is assigned outside of the intended domain of definition.
$b\in A_a$
. We will see that the following definition does conform with these restrictions. Before this is established, we may simply assume that some default value is assigned outside of the intended domain of definition.
Definition 6.9 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
Consider a type A. For a sequence
![]() $\sigma \in \operatorname {Bad}(A)$
and a term
$\sigma \in \operatorname {Bad}(A)$
and a term
![]() $b\in A_\sigma $
we define
$b\in A_\sigma $
we define
![]() $A[\sigma ]$
and
$A[\sigma ]$
and
![]() $\hat e_A(\sigma ,b)$
by the recursive clauses
$\hat e_A(\sigma ,b)$
by the recursive clauses
 $$ \begin{align*} A[\langle\rangle]&=A, & A[\sigma^\frown a]&=A[\sigma](\hat e_A(\sigma,a)),\\ \hat e_A(\langle\rangle,b)&=b, & \hat e_A(\sigma^\frown a,b)&=e_{A[\sigma]}(\hat e_A(\sigma,a),\hat e_A(\sigma,b)). \end{align*} $$
$$ \begin{align*} A[\langle\rangle]&=A, & A[\sigma^\frown a]&=A[\sigma](\hat e_A(\sigma,a)),\\ \hat e_A(\langle\rangle,b)&=b, & \hat e_A(\sigma^\frown a,b)&=e_{A[\sigma]}(\hat e_A(\sigma,a),\hat e_A(\sigma,b)). \end{align*} $$
In order to justify the recursion in detail, we consider
![]() $\sigma =\langle a_0,\dots ,a_{n-1}\rangle $
and write
$\sigma =\langle a_0,\dots ,a_{n-1}\rangle $
and write
![]() $\sigma \!\restriction \!i=\langle a_0,\dots ,a_{i-1}\rangle $
. Then
$\sigma \!\restriction \!i=\langle a_0,\dots ,a_{i-1}\rangle $
. Then
![]() $A[\sigma \!\restriction \!i]$
and the values
$A[\sigma \!\restriction \!i]$
and the values
![]() $\hat e_A(\sigma \!\restriction \!i,a_j)$
for
$\hat e_A(\sigma \!\restriction \!i,a_j)$
for
![]() $i\leq j<n$
are constructed simultaneously by recursion on
$i\leq j<n$
are constructed simultaneously by recursion on
![]() $i<n$
. For
$i<n$
. For
![]() $\sigma ':=\sigma ^\frown a_n$
with
$\sigma ':=\sigma ^\frown a_n$
with
![]() $a_n:=b$
this also explains the value
$a_n:=b$
this also explains the value
![]() $\hat e_A(\sigma ,b)=\hat e_A(\sigma '\!\restriction \!n,a_n)$
.
$\hat e_A(\sigma ,b)=\hat e_A(\sigma '\!\restriction \!n,a_n)$
.
Corollary 6.10 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
If
![]() $\sigma $
is a finite bad sequence in the type A, then
$\sigma $
is a finite bad sequence in the type A, then
![]() $A[\sigma ]$
is a type. For any
$A[\sigma ]$
is a type. For any
![]() $b\in A_\sigma $
the value
$b\in A_\sigma $
the value
![]() $\hat e_A(\sigma ,b)$
is a term of this type. Furthermore we have
$\hat e_A(\sigma ,b)$
is a term of this type. Furthermore we have
for any terms
![]() $b,b'\in A_\sigma $
.
$b,b'\in A_\sigma $
.
Proof. We use induction on
![]() $\sigma $
to verify all claims simultaneously. The case of
$\sigma $
to verify all claims simultaneously. The case of
![]() $\sigma =\langle \rangle $
is immediate. Now assume that we have
$\sigma =\langle \rangle $
is immediate. Now assume that we have
![]() $\sigma ={\sigma _0}^\frown a$
. The induction hypothesis tells us that
$\sigma ={\sigma _0}^\frown a$
. The induction hypothesis tells us that
![]() $\hat e_A(\sigma _0,a)$
is a term of type
$\hat e_A(\sigma _0,a)$
is a term of type
![]() $A[\sigma _0]$
. In view of Definition 6.7 it follows that
$A[\sigma _0]$
. In view of Definition 6.7 it follows that
![]() $A[\sigma ]=A[\sigma _0](\hat e_A(\sigma _0,a))$
is a type. For
$A[\sigma ]=A[\sigma _0](\hat e_A(\sigma _0,a))$
is a type. For
![]() $b\in A_\sigma $
we have
$b\in A_\sigma $
we have
![]() $a\not \leq _A b$
, so that the induction hypothesis yields
$a\not \leq _A b$
, so that the induction hypothesis yields
![]() $\hat e_A(\sigma _0,a)\not \leq _{A[\sigma _0]}\hat e_A(\sigma _0,b)$
. By Proposition 6.8 we get
$\hat e_A(\sigma _0,a)\not \leq _{A[\sigma _0]}\hat e_A(\sigma _0,b)$
. By Proposition 6.8 we get
From
![]() $\hat e_A(\sigma ,b)\leq _{A[\sigma ]}\hat e_A(\sigma ,b')$
we get
$\hat e_A(\sigma ,b)\leq _{A[\sigma ]}\hat e_A(\sigma ,b')$
we get
![]() $\hat e_A(\sigma _0,b)\leq _{A[\sigma _0]}\hat e_A(\sigma _0,b')$
, also by Proposition 6.8. Then
$\hat e_A(\sigma _0,b)\leq _{A[\sigma _0]}\hat e_A(\sigma _0,b')$
, also by Proposition 6.8. Then
![]() $b\leq _A b'$
follows by induction hypothesis.□
$b\leq _A b'$
follows by induction hypothesis.□
In order to obtain a reification, it remains to assign a suitable ordinal to each type. Let us write
![]() $\alpha \oplus \beta $
and
$\alpha \oplus \beta $
and
![]() $\alpha \otimes \beta $
for the natural (“Hessenberg”) sum and product of ordinals
$\alpha \otimes \beta $
for the natural (“Hessenberg”) sum and product of ordinals
![]() $\alpha ,\beta \prec \varepsilon _0$
(see, e.g., [Reference Simpson39, sec. 4]). In contrast to the usual operations of ordinal arithmetic, the natural variants are commutative and strictly increasing in both arguments. Ordinals of the form
$\alpha ,\beta \prec \varepsilon _0$
(see, e.g., [Reference Simpson39, sec. 4]). In contrast to the usual operations of ordinal arithmetic, the natural variants are commutative and strictly increasing in both arguments. Ordinals of the form
![]() $\omega ^\gamma $
are additively indecomposable, in the sense that
$\omega ^\gamma $
are additively indecomposable, in the sense that
![]() $\alpha ,\beta \prec \omega ^\gamma $
implies
$\alpha ,\beta \prec \omega ^\gamma $
implies
![]() $\alpha \oplus \beta \prec \omega ^{\gamma }$
; conversely, any additively indecomposable ordinal
$\alpha \oplus \beta \prec \omega ^{\gamma }$
; conversely, any additively indecomposable ordinal
![]() $\delta \neq 0$
has the form
$\delta \neq 0$
has the form
![]() $\delta =\omega ^\gamma $
. For
$\delta =\omega ^\gamma $
. For
![]() $\alpha ,\beta \prec \omega _2^\gamma :=\omega ^{(\omega ^\gamma )}$
we have
$\alpha ,\beta \prec \omega _2^\gamma :=\omega ^{(\omega ^\gamma )}$
we have
![]() $\alpha \otimes \beta \prec \omega _2^\gamma $
.
$\alpha \otimes \beta \prec \omega _2^\gamma $
.
Definition 6.11 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
Let us say that a type is low if it does not involve the constant symbol
![]() $\mathfrak B$
. We recursively assign an ordinal
$\mathfrak B$
. We recursively assign an ordinal
![]() $o(A)$
to each low type A:
$o(A)$
to each low type A:
 $$ \begin{align*} o(\mathfrak E)&=0, & o(A+B)&=o(A)\oplus o(B),\\ o(A\times B)&=o(A)\otimes o(B), & o(A^*)&=\omega_2^{o(A)}. \end{align*} $$
$$ \begin{align*} o(\mathfrak E)&=0, & o(A+B)&=o(A)\oplus o(B),\\ o(A\times B)&=o(A)\otimes o(B), & o(A^*)&=\omega_2^{o(A)}. \end{align*} $$
The following is crucial for the construction of a reification.
Proposition 6.12 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
If A is a low type and
![]() $a\in A$
is a term, then
$a\in A$
is a term, then
![]() $A(a)$
is a low type and we have
$A(a)$
is a low type and we have
![]() $o(A(a))\prec o(A)$
.
$o(A(a))\prec o(A)$
.
Proof. As preparation we note that
![]() $A\otimes B$
is low if the same holds for A and B. A straightforward induction shows
$A\otimes B$
is low if the same holds for A and B. A straightforward induction shows
![]() $o(A\otimes B)=o(A)\otimes o(B)$
; for example, the distributivity property from [Reference Simpson39, lemma 4.5(8)] accounts for the inductive verification
$o(A\otimes B)=o(A)\otimes o(B)$
; for example, the distributivity property from [Reference Simpson39, lemma 4.5(8)] accounts for the inductive verification
 $$ \begin{align*} &o((C+D)\otimes B)=o(C\otimes B+D\otimes B)=o(C\otimes B)\oplus o(D\otimes B)\\ & \quad =(o(C)\otimes o(B))\oplus(o(D)\otimes o(B))=(o(C)\oplus o(D))\otimes o(B)=o(C+D)\otimes o(B). \end{align*} $$
$$ \begin{align*} &o((C+D)\otimes B)=o(C\otimes B+D\otimes B)=o(C\otimes B)\oplus o(D\otimes B)\\ & \quad =(o(C)\otimes o(B))\oplus(o(D)\otimes o(B))=(o(C)\oplus o(D))\otimes o(B)=o(C+D)\otimes o(B). \end{align*} $$
By induction on A one can show that
![]() $o(A)$
is additively indecomposable when A is an indecomposable type. The most interesting step concerns a type
$o(A)$
is additively indecomposable when A is an indecomposable type. The most interesting step concerns a type
![]() $A=B\times C$
, where B and C are indecomposable according to Definition 6.1. Inductively we may write
$A=B\times C$
, where B and C are indecomposable according to Definition 6.1. Inductively we may write
![]() $o(B)=\omega ^\beta $
and
$o(B)=\omega ^\beta $
and
![]() $o(C)=\omega ^\gamma $
(unless we have
$o(C)=\omega ^\gamma $
(unless we have
![]() $o(A)=0$
). Then
$o(A)=0$
). Then
is an additively indecomposable ordinal as well. The claim of the proposition can now be verified by induction over
![]() $\#a$
, for all types A simultaneously. First consider the case of a term
$\#a$
, for all types A simultaneously. First consider the case of a term
![]() $\iota _0^Ba\in A+B$
. The induction hypothesis tells us that
$\iota _0^Ba\in A+B$
. The induction hypothesis tells us that
![]() $A(a)$
is low with
$A(a)$
is low with
![]() $o(A(a))\prec o(A)$
. Hence
$o(A(a))\prec o(A)$
. Hence
![]() $(A+B)(\iota _0^Ba)=A(a)+B$
is low and we have
$(A+B)(\iota _0^Ba)=A(a)+B$
is low and we have
The case of
![]() $\iota _1^Ab\in A+B$
is analogous. Now consider a term
$\iota _1^Ab\in A+B$
is analogous. Now consider a term
![]() $\langle a,b\rangle \in A\times B$
. In view of the above, the induction hypothesis implies that
$\langle a,b\rangle \in A\times B$
. In view of the above, the induction hypothesis implies that
![]() $A(a)\otimes B$
is low with ordinal
$A(a)\otimes B$
is low with ordinal
In the same way we get
![]() $o(A\otimes B(b))\prec o(A\times B)$
. In view of Definition 6.1, a type of the form
$o(A\otimes B(b))\prec o(A\times B)$
. In view of Definition 6.1, a type of the form
![]() $A\times B$
is always indecomposable. By the above this entails that
$A\times B$
is always indecomposable. By the above this entails that
![]() $o(A\times B)$
is an additively indecomposable ordinal. Hence we obtain
$o(A\times B)$
is an additively indecomposable ordinal. Hence we obtain
 $$ \begin{align*} o((A\times B)(\langle a,b\rangle))&=o(A(a)\otimes B+A\otimes B(b))\\ &=o(A(a)\otimes B)\oplus o(A\otimes B(b))\prec o(A\times B). \end{align*} $$
$$ \begin{align*} o((A\times B)(\langle a,b\rangle))&=o(A(a)\otimes B+A\otimes B(b))\\ &=o(A(a)\otimes B)\oplus o(A\otimes B(b))\prec o(A\times B). \end{align*} $$
Finally, we consider the case of a type
![]() $A^*$
. Concerning the term
$A^*$
. Concerning the term
![]() $\langle \rangle _A\in A^*$
, we note
$\langle \rangle _A\in A^*$
, we note
Now consider a term
![]() $a\star \sigma \in A^*$
(see the proof of Proposition 6.8 for the notation). In view of
$a\star \sigma \in A^*$
(see the proof of Proposition 6.8 for the notation). In view of
![]() $\#a,\#\sigma <\#a\star \sigma $
the induction hypothesis yields
$\#a,\#\sigma <\#a\star \sigma $
the induction hypothesis yields
![]() $o(A^*(\sigma ))\prec o(A^*)=\omega _2^{o(A)}$
and
$o(A^*(\sigma ))\prec o(A^*)=\omega _2^{o(A)}$
and
![]() $o(A(a))\prec o(A)$
. The latter implies
$o(A(a))\prec o(A)$
. The latter implies
![]() $o(A(a)^*)=\omega _2^{o(A(a))}\prec \omega _2^{o(A)}$
. Since we are concerned with ordinals below
$o(A(a)^*)=\omega _2^{o(A(a))}\prec \omega _2^{o(A)}$
. Since we are concerned with ordinals below
![]() $\varepsilon _0$
, we also have
$\varepsilon _0$
, we also have
![]() $o(A)\prec \omega _2^{o(A)}$
. Using the fact that
$o(A)\prec \omega _2^{o(A)}$
. Using the fact that
![]() $\omega _2^{o(A)}$
is additively and multiplicatively indecomposable, we can deduce
$\omega _2^{o(A)}$
is additively and multiplicatively indecomposable, we can deduce
 $$ \begin{align*} o(A^*(a\star\sigma))&=o(A(a)^*+A(a)^*\otimes A\otimes A^*(\sigma))\\ & =o(A(a)^*)\oplus o(A(a)^*)\otimes o(A)\otimes o(A^*(\sigma))\prec\omega_2^{o(A)}=o(A^*), \end{align*} $$
$$ \begin{align*} o(A^*(a\star\sigma))&=o(A(a)^*+A(a)^*\otimes A\otimes A^*(\sigma))\\ & =o(A(a)^*)\oplus o(A(a)^*)\otimes o(A)\otimes o(A^*(\sigma))\prec\omega_2^{o(A)}=o(A^*), \end{align*} $$
as required.□
Recall that the terms of type
![]() $\mathfrak B$
coincide with the finite binary trees, i.e., with the elements of
$\mathfrak B$
coincide with the finite binary trees, i.e., with the elements of
![]() $\mathcal B$
. Below we will show that the type
$\mathcal B$
. Below we will show that the type
![]() $\mathfrak B[\sigma ]$
is low for any non-empty bad sequence
$\mathfrak B[\sigma ]$
is low for any non-empty bad sequence
![]() $\sigma \in \operatorname {Bad}^-(\mathcal B)=\operatorname {Bad}^-(\mathfrak B)$
. To state the following definition, we simply assume that the primitive recursive function
$\sigma \in \operatorname {Bad}^-(\mathcal B)=\operatorname {Bad}^-(\mathfrak B)$
. To state the following definition, we simply assume that the primitive recursive function
![]() $o(\cdot )$
is extended to arbitrary arguments.
$o(\cdot )$
is extended to arbitrary arguments.
Definition 6.13 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
For
![]() $\sigma \in \operatorname {Bad}^-(\mathcal B)$
we put
$\sigma \in \operatorname {Bad}^-(\mathcal B)$
we put
![]() $r(\sigma ):=o(\mathfrak B[\sigma ])$
.
$r(\sigma ):=o(\mathfrak B[\sigma ])$
.
Finally, we can deduce the promised result:
Corollary 6.14 (
 $\mathbf {PA}$
)
$\mathbf {PA}$
)
The primitive recursive function
![]() $r:\operatorname {Bad}^-(\mathcal B)\rightarrow \varepsilon _0$
is a reification, i.e., we have
$r:\operatorname {Bad}^-(\mathcal B)\rightarrow \varepsilon _0$
is a reification, i.e., we have
for any bad sequence
![]() $\langle t_0,\dots ,t_n,t_{n+1}\rangle $
in
$\langle t_0,\dots ,t_n,t_{n+1}\rangle $
in
![]() $\mathcal B$
.
$\mathcal B$
.
Proof. We use induction on
![]() $\sigma \in \operatorname {Bad}^-(\mathfrak B)$
to show that
$\sigma \in \operatorname {Bad}^-(\mathfrak B)$
to show that
![]() $\mathfrak B[\sigma ]$
is a low type. For this purpose it is crucial to recall that the empty sequence was included in
$\mathfrak B[\sigma ]$
is a low type. For this purpose it is crucial to recall that the empty sequence was included in
![]() $\operatorname {Bad}(\mathfrak B)$
but excluded from
$\operatorname {Bad}(\mathfrak B)$
but excluded from
![]() $\operatorname {Bad}^-(\mathfrak B)$
. Hence the base case concerns a sequence of the form
$\operatorname {Bad}^-(\mathfrak B)$
. Hence the base case concerns a sequence of the form
![]() $\sigma =\langle t\rangle $
. In view of Definition 6.9 we have
$\sigma =\langle t\rangle $
. In view of Definition 6.9 we have
Even though the type
![]() $\mathfrak B$
is not low, a straightforward induction on
$\mathfrak B$
is not low, a straightforward induction on
![]() $t\in \mathfrak B$
shows that
$t\in \mathfrak B$
shows that
![]() $\mathfrak B(t)$
is a low type. Now consider a sequence
$\mathfrak B(t)$
is a low type. Now consider a sequence
![]() $\sigma ^\frown t\in \operatorname {Bad}^-(\mathfrak B)$
with
$\sigma ^\frown t\in \operatorname {Bad}^-(\mathfrak B)$
with
![]() $\sigma \neq \langle \rangle $
. The induction hypothesis ensures that
$\sigma \neq \langle \rangle $
. The induction hypothesis ensures that
![]() $\mathfrak B[\sigma ]$
is a low type. According to Corollary 6.10 we have
$\mathfrak B[\sigma ]$
is a low type. According to Corollary 6.10 we have
![]() $\hat e_{\mathfrak B}(\sigma ,t)\in \mathfrak B[\sigma ]$
. By (the easy part of) Proposition 6.12 we conclude that
$\hat e_{\mathfrak B}(\sigma ,t)\in \mathfrak B[\sigma ]$
. By (the easy part of) Proposition 6.12 we conclude that
is a low type as well. The more substantial part of Proposition 6.12 yields
For
![]() $\sigma =\langle t_0,\dots ,t_n\rangle $
and
$\sigma =\langle t_0,\dots ,t_n\rangle $
and
![]() $t=t_{n+1}$
this is the claim of the corollary.□
$t=t_{n+1}$
this is the claim of the corollary.□
7 From reflection to the finite basis property
Working over
![]() $\mathbf {PA}$
, we show that
$\mathbf {PA}$
, we show that
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
entails
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
entails
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
, which does in turn entail
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
, which does in turn entail
![]() $\mathcal K\Sigma ^-_1$
. This completes our proof that all three principles are equivalent. Using Goryachev’s theorem, we can deduce a characterization of the
$\mathcal K\Sigma ^-_1$
. This completes our proof that all three principles are equivalent. Using Goryachev’s theorem, we can deduce a characterization of the
![]() $\Pi ^0_1$
-sentences that are provable in
$\Pi ^0_1$
-sentences that are provable in
![]() $\mathbf {PA}+\mathcal K\Sigma ^-_1$
.
$\mathbf {PA}+\mathcal K\Sigma ^-_1$
.
For the case of uniform reflection and induction with parameters, the following has been shown by Kreisel and Lévy Reference Kreisel and Lévy[27].
Proposition 7.1. Each instance of
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
can be proved in
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
can be proved in
![]() $\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
.
$\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
.
Proof. Consider a
![]() $\Pi ^0_1$
-formula
$\Pi ^0_1$
-formula
![]() $\psi (x)$
with a single free variable. Arguing in the theory
$\psi (x)$
with a single free variable. Arguing in the theory
![]() $\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
, we establish
$\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
, we establish
![]() $\mathcal {TI}(\varepsilon _0,\psi )$
by contraposition: Assume that the conclusion of transfinite induction fails, so that we have
$\mathcal {TI}(\varepsilon _0,\psi )$
by contraposition: Assume that the conclusion of transfinite induction fails, so that we have
![]() $\exists _{\alpha \prec \varepsilon _0}\neg \psi (\alpha )$
. The latter is a
$\exists _{\alpha \prec \varepsilon _0}\neg \psi (\alpha )$
. The latter is a
![]() $\Sigma ^0_1$
-formula, so that its truth can be established by an explicit verification. More formally, we invoke formalized
$\Sigma ^0_1$
-formula, so that its truth can be established by an explicit verification. More formally, we invoke formalized
![]() $\Sigma ^0_1$
-completeness (cf. [Reference Hasegawa, Jones, Hagiya and Sato20, theorem I.1.8]) to obtain
$\Sigma ^0_1$
-completeness (cf. [Reference Hasegawa, Jones, Hagiya and Sato20, theorem I.1.8]) to obtain
This uses Feferman’s dot notation: By
![]() $\psi (\dot \alpha )$
one denotes the closed object formula that results from
$\psi (\dot \alpha )$
one denotes the closed object formula that results from
![]() $\psi (x)$
when we substitute x by the
$\psi (x)$
when we substitute x by the
![]() $\alpha $
-th numeral, where the code
$\alpha $
-th numeral, where the code
![]() $\alpha $
is considered as a natural number (cf. the notation in [Reference Hasegawa, Jones, Hagiya and Sato20, corollary I.1.76]). Gentzen [Reference Hájek and Pudlák19] has shown that
$\alpha $
is considered as a natural number (cf. the notation in [Reference Hasegawa, Jones, Hagiya and Sato20, corollary I.1.76]). Gentzen [Reference Hájek and Pudlák19] has shown that
![]() $\mathbf {PA}$
proves induction up to each fixed ordinal below
$\mathbf {PA}$
proves induction up to each fixed ordinal below
![]() $\varepsilon _0$
. This result can itself be formalized in Peano arithmetic (and in much weaker theories, cf. [Reference Freund, Rathjen and Weiermann13, sec. 3]), which means that we have
$\varepsilon _0$
. This result can itself be formalized in Peano arithmetic (and in much weaker theories, cf. [Reference Freund, Rathjen and Weiermann13, sec. 3]), which means that we have
Together with the above we get
![]() $\operatorname {Pr}_{\mathbf {PA}}(\neg \operatorname {Prog}_{\varepsilon _0}(\psi ))$
. By an instance of
$\operatorname {Pr}_{\mathbf {PA}}(\neg \operatorname {Prog}_{\varepsilon _0}(\psi ))$
. By an instance of
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
we obtain
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
we obtain
![]() $\neg \operatorname {Prog}_{\varepsilon _0}(\psi )$
, which is (provably equivalent to) a closed
$\neg \operatorname {Prog}_{\varepsilon _0}(\psi )$
, which is (provably equivalent to) a closed
![]() $\Sigma ^0_2$
-formula. Hence the premise of
$\Sigma ^0_2$
-formula. Hence the premise of
![]() $\mathcal {TI}(\varepsilon _0,\psi )$
fails, so that our proof by contraposition is complete.□
$\mathcal {TI}(\varepsilon _0,\psi )$
fails, so that our proof by contraposition is complete.□
The following is a consequence of the result that
![]() $(\mathcal B,\leq _{\mathcal B})$
is a well partial order with maximal order type
$(\mathcal B,\leq _{\mathcal B})$
is a well partial order with maximal order type
![]() $\varepsilon _0$
, which is due to de Jongh (unpublished; cf. the introduction to Reference Schmidt[35]) and Diana Schmidt (see [Reference Schmidt36, theorem II.2] in combination with the example after [Reference Schmidt36, definition I.15]). A detailed proof in our setting has been given in the previous section.
$\varepsilon _0$
, which is due to de Jongh (unpublished; cf. the introduction to Reference Schmidt[35]) and Diana Schmidt (see [Reference Schmidt36, theorem II.2] in combination with the example after [Reference Schmidt36, definition I.15]). A detailed proof in our setting has been given in the previous section.
Proposition 7.2. Each instance of
![]() $\mathcal K\Sigma ^-_1$
can be proved in
$\mathcal K\Sigma ^-_1$
can be proved in
![]() $\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
.
$\mathbf {PA}+\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
.
Proof. Let us fix an instance
![]() $\mathcal K\varphi $
, where
$\mathcal K\varphi $
, where
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Sigma ^0_1$
-formula with a single free variable. It is instructive to recall the argument from Remark 3.1, which relies on a notion of
$\Sigma ^0_1$
-formula with a single free variable. It is instructive to recall the argument from Remark 3.1, which relies on a notion of
![]() $\varphi $
-sequence. If
$\varphi $
-sequence. If
![]() $\{n\in \mathbb N\,|\,\varphi (n)\}$
is computably enumerable but not decidable, then it is not decidable whether a given finite sequence is a
$\{n\in \mathbb N\,|\,\varphi (n)\}$
is computably enumerable but not decidable, then it is not decidable whether a given finite sequence is a
![]() $\varphi $
-sequence. For this reason we now introduce a finer notion: Write
$\varphi $
-sequence. For this reason we now introduce a finer notion: Write
![]() $\varphi (x)\equiv \exists _y\theta (x,y)$
with a
$\varphi (x)\equiv \exists _y\theta (x,y)$
with a
![]() $\Delta ^0_0$
-formula
$\Delta ^0_0$
-formula
![]() $\theta $
. As in the previous section we write
$\theta $
. As in the previous section we write
![]() $\operatorname {Bad}^-(\mathcal B)$
for the set of non-empty finite bad sequences in
$\operatorname {Bad}^-(\mathcal B)$
for the set of non-empty finite bad sequences in
![]() $\mathcal B$
. By a certified
$\mathcal B$
. By a certified
![]() $\varphi $
-sequence we mean a finite sequence
$\varphi $
-sequence we mean a finite sequence
such that we have
![]() $\langle t_0,\dots ,t_n\rangle \in \operatorname {Bad}^-(\mathcal B)$
and
$\langle t_0,\dots ,t_n\rangle \in \operatorname {Bad}^-(\mathcal B)$
and
![]() $\theta (t_i,c_i)$
for all
$\theta (t_i,c_i)$
for all
![]() $i\leq n$
. Note that the latter implies
$i\leq n$
. Note that the latter implies
![]() $\varphi (t_i)$
. Since
$\varphi (t_i)$
. Since
![]() $\theta $
contains no further free variables, the notion of certified
$\theta $
contains no further free variables, the notion of certified
![]() $\varphi $
-sequence is defined by a
$\varphi $
-sequence is defined by a
![]() $\Delta ^0_1$
-formula without parameters. By picking the value
$\Delta ^0_1$
-formula without parameters. By picking the value
![]() $f(n)$
with minimal code, we thus obtain a (possibly partial) computable function
$f(n)$
with minimal code, we thus obtain a (possibly partial) computable function
![]() $f:\mathbb N\to \mathcal B\times \mathbb N$
with the following property:
$f:\mathbb N\to \mathcal B\times \mathbb N$
with the following property:
-
• If the sequence
 $\langle f(0),\dots ,f(n-1)\rangle $
is defined and can be extended into a certified
$\langle f(0),\dots ,f(n-1)\rangle $
is defined and can be extended into a certified
 $\varphi $
-sequence of length
$\varphi $
-sequence of length
 $n+1$
, then
$n+1$
, then
 $\langle f(0),\dots ,f(n)\rangle $
is such a sequence.
$\langle f(0),\dots ,f(n)\rangle $
is such a sequence.
Note that the relation
![]() $f(x)=y$
is
$f(x)=y$
is
![]() $\Sigma ^0_1$
-definable without parameters. Working in
$\Sigma ^0_1$
-definable without parameters. Working in
![]() $\mathbf {PA}$
, we now assume that
$\mathbf {PA}$
, we now assume that
![]() $\mathcal K\varphi $
is false and deduce that
$\mathcal K\varphi $
is false and deduce that
![]() $\mathcal {TI}(\varepsilon _0,\psi )$
fails for a suitable formula
$\mathcal {TI}(\varepsilon _0,\psi )$
fails for a suitable formula
![]() $\psi $
. The failure of
$\psi $
. The failure of
![]() $\mathcal K\varphi $
entails that all values
$\mathcal K\varphi $
entails that all values
![]() $f(n)$
are defined: Inductively, we may assume that
$f(n)$
are defined: Inductively, we may assume that
![]() $f(m)=(t_m,c_m)$
is defined for all
$f(m)=(t_m,c_m)$
is defined for all
![]() $m<n$
; in the case of
$m<n$
; in the case of
![]() $n>0$
, the construction of f ensures that
$n>0$
, the construction of f ensures that
![]() $\langle (t_0,c_0),\dots ,(t_{n-1},c_{n-1})\rangle $
is a certified
$\langle (t_0,c_0),\dots ,(t_{n-1},c_{n-1})\rangle $
is a certified
![]() $\varphi $
-sequence. In order to deduce that
$\varphi $
-sequence. In order to deduce that
![]() $f(n)$
is defined as well, we consider the set
$f(n)$
is defined as well, we consider the set
![]() $a:=\{t_0,\dots ,t_{n-1}\}$
. As
$a:=\{t_0,\dots ,t_{n-1}\}$
. As
![]() $\mathcal K\varphi $
is false, we must have
$\mathcal K\varphi $
is false, we must have
For
![]() $s=t_m\in a$
, the construction of f ensures
$s=t_m\in a$
, the construction of f ensures
![]() $\theta (t_m,c_m)$
and thus
$\theta (t_m,c_m)$
and thus
![]() $\varphi (s)$
. Hence the second disjunct yields an element
$\varphi (s)$
. Hence the second disjunct yields an element
![]() $t_n\in \mathcal B$
with
$t_n\in \mathcal B$
with
![]() $\varphi (t_n)$
and
$\varphi (t_n)$
and
![]() $t_m\not \leq _{\mathcal B}t_n$
for all
$t_m\not \leq _{\mathcal B}t_n$
for all
![]() $m<n$
. The latter implies
$m<n$
. The latter implies
![]() $\langle t_0,\dots ,t_n\rangle \in \operatorname {Bad}^-(\mathcal B)$
. Due to
$\langle t_0,\dots ,t_n\rangle \in \operatorname {Bad}^-(\mathcal B)$
. Due to
![]() $\varphi (t_n)$
we can pick a number
$\varphi (t_n)$
we can pick a number
![]() $c_n$
with
$c_n$
with
![]() $\theta (t_n,c_n)$
. Then
$\theta (t_n,c_n)$
. Then
![]() $\langle f(0),\dots ,f(n-1),(t_n,c_n)\rangle $
is a certified
$\langle f(0),\dots ,f(n-1),(t_n,c_n)\rangle $
is a certified
![]() $\varphi $
-sequence, and
$\varphi $
-sequence, and
![]() $f(n)$
is defined as the smallest pair
$f(n)$
is defined as the smallest pair
![]() $\langle t_n,c_n\rangle $
for which this holds. We can now define a total computable function
$\langle t_n,c_n\rangle $
for which this holds. We can now define a total computable function
![]() $g:\mathbb N\rightarrow \operatorname {Bad}^-(\mathcal B)$
by setting
$g:\mathbb N\rightarrow \operatorname {Bad}^-(\mathcal B)$
by setting
According to Corollary 6.14, there is a primitive recursive reification
It follows that the total computable function
![]() $r\circ g:\mathbb N\rightarrow \varepsilon _0$
is strictly decreasing. This is impossible in the presence of
$r\circ g:\mathbb N\rightarrow \varepsilon _0$
is strictly decreasing. This is impossible in the presence of
![]() $\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
. To be more precise, we consider
$\mathcal {TI}(\varepsilon _0,\Pi ^-_1)$
. To be more precise, we consider
which is a
![]() $\Pi ^0_1$
-formula with no other free variables than
$\Pi ^0_1$
-formula with no other free variables than
![]() $\alpha $
. For
$\alpha $
. For
![]() $\alpha =r\circ g(0)+1\prec \varepsilon _0$
we clearly have
$\alpha =r\circ g(0)+1\prec \varepsilon _0$
we clearly have
![]() $\neg \psi (\alpha )$
, which refutes the conclusion of
$\neg \psi (\alpha )$
, which refutes the conclusion of
![]() $\mathcal {TI}(\varepsilon _0,\psi )$
. On the other hand, the premise of this induction statement holds: To derive
$\mathcal {TI}(\varepsilon _0,\psi )$
. On the other hand, the premise of this induction statement holds: To derive
![]() $\operatorname {Prog}_{\varepsilon _0}(\psi )$
by contraposition, we assume that
$\operatorname {Prog}_{\varepsilon _0}(\psi )$
by contraposition, we assume that
![]() $\psi (\gamma )$
fails, i.e., that we have
$\psi (\gamma )$
fails, i.e., that we have
![]() $r\circ g(n)\prec \gamma $
for some
$r\circ g(n)\prec \gamma $
for some
![]() $n\in \mathbb N$
. Since
$n\in \mathbb N$
. Since
![]() $r\circ g$
is strictly decreasing, we obtain
$r\circ g$
is strictly decreasing, we obtain
which yields
![]() $\neg \psi (\beta )$
and thus refutes
$\neg \psi (\beta )$
and thus refutes
![]() $\forall _{\beta \prec \gamma }\psi (\beta )$
.□
$\forall _{\beta \prec \gamma }\psi (\beta )$
.□
Together with Propositions 4.4, 5.1 and 7.1 we obtain the following:
Theorem 7.3. We have
i.e., all three theories prove the same theorems.
Let
![]() $\operatorname {Con}(\mathbf {PA}+\varphi )$
be a reasonable formalization of the statement that
$\operatorname {Con}(\mathbf {PA}+\varphi )$
be a reasonable formalization of the statement that
![]() $\mathbf {PA}+\varphi $
is consistent. We consider the recursively generated
$\mathbf {PA}+\varphi $
is consistent. We consider the recursively generated
![]() $\Pi ^0_1$
-sentences
$\Pi ^0_1$
-sentences
 $$ \begin{align*} \operatorname{Con}_0(\mathbf{PA})&\,:\equiv\, 0=0,\\ \operatorname{Con}_{n+1}(\mathbf{PA})&\,:\equiv\,\operatorname{Con}(\mathbf{PA}+\operatorname{Con}_n(\mathbf{PA})). \end{align*} $$
$$ \begin{align*} \operatorname{Con}_0(\mathbf{PA})&\,:\equiv\, 0=0,\\ \operatorname{Con}_{n+1}(\mathbf{PA})&\,:\equiv\,\operatorname{Con}(\mathbf{PA}+\operatorname{Con}_n(\mathbf{PA})). \end{align*} $$
Note that
![]() $\operatorname {Con}_1(\mathbf {PA})$
is equivalent to the usual consistency statement. As mentioned in the introduction, we obtain the following:
$\operatorname {Con}_1(\mathbf {PA})$
is equivalent to the usual consistency statement. As mentioned in the introduction, we obtain the following:
Corollary 7.4. We have
i.e., the two theories prove the same
![]() $\Pi ^0_1$
-sentences.
$\Pi ^0_1$
-sentences.
Proof. Let us write
![]() $\operatorname {Rfn}_{\mathbf {PA}}$
for the full local reflection principle, i.e., the collection of all formulas
$\operatorname {Rfn}_{\mathbf {PA}}$
for the full local reflection principle, i.e., the collection of all formulas
![]() $\operatorname {Pr}_{\mathbf {PA}}(\varphi )\rightarrow \varphi $
, where
$\operatorname {Pr}_{\mathbf {PA}}(\varphi )\rightarrow \varphi $
, where
![]() $\varphi $
can be any sentence in the language of first order arithmetic. According to Goryachev’s theorem (see, e.g., [Reference Lindström30, theorem IV.5]), any
$\varphi $
can be any sentence in the language of first order arithmetic. According to Goryachev’s theorem (see, e.g., [Reference Lindström30, theorem IV.5]), any
![]() $\Pi ^0_1$
-theorem of
$\Pi ^0_1$
-theorem of
![]() $\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}$
can be proved in
$\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}$
can be proved in
![]() $\mathbf {PA}+\{\operatorname {Con}_n(\mathbf {PA})\,|\,n\in \mathbb N\}$
. A fortiori, this applies to all
$\mathbf {PA}+\{\operatorname {Con}_n(\mathbf {PA})\,|\,n\in \mathbb N\}$
. A fortiori, this applies to all
![]() $\Pi ^0_1$
-theorems of
$\Pi ^0_1$
-theorems of
![]() $\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)\equiv \mathbf {PA}+\mathcal K\Sigma ^-_1$
. In the other direction we have a full inclusion: The theory
$\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)\equiv \mathbf {PA}+\mathcal K\Sigma ^-_1$
. In the other direction we have a full inclusion: The theory
![]() $\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
proves all theorems of
$\mathbf {PA}+\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
proves all theorems of
![]() $\mathbf {PA}+\{\operatorname {Con}_n(\mathbf {PA})\,|\,n\in \mathbb N\}$
, because it proves each statement
$\mathbf {PA}+\{\operatorname {Con}_n(\mathbf {PA})\,|\,n\in \mathbb N\}$
, because it proves each statement
![]() $\operatorname {Con}_n(\mathbf {PA})$
. For
$\operatorname {Con}_n(\mathbf {PA})$
. For
![]() $n=0$
this is trivial. To conclude by meta induction on n, it suffices to observe that the formula
$n=0$
this is trivial. To conclude by meta induction on n, it suffices to observe that the formula
![]() $\operatorname {Con}_n(\mathbf {PA})\rightarrow \operatorname {Con}_{n+1}(\mathbf {PA})$
is the contrapositive of
$\operatorname {Con}_n(\mathbf {PA})\rightarrow \operatorname {Con}_{n+1}(\mathbf {PA})$
is the contrapositive of
which is an instance of
![]() $\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
.□
$\operatorname {Rfn}_{\mathbf {PA}}(\Sigma ^0_2)$
.□
Note that the corollary does not extend to arbitrary formula complexity: In the theory
![]() $\mathbf {PA}+\{\operatorname {Con}_n(\mathbf {PA})\,|\,n\in \mathbb N\}$
one cannot prove all instances of
$\mathbf {PA}+\{\operatorname {Con}_n(\mathbf {PA})\,|\,n\in \mathbb N\}$
one cannot prove all instances of
![]() $\mathcal K\Sigma ^-_1$
, by Corollary 5.4.
$\mathcal K\Sigma ^-_1$
, by Corollary 5.4.
Acknowledgments
I would like to thank Lev Beklemishev for our inspiring discussions and his helpful comments on a first draft. Also, I am very grateful to the anonymous referees, whose detailed feedback has helped me to improve the paper.