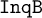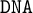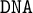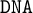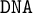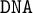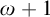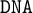1 Introduction
Inquisitive logic was introduced a decade ago as a formal framework to analyse questions. More specifically, inquisitive semantics originates from the so-called “partition semantics” of Groenendijk and Stokhof [Reference Groenendijk and Stokhof25, Reference Groenendijk and Stokhof26] and was formally developed by Ciardelli et al. in [Reference Ciardelli9, Reference Ciardelli11–Reference Ciardelli, Groenendijk and Roelofsen12, Reference Ciardelli and Roelofsen14, Reference Groenendijk, Roelofsen, Larrazabal and Zubeldia27]. In the last decade inquisitive semantics has been widely studied both from the linguistics point of view as well as from the perspective of logic. In particular, inquisitive propositional logic
![]() $\mathtt {InqB}$
has been thoroughly investigated in [Reference Ciardelli9, Reference Frittella, Greco, Palmigiano and Yang21, Reference Punčochář38–Reference Punčochář40]. The recent textbook [Reference Ciardelli, Groenendijk and Roelofsen13] gives the state of the art in the field.
$\mathtt {InqB}$
has been thoroughly investigated in [Reference Ciardelli9, Reference Frittella, Greco, Palmigiano and Yang21, Reference Punčochář38–Reference Punčochář40]. The recent textbook [Reference Ciardelli, Groenendijk and Roelofsen13] gives the state of the art in the field.
It is only recently, however, that an algebraic approach to inquisitive logic has been developed. In [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] algebraic and topological semantics for
![]() $\mathtt {InqB}$
are introduced and investigated (see also [Reference Roelofsen42] for a different algebraic approach to inquisitive logic). Algebraic semantics plays a crucial role in the study of intermediate, modal and other non-classical logics [Reference Blackburn, de Rijke and Venema6, Reference Chagrov and Zakharyaschev8, Reference Font20, Reference Galatos, Jipsen, Kowalski and Ono22]. A development of an algebraic semantics for inquisitive logic is thus an important milestone for better understanding the mathematics behind inquisitive semantics.
$\mathtt {InqB}$
are introduced and investigated (see also [Reference Roelofsen42] for a different algebraic approach to inquisitive logic). Algebraic semantics plays a crucial role in the study of intermediate, modal and other non-classical logics [Reference Blackburn, de Rijke and Venema6, Reference Chagrov and Zakharyaschev8, Reference Font20, Reference Galatos, Jipsen, Kowalski and Ono22]. A development of an algebraic semantics for inquisitive logic is thus an important milestone for better understanding the mathematics behind inquisitive semantics.
In this article we continue the study started in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] and develop a full algebraic apparatus for inquisitive logic
![]() $\mathtt {InqB}$
and related systems. Using this machinery we give, among other things, a full description of the lattice of extensions of
$\mathtt {InqB}$
and related systems. Using this machinery we give, among other things, a full description of the lattice of extensions of
![]() $\mathtt {InqB}$
. Using this algebraic semantics for
$\mathtt {InqB}$
. Using this algebraic semantics for
![]() $\mathtt {InqB}$
we also study the relation between inquisitive logic and intermediate logics.
$\mathtt {InqB}$
we also study the relation between inquisitive logic and intermediate logics.
While inquisitive logic is now widely known and recognized, the related class of
![]() $\mathtt {DNA}$
-logics has not been well investigated yet. In this article we introduce
$\mathtt {DNA}$
-logics has not been well investigated yet. In this article we introduce
![]() $\mathtt {DNA}$
-logics as negative variants of intermediate logics. A
$\mathtt {DNA}$
-logics as negative variants of intermediate logics. A
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
is thus a set of propositional formulas such that, for some intermediate logic L,
$\Lambda $
is thus a set of propositional formulas such that, for some intermediate logic L,
![]() $\varphi \in \Lambda $
if and only if
$\varphi \in \Lambda $
if and only if
![]() . The name
. The name
![]() $\mathtt {DNA}$
stands for double negation atoms, since every
$\mathtt {DNA}$
stands for double negation atoms, since every
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
proves the formula
$\Lambda $
proves the formula
![]() $\neg \neg p\rightarrow p$
for every atomic formula
$\neg \neg p\rightarrow p$
for every atomic formula
![]() $p\in \mathtt {AT}$
. The relation between
$p\in \mathtt {AT}$
. The relation between
![]() $\mathtt {InqB}$
and negative variants of intermediate logics was already pointed out in [Reference Ciardelli9]. Also [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37] establishes several properties of these systems. In this article we provide a systematic study of
$\mathtt {InqB}$
and negative variants of intermediate logics was already pointed out in [Reference Ciardelli9]. Also [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37] establishes several properties of these systems. In this article we provide a systematic study of
![]() $\mathtt {DNA}$
-logics and we investigate the corresponding classes of Heyting algebras, which we call
$\mathtt {DNA}$
-logics and we investigate the corresponding classes of Heyting algebras, which we call
![]() $\mathtt {DNA}$
-varieties.
$\mathtt {DNA}$
-varieties.
The original contributions of this article are therefore twofold. On the one hand, we develop a general algebraic semantics for
![]() $\mathtt {DNA}$
-logics and we prove some fundamental results concerning
$\mathtt {DNA}$
-logics and we prove some fundamental results concerning
![]() $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
![]() $\mathtt {DNA}$
-varieties. In particular, we show that the lattice of
$\mathtt {DNA}$
-varieties. In particular, we show that the lattice of
![]() $\mathtt {DNA}$
-logics is dually isomorphic to the lattice of
$\mathtt {DNA}$
-logics is dually isomorphic to the lattice of
![]() $\mathtt {DNA}$
-varieties. We characterise maximal and minimal intermediate logics with the same negative variant, and we prove a suitable version of Tarski’s and Birkhoff’s classic variety theorems for
$\mathtt {DNA}$
-varieties. We characterise maximal and minimal intermediate logics with the same negative variant, and we prove a suitable version of Tarski’s and Birkhoff’s classic variety theorems for
![]() $\mathtt {DNA}$
-varieties. We also introduce locally finite
$\mathtt {DNA}$
-varieties. We also introduce locally finite
![]() $\mathtt {DNA}$
-varieties and show that these varieties are axiomatised by the analogues of Jankov formulas.
$\mathtt {DNA}$
-varieties and show that these varieties are axiomatised by the analogues of Jankov formulas.
On the other hand, we apply this general algebraic setting to inquisitive logic: we study the lattice of extensions of
![]() $\mathtt {InqB}$
and show that it forms a countable descending chain with an extra bottom element dually isomorphic to the ordinal
$\mathtt {InqB}$
and show that it forms a countable descending chain with an extra bottom element dually isomorphic to the ordinal
![]() $\omega +1$
. We also give an axiomatisation of these logics via the analogues of Jankov formulas. This shows that these extensions coincide with the so-called inquisitive hierarchy considered in [Reference Ciardelli9]. It thus follows from our results that the inquisitive hierarchy comprises all the possible ways in which
$\omega +1$
. We also give an axiomatisation of these logics via the analogues of Jankov formulas. This shows that these extensions coincide with the so-called inquisitive hierarchy considered in [Reference Ciardelli9]. It thus follows from our results that the inquisitive hierarchy comprises all the possible ways in which
![]() $\mathtt {InqB}$
can be extended to other
$\mathtt {InqB}$
can be extended to other
![]() $\mathtt {DNA}$
-logics.
$\mathtt {DNA}$
-logics.
This article is structured as follows. In Section 2 we recall the preliminary notions about varieties, Heyting algebras, intermediate logics and inquisitive semantics which we will make use of in the course of this article. In Section 3 we introduce
![]() $\mathtt {DNA}$
-logics and their algebraic semantics, and we prove that the lattice of
$\mathtt {DNA}$
-logics and their algebraic semantics, and we prove that the lattice of
![]() $\mathtt {DNA}$
-logics is dually isomorphic to the lattice of
$\mathtt {DNA}$
-logics is dually isomorphic to the lattice of
![]() $\mathtt {DNA}$
-varieties. In Section 4 we employ this duality result to make the first steps in the study of
$\mathtt {DNA}$
-varieties. In Section 4 we employ this duality result to make the first steps in the study of
![]() $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
![]() $\mathtt {DNA}$
-varieties: we characterise maximal and minimal intermediate logics with the same negative variant, we prove a suitable version of Birkhoff’s theorems about varieties and we introduce Jankov formulas to axiomatise locally finite
$\mathtt {DNA}$
-varieties: we characterise maximal and minimal intermediate logics with the same negative variant, we prove a suitable version of Birkhoff’s theorems about varieties and we introduce Jankov formulas to axiomatise locally finite
![]() $\mathtt {DNA}$
-varieties. Finally, in Section 5, we continue the work done in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] and we use the methods developed in this article to show that the extensions of
$\mathtt {DNA}$
-varieties. Finally, in Section 5, we continue the work done in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] and we use the methods developed in this article to show that the extensions of
![]() $\mathtt {InqB}$
form a countable descending chain with an extra bottom element. Finally, we provide an axiomatisation of each of these logics and we show that they coincide with the so-called inquisitive hierarchy considered in [Reference Ciardelli9].
$\mathtt {InqB}$
form a countable descending chain with an extra bottom element. Finally, we provide an axiomatisation of each of these logics and we show that they coincide with the so-called inquisitive hierarchy considered in [Reference Ciardelli9].
2 Preliminaries
In this section we briefly discuss some of the basic facts that will be used throughout the article. We use [Reference Chagrov and Zakharyaschev8] as our main reference for the basic theory of intermediate logics. We also use [Reference Burris and Sankappanavar7] for universal algebra, and [Reference Esakia, Bezhanishvili and Holliday18, Reference Sikorski44] for Heyting and Boolean algebras, respectively. Finally, we refer the reader to Ciardelli’s original presentation in [Reference Ciardelli9, Reference Ciardelli, Groenendijk and Roelofsen13] for more details about inquisitive semantics and its applications in linguistics.
2.1 Universal algebra
We write
![]() $f:A\twoheadrightarrow B$
if f is a surjective homomorphism between A and B and we say that B is homomorphic image of A. We denote by
$f:A\twoheadrightarrow B$
if f is a surjective homomorphism between A and B and we say that B is homomorphic image of A. We denote by
![]() $B\preceq A$
that B is a subalgebra of A and by
$B\preceq A$
that B is a subalgebra of A and by
![]() $\prod _{i\in I}A_i$
the product of the family of algebras
$\prod _{i\in I}A_i$
the product of the family of algebras
![]() $\{A_i\}_{i\in I}$
. If I is finite, we also write
$\{A_i\}_{i\in I}$
. If I is finite, we also write
![]() $A_0\times \cdots \times A_n$
for the product
$A_0\times \cdots \times A_n$
for the product
![]() $\prod _{i\in I} A_i$
. For every
$\prod _{i\in I} A_i$
. For every
![]() $i\in I$
we also have a projection function
$i\in I$
we also have a projection function
![]() $\pi _i: \prod _{i\in I} A_i \rightarrow A_i $
such that
$\pi _i: \prod _{i\in I} A_i \rightarrow A_i $
such that
![]() $\pi _i : \alpha \mapsto \alpha (i)$
. It is easy to show that every such projection function is a surjective homomorphism. We introduce the following closure maps.
$\pi _i : \alpha \mapsto \alpha (i)$
. It is easy to show that every such projection function is a surjective homomorphism. We introduce the following closure maps.
Definition 2.1. Let
![]() $\mathcal {K}$
be a set of algebras of the same similarity-type, we then define the following:
$\mathcal {K}$
be a set of algebras of the same similarity-type, we then define the following:
 $$ \begin{align*} & A\in I(\mathcal{K}) \text{ iff } A \text{ is isomorphic to some algebra in } \mathcal{K} \\ & A\in S(\mathcal{K}) \text{ iff } A \text{ is a subalgebra of some algebra in } \mathcal{K} \\ & A\in H(\mathcal{K}) \text{ iff } A \text{ is homomorphic image of some algebra in } \mathcal{K}\\ & A\in P(\mathcal{K}) \text{ iff } A \text{ is product of a nonempty family of algebras in } \mathcal{K}. \end{align*} $$
$$ \begin{align*} & A\in I(\mathcal{K}) \text{ iff } A \text{ is isomorphic to some algebra in } \mathcal{K} \\ & A\in S(\mathcal{K}) \text{ iff } A \text{ is a subalgebra of some algebra in } \mathcal{K} \\ & A\in H(\mathcal{K}) \text{ iff } A \text{ is homomorphic image of some algebra in } \mathcal{K}\\ & A\in P(\mathcal{K}) \text{ iff } A \text{ is product of a nonempty family of algebras in } \mathcal{K}. \end{align*} $$
The following proposition provides a characterisation of how the previous maps interact with one another.
Proposition 2.2. Let
![]() $\mathcal {K}$
be an arbitrary class of algebras, we then have that
$\mathcal {K}$
be an arbitrary class of algebras, we then have that
![]() $SH(\mathcal {K})\subseteq HS(\mathcal {K})$
,
$SH(\mathcal {K})\subseteq HS(\mathcal {K})$
,
![]() $PS(\mathcal {K})\subseteq SP(\mathcal {K})$
and
$PS(\mathcal {K})\subseteq SP(\mathcal {K})$
and
![]() $PH(\mathcal {K})\subseteq HP(\mathcal {K})$
. Moreover, the operators
$PH(\mathcal {K})\subseteq HP(\mathcal {K})$
. Moreover, the operators
![]() $I,S,H,P$
are all idempotent, i.e.,
$I,S,H,P$
are all idempotent, i.e.,
![]() $I^2(\mathcal {K})=I(\mathcal {K})$
,
$I^2(\mathcal {K})=I(\mathcal {K})$
,
![]() $S^2(\mathcal {K})=S(\mathcal {K})$
,
$S^2(\mathcal {K})=S(\mathcal {K})$
,
![]() $H^2(\mathcal {K})=H(\mathcal {K})$
and
$H^2(\mathcal {K})=H(\mathcal {K})$
and
![]() $P^2(\mathcal {K})=P(\mathcal {K})$
.
$P^2(\mathcal {K})=P(\mathcal {K})$
.
A variety is defined as a class of algebras
![]() $\mathcal {V}$
of the same similarity type which is closed under homomorphic images, subalgebras and products. If
$\mathcal {V}$
of the same similarity type which is closed under homomorphic images, subalgebras and products. If
![]() $\mathcal {K}$
is an arbitrary class of algebras of the same similarity type, then we write
$\mathcal {K}$
is an arbitrary class of algebras of the same similarity type, then we write
![]() $\mathcal {V}(\mathcal {K})$
for the variety generated by
$\mathcal {V}(\mathcal {K})$
for the variety generated by
![]() $\mathcal {K}$
, i.e., for the smallest class of algebras containing
$\mathcal {K}$
, i.e., for the smallest class of algebras containing
![]() $\mathcal {K}$
which is closed under subalgebras, homomorphic images and products. An important theorem by Birkhoff establishes that varieties are exactly the classes of algebras which are definable by equations [Reference Burris and Sankappanavar7, Theorem 11.9].
$\mathcal {K}$
which is closed under subalgebras, homomorphic images and products. An important theorem by Birkhoff establishes that varieties are exactly the classes of algebras which are definable by equations [Reference Burris and Sankappanavar7, Theorem 11.9].
Finally, we recall the following important theorems, which provide an internal characterisation of algebraic varieties. The first theorem, due to Tarski, characterizes the variety generated by a set of algebras in terms of the closure maps defined above. The second theorem is an important result by Birkhoff which shows that subdirectly irreducible algebras play an important role as generators of varieties. We use
![]() $\mathcal {V}_{SI}$
to denote the collection of subdirectly irreducible algebras of a variety
$\mathcal {V}_{SI}$
to denote the collection of subdirectly irreducible algebras of a variety
![]() $\mathcal {V}$
. For a proof of these results see [Reference Burris and Sankappanavar7, Theorems 9.5 and 9.7].
$\mathcal {V}$
. For a proof of these results see [Reference Burris and Sankappanavar7, Theorems 9.5 and 9.7].
Theorem 2.3 (Tarski)
Let
![]() $\mathcal {K}$
be a class of algebras of some similarity type, we then have that
$\mathcal {K}$
be a class of algebras of some similarity type, we then have that
![]() $\mathcal {V}(\mathcal {K})= HSP (\mathcal {K})$
.
$\mathcal {V}(\mathcal {K})= HSP (\mathcal {K})$
.
Theorem 2.4 (Birkhoff)
Varieties are generated by their subdirectly irreducible members, i.e., for every variety
![]() $\mathcal {V}$
, we have
$\mathcal {V}$
, we have
![]() $\mathcal {V} = \mathcal {V}(\mathcal {V}_{SI})$
.
$\mathcal {V} = \mathcal {V}(\mathcal {V}_{SI})$
.
2.2 Heyting algebras
A Heyting algebra is a bounded lattice H such that for every
![]() $a,b\in H$
there is some element
$a,b\in H$
there is some element
![]() $a\rightarrow b\in H$
such that for all
$a\rightarrow b\in H$
such that for all
![]() $c\in H$
we have that
$c\in H$
we have that
![]() $c\leq a\rightarrow b \Leftrightarrow c\land a\leq b $
. Given an element
$c\leq a\rightarrow b \Leftrightarrow c\land a\leq b $
. Given an element
![]() $a\in H$
of a Heyting algebra, we define its pseudocomplement
$a\in H$
of a Heyting algebra, we define its pseudocomplement
![]() $\neg a$
as
$\neg a$
as
![]() $\neg a := a \rightarrow 0$
. In case for all
$\neg a := a \rightarrow 0$
. In case for all
![]() $a\in H$
it is the case that
$a\in H$
it is the case that
![]() $a \land \neg a = 0$
and
$a \land \neg a = 0$
and
![]() $a \lor \neg a = 1$
we say that H is a Boolean algebra. It is well known that a Heyting algebra H is subdirectly irreducible iff H has a second greatest element
$a \lor \neg a = 1$
we say that H is a Boolean algebra. It is well known that a Heyting algebra H is subdirectly irreducible iff H has a second greatest element
![]() $s_H$
.
$s_H$
.
A power-set algebra is a Boolean algebra
![]() $B=(\wp (X),\cup ,\cap ,\setminus, \emptyset, X)$
, where the universe is a power-set, the algebraic operations of join and meet are the set-theoretic operations of union and intersection and complementation is the set-theoretic complement. We recall that every finite Boolean algebra B is isomorphic to a power-set algebra, i.e.,
$B=(\wp (X),\cup ,\cap ,\setminus, \emptyset, X)$
, where the universe is a power-set, the algebraic operations of join and meet are the set-theoretic operations of union and intersection and complementation is the set-theoretic complement. We recall that every finite Boolean algebra B is isomorphic to a power-set algebra, i.e.,
![]() $B\cong \wp (X)$
for some finite set X, see e.g., [Reference Davey and Priestley16, Chapter 5]. Thus it follows that finite Boolean algebras are always equivalent up to isomorphism to
$B\cong \wp (X)$
for some finite set X, see e.g., [Reference Davey and Priestley16, Chapter 5]. Thus it follows that finite Boolean algebras are always equivalent up to isomorphism to
![]() $\wp (n)$
for some
$\wp (n)$
for some
![]() $n\in \mathbb {N}$
. It is easy to show that if
$n\in \mathbb {N}$
. It is easy to show that if
![]() $n\leq m$
, then
$n\leq m$
, then
![]() $\wp (n)\preceq \wp (m)$
. Then, by identifying every
$\wp (n)\preceq \wp (m)$
. Then, by identifying every
![]() $\wp (n)$
by
$\wp (n)$
by
![]() $2^n$
, it follows that finite Boolean algebras form an ordered chain of subalgebras:
$2^n$
, it follows that finite Boolean algebras form an ordered chain of subalgebras:
2.3 Intermediate logics
Intermediate logics are a well-studied class of logics with many applications in mathematics and computer science. Fix a countable set
![]() $\mathtt {AT}$
of atomic propositional formulas, we define the set of propositional formulas
$\mathtt {AT}$
of atomic propositional formulas, we define the set of propositional formulas
![]() $\mathcal {L}_P$
inductively as follows.
$\mathcal {L}_P$
inductively as follows.
Definition 2.5. The language
![]() $\mathcal {L}_P$
is defined as follows, where
$\mathcal {L}_P$
is defined as follows, where
![]() $p\in \mathtt {AT}$
:
$p\in \mathtt {AT}$
:
Negation is defined as
![]() $\neg \varphi :=\varphi \rightarrow \bot $
. If
$\neg \varphi :=\varphi \rightarrow \bot $
. If
![]() $\varphi $
is a formula, then we write
$\varphi $
is a formula, then we write
![]() $\varphi (\overline {x})$
or
$\varphi (\overline {x})$
or
![]() $\varphi (x_0,\dots ,x_n)$
to specify that the atomic formulas in
$\varphi (x_0,\dots ,x_n)$
to specify that the atomic formulas in
![]() $\varphi $
are among those of
$\varphi $
are among those of
![]() $\overline {x}$
or respectively of
$\overline {x}$
or respectively of
![]() $x_0,\dots ,x_n$
. A substitution is a function
$x_0,\dots ,x_n$
. A substitution is a function
![]() $\eta : \mathtt {AT} \rightarrow \mathcal {L}_P$
which naturally lifts by induction to formulas by setting, for every connective
$\eta : \mathtt {AT} \rightarrow \mathcal {L}_P$
which naturally lifts by induction to formulas by setting, for every connective
![]() $\odot $
, the map
$\odot $
, the map
![]() $(\psi \odot \chi ) \mapsto \eta (\psi )\odot \eta (\chi ) $
. If
$(\psi \odot \chi ) \mapsto \eta (\psi )\odot \eta (\chi ) $
. If
![]() $\varphi $
is a formula and q occurs in
$\varphi $
is a formula and q occurs in
![]() $\varphi $
, we write
$\varphi $
, we write
![]() for the formula obtained by the substitution
for the formula obtained by the substitution
![]() $\eta : q\mapsto p $
. Similarly, if
$\eta : q\mapsto p $
. Similarly, if
![]() $\overline {q}=q_0,\dots ,q_n$
are variables in
$\overline {q}=q_0,\dots ,q_n$
are variables in
![]() $\varphi $
, then we write
$\varphi $
, then we write
![]() for the formula obtained by the substitution
for the formula obtained by the substitution
![]() $\eta : q_i \mapsto p_i $
for all
$\eta : q_i \mapsto p_i $
for all
![]() $i\leq n$
.
$i\leq n$
.
We denote by
![]() $\mathtt {IPC}$
the intuitionistic propositional calculus and by
$\mathtt {IPC}$
the intuitionistic propositional calculus and by
![]() $\mathtt {CPC}$
the classical propositional calculus. Now, given a propositional language
$\mathtt {CPC}$
the classical propositional calculus. Now, given a propositional language
![]() $\mathcal {L}_P$
, we say that a set of formulas
$\mathcal {L}_P$
, we say that a set of formulas
![]() $L\subseteq \mathcal {L}_P$
is a superintuitionistic logic if
$L\subseteq \mathcal {L}_P$
is a superintuitionistic logic if
![]() $\mathtt {IPC}\subseteq L$
and in addition L is closed under modus ponens and uniform substitution. An intermediate logic is a superintuitionistic logic L which is also consistent, namely
$\mathtt {IPC}\subseteq L$
and in addition L is closed under modus ponens and uniform substitution. An intermediate logic is a superintuitionistic logic L which is also consistent, namely
![]() $\bot \notin L$
. We thus identify every logical system with the sets of its theorems.
$\bot \notin L$
. We thus identify every logical system with the sets of its theorems.
It can be proven that
![]() $\mathtt {CPC}$
is the maximal intermediate logic and that intermediate logics are all the logics L such that
$\mathtt {CPC}$
is the maximal intermediate logic and that intermediate logics are all the logics L such that
![]() $\mathtt {IPC} \subseteq L \subseteq \mathtt {CPC}$
. We denote by
$\mathtt {IPC} \subseteq L \subseteq \mathtt {CPC}$
. We denote by
![]() $L + \varphi $
the closure under substitution and modus ponens of the set of formulas
$L + \varphi $
the closure under substitution and modus ponens of the set of formulas
![]() $L \cup \{\varphi \}$
and by
$L \cup \{\varphi \}$
and by
![]() $L + \Gamma $
the closure under substitution and modus ponens of the set of formulas
$L + \Gamma $
the closure under substitution and modus ponens of the set of formulas
![]() $L \cup \Gamma $
. If L is an intermediate logic and
$L \cup \Gamma $
. If L is an intermediate logic and
![]() $\varphi \in L$
then we write
$\varphi \in L$
then we write
![]() $\vdash _L \varphi $
or
$\vdash _L \varphi $
or
![]() $L\vdash \varphi $
. Moreover, if
$L\vdash \varphi $
. Moreover, if
![]() $\varphi $
can be obtained by closing the set
$\varphi $
can be obtained by closing the set
![]() $L \cup \Gamma $
under modus ponens, then we write
$L \cup \Gamma $
under modus ponens, then we write
![]() $\Gamma \vdash _L \varphi $
and we say that
$\Gamma \vdash _L \varphi $
and we say that
![]() $\varphi $
is derivable from
$\varphi $
is derivable from
![]() $\Gamma $
in L. It is a well-know fact [Reference Chagrov and Zakharyaschev8, Chapter 4.1] that intermediate logics form a bounded lattice
$\Gamma $
in L. It is a well-know fact [Reference Chagrov and Zakharyaschev8, Chapter 4.1] that intermediate logics form a bounded lattice
![]() $ \Lambda (\mathtt {IPC}) $
with
$ \Lambda (\mathtt {IPC}) $
with
![]() $\mathtt {IPC} = \bot $
and
$\mathtt {IPC} = \bot $
and
![]() $\mathtt {CPC} = \top $
and where meet and join are defined as follows
$\mathtt {CPC} = \top $
and where meet and join are defined as follows
 $$ \begin{align*} L_0 \land L_1 \space &=\space L_0 \cap L_1, \\ L_0 \lor L_1 \space &=\space L_0 + L_1. \end{align*} $$
$$ \begin{align*} L_0 \land L_1 \space &=\space L_0 \cap L_1, \\ L_0 \lor L_1 \space &=\space L_0 + L_1. \end{align*} $$
We list here some intermediate logics that will be useful for us in this article:
 $$ \begin{align*} \begin{array}{l @{} l} \mathtt{KC} &\hspace{2pt} = \space \mathtt{IPC} \space + \space \neg p \lor \neg\neg p, \\ \mathtt{KP} &\hspace{2pt} = \space \mathtt{IPC} \space + \space (\neg p \rightarrow q\lor r) \rightarrow (\neg p \rightarrow q) \lor (\neg p \rightarrow r), \\ \mathtt{ND} &\hspace{2pt} =\space \mathtt{IPC} \space + \space \{ (\neg p \rightarrow \bigvee_{i\leq k} \neg q_i )\rightarrow \bigvee_{i\leq k}(\neg p \rightarrow \neg q_i) : k\geq 2 \}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l @{} l} \mathtt{KC} &\hspace{2pt} = \space \mathtt{IPC} \space + \space \neg p \lor \neg\neg p, \\ \mathtt{KP} &\hspace{2pt} = \space \mathtt{IPC} \space + \space (\neg p \rightarrow q\lor r) \rightarrow (\neg p \rightarrow q) \lor (\neg p \rightarrow r), \\ \mathtt{ND} &\hspace{2pt} =\space \mathtt{IPC} \space + \space \{ (\neg p \rightarrow \bigvee_{i\leq k} \neg q_i )\rightarrow \bigvee_{i\leq k}(\neg p \rightarrow \neg q_i) : k\geq 2 \}. \end{array} \end{align*} $$
The logic ND was introduced by Maksimova in [Reference Maksimova34]. The logic
![]() $\mathtt {KP}$
was introduced by Kreisel and Putnam in [Reference Kreisel and Putnam33]. The logic KC is also know as the logic of the weak excluded middle and was introduced by Jankov in [Reference Jankov30]. While the previous logics are defined in axiomatic terms, one can also define logics by specifying the class of structures they correspond to. The logic
$\mathtt {KP}$
was introduced by Kreisel and Putnam in [Reference Kreisel and Putnam33]. The logic KC is also know as the logic of the weak excluded middle and was introduced by Jankov in [Reference Jankov30]. While the previous logics are defined in axiomatic terms, one can also define logics by specifying the class of structures they correspond to. The logic
![]() $\mathtt {ML}$
is the logic of so-called Medvedev frames and it was introduced by Medvedev in [Reference Medvedev36]. A relational structure
$\mathtt {ML}$
is the logic of so-called Medvedev frames and it was introduced by Medvedev in [Reference Medvedev36]. A relational structure
![]() $\mathcal {F}$
is a Medvedev frame if
$\mathcal {F}$
is a Medvedev frame if
![]() $\mathcal {F}\cong (\wp ^+(W),\supseteq )$
, where W is a finite set and
$\mathcal {F}\cong (\wp ^+(W),\supseteq )$
, where W is a finite set and
![]() $\wp ^+(W)=\{X\subseteq W : X\neq \emptyset \}$
. A Medvedev model is then defined as a relational model over a Medvedev frame. Let
$\wp ^+(W)=\{X\subseteq W : X\neq \emptyset \}$
. A Medvedev model is then defined as a relational model over a Medvedev frame. Let
![]() $\mathcal {C}$
be the class of all Medvedev frames, then we have that
$\mathcal {C}$
be the class of all Medvedev frames, then we have that
![]() $ \mathtt {ML}= \{\varphi \in \mathcal {L}_P : \mathcal {C} \Vdash \varphi \}$
, i.e.,
$ \mathtt {ML}= \{\varphi \in \mathcal {L}_P : \mathcal {C} \Vdash \varphi \}$
, i.e.,
![]() $\mathtt {ML}$
is the set of formulas valid in all Medvedev frames (here we assume the reader’s familiarity with the standard Kripke semantics of intuitionistic logic).
$\mathtt {ML}$
is the set of formulas valid in all Medvedev frames (here we assume the reader’s familiarity with the standard Kripke semantics of intuitionistic logic).
We will now briefly recall the algebraic semantics of intermediate logics.
Definition 2.6 (Algebraic Model)
An algebraic model is a pair
![]() $M=(H, V)$
where H is a Heyting algebra and
$M=(H, V)$
where H is a Heyting algebra and
![]() $V:\mathtt {AT} \rightarrow H $
is a valuation of propositional atoms over the elements of H.
$V:\mathtt {AT} \rightarrow H $
is a valuation of propositional atoms over the elements of H.
Given an algebraic model
![]() $M=(H,V)$
, we define by induction the interpretation of any formula
$M=(H,V)$
, we define by induction the interpretation of any formula
![]() $\varphi \in \mathcal {L}_P$
.
$\varphi \in \mathcal {L}_P$
.
Definition 2.7 (Interpretation of Arbitrary Formulas)
Given an algebraic model M and a formula
![]() $\varphi \in \mathcal {L}$
, its interpretation
$\varphi \in \mathcal {L}$
, its interpretation
is defined as follows:

When the valuation V is clear from the context, we simply write
![]() for the interpretation of
for the interpretation of
![]() $\varphi $
in H under V. We say that a formula
$\varphi $
in H under V. We say that a formula
![]() $\varphi $
is true under
$\varphi $
is true under
![]() $ V $
in H or true in the model
$ V $
in H or true in the model
![]() $ M=(H, V) $
and write
$ M=(H, V) $
and write
![]() $M\vDash \varphi $
if
$M\vDash \varphi $
if
![]() . We say that
. We say that
![]() $\varphi $
is valid in H and write
$\varphi $
is valid in H and write
![]() $H\vDash \varphi $
if
$H\vDash \varphi $
if
![]() $\varphi $
is true in every algebraic model
$\varphi $
is true in every algebraic model
![]() $M=(H,V)$
over H. Given a class of Heyting algebras
$M=(H,V)$
over H. Given a class of Heyting algebras
![]() $\mathcal {C}$
, we say that
$\mathcal {C}$
, we say that
![]() $\varphi $
is valid in
$\varphi $
is valid in
![]() $ \mathcal {C} $
and write
$ \mathcal {C} $
and write
![]() $\mathcal {C}\vDash \varphi $
if
$\mathcal {C}\vDash \varphi $
if
![]() $\varphi $
is valid in every Heyting algebra
$\varphi $
is valid in every Heyting algebra
![]() $H\in \mathcal {C}$
. Finally, we say that
$H\in \mathcal {C}$
. Finally, we say that
![]() $\varphi $
is a validity if
$\varphi $
is a validity if
![]() $\varphi $
is valid in any Heyting algebra H.
$\varphi $
is valid in any Heyting algebra H.
We denote by HA the collection of all Heyting algebras. Let
![]() $ \Lambda (\mathrm{HA}) $
be the lattice of varieties of Heyting algebras and
$ \Lambda (\mathrm{HA}) $
be the lattice of varieties of Heyting algebras and
![]() $ \Lambda (\mathtt {IPC}) $
the lattice of intermediate logics, we then define the two maps
$ \Lambda (\mathtt {IPC}) $
the lattice of intermediate logics, we then define the two maps
![]() $Var: \Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathrm{HA}) $
and
$Var: \Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathrm{HA}) $
and
![]() $Log: \Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathtt {IPC}) $
as follows:
$Log: \Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathtt {IPC}) $
as follows:
 $$ \begin{align*} &Var: L\mapsto \{H\in \mathrm{HA} : H\vDash L \};\\ &Log: \mathcal{V} \mapsto \{\varphi\in \mathcal{L}_P : \mathcal{V}\vDash \varphi \}. \end{align*} $$
$$ \begin{align*} &Var: L\mapsto \{H\in \mathrm{HA} : H\vDash L \};\\ &Log: \mathcal{V} \mapsto \{\varphi\in \mathcal{L}_P : \mathcal{V}\vDash \varphi \}. \end{align*} $$
That the two former functions are well defined follows from
![]() $Var(L)$
being a variety of Heyting algebras and
$Var(L)$
being a variety of Heyting algebras and
![]() $Log(\mathcal {V})$
being an intermediate logic. Also, one can prove that both these maps are order-reversing homomorphisms. We say that a variety of Heyting algebras
$Log(\mathcal {V})$
being an intermediate logic. Also, one can prove that both these maps are order-reversing homomorphisms. We say that a variety of Heyting algebras
![]() $\mathcal {V}$
is defined by a set of formulas
$\mathcal {V}$
is defined by a set of formulas
![]() $\Gamma $
if
$\Gamma $
if
![]() $\mathcal {V}=Var(\Gamma )$
and we say
$\mathcal {V}=Var(\Gamma )$
and we say
![]() $\mathcal {V}$
is definable if there exists one such
$\mathcal {V}$
is definable if there exists one such
![]() $\Gamma $
. We say that an intermediate logic L is algebraically complete with respect to a class of Heyting algebras
$\Gamma $
. We say that an intermediate logic L is algebraically complete with respect to a class of Heyting algebras
![]() $\mathcal {C}$
if
$\mathcal {C}$
if
![]() $L=Log(\mathcal {C})$
.
$L=Log(\mathcal {C})$
.
Theorem 2.8 (Definability Theorem)
Every variety of Heyting algebras
![]() $\mathcal {V}$
is defined by its validities, i.e., for every Heyting algebra H,
$\mathcal {V}$
is defined by its validities, i.e., for every Heyting algebra H,
Theorem 2.9 (Algebraic Completeness)
Every intermediate logic L is complete with respect to its corresponding variety of Heyting algebras, i.e., for every
![]() $\varphi \in \mathcal {L}_P$
,
$\varphi \in \mathcal {L}_P$
,
We refer the reader to [Reference Chagrov and Zakharyaschev8, Section 7] for a full proof of the aforementioned two results and the related constructions. Here let us only remark that the first of these two results is an immediate application of the fact that varieties and equational classes coincide. The second result relies essentially on the free-algebra construction, namely on the Lindenbaum–Tarski algebra of intermediate logics. These results together give us the following theorem.
Theorem 2.10 (Dual Isomorphism)
The lattice of intermediate logics is dually isomorphic to the lattice of varieties of Heyting algebras, i.e.,
![]() $\Lambda (\mathtt {IPC}) \cong ^{op}\Lambda (\mathrm{HA}) $
.
$\Lambda (\mathtt {IPC}) \cong ^{op}\Lambda (\mathrm{HA}) $
.
Here, the isomorphisms between
![]() $\Lambda (\mathtt {IPC}) $
and
$\Lambda (\mathtt {IPC}) $
and
![]() $\Lambda (\mathrm{HA}) $
are the two maps
$\Lambda (\mathrm{HA}) $
are the two maps
![]() $Log$
and
$Log$
and
![]() $Var$
. We sometimes refer to the previous theorem as a duality result concerning
$Var$
. We sometimes refer to the previous theorem as a duality result concerning
![]() $\Lambda (\mathtt {IPC}) $
and
$\Lambda (\mathtt {IPC}) $
and
![]() $\Lambda (\mathrm{HA}) $
. Notice that we are implicitly excluding from the lattice
$\Lambda (\mathrm{HA}) $
. Notice that we are implicitly excluding from the lattice
![]() $ \Lambda (\mathrm{HA}) $
the trivial variety generated by a singleton set, for it dually corresponds to the inconsistent logic containing all the formulas of
$ \Lambda (\mathrm{HA}) $
the trivial variety generated by a singleton set, for it dually corresponds to the inconsistent logic containing all the formulas of
![]() $\mathcal {L}_P$
.
$\mathcal {L}_P$
.
2.4 Inquisitive semantics
Inquisitive logic is a formalism extending the repertoire of (classical) propositional logic with questions, in order to study their logical relations. The term question in this context refers to the expressions whose semantics is not completely determined by their truth-conditions (i.e., which evaluations make it true), as it is the case for questions in natural language. And in fact the idea to define the semantics for this logic is to shift from a semantics based on truth-conditions to a semantics based on information (e.g., what pieces of information allow to resolve the question or entail the formula).
In this section we recall the basic definitions of inquisitive logic, which follow the intuition presented above. For an extended exposition on the logic and the idea underlying it we refer to [Reference Ciardelli11, Reference Ciardelli, Groenendijk and Roelofsen13].
Though sometimes inquisitive logic is introduced in a signature containing special question-forming operators—most notably the inquisitive disjunction
![]() , see e.g., [Reference Ciardelli11]—here we follow [Reference Ciardelli9] and present
, see e.g., [Reference Ciardelli11]—here we follow [Reference Ciardelli9] and present
![]() $\mathtt {InqB}$
in the same language
$\mathtt {InqB}$
in the same language
![]() $\mathcal {L}_P$
of intermediate logics. The intended interpretation of the logical operators is the same as for propositional logic (e.g.,
$\mathcal {L}_P$
of intermediate logics. The intended interpretation of the logical operators is the same as for propositional logic (e.g.,
![]() $p \land q$
stands for “both p and q hold”), with one exception: the disjunction operator
$p \land q$
stands for “both p and q hold”), with one exception: the disjunction operator
![]() $\vee $
is used to introduce alternative questions. For example, the formula
$\vee $
is used to introduce alternative questions. For example, the formula
![]() $p \vee \neg p$
is intuitively interpreted as the question “whether p holds,” requesting information on which of the two alternatives holds.
$p \vee \neg p$
is intuitively interpreted as the question “whether p holds,” requesting information on which of the two alternatives holds.
As mentioned above, the semantics of
![]() $\mathtt {InqB}$
is defined in terms of information to properly characterize the logical relations between questions. The usual (classical) valuations (i.e., binary functions
$\mathtt {InqB}$
is defined in terms of information to properly characterize the logical relations between questions. The usual (classical) valuations (i.e., binary functions
![]() $w:\mathtt {AT}\rightarrow \{0,1 \}$
) are interpreted as complete descriptions of the current state of affairs. We refer to the set
$w:\mathtt {AT}\rightarrow \{0,1 \}$
) are interpreted as complete descriptions of the current state of affairs. We refer to the set
![]() $2^{\mathtt {AT}}$
of all classical valuations over
$2^{\mathtt {AT}}$
of all classical valuations over
![]() $\mathtt {AT}$
as the evaluation space over
$\mathtt {AT}$
as the evaluation space over
![]() $\mathtt {AT}$
. To represent pieces of information, inquisitive logic uses information states (or simply states), that is, subsets of the evaluation space. So for example, the information that “the atomic formula p is true” is represented by the set of all and only the evaluations satisfying p:
$\mathtt {AT}$
. To represent pieces of information, inquisitive logic uses information states (or simply states), that is, subsets of the evaluation space. So for example, the information that “the atomic formula p is true” is represented by the set of all and only the evaluations satisfying p:
![]() $\left \{ w \in 2^{\mathtt {AT}} \middle | w(p) = 1 \right \}$
. This allows us to define the notion of support at a state, as follows.
$\left \{ w \in 2^{\mathtt {AT}} \middle | w(p) = 1 \right \}$
. This allows us to define the notion of support at a state, as follows.
Definition 2.11 (Support at a State)
Let
![]() $\varphi $
be a formula of
$\varphi $
be a formula of
![]() $\mathcal {L}_P$
and
$\mathcal {L}_P$
and
![]() $s\in \wp (2^{\mathtt {AT}})$
a state. We say that s supports
$s\in \wp (2^{\mathtt {AT}})$
a state. We say that s supports
![]() $\varphi $
and we define
$\varphi $
and we define
![]() $s\vDash \varphi $
inductively as follows:
$s\vDash \varphi $
inductively as follows:
 $$ \begin{align*} \begin{array}{l @{\hspace{1em}} c @{\hspace{1em}} l} s\vDash p &\Longleftrightarrow & \forall w\in s \ ( w(p)=1) \\ s\vDash \top && \text{always} \\ s\vDash \bot &\Longleftrightarrow & s=\emptyset\\ s\vDash \psi \land \chi &\Longleftrightarrow & s\vDash \psi \text{ and } s\vDash \chi\\ s\vDash \psi \lor \chi &\Longleftrightarrow & s\vDash \psi \text{ or } s\vDash \chi \\ s\vDash \psi \rightarrow \chi &\Longleftrightarrow & \forall t \ ( \text{if }t\subseteq s \text{ and } t\vDash\psi \text{ then } t\vDash \chi ). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l @{\hspace{1em}} c @{\hspace{1em}} l} s\vDash p &\Longleftrightarrow & \forall w\in s \ ( w(p)=1) \\ s\vDash \top && \text{always} \\ s\vDash \bot &\Longleftrightarrow & s=\emptyset\\ s\vDash \psi \land \chi &\Longleftrightarrow & s\vDash \psi \text{ and } s\vDash \chi\\ s\vDash \psi \lor \chi &\Longleftrightarrow & s\vDash \psi \text{ or } s\vDash \chi \\ s\vDash \psi \rightarrow \chi &\Longleftrightarrow & \forall t \ ( \text{if }t\subseteq s \text{ and } t\vDash\psi \text{ then } t\vDash \chi ). \end{array} \end{align*} $$
For
![]() $p\in \mathtt {AT} $
and a state s, we introduce the notation
$p\in \mathtt {AT} $
and a state s, we introduce the notation
![]() , that is,
, that is,
![]() is the set of classical valuations in s that make p true. Since
is the set of classical valuations in s that make p true. Since
![]() $\neg \varphi = \varphi \rightarrow \bot $
, the semantic clause of negation is then the following:
$\neg \varphi = \varphi \rightarrow \bot $
, the semantic clause of negation is then the following:
The valid formulas of inquisitive logic (which with a slight abuse of notation we denote by
![]() $\mathtt {InqB}$
) are the formulas
$\mathtt {InqB}$
) are the formulas
![]() $\varphi \in \mathcal {L}_P$
which are supported in every evaluation state:
$\varphi \in \mathcal {L}_P$
which are supported in every evaluation state:
We present a simple example to show that the support semantics works as intended: let us determine which states support the formula
![]() $p \vee \neg p$
.
$p \vee \neg p$
.
 $$ \begin{align*} \begin{array}{ll} s \vDash p \vee \neg p &\iff\; s \vDash p \text{ or } s \vDash \neg p \\ &\iff\; \forall w\in s\; (w(p) = 1) \text{ or } \forall t\subseteq s\; ( t \nvDash p \text{ or } t = \emptyset ) \\ &\iff\; \forall w\in s\; (w(p) = 1) \text{ or } \forall w\in s\; (w(p) = 0). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} s \vDash p \vee \neg p &\iff\; s \vDash p \text{ or } s \vDash \neg p \\ &\iff\; \forall w\in s\; (w(p) = 1) \text{ or } \forall t\subseteq s\; ( t \nvDash p \text{ or } t = \emptyset ) \\ &\iff\; \forall w\in s\; (w(p) = 1) \text{ or } \forall w\in s\; (w(p) = 0). \end{array} \end{align*} $$
That is, the formula
![]() $p \vee \neg p$
is supported by s if either all the valuations in s satisfy p or all the valuations in s do not satisfy p. This is in line with the intended interpretation of these objects: the question “whether p holds” (represented by
$p \vee \neg p$
is supported by s if either all the valuations in s satisfy p or all the valuations in s do not satisfy p. This is in line with the intended interpretation of these objects: the question “whether p holds” (represented by
![]() $p \vee \neg p$
) is resolved by the pieces of information (represented by the states s) from which we can either infer that p is true (
$p \vee \neg p$
) is resolved by the pieces of information (represented by the states s) from which we can either infer that p is true (
![]() $w(p) = 1$
for every
$w(p) = 1$
for every
![]() $w\in s$
) or that p is false (
$w\in s$
) or that p is false (
![]() $w(p) = 0$
for every
$w(p) = 0$
for every
![]() $w\in s$
).
$w\in s$
).
3
 $\mathtt {DNA}$
-logics and their algebraic semantics
$\mathtt {DNA}$
-logics and their algebraic semantics
In this section we introduce the class of
![]() $\mathtt {DNA}$
-logics and we show that these logics are complete with respect to
$\mathtt {DNA}$
-logics and we show that these logics are complete with respect to
![]() $\mathtt {DNA}$
-varieties, a suitably defined class of Heyting algebras.
$\mathtt {DNA}$
-varieties, a suitably defined class of Heyting algebras.
3.1
 $\mathtt {DNA}$
-logics
$\mathtt {DNA}$
-logics
We proceed by introducing the negative variant of an intermediate logic. Negative variants were first introduced by Miglioli et al. in [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37] and later employed by Ciardelli in [Reference Ciardelli9]. The account of [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37] is slightly different than the one adopted in [Reference Ciardelli9] and in the current paper, since the focus of [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37] is mainly the study of Medvedev’s logic and its properties. The main result of [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37] is, in fact, a new proof of the maximality of Medvedev’s logic among the intermediate logics with the disjunction property.
If
![]() $\varphi \in \mathcal {L}_P$
is an arbitrary formula, we often say that the formula
$\varphi \in \mathcal {L}_P$
is an arbitrary formula, we often say that the formula
![]() obtained by replacing all the atomic letters in
obtained by replacing all the atomic letters in
![]() $\varphi $
with their negation is its negative variant.
$\varphi $
with their negation is its negative variant.
Definition 3.1 (Negative Variant)
For every intermediate logic L, its negative variant
![]() $L^\neg $
is defined as follows:
$L^\neg $
is defined as follows:

A
![]() $\mathtt {DNA}$
-logic is then defined as the negative variant of some intermediate logic L. The name
$\mathtt {DNA}$
-logic is then defined as the negative variant of some intermediate logic L. The name
![]() $\mathtt {DNA}$
stands for double negation atoms, which refers to the fact that, as we will see,
$\mathtt {DNA}$
stands for double negation atoms, which refers to the fact that, as we will see,
![]() $\mathtt {DNA}$
-logics prove
$\mathtt {DNA}$
-logics prove
![]() $\neg \neg p \rightarrow p$
for all atomic formulas
$\neg \neg p \rightarrow p$
for all atomic formulas
![]() $p\in \mathtt {AT}$
. We will use the notation
$p\in \mathtt {AT}$
. We will use the notation
![]() $L^\neg $
to refer to the negative variant of an intermediate logic L. If not specified otherwise, we reserve uppercase greek letters
$L^\neg $
to refer to the negative variant of an intermediate logic L. If not specified otherwise, we reserve uppercase greek letters
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
to denote arbitrary sets of formulas and
$\Delta $
to denote arbitrary sets of formulas and
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Pi $
to denote
$\Pi $
to denote
![]() $\mathtt {DNA}$
-logics. As for an example of this kind of logics, Ciardelli showed in [Reference Ciardelli9, Theorem 3.4.9] that inquisitive logic is indeed a
$\mathtt {DNA}$
-logics. As for an example of this kind of logics, Ciardelli showed in [Reference Ciardelli9, Theorem 3.4.9] that inquisitive logic is indeed a
![]() $\mathtt {DNA}$
-logic: he proved that
$\mathtt {DNA}$
-logic: he proved that
![]() $\mathtt {InqB}$
is the negative variant of all and only the intermediate logics extending Maksimova’s logic
$\mathtt {InqB}$
is the negative variant of all and only the intermediate logics extending Maksimova’s logic
![]() $\texttt {ND}$
and contained in Medvedev’s logic
$\texttt {ND}$
and contained in Medvedev’s logic
![]() $\texttt {ML}$
. A well-known example of intermediate logic in this interval is the Kreisel–Putnam logic
$\texttt {ML}$
. A well-known example of intermediate logic in this interval is the Kreisel–Putnam logic
![]() $\texttt {KP}$
. We refer to [Reference Ciardelli9, Section 3] for an overview of these logics and for further discussion on these results.
$\texttt {KP}$
. We refer to [Reference Ciardelli9, Section 3] for an overview of these logics and for further discussion on these results.
Remark 3.2. Negative variants appear under a different guise in [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37]. Miglioli et al. introduce the class of nonstandard intermediate logics (nsils) as families of formulas extending
![]() $\mathtt {IPC}$
, closed under modus ponens and closed under negative substitutions (i.e., substitutions mapping atoms to negated formulas). They then define and study different operators on nsils, among which the extension operator E mapping a nsil L to the closure of the set
$\mathtt {IPC}$
, closed under modus ponens and closed under negative substitutions (i.e., substitutions mapping atoms to negated formulas). They then define and study different operators on nsils, among which the extension operator E mapping a nsil L to the closure of the set
![]() $L \cup \{ \neg \neg p \to p \;|\; p\in \mathtt {AT} \}$
under modus ponens. It is easy to prove that negative variants as defined in the current paper are exactly the nsils that are fixpoints of the operator E.
$L \cup \{ \neg \neg p \to p \;|\; p\in \mathtt {AT} \}$
under modus ponens. It is easy to prove that negative variants as defined in the current paper are exactly the nsils that are fixpoints of the operator E.
The following proposition provides us with an axiomatisation for every
![]() $\mathtt {DNA}$
-logic.
$\mathtt {DNA}$
-logic.
Proposition 3.3. Let
![]() $\Lambda $
be a
$\Lambda $
be a
![]() $\mathtt {DNA}$
-logic and L an intermediate logic with
$\mathtt {DNA}$
-logic and L an intermediate logic with
![]() $\Lambda = L^\neg $
. Then
$\Lambda = L^\neg $
. Then
![]() $\Lambda $
is the least set of formulas such that:
$\Lambda $
is the least set of formulas such that:
-
1.
 $L \subseteq \Lambda $
.
$L \subseteq \Lambda $
. -
2. For all atomic propositional formulas
 $p\in \mathtt {AT}$
we have that
$p\in \mathtt {AT}$
we have that
 $\neg \neg p \rightarrow p\in \Lambda $
.
$\neg \neg p \rightarrow p\in \Lambda $
. -
3.
 $\Lambda $
is closed under the modus ponens rule: if
$\Lambda $
is closed under the modus ponens rule: if
 $\varphi \in \Lambda $
and
$\varphi \in \Lambda $
and
 $\varphi \to \psi \in \Lambda $
, then
$\varphi \to \psi \in \Lambda $
, then
 $\psi \in \Lambda $
.
$\psi \in \Lambda $
.
Proof. It is trivial to show that
![]() $\Lambda $
satisfies the three conditions; what remains to prove is that
$\Lambda $
satisfies the three conditions; what remains to prove is that
![]() $\Lambda $
is the least such set. So suppose X also validates the three conditions above. What we need to show is that
$\Lambda $
is the least such set. So suppose X also validates the three conditions above. What we need to show is that
![]() $\Lambda \subseteq X$
. To this end, consider a formula
$\Lambda \subseteq X$
. To this end, consider a formula
![]() $\varphi \in \Lambda =L^\neg $
. Then by the definition of negative variant
$\varphi \in \Lambda =L^\neg $
. Then by the definition of negative variant
![]() . Therefore, by uniform substitution,
. Therefore, by uniform substitution,
![]() , and since
, and since
![]() $L\subseteq X$
we also have
$L\subseteq X$
we also have
![]() . Now, since for every
. Now, since for every
![]() $p\in \mathtt {AT}$
we have
$p\in \mathtt {AT}$
we have
![]() $\neg \neg p\rightarrow p\in X$
, and since
$\neg \neg p\rightarrow p\in X$
, and since
![]() $(\neg \neg p\rightarrow p) \to ( p \leftrightarrow \neg \neg p)$
is a theorem of intuitionistic logic, by closure under modus ponens X contains
$(\neg \neg p\rightarrow p) \to ( p \leftrightarrow \neg \neg p)$
is a theorem of intuitionistic logic, by closure under modus ponens X contains
![]() $p \leftrightarrow \neg \neg p$
for every
$p \leftrightarrow \neg \neg p$
for every
![]() $p \in \mathtt {AT}$
. By a straightforward induction argument on the complexity of
$p \in \mathtt {AT}$
. By a straightforward induction argument on the complexity of
![]() $\varphi $
we deduce that
$\varphi $
we deduce that
![]() . Given that X is closed under modus ponens we obtain that
. Given that X is closed under modus ponens we obtain that
![]() $\varphi \in X$
.
$\varphi \in X$
.
As an immediate consequence, we obtain an Hilbert-style axiomatization for
![]() $\mathtt {InqB}$
, based on the fact that
$\mathtt {InqB}$
, based on the fact that
![]() $\mathtt {InqB} = \texttt {KP}^{\neg }$
. This system was originally presented and proved to be sound and complete for
$\mathtt {InqB} = \texttt {KP}^{\neg }$
. This system was originally presented and proved to be sound and complete for
![]() $\mathtt {InqB}$
in [Reference Ciardelli9] (see [Reference Ciardelli9, Definition 3.2.13] and [Reference Ciardelli9, Theorem 3.4.9]). The current formulation was presented in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5].
$\mathtt {InqB}$
in [Reference Ciardelli9] (see [Reference Ciardelli9, Definition 3.2.13] and [Reference Ciardelli9, Theorem 3.4.9]). The current formulation was presented in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5].
 $$ \begin{align*} \mathbf{Axioms } & \hspace{10pt} \mbox{All tautologies of}\ \mathtt{IPC} \\ & \hspace{10pt} (\neg \varphi \rightarrow \psi\lor \chi) \rightarrow (\neg \varphi \rightarrow \psi) \lor (\neg \varphi \rightarrow \chi) \space \text{ for all } \varphi,\psi,\chi\in\mathcal{L}_P \\ &\hspace{10pt} \neg \neg p \rightarrow p \text{ for all } p\in\mathtt{AT} \\ \mathbf{Rule } & \hspace{10pt} \varphi, \varphi\rightarrow \psi \Rightarrow \psi. \end{align*} $$
$$ \begin{align*} \mathbf{Axioms } & \hspace{10pt} \mbox{All tautologies of}\ \mathtt{IPC} \\ & \hspace{10pt} (\neg \varphi \rightarrow \psi\lor \chi) \rightarrow (\neg \varphi \rightarrow \psi) \lor (\neg \varphi \rightarrow \chi) \space \text{ for all } \varphi,\psi,\chi\in\mathcal{L}_P \\ &\hspace{10pt} \neg \neg p \rightarrow p \text{ for all } p\in\mathtt{AT} \\ \mathbf{Rule } & \hspace{10pt} \varphi, \varphi\rightarrow \psi \Rightarrow \psi. \end{align*} $$
As we will see later,
![]() $\mathtt {DNA}$
-logics give rise to a lattice structure ordered by the set-theoretic inclusion. The meet of two
$\mathtt {DNA}$
-logics give rise to a lattice structure ordered by the set-theoretic inclusion. The meet of two
![]() $\mathtt {DNA}$
-logics
$\mathtt {DNA}$
-logics
![]() $\Lambda _0,\Lambda _1$
is just their intersection and their join is the closure of their union under modus ponens. We will thus write
$\Lambda _0,\Lambda _1$
is just their intersection and their join is the closure of their union under modus ponens. We will thus write
![]() $\Lambda _0\land \Lambda _1:=\Lambda _0\cap \Lambda _1$
and
$\Lambda _0\land \Lambda _1:=\Lambda _0\cap \Lambda _1$
and
![]() $\Lambda _0\lor \Lambda _1:=(\Lambda _0\cup \Lambda _1)^{MP}$
, where we denote by
$\Lambda _0\lor \Lambda _1:=(\Lambda _0\cup \Lambda _1)^{MP}$
, where we denote by
![]() $(\Gamma )^{MP}$
the closure under modus ponens of a set
$(\Gamma )^{MP}$
the closure under modus ponens of a set
![]() $\Gamma $
of formulas. If
$\Gamma $
of formulas. If
![]() $\varphi $
can be obtained by closing the set
$\varphi $
can be obtained by closing the set
![]() $ \Gamma $
of formulas under modus ponens, then we write
$ \Gamma $
of formulas under modus ponens, then we write
![]() $\Gamma \vdash \varphi $
and we say that
$\Gamma \vdash \varphi $
and we say that
![]() $\varphi $
is derivable from
$\varphi $
is derivable from
![]() $\Gamma $
. One can show by standard reasoning that
$\Gamma $
. One can show by standard reasoning that
![]() $\Gamma \vdash \varphi $
if and only if there is a finite set of formulas
$\Gamma \vdash \varphi $
if and only if there is a finite set of formulas
![]() $\{\psi _i\}_{i\leq n}\subseteq \Gamma $
such that
$\{\psi _i\}_{i\leq n}\subseteq \Gamma $
such that
![]() $\{\psi _i\}_{i\leq n}\vdash \varphi $
. We often write
$\{\psi _i\}_{i\leq n}\vdash \varphi $
. We often write
![]() $\psi _0,\dots ,\psi _n\vdash \varphi $
for
$\psi _0,\dots ,\psi _n\vdash \varphi $
for
![]() $\{\psi _i\}_{i\leq n}\vdash \varphi $
.
$\{\psi _i\}_{i\leq n}\vdash \varphi $
.
Proposition 3.4. Let
![]() $\Lambda _0$
and
$\Lambda _0$
and
![]() $\Lambda _1$
be two
$\Lambda _1$
be two
![]() $\mathtt {DNA}$
-logics, then:
$\mathtt {DNA}$
-logics, then:
![]() $(i)\ \Lambda _0\land \Lambda _1$
is a
$(i)\ \Lambda _0\land \Lambda _1$
is a
![]() $\mathtt {DNA}$
-logic and it is the infimum of
$\mathtt {DNA}$
-logic and it is the infimum of
![]() $\Lambda _0$
and
$\Lambda _0$
and
![]() $\Lambda _1$
;
$\Lambda _1$
;
![]() $(ii)\ \Lambda _0\lor \Lambda _1$
is a
$(ii)\ \Lambda _0\lor \Lambda _1$
is a
![]() $\mathtt {DNA}$
-logic and it is the supremum of
$\mathtt {DNA}$
-logic and it is the supremum of
![]() $\Lambda _0$
and
$\Lambda _0$
and
![]() $\Lambda _1$
.
$\Lambda _1$
.
Proof. Assume without the loss of generality that
![]() $\Lambda _0 = L_0^\neg $
and
$\Lambda _0 = L_0^\neg $
and
![]() $\Lambda _1 = L_1^\neg $
.
$\Lambda _1 = L_1^\neg $
.
(i) It is straightforward to verify that:

Hence
![]() $\Lambda _0 \land \Lambda _1$
is the least set of formulas satisfying the conditions in Proposition 3.3 with respect to the intermediate logic
$\Lambda _0 \land \Lambda _1$
is the least set of formulas satisfying the conditions in Proposition 3.3 with respect to the intermediate logic
![]() $L_0 \cap L_1$
.
$L_0 \cap L_1$
.
(ii) We show that
![]() $\Lambda _0 \vee \Lambda _1 = (\Lambda _0 \cup \Lambda _1)^{MP}$
is the least set of formulas satisfying the conditions in Proposition 3.3 with respect to the intermediate logic
$\Lambda _0 \vee \Lambda _1 = (\Lambda _0 \cup \Lambda _1)^{MP}$
is the least set of formulas satisfying the conditions in Proposition 3.3 with respect to the intermediate logic
![]() $L_0 \vee L_1 := (L_0 \cup L_1)^{MP}$
.
$L_0 \vee L_1 := (L_0 \cup L_1)^{MP}$
.
It suffices to show that
![]() $(L_0\lor L_1)^\neg = (L_0^\neg \cup L_1^\neg )^{MP}$
. By definition we have that
$(L_0\lor L_1)^\neg = (L_0^\neg \cup L_1^\neg )^{MP}$
. By definition we have that
![]() $(L_0\lor L_1)^\neg = ((L_0\cup L_1)^{MP})^\neg $
and
$(L_0\lor L_1)^\neg = ((L_0\cup L_1)^{MP})^\neg $
and
![]() $ L_0^\neg \lor L_1^\neg = (L_0^\neg \cup L_1^\neg )^{MP}$
. It suffices to show that
$ L_0^\neg \lor L_1^\neg = (L_0^\neg \cup L_1^\neg )^{MP}$
. It suffices to show that
![]() $((L_0\cup L_1)^{MP})^\neg = (L_0^\neg \cup L_1^\neg )^{MP}$
.
$((L_0\cup L_1)^{MP})^\neg = (L_0^\neg \cup L_1^\neg )^{MP}$
.
![]() $(\subseteq )$
Suppose
$(\subseteq )$
Suppose
![]() $\varphi \in ((L_0\cup L_1)^{MP})^\neg $
. It follows that
$\varphi \in ((L_0\cup L_1)^{MP})^\neg $
. It follows that
![]() , hence for some formulas
, hence for some formulas
![]() $\psi _0,\dots ,\psi _n\in L_0\cup L_1$
we have
$\psi _0,\dots ,\psi _n\in L_0\cup L_1$
we have
![]() . We immediately obtain that
. We immediately obtain that
![]() . It follows that
. It follows that
![]() and, since
and, since
![]() $\neg \neg p \rightarrow p \in L_0^\neg \cup L_1^\neg $
for all
$\neg \neg p \rightarrow p \in L_0^\neg \cup L_1^\neg $
for all
![]() $p\in \mathtt {AT}$
, we obtain
$p\in \mathtt {AT}$
, we obtain
![]() $\varphi \in (L_0^\neg \cup L_1^\neg )^{MP}$
.
$\varphi \in (L_0^\neg \cup L_1^\neg )^{MP}$
.
![]() $(\supseteq )$
Suppose that
$(\supseteq )$
Suppose that
![]() $\varphi \in (L_0^\neg \cup L_1^\neg )^{MP} $
. It follows that for some formulas
$\varphi \in (L_0^\neg \cup L_1^\neg )^{MP} $
. It follows that for some formulas
![]() $\psi _0,\dots ,\psi _n\in L_0^\neg \cup L_1^\neg $
we have that
$\psi _0,\dots ,\psi _n\in L_0^\neg \cup L_1^\neg $
we have that
![]() $\psi _0,\dots ,\psi _n\vdash \varphi $
, that is, there is a derivation of
$\psi _0,\dots ,\psi _n\vdash \varphi $
, that is, there is a derivation of
![]() $\varphi $
from
$\varphi $
from
![]() $\psi _0,\dots ,\psi _n$
. Therefore,
$\psi _0,\dots ,\psi _n$
. Therefore,
![]() and by substituting each
and by substituting each
![]() $\psi _i$
with
$\psi _i$
with
![]() in the previous derivation, we obtain
in the previous derivation, we obtain
![]() . So
. So
![]() and consequently
and consequently
![]() $\varphi \in ((L_0\cup L_1)^{MP})^\neg $
.
$\varphi \in ((L_0\cup L_1)^{MP})^\neg $
.
We denote by
![]() $\Lambda (\mathtt {IPC}^\neg ) $
the lattice of
$\Lambda (\mathtt {IPC}^\neg ) $
the lattice of
![]() $\mathtt {DNA}$
-logics. Since intermediate logics also form a lattice
$\mathtt {DNA}$
-logics. Since intermediate logics also form a lattice
![]() $ \Lambda (\mathtt {IPC}) $
, we can then show that the map
$ \Lambda (\mathtt {IPC}) $
, we can then show that the map
![]() $(-)^\neg :\Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathtt {IPC}^\neg ) $
which assigns each intermediate logic to its negative variant is a lattice homomorphism.
$(-)^\neg :\Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathtt {IPC}^\neg ) $
which assigns each intermediate logic to its negative variant is a lattice homomorphism.
Proposition 3.5. The map
![]() $(-)^\neg :\Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathtt {IPC}^\neg ) $
is a bounded lattice homomorphism.
$(-)^\neg :\Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathtt {IPC}^\neg ) $
is a bounded lattice homomorphism.
Proof. Obviously
![]() $(-)^\neg $
sends
$(-)^\neg $
sends
![]() $\bot _{\Lambda (\mathtt {IPC}) }$
to
$\bot _{\Lambda (\mathtt {IPC}) }$
to
![]() $\bot _{\Lambda (\mathtt {IPC}^\neg ) }$
and
$\bot _{\Lambda (\mathtt {IPC}^\neg ) }$
and
![]() $\top _{\Lambda (\mathtt {IPC}) }$
to
$\top _{\Lambda (\mathtt {IPC}) }$
to
![]() $\top _{\Lambda (\mathtt {IPC}^\neg ) }$
. Preservation of meets and joins follows from the proof of Proposition 3.4 above.
$\top _{\Lambda (\mathtt {IPC}^\neg ) }$
. Preservation of meets and joins follows from the proof of Proposition 3.4 above.
3.2 Algebraic semantics for
 $\mathtt {DNA}$
-logics
$\mathtt {DNA}$
-logics
In the existing literature, negative variants have been considered from a syntactic point of view [Reference Ciardelli9, Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37]. An algebraic semantics for inquisitive logic was introduced in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5]. Here we extend this algebraic approach to
![]() $\mathtt {DNA}$
-logics.
$\mathtt {DNA}$
-logics.
Recall that, if H is a Heyting algebra, then we say that an element
![]() $x\in H$
is regular if
$x\in H$
is regular if
![]() $x=\neg \neg x$
. For any Heyting algebra H we then denote by
$x=\neg \neg x$
. For any Heyting algebra H we then denote by
![]() $H_\neg $
the set:
$H_\neg $
the set:
So
![]() $H_\neg $
consists of all regular elements of the Heyting algebra H. Note that since in every Heyting algebras we have that
$H_\neg $
consists of all regular elements of the Heyting algebra H. Note that since in every Heyting algebras we have that
![]() $\neg x = \neg \neg \neg x$
, the set of regular elements of H can also be specified as
$\neg x = \neg \neg \neg x$
, the set of regular elements of H can also be specified as
![]() $H_\neg = \{ y\in H : \exists x \in H (y = \neg x) \}$
. We define
$H_\neg = \{ y\in H : \exists x \in H (y = \neg x) \}$
. We define
![]() $\mathtt {DNA}$
-models as follows.
$\mathtt {DNA}$
-models as follows.
Definition 3.6 (
 $\mathtt {DNA}$
-Model)
$\mathtt {DNA}$
-Model)
A
![]() $\mathtt {DNA}$
-model is a pair
$\mathtt {DNA}$
-model is a pair
![]() $M=(H, \mu )$
where H is a Heyting algebra and
$M=(H, \mu )$
where H is a Heyting algebra and
![]() $\mu : \mathtt {AT} \rightarrow H_\neg $
is a valuation of propositional atoms over the regular elements of H.
$\mu : \mathtt {AT} \rightarrow H_\neg $
is a valuation of propositional atoms over the regular elements of H.
We then say that
![]() $\mu $
is a
$\mu $
is a
![]() $\mathtt {DNA}$
-valuation over the Heyting algebra H. Given a
$\mathtt {DNA}$
-valuation over the Heyting algebra H. Given a
![]() $\mathtt {DNA}$
-model
$\mathtt {DNA}$
-model
![]() $M=(H,\mu )$
, we define by induction the interpretation of any formula
$M=(H,\mu )$
, we define by induction the interpretation of any formula
![]() $\varphi \in \mathcal {L}_P$
.
$\varphi \in \mathcal {L}_P$
.
Definition 3.7 (Interpretation of Arbitrary Formulas)
Given a
![]() $\mathtt {DNA}$
-model
$\mathtt {DNA}$
-model
![]() $M=(H,\mu )$
and a formula
$M=(H,\mu )$
and a formula
![]() $\varphi \in \mathcal {L}_P$
, its interpretation
$\varphi \in \mathcal {L}_P$
, its interpretation
is defined by the following recursive clauses:

When the valuation
![]() $\mu $
is clear from the context, we simply write
$\mu $
is clear from the context, we simply write
![]() for the interpretation of
for the interpretation of
![]() $\varphi $
in H under
$\varphi $
in H under
![]() $\mu $
. From the former definitions it is straightforward to adapt the usual definitions of truth at a model and validity. We say that a formula
$\mu $
. From the former definitions it is straightforward to adapt the usual definitions of truth at a model and validity. We say that a formula
![]() $\varphi $
is true under
$\varphi $
is true under
![]() $ \mu $
in H or true in the model
$ \mu $
in H or true in the model
![]() $ M=(H, \mu ) $
and write
$ M=(H, \mu ) $
and write
![]() $M\vDash ^\neg \varphi $
if
$M\vDash ^\neg \varphi $
if
![]() . We say that
. We say that
![]() $\varphi $
is
$\varphi $
is
![]() $\mathtt {DNA}$
-valid in H and write
$\mathtt {DNA}$
-valid in H and write
![]() $H\vDash ^\neg \varphi $
if
$H\vDash ^\neg \varphi $
if
![]() $\varphi $
is true in every model
$\varphi $
is true in every model
![]() $M=(H,\mu )$
over H. Given a class
$M=(H,\mu )$
over H. Given a class
![]() $\mathcal {C}$
of Heyting algebras, we say that
$\mathcal {C}$
of Heyting algebras, we say that
![]() $\varphi $
is
$\varphi $
is
![]() $\mathtt {DNA}$
-valid in
$\mathtt {DNA}$
-valid in
![]() $ \mathcal {C} $
and write
$ \mathcal {C} $
and write
![]() $\mathcal {C}\vDash ^\neg \varphi $
if
$\mathcal {C}\vDash ^\neg \varphi $
if
![]() $\varphi $
is
$\varphi $
is
![]() $\mathtt {DNA}$
-valid in every Heyting algebra
$\mathtt {DNA}$
-valid in every Heyting algebra
![]() $H\in \mathcal {C}$
. Finally, we say that
$H\in \mathcal {C}$
. Finally, we say that
![]() $\varphi $
is a
$\varphi $
is a
![]() $\mathtt {DNA}$
-validity if
$\mathtt {DNA}$
-validity if
![]() $\varphi $
is valid in any Heyting algebra H. When the context is clear, we drop the qualification
$\varphi $
is valid in any Heyting algebra H. When the context is clear, we drop the qualification
![]() $\mathtt {DNA}$
from the definitions above and talk simply of validity.
$\mathtt {DNA}$
from the definitions above and talk simply of validity.
![]() $\mathtt {DNA}$
-validity and standard validity are closely intertwined. To see how, we first introduce the notion of negative variant of a valuation.
$\mathtt {DNA}$
-validity and standard validity are closely intertwined. To see how, we first introduce the notion of negative variant of a valuation.
Definition 3.8 (Negative Variant of a Valuation)
Let H be a Heyting algebra and V an arbitrary valuation over H. Then we say that
![]() $V^\neg $
is the negative variant of V if for all
$V^\neg $
is the negative variant of V if for all
![]() $p\in \mathtt {AT}$
we have that
$p\in \mathtt {AT}$
we have that
![]() $V^\neg (p)=\neg V(p)$
.
$V^\neg (p)=\neg V(p)$
.
The following lemma, which is easy to prove, shows that the set of
![]() $\mathtt {DNA}$
-valuations and the set of negative variants of standard valuations coincide.
$\mathtt {DNA}$
-valuations and the set of negative variants of standard valuations coincide.
Lemma 3.9. A valuation
![]() $\mu $
is a
$\mu $
is a
![]() $\mathtt {DNA}$
-valuation if and only if it is the negative variant of some valuation V.
$\mathtt {DNA}$
-valuation if and only if it is the negative variant of some valuation V.
By the previous lemma, a generic
![]() $\mathtt {DNA}$
-valuation is always of the form
$\mathtt {DNA}$
-valuation is always of the form
![]() $V^{\neg }$
for some valuation V. We will henceforth write
$V^{\neg }$
for some valuation V. We will henceforth write
![]() $V^\neg $
for an arbitrary
$V^\neg $
for an arbitrary
![]() $\mathtt {DNA}$
-valuation. We can now prove the following important lemma.
$\mathtt {DNA}$
-valuation. We can now prove the following important lemma.
Lemma 3.10. For every Heyting algebra H, for every valuation V and any formula
![]() $\varphi $
, we have
$\varphi $
, we have
Proof. The proof goes by induction on the complexity of
![]() $\varphi $
. The only non-trivial case is
$\varphi $
. The only non-trivial case is
![]() $\varphi = p \in \mathtt {AT}$
:
$\varphi = p \in \mathtt {AT}$
:
From this we can derive the following result.
Proposition 3.11. For any Heyting algebra H we have
![]() $H\vDash ^\neg \varphi $
iff
$H\vDash ^\neg \varphi $
iff
![]() .
.
Proof. We prove both directions by contraposition.
![]() $(\Rightarrow )$
Suppose
$(\Rightarrow )$
Suppose
![]() for some valuation V. Then, given
for some valuation V. Then, given
![]() $V^\neg $
the negative variant of V, it follows by Lemma 3.10 that
$V^\neg $
the negative variant of V, it follows by Lemma 3.10 that
![]() .
.
![]() $(\Leftarrow )$
Suppose
$(\Leftarrow )$
Suppose
![]() for some
for some
![]() $\mathtt {DNA}$
-valuation
$\mathtt {DNA}$
-valuation
![]() $\mu $
. By Lemma 3.9, there exists a valuation V whose negative variant
$\mu $
. By Lemma 3.9, there exists a valuation V whose negative variant
![]() $V^{\neg } \text{ is } \mu $
. Then, by Lemma 3.10, we have that
$V^{\neg } \text{ is } \mu $
. Then, by Lemma 3.10, we have that
![]() .
.
Thus we end up with the following proposition: if a Heyting algebra validates an intermediate logic, then it also validates its negative variant.
Corollary 3.12. Let H be a Heyting algebra and L an intermediate logic. Then we have that
![]() $H\vDash L$
entails
$H\vDash L$
entails
![]() $H\vDash ^\neg L^\neg $
$H\vDash ^\neg L^\neg $
Notice that it is not true in general that
![]() $H\vDash ^\neg L^\neg $
entails
$H\vDash ^\neg L^\neg $
entails
![]() $H\vDash L$
.
$H\vDash L$
.
![]() $\mathtt {DNA}$
-valuations form a subclass of all valuation and it might very well be that a formula is true in a Heyting algebra under all
$\mathtt {DNA}$
-valuations form a subclass of all valuation and it might very well be that a formula is true in a Heyting algebra under all
![]() $\mathtt {DNA}$
-valuations but not under all valuations. However, the next proposition is a weaker version of this fact which we will need later. Let
$\mathtt {DNA}$
-valuations but not under all valuations. However, the next proposition is a weaker version of this fact which we will need later. Let
![]() $\langle H_\neg \rangle $
be the subalgebra of H generated by
$\langle H_\neg \rangle $
be the subalgebra of H generated by
![]() $H_{\neg }$
. First we prove the following lemma.
$H_{\neg }$
. First we prove the following lemma.
Lemma 3.13. For any Heyting algebra H we have that
![]() $H\vDash ^\neg \varphi $
iff
$H\vDash ^\neg \varphi $
iff
![]() $\langle H_\neg \rangle \vDash ^\neg \varphi $
.
$\langle H_\neg \rangle \vDash ^\neg \varphi $
.
Proof. Clearly
![]() $H_\neg =\langle H_\neg \rangle _\neg $
. So we have that
$H_\neg =\langle H_\neg \rangle _\neg $
. So we have that
![]() $V^\neg $
is a
$V^\neg $
is a
![]() $\mathtt {DNA}$
-valuation over H iff it is a
$\mathtt {DNA}$
-valuation over H iff it is a
![]() $\mathtt {DNA}$
-valuation over
$\mathtt {DNA}$
-valuation over
![]() $\langle H_\neg \rangle $
. Since
$\langle H_\neg \rangle $
. Since
![]() $\langle H_\neg \rangle $
is a subalgebra of H, it readily follows that
$\langle H_\neg \rangle $
is a subalgebra of H, it readily follows that
![]() $H\vDash ^\neg \varphi $
iff
$H\vDash ^\neg \varphi $
iff
![]() $\langle H_\neg \rangle \vDash ^\neg \varphi $
.
$\langle H_\neg \rangle \vDash ^\neg \varphi $
.
This allows us to prove the following result.
Proposition 3.14. Let H be a Heyting algebra and L an intermediate logic. Then we have that
![]() $H\vDash ^\neg L^\neg $
entails
$H\vDash ^\neg L^\neg $
entails
![]() $\langle H_\neg \rangle \vDash L$
.
$\langle H_\neg \rangle \vDash L$
.
Proof. Consider any Heyting algebra H, and suppose that
![]() $\langle H_\neg \rangle \nvDash L$
, then there is some formula
$\langle H_\neg \rangle \nvDash L$
, then there is some formula
![]() $\varphi \in L$
and some valuation V such that
$\varphi \in L$
and some valuation V such that
![]() $(\langle H_\neg \rangle ,V)\nvDash \varphi $
. Now, since
$(\langle H_\neg \rangle ,V)\nvDash \varphi $
. Now, since
![]() $\langle H_\neg \rangle $
is the subalgebra generated by
$\langle H_\neg \rangle $
is the subalgebra generated by
![]() $H_{\neg }$
, we can express every element
$H_{\neg }$
, we can express every element
![]() $x\in \langle H_\neg \rangle $
as a polynomial
$x\in \langle H_\neg \rangle $
as a polynomial
![]() $\delta ^x_{H}$
of elements of
$\delta ^x_{H}$
of elements of
![]() $H_{\neg }$
. We thus have
$H_{\neg }$
. We thus have
![]() $ x= \delta ^x_{H}(\overline {y}) $
, where for each
$ x= \delta ^x_{H}(\overline {y}) $
, where for each
![]() $y_i$
we have that
$y_i$
we have that
![]() $y_i \in H_{\neg }$
. By writing for the variables
$y_i \in H_{\neg }$
. By writing for the variables
![]() $p_1,\dots, p_n$
occuring in
$p_1,\dots, p_n$
occuring in
![]() $\varphi $
and
$\varphi $
and
![]() $\overline {\delta ^x_{H}(\overline {y})} $
for the polynomials of the elements
$\overline {\delta ^x_{H}(\overline {y})} $
for the polynomials of the elements
![]() $x_1=V(p_1),\dots, x_n=V(p_n)$
, we get that
$x_1=V(p_1),\dots, x_n=V(p_n)$
, we get that
![]() . Since all the elements
. Since all the elements
![]() $\overline {y}$
in the polynomials
$\overline {y}$
in the polynomials
![]() $\delta _H^x$
are regular elements, we can define a
$\delta _H^x$
are regular elements, we can define a
![]() $\mathtt {DNA}$
-valuation
$\mathtt {DNA}$
-valuation
![]() $U^\neg : \mathtt {AT} \rightarrow H_{\neg }$
such that
$U^\neg : \mathtt {AT} \rightarrow H_{\neg }$
such that
![]() $U^\neg : q_i \mapsto y_i$
for all
$U^\neg : q_i \mapsto y_i$
for all
![]() $i\leq n$
. Then it follows immediately that
$i\leq n$
. Then it follows immediately that
![]() . But then, since we also had
. But then, since we also had
![]() , it follows that
, it follows that
![]() . So since
. So since
![]() $(\langle H_\neg \rangle ,V)\nvDash \varphi $
, we also get that
$(\langle H_\neg \rangle ,V)\nvDash \varphi $
, we also get that
![]() . So it then follows by Lemma 3.13 that
. So it then follows by Lemma 3.13 that
![]() , hence
, hence
![]() . Now, since L is an intermediate logic, it admits free substitution and so, since
. Now, since L is an intermediate logic, it admits free substitution and so, since
![]() $\varphi \in L$
, we also get that
$\varphi \in L$
, we also get that
![]() and therefore as
and therefore as
![]() $L\subseteq L^\neg $
also
$L\subseteq L^\neg $
also
![]() . Finally, this means that
. Finally, this means that
![]() $ H \nvDash ^\neg L^\neg $
, thus proving our claim.
$ H \nvDash ^\neg L^\neg $
, thus proving our claim.
3.3
 $\mathtt {DNA}$
-varieties
$\mathtt {DNA}$
-varieties
The algebraic semantics for
![]() $\mathtt {DNA}$
-logics that we have defined in the previous section motivates the introduction of
$\mathtt {DNA}$
-logics that we have defined in the previous section motivates the introduction of
![]() $\mathtt {DNA}$
-varieties. We will define
$\mathtt {DNA}$
-varieties. We will define
![]() $\mathtt {DNA}$
-varieties as varieties of algebras which are additionally closed under so-called core-superalgebras. This notion plays an important role in the algebraic semantics of
$\mathtt {DNA}$
-varieties as varieties of algebras which are additionally closed under so-called core-superalgebras. This notion plays an important role in the algebraic semantics of
![]() $\mathtt {DNA}$
-logics and is defined as follows.
$\mathtt {DNA}$
-logics and is defined as follows.
Definition 3.15. We say that a Heyting algebra K is a core superalgebra of H if
![]() $ H_{\neg }=K_{\neg } $
and
$ H_{\neg }=K_{\neg } $
and
![]() $ H\preceq K $
.
$ H\preceq K $
.
A core superalgebra K of a Heyting algebra H is thus a subalgebra of H such that K and H share the same regular elements.
![]() $\mathtt {DNA}$
-varieties are then defined as follows.
$\mathtt {DNA}$
-varieties are then defined as follows.
Definition 3.16. A class of Heyting algebras
![]() $\mathcal {C}$
is a
$\mathcal {C}$
is a
![]() $\mathtt {DNA}$
-variety if it is closed under subalgebras, homomorphic images, products and core superalgebras.
$\mathtt {DNA}$
-variety if it is closed under subalgebras, homomorphic images, products and core superalgebras.
Moreover, as
![]() $\mathtt {DNA}$
-logics can be seen also as negative variants of intermediate logic, one can regard
$\mathtt {DNA}$
-logics can be seen also as negative variants of intermediate logic, one can regard
![]() $\mathtt {DNA}$
-varieties as special kinds of closure of standard varieties.
$\mathtt {DNA}$
-varieties as special kinds of closure of standard varieties.
Definition 3.17 (Negative Closure of a Variety)
For every variety of Heyting algebras
![]() $\mathcal {V}$
, its negative closure
$\mathcal {V}$
, its negative closure
![]() $\mathcal {V}^\uparrow $
is defined as follows:
$\mathcal {V}^\uparrow $
is defined as follows:
We use the notation
![]() $\mathcal {V}^\uparrow $
to refer to the negative variant of a variety
$\mathcal {V}^\uparrow $
to refer to the negative variant of a variety
![]() $\mathcal {V}$
and we generally write
$\mathcal {V}$
and we generally write
![]() $\mathcal {X}$
for
$\mathcal {X}$
for
![]() $\mathtt {DNA}$
-varieties. If not specified otherwise, we reserve
$\mathtt {DNA}$
-varieties. If not specified otherwise, we reserve
![]() $\mathcal {C}$
to denote arbitrary classes of Heyting algebras,
$\mathcal {C}$
to denote arbitrary classes of Heyting algebras,
![]() $\mathcal {V}$
or
$\mathcal {V}$
or
![]() $\mathcal {U}$
to denote standard varieties and
$\mathcal {U}$
to denote standard varieties and
![]() $\mathcal {X}$
or
$\mathcal {X}$
or
![]() $\mathcal {Y}$
to denote
$\mathcal {Y}$
to denote
![]() $\mathtt {DNA}$
-varieties.
$\mathtt {DNA}$
-varieties.
The following proposition establishes that every
![]() $\mathtt {DNA}$
-variety is the negative closure of a standard variety.
$\mathtt {DNA}$
-variety is the negative closure of a standard variety.
Proposition 3.18. A class of Heyting algebras
![]() $\mathcal {C}$
is a
$\mathcal {C}$
is a
![]() $\mathtt {DNA}$
-variety if and only if it is the negative closure of a variety.
$\mathtt {DNA}$
-variety if and only if it is the negative closure of a variety.
Proof. (
![]() $\Rightarrow $
) If a set of algebras
$\Rightarrow $
) If a set of algebras
![]() $\mathcal {X}$
is a
$\mathcal {X}$
is a
![]() $\mathtt {DNA}$
-variety, then it is closed under subalgebras, homomorphic images and products and thus it is a variety. Moreover, since it is also closed under core superalgebras, it is straightforward to see that
$\mathtt {DNA}$
-variety, then it is closed under subalgebras, homomorphic images and products and thus it is a variety. Moreover, since it is also closed under core superalgebras, it is straightforward to see that
![]() $\mathcal {X}=\mathcal {X}^\uparrow $
, so that we can see
$\mathcal {X}=\mathcal {X}^\uparrow $
, so that we can see
![]() $\mathcal {X}$
as the negative variant of itself and thus as a
$\mathcal {X}$
as the negative variant of itself and thus as a
![]() $\mathtt {DNA}$
-variety.
$\mathtt {DNA}$
-variety.
(
![]() $\Leftarrow $
) Let
$\Leftarrow $
) Let
![]() $\mathcal {V}^\uparrow $
be the negative variant of some standard variety
$\mathcal {V}^\uparrow $
be the negative variant of some standard variety
![]() $\mathcal {V}$
. To prove that
$\mathcal {V}$
. To prove that
![]() $\mathcal {V}^\uparrow $
is a
$\mathcal {V}^\uparrow $
is a
![]() $\mathtt {DNA}$
-variety we need to check that
$\mathtt {DNA}$
-variety we need to check that
![]() $\mathcal {V}^\uparrow $
is closed under the above four operations.
$\mathcal {V}^\uparrow $
is closed under the above four operations.
(1) We check closure under subalgebras. Suppose
![]() $H\in \mathcal {V}^\uparrow $
and
$H\in \mathcal {V}^\uparrow $
and
![]() $K\preceq H$
. Then by definition of
$K\preceq H$
. Then by definition of
![]() $\mathtt {DNA}$
-variety it follows that there is some
$\mathtt {DNA}$
-variety it follows that there is some
![]() $H'\in \mathcal {V}$
such that
$H'\in \mathcal {V}$
such that
![]() $ H^{\prime }_{\neg }=H_{\neg } $
and
$ H^{\prime }_{\neg }=H_{\neg } $
and
![]() $ H'\preceq H $
. Now consider
$ H'\preceq H $
. Now consider
![]() $K'=H'\cap K$
, since
$K'=H'\cap K$
, since
![]() $K'$
is the intersection of two subalgebras of H, it will also be closed under the Heyting algebra operations. Thus we have that
$K'$
is the intersection of two subalgebras of H, it will also be closed under the Heyting algebra operations. Thus we have that
![]() $K'$
is also a Heyting algebra and
$K'$
is also a Heyting algebra and
![]() $K'\preceq H'$
and
$K'\preceq H'$
and
![]() $K'\preceq K$
. Therefore, by the fact that
$K'\preceq K$
. Therefore, by the fact that
![]() $H'\in \mathcal {V}$
and
$H'\in \mathcal {V}$
and
![]() $\mathcal {V}$
is closed under subalgebras, it then follows that
$\mathcal {V}$
is closed under subalgebras, it then follows that
![]() $K'\in \mathcal {V}$
. Moreover, since
$K'\in \mathcal {V}$
. Moreover, since
![]() $H^{\prime }_\neg =H_\neg \supseteq K_\neg $
, we have that
$H^{\prime }_\neg =H_\neg \supseteq K_\neg $
, we have that
![]() $K^{\prime }_\neg = H^{\prime }_\neg \cap K_\neg = K_\neg $
. Finally, we showed that for
$K^{\prime }_\neg = H^{\prime }_\neg \cap K_\neg = K_\neg $
. Finally, we showed that for
![]() $K'\in \mathcal {V}$
we have
$K'\in \mathcal {V}$
we have
![]() $K'\preceq K$
and
$K'\preceq K$
and
![]() $K^{\prime }_\neg = K_\neg $
, which entails
$K^{\prime }_\neg = K_\neg $
, which entails
![]() $K\in \mathcal {V}^\uparrow $
.
$K\in \mathcal {V}^\uparrow $
.
(2) We check closure under homomorphic images. Suppose
![]() $H\in \mathcal {V}^\uparrow $
and
$H\in \mathcal {V}^\uparrow $
and
![]() $f: H\twoheadrightarrow K$
, then by the definition of
$f: H\twoheadrightarrow K$
, then by the definition of
![]() $\mathtt {DNA}$
-variety we have that for some
$\mathtt {DNA}$
-variety we have that for some
![]() $H'\in \mathcal {V}$
that
$H'\in \mathcal {V}$
that
![]() $ H^{\prime }_{\neg }=H_{\neg } $
and
$ H^{\prime }_{\neg }=H_{\neg } $
and
![]() $ H'\preceq H $
. Consider
$ H'\preceq H $
. Consider
![]() $K'=f[H']$
. Since homomorphic images preserve subalgebras, we have
$K'=f[H']$
. Since homomorphic images preserve subalgebras, we have
![]() $K'\preceq K$
and, by the closure of standard varieties under homomorphic images
$K'\preceq K$
and, by the closure of standard varieties under homomorphic images
![]() $K'\in \mathcal {V}$
. Moreover, since by assumption
$K'\in \mathcal {V}$
. Moreover, since by assumption
![]() $H_\neg = H^{\prime }_\neg $
, we have
$H_\neg = H^{\prime }_\neg $
, we have
![]() $K_\neg =f[H_\neg ]=f[H^{\prime }_\neg ]=K^{\prime }_\neg $
. Thus for
$K_\neg =f[H_\neg ]=f[H^{\prime }_\neg ]=K^{\prime }_\neg $
. Thus for
![]() $K'\in \mathcal {V}$
we have
$K'\in \mathcal {V}$
we have
![]() $K'\preceq K$
and
$K'\preceq K$
and
![]() $K^{\prime }_\neg = K_\neg $
, which yields
$K^{\prime }_\neg = K_\neg $
, which yields
![]() $K\in \mathcal {V}^\uparrow $
.
$K\in \mathcal {V}^\uparrow $
.
(3) We check closure under products. Suppose
![]() $H^i\in \mathcal {V}^\uparrow $
for all
$H^i\in \mathcal {V}^\uparrow $
for all
![]() $i\in I$
of some index-set I. Then we need to check that
$i\in I$
of some index-set I. Then we need to check that
![]() $\prod _{i\in I} H^i\in \mathcal {V}^\uparrow $
. By the definition of
$\prod _{i\in I} H^i\in \mathcal {V}^\uparrow $
. By the definition of
![]() $\mathtt {DNA}$
-variety it immediately follows that there is, for every
$\mathtt {DNA}$
-variety it immediately follows that there is, for every
![]() $i\in I$
, a Heyting algebra
$i\in I$
, a Heyting algebra
![]() $K^i\in \mathcal {V}$
such that
$K^i\in \mathcal {V}$
such that
![]() $H^i_\neg =K^i_\neg $
, and
$H^i_\neg =K^i_\neg $
, and
![]() $K^i\preceq H^i$
. Then by the closure under products of
$K^i\preceq H^i$
. Then by the closure under products of
![]() $\mathcal {V}$
, we have that
$\mathcal {V}$
, we have that
![]() $\prod _{i\in I} K^i\in \mathcal {V}$
. Now, since
$\prod _{i\in I} K^i\in \mathcal {V}$
. Now, since
![]() $K^i\preceq H^i$
holds for every
$K^i\preceq H^i$
holds for every
![]() $i\in I$
, it follows immediately that
$i\in I$
, it follows immediately that
![]() $\prod _{i\in I} K^i\preceq \prod _{i\in I} H^i$
. Similarly, we have that:
$\prod _{i\in I} K^i\preceq \prod _{i\in I} H^i$
. Similarly, we have that:
 $$ \begin{align*}\left(\prod_{i\in I} H^i\right)_\neg=\prod_{i\in I} H^i_\neg=\prod_{i\in I} K^i_\neg=\left(\prod_{i\in I} K^i\right)_\neg.\end{align*} $$
$$ \begin{align*}\left(\prod_{i\in I} H^i\right)_\neg=\prod_{i\in I} H^i_\neg=\prod_{i\in I} K^i_\neg=\left(\prod_{i\in I} K^i\right)_\neg.\end{align*} $$
Hence, by the fact that
![]() $\prod _{i\in I} K^i\in \mathcal {V}$
and the definition of
$\prod _{i\in I} K^i\in \mathcal {V}$
and the definition of
![]() $\mathtt {DNA}$
-variety, it follows that
$\mathtt {DNA}$
-variety, it follows that
![]() $\prod _{i\in I} H^i\in \mathcal {V}^\uparrow $
.
$\prod _{i\in I} H^i\in \mathcal {V}^\uparrow $
.
(4) We check closure under core superalgebras. Suppose
![]() $H\in \mathcal {V}^\uparrow $
and for some K we have that
$H\in \mathcal {V}^\uparrow $
and for some K we have that
![]() $H_\neg =K_\neg $
and
$H_\neg =K_\neg $
and
![]() $H\preceq K $
. By the definition of
$H\preceq K $
. By the definition of
![]() $\mathtt {DNA}$
-varieties we have that there is some
$\mathtt {DNA}$
-varieties we have that there is some
![]() $H'\preceq H $
such that
$H'\preceq H $
such that
![]() $H'\in \mathcal {V}$
and
$H'\in \mathcal {V}$
and
![]() $H^{\prime }_\neg = H_\neg $
. Since
$H^{\prime }_\neg = H_\neg $
. Since
![]() $H'\preceq H $
and
$H'\preceq H $
and
![]() $H\preceq K $
we then have
$H\preceq K $
we then have
![]() $H'\preceq K $
by the transitivity of subalgebra relation. Moreover, since
$H'\preceq K $
by the transitivity of subalgebra relation. Moreover, since
![]() $H^{\prime }_\neg = H_\neg =K_\neg $
and
$H^{\prime }_\neg = H_\neg =K_\neg $
and
![]() $H\in \mathcal {V}$
, it finally follows that
$H\in \mathcal {V}$
, it finally follows that
![]() $K\in \mathcal {V}^\uparrow $
.
$K\in \mathcal {V}^\uparrow $
.
As in the case of standard varieties,
![]() $\mathtt {DNA}$
-varieties give rise to a lattice structure ordered by the set-theoretic inclusion. As it is customary doing, we implicitly exclude from the lattice of
$\mathtt {DNA}$
-varieties give rise to a lattice structure ordered by the set-theoretic inclusion. As it is customary doing, we implicitly exclude from the lattice of
![]() $\mathtt {DNA}$
-varieties the trivial
$\mathtt {DNA}$
-varieties the trivial
![]() $\mathtt {DNA}$
-variety of one-element algebras. The meet of two
$\mathtt {DNA}$
-variety of one-element algebras. The meet of two
![]() $\mathtt {DNA}$
-varieties
$\mathtt {DNA}$
-varieties
![]() $\mathcal {X}_0,\mathcal {X}_1$
is just their intersection and their join is the smallest class containing their union and closed under the
$\mathcal {X}_0,\mathcal {X}_1$
is just their intersection and their join is the smallest class containing their union and closed under the
![]() $\mathtt {DNA}$
-variety operations.
$\mathtt {DNA}$
-variety operations.
For any class
![]() $\mathcal {C}$
of Heyting algebras we say that
$\mathcal {C}$
of Heyting algebras we say that
![]() $\mathcal {X}$
is generated by the class
$\mathcal {X}$
is generated by the class
![]() $\mathcal {C}\subseteq \mathcal {X}$
and we write
$\mathcal {C}\subseteq \mathcal {X}$
and we write
![]() $\mathcal {X}=\mathcal {X}(\mathcal {C})$
if
$\mathcal {X}=\mathcal {X}(\mathcal {C})$
if
![]() $\mathcal {X}$
is the least class of Heyting algebras such that
$\mathcal {X}$
is the least class of Heyting algebras such that
![]() $\mathcal {C}\subseteq \mathcal {X} $
and
$\mathcal {C}\subseteq \mathcal {X} $
and
![]() $\mathcal {X}$
is closed under subalgebras, homomorphic images, products and core superalgebras. It is then clear that
$\mathcal {X}$
is closed under subalgebras, homomorphic images, products and core superalgebras. It is then clear that
![]() $\mathcal {X}(\mathcal {C})$
is the smallest
$\mathcal {X}(\mathcal {C})$
is the smallest
![]() $\mathtt {DNA}$
-variety containing
$\mathtt {DNA}$
-variety containing
![]() $\mathcal {C}$
and that
$\mathcal {C}$
and that
![]() $\mathcal {X}(\mathcal {C})=\mathcal {V}(\mathcal {C})^\uparrow $
. We will thus define
$\mathcal {X}(\mathcal {C})=\mathcal {V}(\mathcal {C})^\uparrow $
. We will thus define
![]() $\mathcal {X}_0\land \mathcal {X}_1:=\mathcal {X}_0\cap \mathcal {X}_1$
and
$\mathcal {X}_0\land \mathcal {X}_1:=\mathcal {X}_0\cap \mathcal {X}_1$
and
![]() $\mathcal {X}_0\lor \mathcal {X}_1:=\mathcal {X}(\mathcal {X}_0\cup \mathcal {X}_1)$
. We proceed to prove the following proposition.
$\mathcal {X}_0\lor \mathcal {X}_1:=\mathcal {X}(\mathcal {X}_0\cup \mathcal {X}_1)$
. We proceed to prove the following proposition.
Proposition 3.19. Let
![]() $\mathcal {X}_0$
and
$\mathcal {X}_0$
and
![]() $\mathcal {X}_1$
be two
$\mathcal {X}_1$
be two
![]() $\mathtt {DNA}$
-varieties. Then:
$\mathtt {DNA}$
-varieties. Then:
![]() $(i)\ \mathcal {X}_0\land \mathcal {X}_1$
is a
$(i)\ \mathcal {X}_0\land \mathcal {X}_1$
is a
![]() $\mathtt {DNA}$
-variety and it is the infimum of
$\mathtt {DNA}$
-variety and it is the infimum of
![]() $\mathcal {X}_0$
and
$\mathcal {X}_0$
and
![]() $\mathcal {X}_1$
;
$\mathcal {X}_1$
;
![]() $(ii)\ \mathcal {X}_0\lor \mathcal {X}_1$
is a
$(ii)\ \mathcal {X}_0\lor \mathcal {X}_1$
is a
![]() $\mathtt {DNA}$
-variety and it is the supremum of
$\mathtt {DNA}$
-variety and it is the supremum of
![]() $\mathcal {X}_0$
and
$\mathcal {X}_0$
and
![]() $\mathcal {X}_1$
.
$\mathcal {X}_1$
.
Proof. (i) By definition
![]() $\mathcal {X}_0\land \mathcal {X}_1:=\mathcal {X}_0\cap \mathcal {X}_1$
. That this is a
$\mathcal {X}_0\land \mathcal {X}_1:=\mathcal {X}_0\cap \mathcal {X}_1$
. That this is a
![]() $\mathtt {DNA}$
-variety follows immediately from the fact that, since both
$\mathtt {DNA}$
-variety follows immediately from the fact that, since both
![]() $\mathcal {X}_0$
and
$\mathcal {X}_0$
and
![]() $\mathcal {X}_1$
are closed under subalgebras, homomorphic images, products and core superalgebras, then also their intersection is closed under these operations. Moreover, since
$\mathcal {X}_1$
are closed under subalgebras, homomorphic images, products and core superalgebras, then also their intersection is closed under these operations. Moreover, since
![]() $\mathcal {X}_0\land \mathcal {X}_1:=\mathcal {X}_0\cap \mathcal {X}_1$
, it follows that
$\mathcal {X}_0\land \mathcal {X}_1:=\mathcal {X}_0\cap \mathcal {X}_1$
, it follows that
![]() $\mathcal {X}_0\land \mathcal {X}_1$
is the infimum of
$\mathcal {X}_0\land \mathcal {X}_1$
is the infimum of
![]() $\mathcal {X}_0$
and
$\mathcal {X}_0$
and
![]() $\mathcal {X}_1$
.
$\mathcal {X}_1$
.
(ii) By definition
![]() $\mathcal {X}_0\lor \mathcal {X}_1=\mathcal {X}(\mathcal {X}_0\cup \mathcal {X}_1)=\mathcal {V}(\mathcal {X}_0\cup \mathcal {X}_1)^\uparrow $
, which is a
$\mathcal {X}_0\lor \mathcal {X}_1=\mathcal {X}(\mathcal {X}_0\cup \mathcal {X}_1)=\mathcal {V}(\mathcal {X}_0\cup \mathcal {X}_1)^\uparrow $
, which is a
![]() $\mathtt {DNA}$
-variety. Now suppose
$\mathtt {DNA}$
-variety. Now suppose
![]() $\mathcal {Y}$
is also a
$\mathcal {Y}$
is also a
![]() $\mathtt {DNA}$
-variety and
$\mathtt {DNA}$
-variety and
![]() $\mathcal {X}_0\cup \mathcal {X}_1\subseteq \mathcal {Y}$
. Then since
$\mathcal {X}_0\cup \mathcal {X}_1\subseteq \mathcal {Y}$
. Then since
![]() $\mathcal {Y}$
is also a variety it follows that
$\mathcal {Y}$
is also a variety it follows that
![]() $\mathcal {V}(\mathcal {X}_0\cup \mathcal {X}_1)\subseteq \mathcal {Y}$
and since
$\mathcal {V}(\mathcal {X}_0\cup \mathcal {X}_1)\subseteq \mathcal {Y}$
and since
![]() $\mathcal {Y}$
is also closed under core superalgebras it follows that
$\mathcal {Y}$
is also closed under core superalgebras it follows that
![]() $\mathcal {V}(\mathcal {X}_0\cup \mathcal {X}_1)^\uparrow =\mathcal {X}(\mathcal {X}_0\cup \mathcal {X}_1)\subseteq \mathcal {Y}$
and in turn gives us
$\mathcal {V}(\mathcal {X}_0\cup \mathcal {X}_1)^\uparrow =\mathcal {X}(\mathcal {X}_0\cup \mathcal {X}_1)\subseteq \mathcal {Y}$
and in turn gives us
![]() $\mathcal {X}(\mathcal {X}_0\cup \mathcal {X}_1 )=\mathcal {X}_0\lor \mathcal {X}_1$
is the supremum of
$\mathcal {X}(\mathcal {X}_0\cup \mathcal {X}_1 )=\mathcal {X}_0\lor \mathcal {X}_1$
is the supremum of
![]() $\mathcal {X}_0$
and
$\mathcal {X}_0$
and
![]() $\mathcal {X}_1$
.
$\mathcal {X}_1$
.
We denote the lattice of
![]() $\mathtt {DNA}$
-varieties by
$\mathtt {DNA}$
-varieties by
![]() $ \Lambda (\mathrm{HA}^\uparrow ) $
. As varieties of Heyting algebras also form a lattice
$ \Lambda (\mathrm{HA}^\uparrow ) $
. As varieties of Heyting algebras also form a lattice
![]() $ \Lambda (\mathrm{HA}) $
, one can then show that the map
$ \Lambda (\mathrm{HA}) $
, one can then show that the map
![]() $(-)^\uparrow :\Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathrm{HA}^\uparrow ) $
which assigns every variety of Heyting algebras to its negative closure is a lattice homomorphism.
$(-)^\uparrow :\Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathrm{HA}^\uparrow ) $
which assigns every variety of Heyting algebras to its negative closure is a lattice homomorphism.
Proposition 3.20. The map
![]() $(-)^\uparrow :\Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathrm{HA}^\uparrow ) $
is a bounded lattice homomorphism.
$(-)^\uparrow :\Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathrm{HA}^\uparrow ) $
is a bounded lattice homomorphism.
Proof. Obviously
![]() $(-)^\uparrow $
sends
$(-)^\uparrow $
sends
![]() $\bot _\Lambda (\mathrm{HA}) $
to
$\bot _\Lambda (\mathrm{HA}) $
to
![]() $\bot _\Lambda (\mathrm{HA}^\uparrow ) $
and
$\bot _\Lambda (\mathrm{HA}^\uparrow ) $
and
![]() $\top _\Lambda (\mathrm{HA}) $
to
$\top _\Lambda (\mathrm{HA}) $
to
![]() $\top _\Lambda (\mathrm{HA}^\uparrow ) $
, so it suffices to check that
$\top _\Lambda (\mathrm{HA}^\uparrow ) $
, so it suffices to check that
![]() $(-)^\uparrow $
preserves meets and joins.
$(-)^\uparrow $
preserves meets and joins.
(i) Consider two standard varieties
![]() $\mathcal {V}_0$
and
$\mathcal {V}_0$
and
![]() $\mathcal {V}_1$
. Notice that if there are
$\mathcal {V}_1$
. Notice that if there are
![]() $A\in \mathcal {V}_0$
and
$A\in \mathcal {V}_0$
and
![]() $B\in \mathcal {V}_1$
such that
$B\in \mathcal {V}_1$
such that
![]() $ A_{\neg }=H_{\neg }$
,
$ A_{\neg }=H_{\neg }$
,
![]() $B_{\neg }=H_{\neg }$
and
$B_{\neg }=H_{\neg }$
and
![]() $A\preceq H$
,
$A\preceq H$
,
![]() $B\preceq H $
, then
$B\preceq H $
, then
![]() $A\cap B\in \mathcal {V}_0\cap \mathcal {V}_1$
,
$A\cap B\in \mathcal {V}_0\cap \mathcal {V}_1$
,
![]() $(A\cap B)_{\neg }=H_{\neg }$
and
$(A\cap B)_{\neg }=H_{\neg }$
and
![]() $A\cap B\preceq H$
.
$A\cap B\preceq H$
.
 $$ \begin{align*} (\mathcal{V}_0\land \mathcal{V}_1)^\uparrow &= \{H: \exists A\in \mathcal{V}_0\cap \mathcal{V}_1 \text{ such that } A_{\neg}=H_{\neg} \text{ and } A\preceq H \}\\ &= \{H: \exists A\in \mathcal{V}_0( A_{\neg}=H_{\neg}, A\preceq H ) \}\cap \{H: \exists A\in \mathcal{V}_1 (A_{\neg}=H_{\neg}, A\preceq H )\}\\ & = \mathcal{V}^\uparrow_0 \land \mathcal{V}^\uparrow_1. \end{align*} $$
$$ \begin{align*} (\mathcal{V}_0\land \mathcal{V}_1)^\uparrow &= \{H: \exists A\in \mathcal{V}_0\cap \mathcal{V}_1 \text{ such that } A_{\neg}=H_{\neg} \text{ and } A\preceq H \}\\ &= \{H: \exists A\in \mathcal{V}_0( A_{\neg}=H_{\neg}, A\preceq H ) \}\cap \{H: \exists A\in \mathcal{V}_1 (A_{\neg}=H_{\neg}, A\preceq H )\}\\ & = \mathcal{V}^\uparrow_0 \land \mathcal{V}^\uparrow_1. \end{align*} $$
which shows that
![]() $(-)^\uparrow $
preserves the meet operator.
$(-)^\uparrow $
preserves the meet operator.
(ii) Consider two standard varieties
![]() $\mathcal {V}_0$
and
$\mathcal {V}_0$
and
![]() $\mathcal {V}_1$
, then we have by definition that
$\mathcal {V}_1$
, then we have by definition that
![]() $(\mathcal {V}_0\lor \mathcal {V}_1)^\uparrow =( \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1))^\uparrow $
and
$(\mathcal {V}_0\lor \mathcal {V}_1)^\uparrow =( \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1))^\uparrow $
and
![]() $ \mathcal {V}^\uparrow _0 \lor \mathcal {V}^\uparrow _1 = \mathcal {X}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)= \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)^\uparrow $
. It thus suffices to show that
$ \mathcal {V}^\uparrow _0 \lor \mathcal {V}^\uparrow _1 = \mathcal {X}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)= \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)^\uparrow $
. It thus suffices to show that
![]() $\mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^\uparrow = \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)^\uparrow $
.
$\mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^\uparrow = \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)^\uparrow $
.
![]() $(\subseteq )$
Let us suppose
$(\subseteq )$
Let us suppose
![]() $H\in (\mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1))^\uparrow $
which implies that there is some
$H\in (\mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1))^\uparrow $
which implies that there is some
![]() $K\in \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)$
such that
$K\in \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)$
such that
![]() $K_\neg = H_\neg $
and
$K_\neg = H_\neg $
and
![]() $K\preceq H$
. Then clearly
$K\preceq H$
. Then clearly
![]() $K\in \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)$
and thus
$K\in \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)$
and thus
![]() $H\in \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)^\uparrow $
.
$H\in \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)^\uparrow $
.
![]() $(\supseteq )$
Suppose now
$(\supseteq )$
Suppose now
![]() $H\in \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)^\uparrow $
, then for some
$H\in \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)^\uparrow $
, then for some
![]() $K\in \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)$
we have that
$K\in \mathcal {V}(\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1)$
we have that
![]() $K_\neg = H_\neg $
and
$K_\neg = H_\neg $
and
![]() $K\preceq H$
. In turn, this means that there exists a family of algebras
$K\preceq H$
. In turn, this means that there exists a family of algebras
![]() $\{A_i : i\in I \} \subseteq \mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1$
such that
$\{A_i : i\in I \} \subseteq \mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1$
such that
![]() $K \in \mathcal {V}(\{A_i : i\in I \})$
. Since each
$K \in \mathcal {V}(\{A_i : i\in I \})$
. Since each
![]() $A_i$
is in
$A_i$
is in
![]() $\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1$
, there exists algebras
$\mathcal {V}^\uparrow _0 \cup \mathcal {V}^\uparrow _1$
, there exists algebras
![]() $B_i\in \mathcal {V}_0 \cup \mathcal {V}_1$
such that
$B_i\in \mathcal {V}_0 \cup \mathcal {V}_1$
such that
![]() $B^i\preceq A^i$
and
$B^i\preceq A^i$
and
![]() $A^i_\neg = B^i_\neg $
for every
$A^i_\neg = B^i_\neg $
for every
![]() $i\leq n$
. Consequently
$i\leq n$
. Consequently
![]() $A_i \in \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^{\uparrow }$
for every
$A_i \in \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^{\uparrow }$
for every
![]() $i \leq n$
; and
$i \leq n$
; and
![]() $K \in \mathcal {V}(\{A_i : i\in I \}) \subseteq \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^{\uparrow }$
. Since
$K \in \mathcal {V}(\{A_i : i\in I \}) \subseteq \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^{\uparrow }$
. Since
![]() $\mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^{\uparrow }$
is a
$\mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^{\uparrow }$
is a
![]() $\mathtt {DNA}$
-variety and H is a core superalgebra of K, we conclude that
$\mathtt {DNA}$
-variety and H is a core superalgebra of K, we conclude that
![]() $H \in \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^{\uparrow }$
.
$H \in \mathcal {V}(\mathcal {V}_0\cup \mathcal {V}_1)^{\uparrow }$
.
We can already give a characterisation of
![]() $\mathtt {DNA}$
-varieties by adapting Tarski’s variety theorem to the case of
$\mathtt {DNA}$
-varieties by adapting Tarski’s variety theorem to the case of
![]() $\mathtt {DNA}$
-varieties.
$\mathtt {DNA}$
-varieties.
Theorem 3.21 (
 $\mathtt {DNA}$
-Tarski)
$\mathtt {DNA}$
-Tarski)
Let
![]() $\mathcal {C}$
be a class of Heyting algebras, then we have that
$\mathcal {C}$
be a class of Heyting algebras, then we have that
![]() $\mathcal {X}(\mathcal {C})=HSP(\mathcal {C})^\uparrow $
.Footnote
2
$\mathcal {X}(\mathcal {C})=HSP(\mathcal {C})^\uparrow $
.Footnote
2
Proof. By definition we have that
![]() $\mathcal {X}(\mathcal {C})=\mathcal {V}(\mathcal {C})^\uparrow $
and by Tarski’s theorem 2.3 we have that
$\mathcal {X}(\mathcal {C})=\mathcal {V}(\mathcal {C})^\uparrow $
and by Tarski’s theorem 2.3 we have that
![]() $\mathcal {V}(\mathcal {C})=HSP(\mathcal {C})$
. Therefore
$\mathcal {V}(\mathcal {C})=HSP(\mathcal {C})$
. Therefore
![]() $\mathcal {X}(\mathcal {C})=HSP(\mathcal {C})^\uparrow $
.
$\mathcal {X}(\mathcal {C})=HSP(\mathcal {C})^\uparrow $
.
Let us remark that we have given to both
![]() $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
![]() $\mathtt {DNA}$
-varieties a twofold characterisation. On the one hand, they can be described in terms of negative variants of some intermediate logics or in terms of negative closure of some variety of Heyting algebras. On the other hand, we can also consider
$\mathtt {DNA}$
-varieties a twofold characterisation. On the one hand, they can be described in terms of negative variants of some intermediate logics or in terms of negative closure of some variety of Heyting algebras. On the other hand, we can also consider
![]() $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
![]() $\mathtt {DNA}$
-varieties as sets of formulas closed under some conditions or as classes of algebras closed under some operations.
$\mathtt {DNA}$
-varieties as sets of formulas closed under some conditions or as classes of algebras closed under some operations.
3.4 The maps
 $Log^\neg $
and
$Log^\neg $
and
 $Var^\neg $
$Var^\neg $
There are two obvious ways to relate formulas and algebras. We define the map
![]() $Var^\neg $
sending sets of formulas to the class of Heyting algebras in which they are
$Var^\neg $
sending sets of formulas to the class of Heyting algebras in which they are
![]() $\mathtt {DNA}$
-valid and the map
$\mathtt {DNA}$
-valid and the map
![]() $Log^\neg $
sending classes of Heyting algebras to the set of their
$Log^\neg $
sending classes of Heyting algebras to the set of their
![]() $\mathtt {DNA}$
-validities. We have:
$\mathtt {DNA}$
-validities. We have:
 $$ \begin{align*} &Var^\neg: \Gamma \mapsto \{H\in \mathrm{HA} : H\vDash^{\neg} \Gamma \}; \\ &Log^\neg: \mathcal{C} \mapsto \{\varphi \in \mathcal{L}_P: \mathcal{C}\vDash^{\neg} \varphi \}. \end{align*} $$
$$ \begin{align*} &Var^\neg: \Gamma \mapsto \{H\in \mathrm{HA} : H\vDash^{\neg} \Gamma \}; \\ &Log^\neg: \mathcal{C} \mapsto \{\varphi \in \mathcal{L}_P: \mathcal{C}\vDash^{\neg} \varphi \}. \end{align*} $$
We say that a
![]() $\mathtt {DNA}$
-variety of Heyting algebras
$\mathtt {DNA}$
-variety of Heyting algebras
![]() $\mathcal {X}$
is
$\mathcal {X}$
is
![]() $\mathtt {DNA}$
-defined by a set of formulas
$\mathtt {DNA}$
-defined by a set of formulas
![]() $\Gamma $
if
$\Gamma $
if
![]() $\mathcal {X}=Var^\neg (\Gamma )$
. A class of Heyting algebras
$\mathcal {X}=Var^\neg (\Gamma )$
. A class of Heyting algebras
![]() $ \mathcal {C} $
is
$ \mathcal {C} $
is
![]() $\mathtt {DNA}$
-definable if there is a set
$\mathtt {DNA}$
-definable if there is a set
![]() $\Gamma $
of formulas such that
$\Gamma $
of formulas such that
![]() $\mathcal {C}=Var^\neg (\Gamma )$
. When the context is clear, we often drop the qualification
$\mathcal {C}=Var^\neg (\Gamma )$
. When the context is clear, we often drop the qualification
![]() $\mathtt {DNA}$
and talk simply of definability. We say that a
$\mathtt {DNA}$
and talk simply of definability. We say that a
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
is algebraically complete with respect to a class of Heyting algebras
$\Lambda $
is algebraically complete with respect to a class of Heyting algebras
![]() $\mathcal {C}$
if
$\mathcal {C}$
if
![]() $\Lambda =Log^\neg (\mathcal {C})$
. We will prove in the next section a definability theorem and an algebraic completeness theorem for
$\Lambda =Log^\neg (\mathcal {C})$
. We will prove in the next section a definability theorem and an algebraic completeness theorem for
![]() $\mathtt {DNA}$
-logics. We will thus establish that every
$\mathtt {DNA}$
-logics. We will thus establish that every
![]() $\mathtt {DNA}$
-variety is defined by its validities and that every
$\mathtt {DNA}$
-variety is defined by its validities and that every
![]() $\mathtt {DNA}$
-logic is complete with respect to its corresponding
$\mathtt {DNA}$
-logic is complete with respect to its corresponding
![]() $\mathtt {DNA}$
-variety.
$\mathtt {DNA}$
-variety.
We will next show that
![]() $Var^\neg (\Gamma )$
is always a
$Var^\neg (\Gamma )$
is always a
![]() $\mathtt {DNA}$
-variety and
$\mathtt {DNA}$
-variety and
![]() $Log^\neg (\mathcal {C})$
is always a
$Log^\neg (\mathcal {C})$
is always a
![]() $\mathtt {DNA}$
-logic. First we prove the following important lemma showing that the
$\mathtt {DNA}$
-logic. First we prove the following important lemma showing that the
![]() $\mathtt {DNA}$
-validity of a formula is preserved by the key operations of a
$\mathtt {DNA}$
-validity of a formula is preserved by the key operations of a
![]() $\mathtt {DNA}$
-variety.
$\mathtt {DNA}$
-variety.
Lemma 3.22 (Preservation of
 $\mathtt {DNA}$
-Validity)
$\mathtt {DNA}$
-Validity)
The
![]() $\mathtt {DNA}$
-validity of a formula
$\mathtt {DNA}$
-validity of a formula
![]() $\varphi $
is preserved by the operations of subalgebras, homomorphic images, products and core superalgebras, i.e.,
$\varphi $
is preserved by the operations of subalgebras, homomorphic images, products and core superalgebras, i.e.,
-
(i) if
 $H\vDash ^\neg \varphi $
and
$H\vDash ^\neg \varphi $
and
 $K\preceq H$
, then
$K\preceq H$
, then
 $K\vDash ^\neg \varphi $
;
$K\vDash ^\neg \varphi $
; -
(ii) if
 $H\vDash ^\neg \varphi $
and
$H\vDash ^\neg \varphi $
and
 $H\twoheadrightarrow K$
, then
$H\twoheadrightarrow K$
, then
 $K\vDash ^\neg \varphi $
;
$K\vDash ^\neg \varphi $
; -
(iii) if
 $A_i\vDash ^\neg \varphi $
for all
$A_i\vDash ^\neg \varphi $
for all
 $i\in I$
of a family
$i\in I$
of a family
 $ \{A_i \}_{i\in I}$
of algebras, then
$ \{A_i \}_{i\in I}$
of algebras, then
 $\prod _{i\in I} A_i \vDash ^\neg \varphi $
; and
$\prod _{i\in I} A_i \vDash ^\neg \varphi $
; and -
(iv) if
 $H\vDash ^\neg \varphi $
and for some K such that
$H\vDash ^\neg \varphi $
and for some K such that
 $K_\neg =H_\neg $
we have that
$K_\neg =H_\neg $
we have that
 $H\preceq K$
, then
$H\preceq K$
, then
 $K\vDash ^\neg \varphi $
.
$K\vDash ^\neg \varphi $
.
Proof. (i) By contraposition: If
![]() $\textrm{(}K,V^{\neg }\textrm{)}\nvDash ^\neg \varphi $
for some
$\textrm{(}K,V^{\neg }\textrm{)}\nvDash ^\neg \varphi $
for some
![]() $\mathtt {DNA}$
-valuation
$\mathtt {DNA}$
-valuation
![]() $V^\neg $
, then
$V^\neg $
, then
![]() $H,V^{\neg }\nvDash ^\neg \varphi $
.
$H,V^{\neg }\nvDash ^\neg \varphi $
.
(ii) Let
![]() $f:H\twoheadrightarrow K$
be a surjective homomorphism. By contraposition: If
$f:H\twoheadrightarrow K$
be a surjective homomorphism. By contraposition: If
![]() $K\nvDash ^\neg \varphi $
, then by Proposition 3.11 it follows that
$K\nvDash ^\neg \varphi $
, then by Proposition 3.11 it follows that
![]() . Since validity is preserved by homomorphic images, it follows that
. Since validity is preserved by homomorphic images, it follows that
![]() and therefore, by Proposition 3.11,
and therefore, by Proposition 3.11,
![]() $H\nvDash ^\neg \varphi $
.
$H\nvDash ^\neg \varphi $
.
(iii) The claim follows readily by noticing
![]() $\left ( \prod _{i\in I} A_i \right )_{\neg } = \prod _{i\in I} \left ( A_i \right )_{\neg }$
, and so
$\left ( \prod _{i\in I} A_i \right )_{\neg } = \prod _{i\in I} \left ( A_i \right )_{\neg }$
, and so
![]() $\mathtt {DNA}$
-valuations over
$\mathtt {DNA}$
-valuations over
![]() $\prod _{i\in I} A_i$
are all and only the functions of the form
$\prod _{i\in I} A_i$
are all and only the functions of the form
![]() $V^\neg (p) = \left \langle V^\neg _i(p) : i\in I \right \rangle $
where every
$V^\neg (p) = \left \langle V^\neg _i(p) : i\in I \right \rangle $
where every
![]() $V^\neg _i$
is some
$V^\neg _i$
is some
![]() $\mathtt {DNA}$
-valuation over
$\mathtt {DNA}$
-valuation over
![]() $A_i$
.
$A_i$
.
(iv) Suppose by reductio ad absurdum that
![]() $K\nvDash ^\neg \varphi $
. Then for some valuation
$K\nvDash ^\neg \varphi $
. Then for some valuation
![]() $V^\neg $
we have
$V^\neg $
we have
![]() $(K,V^{\neg })\nvDash ^\neg \varphi $
. Since
$(K,V^{\neg })\nvDash ^\neg \varphi $
. Since
![]() $H_\neg =K_\neg $
and
$H_\neg =K_\neg $
and
![]() $H\preceq K$
,
$H\preceq K$
,
![]() $V^\neg $
is a valuation over H and
$V^\neg $
is a valuation over H and
![]() .
.
It follows immediately that for every set of formulas
![]() $\Gamma $
the class of Heyting algebras
$\Gamma $
the class of Heyting algebras
![]() $Var^\neg (\Gamma )$
is a
$Var^\neg (\Gamma )$
is a
![]() $\mathtt {DNA}$
-variety.
$\mathtt {DNA}$
-variety.
Proposition 3.23. The class of Heyting algebras
![]() $Var^\neg (\Gamma )$
is a
$Var^\neg (\Gamma )$
is a
![]() $\mathtt {DNA}$
-variety.
$\mathtt {DNA}$
-variety.
Proof. Consider any set of formulas
![]() $\Gamma $
, then by the previous Lemma 3.22 it follows that the corresponding set
$\Gamma $
, then by the previous Lemma 3.22 it follows that the corresponding set
![]() $Var^\neg (\Gamma )$
is closed under the operations of taking subalgebras, homomorphic images, products and core superalgebras. Therefore, it follows by Proposition 3.18 that it is a
$Var^\neg (\Gamma )$
is closed under the operations of taking subalgebras, homomorphic images, products and core superalgebras. Therefore, it follows by Proposition 3.18 that it is a
![]() $\mathtt {DNA}$
-variety.
$\mathtt {DNA}$
-variety.
It is a straightforward consequence of Proposition 3.23 that every
![]() $\mathtt {DNA}$
-definable class of Heyting algebras is also a
$\mathtt {DNA}$
-definable class of Heyting algebras is also a
![]() $\mathtt {DNA}$
-variety. The next proposition shows that for every class
$\mathtt {DNA}$
-variety. The next proposition shows that for every class
![]() $\mathcal {C}$
of Heyting algebras its set of validities
$\mathcal {C}$
of Heyting algebras its set of validities
![]() $Log^\neg (\mathcal {C})$
is a
$Log^\neg (\mathcal {C})$
is a
![]() $\mathtt {DNA}$
-logic.
$\mathtt {DNA}$
-logic.
Proposition 3.24. The class of formulas
![]() $ Log^\neg (\mathcal {C}) $
is a
$ Log^\neg (\mathcal {C}) $
is a
![]() $\mathtt {DNA}$
-logic.
$\mathtt {DNA}$
-logic.
Proof. We check that for any class
![]() $\mathcal {C}$
of Heyting algebras the corresponding set of formulas
$\mathcal {C}$
of Heyting algebras the corresponding set of formulas
![]() $ Log^\neg (\mathcal {C}) $
is a
$ Log^\neg (\mathcal {C}) $
is a
![]() $\mathtt {DNA}$
-logic. In particular, we show that
$\mathtt {DNA}$
-logic. In particular, we show that
![]() $ Log^\neg (\mathcal {C})= Log(\mathcal {C})^\neg $
. We have:
$ Log^\neg (\mathcal {C})= Log(\mathcal {C})^\neg $
. We have:

This shows that
![]() $ Log^\neg (\mathcal {C}) $
is the negative variant of
$ Log^\neg (\mathcal {C}) $
is the negative variant of
![]() $Log(\mathcal {C})$
.
$Log(\mathcal {C})$
.
3.5 Duality between
 $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
 $\mathtt {DNA}$
-varieties
$\mathtt {DNA}$
-varieties
We will now prove our main result about
![]() $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
![]() $\mathtt {DNA}$
-varieties, showing that their lattices are dually isomorphic. Notice that, so far, we have considered
$\mathtt {DNA}$
-varieties, showing that their lattices are dually isomorphic. Notice that, so far, we have considered
![]() $Log^\neg $
as a map defined over arbitrary classes of Heyting algebras and
$Log^\neg $
as a map defined over arbitrary classes of Heyting algebras and
![]() $Var^\neg $
as a map defined over arbitrary sets of propositional formulas. Now we restrict our attention to the case in which the domain of
$Var^\neg $
as a map defined over arbitrary sets of propositional formulas. Now we restrict our attention to the case in which the domain of
![]() $Var^\neg $
is the lattice of
$Var^\neg $
is the lattice of
![]() $\mathtt {DNA}$
-logics
$\mathtt {DNA}$
-logics
![]() $ \Lambda (\mathtt {IPC}^\neg ) $
and the domain of
$ \Lambda (\mathtt {IPC}^\neg ) $
and the domain of
![]() $Log^\neg $
is the lattice of
$Log^\neg $
is the lattice of
![]() $\mathtt {DNA}$
-varieties
$\mathtt {DNA}$
-varieties
![]() $ \Lambda (\mathrm{HA}^\uparrow ) $
.Footnote
3
$ \Lambda (\mathrm{HA}^\uparrow ) $
.Footnote
3
Since we have shown above that
![]() $Var^\neg (\Gamma )$
is always a
$Var^\neg (\Gamma )$
is always a
![]() $\mathtt {DNA}$
-variety and
$\mathtt {DNA}$
-variety and
![]() $Log^\neg (\mathcal {C})$
is always a
$Log^\neg (\mathcal {C})$
is always a
![]() $\mathtt {DNA}$
-logic it follows that we have two maps:
$\mathtt {DNA}$
-logic it follows that we have two maps:
 $$ \begin{align*} &Var^\neg: \Lambda(\mathtt{IPC}^\neg) \rightarrow \Lambda(\text{HA}^\uparrow); \\[2pt] &Log^\neg: \Lambda(\text{HA}^\uparrow) \rightarrow \Lambda(\mathtt{IPC}^\neg). \end{align*} $$
$$ \begin{align*} &Var^\neg: \Lambda(\mathtt{IPC}^\neg) \rightarrow \Lambda(\text{HA}^\uparrow); \\[2pt] &Log^\neg: \Lambda(\text{HA}^\uparrow) \rightarrow \Lambda(\mathtt{IPC}^\neg). \end{align*} $$
We will now prove that these two maps describe a dual isomorphism between the lattice of
![]() $\mathtt {DNA}$
-logics and the lattice of
$\mathtt {DNA}$
-logics and the lattice of
![]() $\mathtt {DNA}$
-varieties. Our proof essentially relies on the standard isomorphism between the lattice of intermediate logics and the lattice of varieties of Heyting algebras. An alternative proof, making use of Lindenbaum–Tarski algebras for
$\mathtt {DNA}$
-varieties. Our proof essentially relies on the standard isomorphism between the lattice of intermediate logics and the lattice of varieties of Heyting algebras. An alternative proof, making use of Lindenbaum–Tarski algebras for
![]() $\mathtt {DNA}$
-logics, was given in [Reference Quadrellaro41]. Let us introduce the following diagram:
$\mathtt {DNA}$
-logics, was given in [Reference Quadrellaro41]. Let us introduce the following diagram:

where the four objects in the diagram are the following:
 $$ \begin{align*} &\Lambda(\mathtt{IPC}) \text{ is the lattice of intermediate logics;} \\ &\Lambda(\text{HA}) \text{ is the lattice of varieties of Heyting algebras;} \\ &\Lambda(\mathtt{IPC}^\neg) \text{ is the lattice of }\mathtt{DNA}\text{-logics;} \\ &\Lambda(\text{HA}^\uparrow) \text{ is the lattice of }\mathtt{DNA}\text{-varieties.} \end{align*} $$
$$ \begin{align*} &\Lambda(\mathtt{IPC}) \text{ is the lattice of intermediate logics;} \\ &\Lambda(\text{HA}) \text{ is the lattice of varieties of Heyting algebras;} \\ &\Lambda(\mathtt{IPC}^\neg) \text{ is the lattice of }\mathtt{DNA}\text{-logics;} \\ &\Lambda(\text{HA}^\uparrow) \text{ is the lattice of }\mathtt{DNA}\text{-varieties.} \end{align*} $$
And the arrows are the following. Firstly,
![]() $(-)^\neg : \Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathtt {IPC}^\neg ) $
is the map we introduced above that assigns to every intermediate logic L its negative variant
$(-)^\neg : \Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathtt {IPC}^\neg ) $
is the map we introduced above that assigns to every intermediate logic L its negative variant
![]() $L^\neg $
. Secondly,
$L^\neg $
. Secondly,
![]() $(-)^\uparrow : \Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathrm{HA}^\uparrow ) $
is the map that assigns to each variety of Heyting algebras
$(-)^\uparrow : \Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathrm{HA}^\uparrow ) $
is the map that assigns to each variety of Heyting algebras
![]() $\mathcal {V}$
its negative closure
$\mathcal {V}$
its negative closure
![]() $\mathcal {V}^\uparrow $
. The isomorphism
$\mathcal {V}^\uparrow $
. The isomorphism
![]() $\Lambda (\mathtt {IPC}) \cong ^{op}\Lambda (\mathrm{HA}) $
is given by the standard duality for intermediate logics and varieties of Heyting algebras. The two maps of this bijection are
$\Lambda (\mathtt {IPC}) \cong ^{op}\Lambda (\mathrm{HA}) $
is given by the standard duality for intermediate logics and varieties of Heyting algebras. The two maps of this bijection are
![]() $Log: \Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathtt {IPC}) $
and
$Log: \Lambda (\mathrm{HA}) \rightarrow \Lambda (\mathtt {IPC}) $
and
![]() $Var: \Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathrm{HA}) $
, which we have defined in the preliminaries. By using the fact that
$Var: \Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathrm{HA}) $
, which we have defined in the preliminaries. By using the fact that
![]() $\Lambda (\mathtt {IPC}) \cong ^{op}\Lambda (\mathrm{HA}) $
we show now that also
$\Lambda (\mathtt {IPC}) \cong ^{op}\Lambda (\mathrm{HA}) $
we show now that also
![]() $\Lambda (\mathtt {IPC}^\neg ) \cong ^{op} \Lambda (\mathrm{HA}^\uparrow ) $
holds. We proceed as follows. First we show that the diagram that we have described commutes, then we show that
$\Lambda (\mathtt {IPC}^\neg ) \cong ^{op} \Lambda (\mathrm{HA}^\uparrow ) $
holds. We proceed as follows. First we show that the diagram that we have described commutes, then we show that
![]() $Var^\neg $
and
$Var^\neg $
and
![]() $Log^\neg $
are inverse maps of each other and finally we prove they are order-reversing homomorphisms between
$Log^\neg $
are inverse maps of each other and finally we prove they are order-reversing homomorphisms between
![]() $ \Lambda (\mathtt {IPC}^\neg ) $
and
$ \Lambda (\mathtt {IPC}^\neg ) $
and
![]() $ \Lambda (\mathrm{HA}^\uparrow ) $
. Thus we will obtain a dual isomorphism
$ \Lambda (\mathrm{HA}^\uparrow ) $
. Thus we will obtain a dual isomorphism
![]() $\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
.
$\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
.
3.5.1 Commutativity of the diagram
We first prove the two following propositions, thereby establishing that our diagram commutes.
Proposition 3.25. For every intermediate logic L we have
![]() $Var^{\neg }(L^{\neg })= Var(L)^\uparrow $
.
$Var^{\neg }(L^{\neg })= Var(L)^\uparrow $
.

Proof.
![]() $(\subseteq )$
Consider any Heyting algebra
$(\subseteq )$
Consider any Heyting algebra
![]() $H\in Var^{\neg }(L^{\neg })$
. We have
$H\in Var^{\neg }(L^{\neg })$
. We have
![]() $H\vDash ^\neg L^{\neg }$
and so by Proposition 3.14 that
$H\vDash ^\neg L^{\neg }$
and so by Proposition 3.14 that
![]() $\langle H_\neg \rangle \vDash L $
. So we have
$\langle H_\neg \rangle \vDash L $
. So we have
![]() $\langle H_\neg \rangle \in Var(L)$
and since
$\langle H_\neg \rangle \in Var(L)$
and since
![]() $\langle H_\neg \rangle _\neg =H_\neg $
and
$\langle H_\neg \rangle _\neg =H_\neg $
and
![]() $\langle H_\neg \rangle \preceq H$
also
$\langle H_\neg \rangle \preceq H$
also
![]() $H\in Var(L)^\uparrow $
.
$H\in Var(L)^\uparrow $
.
![]() $(\supseteq )$
Consider any Heyting algebra
$(\supseteq )$
Consider any Heyting algebra
![]() $H\in Var(L)^\uparrow $
, then there is some
$H\in Var(L)^\uparrow $
, then there is some
![]() $K\in Var(L)$
such that
$K\in Var(L)$
such that
![]() $K\preceq H$
and
$K\preceq H$
and
![]() $H_{\neg }=K_{\neg }$
. Then
$H_{\neg }=K_{\neg }$
. Then
![]() $K\vDash L$
and by Lemma 3.12 we obtain
$K\vDash L$
and by Lemma 3.12 we obtain
![]() $K\vDash ^\neg L^\neg $
, which entails
$K\vDash ^\neg L^\neg $
, which entails
![]() $K\in Var^\neg (L^\neg )$
. Finally, since
$K\in Var^\neg (L^\neg )$
. Finally, since
![]() $\mathtt {DNA}$
-varieties are closed under core superalgebra, it follows that
$\mathtt {DNA}$
-varieties are closed under core superalgebra, it follows that
![]() $H\in Var^\neg (L^\neg )$
.□
$H\in Var^\neg (L^\neg )$
.□
Proposition 3.26. For every variety
![]() $\mathcal {V}$
of Heyting algebras
$\mathcal {V}$
of Heyting algebras
![]() $Log^{\neg }(\mathcal {V}^\uparrow )= Log(\mathcal {V})^\neg $
.
$Log^{\neg }(\mathcal {V}^\uparrow )= Log(\mathcal {V})^\neg $
.

Proof. We prove both directions by contraposition.
![]() $(\subseteq )$
Suppose
$(\subseteq )$
Suppose
![]() $\varphi \notin Log(\mathcal {V})^\neg $
, then
$\varphi \notin Log(\mathcal {V})^\neg $
, then
![]() , so there is some Heyting algebra
, so there is some Heyting algebra
![]() $H\in \mathcal {V}$
such that
$H\in \mathcal {V}$
such that
![]() . By Proposition 3.11 this means that
. By Proposition 3.11 this means that
![]() $H \nvDash ^\neg \varphi $
and so, since
$H \nvDash ^\neg \varphi $
and so, since
![]() $H\in \mathcal {V} \subseteq \mathcal {V}^\uparrow $
, we also have
$H\in \mathcal {V} \subseteq \mathcal {V}^\uparrow $
, we also have
![]() $\varphi \notin Log^{\neg }(\mathcal {V}^\uparrow )$
.
$\varphi \notin Log^{\neg }(\mathcal {V}^\uparrow )$
.
![]() $(\supseteq )$
Suppose
$(\supseteq )$
Suppose
![]() $\varphi \notin Log^{\neg }(\mathcal {V}^\uparrow )$
. It follows that there is some Heyting algebra
$\varphi \notin Log^{\neg }(\mathcal {V}^\uparrow )$
. It follows that there is some Heyting algebra
![]() $H\in \mathcal {V}^\uparrow $
such that
$H\in \mathcal {V}^\uparrow $
such that
![]() $H\nvDash ^\neg \varphi $
, hence by Lemma 3.13 we have that
$H\nvDash ^\neg \varphi $
, hence by Lemma 3.13 we have that
![]() $\langle H_\neg \rangle \nvDash ^\neg \varphi $
. It follows by Proposition 3.11 that
$\langle H_\neg \rangle \nvDash ^\neg \varphi $
. It follows by Proposition 3.11 that
![]() . Now, since
. Now, since
![]() $H\in \mathcal {V}^\uparrow $
, we have for some
$H\in \mathcal {V}^\uparrow $
, we have for some
![]() $K\in \mathcal {V}$
that
$K\in \mathcal {V}$
that
![]() $K\preceq H$
and
$K\preceq H$
and
![]() $K_\neg = H_\neg $
. Therefore
$K_\neg = H_\neg $
. Therefore
![]() $\langle H_\neg \rangle \preceq K$
and
$\langle H_\neg \rangle \preceq K$
and
![]() $\langle H _\neg \rangle \in \mathcal {V}$
. Finally, since
$\langle H _\neg \rangle \in \mathcal {V}$
. Finally, since
![]() we get that
we get that
![]() and hence
and hence
![]() $\varphi \notin Log(\mathcal {V})^\neg $
.
$\varphi \notin Log(\mathcal {V})^\neg $
.
In particular, when
![]() $\mathcal {V}$
is itself a
$\mathcal {V}$
is itself a
![]() $\mathtt {DNA}$
-variety we obtain the following corollary.
$\mathtt {DNA}$
-variety we obtain the following corollary.
Corollary 3.27. For every
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
we have
$\mathcal {X}$
we have
![]() $Log^{\neg }(\mathcal {X})= Log(\mathcal {X})^\neg $
.
$Log^{\neg }(\mathcal {X})= Log(\mathcal {X})^\neg $
.
3.5.2 Definability theorem and algebraic completeness
By relying on the commutativity result described above, we can now prove that the two maps
![]() $Var^\neg $
and
$Var^\neg $
and
![]() $Log^\neg $
are inverse of one another. It is then easy to see that suitable versions of the definability theorem and algebraic completeness follow from this result.
$Log^\neg $
are inverse of one another. It is then easy to see that suitable versions of the definability theorem and algebraic completeness follow from this result.
Proposition 3.28.
![]() $Var^\neg \circ Log^\neg = 1_{\Lambda (\mathrm{HA}^\uparrow ) }$
.
$Var^\neg \circ Log^\neg = 1_{\Lambda (\mathrm{HA}^\uparrow ) }$
.
Proof. For any
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
we have:
$\mathcal {X}$
we have:
 $$ \begin{align*} Var^\neg(Log^\neg (\mathcal{X})) &= Var^\neg(Log (\mathcal{X})^\neg) & \text{(by Corollary 3.27)}\\ &=Var(Log (\mathcal{X}))^\uparrow & \text{(by Proposition 3.25)}\\ &=\mathcal{X}^\uparrow & \text{(by standard duality)}\\ &=\mathcal{X}. & \end{align*} $$
$$ \begin{align*} Var^\neg(Log^\neg (\mathcal{X})) &= Var^\neg(Log (\mathcal{X})^\neg) & \text{(by Corollary 3.27)}\\ &=Var(Log (\mathcal{X}))^\uparrow & \text{(by Proposition 3.25)}\\ &=\mathcal{X}^\uparrow & \text{(by standard duality)}\\ &=\mathcal{X}. & \end{align*} $$
And thus
![]() $Var^\neg \circ Log^\neg = 1_{\Lambda (\mathrm{HA}^\uparrow ) }$
.
$Var^\neg \circ Log^\neg = 1_{\Lambda (\mathrm{HA}^\uparrow ) }$
.
Theorem 3.29 (Definability Theorem)
Every
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
is defined by its
$\mathcal {X}$
is defined by its
![]() $\mathtt {DNA}$
-validities, i.e., for every Heyting algebra H,
$\mathtt {DNA}$
-validities, i.e., for every Heyting algebra H,
We then have that every
![]() $\mathtt {DNA}$
-variety is
$\mathtt {DNA}$
-variety is
![]() $\mathtt {DNA}$
-definable. Moreover, by Proposition 3.23 we have that every
$\mathtt {DNA}$
-definable. Moreover, by Proposition 3.23 we have that every
![]() $\mathtt {DNA}$
-definable class is also a
$\mathtt {DNA}$
-definable class is also a
![]() $\mathtt {DNA}$
-variety, the following corollary also follows.
$\mathtt {DNA}$
-variety, the following corollary also follows.
Corollary 3.30 (Birkhoff Theorem for
 $\mathtt {DNA}$
-Varieties)
$\mathtt {DNA}$
-Varieties)
A class of Heyting algebras
![]() $\mathcal {C}$
is a
$\mathcal {C}$
is a
![]() $\mathtt {DNA}$
-variety if and only if it is
$\mathtt {DNA}$
-variety if and only if it is
![]() $\mathtt {DNA}$
-definable by some set of formulas.
$\mathtt {DNA}$
-definable by some set of formulas.
The algebraic completeness of
![]() $\mathtt {DNA}$
-logics is proved as follows.
$\mathtt {DNA}$
-logics is proved as follows.
Proposition 3.31.
![]() $Log^\neg \circ Var^\neg = 1_{\Lambda (\mathtt {IPC}^\neg ) }$
.
$Log^\neg \circ Var^\neg = 1_{\Lambda (\mathtt {IPC}^\neg ) }$
.
Proof. For any
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\Lambda =L^\neg $
we have:
$\Lambda =L^\neg $
we have:
 $$ \begin{align*} Log^\neg(Var^\neg(\Lambda)) &= Log^\neg(Var^\neg(L^\neg)) &\\[-1pt] &=Log^\neg( Var(L)^\uparrow) & \text{(by Proposition 3.25)}\\[-1pt] &=Log(Var(L))^\neg & \text{(by Proposition 3.26)}\\[-1pt] &=L^\neg & \text{(by standard duality)}\\[-1pt] &=\Lambda. & \end{align*} $$
$$ \begin{align*} Log^\neg(Var^\neg(\Lambda)) &= Log^\neg(Var^\neg(L^\neg)) &\\[-1pt] &=Log^\neg( Var(L)^\uparrow) & \text{(by Proposition 3.25)}\\[-1pt] &=Log(Var(L))^\neg & \text{(by Proposition 3.26)}\\[-1pt] &=L^\neg & \text{(by standard duality)}\\[-1pt] &=\Lambda. & \end{align*} $$
And thus
![]() $Log^\neg \circ Var^\neg = 1_{\Lambda (\mathtt {IPC}^\neg ) }$
.
$Log^\neg \circ Var^\neg = 1_{\Lambda (\mathtt {IPC}^\neg ) }$
.
Theorem 3.32 (Algebraic Completeness)
Every
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
is complete with respect to its corresponding
$\Lambda $
is complete with respect to its corresponding
![]() $\mathtt {DNA}$
-variety, i.e., for every
$\mathtt {DNA}$
-variety, i.e., for every
![]() $\varphi \in \mathcal {L}_P$
,
$\varphi \in \mathcal {L}_P$
,
3.5.3 Dual isomorphism
Finally, by relying on the standard dual isomorphism
![]() $\Lambda (\mathrm{HA}) \cong ^{op}\Lambda (\mathtt {IPC}) $
and the commutative square above, it is easy to show that
$\Lambda (\mathrm{HA}) \cong ^{op}\Lambda (\mathtt {IPC}) $
and the commutative square above, it is easy to show that
![]() $Var^\neg $
and
$Var^\neg $
and
![]() $Log^\neg $
are order-reversing homomorphisms that invert the lattice structure of
$Log^\neg $
are order-reversing homomorphisms that invert the lattice structure of
![]() $ \Lambda (\mathtt {IPC}^\neg ) $
and
$ \Lambda (\mathtt {IPC}^\neg ) $
and
![]() $ \Lambda (\mathrm{HA}^\uparrow ) $
.
$ \Lambda (\mathrm{HA}^\uparrow ) $
.
Proposition 3.33.
![]() $Var^\neg $
is an order-reversing homomorphism.
$Var^\neg $
is an order-reversing homomorphism.
Proof. It suffices to check that
![]() $Var^\neg $
inverts meet and join. Let
$Var^\neg $
inverts meet and join. Let
![]() $\Lambda _0,\Lambda _1$
be two
$\Lambda _0,\Lambda _1$
be two
![]() $\mathtt {DNA}$
-logics such that
$\mathtt {DNA}$
-logics such that
![]() $\Lambda _0=L_0^\neg $
and
$\Lambda _0=L_0^\neg $
and
![]() $\Lambda _1=L_1^\neg $
. The case for
$\Lambda _1=L_1^\neg $
. The case for
![]() $\land $
is as follows:
$\land $
is as follows:
 $$ \begin{align*} Var^\neg(\Lambda_0\land \Lambda_1) &= Var^\neg(L_0^\neg\land L_1^\neg) & \text{ }\\[-1pt] &= Var^\neg((L_0\land L_1)^\neg) & \text{(by Proposition 3.5)}\\[-1pt] &= Var(L_0\land L_1)^\uparrow & \text{(by Proposition 3.25)} \\[-1pt] &= (Var(L_0) \lor Var (L_1) )^\uparrow & \text{(by standard duality)} \\[-1pt] & = Var(L_0)^\uparrow \lor Var (L_1)^\uparrow & \text{(by Proposition 3.20)} \\[-1pt] & =Var^\neg(L_0^\neg) \lor Var^\neg(L_1^\neg) & \text{(by Proposition 3.25)} \\[-1pt] & =Var^\neg(\Lambda_0) \lor Var^\neg(\Lambda_1). & \end{align*} $$
$$ \begin{align*} Var^\neg(\Lambda_0\land \Lambda_1) &= Var^\neg(L_0^\neg\land L_1^\neg) & \text{ }\\[-1pt] &= Var^\neg((L_0\land L_1)^\neg) & \text{(by Proposition 3.5)}\\[-1pt] &= Var(L_0\land L_1)^\uparrow & \text{(by Proposition 3.25)} \\[-1pt] &= (Var(L_0) \lor Var (L_1) )^\uparrow & \text{(by standard duality)} \\[-1pt] & = Var(L_0)^\uparrow \lor Var (L_1)^\uparrow & \text{(by Proposition 3.20)} \\[-1pt] & =Var^\neg(L_0^\neg) \lor Var^\neg(L_1^\neg) & \text{(by Proposition 3.25)} \\[-1pt] & =Var^\neg(\Lambda_0) \lor Var^\neg(\Lambda_1). & \end{align*} $$
The case for
![]() $\lor $
is analogous.
$\lor $
is analogous.
Proposition 3.34
![]() $Log^\neg $
is an order-reversing homomorphism.
$Log^\neg $
is an order-reversing homomorphism.
Proof. It suffices to check that
![]() $Log^\neg $
inverts meet and join. Let
$Log^\neg $
inverts meet and join. Let
![]() $\mathcal {X}_0,\mathcal {X}_1$
be two
$\mathcal {X}_0,\mathcal {X}_1$
be two
![]() $\mathtt {DNA}$
-varieties such that
$\mathtt {DNA}$
-varieties such that
![]() $\mathcal {X}_0=\mathcal {V}^\uparrow _0$
and
$\mathcal {X}_0=\mathcal {V}^\uparrow _0$
and
![]() $\mathcal {X}_1=\mathcal {V}^\uparrow _1$
. The case for
$\mathcal {X}_1=\mathcal {V}^\uparrow _1$
. The case for
![]() $\land $
is as follows:
$\land $
is as follows:
 $$ \begin{align*} Log^\neg(\mathcal{X}_0\land \mathcal{X}_0) &=Log^\neg(\mathcal{V}^\uparrow_0\land \mathcal{V}^\uparrow_1) & \\[-1pt] &= Log^\neg( (\mathcal{V}_0\land \mathcal{V}_1)^\uparrow) & \text{(by Proposition 3.20)}\\[-1pt] & =Log(\mathcal{V}_0\land \mathcal{V}_1)^\neg & \text{(by Proposition 3.26)} \\[-1pt] &= (Log(\mathcal{V}_0)\lor Log(\mathcal{V}_1))^\neg & \text{(by standard duality)} \\[-1pt] & =Log(\mathcal{V}_0)^\neg\lor Log(\mathcal{V}_1)^\neg & \text{(by Proposition 3.5)} \\[-1pt] &= Log^\neg(\mathcal{V}^\uparrow_0)\lor Log^\neg(\mathcal{V}^\uparrow_1) & \text{(by Proposition 3.26)} \\[-1pt] &= Log^\neg(\mathcal{X}_0)\lor Log^\neg(\mathcal{X}_1). & \end{align*} $$
$$ \begin{align*} Log^\neg(\mathcal{X}_0\land \mathcal{X}_0) &=Log^\neg(\mathcal{V}^\uparrow_0\land \mathcal{V}^\uparrow_1) & \\[-1pt] &= Log^\neg( (\mathcal{V}_0\land \mathcal{V}_1)^\uparrow) & \text{(by Proposition 3.20)}\\[-1pt] & =Log(\mathcal{V}_0\land \mathcal{V}_1)^\neg & \text{(by Proposition 3.26)} \\[-1pt] &= (Log(\mathcal{V}_0)\lor Log(\mathcal{V}_1))^\neg & \text{(by standard duality)} \\[-1pt] & =Log(\mathcal{V}_0)^\neg\lor Log(\mathcal{V}_1)^\neg & \text{(by Proposition 3.5)} \\[-1pt] &= Log^\neg(\mathcal{V}^\uparrow_0)\lor Log^\neg(\mathcal{V}^\uparrow_1) & \text{(by Proposition 3.26)} \\[-1pt] &= Log^\neg(\mathcal{X}_0)\lor Log^\neg(\mathcal{X}_1). & \end{align*} $$
The case for
![]() $\lor $
is analogous.
$\lor $
is analogous.
It is a consequence of the previous results that
![]() $Var^\neg $
and
$Var^\neg $
and
![]() $Log^\neg $
are two order-reversing homomorphisms between
$Log^\neg $
are two order-reversing homomorphisms between
![]() $\Lambda (\mathtt {IPC}^\neg ) $
and
$\Lambda (\mathtt {IPC}^\neg ) $
and
![]() $\Lambda (\mathrm{HA}^\uparrow ) $
which are inverse of one another. The following duality theorem follows.
$\Lambda (\mathrm{HA}^\uparrow ) $
which are inverse of one another. The following duality theorem follows.
Theorem 3.35 (Duality)
The lattice of
![]() $\mathtt {DNA}$
-logics is dually isomorphic to the lattice of
$\mathtt {DNA}$
-logics is dually isomorphic to the lattice of
![]() $\mathtt {DNA}$
-varieties of Heyting algebras, i.e.,
$\mathtt {DNA}$
-varieties of Heyting algebras, i.e.,
![]() $\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
.
$\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
.
4
 $\mathtt {DNA}$
-varieties
$\mathtt {DNA}$
-varieties
In this section we prove some further results on
![]() $\mathtt {DNA}$
-varieties. Firstly, we investigate the relation between
$\mathtt {DNA}$
-varieties. Firstly, we investigate the relation between
![]() $\mathtt {DNA}$
-logics and the intermediate logics they are a negative variant of, and we characterize maximal and minimal elements in the sublattice of intermediate logics which have the same negative variant. We introduce regularly generated Heyting algebras and we use them to characterize the maximal logics with a negative variant. We prove for
$\mathtt {DNA}$
-logics and the intermediate logics they are a negative variant of, and we characterize maximal and minimal elements in the sublattice of intermediate logics which have the same negative variant. We introduce regularly generated Heyting algebras and we use them to characterize the maximal logics with a negative variant. We prove for
![]() $\mathtt {DNA}$
-varieties a suitable version of two key results of universal algebra, namely the Tarski and Birkhoff variety theorems. We introduce a suitable notion of local finiteness for
$\mathtt {DNA}$
-varieties a suitable version of two key results of universal algebra, namely the Tarski and Birkhoff variety theorems. We introduce a suitable notion of local finiteness for
![]() $\mathtt {DNA}$
-varieties and of local tabularity for
$\mathtt {DNA}$
-varieties and of local tabularity for
![]() $\mathtt {DNA}$
-logics. Finally, we introduce Jankov
$\mathtt {DNA}$
-logics. Finally, we introduce Jankov
![]() $\mathtt {DNA}$
-formulas and we prove a version of Jankov’s theorem for our setting.
$\mathtt {DNA}$
-formulas and we prove a version of Jankov’s theorem for our setting.
4.1 Connections to intermediate logics
In the previous section we have introduced
![]() $\mathtt {DNA}$
-logics as negative variants of intermediate logics under the map
$\mathtt {DNA}$
-logics as negative variants of intermediate logics under the map
![]() $(-)^\neg :\Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathtt {IPC}^\neg ) $
. Now we will investigate the relation between intermediate logics and
$(-)^\neg :\Lambda (\mathtt {IPC}) \rightarrow \Lambda (\mathtt {IPC}^\neg ) $
. Now we will investigate the relation between intermediate logics and
![]() $\mathtt {DNA}$
-logics in more detail. We will first show that the map
$\mathtt {DNA}$
-logics in more detail. We will first show that the map
![]() $(-)^\neg $
which sends every intermediate logic to its negative variant is not injective. The following proposition was proved by Ciardelli in [Reference Ciardelli9, Lemma 5.2.20] and exemplifies how different intermediate logics can share the same negative variant. We recall that
$(-)^\neg $
which sends every intermediate logic to its negative variant is not injective. The following proposition was proved by Ciardelli in [Reference Ciardelli9, Lemma 5.2.20] and exemplifies how different intermediate logics can share the same negative variant. We recall that
![]() $\mathtt {KC}$
is the logic of the weak excluded middle, i.e.,
$\mathtt {KC}$
is the logic of the weak excluded middle, i.e.,
![]() $ \mathtt {KC} = \mathtt {IPC}+ \neg p \lor \neg \neg p $
.
$ \mathtt {KC} = \mathtt {IPC}+ \neg p \lor \neg \neg p $
.
Lemma 4.1. Let L be any intermediate logic such that
![]() $ \mathtt {KC} \subseteq L$
, then
$ \mathtt {KC} \subseteq L$
, then
![]() $L^\neg = \mathtt {CPC}$
.
$L^\neg = \mathtt {CPC}$
.
Proof. Suppose L is an intermediate logic such that
![]() $ \mathtt {KC} \subseteq L$
. One can show that for every formula
$ \mathtt {KC} \subseteq L$
. One can show that for every formula
![]() $\varphi $
we have
$\varphi $
we have
![]() $\varphi \lor \neg \varphi \in L^\neg $
. We prove this by induction on the complexity of
$\varphi \lor \neg \varphi \in L^\neg $
. We prove this by induction on the complexity of
![]() $\varphi $
. For the base case, suppose that
$\varphi $
. For the base case, suppose that
![]() $p \in \mathtt {AT}$
, then since
$p \in \mathtt {AT}$
, then since
![]() $ \mathtt {KC} \subseteq L$
we have for all
$ \mathtt {KC} \subseteq L$
we have for all
![]() $p\in \mathtt {AT}$
that
$p\in \mathtt {AT}$
that
![]() $\neg p \lor \neg \neg p \in L $
and therefore that
$\neg p \lor \neg \neg p \in L $
and therefore that
![]() $p \lor \neg p \in L^\neg $
. The induction steps follow easily by observing that for every formulas
$p \lor \neg p \in L^\neg $
. The induction steps follow easily by observing that for every formulas
![]() $\psi $
and
$\psi $
and
![]() $\chi $
we have
$\chi $
we have
This shows that
![]() $L^\neg = \mathtt {IPC} + \varphi \lor \neg \varphi =\mathtt {CPC}$
.
$L^\neg = \mathtt {IPC} + \varphi \lor \neg \varphi =\mathtt {CPC}$
.
Therefore, for intermediate logics
![]() $L_0,L_1$
such that
$L_0,L_1$
such that
![]() $\mathtt {KC}\subseteq L_0,L_1$
and
$\mathtt {KC}\subseteq L_0,L_1$
and
![]() $L_0\neq L_1$
we have that
$L_0\neq L_1$
we have that
![]() $L_0^\neg =L_1^\neg =\mathtt {CPC}$
, hence
$L_0^\neg =L_1^\neg =\mathtt {CPC}$
, hence
![]() $(-)^\neg $
is clearly not injective. Every
$(-)^\neg $
is clearly not injective. Every
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
thus determines a subset of the lattice
$\Lambda $
thus determines a subset of the lattice
![]() $ \Lambda (\mathtt {IPC}) $
of those logics which have
$ \Lambda (\mathtt {IPC}) $
of those logics which have
![]() $\Lambda $
as their negative variant. It is easy to see that this subset is also a sublattice, since the map
$\Lambda $
as their negative variant. It is easy to see that this subset is also a sublattice, since the map
![]() $(-)^\neg $
is a homomorphism. Similarly, since also
$(-)^\neg $
is a homomorphism. Similarly, since also
![]() $(-)^\uparrow $
is a homomorphism, we can also consider the sublattice of all varieties
$(-)^\uparrow $
is a homomorphism, we can also consider the sublattice of all varieties
![]() $\mathcal {V}$
in
$\mathcal {V}$
in
![]() $ \Lambda (\mathrm{HA}) $
whose negative closure is
$ \Lambda (\mathrm{HA}) $
whose negative closure is
![]() $\mathcal {X}$
. We then define the preimage of a
$\mathcal {X}$
. We then define the preimage of a
![]() $\mathtt {DNA}$
-logic and the preimage of a
$\mathtt {DNA}$
-logic and the preimage of a
![]() $\mathtt {DNA}$
-variety as follows.
$\mathtt {DNA}$
-variety as follows.
Definition 4.2. Let
![]() $\Lambda $
be a
$\Lambda $
be a
![]() $\mathtt {DNA}$
-logic and
$\mathtt {DNA}$
-logic and
![]() $\mathcal {X}$
be a
$\mathcal {X}$
be a
![]() $\mathtt {DNA}$
-variety. The preimage of
$\mathtt {DNA}$
-variety. The preimage of
![]() $\Lambda $
is the sublattice
$\Lambda $
is the sublattice
![]() $\mathcal {I}(\Lambda )$
of all intermediate logics L such that
$\mathcal {I}(\Lambda )$
of all intermediate logics L such that
![]() $L^\neg =\Lambda $
. The preimage of
$L^\neg =\Lambda $
. The preimage of
![]() $\mathcal {X}$
is the sublattice
$\mathcal {X}$
is the sublattice
![]() $\mathcal {I}(\mathcal {X})$
of all varieties
$\mathcal {I}(\mathcal {X})$
of all varieties
![]() $\mathcal {V}$
such that
$\mathcal {V}$
such that
![]() $\mathcal {V}^\uparrow =\mathcal {X}$
.
$\mathcal {V}^\uparrow =\mathcal {X}$
.
By the duality
![]() $\Lambda (\mathtt {IPC}) \cong ^{op}\Lambda (\mathrm{HA}) $
and the fact that the square introduced in Section 3.5 commutes, we then immediately have the following proposition.
$\Lambda (\mathtt {IPC}) \cong ^{op}\Lambda (\mathrm{HA}) $
and the fact that the square introduced in Section 3.5 commutes, we then immediately have the following proposition.
Proposition 4.3. For every
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
and every
$\Lambda $
and every
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
, we have that if
$\mathcal {X}$
, we have that if
![]() $\mathcal {X}=Var^\neg (\Lambda )$
and
$\mathcal {X}=Var^\neg (\Lambda )$
and
![]() $\Lambda = Log^\neg (\mathcal {X}) $
then
$\Lambda = Log^\neg (\mathcal {X}) $
then
![]() $\mathcal {I}(\Lambda )\cong ^{op}\mathcal {I}(\mathcal {X})$
.
$\mathcal {I}(\Lambda )\cong ^{op}\mathcal {I}(\mathcal {X})$
.
The isomorphism
![]() $\mathcal {I}(\Lambda )\cong ^{op}\mathcal {I}(\mathcal {X})$
above is the restriction of the dual isomorphism
$\mathcal {I}(\Lambda )\cong ^{op}\mathcal {I}(\mathcal {X})$
above is the restriction of the dual isomorphism
![]() $\Lambda (\mathtt {IPC}) \cong \Lambda (\mathrm{HA}) $
. We will now use this duality to characterize the two lattices
$\Lambda (\mathtt {IPC}) \cong \Lambda (\mathrm{HA}) $
. We will now use this duality to characterize the two lattices
![]() $\mathcal {I}(\Lambda )$
and
$\mathcal {I}(\Lambda )$
and
![]() $\mathcal {I}(\mathcal {X})$
.
$\mathcal {I}(\mathcal {X})$
.
First, we prove that the preimage
![]() $\mathcal {I}(\Lambda )$
of some
$\mathcal {I}(\Lambda )$
of some
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
has a greatest element and we provide a characterisation of it. The following notion of schematic fragment of a
$\Lambda $
has a greatest element and we provide a characterisation of it. The following notion of schematic fragment of a
![]() $\mathtt {DNA}$
-logic was first introduced under the name of standardization in [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37, Section 3] and later considered by Ciardelli in [Reference Ciardelli9, Section 3.4].
$\mathtt {DNA}$
-logic was first introduced under the name of standardization in [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37, Section 3] and later considered by Ciardelli in [Reference Ciardelli9, Section 3.4].
Definition 4.4 (Schematic Fragment)
Let
![]() $\Lambda $
be a
$\Lambda $
be a
![]() $\mathtt {DNA}$
-logic, we define its schematic fragment
$\mathtt {DNA}$
-logic, we define its schematic fragment
![]() $Schm(\Lambda )$
as:
$Schm(\Lambda )$
as:
![]() $Schm(\Lambda )$
is the set of all schematic formulas in
$Schm(\Lambda )$
is the set of all schematic formulas in
![]() $\Lambda $
, namely those formulas for which
$\Lambda $
, namely those formulas for which
![]() $\Lambda $
is closed under uniform substitution. One can easily check that
$\Lambda $
is closed under uniform substitution. One can easily check that
![]() $Schm(\Lambda )$
is an intermediate logic and that
$Schm(\Lambda )$
is an intermediate logic and that
![]() $Schm(\Lambda )^\neg = \Lambda $
. Moreover, the following proposition show that
$Schm(\Lambda )^\neg = \Lambda $
. Moreover, the following proposition show that
![]() $Schm(\Lambda )$
is the maximal intermediate logic whose negative variant is
$Schm(\Lambda )$
is the maximal intermediate logic whose negative variant is
![]() $\Lambda $
.
$\Lambda $
.
Proposition 4.5. Let
![]() $\Lambda $
be any
$\Lambda $
be any
![]() $\mathtt {DNA}$
-logic. Then, for every intermediate logic L such that
$\mathtt {DNA}$
-logic. Then, for every intermediate logic L such that
![]() $L^\neg =\Lambda $
we have
$L^\neg =\Lambda $
we have
![]() $L\subseteq Schm(\Lambda )$
.
$L\subseteq Schm(\Lambda )$
.
Proof. By Proposition 3.3
![]() $L\subseteq L^\neg =\Lambda $
. Since L is closed under uniform substitution, for any
$L\subseteq L^\neg =\Lambda $
. Since L is closed under uniform substitution, for any
![]() $\varphi \in L$
we have that any substitution instance
$\varphi \in L$
we have that any substitution instance
![]() of
of
![]() $\varphi $
is also in L. Hence, by the definition of
$\varphi $
is also in L. Hence, by the definition of
![]() $Schm(\Lambda )$
, we obtain
$Schm(\Lambda )$
, we obtain
![]() $\varphi \in Schm(\Lambda )$
. Therefore,
$\varphi \in Schm(\Lambda )$
. Therefore,
![]() $L\subseteq Schm(\Lambda )$
.
$L\subseteq Schm(\Lambda )$
.
The following theorem immediately follows by the previous propositions.
Theorem 4.6. Let
![]() $\Lambda $
be a
$\Lambda $
be a
![]() $\mathtt {DNA}$
-logic. The schematic fragment
$\mathtt {DNA}$
-logic. The schematic fragment
![]() $Schm(\Lambda )$
is the greatest intermediate logic whose negative variant is
$Schm(\Lambda )$
is the greatest intermediate logic whose negative variant is
![]() $\Lambda $
.
$\Lambda $
.
Therefore, the preimage
![]() $\mathcal {I}(\Lambda )$
of a
$\mathcal {I}(\Lambda )$
of a
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
has always a greatest element. By Theorem 3.35 we also obtain a dual characterisation of the corresponding
$\Lambda $
has always a greatest element. By Theorem 3.35 we also obtain a dual characterisation of the corresponding
![]() $\mathtt {DNA}$
-varieties. In fact, we have that
$\mathtt {DNA}$
-varieties. In fact, we have that
![]() $Var(Schm(\Lambda ))$
is the least variety whose negative closure is
$Var(Schm(\Lambda ))$
is the least variety whose negative closure is
![]() $Var^\neg (\Lambda )$
. We define the map
$Var^\neg (\Lambda )$
. We define the map
![]() $least_V: \Lambda (\mathrm{HA}^\uparrow ) \rightarrow \Lambda (\mathrm{HA}) $
as follows:
$least_V: \Lambda (\mathrm{HA}^\uparrow ) \rightarrow \Lambda (\mathrm{HA}) $
as follows:
The following proposition follows easily.
Proposition 4.7. The following diagram commutes in both directions, i.e.,
![]() $Var\circ Schm = least_V \circ Var^\neg $
and
$Var\circ Schm = least_V \circ Var^\neg $
and
![]() $Log\circ least_V = Schm \circ Log^\neg $
.
$Log\circ least_V = Schm \circ Log^\neg $
.

Proof. By the definition of
![]() $least_V$
and the dual isomorphism
$least_V$
and the dual isomorphism
![]() $\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we have
$\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we have
![]() $least_V \circ Var^\neg = Var \circ Schm \circ Log^\neg \circ Var^\neg = Var \circ Schm $
and
$least_V \circ Var^\neg = Var \circ Schm \circ Log^\neg \circ Var^\neg = Var \circ Schm $
and
![]() $Log\circ least_V = Log \circ Var \circ Schm \circ Log^\neg =Schm \circ Log^\neg $
.
$Log\circ least_V = Log \circ Var \circ Schm \circ Log^\neg =Schm \circ Log^\neg $
.
Therefore, for every
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
we have that
$\Lambda $
we have that
![]() $ Schm(\Lambda )$
is the greatest logic in
$ Schm(\Lambda )$
is the greatest logic in
![]() $\mathcal {I}(\Lambda )$
and
$\mathcal {I}(\Lambda )$
and
![]() $ least_V (Var^\neg (\Lambda ))$
is the least variety in
$ least_V (Var^\neg (\Lambda ))$
is the least variety in
![]() $\mathcal {I}(Var^\neg (\Lambda ))$
.
$\mathcal {I}(Var^\neg (\Lambda ))$
.
Similarly, one can show that the lattice
![]() $\mathcal {I}(\Lambda )$
has always a least element, which has so far been neglected in the literature. That this holds follows directly from the fact that for every
$\mathcal {I}(\Lambda )$
has always a least element, which has so far been neglected in the literature. That this holds follows directly from the fact that for every
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
, there is a greatest variety whose negative closure is exactly
$\mathcal {X}$
, there is a greatest variety whose negative closure is exactly
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
Proposition 4.8. For every
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
, there is a greatest variety
$\mathcal {X}$
, there is a greatest variety
![]() $\mathcal {V}$
such that
$\mathcal {V}$
such that
![]() $\mathcal {V}^\uparrow =\mathcal {X}$
.
$\mathcal {V}^\uparrow =\mathcal {X}$
.
Proof. By Proposition 3.18 we have that
![]() $\mathtt {DNA}$
-varieties are also varieties and, moreover,
$\mathtt {DNA}$
-varieties are also varieties and, moreover,
![]() $\mathcal {X}^\uparrow = \mathcal {X}$
for every
$\mathcal {X}^\uparrow = \mathcal {X}$
for every
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
. Hence
$\mathcal {X}$
. Hence
![]() $\mathcal {X}$
is clearly the greatest variety
$\mathcal {X}$
is clearly the greatest variety
![]() $\mathcal {V}$
such that
$\mathcal {V}$
such that
![]() $\mathcal {V}^\uparrow =\mathcal {X}$
.
$\mathcal {V}^\uparrow =\mathcal {X}$
.
The following theorem immediately follows by the previous propositions and
![]() $\mathtt {DNA}$
-duality.
$\mathtt {DNA}$
-duality.
Theorem 4.9. Let
![]() $\mathcal {X}$
be a
$\mathcal {X}$
be a
![]() $\mathtt {DNA}$
-variety. The logic
$\mathtt {DNA}$
-variety. The logic
![]() $Log(\mathcal {X})$
is the least among the intermediate logics whose negative variant is
$Log(\mathcal {X})$
is the least among the intermediate logics whose negative variant is
![]() $Log^\neg (\mathcal {X})$
.
$Log^\neg (\mathcal {X})$
.
We thus define a map
![]() $least_L: \Lambda (\mathtt {IPC}^\neg ) \rightarrow \Lambda (\mathtt {IPC}) $
as follows:
$least_L: \Lambda (\mathtt {IPC}^\neg ) \rightarrow \Lambda (\mathtt {IPC}) $
as follows:
The following proposition follows easily.
Proposition 4.10. The following diagram commutes in both directions, i.e.,
![]() $Var\circ least_L = id \circ Var^\neg $
and
$Var\circ least_L = id \circ Var^\neg $
and
![]() $Log\circ id = least_L \circ Log^\neg $
.
$Log\circ id = least_L \circ Log^\neg $
.

Proof. By the definition of
![]() $least_L$
and the dual isomorphism
$least_L$
and the dual isomorphism
![]() $\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we have
$\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we have
![]() $Var\circ least_L = Var \circ Log \circ Var^\neg = id \circ Var^\neg $
and
$Var\circ least_L = Var \circ Log \circ Var^\neg = id \circ Var^\neg $
and
![]() $least_L \circ Log^\neg = Log \circ Var^\neg \circ Log^\neg = Log \circ id $
.
$least_L \circ Log^\neg = Log \circ Var^\neg \circ Log^\neg = Log \circ id $
.
Therefore, it is the case that for every
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
we have that
$\Lambda $
we have that
![]() $ least_L(\Lambda )$
is the smallest logic in
$ least_L(\Lambda )$
is the smallest logic in
![]() $\mathcal {I}(\Lambda )$
and
$\mathcal {I}(\Lambda )$
and
![]() $ Var^\neg (\Lambda )$
is the greatest variety in
$ Var^\neg (\Lambda )$
is the greatest variety in
![]() $\mathcal {I}(Var^\neg (\Lambda ))$
.
$\mathcal {I}(Var^\neg (\Lambda ))$
.
By the former results above it thus follows that the sublattices
![]() $\mathcal {I}(\Lambda )$
and
$\mathcal {I}(\Lambda )$
and
![]() $\mathcal {I}(\mathcal {X})$
are bounded sublattices of
$\mathcal {I}(\mathcal {X})$
are bounded sublattices of
![]() $ \Lambda (\mathtt {IPC}) $
and
$ \Lambda (\mathtt {IPC}) $
and
![]() $ \Lambda (\mathrm{HA}) $
. We introduce the following definitions.
$ \Lambda (\mathrm{HA}) $
. We introduce the following definitions.
Definition 4.11 (
 $\mathtt {DNA}$
-maximality and
$\mathtt {DNA}$
-maximality and
 $\mathtt {DNA}$
-minimality)
$\mathtt {DNA}$
-minimality)
Let L be an intermediate logic. (i) We say that L is
![]() $\mathtt {DNA}$
-maximal if it is the greatest logic in
$\mathtt {DNA}$
-maximal if it is the greatest logic in
![]() $\mathcal {I}(L^\neg )$
. (ii) We say that L is
$\mathcal {I}(L^\neg )$
. (ii) We say that L is
![]() $\mathtt {DNA}$
-minimal if it is the least logic in
$\mathtt {DNA}$
-minimal if it is the least logic in
![]() $\mathcal {I}(L^\neg )$
.
$\mathcal {I}(L^\neg )$
.
In [Reference Miglioli, Moscato, Ornaghi, Quazza and Usberti37, Section 3] and [Reference Ciardelli9, Section 5.2] intermediate logics L such that
![]() $L=Schm(L^\neg )$
are called stable. The following proposition thus establishes that a logic is
$L=Schm(L^\neg )$
are called stable. The following proposition thus establishes that a logic is
![]() $\mathtt {DNA}$
-maximal iff it is stable. However, we will not use here this terminology, as the notion of stable logic has been employed e.g., in [Reference Ilin28] with a rather different meaning. The following proposition is an immediate consequence of our definition and the previous results.
$\mathtt {DNA}$
-maximal iff it is stable. However, we will not use here this terminology, as the notion of stable logic has been employed e.g., in [Reference Ilin28] with a rather different meaning. The following proposition is an immediate consequence of our definition and the previous results.
Proposition 4.12. Let L be an intermediate logic, then:
-
(i) L is
 $\mathtt {DNA}$
-maximal iff
$\mathtt {DNA}$
-maximal iff
 $L=Schm(L^\neg )$
and
$L=Schm(L^\neg )$
and -
(ii) L is
 $\mathtt {DNA}$
-minimal iff
$\mathtt {DNA}$
-minimal iff
 $Var(L)=Var^\neg (L^\neg )$
.
$Var(L)=Var^\neg (L^\neg )$
.
4.2 Regular Heyting algebras
The previous characterisation of
![]() $\mathtt {DNA}$
-maximal and
$\mathtt {DNA}$
-maximal and
![]() $\mathtt {DNA}$
-minimal logics is in a sense asymmetrical: we have a syntactic criterion for maximality and a semantic one for minimality. We are now after a semantic criterion for maximality. To this sake, we will now define regular Heyting algebras, which also play a major role in the context of
$\mathtt {DNA}$
-minimal logics is in a sense asymmetrical: we have a syntactic criterion for maximality and a semantic one for minimality. We are now after a semantic criterion for maximality. To this sake, we will now define regular Heyting algebras, which also play a major role in the context of
![]() $\mathtt {DNA}$
-logics in general.
$\mathtt {DNA}$
-logics in general.
Definition 4.13 (Regular Heyting Algebras)
A Heyting algebra H is regular if
![]() $H=\langle H_\neg \rangle $
.
$H=\langle H_\neg \rangle $
.
These algebras have been introduced in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] to provide an algebraic semantics to propositional inquisitive logic. A regular Heyting algebra is an algebra generated by its set
![]() $H_\neg $
of regular elements. For this reason we call regular Heyting algebras also regularly generated. Already in the previous section we have described some important properties of regular algebras in Lemma 3.13 and Proposition 3.14. Now we prove two further results showing that varieties
$H_\neg $
of regular elements. For this reason we call regular Heyting algebras also regularly generated. Already in the previous section we have described some important properties of regular algebras in Lemma 3.13 and Proposition 3.14. Now we prove two further results showing that varieties
![]() $\mathcal {V}$
with the same negative closure
$\mathcal {V}$
with the same negative closure
![]() $\mathcal {X}$
have the same collection of regular Heyting algebras. We first show the following proposition.
$\mathcal {X}$
have the same collection of regular Heyting algebras. We first show the following proposition.
Proposition 4.14. Let H be a regular Heyting algebra such that for some
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
we have that
$\Lambda $
we have that
![]() $H\vDash ^\neg \Lambda $
. Then, for every intermediate logic L such that
$H\vDash ^\neg \Lambda $
. Then, for every intermediate logic L such that
![]() $L^\neg =\Lambda $
we have that
$L^\neg =\Lambda $
we have that
![]() $H\vDash L$
.
$H\vDash L$
.
Proof. Suppose that
![]() $H\vDash ^\neg \Lambda $
, then since
$H\vDash ^\neg \Lambda $
, then since
![]() $\Lambda =Schm(\Lambda )^\neg $
it follows that
$\Lambda =Schm(\Lambda )^\neg $
it follows that
![]() $H\vDash ^\neg Schm(\Lambda )^\neg $
and so by Proposition 3.14
$H\vDash ^\neg Schm(\Lambda )^\neg $
and so by Proposition 3.14
![]() $H\vDash Schm(\Lambda )$
. Finally, by Proposition 4.5 we have that
$H\vDash Schm(\Lambda )$
. Finally, by Proposition 4.5 we have that
![]() $L\subseteq Schm(\Lambda )$
and thus
$L\subseteq Schm(\Lambda )$
and thus
![]() $H\vDash L$
.
$H\vDash L$
.
By the dual isomorphism
![]() $\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we then obtain the following proposition.
$\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we then obtain the following proposition.
Proposition 4.15. Let H be a regular Heyting algebra. If
![]() $H\in \mathcal {X}$
, then for every variety
$H\in \mathcal {X}$
, then for every variety
![]() $\mathcal {V}$
such that
$\mathcal {V}$
such that
![]() $ \mathcal {V}^\uparrow =\mathcal {X}$
we have that
$ \mathcal {V}^\uparrow =\mathcal {X}$
we have that
![]() $H\in \mathcal {V}$
.
$H\in \mathcal {V}$
.
Proof. Suppose
![]() $H\in \mathcal {X}$
, then
$H\in \mathcal {X}$
, then
![]() $H\vDash ^\neg Log^\neg (\mathcal {X})$
. Then, since
$H\vDash ^\neg Log^\neg (\mathcal {X})$
. Then, since
![]() $\mathcal {V}^\uparrow = \mathcal {X}$
, it follows by Corollary 3.27 that
$\mathcal {V}^\uparrow = \mathcal {X}$
, it follows by Corollary 3.27 that
![]() $Log(\mathcal {V})^\neg = Log^\neg (\mathcal {X})$
. So
$Log(\mathcal {V})^\neg = Log^\neg (\mathcal {X})$
. So
![]() $H\vDash ^\neg Log(\mathcal {V})^\neg $
and by Proposition 4.14,
$H\vDash ^\neg Log(\mathcal {V})^\neg $
and by Proposition 4.14,
![]() $H\vDash Log(\mathcal {V})$
, which entails
$H\vDash Log(\mathcal {V})$
, which entails
![]() $H\in \mathcal {V}$
.
$H\in \mathcal {V}$
.
We thereby have that all standard varieties whose negative closure is the same
![]() $\mathtt {DNA}$
-variety contain exactly the same regularly generated Heyting algebras. Interestingly, by Proposition 4.15 in order to check whether a regular Heyting algebra H validates an intermediate logic L, it is sufficient to check whether
$\mathtt {DNA}$
-variety contain exactly the same regularly generated Heyting algebras. Interestingly, by Proposition 4.15 in order to check whether a regular Heyting algebra H validates an intermediate logic L, it is sufficient to check whether
![]() $H\ \mathtt {DNA}$
-validates
$H\ \mathtt {DNA}$
-validates
![]() $L^{\neg }$
(i.e., whether H validates
$L^{\neg }$
(i.e., whether H validates
![]() $L^{\neg }$
under
$L^{\neg }$
under
![]() $\mathtt {DNA}$
-valuations).
$\mathtt {DNA}$
-valuations).
Finally, we can strengthen the previous results and show that regular Heyting algebras provide a semantic characterisation of
![]() $\mathtt {DNA}$
-maximal logics. In [Reference Ciardelli, Abramsky, Kontinen, Väänänen and Vollmer10, Section 5.2] a sufficient criterion for
$\mathtt {DNA}$
-maximal logics. In [Reference Ciardelli, Abramsky, Kontinen, Väänänen and Vollmer10, Section 5.2] a sufficient criterion for
![]() $\mathtt {DNA}$
-maximality was given in the context of Kripke frames: Ciardelli established that if L is the logic of a class of finite, everywhere branching trees, then it is
$\mathtt {DNA}$
-maximality was given in the context of Kripke frames: Ciardelli established that if L is the logic of a class of finite, everywhere branching trees, then it is
![]() $\mathtt {DNA}$
-maximal. We propose here a criterion in terms of regular algebras which is both sufficient and necessary.
$\mathtt {DNA}$
-maximal. We propose here a criterion in terms of regular algebras which is both sufficient and necessary.
Theorem 4.16. An intermediate logic L is the logic of a class of regularly generated Heyting algebras if and only if it is
![]() $\mathtt {DNA}$
-maximal.
$\mathtt {DNA}$
-maximal.
Proof.
![]() $(\Rightarrow )$
By Proposition 4.12 this is equivalent to the statement that if an intermediate logic L is such that
$(\Rightarrow )$
By Proposition 4.12 this is equivalent to the statement that if an intermediate logic L is such that
![]() $L=Log(\mathcal {C})$
, where
$L=Log(\mathcal {C})$
, where
![]() $\mathcal {C}$
is a class of regularly generated Heyting algebras, then
$\mathcal {C}$
is a class of regularly generated Heyting algebras, then
![]() $L=Schm(L^\neg )$
. So, suppose that
$L=Schm(L^\neg )$
. So, suppose that
![]() $\mathcal {C} $
is a class of regularly generated Heyting algebras, we need to show that
$\mathcal {C} $
is a class of regularly generated Heyting algebras, we need to show that
![]() $Log(\mathcal {C})= Schm(Log(\mathcal {C})^\neg )$
. Since
$Log(\mathcal {C})= Schm(Log(\mathcal {C})^\neg )$
. Since
![]() $Schm(Log(\mathcal {C})^\neg )$
is
$Schm(Log(\mathcal {C})^\neg )$
is
![]() $\mathtt {DNA}$
-maximal it follows that
$\mathtt {DNA}$
-maximal it follows that
![]() $Log(\mathcal {C})\subseteq Schm(Log(\mathcal {C})^\neg )$
, so that we only need to show that
$Log(\mathcal {C})\subseteq Schm(Log(\mathcal {C})^\neg )$
, so that we only need to show that
![]() $Schm(Log(\mathcal {C})^\neg )\subseteq Log(\mathcal {C})$
. Now suppose by contraposition that
$Schm(Log(\mathcal {C})^\neg )\subseteq Log(\mathcal {C})$
. Now suppose by contraposition that
![]() $\varphi \notin Log(\mathcal {C}) $
, then we have that for some
$\varphi \notin Log(\mathcal {C}) $
, then we have that for some
![]() $H\in \mathcal {C}$
and for some valuation V, we have that
$H\in \mathcal {C}$
and for some valuation V, we have that
![]() $(H, V) \nvDash \varphi $
. Now, since H is regularly generated, every element
$(H, V) \nvDash \varphi $
. Now, since H is regularly generated, every element
![]() $x_i\in H$
can be written out as a polynomial
$x_i\in H$
can be written out as a polynomial
![]() $\delta _i(\overline {y^{k}_{i}})$
of regular elements of H. Then we define the
$\delta _i(\overline {y^{k}_{i}})$
of regular elements of H. Then we define the
![]() $\mathtt {DNA}$
-valuation
$\mathtt {DNA}$
-valuation
![]() $\mu : p^{k}_{i} \mapsto y^{k}_{i}$
so that we then get
$\mu : p^{k}_{i} \mapsto y^{k}_{i}$
so that we then get
![]() . Let
. Let
![]() $q_1,\dots ,q_l$
be a list of the distinct variables appearing in
$q_1,\dots ,q_l$
be a list of the distinct variables appearing in
![]() $\varphi $
, and define indexes
$\varphi $
, and define indexes
![]() $j_1,\dots ,j_l$
such that
$j_1,\dots ,j_l$
such that
![]() $V(q_i) = x_{j_i}$
. Moreover, define
$V(q_i) = x_{j_i}$
. Moreover, define
![]() . We then have that
. We then have that
![]() , and consequently
, and consequently
![]() $(H, \mu ) \nvDash \psi $
. Since
$(H, \mu ) \nvDash \psi $
. Since
![]() $H\in \mathcal {C}\subseteq \mathcal {C}^\uparrow $
, it follows that
$H\in \mathcal {C}\subseteq \mathcal {C}^\uparrow $
, it follows that
![]() $\psi \notin Log^\neg ( \mathcal {C}^\uparrow ) = Log(\mathcal {C})^\neg $
. Finally, since
$\psi \notin Log^\neg ( \mathcal {C}^\uparrow ) = Log(\mathcal {C})^\neg $
. Finally, since
![]() $\psi $
is a substitution instance of
$\psi $
is a substitution instance of
![]() $\varphi $
, it follows that
$\varphi $
, it follows that
![]() $\varphi \notin Schm(Log(\mathcal {C})^\neg )$
.
$\varphi \notin Schm(Log(\mathcal {C})^\neg )$
.
(
![]() $\Leftarrow $
) Suppose that L is a
$\Leftarrow $
) Suppose that L is a
![]() $\mathtt {DNA}$
-maximal logic and consider its corresponding variety
$\mathtt {DNA}$
-maximal logic and consider its corresponding variety
![]() $Var(L)$
. We let
$Var(L)$
. We let
![]() $Var_R(L)$
be the subclass of
$Var_R(L)$
be the subclass of
![]() $Var(L)$
consisting of regular Heyting algebras only. Now, we have that
$Var(L)$
consisting of regular Heyting algebras only. Now, we have that
![]() $Var(L)\subseteq Var_R(L)^\uparrow $
, since for every
$Var(L)\subseteq Var_R(L)^\uparrow $
, since for every
![]() $H\in Var(L)$
, we have
$H\in Var(L)$
, we have
![]() $\langle H_\neg \rangle \in Var_R(L)$
, hence
$\langle H_\neg \rangle \in Var_R(L)$
, hence
![]() $H\in Var_R(L)^\uparrow $
. As obviously
$H\in Var_R(L)^\uparrow $
. As obviously
![]() $Var_R(L)\subseteq Var(L)$
, it immediately follows that
$Var_R(L)\subseteq Var(L)$
, it immediately follows that
![]() $Var(L)^\uparrow = Var_R(L)^\uparrow $
. We thus obtain:
$Var(L)^\uparrow = Var_R(L)^\uparrow $
. We thus obtain:
 $$ \begin{align*} L^\neg &= Log(Var(L))^\neg & \text{ } \\ &= Log^\neg(Var(L)^\uparrow) & \text{(by Proposition 3.26) }\\ &= Log^\neg(Var_R(L)^\uparrow) & \text{(by } Var(L)^\uparrow = Var_R(L)^\uparrow) \\ & = Log^\neg(\mathcal{V}(Var_R(L))^\uparrow) & \text{ (since }\mathcal{V}(Var_R(L))^\uparrow= Var_R(L)^\uparrow ) \\ & = Log(\mathcal{V}(Var_R(L)))^\neg & \text{(by Proposition 3.26)} \\ & = Log(Var_R(L))^\neg. \end{align*} $$
$$ \begin{align*} L^\neg &= Log(Var(L))^\neg & \text{ } \\ &= Log^\neg(Var(L)^\uparrow) & \text{(by Proposition 3.26) }\\ &= Log^\neg(Var_R(L)^\uparrow) & \text{(by } Var(L)^\uparrow = Var_R(L)^\uparrow) \\ & = Log^\neg(\mathcal{V}(Var_R(L))^\uparrow) & \text{ (since }\mathcal{V}(Var_R(L))^\uparrow= Var_R(L)^\uparrow ) \\ & = Log(\mathcal{V}(Var_R(L)))^\neg & \text{(by Proposition 3.26)} \\ & = Log(Var_R(L))^\neg. \end{align*} $$
The last move is justified by the well-known fact that if
![]() $\mathcal {K}$
is a class of Heyting algebras and
$\mathcal {K}$
is a class of Heyting algebras and
![]() $\mathcal {V}(\mathcal {K})$
the variety generated by it, then
$\mathcal {V}(\mathcal {K})$
the variety generated by it, then
![]() $Log(\mathcal {K})=Log(\mathcal {V}(\mathcal {K}))$
(see, e.g., [Reference Chagrov and Zakharyaschev8, Chapter 7]). It follows by the
$Log(\mathcal {K})=Log(\mathcal {V}(\mathcal {K}))$
(see, e.g., [Reference Chagrov and Zakharyaschev8, Chapter 7]). It follows by the
![]() $\mathtt {DNA}$
-maximality of L that
$\mathtt {DNA}$
-maximality of L that
![]() $Log(Var_R(L))\subseteq L $
. Moreover, since we clearly have that
$Log(Var_R(L))\subseteq L $
. Moreover, since we clearly have that
![]() $L \subseteq Log(Var_R(L)) $
it follows that
$L \subseteq Log(Var_R(L)) $
it follows that
![]() $L=Log(Var_R(L)) $
, yielding that L is the logic of a class of regularly generated Heyting algebras.
$L=Log(Var_R(L)) $
, yielding that L is the logic of a class of regularly generated Heyting algebras.
Hence we can restate Proposition 4.12 in purely semantical terms.
Proposition 4.17. Let L be an intermediate logic, then:
-
(i) L is
 $\mathtt {DNA}$
-maximal iff
$\mathtt {DNA}$
-maximal iff
 $L=Log(\mathcal {C})$
, for some class
$L=Log(\mathcal {C})$
, for some class
 $\mathcal {C}$
of regular Heyting algebras and
$\mathcal {C}$
of regular Heyting algebras and -
(ii) L is
 $\mathtt {DNA}$
-minimal iff
$\mathtt {DNA}$
-minimal iff
 $Var(L)=Var^\neg (L^\neg )$
.
$Var(L)=Var^\neg (L^\neg )$
.
4.3 Birkhoff’s theorem for
 $\mathtt {DNA}$
-varieties
$\mathtt {DNA}$
-varieties
We will prove in this section a version of Birkhoff’s theorem for
![]() $\mathtt {DNA}$
-varieties. While in the standard setting Birkhoff’s theorem states that varieties are generated by their subdirectly irreducible algebras, in our context we will prove that
$\mathtt {DNA}$
-varieties. While in the standard setting Birkhoff’s theorem states that varieties are generated by their subdirectly irreducible algebras, in our context we will prove that
![]() $\mathtt {DNA}$
-varieties are generated by their regular, subdirectly irreducible members. Interestingly, another method to generate
$\mathtt {DNA}$
-varieties are generated by their regular, subdirectly irreducible members. Interestingly, another method to generate
![]() $\mathtt {DNA}$
-varieties is by constructing the Lindenbaum–Tarski algebra of their corresponding
$\mathtt {DNA}$
-varieties is by constructing the Lindenbaum–Tarski algebra of their corresponding
![]() $\mathtt {DNA}$
-logic, see for details [Reference Quadrellaro41, Section 3.3.2].
$\mathtt {DNA}$
-logic, see for details [Reference Quadrellaro41, Section 3.3.2].
Recall that if
![]() $\mathcal {X}$
is a
$\mathcal {X}$
is a
![]() $\mathtt {DNA}$
-variety, then we say that
$\mathtt {DNA}$
-variety, then we say that
![]() $\mathcal {X}$
is generated by the class
$\mathcal {X}$
is generated by the class
![]() $\mathcal {C}\subseteq \mathcal {X}$
if
$\mathcal {C}\subseteq \mathcal {X}$
if
![]() $\mathcal {X}=\mathcal {X}(\mathcal {C})=\mathcal {V}(\mathcal {C})^\uparrow $
. We firstly prove the following useful theorem.
$\mathcal {X}=\mathcal {X}(\mathcal {C})=\mathcal {V}(\mathcal {C})^\uparrow $
. We firstly prove the following useful theorem.
Theorem 4.18. Let
![]() $\mathcal {X}$
be a
$\mathcal {X}$
be a
![]() $\mathtt {DNA}$
-variety, then
$\mathtt {DNA}$
-variety, then
![]() $\mathcal {X}=\mathcal {X}(\mathcal {C}) $
iff
$\mathcal {X}=\mathcal {X}(\mathcal {C}) $
iff
![]() $ Log^\neg (\mathcal {X})=Log^\neg (\mathcal {C}).$
$ Log^\neg (\mathcal {X})=Log^\neg (\mathcal {C}).$
Proof.
![]() $(\Rightarrow )$
Since
$(\Rightarrow )$
Since
![]() $\mathcal {C}\subseteq \mathcal {X}$
, the inclusion from left to right is straightforward. Suppose now that
$\mathcal {C}\subseteq \mathcal {X}$
, the inclusion from left to right is straightforward. Suppose now that
![]() $\mathcal {X}\nvDash ^\neg \varphi $
then there is some Heyting algebra
$\mathcal {X}\nvDash ^\neg \varphi $
then there is some Heyting algebra
![]() $H\in \mathcal {X}$
such that
$H\in \mathcal {X}$
such that
![]() $H\nvDash ^\neg \varphi $
. Then since
$H\nvDash ^\neg \varphi $
. Then since
![]() $\mathcal {X}=\mathcal {X}(\mathcal {C})$
, it follows by Theorem 3.21 that
$\mathcal {X}=\mathcal {X}(\mathcal {C})$
, it follows by Theorem 3.21 that
![]() $H\in HSP(\mathcal {C})^\uparrow $
. Thus, since
$H\in HSP(\mathcal {C})^\uparrow $
. Thus, since
![]() $\mathtt {DNA}$
-validities are preserved under homomorphisms, subalgebras, products and core superalgebras, it follows that there is some Heyting algebra
$\mathtt {DNA}$
-validities are preserved under homomorphisms, subalgebras, products and core superalgebras, it follows that there is some Heyting algebra
![]() $A \in \mathcal {C}$
such that
$A \in \mathcal {C}$
such that
![]() $A\nvDash ^\neg \varphi $
.
$A\nvDash ^\neg \varphi $
.
![]() $(\Leftarrow )$
Suppose now that
$(\Leftarrow )$
Suppose now that
![]() $Log^\neg (\mathcal {X})=Log^\neg (\mathcal {C})$
. Then by the Duality Theorem 3.35 it follows
$Log^\neg (\mathcal {X})=Log^\neg (\mathcal {C})$
. Then by the Duality Theorem 3.35 it follows
![]() $Var^\neg (Log^\neg (\mathcal {X}))=Var^\neg (Log^\neg (\mathcal {C}))$
and thus
$Var^\neg (Log^\neg (\mathcal {X}))=Var^\neg (Log^\neg (\mathcal {C}))$
and thus
![]() $\mathcal {X}=Var^\neg (Log^\neg (\mathcal {C}))$
. Now, since
$\mathcal {X}=Var^\neg (Log^\neg (\mathcal {C}))$
. Now, since
![]() $Log^\neg (\mathcal {X}(\mathcal {C}))=Log^\neg (\mathcal {C}))$
it follows by Proposition 3.22 and Duality that
$Log^\neg (\mathcal {X}(\mathcal {C}))=Log^\neg (\mathcal {C}))$
it follows by Proposition 3.22 and Duality that
![]() $Var^\neg (Log^\neg (\mathcal {C})){{\kern-1pt}={\kern-1pt}}Var^\neg (Log^\neg (\mathcal {X}(\mathcal {C})))$
. Thus
$Var^\neg (Log^\neg (\mathcal {C})){{\kern-1pt}={\kern-1pt}}Var^\neg (Log^\neg (\mathcal {X}(\mathcal {C})))$
. Thus
![]() $Var^\neg (Log^\neg (\mathcal {X})){{\kern-1pt}={\kern-1pt}}Var^\neg (Log^\neg (\mathcal {X}(\mathcal {C})))$
, which by duality means
$Var^\neg (Log^\neg (\mathcal {X})){{\kern-1pt}={\kern-1pt}}Var^\neg (Log^\neg (\mathcal {X}(\mathcal {C})))$
, which by duality means
![]() $\mathcal {X}=\mathcal {X}(\mathcal {C})$
.
$\mathcal {X}=\mathcal {X}(\mathcal {C})$
.
A first approximation of a Birkhoff’s theorem for
![]() $\mathtt {DNA}$
-varieties is given by the following result, stating that every
$\mathtt {DNA}$
-varieties is given by the following result, stating that every
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
is generated by its collection of regular Heyting algebras. If
$\mathcal {X}$
is generated by its collection of regular Heyting algebras. If
![]() $\mathcal {X}$
is a
$\mathcal {X}$
is a
![]() $\mathtt {DNA}$
-variety, then we denote by
$\mathtt {DNA}$
-variety, then we denote by
![]() $\mathcal {X}_{R}$
its subclass of regular Heyting algebras.
$\mathcal {X}_{R}$
its subclass of regular Heyting algebras.
Proposition 4.19. Every
![]() $\mathtt {DNA}$
-variety is generated by its collection of regular elements, i.e.,
$\mathtt {DNA}$
-variety is generated by its collection of regular elements, i.e.,
![]() $\mathcal {X} = \mathcal {X}(\mathcal {X}_{R}) $
.
$\mathcal {X} = \mathcal {X}(\mathcal {X}_{R}) $
.
Proof. Let
![]() $\mathcal {X}$
be a
$\mathcal {X}$
be a
![]() $\mathtt {DNA}$
-variety, then for any non-regular
$\mathtt {DNA}$
-variety, then for any non-regular
![]() $H\in \mathcal {X} $
we have that
$H\in \mathcal {X} $
we have that
![]() $\langle H_\neg \rangle \preceq H$
and
$\langle H_\neg \rangle \preceq H$
and
![]() $H_\neg =\langle H_\neg \rangle _\neg $
. So since
$H_\neg =\langle H_\neg \rangle _\neg $
. So since
![]() $\langle H_\neg \rangle \in \mathcal {X}_{R}$
it follows
$\langle H_\neg \rangle \in \mathcal {X}_{R}$
it follows
![]() $H\in \mathcal {X}(\mathcal {X}_{R}) $
.
$H\in \mathcal {X}(\mathcal {X}_{R}) $
.
We thus have, by the standard version of Birkhoff’s theorem, that every
![]() $\mathtt {DNA}$
-variety is generated by its subdirectly irreducible elements and, by the previous proposition, that every
$\mathtt {DNA}$
-variety is generated by its subdirectly irreducible elements and, by the previous proposition, that every
![]() $\mathtt {DNA}$
-variety is generated by its regular elements. We can actually prove more, namely that
$\mathtt {DNA}$
-variety is generated by its regular elements. We can actually prove more, namely that
![]() $\mathtt {DNA}$
-varieties are generated by their regular, subdirectly irreducible elements. Now if
$\mathtt {DNA}$
-varieties are generated by their regular, subdirectly irreducible elements. Now if
![]() $\mathcal {X}$
is a
$\mathcal {X}$
is a
![]() $\mathtt {DNA}$
-variety, we denote by
$\mathtt {DNA}$
-variety, we denote by
![]() $\mathcal {X}_{RSI}$
its subset of regular subdirectly irreducible Heyting algebras. We will thus show that for every
$\mathcal {X}_{RSI}$
its subset of regular subdirectly irreducible Heyting algebras. We will thus show that for every
![]() $\mathtt {DNA}$
-variety we have
$\mathtt {DNA}$
-variety we have
![]() $\mathcal {X}=\mathcal {X}(\mathcal {X}_{RSI})$
. Let us first recall the following result from the literature, originally due to Wronski [Reference Wronski45].
$\mathcal {X}=\mathcal {X}(\mathcal {X}_{RSI})$
. Let us first recall the following result from the literature, originally due to Wronski [Reference Wronski45].
Lemma 4.20. Let
![]() $B\in \mathrm{HA}$
. Then if
$B\in \mathrm{HA}$
. Then if
![]() $b\neq 1_B$
there is a subdirectly irreducible algebra C and a surjective homomorphism
$b\neq 1_B$
there is a subdirectly irreducible algebra C and a surjective homomorphism
![]() $h:B\twoheadrightarrow C$
such that
$h:B\twoheadrightarrow C$
such that
![]() $f(b)=s_C$
, where
$f(b)=s_C$
, where
![]() $s_C$
is the second greatest element of C.
$s_C$
is the second greatest element of C.
By using this fact we can prove Birkhoff theorem for
![]() $\mathtt {DNA}$
-varieties.
$\mathtt {DNA}$
-varieties.
Theorem 4.21 (
 $\mathtt {DNA}$
-Birkhoff)
$\mathtt {DNA}$
-Birkhoff)
Every
![]() $\mathtt {DNA}$
-variety is generated by its collection of regular subdirectly irreducible elements:
$\mathtt {DNA}$
-variety is generated by its collection of regular subdirectly irreducible elements:
![]() $\mathcal {X} = \mathcal {X}(\mathcal {X}_{RSI}) $
.
$\mathcal {X} = \mathcal {X}(\mathcal {X}_{RSI}) $
.
Proof. By the dual isomorphism between
![]() $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
![]() $\mathtt {DNA}$
-varieties it suffices to show that
$\mathtt {DNA}$
-varieties it suffices to show that
![]() $Log^\neg (\mathcal {X})=Log^\neg (\mathcal {X}(\mathcal {X}_{RSI})) $
, which is equivalent by Theorem 4.18 to
$Log^\neg (\mathcal {X})=Log^\neg (\mathcal {X}(\mathcal {X}_{RSI})) $
, which is equivalent by Theorem 4.18 to
![]() $Log^\neg (\mathcal {X})=Log^\neg (\mathcal {X}_{RSI}) $
. The direction
$Log^\neg (\mathcal {X})=Log^\neg (\mathcal {X}_{RSI}) $
. The direction
![]() $Log^\neg (\mathcal {X})\subseteq Log^\neg (\mathcal {X}_{RSI}) $
follows immediately from the inclusion
$Log^\neg (\mathcal {X})\subseteq Log^\neg (\mathcal {X}_{RSI}) $
follows immediately from the inclusion
![]() $\mathcal {X}_{RSI}\subseteq \mathcal {X}$
. It thus suffices to show that
$\mathcal {X}_{RSI}\subseteq \mathcal {X}$
. It thus suffices to show that
![]() $Log^\neg (\mathcal {X}_{RSI}) \subseteq Log^\neg (\mathcal {X})$
.
$Log^\neg (\mathcal {X}_{RSI}) \subseteq Log^\neg (\mathcal {X})$
.
Suppose by contraposition that
![]() $\varphi \notin Log^\neg (\mathcal {X}) $
, then for some
$\varphi \notin Log^\neg (\mathcal {X}) $
, then for some
![]() $H\in \mathcal {X}$
and some
$H\in \mathcal {X}$
and some
![]() $\mathtt {DNA}$
-valuation
$\mathtt {DNA}$
-valuation
![]() $V^\neg $
, we have that
$V^\neg $
, we have that
![]() $(H,V^{\neg })\nvDash ^\neg \varphi $
and so, by reasoning as in the proof of Lemma 3.13, that
$(H,V^{\neg })\nvDash ^\neg \varphi $
and so, by reasoning as in the proof of Lemma 3.13, that
![]() $(\langle H_\neg \rangle, V^{\neg }) \nvDash ^\neg \varphi $
. Then, since
$(\langle H_\neg \rangle, V^{\neg }) \nvDash ^\neg \varphi $
. Then, since
it follows by Lemma 4.20 that there is a subdirectly irreducible algebra C such that there is surjective homomorphism
![]() $h:\langle H_\neg \rangle \twoheadrightarrow C$
with
$h:\langle H_\neg \rangle \twoheadrightarrow C$
with
![]() $h(x )=s_C$
. Then, since homomorphisms preserve regular elements, the valuation
$h(x )=s_C$
. Then, since homomorphisms preserve regular elements, the valuation
![]() $U^\neg = h\circ V^\neg $
is a
$U^\neg = h\circ V^\neg $
is a
![]() $\mathtt {DNA}$
-valuation. Now let
$\mathtt {DNA}$
-valuation. Now let
![]() $p_0,\dots ,p_n$
be the variables in
$p_0,\dots ,p_n$
be the variables in
![]() $\varphi $
, it follows by the properties of homomorphisms that:
$\varphi $
, it follows by the properties of homomorphisms that:

From which it immediately follows that
![]() $ (C,U^\neg )\nvDash \varphi $
and so that
$ (C,U^\neg )\nvDash \varphi $
and so that
![]() $C\nvDash^\neg \varphi $
. Now, since
$C\nvDash^\neg \varphi $
. Now, since
![]() $H\in \mathcal {X}$
, we have that
$H\in \mathcal {X}$
, we have that
![]() $\langle H_\neg \rangle \in \mathcal {X}$
and so since
$\langle H_\neg \rangle \in \mathcal {X}$
and so since
![]() $h:\langle H_\neg \rangle \twoheadrightarrow C$
also that
$h:\langle H_\neg \rangle \twoheadrightarrow C$
also that
![]() $C\in \mathcal {X}$
. Moreover, we have that C is subdirectly irreducible and regular, as it is homomorphic image of
$C\in \mathcal {X}$
. Moreover, we have that C is subdirectly irreducible and regular, as it is homomorphic image of
![]() $\langle H_\neg \rangle $
. Finally, this means that
$\langle H_\neg \rangle $
. Finally, this means that
![]() $C\in \mathcal {X}_{RSI} $
and so that
$C\in \mathcal {X}_{RSI} $
and so that
![]() $\varphi \notin Log^\neg (\mathcal {X}_{RSI}) $
, which proves our claim.
$\varphi \notin Log^\neg (\mathcal {X}_{RSI}) $
, which proves our claim.
4.4 Locally tabular
 $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
 $\mathtt {DNA}$
-varieties
$\mathtt {DNA}$
-varieties
The notions of local tabularity and local finiteness play an important role in the theory of intermediate logics and in universal algebra at large. Here we introduce a suitable notion of local finiteness for
![]() $\mathtt {DNA}$
-varieties and
$\mathtt {DNA}$
-varieties and
![]() $\mathtt {DNA}$
-logics, which we will later employ in our study of inquisitive logic.
$\mathtt {DNA}$
-logics, which we will later employ in our study of inquisitive logic.
We say that a Heyting algebra H is
![]() $\mathtt {DNA}$
-finitely generated if there are finitely many elements
$\mathtt {DNA}$
-finitely generated if there are finitely many elements
![]() $x_0,\dots ,x_n\in H_\neg $
such that
$x_0,\dots ,x_n\in H_\neg $
such that
![]() $\langle x_0,\dots ,x_n \rangle = H$
. We then define locally finite
$\langle x_0,\dots ,x_n \rangle = H$
. We then define locally finite
![]() $\mathtt {DNA}$
-varieties and locally tabular
$\mathtt {DNA}$
-varieties and locally tabular
![]() $\mathtt {DNA}$
-logics.
$\mathtt {DNA}$
-logics.
Definition 4.22. A
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
is
$\mathcal {X}$
is
![]() $\mathtt {DNA}$
-locally finite if every
$\mathtt {DNA}$
-locally finite if every
![]() $\mathtt {DNA}$
-finitely generated
$\mathtt {DNA}$
-finitely generated
![]() $H\in \mathcal {X}$
is also finite. A
$H\in \mathcal {X}$
is also finite. A
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
is
$\Lambda $
is
![]() $\mathtt {DNA}$
-locally tabular if its corresponding
$\mathtt {DNA}$
-locally tabular if its corresponding
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $Var^\neg (\Lambda )$
is locally finite.
$Var^\neg (\Lambda )$
is locally finite.
When the context makes it clear we then drop the prefix
![]() $\mathtt {DNA}$
and talk simply of local finiteness and local tabularity. The following proposition follows straightforwardly and allows us to relate the local finiteness of intermediate logics to the local finiteness of
$\mathtt {DNA}$
and talk simply of local finiteness and local tabularity. The following proposition follows straightforwardly and allows us to relate the local finiteness of intermediate logics to the local finiteness of
![]() $\mathtt {DNA}$
-logics.
$\mathtt {DNA}$
-logics.
Proposition 4.23. Let L be any intermediate logic, if L is locally tabular, then
![]() $L^\neg $
is locally tabular.
$L^\neg $
is locally tabular.
Proof. If L is locally tabular, then every finitely generated
![]() $H\in Var(L)$
is also finite. Now consider any
$H\in Var(L)$
is also finite. Now consider any
![]() $H\in Var^\neg (L^\neg )$
and suppose for some
$H\in Var^\neg (L^\neg )$
and suppose for some
![]() $x_0,\dots ,x_n\in H_\neg $
we have
$x_0,\dots ,x_n\in H_\neg $
we have
![]() $\langle x_0,\dots ,x_n \rangle = H$
. Then it follows that
$\langle x_0,\dots ,x_n \rangle = H$
. Then it follows that
![]() $H=\langle H_\neg \rangle $
and so that H is regular. Then, we have by Proposition 4.15 that
$H=\langle H_\neg \rangle $
and so that H is regular. Then, we have by Proposition 4.15 that
![]() $H\in Var(L)$
and so since H is finitely generated by
$H\in Var(L)$
and so since H is finitely generated by
![]() $x_0,\dots ,x_n$
it also follows that H is finite. This shows that
$x_0,\dots ,x_n$
it also follows that H is finite. This shows that
![]() $L^\neg $
is locally tabular.
$L^\neg $
is locally tabular.
A property of
![]() $\mathtt {DNA}$
-logics which is closely connected to local finiteness is the finite model property (FMP). We introduce it as follows.
$\mathtt {DNA}$
-logics which is closely connected to local finiteness is the finite model property (FMP). We introduce it as follows.
Definition 4.24 (Finite Model Property)
A
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
has the
$\mathcal {X}$
has the
![]() $\mathtt {DNA}$
-finite model property (FMP) if
$\mathtt {DNA}$
-finite model property (FMP) if
![]() $\mathcal {X}=\mathcal {X}(\mathcal {C})$
, where
$\mathcal {X}=\mathcal {X}(\mathcal {C})$
, where
![]() $\mathcal {C}$
is a collection of finite Heyting algebras. A
$\mathcal {C}$
is a collection of finite Heyting algebras. A
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
has the
$\Lambda $
has the
![]() $\mathtt {DNA}$
-finite model property if its corresponding
$\mathtt {DNA}$
-finite model property if its corresponding
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $Var^\neg (\Lambda )$
has the finite model property.
$Var^\neg (\Lambda )$
has the finite model property.
When the context makes it clear we drop the prefix
![]() $\mathtt {DNA}$
and simply talk of finite model property. The finite model property allows, for every formula
$\mathtt {DNA}$
and simply talk of finite model property. The finite model property allows, for every formula
![]() $\varphi \notin \Lambda $
, to find a finite algebra H which validates
$\varphi \notin \Lambda $
, to find a finite algebra H which validates
![]() $\Lambda $
and refutes
$\Lambda $
and refutes
![]() $\varphi $
. Similarly to the case of local finiteness, the finite model property of an intermediate logic entails the finite model property of its negative variant.
$\varphi $
. Similarly to the case of local finiteness, the finite model property of an intermediate logic entails the finite model property of its negative variant.
Proposition 4.25. Let L be any intermediate logic, if L has the finite model property then
![]() $L^\neg $
has the finite model property.
$L^\neg $
has the finite model property.
Proof. Suppose L has the finite model property, then
![]() $Var(L)=\mathcal {V}(\mathcal {C})$
for some class
$Var(L)=\mathcal {V}(\mathcal {C})$
for some class
![]() $\mathcal {C}$
of finite Heyting algebras. Then, we have that
$\mathcal {C}$
of finite Heyting algebras. Then, we have that
![]() $Var^\neg (L^\neg )= Var (L)^\uparrow = \mathcal {V}(\mathcal {C})^\uparrow = \mathcal {X}(\mathcal {C}) $
, which shows that
$Var^\neg (L^\neg )= Var (L)^\uparrow = \mathcal {V}(\mathcal {C})^\uparrow = \mathcal {X}(\mathcal {C}) $
, which shows that
![]() $L^\neg $
also has the finite model property.
$L^\neg $
also has the finite model property.
If a
![]() $\mathtt {DNA}$
-variety has the finite model property we can further refine our version of Birkhoff theorem. We denote by
$\mathtt {DNA}$
-variety has the finite model property we can further refine our version of Birkhoff theorem. We denote by
![]() $\mathcal {X}_{RFSI}$
the collection of finite, regular, subdirectly irreducible elements in
$\mathcal {X}_{RFSI}$
the collection of finite, regular, subdirectly irreducible elements in
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
Theorem 4.26. If a
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
has the finite model property, then it is generated by its finite, regular subdirectly irreducible elements, i.e.,
$\mathcal {X}$
has the finite model property, then it is generated by its finite, regular subdirectly irreducible elements, i.e.,
![]() $\mathcal {X}=\mathcal {X}(\mathcal {X}_{RFSI}) $
.
$\mathcal {X}=\mathcal {X}(\mathcal {X}_{RFSI}) $
.
Proof. By Theorem 4.18 it suffices to check that
![]() $Log^\neg (\mathcal {X}_{RFSI})=Log^\neg (\mathcal {X})$
. The direction
$Log^\neg (\mathcal {X}_{RFSI})=Log^\neg (\mathcal {X})$
. The direction
![]() $Log^\neg (\mathcal {X})\subseteq Log^\neg (\mathcal {X}_{RFSI})$
is obvious, for if
$Log^\neg (\mathcal {X})\subseteq Log^\neg (\mathcal {X}_{RFSI})$
is obvious, for if
![]() $\varphi $
is true in every algebra in
$\varphi $
is true in every algebra in
![]() $\mathcal {X}$
it is also true in
$\mathcal {X}$
it is also true in
![]() $\mathcal {X}_{RFSI}$
. Now, consider the direction
$\mathcal {X}_{RFSI}$
. Now, consider the direction
![]() $Log^\neg (\mathcal {X}_{RFSI})\subseteq Log^\neg (\mathcal {X})$
. First notice that if a
$Log^\neg (\mathcal {X}_{RFSI})\subseteq Log^\neg (\mathcal {X})$
. First notice that if a
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
has the finite model property, then for some class
$\mathcal {X}$
has the finite model property, then for some class
![]() $\mathcal {C}$
of finite Heyting algebras, we have that
$\mathcal {C}$
of finite Heyting algebras, we have that
![]() $\mathcal {X}=\mathcal {X}(\mathcal {C})$
. Suppose now by contradiction that
$\mathcal {X}=\mathcal {X}(\mathcal {C})$
. Suppose now by contradiction that
![]() $\varphi \notin Log^\neg (\mathcal {X})$
, then by Theorem 4.18 there is some finite
$\varphi \notin Log^\neg (\mathcal {X})$
, then by Theorem 4.18 there is some finite
![]() $H\in \mathcal {C}$
such that
$H\in \mathcal {C}$
such that
![]() $H\nvDash ^\neg \varphi $
. Therefore, it follows immediately by Lemma 3.11 that
$H\nvDash ^\neg \varphi $
. Therefore, it follows immediately by Lemma 3.11 that
![]() $\langle H_\neg \rangle \nvDash ^\neg \varphi $
. Then, by the argument of the proof of
$\langle H_\neg \rangle \nvDash ^\neg \varphi $
. Then, by the argument of the proof of
![]() $\mathtt {DNA}$
-Birkhoff Theorem 4.21, we obtain a regular subdirectly irreducible algebra C such that
$\mathtt {DNA}$
-Birkhoff Theorem 4.21, we obtain a regular subdirectly irreducible algebra C such that
![]() $h: \langle H_\neg \rangle \twoheadrightarrow C $
and
$h: \langle H_\neg \rangle \twoheadrightarrow C $
and
![]() $C\nvDash \varphi $
. Moreover, by the fact that C is a homomorphic image of
$C\nvDash \varphi $
. Moreover, by the fact that C is a homomorphic image of
![]() $ \langle H_\neg \rangle $
it also follows that C is finite. We thus obtain that
$ \langle H_\neg \rangle $
it also follows that C is finite. We thus obtain that
![]() $C\in \mathcal {X}_{RFSI}$
and since
$C\in \mathcal {X}_{RFSI}$
and since
![]() $C\nvDash ^\neg \varphi $
that
$C\nvDash ^\neg \varphi $
that
![]() $\varphi \notin Log^\neg (\mathcal {X}_{RFSI})$
, which finishes the proof of the theorem.
$\varphi \notin Log^\neg (\mathcal {X}_{RFSI})$
, which finishes the proof of the theorem.
Moreover, we can also show that if a
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
is locally finite, then it has the finite model property. We denote by
$\mathcal {X}$
is locally finite, then it has the finite model property. We denote by
![]() $\mathcal {X}_F$
the subcollection of finite Heyting algebras in
$\mathcal {X}_F$
the subcollection of finite Heyting algebras in
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
Theorem 4.27. Let
![]() $\mathcal {X}$
be a
$\mathcal {X}$
be a
![]() $\mathtt {DNA}$
-variety. If
$\mathtt {DNA}$
-variety. If
![]() $\mathcal {X}$
is locally finite, then it has the finite model property.
$\mathcal {X}$
is locally finite, then it has the finite model property.
Proof. By Theorem 4.18 it suffices to show that
![]() $Log^\neg (\mathcal {X})=Log^\neg (\mathcal {X}_F)$
. The inclusion
$Log^\neg (\mathcal {X})=Log^\neg (\mathcal {X}_F)$
. The inclusion
![]() $Log^\neg (\mathcal {X})\subseteq Log^\neg (\mathcal {X}_F)$
is obvious, so we show that
$Log^\neg (\mathcal {X})\subseteq Log^\neg (\mathcal {X}_F)$
is obvious, so we show that
![]() $Log^\neg (\mathcal {X}_F)\subseteq Log^\neg (\mathcal {X})$
. Suppose
$Log^\neg (\mathcal {X}_F)\subseteq Log^\neg (\mathcal {X})$
. Suppose
![]() $\varphi \notin Log^\neg (\mathcal {X}) $
, then there is some
$\varphi \notin Log^\neg (\mathcal {X}) $
, then there is some
![]() $H\in \mathcal {X}$
such that for some
$H\in \mathcal {X}$
such that for some
![]() $\mathtt {DNA}$
-valuation
$\mathtt {DNA}$
-valuation
![]() $V^\neg $
we have that
$V^\neg $
we have that
![]() $(H,V^{\neg })\nvDash ^\neg \varphi $
. Let
$(H,V^{\neg })\nvDash ^\neg \varphi $
. Let
![]() $\overline {p}$
be the variables in
$\overline {p}$
be the variables in
![]() $\varphi $
and let
$\varphi $
and let
![]() $V^\neg (\overline {p})$
be their interpretations in H. Then, since
$V^\neg (\overline {p})$
be their interpretations in H. Then, since
![]() $\mathcal {X}$
is locally finite we have that the generated subalgebra
$\mathcal {X}$
is locally finite we have that the generated subalgebra
![]() $\langle V^\neg (\overline {p})\rangle $
is also finite. Moreover, since
$\langle V^\neg (\overline {p})\rangle $
is also finite. Moreover, since
![]() $(H, V^{\neg })\nvDash \varphi $
and by the fact that the interpretation of
$(H, V^{\neg })\nvDash \varphi $
and by the fact that the interpretation of
![]() $\varphi $
lies inside
$\varphi $
lies inside
![]() $\langle V^\neg (\overline {p})\rangle $
, it immediately follows that
$\langle V^\neg (\overline {p})\rangle $
, it immediately follows that
![]() $(\langle V^{\neg}(\overline{p})\rangle, V^{\neg })\nvDash \varphi $
. So, since
$(\langle V^{\neg}(\overline{p})\rangle, V^{\neg })\nvDash \varphi $
. So, since
![]() $\langle V^\neg (\overline {p})\rangle \in \mathcal {X}_F$
, it follows that
$\langle V^\neg (\overline {p})\rangle \in \mathcal {X}_F$
, it follows that
![]() $\varphi \notin Log^\neg (\mathcal {X}_F)$
, which finishes the proof of the theorem.
$\varphi \notin Log^\neg (\mathcal {X}_F)$
, which finishes the proof of the theorem.
One may wonder whether our definition trivializes or if it captures an interesting property that
![]() $\mathtt {DNA}$
-varieties may, or may not, have. That this is the case follows from the fact that one can find
$\mathtt {DNA}$
-varieties may, or may not, have. That this is the case follows from the fact that one can find
![]() $\mathtt {DNA}$
-logics which have the finite model property but that are not locally tabular. Hence, exactly as in the case of intermediate logics, the property of local tabularity is stronger than that of the finite model property. In particular, since
$\mathtt {DNA}$
-logics which have the finite model property but that are not locally tabular. Hence, exactly as in the case of intermediate logics, the property of local tabularity is stronger than that of the finite model property. In particular, since
![]() $\mathtt {IPC}$
has the finite model property, it follows immediately from Proposition 4.25 that
$\mathtt {IPC}$
has the finite model property, it follows immediately from Proposition 4.25 that
![]() $\mathtt {IPC}^\neg $
has the finite model property as well. However, similarly to the case of
$\mathtt {IPC}^\neg $
has the finite model property as well. However, similarly to the case of
![]() $\mathtt {IPC}$
, we can show that
$\mathtt {IPC}$
, we can show that
![]() $\mathtt {IPC}^\neg $
is not locally tabular. This is done by adapting the method of the Rieger–Nishimura ladder to the context of
$\mathtt {IPC}^\neg $
is not locally tabular. This is done by adapting the method of the Rieger–Nishimura ladder to the context of
![]() $\mathtt {DNA}$
-logics. A proof of this result can be found in [Reference Quadrellaro41, Section 4.2.2].
$\mathtt {DNA}$
-logics. A proof of this result can be found in [Reference Quadrellaro41, Section 4.2.2].
4.5 Jankov formulas for
 $\mathtt {DNA}$
-models
$\mathtt {DNA}$
-models
Jankov formulas (or Jankov-de Jongh formulas) play an important role in the study of intermediate logics [Reference Bezhanishvili4, Reference Chagrov and Zakharyaschev8]. These formulas are a sort of counterpart in algebraic logic of what diagrams are in model theory, as they express in syntactic terms some key semantic properties of the corresponding algebra. Jankov introduced these formulas in [Reference Jankov29, Reference Jankov31], where he used them to show that the lattice of intermediate logic has the cardinality of the continuum. Formulas having similar properties have also been introduced around the same time by de Jongh [Reference de Jongh17] (see also [Reference Bezhanishvili4, Section 3.3]) and later by Fine in the context of modal logics [Reference Fine19]. We refer the interested reader to [Reference Bezhanishvili and Bezhanishvili2, Reference Chagrov and Zakharyaschev8, Reference Citkin15] for more information on Jankov formulas and their history.
We introduce a version of Jankov formulas which suits our setting of
![]() $\mathtt {DNA}$
-logics and we show how they can be used to axiomatise locally tabular
$\mathtt {DNA}$
-logics and we show how they can be used to axiomatise locally tabular
![]() $\mathtt {DNA}$
-logics. We adapt the approach originally presented by Wronski in [Reference Wronski45]. First, we show how to decorate a Heyting algebra
$\mathtt {DNA}$
-logics. We adapt the approach originally presented by Wronski in [Reference Wronski45]. First, we show how to decorate a Heyting algebra
![]() $H\in \mathrm{HA}_{RFSI} $
with what we call Jankov representatives. Consider any
$H\in \mathrm{HA}_{RFSI} $
with what we call Jankov representatives. Consider any
![]() $H\in \mathrm{HA}_{RFSI} $
, then we have that
$H\in \mathrm{HA}_{RFSI} $
, then we have that
![]() $H=\langle H_\neg \rangle $
and also that
$H=\langle H_\neg \rangle $
and also that
![]() $H_\neg $
is finite. We can thus assume without loss of generality that H is generated by a finite set of regular elements
$H_\neg $
is finite. We can thus assume without loss of generality that H is generated by a finite set of regular elements
![]() $a_0,\dots ,a_n$
and that every element
$a_0,\dots ,a_n$
and that every element
![]() $x\in H$
can be expressed as a polynomial
$x\in H$
can be expressed as a polynomial
![]() $\delta _H(a_0,\dots ,a_n)$
over the regular elements of H. We then associate every element
$\delta _H(a_0,\dots ,a_n)$
over the regular elements of H. We then associate every element
![]() $x\in H$
to a formula
$x\in H$
to a formula
![]() $\psi _x$
called its Jankov representative.
$\psi _x$
called its Jankov representative.
Definition 4.28 (Jankov Representative)
Let
![]() $H\in \mathrm{HA}_{RFSI} $
and
$H\in \mathrm{HA}_{RFSI} $
and
![]() $x\in H$
, then the Jankov representative of x is a formula
$x\in H$
, then the Jankov representative of x is a formula
![]() $\psi _x$
defined as follows:
$\psi _x$
defined as follows:
-
(i) If
 $x\in H_\neg $
, then
$x\in H_\neg $
, then
 $\psi _x=p_x$
, where
$\psi _x=p_x$
, where
 $p_x\in \mathtt {AT}$
.
$p_x\in \mathtt {AT}$
. -
(ii) If
 $x=\delta _H(a_0,\dots ,a_n)$
with
$x=\delta _H(a_0,\dots ,a_n)$
with
 $a_0,\dots ,a_n\in H_\neg $
, then
$a_0,\dots ,a_n\in H_\neg $
, then
 $\psi _x=\delta (p_{a_0},\dots ,p_{a_n})$
.
$\psi _x=\delta (p_{a_0},\dots ,p_{a_n})$
.
Notice that when we decorate a Heyting algebra H with Jankov representatives we are making a fundamental use of the fact that H is regular. Notice also that the Jankov representative of an element
![]() $x\in H$
is not unique, as there are different polynomials over regular elements characterizing the same element of a regular Heyting algebra. The Jankov representative is thus the formula corresponding to any of those polynomials. Once we have the notion of Jankov representative, we can define Jankov formulas for the setting of
$x\in H$
is not unique, as there are different polynomials over regular elements characterizing the same element of a regular Heyting algebra. The Jankov representative is thus the formula corresponding to any of those polynomials. Once we have the notion of Jankov representative, we can define Jankov formulas for the setting of
![]() $\mathtt {DNA}$
-logics as follows.
$\mathtt {DNA}$
-logics as follows.
Definition 4.29 (Jankov
 $\mathtt {DNA}$
-Formula)
$\mathtt {DNA}$
-Formula)
Let
![]() $H\in \mathrm{HA}_{RFSI} $
, let
$H\in \mathrm{HA}_{RFSI} $
, let
![]() $0$
be the least element of H and s its second greatest element. Then the Jankov
$0$
be the least element of H and s its second greatest element. Then the Jankov
![]() $\mathtt {DNA}$
-Formula
$\mathtt {DNA}$
-Formula
![]() $\chi ^{\mathtt {DNA}}(H)$
is defined as follows:
$\chi ^{\mathtt {DNA}}(H)$
is defined as follows:
where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are the following formulas:
$\beta $
are the following formulas:
 $$ \begin{align*} &\alpha= (\psi_0\leftrightarrow \bot) \land \bigwedge \, \{(\psi_a\land \psi_b) \leftrightarrow \psi_{a\land b} : a,b\in H \} \, \space \land \\ &\hspace{72pt} \bigwedge \, \{(\psi_a\lor \psi_b) \leftrightarrow \psi_{a\lor b} : a,b\in H \} \, \space \land \\ &\hspace{72pt} \bigwedge \, \{(\psi_a\rightarrow \psi_b) \leftrightarrow \psi_{a\rightarrow b} : a,b\in H \} \\ &\beta = \psi_s. \end{align*} $$
$$ \begin{align*} &\alpha= (\psi_0\leftrightarrow \bot) \land \bigwedge \, \{(\psi_a\land \psi_b) \leftrightarrow \psi_{a\land b} : a,b\in H \} \, \space \land \\ &\hspace{72pt} \bigwedge \, \{(\psi_a\lor \psi_b) \leftrightarrow \psi_{a\lor b} : a,b\in H \} \, \space \land \\ &\hspace{72pt} \bigwedge \, \{(\psi_a\rightarrow \psi_b) \leftrightarrow \psi_{a\rightarrow b} : a,b\in H \} \\ &\beta = \psi_s. \end{align*} $$
When its clear from the context that we are working with Jankov
![]() $\mathtt {DNA}$
-formulas and not with the standard Jankov formulas, we drop the superscript and write just
$\mathtt {DNA}$
-formulas and not with the standard Jankov formulas, we drop the superscript and write just
![]() $\chi (H)$
for the Jankov
$\chi (H)$
for the Jankov
![]() $\mathtt {DNA}$
-formula of H. We now prove a lemma which plays an important role in the proof of our Jankov’s theorem.
$\mathtt {DNA}$
-formula of H. We now prove a lemma which plays an important role in the proof of our Jankov’s theorem.
Lemma 4.30. Let
![]() $H\in \mathrm{HA}_{RFSI} $
, then
$H\in \mathrm{HA}_{RFSI} $
, then
![]() $H\nvDash ^\neg \chi (H)$
.
$H\nvDash ^\neg \chi (H)$
.
Proof. Suppose
![]() $H\in \mathrm{HA}_{RFSI} $
and
$H\in \mathrm{HA}_{RFSI} $
and
![]() $\chi (H)$
is its
$\chi (H)$
is its
![]() $\mathtt {DNA}$
-Jankov formula. Then we define the
$\mathtt {DNA}$
-Jankov formula. Then we define the
![]() $\mathtt {DNA}$
-valuation
$\mathtt {DNA}$
-valuation
![]() $V^\neg $
such that for all atomic Jankov representative we have that
$V^\neg $
such that for all atomic Jankov representative we have that
![]() $V^\neg:p_a\mapsto a$
, for all
$V^\neg:p_a\mapsto a$
, for all
![]() $a\in H_\neg $
. Moreover, if an element
$a\in H_\neg $
. Moreover, if an element
![]() $x\in H\setminus H_\neg $
is described by a polynomial
$x\in H\setminus H_\neg $
is described by a polynomial
![]() $ \delta _H(a_0,\dots ,a_n) $
over regular element of H, it follows by the definition of Jankov representative that
$ \delta _H(a_0,\dots ,a_n) $
over regular element of H, it follows by the definition of Jankov representative that
. We then have that for every element
![]() $x\in H$
it is the case that
$x\in H$
it is the case that
. But then it follows straightforwardly that for all
![]() $a,b\in H$
and for any connective
$a,b\in H$
and for any connective
![]() $\odot $
we have
$\odot $
we have
so that the antecedent of the
![]() $\mathtt {DNA}$
-Jankov formula is
$\mathtt {DNA}$
-Jankov formula is
and its consequent is
. Therefore, we have that:
And, therefore, we have that
![]() $(H,V^\neg )\nvDash ^\neg \chi (H)$
and so that
$(H,V^\neg )\nvDash ^\neg \chi (H)$
and so that
![]() $H\nvDash ^\neg \chi (H)$
.
$H\nvDash ^\neg \chi (H)$
.
If A and B are two Heyting algebras, then we define
![]() $ A\leq B \text { iff } A\in HS(B) $
. It is easy to show that this is indeed a partial order—modulo taking isomorphism classes of algebras. We now prove a suitable version of Jankov’s theorem for our setting. We adapt to our setting a similar proof given in [Reference Bezhanishvili and Bezhanishvili2].
$ A\leq B \text { iff } A\in HS(B) $
. It is easy to show that this is indeed a partial order—modulo taking isomorphism classes of algebras. We now prove a suitable version of Jankov’s theorem for our setting. We adapt to our setting a similar proof given in [Reference Bezhanishvili and Bezhanishvili2].
Theorem 4.31 (Jankov’s Theorem for
 $\mathtt {DNA}$
-Models)
$\mathtt {DNA}$
-Models)
Let
![]() $A\in \mathrm{HA}_{RFSI} $
and
$A\in \mathrm{HA}_{RFSI} $
and
![]() $B\in \mathrm{HA}$
then:
$B\in \mathrm{HA}$
then:
Proof.
![]() $(\Rightarrow )$
Suppose that
$(\Rightarrow )$
Suppose that
![]() $B\nvDash ^\neg \chi (A)$
, then for some
$B\nvDash ^\neg \chi (A)$
, then for some
![]() $\mathtt {DNA}$
-valuation
$\mathtt {DNA}$
-valuation
![]() $V^\neg $
we have
$V^\neg $
we have
![]() . It follows from Lemma 4.20 that there is a subdirectly irreducible Heyting algebra C and a surjective homomorphism
. It follows from Lemma 4.20 that there is a subdirectly irreducible Heyting algebra C and a surjective homomorphism
![]() $f:B\twoheadrightarrow C$
such that
$f:B\twoheadrightarrow C$
such that
![]() $f(b)=s_C$
. Hence, since f is a homomorphism, it follows that
$f(b)=s_C$
. Hence, since f is a homomorphism, it follows that
![]() $U^\neg = f\circ V^\neg $
is a
$U^\neg = f\circ V^\neg $
is a
![]() $\mathtt {DNA}$
-valuation. It thus follows that
$\mathtt {DNA}$
-valuation. It thus follows that
![]() . In particular, since
. In particular, since
![]() $s_C$
is the second-greatest element, this implies that
$s_C$
is the second-greatest element, this implies that
![]() and
and
![]() .
.
We now prove that the map
![]() $h: A\rightarrow C$
defined as
$h: A\rightarrow C$
defined as
is an embedding of A into C. First, we show that h is a homomorphism. Since
it follows immediately that
and for every connective
![]() $\odot $
and every element
$\odot $
and every element
![]() $a,b\in C$
, we have
$a,b\in C$
, we have
. From this we immediately get that
and
. So we have the following two identities.

We now want to prove that h is injective. Assume that
![]() $a\nleq b$
. Since under this hypothesis
$a\nleq b$
. Since under this hypothesis
![]() $a\rightarrow b \leq s_A$
—where
$a\rightarrow b \leq s_A$
—where
![]() $s_A$
is the second greatest element of A—and since
$s_A$
is the second greatest element of A—and since
, we have that
![]() $ h(a\rightarrow b) \leq h(s_A) $
. Therefore,
$ h(a\rightarrow b) \leq h(s_A) $
. Therefore,
In particular
![]() $h(a)\nleq h(b)$
, thus proving the injectivity of h.
$h(a)\nleq h(b)$
, thus proving the injectivity of h.
Therefore, we have that h is an embedding and thus
![]() $h[A]\preceq C$
, showing that A is a subalgebra of C up to isomorphism. Since
$h[A]\preceq C$
, showing that A is a subalgebra of C up to isomorphism. Since
![]() $B\twoheadrightarrow C$
it follows that
$B\twoheadrightarrow C$
it follows that
![]() $A\in SH(B)$
and, by Proposition 2.2, that
$A\in SH(B)$
and, by Proposition 2.2, that
![]() $SH(B)\subseteq HS(B)$
. Thus we obtain that
$SH(B)\subseteq HS(B)$
. Thus we obtain that
![]() $A\in HS(B)$
, that is,
$A\in HS(B)$
, that is,
![]() $A\leq B$
.
$A\leq B$
.
![]() $(\Leftarrow )$
Suppose that
$(\Leftarrow )$
Suppose that
![]() $A\leq B$
, namely that
$A\leq B$
, namely that
![]() $A\in HS (B)$
, then we know there is some subalgebra
$A\in HS (B)$
, then we know there is some subalgebra
![]() $B'\preceq B$
such that there is a surjective homomorphism
$B'\preceq B$
such that there is a surjective homomorphism
![]() ${h: B'\twoheadrightarrow A}$
. Moreover, by the previous Lemma 4.30 we have that
${h: B'\twoheadrightarrow A}$
. Moreover, by the previous Lemma 4.30 we have that
![]() $A\nvDash ^\neg \chi (A)$
. Then, since
$A\nvDash ^\neg \chi (A)$
. Then, since
![]() $h: B'\twoheadrightarrow A$
it follows immediately by the fact that the
$h: B'\twoheadrightarrow A$
it follows immediately by the fact that the
![]() $\mathtt {DNA}$
-validity of a formula is preserved by homomorphic images that
$\mathtt {DNA}$
-validity of a formula is preserved by homomorphic images that
![]() $B'\nvDash ^\neg \chi (A)$
. Moreover, since
$B'\nvDash ^\neg \chi (A)$
. Moreover, since
![]() $B'\preceq B$
it follows by the preservation of
$B'\preceq B$
it follows by the preservation of
![]() $\mathtt {DNA}$
-validity under subalgebra that
$\mathtt {DNA}$
-validity under subalgebra that
![]() $B\nvDash ^\neg \chi (A)$
, which proves our claim.
$B\nvDash ^\neg \chi (A)$
, which proves our claim.
Once we have shown that Jankov’s theorem holds for our setting, we can use Jankov’s machinery to characterize the lattice of subvarieties of locally finite
![]() $\mathtt {DNA}$
-varieties. We denote by
$\mathtt {DNA}$
-varieties. We denote by
![]() $\Lambda ^\neg (\mathcal {X})$
the lattice of subvarieties of some
$\Lambda ^\neg (\mathcal {X})$
the lattice of subvarieties of some
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
and we first prove the following useful proposition.
$\mathcal {X}$
and we first prove the following useful proposition.
Definition 4.32 (Hereditary FMP)
We say that a
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
has the hereditary
$\mathcal {X}$
has the hereditary
![]() $\mathtt {DNA}$
-finite model property if every
$\mathtt {DNA}$
-finite model property if every
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {Y}\in \Lambda ^\neg (\mathcal {X} )$
has the finite model property.
$\mathcal {Y}\in \Lambda ^\neg (\mathcal {X} )$
has the finite model property.
As we always do, when the context is clear we drop the prefix
![]() $\mathtt {DNA}$
and talk simply of the hereditary finite model property.
$\mathtt {DNA}$
and talk simply of the hereditary finite model property.
Proposition 4.33. If a
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
is locally finite, then
$\mathcal {X}$
is locally finite, then
![]() $\mathcal {X}$
has the hereditary finite model property.
$\mathcal {X}$
has the hereditary finite model property.
Proof. Suppose that
![]() $\mathcal {X}$
is locally finite and consider any subvariety
$\mathcal {X}$
is locally finite and consider any subvariety
![]() $\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
. Since
$\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
. Since
![]() $\mathcal {X}$
is locally finite we have that every
$\mathcal {X}$
is locally finite we have that every
![]() $\mathtt {DNA}$
-finitely generated
$\mathtt {DNA}$
-finitely generated
![]() $H\in \mathcal {X}$
is also finite and thus since
$H\in \mathcal {X}$
is also finite and thus since
![]() $\mathcal {Y}\subseteq \mathcal {X}$
also that
$\mathcal {Y}\subseteq \mathcal {X}$
also that
![]() $\mathtt {DNA}$
-finitely generated
$\mathtt {DNA}$
-finitely generated
![]() $H\in \mathcal {Y}$
is finite. Hence we have that
$H\in \mathcal {Y}$
is finite. Hence we have that
![]() $\mathcal {Y}$
is locally finite and therefore, by Proposition 4.27, it follows that
$\mathcal {Y}$
is locally finite and therefore, by Proposition 4.27, it follows that
![]() $\mathcal {Y}$
also has the finite model property.
$\mathcal {Y}$
also has the finite model property.
We now prove the following theorem characterising the sublattice of locally finite
![]() $\mathtt {DNA}$
-varieties. We denote by
$\mathtt {DNA}$
-varieties. We denote by
![]() $Dw(\mathcal {X}_{RFSI})$
the downsets of
$Dw(\mathcal {X}_{RFSI})$
the downsets of
![]() $\mathcal {X}_{RFSI}$
under the partial order
$\mathcal {X}_{RFSI}$
under the partial order
![]() $\leq $
defined above.
$\leq $
defined above.
Theorem 4.34. Let
![]() $\mathcal {X}$
be a locally finite
$\mathcal {X}$
be a locally finite
![]() $\mathtt {DNA}$
-variety. Then the lattice of negative subvarieties of
$\mathtt {DNA}$
-variety. Then the lattice of negative subvarieties of
![]() $\mathcal {X}$
is isomorphic to the lattice of downsets over
$\mathcal {X}$
is isomorphic to the lattice of downsets over
![]() $\mathcal {X}_{RFSI}$
, i.e.,
$\mathcal {X}_{RFSI}$
, i.e.,
Proof. Consider the map
![]() $\alpha : \mathcal {Y}\mapsto \mathcal {Y}_{RFSI}$
which sends every subvariety
$\alpha : \mathcal {Y}\mapsto \mathcal {Y}_{RFSI}$
which sends every subvariety
![]() $\mathcal {Y}\subseteq \mathcal {X}$
to its subclass of finite regular subdirectly irreducible elements. We claim that
$\mathcal {Y}\subseteq \mathcal {X}$
to its subclass of finite regular subdirectly irreducible elements. We claim that
![]() $\alpha $
is welldefined and also it is an isomorphism between
$\alpha $
is welldefined and also it is an isomorphism between
![]() $ \Lambda ^\neg (\mathcal {V}) $
and
$ \Lambda ^\neg (\mathcal {V}) $
and
![]() $ Dw(\mathcal {X}_{RFSI})$
. (i) First, we show that
$ Dw(\mathcal {X}_{RFSI})$
. (i) First, we show that
![]() $\mathcal {Y}_{RFSI}\in Dw(\mathcal {X}_{RFSI})$
. Suppose
$\mathcal {Y}_{RFSI}\in Dw(\mathcal {X}_{RFSI})$
. Suppose
![]() $B\in \mathcal {Y}_{RFSI} $
,
$B\in \mathcal {Y}_{RFSI} $
,
![]() $A\in HS(B)$
and
$A\in HS(B)$
and
![]() $A\in \mathcal {X}_{RFSI}$
. As varieties are closed under homomorphic images and subalgebras, we have that
$A\in \mathcal {X}_{RFSI}$
. As varieties are closed under homomorphic images and subalgebras, we have that
![]() $A\in \mathcal {Y}$
and so since
$A\in \mathcal {Y}$
and so since
![]() $A\in \mathcal {X}_{RFSI}$
also that
$A\in \mathcal {X}_{RFSI}$
also that
![]() $A\in \mathcal {Y}_{RFSI}$
. (ii) To show injectivity, consider two subvarieties
$A\in \mathcal {Y}_{RFSI}$
. (ii) To show injectivity, consider two subvarieties
![]() $\mathcal {Y},\mathcal {W}\in \Lambda (\mathcal {V})$
such that
$\mathcal {Y},\mathcal {W}\in \Lambda (\mathcal {V})$
such that
![]() $\mathcal {Y}\neq \mathcal {W}$
. By Proposition 4.33 we have that since
$\mathcal {Y}\neq \mathcal {W}$
. By Proposition 4.33 we have that since
![]() $\mathcal {X}$
is
$\mathcal {X}$
is
![]() $\mathtt {DNA}$
-locally finite then it has the hereditary finite model property. Therefore, it follows from Theorem 4.26 that every subvariety of
$\mathtt {DNA}$
-locally finite then it has the hereditary finite model property. Therefore, it follows from Theorem 4.26 that every subvariety of
![]() $\mathcal {X}$
is generated by its finite regular subdirectly irreducible elements. So we have that
$\mathcal {X}$
is generated by its finite regular subdirectly irreducible elements. So we have that
![]() $\mathcal {Y}=\mathcal {Y}_{RFSI} $
and
$\mathcal {Y}=\mathcal {Y}_{RFSI} $
and
![]() $\mathcal {W}= \mathcal {W}_{RFSI}$
and so it follows that
$\mathcal {W}= \mathcal {W}_{RFSI}$
and so it follows that
![]() $\mathcal {Y}_{RFSI} \neq \mathcal {W}_{RFSI} $
. (iii) For surjectivity, consider any downset
$\mathcal {Y}_{RFSI} \neq \mathcal {W}_{RFSI} $
. (iii) For surjectivity, consider any downset
![]() $D\in Dw(\mathcal {X}_{RFSI})$
. Then this defines a
$D\in Dw(\mathcal {X}_{RFSI})$
. Then this defines a
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {Y}=\mathcal {X}(D)$
. We now claim that
$\mathcal {Y}=\mathcal {X}(D)$
. We now claim that
![]() $D=\mathcal {Y}_{RFSI}$
. For the left-to-right inclusion suppose
$D=\mathcal {Y}_{RFSI}$
. For the left-to-right inclusion suppose
![]() $A\in D$
, then we also have that
$A\in D$
, then we also have that
![]() $A\in \mathcal {X}_{RFSI}$
and
$A\in \mathcal {X}_{RFSI}$
and
![]() $A\in \mathcal {X}(D)=\mathcal {Y}$
, which together imply
$A\in \mathcal {X}(D)=\mathcal {Y}$
, which together imply
![]() $A\in \mathcal {Y}_{RFSI}$
. For the other direction, suppose that
$A\in \mathcal {Y}_{RFSI}$
. For the other direction, suppose that
![]() $A\in \mathcal {Y}_{RFSI}$
, then we have by Lemma 4.30 that
$A\in \mathcal {Y}_{RFSI}$
, then we have by Lemma 4.30 that
![]() $A\nvDash ^\neg \chi ^\neg (A)$
. Then since
$A\nvDash ^\neg \chi ^\neg (A)$
. Then since
![]() $A\in \mathcal {Y}=\mathcal {X}(D)$
it follows that there is some
$A\in \mathcal {Y}=\mathcal {X}(D)$
it follows that there is some
![]() $B\in D$
such that
$B\in D$
such that
![]() $B\nvDash ^\neg \chi ^\neg (A)$
. Finally, it follows by the Jankov’s theorem for
$B\nvDash ^\neg \chi ^\neg (A)$
. Finally, it follows by the Jankov’s theorem for
![]() $\mathtt {DNA}$
-varieties 4.31 that
$\mathtt {DNA}$
-varieties 4.31 that
![]() $A\leq B$
and thus since D is a downset that
$A\leq B$
and thus since D is a downset that
![]() $A\in D$
.
$A\in D$
.
Moreover, we can also use Jankov formulas to axiomatise subvarieties of a locally finite
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $\mathcal {X}$
. To this end, we notice that for every proper subvariety
$\mathcal {X}$
. To this end, we notice that for every proper subvariety
![]() $\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
we have that
$\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
we have that
![]() $\mathcal {Y}_{RFSI}$
is a downset and
$\mathcal {Y}_{RFSI}$
is a downset and
![]() $\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
is a nonempty upset over
$\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
is a nonempty upset over
![]() $\mathcal {X}_{RFSI}$
. Now, since every algebra in
$\mathcal {X}_{RFSI}$
. Now, since every algebra in
![]() $H \in \mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
is finite, we cannot have infinite descending chains of the form
$H \in \mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
is finite, we cannot have infinite descending chains of the form
![]() $H_0\geq H_1\geq H_2\dots $
, for
$H_0\geq H_1\geq H_2\dots $
, for
![]() $|H_n|> |H_{n+1}|$
and
$|H_n|> |H_{n+1}|$
and
![]() $|H_n|$
finite. It follows that every set of the form
$|H_n|$
finite. It follows that every set of the form
![]() $\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
has some minimal element. We thus define the following notion of minimal counterexamples of a subvariety of
$\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
has some minimal element. We thus define the following notion of minimal counterexamples of a subvariety of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
Definition 4.35 (Minimal Counterexample)
Let
![]() $\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
be a subvariety of
$\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
be a subvariety of
![]() $\mathcal {X}$
such that
$\mathcal {X}$
such that
![]() $\mathcal {Y}\neq \mathcal {X}$
. A minimal counterexample to
$\mathcal {Y}\neq \mathcal {X}$
. A minimal counterexample to
![]() $\mathcal {Y}$
is a Heyting algebra
$\mathcal {Y}$
is a Heyting algebra
![]() $H\in \mathcal {X}\setminus \mathcal {Y}$
such that for all
$H\in \mathcal {X}\setminus \mathcal {Y}$
such that for all
![]() $K\leq H$
, if
$K\leq H$
, if
![]() $K\ncong H$
then
$K\ncong H$
then
![]() $K\in \mathcal {Y}$
.
$K\in \mathcal {Y}$
.
For every
![]() $\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
, we denote by
$\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
, we denote by
![]() $min(\mathcal {X}\setminus \mathcal {Y})$
its collection of minimal counterexamples in
$min(\mathcal {X}\setminus \mathcal {Y})$
its collection of minimal counterexamples in
![]() $\mathcal {X}$
. It follows from our previous reasoning that this collection is always nonempty when
$\mathcal {X}$
. It follows from our previous reasoning that this collection is always nonempty when
![]() $\mathcal {Y}$
is a proper subvariety of
$\mathcal {Y}$
is a proper subvariety of
![]() $\mathcal {X}$
. We prove the following theorem.
$\mathcal {X}$
. We prove the following theorem.
Theorem 4.36. Let
![]() $\mathcal {X}$
be a locally finite
$\mathcal {X}$
be a locally finite
![]() $\mathtt {DNA}$
-variety, then for every subvariety
$\mathtt {DNA}$
-variety, then for every subvariety
![]() $\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
such that
$\mathcal {Y}\in \Lambda ^\neg (\mathcal {X})$
such that
![]() $\mathcal {Y}\neq \mathcal {X}$
we have that:
$\mathcal {Y}\neq \mathcal {X}$
we have that:
Proof. It suffices to show that
![]() $\mathcal {Y}_{RFSI}= \{H\in \mathcal {X}_{RFSI} : H\vDash ^\neg \chi (A) \text { for all } A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) \} $
.
$\mathcal {Y}_{RFSI}= \{H\in \mathcal {X}_{RFSI} : H\vDash ^\neg \chi (A) \text { for all } A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) \} $
.
![]() $ (\subseteq ) $
Suppose
$ (\subseteq ) $
Suppose
![]() $H\in \mathcal {Y}_{RFSI}$
, then since
$H\in \mathcal {Y}_{RFSI}$
, then since
![]() $\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
is a nonempty upset it follows that
$\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
is a nonempty upset it follows that
![]() $ min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI})\neq \emptyset $
. But then, for all
$ min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI})\neq \emptyset $
. But then, for all
![]() $A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) $
we have that
$A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) $
we have that
![]() $A\nleq H$
. Therefore, it follows by Jankov’s theorem for
$A\nleq H$
. Therefore, it follows by Jankov’s theorem for
![]() $\mathtt {DNA}$
-varieties (Theorem 4.31) that
$\mathtt {DNA}$
-varieties (Theorem 4.31) that
![]() $H\vDash ^\neg \chi (A)$
and so
$H\vDash ^\neg \chi (A)$
and so
![]() $H\in \{H\in \mathcal {X}_{RFSI} : H\vDash ^\neg \chi (A) \text { for all } A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) \}$
.
$H\in \{H\in \mathcal {X}_{RFSI} : H\vDash ^\neg \chi (A) \text { for all } A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) \}$
.
![]() $(\supseteq )$
Suppose now that
$(\supseteq )$
Suppose now that
![]() $H\in \{H\in \mathcal {X}_{RFSI} : H\vDash ^\neg \chi (A) \text { for all } A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) \}$
, then for all
$H\in \{H\in \mathcal {X}_{RFSI} : H\vDash ^\neg \chi (A) \text { for all } A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) \}$
, then for all
![]() $A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI})$
it follows that
$A\in min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI})$
it follows that
![]() $ H\vDash ^\neg \chi (A)$
, hence by Theorem 4.31 we have that
$ H\vDash ^\neg \chi (A)$
, hence by Theorem 4.31 we have that
![]() $A\nleq H$
. But then, since
$A\nleq H$
. But then, since
![]() $min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) $
is the set of minimal elements in
$min(\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}) $
is the set of minimal elements in
![]() $\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
, it follows that
$\mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
, it follows that
![]() $H\notin \mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
. And since
$H\notin \mathcal {X}_{RFSI}\setminus \mathcal {Y}_{RFSI}$
. And since
![]() $H\in \mathcal {X}_{RFSI} $
, it follows that
$H\in \mathcal {X}_{RFSI} $
, it follows that
![]() $H\in \mathcal {Y}_{RFSI}$
.
$H\in \mathcal {Y}_{RFSI}$
.
The previous theorem provides a set of formulas which axiomatise the subvarieties of a locally finite variety. By the dual isomorphism
![]() $\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we can extend the previous result to the corresponding
$\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we can extend the previous result to the corresponding
![]() $\mathtt {DNA}$
-logics. We say that a
$\mathtt {DNA}$
-logics. We say that a
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Pi $
is an extension of a
$\Pi $
is an extension of a
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Lambda $
if
$\Lambda $
if
![]() $\Lambda \subseteq \Pi $
. Theorem 4.36 thus immediately allows us to axiomatise the extensions of a logic
$\Lambda \subseteq \Pi $
. Theorem 4.36 thus immediately allows us to axiomatise the extensions of a logic
![]() $\Lambda $
which is locally tabular. We denote by
$\Lambda $
which is locally tabular. We denote by
![]() $Var^\neg _{RFSI} (\Lambda )$
the collection of finite, regular, subdirectly irreducible elements of the
$Var^\neg _{RFSI} (\Lambda )$
the collection of finite, regular, subdirectly irreducible elements of the
![]() $\mathtt {DNA}$
-variety
$\mathtt {DNA}$
-variety
![]() $Var^\neg (\Lambda )$
and by
$Var^\neg (\Lambda )$
and by
![]() $\Lambda + \Gamma $
the closure under modus ponens of the set of formulas
$\Lambda + \Gamma $
the closure under modus ponens of the set of formulas
![]() $\Lambda \cup \Gamma $
.
$\Lambda \cup \Gamma $
.
Corollary 4.37. Let
![]() $\Lambda $
be a locally tabular
$\Lambda $
be a locally tabular
![]() $\mathtt {DNA}$
-logic. Then every
$\mathtt {DNA}$
-logic. Then every
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\Pi $
such that
$\Pi $
such that
![]() $\Lambda \subseteq \Pi $
can be axiomatised as follows:
$\Lambda \subseteq \Pi $
can be axiomatised as follows:
Proof. Since
![]() $\Lambda $
is locally tabular we have that
$\Lambda $
is locally tabular we have that
![]() $Var^\neg (\Lambda )$
is locally finite. Moreover, since
$Var^\neg (\Lambda )$
is locally finite. Moreover, since
![]() $\Lambda \subseteq \Pi $
it follows by
$\Lambda \subseteq \Pi $
it follows by
![]() $\mathtt {DNA}$
-duality that
$\mathtt {DNA}$
-duality that
![]() $Var^\neg (\Pi )\subseteq Var^\neg (\Lambda )$
. Let
$Var^\neg (\Pi )\subseteq Var^\neg (\Lambda )$
. Let
![]() $K= \{H\in Var^\neg _{RFSI} (\Lambda ) : H\vDash ^\neg \chi (A) \mbox { for all } A\in min(Var^\neg _{RFSI} (\Lambda )\setminus Var^\neg _{RFSI} (\Pi )) \}$
, then by Theorem 3.32 above it follows that
$K= \{H\in Var^\neg _{RFSI} (\Lambda ) : H\vDash ^\neg \chi (A) \mbox { for all } A\in min(Var^\neg _{RFSI} (\Lambda )\setminus Var^\neg _{RFSI} (\Pi )) \}$
, then by Theorem 3.32 above it follows that
![]() $Var^\neg (\Pi ) = \mathcal {X} (K) $
. Moreover, we have by Theorem 4.18 that
$Var^\neg (\Pi ) = \mathcal {X} (K) $
. Moreover, we have by Theorem 4.18 that
![]() $Log^\neg (\mathcal {X}(K))= Log^\neg (K)$
. By
$Log^\neg (\mathcal {X}(K))= Log^\neg (K)$
. By
![]() $\mathtt {DNA}$
-duality we then have:
$\mathtt {DNA}$
-duality we then have:
Hence, since it is easy to see that
![]() $Log^\neg (K)= \Lambda + \{ \chi (A) : A\in min(Var^\neg _{RFSI} (\Lambda )\setminus Var_{RFSI}^\neg (\Pi ) \} $
, we finally obtain that
$Log^\neg (K)= \Lambda + \{ \chi (A) : A\in min(Var^\neg _{RFSI} (\Lambda )\setminus Var_{RFSI}^\neg (\Pi ) \} $
, we finally obtain that
![]() $\Pi = \Lambda + \{ \chi (A) : A\in min(Var^\neg _{RFSI} (\Lambda )\setminus Var_{RFSI}^\neg (\Pi ) \}$
, which proves our claim
$\Pi = \Lambda + \{ \chi (A) : A\in min(Var^\neg _{RFSI} (\Lambda )\setminus Var_{RFSI}^\neg (\Pi ) \}$
, which proves our claim
We will apply Corollary 4.37 and the method of Jankov formulas in next section to axiomatize the extensions of the system
![]() $\mathtt {InqB}$
of inquisitive logic.
$\mathtt {InqB}$
of inquisitive logic.
5 Linearity of the extensions of
 $\mathtt {InqB}$
$\mathtt {InqB}$
In this section we put to work the general theory of
![]() $\mathtt {DNA}$
-logics that we have developed in the previous sections and we provide a characterisation of the extensions of the system
$\mathtt {DNA}$
-logics that we have developed in the previous sections and we provide a characterisation of the extensions of the system
![]() $\mathtt {InqB}$
of inquisitive logic. In particular, we use the algebraic semantics of
$\mathtt {InqB}$
of inquisitive logic. In particular, we use the algebraic semantics of
![]() $\mathtt {DNA}$
-logics to show that
$\mathtt {DNA}$
-logics to show that
![]() $\mathtt {InqB}$
is locally tabular and it can therefore be studied by using the method of Jankov formulas. We thus prove that the sublattice of
$\mathtt {InqB}$
is locally tabular and it can therefore be studied by using the method of Jankov formulas. We thus prove that the sublattice of
![]() $\mathtt {DNA}$
-logics which extend
$\mathtt {DNA}$
-logics which extend
![]() $\mathtt {InqB}$
is linearly ordered and that it coincides with the inquisitive hierarchy considered by Ciardelli in [Reference Ciardelli9].
$\mathtt {InqB}$
is linearly ordered and that it coincides with the inquisitive hierarchy considered by Ciardelli in [Reference Ciardelli9].
5.1 The method of ND-extensions
We introduce the ND
-extension of a Boolean algebra, in analogy with the KP-extensions of [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5]. Let B be any Boolean algebra and consider the term algebra
![]() $T(B)$
over the signature
$T(B)$
over the signature
![]() $(\dot {\land },\dot {\lor },\dot {\rightarrow },\dot {1},\dot {0})$
. The algebra
$(\dot {\land },\dot {\lor },\dot {\rightarrow },\dot {1},\dot {0})$
. The algebra
![]() $T(B)$
consists of all propositional formulas built over the set of atomic letters B, that is, using the elements of B as propositional formulas:
$T(B)$
consists of all propositional formulas built over the set of atomic letters B, that is, using the elements of B as propositional formulas:
Since
![]() $T(B)$
is a term algebra, we have that its algebraic operations are exactly the signature operations, i.e., we have that
$T(B)$
is a term algebra, we have that its algebraic operations are exactly the signature operations, i.e., we have that
![]() $\varphi \land _{T(B)} \psi = \varphi \dot {\land } \psi $
etc. We now quotient the term algebra
$\varphi \land _{T(B)} \psi = \varphi \dot {\land } \psi $
etc. We now quotient the term algebra
![]() $T(B)$
to obtain an
$T(B)$
to obtain an
![]() $\mathtt {ND}$
-algebra. In order to do this, we define the congruence
$\mathtt {ND}$
-algebra. In order to do this, we define the congruence
![]() $\equiv ^e_{\mathtt {ND}}$
. For any intermediate logic L, we write
$\equiv ^e_{\mathtt {ND}}$
. For any intermediate logic L, we write
![]() $\varphi \equiv _{L}\psi $
if and only if
$\varphi \equiv _{L}\psi $
if and only if
![]() $\varphi \leftrightarrow \psi \in L$
.
$\varphi \leftrightarrow \psi \in L$
.
Definition 5.1. Let B be an arbitrary Boolean algebra, then the congruence
![]() $\equiv ^e_{\mathtt {ND}}$
is the least congruence containing
$\equiv ^e_{\mathtt {ND}}$
is the least congruence containing
![]() $\equiv _{\mathtt {ND}}$
and such that for all
$\equiv _{\mathtt {ND}}$
and such that for all
![]() $p,q\in B$
we have:
$p,q\in B$
we have:
![]() $1_B \equiv ^e_{\mathtt {ND}} \dot {1}, 0_B\equiv ^e_{\mathtt {ND}} \dot {0}$
,
$1_B \equiv ^e_{\mathtt {ND}} \dot {1}, 0_B\equiv ^e_{\mathtt {ND}} \dot {0}$
,
![]() $ p \land _B q \equiv ^e_{\mathtt {ND}} p \dot {\land } q$
,
$ p \land _B q \equiv ^e_{\mathtt {ND}} p \dot {\land } q$
,
![]() $p \rightarrow _B q \equiv ^e_{\mathtt {ND}} p \dot {\rightarrow } q$
.
$p \rightarrow _B q \equiv ^e_{\mathtt {ND}} p \dot {\rightarrow } q$
.
The ND
-extension
![]() $H^{\mathtt {ND}}(B)$
of B is then defined as the quotient algebra
$H^{\mathtt {ND}}(B)$
of B is then defined as the quotient algebra
![]() $T(B)/\equiv ^e_{\mathtt {ND}}$
. Since
$T(B)/\equiv ^e_{\mathtt {ND}}$
. Since
![]() $\equiv _{\mathtt {\mathtt {IPC}}} \,\subseteq \, \equiv _{\mathtt {ND}} \,\subseteq \, \equiv ^e_{\mathtt {ND}}$
, we have that
$\equiv _{\mathtt {\mathtt {IPC}}} \,\subseteq \, \equiv _{\mathtt {ND}} \,\subseteq \, \equiv ^e_{\mathtt {ND}}$
, we have that
![]() $H^{\mathtt {ND}}(B)$
validates all the validities of
$H^{\mathtt {ND}}(B)$
validates all the validities of
![]() $\mathtt {IPC}$
and thus is a Heyting algebra. KP-extensions are introduced analogously in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] by using the equivalence relation
$\mathtt {IPC}$
and thus is a Heyting algebra. KP-extensions are introduced analogously in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] by using the equivalence relation
![]() $\equiv _{\mathtt {KP}}$
instead of
$\equiv _{\mathtt {KP}}$
instead of
![]() $\equiv _{\mathtt {ND}}$
.
$\equiv _{\mathtt {ND}}$
.
Recall that a downset D over a poset
![]() $(P,\leq )$
is finitely generated if there is a nonempty, finite set of elements
$(P,\leq )$
is finitely generated if there is a nonempty, finite set of elements
![]() $x_0,\dots ,x_n$
such that
$x_0,\dots ,x_n$
such that
![]() $D =\, {\downarrow }{\{x_0,\dots ,x_n\}}$
. We denote by
$D =\, {\downarrow }{\{x_0,\dots ,x_n\}}$
. We denote by
![]() $Dw_{fg}(B)$
the set of finitely generated downsets over B and we leave to the reader to verify that this forms a Heyting algebra with the order induced by the set-theoretic inclusion. It was shown in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] that
$Dw_{fg}(B)$
the set of finitely generated downsets over B and we leave to the reader to verify that this forms a Heyting algebra with the order induced by the set-theoretic inclusion. It was shown in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] that
![]() $H^{\mathtt {KP}}(B)\cong Dw_{fg}(B)$
and in [Reference Quadrellaro41] that
$H^{\mathtt {KP}}(B)\cong Dw_{fg}(B)$
and in [Reference Quadrellaro41] that
![]() $H^{\mathtt {ND}}(B)\cong Dw_{fg}(B)$
. Hence we have the following result.
$H^{\mathtt {ND}}(B)\cong Dw_{fg}(B)$
. Hence we have the following result.
Theorem 5.2. Let B be a Boolean algebra, then
![]() $H(B)^{\mathtt {ND}}\cong H(B)^{\mathtt {KP}}\cong Dw_{fg}(B)$
.
$H(B)^{\mathtt {ND}}\cong H(B)^{\mathtt {KP}}\cong Dw_{fg}(B)$
.
We will henceforth drop the superscript and denote the ND-extension of B just by
![]() $H(B)$
. We now recall some important facts about ND-extensions. The proof of the following claims was given in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] for KP-extensions and in [Reference Quadrellaro41] for ND-extensions. The following proposition is an important universal mapping property of such constructions.
$H(B)$
. We now recall some important facts about ND-extensions. The proof of the following claims was given in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] for KP-extensions and in [Reference Quadrellaro41] for ND-extensions. The following proposition is an important universal mapping property of such constructions.
Proposition 5.3 (Universal Mapping Property)
Let B be a Boolean algebra and
![]() $H(B)$
its
ND-extension, then for every Heyting algebra K such that
$H(B)$
its
ND-extension, then for every Heyting algebra K such that
![]() $K\vDash \mathtt {ND}$
and
$K\vDash \mathtt {ND}$
and
![]() $K_\neg = B$
there is a unique homomorphism
$K_\neg = B$
there is a unique homomorphism
![]() $h:H(B)\rightarrow K$
such that
$h:H(B)\rightarrow K$
such that
![]() $h\upharpoonright B = id_B$
. Moreover, if K is regular then h is also surjective.
$h\upharpoonright B = id_B$
. Moreover, if K is regular then h is also surjective.
The following proposition gives us a description of the structure of the
ND-extension
![]() $H(B)$
of a Boolean algebra B. In particular, we show that every element of
$H(B)$
of a Boolean algebra B. In particular, we show that every element of
![]() $H(B)$
can be written in a unique way as a disjunction of elements of B. Following [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] we say that every
$H(B)$
can be written in a unique way as a disjunction of elements of B. Following [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] we say that every
![]() $x\in H(B)$
has a non-redundant representation. With a slight abuse of notation we henceforth drop the square brackets and refer to elements of
$x\in H(B)$
has a non-redundant representation. With a slight abuse of notation we henceforth drop the square brackets and refer to elements of
![]() $H(B)$
as formulas rather than equivalence classes thereof. Also, since the algebra operations of
$H(B)$
as formulas rather than equivalence classes thereof. Also, since the algebra operations of
![]() $H(B)$
agree with the connectives in
$H(B)$
agree with the connectives in
![]() $(\dot {\land },\dot {\lor },\dot {\rightarrow },\dot {1},\dot {0})$
, we drop the dots and use the same symbols both for connectives and operations. The proof of the following two propositions was first given in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] and later adapted to the context of
$(\dot {\land },\dot {\lor },\dot {\rightarrow },\dot {1},\dot {0})$
, we drop the dots and use the same symbols both for connectives and operations. The proof of the following two propositions was first given in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5] and later adapted to the context of
![]() $\mathtt {ND}$
-extensions in [Reference Quadrellaro41].
$\mathtt {ND}$
-extensions in [Reference Quadrellaro41].
Proposition 5.4. For every
![]() $x\in H(B)$
we have that
$x\in H(B)$
we have that
![]() $x= \bigvee _{i\leq n}a_i$
where
$x= \bigvee _{i\leq n}a_i$
where
![]() $a_i\in B$
for all
$a_i\in B$
for all
![]() $i\leq n$
and
$i\leq n$
and
![]() $a_i\nleq a_j$
for
$a_i\nleq a_j$
for
![]() $i\neq j$
. Moreover
$i\neq j$
. Moreover
![]() $a_1,\dots ,a_n$
are uniquely determined.
$a_1,\dots ,a_n$
are uniquely determined.
Moreover
![]() $H(B)$
is well-connected, i.e., we have that for any
$H(B)$
is well-connected, i.e., we have that for any
![]() $x,y\in H(B)$
it is the case that
$x,y\in H(B)$
it is the case that
![]() $x\lor y = 1$
entails
$x\lor y = 1$
entails
![]() $x=1$
or
$x=1$
or
![]() $y=1$
.
$y=1$
.
Proposition 5.5. For any Boolean algebra B, its ND-extension
![]() $H(B)$
is well-connected.
$H(B)$
is well-connected.
We now make a short digression on Medvedev frames (to which we also refer as
![]() $\mathtt {ML}$
-frames). For W a non-empty set, let
$\mathtt {ML}$
-frames). For W a non-empty set, let
![]() $\wp ^+(W)$
be the collection of nonempty subsets of W. A Medvedev frame is a frame of the form
$\wp ^+(W)$
be the collection of nonempty subsets of W. A Medvedev frame is a frame of the form
![]() $\mathcal {F}\cong (\wp ^+(W),\supseteq )$
for a finite W. We recall the following two propositions on
$\mathcal {F}\cong (\wp ^+(W),\supseteq )$
for a finite W. We recall the following two propositions on
![]() $\mathtt {ML}$
-frames. The first connects the validity over a
$\mathtt {ML}$
-frames. The first connects the validity over a
![]() $\mathtt {ML}$
-frame
$\mathtt {ML}$
-frame
![]() $\mathcal {F}$
to the validity of its corresponding downset algebra
$\mathcal {F}$
to the validity of its corresponding downset algebra
![]() $Dw(\mathcal {F})$
(see e.g., [Reference Quadrellaro41, Section 5.1]), and it follows readily from the correspondence between Kripke semantics and algebraic semantics for finite frames [Reference Chagrov and Zakharyaschev8, Reference Esakia, Bezhanishvili and Holliday18]. The second connects validity in
$Dw(\mathcal {F})$
(see e.g., [Reference Quadrellaro41, Section 5.1]), and it follows readily from the correspondence between Kripke semantics and algebraic semantics for finite frames [Reference Chagrov and Zakharyaschev8, Reference Esakia, Bezhanishvili and Holliday18]. The second connects validity in
![]() $\mathtt {ML}$
-frames and validity in state models, and it was already pointed out in [Reference Ciardelli9]. A proof of both these results is contained in [Reference Quadrellaro41].
$\mathtt {ML}$
-frames and validity in state models, and it was already pointed out in [Reference Ciardelli9]. A proof of both these results is contained in [Reference Quadrellaro41].
Proposition 5.6. For every Medvedev frame
![]() $\mathcal {F}$
we have that
$\mathcal {F}$
we have that
![]() $\mathcal {F}\Vdash \varphi $
iff
$\mathcal {F}\Vdash \varphi $
iff
![]() $Dw(\mathcal {F})\vDash \varphi $
.
$Dw(\mathcal {F})\vDash \varphi $
.
Let
![]() $(\wp ^{+}(W),V)$
be a Medvedev model and
$(\wp ^{+}(W),V)$
be a Medvedev model and
![]() $s \in \wp ^{+}(W)$
. Let also
$s \in \wp ^{+}(W)$
. Let also
![]() $X_s^V$
denote the following set of valuations:
$X_s^V$
denote the following set of valuations:
Proposition 5.7. Let
![]() $\mathcal {M}=(\wp ^+(W), \supseteq, V)$
be a Medvedev model, then for any formula
$\mathcal {M}=(\wp ^+(W), \supseteq, V)$
be a Medvedev model, then for any formula
![]() $\varphi \in \mathcal {L}_P$
and any
$\varphi \in \mathcal {L}_P$
and any
![]() $s\in \wp ^+(W)$
we have that
$s\in \wp ^+(W)$
we have that
![]() $ X_s^V\vDash \varphi $
if and only if
$ X_s^V\vDash \varphi $
if and only if
![]()
5.2 Characterisation of
 $Var^\neg (\mathtt {InqB})$
$Var^\neg (\mathtt {InqB})$
We use the results that we recalled in the previous sections to characterise a set of generators of
![]() $Var^\neg (\mathtt {InqB})$
. First, we use the method of the ND
-extension of a Boolean algebra to show that
$Var^\neg (\mathtt {InqB})$
. First, we use the method of the ND
-extension of a Boolean algebra to show that
![]() $\mathtt {InqB}$
is locally tabular. The following theorem also follows as an easy corollary of [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5, Lemmas 4.1 and 4.3]. Recall that
$\mathtt {InqB}$
is locally tabular. The following theorem also follows as an easy corollary of [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5, Lemmas 4.1 and 4.3]. Recall that
![]() $\mathtt {ND}$
is the least intermediate logic whose negative variant is
$\mathtt {ND}$
is the least intermediate logic whose negative variant is
![]() $\mathtt {InqB}$
, hence by Proposition 4.17(ii) we have that
$\mathtt {InqB}$
, hence by Proposition 4.17(ii) we have that
![]() $Var^\neg (\mathtt {InqB}) = Var (\mathtt {ND})^\uparrow $
and
$Var^\neg (\mathtt {InqB}) = Var (\mathtt {ND})^\uparrow $
and
![]() $\mathtt {ND}=Log(Var^\neg (\mathtt {InqB}))$
.
$\mathtt {ND}=Log(Var^\neg (\mathtt {InqB}))$
.
Theorem 5.8.
![]() $\mathtt {InqB}$
is locally tabular.
$\mathtt {InqB}$
is locally tabular.
Proof. We need to show that every
![]() $\mathtt {DNA}$
-finitely generated
$\mathtt {DNA}$
-finitely generated
![]() $\mathtt {InqB}$
-algebra is finite. Consider any
$\mathtt {InqB}$
-algebra is finite. Consider any
![]() $H\in Var^\neg (\mathtt {InqB})$
and suppose H is
$H\in Var^\neg (\mathtt {InqB})$
and suppose H is
![]() $\mathtt {DNA}$
-finitely generated, then there are elements
$\mathtt {DNA}$
-finitely generated, then there are elements
![]() $x_0,\dots ,x_n\in H_\neg $
such that
$x_0,\dots ,x_n\in H_\neg $
such that
![]() $\langle x_0,\dots ,x_n \rangle = H$
. In particular, H is regular. Moreover, by the fact that
$\langle x_0,\dots ,x_n \rangle = H$
. In particular, H is regular. Moreover, by the fact that
![]() $\mathtt {ND}=Log(Var^\neg (\mathtt {InqB}))$
we also have that
$\mathtt {ND}=Log(Var^\neg (\mathtt {InqB}))$
we also have that
![]() $ Var^\neg (\mathtt {InqB}) = Var(\mathtt {ND}) $
and so
$ Var^\neg (\mathtt {InqB}) = Var(\mathtt {ND}) $
and so
![]() $H\in Var(\mathtt {ND})$
.
$H\in Var(\mathtt {ND})$
.
Notice that
![]() $H_{\neg }$
is generated as a Boolean algebra by
$H_{\neg }$
is generated as a Boolean algebra by
![]() $x_0,\dots ,x_n$
and so in particular it is finite. Moreover, by Theorem 5.2,
$x_0,\dots ,x_n$
and so in particular it is finite. Moreover, by Theorem 5.2,
![]() $H(H_{\neg }) \cong Dw_{fg}(H_{\neg })$
is also finite. By Proposition 5.3,
$H(H_{\neg }) \cong Dw_{fg}(H_{\neg })$
is also finite. By Proposition 5.3,
![]() $f: H(H_\neg )\twoheadrightarrow H$
. So it follows that H is finite, as wanted.
$f: H(H_\neg )\twoheadrightarrow H$
. So it follows that H is finite, as wanted.
Since
![]() $\mathtt {InqB}$
is locally tabular, we have by Theorem 4.26 that it is generated by its collection of finite, regular, subdirectly irreducible elements. The next theorem provides a characterisation of this class of
$\mathtt {InqB}$
is locally tabular, we have by Theorem 4.26 that it is generated by its collection of finite, regular, subdirectly irreducible elements. The next theorem provides a characterisation of this class of
![]() $\mathtt {InqB}$
-algebras. Our proof adapts [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5, Theorem 4.6].
$\mathtt {InqB}$
-algebras. Our proof adapts [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5, Theorem 4.6].
Theorem 5.9. Let H be an Heyting algebra. Then
![]() $H\in Var_{RFSI}^\neg (\mathtt {InqB})$
iff there is some finite Boolean algebra B such that
$H\in Var_{RFSI}^\neg (\mathtt {InqB})$
iff there is some finite Boolean algebra B such that
![]() $H\cong H(B)$
.
$H\cong H(B)$
.
Proof.
![]() $(\Leftarrow )$
Suppose
$(\Leftarrow )$
Suppose
![]() $H\cong H(B)$
for some finite Boolean algebra B, then we need to show that H is finite, regular and subdirectly irreducible. Firstly, since
$H\cong H(B)$
for some finite Boolean algebra B, then we need to show that H is finite, regular and subdirectly irreducible. Firstly, since
![]() $H \cong H(B) \cong Dw_{fg}(B)$
, it follows that H is finite. Secondly, by construction
$H \cong H(B) \cong Dw_{fg}(B)$
, it follows that H is finite. Secondly, by construction
![]() $H(B)$
is regular and so H is regular as well. Finally, by Proposition 5.5
$H(B)$
is regular and so H is regular as well. Finally, by Proposition 5.5
![]() $H(B)$
is well-connected and so—since it is finite—it has a second-greatest element, that is, it is a subdirectly irreducible algebra.
$H(B)$
is well-connected and so—since it is finite—it has a second-greatest element, that is, it is a subdirectly irreducible algebra.
(
![]() $\Rightarrow $
) Let
$\Rightarrow $
) Let
![]() $H\in Var_{RFSI}^\neg (\mathtt {InqB})$
, then since H is regular and
$H\in Var_{RFSI}^\neg (\mathtt {InqB})$
, then since H is regular and
![]() $Var^\neg (\mathtt {\mathtt {InqB}})=Var(\mathtt {ND})^\uparrow $
, it follows by Proposition 4.15 that
$Var^\neg (\mathtt {\mathtt {InqB}})=Var(\mathtt {ND})^\uparrow $
, it follows by Proposition 4.15 that
![]() $H\in Var(\mathtt {ND})$
. From the universal mapping property of Proposition 5.3 there is a surjective homomorphism
$H\in Var(\mathtt {ND})$
. From the universal mapping property of Proposition 5.3 there is a surjective homomorphism
![]() $h:H(H_\neg )\twoheadrightarrow H$
, where
$h:H(H_\neg )\twoheadrightarrow H$
, where
![]() $H_\neg $
is a finite Boolean algebra. We prove now that this homomorphism is also injective. Consider
$H_\neg $
is a finite Boolean algebra. We prove now that this homomorphism is also injective. Consider
![]() $x,y\in H$
such that
$x,y\in H$
such that
![]() $h(x)= h(y)$
, then it follows from Proposition 5.4 that we have non-redundant representations
$h(x)= h(y)$
, then it follows from Proposition 5.4 that we have non-redundant representations
![]() $x=\bigvee _{i\leq n} a_i$
and
$x=\bigvee _{i\leq n} a_i$
and
![]() $y=\bigvee _{j\leq m} b_j$
. Since for all
$y=\bigvee _{j\leq m} b_j$
. Since for all
![]() $ i\leq n, j\leq m$
we have
$ i\leq n, j\leq m$
we have
![]() $ a_i,b_j\in H_\neg $
, it follows by Proposition 5.3 that
$ a_i,b_j\in H_\neg $
, it follows by Proposition 5.3 that
![]() $h\upharpoonright H_\neg = id_{H_\neg }$
and so that
$h\upharpoonright H_\neg = id_{H_\neg }$
and so that
![]() $ h(a_i)=a_i$
and
$ h(a_i)=a_i$
and
![]() $h(b_j)= b_j$
, which means that
$h(b_j)= b_j$
, which means that
![]() $h(a_j),h(b_j)\in H_\neg $
. Now, since
$h(a_j),h(b_j)\in H_\neg $
. Now, since
![]() $h(x)= h(y)$
, we have that
$h(x)= h(y)$
, we have that
![]() $h(\bigvee _{i\leq n} a_i)\leq h(\bigvee _{j\leq m} b_j) $
and
$h(\bigvee _{i\leq n} a_i)\leq h(\bigvee _{j\leq m} b_j) $
and
![]() $h(\bigvee _{j\leq m} b_j)\leq h(\bigvee _{i\leq n} a_i) $
. From the former of these claims we have:
$h(\bigvee _{j\leq m} b_j)\leq h(\bigvee _{i\leq n} a_i) $
. From the former of these claims we have:
 $$ \begin{align*} &h\left( \bigvee_{i\leq n} a_i \right) \leq h\left( \bigvee_{j\leq m} b_j \right) \\ \implies & \bigwedge_{i\leq n}\left[ h(a_i)\rightarrow \bigvee_{j\leq m} h(b_{j}) \right] = 1 &\text{(by properties of }\mathtt{IPC}) \\ \implies& \bigwedge_{i\leq n}\left[ \neg\neg h(a_i)\rightarrow \bigvee_{j\leq m} \neg\neg h(b_j) \right] = 1 &\text{(since }h(a_i),h(b_j)\in H_\neg) \\ \implies& \bigwedge_{i\leq n}\bigvee_{j\leq m}\left[ \neg\neg h(a_i)\rightarrow \neg\neg h(b_j) \right] = 1 &\text{(by the axioms of }\mathtt{ND}) \\ \implies& \bigwedge_{i\leq n}\bigvee_{j\leq m}\left[ h(a_i)\rightarrow h(b_{j}) \right] = 1 &\text{(since }h(a_i),h(b_j)\in H_\neg) \\ \implies& \forall i\leq n,\exists j\leq m \text{ such that } h(a_i) \leq h(b_j) &\text{(since }H\text{ is well-connected)} \\ \implies& \forall i\leq n, \exists j\leq m \text{ such that } a_i \leq b_j &\text{(since }h\upharpoonright H_\neg = id_{H_\neg}) \\ \implies& x\leq y. \end{align*} $$
$$ \begin{align*} &h\left( \bigvee_{i\leq n} a_i \right) \leq h\left( \bigvee_{j\leq m} b_j \right) \\ \implies & \bigwedge_{i\leq n}\left[ h(a_i)\rightarrow \bigvee_{j\leq m} h(b_{j}) \right] = 1 &\text{(by properties of }\mathtt{IPC}) \\ \implies& \bigwedge_{i\leq n}\left[ \neg\neg h(a_i)\rightarrow \bigvee_{j\leq m} \neg\neg h(b_j) \right] = 1 &\text{(since }h(a_i),h(b_j)\in H_\neg) \\ \implies& \bigwedge_{i\leq n}\bigvee_{j\leq m}\left[ \neg\neg h(a_i)\rightarrow \neg\neg h(b_j) \right] = 1 &\text{(by the axioms of }\mathtt{ND}) \\ \implies& \bigwedge_{i\leq n}\bigvee_{j\leq m}\left[ h(a_i)\rightarrow h(b_{j}) \right] = 1 &\text{(since }h(a_i),h(b_j)\in H_\neg) \\ \implies& \forall i\leq n,\exists j\leq m \text{ such that } h(a_i) \leq h(b_j) &\text{(since }H\text{ is well-connected)} \\ \implies& \forall i\leq n, \exists j\leq m \text{ such that } a_i \leq b_j &\text{(since }h\upharpoonright H_\neg = id_{H_\neg}) \\ \implies& x\leq y. \end{align*} $$
Similarly, starting from
![]() $h(\bigvee _{j\leq m} b_j)\leq h(\bigvee _{i\leq n} a_i) $
we then get that
$h(\bigvee _{j\leq m} b_j)\leq h(\bigvee _{i\leq n} a_i) $
we then get that
![]() $y\leq x$
and so that
$y\leq x$
and so that
![]() $x=y$
. Finally, this means that the surjective homomorphism
$x=y$
. Finally, this means that the surjective homomorphism
![]() $h:H(H_\neg )\twoheadrightarrow H$
is also injective and so
$h:H(H_\neg )\twoheadrightarrow H$
is also injective and so
![]() $H\cong H(H_\neg )$
.
$H\cong H(H_\neg )$
.
5.3 Extensions of
 $\mathtt {InqB}$
$\mathtt {InqB}$
Finally, we can prove our main result concerning extensions of
![]() $\mathtt {InqB}$
. From the former theorem it is easy to prove the following important lemma. We recall from Section 4.5 that if A and B are two Heyting algebras, the order
$\mathtt {InqB}$
. From the former theorem it is easy to prove the following important lemma. We recall from Section 4.5 that if A and B are two Heyting algebras, the order
![]() $\leq $
between them is defined as
$\leq $
between them is defined as
![]() $ A\leq B \text { iff } A\in HS(B) $
. The next lemma shows that under this ordering the collection of regular, finite, subdirectly irreducible
$ A\leq B \text { iff } A\in HS(B) $
. The next lemma shows that under this ordering the collection of regular, finite, subdirectly irreducible
![]() $\mathtt {InqB}$
-algebras is isomorphic to
$\mathtt {InqB}$
-algebras is isomorphic to
![]() $\omega $
.
$\omega $
.
Lemma 5.10. Let
![]() $Var_{RFSI}^\neg (\mathtt {InqB})$
be the collection of finite, regular, subdirectly irreducible
$Var_{RFSI}^\neg (\mathtt {InqB})$
be the collection of finite, regular, subdirectly irreducible
![]() $\mathtt {InqB}$
-algebras. Then we have that, modulo isomorphism:
$\mathtt {InqB}$
-algebras. Then we have that, modulo isomorphism:
Proof. We show that
![]() $Var_{RFSI}^\neg (\mathtt {InqB})$
is isomorphic to
$Var_{RFSI}^\neg (\mathtt {InqB})$
is isomorphic to
![]() $\omega $
under the order
$\omega $
under the order
![]() $ A\leq B \text { iff } A\in HS(B) $
. First, consider any algebra
$ A\leq B \text { iff } A\in HS(B) $
. First, consider any algebra
![]() $H\in Var_{RFSI}^\neg (\mathtt {InqB})$
, then it follows by Theorem 5.9 that there is some finite Boolean algebra B such that
$H\in Var_{RFSI}^\neg (\mathtt {InqB})$
, then it follows by Theorem 5.9 that there is some finite Boolean algebra B such that
![]() $H=H(B)$
. The representation theorem of the finite Boolean algebras entails that finite Boolean algebras form the following chain of length
$H=H(B)$
. The representation theorem of the finite Boolean algebras entails that finite Boolean algebras form the following chain of length
![]() $\omega $
:
$\omega $
:
Now, we have by the definition of the ND
-extension of a Boolean Algebra
![]() $2^n$
that
$2^n$
that
![]() $H(2^n)$
is regular and
$H(2^n)$
is regular and
![]() $H(2^n)=\langle 2^n \rangle $
. Therefore, since we have that for all
$H(2^n)=\langle 2^n \rangle $
. Therefore, since we have that for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $2^{n}\preceq 2^{n+1}$
, it follows that
$2^{n}\preceq 2^{n+1}$
, it follows that
![]() $H(2^{n})\preceq H(2^{n+1})$
. Finally, since every
$H(2^{n})\preceq H(2^{n+1})$
. Finally, since every
![]() $H\in Var_{RFSI}^\neg (\mathtt {InqB})$
is of the form
$H\in Var_{RFSI}^\neg (\mathtt {InqB})$
is of the form
![]() $H(2^n)$
for some
$H(2^n)$
for some
![]() $n\in \mathbb {N}$
, it follows that:
$n\in \mathbb {N}$
, it follows that:
is a chain of length
![]() $\omega $
ordered by
$\omega $
ordered by
![]() $ A\leq B \Leftrightarrow A\in HS(B) $
which contains every element
$ A\leq B \Leftrightarrow A\in HS(B) $
which contains every element
![]() $H\in Var_{RFSI}^\neg (\mathtt {InqB})$
. Finally, this means that the poset
$H\in Var_{RFSI}^\neg (\mathtt {InqB})$
. Finally, this means that the poset
![]() $(Var_{RFSI}^\neg (\mathtt {InqB}), \leq )$
is isomorphic to
$(Var_{RFSI}^\neg (\mathtt {InqB}), \leq )$
is isomorphic to
![]() $\omega $
.
$\omega $
.
Once we have the previous lemma, we can use the method of Jankov formulas for
![]() $\mathtt {DNA}$
-logics developed in Section 4.5 to show that the lattice of extensions of the system of inquisitive logic
$\mathtt {DNA}$
-logics developed in Section 4.5 to show that the lattice of extensions of the system of inquisitive logic
![]() $\mathtt {InqB}$
is linearly ordered and dually isomorphic to
$\mathtt {InqB}$
is linearly ordered and dually isomorphic to
![]() $\omega +1$
.
$\omega +1$
.
Theorem 5.11. Let
![]() $\Lambda ^\neg (\mathtt {InqB})$
be the lattice of extensions of
$\Lambda ^\neg (\mathtt {InqB})$
be the lattice of extensions of
![]() $\mathtt {InqB}$
. Then there is a dual isomorphism
$\mathtt {InqB}$
. Then there is a dual isomorphism
![]() $\Lambda ^\neg (\mathtt {InqB})\cong ^{op} \omega +1$
.
$\Lambda ^\neg (\mathtt {InqB})\cong ^{op} \omega +1$
.
Proof. By the dual isomorphism
![]() $\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we immediately have that
$\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
we immediately have that
![]() $\Lambda ^\neg (\mathtt {InqB})\cong ^{op}\Lambda ^\neg (Var^\neg (\mathtt {InqB}))$
, where
$\Lambda ^\neg (\mathtt {InqB})\cong ^{op}\Lambda ^\neg (Var^\neg (\mathtt {InqB}))$
, where
![]() $\Lambda ^\neg (Var^\neg (\mathtt {InqB}))$
is the lattice of subvarieties of
$\Lambda ^\neg (Var^\neg (\mathtt {InqB}))$
is the lattice of subvarieties of
![]() $Var^\neg (\mathtt {InqB})$
. Therefore, to show that
$Var^\neg (\mathtt {InqB})$
. Therefore, to show that
![]() $\Lambda ^\neg (\mathtt {InqB})\cong ^{op} \omega +1$
it suffices to show that
$\Lambda ^\neg (\mathtt {InqB})\cong ^{op} \omega +1$
it suffices to show that
![]() $\Lambda ^\neg (Var^\neg (\mathtt {InqB})) \cong \omega +1$
. Now, by Proposition 5.8 we have that
$\Lambda ^\neg (Var^\neg (\mathtt {InqB})) \cong \omega +1$
. Now, by Proposition 5.8 we have that
![]() $\mathtt {InqB}$
is locally tabular and therefore it follows by Theorem 4.34 that
$\mathtt {InqB}$
is locally tabular and therefore it follows by Theorem 4.34 that
![]() $\Lambda ^\neg (Var^\neg (\mathtt {InqB}))\cong Dw(Var_{RFSI}^\neg (\mathtt {InqB}))$
. But then, we have by Lemma 5.10 that
$\Lambda ^\neg (Var^\neg (\mathtt {InqB}))\cong Dw(Var_{RFSI}^\neg (\mathtt {InqB}))$
. But then, we have by Lemma 5.10 that
![]() $Var_{RFSI}^\neg (\mathtt {InqB})\cong \omega $
and therefore that
$Var_{RFSI}^\neg (\mathtt {InqB})\cong \omega $
and therefore that
![]() $Dw(Var_{RFSI}^\neg (\mathtt {InqB}))\cong Dw(\omega )=\omega +1$
. To sum up, we have:
$Dw(Var_{RFSI}^\neg (\mathtt {InqB}))\cong Dw(\omega )=\omega +1$
. To sum up, we have:
which proves our claim.
The method of Jankov formulas allows us also to provide an axiomatisation for all the extensions
![]() $\Lambda $
of
$\Lambda $
of
![]() $\mathtt {InqB}$
. Then by
$\mathtt {InqB}$
. Then by
![]() $\mathtt {DNA}$
-duality and Theorem 4.34 we have that
$\mathtt {DNA}$
-duality and Theorem 4.34 we have that
![]() $\Lambda ^\neg (\mathtt {InqB})\cong ^{op} Dw(Var_{RFSI}^\neg (\mathtt {InqB}))$
. Therefore we have that extensions
$\Lambda ^\neg (\mathtt {InqB})\cong ^{op} Dw(Var_{RFSI}^\neg (\mathtt {InqB}))$
. Therefore we have that extensions
![]() $\Lambda $
of
$\Lambda $
of
![]() $\mathtt {InqB}$
are uniquely identified by specifying a downset of elements of
$\mathtt {InqB}$
are uniquely identified by specifying a downset of elements of
![]() $Var_{RFSI}^\neg (\mathtt {InqB})$
. For any
$Var_{RFSI}^\neg (\mathtt {InqB})$
. For any
![]() $n\in \mathbb {N}$
, we define by
$n\in \mathbb {N}$
, we define by
![]() $\mathtt {InqB}_n$
the
$\mathtt {InqB}_n$
the
![]() $\mathtt {DNA}$
-logic
$\mathtt {DNA}$
-logic
![]() $\mathtt {InqB}_n=Log^\neg (\downarrow H(2^n))$
. We now prove the following proposition.
$\mathtt {InqB}_n=Log^\neg (\downarrow H(2^n))$
. We now prove the following proposition.
Proposition 5.12. Let
![]() $\Lambda $
be a proper extension of
$\Lambda $
be a proper extension of
![]() $\mathtt {InqB}$
, i.e.,
$\mathtt {InqB}$
, i.e.,
![]() $\Lambda $
is a
$\Lambda $
is a
![]() $\mathtt {DNA}$
-logic and
$\mathtt {DNA}$
-logic and
![]() $\mathtt {InqB}\subsetneq \Lambda $
. Then there is some
$\mathtt {InqB}\subsetneq \Lambda $
. Then there is some
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
Proof. Suppose that
![]() $\Lambda $
is a
$\Lambda $
is a
![]() $\mathtt {DNA}$
-logic and
$\mathtt {DNA}$
-logic and
![]() $\mathtt {InqB}\subsetneq \Lambda $
, then it follows by Theorem 4.34 that
$\mathtt {InqB}\subsetneq \Lambda $
, then it follows by Theorem 4.34 that
![]() $Var^\neg (\Lambda )= \mathcal {X}( D ) $
, where
$Var^\neg (\Lambda )= \mathcal {X}( D ) $
, where
![]() $D\in Dw(Var_{RFSI}^\neg (\mathtt {InqB}))$
. Now, since
$D\in Dw(Var_{RFSI}^\neg (\mathtt {InqB}))$
. Now, since
![]() $\Lambda \neq \mathtt {InqB}$
, it follows that
$\Lambda \neq \mathtt {InqB}$
, it follows that
![]() $D\neq Var_{RFSI}^\neg (\mathtt {InqB})$
. Therefore, it follows immediately from Lemma 5.10 that
$D\neq Var_{RFSI}^\neg (\mathtt {InqB})$
. Therefore, it follows immediately from Lemma 5.10 that
![]() $D= {\downarrow }H(2^n)$
for some
$D= {\downarrow }H(2^n)$
for some
![]() $n\in \mathbb {N}$
and hence
$n\in \mathbb {N}$
and hence
![]() $\Lambda = \mathtt {InqB}_n $
. Moreover, it is easy to see that the only minimal counterexample in
$\Lambda = \mathtt {InqB}_n $
. Moreover, it is easy to see that the only minimal counterexample in
![]() $Var^\neg (\mathtt {InqB})\setminus Var^\neg (\mathtt {InqB}_n)$
is
$Var^\neg (\mathtt {InqB})\setminus Var^\neg (\mathtt {InqB}_n)$
is
![]() $H(2^{n+1})$
. Therefore, we have by Corollary 4.37 that
$H(2^{n+1})$
. Therefore, we have by Corollary 4.37 that
![]() $\mathtt {InqB}_n$
is equivalent to
$\mathtt {InqB}_n$
is equivalent to
![]() $ \mathtt {InqB} + \chi (H(2^{n+1}))$
.
$ \mathtt {InqB} + \chi (H(2^{n+1}))$
.
The previous result allows us to present in an alternative way the inquisitive hierarchy originally introduced by Ciardelli [Reference Ciardelli9, Chapter 4]. We define, for every
![]() $n\in \mathbb {N}$
, the system
$n\in \mathbb {N}$
, the system
![]() $\mathtt {InqL}_n$
as follows:
$\mathtt {InqL}_n$
as follows:
We can now show that the inquisitive hierarchy is exactly the sublattice of all the proper extensions of
![]() $\mathtt {InqB}$
. Firstly, we say that a
$\mathtt {InqB}$
. Firstly, we say that a
![]() $\mathtt {DNA}$
-logic is tabular if it is the logic of a finite regular Heyting algebra. Then, since for all
$\mathtt {DNA}$
-logic is tabular if it is the logic of a finite regular Heyting algebra. Then, since for all
![]() $H\in \downarrow H(2^n)$
we have that
$H\in \downarrow H(2^n)$
we have that
![]() $H\preceq H(2^n)$
, it follows immediately that
$H\preceq H(2^n)$
, it follows immediately that
![]() $\mathtt {InqB}_n=Log^\neg (\downarrow H(2^n))=Log^\neg ( H(2^n)) $
, i.e.,
$\mathtt {InqB}_n=Log^\neg (\downarrow H(2^n))=Log^\neg ( H(2^n)) $
, i.e.,
![]() $\mathtt {InqB}_n$
is the logic of
$\mathtt {InqB}_n$
is the logic of
![]() $H(2^n)$
and is thus tabular. Then we obtain the following theorem.
$H(2^n)$
and is thus tabular. Then we obtain the following theorem.
Theorem 5.13. For any
![]() $n\in \mathbb {N}$
, we have that
$n\in \mathbb {N}$
, we have that
![]() $\mathtt {InqB}_n=\mathtt {InqL}_n$
.
$\mathtt {InqB}_n=\mathtt {InqL}_n$
.
Proof. For any
![]() $n\in \mathbb {N}$
, we have the following equalities:
$n\in \mathbb {N}$
, we have the following equalities:

This proves our claim.
Therefore, by defining for every
![]() $n\in \mathbb {N}$
the logic
$n\in \mathbb {N}$
the logic
![]() $\mathtt {ML}_n$
as the set of formulas valid in all Medvedev frames
$\mathtt {ML}_n$
as the set of formulas valid in all Medvedev frames
![]() $\mathcal {F}$
whose cardinality is
$\mathcal {F}$
whose cardinality is
![]() $|\mathcal {F}|\leq n$
, it follows from the previous theorem that
$|\mathcal {F}|\leq n$
, it follows from the previous theorem that
![]() $(\mathtt {ML}_n)^\neg = \mathtt {InqB}_n = \mathtt {InqL}_n$
. The following corollary follows directly from Theorems 5.11 and 5.13 and is an extension of [Reference Ciardelli9, Corollary 4.1.6].
$(\mathtt {ML}_n)^\neg = \mathtt {InqB}_n = \mathtt {InqL}_n$
. The following corollary follows directly from Theorems 5.11 and 5.13 and is an extension of [Reference Ciardelli9, Corollary 4.1.6].
Corollary 5.14.
The results in this section thus provide a characterisation of the extensions of
![]() $\mathtt {InqB}$
and show that they coincide precisely with the inquisitive hierarchy already studied in the literature.
$\mathtt {InqB}$
and show that they coincide precisely with the inquisitive hierarchy already studied in the literature.
6 Conclusion
In this article we developed algebraic semantics for
![]() $\mathtt {DNA}$
-logics and we applied this general setting to inquisitive logic. This semantics allows to apply methods of universal algebra to study
$\mathtt {DNA}$
-logics and we applied this general setting to inquisitive logic. This semantics allows to apply methods of universal algebra to study
![]() $\mathtt {DNA}$
-logics and inquisitive logic from a novel perspective. Let us briefly summarize our main results. In Section 3 we introduced
$\mathtt {DNA}$
-logics and inquisitive logic from a novel perspective. Let us briefly summarize our main results. In Section 3 we introduced
![]() $\mathtt {DNA}$
-logics and their algebraic semantics and we proved the dual isomorphism
$\mathtt {DNA}$
-logics and their algebraic semantics and we proved the dual isomorphism
![]() $\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
between
$\Lambda (\mathtt {IPC}^\neg ) \cong ^{op}\Lambda (\mathrm{HA}^\uparrow ) $
between
![]() $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
![]() $\mathtt {DNA}$
-varieties. In Section 4 we studied closer the relation between
$\mathtt {DNA}$
-varieties. In Section 4 we studied closer the relation between
![]() $\mathtt {DNA}$
-logics and intermediate logics and we proved a suitable version of some classical results for the setting of
$\mathtt {DNA}$
-logics and intermediate logics and we proved a suitable version of some classical results for the setting of
![]() $\mathtt {DNA}$
-varieties. In particular, we showed that every
$\mathtt {DNA}$
-varieties. In particular, we showed that every
![]() $\mathtt {DNA}$
-variety is generated by its regular subdirectly irreducible members and we introduced a suitable version of Jankov formulas in order to axiomatise locally finite
$\mathtt {DNA}$
-variety is generated by its regular subdirectly irreducible members and we introduced a suitable version of Jankov formulas in order to axiomatise locally finite
![]() $\mathtt {DNA}$
-varieties. Finally, in Section 5 we used the algebraic semantics of
$\mathtt {DNA}$
-varieties. Finally, in Section 5 we used the algebraic semantics of
![]() $\mathtt {DNA}$
-logics to study the inquisitive logic
$\mathtt {DNA}$
-logics to study the inquisitive logic
![]() $\mathtt {InqB}$
. In particular, we showed that the sublattice of its extensions is dually isomorphic to
$\mathtt {InqB}$
. In particular, we showed that the sublattice of its extensions is dually isomorphic to
![]() $\omega +1$
and that it actually coincides with the inquisitive hierarchy studied in [Reference Ciardelli9].
$\omega +1$
and that it actually coincides with the inquisitive hierarchy studied in [Reference Ciardelli9].
In addition to these results, in our view one of the main contributions of this article is that it provides a new setting for the study of inquisitive logic. The system
![]() $\mathtt {InqB}$
had so far been considered as the logic of the evaluation states or as the negative variant of the logics between
$\mathtt {InqB}$
had so far been considered as the logic of the evaluation states or as the negative variant of the logics between
![]() $\mathtt {ND}$
and
$\mathtt {ND}$
and
![]() $\mathtt {ML}$
—here we showed that one can also consider
$\mathtt {ML}$
—here we showed that one can also consider
![]() $\mathtt {InqB}$
as the logic of a specific class of Heyting algebras, under a suitable semantics. This new perspective at the propositional system of inquisitive logic allows us to raise new questions and consider new issues.
$\mathtt {InqB}$
as the logic of a specific class of Heyting algebras, under a suitable semantics. This new perspective at the propositional system of inquisitive logic allows us to raise new questions and consider new issues.
One direction for future study is to consider what happens if, instead of the negative substitution
![]() $p\mapsto \neg p$
, we consider the substitution
$p\mapsto \neg p$
, we consider the substitution
![]() $p\mapsto \chi (p)$
for an arbitrary polynomial
$p\mapsto \chi (p)$
for an arbitrary polynomial
![]() $\chi \in \mathcal {L}_P$
. In fact, it seems possible to extend at least part of the theory of
$\chi \in \mathcal {L}_P$
. In fact, it seems possible to extend at least part of the theory of
![]() $\mathtt {DNA}$
-logics to this extended framework. In the case of negative variants we rely on the fact that in intuitionistic logic
$\mathtt {DNA}$
-logics to this extended framework. In the case of negative variants we rely on the fact that in intuitionistic logic
![]() $\neg \neg \neg p= \neg p$
. This property however is shared in a more general form by every polynomial
$\neg \neg \neg p= \neg p$
. This property however is shared in a more general form by every polynomial
![]() $\chi $
. Ruitenberg’s Theorem [Reference Ghilardi and Santocanale23, Reference Ruitenburg43] states that for any polynomial
$\chi $
. Ruitenberg’s Theorem [Reference Ghilardi and Santocanale23, Reference Ruitenburg43] states that for any polynomial
![]() $\chi $
we can find a number
$\chi $
we can find a number
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $\chi ^n=\chi ^{n+2}$
. This allows to introduce the
$\chi ^n=\chi ^{n+2}$
. This allows to introduce the
![]() $\chi $
-variant of an intermediate logic L as
$\chi $
-variant of an intermediate logic L as
![]() and to generalize our study of
and to generalize our study of
![]() $\mathtt {DNA}$
-logics to arbitrary
$\mathtt {DNA}$
-logics to arbitrary
![]() $\chi $
-variants. We refer the reader to the upcoming [Reference Grilletti and Quadrellaro24].
$\chi $
-variants. We refer the reader to the upcoming [Reference Grilletti and Quadrellaro24].
Similarly, the close connection between inquisitive logic and dependence logic that has been studied e.g., in [Reference Ciardelli, Abramsky, Kontinen, Väänänen and Vollmer10–Reference Ciardelli11] suggests that a similar semantics might be developed for the system of propositional dependence logic [Reference Yang and Väänänen46]. This direction, originally hinted at in [Reference Abramsky and Väänänen1], also raises the issue of possible connections between the present framework and the setting of residuated lattices which is employed to give a semantics to separation logic and related formalisms [Reference Jipsen and Litak32].
Finally, a last direction of further research should go towards a deeper understanding of
![]() $\mathtt {DNA}$
-logics and
$\mathtt {DNA}$
-logics and
![]() $\mathtt {DNA}$
-varieties. For instance, a new topological semantics for
$\mathtt {DNA}$
-varieties. For instance, a new topological semantics for
![]() $\mathtt {InqB}$
is introduced in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5]. This raises a question whether it is possible to translate our framework in topological terms and describe a suitable topological semantics for
$\mathtt {InqB}$
is introduced in [Reference Bezhanishvili, Grilletti, Holliday, Iemhoff, Moortgat and de Queiroz5]. This raises a question whether it is possible to translate our framework in topological terms and describe a suitable topological semantics for
![]() $\mathtt {DNA}$
-logics. Moreover, such semantics could be used to give a characterisation of finite regular subdirectly irreducible Heyting algebras. We know by Esakia duality that a finite subdirectly irreducible Heyting algebra is the upset algebra of a finite rooted frame. Can we obtain a similar characterisation for regular finite subdirectly irreducible Heyting algebras? What properties should a rooted frame satisfy in order for its dual Heyting algebra to be regular? Finally, it also seems natural to generalize Jankov formulas for
$\mathtt {DNA}$
-logics. Moreover, such semantics could be used to give a characterisation of finite regular subdirectly irreducible Heyting algebras. We know by Esakia duality that a finite subdirectly irreducible Heyting algebra is the upset algebra of a finite rooted frame. Can we obtain a similar characterisation for regular finite subdirectly irreducible Heyting algebras? What properties should a rooted frame satisfy in order for its dual Heyting algebra to be regular? Finally, it also seems natural to generalize Jankov formulas for
![]() $\mathtt {DNA}$
-models to canonical formulas, as it is the case both for intermediate [Reference Bezhanishvili and Bezhanishvili2] and modal logics [Reference Bezhanishvili and Bezhanishvili3]. These questions are for the moment open problems to be addressed in future investigations.
$\mathtt {DNA}$
-models to canonical formulas, as it is the case both for intermediate [Reference Bezhanishvili and Bezhanishvili2] and modal logics [Reference Bezhanishvili and Bezhanishvili3]. These questions are for the moment open problems to be addressed in future investigations.
Acknowledgments
We would like to thank Dick de Jongh for useful discussions and pointers to the literature. We are also very grateful to the referees for careful reading and useful comments, which have improved considerably both the content and presentation of the paper. The second author was supported by the European Research Council (ERC, grant agreement number 680220) and the Deutsche Forschungsgemeinschaft (DFG, Project number 446711878). The third author was supported by grant 336283 of the Academy of Finland and Research Funds of the University of Helsinki.