Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liz, Eduardo
and
Trofimchuk, Sergei
2000.
Existence and Stability of Almost Periodic Solutions for Quasilinear Delay Systems and the Halanay Inequality.
Journal of Mathematical Analysis and Applications,
Vol. 248,
Issue. 2,
p.
625.
Atici, F. Merdivenci
Cabada, Alberto
and
Ferreiro, Juan B.
2002.
Existence and Comparison Results for First Order Periodic Implicit Difference Equations with Maxima.
Journal of Difference Equations and Applications,
Vol. 8,
Issue. 4,
p.
357.
Ivanov, Anatoli
Liz, Eduardo
and
Trofimchuk, Sergei
2002.
Halanay inequality, Yorke 3/2 stability criterion, and differential equations with maxima.
Tohoku Mathematical Journal,
Vol. 54,
Issue. 2,
Liz, E.
and
Ferreiro, J.B.
2002.
A note on the global stability of generalized difference equations.
Applied Mathematics Letters,
Vol. 15,
Issue. 6,
p.
655.
Liz, Eduardo
Tkachenko, Victor
and
Trofimchuk, Sergei
2003.
A Global Stability Criterion for Scalar Functional Differential Equations.
SIAM Journal on Mathematical Analysis,
Vol. 35,
Issue. 3,
p.
596.
Liz, Eduardo
Ivanov, Anatoli
and
Ferreiro, Juan Bosco
2003.
Discrete Halanay-type inequalities and applications.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 55,
Issue. 6,
p.
669.
Atici, Ferhan M.
Cabada, Alberto
and
Ferreiro, Juan B.
2006.
First order difference equations with maxima and nonlinear functional boundary value conditions.
Journal of Difference Equations and Applications,
Vol. 12,
Issue. 6,
p.
565.
González, Patricio
and
Pinto, Manuel
2007.
Convergent solutions of certain nonlinear differential equations with maxima.
Mathematical and Computer Modelling,
Vol. 45,
Issue. 1-2,
p.
1.
Mishev, D.P.
and
Musa, S.M.
2007.
Distribution of the Zeros of the Solutions of Hyperbolic Differential Equations with Maxima.
Rocky Mountain Journal of Mathematics,
Vol. 37,
Issue. 4,
Huang, Jinhua
and
Liu, Jiqing
2009.
Advances in Neural Networks – ISNN 2009.
Vol. 5551,
Issue. ,
p.
262.
Agarwal, RaviP
Kim, Young-Ho
and
Sen, SK
2009.
Advanced Discrete Halanay-Type Inequalities: Stability of Difference Equations.
Journal of Inequalities and Applications,
Vol. 2009,
Issue. 1,
p.
535849.
Stamova, Ivanka
Stamov, Trayan
and
Li, Xiaodi
2014.
Global exponential stability of a class of impulsive cellular neural networks with supremums.
International Journal of Adaptive Control and Signal Processing,
Vol. 28,
Issue. 11,
p.
1227.
Hakl, R.
Trofimchuk, E.
and
Trofimchuk, S.
2023.
Periodic-Type Solutions for Differential Equations with Positively Homogeneous Functionals.
Journal of Mathematical Sciences,
Vol. 274,
Issue. 1,
p.
126.
Liz, Eduardo
and
Trofimchuk, Sergei
2023.
On a dynamical model of happiness.
Mathematical Modelling of Natural Phenomena,
Vol. 18,
Issue. ,
p.
10.
Shih, Chih-Wen
Tseng, Jui-Pin
and
Wu, Chang-Hong
2023.
Absolute Stability and Synchronization in Second-Order Neural Fields with Conduction Delays.
SIAM Journal on Applied Dynamical Systems,
Vol. 22,
Issue. 2,
p.
878.
Trofymchuk, Olena
Liz, Eduardo
and
Trofimchuk, Sergei
2023.
The peak-end rule and its dynamic realization through differential equations with maxima
*
.
Nonlinearity,
Vol. 36,
Issue. 1,
p.
507.
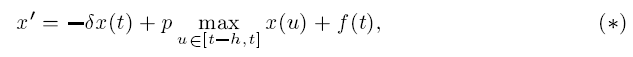 where f(t) is a periodic forcing term and δ,p∈R. We study stability in the first approximation showing that the non-smooth equation (*) can be linearized along some ‘non-singular’ periodic solutions. Then the corresponding variational equation together with the Krasnosel'skij index are used to prove the existence of multiple periodic solutions to (*). Finally, we apply a generalization of Halanay's inequality to establish conditions for global attractivity in equations with maxima.
where f(t) is a periodic forcing term and δ,p∈R. We study stability in the first approximation showing that the non-smooth equation (*) can be linearized along some ‘non-singular’ periodic solutions. Then the corresponding variational equation together with the Krasnosel'skij index are used to prove the existence of multiple periodic solutions to (*). Finally, we apply a generalization of Halanay's inequality to establish conditions for global attractivity in equations with maxima.

