Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-12T08:00:53.299Z Has data issue: false hasContentIssue false
  • English
  • Français

The regularity and stability of solutions to semilinear fourth-order elliptic problems with negative exponents

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  07 January 2016

Baishun Lai
Baishun Lai*
Affiliation:
Institute of Contemporary Mathematics, Henan University, Kaifeng 475004, People's Republic of China (laibaishun@henu.edu.cn)
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We examine the regularity of the extremal solution of the nonlinear eigenvalue problem

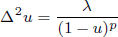
on a general bounded domain Ω in ℝN, with Navier boundary condition u = Δu on ∂Ω. Firstly, we prove the extremal solution is smooth for any p > 1 and N ⩽ 4, which improves the result of Guo and Wei (Discrete Contin. Dynam. Syst. A 34 (2014), 2561–2580). Secondly, if p = 3, N = 3, we prove that any radial weak solution of this nonlinear eigenvalue problem is smooth in the case Ω = 𝔹, which completes the result of Dávila et al. (Math. Annalen348 (2009), 143–193). Finally, we also consider the stability of the entire solution of Δ2u = –l/up in ℝN with u > 0.

Keywords

biharmonic equationentire solutionregularitystability

MSC classification

Secondary: 35J91: Semilinear elliptic equations with Laplacian, bi-Laplacian or poly-Laplacian 35B08: Entire solutions 35B53: Liouville theorems, Phragmén-Lindelöf theorems 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 146 , Issue 1 , February 2016 , pp. 195 - 212
Copyright
Copyright © Royal Society of Edinburgh 2016