Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-06T15:32:26.757Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive solutions for a class of quasilinear problems with critical growth in ℝN

Published online by Cambridge University Press:  02 April 2015

Jun Wang ,
Tianqing An  and
Fubao Zhang
Jun Wang
Affiliation:
Faculty of Science, Jiangsu University, Zhenjiang, Jiangsu 212013, People’s Republic of China, (wangmath2011@126.com)
Tianqing An
Affiliation:
Department of Mathematics, Hohai University, Nanjing 210098, People’s Republic of China, (antq@hhu.edu.cn)
Fubao Zhang
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, People’s Republic of China, (zhangfubao@seu.edu.cn)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the existence, multiplicity and concentration of positive solutions for a class of quasilinear problems

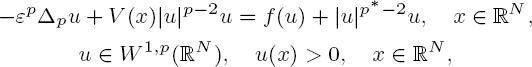
where —Δp is the p-Laplacian operator for 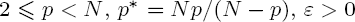is a small parameter, f(u) is a superlinear and subcritical nonlinearity that is continuous in u. Using a variational method, we first prove that for sufficiently small ε > 0 the system has a positive ground state solution uε with some concentration phenomena as ε → 0. Then, by the minimax theorems and Ljusternik–Schnirelmann theory, we investigate the relation between the number of positive solutions and the topology of the set of the global minima of the potentials. Finally, we obtain some sufficient conditions for the non-existence of ground state solutions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 145 , Issue 2 , April 2015 , pp. 411 - 444
Copyright
Copyright © Royal Society of Edinburgh 2015