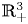1. Introduction
In this article, we continue our study of the Brinkman equations (see [Reference Alarcon and Iório1, Reference Molina Del Sol, Alarcon and Iorio23]) and the references therein). This time we will consider the system
 \begin{gather} \begin{aligned} \partial_{t}\rho+\operatorname{div}\left( \rho v\right) & =F\left( t,\rho\right),\\ \left(1-\Delta\right)v & ={-}\nabla P\left(\rho\right),\\ \left(\rho\left(0\right),v\left(0\right)\right) & =\left(\rho_{0},v_{0}\right), \end{aligned} \end{gather}
\begin{gather} \begin{aligned} \partial_{t}\rho+\operatorname{div}\left( \rho v\right) & =F\left( t,\rho\right),\\ \left(1-\Delta\right)v & ={-}\nabla P\left(\rho\right),\\ \left(\rho\left(0\right),v\left(0\right)\right) & =\left(\rho_{0},v_{0}\right), \end{aligned} \end{gather}
in ![]() $\mathbb {R}_{+}^{3}.$ We assume that the horizontal plane, that is,
$\mathbb {R}_{+}^{3}.$ We assume that the horizontal plane, that is, ![]() $z=0$, to be impenetrable to the fluid. Thus, we must impose a boundary condition at
$z=0$, to be impenetrable to the fluid. Thus, we must impose a boundary condition at ![]() $z=0$, compatible with this assumption. This means that the fluid flow must be zero in the horizontal plane.
$z=0$, compatible with this assumption. This means that the fluid flow must be zero in the horizontal plane.
Now, if ![]() $S$ is a
$S$ is a ![]() $C^{1}$ surface (say), and
$C^{1}$ surface (say), and ![]() $n$ a continuous unit normal to
$n$ a continuous unit normal to ![]() $S$. This orients the surface and determines the sign of the fluid flow, which is defined by the component of the velocity in the direction of
$S$. This orients the surface and determines the sign of the fluid flow, which is defined by the component of the velocity in the direction of ![]() $n$, that is,
$n$, that is, ![]() $v\bullet n.$ where
$v\bullet n.$ where ![]() $\bullet$ denotes the usual inner product in Euclidian spaces. Since we expect
$\bullet$ denotes the usual inner product in Euclidian spaces. Since we expect ![]() $(1-\Delta )$ to be invertible,Footnote 1 we must have
$(1-\Delta )$ to be invertible,Footnote 1 we must have
Let ![]() $S$ be the plane
$S$ be the plane ![]() $z=0.$ We choose
$z=0.$ We choose
In view of the condition at ![]() $z=0$, we have
$z=0$, we have
So,
If ![]() $P^{\prime }(\rho )\neq 0$ for all
$P^{\prime }(\rho )\neq 0$ for all ![]() $\rho \neq 0$ (as we will assume later) it follows that we must have
$\rho \neq 0$ (as we will assume later) it follows that we must have
Thus, ![]() $\rho$ must satisfy a Neumann boundary condition at
$\rho$ must satisfy a Neumann boundary condition at ![]() $z=0$.
$z=0$.
According to [Reference Johari14] ‘the Brinkman equations account for fast-moving fluids in porous media with the kinetic potential from fluid velocity, pressure, and gravity driving the flow. These equations extend Darcy's law to describe the dissipation of the kinetic energy by viscous shear, similar to the Navier–Stokes equations. Therefore, the Brinkman Equations interface is well suited for modelling fast flow in porous media, including transitions between slow flow in porous media governed by Navier–Stokes equations. The Brinkman Equations interface computes both the velocity and pressure’. There are many applications of these equations.
For more information on the Brinkman equations and some of its variants including numerical studies see [Reference Liu21, Reference Xu34], [Reference Brinkman3, Brinkman's original paper], [Reference Alarcon and Iório1, Reference Auriault2, Reference Durlofsky and Brady7, Reference Fuchsberger8, Reference Mansu22, Reference Mosharaf-Dehkordi25, Reference Wiwatanapataphee32, Reference Xie33].
This paper is organized as follows. In § 2 we define the operator ![]() $-\Delta$, mentioned above, and the Sobolev spaces associated with it. In § 3 we establish local well-posedness for the Cauchy problem in question. Section 4 deals with the comparison principle for the solutions of the problem, which in turn is used in § 5 to establish global results.
$-\Delta$, mentioned above, and the Sobolev spaces associated with it. In § 3 we establish local well-posedness for the Cauchy problem in question. Section 4 deals with the comparison principle for the solutions of the problem, which in turn is used in § 5 to establish global results.
2. Distributions and Sobolev spaces
Let ![]() $S(\mathbb {R}_{+}^{3})=S(\mathbb {R}^{2}\times [0,\infty ))$Footnote 2 denote the set of all
$S(\mathbb {R}_{+}^{3})=S(\mathbb {R}^{2}\times [0,\infty ))$Footnote 2 denote the set of all ![]() $C^{\infty }$ functions
$C^{\infty }$ functions ![]() $f:R_+^{3}\longrightarrow C$ such that
$f:R_+^{3}\longrightarrow C$ such that
where ![]() $\alpha ,\beta$, are (tridimensional) multi-indexes,
$\alpha ,\beta$, are (tridimensional) multi-indexes, ![]() $w=(x,y,z) \in R_+^{3},\ D=\frac {1}{i}\nabla$ (see [Reference Cordes6, chap. 1, p. 8], [Reference Iorio and Iorio10, chap. 7, p. 323] and [Reference Schecter30, chap. 1, p. 2]). Moreover, the derivatives with respect to
$w=(x,y,z) \in R_+^{3},\ D=\frac {1}{i}\nabla$ (see [Reference Cordes6, chap. 1, p. 8], [Reference Iorio and Iorio10, chap. 7, p. 323] and [Reference Schecter30, chap. 1, p. 2]). Moreover, the derivatives with respect to ![]() $z$ at
$z$ at ![]() $z=0,$ are taken from above.
$z=0,$ are taken from above.
This defines a countable collection of seminorms in ![]() $S(\mathbb {R} _{+}^{3}),$ which turns this vector space into a Frèchet space (see [Reference Reed and Simon27]). Let
$S(\mathbb {R} _{+}^{3}),$ which turns this vector space into a Frèchet space (see [Reference Reed and Simon27]). Let ![]() $S^{\prime }(\mathbb {R}_{+}^{3})$ denote the topological dual of
$S^{\prime }(\mathbb {R}_{+}^{3})$ denote the topological dual of ![]() $S(\mathbb {R}_{+}^{3})$ that is
$S(\mathbb {R}_{+}^{3})$ that is ![]() $f\in S^{\prime }(\mathbb {R}_{+}^{3})$ if and only if
$f\in S^{\prime }(\mathbb {R}_{+}^{3})$ if and only if ![]() $f:S(\mathbb {R}_{+}^{3})\longrightarrow C$ is linear and is continuous in the following sense,Footnote 3 for any convergent net
$f:S(\mathbb {R}_{+}^{3})\longrightarrow C$ is linear and is continuous in the following sense,Footnote 3 for any convergent net ![]() $f_{\lambda }\in \Lambda$ we have
$f_{\lambda }\in \Lambda$ we have
Now, let ![]() $L^{2}(\mathbb {R}_{+}^{3})=L^{2}(\mathbb {R}^{2}\times [0,\infty )).$ It is not difficult to show that
$L^{2}(\mathbb {R}_{+}^{3})=L^{2}(\mathbb {R}^{2}\times [0,\infty )).$ It is not difficult to show that
where the symbol ![]() $\hookrightarrow$, in the remainder of this article, will always mean that the inclusion is continuous and dense with respect to the relevant topologies involved. Next consider the following operator
$\hookrightarrow$, in the remainder of this article, will always mean that the inclusion is continuous and dense with respect to the relevant topologies involved. Next consider the following operator
 \begin{equation} \begin{aligned} \mathfrak{D}\left(\widetilde{\Delta}\right) & =\left\{\varphi\in\mathfrak{S}\left(\mathbb{R}_{+}^{3}\right)\left\vert \widetilde {\partial}_{z}\varphi\left(x,y,0\right)=0\right.\right\},\\ -\widetilde{\Delta}\varphi\left(x,y,z\right) & =\left(\partial_{x}^{2}+\partial_{y}^{2}+\widetilde{\partial}_{z}^{2}\right)\varphi\left(x,y,z\right). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \mathfrak{D}\left(\widetilde{\Delta}\right) & =\left\{\varphi\in\mathfrak{S}\left(\mathbb{R}_{+}^{3}\right)\left\vert \widetilde {\partial}_{z}\varphi\left(x,y,0\right)=0\right.\right\},\\ -\widetilde{\Delta}\varphi\left(x,y,z\right) & =\left(\partial_{x}^{2}+\partial_{y}^{2}+\widetilde{\partial}_{z}^{2}\right)\varphi\left(x,y,z\right). \end{aligned} \end{equation}
However, it is necessary to explain what the ![]() $z$ derivative means. Define
$z$ derivative means. Define ![]() $\widetilde {d}_{z}^{2}$ by the equations,
$\widetilde {d}_{z}^{2}$ by the equations,
 \begin{equation} \begin{aligned} \mathfrak{D}\left(\widetilde{d}_{z}^{2}\right) & =\left\{f\in\mathcal{S}(\left[0,\infty\right)\right)\left\vert f^{\prime}\left(0\right)=0\right\}\\ -\widetilde{d}_{z}^{2}f & =\frac{\textrm{d}^{2}f}{\textrm{d}z^{2}},\quad f\in\mathfrak{D}\left(\widetilde{d}_{z}^{2}\right), \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \mathfrak{D}\left(\widetilde{d}_{z}^{2}\right) & =\left\{f\in\mathcal{S}(\left[0,\infty\right)\right)\left\vert f^{\prime}\left(0\right)=0\right\}\\ -\widetilde{d}_{z}^{2}f & =\frac{\textrm{d}^{2}f}{\textrm{d}z^{2}},\quad f\in\mathfrak{D}\left(\widetilde{d}_{z}^{2}\right), \end{aligned} \end{equation}where the derivative at zero is taken from above. Using the Fourier cosine transform and its Inversion formula (see [Reference Churchill4, § 54]),
 \begin{equation} \begin{aligned} \left(\mathfrak{F}_{c}f\right)\left(\alpha\right) & =\int_{0}^{\infty}f\left(x\right)\cos\left(\alpha x\right)\textrm{d}x,\ x,\ \alpha \in\left[0,\infty\right),\\ \left(\mathfrak{F}_{c}^{{-}1}g\right)\left(x\right) & =\frac{2}{\pi}\int_{0}^{\infty}g\left(\alpha\right)\cos\left(\alpha x\right)\textrm{d}\alpha, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \left(\mathfrak{F}_{c}f\right)\left(\alpha\right) & =\int_{0}^{\infty}f\left(x\right)\cos\left(\alpha x\right)\textrm{d}x,\ x,\ \alpha \in\left[0,\infty\right),\\ \left(\mathfrak{F}_{c}^{{-}1}g\right)\left(x\right) & =\frac{2}{\pi}\int_{0}^{\infty}g\left(\alpha\right)\cos\left(\alpha x\right)\textrm{d}\alpha, \end{aligned} \end{equation}and the fact that
it is easy to see that ![]() $\widetilde {d}_{z}^{2}$ is essentially self-adjoint. Let
$\widetilde {d}_{z}^{2}$ is essentially self-adjoint. Let ![]() $d_{z}^{2}$ denote its unique self-adjoint extension. Next, if
$d_{z}^{2}$ denote its unique self-adjoint extension. Next, if ![]() $(x,y)\in \mathbb {R}^{2}$ is fixed and
$(x,y)\in \mathbb {R}^{2}$ is fixed and ![]() $\varphi \in S(\mathbb {R}_{+}^{3})$ then
$\varphi \in S(\mathbb {R}_{+}^{3})$ then ![]() $\psi (z) =\varphi (x,y,z)\in S([0,\infty ))$ so we may define
$\psi (z) =\varphi (x,y,z)\in S([0,\infty ))$ so we may define
Once again, it is easy to show that ![]() $(-\widetilde {\Delta })$ is essentially self-adjoint. We will denote its unique self-adjoint extension by
$(-\widetilde {\Delta })$ is essentially self-adjoint. We will denote its unique self-adjoint extension by ![]() $(-\Delta )$. Now, it is necessary to introduce a Fourier transform associated with the operator
$(-\Delta )$. Now, it is necessary to introduce a Fourier transform associated with the operator ![]() $(-\Delta )$. This can be done noting that
$(-\Delta )$. This can be done noting that
satisfies,
So if ![]() $\varphi \in \mathfrak {L}^{1}(\mathbb {R}_{+}^{3})$, we define
$\varphi \in \mathfrak {L}^{1}(\mathbb {R}_{+}^{3})$, we define
 \begin{align} \widehat{\varphi}\left(\xi,\eta,\alpha\right)&=\left(\mathfrak{F}\varphi\right)\left(\xi,\eta,\alpha\right)\nonumber\\ &=\left(\frac{1}{2\pi}\right)\int_{\mathbb{R}_{+}^{3}}\varphi\left(x,y,z\right)\overline{\Theta\left(x,y,z\right)}\,\textrm{d}x\,\textrm{d}y\,\textrm{d}z. \end{align}
\begin{align} \widehat{\varphi}\left(\xi,\eta,\alpha\right)&=\left(\mathfrak{F}\varphi\right)\left(\xi,\eta,\alpha\right)\nonumber\\ &=\left(\frac{1}{2\pi}\right)\int_{\mathbb{R}_{+}^{3}}\varphi\left(x,y,z\right)\overline{\Theta\left(x,y,z\right)}\,\textrm{d}x\,\textrm{d}y\,\textrm{d}z. \end{align} Employing the usual methods [Reference Iorio and Iorio10, Reference Iorio12, Reference Reed and Simon28], we can extend this operator as an unitary map from ![]() $\mathfrak {L}^{2}( \mathbb {R}_{+}^{3})$ into itself. Its inverse is given by
$\mathfrak {L}^{2}( \mathbb {R}_{+}^{3})$ into itself. Its inverse is given by
 \begin{align} \mathop{\omega}\limits^{{\vee}}\left(x,y,z\right)& =\left(\mathfrak{F}^{{-}1}\omega\right)\left(x,y,z\right)\nonumber\\ &=\left(\frac{1}{\pi}\right)^{2}\int_{\mathbb{R}_{+}^{3}}\omega\left(\xi,\eta,\alpha\right)\Theta\left(x,y,z\right)\textrm{d}\xi\,\textrm{d}\eta\,\textrm{d}\alpha. \end{align}
\begin{align} \mathop{\omega}\limits^{{\vee}}\left(x,y,z\right)& =\left(\mathfrak{F}^{{-}1}\omega\right)\left(x,y,z\right)\nonumber\\ &=\left(\frac{1}{\pi}\right)^{2}\int_{\mathbb{R}_{+}^{3}}\omega\left(\xi,\eta,\alpha\right)\Theta\left(x,y,z\right)\textrm{d}\xi\,\textrm{d}\eta\,\textrm{d}\alpha. \end{align}
The usual methods employed to extend the transform Fourier in ![]() $\mathbb {R}^{n}$ can be used in this case to define
$\mathbb {R}^{n}$ can be used in this case to define ![]() $\mathfrak {F}$ in
$\mathfrak {F}$ in ![]() $\mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$ and
$\mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$ and ![]() $\mathfrak {S}^{\prime }(\mathbb {R}_{+}^{3})$. Note that
$\mathfrak {S}^{\prime }(\mathbb {R}_{+}^{3})$. Note that
where ![]() $\Phi$ denotes (with a little abuse of notation) the maximal operator of multiplication by
$\Phi$ denotes (with a little abuse of notation) the maximal operator of multiplication by
in ![]() $\mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$. It deserves remark that the Fourier transform
$\mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$. It deserves remark that the Fourier transform ![]() $\mathfrak {F}$ is a topological isomorphism from
$\mathfrak {F}$ is a topological isomorphism from ![]() $\mathfrak {S}(\mathbb {R}_{+}^{3})$ into itself, so that by the usual duality argument, it has the same property in
$\mathfrak {S}(\mathbb {R}_{+}^{3})$ into itself, so that by the usual duality argument, it has the same property in ![]() $\mathfrak {S}^{\prime }(\mathbb {R}_{+}^{3})$. Moreover, it is a unitary operator in
$\mathfrak {S}^{\prime }(\mathbb {R}_{+}^{3})$. Moreover, it is a unitary operator in ![]() $\mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$.Footnote 4 We are now in position to introduce the resolvent
$\mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$.Footnote 4 We are now in position to introduce the resolvent ![]() $z\longrightarrow R(z)$ of
$z\longrightarrow R(z)$ of ![]() $(-\Delta )$ and the Sobolev spaces associated with it. To begin with, it is not difficult to see that
$(-\Delta )$ and the Sobolev spaces associated with it. To begin with, it is not difficult to see that
and that the function ![]() $z\longrightarrow R(z)$ defined by,
$z\longrightarrow R(z)$ defined by,
 \begin{align} R\left(z\right)f & =\left(-\Delta-z\right)^{{-}1}f,\nonumber\\ &=\mathfrak{F}^{{-}1}\left(\xi^{2}+\eta^{2}+\alpha^{2}-z\right)^{{-}1}\mathfrak{F}f,\nonumber\\ z&\in\mathbb{C}\backslash\left[0,\infty\right),\quad f\in\mathfrak{L}\left(\mathbb{R}_{+}^{3}\right), \end{align}
\begin{align} R\left(z\right)f & =\left(-\Delta-z\right)^{{-}1}f,\nonumber\\ &=\mathfrak{F}^{{-}1}\left(\xi^{2}+\eta^{2}+\alpha^{2}-z\right)^{{-}1}\mathfrak{F}f,\nonumber\\ z&\in\mathbb{C}\backslash\left[0,\infty\right),\quad f\in\mathfrak{L}\left(\mathbb{R}_{+}^{3}\right), \end{align}satisfies,
 \begin{equation} \begin{aligned} R\left(z\right)\left(-\Delta-z\right)f & =f \forall f\in\mathfrak{D}\left(-\Delta\right),\\ \left(-\Delta-z\right)R\left(z\right)g & =g \forall g\in \mathfrak{L}^{2}\left(\mathbb{R}_{+}^{3}\right). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} R\left(z\right)\left(-\Delta-z\right)f & =f \forall f\in\mathfrak{D}\left(-\Delta\right),\\ \left(-\Delta-z\right)R\left(z\right)g & =g \forall g\in \mathfrak{L}^{2}\left(\mathbb{R}_{+}^{3}\right). \end{aligned} \end{equation}
Next, let ![]() $s\in \mathbb {R}$ and denote by
$s\in \mathbb {R}$ and denote by ![]() $\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})$ the Sobolev space of order
$\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})$ the Sobolev space of order ![]() $s$, that is,
$s$, that is,
These spaces have the same properties as the Sobolev spaces in ![]() $\mathbb {R}^{n},$ that is,
$\mathbb {R}^{n},$ that is,
SB1:
 $\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})$ are Hilbert spaces when endowed with the inner product
(2.19)
$\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})$ are Hilbert spaces when endowed with the inner product
(2.19) \begin{equation} \left(f\left\vert g\right.\right)_{s}=\left(\left( 1-\Delta\right)^{{s}/{2}}f\left\vert \left(1-\Delta\right)^{{s}/{2}}g\right. \right),\ \forall f,g\in\mathfrak{H}^{s}\left(\mathbb{R}_{+}^{3}\right).\end{equation}
\begin{equation} \left(f\left\vert g\right.\right)_{s}=\left(\left( 1-\Delta\right)^{{s}/{2}}f\left\vert \left(1-\Delta\right)^{{s}/{2}}g\right. \right),\ \forall f,g\in\mathfrak{H}^{s}\left(\mathbb{R}_{+}^{3}\right).\end{equation}SB2: If
 $s\geqslant \ell$ then
$s\geqslant \ell$ then  $\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})\hookrightarrow \mathfrak {H}^{\ell }(\mathbb {R}_{+} ^{3})$ for all
$\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})\hookrightarrow \mathfrak {H}^{\ell }(\mathbb {R}_{+} ^{3})$ for all  $s,\ell \in \mathbb {R}.$
$s,\ell \in \mathbb {R}.$SB3: (Sobolevś lemma.) Let
 $s>\frac {3}{2}$. Then
$s>\frac {3}{2}$. Then  $\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})\hookrightarrow C_{0}(\mathbb {R}_{+}^{3})$ where
$\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})\hookrightarrow C_{0}(\mathbb {R}_{+}^{3})$ where  $C_{0}(\mathbb {R}_{+}^{3})$ denotes the set of all continuous functions that tend to zero at infinity.
$C_{0}(\mathbb {R}_{+}^{3})$ denotes the set of all continuous functions that tend to zero at infinity.SB4: Let
 $f,g\in \mathfrak {H}^{s}(\mathbb {R}_{+}^{3}),$
$f,g\in \mathfrak {H}^{s}(\mathbb {R}_{+}^{3}),$  $s>\frac {3}{2}.$ Then the pointwise productFootnote 5
$s>\frac {3}{2}.$ Then the pointwise productFootnote 5  $fg\in \mathfrak {H}^{s}(\mathbb {R} _+^{3})$ and
(2.20)where
$fg\in \mathfrak {H}^{s}(\mathbb {R} _+^{3})$ and
(2.20)where \begin{equation} \left\Vert fg\right\Vert_{s}\leq C\left\Vert f\right\Vert _{s}\left\Vert g\right\Vert _{s} \end{equation}
\begin{equation} \left\Vert fg\right\Vert_{s}\leq C\left\Vert f\right\Vert _{s}\left\Vert g\right\Vert _{s} \end{equation} $C>0$ is a constant. Note that this turns
$C>0$ is a constant. Note that this turns  $\mathfrak {H}^{s}(\mathbb {R}_+^{3})$ into a Banach algebra.
$\mathfrak {H}^{s}(\mathbb {R}_+^{3})$ into a Banach algebra.
The proofs of these properties are exactly the same as the corresponding ones in the case of ![]() $\mathbb {R}^{n},$ and will be omitted. The interested reader can consult [Reference Cordes6, Reference Iorio and Iorio10, Reference Reed and Simon28], for example.
$\mathbb {R}^{n},$ and will be omitted. The interested reader can consult [Reference Cordes6, Reference Iorio and Iorio10, Reference Reed and Simon28], for example.
Remark 2.1 Let ![]() $\Omega \subseteq \mathbb {R}^{n}$ be an open set. The Dirichlet Laplacian and the Neumann Laplacian, denoted
$\Omega \subseteq \mathbb {R}^{n}$ be an open set. The Dirichlet Laplacian and the Neumann Laplacian, denoted ![]() $\Delta _{D}^{\Omega }$ and
$\Delta _{D}^{\Omega }$ and ![]() $\Delta _{N}^{\Omega }$ are the unique self-adjoint operators associated with the quadratic form
$\Delta _{N}^{\Omega }$ are the unique self-adjoint operators associated with the quadratic form
with domains ![]() $C_{0}^{\infty }(\Omega )$ and
$C_{0}^{\infty }(\Omega )$ and ![]() $H^{1}(\Omega )$ where
$H^{1}(\Omega )$ where ![]() $\nabla$ denotes the distributional gradient. (See [Reference Reed and Simon29].) This is a very elegant, but rather abstract definition. In many applications one must find the self-adjoint operator in order to deal with actual computations. The Laplacian defined above is the Neumann Laplacian corresponding to
$\nabla$ denotes the distributional gradient. (See [Reference Reed and Simon29].) This is a very elegant, but rather abstract definition. In many applications one must find the self-adjoint operator in order to deal with actual computations. The Laplacian defined above is the Neumann Laplacian corresponding to ![]() $\Omega =\mathbb {R}_{+}^{3}\backslash \{(x,y,z) \left \vert z=0\right .\}$, that is, the interior of
$\Omega =\mathbb {R}_{+}^{3}\backslash \{(x,y,z) \left \vert z=0\right .\}$, that is, the interior of ![]() $\mathbb {R}_{+}^{3}.$
$\mathbb {R}_{+}^{3}.$
3. Local well-posedness
We begin reminding the reader of our definition of well-posedness. The Cauchy problem
![]() $Y\hookrightarrow X,$
$Y\hookrightarrow X,$ ![]() $t\in [0,T_{0}]$,
$t\in [0,T_{0}]$, ![]() $G:[ 0,T_{0}] \times Y\longrightarrow X$ is (at least continuousFootnote 6 ) is said to be locally well-posed if there exists a
$G:[ 0,T_{0}] \times Y\longrightarrow X$ is (at least continuousFootnote 6 ) is said to be locally well-posed if there exists a ![]() $T\in (0,T_{0}]$ and a function
$T\in (0,T_{0}]$ and a function ![]() $u:[0,T] \longrightarrow Y$ such that
$u:[0,T] \longrightarrow Y$ such that ![]() $u(0)=u_{0}$ and satisfies the differential equation with respect to the norm of
$u(0)=u_{0}$ and satisfies the differential equation with respect to the norm of ![]() $X$,
$X$,
Moreover, the solution must depend continuously on the initial data (and on any other relevant parameters occurring in the equation), in appropriate topologies. In what follows, we will consider only the initial data. In that case what we mean is: assume that ![]() $u_{0}^{(j)}\in Y,\ j=1,2,3,\ldots ,\infty ,$ let
$u_{0}^{(j)}\in Y,\ j=1,2,3,\ldots ,\infty ,$ let ![]() $u^{(j)}$ be the corresponding solutions. Suppose that
$u^{(j)}$ be the corresponding solutions. Suppose that
Then, for all ![]() $T^{\prime }\in (0,T)$ we have,
$T^{\prime }\in (0,T)$ we have,
If any of these properties fail, we say that the problem is ill-posed.Footnote 7 In case ![]() $G$ is defined for all
$G$ is defined for all ![]() $t\in \mathbb {R}$ and the preceding properties are valid for all
$t\in \mathbb {R}$ and the preceding properties are valid for all ![]() $T>0$, we say that the problem is globally well-posed.
$T>0$, we say that the problem is globally well-posed.
Using the definitions and notations of the previous section we can solve for ![]() $v$ as indicated in (1.3) and inserting this formula into the first equation of (1.1), we obtain the Cauchy problem
$v$ as indicated in (1.3) and inserting this formula into the first equation of (1.1), we obtain the Cauchy problem
 \begin{align} \partial_{t}\rho & =\operatorname{div}\left(\rho\left(1-\Delta\right)^{{-}1}\nabla P\left(\rho\right)\right)+F\left(t,\rho\right)\nonumber\\ \rho\left(0\right)&=\rho_{0}. \end{align}
\begin{align} \partial_{t}\rho & =\operatorname{div}\left(\rho\left(1-\Delta\right)^{{-}1}\nabla P\left(\rho\right)\right)+F\left(t,\rho\right)\nonumber\\ \rho\left(0\right)&=\rho_{0}. \end{align}Moreover, the compatibility condition
must be satisfied. Note also that the boundary conditions are inserted in the definition of the operators appearing in (3.5).
Now, there are several ways to solve (3.5). We mention our favourites, namely
• Katoś theory of quasilinear Equations
• Parabolic regularization.
3.1 Application of Katoś theory
A very large class of relevant evolution equations can be written in quasilinear form, that is,
 \begin{equation} \begin{cases} \partial_{t}u+A\left(t,u\right)u=F\left(t,u\right)\in X,\\ u\left(0\right)=\phi\in Y. \end{cases} \end{equation}
\begin{equation} \begin{cases} \partial_{t}u+A\left(t,u\right)u=F\left(t,u\right)\in X,\\ u\left(0\right)=\phi\in Y. \end{cases} \end{equation}
Here, ![]() $X$ and
$X$ and ![]() $Y$ are Banach spaces, as before with
$Y$ are Banach spaces, as before with ![]() $Y$
$Y$ ![]() $\hookrightarrow$
$\hookrightarrow$ ![]() $X$ and
$X$ and ![]() $A(t,u)$ is bounded from
$A(t,u)$ is bounded from ![]() $Y$ into
$Y$ into ![]() $X$ (for fixed
$X$ (for fixed ![]() $t$) and is the (negative) generator of a
$t$) and is the (negative) generator of a ![]() $C^{0}$ semigroup for each
$C^{0}$ semigroup for each ![]() $(t,u) \in \lbrack 0.T]\times W,$
$(t,u) \in \lbrack 0.T]\times W,$ ![]() $W$ open in
$W$ open in ![]() $Y$. In its most general formulation,
$Y$. In its most general formulation, ![]() $X$ and
$X$ and ![]() $Y$ may be non-reflexive [Reference Kato18].Footnote 8 Since we will deal exclusively with reflexive spaces, we restrict ourselves to a simpler version, which can be found in [Reference Kato19]. (See also [Reference Iorio12].) The essential assumption of the theory is the existence of an isomorphism
$Y$ may be non-reflexive [Reference Kato18].Footnote 8 Since we will deal exclusively with reflexive spaces, we restrict ourselves to a simpler version, which can be found in [Reference Kato19]. (See also [Reference Iorio12].) The essential assumption of the theory is the existence of an isomorphism ![]() $S$ from
$S$ from ![]() $Y$ onto
$Y$ onto ![]() $X$ such that
$X$ such that
where ![]() $B(t,u)\in \mathcal {B}(X)$, with the strict domain relation implied by the equation. This is, in fact, a condition on the commutator
$B(t,u)\in \mathcal {B}(X)$, with the strict domain relation implied by the equation. This is, in fact, a condition on the commutator ![]() $[S,A(t,u)]$ because (3.8)Footnote 9 can be rewritten as
$[S,A(t,u)]$ because (3.8)Footnote 9 can be rewritten as
There are also lower requirements, involving Lipschitz conditions on the operators in question. For example, ![]() $A(t,u)$ must satisfy
$A(t,u)$ must satisfy
for all pairs ![]() $(t,w),\ (t,\widetilde {w})$ in
$(t,w),\ (t,\widetilde {w})$ in ![]() $[0.T]\times W.$ Both
$[0.T]\times W.$ Both ![]() $B(t,u)$ and
$B(t,u)$ and ![]() $F(t,u)$ must satisfy similar conditions. Once these assumptions are satisfied, Kato tells you that (3.7) is locally well-posed.
$F(t,u)$ must satisfy similar conditions. Once these assumptions are satisfied, Kato tells you that (3.7) is locally well-posed.
Now we must write the integrodifferential equation (3.5) in quasilinear form. Consider the linear operator:
Thus the equation in (3.5) can be written in the form presented in (3.7). Next we choose our function spaces. Due to certain technical estimates needed to control the commutator mentioned above, we take ![]() $Y=\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})$,
$Y=\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})$, ![]() $s>5/2$,
$s>5/2$, ![]() $X=\mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$ and
$X=\mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$ and ![]() $W$ an arbitrary open ball centred at zero in
$W$ an arbitrary open ball centred at zero in ![]() $Y.$
$Y.$
Now assume
•
 $P$ maps
$P$ maps  $\mathfrak {H}^{s}(\mathbb {R})$ into itself,
$\mathfrak {H}^{s}(\mathbb {R})$ into itself,  $P(0)=0$ and is Lipschitz in the following sense:
(3.12)
$P(0)=0$ and is Lipschitz in the following sense:
(3.12) \begin{equation} \left\Vert P\left(\rho\right)-P\left(\widetilde{\rho}\right)\right\Vert _{s}\leq L_{s}\left(\left\Vert \rho\right\Vert _{s},\left\Vert \widetilde{\rho}\right\Vert _{s}\right) \left\Vert \rho-\widetilde{\rho}\right\Vert _{s} \end{equation}
\begin{equation} \left\Vert P\left(\rho\right)-P\left(\widetilde{\rho}\right)\right\Vert _{s}\leq L_{s}\left(\left\Vert \rho\right\Vert _{s},\left\Vert \widetilde{\rho}\right\Vert _{s}\right) \left\Vert \rho-\widetilde{\rho}\right\Vert _{s} \end{equation}•
 $F:[0,T_{0}]\times \mathfrak {H}^{s}(\mathbb {R}) \longrightarrow \mathfrak {H}^{s}(\mathbb {R}),\,F(t,0) =0$ and satisfies the following Lipschitz condition:
(3.13)where
$F:[0,T_{0}]\times \mathfrak {H}^{s}(\mathbb {R}) \longrightarrow \mathfrak {H}^{s}(\mathbb {R}),\,F(t,0) =0$ and satisfies the following Lipschitz condition:
(3.13)where \begin{equation} \left\Vert F\left(t,\rho\right)-F\left(t,\widetilde{\rho}\right)\right\Vert _{s}\leq M_{s}\left(\left\Vert \rho\right\Vert _{s},\left\Vert \widetilde{\rho}\right\Vert _{s}\right)\left\Vert \rho-\widetilde{\rho}\right\Vert_{s}. \end{equation}
\begin{equation} \left\Vert F\left(t,\rho\right)-F\left(t,\widetilde{\rho}\right)\right\Vert _{s}\leq M_{s}\left(\left\Vert \rho\right\Vert _{s},\left\Vert \widetilde{\rho}\right\Vert _{s}\right)\left\Vert \rho-\widetilde{\rho}\right\Vert_{s}. \end{equation} $L_{s},M_{s}:[0,\infty )\times [0,\infty ) \rightarrow [0,\infty )$ are continuous and monotone non-decreasing functions with respect to each of its arguments.
$L_{s},M_{s}:[0,\infty )\times [0,\infty ) \rightarrow [0,\infty )$ are continuous and monotone non-decreasing functions with respect to each of its arguments.
If ![]() $T$ is a linear operator and belongs to the class
$T$ is a linear operator and belongs to the class ![]() $G(X,1,0)$, that is, if
$G(X,1,0)$, that is, if ![]() $(-T)$ generates a contraction semigroup, we say that
$(-T)$ generates a contraction semigroup, we say that ![]() $T$ is maximally accretive (or m-accretive). If
$T$ is maximally accretive (or m-accretive). If ![]() $T\in G(X,1,\beta )$, that is,
$T\in G(X,1,\beta )$, that is, ![]() $T$ generates a semigroup
$T$ generates a semigroup ![]() $U(t)$ such that
$U(t)$ such that ![]() $\Vert U(t)\Vert _{B(X)}\leq M\,\textrm {e}^{-t\beta }$,
$\Vert U(t)\Vert _{B(X)}\leq M\,\textrm {e}^{-t\beta }$, ![]() $T$ is said to be quasi-maximally accretive (or quasi m-accretive). Since
$T$ is said to be quasi-maximally accretive (or quasi m-accretive). Since ![]() $X$ is a Hilbert space, it suffices to prove, in our case, that
$X$ is a Hilbert space, it suffices to prove, in our case, that ![]() $T=A(\rho )$ is maximally accretive in
$T=A(\rho )$ is maximally accretive in ![]() $X$. (See [Reference Kato15, Reference Pazy26, Reference Reed and Simon27]).
$X$. (See [Reference Kato15, Reference Pazy26, Reference Reed and Simon27]).
Let
Integrating by parts and applying Sobolev lemma, we obtain
 \begin{align} \left\langle A(\rho)f,f\right\rangle& =\left\langle-\text{div}\;(f\,\Theta (\rho)),f\right\rangle={-}\sum_{i=1}^{3}\int f\partial_{x_{i}}(f\,\Theta_{i}(\rho))\,\textrm{d}x\nonumber\\ &=\sum_{i=1}^{3}\int f\partial_{x_{i}}f\,\Theta_{i}(\rho)\,\textrm{d}x=\frac{1}{2}\sum_{i=1}^{3}\int\partial_{x_{i}}(f^{2})\Theta_{i}(\rho)\,\textrm{d}x\nonumber\\ &={-}\frac{1}{2}\sum_{i=1}^{3}\int f^{2}\partial_{x_{i}}\Theta_{i}(\rho)\,\textrm{d}x={-}\frac{1}{2}\int(\text{div}\;\vec{\Theta}(\rho))f^{2} \,\textrm{d}x\nonumber\\ &\geq{-}\underbrace{\frac{\Vert\text{div}\;\Theta(\rho)\Vert_{L^{\infty}}}{2}}_{\beta}\Vert f\Vert^{2} \\ R(A(\rho)+\lambda)&=X=\mathfrak{L}^{2}(\mathbb{R}_{+}^{3}),\quad\forall\lambda>\beta \notag\end{align}
\begin{align} \left\langle A(\rho)f,f\right\rangle& =\left\langle-\text{div}\;(f\,\Theta (\rho)),f\right\rangle={-}\sum_{i=1}^{3}\int f\partial_{x_{i}}(f\,\Theta_{i}(\rho))\,\textrm{d}x\nonumber\\ &=\sum_{i=1}^{3}\int f\partial_{x_{i}}f\,\Theta_{i}(\rho)\,\textrm{d}x=\frac{1}{2}\sum_{i=1}^{3}\int\partial_{x_{i}}(f^{2})\Theta_{i}(\rho)\,\textrm{d}x\nonumber\\ &={-}\frac{1}{2}\sum_{i=1}^{3}\int f^{2}\partial_{x_{i}}\Theta_{i}(\rho)\,\textrm{d}x={-}\frac{1}{2}\int(\text{div}\;\vec{\Theta}(\rho))f^{2} \,\textrm{d}x\nonumber\\ &\geq{-}\underbrace{\frac{\Vert\text{div}\;\Theta(\rho)\Vert_{L^{\infty}}}{2}}_{\beta}\Vert f\Vert^{2} \\ R(A(\rho)+\lambda)&=X=\mathfrak{L}^{2}(\mathbb{R}_{+}^{3}),\quad\forall\lambda>\beta \notag\end{align}
The fact that ![]() ${A(\rho )}$ is a closed operator combined with inequality (3.16) shows that
${A(\rho )}$ is a closed operator combined with inequality (3.16) shows that ![]() $(A(\rho )+\lambda )$ has closed range for all
$(A(\rho )+\lambda )$ has closed range for all ![]() $\lambda >\beta$.
$\lambda >\beta$.
Thus it suffices to show that ![]() $(A(\rho )+\lambda )$ has dense range for
$(A(\rho )+\lambda )$ has dense range for ![]() $\lambda >\beta$. For this, is sufficient to prove that
$\lambda >\beta$. For this, is sufficient to prove that ![]() $R(A(\rho )+\lambda )^{\bot }=\{0\}$, because
$R(A(\rho )+\lambda )^{\bot }=\{0\}$, because ![]() $A(\rho )$ is a linear operator.
$A(\rho )$ is a linear operator.
Let ![]() $g\in \mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$ satisfy,
$g\in \mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$ satisfy,
Integrating by parts, yields
 \begin{align} \left\langle(A(\rho)+\lambda)f,g\right\rangle=0&\Rightarrow\left\langle A(\rho)f,g\right\rangle+\left\langle\lambda f,g\right\rangle=0\nonumber\\ &\Rightarrow\left\langle f,\nabla g\,\Theta(\rho)\right\rangle+\left\langle\lambda f,g\right\rangle=0\nonumber\\ &\Rightarrow\left\langle f,\nabla g\,\Theta(\rho)+\lambda g\right\rangle=0,\quad\forall f\in D(A(\rho))=\mathfrak{H}^{s}(\mathbb{R}^{n})\nonumber\\ &\Rightarrow\nabla g\,\Theta(\rho)+\lambda g=0 \end{align}
\begin{align} \left\langle(A(\rho)+\lambda)f,g\right\rangle=0&\Rightarrow\left\langle A(\rho)f,g\right\rangle+\left\langle\lambda f,g\right\rangle=0\nonumber\\ &\Rightarrow\left\langle f,\nabla g\,\Theta(\rho)\right\rangle+\left\langle\lambda f,g\right\rangle=0\nonumber\\ &\Rightarrow\left\langle f,\nabla g\,\Theta(\rho)+\lambda g\right\rangle=0,\quad\forall f\in D(A(\rho))=\mathfrak{H}^{s}(\mathbb{R}^{n})\nonumber\\ &\Rightarrow\nabla g\,\Theta(\rho)+\lambda g=0 \end{align}
Therefore, multiplying by ![]() $g$, integrating by parts, and using (3.16) we have:
$g$, integrating by parts, and using (3.16) we have:
 \begin{align} g\nabla g\,\Theta(\rho)+\lambda g^{2}=0 &\Rightarrow\frac{1}{2}\int\nabla(g^{2})\,\Theta(\rho)\,\textrm{d}x+\lambda\Vert g\Vert^{2}=0\nonumber\\ &\Rightarrow\underbrace{-\frac{1}{2}\int g^{2}\text{div}\;\Theta(\rho)\,\textrm{d}x}_{=\left\langle A(\rho)g,g\right\rangle}+\lambda\Vert g\Vert^{2} =0\nonumber\\ &\Rightarrow\left\langle A(\rho)g,g\right\rangle+\lambda\Vert g\Vert^{2}=0\nonumber\\ &\Rightarrow 0\geq{-}\beta\Vert g\Vert^{2}+\lambda\Vert g\Vert^{2}=(\lambda-\beta)\Vert g\Vert^{2}\nonumber\\ &\Rightarrow g=0 \end{align}
\begin{align} g\nabla g\,\Theta(\rho)+\lambda g^{2}=0 &\Rightarrow\frac{1}{2}\int\nabla(g^{2})\,\Theta(\rho)\,\textrm{d}x+\lambda\Vert g\Vert^{2}=0\nonumber\\ &\Rightarrow\underbrace{-\frac{1}{2}\int g^{2}\text{div}\;\Theta(\rho)\,\textrm{d}x}_{=\left\langle A(\rho)g,g\right\rangle}+\lambda\Vert g\Vert^{2} =0\nonumber\\ &\Rightarrow\left\langle A(\rho)g,g\right\rangle+\lambda\Vert g\Vert^{2}=0\nonumber\\ &\Rightarrow 0\geq{-}\beta\Vert g\Vert^{2}+\lambda\Vert g\Vert^{2}=(\lambda-\beta)\Vert g\Vert^{2}\nonumber\\ &\Rightarrow g=0 \end{align}
Finally, we choose the isomorphism ![]() $S:\mathfrak {D}(S) =\mathfrak {h}^{s}(\mathbb {R}_{+}^{3}) \longrightarrow \mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$ to be
$S:\mathfrak {D}(S) =\mathfrak {h}^{s}(\mathbb {R}_{+}^{3}) \longrightarrow \mathfrak {L}^{2}(\mathbb {R}_{+}^{3})$ to be
Then the proof of (3.8) is exactly the same of the corresponding fact in ![]() $\mathbb {R}^{n}$ (see [Reference Molina Del Sol, Alarcon and Iorio23]).
$\mathbb {R}^{n}$ (see [Reference Molina Del Sol, Alarcon and Iorio23]).
In view of these remarks, Kato's quasilinear theory implies the following result.
Theorem 3.1 The Cauchy problem (3.5) is locally well-posed in ![]() $\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})$ in the sense described at the beginning of this section for all
$\mathfrak {H}^{s}(\mathbb {R}_{+}^{3})$ in the sense described at the beginning of this section for all ![]() $s>5/2$.
$s>5/2$.
3.2 Parabolic regularization
Considering ![]() $F(t,\rho )=0$ in (3.5), for simplicity, it is easy to see that if we integrate with respect to time we obtain
$F(t,\rho )=0$ in (3.5), for simplicity, it is easy to see that if we integrate with respect to time we obtain
 \begin{equation} \mathop{\underbrace{\rho\left(t\right)}}\limits_{\mathfrak{H}^{s}\left(\mathbb{R}_{+}^{3}\right)}=\mathop{\underbrace{\phi}}\limits_{\mathfrak{H}^{s}\left(\mathbb{R}_{+} ^{3}\right)}+\mathop{\underbrace{\int_{0}^{t}\operatorname{div}\left(\rho\left(1-\Delta\right)^{{-}1}\nabla P\left(\rho\right)\right)\left(t'\right)\textrm{d}t'}}\limits_{\mathfrak{H}^{s-1}\left( \mathbb{R}_{+}^{3}\right)}.\end{equation}
\begin{equation} \mathop{\underbrace{\rho\left(t\right)}}\limits_{\mathfrak{H}^{s}\left(\mathbb{R}_{+}^{3}\right)}=\mathop{\underbrace{\phi}}\limits_{\mathfrak{H}^{s}\left(\mathbb{R}_{+} ^{3}\right)}+\mathop{\underbrace{\int_{0}^{t}\operatorname{div}\left(\rho\left(1-\Delta\right)^{{-}1}\nabla P\left(\rho\right)\right)\left(t'\right)\textrm{d}t'}}\limits_{\mathfrak{H}^{s-1}\left( \mathbb{R}_{+}^{3}\right)}.\end{equation}
so we cannot apply Banach's fixed point theorem and Gronwall's inequality to establish local well-posedness. However, we can introduce an artificial viscosity ![]() $\mu >0$ to obtain the regularized Cauchy problem
$\mu >0$ to obtain the regularized Cauchy problem
 \begin{equation} \begin{cases} \partial_{t}\rho_{\mu}=\operatorname{div}\left(\rho_{\mu}\left(1-\Delta\right)^{{-}1}\nabla P\left(\rho_{\mu}\right)\right)+\mu\Delta\rho_{\mu}\\ \rho_{\mu}\left(0\right) =\rho_{0}. \end{cases} \end{equation}
\begin{equation} \begin{cases} \partial_{t}\rho_{\mu}=\operatorname{div}\left(\rho_{\mu}\left(1-\Delta\right)^{{-}1}\nabla P\left(\rho_{\mu}\right)\right)+\mu\Delta\rho_{\mu}\\ \rho_{\mu}\left(0\right) =\rho_{0}. \end{cases} \end{equation}which is equivalent to the integral equation
where ![]() $U_{\mu }(t)$ is the infinitely smoothing
$U_{\mu }(t)$ is the infinitely smoothing ![]() $C^{0}$ semigroup
$C^{0}$ semigroup
Then we can show that (see [Reference Alarcon and Iório1, Reference Molina Del Sol, Alarcon and Iorio23])
Theorem 3.2 Assume that ![]() $\mu >0$ and that
$\mu >0$ and that ![]() $P$ satisfy (3.12) for all (fixed)
$P$ satisfy (3.12) for all (fixed) ![]() $s>3/2$. Then (3.23) is locally well-posed in
$s>3/2$. Then (3.23) is locally well-posed in ![]() $\mathfrak {H} ^{s}(\mathbb {R}_{+}^{3})$. Moreover, if
$\mathfrak {H} ^{s}(\mathbb {R}_{+}^{3})$. Moreover, if ![]() $(0,T_{\mu }]$ is an interval of existence, then
$(0,T_{\mu }]$ is an interval of existence, then ![]() $\rho _{\mu }\in C((0,T_{\mu }];\mathfrak {H}^{\infty }(\mathbb {R}_{+}^{3}))$, where
$\rho _{\mu }\in C((0,T_{\mu }];\mathfrak {H}^{\infty }(\mathbb {R}_{+}^{3}))$, where ![]() $\mathfrak {H}^{\infty }(\mathbb {R}_{+}^{3})=\cap_{s\in \mathbb {R}_{+}^{3}}\mathfrak {H}^{s}(\mathbb {R} _{+}^{3})$ provided with its natural Frechet space topology.
$\mathfrak {H}^{\infty }(\mathbb {R}_{+}^{3})=\cap_{s\in \mathbb {R}_{+}^{3}}\mathfrak {H}^{s}(\mathbb {R} _{+}^{3})$ provided with its natural Frechet space topology.
Proof. It should be noted that the proof (even in ![]() $\mathbb {R}^{3}$) relies heavily on the inequality
$\mathbb {R}^{3}$) relies heavily on the inequality
 \begin{equation} \left\Vert U_{\mu}\left(t\right)\phi\right\Vert_{r+\lambda}\leq K_{\lambda}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right] ^{1/2}\left\Vert \phi\right\Vert _{r} \end{equation}
\begin{equation} \left\Vert U_{\mu}\left(t\right)\phi\right\Vert_{r+\lambda}\leq K_{\lambda}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right] ^{1/2}\left\Vert \phi\right\Vert _{r} \end{equation}
where ![]() $K_{\lambda }>0$ depends only on
$K_{\lambda }>0$ depends only on ![]() $\lambda$ and holds for all
$\lambda$ and holds for all ![]() $\phi \in H^{r}(\mathbb {R}_{+}^{3})$,
$\phi \in H^{r}(\mathbb {R}_{+}^{3})$, ![]() $r\in \mathbb {R}$,
$r\in \mathbb {R}$, ![]() $\lambda \geq 0$, and
$\lambda \geq 0$, and ![]() $\mu ,\,t>0.$ (See [Reference Alarcon and Iório1, Reference Iorio and Iorio10, Reference Iorio13, Reference Molina Del Sol, Alarcon and Iorio23] e.g.).
$\mu ,\,t>0.$ (See [Reference Alarcon and Iório1, Reference Iorio and Iorio10, Reference Iorio13, Reference Molina Del Sol, Alarcon and Iorio23] e.g.).
The next step, is to employ a bootstrapping argument combining (3.23) and (3.25) (with ![]() $\lambda$ fixed in the interval
$\lambda$ fixed in the interval ![]() $(1,2)$), to show that
$(1,2)$), to show that ![]() $\rho _{\mu }\in C((0,T_{\mu }];\mathfrak {H}^{\infty }(\mathbb {R}_{+}^{3}))$.
$\rho _{\mu }\in C((0,T_{\mu }];\mathfrak {H}^{\infty }(\mathbb {R}_{+}^{3}))$.
Let ![]() $t\in (\theta ,\infty ],\,\theta >0$ be fixed (but arbitrary). Then
$t\in (\theta ,\infty ],\,\theta >0$ be fixed (but arbitrary). Then
 \begin{align*} \left\Vert \rho_{\mu}\left(t\right)\right\Vert _{s+\lambda}&\leq\left\Vert U_{\mu}\left(t\right)\rho_{0}\right\Vert _{s+\lambda}+\left\Vert\int_{0} ^{t}U_{\mu} \left(t-t^{\prime}\right)\left[A\left(\rho_{\mu}\left(t^{\prime}\right)\right)\rho_{\mu}\left(t^{\prime}\right) \right] \right\Vert_{s+\lambda}\,\textrm{d}t^{\prime},\\ &\leq\left\Vert U_{\mu}(t) \rho_{0}\right\Vert _{s+\lambda}+\int_{0}^{t}\left\Vert U_{\mu}\left(t-t^{\prime}\right)\left[A\left(\rho_{\mu}\left( t^{\prime}\right)\right)\rho_{\mu}\left(t^{\prime}\right) \right]\right\Vert _{s+\lambda}\,\textrm{d}t^{\prime}\\ &\leq K_{\lambda}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert \rho_{0}\right\Vert _{s}\\ &\quad +\int_{0}^{t}K_{\lambda }\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert A\left(\rho_{\mu}\left(t^{\prime}\right)\right)\rho_{\mu }\left(t^{\prime}\right)\right\Vert _{s}\,\textrm{d}t^{\prime}\\ &\leq K_{\lambda}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert \rho_{0}\right\Vert_{s}\\ &\quad +K_{\lambda}L_{s} \int_{0}^{t}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert \rho_{\mu}\left(t^{\prime}\right)\right\Vert _{s}\,\textrm{d}t^{\prime} \end{align*}
\begin{align*} \left\Vert \rho_{\mu}\left(t\right)\right\Vert _{s+\lambda}&\leq\left\Vert U_{\mu}\left(t\right)\rho_{0}\right\Vert _{s+\lambda}+\left\Vert\int_{0} ^{t}U_{\mu} \left(t-t^{\prime}\right)\left[A\left(\rho_{\mu}\left(t^{\prime}\right)\right)\rho_{\mu}\left(t^{\prime}\right) \right] \right\Vert_{s+\lambda}\,\textrm{d}t^{\prime},\\ &\leq\left\Vert U_{\mu}(t) \rho_{0}\right\Vert _{s+\lambda}+\int_{0}^{t}\left\Vert U_{\mu}\left(t-t^{\prime}\right)\left[A\left(\rho_{\mu}\left( t^{\prime}\right)\right)\rho_{\mu}\left(t^{\prime}\right) \right]\right\Vert _{s+\lambda}\,\textrm{d}t^{\prime}\\ &\leq K_{\lambda}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert \rho_{0}\right\Vert _{s}\\ &\quad +\int_{0}^{t}K_{\lambda }\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert A\left(\rho_{\mu}\left(t^{\prime}\right)\right)\rho_{\mu }\left(t^{\prime}\right)\right\Vert _{s}\,\textrm{d}t^{\prime}\\ &\leq K_{\lambda}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert \rho_{0}\right\Vert_{s}\\ &\quad +K_{\lambda}L_{s} \int_{0}^{t}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert \rho_{\mu}\left(t^{\prime}\right)\right\Vert _{s}\,\textrm{d}t^{\prime} \end{align*}
Since![]() $\ t$ is bounded away from
$\ t$ is bounded away from ![]() $0$ in function
$0$ in function
 \[ f\left(t\right) =\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{{1}/{2}}, \]
\[ f\left(t\right) =\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{{1}/{2}}, \]
is bounded in any interval ![]() $(\theta ,\infty ]$ so that,
$(\theta ,\infty ]$ so that,
 \[ \left\Vert \rho_{\mu}\left(t\right)\right\Vert _{s+\lambda}\leq K_{\lambda}\sup f\left(t\right)\left\Vert \rho_{0}\right\Vert +K_{\lambda }L_{s}\int_{0}^{t}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert \rho_{\mu}\left(t^{\prime}\right)\right\Vert _{s}\,\textrm{d}t \]
\[ \left\Vert \rho_{\mu}\left(t\right)\right\Vert _{s+\lambda}\leq K_{\lambda}\sup f\left(t\right)\left\Vert \rho_{0}\right\Vert +K_{\lambda }L_{s}\int_{0}^{t}\left[1+\left(\frac{1}{2\mu t}\right)^{\lambda}\right]^{1/2}\left\Vert \rho_{\mu}\left(t^{\prime}\right)\right\Vert _{s}\,\textrm{d}t \]Now, the integral on the left-hand side contributes with a term containing
which is finite in every interval ![]() $(\theta ,T^{\prime }], \theta >0, T^{\prime }>0$. Therefore, Gronwall's inequality implies that
$(\theta ,T^{\prime }], \theta >0, T^{\prime }>0$. Therefore, Gronwall's inequality implies that
Next, the, usual limiting process involved in the method of parabolic regularization (see [Reference Iorio and Iorio10, Reference Iorio13]) we are able to show existence and uniqueness of solutions in ![]() $AC([0,T];\mathfrak {H} ^{s-1}({\mathbb {R}_{+}^{3}}))\cap L^{\infty }([0,T] ;\mathfrak {H}^{s}({\mathbb {R}_{+}^{3}}))$. Due to technical reasons (lack of invariance under certain changes of variables, see [Reference Iorio12, Reference Iorio13, Reference Kato20]), so far we were unable to prove that the solution we obtained in this way actually belongs to
$AC([0,T];\mathfrak {H} ^{s-1}({\mathbb {R}_{+}^{3}}))\cap L^{\infty }([0,T] ;\mathfrak {H}^{s}({\mathbb {R}_{+}^{3}}))$. Due to technical reasons (lack of invariance under certain changes of variables, see [Reference Iorio12, Reference Iorio13, Reference Kato20]), so far we were unable to prove that the solution we obtained in this way actually belongs to ![]() $C([0,T];\mathfrak {H}^{s}( {\mathbb {R}_{+}^{3}})) \cap C^{1}([0,T];\mathfrak {H}^{s-1}({\mathbb {R}_{+}^{3}}))$,
$C([0,T];\mathfrak {H}^{s}( {\mathbb {R}_{+}^{3}})) \cap C^{1}([0,T];\mathfrak {H}^{s-1}({\mathbb {R}_{+}^{3}}))$, ![]() $s>3/2$ as we would have liked. However, combining what we already have, with the results in theorem 3.1, proved using Kato's theory when
$s>3/2$ as we would have liked. However, combining what we already have, with the results in theorem 3.1, proved using Kato's theory when ![]() $s>5/2$, we see that the solutions must coincide, due to uniqueness, if
$s>5/2$, we see that the solutions must coincide, due to uniqueness, if ![]() $s>5/2$.
$s>5/2$.
4. Comparison principle
To simplify the notation we will write
In order to state our results, we define of the fractional power spaces associated with Neumann Laplacian ![]() $-\Delta$. Following the arguments found in [Reference Kato and Fujita16, Reference Weissler31]. For
$-\Delta$. Following the arguments found in [Reference Kato and Fujita16, Reference Weissler31]. For ![]() $\alpha >0$ and
$\alpha >0$ and ![]() $f\in L^{2}({\mathbb {R}_{+}^{3}})$, defineFootnote 10
$f\in L^{2}({\mathbb {R}_{+}^{3}})$, defineFootnote 10
Then ![]() $(1-\Delta )^{-\alpha }$ is a bounded, one-to-one operator on
$(1-\Delta )^{-\alpha }$ is a bounded, one-to-one operator on ![]() $\mathfrak {L}^{2}({\mathbb {R}_{+}^{3}})$. We let
$\mathfrak {L}^{2}({\mathbb {R}_{+}^{3}})$. We let ![]() $\mathfrak {J}^{\alpha }=(1-\Delta )^{\alpha }$ be the inverse of
$\mathfrak {J}^{\alpha }=(1-\Delta )^{\alpha }$ be the inverse of ![]() $( 1-\Delta ) ^{-\alpha }$. For
$( 1-\Delta ) ^{-\alpha }$. For ![]() $s>0$, the Hilbert space
$s>0$, the Hilbert space ![]() $\mathfrak {H}^{s}({\mathbb {R}_{+}^{3}})$ is the range of
$\mathfrak {H}^{s}({\mathbb {R}_{+}^{3}})$ is the range of ![]() $(1-\Delta ) ^{-{s/2}}$ with the inner product
$(1-\Delta ) ^{-{s/2}}$ with the inner product
Consider the initial value problem (3.5) with ![]() $F(t,\rho )=0$,Footnote 11
$F(t,\rho )=0$,Footnote 11 ![]() $P(\rho )=\rho ^{2k},\ k=1,2,3\ldots$.
$P(\rho )=\rho ^{2k},\ k=1,2,3\ldots$.
 \begin{equation} \left\{\begin{array}{l} \partial_{t}\rho+ {{\mathrm{div}\,}}(\rho \;\mathbf{v}) =0,\ x \in {\mathbb{R}^{3}_+},\ t\in(0,T_{0}]\\ \mathbf{v} ={-} \mathcal{B}\,\nabla \rho^{2k}={-}\vec{\Theta}(\rho^{2 k})\\ (\rho(0),\ \mathbf{v}(0))=(\rho_{0},\,\mathbf{v}_{0}) \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{l} \partial_{t}\rho+ {{\mathrm{div}\,}}(\rho \;\mathbf{v}) =0,\ x \in {\mathbb{R}^{3}_+},\ t\in(0,T_{0}]\\ \mathbf{v} ={-} \mathcal{B}\,\nabla \rho^{2k}={-}\vec{\Theta}(\rho^{2 k})\\ (\rho(0),\ \mathbf{v}(0))=(\rho_{0},\,\mathbf{v}_{0}) \end{array}\right. \end{equation}Theorem 4.1 (Comparison principle) Let ![]() $(\rho ,v)$ and
$(\rho ,v)$ and ![]() $(\eta ,w)$ be solutions of (3.5) with
$(\eta ,w)$ be solutions of (3.5) with ![]() $P(\rho )=\rho ^{2k},P(\eta )=\eta ^{2k},\ k=1,2,3\ldots$;Footnote 12 and initial values
$P(\rho )=\rho ^{2k},P(\eta )=\eta ^{2k},\ k=1,2,3\ldots$;Footnote 12 and initial values ![]() $(\rho _0,v_0)$ and
$(\rho _0,v_0)$ and ![]() $(\eta _0,w_0)$ respectively. Then
$(\eta _0,w_0)$ respectively. Then
Proof. In this proof, we use the same idea employed by Alarcon, Iorio and Del Sol in the study of Brinkman flow in ![]() $\mathbb {R}^{n}$ [Reference Molina Del Sol, Alarcon and Iorio23]. Let
$\mathbb {R}^{n}$ [Reference Molina Del Sol, Alarcon and Iorio23]. Let
and
where ![]() $\phi (t,y)$ and
$\phi (t,y)$ and ![]() $\psi (t,y)$ satisfy the following ordinary differential equations,
$\psi (t,y)$ satisfy the following ordinary differential equations,
 \begin{align} &\begin{cases} \displaystyle\dfrac{\partial\phi}{\partial t}(t,y)=\mathbf{v}(\phi(t,y),t) & \phi(t,y)=\left(\phi_{1}(t,y),\phi_{2}(t,y), \phi_{3}(t,y)\right)\\ \phi(0,y)=y & v_{i}={-}\partial_{x_{i}}\mathcal{B}(\rho^{2k})\end{cases}, \end{align}
\begin{align} &\begin{cases} \displaystyle\dfrac{\partial\phi}{\partial t}(t,y)=\mathbf{v}(\phi(t,y),t) & \phi(t,y)=\left(\phi_{1}(t,y),\phi_{2}(t,y), \phi_{3}(t,y)\right)\\ \phi(0,y)=y & v_{i}={-}\partial_{x_{i}}\mathcal{B}(\rho^{2k})\end{cases}, \end{align} \begin{align} &\begin{cases} \displaystyle\dfrac{\partial\psi}{\partial t}(t,y)=\mathbf{w}(\psi(t,y),t) & \psi(t,y)=\left(\psi_{1}(t,y),\psi_{2}(t,y),\psi_{3}(t,y)\right)\\ \psi(0,y)=y & w_{i}={-}\partial_{x_{i}}\mathcal{B}(\eta^{2k})\end{cases}, \end{align}
\begin{align} &\begin{cases} \displaystyle\dfrac{\partial\psi}{\partial t}(t,y)=\mathbf{w}(\psi(t,y),t) & \psi(t,y)=\left(\psi_{1}(t,y),\psi_{2}(t,y),\psi_{3}(t,y)\right)\\ \psi(0,y)=y & w_{i}={-}\partial_{x_{i}}\mathcal{B}(\eta^{2k})\end{cases}, \end{align}Now,
 \begin{equation} \left\{\begin{array}{@{}ll} \displaystyle\dfrac{\textrm{d}R}{\textrm{d}t} ={-}R\,\textrm{div}\;\mathbf{v} & \displaystyle\dfrac{\textrm{d}S}{\textrm{d}t}={-}S\,\textrm{div}\;\mathbf{w}\\ R(0,y) = \rho_{0}(y) & S(0,y) = \eta_{0}(y)\end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{@{}ll} \displaystyle\dfrac{\textrm{d}R}{\textrm{d}t} ={-}R\,\textrm{div}\;\mathbf{v} & \displaystyle\dfrac{\textrm{d}S}{\textrm{d}t}={-}S\,\textrm{div}\;\mathbf{w}\\ R(0,y) = \rho_{0}(y) & S(0,y) = \eta_{0}(y)\end{array}\right. \end{equation}Solving (4.8), we obtain:
 \begin{equation} R(t)=R(0)\exp\left[-\int_{0}^{t}\text{div}\;v(\phi(s,y),s)\,\textrm{d}s\right]\overbrace {\Rightarrow}^{\rho_{0}(y)\geq 0}R(t)\geq 0 \end{equation}
\begin{equation} R(t)=R(0)\exp\left[-\int_{0}^{t}\text{div}\;v(\phi(s,y),s)\,\textrm{d}s\right]\overbrace {\Rightarrow}^{\rho_{0}(y)\geq 0}R(t)\geq 0 \end{equation}Analogously, we have that:
 \begin{equation} S(t)=S(0)\exp\left[-\int_{0}^{t}\text{div}\;w(\psi(s,y),s)\,\textrm{d}s\right]\overbrace {\Rightarrow}^{\eta_{0}(y)\geq 0}S(t)\geq 0 \end{equation}
\begin{equation} S(t)=S(0)\exp\left[-\int_{0}^{t}\text{div}\;w(\psi(s,y),s)\,\textrm{d}s\right]\overbrace {\Rightarrow}^{\eta_{0}(y)\geq 0}S(t)\geq 0 \end{equation}
On the other hand, differentiating ![]() $Q(t)$:
$Q(t)$:
 \begin{align} \frac{\textrm{d}Q}{\textrm{d}t}& =\frac{\textrm{d}R}{\textrm{d}t}-\frac{\textrm{d}S}{\textrm{d}t}=(-\text{div}\;v)R(t)+(\text{div}\;\mathbf{w})S(t)\nonumber\\ &={-}\rho\,\text{div}\;v+\eta\,\text{div}\;w\nonumber\\ &={-}(\rho-\eta)\text{div}\;v+\eta(\text{div}\;w-\text{div}\;v)\nonumber\\ &={-}Q(t)(\text{div}\;\mathbf{v})+S(t)(\text{div}\;w-\text{div}\;v) \end{align}
\begin{align} \frac{\textrm{d}Q}{\textrm{d}t}& =\frac{\textrm{d}R}{\textrm{d}t}-\frac{\textrm{d}S}{\textrm{d}t}=(-\text{div}\;v)R(t)+(\text{div}\;\mathbf{w})S(t)\nonumber\\ &={-}\rho\,\text{div}\;v+\eta\,\text{div}\;w\nonumber\\ &={-}(\rho-\eta)\text{div}\;v+\eta(\text{div}\;w-\text{div}\;v)\nonumber\\ &={-}Q(t)(\text{div}\;\mathbf{v})+S(t)(\text{div}\;w-\text{div}\;v) \end{align}where
Substituting (4.12) in (4.11), we obtain a new ordinary differential equation for ![]() $Q(t)$,
$Q(t)$,
 \begin{equation} \left\{\begin{array}{@{}l} \displaystyle\dfrac{\textrm{d}Q}{\textrm{d}t} ={-}\left[\textrm{div}\;\mathbf{v}+ S(t)P(R(t),S(t))\right]Q(t) + B(t,Q(t))\\ Q(0)= \rho_{0}(y)-\eta_{0}(y) \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{@{}l} \displaystyle\dfrac{\textrm{d}Q}{\textrm{d}t} ={-}\left[\textrm{div}\;\mathbf{v}+ S(t)P(R(t),S(t))\right]Q(t) + B(t,Q(t))\\ Q(0)= \rho_{0}(y)-\eta_{0}(y) \end{array}\right. \end{equation}with
 \begin{equation} P(R(t),S(t))=P(\rho,\eta)=\sum_{i=0}^{2k-1}\rho^{2k-1-i}\eta^{i} \end{equation}
\begin{equation} P(R(t),S(t))=P(\rho,\eta)=\sum_{i=0}^{2k-1}\rho^{2k-1-i}\eta^{i} \end{equation}and
Thus,
where
In view of conditions for ![]() ${\rho _{0}}$ and
${\rho _{0}}$ and ![]() $\eta _{0}$, we have that
$\eta _{0}$, we have that ![]() $R(t)\geq 0$ and
$R(t)\geq 0$ and ![]() $S(t)\geq 0$.
$S(t)\geq 0$.
Consider the sequence
 \[ Q_{n}(t)=\left\{\begin{array}{@{}ll} U(t,0)Q(0)+ \int_{0}^{t}U(t,s)B(s,Q_{n-1}(s))\,\textrm{d}s, & \textrm{se}\ n= 1,2,\ldots;\\ \rho_{0}(y)-\eta_{0}(y) , & \textrm{se}\ n=0. \end{array} \right. \]
\[ Q_{n}(t)=\left\{\begin{array}{@{}ll} U(t,0)Q(0)+ \int_{0}^{t}U(t,s)B(s,Q_{n-1}(s))\,\textrm{d}s, & \textrm{se}\ n= 1,2,\ldots;\\ \rho_{0}(y)-\eta_{0}(y) , & \textrm{se}\ n=0. \end{array} \right. \]
If ![]() $Q(0)\geq 0$, then
$Q(0)\geq 0$, then ![]() $Q_{n}(t)\geq 0$, for all
$Q_{n}(t)\geq 0$, for all ![]() $n$. Therefore,
$n$. Therefore,
To complete the proof we need to show the functions ![]() $y\in \Omega \rightarrow \phi (t,y)\in \Omega$ and
$y\in \Omega \rightarrow \phi (t,y)\in \Omega$ and ![]() $y\in \Omega \rightarrow \psi (t,y)\in \Omega$ are onto. To do this, we analyse in detail the map
$y\in \Omega \rightarrow \psi (t,y)\in \Omega$ are onto. To do this, we analyse in detail the map ![]() $y\in \Omega \rightarrow \phi (t,y)\in \Omega$.
$y\in \Omega \rightarrow \phi (t,y)\in \Omega$.
The Neumann boundary condition ![]() $\rho _{z}=0$ for
$\rho _{z}=0$ for ![]() $z=0$ and Brinkman's condition
$z=0$ and Brinkman's condition ![]() $\ v=-\nabla \,\mathcal {B}(\rho ^{2k})$,Footnote 13 implies that
$\ v=-\nabla \,\mathcal {B}(\rho ^{2k})$,Footnote 13 implies that
then ![]() $\phi _3(t,\,(x_1,\,x_2,\,0)=0$ for all
$\phi _3(t,\,(x_1,\,x_2,\,0)=0$ for all ![]() $(x_1,\,x_2)\in \mathbb {R}^{2}$ and
$(x_1,\,x_2)\in \mathbb {R}^{2}$ and ![]() $t\in \lbrack 0,\,T]$.
$t\in \lbrack 0,\,T]$.
We will show that ![]() $\Omega$ it is invariant under the flow
$\Omega$ it is invariant under the flow ![]() $\phi (t,\,y)$, that is,
$\phi (t,\,y)$, that is,
By (4.19), the plane ![]() $\Pi =\{(x_{1},\,x_{2},\,x_{3})\in \mathbb {R}^{3}\colon x_{3}=0\}$ is invariant under the flow
$\Pi =\{(x_{1},\,x_{2},\,x_{3})\in \mathbb {R}^{3}\colon x_{3}=0\}$ is invariant under the flow ![]() $\phi (t,\,y)$, i.e.
$\phi (t,\,y)$, i.e. ![]() $\phi (\Pi )\subset \Pi$. Next we show that (4.20) holds. To this end, it is enough to verify that
$\phi (\Pi )\subset \Pi$. Next we show that (4.20) holds. To this end, it is enough to verify that
If (4.21) does not hold, there is a ![]() $w=(w_{1},\,w_{2},\,w_{3})$ with
$w=(w_{1},\,w_{2},\,w_{3})$ with ![]() $w_{3}>0$ and
$w_{3}>0$ and ![]() $0< t_{1}< t_{2}\leq T$ such that
$0< t_{1}< t_{2}\leq T$ such that ![]() $\phi (t_{1},\,w)\in \Pi$ and
$\phi (t_{1},\,w)\in \Pi$ and ![]() $\phi (t_{2},\,w)\notin \Omega$. But (4.19) implies that
$\phi (t_{2},\,w)\notin \Omega$. But (4.19) implies that
so that ![]() $\phi _{3}(t_{2},\,w)=0$. This contradiction proves (4.20). From (4.6), integrating from 0 to t, we get:
$\phi _{3}(t_{2},\,w)=0$. This contradiction proves (4.20). From (4.6), integrating from 0 to t, we get:
so that
Let ![]() $(z_{1},\,z_{2},\,z_{3})\in {\mathbb {R}_{+}^{3}}$. Taking
$(z_{1},\,z_{2},\,z_{3})\in {\mathbb {R}_{+}^{3}}$. Taking ![]() $y_{i}^{(1)}\ll 0$ for
$y_{i}^{(1)}\ll 0$ for ![]() $i=1,\,2$;
$i=1,\,2$; ![]() $y_{i}^{(2)}\gg 0$ for
$y_{i}^{(2)}\gg 0$ for ![]() $i=1,\,2,\,3$, such that
$i=1,\,2,\,3$, such that ![]() $z_{i}\in (y_{i}^{(1)},y_{i}^{(2)})$ for
$z_{i}\in (y_{i}^{(1)},y_{i}^{(2)})$ for ![]() $i=1,\,2$ and
$i=1,\,2$ and ![]() $0< z_{3}< y_{3}^{(2)}$ we have:
$0< z_{3}< y_{3}^{(2)}$ we have:
and
Therefore
Applying the intermediate value theorem to ![]() $\phi _{i}$ implies that there exists
$\phi _{i}$ implies that there exists ![]() $y_{i}\in (y_{i}^{(1)},y_{i}^{(2)})$ satisfying
$y_{i}\in (y_{i}^{(1)},y_{i}^{(2)})$ satisfying ![]() $\phi _{i}(t,y_{i})=z_{i}$. For
$\phi _{i}(t,y_{i})=z_{i}$. For ![]() $z_{3}=0$ the proof is analogous, since the plane
$z_{3}=0$ the proof is analogous, since the plane ![]() $x_{3}=0$ is invariant by the flow
$x_{3}=0$ is invariant by the flow ![]() $\phi (t,\,y)$, a consequence of (4.19).
$\phi (t,\,y)$, a consequence of (4.19).
5. Global results in  $\mathfrak {H}^{s}({\mathbb {R}_{+}^{3}}),\ s>5/2$
$\mathfrak {H}^{s}({\mathbb {R}_{+}^{3}}),\ s>5/2$
In this section, we obtain the global ![]() $\mathfrak {H}^{s}$-estimate for the solution of the Brinkman flow equation. This will be a consequence of global well-posedness of the regularized problem.
$\mathfrak {H}^{s}$-estimate for the solution of the Brinkman flow equation. This will be a consequence of global well-posedness of the regularized problem.
First, we introduce the following estimates
Lemma 5.1 If ![]() $s>0$, then
$s>0$, then
 \begin{align} &\left\|\sum_{k=1}^{n}\left[\partial_{x_{k}}\mathfrak{J}^{s}(g\partial_{x_{k}}f)-\partial_{x_{k}}f(\partial_{x_{k}}\mathfrak{J}^{s} g)\right]\right\|_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}\nonumber\\ &\quad\leq c\left(\Vert\mathfrak{J}^{2}f\Vert_{L^{\infty}({\mathbb{R}_{+}^{3}})}\Vert \mathfrak{J}^{s}g\Vert_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}+\right. \left.\Vert\mathfrak{J}^{s+2}f\Vert_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}\Vert g\Vert_{L^{\infty}({\mathbb{R}_{+}^{3}})}\right) \end{align}
\begin{align} &\left\|\sum_{k=1}^{n}\left[\partial_{x_{k}}\mathfrak{J}^{s}(g\partial_{x_{k}}f)-\partial_{x_{k}}f(\partial_{x_{k}}\mathfrak{J}^{s} g)\right]\right\|_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}\nonumber\\ &\quad\leq c\left(\Vert\mathfrak{J}^{2}f\Vert_{L^{\infty}({\mathbb{R}_{+}^{3}})}\Vert \mathfrak{J}^{s}g\Vert_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}+\right. \left.\Vert\mathfrak{J}^{s+2}f\Vert_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}\Vert g\Vert_{L^{\infty}({\mathbb{R}_{+}^{3}})}\right) \end{align}Proof. The proof of this lemma is similar to that of lemma X1 in [Reference Kato and Ponce17], is based on the following result due to R. R. Coifman and Y. Meyer (lemma A.1.2). See lemma A.1.3 in [Reference Molina Del Sol24].
Lemma 5.2 If ![]() $s>0$, then
$s>0$, then ![]() $\mathfrak {H}^{s}({\mathbb {R}^{3}_{+}})\cap L^{\infty }({\mathbb {R}^{3}_{+}})$ is a Banach algebra. Moreover
$\mathfrak {H}^{s}({\mathbb {R}^{3}_{+}})\cap L^{\infty }({\mathbb {R}^{3}_{+}})$ is a Banach algebra. Moreover
Proof. See [Reference Kato and Ponce17].
Lemma 5.3 Let ![]() $f\in X^{s}({\mathbb {R}_{+}^{3}})$,
$f\in X^{s}({\mathbb {R}_{+}^{3}})$, ![]() $s>\frac {5}{2},\ k=1,2,\ldots$. Then
$s>\frac {5}{2},\ k=1,2,\ldots$. Then
where ![]() $A\lesssim B$ means that exist a constant
$A\lesssim B$ means that exist a constant ![]() $c > 0$ such that
$c > 0$ such that ![]() $A \leq c\, B$.
$A \leq c\, B$.
Now, we are ready to establish the following result.
Theorem 5.4 (Global solution) Let ![]() $s>5/2,\ P(\rho )=\rho ^{2k},\ F\equiv 0$ and
$s>5/2,\ P(\rho )=\rho ^{2k},\ F\equiv 0$ and ![]() $\rho _{0}\in \mathfrak {H}^{s}({\mathbb {R}_{+}^{3}})$ with
$\rho _{0}\in \mathfrak {H}^{s}({\mathbb {R}_{+}^{3}})$ with ![]() $0\leq \rho _{0} (x)\leq 1$ in
$0\leq \rho _{0} (x)\leq 1$ in ![]() ${\mathbb {R}_{+}^{3}}$. Then (4.2) is globally well-posed in the sense described in § 3 and satisfies
${\mathbb {R}_{+}^{3}}$. Then (4.2) is globally well-posed in the sense described in § 3 and satisfies ![]() $0\leq \rho (x,t)\leq 1,\ \forall t\geq 0$.
$0\leq \rho (x,t)\leq 1,\ \forall t\geq 0$.
Proof. The comparison principle implies that ![]() $0\leq \rho (x,t)\leq 1$. Using the regularized initial value problem, with the simplified notations
$0\leq \rho (x,t)\leq 1$. Using the regularized initial value problem, with the simplified notations ![]() $\rho _{\mu }(t)\equiv \tilde {\rho },\ v\mathbf {_{\mu }}(t)\equiv v$.
$\rho _{\mu }(t)\equiv \tilde {\rho },\ v\mathbf {_{\mu }}(t)\equiv v$.
 \begin{equation} \left\{\begin{array}{@{}l} \partial_{t}\tilde{\rho} - \mu\,\Delta_N\, \tilde{\rho} + \textrm{div}\;[\tilde{\rho}\,\mathbf{v}] = 0 \\ \mathbf{v} ={-}\mathcal{B}\,\nabla \,\tilde{\rho}^{2k}\\ (\tilde{\rho}(0),\mathbf{v}(0)) = (\tilde{\rho}_{0},\mathbf{v}_{0}) \end{array}\right.. \end{equation}
\begin{equation} \left\{\begin{array}{@{}l} \partial_{t}\tilde{\rho} - \mu\,\Delta_N\, \tilde{\rho} + \textrm{div}\;[\tilde{\rho}\,\mathbf{v}] = 0 \\ \mathbf{v} ={-}\mathcal{B}\,\nabla \,\tilde{\rho}^{2k}\\ (\tilde{\rho}(0),\mathbf{v}(0)) = (\tilde{\rho}_{0},\mathbf{v}_{0}) \end{array}\right.. \end{equation}
Applying ![]() $\mathfrak {J}^{s}$ to regularized equation:
$\mathfrak {J}^{s}$ to regularized equation:
Multiplying (5.4) by ![]() $\mathfrak {J}^{s}\tilde {\rho }$ and integrating over
$\mathfrak {J}^{s}\tilde {\rho }$ and integrating over ![]() ${\mathbb {R}_{+}^{3}}$ we get,
${\mathbb {R}_{+}^{3}}$ we get,
so that
 \begin{equation} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x=\underbrace {\mu\int(\mathfrak{J}^{s}\tilde{\rho})\Delta_{N}\,(\mathfrak{J}^{s}\tilde {\rho})\,\textrm{d}x}_{{\leq} 0}-\sum_{i=1}^{3}\int(\mathfrak{J}^{s}\tilde{\rho})\partial_{x_{i}}\mathfrak{J}^{s}(\tilde{\rho}\,v_{i})\,\textrm{d}x. \end{equation}
\begin{equation} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x=\underbrace {\mu\int(\mathfrak{J}^{s}\tilde{\rho})\Delta_{N}\,(\mathfrak{J}^{s}\tilde {\rho})\,\textrm{d}x}_{{\leq} 0}-\sum_{i=1}^{3}\int(\mathfrak{J}^{s}\tilde{\rho})\partial_{x_{i}}\mathfrak{J}^{s}(\tilde{\rho}\,v_{i})\,\textrm{d}x. \end{equation}
Using the commutator ![]() $[\partial _{x_{i}}\mathfrak {J}^{s},v_{i}]\tilde {\rho }=\partial _{x_{i}}\mathfrak {J}^{s}(\tilde {\rho }\,v_{i})-v_{i}\partial _{x_{i}}J^{s}\tilde {\rho }$, we obtain:
$[\partial _{x_{i}}\mathfrak {J}^{s},v_{i}]\tilde {\rho }=\partial _{x_{i}}\mathfrak {J}^{s}(\tilde {\rho }\,v_{i})-v_{i}\partial _{x_{i}}J^{s}\tilde {\rho }$, we obtain:
 \begin{equation} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\int(J^{s}\tilde{\rho})^{2}\,\textrm{d}x\leq{-}\sum_{i=1}^{3} \int(\mathfrak{J}^{s}\tilde{\rho})[\partial_{x_{i}}\mathfrak{J}^{s},v_{i}]\tilde{\rho}\,\textrm{d}x-\sum_{i=1}^{3}\int(\mathfrak{J}^{s}\tilde{\rho} )v_{i}\partial_{x_{i}}\mathfrak{J}^{s}\tilde{\rho}\,\textrm{d}x. \end{equation}
\begin{equation} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\int(J^{s}\tilde{\rho})^{2}\,\textrm{d}x\leq{-}\sum_{i=1}^{3} \int(\mathfrak{J}^{s}\tilde{\rho})[\partial_{x_{i}}\mathfrak{J}^{s},v_{i}]\tilde{\rho}\,\textrm{d}x-\sum_{i=1}^{3}\int(\mathfrak{J}^{s}\tilde{\rho} )v_{i}\partial_{x_{i}}\mathfrak{J}^{s}\tilde{\rho}\,\textrm{d}x. \end{equation}Integration by parts in (5.7) yields,
 \begin{equation} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x\leq{-}\sum_{i=1}^{3}\int(\mathfrak{J}^{s}\tilde{\rho})[\partial_{x_{i}} \mathfrak{J}^{s},v_{i}]\tilde{\rho}\,\textrm{d}x+\frac{1}{2}\int(\mathfrak{J}^{s} \tilde{\rho})^{2}\text{div}\;v\,\textrm{d}x. \end{equation}
\begin{equation} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x\leq{-}\sum_{i=1}^{3}\int(\mathfrak{J}^{s}\tilde{\rho})[\partial_{x_{i}} \mathfrak{J}^{s},v_{i}]\tilde{\rho}\,\textrm{d}x+\frac{1}{2}\int(\mathfrak{J}^{s} \tilde{\rho})^{2}\text{div}\;v\,\textrm{d}x. \end{equation}Taking (4.12) into (5.8) we obtain,
 \begin{align} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x&\leq{-}\sum\limits_{i=1}^{3}\int(\mathfrak{J}^{s}\tilde{\rho})[\partial_{x_{i}}\mathfrak{J}^{s},v_{i}]\tilde{\rho}\,dx+\frac{1}{2}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\tilde{\rho}^{2k}\,\textrm{d}x\nonumber\\ &\quad-\frac{1}{2}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\mathfrak{J}^{{-}1/2}(\tilde{\rho}^{2k})\,\textrm{d}x. \end{align}
\begin{align} \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x&\leq{-}\sum\limits_{i=1}^{3}\int(\mathfrak{J}^{s}\tilde{\rho})[\partial_{x_{i}}\mathfrak{J}^{s},v_{i}]\tilde{\rho}\,dx+\frac{1}{2}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\tilde{\rho}^{2k}\,\textrm{d}x\nonumber\\ &\quad-\frac{1}{2}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\mathfrak{J}^{{-}1/2}(\tilde{\rho}^{2k})\,\textrm{d}x. \end{align}
From the second equation in (5.3) we have ![]() $v_{i}=-\partial _{x_{i}}B_{i}(\tilde {\rho }^{2k})$. Substituting it in (5.9)
$v_{i}=-\partial _{x_{i}}B_{i}(\tilde {\rho }^{2k})$. Substituting it in (5.9)
 \begin{align} \frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x&\leq\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\tilde{\rho}^{2k}\,\textrm{d}x-\overbrace{\int(\mathfrak{J} ^{s}\tilde{\rho})^{2}\mathfrak{J}^{{-}1/2}\tilde{\rho}^{2k}\,\textrm{d}x}^{{\geq} 0}\nonumber\\ &\quad+2\int(\mathfrak{J}^{s}\tilde{\rho})\left(\sum\limits_{i=1}^{3}[\partial_{x_{i}}\mathfrak{J}^{s},\partial_{x_{i}}B_{i}\left(\tilde{\rho} ^{2k}\right)]\tilde{\rho}\right)\,\textrm{d}x. \end{align}
\begin{align} \frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x&\leq\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\tilde{\rho}^{2k}\,\textrm{d}x-\overbrace{\int(\mathfrak{J} ^{s}\tilde{\rho})^{2}\mathfrak{J}^{{-}1/2}\tilde{\rho}^{2k}\,\textrm{d}x}^{{\geq} 0}\nonumber\\ &\quad+2\int(\mathfrak{J}^{s}\tilde{\rho})\left(\sum\limits_{i=1}^{3}[\partial_{x_{i}}\mathfrak{J}^{s},\partial_{x_{i}}B_{i}\left(\tilde{\rho} ^{2k}\right)]\tilde{\rho}\right)\,\textrm{d}x. \end{align}Noting that the third term in (5.10) is non-negative, and applying Cauchy Schwartz inequality in the fourth term we get,
 \begin{align} \frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x&\leq\Vert\tilde{\rho }^{2k}\Vert_{L^{\infty}({\mathbb{R}_{+}^{3}})}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x\nonumber\\ &\quad+2\Vert\mathfrak{J}^{s}\tilde{\rho}\Vert_{\mathfrak{L}\;^{2}({\mathbb{R}_{+}^{3}})}\left\|\sum\limits_{i=1}^{3}\left[\partial_{x_{i}}\mathfrak{J}^{s},\partial_{x_{i}}\mathfrak{J}^{{-}1/2}\tilde{\rho} ^{2k}\right]\tilde{\rho}\right\|_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})} \end{align}
\begin{align} \frac{\textrm{d}}{\textrm{d}t}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x&\leq\Vert\tilde{\rho }^{2k}\Vert_{L^{\infty}({\mathbb{R}_{+}^{3}})}\int(\mathfrak{J}^{s}\tilde{\rho})^{2}\,\textrm{d}x\nonumber\\ &\quad+2\Vert\mathfrak{J}^{s}\tilde{\rho}\Vert_{\mathfrak{L}\;^{2}({\mathbb{R}_{+}^{3}})}\left\|\sum\limits_{i=1}^{3}\left[\partial_{x_{i}}\mathfrak{J}^{s},\partial_{x_{i}}\mathfrak{J}^{{-}1/2}\tilde{\rho} ^{2k}\right]\tilde{\rho}\right\|_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})} \end{align}
Using lemma 5.1 in (5.11), with ![]() $f=J^{-1/2}\tilde {\rho }^{2k}$ and
$f=J^{-1/2}\tilde {\rho }^{2k}$ and ![]() $g=\tilde {\rho }$, we obtain:
$g=\tilde {\rho }$, we obtain:
Applying lemma 5.3 in the term ![]() $\Vert \tilde {\rho }\Vert _{s}^{2}$, in (5.12):
$\Vert \tilde {\rho }\Vert _{s}^{2}$, in (5.12):
Now, we need to estimate ![]() $\Vert \tilde {\rho }\Vert _{L^{\infty }({\mathbb {R} _{+}^{3}})}$. Applying the comparison principle for
$\Vert \tilde {\rho }\Vert _{L^{\infty }({\mathbb {R} _{+}^{3}})}$. Applying the comparison principle for ![]() $\rho$ together with Sobolev's lemma we have
$\rho$ together with Sobolev's lemma we have
Since ![]() $\Vert \tilde {\rho }-\rho \Vert _{s}=\sup _{\Vert \varphi \Vert _{s}=1} |\langle \tilde {\rho }-\rho ,\varphi \rangle _{s}|$ we proceed as follows: in the analysis of the weak convergence of sequence
$\Vert \tilde {\rho }-\rho \Vert _{s}=\sup _{\Vert \varphi \Vert _{s}=1} |\langle \tilde {\rho }-\rho ,\varphi \rangle _{s}|$ we proceed as follows: in the analysis of the weak convergence of sequence ![]() $\rho _{\mu }$ (see the proof of theorem 4.2 in [Reference Molina Del Sol, Alarcon and Iorio23]) we obtained
$\rho _{\mu }$ (see the proof of theorem 4.2 in [Reference Molina Del Sol, Alarcon and Iorio23]) we obtained
 \begin{align} |\langle\rho_{\mu}(t)-\rho_{\eta}(t),\varphi\rangle_{s}|&\leq\Vert\rho_{\mu}(t)-\rho_{\eta}(t)\Vert_{s}\Vert\varphi-\varphi_{\epsilon}\Vert _{s}+\Vert\rho_{\mu}(t)-\rho_{\eta}(t)\Vert_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}\,\Vert\varphi_{\epsilon}\Vert_{2s}\nonumber\\ &\leq 2M\epsilon+\Vert\rho_{\mu}(t)-\rho_{\eta}(t)\Vert_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}\,\Vert\varphi_{\epsilon}\Vert_{2s} \end{align}
\begin{align} |\langle\rho_{\mu}(t)-\rho_{\eta}(t),\varphi\rangle_{s}|&\leq\Vert\rho_{\mu}(t)-\rho_{\eta}(t)\Vert_{s}\Vert\varphi-\varphi_{\epsilon}\Vert _{s}+\Vert\rho_{\mu}(t)-\rho_{\eta}(t)\Vert_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}\,\Vert\varphi_{\epsilon}\Vert_{2s}\nonumber\\ &\leq 2M\epsilon+\Vert\rho_{\mu}(t)-\rho_{\eta}(t)\Vert_{\mathfrak{L}^{2}({\mathbb{R}_{+}^{3}})}\,\Vert\varphi_{\epsilon}\Vert_{2s} \end{align}
Taking the limit as ![]() $\eta \rightarrow 0$ in (5.15), it follows that,
$\eta \rightarrow 0$ in (5.15), it follows that,
Noting that ![]() $\Vert \rho _{\mu }(t)-\rho _{\nu }(t)\Vert _{\mathfrak {L} ^{2}({\mathbb {R}_{+}^{3}})}\leq 2M\sqrt {n\tilde {T}_{s}|\mu -\nu |}\,\textrm {e}^{\tilde {T}_{s}L_{0}(M,M)}$ (see the proof of theorem 4.2 in [Reference Molina Del Sol, Alarcon and Iorio23]) and taking the limit as
$\Vert \rho _{\mu }(t)-\rho _{\nu }(t)\Vert _{\mathfrak {L} ^{2}({\mathbb {R}_{+}^{3}})}\leq 2M\sqrt {n\tilde {T}_{s}|\mu -\nu |}\,\textrm {e}^{\tilde {T}_{s}L_{0}(M,M)}$ (see the proof of theorem 4.2 in [Reference Molina Del Sol, Alarcon and Iorio23]) and taking the limit as ![]() $\nu \rightarrow 0$, it follows that,
$\nu \rightarrow 0$, it follows that,
Substituting (5.17) in (5.16) and noting that ![]() $\Vert \varphi _{\epsilon }\Vert _{2s}\leq \epsilon ^{-s}\Vert \varphi \Vert _{s}$ with
$\Vert \varphi _{\epsilon }\Vert _{2s}\leq \epsilon ^{-s}\Vert \varphi \Vert _{s}$ with ![]() $\varphi _{\epsilon }$ constructed as in [Reference Iorio, Linares and Scialom11, lemma 2.6, p. 900], yields
$\varphi _{\epsilon }$ constructed as in [Reference Iorio, Linares and Scialom11, lemma 2.6, p. 900], yields
Then
and
Since ![]() $r(\tau )=\tau ^{2k}$ is a non-decreasing function, it follows that:
$r(\tau )=\tau ^{2k}$ is a non-decreasing function, it follows that:
Integrating from ![]() $0$ to
$0$ to ![]() $t$ in (5.21)
$t$ in (5.21)
Applying Gronwall's inequality to (5.22), we obtain a priori-estimate in ![]() $H^{s}(R_{+}^{3});\ s>5/2$
$H^{s}(R_{+}^{3});\ s>5/2$
Finally, applying [Reference Yosida35, theorem 1, p. 120] in (5.23) we obtain the final estimate
 \begin{align} \Vert\rho(t)\Vert_{s}^{2}&\leq\liminf_{\mu\rightarrow 0}\Vert\rho_{\mu}(t)\Vert_{s}^{2}\nonumber\\ &\leq\liminf_{\mu\rightarrow 0}\Vert\rho_{0}\Vert_{s}^{2}\,\textrm{e}^{r\left(1+2M\epsilon+\widetilde{C}(n,M,\tilde{T}_{s})\sqrt{\mu} \,\epsilon^{{-}s}\right)\tilde{T}_{s}}\nonumber\\ &=\lim_{\mu\rightarrow 0}\Vert\rho_{0}\Vert_{s}^{2}\,\textrm{e}^{r\left(1+2M\epsilon+\widetilde{C}(n,M,\tilde{T}_{s})\sqrt{\mu}\,\epsilon^{{-}s}\right)\tilde{T}_{s}}\nonumber\\ &=\Vert\rho_{0}\Vert_{s}^{2}\,\textrm{e}^{r(1+2M\epsilon)\tilde{T}_{s}}\ \forall\epsilon>0 \end{align}
\begin{align} \Vert\rho(t)\Vert_{s}^{2}&\leq\liminf_{\mu\rightarrow 0}\Vert\rho_{\mu}(t)\Vert_{s}^{2}\nonumber\\ &\leq\liminf_{\mu\rightarrow 0}\Vert\rho_{0}\Vert_{s}^{2}\,\textrm{e}^{r\left(1+2M\epsilon+\widetilde{C}(n,M,\tilde{T}_{s})\sqrt{\mu} \,\epsilon^{{-}s}\right)\tilde{T}_{s}}\nonumber\\ &=\lim_{\mu\rightarrow 0}\Vert\rho_{0}\Vert_{s}^{2}\,\textrm{e}^{r\left(1+2M\epsilon+\widetilde{C}(n,M,\tilde{T}_{s})\sqrt{\mu}\,\epsilon^{{-}s}\right)\tilde{T}_{s}}\nonumber\\ &=\Vert\rho_{0}\Vert_{s}^{2}\,\textrm{e}^{r(1+2M\epsilon)\tilde{T}_{s}}\ \forall\epsilon>0 \end{align}
Therefore, taking the limit as ![]() $\epsilon$ tends to zero, follows the final estimate
$\epsilon$ tends to zero, follows the final estimate
and the proof is complete.
Acknowledgments
We dedicate this article to our dear friend Eduardo Arbieto Alarcon who left us all too early. Without him our articles about the Brinkman equations would not have been possible. We deeply regret his absence.