Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kostov, V. P.
2018.
A Separation in Modulus Property of the Zeros of a Partial Theta Function.
Analysis Mathematica,
Vol. 44,
Issue. 4,
p.
501.
Kostov, Vladimir Petrov
2019.
О комплексно-сопряженных нулях частичной тэта-функции.
Функциональный анализ и его приложения,
Vol. 53,
Issue. 2,
p.
87.
Rostov, V. P.
2019.
On the Complex Conjugate Zeros of the Partial Theta Function.
Functional Analysis and Its Applications,
Vol. 53,
Issue. 2,
p.
149.
Nguyen, Thu Hien
and
Vishnyakova, Anna
2019.
On a necessary condition for an entire function with the increasing second quotients of Taylor coefficients to belong to the Laguerre-Pólya class.
Journal of Mathematical Analysis and Applications,
Vol. 480,
Issue. 2,
p.
123433.
Kostov, Vladimir Petrov
2020.
Partial Theta Function and Separation in Modulus Property of its Zeros.
Vietnam Journal of Mathematics,
Vol. 48,
Issue. 1,
p.
145.
Nguyen, Thu Hien
and
Vishnyakova, Anna
2020.
On the Closest to Zero Roots and the Second Quotients of Taylor Coefficients of Entire Functions from the Laguerre–Pólya I Class.
Results in Mathematics,
Vol. 75,
Issue. 3,
Nguyen, Thu Hien
and
Vishnyakova, Anna
2021.
On the entire functions from the Laguerre–Pólya I class having the increasing second quotients of Taylor coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 498,
Issue. 1,
p.
124955.
Nguyen, T. H.
and
Vishnyakova, A.
2021.
On entire functions from the Laguerre-Polya I class with non-monotonic second quotients of Taylor coefficients.
Matematychni Studii,
Vol. 56,
Issue. 2,
p.
149.
Nguyen, Thu Hien
2022.
On the Conditions for a Special Entire Function Related to the Partial Theta-Function and the q-Kummer Functions to Belong to the Laguerre–Pólya Class.
Computational Methods and Function Theory,
Vol. 22,
Issue. 1,
p.
7.
Flores, Ramón
and
González-Meneses, Juan
2022.
On the growth of Artin–Tits monoids and the partial theta function.
Journal of Combinatorial Theory, Series A,
Vol. 190,
Issue. ,
p.
105623.
Kostov, V.
2023.
A domain free of the zeros of the partial theta function.
Matematychni Studii,
Vol. 58,
Issue. 2,
p.
142.
Nguyen, Thu Hien
and
Vishnyakova, Anna
2024.
Hutchinson’s intervals and entire functions from the Laguerre–Pólya class.
European Journal of Mathematics,
Vol. 10,
Issue. 1,
 defines a partial theta function. For fixed q (∣q∣ < 1), θ(q, ·) is an entire function. For q ∈ (–1, 0) the function θ(q, ·) has infinitely many negative and infinitely many positive real zeros. There exists a sequence
defines a partial theta function. For fixed q (∣q∣ < 1), θ(q, ·) is an entire function. For q ∈ (–1, 0) the function θ(q, ·) has infinitely many negative and infinitely many positive real zeros. There exists a sequence 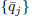 of values of q tending to –1+ such that
of values of q tending to –1+ such that  has a double real zero
has a double real zero  (the rest of its real zeros being simple). For k odd (respectively, k even)
(the rest of its real zeros being simple). For k odd (respectively, k even)  has a local minimum (respectively, maximum) at
has a local minimum (respectively, maximum) at  , and
, and  is the rightmost of the real negative zeros of
is the rightmost of the real negative zeros of  (respectively, for k sufficiently large
(respectively, for k sufficiently large  is the second from the left of the real negative zeros of
is the second from the left of the real negative zeros of  ). For k sufficiently large one has
). For k sufficiently large one has  . One has
. One has 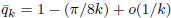 and
and  .
.