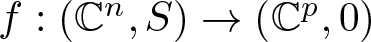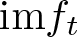1. Introduction
The context of this work is known as Thom–Mather theory: we deal with homology of images of mappings ft that arise as deformations of complex map germs ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, with n < p, and the behaviour of singularities (instabilities) under deformations. The most studied case is
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, with n < p, and the behaviour of singularities (instabilities) under deformations. The most studied case is ![]() $p=n+1$, where there are several long-standing open problems. In contrast, very little is known for p > n, in general (when the deformation fs is locally stable, the homology of
$p=n+1$, where there are several long-standing open problems. In contrast, very little is known for p > n, in general (when the deformation fs is locally stable, the homology of ![]() $\operatorname{im} f_s$ is known, see [Reference Goryunov and Mond10, Reference Goryunov11, Reference Houston16]).
$\operatorname{im} f_s$ is known, see [Reference Goryunov and Mond10, Reference Goryunov11, Reference Houston16]).
We refer to the book [Reference Mond and Nuño-Ballesteros27] for basic definitions and properties about singularities of mappings: instabilities, stability, ![]() $\mathscr{A}$-finiteness, versal unfoldings, etc.
$\mathscr{A}$-finiteness, versal unfoldings, etc.
In §2, we develop the theory of actions of finite groups on a finite simplicial complex M with a good action. We give several statements regarding the isotypical components of the homology ![]() $H_*(M)$ and use it to study the case of icis (isolated complete intersection singularity) and their Milnor fibre.
$H_*(M)$ and use it to study the case of icis (isolated complete intersection singularity) and their Milnor fibre.
This is applied in §4–5 to express the homology of ![]() $\operatorname{im} f_t$ in simple terms, ft being any deformation of a germ f. We do this by means of a well-known spectral sequence, the image-computing spectral sequence (icss), whose input is given by the multiple point spaces,
$\operatorname{im} f_t$ in simple terms, ft being any deformation of a germ f. We do this by means of a well-known spectral sequence, the image-computing spectral sequence (icss), whose input is given by the multiple point spaces, ![]() $D^k(\bullet)$, introduced in §3.
$D^k(\bullet)$, introduced in §3. ![]() $D^k(f)$ are icis if the germ f has corank one, and we use Milnor numbers of a larger set of icis to express
$D^k(f)$ are icis if the germ f has corank one, and we use Milnor numbers of a larger set of icis to express ![]() $H_*(\operatorname{im} f_t)$ in this case.
$H_*(\operatorname{im} f_t)$ in this case.
The deformations that are locally stable stand out among every other deformation, they play the role of Milnor fibres (generic fibres). If we refer only to (locally) stable deformations, it is customary to use fs instead of ft. In §3, we study unstable germs such that the stable deformation fs has contractible image and characterize the dimensions where such mono-germs exist in corank one. This is similar to the concept of rigid singularities, in our context, and their existence was unknown (apart from trivial cases when ![]() $n\ll p$). This also answers negatively a question posed by D. Mond.
$n\ll p$). This also answers negatively a question posed by D. Mond.
The multiple point spaces control the homology of ![]() $\operatorname{im} f_t$ by means of the icss, but very little is known about them. In §4, we give deep results about their behaviour (see theorems 4.8–4.9). This is used in §5 to give a workable way to compute the homology of
$\operatorname{im} f_t$ by means of the icss, but very little is known about them. In §4, we give deep results about their behaviour (see theorems 4.8–4.9). This is used in §5 to give a workable way to compute the homology of ![]() $\operatorname{im} f_s$, in particular two generalizations of the image Milnor number µI defined by Mond, for n < p. This is highly relevant: the homology of
$\operatorname{im} f_s$, in particular two generalizations of the image Milnor number µI defined by Mond, for n < p. This is highly relevant: the homology of ![]() $\operatorname{im} f_s$ is difficult to handle in general and we can translate it into a combination of Milnor numbers of icis (in corank one).
$\operatorname{im} f_s$ is difficult to handle in general and we can translate it into a combination of Milnor numbers of icis (in corank one).
In §5, we also show that there are deformations ft such that ![]() $\operatorname{im} f_t$ has homology in dimensions where the image of the locally stable deformation,
$\operatorname{im} f_t$ has homology in dimensions where the image of the locally stable deformation, ![]() $\operatorname{im} f_s$, has trivial homology. We show when this unexpected homology appears and we give a conservation principle of the homology of images of perturbations, modulo this unexpected homology.
$\operatorname{im} f_s$, has trivial homology. We show when this unexpected homology appears and we give a conservation principle of the homology of images of perturbations, modulo this unexpected homology.
Houston’s conjecture on excellent unfoldings (see [Reference Houston19]) is very relevant for Whitney equisingularity problems (e.g., [Reference Gaffney5, Reference Giménez Conejero and Nuño-Ballesteros8]). In §6, we use the previous developments to show that it is false. We modify the conjecture according to these findings and provide a proof in that adjusted setting. We also show when the converse is true.
Finally, we give some open problems and conjectures to lead the way on the research of this highly unexplored area in §7.
2. Actions on simplicial complexes
2.1. General results
We use several notions of representation theory, such as characters and irreducible representations. The following result is a key idea in this work, and it involves a system of linear equations where the coefficients are given by the characters of some finite group G.
Lemma 2.1. Let G be a finite group and consider the system of linear equations
 \begin{equation*} \sum_{\tau_i} \chi_{\tau_i}(\sigma) x_{\tau_i}=b_\sigma,\end{equation*}
\begin{equation*} \sum_{\tau_i} \chi_{\tau_i}(\sigma) x_{\tau_i}=b_\sigma,\end{equation*} one for each element ![]() $\sigma\in G$, with one unknown
$\sigma\in G$, with one unknown ![]() $x_{\tau_i}$ for each irreducible representation τi of G and bσ the components of a vector
$x_{\tau_i}$ for each irreducible representation τi of G and bσ the components of a vector ![]() $b\in\mathbb{C}^G$. It has a solution if, and only if,
$b\in\mathbb{C}^G$. It has a solution if, and only if, ![]() $b_{\sigma}=b_{\sigma'}$ for σ conjugate to
$b_{\sigma}=b_{\sigma'}$ for σ conjugate to ![]() $\sigma'$, and it is given by
$\sigma'$, and it is given by
 \begin{equation*} |G|x_{\tau_i}= \sum_{\sigma\in G}\overline{\chi_{\tau_i}(\sigma)}b_\sigma.\end{equation*}
\begin{equation*} |G|x_{\tau_i}= \sum_{\sigma\in G}\overline{\chi_{\tau_i}(\sigma)}b_\sigma.\end{equation*}Proof. Recall that the subspace of vectors ![]() $b\in\mathbb{C}^G$ with
$b\in\mathbb{C}^G$ with ![]() $b_\sigma=b_{\sigma'}$ for conjugated σ and
$b_\sigma=b_{\sigma'}$ for conjugated σ and ![]() $\sigma'$ is precisely given by the class functions. Observe that the irreducible characters
$\sigma'$ is precisely given by the class functions. Observe that the irreducible characters ![]() $\chi_{\tau_i}$ of G form an orthonormal basis of the space of class functions for the usual inner product
$\chi_{\tau_i}$ of G form an orthonormal basis of the space of class functions for the usual inner product
 \begin{equation*} \left\langle \phi| \psi\right\rangle:= \frac{1}{|G|}\sum_{\sigma\in G}\phi(\sigma)\overline{\psi(\sigma)}.\end{equation*}
\begin{equation*} \left\langle \phi| \psi\right\rangle:= \frac{1}{|G|}\sum_{\sigma\in G}\phi(\sigma)\overline{\psi(\sigma)}.\end{equation*} Then, we fix one irreducible representation ![]() $\tau'$ and we take the sum of all equations, each one multiplied by the respective
$\tau'$ and we take the sum of all equations, each one multiplied by the respective  $\overline{\chi_{\tau'}(\sigma)}$:
$\overline{\chi_{\tau'}(\sigma)}$:
 \begin{equation*}\begin{array}{ll}
\sum\limits_{\sigma\in G} \overline{\chi_{\tau'}(\sigma)}\sum\limits_{\tau_i} \chi_{\tau_i}(\sigma) x_{\tau_i}&=\sum\limits_{\sigma\in G}\overline{\chi_{\tau'}(\sigma)}b_\sigma\\
\sum\limits_{\tau_i} \sum\limits_{\sigma\in G} \overline{\chi_{\tau'}(\sigma)}\chi_{\tau_i}(\sigma) x_{\tau_i}&=\sum\limits_{\sigma\in G}\overline{\chi_{\tau'}(\sigma)}b_\sigma\\
\sum\limits_{\tau_i} |G|\left\langle \chi_{\tau_i}|\chi_{\tau'}\right\rangle x_{\tau_i}&=\sum\limits_{\sigma\in G}\overline{\chi_{\tau'}(\sigma)}b_\sigma.
\end{array}\end{equation*}
\begin{equation*}\begin{array}{ll}
\sum\limits_{\sigma\in G} \overline{\chi_{\tau'}(\sigma)}\sum\limits_{\tau_i} \chi_{\tau_i}(\sigma) x_{\tau_i}&=\sum\limits_{\sigma\in G}\overline{\chi_{\tau'}(\sigma)}b_\sigma\\
\sum\limits_{\tau_i} \sum\limits_{\sigma\in G} \overline{\chi_{\tau'}(\sigma)}\chi_{\tau_i}(\sigma) x_{\tau_i}&=\sum\limits_{\sigma\in G}\overline{\chi_{\tau'}(\sigma)}b_\sigma\\
\sum\limits_{\tau_i} |G|\left\langle \chi_{\tau_i}|\chi_{\tau'}\right\rangle x_{\tau_i}&=\sum\limits_{\sigma\in G}\overline{\chi_{\tau'}(\sigma)}b_\sigma.
\end{array}\end{equation*}The lemma follows from there.
These kind of systems are very relevant in our study because the solution is completely determined by the bσ, as the coefficients are given by the character table of G. This is one of the main reasons which explain that, as we will see in theorem 5.4, the multiple point spaces control completely the homology of the image of a sufficiently good mapping f.
Another reason is that we use these multiple point spaces in a spectral sequence converging to the homology of their image ![]() $\operatorname{im} f$, the so-called image-computing spectral sequence or icss (see theorem 3.2).
$\operatorname{im} f$, the so-called image-computing spectral sequence or icss (see theorem 3.2).
Nonetheless, the difficulty of using these spectral sequences is that we do not use regular homology to compute the limit of the sequence, but an alternating isotypical component. In many cases, working with this isotypical component is very hard since one needs to have control over the action of the group on a topological space that can be complicated. Hence, instead of this elusive component, one would like to work with the whole homology (or the Euler–Poincaré characteristic), which is easier to control in favourable circumstances. This is where lemma 2.1 plays a role.
Definition 2.2. Consider a simplicial complex M. We say that an action of a group G on M is simplicially good if it maps simplices to simplices and simplices fixed as sets are point-wise fixed.
Let G be a finite group with a simplicially good action on a finite simplicial complex M and let M σ denote the fixed points of the action of σ on M. Then
where χG denotes what we call the (virtual) character of G acting on M and χTop denotes the usual Euler–Poincaré characteristic. More precisely:
 \begin{equation*}
\chi_G(M)(\sigma):= \sum_{i} (-1)^i\operatorname{tr} \left(H_i(M,\mathbb{C})\mathop{\longrightarrow}\limits^{\sigma_*} H_i(M,\mathbb{C})\right).
\end{equation*}
\begin{equation*}
\chi_G(M)(\sigma):= \sum_{i} (-1)^i\operatorname{tr} \left(H_i(M,\mathbb{C})\mathop{\longrightarrow}\limits^{\sigma_*} H_i(M,\mathbb{C})\right).
\end{equation*}Equation (1) links usual homology and the isotypical components of any representation of G, and it can be proven using standard arguments (see, for example, [Reference Hatcher15, theorem 2.44] and Wall’s comments in [Reference Wall34, p. 172]). A detailed account of this can be found in [Reference Giménez Conejero6, Section 6.1.1].
It is convenient to use some notation to work with the different irreducible representations of G.
Definition 2.3. Consider a simplicially good action of a finite group G on a finite simplicial complex M, as in Eq. (1). If τ is an irreducible representation of G, the i-th τ-Betti number is the number of copies of τ in ![]() $H_i(M,\mathbb{C})$, i.e., it is
$H_i(M,\mathbb{C})$, i.e., it is
 \begin{equation*} \beta_{i}^{\tau}(M):= \frac{\operatorname{dim}_{\mathbb{C}} H_i(M,\mathbb{C})^{\tau}}{\operatorname{deg}(\tau)},\end{equation*}
\begin{equation*} \beta_{i}^{\tau}(M):= \frac{\operatorname{dim}_{\mathbb{C}} H_i(M,\mathbb{C})^{\tau}}{\operatorname{deg}(\tau)},\end{equation*} where ![]() $H_i(M,\mathbb{C})^\tau$ denotes the τ-isotypical component of
$H_i(M,\mathbb{C})^\tau$ denotes the τ-isotypical component of ![]() $H_i(M,\mathbb{C})$ and
$H_i(M,\mathbb{C})$ and ![]() $\operatorname{deg}(\tau)$ the degree of τ. Similarly, the τ-characteristic of M is
$\operatorname{deg}(\tau)$ the degree of τ. Similarly, the τ-characteristic of M is
 \begin{equation*}\chi_{\tau}(M):= \sum_{i} (-1)^i \beta_i^\tau(M).\end{equation*}
\begin{equation*}\chi_{\tau}(M):= \sum_{i} (-1)^i \beta_i^\tau(M).\end{equation*} The reason to define ![]() $\beta_i^\tau$ normalized by
$\beta_i^\tau$ normalized by ![]() $\operatorname{deg}(\tau)$ instead of defining it as
$\operatorname{deg}(\tau)$ instead of defining it as ![]() $\operatorname{dim}_{\mathbb{C} }H_i(M,\mathbb{C})^{\tau}$ will become apparent in the following proofs.
$\operatorname{dim}_{\mathbb{C} }H_i(M,\mathbb{C})^{\tau}$ will become apparent in the following proofs.
Proposition 2.4. In the conditions of definition 2.3,
 \begin{equation}
\chi_{\tau}(M)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \chi_{Top}(M^\sigma).
\end{equation}
\begin{equation}
\chi_{\tau}(M)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \chi_{Top}(M^\sigma).
\end{equation}Proof. For each ![]() $\sigma\in G$, we can expand the term
$\sigma\in G$, we can expand the term ![]() $\chi_G(M)(\sigma)$ in Eq. (1) to have
$\chi_G(M)(\sigma)$ in Eq. (1) to have
 \begin{equation*} \sum_{i} (-1)^i \sum_{\tau_j}\chi_{\tau_j}(\sigma) \beta_i^{\tau_j}(M)= \chi_{Top}(M^\sigma),\end{equation*}
\begin{equation*} \sum_{i} (-1)^i \sum_{\tau_j}\chi_{\tau_j}(\sigma) \beta_i^{\tau_j}(M)= \chi_{Top}(M^\sigma),\end{equation*}where τj runs in the irreducible representations of G. Rearranging terms,
 \begin{equation*} \sum_{\tau_j} \chi_{\tau_j}(\sigma)\sum_{i} (-1)^i \beta_i^{\tau_j}(M)= \sum_{\tau_j} \chi_{\tau_j}(\sigma)\chi_{\tau_j}(M)=\chi_{Top}(M^\sigma).\end{equation*}
\begin{equation*} \sum_{\tau_j} \chi_{\tau_j}(\sigma)\sum_{i} (-1)^i \beta_i^{\tau_j}(M)= \sum_{\tau_j} \chi_{\tau_j}(\sigma)\chi_{\tau_j}(M)=\chi_{Top}(M^\sigma).\end{equation*}The statement follows from the previous equation and lemma 2.1.
It is useful to state the case when M and all the M σ are non-empty and have non-trivial homology only in dimension zero and, possibly, in another dimension d and d σ (resp.). To simplify the notation, we set d or d σ to zero if M or M σ only have non-trivial homology in dimension zero (resp.).
Proposition 2.5. With the notation of the previous paragraph,
 \begin{equation}
(-1)^d\beta_{d}^{\tau}(M)+\boldsymbol{\zeta}_{d}\beta_0^{\tau}(M)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \big((-1)^{d^\sigma}\beta_{d^\sigma}(M^\sigma)+\boldsymbol{\zeta}_{d^\sigma}\beta_0(M^\sigma)\big),
\end{equation}
\begin{equation}
(-1)^d\beta_{d}^{\tau}(M)+\boldsymbol{\zeta}_{d}\beta_0^{\tau}(M)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \big((-1)^{d^\sigma}\beta_{d^\sigma}(M^\sigma)+\boldsymbol{\zeta}_{d^\sigma}\beta_0(M^\sigma)\big),
\end{equation} where ![]() $\boldsymbol{\zeta}_a$ is zero when a = 0 and one when a ≠ 0.
$\boldsymbol{\zeta}_a$ is zero when a = 0 and one when a ≠ 0.
Proof. This is an immediate reformulation of proposition 2.4 in terms of τ-Betti numbers.
Example 2.6. For the action of ![]() $\Sigma_2=\left\{\operatorname{id}, (1\: 2)\right\}$ on S 2 given by a reflection on a plane, the fixed point set of the transposition
$\Sigma_2=\left\{\operatorname{id}, (1\: 2)\right\}$ on S 2 given by a reflection on a plane, the fixed point set of the transposition ![]() $(1\: 2)$ are homeomorphic to S 1 (see figure 1). Also, the induced action of Σ2 on
$(1\: 2)$ are homeomorphic to S 1 (see figure 1). Also, the induced action of Σ2 on ![]() $H_2\left(S^2\right)$ is alternating:
$H_2\left(S^2\right)$ is alternating: ![]() $(1\,\: 2)^*\big[S^2\big]=-\big[S^2\big]$. Hence,
$(1\,\: 2)^*\big[S^2\big]=-\big[S^2\big]$. Hence,
 \begin{equation*}\beta_2^{\text{Alt}}\left(S^2\right)+0= \frac{1}{2}\left(\underbrace{1\cdot(1+1)}_{\operatorname{id}}+\underbrace{(-1)(-1+1)}_{(1\: 2)}\right)=1.\end{equation*}
\begin{equation*}\beta_2^{\text{Alt}}\left(S^2\right)+0= \frac{1}{2}\left(\underbrace{1\cdot(1+1)}_{\operatorname{id}}+\underbrace{(-1)(-1+1)}_{(1\: 2)}\right)=1.\end{equation*}In contrast, for the trivial action of Σ2,
 \begin{equation*}\beta_2^{\text{Alt}}\left(S^2\right)+0= \frac{1}{2}\left(\underbrace{1\cdot(1+1)}_{\operatorname{id}}+\underbrace{(-1)(1+1)}_{(1\: 2)}\right)=0.\end{equation*}
\begin{equation*}\beta_2^{\text{Alt}}\left(S^2\right)+0= \frac{1}{2}\left(\underbrace{1\cdot(1+1)}_{\operatorname{id}}+\underbrace{(-1)(1+1)}_{(1\: 2)}\right)=0.\end{equation*}
Figure 1. Diagrams of example 2.6.
2.2. Complete intersections with isolated singularities
Now, we study the interesting situation that arises when M has vanishing homology. This happens, for example, when we consider a sufficiently good action on an icis X that is inherited by its Milnor fibre FX. In that case, we are able to compute the τ-vanishing homology, i.e., the τ-Betti number in middle dimension.
A first approach to this situation can be made by assuming that all the X σ are icis with Milnor fibre ![]() $F_X^\sigma$, including the cases where X σ are empty. However, as we deal with map germs in the following sections, we will have a slightly more general situation that we explain now.
$F_X^\sigma$, including the cases where X σ are empty. However, as we deal with map germs in the following sections, we will have a slightly more general situation that we explain now.
In the context of finite map germs ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$ (in particular, S is a finite set), our icis will be a multiple point space
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$ (in particular, S is a finite set), our icis will be a multiple point space ![]() $X=D^k(f)$ (see definition 3.1) with ambient space
$X=D^k(f)$ (see definition 3.1) with ambient space ![]() $\big(\mathbb{C}^{nk},S^k\big)$. Observe that the icis is a union of germs at several points, so it is rather several icis at several points. In that case, we have an action on the ambient space by reflections that is inherited by
$\big(\mathbb{C}^{nk},S^k\big)$. Observe that the icis is a union of germs at several points, so it is rather several icis at several points. In that case, we have an action on the ambient space by reflections that is inherited by ![]() $D^k(f)$, which is given by invariant equations. In particular, the action is also inherited by the Milnor fibre
$D^k(f)$, which is given by invariant equations. In particular, the action is also inherited by the Milnor fibre ![]() $F_X=D^k(f_s)$.
$F_X=D^k(f_s)$.
The fixed-point spaces X σ of an element ![]() $\sigma\in G$ are
$\sigma\in G$ are ![]() $D^k(f)^\sigma$. In many cases, they are also icis, since the original icis
$D^k(f)^\sigma$. In many cases, they are also icis, since the original icis ![]() $X=D^k(f)$ are given by invariant equations and the equations to find the fixed points are those of the hyperplanes where the reflections take place (i.e., the action of the group). In those cases, their Milnor fibres are the fixed points of FX by σ, i.e.,
$X=D^k(f)$ are given by invariant equations and the equations to find the fixed points are those of the hyperplanes where the reflections take place (i.e., the action of the group). In those cases, their Milnor fibres are the fixed points of FX by σ, i.e., ![]() $F_X^\sigma=D^k(f_s)^\sigma$. However, depending on the dimensions (see definition 3.16), it can happen that
$F_X^\sigma=D^k(f_s)^\sigma$. However, depending on the dimensions (see definition 3.16), it can happen that ![]() $X^\sigma=D^k(f)^\sigma$ does not have the structure of an icis, but it is still a subset of the set of points Sk. In those situations,
$X^\sigma=D^k(f)^\sigma$ does not have the structure of an icis, but it is still a subset of the set of points Sk. In those situations, ![]() $F_X^\sigma=D^k(f_s)^\sigma$ is empty. When we allow this to happen, the computations and results need to carry the information about those isolated points, but the main idea of the results is still the same.
$F_X^\sigma=D^k(f_s)^\sigma$ is empty. When we allow this to happen, the computations and results need to carry the information about those isolated points, but the main idea of the results is still the same.
We extend definition 2.2 about simplicially good actions to include the setting of multiple point spaces that we will have later and we have explained above.
Definition 2.7. Let G be a finite group and ![]() $(X,\mathcal{S})\subset(\mathbb{C}^N,\mathcal{S})$ an icis on the finite set
$(X,\mathcal{S})\subset(\mathbb{C}^N,\mathcal{S})$ an icis on the finite set ![]() $\mathcal{S}$ (one icis for each point of
$\mathcal{S}$ (one icis for each point of ![]() $\mathcal{S}$) with a Milnor fibre FX. We say that G acts in a simplicially excellent way if
$\mathcal{S}$) with a Milnor fibre FX. We say that G acts in a simplicially excellent way if
(i) G has an action on
 $(\mathbb{C}^N,\mathcal{S})$ that is inherited by X and by FX;
$(\mathbb{C}^N,\mathcal{S})$ that is inherited by X and by FX;(ii) the action is simplicially good, i.e., X and FX admit a simplicial decomposition such that simplices fixed as sets are point-wise fixed; and
(iii) for every
 $\sigma\in G$, Xσ are icis with fibre
$\sigma\in G$, Xσ are icis with fibre  $F_X^\sigma$ or, alternatively,
$F_X^\sigma$ or, alternatively,  $X^\sigma\subset \mathcal{S}$ and
$X^\sigma\subset \mathcal{S}$ and  $F_X^\sigma=\varnothing$.
$F_X^\sigma=\varnothing$.
Note. The previous definition has the technical difficulty of choosing a Milnor ball such that the action of G on the ambient is inherited to the Milnor fibre FX. In other words, the ball has to be G-invariant. This happens in many cases, for example when the action is generated by reflections and X is given by G-invariant equations. Indeed, this is the case in the following sections.
Definition 2.8. With the conditions of Definition 2.7, let ![]() $(X,\mathcal{S})$ be an icis of dimension d with a simplicially excellent action of G. Consider an irreducible representation τ of G. Then, the τ-Milnor number of X is
$(X,\mathcal{S})$ be an icis of dimension d with a simplicially excellent action of G. Consider an irreducible representation τ of G. Then, the τ-Milnor number of X is
 \begin{equation*} \mu^\tau(X;\mathcal{S}):= (-1)^d \big(\chi_{\tau}(F_X)-\chi_{\tau}(X)\big).\end{equation*}
\begin{equation*} \mu^\tau(X;\mathcal{S}):= (-1)^d \big(\chi_{\tau}(F_X)-\chi_{\tau}(X)\big).\end{equation*}Example 2.9. Observe that it is not enough to define ![]() $\mu^\tau(X;\mathcal{S})$ as
$\mu^\tau(X;\mathcal{S})$ as ![]() $\beta_d^\tau(F_X)$. The icis X can have dimension zero and, since it is an icis on several points
$\beta_d^\tau(F_X)$. The icis X can have dimension zero and, since it is an icis on several points ![]() $\mathcal{S}$, we need to subtract
$\mathcal{S}$, we need to subtract ![]() $\beta_0^\tau(X)$. E.g., K copies of the same zero-dimensional icis and
$\beta_0^\tau(X)$. E.g., K copies of the same zero-dimensional icis and ![]() $G=\Sigma_K$ the group of permutations of K elements acting by permutation of copies.
$G=\Sigma_K$ the group of permutations of K elements acting by permutation of copies.
In Item (iii) of the definition of simplicially excellent actions, we include the case when ![]() $X^\sigma\subset\mathcal{S}$ is only a set of points such that
$X^\sigma\subset\mathcal{S}$ is only a set of points such that ![]() $F^\sigma=\varnothing$. For this reason, we need to extend the definition of Milnor number to that case:
$F^\sigma=\varnothing$. For this reason, we need to extend the definition of Milnor number to that case:
 \begin{equation}
\widetilde{\mu}(X^\sigma;\mathcal{S}):= \begin{cases}
\mu(X^\sigma;\mathcal{S}), &\text{if }X^\sigma\ \text{is an} \,{\scriptsize{\text{ICIS}}};\\
-\beta_0(X^\sigma), & \text{otherwise.}
\end{cases}
\end{equation}
\begin{equation}
\widetilde{\mu}(X^\sigma;\mathcal{S}):= \begin{cases}
\mu(X^\sigma;\mathcal{S}), &\text{if }X^\sigma\ \text{is an} \,{\scriptsize{\text{ICIS}}};\\
-\beta_0(X^\sigma), & \text{otherwise.}
\end{cases}
\end{equation}Lemma 2.10. Assume that we have a simplicially excellent action of a finite group G on an icis ![]() $(X,\mathcal{S})$. Then, for any irreducible representation τ,
$(X,\mathcal{S})$. Then, for any irreducible representation τ,
 \begin{equation*}\mu^\tau(X;\mathcal{S})=\frac{1}{|G|}\sum_{\sigma\in G}(-1)^{d-d^\sigma}\overline{\chi_{\tau}(\sigma)} \widetilde{\mu}(X^\sigma;\mathcal{S}),\end{equation*}
\begin{equation*}\mu^\tau(X;\mathcal{S})=\frac{1}{|G|}\sum_{\sigma\in G}(-1)^{d-d^\sigma}\overline{\chi_{\tau}(\sigma)} \widetilde{\mu}(X^\sigma;\mathcal{S}),\end{equation*} where dσ is the dimension of X σ, ![]() $d=d^{\operatorname{id}}$ and
$d=d^{\operatorname{id}}$ and ![]() $\widetilde{\mu}$ is given by Equation (4).
$\widetilde{\mu}$ is given by Equation (4).
Proof. Assume that d > 0. By proposition 2.5 for ![]() $M=F_X$; and using that
$M=F_X$; and using that ![]() $\beta_d^\tau(F_X)=\mu^\tau(X)$, and that
$\beta_d^\tau(F_X)=\mu^\tau(X)$, and that ![]() $\beta_0^\tau(F_X)=\beta_0^\tau(X)$ we have
$\beta_0^\tau(F_X)=\beta_0^\tau(X)$ we have
 \begin{equation}
(-1)^d\mu^\tau(X)+\beta_0^{\tau}(X)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \big((-1)^{d^\sigma}\beta_{d^\sigma}(F_X^\sigma)+\boldsymbol{\zeta}_{0d^\sigma}\beta_0(F_X^\sigma)\big).
\end{equation}
\begin{equation}
(-1)^d\mu^\tau(X)+\beta_0^{\tau}(X)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \big((-1)^{d^\sigma}\beta_{d^\sigma}(F_X^\sigma)+\boldsymbol{\zeta}_{0d^\sigma}\beta_0(F_X^\sigma)\big).
\end{equation}We can obtain the desired result by eliminating the zero τ-Betti numbers from the previous equation, which we can do using proposition 2.4 for M = X:
 \begin{equation}
\beta_0^{\tau}(X)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \beta_0(X^\sigma).
\end{equation}
\begin{equation}
\beta_0^{\tau}(X)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \beta_0(X^\sigma).
\end{equation} Subtracting Eq. (6) from Eq. (5) gives the desired result, after taking the notation of ![]() $\widetilde{\mu}$ from Eq. (4) and multiplying by
$\widetilde{\mu}$ from Eq. (4) and multiplying by ![]() $(-1)^d$.
$(-1)^d$.
The case d = 0 follows exactly the same steps, adapting the notation.
Let ![]() $(X,\mathcal{S})$ be an icis with a simplicially excellent action of G. Now, consider a G-equivariant deformation Xt, i.e.,
$(X,\mathcal{S})$ be an icis with a simplicially excellent action of G. Now, consider a G-equivariant deformation Xt, i.e., ![]() $(X_t, G\cdot x)$ is also an icis for any
$(X_t, G\cdot x)$ is also an icis for any ![]() $x\in X_t$ with all the requirements of definition 2.7. Additionally, assume that if
$x\in X_t$ with all the requirements of definition 2.7. Additionally, assume that if ![]() $X_0^\sigma$ is not an icis (so it is only points that vanish when one takes the fibre of X), neither is the deformation
$X_0^\sigma$ is not an icis (so it is only points that vanish when one takes the fibre of X), neither is the deformation ![]() $X_t^\sigma$. This is certainly the case for multiple point spaces in the following sections. Then, we have the conservation principle for the τ-Milnor numbers.
$X_t^\sigma$. This is certainly the case for multiple point spaces in the following sections. Then, we have the conservation principle for the τ-Milnor numbers.
Theorem 2.11. The τ-Milnor numbers are conserved. In other words, if we have a one-parameter family of icis Xt as in definition 2.7, for ![]() $|t|$ small enough,
$|t|$ small enough,
 \begin{equation*} \mu^\tau(X_0;\mathcal{S})=\begin{cases} \beta_d^\tau(X_t)+\sum_{G x\subseteq X_t} \mu^\tau (X_t;\:G x) & \text{if} \,d \gt 0,\\
\beta_0^\tau(X_t)+\sum_{G x\subseteq X_t} \mu^\tau (X_t;\:G x)-\beta_0^\tau(X_0)& \text{if} \,d=0.\end{cases}\end{equation*}
\begin{equation*} \mu^\tau(X_0;\mathcal{S})=\begin{cases} \beta_d^\tau(X_t)+\sum_{G x\subseteq X_t} \mu^\tau (X_t;\:G x) & \text{if} \,d \gt 0,\\
\beta_0^\tau(X_t)+\sum_{G x\subseteq X_t} \mu^\tau (X_t;\:G x)-\beta_0^\tau(X_0)& \text{if} \,d=0.\end{cases}\end{equation*}Proof. If d = 0 the result follows immediately from the definitions, so we assume that d > 0.
Since we have a simplicially excellent action, we can use the conservation principle of the Milnor number for the icis X σ (see [Reference Nuño-Ballesteros, Oréfice-Okamoto and Tomazella29, theorem 4.2]). Lemma 2.10 for X 0 and Xt yields
 \begin{equation}
\mu^{\tau}(X_0;\mathcal{S})=\frac{1}{|G|}\sum_{\sigma\in G}(-1)^{d-d^\sigma}\overline{\chi_{\tau}(\sigma)} \widetilde{\mu}(X_0^\sigma;\mathcal{S})\text{, and}
\end{equation}
\begin{equation}
\mu^{\tau}(X_0;\mathcal{S})=\frac{1}{|G|}\sum_{\sigma\in G}(-1)^{d-d^\sigma}\overline{\chi_{\tau}(\sigma)} \widetilde{\mu}(X_0^\sigma;\mathcal{S})\text{, and}
\end{equation} \begin{equation}
\sum_{G x\subseteq X_t}\mu^{\tau}(X_t;Gx)=\frac{1}{|G|}\sum_{\sigma\in G}(-1)^{d-d^\sigma}\overline{\chi_{\tau}(\sigma)} \sum_{G x\subseteq X_t}\widetilde{\mu}(X_t^\sigma; Gx).
\end{equation}
\begin{equation}
\sum_{G x\subseteq X_t}\mu^{\tau}(X_t;Gx)=\frac{1}{|G|}\sum_{\sigma\in G}(-1)^{d-d^\sigma}\overline{\chi_{\tau}(\sigma)} \sum_{G x\subseteq X_t}\widetilde{\mu}(X_t^\sigma; Gx).
\end{equation} It suffices to prove that subtracting Eq. (8) from Eq. (7) gives ![]() $\beta_d^\tau(X_t)$. Indeed, by the conservation principle for icis, it gives
$\beta_d^\tau(X_t)$. Indeed, by the conservation principle for icis, it gives
 \begin{equation*} \frac{1}{|G|}\left(\sum_{\sigma: d^\sigma \gt 0} (-1)^{d-d^\sigma}\overline{\chi_{\tau}(\sigma)}\beta_{d^\sigma}(X_t^\sigma) + \sum_{\sigma: d^\sigma = 0} (-1)^{d}\overline{\chi_{\tau}(\sigma)}\big(\beta_{0}(X_t^\sigma)-\beta_0(X_0^\sigma)\big) \right).\end{equation*}
\begin{equation*} \frac{1}{|G|}\left(\sum_{\sigma: d^\sigma \gt 0} (-1)^{d-d^\sigma}\overline{\chi_{\tau}(\sigma)}\beta_{d^\sigma}(X_t^\sigma) + \sum_{\sigma: d^\sigma = 0} (-1)^{d}\overline{\chi_{\tau}(\sigma)}\big(\beta_{0}(X_t^\sigma)-\beta_0(X_0^\sigma)\big) \right).\end{equation*} This is equal to ![]() $\beta_d^\tau(X_t)$. To see it, observe that, in positive dimensions,
$\beta_d^\tau(X_t)$. To see it, observe that, in positive dimensions,
 \begin{equation*}\begin{array}{rcl}
\chi_{\tau}(X_0)&=& \beta_0^\tau(X_0)=\beta_0^\tau(X_t),\, \text{and}\\
\chi_{Top}(X_0^\sigma)&=& \beta_0(X_0^\sigma)=\beta_0(X_t^\sigma).
\end{array}
\end{equation*}
\begin{equation*}\begin{array}{rcl}
\chi_{\tau}(X_0)&=& \beta_0^\tau(X_0)=\beta_0^\tau(X_t),\, \text{and}\\
\chi_{Top}(X_0^\sigma)&=& \beta_0(X_0^\sigma)=\beta_0(X_t^\sigma).
\end{array}
\end{equation*}Hence, using proposition 2.4, subtracting
 \begin{equation*} \chi_{\tau}(X_0)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \chi_{Top}(X_0^\sigma) \end{equation*}
\begin{equation*} \chi_{\tau}(X_0)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \chi_{Top}(X_0^\sigma) \end{equation*}from
 \begin{equation*}\chi_{\tau}(X_t)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \chi_{Top}(X_t^\sigma)\end{equation*}
\begin{equation*}\chi_{\tau}(X_t)=\frac{1}{|G|}\sum_{\sigma\in G}\overline{\chi_{\tau}(\sigma)} \chi_{Top}(X_t^\sigma)\end{equation*}one obtains the desired equality
 \begin{align*}\beta_d^\tau(X_t)&= \frac{1}{|G|}\left(\sum_{\sigma: d^\sigma\neq 0}\overline{\chi_{\tau}(\sigma)} (-1)^{d-d^\sigma}\beta_{d^\sigma}(X_t^\sigma)\right.\\ & \quad{}+\left. \sum_{\sigma:d^\sigma = 0}\overline{\chi_{\tau}(\sigma)} (-1)^{d}\big(\beta_{0}(X_t^\sigma)-\beta_0(X_0^\sigma)\big)\right).\end{align*}
\begin{align*}\beta_d^\tau(X_t)&= \frac{1}{|G|}\left(\sum_{\sigma: d^\sigma\neq 0}\overline{\chi_{\tau}(\sigma)} (-1)^{d-d^\sigma}\beta_{d^\sigma}(X_t^\sigma)\right.\\ & \quad{}+\left. \sum_{\sigma:d^\sigma = 0}\overline{\chi_{\tau}(\sigma)} (-1)^{d}\big(\beta_{0}(X_t^\sigma)-\beta_0(X_0^\sigma)\big)\right).\end{align*}Corollary 2.12. In the situation of theorem 2.11, the τ-Milnor numbers are upper semi-continuous:
for all ![]() $x\in X_t$ and
$x\in X_t$ and ![]() $|t|$ small enough.
$|t|$ small enough.
The following example shows that the previous theorem does not hold for non-icis and ![]() $\widetilde{\mu}$. Also, with the same ideas, one also sees that one needs to assume that if
$\widetilde{\mu}$. Also, with the same ideas, one also sees that one needs to assume that if ![]() $X_0^\sigma$ is not an icis, neither is the deformation
$X_0^\sigma$ is not an icis, neither is the deformation ![]() $X_t^\sigma$. This was an observation by the anonymous referee.
$X_t^\sigma$. This was an observation by the anonymous referee.
Example 2.13. The determinantal singularity ![]() $(X,0)\subset(\mathbb{C}^2,0)$ given by the 2-minors of
$(X,0)\subset(\mathbb{C}^2,0)$ given by the 2-minors of
 \begin{equation*}A_0=\begin{bmatrix}
x^2 & y & 0 \\
0 & x & y
\end{bmatrix}\end{equation*}
\begin{equation*}A_0=\begin{bmatrix}
x^2 & y & 0 \\
0 & x & y
\end{bmatrix}\end{equation*} is not an icis, it has dimension zero and its Milnor fibre would be empty (taking a generic preimage of the equations), so ![]() $\widetilde{\mu}(X)=-1$. The deformation Xt given by the 2-minors of
$\widetilde{\mu}(X)=-1$. The deformation Xt given by the 2-minors of
 \begin{equation*}A_t=\begin{bmatrix}
x^2-t^2 & y & 0 \\
0 & x-t & y
\end{bmatrix}\end{equation*}
\begin{equation*}A_t=\begin{bmatrix}
x^2-t^2 & y & 0 \\
0 & x-t & y
\end{bmatrix}\end{equation*} consist of the points ![]() $p=(t,0)$ and
$p=(t,0)$ and ![]() $q=(-t,0)$. It is easy to check that
$q=(-t,0)$. It is easy to check that ![]() $(X_t,q)$ is an icis but
$(X_t,q)$ is an icis but ![]() $(X_t,p)$ is not. So,
$(X_t,p)$ is not. So, ![]() $\widetilde{\mu}(X_t;p)=-1$ and
$\widetilde{\mu}(X_t;p)=-1$ and ![]() $\widetilde{\mu}(X_t;q)=\mu(X_t;q)=1$ (since the icis has multiplicity two). However,
$\widetilde{\mu}(X_t;q)=\mu(X_t;q)=1$ (since the icis has multiplicity two). However,
3. Multiple point spaces and strongly contractible germs
In §4, we use the previous results to study images of stable perturbations of germs ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, where the germs are
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, where the germs are ![]() $\mathscr{A}$-finite and n < p. The link between the previous developments and these objects is the icss, where the multiple point spaces
$\mathscr{A}$-finite and n < p. The link between the previous developments and these objects is the icss, where the multiple point spaces ![]() $D^k(f)$ appear.
$D^k(f)$ appear.
Definition 3.1. The kth-multiple point space of a mapping or a germ f, denoted as ![]() $D^k(f)$, is defined as follows:
$D^k(f)$, is defined as follows:
• Let
 $f\colon X\rightarrow Y$ be a locally stable mapping between complex manifolds. Then,
$f\colon X\rightarrow Y$ be a locally stable mapping between complex manifolds. Then,  $D^k(f)$ is equal to the closure of the set of points
$D^k(f)$ is equal to the closure of the set of points  $\left(x^{(1)},\dots,x^{(k)}\right)$ in Xk such that
$\left(x^{(1)},\dots,x^{(k)}\right)$ in Xk such that  $f\left(x^{(i)}\right)=f\left(x^{(j)}\right)$ but
$f\left(x^{(i)}\right)=f\left(x^{(j)}\right)$ but  $x^{(i)}\neq x^{(j)}$, for all i ≠ j.
$x^{(i)}\neq x^{(j)}$, for all i ≠ j.• When
 $f\colon (\mathbb{C}^n,S)\rightarrow(\mathbb{C}^p,0)$ is a stable germ,
$f\colon (\mathbb{C}^n,S)\rightarrow(\mathbb{C}^p,0)$ is a stable germ,  $D^k(f)$ is defined analogously but in this case it is a set germ in
$D^k(f)$ is defined analogously but in this case it is a set germ in  $\big((\mathbb{C}^n)^k,S^k\big)$.
$\big((\mathbb{C}^n)^k,S^k\big)$.• Let
 $f\colon(\mathbb{C}^n,S)\rightarrow(\mathbb{C}^p,0)$ be finite (which implies the existence of a stable unfolding
$f\colon(\mathbb{C}^n,S)\rightarrow(\mathbb{C}^p,0)$ be finite (which implies the existence of a stable unfolding  $F(x,u)=\big(f_u(x),u\big)$, see [Reference Mond and Nuño-Ballesteros27, proposition 7.2]). Then,
$F(x,u)=\big(f_u(x),u\big)$, see [Reference Mond and Nuño-Ballesteros27, proposition 7.2]). Then,  $D^k(f)$ is the complex space germ in
$D^k(f)$ is the complex space germ in  $\big((\mathbb{C}^n)^k,S^k\big)$ given by
$\big((\mathbb{C}^n)^k,S^k\big)$ given by
 \begin{equation*}
D^k(f)=D^k(F)\cap\left\{u=0\right\}.
\end{equation*}
\begin{equation*}
D^k(f)=D^k(F)\cap\left\{u=0\right\}.
\end{equation*}
Note. For mono-germs of corank one, ![]() $D^k(f)$ can be embedded in
$D^k(f)$ can be embedded in ![]() $\mathbb{C}^{n-1}\times\mathbb{C}^{k}$ (see, for example, [Reference Mond24, end of p. 371] or [Reference Giménez Conejero and Nuño-Ballesteros7, p. 52]).
$\mathbb{C}^{n-1}\times\mathbb{C}^{k}$ (see, for example, [Reference Mond24, end of p. 371] or [Reference Giménez Conejero and Nuño-Ballesteros7, p. 52]).
The theory of icss starts with a theorem given by Goryunov and Mond in [Reference Goryunov and Mond10, proposition 2.3] for rational homology and ![]() $\mathscr{A}$-finite map germs. Goryunov extended the results on icss with [Reference Goryunov11, corollary 1.2.2] for finite maps and integer homology. Years later, Houston proved [Reference Houston18, theorem 5.4] with a bigger class of maps, an action of an additional group, any coefficients and homology of a pair of spaces. Finally, Cisneros Molina and Mond developed a new simple approach in [Reference Cisneros-Molina and Mond1] using double complexes; and Mond and Nuño-Ballesteros gave a self-contained introduction to this topic with the new approach in [Reference Mond and Nuño-Ballesteros27, Section 10].
$\mathscr{A}$-finite map germs. Goryunov extended the results on icss with [Reference Goryunov11, corollary 1.2.2] for finite maps and integer homology. Years later, Houston proved [Reference Houston18, theorem 5.4] with a bigger class of maps, an action of an additional group, any coefficients and homology of a pair of spaces. Finally, Cisneros Molina and Mond developed a new simple approach in [Reference Cisneros-Molina and Mond1] using double complexes; and Mond and Nuño-Ballesteros gave a self-contained introduction to this topic with the new approach in [Reference Mond and Nuño-Ballesteros27, Section 10].
The following theorem is stated for good maps in the sense of [Reference Houston18, definition 5.1], which is a class of maps that contains surjective finite analytic maps between compact subanalytic spaces and also finite and proper simplicial maps between locally-finite simplicial complexes (see [Reference Houston18, propositions 5.2 and 5.3]). This class includes the maps studied in this work.
Theorem 3.2. (see [Reference Houston18, theorem 5.4])
Let ![]() $f:X\to Y$ be a continuous map and
$f:X\to Y$ be a continuous map and ![]() $\tilde{X}$ a subspace of X. Assume that
$\tilde{X}$ a subspace of X. Assume that ![]() $f:X\to Y$ and
$f:X\to Y$ and ![]() $\left.f\right|:\tilde{X}\to Y$ are good maps and that
$\left.f\right|:\tilde{X}\to Y$ are good maps and that ![]() $D^k(\left.f\right|)$ is a subcomplex of
$D^k(\left.f\right|)$ is a subcomplex of ![]() $D^k(f)$ for all
$D^k(f)$ for all ![]() $k\geq 1$. Then, there exists a spectral sequence
$k\geq 1$. Then, there exists a spectral sequence
 \begin{equation*} E^1_{p,q}(f,\left.f\right|)=AH_q\big(D^{p+1}(f),D^{p+1}(\left.f\right|);W\big)\Longrightarrow H_{p+q}\big(f(X),f|(\tilde{X});W\big), \end{equation*}
\begin{equation*} E^1_{p,q}(f,\left.f\right|)=AH_q\big(D^{p+1}(f),D^{p+1}(\left.f\right|);W\big)\Longrightarrow H_{p+q}\big(f(X),f|(\tilde{X});W\big), \end{equation*} where W is a coefficient group and the differential d1 is induced by the projections ![]() $\pi:D^k(f)\to D^{k-1}(f)$ for any k.
$\pi:D^k(f)\to D^{k-1}(f)$ for any k.
Note. In practice, one can apply this result to compute the homology of the image of a stable perturbation, ![]() $\operatorname{im} f_s$, in two similar ways: with the mapping fs or considering the pair
$\operatorname{im} f_s$, in two similar ways: with the mapping fs or considering the pair ![]() $\big( \operatorname{im} F, \operatorname{im} f_s\big)$, where F is a versal unfolding and the mapping
$\big( \operatorname{im} F, \operatorname{im} f_s\big)$, where F is a versal unfolding and the mapping ![]() $\left.f\right|$ in the theorem is
$\left.f\right|$ in the theorem is ![]() $F(\bullet,s)=f_s$.
$F(\bullet,s)=f_s$.
In this theorem, AH denotes the alternating homology, i.e., the homology of the alternating part of the chain complex: chains so that σ acts by ![]() $\operatorname{sgn}(\sigma)$. However, when Hq does not have torsion, we can compute the homology and, only then, consider the alternating part (its isotypical component), which is isomorphic to AHq by [Reference Mond and Nuño-Ballesteros27, proposition 10.1] (cf. [Reference Goryunov11, theorem 2.1.2]). This alternating part of the homology is usually denoted as H Alt. A modern and detailed account of these aspects, multiple point spaces and of the icss can be found in the author’s thesis [Reference Giménez Conejero6, Chapter 2].
$\operatorname{sgn}(\sigma)$. However, when Hq does not have torsion, we can compute the homology and, only then, consider the alternating part (its isotypical component), which is isomorphic to AHq by [Reference Mond and Nuño-Ballesteros27, proposition 10.1] (cf. [Reference Goryunov11, theorem 2.1.2]). This alternating part of the homology is usually denoted as H Alt. A modern and detailed account of these aspects, multiple point spaces and of the icss can be found in the author’s thesis [Reference Giménez Conejero6, Chapter 2].
Obtaining AH, or H Alt, is very difficult in general because one needs to compute the homology and then the action of the group. Hence, it is desirable to work only with the usual homology of the multiple point spaces, since it is easier to compute and the spaces have good properties in some cases (such as being Milnor fibres of icis, see theorem 3.3). However, the homology of the multiple point spaces is not enough to determine the rank of the alternating part, as example 2.6 illustrates. This is discussed in §2.
The multiple point spaces have a very good behaviour in corank one, as the Marar–Mond criterion shows. The first version of this criterion was given for mono-germs by Marar and Mond in [Reference Marar and Mond23, theorem 2.14], for multi-germs it was given by Houston in [Reference Houston19, theorem 2.4 and corollary 2.6], and for germs of maps with an icis in the source by the author and Nuño-Ballesteros in [Reference Giménez Conejero and Nuño-Ballesteros8, lemma 3.2] (see also [Reference Giménez Conejero6, lemma 4.2.3]).
Theorem 3.3. For a finite germ ![]() $f:(\mathbb{C}^n,S)\rightarrow (\mathbb{C}^p,0)$ of corank one with n < p:
$f:(\mathbb{C}^n,S)\rightarrow (\mathbb{C}^p,0)$ of corank one with n < p:
(i) f is stable if, and only if,
 $D^k(f)$ is smooth of dimension
$D^k(f)$ is smooth of dimension  $p-k(p-n)$, or empty, for any
$p-k(p-n)$, or empty, for any  $k\geq1$.
$k\geq1$.(ii)
 $\mathscr{A}_e\text{-codim}(f)$ is finite if, and only if, for each k with
$\mathscr{A}_e\text{-codim}(f)$ is finite if, and only if, for each k with  $p-k(p-n)\geq 0$,
$p-k(p-n)\geq 0$,  $D^k(f)$ is empty or an icis of dimension
$D^k(f)$ is empty or an icis of dimension  $p-k(p-n)$ and if, furthermore, for those k such that
$p-k(p-n)$ and if, furthermore, for those k such that  $p-k(p-n) \lt 0$,
$p-k(p-n) \lt 0$,  $D^k(f)$ is a subset of Sk, possibly empty.
$D^k(f)$ is a subset of Sk, possibly empty.
As theorem 3.2 shows, the multiple point spaces contain all the information about the image of a mapping by means of the alternating homology. In the case of map germs, this information is summed up in the following objects.
Definition 3.4. (cf. [Reference Houston19, definition 3.9])
Let ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be ![]() $\mathscr{A}$-finite of corank one and let
$\mathscr{A}$-finite of corank one and let ![]() $F(x,s)=\big(f_s(x),s\big)$ be a stabilization of f. We set the following notation:
$F(x,s)=\big(f_s(x),s\big)$ be a stabilization of f. We set the following notation:
•
 $s(f)=|S|$,c
$s(f)=|S|$,c•
 $d(f)=\sup\big\{k:\ D^k(f_s)\neq\varnothing\big\}$, where fs is a stable perturbation of f.
$d(f)=\sup\big\{k:\ D^k(f_s)\neq\varnothing\big\}$, where fs is a stable perturbation of f.
The k-th τ-Milnor number of f, denoted by ![]() $\mu_k^\tau(f)$, is defined as
$\mu_k^\tau(f)$, is defined as
 \begin{equation*}
\mu_k^\tau(f):=
\begin{cases}
\mu^\tau\big(D^k(f)\big),& \textrm{if}\, k\leq d(f) \\
\left({s(f)-1} \atop {d(f)}\right),& \textrm{if}\, k=d(f)+1 \,\textrm{and}\, s(f) \gt d(f),\\
0,&\ \textrm{otherwise,}
\end{cases}
\end{equation*}
\begin{equation*}
\mu_k^\tau(f):=
\begin{cases}
\mu^\tau\big(D^k(f)\big),& \textrm{if}\, k\leq d(f) \\
\left({s(f)-1} \atop {d(f)}\right),& \textrm{if}\, k=d(f)+1 \,\textrm{and}\, s(f) \gt d(f),\\
0,&\ \textrm{otherwise,}
\end{cases}
\end{equation*}following definition 2.8.
Recall that the image of a stable perturbation fs of an ![]() $\mathscr{A}$-finite germ
$\mathscr{A}$-finite germ ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^{p},0)$ has the homotopy type of a wedge of spheres. This was proved by Mond for
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^{p},0)$ has the homotopy type of a wedge of spheres. This was proved by Mond for ![]() $p=n+1$ in [Reference Mond25, theorem 1.4] and by Houston for any p > n in [Reference Houston16, theorem 4.24]. For
$p=n+1$ in [Reference Mond25, theorem 1.4] and by Houston for any p > n in [Reference Houston16, theorem 4.24]. For ![]() $p=n+1$, all the spheres are of dimension n and whose number is the image Milnor number
$p=n+1$, all the spheres are of dimension n and whose number is the image Milnor number ![]() $\mu_I(f)$ [Reference Mond and Nuño-Ballesteros27, Section 8.3]. This, and the following proposition, is what motivated the previous definition:
$\mu_I(f)$ [Reference Mond and Nuño-Ballesteros27, Section 8.3]. This, and the following proposition, is what motivated the previous definition:
Proposition 3.5. (see [Reference Houston19, definition 3.11])
Let ![]() $f\colon(\mathbb{C}^n,S)\to(\mathbb{C}^{n+1},0)$ be
$f\colon(\mathbb{C}^n,S)\to(\mathbb{C}^{n+1},0)$ be ![]() $\mathscr{A}$-finite of corank one. Then,
$\mathscr{A}$-finite of corank one. Then,
 \begin{equation*}\mu_I(f)=\sum_k\mu_k^{\text{Alt}}(f).\end{equation*}
\begin{equation*}\mu_I(f)=\sum_k\mu_k^{\text{Alt}}(f).\end{equation*}There is a simple generalization of this result for p > n, in general, that is already known (see [Reference Houston19, remark 3.12]). This is studied further in §5.
Remark 3.6. The origin of definition 3.4 is found in [Reference Houston19, definition 3.9], in more complicated terms and only for the case ![]() $\tau={\text{Alt}}$. The first simplification was already made for
$\tau={\text{Alt}}$. The first simplification was already made for  $\mu_{d(f)+1}^{\text{Alt}}$ in [Reference Giménez Conejero and Nuño-Ballesteros7, definition 3.2] (or [Reference Giménez Conejero6, definition 3.1.14]), after observing a property of binomial numbers. For the remaining
$\mu_{d(f)+1}^{\text{Alt}}$ in [Reference Giménez Conejero and Nuño-Ballesteros7, definition 3.2] (or [Reference Giménez Conejero6, definition 3.1.14]), after observing a property of binomial numbers. For the remaining ![]() $\mu_k^\tau$, it is easy to compute the equivalence between both definitions, using
$\mu_k^\tau$, it is easy to compute the equivalence between both definitions, using
• the long exact sequence of the pair
 $\big(D^k(F), D^k(f_s)\big)$ in
$\big(D^k(F), D^k(f_s)\big)$ in  $H^\tau_*$;
$H^\tau_*$;• the fact that
 $H_0\big(D^k(F),D^k(f_s)\big)$ is also trivial, because there is a point of
$H_0\big(D^k(F),D^k(f_s)\big)$ is also trivial, because there is a point of  $D^k(f_s)$ in every connected component of
$D^k(f_s)$ in every connected component of  $D^k(F)$; and
$D^k(F)$; and• the obvious (equivariant) retraction of
 $D^k(F)$ to
$D^k(F)$ to  $D^k(f)$ for the zero-dimensional case
$D^k(f)$ for the zero-dimensional case  $d_k=0$ (equivalently,
$d_k=0$ (equivalently,  $k=\frac{p}{p-n}$).
$k=\frac{p}{p-n}$).
We omit these details since they are a straightforward computation.
Remark 3.7. It is also very important to notice that the inequality ![]() $s(f) \gt d(f)$ can only happen when d(f) reaches the maximum value possible for that pair of dimensions. This was proven in [Reference Giménez Conejero and Nuño-Ballesteros7, lemma 3.3]. Observe that this maximum is the number
$s(f) \gt d(f)$ can only happen when d(f) reaches the maximum value possible for that pair of dimensions. This was proven in [Reference Giménez Conejero and Nuño-Ballesteros7, lemma 3.3]. Observe that this maximum is the number  $\kappa:= \left\lfloor \frac{p}{p-n}\right\rfloor\in\mathbb{Z}^+$, by theorem 3.3. We shall denote this number always with κ.
$\kappa:= \left\lfloor \frac{p}{p-n}\right\rfloor\in\mathbb{Z}^+$, by theorem 3.3. We shall denote this number always with κ.
Although the Marar–Mond criterion allows us to give a simple way of computing image Milnor numbers ![]() $\mu_I(f)$, it has an unavoidable downside: It could happen that a germ f is unstable but all the spaces
$\mu_I(f)$, it has an unavoidable downside: It could happen that a germ f is unstable but all the spaces ![]() $D^k(f)$ are smooth when
$D^k(f)$ are smooth when ![]() $p-k(p-n)\geq 0$, forcing to have some
$p-k(p-n)\geq 0$, forcing to have some ![]() $D^k(f)\neq\varnothing$ with
$D^k(f)\neq\varnothing$ with ![]() $p-k(p-n) \lt 0$. This is an absolutely bad property to have because, for example, any stable perturbation has contractible image in the mono-germ case. This can be seen from the icss of theorem 3.2 for
$p-k(p-n) \lt 0$. This is an absolutely bad property to have because, for example, any stable perturbation has contractible image in the mono-germ case. This can be seen from the icss of theorem 3.2 for ![]() $\operatorname{im} f_s$ (see also lemma 5.2). By contrast, for
$\operatorname{im} f_s$ (see also lemma 5.2). By contrast, for ![]() $p=n+1$, it is proven that the image of any stable deformation
$p=n+1$, it is proven that the image of any stable deformation ![]() $\operatorname{im}(f_s)$ of an unstable germ f has non-trivial homology, so it cannot be contractible. This is known as the weak form of the Mond conjecture (see [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 3.9] and [Reference Giménez Conejero and Nuño-Ballesteros9, theorem 2.15]).
$\operatorname{im}(f_s)$ of an unstable germ f has non-trivial homology, so it cannot be contractible. This is known as the weak form of the Mond conjecture (see [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 3.9] and [Reference Giménez Conejero and Nuño-Ballesteros9, theorem 2.15]).
Definition 3.8. We will say that a germ ![]() $f:(\mathbb{C}^n,S)\rightarrow (\mathbb{C}^p,0)$, with n < p, is strongly contractible if it is unstable,
$f:(\mathbb{C}^n,S)\rightarrow (\mathbb{C}^p,0)$, with n < p, is strongly contractible if it is unstable, ![]() $d(f)\geq s(f)$ and all the spaces
$d(f)\geq s(f)$ and all the spaces ![]() $D^k(f)$ are smooth (or, more generally, rigid) of dimension
$D^k(f)$ are smooth (or, more generally, rigid) of dimension ![]() $p-k(p-n)$ when
$p-k(p-n)$ when ![]() $p-k(p-n)\geq 0$ (see figure 2, example 3.11, and remark 3.12).
$p-k(p-n)\geq 0$ (see figure 2, example 3.11, and remark 3.12).
Remark 3.9. The key point in the previous definition is that the mentioned multiple point spaces ![]() $D^k(f)$ must have trivial homology (and, therefore, also alternating homology) after the perturbation corresponding to the stable perturbation fs of f. This is the reason we refer to smoothness or rigidity of such spaces, but it would be enough to say that the spaces
$D^k(f)$ must have trivial homology (and, therefore, also alternating homology) after the perturbation corresponding to the stable perturbation fs of f. This is the reason we refer to smoothness or rigidity of such spaces, but it would be enough to say that the spaces ![]() $D^k(f_s)$ have trivial alternating homology (cf. theorem 4.8).
$D^k(f_s)$ have trivial alternating homology (cf. theorem 4.8).

Figure 2. Representation of a strongly contractible instability given by f (left) with its locally stable perturbation fs (right).
Observe that germs of corank one which are strongly contractible are always ![]() $\mathscr{A}$-finite by Item (ii) of the Marar–Mond criterion theorem 3.3.
$\mathscr{A}$-finite by Item (ii) of the Marar–Mond criterion theorem 3.3.
Notation 3.10.
For map germs ![]() $f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$ of corank one, the equations of the multiple point spaces
$f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$ of corank one, the equations of the multiple point spaces ![]() $D^k(f)$ can be given by the divided differences
$D^k(f)$ can be given by the divided differences  $dd^j_i$ for
$dd^j_i$ for ![]() $j\leq k$ and
$j\leq k$ and ![]() $i=1,\dots,p-n+1$ (see [Reference Mond24, Section 3] and [Reference Mond and Nuño-Ballesteros27, Section 9.5]). If
$i=1,\dots,p-n+1$ (see [Reference Mond24, Section 3] and [Reference Mond and Nuño-Ballesteros27, Section 9.5]). If
the divided differences are ![]() $dd^1_i(\underline{x},y_1):= f_i(\underline{x},y_1)$ for
$dd^1_i(\underline{x},y_1):= f_i(\underline{x},y_1)$ for ![]() $i=1,\dots,p-n+1$, and
$i=1,\dots,p-n+1$, and
 \begin{equation*}
dd^k_i(\underline{x},y_1,\dots,y_k):= \frac{dd^{k-1}_i(\underline{x},y_1,\dots,y_{k-2},y_k)-dd^{k-1}_i(\underline{x},y_1,\dots,y_{k-2},y_{k-1})}{y_{k}-y_{k-1}},
\end{equation*}
\begin{equation*}
dd^k_i(\underline{x},y_1,\dots,y_k):= \frac{dd^{k-1}_i(\underline{x},y_1,\dots,y_{k-2},y_k)-dd^{k-1}_i(\underline{x},y_1,\dots,y_{k-2},y_{k-1})}{y_{k}-y_{k-1}},
\end{equation*} for ![]() $i=1,\dots,p-n+1$ and
$i=1,\dots,p-n+1$ and ![]() $j\geq 2$.
$j\geq 2$.
Example 3.11. (cf. example 3.17)
Consider the map germ ![]() $f:(\mathbb{C}^5,0)\to(\mathbb{C}^8,0)$ given by
$f:(\mathbb{C}^5,0)\to(\mathbb{C}^8,0)$ given by
 \begin{equation*} f(x_1,x_2,x_3,x_4,y)=\big(x_1,x_2,x_3,x_4,\ y^3+x_1y, \ y^4+x_2y,\ y^5+x_3y,\ x_4y+x_1y^2\big).\end{equation*}
\begin{equation*} f(x_1,x_2,x_3,x_4,y)=\big(x_1,x_2,x_3,x_4,\ y^3+x_1y, \ y^4+x_2y,\ y^5+x_3y,\ x_4y+x_1y^2\big).\end{equation*} In these dimensions, the unique k such that ![]() $p-k(p-n)\geq0$ (the expected dimension of
$p-k(p-n)\geq0$ (the expected dimension of ![]() $D^k(f)$) is k = 2. On the one hand, the equations of
$D^k(f)$) is k = 2. On the one hand, the equations of ![]() $D^2(f)\subset\mathbb{C}^{5+1}$ are given by the divided differences (see notation 3.10):
$D^2(f)\subset\mathbb{C}^{5+1}$ are given by the divided differences (see notation 3.10):
 \begin{equation}
\begin{array}{ll}
dd^2_1(\underline{x},y_1,y_2)=& x_1+y_1^2+y_1y_2+y_2^2\\
dd^2_2(\underline{x},y_1,y_2)=& x_2+y_1^3+y_1^2y_2+y_1y_2^2+y_2^3\\
dd^2_3(\underline{x},y_1,y_2)=& x_3+y_1^4+y_1^3y_2+y_1^2y_2^2+y_1y_2^3+y_2^4\\
dd^2_4(\underline{x},y_1,y_2)=& x_4+x_1(y_1+y_2).
\end{array}
\end{equation}
\begin{equation}
\begin{array}{ll}
dd^2_1(\underline{x},y_1,y_2)=& x_1+y_1^2+y_1y_2+y_2^2\\
dd^2_2(\underline{x},y_1,y_2)=& x_2+y_1^3+y_1^2y_2+y_1y_2^2+y_2^3\\
dd^2_3(\underline{x},y_1,y_2)=& x_3+y_1^4+y_1^3y_2+y_1^2y_2^2+y_1y_2^3+y_2^4\\
dd^2_4(\underline{x},y_1,y_2)=& x_4+x_1(y_1+y_2).
\end{array}
\end{equation} On the other hand, the equations of ![]() $D^3(f)\subset\mathbb{C}^{5+2}$ are those of
$D^3(f)\subset\mathbb{C}^{5+2}$ are those of ![]() $D^2(f)$ and the new divided differences:
$D^2(f)$ and the new divided differences:
 \begin{equation}
\begin{array}{ll}
dd^3_1(\underline{x},y_1,y_2,y_3)=&y_1+y_2+y_3\\
dd^3_2(\underline{x},y_1,y_2,y_3)=& \sum_{i,j=1,2,3} y_iy_j\\
dd^3_3\underline{x},y_1,y_2,y_3)=& \sum_{i,j,s=1,2,3} y_iy_jy_s\\
dd^3_4(\underline{x},y_1,y_2,y_3)=& x_1.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{ll}
dd^3_1(\underline{x},y_1,y_2,y_3)=&y_1+y_2+y_3\\
dd^3_2(\underline{x},y_1,y_2,y_3)=& \sum_{i,j=1,2,3} y_iy_j\\
dd^3_3\underline{x},y_1,y_2,y_3)=& \sum_{i,j,s=1,2,3} y_iy_jy_s\\
dd^3_4(\underline{x},y_1,y_2,y_3)=& x_1.
\end{array}
\end{equation} A simple observation of Eq. (9) shows that ![]() $D^2(f)$ is smooth, so f is finitely determined by the Marar–Mond criterion, theorem 3.3. Similarly, it is easy to see from Eqs. (9) and (10) that
$D^2(f)$ is smooth, so f is finitely determined by the Marar–Mond criterion, theorem 3.3. Similarly, it is easy to see from Eqs. (9) and (10) that ![]() $(0,0,0)\in D^3(f)\neq\varnothing$, so f is unstable again by the same criterion. This shows that f is strongly contractible.
$(0,0,0)\in D^3(f)\neq\varnothing$, so f is unstable again by the same criterion. This shows that f is strongly contractible.
Remark 3.12. This kind of maps have ![]() $\mu_k^{\text{Alt}}(f)=0$, for every k, because the multiple point spaces
$\mu_k^{\text{Alt}}(f)=0$, for every k, because the multiple point spaces ![]() $D^k(f)$ are smooth, so
$D^k(f)$ are smooth, so ![]() $D^k(f_s)$ do not have alternating homology. Therefore, the image of the stable perturbation is contractible since it has the homotopy type of a wedge of spheres by [Reference Houston16, theorem 4.24] and by lemma 5.2 (which is a simple application of the icss). Furthermore, theorem 4.8 implies that this is, in fact, a characterization of strongly contractible germs in corank one: they are precisely those that have stable perturbation with contractible image (cf. figure 2). This is the reason that these maps provide counterexamples to many statements that involve the topology of the stable perturbation, and the reason we have to restrict many results to germs that are not strongly contractible. In fact, we will use map germs similar to the one given in example 3.11 to give counterexamples to several statements.
$D^k(f_s)$ do not have alternating homology. Therefore, the image of the stable perturbation is contractible since it has the homotopy type of a wedge of spheres by [Reference Houston16, theorem 4.24] and by lemma 5.2 (which is a simple application of the icss). Furthermore, theorem 4.8 implies that this is, in fact, a characterization of strongly contractible germs in corank one: they are precisely those that have stable perturbation with contractible image (cf. figure 2). This is the reason that these maps provide counterexamples to many statements that involve the topology of the stable perturbation, and the reason we have to restrict many results to germs that are not strongly contractible. In fact, we will use map germs similar to the one given in example 3.11 to give counterexamples to several statements.
We can find some dimensions where there are no corank one germs that are strongly contractible. Indeed, as remarked above, when ![]() $p=n+1$, there are no strongly contractible germs (in any corank). To give a better insight of this topic, we introduce now a refinement of the multiple point spaces and the Marar–Mond criterion, which will be important to avoid working with the alternating homology later.
$p=n+1$, there are no strongly contractible germs (in any corank). To give a better insight of this topic, we introduce now a refinement of the multiple point spaces and the Marar–Mond criterion, which will be important to avoid working with the alternating homology later.
Observe that, in definition 3.1, there is a straightforward action of ![]() $\Sigma_k$ in
$\Sigma_k$ in ![]() $D^k(\bullet)$. Indeed, one can give
$D^k(\bullet)$. Indeed, one can give ![]() $\Sigma_k$-invariant equations of
$\Sigma_k$-invariant equations of ![]() $D^k(\bullet)$ (see [Reference Mond and Nuño-Ballesteros27, Section 9.5] or [Reference Marar and Mond23, Section 2]) instead of the divided differences used in example 3.11. This leads to the refinements we were mentioning before for fixed points of these spaces by a permutation
$D^k(\bullet)$ (see [Reference Mond and Nuño-Ballesteros27, Section 9.5] or [Reference Marar and Mond23, Section 2]) instead of the divided differences used in example 3.11. This leads to the refinements we were mentioning before for fixed points of these spaces by a permutation ![]() $\sigma\in\Sigma_k$. The following definition and theorem have a version for other settings: [Reference Marar and Mond23, corollary 2.15] for mono-germs, [Reference Houston19, corollary 2.8] for multi-germs, and [Reference Giménez Conejero and Nuño-Ballesteros8, lemma 3.5] or [Reference Giménez Conejero6, lemma 4.2.10] for germs on icis.
$\sigma\in\Sigma_k$. The following definition and theorem have a version for other settings: [Reference Marar and Mond23, corollary 2.15] for mono-germs, [Reference Houston19, corollary 2.8] for multi-germs, and [Reference Giménez Conejero and Nuño-Ballesteros8, lemma 3.5] or [Reference Giménez Conejero6, lemma 4.2.10] for germs on icis.
Definition 3.13. Let ![]() $\Sigma_k$ be the group of permutations of k elements together with its natural action on
$\Sigma_k$ be the group of permutations of k elements together with its natural action on ![]() $D^k(f)$. For any element
$D^k(f)$. For any element ![]() $\sigma\in\Sigma_k$, we define
$\sigma\in\Sigma_k$, we define ![]() $D^k(f)^\sigma$ as (the isomorphism type of) the subspace of
$D^k(f)^\sigma$ as (the isomorphism type of) the subspace of ![]() $D^k(f)$ given by the fixed points of σ.
$D^k(f)$ given by the fixed points of σ.
Remark 3.14. Also, recall that all the elements in ![]() $\Sigma_k$ can be decomposed into disjoint cycles in a unique way, called the cycle shape. Conversely, if we take a partition of k,
$\Sigma_k$ can be decomposed into disjoint cycles in a unique way, called the cycle shape. Conversely, if we take a partition of k, ![]() $\gamma(k)=(r_1,\dots, r_m)$, and
$\gamma(k)=(r_1,\dots, r_m)$, and ![]() $\alpha_i=\texttt{\#}\left\{j:r_j=i\right\}$, one can find an element
$\alpha_i=\texttt{\#}\left\{j:r_j=i\right\}$, one can find an element ![]() $\sigma\in\Sigma_k$ such that it can be decomposed into αi pair-wise disjoint cycles of length i (e.g., the permutation
$\sigma\in\Sigma_k$ such that it can be decomposed into αi pair-wise disjoint cycles of length i (e.g., the permutation ![]() $\sigma=(1\ 2\ 6\ 3)(4\ 5)(8\ 9)(7)(10)$ has cycle shape
$\sigma=(1\ 2\ 6\ 3)(4\ 5)(8\ 9)(7)(10)$ has cycle shape ![]() $(4,2,2,1,1)$, where
$(4,2,2,1,1)$, where ![]() $\alpha_4=1$,
$\alpha_4=1$, ![]() $\alpha_3=0$,
$\alpha_3=0$, ![]() $\alpha_2=2$ and
$\alpha_2=2$ and ![]() $\alpha_1=2$).
$\alpha_1=2$).
Lemma 3.15. With the hypotheses of theorem 3.3 and ![]() $\sigma\in\Sigma_k$, we have the following.
$\sigma\in\Sigma_k$, we have the following.
(i) If f is stable,
 $D^k(f)^\sigma$ c
$D^k(f)^\sigma$ c  $p-k(p-n)-k+\sum_i\alpha_i$, or empty.
$p-k(p-n)-k+\sum_i\alpha_i$, or empty.(ii)
 $\mathscr{A}_e-codim(f)$ is finite if, and only if:
$\mathscr{A}_e-codim(f)$ is finite if, and only if:(a) for each k with
 $p-k(p-n)-k+\sum_i\alpha_i\geq0$,
$p-k(p-n)-k+\sum_i\alpha_i\geq0$,  $D^k(f)^\sigma$ is empty or an icis of dimension
$D^k(f)^\sigma$ is empty or an icis of dimension  $p-k(p-n)-k+\sum_i\alpha_i$,
$p-k(p-n)-k+\sum_i\alpha_i$,(b) for each k with
 $p-k(p-n)-k+\sum_i\alpha_i \lt 0$,
$p-k(p-n)-k+\sum_i\alpha_i \lt 0$,  $D^k(f)^\sigma$ is a subset of Sk, possibly empty.
$D^k(f)^\sigma$ is a subset of Sk, possibly empty.
The following definition follows naturally from the previous result.
Definition 3.16. We will say that the expected dimension of ![]() $D^k(f)$ (and
$D^k(f)$ (and ![]() $D^k(f_t)$) is
$D^k(f_t)$) is ![]() $d_k:= p-k(p-n)$, and the expected dimension of
$d_k:= p-k(p-n)$, and the expected dimension of ![]() $D^k(f)^\sigma$ (and
$D^k(f)^\sigma$ (and ![]() $D^k(f_t)^\sigma$) is
$D^k(f_t)^\sigma$) is ![]() $d_k^\sigma:= p-k(p-n)-k+\sum_i\alpha_i$. If we want to emphasize the map, we shall write
$d_k^\sigma:= p-k(p-n)-k+\sum_i\alpha_i$. If we want to emphasize the map, we shall write ![]() $d_k(f)$ instead of dk.
$d_k(f)$ instead of dk.
Strongly contractible germs are not very common in corank one when one looks at low dimensions. We restrict to the case of mono-germs for the sake of simplicity, but some of the following results could be generalized to multi-germs using similar ideas. One can see an example of a strongly contractible bi-germ from ![]() $\mathbb{C}^3$ to
$\mathbb{C}^3$ to ![]() $\mathbb{C}^5$ in example 4.2.
$\mathbb{C}^5$ in example 4.2.
Let us complete example 3.11 with another example that is stable to show different behaviours.
Example 3.17. Consider the map germ ![]() $f:(\mathbb{C}^3,0)\to(\mathbb{C}^5,0)$ given by
$f:(\mathbb{C}^3,0)\to(\mathbb{C}^5,0)$ given by
 \begin{equation*} f(x_1,x_2,y)=\big(x_1,x_2,\ y^3 + x_1y, \ y^4 + x_2y,\ x_2y + y^2\big).\end{equation*}
\begin{equation*} f(x_1,x_2,y)=\big(x_1,x_2,\ y^3 + x_1y, \ y^4 + x_2y,\ x_2y + y^2\big).\end{equation*} In this case κ = 2, ![]() $d_2=1$ but
$d_2=1$ but ![]() $d_2-2+1=0$. The equations of
$d_2-2+1=0$. The equations of ![]() $D^2(f)\subset\mathbb{C}^{2+2}$ are
$D^2(f)\subset\mathbb{C}^{2+2}$ are
 \begin{equation}
\begin{array}{ll}
dd^2_1(\underline{x},y_1,y_2)&=x_1 + y_1^2 + y_1 y_2 + y_2^2\\
dd^2_2(\underline{x},y_1,y_2)&=x_2 + y_1^3 + y_1^2 y_2 + y_1 y_2^2 + y_2^3\\
dd^2_3(\underline{x},y_1,y_2)&=x_2 + y_1 + y_2.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{ll}
dd^2_1(\underline{x},y_1,y_2)&=x_1 + y_1^2 + y_1 y_2 + y_2^2\\
dd^2_2(\underline{x},y_1,y_2)&=x_2 + y_1^3 + y_1^2 y_2 + y_1 y_2^2 + y_2^3\\
dd^2_3(\underline{x},y_1,y_2)&=x_2 + y_1 + y_2.
\end{array}
\end{equation} Furthermore, one of the equations of ![]() $D^3(f)$ is
$D^3(f)$ is
 \begin{equation*} dd^3_3(\underline{x},y_1,y_2,y_3)=\frac{dd^2_3(\underline{x},y_1,y_3)-dd^2_3(\underline{x},y_1,y_2)}{y_3-y_2}=1. \end{equation*}
\begin{equation*} dd^3_3(\underline{x},y_1,y_2,y_3)=\frac{dd^2_3(\underline{x},y_1,y_3)-dd^2_3(\underline{x},y_1,y_2)}{y_3-y_2}=1. \end{equation*} Hence, ![]() $D^3(f)=\varnothing$ and
$D^3(f)=\varnothing$ and ![]() $D^2(f)$ is smooth, so f is stable by Marar–Mond criterion theorem 3.3.
$D^2(f)$ is smooth, so f is stable by Marar–Mond criterion theorem 3.3.
This example shows that the same ideas of example 3.11 do not work for any pair of dimensions. Another wrong idea would be considering a strongly contractible germ and taking an unfolding, expecting that it is going to be strongly contractible as well. For example, taking ![]() $f:(\mathbb{C}^5,0)\to(\mathbb{C}^8,0)$ from example 3.11, every unfolding with one parameter,
$f:(\mathbb{C}^5,0)\to(\mathbb{C}^8,0)$ from example 3.11, every unfolding with one parameter, ![]() $F:(\mathbb{C}^{5+1},0)\to(\mathbb{C}^{8+1},0)$, is not strongly contractible because
$F:(\mathbb{C}^{5+1},0)\to(\mathbb{C}^{8+1},0)$, is not strongly contractible because ![]() $D^2(F)$ keeps being smooth but
$D^2(F)$ keeps being smooth but ![]() $D^3(F)$ is always a singular icis of dimension
$D^3(F)$ is always a singular icis of dimension ![]() $d_3(F)=0$.
$d_3(F)=0$.
We present now the characterization of dimensions (n, p) with strongly contractible germs.
Theorem 3.18. Consider unstable germs ![]() $f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$ of corank one, n < p. Then, there are strongly contractible germs in these dimensions if, and only if,
$f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$ of corank one, n < p. Then, there are strongly contractible germs in these dimensions if, and only if,
 \begin{equation*} d_\kappa-\kappa=p- \left\lfloor \frac{p}{p-n}\right\rfloor(p-n+1)\geq0.\end{equation*}
\begin{equation*} d_\kappa-\kappa=p- \left\lfloor \frac{p}{p-n}\right\rfloor(p-n+1)\geq0.\end{equation*}Proof. The proof is based on a careful inspection of the equations of ![]() $D^k(f)$. Examples 3.11 and 3.17 serve as a good references to follow the argument.
$D^k(f)$. Examples 3.11 and 3.17 serve as a good references to follow the argument.
A strongly contractible germ necessarily has ![]() $D^k(f)$ smooth for
$D^k(f)$ smooth for  $k\leq\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor$ and
$k\leq\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor$ and ![]() $D^{\kappa+1}(f)\neq\varnothing$. For this to happen, when we look at the equations of the
$D^{\kappa+1}(f)\neq\varnothing$. For this to happen, when we look at the equations of the ![]() $D^k(f)$ with
$D^k(f)$ with ![]() $k\leq\kappa$ given by divided differences (see notation 3.10), we need to find independent linear terms in each equation.
$k\leq\kappa$ given by divided differences (see notation 3.10), we need to find independent linear terms in each equation.
On the one hand, remember that a corank one germ can be written as
 \begin{equation*} f(x_1,\ldots,x_{n-1},y)=\big(x_1,\ldots,x_{n-1},h_{1}(\underline{x},y),\ldots,h_{p-(n-1)}(\underline{x},y)\big).\end{equation*}
\begin{equation*} f(x_1,\ldots,x_{n-1},y)=\big(x_1,\ldots,x_{n-1},h_{1}(\underline{x},y),\ldots,h_{p-(n-1)}(\underline{x},y)\big).\end{equation*} Also, when we study the divided differences that give ![]() $D^2(f)$, we have
$D^2(f)$, we have ![]() $x_1\ldots,x_{n-1}$ as variables and we introduce y 1 and y 2. The equations of
$x_1\ldots,x_{n-1}$ as variables and we introduce y 1 and y 2. The equations of ![]() $D^k(f)$ are those of
$D^k(f)$ are those of ![]() $D^{k-1}(f)$ and new divided differences, and at each step we add a new variable yk. These new divided differences take the form
$D^{k-1}(f)$ and new divided differences, and at each step we add a new variable yk. These new divided differences take the form
 \begin{equation*}\sum_\delta p_\delta(\underline{x})s_k^\delta(y_1,\dots,y_k),\end{equation*}
\begin{equation*}\sum_\delta p_\delta(\underline{x})s_k^\delta(y_1,\dots,y_k),\end{equation*} where p are polynomials (possibly constant) and ![]() $s_k^\delta$ are the
$s_k^\delta$ are the ![]() $\Sigma_k$-invariant polynomials
$\Sigma_k$-invariant polynomials
 \begin{equation*}s_k^\delta(y_1,\dots,y_k):= \sum_{i_1+\dots+i_k=\delta}y_1^{i_1}\cdots y_k^{i_k}.\end{equation*}
\begin{equation*}s_k^\delta(y_1,\dots,y_k):= \sum_{i_1+\dots+i_k=\delta}y_1^{i_1}\cdots y_k^{i_k}.\end{equation*} Indeed, for ![]() $D^2(f)$ it is obvious, the general case follows from an easy inductive argument on the symmetric part
$D^2(f)$ it is obvious, the general case follows from an easy inductive argument on the symmetric part ![]() $s_k^\delta$:
$s_k^\delta$:
 \begin{equation*}\frac{s_k^\delta(y_1,\ldots,y_{k-1},y_{k+1})-s_k^\delta(y_1,\ldots,y_{k-1},y_{k})}{y_{k+1}-y_k}=s_{k+1}^{\delta-1}(y_1,\dots,y_{k+1}).\end{equation*}
\begin{equation*}\frac{s_k^\delta(y_1,\ldots,y_{k-1},y_{k+1})-s_k^\delta(y_1,\ldots,y_{k-1},y_{k})}{y_{k+1}-y_k}=s_{k+1}^{\delta-1}(y_1,\dots,y_{k+1}).\end{equation*} On the other hand, if sk contains a linear term, then it is easy to see that ![]() $s_{k+1}$ is a unit. Hence, once we find a linear term on the variables
$s_{k+1}$ is a unit. Hence, once we find a linear term on the variables ![]() $y_1,\ldots,y_k$ in the equations of
$y_1,\ldots,y_k$ in the equations of ![]() $D^k(f)$,
$D^k(f)$, ![]() $D^{k+1}(f)=\varnothing$. For this reason, once we have found n − 1 linear terms on
$D^{k+1}(f)=\varnothing$. For this reason, once we have found n − 1 linear terms on ![]() $x_1,\ldots,x_{n-1}$ and a linear term on some yi, the next multiple point space is going to be empty. Also, the number of equations necessary to define
$x_1,\ldots,x_{n-1}$ and a linear term on some yi, the next multiple point space is going to be empty. Also, the number of equations necessary to define ![]() $D^k(f)$ is
$D^k(f)$ is ![]() $\big(p-(n-1)\big)(k-1)$.
$\big(p-(n-1)\big)(k-1)$.
Finally, if the number of equations necessary to define ![]() $D^\kappa(f)$,
$D^\kappa(f)$,
 \begin{equation*}\big(p-(n-1)\big)\left(\left\lfloor \frac{p}{p-n}\right\rfloor-1\right),\end{equation*}
\begin{equation*}\big(p-(n-1)\big)\left(\left\lfloor \frac{p}{p-n}\right\rfloor-1\right),\end{equation*} is less or equal to n − 1, we can use the variables ![]() $x_1,\ldots,x_{n-1}$ to find a germ so that
$x_1,\ldots,x_{n-1}$ to find a germ so that ![]() $D^k(f)$ is smooth for
$D^k(f)$ is smooth for ![]() $k\leq\kappa$ and avoids linear terms on yi except, perhaps, at
$k\leq\kappa$ and avoids linear terms on yi except, perhaps, at ![]() $D^{\kappa+1}(f)$; so it would be a strongly contractible map. Indeed, if one wants that the linear term xi appears in a
$D^{\kappa+1}(f)$; so it would be a strongly contractible map. Indeed, if one wants that the linear term xi appears in a ![]() $(k-1)$-iterated divided difference
$(k-1)$-iterated divided difference ![]() $dd_i^k$ (which define
$dd_i^k$ (which define ![]() $D^k(\bullet)$) it is enough to include the term
$D^k(\bullet)$) it is enough to include the term ![]() $y^{k+1}x_i$ in a component of the map germ (see, for instance, example 3.11). On the other hand,
$y^{k+1}x_i$ in a component of the map germ (see, for instance, example 3.11). On the other hand, ![]() $y^{k+1}$ gives a linear term in the (k)-iterated divided difference. This is enough to give strongly contractible maps whenever
$y^{k+1}$ gives a linear term in the (k)-iterated divided difference. This is enough to give strongly contractible maps whenever
 \begin{equation*} \big(p-(n-1)\big)\left(\left\lfloor \frac{p}{p-n}\right\rfloor-1\right)\leq n-1. \end{equation*}
\begin{equation*} \big(p-(n-1)\big)\left(\left\lfloor \frac{p}{p-n}\right\rfloor-1\right)\leq n-1. \end{equation*}This inequality is equivalent to the inequality of the statement.
Furthermore, any strongly contractible germ needs this condition to hold, otherwise ![]() $D^{\kappa+1}(f)=\varnothing$ or some
$D^{\kappa+1}(f)=\varnothing$ or some ![]() $D^k(f)$ is singular for
$D^k(f)$ is singular for ![]() $k\leq\kappa$ (see, for instance, example 3.17). This proves the result.
$k\leq\kappa$ (see, for instance, example 3.17). This proves the result.
Remark 3.19. D. Mond posed the following question, that we answer now, regarding a generalization of the Mond conjecture for dimension (n, p) with ![]() $p \gt n+1$:
$p \gt n+1$:
Q: Can we define a version of the image Milnor number ![]() $ \widetilde{\mu_I}$ for any dimensions (n, p) as a linear combination of Betti numbers that is independent of any map germ so that
$ \widetilde{\mu_I}$ for any dimensions (n, p) as a linear combination of Betti numbers that is independent of any map germ so that
 \begin{equation*} \widetilde{\mu_I}(f):= \sum_{i \gt 0}a_i\beta_i(\operatorname{im} f_s) \geq \mathscr{A}_e-\operatorname{codim}(f) ?\end{equation*}
\begin{equation*} \widetilde{\mu_I}(f):= \sum_{i \gt 0}a_i\beta_i(\operatorname{im} f_s) \geq \mathscr{A}_e-\operatorname{codim}(f) ?\end{equation*}Remark 3.12 and theorem 3.18 answer negatively to this question, i.e., for a strongly contractible germ f and any linear combination:
 \begin{equation*} \widetilde{\mu_I}(f):= \sum_{i \gt 0}a_i\beta_i(\operatorname{im} f_s) =0 \lt \mathscr{A}_e-\operatorname{codim}(f). \end{equation*}
\begin{equation*} \widetilde{\mu_I}(f):= \sum_{i \gt 0}a_i\beta_i(\operatorname{im} f_s) =0 \lt \mathscr{A}_e-\operatorname{codim}(f). \end{equation*} Note. The condition of theorem 3.18 implies that a germ f cannot have a perturbation with strongly contractible instabilities if ![]() $D^k(f)=\varnothing$ when
$D^k(f)=\varnothing$ when ![]() $d_k \lt 0$. See figure 3 for the overall picture of this issue.
$d_k \lt 0$. See figure 3 for the overall picture of this issue.

Figure 3. Plot of the pair of dimensions without strongly contractible germs of corank one, for ![]() $n\leq20$ (left) and for
$n\leq20$ (left) and for ![]() $n\leq250$ (right).
$n\leq250$ (right).
4. Symmetry of Dk
In this section, we use the results of §2 for the multiple point spaces ![]() $D^k(f)$ with the natural action of
$D^k(f)$ with the natural action of ![]() $\Sigma_k$. We are specially interested in the alternating representation
$\Sigma_k$. We are specially interested in the alternating representation ![]() ${\text{Alt}}$, but we can state the conservation of the
${\text{Alt}}$, but we can state the conservation of the ![]() $\mu^\tau_k(f)$ under deformations of f for any irreducible representation τ of
$\mu^\tau_k(f)$ under deformations of f for any irreducible representation τ of ![]() $\Sigma_k$.
$\Sigma_k$.
Theorem 4.1. Let ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be ![]() $\mathscr{A}$-finite of corank one. Then, the numbers
$\mathscr{A}$-finite of corank one. Then, the numbers ![]() $\mu^\tau_k(f)$ are conserved for
$\mu^\tau_k(f)$ are conserved for  $k\leq\frac{p}{p-n}$. More precisely, if ft is any perturbation of f then, for
$k\leq\frac{p}{p-n}$. More precisely, if ft is any perturbation of f then, for ![]() $|t|$ small enough and
$|t|$ small enough and  $k\leq\frac{p}{p-n}$:
$k\leq\frac{p}{p-n}$:
 \begin{equation*}
\begin{array}{ll}
\mu^\tau_k(f)=&\beta^\tau_{d_k}\big(D^k(f_t)\big)+\sum_{y\in \operatorname{im}(f_t)}\mu_k^\tau(f_t;y),\quad \text{if}\ d_k\neq0 \\
\mu^\tau_k(f)=&\beta^\tau_{d_k}\big(D^k(f_t)\big)+\sum_{y\in \operatorname{im}(f_t)}\mu_k^\tau(f_t;y)-\beta^\tau_{d_k}\big(D^k(f)\big), \quad\text{if}\ d_k=0;
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ll}
\mu^\tau_k(f)=&\beta^\tau_{d_k}\big(D^k(f_t)\big)+\sum_{y\in \operatorname{im}(f_t)}\mu_k^\tau(f_t;y),\quad \text{if}\ d_k\neq0 \\
\mu^\tau_k(f)=&\beta^\tau_{d_k}\big(D^k(f_t)\big)+\sum_{y\in \operatorname{im}(f_t)}\mu_k^\tau(f_t;y)-\beta^\tau_{d_k}\big(D^k(f)\big), \quad\text{if}\ d_k=0;
\end{array}
\end{equation*} where ![]() $\mu_k^\tau(f_t;y)$ is the k-th τ-Milnor number of f at y.
$\mu_k^\tau(f_t;y)$ is the k-th τ-Milnor number of f at y.
Proof. The result follows by Marar–Mond criterion (theorem 3.3), the definition of ![]() $\mu^\tau_k$ (definition 3.4) and the conservation principle for the τ-Milnor numbers (theorem 2.11). Indeed, we can use the conservation principle since
$\mu^\tau_k$ (definition 3.4) and the conservation principle for the τ-Milnor numbers (theorem 2.11). Indeed, we can use the conservation principle since ![]() $D^k(f)$ are icis that can be given by
$D^k(f)$ are icis that can be given by ![]() $\Sigma_k$-invariant equations (see [Reference Mond and Nuño-Ballesteros27, Section 9.5] or [Reference Marar and Mond23, Section 2]) instead of the divided differences and the action is simplicially excellent, definition 2.7. It is easy to see that the action is simplicially good, but a general result showing this is [Reference Houston18, definition 2.8 and proposition 3.4] (Houston uses the word cellular instead of simplicially good).
$\Sigma_k$-invariant equations (see [Reference Mond and Nuño-Ballesteros27, Section 9.5] or [Reference Marar and Mond23, Section 2]) instead of the divided differences and the action is simplicially excellent, definition 2.7. It is easy to see that the action is simplicially good, but a general result showing this is [Reference Houston18, definition 2.8 and proposition 3.4] (Houston uses the word cellular instead of simplicially good).
The previous result omits the case  $ \mu_{d(f)+1}^\tau(f)$, which is non-trivial when
$ \mu_{d(f)+1}^\tau(f)$, which is non-trivial when ![]() $s(f) \gt d(f)$ (so
$s(f) \gt d(f)$ (so  $k \gt \frac{p}{p-n}$ by remark 3.7). It is false, in general, that this quantity is conservative in a good sense, i.e., that we have something as
$k \gt \frac{p}{p-n}$ by remark 3.7). It is false, in general, that this quantity is conservative in a good sense, i.e., that we have something as
 \begin{equation*} \mu_{d(f)+1}^\tau(f)= {\ast} +\sum_{y\in \operatorname{im}(f_t)}\mu_{d(f)+1}^\tau(f_t;y),\end{equation*}
\begin{equation*} \mu_{d(f)+1}^\tau(f)= {\ast} +\sum_{y\in \operatorname{im}(f_t)}\mu_{d(f)+1}^\tau(f_t;y),\end{equation*} with the term ![]() ${\ast}$ lower semi-continuous. The following example illustrates this fact:
${\ast}$ lower semi-continuous. The following example illustrates this fact:  $\mu_{d(f)+1}^{\text{Alt}}$ is neither conservative nor upper semi-continuous.
$\mu_{d(f)+1}^{\text{Alt}}$ is neither conservative nor upper semi-continuous.
Example 4.2. Consider the following perturbation of a map germ ![]() $f:(\mathbb{C}^3,0)\to(\mathbb{C}^5,0)$:
$f:(\mathbb{C}^3,0)\to(\mathbb{C}^5,0)$:
It is not difficult to see (with a mathematical software, such as [33]) that ![]() $D^2(f_t)\subseteq\mathbb{C}^{2+2}$ has singularities at the points
$D^2(f_t)\subseteq\mathbb{C}^{2+2}$ has singularities at the points
 \begin{equation*} \left(0,\ t^2+2 \sqrt{1-t^2}-2,\ \pm\sqrt{1-\sqrt{1-t^2}},\ \mp\sqrt{1-\sqrt{1-t^2}}\right)\end{equation*}
\begin{equation*} \left(0,\ t^2+2 \sqrt{1-t^2}-2,\ \pm\sqrt{1-\sqrt{1-t^2}},\ \mp\sqrt{1-\sqrt{1-t^2}}\right)\end{equation*}and
 \begin{equation*}D^3(f_t)=\big\{(0,0;t,0,0),(0,0;0,t,0),(0,0;0,0,t)\big\}.\end{equation*}
\begin{equation*}D^3(f_t)=\big\{(0,0;t,0,0),(0,0;0,t,0),(0,0;0,0,t)\big\}.\end{equation*} By Marar–Mond criterion, f is ![]() $\mathscr{A}$-finite. Also, for t ≠ 0, as
$\mathscr{A}$-finite. Also, for t ≠ 0, as ![]() $f_t(0,0,t)=f_t(0,0,0)=0$, ft has an instability at the origin given by a bi-germ, which is strongly contractible because
$f_t(0,0,t)=f_t(0,0,0)=0$, ft has an instability at the origin given by a bi-germ, which is strongly contractible because ![]() $D^2(f_t)$ is smooth at
$D^2(f_t)$ is smooth at ![]() $(0,0;0,t)$,
$(0,0;0,t)$, ![]() $(0,0;t,0)$, and
$(0,0;t,0)$, and ![]() $(0,0;0,0)$.
$(0,0;0,0)$.
We can construct a multi-germ ![]() $h=\left\{f,g\right\}:\big(\mathbb{C}^3,\{0,0'\}\big)\to(\mathbb{C}^5,0)$ adding an immersion g to the germ f in a way that h is
$h=\left\{f,g\right\}:\big(\mathbb{C}^3,\{0,0'\}\big)\to(\mathbb{C}^5,0)$ adding an immersion g to the germ f in a way that h is ![]() $\mathscr{A}$-finite, taking g generic enough. A perturbation ht can be given by leaving g unchanged and considering the previous perturbation ft of the non-immersive branch. This perturbation has two unexpected traits:
$\mathscr{A}$-finite, taking g generic enough. A perturbation ht can be given by leaving g unchanged and considering the previous perturbation ft of the non-immersive branch. This perturbation has two unexpected traits:
i.e., it has a free Σ3-orbit of points (so ![]() $D^3(h_t)$ has alternating homology); and
$D^3(h_t)$ has alternating homology); and ![]() $d(h_0)= s(h_0)=2$ but
$d(h_0)= s(h_0)=2$ but ![]() $2=d(h_t;0) \lt s(h_t;0)=3$ for t ≠ 0, so
$2=d(h_t;0) \lt s(h_t;0)=3$ for t ≠ 0, so
 \begin{equation*}\mu_{d(h)+1}^{{\text{Alt}}}(h_0)=0 \lt \mu_{d(h)+1}^{{\text{Alt}}}(h_t)=1, \text{for} t\neq0.\end{equation*}
\begin{equation*}\mu_{d(h)+1}^{{\text{Alt}}}(h_0)=0 \lt \mu_{d(h)+1}^{{\text{Alt}}}(h_t)=1, \text{for} t\neq0.\end{equation*} Hence, this is an example of the non-conservation of the ![]() $\mu_{d(f)+1}^\tau$ and, in particular, that this number is not upper semi-continuous. This solves a question posed by Houston in [Reference Houston19, remarks 4.2 and 6.3].
$\mu_{d(f)+1}^\tau$ and, in particular, that this number is not upper semi-continuous. This solves a question posed by Houston in [Reference Houston19, remarks 4.2 and 6.3].
Since we are interested in alternated homology and the kth alternating-Milnor numbers ![]() $\mu^{\text{Alt}}_k(f)$ (see also lemma 5.2), we can use the previous results to compute them. A very trivial case happens when
$\mu^{\text{Alt}}_k(f)$ (see also lemma 5.2), we can use the previous results to compute them. A very trivial case happens when ![]() $\Sigma_k$ acts freely on an orbit of a connected component of
$\Sigma_k$ acts freely on an orbit of a connected component of ![]() $D^k(f)$, say
$D^k(f)$, say ![]() $D^k(f)_{free}$ (see example 4.3). In that case,
$D^k(f)_{free}$ (see example 4.3). In that case,
 \begin{equation*}\mu^{\text{Alt}}\big(D^k(f)_{free}\big)=\frac{1}{k!}\mu\big(D^k(f)_{free}\big).\end{equation*}
\begin{equation*}\mu^{\text{Alt}}\big(D^k(f)_{free}\big)=\frac{1}{k!}\mu\big(D^k(f)_{free}\big).\end{equation*}If the group does not act freely, things are a bit more complicated and we need to use lemma 2.10.
Example 4.3. It can happen that a germ f has singular ![]() $D^k(f)$ but no fixed points for any
$D^k(f)$ but no fixed points for any ![]() $\sigma\neq\operatorname{id}$. For example, for
$\sigma\neq\operatorname{id}$. For example, for ![]() $f:\big(\mathbb{C}^2,\{0,0'\}\big)\to(\mathbb{C}^3,0)$ given by the tangent double point, i.e.,
$f:\big(\mathbb{C}^2,\{0,0'\}\big)\to(\mathbb{C}^3,0)$ given by the tangent double point, i.e.,
 \begin{equation*} \left\{\begin{array}{ll}
(x,y)&\mapsto (x,y,x^2+y^2)\\
(\widetilde{x},\widetilde{y})&\mapsto\big(\widetilde{x},\widetilde{y}, -(\widetilde{x}^2+\widetilde{y}^2)\big)
\end{array}\right. \end{equation*}
\begin{equation*} \left\{\begin{array}{ll}
(x,y)&\mapsto (x,y,x^2+y^2)\\
(\widetilde{x},\widetilde{y})&\mapsto\big(\widetilde{x},\widetilde{y}, -(\widetilde{x}^2+\widetilde{y}^2)\big)
\end{array}\right. \end{equation*} ![]() $D^2(f)\subset\mathbb{C}^{2+2}$ is given by the equations
$D^2(f)\subset\mathbb{C}^{2+2}$ is given by the equations ![]() $\widetilde{x}=x$,
$\widetilde{x}=x$, ![]() $\widetilde{y}=y$, and
$\widetilde{y}=y$, and ![]() $x^2+y^2=0$. As the notation
$x^2+y^2=0$. As the notation ![]() $\widetilde{x},\widetilde{y}$ is a simplification to denote multi-germs, there is no fixed point by the permutation
$\widetilde{x},\widetilde{y}$ is a simplification to denote multi-germs, there is no fixed point by the permutation ![]() $(1\ 2)$ (see figure 4, cf. figure 10).
$(1\ 2)$ (see figure 4, cf. figure 10).

Figure 4. Diagram of the tangent double point f given in example 4.3 (cf. figure 10).
To tame the sign  $(-1)^{d-d^\sigma}$ in lemma 2.10, observe that the difference of dimensions dk and
$(-1)^{d-d^\sigma}$ in lemma 2.10, observe that the difference of dimensions dk and ![]() $d_k^\sigma$ behaves well in the following sense.
$d_k^\sigma$ behaves well in the following sense.
Lemma 4.4. (see [Reference Giménez Conejero6, lemma 6.3.2])
Given an ![]() $\mathscr{A}$-finite germ
$\mathscr{A}$-finite germ ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, with n < p,
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, with n < p,
 \begin{equation*}(-1)^{d_k-d_k^\sigma}=\operatorname{sgn}(\sigma)=\chi_{\text{Alt}}(\sigma).\end{equation*}
\begin{equation*}(-1)^{d_k-d_k^\sigma}=\operatorname{sgn}(\sigma)=\chi_{\text{Alt}}(\sigma).\end{equation*}Proof. First of all, observe that ![]() $d_k-d_k^\sigma=k-\sum_i\alpha_i$ provided that σ has cycle type
$d_k-d_k^\sigma=k-\sum_i\alpha_i$ provided that σ has cycle type ![]() $(r_1,\dots, r_m)$ and
$(r_1,\dots, r_m)$ and ![]() $\alpha_i=\texttt{\#}\left\{j:r_j=i\right\}$ (see remark 3.14).
$\alpha_i=\texttt{\#}\left\{j:r_j=i\right\}$ (see remark 3.14).
Assume that the lemma is true for the permutations of k − 1 elements. To create a permutation of k elements, say ![]() $\sigma'$, from a permutation of k − 1 elements, say σ, we have to add the new element to any cycle of σ or leave that element invariant by
$\sigma'$, from a permutation of k − 1 elements, say σ, we have to add the new element to any cycle of σ or leave that element invariant by ![]() $\sigma'$.
$\sigma'$.
If we add the element to some cycle, the sum ![]() $\sum_i \alpha^{\sigma}_i$ transforms into
$\sum_i \alpha^{\sigma}_i$ transforms into  $\sum_i\alpha^{\sigma'}_i$, but notice that we are changing two αi. Therefore, the sum does not change because, for some i 0, we have that
$\sum_i\alpha^{\sigma'}_i$, but notice that we are changing two αi. Therefore, the sum does not change because, for some i 0, we have that  $\alpha_{i_0}^\sigma =\alpha_{i_0}^{\sigma'}-1 $ and
$\alpha_{i_0}^\sigma =\alpha_{i_0}^{\sigma'}-1 $ and  $\alpha_{i_0+1}^\sigma =\alpha_{i_0+1}^{\sigma'}+1 $. Hence,
$\alpha_{i_0+1}^\sigma =\alpha_{i_0+1}^{\sigma'}+1 $. Hence,
 \begin{equation*}k-\sum \alpha^{\sigma'}_i=k-\sum \alpha^{\sigma}_i=(k-1)-\sum \alpha^{\sigma}_i+1,\end{equation*}
\begin{equation*}k-\sum \alpha^{\sigma'}_i=k-\sum \alpha^{\sigma}_i=(k-1)-\sum \alpha^{\sigma}_i+1,\end{equation*} so the parity of this number changes. Luckily, this operation changes the sign of the permutation: ![]() $\operatorname{sgn}(\sigma)=-\operatorname{sgn}(\sigma')$.
$\operatorname{sgn}(\sigma)=-\operatorname{sgn}(\sigma')$.
Finally, if we leave the new element invariant neither the sign nor the difference ![]() $k-\sum_i\alpha_i$ changes.
$k-\sum_i\alpha_i$ changes.
We finish the argument by induction, as it is true for Σ2 and ![]() $D^2(f)$.
$D^2(f)$.
Definition 4.5. The positive Milnor characteristic of an icis ![]() $(X,\mathcal{S})$ is defined as
$(X,\mathcal{S})$ is defined as
and the negative Milnor characteristic as
If X is empty, both are zero.
Remark 4.6. For an icis ![]() $(X,\mathcal{S})$ of dimension zero,
$(X,\mathcal{S})$ of dimension zero, ![]() $\mu^{+0}(X;\mathcal{S})$ is equal to the number of points of the fibre. Furthermore,
$\mu^{+0}(X;\mathcal{S})$ is equal to the number of points of the fibre. Furthermore, ![]() $\mu^{-0}(X;\mathcal{S})\geq0$ if each connected component of X has at least one singularity.
$\mu^{-0}(X;\mathcal{S})\geq0$ if each connected component of X has at least one singularity.
Theorem 4.7. Consider an unstable ![]() $\mathscr{A}$-finite germ
$\mathscr{A}$-finite germ ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one, n < p, and a space
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one, n < p, and a space ![]() $D^k(f)\neq\varnothing$ with
$D^k(f)\neq\varnothing$ with ![]() $d_k\geq0$. Then,
$d_k\geq0$. Then,
 \begin{equation}
\mu^{\textrm{Alt}}\big(D^k(f)\big)=\frac{1}{k!}\left(\sum_{d_k^\sigma\geq0}\mu\big(D^k(f)^\sigma\big)-\sum_{d_k^\sigma \lt 0}(-1)^{d_k^\sigma}\beta_0\big(D^k(f)^\sigma\big)\right),
\end{equation}
\begin{equation}
\mu^{\textrm{Alt}}\big(D^k(f)\big)=\frac{1}{k!}\left(\sum_{d_k^\sigma\geq0}\mu\big(D^k(f)^\sigma\big)-\sum_{d_k^\sigma \lt 0}(-1)^{d_k^\sigma}\beta_0\big(D^k(f)^\sigma\big)\right),
\end{equation} where the sums run on the permutations ![]() $\sigma\in\Sigma_k$ such that the condition given on
$\sigma\in\Sigma_k$ such that the condition given on ![]() $d^\sigma_k$ is satisfied.
$d^\sigma_k$ is satisfied.
If, furthermore, the group ![]() $\Sigma_k$ acts freely on the connected components of
$\Sigma_k$ acts freely on the connected components of ![]() $D^k(f)$ (i.e., only by permutation of copies of icis), then
$D^k(f)$ (i.e., only by permutation of copies of icis), then  $\mu^{\textrm{Alt}}\big(D^k(f)\big)=\frac{1}{k!}\mu\big(D^k(f)\big)$. Otherwise, we can consider the orbits of those connected components where the group does not act freely and we have the equivalent expression
$\mu^{\textrm{Alt}}\big(D^k(f)\big)=\frac{1}{k!}\mu\big(D^k(f)\big)$. Otherwise, we can consider the orbits of those connected components where the group does not act freely and we have the equivalent expression
 \begin{equation}
\mu^{\textrm{Alt}}\big(D^k(f)\big)=\frac{1}{k!}\left(\sum_{d_k^\sigma\geq0\;\textrm{even}} \mu^{+0}\big( D^k(f)^\sigma\big)+\sum_{d_k^\sigma \gt 0\;\textrm{odd}} \mu^{-0}\big( D^k(f)^\sigma\big)\right),
\end{equation}
\begin{equation}
\mu^{\textrm{Alt}}\big(D^k(f)\big)=\frac{1}{k!}\left(\sum_{d_k^\sigma\geq0\;\textrm{even}} \mu^{+0}\big( D^k(f)^\sigma\big)+\sum_{d_k^\sigma \gt 0\;\textrm{odd}} \mu^{-0}\big( D^k(f)^\sigma\big)\right),
\end{equation}following definition 4.5.
Proof. We simply have to rewrite lemma 2.10 for ![]() $\tau={\text{Alt}}$ (we can use it since the action is simplicially excellent, see the proof of theorem 4.1):
$\tau={\text{Alt}}$ (we can use it since the action is simplicially excellent, see the proof of theorem 4.1):
 \begin{align}
\begin{array}{ll}
\mu^{\text{Alt}}\big(D^k(f)\big)&= \frac{1}{k!}\sum_{\sigma\in \Sigma_k}(-1)^{d_k-\operatorname{dim} D^k(f)^\sigma}\operatorname{sgn}(\sigma) \widetilde{\mu}\big(D^k(f)^\sigma\big)\\
&= \frac{1}{k!}\left(\sum_{d_k^\sigma\geq0}\mu\big(D^k(f)^\sigma\big)-\sum_{d_k^\sigma \lt 0}(-1)^{d_k}\operatorname{sgn}(\sigma)\beta_0\big(D^k(f)^\sigma\big)\right)
\end{array}\nonumber\\
\end{align}
\begin{align}
\begin{array}{ll}
\mu^{\text{Alt}}\big(D^k(f)\big)&= \frac{1}{k!}\sum_{\sigma\in \Sigma_k}(-1)^{d_k-\operatorname{dim} D^k(f)^\sigma}\operatorname{sgn}(\sigma) \widetilde{\mu}\big(D^k(f)^\sigma\big)\\
&= \frac{1}{k!}\left(\sum_{d_k^\sigma\geq0}\mu\big(D^k(f)^\sigma\big)-\sum_{d_k^\sigma \lt 0}(-1)^{d_k}\operatorname{sgn}(\sigma)\beta_0\big(D^k(f)^\sigma\big)\right)
\end{array}\nonumber\\
\end{align} where we have simplified signs (using the parity given in lemma 4.4) and we have followed the definition  $\widetilde{\mu}\big(D^k(f)^\sigma\big)=-\beta_0\big(D^k(f)^\sigma\big)$ when
$\widetilde{\mu}\big(D^k(f)^\sigma\big)=-\beta_0\big(D^k(f)^\sigma\big)$ when ![]() $d^\sigma_k \lt 0$.
$d^\sigma_k \lt 0$.
Observe that, independently of the parity of dk, we have that
 \begin{equation}
-\sum_{d_k^\sigma \lt 0}(-1)^{d_k}\operatorname{sgn}(\sigma)\beta_0\big(D^k(f)^\sigma\big)= -\sum_{d_k^\sigma \lt 0 \, \text{even }}\beta_0\big(D^k(f)^\sigma\big)+\sum_{d_k^\sigma \lt 0 \, \text{odd }}\beta_0\big(D^k(f)^\sigma\big),
\end{equation}
\begin{equation}
-\sum_{d_k^\sigma \lt 0}(-1)^{d_k}\operatorname{sgn}(\sigma)\beta_0\big(D^k(f)^\sigma\big)= -\sum_{d_k^\sigma \lt 0 \, \text{even }}\beta_0\big(D^k(f)^\sigma\big)+\sum_{d_k^\sigma \lt 0 \, \text{odd }}\beta_0\big(D^k(f)^\sigma\big),
\end{equation}by lemma 4.4.
Equations (14) and (15) give the first equality of the theorem.
To prove the second one, we only have to show that
 \begin{equation}
-\sum_{d_k^\sigma \lt 0}(-1)^{d_k^\sigma}\beta_0\big(D^k(f)^\sigma\big)=\sum_{d_k^\sigma\geq0}(-1)^{d_k^\sigma}\beta_0\big(D^k(f)^\sigma\big).
\end{equation}
\begin{equation}
-\sum_{d_k^\sigma \lt 0}(-1)^{d_k^\sigma}\beta_0\big(D^k(f)^\sigma\big)=\sum_{d_k^\sigma\geq0}(-1)^{d_k^\sigma}\beta_0\big(D^k(f)^\sigma\big).
\end{equation} This follows from the fact that there is no alternating homology on ![]() $H_*\big(D^k(f)\big)$, provided that the group acts non-freely on connected components. Indeed,
$H_*\big(D^k(f)\big)$, provided that the group acts non-freely on connected components. Indeed, ![]() $D^k(f)$ retracts to points of the subset Sk; but points with some entry repeated at least twice by hypothesis, therefore fixed by some transposition. Hence, there cannot be alternated homology in H 0. This and proposition 2.4 applied to
$D^k(f)$ retracts to points of the subset Sk; but points with some entry repeated at least twice by hypothesis, therefore fixed by some transposition. Hence, there cannot be alternated homology in H 0. This and proposition 2.4 applied to ![]() $D^k(f)$ and
$D^k(f)$ and ![]() $\tau={\text{Alt}}$ yield
$\tau={\text{Alt}}$ yield
 \begin{equation*}
\begin{array}{ll}
0 &= \frac{1}{k!}\sum_\sigma \operatorname{sgn}(\sigma)\beta_0 \big(D^k(f)^\sigma\big)\\
0&=\sum_\sigma (-1)^{d_k-d_k^\sigma}\beta_0 \big(D^k(f)^\sigma\big)\\
0&=\sum_\sigma (-1)^{d_k^\sigma}\beta_0 \big(D^k(f)^\sigma\big).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ll}
0 &= \frac{1}{k!}\sum_\sigma \operatorname{sgn}(\sigma)\beta_0 \big(D^k(f)^\sigma\big)\\
0&=\sum_\sigma (-1)^{d_k-d_k^\sigma}\beta_0 \big(D^k(f)^\sigma\big)\\
0&=\sum_\sigma (-1)^{d_k^\sigma}\beta_0 \big(D^k(f)^\sigma\big).
\end{array}
\end{equation*}The following theorem sums up most of the behaviour of multiple point spaces and contains a generalization to multi-germs of the results [Reference Giménez Conejero6, theorems 6.3.1 and 6.3.5] found in the author’s thesis.
Theorem 4.8. For unstable ![]() $\mathscr{A}$-finite germ
$\mathscr{A}$-finite germ ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one, n < p and spaces
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one, n < p and spaces ![]() $D^k(f)\neq\varnothing$ with
$D^k(f)\neq\varnothing$ with ![]() $d_k\geq0$, the following are equivalent:
$d_k\geq0$, the following are equivalent:
(i)
 $D^k(f)$ has a singularity;
$D^k(f)$ has a singularity;(ii)
 $D^k(f_s)$ has non-trivial homology in middle dimension, fs stable;
$D^k(f_s)$ has non-trivial homology in middle dimension, fs stable;(iii)
 $D^{k+j}(f)$ has a singularity if it is not empty, for every
$D^{k+j}(f)$ has a singularity if it is not empty, for every  $j\geq0$ such that
$j\geq0$ such that  $d_{k+j}\geq0$;
$d_{k+j}\geq0$;(iv) every space
 $D^k(f)^\sigma$ has a singularity if it is not empty and
$D^k(f)^\sigma$ has a singularity if it is not empty and  $d_k^\sigma\geq0$;
$d_k^\sigma\geq0$;(v) some space
 $D^k(f)^\sigma$ has a singularity, where
$D^k(f)^\sigma$ has a singularity, where  $d_k^\sigma\geq0$;
$d_k^\sigma\geq0$;(vi)
 $D^k(f_s)$ has non-trivial alternating homology in middle dimension.
$D^k(f_s)$ has non-trivial alternating homology in middle dimension.
Furthermore, if ![]() $d_k^\sigma \lt 0$ and
$d_k^\sigma \lt 0$ and ![]() $D^k(f)^\sigma$ is not empty, we have all of the above.
$D^k(f)^\sigma$ is not empty, we have all of the above.
Proof. We can exclude the orbits of those connected components where the group acts freely, i.e., only by permutation of copies of icis, as the result is trivial there. Hence, we can assume that ![]() $D^k(f)$ is given by a single orbit of a connected component and the group does not act freely on them.
$D^k(f)$ is given by a single orbit of a connected component and the group does not act freely on them.
That Items (i) and (ii) are equivalent is known, a Milnor fibre of an icis is contractible if, and only if, the icis is smooth. See, for example, the classical result on the Milnor–Tjurina inequality [Reference Looijenga and Steenbrink21, theorem].
For the equivalence between Items (i) and (iii), assume that f is a mono-germ. Then, it is given by the fact that the regular sequence defining the icis ![]() $D^{k+j}(f)$ contains the regular sequence of the icis
$D^{k+j}(f)$ contains the regular sequence of the icis ![]() $D^{k}(f)$. For multi-germs, also, this relation is true between components of the multiple point spaces taking into account combinations of branches of the multi-germ. For example, if a component
$D^{k}(f)$. For multi-germs, also, this relation is true between components of the multiple point spaces taking into account combinations of branches of the multi-germ. For example, if a component ![]() $D\subseteq D^k(f)$ is given by points of, say, only one branch, then there is another component
$D\subseteq D^k(f)$ is given by points of, say, only one branch, then there is another component ![]() $D'\subseteq D^{k+1}(f)$ given by the equations of D and adding the intersection with another branch of f.
$D'\subseteq D^{k+1}(f)$ given by the equations of D and adding the intersection with another branch of f.
That Item (i) implies Item (iv) is similar: the regular sequence of the icis ![]() $D^k(f)^\sigma$ (recall the stronger version of the Marar–Mond criterion lemma 3.15) include that of
$D^k(f)^\sigma$ (recall the stronger version of the Marar–Mond criterion lemma 3.15) include that of ![]() $D^k(f)$, since we only need to add equations identifying some variables to have
$D^k(f)$, since we only need to add equations identifying some variables to have ![]() $D^k(f)$ from
$D^k(f)$ from ![]() $D^k(f)^\sigma$. The converse is obvious.
$D^k(f)^\sigma$. The converse is obvious.
Item (i) implies Item (v) with ![]() $\sigma=\operatorname{id}$. For the converse, we can use Eq. (1):
$\sigma=\operatorname{id}$. For the converse, we can use Eq. (1):
 \begin{equation*}\chi_{\Sigma_k}\big(D^k(f)\big)(\sigma)=\chi_{Top}(D^k(f)^\sigma).\end{equation*}
\begin{equation*}\chi_{\Sigma_k}\big(D^k(f)\big)(\sigma)=\chi_{Top}(D^k(f)^\sigma).\end{equation*} Assume, for the sake of the contradiction, that ![]() $D^k(f)$ is smooth but there is some σ such that
$D^k(f)$ is smooth but there is some σ such that ![]() $D^k(f)^\sigma$ is singular,
$D^k(f)^\sigma$ is singular, ![]() $d_k^\sigma\geq0$. Then, because
$d_k^\sigma\geq0$. Then, because ![]() $D^k(f)$ is smooth, the action on the connected components of
$D^k(f)$ is smooth, the action on the connected components of ![]() $D^k(f)$ and its Milnor fibre
$D^k(f)$ and its Milnor fibre ![]() $D^k(f_s)$ are the same, i.e.,
$D^k(f_s)$ are the same, i.e.,
 \begin{equation*}\chi_{\Sigma_k}\big(D^k(f)\big)(\sigma)=\chi_{\Sigma_k}\big(D^k(f_s)\big)(\sigma),\end{equation*}
\begin{equation*}\chi_{\Sigma_k}\big(D^k(f)\big)(\sigma)=\chi_{\Sigma_k}\big(D^k(f_s)\big)(\sigma),\end{equation*}which is a contradiction with
 \begin{equation*}\chi_{Top}(D^k(f)^\sigma)\neq\chi_{Top}(D^k(f_s)^\sigma),\end{equation*}
\begin{equation*}\chi_{Top}(D^k(f)^\sigma)\neq\chi_{Top}(D^k(f_s)^\sigma),\end{equation*} since ![]() $D^k(f_s)^\sigma$ is the Milnor fibre of the icis
$D^k(f_s)^\sigma$ is the Milnor fibre of the icis ![]() $D^k(f)$ (recall lemma 3.15).
$D^k(f)$ (recall lemma 3.15).
The equivalence between Items (i) and (vi) is, now, easy. The converse implication is trivial. The direct implication follows from Item (iv): if every ![]() $D^k(f)^\sigma$ is empty when
$D^k(f)^\sigma$ is empty when ![]() $d_k^\sigma \lt 0$, the implication follows easily from Eq. (12). Otherwise, assume that there exists σ 0 such that
$d_k^\sigma \lt 0$, the implication follows easily from Eq. (12). Otherwise, assume that there exists σ 0 such that ![]() $D^k(f)^{\sigma_0}$ is non-empty and
$D^k(f)^{\sigma_0}$ is non-empty and ![]() $d_k^{\sigma_0}=0$. In that case, the implication follows from Eq. (13) and Item (iv), because (recall remark 4.6)
$d_k^{\sigma_0}=0$. In that case, the implication follows from Eq. (13) and Item (iv), because (recall remark 4.6)
 \begin{equation*}\mu^{\pm0}\big(D^k(f)^\sigma\big)\geq0,\end{equation*}
\begin{equation*}\mu^{\pm0}\big(D^k(f)^\sigma\big)\geq0,\end{equation*} and ![]() $\mu^{+0}\big(D^k(f)^{\sigma_0}\big) \gt 0$.
$\mu^{+0}\big(D^k(f)^{\sigma_0}\big) \gt 0$.
Indeed, the assumption always holds if there is a ![]() $D^k(f)^{\sigma_-}\neq\varnothing$ so that
$D^k(f)^{\sigma_-}\neq\varnothing$ so that  $d_k^{\sigma_-} \lt 0$. If we consider the permutation
$d_k^{\sigma_-} \lt 0$. If we consider the permutation ![]() $\sigma_-$ and we fix one entry of its cycle decomposition to have a new
$\sigma_-$ and we fix one entry of its cycle decomposition to have a new ![]() $\alpha'$, we have another
$\alpha'$, we have another  $D^k(f)^{\sigma'}\neq\varnothing$ and
$D^k(f)^{\sigma'}\neq\varnothing$ and  $0\leq d_k^{\sigma'}-d_k^{\sigma_-}\leq1$ (recall remark 3.14 and lemma 3.15). E.g.,
$0\leq d_k^{\sigma'}-d_k^{\sigma_-}\leq1$ (recall remark 3.14 and lemma 3.15). E.g., ![]() $(1\ 2\ 6\ 3)(4\ 5)(8\ 9)(7)(10)$ fixing 3 and 9 is the permutation
$(1\ 2\ 6\ 3)(4\ 5)(8\ 9)(7)(10)$ fixing 3 and 9 is the permutation ![]() $(1\ 2\ 6)(4\ 5)(3)(8)(9)(7)(10)$. Since
$(1\ 2\ 6)(4\ 5)(3)(8)(9)(7)(10)$. Since ![]() $d_k=d_k^{\operatorname{id}}\geq0$, if we iterate this process we reach at some step a σ 0 so that
$d_k=d_k^{\operatorname{id}}\geq0$, if we iterate this process we reach at some step a σ 0 so that ![]() $D^k(f)^{\sigma_0}\neq\varnothing$ and
$D^k(f)^{\sigma_0}\neq\varnothing$ and ![]() $d_k^{\sigma_0}=0$.
$d_k^{\sigma_0}=0$.
Finally, regarding the last statement, it follows from a similar argument to that of the equivalence between Items (i) and (v).
To complete the previous theorem, we also have this result.
Theorem 4.9. Let ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ be an unstable
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ be an unstable ![]() $\mathscr{A}$-finite germ of corank one, n < p, and ft a perturbation. If
$\mathscr{A}$-finite germ of corank one, n < p, and ft a perturbation. If  $\beta_{d_k}\big(D^k(f_t)\big) \gt 0$, with
$\beta_{d_k}\big(D^k(f_t)\big) \gt 0$, with ![]() $d_k \gt 0$, then
$d_k \gt 0$, then ![]() $D^k(f_t)$ has alternating homology. Furthermore, if
$D^k(f_t)$ has alternating homology. Furthermore, if  $\beta_{d_k}\big(D^k(f_t)\big) \gt 0$,
$\beta_{d_k}\big(D^k(f_t)\big) \gt 0$,
 \begin{equation*} \mu_k^{\textrm{Alt}}(f) \gt \sum_{y\in \operatorname{im} f_t}\mu_k^{\textrm{Alt}}(f_t;y\big).\end{equation*}
\begin{equation*} \mu_k^{\textrm{Alt}}(f) \gt \sum_{y\in \operatorname{im} f_t}\mu_k^{\textrm{Alt}}(f_t;y\big).\end{equation*}Proof. We can assume that the new homology of ![]() $D^k(f_t)$ has appeared in an orbit of a connected component where the group does not act freely, otherwise the group acts by permutation of connected components and the result follows from usual homology arguments. We keep denoting as
$D^k(f_t)$ has appeared in an orbit of a connected component where the group does not act freely, otherwise the group acts by permutation of connected components and the result follows from usual homology arguments. We keep denoting as ![]() $D^k(f)$ and
$D^k(f)$ and ![]() $D^k(f_t)$ this orbit of the connected component.
$D^k(f_t)$ this orbit of the connected component.
For the first statement, then, at least one term of Eq. (13) decreases when we consider f and ft:
 \begin{equation*}\mu^{\pm0}\big(D^k(f)\big) \gt \sum_{x\in D^k(f_t) }\mu^{\pm0}\big(D^k(f_t);x\big),\end{equation*}
\begin{equation*}\mu^{\pm0}\big(D^k(f)\big) \gt \sum_{x\in D^k(f_t) }\mu^{\pm0}\big(D^k(f_t);x\big),\end{equation*} by the conservation principle of the (regular) Milnor number for icis [Reference Nuño-Ballesteros, Oréfice-Okamoto and Tomazella29, theorem 4.2] and the hypothesis  $\beta_{d_k}\big(D^k(f_t)\big) \gt 0$. This implies that
$\beta_{d_k}\big(D^k(f_t)\big) \gt 0$. This implies that ![]() $D^k(f_t)$ must have alternating homology by theorem 2.11, because when we compute
$D^k(f_t)$ must have alternating homology by theorem 2.11, because when we compute ![]() $\mu^{\text{Alt}}\big(D^k(f)\big)$ with Eq. (13) it is strictly bigger than the computation with Eq. (13) of
$\mu^{\text{Alt}}\big(D^k(f)\big)$ with Eq. (13) it is strictly bigger than the computation with Eq. (13) of
 \begin{equation*}\sum_{\Sigma_k x\subseteq D^k(f_t)}\mu^{\text{Alt}}\big(D^k(f_t);\Sigma_k x\big).\end{equation*}
\begin{equation*}\sum_{\Sigma_k x\subseteq D^k(f_t)}\mu^{\text{Alt}}\big(D^k(f_t);\Sigma_k x\big).\end{equation*} This last argument also proves the second statement, recall that ![]() $\mu^{\text{Alt}}\big(D^k(f)\big)=\mu_k^{\text{Alt}}(f)$ and
$\mu^{\text{Alt}}\big(D^k(f)\big)=\mu_k^{\text{Alt}}(f)$ and
 \begin{equation*}\sum_{\Sigma_k x\subseteq D^k(f_t)}\mu^{\text{Alt}}\big(D^k(f_t);\Sigma_k x\big)=\sum_{y\in \operatorname{im} f_t}\mu_k^{\text{Alt}}(f_t;y\big).\end{equation*}
\begin{equation*}\sum_{\Sigma_k x\subseteq D^k(f_t)}\mu^{\text{Alt}}\big(D^k(f_t);\Sigma_k x\big)=\sum_{y\in \operatorname{im} f_t}\mu_k^{\text{Alt}}(f_t;y\big).\end{equation*}5. Homology of deformations and unexpected homology
5.1. Stable deformations
As it has been done several times (see, for example, [Reference Houston19]), we can use the icss given in theorem 3.2 and the ![]() $\mu_k^{\text{Alt}}$ to compute the image Milnor number of germs
$\mu_k^{\text{Alt}}$ to compute the image Milnor number of germs ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{n+1},0)$ (see figure 5). It is not clear what should be the generalization of this object to map germs
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{n+1},0)$ (see figure 5). It is not clear what should be the generalization of this object to map germs ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, for arbitrary n < p. There is not a correct answer to this question but one should consider some definition that allows generalizing properties of germs when
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, for arbitrary n < p. There is not a correct answer to this question but one should consider some definition that allows generalizing properties of germs when ![]() $p=n+1$ to the general case n < p only changing n + 1 by p.
$p=n+1$ to the general case n < p only changing n + 1 by p.

Figure 5. Possibly non-zero entries, with its rank, of the ![]() $E^\infty$-page of the spectral sequence
$E^\infty$-page of the spectral sequence  $E^1_{r,q}= H^{{\text{Alt}}_{r+1}}_q\left(D^{r+1}\left(F\right),D^{r+1}\left(f_s\right)\right)$ for a map germ
$E^1_{r,q}= H^{{\text{Alt}}_{r+1}}_q\left(D^{r+1}\left(F\right),D^{r+1}\left(f_s\right)\right)$ for a map germ ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$. Notice the shift
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$. Notice the shift ![]() $H_{m+1}(\operatorname{im} F,\operatorname{im} f_s)\cong H_m(\operatorname{im} f_s)$ when m > 0.
$H_{m+1}(\operatorname{im} F,\operatorname{im} f_s)\cong H_m(\operatorname{im} f_s)$ when m > 0.
We give, now, two reasonable generalizations. However, we will see later several reasons that make the first definition seemingly better.
Definition 5.1. Consider an ![]() $\mathscr{A}$-finite germ
$\mathscr{A}$-finite germ ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, such that
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, such that ![]() $d_2=2n-p\geq0$. We define its image Milnor number as
$d_2=2n-p\geq0$. We define its image Milnor number as
 \begin{equation*}\mu_I(f):= \sum_{i \gt 0} \beta_i\big(\operatorname{im} f_s\big)\end{equation*}
\begin{equation*}\mu_I(f):= \sum_{i \gt 0} \beta_i\big(\operatorname{im} f_s\big)\end{equation*}for any stable perturbation fs. Similarly, the image vanishing characteristic of f is
 \begin{equation*}\nu_I(f):= (-1)^{d_2+1}\sum_{i \gt 0} (-1)^{i}\beta_i\big(\operatorname{im} f_s\big),\end{equation*}
\begin{equation*}\nu_I(f):= (-1)^{d_2+1}\sum_{i \gt 0} (-1)^{i}\beta_i\big(\operatorname{im} f_s\big),\end{equation*} for any stable perturbation fs. If ![]() $d_2 \lt 0$ (i.e.,
$d_2 \lt 0$ (i.e., ![]() $p \gt 2n$) we say that f is degenerate. In this case, we take as definition
$p \gt 2n$) we say that f is degenerate. In this case, we take as definition ![]() $\mu_I(f)=\nu_I(f)=\beta_0\big(\operatorname{im}(f_s)\big)-1$ (compare figure 5 and figure 6).
$\mu_I(f)=\nu_I(f)=\beta_0\big(\operatorname{im}(f_s)\big)-1$ (compare figure 5 and figure 6).

Figure 6. Comparison between the spectral sequences of non-degenerated and degenerated map germs ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ (where the stable perturbation only has 0-homology, i.e., the expected dimension d 2 is negative). Notice the equality
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ (where the stable perturbation only has 0-homology, i.e., the expected dimension d 2 is negative). Notice the equality ![]() $\beta_{1}\big(\operatorname{im}(F),\operatorname{im}(f_s)\big)+1= \beta_0\big(\operatorname{im}(f_s)\big)$ in the degenerated case.
$\beta_{1}\big(\operatorname{im}(F),\operatorname{im}(f_s)\big)+1= \beta_0\big(\operatorname{im}(f_s)\big)$ in the degenerated case.
The general definition of µI in definition 5.1 is not new. For example, Houston took this definition in [Reference Houston19]. The second definition can also be seen as the difference ![]() $\chi_{Top}(\operatorname{im} f)-\chi_{Top}(\operatorname{im} f_s)$ with a convenient sign (this approach can also be found in, for example, [Reference Nuño Ballesteros, Oréfice-Okamoto and Tomazella28]).
$\chi_{Top}(\operatorname{im} f)-\chi_{Top}(\operatorname{im} f_s)$ with a convenient sign (this approach can also be found in, for example, [Reference Nuño Ballesteros, Oréfice-Okamoto and Tomazella28]).
Lemma 5.2. (cf. [Reference Houston19, remark 3.12])
Given an ![]() $\mathscr{A}$-finite germ
$\mathscr{A}$-finite germ ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one,
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one, ![]() $n \lt p\leq2n$, we have that
$n \lt p\leq2n$, we have that
 \begin{equation*}
\begin{array}{ll}
\mu_I(f)&=\sum_k \mu_k^{\textrm{Alt}}(f), \\
\nu_I(f)&=(-1)^{d_2+1}\left[\sum_{\textrm{{k=2}}}^{\textrm{d(f)}} (-1)^{d_k+k-1}\mu_k^{\textrm{Alt}}(f)\right]+(-1)^{d(f)+d_2}\mu_{d(f)+1}^{\textrm{Alt}}(f).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ll}
\mu_I(f)&=\sum_k \mu_k^{\textrm{Alt}}(f), \\
\nu_I(f)&=(-1)^{d_2+1}\left[\sum_{\textrm{{k=2}}}^{\textrm{d(f)}} (-1)^{d_k+k-1}\mu_k^{\textrm{Alt}}(f)\right]+(-1)^{d(f)+d_2}\mu_{d(f)+1}^{\textrm{Alt}}(f).
\end{array}
\end{equation*} In the degenerate case, they coincide and are equal to  $\mu^{\textrm{Alt}}_{d(f)+1}(f)-1$ if
$\mu^{\textrm{Alt}}_{d(f)+1}(f)-1$ if ![]() $s(f) \gt 1$, and zero otherwise.
$s(f) \gt 1$, and zero otherwise.
Proof. This is a simple application of the icss shown in theorem 3.2 to compute the homology of the pair ![]() $\big(\operatorname{im} F,\operatorname{im} f_s \big)$ and the definition and comments given in definition 3.4 (see also figures 5 and 6).
$\big(\operatorname{im} F,\operatorname{im} f_s \big)$ and the definition and comments given in definition 3.4 (see also figures 5 and 6).
Remark 5.3. For non-degenerated germs, the dimensions where ![]() $\operatorname{im} f_s$ has (possibly) non-trivial homology are (cf. figure 5)
$\operatorname{im} f_s$ has (possibly) non-trivial homology are (cf. figure 5)
•
 $d_k+k-1$ for
$d_k+k-1$ for  $d_k\geq0$, from
$d_k\geq0$, from  $\beta^{\text{Alt}}\big(D^k(f_s)\big)$ or, equivalently, from
$\beta^{\text{Alt}}\big(D^k(f_s)\big)$ or, equivalently, from  $\mu_k^{\text{Alt}}(f)$; and
$\mu_k^{\text{Alt}}(f)$; and•
 $\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor-1$, from
$\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor-1$, from  $\mu_{\kappa+1}^{\text{Alt}}(f)$.
$\mu_{\kappa+1}^{\text{Alt}}(f)$.
Now we can give a workable expression for the image Milnor number µI.
Theorem 5.4. Given an unstable ![]() $\mathscr{A}$-finite germ
$\mathscr{A}$-finite germ ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one,
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one, ![]() $n \lt p\leq2n$,
$n \lt p\leq2n$,
 \begin{equation*}
\mu_I(f)=\sum\limits_{k=2}^{d(f)} \frac{1}{k!}\left(\sum\limits_{d_k^\sigma\geq0}\mu\left(D^k(f)^\sigma\right)-\sum\limits_{d_k^\sigma \lt 0}(-1)^{d_k^\sigma}\beta_0\left(D^k(f)^\sigma\right))+ {({s(f)-1} \atop {d(f)}}\right),
\end{equation*}
\begin{equation*}
\mu_I(f)=\sum\limits_{k=2}^{d(f)} \frac{1}{k!}\left(\sum\limits_{d_k^\sigma\geq0}\mu\left(D^k(f)^\sigma\right)-\sum\limits_{d_k^\sigma \lt 0}(-1)^{d_k^\sigma}\beta_0\left(D^k(f)^\sigma\right))+ {({s(f)-1} \atop {d(f)}}\right),
\end{equation*} where  $({s(f)-1} \atop {d(f)})=0 $ if
$({s(f)-1} \atop {d(f)})=0 $ if ![]() $s(f)\leq d(f)$.
$s(f)\leq d(f)$.
Proof. The proof follows from theorem 4.7 and lemma 5.2.
Remark 5.5. One can give a similar version for ![]() $\nu_I(f)$. Indeed, theorem 5.4 (together with (Eq. 13) of theorem 4.7) should be regarded as the generalization of the Marar–Mond formulae (see [Reference Marar and Mond23], in particular propositions 3.2 and 3.3 and theorem 3.4, cf. [Reference Mond25]), which relate the image Milnor number µI of a mono-germ
$\nu_I(f)$. Indeed, theorem 5.4 (together with (Eq. 13) of theorem 4.7) should be regarded as the generalization of the Marar–Mond formulae (see [Reference Marar and Mond23], in particular propositions 3.2 and 3.3 and theorem 3.4, cf. [Reference Mond25]), which relate the image Milnor number µI of a mono-germ ![]() $f:(\mathbb{C}^2,0)\to(\mathbb{C}^3,0)$ with the number of triple points T, cross-caps C (in
$f:(\mathbb{C}^2,0)\to(\mathbb{C}^3,0)$ with the number of triple points T, cross-caps C (in ![]() $\operatorname{im} f_s$) and the Milnor number of the curve of double points
$\operatorname{im} f_s$) and the Milnor number of the curve of double points ![]() $D(f)\subset \mathbb{C}^2$. A generalization of these formulae was given, only in terms of Euler characteristics (and for mono-germs), by Marar in [Reference Marar22, theorem 3.1], using a combinatorial argument. This argument, however, leaves inaccessible µI because it relies on Euler–Poincaré characteristics. The version of theorem 5.4 for νI would be a reformulation of this generalization by Marar, with a different proof.
$D(f)\subset \mathbb{C}^2$. A generalization of these formulae was given, only in terms of Euler characteristics (and for mono-germs), by Marar in [Reference Marar22, theorem 3.1], using a combinatorial argument. This argument, however, leaves inaccessible µI because it relies on Euler–Poincaré characteristics. The version of theorem 5.4 for νI would be a reformulation of this generalization by Marar, with a different proof.
The ideas that led to theorem 5.4 allow us to prove a modification of the weak version of the Mond conjecture for corank one and n < p. This is proved for corank one in [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 3.9] and for any corank in [Reference Giménez Conejero and Nuño-Ballesteros9, theorem 2.15] when ![]() $p=n+1$.
$p=n+1$.
Theorem 5.6. Let ![]() $f\colon(\mathbb{C}^{n},S)\rightarrow (\mathbb{C}^{p},0)$ be
$f\colon(\mathbb{C}^{n},S)\rightarrow (\mathbb{C}^{p},0)$ be ![]() $\mathscr{A}$-finite of corank one, n < p. Then,
$\mathscr{A}$-finite of corank one, n < p. Then, ![]() $\mu_I(f)=0$ if, and only if, f is stable or, alternatively, strongly contractible.
$\mu_I(f)=0$ if, and only if, f is stable or, alternatively, strongly contractible.
Proof. This follows from theorems 4.7 and 4.8 and lemma 5.2.
Remark 5.7. The germ given in example 3.11 illustrates the need of adding the strongly contractible case. Strongly contractible germs are, precisely, counterexamples to the original formulation of the result: ![]() $\mu_I(f)=0$ if, and only if, f is stable.
$\mu_I(f)=0$ if, and only if, f is stable.
Moreover, it is easy to see why this would fail for ![]() $\nu_I(f)$, as there could be some cancellation. For example, the germ
$\nu_I(f)$, as there could be some cancellation. For example, the germ ![]() $f:(\mathbb{C}^4,0)\to(\mathbb{C}^6,0)$ such that
$f:(\mathbb{C}^4,0)\to(\mathbb{C}^6,0)$ such that
was given in [Reference Houston16, example 4.26] and the ![]() $\operatorname{im} f_s$ (fs stable) has the homotopy type of two 2-spheres and two 3-spheres, so
$\operatorname{im} f_s$ (fs stable) has the homotopy type of two 2-spheres and two 3-spheres, so ![]() $\mu_I(f)=4$ but
$\mu_I(f)=4$ but ![]() $\nu_I(f)=0$ being f unstable (and not strongly contractible).
$\nu_I(f)=0$ being f unstable (and not strongly contractible).
5.2. Unexpected homology
The previous definitions and results deal with the homology of images of stable perturbations, but one can wonder what happens with a deformation ft that is not necessarily locally stable. In this section, we develop what we call unexpected homology. It is homology of ![]() $\operatorname{im}(f_t)$ that is killed when we deform further ft to a locally stable map.
$\operatorname{im}(f_t)$ that is killed when we deform further ft to a locally stable map.
For ![]() $p=n+1$, we have a conservation principle proved in [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 2.8] using a result for hypersurfaces (in particular, [Reference Siersma32, theorem 2.3] together with [Reference Giménez Conejero and Nuño-Ballesteros7, lemma 2.4]). As this result is only for hypersurfaces, the same proof cannot be used when
$p=n+1$, we have a conservation principle proved in [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 2.8] using a result for hypersurfaces (in particular, [Reference Siersma32, theorem 2.3] together with [Reference Giménez Conejero and Nuño-Ballesteros7, lemma 2.4]). As this result is only for hypersurfaces, the same proof cannot be used when ![]() $p \gt n+1$.
$p \gt n+1$.
Indeed, in light of example 4.2, the conservation principle of µI or νI is not true in general: that deformation ht of the bi-germ h has homology that does not come from any of the spaces ![]() $D^k(h_t)$ with
$D^k(h_t)$ with ![]() $d_k\geq0$ or combination of branches (because
$d_k\geq0$ or combination of branches (because ![]() $d(h)\geq s(h)$), hence
$d(h)\geq s(h)$), hence
 \begin{equation*}\begin{array}{ll}
\mu_I(h)& \lt \sum_{i \gt 0} \beta_i\big(\operatorname{im}(h_t)\big) + \sum_{y\in\operatorname{im}(h_t)} \mu_I(h_t;y),\, \text{and}\\
\nu_I(h)&\neq \sum_{i \gt 0} (-1)^{i+d_2+1}\beta_i\big(\operatorname{im}(h_t)\big) + \sum_{y\in\operatorname{im}(h_t)} \nu_I(h_t;y).
\end{array}\end{equation*}
\begin{equation*}\begin{array}{ll}
\mu_I(h)& \lt \sum_{i \gt 0} \beta_i\big(\operatorname{im}(h_t)\big) + \sum_{y\in\operatorname{im}(h_t)} \mu_I(h_t;y),\, \text{and}\\
\nu_I(h)&\neq \sum_{i \gt 0} (-1)^{i+d_2+1}\beta_i\big(\operatorname{im}(h_t)\big) + \sum_{y\in\operatorname{im}(h_t)} \nu_I(h_t;y).
\end{array}\end{equation*}Obviously, if we keep deforming this map ht to have something locally stable, hs, this unexpected homology is killed (see figure 7). This follows from the icss or lemma 5.2.

Figure 7. Creation of unexpected homology in ht and its annihilation in a locally stable perturbation hs.
Let us see the icss for ![]() $(\operatorname{im} H, \operatorname{im} h_t)$, with H a versal unfolding of h. The first page of the spectral sequence
$(\operatorname{im} H, \operatorname{im} h_t)$, with H a versal unfolding of h. The first page of the spectral sequence  $E^1_{r,q}= H^{{\text{Alt}}_{r+1}}_q\left(D^{r+1}\left(H\right),D^{r+1}\left(h_t\right)\right)$ is
$E^1_{r,q}= H^{{\text{Alt}}_{r+1}}_q\left(D^{r+1}\left(H\right),D^{r+1}\left(h_t\right)\right)$ is
We can compare it to the usual icss (after collapsing) for ![]() $(\operatorname{im} A, \operatorname{im} a_s)$ of an arbitrary multi-germ a in the same dimensions with possibly
$(\operatorname{im} A, \operatorname{im} a_s)$ of an arbitrary multi-germ a in the same dimensions with possibly ![]() $s(a) \gt d(a)$, i.e., the
$s(a) \gt d(a)$, i.e., the ![]() $E^\infty$-page of the spectral sequence
$E^\infty$-page of the spectral sequence  $E^1_{r,q}= H^{{\text{Alt}}_{r+1}}_q\left(D^{r+1}\left(A\right),D^{r+1}\left(a_s\right)\right)$:
$E^1_{r,q}= H^{{\text{Alt}}_{r+1}}_q\left(D^{r+1}\left(A\right),D^{r+1}\left(a_s\right)\right)$:


This unexpected homology of example 4.2 comes from alternating homology of ![]() $D^3(h_t)$ that cannot be found on
$D^3(h_t)$ that cannot be found on ![]() $D^3(H)$, which is equivalent to having non-trivial
$D^3(H)$, which is equivalent to having non-trivial
 \begin{equation*}H_1^{\text{Alt}}\big(D^3(H),D^3(h_t)\big), \end{equation*}
\begin{equation*}H_1^{\text{Alt}}\big(D^3(H),D^3(h_t)\big), \end{equation*}by the exact sequence of the pair in alternating homology.
Let us explain this in detail.
For the moment, let us assume that we are in some dimensions where there is no k such that ![]() $d_k=0$ (as it is the case of h in example 4.2). In general, for arbitrary f, we could have several spaces
$d_k=0$ (as it is the case of h in example 4.2). In general, for arbitrary f, we could have several spaces ![]() $D^k(f_t)$ with
$D^k(f_t)$ with ![]() $d_k \lt 0$ such that they have alternating homology that is not found in
$d_k \lt 0$ such that they have alternating homology that is not found in ![]() $D^k(F)$, or, equivalently, non-trivial
$D^k(F)$, or, equivalently, non-trivial ![]() $H_1^{\text{Alt}}$ of the pair. These homologies
$H_1^{\text{Alt}}$ of the pair. These homologies
 \begin{equation*} H_1^{\text{Alt}}\big(D^k(F),D^k(f_t)\big) \end{equation*}
\begin{equation*} H_1^{\text{Alt}}\big(D^k(F),D^k(f_t)\big) \end{equation*} appear in the icss in the first row of the first page,  $E^1_{*,1}(F, f_t)$, and it collapses in the second page leaving a possibly non-trivial term in the column where
$E^1_{*,1}(F, f_t)$, and it collapses in the second page leaving a possibly non-trivial term in the column where ![]() $D^{\kappa+1}$ goes, i.e., on the entry
$D^{\kappa+1}$ goes, i.e., on the entry  $E^2_{\kappa,1}(F,f_t)$, where
$E^2_{\kappa,1}(F,f_t)$, where  $\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor$. For example, if
$\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor$. For example, if ![]() $\ell$ is the maximal multiplicity within the spaces
$\ell$ is the maximal multiplicity within the spaces ![]() $D^{k}(f_t)$ that have
$D^{k}(f_t)$ that have
 \begin{equation*} H_1^{\text{Alt}}\big(D^k(F),D^k(f_t)\big)\ncong 0,\end{equation*}
\begin{equation*} H_1^{\text{Alt}}\big(D^k(F),D^k(f_t)\big)\ncong 0,\end{equation*}we have an exact sequence within the first row of the first page of the icss with the following combinatorial shape:
 \begin{equation}
\mathbb{Z}^{({\ell} \atop {\kappa+1})}\leftarrow \mathbb{Z}^{({\ell} \atop {\kappa+2})} \leftarrow\cdots\leftarrow\mathbb{Z}^{({\ell} \atop {\ell-1})}\leftarrow\mathbb{Z}^{({\ell} \atop {\ell})}\leftarrow 0,\end{equation}
\begin{equation}
\mathbb{Z}^{({\ell} \atop {\kappa+1})}\leftarrow \mathbb{Z}^{({\ell} \atop {\kappa+2})} \leftarrow\cdots\leftarrow\mathbb{Z}^{({\ell} \atop {\ell-1})}\leftarrow\mathbb{Z}^{({\ell} \atop {\ell})}\leftarrow 0,\end{equation} followed by zeroes. Of course, we have more of these sequences as direct sums on the same entries of the icss, depending on the orbits and projections of the ![]() $D^k(f_t)$ with
$D^k(f_t)$ with ![]() $d_k \lt 0$. Indeed, this is the same combinatorial reasoning that is used to prove that the 0-th row of the first page of the icss
$d_k \lt 0$. Indeed, this is the same combinatorial reasoning that is used to prove that the 0-th row of the first page of the icss ![]() $E^r_{*,*}(F,f_s)$ forms an exact sequence and all the homology collapses to give the unique (possibly) non-trivial
$E^r_{*,*}(F,f_s)$ forms an exact sequence and all the homology collapses to give the unique (possibly) non-trivial  $E^2_{\kappa+1,0}$, which defines
$E^2_{\kappa+1,0}$, which defines  $\mu_{d(f)+1}^{\text{Alt}}$. This is proven in [Reference Houston19, lemma 3.3] for rational homology, which is equivalent to integer homology in this case because we only deal with some H 0 of multiple points and the combinatorics of the projections between them (see also [Reference Houston19, figure 2] for a better insight). So we see that the term is non-trivial if there is such alternating homology for some k. See [Reference Houston19, lemmas 3.3 and 3.4] for more details.
$\mu_{d(f)+1}^{\text{Alt}}$. This is proven in [Reference Houston19, lemma 3.3] for rational homology, which is equivalent to integer homology in this case because we only deal with some H 0 of multiple points and the combinatorics of the projections between them (see also [Reference Houston19, figure 2] for a better insight). So we see that the term is non-trivial if there is such alternating homology for some k. See [Reference Houston19, lemmas 3.3 and 3.4] for more details.
In contrast, if n and p are such that ![]() $d_\kappa=0$, all the sequences of the shape of Eq. (17) have an extra term coming from
$d_\kappa=0$, all the sequences of the shape of Eq. (17) have an extra term coming from ![]() $D^\kappa(f_t)$:
$D^\kappa(f_t)$:
 \begin{equation}
\mathbb{Z}^{\ell \choose {\kappa}}\leftarrow\mathbb{Z}^{{\ell} \choose {\kappa+1}}\leftarrow \mathbb{Z}^{{\ell} \choose {\kappa+2}} \leftarrow\cdots\leftarrow\mathbb{Z}^{{\ell} \choose {\ell-1}}\leftarrow\mathbb{Z}^{{\ell} \choose {\ell}}\leftarrow 0.
\end{equation}
\begin{equation}
\mathbb{Z}^{\ell \choose {\kappa}}\leftarrow\mathbb{Z}^{{\ell} \choose {\kappa+1}}\leftarrow \mathbb{Z}^{{\ell} \choose {\kappa+2}} \leftarrow\cdots\leftarrow\mathbb{Z}^{{\ell} \choose {\ell-1}}\leftarrow\mathbb{Z}^{{\ell} \choose {\ell}}\leftarrow 0.
\end{equation} With the same argument, we see that this collapses to give a (possibly) non-trivial  $E^2_{\kappa-1,1}(F,f_t)$, in the column of D κ, and always killing
$E^2_{\kappa-1,1}(F,f_t)$, in the column of D κ, and always killing  $E^2_{\kappa,1}(F,f_t)$ (contributing trivially to the homology of
$E^2_{\kappa,1}(F,f_t)$ (contributing trivially to the homology of ![]() $\operatorname{im}(f_t)$ in the corresponding rank).
$\operatorname{im}(f_t)$ in the corresponding rank).
Definition 5.8. We say that a perturbation ft of an ![]() $\mathscr{A}$-finite map germ
$\mathscr{A}$-finite map germ ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, n < p, has unexpected homology if there are k such that
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, n < p, has unexpected homology if there are k such that
 \begin{equation*} H_1^{\textrm{Alt}}\big( D^k(F), D^k(f_t) \big)\ncong0, \end{equation*}
\begin{equation*} H_1^{\textrm{Alt}}\big( D^k(F), D^k(f_t) \big)\ncong0, \end{equation*} where F is a stable unfolding, and all satisfy that ![]() $d_k(f) \lt 0$ (in contrast with the situation of Eq. (18)). In that case, the unexpected homology is found in a unique rank:
$d_k(f) \lt 0$ (in contrast with the situation of Eq. (18)). In that case, the unexpected homology is found in a unique rank:
with  $\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor$.
$\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor$.
Remark 5.9. An ![]() $\mathscr{A}$-finite map germ
$\mathscr{A}$-finite map germ ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, n < p, such that
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, n < p, such that ![]() $D^k(f)=\varnothing$ for every negative expected dimension dk or such that
$D^k(f)=\varnothing$ for every negative expected dimension dk or such that  $\frac{p}{p-n}\in\mathbb{Z}^+$, has no deformations with unexpected homology.
$\frac{p}{p-n}\in\mathbb{Z}^+$, has no deformations with unexpected homology.
To understand what unexpected homology is, and not only where it is, recall the previous discussion and remark 5.3: if there are no k such that ![]() $d_k+k-1=\kappa$, then the unexpected homology of
$d_k+k-1=\kappa$, then the unexpected homology of ![]() $\operatorname{im}(f_t)$ is
$\operatorname{im}(f_t)$ is
if this is not trivial.
Indeed, the only case where we have a k such that ![]() $d_k+k-1=\kappa$ is when
$d_k+k-1=\kappa$ is when ![]() $d_\kappa= 1$, in which case such k is necessarily κ. This is because
$d_\kappa= 1$, in which case such k is necessarily κ. This is because ![]() $d_k+k-1 \gt d_\kappa+\kappa-1$ and
$d_k+k-1 \gt d_\kappa+\kappa-1$ and ![]() $d_k+k-1 \gt k$ if, simultaneously,
$d_k+k-1 \gt k$ if, simultaneously, ![]() $p \gt n+1$ and
$p \gt n+1$ and ![]() $k \lt \kappa$ (so
$k \lt \kappa$ (so ![]() $d_k \gt 0$). In that case, the unexpected homology is given by the difference
$d_k \gt 0$). In that case, the unexpected homology is given by the difference
 \begin{equation*} \beta_\kappa(\operatorname{im} f_t) - \beta_1^{\text{Alt}} \big( D^\kappa(f_t) \big),\end{equation*}
\begin{equation*} \beta_\kappa(\operatorname{im} f_t) - \beta_1^{\text{Alt}} \big( D^\kappa(f_t) \big),\end{equation*}if it is positive.
Now, we have the best approximation to a conservation principle for µI and νI: we have to eliminate the unexpected homology when necessary. This generalizes [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 2.8].
Theorem 5.10. Let ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ be an
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ be an ![]() $\mathscr{A}$-finite germ of corank one,
$\mathscr{A}$-finite germ of corank one, ![]() $n \lt p\leq2n$. Then, for any perturbation ft, if
$n \lt p\leq2n$. Then, for any perturbation ft, if  $\frac{p}{p-n}\notin\mathbb{Z}^+$:
$\frac{p}{p-n}\notin\mathbb{Z}^+$:
 \begin{equation}
\begin{array}{ll}
\mu_I(f)\!\!&= \sum\limits_{i\neq0,\kappa} \beta_{i}(\operatorname{im} f_t) + \sum\limits_{y\in\operatorname{im}(f_t)} \mu_I(f_t;y) - \beta_\kappa(\operatorname{im} f_t) +\delta,\, \text{and }\\
\nu_I(f)\!\!&= \sum\limits_{i\neq0,\kappa} (-1)^{i+d_2+1}\beta_{i}(\operatorname{im} f_t)\,{+}\, \!\sum\limits_{y\in\operatorname{im}(f_t)} \!\nu_I(f_t;y) \,{-}\, (-1)^{\kappa+d_2+1}\big(\beta_\kappa(\operatorname{im} f_t)\,{-}\,\delta\big);
\end{array}
\end{equation}
\begin{equation}
\begin{array}{ll}
\mu_I(f)\!\!&= \sum\limits_{i\neq0,\kappa} \beta_{i}(\operatorname{im} f_t) + \sum\limits_{y\in\operatorname{im}(f_t)} \mu_I(f_t;y) - \beta_\kappa(\operatorname{im} f_t) +\delta,\, \text{and }\\
\nu_I(f)\!\!&= \sum\limits_{i\neq0,\kappa} (-1)^{i+d_2+1}\beta_{i}(\operatorname{im} f_t)\,{+}\, \!\sum\limits_{y\in\operatorname{im}(f_t)} \!\nu_I(f_t;y) \,{-}\, (-1)^{\kappa+d_2+1}\big(\beta_\kappa(\operatorname{im} f_t)\,{-}\,\delta\big);
\end{array}
\end{equation} where ![]() $\delta=\beta_1^{\text{Alt}}\big(D^\kappa(f_t)\big)$ if
$\delta=\beta_1^{\text{Alt}}\big(D^\kappa(f_t)\big)$ if ![]() $d_\kappa=1$ and 0 otherwise (see remark 5.9).
$d_\kappa=1$ and 0 otherwise (see remark 5.9).
If  $\frac{p}{p-n}\in\mathbb{Z}^+$:
$\frac{p}{p-n}\in\mathbb{Z}^+$:
 \begin{equation}
\begin{array}{ll}
\mu_I(f)&= \sum\limits_{i\neq0} \beta_{i}(\operatorname{im} f_t) + \sum\limits_{y\in\operatorname{im}(f_t)} \mu_I(f_t;y) ,\, \text{and }\\
\nu_I(f)&= \sum\limits_{i\neq0} (-1)^{i+d_2+1}\beta_{i}(\operatorname{im} f_t) + \sum\limits_{y\in\operatorname{im}(f_t)} \nu_I(f_t;y),
\end{array}
\end{equation}
\begin{equation}
\begin{array}{ll}
\mu_I(f)&= \sum\limits_{i\neq0} \beta_{i}(\operatorname{im} f_t) + \sum\limits_{y\in\operatorname{im}(f_t)} \mu_I(f_t;y) ,\, \text{and }\\
\nu_I(f)&= \sum\limits_{i\neq0} (-1)^{i+d_2+1}\beta_{i}(\operatorname{im} f_t) + \sum\limits_{y\in\operatorname{im}(f_t)} \nu_I(f_t;y),
\end{array}
\end{equation}Proof. Assume that  $\frac{p}{p-n}\notin\mathbb{Z}^+$ and let us focus on the case of µI, the case νI is analogous keeping track of the signs.
$\frac{p}{p-n}\notin\mathbb{Z}^+$ and let us focus on the case of µI, the case νI is analogous keeping track of the signs.
Recall that (remark 5.3), in general, ![]() $\mu_k^{\text{Alt}}$ contributes in rank
$\mu_k^{\text{Alt}}$ contributes in rank ![]() $d_k+k-1$ for
$d_k+k-1$ for ![]() $k\leq\kappa$ and
$k\leq\kappa$ and  $\mu_{\kappa+1}^{\text{Alt}}$ in rank
$\mu_{\kappa+1}^{\text{Alt}}$ in rank ![]() $\kappa-1$:
$\kappa-1$:
 \begin{equation} \begin{array}{ll}
\mu_k^{\text{Alt}}(f) &= \beta_{d_k+k-1} (\operatorname{im} f_s) \quad\quad\quad\quad\, \text{for } k=2,\dots,\kappa-1\\
\mu_\kappa^{\text{Alt}}(f) &= \begin{cases}
\beta_{d_\kappa+\kappa-1} (\operatorname{im} f_s) & \, \text{if } d_\kappa\neq0\\
\beta_{d_\kappa+\kappa-1} (\operatorname{im} f_s) -\mu_{\kappa+1}^{\text{Alt}}(f) & \, \text{if } d_\kappa=0
\end{cases}\\
\mu_{\kappa+1}^{\text{Alt}}(f) &= \begin{cases}
\beta_{\kappa-1} (\operatorname{im} f_s) & \quad\quad\text{if } d_\kappa\neq0\\
\beta_{\kappa-1} (\operatorname{im} f_s) -\mu_{\kappa}^{\text{Alt}}(f) & \quad\quad\text{if } d_\kappa=0.
\end{cases}
\end{array}
\end{equation}
\begin{equation} \begin{array}{ll}
\mu_k^{\text{Alt}}(f) &= \beta_{d_k+k-1} (\operatorname{im} f_s) \quad\quad\quad\quad\, \text{for } k=2,\dots,\kappa-1\\
\mu_\kappa^{\text{Alt}}(f) &= \begin{cases}
\beta_{d_\kappa+\kappa-1} (\operatorname{im} f_s) & \, \text{if } d_\kappa\neq0\\
\beta_{d_\kappa+\kappa-1} (\operatorname{im} f_s) -\mu_{\kappa+1}^{\text{Alt}}(f) & \, \text{if } d_\kappa=0
\end{cases}\\
\mu_{\kappa+1}^{\text{Alt}}(f) &= \begin{cases}
\beta_{\kappa-1} (\operatorname{im} f_s) & \quad\quad\text{if } d_\kappa\neq0\\
\beta_{\kappa-1} (\operatorname{im} f_s) -\mu_{\kappa}^{\text{Alt}}(f) & \quad\quad\text{if } d_\kappa=0.
\end{cases}
\end{array}
\end{equation} By the conservation principle, theorem 4.1, and lemma 5.2; ![]() $\beta_k^{\text{Alt}}\big(D^k(f_t)\big)$ for
$\beta_k^{\text{Alt}}\big(D^k(f_t)\big)$ for ![]() $k\leq \kappa$ contributes positively to Eq. (19). This explains most of the positive terms of Eq. (19). It shows that
$k\leq \kappa$ contributes positively to Eq. (19). This explains most of the positive terms of Eq. (19). It shows that
 \begin{equation}
\sum_{k \lt \kappa}\mu_k^{\text{Alt}}(f)= \sum_{k \lt \kappa} \beta_{d_k+k-1}(\operatorname{im} f_t) + \sum_{y\in\operatorname{im}(f_t)} \sum_{k \lt \kappa}\mu_k^{\text{Alt}}(f_t;y),
\end{equation}
\begin{equation}
\sum_{k \lt \kappa}\mu_k^{\text{Alt}}(f)= \sum_{k \lt \kappa} \beta_{d_k+k-1}(\operatorname{im} f_t) + \sum_{y\in\operatorname{im}(f_t)} \sum_{k \lt \kappa}\mu_k^{\text{Alt}}(f_t;y),
\end{equation}and
 \begin{equation}
\mu_\kappa^{\text{Alt}}(f)=
\beta_{d_\kappa}^{\text{Alt}}\big(D^\kappa(f_t)\big)
+ \sum_{y\in\operatorname{im}(f_t)} \mu_\kappa^{\text{Alt}}(f_t;y).
\end{equation}
\begin{equation}
\mu_\kappa^{\text{Alt}}(f)=
\beta_{d_\kappa}^{\text{Alt}}\big(D^\kappa(f_t)\big)
+ \sum_{y\in\operatorname{im}(f_t)} \mu_\kappa^{\text{Alt}}(f_t;y).
\end{equation} If ![]() $d_\kappa\neq0$, we also have
$d_\kappa\neq0$, we also have
 \begin{equation*}\mu_\kappa^{\text{Alt}}(f)= \beta_{d_\kappa+\kappa-1}(\operatorname{im} f_t)+ \sum_{y\in\operatorname{im}(f_t)} \mu_\kappa^{\text{Alt}}(f_t;y).\end{equation*}
\begin{equation*}\mu_\kappa^{\text{Alt}}(f)= \beta_{d_\kappa+\kappa-1}(\operatorname{im} f_t)+ \sum_{y\in\operatorname{im}(f_t)} \mu_\kappa^{\text{Alt}}(f_t;y).\end{equation*} However, if ![]() $d_\kappa=0$, it can happen that
$d_\kappa=0$, it can happen that ![]() $\beta_{d_\kappa+\kappa-1}(\operatorname{im} f_t)$ is equal to
$\beta_{d_\kappa+\kappa-1}(\operatorname{im} f_t)$ is equal to  $\beta_{d_\kappa}^{\text{Alt}}\big(D^\kappa(f_t)\big) $ plus a contribution from the spaces
$\beta_{d_\kappa}^{\text{Alt}}\big(D^\kappa(f_t)\big) $ plus a contribution from the spaces ![]() $H_0^{\text{Alt}}\big(D^k(f_t)\big)$ for
$H_0^{\text{Alt}}\big(D^k(f_t)\big)$ for ![]() $k \gt \kappa$ (see Eq. (21)), similarly to the case for the stable perturbation but with
$k \gt \kappa$ (see Eq. (21)), similarly to the case for the stable perturbation but with ![]() $\mu_\kappa^{\text{Alt}}(f)$ and
$\mu_\kappa^{\text{Alt}}(f)$ and  $\mu_{\kappa+1}^{\text{Alt}}(f)$ (both contribute in rank
$\mu_{\kappa+1}^{\text{Alt}}(f)$ (both contribute in rank ![]() $\kappa-1$).
$\kappa-1$).
Hence, to prove Eq. (19), it is sufficient to show that
 \begin{align}
\mu_{\kappa+1}^{\text{Alt}}(f)=
\begin{cases}\beta_{\kappa-1}(\operatorname{im} f_t) +\sum_{y\in\operatorname{im}(f_t)} \mu_{\kappa+1}^{\text{Alt}}(f_t;y) -\beta_{\kappa}\big(\operatorname{im}(f_t)\big)+\delta \\ \qquad\qquad \text{if }d_\kappa\neq0\\
\beta_{\kappa-1}(\operatorname{im} f_t) -\beta_{d_\kappa}^{\text{Alt}}\big(D^\kappa(f_t)\big)+\sum_{y\in\operatorname{im}(f_t)} \mu_{\kappa+1}^{\text{Alt}}(f_t;y) -\beta_{\kappa}\big(\operatorname{im}(f_t)\big)+\delta \\ \qquad\qquad \text{if }d_\kappa=0
\end{cases}\!\!\!\!.\nonumber\\
\end{align}
\begin{align}
\mu_{\kappa+1}^{\text{Alt}}(f)=
\begin{cases}\beta_{\kappa-1}(\operatorname{im} f_t) +\sum_{y\in\operatorname{im}(f_t)} \mu_{\kappa+1}^{\text{Alt}}(f_t;y) -\beta_{\kappa}\big(\operatorname{im}(f_t)\big)+\delta \\ \qquad\qquad \text{if }d_\kappa\neq0\\
\beta_{\kappa-1}(\operatorname{im} f_t) -\beta_{d_\kappa}^{\text{Alt}}\big(D^\kappa(f_t)\big)+\sum_{y\in\operatorname{im}(f_t)} \mu_{\kappa+1}^{\text{Alt}}(f_t;y) -\beta_{\kappa}\big(\operatorname{im}(f_t)\big)+\delta \\ \qquad\qquad \text{if }d_\kappa=0
\end{cases}\!\!\!\!.\nonumber\\
\end{align}If we show this equation, the result follows by taking the sum of Eqs. (22)–(24).
Finally, we use the spectral sequence to compute the terms of Eq. (24):
• To compute
 $\mu_{\kappa+1}^{\text{Alt}}(f)$, we need the homologies
$\mu_{\kappa+1}^{\text{Alt}}(f)$, we need the homologies
 \begin{equation*}H_0^{\text{Alt}}\big(D^k(f)\big)\cong H_0^{\text{Alt}}\big(D^k(F)\big)\cong H_0^{\text{Alt}}\big(D^k(F),D^k(f_s)\big),\end{equation*}
\begin{equation*}H_0^{\text{Alt}}\big(D^k(f)\big)\cong H_0^{\text{Alt}}\big(D^k(F)\big)\cong H_0^{\text{Alt}}\big(D^k(F),D^k(f_s)\big),\end{equation*}for a versal unfolding F, a stable perturbation fs and
 $k \gt \kappa$ (therefore
$k \gt \kappa$ (therefore  $D^k(f_s)=\varnothing$).
$D^k(f_s)=\varnothing$).• To compute
 $\beta_{\kappa-1}(\operatorname{im} f_t)$, or
$\beta_{\kappa-1}(\operatorname{im} f_t)$, or  $\beta_{\kappa-1}(\operatorname{im} f_t) -\beta_{d_\kappa}^{\text{Alt}}\big(D^\kappa(f_t)\big)$ if
$\beta_{\kappa-1}(\operatorname{im} f_t) -\beta_{d_\kappa}^{\text{Alt}}\big(D^\kappa(f_t)\big)$ if  $d_\kappa=0$, we need the cokernels
$d_\kappa=0$, we need the cokernels
 \begin{equation*} C:= \operatorname{coker}\left( H_0^{\text{Alt}}\big(D^k(f_t)\big)\to H_0^{\text{Alt}}\big(D^k(F)\big)\right)\cong H_0^{\text{Alt}}\big( D^k(F), D^k(f_t) \big).\end{equation*}
\begin{equation*} C:= \operatorname{coker}\left( H_0^{\text{Alt}}\big(D^k(f_t)\big)\to H_0^{\text{Alt}}\big(D^k(F)\big)\right)\cong H_0^{\text{Alt}}\big( D^k(F), D^k(f_t) \big).\end{equation*}• To compute
 $\sum_y\mu_{\kappa+1}^{\text{Alt}}(f_t;y)$, we need the spaces
$\sum_y\mu_{\kappa+1}^{\text{Alt}}(f_t;y)$, we need the spaces
 \begin{equation*}H_0^{\text{Alt}}\big(D^k(f_t)\big)\cong I\oplus K\end{equation*}
\begin{equation*}H_0^{\text{Alt}}\big(D^k(f_t)\big)\cong I\oplus K\end{equation*}with
 $k \gt \kappa$ and
$k \gt \kappa$ and
 \begin{equation*}\begin{array}{l}
I := \operatorname{im}\left( H_0^{\text{Alt}}\big(D^k(f_t)\big)\to H_0^{\text{Alt}}\big(D^k(F)\big)\right),\\
K := \text{ker} \left( H_0^{\text{Alt}}\big(D^k(f_t)\big)\to H_0^{\text{Alt}}\big(D^k(F)\big)\right)\cong H_1^{\text{Alt}}\big( D^k(F), D^k(f_t) \big),
\end{array}\end{equation*}
\begin{equation*}\begin{array}{l}
I := \operatorname{im}\left( H_0^{\text{Alt}}\big(D^k(f_t)\big)\to H_0^{\text{Alt}}\big(D^k(F)\big)\right),\\
K := \text{ker} \left( H_0^{\text{Alt}}\big(D^k(f_t)\big)\to H_0^{\text{Alt}}\big(D^k(F)\big)\right)\cong H_1^{\text{Alt}}\big( D^k(F), D^k(f_t) \big),
\end{array}\end{equation*}• To compute
 $\beta_{\kappa}\big(\operatorname{im}(f_t)\big)+\delta$, which is precisely the unexpected homology, we need the spaces K.
$\beta_{\kappa}\big(\operatorname{im}(f_t)\big)+\delta$, which is precisely the unexpected homology, we need the spaces K.
Hence, since
 \begin{equation} \operatorname{dim} H_0^{\text{Alt}}\big(D^k(F)\big) = \operatorname{dim} C + \operatorname{dim} I = \operatorname{dim} C + \operatorname{dim} H_0^{\text{Alt}}\big(D^k(f_t)\big) - \operatorname{dim} K,
\end{equation}
\begin{equation} \operatorname{dim} H_0^{\text{Alt}}\big(D^k(F)\big) = \operatorname{dim} C + \operatorname{dim} I = \operatorname{dim} C + \operatorname{dim} H_0^{\text{Alt}}\big(D^k(f_t)\big) - \operatorname{dim} K,
\end{equation}we can show that Eq. (24) holds, after a combinatorial argument.
The Eq. (20) follows from the previous argument, since there is no unexpected homology.
Example 5.11. In the deformation ht of example 4.2, there is an instability at the origin with ![]() $\mu_I(h_t;0)=1$ given only by
$\mu_I(h_t;0)=1$ given only by  $\mu_{d(h)+1}^{\text{Alt}}(h_t)$, but also unexpected homology
$\mu_{d(h)+1}^{\text{Alt}}(h_t)$, but also unexpected homology ![]() $\beta_{\kappa}(\operatorname{im} h_t)=1$. Cancelling these quantities we recover the conservation of the µI (this is illustrated in figure 8).
$\beta_{\kappa}(\operatorname{im} h_t)=1$. Cancelling these quantities we recover the conservation of the µI (this is illustrated in figure 8).

Figure 8. Comparison between unexpected homology and  $\mu_{d(h)+1}^{\text{Alt}}(h_t)$: the homology of
$\mu_{d(h)+1}^{\text{Alt}}(h_t)$: the homology of ![]() $\operatorname{im} h_t$ is killed when we take the stable perturbation hs, and this unexpected homology is reflected in the
$\operatorname{im} h_t$ is killed when we take the stable perturbation hs, and this unexpected homology is reflected in the  $\mu_{d(h)+1}^{\text{Alt}}(h_t)$ at the new instability (red dot). See example 5.11.
$\mu_{d(h)+1}^{\text{Alt}}(h_t)$ at the new instability (red dot). See example 5.11.
6. Houston’s conjecture on excellent unfoldings
Houston conjectured in [Reference Houston19, conjecture 6.2] that excellency in families can be controlled by means of the image Milnor number, for any p > n, in corank one. In the same article, Houston gave a partial answer in [Reference Houston19, corollary 5.9], where the family has to be good (and more assumptions). This conjecture was proved by the author and Nuño-Ballesteros for ![]() $p=n+1$ in [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 4.3]. We present now a complete answer using our new approach, giving counterexamples and providing a correct modification of the statement of the conjecture which we also prove. An answer to the conjecture [Reference Giménez Conejero and Nuño-Ballesteros7, conjecture 4.6], which asks about the converse, is also given.
$p=n+1$ in [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 4.3]. We present now a complete answer using our new approach, giving counterexamples and providing a correct modification of the statement of the conjecture which we also prove. An answer to the conjecture [Reference Giménez Conejero and Nuño-Ballesteros7, conjecture 4.6], which asks about the converse, is also given.
Definition 6.1. Let ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ be an
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ be an ![]() $\mathscr{A}$-finite germ. We say that an origin-preserving one-parameter unfolding
$\mathscr{A}$-finite germ. We say that an origin-preserving one-parameter unfolding ![]() $F(x,t)=\big(f_t(x),t\big)$ is good if there exists a representative
$F(x,t)=\big(f_t(x),t\big)$ is good if there exists a representative ![]() $F:U\to W\times T$, where U is an open neighbourhood of
$F:U\to W\times T$, where U is an open neighbourhood of ![]() $S\times\{0\}$ in
$S\times\{0\}$ in ![]() $\mathbb{C}^n\times\mathbb{C}$ and
$\mathbb{C}^n\times\mathbb{C}$ and ![]() $W,$ T are open neighbourhoods of the origin in
$W,$ T are open neighbourhoods of the origin in ![]() $\mathbb{C}^{p},$
$\mathbb{C}^{p},$ ![]() $\mathbb{C}$ respectively, such that
$\mathbb{C}$ respectively, such that
(i) F is finite,
(ii)
 $f_t^{-1}(0)=S$, for all
$f_t^{-1}(0)=S$, for all  $t\in T$,
$t\in T$,(iii) ft is locally stable on
 $W-\left\{0\right\}$, for all
$W-\left\{0\right\}$, for all  $t\in T$.
$t\in T$.
If, in addition, ft has no 0-stable singularities on ![]() $W-\{0\}$ (i.e., stable singularities whose isosingular locus is zero-dimensional, see [Reference Houston19, definition 5.2] or [Reference Mond and Nuño-Ballesteros27, p. 93]) we say that ft is excellent (in Gaffney’s sense).
$W-\{0\}$ (i.e., stable singularities whose isosingular locus is zero-dimensional, see [Reference Houston19, definition 5.2] or [Reference Mond and Nuño-Ballesteros27, p. 93]) we say that ft is excellent (in Gaffney’s sense).
Excellent unfoldings play an important role in the theory of equisingularity of families of germs (see, for example, [Reference Gaffney5]). See figure 9 for a representation of an excellent unfolding.

Figure 9. A non-excellent unfolding (left) due to the presence of a one-dimensional stratum, of stable or unstable points, distinct from the parameter axis (red and green, respectively), and an excellent unfolding (right) with only one stratum of dimension one (green).
Now we can state Houston’s conjecture on excellent unfoldings (see [Reference Houston19, conjecture 6.2]).
Conjecture 6.2. (Houston’s conjecture)
Let ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be ![]() $\mathscr{A}$-finite of corank one and let
$\mathscr{A}$-finite of corank one and let ![]() $F(x,t)=\big(f_t(x),t\big)$ be an origin-preserving one-parameter unfolding. Then, if
$F(x,t)=\big(f_t(x),t\big)$ be an origin-preserving one-parameter unfolding. Then, if ![]() $\widetilde{f_t}$ are the germs
$\widetilde{f_t}$ are the germs ![]() $f_t:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$,
$f_t:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$,  $\mu_I(\widetilde{f_t})$ constant implies F excellent.
$\mu_I(\widetilde{f_t})$ constant implies F excellent.
We give a counterexample to this conjecture in example 6.3. We also give the correct modification of the conjecture, which we also prove, in theorem 6.4.
Example 6.3. The map germ ![]() $f:(\mathbb{C}^7,0)\to(\mathbb{C}^{11},0)$ with one-parameter unfolding given by
$f:(\mathbb{C}^7,0)\to(\mathbb{C}^{11},0)$ with one-parameter unfolding given by
 \begin{equation*} f_t(\underline{x},y)=\big(\underline{x},\ x_6y+y^6,\ x_5y+y^5,\ x_4y+y^4,\ x_3^2y+y^3,\ x_2y+y^2(x_1^2-tx_1)\big)\end{equation*}
\begin{equation*} f_t(\underline{x},y)=\big(\underline{x},\ x_6y+y^6,\ x_5y+y^5,\ x_4y+y^4,\ x_3^2y+y^3,\ x_2y+y^2(x_1^2-tx_1)\big)\end{equation*} has ![]() $D^2(f_t)$ with constant Milnor number (at the origin) for all t and
$D^2(f_t)$ with constant Milnor number (at the origin) for all t and
so ft has two instabilities when t ≠ 0 and ![]() $\mu_I(f_t;0) \gt 0$ is constant (see theorem 5.4).
$\mu_I(f_t;0) \gt 0$ is constant (see theorem 5.4).
Theorem 6.4. (cf. [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 4.3])
Let ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be ![]() $\mathscr{A}$-finite of corank one and let
$\mathscr{A}$-finite of corank one and let ![]() $F(x,t)=\big(f_t(x),t\big)$ be an origin-preserving one-parameter unfolding. Assume that ft has neither strongly contractible instabilities nor unexpected homology. Then, if
$F(x,t)=\big(f_t(x),t\big)$ be an origin-preserving one-parameter unfolding. Assume that ft has neither strongly contractible instabilities nor unexpected homology. Then, if ![]() $\widetilde{f_t}$ are the germs
$\widetilde{f_t}$ are the germs ![]() $f_t:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$,
$f_t:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$,  $\mu_I(\widetilde{f_t})$ constant implies F excellent.
$\mu_I(\widetilde{f_t})$ constant implies F excellent.
Proof. We can assume that f is unstable, otherwise it is trivial. By [Reference Houston19, corollary 5.9], we only need to prove goodness of the unfolding and that, for the induced germ from ft at zero (not necessarily equal to ![]() $\widetilde{f_t}$), either
$\widetilde{f_t}$), either ![]() $s(f_t;0)\leq d(f_t;0)$ for all t or both are constant.
$s(f_t;0)\leq d(f_t;0)$ for all t or both are constant.
That the unfolding F is good follows from the hypotheses. Indeed, we have conservation of the µI because there is no unexpected homology (see theorem 5.10) and every instability has positive µI, by the absence of strongly contractible instabilities. Hence, the constancy of the image Milnor number implies that there is only one instability (the origin) for each ft, this confirms Item (iii) of definition 6.1.
If ![]() $s(f_t;0) \gt d(f_t;0)$ for some t, then
$s(f_t;0) \gt d(f_t;0)$ for some t, then  $d(f_t)=\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor$ by remark 3.7 and
$d(f_t)=\kappa=\left\lfloor \frac{p}{p-n}\right\rfloor$ by remark 3.7 and
 \begin{equation*}\mu_{d(f)+1}^{\text{Alt}}(f_t;0) \gt 0.\end{equation*}
\begin{equation*}\mu_{d(f)+1}^{\text{Alt}}(f_t;0) \gt 0.\end{equation*} Because we are in conditions of conservation of µI, µI and every ![]() $\mu_k^{\text{Alt}}$ is upper semi-continuous; so necessarily
$\mu_k^{\text{Alt}}$ is upper semi-continuous; so necessarily
 \begin{equation*}\mu_{d(f)+1}^{\text{Alt}}(f;0) \gt 0\end{equation*}
\begin{equation*}\mu_{d(f)+1}^{\text{Alt}}(f;0) \gt 0\end{equation*} and ![]() $s(f) \gt d(f)=\kappa$. We only need to prove that
$s(f) \gt d(f)=\kappa$. We only need to prove that ![]() $s(f_t;0)=s(f)$. As F is origin-preserving, we already know that
$s(f_t;0)=s(f)$. As F is origin-preserving, we already know that  $s(f_t;0)\geq s\big(\widetilde{f_t}\big)=s(f)$ but, if the inequality is strict, then
$s(f_t;0)\geq s\big(\widetilde{f_t}\big)=s(f)$ but, if the inequality is strict, then
 \begin{equation*} \mu_{d(f)+1}^{\text{Alt}}(f_t;0) \gt \mu_{d(f)+1}^{\text{Alt}}(f), \end{equation*}
\begin{equation*} \mu_{d(f)+1}^{\text{Alt}}(f_t;0) \gt \mu_{d(f)+1}^{\text{Alt}}(f), \end{equation*}which is absurd by upper semi-continuity of µI.
It is not difficult to see the reason to add the hypothesis on strongly contractible instabilities: once we know that there are instabilities with ![]() $\mu_I=0$, we could find perturbations ft with strongly contractible instabilities splitting from the instability at the origin (see a non-trivial example in example 6.3).
$\mu_I=0$, we could find perturbations ft with strongly contractible instabilities splitting from the instability at the origin (see a non-trivial example in example 6.3).
The condition on unexpected homology is also easy to understand: there could be constancy of the µI while having instabilities away from the origin because of the creation of unexpected homology (that makes instabilities with ![]() $s(\bullet) \gt d(\bullet)$, possibly at the origin, by theorem 5.10). In other words, without strongly contractible instabilities and unexpected homology, the presence of one instability away from the origin implies that µI cannot be constant at the origin; but, with unexpected homology, it could happen that the reduction of the µI at the origin is counterbalanced with more branches because of the creation of unexpected homology.
$s(\bullet) \gt d(\bullet)$, possibly at the origin, by theorem 5.10). In other words, without strongly contractible instabilities and unexpected homology, the presence of one instability away from the origin implies that µI cannot be constant at the origin; but, with unexpected homology, it could happen that the reduction of the µI at the origin is counterbalanced with more branches because of the creation of unexpected homology.
Corollary 6.5. Let ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$, n < p, be ![]() $\mathscr{A}$-finite of corank one and let
$\mathscr{A}$-finite of corank one and let ![]() $F(x,t)=\big(f_t(x),t\big)$ be an origin-preserving one-parameter unfolding. Assume that
$F(x,t)=\big(f_t(x),t\big)$ be an origin-preserving one-parameter unfolding. Assume that ![]() $D^k(f)=\varnothing$ for
$D^k(f)=\varnothing$ for ![]() $d_k \lt 0$. Then, if
$d_k \lt 0$. Then, if ![]() $\widetilde{f_t}$ are the germs
$\widetilde{f_t}$ are the germs ![]() $f_t:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$,
$f_t:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$,  $\mu_I(\widetilde{f_t})$ constant implies F excellent.
$\mu_I(\widetilde{f_t})$ constant implies F excellent.
Proof. In this case, there are no strongly contractible instabilities nor unexpected homology in any perturbation (see Section 3 and remark 5.9).
We can ask about the converse of this result, i.e., if excellency implies the constancy of the image Milnor number. This was addressed in [Reference Giménez Conejero and Nuño-Ballesteros7, proposition 4.4], where the author and Nuño-Ballesteros provide a proof for the case ![]() $(n,p)=(1,2)$ and
$(n,p)=(1,2)$ and ![]() $(n,p)=(2,3)$. There is, however, a small mistake in the proof of the case
$(n,p)=(2,3)$. There is, however, a small mistake in the proof of the case ![]() $(n,p)=(2,3)$: one needs to assume that ft has an instability, as the following example shows.
$(n,p)=(2,3)$: one needs to assume that ft has an instability, as the following example shows.
Example 6.6. The tangent double point germ given in example 4.3, ![]() $f:\big(\mathbb{C}^2,\{0,0'\}\big)\to(\mathbb{C}^3,0)$ given by
$f:\big(\mathbb{C}^2,\{0,0'\}\big)\to(\mathbb{C}^3,0)$ given by
 \begin{equation*} \left\{\begin{array}{ll}
(x,y)&\mapsto (x,y,x^2+y^2)\\
(x',y')&\mapsto(x',y',0)
\end{array}\right. \end{equation*}
\begin{equation*} \left\{\begin{array}{ll}
(x,y)&\mapsto (x,y,x^2+y^2)\\
(x',y')&\mapsto(x',y',0)
\end{array}\right. \end{equation*}has an excellent one-parameter unfolding such that ft is stable at every point and which also preserves the origin (see figure 10):
 \begin{equation*} \left\{\begin{array}{ll}
(x,y)&\mapsto \big(x,y\cos(t)-\sin(t)(x^2+y^2),\cos(t)(x^2+y^2)-\sin(t)y\big)\\
(x',y')&\mapsto(x',y',0)
\end{array}.\right. \end{equation*}
\begin{equation*} \left\{\begin{array}{ll}
(x,y)&\mapsto \big(x,y\cos(t)-\sin(t)(x^2+y^2),\cos(t)(x^2+y^2)-\sin(t)y\big)\\
(x',y')&\mapsto(x',y',0)
\end{array}.\right. \end{equation*}@@
This implies that there are excellent families ft with ![]() $\mu_I(f_t;0)$ not constant. However, the tangent double point is the only example of this phenomenon in these dimensions, any other excellent family has an instability.
$\mu_I(f_t;0)$ not constant. However, the tangent double point is the only example of this phenomenon in these dimensions, any other excellent family has an instability.

Figure 10. Deformation ft that is excellent but does not have constant image Milnor number.
The same authors presented [Reference Giménez Conejero and Nuño-Ballesteros7, conjecture 4.6] for the remaining cases, which we prove now false by a counterexample:
Example 6.7. A fold singularity is an ![]() $\mathscr{A}$-finite germ
$\mathscr{A}$-finite germ ![]() $f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$ that is
$f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$ that is ![]() $\mathscr{A}$-equivalent to
$\mathscr{A}$-equivalent to ![]() $f(\underline{x},y)=\big(\underline{x},y^2,yp_{n+1}(\underline{x},y),\dots,yp_{p}(\underline{x},y)\big)$, where
$f(\underline{x},y)=\big(\underline{x},y^2,yp_{n+1}(\underline{x},y),\dots,yp_{p}(\underline{x},y)\big)$, where ![]() $p_i(\underline{x},y)$ are polynomials.
$p_i(\underline{x},y)$ are polynomials.
If we consider a fold germ ![]() $f:(\mathbb{C}^{3},0)\rightarrow(\mathbb{C}^{4},0)$, none of its perturbations has zero-stable points (stable singularities whose isosingular locus is zero-dimensional). This comes from the fact that zero-stable points in corank one are in one-to-one correspondence with multiple point spaces
$f:(\mathbb{C}^{3},0)\rightarrow(\mathbb{C}^{4},0)$, none of its perturbations has zero-stable points (stable singularities whose isosingular locus is zero-dimensional). This comes from the fact that zero-stable points in corank one are in one-to-one correspondence with multiple point spaces ![]() $D^k(\bullet)^\sigma$ such that
$D^k(\bullet)^\sigma$ such that ![]() $d_k^\sigma=0$. However, these germs only have double points, so
$d_k^\sigma=0$. However, these germs only have double points, so ![]() $D^{2+\ell}(f)=\varnothing$ for
$D^{2+\ell}(f)=\varnothing$ for ![]() $\ell \gt 0$, and
$\ell \gt 0$, and  $d_2,d_2^{(1\; 2)}\geq1$.
$d_2,d_2^{(1\; 2)}\geq1$.
One can certainly find many excellent families, for example given by stable perturbations fs that fix the origin (which can be assumed), such that ![]() $\mu_I(f) \gt \mu_I(f_s)=0$.
$\mu_I(f) \gt \mu_I(f_s)=0$.
Example 6.7 works for any pair ![]() $(n,n+1)\neq(1,2),(2,3)$, so [Reference Giménez Conejero and Nuño-Ballesteros7, proposition 4.4] is, indeed, optimal if we add the detail about the presence of an instability in every ft.
$(n,n+1)\neq(1,2),(2,3)$, so [Reference Giménez Conejero and Nuño-Ballesteros7, proposition 4.4] is, indeed, optimal if we add the detail about the presence of an instability in every ft.
Note. This kind of counterexamples with fold maps was found, independently but also simultaneously, by the author, Oset Sinha and Nuño-Ballesteros after fruitful conversations between them.
Regarding the general question in dimensions (n, p), we can give a complete answer.
Proposition 6.8. In the context of ![]() $\mathscr{A}$-finite map germs
$\mathscr{A}$-finite map germs ![]() $f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one, for
$f:(\mathbb{C}^{n},S)\rightarrow(\mathbb{C}^{p},0)$ of corank one, for ![]() $n \lt p \lt 2n$, there are excellent families with non-constant image Milnor number. Furthermore, for
$n \lt p \lt 2n$, there are excellent families with non-constant image Milnor number. Furthermore, for ![]() $n=2p$, excellency implies constancy of µI.
$n=2p$, excellency implies constancy of µI.
Proof. Observe that ![]() $p=2n$ is equivalent to
$p=2n$ is equivalent to ![]() $d_2=0$, and
$d_2=0$, and ![]() $p \lt 2n$ to
$p \lt 2n$ to ![]() $d_2 \gt 0$. Hence, we can divide by cases depending on d 2.
$d_2 \gt 0$. Hence, we can divide by cases depending on d 2.
If ![]() $d_2 \gt 1$, one can always find fold germs that are unstable and they all give counterexamples (as we have seen in example 6.7).
$d_2 \gt 1$, one can always find fold germs that are unstable and they all give counterexamples (as we have seen in example 6.7).
If ![]() $d_2=0,1$, the presence of strongly contractible instabilities is not a problem: they do not change the image Milnor number. The case
$d_2=0,1$, the presence of strongly contractible instabilities is not a problem: they do not change the image Milnor number. The case ![]() $d_2=0$ is easy, µI only depends on the number of points in the fibre of the zero-dimensional icis
$d_2=0$ is easy, µI only depends on the number of points in the fibre of the zero-dimensional icis ![]() $D^2(f)$ (see theorem 4.7), so a change in µI implies presence of more than one instability or some zero-dimensional stable points, making the unfolding not excellent.
$D^2(f)$ (see theorem 4.7), so a change in µI implies presence of more than one instability or some zero-dimensional stable points, making the unfolding not excellent.
If ![]() $d_2=1$, then
$d_2=1$, then ![]() $p=2n-1$. We take the idea of example 6.6. Hence, we consider the germ
$p=2n-1$. We take the idea of example 6.6. Hence, we consider the germ ![]() $f:\big(\mathbb{C}^n,\{0,0'\}\big)\to(\mathbb{C}^{2n-1},0)$ given by the generalization of the tangent double point given in examples 4.3 and 6.6, i.e.,
$f:\big(\mathbb{C}^n,\{0,0'\}\big)\to(\mathbb{C}^{2n-1},0)$ given by the generalization of the tangent double point given in examples 4.3 and 6.6, i.e.,
 \begin{equation*} \left\{\begin{array}{ll}
(x_1,\dots,x_n)&\mapsto (x_1,\dots,x_{n},x_1,\dots,x_{n-2},x_{n-1}^2+x_{n}^2)\\
(x_1',\dots,x_n')&\mapsto(x_1',\dots,x_{n}',0,\dots,0)
\end{array}.\right. \end{equation*}
\begin{equation*} \left\{\begin{array}{ll}
(x_1,\dots,x_n)&\mapsto (x_1,\dots,x_{n},x_1,\dots,x_{n-2},x_{n-1}^2+x_{n}^2)\\
(x_1',\dots,x_n')&\mapsto(x_1',\dots,x_{n}',0,\dots,0)
\end{array}.\right. \end{equation*} The equations of ![]() $D^2(f)\subset\mathbb{C}^{n+n}$ are
$D^2(f)\subset\mathbb{C}^{n+n}$ are ![]() $x_i=x_i'$,
$x_i=x_i'$, ![]() $x_1=\dots=x_{n-2}=0$ and
$x_1=\dots=x_{n-2}=0$ and ![]() $x_{n-1}^2+x_{n}^2=0$, which gives an icis of dimension one. Furthermore,
$x_{n-1}^2+x_{n}^2=0$, which gives an icis of dimension one. Furthermore, ![]() $D^k(f)=\varnothing$ for k > 2, so f is
$D^k(f)=\varnothing$ for k > 2, so f is ![]() $\mathscr{A}$-finite by the Marar–Mond criterion theorem 3.3. Since there are no points fixed by the permutation
$\mathscr{A}$-finite by the Marar–Mond criterion theorem 3.3. Since there are no points fixed by the permutation ![]() $(1\: 2)\in\Sigma_2$ (as in the tangent double point example 4.3), i.e.,
$(1\: 2)\in\Sigma_2$ (as in the tangent double point example 4.3), i.e., ![]() $D^2(f)^{(1\:2)}=\varnothing$, any stable deformation on one parameter fs is excellent because there are no 0-stable singularities (similarly to what was explained in example 6.6).
$D^2(f)^{(1\:2)}=\varnothing$, any stable deformation on one parameter fs is excellent because there are no 0-stable singularities (similarly to what was explained in example 6.6).
7. Conclusions and open problems
As we have seen, the technique leading to theorems 4.7 and 5.4 allows us to translate the invariants µI and νI into Milnor numbers of icis in corank one. In corank two or higher one could do something similar, but Euler–Poincaré characteristics of some varieties would need to be used. Indeed, as we have pointed out in remark 5.5, this is the correct generalization of the Marar–Mond formulae for µI, see [Reference Marar and Mond23].
Several applications of this technique were shown, such as the proof Houston’s conjecture theorem 6.4. The main goal of this article is being able to bypass the difficulty of working with µI and use the easier-to-handle Milnor numbers of icis. Furthermore, we have clarified many traits of deformations of ![]() $\mathscr{A}$-finite germs
$\mathscr{A}$-finite germs ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, with n < p, using these ideas. However, we have only seen the corank one case. It seems natural to conjecture the following, generalizing the notion of strongly contractible germs to any corank.
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, with n < p, using these ideas. However, we have only seen the corank one case. It seems natural to conjecture the following, generalizing the notion of strongly contractible germs to any corank.
Open Problem 7.1. Show that there are unstable ![]() $\mathscr{A}$-finite germs
$\mathscr{A}$-finite germs ![]() $f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$, n < p, of corank bigger than one such that have contractible stable perturbation.
$f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$, n < p, of corank bigger than one such that have contractible stable perturbation.
Moreover, it is unclear what are the dimensions where we can find strongly contractible multi-germs (even of corank one). We know, by example 4.2, that theorem 3.18 is not sharp for multi-germs. There are some results regarding this: by [Reference Giménez Conejero and Nuño-Ballesteros9, theorem 2.15] (corank one case was also given in [Reference Giménez Conejero and Nuño-Ballesteros7, theorem 3.9]), if ![]() $p=n+1$ then every stable perturbation of an unstable germ f has non-trivial homology, i.e.,
$p=n+1$ then every stable perturbation of an unstable germ f has non-trivial homology, i.e., ![]() $\mu_I(f) \gt 0$.
$\mu_I(f) \gt 0$.
It is, however, reasonable to think that there are no strongly contractible germs if, and only if, ![]() $d_\kappa=0$ (i.e., if
$d_\kappa=0$ (i.e., if  $\frac{p}{p-n}\in\mathbb{Z}^+$) because it seems that strongly contractible germs and unexpected homology (controlled by theorem 4.8) have something in common: see example 4.2 where a strongly contractible bi-germ given from ft at the origin appears together with some unexpected homology of a deformation of another germ h (recall the discussion on §5.2).
$\frac{p}{p-n}\in\mathbb{Z}^+$) because it seems that strongly contractible germs and unexpected homology (controlled by theorem 4.8) have something in common: see example 4.2 where a strongly contractible bi-germ given from ft at the origin appears together with some unexpected homology of a deformation of another germ h (recall the discussion on §5.2).
Open Problem 7.2. There are unstable ![]() $\mathscr{A}$-finite germs
$\mathscr{A}$-finite germs ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, n < p, such that
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, n < p, such that ![]() $\operatorname{im} f_s$ is contractible if, and only if,
$\operatorname{im} f_s$ is contractible if, and only if,  $\frac{p}{p-n}\notin\mathbb{Z}^+$; for fs the stable perturbation.
$\frac{p}{p-n}\notin\mathbb{Z}^+$; for fs the stable perturbation.
Open Problem 7.3. Also, the weakened version of this conjecture for corank one is the generalization of theorem 3.18:
There are strongly contractible multi-germs ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$ of corank one, n < p, if, and only if,
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$ of corank one, n < p, if, and only if,  $\frac{p}{p-n}\notin\mathbb{Z}^+$.
$\frac{p}{p-n}\notin\mathbb{Z}^+$.
Going back to the corank one case, and regarding unexpected homology, it is not clear that mono-germs have deformations with unexpected homology. Indeed, every example, such as example 4.2, seems to need more than one branch to find a deformation with unexpected homology.
Open Problem 7.4. There are no ![]() $\mathscr{A}$-finite mono-germs
$\mathscr{A}$-finite mono-germs ![]() $f:(\mathbb{C}^{n},0)\rightarrow(\mathbb{C}^{p},0)$, with n < p, such that they have a deformation with unexpected homology.
$f:(\mathbb{C}^{n},0)\rightarrow(\mathbb{C}^{p},0)$, with n < p, such that they have a deformation with unexpected homology.
This would eliminate the hypothesis of unexpected homology of theorem 6.4 for the case of mono-germs and, indeed, example 4.2 is not a counterexample since it is a bi-germ.
Finally, the initial motivation of this article was solving the following conjecture.
Conjecture 7.5.
For ![]() $\mathscr{A}$-finite germs
$\mathscr{A}$-finite germs ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^{n+1},0)$, there cannot be coalescence of instabilities in one-parameter deformations. In other words, a one-parameter deformation ft of f cannot have more than one instability and contractible image,
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^{n+1},0)$, there cannot be coalescence of instabilities in one-parameter deformations. In other words, a one-parameter deformation ft of f cannot have more than one instability and contractible image, ![]() $\operatorname{im} f_t$, at the same time.
$\operatorname{im} f_t$, at the same time.
Regarding coalescence of instabilities in the general case n < p, it is not clear that there are mono-germs with coalescence of strongly contractible germs when theorem 3.18 holds with equality: ![]() $d_\kappa-\kappa=0$. The germ given in example 6.3, which has this coalescence, has
$d_\kappa-\kappa=0$. The germ given in example 6.3, which has this coalescence, has ![]() $d_\kappa-\kappa=1$.
$d_\kappa-\kappa=1$.
Open Problem 7.6. There are no ![]() $\mathscr{A}$-finite germs
$\mathscr{A}$-finite germs ![]() $f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$ of corank one such that they have coalescence of strongly contractible instabilities and
$f:(\mathbb{C}^n,0)\to(\mathbb{C}^p,0)$ of corank one such that they have coalescence of strongly contractible instabilities and ![]() $d_\kappa-\kappa=0$.
$d_\kappa-\kappa=0$.
Remark 7.7. The Mond conjecture is a long-standing open problem of map germs ![]() $f:(\mathbb{C}^n,S)\to(\mathbb{C}^{n+1},0)$, stating that the
$f:(\mathbb{C}^n,S)\to(\mathbb{C}^{n+1},0)$, stating that the ![]() $\mathscr{A}_e$-codimension is lower or equal that the µI, with equality in the quasi-homogeneous case. The literature on this problem is vast and points to a positive answer, but the general statement remains open (see [Reference Cooper, Mond and Wik Atique2, Reference de Jong and van Straten3, Reference Houston17, Reference Houston and Kirk20, Reference Mond26, Reference Sharland30, Reference Sharland31] among many others). It seems reasonable to think that there is a version of theorem 5.4 for the
$\mathscr{A}_e$-codimension is lower or equal that the µI, with equality in the quasi-homogeneous case. The literature on this problem is vast and points to a positive answer, but the general statement remains open (see [Reference Cooper, Mond and Wik Atique2, Reference de Jong and van Straten3, Reference Houston17, Reference Houston and Kirk20, Reference Mond26, Reference Sharland30, Reference Sharland31] among many others). It seems reasonable to think that there is a version of theorem 5.4 for the ![]() $\mathscr{A}_e$-codimension, translating it into invariants of icis. This would lead to a possible proof of the conjecture in corank one, based on the known inequality
$\mathscr{A}_e$-codimension, translating it into invariants of icis. This would lead to a possible proof of the conjecture in corank one, based on the known inequality ![]() $\mu\geq\tau$ for icis of positive dimension (see [Reference Greuel12, Reference Greuel14, Reference Looijenga and Steenbrink21] and the nice survey [Reference Greuel13]). In turn, this could lead to a full proof with some ideas from [Reference Fernández de Bobadilla, Nuño Ballesteros and Peñafort Sanchis4]. However, it is not clear what is the analogue of theorem 5.4 for the
$\mu\geq\tau$ for icis of positive dimension (see [Reference Greuel12, Reference Greuel14, Reference Looijenga and Steenbrink21] and the nice survey [Reference Greuel13]). In turn, this could lead to a full proof with some ideas from [Reference Fernández de Bobadilla, Nuño Ballesteros and Peñafort Sanchis4]. However, it is not clear what is the analogue of theorem 5.4 for the ![]() $\mathscr{A}_e$-codimension.
$\mathscr{A}_e$-codimension.
Furthermore, conjecture 7.5 has deep connections with this conjecture as both relate the same invariants (see [Reference Giménez Conejero6, Section 7.3]): one-parameter unfoldings correspond to curves in the parameter space of a versal unfolding.
Acknowledgements
The author thanks Joan Francesc Tent Jorques and Alexander Moretó Quintana for useful indications regarding representation theory. A special mention is to be made about very fruitful conversations between the author and David Mond.
Funding
This work was supported by Ministerio de Ciencia, Innovación y Universidades (MICINN) [PID2021-124577NB-I00].