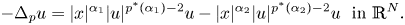1. Introduction
In this paper, we consider the ![]() $p$-Hénon equation
$p$-Hénon equation
 \begin{equation} \left\{ \begin{array}{@{}ll} \displaystyle-\Delta_p u=|x|^{\alpha_1}|u|^{p^{*}(\alpha_1)-2}u-|x|^{\alpha_2}|u|^{p^{*}(\alpha_2)-2}u\ \ {\rm in}\ \mathbb{R}^{N},\\ \displaystyle u\in D^{1,p}_r(\mathbb{R}^{N}), \end{array} \right.\end{equation}
\begin{equation} \left\{ \begin{array}{@{}ll} \displaystyle-\Delta_p u=|x|^{\alpha_1}|u|^{p^{*}(\alpha_1)-2}u-|x|^{\alpha_2}|u|^{p^{*}(\alpha_2)-2}u\ \ {\rm in}\ \mathbb{R}^{N},\\ \displaystyle u\in D^{1,p}_r(\mathbb{R}^{N}), \end{array} \right.\end{equation}
where ![]() $1< p< N$,
$1< p< N$, ![]() $\Delta _p u= \hbox {div}(|\nabla u|^{p-2}\nabla u)$,
$\Delta _p u= \hbox {div}(|\nabla u|^{p-2}\nabla u)$, ![]() $\alpha _1>\alpha _2>-p$,
$\alpha _1>\alpha _2>-p$, ![]() $p^{*}(\alpha _i)=\frac {p(N+\alpha _i)}{N-p}\ (i=1,\,2)$, and
$p^{*}(\alpha _i)=\frac {p(N+\alpha _i)}{N-p}\ (i=1,\,2)$, and ![]() $D_r^{1,p}(\mathbb {R}^{N})=\left \{u \in D^{1,p}(\mathbb {R}^{N}): u \ \hbox {is radial}\right \}$,
$D_r^{1,p}(\mathbb {R}^{N})=\left \{u \in D^{1,p}(\mathbb {R}^{N}): u \ \hbox {is radial}\right \}$, ![]() $D^{1,p}(\mathbb {R}^{N})$ is the completion of
$D^{1,p}(\mathbb {R}^{N})$ is the completion of ![]() $C_0^{\infty }(\mathbb {R}^{N})$ under the norm
$C_0^{\infty }(\mathbb {R}^{N})$ under the norm ![]() $\|u\|:=(\int _{\mathbb {R}^{N}} |\nabla u|^{p} {\rm d}x)^{1/p}$,
$\|u\|:=(\int _{\mathbb {R}^{N}} |\nabla u|^{p} {\rm d}x)^{1/p}$, ![]() $C_{0,r}^{\infty }(\mathbb {R}^{N})=\left \{u \in C_0^{\infty }(\mathbb {R}^{N}): \ u \ \hbox {is radial}\right \}$.
$C_{0,r}^{\infty }(\mathbb {R}^{N})=\left \{u \in C_0^{\infty }(\mathbb {R}^{N}): \ u \ \hbox {is radial}\right \}$.
For ![]() $q\geqslant 1$,
$q\geqslant 1$, ![]() $\alpha \in \mathbb {R}$, let
$\alpha \in \mathbb {R}$, let
be the weighted Lebesgue space with the norm ![]() $\|u\|_{q, \alpha }:=(\int _{\mathbb {R}^{N}} |x|^{\alpha } |u|^{q}{\rm d}x)^{1/q}$. For all
$\|u\|_{q, \alpha }:=(\int _{\mathbb {R}^{N}} |x|^{\alpha } |u|^{q}{\rm d}x)^{1/q}$. For all ![]() $\alpha >-p$, the best weighted Sobolev constant
$\alpha >-p$, the best weighted Sobolev constant
 \begin{equation} S_{\alpha}:=\inf_{u\in D_r^{1,p}(\mathbb{R}^{N}){\setminus}\{0\}}\frac{\int_{\mathbb{R}^{N}}|\nabla u|^{p}{\rm d}x}{\left(\int_{\mathbb{R}^{N}}|x|^{\alpha}|u|^{p^{*}(\alpha)}{\rm d}x\right)^{\frac{p}{p^{*}(\alpha)}}}\end{equation}
\begin{equation} S_{\alpha}:=\inf_{u\in D_r^{1,p}(\mathbb{R}^{N}){\setminus}\{0\}}\frac{\int_{\mathbb{R}^{N}}|\nabla u|^{p}{\rm d}x}{\left(\int_{\mathbb{R}^{N}}|x|^{\alpha}|u|^{p^{*}(\alpha)}{\rm d}x\right)^{\frac{p}{p^{*}(\alpha)}}}\end{equation}is achieved by the function (see [Reference Catrina and Wang7, Reference Wang and Su24])
 \[ U_{ \alpha}(x)=\frac{\left(\frac{(N-p)^{p-1}(N+\alpha)} {(p-1)^{p-1}}\right)^{\frac{N-p}{p(p+\alpha)}}} {\left(1 +|x|^{\frac{p+\alpha}{p-1}}\right)^{\frac{N-p}{p+\alpha}}}, \]
\[ U_{ \alpha}(x)=\frac{\left(\frac{(N-p)^{p-1}(N+\alpha)} {(p-1)^{p-1}}\right)^{\frac{N-p}{p(p+\alpha)}}} {\left(1 +|x|^{\frac{p+\alpha}{p-1}}\right)^{\frac{N-p}{p+\alpha}}}, \]which is a positive solution of the critical equation
 \begin{equation} \displaystyle \left\{ \begin{array}{@{}ll} \displaystyle -\Delta_p u=|x|^{\alpha}|u|^{p^{*}(\alpha)-2}u \text{ in } \mathbb{R}^{N},\\ \displaystyle u\in D^{1,p}_r(\mathbb{R}^{N}). \end{array} \right. \end{equation}
\begin{equation} \displaystyle \left\{ \begin{array}{@{}ll} \displaystyle -\Delta_p u=|x|^{\alpha}|u|^{p^{*}(\alpha)-2}u \text{ in } \mathbb{R}^{N},\\ \displaystyle u\in D^{1,p}_r(\mathbb{R}^{N}). \end{array} \right. \end{equation}The weighted Sobolev inequality (1.2) gives the weighted Sobolev embedding
The number ![]() $p^{*}(\alpha ):=\frac {p(N+\alpha )}{N-p}$ is named as the Sobolev (resp. Hardy–Sobolev, Hénon–Sobolev) critical exponent for
$p^{*}(\alpha ):=\frac {p(N+\alpha )}{N-p}$ is named as the Sobolev (resp. Hardy–Sobolev, Hénon–Sobolev) critical exponent for ![]() $\alpha =0$ (resp.
$\alpha =0$ (resp. ![]() $-p<\alpha <0$ (cf. [Reference Ghoussoub and Yuan10]),
$-p<\alpha <0$ (cf. [Reference Ghoussoub and Yuan10]), ![]() $\alpha >0$ (cf. [Reference Su, Wang and Willem20, Reference Su, Wang and Willem21, Reference Wang and Su23])). It should be pointed out that (1.2) and (1.4) are valid on
$\alpha >0$ (cf. [Reference Su, Wang and Willem20, Reference Su, Wang and Willem21, Reference Wang and Su23])). It should be pointed out that (1.2) and (1.4) are valid on ![]() $D^{1,p}(\mathbb {R}^{N})$ for
$D^{1,p}(\mathbb {R}^{N})$ for ![]() $-p<\alpha \leqslant 0$. Equation (1.3) with Hardy–Sobolev or Sobolev or Hénon–Sobolev critical exponent has been extensively investigated, we refer to [Reference Aubin2, Reference Caffarelli, Kohn and Nirenberg5, Reference Catrina and Wang6, Reference Chou and Chu8, Reference Ghoussoub and Yuan10–Reference Gladiali, Grossi and Neves12, Reference Horiuchi15–Reference -L. Lions18, Reference Talenti22] and some references therein.
$-p<\alpha \leqslant 0$. Equation (1.3) with Hardy–Sobolev or Sobolev or Hénon–Sobolev critical exponent has been extensively investigated, we refer to [Reference Aubin2, Reference Caffarelli, Kohn and Nirenberg5, Reference Catrina and Wang6, Reference Chou and Chu8, Reference Ghoussoub and Yuan10–Reference Gladiali, Grossi and Neves12, Reference Horiuchi15–Reference -L. Lions18, Reference Talenti22] and some references therein.
In recent years the double critical elliptic equation
involving with Hardy–Sobolev and Sobolev critical exponents has been researched by a few of authors. Filippucci et al. [Reference Filippucci, Pucci and Robert9, theorem 1] proved the existence of positive solutions of (1.5) for the case ![]() $\lambda =1$,
$\lambda =1$, ![]() $\alpha _1=0,\, -p<\alpha _2<0$. Hsiaet al. [Reference Hsia, Lin and Wadade13, theorem 1.2] established the ground state solutions for (1.5) as
$\alpha _1=0,\, -p<\alpha _2<0$. Hsiaet al. [Reference Hsia, Lin and Wadade13, theorem 1.2] established the ground state solutions for (1.5) as ![]() $p=2$,
$p=2$, ![]() $\lambda =1$,
$\lambda =1$, ![]() $\alpha _1=0$,
$\alpha _1=0$, ![]() $-2<\alpha _2<0$ in the half space
$-2<\alpha _2<0$ in the half space ![]() $\mathbb {R}^{N}_+$. For (1.5) with
$\mathbb {R}^{N}_+$. For (1.5) with ![]() $p=2$,
$p=2$, ![]() $\lambda \in \mathbb {R}$,
$\lambda \in \mathbb {R}$, ![]() $-2<\alpha _2<\alpha _1<0$, Li and Lin [Reference Li and Lin19, theorems 1.3 and 1.4] found the ground state solutions in
$-2<\alpha _2<\alpha _1<0$, Li and Lin [Reference Li and Lin19, theorems 1.3 and 1.4] found the ground state solutions in ![]() $\mathbb {R}^{N}_+$. More recently, we have established in [Reference Wang and Su25] the positive ground state solutions of (1.5) as
$\mathbb {R}^{N}_+$. More recently, we have established in [Reference Wang and Su25] the positive ground state solutions of (1.5) as ![]() $p=2$,
$p=2$, ![]() $\lambda =1$,
$\lambda =1$, ![]() $\alpha _1>\alpha _2>-2$ by using the ideas in [Reference Filippucci, Pucci and Robert9]. To be more precise, the critical exponents in [Reference Wang and Su25] include Hardy–Sobolev, Sobolev and Hénon–Sobolev critical exponents. In the case
$\alpha _1>\alpha _2>-2$ by using the ideas in [Reference Filippucci, Pucci and Robert9]. To be more precise, the critical exponents in [Reference Wang and Su25] include Hardy–Sobolev, Sobolev and Hénon–Sobolev critical exponents. In the case ![]() $p=2,\, \alpha _i>0$, we call (1.5) the Hénon equation which was raised by Hénon [Reference Hénon14] in 1973 in studying the rotating stellar structures. Indeed, the results in [Reference Wang and Su25] can be extended to the quasilinear case (1.5) with
$p=2,\, \alpha _i>0$, we call (1.5) the Hénon equation which was raised by Hénon [Reference Hénon14] in 1973 in studying the rotating stellar structures. Indeed, the results in [Reference Wang and Su25] can be extended to the quasilinear case (1.5) with ![]() $1< p< N$,
$1< p< N$, ![]() $\alpha _1>\alpha _2>-p$. What is more interesting is that whether or not (1.5) with
$\alpha _1>\alpha _2>-p$. What is more interesting is that whether or not (1.5) with ![]() $\lambda =-1$ and
$\lambda =-1$ and ![]() $\alpha _1>\alpha _2>-p$ has nontrivial solutions. It is a new problem and has never been considered before. The following theorem gives a positive answer in radial case.
$\alpha _1>\alpha _2>-p$ has nontrivial solutions. It is a new problem and has never been considered before. The following theorem gives a positive answer in radial case.
Theorem 1.1 Let ![]() $1< p< N$ and
$1< p< N$ and ![]() $\alpha _1>\alpha _2>-p$. Then (1.1) has a nonnegative ground state solution.
$\alpha _1>\alpha _2>-p$. Then (1.1) has a nonnegative ground state solution.
It is worth noting that the existence of nontrivial solutions for (1.1) with ![]() $\alpha _2>\alpha _1>-p$ is still an open problem. In § 2 we give the proof of theorem 1.1.
$\alpha _2>\alpha _1>-p$ is still an open problem. In § 2 we give the proof of theorem 1.1.
2. Proof of theorem 1.1
By the continuous embedding (1.4), weak solutions of (1.1) are exactly critical points of the ![]() $C^{1}$ functional
$C^{1}$ functional
where
There exists a ground state solution of (1.1) provided the minimum
can be achieved, where
is the Nehari manifold for the functional ![]() $\Phi$. Using the similar arguments in [Reference Willem26], we have the following properties about the manifold.
$\Phi$. Using the similar arguments in [Reference Willem26], we have the following properties about the manifold.
Lemma 2.1 Let ![]() $\alpha _1>\alpha _2>-p$. For each
$\alpha _1>\alpha _2>-p$. For each ![]() $u\in D^{1,p}_r(\mathbb {R}^{N}){\setminus} \{0\},$ there exists a unique
$u\in D^{1,p}_r(\mathbb {R}^{N}){\setminus} \{0\},$ there exists a unique ![]() $t_u>0$ such that
$t_u>0$ such that ![]() $t_u u\in \mathcal {N}$ and
$t_u u\in \mathcal {N}$ and ![]() $\Phi (t_u u)=\max _{t \geqslant 0}\Phi (tu)$. The function
$\Phi (t_u u)=\max _{t \geqslant 0}\Phi (tu)$. The function ![]() $u \mapsto t_u$ is continuous and the map
$u \mapsto t_u$ is continuous and the map ![]() $u \mapsto t_u u$ is a homeomorphism of the unit sphere in
$u \mapsto t_u u$ is a homeomorphism of the unit sphere in ![]() $D^{1,p}_r(\mathbb {R}^{N})$ with
$D^{1,p}_r(\mathbb {R}^{N})$ with ![]() $\mathcal {N}$.
$\mathcal {N}$.
Applying the mountain pass theorem in [Reference Ambrosetti and Rabinowitz1], we have the following lemma.
Lemma 2.2 Let ![]() $\alpha _1>\alpha _2>-p$. There exists a sequence
$\alpha _1>\alpha _2>-p$. There exists a sequence ![]() $\{u_n\}\subset D_r^{1,2}(\mathbb {R}^{N})$ such that
$\{u_n\}\subset D_r^{1,2}(\mathbb {R}^{N})$ such that
with
where ![]() $\Gamma :=\left \{\gamma \in C([0,\,1],\,D_r^{1,p}(\mathbb {R}^{N})):\gamma (0)=0,\, \Phi (\gamma (1))<0\right \}.$
$\Gamma :=\left \{\gamma \in C([0,\,1],\,D_r^{1,p}(\mathbb {R}^{N})):\gamma (0)=0,\, \Phi (\gamma (1))<0\right \}.$
By the arguments in [Reference Willem26, chapter 4] and lemma 2.1, we get a key fact that
Now we analyse the properties of the ![]() ${({\rm PS})_{\hat {c}}}$ sequence
${({\rm PS})_{\hat {c}}}$ sequence ![]() $\{u_n\}$ on the
$\{u_n\}$ on the ![]() $\delta$-ball
$\delta$-ball ![]() $B_\delta :=\{x\in \mathbb {R}^{N}: \ |x|<\delta \}$ and on the annular domain
$B_\delta :=\{x\in \mathbb {R}^{N}: \ |x|<\delta \}$ and on the annular domain ![]() $B_{a,b}:=\left \{x\in \mathbb {R}^{N}: \ 0< a<|x|< b\right \}$ which are important to the proof of theorem 1.1. We remark that the discussion below will be carried out in the sense of subsequence which will be denoted by the original sequence.
$B_{a,b}:=\left \{x\in \mathbb {R}^{N}: \ 0< a<|x|< b\right \}$ which are important to the proof of theorem 1.1. We remark that the discussion below will be carried out in the sense of subsequence which will be denoted by the original sequence.
Lemma 2.3 Assume ![]() $u_n\rightharpoonup 0$ in
$u_n\rightharpoonup 0$ in ![]() $D^{1,p}_r(\mathbb {R}^{N})$. Then for any annular domain
$D^{1,p}_r(\mathbb {R}^{N})$. Then for any annular domain ![]() $B_{a,b},$ we have
$B_{a,b},$ we have
Proof. Let ![]() $\eta \in C_{0,r}^{\infty }(\mathbb {R}^{N})$ be such that
$\eta \in C_{0,r}^{\infty }(\mathbb {R}^{N})$ be such that ![]() $0\leqslant \eta \leqslant 1$ and
$0\leqslant \eta \leqslant 1$ and ![]() $\eta |_{B_{a,b}}\equiv 1$. Since
$\eta |_{B_{a,b}}\equiv 1$. Since
for any ![]() $R>\rho >0$,
$R>\rho >0$, ![]() $1 \leqslant q < \infty$ and
$1 \leqslant q < \infty$ and ![]() $\alpha >-p$, see [Reference Su, Wang and Willem21, lemma 6], it follows that
$\alpha >-p$, see [Reference Su, Wang and Willem21, lemma 6], it follows that
By Hölder inequality and (2.7), we get that
 \begin{equation} \int_{\mathbb{R}^{N}}|\nabla u_n|^{p-1}|\nabla (\eta^{p})||u_n|{\rm d}x \leqslant \left(\int_{\mathbb{R}^{N}}|\nabla u_n|^{p}{\rm d}x\right)^{\frac{p-1}{p}} \left(\int_{\mathbb{R}^{N}}|\nabla (\eta^{p})|^{p}|u_n|^{p}{\rm d}x\right)^{\frac{1}{p}}\to 0\end{equation}
\begin{equation} \int_{\mathbb{R}^{N}}|\nabla u_n|^{p-1}|\nabla (\eta^{p})||u_n|{\rm d}x \leqslant \left(\int_{\mathbb{R}^{N}}|\nabla u_n|^{p}{\rm d}x\right)^{\frac{p-1}{p}} \left(\int_{\mathbb{R}^{N}}|\nabla (\eta^{p})|^{p}|u_n|^{p}{\rm d}x\right)^{\frac{1}{p}}\to 0\end{equation}
as ![]() $n\to \infty$. Furthermore, combining (2.3), (2.8), (2.9) and
$n\to \infty$. Furthermore, combining (2.3), (2.8), (2.9) and ![]() $\eta ^{p}u_n\in D^{1,p}_r(\mathbb {R}^{N})$, we get that
$\eta ^{p}u_n\in D^{1,p}_r(\mathbb {R}^{N})$, we get that
 \begin{align*} o(1)=\langle\Phi'(u_n),\eta^{p}u_n\rangle &=\int_{\mathbb{R}^{N}}|\nabla u_n|^{p-2}\nabla u_n\cdot \nabla(\eta^{p}u_n){\rm d}x+o(1)\\ &=\int_{\mathbb{R}^{N}}u_n|\nabla u_n|^{p-2} \nabla u_n\cdot \nabla(\eta^{p})+|\eta\nabla u_n|^{p}{\rm d}x+o(1)\\ &=\int_{\mathbb{R}^{N}}|\eta\nabla u_n|^{p}{\rm d}x+o(1). \end{align*}
\begin{align*} o(1)=\langle\Phi'(u_n),\eta^{p}u_n\rangle &=\int_{\mathbb{R}^{N}}|\nabla u_n|^{p-2}\nabla u_n\cdot \nabla(\eta^{p}u_n){\rm d}x+o(1)\\ &=\int_{\mathbb{R}^{N}}u_n|\nabla u_n|^{p-2} \nabla u_n\cdot \nabla(\eta^{p})+|\eta\nabla u_n|^{p}{\rm d}x+o(1)\\ &=\int_{\mathbb{R}^{N}}|\eta\nabla u_n|^{p}{\rm d}x+o(1). \end{align*}
It follows from ![]() $\eta |_{B_{a, b}}\equiv 1$ that
$\eta |_{B_{a, b}}\equiv 1$ that
and this completes the proof.
For any ![]() $\delta >0$, we set
$\delta >0$, we set
From lemma 2.3 we see that these three quantities are well defined and are independent of the choice of ![]() $\delta >0$. We have the following conclusion.
$\delta >0$. We have the following conclusion.
Lemma 2.4 Assume ![]() $u_n\rightharpoonup 0$ in
$u_n\rightharpoonup 0$ in ![]() $D^{1,p}_r(\mathbb {R}^{N})$. Then
$D^{1,p}_r(\mathbb {R}^{N})$. Then
Proof. Let ![]() $\phi \in C_{0,r}^{\infty }(\mathbb {R}^{N})$ satisfy
$\phi \in C_{0,r}^{\infty }(\mathbb {R}^{N})$ satisfy ![]() $\phi |_{B_\delta }\equiv 1$. Since
$\phi |_{B_\delta }\equiv 1$. Since ![]() $\phi u_n\in D^{1,p}_r(\mathbb {R}^{N})$,
$\phi u_n\in D^{1,p}_r(\mathbb {R}^{N})$,
According to lemma 2.3, we obtain that
 \begin{align*} &\int_{\mathbb{R}^{N}}|\nabla u_n|^{p-2}\nabla u_n\nabla (\phi u_n){\rm d}x=\int_{B_\delta}|\nabla u_n|^{2}{\rm d}x+o(1),\\ &\int_{\mathbb{R}^{N}}|x|^{\alpha_i}|u_n|^{p^{*}(\alpha_i)} \phi {\rm d}x = \int_{B_\delta}|x|^{\alpha_i}|u_n|^{p^{*}(\alpha_i)}{\rm d}x+o(1), \quad i=1,2. \end{align*}
\begin{align*} &\int_{\mathbb{R}^{N}}|\nabla u_n|^{p-2}\nabla u_n\nabla (\phi u_n){\rm d}x=\int_{B_\delta}|\nabla u_n|^{2}{\rm d}x+o(1),\\ &\int_{\mathbb{R}^{N}}|x|^{\alpha_i}|u_n|^{p^{*}(\alpha_i)} \phi {\rm d}x = \int_{B_\delta}|x|^{\alpha_i}|u_n|^{p^{*}(\alpha_i)}{\rm d}x+o(1), \quad i=1,2. \end{align*}Therefore (2.10) leads to
The weighted Sobolev inequality (1.2) shows that
 \[ \left(\int_{\mathbb{R}^{N}} |x|^{\alpha_1}|\phi u_n|^{p^{*}(\alpha_1)}{\rm d}x\right)^{\frac{p}{p^{*}(\alpha_1)}} \leqslant S_{\alpha_1}^{{-}1}\int_{\mathbb{R}^{N}}|\nabla (\phi u_n)|^{p}{\rm d}x. \]
\[ \left(\int_{\mathbb{R}^{N}} |x|^{\alpha_1}|\phi u_n|^{p^{*}(\alpha_1)}{\rm d}x\right)^{\frac{p}{p^{*}(\alpha_1)}} \leqslant S_{\alpha_1}^{{-}1}\int_{\mathbb{R}^{N}}|\nabla (\phi u_n)|^{p}{\rm d}x. \]Using lemma 2.3 and (2.11), we get that
It follows that
and this completes the proof.
We need the following interpolation inequality for proving lemma 2.6.
Lemma 2.5 [Reference Wang and Su24, lemma 2.4]
Assume ![]() $1< p< N,\, \alpha _1>\alpha _2>-p$. For any
$1< p< N,\, \alpha _1>\alpha _2>-p$. For any ![]() $u\in D_r^{1,p}(\mathbb {R}^{N}),$ it holds that
$u\in D_r^{1,p}(\mathbb {R}^{N}),$ it holds that
where ![]() $\theta = \frac {p^{*}(\alpha _1)\alpha _2 -\nu \alpha _1}{p^{*}(\alpha _1)-\nu },$
$\theta = \frac {p^{*}(\alpha _1)\alpha _2 -\nu \alpha _1}{p^{*}(\alpha _1)-\nu },$ ![]() $\tau =\frac {\nu }{p^{*}(\alpha _2)}\in (0,\,\frac {(p+\alpha _2)(N+\alpha _1)} {(p+\alpha _1)(N+\alpha _2)}],$
$\tau =\frac {\nu }{p^{*}(\alpha _2)}\in (0,\,\frac {(p+\alpha _2)(N+\alpha _1)} {(p+\alpha _1)(N+\alpha _2)}],$ ![]() $0<\nu \leqslant \frac {p+\alpha _2}{p+\alpha _1}p^{*}(\alpha _1).$
$0<\nu \leqslant \frac {p+\alpha _2}{p+\alpha _1}p^{*}(\alpha _1).$
Lemma 2.6 There exist ![]() $0<\xi _1<\frac {1}{2}S_{\alpha _1}^{\frac {p^{*}(\alpha _1)}{p^{*}(\alpha _1)-p}}$ and a sequence
$0<\xi _1<\frac {1}{2}S_{\alpha _1}^{\frac {p^{*}(\alpha _1)}{p^{*}(\alpha _1)-p}}$ and a sequence ![]() $\{r_n>0\},$ such that
$\{r_n>0\},$ such that
verifies for all ![]() $\xi \in (0,\, \xi _1)$,
$\xi \in (0,\, \xi _1)$,
Proof. It follows from ![]() $\hat {c}>0$ and lemma 2.5 that
$\hat {c}>0$ and lemma 2.5 that ![]() $\kappa _\infty :=\displaystyle \lim _{n\to \infty }\int _{\mathbb {R}^{N}}|x|^{\alpha _1}|u_n|^{p^{*}(\alpha _1)}{\rm d}x>0$. Let
$\kappa _\infty :=\displaystyle \lim _{n\to \infty }\int _{\mathbb {R}^{N}}|x|^{\alpha _1}|u_n|^{p^{*}(\alpha _1)}{\rm d}x>0$. Let ![]() $\xi _1:=\min \{S_{\alpha _1}^{\frac {p^{*}(\alpha _1)}{p^{*}(\alpha _1)-p}},\, \kappa _\infty \}$, for fixed
$\xi _1:=\min \{S_{\alpha _1}^{\frac {p^{*}(\alpha _1)}{p^{*}(\alpha _1)-p}},\, \kappa _\infty \}$, for fixed ![]() $\xi \in (0,\, \xi _1)$ and any
$\xi \in (0,\, \xi _1)$ and any ![]() $n\in \mathbb {N}$, there exists
$n\in \mathbb {N}$, there exists ![]() $r_n>0$ such that
$r_n>0$ such that
By scaling, it is straightforward to check that ![]() $\{\tilde {u}_n\}$ satisfies (2.12).
$\{\tilde {u}_n\}$ satisfies (2.12).
Proof Proof of theorem 1.1
It is easy to see that ![]() $\{\tilde {u}_n\}$ satisfies (2.3). Since
$\{\tilde {u}_n\}$ satisfies (2.3). Since ![]() $p^{*}(\alpha _1)>p^{*}(\alpha _2)>p$, it follows from (2.3) that
$p^{*}(\alpha _1)>p^{*}(\alpha _2)>p$, it follows from (2.3) that
Thus ![]() $\{\tilde {u}_n\}$ is bounded in
$\{\tilde {u}_n\}$ is bounded in ![]() $D_r^{1,p}(\mathbb {R}^{N})$ and then there exists
$D_r^{1,p}(\mathbb {R}^{N})$ and then there exists ![]() $\tilde {u} \in D_r^{1,p}(\mathbb {R}^{N})$ such that
$\tilde {u} \in D_r^{1,p}(\mathbb {R}^{N})$ such that
 \[ \left\{\begin{array}{l@{}l} & \tilde{u}_n\rightharpoonup \tilde{u} \text{ in } D^{1,p}_r(\mathbb{R}^{N});\\ & \tilde{u}_n\rightharpoonup \tilde{u} \text{ in } L^{p^{*}(\alpha_i)}(\mathbb{R}^{N};|x|^{\alpha_i}), \quad i=1, 2.\\ & \tilde{u}_n(x)\rightarrow \tilde{u}(x) \text{ a.e. on } \mathbb{R}^{N}. \end{array} \right. \]
\[ \left\{\begin{array}{l@{}l} & \tilde{u}_n\rightharpoonup \tilde{u} \text{ in } D^{1,p}_r(\mathbb{R}^{N});\\ & \tilde{u}_n\rightharpoonup \tilde{u} \text{ in } L^{p^{*}(\alpha_i)}(\mathbb{R}^{N};|x|^{\alpha_i}), \quad i=1, 2.\\ & \tilde{u}_n(x)\rightarrow \tilde{u}(x) \text{ a.e. on } \mathbb{R}^{N}. \end{array} \right. \]
Using the ideas of Boccardo and Murat [Reference Boccardo and Murat3] (see details in [Reference Wang and Su24]), we can prove that ![]() $\nabla \tilde {u}_n(x)\to \nabla \tilde {u} (x)$ a.e. on
$\nabla \tilde {u}_n(x)\to \nabla \tilde {u} (x)$ a.e. on ![]() ${{\mathbb {R}^{N}}}$. It follows that
${{\mathbb {R}^{N}}}$. It follows that ![]() $\tilde {u}$ is a critical point of
$\tilde {u}$ is a critical point of ![]() $\Phi$ and
$\Phi$ and ![]() $\Phi (\tilde {u} )\geqslant 0$ by (2.13) again. Let
$\Phi (\tilde {u} )\geqslant 0$ by (2.13) again. Let ![]() $v_n:=\tilde {u}_n-\tilde {u}$, then
$v_n:=\tilde {u}_n-\tilde {u}$, then ![]() $\{v_n\}$ is bounded in
$\{v_n\}$ is bounded in ![]() $D^{1,p}_r(\mathbb {R}^{N})$. Assume
$D^{1,p}_r(\mathbb {R}^{N})$. Assume
Using Brezis–Lieb lemma[Reference Brézis and Lieb4], we get
If ![]() $A_\infty =0$, then
$A_\infty =0$, then ![]() $\tilde {u}$ is ground state solution of (1.1). Assume that
$\tilde {u}$ is ground state solution of (1.1). Assume that ![]() $A_\infty >0$ and
$A_\infty >0$ and ![]() $\tilde {u} =0$. Then lemma 2.4 implies that
$\tilde {u} =0$. Then lemma 2.4 implies that
This contradicts (2.12) with ![]() $0<\xi <\frac {1}{2}S_{\alpha _1}^{\frac {p^{*}(\alpha _1)}{p^{*}(\alpha _1)-p}}$. Thus
$0<\xi <\frac {1}{2}S_{\alpha _1}^{\frac {p^{*}(\alpha _1)}{p^{*}(\alpha _1)-p}}$. Thus ![]() $\tilde {u}$ is nontrivial. If
$\tilde {u}$ is nontrivial. If ![]() $\Phi (\tilde {u})=\hat {c}$, then we finish the proof with (2.5). Otherwise, we get that
$\Phi (\tilde {u})=\hat {c}$, then we finish the proof with (2.5). Otherwise, we get that
Since
we get by (2.14) and (2.15) that
which contradicts (2). It follows that ![]() $\tilde {u}$ is a ground state solution of (1.1).
$\tilde {u}$ is a ground state solution of (1.1).
By the structure of the manifold ![]() $\mathcal {N}$, we get that
$\mathcal {N}$, we get that ![]() $|\tilde {u}|\in \mathcal {N}$, then a nonnegative ground state solution is established.
$|\tilde {u}|\in \mathcal {N}$, then a nonnegative ground state solution is established.
Acknowledgments
The authors would like to thank the referees and editors for carefully reading the manuscript and giving valuable comments to improve the exposition of the paper. This work is supported by KZ202010028048 and NSFC (11771302, 12171326).