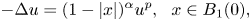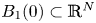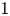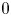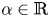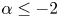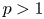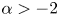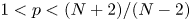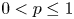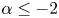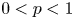1. Introduction
This paper is devoted to the study of positive solutions of the following elliptic equation
\begin{align} -\Delta u=(1-|x|)^{\alpha} u^{p},\quad x\in B_1(0), \end{align}
where 
$p>0$, 
$\alpha \in \mathbb {R}$, and 
$B_1(0)\subset \mathbb {R}^{N}$ 
$(N\geq 3)$ denotes a ball of radius 
$1$ centred at 
$0$. We will establish some estimate, existence and nonexistence of positive solutions of (1.1). In particular, we are interested in the existence and uniqueness of positive solutions of the following Dirichlet problem
\begin{equation} \left\{\begin{array}{@{}ll} \displaystyle -\Delta u=(1-|x|)^{\alpha} u^{p},\ \ & x\in B_1(0),\\ \displaystyle u=0,\ \ & |x|=1. \end{array} \right. \end{equation}
In the equation (1.1), it is clear that 
$d(x,\partial B_1(0)) = 1-|x|$ for 
$x\in B_1(0)$. This weight function 
$(1-|x|)^{\alpha }$ is singular or vanishing on the boundary of 
$B_1(0)$ when 
$\alpha \neq 0$.
Over the last few decades, the following elliptic equation
\begin{align} -\Delta u=a(x)u^{p}\ \ \mbox{in}\ \Omega, \end{align}
where 
$\Omega$ is a domain in 
$\mathbb {R}^{N}$, has been extensively studied under various assumptions. When 
$a(x)\equiv 1$, the equation is the well-known Lane–Emden equation. For the case, there was a great deal of work such as the existence, nonexistence, symmetry and uniqueness of positive solutions. For example, some interesting results in [Reference Chen and Li5, Reference Gidas, Ni and Nirenberg10] are related to the symmetry of positive solutions of (1.3) with 
$\Omega =\mathbb {R}^{N}$. If 
$a(x)=|x|^{\alpha }$ and 
$0\in \Omega$, the equation (1.3) is called Hardy–Hénon equation. When 
$\alpha \leq -2$ and 
$p>1$, the Hardy–Hénon equation (1.3) has no positive solutions in any domain 
$\Omega$ containing the origin (see [Reference Dancer, Du and Guo6]). For the case 
$\alpha >-2$ and 
$p<({N+2+2\alpha })/({N-2})$, the Hardy–Hénon equation (1.3) with 
$\Omega =\mathbb {R}^{N}$ has no positive radial solution (refer to [Reference Phan and Souplet14]). In addition, Du and Guo in [Reference Du and Guo8] investigated the Hardy–Hénon equation (1.3) for the case 
$p<0$ and 
$\alpha >-2$. When 
$a(x)=-d(x,\partial \Omega )^{\alpha }$, there were much well-known study with respect to boundary blow-up solution (also called large solution) of (1.3), for instance, the existence and uniqueness of large solution, and blow-up rate of large solution of (1.3) (see [Reference Du7]). When 
$a(x) = |x|^{\alpha }$ and 
$\Omega = B_1(0)$, Cao–Peng–Yan [Reference Cao, Peng and Yan4] analysed the profile of ground state solution and proved the existence of multi-peaked solutions with their asymptotic behaviour for equation (1.3) subject to Dirichlet boundary condition.
In this paper, we are more interested in
\[ \mbox{the case: the weight function}\ a(x)=(1-|x|)^{\alpha}\ \mbox{and}\ \Omega=B_1(0). \]
In fact, the weight function 
$a(x)=d(x,\partial \Omega )^{\alpha }(=d(x)^{\alpha })$. Clearly, for the case 
$\alpha >0$, 
$(1-|x|)^{\alpha }$ converges to zero as 
$|x|\to 1$, and for the case 
$\alpha <0$, 
$(1-|x|)^{\alpha }$ blows up as 
$|x|\to 1$. Corresponding to the boundary Hardy potential 
${1}/{d(x)^{2}}$, the equation (1.1) is called boundary Hardy–Hénon equation in this paper in order to distinguish from the well-known Hardy–Hénon equations.
Some elliptic equations with coefficient function 
$d(x)$ were extensively considered. Especially, for the Hardy potential 
${1}/{d(x)^{2}}$, there are many interesting problems and results. The well-known Hardy constant and Hardy inequality were established in [Reference Brezis and Marcus3, Reference Marcus, Mizel and Pinchover12]. For elliptic equations with such Hardy potential, in [Reference Bandle, Moroz and Reichel1], Bandle, Moroz and Reichel considered
\begin{align} -\Delta u=\lambda\frac{u}{d(x)^{2}}-d(x)^{\alpha} u^{p}\ \ \mbox{in}\ \Omega, \end{align}
and gave some classification of positive solutions under conditions 
$p>1$, 
$\alpha >-2$, and 
$\lambda \leq 1/4$. For the case 
$\lambda >1/4$, 
$\alpha >-2$ and 
$p>1$, the uniqueness and asymptotic behaviour of positive solutions of (1.4) were obtained in [Reference Du and Wei9]. In [Reference Bandle and Pozio2], Bandle and Pozio investigated the equation (1.4) with the sublinear term. More recently, in [Reference Mercuri and dos Santos13] Mercuri and Santos analysed the quantitative symmetry breaking of ground states for the following weighted Emden–Fowler equations
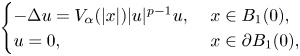\begin{equation} \begin{cases} -\Delta u = V_\alpha (|x|) |u|^{p - 1} u,\ & x\in B_1 (0),\\ u = 0,\ & x \in \partial B_1 (0), \end{cases} \end{equation}
where 
$B_1 (0) \subset \mathbb {R}^{N}$ 
$(N \geq 1)$, 
$p \in (1, 2^{*} - 1)$ with 
$2^{*} = {2N}/({N - 2})$ if 
$N \geq 3$ and 
$2^{*} = +\infty$ if 
$N = 1, 2$, and 
$V_\alpha$ (
$\alpha > 0$) defined as:
(i) for
$R \in (0, 1)$, $V_\alpha (r) = (1 - (r/R))^{\alpha }$ if $r \in [0, R)$ and $V_\alpha (r) = (1 - (({1 - r})/ ({1 - R})))^{\alpha }$ if $r \in [R, 1]$;(ii) for
$R = 0$, $V_\alpha (r) = r^{\alpha }$ if $r \in [0, 1]$; for $R = 1$, $V_\alpha (r) = (1 - r)^{\alpha }$ if $r \in [0, 1]$.
In [Reference Mercuri and dos Santos13], some interesting quantitative results in regard to (1.5) were presented, for example, [Reference Mercuri and dos Santos13, proposition 1.8], which indicate that for the positive ground state solution 
$u_\alpha$ of (1.5) with 
$\alpha > 0$, 
$R = 1$ and 
$N \geq 3$ (i.e. (1.2)), there exist positive constants 
$C_1$ and 
$C_2$ such that 
$C_1 \alpha ^{2/(p - 1)} \leq \max_{x \in \overline {B}(0, 1)} u_\alpha (x) \leq C_2 \alpha ^{2/(p - 1)}$ for large 
$\alpha$. In contrast to [Reference Mercuri and dos Santos13, proposition 1.8], our theorem 1.3 is to establish the existence of positive solutions for (1.2) with 
$\alpha > -2$ and 
$p \in (1, 2^{*} - 1)$.
In consideration of above interesting work, in this article, we consider the following equation
\[ -\Delta u=d(x)^{\alpha} u^{p}\ \mbox{in}\ \Omega. \]
For convenience and brevity, we mainly study the special domain 
$B_1:=B_1(0)$, that is equation (1.1). We will investigate the estimate, existence and nonexistence of positive solutions of (1.1) and (1.2) in view of the weight function 
$(1-|x|)^{\alpha }$. Throughout this paper, unless otherwise stated, a solution 
$u$ of (1.2) is referred to classical solution, that is 
$u\in C^{2}(B_1)\cap C(\bar B_1)$. For all conclusions in this paper, we need the condition 
$N\geq 3$, which plays an important role in some proofs, so we assume always 
$N\geq 3$ throughout this paper.
By using blow-up method and some analysis technique we can obtain the following estimate of positive solutions of (1.1).
Theorem 1.1
(i) If
$1< p<({N+2})/({N-2})$, $\alpha >-2$, then there exists $C=C(N,p,\alpha )$ such that any positive solution $u$ of (1.1) satisfies
(1.6)\begin{align} u(x)\leq C(1-|x|)^{-(({2+\alpha})/({p-1}))}, \ \ x\in B_1. \end{align}(ii) If
$0< p<1$ and $\alpha >-2$, then there exists $C=C(N,p,\alpha )$ such that any positive solution $u$ of (1.1) satisfies
(1.7)\begin{align} u(x)\geq C(1-|x|)^{-(({2+\alpha})/({p-1}))}, \ \ x\in B_1. \end{align}
For the case 
$\alpha \leq -2$, some results on nonexistence of positive solutions of (1.1) are established, which are contained in the following theorem.
Theorem 1.2
For the Dirichelt problem (1.2), under 
$\alpha >-2$ and subcritical nonlinear term, we can obtain the existence of positive classical solutions.
Theorem 1.3 Let 
$-2<\alpha$ and 
$1< p<({N+2})/({N-2})$. Then the problem (1.2) has a positive solution.
For the sublinear case 
$0< p<1$, together with some estimate of positive solutions and some analysis, we can obtain the following two results of nonexistence.
Theorem 1.4 Let 
$0< p<1$ and 
$1+p+\alpha <0$. Then (1.2) has no positive solutions in 
$C^{1}(\bar B_1)$.
Theorem 1.5 Let 
$0< p\leq 1$ and 
$\alpha \leq -2$. Then (1.1) has no positive solutions.
Finally, by using the subsolution and supersolution method, the existence of positive solution is established for the case 
$0< p<1$ and 
$\alpha >-2$, and by the maximum principle and Hopf's Lemma, we can establish the uniqueness of positive solutions. Concretely, we have the following theorem.
Theorem 1.6
(i) Suppose that
$\alpha >-2$ and $p<1$. Then (1.2) has a positive classical solution. Moreover, if $p\leq 0$, the positive solution of (1.2) is unique.(ii) Suppose that
$\psi \in C^{1}(\bar B_1)$ is a nonnegative function, $\alpha \geq 0$ and $0< p<1$. Then the following problem
(1.8)has a unique positive solution in\begin{equation} \left\{\begin{array}{@{}ll} -\Delta u=(1-|x|)^{\alpha} u^{p},\ \ & x\in B_1,\\ \displaystyle u=\psi,\ \ & |x|=1, \end{array} \right. \end{equation}$C^{2}(B_1)\cap C^{1}(\bar B_1)$.
At the end of introduction, we point out that it is challenging to deal with the existence and nonexistence of positive solutions for the more general problem
\[ -\Delta u = a(x) u^{p}\ \mbox{in}\ \Omega, \]
where 
$\Omega$ is a bounded and smooth domain, and 
$a(x)\in C(\Omega )$ satisfies
\[ c_1 d(x)^{\alpha} \leq a(x) \leq c_2 d(x)^{\alpha} \ \mbox{in}\ \Omega, \]
with 
$d(x) = d(x, \partial \Omega )$ and constants 
$c_i > 0$ 
$(i = 1, 2)$. Due to the limited length of the paper, for the more general case we will develop some other technique and methods to establish the similar results to this paper in the near future.
The rest of this paper is organized as follows. In § 2 we mainly consider the equation (1.1) with the superlinear nonlinear term. Firstly, we give estimate of positive solutions, i.e., lemma 2.2, and then give the proof of theorem 1.2. We also establish the estimate of positive radial solutions under small perturbation, i.e., lemma 2.3, and then complete the proof of theorem 1.3. In § 3, we study the existence and nonexistence of positive solutions to (1.1) with sublinear nonlinear term. We establish the estimate of positive solutions, i.e., lemma 3.2. Finally, we prove theorems 1.4–1.6.
2. The case $p>1$
The following lemma can be found in [Reference Phan and Souplet14], which will be used for the estimate of positive solutions.
Lemma 2.1 Let 
$N\geq 3$, 
$1< p<({N+2})/({N-2})$, and 
$\mu \in (0,1]$. Let 
$a\in C^{\mu }(\bar B_1)$ satisfy
\[ \|a\|_{C^{\mu}(\bar B_1)}\leq C_1 \ \mbox{and}\ a(x)\geq C_2, \ x\in\bar B_1, \]
for some constants 
$C_1,C_2>0$. There exists 
$C>0$, depending only on 
$\mu , C_1,C_2,p,N$, such that, for any nonnegative classical solution 
$u$ of
\[ -\Delta u=a(x)u^{p}, \ x\in B_1, \]
$u$ satisfies
\begin{align} |u(x)|^{\frac{p-1}{2}}+|\nabla u(x)|^{(({p-1})/({p+1}))}\leq C\left(1+\frac{1}{1-|x|}\right),\ \ x\in B_1. \end{align}Be based on lemma 2.1, the following lemma 2.2 can be derived.
Lemma 2.2 Let 
$1< p<({N+2})/({N-2})$. There exists 
$C=C(N,p,\alpha )$ such that any nonnegative solution 
$u$ of (1.1) satisfies
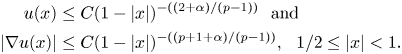\begin{align} u(x)&\leq C(1-|x|)^{-(({2+\alpha})/({p-1}))}\ \ \mbox{and}\notag\\ |\nabla u(x)|&\leq C(1-|x|)^{-(({p+1+\alpha})/({p-1}))},\ \ 1/2\leq|x|<1. \end{align}Proof. Let 
$x_0$ be an arbitrary point in 
$B_1$. We define a function by
\[ U(x)=d(x_0,\partial B_1)^{(({2+\alpha})/({p-1}))}u\left(x_0+\frac{d(x_0,\partial B_1)}{2}x\right),\ \ x\in B_1. \]
Then 
$U$ satisfies
\[ -\Delta U=a(x;x_0)U^{p},\ \ x\in B_1, \]where
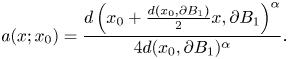\[ a(x;x_0)=\frac{d\left(x_0+\frac{d(x_0,\partial B_1)}{2}x,\partial B_1\right)^{\alpha}}{4d(x_0,\partial B_1)^{\alpha}}. \]
Clearly, for any 
$x\in B_1$, we have that
\[ a(x;x_0)\geq\frac{1}{2^{\alpha+2}}\ \ \mbox{as}\ \alpha\geq 0 \]and
\[ a(x;x_0)\geq\frac{3^{\alpha}}{2^{2+\alpha}}\ \ \mbox{as}\ \alpha<0. \]
We claim that for all 
$x_0$ satisfying 
$|x_0|\geq 1/2$,
\begin{align} \|a({\cdot};x_0)\|_{C^{1}(\bar B_1)}\leq C, \end{align}
where 
$C$ depends only on 
$\alpha$. In fact, for any 
$x\in B_1$ and 
$x_0\in B_1$, 
$a(x;x_0)$ can be written by
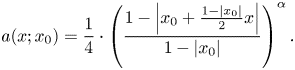\[ a(x; x_0) = \dfrac 14 \cdot \left(\frac{1 - \left| x_0+\frac{1-|x_0|}{2}x \right|}{1-|x_0|} \right)^{\alpha}. \]
It follows that for 
$\alpha \geq 0$
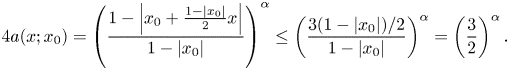\begin{eqnarray*} 4a(x;x_0)=\left(\frac{1-\left|x_0+\frac{1-|x_0|}{2}x\right|}{1-|x_0|}\right)^{\alpha} \leq\left(\frac{3(1-|x_0|)/2}{1-|x_0|}\right)^{\alpha}=\left(\frac{3}{2}\right)^{\alpha}. \end{eqnarray*}
As 
$\alpha <0$, we have
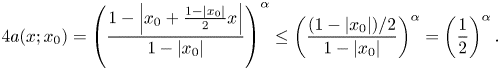\begin{eqnarray*} 4a(x;x_0)=\left(\frac{1-\left|x_0+\frac{1-|x_0|}{2}x\right|}{1-|x_0|}\right)^{\alpha} \leq\left(\frac{(1-|x_0|)/2}{1-|x_0|}\right)^{\alpha}=\left(\frac{1}{2}\right)^{\alpha}. \end{eqnarray*}In addition, it is clear that
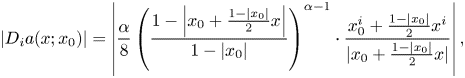\[ |D_ia(x;x_0)|=\left|\frac{\alpha}{8}\left(\frac{1-\left|x_0+\frac{1-|x_0|}{2}x\right|}{1-|x_0|}\right)^{\alpha-1}\cdot \frac{x_0^{i}+\frac{1-|x_0|}{2}x^{i}}{|x_0+\frac{1-|x_0|}{2}x|}\right|, \]
where 
$x^{i}$ and 
$x_0^{i}$ denote the 
$i$-th component of 
$x$ and 
$x_0$ respectively. So, if 
$\alpha \geq 1$ and 
$|x_0|\geq 1/2$, then we obtain that
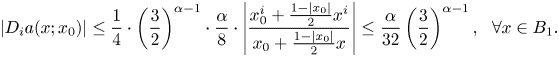\[ |D_ia(x;x_0)|\leq\frac{1}{4}\cdot\left(\frac{3}{2}\right)^{\alpha-1}\cdot\frac{\alpha}{8}\cdot\left|\frac{x_0^{i}+\frac{1-|x_0|}{2}x^{i}}{x_0+\frac{1-|x_0|}{2}x}\right| \leq\frac{\alpha}{32}\left(\frac{3}{2}\right)^{\alpha-1},\ \ \forall x\in B_1. \]
If 
$\alpha <1$ and 
$|x_0|\geq 1/2$, then we have that
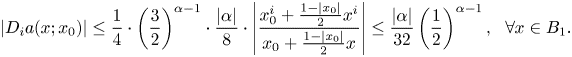\[ |D_ia(x;x_0)|\leq\frac{1}{4}\cdot\left(\frac{3}{2}\right)^{\alpha-1}\cdot\frac{|\alpha|}{8}\cdot\left|\frac{x_0^{i}+\frac{1-|x_0|}{2}x^{i}}{x_0+\frac{1-|x_0|}{2}x}\right| \leq\frac{|\alpha|}{32}\left(\frac{1}{2}\right)^{\alpha-1},\ \ \forall x\in B_1. \]Therefore, applying lemma 2.1, we have
\[ U(0)+|\nabla U(0)|\leq C. \]Further, we obtain
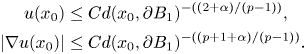\begin{align*} u(x_0)&\leq Cd(x_0,\partial B_1)^{-(({2+\alpha})/({p-1}))},\\ |\nabla u(x_0)|&\leq Cd(x_0,\partial B_1)^{-(({p+1+\alpha})/({p-1}))}. \end{align*}
By the arbitrariness of 
$x_0$ and 
$d(x_0,\partial B_1)=1-|x_0|$, we can obtain the desired conclusion.
Applying lemmas 2.1 and 2.2, we can present a proof of theorem 1.1 (i).
Proof of theorem 1.1 (i). On the one hand, by lemma 2.2 there is 
$C = C (N, p, \alpha )$ such that any positive solution 
$u$ of (1.1) satisfies
\[ u(x) \leq C (1 - |x|)^{- \frac {2 + \alpha}{p - 1}},\quad x \in B_1 \backslash B_{1/2}. \]
On the other hand, noticing that 
$\frac 12 \leq 1 - |x| \leq 1$, 
$\forall x \in \overline {B}_{1/2}$ and that by lemma 2.1 there exists 
$C = C (N, p, \alpha )$ such that 
$|u (x)| \leq C$, 
$\forall x \in \overline {B}_{1/2}$ for any positive solution 
$u$ of (1.1), we know that there is 
$C = C (N, p, \alpha )$ such that
\[ u(x) \leq C (1 - |x|)^{- \frac {2 + \alpha}{p - 1}},\quad x \in \overline{B}_{1/2}. \]The proof is completed.
Next, we are going to prove theorem 1.2 by analysing the corresponding integral average of positive solutions and together with lemma 2.2.
Proof of theorem 1.2. We argue indirectly by assuming that 
$u\in C^{2}(B_1)$ is a positive solution of (1.1). Using spherical coordinates to write 
$u(x)=u(r,\theta )$ with 
$r=|x|$ and 
$\theta =\frac {x}{|x|}$, we have
\begin{align} u_{rr}+\frac{N-1}{r}u_r+\frac{1}{r^{2}}\Delta_{S^{N-1}}u={-}(1-r)^{\alpha} u^{p},\ \ r\in(0,1). \end{align}Let
\[ \tilde u(r)=\frac{1}{|S^{N-1}|}\int_{S^{N-1}}u(r,\theta)\,\textrm{d}\theta. \]
From the above equation for 
$u(r,\theta )$ it follows that
\begin{align} \tilde u_{rr}+\frac{N-1}{r}\tilde u_r={-}\frac{(1-r)^{\alpha}}{|S^{N-1}|}\int_{S^{N-1}}u(r,\theta)^{p}\,\textrm{d}\theta. \end{align}So, we have
\[ (r^{N-1}\tilde u'(r))'<0\ \mbox{for}\ r\in(0,1). \]
Therefore, it is clear that 
$r^{N-1}\tilde u'$ is decreasing, and hence has a limit 
$m\in [-\infty ,+\infty )$ as 
$r\to 1^{-}$. In addition, by Jensen's inequality for (2.5) we obtain
\begin{align} -(r^{N-1}\tilde u')'\geq(1-r)^{\alpha}r^{N-1}\tilde u^{p}\ \mbox{for}\ r\in(0,1). \end{align} We firstly prove the conclusion (i). We divide the proof into two cases for clarity. Suppose that 
$u$ has a positive lower bound.
Case 1. Suppose that 
$m\geq 0$. Then
\[ r^{N-1}\tilde u'(r)>m\ \mbox{for}\ r\in(0,1). \]
Therefore, 
$\tilde u'(r)>0$ holds for all 
$r\in (0,1)$. So, we can assume 
$\tilde u(r)\to m_1>0$ as 
$r\to 1^{-}$. Take 
$r_1\in (0,1)$ such that 
$\tilde u(r)>{m_1}/{2}$ for all 
$r\in (r_1,1)$. From (2.6) it follows that for 
$r\in (r_1,1)$
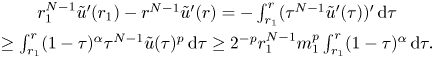\begin{eqnarray*} &r_1^{N-1}\tilde u'(r_1)-r^{N-1}\tilde u'(r)={-}\int_{r_1}^{r}(\tau^{N-1}\tilde u'(\tau))'\,\textrm{d}\tau\\ &\geq\int_{r_1}^{r}(1-\tau)^{\alpha}\tau^{N-1}\tilde u(\tau)^{p}\,\textrm{d}\tau\geq 2^{{-}p}r_1^{N-1}m_1^{p}\int_{r_1}^{r}(1-\tau)^{\alpha}\,\textrm{d}\tau. \end{eqnarray*}Hence, we have
\[ r_1^{N-1}\tilde u'(r_1)\geq 2^{{-}p}r_1^{N-1}m_1^{p} \int_{r_1}^{r}(1-\tau)^{\alpha}\,\textrm{d}\tau. \]
Letting 
$r\to 1^{-}$, in view of 
$\alpha \leq -2$, we obtain a contradiction.
Case 2. 
$m\in [-\infty ,0)$. For the case, there exist 
$r_*>0$ and 
$m_2>0$ such that
\[ r^{N-1}\tilde u'(r)<{-}m_2\ \mbox{for all}\ r\in(r_*,1), \]
and hence there is 
$m_* \in (0, m_2]$ such that
\[ \tilde u'(r)<{-}m_*\ \ \mbox{for}\ r\in(r_*,1). \]
Since 
$u$ has a positive lower bound, we can assume
\[ \tilde u(r)\to m_3\in(0,\infty)\ \mbox{as}\ r\to 1^{-}. \]Clearly,
\[ \tilde u(r)>m_3\ \ \mbox{for all}\ r\in(r_*,1). \]From (2.6) it follows that
\[ r_*^{N-1}\tilde u'(r_*)-r^{N-1}\tilde u'(r)\geq m_3^{p}\int_{r_*}^{r}(1-\tau)^{\alpha}\tau^{N-1} \,\textrm{d}\tau\ \mbox{for}\ r\in(r_*,1). \]Further, we have
\[{-}r^{N-1}\tilde u'(r)\geq m_3^{p}\int_{r_*}^{r}(1-\tau)^{\alpha}\tau^{N-1} \,\textrm{d}\tau\geq m_3^{p}r_*^{N-1}\int_{r_*}^{r}(1-\tau)^{\alpha}\,\textrm{d}\tau\ \mbox{for}\ r\in(r_*,1). \]So, we obtain
\[ \tilde u'(r)\leq{-}m_3^{p}r_*^{N-1}r^{1-N}\int_{r_*}^{r}(1-\tau)^{\alpha} \,\textrm{d}\tau\leq{-}m_3^{p}r_*^{N-1}\int_{r_*}^{r}(1-\tau)^{\alpha} \,\textrm{d}\tau\ \mbox{for}\ r\in(r_*,1). \]
Integrating the above inequality from 
$r_*$ to 
$r$, we see
\[ \tilde u(r)-\tilde u(r_*)\leq{-}m_3^{p}r_*^{N-1}\int_{r_*}^{r}\left(\int_{r_*}^{t}(1-\tau)^{\alpha} \,\textrm{d}\tau\right)\,\textrm{d}t. \]
By the condition 
$\alpha \leq -2$, the right-hand side converges to 
$-\infty$ as 
$r\to 1^{-}$. Therefore, we obtain a contradiction, and hence complete the proof of the conclusion (i).
Now, we prove the conclusion (ii). As the arguments of the proof for conclusion (i), we can derive a contradiction for the case 1. For the case 2, we have that
\[ \tilde u'(r)<{-}m_*\ \mbox{for}\ r\in(r_*,1),\ \mbox{and}\ \tilde u(r)\to m_3\in[0,+\infty)\ \mbox{as}\ r\to 1^{-}. \]
If 
$m_3\neq 0$ holds, we can obtain a contradiction as the arguments for case 2 in the proof of (i). Now, we assume 
$m_3=0$. By the differential mean value theorem, there holds
\[ \tilde u(r)\geq m_*(1-r)\ \mbox{for}\ r\in(r_*,1). \]
From (2.6) it follows that for 
$r\in (r_*,1)$
\[ r_*^{N-1}\tilde u'(r_*)-r^{N-1}\tilde u'(r)\geq m_*^{p}\int_{r_*}^{r}(1-\tau)^{\alpha+p}\tau^{N-1}\,\textrm{d}\tau. \]Hence, we see
\[ -\tilde u'(r)\geq m_*^{p}r^{1-N}\int_{r_*}^{r}(1-\tau)^{\alpha+p}\tau^{N-1}\,\textrm{d}\tau\geq m_*^{p}\int_{r_*}^{r}(1-\tau)^{\alpha+p}\tau^{N-1}\,\textrm{d}\tau. \]Therefore, we obtain that
\[ \tilde u(r_*)-\tilde u(r)\geq m_*^{p}r_*^{N-1}\int_{r_*}^{r}\int_{r_*}^{t}(1-\tau)^{\alpha+p}\,\textrm{d}\tau\,\textrm{d}t. \]
Since 
$\alpha +p+2\leq 0$, letting 
$r\to 1^{-}$, we can derive a contradiction.
For the proof of the conclusion (iii), it suffices to deduce a contradiction for the case 
$m_3=0$ as the proof of conclusion (ii). Since 
$1< p<({N+2})/({N-2})$ holds, together with lemma 2.2, (2.5) and (2.6), we have
\[ (1-r)^{\alpha} r^{N-1}\tilde u^{p}\leq{-}(r^{N-1}\tilde u')'\leq r^{N-1}(1-r)^{\alpha} C(1-r)^{-(({2+\alpha})/({p-1}))p}\ \ \mbox{in}\ (0,1), \]
where 
$C>0$ is a positive constant. So, we obtain
\[ r^{N-1}(1-r)^{\alpha} C(1-r)^{-(({2+\alpha})/({p-1}))p}\geq m_*^{p}(1-r)^{\alpha} r^{N-1}(1-r)^{p}\ \ \mbox{in}\ (r_*,1). \]Therefore, we have
\[ (1-r)^{-(({2+\alpha})/({p-1}))p-p}\geq\frac{m_*^{p}}{C}\ \ \mbox{in}\ (r_*,1). \]
By the condition 
$p+1+\alpha <0$, it is clear that 
$-(({2+\alpha })/({p-1}))p-p>0$, and hence we can deduce a contradiction.
In order to obtain the existence of positive solution of (1.2), we need to consider the corresponding perturbation problem, which has no singularity at the boundary, and establish the estimate of its solutions.
Lemma 2.3 Suppose that 
$1< p<({N+2})/({N-2})$, 
$\alpha >-2$, 
$\epsilon _0>0$ and 
$\epsilon \in (0,\epsilon _0]$. Then there exists 
$C>0$ depending only on 
$\alpha ,p,\epsilon _0,N$ such that any positive radial solution 
$u_\epsilon \in C^{2}(B_1)\cap C^{1}(\bar B_1)$ of
\begin{equation} \left\{\begin{array}{@{}ll}\displaystyle -\Delta u=(1+\epsilon-|x|)^{\alpha} u^{p},\ \ & x\in B_1(0),\\ \displaystyle u=0,\ \ & |x|=1 \end{array} \right. \end{equation}satisfies
\begin{align} \|\nabla u_\epsilon\|_{L^{\infty}(B_1)}+\|u_\epsilon\|_{L^{\infty}(B_1)}\leq C. \end{align}Proof. We divide the proof into two steps.
Step 1. We prove that
\[ \|u_\epsilon\|_{L^{\infty}(B_1)}\leq C, \]
where 
$C>0$ depends only on 
$\alpha ,p,\epsilon _0, N$. We use indirect method to prove the conclusion. Suppose that the assertion is false. Then there is a sequence of solutions 
$u_k$, 
$\epsilon _k$ and 
$P_k\in B_1$ such that
\[ M_k=\max_{x\in\bar B_1} u_k(x)=u_k(P_k)\to+\infty\ \ \mbox{as}\ k\to\infty. \]
Since 
$u_k$ is a radially symmetric function, by the maximum principle we claim 
$P_k=0$. In fact, if 
$P_k\neq 0$, then the symmetric property implies that there exists 
$Q_k\in B_1$ such that 
$u_k$ takes minimum at 
$Q_k$ and 
$|P_k|>|Q_k|$. So, we see
\[ 0\geq{-}\Delta u_k(Q_k)=(1+\epsilon_k-|Q_k|)^{\alpha} u_k(Q_k)^{p}>0. \]This is a contradiction.
Without loss of generality, we assume 
$\epsilon _k\to \tilde \epsilon \in [0,\epsilon _0]$. We define
\[ U_k(y)=\frac{1}{M_k}u_k(M_k^{-(({p-1})/{2})}y). \]
Then 
$U_k$ satisfies
\[ -\Delta U_k=\left(1+\epsilon_k-|M_k^{-({p-1})/{2})}y|\right)^{\alpha} U_k^{p} \]
with 
$0\leq U_k\leq 1$ and 
$U_k(0)=1$. By the standard arguments of elliptic equations, we can extract a subsequence of 
$\{U_k\}$ converging to a function 
$U$ in 
$C^{2}_\textrm {loc}(\mathbb {R}^{N})$, which satisfies
\[ -\Delta U=(1+\tilde\epsilon)^{\alpha} U^{p}\ \ \mbox{in}\ \mathbb{R}^{N}\ \mbox{and}\ U(0)=1. \]
Since 
$1< p<({N+2})/({N-2})$, this contradicts the corresponding Liouville-type results [Reference Gidas and Spruck11].
Step 2. We prove that
\[ \|\nabla u_\epsilon\|_{L^{\infty}(B_1)}\leq C, \]
where 
$C>0$ depends only on 
$\alpha ,p,\epsilon _0,N$. By step 1, we assume that 
$\|u_\epsilon \|_{L^{\infty }(B_1)}\leq C$ for any 
$\epsilon \in (0,\epsilon _0]$. Since 
$u_\epsilon$ is radially symmetric, we also denote 
$u_\epsilon (r)=u_\epsilon (x)$ as 
$|x|=r$. For the case 
$\alpha \geq 0$, according to the regularity of elliptic equations, the conclusion can be obtained directly.
Now, we consider the case 
$-2<\alpha <0$. We still use indirect method to prove it. Suppose that the assertion is false. Then, there exist 
$\epsilon _k\in (0,\epsilon _0]$ and positive solution 
$u_k$ of (2.7) with 
$\epsilon =\epsilon _k$ such that
\[ \|\nabla u_k\|_{L^{\infty}(B_1)}\to\infty\ \mbox{as}\ k\to\infty. \]
Since 
$u_k'(0)=0$ and
\[{-}r^{N-1}u_k'(r)=\int_0^{r}(1+\epsilon_k-\tau)^{\alpha}\tau^{N-1}u_k(\tau)^{p}\,\textrm{d}\tau, \]
we can deduce 
$u_k'(r)<0$ for all 
$r\in (0,1]$. Let 
$r_k\in (0,1]$ be the minimum point of 
$u_k'$. From the interior estimate of elliptic equations it follows that 
$\{r_k\}$ has a subsequence, which converges to 
$1$. Without loss of generality, we assume 
$r_k\to 1$ as 
$k\to \infty$. Hence, we have
\[{-}u_k'(r_k)\to+\infty\ \ (k\to\infty). \]From the equation (2.7), it follows that
\[{-}u_k'(r)=r^{1-N}\int_0^{r}\tau^{N-1}(1+\epsilon_k-\tau)^{\alpha} u_k(\tau)^{p}\,\textrm{d}\tau. \]
By 
$\alpha >-2$, we can take a small constant 
$\eta >0$ such that 
$\alpha +1-\eta >-1$. By the differential mean value theorem, it follows that
\[ u_k(r)\leq (1-r)|u_k'(r_k)|\ \mbox{for any}\ r\in(0,1). \]Therefore, we have
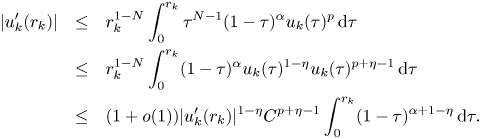\begin{eqnarray*} |u_k'(r_k)|&\leq& r_k^{1-N}\int_0^{r_k}\tau^{N-1}(1-\tau)^{\alpha} u_k(\tau)^{p}\,\textrm{d}\tau\\ &\leq& r_k^{1-N}\int_0^{r_k}(1-\tau)^{\alpha} u_k(\tau)^{1-\eta}u_k(\tau)^{p+\eta-1}\,\textrm{d}\tau\\ &\leq&(1+o(1))|u_k'(r_k)|^{1-\eta}C^{p+\eta-1}\int_0^{r_k}(1-\tau)^{\alpha+1-\eta}\,\textrm{d}\tau. \end{eqnarray*}
Since 
$\alpha +1-\eta >-1$ and 
$\eta >0$, we can obtain
\[ |u_k'(r_k)|\leq K|u_k'(r_k)|^{1-\eta}\ \ \mbox{for all}\ k, \]
where 
$K$ is a positive constant. This contradicts 
$|u_k'(r_k)|\to \infty \ (k\to \infty )$.
Next, we prove theorem 1.3 by using Nehari manifold method and together with lemma 2.3.
Proof of theorem 1.3. Case 1. 
$-2<\alpha \leq 0$. Consider the following problem
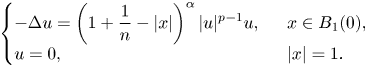\begin{equation} \left\{\begin{array}{@{}ll} \displaystyle -\Delta u=\left(1+\dfrac{1}{n}-|x|\right)^{\alpha} |u|^{p - 1} u,\ \ & x\in B_1(0),\\ \displaystyle u=0,\ \ & |x|=1. \end{array} \right. \end{equation}Define a functional by
\[ F_n(u)=\frac{1}{2}\int_{B_1}|\nabla u|^{2}\,\textrm{d}x-\frac{1}{p+1}\int_{B_1}\left(1+\frac{1}{n}-|x|\right)^{\alpha} (u^{+})^{p+1}\,\textrm{d}x,\ u\in H_0^{1}(B_1), \]
where 
$u^{+} = \max \{u, 0\}$.
We will show that 
$F_n$ has a radially symmetric critical point in 
$H_0^{1}(B_1)$. We denote the norm in 
$H_0^{1}(B_1)$ by
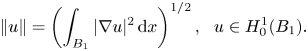\[ \|u\|=\left(\int_{B_1}|\nabla u|^{2}\,\textrm{d}x\right)^{1/2},\ \ u\in H_0^{1}(B_1). \]Let
\[ X=\{u\in H^{1}_0(B_1): u\ \mbox{is a radially symmetric function}\ \}. \]
Clearly, for any given 
$n$, 
$F_n$ satisfies the condition of mountain-pass lemma in 
$X$. By the theory of critical points on symmetric function space, 
$F_n$ has a critical point, which is a radially symmetric function in 
$H_0^{1}(B_1)$. By the standard arguments, we assume that 
$u_n$ is a nontrivial nonnegative solution of (2.9), and 
$u_n$ is a radially symmetric function.
By the regularity and strong maximum principle, it follows that 
$u_n\in C^{2}(B_1)\cap C^{1}(\bar B_1)$ and 
$u_n>0$. From lemma 2.3, there exists 
$C>0$ such that for all 
$n$
\[ \|u_n\|_{C^{1}(\bar B_1)}\leq C. \]
By the regularity of elliptic equations, 
$\{u_n\}$ is bounded in 
$C_\textrm {loc}^{2+\mu }(B_1)$, where 
$\mu \in (0,1)$. In view of Arzela–Ascoli theorem, without loss of generality, we assume 
$u_n\to u$ in 
$C^{2}_\textrm {loc}(B_1)$. So, we can obtain that 
$u\in C^{2}(B_1)\cap C(\bar B_1)$ is a radially symmetric solution of (1.2).
We claim that 
$u$ is a nontrivial solution. Without loss of generality, we assume that 
$u_n\to u$ in 
$C^{1}_\textrm {loc}(B_1)$. Suppose that 
$u\equiv 0$ holds. Since 
$u_n\to u$ in 
$C(\bar B_1)$, we have
\[ \|u_n\|_{L^{\infty}(B_1)}=o(1)\ \ (n\to\infty). \]
From the equations for 
$u_n$ and 
$u_{n+1}$, it follows that
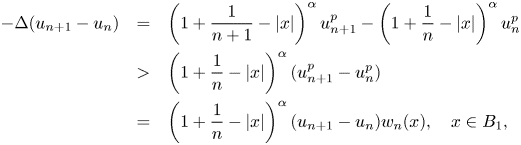\begin{eqnarray*} -\Delta(u_{n+1}-u_n)&=&\left(1+\frac{1}{n+1}-|x|\right)^{\alpha} u_{n+1}^{p}-\left(1+\frac{1}{n}-|x|\right)^{\alpha} u_n^{p}\\ &>&\left(1+\frac{1}{n}-|x|\right)^{\alpha} (u_{n+1}^{p}-u_n^{p})\\ &=&\left(1+\frac{1}{n}-|x|\right)^{\alpha}(u_{n+1}-u_n)w_n(x),\quad x\in B_1, \end{eqnarray*}
where 
$\|w_n\|_{L^{\infty }(B_1)}=o(1)\ (n\to \infty )$. So, we have
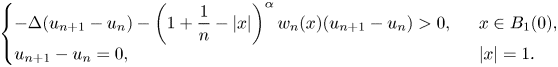\begin{align} \left\{\begin{array}{@{}ll} \displaystyle -\Delta (u_{n+1}-u_n)-\left(1+\dfrac{1}{n}-|x|\right)^{\alpha} w_n(x)(u_{n+1}-u_n)>0,\ \ & x\in B_1(0),\\ \displaystyle u_{n+1}-u_n=0,\ \ & |x|=1. \end{array} \right. \end{align}
Denote by 
$\lambda _1[b(x),\omega ]$ the first eigenvalue of
\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta \phi+b(x)\phi=\lambda \phi,\ \ & x\in \omega,\\ \displaystyle \phi=0,\ \ & x\in \partial\omega. \end{array} \right. \end{eqnarray*}
When 
$b(x)=-\frac {1}{4}(1+\frac {1}{n}-|x|)^{-2}$, by lemma 2.3 in [Reference Du and Wei9] it follows that
\[ \lambda_1[b(x),B_1]>0. \]
Since 
$\|w_n\|_{L^{\infty }(B_1)}$ is sufficiently small for sufficiently large 
$n$, by 
$\alpha >-2$ it follows that
\[ \left(1+\frac{1}{n}-|x|\right)^{\alpha} w_n(x)\leq \frac{1}{4}\left(1+\frac{1}{n}-|x|\right)^{{-}2}\ \mbox{in}\ B_1. \]So, we have
\[ \lambda_1\left[-\left(1+\frac{1}{n}-|x|\right)^{\alpha} w_n(x), B_1\right]>0\ \mbox{for large}\ n. \]Together with (2.10) and the strong maximum principle, we obtain
\[ u_{n+1}(x)>u_n(x)\ \mbox{in}\ B_1 \ \mbox{for large}\ n. \]
This contradicts 
$u_n\to 0$ in 
$C(\bar B_1)$ as 
$n\to \infty$.
Case 2. Suppose 
$\alpha >0$. Define a functional 
$F$ in 
$H^{1}_0(B_1(0))$ by
\[ F(u)=\frac{1}{2}\int_{B_1}|\nabla u|^{2}\,\textrm{d}x-\frac{1}{p+1}\int_{B_1}(1-|x|)^{\alpha} (u^{+})^{p+1}\,\textrm{d}x. \]
By the mountain pass lemma and the standard arguments, 
$F$ has a positive critical point 
$v\in H_0^{1}(B_1(0))$. In view of 
$1< p<({N+2})/({N-2})$ and 
$\alpha >0$, together with the regularity of elliptic equations, 
$v\in C^{2}(B_1)\cap C^{1}(\bar B_1)$ is a positive solution of (1.2).
3. The case $0< p\leq 1$
Here, we firstly establish the following Liouville-type result and estimate of positive solutions, which should be useful for some estimates of positive solutions of some sublinear or negative exponent problems. We are not sure whether the following result is new, but we did not find it in some existing references, and here the method of study is basic.
Theorem 3.1 Suppose that 
$p<1$, 
$\gamma < 2$, 
$\epsilon >0$ and 
$a(x)\geq \epsilon |x|^{-\gamma }$ in 
$\mathbb {R}^{N}$. For the differential inequality
\begin{align} -\Delta v\geq a(x)v^{p}\ \ \mbox{in}\ \mathbb{R}^{N}, \end{align}the following conclusions hold:
(i) for
$0\leq \gamma <2$, (3.1) has no positive classical solutions;(ii) for
$\gamma <0$, any positive solution $v\in C^{2}(\mathbb {R}^{N}{\setminus} \{0\})$ of (3.1) satisfies
where\[ v(x)\geq C|x|^{({2-\gamma})/({1-p})}\ \ \mbox{for all}\ \ x\neq 0, \]$C$ depends only on $\epsilon ,\gamma ,p$.
Proof. We firstly prove the conclusion (i). For 
$0\leq \gamma <2$, we suppose that (3.1) has a positive classical solution 
$v$. We are going to deduce a contradiction. For any positive integer 
$n$, we consider the following problem
\begin{align} \left\{\begin{array}{@{}ll} \displaystyle -\Delta w=c_nw^{p},\ \ & x\in B_n(0),\\ \displaystyle w=m_n,\ \ & x\in \partial B_n(0), \end{array} \right. \end{align}
where 
$m_n=\min _{|x|\leq n}v(x)$ and 
$c_n=\inf _{|x|\leq n}a(x)$. Clearly, 
$m_n$ and 
$v$ can act as a subsolution and supersolution of (3.2). By the supersolution and subsolution method, (3.2) has a minimal positive solution 
$v_n$ in the interval 
$[m_n,v]$. This means that for any positive solution 
$w$ of (3.2) with 
$m_n\leq w\leq v$ must satisfy 
$w(x)\geq v_n(x)$ in 
$B_n(0)$. In fact, 
$v_n$ is the limit of the iteration sequence with the initial value 
$m_n$. Take 
$K>0$ such that
\[ |c_ns^{p}-c_nt^{p}|\leq K|s-t| \ \mbox{for all}\ s,t\in[m_n,M_n], \]
where 
$M_n=\max _{|x|\leq n}v(x)$. Let 
$w_1$ be the unique positive solution of
\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta w+Kw=Km_n+c_nm_n^{p},\ \ & x\in B_n(0),\\ \displaystyle w=m_n,\ \ & x\in \partial B_n(0). \end{array} \right. \end{eqnarray*}
By the maximum principle, we obtain 
$w_1(x)>m_n$ in 
$B_n(0)$. By the uniqueness of solutions and invariant property of rotations for the operator 
$\Delta$, it follows that 
$w_1$ is a radially symmetric function. Let 
$w_2$ be the unique positive solution of
\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta w+Kw=Kw_1+c_nw_1^{p},\ \ & x\in B_n(0),\\ \displaystyle w=m_n,\ \ & x\in \partial B_n(0). \end{array} \right. \end{eqnarray*}
By the maximum principle, we obtain 
$w_2(x)\geq w_1(x)$ in 
$B_n$. By using the uniqueness and invariant property of rotations for the operator 
$\Delta$ again, it follows that 
$w_2$ is a radially symmetric function. Successively, by 
$w_{k+1}$ denote the unique positive solution of
\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta w+Kw=Kw_k+c_nw_k^{p},\ \ & x\in B_n(0),\\ \displaystyle w=m_n,\ \ & x\in \partial B_n(0). \end{array} \right. \end{eqnarray*}
Similarly, any term of the iteration sequence 
$\{w_k\}$ is a radially symmetric function. By the standard arguments, 
$v_n(x):=\lim _{k\to \infty }w_k(x)$ is a minimal positive solution of (3.2) in the interval 
$[m_n,v]$. Clearly, 
$v_n$ is radially symmetric. By the maximum principle, it is easy to show that 
$v_n$ is the minimal positive solution in 
$[m_n,v]$.
For convenience, by 
$\lambda (n)$ and 
$\psi _n$ denote the first eigenvalue and the first eigenfunction of
\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta\psi=\lambda\psi,\ \ & x\in \ B_{n}(0),\\ \displaystyle \psi(x)=0,\ \ & |x|=n. \end{array} \right. \end{eqnarray*}So, we have
\[ \int_{B_n}\lambda(n)\psi_n v_n+\int_{|x|=n}m_n\frac{\partial\psi_n}{\partial\nu}=c_n\int_{B_n}v_n^{p}\psi_n. \]
By Hopf's lemma, we have 
${\partial \psi _n}/{\partial \nu }<0$ on 
$\partial B_n$, where 
$\nu$ is the outer unit normal vector. Therefore, we obtain
\[ \int_{B_n}\psi_n v_n[\lambda(n)-c_nv_n^{p-1}]>0. \]
By the maximum principle and the symmetric property, the origin is the maximum point of 
$v_n$. So, there holds
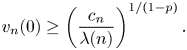\[ v_n(0)\geq \left(\frac{c_n}{\lambda(n)}\right)^{{1}/({1-p})}. \]
It is well-known that 
$\lambda (1)=n^{2}\lambda (n)$. By 
$a(x)\geq \epsilon |x|^{-\gamma }$, it follows that
\[ c_n\geq\epsilon n^{-\gamma}. \]Hence, we have
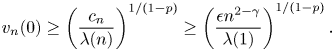\[ v_n(0)\geq \left(\frac{c_n}{\lambda(n)}\right)^{{1}/({1-p})}\geq\left(\frac{\epsilon n^{2-\gamma}}{\lambda(1)}\right)^{{1}/({1-p})}. \]So, we obtain
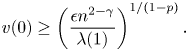\[ v(0)\geq\left(\frac{\epsilon n^{2-\gamma}}{\lambda(1)}\right)^{{1}/({1-p})}. \]
Letting 
$n\to \infty$, we obtain a contradiction. Therefore, the conclusion (i) is proved.
Now, we prove the conclusion (ii). Suppose that 
$v\in C^{2}(\mathbb {R}^{N}{\setminus} \{0\})$ is any positive solution of (3.1) with 
$\gamma <0$. Let 
$x_R$ be an arbitrary point, where 
$R>0$ and 
$|x_R|=2R$. Denote
\[ \tilde m_R=\min_{|x-x_R|\leq \frac{3}{2}R}v(x),\ \ \tilde c_R=\inf_{|x-x_R|< R}a(x). \]We consider the Dirichlet problem
\begin{align} \left\{\begin{array}{@{}ll} \displaystyle -\Delta \vartheta=\tilde c_R\vartheta^{p},\ \ & x\in B_R(x_R),\\ \displaystyle \vartheta=\tilde m_R,\ \ & x\in \partial B_R(x_R). \end{array} \right. \end{align}
Similar to the proof of (i), it follows that (3.3) has a minimal solution 
$\eta _R(x)$ in 
$[\tilde m_R,v]$. Denote
\[ \tilde v_R(x)=\eta_R(x+x_R)\ \mbox{for}\ x\in B_R(0). \]Then we have
\[ \tilde v_R(x)\leq v(x+x_R)\ \mbox{for}\ x\in B_R(0). \]By the similar arguments of (i), it follows that
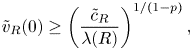\[ \tilde v_R(0)\geq \left(\frac{\tilde c_R}{\lambda(R)}\right)^{{1}/({1-p})}, \]
where 
$\lambda (R)$ denotes the first eigenvalue of 
$-\Delta$ with Dirichlet boundary condition on 
$B_R$. By 
$a(x+x_R)\geq \epsilon |x+x_R|^{-\gamma }$, it follows that
\[ \tilde c_R\geq\epsilon R^{-\gamma}. \]So, we can obtain that
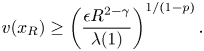\[ v(x_R)\geq\left(\frac{\epsilon R^{2-\gamma}}{\lambda(1)}\right)^{{1}/({1-p})}. \]
By the arbitrariness of 
$x_R$, it follows that
\[ v(x)\geq\left(\frac{\epsilon }{2^{2-\gamma}\lambda(1)}\right)^{{1}/({1-p})}|x|^{({2-\gamma})/({1-p})}\ \ \mbox{for all}\ \ x\neq 0. \]In order to establish the lower estimate of positive solutions of (1.1). We need the following lemma.
Lemma 3.2 Let 
$N\geq 3$, 
$p<1$, and 
$\mu \in (0,1)$. Let 
$a\in C^{\mu }(\bar B_1)$ satisfy
\[ a(x)\geq C, \quad x\in\bar B_1, \]
for some constants 
$C>0$. Then for any positive classical solution 
$u$ of
\[ -\Delta u=a(x)u^{p}, \quad x\in B_1, \]
$u$ satisfies
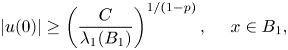\begin{align} |u(0)|\geq \left(\frac{C}{\lambda_1(B_1)}\right)^{{1}/({1-p})},\quad \ x\in B_1, \end{align}
where 
$\lambda _1(B_1)$ is the first eigenvalue of 
$-\Delta$ with Dirichlet boundary condition on 
$B_1(0)$.
Proof. Fix a small positive constant 
$\delta >0$. For any large positive integer 
$n$, we consider
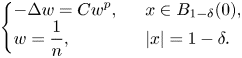\begin{align} \left\{\begin{array}{@{}ll} \displaystyle -\Delta w=Cw^{p},\ \ & x\in B_{1-\delta}(0),\\ \displaystyle w=\dfrac{1}{n},\ \ & |x|=1-\delta. \end{array} \right. \end{align}
Let 
$e$ satisfy
\[ -\Delta e=1\ \mbox{in}\ B_1,\quad e=0\ \mbox{on}\ \partial B_1. \]
Then we can take a large constant 
$M>0$ such that
\[ -\Delta (Me)=M>CM^{p}e^{p}\ \mbox{in}\ B_1 \]and
\[ Me>\frac{1}{n}\ \mbox{as}\ |x|\leq 1-\delta. \]
So, 
$(\frac {1}{n},Me)$ is a pair of subsolution and supersolution of (3.5). As the arguments in the proof of theorem 3.1, (3.5) has a minimal positive solution in 
$[\frac {1}{n},Me]$, and denote it by 
$w_n$. Clearly, 
$w_n$ is a radial function. By the iteration method and maximum principle, it follows that
\[ w_{n+1}(x)\leq w_n(x)\ \mbox{for all}\ x\in B_{1 - \delta}, \]
where 
$w_{n+1}$ is the minimal solution in 
$[({1}/({n+1})),Me]$ of (3.5) with 
$w={1}/({n+1})$ on 
$|x|=1-\delta$. By the maximum principle, the origin is the maximum value point of 
$w_n$. Let 
$\phi _\delta >0$ and 
$\lambda _\delta$ be the first eigenfunction and the first eigenvalue of
\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta\phi=\lambda_1\phi,\ \ & x\in B_{1-\delta},\\ \displaystyle \phi=0,\ \ & |x|=1-\delta. \end{array} \right. \end{eqnarray*}
So, for any 
$n$, we have
\[ \int_{|x|<1-\delta}\lambda_\delta w_n\phi_\delta\,\textrm{d}x+\int_{|x|=1-\delta}w_n\frac{\partial\phi_\delta}{\partial\nu}=C\int_{|x|<1-\delta}w_n^{p}\phi_\delta. \]Hence we see
\[ \int_{|x|<1-\delta}w_n\phi_\delta[\lambda_\delta-Cw_n^{p-1}]>0. \]
By the maximum principle, it follows that the origin is the maximum point of 
$w_n$. Therefore we obtain
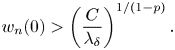\[ w_n(0)>\left(\frac{C}{\lambda_\delta}\right)^{{1}/({1-p})}. \]
By the monotone property of 
$\{w_n\}$ in 
$n$, 
$w_\delta :=\lim _{n\to \infty }w_n$ is well-defined in 
$B_{1-\delta }$ and 
$w_\delta (0)>0$. By the regularity and the strong maximum principle, 
$w_\delta$ is a positive radially symmetric function in 
$B_{1-\delta }$. Clearly, 
$w_\delta$ satisfies
\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta w_\delta=Cw_\delta^{p},\ \ & x\in B_{1-\delta},\\ \displaystyle w_\delta=0,\ \ & |x|=1-\delta \end{array} \right. \end{eqnarray*}and
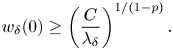\[ w_\delta(0)\geq\left(\frac{C}{\lambda_\delta}\right)^{{1}/({1-p})}. \]
For any positive classical function 
$u$ satisfying
\[ -\Delta u=a(x)u^{p},\ \ x\in B_1, \]
when 
$n$ is sufficiently large, it follows that
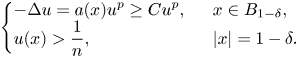\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta u=a(x)u^{p}\geq Cu^{p},\ \ & x\in B_{1-\delta},\\ \displaystyle u(x)>\dfrac{1}{n},\ \ & |x|=1-\delta. \end{array} \right. \end{eqnarray*}So, we obtain that
\[ w_n(x)\leq u(x)\ \mbox{in}\ B_{1-\delta}. \]Therefore, we have
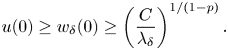\[ u(0)\geq w_\delta(0)\geq\left(\frac{C}{\lambda_\delta}\right)^{{1}/({1-p})}. \]
Letting 
$\delta \to 0^{+}$, we can obtain (3.4).
The conclusion (ii) in theorem 1.1 can be expressed by the following theorem.
Theorem 3.3 Let 
$N\geq 3$, 
$\alpha >-2$ and 
$p<1$. Then there exists 
$C=C(N,p,\alpha )$ such that any nonnegative solution 
$u$ of (1.1) satisfies
\begin{align} u(x)\geq C(1-|x|)^{-(({2+\alpha})/({p-1}))} \ \mbox{for all} \ x\in B_1. \end{align}Proof. Let 
$x_0$ be an arbitrary point in 
$B_1$. We define a function by
\[ U(x)=(1-|x_0|)^{({2+\alpha})/({p-1})}u\left(x_0+\frac{1-|x_0|}{2}x\right),\quad \ x\in B_1. \]
Then 
$U$ satisfies
\[ -\Delta U=a(x)U^{p},\ \ x\in B_1, \]where
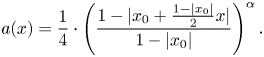\[ a(x) = \dfrac 14 \cdot \left(\frac{1 - |x_0 + \frac{1 - |x_0|}{2}x|}{1 - |x_0|}\right)^{\alpha}. \]
Clearly, for any 
$x\in B_1$, we have
\[ a(x)\geq\frac{1}{2^{\alpha + 2}}\ \ \mbox{as}\ \alpha\geq 0 \]and
\[ a(x)\geq \frac{3^{\alpha}}{2^{\alpha + 2}}\ \ \mbox{as} - 2<\alpha<0. \]Therefore, applying lemma 3.2, we have
\[ U(0)\geq C. \]Hence,
\[ (1-|x_0|)^{({2+\alpha})/({p-1})}u(x_0)\geq C. \]
By the arbitrariness of 
$x_0$, we can obtain (3.6).
Proof of theorem 1.4. Suppose that 
$u\in C^{1}(\bar B_1)$ is a positive solution of (1.2). By Hopf's Lemma, there exist 
$c_1,c_2>0$ such that
\[ c_1(1-|x|)\leq u(x)\leq c_2(1-|x|)\ \mbox{in}\ B_1. \]
By the condition 
$1+p+\alpha <0$, it follows that 
$-(({2+\alpha })/({p-1}))<1$. By theorem 3.3, we see that
\[ C(1-|x|)^{-(({2+\alpha})/({p-1}))}\leq u(x)\leq c_2(1-|x|)\ \mbox{in}\ B_1. \]This is impossible, and hence we obtain a contradiction.
Remark 3.4 In fact, under the condition of theorem 1.4, problem (1.2) has no positive solution 
$u\in C^{1}(B_1)\cap C(\bar B_1)$, which has differential points on 
$\partial B_1$.
Proof of theorem 1.5. We prove this conclusion by using the indirect method. Suppose that (1.1) has a positive solution 
$u$.
Case 1. 
$p\in (0,1)$. According to theorem 3.3 and 
$\alpha \leq -2$, there is a positive constant 
$C>0$ such that
\[ u(x)\geq C\ \ \mbox{for all}\ \ x\in B_1(0). \]Denote
\[ \tilde u(r):=\frac{1}{|S^{N-1}|}\int_{S^{N-1}}u(r,\theta)\,\textrm{d}\theta, \]
and then 
$\tilde u$ satisfies
\[ -(r^{N-1}\tilde u'(r))'\geq C^{p}(1-r)^{\alpha} r^{N-1}\ \mbox{in}\ (0,1), \]As the arguments of the proof of the conclusion (i) in theorem 1.2, we can derive a contradiction.
Case 2. 
$p=1$. For such case, there holds
\[ -\Delta u\geq\frac{u}{(1-|x|)^{2}}\ \ \mbox{in}\ B_1(0). \]
This implies that the first eigenvalue 
$\lambda _1(n)$ of
\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta \phi=\lambda\dfrac{\phi}{(1-|x|)^{2}},\ \ & x\in B_{1-({1}/{n})}(0),\\ \displaystyle \phi=0,\ \ & |x|=1-\dfrac{1}{n}. \end{array} \right. \end{eqnarray*}
is larger than 
$1$. This is a contradiction to 
$\lim _{n\to \infty }\lambda _1(n)=\frac {1}{4}$, which can be found in [Reference Du and Wei9].
Remark 3.5 In fact, when the conditions 
$p<0$ and 
$\alpha \leq -2$ hold, we can also prove that (1.1) has no positive solutions in 
$C^{2}(B_1)\cap C(\bar B_1)$. Suppose that 
$u\in C^{2}(B_1)\cap C(\bar B_1)$ is a positive solution of (1.1). For this case, by the equation and 
$f(t)=t^{p}$ is convex in 
$t$, we also can obtain
\begin{align} (r^{N}\tilde u'(r))'<0\ \mbox{and} - (r^{N-1}\tilde u')'\geq(1-r)^{\alpha} r^{N-1}\tilde u^{p} \ \ \mbox{in}\ (0,1). \end{align}
So we obtain 
$r^{N-1}\tilde u'(r)\to m\in [-\infty ,+\infty )$ as 
$(r\to 1)$. If 
$m<0$ holds, by the similar argument in the proof of theorem 1.2 there exist 
$r_*>0$, 
$m_*>0$ and 
$m_1\geq 0$ such that
\[ \tilde u(r)\to m_1 \ (r\to 1)\ \mbox{and}\ \tilde u'(r)<{-}m_*\ \mbox{in}\ (r_*,1). \]
Therefore, we can choose a small constant 
$\epsilon >0$ such that 
$\tilde u(r)^{p}\geq \epsilon$ in 
$(r_*,1)$. By integral for the second inequality in (3.7), it follows that
\begin{eqnarray*} \tilde u(r)-\tilde u(r_*)\leq{-}\epsilon r_*^{N-1}\int_{r_*}^{r}\left(\int_{r_*}^{r}(1-\tau)^{\alpha}\right)\,\textrm{d}t. \end{eqnarray*}
By 
$\alpha \leq -2$, letting 
$r\to 1$, we can derive a contradiction. If 
$m\geq 0$ holds, then there holds 
$\tilde u'(r)>0$ in 
$(0,1)$. Since 
$u\in C(\bar B_1)$ is a positive function, 
$\tilde u(r)^{p}\geq m_0$ for all 
$r\in (0,1)$, where 
$m_0$ is a positive constant. For any fixed 
$r_1\in (0,1)$, we obtain that for 
$r\in (r_1,1)$
\[ \tilde u'(r_1)\geq m_0\int_{r_1}^{r}(1-\tau)^{\alpha} \,\textrm{d}\tau. \]
In view of 
$\alpha \leq -2$, letting 
$r\to 1$, we can see a contradiction.
Remark 3.6 When 
$p=1$, there exists a unique 
$\alpha >-2$ such that (1.2) has a positive solution. In fact, let 
$\lambda _1(n,\alpha )$ be the first eigenvalue of
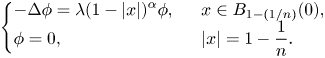\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta \phi=\lambda {(1-|x|)^{\alpha}}{\phi},\ \ & x\in B_{1-({1}/{n})}(0),\\ \displaystyle \phi=0,\ \ & |x|=1-\dfrac{1}{n}. \end{array} \right. \end{eqnarray*}
It is well-known that 
$\lim _{n\to \infty }\lambda _1(n,-2)=\frac {1}{4}$ and 
$\lambda _1(n,0)>5$ for sufficiently large 
$n$ (refer to [Reference Du and Wei9]). By the continuity property and monotone property of the first eigenvalue for weigh functions, we can choose 
$\gamma >-2$ satisfying 
$1>\lambda _1(n,\gamma )>\frac {1}{2}$ for large 
$n$, and hence there exists a unique 
$\alpha _n\in (\gamma , 0)$ such that 
$\lambda _1(n,\alpha _n)=1$. Clearly, 
$\{\alpha _n\}$ is an increasing sequence in 
$n$. Then it is clear that 
$\tilde \alpha :=\lim _{n\to \infty }\alpha _n\in (\gamma ,0)$. By the regularity of elliptic equations, for the case 
$\alpha =\tilde \alpha$, (1.2) with 
$p=1$ has positive solutions.
Finally, we prove the existence and uniqueness of positive solutions of (1.8).
Proof of theorem 1.6. Step 1 We show the existence of positive solutions of (1.2) for the conclusion (i). Denote the first eigenfunction and eigenvalue by 
$\phi _1$ and 
$\lambda _1(B_1)$ of
\[ -\Delta \phi=\lambda\phi\ \mbox{in}\ B_1,\ \ \phi=0 \ \mbox{on}\ \partial B_1. \]
Define 
$\underline u=m\phi _1^{\beta }$, where 
$\beta =({2+\alpha })/({1-p})$. Clearly, we can choose 
$c_1,c_2>0$ such that
\[ c_1\phi_1(x)\leq 1-|x|\leq c_2\phi_1(x)\ \mbox{in}\ B_1(0). \]
When 
$m$ is a small positive constant, we obtain
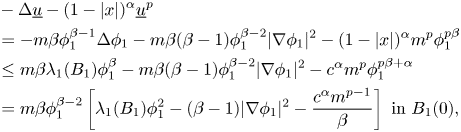\begin{align*} & -\Delta\underline u-(1-|x|)^{\alpha}\underline u^{p}\\ &={-}m\beta\phi_1^{\beta-1}\Delta\phi_1-m\beta(\beta-1)\phi_1^{\beta-2}|\nabla\phi_1|^{2}-(1-|x|)^{\alpha} m^{p}\phi_1^{p\beta}\\ &\leq m\beta\lambda_1(B_1)\phi_1^{\beta}-m\beta(\beta-1)\phi_1^{\beta-2}|\nabla\phi_1|^{2}-c^{\alpha} m^{p}\phi_1^{p\beta+\alpha}\\ &= m\beta\phi_1^{\beta-2}\left[\lambda_1(B_1)\phi_1^{2}-(\beta-1)|\nabla\phi_1|^{2}-\frac{c^{\alpha} m^{p-1}}{\beta}\right]\ \mbox{in}\ B_1(0), \end{align*}
where 
$c$ is a positive constant. According to 
$p-1<0$, 
$\beta >0$, it holds that
\[ -\Delta\underline u-(1-|x|)^{\alpha}\underline u^{p}\leq 0\ \mbox{in}\ B_1(0). \]
In addition, let 
$\bar u=K\phi _1^{\rho }$, where 
$K>0$ and 
$\rho >0$ are constants. We can take large 
$M>0$ and 
$0<\rho \leq \min \{1,(({2+\alpha })/({1-p}))\}$, then by a similar calculation we have
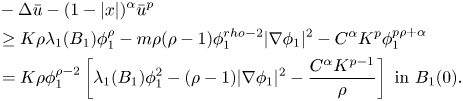\begin{align*} & -\Delta\bar u-(1-|x|)^{\alpha}\bar u^{p}\\ &\geq K\rho\lambda_1(B_1)\phi_1^{\rho}-m\rho(\rho-1)\phi_1^{rho-2}|\nabla\phi_1|^{2}-C^{\alpha} K^{p}\phi_1^{p\rho+\alpha}\\ &= K\rho\phi_1^{\rho-2}\left[\lambda_1(B_1)\phi_1^{2}-(\rho-1)|\nabla\phi_1|^{2}-\frac{C^{\alpha} K^{p-1}}{\rho}\right]\ \mbox{in}\ B_1(0). \end{align*}
So, for sufficiently large 
$K$, it follows that
\[ -\Delta\bar u-(1-|x|)^{\alpha}\bar u^{p}\geq 0 \ \mbox{in}\ B_1(0). \]
By the supersolution and subsolution method, and together with the regularity of elliptic equations, (1.2) has a positive solution in 
$C^{2}(B_1)\cap C(\bar B_1)$.
Step 2 Prove the uniqueness of positive solution of (1.2) with 
$p<0$ and 
$\alpha >-2$. By the estimate of positive solutions, there exists a constant 
$c_*>0$ such that for any positive solution 
$u$ of (1.2)
\[ u(x)\geq c_*\phi_1^{({2+\alpha})/({1-p})} \ \mbox{for all}\ x\in B_1(0). \]
When we take a small positive constant 
$m$ satisfying 
$m< c_*$ in the step 1, then there is a minimal positive solution 
$v_*$ in 
$[m\phi _1^{\beta },K\phi _1^{\rho }]$. Suppose that 
$v$ is any positive solution of (1.2). Then we have 
$v(x)\geq m\phi _1^{\beta }$. Therefore, 
$\min \{v,K\phi _1^{\rho }\}$ is a supersolution of (1.2) and 
$m\phi _1^{\beta }\leq \min \{v,K\phi _1^{\rho }\}$. So, it follows that 
$v_*\leq \min \{v,K\phi _1^{\rho }\}$, and hence we obtain 
$v_*\leq v$. This implies that 
$v_*$ is a minimal positive solution. For the uniqueness, we need to show 
$v_*=v$. If it is not true, there exists 
$x_0\in B_1(0)$ such that
\[ v_*(x_0)-v(x_0)=\min\{v_*(x)-v(x):x\in B_1(0)\}<0. \]
In view of 
$p<0$, we see
\[ 0\geq{-}\Delta(v_*-v)(x_0)=(1-|x_0|)^{\alpha}(v_*(x_0)^{p}-v(x_0)^{p})>0. \]This is a contradiction.
Step 3 Prove the existence of positive solution of (1.8). Take a positive constant 
$\delta >0$ and 
$1< q<({N+2})/({N-2})$. Then the problem
\[ -\Delta u=u^{q}\ \mbox{in}\ B_{1+\delta}(0),\ u=0\ \mbox{on}\ \partial B_{1+\delta}(0) \]
has a positive solution, and denote it by 
$u_\delta$. We can choose a sufficiently large 
$M>0$ such that 
$\bar u:=Mu_\delta$ satisfies
\[ -\Delta\bar u=Mu_\delta^{q}\geq (1-|x|)^{\alpha} (Mu_\delta)^{p}=(1-|x|)^{\alpha}\bar u^{p}\ \mbox{in}\ B_1, \]
\[ \bar u(x)\geq \underline u(x)\ \mbox{in}\ B_1 \ \mbox{and}\ \bar u(x)\geq \psi(x)\ \mbox{on}\ \partial B_1. \]
Then by the supersolution and subsolution method and the standard arguments, there exists a minimal positive solution 
$u_*$ and a maximal positive solution 
$u^{*}$ of the interval 
$[m\phi _1^{\beta },Mu_\delta ]$.
Step 4 We show the uniqueness of the positive solutions for the case 
$\alpha \geq 0$ and 
$p\in (0,1)$. Suppose that 
$v$ is an arbitrary positive solution of (1.1). From theorem 3.3 it follows that there is a positive constant 
$C$ such that
\[ v(x) \geq C(1-|x|)^{\beta} \ \mbox{in} \ B_1. \]
Without loss of generality, we assume 
$m>0$ satisfying
\[ m\phi_1(x)^{\beta}\leq C(1-|x|)^{\beta}\ \mbox{in}\ B_1(0). \]
So, we obtain that 
$m\phi _1^{\beta }$ and 
$\min \{v, \bar {u}\}$ are a pair of subsolution and supersolution of (1.1). Therefore, we have
\[ u_*(x)\leq v(x)\ \mbox{in} \ B_1(0). \]
By the arbitrariness of 
$v$, 
$u_*$ is the minimal positive solution of (1.8).
Next we show that 
$v=u_*$. For the given solution 
$v$, we can take a suitable large 
$M>0$ such that
\[ M u_\delta (x)\geq v(x)\ \mbox{in}\ B_1(0). \]So we have
\[ u_*(x)\leq v(x)\leq u^{*}(x)\ \mbox{in}\ B_1(0). \]
By 
$\alpha \geq 0$ and the regularity, 
$u_*$ and 
$u^{*}$ belong to 
$C^{1}(\bar B_1)\cap C^{2}(B_1)$. For our aim, it is sufficient to show 
$u_*=u^{*}$. Suppose that this conclusion is false. From the equation it follows that
\begin{eqnarray*} \left\{\begin{array}{@{}ll} \displaystyle -\Delta(u_*-u^{*})=(1-|x|)^{\alpha}[u_*^{p}-(u^{*})^{p}],\ \ & x\in B_{1}(0),\\ \displaystyle u_*-u^{*}=0,\ \ & |x|=1. \end{array} \right. \end{eqnarray*}
Since 
$u^{*}\geq u_*$ and 
$u^{*}\not \equiv u_*$, in view of the strong maximum principle, we have
\[ u^{*}(x)>u_*(x)\ \mbox{in}\ B_1. \]By Hopf's Lemma, we see
\[ \frac{\partial (u^{*}-u_*)}{\partial\nu}<0\ \mbox{on}\ \partial B_1(0), \]
where 
$\nu$ is the exterior unit normal on 
$\partial B_1(0)$. Multiplying the equation which 
$u_*$ satisfies by 
$u^{*}$ and multiplying the equation which 
$u^{*}$ satisfies by 
$u_*$, respectively, and then integrating by parts the resulting identities over 
$B_1(0)$ , we have that
\[ \int_{\partial B_1}\psi\left[\frac{\partial u^{*}}{\partial\nu}-\frac{\partial u_*}{\partial\nu}\right]=\int_{B_1}(1-|x|)^{\alpha} u_*u^{*}\left[u_*^{p-1}-(u^{*})^{p-1}\right]. \]From the sign of the two side, we can see a contradiction. Therefore, we deduce the uniqueness.
Remark 3.7
(a) In this paper, we assume always
$N\geq 3$. For the case $N=2$, some estimate of positive solutions similar to lemma 2.1 should be established, which may be a challenge.(b) With respect to theorem 1.2 part (i), we conjecture that (1.1) has no positive solutions when
$p>1$ and $\alpha \leq -2$, but we have not known how to prove it up to now.(c) For the case
$\alpha \in \mathbb {R}$, $p\geq ({N+2})/({N-2})$ and $N\geq 3$, we have still made no progress.(d) When domain
$\Omega$ is a ball, this paper has revealed some interesting conclusions. For a general bounded smooth domain $\Omega$, we guess that the corresponding conclusions should be also valid in which some new methods are perhaps developed.
Acknowledgments
The authors express their gratitude to anonymous referee for some valuable comments and suggestions. The research was supported by NSFC grants 11671394, 11771127, 11871250 and the Fundamental Research Funds for the Central Universities (WUT: 2019IB009, 2020IB011, 2020IB019).
