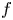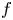1. Introduction
Frei [Reference Frei2] has proved that the differential equation
has a subnormal solution ![]() $f$, which is non-trivial and satisfies
$f$, which is non-trivial and satisfies
if and only if ![]() $\alpha =-m^{2}$ for a positive integer
$\alpha =-m^{2}$ for a positive integer ![]() $m$. The subnormal solution
$m$. The subnormal solution ![]() $f$ is a polynomial in
$f$ is a polynomial in ![]() $\textrm {e}^{z}$ of degree
$\textrm {e}^{z}$ of degree ![]() $m$, that is, an exponential sum of the form
$m$, that is, an exponential sum of the form
It was discovered in [Reference Wen, Gundersen and Heittokangas18, lemma 1] that in this representation one has ![]() $C_j\neq 0$ for
$C_j\neq 0$ for ![]() $1\leq j\leq m$. Substituting the subnormal solution
$1\leq j\leq m$. Substituting the subnormal solution ![]() $f$ into (1.1), we get
$f$ into (1.1), we get
 \[ \sum_{j=1}^{m}C_j j^{2}\textrm{e}^{jz}+\sum_{j=1}^{m}C_j j\textrm{e}^{(\,j-1)z} -m^{2}\sum_{j=1}^{m}C_j \textrm{e}^{jz}=m^{2}. \]
\[ \sum_{j=1}^{m}C_j j^{2}\textrm{e}^{jz}+\sum_{j=1}^{m}C_j j\textrm{e}^{(\,j-1)z} -m^{2}\sum_{j=1}^{m}C_j \textrm{e}^{jz}=m^{2}. \]
By the Borel–Nevanlinna theorem [Reference Gross3, pp. 70, 108], or simply by an elementary observation on three polynomials in ![]() $\textrm {e}^{z}$, this gives rise to the recursive formula
$\textrm {e}^{z}$, this gives rise to the recursive formula
from which ![]() $C_j=\frac {1}{j!}\prod _{k=0}^{j-1}(m^{2}-k^{2})$ for
$C_j=\frac {1}{j!}\prod _{k=0}^{j-1}(m^{2}-k^{2})$ for ![]() $1\leq j \leq m$. Due to the presence of the transcendental coefficient
$1\leq j \leq m$. Due to the presence of the transcendental coefficient ![]() $\textrm {e}^{-z}$, any solution of (1.1) linearly independent with
$\textrm {e}^{-z}$, any solution of (1.1) linearly independent with ![]() $f$ in (1.2) must be of infinite order [Reference Gundersen, Steinbart and Wang7]. For example, when
$f$ in (1.2) must be of infinite order [Reference Gundersen, Steinbart and Wang7]. For example, when ![]() $\alpha =-1$, the function
$\alpha =-1$, the function ![]() $g(z)=\exp (\textrm {e}^{-z}+z)$ is an infinite order solution of (1.1) and linearly independent with
$g(z)=\exp (\textrm {e}^{-z}+z)$ is an infinite order solution of (1.1) and linearly independent with ![]() $f(z)=1+\textrm {e}^{z}$.
$f(z)=1+\textrm {e}^{z}$.
Ozawa [Reference Ozawa15] showed that if ![]() $a\neq 0$, then the non-trivial solutions of
$a\neq 0$, then the non-trivial solutions of
are of infinite order of growth. If ![]() $P(z)$ is a non-constant polynomial, the question whether all non-trivial solutions of
$P(z)$ is a non-constant polynomial, the question whether all non-trivial solutions of
are of infinite order of growth has been known as the Ozawa problem. This problem has been answered affirmatively for particular polynomials ![]() $P(z)$ by Amemiya–Ozawa [Reference Amemiya and Ozawa1] and by Gundersen [Reference Gundersen4], while the complete solution is by Langley [Reference Langley12].
$P(z)$ by Amemiya–Ozawa [Reference Amemiya and Ozawa1] and by Gundersen [Reference Gundersen4], while the complete solution is by Langley [Reference Langley12].
We proceed to state three new examples of Frei–Ozawa type.
Example 1.1 If ![]() $H$ is an arbitrary entire function, then
$H$ is an arbitrary entire function, then ![]() $f(z)=\textrm {e}^{z}+1$ solves
$f(z)=\textrm {e}^{z}+1$ solves
Of particular interest is the case when ![]() $H$ is a polynomial.
$H$ is a polynomial.
Example 1.2 The function ![]() $f(z)=1+(1-3c)(\textrm {e}^{z}+(1-(3/4)c))\textrm {e}^{2z}$,
$f(z)=1+(1-3c)(\textrm {e}^{z}+(1-(3/4)c))\textrm {e}^{2z}$, ![]() $c\in \mathbb {C}\setminus \{1/3,4/3\}$, with two exponential terms solves
$c\in \mathbb {C}\setminus \{1/3,4/3\}$, with two exponential terms solves
Example 1.3 The function ![]() $f(z)=1+3\textrm {e}^{2z}+\sqrt {6}i\textrm {e}^{3z}$ with two exponential terms solves
$f(z)=1+3\textrm {e}^{2z}+\sqrt {6}i\textrm {e}^{3z}$ with two exponential terms solves
where the transcendental coefficient has two exponential terms also. By making a change of variable ![]() $z\to wz$, where
$z\to wz$, where ![]() $w\in \mathbb {C}\setminus \{0\}$, we see that
$w\in \mathbb {C}\setminus \{0\}$, we see that
has a solution ![]() $g(z)=1+3\textrm {e}^{2wz}+\sqrt {6}i\textrm {e}^{3wz}=f(wz)$.
$g(z)=1+3\textrm {e}^{2wz}+\sqrt {6}i\textrm {e}^{3wz}=f(wz)$.
One might wonder about possible examples of solutions ![]() $f$ with a single exponential term and of transcendental coefficients
$f$ with a single exponential term and of transcendental coefficients ![]() $A(z)$ having at least two exponential terms. The non-existence of such examples will be confirmed in theorem 3.2 below. For example, it will be shown that a function
$A(z)$ having at least two exponential terms. The non-existence of such examples will be confirmed in theorem 3.2 below. For example, it will be shown that a function ![]() $f(z)=1+b\textrm {e}^{w z}$ for
$f(z)=1+b\textrm {e}^{w z}$ for ![]() $b, w \in \mathbb {C}$ is a solution of
$b, w \in \mathbb {C}$ is a solution of
for ![]() $P(z), P_1(z), P_2(z)\in \mathbb {C}[z]$ if and only if
$P(z), P_1(z), P_2(z)\in \mathbb {C}[z]$ if and only if ![]() $P_1(z)=({1}/{w})P(z)$ and
$P_1(z)=({1}/{w})P(z)$ and ![]() $P_2(z)=({1}/{bw})P(z)$.
$P_2(z)=({1}/{bw})P(z)$.
In contrast to Ozawa's problem and complementing the three examples above, our primary focus is on exponential polynomial solutions of linear differential equations, in particular of second-order equations
where ![]() $A(z)$ and
$A(z)$ and ![]() $B(z)$ are entire. An exponential polynomial is a function of the form
$B(z)$ are entire. An exponential polynomial is a function of the form
where ![]() $P_j$,
$P_j$, ![]() $Q_j$ are polynomials for
$Q_j$ are polynomials for ![]() $1 \leq j \leq k$. Observe that a polynomial is a special case of an exponential polynomial. A transcendental exponential polynomial
$1 \leq j \leq k$. Observe that a polynomial is a special case of an exponential polynomial. A transcendental exponential polynomial ![]() $f$ can be written in the normalized form
$f$ can be written in the normalized form
where ![]() $q=\max \{\deg (Q_j)\}\geq 1$ is the order of
$q=\max \{\deg (Q_j)\}\geq 1$ is the order of ![]() $f$, the frequencies
$f$, the frequencies ![]() $w_j$ are non-zero and pairwise distinct, the multipliers
$w_j$ are non-zero and pairwise distinct, the multipliers ![]() $F_j$ are exponential polynomials of order
$F_j$ are exponential polynomials of order ![]() $\leq q-1$ such that
$\leq q-1$ such that ![]() $F_j(z)\not \equiv 0$ for
$F_j(z)\not \equiv 0$ for ![]() $1\leq j\leq m$, and
$1\leq j\leq m$, and ![]() $m\leq k$ [Reference Heittokangas, Ishizaki, Tohge and Wen8, Reference Steinmetz16].
$m\leq k$ [Reference Heittokangas, Ishizaki, Tohge and Wen8, Reference Steinmetz16].
Definition 1.4 ([18]) Let ![]() $f$ be given in the normalized form (1.5). If the non-zero frequencies
$f$ be given in the normalized form (1.5). If the non-zero frequencies ![]() ${w}_1,\ldots ,{w}_m$ of
${w}_1,\ldots ,{w}_m$ of ![]() $f$ all lie on a fixed ray
$f$ all lie on a fixed ray ![]() $\arg (w)=\theta$, then
$\arg (w)=\theta$, then ![]() $f$ is called a simple exponential polynomial. If
$f$ is called a simple exponential polynomial. If ![]() $g$ is another simple exponential polynomial of the same order
$g$ is another simple exponential polynomial of the same order ![]() $q$ as
$q$ as ![]() $f$ such that the non-zero frequencies of
$f$ such that the non-zero frequencies of ![]() $g$ all lie on the opposite ray
$g$ all lie on the opposite ray ![]() $\arg (w)=\theta +\pi$, then
$\arg (w)=\theta +\pi$, then ![]() $f$ and
$f$ and ![]() $g$ are called dual exponential polynomials.
$g$ are called dual exponential polynomials.
For example, the functions ![]() $f(z)=z^{2}\textrm {e}^{-iz}+z\textrm {e}^{z^{2}}+\textrm {e}^{2z^{2}+(1-i)z}$ and
$f(z)=z^{2}\textrm {e}^{-iz}+z\textrm {e}^{z^{2}}+\textrm {e}^{2z^{2}+(1-i)z}$ and ![]() $g(z)=2\textrm {e}^{-z^{2}+(1+i)z}+z^{2}\textrm {e}^{-4z^{2}+iz}$ are dual exponential polynomials of order 2.
$g(z)=2\textrm {e}^{-z^{2}+(1+i)z}+z^{2}\textrm {e}^{-4z^{2}+iz}$ are dual exponential polynomials of order 2.
In studying the differential equation (1.3) with entire coefficients ![]() $A(z)$ and
$A(z)$ and ![]() $B(z)$, it is fundamental that each of its solutions
$B(z)$, it is fundamental that each of its solutions ![]() $f$ is an entire function also. In this paper, we study cases when
$f$ is an entire function also. In this paper, we study cases when ![]() $f$ can be an exponential polynomial assuming that
$f$ can be an exponential polynomial assuming that ![]() $A(z)$ is an exponential polynomial and that
$A(z)$ is an exponential polynomial and that ![]() $B(z)$ grows slowly compared to
$B(z)$ grows slowly compared to ![]() $A(z)$. Naturally, the set
$A(z)$. Naturally, the set ![]() ${\mathcal {E}}$ of entire functions is a ring closed under differentiation, and the set
${\mathcal {E}}$ of entire functions is a ring closed under differentiation, and the set ![]() $\operatorname {Exp}_q$ of exponential polynomials of order
$\operatorname {Exp}_q$ of exponential polynomials of order ![]() $\leq q\in \mathbb {N}$ together with constants in
$\leq q\in \mathbb {N}$ together with constants in ![]() $\mathbb {C}$ and ordinary polynomials in
$\mathbb {C}$ and ordinary polynomials in ![]() $\mathbb {C}[z]=:\operatorname {Exp}_0$ becomes a differential subring of
$\mathbb {C}[z]=:\operatorname {Exp}_0$ becomes a differential subring of ![]() $\mathcal {E}$. On the other hand,
$\mathcal {E}$. On the other hand, ![]() $\operatorname {Exp}_q$ is not closed under integration in general except for the set
$\operatorname {Exp}_q$ is not closed under integration in general except for the set ![]() $\operatorname {Exp}_1$ of exponential polynomials of order
$\operatorname {Exp}_1$ of exponential polynomials of order ![]() $\leq 1$, which plays a role in our discussions.
$\leq 1$, which plays a role in our discussions.
To identify a primitive of each element in ![]() $\operatorname {Exp}_1$, it is convenient to use the formula
$\operatorname {Exp}_1$, it is convenient to use the formula
 \[ \int z^{n} \textrm{e}^{w z}\, \textrm{d}z =\left(\frac{1}{w }z^{n} + \sum_{\nu=0}^{n-1}\frac{({-}1)^{n-\nu}n!}{w^{n-\nu+1}\nu!}z^{\nu}\right) \textrm{e}^{w z}+\text{constant} \]
\[ \int z^{n} \textrm{e}^{w z}\, \textrm{d}z =\left(\frac{1}{w }z^{n} + \sum_{\nu=0}^{n-1}\frac{({-}1)^{n-\nu}n!}{w^{n-\nu+1}\nu!}z^{\nu}\right) \textrm{e}^{w z}+\text{constant} \]
for ![]() $n\in \mathbb {N}\cup \{0\}$ and
$n\in \mathbb {N}\cup \{0\}$ and ![]() $w\in \mathbb {C}\setminus \{0\}$. Of course, an analogous formula is not in general available for
$w\in \mathbb {C}\setminus \{0\}$. Of course, an analogous formula is not in general available for ![]() $z^{n} \textrm {e}^{w z^{q}}$ when
$z^{n} \textrm {e}^{w z^{q}}$ when ![]() $q\geq 2$. Indeed, recall the error function
$q\geq 2$. Indeed, recall the error function ![]() $\mathrm {erf}(z)$ defined also for complex argument
$\mathrm {erf}(z)$ defined also for complex argument ![]() $z$ by
$z$ by
It is the primitive of ![]() $({2}/{\sqrt {\pi }})\textrm {e}^{-z^{2}}\in \operatorname {Exp}_2$, but the function itself is not an exponential polynomial. For this reason one needs the special expression
$({2}/{\sqrt {\pi }})\textrm {e}^{-z^{2}}\in \operatorname {Exp}_2$, but the function itself is not an exponential polynomial. For this reason one needs the special expression ![]() $\mathrm {erf}(z)$ for this function as in the real argument case. This is also the case when
$\mathrm {erf}(z)$ for this function as in the real argument case. This is also the case when ![]() $q\geq 3$. The value distribution of the functions
$q\geq 3$. The value distribution of the functions ![]() $\int _0^{z} \textrm {e}^{-\zeta ^{q}}\textrm {d}\zeta$,
$\int _0^{z} \textrm {e}^{-\zeta ^{q}}\textrm {d}\zeta$, ![]() $q\in \mathbb {N}$, as described in Nevanlinna's monograph [Reference Nevanlinna14, pp. 168–170], is quite different from that of exponential polynomials [Reference Heittokangas, Ishizaki, Tohge and Wen8, Reference Heittokangas and Wen10, Reference Steinmetz16].
$q\in \mathbb {N}$, as described in Nevanlinna's monograph [Reference Nevanlinna14, pp. 168–170], is quite different from that of exponential polynomials [Reference Heittokangas, Ishizaki, Tohge and Wen8, Reference Heittokangas and Wen10, Reference Steinmetz16].
Along with ![]() $\operatorname {Exp}_{q-1}$, the set
$\operatorname {Exp}_{q-1}$, the set ![]() $\mathcal {S}_q(\theta )$ of simple exponential polynomials of order
$\mathcal {S}_q(\theta )$ of simple exponential polynomials of order ![]() $q$ with respect to a fixed angle
$q$ with respect to a fixed angle ![]() $\theta \in [0,2\pi )$ forms a differential subring of
$\theta \in [0,2\pi )$ forms a differential subring of ![]() $\operatorname {Exp}_q$. A unit element in
$\operatorname {Exp}_q$. A unit element in ![]() $\mathcal {S}_q(\theta )$ is a single exponential term
$\mathcal {S}_q(\theta )$ is a single exponential term ![]() $\textrm {e}^{wz^{q}+p(z)}$ with
$\textrm {e}^{wz^{q}+p(z)}$ with ![]() $\arg (w)=\theta$,
$\arg (w)=\theta$, ![]() $p(z)\in \mathbb {C}[z]$ and
$p(z)\in \mathbb {C}[z]$ and ![]() $\deg (p)\leq q-1$, whose multiplicative inverse belongs to the set
$\deg (p)\leq q-1$, whose multiplicative inverse belongs to the set ![]() $\mathcal {S}_q(\theta +\pi )$ as its dual exponential polynomial. It should be observed that if
$\mathcal {S}_q(\theta +\pi )$ as its dual exponential polynomial. It should be observed that if ![]() $f\in \mathcal {S}_q(\theta )$ and
$f\in \mathcal {S}_q(\theta )$ and ![]() $g\in \mathcal {S}_q(\theta +\pi )$ are dual exponential polynomials, then
$g\in \mathcal {S}_q(\theta +\pi )$ are dual exponential polynomials, then ![]() $fg\in \operatorname {Exp}_{q-1}$ might not hold, but even so, the growth of
$fg\in \operatorname {Exp}_{q-1}$ might not hold, but even so, the growth of ![]() $fg$ in terms of the characteristic function could be somewhat reduced from that of
$fg$ in terms of the characteristic function could be somewhat reduced from that of ![]() $f$ or
$f$ or ![]() $g$.
$g$.
Example 1.5 If ![]() $f(z)= \textrm {e}^{z} + \textrm {e}^{2z}$ and
$f(z)= \textrm {e}^{z} + \textrm {e}^{2z}$ and ![]() $g(z) = \textrm {e}^{-4z}$, then
$g(z) = \textrm {e}^{-4z}$, then ![]() $T(r,f)=({2}/{\pi })r+O(\log r)$ and
$T(r,f)=({2}/{\pi })r+O(\log r)$ and ![]() $T(r,g)=({4}/{\pi })r+O(\log r)$, while
$T(r,g)=({4}/{\pi })r+O(\log r)$, while ![]() $T(r,fg)=({3}/{\pi })r+O(\log r)$, see [Reference Heittokangas and Wen10]. Alternatively, the choice
$T(r,fg)=({3}/{\pi })r+O(\log r)$, see [Reference Heittokangas and Wen10]. Alternatively, the choice ![]() $g(z)=\textrm {e}^{-z}$ gives
$g(z)=\textrm {e}^{-z}$ gives ![]() $T(r,g)=({1}/{\pi })r$ and
$T(r,g)=({1}/{\pi })r$ and ![]() $T(r,fg)=({1}/{\pi })r+O(1)$.
$T(r,fg)=({1}/{\pi })r+O(1)$.
In our setting, the duality of two exponential polynomials is an interdependence among them in order to reduce the growth under multiplication, especially when combined with differentiation. For example, if ![]() $A$ and
$A$ and ![]() $f$ are dual exponential polynomials of order
$f$ are dual exponential polynomials of order ![]() $q$, then
$q$, then ![]() $A$ and
$A$ and ![]() $f'$ are also dual, and at times the growth of
$f'$ are also dual, and at times the growth of ![]() $Af'$ is reduced to
$Af'$ is reduced to ![]() $\rho (Af')< q$.
$\rho (Af')< q$.
The motivation for studying exponential polynomial solutions of (1.3) arises from the following previous result.
Theorem 1.6 ([18]) Suppose that ![]() $f$ is a transcendental exponential polynomial solution of (1.3), where
$f$ is a transcendental exponential polynomial solution of (1.3), where ![]() $A(z)$ and
$A(z)$ and ![]() $B(z)$ are exponential polynomials satisfying
$B(z)$ are exponential polynomials satisfying ![]() $\rho (B)<\rho (A)$. Then the following assertions hold.
$\rho (B)<\rho (A)$. Then the following assertions hold.
(a)
 $f$ and
$f$ and  $A(z)$ are dual exponential polynomials of order
$A(z)$ are dual exponential polynomials of order  $q\in \mathbb {N}$, and
$q\in \mathbb {N}$, and  $f$ has the normalized representation
(1.6)where
$f$ has the normalized representation
(1.6)where \begin{equation} f(z)=c+F_1(z)\textrm{e}^{w_1z^{q}}+\cdots +F_m(z)\textrm{e}^{w_mz^{q}}, \end{equation}
\begin{equation} f(z)=c+F_1(z)\textrm{e}^{w_1z^{q}}+\cdots +F_m(z)\textrm{e}^{w_mz^{q}}, \end{equation} $m\in \mathbb {N}$ and
$m\in \mathbb {N}$ and  $c\in \mathbb {C}\setminus \{0\}$.
$c\in \mathbb {C}\setminus \{0\}$.(b) If
 $\rho (Af')< q$, then
$\rho (Af')< q$, then  $q=1$ and
(1.7)where
$q=1$ and
(1.7)where \begin{equation} A(z)=a \textrm{e}^{{-}wz}, \quad B(z)={-}w^{2} \quad\text{and} \quad f(z)=c\left(1+\frac{w}{a}\textrm{e}^{wz}\right), \end{equation}
\begin{equation} A(z)=a \textrm{e}^{{-}wz}, \quad B(z)={-}w^{2} \quad\text{and} \quad f(z)=c\left(1+\frac{w}{a}\textrm{e}^{wz}\right), \end{equation} $w=w_1$ and
$w=w_1$ and  $a \in \mathbb {C}\setminus \{0\}$.
$a \in \mathbb {C}\setminus \{0\}$.
If ![]() $a=c=w=1$, then (1.7) reduces to Frei's equation (1.1) and Frei's solution (1.2) in the case
$a=c=w=1$, then (1.7) reduces to Frei's equation (1.1) and Frei's solution (1.2) in the case ![]() $m=1$. The following example illustrates that it is not always the case that the differential equation (1.3) possesses a non-trivial exponential polynomial solution when
$m=1$. The following example illustrates that it is not always the case that the differential equation (1.3) possesses a non-trivial exponential polynomial solution when ![]() $A(z)$ and
$A(z)$ and ![]() $B(z)$ are exponential polynomials satisfying
$B(z)$ are exponential polynomials satisfying ![]() $\rho (B)<\rho (A)$.
$\rho (B)<\rho (A)$.
Example 1.7 For a fixed ![]() $n\in \mathbb {Z}$, let
$n\in \mathbb {Z}$, let ![]() $A(z)=-{5}/{3}+n+({2}/{3})\textrm {e}^{-z}$ and
$A(z)=-{5}/{3}+n+({2}/{3})\textrm {e}^{-z}$ and ![]() $B(z)=-{8}/{3}+n$. Then (1.3) has a zero-free solution
$B(z)=-{8}/{3}+n$. Then (1.3) has a zero-free solution
Note that ![]() $f$ is an exponential of an exponential polynomial. Another solution of (1.3), linearly independent with
$f$ is an exponential of an exponential polynomial. Another solution of (1.3), linearly independent with ![]() $f$, is
$f$, is
 \begin{eqnarray*} g(z)&=& f(z)\int^{z} \frac{\textrm{e}^{-\zeta}}{f(\zeta)}\textrm{d}\zeta \\ &=& \exp\left\{\frac{2}{3}\textrm{e}^{{-}z}+\left(\frac{8}{3}-n\right)z\right\} \int^{z} \exp\left\{\frac{2}{3}\textrm{e}^{-\zeta}+\left(\frac{5}{3}-n\right)\zeta\right\} \textrm{d}\zeta, \end{eqnarray*}
\begin{eqnarray*} g(z)&=& f(z)\int^{z} \frac{\textrm{e}^{-\zeta}}{f(\zeta)}\textrm{d}\zeta \\ &=& \exp\left\{\frac{2}{3}\textrm{e}^{{-}z}+\left(\frac{8}{3}-n\right)z\right\} \int^{z} \exp\left\{\frac{2}{3}\textrm{e}^{-\zeta}+\left(\frac{5}{3}-n\right)\zeta\right\} \textrm{d}\zeta, \end{eqnarray*}where the integral represents an arbitrary primitive function. We may re-write this as
to see that ![]() $g$ solves a first-order equation
$g$ solves a first-order equation
This shows that ![]() $g$ cannot be any exponential polynomial as a function of infinite order. Hence it is necessary in theorem 1.6 to assume that (1.3) has a nontrivial exceptional polynomial solution
$g$ cannot be any exponential polynomial as a function of infinite order. Hence it is necessary in theorem 1.6 to assume that (1.3) has a nontrivial exceptional polynomial solution ![]() $f$.
$f$.
One may also observe that a small perturbation in the above coefficients ![]() $A(z)$ and
$A(z)$ and ![]() $B(z)$ brings our desired case. In fact, by choosing
$B(z)$ brings our desired case. In fact, by choosing ![]() $A(z)=-{5}/{3}-n+({2}/{3})\textrm {e}^{-z}$ and
$A(z)=-{5}/{3}-n+({2}/{3})\textrm {e}^{-z}$ and ![]() $B(z)=-{2}/{3}+2n$ for any
$B(z)=-{2}/{3}+2n$ for any ![]() $n\in \mathbb {Z}$, equation (1.3) permits the exponential polynomial solution
$n\in \mathbb {Z}$, equation (1.3) permits the exponential polynomial solution
A difference between these two cases can also be observed in the logarithmic derivatives: If ![]() $f$ is the function in (1.8), then
$f$ is the function in (1.8), then ![]() ${f'(z)}/{f(z)}=-({2}/{3})\textrm {e}^{-z}+{8}/{3}-n$, while if
${f'(z)}/{f(z)}=-({2}/{3})\textrm {e}^{-z}+{8}/{3}-n$, while if ![]() $f$ is the function in (1.9), then
$f$ is the function in (1.9), then ![]() ${f'(z)}/{f(z)}$ is not an exponential polynomial but an irreducible rational function in
${f'(z)}/{f(z)}$ is not an exponential polynomial but an irreducible rational function in ![]() $\textrm {e}^{z}$.
$\textrm {e}^{z}$.
After discussing some properties of exponential polynomials in § 2, we will show in § 3 that the conclusions in theorem 1.6(a) can be made stronger under weaker assumptions. Complementing the condition ![]() $\rho (Af')< q$ in theorem 1.6(b), some new conditions implying the conclusion
$\rho (Af')< q$ in theorem 1.6(b), some new conditions implying the conclusion ![]() $q=1$ will be discovered. Examples on higher order duality as well as on the cases where a solution is dual to more than one coefficient will be discussed in § 4 and 5, respectively. Two open problems are formulated in the hope that these findings would give raise to further discussions in the future.
$q=1$ will be discovered. Examples on higher order duality as well as on the cases where a solution is dual to more than one coefficient will be discussed in § 4 and 5, respectively. Two open problems are formulated in the hope that these findings would give raise to further discussions in the future.
2. Preliminaries on exponential polynomials
We need to introduce several concepts some of which are new.
Definition 2.1 ([11, p. 214]) Let ![]() $f$ in (1.5) be a simple exponential polynomial. If there exists a constant
$f$ in (1.5) be a simple exponential polynomial. If there exists a constant ![]() $w\in \mathbb {C}\setminus \{0\}$ such that
$w\in \mathbb {C}\setminus \{0\}$ such that ![]() $w_j/w$ is a positive integer for every
$w_j/w$ is a positive integer for every ![]() $j=1,2,\ldots ,m$, then the (non-zero) frequencies of
$j=1,2,\ldots ,m$, then the (non-zero) frequencies of ![]() $f$ are said to be commensurable, and
$f$ are said to be commensurable, and ![]() $w$ is called a common factor.
$w$ is called a common factor.
For example, ![]() $f(z)=\textrm {e}^{\pi z}+3\textrm {e}^{2\pi z}+z\textrm {e}^{3\pi z}$ and
$f(z)=\textrm {e}^{\pi z}+3\textrm {e}^{2\pi z}+z\textrm {e}^{3\pi z}$ and ![]() $g(z)=\textrm {e}^{4iz}+\textrm {e}^{6iz}$ are simple exponential polynomials, both of their frequencies are commensurable, and examples for common factors are
$g(z)=\textrm {e}^{4iz}+\textrm {e}^{6iz}$ are simple exponential polynomials, both of their frequencies are commensurable, and examples for common factors are ![]() $\pi ,\pi /2$ for
$\pi ,\pi /2$ for ![]() $f$ and
$f$ and ![]() $i,2i$ for
$i,2i$ for ![]() $g$. In particular, a common factor is not unique.
$g$. In particular, a common factor is not unique.
Note that it is usual to say that non-zero real numbers ![]() $a$ and
$a$ and ![]() $b$ are commensurable if their ratio
$b$ are commensurable if their ratio ![]() $a/b$ is a rational number. Equivalently, there exist a real number
$a/b$ is a rational number. Equivalently, there exist a real number ![]() $c$ and integers
$c$ and integers ![]() $m$ and
$m$ and ![]() $n$ such that
$n$ such that ![]() $a=mc$ and
$a=mc$ and ![]() $b=nc$. In definition 2.1 we are concerned with a simple exponential polynomial and a fixed
$b=nc$. In definition 2.1 we are concerned with a simple exponential polynomial and a fixed ![]() $\theta \in [0, 2\pi )$, and thus all the non-zero frequencies are of the form
$\theta \in [0, 2\pi )$, and thus all the non-zero frequencies are of the form ![]() $w_j=r_j\textrm {e}^{i\theta }$ for
$w_j=r_j\textrm {e}^{i\theta }$ for ![]() $r_j>0$, and the ratio of
$r_j>0$, and the ratio of ![]() $w_j$ and
$w_j$ and ![]() $w_i$ is
$w_i$ is
This is a positive rational number for a common factor ![]() $w$. If we consider the dual exponential polynomial which are both commensurable with the same common factor, all those frequencies are commensurable in the usual sense, that is, each ratio of the frequencies can be an integer not restricted to a positive integer any more.
$w$. If we consider the dual exponential polynomial which are both commensurable with the same common factor, all those frequencies are commensurable in the usual sense, that is, each ratio of the frequencies can be an integer not restricted to a positive integer any more.
If ![]() $f$ is a simple exponential polynomial of order one with constant multipliers, and if its frequencies are commensurable as in Frei's case (1.2), then by the fundamental theorem of algebra,
$f$ is a simple exponential polynomial of order one with constant multipliers, and if its frequencies are commensurable as in Frei's case (1.2), then by the fundamental theorem of algebra, ![]() $f$ can be written as
$f$ can be written as
 \[ f(z)=A\prod_{j=1}^{m}\left(\textrm{e}^{wz}-\alpha_j\right), \]
\[ f(z)=A\prod_{j=1}^{m}\left(\textrm{e}^{wz}-\alpha_j\right), \]
where ![]() $A\neq 0$,
$A\neq 0$, ![]() $\alpha _j$'s are complex constants and
$\alpha _j$'s are complex constants and ![]() $m$ is a positive integer. In particular, all the zeros of
$m$ is a positive integer. In particular, all the zeros of ![]() $f$ lie on at most
$f$ lie on at most ![]() $m$ lines.
$m$ lines.
We note that if the non-zero frequencies of ![]() $f$ are commensurable, then they are clearly linearly dependent over rationals (see [Reference Moreno13] for results in this direction), but not the other way around. For example, the points
$f$ are commensurable, then they are clearly linearly dependent over rationals (see [Reference Moreno13] for results in this direction), but not the other way around. For example, the points ![]() $w_1=1, w_2=\sqrt {2}, w_3=\sqrt {2}-1$ are linearly dependent over rationals but not commensurable.
$w_1=1, w_2=\sqrt {2}, w_3=\sqrt {2}-1$ are linearly dependent over rationals but not commensurable.
Definition 2.2 Suppose that ![]() $f$ and
$f$ and ![]() $g$ are dual exponential polynomials with commensurable frequencies
$g$ are dual exponential polynomials with commensurable frequencies ![]() $\{w_j\}$
$\{w_j\}$ ![]() $(\,j>0)$ and
$(\,j>0)$ and ![]() $\{\lambda _i\}$
$\{\lambda _i\}$ ![]() $(i>0)$, respectively, sharing the same common factor
$(i>0)$, respectively, sharing the same common factor ![]() $w$ but with opposite signs. If the points
$w$ but with opposite signs. If the points ![]() $w_j+\lambda _i$ are on one ray including the origin for all
$w_j+\lambda _i$ are on one ray including the origin for all ![]() $i,j>0$, then
$i,j>0$, then ![]() $f$ and
$f$ and ![]() $g$ are called strongly dual exponential polynomials.
$g$ are called strongly dual exponential polynomials.
For example, the functions ![]() $f(z)=1+z\textrm {e}^{z}+2\textrm {e}^{3z}$ and
$f(z)=1+z\textrm {e}^{z}+2\textrm {e}^{3z}$ and ![]() $g(z)=1-\textrm {e}^{-z}$ are strongly dual exponential polynomials, while
$g(z)=1-\textrm {e}^{-z}$ are strongly dual exponential polynomials, while ![]() $f(z)$ and
$f(z)$ and ![]() $h(z)=g(z)+2z^{2}\textrm {e}^{-2z}$ are not. Note that if
$h(z)=g(z)+2z^{2}\textrm {e}^{-2z}$ are not. Note that if ![]() $\arg (w_j)=\theta$, then
$\arg (w_j)=\theta$, then ![]() $\arg (\lambda _j)=\theta +\pi$ by duality, and moreover, if
$\arg (\lambda _j)=\theta +\pi$ by duality, and moreover, if ![]() $w_j+\lambda _i\neq 0$, then precisely one of
$w_j+\lambda _i\neq 0$, then precisely one of ![]() $\arg (w_j+\lambda _i)=\theta$ or
$\arg (w_j+\lambda _i)=\theta$ or ![]() $\arg (w_j+\lambda _i)=\theta +\pi$ holds for all
$\arg (w_j+\lambda _i)=\theta +\pi$ holds for all ![]() $i,j>0$. Alternatively, strong duality of
$i,j>0$. Alternatively, strong duality of ![]() $f$ and
$f$ and ![]() $g$ of order
$g$ of order ![]() $q$ can be expressed as follows: there exists a non-zero constant
$q$ can be expressed as follows: there exists a non-zero constant ![]() $w$ such that
$w$ such that
 \begin{equation} f(z) = \sum_{j = 0}^{m} F_j(z)(\textrm{e}^{wz^{q}})^{j}\quad \textrm{and}\quad g(z) = \sum_{i = 0}^{m} G_i(z)(\textrm{e}^{{-}wz^{q}})^{i}, \end{equation}
\begin{equation} f(z) = \sum_{j = 0}^{m} F_j(z)(\textrm{e}^{wz^{q}})^{j}\quad \textrm{and}\quad g(z) = \sum_{i = 0}^{m} G_i(z)(\textrm{e}^{{-}wz^{q}})^{i}, \end{equation}
where ![]() $F_j, G_i$ are exponential polynomials of order
$F_j, G_i$ are exponential polynomials of order ![]() $\leq q-1$. Hence
$\leq q-1$. Hence ![]() $f$ is a polynomial in
$f$ is a polynomial in ![]() $\textrm {e}^{wz^{q}}$ and
$\textrm {e}^{wz^{q}}$ and ![]() $g$ is a polynomial in
$g$ is a polynomial in ![]() $\textrm {e}^{-wz^{q}}$, with smaller exponential polynomials as multipliers. Using the notation above,
$\textrm {e}^{-wz^{q}}$, with smaller exponential polynomials as multipliers. Using the notation above, ![]() $f\in \operatorname {Exp}_{q-1}[\textrm {e}^{wz^{q}}]$ and
$f\in \operatorname {Exp}_{q-1}[\textrm {e}^{wz^{q}}]$ and ![]() $g\in \operatorname {Exp}_{q-1}[\textrm {e}^{-wz^{q}}]$. Differing from the situation in (1.5), some of the multipliers
$g\in \operatorname {Exp}_{q-1}[\textrm {e}^{-wz^{q}}]$. Differing from the situation in (1.5), some of the multipliers ![]() $F_j, G_i$
$F_j, G_i$ ![]() $(i, j>0)$ in (2.1) must suitably vanish identically so that either of
$(i, j>0)$ in (2.1) must suitably vanish identically so that either of ![]() $j-i\geq 0$ or
$j-i\geq 0$ or ![]() $j-i\leq 0$ always holds for all non-vanishing multipliers
$j-i\leq 0$ always holds for all non-vanishing multipliers ![]() $F_j, G_i$
$F_j, G_i$ ![]() $(i, j>0)$. This is a consequence of definition 2.2.
$(i, j>0)$. This is a consequence of definition 2.2.
We may think that being strong in our duality means that the product of ![]() $f(z)-F_0(z)$ and
$f(z)-F_0(z)$ and ![]() $g(z)-G_0(z)$ becomes again a commensurable exponential polynomial with either
$g(z)-G_0(z)$ becomes again a commensurable exponential polynomial with either ![]() $w$ or
$w$ or ![]() $-w$ as a common factor. In the case when both
$-w$ as a common factor. In the case when both ![]() $F_0(z)$ and
$F_0(z)$ and ![]() $G_0(z)$ are constant, each product of the derivatives
$G_0(z)$ are constant, each product of the derivatives ![]() $f^{(k)}(z)$ and
$f^{(k)}(z)$ and ![]() $g^{(\ell )}(z)$,
$g^{(\ell )}(z)$, ![]() $k, \ell \in \mathbb {N}$, is a commensurable exponential polynomial with the same common factor as the product of
$k, \ell \in \mathbb {N}$, is a commensurable exponential polynomial with the same common factor as the product of ![]() $f(z)-F_0(z)$ and
$f(z)-F_0(z)$ and ![]() $g(z)-G_0(z)$.
$g(z)-G_0(z)$.
Definition 2.3 ([18]) Denote the set of complex conjugate frequencies of the function ![]() $f$ in (1.5) by
$f$ in (1.5) by ![]() $W_f=\{\overline {w}_0,\overline {w}_1,\ldots ,\overline {w}_m\}$, where
$W_f=\{\overline {w}_0,\overline {w}_1,\ldots ,\overline {w}_m\}$, where ![]() $\overline {w}_0=0$ is related to the multiplier
$\overline {w}_0=0$ is related to the multiplier ![]() $F_0(z)\not \equiv 0$, and
$F_0(z)\not \equiv 0$, and ![]() $W_f=\{\overline {w}_1,\ldots ,\overline {w}_m\}$ when
$W_f=\{\overline {w}_1,\ldots ,\overline {w}_m\}$ when ![]() $F_0(z)\equiv 0$. Denote the convex hull of the set
$F_0(z)\equiv 0$. Denote the convex hull of the set ![]() $W_f$ by
$W_f$ by ![]() $\operatorname {co} (W_f)$, and let
$\operatorname {co} (W_f)$, and let ![]() $C(\operatorname {co}(W_f))$ denote the circumference of
$C(\operatorname {co}(W_f))$ denote the circumference of ![]() $\operatorname {co}(W_f)$.
$\operatorname {co}(W_f)$.
The set ![]() $\operatorname {co}(W_f)$ is defined as the intersection of all closed convex sets containing
$\operatorname {co}(W_f)$ is defined as the intersection of all closed convex sets containing ![]() $W_f$, and as such it is either a convex polygon or a line segment. The latter occurs when
$W_f$, and as such it is either a convex polygon or a line segment. The latter occurs when ![]() $f$ is simple, and, in particular, when
$f$ is simple, and, in particular, when ![]() $w_1, \ldots , w_m$ are commensurable. The vertices of
$w_1, \ldots , w_m$ are commensurable. The vertices of ![]() $\operatorname {co} (W_f)$ are formed by some (possibly all) of the points
$\operatorname {co} (W_f)$ are formed by some (possibly all) of the points ![]() $\overline {w}_0,\overline {w}_1,\ldots ,\overline {w}_m$. The circumference
$\overline {w}_0,\overline {w}_1,\ldots ,\overline {w}_m$. The circumference ![]() $C(\operatorname {co}(W_f))$ of
$C(\operatorname {co}(W_f))$ of ![]() $\operatorname {co}(W_f)$ plays an important role in describing the value distribution of
$\operatorname {co}(W_f)$ plays an important role in describing the value distribution of ![]() $f$, see [Reference Heittokangas, Ishizaki, Tohge and Wen8, Reference Heittokangas and Wen10, Reference Steinmetz16].
$f$, see [Reference Heittokangas, Ishizaki, Tohge and Wen8, Reference Heittokangas and Wen10, Reference Steinmetz16].
Let ![]() $h$ be a quotient of two transcendental exponential polynomials, say
$h$ be a quotient of two transcendental exponential polynomials, say
where ![]() $f$ is of the form (1.5) and
$f$ is of the form (1.5) and ![]() $g$ is an exponential polynomial of the normalized form
$g$ is an exponential polynomial of the normalized form
In these representations of ![]() $f$ and
$f$ and ![]() $g$ for the quotient
$g$ for the quotient ![]() $h$, we allow that some of the multipliers
$h$, we allow that some of the multipliers ![]() $F_j$ or
$F_j$ or ![]() $G_j$ may vanish identically, but we suppose that the matching multipliers
$G_j$ may vanish identically, but we suppose that the matching multipliers ![]() $F_j$ and
$F_j$ and ![]() $G_j$ do not both vanish identically for any
$G_j$ do not both vanish identically for any ![]() $j$.
$j$.
For the quotient ![]() $h=f/g$, define the set
$h=f/g$, define the set ![]() $W_h=\{\overline {w}_0,\overline {w}_1,\ldots ,\overline {w}_m\}$. The proximity function of
$W_h=\{\overline {w}_0,\overline {w}_1,\ldots ,\overline {w}_m\}$. The proximity function of ![]() $h$ satisfies
$h$ satisfies
see [Reference Steinmetz17, satz 1]. In particular, if ![]() $g\equiv 1$, then
$g\equiv 1$, then ![]() $W_g=\{0\}$ and
$W_g=\{0\}$ and ![]() $C(\operatorname {co}(W_g))=0$. This yields [Reference Steinmetz16, satz 1] as a special case, namely
$C(\operatorname {co}(W_g))=0$. This yields [Reference Steinmetz16, satz 1] as a special case, namely
where ![]() $W^{0}_f=W_f\cup \{0\}$. The estimates (2.2) and (2.3) are consistent with the estimate
$W^{0}_f=W_f\cup \{0\}$. The estimates (2.2) and (2.3) are consistent with the estimate
known as the lemma on the logarithmic derivative, since ![]() $W_{f'/f}=W_f$ holds for any given exponential polynomial
$W_{f'/f}=W_f$ holds for any given exponential polynomial ![]() $f$ of the form (1.5). We also point out that
$f$ of the form (1.5). We also point out that ![]() $W_{f/f'}=W_{f'}$. This fact will be used in proving our main results in § 3.
$W_{f/f'}=W_{f'}$. This fact will be used in proving our main results in § 3.
3. The main results
Motivated by example 1.3, we improve theorem 1.6(a) under weaker assumptions on ![]() $B(z)$.
$B(z)$.
Theorem 3.1 Suppose that ![]() $f$ and
$f$ and ![]() $A(z)$ in (1.3) are transcendental exponential polynomials, and that
$A(z)$ in (1.3) are transcendental exponential polynomials, and that ![]() $B(z)$ is an entire function satisfying
$B(z)$ is an entire function satisfying ![]() $T(r,B)=o(T(r,A))$. Then the following assertions hold:
$T(r,B)=o(T(r,A))$. Then the following assertions hold:
(a)
 $f$ and
$f$ and  $A(z)$ are dual exponential polynomials of order
$A(z)$ are dual exponential polynomials of order  $q\in \mathbb {N}$,
$q\in \mathbb {N}$,  $f$ has the normalized representation (1.6), and
$f$ has the normalized representation (1.6), and  $B(z)$ is an exponential polynomial of order
$B(z)$ is an exponential polynomial of order  $\rho (B)\leq q-1$.
$\rho (B)\leq q-1$.(b) The frequencies of
 $f$ are commensurable if and only if the frequencies of
$f$ are commensurable if and only if the frequencies of  $A(z)$ are commensurable. In both cases,
$A(z)$ are commensurable. In both cases,  $f$ and
$f$ and  $A(z)$ are strongly dual exponential polynomials.
$A(z)$ are strongly dual exponential polynomials.
Proof. (a) Suppose that ![]() $0\leq \rho (f)\leq \rho (A)-1$. The case
$0\leq \rho (f)\leq \rho (A)-1$. The case ![]() $\rho (f)=0$ is not possible because
$\rho (f)=0$ is not possible because ![]() $f$ is transcendental. Hence
$f$ is transcendental. Hence ![]() $\rho (f)\geq 1$. But now
$\rho (f)\geq 1$. But now
and the assumption ![]() $T(r,B)=o(T(r,A))$ imply
$T(r,B)=o(T(r,A))$ imply
which is a contradiction. Here we have used (2.2) for ![]() $h=f/f'$ and
$h=f/f'$ and ![]() $g=f'$, as well as (2.3) for
$g=f'$, as well as (2.3) for ![]() $A$ in place of
$A$ in place of ![]() $f$. The following two cases are also impossible by the proof of [Reference Heittokangas, Laine, Tohge and Wen9, theorem 3.6]:
$f$. The following two cases are also impossible by the proof of [Reference Heittokangas, Laine, Tohge and Wen9, theorem 3.6]:
(1)
 $\rho (f)=\rho (A)$ and either
$\rho (f)=\rho (A)$ and either  $F_0(z)\equiv 0$ or
$F_0(z)\equiv 0$ or  $F'_0(z)\not \equiv 0$.
$F'_0(z)\not \equiv 0$.(2)
 $\rho (f)\geq \rho (A)+1$.
$\rho (f)\geq \rho (A)+1$.
Thus ![]() $\rho (f)=\rho (A)=q\geq 1$ and
$\rho (f)=\rho (A)=q\geq 1$ and ![]() $f$ has the representation (1.6).
$f$ has the representation (1.6).
We proceed to prove that ![]() $f$ and
$f$ and ![]() $A(z)$ are dual exponential polynomials. Using (1.3), we find that
$A(z)$ are dual exponential polynomials. Using (1.3), we find that
Formula (7.3) in [Reference Wen, Gundersen and Heittokangas18] should be replaced by this. Thus formula (7.7) in [Reference Wen, Gundersen and Heittokangas18] holds, and the reasoning in [Reference Wen, Gundersen and Heittokangas18] shows that ![]() $f$ and
$f$ and ![]() $A(z)$ are dual exponential polynomials.
$A(z)$ are dual exponential polynomials.
To complete the proof of (a), it suffices to prove that ![]() $B(z)$ is an exponential polynomial of order
$B(z)$ is an exponential polynomial of order ![]() $\rho (B)\leq q-1$. Since the frequencies
$\rho (B)\leq q-1$. Since the frequencies ![]() $w_j$ of
$w_j$ of ![]() $f$ are all on one ray, we may appeal to a rotation, and suppose that
$f$ are all on one ray, we may appeal to a rotation, and suppose that ![]() $w_1,\ldots ,w_m\in \mathbb {R}_+$. By renaming the frequencies
$w_1,\ldots ,w_m\in \mathbb {R}_+$. By renaming the frequencies ![]() $w_j$, if necessary, we may further suppose that
$w_j$, if necessary, we may further suppose that ![]() $0< w_1<\cdots < w_m$. Thus the dual coefficient must be of the form
$0< w_1<\cdots < w_m$. Thus the dual coefficient must be of the form
 \begin{equation} A(z)=A_0(z)+\sum_{j=1}^{k} A_j(z)\textrm{e}^{-\lambda_j z^{q}}, \end{equation}
\begin{equation} A(z)=A_0(z)+\sum_{j=1}^{k} A_j(z)\textrm{e}^{-\lambda_j z^{q}}, \end{equation}
where ![]() $A_j(z)\not \equiv 0$ for all
$A_j(z)\not \equiv 0$ for all ![]() $j\in \{1,\ldots ,k\}$ and
$j\in \{1,\ldots ,k\}$ and ![]() $\lambda _1,\ldots ,\lambda _k\in \mathbb {R}_+$. Renaming the frequencies
$\lambda _1,\ldots ,\lambda _k\in \mathbb {R}_+$. Renaming the frequencies ![]() $\lambda _j$, if necessary, we may suppose that
$\lambda _j$, if necessary, we may suppose that ![]() $0<\lambda _1<\cdots <\lambda _k$. Write
$0<\lambda _1<\cdots <\lambda _k$. Write
 \[ f'(z)=\sum_{j=1}^{m} G_j(z)\textrm{e}^{w_jz^{q}}\quad \textrm{and}\quad f''(z)=\sum_{j=1}^{m} H_j(z)\textrm{e}^{w_jz^{q}}, \]
\[ f'(z)=\sum_{j=1}^{m} G_j(z)\textrm{e}^{w_jz^{q}}\quad \textrm{and}\quad f''(z)=\sum_{j=1}^{m} H_j(z)\textrm{e}^{w_jz^{q}}, \]
where ![]() $G_j(z)=F_j'(z)+qw_jz^{q-1}F_j(z)\not \equiv 0$ and
$G_j(z)=F_j'(z)+qw_jz^{q-1}F_j(z)\not \equiv 0$ and ![]() $H_j(z)=G_j'(z)+qw_jz^{q-1}G_j(z)\not \equiv 0$. Next, write
$H_j(z)=G_j'(z)+qw_jz^{q-1}G_j(z)\not \equiv 0$. Next, write ![]() $-Af'=Bf+f''$ in the form
$-Af'=Bf+f''$ in the form
 \begin{equation} -\left(\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right)\left(\sum_{j=1}^{m} G_j\textrm{e}^{w_jz^{q}}\right)=cB+\sum_{j=1}^{m} (A_0G_j+BF_j+H_j)\textrm{e}^{w_jz^{q}}. \end{equation}
\begin{equation} -\left(\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right)\left(\sum_{j=1}^{m} G_j\textrm{e}^{w_jz^{q}}\right)=cB+\sum_{j=1}^{m} (A_0G_j+BF_j+H_j)\textrm{e}^{w_jz^{q}}. \end{equation}
From (3.2) we find that ![]() $B$ is an exponential polynomial of order
$B$ is an exponential polynomial of order ![]() $\rho (B)\leq q$. In fact, from (2.3) and the assumption
$\rho (B)\leq q$. In fact, from (2.3) and the assumption ![]() $T(r,B)=o(T(r,A))$, it follows that
$T(r,B)=o(T(r,A))$, it follows that ![]() $\rho (B)\leq q-1$.
$\rho (B)\leq q-1$.
(b) We begin with some preparations. From [Reference Steinmetz16] and [Reference Steinmetz17], we have
 \[ m\left(r,\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right)=T\left(r,\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right) =\frac{\lambda_k}{\pi}r^{q}+o(r^{q}), \]
\[ m\left(r,\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right)=T\left(r,\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right) =\frac{\lambda_k}{\pi}r^{q}+o(r^{q}), \]and
 \begin{eqnarray*} &m\left(r,\bigg\{cB+\sum_{j=1}^{m} (A_0G_j+BF_j+H_j)\textrm{e}^{w_jz^{q}}\bigg\}\Big/\sum_{j=1}^{m} G_j\textrm{e}^{w_jz^{q}}\right)\\ &\quad= \frac{2w_m-2(w_m-w_1)}{2\pi}r^{q}+o(r^{q})= \frac{w_1}{\pi}r^{q}+o(r^{q}). \end{eqnarray*}
\begin{eqnarray*} &m\left(r,\bigg\{cB+\sum_{j=1}^{m} (A_0G_j+BF_j+H_j)\textrm{e}^{w_jz^{q}}\bigg\}\Big/\sum_{j=1}^{m} G_j\textrm{e}^{w_jz^{q}}\right)\\ &\quad= \frac{2w_m-2(w_m-w_1)}{2\pi}r^{q}+o(r^{q})= \frac{w_1}{\pi}r^{q}+o(r^{q}). \end{eqnarray*}Therefore, we deduce that
Thus from (3.2), it follows that
If ![]() $A_0G_m+BF_m+H_m\not \equiv 0$, then from [Reference Heittokangas and Wen10, theorem 2.2] and (3.3), we get
$A_0G_m+BF_m+H_m\not \equiv 0$, then from [Reference Heittokangas and Wen10, theorem 2.2] and (3.3), we get
 \begin{eqnarray*} N(r,0,L)&=&\frac{2(w_m-w_1)+2(\lambda_k-\lambda_1)}{2\pi}r^{q}+O(r^{q-1}+\log r)\\ &=&\frac{w_m-\lambda_1}{\pi}r^{q}+O(r^{q-1}+\log r),\\ N(r,0,R)&=&\frac{w_m}{\pi}r^{q}+O(r^{q-1}+\log r), \end{eqnarray*}
\begin{eqnarray*} N(r,0,L)&=&\frac{2(w_m-w_1)+2(\lambda_k-\lambda_1)}{2\pi}r^{q}+O(r^{q-1}+\log r)\\ &=&\frac{w_m-\lambda_1}{\pi}r^{q}+O(r^{q-1}+\log r),\\ N(r,0,R)&=&\frac{w_m}{\pi}r^{q}+O(r^{q-1}+\log r), \end{eqnarray*}
where ![]() $N(r,0,L)$ and
$N(r,0,L)$ and ![]() $N(r,0,R)$ are the counting functions of zeros of the exponential polynomials on the left-hand side and on the right-hand side of (3.2), respectively. This implies
$N(r,0,R)$ are the counting functions of zeros of the exponential polynomials on the left-hand side and on the right-hand side of (3.2), respectively. This implies ![]() $w_m=w_m-\lambda _1$, which is impossible. Thus we have
$w_m=w_m-\lambda _1$, which is impossible. Thus we have
Now (3.2) reduces to
 \begin{equation} -\left(\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right)\left(\sum_{j=1}^{m} G_j\textrm{e}^{w_jz^{q}}\right) =cB+\sum_{j=1}^{m-1} (A_0G_j+BF_j+H_j)\textrm{e}^{w_jz^{q}}. \end{equation}
\begin{equation} -\left(\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right)\left(\sum_{j=1}^{m} G_j\textrm{e}^{w_jz^{q}}\right) =cB+\sum_{j=1}^{m-1} (A_0G_j+BF_j+H_j)\textrm{e}^{w_jz^{q}}. \end{equation}
From the Borel–Nevanlinna theorem, and from ![]() $A_iG_j\not \equiv 0$ for
$A_iG_j\not \equiv 0$ for ![]() $j\in \{1,2,\ldots ,m\}$ and
$j\in \{1,2,\ldots ,m\}$ and ![]() $i\in \{1,2,\ldots ,k\}$, it follows that there are only two possibilities:
$i\in \{1,2,\ldots ,k\}$, it follows that there are only two possibilities:
(I) For some pairs
 $(\,j,i)$, where
$(\,j,i)$, where  $j\in \{1,2,\ldots ,m\}$ and
$j\in \{1,2,\ldots ,m\}$ and  $i\in \{1,2,\ldots ,k\}$, there exists
$i\in \{1,2,\ldots ,k\}$, there exists  $\ell \in \{0,1,\ldots ,m-1\}$ such that
(3.7)
$\ell \in \{0,1,\ldots ,m-1\}$ such that
(3.7) \begin{equation} w_j-\lambda_i=w_\ell. \end{equation}
\begin{equation} w_j-\lambda_i=w_\ell. \end{equation}(II) For some pairs
 $(\,j,i)$, where
$(\,j,i)$, where  $j\in \{1,2,\ldots ,m\}$ and
$j\in \{1,2,\ldots ,m\}$ and  $i\in \{1,2,\ldots ,k\}$, there exist
$i\in \{1,2,\ldots ,k\}$, there exist  $s\in \{1,2,\ldots ,m\}\setminus \{j\}$ and
$s\in \{1,2,\ldots ,m\}\setminus \{j\}$ and  $t\in \{1,2,\ldots ,k\}\setminus \{i\}$ such that
(3.8)
$t\in \{1,2,\ldots ,k\}\setminus \{i\}$ such that
(3.8) \begin{equation} w_j-\lambda_i=w_s-\lambda_t. \end{equation}
\begin{equation} w_j-\lambda_i=w_s-\lambda_t. \end{equation}
After these preparations we proceed to prove that the frequencies of ![]() $f$ are commensurable if and only if the frequencies of
$f$ are commensurable if and only if the frequencies of ![]() $A(z)$ are commensurable. By appealing to (3.3) and to a change of variable as in example 1.3, we may suppose that
$A(z)$ are commensurable. By appealing to (3.3) and to a change of variable as in example 1.3, we may suppose that ![]() $w_1=\lambda _k\in \mathbb {N}$. Thus we prove that
$w_1=\lambda _k\in \mathbb {N}$. Thus we prove that ![]() $w_j\in \mathbb {N}$ for
$w_j\in \mathbb {N}$ for ![]() $j\in \{1,\ldots ,m\}$ if and only if
$j\in \{1,\ldots ,m\}$ if and only if ![]() $\lambda _i\in \mathbb {N}$ for
$\lambda _i\in \mathbb {N}$ for ![]() $i\in \{1,\ldots ,k\}$.
$i\in \{1,\ldots ,k\}$.
(i) Suppose that
 $w_j\in \mathbb {N}$ for
$w_j\in \mathbb {N}$ for  $j\in \{1,\ldots ,m\}$. From (3.3), we see that
$j\in \{1,\ldots ,m\}$. From (3.3), we see that  $w_m-\lambda _1=\max _{j,i}\{w_j-\lambda _i\}$ and
$w_m-\lambda _1=\max _{j,i}\{w_j-\lambda _i\}$ and  $w_m-\lambda _1>w_j-\lambda _i$ for any
$w_m-\lambda _1>w_j-\lambda _i$ for any  $j\neq m$ and
$j\neq m$ and  $i\neq 1$. Hence, from (3.7) and (3.8), there exists
$i\neq 1$. Hence, from (3.7) and (3.8), there exists  $p< m$ such that
$p< m$ such that  $w_m-\lambda _1=w_p$, which implies that
$w_m-\lambda _1=w_p$, which implies that  $\lambda _1\in \mathbb {N}$. In addition, from (3.3), we have
$\lambda _1\in \mathbb {N}$. In addition, from (3.3), we have  $w_m-\lambda _2>w_j-\lambda _i$ for any
$w_m-\lambda _2>w_j-\lambda _i$ for any  $j\neq m$ and
$j\neq m$ and  $i>2$. Thus, from (3.7) and (3.8), there are only two possibilities: (1) there exists
$i>2$. Thus, from (3.7) and (3.8), there are only two possibilities: (1) there exists  $p< m$ such that
$p< m$ such that  $w_m-\lambda _2=w_p-\lambda _1$ and (2) there exists
$w_m-\lambda _2=w_p-\lambda _1$ and (2) there exists  $p< m$ such that
$p< m$ such that  $w_m-\lambda _2=w_p$. In both cases, it follows that
$w_m-\lambda _2=w_p$. In both cases, it follows that  $\lambda _2\in \mathbb {N}$. Repeating this argument for
$\lambda _2\in \mathbb {N}$. Repeating this argument for  $k$ times gives us
$k$ times gives us  $\lambda _i\in \mathbb {N}$ for
$\lambda _i\in \mathbb {N}$ for  $i\in \{1,\ldots ,k\}$.
$i\in \{1,\ldots ,k\}$.(ii) Suppose that
 $\lambda _i\in \mathbb {N}$ for
$\lambda _i\in \mathbb {N}$ for  $i\in \{1,\ldots ,k\}$. From (3.3), we have
$i\in \{1,\ldots ,k\}$. From (3.3), we have  $\lambda _k=w_1$, and consequently
$\lambda _k=w_1$, and consequently  $w_1\in \mathbb {N}$. Moreover, from (3.3), we have
$w_1\in \mathbb {N}$. Moreover, from (3.3), we have  $w_2-\lambda _k< w_j-\lambda _i$ for any
$w_2-\lambda _k< w_j-\lambda _i$ for any  $j>1$ and
$j>1$ and  $i\neq k$. Thus, from (3.7) and (3.8), there are only two possibilities: there exists
$i\neq k$. Thus, from (3.7) and (3.8), there are only two possibilities: there exists  $p< k$ such that either
$p< k$ such that either  $w_2-\lambda _k=w_1-\lambda _p$ or
$w_2-\lambda _k=w_1-\lambda _p$ or  $w_2-\lambda _k=w_1$. In both cases, we have
$w_2-\lambda _k=w_1$. In both cases, we have  $w_2\in \mathbb {N}$. Repeating this argument for
$w_2\in \mathbb {N}$. Repeating this argument for  $m$ times gives us
$m$ times gives us  $w_j\in \mathbb {N}$ for
$w_j\in \mathbb {N}$ for  $i\in \{1,\ldots ,m\}$.
$i\in \{1,\ldots ,m\}$.
If the frequencies are commensurable for one of ![]() $f,A(z)$, then they are commensurable for both of
$f,A(z)$, then they are commensurable for both of ![]() $f,A(z)$ by the reasoning above. The remaining fact that
$f,A(z)$ by the reasoning above. The remaining fact that ![]() $f$ and
$f$ and ![]() $A(z)$ are strongly dual exponential polynomials now follows by (3.3).
$A(z)$ are strongly dual exponential polynomials now follows by (3.3).
The assumption ![]() $\rho (Af')<\rho (f)$ in theorem 1.6(b) seems to be the only known sufficient condition for the conclusion
$\rho (Af')<\rho (f)$ in theorem 1.6(b) seems to be the only known sufficient condition for the conclusion ![]() $q=1$. However, in the case of Frei's result (1.1), we have
$q=1$. However, in the case of Frei's result (1.1), we have
 \[ A(z)f'(z)=\textrm{e}^{{-}z}\sum_{j=1}^{m} jC_j\textrm{e}^{jz}=\sum_{j=0}^{m-1}(\,j+1)C_{j+1}\textrm{e}^{jz}, \]
\[ A(z)f'(z)=\textrm{e}^{{-}z}\sum_{j=1}^{m} jC_j\textrm{e}^{jz}=\sum_{j=0}^{m-1}(\,j+1)C_{j+1}\textrm{e}^{jz}, \]
and so ![]() $\rho (Af')=\rho (f)=1$. This shows that
$\rho (Af')=\rho (f)=1$. This shows that ![]() $q=1$ may happen even if
$q=1$ may happen even if ![]() $\rho (Af')=\rho (f)$. Theorem 3.2 shows that
$\rho (Af')=\rho (f)$. Theorem 3.2 shows that ![]() $f$ having only one large exponential term is also a sufficient condition for
$f$ having only one large exponential term is also a sufficient condition for ![]() $q=1$. In contrast, if
$q=1$. In contrast, if ![]() $A(z)$ has only one large exponential term, then
$A(z)$ has only one large exponential term, then ![]() $f$ can have multiple large exponential terms as in (1.1).
$f$ can have multiple large exponential terms as in (1.1).
Theorem 3.2 Suppose that ![]() $f(z)=F_0(z)+F_1(z)\textrm {e}^{wz^{q}}$ is a solution of (1.3), where
$f(z)=F_0(z)+F_1(z)\textrm {e}^{wz^{q}}$ is a solution of (1.3), where ![]() $A(z)$ is an exponential polynomial and
$A(z)$ is an exponential polynomial and ![]() $B(z)$ is an entire function satisfying
$B(z)$ is an entire function satisfying ![]() $T(r,B)=o(T(r,A))$. Then
$T(r,B)=o(T(r,A))$. Then ![]() $q=1$, and there are constants
$q=1$, and there are constants ![]() $c,b\in \mathbb {C}\setminus \{0\}$ and a non-trivial polynomial
$c,b\in \mathbb {C}\setminus \{0\}$ and a non-trivial polynomial ![]() $P(z)$ such that
$P(z)$ such that
Proof. We proceed similarly as in the proof of theorem 3.1 until (3.6), which now reduces to the form
 \begin{equation} -\left(\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right)G_1\textrm{e}^{wz^{q}}=cB, \end{equation}
\begin{equation} -\left(\sum_{j=1}^{k}A_j\textrm{e}^{-\lambda_jz^{q}}\right)G_1\textrm{e}^{wz^{q}}=cB, \end{equation}
where ![]() $F_0(z)\equiv c\in \mathbb {C}\setminus \{0\}$. Hence
$F_0(z)\equiv c\in \mathbb {C}\setminus \{0\}$. Hence ![]() $k=1$, and consequently
$k=1$, and consequently ![]() $A(z)$ reduces to the form
$A(z)$ reduces to the form
From (3.9) and (3.5), with ![]() $k=1=m$, we find that
$k=1=m$, we find that
In other words,
Dividing both sides of (3.10) by ![]() $G_1$, we observe that at every zero of
$G_1$, we observe that at every zero of ![]() $G_1$ the right-hand side has a pole but the left-hand side does not. Thus
$G_1$ the right-hand side has a pole but the left-hand side does not. Thus ![]() $G_1$ has no zeros, and so we may write it in the form
$G_1$ has no zeros, and so we may write it in the form ![]() $G_1=\textrm {e}^{g}$, where
$G_1=\textrm {e}^{g}$, where ![]() $g(z)=a_{q-1}z^{q-1}+\cdots +a_0$ is a polynomial of degree
$g(z)=a_{q-1}z^{q-1}+\cdots +a_0$ is a polynomial of degree ![]() $\leq q-1$. Since
$\leq q-1$. Since
we obtain ![]() $(F_1(z)\textrm {e}^{wz^{q}})'=\textrm {e}^{wz^{q}+g(z)}$, and consequently
$(F_1(z)\textrm {e}^{wz^{q}})'=\textrm {e}^{wz^{q}+g(z)}$, and consequently
Here the right-hand side is an exponential polynomial, which happens only if ![]() $q=1$.
$q=1$.
Since ![]() $q=1$, we see from (3.11) that
$q=1$, we see from (3.11) that ![]() $F_1(z)$ reduces to a non-zero constant, say
$F_1(z)$ reduces to a non-zero constant, say ![]() $F_1(z)\equiv b$. Thus
$F_1(z)\equiv b$. Thus ![]() $f(z)=c+b\textrm {e}^{wz}$, and we have
$f(z)=c+b\textrm {e}^{wz}$, and we have ![]() $G_1(z)\equiv w b$ and
$G_1(z)\equiv w b$ and ![]() $H_1(z)\equiv w^{2}b$. A substitution to (3.10) followed by a simplification gives
$H_1(z)\equiv w^{2}b$. A substitution to (3.10) followed by a simplification gives
There is no restriction for ![]() $A_1$ other than the fact that
$A_1$ other than the fact that ![]() $A$ is an exponential polynomial. Thus we may suppose that
$A$ is an exponential polynomial. Thus we may suppose that ![]() $A_1$ is any non-trivial polynomial, say
$A_1$ is any non-trivial polynomial, say ![]() $A_1=P$. This gives us
$A_1=P$. This gives us ![]() $A_0=({b}/{c})P-w$, and finally
$A_0=({b}/{c})P-w$, and finally ![]() $B=-({wb}/{c})P$.
$B=-({wb}/{c})P$.
Example 1.1 shows that the coefficient ![]() $B(z)$ in (1.3) can be a polynomial. Next, we prove that this is equivalent to
$B(z)$ in (1.3) can be a polynomial. Next, we prove that this is equivalent to ![]() $A_0(z)$ in (3.1) being a polynomial, and reveal another sufficient condition for the conclusion
$A_0(z)$ in (3.1) being a polynomial, and reveal another sufficient condition for the conclusion ![]() $q=1$.
$q=1$.
Proposition 3.3 Under the assumptions of theorem 3.1, the term ![]() $A_0(z)$ of
$A_0(z)$ of ![]() $A(z)$ in (3.1) is a polynomial if and only if
$A(z)$ in (3.1) is a polynomial if and only if ![]() $B(z)$ is a polynomial. Moreover, if the multipliers of
$B(z)$ is a polynomial. Moreover, if the multipliers of ![]() $f$ and of
$f$ and of ![]() $A(z)$ are constants, then
$A(z)$ are constants, then ![]() $q=1$ and
$q=1$ and ![]() $B(z)$ is a constant function.
$B(z)$ is a constant function.
Proof. From the proof of theorem 3.1 we find that (3.5) holds, that is,
where
 \begin{eqnarray*} G_m &=& F_m'+w_mqz^{q-1}F_m,\\ H_m &=& F_m''+2w_mqz^{q-1}F_m'+\left(w_mq(q-1)z^{q-2}+w_m^{2}q^{2}z^{2q-2}\right)F_m. \end{eqnarray*}
\begin{eqnarray*} G_m &=& F_m'+w_mqz^{q-1}F_m,\\ H_m &=& F_m''+2w_mqz^{q-1}F_m'+\left(w_mq(q-1)z^{q-2}+w_m^{2}q^{2}z^{2q-2}\right)F_m. \end{eqnarray*}
Thus ![]() $F_m$ solves the second-order differential equation
$F_m$ solves the second-order differential equation
where
 \begin{eqnarray*} P(z) &=& 2w_mqz^{q-1}+A_0,\\ Q(z) &=& w_mqz^{q-1}A_0+w_mq(q-1)z^{q-2}+w_m^{2}q^{2}z^{2(q-1)}+B. \end{eqnarray*}
\begin{eqnarray*} P(z) &=& 2w_mqz^{q-1}+A_0,\\ Q(z) &=& w_mqz^{q-1}A_0+w_mq(q-1)z^{q-2}+w_m^{2}q^{2}z^{2(q-1)}+B. \end{eqnarray*}
Suppose first that ![]() $A_0(z)$ is a polynomial. If
$A_0(z)$ is a polynomial. If ![]() $B(z)$ is transcendental, then it follows from (3.13) and [Reference Gundersen5, corollary 1] that
$B(z)$ is transcendental, then it follows from (3.13) and [Reference Gundersen5, corollary 1] that ![]() $\rho (F_m)=\infty$, which is a contradiction. Hence
$\rho (F_m)=\infty$, which is a contradiction. Hence ![]() $B(z)$ must be a polynomial. Conversely, suppose that
$B(z)$ must be a polynomial. Conversely, suppose that ![]() $B(z)$ is a polynomial. Suppose on the contrary to the assertion that
$B(z)$ is a polynomial. Suppose on the contrary to the assertion that ![]() $A_0(z)$ is a transcendental exponential polynomial. Then there exists an open sector
$A_0(z)$ is a transcendental exponential polynomial. Then there exists an open sector ![]() $S$ such that
$S$ such that ![]() $A_0(z)$ blows up exponentially in
$A_0(z)$ blows up exponentially in ![]() $S$. Using [Reference Gundersen6, corollary 1] and
$S$. Using [Reference Gundersen6, corollary 1] and ![]() $\rho (F_m)\leq q-1$ in (3.13), we obtain on almost every ray in
$\rho (F_m)\leq q-1$ in (3.13), we obtain on almost every ray in ![]() $S$ that
$S$ that
However, this is obviously a contradiction, and hence ![]() $A_0(z)$ is a polynomial.
$A_0(z)$ is a polynomial.
Finally, suppose that the multipliers of ![]() $f$ and of
$f$ and of ![]() $A(z)$ are constants. From (3.4), we find that
$A(z)$ are constants. From (3.4), we find that ![]() $B(z)=Cz^{q-1}$ for some constant
$B(z)=Cz^{q-1}$ for some constant ![]() $C\in \mathbb {C}\setminus \{0\}$. Since
$C\in \mathbb {C}\setminus \{0\}$. Since ![]() $F_m(z)$ is a non-zero constant function, it follows that the coefficient
$F_m(z)$ is a non-zero constant function, it follows that the coefficient ![]() $Q(z)$ in (3.13) vanishes identically. But this is not possible because
$Q(z)$ in (3.13) vanishes identically. But this is not possible because ![]() $A_0(z)$ is a constant function, unless
$A_0(z)$ is a constant function, unless ![]() $q=1$.
$q=1$.
Remark 3.4 (a) Equation (3.13) implies that every possible zero of ![]() $F_m$ is simple.
$F_m$ is simple.
(b) Assuming that ![]() $A_0(z)$ is a polynomial, we give an alternative proof for the fact that
$A_0(z)$ is a polynomial, we give an alternative proof for the fact that ![]() $B(z)$ is a polynomial. We already know from theorem 3.1 that
$B(z)$ is a polynomial. We already know from theorem 3.1 that ![]() $B(z)$ is of order
$B(z)$ is of order ![]() $\leq q-1$. Since the non-zero frequencies of
$\leq q-1$. Since the non-zero frequencies of ![]() $A(z)$ are all on one ray by duality, it follows that the plane divides into
$A(z)$ are all on one ray by duality, it follows that the plane divides into ![]() $2q$ sectors of opening
$2q$ sectors of opening ![]() $\pi /q$ such that in every other sector
$\pi /q$ such that in every other sector ![]() $A(z)$ either blows up exponentially or is asymptotic to the polynomial
$A(z)$ either blows up exponentially or is asymptotic to the polynomial ![]() $A_0(z)$. In the latter case, if
$A_0(z)$. In the latter case, if ![]() $A_0(z)\equiv 0$, then
$A_0(z)\equiv 0$, then ![]() $A(z)$ decays to zero exponentially. Thus, from [Reference Gundersen5, theorem 7], we deduce that
$A(z)$ decays to zero exponentially. Thus, from [Reference Gundersen5, theorem 7], we deduce that ![]() $B(z)$ is a polynomial. Note, in particular, that the constant
$B(z)$ is a polynomial. Note, in particular, that the constant ![]() $\mu$ in [Reference Gundersen5, theorem 7] satisfies
$\mu$ in [Reference Gundersen5, theorem 7] satisfies ![]() $\mu =\pi /q$.
$\mu =\pi /q$.
Open problem 1. Under the assumptions of theorem 3.1, is it always true that ![]() $q=1$ and
$q=1$ and ![]() $B(z)$ is a polynomial?
$B(z)$ is a polynomial?
This problem is fragile in the sense that the desired conclusion is not valid if a minor modification in the assumptions of theorem 3.1 is performed. For example, the differential equation
possesses an exponential polynomial solution ![]() $f(z)=\textrm {e}^{wz^{q}}-1/(q-1)$ for any
$f(z)=\textrm {e}^{wz^{q}}-1/(q-1)$ for any ![]() $q\geq 2$. Moreover, the function
$q\geq 2$. Moreover, the function ![]() $f(z)=\textrm {e}^{z^{2}}+1$ satisfies the differential equations
$f(z)=\textrm {e}^{z^{2}}+1$ satisfies the differential equations
 \begin{equation} \begin{split} & f''+\left(\frac{\textrm{e}^{{-}z^{2}}-1}{2z}-2z\right)f'-f = 0,\\ & f''-\frac{\textrm{e}^{{-}z^{2}}(z-1)+4z^{2}+z+1}{2z}f'+(z-1)f = 0.\end{split} \end{equation}
\begin{equation} \begin{split} & f''+\left(\frac{\textrm{e}^{{-}z^{2}}-1}{2z}-2z\right)f'-f = 0,\\ & f''-\frac{\textrm{e}^{{-}z^{2}}(z-1)+4z^{2}+z+1}{2z}f'+(z-1)f = 0.\end{split} \end{equation}
The transcendental coefficients in (3.14) are entire exponential polynomials with rational multipliers because ![]() $z=0$ is a removable singularity for both.
$z=0$ is a removable singularity for both.
4. Duality for higher order functions
Next we construct examples of differential equations of order ![]() $n\geq 2$ having an exponential polynomial solution
$n\geq 2$ having an exponential polynomial solution ![]() $f$ of order
$f$ of order ![]() $\rho (f)=n-1$ which is dual with one of the coefficients.
$\rho (f)=n-1$ which is dual with one of the coefficients.
Example 4.1 If ![]() $H$ is an arbitrary entire function, then
$H$ is an arbitrary entire function, then ![]() $f(z)=\textrm {e}^{z^{2}}+1$ solves
$f(z)=\textrm {e}^{z^{2}}+1$ solves
 \begin{equation} \begin{split} & f'''+\left(1+\textrm{e}^{{-}z^{2}}\right)Hf''-(6+4z^{2})f'-(2+4z^{2})Hf=0,\\ & f'''-2zf''+(H-4+H\textrm{e}^{{-}z^{2}})f'-2zHf = 0. \end{split} \end{equation}
\begin{equation} \begin{split} & f'''+\left(1+\textrm{e}^{{-}z^{2}}\right)Hf''-(6+4z^{2})f'-(2+4z^{2})Hf=0,\\ & f'''-2zf''+(H-4+H\textrm{e}^{{-}z^{2}})f'-2zHf = 0. \end{split} \end{equation}
A particularly interesting case is when ![]() $H$ is either a polynomial or an exponential polynomial of order one. Thus either of the two possible coefficients can be dual with
$H$ is either a polynomial or an exponential polynomial of order one. Thus either of the two possible coefficients can be dual with ![]() $f$. Examples of second-order dual solutions for third-order equations can be found in [Reference Wen, Gundersen and Heittokangas18] but for polynomial coefficients only.
$f$. Examples of second-order dual solutions for third-order equations can be found in [Reference Wen, Gundersen and Heittokangas18] but for polynomial coefficients only.
We can use the relation ![]() $zf''(z)=(2z^{2}+1)f'$ to see that, in addition to (4.1), the function
$zf''(z)=(2z^{2}+1)f'$ to see that, in addition to (4.1), the function ![]() $f(z)=\textrm {e}^{z^{2}}+1$ satisfies the equations
$f(z)=\textrm {e}^{z^{2}}+1$ satisfies the equations
 \begin{eqnarray*} f'''(z)-2zf'(z)-4f'(z)&=&0,\\ (1+\textrm{e}^{{-}z^{2}})f'(z)-2zf(z)&=&0,\\ (1+\textrm{e}^{{-}z^{2}})f''(z)-(2+4z^{2})f(z)&=&0. \end{eqnarray*}
\begin{eqnarray*} f'''(z)-2zf'(z)-4f'(z)&=&0,\\ (1+\textrm{e}^{{-}z^{2}})f'(z)-2zf(z)&=&0,\\ (1+\textrm{e}^{{-}z^{2}})f''(z)-(2+4z^{2})f(z)&=&0. \end{eqnarray*}Example 4.2 If ![]() $H$ is an arbitrary entire function, then
$H$ is an arbitrary entire function, then ![]() $f(z)=\textrm {e}^{z^{3}}+1$ solves
$f(z)=\textrm {e}^{z^{3}}+1$ solves
 \begin{eqnarray*} f^{(4)}+\left(1+\textrm{e}^{{-}z^{3}}\right)Hf'''-9z^{4}f''-30\left(2+3z^{3}\right)f'-\left(6+54z^{3}+27z^{6}\right)Hf &=& 0,\\ f^{(4)}-3z^{2}f'''+\left(H-18z+H\textrm{e}^{{-}z^{3}}\right)f''-18f'-H\left(6z+9z^{4}\right)f &=& 0,\\ f^{(4)}-3z^{2}f'''-27zf''+\left(H+27z^{3}+H\textrm{e}^{{-}z^{3}}\right)f'-3z^{2}Hf &=& 0. \end{eqnarray*}
\begin{eqnarray*} f^{(4)}+\left(1+\textrm{e}^{{-}z^{3}}\right)Hf'''-9z^{4}f''-30\left(2+3z^{3}\right)f'-\left(6+54z^{3}+27z^{6}\right)Hf &=& 0,\\ f^{(4)}-3z^{2}f'''+\left(H-18z+H\textrm{e}^{{-}z^{3}}\right)f''-18f'-H\left(6z+9z^{4}\right)f &=& 0,\\ f^{(4)}-3z^{2}f'''-27zf''+\left(H+27z^{3}+H\textrm{e}^{{-}z^{3}}\right)f'-3z^{2}Hf &=& 0. \end{eqnarray*}
A particularly interesting case is when ![]() $H$ is an exponential polynomial of order at most two. Thus all three of the possible coefficients can be dual with
$H$ is an exponential polynomial of order at most two. Thus all three of the possible coefficients can be dual with ![]() $f$. Previous examples of third-order dual solutions do not seem to be known.
$f$. Previous examples of third-order dual solutions do not seem to be known.
As in the previous example, we can use the relations ![]() $zf''(z)=(3z^{3}+2)f'(z)$ and
$zf''(z)=(3z^{3}+2)f'(z)$ and ![]() $zf'''(z)=(3z^{3}+1)f''(z)+9z^{2}f'(z)$ to see that
$zf'''(z)=(3z^{3}+1)f''(z)+9z^{2}f'(z)$ to see that ![]() $f(z)=\textrm {e}^{z^{3}}+1$ satisfies the equations
$f(z)=\textrm {e}^{z^{3}}+1$ satisfies the equations
 \begin{eqnarray*} f^{(4)}(z)-3z^{2}f'''(z)-18zf''(z)-18f'(z)&=&0,\\ (1+\textrm{e}^{{-}z^{3}})f'(z)-3z^{2}f(z)&=&0,\\ (1+\textrm{e}^{{-}z^{3}})f''(z)-(6z+9z^{4})f(z)&=&0,\\ (1+\textrm{e}^{{-}z^{3}})f'''(z)-(6+54z^{3}+27z^{6})f(z)&=&0. \end{eqnarray*}
\begin{eqnarray*} f^{(4)}(z)-3z^{2}f'''(z)-18zf''(z)-18f'(z)&=&0,\\ (1+\textrm{e}^{{-}z^{3}})f'(z)-3z^{2}f(z)&=&0,\\ (1+\textrm{e}^{{-}z^{3}})f''(z)-(6z+9z^{4})f(z)&=&0,\\ (1+\textrm{e}^{{-}z^{3}})f'''(z)-(6+54z^{3}+27z^{6})f(z)&=&0. \end{eqnarray*}In light of open problem 1 and the examples just discussed, it is natural to pose our second open problem.
Open problem 2. If a solution and the dominant coefficient are dual exponential polynomials of order ![]() $q$, then is the differential equation in question of order at least
$q$, then is the differential equation in question of order at least ![]() $q+1$?
$q+1$?
For the fragility of this problem, recall equations (3.14) satisfied by ![]() $f(z)=\textrm {e}^{z^{2}}+1$. Moreover, the function
$f(z)=\textrm {e}^{z^{2}}+1$. Moreover, the function ![]() $f(z)=\textrm {e}^{z^{3}}+1$ satisfies the third-order equation
$f(z)=\textrm {e}^{z^{3}}+1$ satisfies the third-order equation
 \begin{equation*} f'''+\left(\frac{\textrm{e}^{{-}z^{3}}-1}{2z}\right)f''-3z(3z^{3}+5)f'-\frac{3}{2}(3z^{3}+2)f=0 \end{equation*}
\begin{equation*} f'''+\left(\frac{\textrm{e}^{{-}z^{3}}-1}{2z}\right)f''-3z(3z^{3}+5)f'-\frac{3}{2}(3z^{3}+2)f=0 \end{equation*}with entire coefficients.
As the first initial step to knowing more about open problem 2, we make a summary of the fundamental ideas in constructing examples 4.1 and 4.2.
Lemma 4.3 The function ![]() $f(z)=\textrm {e}^{z^{q}}+1$,
$f(z)=\textrm {e}^{z^{q}}+1$, ![]() $q\in \mathbb {N}$, possesses the following two properties:
$q\in \mathbb {N}$, possesses the following two properties:
(i)
 $\displaystyle (1+\textrm {e}^{-z^{q}})f^{(\,j+1)}(z)=\sum _{k=0}^{j} P_{j,k}(z)f^{(k)}(z), \quad j\in \mathbb {N}\cup \{0\}$,
$\displaystyle (1+\textrm {e}^{-z^{q}})f^{(\,j+1)}(z)=\sum _{k=0}^{j} P_{j,k}(z)f^{(k)}(z), \quad j\in \mathbb {N}\cup \{0\}$,(ii)
 $\displaystyle f^{(q+1)}(z)=\sum _{\ell =1}^{q} Q_{\ell }(z)f^{(\ell )}(z)$,
$\displaystyle f^{(q+1)}(z)=\sum _{\ell =1}^{q} Q_{\ell }(z)f^{(\ell )}(z)$,
where the ![]() $P_{j,k}(z)$ and
$P_{j,k}(z)$ and ![]() $Q_{\ell }(z)$ are non-zero polynomials satisfying
$Q_{\ell }(z)$ are non-zero polynomials satisfying
(a)
 $\displaystyle \left \{ \begin {array}{l} P_{j+1,j+1}(z)=P_{j,j}(z)-qz^{q-1}, \quad P_{0,0}(z)=qz^{q-1}, \\ P_{j+1,k}(z)=P_{j,k}'(z)+qz^{q-1}P_{j,k}(z)+P_{j, k-1}(z),\\ P_{j,-1}(z)\equiv 0, \quad 1\leq k\leq j, \\ P_{j+1,0}(z)=P_{j,0}'(z)+qz^{q-1}P_{j,0}(z), \end {array} \right .$
$\displaystyle \left \{ \begin {array}{l} P_{j+1,j+1}(z)=P_{j,j}(z)-qz^{q-1}, \quad P_{0,0}(z)=qz^{q-1}, \\ P_{j+1,k}(z)=P_{j,k}'(z)+qz^{q-1}P_{j,k}(z)+P_{j, k-1}(z),\\ P_{j,-1}(z)\equiv 0, \quad 1\leq k\leq j, \\ P_{j+1,0}(z)=P_{j,0}'(z)+qz^{q-1}P_{j,0}(z), \end {array} \right .$(b)
 $\displaystyle Q_{\ell }(z)=-\binom{q}{\ell -1}(\textrm {e}^{-z^{q}})^{(q-\ell +1)}\textrm {e}^{z^{q}}.$
$\displaystyle Q_{\ell }(z)=-\binom{q}{\ell -1}(\textrm {e}^{-z^{q}})^{(q-\ell +1)}\textrm {e}^{z^{q}}.$
Proof. First, let us prove (i) by induction on ![]() $j$. Of course, by taking their logarithmic derivatives, we have
$j$. Of course, by taking their logarithmic derivatives, we have ![]() $(1+\textrm {e}^{-z^{q}})f'(z)=qz^{q-1}f(z)$ immediately, that is, the case when
$(1+\textrm {e}^{-z^{q}})f'(z)=qz^{q-1}f(z)$ immediately, that is, the case when ![]() $j=0$ follows with
$j=0$ follows with ![]() $P_{0,0}(z)=qz^{q-1}$. Assume (i) is true for each
$P_{0,0}(z)=qz^{q-1}$. Assume (i) is true for each ![]() $j=0, 1, \ldots , n$. Then
$j=0, 1, \ldots , n$. Then
 \begin{eqnarray*} (1+\textrm{e}^{{-}z^{q}})f^{(n+2)}(z) &=& qz^{q-1}\textrm{e}^{{-}z^{q}}f^{(n+1)}+\sum_{k=0}^{n} \bigl\{ P_{n,k}'(z)f^{(k)}(z)+P_{n,k}(z)f^{(k+1)}(z)\bigr\}\\ &=& qz^{q-1}(1+\textrm{e}^{{-}z^{q}})f^{(n+1)}(z)+\bigl\{P_{n,n}(z)-qz^{q-1}\bigr\}f^{(n+1)}(z)\\ & & +\sum_{k=1}^{n} \bigl\{ P_{n,k}'(z)f^{(k)}(z)+P_{n,k-1}(z)\bigr\} f^{(k)}(z)+P_{n,0}'(z)f(z) \\ &=& qz^{q-1} \sum_{k=0}^{n} P_{n,k}(z)f^{(k)}(z) + \bigl\{P_{n,n}(z)-qz^{q-1}\bigr\}f^{(n+1)}(z)\\ & & +\sum_{k=1}^{n} \bigl\{ P_{n,k}'(z)f^{(k)}(z)+P_{n,k-1}(z)\bigr\} f^{(k)}(z)+P_{n,0}'(z)f(z) \\ &=& \bigl\{P_{n,n}(z)-qz^{q-1}\bigr\}f^{(n+1)}(z) \\ & & +\sum_{k=1}^{n} \bigl\{ P_{n,k}'(z)f^{(k)}(z)+qz^{q-1}P_{n,k}(z)+P_{n,k-1}(z)\bigr\}f^{(k)}(z)\\ & & +\bigl\{P_{n,0}'(z)+qz^{q-1}P_{n,0}(z)\bigr\}f(z), \end{eqnarray*}
\begin{eqnarray*} (1+\textrm{e}^{{-}z^{q}})f^{(n+2)}(z) &=& qz^{q-1}\textrm{e}^{{-}z^{q}}f^{(n+1)}+\sum_{k=0}^{n} \bigl\{ P_{n,k}'(z)f^{(k)}(z)+P_{n,k}(z)f^{(k+1)}(z)\bigr\}\\ &=& qz^{q-1}(1+\textrm{e}^{{-}z^{q}})f^{(n+1)}(z)+\bigl\{P_{n,n}(z)-qz^{q-1}\bigr\}f^{(n+1)}(z)\\ & & +\sum_{k=1}^{n} \bigl\{ P_{n,k}'(z)f^{(k)}(z)+P_{n,k-1}(z)\bigr\} f^{(k)}(z)+P_{n,0}'(z)f(z) \\ &=& qz^{q-1} \sum_{k=0}^{n} P_{n,k}(z)f^{(k)}(z) + \bigl\{P_{n,n}(z)-qz^{q-1}\bigr\}f^{(n+1)}(z)\\ & & +\sum_{k=1}^{n} \bigl\{ P_{n,k}'(z)f^{(k)}(z)+P_{n,k-1}(z)\bigr\} f^{(k)}(z)+P_{n,0}'(z)f(z) \\ &=& \bigl\{P_{n,n}(z)-qz^{q-1}\bigr\}f^{(n+1)}(z) \\ & & +\sum_{k=1}^{n} \bigl\{ P_{n,k}'(z)f^{(k)}(z)+qz^{q-1}P_{n,k}(z)+P_{n,k-1}(z)\bigr\}f^{(k)}(z)\\ & & +\bigl\{P_{n,0}'(z)+qz^{q-1}P_{n,0}(z)\bigr\}f(z), \end{eqnarray*}which is the one to be proved.
Second, let us calculate the ![]() $q$-th order derivative of the product
$q$-th order derivative of the product ![]() $f'(z)\textrm {e}^{-z^{q}}=qz^{q-1}$. The Leibniz rule gives
$f'(z)\textrm {e}^{-z^{q}}=qz^{q-1}$. The Leibniz rule gives
 \[ \sum_{\ell=0}^{q} \binom{q}{\ell} f^{(\ell+1)}(z)(\textrm{e}^{{-}z^{q}})^{(q-\ell)}\equiv 0. \]
\[ \sum_{\ell=0}^{q} \binom{q}{\ell} f^{(\ell+1)}(z)(\textrm{e}^{{-}z^{q}})^{(q-\ell)}\equiv 0. \]
Denoting ![]() $Q_{\ell +1}(z)=-\binom{q}{\ell }(\textrm {e}^{-z^{q}})^{(q-\ell )}\textrm {e}^{z^{q}}$ for
$Q_{\ell +1}(z)=-\binom{q}{\ell }(\textrm {e}^{-z^{q}})^{(q-\ell )}\textrm {e}^{z^{q}}$ for ![]() $0\leq \ell \leq q-1$, we have
$0\leq \ell \leq q-1$, we have
 \[ f^{(q+1)}(z)=\sum_{\ell=0}^{q-1}Q_{\ell+1}(z)f^{(\ell+1)}(z)=\sum_{\ell=1}^{q}Q_{\ell}(z)f^{(\ell)}(z), \]
\[ f^{(q+1)}(z)=\sum_{\ell=0}^{q-1}Q_{\ell+1}(z)f^{(\ell+1)}(z)=\sum_{\ell=1}^{q}Q_{\ell}(z)f^{(\ell)}(z), \]as desired.
Example 4.4 We may apply the two identities in lemma 4.3 to construct differential equations of arbitrary order. Given any entire function ![]() $H$, we have the identity
$H$, we have the identity
 \[ f^{(q+1)}(z)-\sum_{\ell=1}^{q} Q_{\ell}(z)f^{(\ell)}(z)=H(z)\left( (1+\textrm{e}^{{-}z^{q}})f^{(\,j)}(z)-\sum_{k=0}^{j-1} P_{j-1,k}(z)f^{(k)}(z) \right), \]
\[ f^{(q+1)}(z)-\sum_{\ell=1}^{q} Q_{\ell}(z)f^{(\ell)}(z)=H(z)\left( (1+\textrm{e}^{{-}z^{q}})f^{(\,j)}(z)-\sum_{k=0}^{j-1} P_{j-1,k}(z)f^{(k)}(z) \right), \]
that is, ![]() $f(z)=\textrm {e}^{z^{q}}+1$ solves
$f(z)=\textrm {e}^{z^{q}}+1$ solves
 \begin{eqnarray*} f^{(q+1)}(z) &-&\sum_{\ell=j+1}^{q} Q_{\ell}(z)f^{(\ell)}(z)- \left( (1+\textrm{e}^{{-}z^{q}})H(z) +Q_j(z) \right) f^{(\,j)}(z)\\ &+&\sum_{\ell=1}^{j-1} \bigl(P_{j-1,\ell}(z) H(z)-Q_{\ell}(z)\bigr)f^{(\ell)}(z) +P_{j-1,0}(z)H(z)f(z)=0, \end{eqnarray*}
\begin{eqnarray*} f^{(q+1)}(z) &-&\sum_{\ell=j+1}^{q} Q_{\ell}(z)f^{(\ell)}(z)- \left( (1+\textrm{e}^{{-}z^{q}})H(z) +Q_j(z) \right) f^{(\,j)}(z)\\ &+&\sum_{\ell=1}^{j-1} \bigl(P_{j-1,\ell}(z) H(z)-Q_{\ell}(z)\bigr)f^{(\ell)}(z) +P_{j-1,0}(z)H(z)f(z)=0, \end{eqnarray*}
where ![]() $1\leq j \leq q$, the sum
$1\leq j \leq q$, the sum ![]() $\sum _{\ell =1}^{j-1}$ is empty if
$\sum _{\ell =1}^{j-1}$ is empty if ![]() $j=1$ and the sum
$j=1$ and the sum ![]() $\sum _{\ell =j+1}^{q}$ is empty if
$\sum _{\ell =j+1}^{q}$ is empty if ![]() $j=q$.
$j=q$.
5. Multiple duality
The possibility that a solution ![]() $f$ would be dual to more than one coefficient has not been studied rigorously. In this case there would be at least two equally strong dominant coefficients, or, in the case of (1.3), both coefficients
$f$ would be dual to more than one coefficient has not been studied rigorously. In this case there would be at least two equally strong dominant coefficients, or, in the case of (1.3), both coefficients ![]() $A(z),B(z)$ would be equally strong. For example,
$A(z),B(z)$ would be equally strong. For example, ![]() $f(z)=\textrm {e}^{-z}$ solves
$f(z)=\textrm {e}^{-z}$ solves
and is dual to both coefficients. Obviously the coefficients are not dual to each other. More examples can be produced from example 1.1. Note that ![]() $f(z)=\textrm {e}^{z}$ solves (1.3) if
$f(z)=\textrm {e}^{z}$ solves (1.3) if ![]() $A(z)=-B(z)-1$. Hence
$A(z)=-B(z)-1$. Hence ![]() $f$ is not necessarily dual with either of
$f$ is not necessarily dual with either of ![]() $A(z),B(z)$.
$A(z),B(z)$.
If ![]() $H$ is any entire function, then
$H$ is any entire function, then ![]() $f(z)=\textrm {e}^{z^{q}}$ solves
$f(z)=\textrm {e}^{z^{q}}$ solves
This example is from [Reference Gundersen5]. Note that ![]() $f(z)=\textrm {e}^{z^{q}}$ satisfies both
$f(z)=\textrm {e}^{z^{q}}$ satisfies both ![]() $f'(z)-qz^{q-1}f(z)=0$ and
$f'(z)-qz^{q-1}f(z)=0$ and ![]() $f''(z)-qz^{q-1}f'(z)-q(q-1)z^{q-2}f(z)=0$.
$f''(z)-qz^{q-1}f'(z)-q(q-1)z^{q-2}f(z)=0$.
Recall [Reference Heittokangas, Laine, Tohge and Wen9, theorem 2.1], according to which there cannot be even one ray on which ![]() $B(z)$ would be stronger than
$B(z)$ would be stronger than ![]() $A(z)$ in the sense of the Phragmén–Lindelöf indicator, for otherwise all solutions of (1.3) are of infinite order. This happens, for example, when
$A(z)$ in the sense of the Phragmén–Lindelöf indicator, for otherwise all solutions of (1.3) are of infinite order. This happens, for example, when ![]() $A(z)$ and
$A(z)$ and ![]() $B(z)$ are dual to each other.
$B(z)$ are dual to each other.
Example 5.1 One may observe the necessity of the assumption on the duality of ![]() $f$ and
$f$ and ![]() $A(z)$ as well as that on the dominance of
$A(z)$ as well as that on the dominance of ![]() $A(z)$ over
$A(z)$ over ![]() $B(z)$ by the following example: the function
$B(z)$ by the following example: the function ![]() $f(z)=\bigl (\textrm {e}^{z}+\textrm {e}^{-z}\bigr )\textrm {e}^{z^{q}}$,
$f(z)=\bigl (\textrm {e}^{z}+\textrm {e}^{-z}\bigr )\textrm {e}^{z^{q}}$, ![]() $q\in \mathbb {N}$, satisfies
$q\in \mathbb {N}$, satisfies
 \begin{eqnarray*} f''&+&\bigl\{H\textrm{e}^{z}+H\textrm{e}^{{-}z}-2qz^{q-1}\bigr\}f' \\ &-&\bigl\{(qz^{q-1}+1)H\textrm{e}^{z}+(qz^{q-1}-1)H\textrm{e}^{{-}z}-q^{2}z^{2(q-1)}+q(q-1)z^{q-2}+1 \bigr\}f=0 \end{eqnarray*}
\begin{eqnarray*} f''&+&\bigl\{H\textrm{e}^{z}+H\textrm{e}^{{-}z}-2qz^{q-1}\bigr\}f' \\ &-&\bigl\{(qz^{q-1}+1)H\textrm{e}^{z}+(qz^{q-1}-1)H\textrm{e}^{{-}z}-q^{2}z^{2(q-1)}+q(q-1)z^{q-2}+1 \bigr\}f=0 \end{eqnarray*}
for any entire function ![]() $H$. When
$H$. When ![]() $q=1$, this becomes
$q=1$, this becomes
with ![]() $f(z)=\textrm {e}^{2z}+1$. Thus we may use it in order to observe the duality of
$f(z)=\textrm {e}^{2z}+1$. Thus we may use it in order to observe the duality of ![]() $A(z)$ and
$A(z)$ and ![]() $B(z)$ by several choices of
$B(z)$ by several choices of ![]() $H$ such as
$H$ such as ![]() $H(z)=\textrm {e}^{nz}$ for
$H(z)=\textrm {e}^{nz}$ for ![]() $n\in \mathbb {Z}$ or
$n\in \mathbb {Z}$ or ![]() $H(z)=\textrm {e}^{iz}$.
$H(z)=\textrm {e}^{iz}$.
Here we note that ![]() $f(z)=F(z)\textrm {e}^{z^{q}}$ satisfies
$f(z)=F(z)\textrm {e}^{z^{q}}$ satisfies ![]() ${f'}/{f}={F'}/{F}+qz^{q-1}$ and
${f'}/{f}={F'}/{F}+qz^{q-1}$ and
so that there is no large freedom to choose the function ![]() $F$. For example, taking an Airy function as
$F$. For example, taking an Airy function as ![]() $F$, we cannot have our desired equation
$F$, we cannot have our desired equation ![]() $f''+A(z)f'+B(z)f=0$ with the exponential polynomial coefficients
$f''+A(z)f'+B(z)f=0$ with the exponential polynomial coefficients ![]() $A(z)$ and
$A(z)$ and ![]() $B(z)$.
$B(z)$.
Acknowledgements
Ishizaki was supported by JSPS KAKENHI Grant Number 20K03658. Wen was supported by the National Natural Science Foundation of China (Nos. 11971288 and 11771090) and Shantou University SRFT (NTF18029).