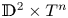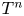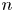1. Introduction
An important question in modern differential geometry is about the connection between the curvatures and topology of a manifold. A very significant and historic result on this is the famous Gauss–Bonnet theorem. As a consequence of that theorem, we note that the topological invariant, named Euler characteristic, gives a topological obstruction to the existence of a certain type of Riemannian metrics on surfaces. In higher dimensions, the relationship between curvatures and the topology of a manifold is much more complicated. However, Schoen and Yau, in their celebrated joint work, discovered interesting relations between the scalar curvature of a three-dimensional manifold and the topology of stable minimal surfaces inside it, which emerge when one uses the second variation formula for the area, the Gauss equation and the Gauss–Bonnet theorem.
In a very recent paper Bray, Brendle and Neves [Reference Bray, Brendle and Neves3] proved an elegant rigidity result concerning to an area-minimizing two-sphere embedded in a closed three-dimensional manifold 
$(M^{3},g)$ with positive scalar curvature and 
$\pi _2(M)\neq 0$. In that work, they showed the following result. Denote by 
$\mathcal {F}$ the set of all smooth maps 
$f:\mathbb {S}^{2}\rightarrow M$ which represent a non-trivial element in 
$\pi _2(M)$. Define
\[ \mathcal{A}(M,g)=\inf \{ Area(\mathbb{S}^{2}, f^{*}g): f\in \mathcal{F} \}. \]
If 
$R_g\geq 2$, the following inequality holds:
\[ \mathcal{A}(M,g)\leq 4\pi, \]
where 
$R_g$ denote the scalar curvature of 
$(M,g)$. Moreover, if the equality holds then the universal cover of 
$(M,g)$ is isometric to the standard cylinder 
$\mathbb {S}^{2}\times \mathbb {R}$ up to scaling. For more results concerning to rigidity of three-dimensional closed manifolds coming from area-minimizing surfaces, see [Reference Bray, Brendle, Eichmair and Neves2, Reference Cai and Galloway4, Reference Mazet and Rosenberg16, Reference Micallef and Moraru18, Reference Nunes19]. In [Reference Zhu21], Zhou showed a version of Bray, Brendle and Neves [Reference Bray, Brendle and Neves3] result for high co-dimension: for 
$n + 2 \leq 7$, let 
$(M^{n+2}, g)$ be an oriented closed Riemannian manifold with 
$R_g \geq 2$, which admits a non-zero degree map 
$F:M\rightarrow \mathbb {S}^{2}\times T^{n}$. Then 
$\mathcal {A}(M,g)\leq 4\pi$. Furthermore, the equality implies that the universal covering of 
$(M^{n+2},g)$ is 
$\mathbb {S}^{2}\times \mathbb {R}^{n}$.
In the same direction as the results mentioned above for the closed manifolds, let 
$M$ be a Riemannian manifold with non-empty boundary 
$\partial M$. A free boundary minimal surface in 
$M$ is a minimal surface in 
$M$ with boundary contained in the boundary 
$\partial M$ and meeting it orthogonally. Such surfaces arise variationally as critical points of the area among surfaces in 
$M$ whose boundaries lie on 
$\partial M$ but are free to vary on 
$\partial M$. The simplest examples, considering 
$M$ as the unit ball with centre at the origin in the Euclidean space, are an equatorial plane disc and the critical catenoid, the unique piece of a suitably scaled catenoid in the unit ball. Fraser and Schoen [Reference Fraser and Schoen12] established a connection between free-boundary minimal surfaces and the Steklov eigenvalue problem, and proved existence of an embedded free-boundary minimal surface of genus zero with any number of boundary components. Since then, many works was developed to study free-boundary minimal surfaces. For more results concerning free-boundary minimal surfaces, see the following references and the references therein: [Reference Ambrozio1, Reference Chen, Fraser and Pang5–Reference Li14].
Consider now a Riemannian 
$n$-manifold with non-empty boundary 
$(M,\partial M,g)$. Let 
$\mathcal {F}_M$ be the set of all immersed discs in 
$M$ whose boundaries are curves in 
$\partial M$ that are homotopically non-trivial in 
$\partial M$. If 
$\mathcal {F}_M\not =\emptyset$, we define
\[ \mathcal{A}(M,g)=\inf_{\Sigma\in \mathcal{F}_M} |\Sigma|_g \quad\text{and}\quad \mathcal{L}(M,g)=\inf_{\Sigma\in \mathcal{F}_M} |\partial \Sigma|_g \]In [Reference Ambrozio1], Ambrózio proved the following result.
Theorem 1.1 Let 
$(M,g)$ be a compact Riemannian three-manifold with mean convex boundary. Assume that 
$\mathcal {F}_M\not =\emptyset$. Then
\begin{equation} \frac{1}{2}\inf R_g^{M} \mathcal{A}(M,g)+\inf H_g^{\partial M}\mathcal{L}(M,g)\leq 2\pi. \end{equation}
Moreover, if equality holds, then the universal covering of 
$(M,g)$ is isometric to 
$(\mathbb {R}\times \Sigma _0,\,\textrm {d}t^{2}+g_0)$, where 
$(\Sigma _0,g_0)$ is a disc with constant Gaussian curvature 
$\frac {1}{2}\inf R_g$ and 
$\partial \Sigma _0$ has constant geodesic curvature 
$\inf H_g^{\partial M}$ in 
$(\Sigma _0,g_0)$.
A question that arises here is the following: Is it possible to obtain similar result for high co-dimension? Unfortunately, a general result cannot be true as we can see with the following example. Consider 
$(M,g)=(\mathbb {S}^{2}_+(r)\times \mathbb {S}^{m}(R), h_0+g_0),$ where 
$(\mathbb {S}^{2}_+(r),h_0)$ is the half two-sphere of radius 
$r$ with the standard metric, and 
$(\mathbb {S}^{m}(R),g_0)$ is the 
$m$-sphere of radius 
$R$ with the standard metric, 
$m\geq 2$. This case, we have that
\[ \frac{1}{2}\inf R_g^{M} \mathcal{A}(M,g)+\inf H_g^{\partial M}\mathcal{L}(M,g) >2\pi. \]
On the other hand, consider 
$(M,g)=(\mathbb {S}^{2}_+(r)\times T^{m}, g_0+\delta ),$ where 
$(T^{m},\delta )$ is the flat 
$m$-torus, 
$m\geq 2$. Note that the equality holds in (1.1). However, we can see that in this case the universal covering of 
$(M,g)$ is isometric to 
$(\mathbb {S}^{2}_+(r)\times \mathbb {R}^{m}, g_0+\delta _0)$, where 
$\delta _0$ is a standard metric in 
$\mathbb {R}^{m}$.
In the first example above, note that there is no map 
$F:(M,\partial M)\rightarrow (\mathbb {D}^{2}\times T^{n},\partial \mathbb {D}^{2}\times T^{n})$ with non-zero degree. However, this is a condition that we need in order to obtain a similar result as in [Reference Ambrozio1]. However, for the rigidity part, we will assume that the manifold has strongly totally geodesic boundary. We say that 
$(M,g)$ has strongly totally geodesic boundary if the following two conditions hold simultaneously:
(a)
$\partial M$ is a totally geodesic hypersurface of $(M, g)$, i.e. $\nabla _{\partial _n} \partial _i=0$ on $\partial M$ for $i=1,\ldots , n - 1$;(b)
$\nabla ^{2k+1}_{\partial _n} \partial _i=0$ for all positive integers $k$ and $i=1,\ldots , n -1$ on $\partial M$.
Our main result of this work is the following.
Theorem 1.2 Let 
$(M,\partial M,g)$ be a Riemannian 
$(n+2)$-manifold, 
$3\leq n+2\leq 7$, with positive scalar curvature and mean convex boundary. Assume that there is a map 
$F:(M,\partial M)\rightarrow (\mathbb {D}^{2}\times T^{n},\partial \mathbb {D}^{2}\times T^{n})$ with non-zero degree. Then,
\begin{equation} \frac{1}{2}\inf R_g^{M} \mathcal{A}(M,g)+\inf H_g^{\partial M}\mathcal{L}(M,g)\leq 2\pi. \end{equation}
Moreover, if the boundary 
$\partial M$ is strongly totally geodesic and the equality holds in (1.2), then the universal covering of 
$(M,g)$ is isometric to 
$(\mathbb {R}^{n}\times \Sigma _0, \delta +g_0)$, where 
$\delta$ is the standard metric in 
$\mathbb {R}^{n}$ and 
$(\Sigma _0,g_0)$ is a disc with constant Gaussian curvature 
$\frac {1}{2}\inf R^{M}_g$ and 
$\partial \Sigma _0$ has null geodesic curvature in 
$(\Sigma _0,g_0)$.
Remark 1.3 In order to prove the rigidity part of the above result, we consider the double manifold (
$DM$). However, such a double manifold does not inherit a smooth Riemannian metric in general. If the manifold has strongly totally geodesic boundary, we obtain that the double metric is smooth. Hence we apply the theorem 1.1 in [Reference Zhu21] and obtain the rigidity. If we consider only the totally geodesic condition on the boundary, we think it is also enough to obtain the rigidity. Actually, if the boundary is totally geodesic, the double metric is smooth and it fails to be smooth only across a hypersurface given by the double of the boundary. As in the work of Miao [Reference Miao17], related to non-smooth versions of the positive mass theorem, we think is it possible to obtain theorem 1.1 in [Reference Zhu21] for this type of metrics: smooth metrics which fails to be smooth only across a hypersurface. Hence, applying the conclusion of theorem 1.1 in [Reference Zhu21], we obtain the rigidity part.
This work is organized as follows. In § 2, we present some auxiliaries results to be used in the proof of the main results. In § 3, we present the proof of the inequality in our main theorem 1.2. Finally, in § 4, we present the proof of the rigidity part for the case where the equality is achieved and the manifold has strongly totally geodesic boundary.
2. Free-boundary minimal $k$-slicings
All the manifolds considered here are compact and orientable.
2.1 Definition and examples
Let 
$(M,\partial M,g)$ be a Riemannian 
$n$-manifold and 
$\eta$ the outward unit vector field on the boundary 
$\partial M$ in 
$(M,g)$. Assume there is a properly embedded free-boundary smooth hypersurface 
$\Sigma _{n-1}\subset M$ which minimizes volume in 
$(M,g)$. Choose 
$u_{n-1}>0$ a first eigenfunction for the second variation 
$S_{n-1}$ of the volume of 
$\Sigma _{n-1}$ in 
$(M,g)$ satisfying
\[ \frac{\partial u_{n-1}}{\partial \eta_{n-1}}=u_{n-1}B^{\partial M}(\nu_{n-1},\nu_{n-1})\ \text{on}\ \partial\Sigma_{n-1} \]
where 
$\nu _{n-1}$ is the unit normal vector field of 
$\Sigma _{n-1}$ on 
$(M,g)$, 
$\eta _{n-1}$ is the outward unit normal vector field on the boundary 
$\partial \Sigma _{n-1}$ in 
$(\Sigma _{n-1},g)$ and 
$B^{\partial M}$ is the second fundamental form of 
$\partial M$ in 
$(M,g)$ with respect to 
$\eta$. Define 
$\rho _{n-1}=u_{n-1}$ and the weighted volume functional 
$V_{\rho _{n-1}}$ for hypersurfaces of 
$\Sigma _{n-1}$,
\[ V_{\rho_{n-1}}(\Sigma)=\int_{\Sigma} \rho_{n-1}\,\textrm{d}v_{\Sigma}, \]
where 
$\textrm {d}v_{\Sigma }$ is the volume form on 
$(\Sigma ,g)$. Assume that there is a properly embedded free-boundary smooth hypersurface 
$\Sigma _{n-2}\subset \Sigma _{n-1}$ which minimizes the weighted volume functional 
$V_{\rho _{n-1}}$. Choose a first eigenfunction 
$u_{n-2}>0$ for the second variation 
$S_{n-2}$ of the weighted volume functional 
$V_{\rho _{n-1}}$ in 
$\Sigma _{n-2}$ satisfying
\[ \frac{\partial u_{n-2}}{\partial \eta_{n-2}}=u_{n-2}B^{\partial\Sigma_{n-1}}(\nu_{n-2},\nu_{n-2})\ \text{on}\ \partial\Sigma_{n-2}, \]
where 
$\nu _{n-2}$ is the unit normal vector field of 
$\Sigma _{n-2}$ on 
$(\Sigma _{n-1},g)$, 
$\eta _{n-2}$ is the outward unit normal vector field on the boundary 
$\partial \Sigma _{n-2}$ in 
$(\Sigma _{n-2},g)$ and 
$B^{\partial \Sigma _{n-1}}$ is the second fundamental form of 
$\partial \Sigma _{n-1}$ in 
$(\Sigma _{n-1},g)$ with respect to 
$\eta _{n-1}$. Define 
$\rho _{n-2}=\rho _{n-1}u_{n-2}$. Assume that we can keep doing this, inductively. Hence, we obtain a family of smooth free-boundary minimal submanifolds
\[ \Sigma_k\subset \Sigma_{k+1}\subset\cdots\subset\Sigma_{n-1}\subset(\Sigma_n,g):=(M,g), \]
which was constructed by choosing, for each 
$j\in \{k,\ldots ,n-1\}$, a smooth properly embedded free-boundary hypersurface 
$\Sigma _j\subset \Sigma _{j+1}$ which minimizes the weighted volume functional 
$V_{\rho _{j+1}}$, where 
$\rho _{j+1}:=u_{j+1}u_{j+2}\cdots u_{n-1}$ and
\[ \frac{\partial u_{j}}{\partial \eta_{j}}=u_{j}B^{\partial\Sigma_{j+1}}(\nu_{j},\nu_{j})\ \text{on}\ \partial\Sigma_{j}. \]
We call such family of free-boundary minimal hypersurfaces a free-boundary minimal 
$k$-slicing in 
$(M,g)$.
Example 2.1 Let 
$(N,\partial N,g)$ be a Riemannian 
$k$-manifold. Consider the following Riemannian 
$n$-manifold 
$(N\times T^{n-k},g+\delta )$, where 
$\delta$ is the flat metric on the torus 
$T^{n-k}$. The family of smooth hypersurfaces
\[ N\subset N\times S^{1}\subset N\times T^{2}\subset \cdots \subset N\times T^{n-k-1}\subset (N\times T^{n-k},g+\delta), \]
where 
$\rho _j\equiv u_j\equiv 1$, for every 
$j=k,\ldots ,n-1$, is a free-boundary minimal 
$k$-slicing in 
$(N\times T^{n-k},g+\delta )$.
2.2 Geometric formulas for free-boundary minimal $k$-slicing
Let 
$(M,\partial M,g)$ be a Riemannian 
$n$-manifold. Consider a free-boundary 
$k$-slicing in 
$M$:
\[ \Sigma_k\subset \cdots \subset \Sigma_{n-1}\subset (\Sigma_n,g):=(M,g). \]Notation
•
$Ric_j$ := Ricci curvature of $(\Sigma _j,g)$•
$R_j$ := Scalar curvature of $(\Sigma _j,g)$•
$\nu _j$ := Unit normal vector field of $\Sigma _j$ in $(\Sigma _{j+1},g)$•
$B_j$ := Second fundamental form of $\Sigma _j$ in $(\Sigma _{j+1},g)$•
$H_j$ := Mean curvature of $\Sigma _j$ in $(\Sigma _{j+1},g)$•
$\eta _j$ := Outward unit normal vector field on the boundary $\partial \Sigma _j$ in $(\Sigma _j,g)$•
$B^{\partial \Sigma _j}$ := Second fundamental form of $\partial \Sigma _j$ in $(\Sigma _j,g)$ with respect to $\eta _j$•
$H^{\partial \Sigma _j}$ := Mean curvature of $\partial \Sigma _j$ in $(\Sigma _j,g)$ with respect to $\eta _j$
Remark 2.2 Since 
$\Sigma _j$ is a free-boundary hypersurface in 
$(\Sigma _{j+1},g)$, for every 
$j=k,\ldots ,n-1$, we have that
(1)
$\eta _j=\eta _p$ in $\partial \Sigma _j$, for every $p\geq j$.(2)
$H^{\partial \Sigma _j}=H^{\partial \Sigma _{j+1}}-B^{\partial \Sigma _{j+1}}(\nu _j,\nu _j)=H^{\partial M}-\sum _{p=j}^{n-1}B^{\partial \Sigma _{p+1}}(\nu _p,\nu _p).$
For each 
$j\in \{k,\ldots ,n-1\}$, define on 
$\Sigma _j\times T^{n-j}$ the Riemannian metric
\[ \hat{g}_j=g+\sum_{p=j}^{n-1}u_p^{2}\,\textrm{d}t_p^{2}. \]We define
\[ \hat{\Sigma}_j=\Sigma_j\times T^{n-j}\quad\text{and}\quad \tilde{\Sigma}_j=\Sigma_j\times T^{n-j-1}. \]
Note that, since 
$\Sigma _j$ is free-boundary hypersurface in 
$(\Sigma _{j+1},g)$, we have that 
$\tilde {\Sigma }_j$ is a free-boundary hypersurface in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$. With the next lemmas and propositions, we will prove that 
$\Sigma _j \times T^{n-j-1}$ is a stable free boundary minimal hypersurface in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$.
Proposition 2.3 Let 
$(M,g)$ be a 
$n$-dimensional Riemannian manifold, 
$\Sigma \subset M$ be a hypersurface and 
$0< u\in C^{\infty }(M)$. Then, the second fundamental form of 
$\Sigma \times \mathbb {S}^{1}$ in 
$(M\times \mathbb {S}^{1},\tilde {g}=g+ u^{2}\,\textrm {d}t^{2})$ is given by
\[ \tilde{B}=B-u\nu(u)\,\textrm{d}t^{2}, \]
where 
$\nu$ is a globally defined unit normal vector field on 
$\Sigma$ and 
$B$ is the second fundamental form of 
$\Sigma$ in 
$(M,g)$.
Proof. Consider 
$(x_1,\ldots ,x_{n-1},t=x_{n})$ a local chart in 
$\Sigma \times \mathbb {S}^{1}$ such that 
$(x_1,\ldots ,x_{n-1})$ is a local chart in 
$\Sigma$. Denote by 
$\tilde {\nabla }$ and 
$\nabla$ the Riemannian connections of 
$(M\times \mathbb {S}^{1},\tilde {g})$ and 
$(M,g)$, respectively. For 
$i,j=1,\ldots , n-1$, we have that
\[ \tilde{\nabla}_{\partial_i}\partial_j=\nabla_{\partial_i}\partial_j,\quad \tilde{\nabla}_{\partial_i}\partial_t=\frac{\partial_i(u)}{u}\partial_t\quad\text{and}\quad \tilde{\nabla}_{\partial_t}\partial_t={-}u\nabla_gu. \]It follows that
\begin{align*} \tilde{B}_{ij}&= \tilde{g}(\tilde{\nabla}_{\partial_i}\partial_j,\nu)=g(\nabla_{\partial_i}\partial_j,\nu)=B_{ij},\\ \tilde{B}_{in}&= \tilde{g}(\tilde{\nabla}_{\partial_i}\partial_t,\nu)=\frac{\partial_i(u)}{u}\tilde{g}(\partial_t,\nu)=0 \end{align*}and
\[ \tilde{B}_{nn}= \tilde{g}(\tilde{\nabla}_{\partial_t}\partial_t,\nu)={-}ug(\nabla_gu,\nu)={-}u\nu(u). \]Lemma 2.4 For every 
$j=k,\ldots ,n-1$, the second fundamental form 
$\tilde {B}_j$ of 
$\tilde {\Sigma }_j$ in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$ is given by
\begin{equation} \tilde{B}_j=B_j-\sum_{p=j+1}^{n-1}u_p\nu_j(u_p)\,\textrm{d}t_p^{2}. \end{equation}In particular,
\[ |\tilde{B}_j|^{2}=|B_j|^{2}+\sum_{p=j+1}^{n-1}(\nu_j(\log u_p))^{2}. \]Proof. To prove (2.1), for 
$m\in \{j+1,\ldots ,n-1$}, define on 
$\Sigma _{j+1}\times T^{n-m}$ the following Riemannian metric
\[ \overline{g}_m=g+\sum_{p=m}^{n-1}u_p^{2}\,\textrm{d}t_p^{2}. \]
We will prove that the second fundamental form of 
$\Sigma _{j}\times T^{n-m}$ in 
$(\Sigma _{j+1}\times T^{n-m},\overline {g}_m)$ is
\begin{equation} \overline{B}_m= B_j-\sum_{p=m}^{n-1}u_p\nu_j(u_p)\,\textrm{d}t_p^{2} \end{equation}
by a finite reverse induction on 
$m$. When 
$m=n-1$ equality (2.2) follows directly from proposition 2.3. Now suppose that (2.2) is valid for 
$m+1$. Note that 
$\overline {g}_m=\overline {g}_{m+1}+u_m^{2}\,\textrm {d}t_m^{2}$. It follows from proposition 2.3 that 
$\overline {B}_m=\overline {B}_{m+1}-u_m\nu _j(u_m)\,\textrm {d}t_m^{2}.$ Equality (2.2) now follows from the inductive assumption. Since 
$\overline {g}_{j+1}=\hat {g}_{j+1}$, we have showed equality (2.1).
Lemma 2.5 For every 
$j=k,\ldots ,n-1$, the second fundamental form 
$\hat {B}_{j+1}$ of 
$\partial \hat {\Sigma }_{j+1}$ in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$ with respect to 
$\eta _j$ satisfies
\[ \hat{B}_{j+1}(\nu_{j},\nu_{j})=B^{\partial\Sigma_{j+1}}(\nu_{j},\nu_j). \]Proof. Using a similar argument used to prove (2.1), we can prove that
\[ \hat{B}_{j+1}=B^{\partial\Sigma_{j+1}}-\sum_{p=j+1}^{n-1}u_p\eta_{j+1}(u_p)\,\textrm{d}t_p^{2}. \]In particular,
\[ \hat{B}_{j+1}(\nu_{j},\nu_{j})=B^{\partial\Sigma_{j+1}}(\nu_{j},\nu_j). \]Proposition 2.6 Let 
$(M,g)$ be a 
$n$-dimensional Riemannian manifold and 
$0< u\in C^{\infty }(M)$. Then the Ricci curvature of 
$(M\times \mathbb {S}^{1},\tilde {g}=g+u^{2}\,\textrm {d}t^{2})$ is given by
\[ Ric_{\tilde{g}}=Ric_g-u^{{-}1}\left(\nabla_g^{2}u\right)-u\Delta_gu\,\textrm{d}t^{2}, \]
where 
$Ric_g$ is the Ricci curvature of 
$(M,g)$.
Proof. Consider 
$(x_1,\ldots ,x_{n},t=x_{n+1})$ a local chart in 
$M\times \mathbb {S}^{1}$ such that 
$(x_1,\ldots ,x_{n})$ is a local chart in 
$M$. Denote by 
$\nabla$ the Riemannian connection of 
$(M,g)$ and 
$\tilde {R}$, 
$R$ the curvature tensors of 
$(M\times \mathbb {S}^{1},\tilde {g})$ and 
$(M,g)$, respectively. Note that
\[ (Ric_{\tilde{g}})_{ij}=\sum_{k,l=1}^{n+1}\tilde{g}^{kl}\tilde{R}_{kijl}=\sum_{k,l=1}^{n}g^{kl}\tilde{R}_{kijl}+u^{{-}2}\tilde{R}_{tijt}. \]
Since, for 
$i,j,k,l=1,\ldots , n$, we have that
\[ \tilde{R}_{kijl}=R_{kijl},\quad \tilde{R}_{tijt}={-}u\left(\nabla_{g}^{2}u\right)_{ij}\quad \text{and}\quad\tilde{R}_{kitl}=0 \]then
\begin{align*} (Ric_{\tilde{g}})_{ij}&= \sum_{k,l=1}^{n}g^{kl}R_{kijl}-u^{{-}1}\left(\nabla_{g}^{2}u\right)_{ij}= (Ric_{g})_{ij}-u^{{-}1}\left(\nabla_{g}^{2}u\right)_{ij},\\ (Ric_{\tilde{g}})_{tt} &={-}u\sum_{k,l=1}^{n} g^{kl}\left(\nabla_{g}^{2}u\right)_{kl}={-}u\Delta_{g}u \end{align*}and
\[ (Ric_{\tilde{g}})_{it}=0 \]
for every 
$i,j=1,\ldots , n$.
Lemma 2.7 For every 
$j=k,\ldots ,n-2$, the Ricci curvature 
$Ric_{\hat {g}_{j+1}}$ of 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$ satisfies
\[ Ric_{\hat{g}_{j+1}}(\nu_j,\nu_j)=Ric_{j+1}(\nu_j,\nu_j)- \sum_{p=j+1}^{n-1} u_p^{{-}1} \left(\nabla_{j+1}^{2}u_p\right)(\nu_j,\nu_j) \]
where 
$\nabla _{j+1}^{2}$ is the Hessian in 
$(\Sigma _{j+1},g)$.
Proof. For 
$m\in \{j+1,\ldots ,n-1$}, define in 
$\Sigma _{j+1}\times T^{n-m}$ the Riemannian metric
\[ \overline{g}_m=g+\sum_{p=m}^{n-1}u_p^{2}\,\textrm{d}t_p^{2}. \]
We will prove that the Ricci curvature 
$\overline {Ric}_m$ of 
$(\Sigma _{j+1}\times T^{n-m},\overline {g}_m)$ satisfies
\begin{equation} \overline{Ric}_m(\nu_j,\nu_j)=Ric_{j+1}(\nu_j,\nu_j)- \sum_{p=m}^{n-1} u_p^{{-}1} \left(\nabla_{j+1}^{2}u_p\right)(\nu_j,\nu_j) \end{equation}
by a finite reverse induction on 
$m$. When 
$m=n-1$ equality (2.3) follows directly from proposition 2.6. Now suppose (2.3) is valid for 
$m+1$. Since 
$\overline {g}_m=\overline {g}_{m+1}+u_m^{2}\textrm {d}t_m^{2}$, it follows from proposition 2.6 that
\[ \overline{Ric}_m(\nu_j,\nu_j)=\overline{Ric}_{m+1}(\nu_j,\nu_j)- u_m^{{-}1} \left(\overline{\nabla}_{m+1}^{2}u_m\right)(\nu_j,\nu_j). \]
where 
$\overline {\nabla }_{m+1}^{2}$ denote the Hessian in 
$(\Sigma _{j+1}\times T^{n-m-1},\overline {g}_{m+1}).$ Note that
\[ \left(\overline{\nabla}_{m+1}^{2}u_m\right)(\nu_j,\nu_j)=\left(\nabla_{j+1}^{2}u_m\right)(\nu_j,\nu_j). \]
Equality (2.3) now follows from the inductive assumption and the last two equalities. Since 
$\overline {g}_{j+1}=\hat {g}_{j+1}$, we have proven the lemma.
Proposition 2.8 For every 
$j=k,\ldots ,n-1$, 
$\tilde {\Sigma }_j$ is a free-boundary minimal hypersurfaces in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$.
Proof. Consider 
$(x_1,\ldots , x_j, t_{j+1}, \ldots , t_{n-1})$ a local chart in 
$\tilde {\Sigma }_j$ such that 
$(x_1,\ldots , x_j)$ is a local chart in 
$\Sigma _j$. Denote by 
$\tilde {H}_j$ the mean curvature of 
$\tilde {\Sigma }_j$ in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$. It follows from lemma 2.4 that
\begin{align*} \tilde{H}_j &= \sum_{i,k=1}^{n-1}\hat{g}_{j+1}^{ik}(\tilde{B}_j)_{ik}\\ &= \sum_{i,k=1}^{j}g^{ik}(B_j)_{ik}-\sum_{p=j+1}^{n-1}\frac{\nu_j(u_p)}{u_p}\\ &= H_j-\sum_{p=j+1}^{n-1}\nu_j(\ln u_p)\\ &= H_j-\nu_j(\ln \rho_{j+1})\\ &= H_j-\langle \nabla_{j+1} \ln \rho_{j+1},\nu_j\rangle \end{align*}
where 
$\nabla _{j+1}$ is the gradient in 
$(\Sigma _{j+1},g)$. We have that 
$\Sigma _j$ minimizes the weight volume functional 
$V_{\rho _{j+1}}$, in particular, the 
$(\ln \rho _{j+1})$-mean curvature of 
$\Sigma _j$ in 
$(\Sigma _{j+1},g)$ vanishes everywhere, this is, 
$H_j=\langle \nabla _{j+1} \ln \rho _{j+1},\nu _j\rangle .$ (See [Reference Li and Xiong15].) This implies that 
$\tilde {H}_j=0$. Therefore, 
$\tilde {\Sigma }_j$ is a free-boundary minimal hypersurfaces in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$.
Denote by 
$S_j$ the second variation for weight volume functional 
$V_{\rho _{j+1}}$ in 
$\Sigma _{j}$, 
$\tilde {S}_j$ the second variation for volume functional of 
$\tilde {\Sigma }_j$ in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$ and 
$\tilde {g}_j=\left .\hat {g}_{j+1}\right |_{\tilde {\Sigma }_j}$.
Proposition 2.9 For every 
$j=k,\ldots ,n-1$, 
$\tilde {\Sigma }_j$ is a free-boundary stable minimal hypersurfaces in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$.
Proof. Let 
$\varphi \in C^{\infty }(\Sigma _j)$. We have that
\begin{align*} S_j(\varphi)&=\int_{\Sigma_j}\left[|\nabla_j\varphi|^{2}-(|B_j|^{2}+Ric_{f_{j+1}}(\nu_j,\nu_j))\varphi^{2}\right]\rho_{j+1}\,\textrm{d}v_j\\ &\quad-\int_{\partial\Sigma_j}\varphi^{2}B^{\partial\Sigma_{j+1}}(\nu_j,\nu_j)\rho_{j+1}\,\textrm{d}\sigma _j \end{align*}
where 
$Ric_{f_{j+1}}(\nu _j,\nu _j)=Ric_{j+1}(\nu _j,\nu _j)-(\nabla _{j+1}^{2}f_{j+1})(\nu _j,\nu _j)$, 
$f_{j+1}=\ln \rho _{j+1}$ (see [Reference Li and Xiong15]). Here, 
$\textrm {d}v_j$ and 
$\textrm {d}\sigma _j$ are the volume forms of 
$(\Sigma _j,g)$ and 
$(\partial \Sigma _j,g)$, respectively. Note that
\begin{align*} \nabla_{j+1}f_{j+1} &=\nabla_{j+1}\ln \rho_{j+1}\\ &=\nabla_{j+1}\left(\sum_{p=j+1}^{n-1}\ln u_p\right)\\ &=\sum_{p=j+1}^{n-1}\nabla_{j+1}\ln u_p\\ &=\sum_{p=j+1}^{n-1}\frac{1}{u_p}\nabla_{j+1} u_p. \end{align*}It follows that
\begin{align*} (\nabla_{j+1}^{2}f_{j+1})(\nu_j,\nu_j) &=\left\langle \nabla_{\nu_j}\left(\nabla_{j+1}f_{j+1}\right),\nu_j\right\rangle\\ &=\left\langle \nabla_{\nu_j}\left( \sum_{p=j+1}^{n-1}\frac{1}{u_p}\nabla_{j+1} u_p \right),\nu_j\right\rangle\\ &=\sum_{p=j+1}^{n-1} \left\langle \frac{1}{u_p}\nabla_{\nu_j}\left(\nabla_{j+1} u_p\right) -\frac{\nu_j(u_p)}{u_p^{2}}\nabla_{j+1} u_p,\nu_j\right\rangle\\ &=\sum_{p=j+1}^{n-1} \frac{1}{u_p} \left\langle \nabla_{\nu_j}\left(\nabla_{j+1} u_p\right),\nu_j\right\rangle- \sum_{p=j+1}^{n-1}\frac{1}{u_p^{2}}[\nu_j(u_p)]^{2}\\ &=\sum_{p=j+1}^{n-1} \frac{1}{u_p} \left(\nabla_{j+1}^{2}u_p\right)(\nu_j,\nu_j)- \sum_{p=j+1}^{n-1}[\nu_j(\ln u_p)]^{2} \end{align*}From lemmas 2.4 and 2.7 we obtain
\[ Ric_{f_{j+1}}(\nu_j,\nu_j)+|B_j|^{2}=Ric_{\hat{g}_{j+1}}(\nu_j,\nu_j)+|\tilde{B}_j|^{2}. \]This implies that
\[ S_j(\varphi)=\int_{\Sigma_j}\left(|\nabla_j\varphi|^{2}-Q_j\varphi^{2}\right)\rho_{j+1}\,\textrm{d}v_j-\int_{\partial\Sigma_j}\varphi^{2}B^{\partial\Sigma_{j+1}}(\nu_j,\nu_j)\rho_{j+1}\,\textrm{d}\sigma _j. \]where
\[ Q_j=Ric_{\hat{g}_{j+1}}(\nu_j,\nu_j)+|\tilde{B}_j|^{2}. \]
Consider now 
$\Psi \in C^{\infty }(\tilde {\Sigma }_j)$. We have that
\[ \tilde{S}_j(\Psi)=\int_{\tilde{\Sigma}_j}\left[|\nabla_{\tilde{g}_j}\Psi|^{2}-Q_j \Psi^{2}\right]\textrm{d}v_{\tilde{g}_j}-\int_{\partial\tilde{\Sigma}_j}\Psi^{2}\hat{B}_{j+1}(\nu_j,\nu_j)\,\textrm{d}\sigma _{\tilde{g}_j} \]
where 
$\textrm {d}v_{\tilde {g}_j}$ and 
$\textrm {d}\sigma _{\tilde {g}_j}$ are the volume forms of 
$(\tilde {\Sigma _j},\tilde {g}_j)$ and 
$(\partial \tilde {\Sigma _j},\tilde {g}_j)$, respectively. From lemma 2.5 we have that
\[ \tilde{S}_j(\Psi) = \int_{\tilde{\Sigma}_j}\left(|\nabla_{\tilde{g}_j}\Psi|^{2}-Q_j \Psi^{2}\right)\textrm{d}v_{\tilde{g}_j} - \int_{\partial\tilde{\Sigma}_j}\Psi^{2}B^{\partial \Sigma_{j+1}}(\nu_j,\nu_j)\,\textrm{d}\sigma _{\tilde{g}_j} \] Furthermore, since 
$\textrm {d}v_{\tilde {g}_j}=\rho _{j+1}\,\textrm {d}v_j\,\textrm {d}t$ and 
$\textrm {d}\sigma _{\tilde {g}_j}=\rho _{j+1}\,\textrm {d}\sigma _j\,\textrm {d}t$, where 
$\textrm {d}t=\textrm {d}t_{j+2}\cdots \textrm {d}t_{n-1}$, we have that
\begin{align*} \tilde{S}_j(\Psi)&=\int_{T^{n-j-1}}\left( \int_{{\Sigma}_j}\left(|\nabla_{\tilde{g}_j}\Psi|^{2}-Q_j\Psi^{2}\right)\rho_{j+1}\,\textrm{d}v_{j}\right)\textrm{d}t\\ &\quad-\int_{T^{n-j-1}}\left(\int_{\partial{\Sigma}_j}\Psi^{2}B^{\partial \Sigma_{j+1}}(\nu_j,\nu_j)\rho_{j+1}\,\textrm{d}\sigma _{j}\right)\textrm{d}t \end{align*} For each 
$\Psi \in C^{\infty }(\tilde {\Sigma }_j)$ define 
$F_{\Psi }: T^{n-j-1}\rightarrow \mathbb {R}$ by 
$F_{\Psi }(t)=S_j(\Psi _t)$, where for each 
$t\in T^{n-j-1}$ the function 
$\Psi _t\in C^{\infty }(\Sigma _j)$ is defined by 
$\Psi _t(x)=\Psi (x,t)$, 
$x\in \Sigma _j$. Note that
\begin{equation} \tilde{S}_j(\Psi) \geq \int_{T^{n-j-1}}F_{\Psi}\,\textrm{d}t. \end{equation} Since 
$\Sigma _j$ minimizes the weight volume functional 
$V_{\rho _{j+1}}$ we have that 
$F_{\Psi }>0$ for every 
$\Psi \in C^{\infty }(\tilde {\Sigma }_j)$. It follows that 
$\tilde {S}_j(\Psi )>0$ for every 
$\Psi \in C^{\infty }(\tilde {\Sigma }_j)$. Hence, 
$\tilde {\Sigma }_j$ is a free-boundary stable minimal hypersurface in 
$(\hat {\Sigma }_{j+1},\hat {g}_{j+1})$.
Note that the equality holds in (2.4) if and only if 
$\Psi \in C^{\infty }({\Sigma }_j)$. So 
$S_j(\varphi )=\tilde {S}_j(\varphi ),$ for every 
$\varphi \in C^{\infty }(\Sigma _j)$. It follows that
\begin{align*} S_j(\varphi)&=\int_{\Sigma_j}(|\nabla_j\varphi|^{2}-Q_j\varphi^{2})\rho_{j+1}\,\textrm{d}v_j -\int_{\partial \Sigma_{j}}\varphi^{2}B^{\partial\Sigma_{j+1}}(\nu_j,\nu_j)\rho_{j+1}\,\textrm{d}\sigma_j\\ &={-}\int_{\Sigma_j}\varphi \tilde{L}_j(\varphi)\rho_{j+1}\,\textrm{d}v_j+ \int_{\partial\Sigma_j}\varphi\left(\frac{\partial \varphi}{\partial \eta_j}-\varphi B^{\partial\Sigma_{j+1}}(\nu_j,\nu_j)\right)\rho_{j+1}\,\textrm{d}\sigma_j \end{align*}
for every 
$\varphi \in C^{\infty }(\Sigma _j)$, where 
$\tilde {L}_j:C^{\infty }(\Sigma _j)\rightarrow C^{\infty }(\Sigma _j)$ is a differential operator given by 
$\tilde {L}(\varphi )=\tilde {\Delta }_j\varphi +Q_j\varphi ,$ where 
$\tilde {\Delta }_j$ denote the Laplacian operator of 
$(\tilde {\Sigma }_j,\hat {g}_{j+1})$.
Consider 
$\lambda _j$ the first eigenvalue of 
$S_j$ associated with the first eigenfunction 
$u_j$. We have that,
\begin{equation} \begin{cases} \tilde{L}_j(u_j)={-}\lambda_ju_j\ \text{on}\ \Sigma_j\\ \displaystyle\dfrac{\partial u_j}{\partial \eta_j} = u_j B^{\partial\Sigma_{j+1}}(\nu_j,\nu_j)\ \text{on}\ \partial\Sigma_j \end{cases} \end{equation}Lemma 2.10 For every 
$j\leq p\leq n-1$, we have that, in 
$\partial \Sigma _j$,
\[ B^{\partial \Sigma_{p+1}}(\nu_p,\nu_p)=\langle \nabla_j\log u_p, \eta_j\rangle. \]Proof. It follows from (2.5) that, in 
$\partial \Sigma _p$,
\[ B^{\partial\Sigma_{p+1}}(\nu_p,\nu_p)=\frac{1}{u_p}\frac{\partial u_p}{\partial \eta_p}=\langle \nabla_p\log u_p,\eta_p\rangle, \]
for every 
$p=k,\ldots ,n-1$. Consider 
$j\leq p\leq n-1$. Note that, in 
$\partial \Sigma _j$,
\[ B^{\partial\Sigma_{p+1}}(\nu_p,\nu_p)=\langle \nabla_p\log u_p,\eta_j\rangle, \]
because we have 
$\eta _p=\eta _j$ in 
$\partial \Sigma _j$ (see remark 2.2). In 
$\Sigma _j$, we can write
\[ \nabla_p\log u_p=\nabla_j\log u_p+\sum_{l=j}^{p-1}\langle \nabla_p\log u_p,\nu_l\rangle \nu_l. \]
Hence, in 
$\partial \Sigma _j$, we have that
\[ B^{\partial\Sigma_{p+1}}(\nu_p,\nu_p)=\langle \nabla_j\log u_p,\eta_j\rangle +\sum_{l=j}^{p-1}\langle \nabla_p\log u_p,\nu_l\rangle\langle \nu_l,\eta_j\rangle. \]
However, we have 
$\eta _j\perp \nu _l$ in 
$\partial \Sigma _j$, for every 
$j\leq l \leq n-1$. Therefore,
\[ B^{\partial\Sigma_{p+1}}(\nu_p,\nu_p)=\langle \nabla_j\log u_p,\eta_j\rangle \]Proposition 2.11 Let 
$(M,g)$ be a 
$n$-dimensional Riemannian manifold and 
$0< u\in C^{\infty }(M)$. Then the scalar curvature of 
$(M\times \mathbb {S}^{1},\tilde {g}=g+u^{2}\,\textrm {d}t^{2})$ is
\[ R_{\tilde{g}}=R_g-\frac{2}{u}\Delta_{g}u, \]
where 
$R_g$ is the scalar curvature of 
$(M,g)$.
Proof. Consider 
$(x_1,\ldots ,x_n,t=x_{n+1})$ a local chart in 
$M\times \mathbb {S}^{1}$ such that 
$(x_1,\ldots ,x_{n})$ is a local chart in 
$M$. From proposition 2.6, we have that
\begin{align*} R_{\tilde{g}} & =\sum_{i,j=1}^{n+1} \tilde{g}^{ij} (Ric_{\tilde{g}})_{ij}\\ &= \sum_{i,j=1}^{n} \tilde{g}^{ij}(Ric_{\tilde{g}})_{ij}+\frac{1}{u^{2}}(Ric_{\tilde{g}})_{tt}\\ &= \sum_{i,j=1}^{n}g^{ij}(Ric_g)_{ij}-\frac{1}{u}\sum_{i,j=1}^{n}g^{ij}\left(\nabla_{g}^{2}u\right)_{ij}-\frac{1}{u}\Delta_{g}u\\ &= R_{g}-\frac{2}{u}\Delta_{g}u. \end{align*}Lemma 2.12 For 
$k\leq j\leq n-1$, the scalar curvature 
$\tilde {R}_j$ of 
$(\tilde {\Sigma }_j,\tilde {g}_{j})$ is given by
\begin{equation} \tilde{R}_j=R_j-2\sum_{p=j+1}^{n-1}u_p^{{-}1}\Delta_ju_p-2\sum_{j+1\leq p< q\leq n-1}\langle \nabla_j\log u_p,\nabla_j\log u_q\rangle. \end{equation}Equivalently,
\begin{equation} \tilde{R}_j=R_j-4\rho_{j+1}^{-({1}/{2})}\Delta_j(\rho_{j+1}^{{1}/{2}})-\sum_{p=j+1}^{n-1}|\nabla_j\log u_p|^{2}. \end{equation}Proof. To prove (2.6), for 
$m\in \{j+1,\ldots ,n-1$}, define in 
$\Sigma _{j}\times T^{n-m}$ the Riemannian metric
\[ \overline{g}_m=g+\sum_{p=m}^{n-1}u_p^{2}\,\textrm{d}t_p^{2}. \]
We will prove that the scalar curvature of 
$(\Sigma _{j}\times T^{n-m},\overline {g}_m)$ is
\begin{equation} \overline{R}_m=R_j-2\sum_{p=m}^{n-1}u_p^{{-}1}\Delta_ju_p-2\sum_{m\leq p< q\leq n-1}\langle \nabla_j\log u_p,\nabla_j\log u_q\rangle \end{equation}
by a finite reverse induction on 
$m$. When 
$m=n-1$ formula (2.8) follows directly from proposition 2.11. Now suppose formula (2.8) is valid for 
$m+1$. Note that 
$\overline {g}_m=\overline {g}_{m+1}+u_m^{2}\,\textrm {d}t_m^{2}$. It follows from proposition 2.11 that
\[ \overline{R}_m=\overline{R}_{m+1}-2u_m^{{-}1}\overline{\Delta}_{m+1}u_m \]
where 
$\overline {\Delta }_{m+1}$ denote the Laplacian operator of 
$(\Sigma _{j}\times T^{n-m-1},\overline {g}_{m+1})$. Note that
\[ \overline{\Delta}_{m+1}u_m=\Delta_ju_m+\sum_{p=m+1}^{n-1}g(\nabla_j\log u_p,\nabla_ju_m). \]
Equality (2.8) now follows from the inductive assumption and the last two equalities. Since 
$\overline {g}_{j+1}=\tilde {g}_{j}$, we have proven equality (2.6).
To prove (2.7), note that
\[ \left|\sum_{p={j+1}}^{n-1}\nabla_j\log u_p\right|^{2} = \sum_{p={j+1}}^{n-1}|\nabla_j\log u_p |^{2} + 2\sum_{j+1\leq p< q\leq n-1}\left\langle \nabla_j\log u_p,\nabla_j\log u_q \right\rangle \]It follows from (2.6) that
\[ \tilde{R}_j = R_j-2\sum_{p=j+1}^{n-1}u_p^{{-}1}\Delta_ju_p-\left|\sum_{p={j+1}}^{n-1}\nabla_j\log u_p\right|^{2}+\sum_{p={j+1}}^{n-1}|\nabla_j\log u_p|^{2}. \]Since
\[ 2\Delta_j\log u_p=2u_p^{{-}1}\Delta_ju_p-2|\nabla_j\log u_p|^{2}\quad \text{and}\quad\sum_{p={j+1}}^{n-1}\log u_p=\log \rho_{j+1} \]we have that
\begin{align*} \tilde{R}_j &= R_j-\sum_{p=j+1}^{n-1}|\nabla_j\log u_p|^{2}-2\Delta_j\left(\sum_{p=j+1}^{n-1}\log u_p\right)-\left|\nabla_j\left(\sum_{p={j+1}}^{n-1}\log u_p\right)\right|^{2}\\ &=R_j-\sum_{p=j+1}^{n-1}|\nabla_j\log u_p|^{2}-2\Delta_j\log \rho_{j+1}-|\nabla_j\log \rho_{j+1}|^{2}\\ &= R_j-4\rho_{j+1}^{-({1}/{2})}\Delta_j(\rho_{j+1}^{{1}/{2}})-\sum_{p=j+1}^{n-1}|\nabla_j\log u_p|^{2}. \end{align*}Lemma 2.13 For 
$k\leq j\leq n-1$, the scalar curvature 
$\hat {R}_j$ of 
$(\hat {\Sigma }_{j},\hat {g}_{j})$ is given by
\begin{align} \hat{R}_j &= R_j-2\sum_{p=j}^{n-1}u_p^{{-}1}\Delta_ju_p-2\sum_{j\leq p< q\leq n-1}\langle \nabla_j\log u_p,\nabla_j\log u_q\rangle \end{align}
\begin{align} &=\hat{R}_{j+1}+|\tilde{B}_j|^{2}+2\lambda_j \end{align}
\begin{align} &=R^{M}+\sum_{p=j}^{n-1}|\tilde{B}_p|^{2}+2\sum_{p=j}^{n-1}\lambda_p. \end{align}Proof. We can prove (2.9) using a similar argument used to prove (2.6). To prove (2.10), note that 
$(\hat {\Sigma }_j, \hat {g}_j)=(\tilde {\Sigma }_j\times \mathbb {S}^{1},\tilde {g}_{j}+u_j^{2}\,\textrm {d}t_j^{2})$. It follows from proposition 2.11 that
\[ \hat{R}_j=\tilde{R}_j-2u_j^{{-}1}\tilde{\Delta}_ju_j \]
where 
$\tilde {\Delta _j}$ denote the Laplacian operator of 
$(\tilde {\Sigma }_j,\tilde {g}_{j})$. So, from (2.5) we have that
\[ 2\lambda_{j}={-}2u_j^{{-}1}\tilde{\Delta}_{j}u_{j}-\hat{R}_{j+1}+\tilde{R}_{j}-|\tilde{B}_{j}|^{2}= \hat{R}_j -\hat{R}_{j+1}-|\tilde{B}_{j}|^{2} \]
Hence, it follows equality (2.10). To get (2.11) we iterate (2.10) 
$n-j$ times.
Proposition 2.14 If 
$R^{M}>0$ and 
$H^{\partial M}\geq 0$ then
\[ 4\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j>{-}2\int_{\partial\Sigma_j}\varphi^{2} H^{\partial\Sigma_j}\,\textrm{d}\sigma_j -\int_{\Sigma_j}\varphi^{2}R_j\,\textrm{d}v_j, \]
for every 
$\varphi \in C^{\infty }(\Sigma _j)$ and 
$j=k,\ldots ,n-1$.
Proof. Since 
$\Sigma _{j}$ minimizes the weighted volume functional 
$V_{\rho _{j+1}}$, we have that 
$S_j(\varphi )\geq 0,$ for every 
$\varphi \in C^{\infty }(\Sigma _j)$. It follows that,
\[ 4\int_{\Sigma_j}|\nabla_j\varphi|^{2}\rho_{j+1}\,\textrm{d}v_j\geq 2\int_{\Sigma_j}c_j\varphi^{2}\rho_{j+1}\,\textrm{d}v_j+2\int_{\partial \Sigma_{j}}\varphi^{2}B^{\partial\Sigma_{j+1}}(\nu_j,\nu_j)\rho_{j+1}\,\textrm{d}\sigma_j, \]
for every 
$\varphi \in C^{\infty }(\Sigma _j).$ From Gauss equation we have that
\[ Q_j=\frac{1}{2}(\hat{R}_{j+1}-\tilde{R}_j+|\tilde{B}_j|^{2}). \]
Since 
$R^{M}>0$, from lemma 2.13, we have that 
$\hat {R}_{i}>0$, for every 
$k\leq i\leq n-1$. It follows from lemma 2.12 that
\[ 2Q_j>{-}R_j+4\rho_{j+1}^{-({1}/{2})}\Delta_j(\rho_{j+1}^{{1}/{2}}) \]Thus,
\begin{align*} 4\int_{\Sigma_j}|\nabla_j\varphi|^{2}\rho_{j+1}\,\textrm{d}v_j & >{-}\int_{\Sigma_j}R_j\varphi^{2}\rho_{j+1}\,\textrm{d}v_j+ 4\int_{\Sigma_j}\rho_{j+1}^{{1}/{2}}\Delta_j(\rho_{j+1}^{{1}/{2}})\varphi^{2}\,\textrm{d}v_j\\ &\quad+ 2\int_{\partial \Sigma_{j}}\varphi^{2}B^{\partial\Sigma_{j+1}}(\nu_j,\nu_j)\rho_{j+1}\,\textrm{d}\sigma_j, \end{align*}
for every 
$\varphi \in C^{\infty }(\Sigma _j).$ Replacing 
$\varphi$ by 
$\varphi \rho _{j+1}^{-({1}/{2})}$ at the last inequality, we obtain that
\begin{align*} 4\int_{\Sigma_j}|\nabla_j(\varphi\rho_{j+1}^{-({1}/{2})})|^{2}\rho_{j+1}\,\textrm{d}v_j & >{-} \int_{\Sigma_j}R_j\varphi^{2}\,\textrm{d}v_j + 4\int_{\Sigma_j}\rho_{j+1}^{-({1}/{2})}\Delta_j(\rho_{j+1}^{{1}/{2}})\varphi^{2}\,\textrm{d}v_j \nonumber\\ &\quad+2\int_{\partial \Sigma_{j}}\varphi^{2}B^{\partial\Sigma_{j+1}}(\nu_j,\nu_j)\,\textrm{d}\sigma_j. \end{align*}Observe that
\[ \nabla_j(\varphi\rho_{j+1}^{-({1}/{2})})=\varphi\nabla_j\rho_{j+1}^{-({1}/{2})}+\rho_{j+1}^{-({1}/{2})}\nabla_j\varphi \]This implies that
\[ |\nabla_j(\varphi\rho_{j+1}^{-({1}/{2})})|^{2}=\rho_{j+1}^{{-}1}|\nabla_j\varphi|^{2}+\varphi^{2}|\nabla_j\rho_{j+1}^{-({1}/{2})}|^{2}+2\varphi\rho_{j+1}^{-({1}/{2})}\langle \nabla_j\rho_{j+1}^{-({1}/{2})},\nabla_j \varphi\rangle \]Thus,
\[ \rho_{j+1}|\nabla_j(\varphi\rho_{j+1}^{-({1}/{2})})|^{2}=|\nabla_j\varphi|^{2}+\varphi^{2}\rho_{j+1}|\nabla_j\rho_{j+1}^{-({1}/{2})}|^{2}+\langle \nabla_j\log\rho_{j+1}^{-({1}/{2})},\nabla_j (\varphi^{2})\rangle \]Using integration by parts, we have that
\begin{align*} &\int_{\Sigma_j} \langle \nabla_j\log\rho_{j+1}^{-({1}/{2})},\nabla_j (\varphi^{2})\rangle\,\textrm{d}v_j\\ & \quad ={-}\int_{\Sigma_j}\varphi^{2}\Delta_j\log \rho_{j+1}^{-({1}/{2})}\,\textrm{d}v_j +\int_{\partial \Sigma_j}\varphi^{2}\frac{\partial(\log\rho_{j+1}^{-({1}/{2})})}{\partial \eta_j}\,\textrm{d}\sigma_j\\ & \quad=+\int_{\Sigma_j}\varphi^{2}\rho_{j+1}^{-({1}/{2})}\Delta_j \rho_{j+1}^{{1}/{2}}\,\textrm{d}v_j -\int_{\Sigma_j}\varphi^{2}|\nabla_j\log \rho_{j+1}^{{1}/{2}}|^{2})\,\textrm{d}v_j\\ &\qquad-\frac{1}{2}\int_{\partial \Sigma_j}\varphi^{2}\langle \nabla_j \log \rho_{j+1},\eta_j\rangle\,\textrm{d}\sigma_j\\ & \quad ={-}\int_{\Sigma_j}\varphi^{2}|\nabla_j\log \rho_{j+1}^{{1}/{2}}|^{2}\,\textrm{d}v_j + \int_{\Sigma_j}\varphi^{2}\rho_{j+1}^{-({1}/{2})}\Delta_j \rho_{j+1}^{{1}/{2}}\,\textrm{d}v_j\\ &\qquad -\frac{1}{2}\int_{\partial \Sigma_j}\varphi^{2}\langle \nabla_j \log \rho_{j+1},\eta_j\rangle\,\textrm{d}\sigma_j \end{align*}Then,
\begin{align*} &4\int_{\Sigma_j} \rho_{j+1}|\nabla_j(\varphi\rho_{j+1}^{-({1}/{2})})|^{2}\,\textrm{d}v_j \\ &\quad = 4\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j +4\int_{\Sigma_j}\varphi^{2}\rho_{j+1}|\nabla_j\rho_{j+1}^{-({1}/{2})}|^{2}\,\textrm{d}v_j\\ &\qquad- 4\int_{\Sigma_j}\varphi^{2}|\nabla_j\log \rho_{j+1}^{{1}/{2}}|^{2}\,\textrm{d}v_j + 4\int_{\Sigma_j}\varphi^{2}\rho_{j+1}^{-({1}/{2})}\Delta_j \rho_{j+1}^{{1}/{2}}\,\textrm{d}v_j\\ &\qquad- 2\int_{\partial \Sigma_j}\varphi^{2}\langle \nabla_j \log \rho_{j+1},\eta_j\rangle\,\textrm{d}\sigma_j\\ \end{align*}Since,
\[ \nabla_j \rho_{j+1}^{-({1}/{2})}={-}\rho_{j+1}^{{-}1}\nabla_j\rho_{j+1}^{{1}/{2}}, \]we obtain that
\[ \rho_{j+1}|\nabla_j\rho_{j+1}^{-({1}/{2})}|^{2}=|\nabla_j\log \rho_{j+1}^{{1}/{2}}|^{2}. \]This implies that
\begin{align*} 4\int_{\Sigma_j} \rho_{j+1}|\nabla_j(\varphi\rho_{j+1}^{-({1}/{2})})|^{2}\,\textrm{d}v_j & = 4\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j + 4\int_{\Sigma_j}\varphi^{2}\rho_{j+1}^{-({1}/{2})}\Delta_j \rho_{j+1}^{{1}/{2}}\,\textrm{d}v_j\\ &\quad - 2\int_{\partial \Sigma_j}\varphi^{2}\langle \nabla_j \log \rho_{j+1},\eta_j\rangle\,\textrm{d}\sigma_j \end{align*}Consequently,
\begin{align*} 4\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j &> 2\int_{\partial \Sigma_{j}}\varphi^{2}\left(B^{\partial\Sigma_{j+1}}(\nu_j,\nu_j)+\langle \nabla_j \log\rho_{j+1},\eta_j\rangle\right)\textrm{d}\sigma_j\\ &\quad -\int_{\Sigma_j}R_j\varphi^{2}\,\textrm{d}v_j \end{align*} Since 
$H^{\partial M}_g\geq 0$, from remark 2.2 and lemma 2.10 that
\begin{align*} 4\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j& >2\int_{\partial \Sigma_{j}}\varphi^{2}\left(\sum_{p=j}^{n-1}B^{\partial\Sigma_{p+1}}(\nu_p,\nu_p)\right)\textrm{d}\sigma_j -\int_{\Sigma_j}R_j\varphi^{2}\,\textrm{d}v_j\\ & =2\int_{\partial \Sigma_{j}}\varphi^{2}\left( H^{\partial M}_g-H^ {\partial \Sigma_j}\right)\textrm{d}\sigma_j - \int_{\Sigma_j}R_j\varphi^{2}\,\textrm{d}v_j\\ &\geq{-}2\int_{\partial \Sigma_{j}}\varphi^{2}H^ {\partial \Sigma_j}\,\textrm{d}\sigma_j-\int_{\Sigma_j}R_j\varphi^{2}\,\textrm{d}v_j \end{align*}Therefore,
\[ 4\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j>{-}2\int_{\partial\Sigma_j}\varphi^{2} H^{\partial\Sigma_j}\,\textrm{d}\sigma_j-\int_{\Sigma_j}\varphi^{2}R_j\,\textrm{d}v_j, \]
for every 
$\varphi \in C^{\infty }(\Sigma _j)$.
Theorem 2.15 Let 
$(M,\partial M,g)$ be a Riemannian 
$n$-manifold such that 
$R^{M}>0$ and 
$H^{\partial M}\geq 0$. Consider the free-boundary minimal 
$k$-slicing in 
$(M,g)$
\[ \Sigma_k\subset \cdots \subset \Sigma_{n-1}\subset \Sigma_n=M. \]Then:
(1) The manifold
$\Sigma _j$ has a metric with positive scalar curvature and minimal boundary, for every $3\leq k\leq j\leq n-1$.(2) If
$k=2$, then the connected components of $\Sigma _2$ are discs.
Proof.
(1) Consider
$j\in \{k,\ldots ,n-1\}$, here $k\geq 3$. It follows from proposition 2.14 that
\[{-}4k_j\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j < 2k_j\int_{\partial\Sigma_j}\varphi^{2} H^{\partial\Sigma_j}\,\textrm{d}\sigma_j+k_j\int_{\Sigma_j}\varphi^{2} R_j\,\textrm{d}v_j, \]
for every 
$\varphi \in C^{\infty }(\Sigma _j)$ such that 
$\varphi \not \equiv 0$ and 
$k_j=({j-2})/({4(j-1)})>0.$ This implies that
\begin{align*} &\displaystyle\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j +2k_j\displaystyle\int_{\partial\Sigma_j}\varphi^{2} H^{\partial\Sigma_j}\,\textrm{d}\sigma_j+k_j\displaystyle\int_{\Sigma_j}\varphi^{2} R_j\,\textrm{d}v_j\\ &\quad > (1-4k_j)\displaystyle\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j, \end{align*}
for every 
$\varphi \in H^{1}(\Sigma _j)$ such that 
$\varphi \not \equiv 0$. It follows that
\[ \lambda_j=\inf_{0\not\equiv \varphi\in H^{1}(\Sigma_j)}\displaystyle\frac{\displaystyle\int_{\Sigma_j}|\nabla_j\varphi|^{2}\,\textrm{d}v_j +2k_j\displaystyle\int_{\partial\Sigma_j}\varphi^{2} H^{\partial\Sigma_j}\,\textrm{d}\sigma_j+k_j\displaystyle\int_{\Sigma_j}\varphi^{2} R_j\,\textrm{d}v_j}{\displaystyle\int_{\Sigma_j}\varphi^{2}\,\textrm{d}v_j}>0. \]
Therefore, there exists a metric in 
$\Sigma _j$ with positive scalar curvature and minimal boundary.
(2) From proposition 2.14 we have that
\[ 4\int_{\Sigma_2}|\nabla_2\varphi|^{2}\,\textrm{d}v_2>{-}2\int_{\partial\Sigma_2}\varphi^{2} H^{\partial\Sigma_2}\,\textrm{d}\sigma_2-2\int_{\Sigma_2}\varphi^{2} K\,\textrm{d}v_2, \]
for every 
$\varphi \in C^{\infty }(\Sigma _2)$ such that 
$\varphi \not \equiv 0$, because 
$R_2=2K_2$, where 
$K_2$ is the Gaussian curvature of 
$(\Sigma _2,g)$. In particular, for 
$\varphi \equiv 1$ we have that
\begin{equation} \int_{\partial\Sigma_2} H^{\partial\Sigma_2}\,\textrm{d}\sigma_2+\int_{\Sigma_2}K\,\textrm{d}v_2>0. \end{equation} Let 
$S$ be a connected component of 
$\Sigma _2$. From inequality (2.12) and from Gauss–Bonnet theorem, we have that 
$\chi (S)>0.$ Therefore 
$S$ is a disc.
3. Proof of inequality
Proposition 3.1 There is a free-boundary minimal two-slicing
\[ \Sigma_2\subset \Sigma_3\subset \cdots \subset \Sigma_{n+1}\subset (M,g), \]
such that 
$\Sigma _k$ is connected and the map 
$F_k:=\left .F\right |_{\Sigma _k}:(\Sigma _k,\partial \Sigma _k)\rightarrow (\mathbb {D}^{2}\times T^{k-2},\partial \mathbb {D}^{2}\times T^{k-2})$ has non-zero degree, for every 
$k=2,\ldots ,n+1.$
Proof. Without loss of generality, we assume that 
$F$ is a smooth function. Consider the projection 
$p_{j}:\mathbb {D}^{2}\times T^{j}\rightarrow S^{1}$ given by
\[ p_{j}(x,(t_1,\ldots,t_j))=t_{j}, \]
for every 
$x\in \Sigma$ and 
$(t_1,\ldots ,t_{j})\in T^{j}=\mathbb {S}^{1}\times \cdots \times \mathbb {S}^{1}$.
We will start constructing the manifold 
$\Sigma _{n+1}$. For this, define 
$f_{n}=p_{n}\circ F.$ It follows from the Sard's theorem that there is 
$\theta _n\in S^{1}$ which is a regular value of 
$f_{n}$ and 
$\partial f_{n}$. Define
\[ S_{n+1}:=f_{n}^{{-}1}(\theta_n)=F^{{-}1}(\mathbb{D}^{2}\times T^{n-1}\times\{\theta_n\}). \]
Note that 
$S_{n+1}\subset M$ is a properly embedded hypersurface which represents a non-trivial class in 
$H_{n+1}(M,\partial M)$ and
\[ \left.F\right|_{S_{n+1}}:(S_{n+1},\partial S_{n+1})\rightarrow (\mathbb{D}^{2} \times T^{n-1}, \partial \mathbb{D}^{2}\times T^{n-1}) \]
is a non-zero degree map. It follows from geometric measure theory that there is a properly embedded free-boundary smooth hypersufrace 
$\Sigma _{n+1}'\subset M$ which minimizes volume in 
$(M,g)$ and represents the class 
$[S_{n+1}]\in H_{n+1}(M,\partial M)$. Since 
$\Sigma _{n+1}'$ and 
$S_{n+1}$ represent the same homology class in 
$H_{n+1}(M,\partial M)$, we have that
\[ \left.F\right|_{\Sigma_{n+1}'}:(\Sigma_{n+1}',\partial \Sigma_{n+1}')\rightarrow (\mathbb{D}^{2} \times T^{n-1}, \partial \mathbb{D}^{2}\times T^{n-1}) \]
has non-zero degree. Consider 
$\Sigma _{n+1}$ a connected component of 
$\Sigma _{n+1}'$ such that 
$F_{n+1}:=\left .F\right |_{\Sigma _{n+1}}:(\Sigma _{n+1},\partial \Sigma _{n+1})\rightarrow (\mathbb {D}^{2} \times T^{n-1}, \partial \mathbb {D}^{2}\times T^{n-1})$ has non-zero degree. It follows from lemma 33.4 in [Reference Simon20] that 
$\Sigma _{n+1}$ is still a properly embedded free-boundary hypersurface which minimizes volume in 
$(M,g)$. Consider 
$u_{n+1}\in C^{\infty }(\Sigma _{n+1})$ a positive first eigenfunction for the second variation 
$S_{n+1}$ of the volume of 
$\Sigma _{n+1}$ in 
$(M,g)$. Define 
$\rho _{n+1}=u_{n+1}$.
By a similar reasoning used to construct 
$\Sigma _{n+1}$, we obtain a properly embedded free-boundary connected smooth hypersurface 
$\Sigma _{n}\subset \Sigma _{n+1}$ which minimizes the weighted volume functional 
$V_{\rho _{n+1}}$ and
\[ F_{n}:=\left.F\right|_{\Sigma_{n}}:(\Sigma_{n},\partial \Sigma_{n})\rightarrow (\mathbb{D}^{2} \times T^{n-2}, \partial \mathbb{D}^{2}\times T^{n-2}) \]
has non-zero degree. Consider 
$u_{n}\in C^{\infty }(\Sigma _{n+1})$ a positive first eigenfunction for the second variation 
$S_{n}$ of 
$V_{\rho _{n+1}}$ on 
$\Sigma _{n}$. We then define 
$\rho _{n}=u_{n}\rho _{n+1}$ and we continue this process.
Lemma 3.2 We have that 
$\Sigma _2\in \mathcal {F}_M$.
Proof. From theorem 2.15 that 
$\Sigma _2$ is a disc. Since there is a non-zero degree map 
$F_2:(\Sigma _2,\partial \Sigma _2)\rightarrow (\mathbb {D}^{2},\partial \mathbb {D}^{2})$, we have that 
$\partial \Sigma _2$ is a curve homotopically non-trivial in 
$\partial M$. Therefore, 
$\Sigma _2\in \mathcal {F}_M$.
Lemma 3.3 We have that,
\[ \frac{1}{2}\inf R^{M} |\Sigma_2|_g+\inf H^{\partial M}|\Sigma_2|_g \leq 2\pi. \]
Moreover, if equality holds then 
$R_2=\inf R^{M}$, 
$H^{\partial \Sigma _2}=\inf H^{\partial M}$ and 
$\left .u_k\right |_{\Sigma _2}$ are positive constants for every 
$k=2,\ldots , n+1$.
Proof. From remark 2.2 and lemma 2.10
\[ \inf H^{\partial M}\leq \sum_{p=2}^{n+1}\langle \nabla_2\log u_p,\eta_2\rangle + H^{\partial\Sigma_2}. \]This implies that
\begin{equation} \inf H^{\partial M}|\partial \Sigma_2|_g\leq \sum_{p=2}^{n+1}\int_{\partial \Sigma_2}\langle \nabla_2\log u_p\,\textrm{d}\sigma_2,\eta_2\rangle + \int_{\partial \Sigma_2} H^{\partial\Sigma_2}\,\textrm{d}\sigma_2. \end{equation}From lemma 2.13, we have that
\begin{align*} \hat{R}_2&= R_2-2\sum_{p=2}^{n+1}u_p^{{-}1}\Delta_2u_p-2\sum_{2\leq p< q\leq n+1}\langle\nabla_2\log u_p,\nabla_2\log u_q\rangle\\ &= R_2-2\sum_{p=2}^{n+1}u_p^{{-}1}\Delta_2u_p-\left|\sum_{p=2}^{n+1} X_p\right|^{2}+\sum_{p=2}^{n+1}|X_p|^{2}, \end{align*}
where 
$X_p:=\nabla _2\log u_p$. Since
\[ u_p^{{-}1}\Delta_2u_p=\Delta_2\log u_p+|X_p|^{2}, \]we have that
\[ \hat{R}_2=R_2-2\sum_{p=2}^{n+1}\Delta_2\log u_p-\left|\sum_{p=2}^{n+1} X_p\right|^{2}-\sum_{p=2}^{n+1} |X_p|^{2}. \]
Since 
$\hat {R}_2\geq \inf R^{M}$, we obtain
\begin{align*} \frac{1}{2}\inf R^{M}|\Sigma_2|_g &\leq \frac{1}{2}\int_{\Sigma_2}\hat{R}_2\,\textrm{d}v_2\\ &=\frac{1}{2}\int_{\Sigma_2}R_2\,\textrm{d}v_2-\sum_{p=2}^{n+1}\int_{\Sigma_2}\Delta_2\log u_p\,\textrm{d}v_2\\ &\quad -\frac{1}{2}\int_{\Sigma_2}\left|\sum_{p=2}^{n+1} X_p\right|^{2}\,\textrm{d}v_2-\frac{1}{2}\sum_{p=2}^{n+1}\int_{\Sigma_2} |X_p|^{2}\,\textrm{d}v_2\\ &\leq \frac{1}{2}\int_{\Sigma_2}R_2\,\textrm{d}v_2-\sum_{p=2}^{n+1}\int_{\Sigma_2}\Delta_2\log u_p\,\textrm{d}v_2. \end{align*}It follows from divergence theorem that
\begin{equation} \frac{1}{2}\inf R^{M}|\Sigma_2|_g \leq \frac{1}{2}\int_{\Sigma_2}R_2\,\textrm{d}v_2-\sum_{p=2}^{n+1}\int_{\partial\Sigma_2}\langle \nabla_2\log u_p,\eta_2\rangle\,\textrm{d}\sigma_2. \end{equation}By inequalities (3.1) and (3.2), we have that
\[ \frac{1}{2}\inf R^{M}|\Sigma_2|_g +\inf H^{\partial M}|\partial\Sigma_2|_g \leq \frac{1}{2}\int_{\Sigma_2}R_2\,\textrm{d}v_2+\int_{\partial \Sigma_2} H^{\partial\Sigma_2}\,\textrm{d}\sigma_2. \]Therefore, from Gauss–Bonnet theorem, we obtain
\[ \frac{1}{2}\inf R^{M}|\Sigma_2|_g +\inf H^{\partial M}|\partial\Sigma_2|_g \leq 2\pi\mathcal{X}(\Sigma_2)=2\pi. \]
However, note that if holds equality then the field 
$X_p=0$ for every 
$p=2,\ldots ,n+1.$ It follows that 
$\left .u_p\right |_{\Sigma _2}$ are positive constants for every 
$p=2,\ldots , n+1$. Consequently, 
$R_2=\hat {R}_2\geq \inf R^{M}$ and 
$H^{\partial \Sigma _2}\geq \inf H^{\partial M}$. Therefore, from Gauss–Bonnet theorem, we have that 
$R_2= \inf R^{M}$ and 
$H^{\partial \Sigma _2}=\inf H^{\partial M}$.
Corollary 3.4 We have that,
\[ \frac{1}{2}\inf R^{M} \mathcal{A}(M,g)+\inf H^{\partial M}\mathcal{L}(M,g)\leq 2\pi. \]
Moreover, if equality holds then 
$R_2=\inf R^{M}$, 
$H^{\partial \Sigma _2}=\inf H^{\partial M}$ and 
$\left .u_k\right |_{\Sigma _2}$ are positive constants for every 
$k=2,\ldots , n+1$.
Proof. We have that
\[ \frac{1}{2}\inf R^{M} \mathcal{A}(M,g)+\inf H^{\partial M}\mathcal{L}(M,g)\leq \frac{1}{2}\inf R^{M} |\Sigma|_g+\inf H^{\partial M}|\partial\Sigma|_g \]
for every 
$\Sigma \in \mathcal {F}_M$. From proposition 3.1 and lemmas 3.2 and 3.3 we have that there is 
$\Sigma _2\in \mathcal {F}_M$ such that
\begin{equation} \frac{1}{2}\inf R^{M} |\Sigma_2|_g+\inf H^{\partial M}|\Sigma_2|_g \leq 2\pi. \end{equation}It follows that
\begin{equation} \frac{1}{2}\inf R^{M} \mathcal{A}(M,g)+\inf H^{\partial M}\mathcal{L}(M,g)\leq 2\pi. \end{equation}
If the equality holds in (3.4) then the equality holds in (3.3). Therefore, from lemma 3.3 we have that 
$R_2=\inf R^{M}$, 
$H^{\partial \Sigma _2}=\inf H^{\partial M}$ and 
$\left .u_k\right |_{\Sigma _2}$ are positive constants for every 
$k=2,\ldots , n+1$.
4. Proof of the rigidity
Proof. Without loss of generality, we can assume that 
$R_g\geq 2$. Using an idea in the Gromov–Lawsons paper on positive scalar curvature and mean-convex manifolds, we obtain that the doubling 
$DM$ of 
$M$ has a metric 
$g$ with 
$R_g\geq 2$. Moreover, if 
$F:(M,\partial M) \rightarrow (\mathbb {D}^{2} \times T^{n}, \partial \mathbb {D}^{2} \times T^{n})$ is a non-zero degree map, then the induced map 
$DF: DM \rightarrow D\mathbb {D}^{2} \times T^{n}$ has the same non-zero degree, simply by looking at the preimage of a non-singular point. Hence, 
$DM$ admits a map to 
$\mathbb {S}^{2}\times T^{n}$ with non-zero degree, since 
$D\mathbb {D}^{2}=\mathbb {S}^{2}$. Note that such a double manifold does not inherit a smooth Riemannian metric in general. However, since the boundary 
$\partial M$ is strongly totally geodesic, we obtain that the double metric is a smooth metric. Now, we obtain that equality in (1.2) implies that the equality is achieved in the main inequality of theorem 1.1 in [Reference Zhu21] for our doubling manifold 
$DM$. Therefore, the rigidity part can be obtained from theorem 1.1 in [Reference Zhu21].
Acknowledgments
The first author was partially supported by CNPq, Brazil (Grant 312598/ 2018-1). The second author was partially supported by CAPES, Brazil (Grant 88882.184181/2018-01) and CNPq, Brazil (Grant 141904/2018-6).
