Compact embedding results of Sobolev spaces and positive solutions to an elliptic equation

Qi Han

doi:10.1017/S0308210515000670

Compact embedding results of Sobolev spaces and positive solutions to an elliptic equation

Part of: Elliptic equations and systems Linear function spaces and their duals Classical measure theory

Published online by Cambridge University Press: 11 April 2016

Qi Han

Show author details

Qi Han*: Affiliation:
Department of Mathematical Sciences, Worcester Polytechnic Institute, Worcester, MA 01609-2280, USA (qhan@wpi.edu)

Article contents

Extract

Rights & Permissions

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using a regular Borel measure μ ⩾ 0 we derive a proper subspace of the commonly used Sobolev space D1(ℝN) when N ⩾ 3. The space resembles the standard Sobolev space H1(Ω) when Ω is a bounded region with a compact Lipschitz boundary ∂Ω. An equivalence characterization and an example are provided that guarantee that is compactly embedded into L1(RN). In addition, as an application we prove an existence result of positive solutions to an elliptic equation in ℝN that involves the Laplace operator with the critical Sobolev nonlinearity, or with a general nonlinear term that has a subcritical and superlinear growth. We also briefly discuss the compact embedding of 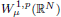to Lp(ℝN) when N ⩾ 2 and 2 ⩽ p ⩽ N.