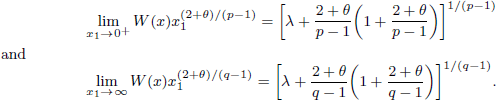Asymptotic behaviour and symmetry of positive solutions to nonlinear elliptic equations in a half-space

Lei Wei

doi:10.1017/S0308210515000876

Asymptotic behaviour and symmetry of positive solutions to nonlinear elliptic equations in a half-space

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press: 25 October 2016

Lei Wei

Show author details

Lei Wei*: Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, People's Republic of China (wlxznu@163.com)

Article contents

Extract

Rights & Permissions

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the following equation:

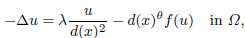
where d(x) = d(x, ∂Ω), θ > –2 and Ω is a half-space. The existence and non-existence of several kinds of positive solutions to this equation when 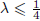, f(u) = up (p > 1) and Ω is a bounded smooth domain were studied by Bandle, Moroz and Reichel in 2008. Here, we study exact the behaviour of positive solutions to this equation as d(x) → 0+ and d(x) → ∞, respectively, and the symmetry of positive solutions when 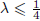, Ω is a half-space and f(u) is a more general nonlinearity term than up . Under suitable conditions for f, we show that the equation has a unique positive solution W, which is a function of x 1 only, and W satisfies