Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-18T19:30:45.021Z Has data issue: false hasContentIssue false
  • English
  • Français

A Lebesgue–Lusin property for linear operators of first and second order

Part of: Manifolds Miscellaneous topics - Partial differential equations General theory of linear operators

Published online by Cambridge University Press:  06 November 2023

Adolfo Arroyo-Rabasa Open the ORCID record for Adolfo Arroyo-Rabasa [Opens in a new window]
Adolfo Arroyo-Rabasa*
Affiliation:
Université catholique de Louvain, Louvain La Neuve, Belgium (adolforabasa@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for a homogeneous linear partial differential operator $\mathcal {A}$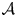 of order $k \le 2$ 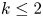and an integrable map $f$ 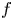taking values in the essential range of that operator, there exists a function $u$ 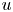of special bounded variation satisfying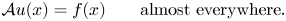

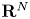\[ \mathcal{A} u(x)= f(x) \qquad \text{almost everywhere}. \]
This extends a result of G. Alberti for gradients on $\mathbf {R}^N$. In particular, for $0 \le m < N$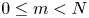, it is shown that every integrable $m$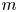-vector field is the absolutely continuous part of the boundary of a normal $(m+1)$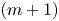-current.

Keywords

bounded variationLusin propertyfirst-ordersecond-orderdifferential operator

MSC classification

Primary: 35R06: Partial differential equations with measure
Secondary: 47A50: Equations and inequalities involving linear operators, with vector unknowns 49Q15: Geometric measure and integration theory, integral and normal currents 49Q20: Variational problems in a geometric measure-theoretic setting
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 11
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alberti, G.. A Lusin type theorem for gradients. J. Funct. Anal. 100 (1991), 110–118.CrossRefGoogle Scholar
Alberti, G.. Integral representation of local functionals. Ann. Mat. Pura Appl. (4) 165 (1993), 49–86.CrossRefGoogle Scholar
Alberti, G.. Rank one property for derivatives of functions with bounded variation. Proc. Roy. Soc. Edinburgh Sect. A 123 (1993), 239–274.CrossRefGoogle Scholar
Ambrosio, L., Coscia, A. and Dal Maso, G.. Fine properties of functions with bounded deformation. Arch. Rational Mech. Anal. 139 (1997), 201–238.CrossRefGoogle Scholar
Ambrosio, L., Fusco, N. and Pallara, D.. Functions of bounded variation and free discontinuity problems. Oxford Mathematical Monographs (The Clarendon Press, Oxford University Press, New York, 2000).Google Scholar
Arroyo-Rabasa, A.. Slicing and fine properties for functions with bounded $\mathcal {A}$-variation, 2020.Google Scholar
Arroyo-Rabasa, A., De Philippis, G. and Rindler, F.. Lower semicontinuity and relaxation of linear-growth integral functionals under pde constraints. Adv. Calc. Var. 13 (2020), 219–255.CrossRefGoogle Scholar
Arroyo-Rabasa, A. and Simental, J.. An elementary approach to the homological properties of constant-rank operators. C. R. Math. Acad. Sci. Paris (2023).Google Scholar
Arroyo-Rabasa, A. and Skorobogatova, A.. A look into some of the fine properties of functions with bounded $\mathcal {A}$-variation, 2019.Google Scholar
Breit, D., Diening, L. and Gmeineder, F.. The Lipschitz truncation of functions of bounded variation. Indiana Univ. Math. J. 70 (2021), 2237–2260.CrossRefGoogle Scholar
De Philippis, G. and Rindler, F.. On the structure of ${\mathcal {A}}$-free measures and applications. Ann. Math. (2) 184 (2016), 1017–1039.CrossRefGoogle Scholar
Delladio, S.. The identity G(D)f = F for a linear partial differential operator G(D). Lusin type and structure results in the non-integrable case. Proceedings of the Royal Society of Edinburgh: Section A Mathematics 151(6) (2021), 1893–1919. http://dx.doi.org/10.1017/prm.2020.85.CrossRefGoogle Scholar
Diening, L. and Gmeineder, F.. Continuity points via Riesz potentials for $\mathbb{C}$-elliptic operators. Q. J. Math. 71 (2021), 1201–1218.CrossRefGoogle Scholar
Federer, H.. Geometric measure theory. xiv+676, 1969.Google Scholar
Fonseca, I., Leoni, G. and Paroni, R.. On Hessian matrices in the space $BH$. Commun. Contemp. Math. 7 (2005), 401–420.CrossRefGoogle Scholar
Francos, G.. The Lusin theorem for higher-order derivatives. Michigan Math. J. 61 (2012), 507–516.CrossRefGoogle Scholar
Moonens, L. and Pfeffer, W. F.. The multidimensional Lusin theorem. J. Math. Anal. Appl. 339 (2008), 746–752.CrossRefGoogle Scholar
Murat, F.. Compacité par compensation: condition nécessaire et suffisante de continuité faible sous une hypothèse de rang constant. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 8 (1981), 69–102.Google Scholar
Raiţă, B.. Potentials for ${\mathcal {A}}$-quasiconvexity. Calc. Var. Partial Differ. Equ. 58 (2019), 105–116.CrossRefGoogle Scholar