Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lopes, Orlando
2006.
Stability of solitary waves of some coupled systems.
Nonlinearity,
Vol. 19,
Issue. 1,
p.
95.
Chang, Qianshun
Wong, Yau-Shu
and
Lin, Chi-Kun
2008.
Numerical computations for long-wave short-wave interaction equations in semi-classical limit.
Journal of Computational Physics,
Vol. 227,
Issue. 19,
p.
8489.
Bai, Dongmei
and
Zhang, Luming
2009.
The finite element method for the coupled Schrödinger–KdV equations.
Physics Letters A,
Vol. 373,
Issue. 26,
p.
2237.
Dias, João-Paulo
Figueira, Mário
and
Oliveira, Filipe
2010.
Existence of bound states for the coupled Schrödinger–KdV system with cubic nonlinearity.
Comptes Rendus. Mathématique,
Vol. 348,
Issue. 19-20,
p.
1079.
Deng, Shengfu
and
Sun, Shu-Ming
2010.
Exact Theory of Three-Dimensional Water Waves at the Critical Speed.
SIAM Journal on Mathematical Analysis,
Vol. 42,
Issue. 6,
p.
2721.
Bai, Dongmei
and
Zhang, Luming
2011.
Numerical studies on a novel split-step quadratic B-spline finite element method for the coupled Schrödinger–KdV equations.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 16,
Issue. 3,
p.
1263.
Bhattarai, Santosh
2012.
Solitary waves and a stability analysis of an equation of short and long dispersive waves.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 18,
p.
6506.
Liu, Chungen
and
Zheng, Youquan
2013.
On soliton solutions to a class of Schrödinger-K𝐝V systems.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 10,
p.
3477.
Xia, Yinhua
and
Xu, Yan
2014.
A Conservative Local Discontinuous Galerkin Method for the Schrödinger-KdV System.
Communications in Computational Physics,
Vol. 15,
Issue. 4,
p.
1091.
Zhang, Hong
Song, Song-He
Zhou, Wei-En
and
Chen, Xu-Dong
2014.
Multi-symplectic method for the coupled Schrödinger—KdV equations.
Chinese Physics B,
Vol. 23,
Issue. 8,
p.
080204.
Sun, Shu-Ming
2014.
Existence theory of capillary-gravity waves on water of finite depth.
Mathematical Control & Related Fields,
Vol. 4,
Issue. 3,
p.
315.
Bhattarai, Santosh
2015.
Stability of normalized solitary waves for three coupled nonlinear Schrödinger equations.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 4,
p.
1789.
Bhattarai, Santosh
2017.
On fractional Schrödinger systems of Choquard type.
Journal of Differential Equations,
Vol. 263,
Issue. 6,
p.
3197.
Álvarez-Caudevilla, P.
Colorado, Eduardo
and
Fabelo, Rasiel
2017.
A higher order system of some coupled nonlinear Schrödinger and Korteweg-de Vries equations.
Journal of Mathematical Physics,
Vol. 58,
Issue. 11,
Colorado, Eduardo
2017.
On the existence of bound and ground states for some coupled nonlinear Schrödinger–Korteweg–de Vries equations.
Advances in Nonlinear Analysis,
Vol. 6,
Issue. 4,
p.
407.
Ardila, Alex H.
2018.
Orbital stability of standing waves for a system of nonlinear Schrödinger equations with three wave interaction.
Nonlinear Analysis,
Vol. 167,
Issue. ,
p.
1.
Bhattarai, Santosh
Corcho, Adán J.
and
Panthee, Mahendra
2018.
Well-Posedness for Multicomponent Schrödinger–gKdV Systems and Stability of Solitary Waves with Prescribed Mass.
Journal of Dynamics and Differential Equations,
Vol. 30,
Issue. 2,
p.
845.
Ardila, Alex H.
2019.
Existence and stability of a two-parameter family of solitary waves for a logarithmic NLS–KdV system.
Nonlinear Analysis,
Vol. 189,
Issue. ,
p.
111563.
Geng, Xianguo
and
Li, Ruomeng
2019.
On a Vector Modified Yajima–Oikawa Long-Wave–Short-Wave Equation.
Mathematics,
Vol. 7,
Issue. 10,
p.
958.
Geng, Qiuping
Liao, Mian
Wang, Jun
and
Xiao, Lu
2020.
Existence and bifurcation of nontrivial solutions for the coupled nonlinear Schrödinger–Korteweg–de Vries system.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 71,
Issue. 1,
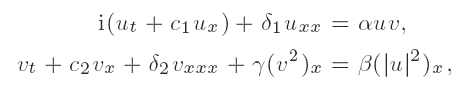 which arises in various physical contexts as a model for the interaction of long and short nonlinear waves. Ground states of the system are, by definition, minimizers of the energy functional subject to constraints on conserved functionals associated with symmetries of the system. In particular, ground states have a simple time dependence because they propagate via those symmetries. For a range of values of the parameters α, β, γ, δi, ci, we prove the existence and stability of a two-parameter family of ground states associated with a two-parameter family of symmetries.
which arises in various physical contexts as a model for the interaction of long and short nonlinear waves. Ground states of the system are, by definition, minimizers of the energy functional subject to constraints on conserved functionals associated with symmetries of the system. In particular, ground states have a simple time dependence because they propagate via those symmetries. For a range of values of the parameters α, β, γ, δi, ci, we prove the existence and stability of a two-parameter family of ground states associated with a two-parameter family of symmetries.

