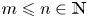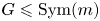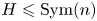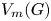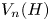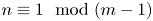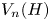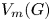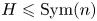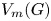1. Introduction
This article concerns embeddability conditions for pairs of groups from the family of symmetric R. Thompson groups $\{{V_m(G)}\}$![]() . The group ${V_m(G)}$
. The group ${V_m(G)}$![]() is the group ${V_m(G)}=\langle V_m\cup G\rangle$
is the group ${V_m(G)}=\langle V_m\cup G\rangle$![]() , where $V_m\leqslant \operatorname {Aut}(\mathfrak {C}_m)$
, where $V_m\leqslant \operatorname {Aut}(\mathfrak {C}_m)$![]() is the Higman–Thompson group denoted $G_{m,1}$
is the Higman–Thompson group denoted $G_{m,1}$![]() by Higman in [Reference Higman9], acting on the Cantor space $\mathfrak {C}_m{:=} \{0,\,1,\,\ldots ,\, m-1\}^{\omega }$
by Higman in [Reference Higman9], acting on the Cantor space $\mathfrak {C}_m{:=} \{0,\,1,\,\ldots ,\, m-1\}^{\omega }$![]() , while $G$
, while $G$![]() is a particular faithful representation of a finite group $\widetilde {G}\leqslant \operatorname {Sym}(m)$
is a particular faithful representation of a finite group $\widetilde {G}\leqslant \operatorname {Sym}(m)$![]() in $\operatorname {Aut}(\mathfrak {C}_m)$
in $\operatorname {Aut}(\mathfrak {C}_m)$![]() .
.
The groups $\{{V_m(G)}\}$![]() have developed as groups of interest for a variety of reasons. Firstly, they were singled out as natural groups of interest in [Reference Nekrashevych14, Reference Röver15], and they arise naturally as a fundamental subfamily of Hughes’ $\mathcal {F}\mathcal {S}\mathcal {S}$
have developed as groups of interest for a variety of reasons. Firstly, they were singled out as natural groups of interest in [Reference Nekrashevych14, Reference Röver15], and they arise naturally as a fundamental subfamily of Hughes’ $\mathcal {F}\mathcal {S}\mathcal {S}$![]() groups [Reference Hughes11]. The paper [Reference Bleak, Donoven and Jonušas3] shows that for $n\geq 2$
groups [Reference Hughes11]. The paper [Reference Bleak, Donoven and Jonušas3] shows that for $n\geq 2$![]() , $V_m\cong {V_m(G)}$
, $V_m\cong {V_m(G)}$![]() if and only if $\widetilde {G}$
if and only if $\widetilde {G}$![]() is semiregular (the non-trivial elements of $\widetilde {G}$
is semiregular (the non-trivial elements of $\widetilde {G}$![]() have no fixed points), and also, that for $m>3$
have no fixed points), and also, that for $m>3$![]() there exists $\widetilde {G},\,\widetilde {H}\in \operatorname {Sym}(m)$
there exists $\widetilde {G},\,\widetilde {H}\in \operatorname {Sym}(m)$![]() with $\widetilde {G}\cong \widetilde {H}$
with $\widetilde {G}\cong \widetilde {H}$![]() but where the induced groups ${V_m(G)}$
but where the induced groups ${V_m(G)}$![]() and $V_m(H)$
and $V_m(H)$![]() are not isomorphic (the orbit structure of the actions of the elements of the groups $\widetilde {G}$
are not isomorphic (the orbit structure of the actions of the elements of the groups $\widetilde {G}$![]() and $\widetilde {H}$
and $\widetilde {H}$![]() impacts the isomorphism types of the groups ${V_m(G)}$
impacts the isomorphism types of the groups ${V_m(G)}$![]() and $V_m(H)$
and $V_m(H)$![]() ). In another direction, in [Reference Farley7], Farley shows that the symmetric R. Thompson groups are CoCF groups (see [Reference Holt, Rees, Röver and Thomas10] for the definition of CoCF groups). Thus, if one can show that some group in the family $\{{V_m(G)}\}$
). In another direction, in [Reference Farley7], Farley shows that the symmetric R. Thompson groups are CoCF groups (see [Reference Holt, Rees, Röver and Thomas10] for the definition of CoCF groups). Thus, if one can show that some group in the family $\{{V_m(G)}\}$![]() fails to embed in $V=V_2$
fails to embed in $V=V_2$![]() , then Lehnert's conjecture will be shown to be false (see [Reference Bleak, Matucci and Neunhöffer4, Reference Lehnert12, Reference Lehnert and Schweitzer13]).
, then Lehnert's conjecture will be shown to be false (see [Reference Bleak, Matucci and Neunhöffer4, Reference Lehnert12, Reference Lehnert and Schweitzer13]).
We investigate conditions on $m\leqslant n$![]() , $G\leqslant \operatorname {Sym}(m)$
, $G\leqslant \operatorname {Sym}(m)$![]() , and $H\leqslant \operatorname {Sym}(n)$
, and $H\leqslant \operatorname {Sym}(n)$![]() that guarantee the existence of embeddings between the groups ${V_m(G)}$
that guarantee the existence of embeddings between the groups ${V_m(G)}$![]() and ${V_n(H)}$
and ${V_n(H)}$![]() (we now drop the ‘tilde’ notation on the groups $G$
(we now drop the ‘tilde’ notation on the groups $G$![]() and $H$
and $H$![]() when thinking of them as subgroups of $\operatorname {Sym}(m)$
when thinking of them as subgroups of $\operatorname {Sym}(m)$![]() and $\operatorname {Sym}(n)$
and $\operatorname {Sym}(n)$![]() , respectively). Thus, this note can be thought of as a continuation of the investigations in [Reference Bleak, Donoven and Jonušas3] and is partly inspired by the work of Birget (in [Reference Birget1], he gives a method to embed $V_2$
, respectively). Thus, this note can be thought of as a continuation of the investigations in [Reference Bleak, Donoven and Jonušas3] and is partly inspired by the work of Birget (in [Reference Birget1], he gives a method to embed $V_2$![]() into $V_m$
into $V_m$![]() for $2\leqslant m$
for $2\leqslant m$![]() ), and partly by considering some of the questions alluded to in the previous paragraph. In this context, our two embedding results depend on the direction of the embedding (${V_m(G)}\rightarrowtail {V_n(H)}$
), and partly by considering some of the questions alluded to in the previous paragraph. In this context, our two embedding results depend on the direction of the embedding (${V_m(G)}\rightarrowtail {V_n(H)}$![]() or ${V_n(H)}\rightarrowtail {V_m(G)}$
or ${V_n(H)}\rightarrowtail {V_m(G)}$![]() ), and our constructed embeddings require in both cases the Higman condition $n\equiv 1\mod (m-1)$
), and our constructed embeddings require in both cases the Higman condition $n\equiv 1\mod (m-1)$![]() .
.
To our knowledge, the first case of a proof that all $V_n$![]() embed into each other is by Nicolás Matte Bon [Reference Bon5, Coroll. 11.16], although it was almost a folklore statement that such embeddings existed. Before that, the only such embedding theorems that we know of in the literature were those of Higman from [Reference Higman9, Thm. 7.2] ($V_n\rightarrowtail V_m$
embed into each other is by Nicolás Matte Bon [Reference Bon5, Coroll. 11.16], although it was almost a folklore statement that such embeddings existed. Before that, the only such embedding theorems that we know of in the literature were those of Higman from [Reference Higman9, Thm. 7.2] ($V_n\rightarrowtail V_m$![]() when $m$
when $m$![]() and $n$
and $n$![]() satisfy the Higman condition). We leverage Birget's construction [Reference Birget1] in this paper because of the utility of his successor function, which we are able to generalize effectively for embeddings in our enriched context ($V_m(G$
satisfy the Higman condition). We leverage Birget's construction [Reference Birget1] in this paper because of the utility of his successor function, which we are able to generalize effectively for embeddings in our enriched context ($V_m(G$![]() ) and $V_n(H)$
) and $V_n(H)$![]() as opposed to $V_m$
as opposed to $V_m$![]() and $V_n$
and $V_n$![]() ).
).
The embedding ${V_m(G)}\rightarrowtail {V_n(H)}$![]() is algebraic in nature and is the one which is inspired by the embeddings of Birget, while the embedding ${V_n(H)}\rightarrowtail {V_m(G)}$
is algebraic in nature and is the one which is inspired by the embeddings of Birget, while the embedding ${V_n(H)}\rightarrowtail {V_m(G)}$![]() uses a topological conjugacy by rational group elements (see [Reference Grigorchuk, Nekrashevych and Sushchanskiĭ8]).
uses a topological conjugacy by rational group elements (see [Reference Grigorchuk, Nekrashevych and Sushchanskiĭ8]).
We can now state and discuss the main results of this chapter. For the topological embedding ${V_n(H)}\rightarrowtail {V_m(G)}$![]() , we need to define a group $\mathcal {R}_{G}(\widetilde {S})\leqslant \operatorname {Sym}(n)$
, we need to define a group $\mathcal {R}_{G}(\widetilde {S})\leqslant \operatorname {Sym}(n)$![]() (where $G \leqslant \operatorname {Sym}(m)$
(where $G \leqslant \operatorname {Sym}(m)$![]() and $\widetilde {S}$
and $\widetilde {S}$![]() is a prefix code of $\mathfrak {C}_m$
is a prefix code of $\mathfrak {C}_m$![]() of length $n$
of length $n$![]() ). The group $\mathcal {R}_{G}(\widetilde {S})$
). The group $\mathcal {R}_{G}(\widetilde {S})$![]() is well defined if there is an $n$
is well defined if there is an $n$![]() -element prefix code $\widetilde {S}$
-element prefix code $\widetilde {S}$![]() in $\mathcal {A}_m^{*}$
in $\mathcal {A}_m^{*}$![]() which is preserved by the action of the iterated permutations of $G$
which is preserved by the action of the iterated permutations of $G$![]() on $\mathcal {A}_m^{*}$
on $\mathcal {A}_m^{*}$![]() . In this case, $\mathcal {R}_{G}(\widetilde {S})$
. In this case, $\mathcal {R}_{G}(\widetilde {S})$![]() is the subgroup of $\operatorname {Sym}(n)$
is the subgroup of $\operatorname {Sym}(n)$![]() induced from the action of $G$
induced from the action of $G$![]() on the elements of $\widetilde {S}$
on the elements of $\widetilde {S}$![]() under a bijection to $\{1,\,2,\,\ldots ,\,n\}$
under a bijection to $\{1,\,2,\,\ldots ,\,n\}$![]() .
.
Theorem 1.1 (Topological Embedding)
Let $n,\,m \geq 2$![]() be natural numbers such that $m< n,$
be natural numbers such that $m< n,$![]() and let $G \leqslant \operatorname {Sym}(m),$
and let $G \leqslant \operatorname {Sym}(m),$![]() $H \leqslant \operatorname {Sym}(n)$
$H \leqslant \operatorname {Sym}(n)$![]() . Suppose that:
. Suppose that:
(1) There exists a prefix code $\widetilde {S}$
 of $\mathfrak {C}_m$
of $\mathfrak {C}_m$ such that $\vert \widetilde {S} \vert = n$
such that $\vert \widetilde {S} \vert = n$ ,
,(2) the group $\mathcal {R}_{G}(\widetilde {S})$
 is well defined, and
is well defined, and(3) $\mathcal {R}_{G}(\widetilde {S})$
 and $H$
and $H$ are cyclically isomorphic.
are cyclically isomorphic.
Then ${V_n(H)}$![]() embeds in ${V_m(G)}$
embeds in ${V_m(G)}$![]() .
.
Thus, we have the following general observation.
Observation 1.1 In practical terms, natural applications of Theorem 1.1 occur by choosing $m$![]() and a prefix code that is closed under the action of iterated permutations from some $G\leqslant \operatorname {Sym}(m)$
and a prefix code that is closed under the action of iterated permutations from some $G\leqslant \operatorname {Sym}(m)$![]() . Then, one immediately obtains a cyclically isomorphic group $H$
. Then, one immediately obtains a cyclically isomorphic group $H$![]() in $\operatorname {Sym}(n)$
in $\operatorname {Sym}(n)$![]() .
.
Theorem 1.2 (Algebraic Embedding)
Let $n,\,m \geq 2$![]() be natural numbers such that $n = k(m-1)+ m$
be natural numbers such that $n = k(m-1)+ m$![]() for some $k \geq 1,$
for some $k \geq 1,$![]() and let $G \leqslant \operatorname {Sym}(m)$
and let $G \leqslant \operatorname {Sym}(m)$![]() . Let $H = G_{ext} \leqslant \operatorname {Sym}(n)$
. Let $H = G_{ext} \leqslant \operatorname {Sym}(n)$![]() the extended symmetric group of $H,$
the extended symmetric group of $H,$![]() whose elements act as the elements of $H$
whose elements act as the elements of $H$![]() on the first $m$
on the first $m$![]() elements and act as the identity on the remaining $n-m$
elements and act as the identity on the remaining $n-m$![]() .
.
Then ${V_m(G)}$![]() embeds in ${V_n(H)}$
embeds in ${V_n(H)}$![]() .
.
Thus, to achieve such an embedding, the main obstruction is that $m$![]() and $n$
and $n$![]() satisfy the Higman Condition, i.e.:
satisfy the Higman Condition, i.e.:
Corollary 1.2 Let $m\leqslant n$![]() so that $n\equiv m\mod (m-1),$
so that $n\equiv m\mod (m-1),$![]() and let $G\leqslant \operatorname {Sym}(m)$
and let $G\leqslant \operatorname {Sym}(m)$![]() . Then, there exists $H\leqslant \operatorname {Sym}(n)$
. Then, there exists $H\leqslant \operatorname {Sym}(n)$![]() so that ${V_m(G)}\rightarrowtail {V_n(H)}$
so that ${V_m(G)}\rightarrowtail {V_n(H)}$![]() .
.
As mentioned above, for given $m$![]() and $G$
and $G$![]() semiregular, the paper [Reference Bleak, Donoven and Jonušas3] shows ${V_m(G)}\cong V_m$
semiregular, the paper [Reference Bleak, Donoven and Jonušas3] shows ${V_m(G)}\cong V_m$![]() , while Higman's book [Reference Higman9] gives an embedding of $V_m$
, while Higman's book [Reference Higman9] gives an embedding of $V_m$![]() into R. Thompson's group $V=V_2$
into R. Thompson's group $V=V_2$![]() . The semiregularity condition above has to do with local groups of germs of the action of ${V_m(G)}$
. The semiregularity condition above has to do with local groups of germs of the action of ${V_m(G)}$![]() on $\mathfrak {C}_m$
on $\mathfrak {C}_m$![]() (see [Reference Bleak and Lanoue2, Reference Bleak, Donoven and Jonušas3]). Our topological embedding preserves the local groups of germs, while the algebraic embeddings (for $G$
(see [Reference Bleak and Lanoue2, Reference Bleak, Donoven and Jonušas3]). Our topological embedding preserves the local groups of germs, while the algebraic embeddings (for $G$![]() non-trivial) produce complicated local groups of germs. Thus, it is impossible to chain our families of embeddings together to get an embedding from ${V_m(G)}$
non-trivial) produce complicated local groups of germs. Thus, it is impossible to chain our families of embeddings together to get an embedding from ${V_m(G)}$![]() into $V_2$
into $V_2$![]() when $G$
when $G$![]() is not semiregular.
is not semiregular.
We therefore ask the following question:
Question 1.3 Does there exist $m\in \mathbb {N}$![]() and $G\in \operatorname {Sym}(m)$
and $G\in \operatorname {Sym}(m)$![]() so that $G$
so that $G$![]() is not semiregular, but where there is an embedding from ${V_m(G)}$
is not semiregular, but where there is an embedding from ${V_m(G)}$![]() into $V_2$
into $V_2$![]() ?
?
2. Symmetric Thompson's groups
In this section, we introduce symmetric Thompson's groups, giving an easy way to express its elements as tables (this corresponds to a generalized construction of Higman used by Scott and Röver in the creation of their extensions of $V$![]() [Reference Röver15–Reference Scott18].
[Reference Röver15–Reference Scott18].
2.1. Tables
For natural $n>1$![]() , let $\mathfrak {C}_n$
, let $\mathfrak {C}_n$![]() be the $n$
be the $n$![]() -adic Cantor set, which is constructed inductively as follows: $\mathfrak {C}_n^{1}$
-adic Cantor set, which is constructed inductively as follows: $\mathfrak {C}_n^{1}$![]() corresponds to first subdividing $\mathfrak {C}_n^{0}= [0,\,1]$
corresponds to first subdividing $\mathfrak {C}_n^{0}= [0,\,1]$![]() into $2n-1$
into $2n-1$![]() closed intervals of equal length (so, sharing endpoints with neighbours), numbered $1,\, \ldots ,\, 2n-1$
closed intervals of equal length (so, sharing endpoints with neighbours), numbered $1,\, \ldots ,\, 2n-1$![]() from left to right, and then taking the collection of odd-numbered sub-intervals. Next, $\mathfrak {C}_n^{2}$
from left to right, and then taking the collection of odd-numbered sub-intervals. Next, $\mathfrak {C}_n^{2}$![]() is obtained from $\mathfrak {C}_n^{1}$
is obtained from $\mathfrak {C}_n^{1}$![]() by applying the same procedure to each of the intervals forming $\mathfrak {C}_n^{1}$
by applying the same procedure to each of the intervals forming $\mathfrak {C}_n^{1}$![]() , and so on. Then, $C_n$
, and so on. Then, $C_n$![]() is the limit of this process, so that
is the limit of this process, so that
Now, let $\mathcal {A}_n = \{0,\,\ldots ,\,n-1\}$![]() and give it the discrete topology. It is easy to build a direct homeomorphism from the space $\mathcal {A}_n^\mathbb{N}$
and give it the discrete topology. It is easy to build a direct homeomorphism from the space $\mathcal {A}_n^\mathbb{N}$![]() equipped with the product topology to $\mathfrak {C}_n$
equipped with the product topology to $\mathfrak {C}_n$![]() , so every element $\zeta \in \mathfrak {C}_n$
, so every element $\zeta \in \mathfrak {C}_n$![]() can be expressed as an infinite word $\zeta = w_1w_2\ldots$
can be expressed as an infinite word $\zeta = w_1w_2\ldots$![]() , where $w_i \in \mathcal {A}_n$
, where $w_i \in \mathcal {A}_n$![]() . It is a classical result of Brouwer from [Reference Brouwer6] that all of the spaces in the set $\{\mathfrak {C}_n\}$
. It is a classical result of Brouwer from [Reference Brouwer6] that all of the spaces in the set $\{\mathfrak {C}_n\}$![]() are abstractly homeomorphic to each other.
are abstractly homeomorphic to each other.
We denote by $\mathcal {A}_n^{*}$![]() the set of finite words in $\mathcal {A}_n$
the set of finite words in $\mathcal {A}_n$![]() . The empty word $\varepsilon$
. The empty word $\varepsilon$![]() is also in $\mathcal {A}_n^{*}$
is also in $\mathcal {A}_n^{*}$![]() .
.
Definition 2.1 (Concatenation)
Let $u = u_1u_2\ldots u_k,\, u_i \in \mathcal {A}_n$![]() be a finite word and $v \in \mathcal {A}_n^{*} \cup \mathcal {A}_n^{\mathbb {N}}$
be a finite word and $v \in \mathcal {A}_n^{*} \cup \mathcal {A}_n^{\mathbb {N}}$![]() with $v=v_1v_2\ldots$
with $v=v_1v_2\ldots$![]() (where for all valid indices $i$
(where for all valid indices $i$![]() we have $v_i\in \mathcal {A}_n$
we have $v_i\in \mathcal {A}_n$![]() ). The concatenation of $u$
). The concatenation of $u$![]() with $v$
with $v$![]() is the (finite or infinite) word:
is the (finite or infinite) word:
With concatenation being a fundamental operation, we will often just write the concatenation of two strings without the formal concatenation operator, that is, we might write $u\vert \!\vert v$![]() as simply $uv$
as simply $uv$![]() , reserving the formal use of ‘$\vert \!\vert$
, reserving the formal use of ‘$\vert \!\vert$![]() ’ for situations where we wish to stress that a concatenation is occurring.
’ for situations where we wish to stress that a concatenation is occurring.
Definition 2.2 (Prefix order)
Let $u \in \mathcal {A}_n^{*}$![]() and $v \in \mathcal {A}_n^{*}\cup \mathcal {A}_n^{\mathbb {N}}$
and $v \in \mathcal {A}_n^{*}\cup \mathcal {A}_n^{\mathbb {N}}$![]() . We say that $u$
. We say that $u$![]() is a prefix of $v$
is a prefix of $v$![]() ($u \leqslant _{pref} v$
($u \leqslant _{pref} v$![]() ) if $v = u\vert \!\vert w$
) if $v = u\vert \!\vert w$![]() , for some $w \in \mathcal {A}_n^{*}\cup \mathcal {A}_n^{\mathbb {N}}$
, for some $w \in \mathcal {A}_n^{*}\cup \mathcal {A}_n^{\mathbb {N}}$![]() .
.
Note that this property is transitive for finite length words: If $u \leqslant _{pref} v$![]() and $v \leqslant _{pref} w$
and $v \leqslant _{pref} w$![]() then $u \leqslant _{pref} w$
then $u \leqslant _{pref} w$![]() . In addition, $u \leqslant _{pref} u$
. In addition, $u \leqslant _{pref} u$![]() , as $\varepsilon \in \mathcal {A}_n^{*}$
, as $\varepsilon \in \mathcal {A}_n^{*}$![]() . That is, $\leqslant _{pref}$
. That is, $\leqslant _{pref}$![]() provides a partial order on $\mathcal {A}_n^{*}$
provides a partial order on $\mathcal {A}_n^{*}$![]() .
.
Definition 2.3 (Prefix code)
Let $S$![]() be a finite set of words in $\mathcal {A}_n^{*}$
be a finite set of words in $\mathcal {A}_n^{*}$![]() . Then $S$
. Then $S$![]() is a prefix code of $\mathfrak {C}_n$
is a prefix code of $\mathfrak {C}_n$![]() if for every infinite word $\zeta \in \mathcal {A}_n^{\mathbb {N}}$
if for every infinite word $\zeta \in \mathcal {A}_n^{\mathbb {N}}$![]() there exists one and only one word $s \in S$
there exists one and only one word $s \in S$![]() such that $s \leqslant _{pref} \zeta$
such that $s \leqslant _{pref} \zeta$![]() . (Specifically, a prefix code is a complete anti-chain for the partial order $\leqslant _{pref}$
. (Specifically, a prefix code is a complete anti-chain for the partial order $\leqslant _{pref}$![]() .)
.)
For convenience, we will use the following notation: let $\sigma \in \operatorname {Sym}(n)$![]() be an element of the symmetric group of $n$
be an element of the symmetric group of $n$![]() elements. Given any word $\zeta = z_1z_2z_3 \ldots \in \mathcal {A}_n^\mathbb{*} \cup \mathcal {A}_n^\mathbb{N}$
elements. Given any word $\zeta = z_1z_2z_3 \ldots \in \mathcal {A}_n^\mathbb{*} \cup \mathcal {A}_n^\mathbb{N}$![]() we define $\sigma (\zeta ) = \sigma (z_1)\sigma (z_2)\sigma (z_3)\ldots \in \mathcal {A}_n^\mathbb{*} \cup \mathcal {A}_n^\mathbb{N}$
we define $\sigma (\zeta ) = \sigma (z_1)\sigma (z_2)\sigma (z_3)\ldots \in \mathcal {A}_n^\mathbb{*} \cup \mathcal {A}_n^\mathbb{N}$![]() . Let $\sigma _i \in H \leqslant \operatorname {Sym}(n)$
. Let $\sigma _i \in H \leqslant \operatorname {Sym}(n)$![]() . (Note that we are using left actions here, so if $\sigma ,\,\tau \in \operatorname {Sym}(n)$
. (Note that we are using left actions here, so if $\sigma ,\,\tau \in \operatorname {Sym}(n)$![]() then the product $\tau \sigma$
then the product $\tau \sigma$![]() means to employ the permutation $\sigma$
means to employ the permutation $\sigma$![]() first, and then employ $\tau$
first, and then employ $\tau$![]() ).
).
With the above notation, an element of ${V_n(H)}$![]() is a homeomorphism of $\mathfrak {C}_n$
is a homeomorphism of $\mathfrak {C}_n$![]() that can be (non-uniquely) described by a table as follows:
that can be (non-uniquely) described by a table as follows:

where $p_i,\,q_i \in \mathcal {A}_n^{*}$![]() , $\sigma _i,\, \tau _i \in H$
, $\sigma _i,\, \tau _i \in H$![]() and such that the sets $P = \{p_i\}_{i=1}^{k}$
and such that the sets $P = \{p_i\}_{i=1}^{k}$![]() and $Q = \{q_i\}_{i=1}^{k}$
and $Q = \{q_i\}_{i=1}^{k}$![]() are prefix codes of $\mathfrak {C}_n$
are prefix codes of $\mathfrak {C}_n$![]() . We say that $k \geq 1$
. We say that $k \geq 1$![]() is the length of the table. The homeomorphism of $\mathfrak {C}_n$
is the length of the table. The homeomorphism of $\mathfrak {C}_n$![]() induced can be defined as follows: for every infinite word $\zeta$
induced can be defined as follows: for every infinite word $\zeta$![]() such that $p_i\leqslant _{pref}\zeta$
such that $p_i\leqslant _{pref}\zeta$![]() , that is $\zeta = p_i \vert \!\vert u$
, that is $\zeta = p_i \vert \!\vert u$![]() for some $u \in \mathcal {A}_n^\mathbb{N}$
for some $u \in \mathcal {A}_n^\mathbb{N}$![]() , we have
, we have
There are infinitely many tables that induce the same homeomorphism of $\mathfrak {C}_n$![]() . We proceed to define the four basic moves we can perform on a table in order to obtain an equivalent one (the four basic moves naturally split as two essential sorts of moves, together with their inverse (or ‘near-inverse’) moves).
. We proceed to define the four basic moves we can perform on a table in order to obtain an equivalent one (the four basic moves naturally split as two essential sorts of moves, together with their inverse (or ‘near-inverse’) moves).
The first basic move is expansion: for a given prefix code
we can consider
by expanding the word $p_i$![]() . This expansion not only occurs in $P$
. This expansion not only occurs in $P$![]() , as the image of $p_i$
, as the image of $p_i$![]() must be also expanded. So we have
must be also expanded. So we have
It is easy to see that both $\widetilde {P}$![]() and $\widetilde {Q}$
and $\widetilde {Q}$![]() are also prefix codes. Then:
are also prefix codes. Then:

One can always perform an expansion, but not all tables look like the result of an expansion. Naturally, the inverse of an expansion (when it is defined) is called a reduction.
The second move we can perform on a table is pushing down (respectively pushing up) the action of all $\sigma _i$![]() such that $\sigma _i = Id$
such that $\sigma _i = Id$![]() for every $i \in \{1,\, \ldots ,\, k\}$
for every $i \in \{1,\, \ldots ,\, k\}$![]() (respectively $\tau _i = Id$
(respectively $\tau _i = Id$![]() for every $i \in \{1,\, \ldots ,\, k\}$
for every $i \in \{1,\, \ldots ,\, k\}$![]() ):
):

It is not hard to see that a table gives a well-defined homeomorphism of the appropriate Cantor space, and if two tables are related by a finite sequence of our four moves then they represent the same homeomorphism. The reader can also check that if a homeomorphism of an appropriate Cantor space is represented by two tables, then in fact these tables are in the same equivalence class under our four basic moves on tables. Thus, we can just consider our group elements to be the equivalence classes of tables with the aforementioned relations.
The composition of two different elements $u,\,v\in {V_n(H)}$![]() is easy to compute using the equivalences. Let $u$
is easy to compute using the equivalences. Let $u$![]() , $v \in {V_n(H)}$
, $v \in {V_n(H)}$![]() , such that $u$
, such that $u$![]() takes the prefix code $P$
takes the prefix code $P$![]() to the prefix code $Q$
to the prefix code $Q$![]() (respectively $v$
(respectively $v$![]() takes $P'$
takes $P'$![]() to $Q'$
to $Q'$![]() ). We need to find a prefix code $S$
). We need to find a prefix code $S$![]() such that, for every element $s \in S$
such that, for every element $s \in S$![]() , there exists one element $q \in Q$
, there exists one element $q \in Q$![]() and one element $p' \in P'$
and one element $p' \in P'$![]() such that $q\leqslant _{pref} s$
such that $q\leqslant _{pref} s$![]() and $p'\leqslant _{pref} s$
and $p'\leqslant _{pref} s$![]() . This can always be done by expanding $P'$
. This can always be done by expanding $P'$![]() and $Q$
and $Q$![]() until we obtain the same prefix code $S$
until we obtain the same prefix code $S$![]() . Thus, without loss of generality:
. Thus, without loss of generality:

Finally, we push up the action of $u$![]() and push down the action of $v$
and push down the action of $v$![]() :
:

so

We sum up the previous discussion in the following proposition:
Proposition 2.4 ${V_n(H)}$![]() is a group with the composition.
is a group with the composition.
3. Topological embeddings
In this section, we present topological embeddings between symmetric Thompson's groups. The key idea is, given any group ${V_n(H)}$![]() , to translate the action of an element $\sigma \in H$
, to translate the action of an element $\sigma \in H$![]() into a permutation $\widetilde {\sigma }$
into a permutation $\widetilde {\sigma }$![]() of the elements of some prefix code of $\mathfrak {C}_m$
of the elements of some prefix code of $\mathfrak {C}_m$![]() . Therefore, $\widetilde {\sigma } \in {V_m(G)}$
. Therefore, $\widetilde {\sigma } \in {V_m(G)}$![]() for some $G$
for some $G$![]() .
.
Our method will be first to understand when actions on prefix codes over smaller alphabets can represent embeddings of permutations on larger alphabets which commute with our core operations of expansion and contraction of prefix codes. With that understanding in hand, we can then build the desired embedding from a group ${V_n(H)}$![]() to a group ${V_m(G)}$
to a group ${V_m(G)}$![]() for $m\leqslant n$
for $m\leqslant n$![]() .
.
We first establish some useful definitions.
3.1. The root group $\boldsymbol {\mathcal {R}_{G}(S)}$
Given a linear order $\leq$![]() on $\mathcal {A}_n$
on $\mathcal {A}_n$![]() (we choose $0<1<\ldots < n-1$
(we choose $0<1<\ldots < n-1$![]() ), there is an induced standard dictionary order:
), there is an induced standard dictionary order:
Definition 3.1 (Dictionary order)
Let $\mathcal {A}_n = \{a_0,\, \ldots ,\, a_{n-1}\}$![]() be an alphabet with linear order $\leq$
be an alphabet with linear order $\leq$![]() . We define the dictionary order on $\mathcal {A}_n^{*}$
. We define the dictionary order on $\mathcal {A}_n^{*}$![]() as follows. Let $u,\,v \in \mathcal {A}_n^{*}$
as follows. Let $u,\,v \in \mathcal {A}_n^{*}$![]() , then $u \leqslant _{dict} v$
, then $u \leqslant _{dict} v$![]() if and only if:
if and only if:
(1) $u \leqslant _{pref} v$
 ,
,(2) $u \not \leqslant _{pref} v$
 and there exist $p,\, s,\, t \in \mathcal {A}_n^{*}$
and there exist $p,\, s,\, t \in \mathcal {A}_n^{*}$ and $\alpha ,\, \beta \in \mathcal {A}_n$
and $\alpha ,\, \beta \in \mathcal {A}_n$ such that $u = p\alpha s,\, v = p \beta t$
such that $u = p\alpha s,\, v = p \beta t$ , and $\alpha < \beta$
, and $\alpha < \beta$ .
.
Let $2\leqslant m < n\in \mathbb {N}$![]() be fixed, and let $G \leqslant \operatorname {Sym}(m)$
be fixed, and let $G \leqslant \operatorname {Sym}(m)$![]() . We assume for the construction Higman's condition: $n = k(m-1)+ 1$
. We assume for the construction Higman's condition: $n = k(m-1)+ 1$![]() for some $k \geq 0$
for some $k \geq 0$![]() (so, $n\equiv 1\mod (m-1)$
(so, $n\equiv 1\mod (m-1)$![]() ). Then, we can find $S = \{s_0,\, \ldots ,\, s_{n-1}\}$
). Then, we can find $S = \{s_0,\, \ldots ,\, s_{n-1}\}$![]() an ordered prefix code of $\mathfrak {C}_m$
an ordered prefix code of $\mathfrak {C}_m$![]() of length $n$
of length $n$![]() (using the dictionary order). Observe for now that if $\sigma (S) = S \ \forall \sigma \in G$
(using the dictionary order). Observe for now that if $\sigma (S) = S \ \forall \sigma \in G$![]() , then $\sigma : S \rightarrow S$
, then $\sigma : S \rightarrow S$![]() will induce the desired rearrangement $\widetilde {\sigma }$
will induce the desired rearrangement $\widetilde {\sigma }$![]() of the elements of $S$
of the elements of $S$![]() , that is, $\widetilde {\sigma } \in \operatorname {Sym}_S\cong \operatorname {Sym}(n)$
, that is, $\widetilde {\sigma } \in \operatorname {Sym}_S\cong \operatorname {Sym}(n)$![]() .
.
We will be interested in the set $\mathcal {T}$![]() of triples $(m,\,n,\,G)$
of triples $(m,\,n,\,G)$![]() where $m\leqslant n$
where $m\leqslant n$![]() , $n\equiv 1\mod (m-1)$
, $n\equiv 1\mod (m-1)$![]() , and $G\in \operatorname {Sym}(m)$
, and $G\in \operatorname {Sym}(m)$![]() . We will say a triple $(m,\,n,\,G)\in \mathcal {T}$
. We will say a triple $(m,\,n,\,G)\in \mathcal {T}$![]() is satisfiable if there is a prefix code $S\subset X_m^{*}$
is satisfiable if there is a prefix code $S\subset X_m^{*}$![]() with $|S|=n$
with $|S|=n$![]() and where for each $\sigma \in G$
and where for each $\sigma \in G$![]() the action of $\sigma$
the action of $\sigma$![]() on $X_m^{*}$
on $X_m^{*}$![]() preserves $S$
preserves $S$![]() . In this case, we say $S$
. In this case, we say $S$![]() is a solution for the triple $(m,\,n,\,G)$
is a solution for the triple $(m,\,n,\,G)$![]() .
.
Definition 3.2 (Root group)
Given a triple $(m,\,n,\,G)\in \mathcal {T}$![]() and a solution $S$
and a solution $S$![]() , we define the root group $\mathcal {R}_{G}(S)$
, we define the root group $\mathcal {R}_{G}(S)$![]() to be the group of permutations of $S$
to be the group of permutations of $S$![]() induced by the action of $G$
induced by the action of $G$![]() on $S$
on $S$![]() .
.
It is the case that not every triple $(m,\,n,\,G)\in \mathcal {T}$![]() admits a solution $S$
admits a solution $S$![]() . However, when it does admit a solution $S$
. However, when it does admit a solution $S$![]() , it is immediate that $\mathcal {R}_{G}(S)$
, it is immediate that $\mathcal {R}_{G}(S)$![]() is isomorphic to $G$
is isomorphic to $G$![]() .
.
Definition 3.3 (Cycle type)
Let $\sigma \in \operatorname {Sym}(n)$![]() . The cycle type c of $\sigma$
. The cycle type c of $\sigma$![]() is the multiset (a set, but allowing multiple elements that are equal) of lengths of the cycles in the cycle decomposition of $\sigma$
is the multiset (a set, but allowing multiple elements that are equal) of lengths of the cycles in the cycle decomposition of $\sigma$![]() . We say that two subgroups $H,\, H' \in \operatorname {Sym}(n)$
. We say that two subgroups $H,\, H' \in \operatorname {Sym}(n)$![]() are cyclically isomorphic if there exists an isomorphism $\psi : H \rightarrow H'$
are cyclically isomorphic if there exists an isomorphism $\psi : H \rightarrow H'$![]() which preserves the cycle type of every permutation, that is, $c(\sigma ) = c(\psi (\sigma ))$
which preserves the cycle type of every permutation, that is, $c(\sigma ) = c(\psi (\sigma ))$![]() for all $\sigma \in H$
for all $\sigma \in H$![]() .
.
Remark 3.4 Subgroups $H$![]() and $H'$
and $H'$![]() are cyclically isomorphic if and only if they are conjugate in $\operatorname {Sym}(n)$
are cyclically isomorphic if and only if they are conjugate in $\operatorname {Sym}(n)$![]() , but our focus is on cycle structure and that is why we are using the language we have chosen. (N.B., there exist exotic automorphisms of $\operatorname {Sym}(6)$
, but our focus is on cycle structure and that is why we are using the language we have chosen. (N.B., there exist exotic automorphisms of $\operatorname {Sym}(6)$![]() which do not arise by conjugation, but these automorphisms change the cycle structure of some elements of order two.)
which do not arise by conjugation, but these automorphisms change the cycle structure of some elements of order two.)
3.2. The induced group $\boldsymbol {\mathcal {G}}$
We proceed to define the group $\mathcal {G} < {V_m(G)}$![]() such that ${V_n(H)}$
such that ${V_n(H)}$![]() is isomorphic to $\mathcal {G}$
is isomorphic to $\mathcal {G}$![]() .
.
Let ${V_m(G)}$![]() and ${V_n(H)}$
and ${V_n(H)}$![]() be two symmetric Thompson's groups such that $m$
be two symmetric Thompson's groups such that $m$![]() and $n$
and $n$![]() fulfil Higman's condition. Let $\widetilde {\mathcal {A}}_m = \{a_0,\,a_1,\,\ldots ,\,a_{n-1}\}$
fulfil Higman's condition. Let $\widetilde {\mathcal {A}}_m = \{a_0,\,a_1,\,\ldots ,\,a_{n-1}\}$![]() be an ordered prefix code of $\mathfrak {C}_m$
be an ordered prefix code of $\mathfrak {C}_m$![]() of length $n$
of length $n$![]() , such that $\mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$
, such that $\mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$![]() is well defined. We may think of $\mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$
is well defined. We may think of $\mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$![]() as a subgroup of $\operatorname {Sym}(n)$
as a subgroup of $\operatorname {Sym}(n)$![]() by using the bijection from $\widetilde {\mathcal {A}}_m$
by using the bijection from $\widetilde {\mathcal {A}}_m$![]() to $\mathcal {A}_n$
to $\mathcal {A}_n$![]() induced by the lexicographic ordering of $\widetilde {\mathcal {A}}_m$
induced by the lexicographic ordering of $\widetilde {\mathcal {A}}_m$![]() . Thus, we can define $\mathcal {G}$
. Thus, we can define $\mathcal {G}$![]() as the set of equivalence classes of tables of the form:
as the set of equivalence classes of tables of the form:

where $\sigma _i,\,\tau _i \in \mathcal {R}_{G}(\widetilde {\mathcal {A}}_m) \ \forall i$![]() and the prefix codes $P$
and the prefix codes $P$![]() and $Q$
and $Q$![]() consist of words in the alphabet $\widetilde {\mathcal {A}}_m$
consist of words in the alphabet $\widetilde {\mathcal {A}}_m$![]() , that is, every $p_i$
, that is, every $p_i$![]() and $q_i$
and $q_i$![]() is a non-empty concatenation of elements of $\widetilde {\mathcal {A}}_m$
is a non-empty concatenation of elements of $\widetilde {\mathcal {A}}_m$![]() .
.
It is straightforward to check that $\mathcal {G}$![]() is a group, since the concatenation of two words in $\widetilde {\mathcal {A}}_m^{*}$
is a group, since the concatenation of two words in $\widetilde {\mathcal {A}}_m^{*}$![]() is another word in $\widetilde {\mathcal {A}}_m^{*}$
is another word in $\widetilde {\mathcal {A}}_m^{*}$![]() . Tables of $\mathcal {G}$
. Tables of $\mathcal {G}$![]() are well defined by expansions and pushings, and the action of an element $\sigma \in \mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$
are well defined by expansions and pushings, and the action of an element $\sigma \in \mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$![]() on a word in $\mathcal {\widetilde {\mathcal {A}}}_m$
on a word in $\mathcal {\widetilde {\mathcal {A}}}_m$![]() gives another word in $\mathcal {\widetilde {\mathcal {A}}}_m$
gives another word in $\mathcal {\widetilde {\mathcal {A}}}_m$![]() by the definition of root group, so the composition of any two elements in $\mathcal {G}$
by the definition of root group, so the composition of any two elements in $\mathcal {G}$![]() gives another element of $\mathcal {G}$
gives another element of $\mathcal {G}$![]() .
.
We recall and prove our topological embedding theorem:
Theorem 1.1 (Topological Embedding)
Let $n,\,m \geq 2$![]() be natural numbers such that $m< n,$
be natural numbers such that $m< n,$![]() and let $G \leqslant \operatorname {Sym}(m),$
and let $G \leqslant \operatorname {Sym}(m),$![]() $H \leqslant \operatorname {Sym}(n)$
$H \leqslant \operatorname {Sym}(n)$![]() . Suppose that:
. Suppose that:
(1) There exists a prefix code $\widetilde {S}$
 of $\mathfrak {C}_m$
of $\mathfrak {C}_m$ such that $\vert \widetilde {S} \vert = n$
such that $\vert \widetilde {S} \vert = n$ ,
,(2) the group $\mathcal {R}_{G}(\widetilde {S})$
 is well defined, and
is well defined, and(3) $\mathcal {R}_{G}(\widetilde {S})$
 and $H$
and $H$ are cyclically isomorphic.
are cyclically isomorphic.
Then ${V_n(H)}$![]() embeds in ${V_m(G)}$
embeds in ${V_m(G)}$![]() .
.
Proof. Let ${V_m(G)}$![]() and ${V_n(H)}$
and ${V_n(H)}$![]() two symmetric Thompson's groups. Let $\mathcal {A}_n = \{0,\,1,\,\ldots ,\,n-1\}$
two symmetric Thompson's groups. Let $\mathcal {A}_n = \{0,\,1,\,\ldots ,\,n-1\}$![]() and $\widetilde {\mathcal {A}}_m = \{a_0,\,a_1,\,\ldots ,\,a_{n-1}\}$
and $\widetilde {\mathcal {A}}_m = \{a_0,\,a_1,\,\ldots ,\,a_{n-1}\}$![]() such that $\mathcal {R}_G(\widetilde {\mathcal {A}}_m)$
such that $\mathcal {R}_G(\widetilde {\mathcal {A}}_m)$![]() is well defined. We define the following translating map:
is well defined. We define the following translating map:
and
where $t$![]() is the isomorphism between $H$
is the isomorphism between $H$![]() and $\mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$
and $\mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$![]() . Note that $t$
. Note that $t$![]() and $\widetilde {t}$
and $\widetilde {t}$![]() have the following property:
have the following property:
as $\widetilde {\sigma }(a_i) = a_{\sigma (i)},\, \forall \sigma \in H,\, \forall i \in \mathcal {A}_n$![]() , since $\mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$
, since $\mathcal {R}_{G}(\widetilde {\mathcal {A}}_m)$![]() and $H$
and $H$![]() are cyclically isomorphic.
are cyclically isomorphic.
Our embedding is as follows:

We see that $\iota$![]() commutes with expansions and pushings, that is, $\iota (\operatorname {exp}(v)) = \operatorname {exp}(\iota (v))$
commutes with expansions and pushings, that is, $\iota (\operatorname {exp}(v)) = \operatorname {exp}(\iota (v))$![]() and $\iota (\operatorname {push}(v)) = \operatorname {push}(\iota (v)) \ \forall v \in {V_n(H)}$
and $\iota (\operatorname {push}(v)) = \operatorname {push}(\iota (v)) \ \forall v \in {V_n(H)}$![]() :
:

As $t$![]() is an isomorphism of groups, the commutativity follows. On the other hand, suppose that we expand the prefix code $P = \{p_1,\, \ldots ,\, p_k\}$
is an isomorphism of groups, the commutativity follows. On the other hand, suppose that we expand the prefix code $P = \{p_1,\, \ldots ,\, p_k\}$![]() on $p_i$
on $p_i$![]() (we argue below that $\iota$
(we argue below that $\iota$![]() commutes with expanding, but our argument uses the pushed version of $v$
commutes with expanding, but our argument uses the pushed version of $v$![]() : it is easy to see that this is sufficient):
: it is easy to see that this is sufficient):

The table for $\iota (\operatorname {exp}(v))$![]() is:
is:

Finally, the table for $\operatorname {exp}(\iota (v))$![]() is:
is:

Both tables $\operatorname {exp}(\iota (v)) = \iota (\operatorname {exp}(v))$![]() are equal as:
are equal as:

(We have used the concat symbol ‘$\vert \!\vert$![]() ’ in these tables and the immediate discussion after, wherever we think it makes terms easier to read. In our later explanations we will generally refrain from using it.)
’ in these tables and the immediate discussion after, wherever we think it makes terms easier to read. In our later explanations we will generally refrain from using it.)
To finish the proof, we need to show that $\iota (v) \circ \iota (u) = \iota (v \circ u)$![]() . This follows easily from the fact that $\iota$
. This follows easily from the fact that $\iota$![]() commutes with expansions and pushings. Without loss of generality, consider:
commutes with expansions and pushings. Without loss of generality, consider:

Thus:

4. Algebraic embeddings
In this section, we present some algebraic embeddings ${V_m(G)}\rightarrowtail {V_n(H)}$![]() between symmetric Thompson's groups (recall here $n-m=k(m-1)$
between symmetric Thompson's groups (recall here $n-m=k(m-1)$![]() for some positive $k$
for some positive $k$![]() , $G\leqslant \operatorname {Sym}(m)$
, $G\leqslant \operatorname {Sym}(m)$![]() and with $H$
and with $H$![]() a particular extended version of $G$
a particular extended version of $G$![]() in $\operatorname {Sym}(n)$
in $\operatorname {Sym}(n)$![]() ).
).
We call these embeddings ‘algebraic’ as they do not arise via topological conjugacy. In particular, these embeddings do not preserve the orbit lengths of the points of $\mathfrak {C}_n$![]() (when $n>m$
(when $n>m$![]() , which is our primary case of interest).
, which is our primary case of interest).
4.1. Successors
Here, we give the key idea for our algebraic embeddings, which relies on extending an idea of Birget into our context.
The successor of an element, expressed as a table, was defined in [Reference Birget1] in order to embed $V_2(Id)$![]() in $V_n(Id)$
in $V_n(Id)$![]() , for all $n \geq 2$
, for all $n \geq 2$![]() . We generalize Birget's definition.
. We generalize Birget's definition.
Definition 4.1 (Set of prefixes)
[Reference Birget1] Let $P \subset \mathcal {A}_n^{*}$![]() be a prefix code of $\mathfrak {C}_n$
be a prefix code of $\mathfrak {C}_n$![]() . We define the set of prefixes of $P$
. We define the set of prefixes of $P$![]() , $\operatorname {spref}(P)$
, $\operatorname {spref}(P)$![]() as follows:
as follows:
In other words, $\operatorname {spref}(P)$![]() is the set of strict prefixes of the elements of $P$
is the set of strict prefixes of the elements of $P$![]() .
.
We are embedding a symmetric Thompson's group on alphabet $\mathcal {A}_m$![]() into a symmetric Thompson's group on alphabet $\mathcal {A}_n$
into a symmetric Thompson's group on alphabet $\mathcal {A}_n$![]() , where $m\leqslant n$
, where $m\leqslant n$![]() . For this, we will assume $\mathcal {A}_m\subseteq \mathcal {A}_n$
. For this, we will assume $\mathcal {A}_m\subseteq \mathcal {A}_n$![]() . And, in particular, we set $\mathcal {A}_m=\{a_0,\,a_1,\,\ldots ,\,a_{m-1}\}$
. And, in particular, we set $\mathcal {A}_m=\{a_0,\,a_1,\,\ldots ,\,a_{m-1}\}$![]() and $\mathcal {A}_n=\mathcal {A}_m\cup \{a_m,\,a_{m+1},\,\ldots ,\,a_{n-1}\}$
and $\mathcal {A}_n=\mathcal {A}_m\cup \{a_m,\,a_{m+1},\,\ldots ,\,a_{n-1}\}$![]() with symbols with distinct indices being distinct (so that $|\mathcal {A}_n|=n$
with symbols with distinct indices being distinct (so that $|\mathcal {A}_n|=n$![]() ).
).
In what follows, we take a prefix code $P\subset a_{m-1}\vert \!\vert \mathcal {A}_m^{*}$![]() (so each element of $P$
(so each element of $P$![]() begins with the letter $a_{m-1}$
begins with the letter $a_{m-1}$![]() ) and transform it to a new prefix code $\operatorname {Succ}({P})\subset \mathcal {A}_n^{*}$
) and transform it to a new prefix code $\operatorname {Succ}({P})\subset \mathcal {A}_n^{*}$![]() by appending letters from the set $\{a_{m},\,a_{m+1},\,\ldots ,\,a_n\}$
by appending letters from the set $\{a_{m},\,a_{m+1},\,\ldots ,\,a_n\}$![]() .
.
Definition 4.2 (Successor)
Let $P \subset a_{m-1}\vert \!\vert \{a_0,\, \ldots ,\, a_{m-1}\}^{*}$![]() be a prefix code (complete, were we to remove the initial prefix letter $a_{m-1}$
be a prefix code (complete, were we to remove the initial prefix letter $a_{m-1}$![]() , so that $|P|\equiv 1\mod (m-1)$
, so that $|P|\equiv 1\mod (m-1)$![]() ) with $\vert P \vert = l \geq 1$
) with $\vert P \vert = l \geq 1$![]() , and let $\{p_1,\, \ldots ,\, p_l\}$
, and let $\{p_1,\, \ldots ,\, p_l\}$![]() be the ordered list of all the elements of $P$
be the ordered list of all the elements of $P$![]() , using the reverse dictionary order.
, using the reverse dictionary order.
We build a new prefix code $\operatorname {Succ}({P})$![]() inductively using our ordered list $(p_1,\,p_2,\,\ldots ,\,p_l)$
inductively using our ordered list $(p_1,\,p_2,\,\ldots ,\,p_l)$![]() .
.
Let $k$![]() be the smallest non-negative integer so that $n-m=k(m-1)$
be the smallest non-negative integer so that $n-m=k(m-1)$![]() (this $k$
(this $k$![]() will exist when $m$
will exist when $m$![]() and $n$
and $n$![]() satisfy Higman's condition, which we require to build our embeddings).
satisfy Higman's condition, which we require to build our embeddings).
We define (inductively) nested sets $P_{s,i}$![]() , where $s$
, where $s$![]() will grow from $1$
will grow from $1$![]() to $l$
to $l$![]() , and for each value of $s$
, and for each value of $s$![]() , we will have $i$
, we will have $i$![]() grow from $1$
grow from $1$![]() to $k$
to $k$![]() .
.
Set $\mathcal {A}_{m,n}:= \{a_m,\,a_{m+1},\,\ldots ,\,a_{n-1}\}$![]() . For every $p_s \in P$
. For every $p_s \in P$![]() , and $i\in \{1,\,2,\,\ldots ,\, k\}$
, and $i\in \{1,\,2,\,\ldots ,\, k\}$![]() the $i$
the $i$![]() -th successor $(p_s)'_i$
-th successor $(p_s)'_i$![]() of $p_s$
of $p_s$![]() is the element of $\operatorname {spref}(P)\vert \!\vert \mathcal {A}_{m,n}$
is the element of $\operatorname {spref}(P)\vert \!\vert \mathcal {A}_{m,n}$![]() defined as follows, assuming that
defined as follows, assuming that

has already been defined, we set:
where $\min$![]() uses the dictionary order in $\{a_0,\, \ldots ,\, a_{n-1}\}$
uses the dictionary order in $\{a_0,\, \ldots ,\, a_{n-1}\}$![]() .
.
Example 4.3 Suppose $m=3$![]() and $n=5$
and $n=5$![]() , so that $k=1$
, so that $k=1$![]() . In the definition above, $a_{m-1}=2$
. In the definition above, $a_{m-1}=2$![]() . So, consider the set $P=\{20,\,210,\,211,\,212,\,22\}$
. So, consider the set $P=\{20,\,210,\,211,\,212,\,22\}$![]() . Now, $k=1$
. Now, $k=1$![]() and $\operatorname {spref}(P)=\{\varepsilon ,\,2,\,21\}$
and $\operatorname {spref}(P)=\{\varepsilon ,\,2,\,21\}$![]() . We obtain
. We obtain

Remark 4.4 The three constants, $n,\,m,\,k$![]() are not arbitrary, as the system of successors needs to be well defined. If every element has $k$
are not arbitrary, as the system of successors needs to be well defined. If every element has $k$![]() successors, then:
successors, then:
which is Higman's condition.
Proof. If we expand an element $p_i \in P$![]() , we need to assign successors to each element $p_ia_j$
, we need to assign successors to each element $p_ia_j$![]() for every $0 \leqslant j \leqslant m-1$
for every $0 \leqslant j \leqslant m-1$![]() . In particular, the number of successors $k$
. In particular, the number of successors $k$![]() of every leaf does not vary, and each element $p_ia_r$
of every leaf does not vary, and each element $p_ia_r$![]() for every $m \leqslant r \leqslant n-1$
for every $m \leqslant r \leqslant n-1$![]() needs to be the successor of some element in $\widetilde {P} = (P \backslash \{p_i\}) \cup \{p_ia_0,\, \ldots ,\,p_ia_{m-1}\}$
needs to be the successor of some element in $\widetilde {P} = (P \backslash \{p_i\}) \cup \{p_ia_0,\, \ldots ,\,p_ia_{m-1}\}$![]() . Then $\widetilde {P}$
. Then $\widetilde {P}$![]() has $m-1$
has $m-1$![]() more elements than $P$
more elements than $P$![]() and there are $n-m$
and there are $n-m$![]() new elements $p_ia_r$
new elements $p_ia_r$![]() for $m \leqslant r \leqslant n-1$
for $m \leqslant r \leqslant n-1$![]() . Thus, we need $m-1$
. Thus, we need $m-1$![]() to evenly divide $n-m$
to evenly divide $n-m$![]() , and $k$
, and $k$![]() is the factor of this division.
is the factor of this division.
We proceed to prove the following lemma, essential for the proof of Theorem 1.2:
Lemma 4.5 Suppose $m\leqslant n$![]() are naturals so that there is $k$
are naturals so that there is $k$![]() natural with $n-m=k(m-1)$
natural with $n-m=k(m-1)$![]() . Suppose $l$
. Suppose $l$![]() is a positive integer congruent to $m$
is a positive integer congruent to $m$![]() modulo $m-1$
modulo $m-1$![]() . Let $S= \{ a_m ,\, \ldots ,\, a_{n-1}\}$
. Let $S= \{ a_m ,\, \ldots ,\, a_{n-1}\}$![]() and let $P \subset a_{m-1}\vert \!\vert \{a_0,\, \ldots ,\, a_{m-1}\}^{*}$
and let $P \subset a_{m-1}\vert \!\vert \{a_0,\, \ldots ,\, a_{m-1}\}^{*}$![]() be an $l$
be an $l$![]() -element prefix code, ordered as $p_l <_{dict} p_{l-1}<_{dict}\ldots <_{dict} p_1$
-element prefix code, ordered as $p_l <_{dict} p_{l-1}<_{dict}\ldots <_{dict} p_1$![]() . Let $i$
. Let $i$![]() with $1\leqslant i\leqslant l$
with $1\leqslant i\leqslant l$![]() . Then, the successors $(p_i)'_1$
. Then, the successors $(p_i)'_1$![]() , $(p_i)'_2,\,\ldots ,\, (p_i)'_k$
, $(p_i)'_2,\,\ldots ,\, (p_i)'_k$![]() are well defined, and furthermore, the expansion in which we replace $P$
are well defined, and furthermore, the expansion in which we replace $P$![]() by $\widetilde {P} = (P \backslash \{p_i\} ) \cup p_i\{a_0,\, \ldots ,\, a_{m-1}\}$
by $\widetilde {P} = (P \backslash \{p_i\} ) \cup p_i\{a_0,\, \ldots ,\, a_{m-1}\}$![]() has successors $(p_ia_j)'_i$
has successors $(p_ia_j)'_i$![]() uniquely determined as follows:
uniquely determined as follows:

Proof. We prove the two statements by induction on $l$![]() .
.
Base Case ( $l=1$![]() ):
):
If $l=1$![]() then $P=\{a_{m-1}\}$
then $P=\{a_{m-1}\}$![]() . We have $\operatorname {spref}{P}=\{\varepsilon \}$
. We have $\operatorname {spref}{P}=\{\varepsilon \}$![]() . It then follows that the $k$
. It then follows that the $k$![]() successors are, the set $\{a_m,\,a_{m+1},\,\ldots ,\,a_{m+k-1}\}$
successors are, the set $\{a_m,\,a_{m+1},\,\ldots ,\,a_{m+k-1}\}$![]() , noting that these are given in order and are the results of the inductive definition of the $k$
, noting that these are given in order and are the results of the inductive definition of the $k$![]() successors of $a_{m-1}$
successors of $a_{m-1}$![]() . Thus, we have in the base case that the successors are well defined. We need to verify the existence of well-defined successors for an expansion of $P=\{a_{m-1}\}$
. Thus, we have in the base case that the successors are well defined. We need to verify the existence of well-defined successors for an expansion of $P=\{a_{m-1}\}$![]() . In this case, $P$
. In this case, $P$![]() admits only one expansion, which is precisely the set $\widetilde {P}=\{a_{m-1}a_{m-1},\,a_{m-1}a_{m-2},\,\ldots ,\,a_{m-1}a_0\}.$
admits only one expansion, which is precisely the set $\widetilde {P}=\{a_{m-1}a_{m-1},\,a_{m-1}a_{m-2},\,\ldots ,\,a_{m-1}a_0\}.$![]() We have $\operatorname {spref}({\widetilde {P}})=\{\varepsilon ,\,a_{m-1}\}$
We have $\operatorname {spref}({\widetilde {P}})=\{\varepsilon ,\,a_{m-1}\}$![]() and we have
and we have

We can directly observe these successors are well defined and distinct. Thus, the statement is true for $l=1$![]() .
.
Inductive Case ( $l>1$![]() ):
):
Now let us assume that $\widetilde {P}$![]() is a result of $v$
is a result of $v$![]() expansions from the one-element prefix code $\{a_{m-1}\}$
expansions from the one-element prefix code $\{a_{m-1}\}$![]() , for some $v\geq 1$
, for some $v\geq 1$![]() , where for any prefix code resulting from $u$
, where for any prefix code resulting from $u$![]() expansions from $\{a_{m-1}\}$
expansions from $\{a_{m-1}\}$![]() for $0\leqslant u< v$
for $0\leqslant u< v$![]() the statement of the lemma holds. We will show that the successors of our expansion $\widetilde {P}$
the statement of the lemma holds. We will show that the successors of our expansion $\widetilde {P}$![]() are well defined. In particular, if $P$
are well defined. In particular, if $P$![]() is the prefix code (of size $l$
is the prefix code (of size $l$![]() ) arising from doing only the first $t-1$
) arising from doing only the first $t-1$![]() expansions from $\{a_{m-1}\}$
expansions from $\{a_{m-1}\}$![]() towards the prefix code $\widetilde {P}$
towards the prefix code $\widetilde {P}$![]() , and $p_i$
, and $p_i$![]() is the element of $P$
is the element of $P$![]() which is being replaced by and $m$
which is being replaced by and $m$![]() -fold expansion to create $\widetilde {P}$
-fold expansion to create $\widetilde {P}$![]() , then by induction, the successors $(p_i)'_1$
, then by induction, the successors $(p_i)'_1$![]() , $(p_i)'_2$
, $(p_i)'_2$![]() , $\ldots$
, $\ldots$![]() , $(p_i)'_k$
, $(p_i)'_k$![]() of $p_i\in P$
of $p_i\in P$![]() are well defined.
are well defined.
Note that $P_{i-1,k} = \widetilde {P}_{i-1,k}$![]() , as the involved subsets of both $P$
, as the involved subsets of both $P$![]() and $\widetilde {P}$
and $\widetilde {P}$![]() are equal. Thus, the first successor to assign is $(p_ia_{m-1})'_1$
are equal. Thus, the first successor to assign is $(p_ia_{m-1})'_1$![]() . Suppose that $(p_ia_{m-1})'_1 <_{dict} p_ia_m$
. Suppose that $(p_ia_{m-1})'_1 <_{dict} p_ia_m$![]() , then $(p_ia_{m-1})'_1 = pa_t$
, then $(p_ia_{m-1})'_1 = pa_t$![]() for some $p \in \operatorname {spref}(P): p <_{dict} p_i$
for some $p \in \operatorname {spref}(P): p <_{dict} p_i$![]() and $a_t \in \{a_m,\, \ldots ,\,a_{n-1} \}$
and $a_t \in \{a_m,\, \ldots ,\,a_{n-1} \}$![]() . Thus, before expanding $P$
. Thus, before expanding $P$![]() , $pa_t$
, $pa_t$![]() is one of the successors of some $p_r \in P$
is one of the successors of some $p_r \in P$![]() .
.
If $p_r <_{dict} p_i$![]() , then the set of successors of $p_i$
, then the set of successors of $p_i$![]() is defined before the set of successors of $p_r$
is defined before the set of successors of $p_r$![]() . Because $p_i$
. Because $p_i$![]() is expanded, the set of $k$
is expanded, the set of $k$![]() successors of $p_ia_{m-1}$
successors of $p_ia_{m-1}$![]() is equal to the set of successors of $p_i$
is equal to the set of successors of $p_i$![]() , and this set does not contain $pa_t$
, and this set does not contain $pa_t$![]() , which is a contradiction. On the other hand, if $p_r >_{dict} p_i$
, which is a contradiction. On the other hand, if $p_r >_{dict} p_i$![]() , then $pa_t \in P_{i-1,k} = \widetilde {P}_{i-1,k}$
, then $pa_t \in P_{i-1,k} = \widetilde {P}_{i-1,k}$![]() , which is also a contradiction. Thus, $(p_ia_{m-1})'_1 = p_ia_m$
, which is also a contradiction. Thus, $(p_ia_{m-1})'_1 = p_ia_m$![]() . We can use a similar argument for all $(p_ia_{m-1})'_1 \ldots (p_ia_{1})'_k$
. We can use a similar argument for all $(p_ia_{m-1})'_1 \ldots (p_ia_{1})'_k$![]() .
.
For $p_ia_0$![]() , all successors of the form $p_ia_s,\, a_s \in \{a_m ,\,\ldots ,\, a_{n-1}\}$
, all successors of the form $p_ia_s,\, a_s \in \{a_m ,\,\ldots ,\, a_{n-1}\}$![]() have already been assigned. Thus, the remaining $k$
have already been assigned. Thus, the remaining $k$![]() successors are precisely the $k$
successors are precisely the $k$![]() successors of $p_i$
successors of $p_i$![]() , taken in order.
, taken in order.
Remark 4.6 Birget in [Reference Birget1] gives a formula for the $i$![]() -th successor of an element, for the case of $m=2$
-th successor of an element, for the case of $m=2$![]() . The statement of Lemma 4.5 above shows the natural generalization of that formula holds when we have the Higman Condition (as we must for successors to be well defined). The resulting formula is given as follows:
. The statement of Lemma 4.5 above shows the natural generalization of that formula holds when we have the Higman Condition (as we must for successors to be well defined). The resulting formula is given as follows:
Let $P \subset a_{m-1}\vert \!\vert \{a_0,\, \ldots ,\, a_{m-1}\}^{*}$![]() be a prefix code with $\vert P \vert \geq 2$
be a prefix code with $\vert P \vert \geq 2$![]() , such that the elements of $P$
, such that the elements of $P$![]() are ordered in reverse dictionary order. Then every element of $w \in P$
are ordered in reverse dictionary order. Then every element of $w \in P$![]() can be written uniquely in the form $ua_ia_0^{t}$
can be written uniquely in the form $ua_ia_0^{t}$![]() , where $u\in \{a_0 ,\, \ldots ,\, a_{m-1}\}^{*}$
, where $u\in \{a_0 ,\, \ldots ,\, a_{m-1}\}^{*}$![]() and $t \geq 0$
and $t \geq 0$![]() . The $i$
. The $i$![]() -th successor of $w$
-th successor of $w$![]() is:
is:
We stress that this formula is only valid if $P$![]() is ordered in reverse dictionary order.
is ordered in reverse dictionary order.
4.2. The algebraic embedding
We proceed to define the algebraic embedding of ${V_m(G)}$![]() in ${V_n(H)} = V_n(G_{ext})$
in ${V_n(H)} = V_n(G_{ext})$![]() . Let $g \in {V_m(G)}$
. Let $g \in {V_m(G)}$![]() , given by the following table:
, given by the following table:

We define the embedding $\iota (g)$![]() below. The resulting tables are large, and our notation requires some explanation. The idea of the embedding is to use the identity map initially, and at $a_{m+k}$
below. The resulting tables are large, and our notation requires some explanation. The idea of the embedding is to use the identity map initially, and at $a_{m+k}$![]() and later letters, but under the address $a_{m-1}$
and later letters, but under the address $a_{m-1}$![]() , we place the prefix code $p_1$
, we place the prefix code $p_1$![]() to $p_l$
to $p_l$![]() , and we also require action under the successors. The first row then has entries following the ordered list given here (wrapped at natural locations due to page length constraints):
, and we also require action under the successors. The first row then has entries following the ordered list given here (wrapped at natural locations due to page length constraints):

We use vertical bars ‘$\vert$![]() ’ in our table at the same locations that we placed line-wraps in the row detailed above, for clarity of grouping. The element $\iota (g)$
’ in our table at the same locations that we placed line-wraps in the row detailed above, for clarity of grouping. The element $\iota (g)$![]() is now given by the following table:
is now given by the following table:

Note that the set of successors of $P = \{p_1,\, \ldots ,\, p_l\}$![]() are assigned supposing that $p_l <_{dict} \ldots <_{dict} p_1$
are assigned supposing that $p_l <_{dict} \ldots <_{dict} p_1$![]() . Therefore, the set of successors of $Q = \{q_1,\, \ldots ,\, q_l\}$
. Therefore, the set of successors of $Q = \{q_1,\, \ldots ,\, q_l\}$![]() is assigned following the order $q_l \rightarrow \ldots \rightarrow q_1$
is assigned following the order $q_l \rightarrow \ldots \rightarrow q_1$![]() , which does not need to follow the dictionary order on $Q$
, which does not need to follow the dictionary order on $Q$![]() .
.
Indeed, the first and third rows of $\iota (g)$![]() are both prefix codes of $\mathfrak {C}_n$
are both prefix codes of $\mathfrak {C}_n$![]() . On the one hand, suppose that the number of columns of $g$
. On the one hand, suppose that the number of columns of $g$![]() is $l = m + d(m-1)$
is $l = m + d(m-1)$![]() for some $d \geq 0$
for some $d \geq 0$![]() . It follows that the number of columns of $\iota (g)$
. It follows that the number of columns of $\iota (g)$![]() whose elements of the first row start with $a_{m-1}$
whose elements of the first row start with $a_{m-1}$![]() is $n+ d(n-1)$
is $n+ d(n-1)$![]() (observe that the last $k$
(observe that the last $k$![]() terms from the successor substitution will not begin with $a_{m-1}$
terms from the successor substitution will not begin with $a_{m-1}$![]() ). On the other hand, as the number of columns of $g$
). On the other hand, as the number of columns of $g$![]() is $(m + d(m-1))$
is $(m + d(m-1))$![]() , and we assign $k$
, and we assign $k$![]() successors to every column, we have $(m+d(m-1))(k+1)$
successors to every column, we have $(m+d(m-1))(k+1)$![]() columns on $\iota (g)$
columns on $\iota (g)$![]() . As we have Higman's Condition, the reader can verify that $(m+d(m-1))(k+1) = n+ d(n-1) +k$
. As we have Higman's Condition, the reader can verify that $(m+d(m-1))(k+1) = n+ d(n-1) +k$![]() . From this, we see firstly that $(n-1)\vert k$
. From this, we see firstly that $(n-1)\vert k$![]() , but more importantly, this embedding/successor operation does not place any constraints on the number of expansions $d$
, but more importantly, this embedding/successor operation does not place any constraints on the number of expansions $d$![]() that were used to create the original prefix code for the domain of $g$
that were used to create the original prefix code for the domain of $g$![]() .
.
We now recall and prove our algebraic embedding theorem:
Theorem 1.2 (Algebraic Embedding)
Let $n,\,m \geq 2$![]() be natural numbers such that $n = k(m-1)+ m$
be natural numbers such that $n = k(m-1)+ m$![]() for some $k \geq 1,$
for some $k \geq 1,$![]() and let $G \leqslant \operatorname {Sym}(m)$
and let $G \leqslant \operatorname {Sym}(m)$![]() . Let $H = G_{ext} \leqslant \operatorname {Sym}(n)$
. Let $H = G_{ext} \leqslant \operatorname {Sym}(n)$![]() the extended symmetric group of $H,$
the extended symmetric group of $H,$![]() whose elements act as the elements of $H$
whose elements act as the elements of $H$![]() on the first $m$
on the first $m$![]() elements and act as the identity on the remaining $n-m$
elements and act as the identity on the remaining $n-m$![]() .
.
Then ${V_m(G)}$![]() embeds in ${V_n(H)}$
embeds in ${V_n(H)}$![]() .
.
Proof. If we push down the action of every $\sigma _i$![]() , we have:
, we have:

Thus, the table for $\iota (\operatorname {push}(g))$![]() is:
is:

On the other hand, the table for $\operatorname {push}(\iota (g))$![]() is:
is:

Recall from the statement of Theorem 1.2 that for an element $\tau \in \operatorname {Sym}(m)$![]() , the extended version $\tau '$
, the extended version $\tau '$![]() of $\tau$
of $\tau$![]() in $\operatorname {Sym}(n)$
in $\operatorname {Sym}(n)$![]() is that element of $\operatorname {Sym}(n)$
is that element of $\operatorname {Sym}(n)$![]() which agrees with $\tau$
which agrees with $\tau$![]() on the set $\mathcal {A}_m$
on the set $\mathcal {A}_m$![]() and acts as the identity on the points of $\mathcal {A}_{m,n}$
and acts as the identity on the points of $\mathcal {A}_{m,n}$![]() in $\mathcal {A}_n$
in $\mathcal {A}_n$![]() . Thus, both tables are equal, as $(\tau _i\sigma _i^{-1})' = (\tau '_i)(\sigma '_i)^{-1},\, \forall i \in \{i,\,\ldots ,\,l\}$
. Thus, both tables are equal, as $(\tau _i\sigma _i^{-1})' = (\tau '_i)(\sigma '_i)^{-1},\, \forall i \in \{i,\,\ldots ,\,l\}$![]() . If we expand $g$
. If we expand $g$![]() on $p_i$
on $p_i$![]() :
:

Then the table for $\iota (\operatorname {exp}(g))$![]() is:
is:

On the other hand, the table for $\operatorname {exp}(\iota (g))$![]() is:
is:

It is straightforward to check that for both tables, the columns starting at $a_{m-1}p_ia_s$![]() for $0 \leqslant s \leqslant m-1$
for $0 \leqslant s \leqslant m-1$![]() are equal, as $\tau '_i(s) = \tau _i(s),\, \forall s \in \{0,\,\ldots ,\, m-1\}$
are equal, as $\tau '_i(s) = \tau _i(s),\, \forall s \in \{0,\,\ldots ,\, m-1\}$![]() .
.
For $m \leqslant s \leqslant n-1$![]() by Lemma 4.5, we know there is a correspondence between the first two rows of $\iota (\operatorname {exp}(g))$
by Lemma 4.5, we know there is a correspondence between the first two rows of $\iota (\operatorname {exp}(g))$![]() and the first two rows of $\operatorname {exp}(\iota (g))$
and the first two rows of $\operatorname {exp}(\iota (g))$![]() . On the other hand, from the description of the algebraic embedding, the order in which successors for every $q_j$
. On the other hand, from the description of the algebraic embedding, the order in which successors for every $q_j$![]() are selected depends only on the order of $\{p_1,\, \ldots ,\, p_l\}$
are selected depends only on the order of $\{p_1,\, \ldots ,\, p_l\}$![]() , so we have the following calculations:
, so we have the following calculations:

That is, e.g., $(a_{m-1}q_i\tau _i(a_{m-1}))'_1$![]() comes first in the choice of a successor as $(a_{m-1}p_ia_{m-1})'_1$
comes first in the choice of a successor as $(a_{m-1}p_ia_{m-1})'_1$![]() appears first under the order of the $p_i$
appears first under the order of the $p_i$![]() , independent of $\tau _i$
, independent of $\tau _i$![]() . Thus, the latter two rows of these tables are also equivalent.
. Thus, the latter two rows of these tables are also equivalent.
Finally, it is easy to see that $\iota (h \circ g) = \iota (h) \circ \iota (g)$![]() , as $\iota$
, as $\iota$![]() commutes with expansions and pushings. We only need to obtain row equality on the first part of the table as the remaining part depends entirely on $P$
commutes with expansions and pushings. We only need to obtain row equality on the first part of the table as the remaining part depends entirely on $P$![]() (respectively, on $Q$
(respectively, on $Q$![]() for the element $h$
for the element $h$![]() ):
):

Thus, the result follows.
Acknowledgements
The authors would like to thank Javier Aramayona, Jim Belk, and Matthew G. Brin for numerous and enjoyable conversations around the material in this note. We also wish to thank an anonymous referee for helpful comments on exposition. The first author wants to acknowledge financial support from the Spanish Ministry of Economy and Competitiveness, through the ‘Severo Ochoa Program for Centres of Excellence in R&D’ (SEV-2015-0554). The second author wishes to acknowledge support from EPSRC grant EP/R032866/1 during the creation of this paper.