Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-11T09:13:40.874Z Has data issue: false hasContentIssue false
  • English
  • Français

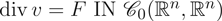Solving the Equation $\hbox{div}\, v = F\, \hbox{IN} {\cal C}_0(\open{R}^N, \open{R}^N)$

Part of: Partial differential equations Linear function spaces and their duals General first-order equations and systems Representations of solutions

Published online by Cambridge University Press:  24 July 2018

Laurent Moonens  and
Tiago H. Picon
Laurent Moonens*
Affiliation:
Université Paris-Sud, Laboratoire de Mathématique UMR 8628, Université Paris-Saclay, Bâtiment 307, F-91405 Orsay Cedex, France (Laurent.Moonens@math.u-psud.fr)
Tiago H. Picon
Affiliation:
University of São Paulo, Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto, Departamento de Computação e Matemática, Avenida Bandeirantes 3900, CEP 1404-040, Ribeirão Preto, Brazil (picon@ffclrp.usp.br)
*
*Corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the following note, we focus on the problem of existence of continuous solutions vanishing at infinity to the equation div v = f for f ∈ Ln(ℝn) and satisfying an estimate of the type ||v||∞ ⩽ C||f||n for any f ∈ Ln(ℝn), where C > 0 is related to the constant appearing in the Sobolev–Gagliardo–Nirenberg inequality for functions with bounded variation (BV functions).

Keywords

continuous solvabilitydivergence equationSobolev–Gagliardo–Nirenberg inequality

MSC classification

Primary: 46E40: Spaces of vector- and operator-valued functions
Secondary: 35A23: Inequalities involving derivatives and differential and integral operators, inequalities for integrals 35F05: Linear first-order equations 35D30: Weak solutions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 4 , November 2018 , pp. 1055 - 1061
Copyright
Copyright © Edinburgh Mathematical Society 2018 

References

1.Bourgain, J. and Brezis, H., On the equation div Y = f and application to control of phases, J. Amer. Math. Soc. 16(2) (2003), 393–426.Google Scholar
2.Brezis, H., Functional analysis, Sobolev spaces and partial differential equations, Universitext (Springer, New York, 2011).Google Scholar
3.De Pauw, T. and Torres, M., On the distributional divergence of vector fields vanishing at infinity, Proc. Roy. Soc. Edinburgh Sect. A 141(1) (2011), 65–76.Google Scholar
4.Evans, L. C. and Gariepy, R. F., Measure theory and fine properties of functions, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1992).Google Scholar