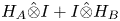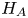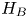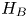1. Introduction
In*Address at the time of publication: IST Austria, Klosterneuburg, Austria. quantum mechanics, the dynamics of a system is governed by the Schrödinger equation
where $H$
is a self-adjoint operator on a Hilbert space $\mathcal {H}$
, called the Hamiltonian, and $\psi _t\in \mathcal {H}$
is the wave function at time $t$
. Its time evolution is given by
In many situations however, physical reasoning yields merely a symmetric, rather than self-adjoint, operator, defined on a subspace of sufficiently regular functions. It is then natural to ask whether this operator has self-adjoint extensions, and if so, how many.
This question was completely answered by von Neumann, whose extension theory states the following: A symmetric operator $H$
has self-adjoint extensions if and only if the dimensions of the deficiency spaces ${\mathcal {N}}(H^{\ast }-i)$
and ${\mathcal {N}}(H^{\ast }+i)$
coincide, and in this case, the self-adjoint extensions of $H$
are parametrized by the unitary operators from ${\mathcal {N}}(H^{\ast }-i)$
to ${\mathcal {N}}(H^{\ast }+i)$
.
Now, given two systems $A$
and $B$
, we can consider the composite system $AB$
. It is modelled on the tensor product of the Hilbert spaces of the individual systems $A$
and $B$
. In the simplest case when there is no interaction between $A$
and $B$
, the time evolution of the composite system is separable, that is,
The corresponding Hamiltonian is
As such, operators of this form are the prototype of Hamiltonians governing the time evolution of composite systems with interactions and are therefore key in understanding the self-adjoint realizations of Hamiltonians of quantum many-particle systems and, in particular, open quantum systems [Reference Breuer and Petruccione2, Reference Davies3].
In the light of the discussion above, one is lead to study self-adjoint extensions of operators of the form $H_A\otimes {{I}}+{{I}}\otimes H_B$
when $H_A$
and $H_B$
are merely symmetric (in general, the time evolution generated by such a self-adjoint extension will not be separable).
In the case when one of the operators is self-adjoint, this problem was considered by Ibort, Marmo and Pérez-Pardo. They state the following result ([Reference Ibort and Pérez-Pardo4, Theorem 2.3], [Reference Ibort, Marmo and Pérez-Pardo5, Theorem 1]).
Theorem Let $H_A$
be a symmetric operator on ${\mathcal {H}}_A$
, $H_B$
a self-adjoint operator on ${\mathcal {H}}_B$
and define $H_{AB}$
on ${\mathcal {H}}_{AB}={\mathcal {H}}_A\hat {\otimes } {\mathcal {H}}_B$
by
Let $\mathcal {N}_{A\pm }={\mathcal {N}}(H_A^{\ast }\mp i)$
be the deficiency spaces of system $H_A$
. The deficiency spaces $\mathcal {N}_{AB\pm }={\mathcal {N}}(H_{AB}^{\ast }\mp i)$
of $H_{AB}$
then satisfy
However, in their proof, they restrict themselves to the case when the spectrum of $H_B$
consists solely of simple eigenvalues, and only state that the general case can be treated by a judicious use of the spectral theorem. In this article, we give a complete proof of he preceding theorem for general self-adjoint $H_B$
.
In the case when the operator $H_B$
is (a restriction of) the Laplacian, the assumption of discrete spectrum covers only compact geometries, while our proof justifies the result also for non-compact geometries. For example, if the system $B$
consists of a single free particle in ${\mathbb {R}}^{n}$
, then the Hamiltonian $H_B$
is the Laplacian, which is essentially self-adjoint on $C_c^{\infty }({\mathbb {R}}^{n})$
, but the spectrum of its closure is not discrete.
Let us outline the proof strategy. First, the spectral theorem allows us to view $H_B$
as a multiplication operator $M_\phi$
on $L^{2}(\Omega ,\,\mu )$
for some measure $\mu$
. The tensor product ${\mathcal {H}}_A\hat \otimes L^{2}(\Omega ,\,\mu )$
can be identified with the Bochner Lebesgue space $L^{2}(\Omega ,\,\mu ;{\mathcal {H}}_A)$
. Under this identification, the operator $H_{AB}$
acts as
These identifications make it possible to reduce the asserted isomorphism for the deficiency spaces to a similar computation as in the proof of Ibort, Marmo and Pérez-Pardo.
There are two main difficulties to overcome. First, while the identification of tensor products of operators on ${\mathcal {H}}_A\hat {\otimes } L^{2}(\Omega ,\,\mu )$
with operators on $L^{2}(\Omega ,\,\mu ;{\mathcal {H}}_A)$
is fairly obvious in the bounded case, we deal with unbounded operators and, as usual, more care is required to determine the correct domains. This is done in §3.
Second, the asserted isomorphism for the deficiency spaces comes from fiberwise isomorphisms. Then one has to prove that these isomorphisms can be chosen so that they depend measurably on the base point. In the discrete case this is of course obvious, but it becomes non-trivial in the general case at hand. This problem is resolved in §4. Finally, the proof is completed in §5.
The self-adjoint extensions of operators of the form $H_{AB}$
as above were also described in [Reference Boitsev, Brasche, Malamud, Neidhardt and Yu. Popov1], using a completely different approach based on boundary triplets. More precisely, given a boundary triplet for $H_A^{\ast }$
, they construct a boundary triplet for $H_{AB}^{\ast }$
that respects the tensor structure.
2. Preliminaries
Throughout this article, all Hilbert spaces are assumed to be separable. An operator $A$
is called symmetric if it is densely defined and $A\subseteq A^{\ast }$
.
Definition 2.1 deficiency spaces
Let $A$
be a symmetric operator. We call
the deficiency spaces of $A$
and their dimensions
the deficiency indices of $A$
.
In case we can rule out confusion, we shall write ${\mathcal {N}}_\pm$
instead of ${\mathcal {N}}_\pm (A)$
.
Next, we state the central theorem of von Neumann's extension theory (see, for instance, [Reference Weidmann and Teubner7, Chapter 10] for an extensive treatment). In the following, $U\dot{+}V$
denotes the algebraic direct sum of subspaces $U$
and $V$
, not necessarily orthogonal, while $U\oplus V$
is reserved for the orthogonal direct sum of closed subspaces.
Theorem 2.2 von Neumann's extension theorem
Let $A$
be a closed, symmetric operator on ${\mathcal {H}}$
. Then $A$
has self-adjoint extensions if and only if $d_+(A)=d_-(A)$
. In this case, let $U\colon {\mathcal {N}}_+\to {\mathcal {N}}_-$
be unitary. Define the operator $B$
by
Then $A{\subseteq } B=B^{*}$
, and all self-adjoint extensions of $A$
arise this way.
This theorem yields a one-to-one correspondence between the set of self-adjoint extensions of the operator $A$
and the set of unitary operators ${\mathcal {N}}_+\to {\mathcal {N}}_-$
, hence reduces the problem of finding self-adjoint extensions of $A$
to constructing unitary operators between the deficiency spaces. We will therefore be interested in computing the deficiency spaces of symmetric closed operators.
We also recall the spectral theorem in multiplication operator form (see for example [Reference Weidmann and Teubner7, Chapter 8]).
Theorem 2.3 spectral theorem
Let $H$
be a self-adjoint operator on the Hilbert space ${\mathcal {H}}$
. There exists a $\sigma$
-finite measure space $(X,\,\mu )$
, a measurable function $\varphi \colon X\to {\mathbb {R}}$
and a unitary operator $U\colon {\mathcal {H}}\to L^{2}(X,\,\mu )$
such that
Let ${\mathcal {H}}$
and ${\mathcal {K}}$
be Hilbert spaces. We denote by ${\mathcal {H}}\otimes {\mathcal {K}}$
their algebraic tensor product and by ${\mathcal {H}}\hat {\otimes }{\mathcal {K}}$
their Hilbert space tensor product.
Definition 2.4 For operators $A$
on ${\mathcal {H}}$
and $B$
on ${\mathcal {K}}$
, we define the operator $A\otimes B$
on ${\mathcal {H}}\hat {\otimes }{\mathcal {K}}$
by
If $A$
and $B$
are closable, then so is $A\otimes B$
, and we denote its closure by $A\hat {\otimes } B$
.
Let $(\Omega ,\,{\mathcal {F}},\,\mu )$
be a measure space, ${\mathcal {H}}$
a Hilbert space and $f\colon \Omega \to {\mathcal {H}}$
measurable. We write $L^{2}(\Omega ;{\mathcal {H}})$
for the Bochner–Lebesgue space of square-integrable ${\mathcal {H}}$
-valued functions.
One can construct a unitary operator ${\mathcal {H}}\hat {\otimes } L^{2}(\Omega )\to L^{2}(\Omega ;{\mathcal {H}})$
by linearly and continuously extending $e\otimes f \mapsto (\omega \mapsto f(\omega )e)$
, thus justifying the identification of ${\mathcal {H}}\hat {\otimes } L^{2}(\Omega )$
with $L^{2}(\Omega ;{\mathcal {H}})$
.
3. Finding the adjoint
Let $H_A$
be a symmetric operator on ${\mathcal {H}}_A$
and let $H_B$
be a self-adjoint operator on ${\mathcal {H}}_B$
. We define the operator $H_{AB}$
on ${\mathcal {H}}_A\hat {\otimes }{\mathcal {H}}_B$
by $H_{AB}=\overline {H_A\hat {\otimes } I + I \hat {\otimes } H_B}$
.
The straightforward way to compute the deficiency spaces ${\mathcal {N}}_\pm (H_{AB})={\mathcal {N}}(H_{AB}^{*}\mp i)$
of the operator $H_{AB}$
is, of course, to compute the adjoint of $H_{AB}$
and then the kernel of $H_{AB}^{*}\mp i$
.
First, note the following:
Hence $H_A\hat {\otimes } I + I \hat {\otimes } H_B$
is densely defined and it makes sense to consider its adjoint. Since $(H_A\hat {\otimes } I)^{*}=(H_A\otimes I)^{*}{\supseteq } H_A^{*}\otimes I$
, we have $(H_A\hat {\otimes } I)^{*}{\supseteq } H_A^{*}\hat {\otimes } I$
and similarly $(I\hat {\otimes } H_B)^{*}{\supseteq } I\hat {\otimes } H_B$
. Combined, this means that $(H_A\hat {\otimes } I + I \hat {\otimes } H_B)^{*}{\supseteq } H_A^{*}\hat {\otimes } I+I\hat {\otimes } H_B$
, and furthermore $(H_A\hat {\otimes } I + I \hat {\otimes } H_B)^{*}{\supseteq } \overline {H_A^{*}\hat {\otimes } I+I\hat {\otimes } H_B}$
. In fact, we will see that these two operators are equal.
Before proving this, let us simplify our notation. Without loss of generality, we can assume, due to the spectral theorem, that ${\mathcal {H}}_B=L^{2}(\Omega )$
and $H_B=M_\varphi$
for some $\sigma$
-finite measure space $\Omega$
and a measurable function $\varphi \colon \Omega \to {\mathbb {R}}$
. Instead of $H_A$
and ${\mathcal {H}}_A$
, we will simply write $H$
and ${\mathcal {H}}$
respectively. As we have seen, we can identify ${\mathcal {H}}\hat {\otimes } L^{2}(\Omega )$
with the Bochner–Lebesgue space $L^{2}(\Omega ;{\mathcal {H}})$
.
Theorem 3.1 Let $K$
be a closed operator on ${\mathcal {H}}$
and let $(\Omega ,\,{\mathcal {F}},\,\mu )$
be a measure space. The domain of the operator $K\hat {\otimes } I$
on ${\mathcal {H}}\hat {\otimes } L^{2}(\Omega )$
is given by
and the operator acts as
for $f\in {\mathcal {D}}(K\hat {\otimes } {{I}})$
and a.e. $\omega \in \Omega$
.
Proof. Since $K$
is closed, the space ${\mathcal {D}}(K)$
equipped with the inner product $\langle {\cdot },\,{\cdot }\rangle _K$
given by
for $f,\,g\in {\mathcal {D}}(A)$
, is a Hilbert space.
Since $K\hat {\otimes } I$
is the closure of the operator $K\otimes I$
, the domain ${\mathcal {D}}(K\hat {\otimes } I)$
is the closure of ${\mathcal {D}}(K\otimes I)={\mathcal {D}}(K)\otimes L^{2}(\Omega )$
with respect to the norm $\left \lVert {\cdot }\right \rVert _{K\hat {\otimes } I}=\sqrt {\Vert {\cdot }\Vert ^{2}+\Vert (K\hat {\otimes } I)\cdot \Vert ^{2}}$
.
This norm, however, coincides with the norm defined on the Bochner–Lebesgue space $L^{2}(\Omega ;({\mathcal {D}}(K),\,\langle {\cdot },\,{\cdot }\rangle _K))={\mathcal {D}}(K)\hat {\otimes } L^{2}(\Omega )$
. Since ${\mathcal {D}}(K)\hat {\otimes } L^{2}(\Omega )$
is defined as the closure of ${\mathcal {D}}(K)\otimes L^{2}(\Omega )$
with respect to $\left \lVert {\cdot }\right \rVert _{K\hat {\otimes } I}$
, we have
Since $\int \left \lVert {f(\omega )}\right \rVert ^{2}_K d\mu (\omega )=\int (\left \lVert {f(\omega )}\right \rVert ^{2}+\left \lVert {Kf(\omega )}\right \rVert ^{2} )d\mu (\omega )<\infty$
if and only if both $\int \left \lVert {f(\omega )}\right \rVert ^{2} d\mu (\omega )<\infty$
and $\int \left \lVert {Kf(\omega )}\right \rVert ^{2} d\mu (\omega )<\infty$
, we can make the following identification
proving the statement about the domain. It remains to show how $K\hat {\otimes } I$
acts.
Let $f\in {\mathcal {D}}(K\otimes I)={\mathcal {D}}(K)\otimes {\mathcal {D}}(M_\psi )$
, that is $f$
, decomposes as a finite linear combination $f=\sum \nolimits _k e_k\otimes f_k$
. Then
for almost every $\omega \in \Omega$
.
Now let $f\in {\mathcal {D}}(K\hat {\otimes } I)$
. Since ${\mathcal {D}}(K\otimes I )$
is a core for $K\hat {\otimes } I$
, i.e. ${{\mathcal {D}}(K\otimes M_\psi )}$
is dense in ${\mathcal {D}}(K\hat {\otimes } M_\psi )$
with respect to the graph norm, there is a sequence $(\phi _n)_n$
in ${\mathcal {D}}(K\otimes I )={\mathcal {D}}(K)\otimes {\mathcal {D}}( I )$
that converges in $\left \lVert {\cdot }\right \rVert _{K\hat {\otimes } I}=\sqrt {\Vert {\cdot }\Vert ^{2}+\Vert (K\hat {\otimes } I)\cdot \Vert ^{2}}$
to $f$
. In particular, there is a subsequence $(\phi _{n_l})_l$
of $(\phi _n)_n$
such that $\phi _{n_l}(\omega )\to f(\omega )$
for almost every $\omega \in \Omega$
, and a subsequence $(\phi _{n_{l_j}})_j$
of $(\phi _{n_l})_l$
such that almost everywhere we have $(K\hat {\otimes } I\phi _{n_{l_j}})(\omega )\to (K\hat {\otimes } I f)(\omega )$
.
Since $(K\hat {\otimes } I\phi _{n_{l_j}})(\omega )= K(\phi _{n_{l_j}}(\omega ))$
, this convergence implies that for almost every $\omega$
, we have $K(\phi _{n_{l_j}}(\omega ))\to (K\hat {\otimes } I f)(\omega )$
.
Hence $K(\phi _{n_{l_j}}(\omega ))\to (K\hat {\otimes } I f)(\omega )$
almost everywhere. Closedness of $K$
yields $f(\omega )\in {\mathcal {D}}(K)$
and
almost everywhere, which concludes the proof.
Proposition 3.2 Let $M_\psi$
be the operator of multiplication by the measurable function $\psi \colon \Omega \to {\mathbb {C}}$
on $L^{2}(\Omega )$
. The operator $I\hat {\otimes } M_\psi$
has domain
and acts by
almost everywhere.
Proof. To see how the operator acts, consider the following. Let $f\in {\mathcal {D}}(I\otimes M_\psi )={\mathcal {H}}\otimes {\mathcal {D}}( M_\psi )$
, then
Now, let $f\in {\mathcal {D}}(I\hat {\otimes } M_\psi )$
. Since ${\mathcal {D}}(I\otimes M_\psi )$
is a core for $I\hat {\otimes } M_\psi$
, i.e. ${{\mathcal {D}}(I\otimes M_\psi )}$
is dense in ${\mathcal {D}}(I\hat {\otimes } M_\psi )$
with respect to the graph norm, there is a sequence $(\phi _n)_n$
in ${\mathcal {D}}(I\otimes M_\psi )={\mathcal {D}}(I)\otimes {\mathcal {D}}( M_\psi )$
that converges in $\left \lVert {\cdot }\right \rVert _{I\hat {\otimes } M_\psi }=\sqrt {\Vert {\cdot }\Vert ^{2}+\Vert (I\hat {\otimes } M_\psi )\cdot \Vert ^{2}}$
to $f$
. In particular, there is a subsequence $(\phi _{n_l})_l$
of $(\phi _n)_n$
such that $\phi _{n_l}(\omega )\to f(\omega )$
almost everywhere, hence $(I\hat {\otimes } M_\psi \phi _{n_{l}})(\omega )=\psi (\omega )\phi _{n_{l}}(\omega )\to (I\hat {\otimes } M_\psi f)(\omega )$
almost everywhere.
It remains to prove our claim about the domain.
Since $I\hat {\otimes } M_\psi$
acts by $I\hat {\otimes } M_\psi f =(\omega \mapsto \psi (\omega )f(\omega ))$
, the inclusion ‘${\subseteq }$
’ holds.
Now, let $f\in \{g\in L^{2}(\Omega ;{\mathcal {H}})\colon \omega \mapsto \left \lVert {g(\omega )}\right \rVert \in {\mathcal {D}}(M_\psi )\}$
. Let $(\xi _n)$
be an orthonormal basis of ${\mathcal {H}}$
, then there are $\phi _n\in L^{2}(\Omega )$
, such that
Since
for all $n_0\in {\mathbb {N}}$
, the fact that $\left \lVert {f(\cdot )\in {\mathcal {D}}(M_\psi )}\right \rVert$
implies $\phi _n\in L^{2}(\Omega )$
for all $n\in {\mathbb {N}}$
. Now, let $f_N$
be given by $f_N=\sum \nolimits _{n=1}^{N}\phi _n(\cdot )\xi _n\in {\mathcal {H}}\otimes {\mathcal {D}}(M_\psi )$
. Obviously, we have
In particular, there is a subsequence $(f_{N_l})$
of $(f_N)$
such that $f_{N_l}(\omega )\xrightarrow {l\to \infty }f(\omega )$
almost everywhere.
Let $g=\phi f\in L^{2}(\Omega ;{\mathcal {H}})$
. Since
Lebesgue's dominated convergence theorem yields
In summary $\left \lVert {f_{N_l}-f}\right \rVert \to 0$
and $\left \lVert {I\hat {\otimes } M_\psi f_{N_l}-g}\right \rVert \to 0$
. Since $I\hat {\otimes } M_\psi$
is closed, $f\in {\mathcal {D}}(I\hat {\otimes } M_\psi )$
, which proves the inclusion ‘${\supseteq }$
’ and hence concludes the proof.
In summary, we now know that $H^{*}\hat {\otimes } I$
and $I\hat {\otimes } M_\varphi$
act in the following way
almost everywhere, for all $f\in {\mathcal {D}}(H^{*}\hat {\otimes } I)$
and $g\in {\mathcal {D}}(I\hat {\otimes } M_\varphi )$
. Therefore, the operator $H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi$
acts on $f\in {\mathcal {D}}(H^{*}\hat {\otimes } I)\cap {\mathcal {D}}(I\hat {\otimes } M_\varphi )$
by
almost everywhere. This extends to $\overline {H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi }$
, as the next lemma shows.
Lemma 3.3 For every $f\in {\mathcal {D}}(\overline {H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi })$
we have
almost everywhere.
Proof. Let $\tilde H=\overline {H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi }$
. Take $f\in {\mathcal {D}}(\tilde {H})$
. Then there is a sequence $(f_n)$
in the space ${\mathcal {D}}({H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi })$
such that $\left \lVert {f_n-f}\right \rVert _{\tilde {H}}\to 0$
. In particular, there is a subsequence $(f_{n_l})$
such that $(\tilde {H}f_{n_l})\xrightarrow {l\to \infty }(\tilde {H}f)$
and $f_{n_{l}}\xrightarrow {l\to \infty } f$
almost everywhere. This yields
almost everywhere. In particular, the limit $\lim _l H^{*}(f_{n_{l}}(\omega ))$
exists almost everywhere. Since $H^{*}$
is closed, $f(\omega )\in {\mathcal {D}}(H^{*})$
and $H^{*}(f(\omega ))=\lim _l H^{*}(f_{n_{l}}(\omega ))$
almost everywhere. This concludes the proof.
Proposition 3.4 The domain of $\overline {H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi }$
is given as follows
Proof. Let $\tilde {H}=\overline {H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi }$
. Again, ${\mathcal {D}}(\tilde {H}){\subseteq } {\mathcal {D}}$
is obvious.
Let $f\in {\mathcal {D}}$
and define the sequence $(E_k)$
of measurable subsets of $\Omega$
as follows
Define $f_k=\chi (\cdot )_{E_k}f$
. Since $\left \lVert {H^{*}(f_k(\omega ))}\right \rVert \le k\left \lVert {f_k(\omega )}\right \rVert$
, it is $f_k\in {\mathcal {D}}(H^{*}\hat {\otimes } I)$
and since $\left \lVert {\varphi (\omega )f_k(\omega )}\right \rVert \le k\left \lVert {f_k(\omega )}\right \rVert$
we have $f_k\in {\mathcal {D}}(I\hat {\otimes } M_\varphi )$
, hence $f_k\in {\mathcal {D}}(H^{*}\hat {\otimes } I+I\hat {\otimes } M_\varphi )$
. Now, $\left \lVert {f_k(\omega )-f(\omega )}\right \rVert =\chi (\omega )_{\Omega \setminus E_k}\left \lVert {f(\omega )}\right \rVert \le \left \lVert {f(\omega )}\right \rVert$
and $\left \lVert {f_k(\omega )-f(\omega )}\right \rVert \xrightarrow {k\to \infty }0$
almost everywhere. Therefore, by Lebesgue's theorem
Similarly, $\left \lVert {(H^{*}+\varphi (\omega )I)(f_k(\omega )-f(\omega ))}\right \rVert \le \left \lVert {(H^{*}+\varphi (\omega )I)f(\omega )}\right \rVert$
, once again applying Lebesgue's theorem yields
where $g=(\omega \mapsto (H^{*}+\varphi (\omega )I)f(\omega ))$
. Since $\tilde {H}$
is closed, we have $f\in {\mathcal {D}}(\tilde {H})$
.
Before we can prove that $(H\hat {\otimes } I +I\hat {\otimes } M_\varphi )^{*}{\subseteq }\overline {H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi }$
, we need a general fact about adjoints (see [Reference Schmüdgen6, Prop. 7.26]).
Lemma 3.5 Let $A$
and $B$
be densely defined, closable operators on the Hilbert spaces ${\mathcal {K}}$
and ${\mathcal {L}}$
, respectively. The operator $A\hat {\otimes } B$
on ${\mathcal {K}}\hat {\otimes } {\mathcal {L}}$
satisfies the following identity for its adjoint
Theorem 3.6 The following identity holds
Proof. Let $\tilde H=\overline {H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi }$
. Only the inclusion ${\mathcal {D}}((H\hat {\otimes } I + I\hat {\otimes } M_\varphi )^{*}){\subseteq }{\mathcal {D}}(\tilde {H})$
is left to prove.
Let $f\in {\mathcal {D}}((H\hat {\otimes } I + I\hat {\otimes } M_\varphi )^{*})$
, that is there is an ${f^{*}}\in L^{2}(\Omega ;{\mathcal {H}})$
such that for all $g\in {\mathcal {D}}(H\hat {\otimes } I + I\hat {\otimes } M_\varphi )$
the following holds
Let $E_k=\{\omega \in \Omega \colon \left \lvert {\varphi (\omega )}\right \rvert \le k\}$
for $k\in {\mathbb {N}}$
. Since
for $g\in {\mathcal {D}}(H\hat {\otimes } I + I\hat {\otimes } M_\varphi )$
also $g_k=\chi _{E_k}g\in {\mathcal {D}}(H\hat {\otimes } I + I\hat {\otimes } M_\varphi )$
, hence
Obviously all functions in ${\mathcal {D}}(H\hat {\otimes } I_{L^{2}(E_k)} + I\hat {\otimes } M_{\varphi \upharpoonright _{E_k}})$
can be extended by $0$
to functions in ${\mathcal {D}}(H\hat {\otimes } I_{L^{2}(\Omega )} + I\hat {\otimes } M_{\varphi })$
, and are therefore representable by restrictions of elements of ${\mathcal {D}}(H\hat {\otimes } I_{L^{2}(\Omega )} + I\hat {\otimes } M_{\varphi })$
. Consequently, the above computation yields
for all $h\in {\mathcal {D}}(H\hat {\otimes } I_{L^{2}(E_k)} + I\hat {\otimes } M_{\varphi \upharpoonright _{E_k}})$
, hence $f\upharpoonright _{E_k}\in {\mathcal {D}}((H\hat {\otimes } I_{L^{2}(E_k)} + I\hat {\otimes } M_{\varphi \upharpoonright _{E_k}})^{*})$
. By the very definition of $E_k$
, the map $\varphi \upharpoonright _{E_k}$
is bounded, hence $M_{\varphi \upharpoonright _{E_k}}$
is bounded, hence $I\hat {\otimes } M_{\varphi \upharpoonright _{E_k}}$
is bounded by the closed graph theorem, since
Therefore
Now let $h\in {\mathcal {D}}(H\hat {\otimes } I_{L^{2}(E_k,)} + I\hat {\otimes } M_{\varphi \upharpoonright _{E_k}})$
, then
Hence
In summary, we have $f(\omega )\in {\mathcal {D}}(H^{*})$
and $f^{*}(\omega )=H^{*}(f(\omega ))+\varphi (\omega )$
for almost every $\omega \in E_k$
. Since $\Omega$
is covered by the $E_k$
, $k\in {\mathbb {N}}$
, we have
However, by Proposition 3.4, this means $f\in {\mathcal {D}}(\tilde {H})$
.
4. Constructing a measurable family of orthonormal bases
Definition 4.1 domain of regularity
Let $A$
be an operator on the Hilbert space ${\mathcal {H}}$
. The set
is called domain of regularity of the operator $A$
.
Note that for all closed operators $A$
, the number
is constant on each connected component of the domain of regularity $\chi (A)$
of $A$
(see [Reference Weidmann and Teubner7, Chapter 10]). That is, for each pair of complex numbers $z,\,w\in \chi (A)$
, there is an isometric isomorphism between ${\mathcal {R}}(A-z)^{\perp }$
and ${\mathcal {R}}(A-w)^{\perp }$
. Our goal is to construct such an isomorphism more or less explicitly. We will restrict ourselves here to closed symmetric operators.
Let $A$
be a closed symmetric operator on the separable Hilbert space ${\mathcal {H}}$
. Since ${\mathcal {R}}(A+i)$
is a closed subspace of ${\mathcal {H}}$
, there exists $N\in {\mathbb {N}}\cup \{\infty \}$
and $\xi _n\in {\mathcal {D}}(A)$
, $n < N$
, such that $((A+i)\xi _n)_n$
is an orthonormal basis of ${\mathcal {R}}(A+i)$
.
By symmetry of $A$
we have $i\in \chi (A)$
, hence $(A+i)^{-1}\colon {\mathcal {R}}(A+i)\to {\mathcal {D}}(A)$
is bounded. Therefore, the span of the $\xi _n=(A+i)^{-1}(A+i)\xi _n$
, $n < N$
, is dense in ${\mathcal {D}}(A)$
. This gives rise to a total set in ${\mathcal {R}}(A+z)$
for $z\in {\mathbb {C}}^{+}$
, as we will show next.
Proposition 4.2 For every $f\in {\mathcal {D}}(A)$
there are $\lambda _n\in {\mathbb {C}}$
, $n < N$
, such that
Proof. Since $((A+i)\xi _n)_{n < N}$
is an orthonormal basis of ${\mathcal {R}}(A+i)$
, there are $\lambda _n\in {\mathbb {C}}$
, $n < N$
, such that $\sum \nolimits _n\left \lvert {\lambda _n}\right \rvert ^{2}<\infty$
and
Thus, for all $k < N$
,
Taking $k=N-1$
if $N<\infty$
or passing to the limit $k\to \infty$
if $N=\infty$
, we obtain
□
Note that since $(A+z)(A+i)^{-1}$
is injective, the vectors $(A+z)\xi _1,\,\dots ,\,(A+z)\xi _m$
are linearly independent for every $m < N$
. We can therefore apply Gram–Schmidt orthonormalization to $((A+z)\xi _n)_{n < N}$
to obtain an orthonormal basis $(\eta _m(z))_{m < N}$
of ${\mathcal {R}}(A+z)$
. Note that all the operations in the Gram–Schmidt algorithm are continuous, in particular, measurable in $z$
. Thus, the map $z\mapsto \eta _m(z)$
is measurable.
Denote the projection onto ${\mathcal {R}}(A+z)$
by $P_z$
, that is,
Now $I-P_z$
is the projection onto ${\mathcal {R}}(A+z)^{\perp }={\mathcal {N}}(A^{*}+\overline {z})$
and $((I-P_z)\zeta _n)$
is total in ${\mathcal {N}}(A^{*}+\overline {z})$
for every orthonormal basis of $(\zeta _n)$
of ${\mathcal {H}}$
. Fix an orthonormal basis $(\zeta _n)$
of ${\mathcal {H}}$
and set $\rho _n(z)=(I-P_z)\zeta _n$
for $n\in {\mathbb {N}}$
. We now introduce a modified Gram–Schmidt algorithm which does not require the input vectors to be linearly independent.
Consider the map $\kappa \colon {\mathbb {R}}\to {\mathbb {R}}$
given by
and note that it is obviously measurable. Define $(\sigma _n)$
inductively by
By the original Gram–Schmidt algorithm, it is easy to see that those of the $\sigma _n(z)$
that do not vanish form an orthonormal basis of ${\mathcal {N}}(A^{*}+\overline {z})$
. Furthermore, it is evident that $z\to \sigma _n(z)$
is measurable for every $n\in {\mathbb {N}}$
. We now want to prove that we can ‘extract’ those not-vanishing $\sigma _n(z)$
in a measurable manner with respect to $z$
. Remember that $d_+=\dim {\mathcal {N}}(A^{*}-i)=\dim {\mathcal {N}}(A^{*}+\overline {z})$
.
Definition 4.3 Let $n_j\colon {\mathbb {C}}^{+}\to {\mathbb {N}}$
for $j<d_+$
be defined inductively by
Lemma 4.4 For every $j<d_++1$
, the map $z\mapsto n_j(z)$
is measurable.
Proof. We proceed inductively: $n_1$
is constant, hence measurable. In order to prove that $n_{j+1}$
is measurable, it suffices to show that the set $\{z\in {\mathbb {C}}^{+}\colon n_{j+1}=k\}$
is measurable for every $k\in {\mathbb {N}}$
. Note the following
By induction hypothesis, $\{z\in {\mathbb {C}}^{+}\colon n_{j}(z)=m\}$
is measurable and therefore the set $\{z\in {\mathbb {C}}^{+}\colon n_{j+1}(z)=k\}$
is measurable as well.
Lemma 4.5 The map $z\mapsto \sigma _{n_j(z)}(z)$
is measurable.
Proof. Let ${\mathcal {A}}{\subseteq } {\mathcal {H}}$
be measurable.
By the above lemma, this set is measurable.
Note that $(\sigma _{n_j(z)}(z))_{j< d_++1}$
is an orthonormal basis of ${\mathcal {N}}(A^{*}+\overline {z})$
.
Let us fix an orthonormal basis $(\tau _j)_{j< d_++1}$
of ${\mathcal {N}}(A^{*}-i)$
. Define the unitary operator $U_z\colon {\mathcal {N}}(A^{*}+\overline {z})\to {\mathcal {N}}(A^{*}-i)$
by linearly and continuously extending the operator $U_z\sigma _{n_j(z)}(z)=\tau _j$
. Note that
for all $f\in {\mathcal {N}}(A^{*}+\overline {z})$
. Since the inner product is continuous, for a measurable curve ${\mathbb {C}}^{+}\to {\mathcal {H}}$
, $z\mapsto f(z)\in {\mathcal {N}}(A^{*}+\overline {z})$
, the map $z\mapsto U_z f(z)$
is measurable. In summary:
Theorem 4.6 There is a family of unitary operators $(U_z)_{z\in {\mathbb {C}}^{+}}$
,
such that for all measurable $f\colon {\mathbb {C}}^{+}\to {\mathcal {H}}$
, satisfying $f(z)\in {\mathcal {N}}(A^{*}+\overline {z})$
, the map $z\mapsto U_z f(z)$
is measurable.
5. Computing the deficiency spaces
We finally dealt with sufficiently many technicalities so that we can prove our main result.
Theorem 5.1 Let $H_A$
and $H_B$
be a symmetric and a self-adjoint operator on the Hilbert space ${\mathcal {H}}_A$
and ${\mathcal {H}}_B$
, respectively. If $H_{AB}=\overline {H_A\hat {\otimes } I+I\hat {\otimes } H_B}$
, then
Proof. Without loss of generality let ${\mathcal {H}}_B=L^{2}(\Omega )$
for a $\sigma$
-finite measure space $(\Omega ,\,{\mathcal {F}},\,\mu )$
and let $H_B=M_\varphi$
be the operator of multiplication by a real-valued measurable function $\varphi \colon \Omega \to {\mathbb {R}}$
. For simplicity, denote ${\mathcal {H}}={\mathcal {H}}_A$
and $H=H_A$
and $\tilde {H}=\overline {H^{*}\hat {\otimes } I +I\hat {\otimes } M_\varphi }$
.
We will prove the existence of an isomorphism for the ${\mathcal {N}}_+$
only; for the ${\mathcal {N}}_-$
the proof works analogously.
If $f\in {\mathcal {N}}_+(H_{AB})={\mathcal {N}}(H^{*}_{AB}-i)={\mathcal {N}}(\tilde {H}-i)$
, then
that is,
Hence $f(\omega )\in {\mathcal {N}}(H^{*}-(i-\varphi (\omega )))$
almost everywhere. Since $\varphi$
is real-valued $i-\varphi (\omega )\in {\mathbb {C}}^{+}$
, thus by Theorem 4.6, there is a family of unitaries
such that the map $\omega \mapsto V_\omega f(\omega )$
is measurable. Since the $V_\omega$
are unitary, we have
In summary, $\omega \mapsto V_\omega f(\omega )$
is in $L^{2}(\Omega ;{\mathcal {N}}(H^{*}-i))$
. On the other hand, because the $V_\omega$
are onto, every $g\in L^{2}(\Omega ;{\mathcal {N}}(H^{*}-i))$
admits a representation $g(\omega )=V_\omega f(\omega )$
for some $f\in L^{2}(\Omega ;{\mathcal {H}})$
satisfying $f(\omega )\in {\mathcal {N}}(H^{*}-(i-\varphi (\omega )))$
almost everywhere, therefore
By closedness of $H^{*}$
, the space ${\mathcal {N}}(H^{*}-i)$
, equipped with the inner product inherited from ${\mathcal {H}}$
, is a Hilbert space. In particular,
□
Remark 5.2
(i) Having constructed the deficiency spaces of $H_{AB}$
, we can answer the question of existence of self-adjoint extensions of $H_{AB}$ and in case of existence, construct them by the means we examined in §2.(ii) Note that, because of the fact that there is a one-to-one correspondence between self-adjoint extensions of a symmetric operator and unitary extensions of its Cayley transform, there are ‘more’ self-adjoint extensions of $H_{AB}$
than there are of $H_A$.(iii) It still remains open to determine the deficiency spaces of $H_{AB}=H_A\otimes I+I\otimes H_B$
in the case when both $H_A$ and $H_B$ are only assumed to be symmetric. As stated in [Reference Ibort and Pérez-Pardo4], it is quite natural to conjecture that
\[ {\mathcal{N}}_{AB\pm}\simeq {\mathcal{N}}_{A\pm}\hat\otimes {\mathcal{H}}_B\oplus {\mathcal{H}}_A\hat\otimes {\mathcal{N}}_{B\pm}. \]
Acknowledgments
M. W. gratefully acknowledges financial support by the German Academic Scholarship Foundation (Studienstiftung des deutschen Volkes). T.W. thanks PAO Gazprom Neft, the Euler International Mathematical Institute in Saint Petersburg and ORISA GmbH for their financial support in the form of scholarships during his Master's and Bachelor's studies respectively. The authors want to thank Mark Malamud for pointing out the reference [Reference Boitsev, Brasche, Malamud, Neidhardt and Yu. Popov1] to them. This work was supported by the Ministry of Science and Higher Education of the Russian Federation, agreement No 075-15-2019-1619.
