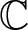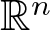1. Introduction
Let ![]() $\mathbb{B}_{n}$ be the open unit ball and
$\mathbb{B}_{n}$ be the open unit ball and ![]() $\mathrm{\mathbb{H}}_{n}$ be the upper half-space in
$\mathrm{\mathbb{H}}_{n}$ be the upper half-space in ![]() $\mathbb{R}^{n}$, respectively. Specially,
$\mathbb{R}^{n}$, respectively. Specially, ![]() $\mathbb{B}_{2}$ and
$\mathbb{B}_{2}$ and ![]() $\mathrm{\mathbb{H}}_{2}$ are denoted as
$\mathrm{\mathbb{H}}_{2}$ are denoted as ![]() $\mathbb{D}$ and
$\mathbb{D}$ and ![]() $\mathbb{H}$, identified with the open unit disc and the upper half-plane of
$\mathbb{H}$, identified with the open unit disc and the upper half-plane of ![]() $\mathbb{C}$. The classical Schwarz–Pick lemma states that holomorphic functions
$\mathbb{C}$. The classical Schwarz–Pick lemma states that holomorphic functions ![]() $f: \mathbb{D}\rightarrow \mathbb{D}$ satisfy
$f: \mathbb{D}\rightarrow \mathbb{D}$ satisfy
 \begin{eqnarray}
|f'(z)|\leq \frac{1-|f(z)| ^{2}}{1-|z| ^{2}}, \quad z\in \mathbb{D},
\end{eqnarray}
\begin{eqnarray}
|f'(z)|\leq \frac{1-|f(z)| ^{2}}{1-|z| ^{2}}, \quad z\in \mathbb{D},
\end{eqnarray}and
where ![]() $\varphi_{w}(z)=(w-z)(1-\overline{w}z)^{-1}$ is the Möbius transformation of
$\varphi_{w}(z)=(w-z)(1-\overline{w}z)^{-1}$ is the Möbius transformation of ![]() $\mathbb{D}$ onto itself.
$\mathbb{D}$ onto itself.
Recall that the hyperbolic metric on ![]() $\mathbb{D}$ is given by
$\mathbb{D}$ is given by
 \begin{equation*} d_{\mathbb{D}}(z,w)=\log \frac{1+|\varphi_{w}(z)|}{1-|\varphi_{w}(z)|}=2\tanh^{-1}(|\varphi_{w}(z)|), \quad z,w\in \mathbb{D}.\end{equation*}
\begin{equation*} d_{\mathbb{D}}(z,w)=\log \frac{1+|\varphi_{w}(z)|}{1-|\varphi_{w}(z)|}=2\tanh^{-1}(|\varphi_{w}(z)|), \quad z,w\in \mathbb{D}.\end{equation*} Note that ![]() $\tanh^{-1}$ is monotone increasing, then (1.2) can be rewritten as
$\tanh^{-1}$ is monotone increasing, then (1.2) can be rewritten as
That is to say every holomorphic function ![]() $f:\mathbb{D}\rightarrow \mathbb{D}$ is a contraction with respect to the hyperbolic metric on
$f:\mathbb{D}\rightarrow \mathbb{D}$ is a contraction with respect to the hyperbolic metric on ![]() $\mathbb{D}$.
$\mathbb{D}$.
In 2012, Kalaj and Vuorinen in [7, Theorem 1.12] proved that, for harmonic functions ![]() $f:\mathbb{D} \rightarrow (-1,1)$,
$f:\mathbb{D} \rightarrow (-1,1)$,
 \begin{eqnarray}
|\triangledown f (z)|\leq \frac{4}{\pi} \frac{1-|f(z)| ^{2}}{1-|z| ^{2}}, \quad z\in \mathbb{D},
\end{eqnarray}
\begin{eqnarray}
|\triangledown f (z)|\leq \frac{4}{\pi} \frac{1-|f(z)| ^{2}}{1-|z| ^{2}}, \quad z\in \mathbb{D},
\end{eqnarray} where the constant ![]() $4/\pi$ is sharp.
$4/\pi$ is sharp.
Equivalently, harmonic functions ![]() $f:\mathbb{D} \rightarrow (-1,1)$ are Lipschitz in the hyperbolic metric, i.e.
$f:\mathbb{D} \rightarrow (-1,1)$ are Lipschitz in the hyperbolic metric, i.e.
 \begin{equation*}d_{\mathbb{D}}(f(z),f(w))\leq \frac{4}{\pi} d_{\mathbb{D}}(z,w), \quad z,w\in \mathbb{D},\end{equation*}
\begin{equation*}d_{\mathbb{D}}(f(z),f(w))\leq \frac{4}{\pi} d_{\mathbb{D}}(z,w), \quad z,w\in \mathbb{D},\end{equation*}which holds also for harmonic functions defined in hyperbolic plane domains (see [Reference Mateljević15, Theorem 4]).
In 2013, Chen in [Reference Chen3, Theorem 1.2] obtained a sharper version of (1.3)
 \begin{equation*}|\triangledown f (z)|\leq \frac{4}{\pi} \frac{\cos \frac{\pi|f(z)|}{2} }{1-|z| ^{2}}, \quad z\in \mathbb{D},\end{equation*}
\begin{equation*}|\triangledown f (z)|\leq \frac{4}{\pi} \frac{\cos \frac{\pi|f(z)|}{2} }{1-|z| ^{2}}, \quad z\in \mathbb{D},\end{equation*}which was generalized into pluriharmonic functions (see [Reference Xu26, Theorem 1.5]).
Motivated by the result of Kalaj and Vuorinen, Marković in 2015 showed [Reference Marković14, Theorem 1.1] that harmonic functions ![]() $f:\mathbb{H} \rightarrow \mathbb{R}^{+}=(0,+\infty)$ are contractible in the hyperbolic metric, i.e.
$f:\mathbb{H} \rightarrow \mathbb{R}^{+}=(0,+\infty)$ are contractible in the hyperbolic metric, i.e.
where the hyperbolic metric ![]() $d_{\mathbb{H}}$ on the upper half-plane
$d_{\mathbb{H}}$ on the upper half-plane ![]() $\mathbb{H}$ is given by
$\mathbb{H}$ is given by
 \begin{equation*}d_{\mathbb{H}}(z,w)=2\tanh^{-1}\Big| \frac{z-w}{\overline{z}-w}\Big|, \quad z,w\in \mathbb{H}.\end{equation*}
\begin{equation*}d_{\mathbb{H}}(z,w)=2\tanh^{-1}\Big| \frac{z-w}{\overline{z}-w}\Big|, \quad z,w\in \mathbb{H}.\end{equation*} In particular, the hyperbolic distance ![]() $d_{\mathbb{R}^{+}}$ on
$d_{\mathbb{R}^{+}}$ on ![]() $\mathbb{R}^{+}$ is
$\mathbb{R}^{+}$ is
 \begin{equation*} d_{\mathbb{R}^{+}}(x,y)=d_{\mathbb{H}}(ix,iy)=|\log\frac{x}{y}|, \quad x,y\in \mathbb{R}^{+}.\end{equation*}
\begin{equation*} d_{\mathbb{R}^{+}}(x,y)=d_{\mathbb{H}}(ix,iy)=|\log\frac{x}{y}|, \quad x,y\in \mathbb{R}^{+}.\end{equation*} In [Reference Melentijević16], Melentijević established some refinements of Schwarz’s lemma for holomorphic functions with the invariant gradient and gave another proof of (1.4) based on Harnack inequality. By using the same strategy, one can show that harmonic functions ![]() $f:\mathbb{D} \rightarrow \mathbb{R}^{+}$ are also contractible in the hyperbolic metric,
$f:\mathbb{D} \rightarrow \mathbb{R}^{+}$ are also contractible in the hyperbolic metric,
Furthermore, Melentijević provide counterexamples to show that these results in (1.4) and (1.5) do not hold in higher dimensions for positive harmonic functions defined in ![]() $\mathbb{B}_n$ or
$\mathbb{B}_n$ or ![]() $\mathbb{H}_n$ when
$\mathbb{H}_n$ when ![]() $n\geq3$; see [Reference Melentijević16, Example 1 and Example 2].
$n\geq3$; see [Reference Melentijević16, Example 1 and Example 2].
In fact, up to multiplying a constant depending on the dimension, these results in (1.4) and (1.5) still hold for positive harmonic functions defined in higher dimensions. To be more precise, we shall establish the following result in this paper.
Theorem 1.1. Let ![]() $n\geq2$ be integer and
$n\geq2$ be integer and ![]() $f:\mathbb{B}_{n} \rightarrow \mathbb{R}^{+}$ be a harmonic function. Then
$f:\mathbb{B}_{n} \rightarrow \mathbb{R}^{+}$ be a harmonic function. Then
where ![]() $d_{\mathbb{B}_{n}}$ is the hyperbolic metric on
$d_{\mathbb{B}_{n}}$ is the hyperbolic metric on ![]() $\mathbb{B}_{n}$ given by
$\mathbb{B}_{n}$ given by  $d_{\mathbb{B}_{n}}(x,y) =2\tanh^{-1}(|\varphi_{y}(x)|)$, and
$d_{\mathbb{B}_{n}}(x,y) =2\tanh^{-1}(|\varphi_{y}(x)|)$, and ![]() $\varphi_{y}(x)$ is the Möbius transformation of
$\varphi_{y}(x)$ is the Möbius transformation of ![]() $\mathbb{B}_{n}$ defined by (2.1).
$\mathbb{B}_{n}$ defined by (2.1).
The proof of Theorem 1.1 is built on the following estimate. Moreover, this estimate is sharp.
Theorem 1.2. Let ![]() $n\geq2$ be integer and
$n\geq2$ be integer and ![]() $f:\mathbb{B}_{n} \rightarrow \mathbb{R}^{+}$ be a harmonic function. Then
$f:\mathbb{B}_{n} \rightarrow \mathbb{R}^{+}$ be a harmonic function. Then
If the equality in (1.7) is attained for some ![]() $a \in \mathbb{B}_{n}$, then there is a point
$a \in \mathbb{B}_{n}$, then there is a point ![]() $\xi \in \partial \mathbb{B}_{n}$ such that
$\xi \in \partial \mathbb{B}_{n}$ such that
 \begin{eqnarray}
f(x)=f(a)|1-\varphi_{a}(x)\overline{a}|^{n-2}P_{\xi}\circ \varphi_{a}(x), \quad x\in \mathbb{B}_{n},
\end{eqnarray}
\begin{eqnarray}
f(x)=f(a)|1-\varphi_{a}(x)\overline{a}|^{n-2}P_{\xi}\circ \varphi_{a}(x), \quad x\in \mathbb{B}_{n},
\end{eqnarray}where Pξ is the Poisson kernel given by
 \begin{equation*}P_{\xi}(x)=P(x, \xi)=\frac{1-|x|^{2}}{|x-\xi|^{n}}.\end{equation*}
\begin{equation*}P_{\xi}(x)=P(x, \xi)=\frac{1-|x|^{2}}{|x-\xi|^{n}}.\end{equation*} Moreover, every positive and harmonic function f defined by (1.8) satisfies the equality in (1.7) for all ![]() $x \in \mathbb{B}_{n}$ and
$x \in \mathbb{B}_{n}$ and ![]() $\xi \in \partial \mathbb{B}_{n}$.
$\xi \in \partial \mathbb{B}_{n}$.
The natural question is to ask: what is the analogue of Theorem 1.1 for bounded harmonic functions ![]() $f:\mathbb{B}_{n} \rightarrow (-1,1)$? Based on the proved Khavinson conjecture in [11], Liu very recently has given an answer to this question by established the following Schwarz–Pick type inequality [Reference Liu12, Theorem 1], which can be viewed as a counterpart of Theorem 1.2 for bounded harmonic functions.
$f:\mathbb{B}_{n} \rightarrow (-1,1)$? Based on the proved Khavinson conjecture in [11], Liu very recently has given an answer to this question by established the following Schwarz–Pick type inequality [Reference Liu12, Theorem 1], which can be viewed as a counterpart of Theorem 1.2 for bounded harmonic functions.
Theorem 1.3. Let ![]() $n\geq4$ be integer and
$n\geq4$ be integer and ![]() $f:\mathbb{B}_{n} \rightarrow (-1,1)$ be a harmonic function. Then
$f:\mathbb{B}_{n} \rightarrow (-1,1)$ be a harmonic function. Then
 \begin{eqnarray}
|\nabla f(x)|\leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}},\quad x\in \mathbb{B}_{n},
\end{eqnarray}
\begin{eqnarray}
|\nabla f(x)|\leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}},\quad x\in \mathbb{B}_{n},
\end{eqnarray} where ![]() $|\mathbb{B}_{n}|$ denotes the volume of the unit ball
$|\mathbb{B}_{n}|$ denotes the volume of the unit ball ![]() $\mathbb{B}_{n}$. The equality in (1.9) holds if and only if x = 0 and
$\mathbb{B}_{n}$. The equality in (1.9) holds if and only if x = 0 and ![]() $f=U \circ T$ for some
$f=U \circ T$ for some ![]() $T\in O(n)$, where U is the Poisson integral of the function that equals 1 on a hemisphere and −1 on the remaining hemisphere and O(n) denotes the set of orthogonal transformations of
$T\in O(n)$, where U is the Poisson integral of the function that equals 1 on a hemisphere and −1 on the remaining hemisphere and O(n) denotes the set of orthogonal transformations of ![]() $\mathbb{R}^{n}$.
$\mathbb{R}^{n}$.
Note that, for n = 2, (1.9) can be obtained directly from (1.3). Curiously, for n = 3, (1.9) should be replaced by
 \begin{equation*}|\nabla f(x)| \lt \frac{8}{3\sqrt{3}}\frac{1}{1-|x|^{2}},\quad x\in \mathbb{B}_{3},\end{equation*}
\begin{equation*}|\nabla f(x)| \lt \frac{8}{3\sqrt{3}}\frac{1}{1-|x|^{2}},\quad x\in \mathbb{B}_{3},\end{equation*} where  $\frac{8}{3\sqrt{3}} ( \gt 2\frac{|\mathbb{B}_{2}|}{|\mathbb{B}_{3}|}=1.5)$ is the best possible; see [Reference Khavinson10, Note] and [11, Remark 1]. Until 2019, Melentijević in [Reference Melentijević17, Theorem 2] established the following sharp inequality:
$\frac{8}{3\sqrt{3}} ( \gt 2\frac{|\mathbb{B}_{2}|}{|\mathbb{B}_{3}|}=1.5)$ is the best possible; see [Reference Khavinson10, Note] and [11, Remark 1]. Until 2019, Melentijević in [Reference Melentijević17, Theorem 2] established the following sharp inequality:
 \begin{equation*}|\nabla f(x)|\leq \frac{1}{|x|^{2}}\Big(\frac{(1+\frac{1}{3}|x|^{2})^{\frac{3}{2}}}{1-|x|^{2}}-1\Big),\quad x\in \mathbb{B}_{3},\end{equation*}
\begin{equation*}|\nabla f(x)|\leq \frac{1}{|x|^{2}}\Big(\frac{(1+\frac{1}{3}|x|^{2})^{\frac{3}{2}}}{1-|x|^{2}}-1\Big),\quad x\in \mathbb{B}_{3},\end{equation*} for every harmonic function ![]() $f:\mathbb{B}_{3} \rightarrow (-1,1)$.
$f:\mathbb{B}_{3} \rightarrow (-1,1)$.
Remark 1.4. Factually, (1.9) at x = 0 holds for all ![]() $n\geq2$ and the constant
$n\geq2$ and the constant ![]() $2 |\mathbb{B}_{n-1}|/|\mathbb{B}_{n}|$ is optimal in this case; see [Reference Axler, Bourdon and Ramey2, Theorem 6.26] or [Reference Kalaj6, Corollary 2.2]. Furthermore, the requirement that f is real-valued is crucial in the validity of (1.9). In fact, (1.9) fails even at x = 0 for complex-valued harmonic functions [Reference Axler, Bourdon and Ramey2, p. 126]. In this paper, for vector-valued harmonic functions
$2 |\mathbb{B}_{n-1}|/|\mathbb{B}_{n}|$ is optimal in this case; see [Reference Axler, Bourdon and Ramey2, Theorem 6.26] or [Reference Kalaj6, Corollary 2.2]. Furthermore, the requirement that f is real-valued is crucial in the validity of (1.9). In fact, (1.9) fails even at x = 0 for complex-valued harmonic functions [Reference Axler, Bourdon and Ramey2, p. 126]. In this paper, for vector-valued harmonic functions ![]() $f:\mathbb{B}_{n}\rightarrow \mathbb{R}^{m}$, we find that (1.9) still hold by using the matrix (operator) norm of the Jacobian matrix
$f:\mathbb{B}_{n}\rightarrow \mathbb{R}^{m}$, we find that (1.9) still hold by using the matrix (operator) norm of the Jacobian matrix ![]() $\nabla f(x)\in \mathbb{R}^{m\times n}$, that is the square root of the biggest eigenvalue of
$\nabla f(x)\in \mathbb{R}^{m\times n}$, that is the square root of the biggest eigenvalue of ![]() $(\nabla f(x))^{T} \nabla f(x)$.
$(\nabla f(x))^{T} \nabla f(x)$.
Theorem 1.5. Let ![]() $f:\mathbb{B}_{n}\rightarrow \mathbb{B}_{m}$ be harmonic functions with
$f:\mathbb{B}_{n}\rightarrow \mathbb{B}_{m}$ be harmonic functions with ![]() $n=2,$ or
$n=2,$ or ![]() $n\geq4$. Then
$n\geq4$. Then
 \begin{eqnarray}
\|\nabla f(x)\|\leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}},\quad x\in \mathbb{B}_{n},
\end{eqnarray}
\begin{eqnarray}
\|\nabla f(x)\|\leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}},\quad x\in \mathbb{B}_{n},
\end{eqnarray} where ![]() $\|\nabla f(x)\|$ denotes the matrix norm of
$\|\nabla f(x)\|$ denotes the matrix norm of ![]() $\nabla f(x)\in \mathbb{R}^{m\times n}$.
$\nabla f(x)\in \mathbb{R}^{m\times n}$.
We restate (1.10) in the terms of the hyperbolic metric as follows. The proof is standard and omitted here.
Theorem 1.6. Let ![]() $f:\mathbb{B}_{n}\rightarrow \mathbb{B}_{m}$ be harmonic functions with
$f:\mathbb{B}_{n}\rightarrow \mathbb{B}_{m}$ be harmonic functions with ![]() $n=2,$ or
$n=2,$ or ![]() $n\geq4$. Then
$n\geq4$. Then
 \begin{eqnarray}
|f(x)-f(y)| \leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|} d_{\mathbb{B}_{n}}(x,y), \quad x,y\in \mathbb{B}_{n}.
\end{eqnarray}
\begin{eqnarray}
|f(x)-f(y)| \leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|} d_{\mathbb{B}_{n}}(x,y), \quad x,y\in \mathbb{B}_{n}.
\end{eqnarray}Remark 1.7. The distance in the left side of (1.11) is Euclidean but not hyperbolic. Based on the inequality (1.3) and Theorem 1.1, one would conjecture a sharper version of (1.9) that, for harmonic functions ![]() $f:\mathbb{B}_{n}\rightarrow(-1,1)$ with
$f:\mathbb{B}_{n}\rightarrow(-1,1)$ with ![]() $n\geq4$,
$n\geq4$,
 \begin{equation*} \frac{|\nabla f(x)|}{1-|f(x)|^{2}}\leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}}, \quad x\in \mathbb{B}_{n}.\end{equation*}
\begin{equation*} \frac{|\nabla f(x)|}{1-|f(x)|^{2}}\leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}}, \quad x\in \mathbb{B}_{n}.\end{equation*}However, it is not the case as shown by a counter-example [Reference Khalfallah, Mateljević and Purtić9, Theorem 2.1].
Remark 1.8. Let ![]() $f:\mathbb{B}_{n}\rightarrow \mathbb{R}^{m}$. When m = 1, the matrix norm concises with the Euclidean norm of
$f:\mathbb{B}_{n}\rightarrow \mathbb{R}^{m}$. When m = 1, the matrix norm concises with the Euclidean norm of ![]() $\nabla f(x)\in \mathbb{R}^{n}$, i.e.
$\nabla f(x)\in \mathbb{R}^{n}$, i.e. ![]() $\|\nabla f(x) \|=|\nabla f(x)|$. Furthermore, it holds that
$\|\nabla f(x) \|=|\nabla f(x)|$. Furthermore, it holds that
where  $\triangledown |f| (x) =(\frac{\partial |f|}{\partial x_{1}},\frac{\partial |f|}{\partial x_{2}},\ldots\frac{\partial |f|}{\partial x_{n}})$ denotes the gradient of the Euclidean norm of f(x).
$\triangledown |f| (x) =(\frac{\partial |f|}{\partial x_{1}},\frac{\partial |f|}{\partial x_{2}},\ldots\frac{\partial |f|}{\partial x_{n}})$ denotes the gradient of the Euclidean norm of f(x).
In the study of the Schwarz–Pick inequality for holomorphic functions, the quantity ![]() $|\triangledown |f||$ was first adopted by Pavlović [Reference Pavlović18] due to that the classical form in (1.1) does not hold generally for vector-valued holomorphic functions. To obtain analogous form of (1.1), Pavlović gave that, for holomorphic mappings
$|\triangledown |f||$ was first adopted by Pavlović [Reference Pavlović18] due to that the classical form in (1.1) does not hold generally for vector-valued holomorphic functions. To obtain analogous form of (1.1), Pavlović gave that, for holomorphic mappings ![]() $f=(f_{1}, \ldots, f_{n}): \mathbb{D} \rightarrow \mathbb{C}^{n}$ with
$f=(f_{1}, \ldots, f_{n}): \mathbb{D} \rightarrow \mathbb{C}^{n}$ with ![]() $|f|=(|f_{1}|^{2}+\cdots +|f_{n}|^{2})^{1/2} \lt 1$,
$|f|=(|f_{1}|^{2}+\cdots +|f_{n}|^{2})^{1/2} \lt 1$,
 \begin{equation}
|\triangledown |f| (z)|\leq \frac{1-|f(z)| ^{2}}{1-|z| ^{2}}, \quad z\in \mathbb{D}.
\end{equation}
\begin{equation}
|\triangledown |f| (z)|\leq \frac{1-|f(z)| ^{2}}{1-|z| ^{2}}, \quad z\in \mathbb{D}.
\end{equation} Following the idea of Pavlović, Chen and Hamada established the vector-valued version of the Khavinson conjecture for the norm of harmonic functions from the Euclidean unit ball ![]() $\mathbb{B}_{n}$ into the unit ball of the real Minkowski space by complicated calculations [Reference Chen and Hamada4]. By the same technique, they gave several sharp Schwarz–Pick type inequalities for pluriharmonic functions from the Euclidean unit ball (or the unit polydisc) in
$\mathbb{B}_{n}$ into the unit ball of the real Minkowski space by complicated calculations [Reference Chen and Hamada4]. By the same technique, they gave several sharp Schwarz–Pick type inequalities for pluriharmonic functions from the Euclidean unit ball (or the unit polydisc) in ![]() $\mathbb{C}^{n}$ into the unit ball of the Minkowski space. Very recently, using the technique of the present author [Reference Xu27], Chen et al. have provided some improvements and generalizations of the corresponding results in [Reference Chen and Hamada4] into Banach spaces by a relatively simple proof [Reference Chen, Hamada, Ponnusamy and Vijayakumar5].
$\mathbb{C}^{n}$ into the unit ball of the Minkowski space. Very recently, using the technique of the present author [Reference Xu27], Chen et al. have provided some improvements and generalizations of the corresponding results in [Reference Chen and Hamada4] into Banach spaces by a relatively simple proof [Reference Chen, Hamada, Ponnusamy and Vijayakumar5].
As a large subclass of the harmonic functions, the concept of monogenic functions appears in Clifford analysis, which is also a natural generalization of complex analysis into higher dimensions over non-commutative algebras. For monogenic functions, the Schwarz lemma does not hold at least in the original form, observed by Yang and Qian [Reference Yang and Qian23, Remark 2] and they established a Schwarz lemma outside of the unit ball in ![]() $\mathbb{R}^{n+1}$. Recently, some analogues of Schwarz lemma inside the unit ball were obtained in Clifford analysis [Reference Zhang24, Reference Zhang25], quaternionic analysis [Reference Gu13, Reference Wang, Sun and Bian22] and octonionic analysis [Reference Wang, Bian and Liu21]. For example, by integral representations of harmonic functions and Möbius transformations with Clifford coefficients, Zhang established the following Schwarz type lemma.
$\mathbb{R}^{n+1}$. Recently, some analogues of Schwarz lemma inside the unit ball were obtained in Clifford analysis [Reference Zhang24, Reference Zhang25], quaternionic analysis [Reference Gu13, Reference Wang, Sun and Bian22] and octonionic analysis [Reference Wang, Bian and Liu21]. For example, by integral representations of harmonic functions and Möbius transformations with Clifford coefficients, Zhang established the following Schwarz type lemma.
Theorem 1.9. [Reference Zhang25, Theorem 3.2]
Let ![]() $f:\mathbb{B}_{n+1} \rightarrow \mathbb{R}_{0,n}$ be a Clifford algebra valued monogenic function with
$f:\mathbb{B}_{n+1} \rightarrow \mathbb{R}_{0,n}$ be a Clifford algebra valued monogenic function with ![]() $|f(x)|\leq1, x \in \mathbb{B}_{n+1}$. If
$|f(x)|\leq1, x \in \mathbb{B}_{n+1}$. If ![]() $f(a)=0$ for some
$f(a)=0$ for some ![]() $a\in \mathbb{B}_{n+1}$, then
$a\in \mathbb{B}_{n+1}$, then
 \begin{eqnarray}
|f(x)| \leq \frac{(1+|a|)^{n}}{\sqrt[n+1]{2}-1} \frac{|x-a|}{|1-\overline{a}x|^{n+1}}, \quad x \in \mathbb{B}_{n+1},
\end{eqnarray}
\begin{eqnarray}
|f(x)| \leq \frac{(1+|a|)^{n}}{\sqrt[n+1]{2}-1} \frac{|x-a|}{|1-\overline{a}x|^{n+1}}, \quad x \in \mathbb{B}_{n+1},
\end{eqnarray} where ![]() $|\cdot |$ is the norm and
$|\cdot |$ is the norm and ![]() $\overline{\cdot } $ is the conjugate in
$\overline{\cdot } $ is the conjugate in ![]() $\mathbb{R}_{0,n}$.
$\mathbb{R}_{0,n}$.
By the same technique as in the prove of Theorem 1.1, we shall offer a unify method to establish Schwarz type inequalities for harmonic functions in Clifford analysis and octonionic analysis as follows, instead of monogenic functions.
Theorem 1.10. Let ![]() $f:\mathbb{B}_{n+1} \rightarrow \mathbb{R}_{0,n}$ be a Clifford algebra valued harmonic function with
$f:\mathbb{B}_{n+1} \rightarrow \mathbb{R}_{0,n}$ be a Clifford algebra valued harmonic function with ![]() $|f(x)|\leq1, x \in \mathbb{B}_{n+1}$. If
$|f(x)|\leq1, x \in \mathbb{B}_{n+1}$. If ![]() $f(a)=0$ for some
$f(a)=0$ for some ![]() $a\in \mathbb{B}_{n+1}$, then
$a\in \mathbb{B}_{n+1}$, then
 \begin{eqnarray}
|f(x)| \leq \frac{(1+|a|)^{n-1}}{\sqrt[n+1]{2}-1} \frac{|x-a|}{|1-\overline{a}x|^{n}}, \quad x \in \mathbb{B}_{n+1},
\end{eqnarray}
\begin{eqnarray}
|f(x)| \leq \frac{(1+|a|)^{n-1}}{\sqrt[n+1]{2}-1} \frac{|x-a|}{|1-\overline{a}x|^{n}}, \quad x \in \mathbb{B}_{n+1},
\end{eqnarray}and as a corollary
 \begin{equation*}|\nabla f(a)| \leq \frac{1}{\sqrt[n+1]{2}-1} \frac{1}{(1+|a|)(1- |a|)^{n}}.\end{equation*}
\begin{equation*}|\nabla f(a)| \leq \frac{1}{\sqrt[n+1]{2}-1} \frac{1}{(1+|a|)(1- |a|)^{n}}.\end{equation*}Theorem 1.11. Let ![]() $f:\mathbb{B}_{8} \rightarrow \mathbb{O}$ be an octonion valued harmonic function with
$f:\mathbb{B}_{8} \rightarrow \mathbb{O}$ be an octonion valued harmonic function with ![]() $|f(x)|\leq1, x \in \mathbb{B}_{8}$. If
$|f(x)|\leq1, x \in \mathbb{B}_{8}$. If ![]() $f(a)=0$ for some
$f(a)=0$ for some ![]() $a\in \mathbb{B}_{8}$, then
$a\in \mathbb{B}_{8}$, then
 \begin{equation*}|f(x)| \leq \frac{(1+|a|)^{6}}{\sqrt[8]{2}-1} \frac{|x-a|}{|1-\overline{a}x|^{7}}, \quad x \in \mathbb{B}_{8}.\end{equation*}
\begin{equation*}|f(x)| \leq \frac{(1+|a|)^{6}}{\sqrt[8]{2}-1} \frac{|x-a|}{|1-\overline{a}x|^{7}}, \quad x \in \mathbb{B}_{8}.\end{equation*} where ![]() $|\cdot |$ is the norm and
$|\cdot |$ is the norm and ![]() $\overline{\cdot } $ is the conjugate in
$\overline{\cdot } $ is the conjugate in ![]() $\mathbb{O}$.
$\mathbb{O}$.
Note that ![]() $|1-\overline{a}x| \lt 1+|a|$ for
$|1-\overline{a}x| \lt 1+|a|$ for ![]() $a,x \in \mathbb{B}_{n+1}$. Hence, in a broader function class being harmonic, the obtained results in Theorems 1.10 and 1.11 are essential improvements of monogenic versions in [Reference Zhang24, Theorem 4.8], [Reference Zhang25, Theorem 3.2] and [Reference Wang, Bian and Liu21, Theorem 4], respectively.
$a,x \in \mathbb{B}_{n+1}$. Hence, in a broader function class being harmonic, the obtained results in Theorems 1.10 and 1.11 are essential improvements of monogenic versions in [Reference Zhang24, Theorem 4.8], [Reference Zhang25, Theorem 3.2] and [Reference Wang, Bian and Liu21, Theorem 4], respectively.
The remaining part of the paper is organized as follows. The next section shall recall preliminaries on Clifford algebras and use it to rewrite some known properties of Möbius transformations of ![]() $\mathbb{B}_{n}$, which shall be used in the proof of main results. The § 3 is devoted to the proof of Theorems 1.1, 1.2 and 1.5. In § 4, we recall the concepts of monogenic functions in Clifford analysis and octonionic analysis and show that they are subclasses of harmonic functions. Finally, we give the proof of Theorems 1.10 and 1.11.
$\mathbb{B}_{n}$, which shall be used in the proof of main results. The § 3 is devoted to the proof of Theorems 1.1, 1.2 and 1.5. In § 4, we recall the concepts of monogenic functions in Clifford analysis and octonionic analysis and show that they are subclasses of harmonic functions. Finally, we give the proof of Theorems 1.10 and 1.11.
2. Preliminaries
In this section, we first recall preliminaries on Clifford algebras; see e.g. [Reference Gürlebeck, Habetha and Sprößig19].
Denote by ![]() $\mathbb{R}_{0,n}$ the real Clifford algebra over imaginary units
$\mathbb{R}_{0,n}$ the real Clifford algebra over imaginary units ![]() $\{e_1,e_2,\ldots,e_n\}$ which satisfy
$\{e_1,e_2,\ldots,e_n\}$ which satisfy
where e 0 is identify with 1, δij is Kronecker function.
Each element ![]() $a\in \mathbb{R}_{0,n}$ has the form of
$a\in \mathbb{R}_{0,n}$ has the form of
 \begin{equation*}a=\sum_{A}a_{A}e_{A},\quad a_A \in \mathbb{R},\end{equation*}
\begin{equation*}a=\sum_{A}a_{A}e_{A},\quad a_A \in \mathbb{R},\end{equation*} where ![]() $A = h_{1}h_{2} \cdots h_{r}$ with
$A = h_{1}h_{2} \cdots h_{r}$ with ![]() $ 1\leq h_{1} \lt h_{2} \lt \cdots \lt h_{r}\leq n, e_{A}=e_{h_{1}}e_{h_{2}}\cdots e_{h_{r}}$ and
$ 1\leq h_{1} \lt h_{2} \lt \cdots \lt h_{r}\leq n, e_{A}=e_{h_{1}}e_{h_{2}}\cdots e_{h_{r}}$ and ![]() $e_{\emptyset}=e_{0}=1$. The real part of
$e_{\emptyset}=e_{0}=1$. The real part of ![]() $a\in \mathbb{R}_{0,n}$ is
$a\in \mathbb{R}_{0,n}$ is ![]() ${\rm{Re}}\, a=a_{\emptyset}=a_0$. The norm of a is defined by
${\rm{Re}}\, a=a_{\emptyset}=a_0$. The norm of a is defined by  $|a|= ({\sum_{A}|a_{A}|^{2}} )^{\frac{1}{2}}.$ As a real vector space, the dimension of Clifford algebra
$|a|= ({\sum_{A}|a_{A}|^{2}} )^{\frac{1}{2}}.$ As a real vector space, the dimension of Clifford algebra ![]() $\mathbb{R}_{0,n}$ is 2n. The paravector x in
$\mathbb{R}_{0,n}$ is 2n. The paravector x in ![]() $\mathbb{R}_{0,n}$ is given by
$\mathbb{R}_{0,n}$ is given by
 \begin{equation*}x = \sum _{i=0}^{n} x_{i}e_{i}, \quad x_{i}\in \mathbb{R}.\end{equation*}
\begin{equation*}x = \sum _{i=0}^{n} x_{i}e_{i}, \quad x_{i}\in \mathbb{R}.\end{equation*} Hence, the space ![]() $\mathbb R^{n+1}$ can be identified as the set of all paravector in Clifford algebra
$\mathbb R^{n+1}$ can be identified as the set of all paravector in Clifford algebra ![]() $\mathbb{R}_{0,n}$. For paravector x ≠ 0, it inverse is given by
$\mathbb{R}_{0,n}$. For paravector x ≠ 0, it inverse is given by
 \begin{equation*}x^{-1}= \frac{\overline{x}}{|x|^{2}}, \end{equation*}
\begin{equation*}x^{-1}= \frac{\overline{x}}{|x|^{2}}, \end{equation*} where ![]() $\overline{x}$ denotes the conjugate of x, that is
$\overline{x}$ denotes the conjugate of x, that is ![]() $\overline{x}= \sum _{i=0}^{n} x_{i}\overline{e_{i}}
= x_{0}-\sum _{i=1}^{n} x_{i}{e_{i}}$. Note that Clifford algebra is associative and non-commutative, but not divisible generally. The equality
$\overline{x}= \sum _{i=0}^{n} x_{i}\overline{e_{i}}
= x_{0}-\sum _{i=1}^{n} x_{i}{e_{i}}$. Note that Clifford algebra is associative and non-commutative, but not divisible generally. The equality ![]() $|ab|=|a| |b|$ does not hold generally for
$|ab|=|a| |b|$ does not hold generally for ![]() $a, b \in \mathbb{R}_{0,n}$ when
$a, b \in \mathbb{R}_{0,n}$ when ![]() $n\geq 3$. However, it is holds for in the following special case in Clifford algebras (see [Reference Gürlebeck, Habetha and Sprößig19, Theorem 3.14]).
$n\geq 3$. However, it is holds for in the following special case in Clifford algebras (see [Reference Gürlebeck, Habetha and Sprößig19, Theorem 3.14]).
Lemma 2.1. Let ![]() $a\in \mathbb{R}_{0,n} $ and
$a\in \mathbb{R}_{0,n} $ and ![]() $x\in \mathbb R^{n+1}$. Then
$x\in \mathbb R^{n+1}$. Then
Now we introduce some known properties of Möbius transformations of ![]() $\mathbb{B}_{n}$ by using the language of Clifford algebras, which shall be used in the sequel. These results can be founded in [Reference Ahlfors1, Reference Stoll20].
$\mathbb{B}_{n}$ by using the language of Clifford algebras, which shall be used in the sequel. These results can be founded in [Reference Ahlfors1, Reference Stoll20].
It is known that any Möbius transformation ψ of ![]() $\mathbb{B}_{n}$ onto itself has the form
$\mathbb{B}_{n}$ onto itself has the form ![]() $\psi=T \varphi_{a}$, where
$\psi=T \varphi_{a}$, where ![]() $T\in O(n)$ and φa is Möbius transformations of
$T\in O(n)$ and φa is Möbius transformations of ![]() $\mathbb{B}_{n}$ with
$\mathbb{B}_{n}$ with ![]() $\varphi_{a}(0)=a\in \mathbb{B}_{n}$, given by
$\varphi_{a}(0)=a\in \mathbb{B}_{n}$, given by
 \begin{eqnarray}
\varphi_{a}(x)=\frac{(1-|a|^{2})(a-x)+|a-x|^{2}a}{[x,a]^{2}},\quad x\in \mathbb{B}_{n},
\end{eqnarray}
\begin{eqnarray}
\varphi_{a}(x)=\frac{(1-|a|^{2})(a-x)+|a-x|^{2}a}{[x,a]^{2}},\quad x\in \mathbb{B}_{n},
\end{eqnarray}where
 \begin{equation*} [x,a]=\sqrt{1+|a|^{2}|x|^{2}-2\langle a, x\rangle}.\end{equation*}
\begin{equation*} [x,a]=\sqrt{1+|a|^{2}|x|^{2}-2\langle a, x\rangle}.\end{equation*} Here ![]() $\langle \cdot, \cdot\rangle$ is real inner product in
$\langle \cdot, \cdot\rangle$ is real inner product in ![]() $\mathbb{R}^{n}$.
$\mathbb{R}^{n}$.
The vector space ![]() $\mathbb{R}^{n}$ can be viewed as the paravector in
$\mathbb{R}^{n}$ can be viewed as the paravector in ![]() $\mathbb{R}_{0,n-1}$, and then
$\mathbb{R}_{0,n-1}$, and then
Hence,
 \begin{equation*}[x,a]=\sqrt{1+|a|^{2}|x|^{2}-2{\rm{Re}}\,(x\overline{a})}=|1-x\overline{a}|.\end{equation*}
\begin{equation*}[x,a]=\sqrt{1+|a|^{2}|x|^{2}-2{\rm{Re}}\,(x\overline{a})}=|1-x\overline{a}|.\end{equation*}Consequently, the mapping φa can be expressed as
 \begin{equation*}\varphi_{a}(x)=\frac{(1-|a|^{2}+a\overline{(a-x)})(a-x)}{|1-x\overline{a}|^{2}}=\frac{(1 -a\overline{x})(a-x)}{|1-x\overline{a}|^{2}}
=(1 -x\overline{a})^{-1}(a-x).\end{equation*}
\begin{equation*}\varphi_{a}(x)=\frac{(1-|a|^{2}+a\overline{(a-x)})(a-x)}{|1-x\overline{a}|^{2}}=\frac{(1 -a\overline{x})(a-x)}{|1-x\overline{a}|^{2}}
=(1 -x\overline{a})^{-1}(a-x).\end{equation*}Furthermore, it holds that
To see this, we should notice that
Let ![]() $y=\varphi_{a}(x)$. Then
$y=\varphi_{a}(x)$. Then
which implies that
Denote by ![]() $\mathcal{M}(\mathbb{B}_{n})$ Möbius transformations of
$\mathcal{M}(\mathbb{B}_{n})$ Möbius transformations of ![]() $\mathbb{B}_{n}$ onto
$\mathbb{B}_{n}$ onto ![]() $\mathbb{B}_{n}$. Recall a useful identity [Reference Stoll20, Theorem 2.1.3]
$\mathbb{B}_{n}$. Recall a useful identity [Reference Stoll20, Theorem 2.1.3]
 \begin{equation*}\frac{|\varphi_{(x)}-\varphi_{(y)}|^{2}}{(1-|\varphi_{(x)}|^{2})(1-|\varphi_{(y)}|^{2})}=\frac{|x-y|^{2}}{(1-|x|^{2})(1-|y|^{2})}, \quad \varphi\in \mathcal{M}(\mathbb{B}_{n}).\end{equation*}
\begin{equation*}\frac{|\varphi_{(x)}-\varphi_{(y)}|^{2}}{(1-|\varphi_{(x)}|^{2})(1-|\varphi_{(y)}|^{2})}=\frac{|x-y|^{2}}{(1-|x|^{2})(1-|y|^{2})}, \quad \varphi\in \mathcal{M}(\mathbb{B}_{n}).\end{equation*}This formula implies that
 \begin{eqnarray}
\|\nabla \varphi_{a} (x)\|= \overline{\lim}_{y\rightarrow x} \frac{|\varphi_{a}(x)-\varphi_{a}(y)|}{|x-y|}= \frac{1-|\varphi_{a} (x)|^{2}}{1-|x|^{2}}.
\end{eqnarray}
\begin{eqnarray}
\|\nabla \varphi_{a} (x)\|= \overline{\lim}_{y\rightarrow x} \frac{|\varphi_{a}(x)-\varphi_{a}(y)|}{|x-y|}= \frac{1-|\varphi_{a} (x)|^{2}}{1-|x|^{2}}.
\end{eqnarray}From the identity
 \begin{eqnarray}
1-|\varphi_{a}(x)|^{2}=1-|a-x|^{2}|1-x\overline{a}|^{-2}=\frac{(1-|a|^{2})(1-|x|^{2})}{|1-x\overline{a}|^{2}},
\end{eqnarray}
\begin{eqnarray}
1-|\varphi_{a}(x)|^{2}=1-|a-x|^{2}|1-x\overline{a}|^{-2}=\frac{(1-|a|^{2})(1-|x|^{2})}{|1-x\overline{a}|^{2}},
\end{eqnarray}it is easy to see that
 \begin{eqnarray}
\|\nabla \varphi_{a} (x)\|=\frac{1-|a|^{2}}{|1-x\overline{a}|^{2}}\in (\frac{1-|a|}{1+|a|},\frac{1+|a|}{1-|a|}).
\end{eqnarray}
\begin{eqnarray}
\|\nabla \varphi_{a} (x)\|=\frac{1-|a|^{2}}{|1-x\overline{a}|^{2}}\in (\frac{1-|a|}{1+|a|},\frac{1+|a|}{1-|a|}).
\end{eqnarray}3. Proof of Theorems 1.1, 1.2 and 1.5
To prove main results, we recall the invariance of the Laplace equation [Reference Hua8, Chapter 1.10, p. 22].
Lemma 3.1. Let ![]() $a\in \mathbb{B}_n$. If an independent variable undergoes the transformation
$a\in \mathbb{B}_n$. If an independent variable undergoes the transformation ![]() $y=\varphi_{a}(x), x\in \mathbb{B}_n,$ and the function is transformed by
$y=\varphi_{a}(x), x\in \mathbb{B}_n,$ and the function is transformed by
 \begin{eqnarray}
Y(y)=\Big(\frac{|1-x\overline{a}|^{2}}{1-|a|^{2}}\Big)^{\frac{n}{2}-1} X(x),
\end{eqnarray}
\begin{eqnarray}
Y(y)=\Big(\frac{|1-x\overline{a}|^{2}}{1-|a|^{2}}\Big)^{\frac{n}{2}-1} X(x),
\end{eqnarray}then
 \begin{equation*} (1-|x|^{2})^{\frac{n}{2}+1}\sum _{i=0}^{n-1} \frac{\partial^{2} X}{\partial x_{i}^{2}}=(1-|y|^{2})^{\frac{n}{2}+1}\sum _{i=0}^{n-1} \frac{\partial^{2} Y}{\partial y_{i}^{2}}.\end{equation*}
\begin{equation*} (1-|x|^{2})^{\frac{n}{2}+1}\sum _{i=0}^{n-1} \frac{\partial^{2} X}{\partial x_{i}^{2}}=(1-|y|^{2})^{\frac{n}{2}+1}\sum _{i=0}^{n-1} \frac{\partial^{2} Y}{\partial y_{i}^{2}}.\end{equation*} Let ![]() $y=\varphi_{a}(x)$. From the identity
$y=\varphi_{a}(x)$. From the identity
and (2.2), the transformation in (3.1) can be rewritten as
 \begin{equation*}Y (y)=\Big(\frac{1-|a|^{2}}{|1-y\overline{a}|^{2}}\Big)^{\frac{n}{2}-1} X( \varphi_{a}^{-1} (y) )=\Big(\frac{1-|a|^{2}}{|1-y\overline{a}|^{2}}\Big)^{\frac{n}{2}-1} X( \varphi_{a} (y) ).\end{equation*}
\begin{equation*}Y (y)=\Big(\frac{1-|a|^{2}}{|1-y\overline{a}|^{2}}\Big)^{\frac{n}{2}-1} X( \varphi_{a}^{-1} (y) )=\Big(\frac{1-|a|^{2}}{|1-y\overline{a}|^{2}}\Big)^{\frac{n}{2}-1} X( \varphi_{a} (y) ).\end{equation*}Hence, Reference HuaLemma 3.1 gives directly the following result.
Lemma 3.2. Let ![]() $a\in \mathbb{B}_n$ and f be a harmonic function in
$a\in \mathbb{B}_n$ and f be a harmonic function in ![]() $\mathbb{B}_n$. Then the function
$\mathbb{B}_n$. Then the function
 \begin{equation*}f[\varphi_{a}](x):=\Big(\frac{1-|a|^{2}}{|1-x\overline{a}|^{2}}\Big)^{\frac{n}{2}-1} f\circ \varphi_{a}(x)\end{equation*}
\begin{equation*}f[\varphi_{a}](x):=\Big(\frac{1-|a|^{2}}{|1-x\overline{a}|^{2}}\Big)^{\frac{n}{2}-1} f\circ \varphi_{a}(x)\end{equation*} is still harmonic in ![]() $\mathbb{B}_{n}$.
$\mathbb{B}_{n}$.
Now we are in a position to prove Theorem 1.2.
Proof of Theorem 1.2
Firstly, let us prove the estimate (1.7) in the special case x = 0, i.e.
for the positive harmonic function f defined in ![]() $\mathbb{B}_{n}$.
$\mathbb{B}_{n}$.
From the Poisson–Herglotz representation, it holds that
 \begin{equation*}f(x)=\int_{\partial \mathbb{B}_{n}}P(x, \xi)\,\mathrm{d}\mu(\xi), \quad x\in \mathbb{B}_{n},\end{equation*}
\begin{equation*}f(x)=\int_{\partial \mathbb{B}_{n}}P(x, \xi)\,\mathrm{d}\mu(\xi), \quad x\in \mathbb{B}_{n},\end{equation*} where µ is a positive Borel measure on ![]() $\partial \mathbb{B}_{n}$ such that
$\partial \mathbb{B}_{n}$ such that  $\int_{\partial \mathbb{B}_{n}} \,\mathrm{d}\mu(\xi)=f(0)$.
$\int_{\partial \mathbb{B}_{n}} \,\mathrm{d}\mu(\xi)=f(0)$.
Note that
 \begin{eqnarray}
\nabla P_{\xi}(x)=-\frac{2x}{|x-\xi|^{n}}-\frac{n(1-|x|^{2})}{|x-\xi|^{n+2}}(x-\xi), \quad (x, \xi)\in \mathbb{B}_{n} \times \partial \mathbb{B}_{n}.
\end{eqnarray}
\begin{eqnarray}
\nabla P_{\xi}(x)=-\frac{2x}{|x-\xi|^{n}}-\frac{n(1-|x|^{2})}{|x-\xi|^{n+2}}(x-\xi), \quad (x, \xi)\in \mathbb{B}_{n} \times \partial \mathbb{B}_{n}.
\end{eqnarray}In particular,
Hence,
 \begin{equation*}|\nabla f(0)|=n|\int_{\partial \mathbb{B}_{n}} \xi\,\mathrm{d}\mu(\xi)|\leq n\int_{\partial \mathbb{B}_{n}} \,\mathrm{d}\mu(\xi)=nf(0),\end{equation*}
\begin{equation*}|\nabla f(0)|=n|\int_{\partial \mathbb{B}_{n}} \xi\,\mathrm{d}\mu(\xi)|\leq n\int_{\partial \mathbb{B}_{n}} \,\mathrm{d}\mu(\xi)=nf(0),\end{equation*} where the equality is attained if and only if the measure µ is a singleton, that is to say, there exits some ![]() $\xi \in \partial \mathbb{B}_{n}$ such that
$\xi \in \partial \mathbb{B}_{n}$ such that
This shows (3.3) and that the equality in (3.3) is attained if and only if ![]() $f(x)=f(0)P_{\xi}(x)$ for some
$f(x)=f(0)P_{\xi}(x)$ for some ![]() $\xi \in \partial \mathbb{B}_{n}$, and in this case, we have, by (3.4),
$\xi \in \partial \mathbb{B}_{n}$, and in this case, we have, by (3.4),
 \begin{eqnarray*}
& & (|x|^{2}-1)\nabla f(x)+(n-2)xf(x)
\\
&=& f(0)(|x|^{2}-1)\Big( -\frac{2x}{|x-\xi|^{n}}-\frac{n(1-|x|^{2})}{|x-\xi|^{n+2}}(x-\xi) -\frac{(n-2)x}{|x-\xi|^{n}} \Big)
\\
&=&f(0) \frac{n(|x|^{2}-1)}{|x-\xi|^{n+2}} ((|x|^{2}-1)(x-\xi)-x |x-\xi|^{2})
\\
&=& f(0) \frac{n(|x|^{2}-1)}{|x-\xi|^{n+2}} ( |x|^{2}-1 -x \overline{(x-\xi)})(x-\xi)
\\
&=& f(0) \frac{n(|x|^{2}-1)}{|x-\xi|^{n+2}} ( x \overline{\xi}-1)(x-\xi).
\end{eqnarray*}
\begin{eqnarray*}
& & (|x|^{2}-1)\nabla f(x)+(n-2)xf(x)
\\
&=& f(0)(|x|^{2}-1)\Big( -\frac{2x}{|x-\xi|^{n}}-\frac{n(1-|x|^{2})}{|x-\xi|^{n+2}}(x-\xi) -\frac{(n-2)x}{|x-\xi|^{n}} \Big)
\\
&=&f(0) \frac{n(|x|^{2}-1)}{|x-\xi|^{n+2}} ((|x|^{2}-1)(x-\xi)-x |x-\xi|^{2})
\\
&=& f(0) \frac{n(|x|^{2}-1)}{|x-\xi|^{n+2}} ( |x|^{2}-1 -x \overline{(x-\xi)})(x-\xi)
\\
&=& f(0) \frac{n(|x|^{2}-1)}{|x-\xi|^{n+2}} ( x \overline{\xi}-1)(x-\xi).
\end{eqnarray*}By Lemma 2.1, it follows that
Therefore, the harmonic function ![]() $f(x)=f(0)P_{\xi}(x)$ satisfies the following identity
$f(x)=f(0)P_{\xi}(x)$ satisfies the following identity
 \begin{eqnarray}
|(|x|^{2}-1)\nabla f(x)+(n-2)xf(x)|=nf(0)\frac{1-|x|^{2}}{|x-\xi|^{n}} =nf(x), \quad (x, \xi)\in \mathbb{B}_{n} \times \partial \mathbb{B}_{n}.\qquad
\end{eqnarray}
\begin{eqnarray}
|(|x|^{2}-1)\nabla f(x)+(n-2)xf(x)|=nf(0)\frac{1-|x|^{2}}{|x-\xi|^{n}} =nf(x), \quad (x, \xi)\in \mathbb{B}_{n} \times \partial \mathbb{B}_{n}.\qquad
\end{eqnarray} Secondly, we prove the conclusion in the general case x = a. Fix ![]() $a\in \mathbb{B}_{n}$. By Lemma 3.2, the function
$a\in \mathbb{B}_{n}$. By Lemma 3.2, the function ![]() $f[\varphi_{a}](x)$ is harmonic in
$f[\varphi_{a}](x)$ is harmonic in ![]() $\mathbb{B}_{n}$. Hence, by applying the inequality (3.3) to the positive and harmonic function
$\mathbb{B}_{n}$. Hence, by applying the inequality (3.3) to the positive and harmonic function ![]() $f[\varphi_{a}](x)$, we have
$f[\varphi_{a}](x)$, we have
Direct calculations gives that
 \begin{equation*}\nabla \frac{1}{|1-x\overline{a}|^{n-2}}=\frac{(2-n)(|a|^{2}x-a)}{|1-x\overline{a}|^{n-2}}, \quad x\in \mathbb{B}_{n},\end{equation*}
\begin{equation*}\nabla \frac{1}{|1-x\overline{a}|^{n-2}}=\frac{(2-n)(|a|^{2}x-a)}{|1-x\overline{a}|^{n-2}}, \quad x\in \mathbb{B}_{n},\end{equation*}and
 \begin{equation*} \nabla (\frac{1}{|1-x\overline{a}|^{n-2}} f\circ \varphi_{a}(x))|_{x=0}= (|a|^{2}-1)\nabla f(a)+(n-2)af(a),\end{equation*}
\begin{equation*} \nabla (\frac{1}{|1-x\overline{a}|^{n-2}} f\circ \varphi_{a}(x))|_{x=0}= (|a|^{2}-1)\nabla f(a)+(n-2)af(a),\end{equation*}then (3.6) reduces into
Let us consider the case of the equality in (1.7) is attained at x = a, that is
Therefore, the previously obtained result of x = 0 gives that ![]() $f[\varphi_{a}](x)=f[\varphi_{a}](0)P_{\xi}(x)$ for some
$f[\varphi_{a}](x)=f[\varphi_{a}](0)P_{\xi}(x)$ for some ![]() $\xi \in \partial \mathbb{B}_{n}$. More precisely,
$\xi \in \partial \mathbb{B}_{n}$. More precisely,
 \begin{equation*}\Big(\frac{1-|a|^{2}}{|1-x\overline{a}|^{2}}\Big)^{\frac{n}{2}-1} f\circ \varphi_{a}(x)=(1-|a|^{2})^{\frac{n}{2}-1} f(a)P_{\xi}(x),\quad x\in \mathbb{B}_{n}.\end{equation*}
\begin{equation*}\Big(\frac{1-|a|^{2}}{|1-x\overline{a}|^{2}}\Big)^{\frac{n}{2}-1} f\circ \varphi_{a}(x)=(1-|a|^{2})^{\frac{n}{2}-1} f(a)P_{\xi}(x),\quad x\in \mathbb{B}_{n}.\end{equation*}Thus
 \begin{equation*} f\circ \varphi_{a}(x)= f(a)|1-x\overline{a}|^{n-2}P_{\xi}(x), \quad x\in \mathbb{B}_{n}.\end{equation*}
\begin{equation*} f\circ \varphi_{a}(x)= f(a)|1-x\overline{a}|^{n-2}P_{\xi}(x), \quad x\in \mathbb{B}_{n}.\end{equation*} Replacing x with ![]() $\varphi_{a}(x)$ in the above formula and noticing (2.2), we obtain
$\varphi_{a}(x)$ in the above formula and noticing (2.2), we obtain
 \begin{equation*}f(x)=f(a)|1-\varphi_{a}(x)\overline{a}|^{n-2}P_{\xi}\circ \varphi_{a}(x), \quad x\in \mathbb{B}_{n}. \end{equation*}
\begin{equation*}f(x)=f(a)|1-\varphi_{a}(x)\overline{a}|^{n-2}P_{\xi}\circ \varphi_{a}(x), \quad x\in \mathbb{B}_{n}. \end{equation*} Finally, we verify that every positive harmonic function f defined by (1.8) satisfies the equality in (1.7) for all ![]() $x \in \mathbb{B}_{n}$ and
$x \in \mathbb{B}_{n}$ and ![]() $\xi \in \partial \mathbb{B}_{n}$. Observing (3.2) and (2.4), straightforward calculations give
$\xi \in \partial \mathbb{B}_{n}$. Observing (3.2) and (2.4), straightforward calculations give
 \begin{align*}
&\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1} f(x))\\
&\qquad=\nabla\log\Big(f(a)(1-|x|^{2})^{\frac{n}{2}-1} \Big(\frac{1-|a|^{2}}{|1-x\overline{a}|}\Big)^{n-2}P_{\xi}\circ \varphi_{a}(x)\Big)\\
&\qquad=\nabla\log\Big(\Big(\frac{(1-|a|^{2})(1-|x|^{2})}{|1-x\overline{a}|^{2}}\Big)^{\frac{n}{2}-1}P_{\xi}\circ \varphi_{a}(x)\Big)\\
&\qquad=\nabla\log( (1-|\varphi_{a}(x)|^{2})^{\frac{n}{2}-1}P_{\xi}\circ \varphi_{a}(x))\\
&\qquad=\frac{n}{2}\nabla\log \frac{1-|\varphi_{a}(x)|^{2} }{|\varphi_{a}(x)-\xi |^{2}}\\
&\qquad=(\nabla\log ((1-|\cdot|^{2})^{\frac{n}{2}-1}P_{\xi}(\cdot)) )(\varphi_{a}(x)) \nabla \varphi_{a}(x).
\end{align*}
\begin{align*}
&\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1} f(x))\\
&\qquad=\nabla\log\Big(f(a)(1-|x|^{2})^{\frac{n}{2}-1} \Big(\frac{1-|a|^{2}}{|1-x\overline{a}|}\Big)^{n-2}P_{\xi}\circ \varphi_{a}(x)\Big)\\
&\qquad=\nabla\log\Big(\Big(\frac{(1-|a|^{2})(1-|x|^{2})}{|1-x\overline{a}|^{2}}\Big)^{\frac{n}{2}-1}P_{\xi}\circ \varphi_{a}(x)\Big)\\
&\qquad=\nabla\log( (1-|\varphi_{a}(x)|^{2})^{\frac{n}{2}-1}P_{\xi}\circ \varphi_{a}(x))\\
&\qquad=\frac{n}{2}\nabla\log \frac{1-|\varphi_{a}(x)|^{2} }{|\varphi_{a}(x)-\xi |^{2}}\\
&\qquad=(\nabla\log ((1-|\cdot|^{2})^{\frac{n}{2}-1}P_{\xi}(\cdot)) )(\varphi_{a}(x)) \nabla \varphi_{a}(x).
\end{align*}Observe that (3.5) has an equivalent representation
 \begin{equation*}|\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1}P_{\xi}(x)) |= \frac{n}{1-|x|^{2}}, \quad (x, \xi)\in \mathbb{B}_{n} \times \partial \mathbb{B}_{n}.\end{equation*}
\begin{equation*}|\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1}P_{\xi}(x)) |= \frac{n}{1-|x|^{2}}, \quad (x, \xi)\in \mathbb{B}_{n} \times \partial \mathbb{B}_{n}.\end{equation*} Combining this with ![]() $\nabla \varphi_{a}(x)/\|\nabla \varphi_{a}(x)\| \in O(n)$ and (2.3), we infer that, for all
$\nabla \varphi_{a}(x)/\|\nabla \varphi_{a}(x)\| \in O(n)$ and (2.3), we infer that, for all ![]() $(x, \xi)\in \mathbb{B}_{n} \times \partial \mathbb{B}_{n}$,
$(x, \xi)\in \mathbb{B}_{n} \times \partial \mathbb{B}_{n}$,
 \begin{align*}
&|\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1} f(x))|\\
&\qquad= |\nabla\log ((1-|\cdot|^{2})^{\frac{n}{2}-1}P_{\xi}(\cdot)) )(\varphi_{a}(x))| \| \nabla \varphi_{a}(x)\|\\
&\qquad=\frac{n}{1-| \varphi_{a}(x)|^{2}} \| \nabla \varphi_{a}(x)\|\\
&\qquad=\frac{n}{1-|x|^{2}},
\end{align*}
\begin{align*}
&|\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1} f(x))|\\
&\qquad= |\nabla\log ((1-|\cdot|^{2})^{\frac{n}{2}-1}P_{\xi}(\cdot)) )(\varphi_{a}(x))| \| \nabla \varphi_{a}(x)\|\\
&\qquad=\frac{n}{1-| \varphi_{a}(x)|^{2}} \| \nabla \varphi_{a}(x)\|\\
&\qquad=\frac{n}{1-|x|^{2}},
\end{align*}which completes the proof.
With the help of Theorem 1.2, we turn back to prove Theorem 1.1.
Proof of Theorem 1.1
By Theorem 1.2, it holds that, for the harmonic function ![]() $f:\mathbb{B}_{n} \rightarrow \mathbb{R}^{+}$,
$f:\mathbb{B}_{n} \rightarrow \mathbb{R}^{+}$,
which has an equivalent representation
 \begin{equation*}|\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1} f(x)) |\leq \frac{n}{1-|x|^{2}}, \quad x\in \mathbb{B}_{n}.\end{equation*}
\begin{equation*}|\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1} f(x)) |\leq \frac{n}{1-|x|^{2}}, \quad x\in \mathbb{B}_{n}.\end{equation*}Hence, by Cauchy–Schwarz inequality,
 \begin{equation*}|d (\log ((1-|x|^{2})^{\frac{n}{2}-1} f(x)) ) |\leq |\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1} f(x)) | |dx|\leq \frac{n|dx|}{1-|x|^{2}}.\end{equation*}
\begin{equation*}|d (\log ((1-|x|^{2})^{\frac{n}{2}-1} f(x)) ) |\leq |\nabla\log( (1-|x|^{2})^{\frac{n}{2}-1} f(x)) | |dx|\leq \frac{n|dx|}{1-|x|^{2}}.\end{equation*} Recall that the hyperbolic metric on ![]() $\mathbb{B}_n$ is given by
$\mathbb{B}_n$ is given by
 \begin{equation*} d_{\mathbb{B}_{n}}(x,y)=2\tanh^{-1}(|\varphi_{y}(x)|)=\log \frac{1+|\varphi_{y}(x)|}{1-|\varphi_{y}(x)|},\end{equation*}
\begin{equation*} d_{\mathbb{B}_{n}}(x,y)=2\tanh^{-1}(|\varphi_{y}(x)|)=\log \frac{1+|\varphi_{y}(x)|}{1-|\varphi_{y}(x)|},\end{equation*}and its responding element of arclength is
 \begin{equation*}ds=\frac{2|dx|}{1-|x|^{2}}.\end{equation*}
\begin{equation*}ds=\frac{2|dx|}{1-|x|^{2}}.\end{equation*}Integrating both sides of the above inequality along geodesics for the hyperbolic metric from x to y, we have
 \begin{equation*}| \log \frac{(1-|x|^{2})^{\frac{n}{2}-1}f(x)}{(1-|y|^{2})^{\frac{n}{2}-1}f(y)} | \leq \frac{n}{2}d_{\mathbb{B}_{n}}(x,y),\end{equation*}
\begin{equation*}| \log \frac{(1-|x|^{2})^{\frac{n}{2}-1}f(x)}{(1-|y|^{2})^{\frac{n}{2}-1}f(y)} | \leq \frac{n}{2}d_{\mathbb{B}_{n}}(x,y),\end{equation*}which implies that
 \begin{equation*}d_{\mathbb{R}^{+}}(f(x),f(y))=| \log \frac{f(x)}{f(y)} | \leq \frac{n}{2}d_{\mathbb{B}_{n}}(x,y)+(\frac{n}{2}-1)| \log \frac{1-|y|^{2}}{1-|x|^{2}} |. \end{equation*}
\begin{equation*}d_{\mathbb{R}^{+}}(f(x),f(y))=| \log \frac{f(x)}{f(y)} | \leq \frac{n}{2}d_{\mathbb{B}_{n}}(x,y)+(\frac{n}{2}-1)| \log \frac{1-|y|^{2}}{1-|x|^{2}} |. \end{equation*}Combining this with the inequality
 \begin{eqnarray}
\frac{1+|\varphi_{y}(x)|}{1-|\varphi_{y}(x)|}\geq \frac{1-|y|^{2}}{1-|x|^{2}}, \quad x, y \in \mathbb{B}_{n},
\end{eqnarray}
\begin{eqnarray}
\frac{1+|\varphi_{y}(x)|}{1-|\varphi_{y}(x)|}\geq \frac{1-|y|^{2}}{1-|x|^{2}}, \quad x, y \in \mathbb{B}_{n},
\end{eqnarray}we get
To see (3.7), using the identity (2.4), we first obtain
 \begin{equation*}\frac{ 1+|\varphi_{y}(x)| }{1-|\varphi_{y}(x)| } = \frac{(1+|\varphi_{y}(x)|)^{2}}{1-|\varphi_{y}(x)|^{2}}=\frac{(1+|\varphi_{y}(x)|)^{2}|1-x\overline{y}|^{2}}{(1-|x|^{2})(1-|y|^{2})},\end{equation*}
\begin{equation*}\frac{ 1+|\varphi_{y}(x)| }{1-|\varphi_{y}(x)| } = \frac{(1+|\varphi_{y}(x)|)^{2}}{1-|\varphi_{y}(x)|^{2}}=\frac{(1+|\varphi_{y}(x)|)^{2}|1-x\overline{y}|^{2}}{(1-|x|^{2})(1-|y|^{2})},\end{equation*} then the question reduces into proving that, for ![]() $x, y \in \mathbb{B}_{n}$ with
$x, y \in \mathbb{B}_{n}$ with ![]() $|x| \gt |y|$,
$|x| \gt |y|$,
If ![]() $|x-y|\geq1-|y|^{2}$, it is a trivial assertion. Otherwise, for
$|x-y|\geq1-|y|^{2}$, it is a trivial assertion. Otherwise, for ![]() $|x-y| \lt 1-|y|^{2}$,
$|x-y| \lt 1-|y|^{2}$,
 \begin{eqnarray*}
&\Leftrightarrow& |1-x\overline{y}|^{2}\geq(1-|y|^{2}-|x-y|)^{2}=(1-|y|^{2})^{2}+|x-y|^{2}-2|x-y|(1-|y|^{2})
\\
&\Leftrightarrow&(1-|x|^{2})(1-|y|^{2})\geq (1-|y|^{2})^{2}-2|x-y|(1-|y|^{2})
\\
&\Leftrightarrow& 1-|x|^{2} \geq 1-|y|^{2}-2|x-y|
\\
&\Leftrightarrow& |x|^{2}-|y|^{2} \leq2|x-y|.
\end{eqnarray*}
\begin{eqnarray*}
&\Leftrightarrow& |1-x\overline{y}|^{2}\geq(1-|y|^{2}-|x-y|)^{2}=(1-|y|^{2})^{2}+|x-y|^{2}-2|x-y|(1-|y|^{2})
\\
&\Leftrightarrow&(1-|x|^{2})(1-|y|^{2})\geq (1-|y|^{2})^{2}-2|x-y|(1-|y|^{2})
\\
&\Leftrightarrow& 1-|x|^{2} \geq 1-|y|^{2}-2|x-y|
\\
&\Leftrightarrow& |x|^{2}-|y|^{2} \leq2|x-y|.
\end{eqnarray*} Under the assumption that ![]() $x, y \in \mathbb{B}_{n}$ with
$x, y \in \mathbb{B}_{n}$ with ![]() $|x| \gt |y|$, it holds naturally that
$|x| \gt |y|$, it holds naturally that
Now the proof is complete.
Remark 3.3. In the proof of Theorem 1.1, we give a direct and basic proof of inequality (3.7). As pointed out by an anonymous reader, (3.7) is a consequence of the known inequality
 \begin{eqnarray}
\frac{|\rho(x,z)-\rho(z,y)|}{1-\rho(x,z)\rho(z,y)} \leq \rho(x,y) \leq \frac{\rho(x,z)+\rho(z,y)}{1+\rho(x,z)\rho(z,y)}, \quad x,y,z\in \mathbb{B}_{n},
\end{eqnarray}
\begin{eqnarray}
\frac{|\rho(x,z)-\rho(z,y)|}{1-\rho(x,z)\rho(z,y)} \leq \rho(x,y) \leq \frac{\rho(x,z)+\rho(z,y)}{1+\rho(x,z)\rho(z,y)}, \quad x,y,z\in \mathbb{B}_{n},
\end{eqnarray} where ![]() $\rho(x,y)=|\varphi_{y}(x)|$ is the so-called pseudo-hyperbolic metric on
$\rho(x,y)=|\varphi_{y}(x)|$ is the so-called pseudo-hyperbolic metric on ![]() $\mathbb{B}_{n}$.
$\mathbb{B}_{n}$.
To see this, we need only to consider ![]() $x,y\in \mathbb{B}_{n}$ with
$x,y\in \mathbb{B}_{n}$ with ![]() $|x|\geq |y|$. In this case, it follows that
$|x|\geq |y|$. In this case, it follows that
 \begin{eqnarray}
\frac{1-|y|^{2}}{1-|x|^{2}}\leq \frac{(1+|x|)(1-|y|)}{(1-|x|)(1+|y|)}
=\frac{1+\frac{|x|-|y|}{1-|x||y|}}{1-\frac{|x|-|y|}{1-|x||y|}}.
\end{eqnarray}
\begin{eqnarray}
\frac{1-|y|^{2}}{1-|x|^{2}}\leq \frac{(1+|x|)(1-|y|)}{(1-|x|)(1+|y|)}
=\frac{1+\frac{|x|-|y|}{1-|x||y|}}{1-\frac{|x|-|y|}{1-|x||y|}}.
\end{eqnarray}According to (3.9), it holds that
 \begin{eqnarray}\frac{|x|-|y|}{1-|x||y|} =\frac{|\rho(x,0)-\rho(0,y)|}{1-\rho(x,0)\rho(0,y)} \leq \rho(x,y).
\end{eqnarray}
\begin{eqnarray}\frac{|x|-|y|}{1-|x||y|} =\frac{|\rho(x,0)-\rho(0,y)|}{1-\rho(x,0)\rho(0,y)} \leq \rho(x,y).
\end{eqnarray} Note that ![]() $(1+t)(1-t)^{-1}$ is an increasing function for
$(1+t)(1-t)^{-1}$ is an increasing function for ![]() $t\in (0,1)$, then (3.10) and (3.11) give the desired inequality (3.7).
$t\in (0,1)$, then (3.10) and (3.11) give the desired inequality (3.7).
Proof of Theorem 1.5
Let ![]() $l\in \partial \mathbb{B}_{m}$. For the harmonic
$l\in \partial \mathbb{B}_{m}$. For the harmonic ![]() $f:\mathbb{B}_{n}\rightarrow \mathbb{B}_{m}$, consider the scalar harmonic function
$f:\mathbb{B}_{n}\rightarrow \mathbb{B}_{m}$, consider the scalar harmonic function ![]() $g=\langle f, l \rangle$, where
$g=\langle f, l \rangle$, where ![]() $\langle \cdot, \cdot\rangle$ is real inner product in
$\langle \cdot, \cdot\rangle$ is real inner product in ![]() $\mathbb{R}^{m}$. Now the scalar harmonic function
$\mathbb{R}^{m}$. Now the scalar harmonic function ![]() $g:\mathbb{B}_{n}\rightarrow (-1,1)$ satisfies the condition of (1.9). Hence,
$g:\mathbb{B}_{n}\rightarrow (-1,1)$ satisfies the condition of (1.9). Hence,
 \begin{equation*}|\nabla \langle f(x), l \rangle| = |(\nabla f(x))^{T}\cdot l | \leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}},\quad x\in \mathbb{B}_{n},\end{equation*}
\begin{equation*}|\nabla \langle f(x), l \rangle| = |(\nabla f(x))^{T}\cdot l | \leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}},\quad x\in \mathbb{B}_{n},\end{equation*} where · denotes the matrix product of ![]() $(\nabla f(x))^{T}\in \mathbb{R}^{n\times m}$ with
$(\nabla f(x))^{T}\in \mathbb{R}^{n\times m}$ with ![]() $l\in \mathbb{R}^{m\times1}$. Due to the arbitrariness of
$l\in \mathbb{R}^{m\times1}$. Due to the arbitrariness of ![]() $l\in \partial \mathbb{B}_{m}$, we obtain
$l\in \partial \mathbb{B}_{m}$, we obtain
 \begin{equation*}\|\nabla f(x)\|\leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}},\quad x\in \mathbb{B}_{n},\end{equation*}
\begin{equation*}\|\nabla f(x)\|\leq \frac{|\mathbb{B}_{n-1}|}{|\mathbb{B}_{n}|}\frac{2}{1-|x|^{2}},\quad x\in \mathbb{B}_{n},\end{equation*}as desired.
4. Proof of Theorems 1.10 and 1.11
Before proving the theorem, we recall the concepts of monogenic functions in Clifford analysis and octonionic analysis and show that they are subclasses of harmonic functions.
First, we give the definition of monogenic functions in Clifford analysis [Reference Gürlebeck, Habetha and Sprößig19].
Definition 4.1. Let ![]() $\Omega \subset \mathbb{R}^{n+1}$ and
$\Omega \subset \mathbb{R}^{n+1}$ and ![]() $f:\Omega \rightarrow \mathbb{R}_{0,n}$ be a Clifford algebra valued C1 function. The function
$f:\Omega \rightarrow \mathbb{R}_{0,n}$ be a Clifford algebra valued C1 function. The function ![]() $f=\sum_{A} e_{A} f_{A}$ is called (left) monogenic in Ω if
$f=\sum_{A} e_{A} f_{A}$ is called (left) monogenic in Ω if
 \begin{equation*} Df(x):=\sum _{i=0}^{n}e_{i} \frac{\partial f}{\partial x_{i}}(x)
= \sum _{i=0}^{n} \sum_{A} e_{i}e_{A} \frac{\partial f_{A}}{\partial x_{i}}(x)=0, \quad x\in \Omega. \end{equation*}
\begin{equation*} Df(x):=\sum _{i=0}^{n}e_{i} \frac{\partial f}{\partial x_{i}}(x)
= \sum _{i=0}^{n} \sum_{A} e_{i}e_{A} \frac{\partial f_{A}}{\partial x_{i}}(x)=0, \quad x\in \Omega. \end{equation*}And the function f is called (left) anti-monogenic in Ω if
 \begin{equation*} \overline{D}f(x):=\sum _{i=0}^{n}\overline{e_{i}} \frac{\partial f}{\partial x_{i}}(x)= \sum _{i=0}^{n} \sum_{A}\overline{e_{i}}e_{A} \frac{\partial f_{A}}{\partial x_{i}}(x)=0, \quad x\in \Omega. \end{equation*}
\begin{equation*} \overline{D}f(x):=\sum _{i=0}^{n}\overline{e_{i}} \frac{\partial f}{\partial x_{i}}(x)= \sum _{i=0}^{n} \sum_{A}\overline{e_{i}}e_{A} \frac{\partial f_{A}}{\partial x_{i}}(x)=0, \quad x\in \Omega. \end{equation*} Due to the non-commutation of Clifford algebra, the right monogenic functions could be defined similarly. Note that all monogenic functions on ![]() $\mathbb{B}_{n+1}$ is real analytic. For the Clifford algebra valued C 2 functions f, by the association of Clifford algebra, it holds that
$\mathbb{B}_{n+1}$ is real analytic. For the Clifford algebra valued C 2 functions f, by the association of Clifford algebra, it holds that
where ![]() $\Delta _{n+1} $ is Laplace operator in
$\Delta _{n+1} $ is Laplace operator in ![]() $\mathbb{R}^{n+1}$.
$\mathbb{R}^{n+1}$.
In fact, Definition 4.1 can also be built in octonionic analysis.
Definition 4.2. Denote by ![]() $\mathbb{O}$ the non-commutative and non-associative algebra with canonical vector basis
$\mathbb{O}$ the non-commutative and non-associative algebra with canonical vector basis ![]() $\{e_{0}=1, e_1,e_2,\ldots,e_7\}$. Let
$\{e_{0}=1, e_1,e_2,\ldots,e_7\}$. Let ![]() $\Omega \subset \mathbb{O}$ and
$\Omega \subset \mathbb{O}$ and ![]() $f:\Omega \rightarrow \mathbb{O}$ be a octonionic valued C 1 function. The function
$f:\Omega \rightarrow \mathbb{O}$ be a octonionic valued C 1 function. The function  $f=\sum_{i=0}^{7} e_{i} f_{i}$ is called (left) monogenic in Ω if
$f=\sum_{i=0}^{7} e_{i} f_{i}$ is called (left) monogenic in Ω if
 \begin{equation*} \mathcal{D}f(x):=\sum _{i=0}^{7} e_{i} \frac{\partial f}{\partial x_{i}}(x)
= \sum _{i=0}^{7} \sum_{j=0}^{7} e_{i}e_{j} \frac{\partial f_{j}}{\partial x_{i}}(x)=0, \quad x\in \Omega. \end{equation*}
\begin{equation*} \mathcal{D}f(x):=\sum _{i=0}^{7} e_{i} \frac{\partial f}{\partial x_{i}}(x)
= \sum _{i=0}^{7} \sum_{j=0}^{7} e_{i}e_{j} \frac{\partial f_{j}}{\partial x_{i}}(x)=0, \quad x\in \Omega. \end{equation*}And the function f is called (left) anti-monogenic in Ω if
 \begin{equation*} \overline{\mathcal{D}}f(x):=\sum _{i=0}^{7}\overline{e_{i} }\frac{\partial f}{\partial x_{i}}(x)
= \sum _{i=0}^{7} \sum_{j=0}^{7}\overline{e_{i}}e_{j} \frac{\partial f_{j}}{\partial x_{i}}(x)=0, \quad x\in \Omega. \end{equation*}
\begin{equation*} \overline{\mathcal{D}}f(x):=\sum _{i=0}^{7}\overline{e_{i} }\frac{\partial f}{\partial x_{i}}(x)
= \sum _{i=0}^{7} \sum_{j=0}^{7}\overline{e_{i}}e_{j} \frac{\partial f_{j}}{\partial x_{i}}(x)=0, \quad x\in \Omega. \end{equation*} Even though the algebra of octonions is non-associative, (4.1) still holds in the octonionic setting. Indeed, the Artin theorem shows that the subalgebra generated by two elements (![]() $\mathcal{D}$ and f) in octonions is associative, which implies
$\mathcal{D}$ and f) in octonions is associative, which implies
where Δ is Laplace operator in ![]() $\mathbb{R}^{8}$.
$\mathbb{R}^{8}$.
Hence, monogenic functions in Clifford analysis and octonionic analysis belong to harmonic functions from (4.1) and (4.2).
Since the proof of Theorem 1.11 is completely similar to Theorem 1.10, we only show Theorem 1.10 in this section.
Proof of Theorem 1.10
Let f be as described in Theorem 1.10. First, if a = 0 (that is ![]() $f(0)=0$), then [Reference Zhang25, Theorem 3.1] gives that
$f(0)=0$), then [Reference Zhang25, Theorem 3.1] gives that
 \begin{eqnarray}
|f(x)| \leq \frac{1}{\sqrt[n+1]{2}-1} |x|, \quad x \in \mathbb{B}_{n+1}.
\end{eqnarray}
\begin{eqnarray}
|f(x)| \leq \frac{1}{\sqrt[n+1]{2}-1} |x|, \quad x \in \mathbb{B}_{n+1}.
\end{eqnarray}Now (1.14) at x = 0 is obtained. Otherwise, as in the prove of Theorem 1.1, consider the Clifford algebra valued harmonic function
 \begin{equation*}g_{1}(x)=\Big(\frac{1-|a|^{2}}{|1-x\overline{a}|^{2}}\Big)^{\frac{n+1}{2}-1} f\circ \varphi_{a}(x), \quad x\in \mathbb{B}_{n+1}.\end{equation*}
\begin{equation*}g_{1}(x)=\Big(\frac{1-|a|^{2}}{|1-x\overline{a}|^{2}}\Big)^{\frac{n+1}{2}-1} f\circ \varphi_{a}(x), \quad x\in \mathbb{B}_{n+1}.\end{equation*}In view of the estimate (2.5), set
 \begin{equation*}g(x)= \Big(\frac{1-|a|}{1+|a|}\Big)^{\frac{n-1}{2}}g_{1}(x)=\Big(\frac{1-|a|}{|1-x\overline{a}|}\Big)^{n-1 } f\circ \varphi_{a}(x)\end{equation*}
\begin{equation*}g(x)= \Big(\frac{1-|a|}{1+|a|}\Big)^{\frac{n-1}{2}}g_{1}(x)=\Big(\frac{1-|a|}{|1-x\overline{a}|}\Big)^{n-1 } f\circ \varphi_{a}(x)\end{equation*} with ![]() $|g(x)| \lt 1$ for
$|g(x)| \lt 1$ for ![]() $x\in \mathbb{B}_{n+1}$. Applying the inequality (4.3) to the harmonic function g(x), we obtain
$x\in \mathbb{B}_{n+1}$. Applying the inequality (4.3) to the harmonic function g(x), we obtain
 \begin{equation*} \Big(\frac{1-|a|}{|1-x\overline{a}|}\Big)^{n-1 } |f\circ \varphi_{a}(x)|\leq \frac{1}{\sqrt[n+1]{2}-1} |x|, \quad x\in \mathbb{B}_{n+1}.\end{equation*}
\begin{equation*} \Big(\frac{1-|a|}{|1-x\overline{a}|}\Big)^{n-1 } |f\circ \varphi_{a}(x)|\leq \frac{1}{\sqrt[n+1]{2}-1} |x|, \quad x\in \mathbb{B}_{n+1}.\end{equation*} Let ![]() $y=\varphi_{a}(x)$. From the identity (3.2), we have
$y=\varphi_{a}(x)$. From the identity (3.2), we have
 \begin{equation*} |f (y)|\leq \frac{1}{\sqrt[n+1]{2}-1} \Big(\frac{1+|a|}{|1-y\overline{a}|}\Big)^{n-1 } |\varphi_{a}^{-1}(y)|, \quad y\in \mathbb{B}_{n+1}.\end{equation*}
\begin{equation*} |f (y)|\leq \frac{1}{\sqrt[n+1]{2}-1} \Big(\frac{1+|a|}{|1-y\overline{a}|}\Big)^{n-1 } |\varphi_{a}^{-1}(y)|, \quad y\in \mathbb{B}_{n+1}.\end{equation*} Thus the fact ![]() $\varphi_{a}=\varphi_{a}^{-1}$ in (2.2) gives the desired inequality
$\varphi_{a}=\varphi_{a}^{-1}$ in (2.2) gives the desired inequality
 \begin{equation*}|f(x)| \leq \frac{(1+|a|)^{n}}{\sqrt[n+1]{2}-1} \frac{|x-a|}{|1-\overline{a}x|^{n+1}}, \quad x \in \mathbb{B}_{n+1}.\end{equation*}
\begin{equation*}|f(x)| \leq \frac{(1+|a|)^{n}}{\sqrt[n+1]{2}-1} \frac{|x-a|}{|1-\overline{a}x|^{n+1}}, \quad x \in \mathbb{B}_{n+1}.\end{equation*}The proof is completed.
Data availability statement
Data sharing is not applicable to this article as no datasets were generated during the current study.
Funding statement
This work was supported by the Anhui Provincial Natural Science Foundation (No. 2308085MA04), the National Natural Science Foundation of China (Nos. 11801125, 12301097) and the Fundamental Research Funds for the Central Universities (Nos. JZ2023HGQA0117, JZ2023HGTA0169).
Competing interests
There is no financial or non-financial interests that are directly or indirectly related to the work submitted for publication.