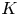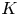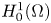1. Introduction
In the last decade, non-local Kirchhoff problems have turned into an extremely active field of research in nonlinear partial differential equations. In particular, from different perspectives and approaches, many authors have investigated problems like (or its variations)

where $\Omega \subset {\rm I}\hskip -0.85mm{\rm R} ^{N}$![]() ($N\geq 1$
($N\geq 1$![]() ) is a smooth bounded domain, $\|u\|:=|\nabla u|_{2}$
) is a smooth bounded domain, $\|u\|:=|\nabla u|_{2}$![]() is the usual norm in the Sobolev space $H^{1}_{0}(\Omega )$
is the usual norm in the Sobolev space $H^{1}_{0}(\Omega )$![]() , $m:[0,\infty )\to {\rm I}\hskip -0.85mm{\rm R}$
, $m:[0,\infty )\to {\rm I}\hskip -0.85mm{\rm R}$![]() and $f:{\rm I}\hskip -0.85mm{\rm R} \to {\rm I}\hskip -0.85mm{\rm R}$
and $f:{\rm I}\hskip -0.85mm{\rm R} \to {\rm I}\hskip -0.85mm{\rm R}$![]() are continuous functions with $m$
are continuous functions with $m$![]() positive and away from zero. Without any intention to provide a complete overview about the matter, we just refer the reader to the following references [Reference Alves, Corrêa and Ma1, Reference He and Zou7, Reference Kirchhoff9–Reference Perera and Zhang12] which can give a first glimpse about mathematical, physical and historical aspects involving stationary Kirchhoff models.
positive and away from zero. Without any intention to provide a complete overview about the matter, we just refer the reader to the following references [Reference Alves, Corrêa and Ma1, Reference He and Zou7, Reference Kirchhoff9–Reference Perera and Zhang12] which can give a first glimpse about mathematical, physical and historical aspects involving stationary Kirchhoff models.
Nevertheless, most recently, it has grown the interest of some authors, attracted by inherent mathematical difficulties, in investigating the case in which $m$![]() is a degenerate function, i.e., when $m$
is a degenerate function, i.e., when $m$![]() is not required to be bounded from below by a positive constant. In fact, Ambrosetti and Arcoya [Reference Ambrosetti and Arcoya2, Reference Ambrosetti and Arcoya3] took a first step towards the understanding of this class of problems. In [Reference Ambrosetti and Arcoya3], the function $m$
is not required to be bounded from below by a positive constant. In fact, Ambrosetti and Arcoya [Reference Ambrosetti and Arcoya2, Reference Ambrosetti and Arcoya3] took a first step towards the understanding of this class of problems. In [Reference Ambrosetti and Arcoya3], the function $m$![]() is allowed to verify $m(0)=0$
is allowed to verify $m(0)=0$![]() and/or $\lim _{t\to +\infty }m(t)=0$
and/or $\lim _{t\to +\infty }m(t)=0$![]() . It is worth to point out that in such a paper remains the assumption $m(t)>0$
. It is worth to point out that in such a paper remains the assumption $m(t)>0$![]() for $t>0$
for $t>0$![]() . On the other hand, Theorem 2.1 (see also Remark 2.2) in [Reference Ambrosetti and Arcoya2] assures the existence of a non-trivial solution even if $m(t)=0$
. On the other hand, Theorem 2.1 (see also Remark 2.2) in [Reference Ambrosetti and Arcoya2] assures the existence of a non-trivial solution even if $m(t)=0$![]() for some $t>0$
for some $t>0$![]() .
.
Inspired by [Reference Brown and Budin5, Reference Hess8], in [Reference Santos Júnior and Siciliano13], the authors considered the case in which $m$![]() has many different positive zeroes and they proved that the number of positive solutions of (P) is related to the number of points which vanish $m$
has many different positive zeroes and they proved that the number of positive solutions of (P) is related to the number of points which vanish $m$![]() . In order to state the result, we denote by $t_k$
. In order to state the result, we denote by $t_k$![]() , $k=1,2,\ldots K$
, $k=1,2,\ldots K$![]() , the zeroes of $m$
, the zeroes of $m$![]() , $F(t): = \int _0^{t} f$
, $F(t): = \int _0^{t} f$![]() , for every $t\geq 0$
, for every $t\geq 0$![]() , $\lambda _1$
, $\lambda _1$![]() the first eigenvalue of Laplacian operator with homogeneous Dirichlet boundary condition and
the first eigenvalue of Laplacian operator with homogeneous Dirichlet boundary condition and
where
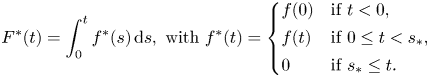
and $s_{\ast }>0$![]() such that $f(t)>0$
such that $f(t)>0$![]() in $(0, s_{\ast })$
in $(0, s_{\ast })$![]() and $f(s_{\ast })=0$
and $f(s_{\ast })=0$![]() .
.
It is proved the following theorem.
Theorem 1.1 Santos Júnior and Siciliano [Reference Santos Júnior and Siciliano13]
If $m:[0, \infty )\to {\rm I}\hskip -0.85mm{\rm R}$![]() is a continuous function and $f:[0, \infty )\to {\rm I}\hskip -0.85mm{\rm R}$
is a continuous function and $f:[0, \infty )\to {\rm I}\hskip -0.85mm{\rm R}$![]() is a locally Lipschitz continuous function satisfying$:$
is a locally Lipschitz continuous function satisfying$:$![]()
(m) there exist positive numbers $0=:t_{0}< t_{1}< t_{2}<\cdots < t_{K}$
 such that
\[ m(t_{k})=0 \ \mbox{and} m>0 \mbox{in} (t_{k-1}, t_{k}), \mbox{for all} k=1,\ldots, K; \]
such that
\[ m(t_{k})=0 \ \mbox{and} m>0 \mbox{in} (t_{k-1}, t_{k}), \mbox{for all} k=1,\ldots, K; \]
(f) there exists $s_{\ast }>0$
 such that $f(t)>0$
such that $f(t)>0$ in $(0, s_{\ast })$
in $(0, s_{\ast })$ and $f(s_{\ast })=0;$
and $f(s_{\ast })=0;$
(A) $\alpha _{k}<\frac 12\int _{t_{k-1}}^{t_{k}}m(s)\,{\textrm {d}}s< |\Omega | \int _0^{s_{\ast }} f$
 , for all $k=1,\ldots , K$
, for all $k=1,\ldots , K$ ,
,
then$,$![]() problem (P) possesses at least $K$
problem (P) possesses at least $K$![]() non-trivial positive solutions. Furthermore$,$
non-trivial positive solutions. Furthermore$,$![]() these solutions are ordered in the $H_{0}^{1}(\Omega )$
these solutions are ordered in the $H_{0}^{1}(\Omega )$![]() -norm$,$
-norm$,$![]() i.e.$,$
i.e.$,$![]()
In this paper, we improve Theorem 1.1 by proving under some appropriated conditions on functions $m$![]() and $f$
and $f$![]() , the existence of $K$
, the existence of $K$![]() further positive solutions for (1.1). Moreover, we show concentration phenomena of these solutions at the zeroes of $m$
further positive solutions for (1.1). Moreover, we show concentration phenomena of these solutions at the zeroes of $m$![]() , when the area $F(s_\ast )=\int _0^{s_{\ast }} f$
, when the area $F(s_\ast )=\int _0^{s_{\ast }} f$![]() tends to zero. Specifically, we have the following result.
tends to zero. Specifically, we have the following result.
Theorem 1.2 Suppose that hypotheses (m) and (f) hold.
(i) If $\alpha _k$
 given by (1.1) satisfies that
given by (1.1) satisfies that
(A’) $\alpha _{k}\leq \frac 12\int _{t_{k-1}}^{t_{k}}m(s)\,{\textrm {d}}s,$
 for all $k=1, \ldots , K,$
for all $k=1, \ldots , K,$
then$,$
 problem (P) possesses at least $K-1$
problem (P) possesses at least $K-1$ positive solutions which are ordered in $H_{0}^{1}(\Omega )$
positive solutions which are ordered in $H_{0}^{1}(\Omega )$ -norm$,$
-norm$,$ i.e.$,$
i.e.$,$ \[ t_{1}<\|v_{2}\|^{2}< t_{2}<\cdots< t_{K-1}<\|v_{K}\|^{2}< t_{K}. \]
\[ t_{1}<\|v_{2}\|^{2}< t_{2}<\cdots< t_{K-1}<\|v_{K}\|^{2}< t_{K}. \]
(ii) Furthermore$,$
 if$,$
if$,$ in addition$,$
in addition$,$ the following condition holds
the following condition holds
(mf) there exists $\gamma :=\lim _{t\searrow 0} \frac {f(t)}{t}\in (0, \infty )$
 and $m(0)<\gamma /\lambda _1,$
and $m(0)<\gamma /\lambda _1,$
then there is one more positive solution $v_{1}\in H_{0}^{1}(\Omega )$
 with
\[ 0<\|v_{1}\|^{2}< t_{1}. \]
with
\[ 0<\|v_{1}\|^{2}< t_{1}. \]
(iii) If we assume the stronger condition (A) instead of (A’), then for every $k=1, \ldots , K,$
 the solution $u_k$
the solution $u_k$ provided in Theorem 1.1 verifies $u_k\not = v_k$
provided in Theorem 1.1 verifies $u_k\not = v_k$ and hence problem (P) has at least $2\,K$
and hence problem (P) has at least $2\,K$ positive solutions.
positive solutions.(iv) Moreover$,$
 if for each $\lambda >0,$
if for each $\lambda >0,$ we denote by $(P_{\lambda })$
we denote by $(P_{\lambda })$ the problem (P) with $F(s_{\ast })=\lambda$
the problem (P) with $F(s_{\ast })=\lambda$ and by $v_{k, \lambda },\ k=1, \ldots , K,$
and by $v_{k, \lambda },\ k=1, \ldots , K,$ the solutions of $(P_{\lambda })$
the solutions of $(P_{\lambda })$ obtained in (i)–(ii), then$,$
obtained in (i)–(ii), then$,$ \[ \lim_{\lambda\searrow 0}\|v_{k, \lambda}\|^{2}=t_{k-1},\quad \forall\,k=1, \ldots, K. \]
\[ \lim_{\lambda\searrow 0}\|v_{k, \lambda}\|^{2}=t_{k-1},\quad \forall\,k=1, \ldots, K. \]
Observe that hypothesis (A’) is weaker than (A).
Let $f_{\lambda }$![]() be a function $f$
be a function $f$![]() satisfying (f), (mf), (A’) and $F(s_{\ast })=\lambda$
satisfying (f), (mf), (A’) and $F(s_{\ast })=\lambda$![]() , where $\lambda$
, where $\lambda$![]() is a positive parameter. In Theorem 1.2-iv), we are interested in proving that if $f^{\ast }_{\lambda }:=(f_{\lambda })^{\ast }$
is a positive parameter. In Theorem 1.2-iv), we are interested in proving that if $f^{\ast }_{\lambda }:=(f_{\lambda })^{\ast }$![]() and $\lambda$
and $\lambda$![]() goes to zero, then the square of the $H_{0}^{1}$
goes to zero, then the square of the $H_{0}^{1}$![]() -norm of the solutions of
-norm of the solutions of
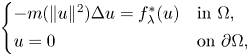
are concentrating at the points which vanish function $m$![]() . This concentration result is somewhat more general than those commonly found in the literature, mainly because the nonlinearity is not required tending to zero in a uniform way. In fact, in [Reference Clément and Sweers6], for example, in order to study concentration phenomena of the solutions, when $\lambda$
. This concentration result is somewhat more general than those commonly found in the literature, mainly because the nonlinearity is not required tending to zero in a uniform way. In fact, in [Reference Clément and Sweers6], for example, in order to study concentration phenomena of the solutions, when $\lambda$![]() tends to infinity, of the problem
tends to infinity, of the problem
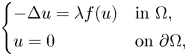
the authors require $\lambda f$![]() goes uniformly to infinity. Instead, we are just assuming $F(s_{\ast })\to 0$
goes uniformly to infinity. Instead, we are just assuming $F(s_{\ast })\to 0$![]() . This assumption allows $f^{\ast }_\lambda$
. This assumption allows $f^{\ast }_\lambda$![]() going to zero in different ways for each $t\in (0, s_{\ast })$
going to zero in different ways for each $t\in (0, s_{\ast })$![]() .
.
The paper is organized as follows. In §2, we provide a technical lemma which plays an important role in the existence result. In §3, we prove items (i), (ii) and (iii) of Theorem 1.2 by looking for critical points with norm in the interval $(t_{k-1}^{1/2}, t_k^{1/2})$![]() of a truncated functional $I_{k}$
of a truncated functional $I_{k}$![]() defined in $H_0^{1}(\Omega )$
defined in $H_0^{1}(\Omega )$![]() . In §4, we study the part (iv) of the cited theorem, that is, the concentration phenomena of the solutions obtained in Theorem 1.2 as $\lambda =F(s_{\ast })$
. In §4, we study the part (iv) of the cited theorem, that is, the concentration phenomena of the solutions obtained in Theorem 1.2 as $\lambda =F(s_{\ast })$![]() tends to zero.
tends to zero.
2. A technical lemma
Taking into account that $f^{\ast }$![]() is continuous and bounded, we deduce by the compact embedding Rellich–Kondrachov theorem that the function $J: H_{0}^{1}(\Omega )\to {\rm I}\hskip -0.85mm{\rm R}$
is continuous and bounded, we deduce by the compact embedding Rellich–Kondrachov theorem that the function $J: H_{0}^{1}(\Omega )\to {\rm I}\hskip -0.85mm{\rm R}$![]() defined by
defined by
is weakly continuous and then it attains its maximum in any closed ball in $H_0^{1}(\Omega )$![]() . In particular, the map $\alpha :[0, \infty )\to {\rm I}\hskip -0.85mm{\rm R}$
. In particular, the map $\alpha :[0, \infty )\to {\rm I}\hskip -0.85mm{\rm R}$![]() given by
given by
is well defined; i.e., the set
is non-empty for every $t\geq 0$![]() .
.
The following technical lemma collects the main properties of $\alpha$![]() and $S_t$
and $S_t$![]() . In order to state it, we define the function $M_{k} :{\rm I}\hskip -0.85mm{\rm R} \to {\rm I}\hskip -0.85mm{\rm R}$
. In order to state it, we define the function $M_{k} :{\rm I}\hskip -0.85mm{\rm R} \to {\rm I}\hskip -0.85mm{\rm R}$![]() by
by
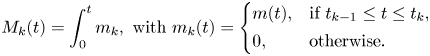
Lemma 2.1 Assume that (f) holds and consider the map $\alpha :[0, \infty )\to {\rm I}\hskip -0.85mm{\rm R}$![]() defined by (2.1) and the set $S_t$
defined by (2.1) and the set $S_t$![]() given by (2.2) for $t\geq 0$
given by (2.2) for $t\geq 0$![]() . We have$:$
. We have$:$![]()
(i) for every $t>0,$
 $\alpha (t)>0$
$\alpha (t)>0$ and each maximizer $u\in S_t,$
and each maximizer $u\in S_t,$ satisfies
satisfies
• $\|u\|^{2}=t$
 , $0< u\leq s_{\ast },$
, $0< u\leq s_{\ast },$
• $u\in C^{2, \beta }(\overline {\Omega })$
 for some $\beta \in (0, 1)$
for some $\beta \in (0, 1)$ and
and• $\partial u/\partial \tau <0$
 on $\partial \Omega ,$
on $\partial \Omega ,$ where $\tau$
where $\tau$ stands for the outward unit normal vector$;$
stands for the outward unit normal vector$;$
(ii) the map $\alpha$
 is differentiable in $(0,\infty )$
is differentiable in $(0,\infty )$ with $\alpha '(t)=(1/2t)\max _{u\in S_t}\int _{\Omega }f^{\ast }(u)u\,{\textrm {d}}x$
with $\alpha '(t)=(1/2t)\max _{u\in S_t}\int _{\Omega }f^{\ast }(u)u\,{\textrm {d}}x$ and $\alpha '$
and $\alpha '$ is upper semicontinuous. In particular$,$
is upper semicontinuous. In particular$,$ $\alpha$
$\alpha$ is increasing. Moreover$,$
is increasing. Moreover$,$ if there exists $\gamma = \lim _{t\to 0} f(t)/t,$
if there exists $\gamma = \lim _{t\to 0} f(t)/t,$ then
\[ \lim_{t\searrow 0}\alpha'(t)=\frac{\gamma}{2\lambda_1} \quad \mbox{and} \quad {\liminf_{t\to t_{{\ast}}}\alpha'(t)>0},\quad \forall\,t_{{\ast}}>0; \]
then
\[ \lim_{t\searrow 0}\alpha'(t)=\frac{\gamma}{2\lambda_1} \quad \mbox{and} \quad {\liminf_{t\to t_{{\ast}}}\alpha'(t)>0},\quad \forall\,t_{{\ast}}>0; \]
(iii) if$,$
 in addition$,$
in addition$,$ condition (m) holds$,$
condition (m) holds$,$ then for every $k\in \{2, \ldots , K\}$
then for every $k\in \{2, \ldots , K\}$ , there exists $\delta _{k-1}>0$
, there exists $\delta _{k-1}>0$ such that the map $g_{k}(t)=(1/2)M_{k}(t)-\alpha (t)$
such that the map $g_{k}(t)=(1/2)M_{k}(t)-\alpha (t)$ is decreasing in $(0, t_{k-1}+\delta _{k-1})$
is decreasing in $(0, t_{k-1}+\delta _{k-1})$ . Moreover$,$
. Moreover$,$ if (mf) holds$,$
if (mf) holds$,$ the same is true in the case $k=1$
the same is true in the case $k=1$ .
.
Proof. (i) Fix $t>0$![]() . For any positive function $\varphi \in H_{0}^{1}(\Omega )$
. For any positive function $\varphi \in H_{0}^{1}(\Omega )$![]() with $\|\varphi \|^{2}\leq t$
with $\|\varphi \|^{2}\leq t$![]() , we have
, we have
and then $\alpha (t) >0$![]() . In particular, if $u\in S_t$
. In particular, if $u\in S_t$![]() , then $u \not = 0$
, then $u \not = 0$![]() . Since
. Since
with strict inequality if $v\not \equiv |v|$![]() , we derive that a maximizer $u\in S_t$
, we derive that a maximizer $u\in S_t$![]() is also non-negative.
is also non-negative.
In addition, we have $\|u \|=t^{1/2}$![]() . Indeed, if, by contradiction, it would be satisfied that $\|u\|< t^{1/2}$
. Indeed, if, by contradiction, it would be satisfied that $\|u\|< t^{1/2}$![]() , then $u$
, then $u$![]() would be a local maximum point in the interior of the ball $B_{t^{1/2}}(0)$
would be a local maximum point in the interior of the ball $B_{t^{1/2}}(0)$![]() of the functional $J\in C^{1}( H_{0}^{1}(\Omega ))$
of the functional $J\in C^{1}( H_{0}^{1}(\Omega ))$![]() . We would get
. We would get
and then $f^{\ast }(u)=0$![]() , contradicting that $u$
, contradicting that $u$![]() is non-negative and non-trivial and proving the claim.
is non-negative and non-trivial and proving the claim.
In particular, by Lagrange multipliers theorem, there exists $\lambda \in {\rm I}\hskip -0.85mm{\rm R}$![]() verifying
verifying
Choosing $v=u$![]() in the previous equality, we obtain
in the previous equality, we obtain
Thus, $u$![]() is a non-trivial and non-negative weak solution of
is a non-trivial and non-negative weak solution of
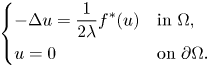
To see that $u\leq s_{\ast }$![]() , it is sufficient to choose $v=(u-s_{\ast })^{+}$
, it is sufficient to choose $v=(u-s_{\ast })^{+}$![]() as test function in the above boundary value problem. Since $f^{\ast }(u)=f(u)\in L^{\infty }(\Omega )$
as test function in the above boundary value problem. Since $f^{\ast }(u)=f(u)\in L^{\infty }(\Omega )$![]() , it also follows from [Reference Ambrosetti and Prodi4, Theorem 0.5(ii)] that $u\in C^{1, \beta }(\overline {\Omega })$
, it also follows from [Reference Ambrosetti and Prodi4, Theorem 0.5(ii)] that $u\in C^{1, \beta }(\overline {\Omega })$![]() for some $0<\beta <1$
for some $0<\beta <1$![]() . Now, since $f$
. Now, since $f$![]() is locally Lipschitz continuous, we get $f(u)\in C^{0,\beta }(\overline {\Omega })$
is locally Lipschitz continuous, we get $f(u)\in C^{0,\beta }(\overline {\Omega })$![]() . Hence, by [Reference Ambrosetti and Prodi4, Theorem 0.5(iii)], we have $u\in C^{2, \beta }(\overline {\Omega })$
. Hence, by [Reference Ambrosetti and Prodi4, Theorem 0.5(iii)], we have $u\in C^{2, \beta }(\overline {\Omega })$![]() . Applying then the strong maximum principle and Hopf lemma, we obtain $u>0$
. Applying then the strong maximum principle and Hopf lemma, we obtain $u>0$![]() in $\Omega$
in $\Omega$![]() and $\partial u/\partial \tau <0$
and $\partial u/\partial \tau <0$![]() on $\partial \Omega$
on $\partial \Omega$![]() and case (i) is proved.
and case (i) is proved.
(ii) We begin by proving the continuity of $\alpha$![]() in $(0, \infty )$
in $(0, \infty )$![]() . Let $\{t_{n}\}$
. Let $\{t_{n}\}$![]() be a sequence of positive numbers with $t_{n}\to t_{\ast }$
be a sequence of positive numbers with $t_{n}\to t_{\ast }$![]() , $t_{\ast }>0$
, $t_{\ast }>0$![]() , and $u_{n}\in S_{t_{n}}$
, and $u_{n}\in S_{t_{n}}$![]() . Since $\{u_{n}\}$
. Since $\{u_{n}\}$![]() is bounded in $H_{0}^{1}(\Omega )$
is bounded in $H_{0}^{1}(\Omega )$![]() , there exists $u_{\ast }\in H_{0}^{1}(\Omega )$
, there exists $u_{\ast }\in H_{0}^{1}(\Omega )$![]() such that, up to a subsequence, $\{ u_n\}$
such that, up to a subsequence, $\{ u_n\}$![]() is weakly convergent to $u_{\ast }$
is weakly convergent to $u_{\ast }$![]() . Using that the norm is weakly lower semicontinuous and the weak continuity of $J$
. Using that the norm is weakly lower semicontinuous and the weak continuity of $J$![]() , we get
, we get
Hence, by definition of $\alpha$![]() , it is clear that
, it is clear that
On the other hand, for the converse inequality, choosing $u_{0}\in S_{t_{\ast }}$![]() we have
we have
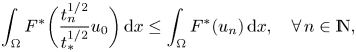
and passing to the limit as $n$![]() goes to infinity, we get
goes to infinity, we get
concluding that
and the continuity of $\alpha$![]() has been proved.
has been proved.
Fix now $t_{0}>0$![]() . For each $t\in (-t_0,\infty )$
. For each $t\in (-t_0,\infty )$![]() , we take a function $u_{t_{0}}$
, we take a function $u_{t_{0}}$![]() (respectively, $u_{t_{0}+t}$
(respectively, $u_{t_{0}+t}$![]() ) in $S_{t_{0}}$
) in $S_{t_{0}}$![]() (respectively, in $S_{t+t_{0}}$
(respectively, in $S_{t+t_{0}}$![]() ). Thus, by definition of $S_{t+t_{0}}$
). Thus, by definition of $S_{t+t_{0}}$![]() ,
,
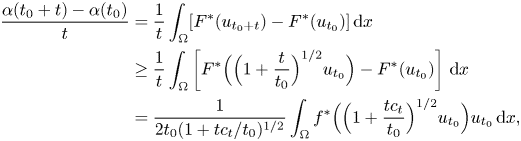
where $0<|c_{t}|<1$![]() . Consequently,
. Consequently,
Since $f^{\ast }$![]() is bounded, it is a consequence of the definition of $S_t$
is bounded, it is a consequence of the definition of $S_t$![]() that $\max _{u\in S_{t_{0}}}\int _{\Omega }f^{\ast }(u)u\,{\textrm {d}}x$
that $\max _{u\in S_{t_{0}}}\int _{\Omega }f^{\ast }(u)u\,{\textrm {d}}x$![]() is attained. Therefore,
is attained. Therefore,
On the other hand, by definition of $S_{t_{0}}$![]() , we get
, we get
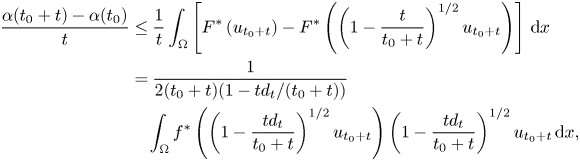
where $0<|d_{t}|<1$![]() . Therefore,
. Therefore,
Claim $\limsup _{t\to 0}[\max _{u\in S_{t_{0}+t(1-d_{t})}}\int _{\Omega }f^{\ast }(u)u\,{\textrm {d}}x]\leq \max _{u\in S_{t_{0}}}\int _{\Omega }f^{\ast }(u)u\,{\textrm {d}}x$![]() .
.
Let $\{t_{n}\}$![]() be a sequence of real numbers converging to zero. For each $n$
be a sequence of real numbers converging to zero. For each $n$![]() , choose $u_{n}\in S_{t_{0}+t_{n}(1-d_{t_{n}})}$
, choose $u_{n}\in S_{t_{0}+t_{n}(1-d_{t_{n}})}$![]() such that
such that
Since $\|u_{n}\|^{2}\leq t_{0}+t_{n}(1-d_{t_{n}}),$![]() we have that $\{u_{n}\}$
we have that $\{u_{n}\}$![]() is bounded in $H_{0}^{1}(\Omega )$
is bounded in $H_{0}^{1}(\Omega )$![]() and, as before, there exists $u_{0}\in H_{0}^{1}(\Omega )$
and, as before, there exists $u_{0}\in H_{0}^{1}(\Omega )$![]() such that, up to a subsequence,
such that, up to a subsequence,
and
Moreover, by the continuity of $\alpha$![]() ,
,
Consequently, $u_{0}\in S_{t_{0}}$![]() and, by $(i)$
and, by $(i)$![]() , $\|u_{0}\|^{2}=t_{0}$
, $\|u_{0}\|^{2}=t_{0}$![]() . The claim follows now by observing that the weak convergence of $u_n$
. The claim follows now by observing that the weak convergence of $u_n$![]() to $u_0$
to $u_0$![]() implies that
implies that
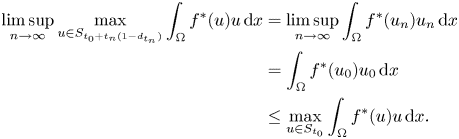
Now, by previous claim, passing to the upper limit as $t$![]() tends to zero in (2.5), we get
tends to zero in (2.5), we get
By comparing this inequality with (2.4), we conclude that $\alpha$![]() is differentiable in $t_{0}$
is differentiable in $t_{0}$![]() and
and
To prove the upper semicontinuity of the derivative, let $\{t_{n}\}$![]() be a sequence of real numbers converging to a positive number $t_{0}$
be a sequence of real numbers converging to a positive number $t_{0}$![]() . For each $n$
. For each $n$![]() , choose $u_{n}\in S_{t_{n}}$
, choose $u_{n}\in S_{t_{n}}$![]() such that
such that
Since $u_{n}\in S_{t_{n}}$![]() , as previously, it follows that there exists $u_{0}\in H_{0}^{1}(\Omega )$
, as previously, it follows that there exists $u_{0}\in H_{0}^{1}(\Omega )$![]() such that, up to a subsequence,
such that, up to a subsequence,
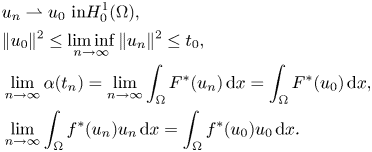
Using the continuity of $\alpha$![]() ,
,
and consequently
and by the computation of the derivative $\alpha '(t_0)$![]() , we obtain
, we obtain
To prove the last part of $(ii)$![]() , let $t_{n}\searrow 0$
, let $t_{n}\searrow 0$![]() and $u_{n}\in S_{t_{n}}$
and $u_{n}\in S_{t_{n}}$![]() be such that
be such that
Define $v_{n}:=u_{n}/t_{n}^{1/2}$![]() and observe that, by (i), $\|u_{n}\|=t_{n}^{1/2}$
and observe that, by (i), $\|u_{n}\|=t_{n}^{1/2}$![]() and thus $\{v_{n}\}$
and thus $\{v_{n}\}$![]() is bounded in $H_{0}^{1}(\Omega )$
is bounded in $H_{0}^{1}(\Omega )$![]() . Consequently, there exists $v_{\ast }$
. Consequently, there exists $v_{\ast }$![]() such that, up to a subsequence,
such that, up to a subsequence,
Thus, by Lebesgue Dominated Convergence Theorem and the definition of $\gamma$![]() , we get
, we get
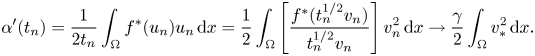
Moreover, by the definition of $\gamma$![]() again and the L'Hospital rule, we have $\lim _{t\searrow 0}F^{\ast }(t)/t^{2}=\gamma /2$
again and the L'Hospital rule, we have $\lim _{t\searrow 0}F^{\ast }(t)/t^{2}=\gamma /2$![]() . Thence, from (2.6), up to a subsequence, we obtain
. Thence, from (2.6), up to a subsequence, we obtain
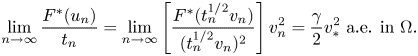
and

for some $h\in L^{1}(\Omega )$![]() . (Observe that the convergence (2.6) implies, passing to a subsequence if necessary, the existence of such a function $h(x)$
. (Observe that the convergence (2.6) implies, passing to a subsequence if necessary, the existence of such a function $h(x)$![]() ). Therefore, by Lebesgue Dominated Convergence Theorem
). Therefore, by Lebesgue Dominated Convergence Theorem
If it were $v_{\ast }=0$![]() , then by (2.7) and (2.8), we would conclude that
, then by (2.7) and (2.8), we would conclude that
On the other hand, since $u_{n}\in S_{t_{n}}$![]() , it follows again from Lebesgue Dominated Convergence Theorem and L'Hospital rule, that
, it follows again from Lebesgue Dominated Convergence Theorem and L'Hospital rule, that
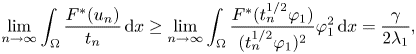
where $\varphi _{1}$![]() is the eigenfunction of Laplacian operator with homogeneous Dirichlet boundary condition, associated with $\lambda _1$
is the eigenfunction of Laplacian operator with homogeneous Dirichlet boundary condition, associated with $\lambda _1$![]() with $\|\varphi _{1}\|=1$
with $\|\varphi _{1}\|=1$![]() . By comparing (2.9) and (2.10), we get a contradiction proving that $v_{\ast }\neq 0$
. By comparing (2.9) and (2.10), we get a contradiction proving that $v_{\ast }\neq 0$![]() $(v_{\ast }\geq 0)$
$(v_{\ast }\geq 0)$![]() .
.
Finally, since $u_{n}\in S_{t_{n}}$![]() and $\|u_{n}\|=t_{n}^{1/2}$
and $\|u_{n}\|=t_{n}^{1/2}$![]() , we can again use the Lagrange multipliers theorem (see proof of item $(i)$
, we can again use the Lagrange multipliers theorem (see proof of item $(i)$![]() ) to conclude that
) to conclude that
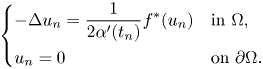
Consequently,
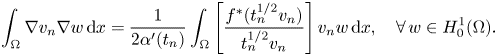
By passing to the limit as $n$![]() goes to infinity in (2.11), it follows from (2.6) and (2.7) that
goes to infinity in (2.11), it follows from (2.6) and (2.7) that
Since $v^{*}\geq 0$![]() , $v^{*}\not \equiv 0$
, $v^{*}\not \equiv 0$![]() , we have $\int _{\Omega }v_{\ast }^{2}\,{\textrm {d}}x=1/\lambda _{1}$
, we have $\int _{\Omega }v_{\ast }^{2}\,{\textrm {d}}x=1/\lambda _{1}$![]() and (2.7) implies that $\lim _{n\to \infty } \alpha ' (t_n) = \gamma /(2\lambda _1)$
and (2.7) implies that $\lim _{n\to \infty } \alpha ' (t_n) = \gamma /(2\lambda _1)$![]() .
.
Finally, suppose by contradiction that there exists a sequence of positive numbers $\{t_{n}\}$![]() and $\{u_{n}\} \subset S_{t_n}$
and $\{u_{n}\} \subset S_{t_n}$![]() such that $t_{n}\to t_{\ast }$
such that $t_{n}\to t_{\ast }$![]() (for some $t_{\ast }>0$
(for some $t_{\ast }>0$![]() ), $\|u_{n}\|= t_{n}^{1/2}$
), $\|u_{n}\|= t_{n}^{1/2}$![]() , $\int _{\Omega }F^{\ast }(u_{n})\,{\textrm {d}}x=\alpha (t_{n})$
, $\int _{\Omega }F^{\ast }(u_{n})\,{\textrm {d}}x=\alpha (t_{n})$![]() and
and
In particular, $\{u_{n}\}$![]() is bounded and hence there exists $u_{\ast }\in H_{0}^{1}(\Omega )$
is bounded and hence there exists $u_{\ast }\in H_{0}^{1}(\Omega )$![]() with $u_{\ast }\geq 0$
with $u_{\ast }\geq 0$![]() (because $u_{n}>0$
(because $u_{n}>0$![]() ) and such that, up to a subsequence,
) and such that, up to a subsequence,
The weak continuity of $J$![]() and of the map $\int _{\Omega }f^{\ast }(v)v\,{\textrm {d}}x$
and of the map $\int _{\Omega }f^{\ast }(v)v\,{\textrm {d}}x$![]() , (2.12), $(i)$
, (2.12), $(i)$![]() and the continuity of $\alpha$
and the continuity of $\alpha$![]() imply by taking limits when $n$
imply by taking limits when $n$![]() tends to infinity that
tends to infinity that
and
Identity (2.14) implies that $u_{\ast }=0$![]() , but that leads us to a contradiction with (2.13). The result is now proved.
, but that leads us to a contradiction with (2.13). The result is now proved.
(iii) Let us consider first $k=2,\ldots , K$![]() . By (ii), $g_{k}: (0, \infty )\to {\rm I}\hskip -0.85mm{\rm R}$
. By (ii), $g_{k}: (0, \infty )\to {\rm I}\hskip -0.85mm{\rm R}$![]() is differentiable with $g'_k (t) =m_k (t) - \alpha '(t)$
is differentiable with $g'_k (t) =m_k (t) - \alpha '(t)$![]() for every $t>0$
for every $t>0$![]() . If $t\in (0, t_{k-1}]$
. If $t\in (0, t_{k-1}]$![]() , by the definition of $m_k$
, by the definition of $m_k$![]() we have $g_{k}(t)=-\alpha (t)$
we have $g_{k}(t)=-\alpha (t)$![]() and thus
and thus
On the other hand, by (m), $\lim _{t\searrow t_{k-1}} m_k(t)= m_k(t_{k-1})=0$![]() and $(ii)$
and $(ii)$![]()
Finally, assuming hypothesis (mf), if $k=1$![]() then, by $g_{1}(0)=0$
then, by $g_{1}(0)=0$![]() and $(ii)$
and $(ii)$![]() , we have
, we have
The result follows.
3. Existence of $K$ further solutions for (P)
further solutions for (P)
As in [Reference Santos Júnior and Siciliano13], our approach to prove the existence of a solution $v_k$![]() for each $k\in \{1,\ldots ,K\}$
for each $k\in \{1,\ldots ,K\}$![]() is based on looking for critical points with norm in the interval $(t_{k-1}^{1/2}, t_k^{1/2})$
is based on looking for critical points with norm in the interval $(t_{k-1}^{1/2}, t_k^{1/2})$![]() of the truncated functional $I_{k}: H_{0}^{1}(\Omega )\to {\rm I}\hskip -0.85mm{\rm R}$
of the truncated functional $I_{k}: H_{0}^{1}(\Omega )\to {\rm I}\hskip -0.85mm{\rm R}$![]() defined by
defined by
where $F^{\ast }$![]() is given by (1.2) and $M_{k}$
is given by (1.2) and $M_{k}$![]() by (2.3).
by (2.3).
Indeed, every critical point $v_{k}\in H_{0}^{1}(\Omega )$![]() of $I_k$
of $I_k$![]() with $\| v_{k}\|^{2}\in (t_{k-1}, t_k)$
with $\| v_{k}\|^{2}\in (t_{k-1}, t_k)$![]() satisfies
satisfies
(because $m_k(\|v_{k}\|^{2})=m(\|v_{k}\|^{2})$![]() ). Hence, by the maximum principle, we conclude that $v_{k}\geq 0$
). Hence, by the maximum principle, we conclude that $v_{k}\geq 0$![]() in $\Omega$
in $\Omega$![]() . In addition, by choosing $\varphi = (v_{k}-s_{\ast })^{+}$
. In addition, by choosing $\varphi = (v_{k}-s_{\ast })^{+}$![]() as a test function, we get
as a test function, we get
Since $m(\|v_{k}\|^{2})>0$![]() (by (m)), we conclude that $0\leq v_{k}\leq s_{\ast }$
(by (m)), we conclude that $0\leq v_{k}\leq s_{\ast }$![]() is a weak solution of (P). By elliptic regularity and the maximum principle, $v_{k}>0$
is a weak solution of (P). By elliptic regularity and the maximum principle, $v_{k}>0$![]() is a classical solution.
is a classical solution.
Proof of case (i) of Theorem 1.2. Fix $k=2, \ldots , K$![]() . It follows from (m) that $M_k\geq 0$
. It follows from (m) that $M_k\geq 0$![]() and thus by the definition of $\alpha _k$
and thus by the definition of $\alpha _k$![]() that
that
for all $u\in H_{0}^{1}(\Omega )$![]() with $\|u\|\leq t_{k}^{1/2}$
with $\|u\|\leq t_{k}^{1/2}$![]() . Consequently, it makes sense to define the real number
. Consequently, it makes sense to define the real number
We deduce from (iii) of Lemma 2.1 that
To conclude the proof, it suffices to show that $b_k$![]() is a critical value of $I_k$
is a critical value of $I_k$![]() with an associated critical point $v_k \in H_{0}^{1}(\Omega )$
with an associated critical point $v_k \in H_{0}^{1}(\Omega )$![]() of norm $t_{k-1}^{1/2} < \|v_k\| < t_{k}^{1/2}$
of norm $t_{k-1}^{1/2} < \|v_k\| < t_{k}^{1/2}$![]() . To prove it, let $\{u_{n}\}\subset H_{0}^{1}(\Omega )$
. To prove it, let $\{u_{n}\}\subset H_{0}^{1}(\Omega )$![]() be a minimizing sequence: i.e., such that
be a minimizing sequence: i.e., such that
Hence, up to a subsequence, there exists $v_{k}\in H_{0}^{1}(\Omega )$![]() and $\tau _k\in [0, t_k]$
and $\tau _k\in [0, t_k]$![]() such that
such that
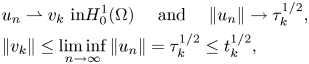
and, by the weak continuity of $J$![]() ,
,
Observe that
Moreover, it is worth to point out that
because in the contrary case we will have $M_{k}(\tau _k)=0$![]() , $\|v_k\|^{2} \leq t_{k-1}$
, $\|v_k\|^{2} \leq t_{k-1}$![]() and we will deduce by (3.3) and the definition of $\alpha _{k-1}$
and we will deduce by (3.3) and the definition of $\alpha _{k-1}$![]() that
that
contradicting (3.2). Therefore, (3.4) holds. Now, we can prove that $\|v_k \|^{2}= \tau _k$![]() . Indeed, we get a contradiction if we assume that $\| v_k\|^{2} < \tau _k$
. Indeed, we get a contradiction if we assume that $\| v_k\|^{2} < \tau _k$![]() because this implies by (m) and (3.4) that $M_k(\tau _k)>M_k(\| v_k\|^{2})$
because this implies by (m) and (3.4) that $M_k(\tau _k)>M_k(\| v_k\|^{2})$![]() and hence (3.3) gives
and hence (3.3) gives
a contradiction with the definition of $b_k$![]() . Therefore, $\{u_n\}$
. Therefore, $\{u_n\}$![]() is weakly convergent to $v_k$
is weakly convergent to $v_k$![]() with the norms $\{\| u_n\| \}$
with the norms $\{\| u_n\| \}$![]() converging also to $\|v_k\|$
converging also to $\|v_k\|$![]() , which is equivalent to the strong convergence of $\{u_n\}$
, which is equivalent to the strong convergence of $\{u_n\}$![]() to $v_k$
to $v_k$![]() . As a consequence,
. As a consequence,
and $v_k$![]() is a minimum point of $I_k$
is a minimum point of $I_k$![]() on the ball with radio $\tau _k^{1/2}$
on the ball with radio $\tau _k^{1/2}$![]() and centered at the origin. To prove that $v_k$
and centered at the origin. To prove that $v_k$![]() is a critical point of $I_k$
is a critical point of $I_k$![]() with level $b_k<0$
with level $b_k<0$![]() (by (3.2) and (i) of Lemma 2.1), it remains us to show that $\|v_{k}\|< t_k^{1/2}$
(by (3.2) and (i) of Lemma 2.1), it remains us to show that $\|v_{k}\|< t_k^{1/2}$![]() . Suppose by contradiction that $\|v_{k}\|=t_{k}^{1/2}$
. Suppose by contradiction that $\|v_{k}\|=t_{k}^{1/2}$![]() . It follows from (A’) that
. It follows from (A’) that
which contradicts that $b_k<0$![]() and therefore we have proved that $v_{k}$
and therefore we have proved that $v_{k}$![]() is a critical point of $I_{k}$
is a critical point of $I_{k}$![]() with $t_{k-1}<\|v_{k}\|^{2}< t_{k}$
with $t_{k-1}<\|v_{k}\|^{2}< t_{k}$![]() .
.
Proof of case (ii) of Theorem 1.2. In this case, we can give exactly the same proof as in the previous case. The hypothesis (mf) is only required due to item (iii) of the Lemma 2.1.
Proof of case (iii) of Theorem 1.2. For every $k=1,\ldots , K$![]() , the solution $v_k$
, the solution $v_k$![]() , provided by items (i) and (ii) in Theorem 1.2, corresponds with a critical point of the truncated functional $I_{k}: H_{0}^{1}(\Omega )\to {\rm I}\hskip -0.85mm{\rm R}$
, provided by items (i) and (ii) in Theorem 1.2, corresponds with a critical point of the truncated functional $I_{k}: H_{0}^{1}(\Omega )\to {\rm I}\hskip -0.85mm{\rm R}$![]() given by (3.1) with $I_{k}(v_{k})<0$
given by (3.1) with $I_{k}(v_{k})<0$![]() . On the other hand, the solution $u_k$
. On the other hand, the solution $u_k$![]() provided in [Reference Santos Júnior and Siciliano13, Theorem 1.1] corresponds with a critical point of the truncated functional $I_{k}$
provided in [Reference Santos Júnior and Siciliano13, Theorem 1.1] corresponds with a critical point of the truncated functional $I_{k}$![]() with $0< I_{k}(u_{k})$
with $0< I_{k}(u_{k})$![]() . Since $I_{k}(v_{k})<0< I_{k}(u_{k})$
. Since $I_{k}(v_{k})<0< I_{k}(u_{k})$![]() , we deduce that $v_{k } \not = u_{k}$
, we deduce that $v_{k } \not = u_{k}$![]() obtaining then 2 K positive solutions of (P).
obtaining then 2 K positive solutions of (P).
4. Concentration phenomena of solutions
Throughout this section, we are going to denote by $f_{\lambda }$![]() a function $f$
a function $f$![]() which satisfies (f), (mf), (A$'$
which satisfies (f), (mf), (A$'$![]() ) and $F(s_{\ast })=\lambda$
) and $F(s_{\ast })=\lambda$![]() , where $\lambda$
, where $\lambda$![]() is a positive parameter. We also denote the dependence on this parameter $\lambda$
is a positive parameter. We also denote the dependence on this parameter $\lambda$![]() of the functional $I_k=I_{k, \lambda }$
of the functional $I_k=I_{k, \lambda }$![]() given by (3.1). It follows from previous section that problem (Pλ) has $K$
given by (3.1). It follows from previous section that problem (Pλ) has $K$![]() positive solutions $v_{k, \lambda }$
positive solutions $v_{k, \lambda }$![]() , with $I_{k, \lambda }(v_k)<0$
, with $I_{k, \lambda }(v_k)<0$![]() , $k=1, \ldots , K$
, $k=1, \ldots , K$![]() . Before proving the main result of this section, we need the following lemma
. Before proving the main result of this section, we need the following lemma
Lemma 4.1 Let $b_{k, \lambda }=\inf _{u\in H_{0}^{1}(\Omega ), \|u\|\leq t_{k}^{1/2}}I_{k, \lambda }(u)$![]() , where $I_{k, \lambda }$
, where $I_{k, \lambda }$![]() is the truncated functional associated with the problem (Pλ) (and given in (3.1)). Then,
is the truncated functional associated with the problem (Pλ) (and given in (3.1)). Then,
Proof. It is sufficient to note that
where $F^{\ast }_\lambda$![]() is the primitive of $f^{\ast }_\lambda$
is the primitive of $f^{\ast }_\lambda$![]() . The proof will be finished by passing to the limit as $\lambda \searrow 0$
. The proof will be finished by passing to the limit as $\lambda \searrow 0$![]() in the previous inequality.
in the previous inequality.
Proof of case (iv) of Theorem 1.2. Assume by contradiction that for some fixed $k=1, \ldots , K$![]() there exists a sequence of positive numbers such that $\lambda _{n}\searrow 0$
there exists a sequence of positive numbers such that $\lambda _{n}\searrow 0$![]() and
and
for some $t_{k-1}< \tau _{k-1}\leq t_{k}$![]() . Since
. Since
there exists $v_{k, 0}\in H_{0}^{1}(\Omega )$![]() such that, up to a subsequence, as $n$
such that, up to a subsequence, as $n$![]() tends to infinity, we obtain
tends to infinity, we obtain
By Lemma 4.1, we deduce that
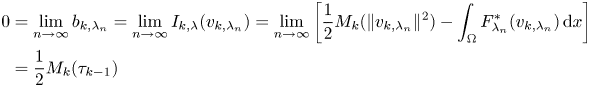
and taking into account that by hypothesis (m), we have $M_{k}(\tau _{k-1})> M_{k}(t_{k-1})=0$![]() , contradicting the previous inequality.
, contradicting the previous inequality.
Acknowledgements
D. Arcoya was supported by MINECO-FEDER Grant MTM2015-68210-P and Junta de Andalucía FQM-116. J. R. Santos J. was partially supported by CNPq-Proc. 302698/2015-9 and CAPES-Proc. 88881.120045/2016-01, Brazil. A. Suárez was supported by MINECO/ FEDER Grant MTM2015-69875-P and Junta de Andalucía FQM-131. Finally, we would like to acknowledge the anonymous referee for her/his comments which have improved the present paper.