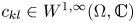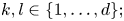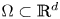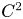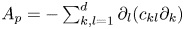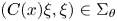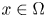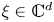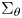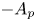1. Introduction
In his book, Kato [Reference Kato11] showed that an 
$m$-sectorial operator in a Hilbert space generates a (quasi-)contraction holomorphic semigroup. One can generalize the notion of sectorial operators to 
$L_p$-spaces as follows (cf. [Reference Goldstein10, Definition 1.5.8, Reference Kato11, Subsection V.3.10, Reference Cialdea and Maz'ya2, Definition 1]).
Definition 1.1 Let 
$d \in \mathbb{N}$, 
$\Omega \subset \mathbb{R}^{d}$ be open and 
$p \in (1, \infty )$. Let 
$A_p$ be an operator in 
$L_p(\Omega )$. Then 
$A_p$ is said to be sectorial if there exists a 
$K > 0$ such that
\begin{equation} |\mathrm{Im} \, (A_p u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]})| \leq K \mathrm{Re} \, (A_p u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]}) \end{equation}
for all 
$u \in D(A_p)$.
There are certain interests in showing that an operator is sectorial in this generalized sense. The significance of these estimates lies in the fact that they are useful in showing that the operators under consideration satisfy a necessary condition to generate holomorphic contraction semigroups. In particular, the estimate (1) can be established for certain second-order differential operators in divergence form. In the proof of [Reference Pazy16, Theorem 7.3.6], Pazy showed that (1) holds when the operator is strongly elliptic with symmetric real-valued 
$C^{1}$-coefficients, with an explicit constant 
$K$ which depends on the coefficients, the ellipticity constant and 
$p$. Okazawa improved Pazy's result and showed that the estimate also holds for degenerate elliptic operators with symmetric real-valued 
$C^{1}$-coefficients, with 
$K = ({|p-2|}/{2 \sqrt {p-1}})$ (cf. [Reference Okazawa14]). Ouhabaz in [Reference Ouhabaz15, Theorem 3.9] proved that (1) is true for generators of sub-Markovian semigroups. It is interesting to note that [Reference Ouhabaz15, Theorem 3.9] gives the same constant 
$K$ in (1) as in [Reference Okazawa14].
In this paper, we will prove the sectorial estimate (1) for degenerate elliptic second-order differential operators with bounded complex-valued coefficients. The results are generalizations of [Reference Okazawa14]. In comparison to [Reference Ouhabaz15, Theorem 3.9], we note that the operators we consider here are, in general, no longer generators of sub-Markovian semigroups. We will then apply the estimate to show that degenerate elliptic operators with smooth enough coefficients generate contraction holomorphic semigroups.
In order to formulate the main theorem, we need to introduce some notation. Let 
$d \in \mathbb{N}$, 
$\Omega \subset \mathbb{R}^{d}$ be open with uniformly 
$C^{2}$ boundary and 
$\theta \in [0, {\pi }/{2})$. Let 
$c_{kl} \in W^{1,\infty }(\Omega , \mathbb{C})$ for all 
$k, l \in \{1, \ldots , d\}$. Define 
$C = (c_{kl})_{1 \leq k,l \leq d}$ and
\begin{equation} \Sigma_\theta = \{r e^{i \beta}: r \geq 0 \mbox{ and } |\beta| \leq \theta\}. \end{equation}Assume that
\begin{equation} (C(x) \xi, \xi) \in \Sigma_\theta \end{equation}
for all 
$x \in \Omega$ and 
$\xi \in \mathbb{C}^{d}$. For convenience, we will usually refer to (3) as 
$C$ takes values in the sector 
$\Sigma _\theta$.
Let 
$p \in (1, \infty )$. Consider the operator 
$A_p$ in 
$L_p(\Omega )$ defined by
\[ A_p u ={-} \sum_{k,l=1}^{d} \partial_l (c_{kl} \partial_k u) \]on the domain
\[ D(A_p) = W^{2,p}(\Omega) \cap W^{1,p}_0(\Omega). \]
If 
$p=2$ then
\begin{equation} |\mathrm{Im} \, (A_2 u, u)| \leq (\tan\theta) \mathrm{Re} \, (A_2 u, u) \end{equation}
for all 
$u \in D(A_2)$. This follows immediately from integration by parts. If 
$p \neq 2$, the situation is quite different. Write 
$C = R + i B$, where 
$R$ and 
$B$ are real matrices. Let 
$R_a$ and 
$B_a$ be the anti-symmetric parts of 
$R$ and 
$B$, respectively, that is, 
$R_a = {(R - R^{T})}/{2}$ and 
$B_a = {(B - B^{T})}/{2}$.
The main result of this paper is as follows.
Theorem 1.2 Let 
$p \in (1, \infty ),$ 
$\theta \in [0, {\pi }/{2}),$ 
$c_{kl} \in W^{1,\infty }(\Omega ,\mathbb{C})$ for all 
$k,l \in \{1,\ldots ,d\}$ and 
$C = (c_{kl})_{1 \leq k,l \leq d}$ take values in the sector 
$\Sigma _\theta$. Suppose 
$|1 - {2}/{p}| < \cos \theta$ and 
$B_a = 0$. Then
\[ |\mathrm{Im} \, (A_p u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]})| \leq K \mathrm{Re} \, (A_p u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]}) \]
for all 
$u \in D(A_p)$, where
\begin{equation} K = \left\{ \begin{array}{@{}ll} \tan \left(\dfrac{\pi}{2} - \phi + \theta\right) & \mbox{if } R_a = 0,\\ \dfrac{\big( {2}/{\sin\phi} - 1 \big) \tan\theta + \cot\phi}{1 - (\tan \theta) \cot\phi} & \mbox{if } R_a \neq 0 \end{array} \right. \end{equation}
and 
$\phi = \arccos |1 - {2}/{p}|$.
Note that when the coefficient matrix 
$C$ consists of real entries and is symmetric, then one can choose 
$\theta = 0$ and (5) gives
\[ K = \tan \bigg(\frac{\pi}{2} - \phi\bigg) = \cot\phi = \frac{|p-2|}{2 \sqrt{p-1}}, \]which is the constant obtained by Okazawa in [Reference Okazawa14].
Remark 1.3 The conditions, conclusion and some implications can be rephrased in the recently introduced terminology of Carbonaro and Dragičević [Reference Carbonaro and Dragičević1]. For every 
$p \in (1,\infty )$ and bounded 
$d \times d$ matrix valued function 
$M: \Omega \longrightarrow \mathbb{C}^{d\times d}$ define
\begin{equation} \Delta_p(M) := ess\,inf_{x \in \Omega} \min_{\stackrel{\xi \in \mathbb{C}^{d}}{\|\xi\|=1}} \mathrm{Re} \, \big( M(x) \xi, \mathcal{J}_p \xi \big), \end{equation}
where 
$\mathcal {J}_p: \mathbb{C}^{d} \longrightarrow \mathbb{C}^{d}$ is defined by
\begin{equation} \mathcal{J}_p \xi = \xi + \left( 1 - \frac{2}{p} \right) \overline{\xi}. \end{equation}
Suppose merely 
$c_{kl} \in L_\infty (\Omega ,\mathbb{C})$ for all 
$k,l \in \{1,\ldots ,d\}$. Then 
$C$ takes values in the sector 
$\Sigma _\theta$ if and only if 
$\Delta _2(e^{\pm i\psi } C) \ge 0$ for all 
$\psi \in [0,{\pi }/{2}-\theta )$. Also, 
$|1-{2}/{p}| < \cos \theta$ if and only if 
$\Delta _p(e^{i\theta }I) > 0$ (cf. [Reference Carbonaro and Dragičević1, (5.18)]).
Now 
$\phi > 0$ by assumption and
\[ \big( e^{i\gamma} C(x) \xi, \xi \big) \in \Sigma_{\theta + |\gamma|} \subset \Sigma_\phi \]
for all 
$x \in \Omega$, 
$\xi \in \mathbb{C}^{d}$ and 
$\gamma \in \mathbb{R}$ with 
$|\gamma | \le \phi - \theta$.
If both 
$B_a = 0$ and 
$R_a = 0$, then [Reference Carbonaro and Dragičević1, Proposition 5.18 (
$3 \Rightarrow 1$)] implies that
\begin{equation} \Delta_p\left( e^{{\pm} i (\phi-\theta)} C \right) \ge 0. \end{equation} On the other hand, if 
$\Delta _2(C) > 0$ (the operator is strongly elliptic) then [Reference Carbonaro and Dragičević1, Theorem 1.3 (a 
$\Rightarrow$ b)] together with the Lumer–Phillips theorem establishes that (8) implies (1), where 
$K = \tan ({\pi }/{2}-\phi +\theta )$ which coincides with (5) if 
$R_a = B_a = 0$.
If 
$R_a = B_a = 0$ then one has equivalence in [Reference Carbonaro and Dragičević1, Proposition 5.18 (
$3 \Leftrightarrow 1$)] and in the strongly elliptic case one also has equivalence in [Reference Carbonaro and Dragičević1, Theorem 1.3 (a 
$\Leftrightarrow$ b)]. Hence, the angle of the sector of contractivity in 
$L_p(\Omega )$, that is 
${\pi }/{2}-\arctan K$, is optimal. Consequently, also 
$K$ is optimal if 
$R_a = B_a = 0$.
In Theorem 1.2, we do not require that 
$R_a = 0$ nor strong ellipticity, but we require Lipschitz continuity of the 
$c_{kl}$.
It is not difficult to see that 
$A_p$ is closable. Let 
$\overline {A_p}$ be the closure of 
$A_p$. Under the current conditions imposed on the coefficient matrix 
$C$ and the domain 
$\Omega$, we do not know whether 
$-\overline {A_p}$ is a generator of a 
$C_0$-semigroup. If 
$\Omega = \mathbb{R}^{d}$ and 
$C$ consists of twice differentiable entries, then we prove the following generation result for 
$-\overline {A_p}$ based on Theorem 1.2.
Theorem 1.4 Let 
$p \in (1, \infty ),$ 
$\theta \in [0, {\pi }/{2})$, 
$c_{kl} \in W^{2,\infty }(\mathbb{R}^{d},\mathbb{C})$ for all 
$k,l \in \{1,\ldots ,d\}$ and 
$C = (c_{kl})_{1 \leq k,l \leq d}$ take values in the sector 
$\Sigma _\theta$. Suppose 
$|1 - {2}/{p}| < \cos \theta$ and 
$B_a = 0$. Set 
$\phi = \arccos |1 - {2}/{p}|$. Then the closure 
$-\overline {A_p}$ generates a holomorphic semigroup on 
$L_p(\mathbb{R}^{d})$ with angle 
$\psi$ given by
\begin{equation} \psi = \left\{ \begin{array}{@{}ll} \phi - \theta, & \mbox{if } R_a = 0,\\ \dfrac{\pi}{2} - \arctan \bigg(\dfrac{\big( {2}/{\sin\phi} - 1 \big) \tan\theta + \cot\phi}{1 - (\tan \theta) \cot\phi} \bigg), & \mbox{if } R_a \neq 0. \end{array} \right. \end{equation}Note that
\[ \psi_1 := \frac{\pi}{2} - \arctan \bigg(\frac{\big( {2}/{\sin\phi} - 1 \big) \tan\theta + \cot\phi}{1 - (\tan \theta) \cot\phi} \bigg) \leq \phi - \theta \]since
\begin{equation} \tan \psi_1 = \frac{1 - (\tan\theta) \cot\phi}{\big( {2}/{\sin\phi} - 1 \big) \tan\theta + \cot\phi} \leq \frac{1 - (\tan \theta) \cot\phi}{\tan\theta + \cot\phi} = \tan(\phi - \theta). \end{equation} It is also interesting that in the case when 
$R_a=0$, Theorem 1.4 provides better angles of holomorphy compared with those of Stein's interpolations [Reference Ouhabaz15, Proposition 3.12] and [Reference Stein18, Theorem 1]. In the one-dimensional case, these better angles were also obtained in [Reference Do and ter Elst5, Corollary 1.3].
Along the same line as our results, [Reference ter Elst, Liskevich, Sobol and Vogt8] considered a type of second-order degenerate elliptic operator in divergence form whose coefficients of the principle part need not satisfy the sectorial condition (3). Other results about angles of holomorphy were considered in [Reference Weissler19, Theorem 1, Reference Epperson9, Theorem 1.1, Reference Davies3, Theorem 1.4.2, Reference Reed and Simon17, Theorem X.55, Reference Liskevich and Perelmuter12, Reference Ouhabaz15, Theorems 3.12 and 3.13].
The holomorphic semigroup generated by 
$-\overline {A_p}$ in Theorem 1.4 also possesses nice contractivity and consistency properties.
Theorem 1.5 Adopt the assumptions and notation as in Theorem 1.4. Let 
$S^{(p)}$ be the semigroup generated by 
$-\overline {A_p}$ and 
$S$ the semigroup generated by 
$-\overline {A_2}$. Then the following hold.
(i)
$S^{(p)}$ is contractive on $\Sigma _\gamma$, where
(11)\begin{equation} \gamma = \left\{ \begin{array}{@{}ll} \psi & \mbox{if } R_a = 0,\\ \psi \wedge \sup \left\{ \beta \in \left[0, \dfrac{\pi}{2}\right): (\tan\theta) \tan\beta < \dfrac{1}{3} \right\}& \mbox{if } R_a \neq 0. \end{array}\right. \end{equation}(ii)
$S^{(p)}$ is consistent with $S$ on $\Sigma _\psi$.
Recently, there is a lot of interest in differential operators with complex coefficients which are accretive on 
$L_p(\Omega )$ with 
$p \ne 2$ and then are the minus generator of a 
$C_0$-semigroup on 
$L_p(\Omega )$. Strongly elliptic operators with mixed boundary conditions are considered in [Reference Egert6, Reference ter Elst, Haller-Dintelmann, Rehberg and Tolksdorf7]. All results in [Reference Carbonaro and Dragičević1] for 
$C_0$-semigroups are for strongly elliptic operators. The main emphasis in this paper is to consider degenerate elliptic operators. In [Reference ter Elst, Liskevich, Sobol and Vogt8], the operator is allowed to be degenerate elliptic, but the coefficient matrix cannot degenerate on a set with positive measure. For 
$W^{1,\infty }$-coefficients in one dimension, the coefficient function cannot vanish at any point in [Reference ter Elst, Liskevich, Sobol and Vogt8]. In contrast, our operators may degenerate on a set with positive measure. The domain of the operator is delicate for proving the range condition for the 
$C_0$-semigroup and this is even more delicate for degenerate operators.
The outline of subsequent sections is as follows. In §2, we provide some estimates on the coefficient matrix 
$C$. These estimates are used to prove Theorem 1.2 in §3. Theorems 1.4 and 1.5 are proved in §4, in the proof of which we use a density result [Reference Do4, Proposition 4.9] that is valid if 
$\Omega = \mathbb{R}^{d}$. This explains why we require 
$\Omega = \mathbb{R}^{d}$ in Theorems 1.4 and 1.5.
2. Estimates on coefficients
Let 
$\Omega$, 
$\theta$ and 
$C$ be as in §1. In this section, we provide some preliminary estimates on the coefficient matrix 
$C$ for later use.
Define
\[ \mathrm{Re} \, C = \frac{C + C^{*}}{2} \quad \textrm{and} \quad \mathrm{Im} \, C = \frac{C - C^{*}}{2i}, \]
where 
$C^{*}$ is the conjugate transpose of 
$C$. Then 
$(\mathrm {Re} \, C)(x)$ and 
$(\mathrm {Im} \, C)(x)$ are self-adjoint for all 
$x \in \Omega$ and
\begin{equation} C = \mathrm{Re} \, C + i \mathrm{Im} \, C. \end{equation}
It is important to keep in mind that 
$\mathrm {Re} \, C$ and 
$\mathrm {Im} \, C$ defined in this manner are not necessarily real-valued.
We will also decompose the coefficient matrix 
$C$ into
\begin{equation} C = R + i B, \end{equation}
where 
$R$ and 
$B$ are matrices with real entries. Write 
$R = R_s + R_a$, where 
$R_s = {(R + R^{T})}/{2}$ is the symmetric part of 
$R$ and 
$R_a = {(R - R^{T})}/{2}$ is the anti-symmetric part of 
$R$. Similarly 
$B = B_s + B_a$, where 
$B_s = {(B + B^{T})}/{2}$ and 
$B_a = {(B - B^{T})}/{2}$. It follows from (12) and (13) that
\[ \mathrm{Re} \, C = R_s + i B_a \quad \textrm{and} \quad \mathrm{Im} \, C = B_s - i R_a. \]Lemma 2.1 We have
\[ |(R_s \xi, \eta)| \leq \frac{1}{2} \Big( (R_s \xi, \xi) + (R_s \eta, \eta) \Big) \]
for all 
$\xi , \eta \in \mathbb{R}^{d}$.
Proof. By hypothesis, 
$C$ takes values in 
$\Sigma _\theta$. This implies 
$((\mathrm {Re} \, C) \xi , \xi ) \geq 0$ for all 
$\xi \in \mathbb{C}^{d}$. We deduce that 
$(R_s \xi , \xi ) \geq 0$ for all 
$\xi \in \mathbb{R}^{d}$. Finally, we use polarization to obtain the lemma.
Lemma 2.2 We have
\[ |(B_s \xi, \eta)| \leq \frac{1}{2} (\tan \theta) \Big( (R_s \xi, \xi) + (R_s \eta, \eta) \Big) \]
for all 
$\xi , \eta \in \mathbb{R}^{d}$.
Proof. Since 
$C$ takes values in 
$\Sigma _\theta$, we have
\begin{equation} \big| \big( (\mathrm{Im} \, C) \xi, \xi \big) \big| \leq (\tan \theta) \big( (\mathrm{Re} \, C) \xi, \xi \big) \end{equation}
for all 
$\xi \in \mathbb{C}^{d}$. It follows that
\[ |(B_s \xi, \xi)| \leq (\tan \theta) (R_s \xi, \xi) \]
for all 
$\xi \in \mathbb{R}^{d}$. Finally, we use polarization to obtain
\[ |(B_s \xi, \eta)| \leq (\tan \theta) (R_s \xi, \xi)^{1/2} (R_s \eta, \eta)^{1/2} \leq \frac{1}{2} (\tan \theta) \Big( (R_s \xi, \xi) + (R_s \eta, \eta) \Big) \]
for all 
$\xi , \eta \in \mathbb{R}^{d}$ as required.
Lemma 2.3 We have
\[ \big| (B_s \xi, \xi) + (B_s \eta, \eta) - 2 (R_a \xi, \eta) \big| \leq (\tan\theta) \Big( (R_s \xi, \xi) + (R_s \eta, \eta) + 2 (B_a \xi, \eta) \Big) \]
for all 
$\xi , \eta \in \mathbb{R}^{d}$.
Proof. Let 
$\xi , \eta \in \mathbb{R}^{d}$. Then
\[ \big( (\mathrm{Im} \, C) (\xi + i \eta), \xi + i \eta \big) = (B_s \xi, \xi) + (B_s \eta, \eta) - 2 (R_a \xi, \eta) \]and
\[ \big( (\mathrm{Re} \, C) (\xi + i \eta), \xi + i \eta \big) = (R_s \xi, \xi) + (R_s \eta, \eta) + 2 (B_a \xi, \eta). \]The claim is now immediate from (14).
Lemma 2.4 Suppose 
$B_a = 0$. Then
\[ \big| (R_a \xi, \eta) \big| \leq (\tan \theta) \Big( (R_s \xi, \xi) + (R_s \eta, \eta) \Big) \]
for all 
$\xi , \eta \in \mathbb{R}^{d}$.
Proof. Since 
$B_a = 0$, Lemma 2.3 gives
\[ \big| (B_s \xi, \xi) + (B_s \eta, \eta) - 2 (R_a \xi, \eta) \big| \leq (\tan\theta) \Big( (R_s \xi, \xi) + (R_s \eta, \eta) \Big). \]The result now follows from the triangle inequality and Lemma 2.2.
Lemma 2.5 Let 
$Q$ be a positive matrix and 
$U$ a complex 
$d \times d$ matrix. Then
\[ (Q U \xi, U \xi) \leq \mathrm{tr} \,(U^{*} Q U) \|\xi\|^{2} \]
for all 
$\xi \in \mathbb{C}^{d}$.
Proof. Since 
$Q$ is a positive matrix, we have 
$(Q U \xi , U \xi ) \geq 0$ for all 
$\xi \in \mathbb{C}^{d}$. It follows that 
$U^{*} Q U \geq 0$. Hence 
$U^{*} Q U \leq \mathrm {tr} \,(U^{*} Q U) I$, where 
$I$ denotes the identity matrix. This justifies the claim.
Lemma 2.6 We have the following.
(a)
$(R_s \xi , \xi ) \geq 0$ for all $\xi \in \mathbb{C}^{d}$.(b)
$( ( (\tan \theta ) R_s \pm B_s ) \xi , \xi ) \geq 0$ for all $\xi \in \mathbb{C}^{d}$.(c) Suppose
$B_a = 0$. Then $( ( 2 (\tan \theta ) R_s \pm i R_a ) \xi , \xi ) \geq 0$ for all $\xi \in \mathbb{C}^{d}$.
Proof. Let 
$\xi \in \mathbb{C}^{d}$. Write 
$\xi = \xi _1 + i \xi _2$, where 
$\xi _1, \xi _2 \in \mathbb{R}^{d}$. We note that
\[ (R_s \xi, \xi) = (R_s \xi_1, \xi_1) + (R_s \xi_2, \xi_2) \]and
\[ (B_s \xi, \xi) = (B_s \xi_1, \xi_1) + (B_s \xi_2, \xi_2). \]Also,
\[ (R_a \xi, \xi) ={-}2i (R_a \xi_1, \xi_2). \] Next, let 
$\alpha \in (-{\pi }/{2} + \theta , {\pi }/{2} - \theta )$ and write 
$C_\alpha = e^{i \alpha } C$. In a similar manner as above, we define 
$\mathrm {Re} \, (C_\alpha )$, 
$\mathrm {Im} \, (C_\alpha )$, 
$R_\alpha$, 
$B_\alpha$, 
$R_{s,\alpha }$, 
$R_{a,\alpha }$, 
$B_{s,\alpha }$ and 
$B_{a,\alpha }$. Note that we also have
\[ \mathrm{Re} \, (C_\alpha) = R_{s,\alpha} + i B_{a,\alpha} \quad \textrm{and} \quad \mathrm{Im} \, (C_\alpha) = B_{s,\alpha} - i R_{a,\alpha}. \]Lemma 2.7 Let 
$j \in \{1, \ldots , d\}$. Suppose 
$U$ is a complex 
$d \times d$ matrix with 
$U^{T} = U$. Then
\[ |\mathrm{tr} \, ((\partial_j C_\alpha) U)|^{2} \leq M \mathrm{tr} \,(U R_{s,\alpha} \overline{U}), \]where
\[ M = 32 d \big( 1 + \tan(\theta + \alpha) \big)^{2} \|\partial_l^{2} C\|_\infty. \]Proof. It follows from [Reference Do4, Corollary 2.6] that
\begin{align*} |\mathrm{tr} \, ((\partial_j C_\alpha) U)|^{2} &\leq 32 d \big( 1 + \tan(\theta + \alpha) \big)^{2} \|\partial_l^{2} (e^{i \alpha} C)\|_\infty \mathrm{tr} \,(U R_{s,\alpha} \overline{U})\\ &\leq 32 d \big( 1 + \tan(\theta + \alpha) \big)^{2} \|\partial_l^{2} C\|_\infty \mathrm{tr} \,(U R_{s,\alpha} \overline{U}) \end{align*}as required.
Lemma 2.8 Suppose 
$B_a = 0$. Then the following hold.
(i)
$\mathrm {Re} \, (C_\alpha ) = R_s \cos \alpha - B_s \sin \alpha + i R_a \sin \alpha$.(ii)
$\mathrm {Im} \, (C_\alpha ) = R_s \sin \alpha + B_s \cos \alpha - i R_a \cos \alpha$.(iii)
$R_\alpha = R_s \cos \alpha + R_a \cos \alpha - B_s \sin \alpha$, $R_{s,\alpha } = R_s \cos \alpha - B_s \sin \alpha$, $R_{a,\alpha } = R_a \cos \alpha$.(iv)
$B_\alpha = R_s \sin \alpha + R_a \sin \alpha + B_s \cos \alpha$, $B_{s,\alpha } = R_s \sin \alpha + B_s \cos \alpha$, $B_{a,\alpha } = R_a \sin \alpha$.
Proof. These identities follow directly from the definition of 
$C$ and 
$C_\alpha$.
3. Sectorial property
Let 
$p \in (1, \infty )$. Let 
$\Omega$, 
$\theta$, 
$C$ and 
$A_p$ be as in §1. In this section, we prove Theorem 1.2. A convenient tool that we will use repeatedly is the formula of integration by parts in Sobolev spaces given in the next theorem. The theorem is immediate from the proof of [Reference Metafune and Spina13, Proposition 3.5]. We emphasize that we do not require 
$C = C^{T}$ in this theorem (cf. [Reference Metafune and Spina13, Theorem 3.1] for the same result but with extra assumption that 
$C = C^{T}$).
Theorem 3.1 Let 
$u \in D(A_p)$. Then
\begin{align} \int_{[u \neq 0]} (A_p u) |u|^{p-2} \overline{u} & = \int_{[u \neq 0]} |u|^{p-2} (C \nabla \overline{u}, \nabla \overline{u})\nonumber\\ &\quad + (p - 2) \int_{[u \neq 0]} |u|^{p-4}\big( C \mathrm{Re} \,(u \nabla \overline{u}), \mathrm{Re} \,(u \nabla \overline{u}) \big)\nonumber\\ &\quad - i (p - 2) \int_{[u \neq 0]} |u|^{p-4} \big( C \mathrm{Re} \,(u \nabla \overline{u}), \mathrm{Im} \,(u \nabla \overline{u}) \big). \end{align}An immediate remark is in order.
Remark 3.2 Recently, [Reference Carbonaro and Dragičević1] introduced the concept of 
$p$-ellipticity. Let 
$\Delta _p$ and 
$\mathcal {J}_p$ be given by (6) and (7). A matrix 
$C$ is said to be 
$p$-elliptic if
\begin{equation} \Delta_p(C) > 0. \end{equation}
Using the operator 
$\mathcal {J}_p$, the formula of integration by parts (15) can be rephrased as
\[ \int_{[u \neq 0]} (A_p u) |u|^{p-2} \overline{u} = \frac{p}{2} \int_{[u \neq 0]} |u|^{p-4} \big(C u \nabla \overline{u}, \mathcal{J}_p(u \nabla \overline{u}) \big). \]Following this, the sectorial condition (1) can be rewritten as
\[ \left\langle |u|^{p-4} C u \nabla \overline{u}, \mathcal{J}_p(\overline{u} \nabla u) {\mathbb 1}_{[u \neq 0]} \right\rangle_{L_2(\Omega)} \in \Sigma_{\arctan K}, \]and hence can be viewed as a degenerate case of (16).
Using Theorem 3.1, we obtain the following proposition, the first part of which is along the same line as [Reference Carbonaro and Dragičević1, Proposition 7.6 and (5.7)]. Nevertheless, in general, the domain for the accretivity (dissipativity) in [Reference Carbonaro and Dragičević1, Proposition 7.6] on 
$L_p(\Omega )$ has no relation with our domain 
$D(A_p)$. Moreover, [Reference Carbonaro and Dragičević1, Proposition 7.6] is only valid for 
$p \ge 2$.
For the sake of clarity, we present here a proof that holds for all 
$p \in (1,\infty )$ under our current setting.
Proposition 3.3 Let 
$u \in D(A_p)$. Write 
$u \nabla \overline {u} = \xi + i \eta$, where 
$\xi ,\eta \in \mathbb{R}^{d}$. Then
\begin{align*} \mathrm{Re} \, (A_p u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]}) &= \int_{[u \neq 0]} |u|^{p-4} \Big( (p-1) (R_s \xi, \xi) + (R_s \eta, \eta) \Big.\\ &\quad \Big. + (p-2) (B_s \xi, \eta) + p (B_a \xi, \eta) \Big) \end{align*}and
\begin{align*} \mathrm{Im} \, (A_p u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]}) &= \int_{[u \neq 0]} |u|^{p-4} \Big( (p-1) (B_s \xi, \xi) + (B_s \eta, \eta) \Big.\\ &\quad \Big. - (p-2) (R_s \xi, \eta) - p (R_a \xi, \eta) \Big). \end{align*}Proof. We will prove the first inequality only. The second is similar.
Consider (15). We have
\begin{align*} |u|^{2} (C \nabla \overline{u}, \nabla \overline{u}) & = (C u \nabla \overline{u}, u \nabla \overline{u}) = \big( C (\xi + i \eta), \xi + i \eta \big)\\ & = (R \xi, \xi) + (R \eta, \eta) + (B \xi, \eta) - (B \eta, \xi)\\ &\quad - i \big( (R \eta, \xi) - (R \xi, \eta) + (B \xi, \xi) + (B \eta, \eta) \big). \end{align*}Therefore,
\begin{align*} \mathrm{Re} \, \big( |u|^{2} (C \nabla \overline{u}, \nabla \overline{u}) \big) & = (R \xi, \xi) + (R \eta, \eta) + (B \xi, \eta) - (B \eta, \xi)\\ & = (R_s \xi, \xi) + (R_s \eta, \eta) + 2 (B_a \xi, \eta). \end{align*}Also,
\[ \mathrm{Re} \, \big( C \mathrm{Re} \,(u \nabla \overline{u}), \mathrm{Re} \,(u \nabla \overline{u}) \big) = \mathrm{Re} \, (C \xi, \xi) = (R \xi, \xi) = (R_s \xi, \xi). \]Similarly
\[ \mathrm{Re} \, \big( i \big( C \mathrm{Re} \,(u \nabla \overline{u}), \mathrm{Im} \,(u \nabla \overline{u}) \big) \big) = \mathrm{Re} \, \big( i (C \xi, \eta) \big) ={-}(B \xi, \eta) ={-}(B_s \xi , \eta) -(B_a \xi , \eta). \]Hence taking the real parts on both sides of (15) yields the result.
The following lemma is essential in the proof of Theorem 1.2.
Lemma 3.4 Suppose 
$|1 - {2}/{p}| < \cos \theta$. Let 
$\phi = \arccos |1 - {2}/{p}|$. Then
\begin{align*} & \bigg( \tan \bigg(\frac{\pi}{2} - \phi\bigg) + \tan\theta \bigg) \big( (R_s \xi, \xi) + (R_s \eta, \eta) \big)\\ &\quad \leq \tan \bigg(\frac{\pi}{2} - \phi + \theta\bigg) \big( (R_s \xi, \xi) + (R_s \eta, \eta) + \frac{p-2}{\sqrt{p-1}} (B_s \xi, \eta) \big) \end{align*}
for all 
$\xi , \eta \in \mathbb{R}^{d}$.
Proof. First, note that
\begin{align} & \tan\bigg(\frac{\pi}{2} - \phi\bigg) (\tan\theta) \big( (R_s \xi, \xi) + (R_s \eta, \eta) \big) + \frac{p-2}{\sqrt{p-1}} (B_s \xi', \eta)\nonumber \\ &\quad \geq \tan\bigg(\frac{\pi}{2} - \phi\bigg) (\tan\theta) \big( (R_s \xi, \xi) + (R_s \eta, \eta) \big) - \frac{|p-2|}{\sqrt{p-1}} |(B_s \xi, \eta)|\nonumber\\ &\quad= \tan\bigg(\frac{\pi}{2} - \phi\bigg) \Big( (\tan\theta) \big( (R_s \xi, \xi) + (R_s \eta, \eta) \big) - 2 |(B_s \xi, \eta)| \Big) \geq 0 \end{align}
as 
$\tan ({\pi }/{2} - \phi ) = \cot (\phi ) = {|p-2|}/{2 \sqrt {p-1}}$ and we used Lemma 2.2 in the last step. We also deduce from the hypotheses that 
$\tan ({\pi }/{2} - \phi + \theta ) \geq 0$. Therefore,
\begin{align*} & \bigg( \tan \bigg(\frac{\pi}{2} - \phi\bigg) + \tan\theta \bigg) \big( (R_s \xi, \xi) + (R_s \eta, \eta) \big)\\ &\quad\leq \left( \tan\bigg(\frac{\pi}{2} - \phi\bigg) + \tan\theta \right) \big( (R_s \xi, \xi) + (R_s \eta, \eta) \big)\\ &\qquad + \tan \bigg(\frac{\pi}{2} - \phi + \theta\bigg) \Big( \tan\bigg(\frac{\pi}{2} - \phi\bigg) (\tan\theta) \big( (R_s \xi, \xi) + (R_s \eta, \eta) \big) + \frac{p-2}{\sqrt{p-1}} (B_s \xi, \eta) \Big)\\ &\quad = \tan \bigg(\frac{\pi}{2} - \phi + \theta\bigg) \big( (R_s \xi, \xi) + (R_s \eta, \eta) + \frac{p-2}{\sqrt{p-1}} (B_s \xi, \eta) \big), \end{align*}where we used (17) in the first step.
Next, we prove Theorem 1.2.
Proof of Theorem 1.2. Let 
$u \in D(A_p)$. Write 
$u \nabla \overline {u} = \xi + i \eta$, where 
$\xi , \eta \in \mathbb{R}^{d}$. By Proposition 3.3, it suffices to show that
\begin{align} & \big| (p-1) (B_s \xi, \xi) + (B_s \eta, \eta) - (p-2) (R_s \xi, \eta) - p (R_a \xi, \eta) \big|\nonumber\\ &\quad \leq K \big( (p-1) (R_s \xi, \xi) + (R_s \eta, \eta) + (p-2) (B_s \xi, \eta) \big), \end{align}
where 
$K$ is defined by (5). Set 
$\xi ' = \sqrt {p-1} \xi$. Then (18) is equivalent to
\begin{align} &\big| (B_s \xi', \xi') + (B_s \eta, \eta) - \frac{p-2}{\sqrt{p-1}} (R_s \xi', \eta) - \frac{p}{\sqrt{p-1}} (R_a \xi', \eta) \big|\nonumber\\ &\quad \leq K \Big( (R_s \xi', \xi') + (R_s \eta, \eta) + \frac{p-2}{\sqrt{p-1}} (B_s \xi', \eta) \Big). \end{align}Note that by Lemma 2.1, we have
\begin{equation} \frac{|p-2|}{\sqrt{p-1}} \big| (R_s \xi', \eta) \big| \leq \tan \bigg(\frac{\pi}{2} - \phi\bigg) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big) \end{equation}
as 
$\tan ({\pi }/{2} - \phi ) = \cot (\phi ) = {|p-2|}/{2 \sqrt {p-1}}$.
Now we consider two cases.
Case 3.5. Suppose 
$R_a = 0$. Using Lemma 2.2 again, we obtain
\begin{equation} \big| (B_s \xi', \xi') + (B_s \eta, \eta) \big| \leq (\tan\theta) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big). \end{equation}It follows that
\begin{align*} & \big| (B_s \xi', \xi') + (B_s \eta, \eta) - \frac{p-2}{\sqrt{p-1}} (R_s \xi', \eta) - \frac{p}{\sqrt{p-1}} (R_a \xi', \eta) \big|\\ &\quad= \big| (B_s \xi', \xi') + (B_s \eta, \eta) - \frac{p-2}{\sqrt{p-1}} (R_s \xi', \eta) \big|\\ &\quad \leq \big( \tan \bigg(\frac{\pi}{2} - \phi\bigg) + \tan\theta \big) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big)\\ &\quad\leq \tan \bigg(\frac{\pi}{2} - \phi + \theta\bigg) \big( (R_s \xi', \xi') + (R_s \eta, \eta) + \frac{p-2}{\sqrt{p-1}} (B_s \xi', \eta) \big), \end{align*}
where we used 
$R_a = 0$ in the first step, ( 21) and ( 20) in the second step and Lemma 3.4 in the last step.
Hence, ( 19) is valid and the result follows in this case.
Case 3.6. Suppose 
$R_a \neq 0$. We rewrite the left-hand side of (19) as
\begin{align*} L &:= \Big| \Big( (B_s \xi', \xi') + (B_s \eta, \eta) - 2 (R_a \xi', \eta) \Big) - \frac{p-2}{\sqrt{p-1}} (R_s \xi', \eta)\\ &\quad - \bigg(\frac{p}{\sqrt{p-1}} - 2 \bigg) (R_a \xi', \eta) \Big|. \end{align*}
(Note that 
${p}/{\sqrt {p-1}} \geq 2$ for all 
$p \in (1, \infty )$.) Since 
$B_a = 0$, it follows from Lemma 2.3 that
\begin{equation} \big| (B_s \xi', \xi') + (B_s \eta, \eta) - 2 (R_a \xi', \eta) \big| \leq (\tan\theta) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big). \end{equation}Next, we deduce from Lemma 2.4 that
\begin{equation} \bigg(\frac{p}{\sqrt{p-1}} - 2 \bigg) \big| (R_a \xi', \eta) \big| \leq \bigg(\frac{2}{\sin\phi} - 2 \bigg) (\tan\theta) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big) \end{equation}
as 
$\sin \phi = {2 \sqrt {p-1}}/{p}$. Now it follows from ( 20), ( 22) and ( 23) that
\begin{align*} L &\leq \bigg( \bigg(\frac{2}{\sin\phi} - 1 \bigg) \tan\theta + \tan\bigg(\frac{\pi}{2} - \phi\bigg) \bigg) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big)\\ &= \frac{\big( {2}/{\sin\phi} - 1 \big) \tan\theta + \tan\left({\pi}/{2} - \phi\right)}{\tan\theta + \tan \left({\pi}/{2} - \phi\right)} \bigg( \tan\theta + \tan \bigg(\frac{\pi}{2} - \phi\bigg) \bigg) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big)\\ &\leq \frac{\big( {2}/{\sin\phi} - 1 \big) \tan\theta + \tan\left({\pi}/{2} - \phi\right)}{\tan\theta + \tan \left({\pi}/{2} - \phi\right)} \tan \bigg(\frac{\pi}{2} - \phi + \theta\bigg)\\ &\quad \times \bigg( (R_s \xi', \xi') + (R_s \eta, \eta) + \frac{p-2}{\sqrt{p-1}} (B_s \xi', \eta) \bigg)\\ &= \frac{\big( {2}/{\sin\phi} - 1 \big) \tan\theta + \tan\left({\pi}/{2} - \phi\right)}{1 - (\tan \theta) \tan \left({\pi}/{2}-\phi\right)} \Big( (R_s \xi', \xi') + (R_s \eta, \eta) + \frac{p-2}{\sqrt{p-1}} (B_s \xi', \eta) \Big), \end{align*}where we used Lemma 3.4 in the second step.
Hence, ( 19) is also valid in this case.
4. Generation of contraction holomorphic semigroup
Let 
$\Omega = \mathbb{R}^{d}$ and 
$\theta \in [0, {\pi }/{2})$. We assume 
$c_{kl} \in W^{2,\infty }(\mathbb{R}^{d}, \mathbb{C})$ for all 
$k, l \in \{1, \ldots , d\}$. Assume further that 
$(C(x) \xi , \xi ) \in \Sigma _\theta$ for all 
$x \in \mathbb{R}^{d}$ and 
$\xi \in \mathbb{C}^{d}$, where 
$C = (c_{kl})_{1 \leq k,l \leq d}$ and 
$\Sigma _\theta$ is defined by (2).
Let 
$p \in (1, \infty )$. We will prove in Proposition 4.1 that 
$A_p$ is closable. Let 
$\overline {A_p}$ be the closure of 
$A_p$. We will show in this section that 
$-\overline {A_p}$ generates a holomorphic semigroup on 
$L_p(\mathbb{R}^{d})$ which is contractive on a sector. This is the content of Theorems 1.4 and 1.5.
First, we introduce some more definitions. Let 
$q$ be such that 
${1}/{p} + {1}/{q} = 1$. Define
\begin{equation} H_q u ={-} \sum_{k,l=1}^{d} \partial_k (\overline{c_{kl}} \partial_l u) \end{equation}on the domain
\[ D(H_q) = C_c^{\infty}(\mathbb{R}^{d}). \]Define
\[ X_p = (H_q)^{*}, \]
which is the dual of 
$H_q$. Then 
$X_p$ is closed by [Reference Kato11, Theorem III.5.29]. Also note that 
$W^{2,p}(\mathbb{R}^{d}) \subset D(X_p)$ and
\[ X_p u ={-} \sum_{k,l=1}^{d} \partial_l (c_{kl} \partial_k u) \]
for all 
$u \in W^{2,p}(\mathbb{R}^{d})$.
Proposition 4.1 The operator 
$A_p$ is closable.
Proof. Since 
$A_p \subset X_p$ and 
$X_p$ are closed, the operator 
$A_p$ is closable.
It turns out that 
$X_p = \overline {A_p}$ under certain conditions, as shown in the following proposition.
Proposition 4.2 Suppose 
$|1 - {2}/{p}| \leq \cos \theta$ and 
$B_a = 0$. Then 
$\overline {A_p} = X_p$. Moreover, 
$\overline {A_p}$ is 
$m$-accretive.
Proof. By [Reference Do4, Proposition 4.9] the operator 
$X_p$ is 
$m$-accretive and the space 
$C_c^{\infty }(\mathbb{R}^{d})$ of test functions is a core for 
$X_p$. It follows that 
$\overline {A_p} = X_p$ and 
$A_p$ is 
$m$-accretive as claimed.
Using Theorem 1.2, we are now able to prove the generation result in Theorem 1.4.
Proof of Theorem 1.4. It follows from Theorem 1.2 that
\[ |\mathrm{Im} \, (\overline{A_p} u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]})| \leq K \mathrm{Re} \, (\overline{A_p} u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]}) \]
for all 
$u \in D(\overline {A_p})$, where 
$K$ is defined by (5). Therefore, the interior 
$\Sigma _{\pi - \arctan (K)}^{\circ } \subset \rho (-\overline {A_p})$ by [Reference Pazy16, Theorem 1.3.9] and Proposition 4.2, where 
$\rho (-\overline {A_p})$ denotes the resolvent set of 
$-\overline {A_p}$. Moreover,
\begin{equation} \|(\lambda + \overline{A_p})^{{-}1}\|_{p \to p} \leq \frac{1}{\mathrm{dist} \,(\lambda,S(-\overline{A_p}))} \end{equation}
for all 
$\lambda \in \Sigma _{\pi - \arctan (K)}^{\circ }$, where 
$S(-\overline {A_p})$ is the numerical range of 
$-\overline {A_p}$ defined by
\[ S(-\overline{A_p}) = \big\{ - \big( \overline{A_p} u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]} \big): u \in D(\overline{A_p}) \mbox{ and } \|u\|_p = 1 \big\}. \]
Let 
$\varepsilon \in (0, \pi - \arctan (K))$. Then 
$\mathrm {dist} \,(\lambda ,S(-\overline {A_p})) \geq (\sin \varepsilon ) |\lambda |$ for all 
$\lambda \in \Sigma _{\pi - \arctan (K) - \varepsilon }$. Therefore, (25) implies
\[ \|(\lambda + \overline{A_p})^{{-}1}\|_{p \to p} \leq \frac{1}{(\sin\varepsilon) |\lambda|} \]
for all 
$\lambda \in \Sigma _{\pi - \arctan (K) - \varepsilon }$. Hence we deduce from [Reference Pazy16, Theorem 2.5.2(c)] that 
$-\overline {A_p}$ generates a holomorphic semigroup on 
$L_p(\mathbb{R}^{d})$ with angle 
$\psi = {\pi }/{2} - \arctan (K)$.
Our next aim is to show Theorem 1.5. We will do this by first showing that 
$-X_p$ generates a holomorphic semigroup which is contractive on a sector. This together with Proposition 4.2 implies the theorem. We first obtain some preliminary results.
In what follows we let 
$X_{p,\alpha } = e^{i \alpha } X_p$ for all 
$\alpha \in (-{\pi }/{2} + \theta , {\pi }/{2} - \theta )$ and adopt the notation used in Lemmas 2.7 and 2.8. We aim to show that 
$X_{p,\alpha }$ is an 
$m$-accretive operator for all 
$\alpha$ in a suitable range. Following [Reference Do4, Reference Wong-Dzung20], we need two crucial inequalities for 
$X_{p,\alpha }$ in order to do this which are given in Propositions 4.3 and 4.5, respectively.
The first inequality is as follows.
Proposition 4.3 Suppose 
$B_a = 0$. Let 
$p \in (1, \infty )$ be such that 
$|1 - {2}/{p}| < \cos \theta$. Let 
$\alpha \in (-\psi , \psi )$, where 
$\psi$ is given by (9). Then
\[ \mathrm{Re} \, (X_{p,\alpha} u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]}) \geq 0 \]
for all 
$u \in W^{2,p}(\mathbb{R}^{d})$.
Proof. Let 
$u \in W^{2,p}(\mathbb{R}^{d})$. It follows from Theorem 3.1 that
\begin{align} (X_{p,\alpha} u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]}) & = \int_{[u \neq 0]} |u|^{p-2} (C_\alpha \nabla \overline{u}, \nabla \overline{u})\nonumber\\ &\quad + (p - 2) \int_{[u \neq 0]} |u|^{p-4} \big( C_\alpha \mathrm{Re} \,(u \nabla \overline{u}), \mathrm{Re} \,(u \nabla \overline{u}) \big)\nonumber\\ &\quad - i (p - 2) \int_{[u \neq 0]} |u|^{p-4} \big( C_\alpha \mathrm{Re} \,(u \nabla \overline{u}), \mathrm{Im} \,(u \nabla \overline{u}) \big). \end{align}
Write 
$u \nabla \overline {u} = \xi + i \eta$, where 
$\xi , \eta \in \mathbb{R}^{d}$. Then
\begin{align*} |u|^{2} (C_\alpha \nabla \overline{u}, \nabla \overline{u})& = (C_\alpha u \nabla \overline{u}, u \nabla \overline{u}) = \big( C_\alpha (\xi + i \eta), \xi + i \eta \big)\\ & = (R_\alpha \xi, \xi) + (R_\alpha \eta, \eta) + (B_\alpha \xi, \eta) - (B_\alpha \eta, \xi)\\ &\quad + i \big( (R_\alpha \eta, \xi) - (R_\alpha \xi, \eta) + (B_\alpha \xi, \xi) + (B_\alpha \eta, \eta) \big). \end{align*}Therefore,
\begin{align*} \mathrm{Re} \, \big( |u|^{2} (C_\alpha \nabla \overline{u}, \nabla \overline{u}) \big) & = (R_\alpha \xi, \xi) + (R_\alpha \eta, \eta) + (B_\alpha \xi, \eta) - (B_\alpha \eta, \xi)\\ & = (R_{s,\alpha} \xi, \xi) + (R_{s,\alpha} \eta, \eta) + 2 (B_{a,\alpha} \xi, \eta). \end{align*}We also have
\[ \mathrm{Re} \, \big( C_\alpha \mathrm{Re} \,(u \nabla \overline{u}), \mathrm{Re} \,(u \nabla \overline{u}) \big) = \mathrm{Re} \, (C_\alpha \xi, \xi) = (R_\alpha \xi, \xi) = (R_{s,\alpha} \xi , \xi). \]Similarly
\begin{align*} \mathrm{Re} \, \big( i \big( C_\alpha \mathrm{Re} \,(u \nabla \overline{u}), \mathrm{Im} \,(u \nabla \overline{u}) \big) \big) &= \mathrm{Re} \, \big( i (C_\alpha \xi, \eta) \big) ={-}(B_\alpha \xi, \eta)\\ &={-}(B_{s,\alpha} \xi , \eta) - (B_{a,\alpha} \xi , \eta). \end{align*}Hence taking the real parts on both sides of (26) yields
\begin{align} & \mathrm{Re} \, (X_{p,\alpha} u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]})\nonumber\\ &\quad= \int_{[u \neq 0]} |u|^{p-4} \Big( (p-1) (R_{s,\alpha} \xi, \xi) + (R_{s,\alpha} \eta, \eta) + p (B_{a,\alpha} \xi, \eta) + (p-2) (B_{s,\alpha} \xi, \eta) \Big)\nonumber\\ &\quad = \int_{[u \neq 0]} |u|^{p-4} \Big( (R_{s,\alpha} \xi', \xi') + (R_{s,\alpha} \eta, \eta) + \frac{p}{\sqrt{p-1}} (B_{a,\alpha} \xi', \eta) + \frac{p-2}{\sqrt{p-1}} (B_{s,\alpha} \xi', \eta) \Big), \end{align}
where 
$\xi ' = \sqrt {p-1} \xi$. Set
\begin{equation} P = (R_{s,\alpha} \xi', \xi') + (R_{s,\alpha} \eta, \eta) + \frac{p}{\sqrt{p-1}} (B_{a,\alpha} \xi', \eta) + \frac{p-2}{\sqrt{p-1}} (B_{s,\alpha} \xi', \eta). \end{equation}
We will show that 
$P \geq 0$. We consider 2 cases.
Case 4.4. Suppose 
$R_a = 0$. Note that 
$\cot \phi = {|p-2|}/{2 \sqrt {p-1}}$. We have
\begin{equation} \big| (\sin\alpha) \big( (B_s \xi', \xi') + (B_s \eta, \eta) \big) \big| \leq \sin(|\alpha|) (\tan\theta) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big) \end{equation}and
\begin{equation} \Big| \frac{p-2}{\sqrt{p-1}} (\cos\alpha) (B_s \xi', \eta) \Big| \leq (\cot\phi) (\cos\alpha) (\tan\theta) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big). \end{equation}by Lemma 2.2. Also,
\begin{equation} \Big| \frac{p-2}{\sqrt{p-1}} (\sin\alpha) (R_s \xi', \eta) \Big| \leq (\cot\phi) \sin(|\alpha|) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big) \end{equation}
by Lemma 2.1. Since 
$R_a = 0$, Lemma 2.8(iv) gives 
$B_{a,\alpha } = (\sin \alpha ) R_a = 0$. It follows from Lemma 2.8, ( 28)–( 31) that
\begin{align*} P&= (R_{s,\alpha} \xi', \xi') + (R_{s,\alpha} \eta, \eta) + \frac{p-2}{\sqrt{p-1}} (B_{s,\alpha} \xi', \eta)\\ &= (\cos\alpha) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big) - (\sin\alpha) \big( (B_s \xi', \xi') + (B_s \eta, \eta) \big) \\ &\quad + \frac{p-2}{\sqrt{p-1}} (\sin\alpha) (R_s \xi', \eta) + \frac{p-2}{\sqrt{p-1}} (\cos\alpha) (B_s \xi', \eta)\\ &\geq \big( \cos\alpha - \sin(|\alpha|) \tan\theta - (\cot\phi) \sin(|\alpha|) - (\cot\phi) (\cos\alpha) \tan\theta \big) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big)\\ &\geq 0, \end{align*}
where we used the fact that 
$\alpha \in (-\psi ,\psi )$ in the last step. Hence, we deduce from ( 27) that 
$\mathrm {Re} \, (X_{p,\alpha } u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]}) \geq 0$ in this case.
Case 4.5. Suppose 
$R_a \neq 0$. Expanding (28) using Lemma 2.8 gives
\begin{align} P&= (R_{s,\alpha} \xi', \xi') + (R_{s,\alpha} \eta, \eta) + \frac{p}{\sqrt{p-1}} (B_{a,\alpha} \xi', \eta) + \frac{p-2}{\sqrt{p-1}} (B_{s,\alpha} \xi', \eta)\nonumber\\ &= (\cos\alpha) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big) - (\sin\alpha) \big( (B_s \xi', \xi') + (B_s \eta, \eta) \big)\nonumber\\ &\quad + \frac{p}{\sqrt{p-1}} (\sin\alpha) (R_a \xi', \eta) + \frac{p-2}{\sqrt{p-1}} (\sin\alpha) (R_s \xi', \eta) + \frac{p-2}{\sqrt{p-1}} (\cos\alpha) (B_s \xi', \eta)\nonumber\\ &= (\cos\alpha) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big) - (\sin\alpha) \big( (B_s \xi', \xi') + (B_s \eta, \eta) - 2 (R_a \xi', \eta) \big) \nonumber\\ &\quad + \bigg(\frac{p}{\sqrt{p-1}} - 2 \bigg) (\sin\alpha) (R_a \xi', \eta) + \frac{p-2}{\sqrt{p-1}} (\sin\alpha) (R_s \xi', \eta)\nonumber\\ &\quad + \frac{p-2}{\sqrt{p-1}} (\cos\alpha) (B_s \xi', \eta), \end{align}where we used Lemma 2.8(iii) and (iv) in the second step. Next, we estimate the terms in ( 32). By Lemma 2.3, we have
\begin{equation} \Big| (\sin\alpha) \big( (B_s \xi', \xi') + (B_s \eta, \eta) - 2 (R_a \xi', \eta) \big) \Big| \leq \sin(|\alpha|) (\tan\theta) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big) \end{equation}
since 
$B_a = 0$ by hypothesis. Using Lemma 2.4 and the fact that 
$\sin \phi = \frac {2 \sqrt {p-1}}{p}$, we deduce that
\begin{equation} \bigg| \bigg(\frac{p}{\sqrt{p-1}} - 2 \bigg) (\sin\alpha) (R_a \xi', \eta) \bigg| \leq \bigg(\frac{2}{\sin\phi} - 2 \bigg) \sin(|\alpha|) (\tan\theta) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big). \end{equation}
Next note that 
$\cot \phi = {|p-2|}/{2 \sqrt {p-1}}$. Therefore,
\begin{equation} \bigg| \frac{p-2}{\sqrt{p-1}} (\sin\alpha) (R_s \xi', \eta) \bigg| \leq (\cot\phi) \sin(|\alpha|) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big) \end{equation}by Lemma 2.1. It follows from Lemma 2.2 that
\begin{equation} \bigg| \frac{p-2}{\sqrt{p-1}} (\cos\alpha) (B_s \xi', \eta) \bigg| \leq (\cot\phi) (\cos\alpha) (\tan\theta) \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big). \end{equation}Next, ( 32)–( 36) together imply
\begin{align} P&\geq \bigg( \big( 1 - (\tan\theta) \cot\phi \big) \cos\alpha - \bigg( \bigg(\frac{2}{\sin\phi} - 1\bigg) \tan\theta + \cot\phi \bigg) \sin(|\alpha|) \bigg)\notag\\ &\quad \times \big( (R_s \xi', \xi') + (R_s \eta, \eta) \big)\nonumber\\ &\geq 0, \end{align}
where we used that fact that 
$\alpha \in (-\psi , \psi )$ and Lemma 2.1 in the last step. Combining ( 27) and ( 37) yields 
$\mathrm {Re} \, (X_{p,\alpha } u, |u|^{p-2} u {\mathbb 1}_{[u \neq 0]}) \geq 0$ in this case.
Next, we prove the second inequality for 
$X_{p,\alpha }$. We need the following density result.
Proposition 4.4 Let 
$\alpha \in (-\psi , \psi )$, where 
$\psi$ is given by (9). Then the space 
$C_c^{\infty }(\mathbb{R}^{d})$ is dense in 
$(D(X_{p,\alpha }) \cap W^{1,p}(\mathbb{R}^{d}), \|\cdot \|_{D(X_{p,\alpha })})$.
Proof. The claim follows from [Reference Do4, Proposition 4.7].
The second inequality is as follows (see [Reference Wong-Dzung20, proposition 6.1] for the case when 
$\alpha = 0$ and 
$X_p$ has real symmetric coefficients as well as [Reference Do4, Proposition 4.8] for the case when 
$\alpha = 0$ and 
$X_p$ has complex coefficients).
Proposition 4.5 Suppose 
$B_a = 0$. Let 
$p \in (1, \infty )$ be such that 
$|1 - {2}/{p}| < \cos \theta$. Let 
$\alpha \in (-\gamma , \gamma )$, where 
$\gamma$ is given by (11). Then there exists an 
$M > 0$ such that
\[ \mathrm{Re} \, (\nabla (X_{p,\alpha} u), |\nabla u|^{p-2} \nabla u {\mathbb 1}_{[\nabla u \neq 0]}) \geq{-} M \|\nabla u\|_p^{p} \]
for all 
$u \in W^{2,p}(\mathbb{R}^{d})$ such that 
$\nabla (X_{p,\alpha } u) \in (L_p(\mathbb{R}^{d}))^{d}$.
Proof. We consider two cases.
Case 4.8 Suppose 
$R_a = 0$. Then it follows from Lemma 2.8 that 
$B_{a,\alpha } = R_a \sin \alpha = 0$. Moreover, the condition 
$\alpha \in (-\psi , \psi )$ implies 
$\tan (\theta +|\alpha |) < \tan \phi$. Therefore, [Reference Do4, Proposition 4.8] still applies to yield the result.
Case 4.9 Suppose 
$R_a \neq 0$. If 
$\alpha = 0$, the claim follows from [Reference Do4, Proposition 4.8]. Therefore, we may assume that 
$\alpha \neq 0$ for the rest of the proof. Note that 
$\alpha \in (-\gamma , \gamma )$ implies 
$(\tan \theta ) \tan (|\alpha |) < \frac {1}{3}$ and 
$K \tan (|\alpha |) < 1$, where 
$K$ is defined by (5). Let 
$\varepsilon _0 \in (0, 1 \wedge (p-1))$ be such that
\begin{equation} (\tan\theta) \tan(|\alpha|) \leq \frac{1 - \varepsilon}{3 - \varepsilon} \end{equation}and
\begin{align} & \left( \bigg(\frac{p}{\sqrt{\bigg(1-\varepsilon\bigg)(p-1-\varepsilon)}} - 1 \bigg) \tan\theta + \frac{|p-2|}{2 \sqrt{(1-\varepsilon)(p-1-\varepsilon)}} \right) \tan(|\alpha|)\nonumber\\ &\quad\leq 1 - (\tan\theta) \frac{|p-2|}{2 \sqrt{(1-\varepsilon)(p-1-\varepsilon)}} \end{align}
for all 
$\varepsilon \in (0, \varepsilon _0)$. Let 
$\varepsilon \in (0, \varepsilon _0)$ be such that
\begin{equation} \varepsilon < \frac{\varepsilon_0}{32 d \big( 1 + \tan(\theta + |\alpha|) \big)^{2} \sup_{1 \leq l \leq d} \|\partial_l^{2} C\|_\infty}. \end{equation} Let 
$u \in W^{2,p}(\mathbb{R}^{d})$. By Lemma 4.4, we can assume without loss of generality that 
$u$ has a compact support. For the rest of the proof, all integrations are over the set 
$\{x \in \mathbb{R}^{d}: |(\nabla u)(x)| \neq 0 \}$. We have
\begin{align*} (\nabla (X_{p,\alpha} u), |\nabla u|^{p-2} \nabla u) & ={-} \sum_{k,l,j=1}^{d} \int \Big( \partial_j \partial_l (e^{i \alpha} c_{kl} \partial_k u) \Big) |\nabla u|^{p-2} \partial_j \overline{u}\\ & ={-} \sum_{k,l,j=1}^{d} \int e^{i \alpha} \Big( \partial_l \big( (\partial_j c_{kl}) (\partial_k u) + c_{kl} (\partial_j \partial_k u) \big) \Big) |\nabla u|^{p-2} \partial_j \overline{u}\\ & ={-} \sum_{k,l,j=1}^{d} \int e^{i \alpha} \Big( \partial_l \big( (\partial_j c_{kl}) (\partial_k u) \big) \Big) |\nabla u|^{p-2} \partial_j \overline{u}\\ &\quad + \sum_{k,l,j=1}^{d} \int e^{i \alpha} c_{kl} (\partial_j \partial_k u) \partial_l \big( |\nabla u|^{p-2} \partial_j \overline{u} \big)\\ & = (\textrm{I}) + (\textrm{II}). \end{align*}We first consider the real part of (I). We have
\begin{align*} & -\mathrm{Re} \, \sum_{k,l,j=1}^{d} \int e^{i \alpha} \Big( \partial_l \big( (\partial_j c_{kl}) (\partial_k u) \big) \Big) |\nabla u|^{p-2} \partial_j \overline{u}\\ &\quad={-} \mathrm{Re} \, \sum_{k,l,j=1}^{d} \int e^{i \alpha} (\partial_l \partial_j c_{kl}) (\partial_k u) (\partial_j \overline{u}) |\nabla u|^{p-2}\\ &- \mathrm{Re} \, \sum_{k,l,j=1}^{d} \int e^{i \alpha} (\partial_j c_{kl}) (\partial_l \partial_k u) (\partial_j \overline{u}) |\nabla u|^{p-2}\\ &\quad = (\textrm{Ia}) + (\textrm{Ib}). \end{align*}For (Ia), we have
\[ (\textrm{Ia}) \geq{-} \frac{1}{2} \sum_{k,l,j=1}^{d} \|c_{kl}\|_{W^{2,\infty}} \int (|\partial_k u|^{2} + |\partial_j u|^{2}) |\nabla u|^{p-2} \geq{-} M_1 \|\nabla u\|_p^{p}, \]
where 
$M_1 = d^{2} \sup \{\|c_{kl}\|_{W^{2,\infty }}: 1 \leq k,l \leq d\}$. Let 
$U = (\partial _l \partial _k u)_{1 \leq k,l \leq d}$. For (Ib), we estimate
\begin{align*} (\textrm{Ib})& ={-} \mathrm{Re} \, \sum_{j=1}^{d} \int \mathrm{tr} \,((\partial_j C_\alpha) U) (\partial_j \overline{u}) |\nabla u|^{p-2}\\ & \geq{-} \sum_{j=1}^{d} \int \Big( \varepsilon |\mathrm{tr} \,((\partial_j C_\alpha) U)|^{2} |\nabla u|^{p-2} + \frac{1}{4 \varepsilon} |\partial_j \overline{u}|^{2} |\nabla u|^{p-2} \Big)\\ & \geq{-} \varepsilon' \int \mathrm{tr} \,(U R_{s,\alpha} \overline{U}) |\nabla u|^{p-2}- M_2 \|\nabla u\|_p^{p}\\ & ={-} \varepsilon' \int \mathrm{tr} \,(\overline{U} R_{s,\alpha} U) |\nabla u|^{p-2} - M_2 \|\nabla u\|_p^{p}, \end{align*}where we used Lemma 2.7 in the third step with
\[ \varepsilon' = 32 \varepsilon d \big( 1 + \tan(\theta + |\alpha|) \big)^{2} \sup_{1 \leq l \leq d} \|\partial_l^{2} C\|_\infty \]
and 
$M_2 = {1}/{4 \varepsilon }$. Note that 
$\varepsilon ' \in (0, \varepsilon _0)$ by ( 40).
Next, we consider the real part of (II). Note that
\begin{align*} &\mathrm{Re} \, \sum_{k,l,j=1}^{d} \int e^{i \alpha} c_{kl} (\partial_j \partial_k u) \partial_l \big( |\nabla u|^{p-2} \partial_j \overline{u} \big)\\ & \quad = \mathrm{Re} \, \sum_{k,l,j=1}^{d} \int e^{i \alpha} c_{kl} (\partial_j \partial_k u) (\partial_l \partial_j \overline{u}) |\nabla u|^{p-2}\\ & \qquad + \mathrm{Re} \, \sum_{k,l,j=1}^{d} \int e^{i \alpha} c_{kl} (\partial_j \partial_k u) (\partial_j \overline{u}) \partial_l(|\nabla u|^{p-2})\\ & \quad = (\textrm{IIa}) + (\textrm{IIb}). \end{align*}
In what follows we let 
$U \nabla \overline {u} = \xi + i \eta$, where 
$\xi , \eta \in \mathbb{R}^{d}$. For (IIa), we have
\[ (\textrm{IIa}) = \int \mathrm{tr} \,(\overline{U} \mathrm{Re} \, (C_\alpha) U) |\nabla u|^{p-2} = \int \mathrm{tr} \,(\overline{U} R_{s,\alpha} U) |\nabla u|^{p-2} + i \int \mathrm{tr} \,(\overline{U} B_{a,\alpha} U) |\nabla u|^{p-2}. \]For (IIb), we have
\begin{align*} (\textrm{IIb})& = \mathrm{Re} \, \sum_{k,l,i,j=1}^{d} \frac{p-2}{2} \int e^{i \alpha} c_{kl} (\partial_j \partial_k u) (\partial_j \overline{u}) \Big( (\partial_l \partial_i u) (\partial_i \overline{u}) + (\partial_l \partial_i \overline{u}) (\partial_i u) \Big) |\nabla u|^{p-4}\\ & = \frac{p-2}{2} \int \mathrm{Re} \, \Big( \big( C_\alpha U \nabla \overline{u}, \overline{U \nabla \overline{u}} \big) + \big( C_\alpha U \nabla \overline{u}, U \nabla \overline{u} \big) \Big) |\nabla u|^{p-4}\\ & = (p-2) \int \Big( (R_\alpha \xi, \xi) - (B_\alpha \eta, \xi) \Big) |\nabla u|^{p-4}\\ & = (p-2) \int \Big( (R_{s,\alpha} \xi, \xi) - (B_{s,\alpha} \xi, \eta) + (B_{a,\alpha} \xi, \eta) \Big) |\nabla u|^{p-4}, \end{align*}
where 
$\xi , \eta \in \mathbb{R}^{d}$ and 
$U \nabla \overline {u} = \xi + i \eta$.
In total, we obtain
\begin{align} \mathrm{Re} \, (\nabla (X_{p,\alpha} u), |\nabla u|^{p-2} \nabla u) & \geq{-} (M_1 + M_2) \|\nabla u\|_p^{p} + (1-\varepsilon') \int \mathrm{tr} \,(U R_{s,\alpha} \overline{U}) |\nabla u|^{p-2}\nonumber\\ &\quad + i \int \mathrm{tr} \,(U B_{a,\alpha} \overline{U}) |\nabla u|^{p-2}\nonumber\\ &\quad + (p-2) \int \Big( (R_{s,\alpha} \xi, \xi) - (B_{s,\alpha} \xi, \eta) + (B_{a,\alpha} \xi, \eta) \Big) |\nabla u|^{p-4}\nonumber\\ & ={-} (M_1 + M_2) \|\nabla u\|_p^{p} + P, \end{align}where
\begin{align*} P&= (1-\varepsilon') \int \mathrm{tr} \,(U R_{s,\alpha} \overline{U}) |\nabla u|^{p-2} + i \int \mathrm{tr} \,(U B_{a,\alpha} \overline{U}) |\nabla u|^{p-2}\\ &\quad + (p-2) \int \Big( (R_{s,\alpha} \xi, \xi) - (B_{s,\alpha} \xi, \eta) + (B_{a,\alpha} \xi, \eta) \Big) |\nabla u|^{p-4}. \end{align*}
Next, we will show that 
$P \geq 0$. First note that 
$(1-\varepsilon ') (\cos \alpha ) - (3 - \varepsilon ') \sin (|\alpha |) \tan \theta \geq 0$ due to (38). It follows that
\begin{align*} & (1-\varepsilon') \mathrm{tr} \,(\overline{U} R_{s,\alpha} U) |\nabla u|^{2} + i \mathrm{tr} \,(\overline{U} B_{a,\alpha} U) |\nabla u|^{2}\\ &\quad= (1-\varepsilon') (\cos\alpha) \mathrm{tr} \,(\overline{U} R_s U) |\nabla u|^{2} - (1-\varepsilon') (\sin\alpha) \mathrm{tr} \,(\overline{U} B_s U) |\nabla u|^{2}\\ &\qquad + i (\sin\alpha) \mathrm{tr} \,(\overline{U} R_a U) |\nabla u|^{2}\\ &\quad= \Big( (1-\varepsilon') \cos\alpha - (3 - \varepsilon') \sin(|\alpha|) \tan\theta \Big) \mathrm{tr} \,(\overline{U} R_s U) |\nabla u|^{2} \\ &\qquad + (1-\varepsilon') \sin(|\alpha|) \mathrm{tr} \, \left( \overline{U} \bigg( (\tan\theta) R_s - \frac{\sin\alpha}{\sin(|\alpha|)} B_s \bigg) U \right) |\nabla u|^{2}\\ &\qquad + \sin(|\alpha|) \mathrm{tr} \, \left( \overline{U} \bigg( 2 (\tan\theta) R_s + i \frac{\sin\alpha}{\sin(|\alpha|)} R_a \bigg) U \right) |\nabla u|^{2}\\ &\quad\geq \Big( (1-\varepsilon') (\cos\alpha) - (3 - \varepsilon') \sin(|\alpha|) \tan\theta \Big) (R_s U \nabla \overline{u}, U \nabla \overline{u})\\ &\qquad + (1-\varepsilon') \sin(|\alpha|) \bigg( \bigg( (\tan\theta) R_s - \frac{\sin\alpha}{\sin(|\alpha|)} B_s \bigg) U \nabla \overline{u}, U \nabla \overline{u} \bigg)\\ &\qquad + \sin(|\alpha|) \bigg( \bigg( 2 (\tan\theta) R_s + i \frac{\sin\alpha}{\sin(|\alpha|)} R_a \bigg) U \nabla \overline{u}, U \nabla \overline{u} \bigg)\\ &\quad= (1-\varepsilon') (\cos\alpha) (R_s U \nabla \overline{u}, U \nabla \overline{u}) - (1-\varepsilon') (\sin\alpha) (B_s U \nabla \overline{u}, U \nabla \overline{u})\\ &\qquad + i (\sin\alpha) (R_a U \nabla \overline{u}, U \nabla \overline{u})\\ &\quad= (1-\varepsilon') (\cos\alpha) \Big( (R_s \xi, \xi) + (R_s \eta, \eta) \Big) - (1-\varepsilon') (\sin\alpha) \Big( (B_s \xi, \xi) + (B_s \eta, \eta) \Big)\\ &\qquad + 2 (\sin\alpha) (R_a \xi, \eta), \end{align*}where we used Lemmas 2.5 and 2.6 in the third step. Hence we obtain
\begin{align} P&\geq \int \bigg( (1-\varepsilon') (\cos\alpha) \Big( (R_s \xi, \xi) + (R_s \eta, \eta) \Big) - (1-\varepsilon') (\sin\alpha) \Big( (B_s \xi, \xi) + (B_s \eta, \eta) \Big)\nonumber\\ &\quad + 2 (\sin\alpha) (R_a \xi, \eta) \bigg) |\nabla u|^{p-4}\nonumber\\ &\quad + (p-2) \int \Big( (R_{s,\alpha} \xi, \xi) - (B_{s,\alpha} \xi, \eta) + (B_{a,\alpha} \xi, \eta) \Big) |\nabla u|^{p-4}\nonumber\\ &= \int \bigg( (\cos\alpha) \big( (p-1-\varepsilon') (R_s \xi, \xi)+ (1-\varepsilon') (R_s \eta, \eta) \big)\nonumber\\ &\quad - (\sin\alpha) \big( (p-1-\varepsilon') (B_s \xi, \xi) + (1-\varepsilon') (B_s \eta, \eta) \big)\nonumber\\ &\quad + p (\sin\alpha) (R_a \xi, \eta) - (p-2) (\sin\alpha) (R_s \xi, \eta) - (p-2) (\cos\alpha) (B_s \xi, \eta) \bigg) |\nabla u|^{p-4}\nonumber\\ &= \int \bigg( (\cos\alpha) \big( (R_s \xi', \xi') + (R_s \eta', \eta') \big) - (\sin\alpha) \big( (B_s \xi', \xi') + (B_s \eta', \eta') \big)\nonumber\\ &\quad + \frac{p}{\sqrt{(1-\varepsilon') (p-1-\varepsilon')}} (\sin\alpha) (R_a \xi', \eta') - \frac{p-2}{\sqrt{(1-\varepsilon') (p-1-\varepsilon')}} (\sin\alpha) (R_s \xi', \eta')\nonumber\\ &\quad - \frac{p-2}{\sqrt{(1-\varepsilon') (p-1-\varepsilon')}} (\cos\alpha) (B_s \xi', \eta') \bigg) |\nabla u|^{p-4}, \end{align}
where we used Lemma 2.8(iii) and (iv) in the second step, 
$\xi ' = \sqrt {p-1-\varepsilon '} \xi$ and 
$\eta ' = \sqrt {1-\varepsilon '} \eta$. Finally, using (39), we argue in a similar manner to that used in Case 2 of the proof of Proposition 4.3 to derive 
$P \geq 0$. Thus, it follows from (41) that
\[ \mathrm{Re} \, (\nabla (X_{p,\alpha} u), |\nabla u|^{p-2} \nabla u) \geq{-} (M_1 + M_2) \|\nabla u\|_p^{p} \]as claimed.
Next, we use the two inequalities obtained in Propositions 4.3 and 4.5 to show that 
$X_{p,\alpha }$ is 
$m$-accretive for all 
$\alpha$ in a suitable range.
Proposition 4.6 Suppose 
$B_a = 0$. Let 
$p \in (1, \infty )$ be such that 
$|1 - {2}/{p}| < \cos \theta$. Let 
$\alpha \in (-\gamma , \gamma )$, where 
$\gamma$ is given by (11). Then 
$X_{p,\alpha }$ is 
$m$-accretive.
Proof. The result follows from the arguments used in the proof of [Reference Do4, Proposition 4.9]. Note that [Reference Do4, Propositions 4.1, 4.7 and 4.8] used in the proof of [Reference Do4, Proposition 4.9] are now replaced by Propositions 4.3, 4.4 and 4.5 respectively.
We are now ready to prove Theorem 1.5.
Proof of Theorem 1.5. We consider two parts.
(i) Contractivity: Using Proposition 4.6 and [Reference Kato11, Theorem IX.1.23], we deduce that
$-X_p$ generates a holomorphic semigroup with angle $\psi$ given by (9) which is contractive on the sector $\Sigma _\gamma$, where $\gamma$ is given by (11). Note that $X_p = \overline {A_p}$ by Proposition 4.2. Hence $S^{(p)}$ is contractive on $\Sigma _\gamma$.(ii) Consistency: It suffices to show that
$S^{(p)}$ is consistent with $S$. It follows from [Reference Do4, Propositions 1.1 and 5.1] that the $C_0$-semigroup generated by $-B_2$ is consistent with the $C_0$-semigroup generated by $-X_p$. Since $B_2 = \overline {A_2}$ and $X_p = \overline {A_p}$ by Proposition 4.2, the semigroup $S^{(p)}$ is consistent with $S$ as required.
Acknowledgements
I wish to thank Tom ter Elst and the referees for giving detailed and valuable comments. I also thank the referees for informing about Remark 1.3.
