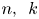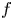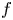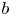1. Introduction and main results
The main purpose of this paper is to characterize meromorphic solutions of functional-differential equation
where $n,\,~k$![]() are two positive integers and $a(\neq 0)$
are two positive integers and $a(\neq 0)$![]() , $b$
, $b$![]() , $c$
, $c$![]() are constants, or more generally, polynomials in $\mathbb {C}$
are constants, or more generally, polynomials in $\mathbb {C}$![]() . The equation is a generalization of the following equation
. The equation is a generalization of the following equation
which include the pantograph equations $f'(z)=af(\alpha z)+bf(z)$![]() and the extensively studied equation
and the extensively studied equation
These differential equations with proportional delays are usually referred to as pantograph ones, which have been studied for both real and complex variables by many authors both numerically and analytically owing to numerous practical applications in various fields, such as electrodynamics, astrophysics and cell growth. See, for example [Reference Ockendon and Taylor12, Reference Wake, Cooper, Kim and van Brunt18] and the references cited therein. And the special case $f'(z)=af(z-k)$![]() is the well-known time delay differential equation (DDE), see monograph [Reference Bellman and Cooke1]. The general form of the time DDE is
is the well-known time delay differential equation (DDE), see monograph [Reference Bellman and Cooke1]. The general form of the time DDE is
where $F(z,\, u,\, w)$![]() and $g(z)$
and $g(z)$![]() are given analytic functions and $f(z)$
are given analytic functions and $f(z)$![]() is an unknown function. In [Reference Utz15], Utz proposed the problem of determining conditions for the existence of a real function $f$
is an unknown function. In [Reference Utz15], Utz proposed the problem of determining conditions for the existence of a real function $f$![]() (not identically zero) satisfying Equation (1.3). The problem was solved by Siu in [Reference Siu13]. Actually, by applying elementary operator theory in Banach spaces, Siu gave existence and uniqueness results for Equation (1.3) under certain conditions. The problems of local existence and uniqueness for the general Equation (1.4) were studied by Oberg in [Reference Oberg10] for local real solutions and in [Reference Oberg11] for local complex solutions. Corresponding to the global solutions (entire solutions) of Equation (1.3), it was Gross in [Reference Gross5] who deduced that $g$
(not identically zero) satisfying Equation (1.3). The problem was solved by Siu in [Reference Siu13]. Actually, by applying elementary operator theory in Banach spaces, Siu gave existence and uniqueness results for Equation (1.3) under certain conditions. The problems of local existence and uniqueness for the general Equation (1.4) were studied by Oberg in [Reference Oberg10] for local real solutions and in [Reference Oberg11] for local complex solutions. Corresponding to the global solutions (entire solutions) of Equation (1.3), it was Gross in [Reference Gross5] who deduced that $g$![]() must be linear when entire functions $f$
must be linear when entire functions $f$![]() and $g$
and $g$![]() in $\mathbb {C}$
in $\mathbb {C}$![]() satisfy Equation (1.3) with $a$
satisfy Equation (1.3) with $a$![]() being a constant. The follow-up work was due to van Brunt–Marshall–Wake in [Reference van Brunt, Marshall and Wake16], who generalized the above result to Equation (1.2) with the condition $c=0$
being a constant. The follow-up work was due to van Brunt–Marshall–Wake in [Reference van Brunt, Marshall and Wake16], who generalized the above result to Equation (1.2) with the condition $c=0$![]() . For describing meromorphic solutions of more general equations, Gross and Yang in [Reference Gross and Yang6] obtained that the entire function $g$
. For describing meromorphic solutions of more general equations, Gross and Yang in [Reference Gross and Yang6] obtained that the entire function $g$![]() is a polynomial if $f$
is a polynomial if $f$![]() is meromorphic. But, the specific form of $g$
is meromorphic. But, the specific form of $g$![]() is not given there. In 2007, Li in [Reference Li and Saleeby8] further studied this kind of equation by characterizing entire functions $g$
is not given there. In 2007, Li in [Reference Li and Saleeby8] further studied this kind of equation by characterizing entire functions $g$![]() to Equation (1.2) when $f$
to Equation (1.2) when $f$![]() is a meromorphic function in $\mathbb {C}$
is a meromorphic function in $\mathbb {C}$![]() and $a,\,~ b,\,~ c$
and $a,\,~ b,\,~ c$![]() are constants or, more generally, polynomials. More precisely, Li proved the following theorem.
are constants or, more generally, polynomials. More precisely, Li proved the following theorem.
Theorem A Suppose that $f$![]() is a non-constant meromorphic function in $\mathbb {C}$
is a non-constant meromorphic function in $\mathbb {C}$![]() and $g$
and $g$![]() is an entire function satisfying the equation
is an entire function satisfying the equation
where $a(\neq 0),$![]() $b,$
$b,$![]() $c$
$c$![]() are constants. Then,
are constants. Then,
(i) $g$
 must be linear, if $f$
must be linear, if $f$ is transcendental;
is transcendental;(ii) $g$
 must be a polynomial of degree less than or equal to 2, if $f$
must be a polynomial of degree less than or equal to 2, if $f$ is rational; furthermore, the degree of $g$
is rational; furthermore, the degree of $g$ is 2 if and only if $f=\frac {\alpha }{z-w_0}+\beta,$
is 2 if and only if $f=\frac {\alpha }{z-w_0}+\beta,$ $g=w_0-a(z-w_0)^{2}$
$g=w_0-a(z-w_0)^{2}$ and $b = a\beta + c = 0,$
and $b = a\beta + c = 0,$ where $\alpha (\neq 0),$
where $\alpha (\neq 0),$ $\beta,$
$\beta,$ $w_0$
$w_0$ are complex numbers.
are complex numbers.
By studying (ii) of Theorem A, one wants to know whether the same conclusion holds for the equation $f^{(k)}(z)=a(f^{n}\circ g)(z)+bf(z)+c$![]() if $f$
if $f$![]() is a rational function, where the left side is the $k$
is a rational function, where the left side is the $k$![]() -th derivative of $f$
-th derivative of $f$![]() and the right side is nonlinear item. Unfortunately, the answer is negative, which is shown by the following example.
and the right side is nonlinear item. Unfortunately, the answer is negative, which is shown by the following example.
Consider the functions $g(z)=z^{2}$![]() and $f=\frac {1}{z^{2}}$
and $f=\frac {1}{z^{2}}$![]() . Obviously, $f$
. Obviously, $f$![]() and $g$
and $g$![]() satisfy the equation $f''(z)=6(f\circ g)(z)$
satisfy the equation $f''(z)=6(f\circ g)(z)$![]() . However, the form of $f$
. However, the form of $f$![]() does not satisfy the conclusion of Theorem A. Observe that the only zero of $g$
does not satisfy the conclusion of Theorem A. Observe that the only zero of $g$![]() and the only pole of $f$
and the only pole of $f$![]() are coincident, which leads us to ask whether this always happens or not when $g$
are coincident, which leads us to ask whether this always happens or not when $g$![]() is nonlinear. In this present paper, we firstly pay attention to this question. More specifically, using an elementary method, we completely characterize the rational solutions of the following Equation (1.5) when $g$
is nonlinear. In this present paper, we firstly pay attention to this question. More specifically, using an elementary method, we completely characterize the rational solutions of the following Equation (1.5) when $g$![]() is nonlinear.
is nonlinear.
Theorem 1 Suppose that $f$![]() is a non-constant rational function in $\mathbb {C}$
is a non-constant rational function in $\mathbb {C}$![]() and $g$
and $g$![]() is a non-constant entire function satisfying the equation
is a non-constant entire function satisfying the equation
where $a(\neq 0),$![]() $b,$
$b,$![]() $c$
$c$![]() are constant. Then, $g$
are constant. Then, $g$![]() is a polynomial. If $g$
is a polynomial. If $g$![]() is nonlinear, then
is nonlinear, then

where $a_1,$![]() $A,$
$A,$![]() $A_0$
$A_0$![]() and $A_j$
and $A_j$![]() are constants, $\mu \in \{2,\, ~3,\,\ldots,\,~[\tfrac {k+1}{n}]\},$
are constants, $\mu \in \{2,\, ~3,\,\ldots,\,~[\tfrac {k+1}{n}]\},$![]() $q=\frac {k}{n\mu -1}$
$q=\frac {k}{n\mu -1}$![]() is an integer.
is an integer.
In particular, if $q=\frac {k}{n\mu -1}$![]() is not an integer for any $\mu \in \{2,\,\ldots,\,~[\tfrac {k+1}{n}]\}$
is not an integer for any $\mu \in \{2,\,\ldots,\,~[\tfrac {k+1}{n}]\}$![]() or $n>k+1$
or $n>k+1$![]() , then Equation (1.5) does not admit any non-polynomial rational solution.
, then Equation (1.5) does not admit any non-polynomial rational solution.
Remark 1 For the special case $n=k=1$![]() , from Theorem 1, it follows that $\mu =\frac {k+1}{n}=2$
, from Theorem 1, it follows that $\mu =\frac {k+1}{n}=2$![]() and $q=\frac {k}{n\mu -1}=\frac {1}{2-1}=1$
and $q=\frac {k}{n\mu -1}=\frac {1}{2-1}=1$![]() if $g$
if $g$![]() is nonlinear. Further, $g(z)=A(z-a_1)^{2}+a_1$
is nonlinear. Further, $g(z)=A(z-a_1)^{2}+a_1$![]() and $f(z)=\frac {\alpha }{z-a_1}+\beta$
and $f(z)=\frac {\alpha }{z-a_1}+\beta$![]() with two constants $\alpha (\neq 0)$
with two constants $\alpha (\neq 0)$![]() , $\beta$
, $\beta$![]() . This is the conclusion (ii) of Theorem A. Therefore, Theorem 1 is an improvement of Theorem 1 when $f$
. This is the conclusion (ii) of Theorem A. Therefore, Theorem 1 is an improvement of Theorem 1 when $f$![]() is a rational function.
is a rational function.
Remark 2 We point out that (1.5) may admit more than one rational solution when $g$![]() is nonlinear, as seen by the following example. Observe that the functions $f(z)=\frac {1}{z^{5}}$
is nonlinear, as seen by the following example. Observe that the functions $f(z)=\frac {1}{z^{5}}$![]() and $g(z)=z^{2}$
and $g(z)=z^{2}$![]() satisfy an equation of the form (1.5), namely $f^{(15)}(z)=a(f^{2}\circ g)(z)$
satisfy an equation of the form (1.5), namely $f^{(15)}(z)=a(f^{2}\circ g)(z)$![]() , where $a=-19!/24$
, where $a=-19!/24$![]() . Moreover, the functions $f(z)=\frac {1}{z^{3}}$
. Moreover, the functions $f(z)=\frac {1}{z^{3}}$![]() and $g(z)=Az^{3}$
and $g(z)=Az^{3}$![]() also satisfy $f^{(15)}(z)=a(f^{2}\circ g)(z)$
also satisfy $f^{(15)}(z)=a(f^{2}\circ g)(z)$![]() , where $A^{6}=\frac {57}{2}$
, where $A^{6}=\frac {57}{2}$![]() .
.
Remark 3 From Theorem 1, we observe that $f$![]() just has one pole when $g$
just has one pole when $g$![]() is nonlinear. The observation is false if $g$
is nonlinear. The observation is false if $g$![]() is linear. We offer an example to show this point. Let $t_0=\frac {1}{2}+i\frac {\sqrt {3}}{2}$
is linear. We offer an example to show this point. Let $t_0=\frac {1}{2}+i\frac {\sqrt {3}}{2}$![]() . Then $t_0^{3}=-1$
. Then $t_0^{3}=-1$![]() . Consider the functions $f(z)=\frac {-t_0}{2(t_0+1)}+\frac {t_0}{z+1}-\frac {1}{z-1}$
. Consider the functions $f(z)=\frac {-t_0}{2(t_0+1)}+\frac {t_0}{z+1}-\frac {1}{z-1}$![]() and $g(z)=-z$
and $g(z)=-z$![]() . Then, a calculation yields the following equation
. Then, a calculation yields the following equation
Remark 4 We emphasize that $a(\neq 0)$![]() , $b$
, $b$![]() , $c$
, $c$![]() cannot be generalized to polynomials, as seen by the following example. Consider $f(z)=\frac {1}{z}$
cannot be generalized to polynomials, as seen by the following example. Consider $f(z)=\frac {1}{z}$![]() , $g(z)=z^{3}$
, $g(z)=z^{3}$![]() and $a(z)=-z$
and $a(z)=-z$![]() . Then, the equation $f'(z)=a(z)(f\circ g)(z)$
. Then, the equation $f'(z)=a(z)(f\circ g)(z)$![]() holds. But $f$
holds. But $f$![]() and $g$
and $g$![]() cannot satisfy the conclusion of Theorem 1.
cannot satisfy the conclusion of Theorem 1.
Next, we turn our attention to transcendental solutions of the following functional-differential Equation (1.6) with polynomial coefficients. As a matter of fact, we generalize the conclusion (i) of Theorem A to Equation (1.6) as follows.
Theorem 2 Suppose that $f$![]() is a transcendental meromorphic function in $\mathbb {C}$
is a transcendental meromorphic function in $\mathbb {C}$![]() and $g$
and $g$![]() is a non-constant entire function satisfying the equation
is a non-constant entire function satisfying the equation
where $a(\neq 0),$![]() $b,$
$b,$![]() $c$
$c$![]() are polynomials in $\mathbb {C}$
are polynomials in $\mathbb {C}$![]() . Then $g$
. Then $g$![]() must be linear. Further, Equation (1.6) does not admit any transcendental meromorphic solution if $n\geq 2$
must be linear. Further, Equation (1.6) does not admit any transcendental meromorphic solution if $n\geq 2$![]() and $\frac {k}{n-1}$
and $\frac {k}{n-1}$![]() is not an integer.
is not an integer.
Remark 5 The conditions that $n\geq 2$![]() and $\frac {k}{n-1}$
and $\frac {k}{n-1}$![]() is not integer are needed in Theorem 2. If one of them is invalid, then Equation (1.6) may admit transcendental meromorphic solutions, which is shown by the following examples.
is not integer are needed in Theorem 2. If one of them is invalid, then Equation (1.6) may admit transcendental meromorphic solutions, which is shown by the following examples.
Consider the equation $f^{(k)}(z)=(f^{n}\circ g)(z)$![]() , where $k$
, where $k$![]() is a positive integer and $g(z)=z+2\pi i$
is a positive integer and $g(z)=z+2\pi i$![]() . When $n=1$
. When $n=1$![]() , the equation admits the solution $f(z)=e^{z}$
, the equation admits the solution $f(z)=e^{z}$![]() . Consider the entire functions $f(z)=A(\sin (az)+\cos (az))$
. Consider the entire functions $f(z)=A(\sin (az)+\cos (az))$![]() and $f(z)=A\cosh (az)+B\sin (az))$
and $f(z)=A\cosh (az)+B\sin (az))$![]() , which satisfy the equations $f'(z)=a(f\circ g)(z)$
, which satisfy the equations $f'(z)=a(f\circ g)(z)$![]() and $f''(z)=a^{2}(f\circ g)(z)$
and $f''(z)=a^{2}(f\circ g)(z)$![]() respectively, where $g(z)=-z$
respectively, where $g(z)=-z$![]() and $A,\,~B$
and $A,\,~B$![]() are arbitrary complex constants. These examples can be found in [Reference Utz15]. Consider the equation $f'(z)=-(f^{2}\circ g)(z)-f(z)$
are arbitrary complex constants. These examples can be found in [Reference Utz15]. Consider the equation $f'(z)=-(f^{2}\circ g)(z)-f(z)$![]() , where $g(z)=z+2\pi i$
, where $g(z)=z+2\pi i$![]() . Clearly, $n=2$
. Clearly, $n=2$![]() and $\frac {k}{n-1}=1$
and $\frac {k}{n-1}=1$![]() . Moreover, the equation admits the solution $f(z)=\frac {1}{e^{z}-1}$
. Moreover, the equation admits the solution $f(z)=\frac {1}{e^{z}-1}$![]() .
.
The same argument in Theorem 2 yields the following corollary. And we omit its proof here.
Corollary 1 Suppose that $f$![]() is a transcendental meromorphic function in $\mathbb {C}$
is a transcendental meromorphic function in $\mathbb {C}$![]() and $g$
and $g$![]() is a non-constant entire function satisfying the equation
is a non-constant entire function satisfying the equation
where $L(f)=a_kf^{(k)}+\cdots +a_{1}f'+a_0$![]() $(a_k\neq 0)$
$(a_k\neq 0)$![]() is a linear differential polynomial in $f$
is a linear differential polynomial in $f$![]() with rational coefficients. Then $g$
with rational coefficients. Then $g$![]() must be linear. Further, Equation (1.7) does not admit any transcendental meromorphic solution if $n\geq 2$
must be linear. Further, Equation (1.7) does not admit any transcendental meromorphic solution if $n\geq 2$![]() and $\frac {k}{n-1}$
and $\frac {k}{n-1}$![]() is not integer.
is not integer.
Proof of Theorem 1. Clearly, $g$![]() is a polynomial, since $f$
is a polynomial, since $f$![]() is a rational function. Firstly, suppose that $f$
is a rational function. Firstly, suppose that $f$![]() is a polynomial. Comparing the degrees of both sides of Equation (1.5), one has $n=1$
is a polynomial. Comparing the degrees of both sides of Equation (1.5), one has $n=1$![]() and $\deg g=1$
and $\deg g=1$![]() , which means that $g$
, which means that $g$![]() is linear. Next, we assume $f$
is linear. Next, we assume $f$![]() is a non-polynomial rational function, which means that $f$
is a non-polynomial rational function, which means that $f$![]() has at least one pole. We below characterize the forms of $f$
has at least one pole. We below characterize the forms of $f$![]() and $g$
and $g$![]() . Set $f(z)=\frac {P_1(z)}{Q(z)}$
. Set $f(z)=\frac {P_1(z)}{Q(z)}$![]() , where $P_1,\,~Q$
, where $P_1,\,~Q$![]() are two co-prime polynomials. By decomposition of rational function, we then can set
are two co-prime polynomials. By decomposition of rational function, we then can set

where $P(z)$![]() is a polynomial, $s$
is a polynomial, $s$![]() and $m_i$
and $m_i$![]() are positive integers and $A_{ij}$
are positive integers and $A_{ij}$![]() and $a_i~ (i=1,\,\ldots ~s)$
and $a_i~ (i=1,\,\ldots ~s)$![]() are constant with $A_{i m_i}\neq 0$
are constant with $A_{i m_i}\neq 0$![]() for all $i=1,\,\ldots,\,~s$
for all $i=1,\,\ldots,\,~s$![]() . In addition, without loss of generality, we suppose that $a_i$
. In addition, without loss of generality, we suppose that $a_i$![]() and $a_j$
and $a_j$![]() are distinct for any $1\leq i\neq j\leq s$
are distinct for any $1\leq i\neq j\leq s$![]() , and $m_1 \leq m_2 \leq m_3 \leq \ldots \leq m_s$
, and $m_1 \leq m_2 \leq m_3 \leq \ldots \leq m_s$![]() . The above form of $f$
. The above form of $f$![]() implies that $f$
implies that $f$![]() has distinct poles $a_1,\,~a_2,\,\ldots,\, ~a_s$
has distinct poles $a_1,\,~a_2,\,\ldots,\, ~a_s$![]() , with orders (or multiplicities) $m_1,\,~ m_2,\,\ldots,\, ~ m_s$
, with orders (or multiplicities) $m_1,\,~ m_2,\,\ldots,\, ~ m_s$![]() respectively. By differentiating the function $f(z)$
respectively. By differentiating the function $f(z)$![]() $k$
$k$![]() -times, we obtain
-times, we obtain

where $B_{ij}$![]() are constants and $B_{i (m_i+k)}\neq 0$
are constants and $B_{i (m_i+k)}\neq 0$![]() for $i=1,\,\ldots,\,s$
for $i=1,\,\ldots,\,s$![]() . Combining (1.8) and (1.9) yields
. Combining (1.8) and (1.9) yields

(In fact, if $b\neq 0$![]() , then $\deg [f^{(k)}-bf-c]=\deg f +ks$
, then $\deg [f^{(k)}-bf-c]=\deg f +ks$![]() .) On the other hand, $\deg [(f^{n}\circ g)]=n m\deg f$
.) On the other hand, $\deg [(f^{n}\circ g)]=n m\deg f$![]() , where $m=\deg g$
, where $m=\deg g$![]() . Plus $s\leq \deg f-\deg P\leq \deg f$
. Plus $s\leq \deg f-\deg P\leq \deg f$![]() , one has that
, one has that

which implies that $m\leq \frac {1+k}{n}$![]() . Clearly, if $n>k+1$
. Clearly, if $n>k+1$![]() , the above inequality is invalid and Equation (1.5) does not admit any rational function $f$
, the above inequality is invalid and Equation (1.5) does not admit any rational function $f$![]() . Below, we will prove the theorem under the condition $n\leq k+1$
. Below, we will prove the theorem under the condition $n\leq k+1$![]() .
.
From Equation (1.5), we see that all the zeros of $g(z)-a_1$![]() must be the poles of $f(z)$
must be the poles of $f(z)$![]() , which implies that each zero of $g(z)-a_1$
, which implies that each zero of $g(z)-a_1$![]() belongs to set $\{a_1,\,~a_2,\,\ldots,\, ~a_s\}$
belongs to set $\{a_1,\,~a_2,\,\ldots,\, ~a_s\}$![]() . Without loss of generality, assume that $g(a_t)=a_1$
. Without loss of generality, assume that $g(a_t)=a_1$![]() , where $t$
, where $t$![]() is a fixed integer such that $t\in \{1,\,\ldots,\,s\}$
is a fixed integer such that $t\in \{1,\,\ldots,\,s\}$![]() . Suppose that $a_t$
. Suppose that $a_t$![]() is a zero of $g(z)-a_1$
is a zero of $g(z)-a_1$![]() with multiplicity $\mu$
with multiplicity $\mu$![]() . We consider the following cases.
. We consider the following cases.
Case 1. $\mu =1$![]() . Then, we can assume that $g(z)=a_1+h(z)(z-a_t)$
. Then, we can assume that $g(z)=a_1+h(z)(z-a_t)$![]() , where $h(z)$
, where $h(z)$![]() is a polynomial and $h(a_t)\neq 0$
is a polynomial and $h(a_t)\neq 0$![]() . Further, substituting the forms of $f$
. Further, substituting the forms of $f$![]() and $g$
and $g$![]() into Equation (1.5), one has
into Equation (1.5), one has

The first line of (1.11) implies that $a_t$![]() is a pole of $f^{(k)}(z)-bf(z)-c$
is a pole of $f^{(k)}(z)-bf(z)-c$![]() with multiplicity $m_t+k$
with multiplicity $m_t+k$![]() . And the last line of (1.11) yields that $a_t$
. And the last line of (1.11) yields that $a_t$![]() is a pole of $f^{(k)}(z)-bf(z)-c=a(f^{n}\circ g)(z)$
is a pole of $f^{(k)}(z)-bf(z)-c=a(f^{n}\circ g)(z)$![]() with multiplicity $n m_1$
with multiplicity $n m_1$![]() . Therefore, Equation (1.5) leads to
. Therefore, Equation (1.5) leads to
The above equality does not hold for $n=1$![]() . So $n\geq 2$
. So $n\geq 2$![]() and $m_1\geq \frac {k}{n-1}$
and $m_1\geq \frac {k}{n-1}$![]() , which implies that $f$
, which implies that $f$![]() has poles with multiplicity at least $q$
has poles with multiplicity at least $q$![]() , where
, where

where $[x]$![]() denotes the greatest integer less than or equal to $x$
denotes the greatest integer less than or equal to $x$![]() . Thus, $s\leq \frac {\deg f-\deg P}{q}\leq \frac {\deg f}{q}$
. Thus, $s\leq \frac {\deg f-\deg P}{q}\leq \frac {\deg f}{q}$![]() . By the first part of (1.10), we then have
. By the first part of (1.10), we then have
Clearly, if $\frac {k}{n-1}$![]() is an integer, then $(1+\frac {k}{q})=n$
is an integer, then $(1+\frac {k}{q})=n$![]() . Together with the above inequality (1.12), one gets that $\deg g=m=1$
. Together with the above inequality (1.12), one gets that $\deg g=m=1$![]() . Further, the above inequalities in (1.12) become equations. So, $s=\frac {\deg f}{q}$
. Further, the above inequalities in (1.12) become equations. So, $s=\frac {\deg f}{q}$![]() , which implies that $\deg P=0$
, which implies that $\deg P=0$![]() and $P$
and $P$![]() reduces a constant. If $\frac {k}{n-1}$
reduces a constant. If $\frac {k}{n-1}$![]() is not an integer, then $(1+\tfrac {k}{q})< n$
is not an integer, then $(1+\tfrac {k}{q})< n$![]() . Plus the above inequality (1.12), one gets that $\deg g=m<1$
. Plus the above inequality (1.12), one gets that $\deg g=m<1$![]() , a contradiction.
, a contradiction.
Case 2. $\mu =2$![]() . We then set
. We then set
where $h(z)$![]() is a polynomial and $h(a_t)\neq 0$
is a polynomial and $h(a_t)\neq 0$![]() (For the sake of simplicity, we still use this notation $h$
(For the sake of simplicity, we still use this notation $h$![]() ). Similarly as in Case 1, comparing the multiplicities of both sides of equation $f^{(k)}(z)-bf(z)-c=a(f^{n}\circ g)(z)$
). Similarly as in Case 1, comparing the multiplicities of both sides of equation $f^{(k)}(z)-bf(z)-c=a(f^{n}\circ g)(z)$![]() at the pole-point $a_t$
at the pole-point $a_t$![]() we can get
we can get
which implies that $m_1\geq \frac {k}{2n-1}$![]() . The same argument as in Case 1 yields that $f$
. The same argument as in Case 1 yields that $f$![]() has poles with multiplicity at least $p$
has poles with multiplicity at least $p$![]() , where
, where

Thus, $s\leq \frac {\deg f-\deg P}{p}\leq \frac {\deg f}{p}$![]() . Again by the first part of (1.10), we have
. Again by the first part of (1.10), we have
Obviously, if $\frac {k}{2n-1}$![]() is an integer, then $(1+\frac {k}{p})=2n$
is an integer, then $(1+\frac {k}{p})=2n$![]() . Then, the above inequality (1.14) yields that $\deg g=m\leq 2$
. Then, the above inequality (1.14) yields that $\deg g=m\leq 2$![]() . Together with the form of $g$
. Together with the form of $g$![]() in (1.13), we have that $\deg g=2$
in (1.13), we have that $\deg g=2$![]() and
and
where $h$![]() reduces to a constant. Further, $\deg P=0$
reduces to a constant. Further, $\deg P=0$![]() and $P$
and $P$![]() reduces to a constant. We claim that $a_t=a_1$
reduces to a constant. We claim that $a_t=a_1$![]() . Otherwise, suppose that $a_t\neq a_1$
. Otherwise, suppose that $a_t\neq a_1$![]() . Below we derive a contradiction. It is pointed out that all the inequalities in (1.14) become equations. Thus, $s=\frac {\deg f}{p}$
. Below we derive a contradiction. It is pointed out that all the inequalities in (1.14) become equations. Thus, $s=\frac {\deg f}{p}$![]() . Plus the fact $f$
. Plus the fact $f$![]() has poles with multiplicity at least $p=\frac {k}{2n-1}$
has poles with multiplicity at least $p=\frac {k}{2n-1}$![]() , we derive that any pole of $f$
, we derive that any pole of $f$![]() has multiplicity $p=\frac {k}{2n-1}$
has multiplicity $p=\frac {k}{2n-1}$![]() . This means $m_1=m_2=\cdots =m_s=p$
. This means $m_1=m_2=\cdots =m_s=p$![]() . Observe that all the zeros of $g(z)-a_t$
. Observe that all the zeros of $g(z)-a_t$![]() must be the poles of $f$
must be the poles of $f$![]() . Then, there exists an index $\nu \in \{2,\,\ldots,\, t\}$
. Then, there exists an index $\nu \in \{2,\,\ldots,\, t\}$![]() such that $g(a_{\mu })=a_t$
such that $g(a_{\mu })=a_t$![]() . Clearly, $a_{\mu }$
. Clearly, $a_{\mu }$![]() is a simple zero of $g(z)-a_t$
is a simple zero of $g(z)-a_t$![]() . Then, Similarly as above discussion, again comparing the multiplicities of both sides of the equation $f^{(k)}(z)-bf(z)-c=a(f^{n}\circ g)(z)$
. Then, Similarly as above discussion, again comparing the multiplicities of both sides of the equation $f^{(k)}(z)-bf(z)-c=a(f^{n}\circ g)(z)$![]() at the pole-point $a_{\mu }$
at the pole-point $a_{\mu }$![]() , we have
, we have
which implies that $p=\frac {k}{n-1}$![]() , a contradiction. Therefore, $a_t=a_1$
, a contradiction. Therefore, $a_t=a_1$![]() and $g(z)=h(z-a_1)^{2}+a_1$
and $g(z)=h(z-a_1)^{2}+a_1$![]() . Below, we will derive that $f$
. Below, we will derive that $f$![]() just has one pole. Without loss of generality, we assume $f$
just has one pole. Without loss of generality, we assume $f$![]() has another pole $a_2$
has another pole $a_2$![]() $(\neq a_1)$
$(\neq a_1)$![]() . Then, Equation (1.5) leads to that $g(a_2)$
. Then, Equation (1.5) leads to that $g(a_2)$![]() is also a pole of $f$
is also a pole of $f$![]() . Assume that $g(a_2)=a_{\omega }$
. Assume that $g(a_2)=a_{\omega }$![]() . Obviously, $a_2$
. Obviously, $a_2$![]() is a simple zero of $g(z)-a_\omega$
is a simple zero of $g(z)-a_\omega$![]() and $\omega \in \{2,\,\ldots,\,~t\}$
and $\omega \in \{2,\,\ldots,\,~t\}$![]() . Again comparing the multiplicities of both sides of equation $f^{(k)}(z)-bf(z)-c=a(f^{n}\circ g)(z)$
. Again comparing the multiplicities of both sides of equation $f^{(k)}(z)-bf(z)-c=a(f^{n}\circ g)(z)$![]() at the pole-point $a_{2}$
at the pole-point $a_{2}$![]() , one has
, one has
which implies that $p=\frac {k}{n-1}$![]() , a contradiction. Thus, $f$
, a contradiction. Thus, $f$![]() has just a pole $a_1$
has just a pole $a_1$![]() with multiplicity $p=\frac {k}{2n-1}$
with multiplicity $p=\frac {k}{2n-1}$![]() .
.
If $\frac {k}{2n-1}$![]() is not an integer, then $(1+\tfrac {k}{p})<2n$
is not an integer, then $(1+\tfrac {k}{p})<2n$![]() . Plus the above inequality (1.14), one has that $\deg g< 2$
. Plus the above inequality (1.14), one has that $\deg g< 2$![]() , which contradicts the fact $\mu =2$
, which contradicts the fact $\mu =2$![]() .
.
Case 3. $\mu \in \{3,\,\ldots,\,~[\tfrac {k+1}{n}]\}$![]() . Then, the same argument as in Case 2 yields that $g(z)=h(z-a_1)^{\mu }+a_1$
. Then, the same argument as in Case 2 yields that $g(z)=h(z-a_1)^{\mu }+a_1$![]() , $\tfrac {k}{n\mu -1}$
, $\tfrac {k}{n\mu -1}$![]() is an integer and $Q$
is an integer and $Q$![]() is a constant. At the same time, $f$
is a constant. At the same time, $f$![]() has just one pole $a_1$
has just one pole $a_1$![]() with multiplicity $\tfrac {k}{n\mu -1}$
with multiplicity $\tfrac {k}{n\mu -1}$![]() . When $\tfrac {k}{n\mu -1}$
. When $\tfrac {k}{n\mu -1}$![]() is not an integer, we can get a contradiction.
is not an integer, we can get a contradiction.
Therefore, all the above discussions yield the desired result and the proof is finished.
To prove Theorem 2, we will employ Nevanlinna theory. For the reader's convenience, we recall some notation and results in Nevanlinna theory. For a meromorphic function $f$![]() , the Nevanlinna characteristic $T(r,\,f)$
, the Nevanlinna characteristic $T(r,\,f)$![]() is defined as
is defined as
where
and
$n(t,\, f)$![]() denotes the number of poles of $f$
denotes the number of poles of $f$![]() (counting multiplicity) in $|z|\leq t$
(counting multiplicity) in $|z|\leq t$![]() . We also need the notation $\overline {N}(r,\,f)$
. We also need the notation $\overline {N}(r,\,f)$![]() , which is defined as
, which is defined as
$\overline {n}(t,\, f)$![]() denotes the number of poles of $f$
denotes the number of poles of $f$![]() (ignoring multiplicity) in $|z|\leq t$
(ignoring multiplicity) in $|z|\leq t$![]() . Obviously, $\overline {N}(r,\,f)\leq N(r,\,f)$
. Obviously, $\overline {N}(r,\,f)\leq N(r,\,f)$![]() . Further, for any positive integer $k$
. Further, for any positive integer $k$![]() ,
,
since $n(t,\,f^{(k)})\leq n(t,\,f)+k\overline {n}(t,\,f)$![]() for any positive constant $t$
for any positive constant $t$![]() . Further, we recall the following known facts (see, e.g. [Reference Li and Saleeby8, Reference Stoll14, Reference Vitter17].)
. Further, we recall the following known facts (see, e.g. [Reference Li and Saleeby8, Reference Stoll14, Reference Vitter17].)
(1) If $f$
 (meromorphic) and $g$
(meromorphic) and $g$ (entire) are transcendental, then
\[ \limsup_{r\not\in E,~r\rightarrow\infty}\frac{T (r, f\circ g)}{T (r, f )}=\infty, \]where $E$
(entire) are transcendental, then
\[ \limsup_{r\not\in E,~r\rightarrow\infty}\frac{T (r, f\circ g)}{T (r, f )}=\infty, \]where $E$
 is a set of finite Lebesgue measure (see [Reference Clunie2, Theorem 2] and [Reference Gross and Yang6, p. 370]).
is a set of finite Lebesgue measure (see [Reference Clunie2, Theorem 2] and [Reference Gross and Yang6, p. 370]).(2) The logarithmic derivative lemma $m(r,\, \frac {f^{(k)}}{f})=S(r,\,f)$
 for any positive integer $k$
for any positive integer $k$ , where $S(r,\,f)$
, where $S(r,\,f)$ denotes any quantity satisfying that $S(r,\,f)=o\{T(r,\,f)\}$
denotes any quantity satisfying that $S(r,\,f)=o\{T(r,\,f)\}$ as $r\rightarrow \infty$
as $r\rightarrow \infty$ outside a set of $r$
outside a set of $r$ of finite Lebesgue measure.
of finite Lebesgue measure.(3) If $f$
 is transcendental, then $lim_{r\rightarrow \infty } \frac {T(r,\, f)}{\log r}=\infty ;$
is transcendental, then $lim_{r\rightarrow \infty } \frac {T(r,\, f)}{\log r}=\infty ;$ And if $h$
And if $h$ is a rational function, then $T(r,\,h)=O(\log r)=S(r,\,f)$
is a rational function, then $T(r,\,h)=O(\log r)=S(r,\,f)$ .
.(4) Suppose that $g = a_m z^{m}+ a_{m_1}z^{m-1}+\ldots + a_1 z + a_0$
 is a non-constant polynomial, then for any $\epsilon _1 > 0$
is a non-constant polynomial, then for any $\epsilon _1 > 0$ and $\epsilon _2 > 0$
and $\epsilon _2 > 0$ ,
\begin{align*} & T (r, f\circ g)\geq (1 -\epsilon_2 )T\bigg(\frac{|a_m|}{2}r^{m}, f\bigg),\\ & T (r, f)\leq \frac{1}{m}(1+\epsilon_1)T\bigg(\frac{|a_m|}{2}r^{m}, f\bigg), \end{align*}for large $r$
,
\begin{align*} & T (r, f\circ g)\geq (1 -\epsilon_2 )T\bigg(\frac{|a_m|}{2}r^{m}, f\bigg),\\ & T (r, f)\leq \frac{1}{m}(1+\epsilon_1)T\bigg(\frac{|a_m|}{2}r^{m}, f\bigg), \end{align*}for large $r$
 outside possibly a set of finite Lebesgue measure. The above inequalities can be seen in [Reference Gross and Yang6, (19)]) and [Reference Li and Saleeby8, (2.7)]), respectively.
outside possibly a set of finite Lebesgue measure. The above inequalities can be seen in [Reference Gross and Yang6, (19)]) and [Reference Li and Saleeby8, (2.7)]), respectively.(5) Combining the above two inequalities yields that
\[ T (r, f)\leq \frac{1}{m}\bigg(\frac{1+\epsilon_1}{1-\epsilon_2}\bigg)T(r, f\circ g)=\frac{1}{m}(1+\varepsilon)T(r, f\circ g), \]for large $r$
 outside possibly a set of finite Lebesgue measure, where $\varepsilon =\frac {\epsilon _1+\epsilon _2}{1-\epsilon _2}$
outside possibly a set of finite Lebesgue measure, where $\varepsilon =\frac {\epsilon _1+\epsilon _2}{1-\epsilon _2}$ is a positive constant. The form of $\varepsilon$
is a positive constant. The form of $\varepsilon$ implies that $\varepsilon$
implies that $\varepsilon$ can be chosen for any arbitrary positive number.
can be chosen for any arbitrary positive number.(6) $T(r,\,f)=T(r,\,\tfrac {1}{f})+O(1)$
 , $T(r,\, fg)\leq T(r,\,f)+T(r,\,g)$
, $T(r,\, fg)\leq T(r,\,f)+T(r,\,g)$ , $T(r,\, f+g)\leq T(r,\,f)+T(r,\,g)+O(1)$
, $T(r,\, f+g)\leq T(r,\,f)+T(r,\,g)+O(1)$ . The last two inequalities also hold for $m(r,\, \cdot )$
. The last two inequalities also hold for $m(r,\, \cdot )$ .
.
Proof of Theorem 2. Based on the idea in [Reference Li and Saleeby8], we will prove the theorem. Assume the functions $f$![]() and $g$
and $g$![]() satisfy Equation (1.6). From Equation (1.6), the facts (2), (3) and (6), one has that
satisfy Equation (1.6). From Equation (1.6), the facts (2), (3) and (6), one has that

outside possibly a set of finite Lebesgue measure. Notice that $f$![]() is transcendental. We then see that $g$
is transcendental. We then see that $g$![]() must be a polynomial, since if $g$
must be a polynomial, since if $g$![]() were transcendental, then it is easy to get a contradiction from the fact (1) and (1.15). Suppose that $g=a_m z^{m}+ a_{m_1}z^{m-1}+\cdots + a_1 z + a_0$
were transcendental, then it is easy to get a contradiction from the fact (1) and (1.15). Suppose that $g=a_m z^{m}+ a_{m_1}z^{m-1}+\cdots + a_1 z + a_0$![]() with $a_m\neq 0$
with $a_m\neq 0$![]() . Combining the fact (5) and (1.15) yields
. Combining the fact (5) and (1.15) yields
outside possibly a set of finite Lebesgue measure. This implies that
If $\frac {1+k}{n}<2$![]() , then we get that $m=1$
, then we get that $m=1$![]() and $g$
and $g$![]() is linear, since $\varepsilon$
is linear, since $\varepsilon$![]() can be chosen small enough. For the proof of Theorem 2, it suffices to consider the case $\frac {1+k}{n}\geq 2$
can be chosen small enough. For the proof of Theorem 2, it suffices to consider the case $\frac {1+k}{n}\geq 2$![]() . Below we consider two cases.
. Below we consider two cases.
Case 1. For any positive integer $q$![]() , $f$
, $f$![]() just has finitely many poles with multiplicity $q$
just has finitely many poles with multiplicity $q$![]() .
.
Then, for any fixed integer $q$![]() , we can say that $f$
, we can say that $f$![]() has poles with multiplicity at least $q$
has poles with multiplicity at least $q$![]() except finitely many points. Further,
except finitely many points. Further,
Substituting the above inequality into (1.15) yields that

outside possibly a set of finite Lebesgue measure. Furthermore, by the fact (5) again, one has
outside possibly a set of finite Lebesgue measure. Let $q\rightarrow \infty$![]() , we can derive that $m=n=1$
, we can derive that $m=n=1$![]() and $g$
and $g$![]() is linear.
is linear.
Case 2. There exists a positive integer $q$![]() such that $f$
such that $f$![]() has infinitely many poles with multiplicity $q$
has infinitely many poles with multiplicity $q$![]() .
.
Suppose that $P$![]() is an integer such that $f$
is an integer such that $f$![]() has finitely many poles with multiplicity $< P$
has finitely many poles with multiplicity $< P$![]() and infinitely many poles with multiplicity $P$
and infinitely many poles with multiplicity $P$![]() . In fact, the number $P$
. In fact, the number $P$![]() is the minimum integer which satisfies the assumption of Case 2. We define a set $S$
is the minimum integer which satisfies the assumption of Case 2. We define a set $S$![]() as follows:
as follows:
Clearly, $S$![]() is a finite set, since $a$
is a finite set, since $a$![]() , $b$
, $b$![]() , $c$
, $c$![]() and $g'$
and $g'$![]() are polynomials. Set $L=\max \{|z|:z\in S\}.$
are polynomials. Set $L=\max \{|z|:z\in S\}.$![]()
Assume that $\{z_n\}_{n=1}^{\infty }$![]() are the poles of $f$
are the poles of $f$![]() with multiplicity $P$
with multiplicity $P$![]() such that $|z_1|\leq |z_2|\leq \ldots \leq |z_n|\leq \ldots$
such that $|z_1|\leq |z_2|\leq \ldots \leq |z_n|\leq \ldots$![]() and $|z_n|\rightarrow \infty$
and $|z_n|\rightarrow \infty$![]() as $n\rightarrow \infty$
as $n\rightarrow \infty$![]() . Note that $g$
. Note that $g$![]() is a polynomial. Without loss of generality, we can assume that the modulus of any zero of $g(z)-z_n$
is a polynomial. Without loss of generality, we can assume that the modulus of any zero of $g(z)-z_n$![]() is bigger than $L$
is bigger than $L$![]() for any $n>N$
for any $n>N$![]() , where $N$
, where $N$![]() is an fixed integer. Suppose that $g(a_0)=z_n$
is an fixed integer. Suppose that $g(a_0)=z_n$![]() with $n>N$
with $n>N$![]() . Then, it follows $a_0\not \in S$
. Then, it follows $a_0\not \in S$![]() , which implies that $a_0$
, which implies that $a_0$![]() is neither the pole of $f$
is neither the pole of $f$![]() with multiplicity $< P$
with multiplicity $< P$![]() nor the zeros of the coefficients $a,\,~b,\,~c$
nor the zeros of the coefficients $a,\,~b,\,~c$![]() and $g'$
and $g'$![]() . Moreover, $a_0$
. Moreover, $a_0$![]() is a simple zero of $g(z)-z_n$
is a simple zero of $g(z)-z_n$![]() . Assume that $g(z)-z_n=h(z)(z-a_0)$
. Assume that $g(z)-z_n=h(z)(z-a_0)$![]() , where $h(z)$
, where $h(z)$![]() is a polynomial with $h(a_0)\neq 0$
is a polynomial with $h(a_0)\neq 0$![]() . Equation (1.6) implies that $a_0$
. Equation (1.6) implies that $a_0$![]() is also a pole of $f$
is also a pole of $f$![]() . Suppose that the multiplicity of $f$
. Suppose that the multiplicity of $f$![]() at $a_0$
at $a_0$![]() is $s$
is $s$![]() . The fact $a_0\not \in S$
. The fact $a_0\not \in S$![]() yields that $s\geq P$
yields that $s\geq P$![]() . Then, the Laurent series expansions of $f(z)$
. Then, the Laurent series expansions of $f(z)$![]() and $f^{(k)}(z)$
and $f^{(k)}(z)$![]() at $a_{0}$
at $a_{0}$![]() are as follows
are as follows
where $\alpha _{i}~(i=s,\,~s-1,\,\cdots )$![]() and $\beta _{i}~(i=s,\,~s-1,\,\cdots )$
and $\beta _{i}~(i=s,\,~s-1,\,\cdots )$![]() are finite complex numbers with $\alpha _{s}\neq 0$
are finite complex numbers with $\alpha _{s}\neq 0$![]() and $\beta _{s}\neq 0$
and $\beta _{s}\neq 0$![]() . In fact, $\beta _{s}=(-1)^{k} \alpha _{s} s(s+1)\ldots (s+k-1)$
. In fact, $\beta _{s}=(-1)^{k} \alpha _{s} s(s+1)\ldots (s+k-1)$![]() . Suppose that the Laurent series expansion of $f(z)$
. Suppose that the Laurent series expansion of $f(z)$![]() at $z_{n}$
at $z_{n}$![]() is
is
where $\theta _{i}~(i=P,\,~P-1,\,\cdots )$![]() are finite complex numbers with $\theta _{P}\neq 0$
are finite complex numbers with $\theta _{P}\neq 0$![]() . Furthermore, by the form of $g(z)$
. Furthermore, by the form of $g(z)$![]() and (1.19), one has
and (1.19), one has

where $A_1,\,~A_2,\,\ldots$![]() are constants and $A_1\neq 0$
are constants and $A_1\neq 0$![]() . In fact, $A_1=\left [\frac {\theta _P}{h(a_0)}\right ]^{n}$
. In fact, $A_1=\left [\frac {\theta _P}{h(a_0)}\right ]^{n}$![]() . We rewrite Equation (1.6) as
. We rewrite Equation (1.6) as
Substitute (1.17), (1.18) and (1.20) into (1.21). Then, by comparing the multiplicities of both sides of Equation (1.21) at the pole-point $a_0$![]() , one has
, one has
which is impossible if $n=1$![]() . When $n\geq 2$
. When $n\geq 2$![]() , it implies that
, it implies that
where

The above discussion yields that $f$![]() has poles with multiplicity at least $t$
has poles with multiplicity at least $t$![]() except for finitely many points. Then, it follows that
except for finitely many points. Then, it follows that
The similar argument as in (1.16) yields

outside possibly a set of finite Lebesgue measure. Furthermore, plus the fact (5) again, one has
outside possibly a set of finite Lebesgue measure. If $\frac {k}{n-1}$![]() is an integer, then $1+\frac {k}{t}=n$
is an integer, then $1+\frac {k}{t}=n$![]() . Together with the above inequality, we get that
. Together with the above inequality, we get that
which implies that $m=1$![]() and $g$
and $g$![]() is linear, since $\varepsilon$
is linear, since $\varepsilon$![]() can be taken small enough. Moreover, if $\frac {k}{n-1}$
can be taken small enough. Moreover, if $\frac {k}{n-1}$![]() is not an integer, then $t=[\tfrac {k}{n-1}]+1$
is not an integer, then $t=[\tfrac {k}{n-1}]+1$![]() and $1+\frac {k}{t}= \lambda n< n$
and $1+\frac {k}{t}= \lambda n< n$![]() , where $0<\lambda <1$
, where $0<\lambda <1$![]() is a fixed constant. Again plus the above inequality, one has
is a fixed constant. Again plus the above inequality, one has
By choosing $\varepsilon$![]() small enough such that $\lambda (1+\varepsilon )(1+o(1))<1$
small enough such that $\lambda (1+\varepsilon )(1+o(1))<1$![]() , then it follows $m <1$
, then it follows $m <1$![]() , which is impossible. Thus, when $\frac {k}{n-1}$
, which is impossible. Thus, when $\frac {k}{n-1}$![]() is not integer, the equation does not admit any transcendental meromorphic function.
is not integer, the equation does not admit any transcendental meromorphic function.
Therefore, the proof is finished.
2. Growth of meromorphic solutions of FDE
In this section, we turn our attention to the growth of the meromorphic solutions of the general functional-differential equations (FDE). This is motivated by a result of Gross and Yang in [Reference Gross and Yang6]. In fact, they proved that
Theorem B Let $g$![]() be a given non-constant entire function and $P(z,\,y'(z), y''(z),\,\ldots,\,y^{(k)}(z))$
be a given non-constant entire function and $P(z,\,y'(z), y''(z),\,\ldots,\,y^{(k)}(z))$![]() be a given polynomial in variables $z,\,~y(z),\,~y'(z)\ldots,\,y^{(k)}(z)$
be a given polynomial in variables $z,\,~y(z),\,~y'(z)\ldots,\,y^{(k)}(z)$![]() . If $f$
. If $f$![]() is a transcendental meromorphic solutions of the equation
is a transcendental meromorphic solutions of the equation
then $g$![]() must be polynomial. Furthermore, if $g$
must be polynomial. Furthermore, if $g$![]() is nonlinear, then $T(r,\,f)=O((\log r)^{\beta })$
is nonlinear, then $T(r,\,f)=O((\log r)^{\beta })$![]() as $r\rightarrow \infty$
as $r\rightarrow \infty$![]() for some constant $\beta >1$
for some constant $\beta >1$![]() .
.
In Theorem B, we see that the characteristic function $T(r,\,f)$![]() is estimated and a lower bound for $\beta$
is estimated and a lower bound for $\beta$![]() is given. So, it is natural to ask whether one can give an upper bound for $\beta$
is given. So, it is natural to ask whether one can give an upper bound for $\beta$![]() . In this section, we consider the problem by deriving an upper bound for $\beta$
. In this section, we consider the problem by deriving an upper bound for $\beta$![]() . In order to state the main result, we need the following definitions.
. In order to state the main result, we need the following definitions.
Let $f$![]() be a non-constant meromorphic function on $\mathbb {C}$
be a non-constant meromorphic function on $\mathbb {C}$![]() , and let $n_0$
, and let $n_0$![]() , $n_1,\,\ldots,\,n_k$
, $n_1,\,\ldots,\,n_k$![]() be $k+1$
be $k+1$![]() non-negative integers. We call
non-negative integers. We call
a monomial in $f$![]() of degree $\lambda _M=n_0+n_1+\cdots +n_k$
of degree $\lambda _M=n_0+n_1+\cdots +n_k$![]() and weight $\gamma _{M}=n_0+2n_1+\ldots +(k+1)n_k$
and weight $\gamma _{M}=n_0+2n_1+\ldots +(k+1)n_k$![]() , respectively. Now, let $M_1[f]$
, respectively. Now, let $M_1[f]$![]() , $M_2[f],\,\ldots,\,M_l[f]$
, $M_2[f],\,\ldots,\,M_l[f]$![]() be $l$
be $l$![]() monomials in $f$
monomials in $f$![]() of degree $\lambda _{M_j}$
of degree $\lambda _{M_j}$![]() and weight $\gamma _{M_j}$
and weight $\gamma _{M_j}$![]() $j=1,\,2,\,\ldots,\, l$
$j=1,\,2,\,\ldots,\, l$![]() respectively; and let $b_1$
respectively; and let $b_1$![]() , $b_2,\,\ldots,\,b_l$
, $b_2,\,\ldots,\,b_l$![]() be $l$
be $l$![]() polynomials. We call
polynomials. We call
is a differential polynomial in $f$![]() of total degree $\lambda _Q=\max \{\lambda _{M_1},\, \lambda _{M_2},\, \ldots,\, \lambda _{M_l}\}$
of total degree $\lambda _Q=\max \{\lambda _{M_1},\, \lambda _{M_2},\, \ldots,\, \lambda _{M_l}\}$![]() and total weight $\gamma _Q=\max \{\gamma _{M_1},\, \gamma _{M_2},\, \ldots,\, \gamma _{M_l}\}$
and total weight $\gamma _Q=\max \{\gamma _{M_1},\, \gamma _{M_2},\, \ldots,\, \gamma _{M_l}\}$![]() . More precisely, we get the following.
. More precisely, we get the following.
Theorem 3 Suppose that $f$![]() is a transcendental meromorphic function in $\mathbb {C}$
is a transcendental meromorphic function in $\mathbb {C}$![]() and $g$
and $g$![]() is a non-constant entire function satisfying the equation
is a non-constant entire function satisfying the equation
where $n$![]() is a positive integer and $Q[f]$
is a positive integer and $Q[f]$![]() is a differential polynomial of total degree $\Lambda$
is a differential polynomial of total degree $\Lambda$![]() and total weight $\Gamma,$
and total weight $\Gamma,$![]() respective. Let $\omega =\max \{\Lambda,\, \Gamma \}$
respective. Let $\omega =\max \{\Lambda,\, \Gamma \}$![]() . Then $g$
. Then $g$![]() must be a polynomial and the following assertions hold.
must be a polynomial and the following assertions hold.
(i) If $\omega <2n$
 , then $g$
, then $g$ must be linear;
must be linear;(ii) If $g$
 is a polynomial with degree $m\geq 2,$
is a polynomial with degree $m\geq 2,$ then
\[ T(r,f)=O((\log r)^{\beta}), \]where $\beta =\frac {\log \frac {\omega }{n}(1+\varepsilon )}{\log m}$
then
\[ T(r,f)=O((\log r)^{\beta}), \]where $\beta =\frac {\log \frac {\omega }{n}(1+\varepsilon )}{\log m}$
 and $\varepsilon$
and $\varepsilon$ is any arbitrary positive number.
is any arbitrary positive number.
Unfortunately, we don't know whether this upper bound is sharp or not.
Proof of Theorem 3. Note that $f$![]() is transcendental. It is well known that
is transcendental. It is well known that
outside possibly a set of finite Lebesgue measure. The fact can be found in [Reference Doeringer3, Lemma 1] and given by Doeringer. Further, from Equation (2.2), one has that

outside possibly a set of finite Lebesgue measure. Then, together with the fact (1), we then see that $g$![]() must be a polynomial. Still set $g = a_m z^{m}+ a_{m_1}z^{m-1}+\cdots + a_1 z + a_0$
must be a polynomial. Still set $g = a_m z^{m}+ a_{m_1}z^{m-1}+\cdots + a_1 z + a_0$![]() with $a_m\neq 0$
with $a_m\neq 0$![]() . Then, combining the fact (5) and (2.3) yields
. Then, combining the fact (5) and (2.3) yields
outside possibly a set of finite Lebesgue measure. It implies that
If $\frac {\omega }{n}<2$![]() , then we see that $m=1$
, then we see that $m=1$![]() and $g$
and $g$![]() is linear by choosing $\varepsilon$
is linear by choosing $\varepsilon$![]() small enough. Thus, the proof of (i) is finished.
small enough. Thus, the proof of (i) is finished.
Now, we prove the conclusion (ii) under the condition $\omega \geq 2n$![]() . With the above discussion and the fact (4), one has
. With the above discussion and the fact (4), one has

outside possibly a set of finite Lebesgue measure, where $\varepsilon _1$![]() is an arbitrary positive constant and $\varepsilon =\frac {\varepsilon _1+\epsilon _2}{1-\epsilon _2}$
is an arbitrary positive constant and $\varepsilon =\frac {\varepsilon _1+\epsilon _2}{1-\epsilon _2}$![]() . The form of $\varepsilon$
. The form of $\varepsilon$![]() implies that $\varepsilon$
implies that $\varepsilon$![]() is also a arbitrary positive number. Next, we need the following result, which is Lemma 1.1.1 in [Reference Laine7].
is also a arbitrary positive number. Next, we need the following result, which is Lemma 1.1.1 in [Reference Laine7].
Lemma 2.1 Let $g(r),\, h(r):(0,\, +\infty )\rightarrow \mathbb {R}$![]() be monotone non-decreasing functions such that $g(r)\leq h(r)$
be monotone non-decreasing functions such that $g(r)\leq h(r)$![]() outside possibly a set of finite Lebesgue measure. Then for any real number $\alpha >1,$
outside possibly a set of finite Lebesgue measure. Then for any real number $\alpha >1,$![]() there exists $r_0>0$
there exists $r_0>0$![]() such that $g(r)\leq h(\alpha r)$
such that $g(r)\leq h(\alpha r)$![]() for all $r>r_0$
for all $r>r_0$![]() .
.
Set $g(r)=T(\tfrac {|a_m|}{2}r^{m},\, f)$![]() and $\tfrac {\omega }{n}(1+\varepsilon )T(r,\,f)=h(r)$
and $\tfrac {\omega }{n}(1+\varepsilon )T(r,\,f)=h(r)$![]() . Obviously, $g(r)\leq h(r)$
. Obviously, $g(r)\leq h(r)$![]() outside possibly a set of finite Lebesgue measure. By Lemma 2.1, for any $\alpha >1$
outside possibly a set of finite Lebesgue measure. By Lemma 2.1, for any $\alpha >1$![]() , there exists a positive number $r_0$
, there exists a positive number $r_0$![]() such that $g(r)\leq h(\alpha r)$
such that $g(r)\leq h(\alpha r)$![]() for all $r>r_0$
for all $r>r_0$![]() . That is
. That is
Set $\alpha r=R$![]() . Then, we rewrite (2.5) as
. Then, we rewrite (2.5) as
To end the proof, we will employ a result of Goldstein, which can be found in [Reference Goldstein4, Lemma 3].
Lemma 2.2 Let $\psi (r)$![]() be a function of $r$
be a function of $r$![]() ($r\geq r_0$
($r\geq r_0$![]() ), positive and bounded in every finite interval. Suppose that
), positive and bounded in every finite interval. Suppose that
where $\mu (>0),$![]() $m(>1),$
$m(>1),$![]() $A(>1),$
$A(>1),$![]() $B$
$B$![]() are constants. Then
are constants. Then
Applying Lemma 2.2 to the function $T(R,\,f)$![]() , plus the inequality (2.6), we have
, plus the inequality (2.6), we have
where $\alpha =\frac {\log \frac {\omega }{n}(1+\varepsilon )}{\log m}$![]() .
.
Thus, the proof is finished.
To end this section, we give a simple application of Theorem 3 by considering a special functional-differential equation as follows.
It is known that the Weierstrass $\wp$![]() function is constructed in the most obvious way. Let $\omega _1$
function is constructed in the most obvious way. Let $\omega _1$![]() and $\omega _2$
and $\omega _2$![]() be two complex numbers such that ${\sf Im(\omega _2/\omega _1)\neq 0 }$
be two complex numbers such that ${\sf Im(\omega _2/\omega _1)\neq 0 }$![]() . The Weierstrass $\wp$
. The Weierstrass $\wp$![]() function is defined by
function is defined by

where $\Omega _{mn}=m\omega _1+n\omega _2$![]() and $\sum \nolimits _{m,~n}$
and $\sum \nolimits _{m,~n}$![]() denotes the sum over all integer $m$
denotes the sum over all integer $m$![]() and $n$
and $n$![]() excluding $(m,\,n)=(0,\,0)$
excluding $(m,\,n)=(0,\,0)$![]() . The Weierstrass $\wp$
. The Weierstrass $\wp$![]() function is an even meromorphic function with periods $\omega _1$
function is an even meromorphic function with periods $\omega _1$![]() and $\omega _2$
and $\omega _2$![]() and satisfies the ODE
and satisfies the ODE
where $g_2=60\sum \nolimits _{m,~n}\Omega _{mn}^{-4}$![]() and $g_3=140\sum \nolimits _{m,~n}\Omega _{mn}^{-6}$
and $g_3=140\sum \nolimits _{m,~n}\Omega _{mn}^{-6}$![]() . Naturally, one wants to know whether Weierstrass $\wp$
. Naturally, one wants to know whether Weierstrass $\wp$![]() function satisfies another functional-differential equation as follows, which maybe different from Equation (2.7).
function satisfies another functional-differential equation as follows, which maybe different from Equation (2.7).
where $a(\neq 0)$![]() , $b$
, $b$![]() , $c$
, $c$![]() are three constants. Actually, we below prove that if Equation (2.8) holds, then it reduces to (2.7).
are three constants. Actually, we below prove that if Equation (2.8) holds, then it reduces to (2.7).
Now, we give the proof. Suppose that Weierstrass $\wp$![]() function satisfies (2.8). We know that the characteristic function of $\wp$
function satisfies (2.8). We know that the characteristic function of $\wp$![]() is $T(r,\,\wp )=\frac {\pi }{A}r^{2}(1+o(1))$
is $T(r,\,\wp )=\frac {\pi }{A}r^{2}(1+o(1))$![]() with a positive constant $A$
with a positive constant $A$![]() . Then, we can get that $g$
. Then, we can get that $g$![]() is linear, no matter from the conclusions (i) or (ii) of Theorem 3. Assume that $g(z)=\alpha z+\beta$
is linear, no matter from the conclusions (i) or (ii) of Theorem 3. Assume that $g(z)=\alpha z+\beta$![]() . Substitute the forms of $g(z)$
. Substitute the forms of $g(z)$![]() and $\wp$
and $\wp$![]() into Equation (2.8), we can easily get that
into Equation (2.8), we can easily get that
where $m_0$![]() and $n_0$
and $n_0$![]() are two fixed integers. Therefore, $(\wp \circ g)(z)=\wp (\pm z+m_0\omega _1+n_0\omega _2)=\wp (z)$
are two fixed integers. Therefore, $(\wp \circ g)(z)=\wp (\pm z+m_0\omega _1+n_0\omega _2)=\wp (z)$![]() , since $\wp$
, since $\wp$![]() is an even meromorphic function with periods $\omega _1$
is an even meromorphic function with periods $\omega _1$![]() and $\omega _2$
and $\omega _2$![]() . Furthermore, we have $a=4$
. Furthermore, we have $a=4$![]() , $b=g_2$
, $b=g_2$![]() and $c=g_3$
and $c=g_3$![]() .
.
Thus, the proof is finished.
Acknowledgements
The author would like to thank the referee for helpful suggestions.