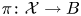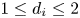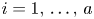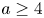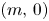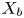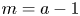1. Introduction
A family of $n$![]() -dimensional complex varieties is a flat, smooth proper morphism $\pi \colon \mathcal {X}\rightarrow B$
-dimensional complex varieties is a flat, smooth proper morphism $\pi \colon \mathcal {X}\rightarrow B$![]() such that the fibre $X_b :=\pi ^{-1}(b)$
such that the fibre $X_b :=\pi ^{-1}(b)$![]() over a point $b$
over a point $b$![]() on the base $B$
on the base $B$![]() has dimension $n$
has dimension $n$![]() . In this paper, we assume that $B$
. In this paper, we assume that $B$![]() is a smooth connected open complex variety of dimension $1$
is a smooth connected open complex variety of dimension $1$![]() . We will also assume that $X_{b}$
. We will also assume that $X_{b}$![]() is an irregular smooth variety of general type such that its Albanese morphism ${\rm {alb}}(X_b):X_{b}\rightarrow {\rm {Alb}}(X_{b})$
is an irregular smooth variety of general type such that its Albanese morphism ${\rm {alb}}(X_b):X_{b}\rightarrow {\rm {Alb}}(X_{b})$![]() is of degree $1$
is of degree $1$![]() . We want to study conditions which ensure that the fibres of $\pi \colon \mathcal {X}\rightarrow B$
. We want to study conditions which ensure that the fibres of $\pi \colon \mathcal {X}\rightarrow B$![]() are of the same birational type.
are of the same birational type.
It is well known that, up to base change, we can associate with $\pi \colon \mathcal {X}\rightarrow B$![]() the family of corresponding Albanese varieties. In fact, we can work in the more general setup of families of Albanese type (cf. [Reference Pirola and Zucconi23, Definition 1.1.1]), for which we recall the basic definition.
the family of corresponding Albanese varieties. In fact, we can work in the more general setup of families of Albanese type (cf. [Reference Pirola and Zucconi23, Definition 1.1.1]), for which we recall the basic definition.
Let $p\colon \mathcal {A}\rightarrow B$![]() be a family of abelian varieties; that is, the fibre $A_{b}:=p^{-1}(b)$
be a family of abelian varieties; that is, the fibre $A_{b}:=p^{-1}(b)$![]() is an abelian variety of dimension $a>0$
is an abelian variety of dimension $a>0$![]() . We say that a morphism $\varPhi \colon \mathcal {X}{\rightarrow }\mathcal {A}$
. We say that a morphism $\varPhi \colon \mathcal {X}{\rightarrow }\mathcal {A}$![]() is a family of Albanese type over $B$
is a family of Albanese type over $B$![]() if:
if:
1. $\varPhi$
 fits into the commutative diagram:
fits into the commutative diagram:

2. the induced map $\phi _{b}\colon X_{b}\rightarrow A_{b}$
 of $\varPhi$
of $\varPhi$ on $X_{b}$
on $X_{b}$ is birational onto its image $Z_{b}$
is birational onto its image $Z_{b}$ for general $b$
for general $b$ ;
;3. the cycle $Z_{b}$
 generates the fibre $A_{b}$
generates the fibre $A_{b}$ as a group for general $b$
as a group for general $b$ .
.
A family of Albanese type comes equipped with a global object: its relative homologically trivial cycle. Indeed, let $-{\rm {Id}}_{\mathcal {A}}\colon \mathcal {A}\rightarrow \mathcal {A}$![]() be the natural involution induced on $p:\mathcal {A}\rightarrow B$
be the natural involution induced on $p:\mathcal {A}\rightarrow B$![]() by the multiplication by $(-1)$
by the multiplication by $(-1)$![]() on the fibres. The composition $(-{\rm {Id}}_{\mathcal {A}})\circ \varPhi \colon \mathcal {X}\rightarrow \mathcal {A}$
on the fibres. The composition $(-{\rm {Id}}_{\mathcal {A}})\circ \varPhi \colon \mathcal {X}\rightarrow \mathcal {A}$![]() is an Albanese type family. We set $(-{\rm {Id}}_{\mathcal {A}})\circ \varPhi :=\varPhi ^{-}$
is an Albanese type family. We set $(-{\rm {Id}}_{\mathcal {A}})\circ \varPhi :=\varPhi ^{-}$![]() . Then, we can construct two cycles $[\varPhi \colon \mathcal {X}\rightarrow \mathcal {A}]$
. Then, we can construct two cycles $[\varPhi \colon \mathcal {X}\rightarrow \mathcal {A}]$![]() and $[\varPhi ^{-}\colon \mathcal {X}\rightarrow \mathcal {A}]$
and $[\varPhi ^{-}\colon \mathcal {X}\rightarrow \mathcal {A}]$![]() in the relative group $Z^{a-n}_{}(\mathcal {A}/B)$
in the relative group $Z^{a-n}_{}(\mathcal {A}/B)$![]() , which we denote, respectively, by $[\mathcal {X}]^{+}$
, which we denote, respectively, by $[\mathcal {X}]^{+}$![]() and $[\mathcal {X}]^{-}$
and $[\mathcal {X}]^{-}$![]() . The following cycle will be called the basic cycle of the Albanese type family $\varPhi \colon \mathcal {X}{\rightarrow }\mathcal {A}$
. The following cycle will be called the basic cycle of the Albanese type family $\varPhi \colon \mathcal {X}{\rightarrow }\mathcal {A}$![]() :
:
It is well known that the cycle $[\mathcal {Z}]$![]() is relatively homologically trivial; that is $[\mathcal {Z}]\in Z^{a-n}_{h}(\mathcal {A}/B)$
is relatively homologically trivial; that is $[\mathcal {Z}]\in Z^{a-n}_{h}(\mathcal {A}/B)$![]() . By the theory of normal functions and its infinitesimal invariant $\delta _{\mathcal {Z}}$
. By the theory of normal functions and its infinitesimal invariant $\delta _{\mathcal {Z}}$![]() , see [Reference Griffiths13, Reference Griffiths14, Reference Voisin31], we know that Albanese type families come into two types: those whose infinitesimal invariant is non-zero and those which have $\delta _{\mathcal {Z}}=0$
, see [Reference Griffiths13, Reference Griffiths14, Reference Voisin31], we know that Albanese type families come into two types: those whose infinitesimal invariant is non-zero and those which have $\delta _{\mathcal {Z}}=0$![]() . The latter are called Nori trivial families.
. The latter are called Nori trivial families.
Another piece of information carried by the morphism $\phi _{b}\colon X_{b}\rightarrow A_{b}$![]() is a splitting of $H^{n,0}(X_b)$
is a splitting of $H^{n,0}(X_b)$![]() . Indeed let $\phi _b^{*} \colon H^{n,0}(A_b)\to H^{n,0}(X_b)$
. Indeed let $\phi _b^{*} \colon H^{n,0}(A_b)\to H^{n,0}(X_b)$![]() and set $V_b:= {\rm {Im}}(\phi _b^{*})$
and set $V_b:= {\rm {Im}}(\phi _b^{*})$![]() . Inside the dual $H^{0,n}(X_b)$
. Inside the dual $H^{0,n}(X_b)$![]() of $H^{n,0}(X_b)$
of $H^{n,0}(X_b)$![]() , we can define:
, we can define:
and we know that
where ${\overline {V_b}}\subset H^{0,n}(X)$![]() is the conjugate space of $V_b$
is the conjugate space of $V_b$![]() . It also holds:
. It also holds:
which in turns gives a decomposition of the symmetric product
The standard multiplication map $H^{n,0}(X_b)\otimes H^{n,0}(X_b)\to H^{0}(X,\,\omega _{X_b}^{\otimes 2})$![]() factors on the symmetric product
factors on the symmetric product
and induces homomorphisms
and
Finally, we say that a family of relative dimension $n$![]() satisfies the extremal liftability assumptions if the natural restriction homomorphisms $H^{0}({\mathcal {X}},\,\varOmega _{{\mathcal {X}}}^{1}) \to H^{0}(X_{b},\,\varOmega _{X_{b}}^{1})$
satisfies the extremal liftability assumptions if the natural restriction homomorphisms $H^{0}({\mathcal {X}},\,\varOmega _{{\mathcal {X}}}^{1}) \to H^{0}(X_{b},\,\varOmega _{X_{b}}^{1})$![]() and $H^{0}({\mathcal {X}},\,\varOmega _{{\mathcal {X}}}^{n}) \to H^{0}(X_{b},\,\varOmega _{X_{b}}^{n})$
and $H^{0}({\mathcal {X}},\,\varOmega _{{\mathcal {X}}}^{n}) \to H^{0}(X_{b},\,\varOmega _{X_{b}}^{n})$![]() are surjective for every $b$
are surjective for every $b$![]() on $B$
on $B$![]() . The case where the map $H^{0}(X_b,\,\varOmega _{{\mathcal {X}|X_b}}^{n}) \to H^{0}(X_{b},\,\varOmega _{X_{b}}^{n})$
. The case where the map $H^{0}(X_b,\,\varOmega _{{\mathcal {X}|X_b}}^{n}) \to H^{0}(X_{b},\,\varOmega _{X_{b}}^{n})$![]() is surjective is deeply studied in [Reference Peters19, Reference Reider24]. Hence, our results must be read and applied jointly to the results in [Reference Peters19, Reference Reider24]. We show:
is surjective is deeply studied in [Reference Peters19, Reference Reider24]. Hence, our results must be read and applied jointly to the results in [Reference Peters19, Reference Reider24]. We show:
Theorem 1 Let $\varPhi \colon \mathcal {X}\rightarrow \mathcal {A}$![]() be a Nori family. If it satisfies extremal liftability assumptions and for each non-zero element $\eta$
be a Nori family. If it satisfies extremal liftability assumptions and for each non-zero element $\eta$![]() in $\overline {{\rm {Ann}}(V_b)}$
in $\overline {{\rm {Ann}}(V_b)}$![]() its square is not contained in the image of $\gamma _{X_b},$
its square is not contained in the image of $\gamma _{X_b},$![]() then its fibres belong to the same birational class.
then its fibres belong to the same birational class.
The proof is a direct consequence of the new notion of adjoint quadric introduced in [Reference Rizzi and Zucconi28]. By the extremal liftability assumptions, we are actually concerned with families of varieties equipped with a morphism to a fixed abelian variety; see Proposition 3.4. Nevertheless, our result should be considered in light of the theory of families of varieties of general type as described in [Reference Kollár15]; for this reason, we present the theorem in the above general set up, which strongly relies on the theory exposed in [Reference Pirola and Zucconi23]. In particular, we use the Volumetric Theorem [Reference Pirola and Zucconi23, Theorem 1.5.3] recalled in Theorem 3.7.
As an immediate consequence of Theorem [A] and of the well-known fact that, if $C$![]() is a hyperelliptic curve then the Ceresa's cycle $C-C^{-}$
is a hyperelliptic curve then the Ceresa's cycle $C-C^{-}$![]() is trivial in its Jacobian, we have the well-known Torelli Theorem for hyperelliptic deformations of hyperelliptic curves, see [Reference Oort and Steenbrink18]; this is a case where ${\overline {{\rm {Ann}}(V_b)}}=0$
is trivial in its Jacobian, we have the well-known Torelli Theorem for hyperelliptic deformations of hyperelliptic curves, see [Reference Oort and Steenbrink18]; this is a case where ${\overline {{\rm {Ann}}(V_b)}}=0$![]() .
.
More deeply, by a famous Theorem of Nori [Reference Nori17, pp. 372] (see also [Reference Fakhruddin8]), Theorem [A] applies to the case where the family $\mathcal {X}$![]() is given by a family of cycles inside a general abelian variety of dimension $a\geq 4$
is given by a family of cycles inside a general abelian variety of dimension $a\geq 4$![]() such that for each element $\eta$
such that for each element $\eta$![]() contained in $\overline {{\rm {Ann}}(V_b)}$
contained in $\overline {{\rm {Ann}}(V_b)}$![]() , its square is not contained in the image of $\gamma _{X_b}$
, its square is not contained in the image of $\gamma _{X_b}$![]() .
.
In the particular case of families of divisors, the above-mentioned theorem by Nori does not apply. However, by using techniques which are analogous to those we use to prove Theorem [A], we can show another result.
Let $(A,\,\mathcal {L})$![]() be a $(d_1,\,d_2,\,\ldots,\, d_a)$
be a $(d_1,\,d_2,\,\ldots,\, d_a)$![]() polarized abelian variety which is general inside its moduli space and $1\leq d_i\leq 2$
polarized abelian variety which is general inside its moduli space and $1\leq d_i\leq 2$![]() , $i=1,\,\ldots,\, a$
, $i=1,\,\ldots,\, a$![]() . Let $X\subset A$
. Let $X\subset A$![]() be a smooth divisor in $|\mathcal {L}|$
be a smooth divisor in $|\mathcal {L}|$![]() . Consider the incidence variety inside $|\mathcal {L}|\times A$
. Consider the incidence variety inside $|\mathcal {L}|\times A$![]() and $\hat {B}$
and $\hat {B}$![]() a curve inside $|\mathcal {L}|$
a curve inside $|\mathcal {L}|$![]() passing and smooth through $X$
passing and smooth through $X$![]() . Possibly after resolution of singularities, we obtain a fibration $\mathcal {Y}\to \hat {B}$
. Possibly after resolution of singularities, we obtain a fibration $\mathcal {Y}\to \hat {B}$![]() with $\mathcal {Y}$
with $\mathcal {Y}$![]() smooth. We say that a (local) family $\pi \colon \mathcal {X}\to B$
smooth. We say that a (local) family $\pi \colon \mathcal {X}\to B$![]() is induced by embedded deformations if it is obtained by the restriction of $\mathcal {Y}\to \hat {B}$
is induced by embedded deformations if it is obtained by the restriction of $\mathcal {Y}\to \hat {B}$![]() over an open contractible set $B\subset \hat {B}$
over an open contractible set $B\subset \hat {B}$![]() contained in the subset of smooth elements of $|\mathcal {L}|$
contained in the subset of smooth elements of $|\mathcal {L}|$![]() .
.
Theorem 2 Let $(A,\,\mathcal {L})$![]() be a $(d_1,\,d_2,\,\ldots,\, d_a)$
be a $(d_1,\,d_2,\,\ldots,\, d_a)$![]() polarized abelian variety which is general inside its moduli space and $1\leq d_i\leq 2,$
polarized abelian variety which is general inside its moduli space and $1\leq d_i\leq 2,$![]() $i=1,\,\ldots,\, a$
$i=1,\,\ldots,\, a$![]() . Let $\pi \colon \mathcal {X}\to B$
. Let $\pi \colon \mathcal {X}\to B$![]() be a family induced by embedded deformations. If $\pi \colon \mathcal {X}\to B$
be a family induced by embedded deformations. If $\pi \colon \mathcal {X}\to B$![]() satisfies the extremal liftability conditions then the fibres belong to the same birational class.
satisfies the extremal liftability conditions then the fibres belong to the same birational class.
Theorem [B], see § (4.5), follows by a careful study of the map
where $X_b$![]() is an element of the linear system associated with a $(d_1,\,d_2,\,\ldots,\, d_a)$
is an element of the linear system associated with a $(d_1,\,d_2,\,\ldots,\, d_a)$![]() -polarization, and $b\in B$
-polarization, and $b\in B$![]() .
.
This problem has turned out to be quite involved. Actually, the well-known problem to determine conditions for the surjectivity of $\mu _{X_b}$![]() , as well as of the maps
, as well as of the maps
are still of research interest. For instance, the surjectivity of $\mu _{a-1}$![]() implies that the Infinitesimal Torelli Theorem holds for the smooth hypersurfaces of $A$
implies that the Infinitesimal Torelli Theorem holds for the smooth hypersurfaces of $A$![]() of the linear system $|\mathcal {L}|$
of the linear system $|\mathcal {L}|$![]() , and it has been recently proved (see [Reference Bloss4]) that $\mu _{n}$
, and it has been recently proved (see [Reference Bloss4]) that $\mu _{n}$![]() is surjective, provided that $h^{0}(A,\, \mathcal {L}) > (\frac {n+1}{n})^{a} \cdot a!$
is surjective, provided that $h^{0}(A,\, \mathcal {L}) > (\frac {n+1}{n})^{a} \cdot a!$![]() and $A$
and $A$![]() is simple.
is simple.
As a first step in this direction, in § 4, we study the loci in the moduli space of polarized abelian varieties of type $(1,\,\dots,\,1,\,2,\,\dots,\,2)$![]() where
where
is not injective. Note that the injectivity of $\mu _b$![]() is equivalent to the injectivity of $\nu _{X_b}$
is equivalent to the injectivity of $\nu _{X_b}$![]() , since there is the following commutative diagram:
, since there is the following commutative diagram:

We prove:
Theorem 3 Let $(A,\,\mathcal {L})$![]() be a general polarized abelian variety of type $(1,\,\dots,\,1,\,2,\,\dots,\,2)$
be a general polarized abelian variety of type $(1,\,\dots,\,1,\,2,\,\dots,\,2)$![]() and $\mathcal {D}$
and $\mathcal {D}$![]() a general element in $|\mathcal {L}|$
a general element in $|\mathcal {L}|$![]() . For each element $\eta$
. For each element $\eta$![]() contained in $\overline {{\rm {Ann}}(V)},$
contained in $\overline {{\rm {Ann}}(V)},$![]() its square is not contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$
its square is not contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$![]() with respect to the multiplication map
with respect to the multiplication map
Moreover, the natural map
is injective.
See Corollary 4.4 and Theorem 4.5. Theorem [B] is a direct consequence of Theorem [C]. Actually, Theorem [C] is interesting on its own because it proves a condition on the kernel of $\mu _\mathcal {D}$![]() which is strictly stronger that the simple injectivity of $\nu _\mathcal {D}$
which is strictly stronger that the simple injectivity of $\nu _\mathcal {D}$![]() . As the proof of Theorem 4.5 clearly shows the condition on the squares of the elements $\eta$
. As the proof of Theorem 4.5 clearly shows the condition on the squares of the elements $\eta$![]() is independent from the injectivity of $\nu _{\mathcal {D}}$
is independent from the injectivity of $\nu _{\mathcal {D}}$![]() and in the explicit cases that one can consider they are indeed not true at the same time. They must both hold, however, on the general abelian variety described in Theorem [C].
and in the explicit cases that one can consider they are indeed not true at the same time. They must both hold, however, on the general abelian variety described in Theorem [C].
Finally, we have an application of the above circle of ideas to the case of fibrations with maximal relative irregularity. Let $S$![]() , $B$
, $B$![]() be, respectively, a smooth surface and a smooth curve. A fibration $f\colon S\to B$
be, respectively, a smooth surface and a smooth curve. A fibration $f\colon S\to B$![]() is said to be of maximal relative irregularity if $q(S)-g(B)=g(F)-1$
is said to be of maximal relative irregularity if $q(S)-g(B)=g(F)-1$![]() where $q(S)$
where $q(S)$![]() is the irregularity of $S$
is the irregularity of $S$![]() and $g(B),\,g(F)$
and $g(B),\,g(F)$![]() are, respectively, the genus of $B$
are, respectively, the genus of $B$![]() and of a general fibre $F$
and of a general fibre $F$![]() . There are many papers on this topic. Here, we can quote [Reference Möller16, Reference Pirola20] and [Reference Barja, González-Alonso and Naranjo2], which also contains basic references to this problem. In this particular case, it occurs that ${\overline {{\rm {Ann}}(V_b)}}\simeq \mathbb {C}$
. There are many papers on this topic. Here, we can quote [Reference Möller16, Reference Pirola20] and [Reference Barja, González-Alonso and Naranjo2], which also contains basic references to this problem. In this particular case, it occurs that ${\overline {{\rm {Ann}}(V_b)}}\simeq \mathbb {C}$![]() . Indeed, if the natural morphism $F\to {\rm {Alb}}(S)$
. Indeed, if the natural morphism $F\to {\rm {Alb}}(S)$![]() has degree $1$
has degree $1$![]() , we can find a suitable open subset $U\subset B$
, we can find a suitable open subset $U\subset B$![]() contained in the locus where $f\colon S\to B$
contained in the locus where $f\colon S\to B$![]() is smooth, and we can form a family of Albanese type $\varPhi _U\colon S_U\to \mathcal {A}_U$
is smooth, and we can form a family of Albanese type $\varPhi _U\colon S_U\to \mathcal {A}_U$![]() where $p\colon \mathcal {A}\to U$
where $p\colon \mathcal {A}\to U$![]() is such that its fibres are isomorphic to a fixed abelian variety $A$
is such that its fibres are isomorphic to a fixed abelian variety $A$![]() of dimension $g(F)-1$
of dimension $g(F)-1$![]() and $S_U:=f^{-1}(U)$
and $S_U:=f^{-1}(U)$![]() . In Theorem 5.2, which does not depend on Theorem [A], we show that the infinitesimal invariant associated with the basic cycle associated with $f_{|S_U}\colon S_U\to U$
. In Theorem 5.2, which does not depend on Theorem [A], we show that the infinitesimal invariant associated with the basic cycle associated with $f_{|S_U}\colon S_U\to U$![]() is not zero.
is not zero.
2. Adjoint quadrics
We recall some of the results of [Reference Pirola and Zucconi23]. See also [Reference Rizzi and Zucconi26–Reference Rizzi and Zucconi28].
2.1. The Adjoint theorem
2.1.1 The Gauss-type homomorphism
Let $X$![]() be a compact complex smooth variety of dimension $m$
be a compact complex smooth variety of dimension $m$![]() and let $\mathcal {F}$
and let $\mathcal {F}$![]() be a locally free sheaf of rank $n$
be a locally free sheaf of rank $n$![]() . Fix an extension class $\xi \in \text {Ext}^{1}(\mathcal {F},\,\mathcal {O}_X)$
. Fix an extension class $\xi \in \text {Ext}^{1}(\mathcal {F},\,\mathcal {O}_X)$![]() associated with the exact sequence:
associated with the exact sequence:
By the Koszul resolution associated with the section $d\epsilon \in H^{0}(X,\,\mathcal {E})$![]() and by the isomorphisms
and by the isomorphisms

we see that the coboundary homomorphisms

are computed by cup product and interior product with $\xi$![]() , $i=1,\,\dots,\,n$
, $i=1,\,\dots,\,n$![]() .
.
Denote by $H^{n}_{d\epsilon }\colon \det \mathcal {E}\to \det \mathcal {F}$![]() the natural isomorphism and by $\varLambda ^{n+1}$
the natural isomorphism and by $\varLambda ^{n+1}$![]() the natural map
the natural map
By composition, we define a Gauss-type homomorphism:
2.1.2 Adjoint forms
Let $W\subset \mathrm {Ker}\,(\partial _\xi ^{1})\subset H^{0}(X,\,\mathcal {F})$![]() be a vector subspace of dimension $n+1$
be a vector subspace of dimension $n+1$![]() and let $\mathcal {B}:=\{\eta _1,\,\ldots,\,\eta _{n+1}\}$
and let $\mathcal {B}:=\{\eta _1,\,\ldots,\,\eta _{n+1}\}$![]() be a basis of $W$
be a basis of $W$![]() . By definition, we can take liftings $s_1,\,\dots,\,s_{n+1}\in H^{0}(X,\,\mathcal {E})$
. By definition, we can take liftings $s_1,\,\dots,\,s_{n+1}\in H^{0}(X,\,\mathcal {E})$![]() such that $\rho _1(s_i)=\eta _i$
such that $\rho _1(s_i)=\eta _i$![]() , $i=1,\,\ldots,\,n+1$
, $i=1,\,\ldots,\,n+1$![]() .
.
Definition 2.1 The section
is called an adjoint form of $\xi,\,W,\,\mathcal {B}$![]() .
.
If we consider the natural map
we can define the subspace $\lambda ^{n} W\subset H^{0}(X,\,\det \mathcal {F})$![]() generated by
generated by
for $i=1,\,\dots,\,n+1$![]() .
.
Definition 2.2 The class
is called the Massey product of $W$![]() along $\xi$
along $\xi$![]() .
.
In the literature, $[\omega _{\xi,W,\mathcal {B}}]$![]() is also called the adjoint image of $W$
is also called the adjoint image of $W$![]() by $\xi$
by $\xi$![]() . For the main properties of Massey products in our context see [Reference Collino and Pirola7, Reference Pirola and Zucconi23, Reference Rizzi and Zucconi26–Reference Rizzi and Zucconi28]. Here we only recall that while the section $\omega _{\xi,W,\mathcal {B}}$
. For the main properties of Massey products in our context see [Reference Collino and Pirola7, Reference Pirola and Zucconi23, Reference Rizzi and Zucconi26–Reference Rizzi and Zucconi28]. Here we only recall that while the section $\omega _{\xi,W,\mathcal {B}}$![]() depends on the choice of the liftings $s_i$
depends on the choice of the liftings $s_i$![]() , the class $[\omega _{\xi,W,\mathcal {B}}]$
, the class $[\omega _{\xi,W,\mathcal {B}}]$![]() does not. Furthermore, if we choose another basis $\mathcal {B}':=\{\eta '_1,\,\ldots,\,\eta '_{n+1}\}$
does not. Furthermore, if we choose another basis $\mathcal {B}':=\{\eta '_1,\,\ldots,\,\eta '_{n+1}\}$![]() of $W$
of $W$![]() then $[\omega _{\xi,W,\mathcal {B}}]=k[\omega _{\xi,W,\mathcal {B}'}]$
then $[\omega _{\xi,W,\mathcal {B}}]=k[\omega _{\xi,W,\mathcal {B}'}]$![]() where $k$
where $k$![]() is the determinant of the matrix of the change of basis. Since we will be mostly concerned with the condition $[\omega _{\xi,W,\mathcal {B}}]=0$
is the determinant of the matrix of the change of basis. Since we will be mostly concerned with the condition $[\omega _{\xi,W,\mathcal {B}}]=0$![]() , the choice of the basis of $W$
, the choice of the basis of $W$![]() is also not essential and that is why in the above definition, we only highlight the dependence on $W$
is also not essential and that is why in the above definition, we only highlight the dependence on $W$![]() and $\xi$
and $\xi$![]() .
.
Definition 2.3 If $\lambda ^{n}W$![]() is nontrivial we denote by $|\lambda ^{n} W|\subset \mathbb {P}(H^{0}(X,\,\det \mathcal {F}))$
is nontrivial we denote by $|\lambda ^{n} W|\subset \mathbb {P}(H^{0}(X,\,\det \mathcal {F}))$![]() the induced sublinear system. We call $D_W$
the induced sublinear system. We call $D_W$![]() the fixed divisor of this linear system and $Z_W$
the fixed divisor of this linear system and $Z_W$![]() the base locus of its moving part $|M_W|\subset \mathbb {P}(H^{0}(X,\,\det \mathcal {F}(-D_W)))$
the base locus of its moving part $|M_W|\subset \mathbb {P}(H^{0}(X,\,\det \mathcal {F}(-D_W)))$![]() .
.
From the natural map $\epsilon _{D_{W}}\colon \mathcal {F}(-D_W)\to \mathcal {F}$![]() , we have the induced homomorphism in cohomology:
, we have the induced homomorphism in cohomology:
We set
Definition 2.4 We say that $\xi \in H^{1}(X,\,\mathcal {F}^{\vee })$![]() is supported on $D_W$
is supported on $D_W$![]() if $\xi _{D_W}=0$
if $\xi _{D_W}=0$![]()
In [Reference Pirola and Zucconi23, Theorem 1.5.1], see also [Reference Rizzi and Zucconi28], we have shown:
Theorem 2.5 Adjoint Theorem
Let $X$![]() be a compact $m$
be a compact $m$![]() -dimensional complex smooth variety. Let $\mathcal {F}$
-dimensional complex smooth variety. Let $\mathcal {F}$![]() be a rank $n$
be a rank $n$![]() locally free sheaf on $X$
locally free sheaf on $X$![]() and $\xi \in H^{1}(X,\,\mathcal {F}^{\vee })$
and $\xi \in H^{1}(X,\,\mathcal {F}^{\vee })$![]() the extension class of the exact sequence (2.1). Let $W$
the extension class of the exact sequence (2.1). Let $W$![]() be a $n+1$
be a $n+1$![]() -dimensional subspace of $\mathrm {Ker}\,(\partial _\xi ^{1})\subset H^{0}(X,\,\mathcal {F})$
-dimensional subspace of $\mathrm {Ker}\,(\partial _\xi ^{1})\subset H^{0}(X,\,\mathcal {F})$![]() and $\omega$
and $\omega$![]() one of its adjoint forms. If the Massey product $[\omega ]=0$
one of its adjoint forms. If the Massey product $[\omega ]=0$![]() then $\xi$
then $\xi$![]() is supported on $D_W$
is supported on $D_W$![]() .
.
For interesting applications of this theory different from those presented in this paper, we refer to [Reference Barja, González-Alonso and Naranjo2, Reference González-Alonso9–Reference González-Alonso, Stoppino and Torelli12, Reference Pirola and Torelli22, Reference Rizzi25, Reference Rizzi and Zucconi29, Reference Torelli30].
2.2. The notion of Adjoint quadric
We denote by $\lambda ^{n}H^{0}(X,\,\mathcal {F})$![]() the image of
the image of
and we consider the linear subsystem $\mathbb {P}(\lambda ^{n}H^{0}(X,\,\mathcal {F}))$![]() of $|\det \mathcal {F}|$
of $|\det \mathcal {F}|$![]() . Denote by $D_\mathcal {F}$
. Denote by $D_\mathcal {F}$![]() its fixed component and by $|M_{\mathcal {F}}|$
its fixed component and by $|M_{\mathcal {F}}|$![]() its associated mobile linear system. Moreover, we denote $D_{\det \mathcal {F}}$
its associated mobile linear system. Moreover, we denote $D_{\det \mathcal {F}}$![]() , $M_{\det \mathcal {F}}$
, $M_{\det \mathcal {F}}$![]() , respectively, the fixed and the movable part of $|\det \mathcal {F}|$
, respectively, the fixed and the movable part of $|\det \mathcal {F}|$![]() ; that is, $|\det \mathcal {F}|=D_{\det \mathcal {F}}+|M_{\det \mathcal {F}}|$
; that is, $|\det \mathcal {F}|=D_{\det \mathcal {F}}+|M_{\det \mathcal {F}}|$![]() .
.
Take $W=\langle \eta _1,\,\ldots,\,\eta _{n+1}\rangle$![]() and $\omega _i$
and $\omega _i$![]() , $i=1,\,\ldots,\,n+1$
, $i=1,\,\ldots,\,n+1$![]() as above and let $\omega \in H^{0}(X,\, \det \mathcal {F})$
as above and let $\omega \in H^{0}(X,\, \det \mathcal {F})$![]() be a $\xi$
be a $\xi$![]() -adjoint of $W\subset H^{0}(X,\,\mathcal {F})$
-adjoint of $W\subset H^{0}(X,\,\mathcal {F})$![]() . Let
. Let
be the natural multiplication homomorphism. The basic definition of this paper is:
Definition 2.6 An $\omega$![]() -adjoint quadric is an element $Q\in {\rm {Sym}}^{2}(H^{0}(X,\, \det \mathcal {F}))$
-adjoint quadric is an element $Q\in {\rm {Sym}}^{2}(H^{0}(X,\, \det \mathcal {F}))$![]() such that
such that
1. $Q:=\omega \odot \omega -\sum \nolimits _{i=1}^{n+1} \omega _i\odot L_i$
 for some $L_i\in H^{0}(X,\,\det \mathcal {F})$
for some $L_i\in H^{0}(X,\,\det \mathcal {F})$ , $i=1,\,\ldots,\,n+1$
, $i=1,\,\ldots,\,n+1$ ;
;2. $\mu _{\det \mathcal {F}}(Q)=0$
 .
.
The condition $(2)$![]() of this Definition means that $Q$
of this Definition means that $Q$![]() gives an element of ${\rm {Sym}}^{2}(H^{0}(X,\, \det \mathcal {F}))$
gives an element of ${\rm {Sym}}^{2}(H^{0}(X,\, \det \mathcal {F}))$![]() which vanishes on the schematic image $\phi _{|M_{\det \mathcal {F}} |}(X)$
which vanishes on the schematic image $\phi _{|M_{\det \mathcal {F}} |}(X)$![]() . The study of $\omega$
. The study of $\omega$![]() -adjoint quadrics is useful to find extension classes supported on a divisor.
-adjoint quadrics is useful to find extension classes supported on a divisor.
Theorem 2.7 Let $X$![]() be a compact complex smooth variety. Let $\mathcal {F}$
be a compact complex smooth variety. Let $\mathcal {F}$![]() be a locally free sheaf of rank $n$
be a locally free sheaf of rank $n$![]() such that $h^{0}(X,\, \mathcal {F})\geq n+1$
such that $h^{0}(X,\, \mathcal {F})\geq n+1$![]() . Let $\xi \in H^{1}(X,\,\mathcal {F}^{\vee })$
. Let $\xi \in H^{1}(X,\,\mathcal {F}^{\vee })$![]() and $W$
and $W$![]() an $n+1$
an $n+1$![]() -dimensional subspace $W\subset \mathrm {Ker}\,\partial _\xi \subset H^{0}(X,\,\mathcal {F})$
-dimensional subspace $W\subset \mathrm {Ker}\,\partial _\xi \subset H^{0}(X,\,\mathcal {F})$![]() . If $\xi$
. If $\xi$![]() is such that $\partial _{\xi }^{n}(\omega )=0,$
is such that $\partial _{\xi }^{n}(\omega )=0,$![]() where $\omega$
where $\omega$![]() is an adjoint form associated with $W$
is an adjoint form associated with $W$![]() and $\xi,$
and $\xi,$![]() then $[\omega ]=0,$
then $[\omega ]=0,$![]() providing that there are no $\omega$
providing that there are no $\omega$![]() -adjoint quadrics.
-adjoint quadrics.
Proof. Let $\mathcal {B}=\{\eta _{1},\,\ldots,\, \eta _{n+1}\}$![]() be a basis of $W$
be a basis of $W$![]() . Set $\omega _i$
. Set $\omega _i$![]() for $i=1,\,\dots,\,n+1$
for $i=1,\,\dots,\,n+1$![]() as above and denote by $\tilde {\omega }_i\in H^{0}(\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W})$
as above and denote by $\tilde {\omega }_i\in H^{0}(\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W})$![]() the corresponding sections via
the corresponding sections via
Recall that $\lambda ^{n}W:=\left \langle \omega _1,\,\dots,\,\omega _{n+1}\right \rangle \subset H^{0}(X,\,\det \mathcal {F})$![]() is the vector space generated by the sections $\omega _i$
is the vector space generated by the sections $\omega _i$![]() . Note also that the sheaf $\bigwedge ^{n}W\otimes \mathcal {O}_{X}$
. Note also that the sheaf $\bigwedge ^{n}W\otimes \mathcal {O}_{X}$![]() is trivial and choosing $\eta _1\wedge \ldots \wedge \widehat {\eta _i}\wedge \ldots \wedge \eta _{n+1}$
is trivial and choosing $\eta _1\wedge \ldots \wedge \widehat {\eta _i}\wedge \ldots \wedge \eta _{n+1}$![]() , $i=1,\,\dots,\,n+1$
, $i=1,\,\dots,\,n+1$![]() , as a basis for $\bigwedge ^{n}W$
, as a basis for $\bigwedge ^{n}W$![]() we obtain an isomorphism to $\mathcal {O}_X^{n+1}$
we obtain an isomorphism to $\mathcal {O}_X^{n+1}$![]() .
.
The standard evaluation map $\bigwedge ^{n}W\otimes \mathcal {O}_{X}\to \det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_{W}}$![]() given by $\tilde {\omega }_1,\,\dots, \tilde {\omega }_{n+1}$
given by $\tilde {\omega }_1,\,\dots, \tilde {\omega }_{n+1}$![]() gives the following exact sequence
gives the following exact sequence
which is associated with a class $\xi '\in \text {Ext}^{1}(\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W},\,\mathcal {K})$![]() . The sequence (2.4) fits into the following commutative diagram
. The sequence (2.4) fits into the following commutative diagram

where $f$![]() is the map given by the contraction by the sections $(-1)^{n+1-i}s_i$
is the map given by the contraction by the sections $(-1)^{n+1-i}s_i$![]() , for $i=1,\,\dots,\,n+1$
, for $i=1,\,\dots,\,n+1$![]() , and $g$
, and $g$![]() is given by the global section $\sigma \in H^{0}(X,\,\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W})$
is given by the global section $\sigma \in H^{0}(X,\,\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W})$![]() corresponding to the adjoint form $\omega$
corresponding to the adjoint form $\omega$![]() . We have the standard factorization
. We have the standard factorization

where the sequence in the middle is associated with the class $\xi ''\in H^{1}(X,\,\mathcal {K})$![]() which is the image of $\xi \in H^{1}(X,\,\mathcal {F}^{\vee })$
which is the image of $\xi \in H^{1}(X,\,\mathcal {F}^{\vee })$![]() through the map $H^{1}(X,\,\mathcal {F}^{\vee })\to H^{1}(X,\,\mathcal {K})$
through the map $H^{1}(X,\,\mathcal {F}^{\vee })\to H^{1}(X,\,\mathcal {K})$![]() . In particular, we obtain the commutative square:
. In particular, we obtain the commutative square:

By commutativity, we immediately have that the image of $\sigma \in H^{0}(X,\,\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W})$![]() through the coboundary map $H^{0}(X,\,\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W})\to H^{1}(X,\,\mathcal {K})$
through the coboundary map $H^{0}(X,\,\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W})\to H^{1}(X,\,\mathcal {K})$![]() is $\xi ''$
is $\xi ''$![]() . Tensoring by $\det \mathcal {F}$
. Tensoring by $\det \mathcal {F}$![]() , the map $\mathcal {F}^{\vee }\to \mathcal {K}$
, the map $\mathcal {F}^{\vee }\to \mathcal {K}$![]() gives
gives

and, since $\xi \cdot \omega \in H^{1}(X,\,\mathcal {F}^{\vee }\otimes \det \mathcal {F})$![]() is sent to $\xi ''\cdot \omega \in H^{1}(X,\,\mathcal {K}\otimes \det \mathcal {F})$
is sent to $\xi ''\cdot \omega \in H^{1}(X,\,\mathcal {K}\otimes \det \mathcal {F})$![]() , we have that
, we have that
where $\xi \cdot \omega$![]() is the cup product.
is the cup product.
By hypothesis $\partial _\xi ^{n}(\omega )=\xi \cdot \omega =0\in H^{1}(X,\,\bigwedge ^{n-1}\mathcal {F})$![]() , so also $\xi ''\cdot \omega =0\in H^{1}(X,\,\mathcal {K}\otimes \det \mathcal {F})$
, so also $\xi ''\cdot \omega =0\in H^{1}(X,\,\mathcal {K}\otimes \det \mathcal {F})$![]() , hence, the global section $\sigma \cdot \omega \in H^{0}(X,\,\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W}\otimes \det \mathcal {F})$
, hence, the global section $\sigma \cdot \omega \in H^{0}(X,\,\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W}\otimes \det \mathcal {F})$![]() is in the kernel of the coboundary map $H^{0}(X,\,\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W}\otimes \det \mathcal {F})\to H^{1}(X,\, \mathcal {K}\otimes \det \mathcal {F})$
is in the kernel of the coboundary map $H^{0}(X,\,\det \mathcal {F}(-D_W)\otimes \mathcal {I}_{Z_W}\otimes \det \mathcal {F})\to H^{1}(X,\, \mathcal {K}\otimes \det \mathcal {F})$![]() associated to the sequence
associated to the sequence
This occurs if there exist $L^{\sigma }_{i}\in H^{0}(X,\,\det \mathcal {F})$![]() , $i=1,\,\ldots,\, n+1$
, $i=1,\,\ldots,\, n+1$![]() such that
such that

This relation gives the following relation in $H^{0}(X,\,\det \mathcal {F}^{\otimes 2})$![]() :
:

Then, equation (2.12) gives an adjoint quadric. By contradiction, the claim follows.
Corollary 2.8 In the hypothesis of Theorem 2.7 it holds that $\xi$![]() is supported on $D_{W};$
is supported on $D_{W};$![]() that is, $\xi _{D_{W}}$
that is, $\xi _{D_{W}}$![]() is trivial. Moreover, if we further assume that $H^{0}(X,\, \mathcal {F})=\mathrm {Ker}\,\partial _\xi$
is trivial. Moreover, if we further assume that $H^{0}(X,\, \mathcal {F})=\mathrm {Ker}\,\partial _\xi$![]() and $W$
and $W$![]() is generic inside $H^{0}(X,\, \mathcal {F})$
is generic inside $H^{0}(X,\, \mathcal {F})$![]() it follows that $\xi$
it follows that $\xi$![]() is supported on $D_{\mathcal {F}}$
is supported on $D_{\mathcal {F}}$![]() .
.
Proof. The first claim follows by Theorem 2.7 and by Theorem 2.5. To show the second claim, we recall that by [Reference Pirola and Zucconi23, Proposition 3.1.6] $D_{\mathcal {F}}=D_W$![]() since $W$
since $W$![]() is a generic $n+1$
is a generic $n+1$![]() -dimensional subspace of $H^{0}(X,\,\mathcal {F})$
-dimensional subspace of $H^{0}(X,\,\mathcal {F})$![]() . Then, the claim follows.
. Then, the claim follows.
Note that in the rest of the paper, $\mathcal {F}$![]() will be $\varOmega ^{1}_{X}$
will be $\varOmega ^{1}_{X}$![]() and therefore, the assumption $H^{0}(X,\, \mathcal {F})=\mathrm {Ker}\,\partial _\xi$
and therefore, the assumption $H^{0}(X,\, \mathcal {F})=\mathrm {Ker}\,\partial _\xi$![]() of the Corollary comes from the extremal liftability assumptions.
of the Corollary comes from the extremal liftability assumptions.
3. Nori families
We apply the notion of adjoint quadrics to the case where $\mathcal {F}$![]() is the cotangent sheaf $\varOmega ^{1}_{X}$
is the cotangent sheaf $\varOmega ^{1}_{X}$![]() of a smooth variety. We stress that we want to find conditions on a family $\pi \colon \mathcal {X}\rightarrow B$
of a smooth variety. We stress that we want to find conditions on a family $\pi \colon \mathcal {X}\rightarrow B$![]() which ensure that the fibres are in the same birational class.
which ensure that the fibres are in the same birational class.
3.1. A notion of equivalence among families of Albanese type
The notion of Albanese type family behaves well under base change and we can introduce a notion of equivalence for this kind of families. Consider a family of Albanese type $\varPhi \colon \mathcal {X}{\rightarrow }\mathcal {A}$![]() as in § 1.
as in § 1.
3.1.1 Translation equivalence
If $s\colon B\to \mathcal {A}$![]() is a section of $p:\mathcal {A}\rightarrow B$
is a section of $p:\mathcal {A}\rightarrow B$![]() , we define the translated family $\varPhi _{s}:\mathcal {X}\rightarrow \mathcal {A}$
, we define the translated family $\varPhi _{s}:\mathcal {X}\rightarrow \mathcal {A}$![]() of $\varPhi$
of $\varPhi$![]() by the formula:
by the formula:
Notice that $\varPhi _{s}:\mathcal {X}\rightarrow \mathcal {A}$![]() is a family of Albanese type. Two families $\varPhi$
is a family of Albanese type. Two families $\varPhi$![]() and $\varPsi$
and $\varPsi$![]() over $B$
over $B$![]() are said to be translation equivalent if there exists a section $\sigma$
are said to be translation equivalent if there exists a section $\sigma$![]() of $p\colon \mathcal {A}\rightarrow B$
of $p\colon \mathcal {A}\rightarrow B$![]() such that the images of $\varPhi _{\sigma }$
such that the images of $\varPhi _{\sigma }$![]() and $\varPsi$
and $\varPsi$![]() (fibrewise) coincide.
(fibrewise) coincide.
We recall also the following definition given in [Reference Pirola and Zucconi23, definition 1.1.2]:
Definition 3.1 Two families of Albanese type $\varPhi \colon \mathcal {X}{\rightarrow }\mathcal {A}$![]() , $\varPhi '\colon \mathcal {X}^{'} {\rightarrow }\mathcal {A}^{'}$
, $\varPhi '\colon \mathcal {X}^{'} {\rightarrow }\mathcal {A}^{'}$![]() over, respectively, $B$
over, respectively, $B$![]() and $B'$
and $B'$![]() will be said locally translation equivalent, if there exist an open set $U\subset B$
will be said locally translation equivalent, if there exist an open set $U\subset B$![]() an open set $U'\subset B'$
an open set $U'\subset B'$![]() and a biregular map $\mu \colon U'\to U:=\mu (U')\subset B$
and a biregular map $\mu \colon U'\to U:=\mu (U')\subset B$![]() such that the pull-back families $\mu ^{\ast }( \varPhi _{U})$
such that the pull-back families $\mu ^{\ast }( \varPhi _{U})$![]() and $\varPhi ^{'}_{U^{'}}$
and $\varPhi ^{'}_{U^{'}}$![]() are translation equivalent where $U$
are translation equivalent where $U$![]() , $U'$
, $U'$![]() are dense with respect to the classical topology on $B$
are dense with respect to the classical topology on $B$![]() , respectively, $B'$
, respectively, $B'$![]() . We will say that $\varPhi$
. We will say that $\varPhi$![]() is trivial if $\mathcal {X}=X\times B$
is trivial if $\mathcal {X}=X\times B$![]() , $\mathcal {A}=A\times B$
, $\mathcal {A}=A\times B$![]() and $\pi _{A}(\varPhi ({X_{b}}))=\pi _{A}(\varPhi (X_{b_{0}}))$
and $\pi _{A}(\varPhi ({X_{b}}))=\pi _{A}(\varPhi (X_{b_{0}}))$![]() for all $b$
for all $b$![]() where $\pi _{A}\colon A\times B\to A$
where $\pi _{A}\colon A\times B\to A$![]() is the natural projection.
is the natural projection.
We will use the following:
Proposition 3.2 An Albanese type family $\varPhi \colon \mathcal {X}\to \mathcal {A}$![]() is locally translation equivalent to a trivial family if and only if the fibres $X_{b}$
is locally translation equivalent to a trivial family if and only if the fibres $X_{b}$![]() are birationally equivalent.
are birationally equivalent.
Proof. See [Reference Pirola and Zucconi23, Proposition 1.1.3].
3.2. Liftability assumptions
The following conditions are natural in order to find families locally translation equivalent to trivial families.
Definition 3.3 We say that a family $\pi \colon \mathcal {X} {\rightarrow }B$![]() of relative dimension $n$
of relative dimension $n$![]() satisfies the extremal liftability conditions over a one-dimensional variety $B$
satisfies the extremal liftability conditions over a one-dimensional variety $B$![]() if
if
1. $H^{0}({\mathcal {X}},\,\varOmega _{{\mathcal {X}}}^{1}) \twoheadrightarrow H^{0}(X_{b},\,\varOmega _{X_{b}}^{1})$
 ;
;2. $H^{0}({\mathcal {X}},\,\varOmega _{{\mathcal {X}}}^{n}) \twoheadrightarrow H^{0}(X_{b},\,\varOmega _{X_{b}}^{n})$

where the symbol $\twoheadrightarrow$![]() means that the homomorphism is surjective.
means that the homomorphism is surjective.
The above definition says that all the $1$![]() -forms and all the $n$
-forms and all the $n$![]() -forms of the fibre $X_b$
-forms of the fibre $X_b$![]() are obtained by restriction of forms defined on the family $\mathcal {X}$
are obtained by restriction of forms defined on the family $\mathcal {X}$![]() . Comparing the two conditions with the hypotheses of Theorem 2.7, we see that they ensure that $\partial ^{1}_{\xi _b}=0$
. Comparing the two conditions with the hypotheses of Theorem 2.7, we see that they ensure that $\partial ^{1}_{\xi _b}=0$![]() and $\partial _{\xi _{b}}^{n}=0$
and $\partial _{\xi _{b}}^{n}=0$![]() , where $\xi _b\in H^{1}(X_b,\, \varTheta _{X_{b}})$
, where $\xi _b\in H^{1}(X_b,\, \varTheta _{X_{b}})$![]() is an infinitesimal deformation in the image of the Kodaira–Spencer map associated with $\pi \colon \mathcal {X} {\rightarrow }B$
is an infinitesimal deformation in the image of the Kodaira–Spencer map associated with $\pi \colon \mathcal {X} {\rightarrow }B$![]() .
.
Proposition 3.4 Let $\varPhi \colon \mathcal {X}\to \mathcal {A}$![]() be an Albanese type family such that for every $b\in B$
be an Albanese type family such that for every $b\in B$![]() it holds that $H^{0}({\mathcal {X}},\,\varOmega _{{\mathcal {X}}}^{1}) \twoheadrightarrow H^{0}(X_{b},\,\varOmega _{X_{b}}^{1})$
it holds that $H^{0}({\mathcal {X}},\,\varOmega _{{\mathcal {X}}}^{1}) \twoheadrightarrow H^{0}(X_{b},\,\varOmega _{X_{b}}^{1})$![]() . Then up to shrinking $B$
. Then up to shrinking $B$![]() , the fibres of $p\colon \mathcal {A}\to B$
, the fibres of $p\colon \mathcal {A}\to B$![]() are isomorphic.
are isomorphic.
Proof. Let $\mu _b\in {{\rm Ext}}^{1}(\varOmega ^{1}_{A_b},\,\mathcal {O}_{A_b})$![]() be the class given by the family $p\colon \mathcal {A}\to B$
be the class given by the family $p\colon \mathcal {A}\to B$![]() , that is the class of the following extension:
, that is the class of the following extension:
Now $\phi _b^{*}\mathcal {O}_{A_{b}}=\mathcal {O}_{X_b}$![]() and the map $\phi _b^{*}\mathcal {O}_{A_{b}}\to \phi _b^{*}\varOmega ^{1}_{\mathcal {A}|A_{b}}$
and the map $\phi _b^{*}\mathcal {O}_{A_{b}}\to \phi _b^{*}\varOmega ^{1}_{\mathcal {A}|A_{b}}$![]() is generically injective; hence, it is injective because otherwise the kernel would be a torsion subsheaf of $\mathcal {O}_{X_b}$
is generically injective; hence, it is injective because otherwise the kernel would be a torsion subsheaf of $\mathcal {O}_{X_b}$![]() . Thus, we have the following exact sequence
. Thus, we have the following exact sequence
which fits into the following diagram

In cohomology, we have

so, by commutativity and by the hypothesis $H^{0}({\mathcal {X}},\,\varOmega _{{\mathcal {X}}}^{1}) \twoheadrightarrow H^{0}(X_{b},\,\varOmega _{X_{b}}^{1})$![]() , we immediately obtain $H^{0}(X_b,\,\phi _b^{*}\varOmega ^{1}_{\mathcal {A}|A_{b}}) \twoheadrightarrow H^{0}(X_{b},\,\phi _b^{*}\varOmega ^{1}_{A_{b}})$
, we immediately obtain $H^{0}(X_b,\,\phi _b^{*}\varOmega ^{1}_{\mathcal {A}|A_{b}}) \twoheadrightarrow H^{0}(X_{b},\,\phi _b^{*}\varOmega ^{1}_{A_{b}})$![]() and hence the coboundary $\partial _{\mu _{b}}\colon H^{0}(A_b ,\,\varOmega ^{1}_{A_{b}})\to H^{1}(A_b,\, \mathcal {O}_{A_{b}})$
and hence the coboundary $\partial _{\mu _{b}}\colon H^{0}(A_b ,\,\varOmega ^{1}_{A_{b}})\to H^{1}(A_b,\, \mathcal {O}_{A_{b}})$![]() is trivial. Then we can apply the argument in cf. [Reference Collino and Pirola7, Page 77, 78] on a conveniently small $B$
is trivial. Then we can apply the argument in cf. [Reference Collino and Pirola7, Page 77, 78] on a conveniently small $B$![]() .
.
3.3. Nori families
Let $\varPhi :\mathcal {X}\rightarrow \mathcal {A}$![]() be an Albanese type family over the unitary disc $\Delta$
be an Albanese type family over the unitary disc $\Delta$![]() . From $\varPhi (\mathcal {X})\hookrightarrow \mathcal {A}$
. From $\varPhi (\mathcal {X})\hookrightarrow \mathcal {A}$![]() , we obtain the basic cycle $[\mathcal {Z}]=[\mathcal {X}]^{+}-[\mathcal {X}]^{-}$
, we obtain the basic cycle $[\mathcal {Z}]=[\mathcal {X}]^{+}-[\mathcal {X}]^{-}$![]() as in § 1; see (1.1). Note that $[\mathcal {Z}]\in Z^{a-n}_{h}(\mathcal {A}/B)$
as in § 1; see (1.1). Note that $[\mathcal {Z}]\in Z^{a-n}_{h}(\mathcal {A}/B)$![]() . To the normal function defined by $\mathcal {Z}$
. To the normal function defined by $\mathcal {Z}$![]() , it is associated with its infinitesimal invariant $\delta _{\mathcal {Z}}$
, it is associated with its infinitesimal invariant $\delta _{\mathcal {Z}}$![]() ; see cf.[Reference Voisin31].
; see cf.[Reference Voisin31].
Definition 3.5 An Albanese type family $\varPhi$![]() is called Nori trivial if the infinitesimal invariant $\delta _{\mathcal {Z}}$
is called Nori trivial if the infinitesimal invariant $\delta _{\mathcal {Z}}$![]() induced by the cycle $[\mathcal {Z}]$
induced by the cycle $[\mathcal {Z}]$![]() is zero for the generic $b\in B$
is zero for the generic $b\in B$![]() (hence for all $b$
(hence for all $b$![]() ).
).
Transversality. Fix $s_{1},\,\dots,\,s_{n+1}\in H^{0}(\mathcal {A},\,\varOmega ^{1}_{\mathcal {A}_{}}\,)$![]() such that $s_{1}\wedge \dots \wedge s_{n+1}$
such that $s_{1}\wedge \dots \wedge s_{n+1}$![]() induces, by fibre restriction, a non-trivial form $\varOmega \in H^{0}(A_{b},\,\varOmega ^{1+n}_{\mathcal {A}\mid A_{b}}\,).$
induces, by fibre restriction, a non-trivial form $\varOmega \in H^{0}(A_{b},\,\varOmega ^{1+n}_{\mathcal {A}\mid A_{b}}\,).$![]() Let $\xi _b\in H^{1}(X_{b},\,T_{X_{b}})$
Let $\xi _b\in H^{1}(X_{b},\,T_{X_{b}})$![]() be an infinitesimal deformation given by the Kodaira–Spencer map. We remind the reader that, as in the previous Proposition 3.4, $\phi _b$
be an infinitesimal deformation given by the Kodaira–Spencer map. We remind the reader that, as in the previous Proposition 3.4, $\phi _b$![]() is the map $\phi _b\colon X_b\to A_b$
is the map $\phi _b\colon X_b\to A_b$![]() and we have the diagram
and we have the diagram

Let
be the restriction map and set $\eta _{i}=r(\varPhi _{b}^{\ast }(s_{i}))$![]() , $i=1,\,\ldots,\,n+1.$
, $i=1,\,\ldots,\,n+1.$![]() In our case, the set $\mathcal {B}=\{\eta _{i}\}_{i=1}^{n+1}$
In our case, the set $\mathcal {B}=\{\eta _{i}\}_{i=1}^{n+1}$![]() is a basis of a vector space $W\subset H^{0}(X_{b},\,\varOmega ^{1}_{X_b}\,)$
is a basis of a vector space $W\subset H^{0}(X_{b},\,\varOmega ^{1}_{X_b}\,)$![]() . Suppose that $W\subset {\rm {Ker}}\partial _{\xi _b}.$
. Suppose that $W\subset {\rm {Ker}}\partial _{\xi _b}.$![]() Then the element $\varPhi _{b}^{\ast }(s_{1}\wedge \dots \wedge s_{n+1})$
Then the element $\varPhi _{b}^{\ast }(s_{1}\wedge \dots \wedge s_{n+1})$![]() gives precisely an adjoint form $\omega _{_{\xi _b,W,\mathcal {B}}}$
gives precisely an adjoint form $\omega _{_{\xi _b,W,\mathcal {B}}}$![]() once it is restricted to $X_b$
once it is restricted to $X_b$![]() . In [Reference Pirola and Zucconi23, Theorem 5.2.5], it is proved:
. In [Reference Pirola and Zucconi23, Theorem 5.2.5], it is proved:
Theorem 3.6 Transversality Criteria.
If $\delta _{\mathcal {Z}}(b)=0$![]() then for every $\sigma \in H^{0}(A_{b},\,\varOmega ^{n}_{A_{b}}\,)$
then for every $\sigma \in H^{0}(A_{b},\,\varOmega ^{n}_{A_{b}}\,)$![]() it holds:
it holds:
3.4. Proof of Theorem [A]
The main tool for the proof is the Volumetric Theorem [Reference Pirola and Zucconi23, Theorem 1.5.3] that we recall here for convenience.
Theorem 3.7 Let $\varPhi \colon \mathcal {X}\to \mathcal {A}$![]() be an Albanese type family such that $p\colon \mathcal {A}\rightarrow B$
be an Albanese type family such that $p\colon \mathcal {A}\rightarrow B$![]() has fibres isomorphic to a fixed abelian variety $A$
has fibres isomorphic to a fixed abelian variety $A$![]() . Let $W\subset H^{0}(A,\,\varOmega ^{1}_{A})$
. Let $W\subset H^{0}(A,\,\varOmega ^{1}_{A})$![]() be a generic $(n+1)$
be a generic $(n+1)$![]() -dimensional subspace and $W_{b}\subset H^{0}(X_{b},\,\varOmega ^{1}_{X_{b}})$
-dimensional subspace and $W_{b}\subset H^{0}(X_{b},\,\varOmega ^{1}_{X_{b}})$![]() its pull-back over the fibre $X_{b}$
its pull-back over the fibre $X_{b}$![]() . Assume that for every point $b\in B$
. Assume that for every point $b\in B$![]() it holds that $\omega _{_{\xi _{b},\,W_{b},\, \mathcal {B}_{b}}}\in \lambda ^{n}W_{b}$
it holds that $\omega _{_{\xi _{b},\,W_{b},\, \mathcal {B}_{b}}}\in \lambda ^{n}W_{b}$![]() where $\xi _{b}\in H^{1}(X_{b},\,\varTheta _{X_{b}})$
where $\xi _{b}\in H^{1}(X_{b},\,\varTheta _{X_{b}})$![]() is the class given on $X_{b}$
is the class given on $X_{b}$![]() by $\pi \colon \mathcal {X}\to B$
by $\pi \colon \mathcal {X}\to B$![]() , then the fibres of $\pi \colon \mathcal {X}\to B$
, then the fibres of $\pi \colon \mathcal {X}\to B$![]() are birational.
are birational.
We now prove Theorem [A] of the introduction.
Proof. By Proposition, 3.4 we can assume that $p\colon \mathcal {A}\to B$![]() is trivial, that is $\mathcal {A}\simeq A\times B$
is trivial, that is $\mathcal {A}\simeq A\times B$![]() and $p\colon \mathcal {A}\to B$
and $p\colon \mathcal {A}\to B$![]() is the first projection. Up to base change, the Albanese family ${{\rm alb}}(\mathcal {X})\colon \mathcal {X}\to {{\rm Alb}}(\mathcal {X})$
is the first projection. Up to base change, the Albanese family ${{\rm alb}}(\mathcal {X})\colon \mathcal {X}\to {{\rm Alb}}(\mathcal {X})$![]() exists and by Proposition 3.2, our claim is equivalent to show that the Albanese family ${{\rm alb}} (\mathcal {X}) \colon \mathcal {X}\to {{\rm Alb}} (\mathcal {X})$
exists and by Proposition 3.2, our claim is equivalent to show that the Albanese family ${{\rm alb}} (\mathcal {X}) \colon \mathcal {X}\to {{\rm Alb}} (\mathcal {X})$![]() is locally translation equivalent to the trivial family. Hence, it is not restrictive to assume that ${{\rm Alb}}(\mathcal {X})=A\times B$
is locally translation equivalent to the trivial family. Hence, it is not restrictive to assume that ${{\rm Alb}}(\mathcal {X})=A\times B$![]() too. In particular, we can restrict to consider only the case where ${{\rm Alb}}(X_b)=A$
too. In particular, we can restrict to consider only the case where ${{\rm Alb}}(X_b)=A$![]() and the map $\phi _b\colon X_b\to A$
and the map $\phi _b\colon X_b\to A$![]() is of degree one for every $b\in B$
is of degree one for every $b\in B$![]() .
.
Denote by $\xi _b\in H^{1}(X_b,\,\varTheta _{X_b})$![]() a class associated with an infinitesimal deformation of $X_b$
a class associated with an infinitesimal deformation of $X_b$![]() induced by the fibration $\pi \colon \mathcal {X}\rightarrow B$
induced by the fibration $\pi \colon \mathcal {X}\rightarrow B$![]() . We know that $q\geq n+1$
. We know that $q\geq n+1$![]() where $q={{\rm dim}}_\mathbb {C} A$
where $q={{\rm dim}}_\mathbb {C} A$![]() . Let $\mathcal {B}:=\{dz_1,\,\ldots,\,dz_{n+1}\}$
. Let $\mathcal {B}:=\{dz_1,\,\ldots,\,dz_{n+1}\}$![]() be a basis of an $n+1$
be a basis of an $n+1$![]() -dimensional generic subspace $W$
-dimensional generic subspace $W$![]() of $H^{0}( A,\,\varOmega ^{1}_{A})$
of $H^{0}( A,\,\varOmega ^{1}_{A})$![]() , (if $q=n+1$
, (if $q=n+1$![]() we can take $H^{0}( A,\,\varOmega ^{1}_{A})=W$
we can take $H^{0}( A,\,\varOmega ^{1}_{A})=W$![]() ). For every $b\in B$
). For every $b\in B$![]() let $\eta _i(b):= {{\rm alb}}(X_b)^{*}dz_i$
let $\eta _i(b):= {{\rm alb}}(X_b)^{*}dz_i$![]() , $i=1,\,\ldots,\, n+1$
, $i=1,\,\ldots,\, n+1$![]() . By standard theory of the Albanese morphism, it holds that $\mathcal {B}_b:=\{ \eta _1(b),\,\ldots,\, \eta _{n+1}(b)\}$
. By standard theory of the Albanese morphism, it holds that $\mathcal {B}_b:=\{ \eta _1(b),\,\ldots,\, \eta _{n+1}(b)\}$![]() is a basis of the pull-back $W_{b}$
is a basis of the pull-back $W_{b}$![]() of $W$
of $W$![]() inside $H^{0}(X_b,\,\varOmega _{X_{b}}^{1})$
inside $H^{0}(X_b,\,\varOmega _{X_{b}}^{1})$![]() . Let
. Let
for $i=1,\,\ldots,\, n+1$![]() . Note that if $\omega '_i:=dz_1\wedge \ldots \wedge dz_{i-1} \wedge {\widehat {dz_i}} \wedge \ldots \wedge dz_{n+1}$
. Note that if $\omega '_i:=dz_1\wedge \ldots \wedge dz_{i-1} \wedge {\widehat {dz_i}} \wedge \ldots \wedge dz_{n+1}$![]() then $\omega _i (b):=\phi _{b}^{}\omega _i'$
then $\omega _i (b):=\phi _{b}^{}\omega _i'$![]() , $i=1,\,\ldots,\,n$
, $i=1,\,\ldots,\,n$![]() . Since $\varPhi \colon \mathcal {X}\to \mathcal {A}$
. Since $\varPhi \colon \mathcal {X}\to \mathcal {A}$![]() is a family of Albanese type, ${{\rm dim}}\lambda ^{n}W_{b}\geq 1$
is a family of Albanese type, ${{\rm dim}}\lambda ^{n}W_{b}\geq 1$![]() , (actually if $q>n+1$
, (actually if $q>n+1$![]() by [Reference Pirola and Zucconi23, Theorem 1.3.3] it follows that $\lambda ^{n}W_{b}$
by [Reference Pirola and Zucconi23, Theorem 1.3.3] it follows that $\lambda ^{n}W_{b}$![]() has dimension $n+1$
has dimension $n+1$![]() ), and we can write: $\lambda ^{n}W_{b}=\langle \omega _1(b),\,\ldots,\,\omega _{n+1}(b)\rangle$
), and we can write: $\lambda ^{n}W_{b}=\langle \omega _1(b),\,\ldots,\,\omega _{n+1}(b)\rangle$![]() .
.
By extremal liftability assumptions, we can form the Massey class for every $[W]\in \mathbb {G}(n+1,\,q)$![]() where we denote by $\mathbb {G}(n+1,\,q)$
where we denote by $\mathbb {G}(n+1,\,q)$![]() the Grassmannian of $n+1$
the Grassmannian of $n+1$![]() -dimensional subspaces of $H^{0}(X_b,\,\varOmega ^{1}_{X_b})$
-dimensional subspaces of $H^{0}(X_b,\,\varOmega ^{1}_{X_b})$![]() .
.
Consider the following diagram in Dolbeaut's cohomology:

By the identification $H^{0}(X_b,\,\phi _{b}^{*}(\varOmega ^{n}_{A})\otimes \omega _{X_b})=H^{n,0}(A)\otimes H^{n,0}(X_b)$![]() , it follows that
, it follows that
Now, we can consider the induced diagram of the symmetric part:

We set $V_b:= {{\rm Im}}\phi _b^{*}\subset H^{n,0}(X_b)$![]() . Recall the decomposition (1.4) in § 1
. Recall the decomposition (1.4) in § 1
and that this direct sum induces homomorphisms
and
Now assume that for the generic $W_b$![]() , the generic adjoint form $\omega$
, the generic adjoint form $\omega$![]() has an adjoint quadric
has an adjoint quadric

By Definition 2.6, $Q$![]() is in ${{\rm Ker}}(\mu )$
is in ${{\rm Ker}}(\mu )$![]() .
.
By the Transversality Theorem 3.6, $\omega$![]() vanishes on $\overline {V_b}$
vanishes on $\overline {V_b}$![]() , hence $\omega \odot \omega$
, hence $\omega \odot \omega$![]() is an element of ${{\rm Sym}}^{2}(\overline {\text {Ann}(V_b)})$
is an element of ${{\rm Sym}}^{2}(\overline {\text {Ann}(V_b)})$![]() . On the other hand, recall that by definition the forms $\omega _i(b)$
. On the other hand, recall that by definition the forms $\omega _i(b)$![]() are in $V$
are in $V$![]() , hence $\sum \nolimits _{i=1}^{n+1} \omega _i(b)\odot L_i$
, hence $\sum \nolimits _{i=1}^{n+1} \omega _i(b)\odot L_i$![]() is an element of $V_b\odot H^{n,0}(X_b)$
is an element of $V_b\odot H^{n,0}(X_b)$![]() . By the hypothesis that for each element $\eta$
. By the hypothesis that for each element $\eta$![]() contained in $\overline {{{\rm Ann}}(V_b)}$
contained in $\overline {{{\rm Ann}}(V_b)}$![]() , its square is not contained in the image of $\gamma _{X_b}$
, its square is not contained in the image of $\gamma _{X_b}$![]() , we get that $\omega \odot \omega =0$
, we get that $\omega \odot \omega =0$![]() . By the Volumetric Theorem 3.7, the claim follows easily.
. By the Volumetric Theorem 3.7, the claim follows easily.
Remark 3.8 We stress that the argument above is a local argument applied to the differential forms $\omega _i(b)$![]() .
.
Corollary 3.9 Let $\varPhi :\mathcal {X}\rightarrow \mathcal {A}$![]() be a family of Albanese type where the general fibre $A_{b}$
be a family of Albanese type where the general fibre $A_{b}$![]() of $p:\mathcal {A}\rightarrow B$
of $p:\mathcal {A}\rightarrow B$![]() is a generic abelian variety of dimension $a\geq 4,$
is a generic abelian variety of dimension $a\geq 4,$![]() the general fibre $X_b$
the general fibre $X_b$![]() of $\pi \colon \mathcal {X}\to B$
of $\pi \colon \mathcal {X}\to B$![]() is such that $a-{\rm {dim}}X_b>1$
is such that $a-{\rm {dim}}X_b>1$![]() , and for each element $\eta$
, and for each element $\eta$![]() contained in $\overline {{\rm {Ann}}(V_b)},$
contained in $\overline {{\rm {Ann}}(V_b)},$![]() its square is not contained in the image of $\gamma _{X_b}$
its square is not contained in the image of $\gamma _{X_b}$![]() . If it satisfies the liftability conditions then the fibres of $\pi \colon \mathcal {X}\to B$
. If it satisfies the liftability conditions then the fibres of $\pi \colon \mathcal {X}\to B$![]() are in the same birational class. In particular, the fibres of a family $\pi \colon \mathcal {X}\to B$
are in the same birational class. In particular, the fibres of a family $\pi \colon \mathcal {X}\to B$![]() of smooth varieties of general type all contained inside a fixed generic abelian variety of dimension $\geq 4$
of smooth varieties of general type all contained inside a fixed generic abelian variety of dimension $\geq 4$![]() as cycles of codimension $\geq 2$
as cycles of codimension $\geq 2$![]() are in the same birational class if $\pi \colon \mathcal {X}\to B$
are in the same birational class if $\pi \colon \mathcal {X}\to B$![]() satisfies the liftability assumptions and for each element $\eta$
satisfies the liftability assumptions and for each element $\eta$![]() contained in $\overline {{\rm {Ann}}(V_b)},$
contained in $\overline {{\rm {Ann}}(V_b)},$![]() its square is not contained in the image of $\gamma _{X_b}$
its square is not contained in the image of $\gamma _{X_b}$![]() .
.
Proof. By [Reference Pirola and Zucconi23, Proposition 6.2.2], we know that $\varPhi :\mathcal {X}\rightarrow \mathcal {A}$![]() is equivalent to a Nori trivial family. By Theorem [A], the claim follows.
is equivalent to a Nori trivial family. By Theorem [A], the claim follows.
Remark 3.10 The necessary ‘genericity conditions’ on the abelian variety $A_b$![]() of Corollary 3.9 are those which make it possible to apply the fundamental theorem which claims that the Abel–Jacobi map of a homologically trivial cycle of a generic abelian variety of dimension $\geq 4$
of Corollary 3.9 are those which make it possible to apply the fundamental theorem which claims that the Abel–Jacobi map of a homologically trivial cycle of a generic abelian variety of dimension $\geq 4$![]() is torsion modulo the largest abelian subvariety of the intermediate Jacobian; see [Reference Nori17, section 7.5] or the very clear exposition [Reference Pirola21]. Actually, we can understand that genericity here means that $A_b$
is torsion modulo the largest abelian subvariety of the intermediate Jacobian; see [Reference Nori17, section 7.5] or the very clear exposition [Reference Pirola21]. Actually, we can understand that genericity here means that $A_b$![]() is outside a countable union of proper Zariski's closed sets.
is outside a countable union of proper Zariski's closed sets.
Remark 3.11 We point out to the reader that since the Ceresa's cycle of an hyperelliptic curve $C$![]() is trivial, Theorem [A] implies that a family $\pi \colon \mathcal {C}\to B$
is trivial, Theorem [A] implies that a family $\pi \colon \mathcal {C}\to B$![]() of hyperelliptic curves satisfying liftability assumptions is a locally trivial family.
of hyperelliptic curves satisfying liftability assumptions is a locally trivial family.
4. Families of divisors of a polarized abelian variety
We cannot use Nori's theorem in the case of Albanese type families of divisors. Nevertheless a statement as the one of Theorem [A] holds also in this case. First, we review some facts on divisors of an abelian variety.
4.1. Theta functions
Let $({{A}},\, \mathcal {L})$![]() be a $(d_1 \cdots d_a)$
be a $(d_1 \cdots d_a)$![]() -polarized abelian variety, where ${{A}}$
-polarized abelian variety, where ${{A}}$![]() is a complex torus defined as a quotient of a vector space ${V}$
is a complex torus defined as a quotient of a vector space ${V}$![]() of rank $a$
of rank $a$![]() by a lattice $\varLambda$
by a lattice $\varLambda$![]() , and $\mathcal {L}$
, and $\mathcal {L}$![]() an ample line bundle on it. The algebraic equivalence class of line bundles of $\mathcal {L}$
an ample line bundle on it. The algebraic equivalence class of line bundles of $\mathcal {L}$![]() is defined by a non-degenerate hermitian bilinear form $H$
is defined by a non-degenerate hermitian bilinear form $H$![]() on ${V}$
on ${V}$![]() , whose imaginary part $E$
, whose imaginary part $E$![]() is a bilinear form integer-valued on $\varLambda$
is a bilinear form integer-valued on $\varLambda$![]() . Since we are interested in the algebraic equivalence class of line bundles on ${{A}}$
. Since we are interested in the algebraic equivalence class of line bundles on ${{A}}$![]() defined by $\mathcal {L}$
defined by $\mathcal {L}$![]() , we may assume the characteristic of $\mathcal {L}$
, we may assume the characteristic of $\mathcal {L}$![]() to be $0$
to be $0$![]() . We also recall that $\mathcal {L}$
. We also recall that $\mathcal {L}$![]() determines an isogeny
determines an isogeny
which is defined as follows:
A decomposition of $V$![]() for $\mathcal {L}$
for $\mathcal {L}$![]() is a decomposition of ${V} = {V}_1 \oplus {V}_2$
is a decomposition of ${V} = {V}_1 \oplus {V}_2$![]() into real vector spaces of rank $a$
into real vector spaces of rank $a$![]() which induces a decomposition for $\varLambda = \varLambda _1 \oplus \varLambda _2$
which induces a decomposition for $\varLambda = \varLambda _1 \oplus \varLambda _2$![]() into $E$
into $E$![]() -isotropic free $\mathbb {Z}$
-isotropic free $\mathbb {Z}$![]() -modules of rank $a$
-modules of rank $a$![]() . Such a decomposition of $V$
. Such a decomposition of $V$![]() for $\mathcal {L}$
for $\mathcal {L}$![]() induces moreover a decomposition of the lattice
induces moreover a decomposition of the lattice
into $E$![]() -isotropic free $\mathbb {Z}$
-isotropic free $\mathbb {Z}$![]() -modules of rank $a$
-modules of rank $a$![]() , which we, respectively, denote by $\varLambda (\mathcal {L})_1$
, which we, respectively, denote by $\varLambda (\mathcal {L})_1$![]() and $\varLambda (\mathcal {L})_2$
and $\varLambda (\mathcal {L})_2$![]() . The latter decomposition naturally induces a decomposition of the kernel of $\phi _{\mathcal {L}}$
. The latter decomposition naturally induces a decomposition of the kernel of $\phi _{\mathcal {L}}$![]() , which we denote by $K$
, which we denote by $K$![]() . It is known, see cf. [Reference Birkenhake and Lange3, Theorem 2.7 p.55], that
. It is known, see cf. [Reference Birkenhake and Lange3, Theorem 2.7 p.55], that
is a basis for $H^{0}({{A}},\, \mathcal {L})$![]() , where
, where
Here $B$![]() denotes the $\mathbb {C}$
denotes the $\mathbb {C}$![]() -linear extension of $H|_{{V}_2 \times {V}_2}$
-linear extension of $H|_{{V}_2 \times {V}_2}$![]() , and for every $x$
, and for every $x$![]() in $K_1$
in $K_1$![]()
where $\{\psi _{\lambda }\}_{\lambda }$![]() is the cocycle in $Z^{1}(\varLambda,\, \mathcal {O}_{{V}})$
is the cocycle in $Z^{1}(\varLambda,\, \mathcal {O}_{{V}})$![]() such that, for every $\lambda$
such that, for every $\lambda$![]() in the lattice $\varLambda$
in the lattice $\varLambda$![]() and $z$
and $z$![]() in ${V}$
in ${V}$![]() , we have
, we have
Proposition 4.1 Let $({{A}},\, \mathcal {L})$![]() be an abelian variety, and $\mathcal {D}$
be an abelian variety, and $\mathcal {D}$![]() be a divisor in the linear system $|\mathcal {L}|$
be a divisor in the linear system $|\mathcal {L}|$![]() . Then there is a commutative diagram
. Then there is a commutative diagram

where the arrow on the right side of diagram
4.3 is the connecting homomorphism in the long exact cohomology sequence of the fundamental sequence of $\mathcal {D}$![]()
Proof. We assume that $\mathcal {D}$![]() is the zero locus of a holomorphic section $s$
is the zero locus of a holomorphic section $s$![]() of $\mathcal {L}$
of $\mathcal {L}$![]() . The complex space $V$
. The complex space $V$![]() can be naturally identified with the space of holomorphic vector fields $\varTheta _{{{A}}}$
can be naturally identified with the space of holomorphic vector fields $\varTheta _{{{A}}}$![]() on ${{A}}$
on ${{A}}$![]() . Fixed $\omega$
. Fixed $\omega$![]() a non-zero $(a,\,0)$
a non-zero $(a,\,0)$![]() -form on ${{A}}$
-form on ${{A}}$![]() , recall that the map
, recall that the map
sends under this identification a vector $v$![]() of $V$
of $V$![]() to the holomorphic $(a-1)$
to the holomorphic $(a-1)$![]() -form $w$
-form $w$![]() obtained by contracting the $(a,\,0)$
obtained by contracting the $(a,\,0)$![]() -form $\omega$
-form $\omega$![]() with the vector field $\frac {\partial }{\partial v}$
with the vector field $\frac {\partial }{\partial v}$![]() .
.
The holomorphic function $\frac {\partial s}{\partial v}$![]() can be seen by adjunction as a holomorphic section of the canonical bundle of $\mathcal {D}$
can be seen by adjunction as a holomorphic section of the canonical bundle of $\mathcal {D}$![]() , which coincides with the restriction to $\mathcal {D}$
, which coincides with the restriction to $\mathcal {D}$![]() of the $(a-1)$
of the $(a-1)$![]() -form $w$
-form $w$![]() defined above. On the other side, the connecting homomorphism can be computed by using the fact that there is a canonical isomorphism of cohomology groups sequences
defined above. On the other side, the connecting homomorphism can be computed by using the fact that there is a canonical isomorphism of cohomology groups sequences
where $\pi$![]() denotes the projection of ${V}$
denotes the projection of ${V}$![]() onto ${{A}}$
onto ${{A}}$![]() , and it holds (see also: [Reference Cesarano6] Proposition 1.1, p. 4):
, and it holds (see also: [Reference Cesarano6] Proposition 1.1, p. 4):
It remains to compute $d_0\phi _{\mathcal {L}}(\tfrac {\partial }{\partial v} )$![]() . Let us consider $S := Spec(\mathbb {C}[\epsilon]/{\epsilon^{2}})$
. Let us consider $S := Spec(\mathbb {C}[\epsilon]/{\epsilon^{2}})$![]() the scheme of dual numbers over $\mathbb {C}$
the scheme of dual numbers over $\mathbb {C}$![]() and ${{A}}_S$
and ${{A}}_S$![]() the base change. We have the exact sequence of sheaves
the base change. We have the exact sequence of sheaves
Its long cohomology sequence identifies $H^{1}({{A}},\, \mathcal {O}_{{{A}}})$![]() with the kernel of the map ${{\rm Pic}}({{A}}_S) \longrightarrow {{\rm Pic}}({{A}})$
with the kernel of the map ${{\rm Pic}}({{A}}_S) \longrightarrow {{\rm Pic}}({{A}})$![]() , which to a line bundle on ${{A}}_S$
, which to a line bundle on ${{A}}_S$![]() whose transition functions $g_{\alpha \beta }=g'_{\alpha \beta } + \epsilon g''_{\alpha \beta }$
whose transition functions $g_{\alpha \beta }=g'_{\alpha \beta } + \epsilon g''_{\alpha \beta }$![]() associates the line bundle on ${{A}}$
associates the line bundle on ${{A}}$![]() with transition functions $g'_{\alpha \beta }$
with transition functions $g'_{\alpha \beta }$![]() . Moreover, under the identification $H^{1}({{A}},\, \mathcal {O}_{{{A}}}^{*}) \cong H^{1}(\varLambda,\, H^{0}({V},\, \mathcal {O}_{{V}}^{*}))$
. Moreover, under the identification $H^{1}({{A}},\, \mathcal {O}_{{{A}}}^{*}) \cong H^{1}(\varLambda,\, H^{0}({V},\, \mathcal {O}_{{V}}^{*}))$![]()
since ${{A}}_S$![]() is defined through a flat base change. Now, for every $z$
is defined through a flat base change. Now, for every $z$![]() on $A$
on $A$![]() , $\phi _{\mathcal {L}}(z)$
, $\phi _{\mathcal {L}}(z)$![]() is the line bundle of degree $0$
is the line bundle of degree $0$![]() with cocycles $[\{e^{2 \pi i E(z, \lambda )}\}_{\lambda }]$
with cocycles $[\{e^{2 \pi i E(z, \lambda )}\}_{\lambda }]$![]() . Hence, $d_0\phi _{\mathcal {L}}(\tfrac {\partial }{\partial v} )$
. Hence, $d_0\phi _{\mathcal {L}}(\tfrac {\partial }{\partial v} )$![]() is the line bundle on ${{A}}_S$
is the line bundle on ${{A}}_S$![]() whose cocycles, according to identification 4.7, are precisely
whose cocycles, according to identification 4.7, are precisely
In conclusion, we have
It is now easy to see that the two elements in the cohomology group $H^{1}(\varLambda,\, H^{0}({V},\,\mathcal {O}_{{V}}^{*}))$![]() are the same. Indeed, it is enough to show, by the definitions of group cohomology, that there exists a holomorphic function $F$
are the same. Indeed, it is enough to show, by the definitions of group cohomology, that there exists a holomorphic function $F$![]() on $V$
on $V$![]() such that, for every $z$
such that, for every $z$![]() on $V$
on $V$![]() and every $\lambda$
and every $\lambda$![]() on $\varLambda$
on $\varLambda$![]() , it holds that
, it holds that
But $E$![]() is defined as the imaginary part of $H$
is defined as the imaginary part of $H$![]() , which is an alternating $\mathbb {R}$
, which is an alternating $\mathbb {R}$![]() -bilinear form on ${V}$
-bilinear form on ${V}$![]() , and $H$
, and $H$![]() can be recovered by $E$
can be recovered by $E$![]() . Indeed, for every $z$
. Indeed, for every $z$![]() and $w$
and $w$![]() on ${V}$
on ${V}$![]() it holds:
it holds:
In conclusion, with $F(z) := -\pi (i E(v,\,z) - E(iv,\, z))$![]() , it is easily seen that $F$
, it is easily seen that $F$![]() is $\mathbb {C}$
is $\mathbb {C}$![]() -linear on ${V}$
-linear on ${V}$![]() and that 4.9 holds true.
and that 4.9 holds true.
4.2. The multiplication map
From diagram (4.3) and the long cohomology sequence of (4.4), it follows easily that

Moreover, we have clearly a commutative diagram

Note that ${\rm {Sym}}^{2}{H^{0}({{A}},\, \mathcal {L})}\cong s^{\otimes 2}\mathbb {C}\oplus s\otimes {\overline {\text {Ann}(V)}} \oplus {\rm {Sym}}^{2}{\overline {\text {Ann}(V)}}$![]() . In particular, when the divisor $\mathcal {D}= (s=0)$
. In particular, when the divisor $\mathcal {D}= (s=0)$![]() is reduced and irreducible, the map $\nu$
is reduced and irreducible, the map $\nu$![]() is injective if and only if the multiplication map $\mu$
is injective if and only if the multiplication map $\mu$![]() is injective. Indeed if $\mu$
is injective. Indeed if $\mu$![]() is not injective, then there exists a non-zero element $w = s \otimes t + \sum \nolimits _{j} u_j \otimes v_j$
is not injective, then there exists a non-zero element $w = s \otimes t + \sum \nolimits _{j} u_j \otimes v_j$![]() in ${\rm {Sym}}^{2}{H^{0}({{A}},\, \mathcal {L})}$
in ${\rm {Sym}}^{2}{H^{0}({{A}},\, \mathcal {L})}$![]() in the kernel of the multiplication map $\mu$
in the kernel of the multiplication map $\mu$![]() , and by the above decomposition, we can assume $(\sum \nolimits _{j} u_j \otimes v_j)_{|\mathcal {D}}\neq 0$
, and by the above decomposition, we can assume $(\sum \nolimits _{j} u_j \otimes v_j)_{|\mathcal {D}}\neq 0$![]() in ${\rm {Sym}}^{2}{\overline {\text {Ann}(V)}}$
in ${\rm {Sym}}^{2}{\overline {\text {Ann}(V)}}$![]() . Since the diagram (4.11) is commutative, this implies $\nu (\sum \nolimits _{j} u_j \otimes v_j)_{|\mathcal {D}}=0$
. Since the diagram (4.11) is commutative, this implies $\nu (\sum \nolimits _{j} u_j \otimes v_j)_{|\mathcal {D}}=0$![]() , and thus, $\nu$
, and thus, $\nu$![]() is not injective. On the other side, let us assume that $\sum \nolimits _{j} u_j|_{\mathcal {D}} \otimes v_j|_{\mathcal {D}}$
is not injective. On the other side, let us assume that $\sum \nolimits _{j} u_j|_{\mathcal {D}} \otimes v_j|_{\mathcal {D}}$![]() is non-zero and belong to the kernel of $\nu$
is non-zero and belong to the kernel of $\nu$![]() , where $u_j$
, where $u_j$![]() and $v_j$
and $v_j$![]() are non-zero holomorphic sections of $\mathcal {L}$
are non-zero holomorphic sections of $\mathcal {L}$![]() . Then we have that $\mu (\sum \nolimits _{j} u_j\otimes v_j) = \sum \nolimits _j u_jv_j$
. Then we have that $\mu (\sum \nolimits _{j} u_j\otimes v_j) = \sum \nolimits _j u_jv_j$![]() vanishes along $\mathcal {D}$
vanishes along $\mathcal {D}$![]() . Hence, there exists $t \in H^{0}({{A}},\, \mathcal {L})$
. Hence, there exists $t \in H^{0}({{A}},\, \mathcal {L})$![]() such that $st=\sum \nolimits _j u_jv_j$
such that $st=\sum \nolimits _j u_jv_j$![]() . It follows that $\mu$
. It follows that $\mu$![]() is not injective.
is not injective.
4.3. On the injectivity of the multiplication map
Given now an abelian variety $(A,\, \mathcal {L})$![]() , we want to give conditions which ensure the injectivity of the multiplication map $\mu$
, we want to give conditions which ensure the injectivity of the multiplication map $\mu$![]() . We begin by fixing a decomposition of ${V}$
. We begin by fixing a decomposition of ${V}$![]() for $\mathcal {L}^{2}$
for $\mathcal {L}^{2}$![]() which, according to our previous discussion, induces a decomposition $K_1 \oplus K_2$
which, according to our previous discussion, induces a decomposition $K_1 \oplus K_2$![]() of $K:=Ker(\phi _{\mathcal {L}^{2}})$
of $K:=Ker(\phi _{\mathcal {L}^{2}})$![]() . In particular, the same decomposition induces a decomposition $2K_1 \oplus 2K_2$
. In particular, the same decomposition induces a decomposition $2K_1 \oplus 2K_2$![]() for the kernel of $\phi _{\mathcal {L}}$
for the kernel of $\phi _{\mathcal {L}}$![]() .
.
Let us assume that $H$![]() is the non-degenerate hermitian form which corresponds to $\mathcal {L}$
is the non-degenerate hermitian form which corresponds to $\mathcal {L}$![]() according to Appell–Humbert theorem. We recall that, by [Reference Birkenhake and Lange3, Lemma 1.2 p. 48], $K(\mathcal {L}) = {\varLambda(\mathcal{L})}/{\varLambda}$
according to Appell–Humbert theorem. We recall that, by [Reference Birkenhake and Lange3, Lemma 1.2 p. 48], $K(\mathcal {L}) = {\varLambda(\mathcal{L})}/{\varLambda}$![]() and $K(\mathcal {L}^{2}) = {\varLambda (\mathcal {L}^{2})}/{\varLambda}$
and $K(\mathcal {L}^{2}) = {\varLambda (\mathcal {L}^{2})}/{\varLambda}$![]() , where
, where

are lattices in ${V}$![]() , and $K(\mathcal {L})_i \cong \mathbb {Z}_{d_1} \oplus \cdots \cdots \mathbb {Z}_{d_a}$
, and $K(\mathcal {L})_i \cong \mathbb {Z}_{d_1} \oplus \cdots \cdots \mathbb {Z}_{d_a}$![]() ($i=1,\,2$
($i=1,\,2$![]() ), where $(d_1 \cdots d_a)$
), where $(d_1 \cdots d_a)$![]() is the polarization type of $\mathcal {L}$
is the polarization type of $\mathcal {L}$![]() ; see [Reference Birkenhake and Lange3, Lemma 1.4 p. 50].
; see [Reference Birkenhake and Lange3, Lemma 1.4 p. 50].
Moreover, $\varLambda (\mathcal {L}^{2})$![]() contains the sublattice $\varLambda (\mathcal {L})$
contains the sublattice $\varLambda (\mathcal {L})$![]() , and the quotient is isomorphic to $\mathbb {Z}_2^{2a}$
, and the quotient is isomorphic to $\mathbb {Z}_2^{2a}$![]() , with $2\varLambda (\mathcal {L}^{2}) = \varLambda (\mathcal {L})$
, with $2\varLambda (\mathcal {L}^{2}) = \varLambda (\mathcal {L})$![]() . On the other side, $K(\mathcal {L}^{2})_i \cong \mathbb {Z}_{2d_1} \oplus \cdots \cdots \mathbb {Z}_{2d_a}$
. On the other side, $K(\mathcal {L}^{2})_i \cong \mathbb {Z}_{2d_1} \oplus \cdots \cdots \mathbb {Z}_{2d_a}$![]() it contains $K(\mathcal {L})_i$
it contains $K(\mathcal {L})_i$![]() , and the quotient is isomorphic to $\mathbb {Z}_2^{a}$
, and the quotient is isomorphic to $\mathbb {Z}_2^{a}$![]() .
.
Hence, the following is a basis for $H^{0}({{A}},\, \mathcal {L})$![]() :
:
Let us denote by $Z_2:={{A}}[2] \cap K_1 \cong \mathbb {Z}_2^{a}$![]() . For every $(x_1,\, x_2) \in 2K_1 \oplus 2K_1$
. For every $(x_1,\, x_2) \in 2K_1 \oplus 2K_1$![]() , and $(y_1,\, y_2) \in K_1 \oplus K_1$
, and $(y_1,\, y_2) \in K_1 \oplus K_1$![]() such that $y_1 + y_2 = x_1$
such that $y_1 + y_2 = x_1$![]() and $y_1 - y_2 = x_2$
and $y_1 - y_2 = x_2$![]() , it holds the following multiplication formula cf. [Reference Birkenhake and Lange3, 1.3 Multiplication Formula, p. 182]:
, it holds the following multiplication formula cf. [Reference Birkenhake and Lange3, 1.3 Multiplication Formula, p. 182]:
Let us denote $Z_2':=Z_2 \cap 2K_1 \cong \mathbb {Z}_2^{a-s}$![]() , where $s$
, where $s$![]() is the number of odd indexes among $(d_1 \cdots d_a)$
is the number of odd indexes among $(d_1 \cdots d_a)$![]() . For a character $\rho \colon Z_2' \to \mathbb {C}^{*}$
. For a character $\rho \colon Z_2' \to \mathbb {C}^{*}$![]() of $Z_2'$
of $Z_2'$![]() we can define:
we can define:
This is an element of $H^{0}({{A}},\,\mathcal {L})\otimes H^{0}({{A}},\,\mathcal {L})$![]() . We point out to the reader that the diagonal action of $Z_2'$
. We point out to the reader that the diagonal action of $Z_2'$![]() on $2K_2 \times 2K_2$
on $2K_2 \times 2K_2$![]() leaves every holomorphic section in 4.13 invariant up to the multiplication by a non-zero constant, since
leaves every holomorphic section in 4.13 invariant up to the multiplication by a non-zero constant, since
Hence, we have the following basis for the vector space $H^{0}({{A}},\, \mathcal {L}) \otimes H^{0}({{A}},\, \mathcal {L})$![]() :
:
where $\Delta _{Z_2'}$![]() denotes the diagonal subgroup of $Z_2' \times Z_2' \subseteq 2K_1 \oplus 2K_1$
denotes the diagonal subgroup of $Z_2' \times Z_2' \subseteq 2K_1 \oplus 2K_1$![]() .
.
We can now choose a complement $W$![]() of $Z_2'$
of $Z_2'$![]() in $Z_2$
in $Z_2$![]() ; that is $Z_2=Z_2'\oplus W$
; that is $Z_2=Z_2'\oplus W$![]() as $\mathbb {Z}_2$
as $\mathbb {Z}_2$![]() -vector spaces. Now choose $U$
-vector spaces. Now choose $U$![]() a transversal subset for $Z_2$
a transversal subset for $Z_2$![]() in $K_1$
in $K_1$![]() , that is $U$
, that is $U$![]() is a subset of $K_1$
is a subset of $K_1$![]() such that every (right or left) coset of $Z_2$
such that every (right or left) coset of $Z_2$![]() contains precisely one element of $U$
contains precisely one element of $U$![]() . Thus, the set $U$
. Thus, the set $U$![]() contains $\prod _{i=j}^{a} d_j$
contains $\prod _{i=j}^{a} d_j$![]() elements and the quotient $2K_1/Z_2'$
elements and the quotient $2K_1/Z_2'$![]() contains $\prod _{i=j}^{a} d_j/2^{a-s}$
contains $\prod _{i=j}^{a} d_j/2^{a-s}$![]() elements.
elements.
By means of this choice, we can fix the following basis for $H^{0}({{A}},\, \mathcal {L}^{2})$![]() :
:
where
We aim to express the multiplication map $\mu$![]() with respect to the basis (4.14) and (4.15). We have:
with respect to the basis (4.14) and (4.15). We have:

where, in the third equality, we decompose the summation variable by using the complement $W$![]() . If in the last summation above, we replace $z$
. If in the last summation above, we replace $z$![]() by $z'+z$
by $z'+z$![]() , we get an expression of the multiplication map in terms of the elements of the canonical basis for the vector space $H^{0}({{A}},\, \mathcal {L}^{2})$
, we get an expression of the multiplication map in terms of the elements of the canonical basis for the vector space $H^{0}({{A}},\, \mathcal {L}^{2})$![]() :
:

where we set:
where $w \in W$![]() and $t \in K_1$
and $t \in K_1$![]() . We consider moreover the following set:
. We consider moreover the following set:
Let us consider the function ![]() , which sends $(y,\,t)$
, which sends $(y,\,t)$![]() to $(y+t,\, y-t)$
to $(y+t,\, y-t)$![]() . We now show that $\psi$
. We now show that $\psi$![]() is a bijection.
is a bijection.
Indeed let $\overline {(u,\,v)}$![]() be a pair in the quotient ${2K_1 \times 2K_1}/{\Delta _{Z_2'}}$
be a pair in the quotient ${2K_1 \times 2K_1}/{\Delta _{Z_2'}}$![]() . We show that there exists a unique element $y$
. We show that there exists a unique element $y$![]() of the transversal $U$
of the transversal $U$![]() and a unique class $\overline {t}$
and a unique class $\overline {t}$![]() in the quotient group ${K_1}/{Z_2'}$
in the quotient group ${K_1}/{Z_2'}$![]() such that $\overline {(y + t,\, y - t)} = \overline {(u,\, v)}$
such that $\overline {(y + t,\, y - t)} = \overline {(u,\, v)}$![]() .
.
The sum $u+v$![]() belongs to $2K_1$
belongs to $2K_1$![]() . Thus, $u + v = 2r$
. Thus, $u + v = 2r$![]() for a certain $r$
for a certain $r$![]() of $K_1$
of $K_1$![]() . However, $r$
. However, $r$![]() belongs to a unique coset of the form $y + Z_2$
belongs to a unique coset of the form $y + Z_2$![]() with $y$
with $y$![]() in $U$
in $U$![]() . Thus, $y$
. Thus, $y$![]() is uniquely determined, and it holds that $u+v = 2y$
is uniquely determined, and it holds that $u+v = 2y$![]() . By the same procedure, we determine a $t$
. By the same procedure, we determine a $t$![]() of $K_1$
of $K_1$![]() such that $u-v = 2t$
such that $u-v = 2t$![]() . Note that $t$
. Note that $t$![]() is unique up to a $2$
is unique up to a $2$![]() -torsion in $2K_1$
-torsion in $2K_1$![]() , since both $u$
, since both $u$![]() and $v$
and $v$![]() belong to $2K_1$
belong to $2K_1$![]() . Hence, we have:
. Hence, we have:

In particular there exist two $2$![]() -torsion elements of $Z_2'$
-torsion elements of $Z_2'$![]() , $p$
, $p$![]() and $q$
and $q$![]() , in such that:
, in such that:

Since $u + v = 2y$![]() , we conclude that $p = q$
, we conclude that $p = q$![]() and our claim that the elements $\overline {(y + t,\, y - t)}$
and our claim that the elements $\overline {(y + t,\, y - t)}$![]() and $\overline {(u,\, v)}$
and $\overline {(u,\, v)}$![]() coincide is proved. We conclude that:
coincide is proved. We conclude that:
It can be easily seen that the matrix of multiplication map $\mu$![]() with respect to the basis (4.14) and (4.15) splits into blocks, each for every character $\rho$
with respect to the basis (4.14) and (4.15) splits into blocks, each for every character $\rho$![]() inside the group of characters $\widehat {Z_2'}$
inside the group of characters $\widehat {Z_2'}$![]() . Moreover, the multiplication map is injective if and only if the restriction to the subspaces associated with the characters $\rho$
. Moreover, the multiplication map is injective if and only if the restriction to the subspaces associated with the characters $\rho$![]() of $Z_2'$
of $Z_2'$![]() is injective. We can denote the latter subspaces as follows:
is injective. We can denote the latter subspaces as follows:

and the restrictions, respectively, by
We point out to the reader that even if we exchange $x_1$![]() and $x_2$
and $x_2$![]() in definition (4.13), we get the same element inside the image of the projection $H^{0}({{A}},\, \mathcal {L})\otimes H^{0}({{A}},\, \mathcal {L})\to \text {Sym}^{2}(H^{0}({{A}},\, \mathcal {L}))$
in definition (4.13), we get the same element inside the image of the projection $H^{0}({{A}},\, \mathcal {L})\otimes H^{0}({{A}},\, \mathcal {L})\to \text {Sym}^{2}(H^{0}({{A}},\, \mathcal {L}))$![]() and this exchange is induced by the change $t\mapsto -t$
and this exchange is induced by the change $t\mapsto -t$![]() . Hence, the restriction of the multiplication map on the symmetric part $\text {Sym}(H^{0}({{A}},\, \mathcal {L}))$
. Hence, the restriction of the multiplication map on the symmetric part $\text {Sym}(H^{0}({{A}},\, \mathcal {L}))$![]() can be described on the different blocks, each corresponding to $y$
can be described on the different blocks, each corresponding to $y$![]() and $\rho$
and $\rho$![]() , with the matrix:
, with the matrix:
where the sign can be arbitrarily chosen, since the obtained element of $\text {Sym}^{2}(H^{0}({{A}},\, \mathcal {L}))$![]() obtained is independent from this choice.
obtained is independent from this choice.
Remark 4.2 The theorem below describes the loci in the moduli space of polarized abelian varieties where the multiplication map is not injective. Indeed $\mu$![]() is injective precisely when for every $y$
is injective precisely when for every $y$![]() and for every character $\rho$
and for every character $\rho$![]() the matrix $M_{\rho }$
the matrix $M_{\rho }$![]() has maximal rank.
has maximal rank.
Theorem 4.3 Let $(A,\, \mathcal {L})$![]() be a general $(1,\, 1,\, \cdots,\, 2,\, \cdots 2)$
be a general $(1,\, 1,\, \cdots,\, 2,\, \cdots 2)$![]() -polarized abelian variety of dimension $a$
-polarized abelian variety of dimension $a$![]() . Then the multiplication map $\mu$
. Then the multiplication map $\mu$![]() is injective.
is injective.
Proof. Let us begin by the case in which the polarization type is $(2,\,\cdots 2)$![]() . For such a polarization, the matrix $M_{\rho }$
. For such a polarization, the matrix $M_{\rho }$![]() in 4.18 with $\rho \in Hom(\mathbb {Z}_2^{g},\, \mathbb {C}^{*})$
in 4.18 with $\rho \in Hom(\mathbb {Z}_2^{g},\, \mathbb {C}^{*})$![]() is just the scalar:
is just the scalar:
Now inside the moduli space of $(2,\,2,\, \cdots 2)$![]() -polarized abelian variety it is easy to conclude that $C_{\rho } \neq 0$
-polarized abelian variety it is easy to conclude that $C_{\rho } \neq 0$![]() holds for the general abelian variety since it holds for the product of $2$
holds for the general abelian variety since it holds for the product of $2$![]() -polarized elliptic curves. If we now take a general $(1,\,1,\,\cdots 1,\, 2,\, \cdots 2)$
-polarized elliptic curves. If we now take a general $(1,\,1,\,\cdots 1,\, 2,\, \cdots 2)$![]() -polarization we can consider $(A',\, \mathcal {L}')$
-polarization we can consider $(A',\, \mathcal {L}')$![]() a $(2,\,\cdots,\,2)$
a $(2,\,\cdots,\,2)$![]() -polarized abelian variety with an isogeny $h \colon A' \longrightarrow A$
-polarized abelian variety with an isogeny $h \colon A' \longrightarrow A$![]() such that $h^{*}\mathcal {L} = \mathcal {L}'$
such that $h^{*}\mathcal {L} = \mathcal {L}'$![]() . Then the multiplication map $\mu$
. Then the multiplication map $\mu$![]() on the sections of $\mathcal {L}$
on the sections of $\mathcal {L}$![]() is just the restriction of the multiplication map
is just the restriction of the multiplication map
to the symmetric product of the subvector space of the $Ker(h)$![]() -invariant sections of $\mathcal {L}'$
-invariant sections of $\mathcal {L}'$![]() .
.
Corollary 4.4 Let $(A,\,\mathcal {L})$![]() be as above and $\mathcal {D}$
be as above and $\mathcal {D}$![]() a general element in $|\mathcal {L}|$
a general element in $|\mathcal {L}|$![]() . The natural map
. The natural map
is injective.
Proof. This follows immediately by the above theorem and Diagram (4.11).
4.4. The divisorial case
The following theorem, together with Corollary 4.4, is Theorem [C] from § 1.
Theorem 4.5 Let $\mathcal {D}$![]() be a general divisor on a general $(1,\,1,\, \cdots,\, 1,\, 2,\, \cdots,\, 2)$
be a general divisor on a general $(1,\,1,\, \cdots,\, 1,\, 2,\, \cdots,\, 2)$![]() -polarized abelian variety of dimension $a$
-polarized abelian variety of dimension $a$![]() . Then for each element $\eta$
. Then for each element $\eta$![]() contained in $\overline {{\rm {Ann}}(V)}$
contained in $\overline {{\rm {Ann}}(V)}$![]() , its square is not contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$
, its square is not contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$![]() with respect to the multiplication map
with respect to the multiplication map
Proof. As in the proof of Theorem 4.3, it is enough to work on $(2,\,\dots,\,2)$![]() -polarizations. First, we prove that the locus in the moduli space of polarized abelian varieties $({{A}},\, \mathcal {D})$
-polarizations. First, we prove that the locus in the moduli space of polarized abelian varieties $({{A}},\, \mathcal {D})$![]() such that there is no element $\eta$
such that there is no element $\eta$![]() in $\overline {{{\rm Ann}}(V)} \cong H^{0}({{A}},\, \mathcal {D})$
in $\overline {{{\rm Ann}}(V)} \cong H^{0}({{A}},\, \mathcal {D})$![]() whose square is contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$
whose square is contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$![]() is open.
is open.
Indeed, the moduli space $U$![]() of smooth divisors in the polarization of an $a$
of smooth divisors in the polarization of an $a$![]() -dimensional $(2,\, \cdots,\,2)$
-dimensional $(2,\, \cdots,\,2)$![]() -polarized abelian variety is an open subset of a $\mathbb {P}^{d - 1}$
-polarized abelian variety is an open subset of a $\mathbb {P}^{d - 1}$![]() -bundle on the moduli space $\mathcal {A}_a$
-bundle on the moduli space $\mathcal {A}_a$![]() of $(2,\, \cdots,\,2)$
of $(2,\, \cdots,\,2)$![]() -polarized abelian varieties of dimension $a$
-polarized abelian varieties of dimension $a$![]() , where $d = 2^{a}$
, where $d = 2^{a}$![]() . Note that $U$
. Note that $U$![]() is a smooth Kuranishi family, in fact
is a smooth Kuranishi family, in fact
and for every element $[{{A}},\,\mathcal {D}]$![]() of $U$
of $U$![]() , it is known that
, it is known that

Now for every element $[{{A}},\,\mathcal {D}]$![]() of $U$
of $U$![]() , the canonical bundle of $\mathcal {D}$
, the canonical bundle of $\mathcal {D}$![]() is very ample and we can choose uniformizing coordinates $[X_1,\, \cdots,\, X_a,\, Y_0,\, Y_1,\, \cdots,\,Y_{d-1}]$
is very ample and we can choose uniformizing coordinates $[X_1,\, \cdots,\, X_a,\, Y_0,\, Y_1,\, \cdots,\,Y_{d-1}]$![]() on $\mathbb {P}^{N} \cong \mathbb {P}(H^{0}(\mathcal {D},\, \omega _{\mathcal {D}}))$
on $\mathbb {P}^{N} \cong \mathbb {P}(H^{0}(\mathcal {D},\, \omega _{\mathcal {D}}))$![]() , where $N = d + a$
, where $N = d + a$![]() . Let $H$
. Let $H$![]() be the Hilbert scheme of closed subvarieties of $\mathbb {P}^{N}$
be the Hilbert scheme of closed subvarieties of $\mathbb {P}^{N}$![]() with Hilbert polynomial $p(n) = (2n)^{a} - (2n-1)^{a}$
with Hilbert polynomial $p(n) = (2n)^{a} - (2n-1)^{a}$![]() . The natural morphism of schemes $\phi \colon U\to H$
. The natural morphism of schemes $\phi \colon U\to H$![]() is smooth and finite onto a locally closed subscheme $Z\subset H$
is smooth and finite onto a locally closed subscheme $Z\subset H$![]() by (4.22).
by (4.22).
The decomposition of $H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$![]() for every divisor $\mathcal {D}$
for every divisor $\mathcal {D}$![]() into the direct sum $V \oplus \overline {{{\rm Ann}}(V)}$
into the direct sum $V \oplus \overline {{{\rm Ann}}(V)}$![]() induces a decomposition $\mathbb {P}^{N} = \mathbb {P}(V' \oplus W')$
induces a decomposition $\mathbb {P}^{N} = \mathbb {P}(V' \oplus W')$![]() , where $V$
, where $V$![]() is generated by the forms $X_1 \cdots X_a$
is generated by the forms $X_1 \cdots X_a$![]() , and $W$
, and $W$![]() by the remaining forms $Y_0 \cdots Y_{d-1}$
by the remaining forms $Y_0 \cdots Y_{d-1}$![]() .
.
The set $Q$![]() of points of $Z$
of points of $Z$![]() which are contained in a quadric of the form $w^{2} - \sum \nolimits _{i} v_i z_i$
which are contained in a quadric of the form $w^{2} - \sum \nolimits _{i} v_i z_i$![]() in $H^{0}(\mathbb {P}^{N},\, \mathcal {O}_{\mathbb {P}}(2))$
in $H^{0}(\mathbb {P}^{N},\, \mathcal {O}_{\mathbb {P}}(2))$![]() , where $w \in W'$
, where $w \in W'$![]() and the elements $v_i$
and the elements $v_i$![]() are forms of $V'$
are forms of $V'$![]() not all equal to $0$
not all equal to $0$![]() , is a proper locally closed subset of $Z$
, is a proper locally closed subset of $Z$![]() . Since $\phi$
. Since $\phi$![]() is flat, the scheme theoretic counterimage of $Q$
is flat, the scheme theoretic counterimage of $Q$![]() is also a proper locally closed subset of $U$
is also a proper locally closed subset of $U$![]() .
.
We have shown that the locus in the moduli space of polarized abelian varieties $({{A}},\, \mathcal {D})$![]() such that there is no element $\eta$
such that there is no element $\eta$![]() in $\overline {{{\rm Ann}}(V)} \cong H^{0}({{A}},\, \mathcal {D})$
in $\overline {{{\rm Ann}}(V)} \cong H^{0}({{A}},\, \mathcal {D})$![]() whose square is contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$
whose square is contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$![]() is open. Therefore, it suffices to prove that the claim of the Theorem holds true in the case of a smooth divisor $\mathcal {D}$
is open. Therefore, it suffices to prove that the claim of the Theorem holds true in the case of a smooth divisor $\mathcal {D}$![]() in a product of $a$
in a product of $a$![]() $(2)$
$(2)$![]() -polarized elliptic curves.
-polarized elliptic curves.
To this purpose, we denote by $A$![]() the product of $E_1,\, \cdots,\, E_a$
the product of $E_1,\, \cdots,\, E_a$![]() elliptic curves, each of them considered as the quotient of the complex plane by the lattice ${\tau _i \mathbb {Z} \oplus 2\mathbb {Z}}$
elliptic curves, each of them considered as the quotient of the complex plane by the lattice ${\tau _i \mathbb {Z} \oplus 2\mathbb {Z}}$![]() , where $\tau _i$
, where $\tau _i$![]() denotes a certain element in the Siegel upper half-space, and equipped with the polarization $\mathcal {L}_i$
denotes a certain element in the Siegel upper half-space, and equipped with the polarization $\mathcal {L}_i$![]() of type $(2)$
of type $(2)$![]() induced by the divisor $2\cdot 0$
induced by the divisor $2\cdot 0$![]() . For each $i$
. For each $i$![]() , we denote moreover by $\theta ^{(i)}_{0}$
, we denote moreover by $\theta ^{(i)}_{0}$![]() and $\theta ^{(i)}_{1}$
and $\theta ^{(i)}_{1}$![]() the canonical theta functions which span the vector space of the global holomorphic sections of the polarization $\mathcal {L}_i$
the canonical theta functions which span the vector space of the global holomorphic sections of the polarization $\mathcal {L}_i$![]() on $E_i$
on $E_i$![]() .
.
Considering $\mathcal {L}$![]() to be the induced product polarization on $A$
to be the induced product polarization on $A$![]() , we first fix a basis for the vector space of the global holomorphic sections of $\mathcal {L}$
, we first fix a basis for the vector space of the global holomorphic sections of $\mathcal {L}$![]() and a convenient notation for its elements. Since $\mathcal {L}$
and a convenient notation for its elements. Since $\mathcal {L}$![]() is the product of all the polarizations on the factors $E_i$
is the product of all the polarizations on the factors $E_i$![]() , a basis for the global sections of $\mathcal {L}$
, a basis for the global sections of $\mathcal {L}$![]() can be easily defined by considering all the possible products of sections on each factor $E_i$
can be easily defined by considering all the possible products of sections on each factor $E_i$![]() , arising by selecting $\theta ^{(i)}_{0}$
, arising by selecting $\theta ^{(i)}_{0}$![]() or $\theta ^{(i)}_{1}$
or $\theta ^{(i)}_{1}$![]() for each index $i$
for each index $i$![]() . Every global section of this basis corresponds to a unique subset of $\{1,\, \cdots,\, a\}$
. Every global section of this basis corresponds to a unique subset of $\{1,\, \cdots,\, a\}$![]() containing the indices $i$
containing the indices $i$![]() of the factors on which $\theta ^{(i)}_{1}$
of the factors on which $\theta ^{(i)}_{1}$![]() has been selected. Hence, if we consider $\mathcal {P}$
has been selected. Hence, if we consider $\mathcal {P}$![]() to be the power set of $\{1,\, \cdots,\, a\}$
to be the power set of $\{1,\, \cdots,\, a\}$![]() , we can denote for every $S \in \mathcal {P}$
, we can denote for every $S \in \mathcal {P}$![]() the following global section of $\mathcal {L}$
the following global section of $\mathcal {L}$![]() :
:

where $\chi _S(i)$![]() is the characteristic function of $S$
is the characteristic function of $S$![]() . It can be now easily seen that $\{\theta _S\}_{S \in \mathcal {P}}$
. It can be now easily seen that $\{\theta _S\}_{S \in \mathcal {P}}$![]() is a basis for $H^{0}(A,\,\mathcal {L})$
is a basis for $H^{0}(A,\,\mathcal {L})$![]() . For the reader's convenience, we remark that $\theta _{\emptyset }$
. For the reader's convenience, we remark that $\theta _{\emptyset }$![]() is the element of the latter basis obtained by multiplying on every factor $E_i$
is the element of the latter basis obtained by multiplying on every factor $E_i$![]() the section $\theta ^{(i)}_{0}$
the section $\theta ^{(i)}_{0}$![]() :
:

Let us consider now a general non-zero section
for some complex coefficients $a_S$![]() such that its zero locus $\mathcal {D}$
such that its zero locus $\mathcal {D}$![]() is smooth.
is smooth.
We prove that the kernel of the multiplication map (4.21) is generated by elements of $\text {Sym}^{2}\overline {{{\rm Ann}}(V)}$![]() of the form:
of the form:
with $S \cup T = A \cup B$![]() and $S \cap T = A \cap B$
and $S \cap T = A \cap B$![]() . This will immediately imply our thesis that for each element $\eta$
. This will immediately imply our thesis that for each element $\eta$![]() contained in $\overline {{{\rm Ann}}(V)}$
contained in $\overline {{{\rm Ann}}(V)}$![]() , its square is not contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$
, its square is not contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$![]() , since we recall that the intersection of this space with $\text {Sym}^{2}\overline {{{\rm Ann}}(V)}$
, since we recall that the intersection of this space with $\text {Sym}^{2}\overline {{{\rm Ann}}(V)}$![]() is trivial.
is trivial.
This statement can be proven on a suitable affine open subset of $\mathcal {D}$![]() .
.
On each factor, the canonical theta functions $\theta ^{(i)}_{0}$![]() and $\theta ^{(i)}_{1}$
and $\theta ^{(i)}_{1}$![]() induce a covering $x_i: E_i \longrightarrow \mathbb {P}^{1}$
induce a covering $x_i: E_i \longrightarrow \mathbb {P}^{1}$![]() , where:
, where:

This covering is of degree $2$![]() , branched over four distinct points $1$
, branched over four distinct points $1$![]() , $-1$
, $-1$![]() , $\delta _{i}$
, $\delta _{i}$![]() , $-\delta _{i}$
, $-\delta _{i}$![]() , which are, respectively, the images of the points $0$
, which are, respectively, the images of the points $0$![]() , $1$
, $1$![]() , $\frac {\tau _i}{2}$
, $\frac {\tau _i}{2}$![]() , $1 + \frac {\tau _i}{2}$
, $1 + \frac {\tau _i}{2}$![]() .
.
Hence, the elliptic curve $E_i$![]() is the Riemann surface which on an affine neighbourhood $\mathcal {U}_{i}$
is the Riemann surface which on an affine neighbourhood $\mathcal {U}_{i}$![]() with local coordinates ($x_{i}$
with local coordinates ($x_{i}$![]() ,$y_{i}$
,$y_{i}$![]() ) is defined by the equation:
) is defined by the equation:
The affine model in (4.26) is called the Legendre normal form of $E_{i}$![]() (see also [Reference Catanese5]).
(see also [Reference Catanese5]).
Let us consider the affine neighbourhood of $\mathcal {U}$![]() of $\mathcal {D}$
of $\mathcal {D}$![]() defined as:
defined as:
Then $\mathcal {U}$![]() can be described as the Zariski closed subsed of the affine space $\mathbb {A}^{2a}$
can be described as the Zariski closed subsed of the affine space $\mathbb {A}^{2a}$![]() with coordinates $x_1 \cdots,\, x_a,\, y_1,\, \cdots,\, y_a$
with coordinates $x_1 \cdots,\, x_a,\, y_1,\, \cdots,\, y_a$![]() with defining equations (4.26) together with the local equation of $\mathcal {D}$
with defining equations (4.26) together with the local equation of $\mathcal {D}$![]() , which can we obtain from (4.23) by dividing by $\theta ^{(0)}_i$
, which can we obtain from (4.23) by dividing by $\theta ^{(0)}_i$![]() for each $i$
for each $i$![]() (according to the definition of $x_i$
(according to the definition of $x_i$![]() in (4.25)). Hence, the local equation of $\mathcal {D}$
in (4.25)). Hence, the local equation of $\mathcal {D}$![]() on $\mathcal {U}$
on $\mathcal {U}$![]() is $f(x_1,\, \cdots,\, x_a) = 0$
is $f(x_1,\, \cdots,\, x_a) = 0$![]() , where
, where

for some complex coefficients $b_S$![]() . For every $j$
. For every $j$![]() in $\{1,\, \cdots,\, a\}$
in $\{1,\, \cdots,\, a\}$![]() , the tangent vector $\frac {\partial }{\partial z_j}$
, the tangent vector $\frac {\partial }{\partial z_j}$![]() is naturally identified with the holomorphic $a-1$
is naturally identified with the holomorphic $a-1$![]() -form
-form

(see (4.4) in the proof of Proposition 4.1).
Hence, on the affine subset $\mathcal {V}$![]() of $\mathcal {U}$
of $\mathcal {U}$![]() where $f_a:= \frac {\partial f}{\partial x_a}$
where $f_a:= \frac {\partial f}{\partial x_a}$![]() does not vanish, we obtain, up to a sign:
does not vanish, we obtain, up to a sign:
where $f_j$![]() denotes the derivative of $f$
denotes the derivative of $f$![]() with respect to $x_j$
with respect to $x_j$![]() .
.
The global holomorphic differentials on $\mathcal {D}$![]() obtained by restricting the global sections of the polarization of $A$
obtained by restricting the global sections of the polarization of $A$![]() to $\mathcal {D}$
to $\mathcal {D}$![]() can be computed by applying the residue map $H^{0}(A,\, \mathcal {O}_{A}(\mathcal {D})) = H^{0}(A,\, \omega _{A}(\mathcal {D})) \longrightarrow H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$
can be computed by applying the residue map $H^{0}(A,\, \mathcal {O}_{A}(\mathcal {D})) = H^{0}(A,\, \omega _{A}(\mathcal {D})) \longrightarrow H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$![]() . When restricted to $\mathcal {V}$
. When restricted to $\mathcal {V}$![]() this gives, for each element $S$
this gives, for each element $S$![]() of $\mathcal {P}$
of $\mathcal {P}$![]() ,
,
where $\neg$![]() is the contraction operator. We have in conclusion
is the contraction operator. We have in conclusion

and since $X_S$![]() as in (4.27) is equal to $\frac {\theta _S}{\theta _{\emptyset }}$
as in (4.27) is equal to $\frac {\theta _S}{\theta _{\emptyset }}$![]() (up to a non-zero constant):
(up to a non-zero constant):
Hence, if we multiply the expressions (4.28) and (4.31) by $f_a y_1 \cdots y_a$![]() , we see that the elements in (4.24) become, up to a constant
, we see that the elements in (4.24) become, up to a constant
which are mapped by the multiplication map to
by the assumptions that $S \cup T = A \cup B$![]() and $S \cap T = A \cap B$
and $S \cap T = A \cap B$![]() .
.
On the other side, if a linear combination of tensor elements $X_S\otimes X_T$![]() , say
, say
is mapped to zero by the multiplication map, then we have

This implies that for every couple of subsets $U$![]() and $V$
and $V$![]() of $\{1,\, \cdots,\, a\}$
of $\{1,\, \cdots,\, a\}$![]() with $U \subseteq V$
with $U \subseteq V$![]() , we have:
, we have:

since $x_j$![]() appears in every term $X_U \cdot X_V$
appears in every term $X_U \cdot X_V$![]() with degree $0$
with degree $0$![]() , $1$
, $1$![]() or $2$
or $2$![]() , according to whether $j \notin V$
, according to whether $j \notin V$![]() , $j \in V-U$
, $j \in V-U$![]() or $j \in U$
or $j \in U$![]() , which implies that the tensor element
, which implies that the tensor element

is linear combination of elements of the form (4.32) with $S \cap T = U = A \cap B$![]() and $S \cup T = V = A \cup B$
and $S \cup T = V = A \cup B$![]() . Finally, also $K$
. Finally, also $K$![]() must be linear combination of such elements, since clearly $K = \sum \nolimits _{U \subseteq V}K_{UV}$
must be linear combination of such elements, since clearly $K = \sum \nolimits _{U \subseteq V}K_{UV}$![]() .
.
Hence, our claim that the kernel of the multiplication map is generated by elements of the form as in (4.24) holds true once we prove that there are no other quadratic relations between the polynomials $X_S$![]() for all $S \in \mathcal {P}$
for all $S \in \mathcal {P}$![]() and $Q_j := f_j y_j$
and $Q_j := f_j y_j$![]() for $j \in \{1,\, \cdots,\, a\}$
for $j \in \{1,\, \cdots,\, a\}$![]() in the quotient ring:
in the quotient ring:
We stress here that $V$![]() corresponds to the vector space spanned by all polynomials $Q_j$
corresponds to the vector space spanned by all polynomials $Q_j$![]() , while the polynomials $X_S$
, while the polynomials $X_S$![]() span a vector subspace which, according to (4.10), corresponds precisely to the subspace $\overline {{{\rm Ann}}(V)}$
span a vector subspace which, according to (4.10), corresponds precisely to the subspace $\overline {{{\rm Ann}}(V)}$![]() . In particular, $V$
. In particular, $V$![]() is generated by elements which involve the letters $y_j$
is generated by elements which involve the letters $y_j$![]() .
.
Since $X_{\emptyset } = 1$![]() , we can define also the vector space $W$
, we can define also the vector space $W$![]() inside $R$
inside $R$![]() generated as $\mathbb {C}$
generated as $\mathbb {C}$![]() -vector space by all monomials in the letters $x_j$
-vector space by all monomials in the letters $x_j$![]() of degree at most $2$
of degree at most $2$![]() in each letter $x_j$
in each letter $x_j$![]() .
.
A quadratic relation among the polynomials $X_S$![]() and $Q_j$
and $Q_j$![]() would give in $R$
would give in $R$![]() the following relation:
the following relation:

where $\beta,\, \gamma _j,\, \eta _{ij}\in W$![]() since for $\eta _{ij}$
since for $\eta _{ij}$![]() we have the form
we have the form
where $c_{ij}$![]() are constants depending on the definition of the polynomials $Q_j$
are constants depending on the definition of the polynomials $Q_j$![]() .
.
If we rearrange the terms of the equation (4.33) and we express it in the form of an algebraic relation between $y_a$![]() and the remaining generators of $R$
and the remaining generators of $R$![]() , we obtain:
, we obtain:

However, since by (4.26), the equality $y_a^{2} = (x_{a}^{2} - 1)(x_{a}^{2} - \delta _{a}^{2})$![]() holds in $R$
holds in $R$![]() , we obtain:
, we obtain:

Since this holds in $R$![]() and the polynomial which in the latter equation (4.35) multiplies $y_a$
and the polynomial which in the latter equation (4.35) multiplies $y_a$![]() is of degree at most $1$
is of degree at most $1$![]() in $x_a$
in $x_a$![]() , it must be $0$
, it must be $0$![]() in $R$
in $R$![]() , since the only relation involving $y_a$
, since the only relation involving $y_a$![]() is $h_a$
is $h_a$![]() , which is of degree $2$
, which is of degree $2$![]() in $y_a$
in $y_a$![]() and $4$
and $4$![]() in $x_a$
in $x_a$![]() . Hence, $\eta _{ia} = 0$
. Hence, $\eta _{ia} = 0$![]() for every $i \neq a$
for every $i \neq a$![]() and $\gamma _{a} = 0$
and $\gamma _{a} = 0$![]() . By applying the same procedure to each index, it follows that $\eta _{ij} = 0$
. By applying the same procedure to each index, it follows that $\eta _{ij} = 0$![]() for every $i$
for every $i$![]() and $j$
and $j$![]() with $i \neq j$
with $i \neq j$![]() , and $\gamma _{i} = 0$
, and $\gamma _{i} = 0$![]() for every $i$
for every $i$![]() .
.
It follows that the quadratic relation (4.33) can be written in the following form:

Using again the relations $h_1,\, \cdots,\, h_a$![]() , we can write:
, we can write:

If at least one of the coefficients $c_{jj}$![]() is non-zero, say $c_{aa}$
is non-zero, say $c_{aa}$![]() , then there exists a polynomial $u = u(x_1 \cdots x_a)$
, then there exists a polynomial $u = u(x_1 \cdots x_a)$![]() such that, the following relation holds in the polynomial ring $\mathbb {C}[x_1,\, \cdots,\, x_a]$
such that, the following relation holds in the polynomial ring $\mathbb {C}[x_1,\, \cdots,\, x_a]$![]() :
:

We recall that the variable $x_a$![]() occurs in $\beta$
occurs in $\beta$![]() with an exponent at most 2, hence it occurs in degree 4 in the left side of (4.36). Clearly, if $u$
with an exponent at most 2, hence it occurs in degree 4 in the left side of (4.36). Clearly, if $u$![]() is equal to zero, then $c_{aa}=0$
is equal to zero, then $c_{aa}=0$![]() is a contradiction. Hence, assume $u\neq 0$
is a contradiction. Hence, assume $u\neq 0$![]() . By definition, we can write $f = p + qx_a$
. By definition, we can write $f = p + qx_a$![]() , where $x_a$
, where $x_a$![]() does not occur neither in $p$
does not occur neither in $p$![]() nor in $q$
nor in $q$![]() . This forces that $u$
. This forces that $u$![]() must have degree 3 in $x_a$
must have degree 3 in $x_a$![]() . On the other hand, the left side of (4.36) does not contain monomials of degree 3 in $x_a$
. On the other hand, the left side of (4.36) does not contain monomials of degree 3 in $x_a$![]() . This implies $p=0$
. This implies $p=0$![]() . Hence, $x_a$
. Hence, $x_a$![]() divides $f$
divides $f$![]() and $\mathcal {D}$
and $\mathcal {D}$![]() is reducible, which contradicts our hypothesis.
is reducible, which contradicts our hypothesis.
4.5. The proof of Theorem [B]
We can show Theorem [B] by a direct argument not relying on Theorem 3.6, which we used in the case of Nori's families.
We consider, as in § 1, a family induced by embedded deformations $\pi \colon \mathcal {X}\to B$![]() . By construction, it is obtained by shrinking to $B$
. By construction, it is obtained by shrinking to $B$![]() a fibration ${\Pi }\colon \mathcal {Y}\to \hat {B}$
a fibration ${\Pi }\colon \mathcal {Y}\to \hat {B}$![]() where $\mathcal {Y}$
where $\mathcal {Y}$![]() is smooth and $\hat {B}$
is smooth and $\hat {B}$![]() is a curve. If $X\subset \mathcal {X}$
is a curve. If $X\subset \mathcal {X}$![]() is a fibre and $U:=\mathcal {Y}\setminus X$
is a fibre and $U:=\mathcal {Y}\setminus X$![]() , by the composition of the residue homomorphism $H^{2n+1}(U,\,\mathbb {Z})\to H^{2n}(X,\,\mathbb {Z})$
, by the composition of the residue homomorphism $H^{2n+1}(U,\,\mathbb {Z})\to H^{2n}(X,\,\mathbb {Z})$![]() with the Gysin homomorphism $l_{*}\colon H^{2n}(X,\,\mathbb {Z})\to H^{2n+2} (\mathcal {Y},\,\mathbb {Z})$
with the Gysin homomorphism $l_{*}\colon H^{2n}(X,\,\mathbb {Z})\to H^{2n+2} (\mathcal {Y},\,\mathbb {Z})$![]() , we obtain the exact sequence
, we obtain the exact sequence
We also recall the compatible identifications $\int _{X}\colon H^{2n}(X,\,\mathbb {C})\to \mathbb {C}$![]() , $\int _{\mathcal {Y}}\colon H^{2n+2} (\mathcal {Y},\,\mathbb {C})\to \mathbb {C}$
, $\int _{\mathcal {Y}}\colon H^{2n+2} (\mathcal {Y},\,\mathbb {C})\to \mathbb {C}$![]() .
.
4.5.1 The proof
By the assumptions of Theorem [B], $\pi \colon \mathcal {X}{\rightarrow }B$![]() satisfies extremal liftability conditions. Call $\varPhi \colon \mathcal {X}\to A$
satisfies extremal liftability conditions. Call $\varPhi \colon \mathcal {X}\to A$![]() the morphism induced by the projection from the incidence variety. We stress that $\varPhi$
the morphism induced by the projection from the incidence variety. We stress that $\varPhi$![]() induces the natural inclusion $X_b\hookrightarrow A$
induces the natural inclusion $X_b\hookrightarrow A$![]() . Let $W:=\langle \varPhi ^{*}\sigma _{1},\,\dots,\,\varPhi ^{*}\sigma _{n+1}\rangle$
. Let $W:=\langle \varPhi ^{*}\sigma _{1},\,\dots,\,\varPhi ^{*}\sigma _{n+1}\rangle$![]() , where $\sigma _1,\,\dots,\,\sigma _{n+1}$
, where $\sigma _1,\,\dots,\,\sigma _{n+1}$![]() are independent 1-forms on $A$
are independent 1-forms on $A$![]() . Set $s_i:=\varPhi ^{*}\sigma _{n+1}$
. Set $s_i:=\varPhi ^{*}\sigma _{n+1}$![]() , $i=1,\,\dots,\,n+1$
, $i=1,\,\dots,\,n+1$![]() . Let $\varOmega \in H^{0}(\mathcal {X},\,\varOmega ^{n+1}_{\mathcal {X}})$
. Let $\varOmega \in H^{0}(\mathcal {X},\,\varOmega ^{n+1}_{\mathcal {X}})$![]() be the form induced by $s_1\wedge s_2\wedge \cdots \wedge s_{n+1}$
be the form induced by $s_1\wedge s_2\wedge \cdots \wedge s_{n+1}$![]() and $\xi _b\in H^{1}(X_{b},\,T_{X_{b}})$
and $\xi _b\in H^{1}(X_{b},\,T_{X_{b}})$![]() be an infinitesimal deformation given by the Kodaira–Spencer map. Let
be an infinitesimal deformation given by the Kodaira–Spencer map. Let
be the restriction map and set $\eta _{i}=r(s_{i})$![]() , $i=1,\,\ldots,\,n+1$
, $i=1,\,\ldots,\,n+1$![]() . In this case, the set $\mathcal {B}=\{\eta _{i}\}_{i=1}^{n+1}$
. In this case, the set $\mathcal {B}=\{\eta _{i}\}_{i=1}^{n+1}$![]() is a basis of $H^{0}(X_{b},\,\varOmega ^{1}_{X_b}\,)$
is a basis of $H^{0}(X_{b},\,\varOmega ^{1}_{X_b}\,)$![]() . Now we work on the fibre $X$
. Now we work on the fibre $X$![]() and we denote $\phi \colon X\to A$
and we denote $\phi \colon X\to A$![]() the morphism induced by $\varPhi$
the morphism induced by $\varPhi$![]() . Let $t$
. Let $t$![]() be a local parameter on $B$
be a local parameter on $B$![]() such that $( \pi ^{*}(t)=0)$
such that $( \pi ^{*}(t)=0)$![]() is the equation of $X$
is the equation of $X$![]() . We know that by the sheaf-homomorphism $\varOmega _{\mathcal {X}}^{n+1}({\rm {log}}(X))\to \omega _X$
. We know that by the sheaf-homomorphism $\varOmega _{\mathcal {X}}^{n+1}({\rm {log}}(X))\to \omega _X$![]() , the residue of the form locally given by $\frac {\varOmega }{\pi ^{*}(t)}$
, the residue of the form locally given by $\frac {\varOmega }{\pi ^{*}(t)}$![]() is the adjoint form $\omega _{_{\xi _b,W,\mathcal {B}}}$
is the adjoint form $\omega _{_{\xi _b,W,\mathcal {B}}}$![]() , see Definition 2.1. We consider $H^{0}(\mathcal {X},\,\varOmega _{\mathcal {X}}^{n})\ni \varOmega _i$
, see Definition 2.1. We consider $H^{0}(\mathcal {X},\,\varOmega _{\mathcal {X}}^{n})\ni \varOmega _i$![]() the forms induced by $s_1\wedge s_2\wedge \dots \wedge {\widehat {s_i}}\wedge \dots \wedge s_{n+1}$
the forms induced by $s_1\wedge s_2\wedge \dots \wedge {\widehat {s_i}}\wedge \dots \wedge s_{n+1}$![]() , $i=1,\,\ldots,\,n+1$
, $i=1,\,\ldots,\,n+1$![]() . For every $i=1,\,\ldots,\,n+1$
. For every $i=1,\,\ldots,\,n+1$![]() the form locally given by $\frac {\varOmega }{\pi ^{*}(t)}\wedge {\overline {\varOmega _i}}$
the form locally given by $\frac {\varOmega }{\pi ^{*}(t)}\wedge {\overline {\varOmega _i}}$![]() , gives an element of $H^{2n+1} (U,\,\mathbb {C})$
, gives an element of $H^{2n+1} (U,\,\mathbb {C})$![]() whose residue in $H^{2n}(X,\,\mathbb {C})$
whose residue in $H^{2n}(X,\,\mathbb {C})$![]() is $\omega _{_{\xi _b,W,\mathcal {B}}}\wedge \phi ^{*}{\overline {\omega _i}}$
is $\omega _{_{\xi _b,W,\mathcal {B}}}\wedge \phi ^{*}{\overline {\omega _i}}$![]() . By the compatibility of the sequence (4.37) with both $\int _{\mathcal {Y}}$
. By the compatibility of the sequence (4.37) with both $\int _{\mathcal {Y}}$![]() and $\int _{X}$
and $\int _{X}$![]() it follows that for every $\sigma \in H^{0}(A_{b},\,\varOmega ^{n}_{A_{b}}\,)$
it follows that for every $\sigma \in H^{0}(A_{b},\,\varOmega ^{n}_{A_{b}}\,)$![]() it holds:
it holds:
(in other words, the Transversality criteria applies also under the hypothesis of Theorem [B]). Finally, by Theorem 4.5, we have that for each element $\eta$![]() contained in $\overline {{\rm {Ann}}(V)}$
contained in $\overline {{\rm {Ann}}(V)}$![]() , its square is not contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$
, its square is not contained in the image of $V \odot H^{0}(\mathcal {D},\, \omega _{\mathcal {D}})$![]() . Hence, we can conclude as in the proof of Theorem [A].
. Hence, we can conclude as in the proof of Theorem [A].
Remark 4.6 We stress that the above proof of the Transversality claim in the case of divisors of an abelian variety does not make any generality assumption on the abelian variety.
5. The case of maximal relative irregularity for a fibred surface
We can use the strategy behind the proof of Theorem [A] to study a class of surfaces too. Let $S$![]() be a smooth surface and let $f\colon S\to B$
be a smooth surface and let $f\colon S\to B$![]() be a fibration to a smooth curve $B$
be a fibration to a smooth curve $B$![]() with general fibre $F$
with general fibre $F$![]() . Let $g(F)$
. Let $g(F)$![]() be the genus of $F$
be the genus of $F$![]() . In [Reference Xiao32, Corollary 3 and 4], it is shown that a non-isotrivial fibration satisfies $q(S)-g(B)\leq \frac {5g(F)+1}{6}$
. In [Reference Xiao32, Corollary 3 and 4], it is shown that a non-isotrivial fibration satisfies $q(S)-g(B)\leq \frac {5g(F)+1}{6}$![]() . A very interesting class of fibrations is the one where $q(S)-g(B) =g(F)-1$
. A very interesting class of fibrations is the one where $q(S)-g(B) =g(F)-1$![]() . These fibrations are called fibrations with maximal relative irregularity. In the same paper, Xiao showed that they can exist only for $g(F)\leq 7$
. These fibrations are called fibrations with maximal relative irregularity. In the same paper, Xiao showed that they can exist only for $g(F)\leq 7$![]() . These fibrations have received a lot of attention in recent years thanks to the beauty of the interplay between surface theory and the theory of abelian varieties which they help to see [Reference Möller16, Reference Torelli30] and the bibliography there quoted. In order to understand the geometry of any fibration, it is natural to try to obtain information by relating the invariants of $B$
. These fibrations have received a lot of attention in recent years thanks to the beauty of the interplay between surface theory and the theory of abelian varieties which they help to see [Reference Möller16, Reference Torelli30] and the bibliography there quoted. In order to understand the geometry of any fibration, it is natural to try to obtain information by relating the invariants of $B$![]() and of (the general fibre) $F$
and of (the general fibre) $F$![]() to those of $S$
to those of $S$![]() . By definition, if $q(S)-g(B)=g(F)-1$
. By definition, if $q(S)-g(B)=g(F)-1$![]() , there exists a hyperplane $V$
, there exists a hyperplane $V$![]() of $H^{0}(F,\,\omega _F)$
of $H^{0}(F,\,\omega _F)$![]() such that the standard restriction homomorphisms $H^{0}(S,\,\varOmega ^{1}_{S})\to H^{0}(F,\,\omega _{F})$
such that the standard restriction homomorphisms $H^{0}(S,\,\varOmega ^{1}_{S})\to H^{0}(F,\,\omega _{F})$![]() has $V$
has $V$![]() as its own image. We need the following:
as its own image. We need the following:
Lemma 5.1 Let $f\colon S\to B$![]() be a non-isotrivial fibration with a general fibre of genus $\geq 3$
be a non-isotrivial fibration with a general fibre of genus $\geq 3$![]() and such that $q(S)-g(B)=g(F)-1$
and such that $q(S)-g(B)=g(F)-1$![]() . Then, the sublinear system induced by $V$
. Then, the sublinear system induced by $V$![]() is base point free.
is base point free.
Proof. Take an infinitesimal deformation $\xi \in H^{1}(F,\,T_F)$![]() of $F$
of $F$![]() given by the Kodaira–Spencer map. Assume that for the general fibre $F$
given by the Kodaira–Spencer map. Assume that for the general fibre $F$![]() the image $V$
the image $V$![]() of $H^{0}(S,\,\varOmega ^{1}_{S})\to H^{0}(F,\,\omega _{F})$
of $H^{0}(S,\,\varOmega ^{1}_{S})\to H^{0}(F,\,\omega _{F})$![]() has base points. Since $V$
has base points. Since $V$![]() is a hyperplane then Riemann–Roch theorem on curves implies that there exists a unique point $p_F\in F$
is a hyperplane then Riemann–Roch theorem on curves implies that there exists a unique point $p_F\in F$![]() which is the base point of the linear system $|V|$
which is the base point of the linear system $|V|$![]() . By the viceversa of the Adjoint theorem in the case of one-dimensional varieties, see [Reference Collino and Pirola7], it follows that $\xi$
. By the viceversa of the Adjoint theorem in the case of one-dimensional varieties, see [Reference Collino and Pirola7], it follows that $\xi$![]() is the Shiffer variation supported on $p_F$
is the Shiffer variation supported on $p_F$![]() . This is a contradiction to [Reference Arbarello and Cornalba1, Corollary 6.11]; see also [Reference González-Alonso9, Prop. 6.3.9]
. This is a contradiction to [Reference Arbarello and Cornalba1, Corollary 6.11]; see also [Reference González-Alonso9, Prop. 6.3.9]
Our basic reference for this last part [Reference Pirola and Zucconi23, Section V]. Since $q(S)-g(B)=g(F)-1$![]() the Jacobians of the fibres have an abelian variety $A'$
the Jacobians of the fibres have an abelian variety $A'$![]() of dimension $g-1$
of dimension $g-1$![]() in common. Let $B^{0}$
in common. Let $B^{0}$![]() the open subscheme of $B$
the open subscheme of $B$![]() where $f\colon S\to B$
where $f\colon S\to B$![]() is smooth. By shrinking to open subsets $U\subset B^{0}$
is smooth. By shrinking to open subsets $U\subset B^{0}$![]() , the family ${\rm {Alb}}(S)\times _{\rm {Alb}(B)}B\to B$
, the family ${\rm {Alb}}(S)\times _{\rm {Alb}(B)}B\to B$![]() obtained by standard universal properties restricts to a family $p\colon \mathcal {A}_U\to U$
obtained by standard universal properties restricts to a family $p\colon \mathcal {A}_U\to U$![]() whose fibres are all isomorphic to the dual $A$
whose fibres are all isomorphic to the dual $A$![]() of $A'$
of $A'$![]() . Note that $p\colon \mathcal {A}_U\to U$
. Note that $p\colon \mathcal {A}_U\to U$![]() is a family of polarized abelian varieties where the fibre is always isomorphic to $A$
is a family of polarized abelian varieties where the fibre is always isomorphic to $A$![]() but the polarization on $A\times \{b\}$
but the polarization on $A\times \{b\}$![]() is given by:
is given by:
where $\phi _b\colon F_b\to A_b$![]() is given by the composition ${\rm {alb}}(S)\circ j_{b}\colon F_b\to {\rm {Alb}}(S)$
is given by the composition ${\rm {alb}}(S)\circ j_{b}\colon F_b\to {\rm {Alb}}(S)$![]() , and $j_b\colon F_b\to S$
, and $j_b\colon F_b\to S$![]() is the natural inclusion and $A_b$
is the natural inclusion and $A_b$![]() is a translate of $A$
is a translate of $A$![]() inside ${\rm {Alb}}(S)$
inside ${\rm {Alb}}(S)$![]() .
.
Theorem 5.2 Let $f\colon S\to B$![]() be a non-isotrivial fibration of maximal relative irregularity $> 2$
be a non-isotrivial fibration of maximal relative irregularity $> 2$![]() with fixed abelian variety $A$
with fixed abelian variety $A$![]() and let $B^{0}$
and let $B^{0}$![]() the open subscheme where it is smooth. If $\phi _b\colon F_b\to A$
the open subscheme where it is smooth. If $\phi _b\colon F_b\to A$![]() has degree $1$
has degree $1$![]() then the infinitesimal invariant associated with the basic cycle of the Albanese type family obtained by restricting over open subschemes, $U\subset B^{0}$
then the infinitesimal invariant associated with the basic cycle of the Albanese type family obtained by restricting over open subschemes, $U\subset B^{0}$![]() is not zero.
is not zero.
Proof. The problem is local over $B$![]() . We can write $H^{0}(F_b,\,\varOmega ^{1}_{F_b})=V\oplus ^{\perp } s\cdot \mathbb {C}$
. We can write $H^{0}(F_b,\,\varOmega ^{1}_{F_b})=V\oplus ^{\perp } s\cdot \mathbb {C}$![]() where $V=\phi _b^{*}H^{0}(A,\,\varOmega ^{1}_A)$
where $V=\phi _b^{*}H^{0}(A,\,\varOmega ^{1}_A)$![]() and $s$
and $s$![]() is a nontrivial section. The decomposition is an orthogonal one with respect to the standard pairing on $F_b$
is a nontrivial section. The decomposition is an orthogonal one with respect to the standard pairing on $F_b$![]() . In particular ${\overline {{{\rm Ann}}(V)}}=s\cdot \mathbb {C}$
. In particular ${\overline {{{\rm Ann}}(V)}}=s\cdot \mathbb {C}$![]() . By contradiction assume that the infinitesimal invariant associated with an Albanese type family over a neighbourhood $U$
. By contradiction assume that the infinitesimal invariant associated with an Albanese type family over a neighbourhood $U$![]() of $b$
of $b$![]() is zero. Let $\xi \in H^{1}(F,\,T_F)$
is zero. Let $\xi \in H^{1}(F,\,T_F)$![]() be an infinitesimal deformation of $F$
be an infinitesimal deformation of $F$![]() given by the Kodaira–Spencer map of $f_{|f^{-1}(U)}\colon f^{-1}(U)\to U$
given by the Kodaira–Spencer map of $f_{|f^{-1}(U)}\colon f^{-1}(U)\to U$![]() . By Theorem 3.6, this means that all the adjoints obtained by $\xi$
. By Theorem 3.6, this means that all the adjoints obtained by $\xi$![]() and by two-dimensional subspaces $W\subset V$
and by two-dimensional subspaces $W\subset V$![]() belongs to $V^{\perp }=s\cdot \mathbb {C}$
belongs to $V^{\perp }=s\cdot \mathbb {C}$![]() . This means that if $W=\langle \eta _1,\,\eta _2\rangle$
. This means that if $W=\langle \eta _1,\,\eta _2\rangle$![]() then there exists a constant $c\in \mathbb {C}$
then there exists a constant $c\in \mathbb {C}$![]() such that $c \cdot s$
such that $c \cdot s$![]() is an adjoint form associated with $W$
is an adjoint form associated with $W$![]() , in other words $[c\cdot s]\in H^{0}(F,\,\omega _F)/W$
, in other words $[c\cdot s]\in H^{0}(F,\,\omega _F)/W$![]() is the Massey product of $\eta _{1}$
is the Massey product of $\eta _{1}$![]() and $\eta _{2}$
and $\eta _{2}$![]() . This implies that if we take a general $\eta \in V$
. This implies that if we take a general $\eta \in V$![]() and a general two-dimensional subspace $\langle \eta _1,\,\eta _2\rangle =W\subset V$
and a general two-dimensional subspace $\langle \eta _1,\,\eta _2\rangle =W\subset V$![]() (in particular $\eta \not \in W$
(in particular $\eta \not \in W$![]() , here we need $q(S)-g(B)>2$
, here we need $q(S)-g(B)>2$![]() , that is $g(F)\geq 4$
, that is $g(F)\geq 4$![]() ), we can find a $\sigma \in W$
), we can find a $\sigma \in W$![]() such that the Massey product of the two-dimensional subspace $\langle \eta,\,\sigma \rangle$
such that the Massey product of the two-dimensional subspace $\langle \eta,\,\sigma \rangle$![]() along $\xi$
along $\xi$![]() is zero. Indeed if $[c_i\cdot s]\in H^{0}(F,\,\omega _F)/W_i$
is zero. Indeed if $[c_i\cdot s]\in H^{0}(F,\,\omega _F)/W_i$![]() is the Massey product of $W_i=\langle \eta,\,\eta _i\rangle$
is the Massey product of $W_i=\langle \eta,\,\eta _i\rangle$![]() , $i=1,\,2$
, $i=1,\,2$![]() then $\sigma =c_1\eta _2-c_2\eta _1\in W$
then $\sigma =c_1\eta _2-c_2\eta _1\in W$![]() . By the Adjoint theorem, it follows that $\xi =0$
. By the Adjoint theorem, it follows that $\xi =0$![]() if the linear system $\langle \eta,\,\sigma \rangle$
if the linear system $\langle \eta,\,\sigma \rangle$![]() has no base points or that $\xi$
has no base points or that $\xi$![]() is supported on the base points of $\langle \eta,\,\sigma \rangle$
is supported on the base points of $\langle \eta,\,\sigma \rangle$![]() . By the genericity of $\eta$
. By the genericity of $\eta$![]() and $W$
and $W$![]() it follows that $\xi$
it follows that $\xi$![]() is supported on the base points of the linear subsystem $V\subset H^{0}(F,\,\omega _F)$
is supported on the base points of the linear subsystem $V\subset H^{0}(F,\,\omega _F)$![]() . By Lemma 5.1, we conclude that $\xi =0$
. By Lemma 5.1, we conclude that $\xi =0$![]() . This means that $f\colon S\to B$
. This means that $f\colon S\to B$![]() has constant moduli; a contradiction.
has constant moduli; a contradiction.
Acknowledgements
F.Z. has been supported by the grant DIMAGeometry PRIDZUCC, L.C. by the ERC Advanced grant no. 340258, ‘TADMICANT’, and L.R. by the JSPS-Japan Society for the Promotion of Science (Postdoctoral Research Fellowship, The University of Tokyo) and the IBS Center for Complex Geometry. The authors thank Gian Pietro Pirola because he pointed out two unclear deductions contained in a preliminary version of this work, and Claire Voisin for her useful advice. Last but not least, they also thank Ingrid Bauer, Fabrizio Catanese, and Yujiro Kawamata because they gave the opportunity to show some of our results in the workshop ‘Differential, Algebraic and Topological Methods in Complex Algebraic Geometry’, Grand Hotel San Michele, Cetraro, 6–15 September 2018: actually, the idea behind this paper was conceived in Cetraro.
We are deeply grateful to the referee for pointing out a mistake, for providing valuable comments, and critical feedback to help us significantly improve the quality of the paper.