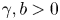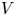1. Introduction
This work deals with the existence of positive solutions of Schrödinger–Poisson systems of the form
where we assume $b>0$![]() , the nonlinearity $p\ge 4$
, the nonlinearity $p\ge 4$![]() , the coupling coefficient $\gamma >0$
, the coupling coefficient $\gamma >0$![]() and the potential $V$
and the potential $V$![]() is a positive measurable function.
is a positive measurable function.
For their relevance in physics, Schrödinger–Poisson systems have been extensively studied in the three-dimensional case, see, for example, the survey paper [Reference Ambrosetti1], the recent paper [Reference Dutko, Mercuri and Tyler15] or also [Reference Azzollini and Pomponio2, Reference Bellazzini, Jeanjean and Luo3, Reference Cerami and Molle8, Reference Cerami and Molle9, Reference Ruiz25] and the references therein. On the contrary, in dimension two they are much less studied, also due to some difficulties intrinsic to the planar case (see [Reference Bonheure, Cingolani and Secchi4, Reference Cingolani and Weth10, Reference Chen and Pan11, Reference Choquard, Stubbe and Vuffray13, Reference Du and Weth14, Reference Masaki20, Reference Masaki21, Reference Stubbe27] and references therein).
Concerning the semiclassical analysis related to (S), very little is known. The autonomous case has been treated first in [Reference Masaki20], while the case where a potential is involved has been studied only recently, in [Reference Bonheure, Cingolani and Secchi4], where the problem is fronted by perturbation methods.
We observe that in the two-dimensional Choquard problem with logarithmic kernel, analogous difficulties come out. We refer the reader to the recent paper [Reference Cassani and Tarsi7] for more details and references on this subject. In [Reference Cassani and Tarsi7], the authors considered non homogeneous nonlinearities and the positive potential is assumed to be continuous and one-periodic.
Since the Poisson equation in (S) gives
the system (S) can be reduced to the single nonlocal equation
It is natural to expect that the solutions of equation (E) correspond to the critical points of the following action functional, where we have normalized the constants:

However, a first difficulty is that $I$![]() is not well defined on the usual Sobolev space $H^1(\mathbb {R}^2)$
is not well defined on the usual Sobolev space $H^1(\mathbb {R}^2)$![]() , for the presence of the sign-changing and unbounded logarithmic kernel. Moreover, in the framework considered in this paper, another point to be fixed is related to the potential, that is assumed to be unbounded and possibly not coercive at infinity. To overcome the difficulty related to the Newtonian kernel, Stubbe in [Reference Stubbe27] introduced the following Hilbert space, to study (S) in the autonomous case $V\equiv 0$
, for the presence of the sign-changing and unbounded logarithmic kernel. Moreover, in the framework considered in this paper, another point to be fixed is related to the potential, that is assumed to be unbounded and possibly not coercive at infinity. To overcome the difficulty related to the Newtonian kernel, Stubbe in [Reference Stubbe27] introduced the following Hilbert space, to study (S) in the autonomous case $V\equiv 0$![]() , $b=0$
, $b=0$![]() ,
,
The variational framework introduced in [Reference Stubbe27] was then developed in detail by Cingolani and Weth in [Reference Cingolani and Weth10] to front non-autonomous problems of the form (S), with $b>0$![]() , when the potential is assumed to be $\mathbb {Z}^2$
, when the potential is assumed to be $\mathbb {Z}^2$![]() -periodic or constant. The Cerami condition turns out to be the more convenient compactness condition to tackle the two-dimensional case in a variational way, indeed it is not evident how to show the boundedness of the Palais–Smale sequences. However, since the logarithmic convolution term does not have a definite sign on $\widetilde X$
-periodic or constant. The Cerami condition turns out to be the more convenient compactness condition to tackle the two-dimensional case in a variational way, indeed it is not evident how to show the boundedness of the Palais–Smale sequences. However, since the logarithmic convolution term does not have a definite sign on $\widetilde X$![]() , also the boundedness of Cerami sequences becomes a major difficulty. The idea, developed in [Reference Stubbe27], to handle the different signs of the kernel is to take advantage of the relation $\log r=\log (1+r)-\log (1+\frac 1r)$
, also the boundedness of Cerami sequences becomes a major difficulty. The idea, developed in [Reference Stubbe27], to handle the different signs of the kernel is to take advantage of the relation $\log r=\log (1+r)-\log (1+\frac 1r)$![]() , for all $r>0$
, for all $r>0$![]() , to work in $\widetilde X$
, to work in $\widetilde X$![]() and decompose the action of the nonlocal part in its positive and negative contribution. Once obtained the boundedness of the Cerami sequences, another difficulty is to prove that the weak limit actually is a strong limit for the Cerami sequences. To this aim, some more assumptions on the potential has been done; for example, its $\mathbb {Z}^2$
and decompose the action of the nonlocal part in its positive and negative contribution. Once obtained the boundedness of the Cerami sequences, another difficulty is to prove that the weak limit actually is a strong limit for the Cerami sequences. To this aim, some more assumptions on the potential has been done; for example, its $\mathbb {Z}^2$![]() periodicity considered in [Reference Cingolani and Weth10] (see also [Reference Cao, Dai and Zhang6] and references therein), or its axial symmetry, assumed for example in [Reference Chen and Pan11, Reference Chen and Tang12].
periodicity considered in [Reference Cingolani and Weth10] (see also [Reference Cao, Dai and Zhang6] and references therein), or its axial symmetry, assumed for example in [Reference Chen and Pan11, Reference Chen and Tang12].
To the best of our knowledge, up to the semiclassical analysis performed in [Reference Bonheure, Cingolani and Secchi4], there are not works concerning problem (S) without any periodicity or symmetry assumption on the potential. Our contribution in this paper is to consider a class of problems of the form (S), where $V$![]() does not enjoy those assumptions. On $V$
does not enjoy those assumptions. On $V$![]() , we assume the following conditions
, we assume the following conditions

If the potential verifies (V), the functional $I$![]() could be not well defined on $\widetilde X$
could be not well defined on $\widetilde X$![]() , so that its natural domain turns out to be the weighted Hilbert space
, so that its natural domain turns out to be the weighted Hilbert space
endowed with the norm
We assume (V)$(a)$![]() to avoid pathological potentials such that $X=\emptyset$
to avoid pathological potentials such that $X=\emptyset$![]() and to guarantee that ${\mathcal {C}}^\infty _c(\mathbb {R}^2)\subseteq X$
and to guarantee that ${\mathcal {C}}^\infty _c(\mathbb {R}^2)\subseteq X$![]() , so that the weak formulation of problem (E) is meaningful.
, so that the weak formulation of problem (E) is meaningful.
In Proposition 3.2, we employ assumption (V)$(c)$![]() to get the compactness condition. In this regard, it is worth to observe that even if the coercivity of the logarithmic weight in the definition of $\widetilde X$
to get the compactness condition. In this regard, it is worth to observe that even if the coercivity of the logarithmic weight in the definition of $\widetilde X$![]() guarantees the compactness of the embedding of $\widetilde X$
guarantees the compactness of the embedding of $\widetilde X$![]() in the Lebesgue spaces $L^p$
in the Lebesgue spaces $L^p$![]() , for $p\in [2,+\infty )$
, for $p\in [2,+\infty )$![]() , the logarithmic weight in the functional $I$
, the logarithmic weight in the functional $I$![]() does not work in the compactness of the functional, because its contribution is invariant by translation.
does not work in the compactness of the functional, because its contribution is invariant by translation.
We prove the following result.
Theorem 1.1 If $p\ge 4,$![]() and $V$
and $V$![]() verifies (V), then equation (E) has at least a non-trivial weak solution $\bar u\in X$
verifies (V), then equation (E) has at least a non-trivial weak solution $\bar u\in X$![]() , with $\bar u\ge 0$
, with $\bar u\ge 0$![]() . Moreover, if $p>4$
. Moreover, if $p>4$![]() then the solution $\bar u$
then the solution $\bar u$![]() is a ground state solution:
is a ground state solution:
If $V\in L^q_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() for some $q>1,$
for some $q>1,$![]() then $\bar u\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$
then $\bar u\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() and $\bar u(x)>0,$
and $\bar u(x)>0,$![]() for all $x\in \mathbb {R}^2$
for all $x\in \mathbb {R}^2$![]() .
.
If $V\in L^q_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() for some $q>2,$
for some $q>2,$![]() then $\bar u\in {\mathcal {C}}^{1,\alpha }_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$
then $\bar u\in {\mathcal {C}}^{1,\alpha }_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() .
.
If $V\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2),$![]() then $\bar u\in {\mathcal {C}}^2(\mathbb {R}^2)$
then $\bar u\in {\mathcal {C}}^2(\mathbb {R}^2)$![]() is a classical solution.
is a classical solution.
To prove Theorem 1.1, we use a variant of the mountain pass Theorem (see Theorem 2.6). Indeed, it is not convenient to try a direct application of the mountain pass Theorem because it is not straightforward to see that $I$![]() is a positive quadratic form near 0 with respect to the $X$
is a positive quadratic form near 0 with respect to the $X$![]() -norm. On the contrary, it is easy to see that $I$
-norm. On the contrary, it is easy to see that $I$![]() is quadratic in zero with respect to the usual $H^1$
is quadratic in zero with respect to the usual $H^1$![]() -norm. Let us remark that for $p=4$
-norm. Let us remark that for $p=4$![]() , the analysis of I on the fiber $t\mapsto t u(\cdot )$
, the analysis of I on the fiber $t\mapsto t u(\cdot )$![]() is not sufficient to guarantee the mountain pass structure, so for $p=4$
is not sufficient to guarantee the mountain pass structure, so for $p=4$![]() a different fiber $t\mapsto u_t$
a different fiber $t\mapsto u_t$![]() has to be considered. Moreover, the assumption $p>4$
has to be considered. Moreover, the assumption $p>4$![]() is necessary to apply the fibering techniques that guarantee that the mountain pass solution is a ground state. To apply Theorem 2.6, a basic tool is the Cerami compactness condition, that can be verified because of (V) and $p\ge 4$
is necessary to apply the fibering techniques that guarantee that the mountain pass solution is a ground state. To apply Theorem 2.6, a basic tool is the Cerami compactness condition, that can be verified because of (V) and $p\ge 4$![]() .
.
The paper is organized as follows: in § 2, we introduce the main notation and some preliminary results, in § 3, we prove the compactness condition and in § 4, we prove Theorem 1.1.
2. Variational framework and preliminary facts
Since in the present work we focus on (E) in the case $\gamma,b,\inf V > 0$![]() , to simplify the notation, we assume
, to simplify the notation, we assume
We use the following notation:
• $\int =\int _{\mathbb {R}^2}$
 .
.• $B_r(y)$
 denotes the open ball of radius $r>0$
denotes the open ball of radius $r>0$ and centre $y\in \mathbb {R}^2$
and centre $y\in \mathbb {R}^2$ .
.• $L^p$
 , $1\leq p<+\infty$
, $1\leq p<+\infty$ , and $H^1$
, and $H^1$ are the usual Lebesgue and Sobolev spaces in $\mathbb {R}^2$
are the usual Lebesgue and Sobolev spaces in $\mathbb {R}^2$ , with norm $|u|_{p}=(\int |u|^p{\rm d}x)^{1/p}$
, with norm $|u|_{p}=(\int |u|^p{\rm d}x)^{1/p}$ and $\|u\|=(\int (|\nabla u|^2+u^2)\,{\rm d}x)^{1/2}$
and $\|u\|=(\int (|\nabla u|^2+u^2)\,{\rm d}x)^{1/2}$ , respectively.
, respectively.• We denote by $C, c_1, c_2,\ldots$
 various constants that can also vary from one line to another.
various constants that can also vary from one line to another.
First, in Lemma 2.1, we recall from [Reference Cingolani and Weth10, Reference Stubbe27] that the nonlocal term is well defined and regular in $\widetilde X$![]() . To state this result, let us introduce the following bilinear forms:
. To state this result, let us introduce the following bilinear forms:

where $u, v:\mathbb {R}^2 \to \mathbb {R}$![]() are measurable functions such that the integrals are well defined. Correspondingly, let
are measurable functions such that the integrals are well defined. Correspondingly, let
With this notation, the functional related to problem (E) takes the form
Lemma 2.1 The functional $I$![]() is a well-defined $C^2$
is a well-defined $C^2$![]() functional on the Hilbert space X. Moreover, $V_2$
functional on the Hilbert space X. Moreover, $V_2$![]() is of class $C^1$
is of class $C^1$![]() on $L^\frac 83 (\mathbb {R}^2)$
on $L^\frac 83 (\mathbb {R}^2)$![]() and the following formulas hold
and the following formulas hold
In particular,
For the proof, see [Reference Cingolani and Weth10, Lemma 2.2] and [Reference Sardilli26, Lemma 3.1.5].
Moreover, let us recall the Hardy–Littlewood–Sobolev inequality (see [Reference Lieb and Loss18, Theorem 4.3]):
where $p,r>1$![]() and $0 <\lambda < N$
and $0 <\lambda < N$![]() are such that $\frac {1}{p} + \frac {\lambda }{N} + \frac {1}{r} = 2$
are such that $\frac {1}{p} + \frac {\lambda }{N} + \frac {1}{r} = 2$![]() . Then, by (2.2) and $\log (1+r)\le r$
. Then, by (2.2) and $\log (1+r)\le r$![]() , $\forall r>0$
, $\forall r>0$![]() , it is readily seen that
, it is readily seen that
Next, we introduce the Cerami compactness condition.
Definition 2.2 Let $X$![]() be a Banach space, $I\in C^1(X)$
be a Banach space, $I\in C^1(X)$![]() and $c \in \mathbb {R}$
and $c \in \mathbb {R}$![]() . A sequence $\{x_n\}_n$
. A sequence $\{x_n\}_n$![]() is called a $(C)$
is called a $(C)$![]() sequence for $I$
sequence for $I$![]() at the level $c$
at the level $c$![]() if
if
We say that $I$![]() satisfies the Palais–Smale–Cerami condition (at the level $c$
satisfies the Palais–Smale–Cerami condition (at the level $c$![]() ), $(C)$
), $(C)$![]() condition for short, if any $(C)$
condition for short, if any $(C)$![]() sequence (at the level $c$
sequence (at the level $c$![]() ) possesses a converging subsequence.
) possesses a converging subsequence.
To analyse the compactness condition, we report some known facts: Lemma 2.3 is Lemma 2.6 in [Reference Cingolani and Weth10] and states a continuity property of the bilinear form $B_1$![]() , Lemma 2.4 provides the compactness of the embedding of $X$
, Lemma 2.4 provides the compactness of the embedding of $X$![]() in the Lebesgue spaces.
in the Lebesgue spaces.
Lemma 2.3 Let $\{u_n\}_n, \{v_n\}_n, \{w_n\}_n$![]() be bounded sequences in X such that $u_n \to u$
be bounded sequences in X such that $u_n \to u$![]() weakly in X. Then, for every $z\in X$
weakly in X. Then, for every $z\in X$![]() , we have $B_1(v_nw_n, z(u_n - u)) \to 0$
, we have $B_1(v_nw_n, z(u_n - u)) \to 0$![]() as $n\to \infty$
as $n\to \infty$![]() .
.
Lemma 2.4 The space $X$![]() is compactly embedded in $L^q(\mathbb {R}^2)$
is compactly embedded in $L^q(\mathbb {R}^2)$![]() for all $q \in [2, +\infty )$
for all $q \in [2, +\infty )$![]() .
.
Since bounded sets in $X$![]() are also bounded sets in $\widetilde X$
are also bounded sets in $\widetilde X$![]() (see (1.2), (1.3)), to verify Lemma 2.4 it is sufficient to exploit the coercivity of the map $|x|\mapsto \log (1+|x|)$
(see (1.2), (1.3)), to verify Lemma 2.4 it is sufficient to exploit the coercivity of the map $|x|\mapsto \log (1+|x|)$![]() and apply, for example, Theorem XIII.65 in [Reference Reed and Simon24] (see also [Reference Rabinowitz23]).
and apply, for example, Theorem XIII.65 in [Reference Reed and Simon24] (see also [Reference Rabinowitz23]).
Finally, let us state the topological tools we will use in the proof of Theorem 1.1.
Lemma 2.5 see [Reference Li and Wang17, Lemma 2.6]
Let $X$![]() be a Banach space, $I \in C^{1}(X),$
be a Banach space, $I \in C^{1}(X),$![]() $c \in \mathbb {R},$
$c \in \mathbb {R},$![]() $\varepsilon >0$
$\varepsilon >0$![]() and suppose that there exists $\alpha >0$
and suppose that there exists $\alpha >0$![]() such that
such that
Then there exists a continuous map $\eta :X \to X$![]() , such that:
, such that:
1. $\eta (I^{c+\epsilon }) \subset (I^{c-\epsilon });$

2. $\eta (x) = x,$
 for all $x \not \in I^{c+2\epsilon }_{c-2\epsilon },$
for all $x \not \in I^{c+2\epsilon }_{c-2\epsilon },$
where $I^a=\{x\in X\ :\ I(x)\le a\}$![]() and $I^b_a=\{x\in X\ :\ a\le I(x)\le b\}$
and $I^b_a=\{x\in X\ :\ a\le I(x)\le b\}$![]() , for all $a< b$
, for all $a< b$![]() .
.
From Lemma 2.5 there follows the following variant of the Mountain Pass Theorem.
Theorem 2.6 Let $I \in C^{1}(X)$![]() , X a Banach space. We suppose that $I(0) = 0$
, X a Banach space. We suppose that $I(0) = 0$![]() and there exists a closed subspace $S \subset X$
and there exists a closed subspace $S \subset X$![]() that disconnects $X$
that disconnects $X$![]() in two path-connected components $X_1$
in two path-connected components $X_1$![]() and $X_2$
and $X_2$![]() . We assume that $0 \in X_1$
. We assume that $0 \in X_1$![]() and there exists $A>0$
and there exists $A>0$![]() , $\bar u \in X_2$
, $\bar u \in X_2$![]() such that
such that
• $I\big |_S\geq A;$

• $I(\bar u)\leq 0$
 .
.
Set
where $\Gamma :=\{\gamma : [0,1] \to X: \gamma\mbox{ is continuous,}\ \gamma (0)=0,\ \gamma (1) \in X_2,\ I(\gamma (1))\leq 0 \}$![]() . If $I$
. If $I$![]() verifies the (C) condition at $c,$
verifies the (C) condition at $c,$![]() then $c$
then $c$![]() is a critical value for $I$
is a critical value for $I$![]() .
.
The proof of Theorem 2.6 is standard so we give here only a sketch of it, for the sake of completeness.
If, by contradiction, $c$![]() is not a critical value for $I$
is not a critical value for $I$![]() , then (2.4) has to be verified for suitable $\varepsilon,\alpha >0$
, then (2.4) has to be verified for suitable $\varepsilon,\alpha >0$![]() , because $I$
, because $I$![]() verifies the (C) condition at the level $c$
verifies the (C) condition at the level $c$![]() . We can choose $\varepsilon < A$
. We can choose $\varepsilon < A$![]() . Now, let $\gamma _\varepsilon \in \Gamma$
. Now, let $\gamma _\varepsilon \in \Gamma$![]() be such that $\max _{[0,1]}I(\gamma _\varepsilon (t))\le c+\varepsilon$
be such that $\max _{[0,1]}I(\gamma _\varepsilon (t))\le c+\varepsilon$![]() . If we consider $\tilde \gamma _\varepsilon :=\eta \circ \gamma _\varepsilon$
. If we consider $\tilde \gamma _\varepsilon :=\eta \circ \gamma _\varepsilon$![]() , where $\eta$
, where $\eta$![]() is the deformation provided by Lemma 2.5, it turns out that
is the deformation provided by Lemma 2.5, it turns out that
contrary to the definition of $c$![]() .
.
3. Compactness
This section is devoted to prove that the (C) condition holds at positive values, that is the range where we are looking for critical levels:
Remark 3.1 Let $u$![]() be a nontrivial critical point of $I$
be a nontrivial critical point of $I$![]() , then $I(u)>0$
, then $I(u)>0$![]() .
.
Indeed, by $p\ge 4$![]() and assumption (V)$(b)$
and assumption (V)$(b)$![]() ,
,

Proposition 3.2 Assume that $p\ge 4$![]() and $V$
and $V$![]() satisfies (V), and let $\{u_n\}_n$
satisfies (V), and let $\{u_n\}_n$![]() be a $(C)$
be a $(C)$![]() sequence at the level $c$
sequence at the level $c$![]() . If $c>0$
. If $c>0$![]() then $\{u_n\}_n$
then $\{u_n\}_n$![]() is relatively compact.
is relatively compact.
A key point to prove the proposition is the following lemma that states the boundedness of the $(C)$![]() sequences at the positive levels.
sequences at the positive levels.
Lemma 3.3 Under the assumptions of Proposition 3.2, the sequence $\{u_n\}_n$![]() is bounded in $X$
is bounded in $X$![]() . Moreover, there exist a ball $B_2(\bar x)$
. Moreover, there exist a ball $B_2(\bar x)$![]() and a constant $d>0$
and a constant $d>0$![]() such that, up to a subsequence,
such that, up to a subsequence,
Proof. Since $\{u_n\}_n$![]() is a (C) sequence, it turns out that
is a (C) sequence, it turns out that
and so we have

Therefore, $\{u_n\}_n$![]() is bounded in $H^1(\mathbb {R}^2)$
is bounded in $H^1(\mathbb {R}^2)$![]() , hence in $L^q(\mathbb {R}^2)$
, hence in $L^q(\mathbb {R}^2)$![]() for all $q\in [2, +\infty )$
for all $q\in [2, +\infty )$![]() , and
, and
So, we are left to prove that
Let us define

We claim that $\delta >0$![]() . Assume, by contradiction, that $\delta = 0$
. Assume, by contradiction, that $\delta = 0$![]() . Then by [Reference Lions19, Lemma I.1] there follows
. Then by [Reference Lions19, Lemma I.1] there follows
and so, by (2.3), we get
From (3.2), (3.4) and (3.5), we infer
that, by the positivity of $V_1$![]() , implies
, implies
Summarizing, from (3.4), (3.5) and (3.6), we infer
contrary to $I(u_n)\to c>0$![]() , and the claim follows.
, and the claim follows.
Then, $\delta > 0$![]() and there exists a sequence $\{x_n\}_n \subset \mathbb {R}^2$
and there exists a sequence $\{x_n\}_n \subset \mathbb {R}^2$![]() such that
such that
for n large enough.
The task is now to prove that $\{x_n\}$![]() is bounded. Assume by contradiction that $|x_n| \to \infty$
is bounded. Assume by contradiction that $|x_n| \to \infty$![]() , up to a subsequence.
, up to a subsequence.
Let us fix an arbitrary $M>0$![]() and call
and call
By (V) $(c)$![]() and $|x_n| \to \infty$
and $|x_n| \to \infty$![]() , we obtain
, we obtain
Observe that from (3.8) we infer, for any fixed $q>2$![]() ,
,
As a consequence
Then, taking into account (2.3), we have

where $C_2$![]() is a constant independent of $M$
is a constant independent of $M$![]() . Letting $M\to \infty$
. Letting $M\to \infty$![]() in (3.9), we get a contradiction, hence $\{x_n\}$
in (3.9), we get a contradiction, hence $\{x_n\}$![]() has to be bounded.
has to be bounded.
Therefore, there exists $\bar {x}\in \mathbb {R}^2$![]() such that $x_n\to \bar {x}$
such that $x_n\to \bar {x}$![]() , up to a subsequence. Taking into account (3.7), we can also assume that
, up to a subsequence. Taking into account (3.7), we can also assume that
that proves (3.1).
Now, observe that for every $R>0$![]()
Then, fixing $\bar R>|\bar x|+2$![]() and taking into account (3.10), we get
and taking into account (3.10), we get

Thus, we conclude that
Since $\{|u_n|_2\}_n$![]() is bounded, if we prove that $\{V_1(u_n)\}_n$
is bounded, if we prove that $\{V_1(u_n)\}_n$![]() is bounded, we are done.
is bounded, we are done.
Observe that
from which we infer, taking into account (2.3),
that is the desired result.
Proof of Proposition 3.2. By Lemma 3.3, $\{u_n\}_n$![]() is bounded in the Hilbert space $X$
is bounded in the Hilbert space $X$![]() , so, taking also into account Lemma 2.4, there exists $\bar u\in X$
, so, taking also into account Lemma 2.4, there exists $\bar u\in X$![]() such that, up to a subsequence,
such that, up to a subsequence,
Clearly, the sequence $\{u_n\}$![]() is bounded also in the weighted Hilbert space
is bounded also in the weighted Hilbert space
Hence, we can assume that $\{u_n\}$![]() weakly converges in $H_V$
weakly converges in $H_V$![]() to a function $\tilde u\in H_V$
to a function $\tilde u\in H_V$![]() . Observe that $\tilde u=\bar u$
. Observe that $\tilde u=\bar u$![]() . Indeed for every fixed $\varphi \in {\mathcal {C}}^\infty _0(\mathbb {R}^2)$
. Indeed for every fixed $\varphi \in {\mathcal {C}}^\infty _0(\mathbb {R}^2)$![]() the map
the map
is a continuous linear form on $X$![]() and on $H_V$
and on $H_V$![]() , so that
, so that
Then we can conclude that
and the assertion follows by the fundamental lemma of Calculus of Variations (see e.g. [Reference Brezis5, Corollary 4.24]).
Now, from the boundedness in $X$![]() of the (C) sequence $\{u_n\}_n$
of the (C) sequence $\{u_n\}_n$![]() , we get
, we get

The weak convergence in $H_V$![]() yields
yields


By (3.15),
From (3.16), taking into account (3.17), (3.18), (3.19) and (3.20), we infer

Thus, it follows that
and
Taking into account (3.1) and arguing exactly as in (3.11), we get
From (3.23), (3.22) and $u_n\to \bar u$![]() in $L^2$
in $L^2$![]() , there follows
, there follows
that, together with (3.21), gives $\|u_n-\bar u\|_X\to 0$![]() .
.
4. Proof of Theorem 1.1
To prove Theorem 1.1, we are going to apply Theorem 2.6. Since condition $(C)$![]() holds on $(0,+\infty )$
holds on $(0,+\infty )$![]() by Proposition 3.2, we are left to show that also the geometric conditions hold.
by Proposition 3.2, we are left to show that also the geometric conditions hold.
Observe that, by (2.3) and by the Sobolev inequality, for every $u \in X \setminus \{0\}$![]()

Since $p\ge 4$![]() , there exist $A >0$
, there exist $A >0$![]() and $\bar {\rho }>0$
and $\bar {\rho }>0$![]() such that $I_{|_{S }}\geq A$
such that $I_{|_{S }}\geq A$![]() , where $S :=\{u \in X: \|u\| = \bar \rho \}$
, where $S :=\{u \in X: \|u\| = \bar \rho \}$![]() . The closed set $S$
. The closed set $S$![]() disconnects $X$
disconnects $X$![]() in the two path-connected components
in the two path-connected components
Clearly, $0 \in X_1$![]() and $I(0)=0$
and $I(0)=0$![]() .
.
Now, we are going to show that there exists $\bar u\in X_2$![]() such that $I(\bar u)<0$
such that $I(\bar u)<0$![]() . If $p>4$
. If $p>4$![]() , let us fix $\tilde u\in X\setminus \{0\}$
, let us fix $\tilde u\in X\setminus \{0\}$![]() and observe that $\lim \limits _{t\to \infty }I(t\tilde u)=-\infty$
and observe that $\lim \limits _{t\to \infty }I(t\tilde u)=-\infty$![]() , so the claim follows.
, so the claim follows.
If $p=4$![]() , then let us fix $\tilde u\in {\mathcal {C}} (\mathbb {R}^2)$
, then let us fix $\tilde u\in {\mathcal {C}} (\mathbb {R}^2)$![]() with compact support and define $u_t:=t^2\tilde u(t\,\cdot )$
with compact support and define $u_t:=t^2\tilde u(t\,\cdot )$![]() , for $t>0$
, for $t>0$![]() . We can assume that $0$
. We can assume that $0$![]() is a Lebesgue point for $V$
is a Lebesgue point for $V$![]() , then, by standard computations,
, then, by standard computations,

where $o(1)\to 0$![]() as $t\to \infty$
as $t\to \infty$![]() . Since (4.2) implies $\lim \limits _{t\to \infty }I( u_t)=-\infty$
. Since (4.2) implies $\lim \limits _{t\to \infty }I( u_t)=-\infty$![]() , and $\|u_t\|\to \infty$
, and $\|u_t\|\to \infty$![]() as $t\to \infty$
as $t\to \infty$![]() , the existence of $\bar u\in X_2$
, the existence of $\bar u\in X_2$![]() such that $I(\bar u)<0$
such that $I(\bar u)<0$![]() follows.
follows.
Then, the value
where $\Gamma := \{\gamma :[0,1] \to X: \gamma\mbox{ is continuous,}\ \gamma (0)=0, \gamma (1) \in X_2, I(\gamma (1))\leq 0 \}$![]() , is a critical value for $I$
, is a critical value for $I$![]() , according to Theorem 2.6, with $c\ge A>0$
, according to Theorem 2.6, with $c\ge A>0$![]() .
.
Now, let $p>4$![]() . To verify that $c$
. To verify that $c$![]() is a ground state level, let us fix any nontrivial solution $\tilde u$
is a ground state level, let us fix any nontrivial solution $\tilde u$![]() and consider the path $t\mapsto t\tilde u$
and consider the path $t\mapsto t\tilde u$![]() . A direct computation shows that the real function $t\mapsto I( t\tilde u)$
. A direct computation shows that the real function $t\mapsto I( t\tilde u)$![]() has a unique critical point $t_{\tilde u}$
has a unique critical point $t_{\tilde u}$![]() , that corresponds to a maximum. From $\frac {d\,}{dt}I(t\tilde u)=I'(t\tilde u)[\tilde u]$
, that corresponds to a maximum. From $\frac {d\,}{dt}I(t\tilde u)=I'(t\tilde u)[\tilde u]$![]() we infer $t_{\tilde u}=1$
we infer $t_{\tilde u}=1$![]() . Then, taking into account that $\lim \limits _{t\to \infty }I(t\tilde u)=-\infty$
. Then, taking into account that $\lim \limits _{t\to \infty }I(t\tilde u)=-\infty$![]() and (4.3), it is readily seen that
and (4.3), it is readily seen that
that is our claim.
Our next goal is to show that there exists a constant sign solution. Let $u$![]() be a critical point for $I$
be a critical point for $I$![]() at the level $c$
at the level $c$![]() and consider the path $t\mapsto t|u|$
and consider the path $t\mapsto t|u|$![]() . Since the functional is even, $c=\max _{t\ge 0}I(t|u|)=I(|u|)$
. Since the functional is even, $c=\max _{t\ge 0}I(t|u|)=I(|u|)$![]() from which we infer that $\bar u:=|u|$
from which we infer that $\bar u:=|u|$![]() is a critical point for $I$
is a critical point for $I$![]() , too. So, $\bar u$
, too. So, $\bar u$![]() is the weak solution we are looking for.
is the weak solution we are looking for.
Now, we consider the regularity issue. For classical regularity results, we refer the reader to [Reference Lieb and Loss18, §10] (in particular Theorems 10.2 and 10.3), or to [Reference Gilbarg and Trudinger16, §8].
Observe that
(see (1.1)).
Assume $V\in L^q_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() for some $q>1$
for some $q>1$![]() . Since $\bar u\in L^r(\mathbb {R}^2)$
. Since $\bar u\in L^r(\mathbb {R}^2)$![]() for every $r\in [2,\infty )$
for every $r\in [2,\infty )$![]() , and $\phi _u\in {\mathcal {C}}^3(\mathbb {R}^2)$
, and $\phi _u\in {\mathcal {C}}^3(\mathbb {R}^2)$![]() (see [Reference Cingolani and Weth10, Proposition 2.3]), we get $\varphi \in L^s_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$
(see [Reference Cingolani and Weth10, Proposition 2.3]), we get $\varphi \in L^s_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() for every $s\in [1,q)$
for every $s\in [1,q)$![]() . So we are in position to apply classical regularity results and obtain $\bar u\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$
. So we are in position to apply classical regularity results and obtain $\bar u\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() . Moreover, we can also write
. Moreover, we can also write
and then, since $\psi \in L^q_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() , by the Harnack inequality, we can conclude $\bar u>0$
, by the Harnack inequality, we can conclude $\bar u>0$![]() (see [Reference Pucci and Serrin22, Theorem 7.2.1]).
(see [Reference Pucci and Serrin22, Theorem 7.2.1]).
If $V\in L^q_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() for some $q>2$
for some $q>2$![]() , then we can argue as before and conclude $\varphi \in L^s_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$
, then we can argue as before and conclude $\varphi \in L^s_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() for every $s\in [1,q)$
for every $s\in [1,q)$![]() , so that $\bar u\in {\mathcal {C}}_{\mathop {\rm loc}\nolimits }^{1,\alpha }(\mathbb {R}^2)$
, so that $\bar u\in {\mathcal {C}}_{\mathop {\rm loc}\nolimits }^{1,\alpha }(\mathbb {R}^2)$![]() .
.
If $V\in {\mathcal {C}}^{0,\alpha }_{\mathop {\rm loc}\nolimits }(\mathbb {R}^2)$![]() , then the RHS in (4.4) is locally Hölder continuous, so $u\in {\mathcal {C}}^2(\mathbb {R}^2)$
, then the RHS in (4.4) is locally Hölder continuous, so $u\in {\mathcal {C}}^2(\mathbb {R}^2)$![]() by standard elliptic regularity (see, for example, [Reference Lieb and Loss18, §10]).
by standard elliptic regularity (see, for example, [Reference Lieb and Loss18, §10]).
Acknowledgements
R.M. has been supported by the INdAM-GNAMPA group. He acknowledges also the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006.