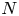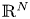Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T10:02:23.106Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of critical N-Laplacian problems

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  27 June 2022

Tsz Chung Ho  and
Kanishka Perera
Tsz Chung Ho
Affiliation:
Department of Mathematical Sciences, Florida Institute of Technology, Melbourne, FL 32901, USA (tho2011@my.fit.edu; kperera@fit.edu)
Kanishka Perera
Affiliation:
Department of Mathematical Sciences, Florida Institute of Technology, Melbourne, FL 32901, USA (tho2011@my.fit.edu; kperera@fit.edu)
Rights & Permissions [Opens in a new window]

Abstract

We establish some existence results for a class of critical $N$-Laplacian problems in a bounded domain in $\mathbb {R}^{N}$. In the absence of a suitable direct sum decomposition of the underlying Sobolev space to which the classical linking theorem can be applied, we use an abstract linking theorem based on the $\mathbb {Z}_2$-cohomological index to obtain a non-trivial critical point.

Keywords

critical N-Laplacian problemsexistencecritical pointslinkingℤ2-cohomological index

MSC classification

Primary: 35J92: Quasilinear elliptic equations with $p$-Laplacian
Secondary: 35B33: Critical exponents 35B38: Critical points
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 2 , May 2022 , pp. 556 - 576
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

1. Introduction

In this paper, we establish some existence results for the class of critical $N$-Laplacian problems

(1.1)\begin{equation} \left\{\begin{array}{@{}cc} - \Delta_N\, u = h(u)\, e^{\alpha\, |u|^{N'}} & \text{in } \Omega\\ u = 0 & \text{on } \partial {\Omega}, \end{array}\right. \end{equation}

where $\Omega$ is a smooth-bounded domain in $\mathbb {R}^{N},\, N \ge 2$, $\alpha > 0$, $N' = N/(N - 1)$ is the Hölder conjugate of $N$, and $h$ is a continuous function such that

(1.2)\begin{equation} \lim_{|t| \to \infty}\, h(t) = 0 \end{equation}

and

(1.3)\begin{equation} 0 < \beta := \liminf_{|t| \to \infty}\, th(t) < \infty. \end{equation}

This problem is motivated by the Trudinger–Moser inequality

(1.4)\begin{equation} \sup_{\substack{u \in W^{1,N}_0(\Omega)\\ \left\|u\right\| \le 1}}\, \displaystyle\int_\Omega e^{\alpha_N\, |u|^{N'}} \,{\rm d}x < \infty, \end{equation}

where $W^{1,N}_0(\Omega )$ is the usual Sobolev space with the norm

\begin{align*} \left\|u\right\| = \left(\int_\Omega |\nabla u|^{N} \,{\rm d}x\right)^{1/N},\\ \alpha_N = N\, \omega_{N-1}^{1/(N-1)}, \end{align*}

and

\[ \omega_{N-1} = \frac{2 \pi^{N/2}}{\Gamma(N/2)} \]

is the area of the unit sphere in $\mathbb {R}^{N}$ (see Trudinger [Reference Trudinger14] and Moser [Reference Moser10]). Problem (1.1) is critical with respect to this inequality and hence lacks compactness. Indeed, the associated variational functional satisfies the Palais–Smale compactness condition only at energy levels below a certain threshold (see Proposition 2.1 in the next section).

In dimension $N = 2$, problem (1.1) is semilinear and has been extensively studied in the literature (see, e.g., [Reference Adimurthi and Yadava2–Reference de Figueiredo, Miyagaki and Ruf4, Reference de Figueiredo, do Ó and Ruf6]). In dimensions $N \ge 3$, this problem is quasilinear and has been studied mainly when

(1.5)\begin{equation} G(t) := \displaystyle\int_0^{t} h(s)\, e^{\alpha\, |s|^{N'}} {\rm d}s \le \lambda\, |t|^{N} \quad \text{for small } t \end{equation}

for some $\lambda \in (0,\lambda _1)$ (see, e.g., [Reference Adimurthi1, Reference de Figueiredo, do Ó and Ruf5, Reference do Ó8]). Here,

(1.6)\begin{equation} \lambda_1 = \inf_{u \in W^{1,N}_0(\Omega) {\setminus} \left\{{0}\right\}}\, \displaystyle\frac{\displaystyle{\int}_\Omega |\nabla u|^{N} \,{\rm d}x}{\displaystyle{\int}_\Omega |u|^{N} \,{\rm d}x} \end{equation}

is the first eigenvalue of the eigenvalue problem

(1.7)\begin{equation} \left\{\begin{array}{@{}cc} - \Delta_N\, u = \lambda\, |u|^{N-2}\, u & \text{in } \Omega\\ u= 0 & \text{on } \partial {\Omega}. \end{array}\right. \end{equation}

The case $h(t) = \lambda \, |t|^{N-2}\, t$ with $\lambda > 0$, for which $\beta = \infty$, was recently studied in Yang and Perera [Reference Yang and Perera15]. The remaining case, where $N \ge 3$, $\lambda \ge \lambda _1$, and $\beta < \infty$, does not seem to have been studied in the literature. This case is covered in our results here, which are for large $\beta < \infty$ and allow $N \ge 3$ and $\lambda \ge \lambda _1$ in (1.5).

Let $d$ be the radius of the largest open ball contained in $\Omega$. Our first result is the following theorem.

Theorem 1.1 Assume that $\alpha > 0,$ $h$ satisfies (1.2) and (1.3) , and $G$ satisfies

(1.8)\begin{align} G(t) & \ge - \frac{1}{N}\, \sigma_0\, |t|^{N} \quad \text{for } t \ge 0, \end{align}
(1.9)\begin{align} G(t) & \le \frac{1}{N}\, (\lambda_1 - \sigma_1)\, |t|^{N} \quad \text{for } |t| \le \delta \end{align}

for some $\sigma _0 \ge 0$ and $\sigma _1, \delta > 0$. If

(1.10)\begin{equation} \beta > \displaystyle\frac{1}{N \alpha^{N-1}} \left(\frac{N}{d}\right)^{N}\! e^{\sigma_0/(N-1)\, \kappa}, \end{equation}

where $\kappa = \dfrac {1}{N!} \left(\dfrac {N}{d}\right)^{N},$ then problem (1.1) has a non-trivial solution.

In particular, we have the following corollary for $\sigma _0 = 0$.

Corollary 1.2 Assume that $\alpha > 0,$ $h$ satisfies (1.2) and (1.3), and $G$ satisfies

\begin{align*} G(t) & \ge 0 \quad \text{for } t \ge 0,\\ G(t) & \le \frac{1}{N}\, (\lambda_1 - \sigma_1)\, |t|^{N} \quad \text{for } |t| \le \delta \end{align*}

for some $\sigma _1, \delta > 0$. If

\[ \beta > \frac{1}{N \alpha^{N-1}} \left(\frac{N}{d}\right)^{N}, \]

then problem (1.1) has a non-trivial solution.

Corollary 1.2 should be compared with Theorem 1 of do Ó [Reference do Ó8], where this result is proved under the stronger assumption $h(t) \ge 0$ for $t \ge 0$.

To state our second result, let $\left ({\lambda _k}\right )$ be the sequence of eigenvalues of problem (1.7) based on the $\mathbb {Z}_2$-cohomological index that was introduced in Perera [Reference Perera11] (see Proposition 2.3 in the next section). We have the following theorem.

Theorem 1.3 Assume that $\alpha > 0,$ $h$ satisfies (1.2) and (1.3), and $G$ satisfies

(1.11)\begin{align} G(t) & \ge \frac{1}{N}\, (\lambda_{k-1} + \sigma_0)\, |t|^{N} \quad \forall t, \end{align}
(1.12)\begin{align} G(t) & \le \frac{1}{N}\, (\lambda_k - \sigma_1)\, |t|^{N} \quad \text{for } |t| \le \delta \end{align}

for some $k \ge 2$ and $\sigma _0, \sigma _1, \delta > 0$. Then there exists a constant $c > 0$ depending on $\Omega$, $\alpha$, and $k$, but not on $\sigma _0$, $\sigma _1$, or $\delta$, such that if

\[ \beta > \frac{1}{\alpha^{N-1}} \left(\frac{N}{d}\right)^{N}\! e^{c/\sigma_0^{N-1}}, \]

then problem (1.1) has a non-trivial solution.

Theorem 1.3 should be compared with Theorem 1.4 of de Figueiredo et al. [Reference de Figueiredo, Miyagaki and Ruf3, Reference de Figueiredo, Miyagaki and Ruf4], where this result is proved in the case $N = 2$ under the additional assumption that $0 < 2G(t) \le th(t)\, e^{\alpha t^{2}}$ for all $t \in \mathbb {R} {\setminus} \left \{{0}\right \}$. However, the linking argument used in [Reference de Figueiredo, Miyagaki and Ruf3, Reference de Figueiredo, Miyagaki and Ruf4] is based on a splitting of $H^{1}_0(\Omega )$ that involves the eigenspaces of the Laplacian, and this argument does not extend to the case $N \ge 3$ where the $N$-Laplacian is a nonlinear operator and therefore has no linear eigenspaces. We will prove Theorem 1.3 using an abstract critical point theorem based on the $\mathbb {Z}_2$-cohomological index that was proved in Yang and Perera [Reference Yang and Perera15] (see § 2.4).

In the proofs of Theorems 1.1 and 1.3, the inner radius $d$ of $\Omega$ comes into play when verifying that certain minimax levels are below the compactness threshold given in Proposition 2.1.

2. Preliminaries

2.1. A compactness result

Weak solutions of problem (1.1) coincide with critical points of the $C^{1}$-functional

\[ E(u) = \frac{1}{N} \int_\Omega |\nabla u|^{N} \,{\rm d}x - \int_\Omega G(u)\,{\rm d}x, \quad u \in W^{1,N}_0(\Omega). \]

We recall that a $(\text {PS})_{c}$ sequence of $E$ is a sequence $\left ({u_j}\right ) \subset W^{1,N}_0(\Omega )$ such that $E(u_j) \to c$ and $E'(u_j) \to 0$. Proofs of Theorem 1.1 and Theorem 1.3 will be based on the following compactness result.

Proposition 2.1 Assume that $\alpha > 0$ and $h$ satisfies (1.2) and (1.3). Then for all $c \ne 0$ satisfying

\[ c < \frac{1}{N} \left(\frac{\alpha_N}{\alpha}\right)^{N-1}, \]

every $(\text {PS})_{c}$ sequence of $E$ has a subsequence that converges weakly to a non-trivial solution of problem (1.1).

Proof. Let $\left ({u_j}\right ) \subset W^{1,N}_0(\Omega )$ be a $(\text {PS})_{c}$ sequence of $E$. Then,

(2.1)\begin{equation} E(u_j) = \displaystyle\frac{1}{N} \left\|u_j\right\|^{N} - \displaystyle\int_\Omega G(u_j)\,{\rm d}x = c + \text{o}(1) \end{equation}

and

(2.2)\begin{equation} E'(u_j)\, u_j = \left\|u_j\right\|^{N} - \displaystyle\int_\Omega u_j\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} \,{\rm d}x = \text{o}(\left\|u_j\right\|). \end{equation}

First, we show that $\left ({u_j}\right )$ is bounded in $W^{1,N}_0(\Omega )$. Multiplying (2.1) by $2N$ and subtracting (2.2) gives

\[ \left\|u_j\right\|^{N} + \int_\Omega \left(u_j\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} - 2N G(u_j)\right) \,{\rm d}x = 2Nc + \text{o}(\left\|u_j\right\| + 1), \]

so it suffices to show that $th(t)\, e^{\alpha \, |t|^{N'}} - 2N G(t)$ is bounded from below. Let $0 < \varepsilon < \beta /(2N + 1)$. By (1.2) and (1.3), for some constant $C_\varepsilon > 0$,

(2.3)\begin{equation} |G(t)| \le \varepsilon\, e^{\alpha\, |t|^{N'}} + C_\varepsilon \end{equation}

and

(2.4)\begin{equation} th(t)\, e^{\alpha\, |t|^{N'}} \ge (\beta - \varepsilon)\, e^{\alpha\, |t|^{N'}} - C_\varepsilon \end{equation}

for all $t$. So

\[ th(t)\, e^{\alpha\, |t|^{N'}} - 2N G(t) \ge [\beta - (2N + 1)\, \varepsilon]\, e^{\alpha\, |t|^{N'}} - (2N + 1)\, C_\varepsilon, \]

which is bounded from below.

Since $\left ({u_j}\right )$ is bounded in $W^{1,N}_0(\Omega )$, a renamed subsequence converges to some $u$ weakly in $W^{1,N}_0(\Omega )$, strongly in $L^{p}(\Omega )$ for all $p \in [1,\infty )$, and a.e.in $\Omega$. We have

(2.5)\begin{equation} E'(u_j)\, v = \displaystyle\int_\Omega |\nabla u_j|^{N-2}\, \nabla u_j \cdot \nabla v\,{\rm d}x - \int_\Omega v\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} \,{\rm d}x \to 0 \end{equation}

for all $v \in W^{1,N}_0(\Omega )$. By (1.2), given any $\varepsilon > 0$, there exists a constant $C_\varepsilon > 0$ such that

(2.6)\begin{equation} |h(t)\, e^{\alpha\, |t|^{N'}}| \le \varepsilon\, e^{\alpha\, |t|^{N'}} + C_\varepsilon \quad \forall t. \end{equation}

By (2.2),

\[ \sup_j\, \int_\Omega u_j\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} \,{\rm d}x < \infty, \]

which together with (2.4) gives

(2.7)\begin{equation} \sup_j\, \displaystyle\int_\Omega e^{\alpha\, |u_j|^{N'}} \,{\rm d}x < \infty. \end{equation}

For $v \in C^{\infty }_0(\Omega )$, it follows from (2.6) and (2.7) that the sequence $(v\, h(u_j)\, e^{\alpha \, |u_j|^{N'}})$ is uniformly integrable and hence

\[ \int_\Omega v\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} \,{\rm d}x \to \int_\Omega v\, h(u)\, e^{\alpha\, |u|^{N'}} \,{\rm d}x \]

by Vitali's convergence theorem, so it follows from (2.5) that

\[ \int_\Omega |\nabla u|^{N-2}\, \nabla u \cdot \nabla v\,{\rm d}x - \int_\Omega v\, h(u)\, e^{\alpha\, |u|^{N'}} \,{\rm d}x = 0. \]

Then this holds for all $v \in W^{1,N}_0(\Omega )$ by density, so the weak limit $u$ is a solution of problem (1.1).

Suppose that $u = 0$. Then

\[ \int_\Omega G(u_j)\,{\rm d}x \to 0 \]

since (2.3) and (2.7) imply that the sequence $\left ({G(u_j)}\right )$ is uniformly integrable, so (2.1) gives $c \ge 0$ and

(2.8)\begin{equation} \left\|u_j\right\| \to (Nc)^{1/N}. \end{equation}

Let $Nc < \nu < (\alpha _N/\alpha )^{N-1}$. Then $\left \|u_j\right \| \le \nu ^{1/N}$ for all $j \ge j_0$ for some $j_0$. Let $q = \alpha _N/\alpha \nu ^{1/(N-1)} > 1$. By the Hölder inequality,

\[ \left|{\int_\Omega u_j\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} \,{\rm d}x}\right| \le \left(\int_\Omega |u_j\, h(u_j)|^{p}\,{\rm d}x\right)^{1/p}\! \left(\int_\Omega e^{q \alpha\, |u_j|^{N'}} \,{\rm d}x\right)^{1/q}, \]

where $1/p + 1/q = 1$. The first integral on the right-hand side converges to zero since $h$ is bounded and $u_j \to 0$ in $L^{p}(\Omega )$, and the second integral is bounded by (1.4) since $q \alpha \, |u_j|^{N'} = \alpha _N\, |\widetilde {u}_j|^{N'}$, where $\widetilde {u}_j = u_j/\nu ^{1/N}$ satisfies $\left \|\widetilde {u}_j\right \| \le 1$ for $j \ge j_0$, so

\[ \int_\Omega u_j\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} \,{\rm d}x \to 0. \]

Then, $u_j \to 0$ by (2.2) and hence $c = 0$ by (2.8), contrary to assumption. So $u$ is a non-trivial solution.

2.2. $\mathbb {Z}_2$-cohomological index

The $\mathbb {Z}_2$-cohomological index of Fadell and Rabinowitz [Reference Fadell and Rabinowitz9] is defined as follows. Let $W$ be a Banach space and let $\mathcal {A}$ denote the class of symmetric subsets of $W {\setminus} \left \{{0}\right \}$. For $A \in \mathcal {A}$, let $\overline {A} = A/\mathbb {Z}_2$ be the quotient space of $A$ with each $u$ and $-u$ identified, let $f : \overline {A} \to \mathbb {R} \text {P}^{\infty }$ be the classifying map of $\overline {A}$, and let $f^{\ast } : H^{\ast }(\mathbb {R} \text {P}^{\infty }) \to H^{\ast }(\overline {A})$ be the induced homomorphism of the Alexander–Spanier cohomology rings. The cohomological index of $A$ is defined by

\[ i(A) = \begin{cases} \sup \left\{{m \ge 1 : f^{{\ast}}(\omega^{m-1}) \ne 0}\right\}, & A \ne \emptyset\\ 0, & A = \emptyset, \end{cases} \]

where $\omega \in H^{1}(\mathbb {R} \text {P}^{\infty })$ is the generator of the polynomial ring $H^{\ast }(\mathbb {R} \text {P}^{\infty }) = \mathbb {Z}_2[\omega ]$. For example, the classifying map of the unit sphere $S^{m-1}$ in $\mathbb {R}^{m},\, m \ge 1$ is the inclusion $\mathbb {R} \text {P}^{m-1} \subset \mathbb {R} \text {P}^{\infty }$, which induces isomorphisms on $H^{q}$ for $q \le m - 1$, so $i(S^{m-1}) = m$.

The following proposition summarizes the basic properties of the cohomological index (see Fadell and Rabinowitz [Reference Fadell and Rabinowitz9]).

Proposition 2.2 The index $i : \mathcal {A} \to \mathbb {N} \cup \left \{{0,\infty }\right \}$ has the following properties:

  1. (i) Definiteness: $i(A) = 0$ if and only if $A = \emptyset$.

  2. (ii) Monotonicity: If there is an odd continuous map from $A$ to $B$ (in particular, if $A \subset B$), then $i(A) \le i(B)$. Thus, equality holds when the map is an odd homeomorphism.

  3. (iii) Dimension: $i(A) \le \dim W$.

  4. (iv) Continuity: If $A$ is closed, then there is a closed neighbourhood $N \in \mathcal {A}$ of $A$ such that $i(N) = i(A)$. When $A$ is compact, $N$ may be chosen to be a $\delta$-neighbourhood $N_\delta (A) = \left \{{u \in W : \text {dist}\, ({u}, {A}) \le \delta }\right \}$.

  5. (v) Subadditivity: If $A$ and $B$ are closed, then $i(A \cup B) \le i(A) + i(B)$.

  6. (vi) Stability: If $SA$ is the suspension of $A \ne \emptyset$, obtained as the quotient space of $A \times [-1,1]$ with $A \times \left \{{1}\right \}$ and $A \times \left \{{-1}\right \}$ collapsed to different points, then $i(SA) = i(A) + 1$.

  7. (vii) Piercing property: If $A$, $A_0$ and $A_1$ are closed, and $\varphi : A \times [0,1] \to A_0 \cup A_1$ is a continuous map such that $\varphi (-u,t) = - \varphi (u,t)$ for all $(u,t) \in A \times [0,1]$, $\varphi (A \times [0,1])$ is closed, $\varphi (A \times \left \{{0}\right \}) \subset A_0$ and $\varphi (A \times \left \{{1}\right \}) \subset A_1,$ then $i(\varphi (A \times [0,1]) \cap A_0 \cap A_1) \ge i(A)$.

  8. (viii) Neighborhood of zero: If $U$ is a bounded closed symmetric neighbourhood of $0$, then $i(\partial {U}) = \dim W$.

2.3. Eigenvalues

Eigenvalues of problem (1.7) coincide with critical values of the functional

\[ \Psi(u) = \frac{1}{\displaystyle{\int}_\Omega |u|^{N} \,{\rm d}x}, \quad u \in S = \left\{{u \in W^{1,N}_0(\Omega) : \int_\Omega |\nabla u|^{N} \,{\rm d}x = 1}\right\}. \]

We have the following proposition (see Perera [Reference Perera11] and Perera $et al.$[Reference Perera, Agarwal and O'Regan12, Proposition 3.52 and Proposition 3.53]).

Proposition 2.3 Let $\mathcal {F}$ denote the class of symmetric subsets of $S$ and set

\[ \lambda_k := \inf_{\substack{M \in \mathcal{F}\\ i(M) \ge k}}\, \sup_{u \in M}\, \Psi(u), \quad k \in \mathbb{N}. \]

Then $0 < \lambda _1 < \lambda _2 \le \lambda _3 \le \cdots \to + \infty$ is a sequence of eigenvalues of problem (1.7). Moreover, if $\lambda _{k-1} < \lambda _k,$ then

\[ i(\Psi^{\lambda_{k-1}}) = i(S {\setminus} \Psi_{\lambda_k}) = k - 1, \]

where $\Psi ^{a} = \left \{{u \in S : \Psi (u) \le a}\right \}$ and $\Psi _a = \left \{{u \in S : \Psi (u) \ge a}\right \}$ for $a \in \mathbb {R}$.

We will also need the following result of Degiovanni and Lancelotti [Reference Degiovanni and Lancelotti7, Theorem 2.3].

Proposition 2.4 If $\lambda _{k-1} < \lambda _k,$ then $\Psi ^{\lambda _{k-1}}$ contains a compact symmetric set $C$ of index $k - 1$ that is bounded in $C^{1}(\overline {\Omega })$.

2.4. An abstract critical point theorem

We will use the following abstract critical point theorem proved in Yang and Perera [Reference Yang and Perera15, Theorem 2.2] to prove Theorem 1.3. This result generalizes the linking theorem of Rabinowitz [Reference Rabinowitz13].

Theorem 2.5 Let $E$ be a $C^{1}$-functional defined on a Banach space $W$ and let $A_0$ and $B_0$ be disjoint non-empty closed symmetric subsets of the unit sphere $S = \left \{{u \in W : \left \|u\right \| = 1}\right \}$ such that

(2.9)\begin{equation} i(A_0) = i(S {\setminus} B_0) < \infty. \end{equation}

Assume that there exist $R > \rho > 0$ and $\omega \in S {\setminus} A_0$ such that

\[ \sup E(A) \le \inf E(B), \quad \sup E(X) < \infty, \]

where

\begin{align*} A & = \left\{{sv : v \in A_0,\, 0 \le s \le R}\right\} \cup \left\{{R\, \pi((1 - t)\, v + t \omega) : v \in A_0,\, 0 \le t \le 1}\right\},\\ B & = \left\{{\rho u : u \in B_0}\right\},\\ X & = \left\{{sv + t \omega : v \in A_0,\, s, t \ge 0,\, \left\|{sv + t \omega}\right\| \le R}\right\}, \end{align*}

and $\pi : W {\setminus} \left \{{0}\right \} \to S,\, u \mapsto u/\left \|u\right \|$ is the radial projection onto $S$. Let

\[ \Gamma = \left\{{\gamma \in C(X,W) : \gamma(X) \text{ is closed and } \left.{\gamma}\right|_{A} = id_{A}}\right\}, \]

and set

\[ c := \inf_{\gamma \in \Gamma}\, \sup_{u \in \gamma(X)}\, E(u). \]

Then, $\inf E(B) \le c \le \sup E(X),$ and $E$ has a $(\text {PS})_{c}$ sequence.

2.5. Moser sequence

For $j \ge 2$, let

(2.10)\begin{equation} \omega_j(x) = \displaystyle\frac{1}{\omega_{N-1}^{1/N}} \begin{cases} (\log j)^{(N-1)/N}, & |x| \le d/j\\ \dfrac{\log\, (d/|x|)}{(\log j)^{1/N}}, & d/j < |x| < d\\ 0, & |x| \ge d \end{cases} \end{equation}

(see Moser [Reference Moser10]).

Proposition 2.6 We have

(2.11)\begin{equation} \displaystyle\int_\Omega \omega_j^{m}\,{\rm d}x = \displaystyle\frac{m!\, \omega_{N-1}^{1-m/N} d^{N}}{N^{m+1}\, (\log j)^{m/N}} \left[1 - \frac{1}{j^{N}} \displaystyle\sum_{l=1}^{m} \frac{(N \log j)^{m-l}}{(m - l)!}\right], \quad m = 1,\dots,N \end{equation}

and

(2.12)\begin{equation} \displaystyle\int_\Omega |\nabla \omega_j|^{m}\,{\rm d}x = \begin{cases} \dfrac{\omega_{N-1}^{1-m/N} d^{N-m}}{(N - m)\, (\log j)^{m/N}} \left(1 - \dfrac{1}{j^{N-m}}\right), & m = 1,\dots,N - 1\\ 1, & m = N. \end{cases} \end{equation}

Proof. We have

\[ \int_\Omega \omega_j^{m}\,{\rm d}x = \frac{\omega_{N-1}^{1-m/N} d^{N}}{(\log j)^{m/N}} \left[I_m + \frac{(\log j)^{m}}{N j^{N}}\right], \]

where

\[ I_m = \int_{1/j}^{1} (- \log s)^{m}\, s^{N-1}\, {\rm d}s. \]

We have

\[ I_1 = \frac{1}{N^{2}} \left[1 - \frac{1}{j^{N}}\, (N \log j + 1)\right], \]

and integrating by parts gives the recurrence relation

\[ I_m = \frac{m}{N}\, I_{m-1} - \frac{(\log j)^{m}}{N j^{N}}, \quad m \ge 2. \]

So

\[ I_m = \frac{m!}{N^{m+1}} \left[1 - \frac{1}{j^{N}} \sum_{l=0}^{m} \frac{(N \log j)^{m-l}}{(m - l)!}\right], \]

and (2.11) follows. The integral in (2.12) is easily evaluated.

2.6. A limit calculation

We will need the following limit in the proof of Theorem 1.1.

Proposition 2.7 We have

\[ \lim_{n \to \infty}\, \int_0^{1} ne^{- n\, (t - t^{N'})}\, {\rm d}t = N. \]

Proof. Let $f_n(t) = ne^{- n\, (t - t^{N'})}$ and set $t_0 = (N')^{-1/(N'-1)}$. For $t \ne t_0$,

(2.13)\begin{equation} f_n(t) = g_n(t) - \displaystyle\frac{d}{{\rm d}t} \left(\frac{e^{- n\, (t - t^{N'})}}{1 - N'\, t^{N'-1}}\right), \end{equation}

where

\[ g_n(t) = \frac{N' (N' - 1)\, t^{N'-2}\, e^{- n\, (t - t^{N'})}}{(1 - N'\, t^{N'-1})^{2}}. \]

Fix $\delta$ so small that $0 < \delta < t_0 < 1 - \delta < 1$ and write

(2.14)\begin{equation} \displaystyle\int_0^{1} f_n(t)\, {\rm d}t = \int_0^{\delta} f_n(t)\, {\rm d}t + \int_\delta^{1 - \delta} f_n(t)\, {\rm d}t + \int_{1 - \delta}^{1} f_n(t)\, {\rm d}t. \end{equation}

By (2.13),

(2.15)\begin{equation} \displaystyle\int_0^{\delta} f_n(t)\, {\rm d}t = \int_0^{\delta} g_n(t)\, {\rm d}t - \displaystyle\frac{e^{- n\, (\delta - \delta^{N'})}}{1 - N'\, \delta^{N'-1}} + 1. \end{equation}

For all $t \in (0,\delta )$, $g_n(t) \to 0$ as $n \to \infty$ and $\left |{g_n(t)}\right | \le N' (N' - 1)\, t^{N'-2}/(1 - N'\, \delta ^{N'-1})^{2}$, so $\int _0^{\delta } g_n(t)\, {\rm d}t \to 0$ by the dominated convergence theorem. So $\int _0^{1} f_n(t)\, {\rm d}t \to 1$ by (2.15). A similar calculation shows that $\int _{1 - \delta }^{1} f_n(t)\, {\rm d}t \to N - 1$. On the other hand, it is easily seen that $\int _\delta ^{1 - \delta } f_n(t)\, {\rm d}t \to 0$. So $\int _0^{1} f_n(t)\, {\rm d}t \to N$ by (2.14).

3. Proof of Theorem 1.1

In this section, we prove Theorem 1.1 by showing that the functional $E$ has the mountain pass geometry with the mountain pass level $c \in (0,(1/N)(\alpha _N/\alpha )^{N-1})$ and applying Proposition 2.1.

Lemma 3.1 There exists a $\rho > 0$ such that

\[ \inf_{\left\|u\right\| = \rho}\, E(u) > 0. \]

Proof. Since (1.2) implies that $h$ is bounded, there exists a constant $C_\delta > 0$ such that

\[ |G(t)| \le C_\delta\, |t|^{N+1}\, e^{\alpha\, |t|^{N'}} \quad \text{for } |t| > \delta, \]

which together with (1.9) gives

(3.1)\begin{equation} \displaystyle\int_\Omega G(u)\,{\rm d}x \le \displaystyle\frac{1}{N}\, (\lambda_1 - \sigma_1) \int_\Omega |u|^{N} \,{\rm d}x + C_\delta \int_\Omega |u|^{N+1}\, e^{\alpha\, |u|^{N'}} \,{\rm d}x. \end{equation}

By (1.6),

(3.2)\begin{equation} \displaystyle\int_\Omega |u|^{N} \,{\rm d}x \le \displaystyle\frac{\rho^{N}}{\lambda_1},\end{equation}

where $\rho = \left \|u\right \|$. By the Hölder inequality,

(3.3)\begin{equation} \displaystyle\int_\Omega |u|^{N+1}\, e^{\alpha\, |u|^{N'}} \,{\rm d}x \le \left(\int_\Omega |u|^{2\, (N+1)}\,{\rm d}x\right)^{1/2} \left(\int_\Omega e^{2 \alpha\, |u|^{N'}} \,{\rm d}x\right)^{1/2}. \end{equation}

The first integral on the right-hand side is bounded by $C \rho ^{2\, (N+1)}$ for some constant $C > 0$ by the Sobolev embedding theorem. Since $2 \alpha \, |u|^{N'} = 2 \alpha \, \rho ^{N'} |\widetilde {u}|^{N'}$, where $\widetilde {u} = u/\rho$ satisfies $\left \|\widetilde {u}\right \| = 1$, the second integral is bounded when $\rho ^{N'} \le \alpha _N/2 \alpha$ by (1.4). So combining (3.1)–(3.3) gives

\[ \int_\Omega G(u)\,{\rm d}x \le \frac{1}{N} \left(1 - \frac{\sigma_1}{\lambda_1}\right) \rho^{N} + \text{O}(\rho^{N+1}) \quad \text{as } \rho \to 0. \]

Then,

\[ E(u) \ge \frac{1}{N}\, \frac{\sigma_1}{\lambda_1}\, \rho^{N} + \text{O}(\rho^{N+1}), \]

and the desired conclusion follows from this for sufficiently small $\rho > 0$.

We may assume without loss of generality that $B_d(0) \subset \Omega$. Let $\left ({\omega _j}\right )$ be the sequence of functions defined in (2.10).

Lemma 3.2 We have

  1. (i) $E(t \omega _j) \to - \infty$ as $t \to \infty$ for all $j \ge 2,$

  2. (ii) $\exists j_0 \ge 2$ such that

    \[ \sup_{t \ge 0}\, E(t \omega_{j_0}) < \frac{1}{N} \left(\frac{\alpha_N}{\alpha}\right)^{N-1}. \]

Proof. ${\rm (i)}$ Fix $0 < \varepsilon < \beta$. By (1.3), $\exists M_\varepsilon > 0$ such that

(3.4)\begin{equation} th(t)\, e^{\alpha\, |t|^{N'}} > (\beta - \varepsilon)\, e^{\alpha\, |t|^{N'}} \quad \text{for } |t| > M_\varepsilon. \end{equation}

Since $e^{\alpha \, |t|^{N'}} > \alpha ^{2N-2}\, t^{2N}/(2N - 2)!$ for all $t$, then there exists a constant $C_\varepsilon > 0$ such that

(3.5)\begin{equation} th(t)\, e^{\alpha\, |t|^{N'}} \ge \displaystyle\frac{1}{(2N - 2)!}\, (\beta - \varepsilon)\, \alpha^{2N-2}\, t^{2N} - C_\varepsilon\, |t| \end{equation}

and

(3.6)\begin{equation} G(t) \ge \displaystyle\frac{2N - 1}{(2N)!}\, (\beta - \varepsilon)\, \alpha^{2N-2}\, t^{2N} - C_\varepsilon\, |t| \end{equation}

for all $t$. Since $\left \|{\omega _j}\right \| = 1$ and $\omega _j \ge 0$, then

\[ E(t \omega_j) \le \frac{t^{N}}{N} - \frac{2N - 1}{(2N)!}\, (\beta - \varepsilon)\, \alpha^{2N-2}\, t^{2N} \int_\Omega \omega_j^{2N}\,{\rm d}x + C_\varepsilon\, t \int_\Omega \omega_j\,{\rm d}x, \]

and the conclusion follows.

${\rm (ii)}$ Set

\[ H_j(t) = E(t \omega_j) = \frac{t^{N}}{N} - \int_\Omega G(t \omega_j)\,{\rm d}x, \quad t \ge 0. \]

If the conclusion is false, then it follows from ${\rm (i)}$ that for all $j \ge 2$, $\exists t_j > 0$ such that

(3.7)\begin{align} H_j(t_j) & = \frac{t_j^{N}}{N} - \int_\Omega G(t_j \omega_j)\,{\rm d}x = \sup_{t \ge 0}\, H_j(t) \ge \frac{1}{N} \left(\frac{\alpha_N}{\alpha}\right)^{N-1}, \end{align}
(3.8)\begin{align} H_j'(t_j) & = t_j^{N-1} - \int_\Omega \omega_j\, h(t_j \omega_j)\, e^{\alpha\, t_j^{N'} \omega_j^{N'}} \,{\rm d}x = 0. \end{align}

Since $G(t) \ge - C_\varepsilon \, t$ for all $t \ge 0$ by (3.6), (3.7) gives

(3.9)\begin{equation} t_j^{N} \ge t_0^{N} - N \delta_j\, t_j, \end{equation}

where

\[ t_0 = \left(\frac{\alpha_N}{\alpha}\right)^{(N-1)/N} \]

and

(3.10)\begin{equation} \delta_j = C_\varepsilon \displaystyle\int_\Omega \omega_j\,{\rm d}x \to 0 \quad \text{as } j \to \infty \end{equation}

by Proposition 2.6. First, we will show that $t_j \to t_0$.

By (3.9) and the Young's inequality,

\[ (1 + \nu)\, t_j^{N} \ge t_0^{N} - \frac{N - 1}{\nu^{1/(N-1)}}\, \delta_j^{N'} \quad \forall \nu > 0, \]

which together with (3.10) gives

(3.11)\begin{equation} \liminf_{j \to \infty}\, t_j \ge t_0. \end{equation}

Write (3.8) as

(3.12)\begin{equation} t_j^{N} = \displaystyle\int_{\left\{{t_j \omega_j \!>\! M_\varepsilon}\right\}} t_j \omega_j\, h(t_j \omega_j)\, e^{\alpha\, t_j^{N'} \omega_j^{N'}} \,{\rm d}x \!+\! \int_{\left\{{t_j \omega_j \le M_\varepsilon}\right\}} t_j \omega_j\, h(t_j \omega_j)\, e^{\alpha\, t_j^{N'} \omega_j^{N'}} \,{\rm d}x =: I_1 \!+\! I_2. \end{equation}

Set $r_j = de^{- M_\varepsilon \, (\omega _{N-1} \log j)^{1/N}/t_j}$. Since $\liminf t_j > 0$, for all sufficiently large $j$, $d/j < r_j < d$ and $t_j \omega _j(x) > M_\varepsilon$ if and only if $|x| < r_j$. So, (3.4) gives

(3.13)\begin{align} I_1 & \ge (\beta - \varepsilon) \displaystyle\int_{\left\{{|x| < r_j}\right\}} e^{\alpha\, t_j^{N'} \omega_j^{N'}} \,{\rm d}x = (\beta - \varepsilon) \left(\int_{\left\{{|x| \le d/j}\right\}} e^{\alpha\, t_j^{N'} \omega_j^{N'}}\right. \,{\rm d}x \end{align}
(3.14)\begin{align} & \quad+ \left.\int_{\left\{{d/j < |x| < r_j}\right\}} e^{\alpha\, t_j^{N'} \omega_j^{N'}} \,{\rm d}x\right) =: (\beta - \varepsilon)\, (I_3 + I_4). \end{align}

We have

(3.15)\begin{equation} I_3 = \displaystyle\frac{\omega_{N-1}}{N} \left(\frac{d}{j}\right)^{N} e^{\alpha\, t_j^{N'} \log j/\omega_{N-1}^{1/(N-1)}} = \frac{\omega_{N-1}}{N}\, d^{N} j^{\alpha\, (t_j^{N'} - t_0^{N'})/\omega_{N-1}^{1/(N-1)}}.\end{equation}

Since $th(t)\, e^{\alpha \, |t|^{N'}} \ge - C_\varepsilon \, t$ for all $t \ge 0$ by (3.5),

(3.16)\begin{equation} I_2 \ge - C_\varepsilon\, t_j \displaystyle\int_{\left\{{t_j \omega_j \le M_\varepsilon}\right\}} \omega_j\,{\rm d}x \ge - \delta_j\, t_j. \end{equation}

Combining (3.12)–(3.16) and noting that $I_4 \ge 0$ gives

\[ t_j^{N} \ge (\beta - \varepsilon)\, \frac{\omega_{N-1}}{N}\, d^{N} j^{\alpha\, (t_j^{N'} - t_0^{N'})/\omega_{N-1}^{1/(N-1)}} - \delta_j\, t_j. \]

It follows from this that

\[ \limsup_{j \to \infty}\, t_j \le t_0, \]

which together with (3.11) shows that $t_j \to t_0$.

Next, we estimate $I_4$. We have

(3.17)\begin{align} I_4 & = \displaystyle\int_{\left\{{d/j < |x| < r_j}\right\}} e^{\alpha\, t_j^{N'} [\log\, (d/|x|)]^{N'}/(\omega_{N-1} \log j)^{1/(N-1)}}\,{\rm d}x \nonumber\\ & = \omega_{N-1}\, \left(\int_{d/j}^{d} e^{\alpha\, t_j^{N'} [\log\, (d/r)]^{N'}/(\omega_{N-1} \log j)^{1/(N-1)}}\, r^{N-1}\, {\rm d}r\right.\nonumber\\ & \quad- \left.\int_{r_j}^{d} e^{\alpha\, t_j^{N'} [\log\, (d/r)]^{N'}/(\omega_{N-1} \log j)^{1/(N-1)}}\, r^{N-1}\, {\rm d}r\right) \nonumber\\ & = \omega_{N-1}\, d^{N} (\log j \int_0^{1} e^{- Nt\, [1 - (t_j/t_0)^{N'} t^{1/(N-1)}] \log j}\, {\rm d}t \nonumber\\ & \quad- \int_{s_j}^{1} s^{N-1}\, e^{\alpha\, t_j^{N'} (- \log s)^{N'}/(\omega_{N-1} \log j)^{1/(N-1)}}\, {\rm d}s), \end{align}

where $t = \log \, (d/r)/\log j$, $s = r/d$, and $s_j = r_j/d = e^{- M_\varepsilon \, (\omega _{N-1} \log j)^{1/N}/t_j} \to 0$. For $s_j < s < 1$, $\alpha \, t_j^{N'} (- \log s)^{N'}/(\omega _{N-1} \log j)^{1/(N-1)}$ is bounded by $\alpha M_\varepsilon ^{N'}$ and goes to zero as $j \to \infty$, so the last integral converges to

\[ \int_0^{1} s^{N-1}\, {\rm d}s = \frac{1}{N}. \]

So, combining (3.12)–(3.17) and letting $j \to \infty$ gives

\[ t_0^{N} \ge (\beta - \varepsilon)\, \frac{\omega_{N-1}}{N}\, d^{N} (L_1 + L_2 - 1), \]

where

\begin{align*} L_1 & = \liminf_{j \to \infty}\, e^{- n\, [1 - (t_j/t_0)^{N'}]},\\ L_2 & = \liminf_{j \to \infty}\, \int_0^{1} ne^{- n\, [t - (t_j/t_0)^{N'} t^{N'}]}\, {\rm d}t, \end{align*}

and $n = N \log j \to \infty$. Letting $\varepsilon \to 0$ in this inequality gives

(3.18)\begin{equation} \beta \le \displaystyle\frac{1}{\alpha^{N-1}} \left(\frac{N}{d}\right)^{N} \frac{1}{L_1 + L_2 - 1}. \end{equation}

By (3.7), (1.8), and Proposition 2.6,

\[ t_j^{N} - t_0^{N} \ge N \int_\Omega G(t_j \omega_j)\,{\rm d}x \ge - \sigma_0\, t_j^{N} \int_\Omega \omega_j^{N}\,{\rm d}x \ge - \frac{\sigma_0\, t_j^{N}}{\kappa n}, \]

so

\[ \left(\frac{t_j}{t_0}\right)^{N'} \ge \left(1 + \frac{\sigma_0}{\kappa n}\right)^{- 1/(N-1)} \ge 1 - \frac{\sigma_0}{(N - 1)\, \kappa n}. \]

This gives

\[ L_1 \ge e^{- \sigma_0/(N-1)\, \kappa} \]

and

\[ L_2 \ge \lim_{n \to \infty}\, \int_0^{1} ne^{- n\, (t - t^{N'}) - \sigma_0\, t^{N'}/(N-1)\, \kappa}\, {\rm d}t \ge Ne^{- \sigma_0/(N-1)\, \kappa} \]

by Proposition 2.7. So (3.18) gives

\[ \beta \le \frac{1}{\alpha^{N-1}} \left(\frac{N}{d}\right)^{N} \frac{1}{Ne^{- \sigma_0/(N-1)\, \kappa} - (1 - e^{- \sigma_0/(N-1)\, \kappa})} \le \frac{1}{N \alpha^{N-1}} \left(\frac{N}{d}\right)^{N}\! e^{\sigma_0/(N-1)\, \kappa}, \]

contradicting (1.10).

We are now ready to prove Theorem 1.1.

Proof of Theorem 1.1. Let $j_0$ be as in Lemma 3.2 ${\rm (ii)}$. By Lemma 3.2 ${\rm (i)}$, $\exists R > \rho$ such that $E(R \omega _{j_0}) \le 0$, where $\rho$ is as in Lemma 3.1. Let

\[ \Gamma = \left\{{\gamma \in C([0,1],W^{1,N}_0(\Omega)) : \gamma(0) = 0,\, \gamma(1) = R \omega_{j_0}}\right\} \]

be the class of paths joining the origin to $R \omega _{j_0}$, and set

\[ c := \inf_{\gamma \in \Gamma}\, \max_{u \in \gamma([0,1])}\, E(u). \]

By Lemma 3.1, $c > 0$. Since the path $\gamma _0(t) = tR \omega _{j_0},\, t \in [0,1]$ is in $\Gamma$,

\[ c \le \max_{u \in \gamma_0([0,1])}\, E(u) \le \sup_{t \ge 0}\, E(t \omega_{j_0}) < \frac{1}{N} \left(\frac{\alpha_N}{\alpha}\right)^{N-1}. \]

If there are no $(\text {PS})_{c}$ sequences of $E$, then $E$ satisfies the $(\text {PS})_{c}$ condition vacuously and hence has a critical point $u$ at the level $c$ by the mountain pass theorem. Then $u$ is a solution of problem (1.1) and $u$ is non-trivial since $c > 0$. So we may assume that $E$ has a $(\text {PS})_{c}$ sequence. Then this sequence has a subsequence that converges weakly to a non-trivial solution of problem (1.1) by Proposition 2.1.

4. Proof of Theorem 1.3

In this section, we prove Theorem 1.3 using Theorem 2.5. We take $A_0$ to be the set $C$ in Proposition 2.4 and $B_0 = \Psi _{\lambda _k}$. Since $i(S {\setminus} B_0) = k - 1$ by Proposition 2.3, (2.9) holds.

Lemma 4.1 There exists a $\rho > 0$ such that $\inf E(B) > 0,$ where $B = \left \{{\rho u : u \in B_0}\right \}$.

Proof. As in the proof of Lemma 3.1, there exists a constant $C_\delta > 0$ such that

\[ |G(t)| \le C_\delta\, |t|^{N+1}\, e^{\alpha\, |t|^{N'}} \quad \text{for } |t| > \delta, \]

which together with (1.12) gives

(4.1)\begin{equation} G(t)\le \displaystyle\frac{1}{N}\, (\lambda_k - \sigma_1)\, |t|^{N} + C_\delta\, |t|^{N+1}\, e^{\alpha\, |t|^{N'}} \quad \forall t. \end{equation}

For $u \in B_0$ and $\rho > 0$,

(4.2)\begin{equation} \displaystyle\int_\Omega |\rho u|^{N} \,{\rm d}x \le \displaystyle\frac{\rho^{N}}{\lambda_k}\end{equation}

and

(4.3)\begin{equation} \displaystyle\int_\Omega |\rho u|^{N+1}\, e^{\alpha\, |\rho u|^{N'}} \,{\rm d}x \le \rho^{N+1} \left(\int_\Omega |u|^{2\, (N+1)}\,{\rm d}x\right)^{1/2} \left(\int_\Omega e^{2 \alpha\, \rho^{N'} |u|^{N'}} \,{\rm d}x\right)^{1/2}. \end{equation}

The first integral on the right-hand side of (4.3) is bounded by the Sobolev embedding theorem, and the second integral is bounded when $\rho ^{N'} \le \alpha _N/2 \alpha$ by (1.4). So, combining (4.1)–(4.3) gives

\[ \int_\Omega G(\rho u)\,{\rm d}x \le \frac{1}{N} \left(1 - \frac{\sigma_1}{\lambda_k}\right) \rho^{N} + \text{O}(\rho^{N+1}) \quad \text{as } \rho \to 0. \]

Then,

\[ E(\rho u) \ge \frac{1}{N}\, \frac{\sigma_1}{\lambda_k}\, \rho^{N} + \text{O}(\rho^{N+1}), \]

and the desired conclusion follows from this for sufficiently small $\rho$.

We may assume without loss of generality that $B_d(0) \subset \Omega$. Let $\left ({\omega _j}\right )$ be the sequence of functions defined in (2.10).

Lemma 4.2 We have

  1. (i) $E(sv) \le 0 \hspace {0.08in} \forall v \in A_0,\, s \ge 0,$

  2. (ii) for all $j \ge 2,$

    \[ \sup \left\{{E(R\, \pi((1 - t)\, v + t \omega_j)) : v \in A_0,\, 0 \le t \le 1}\right\} \to - \infty \text{ as }R \to \infty, \]

  3. (iii) $\exists j_0 \ge 2$ such that

    \[ \sup \left\{{E(sv + t \omega_{j_0}) : v \in A_0,\, s, t \ge 0}\right\} < \frac{1}{N} \left(\frac{\alpha_N}{\alpha}\right)^{N-1}. \]

Proof. ${\rm (i)}$ By (1.11),

(4.4)\begin{equation} E(u) \le \displaystyle\frac{1}{N}\left [\displaystyle\int_\Omega |\nabla u|^{N} \,{\rm d}x - (\lambda_{k-1} + \sigma_0) \int_\Omega |u|^{N} \,{\rm d}x\right]. \end{equation}

For $v \in A_0$ and $s \ge 0$,

\[ \int_\Omega |sv|^{N} \,{\rm d}x \ge \frac{s^{N}}{\lambda_{k-1}} \]

since $A_0 \subset \Psi ^{\lambda _{k-1}}$, so (4.4) gives

\[ E(sv) \le - \frac{1}{N}\, \frac{\sigma_0}{\lambda_{k-1}}\, s^{N} \le 0. \]

${\rm (ii)}$ Fix $0 < \varepsilon < \beta$. As in the proof of Lemma 3.2 ${\rm (i)}$, $\exists M_\varepsilon > 0$ such that

(4.5)\begin{equation} th(t)\, e^{\alpha\, |t|^{N'}} > (\beta - \varepsilon)\, e^{\alpha\, |t|^{N'}} \quad \text{for } |t| > M_\varepsilon \end{equation}

and there exists a constant $C_\varepsilon > 0$ such that

(4.6)\begin{equation} th(t)\, e^{\alpha\, |t|^{N'}} \ge \displaystyle\frac{1}{(2N - 2)!}\, (\beta - \varepsilon)\, \alpha^{2N-2}\, t^{2N} - C_\varepsilon\, |t| \end{equation}

and

(4.7)\begin{equation} G(t) \ge \displaystyle\frac{2N - 1}{(2N)!}\, (\beta - \varepsilon)\, \alpha^{2N-2}\, t^{2N} - C_\varepsilon\, |t| \end{equation}

for all $t$. Let $A_1 = \left \{{\pi ((1 - t)\, v + t \omega _j) : v \in A_0,\, 0 \le t \le 1}\right \}$. For $u \in A_1$ and $R > 0$, (4.7) gives

\[ E(Ru) \le \frac{R^{N}}{N} - \frac{2N - 1}{(2N)!}\, (\beta - \varepsilon)\, \alpha^{2N-2}\, R^{2N} \int_\Omega |u|^{2N} \,{\rm d}x + C_\varepsilon R \int_\Omega |u|\,{\rm d}x. \]

The set $A_1$ is compact since $A_0$ is compact, so the first integral on the right-hand side is bounded away from zero on $A_1$. Since the second integral is bounded, the desired conclusion follows.

${\rm (iii)}$ If the conclusion is false, then it follows from ${\rm (i)}$ and ${\rm (ii)}$ that for all $j \ge 2$, there exist $v_j \in A_0,\, s_j \ge 0,\, t_j > 0$ such that

\[ E(s_j v_j + t_j \omega_j) = \sup \left\{{E(sv + t \omega_j) : v \in A_0,\, s, t \ge 0}\right\} \ge \frac{1}{N} \left(\frac{\alpha_N}{\alpha}\right)^{N-1}. \]

Set $u_j = s_j v_j + t_j \omega _j$. Then

(4.8)\begin{equation} E(u_j)= \displaystyle\frac{1}{N} \left\|u_j\right\|^{N} - \displaystyle\int_\Omega G(u_j)\,{\rm d}x \ge \frac{1}{N} \left(\frac{\alpha_N}{\alpha}\right)^{N-1}. \end{equation}

Moreover, $\tau u_j \in \left \{{sv + t \omega _j : v \in A_0,\, s, t \ge 0}\right \}$ for all $\tau \ge 0$ and $E(\tau u_j)$ attains its maximum at $\tau = 1$, so

(4.9)\begin{equation} \left.{\displaystyle\frac{\partial}{\partial \tau}\, E(\tau u_j)}\right|_{\tau = 1} = E'(u_j)\, u_j = \left\|u_j\right\|^{N} - \displaystyle\int_\Omega u_j\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} \,{\rm d}x = 0. \end{equation}

Since $\left \|{v_j}\right \| = \left \|{\omega _j}\right \| = 1$ and $G(t) \ge 0$ for all $t$ by (1.11), (4.8) gives

\[ s_j + t_j \ge t_0, \]

where

\[ t_0 = \left(\frac{\alpha_N}{\alpha}\right)^{(N-1)/N}. \]

First, we show that $s_j \to 0$ and $t_j \to t_0$ as $j \to \infty$.

Combining (4.8) with (1.11) gives

\[ \left\|{s_j v_j + t_j \omega_j}\right\|^{N} \ge (\lambda_{k-1} + \sigma_0) \int_\Omega |s_j v_j + t_j \omega_j|^{N} \,{\rm d}x + t_0^{N}. \]

Set $\tau _j = s_j/t_j$. Then,

(4.10)\begin{equation} \left\|{\tau_j v_j + \omega_j}\right\|^{N} \ge (\lambda_{k-1} + \sigma_0) \displaystyle\int_\Omega |\tau_j v_j + \omega_j|^{N} \,{\rm d}x + (\displaystyle\frac{t_0}{t_j})^{N}. \end{equation}

Since $\left ({v_j}\right )$ is bounded in $C^{1}(\overline {\Omega })$, Proposition 2.6 gives

\begin{align*} \left\|{\tau_j v_j + \omega_j}\right\|^{N} & \le \displaystyle\int_\Omega (\tau_j\, |\nabla v_j| + |\nabla \omega_j|)^{N} \,{\rm d}x = \tau_j^{N} \int_\Omega |\nabla v_j|^{N} \,{\rm d}x + \int_\Omega |\nabla \omega_j|^{N} \,{\rm d}x\\ & \quad+ \displaystyle\sum_{m=1}^{N-1} \binom{N}{m}\, \tau_j^{N-m} \int_\Omega |\nabla v_j|^{N-m}\, |\nabla \omega_j|^{m}\,{\rm d}x \le \tau_j^{N} \!+\! 1 \!+\! c_1 \sum_{m=1}^{N-1} \displaystyle\frac{\tau_j^{N-m}}{(\log j)^{m/N}} \end{align*}

and

\begin{align*} & \displaystyle\int_\Omega |\tau_j v_j + \omega_j|^{N} \,{\rm d}x \ge \int_\Omega (\tau_j\, |v_j| - \omega_j)^{N} \,{\rm d}x = \tau_j^{N} \int_\Omega |v_j|^{N} \,{\rm d}x\\ & \quad+ \displaystyle\sum_{m=1}^{N} ({-}1)^{m}\, \binom{N}{m}\, \tau_j^{N-m} \int_\Omega |v_j|^{N-m}\, \omega_j^{m}\,{\rm d}x \ge \displaystyle\frac{\tau_j^{N}}{\lambda_{k-1}} - c_2 \sum_{m=1}^{N} \frac{\tau_j^{N-m}}{(\log j)^{m/N}} \end{align*}

for some constants $c_1, c_2 > 0$. So (4.10) gives

(4.11)\begin{equation} \displaystyle\frac{\sigma_0}{\lambda_{k-1}}\, \tau_j^{N} + \left(\frac{t_0}{t_j}\right)^{N} \le 1 + c_3 \displaystyle\sum_{m=1}^{N} \frac{\tau_j^{N-m}}{(\log j)^{m/N}} \end{equation}

for some constant $c_3 > 0$, which implies that $\left ({\tau _j}\right )$ is bounded and

(4.12)\begin{equation} \liminf_{j \to \infty}\, t_j \ge t_0. \end{equation}

Next, combining (4.9) with (4.5) and (4.6) gives

(4.13)\begin{align} \left\|u_j\right\|^{N} & = \displaystyle\int_{\left\{{|u_j| > M_\varepsilon}\right\}} u_j\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} \,{\rm d}x + \int_{\left\{{|u_j| \le M_\varepsilon}\right\}} u_j\, h(u_j)\, e^{\alpha\, |u_j|^{N'}} \,{\rm d}x\nonumber\\ & \ge (\beta - \varepsilon) \int_{\left\{{|u_j| > M_\varepsilon}\right\}} e^{\alpha\, |u_j|^{N'}} \,{\rm d}x - C_\varepsilon \int_{\left\{{|u_j| \le M_\varepsilon}\right\}} |u_j|\,{\rm d}x. \end{align}

For $|x| \le d/j$,

\[ |u_j| \ge t_j \omega_j - s_j\, |v_j| \ge \frac{t_j}{\omega_{N-1}^{1/N}} \left[(\log j)^{(N-1)/N} - c_4 \tau_j\right] \]

for some constant $c_4 > 0$, and the last expression is greater than $M_\varepsilon$ for all sufficiently large $j$ since $\left ({\tau _j}\right )$ is bounded and $\liminf t_j > 0$. So

\begin{align*} \displaystyle\int_{\left\{{|u_j| > M_\varepsilon}\right\}} e^{\alpha\, |u_j|^{N'}} \,{\rm d}x & \ge e^{\alpha\, t_j^{N'} [(\log j)^{(N-1)/N} - c_4 \tau_j]^{N'}/\omega_{N-1}^{1/(N-1)}} \int_{\left\{{|x| \le d/j}\right\}} \,{\rm d}x\\ & = \displaystyle\frac{\omega_{N-1}\, d^{N}}{N}\, j^{\alpha\, [t_j^{N'} (1 - c_4 \tau_j/(\log j)^{(N-1)/N})^{N'} - t_0^{N'}]/\omega_{N-1}^{1/(N-1)}} \end{align*}

for large $j$. On the contrary,

\[ \int_{\left\{{|u_j| \le M_\varepsilon}\right\}} |u_j|\,{\rm d}x \le \int_\Omega (s_j\, |v_j| + t_j \omega_j)\,{\rm d}x \le c_5\, t_j \left[\tau_j + \frac{1}{(\log j)^{1/N}}\right] \]

for some constant $c_5 > 0$ by Proposition 2.6. So, (4.13) gives

(4.14)\begin{align} & (\beta - \varepsilon)\, j^{\alpha\, [t_j^{N'} (1 - c_4 \tau_j/(\log j)^{(N-1)/N})^{N'} - t_0^{N'}]/\omega_{N-1}^{1/(N-1)}} \le \displaystyle\frac{N t_j^{N} (\tau_j + 1)^{N}}{\omega_{N-1}\, d^{N}}\nonumber\\ & \quad+ c_6\, t_j \left[\tau_j + \frac{1}{(\log j)^{1/N}}\right] \end{align}

for some constant $c_6 > 0$. Since $\left ({\tau _j}\right )$ is bounded, it follows from this that

\[ \limsup_{j \to \infty}\, t_j \le t_0, \]

which together with (4.12) shows that $t_j \to t_0$. Then (4.11) implies that $\tau _j \to 0$, so $s_j = \tau _j\, t_j \to 0$.

Now, we show that there exists a constant $c > 0$ depending only on $\Omega$, $\alpha$, and $k$ such that

(4.15)\begin{equation} \beta \le \displaystyle\frac{1}{\alpha^{N-1}} \left(\frac{N}{d}\right)^{N}\! e^{c/\sigma_0^{N-1}}. \end{equation}

The right-hand side of (4.14) goes to $(N/d)^{N}/\alpha ^{N-1}$ as $j \to \infty$. If $\beta \le (N/d)^{N}/\alpha ^{N-1}$, then we may take any $c > 0$, so suppose $\beta > (N/d)^{N}/\alpha ^{N-1}$. Then for $\varepsilon < \beta - (N/d)^{N}/\alpha ^{N-1}$ and all sufficiently large $j$, (4.14) gives $j^{\alpha \, [t_j^{N'} (1 - c_4 \tau _j/(\log j)^{(N-1)/N})^{N'} - t_0^{N'}]/\omega _{N-1}^{1/(N-1)}} \le 1$, so

\[ \frac{t_0}{t_j} \ge 1 - \frac{c_4 \tau_j}{(\log j)^{(N-1)/N}}. \]

Combining this with (4.11) gives

\[ \frac{\sigma_0}{\lambda_{k-1}}\, \tau_j^{N} - \frac{N c_4 \tau_j}{(\log j)^{(N-1)/N}} \le c_3 \sum_{m=1}^{N} \frac{\tau_j^{N-m}}{(\log j)^{m/N}}, \]

so

\[ \sigma_0 \tau_j^{N} \le c_7 \sum_{m=1}^{N} \frac{\tau_j^{N-m}}{(\log j)^{m/N}} \]

for some constant $c_7 > 0$. Set $\widetilde {\tau }_j = \tau _j\, (\log j)^{1/N}$. Then

(4.16)\begin{equation} \sigma_0 \widetilde{\tau}_j^{N} \le c_7 \displaystyle\sum_{m=1}^{N} \widetilde{\tau}_j^{N-m}. \end{equation}

We claim that

(4.17)\begin{equation} \widetilde{\tau}_j \le \displaystyle\frac{c_8}{\sigma_0} \end{equation}

for some constant $c_8 > 0$. Taking $\sigma _0$ smaller in (1.11) if necessary, we may assume that $\sigma _0 \le 1$. So if $\widetilde {\tau }_j < 1$, then (4.17) holds with $c_8 = 1$, so suppose $\widetilde {\tau }_j \ge 1$. Then (4.16) gives (4.17) with $c_8 = N c_7$. Now (4.11) gives

\[ \left(\frac{t_0}{t_j}\right)^{N} \le 1 + \frac{c_3}{\log j}\, \sum_{m=1}^{N} \widetilde{\tau}_j^{N-m} \le 1 + \frac{c_9}{\sigma_0^{N-1} \log j} \]

for some constant $c_9 > 0$, so

\[ \left(\frac{t_0}{t_j}\right)^{N'} \le \left(1 + \frac{c_9}{\sigma_0^{N-1} \log j}\right)^{1/(N-1)} \le 1 + \frac{c_9}{\sigma_0^{N-1} \log j}. \]

Then,

\begin{align*} & t_j^{N'} \left[1 - \displaystyle\frac{c_4 \tau_j}{(\log j)^{(N-1)/N}}\right]^{N'} - t_0^{N'} = t_j^{N'} \left[\left(1 - \frac{c_4 \widetilde{\tau}_j}{\log j}\right)^{N'} - \left(\frac{t_0}{t_j}\right)^{N'}\right]\\ & \quad\ge t_j^{N'} \left[(1 - \frac{c_{10}}{\sigma_0 \log j})^{N'} - \left(1 + \frac{c_9}{\sigma_0^{N-1} \log j}\right)\right] \ge - t_j^{N'} \left(\frac{N' c_{10}}{\sigma_0 \log j} + \frac{c_9}{\sigma_0^{N-1} \log j}\right)\\ & \quad\ge - \frac{c_{11}}{\sigma_0^{N-1} \log j} \end{align*}

for some constants $c_{10}, c_{11} > 0$, so

\[ j^{\alpha\, [t_j^{N'} (1 - c_4 \tau_j/(\log j)^{(N-1)/N})^{N'} - t_0^{N'}]/\omega_{N-1}^{1/(N-1)}} \ge j^{- c/\sigma_0^{N-1} \log j} = e^{- c/\sigma_0^{N-1}} \]

for some constant $c > 0$. Combining this with (4.14) and passing to the limit gives

\[ (\beta - \varepsilon)\, e^{- c/\sigma_0^{N-1}} \le \frac{1}{\alpha^{N-1}} \left(\frac{N}{d}\right)^{N}, \]

and letting $\varepsilon \to 0$ gives (4.15).

We are now ready to prove Theorem 1.3.

Proof of Theorem 1.3. Let $j_0 \ge 2$ be as in Lemma 4.2 ${\rm (iii)}$. By Lemma 4.2 ${\rm (ii)}$, $\exists R > \rho$ such that

(4.18)\begin{equation} \sup \left\{{E(R\, \pi((1 - t)\, v + t \omega_{j_0})) : v \in A_0,\, 0 \le t \le 1}\right\} \le 0, \end{equation}

where $\rho > 0$ is as in Lemma 4.1. Let

\begin{align*} A & = \left\{{sv : v \in A_0,\, 0 \le s \le R}\right\} \cup \left\{{R\, \pi((1 - t)\, v + t \omega_{j_0}) : v \in A_0,\, 0 \le t \le 1}\right\},\\ X & = \left\{{sv + t \omega_{j_0} : v \in A_0,\, s, t \ge 0,\, \left\|{sv + t \omega_{j_0}}\right\| \le R}\right\}. \end{align*}

Combining Lemma 4.2 ${\rm (i)}$, (4.18), and Lemma 4.1 gives

(4.19)\begin{equation} \sup E(A) \le 0 < \inf E(B), \end{equation}

while Lemma 4.2 ${\rm (iii)}$ gives

(4.20)\begin{equation} \sup E(X) \le \sup \left\{{E(sv + t \omega_{j_0}) : v \in A_0,\, s, t \ge 0}\right\} < \displaystyle\frac{1}{N} \left(\frac{\alpha_N}{\alpha}\right)^{N-1}. \end{equation}

Let

\[ \Gamma = \left\{{\gamma \in C(X,W) : \gamma(X) \text{ is closed and} \left.{\gamma}\right|_{A} = id_{A}}\right\}, \]

and set

\[ c := \inf_{\gamma \in \Gamma}\, \sup_{u \in \gamma(X)}\, E(u). \]

By Theorem 2.5, $\inf E(B) \le c \le \sup E(X)$, and $E$ has a $(\text {PS})_{c}$ sequence. By (4.19) and (4.20),

\[ 0 < c < \frac{1}{N} \left(\frac{\alpha_N}{\alpha}\right)^{N-1}, \]

so a subsequence of this $(\text {PS})_{c}$ sequence converges weakly to a non-trivial solution of problem (1.1) by Proposition 2.1.

Competing interests declaration

The authors declare no competing interests.

References

Adimurthi, A., Existence of positive solutions of the semilinear Dirichlet problem with critical growth for the $n$-Laplacian, Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 17(3) (1990), 393–413.Google Scholar
Adimurthi, A. and Yadava, S. L., Bifurcation results for semilinear elliptic problems with critical exponent in $R^{2}$, Nonlinear Anal. 14(7) (1990), 607–612.CrossRefGoogle Scholar
de Figueiredo, D. G., Miyagaki, O. H. and Ruf, B., Elliptic equations in $R^{2}$ with nonlinearities in the critical growth range, Calc. Var. Partial Differ. Equ. 3(2) (1995), 139–153.CrossRefGoogle Scholar
de Figueiredo, D. G., Miyagaki, O. H. and Ruf, B., Corrigendum: Elliptic equations in $R^{2}$ with nonlinearities in the critical growth range, Calc. Var. Partial Differ. Equ. 4(2) (1996), 203.Google Scholar
de Figueiredo, D. G., do Ó, J. M. and Ruf, B., On an inequality by N. Trudinger and J. Moser and related elliptic equations, Comm. Pure Appl. Math. 55(2) (2002), 135–152.CrossRefGoogle Scholar
de Figueiredo, D. G., do Ó, J. M. and Ruf, B., Elliptic equations and systems with critical Trudinger–Moser nonlinearities, Discrete Contin. Dyn. Syst. 30(2) (2011), 455–476.CrossRefGoogle Scholar
Degiovanni, M. and Lancelotti, S., Linking solutions for $p$-Laplace equations with nonlinearity at critical growth, J. Funct. Anal. 256(11) (2009), 3643–3659.CrossRefGoogle Scholar
do Ó, J. M. B., Semilinear Dirichlet problems for the $N$-Laplacian in $\mathbb {R}^{N}$ with nonlinearities in the critical growth range, Differ. Int. Equ. 9(5) (1996), 967–979.Google Scholar
Fadell, E. R. and Rabinowitz, P. H., Generalized cohomological index theories for Lie group actions with an application to bifurcation questions for Hamiltonian systems, Invent. Math. 45(2) (1978), 139–174.CrossRefGoogle Scholar
Moser, J., A sharp form of an inequality by N. Trudinger, Indiana Univ. Math. J. 20 (1970), 1077/71–1092.Google Scholar
Perera, K., Nontrivial critical groups in $p$-Laplacian problems via the Yang index, Topol. Methods Nonlinear Anal. 21(2) (2003), 301–309.CrossRefGoogle Scholar
Perera, K., Agarwal, R. P. and O'Regan, D., Morse theoretic aspects of $p$-Laplacian type operators, Mathematical Surveys and Monographs, Volume 161 (American Mathematical Society, Providence, RI, 2010).CrossRefGoogle Scholar
Rabinowitz, P. H., Some critical point theorems and applications to semilinear elliptic partial differential equations, Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 5(1) (1978), 215–223.Google Scholar
Trudinger, N. S., On imbeddings into Orlicz spaces and some applications, J. Math. Mech. 17 (1967), 473–483.Google Scholar
Yang, Y. and Perera, K., $N$-Laplacian problems with critical Trudinger–Moser nonlinearities, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 16(4) (2016), 1123–1138.Google Scholar