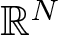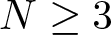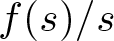1. Introduction
We investigate the existence of a non-trivial solution of the elliptic problem
with  $g(s)=\mu f(s) + |s|^{2^*-2}s$,
$g(s)=\mu f(s) + |s|^{2^*-2}s$, ![]() $N\geq 3$, µ > 0, under no periodicity condition on V that changes sign, and
$N\geq 3$, µ > 0, under no periodicity condition on V that changes sign, and ![]() $s\mapsto f(s)/s$ is bounded.
$s\mapsto f(s)/s$ is bounded.
This problem has been extensively studied considering several potentials V and non-linearities g. For the case where V and ![]() $g(s)=g(x,s)$ are periodic functions in the variable x and g have a subcritical growth, we refer the reader to [Reference Jeanjean7–Reference Li and Szulkin9, Reference Pankov and Pflüger13, Reference Stuart and Zhou16, Reference Szulkin and Weth17 ] and references therein.
$g(s)=g(x,s)$ are periodic functions in the variable x and g have a subcritical growth, we refer the reader to [Reference Jeanjean7–Reference Li and Szulkin9, Reference Pankov and Pflüger13, Reference Stuart and Zhou16, Reference Szulkin and Weth17 ] and references therein.
The case when g possesses critical growth and potential V changes sign, we refer the works of [Reference Alves and Germano2, Reference Chabrowski and Szulkin4, Reference Schechter and Zou14, Reference Zhang, Xu and Zhang18 ], which are more closely related to this article. In all of them, the condition of periodicity is crucial in order to overcome the lack of compactness in ![]() $\mathbb{R}^N$.
$\mathbb{R}^N$.
On the other side, Maia e Soares in [Reference Maia and Soares12] considered the case when V is not periodic (namely, ![]() $V(x)\to V_\infty \gt 0$ as
$V(x)\to V_\infty \gt 0$ as ![]() $|x|\to \infty$) and g is asymptotically linear at infinity, without any monotonicity condition on
$|x|\to \infty$) and g is asymptotically linear at infinity, without any monotonicity condition on ![]() $s\mapsto g(s)/s$. The framework that the authors deal with the problem makes possible to apply the celebrated result due to Berestycki and Lions in [Reference Berestycki and Lions3] and ensures that the limit problem associated to
$s\mapsto g(s)/s$. The framework that the authors deal with the problem makes possible to apply the celebrated result due to Berestycki and Lions in [Reference Berestycki and Lions3] and ensures that the limit problem associated to ![]() $(P_\mu)$
$(P_\mu)$
has a non-trivial ground state solution ![]() $u_0\in C^2(\mathbb{R}^N,\mathbb{R})$, which is positive, radially symmetric and decays exponentially, namely,
$u_0\in C^2(\mathbb{R}^N,\mathbb{R})$, which is positive, radially symmetric and decays exponentially, namely,
 \begin{equation}
u_0(x)\leq {\rm e}^{-\sqrt{V_\infty}|x|} \quad \text{for all} \ x\in\mathbb{R}^N.
\end{equation}
\begin{equation}
u_0(x)\leq {\rm e}^{-\sqrt{V_\infty}|x|} \quad \text{for all} \ x\in\mathbb{R}^N.
\end{equation} As quoted by the authors in page 21, after some interactions between the energy functionals associated to ![]() $(P_\mu)$ and
$(P_\mu)$ and ![]() $(P_{\mu,\infty})$, property (1.1) of the solution u 0 was strongly needed in order to prove that the weak solution of
$(P_{\mu,\infty})$, property (1.1) of the solution u 0 was strongly needed in order to prove that the weak solution of ![]() $(P_\mu)$ is non-trivial (see Section 5 in [Reference Maia and Soares12], p. 19).
$(P_\mu)$ is non-trivial (see Section 5 in [Reference Maia and Soares12], p. 19).
Our work complements all results cited above. Differently from them, the potential V is non-periodic and changes sign and the non-linearity  $g(s)=\mu f(s) + |s|^{2^*-2}s$ possesses a critical growth, with
$g(s)=\mu f(s) + |s|^{2^*-2}s$ possesses a critical growth, with ![]() $s\mapsto f(s)/s$ bounded. This scenario brings several difficulties.
$s\mapsto f(s)/s$ bounded. This scenario brings several difficulties.
The central idea of our approach is to apply the version of the Linking Theorem due to Maia and Soares in [Reference Maia and Soares12, Theorem 1.2] and, for that purpose, takes a positive ground state solution of ![]() $(P_{\mu,\infty})$ that has an exponential decay and makes some suitable interactions with problem
$(P_{\mu,\infty})$ that has an exponential decay and makes some suitable interactions with problem ![]() $(P_\mu)$. Since our problem is critical, we cannot apply [Reference Berestycki and Lions3] directly as the authors do in [Reference Maia and Soares12]. Therefore, how to guarantee that
$(P_\mu)$. Since our problem is critical, we cannot apply [Reference Berestycki and Lions3] directly as the authors do in [Reference Maia and Soares12]. Therefore, how to guarantee that ![]() $(P_{\mu,\infty})$ has some non-trivial ground state solution? And, then, is it possible to show that this solution has exponential decay as (1.1)?
$(P_{\mu,\infty})$ has some non-trivial ground state solution? And, then, is it possible to show that this solution has exponential decay as (1.1)?
In this paper, to prove that problem ![]() $(P_\mu)$ has a non-trivial solution, we first answer these two question, considering the elliptic problem
$(P_\mu)$ has a non-trivial solution, we first answer these two question, considering the elliptic problem
 \begin{equation}
-\Delta u + V(x) u = \mu f(u) + |u|^{2^*-2}u, \quad u\in H^1(\mathbb{R}^N), \ u\neq 0
\end{equation}
\begin{equation}
-\Delta u + V(x) u = \mu f(u) + |u|^{2^*-2}u, \quad u\in H^1(\mathbb{R}^N), \ u\neq 0
\end{equation}with ![]() $N\geq 3$, µ > 0 and
$N\geq 3$, µ > 0 and ![]() $u\in E:= H^1(\mathbb{R}^N)$ and
$u\in E:= H^1(\mathbb{R}^N)$ and ![]() $V:\mathbb{R}^N\to\mathbb{R}$ is a potential satisfying the conditions:
$V:\mathbb{R}^N\to\mathbb{R}$ is a potential satisfying the conditions:
![]() $(V_1)$
$(V_1)$ ![]() $V\in L^\infty(\mathbb{R}^N)$;
$V\in L^\infty(\mathbb{R}^N)$;
![]() $(V_2)$
$(V_2)$  $\displaystyle\lim_{|x|\rightarrow +\infty}V(x)=V_\infty \gt 0$;
$\displaystyle\lim_{|x|\rightarrow +\infty}V(x)=V_\infty \gt 0$;
![]() $(V_3)$
$(V_3)$![]() $0\notin \sigma(L)$ and
$0\notin \sigma(L)$ and ![]() $\inf\sigma(L) \lt 0$, where
$\inf\sigma(L) \lt 0$, where ![]() $\sigma(L)$ is the spectrum of the operator
$\sigma(L)$ is the spectrum of the operator ![]() $L=-\Delta+V$.
$L=-\Delta+V$.
![]() $(V_4)$
$(V_4)$ $V(x) \leq V_\infty - Ce^{-\gamma_1|x|^{\gamma_2}}$, with
$V(x) \leq V_\infty - Ce^{-\gamma_1|x|^{\gamma_2}}$, with ![]() $\gamma_1 \gt 0$ and
$\gamma_1 \gt 0$ and ![]() $\gamma_2\in (0,1)$.
$\gamma_2\in (0,1)$.
The conditions that we consider on the non-linearity ![]() $f\in C(\mathbb{R},\mathbb{R})$ are the following:
$f\in C(\mathbb{R},\mathbb{R})$ are the following:
![]() $(f_1)$
$(f_1)$  $\displaystyle\lim_{s\rightarrow 0}\displaystyle\frac{f(s)}{s}=0$ and
$\displaystyle\lim_{s\rightarrow 0}\displaystyle\frac{f(s)}{s}=0$ and ![]() $f(s)=0$, for all
$f(s)=0$, for all ![]() $s\in(-\infty, 0]$ ;
$s\in(-\infty, 0]$ ;
![]() $(f_2)$ We have
$(f_2)$ We have ![]() $f(s)=0$ for
$f(s)=0$ for ![]() $s\leq 0$ and
$s\leq 0$ and  $\displaystyle\frac{|f(s)|}{|s|} \lt m$ for all s ≠ 0;
$\displaystyle\frac{|f(s)|}{|s|} \lt m$ for all s ≠ 0;
![]() $(f_3)$ If
$(f_3)$ If  $F(s):=\displaystyle\int_{0}^{s}f(t)\,{\rm d}t$ and
$F(s):=\displaystyle\int_{0}^{s}f(t)\,{\rm d}t$ and  $Q(s):=\displaystyle\frac{1}{2}f(s)s-F(s)$, then for all
$Q(s):=\displaystyle\frac{1}{2}f(s)s-F(s)$, then for all ![]() $s\in\mathbb{R}\setminus\{0\}$,
$s\in\mathbb{R}\setminus\{0\}$,
 \begin{equation*}
F(s)\geq 0, \ Q(s) \gt 0 \quad \textrm{and} \quad \displaystyle\lim_{s\rightarrow \infty} Q(s)= + \infty.
\end{equation*}
\begin{equation*}
F(s)\geq 0, \ Q(s) \gt 0 \quad \textrm{and} \quad \displaystyle\lim_{s\rightarrow \infty} Q(s)= + \infty.
\end{equation*} An important consequence of assumptions ![]() $(f_1)$ and
$(f_1)$ and ![]() $(f_2)$ is that, given ɛ > 0 and
$(f_2)$ is that, given ɛ > 0 and ![]() $2\leq p\leq 2^*$, there exists
$2\leq p\leq 2^*$, there exists ![]() $C_\varepsilon \gt 0$ such that
$C_\varepsilon \gt 0$ such that
for all ![]() $s\in\mathbb{R}$.
$s\in\mathbb{R}$.
One of our main results is the next theorem.
Theorem 1.1. Suppose that assumptions ![]() $(V_1)-(V_4)$ and
$(V_1)-(V_4)$ and ![]() $(f_1)-(f_3)$ hold. Then, there exists
$(f_1)-(f_3)$ hold. Then, there exists ![]() $\mu^* \gt 0$ such that, if
$\mu^* \gt 0$ such that, if ![]() $\mu\geq \mu^*$, problem
$\mu\geq \mu^*$, problem ![]() $(P_\mu)$ has a nontrivial and nonnegative solution uµ in
$(P_\mu)$ has a nontrivial and nonnegative solution uµ in ![]() $H^1(\mathbb{R}^N)$. Moreover, the limit problem
$H^1(\mathbb{R}^N)$. Moreover, the limit problem
 \begin{equation}
\left\{
\begin{array}{l}
- \Delta u+V_{\infty}u= \mu f(u)+|u|^{2^*-2}u \quad \mbox{in}\ \mathbb{R}^{N}\\
u\in H^1(\mathbb{R}^N),
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{l}
- \Delta u+V_{\infty}u= \mu f(u)+|u|^{2^*-2}u \quad \mbox{in}\ \mathbb{R}^{N}\\
u\in H^1(\mathbb{R}^N),
\end{array}
\right.
\end{equation}has a ground state solution u 0 such that, if ![]() $\nu\in\left(0,\sqrt{V_\infty}\right)$, then there exists
$\nu\in\left(0,\sqrt{V_\infty}\right)$, then there exists ![]() $C=C(m,\nu) \gt 0$ satisfying
$C=C(m,\nu) \gt 0$ satisfying
We stress here that, in order to prove Theorem 1.1, we do not need any monotonicity hypothesis on function ![]() $s\mapsto f(s)/s$, as one can find in the literature about similar problems. One example of non-linearity that satisfies our assumptions but
$s\mapsto f(s)/s$, as one can find in the literature about similar problems. One example of non-linearity that satisfies our assumptions but ![]() $f(s)/s$, s ≠ 0, is not increasing is
$f(s)/s$, s ≠ 0, is not increasing is  $f(s)=\dfrac{s^7-1,5s^5+2s^3}{1+s^6}$ for
$f(s)=\dfrac{s^7-1,5s^5+2s^3}{1+s^6}$ for ![]() $s\in\mathbb{R}$. Then f satisfies our hypotheses; however,
$s\in\mathbb{R}$. Then f satisfies our hypotheses; however, ![]() $f(s)/s$, s ≠ 0, is not increasing.
$f(s)/s$, s ≠ 0, is not increasing.
This paper is organized into seven sections as follows. In § 2, we focus on providing the appropriate variational setting for the problem. In § 3, we obtain the geometry of a version of the Linking Theorem, and as a result, we obtain an appropriate Cerami sequence. This sequence is proven to be bounded in § 4. In § 5, we present the first part of the proof of Theorem 1.1, and in § 6, Appendix A, we present the second part of the proof and we also discuss the limit problem ![]() $(P_{\mu,\infty})$ and its ground state solution in detail. Finally, in Appendix B, § 7, we present a technical result on significant convergences.
$(P_{\mu,\infty})$ and its ground state solution in detail. Finally, in Appendix B, § 7, we present a technical result on significant convergences.
2. Variational setting
Let ![]() $E:=H^1(\mathbb{R}^N)$. The energy functional
$E:=H^1(\mathbb{R}^N)$. The energy functional ![]() $I:E\rightarrow\mathbb{R}$ associated with equation (P) is given by
$I:E\rightarrow\mathbb{R}$ associated with equation (P) is given by
 \begin{equation*}
I_\mu(u)=\displaystyle\frac{1}{2}\int_{\mathbb{R}^N}\left( |\nabla u |^2 + V(x) u^2 \right)\,{\rm d}x - \mu\int_{\mathbb{R}^N} F(u)\,{\rm d}x - \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |u|^{2^*}\,{\rm d}x,
\end{equation*}
\begin{equation*}
I_\mu(u)=\displaystyle\frac{1}{2}\int_{\mathbb{R}^N}\left( |\nabla u |^2 + V(x) u^2 \right)\,{\rm d}x - \mu\int_{\mathbb{R}^N} F(u)\,{\rm d}x - \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |u|^{2^*}\,{\rm d}x,
\end{equation*}with ![]() $u\in E$. It is well known from conditions
$u\in E$. It is well known from conditions ![]() $(V_2)$ and
$(V_2)$ and ![]() $(V_3)$ that the eigenvalue problem
$(V_3)$ that the eigenvalue problem
has a sequence of eigenvalues ![]() $\lambda_1 \lt \lambda_2\leq \cdots\leq \lambda_k \lt 0$ (see [Reference Egorov and Kondratiev6], Theorem 30, p. 150). We denote by ϕi the eigenfunction corresponding to λi,
$\lambda_1 \lt \lambda_2\leq \cdots\leq \lambda_k \lt 0$ (see [Reference Egorov and Kondratiev6], Theorem 30, p. 150). We denote by ϕi the eigenfunction corresponding to λi, ![]() $i\in\{1,2,\ldots,k\}$ in
$i\in\{1,2,\ldots,k\}$ in ![]() $H^1(\mathbb{R}^N)$. Setting
$H^1(\mathbb{R}^N)$. Setting
 \begin{equation*}
E^-:=\textrm{span}\{\phi_i, \ i=1,2,\ldots, k\} \quad \textrm{and} \quad E^+:=\left(E^-\right)^{\perp},
\end{equation*}
\begin{equation*}
E^-:=\textrm{span}\{\phi_i, \ i=1,2,\ldots, k\} \quad \textrm{and} \quad E^+:=\left(E^-\right)^{\perp},
\end{equation*}we see that ![]() $E=E^+ \oplus E^-$. According to Stuart in [Reference Stuart15], Theorem 3.15, the essential spectrum of
$E=E^+ \oplus E^-$. According to Stuart in [Reference Stuart15], Theorem 3.15, the essential spectrum of ![]() $-\Delta +V$ is the interval
$-\Delta +V$ is the interval ![]() $[V_\infty,+\infty)$, and this implies that
$[V_\infty,+\infty)$, and this implies that ![]() $\dim E^- \lt \infty$. Having made these considerations, every function
$\dim E^- \lt \infty$. Having made these considerations, every function ![]() $u\in E$ may be written as
$u\in E$ may be written as ![]() $u=u^+ + u^-$ uniquely, where
$u=u^+ + u^-$ uniquely, where ![]() $u^+\in E^+$ and
$u^+\in E^+$ and ![]() $u^-\in E^-$. Hence, by using the arguments in Lemma 1.2 of [Reference Costa and Tehrani5], we may introduce the new inner product
$u^-\in E^-$. Hence, by using the arguments in Lemma 1.2 of [Reference Costa and Tehrani5], we may introduce the new inner product ![]() $\langle \cdot, \cdot\rangle$ in E, namely,
$\langle \cdot, \cdot\rangle$ in E, namely,
 \begin{equation*}
\langle u,v \rangle =
\left\{\begin{array}{cl}
\displaystyle\int_{\mathbb{R}^N} (\nabla u\cdot\nabla v + V(x)uv)\,{\rm d}x & \textrm{if} \ u,v \in E^+,\\
-\displaystyle\int_{\mathbb{R}^N} (\nabla u\cdot\nabla v + V(x)uv)\,{\rm d}x & \textrm{if} \ u,v \in E^-,\\
0 & \textrm{if} \ u\in E^+ \ \textrm{and} \ v\in E^-.
\end{array}\right.
\end{equation*}
\begin{equation*}
\langle u,v \rangle =
\left\{\begin{array}{cl}
\displaystyle\int_{\mathbb{R}^N} (\nabla u\cdot\nabla v + V(x)uv)\,{\rm d}x & \textrm{if} \ u,v \in E^+,\\
-\displaystyle\int_{\mathbb{R}^N} (\nabla u\cdot\nabla v + V(x)uv)\,{\rm d}x & \textrm{if} \ u,v \in E^-,\\
0 & \textrm{if} \ u\in E^+ \ \textrm{and} \ v\in E^-.
\end{array}\right.
\end{equation*}such that the corresponding norm ![]() $\|\cdot\|$ is equivalent to
$\|\cdot\|$ is equivalent to ![]() $\|\cdot\|_E$, the usual norm in
$\|\cdot\|_E$, the usual norm in ![]() $E=H^1(\mathbb{R}^N)$. In addition, the functional I may be written as
$E=H^1(\mathbb{R}^N)$. In addition, the functional I may be written as
 \begin{equation*}
I_\mu(u) = \displaystyle\frac{1}{2}\|u^+\|^2 - \displaystyle\frac{1}{2}\|u^-\|^2 - \mu\displaystyle\int_{\mathbb{R}^N} F(u)\,{\rm d}x {-\displaystyle\frac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |u|^{2^*}\,{\rm d}x}
\end{equation*}
\begin{equation*}
I_\mu(u) = \displaystyle\frac{1}{2}\|u^+\|^2 - \displaystyle\frac{1}{2}\|u^-\|^2 - \mu\displaystyle\int_{\mathbb{R}^N} F(u)\,{\rm d}x {-\displaystyle\frac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |u|^{2^*}\,{\rm d}x}
\end{equation*}for every function ![]() $u=u^++u^-\in E$. We call the attention to the fact that, since
$u=u^++u^-\in E$. We call the attention to the fact that, since ![]() $\lambda_i\neq 0$ for all
$\lambda_i\neq 0$ for all ![]() $i\in\{1,2,\ldots,k\}$, it follows from (2.1) and the definition of ϕi that
$i\in\{1,2,\ldots,k\}$, it follows from (2.1) and the definition of ϕi that
 \begin{equation}
\displaystyle\int_{\mathbb{R}^N} u^+(x)v^-(x)\, {\rm d}x = 0
\end{equation}
\begin{equation}
\displaystyle\int_{\mathbb{R}^N} u^+(x)v^-(x)\, {\rm d}x = 0
\end{equation}for all functions ![]() $u^+\in E^+$ and
$u^+\in E^+$ and ![]() $v^-\in E^-$.
$v^-\in E^-$.
To deal with compactness issues, we will prove several auxiliary results concerning the limit problem associated to ![]() $(P_\mu)$, namely,
$(P_\mu)$, namely,
 \begin{equation}
\left\{
\begin{array}{l}
- \Delta u+V_{\infty}u= \mu f(u)+|u|^{2^*-2}u \quad \mbox{in}\ \mathbb{R}^{N}\\\\
u\in H^1(\mathbb{R}^N).
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{l}
- \Delta u+V_{\infty}u= \mu f(u)+|u|^{2^*-2}u \quad \mbox{in}\ \mathbb{R}^{N}\\\\
u\in H^1(\mathbb{R}^N).
\end{array}
\right.
\end{equation} Hereafter, let us denote by ![]() $J_{\mu}: H^1(\mathbb{R}^N) \to \mathbb{R}$ the associated functional given by
$J_{\mu}: H^1(\mathbb{R}^N) \to \mathbb{R}$ the associated functional given by
 \begin{equation*}
J_{\mu}(u):=\displaystyle\frac{1}{2}\int_{\mathbb{R}^N}\left( |\nabla u |^2 + V_\infty u^2 \right)\, {\rm d}x - \mu\int_{\mathbb{R}^N} F(u)\,{\rm d}x - \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |u|^{2^*}\, {\rm d}x.
\end{equation*}
\begin{equation*}
J_{\mu}(u):=\displaystyle\frac{1}{2}\int_{\mathbb{R}^N}\left( |\nabla u |^2 + V_\infty u^2 \right)\, {\rm d}x - \mu\int_{\mathbb{R}^N} F(u)\,{\rm d}x - \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |u|^{2^*}\, {\rm d}x.
\end{equation*} Also, let us consider the level  $d_\mu:=\inf\limits_{u\in\mathcal{N}_\mu}J_\mu(u)$, where
$d_\mu:=\inf\limits_{u\in\mathcal{N}_\mu}J_\mu(u)$, where
 \begin{equation*}
\mathcal{N}_\mu:=\left\{u\in H^{1}(\mathbb{R}^N)/\{0\}:~J^\prime_\mu(u)=0 \right\}.
\end{equation*}
\begin{equation*}
\mathcal{N}_\mu:=\left\{u\in H^{1}(\mathbb{R}^N)/\{0\}:~J^\prime_\mu(u)=0 \right\}.
\end{equation*}3. Geometry of the Linking Theorem
In this section, we are going to show that functional Iµ satisfies the geometry of the following version of the Linking Theorem.
Theorem 3.1. [Reference Maia and Soares12, Theorem 1.2] Let E be a real Banach space with ![]() $E=V \oplus X$, where V is finite dimensional. Suppose there exist real constants
$E=V \oplus X$, where V is finite dimensional. Suppose there exist real constants ![]() $R \gt \rho \gt 0,\ \alpha \gt \beta$ and there exists an
$R \gt \rho \gt 0,\ \alpha \gt \beta$ and there exists an ![]() $e \in \partial B_{1} \cap X$ such that
$e \in \partial B_{1} \cap X$ such that ![]() $I \in C^{1}(E, \mathbb{R})$ satisfies
$I \in C^{1}(E, \mathbb{R})$ satisfies
(I
 $\left._{1}\right)$
$\left._{1}\right)$  $\left.\quad I\right|_{\partial B_{\rho} \cap X} \geq \alpha ;$
$\left.\quad I\right|_{\partial B_{\rho} \cap X} \geq \alpha ;$(I2) Setting
 $M:=\left(\bar{B}_{R} \cap V\right) \oplus\{$re
$M:=\left(\bar{B}_{R} \cap V\right) \oplus\{$re  $: 0 \leq r \leq R\}$, there exists an h
$: 0 \leq r \leq R\}$, there exists an h $_{0} \in C(M, E)$ such that
$_{0} \in C(M, E)$ such that
(i)
 $\sup\limits_{w \in M} I\left(h_{0}(w)\right) \lt +\infty$,
$\sup\limits_{w \in M} I\left(h_{0}(w)\right) \lt +\infty$,(ii)
 $\sup\limits_{w \in \partial M} I\left(h_{0}(w)\right)=\beta$,
$\sup\limits_{w \in \partial M} I\left(h_{0}(w)\right)=\beta$,(iii)
 $h_{0}(\partial M) \cap\left(\partial B_{\rho} \cap X\right)=\emptyset$,
$h_{0}(\partial M) \cap\left(\partial B_{\rho} \cap X\right)=\emptyset$,(iv) There exists a unique
 $u\in h_{0}(M) \cap\left(\partial B_{\rho} \cap X\right)$ such that
$u\in h_{0}(M) \cap\left(\partial B_{\rho} \cap X\right)$ such that
 \begin{equation*}\operatorname{deg}\left(h_{0}, \operatorname{int}(M), u\right) \neq 0.\end{equation*}
\begin{equation*}\operatorname{deg}\left(h_{0}, \operatorname{int}(M), u\right) \neq 0.\end{equation*}
Then I possess a Cerami sequence on a level ![]() $c \geq \alpha$, which can be characterized as
$c \geq \alpha$, which can be characterized as
 \begin{equation*}
c:=\inf _{h \in \Gamma} \max _{w \in M} I(h(w)),
\end{equation*}
\begin{equation*}
c:=\inf _{h \in \Gamma} \max _{w \in M} I(h(w)),
\end{equation*}where ![]() $\Gamma:=\left\{h \in C(M, E):\left.h\right|_{\partial M}=h_{0}\right\}$.
$\Gamma:=\left\{h \in C(M, E):\left.h\right|_{\partial M}=h_{0}\right\}$.
To prove that functional Iµ has the geometry of Theorem 3.1, let ![]() $u_0\in H^1(\mathbb{R}^N)$ be a non-trivial ground state solution of problem
$u_0\in H^1(\mathbb{R}^N)$ be a non-trivial ground state solution of problem ![]() $(P_{\mu,\infty})$ given by Proposition 6.7 in Appendix A. By hypothesis
$(P_{\mu,\infty})$ given by Proposition 6.7 in Appendix A. By hypothesis ![]() $(f_2)$, u 0 is nonnegative.
$(f_2)$, u 0 is nonnegative.
Given ![]() $w\in E$ and
$w\in E$ and ![]() $y\in\mathbb{R}^N$, to simplify the notation, we write
$y\in\mathbb{R}^N$, to simplify the notation, we write ![]() $w^+(\cdot-y)$ (or
$w^+(\cdot-y)$ (or ![]() $w^-(\cdot - y)$) referring to the projection in
$w^-(\cdot - y)$) referring to the projection in ![]() $E^+$ (respectively, in
$E^+$ (respectively, in ![]() $E^-$) of the translated function
$E^-$) of the translated function ![]() $w(\cdot-y)$.
$w(\cdot-y)$.
Proceeding as Claim 4.5 in [Reference Maia, Junior and Ruviaro11], we may prove that ![]() $u_0^+(\cdot-y)$ is a non-trivial function just choosing
$u_0^+(\cdot-y)$ is a non-trivial function just choosing ![]() $y\in\mathbb{R}^N$ with norm sufficiently large. Now, let us consider R > 0, any non-trivial function
$y\in\mathbb{R}^N$ with norm sufficiently large. Now, let us consider R > 0, any non-trivial function ![]() $e\in E^+$ with
$e\in E^+$ with ![]() $\|e\|=1$ and the sets
$\|e\|=1$ and the sets
and
Defining
 \begin{equation*}
h_0(w) = h_0\left(tRe+v^-\right):=u_0^+\left(\frac{\cdot - y}{tL}\right)+|v^-|, \ \text{for} \ t\in (0,1]
\end{equation*}
\begin{equation*}
h_0(w) = h_0\left(tRe+v^-\right):=u_0^+\left(\frac{\cdot - y}{tL}\right)+|v^-|, \ \text{for} \ t\in (0,1]
\end{equation*}and ![]() $h_0(v^-) = |v^-|$, where
$h_0(v^-) = |v^-|$, where ![]() $u_0\in E$ is the non-trivial solution to the limit problem
$u_0\in E$ is the non-trivial solution to the limit problem ![]() $(P_\infty)$ found before and L > 0 to be chosen, we have the following lemmas. The first one proves item
$(P_\infty)$ found before and L > 0 to be chosen, we have the following lemmas. The first one proves item ![]() $(I_1)$ from Theorem 3.1.
$(I_1)$ from Theorem 3.1.
Lemma 3.2. There exists ρ > 0 such that
 \begin{equation*}
\displaystyle\inf_{w\in \partial B_\rho\cap E^+} I_\mu(w) \gt 0.
\end{equation*}
\begin{equation*}
\displaystyle\inf_{w\in \partial B_\rho\cap E^+} I_\mu(w) \gt 0.
\end{equation*}Proof. For ρ > 0, let ![]() $w^+\in E^+$ with
$w^+\in E^+$ with ![]() $\|w^+\|=\rho$. Then, from (1.2), for all ɛ > 0, there exists
$\|w^+\|=\rho$. Then, from (1.2), for all ɛ > 0, there exists ![]() $C_\varepsilon \gt 0$ such that
$C_\varepsilon \gt 0$ such that
 \begin{equation*}
I_\mu(w^+) \geq \dfrac{1}{2}\rho^2 - \mu\varepsilon C\rho^2 - \mu C_\varepsilon C \rho^{2^*} - \dfrac{1}{2^*}\rho^{2^*},
\end{equation*}
\begin{equation*}
I_\mu(w^+) \geq \dfrac{1}{2}\rho^2 - \mu\varepsilon C\rho^2 - \mu C_\varepsilon C \rho^{2^*} - \dfrac{1}{2^*}\rho^{2^*},
\end{equation*}where we used Sobolev embeddings and the equivalence of the norms. It follows that, for  $\varepsilon \lt \dfrac{1}{4\mu C}$,
$\varepsilon \lt \dfrac{1}{4\mu C}$,
 \begin{equation*}
I_\mu(w^+) \geq \dfrac{1}{4}\rho^2 - \left( \dfrac{1}{2^*} + \mu C_\varepsilon C\right)\rho^{2^*}.
\end{equation*}
\begin{equation*}
I_\mu(w^+) \geq \dfrac{1}{4}\rho^2 - \left( \dfrac{1}{2^*} + \mu C_\varepsilon C\right)\rho^{2^*}.
\end{equation*} Now, choosing  $0 \lt \rho \lt \left( \dfrac{2^*}{4(1+2^*\mu C_\varepsilon C)} \right)^{\frac{1}{2^*-2}}$, the result follows.
$0 \lt \rho \lt \left( \dfrac{2^*}{4(1+2^*\mu C_\varepsilon C)} \right)^{\frac{1}{2^*-2}}$, the result follows.
The next result shows that item (ii) from Theorem 3.1 holds, choosing β = 0. Before stating this result, we remember an important result from spectral theory that characterizes the functions that belong to ![]() $E^-$ as follows:
$E^-$ as follows: ![]() $u\in E^-$ if and only if
$u\in E^-$ if and only if
 \begin{equation*}
\displaystyle\int_{\mathbb{R}^N} \left(|\nabla u|^2 + V(x)u^2\right) \,{\rm d}x \lt 0.
\end{equation*}
\begin{equation*}
\displaystyle\int_{\mathbb{R}^N} \left(|\nabla u|^2 + V(x)u^2\right) \,{\rm d}x \lt 0.
\end{equation*} Thus, if ![]() $u\in E^-$, then
$u\in E^-$, then ![]() $|u|\in E^-$.
$|u|\in E^-$.
In the sequel, we will denote  $\|w\|^2_{V_\infty} = \displaystyle\int_{\mathbb{R}^N} (|\nabla w|^2+V_\infty w^2)\,{\rm d}x$ for any
$\|w\|^2_{V_\infty} = \displaystyle\int_{\mathbb{R}^N} (|\nabla w|^2+V_\infty w^2)\,{\rm d}x$ for any ![]() $w\in H^1(\mathbb{R}^N)$.
$w\in H^1(\mathbb{R}^N)$.
Lemma 3.3. There exist R > 0 sufficiently large, which does not depend on µ, such that, for all µ > 0,
 \begin{equation*}
\sup_{w\in M_0} I_\mu(h_0(w)) = 0.
\end{equation*}
\begin{equation*}
\sup_{w\in M_0} I_\mu(h_0(w)) = 0.
\end{equation*}Proof. Denoting by  $\Upsilon^+(t)(x) = u_0^+\left(\frac{x - y}{tL}\right)$, let us separate this proof in three possible cases. If
$\Upsilon^+(t)(x) = u_0^+\left(\frac{x - y}{tL}\right)$, let us separate this proof in three possible cases. If ![]() $w=tRe+v^-$ with
$w=tRe+v^-$ with ![]() $t\in [0,1]$ and
$t\in [0,1]$ and ![]() $\|v^-\|=R$, we have
$\|v^-\|=R$, we have
 \begin{equation*}
\begin{aligned}
I_\mu\left(h_{0}(w)\right) &\leq \frac{1}{2}\left[\left\|\Upsilon^{+}(t)\right\|^{2}-R^{2}\right] \\
& \leq \frac{1}{2}\left[\left\|\Upsilon(t)\right\|_{V_\infty}^{2}-R^{2}\right] \\
& \leq \frac{1}{2}\left[\max _{t \in[0,1]}\|\Upsilon(t)\|_{V_\infty}^{2}-R^{2}\right] \lt 0
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
I_\mu\left(h_{0}(w)\right) &\leq \frac{1}{2}\left[\left\|\Upsilon^{+}(t)\right\|^{2}-R^{2}\right] \\
& \leq \frac{1}{2}\left[\left\|\Upsilon(t)\right\|_{V_\infty}^{2}-R^{2}\right] \\
& \leq \frac{1}{2}\left[\max _{t \in[0,1]}\|\Upsilon(t)\|_{V_\infty}^{2}-R^{2}\right] \lt 0
\end{aligned}
\end{equation*}for R > 0 large enough. Second, if ![]() $w=v^- \in \bar{B}_{R}(0) \cap E^-$, one has
$w=v^- \in \bar{B}_{R}(0) \cap E^-$, one has
To finish the proof, if ![]() $w=Re + v^-$, with
$w=Re + v^-$, with ![]() $\|v^-\|\leq R$, then
$\|v^-\|\leq R$, then
 \begin{equation*}
\begin{aligned}
I_\mu\left(h_{0}(w)\right) &=\frac{1}{2}\left[\left\|\Upsilon^{+}(1)\right\|^{2}-\|v^-\|^{2}\right]-\mu\int_{\mathbb{R}^{N}} F\left(\Upsilon^{+}(1)+|v^-|\right)\,{\rm d} x \\
&\quad- \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} \left|\Upsilon^{+}(1)+|v^-|\right|^{2^*}\,{\rm d}x \\
& \leq J_\mu\left(\Upsilon^+(1)\right)+\mu\int_{\mathbb{R}^{N}} [F\left(\Upsilon^{+}(1)\right) - F\left(\Upsilon^{+}(1)+|v|\right)]\,{\rm d} x \\
& \quad+ \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} \left[\left| \Upsilon^+(1)\right|^{2^*} - \left|\Upsilon^{+}(1)+|v^-|\right|^{2^*}\right]\,{\rm d}x\\
& \leq 0,
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
I_\mu\left(h_{0}(w)\right) &=\frac{1}{2}\left[\left\|\Upsilon^{+}(1)\right\|^{2}-\|v^-\|^{2}\right]-\mu\int_{\mathbb{R}^{N}} F\left(\Upsilon^{+}(1)+|v^-|\right)\,{\rm d} x \\
&\quad- \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} \left|\Upsilon^{+}(1)+|v^-|\right|^{2^*}\,{\rm d}x \\
& \leq J_\mu\left(\Upsilon^+(1)\right)+\mu\int_{\mathbb{R}^{N}} [F\left(\Upsilon^{+}(1)\right) - F\left(\Upsilon^{+}(1)+|v|\right)]\,{\rm d} x \\
& \quad+ \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} \left[\left| \Upsilon^+(1)\right|^{2^*} - \left|\Upsilon^{+}(1)+|v^-|\right|^{2^*}\right]\,{\rm d}x\\
& \leq 0,
\end{aligned}
\end{equation*}where we used the facts that, for L > 0 large enough, it holds that ![]() $J_\mu(\Upsilon(1)) \lt 0$; we also have for
$J_\mu(\Upsilon(1)) \lt 0$; we also have for ![]() $|y|$ sufficiently large that
$|y|$ sufficiently large that ![]() $\left\|\Upsilon^{-}(1)\right\|$ is small enough such that
$\left\|\Upsilon^{-}(1)\right\|$ is small enough such that ![]() $J_\mu(\Upsilon(1)) \lt 0$ implies
$J_\mu(\Upsilon(1)) \lt 0$ implies ![]() $J_\mu\left(\Upsilon^{+}(1)\right) \leq 0$ and
$J_\mu\left(\Upsilon^{+}(1)\right) \leq 0$ and
 \begin{equation*}
\displaystyle\int_{\mathbb{R}^N} \left[\left| \Upsilon^+(1)\right|^{2^*} - \left|\Upsilon^{+}(1)+|v^-|\right|^{2^*}\right]\,{\rm d}x \approx \displaystyle\int_{\mathbb{R}^N} \left[\left| \Upsilon(1)\right|^{2^*} - \left|\Upsilon(1)+|v^-|\right|^{2^*}\right]\,{\rm d}x.
\end{equation*}
\begin{equation*}
\displaystyle\int_{\mathbb{R}^N} \left[\left| \Upsilon^+(1)\right|^{2^*} - \left|\Upsilon^{+}(1)+|v^-|\right|^{2^*}\right]\,{\rm d}x \approx \displaystyle\int_{\mathbb{R}^N} \left[\left| \Upsilon(1)\right|^{2^*} - \left|\Upsilon(1)+|v^-|\right|^{2^*}\right]\,{\rm d}x.
\end{equation*} Moreover, we applied the non-decreasing condition for function F since ![]() $f(s)\geq 0$ for all s and for function
$f(s)\geq 0$ for all s and for function ![]() $s\mapsto s^{2^*}$, for s > 0.
$s\mapsto s^{2^*}$, for s > 0.
Now, let us demonstrate that item (iii) from Theorem 3.1 also is valid.
Lemma 3.4. It holds that ![]() $h_{0}(\partial M) \cap\left(\partial B_{\rho} \cap E^+\right)=\emptyset$.
$h_{0}(\partial M) \cap\left(\partial B_{\rho} \cap E^+\right)=\emptyset$.
Proof. Observe that
and that
In addition, to guarantee that ![]() $\left(\bar{B}_{R} \cap E^-\right) \oplus\left\{\Upsilon^{+}(1)\right\} \cap E^+ \cap \partial B_{\rho}=\emptyset$, it is enough to choose a sufficiently large
$\left(\bar{B}_{R} \cap E^-\right) \oplus\left\{\Upsilon^{+}(1)\right\} \cap E^+ \cap \partial B_{\rho}=\emptyset$, it is enough to choose a sufficiently large ![]() $L,|y| \gt 0$ such that
$L,|y| \gt 0$ such that ![]() $I_\mu(\Upsilon^{+}(1))\approx I_\mu(\Upsilon(1))\leq J_\mu(\Upsilon(1)) \lt -1$. Therefore, by Lemma 3.2, necessarily
$I_\mu(\Upsilon^{+}(1))\approx I_\mu(\Upsilon(1))\leq J_\mu(\Upsilon(1)) \lt -1$. Therefore, by Lemma 3.2, necessarily
 \begin{equation}
\left\|\Upsilon^{+}(1)\right\|^{2} \gt \rho^{2},
\end{equation}
\begin{equation}
\left\|\Upsilon^{+}(1)\right\|^{2} \gt \rho^{2},
\end{equation}where  $\Upsilon^{+}(1)=u_0^{+}\left(\frac{x-y}{L}\right)$. Then, we conclude that
$\Upsilon^{+}(1)=u_0^{+}\left(\frac{x-y}{L}\right)$. Then, we conclude that
The lemma follows.
Finally, let us prove that item (iv) from Theorem 3.1 is true.
Lemma 3.5. There exists a unique ![]() $u\in h_{0}(M) \cap\left(\partial B_{\rho} \cap E^+\right)$ such that
$u\in h_{0}(M) \cap\left(\partial B_{\rho} \cap E^+\right)$ such that
Proof. Consider the function ![]() $\psi:[0,1] \rightarrow \mathbb{R}$, given by
$\psi:[0,1] \rightarrow \mathbb{R}$, given by ![]() $\psi(t)=\left\|\Upsilon^{+}(t)\right\|$, is strictly increasing and hence injective. Moreover, ψ is continuous,
$\psi(t)=\left\|\Upsilon^{+}(t)\right\|$, is strictly increasing and hence injective. Moreover, ψ is continuous, ![]() $\psi(0)=0$, and from (3.1), we have
$\psi(0)=0$, and from (3.1), we have ![]() $\psi(1) \gt \rho$. Thus, from the Intermediate Value Theorem, there exists some (unique, since ψ is injective)
$\psi(1) \gt \rho$. Thus, from the Intermediate Value Theorem, there exists some (unique, since ψ is injective) ![]() $t_{0} \in(0,1)$ such that
$t_{0} \in(0,1)$ such that ![]() $\psi\left(t_{0}\right)=\rho$. Hence,
$\psi\left(t_{0}\right)=\rho$. Hence,
and there exists an unique ![]() $w=\Upsilon^{+}\left(t_{0}\right) \in h_{0}(M) \cap\left(\partial B_{\rho} \cap E^+\right)$. Since
$w=\Upsilon^{+}\left(t_{0}\right) \in h_{0}(M) \cap\left(\partial B_{\rho} \cap E^+\right)$. Since ![]() $Rte \mapsto h_{0}( Rte )=\Upsilon^{+}(t)$ is injective, there exists a unique
$Rte \mapsto h_{0}( Rte )=\Upsilon^{+}(t)$ is injective, there exists a unique ![]() $u_{0}=R t_{0} e \in \operatorname{int}(M)$ such that
$u_{0}=R t_{0} e \in \operatorname{int}(M)$ such that ![]() $h_{0}\left(u_{0}\right)=\Upsilon^{+}\left(t_{0}\right)$. Therefore,
$h_{0}\left(u_{0}\right)=\Upsilon^{+}\left(t_{0}\right)$. Therefore, ![]() $\operatorname{deg}\left(h_{0}, \operatorname{int}(M), w\right) \neq 0$, proving (iv).
$\operatorname{deg}\left(h_{0}, \operatorname{int}(M), w\right) \neq 0$, proving (iv).
4. Boundedness of Cerami sequences
We say that a sequence ![]() $(u_n)\subset E$ is a Cerami sequence at level c for functional Iµ if
$(u_n)\subset E$ is a Cerami sequence at level c for functional Iµ if
 \begin{equation*}
I_\mu(u_n)\to c~\text{in}~\mathbb{R} \quad\text{and}\quad \|I_\mu^{\prime}(u_n)\|_{E^*}(1+\|u_n\|)\to 0~\in~\mathbb{R},
\end{equation*}
\begin{equation*}
I_\mu(u_n)\to c~\text{in}~\mathbb{R} \quad\text{and}\quad \|I_\mu^{\prime}(u_n)\|_{E^*}(1+\|u_n\|)\to 0~\in~\mathbb{R},
\end{equation*}as ![]() $n\rightarrow +\infty$. Before we state the next result, we note that, if
$n\rightarrow +\infty$. Before we state the next result, we note that, if ![]() $(v_n)$ is a bounded sequence in E, then
$(v_n)$ is a bounded sequence in E, then ![]() $(v_n)$ satisfies either
$(v_n)$ satisfies either
(i) vanishing: for all r > 0,
 $\displaystyle\limsup_{n\rightarrow \infty} \sup_{y\in\mathbb{R}^N}\int_{B(y,r)}|v_n|^2\,{\rm d}x = 0$
$\displaystyle\limsup_{n\rightarrow \infty} \sup_{y\in\mathbb{R}^N}\int_{B(y,r)}|v_n|^2\,{\rm d}x = 0$or
(ii) non-vanishing: there exist
 $r,\eta \gt 0$ and a sequence
$r,\eta \gt 0$ and a sequence  $(y_n)\subset\mathbb{R}^N$ such that
$(y_n)\subset\mathbb{R}^N$ such that
 \begin{equation*}
\displaystyle\limsup_{n\rightarrow \infty} \int_{B(y_n,r)}|v_n|^2\,{\rm d}x \gt \eta.
\end{equation*}
\begin{equation*}
\displaystyle\limsup_{n\rightarrow \infty} \int_{B(y_n,r)}|v_n|^2\,{\rm d}x \gt \eta.
\end{equation*}
Lemma 4.1. Let ![]() $(u_n)\subset E$ be a Cerami sequence at level c > 0. Then,
$(u_n)\subset E$ be a Cerami sequence at level c > 0. Then, ![]() $(u_n)$ has a bounded subsequence.
$(u_n)$ has a bounded subsequence.
Proof. Suppose by contradiction that ![]() $1\leq \|u_n\|\rightarrow \infty$ as
$1\leq \|u_n\|\rightarrow \infty$ as ![]() $n\to+\infty$. Consider
$n\to+\infty$. Consider
 \begin{equation*}v_n=\displaystyle\frac{u_n}{\|u_n\|}\end{equation*}
\begin{equation*}v_n=\displaystyle\frac{u_n}{\|u_n\|}\end{equation*}and note that ![]() $\|v_n\|=1$. The sequence
$\|v_n\|=1$. The sequence ![]() $(v_n)$ is bounded; however, we will show that neither (i) or (ii) is true. First, notice that from hypothesis
$(v_n)$ is bounded; however, we will show that neither (i) or (ii) is true. First, notice that from hypothesis ![]() $(f_3)$,
$(f_3)$,
 \begin{align*}
c+o_n(1) &= I_\mu(u_n)-\dfrac{1}{2}I^{\prime}_\mu(u_n)u_n
\nonumber\\
&= \mu \displaystyle\int_{\mathbb{R}^N}\left( \dfrac{f(u_n)u_n}{2}-F(u_n) \right) \,{\rm d}x + \left( \dfrac{1}{2} - \dfrac{1}{2^*} \right)\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*}\,{\rm d}x
\nonumber\\
&\geq \left( \dfrac{1}{2} - \dfrac{1}{2^*} \right)\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*}\,{\rm d}x,
\end{align*}
\begin{align*}
c+o_n(1) &= I_\mu(u_n)-\dfrac{1}{2}I^{\prime}_\mu(u_n)u_n
\nonumber\\
&= \mu \displaystyle\int_{\mathbb{R}^N}\left( \dfrac{f(u_n)u_n}{2}-F(u_n) \right) \,{\rm d}x + \left( \dfrac{1}{2} - \dfrac{1}{2^*} \right)\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*}\,{\rm d}x
\nonumber\\
&\geq \left( \dfrac{1}{2} - \dfrac{1}{2^*} \right)\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*}\,{\rm d}x,
\end{align*}which shows the boundedness of the sequence ![]() $\left(|u_n|_{2^*}\right)$. It will be used in the calculations that follows.
$\left(|u_n|_{2^*}\right)$. It will be used in the calculations that follows.
First, suppose that hypothesis (i) is satisfied for sequence ![]() $(v_n)$. Since the sequence
$(v_n)$. Since the sequence ![]() $(u_n)$ is a Cerami sequence, we have
$(u_n)$ is a Cerami sequence, we have
 \begin{align}
o_n(1)=I^{\prime}_\mu(u_n)\displaystyle\frac{u_n^+}{\|u_n\|^2}&=\displaystyle\frac{1}{\|u_n\|}I^{\prime}_\mu(u_n)v_n^+ \nonumber\\
&= \|v_n^+\|^2 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_nv_n^+\right)\,{\rm d}x
\end{align}
\begin{align}
o_n(1)=I^{\prime}_\mu(u_n)\displaystyle\frac{u_n^+}{\|u_n\|^2}&=\displaystyle\frac{1}{\|u_n\|}I^{\prime}_\mu(u_n)v_n^+ \nonumber\\
&= \|v_n^+\|^2 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_nv_n^+\right)\,{\rm d}x
\end{align}and
 \begin{align}
o_n(1)=I^{\prime}_\mu(u_n)\displaystyle\frac{u_n^-}{\|u_n\|^2}&=\displaystyle\frac{1}{\|u_n\|}I_\mu^{\prime}(u_n)v_n^- \nonumber\\
&= -\|v_n^-\|^2 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_nv_n^-\right)\,{\rm d}x .
\end{align}
\begin{align}
o_n(1)=I^{\prime}_\mu(u_n)\displaystyle\frac{u_n^-}{\|u_n\|^2}&=\displaystyle\frac{1}{\|u_n\|}I_\mu^{\prime}(u_n)v_n^- \nonumber\\
&= -\|v_n^-\|^2 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_nv_n^-\right)\,{\rm d}x .
\end{align}Subtracting equation (4.2) from (4.1), we have
 \begin{align*}
o_n(1) & = \|v_n^+\|^2 + \|v_n^-\|^2 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x\\\\
& = \|v_n\|^2 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x\\\\
&= 1 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x.
\end{align*}
\begin{align*}
o_n(1) & = \|v_n^+\|^2 + \|v_n^-\|^2 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x\\\\
& = \|v_n\|^2 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x\\\\
&= 1 - {\mu}\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x.
\end{align*}Thus,
 \begin{equation}
\mu\displaystyle\int_{\Omega^+_n}\left( \displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x=\mu\displaystyle\int_{\mathbb{R}^N}\left( \displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x \rightarrow 1,
\end{equation}
\begin{equation}
\mu\displaystyle\int_{\Omega^+_n}\left( \displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x=\mu\displaystyle\int_{\mathbb{R}^N}\left( \displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x \rightarrow 1,
\end{equation}provided ![]() $f(s)=0$ if
$f(s)=0$ if ![]() $s\leq 0$, where we define
$s\leq 0$, where we define ![]() $\Omega_n^+=\{x\in\mathbb{R}^N; \ u_n(x) \gt 0\}$. By equivalence of the norms, there exists a constant
$\Omega_n^+=\{x\in\mathbb{R}^N; \ u_n(x) \gt 0\}$. By equivalence of the norms, there exists a constant ![]() $\nu_0 \gt 0$ such that
$\nu_0 \gt 0$ such that
 \begin{equation}
\|w\|^2\geq \nu_0\|w\|^2_{L^2(\mathbb{R}^N)}
\end{equation}
\begin{equation}
\|w\|^2\geq \nu_0\|w\|^2_{L^2(\mathbb{R}^N)}
\end{equation}for any ![]() $w\in E$. Given
$w\in E$. Given  $0 \lt \varepsilon \lt \frac{1}{2}\nu_0$, by hypothesis
$0 \lt \varepsilon \lt \frac{1}{2}\nu_0$, by hypothesis ![]() $(f_1)$, there exists δ > 0 such that
$(f_1)$, there exists δ > 0 such that
 \begin{equation*}
\mu\displaystyle\frac{|f(s)|}{|s|}\leq\varepsilon \quad \textrm{for} \quad 0\neq |s| \lt \delta.
\end{equation*}
\begin{equation*}
\mu\displaystyle\frac{|f(s)|}{|s|}\leq\varepsilon \quad \textrm{for} \quad 0\neq |s| \lt \delta.
\end{equation*} For each ![]() $n\in\mathbb{N}$, consider the set
$n\in\mathbb{N}$, consider the set
Thus, from (4.4) and by Hölder’s inequality,
 \begin{equation*}
\begin{array}{rcl}
\mu\displaystyle\int_{\tilde{\Omega}_n} \left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x& \leq &\varepsilon\displaystyle\int_{\tilde{\Omega}_n}|v_n||v_n^+-v_n^-|\,{\rm d}x\\ \\
& \leq & \varepsilon\|v_n\|_{L^2(\mathbb{R}^N)}\left(\|v_n^+\|_{L^2(\mathbb{R}^N)} + \|v_n^-\|_{L^2(\mathbb{R}^N)} \right)\\\\
& \leq & 2\varepsilon\|v_n\|_{L^2(\mathbb{R}^N)}^2\\\\
& \leq & \displaystyle\frac{2\varepsilon}{\nu_0}\|v_n\|^2 = \displaystyle\frac{2\varepsilon}{\nu_0} \lt 1,
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{rcl}
\mu\displaystyle\int_{\tilde{\Omega}_n} \left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x& \leq &\varepsilon\displaystyle\int_{\tilde{\Omega}_n}|v_n||v_n^+-v_n^-|\,{\rm d}x\\ \\
& \leq & \varepsilon\|v_n\|_{L^2(\mathbb{R}^N)}\left(\|v_n^+\|_{L^2(\mathbb{R}^N)} + \|v_n^-\|_{L^2(\mathbb{R}^N)} \right)\\\\
& \leq & 2\varepsilon\|v_n\|_{L^2(\mathbb{R}^N)}^2\\\\
& \leq & \displaystyle\frac{2\varepsilon}{\nu_0}\|v_n\|^2 = \displaystyle\frac{2\varepsilon}{\nu_0} \lt 1,
\end{array}
\end{equation*}From (4.3), we conclude that
 \begin{equation}
\displaystyle\liminf_{n\rightarrow \infty} \int_{\Omega_n^+\setminus\tilde{\Omega}_n}\left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x \gt 0.
\end{equation}
\begin{equation}
\displaystyle\liminf_{n\rightarrow \infty} \int_{\Omega_n^+\setminus\tilde{\Omega}_n}\left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x \gt 0.
\end{equation} Since the function  $\displaystyle\frac{|f(\cdot)|}{|\cdot|}$ is bounded by
$\displaystyle\frac{|f(\cdot)|}{|\cdot|}$ is bounded by ![]() $(f_2)$, by Hölder’s inequality with exponent
$(f_2)$, by Hölder’s inequality with exponent  $\displaystyle\frac{p}{2} \gt 1$, we obtain
$\displaystyle\frac{p}{2} \gt 1$, we obtain
 \begin{equation}
\int_{\Omega_n^+\setminus\tilde{\Omega}_n}\left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x\leq C| \Omega_n^+\setminus\tilde{\Omega}_n|^{\frac{p-2}{p}}\|v_n\|_{L^p(\mathbb{R}^N)}^{\frac{2}{p}}.
\end{equation}
\begin{equation}
\int_{\Omega_n^+\setminus\tilde{\Omega}_n}\left(\displaystyle\frac{f(u_n)}{u_n}v_n(v_n^+-v_n^-)\right)\,{\rm d}x\leq C| \Omega_n^+\setminus\tilde{\Omega}_n|^{\frac{p-2}{p}}\|v_n\|_{L^p(\mathbb{R}^N)}^{\frac{2}{p}}.
\end{equation} Assumption (i) and Lions’s Lemma ensure that  $\|v_n\|_{L^p(\mathbb{R}^N)}\rightarrow 0$. Therefore, up to a subsequence, from (4.5), we obtain
$\|v_n\|_{L^p(\mathbb{R}^N)}\rightarrow 0$. Therefore, up to a subsequence, from (4.5), we obtain
Now we consider two disjoint subsets of ![]() $\Omega_n^+\setminus\tilde{\Omega}_n$. Hypothesis
$\Omega_n^+\setminus\tilde{\Omega}_n$. Hypothesis ![]() $(f_3)$ implies that there exists R > 0 such that, if s > R,
$(f_3)$ implies that there exists R > 0 such that, if s > R,
 \begin{equation*}
\displaystyle\frac{1}{2}f(s)s - F(s) \gt 1.
\end{equation*}
\begin{equation*}
\displaystyle\frac{1}{2}f(s)s - F(s) \gt 1.
\end{equation*} Without loss of generality, we assume ![]() $0 \lt \delta \lt R$. For each
$0 \lt \delta \lt R$. For each ![]() $n\in\mathbb{N}$, let
$n\in\mathbb{N}$, let
and thus, by (4.1),
 \begin{equation*}
c+o_n(1) \geq \displaystyle\mu\int_{A_n}\left(\displaystyle\frac{1}{2}f(u_n(x))u_n(x) - F(u_n(x))\right)\, {\rm d}x \gt \mu |A_n|,
\end{equation*}
\begin{equation*}
c+o_n(1) \geq \displaystyle\mu\int_{A_n}\left(\displaystyle\frac{1}{2}f(u_n(x))u_n(x) - F(u_n(x))\right)\, {\rm d}x \gt \mu |A_n|,
\end{equation*}which implies that the sequence ![]() $(|A_n|)$ is bounded. Consider also
$(|A_n|)$ is bounded. Consider also
Since ![]() $B_n = (\Omega_n^+\setminus\tilde{\Omega}_n)\setminus A_n$, we have
$B_n = (\Omega_n^+\setminus\tilde{\Omega}_n)\setminus A_n$, we have
It follows from (4.7) and the boundedness of the sequence ![]() $(|A_n|)$ that
$(|A_n|)$ that
Since the interval ![]() $[\delta, R]$ is compact and the functions f and F are continuous, we have by hypothesis
$[\delta, R]$ is compact and the functions f and F are continuous, we have by hypothesis ![]() $(f_3)$ that
$(f_3)$ that  $\overline{\delta}:=\displaystyle\inf_{s\in[\delta,R]}\left(\displaystyle\frac{1}{2}f(s)s - F(s)\right) \gt 0$. Thus, from (4.8),
$\overline{\delta}:=\displaystyle\inf_{s\in[\delta,R]}\left(\displaystyle\frac{1}{2}f(s)s - F(s)\right) \gt 0$. Thus, from (4.8),
 \begin{align*}
\mu\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{1}{2}f(u_n)u_n - F(u_n)\right)\,{\rm d}x & \geq \mu\displaystyle\int_{B_n}\left(\displaystyle\frac{1}{2}f(u_n)u_n - F(u_n)\right)\,{\rm d}x\\\\
& \geq \mu\overline{\delta}| B_n| \rightarrow \infty.
\end{align*}
\begin{align*}
\mu\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{1}{2}f(u_n)u_n - F(u_n)\right)\,{\rm d}x & \geq \mu\displaystyle\int_{B_n}\left(\displaystyle\frac{1}{2}f(u_n)u_n - F(u_n)\right)\,{\rm d}x\\\\
& \geq \mu\overline{\delta}| B_n| \rightarrow \infty.
\end{align*}We have a contradiction with the fact that
 \begin{equation*}
\mu\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{1}{2}f(u_n)u_n - F(u_n)\right)\,{\rm d}x \leq I_\mu(u_n)-\displaystyle\frac{1}{2}I^{\prime}_\mu(u_n)u_n = c + o_n(1).
\end{equation*}
\begin{equation*}
\mu\displaystyle\int_{\mathbb{R}^N} \left(\displaystyle\frac{1}{2}f(u_n)u_n - F(u_n)\right)\,{\rm d}x \leq I_\mu(u_n)-\displaystyle\frac{1}{2}I^{\prime}_\mu(u_n)u_n = c + o_n(1).
\end{equation*} Therefore, (i) does not hold for sequence ![]() $(v_n)$. Now, suppose that (ii) holds for sequence
$(v_n)$. Now, suppose that (ii) holds for sequence ![]() $(v_n)$. By equivalence of the norms, there exist constants
$(v_n)$. By equivalence of the norms, there exist constants ![]() $C_1,C_2 \gt 0$ such that
$C_1,C_2 \gt 0$ such that
 \begin{equation}
\| w\|\leq C_1\| w\|_{H^1(\mathbb{R}^N)}\leq C_2\|w\|, \ \textrm{for all functions} \ w\in E.
\end{equation}
\begin{equation}
\| w\|\leq C_1\| w\|_{H^1(\mathbb{R}^N)}\leq C_2\|w\|, \ \textrm{for all functions} \ w\in E.
\end{equation} Let ![]() $(y_n)\subset\mathbb{R}^N$ be the sequence given by hypothesis (ii). Consider
$(y_n)\subset\mathbb{R}^N$ be the sequence given by hypothesis (ii). Consider ![]() $\tilde{v}_n(x)=v_n(x+y_n)$ and
$\tilde{v}_n(x)=v_n(x+y_n)$ and ![]() $\tilde{u}_n(x)=u_n(x+y_n)$. Note that
$\tilde{u}_n(x)=u_n(x+y_n)$. Note that ![]() $(\tilde{v}_n)$ is bounded in E. In fact, from (4.9), it follows that
$(\tilde{v}_n)$ is bounded in E. In fact, from (4.9), it follows that
 \begin{equation*}
\|\tilde{v}_n\| \leq C_1\|\tilde{v}_n\|_{H^1(\mathbb{R}^N)}=C_1\|v_n\|_{H^1(\mathbb{R}^N)}\leq C_2\|v_n\|=C_2.
\end{equation*}
\begin{equation*}
\|\tilde{v}_n\| \leq C_1\|\tilde{v}_n\|_{H^1(\mathbb{R}^N)}=C_1\|v_n\|_{H^1(\mathbb{R}^N)}\leq C_2\|v_n\|=C_2.
\end{equation*}Thus, up to a subsequence,
 \begin{equation}
\left\{\begin{array}{lllll}
\tilde{v}_n\rightharpoonup \tilde{v} &\textrm{weakly in} \ E, \\
\tilde{v}_n \rightarrow \tilde{v} &\textrm{strongly in} \ L^2_{\rm loc}(\mathbb{R}^N).
\end{array} \right.
\end{equation}
\begin{equation}
\left\{\begin{array}{lllll}
\tilde{v}_n\rightharpoonup \tilde{v} &\textrm{weakly in} \ E, \\
\tilde{v}_n \rightarrow \tilde{v} &\textrm{strongly in} \ L^2_{\rm loc}(\mathbb{R}^N).
\end{array} \right.
\end{equation} We note that ![]() $\tilde{v}\neq 0$, since by (ii) and (4.10),
$\tilde{v}\neq 0$, since by (ii) and (4.10),
 \begin{equation*}
\displaystyle\int_{B(0,r)} \tilde{v}^2\,{\rm d}x = \limsup_{n\rightarrow \infty}\int_{B(0,r)}\tilde{v}_n^2\,{\rm d}x = \limsup_{n\rightarrow \infty}\int_{B(y_n,r)}v_n^2\,{\rm d}x \gt \eta \gt 0.
\end{equation*}
\begin{equation*}
\displaystyle\int_{B(0,r)} \tilde{v}^2\,{\rm d}x = \limsup_{n\rightarrow \infty}\int_{B(0,r)}\tilde{v}_n^2\,{\rm d}x = \limsup_{n\rightarrow \infty}\int_{B(y_n,r)}v_n^2\,{\rm d}x \gt \eta \gt 0.
\end{equation*} By (4.9),  $\|\tilde{u}_n\|\geq \displaystyle\frac{C_1}{C_2}\|u_n\|$, which goes to infinity as
$\|\tilde{u}_n\|\geq \displaystyle\frac{C_1}{C_2}\|u_n\|$, which goes to infinity as ![]() $n\rightarrow \infty$. It follows from (4.10) that
$n\rightarrow \infty$. It follows from (4.10) that
 \begin{equation*}
0 \neq |\tilde{v}(x)|=\displaystyle\lim_{n\rightarrow \infty}|\tilde{v}_n(x)|=\lim_{n\rightarrow \infty}\displaystyle\frac{|\tilde{u}_n(x)|}{\|\tilde{u}_n\|} \quad \textrm{a.e. in} \ \Omega,
\end{equation*}
\begin{equation*}
0 \neq |\tilde{v}(x)|=\displaystyle\lim_{n\rightarrow \infty}|\tilde{v}_n(x)|=\lim_{n\rightarrow \infty}\displaystyle\frac{|\tilde{u}_n(x)|}{\|\tilde{u}_n\|} \quad \textrm{a.e. in} \ \Omega,
\end{equation*}with ![]() $|\Omega| \gt 0$ and
$|\Omega| \gt 0$ and ![]() $\Omega\subset B(0,r)$. Since
$\Omega\subset B(0,r)$. Since ![]() $\|\tilde{u}_n\|\rightarrow\infty$, we have
$\|\tilde{u}_n\|\rightarrow\infty$, we have ![]() $|\tilde{u}_n(x)|\rightarrow\infty$ a.e. in Ω. Thus, Fatou’s Lemma yields
$|\tilde{u}_n(x)|\rightarrow\infty$ a.e. in Ω. Thus, Fatou’s Lemma yields
 \begin{align*}
\displaystyle\liminf_{n\rightarrow \infty}\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*}\,{\rm d}x &= \displaystyle\liminf_{n\rightarrow \infty}\displaystyle\int_{\mathbb{R}^N} |\tilde{u}_n|^{2^*}\,{\rm d}x\\\\
& \geq \displaystyle\liminf_{n\rightarrow \infty}\int_{{\Omega}}|\tilde{u}_n|^{2^*}\,{\rm d}x\\\\
& \geq \displaystyle\int_{{\Omega}}\displaystyle\liminf_{n\rightarrow \infty}|\tilde{u}_n|^{2^*}\,{\rm d}x\\\\
& = +\infty.
\end{align*}
\begin{align*}
\displaystyle\liminf_{n\rightarrow \infty}\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*}\,{\rm d}x &= \displaystyle\liminf_{n\rightarrow \infty}\displaystyle\int_{\mathbb{R}^N} |\tilde{u}_n|^{2^*}\,{\rm d}x\\\\
& \geq \displaystyle\liminf_{n\rightarrow \infty}\int_{{\Omega}}|\tilde{u}_n|^{2^*}\,{\rm d}x\\\\
& \geq \displaystyle\int_{{\Omega}}\displaystyle\liminf_{n\rightarrow \infty}|\tilde{u}_n|^{2^*}\,{\rm d}x\\\\
& = +\infty.
\end{align*} However, this contradicts the fact that ![]() $(|u_n|_{2^*})$ is bounded. This implies that hypothesis (ii) does not hold for sequence
$(|u_n|_{2^*})$ is bounded. This implies that hypothesis (ii) does not hold for sequence ![]() $(v_n)$. We conclude that, up to a subsequence,
$(v_n)$. We conclude that, up to a subsequence, ![]() $(u_n)$ is bounded.
$(u_n)$ is bounded.
In the sequel, since M is a closed and bounded subset of a finite dimensional space, we have that M is compact. Therefore, by the continuity of h 0 and Iµ, for each µ > 0, there exist ![]() $t_\mu \gt 0$ and
$t_\mu \gt 0$ and ![]() $v_\mu^-\in E^-$ such that
$v_\mu^-\in E^-$ such that
 \begin{equation*}
\displaystyle\max_{u\in M} I_\mu(h_0(u)) = I_\mu(h_0(t_\mu Re+v_\mu^-)) = I_\mu\left(u_0^+\left(\frac{\cdot - y}{t_\mu L}\right) + |v_\mu^-|\right),
\end{equation*}
\begin{equation*}
\displaystyle\max_{u\in M} I_\mu(h_0(u)) = I_\mu(h_0(t_\mu Re+v_\mu^-)) = I_\mu\left(u_0^+\left(\frac{\cdot - y}{t_\mu L}\right) + |v_\mu^-|\right),
\end{equation*}with ![]() $t_\mu Re+v_\mu^-\in M$. Let us prove that in fact
$t_\mu Re+v_\mu^-\in M$. Let us prove that in fact ![]() $t_\mu \gt 0$. Otherwise, if
$t_\mu \gt 0$. Otherwise, if ![]() $t_\mu=0$, then by the definition of Iµ, we have
$t_\mu=0$, then by the definition of Iµ, we have ![]() $I_\mu(|v_\mu^-|)\leq 0$. However, by the proof of Lemma 3.2, we may choose several small values of t > 0 such that
$I_\mu(|v_\mu^-|)\leq 0$. However, by the proof of Lemma 3.2, we may choose several small values of t > 0 such that ![]() $tRe \in M$ and
$tRe \in M$ and  $\left\|u_0^+\left(\dfrac{\cdot-y}{tL} \right)\right\| \lt \rho$, satisfying
$\left\|u_0^+\left(\dfrac{\cdot-y}{tL} \right)\right\| \lt \rho$, satisfying  $I_\mu(h_0(tRe)) = I_\mu\left( u_0^+\left(\dfrac{\cdot-y}{tL} \right)\right) \gt 0$, contradicting the maximality of
$I_\mu(h_0(tRe)) = I_\mu\left( u_0^+\left(\dfrac{\cdot-y}{tL} \right)\right) \gt 0$, contradicting the maximality of ![]() $I_\mu(|v_\mu^-|)$. Therefore,
$I_\mu(|v_\mu^-|)$. Therefore, ![]() $t_\mu \gt 0$.
$t_\mu \gt 0$.
Lemma 4.2. It holds that ![]() $c_\mu\to 0$ as
$c_\mu\to 0$ as ![]() $\mu\to+\infty$, where
$\mu\to+\infty$, where  $
c_\mu=\displaystyle\inf _{h \in \Gamma} \max _{w \in M} I_\mu(h(w)),
$ with
$
c_\mu=\displaystyle\inf _{h \in \Gamma} \max _{w \in M} I_\mu(h(w)),
$ with ![]() $\Gamma:=\left\{h \in C(M, E):\left.h\right|_{\partial M}=h_{0}\right\}$.
$\Gamma:=\left\{h \in C(M, E):\left.h\right|_{\partial M}=h_{0}\right\}$.
Proof. First, remember that ![]() $t_\mu \gt 0$ is not equal to zero. We claim that
$t_\mu \gt 0$ is not equal to zero. We claim that ![]() $t_\mu Re+v_\mu^- \to 0$ as
$t_\mu Re+v_\mu^- \to 0$ as ![]() $\mu\to +\infty$. In fact, since
$\mu\to +\infty$. In fact, since ![]() $t_\mu Re+v_\mu^-\in M$ and M is a compact set, passing to a subsequence if necessary, we may suppose that
$t_\mu Re+v_\mu^-\in M$ and M is a compact set, passing to a subsequence if necessary, we may suppose that ![]() $t_\mu Re+v_\mu^-\to w_0:=t_0Re+v^-_0\in M$ strongly as
$t_\mu Re+v_\mu^-\to w_0:=t_0Re+v^-_0\in M$ strongly as ![]() $\mu\to +\infty$. Let us show that
$\mu\to +\infty$. Let us show that ![]() $w_0=0$. Otherwise, suppose
$w_0=0$. Otherwise, suppose ![]() $w_0\neq 0$ and note that, by the equivalence of the norms,
$w_0\neq 0$ and note that, by the equivalence of the norms,
 \begin{eqnarray*}
0\leq c_\mu \leq \displaystyle\max_{u\in M} I_\mu(h_0(u)) &=& I_\mu(h_0(t_\mu Re +v_\mu^-)) \\
& \leq & \dfrac{C}{2}\left\|u_0\left(\dfrac{\cdot-y}{t_\mu L}\right)\right\|_{H^1(\mathbb{R}^N)}^2 - \mu\displaystyle\int_{\mathbb{R}^N} F(h_0(t_\mu Re+v_\mu^-)) \,{\rm d}x.
\end{eqnarray*}
\begin{eqnarray*}
0\leq c_\mu \leq \displaystyle\max_{u\in M} I_\mu(h_0(u)) &=& I_\mu(h_0(t_\mu Re +v_\mu^-)) \\
& \leq & \dfrac{C}{2}\left\|u_0\left(\dfrac{\cdot-y}{t_\mu L}\right)\right\|_{H^1(\mathbb{R}^N)}^2 - \mu\displaystyle\int_{\mathbb{R}^N} F(h_0(t_\mu Re+v_\mu^-)) \,{\rm d}x.
\end{eqnarray*} After a change of variables, since ![]() $0\leq t_\mu\leq 1$, it is possible to find a constant C > 0, which does not depend on µ, such that
$0\leq t_\mu\leq 1$, it is possible to find a constant C > 0, which does not depend on µ, such that
 \begin{equation*}
\dfrac{C}{2}\left\|u_0\left(\dfrac{\cdot-y}{t_\mu L}\right)\right\|_{H^1(\mathbb{R}^N)}^2 \leq C
\end{equation*}
\begin{equation*}
\dfrac{C}{2}\left\|u_0\left(\dfrac{\cdot-y}{t_\mu L}\right)\right\|_{H^1(\mathbb{R}^N)}^2 \leq C
\end{equation*}for all µ > 0. At this moment, supposing ![]() $t_0 \gt 0$, since u 0 is positive and
$t_0 \gt 0$, since u 0 is positive and ![]() $u_0^-(\cdot - y)\to 0$ strongly in E as
$u_0^-(\cdot - y)\to 0$ strongly in E as ![]() $|y|\to \infty$, we choose
$|y|\to \infty$, we choose ![]() $y\in\mathbb{R}^N$ with norm large enough to get
$y\in\mathbb{R}^N$ with norm large enough to get  $F(h_0(w_0))=F(h_0(t_0Re+v^-_0))=F(u^+_0((\cdot - y)/t_0L)+|v_0^-|)\approx F(u_0((\cdot-y)/t_0L)+|v_0^-|) \gt 0$. Therefore, Fatou’s lemma provides
$F(h_0(w_0))=F(h_0(t_0Re+v^-_0))=F(u^+_0((\cdot - y)/t_0L)+|v_0^-|)\approx F(u_0((\cdot-y)/t_0L)+|v_0^-|) \gt 0$. Therefore, Fatou’s lemma provides
 \begin{equation*}
0 \lt \displaystyle\int_{\mathbb{R}^N} F(h_0(w_0))\,{\rm d}x \leq \displaystyle\liminf_{\mu\to \infty} \displaystyle\int_{\mathbb{R}^N} F(h_0(t_\mu Re +v_\mu^-)) \,{\rm d}x.
\end{equation*}
\begin{equation*}
0 \lt \displaystyle\int_{\mathbb{R}^N} F(h_0(w_0))\,{\rm d}x \leq \displaystyle\liminf_{\mu\to \infty} \displaystyle\int_{\mathbb{R}^N} F(h_0(t_\mu Re +v_\mu^-)) \,{\rm d}x.
\end{equation*}Then, we obtain for µ > 0 sufficiently large that
 \begin{equation*}
0\leq c_\mu \leq C - \mu\displaystyle\int_{\mathbb{R}^N} F(h_0(t_\mu Re +v_\mu^-))\,{\rm d}x \lt 0,
\end{equation*}
\begin{equation*}
0\leq c_\mu \leq C - \mu\displaystyle\int_{\mathbb{R}^N} F(h_0(t_\mu Re +v_\mu^-))\,{\rm d}x \lt 0,
\end{equation*}which is an absurd. This contradiction shows that ![]() $w_0=0$ and proves our claim.
$w_0=0$ and proves our claim.
It follows from the continuity of the norm and of the function h 0 (using also that ![]() $h_0(0)=0$) that
$h_0(0)=0$) that
 \begin{eqnarray*}
0\leq c_\mu \leq \displaystyle\max_{u\in M} I_\mu(u) &=& I_\mu(h_0(t_\mu Re+v_\mu^-)) \\
&\leq & \dfrac{1}{2}\|h_0(t_\mu Re + v_\mu^-)\|^2 \\
&\to& 0
\end{eqnarray*}
\begin{eqnarray*}
0\leq c_\mu \leq \displaystyle\max_{u\in M} I_\mu(u) &=& I_\mu(h_0(t_\mu Re+v_\mu^-)) \\
&\leq & \dfrac{1}{2}\|h_0(t_\mu Re + v_\mu^-)\|^2 \\
&\to& 0
\end{eqnarray*}as ![]() $\mu\to \infty$, and the result follows.
$\mu\to \infty$, and the result follows.
5. A nontrivial solution for  $(P_\mu)$
$(P_\mu)$
We begin with a technical result.
Lemma 5.1. If ![]() $\mu_{2} \gt \mu_{1}\geq0,$ there exists C > 0 such that, for all
$\mu_{2} \gt \mu_{1}\geq0,$ there exists C > 0 such that, for all ![]() $x_{1},x_{2}\in\mathbb{R}^{N}$,
$x_{1},x_{2}\in\mathbb{R}^{N}$,
 \begin{equation*}
\int_{\mathbb{R}^{N}}{\rm e}^{-\mu_{1}|x-x_{1}|}{\rm e}^{-\mu_{2}|x-x_{2}|}\,{|rm d}x\leq
C\,{\rm e}^{-\mu_{1}|x_{1}-x_{2}|}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{R}^{N}}{\rm e}^{-\mu_{1}|x-x_{1}|}{\rm e}^{-\mu_{2}|x-x_{2}|}\,{|rm d}x\leq
C\,{\rm e}^{-\mu_{1}|x_{1}-x_{2}|}.
\end{equation*}Proof. Since
 \begin{equation*}
\begin{array}{llllll}
\mu_{1}\left\vert x_{1}-x_{2}\right\vert +(\mu_{2}-\mu_{1})\left\vert
x-x_{2}\right\vert &\leq&\mu_{1}\left( \left\vert x-x_{1}\right\vert
+\left\vert x-x_{2}\right\vert \right) +(\mu_{2}-\mu_{1})\left\vert
x-x_{2}\right\vert \\
&=&\mu_{1}\left\vert x-x_{1}\right\vert +\mu_{2}\left\vert
x-x_{2}\right\vert ,
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{llllll}
\mu_{1}\left\vert x_{1}-x_{2}\right\vert +(\mu_{2}-\mu_{1})\left\vert
x-x_{2}\right\vert &\leq&\mu_{1}\left( \left\vert x-x_{1}\right\vert
+\left\vert x-x_{2}\right\vert \right) +(\mu_{2}-\mu_{1})\left\vert
x-x_{2}\right\vert \\
&=&\mu_{1}\left\vert x-x_{1}\right\vert +\mu_{2}\left\vert
x-x_{2}\right\vert ,
\end{array}
\end{equation*}we have
 \begin{equation*}
\int_{\mathbb{R}^{N}}{\rm e}^{-\mu_{1}|x-x_{1}|}{\rm e}^{-\mu_{2}|x-x_{2}|}\,{\rm d}x\leq
\int_{\mathbb{R}^{N}}{\rm e}^{-\mu_{1}\left\vert x_{1}-x_{2}\right\vert }
{\rm e}^{-(\mu_{2}-\mu_{1})\left\vert x-x_{2}\right\vert }\,{\rm d}x=C\,{\rm e}^{-\mu_{1}
|x_{1}-x_{2}|}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{R}^{N}}{\rm e}^{-\mu_{1}|x-x_{1}|}{\rm e}^{-\mu_{2}|x-x_{2}|}\,{\rm d}x\leq
\int_{\mathbb{R}^{N}}{\rm e}^{-\mu_{1}\left\vert x_{1}-x_{2}\right\vert }
{\rm e}^{-(\mu_{2}-\mu_{1})\left\vert x-x_{2}\right\vert }\,{\rm d}x=C\,{\rm e}^{-\mu_{1}
|x_{1}-x_{2}|}.
\end{equation*}The proof follows.
Lemma 5.2. For every µ > 0, it holds that ![]() $c_\mu \lt d_\mu$.
$c_\mu \lt d_\mu$.
Proof. For simplicity, C will denote a positive constant, not necessarily the same one. By the definitions of the functionals Iµ and Jµ and fixing ![]() $u_{\mu}=v_\mu^- + t_\mu R e$, we have
$u_{\mu}=v_\mu^- + t_\mu R e$, we have
 \begin{eqnarray}
I_\mu(h_0(u_\mu)) & = & \displaystyle\frac{1}{2}\|\Upsilon^+(t_\mu)\|^2 - \displaystyle\frac{1}{2}\|v_\mu^-\|^2 - \mu\displaystyle\int_{\mathbb{R}^N} F(\Upsilon^+(t_\mu)+|v^-|)\,{\rm d}x \nonumber\\
&&- \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |\Upsilon^+(t_\mu)+|v^-||^{2^*}\,{\rm d}x\nonumber \\
& \leq & \displaystyle\frac{1}{2}\|\Upsilon^+(t_\mu)\|_{V_\infty}^2 - \displaystyle\int_{\mathbb{R}^N} F(\Upsilon^+(t_\mu))\,{\rm d}x - \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |\Upsilon^+(t_\mu)|^{2^*}\, {\rm d}x \nonumber \\
&&- \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |\Upsilon^+(t_\mu)+|v^-||^{2^*}\, {\rm d}x \nonumber \\
& & + \displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon^+(t_\mu)) - F(\Upsilon^+(t_\mu)+|v^-|) \right)\,{\rm d}x + \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |\Upsilon^+(t_\mu)|^{2^*}\, {\rm d}x\nonumber \\
& & + \displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x \nonumber\\
& \leq & J_{\mu}(\Upsilon^+(t_\mu)) + \displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x \nonumber \\
& & + \displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon^+(t_\mu)) - F(\Upsilon^+(t_\mu)+|v^-|) \right)\,{\rm d}x \nonumber\\
& & +\dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} \left( |\Upsilon^+(t_\mu)|^{2^*} - |\Upsilon^+(t_\mu)+|v^-||^{2^*} \right) \,{\rm d}x\nonumber \\
&\leq & J_{\mu}(\Upsilon^+(t_\mu)) + \displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x
\end{eqnarray}
\begin{eqnarray}
I_\mu(h_0(u_\mu)) & = & \displaystyle\frac{1}{2}\|\Upsilon^+(t_\mu)\|^2 - \displaystyle\frac{1}{2}\|v_\mu^-\|^2 - \mu\displaystyle\int_{\mathbb{R}^N} F(\Upsilon^+(t_\mu)+|v^-|)\,{\rm d}x \nonumber\\
&&- \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |\Upsilon^+(t_\mu)+|v^-||^{2^*}\,{\rm d}x\nonumber \\
& \leq & \displaystyle\frac{1}{2}\|\Upsilon^+(t_\mu)\|_{V_\infty}^2 - \displaystyle\int_{\mathbb{R}^N} F(\Upsilon^+(t_\mu))\,{\rm d}x - \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |\Upsilon^+(t_\mu)|^{2^*}\, {\rm d}x \nonumber \\
&&- \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |\Upsilon^+(t_\mu)+|v^-||^{2^*}\, {\rm d}x \nonumber \\
& & + \displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon^+(t_\mu)) - F(\Upsilon^+(t_\mu)+|v^-|) \right)\,{\rm d}x + \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |\Upsilon^+(t_\mu)|^{2^*}\, {\rm d}x\nonumber \\
& & + \displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x \nonumber\\
& \leq & J_{\mu}(\Upsilon^+(t_\mu)) + \displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x \nonumber \\
& & + \displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon^+(t_\mu)) - F(\Upsilon^+(t_\mu)+|v^-|) \right)\,{\rm d}x \nonumber\\
& & +\dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} \left( |\Upsilon^+(t_\mu)|^{2^*} - |\Upsilon^+(t_\mu)+|v^-||^{2^*} \right) \,{\rm d}x\nonumber \\
&\leq & J_{\mu}(\Upsilon^+(t_\mu)) + \displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x
\end{eqnarray}provided ![]() $|y|$ is large enough and F and
$|y|$ is large enough and F and ![]() $s\mapsto s^{2^*}$, for s > 0, are non-decreasing.
$s\mapsto s^{2^*}$, for s > 0, are non-decreasing.
Let us estimate the integral  $\displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x$. We begin remembering that
$\displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x$. We begin remembering that
 \begin{equation*}
u_0\left(\dfrac{x-y}{t_\mu L}\right)=\Upsilon(t_\mu)(x) = \Upsilon^+(t_\mu)(x) + \Upsilon^-(t_\mu)(x)
\end{equation*}
\begin{equation*}
u_0\left(\dfrac{x-y}{t_\mu L}\right)=\Upsilon(t_\mu)(x) = \Upsilon^+(t_\mu)(x) + \Upsilon^-(t_\mu)(x)
\end{equation*}for all ![]() $x,y\in\mathbb{R}^N$. Thus, replacing x by x + y, we get
$x,y\in\mathbb{R}^N$. Thus, replacing x by x + y, we get
 \begin{equation*}
u_0\left(\dfrac{x}{t_\mu L}\right)=\Upsilon(t_\mu)(x+y) = \Upsilon^+(t_\mu)(x+y) + \Upsilon^-(t_\mu)(x+y)
\end{equation*}
\begin{equation*}
u_0\left(\dfrac{x}{t_\mu L}\right)=\Upsilon(t_\mu)(x+y) = \Upsilon^+(t_\mu)(x+y) + \Upsilon^-(t_\mu)(x+y)
\end{equation*}for all ![]() $x,y\in\mathbb{R}^N$. Since
$x,y\in\mathbb{R}^N$. Since ![]() $\|\Upsilon^-(t)(x+y)\|_2=\|\Upsilon^-(t)\|_2\to 0$ as
$\|\Upsilon^-(t)(x+y)\|_2=\|\Upsilon^-(t)\|_2\to 0$ as ![]() $|y|\to\infty$ uniformly on
$|y|\to\infty$ uniformly on ![]() $t\in [0,1]$ (see (3.8) and (3.9) in [Reference Maia and Soares12] and note that we are considering for t = 0,
$t\in [0,1]$ (see (3.8) and (3.9) in [Reference Maia and Soares12] and note that we are considering for t = 0, ![]() $\Upsilon^-(0)=0$), it yields the pointwise convergence
$\Upsilon^-(0)=0$), it yields the pointwise convergence
 \begin{equation}
\Upsilon^+(t_\mu)(x+y) \to u_0\left(\dfrac{x}{t_\mu L} \right) \ \textrm{as} \ |y|\to \infty.
\end{equation}
\begin{equation}
\Upsilon^+(t_\mu)(x+y) \to u_0\left(\dfrac{x}{t_\mu L} \right) \ \textrm{as} \ |y|\to \infty.
\end{equation}We have from assumption ![]() $(V_4)$ that
$(V_4)$ that
 \begin{eqnarray}
\displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x & = &\displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x+y) - V_\infty \right) (\Upsilon^+(t_\mu))^2(x+y)\,{\rm d}x \nonumber \\
&\leq & -C\displaystyle\int_{\mathbb{R}^N} {\rm e}^{-\gamma_1|x+y|^{\gamma_2}}(\Upsilon^+(t_\mu))^2(x+y)\,{\rm d}x.\\
&\leq & - C\,{\rm e}^{-C|y|^{\gamma_2}}\displaystyle\int_{\mathbb{R}^N} {\rm e}^{-C|x|^{\gamma_2}}(\Upsilon^+(t_\mu))^2(x+y) \,{\rm d}x,\nonumber
\end{eqnarray}
\begin{eqnarray}
\displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x & = &\displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x+y) - V_\infty \right) (\Upsilon^+(t_\mu))^2(x+y)\,{\rm d}x \nonumber \\
&\leq & -C\displaystyle\int_{\mathbb{R}^N} {\rm e}^{-\gamma_1|x+y|^{\gamma_2}}(\Upsilon^+(t_\mu))^2(x+y)\,{\rm d}x.\\
&\leq & - C\,{\rm e}^{-C|y|^{\gamma_2}}\displaystyle\int_{\mathbb{R}^N} {\rm e}^{-C|x|^{\gamma_2}}(\Upsilon^+(t_\mu))^2(x+y) \,{\rm d}x,\nonumber
\end{eqnarray}where we used that, for all ![]() $x,y\in\mathbb{R}^N$,
$x,y\in\mathbb{R}^N$, ![]() $|t_\mu L x+y|^{\gamma_2}\leq Ct_\mu^{\gamma_2} L^{\gamma_2} |x|^{\gamma_2} + C|y|^{\gamma_2}\leq C|x|^{\gamma_2}+C|y|^{\gamma_2}$ and the function
$|t_\mu L x+y|^{\gamma_2}\leq Ct_\mu^{\gamma_2} L^{\gamma_2} |x|^{\gamma_2} + C|y|^{\gamma_2}\leq C|x|^{\gamma_2}+C|y|^{\gamma_2}$ and the function ![]() $s\mapsto -e^{-\gamma_1 s}, \ s \gt 0$, is increasing.
$s\mapsto -e^{-\gamma_1 s}, \ s \gt 0$, is increasing.
Now using (5.2) and the Lebesgue Theorem, we obtain as ![]() $|y|\to \infty$ that
$|y|\to \infty$ that
 \begin{equation*}
\displaystyle\int_{\mathbb{R}^N} {\rm e}^{-C|x|^{\gamma_2}}(\Upsilon^+(t_\mu))^2(x+y)\,{\rm d}x \to \displaystyle\int_{\mathbb{R}^N} {\rm e}^{-C|x|^{\gamma_2}}\left(u_0\left(\dfrac{x}{t_\mu L} \right)\right)^2\,{\rm d}x := \alpha_0 \gt 0,
\end{equation*}
\begin{equation*}
\displaystyle\int_{\mathbb{R}^N} {\rm e}^{-C|x|^{\gamma_2}}(\Upsilon^+(t_\mu))^2(x+y)\,{\rm d}x \to \displaystyle\int_{\mathbb{R}^N} {\rm e}^{-C|x|^{\gamma_2}}\left(u_0\left(\dfrac{x}{t_\mu L} \right)\right)^2\,{\rm d}x := \alpha_0 \gt 0,
\end{equation*}with ![]() $\alpha_0 \gt 0$ does not depending on y. It follows from this and (5.3) that
$\alpha_0 \gt 0$ does not depending on y. It follows from this and (5.3) that
 \begin{equation}
\displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x \leq -C\,{\rm e}^{-C|y|^{\gamma_2}}
\end{equation}
\begin{equation}
\displaystyle\frac{1}{2}\displaystyle\int_{\mathbb{R}^N} \left(V(x) - V_\infty \right)(\Upsilon^+(t_\mu))^2\,{\rm d}x \leq -C\,{\rm e}^{-C|y|^{\gamma_2}}
\end{equation}for ![]() $|y|$ large enough.
$|y|$ large enough.
Therefore, from (5.1), we obtain
 \begin{eqnarray}
I_\mu(h_0(u_\mu)) \leq J_\mu(\Upsilon^+(t_\mu)) - C\,{\rm e}^{-C|y|^{\gamma_2}}.
\end{eqnarray}
\begin{eqnarray}
I_\mu(h_0(u_\mu)) \leq J_\mu(\Upsilon^+(t_\mu)) - C\,{\rm e}^{-C|y|^{\gamma_2}}.
\end{eqnarray} By Mean Value Theorem (choosing the points ![]() $a:=\Upsilon(t_\mu)$ and
$a:=\Upsilon(t_\mu)$ and ![]() $h:=-\Upsilon^-(t_\mu)$ that implies
$h:=-\Upsilon^-(t_\mu)$ that implies ![]() $a+h=\Upsilon^+(t_\mu)$) and the growth of f, we have for
$a+h=\Upsilon^+(t_\mu)$) and the growth of f, we have for ![]() $2 \lt p \lt 2^*$ that
$2 \lt p \lt 2^*$ that
 \begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon(t_\mu)) - F(\Upsilon^+(t_\mu)) \right)\,{\rm d}x & \leq & \displaystyle\int_{\mathbb{R}^N} \left| f(\Upsilon(t_\mu) + r_t\Upsilon^-(t_\mu)) \right||\Upsilon^-(t_\mu)|\,{\rm d}x \nonumber \\
& \leq & \varepsilon \displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)||\Upsilon^-(t_\mu)|\,{\rm d}x + \varepsilon\displaystyle\int_{\mathbb{R}^N} (\Upsilon^-(t_\mu))^2\,{\rm d}x \nonumber \\
& & + C_\varepsilon \displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)|^{p-1}|\Upsilon^-(t_\mu)|\,{\rm d}x\\
&& + C_\varepsilon\displaystyle\int_{\mathbb{R}^N} |\Upsilon^-(t_\mu)|^p \,{\rm d}x, \nonumber
\end{eqnarray}
\begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon(t_\mu)) - F(\Upsilon^+(t_\mu)) \right)\,{\rm d}x & \leq & \displaystyle\int_{\mathbb{R}^N} \left| f(\Upsilon(t_\mu) + r_t\Upsilon^-(t_\mu)) \right||\Upsilon^-(t_\mu)|\,{\rm d}x \nonumber \\
& \leq & \varepsilon \displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)||\Upsilon^-(t_\mu)|\,{\rm d}x + \varepsilon\displaystyle\int_{\mathbb{R}^N} (\Upsilon^-(t_\mu))^2\,{\rm d}x \nonumber \\
& & + C_\varepsilon \displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)|^{p-1}|\Upsilon^-(t_\mu)|\,{\rm d}x\\
&& + C_\varepsilon\displaystyle\int_{\mathbb{R}^N} |\Upsilon^-(t_\mu)|^p \,{\rm d}x, \nonumber
\end{eqnarray}where ![]() $r_t(x) \in (0,1)$. Following the same arguments, we arrive at
$r_t(x) \in (0,1)$. Following the same arguments, we arrive at
 \begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} \left( (\Upsilon(t_\mu))^{2^*} - (\Upsilon^+(t_\mu))^{2^*} \right)\,{\rm d}x &\leq & C \displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)|^{2^*-1}|\Upsilon^-(t_\mu)|\,{\rm d}x\\
&&+ C\displaystyle\int_{\mathbb{R}^N} |\Upsilon^-(t_\mu)|^{2^*} \,{\rm d}x. \nonumber
\end{eqnarray}
\begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} \left( (\Upsilon(t_\mu))^{2^*} - (\Upsilon^+(t_\mu))^{2^*} \right)\,{\rm d}x &\leq & C \displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)|^{2^*-1}|\Upsilon^-(t_\mu)|\,{\rm d}x\\
&&+ C\displaystyle\int_{\mathbb{R}^N} |\Upsilon^-(t_\mu)|^{2^*} \,{\rm d}x. \nonumber
\end{eqnarray} Now using the exponential decay of ![]() $\Upsilon(t_\mu)$ given by Proposition 6.10 in Appendix A, with ν > 0 to be chosen, we get from Lemma 5.1 that
$\Upsilon(t_\mu)$ given by Proposition 6.10 in Appendix A, with ν > 0 to be chosen, we get from Lemma 5.1 that
 \begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)|^{2^*-1}|\Upsilon^-(t_\mu)|\,{\rm d}x & \leq & C \displaystyle\int_{\mathbb{R}^N} \left( {\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|x-y\right|}{\rm e}^{-\delta\left|x\right|} \right)\,{\rm d}x\nonumber \\
& \leq & C\,{\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|},
\end{eqnarray}
\begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)|^{2^*-1}|\Upsilon^-(t_\mu)|\,{\rm d}x & \leq & C \displaystyle\int_{\mathbb{R}^N} \left( {\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|x-y\right|}{\rm e}^{-\delta\left|x\right|} \right)\,{\rm d}x\nonumber \\
& \leq & C\,{\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|},
\end{eqnarray}just choosing ν > 0 small enough. By the same arguments, we also have
 \begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)|^{p-1}|\Upsilon^-(t_\mu)|\,{\rm d}x & \leq & C \displaystyle\int_{\mathbb{R}^N} \left( {\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|x-y\right|}{\rm e}^{-\delta\left|x\right|} \right)\,{\rm d}x\nonumber \\
& \leq & C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|}
\end{eqnarray}
\begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)|^{p-1}|\Upsilon^-(t_\mu)|\,{\rm d}x & \leq & C \displaystyle\int_{\mathbb{R}^N} \left( {\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|x-y\right|}{\rm e}^{-\delta\left|x\right|} \right)\,{\rm d}x\nonumber \\
& \leq & C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|}
\end{eqnarray}and
 \begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)||\Upsilon^-(t_\mu)|{\rm d}x & \leq & C \displaystyle\int_{\mathbb{R}^N} \left( {\rm e}^{-\frac{\nu}{t_\mu L}\left|x-y\right|}{\rm e}^{-\delta\left|x\right|} \right) \,{\rm d}x\nonumber \\
& \leq & C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|}.
\end{eqnarray}
\begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} |\Upsilon(t_\mu)||\Upsilon^-(t_\mu)|{\rm d}x & \leq & C \displaystyle\int_{\mathbb{R}^N} \left( {\rm e}^{-\frac{\nu}{t_\mu L}\left|x-y\right|}{\rm e}^{-\delta\left|x\right|} \right) \,{\rm d}x\nonumber \\
& \leq & C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|}.
\end{eqnarray} Now applying (5.8)–(5.10) in (5.6) and (5.7), and defining ![]() $\|\Upsilon^-(t_\mu)\|_{V_\infty}:=\beta_y$, one has
$\|\Upsilon^-(t_\mu)\|_{V_\infty}:=\beta_y$, one has
 \begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon(t_\mu)) - F(\Upsilon^+(t_\mu)) \right)\,{\rm d}x \leq \varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} + \varepsilon\beta_y^2 + C_\varepsilon C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|} + C_\varepsilon C\beta_y^p \nonumber\\
\end{eqnarray}
\begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon(t_\mu)) - F(\Upsilon^+(t_\mu)) \right)\,{\rm d}x \leq \varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} + \varepsilon\beta_y^2 + C_\varepsilon C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|} + C_\varepsilon C\beta_y^p \nonumber\\
\end{eqnarray}and
 \begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} \left( (\Upsilon(t_\mu))^{2^*} - (\Upsilon^+(t_\mu))^{2^*} \right)\,{\rm d}x \leq C\,{\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|} + C\beta_y^{2^*}.
\end{eqnarray}
\begin{eqnarray}
\displaystyle\int_{\mathbb{R}^N} \left( (\Upsilon(t_\mu))^{2^*} - (\Upsilon^+(t_\mu))^{2^*} \right)\,{\rm d}x \leq C\,{\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|} + C\beta_y^{2^*}.
\end{eqnarray} Choosing  $0 \lt \varepsilon \lt \frac{1}{2}$, inequalities (5.11) and (5.12) provide
$0 \lt \varepsilon \lt \frac{1}{2}$, inequalities (5.11) and (5.12) provide
 \begin{eqnarray}
J_{\mu}(\Upsilon(t_\mu)) & = & \dfrac{1}{2}\|\Upsilon^+(t_\mu)\|^2 -\mu\displaystyle\int_{\mathbb{R}^N} F(\Upsilon^+(t_\mu))\,{\rm d}x -\dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} (\Upsilon^+(t_\mu))^{2^*}\,{\rm d}x \nonumber\\
& & + \dfrac{1}{2}\beta_y^2 - \mu\displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon(t_\mu)) - F(\Upsilon^+(t_\mu))\right)\,{\rm d}x \nonumber\\
& & -\dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} \left( (\Upsilon(t_\mu))^{2^*} - (\Upsilon^+(t_\mu))^{2^*} \right)\,{\rm d}x \nonumber \\
& \geq & J_{\mu}(\Upsilon^+(t_\mu)) -\left[\varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} + \varepsilon\beta_y^2 + C_\varepsilon C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|} + C_\varepsilon C\beta_y^p\right]\nonumber \\
& & -\left[ C \,{\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|} + C\beta_y^{2^*} \right] +\dfrac{1}{2}\beta_y^2 \nonumber \\
& \geq &{J_{\mu}(\Upsilon^+(t_\mu)) + \left(\dfrac{1}{2}-\varepsilon \right)\beta_y^2 - \varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} - C_\varepsilon C \,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|}- C_\varepsilon C\beta_y^p} \nonumber \\
& & {-C\,{\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|} - C\beta_y^{2^*} } \nonumber
\end{eqnarray}
\begin{eqnarray}
J_{\mu}(\Upsilon(t_\mu)) & = & \dfrac{1}{2}\|\Upsilon^+(t_\mu)\|^2 -\mu\displaystyle\int_{\mathbb{R}^N} F(\Upsilon^+(t_\mu))\,{\rm d}x -\dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} (\Upsilon^+(t_\mu))^{2^*}\,{\rm d}x \nonumber\\
& & + \dfrac{1}{2}\beta_y^2 - \mu\displaystyle\int_{\mathbb{R}^N} \left( F(\Upsilon(t_\mu)) - F(\Upsilon^+(t_\mu))\right)\,{\rm d}x \nonumber\\
& & -\dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} \left( (\Upsilon(t_\mu))^{2^*} - (\Upsilon^+(t_\mu))^{2^*} \right)\,{\rm d}x \nonumber \\
& \geq & J_{\mu}(\Upsilon^+(t_\mu)) -\left[\varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} + \varepsilon\beta_y^2 + C_\varepsilon C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|} + C_\varepsilon C\beta_y^p\right]\nonumber \\
& & -\left[ C \,{\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|} + C\beta_y^{2^*} \right] +\dfrac{1}{2}\beta_y^2 \nonumber \\
& \geq &{J_{\mu}(\Upsilon^+(t_\mu)) + \left(\dfrac{1}{2}-\varepsilon \right)\beta_y^2 - \varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} - C_\varepsilon C \,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|}- C_\varepsilon C\beta_y^p} \nonumber \\
& & {-C\,{\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|} - C\beta_y^{2^*} } \nonumber
\end{eqnarray} Since ![]() $\beta_y\to 0$, we have
$\beta_y\to 0$, we have
 \begin{equation*}
\left(\dfrac{1}{2}-\varepsilon \right)\beta_y^2 - C_\varepsilon C\beta_y^p - C\beta_y^{2^*} \geq 0
\end{equation*}
\begin{equation*}
\left(\dfrac{1}{2}-\varepsilon \right)\beta_y^2 - C_\varepsilon C\beta_y^p - C\beta_y^{2^*} \geq 0
\end{equation*}taking ![]() $|y|$ sufficiently large. It follows that
$|y|$ sufficiently large. It follows that
 \begin{eqnarray}
J_{\mu}(\Upsilon(t_\mu)) \geq J_{\mu}(\Upsilon^+(t_\mu)) - \varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} - C_\varepsilon C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|}-C\, {\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|}.\nonumber\\
\end{eqnarray}
\begin{eqnarray}
J_{\mu}(\Upsilon(t_\mu)) \geq J_{\mu}(\Upsilon^+(t_\mu)) - \varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} - C_\varepsilon C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|}-C\, {\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|}.\nonumber\\
\end{eqnarray}Thus, returning to (5.1) with (5.4) and (5.13), we get
 \begin{align}
I_\mu(h_0(u_\mu))& \leq J_{\mu}(\Upsilon(t_\mu)) -C\,{\rm e}^{-C|y|^{\gamma_2}} + \varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} + C_\varepsilon C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|}\nonumber\\ & \quad + C\, {\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|}
\end{align}
\begin{align}
I_\mu(h_0(u_\mu))& \leq J_{\mu}(\Upsilon(t_\mu)) -C\,{\rm e}^{-C|y|^{\gamma_2}} + \varepsilon C\,{\rm e}^{-\frac{\nu}{t_\mu L}\left|y\right|} + C_\varepsilon C\,{\rm e}^{-(p-1)\frac{\nu}{t_\mu L}\left|y\right|}\nonumber\\ & \quad + C\, {\rm e}^{-(2^*-1)\frac{\nu}{t_\mu L}\left|y\right|}
\end{align}with ![]() $|y|$ large enough. Since the function
$|y|$ large enough. Since the function ![]() ${\rm e}^{-C|y|^{\gamma_2}}$ decays more slowly than the other terms of exponential functions (because
${\rm e}^{-C|y|^{\gamma_2}}$ decays more slowly than the other terms of exponential functions (because ![]() $0 \lt \gamma_2 \lt 1$), we conclude from (5.14) that
$0 \lt \gamma_2 \lt 1$), we conclude from (5.14) that
To finish the proof, we proceed as follows.
 \begin{eqnarray*}
c_\mu \leq \max_{u\in M} I_\mu(h_0(u)) = I_\mu(h_0(u_\mu)) \lt J_{\mu}(\Upsilon(t_\mu)) \leq \max_{t\in [0,1]} J_{\mu}(\Upsilon(t)) = J_{\mu}(u_0) = d_\mu.
\end{eqnarray*}
\begin{eqnarray*}
c_\mu \leq \max_{u\in M} I_\mu(h_0(u)) = I_\mu(h_0(u_\mu)) \lt J_{\mu}(\Upsilon(t_\mu)) \leq \max_{t\in [0,1]} J_{\mu}(\Upsilon(t)) = J_{\mu}(u_0) = d_\mu.
\end{eqnarray*} We used the fact that the maximum  $\displaystyle\max_{t\in [0,1]} J_{\mu}(\Upsilon(t))$ is achieved at the unique point t 0, where
$\displaystyle\max_{t\in [0,1]} J_{\mu}(\Upsilon(t))$ is achieved at the unique point t 0, where ![]() $J_{\mu}^{\prime}(\Upsilon(t_0))\Upsilon(t_0) =0.$ This point t 0 is unique once
$J_{\mu}^{\prime}(\Upsilon(t_0))\Upsilon(t_0) =0.$ This point t 0 is unique once ![]() $J_{\mu}^{\prime}(\Upsilon(t_0))\Upsilon(t_0) =0$ is equivalent to
$J_{\mu}^{\prime}(\Upsilon(t_0))\Upsilon(t_0) =0$ is equivalent to
 \begin{equation*}
t_0^{N-2}L^{N-2}\|\nabla u_0\|_2^2 + t_0^NL^N\|u_0\|_2^2 = t_0^NL^N \displaystyle\int_{\mathbb{R}^N} f(u_0)u_0\,{\rm d}x + t_0^NL^N \|u_0\|_{2^*}^{2^*},
\end{equation*}
\begin{equation*}
t_0^{N-2}L^{N-2}\|\nabla u_0\|_2^2 + t_0^NL^N\|u_0\|_2^2 = t_0^NL^N \displaystyle\int_{\mathbb{R}^N} f(u_0)u_0\,{\rm d}x + t_0^NL^N \|u_0\|_{2^*}^{2^*},
\end{equation*}which has only one solution in t 0. Since u 0 is a non-trivial solution of ![]() $(P_{\mu,\infty})$, we can infer that the value of t 0 is
$(P_{\mu,\infty})$, we can infer that the value of t 0 is  $t_0=\dfrac{1}{L}$. The proof is complete.
$t_0=\dfrac{1}{L}$. The proof is complete.
Lemma 5.3. Consider ![]() $(u_n)\subset E$, a
$(u_n)\subset E$, a ![]() $(Ce)_c$ sequence for functional Iµ such that
$(Ce)_c$ sequence for functional Iµ such that
 \begin{equation*}
u_n\rightharpoonup 0 ~\text{in}~ H^1(\mathbb{R}^N)\quad \text{and} \quad c\in\left(0,\dfrac{1}{N{C_1^{\frac{N}{2}}}}S^\frac{N}{2}\right),
\end{equation*}
\begin{equation*}
u_n\rightharpoonup 0 ~\text{in}~ H^1(\mathbb{R}^N)\quad \text{and} \quad c\in\left(0,\dfrac{1}{N{C_1^{\frac{N}{2}}}}S^\frac{N}{2}\right),
\end{equation*}where C 1 is given by (4.9). Then, there exist a sequence ![]() $(y_n)\subset E$ and
$(y_n)\subset E$ and ![]() $\rho,\eta \gt 0$, satisfying
$\rho,\eta \gt 0$, satisfying
 \begin{eqnarray}
\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(y_n)}|u_n|^2\,{\rm d}x\geq\eta.
\end{eqnarray}
\begin{eqnarray}
\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(y_n)}|u_n|^2\,{\rm d}x\geq\eta.
\end{eqnarray}Proof. Suppose, by contradiction, that (5.15) does not hold. Then, by [Reference Lions10, Lemma 8.4], we have, for ![]() $p\in(2,2^*)$, that
$p\in(2,2^*)$, that
 \begin{eqnarray*}
\lim\limits_{n\rightarrow\infty}\displaystyle\int_{\mathbb{R}^N}|u_n|^p\,{\rm d}x=0.
\end{eqnarray*}
\begin{eqnarray*}
\lim\limits_{n\rightarrow\infty}\displaystyle\int_{\mathbb{R}^N}|u_n|^p\,{\rm d}x=0.
\end{eqnarray*} Consequently, by (1.2) and ![]() $(f_3)$,
$(f_3)$,
 \begin{eqnarray}
\lim\limits_{n\rightarrow\infty}\displaystyle\int_{\mathbb{R}^N}F(u_n)dx=\lim\limits_{n\rightarrow\infty}\displaystyle\int_{\mathbb{R}^N}f(u_n)u_n\,{\rm d}x=0.
\end{eqnarray}
\begin{eqnarray}
\lim\limits_{n\rightarrow\infty}\displaystyle\int_{\mathbb{R}^N}F(u_n)dx=\lim\limits_{n\rightarrow\infty}\displaystyle\int_{\mathbb{R}^N}f(u_n)u_n\,{\rm d}x=0.
\end{eqnarray} Since ![]() $u_n\rightharpoonup 0$ in
$u_n\rightharpoonup 0$ in ![]() $H^1(\mathbb{R}^N)$ and
$H^1(\mathbb{R}^N)$ and ![]() $\dim E^- \lt \infty$, then
$\dim E^- \lt \infty$, then ![]() $\|u^-_n\|\rightarrow 0$. Thus, using that
$\|u^-_n\|\rightarrow 0$. Thus, using that ![]() $I_\mu^{\prime}(u_n)u_n=o_n(1)$ and
$I_\mu^{\prime}(u_n)u_n=o_n(1)$ and ![]() $(u_n)$ is bounded in
$(u_n)$ is bounded in ![]() $H^1(\mathbb{R}^N)$, we obtain by (5.16)
$H^1(\mathbb{R}^N)$, we obtain by (5.16)
 \begin{eqnarray*}
l:=\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*} \,{\rm d}x+o_n(1)=\|u_n^+\|^2-\|u_n^-\|^2+o_n(1)=\|u_n^+\|^2+o_n(1).
\end{eqnarray*}
\begin{eqnarray*}
l:=\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*} \,{\rm d}x+o_n(1)=\|u_n^+\|^2-\|u_n^-\|^2+o_n(1)=\|u_n^+\|^2+o_n(1).
\end{eqnarray*} Hence, by ![]() $(5.16)$ and inequality above,
$(5.16)$ and inequality above,
 \begin{eqnarray}
o_n(1)+c=I_\mu(u_n)= \dfrac{1}{N}\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*} \,{\rm d}x+o_n(1)=\dfrac{1}{N}l.
\end{eqnarray}
\begin{eqnarray}
o_n(1)+c=I_\mu(u_n)= \dfrac{1}{N}\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*} \,{\rm d}x+o_n(1)=\dfrac{1}{N}l.
\end{eqnarray} This implies that ![]() $l=Nc \gt 0$. Now considering S the best constant of the Sobolev embedding
$l=Nc \gt 0$. Now considering S the best constant of the Sobolev embedding  $D^{1,2}(\mathbb{R}^N)\hookrightarrow L^{2^*}(\mathbb{R}^N$), we can conclude, by (4.9), that
$D^{1,2}(\mathbb{R}^N)\hookrightarrow L^{2^*}(\mathbb{R}^N$), we can conclude, by (4.9), that
 \begin{eqnarray*}
l^\frac{2}{2^*}S\leq \displaystyle\int\limits_{\mathbb{R}^N}|\nabla u_n|^2\,{\rm d}x\leq C_1\|u_n^+\|^2+o_n(1)=C_1l+o_n(1).
\end{eqnarray*}
\begin{eqnarray*}
l^\frac{2}{2^*}S\leq \displaystyle\int\limits_{\mathbb{R}^N}|\nabla u_n|^2\,{\rm d}x\leq C_1\|u_n^+\|^2+o_n(1)=C_1l+o_n(1).
\end{eqnarray*} Using that l = Nc and inequality above, we obtain  $c\geq\dfrac{1}{N{C_1^{\frac{N}{2}}}}S^\frac{N}{2}$, which contradicts our hypothesis.
$c\geq\dfrac{1}{N{C_1^{\frac{N}{2}}}}S^\frac{N}{2}$, which contradicts our hypothesis.
Proposition 5.4. Let ![]() $(u_n)\subset E$ be a
$(u_n)\subset E$ be a ![]() $(Ce)_c$ sequence for functional Iµ. If
$(Ce)_c$ sequence for functional Iµ. If
 \begin{eqnarray*}
c\in\left(0,\min\left\{d_\mu, \dfrac{1}{{C_1^{\frac{N}{2}}}N}S^\frac{N}{2}\right\} \right),
\end{eqnarray*}
\begin{eqnarray*}
c\in\left(0,\min\left\{d_\mu, \dfrac{1}{{C_1^{\frac{N}{2}}}N}S^\frac{N}{2}\right\} \right),
\end{eqnarray*}then problem ![]() $(P_\mu)$ has a non-trivial solution uµ.
$(P_\mu)$ has a non-trivial solution uµ.
Proof. Using Lemma 4, there is ![]() $u_\mu\in E$ such that
$u_\mu\in E$ such that ![]() $u_n\rightharpoonup u_\mu$ in E and
$u_n\rightharpoonup u_\mu$ in E and ![]() $I^{\prime}_\mu(u_\mu)=0$. Suppose, by contradiction, that
$I^{\prime}_\mu(u_\mu)=0$. Suppose, by contradiction, that ![]() $u_\mu\equiv 0$. Then, by Lemma 5.3, there are
$u_\mu\equiv 0$. Then, by Lemma 5.3, there are ![]() $(y_n)\subset\mathbb{R}^N$ and
$(y_n)\subset\mathbb{R}^N$ and ![]() $\rho,\;\eta \gt 0$ such that (5.15) holds. Note that since
$\rho,\;\eta \gt 0$ such that (5.15) holds. Note that since ![]() $\dim E^-$ is finite,
$\dim E^-$ is finite, ![]() $\|u_n^-\|\rightarrow 0$ and, consequently, for all
$\|u_n^-\|\rightarrow 0$ and, consequently, for all ![]() $v\in E$,
$v\in E$,
 \begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} \left(\nabla u_n \nabla v+V(x)u_n v\right)\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} \left(\nabla u^+_n \nabla v+V(x)u^+_n v\right)\,{\rm d}x+o_n(1),\\
\displaystyle\int_{\mathbb{R}^N} f(u_n)v\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} f(u_n^+)v\,{\rm d}x+o_n(1),\\
\displaystyle\int_{\mathbb{R}^N} F(u_n)\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} F(u_n^+)\,{\rm d}x+o_n(1),\\
\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*-1}u_nv\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} |u^+_n|^{2^*-1}u^+_nv\,{\rm d}x+o_n(1),\\
\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*}\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} |u^+_n|^{2^*}\,{\rm d}x+o_n(1),
\end{eqnarray*}
\begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} \left(\nabla u_n \nabla v+V(x)u_n v\right)\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} \left(\nabla u^+_n \nabla v+V(x)u^+_n v\right)\,{\rm d}x+o_n(1),\\
\displaystyle\int_{\mathbb{R}^N} f(u_n)v\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} f(u_n^+)v\,{\rm d}x+o_n(1),\\
\displaystyle\int_{\mathbb{R}^N} F(u_n)\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} F(u_n^+)\,{\rm d}x+o_n(1),\\
\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*-1}u_nv\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} |u^+_n|^{2^*-1}u^+_nv\,{\rm d}x+o_n(1),\\
\displaystyle\int_{\mathbb{R}^N} |u_n|^{2^*}\,{\rm d}x&=&\displaystyle\int_{\mathbb{R}^N} |u^+_n|^{2^*}\,{\rm d}x+o_n(1),
\end{eqnarray*}which imply ![]() $I_\mu(u_n)=I_\mu(u^+_n)+o_n(1)$ and
$I_\mu(u_n)=I_\mu(u^+_n)+o_n(1)$ and ![]() $I^{\prime}_\mu(u_n^+)=o_n(1)$.
$I^{\prime}_\mu(u_n^+)=o_n(1)$.
Let us prove that  $\lim\limits_{n\to+\infty}|y_n|\rightarrow+\infty$ occurs. In fact, if there exists
$\lim\limits_{n\to+\infty}|y_n|\rightarrow+\infty$ occurs. In fact, if there exists ![]() $\overline{R} \gt 0$ such that
$\overline{R} \gt 0$ such that ![]() $B_{\rho}(y_n)\subset B_{\overline{R}}(0)\subset\mathbb{R}^N$, for all
$B_{\rho}(y_n)\subset B_{\overline{R}}(0)\subset\mathbb{R}^N$, for all ![]() $n\in\mathbb{N}$, then, since
$n\in\mathbb{N}$, then, since ![]() $(u_n)$ converges strongly to 0 in
$(u_n)$ converges strongly to 0 in ![]() $L^2_{\rm loc}(\mathbb{R}^N)$, we see that
$L^2_{\rm loc}(\mathbb{R}^N)$, we see that
 \begin{eqnarray*}
\limsup\limits_{n\to+\infty}\int_{B_{\rho}(y_n)}\hspace{-0,5cm} u_n^2\,{\rm d}x&\leq& \limsup\limits_{n\to+\infty}\int_{B_{\overline{R}}(0)}\hspace{-0,5cm}u_n^2\,{\rm d}x=0,
\end{eqnarray*}
\begin{eqnarray*}
\limsup\limits_{n\to+\infty}\int_{B_{\rho}(y_n)}\hspace{-0,5cm} u_n^2\,{\rm d}x&\leq& \limsup\limits_{n\to+\infty}\int_{B_{\overline{R}}(0)}\hspace{-0,5cm}u_n^2\,{\rm d}x=0,
\end{eqnarray*}contradicting (5.15).
Now define ![]() $w_n(x):=u_n^+(x+y_n)$, for all
$w_n(x):=u_n^+(x+y_n)$, for all ![]() $x\in \mathbb{R}^N$. Therefore,
$x\in \mathbb{R}^N$. Therefore, ![]() $(w_n)$ is bounded in E, and there exists
$(w_n)$ is bounded in E, and there exists ![]() $w_n \rightharpoonup w_\mu\in E$. Using the arguments above, we have
$w_n \rightharpoonup w_\mu\in E$. Using the arguments above, we have
 \begin{eqnarray}
I_{\mu}(u^+_n)= J_{\mu}(w_n)+o_n(1)&\quad \text{and}&\quad J^{\prime}_{\mu}(w_\mu)=0.
\end{eqnarray}
\begin{eqnarray}
I_{\mu}(u^+_n)= J_{\mu}(w_n)+o_n(1)&\quad \text{and}&\quad J^{\prime}_{\mu}(w_\mu)=0.
\end{eqnarray} We claim that ![]() $w_\mu\neq0$. In fact, by (5.15),
$w_\mu\neq0$. In fact, by (5.15),
 \begin{equation*}
\begin{array}{llllllll}
\eta\leq \limsup\limits_{n\to+\infty}\displaystyle\int\limits_{B_\rho(y_n)}|u_n|^2\,{\rm d}x&=&\limsup\limits_{n\to+\infty}\displaystyle\int\limits_{B_\rho(y_n)}|u^+_n|^2\,{\rm d}x +o_n(1)\\
&=&\limsup\limits_{n\to+\infty}\displaystyle\int\limits_{B_\rho(0)}|w_n|^2\,{\rm d}x+o_n(1)\\
&=&\displaystyle\int\limits_{B_\rho(0)}|w_\mu|^2\,{\rm d}x.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{llllllll}
\eta\leq \limsup\limits_{n\to+\infty}\displaystyle\int\limits_{B_\rho(y_n)}|u_n|^2\,{\rm d}x&=&\limsup\limits_{n\to+\infty}\displaystyle\int\limits_{B_\rho(y_n)}|u^+_n|^2\,{\rm d}x +o_n(1)\\
&=&\limsup\limits_{n\to+\infty}\displaystyle\int\limits_{B_\rho(0)}|w_n|^2\,{\rm d}x+o_n(1)\\
&=&\displaystyle\int\limits_{B_\rho(0)}|w_\mu|^2\,{\rm d}x.
\end{array}
\end{equation*}Hence,
 \begin{equation*}
\begin{array}{lllllll}
d_{\mu}\leq J_{\mu}(w_\mu) &=& J_{\mu}(w_\mu)-\dfrac{1}{2}J^{\prime}_{\mu}(w_\mu)w_\mu\\
&\leq & \liminf\limits_{n\to\infty} \left[I_{\mu}(w_n)-\dfrac{1}{2}I^{\prime}_{\mu}(w_n)w_n\right]\\
&=&\liminf\limits_{n\to\infty} \left[I_{\mu}(u_n)-\dfrac{1}{2}I^{\prime}_{\mu}(u_n)u_n\right]\\
&\leq & I_{\mu}(u_n)+o_n(1) \\
&=& c_\mu.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllllll}
d_{\mu}\leq J_{\mu}(w_\mu) &=& J_{\mu}(w_\mu)-\dfrac{1}{2}J^{\prime}_{\mu}(w_\mu)w_\mu\\
&\leq & \liminf\limits_{n\to\infty} \left[I_{\mu}(w_n)-\dfrac{1}{2}I^{\prime}_{\mu}(w_n)w_n\right]\\
&=&\liminf\limits_{n\to\infty} \left[I_{\mu}(u_n)-\dfrac{1}{2}I^{\prime}_{\mu}(u_n)u_n\right]\\
&\leq & I_{\mu}(u_n)+o_n(1) \\
&=& c_\mu.
\end{array}
\end{equation*}Therefore, uµ may not be trivial, and the proof of the lemma is complete.
At this moment, the first part of the proof of Theorem 1.1 may be presented. In § 2, we proved that Iµ satisfies all conditions in Theorem 3.1, what implies the existence of a Cerami sequence ![]() $(u_n)$ at level
$(u_n)$ at level ![]() $c_\mu \gt 0$, where
$c_\mu \gt 0$, where  $
\displaystyle c_\mu=\inf _{h \in \Gamma} \max _{w \in M} I_\mu(h_0(w))
$ with
$
\displaystyle c_\mu=\inf _{h \in \Gamma} \max _{w \in M} I_\mu(h_0(w))
$ with ![]() $\Gamma:=\left\{h \in C(M, E):\left.h\right|_{\partial M}=h_{0}\right\}$. This sequence is bounded by Lemma 4 and then
$\Gamma:=\left\{h \in C(M, E):\left.h\right|_{\partial M}=h_{0}\right\}$. This sequence is bounded by Lemma 4 and then ![]() $(u_n)$ converges weakly to a solution uµ of
$(u_n)$ converges weakly to a solution uµ of ![]() $(P_\mu)$. To show that uµ is non-trivial, we have from Lemma 5.2 that
$(P_\mu)$. To show that uµ is non-trivial, we have from Lemma 5.2 that ![]() $c_\mu \lt d_\mu$ and, from Lemma 4.2, we choose µ > 0 large enough to obtain
$c_\mu \lt d_\mu$ and, from Lemma 4.2, we choose µ > 0 large enough to obtain  $c_\mu \lt \dfrac{1}{{C_1^{\frac{N}{2}}}N}S^\frac{N}{2}$ and apply Proposition 5.4 to get a non-trivial solution uµ of problem
$c_\mu \lt \dfrac{1}{{C_1^{\frac{N}{2}}}N}S^\frac{N}{2}$ and apply Proposition 5.4 to get a non-trivial solution uµ of problem ![]() $(P_\mu)$, which is non-negative because of hypothesis
$(P_\mu)$, which is non-negative because of hypothesis ![]() $(f_2)$, as we wished to prove.
$(f_2)$, as we wished to prove.
6. Appendix A: One ground state solution to the Limit Problem  $(P_{\mu,\infty})$ and some of its properties
$(P_{\mu,\infty})$ and some of its properties
To prove the existence of ground state solution to the limit problem ![]() $(P_{\mu,\infty})$, we consider
$(P_{\mu,\infty})$, we consider
 \begin{equation}
\left\{
\begin{array}{l}
- \Delta u+V_{\infty}u= \mu f(u)+|u|^{2^*-2}u \quad \mbox{in}\ \mathbb{R}^{N}\\\\
u\in H^1(\mathbb{R}^N).
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{l}
- \Delta u+V_{\infty}u= \mu f(u)+|u|^{2^*-2}u \quad \mbox{in}\ \mathbb{R}^{N}\\\\
u\in H^1(\mathbb{R}^N).
\end{array}
\right.
\end{equation} Hereafter, let us denote by ![]() $J_{\mu}: H^1(\mathbb{R}^N) \to \mathbb{R}$ the associated functional given by
$J_{\mu}: H^1(\mathbb{R}^N) \to \mathbb{R}$ the associated functional given by
 \begin{equation*}
J_{\mu}(u):=\displaystyle\frac{1}{2}\int_{\mathbb{R}^N}\left( |\nabla u |^2 + V_\infty u^2 \right) \,{\rm d}x - \mu\int_{\mathbb{R}^N} F(u)\,{\rm d}x - \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |u|^{2^*}\,{\rm d}x.
\end{equation*}
\begin{equation*}
J_{\mu}(u):=\displaystyle\frac{1}{2}\int_{\mathbb{R}^N}\left( |\nabla u |^2 + V_\infty u^2 \right) \,{\rm d}x - \mu\int_{\mathbb{R}^N} F(u)\,{\rm d}x - \dfrac{1}{2^*}\displaystyle\int_{\mathbb{R}^N} |u|^{2^*}\,{\rm d}x.
\end{equation*} In this section, we consider ![]() $H^1(\mathbb{R}^N)$ endowed with the following norm
$H^1(\mathbb{R}^N)$ endowed with the following norm
 \begin{equation*}
\|u\|^2_{H^1}:=\displaystyle\int_{\mathbb{R}^N}\left(|\nabla u|^2+V_\infty|u|^2 \right) \,{\rm d}x.
\end{equation*}
\begin{equation*}
\|u\|^2_{H^1}:=\displaystyle\int_{\mathbb{R}^N}\left(|\nabla u|^2+V_\infty|u|^2 \right) \,{\rm d}x.
\end{equation*} Notice that weak solutions of problem ![]() $(P_{\mu,\infty})$ in
$(P_{\mu,\infty})$ in ![]() $H^1(\mathbb{R}^N)$ are critical points of functional
$H^1(\mathbb{R}^N)$ are critical points of functional ![]() $J_\mu\in C^1(H^1(\mathbb{R}^N),\mathbb{R})$.
$J_\mu\in C^1(H^1(\mathbb{R}^N),\mathbb{R})$.
Let us show that functional Jµ has a mountain pass geometry.
Proposition 6.1. The following statements hold.
(i) There exist
 $\alpha,\;\rho \gt 0$ such that
$\alpha,\;\rho \gt 0$ such that
 \begin{equation*}
J_\mu(u)\geq\alpha,\ \text{for all} \ u\in H^1(\mathbb{R}^N), \ \text{with} \ \|u\|_{H^1}=\rho.
\end{equation*}
\begin{equation*}
J_\mu(u)\geq\alpha,\ \text{for all} \ u\in H^1(\mathbb{R}^N), \ \text{with} \ \|u\|_{H^1}=\rho.
\end{equation*}(ii) For all
 $u\in H^1(\mathbb{R}^N)\setminus\{0\}$, we have
$u\in H^1(\mathbb{R}^N)\setminus\{0\}$, we have
 \begin{equation*}
\limsup\limits_{t\to+\infty}J_\mu(tu)\leq -\infty.
\end{equation*}
\begin{equation*}
\limsup\limits_{t\to+\infty}J_\mu(tu)\leq -\infty.
\end{equation*}
Proof. Using ![]() $(1.2)$ and Sobolev embeddings, we obtain
$(1.2)$ and Sobolev embeddings, we obtain
 \begin{equation*}
\begin{array}{lllll}
J_\mu(u)&\geq & \dfrac{1}{2}\|u\|_{H^1}^2-\mu\left(\dfrac{\epsilon}{2}\displaystyle\int_{\mathbb{R}^N}|u|^2\,{\rm d}x + C_\epsilon\displaystyle\int_{\mathbb{R}^N}|u|^p\,{\rm d}x \right)-\dfrac{1}{2^*} \displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x
\\
\\
&\geq& \dfrac{1}{2}\|u\|_{H^1}^2-\dfrac{\mu \epsilon}{2}C\|u\|^2_{H^1}-\mu C C_\epsilon\|u\|^p_{H^1}-C \|u\|^{2^*}_{H^1} \\
\\
&=& \|u\|_{H^1}^2\left[ \left(\dfrac{1}{2}-\dfrac{\mu \epsilon}{2}C\right)-\mu C C_\epsilon\|u\|^{p-2}_{H^1}-C \|u\|_{H^1}^{2^*-2}\right]
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllll}
J_\mu(u)&\geq & \dfrac{1}{2}\|u\|_{H^1}^2-\mu\left(\dfrac{\epsilon}{2}\displaystyle\int_{\mathbb{R}^N}|u|^2\,{\rm d}x + C_\epsilon\displaystyle\int_{\mathbb{R}^N}|u|^p\,{\rm d}x \right)-\dfrac{1}{2^*} \displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x
\\
\\
&\geq& \dfrac{1}{2}\|u\|_{H^1}^2-\dfrac{\mu \epsilon}{2}C\|u\|^2_{H^1}-\mu C C_\epsilon\|u\|^p_{H^1}-C \|u\|^{2^*}_{H^1} \\
\\
&=& \|u\|_{H^1}^2\left[ \left(\dfrac{1}{2}-\dfrac{\mu \epsilon}{2}C\right)-\mu C C_\epsilon\|u\|^{p-2}_{H^1}-C \|u\|_{H^1}^{2^*-2}\right]
\end{array}
\end{equation*} Choosing  $\epsilon\in\left(0,\dfrac{1}{\mu C}\right)$ and taking
$\epsilon\in\left(0,\dfrac{1}{\mu C}\right)$ and taking ![]() $\|u\|_{H^1}$ small enough, we can determine positive numbers α and ρ such that
$\|u\|_{H^1}$ small enough, we can determine positive numbers α and ρ such that
 \begin{equation*}
J_\mu(u)\geq\alpha,\ \text{for all} \ u\in H^1(\mathbb{R}^N), \quad \text{with} \ \|u\|_{H^1}=\rho.
\end{equation*}
\begin{equation*}
J_\mu(u)\geq\alpha,\ \text{for all} \ u\in H^1(\mathbb{R}^N), \quad \text{with} \ \|u\|_{H^1}=\rho.
\end{equation*} To prove the second item, let us consider u ≠ 0 and t > 0. Then, by ![]() $(f_3)$,
$(f_3)$,
 \begin{equation*}
\begin{array}{lllll}
J_\mu(tu)&=&\dfrac{t^2}{2}\|u\|_{H^1}^2-\mu\displaystyle\int_{\mathbb{R}^N}F(tu)\,{\rm d}x-\dfrac{t^{2^*}}{2^*}\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\\\\
& \lt & t^2\left[\dfrac{1}{2}\|u\|_{H^1}^2-\dfrac{t^{2^*-2}}{2^*}\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x \right].
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllll}
J_\mu(tu)&=&\dfrac{t^2}{2}\|u\|_{H^1}^2-\mu\displaystyle\int_{\mathbb{R}^N}F(tu)\,{\rm d}x-\dfrac{t^{2^*}}{2^*}\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\\\\
& \lt & t^2\left[\dfrac{1}{2}\|u\|_{H^1}^2-\dfrac{t^{2^*-2}}{2^*}\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x \right].
\end{array}
\end{equation*} Letting ![]() $t\to+\infty$, we obtain
$t\to+\infty$, we obtain
 \begin{equation*}
\limsup\limits_{t\to+\infty}J_\mu(tu)\leq t^2\left[\dfrac{1}{2}\|u\|_{H^1}^2-\dfrac{t^{2^*-2}}{2^*}\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x \right]\to -\infty.
\end{equation*}
\begin{equation*}
\limsup\limits_{t\to+\infty}J_\mu(tu)\leq t^2\left[\dfrac{1}{2}\|u\|_{H^1}^2-\dfrac{t^{2^*-2}}{2^*}\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x \right]\to -\infty.
\end{equation*} We say that a sequence ![]() $(u_{n})\subset H^1(\mathbb{R}^N)$ is a Palais-Smale sequence at level bµ for the functional Jµ if
$(u_{n})\subset H^1(\mathbb{R}^N)$ is a Palais-Smale sequence at level bµ for the functional Jµ if
 \begin{eqnarray*}
J_{\mu}(u_{n})\rightarrow b_\mu &\quad \text{and} &\quad
\|J^\prime_{\mu}(u_{n})\|\rightarrow 0 \quad
\mbox{in} \ H^{-1}(\mathbb{R}^N),
\end{eqnarray*}
\begin{eqnarray*}
J_{\mu}(u_{n})\rightarrow b_\mu &\quad \text{and} &\quad
\|J^\prime_{\mu}(u_{n})\|\rightarrow 0 \quad
\mbox{in} \ H^{-1}(\mathbb{R}^N),
\end{eqnarray*}as ![]() $n\to\infty$, where
$n\to\infty$, where
 \begin{equation*}
b_\mu := \inf_{\eta \in \Gamma} \max_{t \in [0,1]}
J_{\mu}(\eta(t)) \gt 0
\end{equation*}
\begin{equation*}
b_\mu := \inf_{\eta \in \Gamma} \max_{t \in [0,1]}
J_{\mu}(\eta(t)) \gt 0
\end{equation*}and
 \begin{equation*}
\Gamma := \{\eta \in
C([0,1],H^1(\mathbb{R}^N)) : \eta(0)=0, ~J_{\mu}(\eta(1)) \lt 0\}.
\end{equation*}
\begin{equation*}
\Gamma := \{\eta \in
C([0,1],H^1(\mathbb{R}^N)) : \eta(0)=0, ~J_{\mu}(\eta(1)) \lt 0\}.
\end{equation*} Notice that Proposition 6.1 implies the existence of a Palais-Smale sequence at level bµ for the functional Jµ. Using this Palais-Smale sequence, we show the existence of non-trivial critical point for Jµ, but we need to show some technical results. First, let S > 0 be the best constant to the Sobolev embedding  $D^{1,2}(\mathbb{R}^N)\hookrightarrow L^{2^*}(\mathbb{R}^N)$.
$D^{1,2}(\mathbb{R}^N)\hookrightarrow L^{2^*}(\mathbb{R}^N)$.
Lemma 6.2. Consider ![]() $(u_n)\subset H^1(\mathbb{R}^N)$ a Palais-Smale sequence at level bµ for the functional Jµ such that
$(u_n)\subset H^1(\mathbb{R}^N)$ a Palais-Smale sequence at level bµ for the functional Jµ such that
 \begin{equation*}
u_n\rightharpoonup 0 ~\text{in}~ H^1(\mathbb{R}^N)\quad \text{and} \quad b_\mu\in\left(0,\frac{1}{N}S^\frac{N}{2}\right).
\end{equation*}
\begin{equation*}
u_n\rightharpoonup 0 ~\text{in}~ H^1(\mathbb{R}^N)\quad \text{and} \quad b_\mu\in\left(0,\frac{1}{N}S^\frac{N}{2}\right).
\end{equation*} Then, there exist a sequence ![]() $(y_n)\subset\mathbb{R}^N$ and
$(y_n)\subset\mathbb{R}^N$ and ![]() $\rho,\eta \gt 0$ such that
$\rho,\eta \gt 0$ such that
 \begin{eqnarray}
\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(y_n)}|u_n|^2\,{\rm d}x\geq\eta.
\end{eqnarray}
\begin{eqnarray}
\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(y_n)}|u_n|^2\,{\rm d}x\geq\eta.
\end{eqnarray}Proof. One proceeds exactly as in Proposition 5.4.
Lemma 6.3. If ![]() $\mu \to +\infty$, then
$\mu \to +\infty$, then ![]() $b_\mu\to 0$.
$b_\mu\to 0$.
Proof. Consider a function ![]() $\varphi\in C^\infty_0(\mathbb{R}^N)$ such that
$\varphi\in C^\infty_0(\mathbb{R}^N)$ such that  $\|\varphi\|^2_{H^1}=2$. Then, by Lemma 6.1, there exists
$\|\varphi\|^2_{H^1}=2$. Then, by Lemma 6.1, there exists ![]() $t_\mu \gt 0$ such that
$t_\mu \gt 0$ such that
 \begin{equation*}
J_\mu(t_\mu \varphi)=\max\limits_{t\geq 0}J_\mu(t\varphi).
\end{equation*}
\begin{equation*}
J_\mu(t_\mu \varphi)=\max\limits_{t\geq 0}J_\mu(t\varphi).
\end{equation*} We are going to show that, up to subsequence, ![]() $t_\mu\to 0$ when
$t_\mu\to 0$ when ![]() $\mu\to+\infty$. First, using the characterization of bµ and
$\mu\to+\infty$. First, using the characterization of bµ and ![]() $(f_3)$, we have
$(f_3)$, we have
 \begin{equation*}
\begin{array}{lllllll}
0 \lt b_\mu &\leq & t_\mu^2-\mu \displaystyle\int_{\mathbb{R}^N} F(t_\mu \varphi)\,{\rm d}x- \dfrac{t_\mu^{2^*}}{2^*} \displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x\\
\\
&\leq & t_\mu^{2} \left(\dfrac{1}{2}- \dfrac{t_\mu^{2^*-2}}{2^*}\displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x\right),
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllllll}
0 \lt b_\mu &\leq & t_\mu^2-\mu \displaystyle\int_{\mathbb{R}^N} F(t_\mu \varphi)\,{\rm d}x- \dfrac{t_\mu^{2^*}}{2^*} \displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x\\
\\
&\leq & t_\mu^{2} \left(\dfrac{1}{2}- \dfrac{t_\mu^{2^*-2}}{2^*}\displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x\right),
\end{array}
\end{equation*}and this implies that ![]() $(t_\mu)\subset\mathbb{R}$ is bounded. Hence, up to a subsequence,
$(t_\mu)\subset\mathbb{R}$ is bounded. Hence, up to a subsequence, ![]() $(t_\mu)$ converges to some
$(t_\mu)$ converges to some ![]() $t_0\geq0$. To prove that
$t_0\geq0$. To prove that ![]() $t_0=0$, let us suppose, by contradiction, that
$t_0=0$, let us suppose, by contradiction, that ![]() $t_0 \gt 0$. Then, by
$t_0 \gt 0$. Then, by ![]() $(f_3)$,
$(f_3)$,
 \begin{equation*}
\begin{array}{lllllll}
0 \lt b_\mu &\leq & t_\mu^2-\mu \displaystyle\int_{\mathbb{R}^N} F(t_\mu \varphi)\,{\rm d}x- \dfrac{t_\mu^{2^*}}{2^*} \displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x\\
\\
&\leq & t_0^2-\dfrac{\mu}{2} \displaystyle\int_{\mathbb{R}^N} F(t_0 \varphi)\,{\rm d}x- \dfrac{t_0^{2^*}}{2^*} \displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x+o_\mu(1),
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllllll}
0 \lt b_\mu &\leq & t_\mu^2-\mu \displaystyle\int_{\mathbb{R}^N} F(t_\mu \varphi)\,{\rm d}x- \dfrac{t_\mu^{2^*}}{2^*} \displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x\\
\\
&\leq & t_0^2-\dfrac{\mu}{2} \displaystyle\int_{\mathbb{R}^N} F(t_0 \varphi)\,{\rm d}x- \dfrac{t_0^{2^*}}{2^*} \displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x+o_\mu(1),
\end{array}
\end{equation*}which implies that
 \begin{equation*}
\begin{array}{lllllll}
0\leq \limsup\limits_{\mu\to+\infty} b_\mu\leq -\infty.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllllll}
0\leq \limsup\limits_{\mu\to+\infty} b_\mu\leq -\infty.
\end{array}
\end{equation*} Therefore, up to a subsequence, ![]() $(t_\mu)$ converges to 0. Hence, by
$(t_\mu)$ converges to 0. Hence, by ![]() $(f_3)$ one more time,
$(f_3)$ one more time,
 \begin{equation*}
\begin{array}{lllllll}
0 \lt b_\mu\leq t_\mu^2-\mu \displaystyle\int_{\mathbb{R}^N} F(t_\mu \varphi)\,{\rm d}x- \dfrac{t_\mu^{2^*}}{2^*} \displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x\leq t_\mu^2,
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllllll}
0 \lt b_\mu\leq t_\mu^2-\mu \displaystyle\int_{\mathbb{R}^N} F(t_\mu \varphi)\,{\rm d}x- \dfrac{t_\mu^{2^*}}{2^*} \displaystyle\int_{\mathbb{R}^N}|\varphi|^{2^*}\,{\rm d}x\leq t_\mu^2,
\end{array}
\end{equation*}for all µ > 0. This proves the lemma.
Proposition 6.4. There exists ![]() $\mu^* \gt 0$ such that the limit problem
$\mu^* \gt 0$ such that the limit problem ![]() $(P_{\mu, \infty})$ has a nontrivial solution.
$(P_{\mu, \infty})$ has a nontrivial solution.
Proof. By Proposition 6.1, we get a Palais-Smale sequence ![]() $(u_n)\subset H^1(\mathbb{R}^N)$ at level
$(u_n)\subset H^1(\mathbb{R}^N)$ at level ![]() $b_\mu \gt 0$. Using the proof of Lemma 4 with a slight modification, we can show that the sequence
$b_\mu \gt 0$. Using the proof of Lemma 4 with a slight modification, we can show that the sequence ![]() $(u_n)$ is bounded in
$(u_n)$ is bounded in ![]() $H^1(\mathbb{R}^N)$. Then, there exists
$H^1(\mathbb{R}^N)$. Then, there exists ![]() $u_\infty\in H^1(\mathbb{R}^N)$ such that, up to a subsequence,
$u_\infty\in H^1(\mathbb{R}^N)$ such that, up to a subsequence, ![]() $u_n\rightharpoonup u_0 \in H^1(\mathbb{R}^N)$.
$u_n\rightharpoonup u_0 \in H^1(\mathbb{R}^N)$.
If ![]() $u_0\neq 0$ then, using a density argument, we have a nontrivial solution of
$u_0\neq 0$ then, using a density argument, we have a nontrivial solution of ![]() $(P_{\mu,\infty})$. On the other hand, if
$(P_{\mu,\infty})$. On the other hand, if ![]() $u_0\equiv 0$, we can find
$u_0\equiv 0$, we can find ![]() $\mu^* \gt 0$ such that, by Lemma 6.3,
$\mu^* \gt 0$ such that, by Lemma 6.3,
 \begin{equation*}
0 \lt b_\mu \lt \dfrac{1}{N}S^{\frac{N}{2}},\quad \forall~~\mu\geq\mu^*.
\end{equation*}
\begin{equation*}
0 \lt b_\mu \lt \dfrac{1}{N}S^{\frac{N}{2}},\quad \forall~~\mu\geq\mu^*.
\end{equation*} Then, by Lemma 6.2, there exist a sequence ![]() $(y_n)\subset\mathbb{R}^N$ and
$(y_n)\subset\mathbb{R}^N$ and ![]() $\rho,\eta \gt 0$ such that
$\rho,\eta \gt 0$ such that
 \begin{eqnarray}
\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(y_n)}|u_n|^2\,{\rm d}x\geq\eta.
\end{eqnarray}
\begin{eqnarray}
\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(y_n)}|u_n|^2\,{\rm d}x\geq\eta.
\end{eqnarray} Setting ![]() $w_n:=u_n(x+y_n)$ and, since the problem is invariant under translations, we have that
$w_n:=u_n(x+y_n)$ and, since the problem is invariant under translations, we have that ![]() $(w_n)\subset\mathbb{R}^N$ is a bounded Palais-Smale sequence. Hence, there exists
$(w_n)\subset\mathbb{R}^N$ is a bounded Palais-Smale sequence. Hence, there exists ![]() $w_0\in H^1(\mathbb{R}^N)$ such that, up to a subsequence,
$w_0\in H^1(\mathbb{R}^N)$ such that, up to a subsequence, ![]() $w_n\rightharpoonup w_0 \in H^1(\mathbb{R}^N)$ and, by
$w_n\rightharpoonup w_0 \in H^1(\mathbb{R}^N)$ and, by ![]() $(6.2)$ and Sobolev embeddings,
$(6.2)$ and Sobolev embeddings,
 \begin{eqnarray*}
\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(0)}|w_0|^2\,{\rm d}x=\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(0)}|w_n|^2\,{\rm d}x\geq\eta,
\end{eqnarray*}
\begin{eqnarray*}
\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(0)}|w_0|^2\,{\rm d}x=\limsup\limits_{n\rightarrow\infty}\displaystyle\int_{B_\rho(0)}|w_n|^2\,{\rm d}x\geq\eta,
\end{eqnarray*}which implies that ![]() $w_0\neq 0$ and, using a density argument one more time, we have a non-trivial solution of
$w_0\neq 0$ and, using a density argument one more time, we have a non-trivial solution of ![]() $(P_{\mu,\infty})$.
$(P_{\mu,\infty})$.
At this moment, we will concentrate in showing that the limit problem has a ground state solution. For this, let us consider
 \begin{equation*}
\mathcal{N}_\mu:=\left\{~u\in H^{1}(\mathbb{R}^N)\setminus\{0\}:~J^\prime_\mu(u)=0 \right\}.
\end{equation*}
\begin{equation*}
\mathcal{N}_\mu:=\left\{~u\in H^{1}(\mathbb{R}^N)\setminus\{0\}:~J^\prime_\mu(u)=0 \right\}.
\end{equation*} Before stating the results, observe that Lemmas 5.4 and 6.2 are still valid when we consider a sequence ![]() $(u_n)\subset\mathcal{N}_\mu$ instead of a
$(u_n)\subset\mathcal{N}_\mu$ instead of a ![]() $(Ce)_c$ sequence for functional Jµ.
$(Ce)_c$ sequence for functional Jµ.
Lemma 6.5. Consider ![]() $\mu^* \gt 0$ given by Proposition 6.4. If
$\mu^* \gt 0$ given by Proposition 6.4. If ![]() $\mu\geq\mu^*$, then the following proprieties hold.
$\mu\geq\mu^*$, then the following proprieties hold.
(i)
 $\mathcal{N}_\mu\neq \emptyset$.
$\mathcal{N}_\mu\neq \emptyset$.(ii) There exists
 $\rho_{\mu} \gt 0$ such that
$\rho_{\mu} \gt 0$ such that
 \begin{equation*}
\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\geq\rho_{\mu} \gt 0,\quad \forall\ u\in\mathcal{N}_\mu.
\end{equation*}
\begin{equation*}
\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\geq\rho_{\mu} \gt 0,\quad \forall\ u\in\mathcal{N}_\mu.
\end{equation*}(iii) If
 $u\in\mathcal{N}_\mu$, then
$u\in\mathcal{N}_\mu$, then  $J_\mu (u)\geq\dfrac{1}{N}\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\geq \dfrac{\rho_\mu}{N} \gt 0$.
$J_\mu (u)\geq\dfrac{1}{N}\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\geq \dfrac{\rho_\mu}{N} \gt 0$.
Proof. We deduce immediately item (i) from the existence of a non-trivial solution obtained by Proposition 6.4. To prove the second item, we are going to use ![]() $(1.2)$ to ensure that
$(1.2)$ to ensure that
 \begin{equation*}
|f(s)|\leq \epsilon|s|+C_\epsilon|s|^{2^*-1},\quad \forall\ s\in\mathbb{R}.
\end{equation*}
\begin{equation*}
|f(s)|\leq \epsilon|s|+C_\epsilon|s|^{2^*-1},\quad \forall\ s\in\mathbb{R}.
\end{equation*} Then, considering ![]() $u\in\mathcal{N}_\mu$ and using Sobolev embeddings,
$u\in\mathcal{N}_\mu$ and using Sobolev embeddings,
 \begin{equation}
\begin{array}{llll}
\|u\|_{H^1}^2&=&\mu\displaystyle\int_{\mathbb{R}^N}f(u)u \,{\rm d}x+\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\\
\\
&\leq&\epsilon \mu \displaystyle\int_{\mathbb{R}^N}|u|^2\,{\rm d}x+(\mu C_\epsilon+1)\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\\
\\
&\leq &
\epsilon \mu\|u\|_{H^1}^2+C_{\epsilon,\mu}\|u\|_{H^1}^{2^*}.
\end{array}
\end{equation}
\begin{equation}
\begin{array}{llll}
\|u\|_{H^1}^2&=&\mu\displaystyle\int_{\mathbb{R}^N}f(u)u \,{\rm d}x+\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\\
\\
&\leq&\epsilon \mu \displaystyle\int_{\mathbb{R}^N}|u|^2\,{\rm d}x+(\mu C_\epsilon+1)\displaystyle\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\\
\\
&\leq &
\epsilon \mu\|u\|_{H^1}^2+C_{\epsilon,\mu}\|u\|_{H^1}^{2^*}.
\end{array}
\end{equation} Choosing  $\epsilon\in\left(0,\dfrac{1}{\mu} \right) $, then there exists
$\epsilon\in\left(0,\dfrac{1}{\mu} \right) $, then there exists ![]() $K_\mu \gt 0$ such that
$K_\mu \gt 0$ such that
 \begin{equation}
\|u\|_{H^1}^2\geq K_\mu,\quad \forall\ u\in\mathcal{N}_\mu.
\end{equation}
\begin{equation}
\|u\|_{H^1}^2\geq K_\mu,\quad \forall\ u\in\mathcal{N}_\mu.
\end{equation} Using again (6.3) and (6.4), we can find ![]() $\rho_\mu \gt 0$ such that
$\rho_\mu \gt 0$ such that
 \begin{equation*}
\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\geq\rho_{\mu} \gt 0,\quad \forall \ u\in\mathcal{N}_\mu.
\end{equation*}
\begin{equation*}
\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\geq\rho_{\mu} \gt 0,\quad \forall \ u\in\mathcal{N}_\mu.
\end{equation*} Let us show item (iii). Using ![]() $(f_3)$ and item (ii), we obtain, for
$(f_3)$ and item (ii), we obtain, for ![]() $u\in\mathcal{N}_\mu$,
$u\in\mathcal{N}_\mu$,
 \begin{equation*}
\begin{split}
J_\mu(u)&=J_\mu(u)-\dfrac{1}{2} J_\mu(u)u\\
&=\mu\int_{\mathbb{R}^N}\left(\dfrac{f(u)u}{2}-F(u)\right)\,{\rm d}x+\left(\dfrac{1}{2}-\dfrac{1}{2^*}\right)\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\\
&\geq \dfrac{\rho_\mu}{N} \gt 0
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
J_\mu(u)&=J_\mu(u)-\dfrac{1}{2} J_\mu(u)u\\
&=\mu\int_{\mathbb{R}^N}\left(\dfrac{f(u)u}{2}-F(u)\right)\,{\rm d}x+\left(\dfrac{1}{2}-\dfrac{1}{2^*}\right)\int_{\mathbb{R}^N}|u|^{2^*}\,{\rm d}x\\
&\geq \dfrac{\rho_\mu}{N} \gt 0
\end{split}
\end{equation*}The above Lemma ensures that
 \begin{equation}
0 \lt d_\mu:=\inf\limits_{u\in\mathcal{N}_\mu}J_\mu(u).
\end{equation}
\begin{equation}
0 \lt d_\mu:=\inf\limits_{u\in\mathcal{N}_\mu}J_\mu(u).
\end{equation} The next result establishes the existence of a non-trivial ground state solution ![]() $w_\infty$ to problem
$w_\infty$ to problem ![]() $(P_{\mu,\infty})$.
$(P_{\mu,\infty})$.
Lemma 6.6. If ![]() $\mathcal{N}_\mu\neq \emptyset$, let
$\mathcal{N}_\mu\neq \emptyset$, let ![]() $(u_n)\subset \mathcal{N}_\mu$ be a minimizing sequence for Jµ. Then
$(u_n)\subset \mathcal{N}_\mu$ be a minimizing sequence for Jµ. Then ![]() $(u_n)$ is bounded in
$(u_n)$ is bounded in ![]() $H^1(\mathbb{R}^N)$. Moreover, there exists
$H^1(\mathbb{R}^N)$. Moreover, there exists ![]() $\mu^* \gt 0$ such that the infimum of Jµ on
$\mu^* \gt 0$ such that the infimum of Jµ on ![]() $\mathcal{N}_\mu$ is attained for all
$\mathcal{N}_\mu$ is attained for all ![]() $\mu \gt \mu^*$.
$\mu \gt \mu^*$.
Proof. The existence of a minimizing sequence ![]() $(u_n)\subset\mathcal{N}_\mu$ is assured by Lemma 6.5. Using the same arguments as in Lemma 4.1, we show that
$(u_n)\subset\mathcal{N}_\mu$ is assured by Lemma 6.5. Using the same arguments as in Lemma 4.1, we show that ![]() $(u_n)$ is bounded in
$(u_n)$ is bounded in ![]() $H^1(\mathbb{R}^N)$. Hence, by usual arguments and Sobolev embeddings, there exists
$H^1(\mathbb{R}^N)$. Hence, by usual arguments and Sobolev embeddings, there exists ![]() $w_{\infty}\in H^1(\mathbb{R}^N)$ such that, up to a subsequence,
$w_{\infty}\in H^1(\mathbb{R}^N)$ such that, up to a subsequence,
 \begin{eqnarray}
\left\{\begin{array}{llllll}
\nabla u_n(x)\rightarrow \nabla w_\infty(x)\quad a.e\ \text{in}\ \mathbb{R}^N.\\\\
u_n\rightarrow w_\infty \ \text{in}\ L^s_{\rm loc}(\mathbb{R}^N)\quad \text{for any}\ 1\leq s \lt 2^*,\\\\
u_n(x)\rightarrow w_\infty(x)\quad \text{for a.e}\ x\in\mathbb{R}^N.\\
\end{array}\right.
\end{eqnarray}
\begin{eqnarray}
\left\{\begin{array}{llllll}
\nabla u_n(x)\rightarrow \nabla w_\infty(x)\quad a.e\ \text{in}\ \mathbb{R}^N.\\\\
u_n\rightarrow w_\infty \ \text{in}\ L^s_{\rm loc}(\mathbb{R}^N)\quad \text{for any}\ 1\leq s \lt 2^*,\\\\
u_n(x)\rightarrow w_\infty(x)\quad \text{for a.e}\ x\in\mathbb{R}^N.\\
\end{array}\right.
\end{eqnarray}The pointwise convergence of the gradient in (6.6) is guaranteed by Lemma 7.1 in the Appendix B.
By density arguments, ![]() $J_{\mu}^{\prime}(w_\infty)(w_\infty)=0$. Observe that, if
$J_{\mu}^{\prime}(w_\infty)(w_\infty)=0$. Observe that, if ![]() $w_\infty\neq 0$, then
$w_\infty\neq 0$, then ![]() $w_\infty\in\mathcal{N}_\mu$, and hence, by Fatou’s Lemma and
$w_\infty\in\mathcal{N}_\mu$, and hence, by Fatou’s Lemma and ![]() $(f_3)$,
$(f_3)$,
 \begin{equation*}
\begin{array}{lllllllllll}
d_\mu &\leq& J_\mu(w_\infty)= J_\mu(w_\infty)-\dfrac{1}{2}J^\prime_\mu(w_\infty)w_\infty\\
\\
&=&\mu\displaystyle\int_{\mathbb{R}^N}\left(\dfrac{f(w_\infty)w_\infty}{2}-F(w_\infty)\right)\,{\rm d}x+\left(\dfrac{1}{2}-\dfrac{1}{2^*}\right)\int_{\mathbb{R}^N}|w_\infty|^{2^*}\,{\rm d}x\\
\\
& \leq & \mu\displaystyle\int_{\mathbb{R}^N}\left(\dfrac{f(u_n)u_n}{2}-F(u_n)\right)\,{\rm d}x+\left(\dfrac{1}{2}-\dfrac{1}{2^*}\right)\int_{\mathbb{R}^N}|u_n|^{2^*}\,{\rm d}x+o_n(1)\\
\\
& \leq &J_\mu(u_n)-\dfrac{1}{2}J^\prime_\mu(u_n)u_n+o_n(1)=J_\mu(u_n)+o_n(1)=d_\mu+o_n(1).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllllllllll}
d_\mu &\leq& J_\mu(w_\infty)= J_\mu(w_\infty)-\dfrac{1}{2}J^\prime_\mu(w_\infty)w_\infty\\
\\
&=&\mu\displaystyle\int_{\mathbb{R}^N}\left(\dfrac{f(w_\infty)w_\infty}{2}-F(w_\infty)\right)\,{\rm d}x+\left(\dfrac{1}{2}-\dfrac{1}{2^*}\right)\int_{\mathbb{R}^N}|w_\infty|^{2^*}\,{\rm d}x\\
\\
& \leq & \mu\displaystyle\int_{\mathbb{R}^N}\left(\dfrac{f(u_n)u_n}{2}-F(u_n)\right)\,{\rm d}x+\left(\dfrac{1}{2}-\dfrac{1}{2^*}\right)\int_{\mathbb{R}^N}|u_n|^{2^*}\,{\rm d}x+o_n(1)\\
\\
& \leq &J_\mu(u_n)-\dfrac{1}{2}J^\prime_\mu(u_n)u_n+o_n(1)=J_\mu(u_n)+o_n(1)=d_\mu+o_n(1).
\end{array}
\end{equation*} Then, we conclude that ![]() $(u_n)$ converges strongly to
$(u_n)$ converges strongly to ![]() $w_\infty$ in
$w_\infty$ in ![]() $H^1(\mathbb{R}^N)$ and hence
$H^1(\mathbb{R}^N)$ and hence ![]() $J_{\mu}(w_\infty)=d_\mu$.
$J_{\mu}(w_\infty)=d_\mu$.
On the other hand, if ![]() $w_\infty\equiv 0$, we define
$w_\infty\equiv 0$, we define ![]() $w_n(x):=u_n(x+y_n)$. Then, arguing as we did in Lemmas 5.3, 5.4 and 6.3, there exists
$w_n(x):=u_n(x+y_n)$. Then, arguing as we did in Lemmas 5.3, 5.4 and 6.3, there exists ![]() $\mu^* \gt 0$ such that if
$\mu^* \gt 0$ such that if ![]() $\mu \gt \mu^*$, then there is
$\mu \gt \mu^*$, then there is ![]() $\widetilde{w_{\mu,\infty}}\in\mathcal{N}_{\mu,\infty}$ satisfying, up to a subsequence,
$\widetilde{w_{\mu,\infty}}\in\mathcal{N}_{\mu,\infty}$ satisfying, up to a subsequence,
 \begin{equation}
\left\{\begin{array}{llllllllll}
\nabla w_n(x)\rightarrow \nabla \widetilde{w_\infty}(x)\quad a.e\ \text{in}\ \mathbb{R}^N,\\\\
w_n\rightarrow \widetilde{w_\infty} \ \text{in}\ L^s_{\rm loc}(\mathbb{R}^N)\quad \text{for any}\ 2\leq s \lt 2^*,\\\\
w_n(x)\rightarrow \widetilde{w_\infty}(x)\quad \text{a.e}\ x\in\mathbb{R}^N,\\\\
J_\mu(u_n)=J_{\mu}(w_n).
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{llllllllll}
\nabla w_n(x)\rightarrow \nabla \widetilde{w_\infty}(x)\quad a.e\ \text{in}\ \mathbb{R}^N,\\\\
w_n\rightarrow \widetilde{w_\infty} \ \text{in}\ L^s_{\rm loc}(\mathbb{R}^N)\quad \text{for any}\ 2\leq s \lt 2^*,\\\\
w_n(x)\rightarrow \widetilde{w_\infty}(x)\quad \text{a.e}\ x\in\mathbb{R}^N,\\\\
J_\mu(u_n)=J_{\mu}(w_n).
\end{array}\right.
\end{equation} Then, by Fatou’s Lemma and ![]() $(f_3)$,
$(f_3)$,
 \begin{eqnarray*}
d_\mu\leq J_{\mu}(\widetilde{w_{\mu,\infty}}) &=& J_{\mu}(\widetilde{w_{\mu,\infty}})-\dfrac{1}{2}J^\prime_{\mu}(\widetilde{w_{\mu,\infty}})\widetilde{w_{\mu,\infty}}\\
&\leq & \liminf\limits_{n\to\infty} \left[J_{\mu}(w_n)-\dfrac{1}{2}J^\prime_{\mu}(w_n)w_n\right]\\
&=&\liminf\limits_{n\to\infty} \left[J_{\mu}(u_n)-\dfrac{1}{2}J^\prime_{\mu}(u_n)u_n\right]\\
&\leq & J_{\mu}(u_n)+o_n(1) \\
&=& d_\mu,
\end{eqnarray*}
\begin{eqnarray*}
d_\mu\leq J_{\mu}(\widetilde{w_{\mu,\infty}}) &=& J_{\mu}(\widetilde{w_{\mu,\infty}})-\dfrac{1}{2}J^\prime_{\mu}(\widetilde{w_{\mu,\infty}})\widetilde{w_{\mu,\infty}}\\
&\leq & \liminf\limits_{n\to\infty} \left[J_{\mu}(w_n)-\dfrac{1}{2}J^\prime_{\mu}(w_n)w_n\right]\\
&=&\liminf\limits_{n\to\infty} \left[J_{\mu}(u_n)-\dfrac{1}{2}J^\prime_{\mu}(u_n)u_n\right]\\
&\leq & J_{\mu}(u_n)+o_n(1) \\
&=& d_\mu,
\end{eqnarray*}which completes the proof.
Proposition 6.7. There exists ![]() $\mu^* \gt 0$ such that problem
$\mu^* \gt 0$ such that problem ![]() $(P_{\mu,\infty})$ has a ground state solution
$(P_{\mu,\infty})$ has a ground state solution ![]() $u_0\in H^1(\mathbb{R}^N)$ for all
$u_0\in H^1(\mathbb{R}^N)$ for all ![]() $\mu \gt \mu^*$.
$\mu \gt \mu^*$.
Without loss of generality, we may suppose that ![]() $u_0\geq 0$ in
$u_0\geq 0$ in ![]() $\mathbb{R}^N$. To see this, it is enough to truncate the functional Jµ, considering
$\mathbb{R}^N$. To see this, it is enough to truncate the functional Jµ, considering  $(\max\{w,0\})^{2^*}$ in place of
$(\max\{w,0\})^{2^*}$ in place of  $|w|^{2^*}$ and using hypothesis
$|w|^{2^*}$ and using hypothesis ![]() $(f_2)$.
$(f_2)$.
The next lemma is an important consequence of the standard regularity arguments. It will be used to apply the Divergence Theorem in the sequel.
Lemma 6.8. It holds that ![]() $u_0\in H^2(\mathbb{R}^N)$.
$u_0\in H^2(\mathbb{R}^N)$.
We also may suppose that ![]() $u_0\in H^1_{\text{rad}}(\mathbb{R}^N)$. Indeed, it is enough to solve problem
$u_0\in H^1_{\text{rad}}(\mathbb{R}^N)$. Indeed, it is enough to solve problem ![]() $(P_{\mu,\infty})$ in
$(P_{\mu,\infty})$ in ![]() $H^1_{\text{rad}}(\mathbb{R}^N)$ and use the Symmetric Criticality Principle. This implies the following lemma whose proof is an immediate consequence of Strauss inequality.
$H^1_{\text{rad}}(\mathbb{R}^N)$ and use the Symmetric Criticality Principle. This implies the following lemma whose proof is an immediate consequence of Strauss inequality.
Lemma 6.9. There exists ![]() $C=C(N) \gt 0$ such that, for all x ≠ 0,
$C=C(N) \gt 0$ such that, for all x ≠ 0,
 \begin{equation*}
|u_0(x)|\leq C|u_0|_\infty\dfrac{1}{|x|^{\frac{N-1}{2}}}.
\end{equation*}
\begin{equation*}
|u_0(x)|\leq C|u_0|_\infty\dfrac{1}{|x|^{\frac{N-1}{2}}}.
\end{equation*} The next result is the most important concerning the qualitative properties of u 0. It will guarantee that the solution u 0 has an appropriate exponential decay, which was used before to relate two important levels in order to obtain a strong convergence of a Cerami sequence. Recall that  $\dfrac{|f(s)|}{|s|} \lt m$ for all
$\dfrac{|f(s)|}{|s|} \lt m$ for all ![]() $s\in\mathbb{R}$ from hypothesis
$s\in\mathbb{R}$ from hypothesis ![]() $(f_2)$.
$(f_2)$.
Proposition 6.10. If ![]() $\nu\in\left(0,\sqrt{V_\infty}\right)$ and
$\nu\in\left(0,\sqrt{V_\infty}\right)$ and ![]() $\mu\geq \mu^*$, then there exists
$\mu\geq \mu^*$, then there exists ![]() $C=C(m,\nu) \gt 0$ such that
$C=C(m,\nu) \gt 0$ such that
Proof. For x ≠ 0, we have that
 \begin{equation}
\Delta \left( {\rm e}^{-\nu|x|}\right) = \left( \nu^2 - \dfrac{N-1}{|x|}\nu \right){\rm e}^{-\nu|x|}.
\end{equation}
\begin{equation}
\Delta \left( {\rm e}^{-\nu|x|}\right) = \left( \nu^2 - \dfrac{N-1}{|x|}\nu \right){\rm e}^{-\nu|x|}.
\end{equation} Define ![]() $C:= {\rm e}^{\nu R} \gt 0$, where R > 0 to be chosen, and
$C:= {\rm e}^{\nu R} \gt 0$, where R > 0 to be chosen, and
By the definition of C, we get ![]() $w(x)\leq 0$ for
$w(x)\leq 0$ for ![]() $|x|\leq R$. Let us prove that this inequality still holds for
$|x|\leq R$. Let us prove that this inequality still holds for ![]() $|x| \gt R$. For this end, consider the set
$|x| \gt R$. For this end, consider the set
where ![]() $w_+(x)=\max\{w(x),0\}$. Suppose, by contradiction, that
$w_+(x)=\max\{w(x),0\}$. Suppose, by contradiction, that ![]() $\Omega\neq \emptyset$. Since
$\Omega\neq \emptyset$. Since ![]() $w_+\in H^1(\mathbb{R}^N)$, it follows that Ω is a Lebesgue measurable set, which satisfies
$w_+\in H^1(\mathbb{R}^N)$, it follows that Ω is a Lebesgue measurable set, which satisfies
Therefore, by the Divergence Theorem (note that ![]() $w_+ =0$ on
$w_+ =0$ on ![]() $\partial D(R)$), we get
$\partial D(R)$), we get
 \begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x & = & \displaystyle\int_{D(R)} \nabla w_+\cdot\nabla w_+\, {\rm d}x\\
&=& \displaystyle\int_{\mathbb{R}^N} \nabla w\cdot\nabla w_+\,{\rm d}x \\
& = & \displaystyle\int_{\mathbb{R}^N} \nabla u_0\cdot\nabla w_+ \,{\rm d}x - C|u|_{\infty} \displaystyle\int_{\mathbb{R}^N} \nabla (e^{-\nu|x|})\cdot\nabla w_+ \,{\rm d}x \\
& = & \displaystyle\int_{\mathbb{R}^N} \nabla u_0\cdot\nabla w_+ \,{\rm d}x + C|u|_{\infty} \displaystyle\int_{\mathbb{R}^N} \Delta (e^{-\nu|x|}) w_+\,{\rm d}x.
\end{eqnarray*}
\begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x & = & \displaystyle\int_{D(R)} \nabla w_+\cdot\nabla w_+\, {\rm d}x\\
&=& \displaystyle\int_{\mathbb{R}^N} \nabla w\cdot\nabla w_+\,{\rm d}x \\
& = & \displaystyle\int_{\mathbb{R}^N} \nabla u_0\cdot\nabla w_+ \,{\rm d}x - C|u|_{\infty} \displaystyle\int_{\mathbb{R}^N} \nabla (e^{-\nu|x|})\cdot\nabla w_+ \,{\rm d}x \\
& = & \displaystyle\int_{\mathbb{R}^N} \nabla u_0\cdot\nabla w_+ \,{\rm d}x + C|u|_{\infty} \displaystyle\int_{\mathbb{R}^N} \Delta (e^{-\nu|x|}) w_+\,{\rm d}x.
\end{eqnarray*} Using the definition of w and that u 0 is a solution of ![]() $(P_{\beta,\infty})$, we obtain
$(P_{\beta,\infty})$, we obtain
 \begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x & = & \displaystyle\int_\Omega \left( \mu f(u_0) - V_\infty u_0 + (u_0)^{2^*-1} + C\|u_0\|_\infty \Delta ({\rm e}^{-\nu|x|}) \right)w\,{\rm d}x \\
& = & \displaystyle\int_\Omega \left[\left(\mu \dfrac{f(u_0)}{u_0} - V_\infty + (u_0)^{2^*-2}\right)u_0 \right. \\
& & \left. + \ C|u_0|_\infty\left( \nu^2-\dfrac{N-1}{|x|}\nu \right){\rm e}^{-\nu|x|} \right]w\,{\rm d}x \\
&\leq & \displaystyle\int_\Omega \left[\left(\mu \varepsilon + C_\varepsilon (u_0)^{p-2}- V_\infty + (u_0)^{2^*-2}\right)u_0 \right. \\
& & \left. + \ C|u_0|_\infty\left( \nu^2-\dfrac{N-1}{|x|}\nu \right){\rm e}^{-\nu|x|} \right]w\,{\rm d}x,
\end{eqnarray*}
\begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x & = & \displaystyle\int_\Omega \left( \mu f(u_0) - V_\infty u_0 + (u_0)^{2^*-1} + C\|u_0\|_\infty \Delta ({\rm e}^{-\nu|x|}) \right)w\,{\rm d}x \\
& = & \displaystyle\int_\Omega \left[\left(\mu \dfrac{f(u_0)}{u_0} - V_\infty + (u_0)^{2^*-2}\right)u_0 \right. \\
& & \left. + \ C|u_0|_\infty\left( \nu^2-\dfrac{N-1}{|x|}\nu \right){\rm e}^{-\nu|x|} \right]w\,{\rm d}x \\
&\leq & \displaystyle\int_\Omega \left[\left(\mu \varepsilon + C_\varepsilon (u_0)^{p-2}- V_\infty + (u_0)^{2^*-2}\right)u_0 \right. \\
& & \left. + \ C|u_0|_\infty\left( \nu^2-\dfrac{N-1}{|x|}\nu \right){\rm e}^{-\nu|x|} \right]w\,{\rm d}x,
\end{eqnarray*}where we used (1.2). Now, choosing ɛ > 0 such that ![]() $\mu\varepsilon+\nu^2-V_\infty \lt 0$, which implies in particular that
$\mu\varepsilon+\nu^2-V_\infty \lt 0$, which implies in particular that ![]() $\mu\varepsilon-V_\infty \lt 0$, we obtain from Lemma 6.9 that
$\mu\varepsilon-V_\infty \lt 0$, we obtain from Lemma 6.9 that
 \begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x & \leq & \displaystyle\int_\Omega \left[\left( {\mu\varepsilon-V_\infty} +\dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} + \dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}}\right)u_0 \right. \\
& & \left. + \ C|u_0|_\infty\left( \nu^2-\dfrac{N-1}{|x|}\nu \right)e^{-\nu|x|} \right]w\,{\rm d}x \\
\end{eqnarray*}
\begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x & \leq & \displaystyle\int_\Omega \left[\left( {\mu\varepsilon-V_\infty} +\dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} + \dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}}\right)u_0 \right. \\
& & \left. + \ C|u_0|_\infty\left( \nu^2-\dfrac{N-1}{|x|}\nu \right)e^{-\nu|x|} \right]w\,{\rm d}x \\
\end{eqnarray*}for some constants ![]() $c_1,c_2 \gt 0$ that do not depend on R > 0. We choose R > 0 sufficiently large such that, for
$c_1,c_2 \gt 0$ that do not depend on R > 0. We choose R > 0 sufficiently large such that, for ![]() $|x| \gt R$,
$|x| \gt R$,
 \begin{equation*}
\mu\varepsilon-V_\infty + \dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} +\dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}} \lt 0.
\end{equation*}
\begin{equation*}
\mu\varepsilon-V_\infty + \dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} +\dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}} \lt 0.
\end{equation*} Noting that ![]() $u_0(x) \gt C|u_0|_\infty {\rm e}^{-\nu|x|}$ in Ω, we get
$u_0(x) \gt C|u_0|_\infty {\rm e}^{-\nu|x|}$ in Ω, we get
 \begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x & \leq & \displaystyle\int_\Omega \left[\left(\mu\varepsilon-V_\infty + \dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} + \dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}}\right)C|u_0|_\infty {\rm e}^{-\nu|x|} \right. \\
& & \left. + \ \left( \nu^2-\dfrac{N-1}{|x|}\nu \right)C|u_0|_\infty {\rm e}^{-\nu|x|} \right]w\,{\rm d}x. \\
& \leq & \displaystyle\int_\Omega \left[\mu\varepsilon-V_\infty+\nu^2+\dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} +\dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}} \right]\\
& & \times C|u_0|_\infty {\rm e}^{-\nu|x|}w\,{\rm d}x.
\end{eqnarray*}
\begin{eqnarray*}
\displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x & \leq & \displaystyle\int_\Omega \left[\left(\mu\varepsilon-V_\infty + \dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} + \dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}}\right)C|u_0|_\infty {\rm e}^{-\nu|x|} \right. \\
& & \left. + \ \left( \nu^2-\dfrac{N-1}{|x|}\nu \right)C|u_0|_\infty {\rm e}^{-\nu|x|} \right]w\,{\rm d}x. \\
& \leq & \displaystyle\int_\Omega \left[\mu\varepsilon-V_\infty+\nu^2+\dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} +\dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}} \right]\\
& & \times C|u_0|_\infty {\rm e}^{-\nu|x|}w\,{\rm d}x.
\end{eqnarray*}If necessary, we take R > 0 even large so that
 \begin{equation*}
\mu\varepsilon-V_\infty+\nu^2+\dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} + \dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}} \lt 0,
\end{equation*}
\begin{equation*}
\mu\varepsilon-V_\infty+\nu^2+\dfrac{c_1}{|x|^{\frac{(N-1)(p-2)}{2}}} + \dfrac{c_2}{|x|^{\frac{(N-1)(2^*-2)}{2}}} \lt 0,
\end{equation*}what is possible in view of ![]() $\mu\varepsilon-V_\infty+\nu^2 \lt 0$. Then, we arrive at
$\mu\varepsilon-V_\infty+\nu^2 \lt 0$. Then, we arrive at
 \begin{eqnarray*}
0 \leq \displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x \lt 0,
\end{eqnarray*}
\begin{eqnarray*}
0 \leq \displaystyle\int_{\mathbb{R}^N} |\nabla w_+|^2\,{\rm d}x \lt 0,
\end{eqnarray*}an absurd. Thus, ![]() $\Omega=\emptyset$ and the proposition follows.
$\Omega=\emptyset$ and the proposition follows.
All this section proves the second and final part of Theorem 1.1.
7. Appendix B: A technical result
Lemma 7.1. Let ![]() $(u_n)\subset \mathcal{N}_\mu$ be a sequence satisfying
$(u_n)\subset \mathcal{N}_\mu$ be a sequence satisfying ![]() $u_n \rightharpoonup w_\infty$ in
$u_n \rightharpoonup w_\infty$ in ![]() $H^1(\mathbb{R}^N)$ for some
$H^1(\mathbb{R}^N)$ for some ![]() $w_\infty\in H^1(\mathbb{R}^N)$. Then, passing to a subsequence,
$w_\infty\in H^1(\mathbb{R}^N)$. Then, passing to a subsequence, ![]() $\nabla u_n \to \nabla w_\infty$ strongly in
$\nabla u_n \to \nabla w_\infty$ strongly in ![]() $[L^2_{\rm loc}(\mathbb{R}^N)]^N$ and
$[L^2_{\rm loc}(\mathbb{R}^N)]^N$ and ![]() $\nabla u_n(x)\to \nabla w_\infty(x)$ almost everywhere
$\nabla u_n(x)\to \nabla w_\infty(x)$ almost everywhere ![]() $x\in\mathbb{R}^N$.
$x\in\mathbb{R}^N$.
Proof. We will adapt some ideas found in [Reference Alves and Figueiredo1]. Since ![]() $u_n\rightharpoonup w_\infty$ in
$u_n\rightharpoonup w_\infty$ in ![]() $H^1(\mathbb{R}^N)$, then, up to a subsequence,
$H^1(\mathbb{R}^N)$, then, up to a subsequence,
 \begin{eqnarray}
\left\{\begin{array}{llllll}
u_n\rightarrow w_\infty \ \text{in}\ L^s_{\rm loc}(\mathbb{R}^N)\quad \text{for any}\ 1\leq s \lt 2^*,\\\\
u_n(x)\rightarrow w_\infty(x)\quad \text{for a.e}\ x\in\mathbb{R}^N.\\\\
\end{array}\right.
\end{eqnarray}
\begin{eqnarray}
\left\{\begin{array}{llllll}
u_n\rightarrow w_\infty \ \text{in}\ L^s_{\rm loc}(\mathbb{R}^N)\quad \text{for any}\ 1\leq s \lt 2^*,\\\\
u_n(x)\rightarrow w_\infty(x)\quad \text{for a.e}\ x\in\mathbb{R}^N.\\\\
\end{array}\right.
\end{eqnarray} Given any R > 0, let ![]() $\psi\in C_0^\infty (\mathbb{R}^N,[0,1])$ be such that
$\psi\in C_0^\infty (\mathbb{R}^N,[0,1])$ be such that ![]() $\psi\equiv 1$ in
$\psi\equiv 1$ in ![]() $B_R(0)$ and
$B_R(0)$ and ![]() $\psi\equiv 0$ in
$\psi\equiv 0$ in ![]() $\mathbb{R}^N\backslash B_{2R}(0)$. Then, by Cauchy–Schwarz inequality and the fact that
$\mathbb{R}^N\backslash B_{2R}(0)$. Then, by Cauchy–Schwarz inequality and the fact that  $\int_{\mathbb{R}^N} \psi \nabla w_\infty \nabla \left(u_n-w_\infty \right) \,{\rm d}x = o_n(1)$ (because of the weak convergence
$\int_{\mathbb{R}^N} \psi \nabla w_\infty \nabla \left(u_n-w_\infty \right) \,{\rm d}x = o_n(1)$ (because of the weak convergence ![]() $u_n \rightharpoonup w_\infty$), we have the following facts:
$u_n \rightharpoonup w_\infty$), we have the following facts:
 \begin{equation*}
\begin{array}{lllll}
\displaystyle\int_{\mathbb{R}^N} \nabla w_\infty \nabla \left(\left(u_n-w_\infty \right)\psi\right)\,{\rm d}x
&=&\displaystyle\int_{\mathbb{R}^N} \psi \nabla w_\infty \nabla \left(u_n-w_\infty \right)\,{|rm d}x\\
\\
&&+ \displaystyle\int_{\mathbb{R}^N} \left(u_n-w_\infty \right)\nabla w_\infty \nabla \psi\,{\rm d}x\\\\
&=& o_n(1),
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllll}
\displaystyle\int_{\mathbb{R}^N} \nabla w_\infty \nabla \left(\left(u_n-w_\infty \right)\psi\right)\,{\rm d}x
&=&\displaystyle\int_{\mathbb{R}^N} \psi \nabla w_\infty \nabla \left(u_n-w_\infty \right)\,{|rm d}x\\
\\
&&+ \displaystyle\int_{\mathbb{R}^N} \left(u_n-w_\infty \right)\nabla w_\infty \nabla \psi\,{\rm d}x\\\\
&=& o_n(1),
\end{array}
\end{equation*} \begin{equation*}
\displaystyle\int_{\mathbb{R}^N}\left(u_n-w_\infty\right) \nabla \left( u_n-w_\infty\right) \nabla \psi \,{\rm d}x =o_n(1),
\end{equation*}
\begin{equation*}
\displaystyle\int_{\mathbb{R}^N}\left(u_n-w_\infty\right) \nabla \left( u_n-w_\infty\right) \nabla \psi \,{\rm d}x =o_n(1),
\end{equation*} \begin{equation*}
\begin{array}{llllllllll}
\displaystyle\int_{\mathbb{R}^N} V_\infty u_n \left(u_n-w_\infty \right)\psi \,{\rm d}x=\displaystyle\int_{B_{2R}(0)} V_\infty u_n \left(u_n-w_\infty \right)\psi \,{\rm d}x=o_n(1)
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{llllllllll}
\displaystyle\int_{\mathbb{R}^N} V_\infty u_n \left(u_n-w_\infty \right)\psi \,{\rm d}x=\displaystyle\int_{B_{2R}(0)} V_\infty u_n \left(u_n-w_\infty \right)\psi \,{\rm d}x=o_n(1)
\end{array}
\end{equation*}and
 \begin{equation*}
\begin{array}{llllllllll}
\displaystyle\int_{\mathbb{R}^N}f(u_n)\left(w_\infty-u_n \right)\psi \,{\rm d}x=\displaystyle\int_{B_{2R}(0)} f(u_n)\left(w_\infty-u_n \right)\psi \,{\rm d}x=o_n(1),
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{llllllllll}
\displaystyle\int_{\mathbb{R}^N}f(u_n)\left(w_\infty-u_n \right)\psi \,{\rm d}x=\displaystyle\int_{B_{2R}(0)} f(u_n)\left(w_\infty-u_n \right)\psi \,{\rm d}x=o_n(1),
\end{array}
\end{equation*}where in the last convergence, we used the growth of f. Moreover, let ![]() $2^*-1 \lt s \lt 2^*$ and consider
$2^*-1 \lt s \lt 2^*$ and consider  $r=\dfrac{s}{2^*-1} \gt 1$. Then,
$r=\dfrac{s}{2^*-1} \gt 1$. Then,  $r^{\prime}:=\dfrac{r}{r-1}$ satisfies
$r^{\prime}:=\dfrac{r}{r-1}$ satisfies  $r^{\prime}=\dfrac{s}{s-2^*+1} \lt 2^*$. By Hölder inequality with exponents r and r ʹ, we get from (7.1) and from the boundedness of
$r^{\prime}=\dfrac{s}{s-2^*+1} \lt 2^*$. By Hölder inequality with exponents r and r ʹ, we get from (7.1) and from the boundedness of ![]() $(u_n)$ in
$(u_n)$ in ![]() $L^s(\mathbb{R}^N)$ that
$L^s(\mathbb{R}^N)$ that
 \begin{equation*}
\begin{array}{llllllllll}
\left|\displaystyle\int_{\mathbb{R}^N}|u_n|^{2^*-1}\left(u_n-w_\infty \right)\psi\,{\rm d}x\right|&=&\left|\displaystyle\int_{B_{2R}(0)}|u_n|^{2^*-1}\left(u_n-w_\infty \right)\psi \,{\rm d}x\right|\\\\
&\leq& \left[\displaystyle\int_{B_{2R}(0)}|u_n|^{r(2^*-1)} \,{\rm d}x\right]^{1/r}\\\\
&& \times\left[\displaystyle\int_{B_{2R}(0)}|u_n-w_\infty|^{r^{\prime}}|\psi|^{r^{\prime}} \,{\rm d}x\right]^{1/r^{\prime}} \\\\
& \leq & \left[\displaystyle\int_{B_{2R}(0)}|u_n|^{s} \,{\rm d}x\right]^{1/r}\left[\displaystyle\int_{B_{2R}(0)}|u_n-w_\infty|^{r^{\prime}}\,{\rm d}x\right]^{1/r^{\prime}} \\\\
&=& o_n(1).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{llllllllll}
\left|\displaystyle\int_{\mathbb{R}^N}|u_n|^{2^*-1}\left(u_n-w_\infty \right)\psi\,{\rm d}x\right|&=&\left|\displaystyle\int_{B_{2R}(0)}|u_n|^{2^*-1}\left(u_n-w_\infty \right)\psi \,{\rm d}x\right|\\\\
&\leq& \left[\displaystyle\int_{B_{2R}(0)}|u_n|^{r(2^*-1)} \,{\rm d}x\right]^{1/r}\\\\
&& \times\left[\displaystyle\int_{B_{2R}(0)}|u_n-w_\infty|^{r^{\prime}}|\psi|^{r^{\prime}} \,{\rm d}x\right]^{1/r^{\prime}} \\\\
& \leq & \left[\displaystyle\int_{B_{2R}(0)}|u_n|^{s} \,{\rm d}x\right]^{1/r}\left[\displaystyle\int_{B_{2R}(0)}|u_n-w_\infty|^{r^{\prime}}\,{\rm d}x\right]^{1/r^{\prime}} \\\\
&=& o_n(1).
\end{array}
\end{equation*} Therefore, remembering that ![]() $u_n\in \mathcal{N}_\mu$, one obtains
$u_n\in \mathcal{N}_\mu$, one obtains
 \begin{equation*}
\begin{array}{llllllllll}
o_n(1)&=&J_\mu^\prime(u_n)u_n\psi-J_\mu^\prime(u_n)w_\infty\psi-\displaystyle\int_{\mathbb{R}^N} \nabla w_\infty \nabla \left(\left(u_n-w_\infty \right)\psi\right) \,{\rm d}x\\\\
&=&\displaystyle\int_{\mathbb{R}^N} \nabla u_n \nabla \left(\left(u_n-w_\infty \right)\psi\right) \,{\rm d}x+\displaystyle\int_{\mathbb{R}^N} V_\infty u_n \left(u_n-w_\infty \right)\psi \,{\rm d}x\\\\
&&+\displaystyle\int_{\mathbb{R}^N}f(u_n)\left(w_\infty-u_n \right)\psi\, {\rm d}x+\displaystyle\int_{\mathbb{R}^N}|u_n|^{2^*-1}\left(w_\infty-u_n \right)\psi \,{\rm d}x\\
\\
&& -\displaystyle\int_{\mathbb{R}^N} \nabla w_\infty \nabla \left(\left(u_n-w_\infty \right)\psi\right) \,{\rm d}x\\
\\
&=& \displaystyle\int_{\mathbb{R}^N} \nabla \left( u_n-w_\infty\right) \nabla \left(\left(u_n-w_\infty \right)\psi\right) \,{\rm d}x +o_n(1)\\\\
&=& \displaystyle\int_{\mathbb{R}^N} \psi |\nabla \left( u_n-w_\infty\right)|^2 \,{\rm d}x + \displaystyle\int_{\mathbb{R}^N}\left(u_n-w_\infty\right) \nabla \left( u_n-w_\infty\right) \nabla \psi\, {\rm d}x +o_n(1)
\\
\\
&\geq &\displaystyle\int_{B_{R}(0)} |\nabla \left( u_n-w_\infty\right)|^2 \,{\rm d}x + o_n(1).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{llllllllll}
o_n(1)&=&J_\mu^\prime(u_n)u_n\psi-J_\mu^\prime(u_n)w_\infty\psi-\displaystyle\int_{\mathbb{R}^N} \nabla w_\infty \nabla \left(\left(u_n-w_\infty \right)\psi\right) \,{\rm d}x\\\\
&=&\displaystyle\int_{\mathbb{R}^N} \nabla u_n \nabla \left(\left(u_n-w_\infty \right)\psi\right) \,{\rm d}x+\displaystyle\int_{\mathbb{R}^N} V_\infty u_n \left(u_n-w_\infty \right)\psi \,{\rm d}x\\\\
&&+\displaystyle\int_{\mathbb{R}^N}f(u_n)\left(w_\infty-u_n \right)\psi\, {\rm d}x+\displaystyle\int_{\mathbb{R}^N}|u_n|^{2^*-1}\left(w_\infty-u_n \right)\psi \,{\rm d}x\\
\\
&& -\displaystyle\int_{\mathbb{R}^N} \nabla w_\infty \nabla \left(\left(u_n-w_\infty \right)\psi\right) \,{\rm d}x\\
\\
&=& \displaystyle\int_{\mathbb{R}^N} \nabla \left( u_n-w_\infty\right) \nabla \left(\left(u_n-w_\infty \right)\psi\right) \,{\rm d}x +o_n(1)\\\\
&=& \displaystyle\int_{\mathbb{R}^N} \psi |\nabla \left( u_n-w_\infty\right)|^2 \,{\rm d}x + \displaystyle\int_{\mathbb{R}^N}\left(u_n-w_\infty\right) \nabla \left( u_n-w_\infty\right) \nabla \psi\, {\rm d}x +o_n(1)
\\
\\
&\geq &\displaystyle\int_{B_{R}(0)} |\nabla \left( u_n-w_\infty\right)|^2 \,{\rm d}x + o_n(1).
\end{array}
\end{equation*} Since R > 0 is arbitrary, this implies that, passing to a subsequence, ![]() $\nabla u_n \to \nabla w_\infty$ in
$\nabla u_n \to \nabla w_\infty$ in ![]() $[L^2_{\rm loc}(\mathbb{R}^N)]^N$.
$[L^2_{\rm loc}(\mathbb{R}^N)]^N$.
To complete the proof of the lemma, let us show that ![]() $\nabla u_n(x)\to \nabla w_\infty(x)$ a.e.
$\nabla u_n(x)\to \nabla w_\infty(x)$ a.e. ![]() $x\in\mathbb{R}^N$ by using a diagonal process. Since
$x\in\mathbb{R}^N$ by using a diagonal process. Since ![]() $\nabla u_n \rightarrow \nabla w_\infty$ in
$\nabla u_n \rightarrow \nabla w_\infty$ in ![]() $[L^2(B_1(0))]^N$, there exists an infinite subset
$[L^2(B_1(0))]^N$, there exists an infinite subset ![]() $\mathbb{N}_1 \subset \mathbb{N}$ such that the subsequence
$\mathbb{N}_1 \subset \mathbb{N}$ such that the subsequence  $\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_1}$ converges to
$\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_1}$ converges to ![]() $\nabla w_\infty(x)$ a.e.
$\nabla w_\infty(x)$ a.e. ![]() $x\in B_1(0)$. Since
$x\in B_1(0)$. Since  $\left(\nabla u_n\right)_{n \in \mathbb{N}_1}$ converges to
$\left(\nabla u_n\right)_{n \in \mathbb{N}_1}$ converges to ![]() $\nabla w_\infty$ in
$\nabla w_\infty$ in ![]() $[L^2(B_2(0))]^N$, we obtain a subsequence
$[L^2(B_2(0))]^N$, we obtain a subsequence  $\left(\nabla u_n\right)_{n \in \mathbb{N}_2} \operatorname{with} \mathbb{N}_2 \subset \mathbb{N}_1$ such that
$\left(\nabla u_n\right)_{n \in \mathbb{N}_2} \operatorname{with} \mathbb{N}_2 \subset \mathbb{N}_1$ such that  $\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_2}$ converges to
$\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_2}$ converges to ![]() $\nabla w_\infty(x)$ a.e.
$\nabla w_\infty(x)$ a.e. ![]() $x\in B_2(0)$. Proceeding in this way, we find infinite subsets of indexes
$x\in B_2(0)$. Proceeding in this way, we find infinite subsets of indexes ![]() $\mathbb{N}_{k+1} \subset \mathbb{N}_k \subset \mathbb{N}$ such that
$\mathbb{N}_{k+1} \subset \mathbb{N}_k \subset \mathbb{N}$ such that  $\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_k}$ converges to
$\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_k}$ converges to ![]() $\nabla w_\infty(x)$ a.e.
$\nabla w_\infty(x)$ a.e. ![]() $x\in B_k(0)$. Consider
$x\in B_k(0)$. Consider ![]() $\mathbb{N}^*=\left\{n_1^*, n_2^*, \ldots, n_k^*, \ldots\right\} \subset \mathbb{N}$ with
$\mathbb{N}^*=\left\{n_1^*, n_2^*, \ldots, n_k^*, \ldots\right\} \subset \mathbb{N}$ with ![]() $n_k^*$ being the kth element of
$n_k^*$ being the kth element of ![]() $\mathbb{N}_k$. Therefore,
$\mathbb{N}_k$. Therefore, ![]() $\left(\nabla u_n(x)\right)_{n \in \mathbb{N} *}$ is, from its kth element, a subsequence of
$\left(\nabla u_n(x)\right)_{n \in \mathbb{N} *}$ is, from its kth element, a subsequence of  $\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_k}$ and hence converges to
$\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_k}$ and hence converges to ![]() $\nabla w_\infty(x)$ a.e.
$\nabla w_\infty(x)$ a.e. ![]() $x\in B_k(0)$. For each
$x\in B_k(0)$. For each ![]() $k \in \mathbb{N}$, there exists
$k \in \mathbb{N}$, there exists ![]() $Z_k \subset B_k(0)$ of zero measure such that
$Z_k \subset B_k(0)$ of zero measure such that  $\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_k}$ converges to
$\left(\nabla u_n(x)\right)_{n \in \mathbb{N}_k}$ converges to ![]() $\nabla w_\infty(x)$ for all
$\nabla w_\infty(x)$ for all ![]() $x \in B_k(0) \backslash Z_k$. Take
$x \in B_k(0) \backslash Z_k$. Take ![]() $Z:=\cup_{m=1}^{\infty} Z_m$. Then, Z has zero measure and, for all
$Z:=\cup_{m=1}^{\infty} Z_m$. Then, Z has zero measure and, for all ![]() $x \in \mathbb{R}^N \backslash Z$, we have
$x \in \mathbb{R}^N \backslash Z$, we have ![]() $x \in B_k(0) \backslash Z_k$ for some
$x \in B_k(0) \backslash Z_k$ for some ![]() $k \in \mathbb{N}$ and
$k \in \mathbb{N}$ and ![]() $\left(\nabla u_n(x)\right)_{n \in \mathbb{N}^*}$ converges to
$\left(\nabla u_n(x)\right)_{n \in \mathbb{N}^*}$ converges to ![]() $\nabla w_\infty(x)$. This shows that, up to a subsequence,
$\nabla w_\infty(x)$. This shows that, up to a subsequence, ![]() $\nabla u_n(x)\to\nabla w_\infty(x)$ a.e.
$\nabla u_n(x)\to\nabla w_\infty(x)$ a.e. ![]() $x\in \mathbb{R}^N$ and completes the proof.
$x\in \mathbb{R}^N$ and completes the proof.
Funding Statement
Gustavo S. A. Costa was supported by CNPq, Conselho Nacional de Desenvolvimento Científico e Tecnológico, Brazil (grant number 163054/2020-7). Giovany M. Figueiredo was supported by FAPDF – Demanda Espontânea 2021 and CNPq Produtividade 2019.