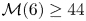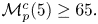1. Introduction
In the last century, Hilbert presented a list of problems that almost all of them are solved. One problem that remains open consists in determining the maximal number $\mathcal {H}(n)$![]() of limit cycles, and their relative positions, of planar polynomial vector fields of degree $n$
of limit cycles, and their relative positions, of planar polynomial vector fields of degree $n$![]() . This problem is known as the second part of the 16th Hilbert's problem. In the year of 1977, Arnol'd in [Reference Arnol'd4] proposed a weakened version, focused on the study of the number of limit cycles bifurcating from the period annulus of Hamiltonian systems.
. This problem is known as the second part of the 16th Hilbert's problem. In the year of 1977, Arnol'd in [Reference Arnol'd4] proposed a weakened version, focused on the study of the number of limit cycles bifurcating from the period annulus of Hamiltonian systems.
In this work, we are interested in another local version, that consists in providing the maximum number $\mathcal {M}(n)$![]() of small amplitude limit cycles bifurcating from an elementary centre or an elementary focus, clearly $\mathcal {M}(n)\leq \mathcal {H}(n).$
of small amplitude limit cycles bifurcating from an elementary centre or an elementary focus, clearly $\mathcal {M}(n)\leq \mathcal {H}(n).$![]() In other words, $\mathcal {M}(n)$
In other words, $\mathcal {M}(n)$![]() is an upper bound of the (local) cyclicity of such equilibrium points. For more details, see [Reference Roussarie49]. For $n=2$
is an upper bound of the (local) cyclicity of such equilibrium points. For more details, see [Reference Roussarie49]. For $n=2$![]() , Bautin proved that $\mathcal {M}(2) = 3,$
, Bautin proved that $\mathcal {M}(2) = 3,$![]() see [Reference Bautin5]. For $n=3$
see [Reference Bautin5]. For $n=3$![]() , the family of cubic systems without quadratic terms was studied in [Reference Blows and Lloyd7, Reference Sibirskiĭ51]. The proof of $\mathcal {M}_h(3)=5$
, the family of cubic systems without quadratic terms was studied in [Reference Blows and Lloyd7, Reference Sibirskiĭ51]. The proof of $\mathcal {M}_h(3)=5$![]() can be found in [Reference Żoła̧dek54]. Żoła̧dek in [Reference Żoła̧dek55] shows the first evidence that $\mathcal {M}(3)\ge 11.$
can be found in [Reference Żoła̧dek54]. Żoła̧dek in [Reference Żoła̧dek55] shows the first evidence that $\mathcal {M}(3)\ge 11.$![]() However, this problem has been recently revisited by himself in [Reference Żoła̧dek57]. The first proof of this fact was obtained some years later by Christopher in [Reference Christopher14], studying first-order perturbations of another cubic centre also provided by Żoła̧dek in [Reference Żoła̧dek56].
However, this problem has been recently revisited by himself in [Reference Żoła̧dek57]. The first proof of this fact was obtained some years later by Christopher in [Reference Christopher14], studying first-order perturbations of another cubic centre also provided by Żoła̧dek in [Reference Żoła̧dek56].
In 2012, Giné conjectures that $\mathcal {M}(n)= n^{2}+3n-7$![]() , see [Reference Giné25, Reference Giné26]. This suggests a higher value for $\mathcal {M}(n)$
, see [Reference Giné25, Reference Giné26]. This suggests a higher value for $\mathcal {M}(n)$![]() for polynomial vector fields of low degree. Gouveia and Torregrosa in [Reference Gouveia and Torregrosa30] show that $\mathcal {M}(5)\geq 33$
for polynomial vector fields of low degree. Gouveia and Torregrosa in [Reference Gouveia and Torregrosa30] show that $\mathcal {M}(5)\geq 33$![]() , $\mathcal {M}(7) \geq 61,$
, $\mathcal {M}(7) \geq 61,$![]() $\mathcal {M}(8) \geq 76,$
$\mathcal {M}(8) \geq 76,$![]() and $\mathcal {M}(9) \geq 88$
and $\mathcal {M}(9) \geq 88$![]() . The first evidence that this conjecture fails is given in [Reference Yu and Tian53]. Recently, a complete proof that $\mathcal {M}(3) \geq 12$
. The first evidence that this conjecture fails is given in [Reference Yu and Tian53]. Recently, a complete proof that $\mathcal {M}(3) \geq 12$![]() is provided by Giné, Gouveia, and Torregrosa in [Reference Giné, Gouveia and Torregrosa27]. Moreover, in the same paper, they show that $\mathcal {M}(4) \geq 21.$
is provided by Giné, Gouveia, and Torregrosa in [Reference Giné, Gouveia and Torregrosa27]. Moreover, in the same paper, they show that $\mathcal {M}(4) \geq 21.$![]() For $n=6$
For $n=6$![]() , the best lower bound was given in [Reference Liang and Torregrosa42], proving that $\mathcal {M}(6)\geq 40$
, the best lower bound was given in [Reference Liang and Torregrosa42], proving that $\mathcal {M}(6)\geq 40$![]() . The first main result of this paper updates this value.
. The first main result of this paper updates this value.
Theorem 1.1 The local cyclicity of monodromic equilibrium points for polynomial vector fields of degree $n=6$![]() is greater than or equal to $44$
is greater than or equal to $44$![]() . That is, $\mathcal {M}(6)\ge 44.$
. That is, $\mathcal {M}(6)\ge 44.$![]()
In this work, we are also interested in piecewise polynomial vector fields. Andronov, in [Reference Andronov, Vitt and Khaikin2] was the first to study such class of systems. In the last years, they have been widely studied, since many problems of engineering, physics, and biology can be modelled by them, see [Reference Acary, Bonnefon and Brogliato1, Reference di Bernardo, Budd, Champneys and Kowalczyk6]. One of the most studied situations in the plane is given by two vector fields defined in two half-planes separated by a straight line. As in the case of the classical qualitative theory of polynomial systems, the study of the number and location of the isolated periodic orbits, also called limit cycles, have received special attention, see for example [Reference Buzzi, Pessoa and Torregrosa11, Reference Coombes17, Reference Giannakopoulos and Pliete24, Reference Han and Zhang34, Reference Leine and van Campen41, Reference Llibre and Ponce43]. In particular, it can be seen as an extension of the 16th-Hilbert problem for planar piecewise polynomial vector fields, see [Reference Ilyashenko38].
Here, we study limit cycles bifurcating from the origin in the class of piecewise differential equations of the form
where $P^{\pm }(x,\,y,\,\lambda )$![]() and $Q^{\pm }(x,\,y,\,\lambda )$
and $Q^{\pm }(x,\,y,\,\lambda )$![]() are polynomials in $x$
are polynomials in $x$![]() and $y$
and $y$![]() . The straight line $\Sigma =\{y=0\}$
. The straight line $\Sigma =\{y=0\}$![]() divides the plane in two half-planes, $\Sigma ^{\pm }=\{(x,\,y) :\pm y>0\},$
divides the plane in two half-planes, $\Sigma ^{\pm }=\{(x,\,y) :\pm y>0\},$![]() and the trajectories on $\Sigma$
and the trajectories on $\Sigma$![]() are defined following the Filippov convention, see [Reference Filippov20]. Here we will consider only limit cycles of crossing type, that is, when both vector fields point out in the same direction on the separation line $\Sigma.$
are defined following the Filippov convention, see [Reference Filippov20]. Here we will consider only limit cycles of crossing type, that is, when both vector fields point out in the same direction on the separation line $\Sigma.$![]() Then, we denote by $\mathcal {H}^{c}_{p}(n)$
Then, we denote by $\mathcal {H}^{c}_{p}(n)$![]() the number of limit cycles of crossing type for piecewise polynomial vector fields of degree $n.$
the number of limit cycles of crossing type for piecewise polynomial vector fields of degree $n.$![]() Similarly, $\mathcal {M}_{p}^{c}(n)$
Similarly, $\mathcal {M}_{p}^{c}(n)$![]() counts the ones of small amplitude bifurcating from a monodromic equilibrium point. The upper index $c$
counts the ones of small amplitude bifurcating from a monodromic equilibrium point. The upper index $c$![]() means for crossing limit cycles and the subscript $p$
means for crossing limit cycles and the subscript $p$![]() for piecewise class. Clearly, $\mathcal {M}(n) \leq \mathcal {H}(n)$
for piecewise class. Clearly, $\mathcal {M}(n) \leq \mathcal {H}(n)$![]() and $\mathcal {M}_{p}^{c}(n) \leq \mathcal {H}_{p}^{c}(n).$
and $\mathcal {M}_{p}^{c}(n) \leq \mathcal {H}_{p}^{c}(n).$![]()
For $n=1$![]() , Huan and Yang in [Reference Huan and Yang37] show a numerical evidence that $\mathcal {H}^{c}_{p}(1) \geq 3.$
, Huan and Yang in [Reference Huan and Yang37] show a numerical evidence that $\mathcal {H}^{c}_{p}(1) \geq 3.$![]() Llibre and Ponce in [Reference Llibre and Ponce43] provide an analytical proof of this property. Using the averaging technique, this lower bound was reobtained by Buzzi, Pessoa, and Torregrosa in [Reference Buzzi, Pessoa and Torregrosa11]. Freire, Ponce, and Torres also obtained the same number in [Reference Freire, Ponce and Torres21]. In this last work, the three limit cycles are explained by studying the full return map, two appear near the origin and the other one far from it. But the three limit cycles appear nested and surrounding one sliding segment. In fact, the two limit cycles of small amplitude appearing from an equilibrium point provide the lower bound $\mathcal {M}^{c}_{p}(1) \geq 2.$
Llibre and Ponce in [Reference Llibre and Ponce43] provide an analytical proof of this property. Using the averaging technique, this lower bound was reobtained by Buzzi, Pessoa, and Torregrosa in [Reference Buzzi, Pessoa and Torregrosa11]. Freire, Ponce, and Torres also obtained the same number in [Reference Freire, Ponce and Torres21]. In this last work, the three limit cycles are explained by studying the full return map, two appear near the origin and the other one far from it. But the three limit cycles appear nested and surrounding one sliding segment. In fact, the two limit cycles of small amplitude appearing from an equilibrium point provide the lower bound $\mathcal {M}^{c}_{p}(1) \geq 2.$![]() This value can be proved with the results in [Reference Freire, Ponce and Torres21] and we will recall it in the next section. Recently in [Reference Freire, Ponce, Torregrosa and Torres23], the three limit cycles have been obtained near infinity in a Hopf type bifurcation.
This value can be proved with the results in [Reference Freire, Ponce and Torres21] and we will recall it in the next section. Recently in [Reference Freire, Ponce, Torregrosa and Torres23], the three limit cycles have been obtained near infinity in a Hopf type bifurcation.
For $n=2$![]() , using averaging theory of fifth-order, and perturbing the linear centre, Llibre and Tang in [Reference Llibre and Tang44] proved that $\mathcal {H}^{c}_{p}(2) \geq 8.$
, using averaging theory of fifth-order, and perturbing the linear centre, Llibre and Tang in [Reference Llibre and Tang44] proved that $\mathcal {H}^{c}_{p}(2) \geq 8.$![]() Recently, da Cruz, Novaes, and Torregrosa in [Reference da Cruz, Novaes and Torregrosa18] improve this lower bound and, using local developments of the difference map, Gouveia and Torregrosa in [Reference Gouveia and Torregrosa29] provide the first high lower bounds for piecewise polynomial classes of degrees three, four and five: $\mathcal {M}_{p}^{c}(3)\geq 26$
Recently, da Cruz, Novaes, and Torregrosa in [Reference da Cruz, Novaes and Torregrosa18] improve this lower bound and, using local developments of the difference map, Gouveia and Torregrosa in [Reference Gouveia and Torregrosa29] provide the first high lower bounds for piecewise polynomial classes of degrees three, four and five: $\mathcal {M}_{p}^{c}(3)\geq 26$![]() , $\mathcal {M}_{p}^{c}(4)\geq 40$
, $\mathcal {M}_{p}^{c}(4)\geq 40$![]() , and $\mathcal {M}_{p}^{c}(5)\geq 58.$
, and $\mathcal {M}_{p}^{c}(5)\geq 58.$![]() Here we update two of these lower bounds using averaging theory in our second main result.
Here we update two of these lower bounds using averaging theory in our second main result.
Theorem 1.2 The local cyclicity for piecewise polynomial vector fields of degree four and five is $\mathcal {M}^{c}_{p}(4) \geq 43$![]() and $\mathcal {M}^{c}_{p}(5) \geq 65,$
and $\mathcal {M}^{c}_{p}(5) \geq 65,$![]() respectively.
respectively.
In this paper, we are interesting also in differential equations containing a privileged $\varepsilon$![]() that acts as a small perturbation of a periodic behaviour. Lagrange, in his study about the three-body problem, formulated the idea of averaging. During some years, this method was used in many fields without people bothering about proofs validity. In 1928, Fatou in [Reference Fatou19] gave the first analytic proof. Nowadays, in planar differential systems, the averaging theory is also used for proving the existence of limit cycles which appear, after perturbation, from a fully periodic neighbourhood. A similar mechanism, when the differential equation is nonautonomous, used for the same purpose is the Melnikov method. Moreover, it is an excellent tool for studying global bifurcations that occur near homoclinic or heteroclinic loops in one-parameter families.
that acts as a small perturbation of a periodic behaviour. Lagrange, in his study about the three-body problem, formulated the idea of averaging. During some years, this method was used in many fields without people bothering about proofs validity. In 1928, Fatou in [Reference Fatou19] gave the first analytic proof. Nowadays, in planar differential systems, the averaging theory is also used for proving the existence of limit cycles which appear, after perturbation, from a fully periodic neighbourhood. A similar mechanism, when the differential equation is nonautonomous, used for the same purpose is the Melnikov method. Moreover, it is an excellent tool for studying global bifurcations that occur near homoclinic or heteroclinic loops in one-parameter families.
Let us consider the perturbation of a Hamiltonian system

Then, the first Melnikov function writes as
where $\Gamma _h=\{H(x,\,y)=h^{2}\}$![]() are closed ovals. This first-order analysis is based on the Implicit Function Theorem. In fact, for $\varepsilon$
are closed ovals. This first-order analysis is based on the Implicit Function Theorem. In fact, for $\varepsilon$![]() small enough, the simple zeros of $M(h)$
small enough, the simple zeros of $M(h)$![]() correspond to limit cycles of the perturbed system (1). That is, if $h^{*}$
correspond to limit cycles of the perturbed system (1). That is, if $h^{*}$![]() satisfies that $M(h^{*})=0$
satisfies that $M(h^{*})=0$![]() and $M'(h^{*})\ne 0$
and $M'(h^{*})\ne 0$![]() then, there exists an hyperbolic limit cycle of (1) that goes to $\Gamma _{h^{*}}$
then, there exists an hyperbolic limit cycle of (1) that goes to $\Gamma _{h^{*}}$![]() when $h$
when $h$![]() goes to $h^{*}.$
goes to $h^{*}.$![]()
This result can be generalized also for the perturbation of centres, $(\dot x,\,\dot y)=(P_c,\,Q_c)$![]() , having an inverse integrating factor $V(x,\,y)$
, having an inverse integrating factor $V(x,\,y)$![]() . Then after a time rescaling the perturbed system
. Then after a time rescaling the perturbed system

can be written as

So, the corresponding generalized first Melnikov function of (4), or also of (3), is
In this paper, we only consider the above Melnikov function for the study of perturbations of periodic orbits near planar autonomous differential systems. In this case, there are some works explaining the equivalence between Melnikov studies and the averaging theory, see [Reference Buică9, Reference Han, Romanovski and Zhang35]. For more details in this theory, we refer the reader to [Reference Buică and Llibre10, Reference Han and Yu33, Reference Sanders and Verhulst50, Reference Verhulst52].
This bifurcation mechanism can be used also in piecewise differential equations, see [Reference Llibre, Novaes and Teixeira45–Reference Llibre, Mereu and Novaes47]. Although this problem can be treated in a more general way, in this work, we will consider a simplified version of it. We will study that only the perturbation in (3) is defined by piecewise functions. This perturbation will be defined in two zones separated by a straight line, that is, the differential equation to consider can be written as

Therefore, the piecewise generalized first Melnikov function of (6) is
where

with $\Gamma _h^{\pm }=\Gamma _h \cap \{\pm y>0\}(x_0,0)\Gamma_hy=0x_0>0.\Gamma _h^{\pm }=\Gamma _h \cap \{\pm y>0\}(x_0,0)\Gamma_hy=0x_0>0.$![]() $\Gamma _h^{\pm }=\Gamma _h \cap \{\pm y>0\}(x_0,0)\Gamma_hy=0x_0\,{>}\,0.\Gamma _h^{\pm }=\Gamma _h \cap \{\pm y>0\}(x_0,0)\Gamma_hy=0x_0\,{>}\,0.$
$\Gamma _h^{\pm }=\Gamma _h \cap \{\pm y>0\}(x_0,0)\Gamma_hy=0x_0\,{>}\,0.\Gamma _h^{\pm }=\Gamma _h \cap \{\pm y>0\}(x_0,0)\Gamma_hy=0x_0\,{>}\,0.$![]() $\Gamma _h^{\pm } =\Gamma _h \cap \{\pm y>0\}(x_0,0)\Gamma_hy=0x_0>0.$
$\Gamma _h^{\pm } =\Gamma _h \cap \{\pm y>0\}(x_0,0)\Gamma_hy=0x_0>0.$![]() Clearly, in both piecewise regions, we have the same centre having $V(x,\,y)$
Clearly, in both piecewise regions, we have the same centre having $V(x,\,y)$![]() as an inverse integrating factor. The main results of this work could be extended to perturbing piecewise centres but this is not the aim of this paper.
as an inverse integrating factor. The main results of this work could be extended to perturbing piecewise centres but this is not the aim of this paper.
From the mechanism described above, the functions (2), (5), and (7) provide the number of limit cycles bifurcating from the period annulus up to first-order analysis. Another tool for obtaining limit cycles bifurcating from the origin comes from the study of the Taylor development of the return map, the so-called Lyapunov constants. In this context, the perturbation terms of the non-degenerate linear centre, $(\dot x,\,\dot y)=(-y,\,x)$![]() , usually have degree at least two because in this case, the Lyapunov constants are polynomials in the perturbation parameters, [Reference Cima, Gasull, Mañosa and Mañosas15]. Another small limit cycle bifurcates from the origin using the classical Hopf bifurcation when the linear coefficients are added in the perturbation terms and the trace parameter change sign adequately. This bifurcation phenomenon is also known as the degenerated Hopf bifurcation. More details on it can be seen in [Reference Andronov, Leontovich, Gordon and Maĭer3]. In piecewise differential equations, a similar bifurcation can also be introduced, but adding two limit cycles instead of only one. The linear terms are responsible for one of them and the other is due to the existence of what is known as the sliding segment that appears when the constant terms are added. The latter is known as the pseudo-Hopf bifurcation and they are summarized in the next result.
, usually have degree at least two because in this case, the Lyapunov constants are polynomials in the perturbation parameters, [Reference Cima, Gasull, Mañosa and Mañosas15]. Another small limit cycle bifurcates from the origin using the classical Hopf bifurcation when the linear coefficients are added in the perturbation terms and the trace parameter change sign adequately. This bifurcation phenomenon is also known as the degenerated Hopf bifurcation. More details on it can be seen in [Reference Andronov, Leontovich, Gordon and Maĭer3]. In piecewise differential equations, a similar bifurcation can also be introduced, but adding two limit cycles instead of only one. The linear terms are responsible for one of them and the other is due to the existence of what is known as the sliding segment that appears when the constant terms are added. The latter is known as the pseudo-Hopf bifurcation and they are summarized in the next result.
Proposition 1.3 Gouveia and Torregrosa [Reference Gouveia and Torregrosa28]
Consider the perturbed system

for $y\ge 0$![]() and $y<0$
and $y<0$![]() , respectively. If $a^{+}_{11}-a^{-}_{11}+2b^{+}_{02}-2b^{-}_{02}+b^{+}_{20}-b^{-}_{20}\ne 0$
, respectively. If $a^{+}_{11}-a^{-}_{11}+2b^{+}_{02}-2b^{-}_{02}+b^{+}_{20}-b^{-}_{20}\ne 0$![]() then there exist $c$
then there exist $c$![]() and $d$
and $d$![]() small enough such that two crossing limit cycles of small amplitude bifurcate from the origin.
small enough such that two crossing limit cycles of small amplitude bifurcate from the origin.
We notice that when $c=d=0,$![]() the expression $a^{+}_{11}-a^{-}_{11}+2b^{+}_{02}-2b^{-}_{02}+b^{+}_{20}-b^{-}_{20}$
the expression $a^{+}_{11}-a^{-}_{11}+2b^{+}_{02}-2b^{-}_{02}+b^{+}_{20}-b^{-}_{20}$![]() defines the stability of the origin. So, we could define it as the first Lyapunov constant for the piecewise perturbation of the linear centre. More details on the pseudo-Hopf bifurcation are collected in [Reference Castillo, Llibre and Verduzco12, Reference Freire, Ponce and Torres21, Reference Freire, Ponce and Torres22]. In [Reference Christopher14, Reference Giné, Gouveia and Torregrosa27, Reference Gouveia and Torregrosa29, Reference Gouveia and Torregrosa30], we can see that a good and simple tool for studying the number of limit cycles of small amplitude bifurcating from the origin is the first-order development of the Lyapunov constants. We notice that, in this case, the Jacobian matrix of the vector field at the origin must be of non-degenerate monodromic type.
defines the stability of the origin. So, we could define it as the first Lyapunov constant for the piecewise perturbation of the linear centre. More details on the pseudo-Hopf bifurcation are collected in [Reference Castillo, Llibre and Verduzco12, Reference Freire, Ponce and Torres21, Reference Freire, Ponce and Torres22]. In [Reference Christopher14, Reference Giné, Gouveia and Torregrosa27, Reference Gouveia and Torregrosa29, Reference Gouveia and Torregrosa30], we can see that a good and simple tool for studying the number of limit cycles of small amplitude bifurcating from the origin is the first-order development of the Lyapunov constants. We notice that, in this case, the Jacobian matrix of the vector field at the origin must be of non-degenerate monodromic type.
Then, a natural question arises. Are there any relation between both mechanisms? Chicone and Jacobs in 1991 provided a positive answer for quadratic families of vector fields, see [Reference Chicone and Jacobs13]. But, their proof is also valid for polynomial vector fields of any degree. Hence, we can say that the next result comes from their original work. These ideas appear also in the works of Han and Yu, see [Reference Han and Yu33, Reference Han, Sheng and Zhang36], where the Melnikov function in the Hopf bifurcation is studied.
Theorem 1.4 Chicone and Jacobs [Reference Chicone and Jacobs13]
Let $(\dot x,\,\dot y)=(P_c(x,\,y),\,Q_c(x,\,y))$![]() be a polynomial vector field of degree $n,$
be a polynomial vector field of degree $n,$![]() with a non degenerated centre at the origin. Consider the perturbed systems, in the class of polynomial vector fields of degree $n,$
with a non degenerated centre at the origin. Consider the perturbed systems, in the class of polynomial vector fields of degree $n,$![]()

and

If we denote by $L_k^{[1]}$![]() the first-order expansion, with respect to the parameters $a_{kl},\, b_{kl}$
the first-order expansion, with respect to the parameters $a_{kl},\, b_{kl}$![]() , for the Taylor series of the Lyapunov constant $L_k$
, for the Taylor series of the Lyapunov constant $L_k$![]() associated with (8) then, for $\rho$
associated with (8) then, for $\rho$![]() small, the first Melnikov function of (9) is
small, the first Melnikov function of (9) is

with the Bautin ideal $\langle L_1,\,\ldots,\,L_N,\,\ldots \rangle =\langle L_1,\,\ldots,\,L_N \rangle.$![]()
We remark that the perturbations in the above result are taken without linear terms. This restriction is due to the fact that the elements in the Bautin ideal should be polynomials. A direct consequence is the first part of the next corollary. For the second part, the classical Hopf bifurcation is necessarily to be used. As usual, $O(\varepsilon ^{2})$![]() denotes the terms of degree at least $2$
denotes the terms of degree at least $2$![]() in the perturbative parameter $\varepsilon$
in the perturbative parameter $\varepsilon$![]() .
.
Corollary 1.5 Let $A_m$![]() be the matrix corresponding to $(L^{[1]}_{1},\,\ldots,\,L^{[1]}_{m})$
be the matrix corresponding to $(L^{[1]}_{1},\,\ldots,\,L^{[1]}_{m})$![]() with respect to the parameters $(a_{20},\,a_{11},\,a_{02},\,\ldots,\,b_{20},\,b_{11},\,b_{02},\,\ldots )\in \mathbb {R}^{n^{2}+3n-4},$
with respect to the parameters $(a_{20},\,a_{11},\,a_{02},\,\ldots,\,b_{20},\,b_{11},\,b_{02},\,\ldots )\in \mathbb {R}^{n^{2}+3n-4},$![]() where each $L^{[1]}_{k}$
where each $L^{[1]}_{k}$![]() is the linear $k$
is the linear $k$![]() -Lyapunov constant of system (8) and $m\leq N$
-Lyapunov constant of system (8) and $m\leq N$![]() . Then, if $\operatorname {rank} A_m=\ell$
. Then, if $\operatorname {rank} A_m=\ell$![]() and for $\varepsilon$
and for $\varepsilon$![]() small enough, system (9) has $\ell -1$
small enough, system (9) has $\ell -1$![]() hyperbolic limit cycles of small amplitude bifurcating from the origin. Additionally, adding the trace parameter, there are polynomial perturbations of the centre $(\dot x,\,\dot y)=(P_c(x,\,y),\,Q_c(x,\,y)),$
hyperbolic limit cycles of small amplitude bifurcating from the origin. Additionally, adding the trace parameter, there are polynomial perturbations of the centre $(\dot x,\,\dot y)=(P_c(x,\,y),\,Q_c(x,\,y)),$![]() exhibiting $\ell$
exhibiting $\ell$![]() hyperbolic limit cycles of small amplitude in a small enough neighbourhood of the origin.
hyperbolic limit cycles of small amplitude in a small enough neighbourhood of the origin.
Recently, see [Reference Giné, Gouveia and Torregrosa27, Reference Gouveia and Torregrosa29, Reference Gouveia and Torregrosa30], a detailed study of the return map of a differential equation near a non-degenerated monodromic point located at the origin has been done. The authors focus their attention not only on first-order Taylor developments, with respect to parameters, of the coefficients of the return map with respect to the initial condition. These papers are a continuation of the work given by Christopher in [Reference Christopher14]. The degenerated Hopf bifurcation technique applies when $L_k^{[1]}=u_k$![]() for $k=1,\,\ldots,\,N,$
for $k=1,\,\ldots,\,N,$![]() and all $u_k$
and all $u_k$![]() are new independent parameters. Then, the existence of $N$
are new independent parameters. Then, the existence of $N$![]() limit cycles of small amplitude bifurcating from the origin is guaranteed. This approach fails when the rank does not increase in each step. That is when at least one $L_k^{[1]}$
limit cycles of small amplitude bifurcating from the origin is guaranteed. This approach fails when the rank does not increase in each step. That is when at least one $L_k^{[1]}$![]() is a linear combination of the previous ones. The main advantage of Theorem 1.4 is that we can compute easier the expressions of $L_k^{[1]}$
is a linear combination of the previous ones. The main advantage of Theorem 1.4 is that we can compute easier the expressions of $L_k^{[1]}$![]() than the coefficients of the series expansion of $M.$
than the coefficients of the series expansion of $M.$![]() In [Reference Han and Yang32], the study of the multiplicity of zeros is also taken into account and moreover it provides upper bounds for the number of limit cycles up to this perturbation order.
In [Reference Han and Yang32], the study of the multiplicity of zeros is also taken into account and moreover it provides upper bounds for the number of limit cycles up to this perturbation order.
This paper is structured as follows. In § 2, for completeness, we prove Theorem 1.1 recovering the original proof for quadratic vector fields obtained in [Reference Chicone and Jacobs13]. As a natural application of it, we also prove Corollary 1.5. Then, we can get limit cycles of small amplitude bifurcating from a centre equilibrium point. Finally, we extend Theorem 1.4 and Corollary 1.5 to the class of piecewise polynomial vector fields. In § 3, we show, with a simple example of a polynomial vector field of degree $6$![]() , that the maximal computed rank of the linear developments does not coincide with the subscript of the corresponding Lyapunov constant. Then, the result using only linear parts given by Christopher in [Reference Christopher14] does not apply. But using Theorem 1.4, we provide more limit cycles of small amplitude. In § 4, we prove our first main result, Theorem 1.1, and we study the local cyclicity problem for some vector fields of degrees $7$
, that the maximal computed rank of the linear developments does not coincide with the subscript of the corresponding Lyapunov constant. Then, the result using only linear parts given by Christopher in [Reference Christopher14] does not apply. But using Theorem 1.4, we provide more limit cycles of small amplitude. In § 4, we prove our first main result, Theorem 1.1, and we study the local cyclicity problem for some vector fields of degrees $7$![]() , $8$
, $8$![]() , and $10,$
, and $10,$![]() proving that $\mathcal {M}(7)\geq 60$
proving that $\mathcal {M}(7)\geq 60$![]() , $\mathcal {M}(8)\geq 70$
, $\mathcal {M}(8)\geq 70$![]() , and $\mathcal {M}(10)\geq 97.$
, and $\mathcal {M}(10)\geq 97.$![]() Finally, § 5 is devoted to piecewise polynomial vector fields of degrees $3,\,4,$
Finally, § 5 is devoted to piecewise polynomial vector fields of degrees $3,\,4,$![]() and $5$
and $5$![]() , proving our second main result Theorem 1.2. We also provide a new proof of $\mathcal {M}_p^{c}(3)\ge 26,$
, proving our second main result Theorem 1.2. We also provide a new proof of $\mathcal {M}_p^{c}(3)\ge 26,$![]() different from the one published in [Reference Gouveia and Torregrosa29], using now only first-order developments.
different from the one published in [Reference Gouveia and Torregrosa29], using now only first-order developments.
2. The proof of Chicone–Jacobs’ result
This section is devoted to the proof of Theorem 1.4 and Corollary 1.5. The proof of Theorem 1.4 for quadratic vector fields can be found in [Reference Chicone and Jacobs13]. You can see it partially also in [Reference Perko48]. Here we reproduce it but extended for every polynomial vector field of degree $n.$![]()
Proof of Theorem 1.4. Proof of Theorem 1.4
To simplify notation, we rewrite the perturbed parameters in (8) and (9) as
After a linear change if necessary, Equations (8) and (9), in the usual polar coordinates, write as
where $R_i$![]() and $\Theta _i$
and $\Theta _i$![]() are homogeneous trigonometric polynomials in $\sin \theta,\,\cos \theta$
are homogeneous trigonometric polynomials in $\sin \theta,\,\cos \theta$![]() of degree $i.$
of degree $i.$![]() We define $r(\theta ;\rho )$
We define $r(\theta ;\rho )$![]() the solution of the initial value problem defined by (11) with initial condition $r(0;\rho )=\rho.$
the solution of the initial value problem defined by (11) with initial condition $r(0;\rho )=\rho.$![]() Then, from the first return map $r(2\pi ;\rho ),$
Then, from the first return map $r(2\pi ;\rho ),$![]() we can define the displacement function associated with (11) as
we can define the displacement function associated with (11) as
Clearly, the zeros of this function provide periodic orbits of the corresponding system in Cartesian coordinates.
The Taylor series in $\rho$![]() of the displacement function $\Delta _1$
of the displacement function $\Delta _1$![]() associated with (8) is
associated with (8) is

with $\beta _{kj}$![]() polynomials vanishing at zero. Similarly, the Taylor series in $\varepsilon$
polynomials vanishing at zero. Similarly, the Taylor series in $\varepsilon$![]() of the displacement function $\Delta _2$
of the displacement function $\Delta _2$![]() associated with (9) is
associated with (9) is

We notice that both Taylor series representation are only local, but with the Global Bifurcation Lemma, see [Reference Chicone and Jacobs13], the coefficients $d_{k}(\rho )$![]() are defined and being analytic on the $\rho$
are defined and being analytic on the $\rho$![]() -domain corresponding to the portion of the $x-$
-domain corresponding to the portion of the $x-$![]() axis cut by the periodic trajectories surrounding the centre at the origin of the system. We observe that the idea of Melnikov theory is determining $d_{k}(\rho )$
axis cut by the periodic trajectories surrounding the centre at the origin of the system. We observe that the idea of Melnikov theory is determining $d_{k}(\rho )$![]() under the condition $d_{j}(\rho )=0$
under the condition $d_{j}(\rho )=0$![]() for all $j< k$
for all $j< k$![]() .
.
Writing the parameters $\lambda$![]() as their Taylor series expansion in terms of a privileged parameter $\varepsilon,$
as their Taylor series expansion in terms of a privileged parameter $\varepsilon,$![]() $\lambda _l(\varepsilon )= \sum \nolimits _{j=1}^{\infty }\lambda _{jl}\varepsilon ^{j},\,$
$\lambda _l(\varepsilon )= \sum \nolimits _{j=1}^{\infty }\lambda _{jl}\varepsilon ^{j},\,$![]() in (12), we have for each $k$
in (12), we have for each $k$![]() and $i$
and $i$![]() ,
,

Rearranging the Taylor series (12), for $\varepsilon$![]() and $\rho$
and $\rho$![]() small enough, it follows that
small enough, it follows that

As the first-orders in $\varepsilon$![]() of Equation (8), changing $\lambda$
of Equation (8), changing $\lambda$![]() by $\varepsilon \lambda,$
by $\varepsilon \lambda,$![]() and Equation (9) coincide, the coefficients of degree one in $\varepsilon$
and Equation (9) coincide, the coefficients of degree one in $\varepsilon$![]() for (14) and (13) are equal. So,
for (14) and (13) are equal. So,

It is well known that in the above expression the odd exponents in $\rho$![]() corresponds to the property that the first non vanishing Lyapunov constant has always an odd index, see [Reference Andronov, Leontovich, Gordon and Maĭer3]. For a proof that the Lyapunov constants of even indices are in the ideal of the odd ones, we refer the reader to [Reference Cima, Gasull and Mañosas16, Reference Han31]. Applying the ideas in [Reference Chicone and Jacobs13, Sect. 4] to differential system (4), we can write
corresponds to the property that the first non vanishing Lyapunov constant has always an odd index, see [Reference Andronov, Leontovich, Gordon and Maĭer3]. For a proof that the Lyapunov constants of even indices are in the ideal of the odd ones, we refer the reader to [Reference Cima, Gasull and Mañosas16, Reference Han31]. Applying the ideas in [Reference Chicone and Jacobs13, Sect. 4] to differential system (4), we can write
where the function $M$![]() is defined in (5).
is defined in (5).
The statement follows because, in our case, $H(x,\,y)=(x^{2}+y^{2})/2+\cdots$![]() .
.
Proof of Corollary 1.5. Proof of Corollary 1.5
We study first the case when the trace parameter is zero. In this case, it is well known that the Lyapunov constants are polynomials in the perturbation parameters, see [Reference Cima, Gasull, Mañosa and Mañosas15]. Then we can compute the linear terms of the Lyapunov constants with, for example, the classical mechanism described in [Reference Liang and Torregrosa42]. Consequently, Theorem 1.4 gets the expression of the first Melnikov function (10). Hence, if the rank of the computed expressions is $\ell$![]() , we have $\ell -1$
, we have $\ell -1$![]() simple zeros near $\rho =0$
simple zeros near $\rho =0$![]() and there exists a perturbed system exhibiting $\ell -1$
and there exists a perturbed system exhibiting $\ell -1$![]() limit cycles of small amplitude. Finally, adding the trace parameter as in the classical Hopf bifurcation (see [Reference Kuznetsov40]), we get the total $\ell$
limit cycles of small amplitude. Finally, adding the trace parameter as in the classical Hopf bifurcation (see [Reference Kuznetsov40]), we get the total $\ell$![]() limit cycles as it is stated in the statement.
limit cycles as it is stated in the statement.
We notice that the above two results can be easily generalized for piecewise vector fields. Let us consider the piecewise version of the perturbed differential systems (8) and (9) given by

and

They are defined for the parameters $a^{+}_{kl},\,b^{+}_{kl}$![]() and $a^{-}_{kl},\,b^{-}_{kl},$
and $a^{-}_{kl},\,b^{-}_{kl},$![]() in the regions $y\ge 0$
in the regions $y\ge 0$![]() and $y<0,$
and $y<0,$![]() respectively. Here, as previously, the unperturbed system $(\dot x,\, \dot y)=(P_c(x,\,y),\,Q_c(x,\,y))$
respectively. Here, as previously, the unperturbed system $(\dot x,\, \dot y)=(P_c(x,\,y),\,Q_c(x,\,y))$![]() has a non-degenerated centre at the origin.
has a non-degenerated centre at the origin.
The next corollary provides the piecewise extension of Theorem 1.4. So, its proof follows closely to the proof of Theorem 1.4. In this case, the return map is also analytic in $\rho$![]() and all the steps are similar. The main difference is that the Taylor series of $d_1$
and all the steps are similar. The main difference is that the Taylor series of $d_1$![]() in $\rho$
in $\rho$![]() have all powers starting in 2, because now we have not the property of symmetry that vanishes all the even terms in the developments. We remark that the perturbation in (16) has no constant nor linear terms.
have all powers starting in 2, because now we have not the property of symmetry that vanishes all the even terms in the developments. We remark that the perturbation in (16) has no constant nor linear terms.
Corollary 2.1 Let $L_k^{[1]}$![]() be the linear terms of the Lyapunov constants of a polynomial piecewise vector field (15) near a monodromic equilibrium point. Then the corresponding first Melnikov function (5) of (16) writes as
be the linear terms of the Lyapunov constants of a polynomial piecewise vector field (15) near a monodromic equilibrium point. Then the corresponding first Melnikov function (5) of (16) writes as

being the Bautin ideal $\langle L_2,\,\ldots,\,L_N,\,\ldots \rangle =\langle L_2,\,\ldots,\,L_N \rangle.$![]()
Finally, similarly as for analytic perturbations here also the rank of the matrix provides a lower bound for the number of limit cycles bifurcating from a monodromic equilibrium point. But, using piecewise perturbations, we have two extra limit cycles of small amplitude as we have shown in Proposition 1.3. Then we have at least as many limit cycles as the number of linearly independent linear parts plus one.
Corollary 2.2 Let $A_m$![]() be the matrix corresponding to $(L^{[1]}_{2},\,\ldots,\,L^{[1]}_{m})$
be the matrix corresponding to $(L^{[1]}_{2},\,\ldots,\,L^{[1]}_{m})$![]() with respect to the parameters $(a_{20}^{\pm },\,a_{11}^{\pm },\,a_{02}^{\pm },\,\ldots,\,b_{20}^{\pm },\,b_{11}^{\pm },\,b_{02}^{\pm },\,\ldots )\in \mathbb {R}^{2n^{2}+6n-8},$
with respect to the parameters $(a_{20}^{\pm },\,a_{11}^{\pm },\,a_{02}^{\pm },\,\ldots,\,b_{20}^{\pm },\,b_{11}^{\pm },\,b_{02}^{\pm },\,\ldots )\in \mathbb {R}^{2n^{2}+6n-8},$![]() where each $L^{[1]}_{k}$
where each $L^{[1]}_{k}$![]() is the linear part of the $k$
is the linear part of the $k$![]() -Lyapunov constant of system (15). Then, if $\operatorname {rank} A_{m}=\ell,$
-Lyapunov constant of system (15). Then, if $\operatorname {rank} A_{m}=\ell,$![]() for $\varepsilon$
for $\varepsilon$![]() small enough, there exist perturbation parameters, $(a^{\pm },\,b^{\pm }),$
small enough, there exist perturbation parameters, $(a^{\pm },\,b^{\pm }),$![]() such that system (16) has $\ell -1$
such that system (16) has $\ell -1$![]() limit cycles of small amplitude bifurcating from the origin. Additionally, adding the trace parameter, there are piecewise polynomial perturbations of $(\dot x,\,\dot y)=(P_c(x,\,y),\,Q_c(x,\,y))$
limit cycles of small amplitude bifurcating from the origin. Additionally, adding the trace parameter, there are piecewise polynomial perturbations of $(\dot x,\,\dot y)=(P_c(x,\,y),\,Q_c(x,\,y))$![]() exhibiting $\ell +1$
exhibiting $\ell +1$![]() hyperbolic limit cycles of small amplitude in a small enough neighbourhood of the origin.
hyperbolic limit cycles of small amplitude in a small enough neighbourhood of the origin.
We remark that the definition of the matrix $A_m$![]() for Corollaries 1.5 and 2.2 does not coincide, because of the different definitions of the subscripts in the nonvanishing coefficients of the respectively Taylor developments in $\rho$
for Corollaries 1.5 and 2.2 does not coincide, because of the different definitions of the subscripts in the nonvanishing coefficients of the respectively Taylor developments in $\rho$![]() . But the important property for the number of the limit cycles of small amplitude is which is the value of its rank.
. But the important property for the number of the limit cycles of small amplitude is which is the value of its rank.
3. A first but not trivial example
In this section, we show the explicit linear developments of the Lyapunov constants in a simple example provided by [Reference Itikawa, Llibre and Oliveira39]. In the proof of the next result, we can see how Corollary 1.5 is better than the direct use of the Lyapunov constants. We remark that, most probably, the number of limit cycles presented will be the maximum using only first-order analysis. We have chosen a vector field of a high degree to see better the effectiveness of our results.
Proposition 3.1 Let us consider the system
Then, there exist polynomial perturbations of degree $6$![]() such that from the origin of the centre (17) bifurcate $16$
such that from the origin of the centre (17) bifurcate $16$![]() limit cycles of small amplitude.
limit cycles of small amplitude.
Proof. System (17) has a time-reversible centre at the origin. Because it is invariant by the change $(x,\,y,\,t)\rightarrow (x,\,-y,\,-t)$![]() . Additionally, it has also a rational first integral obtained from its corresponding inverse integrating factor. They are, respectively,
. Additionally, it has also a rational first integral obtained from its corresponding inverse integrating factor. They are, respectively,
The next step is the computation of the linear terms of the Taylor developments of the Lyapunov constants. We have computed $L_k^{[1]}$![]() for $k=1,\,\ldots,\,40$
for $k=1,\,\ldots,\,40$![]() with, for example, the algorithm described in [Reference Gouveia and Torregrosa30]. As in the previous section, let $A_n$
with, for example, the algorithm described in [Reference Gouveia and Torregrosa30]. As in the previous section, let $A_n$![]() be the matrix corresponding to $(L^{[1]}_{1},\,\ldots,\,L^{[1]}_{n})$
be the matrix corresponding to $(L^{[1]}_{1},\,\ldots,\,L^{[1]}_{n})$![]() with respect to the parameters $(a_{20},\,a_{11},\,a_{02},\,\ldots,\,b_{20},\,b_{11},\,b_{02},\,\ldots )\in \mathbb {R}^{50}.$
with respect to the parameters $(a_{20},\,a_{11},\,a_{02},\,\ldots,\,b_{20},\,b_{11},\,b_{02},\,\ldots )\in \mathbb {R}^{50}.$![]() Then, the proof of the statement follows using Corollary 1.5 because $\operatorname {rank} A_{20}=16.$
Then, the proof of the statement follows using Corollary 1.5 because $\operatorname {rank} A_{20}=16.$![]()
We point out that we have checked that $\operatorname {rank} A_k=k$![]() for $k=1,\,\ldots,\,12,$
for $k=1,\,\ldots,\,12,$![]() but ${\operatorname {rank} A_{13}=12}$
but ${\operatorname {rank} A_{13}=12}$![]() . Additionally, that $\operatorname {rank} A_{14}=13,$
. Additionally, that $\operatorname {rank} A_{14}=13,$![]() $\operatorname {rank} A_{k}=14,$
$\operatorname {rank} A_{k}=14,$![]() for $k=15,\,\ldots,\, 18$
for $k=15,\,\ldots,\, 18$![]() , $\operatorname {rank} A_{19}=15,$
, $\operatorname {rank} A_{19}=15,$![]() and $\operatorname {rank} A_{k}=16,$
and $\operatorname {rank} A_{k}=16,$![]() for $k=20,\,\ldots,\,40.$
for $k=20,\,\ldots,\,40.$![]() From these values, we can say that, up to $k=40$
From these values, we can say that, up to $k=40$![]() , there are no more limit cycles than the ones in the statement. Moreover, without Corollary 1.5, that is with the results in [Reference Christopher14], only $12$
, there are no more limit cycles than the ones in the statement. Moreover, without Corollary 1.5, that is with the results in [Reference Christopher14], only $12$![]() limit cycles of small amplitude can bifurcate from the origin.
limit cycles of small amplitude can bifurcate from the origin.
The explicit expression of the necessary Lyapunov constants to get the statement are:


4. Local cyclicity for systems of degrees $6,\,7,\,8,$ and $10$
and $10$
In this section, we use Corollary 1.5 to study lower bounds for the cyclicity in some centres of low degree, $n=6,\,7,\,8,$![]() and $10$
and $10$![]() . Next result proves Theorem 1.1. The other propositions do not provide better lower bounds for the local cyclicity in the indicated degrees. But we have decided to be added here because the centres and their perturbation studies are new. From the proofs, it seems that the number of limit cycles that bifurcate from the origin will be the maximum values for first-order studies. We have computed some more terms than the necessary to prove the statements. In all cases, we show that only studying first-order developments and using the technique described in [Reference Christopher14] the results on lower bounds for the cyclicity are worst. We have not studied degrees $n=3,\,4,\,5,\,9$
. Next result proves Theorem 1.1. The other propositions do not provide better lower bounds for the local cyclicity in the indicated degrees. But we have decided to be added here because the centres and their perturbation studies are new. From the proofs, it seems that the number of limit cycles that bifurcate from the origin will be the maximum values for first-order studies. We have computed some more terms than the necessary to prove the statements. In all cases, we show that only studying first-order developments and using the technique described in [Reference Christopher14] the results on lower bounds for the cyclicity are worst. We have not studied degrees $n=3,\,4,\,5,\,9$![]() because we do not have new centres having this special property. Unfortunately, we have not improved the lower bounds previously obtained in [Reference Giné, Gouveia and Torregrosa27, Reference Gouveia and Torregrosa30].
because we do not have new centres having this special property. Unfortunately, we have not improved the lower bounds previously obtained in [Reference Giné, Gouveia and Torregrosa27, Reference Gouveia and Torregrosa30].
Proposition 4.1 There are polynomial perturbations of degree $6$![]() such that from the origin of the centre
such that from the origin of the centre

bifurcate at least $44$![]() limit cycles of small amplitude.
limit cycles of small amplitude.
Proof. The vector field in the statement and the proof that it has a centre at the origin is given by Giné in [Reference Giné25]. The proof of the statement follows from Corollary 1.5 computing $L_k^{[1]},$![]() for $k=1,\,\ldots,\,80,$
for $k=1,\,\ldots,\,80,$![]() and checking that $\operatorname {rank} A_{k}=44,$
and checking that $\operatorname {rank} A_{k}=44,$![]() for $k=52,\,\ldots,\,80.$
for $k=52,\,\ldots,\,80.$![]() We notice that $\operatorname {rank} A_{k}=k,$
We notice that $\operatorname {rank} A_{k}=k,$![]() for $k=1,\,\ldots,\,32.$
for $k=1,\,\ldots,\,32.$![]() Because of the size, we only show the linear developments of the first three Lyapunov constants:
Because of the size, we only show the linear developments of the first three Lyapunov constants:

Remark 4.2 We notice that for the centre (18) we have also computed $44$![]() Lyapunov constants up to fourth-order and, using [Reference Gouveia and Torregrosa30], we can prove only the existence of $41$
Lyapunov constants up to fourth-order and, using [Reference Gouveia and Torregrosa30], we can prove only the existence of $41$![]() limit cycles of small amplitude bifurcating from the origin.
limit cycles of small amplitude bifurcating from the origin.
Proposition 4.3 There are polynomial perturbations of degree $7$![]() such that from the origin of the centre
such that from the origin of the centre

bifurcate at least $60$![]() limit cycles of small amplitude.
limit cycles of small amplitude.
Proof. The system in the statement has a centre at the origin because it has a rational first integral of the form $H(x(x^{2}+y^{2}),\,y(x^{2}+y^{2})),$![]() where
where
with $\psi (x,\,y)= 1\,0752 {x}^{3}+29568 {x}^{2}y+17640 x{y}^{2}+3024 {y}^{3}-1600 {x}^{2}-2760 xy-576 {y}^{2}+74 x+57 y-1.$![]() The original cubic polynomial vector field having a centre at the origin is given in [Reference Bondar and Sadovskiĭ8].
The original cubic polynomial vector field having a centre at the origin is given in [Reference Bondar and Sadovskiĭ8].
The proof follows also from Corollary 1.5 computing $L_k^{[1]},$![]() for $k=1,\,\ldots,\,80,$
for $k=1,\,\ldots,\,80,$![]() and checking that $\operatorname {rank} A_{63}=60.$
and checking that $\operatorname {rank} A_{63}=60.$![]() We notice that $\operatorname {rank} A_{k}=k,$
We notice that $\operatorname {rank} A_{k}=k,$![]() for $k=1,\,\ldots,\,55.$
for $k=1,\,\ldots,\,55.$![]() We show only the first three Lyapunov constants:
We show only the first three Lyapunov constants:

Proposition 4.4 There are polynomial perturbations of degree $8$![]() such that from the origin of the centre
such that from the origin of the centre

bifurcate at least $70$![]() limit cycles of small amplitude.
limit cycles of small amplitude.
Proof. We consider the centre with quartic homogeneous nonlinearities given in [Reference Giné25] but written in polar coordinates, $(x,\,y)=(r\cos \theta,\,r\sin \theta ).$![]() Then, with the change $R=r^{3/5}$
Then, with the change $R=r^{3/5}$![]() and recovering again new Cartesian coordinates, we obtain the system in the statement of degree $8.$
and recovering again new Cartesian coordinates, we obtain the system in the statement of degree $8.$![]() Then it has also a centre at the origin. The proof of the statement follows again from Corollary 1.5 computing $L_k^{[1]},$
Then it has also a centre at the origin. The proof of the statement follows again from Corollary 1.5 computing $L_k^{[1]},$![]() for $k=1,\,\ldots,\,130,$
for $k=1,\,\ldots,\,130,$![]() and checking that $\operatorname {rank} A_{87}=70.$
and checking that $\operatorname {rank} A_{87}=70.$![]() We notice that $\operatorname {rank} A_{k}=k,$
We notice that $\operatorname {rank} A_{k}=k,$![]() for $k=1,\,\ldots,\,45.$
for $k=1,\,\ldots,\,45.$![]() The first three Lyapunov constants are
The first three Lyapunov constants are

Proposition 4.5 There are polynomial perturbations of degree $10$![]() such that from the origin of the centre
such that from the origin of the centre

bifurcate at least $97$![]() limit cycles of small amplitude.
limit cycles of small amplitude.
Proof. The centre in the statement is obtained following the same procedure than in the proof of Proposition 4.4 but with the change $R=r^{3/9}.$![]() The proof of the existence of such limit cycles of small amplitude follows again from Corollary 1.5 computing $L_k^{[1]},$
The proof of the existence of such limit cycles of small amplitude follows again from Corollary 1.5 computing $L_k^{[1]},$![]() for $k=1,\,\ldots,\,130,$
for $k=1,\,\ldots,\,130,$![]() and checking that $\operatorname {rank} A_{126}=97.$
and checking that $\operatorname {rank} A_{126}=97.$![]() We notice that $\operatorname {rank} A_{k}=k,$
We notice that $\operatorname {rank} A_{k}=k,$![]() for $k=1,\,\ldots,\,58.$
for $k=1,\,\ldots,\,58.$![]() Curiously, the expressions of the first three Lyapunov constants coincide with the ones of the previous proposition.
Curiously, the expressions of the first three Lyapunov constants coincide with the ones of the previous proposition.
5. Perturbing piecewise systems of degrees $3$ , $4,$
, $4,$ and $5$
and $5$
This section is devoted to proving Theorem 1.2. We also show that there are other cubic centres having cyclicity also higher or equal than $26$![]() as it was proved in [Reference Gouveia and Torregrosa29] but using second-order developments. The following result only uses first-order analysis. The best lower bound for the local cyclicity, up to our knowledge, for piecewise quadratic vector fields is [Reference da Cruz, Novaes and Torregrosa18]. As we have no new nor better results for $n=2$
as it was proved in [Reference Gouveia and Torregrosa29] but using second-order developments. The following result only uses first-order analysis. The best lower bound for the local cyclicity, up to our knowledge, for piecewise quadratic vector fields is [Reference da Cruz, Novaes and Torregrosa18]. As we have no new nor better results for $n=2$![]() we have concentrated our efforts to high degrees. But, the computational difficulties arise for $n\ge 6$
we have concentrated our efforts to high degrees. But, the computational difficulties arise for $n\ge 6$![]() even using the parallelization algorithms. This is why we have stopped in degree five polynomial piecewise differential equations. So we do not write them here again.
even using the parallelization algorithms. This is why we have stopped in degree five polynomial piecewise differential equations. So we do not write them here again.
As in the previous section, we have computed some more Lyapunov constants than the strictly necessary to get the proofs. With the aim to convince ourselves that we have obtained the optimal results for first-order studies. From the proofs, it can be seen also that the classical study using only the return map and the Lyapunov constants provide worse results. See again [Reference Gouveia and Torregrosa29].
The general perturbed system considered in this section is

Proposition 5.1 There exist polynomial piecewise perturbations of degree $n=3$![]() as (20) such that $26$
as (20) such that $26$![]() crossing limit cycles of small amplitude bifurcate from the origin of system
crossing limit cycles of small amplitude bifurcate from the origin of system

Proof. The system in the statement is the Bondar–Sadovskiĭ cubic centre system given by the rational first integral (19), see again [Reference Bondar and Sadovskiĭ8], but rotated with the matrix
The proof of the statement follows from Corollary 2.2 computing $L_k^{[1]},$![]() for $k=2,\,\ldots,\,32,$
for $k=2,\,\ldots,\,32,$![]() and checking that $\operatorname {rank} A_{28}=25.$
and checking that $\operatorname {rank} A_{28}=25.$![]() We notice that $\operatorname {rank} A_{k}=k-1,$
We notice that $\operatorname {rank} A_{k}=k-1,$![]() for $k=2,\,\ldots,\,24.$
for $k=2,\,\ldots,\,24.$![]() Because of the size, we only show the linear developments of the first three Lyapunov constants:
Because of the size, we only show the linear developments of the first three Lyapunov constants:

We remark that, in the above result, we have rotated because, without it, the local cyclicity takes a lower value, up to first-order analysis. We have not proved that this rotation plays any special role. Except that the entries of the matrix are small rational numbers. With other rotation matrices, the result will be generically the same. This example shows how the separation straight line change the local cyclicity of the origin.
Proposition 5.2 There exist polynomial piecewise perturbations of degree $n=4$![]() as (20) such that $43$
as (20) such that $43$![]() crossing limit cycles of small amplitude bifurcate from the origin of system
crossing limit cycles of small amplitude bifurcate from the origin of system

Proof. The above vector field has a centre at the origin because it is the holomorphic system of degree four $\dot z=\operatorname {i} z+z^{2}+z^{3}+z^{4},$![]() but written in Cartesian coordinates, $z=x+\operatorname {i} y$
but written in Cartesian coordinates, $z=x+\operatorname {i} y$![]() . The proof follows also from Corollary 2.2 computing $L_k^{[1]},$
. The proof follows also from Corollary 2.2 computing $L_k^{[1]},$![]() for $k=2,\,\ldots,\,60,$
for $k=2,\,\ldots,\,60,$![]() and checking that $\operatorname {rank} A_{60}=42.$
and checking that $\operatorname {rank} A_{60}=42.$![]() We notice that $\operatorname {rank} A_{k}=k-1,$
We notice that $\operatorname {rank} A_{k}=k-1,$![]() for $k=2,\,\ldots,\,38.$
for $k=2,\,\ldots,\,38.$![]() Because of the size, we only show the linear developments of the first three Lyapunov constants:
Because of the size, we only show the linear developments of the first three Lyapunov constants:

Proposition 5.3 There exist polynomial piecewise perturbations of degree $n=5$![]() as (20) such that $65$
as (20) such that $65$![]() crossing limit cycles of small amplitude bifurcate from the origin of system
crossing limit cycles of small amplitude bifurcate from the origin of system
Proof. The vector field in the statement is, written in Cartesian coordinates ($z=x+\operatorname {i} y$![]() ), the holomorphic system of degree five $\dot z = \operatorname {i} z + z^{2}+z^{3}+z^{4}+z^{5}.$
), the holomorphic system of degree five $\dot z = \operatorname {i} z + z^{2}+z^{3}+z^{4}+z^{5}.$![]() The proof follows again from Corollary 2.2 computing $L_k^{[1]},$
The proof follows again from Corollary 2.2 computing $L_k^{[1]},$![]() for $k=2,\,\ldots,\,80,$
for $k=2,\,\ldots,\,80,$![]() and checking that $\operatorname {rank} A_{72}=64.$
and checking that $\operatorname {rank} A_{72}=64.$![]() We notice that $\operatorname {rank} A_{k}=k-1,$
We notice that $\operatorname {rank} A_{k}=k-1,$![]() for $k=2,\,\ldots,\,58.$
for $k=2,\,\ldots,\,58.$![]() Because of the size, we only show the linear developments of the first three Lyapunov constants:
Because of the size, we only show the linear developments of the first three Lyapunov constants:

Acknowledgements
This work has been realized thanks to the Catalan AGAUR 2017 SGR 1617 grant, the Spanish Ministerio de Ciencia, Innovación y Universidades - Agencia Estatal de Investigación PID2019-104658GB-I00 grant, the Severo Ochoa and María de Maeztu Program for Centers and Units of Excellence in R&D CEX2020-001084-M grant, the European Community H2020-MSCA-RISE-2017-777911 grant, and the Brazilian CNPq 200484/2015-0 and FAPESP 2020/04717-0 grants.
We would like to thank also the referees for their helpful comments and suggestions for improving the final version of this paper.