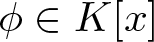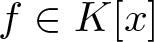1. Introduction
The problem of finding the irreducibility of a given polynomial with integer coefficients has fascinated several mathematicians. Some well-known classical irreducibility criteria such as Schönemann–Eisenstein–Dumas irreducibility criteria have seen various extensions and generalizations over the years. Recently, in [Reference Jakhar and Srinivas8, Reference Jakhar and Srinivas9], Jakhar and Srinivas also extended some of these criteria and provided information about the lower bounds on the degrees of irreducible factors of polynomials over valued fields. In this paper, we improve and generalize these results. To state the main results, we first recall some notation and definitions.
Let (K, v) be a valued field with value group 
$\Gamma_ v,$ valuation ring Ov having maximal ideal Mv and residue field 
$k_{v}=O_v/ M_v.$ An extension w of v to a simple transcendental extension K(x) is called residue-transcendental (abbreviated r. t.) if the corresponding residue field extension 
$k_{w}| k_v$ is transcendental.
Definition 1.1. Let 
$\bar{v}$ be an extension of v to a fixed algebraic closure 
$\overline{K}$ of K with value group 
$\Gamma_{\bar{v}}.$ A pair 
$(\alpha,\delta)$ in 
$\overline{K}\times \Gamma_{\bar{v}}$ is called a (K, v)-minimal pair if for every β in 
$\overline{K}$ satisfying 
$\bar{v}(\alpha-\beta)\geq\delta,$ we have 
$\deg\beta\geq\deg\alpha,$ where by 
$\deg\alpha$ we mean the degree of the extension 
$K(\alpha)|K.$
An extension 
$\overline{w}$ of w to 
$\overline{K}(x)$ which is also an extension of 
$\bar{v}$ is called a common extension of w and 
$\bar{v}.$
For a (K, v)-minimal pair 
$(\alpha,\delta)\in\overline{K}\times\Gamma_{\bar{v}},$ the map 
$\overline{w}_{\alpha,\delta}: \overline{K}[x]\longrightarrow \Gamma_{\bar{v}},$ given by
\begin{align*}
\overline{w}_{\alpha,\delta}\left(\sum_{i\geq 0} c_i (x-\alpha)^i\right):=\min_{i\geq 0}\{\bar{v}(c_i)+i\delta\}, \, c_i\in\overline{K},
\end{align*} is a valuation on 
$\overline{K}[x]$ and extends uniquely to 
$\overline{K}(x)$ [Reference Engler and Prestel3, Theorem 2.2.1]. The valuation 
$\overline{w}_{\alpha,\delta}$ is said to be defined by 
$\min,\, \bar{v},\, \alpha$ and 
$\delta.$
Definition 1.2. If 
$\overline{w}=\overline{w}_{\alpha,\delta},$ then we say that 
$(\alpha,\delta)$ is a minimal pair of definition for 
$\overline{w}$ and denote its restriction to K(x) by 
$w:=w_{\alpha,\delta}.$
Let 
$w=w_{\alpha,\delta}$ and ϕ be the minimal polynomial of α over 
$K,$ then by [Reference Alexandru, Popescu and Zaharescu2, Theorem 2.1], for any polynomial 
$f\in K[x]$ with ϕ-expansion 
$\sum_{i} a_i \phi^i,$ 
$a_i\in K[x],$ 
$\deg a_i \lt \deg \phi,$ we have
\begin{align}
w(f)=\min_{i}\{\bar{v}(a_i(\alpha))+ iw(\phi)\}.
\end{align} Such a valuation w is an r. t. extension and any r. t. extension can be obtained in this way (see [Reference Alexandru, Popescu and Zaharescu2]). In particular, 
$w=w_{0,0}$ is called the Gaussian extension of v to K(x) and is denoted by 
$v^x.$
For an r. t. extension w of v to K(x) and polynomials 
$f,$ g in 
$K[x],$ we say that f and g are w-equivalent if 
$w(f-g) \gt w(f)=w(g);$ g is w-divisible by f (denoted 
$f|_{w} g$) if there exists some polynomial 
$h \in K[x]$ such that g is w-equivalent to 
$fh.$
Let us now recall the definition of key polynomials, introduced by Mac Lane [Reference MacLane11] in 1936 for discrete rank-one valuations and generalized to arbitrary valued fields by Vaquié [Reference Vaquié14] in 2007. Key polynomials have been used to classify all possible extensions of v to K(x) (see [Reference Nart12]). Over the years, key polynomials have been extensively used to find irreducible factors of polynomials over valued fields (for example see [Reference Alberich-Carraminãna, Guàrdia, Nart, Poteaux, Roé and Weimann1], [Reference Guàrdia, Montes and Nart4] and [Reference Jakhar, Khanduja and Sangwan7]).
Definition 1.3. A monic polynomial f is called a key polynomial for w if it is
(i) w-irreducible, i.e. for any
$h,\, q\in K[x],$ whenever
$f\mid_{w} hq,$ then either
$f\mid_{w}h $ or
$f\mid_{w}q,$(ii) and w-minimal, i.e. for every non-zero polynomial
$h\in K[x],$ whenever
$f\mid_{w}h,$ then
$\deg h\geq \deg f.$
We denote by 
$\operatorname{KP}(w)$ the set of all key polynomials for 
$w.$ If 
$w=w_{\alpha,\delta}$ and ϕ the minimal polynomial of α over 
$K,$ then 
$\phi\in\operatorname{KP}(w)$ (see [Reference Popescu and Popescu13, Theorem 4.4]).
For any 
$\phi\in\operatorname{KP}(w),$ consider the subset
\begin{equation*}\Gamma_{w}^{\circ}:=\{w(a)\mid a\in K[x],~\deg a \lt \deg\phi\}\subset\Gamma_{w}.\end{equation*} Then 
$\Gamma_{w} ^{\circ}$ is a subgroup of 
$\Gamma_{w}$ and 
$\Gamma_w=\langle\Gamma_{w} ^{\circ}, w(\phi)\rangle.$ Since w is r. t., so there is a smallest positive integer e such that 
$e w(\phi)\in\Gamma_{w} ^{\circ}.$
Let w be an r. t. extension of v to K(x) and let Γ be the divisible closure of 
$\Gamma_w.$ Any 
$\phi\in\operatorname{KP}(w)$ determines a Newton-polygon operator
\begin{equation*}N_{\phi,w}: K[x]\longrightarrow \mathcal{P}(\mathbb{Q}\times\Gamma),\end{equation*} where 
$\mathcal{P}(\mathbb{Q}\times\Gamma)$ is the power set of the rational vector space 
$\mathbb{Q}\times\Gamma.$ For any 
$A\subseteq\mathbb{Q}\times\Gamma,$ the set
\begin{equation*}L=\{(a,b)\in A\mid b\leq b'~\text{for every}~ (a,b')\in A\}\end{equation*} is called the lower part of 
$A.$
Definition 1.4. For any non-zero polynomial 
$f\in K[x],$ not divisible by 
$\phi,$ with ϕ-expansion 
$\sum_{i=0}^{n} a_i\phi^i,$ 
$a_n\neq 0,$ the ϕ-Newton polygon 
$N_{\phi,w}(f)$ is defined as the lower part of the convex hull in 
$\mathbb{Q}\times\Gamma$ of the finite set 
$\{(i, w(a_i))\mid a_i\neq 0,~0\leq i\leq n\}.$
Therefore, 
$N_{\phi,w}(f)$ is either a single point or a chain of sides (or edges), 
$S_1,\ldots, S_r,$ ordered from left to right by increasing slopes.
Definition 1.5. The principal Newton polygon 
$N^{+} _{\phi,w}(f)$ of f is the polygon formed by the sides of 
$N_{\phi,w}(f)$ of slope less than 
$-w(\phi).$
In 2020, Jakhar and Srinivas proved the following.
Theorem 1.6. ([Reference Jakhar and Srinivas8], Theorem 1.3)
Let 
$\phi\in O_v[x]$ be a monic polynomial of degree m which is irreducible modulo 
$M_v.$ Let 
$f\in O_v[x]$ be a polynomial not divisible by 
$\phi.$ Assume that the ϕ-Newton polygon of f with respect to vx has l many sides with positive slopes 
$\lambda_j,$ 
$1\leq j\leq l.$ If ej is the smallest positive integer such that 
$e_j\lambda_j\in\Gamma_v$ for 
$1\leq j\leq l,$ then f has an irreducible factor of degree at least 
$\max_{1\leq j\leq l}\{e_j m\}$ over 
$K.$
Remark 1.7. It may be pointed out that any monic polynomial which is irreducible modulo Mv is a key polynomial for vx and conversely (see [Reference Popescu and Popescu13, Theorem 4.6, Corollary 4.7]). However, if 
$w(\neq v^x)$ is r. t., then not every key polynomial for w is irreducible modulo Mv (see Example 1.10).
In view of Remark 1.7, Theorem 1.6 follows from our following result.
Theorem 1.8. Let (K, v) be a valued field and w an r. t. extension of v to 
$K(x).$ Let 
$\phi\in \operatorname{KP}(w)$ be of degree 
$m.$ Let 
$f\in K[x]$ be a polynomial not divisible by 
$\phi.$ Assume that 
$N^{+} _{\phi,w}(f) $ has l many sides with slopes 
$-\lambda_j \lt -w(\phi),$ 
$1\leq j\leq l.$ If ej is the smallest positive integer such that 
$e_j\lambda_j\in\Gamma_w ^{\circ},$ then f has an irreducible factor of degree at least 
$\max_{1\leq j\leq l}\{e_j m\}$ over 
$K.$
For 
$(K,v)=(\mathbb{Q},v_p)$ and 
$w=v^x,$ the next result immediately follows from the above theorem, which also generalizes [Reference Jakhar5, Theorem 1.1].
Corollary 1.9. ([Reference Jakhar and Srinivas8], Theorem 1.5)
Let 
$f=\sum_{i=0}^{n} a_ix^i$ with 
$a_0\neq 0$ be a polynomial over 
$\mathbb{Z}.$ Assume that 
$N^{+} _{x,v^x}(f)$ has l many sides with slopes 
$-\lambda_j=-\frac{r_j}{s_j} \lt -v^x(x)=0,$ where 
$\text{gcd}(r_j,s_j)=1,$ 
$1\leq j\leq l,$ then f has an irreducible factor of degree at least 
$\max_{1\leq j\leq l}\{s_j \}$ over 
$\mathbb{Q}.$
The following examples illustrate the importance of our result.
Example 1.10. Let 
$\mathbb{Q}$ be the field of rational numbers with the p-adic valuation 
$v_p,$ p an odd prime, having value group 
$\mathbb{Z},$ valuation ring 
$\mathbb{Z}_{(p)}$ and maximal ideal 
$p\mathbb{Z}_{(p)}.$ Let 
$w=w_{0,1/2}$ be the valuation on 
$\mathbb{Q}(x)$ defined by the minimal pair 
$(0,1/2)$ with 
$\Gamma_w =\frac{1}{2}\mathbb{Z}.$ Take the polynomial 
$\phi=x^2+px+p.$ Then in view of [Reference Popescu and Popescu13, Theorem 4.6], it can be easily shown that 
$\phi\in\operatorname{KP}(w).$ However, ϕ is not irreducible modulo 
$p\mathbb{Z}_{(p)}.$ Clearly 
$\Gamma_w ^{\circ}=\frac{1}{2}\mathbb{Z}.$ Let
\begin{equation*}f=\frac{1}{p^5}\phi^7+\left( x+\frac{1}{p^5}\right) \phi^6+\frac{1}{p^4}\phi^5+\frac{1}{p}\phi^3+(px+p)\phi^2+p^6 x+p^6.\end{equation*} Then 
$N_{\phi,w}(f)$ has slopes
\begin{equation*}-\lambda_1=-\frac{5}{2} \lt -\lambda_2 =-2 \lt -\lambda_3=-\frac{3}{2} \lt -\lambda_4=-1 \lt -\lambda_5=0.\end{equation*} Since 
$w(\phi)=1,$ so 
$N^{+} _{\phi,w}(f)$ has three sides with slope strictly less than 
$-w(\phi)=-1,$ and 
$e_1=2,$ 
$e_2=1$ and 
$e_3=2.$ Therefore, by Theorem 1.8, f has an irreducible factor of degree at least 
$\max\{4,2,4\}=4$ over 
$\mathbb{Q}.$ However, Theorem 1.6 provides no information about the degrees of irreducible factors of 
$f.$
Example 1.11. Let 
$(\mathbb{Q},v_p),$ w and ϕ be as in the above example. Let 
$a,$ b and c be polynomials of degree at most one over 
$\mathbb{Z}$ with w valuation 
$0,~1$ and 6, respectively. Take the polynomial 
$f=a\phi^4+b\phi^3+c\in \mathbb{Z}[x].$ Then 
$N^{+} _{\phi,w}(f)$ has a single side with slope 
$-5/3 \lt -w(\phi),$ which implies that e = 3. Hence by Theorem 1.8, f has an irreducible factor of degree at least 6 over 
$\mathbb{Q}.$
Our next result gives a lower bound on the degrees of all irreducible factors of f over 
$K.$
Theorem 1.12. Let 
$\phi\in K[x]$ be a monic polynomial of degree m which is irreducible modulo 
$M_v.$ Let 
$f=\sum_{i=0}^{n}a_i \phi^i,$ 
$a_0\neq 0,$ be the ϕ-expansion of f with 
$v^x(a_n)=0$ and 
$v^x(a_i) \gt 0$ for 
$0\leq i\leq n-1.$ Assume that 
$N_{\phi, v^x}(f)$ has l many sides with slope 
$-\lambda_j,$ 
$1\leq j\leq l.$ If ej is the smallest positive integer such that 
$e_j\lambda_j\in\Gamma_v$ for 
$1\leq j\leq l,$ then each irreducible factor of f has degree at least 
$\min_{1\leq j\leq l}\{e_j m\}$ over 
$K.$
Remark 1.13. It may be pointed out that the above theorem extends [Reference Jakhar and Srinivas9, Theorem 1.2], which in turn also generalizes Eisenstein–Dumas irreducibility criterion [Reference Jakhar and Srinivas9, Theorem 1.5]. Further, on taking 
$\phi=x$ in the above theorem, if 
$N_{x, v^x}(f)$ has a single side, then we obtain the main result of [Reference Jakhar6].
Example 1.14. Consider the valued field 
$(\mathbb{Q}, v_p)$ and 
$\phi\in \mathbb{Q}[x]$ be a monic polynomial of degree m which is irreducible modulo 
$p\mathbb{Z}_{(p)}.$ For any odd positive integer 
$n,$ take the polynomial 
$f=a_{2n}\phi^{2n}+pa_n\phi^{n}+p^3a_0,$ where 
$a_{2n},$ an and a 0 are polynomials over 
$\mathbb{Q}$ having degree at most m − 1 with Gaussian valuation zero. Then 
$N_{\phi, v^x}(f)$ has slopes 
$-\lambda_1=-\frac{2}{n} \lt -\lambda_2=-\frac{1}{n},$ and therefore, by Theorem 1.12, either f is irreducible or f has two irreducible factors each of degree 
$mn.$ However, if we take p = 3 and 
$\phi=x^2+1,$ then [Reference Jakhar and Srinivas9, Theorem 1.2] provides no information about the degrees of irreducible factors of 
$f.$
The following example highlights the importance of Theorems 1.8 and 1.12.
Example 1.15. Let 
$(\mathbb{Q}, v_p)$ and ϕ be as in the above example. Let 
$q\geq 5$ be prime such that 
$2(q-p) \gt p\geq 3.$ Then clearly, 
$q \gt p.$ Now consider the polynomial 
$f=a_q\phi^q+pa_p\phi^p+p^3 a_0,$ where 
$a_{q},$ ap and a 0 be polynomials over 
$\mathbb{Q}$ of degree at most m − 1 with Gaussian valuation zero. Then for the vertices 
$(0,3),$ 
$(p,1)$ and 
$(q,0),$ 
$N_{\phi, v^x}(f)$ has slopes 
$-\lambda_1=-\frac{2}{p} \lt -\lambda_2=-\frac{1}{q-p},$ which in view of Theorems 1.8 and 1.12 implies that either f is irreducible or f has two irreducible factors of degree mp and 
$m(q-p).$
2. Proof of Theorems 1.8 and 1.12
Let (K, v) and 
$(\overline{K},\bar{v})$ be as in the previous section. Let w be an r. t. extension of v to 
$K(x).$
Definition 2.1. Let 
$\phi\in K[x]$ be a key polynomial for a valuation 
$w'$ on 
$K(x),$ and let 
$\gamma \gt w'(\phi)$ be an element of a totally ordered abelian group Γ containing 
$\Gamma_{w'}$ as an ordered subgroup. The map 
$w: K[x]\longrightarrow \Gamma\cup\{\infty\}$ defined by
\begin{equation*}w(f):=\min_{i\geq 0}\{w'(a_i)+i\gamma\},\end{equation*} where 
$\sum_{i\geq 0}a_i \phi^i, $ 
$\deg a_i \lt \deg \phi,$ is the ϕ-expansion of 
$f\in K[x],$ gives a valuation on K(x) (see [Reference Vaquié14, Section 1.1]) called the ordinary augmentation of w ʹ and is denoted by 
$[w'; \phi,\gamma].$
Remark 2.2. If 
$\phi\in O_v[x]$ is a monic polynomial of degree 
$m\geq 1$ such that ϕ is irreducible modulo Mv and α is a root of 
$\phi,$ then 
$(\alpha,\delta)$ is a (K, v)-minimal pair for each positive 
$\delta\in\Gamma_{\bar{v}}.$ Moreover, for any polynomial 
$g=\sum_{i\geq0} a_i x^i\in K[x]$ having degree less than 
$m,$ we have
\begin{align}
\bar{v}(g(\alpha))=v^x(g).
\end{align} Let 
$(\alpha,\delta)$ be the minimal pair of definition for 
$\overline{w},$ 
$w=\overline{w}|_{K(x)},$ and ϕ the minimal polynomial of α having degree m over 
$K.$ Keeping in mind (1.1), for any non-zero polynomial 
$f\in K[x]$ with ϕ-expansion 
$\sum_{i\geq 0} a_i \phi^i,$ denote
\begin{align}
I_{\phi,w}(f)&:=\min\{i\mid w(f)=\bar{v}(a_i(\alpha))+i w(\phi)\}
\end{align}
\begin{align}
S_{\phi,w}(f)&:=\max\{i\mid w(f)=\bar{v}(a_i(\alpha))+i w(\phi)\}.
\end{align}Theorem 2.3. ([Reference Khanduja and Kumar10], Lemma 2.1)
For any non-zero polynomials 
$f,$ 
$g\in K[x],$ we have
(i)
$I_{\phi,w}(fg)=I_{\phi,w}(f)+I_{\phi,w}(g),$(ii)
$S_{\phi,w}(fg)=S_{\phi,w}(f)+S_{\phi,w}(g).$
The main idea in the proof of Theorems 1.8 and 1.12 is as follows: For the given valuation w (or vx), we first construct suitable augmentations wj with respect to ϕ and slopes λj and show that if λj is the slope of 
$N^{+} _{\phi,w}(f)$ (or 
$N_{\phi,v^x}(f)$) connecting the vertices 
$(k_{j-1}, w(a_{k_{j-1}}))$ and 
$(k_j, w(a_{k_j}))$ (or 
$(k_{j-1}, v^x(a_{k_{j-1}}))$ and 
$(k_j, v^x(a_{k_j}))$) then 
$I_{\phi, w_j}(f)=k_{j-1}$ and 
$S_{\phi, w_j}(f)=k_{j}.$ On applying Theorem 2.3 on the factorization of 
$f,$ we then obtain the desired lower bounds.
Proof of Theorem 1.8.
Let 
$f=\sum_{i=0}^{n} a_i\phi^i$ be the ϕ-expansion of f and let
\begin{equation*}\{(k_0=0, w(a_{k_0})), (k_1, w(a_{k_1})),\ldots, (k_l, w(a_{k_l}))\}\end{equation*} denote the successive vertices corresponding to the sides of 
$N^{+} _{\phi,w}(f)$ with slopes 
$-\lambda_{1},-\lambda_{2},\ldots,-\lambda_{l}.$ Then 
$k_0 \lt k_1 \lt \cdots \lt k_l$ and 
$-\lambda_{1} \lt -\lambda_{2} \lt \cdots \lt -\lambda_{l} \lt -w(\phi).$ For each 
$\lambda_j \gt w(\phi),$ 
$1\leq j\leq l,$ consider the ordinary augmentation of 
$w,$ 
$w_j=[w; \phi,\lambda_j]$ so that 
$w_j(\phi)=\lambda_j.$ Then
\begin{align}
w_j(f)=w_j\left( \sum_{i=0}^{n} a_i \phi^i\right) =\min_{0\leq i\leq n}\{w(a_i)+i\lambda_j\}.
\end{align} Let 
$I_{\phi,w_j}(f)$ and 
$S_{\phi,w_j}(f)$ be as in (2.2) and (2.3). Since −λj is the slope of 
$N^{+} _{\phi,w}(f)$ connecting the vertices 
$(k_{j-1}, w(a_{k_{j-1}}))$ and 
$(k_j, w(a_{k_j})),$ so by definition
\begin{align}
\min_{0\leq i\leq k_{j-1}}\left\{\frac{w(a_{k_j})-w({a_{i})}}{k_j-i}\right\}&\leq -\lambda_j,
\end{align}
\begin{align}
\min_{k_{j-1} \lt i\leq n}\left\{\frac{w(a_{i})-w({a_{k_{j-1}}})}{i-k_{j-1}}\right\}&\geq -\lambda_j.
\end{align} The smallest and largest index i for which equality holds in (2.5) and (2.6) is 
$k_{j-1}$ and 
$k_{j},$ respectively. Consequently, by (2.4), we have
\begin{align*}
w_j(f)=w(a_{k_j})+k_j\lambda_j=w(a_{k_{j-1}})+k_{j-1}\lambda_j.
\end{align*} i.e. 
$I_{\phi,w_j}(f)=k_{j-1}$ and 
$S_{\phi,w_j}(f)=k_j.$ Let 
$f=f_1f_2\cdots f_t$ be the factorization of f into irreducible factors over 
$K.$ Denote 
$I_{\phi,w_j}(f_r)$ by 
$k_{j-1}^{(r)}$ and 
$S_{\phi,w_j}(f_r)$ by 
$k_j ^{(r)}$ for 
$1\leq r\leq t.$ Then by Theorem 2.3,
\begin{align*}
k_j&=k_j ^{(1)}+\cdots+ k_j^{(t)}~\text{and}~
k_{j-1}=k_{j-1} ^{(1)}+\cdots+ k_{j-1}^{(t)}.
\end{align*} Since 
$k_j \gt k_{j-1},$ so 
$k_{j}-k_{j-1}=(k_j ^{(1)}-k_{j-1} ^{(1)})+\cdots+ (k_j ^{(t)}-k_{j-1}^{(t)}) \gt 0,$ implies that 
$k_{j}^{(r)}-k_{j-1}^{(r)} \gt 0$ for some 
$1\leq r\leq t.$ Without loss of generality, we can assume that 
$k_j ^{(1)}-k_{j-1} ^{(1)} \gt 0 .$ Let 
$f_1=\sum_{u=0}^{d_1} b_u \phi^{u}$ be the ϕ-expansion of 
$f_1.$ Then
\begin{equation*}w_j(f_1)=w\left(b_{k_j ^{(1)}}\right)+k_j ^{(1)}\lambda_j=w\left(b_{k_{j-1}^{(1)}}\right)+k_{j-1}^{(1)}\lambda_j,\end{equation*} which implies that 
$(k_j ^{(1)}-k_{j-1}^{(1)})\lambda_j=w(b_{k_j ^{(1)}})-w(b_{k_{j-1} ^{(1)}})\in\Gamma_w ^{\circ}.$ Now ej being the smallest positive integer such that 
$e_j\lambda_j\in \Gamma_w ^{\circ},$ so 
$k_j ^{(1)}-k_{j-1}^{(1)}\geq e_j.$ Since, 
$S_{\phi,w_j}(f_1)=k_j ^{(1)},$ so
\begin{align*}
\deg f_1&\geq \deg b_{k_j ^{(1)}}+k_j ^{(1)}m\geq k_j ^{(1)}m\geq(k_j ^{(1)}-k_{j-1}^{(1)})m\geq e_j m.
\end{align*} As j is arbitrary, so f has an irreducible factor of degree at least 
$\max_{1\leq j\leq l}\{e_j m\}$ over 
$K.$
Remark 2.4. It may be pointed out that the proof of the above theorem is motivated by [Reference Jakhar and Srinivas8, Theorem 1.3]. However, the main difference is the presence of key polynomials and corresponding augmented valuations with their respective value groups.
Proof of Theorem 1.12.
Let 
$(k_0=0, k_1,\ldots, k_{l-1}, k_l=n)$ be integers such that the successive vertices of the sides of 
$N_{\phi, v^x}(f)$ are given by
\begin{equation*}\{(k_0, v^x(a_{k_0})), (k_1, v^x(a_{k_1})),\ldots, (k_l, v^x(a_{k_l}))\}.\end{equation*} Let 
$-\lambda_{1} \lt -\lambda_{2} \lt \cdots \lt -\lambda_{l}$ denote the corresponding slopes in 
$N_{\phi, v^x} (f).$ In particular, 
$-\lambda_j=\frac{v^x(a_{k_j})-v^x(a_{k_{j-1}})}{k_j-k_{j-1}},$ 
$1\leq j\leq l,$ i.e.
\begin{align}
v^x(a_{k_j})+k_j\lambda_j=v^x(a_{k_{j-1}})+k_{j-1}\lambda_j.
\end{align} For a root α of 
$\phi,$ let 
$\phi=c_m(x-\alpha)^m+\cdots+c_1(x-\alpha),~ c_m=1$ and set
\begin{equation*}\delta_j=\max_{1\leq i\leq m}\left\{\frac{\lambda_j-\bar{v}(c_i)}{i}\right\}\in\Gamma_{\bar{v}}.\end{equation*} Since 
$\lambda_j \gt 0,$ 
$\forall j,$ so 
$(\alpha,\delta_j)$ is a (K, v)-minimal pair. Let 
$\overline{w}_{\alpha,\delta_j}$ be the valuation of 
$\overline{K}(x)$ defined by the pair 
$(\alpha,\delta_j)$ and let 
$w_j:= w_{\alpha,\delta_j}$ be its restriction to 
$K(x).$ Then by the choice of 
$\delta_j,$ we have
\begin{align}
w_j(\phi)=\min_{i}\{\bar{v}(c_i)+i\delta_j\}=\lambda_j.
\end{align} As 
$\deg a_i \lt \deg\phi,$ by Remark 2.2, we have 
$v^x(a_i)=\bar{v}(a_i(\alpha))$ and hence 
$w_j(f)=\min_{1\leq i\leq n}\{v^x(a_i)+i\lambda_j\}.$ Again as −λj is the slope of 
$N_{\phi,v^x}(f)$ connecting the vertices 
$(k_{j-1}, v^x(a_{k_{j-1}}))$ and 
$(k_j, v^x(a_{k_j})),$ by definition
\begin{align}
\min_{0\leq i\leq k_{j-1}}\left\{\frac{v^x(a_{k_j})-v^x({a_{i})}}{k_j-i}\right\}&\leq -\lambda_j,
\end{align}
\begin{align}
\min_{k_{j-1} \lt i\leq n}\left\{\frac{v^x(a_{i})-v^x({a_{k_{j-1}}})}{i-k_{j-1}}\right\}&\geq -\lambda_j.
\end{align} The smallest index i for which equality holds in (2.9) is 
$k_{j-1}$ and the largest index i for which equality holds in (2.10) is 
$k_{j}.$ This implies that
\begin{align}
w_j(f)=v^x(a_{k_{j-1}})+k_{j-1}\lambda_j=v^x(a_{k_j})+k_j\lambda_j.
\end{align} Therefore, 
$I_{\phi,w_j}(f)=k_{j-1}$ and 
$S_{\phi,w_j}(f)=k_j.$ Let 
$f=f_1f_2\cdots f_t$ be the factorization of f into irreducible factors over K and let 
$f_s=\sum_{u=0}^{d_s} b_{su}\phi^u,~ b_{sd_s}\neq 0,$ be the ϕ-expansion of 
$f_s.$ Fix any 
$s,$ 
$1\leq s\leq t,$ and assume that for 
$2\leq j\leq l,$ 
$S_{\phi, w_{j-1}}(f_s)=k_{j-1}^{(s)},$ with 
$0\leq k_{j-1} ^{(s)}\leq d_s.$ We claim that 
$I_{\phi, w_j}(f_s)=k_{j-1}^{(s)},$ and
\begin{align}
w_j(f_s)=v^x\left(b_{s k_{j-1}^{(s)}}\right)+k_{j-1} ^{(s)}\lambda_j=v^x\left(b_{s k_{j} ^{(s)}}\right)+k_{j} ^{(s)}\lambda_j,~ 1\leq j\leq l,
\end{align} with 
$0\leq k_{j-1}^{(s)}\leq k_{j}^{(s)}\leq d_s$ and 
$k_{l}^{(s)}=d_s,$ 
$k_{0}^{(s)}=0.$
Since 
$S_{\phi, w_{j-1}}(f_s)=k_{j-1}^{(s)},$ so
\begin{align}
w_{j-1}(f_s)&=\min_{0\leq u\leq d_s}\{v^x({b_{su}})+u\lambda_{j-1}\}
=v^x\left( {b_{sk_{j-1}^{(s)}}}\right) +k_{j-1}^{(s)}\lambda_{j-1}.
\end{align}We first show that
\begin{align}
k_{j-1}=k_{j-1}^{(1)}+\cdots+k_{j-1}^{(t)}.
\end{align} By the choice of 
$k_{j-1}^{(s)},$ we have
\begin{align}
w_{j-1}(f_s)\leq v^{x}(b_{su})+u\lambda_{j-1},
\end{align} for 
$0\leq u\leq d_s$ with strict inequality if 
$u \gt k_{j-1}^{(s)}.$ Keeping in mind (2.15) together with the fact that 
$k_{j-1}$ is the largest index for which 
$w_{j-1}(f)=v^x (a_{k_{j-1}})+k_{j-1}\lambda_{j-1},$ we have that 
$k_{j-1}^{(1)}+\cdots+k_{j-1}^{(t)}$ is the largest at which 
$w_{j-1}(f)=w_{j-1}(f_1)+\cdots+w_{j-1}(f_t)$ is attained and hence (2.14) follows. Now on using Equations (2.11), (2.13) and (2.14), we obtain
\begin{equation}v^x\left(a_{k_{j-1}}\right)=v^x\left(b_{1k_{j-1}^{(1)}}\right)+\cdots+v^x\left(b_{tk_{j-1}^{(t)}}\right).\end{equation} Recall that 
$k_{j-1}$ is the smallest at which 
$w_{j}(f)=v^{x}(a_{k_{j-1}})+k_{j-1}\lambda_{j}$ is attained and 
$w_j(f_s)\leq v^{x}(b_{su})+u\lambda_{j}$ for 
$0\leq u\leq d_s.$ By (2.14) and (2.16), it can be easily varified that 
$k_{j-1}^{(s)}$ is the smallest index at which 
$w_j(f_s)$ is attained which proves that 
$I_{\phi, w_j}(f_s)=k_{j-1}^{(s)}.$ Therefore, we have for 
$1\leq j\leq l,$ 
$w_1(f_s)=v^x(b_{sk_{1}^{(s)}}) +k_{1}^{(s)}\lambda_{1},$
\begin{equation}w_j(f_s)=v^x\left(b_{sk_{j-1}^{(s)}}\right)+k_{j-1}^{(s)}\lambda_j=v^x\left(b_{sk_j^{(s)}}\right)+k_j^{(s)}\lambda_j,\;2\leq j\leq l-1,\end{equation}
\begin{equation}w_l(f_s)=v^x\left(b_{sk_{l-1}^{(s)}}\right)+k_{l-1}^{(s)}\lambda_l,\end{equation} where 
$0\leq k_{j-1}^{(s)}\leq k_{j}^{(s)}\leq d_s$ for 
$2\leq j\leq l-1,$ 
$k_1 ^{(s)}$ is the largest index at which 
$w_1(f_s)$ is attained and 
$k_{l-1}^{(s)}$ is the smallest at which 
$w_l(f_s)$ is attained. Let 
$I_{\phi, w_1}(f_s)=k_0 ^{(s)}$ and 
$S_{\phi, w_l}(f_s)=k_l^{(s)}.$ Clearly, 
$0\leq k_0^{(s)}\leq k_1^{(s)}\leq d_s$ and 
$0\leq k_{l-1}^{(s)}\leq k_l^{(s)}.$ We now show that
\begin{align}
k_l^{(s)}=d_s~\text{and}~ k_0^{(s)}=0.
\end{align} Since, 
$k_l=n$ and 
$v^x(a_n)=0,$ so we may assume that 
$v^x(b_{sd_s}) =0$ for 
$1\leq s\leq t.$ By definition, we have 
$w_l(f_s)=\min_{0\leq u\leq d_s}\{v^x(b_{su})+u\lambda_l\}\leq d_s\lambda_l,$ with
\begin{align}
w_l(f)=w_l(f_1)+\cdots+w_l(f_t).
\end{align} Keeping in mind that 
$v^x(a_n)=0,$ we have 
$w_l(f)=n\lambda_l.$ Since 
$n=d_1+d_2+\cdots+d_t,$ it follows from (2.20) that 
$w_l(f_s)=\min_{0\leq u\leq d_s}\{v^x(b_{su})+u\lambda_{l}\}=d_s\lambda_l,$ which implies that 
$k_l^{(s)}=d_s.$ Now on using (2.11), we have
\begin{align}
w_0(f)=v^x(a_{k_0})=v^x(a_0)
\end{align} and by definition, 
$w_0(f_s)=\min_{0\leq u\leq d_s}\{v^x(b_{su})+u\lambda_0\}\leq v^x(b_{s0})$ and
\begin{align}
w_0(f)=w_0(f_1)+\cdots+ w_0(f_t).
\end{align} Keeping in mind that 
$v^x(a_0)=v^x\left( \prod_{s=1}^{t} b_{s0}\right) =v^x(b_{10})+\cdots+v^x(b_{t0})$ together with (2.21) and (2.22), we obtain that 
$w_0(f_s)=v^x(b_{s0}),$ i.e. 
$k_0^{(s)}=0,$ which completes the claim.
If 
$k_{0}^{(s)}=k_{1}^{(s)}=\cdots=k_{l}^{(s)}, $ then 
$d_s=k_{l}^{(s)}= k_{0}^{(s)}=0$ contradicting the fact that 
$d_s\geq 1.$ Therefore, we must have that 
$k_j ^{(s)} \gt k_{j-1}^{(s)},$ for some 
$j,$ 
$1\leq j\leq l,$ which in view of (2.12) implies that 
$(k_j ^{(s)}-k_{j-1}^{(s)})\lambda_j\in\Gamma_v.$ Since ej is the smallest positive integer such that 
$e_j\lambda_j\in\Gamma_v,$ so 
$(k_j ^{(s)}-k_{j-1}^{(s)})\geq e_j.$ Thus, we have
\begin{equation*}\deg f_s=d_sm\geq d_s m-k_{j-1}^{(s)}\geq k_j ^{(s)}m-k_{j-1}^{(s)}m=(k_j ^{(s)}-k_{j-1}^{(s)})m\geq e_jm.\end{equation*} Since s is arbitrary, so each irreducible factor of f has degree at least 
$\min_{1\leq j\leq l}\{e_j m\}$ over 
$K.$
Acknowledgements
The first author's research is supported by CSIR (Grant no. 09/045(1747)/2019-EMR-I).
