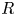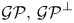Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-11T21:30:03.012Z Has data issue: false hasContentIssue false
  • English
  • Français

FP-injective dimensions and Gorenstein homology

Part of: Homological algebra

Published online by Cambridge University Press:  21 December 2022

Gang Yang  and
Junpeng Wang
Gang Yang
Affiliation:
Department of Mathematics, Lanzhou Jiaotong University, Lanzhou 730070, China (yanggang@mail.lzjtu.cn)
Junpeng Wang*
Affiliation:
Department of Mathematics, Northwest Normal University, Lanzhou 730070, China (wangjunpeng1218@163.com)
*
*Corresponding author
Rights & Permissions [Opens in a new window]

Abstract

Let $R$ be a left coherent ring. It is proven that if an $R$-module $M$ has a finite FP-injective dimension, then the Gorenstein projective (resp. Gorenstein flat) dimension and the projective (resp. flat) dimension coincide. Also, we obtain that the pair ($\mathcal {GP},\, \mathcal {GP}^{\perp }$) forms a projective cotorsion pair under some mild conditions.

Keywords

FP-injective modulesGorenstein projective modulesGorenstein flat modules

MSC classification

Primary: 18G25: Relative homological algebra, projective classes
Secondary: 18G20: Homological dimension
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 4 , November 2022 , pp. 1183 - 1199
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Introduction

Inspired by the work of Auslander and Bridger [Reference Auslander and Bridger1], Enochs, Jenda, and Torrecillas introduced the concept of Gorenstein projective, Gorenstein injective and Gorenstein flat modules [Reference Enochs and Jenda9, Reference Enochs, Jenda and Torrecillas12] for any ring, and then established Gorenstein homological algebra. Such a relative homological algebra has been developed rapidly during the past several years and become a rich theory. In this paper, we will consider the following two topics:

  1. (1) The triviality of Gorenstein projective and Gorenstein flat dimensions.

  2. (2) The complete hereditary cotorsion pair induced by the class of Gorenstein projective modules.

For the first topic, it is well known that the Gorenstein projective dimension ${\rm Gpd}_R(-)$ (resp. Gorenstein flat dimension ${\rm Gfd}_R(-)$) is a refinement of the usual projective dimension ${\rm pd}_R(-)$ (resp. flat dimension ${\rm fd}_R(-)$), that is, for any $R$-module $M$ there is an inequality ${\rm Gpd}_RM\leq {\rm pd}_RM$ (resp. ${\rm Gfd}_RM\leq {\rm fd}_RM$), and if ${\rm pd}_RM$ (resp. ${\rm fd}_RM$) is finite, then there is an equality ${\rm Gpd}_RM={\rm pd}_RM$ (resp. ${\rm Gfd}_RM={\rm fd}_RM$). On the other hand, the equalities are closely related with injective dimensions. Holm proved in [Reference Holm18, Theorem 2.2] that the equality ${\rm Gpd}_RM={\rm pd}_RM$ holds when $M$ has a finite injective dimension; Holm showed in [Reference Holm18, Theorem 2.6] that if $R$ is a left and right coherent ring with finite $\text {RightFPD}(R)$, then the equality ${\rm Gfd}_RM={\rm fd}_RM$ holds when $M$ has a finite injective dimension. Here $\text {RightFPD}(R)$ denotes the right finitistic projective dimension of $R$ and is defined as the supremum of the projective dimensions of all right $R$-modules with finite projective dimension.

The first motivation of the paper is to link the above equalities with FP-injective dimensions. The main results, being shown in § 2, are as follows:

Theorem A Assume that $R$ is a left coherent ring. If ${\rm FP}\hbox{-}{\rm id}_RM<\infty,$ then there is an equality ${\rm Gpd}_RM={\rm pd}_RM$.

Theorem B Assume that $R$ is a left coherent ring. If ${\rm FP}\hbox{-}{\rm id}_RM<\infty,$ then there is an equality ${\rm Gfd}_RM={\rm fd}_RM$.

Let us turn our attention to the second topic. A classical result over Gorenstein rings tells us that, over such a ring $R$, the following claims hold, where $\mathcal {GP}$ (resp. $\mathcal {GI}$ and $\mathcal {GF}$) stands for the class of all Gorenstein projective (resp. Gorenstein injective and Gorenstein flat) left $R$-modules:

  1. (2.1) The pair $(^{\perp }\mathcal {GI},\, \mathcal {GI})$ forms a complete hereditary cotorsion pair.

  2. (2.2) The pair $(\mathcal {GF},\, \mathcal {GF}^{\perp })$ forms a complete hereditary cotorsion pair.

  3. (2.3) The pair $(\mathcal {GP},\, \mathcal {GP}^{\perp })$ forms a complete hereditary cotorsion pair.

In order that Gorenstein homological algebra should work, many authors in [Reference Bravo, Gillespie and Hovey5, Reference Enochs and Lépez-Ramos13, Reference Gillespie15, Reference Jørgensen21, Reference Krause23, Reference Murfet and Salarian25, Reference Šaroch and Št'ovíček27, Reference Yang and Liang32] seek more general rings such that (2.1)–(2.3) hold. It is worth mentioning that, by virtue of the work of Šaroch and Št'ovíček [Reference Šaroch and Št'ovíček27], the claims (2.1) and (2.2) hold for any ring. However, the claim (2.3) for an arbitrary ring remains unknown.

Let $R$ be a ring such that any level left $R$-module has a finite projective dimension. The class of such rings includes strictly the one of right coherent rings $R$ such that any flat left $R$-module has a finite projective dimension (see Remark 3.13). By establishing a link between Gorenstein AC-projective and Gorenstein projective modules, Bravo, Gillespie and Hovey [Reference Bravo, Gillespie and Hovey5, Reference Gillespie15] proved that the claim (2.3) holds true. To compare these facts, the second motivation of the paper is to obtain a condition of left coherent rings such that the claim (2.3) holds.

Let $R$ be a left coherent ring and $n$ be a non-negative integer. Note from Remark 3.1 that ${\rm Ext}_R^{1}(G,\,M)=0$ for all $G\in \mathcal {GP}$ and all $M\in \mathcal {FI}_n$, where $\mathcal {FI}_n$ denotes the class of all left $R$-modules $M$ with ${\rm FP}\hbox{-}{\rm id}_R(M)\leq n$. Our main results in § 3 is as follows, which checks when such two classes form a complete hereditary cotorsion pair, where FFPID$(R)$ denotes the left fintistic FP-injective dimension of $R$, it is defined as the supremum of the FP-injective dimensions of all left $R$-modules with finite FP-injective dimension.

Theorem C Let $R$ be a left coherent ring and $n$ a non-negative integer. Then the following conditions are equivalent.

  1. (1) The pair $(\mathcal {GP},\,\mathcal {FI}_n)$ forms a projective cotorsion pair.

  2. (2) $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\} \leq n$.

As an immediate consequence of Theorem C, we have the claim (2.3) hold whenever $R$ is a left coherent ring with both ${\rm FP}\hbox{-}{\rm id}_R(R)<\infty$ and $\mathrm {FFPID}(R)<\infty$. Note that there exists a ring $R$ with both ${\rm FP}\hbox{-}{\rm id}_R(R)<\infty$ and $\mathrm {FFPID}(R)<\infty$ which neither satisfies that level left $R$-module has a finite projective dimension nor is right coherent (See Remarks 3.10 and 3.11).

As we all know, the famous “Auslander's last theorem” announced that over an arbitrary Gorenstein ring any finitely generated module has a Gorenstein projective cover. We give a sufficient and necessary condition that all modules have a Gorenstein projective cover over a left coherent ring $R$ with both ${\rm FP}\hbox{-}{\rm id}_R(R)<\infty$ and $\mathrm {FFPID}(R)<\infty$. Thus, Gorenstein rings can not guarantee that over them all modules have a Gorenstein projective cover (see Remark 3.6). Furthermore, we obtain that, over such a ring, Gorenstein projective and Ding projective modules coincide with each other, which are exactly modules as some kernel of an exact complex of projective modules (see Proposition 3.9). This improves [Reference Gillespie16, Theorem 1.1(1)]. We then compare the two conditions $`` R \text { is a left coherent ring with both }{\rm FP}\hbox{-}{\rm id}_R(R)<\infty \text { and }\mathrm {FFPID}(R)<\infty ''\text { and }'' R$ is a ring such that any level left $R$-module has finite projective dimension” as well as other well-known conditions such that the claim (2.3) holds (see Remarks 3.12–3.14).

As another application of Theorem C, in § 4 we characterize Gorenstein global dimension of a left coherent ring.

1. Notation and terminology

Throughout the paper, $R$ denotes an associative ring with identity. An $R$-module will mean a left $R$-module, unless stated otherwise. We also refer to right $R$-modules as modules over the opposite ring $R^o$. The category of $R$-modules will be denoted by $R$-Mod.

Recall from [Reference Enochs and Jenda11] that an $R$-module $M$ is called Gorenstein projective if there exists an exact sequence

of projective $R$-modules with $M=\text {Ker}(P_0\rightarrow P_{-1})$, such that it remains exact after applying ${\rm Hom}(-,\,Q)$ for any projective $R$-module $Q$. An $R$-module $N$ is Gorenstein flat if there exists an exact sequence

of flat $R$-modules with $N=\text {Ker}(F_0\rightarrow F_{-1})$ such that $I\otimes _R-$ leaves the sequence exact whenever $I$ is an injective $R^o$-module. As usual, we use the symbol ${\rm pd}_R(-)$, ${\rm fd}_R(-)$, ${\rm Gpd}_R(-)$, and ${\rm Gfd}_R(-)$ to denote the projective, flat, Gorenstein projective and Gorenstein flat dimension, respectively. We use $\mathcal {GP}$ and $\mathcal {GF}$ to denote the class of Gorenstein projective, and Gorenstein flat modules, respectively. We say that $\mathcal {GP}$ is special precovering (resp. covering) if every module has a special Gorenstein projective precover (resp. Gorenstein projective cover), that is, if every module has a special $\mathcal {GP}$-precover (resp. $\mathcal {GP}$-cover).

Recall from [Reference Stenström29] that an $R$-module $E$ is called FP-injective if $\text {Ext}^1_R(A,\, E)=0$ for all finitely presented $R$-modules $A$. The FP-injective dimension of a module $B$, denoted by $\text {FP-id}_R(B)$, is defined to be the least integer $n\geq 0$ such that $\text {Ext}^{n+1}_R(A,\, B)=0$ for all finitely presented $R$-modules $A$. If no such $n$ exists, set $\text {FP-id}(B)=\infty$. FP-injective modules and dimension have a nice description over coherent rings, see Enochs–Jenda's book [Reference Enochs and Jenda11].

Let $\mathcal {C}$ be an abelian category, and $\mathcal {A}$ and $\mathcal {B}$ be classes of objects in $\mathcal {C}$. We think of a cotorsion pair $(\mathcal {A},\, \mathcal {B})$ as being “orthogonal with respect to the functor ${\rm Ext}^1_\mathcal {C}$”. This is often expressed with the notation $\mathcal {A}={^\perp \mathcal {B}}$ and $\mathcal {B}=\mathcal {A}^\perp$. A cotorsion pair $(\mathcal {A},\, \mathcal {B})$ is said to be complete if for any object $X$ there are exact sequences $0 \rightarrow X\rightarrow B\rightarrow A \rightarrow 0$ and $0\rightarrow \widetilde {B}\rightarrow \widetilde {A}\rightarrow X\rightarrow 0$ with $B,\, \widetilde {B}\in \mathcal {B}$ and $A,\, \widetilde {A}\in \mathcal {A}$. A cotorsion pair $(\mathcal {A},\, \mathcal {B})$ is said to be cogenerated by a set $\mathcal {S}\subseteq \mathcal {A}$ whenever $B\in \mathcal {B}$ if and only if $\text {Ext}^1(S,\, B)=0$ for all $S\in \mathcal {S}$. A cotorsion pair $(\mathcal {A},\, \mathcal {B})$ is said to be hereditary if whenever $0 \rightarrow A'\rightarrow A\rightarrow A'' \rightarrow 0$ is exact with $A,\, A''\in \mathcal {A}$ then $A'$ is also in $\mathcal {A}$, or equivalently, if $0 \rightarrow B'\rightarrow B\rightarrow B'' \rightarrow 0$ is exact with $B',\, B\in \mathcal {B}$ then $B''$ is also in $\mathcal {B}$. The notion of a cotorsion pair was first introduced by Salce in [Reference Salce26] and rediscovered by Enochs and coauthors in 1990's (see [Reference Enochs and Jenda11]). Its importance in homological algebra has been shown by its use in the proof of the existence of flat covers of modules over any ring [Reference Bican, El Bashir and Enochs3].

2. The triviality of Gorenstein projective and Gorenstein flat dimensions

Let $R$ be a left coherent ring, and $P$ an acyclic complex of projective $R$-modules. It is proved by Gillespie [Reference Gillespie16, Theorem 3.6] that ${\rm Ext}^1_R(\mathbf {Z}_nP,\, A)=0$ for any FP-injective $R$-module $A$, where $\mathbf {Z}_nP$ is the $n$th cycle of the complex $P$. We shall use this result to show the following lemma.

Lemma 2.1 Let $R$ be a left coherent ring and $G$ a Gorenstein projective $R$-module. Then ${\rm Ext}^{i\geq 1}_R(G,\, B)=0$ for any $R$-module $B$ of finite FP-injective dimension.

Proof. If $B$ is FP-injective, then the result follows directly by [Reference Gillespie16, Theorem 3.6]. Now we assume that $\text {FP-id}_RB=n>0$. By [Reference Stenström29, Lemma 3.1] there exists an exact sequence $0\to B \to E^0 \to \cdots \to E^{n}\to 0$ of $R$-modules with each $E^i$ FP-injective. As $G$ is Gorenstein projective, there is an exact sequence

of projective $R$-modules, such that $G\cong \text {Ker}(P_{0}\to P_{-1})$ and each kernel of $\mathbf {P}$ is Gorenstein projective, and it remains exact after applying the functor ${\rm Hom}_R(-,\,Q)$ for every projective $R$-module $Q$. We get an exact sequence of complexes

It is obvious that each complex ${\rm Hom}_R(\mathbf {P},\,E^j)$ is acyclic since ${\rm Ext}^{i\geq 1}_R(N,\, E^j)=0$ for any kernel $N$ of $\mathbf {P}$ and any $E^{j}$. So we conclude that the complex ${\rm Hom}_R(\mathbf {P},\,B)$ is also acyclic, this implies that ${\rm Ext}^{i\geq 1}_R(G,\, B)=0$, as desired.

It is proved by Holm [Reference Holm18, Theorem 2.2] that if $M$ is an $R$-module with ${\rm id}_RM<\infty$, then ${\rm Gpd}_RM={\rm pd}_RM$. We extend the result as the following.

Theorem 2.2 Assume that $R$ is a left coherent ring and let $M$ be an $R$-module. If ${\rm FP}\hbox{-}{\rm id}_RM<\infty,$ then ${\rm Gpd}_RM={\rm pd}_RM$.

Proof. Clearly ${\rm Gpd}_RM\leq {\rm pd}_RM$ always holds true (for any ring $R$ and any $R$-module $M$). To see the inverse inequality, we may assume that ${\rm Gpd}_RM=n<\infty$. Then [Reference Christensen, Frankild and Holm6, Lemma 2.17] yields a short exact sequence of $R$-modules

with ${\rm pd}_RP=n<\infty$ and $G$ Gorenstein projective. By Lemma 2.1 one has ${{\rm Ext}^1_R(G,\, M)=0}$ since ${\rm FP}\hbox{-}{\rm id}_RM<\infty$. It follows that the above short exact sequence is split, and hence ${\rm pd}_RM\leq {\rm pd}_RP={\rm Gpd}_RM$, as desired.

By introducing the notion of projectively coresolved Gorenstein flat modules, Šaroch and Št'ovíček [Reference Šaroch and Št'ovíček27, Theorem 4.11] have shown that any ring $R$ is GF-closed, that is, the class, $\mathcal {GF}$, of all Gorenstein flat $R$-modules is closed under extensions. Here a left $R$-module $M$ is called projectively coresolved Gorenstein flat [Reference Šaroch and Št'ovíček27] if there exists an exact sequence of projective $R$-modules

such that $M\cong {\rm Ker}(P_0\to P_{-1})$, and such that it remains exact after applying the functor $I\otimes _{R}-$ for every injective $R^o$-module $I$. It is trivial that any projectively coresolved Gorenstein flat module is Gorenstein flat. Note that any projectively coresolved Gorenstein flat module is also Gorenstein projective [Reference Šaroch and Št'ovíček27, Theorem 4.4].

Lemma 2.3 Let $R$ be a ring and $n$ a non-negative integer. If $M$ is an $R$-module with ${\rm Gfd}_R(M)\leq n$, then there is an exact sequence of $R$-modules

with ${\rm fd}_R(F)\leq n$ and $G$ Gorenstein projective.

Proof. Let $M$ be an $R$-module with ${\rm Gfd}_R(M)\leq n$. Since the class $\mathcal {GF}$ is closed under extensions as mentioned above, it follows from [Reference Bouchiba4, Definition 1] and [Reference Bouchiba4, Theorem 4] that there is a short exact sequence of $R$-modules

with ${\rm fd}_R(E)\leq n$ and $N\in \mathcal {GF}$. According to [Reference Šaroch and Št'ovíček27, Theorem 4.11], there exists another short exact sequence of $R$-modules

with $K$ flat and $G$ projectively coresolved Gorenstein flat. Now we consider the following pullback diagram:

Since, in the middle column, $K$ is flat and ${\rm fd}_R(E)\leq n$, it follows that ${\rm fd}_R(F)\leq n$. Besides, $G\in \mathcal {GP}$ as any projectively coresolved Gorenstein flat $R$-module is always Gorenstein projective (see [Reference Šaroch and Št'ovíček27, Theorem 4.4]). Therefore, the middle row is the desired exact sequence.

Assume that $R$ is a left and right coherent ring with finite $\text {RightFPD}(R)$. Here $\text {RightFPD}(R)$ is the right finitistic projective dimension of $R$, it is defined as the supremum of the projective dimensions of all right $R$-modules with finite projective dimension. It is proved by Holm [Reference Holm18, Theorem 2.6] that if $\text {id}_RM<\infty$, then $\text {Gfd}_RM=\text {fd}_RM$. We improve this result by removing the assumption of the finiteness of $\text {RightFPD}(R)$ and the right coherence of $R$ as the following, which is the “flat version” of the previous Theorem 2.2.

Theorem 2.4 Assume that $R$ is a left coherent ring and let $M$ be an $R$-module. If $\text {FP-id}_RM<\infty$, then $\text {Gfd}_RM=\text {fd}_RM$.

Proof. Suppose $\text {FP-id}_RM<\infty$. It is sufficient to show ${\rm fd}_R(M)\leq {\rm Gfd}_R(M)$ since the inverse inequality is clear. For this, let ${\rm Gfd}_R(M)=n<\infty$. Then Lemma 2.3 yields a short exact sequence $0\to M\to F\to G\to 0$ with ${\rm fd}_R(F)\leq n$ and $G$ Gorenstein projective. Thus, by Lemma 2.1, one gets that the above sequence is split. It follows easily that ${\rm fd}_R(M)\leq {\rm fd}_R(F)\leq n$, as desired.

3. Cotorsion pairs induced by gorenstein projective modules

As mentioned in the introduction, it is still open whether the pair $(\mathcal {GP},\, \mathcal {GP}^{\perp })$ forms a complete hereditary cotorsion pair over an arbitrary ring. Let $R$ be a right coherent ring such that all flat $R$-modules have finite projective dimension. It is known from [Reference Gillespie15, Fact 10.2] that, over such a ring the pair $(\mathcal {GP},\, \mathcal {GP}^{\perp })$ forms a complete hereditary cotorsion pair. In this section, we will obtain the same result for certain left coherent rings (see Corollary 3.4). We also compare some conditions of rings (see Remarks 3.12, 3.13, and 3.14).

In what follows, for any non-negative integer $n$, we will denote by $\mathcal {FI}_n$ the class of all $R$-modules $M$ with ${\rm FP}\hbox{-}{\rm id}_R(M)\leq n$. Let us start with a fact proved by Mao and Ding.

Remark 3.1 Let $R$ be a left coherent ring. It follows by [Reference Mao and Ding24, Proposition 3.6(2)] that $(^{\perp }\mathcal {FI}_n,\,\mathcal {FI}_n)$ is a complete hereditary cotorsion pair.

Let $\mathcal {A}$ be an abelian category. We say that a class $\mathcal {X}$ of objects in $\mathcal {A}$ is thick if $\mathcal {X}$ is closed under direct summands and such that if any two out of three of the terms in a short exact sequence are in $\mathcal {X}$, then so is the third.

If $\mathcal {A}$ has enough projectives, then we say that a pair $(\mathcal {X},\,\mathcal {Y})$ of objects in $\mathcal {A}$ is a projective cotorsion pair if $(\mathcal {X},\,\mathcal {Y})$ forms a complete cotorsion pair such that $\mathcal {Y}$ is thick and $\mathcal {X}\cap \mathcal {Y}$ coincides with the subcategory of projective objects. Equivalently, if $(\mathcal {X},\,\mathcal {Y})$ forms a hereditary complete cotorsion pair such that $\mathcal {X}\cap \mathcal {Y}$ coincides with the subcategory of projective objects (see [Reference Gillespie15, Definition 3.4] and [Reference Gillespie15, Proposition 3.7]).

The left finitistic FP-injective dimension FFPID$(R)$ of the ring $R$, is defined as the supremum of the FP-injective dimensions of those $R$-modules that have finite FP-injective dimension.

Lemma 3.2 Let $R$ be a left coherent ring and $n$ a non-negative integer. Then the following conditions are equivalent.

  1. (1) The cotorsion pair $(^{\perp }\mathcal {FI}_n,\,\mathcal {FI}_n)$ is projective.

  2. (2) $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\} \leq n$.

Proof. $(1)\Rightarrow (2)$. Suppose that the cotorsion pair $(^{\perp }\mathcal {FI}_n,\,\mathcal {FI}_n)$ is projective. Then by [Reference Gillespie15, Theorem 5.4], one has $^{\perp }\mathcal {FI}_n\subseteq \mathcal {GP}$. Using the completeness of the cotorsion pair $(^{\perp }\mathcal {FI}_n,\,\mathcal {FI}_n)$, one gets a short exact sequence of $R$-modules

with $E\in \mathcal {FI}_n$ and $N\in {^{\perp }}\mathcal {FI}_n\subseteq \mathcal {GP}$. Note that the short exact sequence is split since ${\rm Ext}_R^1(N,\, R)=0$, and hence ${\rm FP}\hbox{-}{\rm id}_R(R)\leq n$ .

Let $M$ be an $R$-module with ${\rm FP}\hbox{-}{\rm id}_R(M)<\infty$. It follows from Lemma 2.1 that ${\rm Ext}_R^{1}(G,\, M)=0$ for any $G\in \mathcal {GP}$, and then ${\rm Ext}_R^{1}(X,\, M)=0$ for any $X\in {^\perp \mathcal {FI}_n}$ as ${^\perp \mathcal {FI}_n}\subseteq \mathcal {GP}$ by [Reference Gillespie15, Theorem 5.4] and the assumption. This yields that $M\in \mathcal {FI}_n$ via the cotorsion pair $(^{\perp }\mathcal {FI}_n,\,\mathcal {FI}_n)$. That is, ${\rm FP}\hbox{-}{\rm id}_R(M)\leq n$.

$(2)\Rightarrow (1)$. Assume $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\} \leq n$. By Remark 3.1, the pair $(^{\perp }\mathcal {FI}_n,\,\mathcal {FI}_n)$ is a complete hereditary cotorsion pair. Note that $\mathcal {P}\subseteq {^{\perp }}\mathcal {FI}_n\cap \mathcal {FI}_n$ since $\mathcal {P}\subseteq {^{\perp }}\mathcal {FI}_n$ is clear and $\mathcal {P}\subseteq \mathcal {FI}_n$ follows by the equality

\[ {\rm FP}\hbox{-}{\rm id}_R(R)=\sup\{{\rm FP}\hbox{-}{\rm id}_R(P)~|~P~\text{is a projective}~R\text{-module}\} \]

and the assumption ${\rm FP}\hbox{-}{\rm id}_R(R)\leq n$. Now, let $M\in {^{\perp }}\mathcal {FI}_n\cap \mathcal {FI}_n$. Consider the short exact sequence of $R$-modules

with $P$ projective. Noticing that $P$ and $M$ have finite FP-injective dimension, one gets that $K$ has a finite FP-injective dimension as well. The assumption $\mathrm {FFPID}(R)\leq n$ yields $K\in \mathcal {FI}_n$ and so ${\rm Ext}_R^{1}(M,\,K)=0$. Thus, the short exact sequence above splits and so $M$ is projective. Therefore, the cotorsion pair $(^{\perp }\mathcal {FI}_n,\,\mathcal {FI}_n)$ is projective by [Reference Gillespie15, Proposition 3.7].

Now we are able to prove the following theorem.

Theorem 3.3 Let $R$ be a left coherent ring and $n$ a non-negative integer. Then the following conditions are equivalent.

  1. (1) The pair $(\mathcal {GP},\,\mathcal {FI}_n)$ forms a projective cotorsion pair.

  2. (2) $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\} \leq n$.

Proof. $(1)\Rightarrow (2)$. Suppose that the pair $(\mathcal {GP},\,\mathcal {FI}_n)$ forms a projective cotorsion pair. Then one has $^{\perp }\mathcal {FI}_n=\mathcal {GP}$ by Remark 3.1. So according to Lemma 3.2, one has $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\} \leq n$‘.

$(2)\Rightarrow (1)$. Assume $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\} \leq n$. Then Lemma 3.2 yields a projective cotorsion pair $({^\perp \mathcal {FI}_n},\,\mathcal {FI}_n)$. We have to show that $^{\perp }\mathcal {FI}_n=\mathcal {GP}$. Indeed, on the one hand, applying [Reference Gillespie15, Theorem 5.4] to the above projective cotorsion pair, one has ${^{\perp }\mathcal {FI}_n} \subseteq \mathcal {GP}$. On the other hand, Lemma 2.1 yields $\mathcal {GP} \subseteq {^{\perp }}\mathcal {FI}_n$. Thus, $^{\perp }\mathcal {FI}_n=\mathcal {GP}$, as desired.

Using Theorem 3.3, one can deduce easily the following corollary.

Corollary 3.4 Let $R$ be a left coherent ring with both ${\rm FP}\hbox{-}{\rm id}_R(R)$ and $\mathrm {FFPID}(R)$ finite. Then $(\mathcal {GP},\,\mathcal {W})$ forms a projective cotorsion pair, where $\mathcal {W}$ denotes the class of $R$-modules of finite FP-injective dimension. Moreover, every $R$-module has a special Gorenstein projective precover.

Using Theorem 3.3, we can also characterize Gorenstein projective modules as follows.

Corollary 3.5 Let $R$ be a left coherent ring with both ${\rm FP}\hbox{-}{\rm id}_R(R)$ and $\mathrm {FFPID}(R)$ finite. Then the following conditions are equivalent for any $R$-module $M$.

  1. (1) $M$ is Gorenstein projective.

  2. (2) There is an exact sequence of $R$-modules $0\to M\to P^{0}\to P^{1} \to \cdots$ with each $P^{i}$ projective.

Proof. $(1)\Rightarrow (2)$ is clear.

$(2)\Rightarrow (1)$. Assume that $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\} = n<\infty$. Then Theorem 3.3 yields a projective cotorsion pair $(\mathcal {GP},\,\mathcal {FI}_n)$. Now suppose that we are given an exact sequence of $R$-modules $0\to M\to P^{0}\to P^{1} \to \cdots$ with each $P^{i}$ projective. To see $M$ is Gorenstein projective, it is sufficient to show ${\rm Ext}_R^{1}(M,\,F)=0$ for all $F\in \mathcal {FI}_n$ by the above cotorsion pair.

Indeed, combining the exact sequence in (2) with a projective resolution of $M$, one can get an exact sequence of projective $R$-modules

such that $M = {\rm Im}(P_{0} \to P^0).$ For any $F\in \mathcal {FI}_n$, using [Reference Gillespie16, Theorem 3.6.] and applying the arguments used in the proof of Lemma 2.1, one has ${\rm Ext}_R^{1}(M,\,F)=0$, as desired.

Let $R$ be a left coherent ring with both ${\rm FP}\hbox{-}{\rm id}_R(R)$ and $\mathrm {FFPID}(R)$ finite. Then Corollary 3.4 shows that the class $\mathcal {GP}$ is special precovering. The next result considers when the class $\mathcal {GP}$ is covering.

Corollary 3.6 Let $R$ be a left coherent ring with both ${\rm FP}\hbox{-}{\rm id}_R(R)$ and $\mathrm {FFPID}(R)$ finite and $\mathcal {W}$ be as above. Then the following are equivalent:

  1. (1) The class $\mathcal {GP}$ is covering.

  2. (2) The class $\mathcal {GP}$ is closed under direct limits.

  3. (3) The pair $(\mathcal {GP},\, \mathcal {W})$ is a perfect cotorsion pair.

  4. (4) Every Gorenstein flat $R$-module $M$ has a Gorenstein projective cover.

  5. (5) Every flat $R$-module $M$ has a Gorenstein projective cover.

  6. (6) $R$ is left perfect.

Proof. Note that $(2) \Rightarrow (3)$ follows from Corollary 3.4 and [Reference Enochs and Jenda11, Theorem 7.2.6], $(3) \Rightarrow (1) \Rightarrow (4) \Rightarrow (5)$ are trivial.

$(5) \Longrightarrow (6)$. Let $F$ be a flat $R$-module and $\alpha : P\longrightarrow F$ a Gorenstein projective cover of $F$. So $\alpha$ must epic since the class $\mathcal {GP}$ contains all projective $R$-modules. Consider the short exact sequence of $R$-modules

with $K=\mathrm {Ker}\alpha$. Then $K$ belongs to $\mathcal {W}$ by Wakamutsu's Lemma since the class $\mathcal {GP}$ is closed under extensions (see [Reference Holm19, Theorem 2.5]). As $R$ is a left coherent ring with ${\rm FP}\hbox{-}{\rm id}_R(R)<\infty$, it is easy to see that

\[ {\rm FP}\hbox{-}{\rm id}_R(R)=\sup\{{\rm FP}\hbox{-}{\rm id}_R(M)~|~M~\text{is a flat}~R\text{-module}\}. \]

This means every flat $R$-module $F\in \mathcal {W}$. Thus, one has $P\in \mathcal {W}$, and so $P\in \mathcal {W}\cap \mathcal {GP}=\mathcal {GP}^{\perp }\cap \mathcal {GP}=\mathcal {P}$. It follows that $\alpha : P\longrightarrow F$ is also a projective cover of $F$. Therefore, $R$ is left perfect by the proof of $(3)\Rightarrow (1)$ in [Reference Enochs and Jenda11, Theorem 5.3.2].

$(6) \Rightarrow (2)$. Suppose that $R$ is left perfect. To see that the class $\mathcal {GP}$ is closed under direct limits, let $\{(G_j)_{j\in J}\}$ be a family of Gorenstein projective $R$-modules. Then for each $j\in J$, there is an exact sequence of $R$-modules

with all $P^{i}_j\in \mathcal {P}$. Hence, one can obtain an exact sequence of $R$-modules

with all $\lim \limits _{\longrightarrow } P^{i}_j\in \mathcal {P}$ since $R$ is left perfect. Thus, $\lim \limits _{\longrightarrow } G_j$ is Gorenstein projective by Corollary 3.5.

Recall that a ring $R$ is called an $n$-FC ring (resp. $n$-Gorenstein ring) if it is both left and right coherent (resp. Noether) and ${\rm FP}\hbox{-}{\rm id}_R({R})$ and ${\rm FP}\hbox{-}{\rm id}_{R^o}({R})$ (resp. ${\rm id}_R({R})$ and ${\rm id}_{R^o}({R})$) are both less than or equal to $n$. A ring $R$ is called Ding-Chen (resp. Gorenstein) if it is an $n$-FC (resp. $n$-Gorenstein) ring for some non-negative integer $n$. Ding-Chen rings are natural generalizations of Gorenstein rings.

Recall from [Reference Ding, Li and Mao10, Reference Gillespie14] that an $R$-module $M$ is called Ding projective if there exists an exact sequence

of projective $R$-modules with $M=\text {Ker}(P_0\rightarrow P_{-1})$, such that it remains exact after applying ${\rm Hom}(-,\,Q)$ for any flat $R$-module $Q$. It is clear that Ding projective modules are always Gorenstein projective, conversely, it is not known.

Let $R$ be a Ding-Chen ring. Then Gillespie [Reference Gillespie14] showed that $(\mathcal {DP},\,\mathcal {W})$ is a projective cotorsion pair, where $\mathcal {DP}$ denotes the class of Ding projective $R$-modules, and $\mathcal {W}$ denotes the class of $R$-modules of finite FP-injective dimension. Moreover, Gillespie [Reference Gillespie16, Theorem 1.1] has shown recently that the class $\mathcal {DP}$ coincides with $\mathcal {GP}$. It yields the following corollary. Meanwhile, this is obvious by Corollary 3.4 as any Ding-Chen ring $R$ satisfies $\mathrm {FFPID}(R)<\infty$ by [Reference Ding and Chen8, Proposition 3.16].

Corollary 3.7 Let $R$ be a Ding-Chen ring. Then the pair $(\mathcal {GP},\,\mathcal {W})$ forms a projective cotorsion pair, where $\mathcal {W}$ is as above.

Remark 3.8 (1) Let $R$ be a Ding-Chen ring (in particular the case for $R$ is Gorenstein). Then Corollary 3.7 shows that the class $\mathcal {GP}$ is special precovering. Applying Corollary 3.6, one gets that the class $\mathcal {GP}$ is covering if and only if $R$ is left perfect.

(2) Let $R$ be a Gorenstein ring. Then the famous “Auslander's last theorem” (see [Reference Enochs and Jenda11, Theorem 11.6.9]) tells us that every finitely generated $R$-module has a Gorenstein projective cover. However, there exists a Gorenstein ring such that not all modules have a Gorenstein projective cover. Indeed, as we all know, the ring $\mathbb {Z}$ is a commutative 1-Gorenstein ring which is not perfect. Then by (1), over $\mathbb {Z}$ the class $\mathcal {GP}$ is not covering.

The following proposition improves the Gillespie's result [Reference Gillespie16, Theorem 1.1(1)] from a Ding-Chen ring to a left coherent ring $R$ with both ${\rm FP}\hbox{-}{\rm id}_R(R)$ and $\mathrm {FFPID}(R)$ finite (see Remark 3.10 for the existence of that a left coherent ring $R$ with both ${\rm FP}\hbox{-}{\rm id}_R(R)$ and $\mathrm {FFPID}(R)$ finite may not be Ding-Chen ring).

Proposition 3.9 Let $R$ be a left coherent ring with both ${\rm FP}\hbox{-}{\rm id}_R(R)$ and $\mathrm {FFPID}(R)$ finite. Then Ding projective $R$-modules are exactly the Gorenstein projective $R$-modules, and hence are exactly some kernel of an exact complex of projective $R$-modules.

Proof. Since $R$ is a left coherent ring with ${\rm FP}\hbox{-}{\rm id}_R(R)<\infty$, it is easy to see that ${\rm FP}\hbox{-}{\rm id}_R(R)=\sup \{{\rm FP}\hbox{-}{\rm id}_R(M)~|~M~\text {is a flat}~R\text {-module}\}$. This means every flat $R$-module $F\in \mathcal {GP}^{\perp }=\mathcal {W}$ by Corollary 3.4. Therefore, it follows by [Reference Iacob20, Lemma 4] that any Gorenstein projective $R$-module is Ding projective. The last assertion follows then by Corollary 3.5.

Remark 3.10 We notice that there exists a left coherent ring $R$ with both ${\rm FP}\hbox{-}{\rm id}_R(R)$ and $\mathrm {FFPID}(R)$ finite which is not right coherent. For example, let $R_1$ be the oppositive ring of $T$, where $T=\left (\begin {smallmatrix} A & F \\ 0 & A/L \\ \end {smallmatrix}\right )$is constructed by Small [Reference Small28], in which $A$ is an algebra over a field $F$, $L$ is a left ideal of $A$ with ${\rm pd}_A(L)=1$. By virtue of [Reference Small28, Theorem 1], $T$ is a right hereditary ring with $l.\text {gldim}(T)=3$ which is not left coherent. Hence $R_1=T^o$ is a left hereditary ring (hence a left coherent ring) with ${\rm FP}\hbox{-}{\rm id}_{R_1}(R_1)\leq {\rm id}_{R_1}(R_1)\leq 1$ and $\mathrm {FFPID}(R_1)\leq 1$ which is not right coherent. In particular, $R_1$ is not a Ding-Chen ring.

Recall from [Reference Bravo, Gillespie and Hovey5] that a right $R$-module $F$ is of type FP $_\infty$ if $F$ has a projective resolution consisting of finitely generated modules, and that a left $R$-module $M$ is level if ${\rm Tor}_1^{R}(F,\,M)=0$ for all right $R$-modules $F$ of type FP$_\infty$.

Remark 3.11 We notice that there exists a left coherent ring $R$ admitting both finite left self-FP-injective dimension and finite left finitistic FP-injective dimension which is neither right coherent nor satisfies that all level left $R$-modules have finite projective dimension.

We first consider $R_2=F_{\alpha }$, the free Boolean ring on $\aleph _{\alpha }$ generators with $\alpha$ an infinite cardinality. By [Reference Wang30, Example 3.3], $R_2$ is a commutative von Neumann regular ring (hence a commutative coherent ring with ${\rm FP}\hbox{-}{\rm id}_{R_2}(R_2)=0$ and $\mathrm {FFPID}(R_2)=0$) which has infinite (Gorenstein) global dimension. Note that over a commutative von Neumann regular ring every module is flat, and that the global dimension of a commutative ring is finite if and only if every module has a finite projective dimension. These facts imply that there is a flat left $R_2$-module $M$ with infinite projective dimension. On the other hand, note from [Reference Bravo, Gillespie and Hovey5, Corollary 2.11] that, over a right coherent ring the level modules are exactly flat modules. Thus there is a level left $R_2$-module $M$ with infinite projective dimension.

Now we consider $R=R_1\times R_2$, the product ring of $R_1$ and $R_2$, where $R_1$ is as in Remark 3.10. Then $R$ admits both finite left self-FP-injective dimension and finite left finitistic FP-injective dimension since so do $R_1$ and $R_2$. However, $R$ is neither right coherent nor satisfies that all level left $R$-modules have finite projective dimension since $R_1$ is not right coherent and $R_2$ does not satisfy that all level left $R_2$-modules have finite projective dimension.

As mentioned above, whether the pair $(\mathcal {GP},\,\mathcal {GP}^{\perp })$ forms a complete and hereditary cotorsion pair over any associative ring is still open. It is known that over a (commutative) Gorenstein ring the answer of the question is affirmative (see [Reference Enochs and Jenda11, Remark 11.5.10]). Later, many authors extended the result to a more general ring:

  1. (1) For the commutative settings, it is extended to the commutative Noether rings with a dualizing complex or with finite Krull dimension (see [Reference Jørgensen21, Proposition 1.9, Theorem 1.0 and Corollary 2.13]).

  2. (2) For the possibly not commutative settings, it is extended to the following:

  1. (C1) rings such that any level module has a finite projective dimension (see [Reference Gillespie15, Fact 10.2]). Note that such class of rings contains right coherent rings such that any flat module has a finite projective dimension (see [Reference Gillespie15, Fact 10.2]) and hence contains commutative Noether rings with a dualizing complex or with finite Krull dimension.

  2. (C2) rings such that any projective module has a finite injective dimension (see [Reference Wang and Liang31, Theorem 4.2]). Note that such class of rings contains rings with finite left Gorenstein global dimension.

  3. (C3) left coherent rings $R$ such that $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\}<\infty$ (see Corollary 3.4). Note that such class of rings contains strictly Ding-Chen rings (see Remark 3.10).

We end this section by pointing out that the classes of rings in (C1) (resp. (C2))and (C3) above are independent to each other as shown by the following remarks.

Remark 3.12 Let $R_2=F_{\alpha }$ be the free Boolean ring on $\aleph _{\alpha }$ generators with $\alpha$ an infinite cardinality, as in Remark 3.11. Then, $R_2$ is in the class (C3) but not in the class (C1). Furthermore, $R_2$ admits infinite Gorenstein global dimension. it follows by Theorem 4.4 (in § 3) that there exists a projective left $R$-module $M$ with ${\rm id}_R(M)=\infty$. In other words, $R_2$ is not in the class (C2).

Remark 3.13 There exists a commutative ring $R$ with finite global dimension (hence $R$ is in both the classes (C1) and (C2)) which is not coherent, see [Reference Kirkman and Kuzmanovich22, Example in p.128]. Thus, $R$ is not in the class (C3).

Remark 3.14 There exists a commutative Noether ring $R$ with finite Krull dimension (so $R$ is a commutative coherent ring with $\sup \{{\rm pd}_R(M) |~M~\text {is a level}~R\text {-module}\}$ $<\infty$, that is, $R$ is in the class (C1)) which is not Gorenstein. Note that a commutative Noether ring $R$ is Gorenstein if and only if ${\rm FP}\hbox{-}{\rm id}_R(R)={\rm id}_R(R)<\infty$ by the definition, equivalently, if and only if all projective $R$-modules have finite injective dimension (see [Reference Enochs and Jenda11, Theorem 9.1.11]). These facts imply that $R$ is neither in the class (C2) nor in the class (C3).

Remark 3.14 shows that rings in (C1) may not be in (C2). Besides, we know from Lemma 4.3 (in § 3) that any ring in (C2) satisfies that all flat modules have finite projective dimension. So we pose a question below:

Question 3.15 Does the class (C1) strictly contain the class (C2)?

4. Gorenstein global dimensions of coherent rings

As another application of Theorem 3.3, we will characterize Gorenstein global dimensions for left coherent rings.

For a ring $R$, the invariant $\mathrm {silffpi}(R)$ is defined as the supremum of the injective dimensions of $R$-modules with finite FP-injective dimension; the invariant $\mathrm {splfpi}(R)$ is defined as the supremum of the projective dimensions of FP-injective $R$-modules.

It is proved by Bennis and Mahdou [Reference Bennis and Mahdou2, Theorem 1.1] that the equality

\[ \text{sup}\{\text{Gpd}_R(M) \ | \ M \text{ is an }R\text{-module}\}=\text{sup}\{\text{Gid}_R(M) \ | \ M \text{ is an}~R~\text{-module}\} \]

holds. Bennis and Mahdou call the common value of the equality the left Gorenstein global dimension of $R$ and denote it by $l.\text {Ggldim}(R)$.

Proposition 4.1 The following quantities are equal to each other whenever $R$ is a left coherent ring.

  1. (1) $l.\text {Ggldim}(R)$.

  2. (2) $\max \{\mathrm {silffpi}(R),\,{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\}$.

  3. (3) $\max \{\mathrm {splfpi}(R),\,{\rm FP}\hbox{-}{\rm id}_R(R),\,\mathrm {FFPID}(R)\}$.

Proof. Assume $l.\text {Ggldim}(R)=n<\infty$. Then by [Reference Bennis and Mahdou2, Corollary 2.7], the regular module $_RR$ has a finite injective dimension at most $n$, and of course ${\rm FP}\hbox{-}{\rm id}_R(R)\leq n$. Now let $E$ be an FP-injective $R$-module. Then we have a pure short exact sequence of $R$-modules

with $I$ injective. Since ${\rm fd}_R(I)\leq n$ by [Reference Bennis and Mahdou2, Corollary 2.7], one has ${\rm fd}_R(E)\leq n$. Thus one can deduce easily that any $R$-module with finite FP-injective dimension has flat dimension at most $n$. It follows again from [Reference Bennis and Mahdou2, Corollary 2.7] that any $R$-module with finite FP-injective dimension has both injective dimension and projective dimension at most $n$. This means $\mathrm {silffpi}(R)\leq n$ and $\mathrm {splfpi}(R)\leq n$, and also $\mathrm {FFPID}(R)\leq n$. Thus we have shown that $\max \{\mathrm {silffpi}(R),\,{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\}\leq l.\text {Ggldim}(R)$, and $\max \{\mathrm {splfpi}(R),\,{\rm FP}\hbox{-}{\rm id}_R(R),\,\mathrm {FFPID}(R)\}\leq l.\text {Ggldim}(R)$.

In the next, we show that $l.\text {Ggldim}(R)\leq \max \{\mathrm {silffpi}(R),\,{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\}$. Suppose $\max \{\mathrm {silffpi}(R),\,{\rm FP}\hbox{-}{\rm id}_R(R),\,\mathrm {FFPID}(R)\}=n<\infty$. By Theorem 3.3 and $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\,\mathrm {FFPID}(R)\}\leq n$ one has a projective cotorsion pair $(\mathcal {GP},\,\mathcal {FI}_n)$. For any $R$-module $M$, there is an exact sequence of $R$-modules

with each $P_i$ projective. Then by dimension shifting, one gets

\[ {\rm Ext}_R^{1}(K,E)\cong{\rm Ext}_R^{n+1}(M,E) \]

for any $R$-module $E$ with ${\rm FP}\hbox{-}{\rm id}_R(E)\leq n$. But ${\rm Ext}_R^{n+1}(M,\, E)=0$ as $\mathrm {silffpi}(R)\leq n$. Thus, ${\rm Ext}_R^{1}(K,\, E)=0$ for any $R$-module $E$ with ${\rm FP}\hbox{-}{\rm id}_R(E)\leq n$. It follows that $K$ is Gorenstein projective since $(\mathcal {GP},\,\mathcal {FI}_n)$ is a cotorsion pair. Therefore, $M$ has a finite Gorenstein projective dimension at most $n$, as desired.

In the last, we show that $l.\text {Ggldim}(R)\leq \max \{\mathrm {splfpi}(R),\,{\rm FP}\hbox{-}{\rm id}_R(_RR),\, \mathrm {FFPID}(R)\}$. Now suppose $\max \{\mathrm {splfpi}(R),\,{\rm FP}\hbox{-}{\rm id}_R(R),\, \mathrm {FFPID}(R)\}=n<\infty$. Again, by Theorem 3.3 and $\max \{{\rm FP}\hbox{-}{\rm id}_R(R),\,\mathrm {FFPID}(R)\}\leq n$ one obtains a projective cotorsion pair $(\mathcal {GP},\,\mathcal {FI}_n)$. Thus, for any $R$-module $M$, there is a short exact sequence

of $R$-modules with $G$ Gorenstein projective and $N\in \mathcal {FI}_n$. Since $\mathrm {splfpi}(R)\leq n$, it is a routine to see that ${\rm pd}_R(N)\leq n$, and hence, it is a routine to check that $M$ has Gorenstein projective dimension at most $n$, as desired.

Let $R$ be a ring. Then the invariant $\mathrm {silp}(R)$ (respectively, $\mathrm {silf}(R)$) is defined as the supremum of the injective dimensions of projective (respectively, flat) $R$-modules. The invariant $\mathrm {splf}(R)$ is defined as the supremum of the projective dimensions of flat $R$-modules.

Corollary 4.2 Let $R$ be a Ding-Chen ring. Then the following invariants of $R$ coincide with each other.

  1. (1) $l.\text {Ggldim}(R)$.

  2. (2) $\mathrm {silffpi}(R)$.

  3. (3) $\mathrm {splfpi}(R)$.

  4. (4) $\mathrm {splf}(R)$.

  5. (5) $\mathrm {silf}(R)$.

  6. (6) $\mathrm {silp}(R)$.

Proof. Since $R$ is Ding-Chen, [Reference Ding and Chen8, Proposition 3.6] yields $\mathrm {FFPID}(R)<\infty$. Now the quantities (1), (2) and (3) are equal by Proposition 4.1. The quantities (5) and (6) are equal by [Reference Christensen, Foxby and Holm7, Execise 8.5.19], which tells us that $\mathrm {silf}(R)=\mathrm {silp}(R)$ for any ring $R$. Finally, (2)$=$(5) and (3)$=$(4) follow by [Reference Ding and Chen8, Proposition 3.16].

As mentioned in the proof of Corollary 4.2, it is known from [Reference Christensen, Foxby and Holm7, Execise 8.5.19] that $\mathrm {silf}(R)=\mathrm {silp}(R)$ for any ring $R$. In particular, $\mathrm {silf}(R)<\infty$ if and only if $\mathrm {silp}(R)<\infty$. Furthermore, in this case one also gets that $\mathrm {FPD}(R)<\infty$ by [Reference Christensen, Foxby and Holm7, Execise 8.5.14], where $\mathrm {FPD}(R)$ is defined as the supremum of the projective dimensions of all $R$-modules with finite projective dimension.

The next lemma can be viewed as a continuation of these facts.

Lemma 4.3 Let $R$ be a ring. Then the following are equivalent:

  1. (1) Every flat $R$-module has a finite injective dimension.

  2. (2) Every projective $R$-module has a finite injective dimension.

Moreover, $\mathrm {FPD}(R)<\infty$ holds if any one of the above conditions is satisfied.

Proof. $(1)\Rightarrow (2)$ is obvious.

$(2)\Rightarrow (1)$. Assume that every projective $R$-module has a finite injective dimension. Then one gets easily that any $R$-module of finite projective dimension has finite injective dimension. Since $\mathrm {FPD}(R)<\infty$ implies that any flat $R$-module has a finite projective dimension by [Reference Christensen, Foxby and Holm7, Theorem 8.5.17], we need only to show $\mathrm {FPD}(R)<\infty$.

Firstly, we claim that for any $R$-module with ${\rm pd}_R(M)=m<\infty$ and any $R$-module $N$ with a projective presentation $0\to K_N\to P_N\to N\to 0$, there is an inequality $m\leq {\rm id}_R(P_N)$. Otherwise, let $m> {\rm id}_R(P_N)$. Consider the following exact sequence of Abel groups

Note that ${\rm Ext}_R^{m}(M,\,P_N)=0$ as ${\rm id}_R(P_N)< m$, and ${\rm Ext}_R^{m+1}(M,\,K_N)=0$ as ${\rm pd}_R(M)=m$. Hence, one has ${\rm Ext}_R^{m}(M,\,N)=0$, which shows that ${\rm pd}_R(M)< m$, it is a contradiction with ${\rm pd}_R(M)=m$.

Now we prove that $\mathrm {FPD}(R)<\infty$. If $\mathrm {FPD}(R)=\infty$, then for each $n\in \mathbb {N}$, there exists an $R$-module $M_n$ with ${\rm pd}_R(M_n)<\infty$ but ${\rm pd}_R(M_n)\geq n$. Then ${\rm pd}_R(\coprod _{n\in \mathbb {N}}M_n)=\sup \{{\rm pd}_R(M_n)~|~n\in \mathbb {N}\}=\infty.$ For each $n\in \mathbb {N}$, there is a short exact sequence of $R$-modules $0\to K_n\to P_n \to M_n \to 0$ with $P_n$ projective. This induces a projective presentation of $\coprod _{n\in \mathbb {N}}M_n$ of the form

So, by the above claim, we conclude that ${\rm id}_R(\coprod _{n\in \mathbb {N}}P_n)\geq {\rm pd}_R(\coprod _{n\in \mathbb {N}}M_n)=\infty$. This is a contradiction with the assumption as $\coprod _{n\in \mathbb {N}}P_n$ is projective. Therefore, $\mathrm {FPD}(R)<\infty$, and the proof is completed.

Now we can give some characterizations of when the left Gorenstein global dimension of a Ding-Chen ring is finite.

Theorem 4.4 Let $R$ be a Ding-Chen ring. Then the following are equivalent:

  1. (1) $l.\text {Ggldim}(R)<\infty$.

  2. (2) $\mathrm {silffpi}(R)<\infty$.

  3. (3) $\mathrm {splfpi}(R)<\infty$.

  4. (4) $\mathrm {splf}(R)<\infty$.

  5. (5) $\mathrm {silf}(R)<\infty$.

  6. (6) $\mathrm {silp}(R)<\infty$.

  7. (7) Every FP-injective $R$-module has finite injective dimension.

  8. (8) Every FP-injective $R$-module has a finite projective dimension.

  9. (9) Every flat $R$-module has a finite projective dimension.

  10. (10) Every flat $R$-module has finite injective dimension.

  11. (11) Every projective $R$-module has finite injective dimension.

  12. (12) $\mathrm {FPD}(R)<\infty$.

Proof. (1)–(6) are equivalent by Corollary 4.2. $(2)\Rightarrow (7)$, $(3)\Rightarrow (8)$, $(4)\Rightarrow (9)$, $(5)\Rightarrow (10)$, and $(6)\Rightarrow (11)$ are trivial.

$(7)\Rightarrow (2)$. Assume that every FP-injective $R$-module has finite injective dimension. Then there must exist an integer $m$ such that ${\rm id}_R(M)\leq m$ for any FP-injective module $M$. Otherwise, for each positive integer $i$ there is an FP-injective module $M_i$ with $i<{\rm id}_R(M_i)<\infty$, then $\prod M_i$ is an FP-injective module of infinite injective dimension. This is a contradiction. Now one gets easily that $\mathrm {silffpi}(R)<\infty$, since $R$ is Ding-Chen.

Similar arguments applied, one can show that $(8)\Rightarrow (3)$, $(9)\Rightarrow (4)$, and $(10)\Rightarrow (5)$ hold. Now we obtain that 1)-(10) are equivalent.

Finally, (10)$\Leftrightarrow$(11)$\Rightarrow$(12) follows from Lemma 4.3 and (12)$\Rightarrow$(9) holds by [Reference Christensen, Foxby and Holm7, Theorem 8.5.17].

Acknowledgements

The authors thank the referee for his/her careful reading and many considerable suggestions, which have improved the present paper.

The work is partly supported by NSF of China (Grant Nos. 12161049; 12061061; 11861105), NSF of Gansu Province (Grant Nos. 21JR7RA295; 21JR7RA297; 21JR7RA127), and the Foundation of A Hundred Youth Talents Training Program of Lanzhou Jiaotong University, as well as a grant from Northwest Normal University (Grant No. NWNULKQN2019-14).

Competing interests

The authors declare none.

References

Auslander, M. and Bridger, M., Stable module theory, Mem. Amer. Math. Soc. Volume 94 (American Mathematical Society, Providence, RI, 1969).CrossRefGoogle Scholar
Bennis, D. and Mahdou, N., Global Gorenstein dimensions, Proc. Amer. Math. Soc. 138(2) (2010), 461–465.Google Scholar
Bican, L., El Bashir, R. and Enochs, E. E., All modules have flat covers, Bull. Lond. Math. Soc. 33 (2001), 385–390.CrossRefGoogle Scholar
Bouchiba, S., On Gorenstein flat dimension, J. Algebra Appl. 14 (2015), 1550096.CrossRefGoogle Scholar
Bravo, D., Gillespie, J. and Hovey, M., The stable module category of a general ring, arXiv:1405.5768Google Scholar
Christensen, L. W., Frankild, A. and Holm, H., On Gorenstein projective, injective and flat dimensions – a functorial description with applications, J.Algebra 302 (2006), 231–279.CrossRefGoogle Scholar
Christensen, L. W., Foxby, H-B. and Holm, H., Derived category methods in commutative algebra, preprint, 2022.Google Scholar
Ding, N. Q. and Chen, J. L., The flat dimension of injective modules, Manuscritpa Math. 78 (1993), 165–177.CrossRefGoogle Scholar
Enochs, E. E. and Jenda, O. M. G., Gorenstein injective and projective modules, Math. Z. 220 (1995), 611–633.CrossRefGoogle Scholar
Ding, N. Q., Li, Y. L. and Mao, L. X., Strongly Gorenstein flat modules, J. Aust. Math. Soc. 86 (2009), 323–338.CrossRefGoogle Scholar
Enochs, E. E. and Jenda, O. M. G., Relative homological algebra, In de Gruyter Expositions in Mathematics, Volume 30 (Walter de Gruyter and Co, Berlin, 2000).CrossRefGoogle Scholar
Enochs, E. E., Jenda, O. M. G. and Torrecillas, B., Gorenstein flat modules, Nanjing Daxue Xuebao Shuxue Bannian Kan 10 (1993), 1–9.Google Scholar
Enochs, E. E. and Lépez-Ramos, J. A., Gorenstein flat modules (Nova Science Publishers Inc., New York, 2001).Google Scholar
Gillespie, J., Model Structures on Modules over Ding-Chen rings, Homology Homology Appl. 12 (2010), 61–73.Google Scholar
Gillespie, J., Gorenstein complexes and recollements from cotorsion pairs, Adv. Math. 291 (2016), 859–911.CrossRefGoogle Scholar
Gillespie, J., On Ding injective, Ding projective and Ding flat modules and complexes, Rocky Mountain J. Math. 47(8) (2017), 2641–2673.Google Scholar
Holm, H., Gorenstein projective, injective and flat modules, MSc Thesis, Institute for Mathematical Sciences (University of Copenhagen 2000).Google Scholar
Holm, H., Rings with finite Gorenstein injective dimension, Proc. Amer. Math. Soc. 132 (2004), 1279–1283.CrossRefGoogle Scholar
Holm, H., Gorenstein homological dimensions, J. Pure Appl. Algebra 189 (2004), 167–193.CrossRefGoogle Scholar
Iacob, A., Projectively coresolved Gorenstein flat and Ding projective modules, Comm. Algebra 48 (2020), 2883–2893.CrossRefGoogle Scholar
Jørgensen, P., Existence of Gorenstein projective resolutions and Tate cohomology, J. Eur. Math. Soc. 9(1) (2007), 59–76.CrossRefGoogle Scholar
Kirkman, E. and Kuzmanovich, J., On the global dimension of fibre products, Pacific J. Math. 134 (1988), 121–132.CrossRefGoogle Scholar
Krause, H., The stable derived category of a Noetherian scheme, Compos. Math. 141 (2005), 1128–1162.Google Scholar
Mao, L. X. and Ding, N. Q., Envelopes and covers by modules of finite FP-injective and flat dimensions, Comm. Algebra 35 (2007), 833–849.CrossRefGoogle Scholar
Murfet, D. and Salarian, S., Totally acyclic complexes over Noetherian schemes, Adv. Math. 226(2) (2011), 1096–1133.CrossRefGoogle Scholar
Salce, L., Cotorsion theories for abelian groups. Symposia Math. Volume 23 (1979).Google Scholar
Šaroch, J. and Št'ovíček, J., Singular compactness and definability for $\Sigma$-cotorsion and Gorenstein modules, Sel. Math. 26 (2020), 23.Google Scholar
Small, L. W., Hereditary rings, Proc. Amer. Math. Soc. 1(55) (1966), 25–27.Google Scholar
Stenström, B., Coherent rings and FP-injective modules, J. Lond. Math. Soc. 2(2) (1970), 323–329.CrossRefGoogle Scholar
Wang, J. P., Ding projective dimension of Gorenstein flat modules, Bull. Korean Math. Soc. 54 (2017), 1935–1950.Google Scholar
Wang, J. and Liang, L., A characterization of Gorenstein projective modules, Comm. Algebra 44 (2016), 1420–1432.CrossRefGoogle Scholar
Yang, G. and Liang, L., All modules have Gorenstein flat precovers, Comm. Algebra 42 (2014), 3078–3085.CrossRefGoogle Scholar