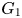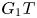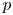1. Introduction
Let $G= SL_{n+1}$![]() with $n\geq 1$
with $n\geq 1$![]() be defined over an algebraically closed field $\Bbbk$
be defined over an algebraically closed field $\Bbbk$![]() of characteristic $p > 2$
of characteristic $p > 2$![]() . We will also assume that $p$
. We will also assume that $p$![]() is a very good prime for $G$
is a very good prime for $G$![]() (i.e. $p\nmid n+1$
(i.e. $p\nmid n+1$![]() for $SL_{n+1}$
for $SL_{n+1}$![]() ). The setting of this paper is centered around the representation theory of the subgroups $G_1$
). The setting of this paper is centered around the representation theory of the subgroups $G_1$![]() and $G_1T$
and $G_1T$![]() , where $G_1$
, where $G_1$![]() is the Frobenius kernel and $T\subseteq G$
is the Frobenius kernel and $T\subseteq G$![]() is the subgroup of diagonal matrices. More specifically, we will focus on an important class of representations known as the baby Verma modules. These are certain finite-dimensional representations, which are highly analogous to the ‘classical’ Verma modules for complex semisimple Lie algebras. We are also interested in an important invariant known as the Loewy series (or the radical series) of a module. The invariant provides a significant amount of information on the submodule structure of a representation but is often impractical to compute.
is the subgroup of diagonal matrices. More specifically, we will focus on an important class of representations known as the baby Verma modules. These are certain finite-dimensional representations, which are highly analogous to the ‘classical’ Verma modules for complex semisimple Lie algebras. We are also interested in an important invariant known as the Loewy series (or the radical series) of a module. The invariant provides a significant amount of information on the submodule structure of a representation but is often impractical to compute.
Determining the Loewy series of baby Verma modules for $G_1T$![]() has been a particularly important topic in the history of representation theory for algebraic groups. Major progress was first made in the 1990s, when Andersen, Jantzen, and Soergel demonstrated that for $p \gg 0$
has been a particularly important topic in the history of representation theory for algebraic groups. Major progress was first made in the 1990s, when Andersen, Jantzen, and Soergel demonstrated that for $p \gg 0$![]() , the Loewy series of any baby Verma module whose highest weight is $p$
, the Loewy series of any baby Verma module whose highest weight is $p$![]() -regular can be expressed in terms of the periodic Kazhdan–Lusztig basis (see [Reference Andersen, Jantzen and Soergel4]). Recently, Abe and Kaneda in [Reference Abe and Kaneda1], building on a 2010 result by Riche [Reference Riche9], were able to extend these results to include baby Verma modules of any highest weight. Their methods depend on the validity of Lusztig's character formula, as well as some additional assumptions from [Reference Riche9] (see [Reference Abe and Kaneda1, Theorem, p. 2]). Unfortunately, by the well-known result of Williamson [Reference Williamson11], these character formulas are often only valid for extremely large primes. It is also worth mentioning that the periodic Kazhdan–Lusztig basis is highly difficult to compute. So even in the case where $p$
-regular can be expressed in terms of the periodic Kazhdan–Lusztig basis (see [Reference Andersen, Jantzen and Soergel4]). Recently, Abe and Kaneda in [Reference Abe and Kaneda1], building on a 2010 result by Riche [Reference Riche9], were able to extend these results to include baby Verma modules of any highest weight. Their methods depend on the validity of Lusztig's character formula, as well as some additional assumptions from [Reference Riche9] (see [Reference Abe and Kaneda1, Theorem, p. 2]). Unfortunately, by the well-known result of Williamson [Reference Williamson11], these character formulas are often only valid for extremely large primes. It is also worth mentioning that the periodic Kazhdan–Lusztig basis is highly difficult to compute. So even in the case where $p$![]() is sufficiently large, it remains challenging to obtain precise information with these methods.
is sufficiently large, it remains challenging to obtain precise information with these methods.
In this article, we take a more specialized approach and restrict ourselves to a particular subcategory of $G_1T$![]() -modules, which is related to an interesting singular block of $G_1$
-modules, which is related to an interesting singular block of $G_1$![]() (see (2.12) for an explicit definition). The most significant result is Theorem 6.3 which gives precise formulas for the Loewy series of every baby Verma module in this subcategory. A key consequence is that these baby Verma modules are rigid (see Proposition 6.5). Our formulas are independent of $p$
(see (2.12) for an explicit definition). The most significant result is Theorem 6.3 which gives precise formulas for the Loewy series of every baby Verma module in this subcategory. A key consequence is that these baby Verma modules are rigid (see Proposition 6.5). Our formulas are independent of $p$![]() , and thus agree with the results of [Reference Abe and Kaneda1], but our techniques differ considerably from loc. cit. Another major result is Theorem 5.1, which gives a complete determination of the extensions between the irreducible objects. Amazingly, we are able to prove all of these results under the mild assumption that $p$
, and thus agree with the results of [Reference Abe and Kaneda1], but our techniques differ considerably from loc. cit. Another major result is Theorem 5.1, which gives a complete determination of the extensions between the irreducible objects. Amazingly, we are able to prove all of these results under the mild assumption that $p$![]() is very good.
is very good.
Finally, in §7, we impose an additional condition on $p$![]() which is known to hold when $p$
which is known to hold when $p$![]() is extremely large (see Remark 7.2). In this case, our methods also lead to an explicit description of the Loewy series for every indecomposable projective module in Theorem 7.3. The strategy of our proof involves combining our baby Verma calculations with the results of [Reference Abe and Kaneda1] and by adapting the techniques from [Reference Andersen and Kaneda3] over to our setting.
is extremely large (see Remark 7.2). In this case, our methods also lead to an explicit description of the Loewy series for every indecomposable projective module in Theorem 7.3. The strategy of our proof involves combining our baby Verma calculations with the results of [Reference Abe and Kaneda1] and by adapting the techniques from [Reference Andersen and Kaneda3] over to our setting.
To the author's best knowledge, this paper gives the first known example of an infinite family of non-trivial singular blocks for $G_1T$![]() with $G = SL_{n+1}$
with $G = SL_{n+1}$![]() (as $n\geq 1$
(as $n\geq 1$![]() varies), in which [Reference Abe and Kaneda1, Theorem, p. 2] holds for ‘reasonable’ primes.Footnote 1 By contrast, recall from [Reference Williamson11] that if we consider the corresponding family of principal blocks and let $p(n)$
varies), in which [Reference Abe and Kaneda1, Theorem, p. 2] holds for ‘reasonable’ primes.Footnote 1 By contrast, recall from [Reference Williamson11] that if we consider the corresponding family of principal blocks and let $p(n)$![]() be the minimal prime for each $n$
be the minimal prime for each $n$![]() such that [Reference Abe and Kaneda1, Theorem, p. 2] holds, then the growth rate of the function $p(n)$
such that [Reference Abe and Kaneda1, Theorem, p. 2] holds, then the growth rate of the function $p(n)$![]() is actually non-polynomial (see [Reference Fiebig5] for an explicit upper bound to $p(n)$
is actually non-polynomial (see [Reference Fiebig5] for an explicit upper bound to $p(n)$![]() ).
).
As a consequence, we can see that even though the principal block is often poorly behaved for smaller primes, there can still exist interesting singular blocks which are well behaved under milder assumptions on the characteristic. These kinds of blocks have also been the subject of a recent preprint [Reference Nandakumar and Zhao8], where the authors studied a family of singular $G_1$![]() -blocks occurring in a categorified $\mathfrak {sl}_2(\mathbb {C})$
-blocks occurring in a categorified $\mathfrak {sl}_2(\mathbb {C})$![]() representation.
representation.
The case of general linear groups: It is important to note that the results of this paper can be adapted to the case where $G = GL_{n+1}$![]() (see Remark 2.3). Moreover, since all primes are very good for $GL_{n+1}$
(see Remark 2.3). Moreover, since all primes are very good for $GL_{n+1}$![]() , it should also be straightforward to check that all of our results from §2 to §6 extend to every odd $p$
, it should also be straightforward to check that all of our results from §2 to §6 extend to every odd $p$![]() in this situation.
in this situation.
2. Notation and preliminaries
Maintaining the same assumptions as in the introduction, we let $B \subseteq G$![]() denote the Borel subgroup consisting of lower triangular matrices. The weight lattice of $G$
denote the Borel subgroup consisting of lower triangular matrices. The weight lattice of $G$![]() is given by
is given by
where $e_1,\ldots, e_{n+1}$![]() are standard basis vectors. Set $\epsilon _i = \overline {e_i} \in \mathbf {X}$
are standard basis vectors. Set $\epsilon _i = \overline {e_i} \in \mathbf {X}$![]() for $i=1,\ldots, n+1$
for $i=1,\ldots, n+1$![]() , and let $\varpi _i = \epsilon _1 + \cdots +\epsilon _i$
, and let $\varpi _i = \epsilon _1 + \cdots +\epsilon _i$![]() for $i=1,\ldots, n$
for $i=1,\ldots, n$![]() be the fundamental weights. The root system is given by
be the fundamental weights. The root system is given by
We take
to be the set of positive roots with basis
We will set $\alpha _i = \epsilon _i-\epsilon _{i+1}$![]() for $i = 1,\ldots, n$
for $i = 1,\ldots, n$![]() .
.
The Weyl group is $W = \Sigma _{n+1}$![]() (the group of permutations on $n+1$
(the group of permutations on $n+1$![]() letters), and its action on $\mathbf {X}$
letters), and its action on $\mathbf {X}$![]() is induced by the natural action of permuting coordinates. The longest element $w_0 \in W$
is induced by the natural action of permuting coordinates. The longest element $w_0 \in W$![]() is the permutation given by
is the permutation given by
for $i=1,\ldots, n+1$![]() .
.
The affine Weyl group is given by
where $\mathbb {Z}\varPhi$![]() acts on $\mathbf {X}$
acts on $\mathbf {X}$![]() by translations (and hence $p\mathbb {Z}\varPhi$
by translations (and hence $p\mathbb {Z}\varPhi$![]() acts by translations of elements in $p\mathbb {Z}\varPhi \subset \mathbb {Z}\varPhi$
acts by translations of elements in $p\mathbb {Z}\varPhi \subset \mathbb {Z}\varPhi$![]() ). We similarly define the extended affine Weyl group
). We similarly define the extended affine Weyl group
As usual, we set $\rho = \frac {1}{2}\sum _{\alpha \in \varPhi ^{+}} \alpha$![]() and define the dot action of ${W_{\mathrm {p}}}$
and define the dot action of ${W_{\mathrm {p}}}$![]() (or ${W^{\mathrm {ext}}_{\mathrm {p}}}$
(or ${W^{\mathrm {ext}}_{\mathrm {p}}}$![]() ) on $\mathbf {X}$
) on $\mathbf {X}$![]() by $w\cdot \lambda = w(\lambda +\rho ) - \rho$
by $w\cdot \lambda = w(\lambda +\rho ) - \rho$![]() for any $w \in {W_{\mathrm {p}}}$
for any $w \in {W_{\mathrm {p}}}$![]() (or ${W^{\mathrm {ext}}_{\mathrm {p}}}$
(or ${W^{\mathrm {ext}}_{\mathrm {p}}}$![]() ) and $\lambda \in \mathbf {X}$
) and $\lambda \in \mathbf {X}$![]() . This extends to an action on $\mathbf {X} \otimes \mathbb {R}$
. This extends to an action on $\mathbf {X} \otimes \mathbb {R}$![]() and defines a system of facets for $\mathbf {X} \otimes \mathbb {R}$
and defines a system of facets for $\mathbf {X} \otimes \mathbb {R}$![]() .
.
For any group scheme $H$![]() , let $\mathsf {Rep}(H)$
, let $\mathsf {Rep}(H)$![]() denote the category of finite-dimensional $H$
denote the category of finite-dimensional $H$![]() -modules, and let $\mathcal {K}(H)$
-modules, and let $\mathcal {K}(H)$![]() denote the Grothendieck group. For an $H$
denote the Grothendieck group. For an $H$![]() -module $M$
-module $M$![]() , let $[M] \in \mathcal {K}(H)$
, let $[M] \in \mathcal {K}(H)$![]() denote its class, and for an $H$
denote its class, and for an $H$![]() -module $N$
-module $N$![]() , take $[M] \leq [N]$
, take $[M] \leq [N]$![]() to mean ${[M:\mathsf {L}] \leq [N:L]}$
to mean ${[M:\mathsf {L}] \leq [N:L]}$![]() for every irreducible $H$
for every irreducible $H$![]() -module $\mathsf {L}$
-module $\mathsf {L}$![]() (where $[M:\mathsf {L}]$
(where $[M:\mathsf {L}]$![]() is the multiplicity of $\mathsf {L}$
is the multiplicity of $\mathsf {L}$![]() in any Jordan–Hölder filtration). In particular, the class of any $H$
in any Jordan–Hölder filtration). In particular, the class of any $H$![]() -module $M$
-module $M$![]() has the unique expansion
has the unique expansion
where $\mathrm {Irr}(H)$![]() denotes the set of (isomorphism classes of) irreducible representations.
denotes the set of (isomorphism classes of) irreducible representations.
The radical of an $H$![]() -module $M$
-module $M$![]() , denoted $\text {rad}\, M$
, denoted $\text {rad}\, M$![]() , is defined to be the intersection of all maximal submodules of $M$
, is defined to be the intersection of all maximal submodules of $M$![]() . For $i\geq 0$
. For $i\geq 0$![]() , $\text {rad}^{i}\,M$
, $\text {rad}^{i}\,M$![]() is given by
is given by

The $i^{th}$![]() -radical layer of $M$
-radical layer of $M$![]() is given by
is given by
Similarly, let $\text {soc}\, M$![]() denote the socle of $M$
denote the socle of $M$![]() , which is the sum of all simple submodules of $M$
, which is the sum of all simple submodules of $M$![]() . For $i\geq 0$
. For $i\geq 0$![]() , $\text {soc}^{i}\, M$
, $\text {soc}^{i}\, M$![]() is given by
is given by

The $i^{th}$![]() -socle layer is the subquotient
-socle layer is the subquotient
We will also set
for $i\geq 0$![]() . Observe that $\text {cap}^{1}\, M = \overline {\text {rad}}_0(M)$
. Observe that $\text {cap}^{1}\, M = \overline {\text {rad}}_0(M)$![]() , this is often called the head of $M$
, this is often called the head of $M$![]() .
.
Suppose $N\subseteq M$![]() is any submodule, then it is easy to verify that for $i\geq 0$
is any submodule, then it is easy to verify that for $i\geq 0$![]() ,
,
In particular, if $\pi : M \twoheadrightarrow M'$![]() is a surjection, then $\pi (\text {rad}^{i}\,M) = \text {rad}^{i}\, M'$
is a surjection, then $\pi (\text {rad}^{i}\,M) = \text {rad}^{i}\, M'$![]() .
.
The Loewy length of $M$![]() is defined to be the smallest integer $r\geq 0$
is defined to be the smallest integer $r\geq 0$![]() such that $\text {rad}^{r}(M) = 0$
such that $\text {rad}^{r}(M) = 0$![]() (or equivalently $\text {soc}^{r}\, M = M$
(or equivalently $\text {soc}^{r}\, M = M$![]() ); we will denote this by $\ell \ell (M)$
); we will denote this by $\ell \ell (M)$![]() (see [Reference Jantzen7, II.D.1]). For all $0 \leq i \leq \ell \ell (M)$
(see [Reference Jantzen7, II.D.1]). For all $0 \leq i \leq \ell \ell (M)$![]() ,
,
The module $M$![]() is said to be rigid whenever equality holds for all $i$
is said to be rigid whenever equality holds for all $i$![]() (see [Reference Andersen and Kaneda3, (4)] or [Reference Jantzen7, D.9]).
(see [Reference Andersen and Kaneda3, (4)] or [Reference Jantzen7, D.9]).
Another useful observation is that if $\pi : M \twoheadrightarrow M'$![]() is surjective and $\ell \ell (M') = r$
is surjective and $\ell \ell (M') = r$![]() , then there is an induced surjection
, then there is an induced surjection
(Equivalently, any surjective map from $M$![]() to a module of Loewy length $r$
to a module of Loewy length $r$![]() factors through $\text {cap}^{r}\, M$
factors through $\text {cap}^{r}\, M$![]() .)
.)
Remark 2.1 If $M$![]() is a $G_1T$
is a $G_1T$![]() -module, then
-module, then
So in particular, $\ell \ell (M) = \ell \ell (M|_{G_1})$![]() .
.
The irreducible representations of $G_1$![]() are indexed by the set of $p$
are indexed by the set of $p$![]() -restricted weights $\mathbf {X}_1 = \{ \sum a_i\varpi _i \mid 0\leq a_i < p\}$
-restricted weights $\mathbf {X}_1 = \{ \sum a_i\varpi _i \mid 0\leq a_i < p\}$![]() and will be denoted by $\mathsf {L}(\lambda )$
and will be denoted by $\mathsf {L}(\lambda )$![]() for $\lambda \in \mathbf {X}_1$
for $\lambda \in \mathbf {X}_1$![]() . The irreducible representations of $G_1T$
. The irreducible representations of $G_1T$![]() will be denoted by $\widehat {\mathsf {L}}(\lambda )$
will be denoted by $\widehat {\mathsf {L}}(\lambda )$![]() for all $\lambda \in \mathbf {X}$
for all $\lambda \in \mathbf {X}$![]() , where we recall that if we write $\lambda = \mu + p\nu$
, where we recall that if we write $\lambda = \mu + p\nu$![]() for some $\mu \in \mathbf {X}_1$
for some $\mu \in \mathbf {X}_1$![]() and $\nu \in \mathbf {X}$
and $\nu \in \mathbf {X}$![]() , then
, then
Let $B^{+}$![]() denote the opposite Borel subgroup consisting of upper triangular matrices. For any $\lambda \in \mathbf {X}$
denote the opposite Borel subgroup consisting of upper triangular matrices. For any $\lambda \in \mathbf {X}$![]() , we define the baby Verma and dual baby Verma modules, respectively, by
, we define the baby Verma and dual baby Verma modules, respectively, by
(see [Reference Jantzen7, II.9] for an overview). We also let ${\widehat {\mathsf {Q}}(\lambda ) }$![]() denote the projective cover of ${\widehat {\mathsf {L}}(\lambda )}$
denote the projective cover of ${\widehat {\mathsf {L}}(\lambda )}$![]() (see [Reference Jantzen7, II.11]). The corresponding $G_1$
(see [Reference Jantzen7, II.11]). The corresponding $G_1$![]() -modules are given by
-modules are given by
for any $\lambda \in \mathbf {X}_1$![]() .
.
Let $\tau : G \rightarrow G$![]() be the anti-automorphism given by matrix transposition. In this specific case, it is obvious that $\tau$
be the anti-automorphism given by matrix transposition. In this specific case, it is obvious that $\tau$![]() fixes $T$
fixes $T$![]() and interchanges $B$
and interchanges $B$![]() and $B^{+}$
and $B^{+}$![]() (see [Reference Jantzen7, Corollary II.1.16] for the more general statement). It is also well known that $\tau$
(see [Reference Jantzen7, Corollary II.1.16] for the more general statement). It is also well known that $\tau$![]() commutes with the Frobenius map, and hence preserves $G_1$
commutes with the Frobenius map, and hence preserves $G_1$![]() and $G_1T$
and $G_1T$![]() .
.
If $H \leq G$![]() is any subgroup scheme preserved by $\tau$
is any subgroup scheme preserved by $\tau$![]() and $M$
and $M$![]() is any $H$
is any $H$![]() -module, then the twist ${ }^{\tau }M$
-module, then the twist ${ }^{\tau }M$![]() is an $H$
is an $H$![]() -module called the $\tau$
-module called the $\tau$![]() -dual of $M$
-dual of $M$![]() (see [Reference Jantzen7, I.2.15]). We also have
(see [Reference Jantzen7, I.2.15]). We also have
for $i\geq 0$![]() , and in particular, ${\ell \ell ({ }^{\tau }M) = \ell \ell (M)}$
, and in particular, ${\ell \ell ({ }^{\tau }M) = \ell \ell (M)}$![]() for any $H$
for any $H$![]() -module $M$
-module $M$![]() .
.
If $H=G_1T$![]() , then by [Reference Jantzen7, II.9.3(5), II.9.6(13), II.11.5(5)],
, then by [Reference Jantzen7, II.9.3(5), II.9.6(13), II.11.5(5)],
for any $\lambda \in \mathbf {X}$![]() . Consequently,
. Consequently,
for $i \geq 0$![]() . (Similar statements hold for $H=G_1$
. (Similar statements hold for $H=G_1$![]() .)
.)
For any $\lambda \in \mathbf {X}$![]() , let $\widehat {\mathcal {C}}(\lambda )$
, let $\widehat {\mathcal {C}}(\lambda )$![]() denote the block of $\mathsf {Rep}(G_1T)$
denote the block of $\mathsf {Rep}(G_1T)$![]() whose irreducible objects are given by $\widehat {\mathsf {L}}(w\cdot \lambda )$
whose irreducible objects are given by $\widehat {\mathsf {L}}(w\cdot \lambda )$![]() for $w \in {W_{\mathrm {p}}}$
for $w \in {W_{\mathrm {p}}}$![]() (cf. [Reference Jantzen7, II.9.22]). Let $\overline {C} \subset \mathbf {X} \otimes \mathbb {R}$
(cf. [Reference Jantzen7, II.9.22]). Let $\overline {C} \subset \mathbf {X} \otimes \mathbb {R}$![]() denote the closure of the bottom alcove $C$
denote the closure of the bottom alcove $C$![]() , and recall from [Reference Jantzen7, II.6.2(5)] that $\overline {C}\cap \mathbf {X}$
, and recall from [Reference Jantzen7, II.6.2(5)] that $\overline {C}\cap \mathbf {X}$![]() is a fundamental domain for the dot action of ${W_{\mathrm {p}}}$
is a fundamental domain for the dot action of ${W_{\mathrm {p}}}$![]() on $\mathbf {X}$
on $\mathbf {X}$![]() . Thus, since $\widehat {\mathcal {C}}(\lambda ) = \widehat {\mathcal {C}}(w\cdot \lambda )$
. Thus, since $\widehat {\mathcal {C}}(\lambda ) = \widehat {\mathcal {C}}(w\cdot \lambda )$![]() for any $w \in {W_{\mathrm {p}}}$
for any $w \in {W_{\mathrm {p}}}$![]() , it follows that $\overline {C}\cap \mathbf {X}$
, it follows that $\overline {C}\cap \mathbf {X}$![]() forms an indexing set for the blocks of $\mathsf {Rep}(G_1T)$
forms an indexing set for the blocks of $\mathsf {Rep}(G_1T)$![]() . For any facet $F \subset \overline {C}$
. For any facet $F \subset \overline {C}$![]() , and any $\lambda, \mu \in F\cap \mathbf {X}$
, and any $\lambda, \mu \in F\cap \mathbf {X}$![]() , the $G_1T$
, the $G_1T$![]() -translation functors $T^{\lambda }_{\mu }(-)$
-translation functors $T^{\lambda }_{\mu }(-)$![]() and $T^{\mu }_{\lambda }(-)$
and $T^{\mu }_{\lambda }(-)$![]() are mutually inverse and induce an equivalence $\widehat {\mathcal {C}}(\lambda ) \cong \widehat {\mathcal {C}}(\mu )$
are mutually inverse and induce an equivalence $\widehat {\mathcal {C}}(\lambda ) \cong \widehat {\mathcal {C}}(\mu )$![]() (see [Reference Jantzen7, II.9.4]).
(see [Reference Jantzen7, II.9.4]).
For any $\lambda \in \mathbf {X}_1$![]() , we similarly let $\mathcal {C}(\lambda )$
, we similarly let $\mathcal {C}(\lambda )$![]() denote the block of $\mathsf {Rep}(G_1)$
denote the block of $\mathsf {Rep}(G_1)$![]() whose irreducible objects are given by $\mathsf {L}(\mu )$
whose irreducible objects are given by $\mathsf {L}(\mu )$![]() for $\mu \in ({W^{\mathrm {ext}}_{\mathrm {p}}}\cdot \lambda ) \cap \mathbf {X}_1$
for $\mu \in ({W^{\mathrm {ext}}_{\mathrm {p}}}\cdot \lambda ) \cap \mathbf {X}_1$![]() (see [Reference Jantzen7, II.9.22(1)]). We also let $\tilde {\mathcal {C}}(\lambda )$
(see [Reference Jantzen7, II.9.22(1)]). We also let $\tilde {\mathcal {C}}(\lambda )$![]() denote the subcategory of $\mathsf {Rep}(G_1T)$
denote the subcategory of $\mathsf {Rep}(G_1T)$![]() generated by blocks of the form $\widehat {\mathcal {C}}(\lambda ')$
generated by blocks of the form $\widehat {\mathcal {C}}(\lambda ')$![]() where $\lambda ' \in ({W^{\mathrm {ext}}_{\mathrm {p}}}\cdot \lambda )\cap \overline {C}$
where $\lambda ' \in ({W^{\mathrm {ext}}_{\mathrm {p}}}\cdot \lambda )\cap \overline {C}$![]() . By (2.6), the $\widehat {\mathsf {L}}(\mu ) \otimes p\nu$
. By (2.6), the $\widehat {\mathsf {L}}(\mu ) \otimes p\nu$![]() for $\mu \in ({W^{\mathrm {ext}}_{\mathrm {p}}}\cdot \lambda ) \cap \mathbf {X}_1$
for $\mu \in ({W^{\mathrm {ext}}_{\mathrm {p}}}\cdot \lambda ) \cap \mathbf {X}_1$![]() and $\nu \in \mathbf {X}$
and $\nu \in \mathbf {X}$![]() (or equivalently, the $\widehat {\mathsf {L}}(w\cdot \lambda )$
(or equivalently, the $\widehat {\mathsf {L}}(w\cdot \lambda )$![]() for $w \in {W^{\mathrm {ext}}_{\mathrm {p}}}$
for $w \in {W^{\mathrm {ext}}_{\mathrm {p}}}$![]() ), form the set of isomorphism classes of irreducible objects of $\tilde {\mathcal {C}}(\mu )$
), form the set of isomorphism classes of irreducible objects of $\tilde {\mathcal {C}}(\mu )$![]() . We will refer to $\tilde {\mathcal {C}}(\mu )$
. We will refer to $\tilde {\mathcal {C}}(\mu )$![]() as the lift of $\mathcal {C}(\mu )$
as the lift of $\mathcal {C}(\mu )$![]() to $\mathsf {Rep}(G_1T)$
to $\mathsf {Rep}(G_1T)$![]() .
.
The subcategory $\tilde {\mathcal {C}}(\lambda _0)$![]() : We will now describe the subcategory under consideration in this paper. For $i=0,\ldots, n$
: We will now describe the subcategory under consideration in this paper. For $i=0,\ldots, n$![]() , set
, set
Each $\mu _i$![]() has a unique representative $\lambda _i \in \mathbf {X}_1$
has a unique representative $\lambda _i \in \mathbf {X}_1$![]() , which is given by
, which is given by
It is easy to verify that
and thus $\mathcal {C}(\lambda _0)$![]() is the block of $\mathsf {Rep}(G_1)$
is the block of $\mathsf {Rep}(G_1)$![]() where $\{\mathsf {L}(\lambda _0), \ldots, \mathsf {L}(\lambda _n)\}$
where $\{\mathsf {L}(\lambda _0), \ldots, \mathsf {L}(\lambda _n)\}$![]() gives the complete set of isomorphism classes of irreducibles. The lift $\tilde {\mathcal {C}}(\lambda _0)$
gives the complete set of isomorphism classes of irreducibles. The lift $\tilde {\mathcal {C}}(\lambda _0)$![]() is the full abelian subcategory of $\mathsf {Rep}(G_1T)$
is the full abelian subcategory of $\mathsf {Rep}(G_1T)$![]() which is generated by the set
which is generated by the set
Remark 2.2 More generally, for $1 \leq a \leq p-1$![]() , we can define the weights
, we can define the weights

and observe that $\lambda ^{1}_i = \lambda _i$![]() for all $i$
for all $i$![]() . Also, for any fixed $i$
. Also, for any fixed $i$![]() and $\nu \in \mathbf {X}$
and $\nu \in \mathbf {X}$![]() , the weights $\lambda ^{a}_i+p\nu$
, the weights $\lambda ^{a}_i+p\nu$![]() defined above are all contained in the same facet for any choice of $a$
defined above are all contained in the same facet for any choice of $a$![]() . It then follows from [Reference Jantzen7, II.9.22(2), II.9.22(4)] that the translation functors $T^{\lambda _i+p\nu }_{\lambda ^{a}_i+p\nu }(-)$
. It then follows from [Reference Jantzen7, II.9.22(2), II.9.22(4)] that the translation functors $T^{\lambda _i+p\nu }_{\lambda ^{a}_i+p\nu }(-)$![]() and $T^{\lambda ^{a}_i +p\nu }_{\lambda _i+p\nu }(-)$
and $T^{\lambda ^{a}_i +p\nu }_{\lambda _i+p\nu }(-)$![]() induce equivalences $\widehat {\mathcal {C}}(\lambda ^{a}_i + p\nu ) \cong \widehat {\mathcal {C}}(\lambda _i+p\nu ),$
induce equivalences $\widehat {\mathcal {C}}(\lambda ^{a}_i + p\nu ) \cong \widehat {\mathcal {C}}(\lambda _i+p\nu ),$![]() and also $\tilde {\mathcal {C}}(\lambda ^{a}_0) \cong \tilde {\mathcal {C}}(\lambda _0).$
and also $\tilde {\mathcal {C}}(\lambda ^{a}_0) \cong \tilde {\mathcal {C}}(\lambda _0).$![]()
Remark 2.3 All of our results extend to any group $G$![]() whose derived subgroup is isomorphic to $SL_{n+1}$
whose derived subgroup is isomorphic to $SL_{n+1}$![]() . This includes the case where $G = GL_{n+1}$
. This includes the case where $G = GL_{n+1}$![]() . Another important example is given by taking $G$
. Another important example is given by taking $G$![]() to be the Levi factor $L_I \subset SL_{n+r+1}$
to be the Levi factor $L_I \subset SL_{n+r+1}$![]() for any $r \geq 1$
for any $r \geq 1$![]() , where
, where
We can then let $\mathcal {C}_I(\lambda _0)$![]() denote the block of $(L_I)_1$
denote the block of $(L_I)_1$![]() whose irreducible objects are given by $\mathsf {L}_I(\lambda _0), \ldots, \mathsf {L}_I(\lambda _n)$
whose irreducible objects are given by $\mathsf {L}_I(\lambda _0), \ldots, \mathsf {L}_I(\lambda _n)$![]() . (Notice that the weights $\epsilon _{1},\ldots, \epsilon _{n+1}$
. (Notice that the weights $\epsilon _{1},\ldots, \epsilon _{n+1}$![]() are linearly independent in this situation.)
are linearly independent in this situation.)
3. Baby Verma modules for parabolic subgroups
In this section, we will review some key properties of baby Verma modules. We will also consider an analogous family of modules associated with arbitrary parabolic subgroups. All of the results in this section should be applicable to arbitrary (connected) reductive algebraic groups.
Let $P_I^{+} \subseteq G$![]() be a (positive) parabolic with Levi decomposition $P^{+}_I = L_I \ltimes U_I^{+}$
be a (positive) parabolic with Levi decomposition $P^{+}_I = L_I \ltimes U_I^{+}$![]() for $I \subseteq S$
for $I \subseteq S$![]() (cf. [Reference Jantzen7, II.1.8]). Also, let $W_I \subseteq W$
(cf. [Reference Jantzen7, II.1.8]). Also, let $W_I \subseteq W$![]() be the Weyl group of $L_I$
be the Weyl group of $L_I$![]() . (We will often write $P = P_I$
. (We will often write $P = P_I$![]() and $L = L_I$
and $L = L_I$![]() when the subset $I$
when the subset $I$![]() is implicit.) Let $\widehat {\mathsf {L}}_I(\lambda )$
is implicit.) Let $\widehat {\mathsf {L}}_I(\lambda )$![]() and $\widehat {\mathsf {Z}}_I(\lambda )$
and $\widehat {\mathsf {Z}}_I(\lambda )$![]() denote the irreducible and baby Verma modules for $L_1T$
denote the irreducible and baby Verma modules for $L_1T$![]() (or $P_1^{+}T$
(or $P_1^{+}T$![]() by inflation), respectively. For any $\lambda \in \mathbf {X}$
by inflation), respectively. For any $\lambda \in \mathbf {X}$![]() , we define the $G_1T$
, we define the $G_1T$![]() -module
-module
If $\lambda \in \mathbf {X}_1$![]() , then $\mathsf {M}_I(\lambda ) = \operatorname {coind}_{P_1^{+}}^{G_1}\, \mathsf {L}_{I}(\lambda )$
, then $\mathsf {M}_I(\lambda ) = \operatorname {coind}_{P_1^{+}}^{G_1}\, \mathsf {L}_{I}(\lambda )$![]() is the restriction of $\widehat {\mathsf {M}}_I(\lambda )$
is the restriction of $\widehat {\mathsf {M}}_I(\lambda )$![]() to $G_1$
to $G_1$![]() .
.
Remark 3.1 The duals of these modules are obtained by applying $\operatorname {ind}_{P_1T}^{G_1T}(-)$![]() to $\widehat {\mathsf {L}}_I(\lambda )$
to $\widehat {\mathsf {L}}_I(\lambda )$![]() , and are denoted by $\widehat {\mathsf {M}}'_I(\lambda )$
, and are denoted by $\widehat {\mathsf {M}}'_I(\lambda )$![]() .
.
We now recall an alternative description of the baby Verma modules. Let $\mathcal {U} = \mathrm {Dist}(G_1) \cong U^{[p]}(\mathfrak {g})$![]() and $\widehat {\mathcal {U}} = \mathrm {Dist}(G_1T)$
and $\widehat {\mathcal {U}} = \mathrm {Dist}(G_1T)$![]() be two subalgebras of $\mathrm {Dist}(G)$
be two subalgebras of $\mathrm {Dist}(G)$![]() , where $U^{[p]}(\mathfrak {g})$
, where $U^{[p]}(\mathfrak {g})$![]() is the restricted universal enveloping algebra of $G$
is the restricted universal enveloping algebra of $G$![]() . Following [Reference Jantzen7, II.1.11], let ${\{X_{\alpha }\}_{\alpha \in \varPhi }}$
. Following [Reference Jantzen7, II.1.11], let ${\{X_{\alpha }\}_{\alpha \in \varPhi }}$![]() and ${\{H_i\}_{i=1,\ldots,n}}$
and ${\{H_i\}_{i=1,\ldots,n}}$![]() denote the Chevalley basis of $\mathfrak {g}_{\mathbb {Z}}$
denote the Chevalley basis of $\mathfrak {g}_{\mathbb {Z}}$![]() .
.
Now by [Reference Jantzen7, II.1.12], $\mathcal {U} \leq \mathrm {Dist}(G)$![]() is the subalgebra generated by $X_{\alpha _i}$
is the subalgebra generated by $X_{\alpha _i}$![]() and $H_i$
and $H_i$![]() for $i=1,\ldots, n$
for $i=1,\ldots, n$![]() . Similarly, $\widehat {\mathcal {U}} \leq \mathrm {Dist}(G)$
. Similarly, $\widehat {\mathcal {U}} \leq \mathrm {Dist}(G)$![]() is the subalgebra generated by ${X_{\alpha _i}}$
is the subalgebra generated by ${X_{\alpha _i}}$![]() and ${H_i\choose m}$
and ${H_i\choose m}$![]() for $i=1,\ldots, n$
for $i=1,\ldots, n$![]() and $m\geq 1$
and $m\geq 1$![]() , where
, where
For any $\lambda = a_1\varpi _1 + \cdots + a_n \varpi _n \in \mathbf {X}$![]() , let $I_{\lambda } \unlhd \mathcal {U}$
, let $I_{\lambda } \unlhd \mathcal {U}$![]() be the left ideal generated by $H_i - a_i\cdot 1$
be the left ideal generated by $H_i - a_i\cdot 1$![]() and $X_{\alpha _i}$
and $X_{\alpha _i}$![]() for $i=1,\ldots, n$
for $i=1,\ldots, n$![]() . There is a well-known isomorphism
. There is a well-known isomorphism
Likewise, let $\widehat {I}_{\lambda } \unlhd \widehat {\mathcal {U}}$![]() be the left ideal generated by $[{H_i \choose m} - {a_i \choose m }] \cdot 1$
be the left ideal generated by $[{H_i \choose m} - {a_i \choose m }] \cdot 1$![]() and $X_{\alpha _i}$
and $X_{\alpha _i}$![]() for $i=1,\ldots, n$
for $i=1,\ldots, n$![]() and $m \geq 1$
and $m \geq 1$![]() . We also have an isomorphism
. We also have an isomorphism
By [Reference Jantzen7, II.9.2], the elements
for $0 \leq n(\alpha ) < p$![]() give a basis of weight vectors for $\widehat {\mathsf {Z}}(\lambda )$
give a basis of weight vectors for $\widehat {\mathsf {Z}}(\lambda )$![]() . (The weight corresponding to the element $\Pi _{\alpha \in \varPhi ^{+}} X_{-\alpha }^{n(\alpha )}$
. (The weight corresponding to the element $\Pi _{\alpha \in \varPhi ^{+}} X_{-\alpha }^{n(\alpha )}$![]() is given by $\lambda - (\sum _{\alpha \in \varPhi ^{+}} n(\alpha )\alpha )$
is given by $\lambda - (\sum _{\alpha \in \varPhi ^{+}} n(\alpha )\alpha )$![]() .)
.)
To obtain a similar description of the $\widehat {\mathsf {M}}_I(\lambda )$![]() , let us first set
, let us first set
where $\mathrm {Dist}((U_I)_1)$![]() is the distribution algebra of $(U_I)_1$
is the distribution algebra of $(U_I)_1$![]() and $U^{[p]}(\mathfrak {u}_I)$
and $U^{[p]}(\mathfrak {u}_I)$![]() is the restricted enveloping algebra of $\mathfrak {u}_I$
is the restricted enveloping algebra of $\mathfrak {u}_I$![]() . We also note that $\mathsf {D}_I$
. We also note that $\mathsf {D}_I$![]() has the natural structure of a $T$
has the natural structure of a $T$![]() -module arising from the conjugation action of $T$
-module arising from the conjugation action of $T$![]() on $(U_I)_1$
on $(U_I)_1$![]() . Following the notation of [Reference Jantzen7, II.1], the elements
. Following the notation of [Reference Jantzen7, II.1], the elements
for $0 \leq n(\alpha ) < p$![]() give a basis of weight vectors for $\mathsf {D}_I$
give a basis of weight vectors for $\mathsf {D}_I$![]() with respect to this action. In particular, the lowest weight of $\mathsf {D}_I$
with respect to this action. In particular, the lowest weight of $\mathsf {D}_I$![]() is given by
is given by
For any $L_1$![]() -module $M$
-module $M$![]() (regarded as a $P_1^{+}$
(regarded as a $P_1^{+}$![]() -module), the arguments from [Reference Jantzen7, II.3.6] give a vector space isomorphism
-module), the arguments from [Reference Jantzen7, II.3.6] give a vector space isomorphism
which is compatible with the natural $(U_I)_1$![]() and $L_1$
and $L_1$![]() module structures on $\mathsf {D}_I \otimes M$
module structures on $\mathsf {D}_I \otimes M$![]() . Specifically, $(U_I)_1$
. Specifically, $(U_I)_1$![]() acts on $\mathsf {D}_I$
acts on $\mathsf {D}_I$![]() by the regular representation and acts on $M$
by the regular representation and acts on $M$![]() trivially, while $L_1$
trivially, while $L_1$![]() acts on $\mathsf {D}_I$
acts on $\mathsf {D}_I$![]() by the adjoint action (induced from conjugation) and on $M$
by the adjoint action (induced from conjugation) and on $M$![]() by left multiplication. Furthermore, these actions are compatible with the conjugation action of $L_1$
by left multiplication. Furthermore, these actions are compatible with the conjugation action of $L_1$![]() on $(U_I)_1$
on $(U_I)_1$![]() , and thus (3.4) is actually an isomorphism of $P_1$
, and thus (3.4) is actually an isomorphism of $P_1$![]() -modules.
-modules.
Likewise, if $M$![]() is a $L_1T$
is a $L_1T$![]() -module (regarded as a $P_1^{+}T$
-module (regarded as a $P_1^{+}T$![]() -module), then the arguments from [Reference Jantzen7, II.9.2] give a $P_1T$
-module), then the arguments from [Reference Jantzen7, II.9.2] give a $P_1T$![]() -module isomorphism
-module isomorphism
Lemma 3.2 Let $\lambda \in \mathbf {X}$![]() .
.
1. $\widehat {\mathsf {M}}_I(\lambda )$
 is a quotient of $\widehat {\mathsf {Z}}(\lambda )$
is a quotient of $\widehat {\mathsf {Z}}(\lambda )$ .
.2. The lowest weight of $\widehat {\mathsf {M}}_I(\lambda )$
 is given by $\mu _I + w_I(\lambda )$
is given by $\mu _I + w_I(\lambda )$ , where $w_I \in W$
, where $w_I \in W$ is the longest element of $W_I$
is the longest element of $W_I$ .
.
Proof. The first claim follows from exactness of coinduction. (In particular, the surjection $\widehat {\mathsf {Z}}(\lambda ) \twoheadrightarrow \widehat {\mathsf {L}}(\lambda )$![]() factors through $\widehat {\mathsf {M}}_I(\lambda )$
factors through $\widehat {\mathsf {M}}_I(\lambda )$![]() .) The second claim can be deduced from (3.5).
.) The second claim can be deduced from (3.5).
Remark 3.3 An immediate consequence of the first statement in this lemma is that
In particular, $\widehat {\mathsf {M}}_I(\lambda )$![]() has an irreducible head, and hence, is indecomposable.
has an irreducible head, and hence, is indecomposable.
We now prove an analogue to [Reference Jantzen7, Lemma II.2.11].
Lemma 3.4 Let $\lambda \in \mathbf {X}$![]() be arbitrary and regard $\widehat {\mathsf {L}}(\lambda )$
be arbitrary and regard $\widehat {\mathsf {L}}(\lambda )$![]() as a $P_1^{+}T$
as a $P_1^{+}T$![]() -module, then there is an $L_1T$
-module, then there is an $L_1T$![]() -module isomorphism
-module isomorphism
Proof. Let $\widehat {\mathsf {M}}'_I(\lambda ) = \operatorname {ind}_{P_1T}^{G_1T}\, \widehat {\mathsf {L}}_I(\lambda )$![]() as in Remark 3.1. The ‘dual’ of (3.5) gives a $P_1^{+}T$
as in Remark 3.1. The ‘dual’ of (3.5) gives a $P_1^{+}T$![]() -module isomorphism
-module isomorphism
where, in particular, $(U_I^{+})_1$![]() acts via the left regular representation on the first term and trivially on the second term. Thus,
acts via the left regular representation on the first term and trivially on the second term. Thus,
where the last isomorphism follows from the fact that $\Bbbk [(U_I^{+})_1]^{(U_I^{+})_1} = \Bbbk$![]() .
.
Moreover, the ‘dual’ of Lemma 3.2 gives an inclusion $\widehat {\mathsf {M}}'_I(\lambda ) \hookrightarrow \widehat {\mathsf {Z}}'(\lambda )$![]() . Thus, there also exists an inclusion $\widehat {\mathsf {L}}(\lambda ) \hookrightarrow \widehat {\mathsf {M}}'_I(\lambda )$
. Thus, there also exists an inclusion $\widehat {\mathsf {L}}(\lambda ) \hookrightarrow \widehat {\mathsf {M}}'_I(\lambda )$![]() since $\widehat {\mathsf {M}}'_I(\lambda )$
since $\widehat {\mathsf {M}}'_I(\lambda )$![]() must contain the (simple) socle of $\widehat {\mathsf {Z}}'(\lambda )$
must contain the (simple) socle of $\widehat {\mathsf {Z}}'(\lambda )$![]() . This implies
. This implies
Finally, since the first term is non-zero (because non-zero $(U_I^{+})_1$![]() invariants always exist), and the middle term is irreducible for $L_1T$
invariants always exist), and the middle term is irreducible for $L_1T$![]() , then we must have equality.
, then we must have equality.
The next proposition will be essential to our Loewy series calculations.
Proposition 3.5 Let $M$![]() be an arbitrary $L_1T$
be an arbitrary $L_1T$![]() -module (regarded as a $P_1^{+}T$
-module (regarded as a $P_1^{+}T$![]() -module with a trivial $(U_I^{+})_1$
-module with a trivial $(U_I^{+})_1$![]() action), and let $N = \operatorname {coind}_{P_1^{+}T}^{G_1T}\, M,$
action), and let $N = \operatorname {coind}_{P_1^{+}T}^{G_1T}\, M,$![]() then
then
for all $\mu \in \mathbf {X}$![]() .
.
Proof. It suffices to show that $\dim \operatorname {Hom}_{G_1T}(N, \widehat {\mathsf {L}}(\mu )) = \dim \operatorname {Hom}_{L_1T}(M, \widehat {\mathsf {L}}_I(\mu ))$![]() for all $\mu \in \mathbf {X}$
for all $\mu \in \mathbf {X}$![]() . Observe,
. Observe,
where the first isomorphism follows from [Reference Jantzen7, I.8.14(4)] and the second isomorphism holds because $(U_I^{+})_1$![]() acts trivially on $M$
acts trivially on $M$![]() , so the image of any morphism must also be $(U_I^{+})_1$
, so the image of any morphism must also be $(U_I^{+})_1$![]() -invariant. Finally, by Lemma 3.4,
-invariant. Finally, by Lemma 3.4,
Therefore, $\dim \operatorname {Hom}_{G_1T}(N, \widehat {\mathsf {L}}(\mu )) = \dim \operatorname {Hom}_{L_1T}(M, \widehat {\mathsf {L}}_I(\mu ))$![]() .
.
4. Multiplicity and dimension formulas
We now fix two subsets $I = \{\epsilon _1-\epsilon _2, \ldots, \epsilon _{n-1}-\epsilon _n\}$![]() and $J = \{\epsilon _2-\epsilon _3, \ldots, \epsilon _{n}-\epsilon _{n+1}\}$
and $J = \{\epsilon _2-\epsilon _3, \ldots, \epsilon _{n}-\epsilon _{n+1}\}$![]() of $S$
of $S$![]() for the rest of this paper. Our first result gives a remarkable property of $\mathcal {C}(\lambda _0)$
for the rest of this paper. Our first result gives a remarkable property of $\mathcal {C}(\lambda _0)$![]() .
.
Proposition 4.1 For $i=0,\ldots, n,$![]()
where $\mathsf {V}(\lambda )$![]() denotes the Weyl module of highest weight $\lambda \in \mathbf {X}$
denotes the Weyl module of highest weight $\lambda \in \mathbf {X}$![]() .
.
Proof. We will use Jantzen's criterion for the simplicity of Weyl modules (cf. [Reference Jantzen7, II.8.21] or [Reference Jantzen6]). Set $\nu _i =\lambda _i + \rho$![]() for $i=0,\ldots,n$
for $i=0,\ldots,n$![]() . It will suffice to show that for any $i = 0, \ldots, n$
. It will suffice to show that for any $i = 0, \ldots, n$![]() and $1 \leq k< j \leq n+1$
and $1 \leq k< j \leq n+1$![]() , the quantity
, the quantity
satisfies the criterion. We will proceed by dividing this problem into the following cases:
Case 1 $i=0$

1.1) $k = 1$
 , $2 \leq j \leq n+1$
, $2 \leq j \leq n+1$
1.2) $2 \leq k < j \leq n+1$

Case 2 $i=n$

2.1) $1\leq k \leq n$
 , $j=n+1$
, $j=n+1$
2.2) $1 \leq k < j \leq n$

Case 3 $1 \leq i \leq n-1$

3.1) $1 \leq k < j \leq i$

3.2) $i+2 \leq k < j \leq n+1$

3.3) $1 \leq k \leq i$
 , $j=i+1$
, $j=i+1$
3.4) $k = i+1$
 , $i+1 < j \leq n+1$
, $i+1 < j \leq n+1$
3.5) $1 \leq k \leq i < i+2 \leq j \leq n+1$
 .
.
(Note that some of these sub-cases may be empty for certain choices of $i$![]() and $n$
and $n$![]() .)
.)
Let us first consider Case 1. We calculate ${\langle \nu _0, \epsilon _1 - \epsilon _{2} \rangle = 1}$![]() , and for $2\leq k\leq n$
, and for $2\leq k\leq n$![]() , ${\langle \nu _0, \epsilon _k - \epsilon _{k+1} \rangle = p}$
, ${\langle \nu _0, \epsilon _k - \epsilon _{k+1} \rangle = p}$![]() . In the situation of 1.1), first observe
. In the situation of 1.1), first observe
for $2 \leq j \leq n+1$![]() . Following the notation in [Reference Jantzen7, II.8.21], set $a = 1$
. Following the notation in [Reference Jantzen7, II.8.21], set $a = 1$![]() , $b = j-2$
, $b = j-2$![]() and $s=0$
and $s=0$![]() . The criterion is satisfied by setting $\beta _0 = \epsilon _1 - \epsilon _{2}$
. The criterion is satisfied by setting $\beta _0 = \epsilon _1 - \epsilon _{2}$![]() and $\beta _r = \epsilon _{r+1}-\epsilon _{r+2}$
and $\beta _r = \epsilon _{r+1}-\epsilon _{r+2}$![]() for $r = 1,\ldots, j-2$
for $r = 1,\ldots, j-2$![]() . Similarly, in the case of 1.2), first note that for $2 \leq k < j \leq n+1$
. Similarly, in the case of 1.2), first note that for $2 \leq k < j \leq n+1$![]() ,
,
If we write ${j-k= ap^{s-1} + bp^{s}}$![]() for some $s \geq 1$
for some $s \geq 1$![]() and $0 < a < p$
and $0 < a < p$![]() , then ${\langle \nu _0, \epsilon _k - \epsilon _{j} \rangle } = ap^{s} + bp^{s+1}$
, then ${\langle \nu _0, \epsilon _k - \epsilon _{j} \rangle } = ap^{s} + bp^{s+1}$![]() . Finally, set ${\beta _0 = \epsilon _k - \epsilon _{k+ ap^{s-1}}}$
. Finally, set ${\beta _0 = \epsilon _k - \epsilon _{k+ ap^{s-1}}}$![]() , and ${\beta _r = \epsilon _{k+ ap^{s-1}+(r-1)p^{s}} - \epsilon _{k+ ap^{s-1} + rp^{s}}}$
, and ${\beta _r = \epsilon _{k+ ap^{s-1}+(r-1)p^{s}} - \epsilon _{k+ ap^{s-1} + rp^{s}}}$![]() for ${r= 1,\ldots, b}.$
for ${r= 1,\ldots, b}.$![]()
Now we consider Case 2. Again, we calculate for $1\leq k\leq n-1$![]() , $\langle \nu _n, \epsilon _k - \epsilon _{k+1} \rangle = p$
, $\langle \nu _n, \epsilon _k - \epsilon _{k+1} \rangle = p$![]() and ${\langle \nu _n, \epsilon _n - \epsilon _{n+1}\rangle =p-1}$
and ${\langle \nu _n, \epsilon _n - \epsilon _{n+1}\rangle =p-1}$![]() . In the situation of 2.1), note that for $1\leq k \leq n$
. In the situation of 2.1), note that for $1\leq k \leq n$![]() ,
,
so $a = p-1$![]() , $b = n-k$
, $b = n-k$![]() and $s=0$
and $s=0$![]() . The criterion is satisfied by setting $\beta _0 = \epsilon _n - \epsilon _{n+1}$
. The criterion is satisfied by setting $\beta _0 = \epsilon _n - \epsilon _{n+1}$![]() and $\beta _r = \epsilon _{r+k-1}-\epsilon _{r+k}$
and $\beta _r = \epsilon _{r+k-1}-\epsilon _{r+k}$![]() for $r = 1,\ldots, n-k$
for $r = 1,\ldots, n-k$![]() . In the situation of 2.2), we get
. In the situation of 2.2), we get
for $1 \leq k < j \leq n$![]() . If we write ${j-k= ap^{s-1} + bp^{s}}$
. If we write ${j-k= ap^{s-1} + bp^{s}}$![]() for some $s \geq 1$
for some $s \geq 1$![]() and $0 < a < p$
and $0 < a < p$![]() , then ${\langle \nu _n, \epsilon _k - \epsilon _{j} \rangle } = ap^{s} + bp^{s+1}$
, then ${\langle \nu _n, \epsilon _k - \epsilon _{j} \rangle } = ap^{s} + bp^{s+1}$![]() . Now set ${\beta _0 = \epsilon _k - \epsilon _{ap^{s-1} +k}}$
. Now set ${\beta _0 = \epsilon _k - \epsilon _{ap^{s-1} +k}}$![]() , and $\beta_{r} = \epsilon _{k+ ap^{s-1}+(r-1)p^{s}} - \epsilon _{k+ ap^{s-1} + rp^{s}}$
, and $\beta_{r} = \epsilon _{k+ ap^{s-1}+(r-1)p^{s}} - \epsilon _{k+ ap^{s-1} + rp^{s}}$![]() for ${r= 1,\ldots, b}$
for ${r= 1,\ldots, b}$![]() as in 1.2).
as in 1.2).
Finally, we consider Case 3. For $1\leq k\leq i-1$![]() and $i+2 \leq k \leq n+1$
and $i+2 \leq k \leq n+1$![]() , we have $\langle \nu _i, \epsilon _k - \epsilon _{k+1} \rangle = p,$
, we have $\langle \nu _i, \epsilon _k - \epsilon _{k+1} \rangle = p,$![]() ${ \langle \nu _i, \epsilon _i - \epsilon _{i+1} \rangle = p-1}$
${ \langle \nu _i, \epsilon _i - \epsilon _{i+1} \rangle = p-1}$![]() and ${ \langle \nu _i, \epsilon _{i+1} - \epsilon _{i+2} \rangle = 1}$
and ${ \langle \nu _i, \epsilon _{i+1} - \epsilon _{i+2} \rangle = 1}$![]() . To handle 3.1) and 3.2), note that in both instances
. To handle 3.1) and 3.2), note that in both instances
These cases then follow by writing ${j-k= ap^{s-1} + bp^{s}}$![]() with $0 < a < p$
with $0 < a < p$![]() , and defining $\beta _0$
, and defining $\beta _0$![]() and $\beta _r$
and $\beta _r$![]() for $r=1,\ldots, b$
for $r=1,\ldots, b$![]() as in 1.2) and 2.2), respectively. Similarly, the verifications of 3.3) and 3.4) are identical to the verifications of 2.1) and 1.1), respectively.
as in 1.2) and 2.2), respectively. Similarly, the verifications of 3.3) and 3.4) are identical to the verifications of 2.1) and 1.1), respectively.
Thus, we only need to consider 3.5). We first observe
and write ${j-k-1= ap^{s-1} + bp^{s}}$![]() where $0 < a < p$
where $0 < a < p$![]() . Now there are two further sub-cases:
. Now there are two further sub-cases:
a) $k + ap^{s-1} \geq i+1$
 ,
,b) $k + ap^{s-1} \leq i$
 .
.
In the situation of a), we set $\beta _0 = \epsilon _k - \epsilon _{k+1+ap^{s-1}}$![]() and $\beta _r = \epsilon _{k+ 1+ ap^{s-1}+(r-1)p^{s}} - \epsilon _{k+ 1+ ap^{s-1} + rp^{s}}$
and $\beta _r = \epsilon _{k+ 1+ ap^{s-1}+(r-1)p^{s}} - \epsilon _{k+ 1+ ap^{s-1} + rp^{s}}$![]() for ${r= 1,\ldots, b}$
for ${r= 1,\ldots, b}$![]() . In the situation of b), we set ${\beta _0 = \epsilon _k - \epsilon _{k+ap^{s-1}}}$
. In the situation of b), we set ${\beta _0 = \epsilon _k - \epsilon _{k+ap^{s-1}}}$![]() and
and

for $r = 1,\ldots, b$![]() .
.
Remark 4.2 If we assume $p > n+1$![]() , then the preceding proof can be dramatically simplified since $\langle \nu _i, \epsilon _k - \epsilon _j \rangle < p^{2}$
, then the preceding proof can be dramatically simplified since $\langle \nu _i, \epsilon _k - \epsilon _j \rangle < p^{2}$![]() for all possible choices of $i$
for all possible choices of $i$![]() , $j$
, $j$![]() , $k$
, $k$![]() .
.
Corollary 4.3 The dimensions and characters of the irreducible modules in $\tilde {\mathcal {C}}(\lambda _0)$![]() can be deduced from Weyl's dimension formula and Weyl's character formula, respectively.
can be deduced from Weyl's dimension formula and Weyl's character formula, respectively.
Observe now that
which implies $\dim _{\Bbbk }\mathsf {D}_I= p^{n}$![]() , and that the lowest weight of $\mathsf {D}_I$
, and that the lowest weight of $\mathsf {D}_I$![]() is
is
The longest element $w_I \in W_I$![]() is the permutation given by
is the permutation given by

Analogously, the lowest weight of $\mathsf {D}_J$![]() is
is
and $w_J \in W_J$![]() is given by
is given by

Our goal is to explicitly describe the modules $\widehat {\mathsf {M}}_I(\lambda _i)$![]() and $\widehat {\mathsf {M}}_J(\lambda _i)$
and $\widehat {\mathsf {M}}_J(\lambda _i)$![]() . We begin with the following dimension formula for the restrictions of these modules to $G_1$
. We begin with the following dimension formula for the restrictions of these modules to $G_1$![]() .
.
Lemma 4.4
1. For $i=0,\ldots, n-1,$
 \[ \dim_{\Bbbk}\mathsf{M}_I(\lambda_i) = \dim_{\Bbbk} \mathsf{L}(\lambda_i) + \dim_{\Bbbk} \mathsf{L}(\lambda_{i+1}). \]
\[ \dim_{\Bbbk}\mathsf{M}_I(\lambda_i) = \dim_{\Bbbk} \mathsf{L}(\lambda_i) + \dim_{\Bbbk} \mathsf{L}(\lambda_{i+1}). \]
2. For $i=1,\ldots, n,$
 \[ \dim_{\Bbbk}\mathsf{M}_J(\lambda_i) = \dim_{\Bbbk} \mathsf{L}(\lambda_i) + \dim_{\Bbbk} \mathsf{L}(\lambda_{i-1}). \]
\[ \dim_{\Bbbk}\mathsf{M}_J(\lambda_i) = \dim_{\Bbbk} \mathsf{L}(\lambda_i) + \dim_{\Bbbk} \mathsf{L}(\lambda_{i-1}). \]
Proof. It will be enough to prove (1), since (2) will follow from the exact same arguments. For notational simplicity, set $\nu _i = \lambda _i + \rho$![]() for $i=0,\ldots, n-1$
for $i=0,\ldots, n-1$![]() . By Corollary 4.3, we can apply the Weyl dimension formula, which gives
. By Corollary 4.3, we can apply the Weyl dimension formula, which gives

where
By (3.4), the description of the weight basis of $\mathsf {D}_I$![]() in (3.3), and the analogue of Corollary 4.3 for the Levi factor $L_I$
in (3.3), and the analogue of Corollary 4.3 for the Levi factor $L_I$![]() (applied to $\mathsf {L}_I(\lambda _i)$
(applied to $\mathsf {L}_I(\lambda _i)$![]() ), we can deduce
), we can deduce
Thus, the equation in the statement of the lemma is equivalent to
for $i=0,\ldots, n-1$![]() . Notice that if we treat $p$
. Notice that if we treat $p$![]() as an indeterminate variable, then the expressions
as an indeterminate variable, then the expressions
are exclusive to the first and second terms appearing in (4.4), respectively. So it will be helpful to introduce the notation
Claim. For $i=0,\ldots, n-1$![]() ,
,
Suppose for now that this claim holds, then by the observation immediately preceding the claim,
Combining this with the following identity:

verifies (4.4).
The remainder of the proof will be devoted to proving the preceding claim. Let
It can be checked that $|X| = 2n-1$![]() and that $X$
and that $X$![]() is the subset of $\Gamma$
is the subset of $\Gamma$![]() consisting of all $(k,j)$
consisting of all $(k,j)$![]() satisfying
satisfying
In particular, the sets ${X\backslash \{(i+1,n+1)\}}$![]() and ${X \backslash \{(1,i+2)\} }$
and ${X \backslash \{(1,i+2)\} }$![]() have precisely $2n-2$
have precisely $2n-2$![]() elements. We get immediately that
elements. We get immediately that
and we only have to check the $(2n-2)$![]() -fold products
-fold products
If $i=0$![]() ,
,

and for $i=n-1$![]() ,
,

Finally, suppose that $1 \leq i \leq n-2$![]() , then
, then

It will now be helpful to recall that if we let $\lambda \in \mathbf {X}$![]() be arbitrary, and write $\lambda = \mu + p\nu$
be arbitrary, and write $\lambda = \mu + p\nu$![]() for $\mu \in \mathbf {X}_1$
for $\mu \in \mathbf {X}_1$![]() , $\nu \in \mathbf {X}$
, $\nu \in \mathbf {X}$![]() , then the lowest weight of $\widehat {\mathsf {L}}(\lambda )$
, then the lowest weight of $\widehat {\mathsf {L}}(\lambda )$![]() is unique to $\lambda$
is unique to $\lambda$![]() and is given by $w_0(\mu ) + p\nu.$
and is given by $w_0(\mu ) + p\nu.$![]()
Lemma 4.5
1. For $i=0,\ldots, n-1,$
 ${ \widehat {\mathsf {L}}(\lambda _{i+1} - p\varpi _n) \subset \widehat {\mathsf {M}}_I(\lambda _i). }$
${ \widehat {\mathsf {L}}(\lambda _{i+1} - p\varpi _n) \subset \widehat {\mathsf {M}}_I(\lambda _i). }$
2. For $i=1,\ldots, n,$
 ${ \widehat {\mathsf {L}}(\lambda _{i-1} - p\varpi _1) \subset \widehat {\mathsf {M}}_J(\lambda _i). }$
${ \widehat {\mathsf {L}}(\lambda _{i-1} - p\varpi _1) \subset \widehat {\mathsf {M}}_J(\lambda _i). }$
Proof. The proofs of (1) and (2) are identical, so we will only prove (1). It will be sufficient to show that the lowest weights of $\widehat {\mathsf {M}}_I(\lambda _i)$![]() and ${\widehat {\mathsf {L}}(\lambda _{i+1}-p\varpi _n)}$
and ${\widehat {\mathsf {L}}(\lambda _{i+1}-p\varpi _n)}$![]() coincide. This is because Lemma 4.4 will then imply that the modules $\widehat {\mathsf {L}}(\lambda _{i+1} - p\varpi _n)$
coincide. This is because Lemma 4.4 will then imply that the modules $\widehat {\mathsf {L}}(\lambda _{i+1} - p\varpi _n)$![]() and $\widehat {\mathsf {L}}(\lambda _{i})$
and $\widehat {\mathsf {L}}(\lambda _{i})$![]() account for the complete set of composition factors (including multiplicity) of $\widehat {\mathsf {M}}_I(\lambda _i)$
account for the complete set of composition factors (including multiplicity) of $\widehat {\mathsf {M}}_I(\lambda _i)$![]() . The fact that $\widehat {\mathsf {L}}(\lambda _{i})$
. The fact that $\widehat {\mathsf {L}}(\lambda _{i})$![]() is the unique simple quotient of $\widehat {\mathsf {M}}_I(\lambda _i)$
is the unique simple quotient of $\widehat {\mathsf {M}}_I(\lambda _i)$![]() by Lemma 3.2 will then force $\widehat {\mathsf {L}}(\lambda _{i+1} - p\varpi _n)$
by Lemma 3.2 will then force $\widehat {\mathsf {L}}(\lambda _{i+1} - p\varpi _n)$![]() to be a submodule.
to be a submodule.
By Lemma 3.2 and (4.1), the lowest weight of $\widehat {\mathsf {M}}_I(\lambda _{i})$![]() is
is
Likewise, the lowest weight of $\widehat {\mathsf {L}}(\lambda _{i+1}-p\varpi _n)$![]() is
is
Hence, the result will follow if we can prove that
(Recall the definitions (2.1), (4.2), and (4.3).)
To verify this identity, let us first define

then

Thus, $w_0(\rho ) = -\rho _I - \frac {(n+1)}{2}\varpi _n$![]() and $w_I(\rho )= -\rho _I + \frac {(n+1)}{2}\varpi _n.$
and $w_I(\rho )= -\rho _I + \frac {(n+1)}{2}\varpi _n.$![]() We also observe that for $i=1,\ldots, n-1$
We also observe that for $i=1,\ldots, n-1$![]() , ${w_I(\varpi _{i}) = \varpi _n - \varpi _{n-1-i}}$
, ${w_I(\varpi _{i}) = \varpi _n - \varpi _{n-1-i}}$![]() and, by recalling the $\mu _i$
and, by recalling the $\mu _i$![]() from (2.10),
from (2.10),

for $i=0,\ldots, n-1$![]() . Finally, we verify (4.5) by substituting the preceding identities into (2.11).
. Finally, we verify (4.5) by substituting the preceding identities into (2.11).
The following proposition will give us some insight into the structure of the modules $\widehat {\mathsf {M}}_I(\lambda _i + p\nu )$![]() and $\widehat {\mathsf {M}}_J(\lambda _i + p\nu )$
and $\widehat {\mathsf {M}}_J(\lambda _i + p\nu )$![]() .
.
Proposition 4.6 Let $\nu \in \mathbf {X}$![]() .
.
1. For $i=0,\ldots,n-1,$
 $\widehat {\mathsf {M}}_I(\lambda _i+p\nu )$
$\widehat {\mathsf {M}}_I(\lambda _i+p\nu )$ is an indecomposable length 2 module where we have $\overline {\text {rad}}_0\,\widehat {\mathsf {M}}_I(\lambda _i + p\nu ) \cong \widehat {\mathsf {L}}(\lambda _i + p\nu )$
is an indecomposable length 2 module where we have $\overline {\text {rad}}_0\,\widehat {\mathsf {M}}_I(\lambda _i + p\nu ) \cong \widehat {\mathsf {L}}(\lambda _i + p\nu )$ and $\overline {\text {rad}}_1\, \widehat {\mathsf {M}}_I(\lambda _i+p\nu ) \cong \widehat {\mathsf {L}}(\lambda _{i+1} +p\nu - p\varpi _n)$
and $\overline {\text {rad}}_1\, \widehat {\mathsf {M}}_I(\lambda _i+p\nu ) \cong \widehat {\mathsf {L}}(\lambda _{i+1} +p\nu - p\varpi _n)$ . Also,
\[ \widehat{\mathsf{M}}_I(\lambda_n + p\nu) \cong \widehat{\mathsf{Z}}(\lambda_n + p\nu). \]
. Also,
\[ \widehat{\mathsf{M}}_I(\lambda_n + p\nu) \cong \widehat{\mathsf{Z}}(\lambda_n + p\nu). \]
2. For $i=1,\ldots,n,$
 $\widehat {\mathsf {M}}_J(\lambda _i + p\nu )$
$\widehat {\mathsf {M}}_J(\lambda _i + p\nu )$ is an indecomposable length 2 module where we have $\overline {\text {rad}}_0\, \widehat {\mathsf {M}}_J(\lambda _i+p\nu ) \cong \widehat {\mathsf {L}}(\lambda _i+p\nu )$
is an indecomposable length 2 module where we have $\overline {\text {rad}}_0\, \widehat {\mathsf {M}}_J(\lambda _i+p\nu ) \cong \widehat {\mathsf {L}}(\lambda _i+p\nu )$ and $\overline {\text {rad}}_1\, \widehat {\mathsf {M}}_J(\lambda _i+p\nu ) \cong \widehat {\mathsf {L}}(\lambda _{i-1} + p\nu - p\varpi _1)$
and $\overline {\text {rad}}_1\, \widehat {\mathsf {M}}_J(\lambda _i+p\nu ) \cong \widehat {\mathsf {L}}(\lambda _{i-1} + p\nu - p\varpi _1)$ . Also,
\[ \widehat{\mathsf{M}}_J(\lambda_0 + p\nu) \cong \widehat{\mathsf{Z}}(\lambda_0 +p\nu). \]
. Also,
\[ \widehat{\mathsf{M}}_J(\lambda_0 + p\nu) \cong \widehat{\mathsf{Z}}(\lambda_0 +p\nu). \]
3. Restricting to $G_1$
 gives similar descriptions for $\mathsf {M}_I(\lambda _i)$
gives similar descriptions for $\mathsf {M}_I(\lambda _i)$ and $\mathsf {M}_J(\lambda _i)$
and $\mathsf {M}_J(\lambda _i)$ .
.
Proof. Without loss of generality, we can assume $\nu =0$![]() . Also, it will be enough to prove (1), since (2) will follow from an identical argument.
. Also, it will be enough to prove (1), since (2) will follow from an identical argument.
The description of $\widehat {\mathsf {M}}_I(\lambda _i)$![]() for $i=0,\ldots, n-1$
for $i=0,\ldots, n-1$![]() follows immediately from Lemmas 4.4 and 4.5. On the other hand, the description of $\widehat {\mathsf {M}}_I(\lambda _n)$
follows immediately from Lemmas 4.4 and 4.5. On the other hand, the description of $\widehat {\mathsf {M}}_I(\lambda _n)$![]() is a consequence of [Reference Jantzen7, Lemma II.11.8]. Namely, since ${\langle \lambda _n + \rho, \alpha ^{\vee }\rangle = p}$
is a consequence of [Reference Jantzen7, Lemma II.11.8]. Namely, since ${\langle \lambda _n + \rho, \alpha ^{\vee }\rangle = p}$![]() for all $\alpha \in I$
for all $\alpha \in I$![]() , then it follows that $\widehat {\mathsf {L}}_I(\lambda _n) \cong \widehat {\mathsf {Z}}_{I}(\lambda _n).$
, then it follows that $\widehat {\mathsf {L}}_I(\lambda _n) \cong \widehat {\mathsf {Z}}_{I}(\lambda _n).$![]() By transitivity of coinduction, we obtain
By transitivity of coinduction, we obtain
We can now compute the composition multiplicities of the baby Verma modules and the indecomposable projective modules of $\mathcal {C}(\lambda _0)$![]() .
.
Proposition 4.7 For $0\leq i,j \leq n,$![]()
Proof. We shall perform induction with respect to $n$![]() , where $G = SL_{n+1}$
, where $G = SL_{n+1}$![]() . For the base case, when $n=1$
. For the base case, when $n=1$![]() , we have
, we have
In this case, $\mathcal {C}(\lambda _0)$![]() is actually the regular block and the claim can be verified through explicit computation (eg. [Reference Jantzen7, II.9.10]). Now suppose $n \geq 2$
is actually the regular block and the claim can be verified through explicit computation (eg. [Reference Jantzen7, II.9.10]). Now suppose $n \geq 2$![]() and that the formula holds for $SL_{r+1}$
and that the formula holds for $SL_{r+1}$![]() with $r \leq n-1$
with $r \leq n-1$![]() . We set $G' = [L_I, L_I]$
. We set $G' = [L_I, L_I]$![]() and note that $G' \cong SL_{n}$
and note that $G' \cong SL_{n}$![]() . Similarly, set $B' = B \cap G' \subset B \cap L_I$
. Similarly, set $B' = B \cap G' \subset B \cap L_I$![]() and $T' = T \cap G'$
and $T' = T \cap G'$![]() , where $B'$
, where $B'$![]() is the (lower) Borel subgroup of $G'$
is the (lower) Borel subgroup of $G'$![]() and $T'$
and $T'$![]() is the torus of $G'$
is the torus of $G'$![]() .
.
By the remark following [Reference Jantzen7, Proposition I.8.20],
and by [Reference Jantzen7, II.2.10(2)]
For $i=0,\ldots, n-1$![]() , set $\lambda '_i = \lambda _i|_{T'}$
, set $\lambda '_i = \lambda _i|_{T'}$![]() . Applying the inductive hypothesis to $G'$
. Applying the inductive hypothesis to $G'$![]() yields
yields
for $0 \leq i,j \leq n-1$![]() . The modules $\mathsf {L}_I(\lambda _0),\ldots, \mathsf {L}_I(\lambda _{n-1})$
. The modules $\mathsf {L}_I(\lambda _0),\ldots, \mathsf {L}_I(\lambda _{n-1})$![]() form the entire set of irreducibles of the $\mathsf {Rep}((L_I)_1)$
form the entire set of irreducibles of the $\mathsf {Rep}((L_I)_1)$![]() block $\mathcal {C}_I(\lambda _0)$
block $\mathcal {C}_I(\lambda _0)$![]() . Now since $\mathsf {Z}_I(\lambda _i)$
. Now since $\mathsf {Z}_I(\lambda _i)$![]() is an object of $\mathcal {C}_I(\lambda _0)$
is an object of $\mathcal {C}_I(\lambda _0)$![]() and for each $i=0,\ldots, n-1$
and for each $i=0,\ldots, n-1$![]() , $\mathsf {L}_I(\lambda _i)$
, $\mathsf {L}_I(\lambda _i)$![]() is the only irreducible of $\mathcal {C}_I(\lambda _0)$
is the only irreducible of $\mathcal {C}_I(\lambda _0)$![]() which satisfies $\mathsf {L}_I(\lambda _i)|_{G_1'}\cong \mathsf {L}(\lambda '_i)$
which satisfies $\mathsf {L}_I(\lambda _i)|_{G_1'}\cong \mathsf {L}(\lambda '_i)$![]() , then we must also have
, then we must also have
If we take any Jordan–Hölder filtration of $\mathsf {Z}_I(\lambda _i)$![]() for $0 \leq i \leq n-1$
for $0 \leq i \leq n-1$![]() and apply the exact functor $\operatorname {coind}_{(P_I)^{+}_1}^{G_1}(-)$
and apply the exact functor $\operatorname {coind}_{(P_I)^{+}_1}^{G_1}(-)$![]() , we will get a filtration whose layers are of the form $\mathsf {M}_I(\lambda _j)$
, we will get a filtration whose layers are of the form $\mathsf {M}_I(\lambda _j)$![]() for $0 \leq j \leq n-1$
for $0 \leq j \leq n-1$![]() . Thus,
. Thus,
where $[\mathsf {Z}(\lambda _i): \mathsf {M}_I(\lambda _j)]$![]() denotes the filtration multiplicity.
denotes the filtration multiplicity.
By Proposition 4.6, each $\mathsf {M}_I(\lambda _j)$![]() contributes a single copy of $\mathsf {L}(\lambda _j)$
contributes a single copy of $\mathsf {L}(\lambda _j)$![]() and $\mathsf {L}(\lambda _{j+1})$
and $\mathsf {L}(\lambda _{j+1})$![]() . Thus, $[\mathsf {Z}(\lambda _i): \mathsf {L}(\lambda _0)] = 1$
. Thus, $[\mathsf {Z}(\lambda _i): \mathsf {L}(\lambda _0)] = 1$![]() and $[\mathsf {Z}(\lambda _i): \mathsf {L}(\lambda _n)] = 1$
and $[\mathsf {Z}(\lambda _i): \mathsf {L}(\lambda _n)] = 1$![]() since by (4.6), $[\mathsf {Z}(\lambda _i): \mathsf {M}_I(\lambda _0)] =1$
since by (4.6), $[\mathsf {Z}(\lambda _i): \mathsf {M}_I(\lambda _0)] =1$![]() and $[\mathsf {Z}(\lambda _i): \mathsf {M}_I(\lambda _{n-1})] =1$
and $[\mathsf {Z}(\lambda _i): \mathsf {M}_I(\lambda _{n-1})] =1$![]() . Likewise, for $1 \leq j \leq n-1$
. Likewise, for $1 \leq j \leq n-1$![]() the multiplicity
the multiplicity
arises from the ${n-1\choose j}$![]() copies of $\mathsf {M}_I(\lambda _j)$
copies of $\mathsf {M}_I(\lambda _j)$![]() and the ${n-1\choose j-1}$
and the ${n-1\choose j-1}$![]() copies of $\mathsf {M}_I(\lambda _{j-1})$
copies of $\mathsf {M}_I(\lambda _{j-1})$![]() . The proposition now follows from the well-known identity
. The proposition now follows from the well-known identity
Thus, we have verified the formula for $\mathsf {Z}(\lambda _i)$![]() when $0 \leq i \leq n-1$
when $0 \leq i \leq n-1$![]() . The $\mathsf {Z}(\lambda _n)$
. The $\mathsf {Z}(\lambda _n)$![]() case can be verified by replacing $I$
case can be verified by replacing $I$![]() with $J$
with $J$![]() and repeating the same arguments.
and repeating the same arguments.
Remark 4.8 An alternative argument is to simply apply Theorem 6.3, whose proof is independent of this proposition.
If we let ${[\mathsf {Q}(\lambda ):\mathsf {Z}(\mu )]}$![]() denote the multiplicity of $\mathsf {Z}(\mu )$
denote the multiplicity of $\mathsf {Z}(\mu )$![]() in any baby Verma filtration as in [Reference Jantzen7, Proposition II.11.4], then the following identity
in any baby Verma filtration as in [Reference Jantzen7, Proposition II.11.4], then the following identity
is known as BGG reciprocity for baby Verma modules.
Corollary 4.9 For $0\leq i,j \leq n,$![]()
Proof. By BGG reciprocity,

where the last equality follows from Proposition 4.7.
5. Extensions between irreducibles
The goal of this section is to prove the following theorem.
Theorem 5.1 Let $V = \mathsf {L}(\varpi _1)$![]() be the standard representation for $G,$
be the standard representation for $G,$![]() then for $0 \leq i,j \leq n$
then for $0 \leq i,j \leq n$![]()

where $(-)^{(-1)}$![]() denotes the inverse Frobenius twist (see [Reference Jantzen7, I.9]).
denotes the inverse Frobenius twist (see [Reference Jantzen7, I.9]).
It will be helpful to recall the identity
for any $\lambda, \mu \in \mathbf {X}_1$![]() and $\nu \in \mathbf {X}$
and $\nu \in \mathbf {X}$![]() , where the right-hand side denotes the $p\nu$
, where the right-hand side denotes the $p\nu$![]() -weight space of the corresponding $G$
-weight space of the corresponding $G$![]() -moduleFootnote 2 (cf. [Reference Jantzen7, I.6.9(4), (5)] and [Reference Jantzen7, II.9.19(3)]).
-moduleFootnote 2 (cf. [Reference Jantzen7, I.6.9(4), (5)] and [Reference Jantzen7, II.9.19(3)]).
We also recall from §1 that our assumption of $p$![]() being very good for $SL_{n+1}$
being very good for $SL_{n+1}$![]() (i.e. $p \nmid n+1$
(i.e. $p \nmid n+1$![]() ) is equivalent to the condition that the quotient $\mathbf {X}/ \mathbb {Z}\varPhi$
) is equivalent to the condition that the quotient $\mathbf {X}/ \mathbb {Z}\varPhi$![]() contains no $p$
contains no $p$![]() -torsion. In particular,
-torsion. In particular,
As a consequence, for any $\mu, \nu \in \mathbf {X}$![]()
Before proceeding to the proof of the theorem, we will record the following corollary.
Corollary 5.2 Let $G=SL_{n+1}$![]() with $n\geq 1$
with $n\geq 1$![]() , then for $0\leq i \leq n$
, then for $0\leq i \leq n$![]() ,
,

and for $i=1,\ldots, n-1$![]() ,
,

where we set $\varpi _0 =0$![]() and $\varpi _{n+1} =0$
and $\varpi _{n+1} =0$![]() for notational simplicity.
for notational simplicity.
Proof. First recall that for any $\lambda, \mu \in \mathbf {X}$![]() ,
,
which we obtain by applying $\operatorname {Hom}_{G_1T}(-, \widehat {\mathsf {L}}(\mu ))$![]() to the short exact sequence
to the short exact sequence
On the other hand, if we combine Theorem 5.1 with (5.1), then we can deduce that the dimensions
for $0 \leq i,j \leq n$![]() and $\nu \in \mathbf {X}$
and $\nu \in \mathbf {X}$![]() are given by the appropriate weight multiplicities of $V$
are given by the appropriate weight multiplicities of $V$![]() and $V^{*}$
and $V^{*}$![]() .
.
Determining the top two radical layers of the $\mathsf {Z}(\lambda _i)$![]() will also be essential to our $\operatorname {Ext}^{1}$
will also be essential to our $\operatorname {Ext}^{1}$![]() -calculation. Before stating this result, we will introduce some additional notation.
-calculation. Before stating this result, we will introduce some additional notation.
First fix $I, J \subset S$![]() as in §4, and for $0 \leq i \leq n-1$
as in §4, and for $0 \leq i \leq n-1$![]() , set
, set
Similarly, for $1 \leq i \leq n$![]() , set
, set
We also set $\overline {\text {F}}_I^{j}(\lambda _i) = \text {F}_I^{j}(\lambda _i)/\text {F}_I^{j+1}(\lambda _i)$![]() and $\overline {\text {F}}_J^{j}(\lambda _i) = \text {F}_J^{j}(\lambda _i)/\text {F}_J^{j+1}(\lambda _i)$
and $\overline {\text {F}}_J^{j}(\lambda _i) = \text {F}_J^{j}(\lambda _i)/\text {F}_J^{j+1}(\lambda _i)$![]() .
.
The exactness of coinduction implies

with a similar statement for $P_J$![]() .
.
Lemma 5.3 Set $\lambda _{-1} = \lambda _{n+1} = 0$![]() and declare that $M^{\oplus 0} = 0$
and declare that $M^{\oplus 0} = 0$![]() for any module $M,$
for any module $M,$![]() then
then
Proof. The case for $n=1$![]() follows from [Reference Jantzen7, II.9.10] and the $n=2$
follows from [Reference Jantzen7, II.9.10] and the $n=2$![]() case follows from [Reference Xi12, Theorems 2.4-2.5]. Now suppose $n > 2$
case follows from [Reference Xi12, Theorems 2.4-2.5]. Now suppose $n > 2$![]() and that the statement of the lemma holds for $SL_{r+1}$
and that the statement of the lemma holds for $SL_{r+1}$![]() whenever $1 \leq r < n$
whenever $1 \leq r < n$![]() . By the same argument as in the proof of Proposition 4.7, we can assume the statement also holds for $\mathsf {Z}_I(\lambda _i)$
. By the same argument as in the proof of Proposition 4.7, we can assume the statement also holds for $\mathsf {Z}_I(\lambda _i)$![]() with $0 \leq i \leq n-1$
with $0 \leq i \leq n-1$![]() (respectively, for $\mathsf {Z}_J(\lambda _i)$
(respectively, for $\mathsf {Z}_J(\lambda _i)$![]() with $1 \leq i \leq n$
with $1 \leq i \leq n$![]() ).
).
The inductive hypothesis gives
for $0 \leq i \leq n-1$![]() , and
, and
for $1 \leq i \leq n$![]() . Now we coinduce to get
. Now we coinduce to get
and
for $0 \leq i \leq n-1$![]() . (The formulas for $\overline {\text {F}}_J^{0}(\lambda _i)$
. (The formulas for $\overline {\text {F}}_J^{0}(\lambda _i)$![]() and $\overline {\text {F}}_J^{1}(\lambda _i)$
and $\overline {\text {F}}_J^{1}(\lambda _i)$![]() are similar.)
are similar.)
Let us focus on $I$![]() for now. By Proposition 4.6,
for now. By Proposition 4.6,
We also have
for $0 \leq i \leq n-1$![]() , where the first isomorphism is a consequence of (5.8) and Proposition 3.5 and the second isomorphism is deduced from (5.9) and Proposition 4.6. It then follows that the surjective map
, where the first isomorphism is a consequence of (5.8) and Proposition 3.5 and the second isomorphism is deduced from (5.9) and Proposition 4.6. It then follows that the surjective map
is an isomorphism since the left- and right-hand sides have the same dimension. Consequently,
Now let $M = \text {rad}^{1}\, \mathsf {Z}(\lambda _i) / \text {rad}^{1}\text {F}_I^{1}(\lambda _i)$![]() and observe
and observe

Thus, if we combine this with (5.10) and (5.11), we deduce the formula
Now observe that $\text {rad}^{1}\,\text {F}_I^{1}(\lambda _i) \subseteq \text {rad}^{2}\, \mathsf {Z}(\lambda _i)$![]() since $\text {F}_I^{1}(\lambda _i) \subseteq \text {rad}^{1}\, \mathsf {Z}(\lambda _i)$
since $\text {F}_I^{1}(\lambda _i) \subseteq \text {rad}^{1}\, \mathsf {Z}(\lambda _i)$![]() . As a consequence,
. As a consequence,
and hence,
Moreover, $\overline {\text {rad}}_0\, \text {F}_I^{1}(\lambda _i) = \text {F}_I^{1}(\lambda _i)/\text {rad}^{1}\text {F}_I^{1}(\lambda _i) \hookrightarrow M.$![]() Thus by (5.11), there exists an injective map
Thus by (5.11), there exists an injective map
whose image must account for every irreducible factor of $M$![]() except for a single copy of $\mathsf {L}(\lambda _{i+1})$
except for a single copy of $\mathsf {L}(\lambda _{i+1})$![]() . Consequently, $M$
. Consequently, $M$![]() fits into a short exact sequence of the form
fits into a short exact sequence of the form
Now let $N = \iota (\mathsf {L}(\lambda _{i-1})^{\oplus i})$![]() so that $[M/N] = (n-i)[\mathsf {L}(\lambda _{i+1})]$
so that $[M/N] = (n-i)[\mathsf {L}(\lambda _{i+1})]$![]() . From [Reference Jantzen7, Proposition II.12.9], we know that any $G_1$
. From [Reference Jantzen7, Proposition II.12.9], we know that any $G_1$![]() -module with precisely one isotypic component must be semisimple. It follows that $M/N \cong \mathsf {L}(\lambda _{i+1})^{\oplus n-i}$
-module with precisely one isotypic component must be semisimple. It follows that $M/N \cong \mathsf {L}(\lambda _{i+1})^{\oplus n-i}$![]() . In particular, we get a surjection
. In particular, we get a surjection
Finally, since every map from $\text {rad}^{1}\, \mathsf {Z}(\lambda _i)$![]() to a semisimple module factors through $\overline {\text {rad}}_1\, \mathsf {Z}(\lambda _i)$
to a semisimple module factors through $\overline {\text {rad}}_1\, \mathsf {Z}(\lambda _i)$![]() (recall that the latter is the head of the former), we get a surjection
(recall that the latter is the head of the former), we get a surjection
(Recall that $\overline {\text {rad}}_0\, M = \overline {\text {rad}}_1\, \mathsf {Z}(\lambda _i)$![]() .) Observe now that if $i=0$
.) Observe now that if $i=0$![]() , then the preceding map must be an isomorphism since every possible factor of $\overline {\text {rad}}_1\, \mathsf {Z}(\lambda _i)$
, then the preceding map must be an isomorphism since every possible factor of $\overline {\text {rad}}_1\, \mathsf {Z}(\lambda _i)$![]() has been accounted for and we are done.
has been accounted for and we are done.
On the other hand, if $1 \leq i \leq n$![]() , then by replacing $I$
, then by replacing $I$![]() with $J$
with $J$![]() and repeating the same arguments, we also obtain a surjection
and repeating the same arguments, we also obtain a surjection
Therefore, the lemma follows by combining (5.13) and (5.14) which account for every possible factor of $\overline {\text {rad}}_1\, \mathsf {Z}(\lambda _i)$![]() .
.
We can now compute the top two radical layers of $\widehat {\mathsf {Z}}(\lambda _i)$![]() .
.
Lemma 5.4 Let us set $\varpi _0=0$![]() and $\varpi _{n+1} =0$
and $\varpi _{n+1} =0$![]() for notational simplicity. We then have
for notational simplicity. We then have

and for $i=1,\ldots, n-1,$![]()

Proof. The $n=1$![]() case follows from [Reference Jantzen7, II.9.10], and the $n=2$
case follows from [Reference Jantzen7, II.9.10], and the $n=2$![]() case is given in [Reference Xi12, Theorems 2.4-2.5]. Suppose now that $n>2$
case is given in [Reference Xi12, Theorems 2.4-2.5]. Suppose now that $n>2$![]() , and that the statement holds for $SL_{r+1}$
, and that the statement holds for $SL_{r+1}$![]() with $2 \leq r < n$
with $2 \leq r < n$![]() . The inductive hypothesis can be applied to $L_I$
. The inductive hypothesis can be applied to $L_I$![]() and $L_J$
and $L_J$![]() as in the proof of Proposition 4.7. More precisely, for $L_I$
as in the proof of Proposition 4.7. More precisely, for $L_I$![]() and $i=0,\ldots, n-1$
and $i=0,\ldots, n-1$![]() , [Reference Jantzen7, Lemma II.9.2(3)] implies that the highest weight of every composition factor of $\widehat {\mathsf {Z}}_I(\lambda _i)$
, [Reference Jantzen7, Lemma II.9.2(3)] implies that the highest weight of every composition factor of $\widehat {\mathsf {Z}}_I(\lambda _i)$![]() is of the form $\lambda _i - \gamma$
is of the form $\lambda _i - \gamma$![]() for various $\gamma \in \mathbb {Z} I$
for various $\gamma \in \mathbb {Z} I$![]() .
.
If we set $G' = [L_I, L_I]\cong SL_n$![]() , and $T' = T\cap G'$
, and $T' = T\cap G'$![]() , we get
, we get
with ${[\widehat {\mathsf {Z}}_I(\lambda _i): \widehat {\mathsf {L}}(\lambda _i - \gamma )] = [\widehat {\mathsf {Z}}(\lambda _i|_{T'}): \widehat {\mathsf {L}}(\lambda _i|_{T'} - \gamma |_{T'})] }$![]() . Furthermore,
. Furthermore,

So the inductive hypothesis is applied to $L_I$![]() by first expressing the irreducibles occurring in the inductive hypothesis for $SL_{n}$
by first expressing the irreducibles occurring in the inductive hypothesis for $SL_{n}$![]() as $\widehat {\mathsf {L}}(\lambda _i|_{T'} - \gamma |_{T'})$
as $\widehat {\mathsf {L}}(\lambda _i|_{T'} - \gamma |_{T'})$![]() for various uniquely determined $\gamma$
for various uniquely determined $\gamma$![]() , and then employing (5.15) to obtain the corresponding formulas for $\overline {\text {rad}}_1\, \widehat {\mathsf {Z}}_I(\lambda _i)$
, and then employing (5.15) to obtain the corresponding formulas for $\overline {\text {rad}}_1\, \widehat {\mathsf {Z}}_I(\lambda _i)$![]() . (The case for $L_J$
. (The case for $L_J$![]() with $i=1,\ldots, n$
with $i=1,\ldots, n$![]() is similar.)
is similar.)
Thus, the inductive hypothesis gives

So the formula for $\overline {\text {rad}}_1\, \widehat {\mathsf {Z}}(\lambda _0)$![]() follows from Proposition 4.6 and the proof of Lemma 5.3. For $i=1,\ldots, n-1$
follows from Proposition 4.6 and the proof of Lemma 5.3. For $i=1,\ldots, n-1$![]() , the hypothesis also gives
, the hypothesis also gives

Now once again, the formula for $\overline {\text {rad}}_1\, \widehat {\mathsf {Z}}(\lambda _i)$![]() is obtained by applying Proposition 4.6 and then proceeding as in the proof of Lemma 5.3.
is obtained by applying Proposition 4.6 and then proceeding as in the proof of Lemma 5.3.
Finally, the formula for $\overline {\text {rad}}_1\, \widehat {\mathsf {Z}}(\lambda _n)$![]() is verified by first applying the inductive hypothesis to $L_J$
is verified by first applying the inductive hypothesis to $L_J$![]() , which gives
, which gives

and then proceeding as above.
The following lemma helps characterize modules which admit a surjective map from a baby Verma module.
Lemma 5.5 If ${E \in \operatorname {Ext}^{1}_{G_1T}(\widehat {\mathsf {L}}(\lambda ), \widehat {\mathsf {L}}(\mu ))}$![]() for $\lambda,\mu \in \mathbf {X}$
for $\lambda,\mu \in \mathbf {X}$![]() is non-trivial and $\lambda \not \leq \mu,$
is non-trivial and $\lambda \not \leq \mu,$![]() then $E$
then $E$![]() is a quotient of $\widehat {\mathsf {Z}}(\lambda )$
is a quotient of $\widehat {\mathsf {Z}}(\lambda )$![]() .
.
Proof. By definition, $E$![]() is an indecomposable length 2 module with head $\widehat {\mathsf {L}}(\lambda )$
is an indecomposable length 2 module with head $\widehat {\mathsf {L}}(\lambda )$![]() and socle $\widehat {\mathsf {L}}(\mu )$
and socle $\widehat {\mathsf {L}}(\mu )$![]() . In particular, $E$
. In particular, $E$![]() is a cyclic module for $\widehat {\mathcal {U}}$
is a cyclic module for $\widehat {\mathcal {U}}$![]() which is generated by some $\lambda$
which is generated by some $\lambda$![]() -weight vector $v_{\lambda }$
-weight vector $v_{\lambda }$![]() . Now every weight $\gamma$
. Now every weight $\gamma$![]() occurring with non-zero multiplicity in $\widehat {\mathsf {L}}(\mu )$
occurring with non-zero multiplicity in $\widehat {\mathsf {L}}(\mu )$![]() satisfies $\gamma \leq \mu$
satisfies $\gamma \leq \mu$![]() , and hence, $\lambda \not \leq \gamma$
, and hence, $\lambda \not \leq \gamma$![]() . On the other hand, any weight $\gamma$
. On the other hand, any weight $\gamma$![]() occurring with non-zero multiplicity in $\widehat {\mathsf {L}}(\lambda )$
occurring with non-zero multiplicity in $\widehat {\mathsf {L}}(\lambda )$![]() with $\gamma \neq \lambda$
with $\gamma \neq \lambda$![]() must also satisfy $\gamma < \lambda$
must also satisfy $\gamma < \lambda$![]() , and thus, $\lambda + \alpha _i \not \leq \gamma$
, and thus, $\lambda + \alpha _i \not \leq \gamma$![]() for $i=1,\ldots,n$
for $i=1,\ldots,n$![]() . Therefore, $\lambda + \alpha _i$
. Therefore, $\lambda + \alpha _i$![]() cannot occur as a weight of $E$
cannot occur as a weight of $E$![]() which forces $X_{\alpha _i}\cdot v_{\lambda } =0$
which forces $X_{\alpha _i}\cdot v_{\lambda } =0$![]() for all $i$
for all $i$![]() . As a result, the surjective map
. As a result, the surjective map

factors through the ideal $\widehat {I}_{\lambda }$![]() , and so it follows that $E$
, and so it follows that $E$![]() is a quotient of ${\widehat {\mathsf {Z}}(\lambda ) \cong \widehat {\mathcal {U}}/\widehat {I}_{\lambda }}$
is a quotient of ${\widehat {\mathsf {Z}}(\lambda ) \cong \widehat {\mathcal {U}}/\widehat {I}_{\lambda }}$![]() .
.
Lemma 5.6 If $M = \operatorname {Ext}^{1}_{G_1}(\mathsf {L}(\lambda _i),\mathsf {L}(\lambda _j))$![]() is non-zero for $|i-j| \geq 2,$
is non-zero for $|i-j| \geq 2,$![]() then there exists $\nu \in \mathbf {X}^{+}$
then there exists $\nu \in \mathbf {X}^{+}$![]() such that ${p\nu \leq \lambda _j - \lambda _i}$
such that ${p\nu \leq \lambda _j - \lambda _i}$![]() .
.
Proof. The $G/G_1$![]() -module $M$
-module $M$![]() is non-zero if and only if $M_{p\nu } \neq 0$
is non-zero if and only if $M_{p\nu } \neq 0$![]() for some $\nu \in \mathbf {X}^{+}$
for some $\nu \in \mathbf {X}^{+}$![]() . By Lemma 5.3, we know that there does not exist an extension $E \in M$
. By Lemma 5.3, we know that there does not exist an extension $E \in M$![]() which is isomorphic to a quotient of $\mathsf {Z}(\lambda _i)$
which is isomorphic to a quotient of $\mathsf {Z}(\lambda _i)$![]() . Hence, there are no extensions $E \in M_{p\nu } = \operatorname {Ext}^{1}_{G_1T}(\widehat {\mathsf {L}}(\lambda _i), \widehat {\mathsf {L}}(\lambda _j - p\nu ))$
. Hence, there are no extensions $E \in M_{p\nu } = \operatorname {Ext}^{1}_{G_1T}(\widehat {\mathsf {L}}(\lambda _i), \widehat {\mathsf {L}}(\lambda _j - p\nu ))$![]() which occur as a quotient of $\widehat {\mathsf {Z}}(\lambda _i)$
which occur as a quotient of $\widehat {\mathsf {Z}}(\lambda _i)$![]() . Thus, by Lemma 5.5, we must have $\lambda _i \leq \lambda _j - p\nu$
. Thus, by Lemma 5.5, we must have $\lambda _i \leq \lambda _j - p\nu$![]() if $M_{p\nu } \neq 0$
if $M_{p\nu } \neq 0$![]() .
.
The vanishing portion of Theorem 5.1 will follow provided that if $|i-j| \geq 2$![]() , then there does not exist any $\nu \in \mathbf {X}^{+}$
, then there does not exist any $\nu \in \mathbf {X}^{+}$![]() which satisfies
which satisfies
Lemma 5.7 If $0\leq i, j \leq n$![]() are such that $|i-j| \neq 1,$
are such that $|i-j| \neq 1,$![]() then
then
Proof. We begin by noting that the $i=j$![]() case immediately follows from [Reference Jantzen7, Proposition II.12.9]. So we only have to consider the case when $|i-j| \geq 2$
case immediately follows from [Reference Jantzen7, Proposition II.12.9]. So we only have to consider the case when $|i-j| \geq 2$![]() . By the comments immediately preceding this lemma, it suffices to show that there exist no dominant weights $\nu$
. By the comments immediately preceding this lemma, it suffices to show that there exist no dominant weights $\nu$![]() such that
such that
whenever $|i-j| \geq 2$![]() . Applying (2.11), we compute
. Applying (2.11), we compute

First suppose that $j>i$![]() , then we can see that
, then we can see that

The $j=n$![]() case is now obvious since $\varpi _{i+1}$
case is now obvious since $\varpi _{i+1}$![]() is minuscule, and thus $p\nu \leq \lambda _n - \lambda _i$
is minuscule, and thus $p\nu \leq \lambda _n - \lambda _i$![]() implies $p\nu < p\varpi _{i+1}.$
implies $p\nu < p\varpi _{i+1}.$![]() Hence by (5.3), $\nu < \varpi _{i+1}$
Hence by (5.3), $\nu < \varpi _{i+1}$![]() which is impossible for $\nu \in \mathbf {X}^{+}$
which is impossible for $\nu \in \mathbf {X}^{+}$![]() . On the other hand, for $i < j < n$
. On the other hand, for $i < j < n$![]() ,
,
where the rightmost inequality comes from the fact that $\varpi _{n+1-(j-i)} = w(-\varpi _{j+1} + \varpi _{i+1})$![]() for some $w \in W$
for some $w \in W$![]() . Now by applying (5.3) as above, we can see that if $p\nu \leq \lambda _j - \lambda _i$
. Now by applying (5.3) as above, we can see that if $p\nu \leq \lambda _j - \lambda _i$![]() , then $\nu < \varpi _{n+1-(j-i)}$
, then $\nu < \varpi _{n+1-(j-i)}$![]() , which is also impossible for $\nu \in \mathbf {X}^{+}$
, which is also impossible for $\nu \in \mathbf {X}^{+}$![]() .
.
Suppose now that $j < i$![]() . When $i=n$
. When $i=n$![]() , we can see that $\lambda _j-\lambda _n \not \in p\mathbf {X}$
, we can see that $\lambda _j-\lambda _n \not \in p\mathbf {X}$![]() so if $p\nu < \lambda _j - \lambda _n$
so if $p\nu < \lambda _j - \lambda _n$![]() (and thus $(\lambda _j - \lambda _n) - p\nu \in \mathbb {Z}_{\geq 0}\varPhi ^{+}$
(and thus $(\lambda _j - \lambda _n) - p\nu \in \mathbb {Z}_{\geq 0}\varPhi ^{+}$![]() ), then
), then
If we set $\gamma = -\varpi _{j+1} - \nu$![]() and then compare both sides of the preceding equation, we can deduce that $p\gamma \in p\mathbf {X}\cap \mathbb {Z}\varPhi = p\mathbb {Z}\varPhi$
and then compare both sides of the preceding equation, we can deduce that $p\gamma \in p\mathbf {X}\cap \mathbb {Z}\varPhi = p\mathbb {Z}\varPhi$![]() , where the equality follows from (5.2). So we can write $p\gamma = \sum _{k=1}^{n} pc_k\alpha _k$
, where the equality follows from (5.2). So we can write $p\gamma = \sum _{k=1}^{n} pc_k\alpha _k$![]() where $c_k \in \mathbb {Z}$
where $c_k \in \mathbb {Z}$![]() for all $k$
for all $k$![]() . Moreover, $\gamma \in \mathbb {Z}_{\geq 0}\varPhi ^{+}$
. Moreover, $\gamma \in \mathbb {Z}_{\geq 0}\varPhi ^{+}$![]() since
since

and thus if $c_k < 0$![]() for some $k$
for some $k$![]() , then $pc_k +1 <0$
, then $pc_k +1 <0$![]() . But this contradicts the assumption that $(\lambda _j - \lambda _n) - p\nu \in \mathbb {Z}_{\geq 0}\varPhi ^{+}$
. But this contradicts the assumption that $(\lambda _j - \lambda _n) - p\nu \in \mathbb {Z}_{\geq 0}\varPhi ^{+}$![]() .
.
Hence,
and so by (5.3), $\nu < \varpi _{n-j}$![]() , which is impossible for $\nu \in \mathbf {X}^{+}$
, which is impossible for $\nu \in \mathbf {X}^{+}$![]() . For $j < i < n$
. For $j < i < n$![]() , the same reasoning shows that if $p\nu \leq \lambda _j - \lambda _i$
, the same reasoning shows that if $p\nu \leq \lambda _j - \lambda _i$![]() , then $p\nu \leq p(-\varpi _{j+1} + \varpi _{i+1}) < p\varpi _{i-j-1}$
, then $p\nu \leq p(-\varpi _{j+1} + \varpi _{i+1}) < p\varpi _{i-j-1}$![]() . This forces $\nu < \varpi _{i-j-1}$
. This forces $\nu < \varpi _{i-j-1}$![]() , which again is impossible for $\nu \in \mathbf {X}^{+}$
, which again is impossible for $\nu \in \mathbf {X}^{+}$![]() .
.
We now have enough information to complete our $\operatorname {Ext}^{1}$![]() -calculation. However, before we get to the proof of Theorem 5.1, it will be helpful to recall [Reference Andersen2, Lemma 5.1]. First, for any $\lambda \in \mathbf {X}^{+}$
-calculation. However, before we get to the proof of Theorem 5.1, it will be helpful to recall [Reference Andersen2, Lemma 5.1]. First, for any $\lambda \in \mathbf {X}^{+}$![]() , we introduce the notation
, we introduce the notation
Now suppose ${M = \operatorname {Ext}^{1}_{G_1}(\mathsf {L}(\lambda ), \mathsf {L}(\mu ))^{(-1)}}$![]() for some $\lambda, \mu \in \mathbf {X}_1$
for some $\lambda, \mu \in \mathbf {X}_1$![]() and suppose there exists an element $\nu \in \mathbf {X}$
and suppose there exists an element $\nu \in \mathbf {X}$![]() such that $M_{\nu } \neq 0$
such that $M_{\nu } \neq 0$![]() , then the aforementioned lemma implies
, then the aforementioned lemma implies
This gives the following lemma.
Lemma 5.8 Let $M = \operatorname {Ext}^{1}_{G_1}(\mathsf {L}(\lambda ), \mathsf {L}(\mu ))^{(-1)}$![]() for some $\lambda, \mu \in \mathbf {X}_1$
for some $\lambda, \mu \in \mathbf {X}_1$![]() . If $\nu, \nu ' \in \mathbf {X}$
. If $\nu, \nu ' \in \mathbf {X}$![]() are such that $M_{\nu } \neq 0$
are such that $M_{\nu } \neq 0$![]() and $M_{\nu '} \neq 0$
and $M_{\nu '} \neq 0$![]() , then $\nu - \nu ' \in \mathbb {Z}\varPhi$
, then $\nu - \nu ' \in \mathbb {Z}\varPhi$![]() .
.
Proof. By the observation immediately preceding the lemma, we know that if $M_{\nu } \neq 0$![]() and $M_{\nu '} \neq 0$
and $M_{\nu '} \neq 0$![]() , then both $p\nu$
, then both $p\nu$![]() and $p\nu '$
and $p\nu '$![]() are in the same root coset since they are both comparable to the weight $\mu ^{0} - \lambda$
are in the same root coset since they are both comparable to the weight $\mu ^{0} - \lambda$![]() . Thus by (5.2),
. Thus by (5.2),
Therefore, $\nu - \nu ' \in \mathbb {Z}\varPhi$![]() and we are done.
and we are done.
We will also need the following technical lemma.
Lemma 5.9 Any $\nu \in (\varpi _1 + \mathbb {Z}\varPhi )\cap \mathbf {X}^{+}$![]() satisfies $\varpi _1 \leq \nu$
satisfies $\varpi _1 \leq \nu$![]() .
.
Proof. Let $\nu = \varpi _1 + \sum _{i=1}^{n} a_i\alpha _i$![]() , where $a_i \in \mathbb {Z}$
, where $a_i \in \mathbb {Z}$![]() is arbitrary for all $i$
is arbitrary for all $i$![]() . The lemma will follow if we can show that
. The lemma will follow if we can show that
(Note that if $n=1$![]() , then the claim is immediate since $\nu = \varpi _1 + a_1\alpha _1 = (2a_1+1)\varpi _1$
, then the claim is immediate since $\nu = \varpi _1 + a_1\alpha _1 = (2a_1+1)\varpi _1$![]() , where $2a_1 +1 \geq 0$
, where $2a_1 +1 \geq 0$![]() implies $a_1 \geq 0$
implies $a_1 \geq 0$![]() because $a_1$
because $a_1$![]() is an integer.)
is an integer.)
In general, write $\nu = c_1\varpi _1 + c_2\varpi _2 + \cdots +c_n \varpi _n$![]() , and observe that $c_1 = 2a_1-a_2+1$
, and observe that $c_1 = 2a_1-a_2+1$![]() , $c_n = -a_{n-1} + 2a_n$
, $c_n = -a_{n-1} + 2a_n$![]() and $c_i = -a_{i-1} + 2a_i -a_{i+1}$
and $c_i = -a_{i-1} + 2a_i -a_{i+1}$![]() for $i=2, \ldots, n-1$
for $i=2, \ldots, n-1$![]() . Thus, the condition $\nu \in \mathbf {X}^{+}$
. Thus, the condition $\nu \in \mathbf {X}^{+}$![]() is given by
is given by

From the above list of inequalities, we can deduce that $a_n \geq \frac {1}{2}a_{n-1}$![]() , $a_{n-1} \geq \frac {2}{3}a_{n-2}$
, $a_{n-1} \geq \frac {2}{3}a_{n-2}$![]() , and generally, that
, and generally, that

Now since $a_1 \in \mathbb {Z}$![]() and $-1 < \frac {-n}{n+1} \leq a_1$
and $-1 < \frac {-n}{n+1} \leq a_1$![]() , we get $a_1 \geq 0$
, we get $a_1 \geq 0$![]() . But then $a_1 \geq 0$
. But then $a_1 \geq 0$![]() implies $a_2 \geq \frac {n-1}{n}a_1 \geq 0$
implies $a_2 \geq \frac {n-1}{n}a_1 \geq 0$![]() , which then implies $a_3 \geq \frac {n-2}{n-1}a_2 \geq 0$
, which then implies $a_3 \geq \frac {n-2}{n-1}a_2 \geq 0$![]() . Proceeding in this way, we conclude that $a_i \geq 0$
. Proceeding in this way, we conclude that $a_i \geq 0$![]() for all $i$
for all $i$![]() .
.
Proof of Theorem 5.1. By Lemma 5.7, we only have to determine
in the case where $|i-j| = 1$![]() .
.
Before proceeding, we note that a $G$![]() -module $M$
-module $M$![]() satisfies $M \cong \mathsf {L}(\varpi _1)$
satisfies $M \cong \mathsf {L}(\varpi _1)$![]() if and only if the following two conditions hold:
if and only if the following two conditions hold:
a) $\dim _{\Bbbk } M_{\varpi _1} = 1,$

b) $M_{\nu } = 0$
 for any $\nu \in \mathbf {X}^{+}$
for any $\nu \in \mathbf {X}^{+}$ with $\nu \neq \varpi _1$
with $\nu \neq \varpi _1$ .
.
To justify this, first note that if $M \cong \mathsf {L}(\varpi _1)$![]() , then a) and b) can be verified by considering the (well-known) weight space multiplicities of $\mathsf {L}(\varpi _1)$
, then a) and b) can be verified by considering the (well-known) weight space multiplicities of $\mathsf {L}(\varpi _1)$![]() and by recalling the fact that $\varpi _1$
and by recalling the fact that $\varpi _1$![]() is minuscule. Conversely, if $M$
is minuscule. Conversely, if $M$![]() is any module satisfying both conditions, then b) ensures that $\varpi _1$
is any module satisfying both conditions, then b) ensures that $\varpi _1$![]() is the only possible highest weight, and a) ensures that it must occur with multiplicity one. In particular, these two conditions force $M$
is the only possible highest weight, and a) ensures that it must occur with multiplicity one. In particular, these two conditions force $M$![]() to have the same weight space dimensions as $\mathsf {L}(\varpi _1)$
to have the same weight space dimensions as $\mathsf {L}(\varpi _1)$![]() , and thus, $M \cong \mathsf {L}(\varpi _1)$
, and thus, $M \cong \mathsf {L}(\varpi _1)$![]() .
.
We now begin by setting
We will first prove that $M$![]() satisfies a). By (2.5), we know that any length two quotient of $\widehat {\mathsf {Z}}(\lambda _i)$
satisfies a). By (2.5), we know that any length two quotient of $\widehat {\mathsf {Z}}(\lambda _i)$![]() factors through the module
factors through the module
whose Loewy series is explicitly described in Lemma 5.4. In fact, from this description, we deduce that there exists (up to isomorphism) precisely one $G_1T$![]() -module $E$
-module $E$![]() which is a quotient of $\widehat {\mathsf {Z}}(\lambda _{i+1})$
which is a quotient of $\widehat {\mathsf {Z}}(\lambda _{i+1})$![]() and which fits into a non-splitFootnote 3 short exact sequence of the form
and which fits into a non-splitFootnote 3 short exact sequence of the form
By (5.1), it then follows that $\dim _{\Bbbk } M_{\varpi _1} \geq 1$![]() .
.
On the other hand, suppose $E'$![]() is an arbitrary $G_1T$
is an arbitrary $G_1T$![]() -module which fits into a short exact sequence as above. Now since we can deduce from (5.17) that
-module which fits into a short exact sequence as above. Now since we can deduce from (5.17) that
then by Lemma 5.5, $E'$![]() is also a quotient of $\widehat {\mathsf {Z}}(\lambda _{i+1})$
is also a quotient of $\widehat {\mathsf {Z}}(\lambda _{i+1})$![]() . Hence $E' \cong E$
. Hence $E' \cong E$![]() , and therefore, $\dim _{\Bbbk } M_{\varpi _1} = 1$
, and therefore, $\dim _{\Bbbk } M_{\varpi _1} = 1$![]() . So we have verified a).
. So we have verified a).
We will now verify b) by contradiction. Suppose there exists $\nu \in \mathbf {X}^{+}$![]() with $\nu \neq \varpi _1$
with $\nu \neq \varpi _1$![]() and $M_{\nu } \neq 0$
and $M_{\nu } \neq 0$![]() . By Lemma 5.8, we know that $\nu \in (\varpi _1 + \mathbb {Z}\varPhi )\cap \mathbf {X}^{+}$
. By Lemma 5.8, we know that $\nu \in (\varpi _1 + \mathbb {Z}\varPhi )\cap \mathbf {X}^{+}$![]() , and hence, $\varpi _1 < \nu$
, and hence, $\varpi _1 < \nu$![]() by Lemma 5.9. In addition, we must also have $p\nu \not \leq \lambda _i - \lambda _{i+1}$
by Lemma 5.9. In addition, we must also have $p\nu \not \leq \lambda _i - \lambda _{i+1}$![]() since $p\varpi _1 \not \leq \lambda _i - \lambda _{i+1}$
since $p\varpi _1 \not \leq \lambda _i - \lambda _{i+1}$![]() . So by Lemma 5.5, there exists a quotient $E'$
. So by Lemma 5.5, there exists a quotient $E'$![]() of $\widehat {\mathsf {Z}}(\lambda _{i+1})$
of $\widehat {\mathsf {Z}}(\lambda _{i+1})$![]() , which fits into a short exact sequence of the form
, which fits into a short exact sequence of the form
In particular, $\widehat {\mathsf {L}}(\lambda _i-p\nu )$![]() must occur as a factor of $\overline {\text {rad}}_1\, \mathsf {Z}(\lambda _{i+1})$
must occur as a factor of $\overline {\text {rad}}_1\, \mathsf {Z}(\lambda _{i+1})$![]() . But from Lemma 5.4, we can see that there are no such factors (i.e. there are no factors of the form $\widehat {\mathsf {L}}(\lambda _i -p\nu )$
. But from Lemma 5.4, we can see that there are no such factors (i.e. there are no factors of the form $\widehat {\mathsf {L}}(\lambda _i -p\nu )$![]() with $\nu > \varpi _1$
with $\nu > \varpi _1$![]() ). It follows that $M_{\nu } =0$
). It follows that $M_{\nu } =0$![]() and we have reached a contradiction.
and we have reached a contradiction.
Similarly, if we set
then by the same reasoning as above, we get $N \cong \mathsf {L}(\varpi _1)^{*}$![]() .
.
6. The Loewy series for $\widehat {\mathsf {Z}}(\lambda _i + p\nu )$ and $\widehat {\mathsf {Z}}'(\lambda _i + p\nu )$
and $\widehat {\mathsf {Z}}'(\lambda _i + p\nu )$
In this section, we will determine Loewy series for $\widehat {\mathsf {Z}}(\lambda _i+p\nu )$![]() and $\widehat {\mathsf {Z}}'(\lambda _i+p\nu )$
and $\widehat {\mathsf {Z}}'(\lambda _i+p\nu )$![]() . We will also deduce the Loewy lengths and establish the rigidity of these modules. We now begin by considering the easier problem involving $\mathsf {Z}(\lambda _i)$
. We will also deduce the Loewy lengths and establish the rigidity of these modules. We now begin by considering the easier problem involving $\mathsf {Z}(\lambda _i)$![]() and $\mathsf {Z}'(\lambda _i)$
and $\mathsf {Z}'(\lambda _i)$![]() .
.
Lemma 6.1 Let $n\geq 2,$![]() then for $0\leq i \leq n$
then for $0\leq i \leq n$![]() and $j\geq 0,$
and $j\geq 0,$![]()
Moreover, for $0 \leq i \leq n-1,$![]()
Also, for $1\leq i \leq n$![]() ,
,
(We set $\overline {\text {F}}^{-1}_I(\lambda _i) = 0$![]() and $\overline {\text {F}}^{-1}_J(\lambda _i) =0$
and $\overline {\text {F}}^{-1}_J(\lambda _i) =0$![]() .)
.)
Proof. As in the proof of Lemma 5.3, we will proceed by induction on $n\geq 2$![]() . The base case again follows from the explicit formulas given in [Reference Xi12, Theorems 2.4-2.5]. Suppose $n > 2$
. The base case again follows from the explicit formulas given in [Reference Xi12, Theorems 2.4-2.5]. Suppose $n > 2$![]() and assume the statement of the lemma holds for all $SL_{r+1}$
and assume the statement of the lemma holds for all $SL_{r+1}$![]() with $2 \leq r < n$
with $2 \leq r < n$![]() . The argument in the proof of Proposition 4.7 implies that the statement also holds for the Levi factor $L_I$
. The argument in the proof of Proposition 4.7 implies that the statement also holds for the Levi factor $L_I$![]() with $\mathsf {Z}_I(\lambda _i)$
with $\mathsf {Z}_I(\lambda _i)$![]() and $0 \leq i \leq n-1$
and $0 \leq i \leq n-1$![]() (respectively, $L_J$
(respectively, $L_J$![]() with $\mathsf {Z}_J(\lambda _i)$
with $\mathsf {Z}_J(\lambda _i)$![]() and $1 \leq i \leq n$
and $1 \leq i \leq n$![]() ).
).
For simplicity, let us begin by fixing $i \in \{0,\ldots, n-1\}$![]() . The inductive hypothesis gives
. The inductive hypothesis gives
where $m^{j}_{ik} \neq 0$![]() implies $k \equiv i + j \mod 2$
implies $k \equiv i + j \mod 2$![]() . Thus,
. Thus,
By Proposition 4.6,
From the inductive hypothesis, we can see that (6.1) will hold on the factors of $\overline {\text {rad}}_j\, \mathsf {Z}(\lambda _i)$![]() , provided we verify (6.2). We will proceed by induction on $j\geq 0$
, provided we verify (6.2). We will proceed by induction on $j\geq 0$![]() . The base case, $j=0$
. The base case, $j=0$![]() , is obvious since ${\overline {\text {rad}}_0\, \mathsf {Z}(\lambda _i) = \mathsf {L}(\lambda _i)}$
, is obvious since ${\overline {\text {rad}}_0\, \mathsf {Z}(\lambda _i) = \mathsf {L}(\lambda _i)}$![]() . Also, the $j=1$
. Also, the $j=1$![]() case follows from Lemma 5.3. Now assume $j\geq 2$
case follows from Lemma 5.3. Now assume $j\geq 2$![]() and that (6.2) holds for $0 \leq l < j$
and that (6.2) holds for $0 \leq l < j$![]() .
.
The inductive hypothesis for $j$![]() gives $\text {F}_I^{j-1}(\lambda _i) \subseteq \text {rad}^{j-1}\, \mathsf {Z}(\lambda _i)$
gives $\text {F}_I^{j-1}(\lambda _i) \subseteq \text {rad}^{j-1}\, \mathsf {Z}(\lambda _i)$![]() , and thus,
, and thus,
Now if we apply the inductive hypothesis for $L_I$![]() and reason as we did in the portion of the proof of Lemma 5.3 between (5.11) and (5.12), we can deduce
and reason as we did in the portion of the proof of Lemma 5.3 between (5.11) and (5.12), we can deduce
and hence, the first claim of (6.2). Moreover, by imitating the arguments immediately following (5.12), we can also show that $\overline {\text {rad}}_j\, \mathsf {Z}(\lambda _i)$![]() is the head of the module
is the head of the module

which fits into a short exact sequence of the form
But now, by the inductive hypothesis and (6.4), we can see that every factor $\mathsf {L}(\lambda _k)$![]() of $M$
of $M$![]() occurring with non-zero multiplicity must satisfy $k \equiv i + j \mod 2$
occurring with non-zero multiplicity must satisfy $k \equiv i + j \mod 2$![]() . In particular, if $\mathsf {L}(\lambda _s)$
. In particular, if $\mathsf {L}(\lambda _s)$![]() and $\mathsf {L}(\lambda _t)$
and $\mathsf {L}(\lambda _t)$![]() are two non-zero factors of $M$
are two non-zero factors of $M$![]() , then $|s-t| \neq 1$
, then $|s-t| \neq 1$![]() . Thus, Theorem 5.1 implies the preceding short exact sequence is split, and hence (6.2) holds for all $j\geq 0$
. Thus, Theorem 5.1 implies the preceding short exact sequence is split, and hence (6.2) holds for all $j\geq 0$![]() .
.
So we have verified (6.1) and (6.2) for $0 \leq i \leq n-1$![]() and $j\geq 0$
and $j\geq 0$![]() . On the other hand, if we replace $I$
. On the other hand, if we replace $I$![]() with $J$
with $J$![]() and fix any $i \in \{1,\ldots, n\}$
and fix any $i \in \{1,\ldots, n\}$![]() , then the same argument as above also verifies (6.1) and (6.3) for all $j\geq 0$
, then the same argument as above also verifies (6.1) and (6.3) for all $j\geq 0$![]() .
.
Before getting to the main results of this section, we recall a simple combinatorial identity obtained from Pascal's triangle. Namely, for any $0 \leq j \leq n$![]() and $0 \leq i \leq j$
and $0 \leq i \leq j$![]() ,
,

where we assume ${n \choose j} =0$![]() unless ${0\leq j \leq n}$
unless ${0\leq j \leq n}$![]() .
.
Proposition 6.2 Let $n\geq 1,$![]() then for $0\leq i \leq n$
then for $0\leq i \leq n$![]() and $j\geq 0,$
and $j\geq 0,$![]()
In particular, ${\ell \ell (\mathsf {Z}'(\lambda _i))=\ell \ell (\mathsf {Z}(\lambda _i)) = n+1}$![]() and $\overline {\text {rad}}_j\, \mathsf {Z}(\lambda _i)$
and $\overline {\text {rad}}_j\, \mathsf {Z}(\lambda _i)$![]() has precisely ${n \choose j}$
has precisely ${n \choose j}$![]() factors.
factors.
Proof. By (2.9), we are reduced to determining the radical layers of $\mathsf {Z}(\lambda _i)$![]() . As usual, we will prove (6.6) by induction on $n\geq 1$
. As usual, we will prove (6.6) by induction on $n\geq 1$![]() . The base case, $n=1$
. The base case, $n=1$![]() , is trivial. Now assume by induction that the formula holds for $SL_{r+1}$
, is trivial. Now assume by induction that the formula holds for $SL_{r+1}$![]() with $1 \leq r < n$
with $1 \leq r < n$![]() and apply this to $L_I$
and apply this to $L_I$![]() . If we fix $i \in \{0,\ldots, n-1\}$
. If we fix $i \in \{0,\ldots, n-1\}$![]() , then by Lemma 6.1 and Proposition 4.6,
, then by Lemma 6.1 and Proposition 4.6,

Similarly, we can verify (6.6) for $i \in \{1,\ldots,n\}$![]() by applying the inductive hypothesis to $L_J$
by applying the inductive hypothesis to $L_J$![]() .
.
Using the same methods as above, we can determine the radical layers of $\widehat {\mathsf {Z}}(\lambda _i + p\nu )$![]() (or equivalently the socle layers of ${\widehat {\mathsf {Z}}'(\lambda _i + p\nu )}$
(or equivalently the socle layers of ${\widehat {\mathsf {Z}}'(\lambda _i + p\nu )}$![]() by (2.9)) for $0 \leq i \leq n$
by (2.9)) for $0 \leq i \leq n$![]() .
.
For any $i \leq j$![]() , set
, set
and for any subset $X \subseteq [1,n+1]$![]() , we define
, we define
where $\epsilon _{\emptyset } = 0$![]() . The $\lambda _0$
. The $\lambda _0$![]() and $\lambda _n$
and $\lambda _n$![]() formulas are now easily obtained by applying Lemma 6.1 and Proposition 4.6. In particular, for any $\nu \in \mathbf {X}$
formulas are now easily obtained by applying Lemma 6.1 and Proposition 4.6. In particular, for any $\nu \in \mathbf {X}$![]() ,
,
To handle the $0 < i < n$![]() case, we introduce the subsets $I_i = \{\epsilon _1-\epsilon _2, \ldots, \epsilon _i-\epsilon _{i+1}\}$
case, we introduce the subsets $I_i = \{\epsilon _1-\epsilon _2, \ldots, \epsilon _i-\epsilon _{i+1}\}$![]() . We then apply (6.8) to $\widehat {\mathsf {Z}}_{I_i}(\lambda _i)$
. We then apply (6.8) to $\widehat {\mathsf {Z}}_{I_i}(\lambda _i)$![]() and get
and get
with $0\leq k \leq i$![]() (it is zero otherwise). The radical layers of $\widehat {\mathsf {Z}}(\lambda _i)$
(it is zero otherwise). The radical layers of $\widehat {\mathsf {Z}}(\lambda _i)$![]() are computed by repeatedly applying Lemma 6.1 and Proposition 4.6 to each radical layer of ${\widehat {\mathsf {Z}}_{I_r}(\lambda _i)}$
are computed by repeatedly applying Lemma 6.1 and Proposition 4.6 to each radical layer of ${\widehat {\mathsf {Z}}_{I_r}(\lambda _i)}$![]() for $i< r \leq n$
for $i< r \leq n$![]() . In particular, applying this procedure to each ${\widehat {\mathsf {L}}_{I_i}(\lambda _{i-k} - p\epsilon _X)}$
. In particular, applying this procedure to each ${\widehat {\mathsf {L}}_{I_i}(\lambda _{i-k} - p\epsilon _X)}$![]() produces an object ‘$M_{i-k, X}$
produces an object ‘$M_{i-k, X}$![]() ’, whose non-zero radical layers are given by
’, whose non-zero radical layers are given by
with $0 \leq s \leq n-i$![]() . The radical layers of $\widehat {\mathsf {Z}}(\lambda _i)$
. The radical layers of $\widehat {\mathsf {Z}}(\lambda _i)$![]() are actually built out of various ‘$k$
are actually built out of various ‘$k$![]() -shifted’ copies of $\overline {\text {rad}}_s\, M_{i-k, X}$
-shifted’ copies of $\overline {\text {rad}}_s\, M_{i-k, X}$![]() , where we have
, where we have
Altogether, we get

Thus, we have proven the following theorem.
Theorem 6.3 Let $n\geq 1,$![]() then for $0\leq i \leq n,$
then for $0\leq i \leq n,$![]() $\nu \in \mathbf {X}$
$\nu \in \mathbf {X}$![]() and any $j\geq 0,$
and any $j\geq 0,$![]()

Remark 6.4 Compare with [Reference Abe and Kaneda1, Theorem, p. 2].
The arguments used in Proposition 6.2 and Theorem 6.3, can also be adapted to compute $\overline {\text {soc}}_j\, \widehat {\mathsf {Z}}(\lambda _i)$![]() for $j \geq 1$
for $j \geq 1$![]() (or equivalently $\overline {\text {rad}}_j\, \widehat {\mathsf {Z}}'(\lambda _i)$
(or equivalently $\overline {\text {rad}}_j\, \widehat {\mathsf {Z}}'(\lambda _i)$![]() for $j\geq 0$
for $j\geq 0$![]() ).
).
Proposition 6.5 Let $n\geq 1,$![]() then for $0\leq i \leq n,$
then for $0\leq i \leq n,$![]() $\nu \in \mathbf {X}$
$\nu \in \mathbf {X}$![]() and any $j\geq 1,$
and any $j\geq 1,$![]()
In particular, $\widehat {\mathsf {Z}}(\lambda _i + p\nu )$![]() and $\widehat {\mathsf {Z}}'(\lambda _i + p\nu )$
and $\widehat {\mathsf {Z}}'(\lambda _i + p\nu )$![]() are rigid modules.
are rigid modules.
7. The Loewy series for $\widehat {\mathsf {Q}}(\lambda _i + p\nu )$
We will now show that the results for $\widehat {\mathsf {Z}}(\lambda _i + p\nu )$![]() from the preceding sections enable us to adapt the arguments from [Reference Andersen and Kaneda3] to our setting and determine Loewy series for the $\widehat {\mathsf {Q}}(\lambda _i + p\nu )$
from the preceding sections enable us to adapt the arguments from [Reference Andersen and Kaneda3] to our setting and determine Loewy series for the $\widehat {\mathsf {Q}}(\lambda _i + p\nu )$![]() . From now on, we will additionally assume that $p$
. From now on, we will additionally assume that $p$![]() is large enough so that the following conjecture holds.
is large enough so that the following conjecture holds.
Conjecture 7.1 Let $n \geq 1,$![]() then for $0 \leq i \leq n$
then for $0 \leq i \leq n$![]() and $\nu \in \mathbf {X},$
and $\nu \in \mathbf {X},$![]() $\ell \ell (\widehat {\mathsf {Q}}(\lambda _i+p\nu )) = 2n+1$
$\ell \ell (\widehat {\mathsf {Q}}(\lambda _i+p\nu )) = 2n+1$![]() .
.
Remark 7.2 This is known to hold for extremely large $p$![]() by [Reference Abe and Kaneda1, Theorem, p. 10].
by [Reference Abe and Kaneda1, Theorem, p. 10].
The remainder of the section will be devoted to proving the following theorem.
Theorem 7.3 Suppose Conjecture 7.1 holds. Let $n\geq 1,$![]() then for $0\leq i \leq n$
then for $0\leq i \leq n$![]() and $\nu \in \mathbf {X},$
and $\nu \in \mathbf {X},$![]() $\widehat {\mathsf {Q}}(\lambda _i + p\nu )$
$\widehat {\mathsf {Q}}(\lambda _i + p\nu )$![]() is rigid and for any $j\geq 0$
is rigid and for any $j\geq 0$![]()

Remark 7.4 Obviously, ${[\overline {\text {rad}}_k\, \widehat {\mathsf {Z}}(\mu ):\widehat {\mathsf {L}}(\lambda _i +p\nu )] = 0}$![]() unless ${\mu = \lambda _t + p\eta }$
unless ${\mu = \lambda _t + p\eta }$![]() for some $0 \leq t \leq n$
for some $0 \leq t \leq n$![]() and $\eta \in \mathbf {X}$
and $\eta \in \mathbf {X}$![]() . So by combining the preceding theorem with Theorem 6.3, we can completely determine the Loewy series of the $\widehat {\mathsf {Q}}(\lambda _i + p\nu )$
. So by combining the preceding theorem with Theorem 6.3, we can completely determine the Loewy series of the $\widehat {\mathsf {Q}}(\lambda _i + p\nu )$![]() .
.
For the remainder of the section, we will fix $I, J \subset S$![]() as in §4. Let us first observe that from the identities (2.7), (2.8) and (2.9), it can be shown that (7.1) holds for all $j\geq 0$
as in §4. Let us first observe that from the identities (2.7), (2.8) and (2.9), it can be shown that (7.1) holds for all $j\geq 0$![]() if and only if
if and only if

for all $j\geq 1$![]() (compare with [Reference Andersen and Kaneda3, Theorem 7.2(ii)]).
(compare with [Reference Andersen and Kaneda3, Theorem 7.2(ii)]).
It turns out that the preceding identity is always ‘partially’ true by the following lemma (adapted from [Reference Andersen and Kaneda3, Proposition 3.7]).
Lemma 7.5 For any $\lambda \in \mathbf {X}$![]() and $j\geq 1,$
and $j\geq 1,$![]()

Proof. We first note that the Lemmas occurring in [Reference Andersen and Kaneda3, 3.5 and 3.6] can be adapted to our setting. This is because their proofs essentially consist of the same types of arguments employed in the proof of [Reference Jantzen7, Proposition II.11.2], as well as certain general results on socle filtrations of modules, and on the basic properties of $\widehat {\mathsf {Z}}'(\lambda )$![]() (e.g. the highest weight structure). In particular, there is no dependence on the $p$
(e.g. the highest weight structure). In particular, there is no dependence on the $p$![]() -regularity of $\lambda \in \mathbf {X}$
-regularity of $\lambda \in \mathbf {X}$![]() , or even on the prime $p$
, or even on the prime $p$![]() . The proof of our result follows by applying the more general versions of these lemmas to imitate the proof of [Reference Andersen and Kaneda3, Proposition 3.7].
. The proof of our result follows by applying the more general versions of these lemmas to imitate the proof of [Reference Andersen and Kaneda3, Proposition 3.7].
Next, we observe that results from §6 imply the following analogue to [Reference Andersen and Kaneda3, Lemma 7.1].
Lemma 7.6 Let $n\geq 1,$![]() then for $0\leq i \leq n$
then for $0\leq i \leq n$![]() and $\nu \in \mathbf {X},$
and $\nu \in \mathbf {X},$![]()

for all $j \geq 1$![]() .
.
Proof of Theorem 7.3. To verify (7.2) (which is equivalent to (7.1)), we will proceed as in the proof of [Reference Andersen and Kaneda3, Theorem 7.2]. Namely, observe that
implies
for all $j\geq 1$![]() . Applying Lemma 7.5, Lemma 7.6, and Proposition 6.5, we get
. Applying Lemma 7.5, Lemma 7.6, and Proposition 6.5, we get

Combining this with Conjecture 7.1 and (2.4), then gives
and hence the rigidity result follows. We are also forced to have both

Acknowledgements
The author would like to thank V. Nandakumar for providing the motivation for this project and a number of key insights, as well as D. Nakano and J. Humphreys for their useful comments and suggestions. The author also expresses his sincere gratitude to the anonymous referee for providing a very thorough report.