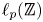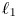1. Introduction
Let $\mathcal {H}$![]() be a separable Banach space and $T: \mathcal {H} \rightarrow \mathcal {H}$
be a separable Banach space and $T: \mathcal {H} \rightarrow \mathcal {H}$![]() a continuous linear operator. $T$
a continuous linear operator. $T$![]() is chaotic if $T$
is chaotic if $T$![]() has a dense orbit and the set of periodic points of $T$
has a dense orbit and the set of periodic points of $T$![]() is dense in $X$
is dense in $X$![]() . Chaotic operators are well studied in linear dynamics and well understood. For example, Grosse-Erdmann in [Reference Grosse-Erdmann12] gave a complete characterization of backward weighted shifts which are chaotic.
. Chaotic operators are well studied in linear dynamics and well understood. For example, Grosse-Erdmann in [Reference Grosse-Erdmann12] gave a complete characterization of backward weighted shifts which are chaotic.
The notion of frequent hypercyclicity is a quantitative version of hypercyclicity. It was introduced by Bayart and Grivaux in [Reference Bayart and Grivaux3] in the linear setting, but it also makes sense for Polish dynamical systems. Although such a notion is purely topological, it is related to measure-theoretical features of the topological dynamical system $(\mathcal {H},\, T)$![]() . More specifically by Birkhoff's Pointwise Ergodic Theorem, it follows that if $T$
. More specifically by Birkhoff's Pointwise Ergodic Theorem, it follows that if $T$![]() admits an invariant ergodic Borel probability measure with full support, then $T$
admits an invariant ergodic Borel probability measure with full support, then $T$![]() is frequently hypercyclic. Conversely, Grivaux and Matheron showed in [Reference Grivaux and Matheron11] that if $\mathcal {H}$
is frequently hypercyclic. Conversely, Grivaux and Matheron showed in [Reference Grivaux and Matheron11] that if $\mathcal {H}$![]() is a reflexive Banach space, then any frequently hypercyclic operator $T$
is a reflexive Banach space, then any frequently hypercyclic operator $T$![]() on $\mathcal {H}$
on $\mathcal {H}$![]() admits a continuous invariant Borel probability measure with full support. The notion of frequent hypercyclicity is tricky: in fact, it took a span of 10 years between the pioneer partial works [Reference Bayart and Grivaux3, Reference Grosse-Erdmann and Peris13] and the full characterization of frequently hypercyclic backward weighted shifts obtained in [Reference Bayart and Ruzsa5].
admits a continuous invariant Borel probability measure with full support. The notion of frequent hypercyclicity is tricky: in fact, it took a span of 10 years between the pioneer partial works [Reference Bayart and Grivaux3, Reference Grosse-Erdmann and Peris13] and the full characterization of frequently hypercyclic backward weighted shifts obtained in [Reference Bayart and Ruzsa5].
An important problem in linear dynamics is distinguishing between chaotic operators and frequently hypercyclic operators. Bayart and Grivaux constructed in [Reference Bayart and Grivaux4] a frequently hypercyclic continuous linear operator that is not chaotic while Menet showed in [Reference Menet16] that there exist chaotic continuous linear operators that are not frequently hypercyclic. However, for many natural classes of operators such as backward weighted shifts on $\ell _p(\mathbb {Z})$![]() , these two notions coincide.
, these two notions coincide.
Another important problem concerning frequently hypercyclic operators is whether the inverse of every invertible frequently hypercyclic operator is frequently hypercyclic. This was solved in the negative very recently by Menet [Reference Menet17]. However, again for natural classes of operators such as backward weighted shifts on $\ell _p(\mathbb {Z})$![]() , the inverse of an invertible frequently hypercyclic operator is frequently hypercyclic.
, the inverse of an invertible frequently hypercyclic operator is frequently hypercyclic.
Our aim in this article is to give a very large class of composition operators for which the notions of chaos and frequent hypercyclicity coincide (see Theorem 3.7 and Corollary 3.9). Moreover, as the inverse of an invertible chaotic operator is chaotic, we also obtain that in our class, the inverse of a frequently hypercyclic operator is also frequently hypercyclic (see Corollary 3.8).
A powerful method for constructing frequently hypercyclic operator is to apply the Frequent Hypercyclicity Criterion (FHC). This criterion was introduced by Bayart and Grivaux in [Reference Bayart and Grivaux3] and strengthened by Bonilla and Grosse-Erdmann in [Reference Grosse-Erdmann12]. We also explore the relationship between operators satisfying (FHC) and chaotic operators. Theorem 3.1 and Theorem 3.2 imply that in our setting, chaotic operators satisfy (FHC). Moreover, we prove the partial converse for composition operators on $L^{p}(X)$![]() , $p \ge 2$
, $p \ge 2$![]() .
.
We specifically study composition operators on $L^{p}(X)$![]() where $(X,\,\mathcal {B},\,\mu )$
where $(X,\,\mathcal {B},\,\mu )$![]() is a $\sigma$
is a $\sigma$![]() -finite measure space and $f:X\to X$
-finite measure space and $f:X\to X$![]() is a bijective, bimeasurable, nonsingular transformation satisfying $\mu (f^{-1}(B))\le c\mu (B)$
is a bijective, bimeasurable, nonsingular transformation satisfying $\mu (f^{-1}(B))\le c\mu (B)$![]() for all $B\in \mathcal {B}$
for all $B\in \mathcal {B}$![]() and some $c>0$
and some $c>0$![]() . The continuous linear operator $T_f:L^{p}(X)\to L^{p}(X)$
. The continuous linear operator $T_f:L^{p}(X)\to L^{p}(X)$![]() defined by $\varphi \mapsto \varphi \circ f$
defined by $\varphi \mapsto \varphi \circ f$![]() is called the composition operator induced by $f$
is called the composition operator induced by $f$![]() . In such a general setting, hypercyclic composition operators and topologically mixing composition operators on $L^{p}$
. In such a general setting, hypercyclic composition operators and topologically mixing composition operators on $L^{p}$![]() -spaces were completely characterized in a joint work of the authors with Bayart in [Reference Bayart, Darji and Pires2]. Li–Yorke chaotic composition operators on $L^{p}$
-spaces were completely characterized in a joint work of the authors with Bayart in [Reference Bayart, Darji and Pires2]. Li–Yorke chaotic composition operators on $L^{p}$![]() -spaces were completely characterized in a joint work of the authors with Bernardes Jr. in [Reference Bernardes, Darji and Pires6]. Recently, generalized hyperbolicity among composition operators was characterized by the first author, D'Aniello and Maiuriello in [Reference D'Aniello, Darji and Maiuriello10].
-spaces were completely characterized in a joint work of the authors with Bernardes Jr. in [Reference Bernardes, Darji and Pires6]. Recently, generalized hyperbolicity among composition operators was characterized by the first author, D'Aniello and Maiuriello in [Reference D'Aniello, Darji and Maiuriello10].
We would also like to point out that in a very different direction, Charpentier, Grosse-Erdmann and Menet [Reference Charpentier, Grosse-Erdmann and Menet9] give conditions under which backward weighted shifts on Köthe sequence spaces have the property that the notions of chaos and frequent hypercyclicity coincide.
The article is organized as follows: In §2, we give definitions and background results. In §3, we state the main results and their consequences. Section 4 consists of examples, §5 of proofs and §6 of open problems.
2. Definitions and background results
2.1. Topological dynamics of linear operators
Let $T:\mathcal {H}\to \mathcal {H}$![]() be a continuous linear operator acting on a separable Banach space $\mathcal {H}$
be a continuous linear operator acting on a separable Banach space $\mathcal {H}$![]() .
.
Definition 2.1 The operator $T$![]() is topologically transitive (or hypercyclic) if for any pair of non-empty open sets $U,\,V \subseteq \mathcal {H}$
is topologically transitive (or hypercyclic) if for any pair of non-empty open sets $U,\,V \subseteq \mathcal {H}$![]() , there is $k > 0$
, there is $k > 0$![]() such that $T^{k}(U)\cap V\neq \emptyset$
such that $T^{k}(U)\cap V\neq \emptyset$![]() . If, in addition, the set of periodic points of $T$
. If, in addition, the set of periodic points of $T$![]() is dense in $\mathcal {H}$
is dense in $\mathcal {H}$![]() , then $T$
, then $T$![]() is said to be chaotic.
is said to be chaotic.
We recall that in the setting of Banach spaces, $T$![]() is topologically transitive if and only if $T$
is topologically transitive if and only if $T$![]() admits a hypercyclic vector $\varphi$
admits a hypercyclic vector $\varphi$![]() , i.e., $\varphi \in \mathcal {H}$
, i.e., $\varphi \in \mathcal {H}$![]() such that the orbit $\{\varphi ,\,T\varphi ,\,T^{2}\varphi \ldots \}$
such that the orbit $\{\varphi ,\,T\varphi ,\,T^{2}\varphi \ldots \}$![]() is dense in $\mathcal {H}$
is dense in $\mathcal {H}$![]() .
.
Definition 2.2 The operator $T$![]() is topologically mixing if for any pair of non-empty open sets $U,\,V\subseteq \mathcal {H}$
is topologically mixing if for any pair of non-empty open sets $U,\,V\subseteq \mathcal {H}$![]() , there exists $k_0\ge 0$
, there exists $k_0\ge 0$![]() such that $T^{k}(U)\cap V\neq \emptyset$
such that $T^{k}(U)\cap V\neq \emptyset$![]() for all $k\ge k_0$
for all $k\ge k_0$![]() .
.
Definition 2.3 A vector $\varphi \in \mathcal {H}$![]() is called frequently hypercyclic if for each non-empty open set $U\subseteq \mathcal {H}$
is called frequently hypercyclic if for each non-empty open set $U\subseteq \mathcal {H}$![]() , the set of integers $\mathcal {N}(\varphi ,\,U)=\{n\in \mathbb {N}: T^{n}\varphi \in U\}$
, the set of integers $\mathcal {N}(\varphi ,\,U)=\{n\in \mathbb {N}: T^{n}\varphi \in U\}$![]() has positive lower density, that is,
has positive lower density, that is,
The operator $T$![]() is called frequently hypercyclic if it admits a frequently hypercyclic vector.
is called frequently hypercyclic if it admits a frequently hypercyclic vector.
The following Frequently Hypercyclic Criterion was provided by Bonilla and Grosse-Erdmann in [Reference Bonilla and Grosse-Erdmann8, theorem 2.1]. It is a strengthened version of the original criterion obtained by Bayart and Grivaux in [Reference Bayart and Grivaux3, theorem 2.1]. Its simplified reformulation is stated below in the context that we use.
Theorem 2.4 (FHC) Let $(\mathcal {H},\,\Vert \cdot \Vert )$![]() be a separable Banach space and let $T:\mathcal {H}\to \mathcal {H}$
be a separable Banach space and let $T:\mathcal {H}\to \mathcal {H}$![]() be a continuous linear operator. Assume there exists a dense subset $\mathcal {H}_0$
be a continuous linear operator. Assume there exists a dense subset $\mathcal {H}_0$![]() of $\mathcal {H}$
of $\mathcal {H}$![]() and a map $S:\mathcal {H}_0\to \mathcal {H}_0$
and a map $S:\mathcal {H}_0\to \mathcal {H}_0$![]() such that, for any $\varphi \in \mathcal {H}_0,$
such that, for any $\varphi \in \mathcal {H}_0,$![]()
(a) The series $\sum \nolimits _{n\ge 1} T^{n} (\varphi )$
 converges unconditionally;
converges unconditionally;(b) The series $\sum \nolimits _{n\ge 1} S^{n}(\varphi )$
 converges unconditionally;
converges unconditionally;(c) $T S(\varphi )=\varphi$
 .
.
Then, $T$![]() is frequently hypercyclic, chaotic and topologically mixing.
is frequently hypercyclic, chaotic and topologically mixing.
2.2. Measurable dynamics
Definition 2.5 A transformation $f:X\to X$![]() on the measure space $(X,\,\mathcal {B},\,\mu )$
on the measure space $(X,\,\mathcal {B},\,\mu )$![]() is
is
(a) bimeasurable if $f(B)\in \mathcal {B}$
 and $f^{-1}(B)\in \mathcal {B}$
and $f^{-1}(B)\in \mathcal {B}$ for all $B\in \mathcal {B}$
for all $B\in \mathcal {B}$ ;
;(b) nonsingular if $\mu (f^{-1}(B))=0$
 if and only if $\mu (B)=0$
if and only if $\mu (B)=0$ .
.
Definition 2.6 A measurable system is a tuple $(X,\,{\mathcal {B}},\,\mu ,\, f)$![]() , where
, where
(1) $(X,\,{\mathcal {B}},\,\mu )$
 is a $\sigma$
is a $\sigma$ -finite measure space with $\mu (X)>0$
-finite measure space with $\mu (X)>0$ ;
;(2) $f : X \to X$
 is a bijective bimeasurable nonsingular transformation;
is a bijective bimeasurable nonsingular transformation;(3) there is $c > 0$
 such that
(\unicode{x002A})\begin{equation} \mu(f^{{-}1}(B)) \leq c \mu(B) \text{ for every } B \in {\mathcal{B}}. \end{equation}
such that
(\unicode{x002A})\begin{equation} \mu(f^{{-}1}(B)) \leq c \mu(B) \text{ for every } B \in {\mathcal{B}}. \end{equation}
If both $f$![]() and $f^{-1}$
and $f^{-1}$![]() satisfy $(*)$
satisfy $(*)$![]() , then we say that the measurable system is invertible.
, then we say that the measurable system is invertible.
Definition 2.7 Let $p\ge 1$![]() . The composition operator $T_f$
. The composition operator $T_f$![]() induced by a measurable system $(X,\,\mathcal {B},\,\mu ,\,f)$
induced by a measurable system $(X,\,\mathcal {B},\,\mu ,\,f)$![]() is the map $T_f:L^{p}(X)\to L^{p}(X)$
is the map $T_f:L^{p}(X)\to L^{p}(X)$![]() defined by
defined by
It is well known that (*) guarantees that $T_f$![]() is a continuous linear operator. We refer the reader to [Reference Singh and Manhas19] for a detailed exposition on compositions operators.
is a continuous linear operator. We refer the reader to [Reference Singh and Manhas19] for a detailed exposition on compositions operators.
Definition 2.8 A measurable transformation $f:X\to X$![]() on the measure space $(X,\,\mathcal {B},\,\mu )$
on the measure space $(X,\,\mathcal {B},\,\mu )$![]() is
is
(a) conservative if for each measurable set $B$
 of positive $\mu$
of positive $\mu$ -measure, there is $n\ge 1$
-measure, there is $n\ge 1$ such that $\mu (B\cap f^{-n}(B))>0$
such that $\mu (B\cap f^{-n}(B))>0$ ;
;(b) dissipative if there exists $W\in \mathcal {B}$
 such that $f^{n}(W)$
such that $f^{n}(W)$ , $n\in \mathbb {Z}$
, $n\in \mathbb {Z}$ , are pairwise disjoint and $X=\bigcup_{n\in \mathbb {Z}} f^{n}(W)$
, are pairwise disjoint and $X=\bigcup_{n\in \mathbb {Z}} f^{n}(W)$ .
.
The measurable system $(X,\,\mathcal {B},\,\mu ,\,f)$![]() is called conservative (respectively, dissipative) if $f$
is called conservative (respectively, dissipative) if $f$![]() is conservative (respectively, dissipative).
is conservative (respectively, dissipative).
We say that a set $A\subseteq X$![]() is $f$
is $f$![]() -invariant if $f^{-1}(A)=A$
-invariant if $f^{-1}(A)=A$![]() .
.
Theorem 2.9 (Hopf [Reference Aaronson1, Reference Krengel15])
Let $(X,\, {\mathcal {B}},\, \mu ,\,f)$![]() be a measurable system. Then, $X$
be a measurable system. Then, $X$![]() is the union of two disjoint $f$
is the union of two disjoint $f$![]() -invariant sets ${\mathcal {C}}(f)$
-invariant sets ${\mathcal {C}}(f)$![]() and ${\mathcal {D}}(f)$
and ${\mathcal {D}}(f)$![]() , called the conservative and the dissipative parts of $f$
, called the conservative and the dissipative parts of $f$![]() , respectively, such that $f\vert _{\mathcal {C}(f)}$
, respectively, such that $f\vert _{\mathcal {C}(f)}$![]() is conservative and $f\vert _{\mathcal {D}(f)}$
is conservative and $f\vert _{\mathcal {D}(f)}$![]() is dissipative.
is dissipative.
Definition 2.10 Let $(X,\,\mathcal {B},\,\mu ,\,f)$![]() be a measurable system. A measurable set $W\subseteq X$
be a measurable system. A measurable set $W\subseteq X$![]() is a wandering set if the sets $f^{n}(W)$
is a wandering set if the sets $f^{n}(W)$![]() , $n\in \mathbb {Z}$
, $n\in \mathbb {Z}$![]() , are pairwise disjoint. The system $(X,\,\mathcal {B},\,\mu ,\,f)$
, are pairwise disjoint. The system $(X,\,\mathcal {B},\,\mu ,\,f)$![]() is said to be generated by a wandering set $W$
is said to be generated by a wandering set $W$![]() if $X=\bigcup_{n\in \mathbb {Z}}f^{n}(W)$
if $X=\bigcup_{n\in \mathbb {Z}}f^{n}(W)$![]() .
.
In the sequel, we let $\mathcal {B}(W)=\{B\cap W: B\in \mathcal {B}\}$![]() .
.
Definition 2.11 We say that a dissipative system $(X,\,{\mathcal {B}},\,\mu ,\, f)$![]() is of bounded distortion if there exist a wandering set $W$
is of bounded distortion if there exist a wandering set $W$![]() of finite positive $\mu$
of finite positive $\mu$![]() -measure and $K>0$
-measure and $K>0$![]() such that
such that
(i) $W$
 generates $(X,\,\mathcal {B},\,\mu ,\,f)$
generates $(X,\,\mathcal {B},\,\mu ,\,f)$ , i.e, $X=\bigcup_{n\in \mathbb {Z}}f^{n}(W)$
, i.e, $X=\bigcup_{n\in \mathbb {Z}}f^{n}(W)$ ;
;(ii) For all $n \in \mathbb {Z}$
 and $C \in {\mathcal {B}}(W)$
and $C \in {\mathcal {B}}(W)$ with positive $\mu$
with positive $\mu$ -measure,
\[ \dfrac{1}{K} \frac{\mu(f^{n}(W))}{\mu(W)} \leq \frac{\mu(f^{n} (C))}{\mu (C)} \leq K \frac{\mu(f^{n}(W))}{\mu(W)}. \]
-measure,
\[ \dfrac{1}{K} \frac{\mu(f^{n}(W))}{\mu(W)} \leq \frac{\mu(f^{n} (C))}{\mu (C)} \leq K \frac{\mu(f^{n}(W))}{\mu(W)}. \]
Notice that in the definition of dissipative system (see Definition 2.8), we do not require that $W$![]() has finite measure.
has finite measure.
3. Statement of the main results
In this section, we introduce a condition called Summability Condition or simply Condition (SC) that is useful for constructing composition operators that are simultaneously chaotic, topologically mixing and frequently hypercyclic. We split our results into two subsections. In the first subsection, we introduce Condition (SC) and we explore its relation to the FHC. In particular, we show that if we add the hypothesis that $f$![]() is dissipative, then we obtain that Condition (SC) is equivalent to $T_f$
is dissipative, then we obtain that Condition (SC) is equivalent to $T_f$![]() being chaotic. In the second subsection, we show that if $f$
being chaotic. In the second subsection, we show that if $f$![]() is a dissipative transformation of bounded distortion, then Condition (SC) is equivalent to $T_f$
is a dissipative transformation of bounded distortion, then Condition (SC) is equivalent to $T_f$![]() being frequently hypercyclic.
being frequently hypercyclic.
3.1. The summability condition and the frequent hypercyclicity criterion
Let $(X,\,\mathcal {B},\,\mu ,\,f)$![]() be a measurable system. We say that $f$
be a measurable system. We say that $f$![]() satisfies the Summability Condition (SC) if for each $\epsilon >0$
satisfies the Summability Condition (SC) if for each $\epsilon >0$![]() and $B\in \mathcal {B}$
and $B\in \mathcal {B}$![]() with $\mu (B)<\infty$
with $\mu (B)<\infty$![]() , there exists a measurable set $B'\subseteq B$
, there exists a measurable set $B'\subseteq B$![]() such that
such that
The following result shows that the Summability Condition (SC) is the natural translation of the FHC to the composition operator framework.
Theorem 3.1 Let $(X,\,\mathcal {B},\,\mu ,\,f)$![]() be a measurable system. For all $p\ge 1,$
be a measurable system. For all $p\ge 1,$![]() (SC) implies (FHC). Moreover, (SC) and (FHC) are equivalent for all $p\ge 2$
(SC) implies (FHC). Moreover, (SC) and (FHC) are equivalent for all $p\ge 2$![]() .
.
Now we will provide a list of results that show how Condition (SC) is useful to characterize when a transformation $f$![]() is dissipative and when the composition operator $T_f$
is dissipative and when the composition operator $T_f$![]() is frequently hypercyclic or chaotic. The results below are true for all $p\ge 1$
is frequently hypercyclic or chaotic. The results below are true for all $p\ge 1$![]() .
.
Theorem 3.2 ((SC) Characterization, General Case) Let $(X,\, \mathcal {B},\, \mu ,\, f)$![]() be a measurable system and $T_f: L^{p}(X) \rightarrow L^{p}(X)$
be a measurable system and $T_f: L^{p}(X) \rightarrow L^{p}(X)$![]() be the associated composition operator. The following statements are equivalent.
be the associated composition operator. The following statements are equivalent.
(a) $f$
 satisfies Condition (SC);
satisfies Condition (SC);(b) $f$
 is dissipative and $T_f$
is dissipative and $T_f$ has a dense set of periodic points.
has a dense set of periodic points.
Moreover, any of the above implies that $T_f$![]() is chaotic, topologically mixing and frequently hypercyclic.
is chaotic, topologically mixing and frequently hypercyclic.
Theorem 3.3 ((SC) Characterization, $\mu (X) < \infty$![]() )
)
Let $(X,\, \mathcal {B},\, \mu ,\, f)$![]() be a measurable system with $\mu (X)<\infty$
be a measurable system with $\mu (X)<\infty$![]() and $T_f: L^{p}(X) \rightarrow L^{p}(X)$
and $T_f: L^{p}(X) \rightarrow L^{p}(X)$![]() be the associated composition operator. Then, the following statements are equivalent.
be the associated composition operator. Then, the following statements are equivalent.
(a) $f$
 satisfies Condition (SC);
satisfies Condition (SC);(b) $f$
 is dissipative.
is dissipative.
Moreover, any of the above implies that $T_f$![]() is chaotic, topologically mixing and frequently hypercyclic.
is chaotic, topologically mixing and frequently hypercyclic.
In the sequel, we will need the following definition. Let $X$![]() be a metric space and $f:X\to X$
be a metric space and $f:X\to X$![]() be a map. We say that $x\in X$
be a map. We say that $x\in X$![]() is recurrent (for $f$
is recurrent (for $f$![]() ) if for every open set $U$
) if for every open set $U$![]() containing $x$
containing $x$![]() , there exists an integer $n\ge 1$
, there exists an integer $n\ge 1$![]() such that $f^{n}(x)\in U$
such that $f^{n}(x)\in U$![]() .
.
Corollary 3.4 Let $(X,\, \mathcal {B},\, \mu ,\, f)$![]() be a measurable system where $X$
be a measurable system where $X$![]() is a metric space and $\mu$
is a metric space and $\mu$![]() is a Borel finite measure. Let $T_f: L^{p}(X) \rightarrow L^{p}(X)$
is a Borel finite measure. Let $T_f: L^{p}(X) \rightarrow L^{p}(X)$![]() be the associated composition operator. If the set of recurrent points of $f$
be the associated composition operator. If the set of recurrent points of $f$![]() has $\mu$
has $\mu$![]() -measure zero, then $f$
-measure zero, then $f$![]() satisfies Condition (SC) and hence $T_f$
satisfies Condition (SC) and hence $T_f$![]() is chaotic, topologically mixing and frequently hypercyclic.
is chaotic, topologically mixing and frequently hypercyclic.
Corollary 3.5 (SC) Characterization, $f$![]() dissipative
dissipative
Let $(X,\, \mathcal {B},\, \mu ,\, f)$![]() be a dissipative system and $T_f: L^{p}(X) \rightarrow L^{p}(X)$
be a dissipative system and $T_f: L^{p}(X) \rightarrow L^{p}(X)$![]() be the associated composition operator. Then, the following statements are equivalent.
be the associated composition operator. Then, the following statements are equivalent.
(a) $f$
 satisfies Condition (SC);
satisfies Condition (SC);(b) $T_f$
 is chaotic;
is chaotic;(c) $T_f$
 has dense set of periodic points.
has dense set of periodic points.
3.2. Bounded distortion and frequent hypercyclicity
Theorem 3.6 (Necessary condition for frequent hypercyclicity) Let $(X,\,\mathcal {B},\,\mu ,\, f)$![]() be a measurable system with associated composition operator $T_f$
be a measurable system with associated composition operator $T_f$![]() frequently hypercyclic. Then for every wandering set $W$
frequently hypercyclic. Then for every wandering set $W$![]() with positive finite $\mu$
with positive finite $\mu$![]() -measure, the following inequality holds
-measure, the following inequality holds

Theorem 3.7 (Frequent Hypercyclicity Characterization) Let $(X,\, \mathcal {B},\, \mu ,\, f)$![]() be a dissipative system of bounded distortion and $T_f: L^{p}(X) \rightarrow L^{p}(X)$
be a dissipative system of bounded distortion and $T_f: L^{p}(X) \rightarrow L^{p}(X)$![]() be the associated composition operator. Then, the following statements are equivalent.
be the associated composition operator. Then, the following statements are equivalent.
(a) $f$
 satisfies Condition (SC);
satisfies Condition (SC);(b) $T_f$
 is frequently hypercyclic;
is frequently hypercyclic;(c) $T_f$
 is chaotic.
is chaotic.
Corollary 3.8 Let $(X,\, \mathcal {B},\, \mu ,\,f )$![]() be an invertible dissipative system of bounded distortion and $T_f ,\,T_{f^{-1}} :L^{p}(X) \rightarrow L^{p}(X)$
be an invertible dissipative system of bounded distortion and $T_f ,\,T_{f^{-1}} :L^{p}(X) \rightarrow L^{p}(X)$![]() be the associated composition operators. Then, $T_f$
be the associated composition operators. Then, $T_f$![]() is frequently hypercyclic (respectively, chaotic) if and only if $(T_f)^{-1}$
is frequently hypercyclic (respectively, chaotic) if and only if $(T_f)^{-1}$![]() is.
is.
Proof. This follows from the fact that $(T_f)^{-1} = T_{f^{-1}}$![]() .
.
We say that $f$![]() is ergodic if every $f$
is ergodic if every $f$![]() -invariant set $A\in \mathcal {B}$
-invariant set $A\in \mathcal {B}$![]() satisfies $\mu (A)=0$
satisfies $\mu (A)=0$![]() or $\mu (X{\setminus }A)=0$
or $\mu (X{\setminus }A)=0$![]() .
.
Corollary 3.9 Let $(X,\,\mathcal {B},\,\mu ,\, f)$![]() be a dissipative system with a purely atomic measure $\mu$
be a dissipative system with a purely atomic measure $\mu$![]() . Furthermore, assume that $f$
. Furthermore, assume that $f$![]() is ergodic. Then the following statements are equivalent.
is ergodic. Then the following statements are equivalent.
(a) $T_f$
 is frequently hypercyclic;
is frequently hypercyclic;(b) $T_f$
 is chaotic;
is chaotic;(c) $\mu$
 is finite.
is finite.
Proof. $(a)\implies (c)$![]() Assume that $T_f$
Assume that $T_f$![]() is frequently hypercyclic. Let $x\in X$
is frequently hypercyclic. Let $x\in X$![]() be an atom of $\mu$
be an atom of $\mu$![]() . Since $f$
. Since $f$![]() is dissipative and ergodic, we have that $W=\{x\}$
is dissipative and ergodic, we have that $W=\{x\}$![]() is a wandering set that generates $X$
is a wandering set that generates $X$![]() , thus $\mu (X)=\sum \nolimits _{n\in \mathbb {Z}}\mu (f^{n}(W))$
, thus $\mu (X)=\sum \nolimits _{n\in \mathbb {Z}}\mu (f^{n}(W))$![]() . Applying Theorem 3.6 and using the fact that $\textrm {d}\mu /\textrm {d}(\mu \circ f^{n})$
. Applying Theorem 3.6 and using the fact that $\textrm {d}\mu /\textrm {d}(\mu \circ f^{n})$![]() on $W$
on $W$![]() is equal to the constant $\mu (W)/\mu (f^{n}(W))$
is equal to the constant $\mu (W)/\mu (f^{n}(W))$![]() , we obtain that
, we obtain that

implying that $\mu$![]() is finite.
is finite.
$(c)\implies (b)$![]() It follows from Theorem 3.3 that $f$
It follows from Theorem 3.3 that $f$![]() satisfies Condition (SC) and hence it is chaotic.
satisfies Condition (SC) and hence it is chaotic.
$(b)\implies (a)$![]() As $f$
As $f$![]() is dissipative and $T_f$
is dissipative and $T_f$![]() chaotic, by Corollary 3.5, we have that $f$
chaotic, by Corollary 3.5, we have that $f$![]() satisfies Condition (SC) and hence it is frequently hypercyclic.
satisfies Condition (SC) and hence it is frequently hypercyclic.
4. Applications and examples
In this section, we give some applications of our main theorems. We also give some examples which show that our theorems are sharp.
The first result is an application of Corollary 3.4. It shows that a large class of natural, simple maps $f$![]() on $\mathbb {R}^{d}$
on $\mathbb {R}^{d}$![]() yields complex behaviour of $T_f$
yields complex behaviour of $T_f$![]() . We recall that a linear isomorphism $L:\mathbb {R}^{d}\to \mathbb {R}^{d}$
. We recall that a linear isomorphism $L:\mathbb {R}^{d}\to \mathbb {R}^{d}$![]() is hyperbolic if $L$
is hyperbolic if $L$![]() has no eigenvalue of modulus $1$
has no eigenvalue of modulus $1$![]() .
.
Theorem 4.1 Consider a measurable system $(\mathbb {R} ^{d},\, \mathcal {B},\,\mu ,\, f)$![]() where $\mu$
where $\mu$![]() is a Borel measure on $\mathbb {R}^{d}$
is a Borel measure on $\mathbb {R}^{d}$![]() , $\mu (\mathbb {R} ^{d}) <\infty ,$
, $\mu (\mathbb {R} ^{d}) <\infty ,$![]() $\mu (\{0\})=0$
$\mu (\{0\})=0$![]() and $f$
and $f$![]() is a hyperbolic linear isomorphism. Then, $T_f$
is a hyperbolic linear isomorphism. Then, $T_f$![]() is chaotic, topologically mixing and frequently hypercyclic.
is chaotic, topologically mixing and frequently hypercyclic.
Proof. By [Reference Palis and de Melo18, Propositions 2.9, 2.10], there exist $f$![]() -invariant subspaces $E^{s}$
-invariant subspaces $E^{s}$![]() and $E^{u}$
and $E^{u}$![]() of $\mathbb {R}^{d}$
of $\mathbb {R}^{d}$![]() with $\mathbb {R} ^{d} = E^{s} {\bigoplus} E^{u}$
with $\mathbb {R} ^{d} = E^{s} {\bigoplus} E^{u}$![]() and an adapted norm $\Vert \cdot \Vert _1$
and an adapted norm $\Vert \cdot \Vert _1$![]() on $\mathbb {R}^{d}$
on $\mathbb {R}^{d}$![]() with respect to which the map $f_s=f\vert _{E^{s}}$
with respect to which the map $f_s=f\vert _{E^{s}}$![]() is a contraction and the map $f_u=f\vert _{E^{u}}$
is a contraction and the map $f_u=f\vert _{E^{u}}$![]() is a dilation (thus its inverse is a contraction). In this way, if $x\in \mathbb {R}^{d}$
is a dilation (thus its inverse is a contraction). In this way, if $x\in \mathbb {R}^{d}$![]() then either $\lim _{n\to \infty } { \| f^{n}(x) \|}=0$
then either $\lim _{n\to \infty } { \| f^{n}(x) \|}=0$![]() or $\lim _{n\to \infty } \Vert f^{n}(x)\Vert =\infty$
or $\lim _{n\to \infty } \Vert f^{n}(x)\Vert =\infty$![]() (with respect to any norm $\Vert \cdot \Vert$
(with respect to any norm $\Vert \cdot \Vert$![]() ). Hence, the set of recurrent points of $f$
). Hence, the set of recurrent points of $f$![]() equals $\{0\}$
equals $\{0\}$![]() , which has $\mu$
, which has $\mu$![]() -measure $0$
-measure $0$![]() by hypothesis. Hence, by Corollary 3.4, the proof follows.
by hypothesis. Hence, by Corollary 3.4, the proof follows.
The following is a concrete application of Corollary 3.4.
Example 4.2 Let $f:\mathbb {R}\to \mathbb {R}$![]() be a non-identity affine map of the form $x\mapsto ax+b$
be a non-identity affine map of the form $x\mapsto ax+b$![]() , $0 < |a| \le 1$
, $0 < |a| \le 1$![]() . Let $\mu$
. Let $\mu$![]() be the probability measure on $\mathbb {R}$
be the probability measure on $\mathbb {R}$![]() defined by $\mu (J)=\tfrac {1}{2}\int _J e^{-\vert t\vert } \mathrm {d}t$
defined by $\mu (J)=\tfrac {1}{2}\int _J e^{-\vert t\vert } \mathrm {d}t$![]() for all interval $J\subseteq \mathbb {R}$
for all interval $J\subseteq \mathbb {R}$![]() . Then, $T_f$
. Then, $T_f$![]() is chaotic, topologically mixing and frequently hypercyclic.
is chaotic, topologically mixing and frequently hypercyclic.
Proof. We first show that $(X,\,\mathcal {B},\,\mu ,\,f)$![]() is a measurable system, i.e., that Condition (*) in Definition 2.6 holds. Indeed, such is the case:
is a measurable system, i.e., that Condition (*) in Definition 2.6 holds. Indeed, such is the case:

where the last inequality follows from the fact $0 < \vert a \vert \le 1$![]() implies that $e^{-\vert a t\vert } \ge {e^{-\vert t\vert }}$
implies that $e^{-\vert a t\vert } \ge {e^{-\vert t\vert }}$![]() for all $t$
for all $t$![]() .
.
The transformation $f$![]() has no recurrent points when $a=1$
has no recurrent points when $a=1$![]() as, in this case, $b\neq 0$
as, in this case, $b\neq 0$![]() and $f^{n}(x)=x+ nb$
and $f^{n}(x)=x+ nb$![]() for all $x\in \mathbb {R}$
for all $x\in \mathbb {R}$![]() and $n\in \mathbb {N}$
and $n\in \mathbb {N}$![]() . For $a \neq 1$
. For $a \neq 1$![]() , some elementary computation shows that $f$
, some elementary computation shows that $f$![]() has exactly one recurrent point, namely the fixed point of $f$
has exactly one recurrent point, namely the fixed point of $f$![]() , $x = {b}/({1-a})$
, $x = {b}/({1-a})$![]() . In either case, as $\mu$
. In either case, as $\mu$![]() is non-atomic, the set of recurrent points has measure zero. By Corollary 3.4, we have that $T_f$
is non-atomic, the set of recurrent points has measure zero. By Corollary 3.4, we have that $T_f$![]() is chaotic, topologically mixing and frequently hypercyclic.
is chaotic, topologically mixing and frequently hypercyclic.
The next example shows that Corollary 3.5 is sharp in the sense that the hypothesis of dissipativity cannot be removed.
Example 4.3 There exists a measurable system $(X,\, \mathcal {B},\, \mu ,\,f)$![]() such that $T_f: L^{p}(X) \rightarrow L^{p}(X)$
such that $T_f: L^{p}(X) \rightarrow L^{p}(X)$![]() is chaotic but $f$
is chaotic but $f$![]() does not satisfy Condition (SC).
does not satisfy Condition (SC).
Proof. We use an example from our earlier work [Reference Bayart, Darji and Pires2]. In particular, our $X$![]() is an odometer and $f$
is an odometer and $f$![]() is the $+1$
is the $+1$![]() -map.
-map.
For $i \ge 1$![]() , we let $\mathbb {Z}_i =\{0,\, \ldots ,\, i-1 \}$
, we let $\mathbb {Z}_i =\{0,\, \ldots ,\, i-1 \}$![]() be integers modulo $i$
be integers modulo $i$![]() . We let $X = \Pi _{i=1}^{\infty } A_i$
. We let $X = \Pi _{i=1}^{\infty } A_i$![]() , where $A_i = \mathbb {Z}_2$
, where $A_i = \mathbb {Z}_2$![]() for $i$
for $i$![]() even and $A_i = \mathbb {Z}_{2i}$
even and $A_i = \mathbb {Z}_{2i}$![]() for $i$
for $i$![]() odd. We put the discrete topology on $A_i$
odd. We put the discrete topology on $A_i$![]() and the associated product topology on $X$
and the associated product topology on $X$![]() . Endowed with this topology, $X$
. Endowed with this topology, $X$![]() is homeomorphic to the Cantor space.
is homeomorphic to the Cantor space.
We let $\mathcal {B}$![]() be the collection of Borel subsets of $X$
be the collection of Borel subsets of $X$![]() . We define a product measure $\mu$
. We define a product measure $\mu$![]() on $X$
on $X$![]() by defining a probability measure $\mu _i$
by defining a probability measure $\mu _i$![]() on $A_i$
on $A_i$![]() as follows:
as follows:
and

Hence, $X=(X,\,\mathcal {B},\,\mu )$![]() becomes a topological Borel probability space.
becomes a topological Borel probability space.
The map $f:X\to X$![]() is simply the $+1$
is simply the $+1$![]() -map with carryover. It was shown in [Reference Bayart, Darji and Pires2] that $T_f$
-map with carryover. It was shown in [Reference Bayart, Darji and Pires2] that $T_f$![]() is a well-defined continuous linear operator which is topologically transitive but not topologically mixing. We will show that $T_f$
is a well-defined continuous linear operator which is topologically transitive but not topologically mixing. We will show that $T_f$![]() has a dense set of periodic points, implying that $T_f$
has a dense set of periodic points, implying that $T_f$![]() is chaotic. As $T_f$
is chaotic. As $T_f$![]() is not topologically mixing, by Theorem 3.2 we have that $f$
is not topologically mixing, by Theorem 3.2 we have that $f$![]() does satisfy Condition (SC).
does satisfy Condition (SC).
We recall that the open subsets of $X$![]() are countable unions of disjoint basic cylinders, i.e., sets of the form
are countable unions of disjoint basic cylinders, i.e., sets of the form
We claim that $\chi _{[a_1,\ldots ,a_i]}$![]() is a periodic point of $T_f$
is a periodic point of $T_f$![]() . In fact, if $N=\vert A_1\vert \cdot \vert A_2\vert \cdots \vert A_i\vert$
. In fact, if $N=\vert A_1\vert \cdot \vert A_2\vert \cdots \vert A_i\vert$![]() , where $\vert A_j\vert$
, where $\vert A_j\vert$![]() denotes the cardinality of $A_j$
denotes the cardinality of $A_j$![]() , and $x=(x_1,\,x_2,\,\ldots )\in [a_1,\,\ldots ,\,a_i]$
, and $x=(x_1,\,x_2,\,\ldots )\in [a_1,\,\ldots ,\,a_i]$![]() , then $f^{N}(x)=(x_1,\,x_2,\,\ldots ,\,x_i,\,y_{i+1},\,\ldots )$
, then $f^{N}(x)=(x_1,\,x_2,\,\ldots ,\,x_i,\,y_{i+1},\,\ldots )$![]() , that is, $f^{N}(x)\in [a_1,\,\ldots ,\,a_i]$
, that is, $f^{N}(x)\in [a_1,\,\ldots ,\,a_i]$![]() . Hence, $f^{-N}([a_1,\,\ldots ,\,a_i])=[a_1,\,\ldots ,\,a_i]$
. Hence, $f^{-N}([a_1,\,\ldots ,\,a_i])=[a_1,\,\ldots ,\,a_i]$![]() . In this way,
. In this way,
implying that $\chi _{[a_1,\ldots ,a_i]}$![]() is a periodic point of $T_f$
is a periodic point of $T_f$![]() .
.
Now it is easy to verify that the characteristic function of the finite union of cylinders is also a periodic point. From this, one can easily show that the collection of simple functions of the form $\sum \nolimits _{i=1}^{m} a_i \cdot \chi _{C_i}$![]() , where $C_i$
, where $C_i$![]() is the finite union of cylinders, is dense in $L^{p}(X)$
is the finite union of cylinders, is dense in $L^{p}(X)$![]() , completing the proof.
, completing the proof.
The following example shows that there are simple situations where the full strength of Theorem 3.2 is realized. It also shows that the hypothesis of ergodicity is necessary in Corollary 3.9.
Example 4.4 There exists a dissipative system $(X,\, \mathcal {B},\, \mu ,\,f)$![]() with a purely atomic measure $\mu$
with a purely atomic measure $\mu$![]() such that $\mu (X)=\infty$
such that $\mu (X)=\infty$![]() and $T_f$
and $T_f$![]() satisfies Condition (SC).
satisfies Condition (SC).
Proof. Let $X=\mathbb {Z}\times \mathbb {Z}$![]() and $f:X\to X$
and $f:X\to X$![]() defined by $f((i,\,j))=(i,\,j+1)$
defined by $f((i,\,j))=(i,\,j+1)$![]() , $i,\,j\in \mathbb {Z}$
, $i,\,j\in \mathbb {Z}$![]() . Let $\mathcal {B}=2^{X}$
. Let $\mathcal {B}=2^{X}$![]() be the discrete $\sigma$
be the discrete $\sigma$![]() -algebra and $\mu :\mathcal {B}\to [0,\,\infty ]$
-algebra and $\mu :\mathcal {B}\to [0,\,\infty ]$![]() be the $\sigma$
be the $\sigma$![]() -finite measure defined by $\mu (\{(i,\,j)\})=2^{-\vert j\vert }$
-finite measure defined by $\mu (\{(i,\,j)\})=2^{-\vert j\vert }$![]() . Clearly, $\mu (X)=\infty$
. Clearly, $\mu (X)=\infty$![]() .
.
Now let us verify Condition (SC). Let $B\in \mathcal {B}$![]() and $\epsilon >0$
and $\epsilon >0$![]() with $\mu (B)<\infty$
with $\mu (B)<\infty$![]() . As $\mu (B)<\infty$
. As $\mu (B)<\infty$![]() , there is $L \ge 1$
, there is $L \ge 1$![]() such that $\mu (B {\setminus } ( [-L,\, L ] \times [-L,\, L ] ) ) < \epsilon$
such that $\mu (B {\setminus } ( [-L,\, L ] \times [-L,\, L ] ) ) < \epsilon$![]() . Let $B' = B \cap ([-L,\, L ] \times [-L,\, L ])$
. Let $B' = B \cap ([-L,\, L ] \times [-L,\, L ])$![]() . Clearly, $\mu (B {\setminus } B' ) < \epsilon$
. Clearly, $\mu (B {\setminus } B' ) < \epsilon$![]() . Next, we observe that for any $(i,\, j) \in X$
. Next, we observe that for any $(i,\, j) \in X$![]() , we have that $\sum \nolimits _{n \in \mathbb {Z}} \mu (f^{n} (i,\,j)) =3$
, we have that $\sum \nolimits _{n \in \mathbb {Z}} \mu (f^{n} (i,\,j)) =3$![]() . As $B' \subseteq [-L,\, L ] \times [-L,\, L ]$
. As $B' \subseteq [-L,\, L ] \times [-L,\, L ]$![]() , we have that $\sum \nolimits _{n \in \mathbb {Z}} \mu (f^{n} (B')) \le 3\cdot (2L+1)^{2}$
, we have that $\sum \nolimits _{n \in \mathbb {Z}} \mu (f^{n} (B')) \le 3\cdot (2L+1)^{2}$![]() .
.
5. Proofs of the main results
Lemma 5.1 (Orlicz [Reference Kadets and Kadets14, Theorem 4.2.1])
Let $(X,\,\mathcal {B},\,\mu )$![]() be a $\sigma$
be a $\sigma$![]() -finite measure space. Let the series $\sum \nolimits _{n\in \mathbb {N}} \varphi _n$
-finite measure space. Let the series $\sum \nolimits _{n\in \mathbb {N}} \varphi _n$![]() of elements of $L^{p}(X)$
of elements of $L^{p}(X)$![]() converge unconditionally. Then for each $1\le p\le 2,$
converge unconditionally. Then for each $1\le p\le 2,$![]() the series $\sum \nolimits _{n\in \mathbb {N}} \Vert \varphi _n\Vert _p^{2}$
the series $\sum \nolimits _{n\in \mathbb {N}} \Vert \varphi _n\Vert _p^{2}$![]() converges, and for each $2\le p<\infty ,$
converges, and for each $2\le p<\infty ,$![]() the series $\sum \nolimits _{n\in \mathbb {N}}\Vert \varphi _n\Vert _p^{p}$
the series $\sum \nolimits _{n\in \mathbb {N}}\Vert \varphi _n\Vert _p^{p}$![]() converges.
converges.
Lemma 5.2 Let $(X,\,\mathcal {B},\,\mu ,\,f)$![]() be a measurable system. If $f$
be a measurable system. If $f$![]() satisfies Condition (SC), then $f$
satisfies Condition (SC), then $f$![]() is dissipative.
is dissipative.
Proof. By the Hopf Decomposition Theorem, we may write $X=\mathcal {C}(f)\cup \mathcal {D}(f)$![]() as the union of the conservative and the dissipative parts of $f$
as the union of the conservative and the dissipative parts of $f$![]() , respectively. We will prove that $\mu (\mathcal {C}(f))=0$
, respectively. We will prove that $\mu (\mathcal {C}(f))=0$![]() . By way of contradiction, suppose that $B\subseteq \mathcal {C}(f)$
. By way of contradiction, suppose that $B\subseteq \mathcal {C}(f)$![]() is a measurable set with $0<\mu (B)<\infty$
is a measurable set with $0<\mu (B)<\infty$![]() .
.
We claim that there exist $W\subseteq {B}$![]() and $N\in \mathbb {N}$
and $N\in \mathbb {N}$![]() such that $\mu (W)>0$
such that $\mu (W)>0$![]() and $f^{n}(W)\cap W=\emptyset$
and $f^{n}(W)\cap W=\emptyset$![]() for all $n\in \mathbb {N}$
for all $n\in \mathbb {N}$![]() satisfying $\vert n\vert \ge N$
satisfying $\vert n\vert \ge N$![]() . By Condition (SC), there exist a measurable set $B'\subseteq B$
. By Condition (SC), there exist a measurable set $B'\subseteq B$![]() and $N\in \mathbb {N}$
and $N\in \mathbb {N}$![]() such that
such that

Let $W=B'{\big \backslash } \bigcup_{\vert n\vert \ge N} f^{n}(B')$![]() . Notice that
. Notice that

In this way, $\mu (B{\setminus } W)<\mu (B)/2$![]() , which yields $\mu (W)>0$
, which yields $\mu (W)>0$![]() . Moreover, $f^{n}(W)\cap W=\emptyset$
. Moreover, $f^{n}(W)\cap W=\emptyset$![]() for all $n\in \mathbb {Z}$
for all $n\in \mathbb {Z}$![]() satisfying $\vert n\vert \ge N$
satisfying $\vert n\vert \ge N$![]() . This proves the claim.
. This proves the claim.
Now let $A=\{x\in W: f^{n}(x)\not \in W,\,\forall n\ge 1\}$![]() . Since $A\subseteq \mathcal {C}(f)$
. Since $A\subseteq \mathcal {C}(f)$![]() , we have that $\mu (A)=0$
, we have that $\mu (A)=0$![]() . Hence, the set $W'=W{\setminus }\bigcup_{n\in \mathbb {Z}}f^{n}(A)$
. Hence, the set $W'=W{\setminus }\bigcup_{n\in \mathbb {Z}}f^{n}(A)$![]() has positive $\mu$
has positive $\mu$![]() -measure. Moreover, if $x\in W'$
-measure. Moreover, if $x\in W'$![]() , then $f^{n}(x)\in W$
, then $f^{n}(x)\in W$![]() for infinitely many positive $n$
for infinitely many positive $n$![]() , contradicting the claim. Therefore, $\mu (C(f))=0$
, contradicting the claim. Therefore, $\mu (C(f))=0$![]() and $f$
and $f$![]() is dissipative.
is dissipative.
5.1. Proof of Theorem 3.1
Proof of $(SC)\implies (FHC)$![]() . Assume that $f$
. Assume that $f$![]() satisfies (SC). We will show that $T_f$
satisfies (SC). We will show that $T_f$![]() satisfies (FHC). By Lemma 5.2, $f$
satisfies (FHC). By Lemma 5.2, $f$![]() is dissipative. Let $W$
is dissipative. Let $W$![]() be a wandering set such that $X=\bigcup_{n\in \mathbb {Z}} f^{n}(W)$
be a wandering set such that $X=\bigcup_{n\in \mathbb {Z}} f^{n}(W)$![]() . Let $\mathcal {H}=L^{p}(X)$
. Let $\mathcal {H}=L^{p}(X)$![]() and $\mathcal {H}_0\subseteq \mathcal {H}$
and $\mathcal {H}_0\subseteq \mathcal {H}$![]() be defined as follows: $\varphi \in \mathcal {H}_0$
be defined as follows: $\varphi \in \mathcal {H}_0$![]() if and only if there exist $m\ge 1,\, a_1,\,\ldots ,\,a_m\in \mathbb {R}$
if and only if there exist $m\ge 1,\, a_1,\,\ldots ,\,a_m\in \mathbb {R}$![]() , $k_1,\,\ldots ,\,k_m\in \mathbb {Z}$
, $k_1,\,\ldots ,\,k_m\in \mathbb {Z}$![]() , and pairwise disjoint measurable sets $B_1,\,\ldots ,\,B_m$
, and pairwise disjoint measurable sets $B_1,\,\ldots ,\,B_m$![]() such that $\varphi =\sum \nolimits _{i=1}^{m} a_i \chi _{B_i}$
such that $\varphi =\sum \nolimits _{i=1}^{m} a_i \chi _{B_i}$![]() and, for each $1\le i\le m$
and, for each $1\le i\le m$![]() , $B_i\subseteq f^{k_i}(W)$
, $B_i\subseteq f^{k_i}(W)$![]() and $\sum \nolimits _{n\in \mathbb {Z}} \mu (f^{n}(B_i) )<\infty$
and $\sum \nolimits _{n\in \mathbb {Z}} \mu (f^{n}(B_i) )<\infty$![]() .
.
We will now show that $\mathcal {H}_0$![]() is dense in $\mathcal {H}$
is dense in $\mathcal {H}$![]() . Given $\epsilon >0$
. Given $\epsilon >0$![]() and $\psi \in \mathcal {H}$
and $\psi \in \mathcal {H}$![]() , let $\varphi =\sum \nolimits _{j=1}^{r} a_j\chi _{D_j}\in \mathcal {H}\backslash \{0\}$
, let $\varphi =\sum \nolimits _{j=1}^{r} a_j\chi _{D_j}\in \mathcal {H}\backslash \{0\}$![]() be such that $D_1,\,\ldots ,\,D_r$
be such that $D_1,\,\ldots ,\,D_r$![]() are pairwise disjoint measurable sets with finite positive $\mu$
are pairwise disjoint measurable sets with finite positive $\mu$![]() -measures and $\Vert \varphi -\psi \Vert _p<\epsilon /2$
-measures and $\Vert \varphi -\psi \Vert _p<\epsilon /2$![]() . Set $M=\max \{\vert a_j\vert : 1\le j\le r\}$
. Set $M=\max \{\vert a_j\vert : 1\le j\le r\}$![]() , then $M>0$
, then $M>0$![]() . As $f$
. As $f$![]() satisfies Condition (SC) and $X=\bigcup_{n\in \mathbb {Z}}f^{n}(W)$
satisfies Condition (SC) and $X=\bigcup_{n\in \mathbb {Z}}f^{n}(W)$![]() , there exist an integer $N>0$
, there exist an integer $N>0$![]() and measurable sets $C_1,\,\ldots ,\,C_r$
and measurable sets $C_1,\,\ldots ,\,C_r$![]() such that, for each $1\le j\le r$
such that, for each $1\le j\le r$![]() , $C_j\subseteq D_j\cap \bigcup_{\vert n\vert \le N} f^{n}(W)$
, $C_j\subseteq D_j\cap \bigcup_{\vert n\vert \le N} f^{n}(W)$![]() ,
,
Let $\varphi ' =\sum \nolimits _{j=1}^{r} a_j \chi _{C_j}$![]() . Since $C_j\subseteq \bigcup_{\vert n\vert \le N} f^{n}(W)$
. Since $C_j\subseteq \bigcup_{\vert n\vert \le N} f^{n}(W)$![]() , we have that each $C_j$
, we have that each $C_j$![]() is the union of finitely many pairwise disjoint sets $B_i$
is the union of finitely many pairwise disjoint sets $B_i$![]() satisfying $B_i\subseteq f^{k_i}(W)$
satisfying $B_i\subseteq f^{k_i}(W)$![]() for some $-N\le k_i\le N$
for some $-N\le k_i\le N$![]() . In this way, $\varphi '\in \mathcal {H}_0$
. In this way, $\varphi '\in \mathcal {H}_0$![]() . Moreover,
. Moreover,

In this way, $\Vert \varphi ' -\psi \Vert _p<\epsilon$![]() , completing the proof of the denseness of $\mathcal {H}_0$
, completing the proof of the denseness of $\mathcal {H}_0$![]() .
.
We next show that $\sum \nolimits _{n\ge 1} T_f^{n}\varphi$![]() is unconditionally convergent for all $\varphi =\sum \nolimits _{i=1}^{m} a_i \chi _{B_i} \in \mathcal {H}_0$
is unconditionally convergent for all $\varphi =\sum \nolimits _{i=1}^{m} a_i \chi _{B_i} \in \mathcal {H}_0$![]() . Since $B_i\subseteq f^{k_i}(W)$
. Since $B_i\subseteq f^{k_i}(W)$![]() , we have that the sets $f^{n}(B_i)$
, we have that the sets $f^{n}(B_i)$![]() , $n\in \mathbb {Z}$
, $n\in \mathbb {Z}$![]() , are pairwise disjoint. Hence, for each sequence of integers $1\le n_1< n_2<\ldots$
, are pairwise disjoint. Hence, for each sequence of integers $1\le n_1< n_2<\ldots$![]() , we have that
, we have that

Since $\sum \nolimits _{n\in \mathbb {Z}}\mu (f^{n}(B_i))<\infty$![]() for all $1\le i\le m$
for all $1\le i\le m$![]() , we have that $\chi _{\bigcup_{j\ge 1}f^{-n_j}(B_i)}\in L^{p}(X)$
, we have that $\chi _{\bigcup_{j\ge 1}f^{-n_j}(B_i)}\in L^{p}(X)$![]() . Thus, $\sum \nolimits _{j\ge 1}T_f^{n_j}\varphi$
. Thus, $\sum \nolimits _{j\ge 1}T_f^{n_j}\varphi$![]() converges for each sequence of integers $1\le n_1< n_2<\ldots\ .$
converges for each sequence of integers $1\le n_1< n_2<\ldots\ .$![]() Therefore, $\sum \nolimits _{n\ge 1} T_f^{n}\varphi$
Therefore, $\sum \nolimits _{n\ge 1} T_f^{n}\varphi$![]() is unconditionally convergent and Condition (a) in Theorem 2.4 is true.
is unconditionally convergent and Condition (a) in Theorem 2.4 is true.
Given $\varphi =\sum \nolimits _{i=1}^{m} a_i \chi _{B_i}\in \mathcal {H}_0$![]() , let $S\varphi =\sum \nolimits _{i=1}^{m} a_i \chi _{f(B_i)}.$
, let $S\varphi =\sum \nolimits _{i=1}^{m} a_i \chi _{f(B_i)}.$![]() Since $f$
Since $f$![]() is bijective, bimeasurable and non-singular, we have that $S\varphi \in \mathcal {H}_0$
is bijective, bimeasurable and non-singular, we have that $S\varphi \in \mathcal {H}_0$![]() and $S:\varphi \to S\varphi$
and $S:\varphi \to S\varphi$![]() is a self-map on $\mathcal {H}_0$
is a self-map on $\mathcal {H}_0$![]() . Moreover, $TS\varphi =\sum \nolimits _{i=1}^{m} a_i \chi _{f^{-1}(f(B_i))}=\varphi$
. Moreover, $TS\varphi =\sum \nolimits _{i=1}^{m} a_i \chi _{f^{-1}(f(B_i))}=\varphi$![]() , showing that Condition (c) in Theorem 2.4 is true. By proceeding as in (5.1), we can show that $\sum \nolimits _{n\ge 1}S^{n}\varphi$
, showing that Condition (c) in Theorem 2.4 is true. By proceeding as in (5.1), we can show that $\sum \nolimits _{n\ge 1}S^{n}\varphi$![]() is unconditionally convergent for all $\varphi \in \mathcal {H}_0$
is unconditionally convergent for all $\varphi \in \mathcal {H}_0$![]() . We have proved that $T_f$
. We have proved that $T_f$![]() satisfies (FHC).
satisfies (FHC).
Proof of $(FHC)\implies (SC)$![]() when $p\ge 2$
when $p\ge 2$![]() . Assume the hypothesis, i.e., $T_f$
. Assume the hypothesis, i.e., $T_f$![]() satisfies the FHC. Let $\mathcal {H}_0 \subseteq L^{p}(X)$
satisfies the FHC. Let $\mathcal {H}_0 \subseteq L^{p}(X)$![]() be as in the statement of (FHC). Let $0<\epsilon <\tfrac {1}{2}$
be as in the statement of (FHC). Let $0<\epsilon <\tfrac {1}{2}$![]() and $B\in \mathcal {B}$
and $B\in \mathcal {B}$![]() with $\mu (B)<\infty$
with $\mu (B)<\infty$![]() . By the denseness of $\mathcal {H}_0$
. By the denseness of $\mathcal {H}_0$![]() , there is $\varphi \in \mathcal {H}_0$
, there is $\varphi \in \mathcal {H}_0$![]() such that
such that
Let
Then,

showing that $\mu (B{\setminus }B')<\epsilon$![]() .
.
We next show that $\sum \nolimits _{n \ge 1} \mu (f^{-n}(B')) < \infty$![]() . Proceeding as earlier we have that for any $n\ge 1$
. Proceeding as earlier we have that for any $n\ge 1$![]() ,
,

implying that

Since $\sum \nolimits _{n\ge 1} T_f^{n}\varphi$![]() converges unconditionally and $p\ge 2$
converges unconditionally and $p\ge 2$![]() , by Theorem 5.1 we have that
, by Theorem 5.1 we have that
We next show that $\sum \nolimits _{n \ge 1} \mu (f^{n}(B')) < \infty$![]() . As $\{\varphi ,\, S\varphi ,\, \ldots ,\, S^{n}\varphi \}\subset \mathcal {H}_0$
. As $\{\varphi ,\, S\varphi ,\, \ldots ,\, S^{n}\varphi \}\subset \mathcal {H}_0$![]() and $T_fS$
and $T_fS$![]() is the identity map on $\mathcal {H}_0$
is the identity map on $\mathcal {H}_0$![]() , we have that $T_f^{n}S^{n}(\varphi ) = \varphi$
, we have that $T_f^{n}S^{n}(\varphi ) = \varphi$![]() for all $n \ge 1$
for all $n \ge 1$![]() . Since $f$
. Since $f$![]() is bijective, bimeasurable and non-singular, we have that
is bijective, bimeasurable and non-singular, we have that
Using this we have that

Since $\sum \nolimits _{n\ge 1} S_f^{n}\varphi$![]() converges unconditionally and $p\ge 2$
converges unconditionally and $p\ge 2$![]() , by Lemma 5.1 we have that
, by Lemma 5.1 we have that
which completes the proof.
5.2. Proof of Theorem 3.2
Proof of $(a) \implies (b)$![]() . Suppose that $f$
. Suppose that $f$![]() satisfies Condition (SC). Then, by Lemma 5.2, $f$
satisfies Condition (SC). Then, by Lemma 5.2, $f$![]() is dissipative. By Theorem 3.1, $T_f$
is dissipative. By Theorem 3.1, $T_f$![]() satisfies (FHC). Hence, by Theorem 2.4, $T_f$
satisfies (FHC). Hence, by Theorem 2.4, $T_f$![]() is frequently hypercyclic, topologically mixing and chaotic. In particular, $T_f$
is frequently hypercyclic, topologically mixing and chaotic. In particular, $T_f$![]() has a dense set of periodic points.
has a dense set of periodic points.
Proof of $(b) \Longrightarrow (a)$![]() . Since $f$
. Since $f$![]() is dissipative, there exist a wandering set $W\in \mathcal {B}$
is dissipative, there exist a wandering set $W\in \mathcal {B}$![]() of positive $\mu$
of positive $\mu$![]() -measure such that $X=\bigcup_{n\in \mathbb {Z}} f^{n}(W)$
-measure such that $X=\bigcup_{n\in \mathbb {Z}} f^{n}(W)$![]() . Let $\epsilon >0$
. Let $\epsilon >0$![]() and $B\in \mathcal {B}$
and $B\in \mathcal {B}$![]() with $\mu (B)<\infty$
with $\mu (B)<\infty$![]() . Let $n_0\in \mathbb {N}$
. Let $n_0\in \mathbb {N}$![]() be such that if
be such that if
By hypothesis, there exists a periodic point $\varphi \in L^{p}(X)$![]() of $T_f$
of $T_f$![]() such that
such that
For $B'=\{x\in B_0: |\varphi (x)|>{3}/{4}\}$![]() , we have that $\mu (B_0{\setminus } B')\le {\epsilon }/{2}$
, we have that $\mu (B_0{\setminus } B')\le {\epsilon }/{2}$![]() because
because
In this way,
Let $N\ge 2n_0+1$![]() be such that $T_f^{N} \varphi =\varphi \circ f^{N}=\varphi$
be such that $T_f^{N} \varphi =\varphi \circ f^{N}=\varphi$![]() $\mu$
$\mu$![]() -a.e. Hence, since $f$
-a.e. Hence, since $f$![]() is bijective, we have that $\varphi \circ f^{kN}=\varphi$
is bijective, we have that $\varphi \circ f^{kN}=\varphi$![]() $\mu$
$\mu$![]() -a.e. for all $k\in \mathbb {Z}$
-a.e. for all $k\in \mathbb {Z}$![]() . Because $B'\subseteq B_0$
. Because $B'\subseteq B_0$![]() and $N\ge 2n_0+1$
and $N\ge 2n_0+1$![]() , we have that the sets in the family $\{ f^{kN}(B'):k\in \mathbb {Z}\}$
, we have that the sets in the family $\{ f^{kN}(B'):k\in \mathbb {Z}\}$![]() are pairwise disjoint. Moreover,
are pairwise disjoint. Moreover,

showing that $\sum \nolimits _{k\in \mathbb {Z}} \mu (f^{kN}(B'))<\infty$![]() . By (*), we have that
. By (*), we have that

This proves that Condition (SC) is true, which concludes the proof of $(b)\implies (a)$![]() .
.
5.3. Proof of Theorem 3.3
Proof of $(a)\implies (b)$![]() . This is Lemma 5.2.
. This is Lemma 5.2.
Proof of $(b)\implies (a)$![]() . Assume $f$
. Assume $f$![]() is dissipative and $\mu (X)<\infty$
is dissipative and $\mu (X)<\infty$![]() . Then, there exists a wandering set $W$
. Then, there exists a wandering set $W$![]() such that $X=\bigcup_{n\in \mathbb {Z}}f^{n}(W)$
such that $X=\bigcup_{n\in \mathbb {Z}}f^{n}(W)$![]() . Let $\epsilon >0$
. Let $\epsilon >0$![]() and $B\in \mathcal {B}$
and $B\in \mathcal {B}$![]() with $\mu (B) < \infty$
with $\mu (B) < \infty$![]() be given. Let us verify Condition (SC). Let $N\in \mathbb {N}$
be given. Let us verify Condition (SC). Let $N\in \mathbb {N}$![]() be such that $\mu (B{\setminus } \bigcup_{\vert n\vert \le N} f^{n}(W))<\epsilon$
be such that $\mu (B{\setminus } \bigcup_{\vert n\vert \le N} f^{n}(W))<\epsilon$![]() . Then $B'=B\cap \bigcup_{\vert n\vert \le N} f^{n}(W)$
. Then $B'=B\cap \bigcup_{\vert n\vert \le N} f^{n}(W)$![]() verifies Condition (SC) because $\mu (B{\setminus }B')<\epsilon$
verifies Condition (SC) because $\mu (B{\setminus }B')<\epsilon$![]() and by the dissipativity of $f$
and by the dissipativity of $f$![]() , we have that
, we have that
which concludes the proof.
5.4. Proof of corollary 3.4
The proof consists in verifying Condition (SC). Hence, to begin with, let $\epsilon >0$![]() and $B\in \mathcal {B}$
and $B\in \mathcal {B}$![]() with $0<\mu (B)<\infty$
with $0<\mu (B)<\infty$![]() be given. We may assume that $B$
be given. We may assume that $B$![]() has no recurrent points. For each $n\ge 1$
has no recurrent points. For each $n\ge 1$![]() , set
, set
where $B(x,\,1/n)=\{y\in X: d(y,\,x)<1/n\}$![]() , where $d$
, where $d$![]() is the metric on $X$
is the metric on $X$![]() . Notice that $A_1\subseteq A_2\subseteq \ldots$
. Notice that $A_1\subseteq A_2\subseteq \ldots$![]() and $B=\bigcup_{n=1}^{\infty } A_n$
and $B=\bigcup_{n=1}^{\infty } A_n$![]() . In this way, there exist $N$
. In this way, there exist $N$![]() large enough so that $\mu (B{\setminus } A_N)<{\epsilon }/{4}$
large enough so that $\mu (B{\setminus } A_N)<{\epsilon }/{4}$![]() . Let $K$
. Let $K$![]() be a compact subset of $A_N$
be a compact subset of $A_N$![]() such that $\mu (A_N{\setminus }K)< {\epsilon }/{4}$
such that $\mu (A_N{\setminus }K)< {\epsilon }/{4}$![]() . Let $U_1,\, U_2,\,\ldots ,\, U_r$
. Let $U_1,\, U_2,\,\ldots ,\, U_r$![]() be a finite collection of balls of radius ${1}/{2N}$
be a finite collection of balls of radius ${1}/{2N}$![]() such that $K\subseteq \bigcup_{i=1}^{r} U_i$
such that $K\subseteq \bigcup_{i=1}^{r} U_i$![]() . Since $U_i\cap K\subseteq A_N$
. Since $U_i\cap K\subseteq A_N$![]() , we have that if $x\in U_i\cap K$
, we have that if $x\in U_i\cap K$![]() , then $\{f(x),\,f^{2}(x),\,\ldots \}\cap U_i=\emptyset$
, then $\{f(x),\,f^{2}(x),\,\ldots \}\cap U_i=\emptyset$![]() . In particular, if $K_i=U_i\cap K$
. In particular, if $K_i=U_i\cap K$![]() , then the following statements are true:
, then the following statements are true:
(a) $K=\bigcup_{i=1}^{r} K_i$
 ;
;(b) $f^{n}(K_i)\cap K_i=\emptyset$
 for all $n\ge 1$
for all $n\ge 1$ .
.
The bijectivity of $f$![]() and (b) imply that $W$
and (b) imply that $W$![]() is a wandering set. Hence,
is a wandering set. Hence,
In this way,
Thus, Condition (SC) is true, which concludes the proof.
5.5. Proof of Theorem 3.6
Throughout this section, $(X,\,\mathcal {B},\,\mu ,\,f)$![]() will denote a measurable system. Given a measurable set $W\subseteq X$
will denote a measurable system. Given a measurable set $W\subseteq X$![]() with finite positive $\mu$
with finite positive $\mu$![]() -measure, let $(d_n(W))_{n\in \mathbb {Z}}$
-measure, let $(d_n(W))_{n\in \mathbb {Z}}$![]() be the sequence defined by
be the sequence defined by

where we set $1/\infty =0$![]() so that $d_n(W)$
so that $d_n(W)$![]() is well defined even in the case in which $\left \Vert {\mathrm {d}\mu }/{\mathrm {d} (\mu \circ f^{n})}\bigg |_W\right \Vert _{\infty }=\infty$
is well defined even in the case in which $\left \Vert {\mathrm {d}\mu }/{\mathrm {d} (\mu \circ f^{n})}\bigg |_W\right \Vert _{\infty }=\infty$![]() .
.
Lemma 5.3 Let $c>0$![]() be as in ($\star$
be as in ($\star$![]() ) and let $W$
) and let $W$![]() be a measurable set with finite positive $\mu$
be a measurable set with finite positive $\mu$![]() -measure. Then, $d_{n+1}(W)\ge c^{-1} d_n(W)$
-measure. Then, $d_{n+1}(W)\ge c^{-1} d_n(W)$![]() for all $n\in \mathbb {Z}$
for all $n\in \mathbb {Z}$![]() .
.
Proof. By ($\star$![]() ), $\mu (f^{n}(B))\le c\mu ( f^{n+1}(B))$
), $\mu (f^{n}(B))\le c\mu ( f^{n+1}(B))$![]() for all $B\in \mathcal {B}$
for all $B\in \mathcal {B}$![]() and $n\in \mathbb {Z}$
and $n\in \mathbb {Z}$![]() . Hence, the Radon–Nikodym derivatives $\textrm {d}(\mu \circ f^{n})/\textrm {d}(\mu \circ f^{n+1})$
. Hence, the Radon–Nikodym derivatives $\textrm {d}(\mu \circ f^{n})/\textrm {d}(\mu \circ f^{n+1})$![]() , $n\in \mathbb {Z}$
, $n\in \mathbb {Z}$![]() , are bounded by $c$
, are bounded by $c$![]() at $\mu \circ f^{n+1}$
at $\mu \circ f^{n+1}$![]() -almost every point, and therefore, $\mu$
-almost every point, and therefore, $\mu$![]() -a.e. In this way, for all $n\in \mathbb {Z}$
-a.e. In this way, for all $n\in \mathbb {Z}$![]() ,
,

Therefore, for all $n\in \mathbb {Z}$![]() , we have that
, we have that

showing that $d_{n+1}(W)\ge c^{-1} d_n(W)$![]() for all $n\in \mathbb {Z}$
for all $n\in \mathbb {Z}$![]() .
.
Lemma 5.4 Suppose that $T_f$![]() is frequently hypercyclic. If $W$
is frequently hypercyclic. If $W$![]() is a wandering set with finite positive $\mu$
is a wandering set with finite positive $\mu$![]() -measure, then there exists a set $A\subset \mathbb {N}$
-measure, then there exists a set $A\subset \mathbb {N}$![]() with positive lower density such that for each $n\in A,$
with positive lower density such that for each $n\in A,$![]()
Proof. Let $\varphi \in L^{p}(X)$![]() be a frequently hypercyclic vector for $T_f$
be a frequently hypercyclic vector for $T_f$![]() and let $W$
and let $W$![]() be a wandering set with finite positive $\mu$
be a wandering set with finite positive $\mu$![]() -measure. Let
-measure. Let
then $A$![]() has positive lower density.
has positive lower density.
By combining the definition of $A$![]() with the fact that $W$
with the fact that $W$![]() is a wandering set, we obtain for each $n\in A$
is a wandering set, we obtain for each $n\in A$![]() ,
,

In particular, the second term of (5.6) satisfies the following inequality for each $n\in A$![]() ,
,

Applying the triangle inequality to the first term of (5.6) yields for each $n\in A$![]() ,
,

Therefore, renaming $n$![]() by $k$
by $k$![]() in (5.8) yields
in (5.8) yields
In what follows, keep $n\in A$![]() fixed and let $m\in A-n$
fixed and let $m\in A-n$![]() be arbitrary. Setting $k=n+m$
be arbitrary. Setting $k=n+m$![]() in (5.9) yields $\int _W \left \vert \varphi \circ f^{n+m}\right \vert ^{p}\textrm {d}\mu > {1}/{2^{p}}\mu (W)$
in (5.9) yields $\int _W \left \vert \varphi \circ f^{n+m}\right \vert ^{p}\textrm {d}\mu > {1}/{2^{p}}\mu (W)$![]() . By combining this with (5.7), we arrive at
. By combining this with (5.7), we arrive at

By the Change of Variables Formula, for all $m\in A-n$![]() ,
,
Replacing (5.11) in (5.10) yields

For all $m\in A-n$![]() ,
,

Replacing (5.13) in (5.12) and cancelling out the nonzero term $\int _W \left \vert \varphi \circ f^{n+m}\right \vert ^{p}\textrm {d}(\mu \circ f^{m})$![]() yields
yields

Therefore, after renaming variables, we obtain

Lemma 5.5 (Bayart-Ruzsa [Reference Bayart and Ruzsa5, Corollary 9])
Let $(\alpha _n)_{n\in \mathbb {Z}}$![]() be a sequence of non-negative real numbers such there exists $C>0$
be a sequence of non-negative real numbers such there exists $C>0$![]() such that either $\alpha _{n+1}\ge C \alpha _{n}$
such that either $\alpha _{n+1}\ge C \alpha _{n}$![]() for all $n\in \mathbb {Z},$
for all $n\in \mathbb {Z},$![]() or $\alpha _{n}\ge C \alpha _{n+1}$
or $\alpha _{n}\ge C \alpha _{n+1}$![]() for all $n\in \mathbb {Z}$
for all $n\in \mathbb {Z}$![]() . Suppose that for some set $A\subset \mathbb {Z}$
. Suppose that for some set $A\subset \mathbb {Z}$![]() with positive upper density the sequence $(\beta _n)_{n\in A}$
with positive upper density the sequence $(\beta _n)_{n\in A}$![]() defined by $\beta _n=\sum \nolimits _{m\in A} \alpha _{m-n}$
defined by $\beta _n=\sum \nolimits _{m\in A} \alpha _{m-n}$![]() is bounded. Then $\sum \nolimits _{n\in \mathbb {Z}} \alpha _n<\infty$
is bounded. Then $\sum \nolimits _{n\in \mathbb {Z}} \alpha _n<\infty$![]() .
.
5.6. Proof of Theorem 3.6
Set $\alpha _n= d_n(W)$![]() for all $n\in \mathbb {Z}$
for all $n\in \mathbb {Z}$![]() . By Lemma 5.3, we have that $\alpha _{n+1}\ge c^{-1} \alpha _n$
. By Lemma 5.3, we have that $\alpha _{n+1}\ge c^{-1} \alpha _n$![]() for all $n\in \mathbb {Z}$
for all $n\in \mathbb {Z}$![]() . Let $A$
. Let $A$![]() be as in Lemma 5.4 and let $(\beta _n)_{n\in {A}}$
be as in Lemma 5.4 and let $(\beta _n)_{n\in {A}}$![]() be defined by $\beta _n=\sum \nolimits _{m\in A} \alpha _{m-n}$
be defined by $\beta _n=\sum \nolimits _{m\in A} \alpha _{m-n}$![]() . Then, by Lemma 5.4, for each $n\in A$
. Then, by Lemma 5.4, for each $n\in A$![]() ,
,
Hence, $(\beta _n)_{n\in {A}}$![]() is bounded. By Lemma 5.5,
is bounded. By Lemma 5.5,
5.7. Proof of Theorem 3.7
Proof of $(a)\implies (b)$![]() . This follows immediately from Theorem 3.2.
. This follows immediately from Theorem 3.2.
Proof of $(b)\implies (a)$![]() . Let $B\in \mathcal {B}$
. Let $B\in \mathcal {B}$![]() with $\mu (B)<\infty$
with $\mu (B)<\infty$![]() and $\epsilon >0$
and $\epsilon >0$![]() be given. We will verify Condition (SC). Let $W$
be given. We will verify Condition (SC). Let $W$![]() be a wandering set of finite positive $\mu$
be a wandering set of finite positive $\mu$![]() -measure satisfying the bounded distortion Conditions (i) and (ii) in Definition 2.11. For each $i\in \mathbb {Z}$
-measure satisfying the bounded distortion Conditions (i) and (ii) in Definition 2.11. For each $i\in \mathbb {Z}$![]() , set $W_i=f^{i}(W)$
, set $W_i=f^{i}(W)$![]() . By (i), there exists $N\in \mathbb {N}$
. By (i), there exists $N\in \mathbb {N}$![]() such that if $B'=B\cap \bigcup_{\vert i\vert \le N}f^{i}(W)$
such that if $B'=B\cap \bigcup_{\vert i\vert \le N}f^{i}(W)$![]() , then $\mu (B{\setminus B'})<\epsilon$
, then $\mu (B{\setminus B'})<\epsilon$![]() . We claim that there exists $K>0$
. We claim that there exists $K>0$![]() such that for each integer $-N\le i\le N$
such that for each integer $-N\le i\le N$![]() , each $D\in \mathcal {B}(W_i)$
, each $D\in \mathcal {B}(W_i)$![]() with positive $\mu$
with positive $\mu$![]() -measure and each $n\in \mathbb {Z}$
-measure and each $n\in \mathbb {Z}$![]() ,
,
In fact, since $f$![]() is bijective, bimeasurable and non-singular, any set $D\in \mathcal {B}(W_i)$
is bijective, bimeasurable and non-singular, any set $D\in \mathcal {B}(W_i)$![]() has positive $\mu$
has positive $\mu$![]() -measure if and only if $D=f^{i}(C)$
-measure if and only if $D=f^{i}(C)$![]() , where $C\in \mathcal {B}(W)$
, where $C\in \mathcal {B}(W)$![]() has positive $\mu$
has positive $\mu$![]() -measure. By Condition (ii) in Definition 2.11, we have that
-measure. By Condition (ii) in Definition 2.11, we have that

which proves the claim.
Hence, since $D\in \mathcal {B}(W_i)$![]() is an arbitrary measurable set of positive $\mu$
is an arbitrary measurable set of positive $\mu$![]() -measure, we obtain
-measure, we obtain
Therefore, since $W_i$![]() is a wandering set and $T_f$
is a wandering set and $T_f$![]() is frequently hypercyclic, by Theorem 3.6 we arrive at
is frequently hypercyclic, by Theorem 3.6 we arrive at

In this way,

Proof of $(a)\iff (c)$![]() . This follows immediately from Corollary 3.5.
. This follows immediately from Corollary 3.5.
6. Problems and final comments
Below we list some problems related to our work.
Problem 6.1 In Theorem 3.1, we show that (FHC) implies (SC) for $p \ge 2$![]() . What happens for $1 \le p <2$
. What happens for $1 \le p <2$![]() ?
?
Problem 6.2 Is the condition of bounded distortion necessary in Theorem 3.7?
Problem 6.3 In Example 4.3 is $T_f$![]() frequently hypercyclic? If not, this would give an alternative solution to a result of Menet [Reference Menet16].
frequently hypercyclic? If not, this would give an alternative solution to a result of Menet [Reference Menet16].
Problem 6.4 We have thoroughly studied the case when the measurable system is dissipative. What happens in the case when the measurable system is conservative? In particular, what can be said when $X$![]() is an odometer endowed with the product measure? Characterizations of hypercyclic and topologically mixing operators of such type were given in [Reference Bongiorno, D'Aniello, Darji and Di Piazza7].
is an odometer endowed with the product measure? Characterizations of hypercyclic and topologically mixing operators of such type were given in [Reference Bongiorno, D'Aniello, Darji and Di Piazza7].
Concerning the extension of our results to the non-bijective case, a slight variation of the proof of Theorem 3.6 leads to the result stated below. We recall that a measurable set $W\subseteq X$![]() is a forward wandering set if $W,\, f(W),\, f^{2}(W),\,\ldots$
is a forward wandering set if $W,\, f(W),\, f^{2}(W),\,\ldots$![]() are pairwise disjoint.
are pairwise disjoint.
Theorem 6.5 (Necessary condition for frequent hypercyclicity) Let $(X,\,\mathcal {B},\,\mu )$![]() be a $\sigma$
be a $\sigma$![]() -finite measure space and $f:X\to X$
-finite measure space and $f:X\to X$![]() be an injective bimeasurable map satisfying $(\star )$
be an injective bimeasurable map satisfying $(\star )$![]() with associated composition operator $T_f$
with associated composition operator $T_f$![]() frequently hypercyclic. Then for every forward wandering set $W$
frequently hypercyclic. Then for every forward wandering set $W$![]() with positive finite $\mu$
with positive finite $\mu$![]() -measure, the following inequality holds
-measure, the following inequality holds

Let $w=(w_i)_{i\in \mathbb {N}}$![]() be a bounded sequence of positive real numbers and $B_{w}$
be a bounded sequence of positive real numbers and $B_{w}$![]() be the backward weighted shift on $\ell _p(\mathbb {N})$
be the backward weighted shift on $\ell _p(\mathbb {N})$![]() . By considering $X=\mathbb {N}$
. By considering $X=\mathbb {N}$![]() , $\mathcal {B}=\mathcal {P}(\mathbb {N})$
, $\mathcal {B}=\mathcal {P}(\mathbb {N})$![]() (the power set of $\mathbb {N}$
(the power set of $\mathbb {N}$![]() ), $f:i\in \mathbb {N}\to i+1\in \mathbb {N}$
), $f:i\in \mathbb {N}\to i+1\in \mathbb {N}$![]() , $W=\{0\}$
, $W=\{0\}$![]() and $\mu (\{i\})={1}/{(w_0\cdots w_i)^{p}}$
and $\mu (\{i\})={1}/{(w_0\cdots w_i)^{p}}$![]() in Theorem 6.5, we obtain the implication $(i)\implies (iii)$
in Theorem 6.5, we obtain the implication $(i)\implies (iii)$![]() in [Reference Bayart and Ruzsa5, Theorem 4], which leads to the known conclusion that frequently hypercyclic backward weighted shifts on $\ell _p(\mathbb {N})$
in [Reference Bayart and Ruzsa5, Theorem 4], which leads to the known conclusion that frequently hypercyclic backward weighted shifts on $\ell _p(\mathbb {N})$![]() are chaotic. Likewise, by means of Corollary 3.9, we obtain the equivalence $(i)\iff (iii)$
are chaotic. Likewise, by means of Corollary 3.9, we obtain the equivalence $(i)\iff (iii)$![]() in [Reference Bayart and Ruzsa5, Theorem 3] and we arrive at the known conclusion that a backward weighted shift on $\ell _p(\mathbb {Z})$
in [Reference Bayart and Ruzsa5, Theorem 3] and we arrive at the known conclusion that a backward weighted shift on $\ell _p(\mathbb {Z})$![]() is frequently hypercyclic if and only if it is chaotic.
is frequently hypercyclic if and only if it is chaotic.
Apart from Theorem 6.5, we do not know if the other results can be generalized to the non-bijective case. Note that we use the hypothesis that $f$![]() is bijective in the Hopf Decomposition Theorem.
is bijective in the Hopf Decomposition Theorem.
Acknowledgements
The authors are very grateful to the reviewer for the careful reading of the manuscript. The first author was supported by grant #2017/19360-8 São Paulo Research Foundation (FAPESP). The second author was partially supported by grants #2018/06916-0 and #2019/10269-3 São Paulo Research Foundation (FAPESP).