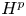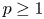Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-11T13:11:22.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation numbers of composition operators on weighted besov spaces of analytic functions

Part of: Spaces and algebras of analytic functions Special classes of linear operators Two-dimensional theory

Published online by Cambridge University Press:  28 February 2022

Stamatis Pouliasis
Stamatis Pouliasis*
Affiliation:
Department of Mathematics and Statistics, Texas Tech University, Lubbock, TX 79409, USA (stamatis.pouliasis@ttu.edu)
Rights & Permissions [Opens in a new window]

Abstract

Li et al. [A spectral radius type formula for approximation numbers of composition operators, J. Funct. Anal. 267(12) (2014), 4753-4774] proved a spectral radius type formula for the approximation numbers of composition operators on analytic Hilbert spaces with radial weights and on $H^{p}$ spaces, $p\geq 1$, involving Green capacity. We prove that their formula holds for a wide class of Banach spaces of analytic functions and weights.

Keywords

composition operatorsapproximation numbersBesov spacescondenser capacityBagby points

MSC classification

Primary: 47B06: Riesz operators; eigenvalue distributions; approximation numbers, $s$-numbers, Kolmogorov numbers, entropy numbers, etc. of operators 47B33: Composition operators
Secondary: 30H25: Besov spaces and $Q_p$-spaces 31A15: Potentials and capacity, harmonic measure, extremal length
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 2 , May 2022 , pp. 311 - 325
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

1. Introduction

Let $\mathbb {D}=\{z\in \mathbb {C}:|z|<1\}$ denote the unit disc and let $\phi :\mathbb {D}\mapsto \mathbb {D}$ be a non-constant analytic self-map of the unit disc. The composition operator with symbol $\phi$ is defined by $C_{\phi }(f):=f\circ \phi$, for every analytic function $f$ on $\mathbb {D}$. The properties of composition operators acting on several analytic function spaces on $\mathbb {D}$ have been studied extensively. The main interest is the connection between the operator theoretic behaviour of $C_{\phi }$ and the function theoretic behaviour of the symbol $\phi$. We refer the interested reader in the books [Reference Cowen and MacCluer5, Reference Shapiro18] and the references therein for more information on composition operators and function theory. In the present paper, we will study the approximation numbers of composition operators.

Let $X$ and $Y$ be two Banach spaces and let $T:X\mapsto Y$ be a bounded linear operator. The approximation numbers $a_{n}(T)$, $n\in \mathbb {N}$, of $T$ are defined by

\[ a_{n}(T)=\inf_{R}\|T-R\|, \]

where $\|\cdot \|$ denotes the operator norm and the infimum is taken over all linear operators $R:X\mapsto Y$ with ${\rm rank}(R):={\rm dim}(R(X))< n$. For the general theory of approximation numbers, see e.g. [Reference Wojtaszczyk23, Section III.G]. Here we will study composition operators acting on weighted Besov spaces of analytic functions on $\mathbb {D}$.

Let $w:\mathbb {D}\mapsto (0,\,+\infty ]$ be a lower semicontinuous function on $L^{1}(\mathbb {D})$. For $p>1$, the weighted Besov space $B_{w}^{p}$ is the family of analytic functions $f$ in $\mathbb {D}$ satisfying

\[ \|f\|_{B_{w}^{p}}:=|f(0)|+\left(\int_{\mathbb{D}}|f'(z)|^{p}w(z)dA(z)\right)^{1/p}<{+}\infty. \]

For $w(z)=(1-|z|^{2})^{p-2}$, we obtain the standard Besov space $B^{p}=B_{w}^{p}$, which is an important Möbius invariant space of analytic functions whose properties have been investigated extensively; see e.g [Reference Zhu24]. For $p>0$, the Hardy space $H^{p}$ consists of the family of analytic functions $f$ on $\mathbb {D}$ satisfying

\[ \left(\sup_{r\in(0,1)}\frac{1}{2\pi}\int_{0}^{2\pi}|f(re^{i\theta})|^{p}d\theta\right)^{1/p}<{+}\infty. \]

We will also use the norm

\[ \|f\|_{\infty}:=\sup_{z\in\mathbb{D}}|f(z)|, \]

for the space $H^{\infty }$ of bounded analytic functions on $\mathbb {D}$.

Our study was initiated by the work of Li et al. [Reference Li, Queffélec and Rodríguez-Piazza14], where a spectral radius type formula was proved for the approximation numbers of composition operators on analytic Hilbert spaces with radial weights and on $H^{p}$ spaces, $p\geq 1$, involving condenser capacity. There are several (equivalent) ways to define condenser capacity; here we will use the logarithmic energy integrals.

A condenser is a pair $(E,\,F)$ where $E$ and $F$ are non-empty disjoint compact subsets of $\mathbb {C}$. We will denote by $S(E,\,F)$ the family of signed measures $\sigma =\sigma _{E}-\sigma _{F}$, where $\sigma _{E}$ and $\sigma _{F}$ are Borel probability measures supported on $E$ and $F$, respectively. The energy of a measure $\sigma \in S(E,\,F)$ is defined by

\[ I(\sigma):=\iint\log\frac{1}{|z-w|}d\sigma(z)d\sigma(w). \]

Although both the measure and the integrand in the above energy integral are not positive, it is true that $I(\sigma )>0$, for every $\sigma \in S(E,\,F)$; see e.g. [Reference Landkof13, p. 80]. Following Bagby [Reference Bagby2], we define the equilibrium energy of $(E,\,F)$ by

\[ I(E,F):=\inf_{\sigma\in S(E,F)}I(\sigma) \]

and the capacity of $(E,\,F)$ is given by

\[ {\rm{Cap}}(E,F):=\frac{2\pi}{I(E,F)}. \]

We note that, in [Reference Li, Queffélec and Rodríguez-Piazza14], the authors define condenser capacity to be the reciprocal of the equilibrium energy. This will explain the slight deviation by a factor $2\pi$ in our statements from the statements of the results in [Reference Li, Queffélec and Rodríguez-Piazza14]. For other definitions, using Green energy integrals or Dirichlet integrals, and for more information about condenser capacity, we refer to [Reference Bagby2, Reference Dubinin6, Reference Landkof13].

In [Reference Li, Queffélec and Rodríguez-Piazza14], the authors considered the case $p=2$ and studied the Hilbert spaces $B_{w}^{2}$, for weights $w\in L^{1}(\mathbb {D})$ that satisfy the following additional properties:

  1. (P1) $w$ is continuous on $\mathbb {D}$,

  2. (P2) $w$ is radial; that is, $w(z)=w(|z|)$, $z\in \mathbb {D}$.

In particular, the well-known Dirichlet-type spaces corresponding to the weights $w(z)=(1-|z|^{2})^{s}$, $s\in (-1,\,+\infty )$, and containing as special cases the standard Bergman space ($s=2$), Hardy space ($s=1$) and Dirichlet space ($s=0$), are covered in the family $B_{w}^{2}$, for weights $w$ satisfying (P1) and (P2). They proved the following equalities for the approximation numbers of composition operators.

Theorem A Li et al.[Reference Li, Queffélec and Rodríguez-Piazza14]

Let $w\in L^{1}(\mathbb {D})$ be a weight satisfying the properties (P1) and (P2) and let $\phi :\mathbb {D}\mapsto \mathbb {D}$ be a non-constant analytic function in $X,$ where $X$ is either $B_{w}^{2}$ or $H^{p},$ $p\in [1,\,+\infty )$. Then the following hold for the approximation numbers of $C_{\phi }:X\mapsto X$.

  1. (1) If $\|\phi \|_{\infty }<1,$

    (1.1)\begin{equation} \lim_{n\to\infty}(a_{n}(C_{\phi}))^{1/n}=\exp({-}2\pi/{\rm{Cap}}(\partial\mathbb{D},\overline{\phi(\mathbb{D})})), \end{equation}

  2. (2) if $\|\phi \|_{\infty }=1,$

    (1.2)\begin{equation} \lim_{n\to\infty}(a_{n}(C_{\phi}))^{1/n}=1. \end{equation}

Our purpose in this paper is to show that Equations (1.1) and (1.2) hold for a wider class of Banach spaces of analytic functions on $\mathbb {D}$. We note that, for $p\neq 2$, the weighted Besov spaces $B_{w}^{p}$ and in particular the standard Besov spaces $B^{p}$ are not covered in Theorem A. Even in the case $p=2$, there are important weighted Hilbert spaces of analytic functions with weights that do not satisfy the properties (P1) or (P2) mentioned above. For example, the harmonically weighted Dirichlet spaces are obtained by weights of the form

\[ w(z)=\int_{\partial\mathbb{D}}\frac{1-|z|^{2}}{|\zeta-z|^{2}}d\mu(\zeta), \]

where $\mu$ is a finite positive Borel measure on $\partial \mathbb {D}$, which in general does not satisfy (P2). In particular, the weights obtained by unit Dirac measures $\mu =\delta _{\zeta }$, $\zeta \in \partial \mathbb {D}$, which generate the well-known local Dirichlet spaces, are not radial; see e.g. [Reference Costara and Ransford4, Reference Richter15–Reference Sarason17] and the book [Reference El-Fallah, Kellay, Mashreghi and Ransford7, Chapter 7] for more information about harmonically weighted Dirichlet spaces. More generally, for weights $w$ that are positive superharmonic functions on $\mathbb {D}$, neither (P1) nor (P2) are satisfied in general; see e.g. [Reference Aleman1, Reference Bao, Göğüş and Pouliasis3, Reference El-Fallah, Kellay, Klaja, Mashreghi and Ransford8, Reference Shimorin19] for more information about Dirichlet spaces with superharmonic weights. We note that, by definition, superharmonic functions are lower semicontinuous but in general may not be continuous.

In [Reference Li, Queffélec and Rodríguez-Piazza14], the authors are expressing the norm of the weighted analytic Hilbert spaces by an infinite series, using the assumption that the weights considered are radial. Then, they use results of Widom [Reference Widom22] on rational approximation of bounded analytic functions, to approximate the truncated power series expansions of the functions in the Hilbert space, on the image of the symbol of the composition operator. Here we adopt the arguments in the proof of Widom's result to approximate functions in $B_{w}^{p}$, using the rational functions corresponding to the Bagby points (see § 2) of the condenser $(\partial \mathbb {D},\,\overline {\phi (\mathbb {D})})$. These rational functions have simple poles $\{a_{i}\}$ and simple zeros $\{b_{i}\}$, $i=1,\,...,\,n$, which are well separated (see [Reference Götz10, Reference Kloke11]) in the sense that

\[ \min_{i\neq j}|a_{i}-a_{j}|\geq\frac{C}{n^{2}}\qquad\mbox{and}\qquad \min_{i\neq j}|b_{i}-b_{j}|\geq\frac{C}{n^{2}}, \]

where $C>0$ depends on the condenser $(\partial \mathbb {D},\,\overline {\phi (\mathbb {D})})$. We obtain an explicit formula for a finite rank operator to estimate the approximation numbers of $C_{\phi }$.

In the following section, we state several known results from function theory and potential theory that will be used in the proofs of our main results. In particular, the approach to condenser capacity via discrete energies will be described and the rational functions corresponding to the extremal points for the discrete energies will be used in our proof to approximate analytic functions on compact subsets of $\mathbb {D}$. In § 3, we will state and prove the result that the equality (1.1) holds for weighted Besov spaces $B_{w}^{p}$ and the validity of the equality (1.2) will be proved in § 4.

2. Background material

In this section, we collect some results from function theory and potential theory.

2.1. Equilibrium measure and potential

The logarithmic potential of a positive Borel measure $\mu$ with compact support in $\mathbb {C}$ is the function

\[ U_{\mu}(z):=\int\log\frac{1}{|z-w|}d\mu(w),\quad z\in\mathbb{C}. \]

We note that the potential $U_{\mu }$ is a harmonic function outside the support of $\mu$. The logarithmic capacity of a compact set $K\subset \mathbb {C}$ is defined by

\[ c(K)=\exp\left(-\inf_{\mu}\iint\log\frac{1}{|z-w|}d\mu(z)d\mu(w)\right), \]

where the above infimum is taken over all Borel probability measures $\mu$ supported on $K$.

Let $(E,\,F)$ be a condenser and let $\sigma =\sigma _{E}-\sigma _{F}\in S(E,\,F)$. The potential of $\sigma$ is defined by

\[ U_{\sigma}(z):=\int\log\frac{1}{|z-w|}d\sigma(w)=U_{\sigma_{E}}(z)-U_{\sigma_{F}}(z),\qquad z\in\mathbb{C}. \]

Since $U_{\sigma _{E}}$ is harmonic on $\mathbb {C}\setminus E$ and $U_{\sigma _{F}}$ is harmonic on $\mathbb {C}\setminus F$, the potential $U_{\sigma }$ is well defined for every $z\in \mathbb {C}$, although it may take the values $\pm \infty$.

Let $(E,\,F)$ be a condenser with finite equilibrium energy. Then, there exists a unique measure $\tau \in S(E,\,F)$ such that $I(E,\,F)=I(\tau )$ and $\tau$ is called the equilibrium measure of $(E,\,F)$. Also, according to the fundamental theorem of potential theory for condensers, there exist real numbers $V_{E}\geq 0$, $V_{F}\leq 0$ and Borel sets $Z_{E}\subset \partial E$, $Z_{F}\subset \partial F$ (possibly empty) having zero logarithmic capacity, such that the following equalities hold for the equilibrium energy and the equilibrium potential $U_{\tau }$:

(2.1)\begin{align} V_{F}& \leq U_{\tau}(z)\leq V_{E},\text{ for every }z\in\mathbb{C}, \end{align}
(2.2)\begin{align} U_{\tau}(z)& =V_{E},\text{ for every }z\in E\setminus Z_{E}, \end{align}
(2.3)\begin{align} U_{\tau}(z)& =V_{F},\text{ for every }z\in F\setminus Z_{F}, \end{align}
(2.4)\begin{align} I(E,F)& =V_{E}-V_{F}. \end{align}

When the open set $\mathbb {C}\setminus (E\cup F)$ is regular for the Dirichlet problem, the equilibrium potential is continuous on $\mathbb {C}$ and $Z_{E}=Z_{F}=\emptyset$. In particular, when the compact sets $E$ and $F$ are connected, the equilibrium potential satisfies a Hölder continuity property described in the following theorem proved by J. Siciak [Reference Siciak20, pp. 205, 210].

Theorem B Siciak [Reference Siciak20]

Let $(E,\,F)$ be a condenser, where $E$ and $F$ are non-degenerate continua. Let $\tau$ be the equilibrium measure of $(E,\,F)$. Then, there exist constants $C_{1}=C_{1}(E,\,F)>0$ and $\alpha =\alpha (E,\,F)\in (0,\,1),$ such that

(2.5)\begin{equation} |U_{\tau}(z)-V_{E}|\leq C_{1}{\rm{dist}}(z,E)^{\alpha} \end{equation}

and

(2.6)\begin{equation} |U_{\tau}(z)-V_{F}|\leq C_{1}{\rm{dist}}(z,F)^{\alpha}, \end{equation}

for every $z\in \mathbb {C}$.

2.2. Discrete energies

Let $(E,\,F)$ be a condenser and suppose that both sets $E$ and $F$ contain infinitely many points. For any integer $n\geq 2$, let

\[ L_{n}(E,F):=\{(\alpha_{1},\ldots,\alpha_{n},\beta_{1},\ldots,\beta_{n})\in E^{n}\times F^{n}: \alpha_{i}\neq \alpha_{j}\text{ and }\beta_{i}\neq \beta_{j}, i\neq j\}. \]

The $n$-th discrete energy of $(E,\,F)$ is defined by

\[ W_{n}(E,F)=\frac{1}{n(n-1)}\inf\left\{\sum_{1\leq i< j\leq n}\log\bigg(\frac{|\alpha_{i}-\beta_{j}||\alpha_{j}-\beta_{i}|}{|\alpha_{i}-\alpha_{j}||\beta_{i}-\beta_{j}|}\bigg)\right\}, \]

where the infimum is taken over all point configurations $(\alpha _{1},\,\ldots,\,\alpha _{n},\,\beta _{1},\,\ldots,\,\beta _{n})\in L_{n}(E,\,F)$. Each configuration $(a_{1},\,\ldots,\,a_{n},\,b_{1},\,\ldots,\,b_{n})\in L_{n}(E,\,F)$ for which the above infimum is attained will be called an extremal configuration for $(E,\,F)$ and the points $a_{1},\,\ldots,\,a_{n}$, $b_{1},\,\ldots,\,b_{n}$ are called $n$-th Bagby points. From the compactness of $E$ and $F$ it follows that, for every integer $n\geq 2$, there exists an extremal configuration in $L_{n}(E,\,F)$.

Although every discrete signed measure in $S(E,\,F)$ has infinite energy, the above sum may be considered as a discrete version of the energy of a discrete measure having point masses at the points $a_{i}$ and $b_{i}$, $i=1,\,\ldots,\,n$. Bagby [Reference Bagby2] proved the following theorem relating the equilibrium energy with the discrete energies $W_{n}(E,\,F)$ of a condenser.

Theorem C Bagby [Reference Bagby2]

Let $(E,\,F)$ be a condenser and suppose that both sets $E$ and $F$ contain infinitely many points. Then the sequence $(W_{n}(E,\,F))$ is increasing and

\[ I(E,F)=\lim_{n\to\infty}W_{n}(E,F). \]

Moreover, assuming that $(a_{1},\,\ldots,\,a_{n},\,b_{1},\,\ldots,\,b_{n})\in L_{n}(E,\,F)$ is an extremal configuration and letting

\[ \sigma_{n}=\frac{1}{n}\bigg(\sum_{i=1}^{n}\delta_{a_{i}}-\sum_{i=1}^{n}\delta_{b_{i}}\bigg)\in S(E,F), \]

it is true (see [Reference Bagby2]) that the sequence of the measures $\sigma _{n}$ converges in the weak-star sense to the equilibrium measure of $(E,\,F)$ and the potentials $U_{\sigma _{n}}$ converge locally uniformly to the equilibrium potential of $(E,\,F)$ in $\mathbb {C}\setminus (E\cup F)$. We will need the following result concerning the rate of convergence of the potentials $U_{\sigma _{n}}$ proved by Kloke [Reference Kloke12, Theorem 2.7, p. 194] (see also [Reference Götz10] for condensers in higher-dimensional Euclidean spaces).

Theorem D Kloke [Reference Kloke12]

Let $(E,\,F)$ be a condenser such that both $E$ and $F$ are unions of a finite number of mutually disjoint and non-degenerate continua. Let $\tau$ be the equilibrium measure of $(E,\,F)$. Also, for every integer $n\geq 2,$ let

\[ (a_{1},\ldots,a_{n},b_{1},\ldots,b_{n})\in L_{n}(E,F) \]

be an extremal configuration for $(E,\,F)$ and let

\[ \sigma_{n}=\frac{1}{n}\bigg(\sum_{i=1}^{n}\delta_{a_{i}}-\sum_{i=1}^{n}\delta_{b_{i}}\bigg)\in S(E,F). \]

Then, there exists a constant $C_{2}=C_{2}(E,\,F)>1$ such that

\[ |U_{\tau}(z)-U_{\sigma_{n}}(z)|\leq\frac{32\log(C_{2}n)}{n}, \]

for every

\[ z\in\left\{w\in\mathbb{C}:{\rm{dist}}(w,\partial E)\geq\frac{1}{n^{2}}\text{ and } {\rm{dist}}(w,\partial F)\geq\frac{1}{n^{2}}\right\}. \]

2.3. Diameters in the space of continuous functions

Let $K$ be a compact subset of $\mathbb {D}$ and let $C(K)$ be the Banach space of continuous functions on $K$, equipped with the norm

\[ \|f\|_{K}=\sup_{z\in K}|f(z)|,\qquad f\in C(K). \]

Let

\[ B:=\{f\in H^{\infty}:\|f\|_{\infty}\leq 1\} \]

be the unit ball in $H^{\infty }$. Taking restrictions on $K$, we may consider $B$ as a subset of $C(K)$. For every $n\in \mathbb {N}$, let $X_{n}$ denote the family of $n$-dimensional linear subspaces of $C(K)$. The $n$-dimensional diameter of $B$ in $C(K)$ is defined by

\[ d_{n}(B,C(K)):=\inf_{E\in X_{n}} \Big[\sup_{f\in B} \Big(\inf_{g\in E}\|f-g\|_{K}\Big) \Big]. \]

We will need the following result about the $n$-dimensional diameter of $B$ in $C(K)$; see [Reference Widom22, Theorem 7, p. 353] or [Reference Fisher9, p. 249].

Theorem E Widom [Reference Widom22]

Let $K$ be a compact subset of $\mathbb {D}$. There exists a constant $C_{3}:=C_{3}(K)>0$ such that

\[ d_{n}(B,C(K))\geq C_{3}\exp\left({-}2\pi n/{\rm{Cap}}(\partial\mathbb{D},K)\right), \quad n\in\mathbb{N}. \]

3. Symbols with compact image in the unit disc

In this section, we will prove that the asymptotic formula (1.1) holds for composition operators on weighted Besov spaces. Before stating and proving our first main result, we will prove some helpful lemmas. The first one is standard, it concerns the norms of the evaluation functionals and it follows from the subharmonicity property of the modulus of an analytic function. We include its proof for the convenience of the reader. We will denote by $D(z,\,r)$ the open disc centred at $z\in \mathbb {C}$ with radius $r>0$.

Lemma 3.1 Let $w:\mathbb {D}\mapsto (0,\,+\infty ]$ be a lower semicontinuous function on $L^{1}(\mathbb {D})$ and let $p>1$. For every $a\in \mathbb {D},$ the linear functionals $L_{a}(f)=f(a)$ and $T_{a}(f)=f'(a)$ are bounded on $B_{w}^{p}$. Also, for every compact subset $K$ of $\mathbb {D},$

\[ \sup_{a\in K}\|L_{a}\|<{+}\infty\text{ and } \sup_{a\in K}\|T_{a}\|<{+}\infty. \]

Proof. Let $K$ be a compact subset of $\mathbb {D}$ and let $d={{\rm dist}}(K,\,\partial \mathbb {D})/2$. Since $w$ is lower semicontinuous on $\mathbb {D},$ it attains its lower bound on any compact subset of $\mathbb {D}$. In particular,

\[ M:=\min\left\{w(z):z\in\overline{D(0,1-d)}\right\}>0. \]

Let $f\in B_{w}^{p}$ and $a\in K$. From the subharmonicity of $|f'|^{p}$,

\begin{align*} |T_{a}(f)|^{p}=|f'(a)|^{p}& \leq\displaystyle\frac{1}{\pi d^{2}}\displaystyle\int_{D(a,d)} |f'(z)|^{p}dA(z)\\ & \leq \frac{1}{\pi d^{2}M}\int_{D(a,d)} |f'(z)|^{p}w(z)dA(z)\\ & \leq \frac{1}{\pi d^{2}M}\int_{\mathbb{D}} |f'(z)|^{p}w(z)dA(z)\end{align*}

and

\[ |T_{a}(f)|\leq\left(\frac{1}{\pi d^{2}M}\right)^{1/p} \left(\int_{\mathbb{D}} |f'(z)|^{p}w(z)dA(z)\right)^{1/p}\leq \left(\frac{1}{\pi d^{2}M}\right)^{1/p}\|f\|_{B_{w}^{p}}. \]

Since $a\in K\subset \mathbb {D}$ were arbitrary, we conclude that $T_{a}$ is bounded on $B_{w}^{p}$ for every $a\in \mathbb {D}$ and

(3.1)\begin{equation} \sup_{a\in K}\|T_{a}\|\leq \left(\displaystyle\frac{1}{\pi d^{2}M}\right)^{1/p}<{+}\infty. \end{equation}

The corresponding results for $L_{a}$ follow from (3.1) and the inequality

\begin{align*} |L_{a}(f)|=|f(a)|& =\left|f(0)+\displaystyle\int_{0}^{a}f'(z)dz\right|\\ & \leq |f(0)|+|a|\Big(\sup_{b\in[0,a]}\|T_{b}\|\Big)\|f\|_{B_{w}^{p}}\\ & \leq \Big(1+\sup_{b\in[0,a]}\|T_{b}\|\Big)\|f\|_{B_{w}^{p}}. \end{align*}

In the following lemma, we will describe the symbols $\phi$, with $\|\phi \|_{\infty }<1$, for which $C_{\phi }:B_{w}^{p}\mapsto B_{w}^{p}$ is bounded.

Lemma 3.2 Let $w:\mathbb {D}\mapsto (0,\,+\infty ]$ be a lower semicontinuous function on $L^{1}(\mathbb {D}),$ let $p>1$ and let $\phi \in H^{\infty }$ satisfying $\|\phi \|_{\infty }<1$. Then $C_{\phi }:B_{w}^{p}\mapsto B_{w}^{p}$ is bounded if and only if $\phi \in B_{w}^{p}$.

Proof. Suppose that $\phi \in B_{w}^{p}$. Then, since $\overline {\phi (\mathbb {D})}$ is a compact subset of $\mathbb {D}$, we have

\begin{align*} \displaystyle\int_{\mathbb{D}}|C_{\phi}(f)'(z)|^{p}w(z)dA(z)& =\int_{\mathbb{D}}|f'(\phi(z))|^{p}|\phi'(z)|^{p}w(z)dA(z)\\ & \leq \left(\sup_{z\in\overline{\phi(\mathbb{D})}}|f'(z)|^{p}\right) \|\phi\|_{B_{w}^{p}}^{p}<{+}\infty, \end{align*}

and $C_{\phi }(f)\in B_{w}^{p}$, for every $f\in B_{w}^{p}$. By Lemma 3.1, we get that convergence in $B_{w}^{p}$ implies uniform convergence on compact subsets of $\mathbb {D}$. From the closed graph theorem, it follows that $C_{\phi }:B_{w}^{p}\mapsto B_{w}^{p}$ is bounded.

Conversely, we have $\phi =C_{\phi }(I)\in B_{w}^{p}$, where $I\in B_{w}^{p}$ is the identity function.

The main step in the proof of the first main result will be the approximation of functions in $B_{w}^{p}$ by rational functions on the closure of the image of the symbol of the composition operator. The success of this approach on getting a lower bound for the approximation numbers is based on the following result.

Let $X$ and $Y$ be two Banach spaces and let $T:X\mapsto Y$ be a bounded linear operator. For every integer $n\geq 1$, we define

\[ \tilde{a}_{n}(T):=\inf\left\{\|T-R\|:R:X\mapsto Y \text{ is linear, }{\rm{rank}}(R)< n \text{ and }R(X)\subset T(X)\right\}. \]

Clearly, $a_{n}(T)\leq \tilde {a}_{n}(T)$. In the other direction, we have the following result.

Proposition 3.3 Let $X$ and $Y$ be two Banach spaces and let $T:X\mapsto Y$ be a bounded linear operator. For every integer $n\geq 1,$ $\tilde {a}_{n}(T)\leq n a_{n}(T)$.

Proof. Let $\epsilon >0$. Let $R:X\mapsto Y$ be a linear operator satisfying ${{\rm rank}}(R)< n$ and $\|T-R\|< a_{n}(T)+\epsilon$. Set $m:={{\rm rank}}(R)$. Then $X/{{\rm ker}}(R)$ is an $m$-dimensional normed space. By Auerbach's lemma (see e.g. [Reference Wojtaszczyk23, II.E.11, p. 75]), there exist $\xi _{1},\,\ldots,\,\xi _{m}\in (X/{{\rm ker}}(R))$ and $\psi _{1},\,\ldots,\,\psi _{m}\in (X/{{\rm ker}}(R))^{*}$ such that, for all $j,\,k=1,\,\ldots,\,m$,

\[ \|\xi_{j}\|=1,\quad\|\psi_{k}\|=1\text{ and } \psi_{k}(\xi_{j})=\delta_{jk}, \]

where

\[ \delta_{jk}=\begin{cases} 0, & \mbox{if } j\neq k, \\ 1, & \mbox{if } j=k. \end{cases} \]

Writing $\pi :X\mapsto X/{{\rm ker}}(R)$ for the quotient map, for each $j$, we may pick $x_{j}\in X$ such that $\pi (x_{j})=\xi _{j}$ and $\|x_{j}\|<1+\epsilon$. Also, for each $k$, define $\varphi _{k}\in X^{*}$ by $\varphi _{k}:=\psi _{k}\circ \pi$. Clearly we have $\|\varphi _{k}\|\leq 1$ for each $k$ and $\varphi _{k}(x_{j})=\delta _{jk}$, for all $j,\,k$. Thus

(3.2)\begin{equation} R=\displaystyle\sum_{k=1}^{m}Rx_{k}\otimes\varphi_{k}, \end{equation}

because every vector in $X$ can be written as a linear combination of $x_{1},\,\ldots,\,x_{m}$ and a vector in ${{\rm ker}}(R)$, and the two sides of (3.2) agree on all such vectors. Define

\[ \tilde{R}:=\sum_{k=1}^{m}Tx_{k}\otimes\varphi_{k}. \]

Clearly $\tilde {R}:X\mapsto Y$ is linear with ${{\rm rank}}(\tilde {R})\leq m$ and $\tilde {R}(X)\subset T(X)$. Hence

\begin{align*} \tilde{a}_{n}(T) & \leq \|T-\tilde{R}\| \\ & \leq \|T-R\|+\|R-\tilde{R}\|\\ & = \|T-R\|+\left\|\displaystyle\sum_{k=1}^{m}(Rx_{k}-Tx_{k})\otimes\varphi_{k}\right\|\\ & \leq \|T-R\|+\sum_{k=1}^{m}\|R-T\|\|x_{k}\|\|\varphi_{k}\|\\ & \leq \|T-R\|(1+m(1+\epsilon))\\ & \leq (a_{n}(T)+\epsilon)n(1+\epsilon). \end{align*}

Letting $\epsilon \to 0$ we obtain the result.

We now proceed to state and prove our first main result.

Theorem 3.4 Let $w:\mathbb {D}\mapsto (0,\,+\infty ]$ be a lower semicontinuous function on $L^{1}(\mathbb {D}),$ let $p>1$ and let $\phi \in B_{w}^{p}$ satisfying $\|\phi \|_{\infty }<1$. Then the formula

(3.3)\begin{equation} \lim_{n\to\infty}(a_{n}(C_{\phi}))^{1/n}=\exp({-}2\pi/{\rm{Cap}}(\partial\mathbb{D},\overline{\phi(\mathbb{D})})) \end{equation}

holds, for the approximation numbers of $C_{\phi }:B_{w}^{p}\mapsto B_{w}^{p}$.

Proof. Let $\partial \mathbb {D}:=\mathbb {T}$, $K:=\overline {\phi (\mathbb {D})}$ and note that both $\mathbb {T}$ and $K$ are non-degenerate continua. Therefore, the condenser $(\mathbb {T},\,K)$ has a positive capacity. Let $\tau$ be the equilibrium measure of $(\mathbb {T},\,K)$. For every integer $n\geq 2$, let $(a_{1},\,\ldots,\,a_{n},\,b_{1},\,\ldots,\,b_{n})\in L_{n}(\mathbb {T},\,K)$ be an extremal configuration and let

\[ \sigma_{n}=\frac{1}{n}\bigg(\sum_{i=1}^{n}\delta_{a_{i}}-\sum_{i=1}^{n}\delta_{b_{i}}\bigg)\in S(\mathbb{T},K). \]

The potential of $\sigma _{n}$ is

\begin{align*} U_{\sigma_{n}}(z)& =\displaystyle\frac{1}{n}(\displaystyle\sum_{i=1}^{n}\log\frac{1}{|z-a_{i}|} -\sum_{i=1}^{n}\log\frac{1}{|z-b_{i}|})\\ & = \displaystyle\frac{1}{n}\log\left|\frac{(z-b_{1})\cdots (z-b_{n})}{(z-a_{1})\cdots (z-a_{n})}\right|. \end{align*}

Consider the rational function

\[ R_{n}(z)=\frac{(z-b_{1})\cdots (z-b_{n})}{(z-a_{1})\cdots (z-a_{n})} \]

and note that $R_{n}$ is analytic on $\mathbb {D}$ and $U_{\sigma _{n}}(z)=\frac {1}{n}\log |R_{n}(z)|$. First, we will use the rational functions $R_{n}$ to obtain finite rank linear operators that will approximate $C_{\phi }$ in order to prove that

(3.4)\begin{equation} \limsup_{n\to\infty}(a_{n}(C_{\phi}))^{1/n}\leq\exp({-}2\pi/{{\rm Cap}}(\mathbb{T},K)). \end{equation}

We start by establishing upper and lower bounds for $|R_{n}|$.

Fix $\epsilon \in (0,\,{{\rm dist}}(\mathbb {T},\,K)/2)$ and $n\in \mathbb {N}$ satisfying $1/n^{2}<{{\rm dist}}(\mathbb {T},\,K)/2$. Let $\gamma _{\epsilon }:=\partial D(0,\,1-\epsilon )$ (positively oriented circle) and $A_{n}:=\{z\in \mathbb {D}:{{\rm dist}}(z,\,K)=1/n^{2}\}$. From Theorem B and Theorem D, it follows that

(3.5)\begin{equation} U_{\sigma_{n}}(z)\leq U_{\tau}(z)+\displaystyle\frac{32\log(C_{2}n)}{n}\leq V_{K}+\frac{C_{1}}{n^{2\alpha}}+\frac{32\log(C_{2}n)}{n}, \end{equation}

for every $z\in A_{n}$ and

(3.6)\begin{equation} U_{\sigma_{n}}(z)\geq U_{\tau}(z)-\displaystyle\frac{32\log(C_{2}n)}{n}\geq V_{\mathbb{T}}-C_{1}\epsilon^{\alpha}-\frac{32\log(C_{2}n)}{n}, \end{equation}

for every $z\in \gamma _{\epsilon }$, where the constants $C_{1}>0$, $C_{2}>1$ and $\alpha \in (0,\,1)$ depend only on the condenser $(\mathbb {T},\,K)$. From (3.5) and (3.6), we obtain the inequalities

(3.7)\begin{equation} |R_{n}(z)|\leq\exp( nV_{K}+C_{1}n^{1-2\alpha}+32\log(C_{2}n)), \end{equation}

for every $z\in A_{n}$ and

(3.8)\begin{equation} |R_{n}(z)|\geq\exp( nV_{\mathbb{T}}-nC_{1}\epsilon^{\alpha}-32\log(C_{2}n)), \end{equation}

for every $z\in \gamma _{\epsilon }$. Also, from the maximum principle, it follows that the inequality (3.7) holds for every $z$ in the component of $\mathbb {C}\setminus A_{n}$ containing $K$.

For $f\in B_{w}^{p}$, let

\[ F_{n}(z,f):=\frac{R_{n}(z)}{2\pi i}\int_{\gamma_{\epsilon}}\frac{f'(\zeta)}{R_{n}(\zeta)(\zeta-z)}d\zeta,\qquad z\in K. \]

From the residue theorem, we get that

(3.9)\begin{equation} F_{n}(z,f)=f'(z)-H_{n}(z,f), \end{equation}

where

\[ H_{n}(z,f):=R_{n}(z)\sum_{i=1}^{n}\frac{f'(b_{i})}{R_{n}'(b_{i})(b_{i}-z)}\cdot \]

Let

\[ I_{n}(z,f):=f(\phi(0))+\sum_{i=1}^{n}f'(b_{i})\int_{0}^{z}\frac{R_{n}(\zeta)}{R_{n}'(b_{i})(b_{i}-\zeta)}d\zeta \]

be a primitive of $H_{n}(\cdot,\,f)$ on $\mathbb {D}$. We note that

\begin{align*} \displaystyle\int_{\mathbb{D}}|(I_{n}(\phi(z),f))'(z)|^{p}w(z)dA(z)& = \int_{\mathbb{D}}|I_{n}'(\phi(z),f)|^{p}|\phi'(z)|^{p}w(z)dA(z)\\ & \leq \left(\sup_{z\in K}|I_{n}'(z,f)|^{p}\right) \|\phi\|_{B_{w}^{p}}^{p}<{+}\infty \end{align*}

and $I_{n}(\cdot,\,f)\circ \phi \in B_{w}^{p}$, for every $f\in B_{w}^{p}$. We consider the operator $J_{n}:B_{w}^{p}\mapsto B_{w}^{p}$, defined by $J_{n}(f):=I_{n}(\cdot,\,f)\circ \phi$. Then $J_{n}$ is a bounded linear operator and $J_{n}(B_{w}^{p})$ is contained in the linear span of the functions

\[ z\mapsto\int_{0}^{\phi(z)}\frac{R_{n}(\zeta)}{R_{n}'(b_{i})(b_{i}-\zeta)}d\zeta\in B_{w}^{p},\quad i=1,\ldots,n. \]

We obtain that ${\rm rank}(J_{n})\leq n$. Therefore, for every $f\in B_{w}^{p}$,

(3.10)\begin{align} a_{n+1}(C_{\phi})& \leq\|C_{\phi}-J_{n}\| \nonumber\\ & =\sup_{\|f\|_{B_{w}^{p}}=1} \left(\displaystyle\int_{\mathbb{D}}|(C_{\phi}(f)-J_{n}(f))'(z)|^{p}w(z)dA(z)\right)^{1/p} \nonumber\\ & =\sup_{\|f\|_{B_{w}^{p}}=1} \left(\int_{\mathbb{D}}|f'(\phi(z))-H_{n}(\phi(z),f)|^{p}|\phi'(z)|^{p}w(z)dA(z)\right)^{1/p} \nonumber\\ & =\sup_{\|f\|_{B_{w}^{p}}=1} \left(\int_{\mathbb{D}}|F_{n}(\phi(z),f)|^{p}|\phi'(z)|^{p}w(z)dA(z)\right)^{1/p}, \end{align}

where in (3.10) the equality (3.9) has been used. From the inequalities (3.7) and (3.8), we get that, for every $z\in K$,

(3.11)\begin{align} |F_{n}(z,f)| & \leq \displaystyle\frac{|R_{n}(z)|}{2\pi}\displaystyle\int_{\gamma_{\epsilon}}\frac{|f'(\zeta)|}{|R_{n}(\zeta)||\zeta-z|}|d\zeta| \nonumber\\ & \leq \displaystyle\frac{\exp( n(V_{K}-V_{\mathbb{T}})+C_{1}n^{1-2\alpha}+nC_{1}\epsilon^{\alpha}+64\log(C_{2}n))}{({{\rm dist}}(\mathbb{T},K)/2)}\cdot \\ & \quad\cdot(1-\epsilon)\sup_{\zeta\in\gamma_{\epsilon}}|f'(\zeta)|. \nonumber \end{align}

We note that (3.11) holds for every analytic function $f$ on $\mathbb {D}$. From (2.4), (3.10) and (3.11), it follows that

(3.12)\begin{align} & a_{n+1}(C_{\phi}) \nonumber\\ & \leq\displaystyle\frac{\exp({-}nI(\mathbb{T},K)+C_{1}n^{1-2\alpha}+nC_{1}\epsilon^{\alpha}+64\log(C_{2}n))}{({{\rm dist}}(\mathbb{T},K)/2)}\cdot \\ & \cdot\left(\displaystyle\int_{\mathbb{D}}|\phi'(z)|^{p}w(z)dA(z)\right)^{1/p}(1-\epsilon)\sup_{\zeta\in\gamma_{\epsilon}}|f'(\zeta)|. \nonumber \end{align}

Raising (3.12) to the power $1/(n+1)$ and letting $n\to +\infty$ we get

\[ \limsup_{n\to+\infty}(a_{n}(C_{\phi}))^{1/n}\leq\exp\left({-}I(\mathbb{T},K)+C_{1}\epsilon^{\alpha}\right). \]

Letting $\epsilon \to 0$, we obtain (3.4).

Next, we will use Proposition 3.3 to get a lower bound for the approximation numbers of $C_{\phi }$. Let $\epsilon >0$, let $n\in \mathbb {N}$ and let $P_{m}:B_{w}^{p}\mapsto B_{w}^{p}$ be a linear operator with ${{\rm rank}}(P_{m})=m< n$, satisfying $P_{m}(B_{w}^{p})\subset C_{\phi }(B_{w}^{p})$. Let $E:=\{h':\mathbb {D}\mapsto \mathbb {C}: h\circ \phi \in P_{m}(B_{w}^{p})\}$ and note that, taking restriction on the set $K$, $E$ is a linear subspace of $C(K)$ with ${{\rm dim}}(E)=m$. Therefore,

(3.13)\begin{equation} d_{m}(B,C(K))\leq\sup_{f\in B}(\inf_{g\in E}\|f-g\|_{K}), \end{equation}

where $B$ is the unit ball in $H^{\infty }$. Let $f_{0}\in B$ such that

(3.14)\begin{equation} \sup_{f\in B}(\inf_{g\in E}\|f-g\|_{K})\leq (1+\epsilon)\inf_{g\in E}\|f_{0}-g\|_{K}. \end{equation}

From Theorem E, there exists $C_{3}>0$ such that

(3.15)\begin{equation} C_{3}\exp({-}n I(\mathbb{T},K))\leq C_{3}\exp({-}m I(\mathbb{T},K))\leq d_{m}(B,C(K)). \end{equation}

From (3.13), (3.14) and (3.15), we obtain that

(3.16)\begin{equation} C_{3}\exp({-}n I(\mathbb{T},K))\leq (1+\epsilon)\inf_{g\in E}\|f_{0}-g\|_{K}. \end{equation}

We will now estimate $\|C_{\phi }-P_{m}\|$. Let $I_{0}$ be a primitive of $f_{0}$ on $\mathbb {D}$, satisfying $I_{0}(\phi (0))=0$. We have

\[ \|I_{0}\|_{B_{w}^{p}}=\left(\int_{\mathbb{D}}|f_{0}(z)|^{p}w(z)dA(z)\right)^{1/p} \leq \left(\int_{\mathbb{D}}w(z\bigg)dA(z)\right)^{1/p}:=C_{w}. \]

Therefore, $I_{0}/C_{w}$ lies in the unit sphere of $B_{w}^{p}$. Let $P_{m}(I_{0}/C_{w})=h_{0}\circ \phi$ and note that $C_{w}h_{0}'\in E$. From (3.16) we obtain that

(3.17)\begin{align} \|C_{\phi}-P_{m}\|& \geq \|C_{\phi}(I_{0}/C_{w})-P_{m}(I_{0}/C_{w})\|_{B_{w}^{p}} \nonumber\\ & =\displaystyle\frac{1}{C_{w}} \left(\displaystyle\int_{\mathbb{D}}|f_{0}(\phi(z))-C_{w}h_{0}'(\phi(z))|^{p}|\phi'(z)|^{p}w(z)dA(z)\right)^{1/p} \nonumber\\ & \geq \frac{1}{C_{w}}\inf_{g\in E}\|f_{0}-g\|_{K} \|\phi\|_{B_{w}^{p}} \nonumber\\ & \geq \frac{C_{3}\|\phi\|_{B_{w}^{p}}}{C_{w}(1+\epsilon)}\exp({-}n I(\mathbb{T},K)). \end{align}

Taking infimum over all linear operators $P_{m}:B_{w}^{p}\mapsto B_{w}^{p}$ with ${{\rm rank}}(P_{m})=m< n$ and $P_{m}(B_{w}^{p})\subset C_{\phi }(B_{w}^{p})$, we obtain that

(3.18)\begin{equation} \tilde{a}_{n}(C_{\phi})\geq \displaystyle\frac{C_{3}\|\phi\|_{B_{w}^{p}}}{C_{w}(1+\epsilon)}\exp({-}n I(\mathbb{T},K)). \end{equation}

From Proposition 3.3 and (3.18), it follows that

(3.19)\begin{equation} a_{n}(C_{\phi})\geq \displaystyle\frac{C_{3}\|\phi\|_{B_{w}^{p}}}{C_{w}(1+\epsilon)n}\exp({-}n I(\mathbb{T},K)). \end{equation}

Raising (3.19) to the power $1/n$ and letting $n\to +\infty$, we get

(3.20)\begin{equation} \liminf_{n\to+\infty}(a_{n}(C_{\phi}))^{1/n}\geq\exp({-}I(\mathbb{T},K)). \end{equation}

Finally, the equality (3.3) follows from (3.4) and (3.20). The proof is complete.

4. Symbols with non-compact image in the unit disc

In this section, we will prove that the asymptotic formula (1.2) holds for composition operators on weighted Besov spaces. We will see that formula (1.2) follows from Theorem 3.4 and the following well-known properties.

The first is a property of approximation numbers (see e.g. [Reference Wojtaszczyk23, III.G.2, p. 237]).

Theorem F Wojtaszczyk [Reference Wojtaszczyk23]

Let $X$ be a Banach space and let $T,\,S:X\mapsto X$ be two bounded linear operators. For all integers $n,\,m\geq 1,$

\[ a_{n+m-1}(T\circ S)\leq a_{n}(T)a_{m}(S). \]

The second property is a lower bound for the capacity of a condenser involving the diameters of its plates and the distance between them; see e.g. [Reference Vuorinen21, Lemma 7.38, p. 95].

Theorem G Vuorinen [Reference Vuorinen21]

There exists a constant $C_{4}>0$ such that, for every condenser $(E,\,F),$ where both $E$ and $F$ are non-degenerate continua, we have

\[ {\rm{Cap}}(E,F)\geq C_{4}\log\left(1+\frac{\min\{{\rm{diam}}(E),{\rm{diam}}(F)\}}{{\rm{dist}}(E,F)}\right). \]

We will now state and prove our second main result.

Theorem 4.1 Let $w:\mathbb {D}\mapsto (0,\,+\infty ]$ be a lower semicontinuous function on $L^{1}(\mathbb {D}),$ let $p>1$ and let $\phi \in B_{w}^{p}$ satisfying $\|\phi \|_{\infty }=1$. Then the formula

(4.1)\begin{equation} \lim_{n\to\infty}(a_{n}(C_{\phi}))^{1/n}=1 \end{equation}

holds, for the approximation numbers of $C_{\phi }:B_{w}^{p}\mapsto B_{w}^{p}$.

Proof. Let $r\in (0,\,1)$ and consider the bounded linear operator $L_{r}:B_{w}^{p}\mapsto B_{w}^{p}$, defined by $L_{r}f(z)=f(rz)$, $f\in B_{w}^{p}$. Also, note that $C_{\phi }\circ L_{r}=C_{r\phi }$, $\|r\phi \|_{\infty }=r$ and $\overline {r\phi (\mathbb {D})}=\overline {\{rz:z\in \phi (\mathbb {D})\}}$ is a compact subset of $\mathbb {D}$. From Theorem F, it follows that

\[ a_{n}(C_{r\phi})=a_{n}(C_{\phi}\circ L_{r})=a_{n+1-1}(C_{\phi}\circ L_{r})\leq a_{n}(C_{\phi}) a_{1}(L_{r})=a_{n}(C_{\phi})\|L_{r}\|, \]

for every $n\in \mathbb {N}$. Therefore,

\[ \displaystyle\frac{a_{n}(C_{r\phi})^{1/n}}{\|L_{r}\|^{1/n}}\leq a_{n}(C_{\phi})^{1/n},\quad n\in\mathbb{N}. \]

Letting $n\to +\infty$, from Theorem 3.4, we obtain that

(4.2)\begin{equation} \exp({-}2\pi/{{\rm Cap}}(\partial\mathbb{D},\overline{r\phi(\mathbb{D})}))\leq\liminf_{n\to +\infty} (a_{n}(C_{\phi}))^{1/n}. \end{equation}

From Theorem G, it follows that

(4.3)\begin{align} {{\rm Cap}}(\partial\mathbb{D},\overline{r\phi(\mathbb{D})})& \geq C_{4}\log(1+\displaystyle\frac{\min\{{{\rm diam}}(\partial\mathbb{D}),{{\rm diam}}(\overline{r\phi(\mathbb{D})})\}}{{{\rm dist}}(\partial\mathbb{D},\overline{r\phi(\mathbb{D})})}) \nonumber\\ & = C_{4}\log(1+\displaystyle\frac{{{\rm diam}}(\overline{r\phi(\mathbb{D})})}{1-r}). \end{align}

Letting $r\to 1$, from (4.2) and (4.3), we get

(4.4)\begin{equation} 1\leq \liminf_{n\to +\infty}(a_{n}(C_{\phi}))^{1/n}. \end{equation}

On the other hand,

(4.5)\begin{equation} \limsup_{n\to +\infty}(a_{n}(C_{\phi}))^{1/n} \leq \limsup_{n\to +\infty}(a_{1}(C_{\phi}))^{1/n}=1. \end{equation}

The conclusion follows from (4.4) and (4.5).

Acknowledgements

The author would like to thank Professor Thomas Ransford for providing and allowing him to use the proof of Proposition 3.3.

References

Aleman, A., The multiplication operator on Hilbert spaces of analytic functions, (Habilitation, FernUniversität Hagen, 1993).Google Scholar
Bagby, T., The modulus of a plane condenser, J. Math. Mech. 17 (1967), 315–329.Google Scholar
Bao, G., Göğüş, N. G. and Pouliasis, S., On Dirichlet spaces with a class of superharmonic weights, Canad. J. Math. 70 (2018), 721–741.CrossRefGoogle Scholar
Costara, C. and Ransford, T., Which de Branges-Rovnyak spaces are Dirichlet spaces (and vice versa)?, J. Funct. Anal. 265 (2013), 3204–3218.CrossRefGoogle Scholar
Cowen, C. C. and MacCluer, B. D., Composition operators on spaces of analytic functions, Studies in Advanced Mathematics (CRC Press, 1995).Google Scholar
Dubinin, V. N., Condenser capacities and symmetrization in geometric function theory, Translated from the Russian by Nikolai G. Kruzhilin (Springer, Basel, 2014).CrossRefGoogle Scholar
El-Fallah, O., Kellay, K., Mashreghi, J. and Ransford, T., A primer on the Dirichlet space, Cambridge Tracts in Mathematics, Volume 203 (Cambridge University Press, 2014).CrossRefGoogle Scholar
El-Fallah, O., Kellay, K., Klaja, H., Mashreghi, J. and Ransford, T., Dirichlet spaces with superharmonic weights and de Branges-Rovnyak spaces, Complex Anal. Operator Theory 10 (2016), 97–107.CrossRefGoogle Scholar
Fisher, S. D., Function theory on planar domains. A second course in complex analysis, Pure and Applied Mathematics (John Wiley and Sons, 1983).Google Scholar
Götz, M., Approximating the condenser equilibrium distribution, Math. Z. 236(4) (2001), 699–715.CrossRefGoogle Scholar
Kloke, H., Punktsysteme mit extremalen Eigenschaften für ebene Kondensatoren, Dissertation Universität Dortmund, 1984.Google Scholar
Kloke, H., On the capacity of a plane condenser and conformal mapping, J. Reine Angew. Math. 358 (1985), 179–201.Google Scholar
Landkof, N. S., Foundations of Modern Potential Theory (Springer-Verlag, 1972).CrossRefGoogle Scholar
Li, D., Queffélec, H. and Rodríguez-Piazza, L., A spectral radius type formula for approximation numbers of composition operators, J. Funct. Anal. 267(12) (2014), 4753–4774.CrossRefGoogle Scholar
Richter, S., A representation theorem for cyclic analytic two-isometries, Trans. Amer. Math. Soc. 328 (1991), 325–349.CrossRefGoogle Scholar
Richter, S. and Sundberg, C., A formula for the local Dirichlet integral, Michigan Math. J. 38 (1991), 355–379.CrossRefGoogle Scholar
Sarason, D., Local Dirichlet spaces as de Branges-Rovnyak spaces, Proc. Amer. Math. Soc. 125 (1997), 2133–2139.CrossRefGoogle Scholar
Shapiro, J. H., Composition operators and classical function theory, Universitext, Tracts in Mathematics (Springer-Verlag, 1993).CrossRefGoogle Scholar
Shimorin, S. M., Complete Nevanlinna-Pick property of Dirichlet-type spaces, J. Funct. Anal. 191 (2002), 276–296.CrossRefGoogle Scholar
Siciak, J., Wiener's type regularity criteria on the complex plane, Ann. Polon. Math. 66 (1997), 203–221.CrossRefGoogle Scholar
Vuorinen, M., Conformal geometry and quasiregular mappings, Lecture Notes in Math. Volume 1319 (Springler-Verlag, 1988).CrossRefGoogle Scholar
Widom, H., Rational approximation and $n$-dimensional diameter, J. Approx. Theory 5 (1972), 343–361.CrossRefGoogle Scholar
Wojtaszczyk, P., Banach spaces for analysts, Cambridge Studies in Advanced Mathematics, Volume 25 (Cambridge University Press, 1991).CrossRefGoogle Scholar
Zhu, K., Operator theory in function spaces, 2nd edn, Mathematical Surveys and Monographs, Volume 138 (American Mathematical Society, 2007).CrossRefGoogle Scholar